Sainavle

Probability

Conditional Probability And Probability Of Independent Events

In this chapter, we shall be dealing with problems based on conditional probability and probability of independent events.

Conditional Probability

Let A and B be two events associated with the same random experiment. Then, the probability of occurrence of A under the condition B has already occurred and P(B) ^ 0, is called conditional probability, denoted by P(A/B).

We define:

⇒ \(P(A / B)=\frac{P(A \cap B)}{P(B)}, \text { where } P(B) \neq 0\)

and \(P(B / A)=\frac{P(B \cap A)}{P(A)}=\frac{P(A \cap B)}{P(A)}, \text { where } P(A) \neq 0\).

Read and Learn More WBCHSE Solutions For Class 12 Maths

Conditional Probability Solved Examples

Example 1. A die is rolled. If the outcome is an odd number, what is the probability that it is prime?
Solution:

When a die is rolled, the sample space is given by S = { 1,2,3,4, 5,6}.

Let A = event of getting a prime number, and

B = event of getting an odd number.

Example 2. Ten cards numbered 1 to 10 are placed in a box, mixed up thoroughly and then one card is drawn randomly. If it is known that the number on the drawn card is more than 3, what is the probability that it is an even number?
Solution:

Clearly, the sample space is S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

Let A =event that the number on the drawn card is even, and
B =event that the number on the drawn card is more than 3.

Then A ={2, 4, 6, 8, 10}, B ={4, 5, 6, 7, 8, 9, 10} and A ∩ B ={4,6, 8, 10}.

∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{5}{10}=\frac{1}{2}\),

P(B)= \(\frac{n(B)}{n(S)}=\frac{7}{10}\) and

P(A∩B)= \(\frac{n(A \cap B)}{n(S)}=\frac{4}{10}=\frac{2}{5}\)

Suppose B has already occurred and then A occurs.

So, we have to find P(A/B).

Now, P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{(2 / 5)}{(7 / 10)}=\left(\frac{2}{5} \times \frac{10}{7}\right)=\frac{4}{7}\).

Hence, the required probability is \(\frac{4}{7}\).

Example 3. A die is thrown twice and the sum of the numbers appearing is observed to be 6. What is the conditional probability that the number 4 has appeared at least once?
Solution:

We know that when a die is thrown twice, then the sample space has 36 possible outcomes.

Let A = event that 4 appears at least once, and
B = event that the sum of the numbers appearing is 6.

Then, A = {(4,1), (4,2), (4,3), (4,4), (4, 5), (4,6), (1,4), (2,4), (3,4), (5,4), (6,4)}

and B = {(1,5), (2,4), (3,3), (4,2), (5,1)}

∴ A∩B = {(2,4), (4,2)}.

So, P(A) = \(\frac{n(A)}{n(S)}=\frac{11}{36}, P(B)=\frac{n(B)}{n(S)}=\frac{5}{36}\)

P(B) = \(\frac{n(B)}{n(S)}=\frac{5}{36}\)

and P(A∩B)= \(\frac{n(A \cap B)}{n(S)}=\frac{2}{36}=\frac{1}{18}\)

Suppose B has already occurred and then A occurs.

So, we have to find P(A/B).

Now, P(A B) = \(\frac{P(A \cap B)}{P(B)}=\frac{(1 / 18)}{(5 / 36)}=\left(\frac{1}{18} \times \frac{36}{5}\right)=\frac{2}{5} \text {. }\)

Hence, the required probability is \(\frac{2}{5}\)

Example 4. Assume that each born child is equally likely to be a boy or a girl. If a family has two children, what is the conditional probability that both are girls given that

1. The youngest child is a girl,
2. At least one of the children is a girl.

Solution:

We may write the sample space as

S = {G₁G₂, G₁B₂, B₁G₂, B₁B₂}, where the youngest child appears later,

1. Let A = event that both the children are girls and B = event that the youngest child is a girl.

Then, A = {G₁G₂}, B = {G₁G₂, B₁G₂} and A∩B = {G₁G₂}.

∴ P(A)= \(\frac{n(A)}{n(S)}=\frac{1}{4}\), \(P(B)=\frac{n(B)}{n(S)}=\frac{2}{4}=\frac{1}{2}\)

and P(A∩B) = \(\frac{n(A \cap B)}{n(S)}=\frac{1}{4}\)

Suppose B has already occurred and then A occurs.

So, we have to find P(A/B).

Now, \(P(A / B)=\frac{P(A \cap B)}{P(B)}=\frac{(1 / 4)}{(1 / 2)}=\left(\frac{1}{4} \times \frac{2}{1}\right)=\frac{1}{2}\).

Hence, the required probability is \(\frac{1}{2}\).

2. Let A = event that both the children are girls, and

E = event that at least one of the children is a girl.

Then, A = {G₁G₂}, E = {G₁B₂, B₁G₂, G₁G₂} and A∩E = {G₁G₂}.

∴ P(A)= \(\frac{n(A)}{n(S)}=\frac{1}{4}\), P(E)= \(\frac{n(E)}{n(S)}=\frac{3}{4}\)

and \(P(A \cap E)=\frac{n(A \cap E)}{n(S)}=\frac{1}{4}\).

Suppose E has already occurred and then A occurs.

So, we have to find P(A/E).

Now, \(P(A / E)=\frac{P(A \cap E)}{P(E)}=\frac{(1 / 4)}{(3 / 4)}=\left(\frac{1}{4} \times \frac{4}{3}\right)=\frac{1}{3}\)

Hence, the required probability is 1/3.

Example 5. An instructor has a question bank consisting of 300 easy true/false questions; 200 difficult true/false questions; 500 easy multiple-choice questions and 400 difficult multiple-choice questions. If a question is selected at random from the question bank, what is the probability that it will be an easy question given that it is a multiple-choice question?
Solution:

Clearly, the sample space consists of 1400 questions.

∴ n(S) = 1400.

Let A = event of selecting an easy question, and

B = event of selecting a multiple-choice question.

Then, A∩B = event of selecting an easy multiple-choice question.

∴ n(A) = (300 +500) = 800, n(B) = (500 +400) = 900 and n(A∩B) = 500.

So, P(A) = \(\frac{n(A)}{n(S)}=\frac{800}{1400}=\frac{4}{7}\), P(B)= \(\frac{n(B)}{n(S)}=\frac{900}{1400}=\frac{9}{14}\)

and \(P(A \cap B)=\frac{n(A \cap B)}{n(S)}=\frac{500}{1400}=\frac{5}{14} \text {. }\)

Hence, the required probability is \(\frac{5}{14}\)

Suppose B has already occurred and then A occurs.

Thus we have to find P(A/B)

Now, P(A/B)= \(\frac{P(A \cap B)}{P(B)}=\frac{(5 / 14)}{(9 / 14)}=\left(\frac{5}{14} \times \frac{14}{9}\right)=\frac{5}{9}\).

Hence, the required probability is \(\frac{5}{9}\).

Example 6. Two numbers are selected at random from the integers 1 through 9. If the sum is even, find the probability that both the numbers are odd.
Solution:

Out of the numbers from 1 to 9, there are 5 odd numbers and 4 even numbers.

Let A = event of choosing two odd numbers, and

B = event of choosing two numbers whose sum is even.

Then, n(A) = number of ways of choosing 2 odd numbers out of = ⁵C₂

n(B) = number of ways of choosing 2 numbers whose sum is even

= (⁴C₂ + ⁵C₂) [2 out of 4 even and 2 out of 5 odd].

n(A∩B) = number of ways of choosing 2 odd numbers out of 5 = ⁵C₂.

Suppose B has already occurred and then A occurs.

Then, we have to find P(A/B).

Now, P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{n(A \cap B)}{n(B)}=\frac{{ }^5 C_2}{{ }^4 C_2+{ }^5 C_2}\)

= \(\frac{5 \times 4}{2} \times \frac{2}{(4 \times 3+5 \times 4)}=\frac{20}{32}=\frac{5}{8}\) .

Hence the required probability is \(\frac{5}{8}\)

Properties Of Conditional Probability

Theorem 1. Let A and B be events of a sample space S of an experiment. Then, prove thatP(S/B) =P(B/B) -1.

Proof: We know that:

P(S/B) = \(\frac{P(S \cap B)}{P(B)}=\frac{P(B)}{P(B)}=1[because S \cap B=B]\)

And, \(P(B / B)=\frac{P(B \cap B)}{P(B)}=\frac{P(B)}{P(B)}=1\).

Hence, P(S/B) -P(B/B) =1.

Theorem 2. Let A and B be two events of a sample space S and let E be an event such that P(E) ≠ 0. Then, prove that P[(A∪B)/E] =P(A/E) +P(B/E) -P[(A∩B)/E].

Proof: We have

P[(A∪B)/E] = \(\frac{P[(A \cup B) \cap E]}{P(E)}\)

= \(\frac{P[(A \cap E) \cup(B \cap E)]}{P(E)}\)

= \(\frac{P(A \cap E)+P(B \cap E)-P[(A \cap E) \cap(B \cap E)]}{P(E)}\)

= \(\frac{P(A \cap E)+P(B \cap E)-P(A \cap B \cap E)}{P(E)}\)

= \(\frac{P(A \cap E)}{P(E)}+\frac{P(B \cap E)}{P(E)}-\frac{P[(A \cap B) \cap E]}{P(E)}\)

= \(P(A / E)+P(B / E)-P[(A \cap B) / E]\).

Hence, \(P(A / E)+P(B / E)-P[(A \cap B) / E]\)

Corollary: If A and B are disjoint events, prove that P[(A∪B)/E] =P(A/E)+P(B/E).

Proof: For any events A and B, we have

P[(A∪B)/E] = P(A/E) +P(B/E) -P[(A∩B)/E].

If A and B are disjoint, then P[(A∩B)/E] = 0.

Hence, in this case, we have P[(A∪B)/E] = P(A/E) +P(B/E).

Theorem 3. For any events A and B of a sample space S, proue Bird P(\(\bar{A}\)/B) = 1 -P(A/B), where \(\bar{A}\) denotes ‘not A’.

Proof: We know that

P(S/B) =1

⇒ P[(Au\(\bar{A}\))/B] =1 [S = \(A \cup \bar{A}]\)]

⇒ P(A/B)+ P(A/B)=1 [A \(\bar{A}\)= ]

⇒ P(\(\bar{A}\)/B) = 1-P(A/B).

Hence, P(\(\bar{A}\)/B) = 1-P(A/B).

Example 1. If A end B are two events such that P(A) = \(\frac{3}{5}\), P(B)= \(\frac{7}{10}\) and P(A∪B) = \(\frac{9}{10}\), then find

1. P(A∩B)
2. P(A/B)
3. P(B/A).

Solution:

1. We know that P(A∩B) =P(A) +P(B) -P(A∪B)

= \(\left(\frac{3}{5}+\frac{7}{10}-\frac{9}{10}\right)=\frac{(6+7-9)}{10}=\frac{4}{10}=\frac{2}{5}\) .

2. \(P(A / B)=\frac{(A \cap B)}{P(B)}=\frac{(2 / 5)}{(7 / 10)}=\left(\frac{2}{5} \times \frac{10}{7}\right)=\frac{4}{7}\).

3. \(P(B / A)=\frac{(B \cap A)}{P(A)}=\frac{P(A \cap B)}{P(A)}=\left(\frac{2 / 5}{3 / 5}\right)=\left(\frac{2}{5} \times \frac{5}{3}\right)=\frac{2}{3}\).

Example 2. Evaluate P(A∪B), if 2P(A) = P(B) = \(\frac{6}{13}\) and P(A/B) = \(\frac{1}{3}\)
Solution:

2P(A) = P(B) = \(\frac{6}{13}\)

⇒ P(A) = \(\frac{3}{13}\) and P(B) = \(\frac{6}{13}\)

∴ P(A/B) = \(\frac{P(A \cap B)}{P(B)}\)

⇒ \(P(A \cap B)=P(A / B) \cdot P(B)=\left(\frac{1}{3} \times \frac{6}{13}\right)=\frac{2}{13}\).

So, P(A∪B) = P(A) + P(B) – P(A∩B)

= \(\left(\frac{3}{13}+\frac{6}{13}-\frac{2}{13}\right)=\frac{(3+6-2)}{13}=\frac{7}{13} .\)

Hence, P(A∪B) = \(\frac{7}{13}\)

Example 3. Let A and B be events such that P(A) = \(\frac{1}{3}\),P(B) = \(\frac{1}{4}\) and P(A∩B) = \(\frac{1}{5}\) Find:

1. P(A/B)
2. P(B/A)
3. P(A∪B)
4. P(B/A)

Solution:

We have:

1. P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{(1 / 5)}{(1 / 4)}=\left(\frac{1}{5} \times \frac{4}{1}\right)=\frac{4}{5}\).

2. P(B/A) = \(\frac{P(B \cap A)}{P(A)}=\frac{P(A \cap B)}{P(A)}=\frac{(1 / 5)}{(1 / 3)}=\left(\frac{1}{5} \times \frac{3}{1}\right)=\frac{3}{5}\)

3. \(P(A \cup B)\) = \(P(A)+P(B)-P(A \cap B)\)

= \(\left(\frac{1}{3}+\frac{1}{4}-\frac{1}{5}\right)=\frac{(20+15-12)}{60}=\frac{23}{60}\)

4. \(P(\bar{B} / \bar{A})=\frac{P(\bar{B} \cap \bar{A})}{P(\bar{A})}=\frac{P(\bar{A} \cap \bar{B})}{P(\bar{A})}=\frac{P(\overline{A \cup B})}{P(\bar{A})}\)

= \(\frac{1-P(A \cup B)}{1-P(A)}=\frac{\left(1-\frac{23}{60}\right)}{\left(1-\frac{1}{3}\right)}=\frac{(37 / 60)}{(2 / 3)}=\left(\frac{37}{60} \times \frac{3}{2}\right)=\frac{37}{40}\).

Conditional Probability Exercise 1A

Question 1. Let A and B be events such that P(A) = \(\frac{7}{13}\), P(B)= \(\frac{9}{13}\) and P(A∩B)= \(\frac{4}{13}\) Find

1. P(A/B)
2. P(B/A)
3. P(A∪B)
4. \(P(\bar{A} / \bar{B}).\)

Solution:

1. 4/9
2. 4/7
3. 12/13
4. 1/6

Question 2. Let A and B be events such that P(A)= \(\frac{5}{11}\) ,P(B)= \(\frac{6}{11}\) and P(A∪B)= \(\frac{7}{11}\). Find

1. P(A∩B)
2. P(A/B)
3. P(B/A)
4. \(P(\bar{A} / \bar{B})\)

Solution:

1. 4/11
2. 2/3
3. 4/5
4. 4/5

Question 3. Let A and B be events such that P(A) = \(\frac{3}{10}\), P(B) = \(\frac{1}{2}\) and P(B/A) = \(\frac{2}{5}\) Find

1. P(A∩B)
2. P(A∪B)
3. P(A/B).

Solution:

1. 3/25
2. 17/25
3. 6/25

Question 4. Let A and B be events such that 2P(A) = P(B) = \(\frac{5}{13}\) and P(A/B) = \(\frac{2}{5}\) Find

1. P(A∩B)
2. P(A∪B)

Solution:

1. 2/13
2. 11/26

Question 5. A die is rolled. If the outcome is an even number, what is the probability that it is a number greater than 2?
Solution: 2/3

Question 6. A coin is tossed twice. If the outcome is at most one tail, what is the probability that both head and tail have appeared?
Solution: 2/3

Question 7. Three coins are tossed simultaneously. Find the probability that all coins show heads if at least one of the coins shows a head.
Solution: 1/7

Question 8. Two unbiased dice are thrown. Find the probability that the sum of the numbers appearing is 8 or greater if 4 appears on the first die.
Solution: 1/2

Hint: Let A =event of getting the sum 8 or greater, and

B = event of getting a 4 on the first die.

∴ A ={(2, 6),(3, 5), (3, 6),(4, 4), (4, 5),(4, 6), (5, 3),(5, 4), (5, 5),(5, 6), (6,2),(6, 3), (6, 4),(6, 5), (6, 6)}

B ={(4,1), (4, 2),(4, 3), (4, 4), (4, 5), (4, 6)}.

(A∩B) ={(4,4), (4, 5), (4, 6)}.

∴ n(A) =15, n(B) =6 and n(A∩B) =3.

Hence, the required probability = P(A/B) = \(\frac{n(A \cap B)}{n(B)}=\frac{3}{6}=\frac{1}{2}\)

Question 9. A die is thrown twice and the sum of the numbers appearing is observed to be 8. What is the conditional probability that the number 5 has appeared at least once?
Solution: 2/5

Question 10. Two dice were thrown and it is known that the numbers which come up were different. Find the probability that the sum of the two numbers was 5.
Solution: 2/15

Hint: Let A =event that the sum of two numbers appeared is 5, and

B =event event that the two dice show different numbers.

Then, A ={(2, 3), (3, 2), (1, 4), (4,1)}.

Thus, n(A) =4, n(B) =30, A∩B=A and so n(A n B) =n(A) =4

∴ the required probability = P(A/B) = \(\frac{n(A \cap B)}{n(B)}=\frac{4}{30}=\frac{2}{15}.\)

Question 11. A coin is tossed and then a die is thrown. Find the probability of obtaining a 6, given that a head came up.
Solution: 1/6

Let A =event that the die shows a 6, and

B =event that a head comes up.

Then, A ={(H, 6), (T, 6)}

and B ={(H,1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6)}.

Then, P(A/B) = \(\frac{n(A \cap B)}{n(B)}=\frac{1}{6}\).

Question 12. A couple has 2 children. Find the probability that both are boys if it is known that

1. One of the children is a boy, and
2. The elder child is a boy.

Solution:

1. 1/3
2. 1/2

Question 13. In a class, 40% of students study mathematics; 25% study biology, and 15% study both mathematics and biology. One student is selected at random. Find the probability that

1. He studies mathematics if it is known that he studies biology
2. He studies biology if it is known that he studies mathematics.

Solution:

1. 3/5
2. 3/8

Hint:

Let M =event of studying mathematics, and

B =event of studying biology.

Then P(M)= \(\frac{40}{100}\) = \(\frac{2}{5}\), P(B)= \(\frac{25}{100}\) = \(\frac{1}{4}\) and P(M nB)= \(\frac{15}{100}\) = \(\frac{3}{20}\)

1. P(M/B) = \(\frac{P(M \cap B)}{P(B)}\)
2. P(B/M) = \(\frac{P(M \cap B)}{P(M)}\)

Question 14. The probability that a student selected at random from a class will pass in Hindi is 4/5 and the probability that he passes in Hindi and English is 1/2. What is the probability that he will pass in English if it is known that he has passed in Hindi?
Solution: 5/8

Hint: Given, P(H)= \(\frac{4}{5}\) and P(H∩E)= \(\frac{1}{2}\)

∴ P(E/H) = \(\frac{P(E \cap H)}{P(H)}=\frac{P(H \cap E)}{P(H)} \text {. }\)

Question 15. The probability that a certain person will buy a shirt is 0.2, the probability that he will buy a coat is 0.3 and the probability that he will buy a shirt given that he buys a coat is 0.4. Find the probability that he will buy both a shirt and a coat.
Solution: 0.12

Hint: P(S) = 02, P(C) = 0.3, P(S/C)= 0.4.

∴ P(S/C) = \(\frac{P(S \cap C)}{P(C)}\)

⇒ P(S∩C)=P(C)·P(S/C).

Question 16. In a hostel, 60% of the students read Hindi newspapers, 40% read English newspapers and 20% read both Hindi and English newspapers. A student is selected at random.

1. Find the probability that he reads neither Hindi nor English newspapers.
2. If he reads Hindi newspaper, what is the probability that he reads English newspaper?
3. If he reads an English newspaper, what is the probability that he reads Hindi newspaper?

Solution:

1. 1/5
2. 1/3
3. 1/2

Question 17. Two integers are selected at random from integers 1 through 11. If the sum is even, find the probability that both the numbers selected are odd.
Solution: 3/5

Hint: Let A =event of choosing both odd numbers,

B =event that sum of chosen numbers is even.

In integers from 1 to 11, there are 5 even and 6 odd integers.

⇒ \(P(A)=\frac{{ }^6 C_2}{{ }^{11} C_2}=\frac{3}{11}, P(B)=\left(\frac{{ }^6 C_2+{ }^5 C_2}{{ }^{11} C_2}\right)=\frac{5}{11}, P(A \cap B)=\frac{{ }^6 C_2}{{ }^{11} C_2}=\frac{3}{11}\)

∴ required probability = P(A/B) = \(\frac{P(A \cap B)}{P(B)}\).

Multiplication Theorem On Probability

Let A and B be two events associated with a sample space S. Then, the simultaneous occurrence of two events A and B is denoted by (A∩B) and also written as AB

Multiplication Theorem: Let A and B be two events associated with a sample space S. Then, prove that

P(AB) = P(A∩B) =P(A)·P(B/A) =P(B)·P(A/B), provided P(A)≠0 and P(B)≠ 0.

Proof: For any events A and B, we have

P(A/B) = \(\frac{P(A \cap B)}{P(B)}\), where P(A)≠0.

∴ P(A∩B)=P(B)·P(A/B)….. (1)

Again, P(B/A) = \(\frac{P(B \cap A)}{P(A)}=\frac{P(A \cap B)}{P(A)}\) where P(B)≠0.

∴ P(A∩B) =P(A)·P(B/A)…….(2)

From (1) and (2), we get

P(A∩B) =P(B)·P(A/B) = P(A)·P(A/B), where P(A)≠0 and P(A)≠0.

Multiplication Rule for Three Events: For any three events A, B, and C of the same sample space, we have P(A∩B∩C) = P(A)·P(B/A)·P[C/(A∩B)]

= P(A)·P(B/A)·(C/AB).

This rule can be extended for four or more events.

Multiplication Theorem On Probability Solved Examples

Example 1. An urn contains 8 white and 4 red balls. Two balls are drawn from the urn one after the other without replacement. What is the probability that both drawn balls are white?
Solution:

Let A and B denote respectively the events that the first and second balls both drawn are white.

Then, we have to find P(A∩B).

Now, P(A) = P (white ball in the first draw) = \(\frac{8}{12}\).

After the occurrence of event A, we are left with 7 white and 4 red balls.

The probability of drawing second white ball, given that the first ball drawn is white, is clearly the conditional probability of occurrence of B, given that A has occurred.

∴ P(B/A) = \(\frac{7}{11}\).

By multiplication rule of probability, we have \(P(A \cap B)=P(A) \cdot P(B / A)=\left(\frac{8}{12} \times \frac{7}{11}\right)=\frac{14}{33}\)

Hence, the required probability is \(\frac{14}{33}\)

Example 2. Three cards are drawn successively without replacement from a pack of 52 well-shuffled cards. What is the probability that first two cards are queens and the third card drawn is a king?
Solution:

Let Q denote the event that the card drawn is a queen and K be the event that the card drawn is a king. Then, we have to find P(QQK).

Probability of drawing first queen is P(Q)= \(\frac{4}{52}\)

Now, there are 3 queens in the remaining 51 cards.

Let P(Q/Q) be the probability of getting the second queen with the condition that one queen has already been drawn.

∴ P(Q/Q)= \(\frac{3}{51}\)

Lastly, P(K/QQ) is the probability of a third drawn card to be a king, with the condition that two queens have already been drawn.

Now, there are 4 kings in remaining 50 cards.

∴ P(K/QQ)= \(\frac{4}{50}\)

By multiplication law of probability, we have P(QQK)=P(Q∩Q∩K)

=P(Q)·P(Q/Q)·P(K/QQ)

= \(\left(\frac{4}{52} \times \frac{3}{51} \times \frac{4}{50}\right)=\left(\frac{1}{13} \times \frac{1}{17} \times \frac{2}{25}\right)=\frac{2}{5525}\)

Hence, the required probability is \(\frac{2}{5525}\)

Independent Events: Two events A and B are said to be independent if

P(A/B) = P(A), where P(B)≠0 and P(B/A) = P(B), where P(A)≠0.

i.e., event A does not depend on the occurence of event B and vice versa.

Condition for Independence of Two Events: For any two events A and B, we have

P(A∩B) = P(A)·P(B/A)…. (1)

If A and B are independent, we have P(B/A) = P(B).

∴ (1) becomes P(A∩B) = P(A) xP(B).

Thus, two events A and B associated with the same random experiment are said to be independent if P(A∩B) =P(A)xP(B).

Note: Two events A and B are said to be dependent if they are not independent, i.e., if P(A∩B)≠P(A)xP(B).

Difference between Two Mutually Exclusive and Independent Events: Two events A and B are said to be mutually exclusive if A∩B = φ and in this case P(A∩B) -P(φ) =0.

Also, we know that two events A and B are independent if P(A nB)= P(A) xP(B).

Clearly, two independent events with nonzero probabilities cannot be mutually exclusive.

Also, two mutually exclusive events with nonzero probabilities cannot be mutually independent.

Three events A, B and C are said to be mutually independent, if

P(A∩B) =P(A) x P(B), P(A∩C) =P(A) x P(C), P(B∩C) =P(B) x P(C) and P(A∩B ∩C) =P(A) x P(B) x P(C).

If at least one of the above is not true for three given events A, B and C, then we say that these events are not independent.

Example 3. Let E₁ and E₂ be two events such that P(E₁) = 0.3, P(\(E_1 \cup E_2\)) =0.4 and P(E₂) = x. Find the value of x such that 

1. E₁ and E₂ are mutually exclusive,
2. E₁ and E₂ are independent.

Solution:

Let E₁ and E₂ be mutually exclusive. Then, E₁ ∩ E₂ = φ.

∴ P(E₁ ∩ E₂)=P(E₁)+P(E₂)

⇒ 0.4 = 0.3+x

⇒ x = 0.1.

Thus, when E₁ and E₂ are mutually exclusive, then x = 0.1.

2. Let E₁ and E₂ be two independent events. Then,

P(E₁ ∩ E₂) =P(E₁) X P(E₂) = 0.3 x x = 0.3x.

∴ P(\(E_1 \cup E_2\)) =P(E₁)+P(E₂)-P(E₁∩E₂)

⇒ 0.4 =0.3+ x-0.3x

⇒ 0.7x = 0.1

⇒ x =\(=\frac{0.1}{0.7}=\frac{1}{7} .\)

Thus, when E₁ and E₂ are independent, then A = \(\frac{1}{7} .\)

Example 4. Let E₁ and E₂ are two independent events such that P(E₁) =0.35 and P(\(E_1 \cup E_2\)) = 0.60,find P(E₂).
Solution:

Let P(E₂)= A.

Then, E₁ and E₂ being independent events, we have

P(E₁∩E₂) =P(E₁) X P(E₂) = 0.35 X x = 0.35x.

Now, P(E₁∪E₂)=P(E₁)+P(E₂)-P(E₁∩E₂)

⇒ 0.60 =0.35 + x – 0.35x

⇒ 0.65A =0.25

⇒ x = \(\frac{0.25}{0.65}=\frac{25}{65}=\frac{5}{13}\) .

Hence, \(P\left(E_2\right)=\frac{5}{13}\).

Example 5. A coin is tossed thrice. Let the event E be ‘the first throw results in a head’, and the event F be ‘the last throw results in a tail’. Find whether the events E and F are independent.
Solution:

When a coin is tossed three times, the sample space is given by S = [HHH, HHT, HTH, THH, TTH, TUT, HTT, TTT}.

Now, E = event that the first throw results in a head.

∴ E = {HHH, HHT, HTH, HTT}.

And, F = event that the last throw results in a tail.

∴ F = {HHT, THT, HTT, TIT}.

So, (E∩F) = {HHT, HIT}.

Clearly, n(E) = 4, n(F) = 4, n(E nF) = 2 and n(S) = 8.

∴ P(E)= \(\frac{n(E)}{n(S)}=\frac{4}{8}=\frac{1}{2}, P(F)=\frac{n(F)}{n(S)}=\frac{4}{8}=\frac{1}{2}\)

and \(P(E \cap F)\)=\(\frac{n(E \cap F)}{n(S)}\)=\(\frac{2}{8}\)=\(\frac{1}{4}\)

Thus, P(E∩F) = P(E )x P(F).

Hence, E and F are independent events.

Example 6. An unbiased die is tossed twice. Find the probability of getting a 4, 5 or 6 on the first toss and a 1, 2,3 or 4 on the second toss.
Solution:

In each case, the sample space is given by S = {1,2,3,4,5,6}.

Let E = event of getting a 4,5 or 6 on the first toss.

And, F = event of getting a 1,2,3 or 4 on the second toss.

Then, P(E) = \(\frac{3}{6}\) = \(\frac{1}{2}\) and P(F)= \(\frac{4}{6}\) = \(\frac{2}{3}\)

Clearly, E and F are independent events.

∴ required probability=P(E∩F) = P(E) x P(F)

[E and F are independent]

= \(\left(\frac{1}{2} \times \frac{2}{3}\right)=\frac{1}{3}\)

Example 7. Ramesh appears for an interview for two posts, A and B, for which the selection is independent. The probability for his selection for Post A is (1/6) and for Post B, it is (1/7). Find the probability that Ramesh is selected for at least one post.
Solution:

Let E₁ = event that Ramesh is selected for tire post A, and

E₂ = event that Ramesh is selected for the post B.

Then, \(P\left(E_1\right)=\frac{1}{6} \text { and } P\left(E_2\right)=\frac{1}{7}\)

Clearly, E₁ and E₂ are independent events.

∴ \(P\left(E_1 \cap E_2\right)=P\left(E_1\right) \times P\left(E_2\right)=\left(\frac{1}{6} \times \frac{1}{7}\right)=\frac{1}{42}\).

∴ P(Ramesh is selected for at least one post) =P(E₁∪E₂)

= P(E₁)+P(E₂)-P(E₁∩E₂)

= \(\left(\frac{1}{6}+\frac{1}{7}-\frac{1}{42}\right)=\frac{12}{42}=\frac{2}{7}\).

Hence, the required probability is \(\frac{2}{7}\)

Example 8. A can solve 90% of the problems given in a book, and B can solve 70%. What is the probability that at least one of them will solve a problem selected at random from the book?
Solution:

Let E₁ =event that A solves the problem,

and E₂ =event that B solves the problem.

Then, \(P\left(E_1\right)=\frac{90}{100}=\frac{9}{10} \text { and } P\left(E_2\right)=\frac{70}{100}=\frac{7}{10}\)

Clearly, E₁ and E₂ are independent events.

∴ \(P\left(E_1 \cap E_2\right)=P\left(E_1\right) \times P\left(E_2\right)=\left(\frac{9}{10} \times \frac{7}{10}\right)=\frac{63}{100}\).

∴ P(at least one of them will solve the problem)

= P(E₁∪E₂)

= P(E₁)+P(E₂)-P(E₁∩E₂)

= \(\left(\frac{9}{10}+\frac{7}{10}-\frac{63}{100}\right)=\frac{(90+70-63)}{100}=\frac{97}{100}\)

Hence, the required probability is 0.97.

Example 9. The probability that A hits a target is (1/3) and the probability that B hits it is (2/5). What is the probability that the target will be hit if both A and B shoot at it?
Solution:

Let E₁ =event that A hits the target,

and E₂ =event that B hits the target.

Then, \(P\left(E_1\right)=\frac{1}{3} \text { and } P\left(E_2\right)=\frac{2}{5} \text {. }\)

Clearly, E₁ and E₂ are independent events.

∴ \(P\left(E_1 \cap E_2\right)=P\left(E_1\right) \times P\left(E_2\right)=\left(\frac{1}{3} \times \frac{2}{5}\right)=\frac{2}{15}\)

∴ P(target is hit) = P(A hits or B hits)

= P(E₁ ∪E₂)

= P(E₁)+P(E₂)-P(E_1∩E₂)

Hence, the required probability is \(\frac{2}{15}\)

Example 10. A and B appear for an interview for two posts. The probability of A’s selection is (1/3) and that of B’s selection is (2/5). Find the probability that only one of them will be selected.
Solution:

Let E₁ = event that A is selected, and E₂ = event that B is selected.

Then, P(E₁)= \(\frac{1}{3}\) and P(E₂) = \(\frac{2}{5}\)

⇒ \(P\left(\bar{E}_1\right)=\left(1-\frac{1}{3}\right)=\frac{2}{3} \text { and } P\left(\bar{E}_2\right)=\left(1-\frac{2}{5}\right)=\frac{3}{5}\)

∴ P(event that only one of them is selected)

=  P[(E₁ and not E₂) or (E₂ and not E₁]

= \(P\left(E_1 \cap \bar{E}_2\right)+P\left(E_2 \cap \bar{E}_1\right) \quad\left[because \quad\left(E_1 \cap \bar{E}_2\right) \cap\left(E_2 \cap \bar{E}_1\right)=\phi\right]\)

= \(P\left(E_1\right) \cdot P\left(\bar{E}_2\right)+P\left(E_2\right) \cdot P\left(\bar{E}_1\right)\)

[because \(E_1 and \bar{E}_2\) are independent, and \(E_1 and \bar{E}_1\) are independent]

= \(\left(\frac{1}{3} \times \frac{3}{5}\right)+\left(\frac{2}{5} \times \frac{2}{3}\right)\)

= \(\left(\frac{1}{5}+\frac{4}{15}\right)=\frac{7}{15}\)

Example 11. A speaks the truth in 60% of the cases, and B m 90% o/ f/zc cases. In what percentage of cases are they likely to contradict each other in stating the same fact?
Solution:

Let E₁ = event that A speaks the truth, and E₂ = event that B speaks the truth.

Then, \(\bar{E}_1\) = event that A tells a lie,

and \(\bar{E}_2\) = event that B tells a lie.

Clearly, E₁ and E₂ are independent events.

Also, (E₁ and \(\bar{E}_2\)) as well as (\(\bar{E}_1\) and E₂) are independent.

Now, \(P\left(E_1\right)=\frac{60}{100}=\frac{3}{5} ; P\left(E_2\right)=\frac{90}{100}=\frac{9}{10} ;\)

⇒ \(P\left(\bar{E}_1\right)=\left(1-\frac{3}{5}\right)=\frac{2}{5} \text { and } P\left(\bar{E}_2\right)=\left(1-\frac{9}{10}\right)=\frac{1}{10}\).

∴ P(A and B contradict each other)

= P[(A speaks the truth and B tells a lie) or (A tells a lie and B speaks the truth)]

= \(P\left[\left(E_1 \cap \bar{E}_2\right) \cup\left(\bar{E}_1 \cap E_2\right)\right]\)

= \(P\left(E_1 \cap \bar{E}_2\right)+P\left(\bar{E}_1 \cap E_2\right) \quad\left[because \quad\left(E_1 \cap \bar{E}_2\right) \cap\left(\bar{E}_1 \cap E_2\right)=\phi\right]\)

= \(\left\{P\left(E_1\right) \times P\left(\bar{E}_2\right)\right\}+\left\{P\left(\bar{E}_1\right) \times P\left(E_2\right)\right\}\)

= \(\left(\frac{3}{5} \times \frac{1}{10}\right)+\left(\frac{2}{5} \times \frac{9}{10}\right)=\left(\frac{3}{50}+\frac{18}{50}\right)=\frac{21}{50}\).

Percentage of cases in which A and B Contradict each other = \(\left(\frac{21}{50} \times 100\right) \%\) = 42%

Example 12. The probabilities of a specific problem being solved independently by A and B are 1/2 and 1/3 respectively. If both try to solve the problem independently, find the probability that

1. The problem is solved
2. Exactly one of them solves the problem.

Solution:

Let E₁ =event that A solves the problem,

and E₂ =event that B solves the problem.

Then, P(E₁) = \(\frac{1}{2}\) and P(E₂) = \(\frac{1}{3}\)

⇒ \(P\left(\bar{E}_1\right)=\left(1-\frac{1}{2}\right)=\frac{1}{2} \text { and } P\left(\bar{E}_2\right)=\left(1-\frac{1}{3}\right)=\frac{2}{3} \text {. }\)

Clearly, E₁ and E₂ are independent events.

⇒ \(P\left(E_1 \cap E_2\right)=P\left(E_1\right) \times P\left(E_2\right)=\left(\frac{1}{2} \times \frac{1}{3}\right)=\frac{1}{6}\).

1. P(the problem is solved)

= P(at least one of A and B solves the problem)

= \(P\left(E_1 \text { or } E_2\right)=P\left(E_1 \cup E_2\right)\)

= \(P\left(E_1\right)+P\left(E_2\right)-P\left(E_1 \cap E_2\right)\)

= \(\left(\frac{1}{2}+\frac{1}{3}-\frac{1}{6}\right)=\frac{4}{6}=\frac{2}{3}\).

2. P(exactly one of them solves the problem)

= \(P\left(E_1 \text { or } E_2\right)=P\left(E_1 \cup E_2\right)\)

= \(P\left(E_1\right)+P\left(E_2\right)-P\left(E_1 \cap E_2\right)\)

= \(=\left(\frac{1}{2} \times \frac{2}{3}\right)+\left(\frac{1}{3} \times \frac{1}{2}\right)=\left(\frac{1}{3}+\frac{1}{6}\right)=\frac{3}{6}=\frac{1}{2}\).

Example 13. Amit and Nisha appear for an interview for two vacancies in a company. The probability of Amit’s selection is 1/5 and that of Nisha’s selection is 1/6. What is the probability that

1. Both of them are selected?
2. Only one of them is selected?
3. None of them is selected?

Solution:

Let E₁ = event that Amit is selected,

and E₂ = event that Nisha is selected.

Then, P(E₁) = \(\frac{1}{5}\) and P(E₂) = \(\frac{1}{6}\)

Clearly, E₁ and E₂ are independent events.

1. P(both are selected) =P(E₁∩E₂)

=P(E₁)xP(E₂) [E₁ and E₂ are independent]

= \(\left(\frac{1}{5} \times \frac{1}{6}\right)=\frac{1}{30}\)

2. P(only one of them is selected)

=P[(E₁ and not E₂) or (E₂ and not E₁]

=P(E₁ and not E₂) +P(E₂ and not E₁)

=P(E₁) -P(not E₂) +P(E₂)-P(not E₁)

=P(E₁)•[1 -P(E₂)] +P(E₂)•[1 -P(E₁)]

= \(\frac{1}{5} \cdot\left(1-\frac{1}{6}\right)+\frac{1}{6} \cdot\left(1-\frac{1}{5}\right)=\left(\frac{1}{5} \times \frac{5}{6}\right)+\left(\frac{1}{6} \times \frac{4}{5}\right)\)

= \(\left(\frac{1}{6}+\frac{2}{15}\right)=\frac{9}{30}=\frac{3}{10}\)

3. P (none of them is selected)

=P(not E₁ and not E₂)

=P(not E₁) and P(not E₂)

=[1-P(E₁)] [1-P(E₂)1]

= \(\left(1-\frac{1}{5}\right) \cdot\left(1-\frac{1}{6}\right)=\left(\frac{4}{5} \times \frac{5}{6}\right)=\frac{2}{3}\)

Example 14. Three groups of children contain 3 girls and 1 boy; 2 girls and 2 boys; and 1 girl and 3 boys. One child is selected at random from each group. Find the chance that the three children selected comprise 1 girl and 2 boys.
Solution:

Let G₁, G₂, and G₃ be the events of selecting a girl from the first, second and third groups respectively, and let B₁, B₂, and B₃ be the events of selecting a boy from the first, second and third groups respectively.

Then,

⇒ \(P\left(G_1\right)=\frac{3}{4} ; P\left(G_2\right)=\frac{2}{4}=\frac{1}{2} ; P\left(G_3\right)=\frac{1}{4}\)

⇒ \(P\left(B_1\right)=\frac{1}{4} ; P\left(B_2\right)=\frac{2}{4}=\frac{1}{2} \text { and } P\left(B_3\right)=\frac{3}{4}\)

∴ P(selecting 1 girl and 2 boys)

= \(P\left[\left(G_1 B_2 B_3\right) \text { or }\left(B_1 G_2 B_3\right) \text { or }\left(B_1 B_2 G_3\right)\right]\)

= \(P\left(G_1 B_2 B_3\right)+P\left(B_1 G_2 B_3\right)+P\left(B_1 B_2 G_3\right)\)

= \(\left\{P\left(G_1\right) \times P\left(B_2\right) \times P\left(B_3\right)\right\}+\left\{P\left(B_1\right) \times P\left(G_2\right) \times P\left(B_3\right)\right\}+\left\{P\left(B_1\right) \times P\left(B_2\right) \times P\left(G_3\right)\right\}\)

= \(\left(\frac{3}{4} \times \frac{1}{2} \times \frac{3}{4}\right)+\left(\frac{1}{4} \times \frac{1}{2} \times \frac{3}{4}\right)+\left(\frac{1}{4} \times \frac{1}{2} \times \frac{1}{4}\right)=\left(\frac{9}{32}+\frac{3}{32}+\frac{1}{32}\right)=\frac{13}{32}\).

Hence, the chances of selecting 1 girl and 2 boys are \(\frac{13}{32}\)

Example 15. A problem is given to three students whose chances of solving it are 1/3, 2/7 and 3/8. What is the probability that the problem will be solved?
Solution:

Let the three students be  A, B, and C respectively. Let E₁/E₂/E₃ be the events that the problem is solved by A, B, and C respectively. Then,

⇒ \(P\left(E_1\right)=\frac{1}{3}, P\left(E_2\right)=\frac{2}{7}, P\left(E_3\right)=\frac{3}{8} .\)

∴ \(P\left(\bar{E}_1\right)=\left(1-\frac{1}{3}\right)=\frac{2}{3} ; P\left(\bar{E}_2\right)=\left(1-\frac{2}{7}\right)=\frac{5}{7} \text { and } P\left(\bar{E}_3\right)=\left(1-\frac{3}{8}\right)=\frac{5}{8}\)

∴ P(none solves the problem)

= P[(not E₁) and (not E₂) and (not E₃)]

= \(P\left(\bar{E}_1 \cap \bar{E}_2 \cap \bar{E}_3\right)\)

= \(P\left(\bar{E}_1\right) \times P\left(\bar{E}_2\right) \times P\left(\bar{E}_3\right) \quad\left[because \bar{E}_1, \bar{E}_2, \bar{E}_3 \text { are independent }\right]\)

= \(\left(\frac{2}{3} \times \frac{5}{7} \times \frac{5}{8}\right)=\frac{25}{84}\).

∴ P(that the problem is solved)

=1-P(none solves the problem)

= \(\left(1-\frac{25}{84}\right)=\frac{59}{84}\) .

Hence, the required probability is \(\frac{59}{84}\).

Example 16. A problem in mathematics is given to three students whose chances of solving it correctly are 1/2, 1/3 and 1/4 respectively. What is the probability that only one of them solves it correctly?
Solution:

Let A, B, and C be the given students and let E₁,E₂ and E₃ be the events that the problem is solved by A, B, and C respectively. Then,

⇒ \(\bar{E}_1, \bar{E}_2 \text { and } \bar{E}_3\)are the events that the given problem is not solved by A, B, C respectively. Then,

⇒ \(P\left(E_1\right)=\frac{1}{2} ; P\left(E_2\right)=\frac{1}{3} ; P\left(E_3\right)=\frac{1}{4} ;\)

⇒ \(P\left(\bar{E}_1\right)=\left(1-\frac{1}{2}\right)=\frac{1}{2} ; P\left(\bar{E}_2\right)=\left(1-\frac{1}{3}\right)=\frac{2}{3} \text { and } P\left(\bar{E}_3\right)=\left(1-\frac{1}{4}\right)=\frac{3}{4}\)

P (exactly one of them solves the problem)

= \(P\left[\left(E_1 \cap \bar{E}_2 \cap \bar{E}_3\right) \text { or }\left(\bar{E}_1 \cap E_2 \cap \bar{E}_3\right) \text { or }\left(\bar{E}_1 \cap \bar{E}_2 \cap E_3\right)\right]\)

= \(P\left(E_1 \cap \bar{E}_2 \cap \bar{E}_3\right)+P\left(\bar{E}_1 \cap E_2 \cap \bar{E}_3\right)+P\left(\bar{E}_1 \cap \bar{E}_2 \cap E_3\right)\)

= \(\left\{P\left(E_1\right) \times P\left(\bar{E}_2\right) \times P\left(\bar{E}_3\right)\right\}+\left\{P\left(\bar{E}_1\right) \times P\left(E_2\right) \times P\left(\bar{E}_3\right)\right\}\quad\)

+ \(\left\{P\left(\bar{E}_1\right) \times P\left(\bar{E}_2\right) \times P\left(E_3\right)\right\}\)

= \(\left(\frac{1}{2} \times \frac{2}{3} \times \frac{3}{4}\right)+\left(\frac{1}{2} \times \frac{1}{3} \times \frac{3}{4}\right)+\left(\frac{1}{2} \times \frac{2}{3} \times \frac{1}{4}\right)\)

= \(\left(\frac{1}{4}+\frac{1}{8}+\frac{1}{12}\right)=\frac{11}{24}\)

Hence, the required probability is \(\frac{11}{24}\)

Example 17. Three critics review a book. For the three critics, the odds in favour of the book are (5:2), (4:3) and (3:4) respectively. Find the probability that the majority is in favour of the book.
Solution:

Let A, B, and C denote the events that the book is favoured by the first, second and third critic respectively. Then,

P(A)= \(\frac{5}{7}\);P(B)= \(\frac{4}{7}\);P(C) = \(\frac{3}{7}\);

⇒ \(P(\bar{A})=\left(1-\frac{5}{7}\right)=\frac{2}{7} ; P(\bar{B})=\left(1-\frac{4}{7}\right)=\frac{3}{7} \text { and } P(\bar{C})=\left(1-\frac{3}{7}\right)=\frac{4}{7}\)

Required probability

= P(2 critics favour the book or 3 critics favour the book)

= P(2 critics favour the book) + P(3 critics favour the book)

= P[{A and B and not C} or A and C and not B or {B and C and not A}] + P(A and B and C)

= \(P(A \cap B \cap \bar{C})+P(A \cap \bar{B} \cap C)+P(\bar{A} \cap B \cap C)+P(A \cap B \cap C)\)

= \(\{P(A) \times P(B) \times P(\bar{C})\}+\{P(A) \times P(\bar{B}) \times P(C)\}+\{P(\bar{A}) \times P(B) \times P(C)\}\)

+ \(\{P(A) \times P(B) \times P(C)\}\)

= \(\left(\frac{5}{7} \times \frac{4}{7} \times \frac{4}{7}\right)\)+\(\left(\frac{5}{7} \times \frac{3}{7} \times \frac{3}{7}\right)\)+\(\left(\frac{2}{7} \times \frac{4}{7} \times \frac{3}{7}\right)\)+\(\left(\frac{5}{7} \times \frac{4}{7} \times \frac{3}{7}\right)\)

= \(\left(\frac{80}{343}+\frac{45}{343}+\frac{24}{343}+\frac{60}{343}\right)=\frac{209}{343}\)

Hence, the required probability is \(\frac{209}{343}\)

Example 18. The odds against a man who is 45 years old, living till he is 70 are 7: 5, and the odds against his wife who is now 36, living till she is 61 are 5 : 3. Find the probability that

1. The couple will be alive 25 years hence
2. At least one of them will be alive 25 years hence.

Solution:

Let E₁ = event that the husband will be alive 25 years hence, and E₂ = event that the wife will be alive 25 years hence.

Then, \(P\left(E_1\right)=\frac{5}{12} and P\left(E_2\right)=\frac{3}{8}\).

∴ \(P\left(\bar{E}_1\right)=\left(1-\frac{5}{12}\right)=\frac{7}{12} \text { and } P\left(\bar{E}_2\right)=\left(1-\frac{3}{8}\right)=\frac{5}{8} \text {. }\)

Clearly, E₁ and E₂ are independent events.

1. P(the couple will be alive 25 years hence) =

= \(P\left(E_1 \text { and } E_2\right)=P\left(E_1 \cap E_2\right)\)

= \(P\left(E_1\right) \cdot P\left(E_2\right)=\left(\frac{5}{12} \times \frac{3}{8}\right)=\frac{5}{32}\).

2. P(at least one of them will be alive 25 years hence)

= 1-P(none will be alive 25 years hence)

= 1-P[(not E₁) and (not E₂)]

= \(1-P\left(\bar{E}_1 \cap \bar{E}_2\right)\)

= \(1-\left[P\left(\bar{E}_1\right) \cdot P\left(\bar{E}_2\right)\right] \quad\left[because \bar{E}_1 \text { and } \bar{E}_2 \text { are independent }\right]\)

= \(1-\left(\frac{7}{12} \times \frac{5}{8}\right)=\left(1-\frac{35}{96}\right)=\frac{61}{96}\)

Example 19. A, B and C shoot to hit a target. If A hits the target 4 times in 5 trials; B hits it 3 times in 4 trials and C hits it 2 times in 3 trials, what is the probability that the target is hit by at least 2 persons?
Solution:

Let E₁, E₂ and E₃ be the events that A hits the target, B hits the target and C hits the target respectively. Then,

⇒ \(P\left(E_1\right)=\frac{4}{5}, P\left(E_2\right)=\frac{3}{4}, P\left(E_3\right)=\frac{2}{3} \)

⇒  \(P\left(\bar{E}_1\right)=\left(1-\frac{4}{5}\right)=\frac{1}{5}, P\left(\bar{E}_2\right)=\left(1-\frac{3}{4}\right)=\frac{1}{4} \text { and } P\left(\bar{E}_3\right)=\left(1-\frac{2}{3}\right)=\frac{1}{3}\)

Case 1 A, B, and C all hit the target

In this case, P(A, B and C) all hit the target)

= \(P\left(E_1\right. and E_2 and \left.E_3\right)\)

= \(P\left(E_1\right) \cdot P\left(E_2\right) \cdot P\left(E_3\right)\) [because \(E_1, E_2, E_3\) are independent]

= \(\left(\frac{4}{5} \times \frac{3}{4} \times \frac{2}{3}\right)=\frac{2}{5}\)

Case 2 A and B hit but not C

In this case, P(A and B hit but not C)

= \(P\left(E_1 \text { and } E_2 \text { and not } E_3\right)\)

= \(P\left(E_1 \cap E_2 \cap \bar{E}_3\right)\)

= \(P\left(E_1\right) \cdot P\left(E_2\right) \cdot P\left(\bar{E}_3\right)\left[because E_1, E_2, \bar{E}_3 \text { are independent }\right]\)

= \(\left(\frac{4}{5} \times \frac{3}{4} \times \frac{1}{3}\right)=\frac{1}{5}\).

Case 3 A and C both hit but not B

In this case, P(A and C hit but not B)

= \(P\left(E_1 \text { and } E_3 \text { and } \bar{E}_2\right)\)

= \(P\left(E_1\right) \cdot P\left(E_3\right) \cdot P\left(\bar{E}_2\right)\left[because E_1, E_3, \bar{E}_2\right. \text { are independent}\)

= \(\left(\frac{4}{5} \times \frac{2}{3} \times \frac{1}{4}\right)=\frac{2}{15}\)

Case 4 B and C both hit but not A

In this case, P(B and C hit but not A)

= \(P\left(E_2 \text { and } E_3 \text { and } E_1\right)\)

= \(P\left(E_2\right) \cdot P\left(E_3\right) \cdot P\left(\bar{E}_1\right)\left[because E_2, E_3, \bar{E}_1 \text { are independent }\right]\)

= \(\left(\frac{3}{4} \times \frac{2}{3} \times \frac{1}{5}\right)=\frac{1}{10}\).

Clearly, all these are mutually exclusive.

Hence, required probability = \(\left(\frac{2}{5}+\frac{1}{5}+\frac{2}{15}+\frac{1}{10}\right)=\frac{5}{6} \text {. }\)

Multiplication Theorem On Probability Excercise 1B

Question 1. A bag contains 17 tickets, numbered from 1 to 17. A ticket is drawn and then another ticket is drawn without replacing the first one. Find the probability that both the tickets may show even numbers.
Solution: 7/34

Question 2. Two marbles are drawn successively from a box containing 3 black and 4 white marbles. Find the probability that both the marbles are black, if the first marble is not replaced before the second draw.
Solution: 1/7

Question 3. A card is drawn from a well-shuffled deck of 52 cards and without replacing this card, a second card is drawn. Find the probability that the first card is a club and the second card is a spade.
Solution: 13/204

Question 4. There is a box containing 30 bulbs of which 5 are defective. If two bulbs are chosen at random from the box in succession without replacing the first, what is the probability that both the bulbs chosen are defective?
Solution: 2/87

Question 5. A bag contains 10 white and 15 black balls. Two balls are drawn in succession without replacement. What is the probability that the first ball is white and the second is black?
Solution:  1/4

Question 6. An urn contains 5 white and 8 black balls. Two successive drawings of 3 balls at a time are made such that the balls drawn in the first draw are not replaced before the second draw. Find the probability that the first draw gives 3 white balls and the second draw gives 3 black balls.
Solution: 7/429

Explanation:

Required Probability = \(\left\{\frac{{ }^5 C_3}{{ }^{13} C_3} \times \frac{{ }^8 C_3}{{ }^{10} C_3}\right\}=\left(\frac{5 \times 4 \times 3}{13 \times 12 \times 11} \times \frac{8 \times 7 \times 6}{10 \times 9 \times 8}\right)\)

Question 7. Let E₁ and E₂ be the events such that P(E₁) = 1/3 and P(E₂) = 3/5 Find:

1. P(E₁∪E₂), when E₁ and E₂ are mutually exclusive,
2. P(E₁∩E₂), when E₁ and E₂ are independent.

Solution:

1. 14/15
2. 1/5

Question 8. If E₁ and E₂ are two events such that P(E₁) =1/4, P(E₂) = 1/3, and P(E₁∪E₂) = 1/2, show that E₁ and E₂ are independent events.
Solution: 4/5

Question 9. If E₁ and E₂ are independent events such that P(E₁) =0.3 and P(E₂) =0.4, find

1. \(P\left(E_1 \cap E_2\right)\)
2. \(P\left(E_1 \cap E_2\right)\)
3. \(P\left(\bar{E}_1 \cap \bar{E}_2\right)\)
4. \(P\left(\bar{E}_1 \cap E_2\right)\).

Solution:

1. 0.12
2. 0.58
3. 0.42
4. 0.28

Question 10. Let A and B be events such that P(A) = 1/2, P(B) = 7/12 and P(not A or not B) = 1/4 State whether A and B are

1. Mutually exclusive,
2. Independent.⇒

Solution:

1. No
2. No

Hint: P({not} A or {not} B) = \(P(\bar{A} \text { or } \bar{B})=P(\bar{A} \cup \bar{B})\)

= \(P(\overline{A \cap B})=1-P(A \cap B)\)

⇒ \(1-P(A \cap B)=\frac{1}{4}\)

⇒ \(P(A \cap B)=\frac{3}{4}\)

1. Since \(P(A \cap B) \neq 0\), so A and B are not mutually exclusive.

2. \(P(A) \times P(B)=\left(\frac{1}{2} \times \frac{7}{12}\right)=\frac{7}{24} \neq P(A \cap B)\)

⇒ A and B are not independent.

Question 11. Kamal and Vimal appeared for an interview for two vacancies. The probability of Kamal’s selection is 1/3 and that of Vimal’s selection is 1/5 Find the probability that only one of them will be selected.
Solution: 2/5

Hint:

Let E₁ = event that kamal is selected,

and E₂ = event that Vimal is selected. Then,

⇒ \(P\left(E_1\right)=\frac{1}{3}, P\left(E_2\right)=\frac{1}{5}, P\left(\bar{E}_1\right)=\left(1-\frac{1}{3}\right)=\frac{2}{3} \text { and } P\left(\bar{E}_2\right)=\left(1-\frac{1}{5}\right)=\frac{4}{5}\)

∴ required probability

= \(P\left[\left(E_1 \text { and }{not} E_2\right) \text { or }\left(E_2 \text { and } {not} E_1\right)\right]\)

= \(P\left[\left(E_1\right.\right. and \left.\bar{E}_2\right) or \left(E_2\right. and \left.\left.\bar{E}_1\right)\right]\)

= \(P\left(E_1 \cap \bar{E}_2\right)+P\left(E_2 \cap \bar{E}_1\right)\)

= \(\left\{P\left(E_1\right) \times P\left(\bar{E}_2\right)\right\}+\left\{P\left(E_2\right) \times P\left(\bar{E}_1\right)\right\}\).

Question 12. Arun and Ved appeared for an interview for two vacancies. The probability of Aran’s selection is 1/4 and that of Ved’s rejection is 2/3. Find the probability that at least one of them will be selected.
Solution: 1/2

Hint:

Let E₁ =event that Arun is selected,

and E₂ =event that Ved is selected.

Then, \(P\left(E_1\right)=\frac{1}{4} \text { and } P\left(E_2\right)=\left(1-\frac{2}{3}\right)=\frac{1}{3} \text {. }\)

Clearly, E₁ and E₂ are independent events.

∴ \(P\left(E_1 \cap E_2\right)=P\left(E_1\right) \times P\left(E_2\right)=\left(\frac{1}{4} \times \frac{1}{3}\right)=\frac{1}{12}\)

Required probability = \(P\left(E_1 \text { or } E_2\right)=P\left(E_1 \cup E_2\right)\)

= \(P\left(E_1\right)+P\left(E_2\right)-P\left(E_1 \cap E_2\right)=\left(\frac{1}{4}+\frac{1}{3}-\frac{1}{12}\right)=\frac{6}{12}=\frac{1}{2}\)

Question 13. A and B appear for an interview for two vacancies in the same post. The probability of A’s selection is 1/6 and that of B’s selection is 1/4. Find the probability that

1. Both of them are selected
2. Only one of them is selected
3. None is selected
4. At least one of them is selected.

Solution:

1. 1/24
2. 1/3
3. 5/8
4. 3/8

Hint:

We have P(A)= \(\frac{1}{6}, P(B)=\frac{1}{4}\).

∴ \(P(\bar{A})=1-P(A)=\left(1-\frac{1}{6}\right)=\frac{5}{6}\) and \(P(\bar{B})=1-P(B)=\left(1-\frac{1}{4}\right)=\frac{3}{4}\).

1. P (both are selected)

= \(P(A \cap B)=P(A) \times P(B) \text {. }\)

2. P(only one of them is selected)

= \(P[(A \text { and not } B) \text { or }(B \text { and not } A)]\)

= \(P(A \cap \bar{B})+P(B \cap \bar{A})\)

= \(\{P(A) \times P(\bar{B})\}+\{P(B) \times P(\bar{A})\}\)

3. P( none is selected )=P(not A and not B)

= \(P(\bar{A} \cap \bar{B})=P(\bar{A}) \times P(\bar{B})\)

4. P (at least one is selected )= 1-P (none is selected).

Question 14. Given the probability that A can solve a problem is 2/3, and the probability that B can solve the same problem is 3/5, find the probability that

1. At least one of a and b will solve the problem
2. None of the two will solve the problem.

Solution:

1. 13/15
2. 2/15

Hint:

Let E₁ =event that A can solve the problem

and E₂ =event that B can solve the problem.

Then, E₁ and E₂ are clearly independent events.

∴ \(P\left(E_1 \cap E_2\right)=P\left(E_1\right) \times P\left(E_2\right)=\left(\frac{2}{3} \times \frac{3}{5}\right)=\frac{2}{5} \text {. }\)

1. P(at least one of A and B can solve the problem)

= \(P\left(E_1 \cup E_2\right)=P\left(E_1\right)+P\left(E_2\right)-P\left(E_1 \cap E_2\right)=\left(\frac{2}{3}+\frac{3}{5}-\frac{2}{5}\right)=\frac{13}{15}\)

2. P(none can solve the problem)

=1-P(at least one can solve the problem)

= \(\left(1-\frac{13}{15}\right)=\frac{2}{15}\)

Question 15. A problem is given to three students whose chances of solving it are 1/4, 1/5, and 1/6 respectively. Find the probability that the problem is solved.
Solution: 1/2

Hint: Let A, B, and C be the events of solving the problem by the 1st, 2nd, and 3rd student respectively. Then,

P(A)= \(\frac{1}{4}\), P(B)= \(\frac{1}{5}\) and P(C)= \(\frac{1}{6}\)

⇒ \(P(\bar{A})=\left(1-\frac{1}{4}\right)=\frac{3}{4}  P(\bar{B})=\left(1-\frac{1}{5}\right)=\frac{4}{5} \text { and } P(\bar{C})=\left(1-\frac{1}{6}\right)=\frac{5}{6}\)

∴ P(none solves the problem)= P({not} A)and{not} B) and }({not} C))

= \(P(\bar{A} \text { and } \bar{B} \text { and } \bar{C})=P(\bar{A}) \times P(\bar{B}) \times P(\bar{C})\)

Question 16. The probabilities of A, B, and C solving a problem are 1/3, 1/4, and 1/6 respectively. If all three try to solve the problem simultaneously, find the probability that exactly one of them will solve it.
Solution: 31/72

Hint:

Given P(A)= \(\frac{1}{3}\), P(B)=\(\frac{1}{4}\) and P(C)= \(\frac{1}{6}\)

⇒ \(P(\bar{A})=\left(1-\frac{1}{3}\right)=\frac{2}{3}, P(\bar{B})=\left(1-\frac{1}{4}\right)=\frac{3}{4} \text { and } P(\bar{C})=\left(1-\frac{1}{6}\right)=\frac{5}{6}\)

∴ required probability

= P(exactly one of them solves the problem)

= \(P[(A \cap \bar{B} \cap \bar{C}) \text { or }(\bar{A} \cap B \cap \bar{C}) \text { or }(\bar{A} \cap \bar{B} \cap C)]\)

= \(P(A \cap \bar{B} \cap \bar{C})+P(\bar{A} \cap B \cap \bar{C})+P(\bar{A} \cap \bar{B} \cap C)\)

= \(\{P(A) \times P(\bar{B}) \times P(\bar{C})\}+\{P(\bar{A}) \times P(B) \times P(\bar{C})\}+\{P(\bar{A}) \times P(\bar{B}) \times P(C)\}\)

Question 17. A can hit a target 4 times in 5 shots, B can hit 3 times in 4 shots, and C can hit 2 times in 3 shots. Calculate the probability that

1. A, B, and C all hit the target
2. B and C hit and A does not hit the target.

Solution:

1. 2/5
2. 1/10

Hint: P(A hits)= 4/5, P(B hits)= 3/4 and P(C hits)= 2/3

1. P(A hits and B hits and C hits) = P(A) x P(B) x P(C).
2. P(B hits C hits and A does not hit) = P(B)xP(C)xP\((\overline{\mathrm{A}})\)

Question 18. Neelam has offered physics, chemistry, and mathematics in Class 12. She estimates that her probabilities of receiving a grade A in these courses are 0.2, 0.3, and 0.9 respectively. Find the probabilities that Neelam receives

1. All a grades
2. No a grade
3. Exactly 2 grades.

Solution:

1. 0.054
2. 0.056
3. 0.348

Hint:

1. P(getting all A grades) = \(P\left(A_1 A_2 A_3\right)=P\left(A_1\right) \times P\left(A_2\right) \times P\left(A_3\right)\)

2. P(getting no A grade) = \(P\left(\bar{A}_1 \bar{A}_2 \bar{A}_3\right)=P\left(\bar{A}_1\right) \times P\left(\bar{A}_2\right) \times P\left(\bar{A}_3\right)\) .

3. P(getting exactly two A grades)

= \(P\left[\left(\bar{A}_1 A_2 A_3\right) \text { or }\left(A_1 \bar{A}_2 A_3\right) {or}\left(A_1 A_2 \bar{A}_3\right)\right]\)

= \(P\left(\bar{A}_1 A_2 A_3\right)+P\left(A_1 \bar{A}_2 A_3\right)+P\left(A_1 A_2 \bar{A}_3\right)\)

= \(\left\{P\left(\bar{A}_1\right) \times P\left(A_2\right) \times P\left(A_3\right)\right\}+\left\{P\left(A_1\right) \times P\left(\bar{A}_2\right) \times P\left(A_3\right)\right\}+\left\{P\left(A_1\right) \times P\left(A_2\right) \times P\left(\bar{A}_3\right)\right\}\)

Question 19. An article manufactured by a company consists of two parts X and Y. In the process of manufacture of part X, 8 out of 100 parts may be defective. Similarly, 5 out of 100 parts of Y may be defective. Calculate the probability that the assembled product will not be defective.
Solution: 437/500

Hint: P(X is defective) = \(\frac{8}{100}\) = \(\frac{2}{25}\)

P(Y is defective) = \(\frac{5}{100}\) = \(\frac{1}{20}\)

P(X is not defective) = (1-\(\frac{2}{25}\)) = \(\frac{23}{25}\)

P(Y is not defective = (1-\(\frac{2}{20}\)) = \(\frac{19}{20}\)

Required probability =P(assembled part is not defective)

= P(X is not defective and Y is not defective)

= \(\left(\frac{23}{25} \times \frac{19}{20}\right)=\frac{437}{500}\).

Question 20. A town has two fire-extinguishing engines, functioning independently. The probability of availability of each engine when needed is 0.95. What is the probability that

1. Neither of them is available when needed.
2. An engine is available when needed?

Solution:

1. 1/400
2. 19/200

Hint: Let E₁ =event of availability of the first engine.

And, E₂ =event of availability of the second engine.

Then, \(P\left(E_1\right)=P\left(E_2\right)=0.95 and P\left(\bar{E}_1\right)=P\left(\bar{E}_2\right)=(1-0.95)=0.05\).

1. P(neither of them is available when needed)

= \(P\left(\bar{E}_1 \text { and } \bar{E}_2\right)=P\left(\bar{E}_1\right) \times P\left(\bar{E}_2\right) \text {. }\)

2. P(an engine is available when needed)

= \(P\left[\left(E_1 \text { and not } E_2\right) \text { or }\left(E_2 \text { and not } E_1\right)\right]\)

= \(P\left[\left(E_1 \text { and } \bar{E}_2\right) \text { or }\left(E_2 \text { and } \bar{E}_1\right)\right] \)

= \(P\left(E_1 \cap \bar{E}_2\right)+P\left(E_2 \cap \bar{E}_1\right)\)

= \(\left\{P\left(E_1\right) \times P\left(\bar{E}_2\right)\right\}+\left\{P\left(E_2\right) \times P\left(\bar{E}_1\right)\right\}\)

Question 21. A machine operates only when all of its three components function. The probabilities of the failures of the first, second, and third components are 0.14, 0.10, and 0.05 respectively. What is the probability that the machine will fail?
Solution: 0.02647

Hint: Let E₁, E₂, and E₃ be the respective events that the 1st, 2nd, and 3rd components function. Then,

⇒ \(P\left(\bar{E}_1\right)=0.14, P\left(\bar{E}_2\right)=0.10 \text { and } P\left(\bar{E}_3\right)=0.05\)

P(E₁) =(1- 0.14) = 0.86, P(E₂) =(1- 0.10) = 0.90 and P(E₃) =(1- 0.05) = 0.95

P(machine fails) =1 -P(machine functions)

=1-P[(E₁ and E₂ and E₃)]

=1-P(E₁)X P(E₂)X P(E₃)].

Question 22. An anti-aircraft gun can take a maximum of 4 shots at an enemy plane moving away from it. The probabilities of hitting the plane at the first, second, third, and fourth shots are 0.4,0.3,0.2 and 0.1 respectively. What is the probability that at least one shot hits the plane?
Solution: 0.6976

Hint: Let E₁, E₂, E₃, and E₄ be the respective events that the plane is hit in the 1st, 2nd, 3rd, and 4th shots. Then,

P(E₁) = 0.4, P(E₂) = 0.3, P(E₃) = 0.2 and P(E₄) = 0.1

∴ \(P\left(\bar{E}_1\right)=(1-0.4)=0.6, P\left(\bar{E}_2\right)=(1-0.3)=0.7,\)

∴ \(P\left(\bar{E}_3\right)=(1-0.2)=0.8, P\left(\bar{E}_4\right)=(1-0.1)=0.9\)

∴ P(at least one shot hits the plane) = \(1-P\left(\bar{E}_1 \text { and } \bar{E}_2 \text { and } \bar{E}_3 \text { and } \bar{E}_4\right)\)

= \(1-\left\{P\left(\bar{E}_1\right) \times P\left(\bar{E}_2\right) \times P\left(\bar{E}_3\right) \times P\left(\bar{E}_4\right)\right\}\)

Question 23. Let S₁ and S₂ be two switches and let their probabilities of working be given by P(S₁) = 4/5 and P(S₂) = 9/10. Find the probability that the current flows from terminal A to terminal B when S₁ and S₂ are installed in series, shown as follows:
Solution: 18/25

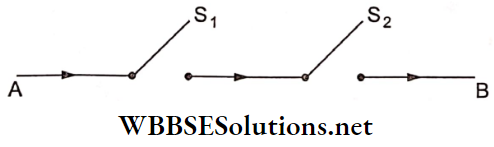
Hint: P(current flows from A to B)

=P(S₁ is closed and S₂ is closed)

=P(S₁ and S₂)=P(S₁) x P(S₂).

Question 24. Let S₁ and S₂ be two switches and let their probabilities of working be given by P(S₁) = 4/5 and P(S₂) = 3/4. Find the probability that the current flows from terminal A to terminal B, when S₁ and S₂ are installed in parallel, as shown below:
Solution: 11/12

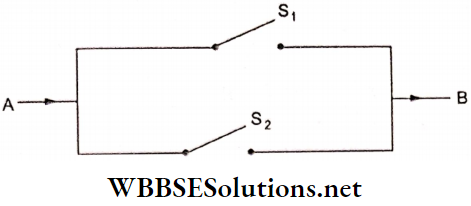
Hint: P(the current flows) =P(S₁ or S₂ )

=P(S₁∪S₂)=P(S₁)+P(S₂)-P(S₁∩S₂)

=P(S₁)+P(S₂)-P(S₁)xP(S₂).

Question 25. A coin is tossed. If a head comes up, a die is thrown but if a tail comes up, the coin is tossed again. Find the probability of obtaining

1. Two tails
2. A head and the number 6
3. A head and an even number.

Solution:

1. 1/8
2. 1/8
3. 1/3

Hint:

S =[H1, HI, H3, HA, H5, H6, TT, TH) → n(S) = 8.

1. P(two tails) = 1/8
2. P(head and the number 6) = 1/8
3. P(head and an even number) = 3/8