Centre Of Mass Multiple Choice Question And Answers
Question 1. The center of mass of a body:
- Lies always at the geometrical center
- Lies always inside the body
- Lies always outside the body
- Lies within or outside the body
Answer: 4. Lies within or outside the body
Question 2. A body has its center of mass at the origin. The x-coordinates of the particles
- Maybe all positive
- Maybe all negative
- It must be all non-negative
- It may be positive for some particles and negative for other particles
Answer: 4. May be positive for some particles and negative in other particles
Centre of Mass MCQs for NEET Physics Class 11 with Answers
Question 3. All the particles of a body are situated at a distance R from the origin. The distance of the center of mass of the body from the origin is
- = R
- ≤ R
- > R
- ≥ R
Answer: 2. ≤ R
Question 4. Where will be the center of mass on combining two masses m and M (M > m):
- Towards m
- Towards M
- In the middle of m and M
- Anywhere
Answer: 2. Towards M
Question 5. Two homogenous spheres A and B of masses m and 2m having radii 2a and a respectively are placed in touch. The distance of the center of mass from the first sphere is :
- a
- 2a
- 3a
- None of these
Answer: 2. 2a
Question 6. In the HCl molecule, the separation between the nuclei of the two atoms is about 1.27 Å (1 Å = 10–10 m). The approximate location of the centre of mass of the molecule, distance from the hydrogen atom assuming the chlorine atom to be about 35.5 times as massive as hydrogen is
- 1Å
- 2.5 Å
- 1.24 Å
- 1.5 Å
Answer: 3. 1.24 Å
Question 7. The distance between the carbon atom and the oxygen atom in a carbon monoxide molecule is 1.1 Å. Given, that the mass of the carbon atom is 12 a.m.u. and the mass of the oxygen atom is 16 a.m.u., calculate the position of the center of mass of the carbon monoxide molecule
- 6.3 Å from the carbon atom
- 1 Å from the oxygen atom
- 0.63 Å from the carbon atom
- 0.12 Å from the oxygen atom
Answer: 3. 0.63 Å from the carbon atom
Question 8. Three identical metal balls each of radius r are placed touching each other on a horizontal surface such that an equilateral triangle is formed when the centers of the three balls are joined. The center of the mass of the system is located at
- Horizontal surface
- The center of one of the balls
- Line joining centers of any two balls
- Point of intersection of the medians
Answer: 4. Point of intersection of the medians
Question 9. Centre of mass is a point
- Which is the geometric center of a body
- From which distance of particles the same
- Where the whole mass of the body is supposed to be concentrated
- Which is the origin of the reference frame
Answer: 3. Where the whole mass of the body is supposed to be concentrated
Question 10. Choose the correct statement about the center of mass (CM) of a system of two particles
- The CM lies on the line joining the two particles midway between them
- The CM lies on the line joining them at a point whose distance from each particle is inversely proportional to the mass of that particle
- The CM lies on the line joining them at a point whose distance from each particle is proportional to the square of the mass of that particle
- The CM is on the line joining them at a point whose distance from each particle is proportional to the mass of that particle
Answer: 2. The CM lies on the line joining them at a point whose distance from each particle is inversely proportional to the mass of that particle
Question 11. The center of mass of a system of two particles divides the distance between them

- In the inverse ratio of the square of masses of particles
- In a direct ratio of the square of masses of particles
- In inverse ratio of masses of particles
- In direct ratio of masses of particles
Answer: 3. In inverse ratio of masses of particles
Question 12. A cricket bat is cut at the location of its center of mass as shown.
- The two pieces will have the same mass
- The bottom piece will have a larger mass
- The handle piece will have a larger mass
- The mass of the handle piece is double the mass of the bottom piece
Answer: 2. The bottom piece will have a larger mass
Question 13. The center of mass of the triangle shown in the figure has coordinates

- \(x=\frac{h}{2}, y=\frac{b}{2}\)
- \(\mathrm{x}=\frac{\mathrm{b}}{2}, \mathrm{y}=\frac{\mathrm{h}}{2}\)
- \(x=\frac{b}{3}, y=\frac{h}{3}\)
- \(x=\frac{h}{3}, y=\frac{b}{3}\)
Answer: 3. \(x=\frac{b}{3}, y=\frac{h}{3}\)
Question 14. Four bodies of equal mass start moving at the same speed as shown in the figure. In which of the following combination the center of mass will remain at the origin

- c and b
- a and d
- a and c
- b and c
Answer: 3. a and c
Question 15. Three identical spheres, each of mass 1 kg are kept as shown in the figure, touching each other, with their centers on a straight line. If their centers are marked P, Q, and R respectively, the distance of the center of mass of the system from P (origin) is

- \(\frac{P Q+P R+Q R}{3}\)
- \(\frac{P Q+P R}{3}\)
- \(\frac{P Q+Q R}{3}\)
- PR+QR
Answer: 2. \(\frac{P Q+P R}{3}\)
Question 16. A uniform square plate ABCD has a mass of 10 kg. If two point masses of 3 kg each are placed at the corners C and D as shown in the adjoining figure, then the center of mass shifts to the point which lies on –

- OC
- OD
- OY
- OX
Answer: 3. OY
Question 17. Three particles of masses 1 kg, 2 kg, and 3 kg are placed at the corners of an equilateral triangle of side 1.0 m as shown in Fig. The coordinates of the center of masses of the system are

- \(\left(\frac{7}{12} m, \frac{\sqrt{3}}{4} m\right)\)
- \(\left(\frac{1}{2} m, \frac{\sqrt{3}}{4} m\right)\)
- \(\left(\frac{3}{12} m, \frac{1}{4} m\right)\)
- \(\left(\frac{3}{12} m, \frac{\sqrt{3}}{4} m\right)\)
Answer: 3. \(\left(\frac{3}{12} m, \frac{1}{4} m\right)\)
Question 18. A non–uniform thin rod of length L is placed along the x-axis as such it is one of the ends at the origin. The linear mass density of the rod is λ = λ0x. The distance of the center of mass of the rod from the origin is:
- L/2
- 2L/3
- L/4
- L/5
Answer: 2. 2L/3
Question 19. The center of mass of the shaded portion of the disc is : (The mass is uniformly distributed in the shaded portion):

- \(\frac{\mathrm{R}}{20}\) to the left of A
- \(\frac{\mathrm{R}}{12}\) to the left of A
- \(\frac{\mathrm{R}}{20}\) to the right of A
- \(\frac{\mathrm{R}}{12}\) to the right of A
Answer: 1. \(\frac{\mathrm{R}}{20}\) to the left of A
Question 20. Four particles of masses m, 2m, 3m, and 4m are arranged at the corners of a parallelogram with each side equal to a, and one of the angles between two adjacent sides is 60º. The parallelogram lies in the x-y plane with mass m at the origin and 4m on the x-axis. The center of mass of the arrangement will be located at
- \(\left(\frac{\sqrt{3}}{2} a, 0.95 a\right)\)
- \(\left(0.95 a, \frac{\sqrt{3}}{4} a,\right)\)
- \(\left(\frac{3 \mathrm{a}}{4}, \frac{\mathrm{a}}{2}\right)\)
- \(\left(\frac{\mathrm{a}}{2}, \frac{3 \mathrm{a}}{4}\right)\)
Answer: 2. \(\left(0.95 a, \frac{\sqrt{3}}{4} a,\right)\)
Question 21. Masses 8, 2, 4, and 2 kg are placed at the corners A, B, C, and D respectively of a square ABCD of diagonal 80 cm. The distance of the center of mass from A will be
- 20 cm
- 30 cm
- 40 cm
- 60 cm
Answer: 2. 30 cm
Question 22. If the linear density of a rod of length 3m varies as λ = 2 + x, then the position of the center of gravity of the rod is
- \(\frac{7}{3} m\)
- \(\frac{12}{7} m\)
- \(\frac{10}{7} m\)
- \(\frac{9}{7} m\)
Answer: 2. \(\frac{12}{7} m\)
Question 23. A circular plate of uniform thickness has a diameter of 56 cm. A circular portion of diameter 42 cm is removed from one edge as shown in the figure. The center of mass of the remaining portion from the center of the plate will be:

- 5 cm
- 7 cm
- 9 cm
- 11 cm
Answer: 3. 9 cm
NEET Physics Chapter 3 Centre of Mass Multiple Choice Questions
Question 24. The coordinate of the center of mass of a system is shown in the figure:

- \(\left(\frac{\mathrm{a}}{3}, 0\right)\)
- \(\left(\frac{\mathrm{a}}{2}, \frac{\mathrm{a}}{2}\right)\)
- \(\left(\frac{\mathrm{a}}{3}, \frac{\mathrm{a}}{3}\right)\)
- \(\left(0, \frac{\mathrm{a}}{3}\right)\)
Answer: 3. \(\left(\frac{\mathrm{a}}{3}, \frac{\mathrm{a}}{3}\right)\)
Question 25. The coordinate of the center of mass of a system is shown in the figure:

- \(\frac{\mathrm{a} \sqrt{3}}{2}, \frac{\mathrm{a}}{2}\)
- \(\frac{a}{2}, \frac{a}{6} \sqrt{3}\)
- \(\frac{a}{4}, \frac{a}{4} \sqrt{3}\)
- \(\frac{\mathrm{a}}{2}, \frac{\mathrm{a}}{\sqrt{3}}\)
Answer: 2. \(\frac{a}{2}, \frac{a}{6} \sqrt{3}\)
Question 26. The center of masses of three particles of mass m1= m2= 1 kg at the corners of an equilateral triangle of side 1 m will be –
- 0.50m, 0.43m
- 0.43m, 0.50m
- 0.25m, 0.25m
- 0.22m, 0.22m
Answer: 1. 0.50m, 0.43m
Question 27. Two bodies of mass 1 kg and 3 kg have position vector \(\hat{i}+2 \hat{j}+\hat{k} \text { and }-3 \hat{i}-2 \hat{j}+\hat{k}\) respectively. The center of mass of this system has a position vector.
- \(-2 \hat{i}+2 \hat{k}\)
- \(-2 \hat{i}-\hat{j}+\hat{k}\)
- \(2 \hat{i}-\hat{j}-2 \hat{k}\)
- \(-\hat{i}+\hat{j}+\hat{k}\)
Answer: 2. \(-2 \hat{i}-\hat{j}+\hat{k}\)
Question 28. A circular disc of radius R is removed from a bigger circular disc of radius 2R such that the circumferences of the discs coincide. The center of mass of the new disc is αR from the center of the bigger disc. The value of α is:
- 1/3
- 1/2
- 1/6
- 1/4
Answer: 1. 1/3
Question 29. Two semicircular rings of linear mass densities λ and 2 λ and of radius ‘R’ each are joined to form a complete ring. The distance of the center of the mass of the complete ring from its geometrical center is:
- \(\frac{3 R}{8 \pi}\)
- \(\frac{2 R}{3 \pi}\)
- \(\frac{3 R}{4 \pi}\)
- None of these
Answer: 2. \(\frac{2 R}{3 \pi}\)
Question 30. A uniform metal disc of radius R is taken and out of it, a disc of diameter R is cut off from the end. The center of mass of the remaining part will be:
- \(\frac{R}{4}\)from the centre
- \(\frac{R}{3}\) from the centre
- \(\frac{R}{5}\) from the centre
- \(\frac{R}{6}\) from the centre
Answer: 4. \(\frac{R}{6}\) from the centre
Question 31. A uniform solid cone of height 40 cm is shown in the figure. The distance of the center of mass of the cone from point B (center of the base) is:

- 20 cm
- 10/3 cm
- 20/3 cm
- 10 cm
Answer: 4. 10 cm
Question 32. A bomb traveling in a parabolic path under the effect of gravity explodes in mid-air. The center of mass of fragments will:
- Move vertically upwards and then downwards
- Move vertically downwards
- Move-in irregular path
- Move-in the parabolic path which the unexploded bomb would have traveled.
Answer: 4. Move in the parabolic path that the unexploded bomb would have traveled.
Question 33. If a ball is thrown upwards from the surface of the earth and during upward motion :
- The earth remains stationary while the ball moves upwards
- The ball remains stationary while the earth moves downwards
- The ball and earth both move toward each other
- The ball and earth both move away from each other
Answer: 4. The ball and earth both move away from each other
Question 34. Internal forces can change :
- The linear momentum but not the kinetic energy of the system.
- The kinetic energy but not the linear momentum of the system.
- Linear momentum as well as kinetic energy of the system.
- Neither the linear momentum nor the kinetic energy of the system.
Answer: 2. The kinetic energy but not the linear momentum of the system.
Question 35. If the external forces acting on a system have zero resultant, the center of mass
- Must not move
- Must accelerate
- May move
- May accelerate
Answer: 3. May accelerate
Question 36. Two balls are thrown in the air. The acceleration of the center of mass of the two balls while in the air (neglect air resistance)
- Depends on the direction of the motion of the balls
- Depends on the masses of the two balls
- Depends on the speeds of the two balls
- Is equal to g
Answer: 4. Is equal to g
Question 37. Two particles of mass 1 kg and 0.5 kg are moving in the same direction with speeds of 2m/s and 6m/s respectively on a smooth horizontal surface. The speed of the center of mass of the system is:
- \(\frac{10}{3} \mathrm{~m} / \mathrm{s}\)
- \(\frac{10}{7} \mathrm{~m} / \mathrm{s}\)
- \(\frac{11}{2} \mathrm{~m} / \mathrm{s}\)
- \(\frac{12}{3} \mathrm{~m} / \mathrm{s}\)
Answer: 1. \(\frac{10}{3} \mathrm{~m} / \mathrm{s}\)
Question 38. The motion of the center of mass of a system of two particles is unaffected by their internal forces:
- Irrespective of the actual direction of the internal forces
- Only if they are along the line joining the particles
- Only if they are at right angles to the line joining the particles
- Only if they are obliquely inclined to the line joining the particles.
Answer: 1. Irrespective of the actual directions of the internal forces
Question 39. Two objects of masses 200 gm and 500 gm possess velocities \(10 \hat{i} \mathrm{~m} / \mathrm{s} \text { and } 3 \hat{i}+5 \hat{j} \mathrm{~m} / \mathrm{s}\) respectively. The velocity of their center of mass in m/s is :
- \(5 \hat{i}-25 \hat{j}\)
- \(\frac{5}{7} \hat{i}-25 \hat{j}\)
- \(5 \hat{i}+\frac{25}{7} \hat{j}\)
- \(25 \hat{i}-\frac{5}{7} \hat{j}\)
Answer: 3. \(5 \hat{i}+\frac{25}{7} \hat{j}\)
Question 40. 2 bodies of different masses of 2kg and 4kg are moving with velocities 20m/s and 10m/s towards each other due to mutual gravitational attraction. What is the velocity of their center of mass?
- 5 m/s
- 6 m/s
- 8 m/s
- Zero
Answer: 4. Zero
Question 41. Two spheres of masses 2M and M are initially at rest at a distance R apart. Due to the mutual force of attraction, they approach each other. When they are at separation R/2, the acceleration of the center of mass of spheres would be
- 0 m / s2
- g m / s2
- 3g m / s2
- 12g m / s2
Answer: 1. 0 m / s2
Question 42. Two bodies A and B have masses M and m respectively, where M > m and they are at a distance d apart. Equal force is applied to them so that they approach each other. The position where they hit each other is
- Nearer to B
- Nearer to A
- At an equal distance from A and B
- Cannot be decided
Answer: 2. Nearer to A
Question 43. Two particles whose masses are 10 kg and 30 kg and their position vectors are respectively would have the center of mass at –
- \(-\frac{(\hat{\mathbf{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}})}{2}\)
- \(\frac{(\hat{i}+\hat{j}+\hat{k})}{2}\)
- \(-\frac{(\hat{i}+\hat{j}+\hat{k})}{4}\)
- \(\frac{(\hat{i}+\hat{j}+\hat{k})}{4}\)
Answer: 1. \(-\frac{(\hat{\mathbf{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}})}{2}\)
Question 44. Two balls A and B of masses 100 gm and 250 gm respectively are connected by a stretched spring of negligible mass and placed on a smooth table. When the balls are released simultaneously the initial acceleration of B is 10 cm/sec2 westward. What is the magnitude and direction of the initial acceleration of the ball A –
- 25 cm/sec2 Eastward
- 25 cm/sec2 Northward
- 25 cm/sec2 Westward
- 25 cm/sec2 Southward
Answer: 1. 25 cm/sec2 Eastward
Question 45. A shell of mass m moving with velocity u suddenly breaks into 2 pieces. The part having mass m/4 remains stationary. The velocity of the other shell will be :
- u
- 2u
- \(\frac{3}{4}\)u
- \(\frac{4}{3}\)u
Answer: 4. \(\frac{4}{3}\)u
Question 46. A stone is projected with an initial velocity at some angle to the horizontal. A small piece separates from the stone before the stone reaches its maximum height. Then the piece will :
- Fall to the ground
- Fly horizontally initially and will then describe a parabolic path
- Fly side by side with the parent stone along a parabolic path
- The lag behind the parent stone increases the distance from it.
Answer: 3. Fly side by side with the parent stone along a parabolic path
Centre of Mass NEET Class 11 MCQs with Detailed Solutions
Question 47. Three particles with masses 10, 20 and 40gm are moving with velocities \(10 \hat{i}, 10 \hat{j}\) and \(10 \hat{k}_{}\) m/sec respectively. If due to some internal force, the first particle comes to rest and the velocity of the second becomes \((3 \hat{i}+4 \hat{j})\)+m/sec. then the velocity of the third particle after the interaction is-
- \(\hat{i}+\hat{j}+5 \hat{k}\)
- \(\hat{j}+10 \hat{k}\)
- \(\hat{\mathrm{i}}+\hat{\mathrm{j}}+10 \hat{\mathrm{k}}\)
- \(\hat{i}+3 \hat{j}+10 \hat{k}\)
Answer: 4. \(\hat{i}+3 \hat{j}+10 \hat{k}\)
Question 48. Two particles having mass ratio n: 1 are interconnected by a light inextensible string that passes over a smooth pulley. If the system is released, then the acceleration of the center of mass of the system is:
- \((n-1)^2 g\)
- \(\left(\frac{n+1}{n-1}\right)^2 g\)
- \(\left(\frac{n-1}{n+1}\right)^2 g\)
- \(\left(\frac{n+1}{n-1}\right) g\)
Answer: 3. \(\left(\frac{n-1}{n+1}\right)^2 g\)
Question 49. A uniform thin rod of mass M and Length L is standing vertically along the y-axis on a smooth horizontal surface, with its lower end at the origin (0,0). A slight disturbance at t = 0 causes the lower end to slip on the smooth surface along the positive x-axis, and the rod starts falling. The acceleration vector of the center of mass of the rod during its fall is :
⇒ [\(\vec{R}\) is reaction from surface]
- \(\vec{a}_{C M}=\frac{M \vec{g}+\vec{R}}{M}\)
- \(\vec{a}_{C M}=\frac{M \vec{g}-\vec{R}}{M}\)
- \(\overrightarrow{\mathrm{a}}_{\mathrm{CM}}=\mathrm{Mg}-\overrightarrow{\mathrm{R}}\)
- None of these
Answer: 1. [\(\vec{R}\) is reaction from surface]
Question 50. In a vertical plane inside a smooth hollow thin tube, a block of the same mass as that of the tube is released as shown in the figure. When it is slightly disturbed it moves towards the right. By the time the block reaches the right end of the tube then the displacement of the tube will be (where ‘R’ is the mean radius of a tube). Assume that the tube remains in the vertical plane.

- \(\frac{2 R}{\pi}\)
- \(\frac{4 R}{\pi}\)
- \(\frac{R}{2}\)
- R
Answer: 3. \(\frac{R}{2}\)
Question 51. A ball kept in a closed box moves in the box making collisions with the walls. The box is kept on a smooth surface. The centre of mass:
- Of the box remains constant
- Of the box plus the ball system remains constant
- If the ball remains constant
- Of the ball relative to the box remains constant
Answer: 2. Of the box plus the ball system remains constant
Question 52. A man of mass M stands at one end of a plank of length L which lies at rest on a frictionless surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the plank moves relative to the ground is :
- 3L/4
- L/4
- 4L/5
- L/3
Answer: 1. 3L/4
Question 53. Two blocks A and B are connected by a massless string (shown in figure) A force of 30 N is applied to block B. The distance traveled by center of mass in 2s starting from rest is :

- 1m
- 2m
- 3m
- None of these
Answer: 2. 2m
Question 54. If the system is released, then the acceleration of the center of mass of the system :

- \(\frac{g}{4}\)
- \(\frac{g}{2}\)
- g
- 2g
Answer: 1. \(\frac{g}{4}\)
Question 55. Three particles of masses 1 kg, 2 kg and 3 kg are subjected to forces \((3 \hat{i}-2 \hat{j}+2 \hat{k}) N,(-\hat{i}+2 \hat{j}-\hat{k}) N\), and \((\hat{i}+\hat{j}+\hat{k}) N\)respectively. The magnitude of the acceleration of the CM of the system is:
- \(\frac{\sqrt{11}}{6} \mathrm{~ms}^{-2}\)
- \(\frac{\sqrt{14}}{6} \mathrm{~ms}^{-2} \)
- \(\frac{11}{6} \mathrm{~ms}^{-2}\)
- \(\frac{22}{6} \mathrm{~ms}^{-2}\)
Answer: 2. \(\frac{\sqrt{14}}{6} \mathrm{~ms}^{-2} \)
Question 56. Two bodies of mass 10 kg and 2 kg are moving with velocity \(2 \hat{i}-7 \hat{j}+3 \hat{k} \mathrm{~m} / \mathrm{s} \text { and }-10 \hat{i}+35 \hat{j}-3 \hat{k} \mathrm{~m} / \mathrm{s}\)respectively. The velocity of their centre of mass is :
- \(2 \hat{i} \mathrm{~ms}\)
- \(2 \hat{k} \text { ms }\)
- \((2 \hat{j}+2 \hat{k}) \mathrm{ms}\)
- \((2 \hat{i}+2 \hat{j}+2 \hat{k}) \mathrm{ms}\)
Answer: 2. \(2 \hat{k} \text { ms }\)
Question 57. Consider a system of two particles having masses m1 and m1. If the particle of mass m1 is pushed towards the mass center of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the mass center of particles at the original position?
- \(\frac{m_1}{m_1+m_2} d\)
- \(\frac{m_1}{m_2} d\)
- d
- \(\frac{m_2}{m_1} d\)
Answer: 2. \(\frac{m_1}{m_2} d\)
Question 58. Two identical particles move towards each other with velocities 2v and v respectively. This velocity of the centre of mass is –
- v
- v/3
- v/2
- Zero
Answer: 3. v/2
Question 59. Two blocks of masses 10kg and 4kg are connected by a spring of negligible mass and are placed on a frictionless horizontal surface. An impulse gives a speed of 14 ms-1 to the heavier block in the direction of the lighter block. Then, the velocity of the centre of mass is
- 30 ms-1
- 20 ms-1
- 10 ms-1
- 5 ms-1
Answer: 3. 10 ms-1
Question 60. A uniform chain of length 2 m is kept on a table such that a length of 60 cm hangs freely from the edge of the table. The total mass of the chain is 4 kg. What is the work done in pulling the entire chain on the table?
- 7.2 J
- 3.6 J
- 120 J
- 1200 J
Answer: 2. 3.6 J
Question 61. A body A of mass M while falling vertically downwards under gravity breaks into two parts; a body B of mass \([\frac{1}{3}\)M and, a body C of mass \([\frac{2}{3}\)M. The centre of mass of bodies B and C taken together shifts compared to that of body A towards:
- Depends on the height of the breaking
- Does not shift
- Shift towards body C
- Shift towards body B
Answer: 2. Does not shift
Question 62. Consider a two-particle system with particles having masses m1 and m2. If the first particle is pushed towards the centre of mass through a distance d, by what distance should the second particle be moved, so as to keep the centre of mass at the same position?
- d
- \(\frac{m_2}{m_1} d\)
- \(\frac{m_1}{m_1+m_2} d\)
- \(\frac{m_1}{m_2} d\)
Answer: 4. \(\frac{m_1}{m_2} d\)
Question 63. A uniform sphere is placed on a smooth horizontal surface and a horizontal force F is applied on it at a distance h above the surface. The acceleration of the center
- Is maximum when h = 0
- Is maximum when h = R
- Is maximum when h = 2R
- Is independent of h
Answer: 4. Is independent of h
Question 64. A can of height h is filled with liquid of uniform density ρ. If the liquid is coming out from the bottom then a centre of mass of the ” can + water in the can “
- First ascends and then descends
- First descends and then ascends
- Always decreases
- None of these
Answer: 2. First descends and then ascends
Question 65. A man of mass M stands at one end of a plank of length L which lies at rest on a frictionless horizontal surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
- 3 L/4
- 4 L/5
- L/4
- None of these
Answer: 3. L/4
Question 66. When a block is placed on a wedge as shown in the figure, the block starts sliding down and the wedge also starts sliding on the ground. All surfaces are rough. The center of mass of the (wedge + block) system will
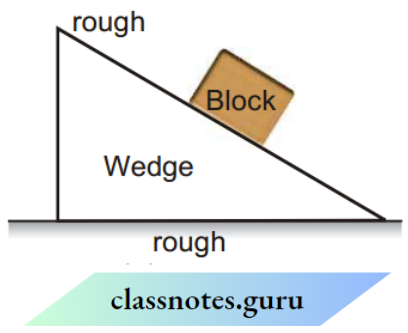
- Leftward and downward.
- Right ward and downward.
- Leftward and upwards.
- Only downward.
Answer: 2. Rightward and downward.
Question 67. A 2 kg body and a 3 kg body are moving along the x-axis. At a particular instant the 2 kg body has a velocity of 3 ms-1 and the 3 kg body has a velocity of 2 ms-1. The velocity of the center of mass at that instant is
- 5 ms-1
- 1 ms-1
- zero
- None of these
Answer: 4. None of these
NEET Class 11 Physics Centre of Mass MCQs for Exam Preparation
Question 68. Two bodies of masses 2 kg and 4 kg are moving with velocities 2 m/s and 10m/s respectively along the same direction. Then the velocity of their centre of mass will be
- 8.1 m/s
- 7.3 m/s
- 6.4 m/s
- 5.3 m/s
Answer: 2. 7.3 m/s
Question 69. Two particles of masses m1 and m2 initially at rest start moving towards each other under their mutual force of attraction. The speed of the centre of mass at any time t, when they are at a distance r apart, is
- Zero
- \(\left(G \frac{m_1 m_2}{r^2} \cdot \frac{1}{m_1}\right) t\)
- \(\left(G \frac{m_1 m_2}{r^2} \cdot \frac{1}{m_2}\right) t\)
- \(\left(G \frac{m_1 m_2}{r^2} \cdot \frac{1}{m_1+m_2}\right) t\)
Answer: 1. Zero
Question 70. A body of mass 20 kg is moving with a velocity of 2ν and another body of mass 10 kg is moving with velocity V along the same direction. The velocity of their center of mass is
- 5ν/3
- 2ν/3
- ν
- Zero
Answer: 1. 5ν/3
Question 71. The two particles X and Y, initially at rest, start moving towards each other under mutual attraction. If at any instant the velocity of X is V and that of Y is 2V, the velocity of their centre of mass will be
- Zero
- V
- 2V
- V/2
Answer: 1. Zero
Question 72. Two particles A and B initially at rest move towards each other under a mutual force of attraction. The speed of the center of mass at the instant when the speed of A is v and the speed of B is 2v is :
- v
- Zero
- 2 v
- 3 v /2
Answer: 2. Zero
Question 73. If the KE of a body becomes four times its initial value, then the new momentum will be more than its initial momentum by;
- 50%
- 100%
- 125%
- 150%
Answer: 2. 100%
Question 74. A particle of mass 4m which is at rest explodes into three fragments. Two of the fragments, each of mass m are found to move with speed v each, in mutually perpendicular directions. The total energy released in the process of explosion is-
- 3mv2/2
- mv2
- 4mv2
- 2mv2
Answer: 1. 3mv2/2
Question 75. A bullet of mass m is being fired from a stationary gun of mass M. If the velocity of the bullet is v, the velocity of the gun is-
- \(\frac{M v}{m+M}\)
- \(\frac{\mathrm{mv}}{\mathrm{M}}\)
- \(\frac{(M+m) v}{M}\)
- \(\frac{\mathrm{M}+\mathrm{m}}{\mathrm{Mv}}\)
Answer: 2. \(\frac{\mathrm{mv}}{\mathrm{M}}\)
Question 76. A bomb explodes in the air in two equal fragments. If one of the fragments is moving vertically upwards with velocity v0, then the other fragment is moving-
- Vertically up with velocity v0
- Vertically downwards with velocity v0
- In any arbitrary direction
- None of these
Answer: 2. Vertically downwards with velocity v0
Question 77. Two particles with equal kinetic energies have masses in the ratio of 1: 2. Then linear momenta will be in the ratio-
- 1
- 4
- 0.707
- 2
Answer: 3. 0.707
Question 78. If a shell fired from a canon explodes in the air then-
- Momentum decreases
- Momentum increases
- Kinetic energy increases
- K.E. decreases
Answer: 3. Kinetic energy increases
Question 79. Three particles A, B and C of equal mass move with equal speeds v along the medians of an equilateral triangle as shown in the figure. They collide at the centroid G of the triangle. After collision A comes to rest, and B retraces its path with speed v. The velocity of C is-

- \(\vec{v} \text {, direction } \vec{G} A\)
- \(\overrightarrow{2} \mathrm{v} \text { and direction } \overrightarrow{\mathrm{G}} \mathrm{A}\)
- \(2 \mathrm{v} \text {, direction } \overrightarrow{\mathrm{GB}}\)
- \(\vec{v} \text {, and direction } \overrightarrow{B G}\)
Answer: 4. \(\vec{v} \text {, and direction } \overrightarrow{B G}\)
Question 80. Under the effect of mutual internal attractions-
- The linear momentum of a system increases
- The linear momentum of a system decreases
- The linear momentum of the system is conserved
- The angular momentum increases
Answer: 3. The linear momentum of the system is conserved
Question 81. A ball of mass 3 kg collides with a wall with a velocity of 10 m/sec at an angle of 30° and after collision reflects at the same angle with the same speed. The change in momentum of the ball in the MKS unit is-
- 20
- 30
- 15
- 45
Answer: 2. 30
Question 82. A particle is moving in X–Y plane under the action of a force \(\vec{F}\) such that at some instant ‘t’ the components of its linear momentum \(\vec{p}\) are px= 2 cos t and py= 2 sin t. At this instant the angle between \(\vec{F} \text { and } \vec{p}\) is
- 90°
- 0°
- 180°
- 30°
Answer: 1. 90°
Question 83. The kinetic energies of a lighter body and a heavier body are the same. Then the value of momentum is-
- Higher for lighter body
- Higher for heavier body
- Same for both
- Additional information is needed to reply to this question
Answer: 2. Higher for heavier body
Centre of Mass Multiple Choice Questions for NEET Class 11
Question 84. A bullet of mass m moving with a velocity v1strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height of h the initial velocity of the bullet is-

- \(\frac{\mathrm{m}+\mathrm{M}}{\mathrm{m}} \sqrt{2 \mathrm{gh}}\)
- \(\sqrt{2 g h}\)
- \(\frac{M+m}{M} \sqrt{2 g h}\)
- \(\frac{m}{M+m} \sqrt{2 g h}\)
Answer: 1. \(\frac{\mathrm{m}+\mathrm{M}}{\mathrm{m}} \sqrt{2 \mathrm{gh}}\)
Question 85. If the mass and kinetic energy of a particle are m and E respectively, then the value of its momentum is-
- \(\sqrt{\mathrm{mE}}\)
- \(\sqrt{2 m E}\)
- \(\sqrt{2 E / m}\)
- \(\sqrt{2 \mathrm{~m} / \mathrm{E}}\)
Answer: 2. \(\sqrt{2 m E}\)
Question 86. If a lighter body (mass M1 and velocity V1) and a heavier body (mass M2 and velocity V2) have the same kinetic energy, then-
- M2V2< M1V1
- M2V2= M1V1
- M2V1= M1V2
- M2V2> M1V1
Answer: 4. M2V2> M1V1
Question 87. A bomb of mass 12kg at rest explodes into two fragments of masses in the ratio 1: 3. The K.E. of the smaller fragment is 216 J. The momentum of heavier fragments is (in kg-m/sec) –
- 36
- 72
- 108
- Insufficient data
Answer: 1. 36
Question 88. A bomb is projected at 200m/s at an angle of 60° with horizontal. At the highest point, it explodes into three particles of equal masses. One goes vertically upward with a velocity of 100m/sec, second particle goes vertically downward with the same velocity as the first. Then what is the velocity of the third one-
- 120 m/sec with 60° angle
- 200 m/sec with 30° angle
- 50 m/sec, in horizontal direction
- 300 m/sec, in horizontal direction
Answer: 4. 300 m/sec, in horizontal direction
Question 89. The law of conservation of energy implies that the
- Total mechanical energy is conserved
- Total kinetic energy is conserved
- Total potential energy is conserved
- Sum of all kinds of energies is conserved
Answer: 4. Sum of all kinds of energies is conserved
Question 90. If the kinetic energy of a body becomes four times its initial value, then new momentum will-
- Become twice its initial value
- Become three times, its initial value
- Become four times, its initial value
- Remains constant
Answer: 1. Become twice its initial value
Question 91. A spacecraft of mass M is travelling in space with velocity v. It then breaks up into two parts such that the smaller part m comes to the rest, then the velocity of the remaining part is-
- \(\frac{M v}{M-m}\)
- \(\frac{M v}{M+m}\)
- \(\frac{\mathrm{mv}}{\mathrm{M}-\mathrm{m}}\)
- \(\frac{\mathrm{Mv}}{\mathrm{m}}\)
Answer: 1. \(\frac{M v}{M-m}\)
Question 92. A bomb at rest has a mass of 60 kg. It explodes and a fragment of 40 kg has a kinetic energy of 96 joules. Then the kinetic energy of the other fragment is-
- 180 J
- 190 J
- 182 J
- 192 J
Answer: 4. 192 J
Question 93. Consider the following two statements-
- The linear momentum of a system of particles is zero
- the kinetic energy of a system of particles is zero. Then
- A does not imply B but B implies A
- A implies B and B implies A
- A does not imply B & B does not imply A
- A implies B but B does not imply A
Answer: 1. A does not imply B but B implies A
Question 94. When a U238 nucleus originally at rest, decays emitting an alpha particle having a speed ‘u’, the recoil speed of the residual nucleus is-
- \(\frac{4 u}{234}\)
- \(-\frac{4 u}{238}\)
- \(\frac{4 u}{238}\)
- \(-\frac{4 u}{234}\)
Answer: 1. \(\frac{4 u}{234}\)
Question 95. A ball of mass 2 kg and another of mass 4 kg are dropped together from a 60-foot-tall building. After a fall of 30 feet each toward Earth, their respective kinetic energies will be in the ratio of-
- \(\sqrt{2}\): 1
- 1: 4
- 1: 2
- 1:\(\sqrt{2}\)
Answer: 3. 1: 2
Question 96. A moving body of mass m and velocity 3 km/hr collides with a body at rest and of mass 2m and then sticks to it. Now the combined mass starts to move, then the combined velocity will be:
- 4 km/hr
- 3 km/hr
- 2 km/hr
- 1 km/hr
Answer: 4. 1 km/hr
Question 97. A 50 g bullet moving with a velocity of 10 m/s strikes a block of mass 950 g at rest and gets embedded into it. The loss in kinetic energy will be
- 100 %
- 95 %
- 5 %
- 50 %
Answer: 2. 95 %
Question 98. A body at rest splits into three parts of mass m, m and 4m respectively. The two equal masses fly off perpendicular to each other and each with a speed of V. The speed of 4m will be
- \(\frac{V}{2 \sqrt{2}}\)
- \(\frac{\mathrm{V}}{\sqrt{2}}\)
- \(\frac{\mathrm{V}}{2}\)
- \(\sqrt{2} \mathrm{~V}\)
Answer: 1. \(\frac{V}{2 \sqrt{2}}\)
Question 99. A stationary body explodes into two fragments of masses m1 and m2. If the momentum of one fragment is p, the minimum energy of the explosion is
- \(\frac{p^2}{2\left(m_1+m_2\right)}\)
- \(\frac{p^2}{2 \sqrt{m_1 m_2}}\)
- \(\frac{p^2\left(m_1+m_2\right)}{2 m_1 m_2}\)
- \(\frac{p^2}{2\left(m_1-m_2\right)}\)
Answer: 3. \(\frac{p^2\left(m_1+m_2\right)}{2 m_1 m_2}\)
Question 100. A train of mass M is moving on a circular track of radius ‘ R ‘ with constant speed V. The length of the train is half of the perimeter of the track. The linear momentum of the train will be
- 0
- \(\frac{2 M V}{\pi}\)
- MVR
- MV
Answer: 2. \(\frac{2 M V}{\pi}\)
Question 101. Two bodies of masses m and 4m are moving with equal linear momentum. The ratio of their kinetic energies is:
- 1: 4
- 4: 1
- 1: 1
- 1: 2
Answer: 2. 4: 1
Question 102. If the momentum of a body increases by 20%, the percentage increase in its kinetic energy is equal to :
- 44
- 88
- 66
- 20
Answer: 1. 44
Question 103. A man is in a moving train, then the train :
- His momentum must not be zero
- His kinetic energy is zero
- His kinetic energy is not zero
- His kinetic energy may be zero
Answer: 4. His kinetic energy may be zero
Question 104. A bomb dropped from an airplane explodes in the air. It’s total :
- Momentum decreases
- Momentum increases
- Kinetic energy increases
- Kinetic energy decreases
Answer: 3. Kinetic energy increases
Question 105. Two blocks of masses m1 and m2 are connected by a massless spring and placed on a smooth surface. The spring initially stretched and released. Then :
- The momentum of each particle remains constant separately
- The momentums of each body are equal
- The magnitude of momentums of each body are equal to each other
- The mechanical energy of a system remains constant
- a and b are correct
- a, b and c are correct
- c and d are correct
- Only C is correct
Answer: 3. c and d are correct
Question 106. A bag of mass M hangs by a long thread and a bullet (mass m) comes horizontally with velocity v and gets caught in the bag. Then for the combined system (bag + bullet):
- Momentum is mMv/(M + m)
- KE is (1/2) Mv2
- Momentum is mv
- KE is m2v2/(M + m)
Answer: 3. Momentum is mv
Question 107. A man of mass ‘m’ climbs on a rope of length L suspended below a balloon of mass M. The balloon is stationary with respect to ground. If the man begins to climb up the rope at a speed vrel (relative to rope). In what direction and with what speed (relative to ground) will the balloon move?
- Downwards, \(\frac{\mathrm{mv}_{\mathrm{rel}}}{\mathrm{m}+\mathrm{M}}\)
- Upwards, \(\frac{\mathrm{Mv}_{\mathrm{rell}}}{\mathrm{m}+\mathrm{M}}\)
- Downwards, \(\frac{\mathrm{mV}_{\mathrm{rel}}}{\mathrm{M}}\)
- Downwards, \(\frac{(M+m) v_{\text {rel }}}{M}\)
Answer: 1. Downwards, \(\frac{\mathrm{mv}_{\mathrm{rel}}}{\mathrm{m}+\mathrm{M}}\)
Question 108. In the figure shown the initial velocity of a boat (30 kg) + person (15 kg ) is 2 m/s. Find the velocity of the person w.r.t. boat so that the velocity of the boat will be 1 m/s in right (Neglect friction between boat and water)

- 3 m/s towards right
- 3 m/s towards left
- 4 m/s towards right
- 4 m/s towards left
Answer: 1. 3 m/s towards right
Question 109. 1 kg body explodes into three fragments. The ratio of their masses is 1: 1 : 3. The fragments of the same mass move perpendicular to each other at speeds of 30 m/s, while the heavier part remains in the initial direction. The speed of the heavier part is :
- \(\frac{10}{\sqrt{2}} \mathrm{~m} / \mathrm{s}\)
- \(10 \sqrt{2} \mathrm{~m} / \mathrm{s}\)
- \(20 \sqrt{2} \mathrm{~m} / \mathrm{s}\)
- \(30 \sqrt{2} \mathrm{~m} / \mathrm{s}\)
Answer: 2. \(10 \sqrt{2} \mathrm{~m} / \mathrm{s}\)
Question 110. A stationary particle explodes into two particles of masses m1 and m2 which move in opposite directions with velocities v1 and v2. The ratio of their kinetic energies E1/E2 is:-
- m2/m1
- m1/m2
- 1
- m1v2/m2 v1
Answer: 1. m1/m2
Question 111. A particle of mass m1 is moving with a velocity v1and another particle of mass m2 is moving with a velocity v2. Both of them have the same momentum but their different kinetic energies are E1 and E2 respectively. If m1> m2 then :
- E1 < E2
- \(\frac{E_1}{E_2}=\frac{m_1}{m_2}\)
- E1 > E2
- E1 = E2
Answer: 1. E1 < E2
Question 112. A bomb of mass 30 kg at rest explodes into two pieces of masses 18 kg and 12 kg. The velocity of 18 kg mass is 6 ms-1. The kinetic energy of the other mass is:
- 256 J
- 486 J
- 524 J
- 324 J
Answer: 2. 486 J
Question 113. A shell of mass 200 g is ejected from a gun of mass 4 kg by an explosion that generates 1.05 kJ of energy. The initial velocity of the shell is
- 100 ms-1
- 80 ms-1
- 40 ms-1
- 120 ms-1
Answer: 1. 100 ms-1
NEET Physics Chapter 3 Centre of Mass MCQs: Key Concepts and Solutions
Question 114. A bomb of mass 3.0 kg explodes in the air into two pieces of masses 2.0 kg and 1.0 kg. The smaller mass goes at a speed of 80 m/s. The total energy imparted to the two fragments is :
- 1.07 kJ
- 2.14 kJ
- 2.4 kJ
- 4.8 kJ
Answer: 4. 4.8 kJ
Question 115. Consider the following two statements :
- A. Linear momentum of a system of particles is zero
- B. Kinetic energy of a system of particles is zero,
Then,
- A does not imply B and B does not imply A
- A implies B but B does not imply A
- A does not imply B but B implies A
- A implies B and B implies A
Answer: 3. A does not imply B but B implies A
Question 116. A bomb of mass 16 kg at rest explodes into two pieces of masses of 4 kg and 12 kg. The velocity of the 12 kg mass is 4 ms-1. The kinetic energy of the other mass is :
- 96 J
- 144 J
- 288 J
- 192 J
Answer: 3. 288 J
Question 117. A block of mass 0.50 kg is moving with a speed of 2.00 ms-1 on a smooth surface. It strikes another mass of 1.00 kg and then they move together as a single body. The energy loss during the collision is :
- 1.00 J
- 0.67 J
- 0.34 J
- 0.16 J
Answer: 2. 0.67 J
Question 118. Which of the following is incorrect?
- If the centre of mass of three particles is at rest, and it is known that two of them are moving along different non-parallel lines then the third particle must also be moving.
- If the centre of mass remains at rest, then the net work done by the forces acting on the system must be zero.
- If the centre of mass remains at rest then the net external force must be zero
- None of this statement is incorrect
Answer: 2. If the centre of mass remains at rest, then the net work done by the forces acting on the system must be zero.
Question 119. A bomb at rest explodes in three segments of unequal masses. The most general description of the final state is that:
- The fragments fly off in any arbitrary direction.
- The fragments fly off in such a way that there directions lie in the same plane.
- Two of the three must go opposite to each other.
- Two of the three must fly off at right angles to each other.
Answer: 2. The fragments fly off in such a way that there directions lie in the same plane.
Question 120. Two particles A and B start moving due to their mutual interaction only. If at any time ‘t’, \(\overrightarrow{\mathrm{a}}_{\mathrm{A}} and \overrightarrow{\mathrm{a}}_{\mathrm{B}}\) respective accelerations, \(\vec{v}_A\) and \(\vec{v}_A\) are their respective velocities, and upto that time wA and B wB are the work done on A and B respectively by the mutual force, mA and mB are their masses respectively, then which of the following is always correct.
- \(\vec{v}_A+\vec{v}_B=0\)
- \(m_A \vec{v}_A+\vec{v}_B m_B=0\)
- \(w_A+w_B=0\)
- \(\vec{a}_A+\vec{a}_B=0\)
Answer: 2. \(m_A \vec{v}_A+\vec{v}_B m_B=0\)
Question 121. In the diagram shown, a block of mass M initially at rest on a frictionless horizontal surface is struck by a bullet of mass m moving with horizontal velocity v. What is the velocity of the bullet-block system after the bullet embeds itself in the block?

- \(\left(\frac{M+m}{M}\right) v\)
- \(\left(\frac{\mathrm{m}}{\mathrm{M}}\right) \mathrm{v}\)
- \(\frac{\mathrm{mv}}{\mathrm{Nm}+\mathrm{M}}\)
- \(\frac{\mathrm{Nm}+\mathrm{M}}{\mathrm{mv}}\)
Answer: 4. \(\frac{\mathrm{Nm}+\mathrm{M}}{\mathrm{mv}}\)
Question 122. A continuous stream of particles of mass m and velocity v, is emitted from a source at a rate of n per second. The particles travel along a straight line, collide with a body of mass M and are buried in this body. If the mass M was originally at rest, its velocity when it has received N particles will be:
- \(\frac{\mathrm{mvn}}{\mathrm{Nm}+\mathrm{n}}\)
- \(\frac{\mathrm{mvN}}{\mathrm{Nm}+\mathrm{M}}\)
- \(\frac{\mathrm{mv}}{\mathrm{Nm}+\mathrm{M}}\)
- \(\frac{\mathrm{Nm}+\mathrm{M}}{\mathrm{mv}}\)
Answer: 2. \(\frac{\mathrm{mvN}}{\mathrm{Nm}+\mathrm{M}}\)
Question 123. On doubling the speed of an object its-
- K.E. is doubled
- P.E. is doubled
- Momentum is doubled
- Acceleration is doubled
Answer: 3. Momentum is doubled
Question 124. A block moving in the air explodes in two parts then just after the explosion
- The total momentum must be conserved
- The total kinetic energy of the two parts must be the same as that of a block before the explosion.
- The total momentum must change
- The total kinetic energy must not be increased
Answer: 1. The total momentum must be conserved
Question 125. A particle of mass m moving with velocity v rebounds with the same speed after making an impact with a wall. The change in its momentum shall be
- –2mv
- mv
- –mv
- Zero
Answer: 1. –2mv
Question 126. A block of mass m slips down an inclined plane as shown in the figure and it presses a spring lying at the bottom. If the length of the spring h >> l and the spring constant is K the compression in the spring will be

- \(\sqrt{\frac{\mathrm{mgh}}{\mathrm{k}}}\)
- \(\sqrt{\frac{2 m g h}{k}}\)
- \(\sqrt{\frac{g h}{m k}}\)
- \(\sqrt{\frac{2 \mathrm{gh}}{\mathrm{mk}}}\)
Answer: 2. \(\sqrt{\frac{2 m g h}{k}}\)
Question 127. One end of a vertical ideal spring is attached to a rigid support and to the other end a weight of 200 gm is suspended. If this weight is doubled then the value of the spring constant is :
- Halved
- Unchanged
- Doubled
- Zero
Answer: 2. Unchanged
Question 128. A mass M is hanging from a spring. If on hanging an additional mass ‘m’ the string further gets stretched by x meters, then the spring constant is :
- mg/x
- (m + M)g/x
- Mg/x
- Mx/m
Answer: 1. mg/x
Question 129. After falling from a height h a mass m compresses a spring of force constant k. The compression produced in the spring is :
- (mgh/k)1/2
- (2mgh/k)1/2
- (k/mgh)1/2
- (2k/mgh)1/2
Answer: 2. (2mgh/k)1/2
Question 130. With how much velocity a block of mass 2 kg should move on a frictionless surface so as to compress a spring with a force constant of 2 newton/meter by 4 meters:
- 4 m/s
- 16 m/s
- 2 m/s
- 8 m/s
Answer: 1. 4 m/s
Question 131. A body of mass 8kg moving with a velocity of 2 m/sec comes to the rest, after compressing a spring placed on a frictionless table. If the spring constant is 5000N/m then compression produced in the spring shall be :
- 4 cm
- 8 cm
- 16 cm
- 32 cm
Answer: 2. 8 cm
Question 132. A mass of 2 kg falls from a height of 0.4 m on a spring of force constant k = 1960 N/m. The maximum distance upto which the string can be compressed is :
- 9 cm
- 4.5 cm
- 12.6 cm
- 6.3 cm
Answer: 1. 9 cm
Question 133. An object is attached to a vertical spring and slowly lowered to its equilibrium position. This stretches the spring by 10 cm. If the same object is attached to the same vertical spring but permitted to fall instead, the maximum distance upto which the spring can be stretched is:
- 5 cm
- 10 cm
- 20 cm
- 40 cm
Answer: 3. 20 cm
Question 134. The figure shows the magnitude of change in momentum of the block when it comes to its initial position if the maximum compression of the spring is x0 will be:

- \(2 \sqrt{k m} x_0\)
- \(\sqrt{\mathrm{km}} x_0\)
- Zero
- None of these
Answer: 1. \(2 \sqrt{k m} x_0\)
Question 135. Two masses are connected by a spring as shown in the figure. One of the masses was given velocity v = 2 k, as shown in the figure where ‘k’ is the spring constant. The maximum extension in the spring will be

- 2 m
- m
- \(\sqrt{2 m k}\)
- \(\sqrt{3 \mathrm{mk}}\)
Answer: 3. \(\sqrt{2 m k}\)
Centre of Mass MCQ Practice Test with Answers for NEET Class 11
Question 136. A force of 50 dynes is acted on a body of mass 5gm which is at rest for an interval of 3 sec, then the impulse is-
- 0.16 × 10-3 N-S
- 0.98 × 10-3 N-S
- 1.5 × 10-3 N-S
- 2.5 × 10-3 N-S
Answer: 3. 1.5 × 10-3 N-S
Question 137. The area of the F-t curve is A, where ‘F’ is the force on one mass due to the other. If one of the colliding bodies of mass M is at rest initially, its speed just after the collision is :
- A/M
- M/A
- AM
- \(\sqrt{\frac{2 A}{M}}\)
Answer: 1. A/M
Question 138. A body of mass 0.5 kg is projected under gravity with a speed of 98 m/s at an angle of 60° with the vertical. The change in momentum [in magnitude] of the body when it returns to the ground is
- 24.5 N-s
- 49.0 N-s
- 98.0 N-s
- 49 \(\sqrt{\frac{2 A}{M}}\)
Answer: 2. 49.0 N-s
Question 139. A body of mass ‘M’ collides against a wall with a velocity υ and retraces its path at the same speed. The change in momentum is (take the initial direction of velocity as positive) :
- zero‘
- 2Mυ
- Mυ
- –2Mυ
Answer: 4. –2Mυ
Question 140. If two balls, each of mass 0.06 kg, moving in opposite directions with a speed of 4m/s, collide and rebound with the same speed, then the impulse imparted to each ball due to the other (in kg-m/s) is :
- 0.48
- 0.53
- 0.81
- 0.92
Answer: 1. 0.48
Question 141. A ball of mass 50 gm is dropped from a height h = 10 m. It rebounds losing 75 percent of its kinetic energy. If it remains in contact with the ground for Δt = 0.01 sec., the impulse of the impact force is :
- 1.3 N–s
- 1.05 N-s
- 1300 N–s
- 105 N–s
Answer: 2. 1.05 N-s
Question 142. The given figure shows a plot of the time-dependent force F acting on a particle in motion along the x-axis. What is the total impulse delivered by this force to the particle from time t = 0 to t = 2second?

- 0
- 1 kg-m/s
- 2 kg-m/s
- 3 kg-m/s
Answer: 3. 2 kg-m/s
Question 143. A ball of mass 3 kg moving with a speed of 100 m/s, strikes a wall at an angle of 60º (as shown in the figure). The ball rebounds at the same speed and remains in contact with the ball for 0.2 seconds, the force exerted by the ball on the wall is :

- 1500
- 1500 N
- 3003N
- 300 N
Answer: 1. 1500
Question 144. In the figure given the position-time graph of a particle of mass 0.1 kg is shown. The impulse at t = 2 s is:

- 0.2 kg m s-1
- – 0.2 kg m s-1
- 0.1 kg m s-1
- – 0.4 kg m s-1
Answer: 2. – 0.2 kg m s-1
Question 145. Two balls of the same mass are dropped from the same height onto the floor. The first ball bounces upwards from the floor elastically. The second ball sticks to the floor. The first applies an impulse to the floor of I1 the second applies an impulse Ι2(for the duration of collision). Then the relation between both impulses is,
- Ι2= 2Ι1
- \(\mathrm{I}_2=\frac{\mathrm{I}_1}{2}\)
- Ι2= 4Ι1
- \(\mathrm{I}_2=\frac{\mathrm{I}_1}{4}\)
Answer: 2. \(\mathrm{I}_2=\frac{\mathrm{I}_1}{2}\)
Question 146. A particle of mass m initially at rest, is acted upon by a variable force F for a brief interval of time T. It attains a velocity u after the force stops acting. F is shown in the graph as a function of time. The curve is a semicircle, find u.

- \(\frac{\pi F_0^2}{2 m}\)
- \(\frac{\pi T^2}{8 \mathrm{~m}}\)
- \(\frac{\pi F_0 T}{4 m}\)
- \(\frac{F_0 T}{2 m}\)
Answer: 3. \(\frac{\pi F_0 T}{4 m}\)
Question 147. A mass of 100g strikes the wall with a speed of 5m/s at an angle as shown in the figure and it rebounds with the same speed. If the contact time is 2 × 10-3 sec., what is the force applied on the mass by the wall:

- 250\(\sqrt{3}\) to right
- 250 N to right
- 250\(\sqrt{3}\)N to left
- 250 N to left
Answer: 3. 250\(\sqrt{3}\)N to left
Question 148. Two particles of masses m1 and m2 in projectile motion have velocities \(\overrightarrow{\mathrm{u}}_1\) and \(\overrightarrow{\mathrm{u}}_2\) respectively at time t = 0. They collide at time t0. Their velocities become \(\overrightarrow{\mathrm{v}}_1\) and \(\overrightarrow{\mathrm{v}}_2\)at time 2t0 while still moving in the air. The value of
⇒ \(\left[\left(m_1 \vec{v}_1+m_2 \vec{v}_2\right)-\left(m_1 \vec{u}_1+m_2 \vec{u}_2\right)\right]\)is
- Zero
- (m1+ m2)gt0
- 2(m1+ m2)gt0
- \(\frac{1}{2}\)(m1+ m2)gt0
Answer: 3. 2(m1+ m2)gt0
Question 149. A body is moving towards a finite body which is initially at rest and collides with it. In the absence of any external impulsive force, it is not possible that
- Both the bodies come to rest
- Both bodies move after the collision
- The moving body comes to rest and the stationary body starts moving
- The stationary body remains stationary, the moving body does not change its velocity.
Answer: 1. Both the bodies come to rest
Question 150. In head-on elastic collision of two bodies of equal masses, it is not possible :
- The velocities are interchanged
- The speeds are interchanged
- The momenta are interchanged
- The faster body speeds up and the slower body slows down
Answer: 4. The faster body speeds up and the slower body slows down
Question 151. A massive ball moving with speed v collides head-on with a tiny ball at rest having a mass very less than the mass of the first ball. If the collision is elastic, then immediately after the impact, the second ball will move with a speed approximately equal to:
- v
- 2v
- v/2
- ∞.
Answer: 2. 2v
Question 152. A ball of mass ‘m’, moving with uniform speed, collides elastically with another stationary ball. The incident ball will lose maximum kinetic energy when the mass of the stationary ball is
- m
- 2m
- 4m
- Infinity
Answer: 1. m
Question 153. In a collision between two solid spheres, the velocity of separation along the line of impact (assume no external forces act on the system of two spheres during impact) :
- Cannot be greater than the velocity of the approach
- Cannot be less than the velocity of the approach
- Cannot be equal to the velocity of the approach
- None of these
Answer: 1. Cannot be greater than the velocity of the approach
Question 154. In the figure shown block A collides head-on with another block B at rest. The mass of B is twice the mass of A. Block A stops after collision. The coefficient of restitution is :
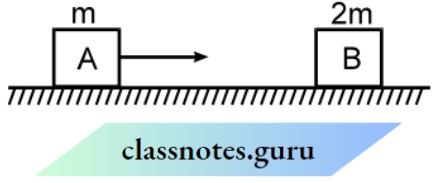
- 0.5
- 1
- 0.25
- It is not possible
Answer: 1. 0.5
Question 155. A sphere of mass m moving with a constant velocity hits another stationary sphere of the same mass. If e is the coefficient of restitution, then the ratio of the speed of the first sphere to the speed of the second sphere after a collision will be :
- \(\left(\frac{1-e}{1+e}\right)\)
- \(\left(\frac{1+e}{1-e}\right)\)
- \(\left(\frac{e+1}{e-1}\right)\)
- \(\left(\frac{e-1}{e+1}\right)\)
Answer: 1. \(\left(\frac{1-e}{1+e}\right)\)
Question 156. A ball rebounds after colliding with the floor, then in case of inelastic collision-
- The momentum of the ball before and after collision is the same
- The mechanical energy of the ball is conserved
- The total momentum of the earth-ball system is conserved
- The total kinetic energy of the earth and ball is conserved
Answer: 3. The total momentum of the earth-ball system is conserved
Question 157. A ball is allowed to fall from a height of 8cm, if the ball is perfectly elastic, how much does it rise after rebound-
- 8 cm
- 1 cm
- 0.5 cm
- 0
Answer: 1. 8 cm
Question 158. A particle of mass m1 moving with a velocity of 5m/s collides head-on with a stationary particle of mass m2. After collision both the particle moves with a common velocity of 4m/s, then the value of m1/m2 is-
- 4: 1
- 2: 1
- 1 : 8
- 1 : 1
Answer: 1. 4: 1
Question 159. A body of mass m1 collides head-on elastically with a stationary body of mass m2. If velocities of m1 before and after the collision are v and –v/3 respectively then the value of m1/m2 is-
- 1
- 2
- 0.5
- 4
Answer: 3. 0.5
Question 160. A sphere of mass 0.1 kg is attached to a cord of 1m in length. Starting from the height of its point of suspension this sphere hits a block of the same mass at rest on a frictionless table. If the impact is elastic, then the kinetic energy of the block after the collision is-
- 1 J
- 10 J
- 0.1 J
- 0.5 J
Answer: 1. 1 J
Question 161. Two identical smooth spheres A and B are moving with the same velocity and collide with similar spheres C and D, then after elastics collision- (Consider dimensional collision)

- D will move with greater speed
- C and D will move with the same velocity v
- C will stop and D will move with velocity v
- All spheres A, B, C, and D will move with velocity v/2
Answer: 2. C and D will move with the same velocity v
Question 162. A ball is allowed to fall from a height of 1.0 m. If the value of the coefficient of restitution is 0.6, then after the impact ball will go up to
- 0.16 m
- 0.36 m
- 0.40 m
- 0.60 m
Answer: 2. 0.36 m
Question 163. A ball of mass m moving with velocity v collides elastically with another ball of identical mass coming from the opposite direction with velocity 2v. Their velocities after collisions are-
- – v, 2v
- – 2v, v
- v, – 2v
- 2v, – v
Answer: 2. – 2v, v
Question 164. A sphere of mass M moving with velocity u collides head-on elastically with a sphere of mass m at rest. After collision their respective velocities are V and v. The value of v is-
- \(2 \mathrm{u} \frac{\mathrm{M}}{\mathrm{m}}\)
- \(2 u \frac{\mathrm{m}}{\mathrm{m}}\)
- \(\frac{2 u}{1+\mathrm{m} / \mathrm{M}}\)
- \(\frac{2 \mathrm{u}}{1+\mathrm{M} / \mathrm{m}}\)
Answer: 3. \(\frac{2 u}{1+\mathrm{m} / \mathrm{M}}\)
Centre of Mass in NEET Physics Class 11 MCQs and Explanations
Question 165. A scooter of 40 kg mass moving with a velocity of 4 m/s collides with another scooter of 60 kg mass and moving with a velocity of 2 m/s. After the collision the two scooters stick to each other the loss in kinetic energy-
- 392 J
- 440 J
- 48 J
- 110 J
Answer: 3. 48 J
Question 166. Two spheres approaching each other collide elastically. Before collision the speed of A is 5m/s and that of B is 10m/s. Their masses are 1kg and 0.5kg. After collision velocities of A and B are respectively-
- 5 m/s –10 m/s
- 10 m/s, –5 m/s
- –10 m/s, –5 m/s
- –5 m/s, 10 m/s
Answer: 4. –5 m/s, 10 m/s
Question 167. After falling from a height of h and striking the ground twice, a ball rises up to the height [e = coefficient of restitution]
- He
- He2
- He3
- He4
Answer: 4. He4
Question 168. A metal ball of mass 2.0kg moving at 36km/hr collides with a stationary ball of mass 3.0kg. If after the collision both balls move together, the loss in kinetic energy will be
- 40 J
- 60 J
- 100 J
- 140 J
Answer: 2. 60 J
Question 169. A rubber ball is dropped from a height of 5m on a plane. On bouncing it rises to 1.8m. The ball loses its velocity on bouncing by a factor of-
- 16/25
- 2/5
- 3/5
- 9/25
Answer: 2. 2/5
Question 170. One sphere collides with another sphere of the same mass at rest inelastically. If the value of the coefficient of restitution is 1/2, the ratio of their speeds after collision shall be-
- 1 : 2
- 2 : 1
- 1 : 3
- 3 : 1
Answer: 3. 1 : 3
Question 171. A steel ball of radius 2cm is initially at rest on a horizontal frictionless surface. It is struck head-on by another steel ball of 4 cm radius travelling with a velocity of 81 cm/s. The velocities of two balls after collision are-
- 72 cm/s and 56 cm/s
- 144 cm/s and 56 cm/s
- 144 cm/s and 63 cm/s
- 63 cm/s and 72 cm/s
Answer: 3. 144 cm/s and 63 cm/s
Question 172. Which of the following statements is true for collisions-
- Momentum is conserved in elastic collisions but not in inelastic collisions
- Total kinetic energy is conserved in elastic collisions but momentum is not conserved
- Total kinetic energy is not conserved in inelastic collisions but momentum is conserved
- Total kinetic energy and momentum both are conserved in all types of collisions
Answer: 3. Total kinetic energy is not conserved in inelastic collisions but momentum is conserved
Question 173. For a two-particle collision, the following quantities are conserved in general-
- Kinetic energy
- Momentum
- Both kinetic energy and momentum
- Neither kinetic energy nor momentum
Answer: 2. Momentum
Question 174. A completely inelastic collision is one in which the two colliding particles-
- Are separated after the collision.
- Remain together after the collision.
- Split into small fragments flying in all directions.
- None of the above.
Answer: 2. Remain together after the collision.
Question 175. A bullet of mass m = 50 gm strikes a sandbag of mass M = 5 kg hanging from a fixed point, with a horizontal velocity \(\overrightarrow{\mathrm{v}}_{\mathrm{p}}\). If the bullet sticks to the sandbag then the ratio of the final and initial kinetic energy of the bullet is (approximately) :
- 10-2
- 10-3
- 10-6
- 10-4
Answer: 4. 10-4
Question 176. There are a hundred identical sliders equally spaced on a frictionless track as shown in the figure. Initially, all the sliders are at rest. Slider 1 is pushed with velocity v towards slider 2. In a collision, the sliders stick together. The final velocity of the set of hundred stuck sliders will be :

- \(\frac{v}{99}\)
- \(\frac{v}{100}\)
- Zero
- v
Answer: 2. \(\frac{v}{100}\)
Question 177. The coefficient of restitution depends upon-
- The masses of the colliding bodies
- The direction of motion of the colliding bodies
- The inclination between the colliding bodies
- The materials of the colliding bodies
Answer: 4. The materials of the colliding bodies
Question 178. In an elastic collision of two particles, the following is conserved :
- Momentum of each particle
- The speed of each particle
- The kinetic energy of each particle
- The total kinetic energy of both the particles
Answer: 4. Total kinetic energy of both the particles
Question 179. A body of mass M1 collides elastically with another mass M2 at rest. There is maximum transfer of energy when :
- M1> M2
- M1< M2
- M1= M2
- Same for all values of M1 and M2
Answer: 3. M1= M2
Question 180. Two putty balls of equal mass moving with equal velocity in mutually perpendicular directions, stick together after collision. If the balls were initially moving with a velocity of \(45 \sqrt{2} \mathrm{~ms}^{-1}\) each, the velocity of their combined mass after a collision is :
- \(45 \sqrt{2} \mathrm{~ms}^{-1}\)
- 45 ms-1
- 90 ms-1
- \(22.5 \sqrt{2} \mathrm{~ms}^{-1}\)
Answer: 2. 45 ms-1
Question 181. The coefficient of restitution e for a perfectly elastic collision is :
- 1
- 0
- ∞
- –1
Answer: 1. 1
Question 182. Two perfectly elastic particles P and Q of equal mass travelling along the joining them with velocities 15m/sec. and 10 m/sec. After the collision, their velocities respectively (in m/sec.) will be :
- 0,25
- 5,20
- 10, 15
- 20, 5
Answer: 3. 10, 15
Question 183. A particle of mass m moving with horizontal speed 6 m/sec. as shown in the figure. If m << M then for one-dimensional elastic collision, the speed of lighter particles after the collision will be :

- 2 m/sec in original direction
- 2 m/sec opposite to the original direction
- 4 m/sec opposite to the original direction
- 4 m/sec in original direction
Answer: 1. 2 m/sec in original direction
Question 184. A particle of mass m moving towards East with a velocity v collides with another particle of the same mass moving towards North with the same speed and adheres to it. The velocity of the combined particle is-
- \(v / \sqrt{2}\) along North-East
- \(v / \sqrt{2}\) along North-West
- 2 \(\sqrt{2 v}\) along North-East
- \(\sqrt{2 v}\) along North-West
Answer: 1. \(v / \sqrt{2}\) along North-East
Question 185. A particle of mass ‘m’ and velocity ‘ \(\) collides oblique elastically with a stationary particle of mass ‘m’. The angle between the velocity vectors of the two particles after the collision is :
- 45°
- 30°
- 90°
- None of these
Answer: 3. 90°
Question 186. An iron ball of mass 100gm moving at a speed of 10m/sec strikes a wall at an angle of 30° and reflects at the same angle. If the ball and wall remain in contact for 0.1 sec, the force exerted on the wall will be
- 10 N
- 100 N
- 1.0 N
- 0.1 N
Answer: 1. 10 N
Question 187. If a ball of mass 10 gm strikes perpendicular on a hard floor with a speed of 5 m/sec. and bounces with the same speed and remains in contact with the floor for 1 sec, then the force applied on the ball by the floor is-
- 100 N
- 10 N
- 1.0 N
- 0.1 N
Answer: 4. 0.1 N
Question 188. For inelastic collision between two spherical rigid bodies :
- The total kinetic energy is conserved
- The linear momentum is not conserved
- The total mechanical energy is not conserved
- The linear momentum is conserved
Answer: 4. The linear momentum is conserved
Question 189. A mass of 20 kg moving with a speed of 10 m/s collides with another stationary mass of 5 kg. As a result of the collision both masses stick together. The kinetic energy of the composite mass will be :
- 600 J
- 800 J
- 1000 J
- 1200 J
Answer: 2. 800 J
Question 190. When two bodies collide elastically, then :
- The kinetic energy of the system alone is conserved
- Only momentum is conserved
- Both energy and momentum are conserved
- Neither energy nor momentum is conserved
Answer: 3. Both energy and momentum are conserved
Question 191. A ball of mass ‘m’ moving with the velocity v collides head-on with another ball of mass m at rest, If the coefficient of restitution is e, then the ratio of the velocities of the first and second ball after the collision
- \(\frac{1-e}{1+e}\)
- \(\frac{1+e}{1-e}\)
- \(\frac{1+e}{2}\)
- \(\frac{1-e}{2}\)
Answer: 1. \(\frac{1-e}{1+e}\)
Question 192. When two bodies collide elastically, the force of interaction between them is :
- Conservative
- Non–conservative
- Either conservative or non–conservative
- Zero
Answer: 1. Conservative
Question 193. In an elastic collision in the absence of external force, which of the following is/are correct :
- The linear momentum is not conserved
- The potential energy is conserved in the collision
- The final kinetic energy is less than the initial kinetic energy
- The final kinetic energy is equal to the initial kinetic energy
Answer: 4. The final kinetic energy is equal to the initial kinetic energy
Question 194. A shell explodes in a region of negligible gravitational field, giving out n fragments of equal mass m. Then it’s total
- Kinetic energy is smaller than that before the explosion
- Kinetic energy is equal to the before the explosion
- Momentum and kinetic energy depend on n
- Momentum is equal to that before the explosion.
Answer: 4. Momentum is equal to that before the explosion.
Question 195. During the head-on collision of two masses 1 kg and 2 kg the maximum energy of deformation is 1003J. If before the collision the masses are moving in the opposite direction, then their velocity of approach before the collision is :
- 10 m/sec.
- 5 m/sec.
- 20 m/sec.
- \(10 \sqrt{2}\) m/sec.
Answer: 1. 10 m/sec.
Question 196. A block A of mass m moving with a velocity ‘ v ‘ along a frictionless horizontal track and blocks of mass m/2 moving with 2 v collide with plank elastically. The final speed of the block A is :

- \(\frac{5 v}{3}\)
- v
- \(\frac{2 v}{3}\)
- None of these
Answer: 2. v
Question 197. A particle of mass m moves with velocity v0= 20 m/sec towards a wall that is moving with velocity v = 5 m/sec. If the particle collides with the wall elastically, the speed of the particle just after the collision is :

- 30 m/s
- 20 m/s
- 25 m/s
- 22 m/s
Answer: 1. 30 m/s
Question 198. A super-ball is to bounce elastically back and forth between two rigid walls at a distance d from each other. Neglecting gravity and assuming the velocity of the super-ball to be v0horizontally, the average force being exerted by the super-ball on one wall is :
- \(\frac{1}{2} \frac{m v_0^2}{d}\)
- \(\frac{\mathrm{mv}_0^2}{\mathrm{~d}}\)
- \(\frac{2 m v_0^2}{d}\)
- \(\frac{4 m v_0^2}{d}\)
Answer: 2. \(\frac{\mathrm{mv}_0^2}{\mathrm{~d}}\)
Question 199. Which of the following relation(s) is/are always correct? [ p = linear momentum ]
- Thrust = \(u_{\text {rel }} \frac{d m}{d t}\)
- F = m \(\mathrm{m} \frac{\mathrm{dp}}{\mathrm{dt}}\)
- F = m \(m \frac{d v}{d t}\)
- F = m \(m \frac{d v}{d t}+v \frac{d m}{d t}\)
Answer: 4. F = m \(m \frac{d v}{d t}+v \frac{d m}{d t}\)
Question 200. Statement-1: In an elastic collision between two bodies, the relative speed of the bodies after a collision is equal to the relative speed before the collision. because Statement 2: In an elastic collision, the linear momentum of the system is conserved
- Statement-1 is True, Statement-2 is True; Statement-2 is a correct explanation for Statement-1
- Statement-1 is True,Statement-2 is True;Statement-2 is NOT a correct explanation for Statement-1
- Statement-1 is True, Statement-2 is False
- Statement-1 is False, and Statement-2 is True.
Answer: 2. Statement-1 is True,Statement-2 is True;Statement-2 is NOT a correct explanation for Statement-1
Question 201. A ball hits a floor and rebounds after an inelastic collision. In this case
- The momentum of the ball just after the collision is the same as that just before the collision
- The mechanical energy of the ball remains the same during the collision
- The total momentum of the ball and the earth is conserved
- The total energy of the ball and the earth remains the same
Answer: 3. The total momentum of the ball and the earth is conserved
Question 202. Two balls having mass of 2 kg and 3 kg are approaching each other with velocities of 3 m/s and 2 m/s respectively on the horizontal frictionless surface. They undergo a head-on elastic collision. Find out the maximum potential energy of deformation.
- Zero
- 12.5 J
- 15 J
- None of these
Answer: 3. 15 J
Question 203. A particle ‘A’ of mass m collides head-on with another stationary particle ‘B’ of the same mass ‘m’. The kinetic energy lost by the colliding particle ‘A’ will be maximum if the coefficient of the restitution is
- 1
- 0
- 0.5
- None
Answer: 1. 1
Question 204. Two particles A and B of masses 10 kg and 38 kg respectively are moving along the same straight line with velocities of 15 m/s and 3 m/s respectively in the same direction. After the elastic collision, the velocities of A and B are vA and vB in the direction of initial motion. Then :

- vA= 20, vB= 8
- vA= − 4, vB= 8
- vA= 16, vB= 28
- vA= − 5, vB= 10
Answer: 2. vA= − 4, vB= 8
NEET Physics Chapter 3 Centre of Mass: MCQs for Revision and Practice
Question 205. Two small spheres of equal mass, heading towards each other with equal speeds, undergo a head-on collision (no external force acts on the system of two spheres). Then which of the following statements is correct?
- Their final velocities must be zero.
- Their final velocities may be zero.
- Each must have a final velocity equal to the other’s initial velocity.
- Their velocities must be reduced in magnitude
Answer: 2. Their final velocities may be zero.
Question 206. In a perfectly inelastic direct collision, maximum transfer of energy takes place if-
- m1>> m2
- m1<< m2
- m1= m2
- m2= 0
Answer: 3. m1= m2
Question 207. Which of the following statements is true for collisions-
- Momentum is conserved in elastic collisions but not in inelastic collisions.
- Total K.E. is conserved in elastic collisions but momentum is not conserved.
- Total K.E. is not conserved in inelastic collisions but momentum is conserved.
- Total K.E. and momentum both are conserved in all types of collisions.
Answer: 3. Total K.E. is not conserved in inelastic collisions but momentum is conserved.
Question 208. A body falls on a surface with a coefficient of restitution of 0.6 from a height of 1m. Then the body rebounds to a height of :
- 0.6 m
- 0.4 m
- 1m
- 0.36 m
Answer: 4. 0.36 m
Question 209. If the force on a rocket which is ejecting gases with a relative velocity of 300 m/s, is 210 N. Then the rate of combustion of the fuel will be :
- 10.7 kg/sec
- 0.07 kg/sec
- 1.4 kg/sec
- 0.7 kg/sec
Answer: 4. 0.7 kg/sec
Question 210. A belt is moving horizontally with a speed of 2m/s and sand is falling on it at the rate of 150 gm/sec. The additional force required to keep the speed of the belt is-
- 0.015 N
- 0.30 N
- 3N
- 300 N
Answer: 2. 0.30 N
Question 211. A rocket with a lift-off mass of 3.5 × 104 kg is blasted upwards with an initial acceleration of 10 m/s2. The initial thrust of the blast is-
- 14.0 × 105 N
- 1.76 × 105 N
- 3.5 × 105 N
- 7.0 × 105 N
Answer: 4. 7.0 × 105 N
Question 212. Fuel is consumed at the rate of 100 kg/sec. in a rocket. The exhaust gases are ejected at a speed of 4.5 × 104 m/s. What is the thrust experience by the rocket-
- 3 × 106 N
- 4.5 × 106 N
- 6 × 106 N
- 9 × 106 N
Answer: 2. 4.5 × 106 N
Question 213. A rocket of initial mass 6000 kg. ejects mass at a constant rate of 16 kg/sec. with a constant relative speed of 11 km/sec. What is the acceleration of the rocket, a minute after the blast-(Consider acceleration due to gravity g = 10msec-2)
- 28.3 m/sec²
- 42 m/sec²
- 34.9 m/sec²
- 24.92 m/sec²
Answer: 4. 24.92 m/sec²
Question 214. A 6000 kg rocket is set for vertical firing. If the exhaust speed is 1000 m/sec. How much gas must be ejected each second to supply the thrust needed to give the rocket an initial upward acceleration of 20 m/sec²- (consider g = 9.8 msec-2 acceleration due to gravity )
- 92.4 kg/sec
- 178.8 kg/sec
- 143.2 kg/sec
- 47.2 kg/sec
Answer: 2. 178.8 kg/sec
Question 215. The rocket works on the principle of conservation of-
- Energy
- Angular momentum
- Momentum
- Mass
Answer: 3. Momentum
Question 216. A rocket with a lift-off mass of 3.5 × 104 kg is blasted upwards with an initial acceleration of 10 m/s2. Then the initial thrust of the blast is :
- 3.5 × 105 N
- 7.0 × 105 N
- 14.0 × 105 N
- 1.75 × 105 N
Answer: 2. 7.0 × 105 N
Question 217. A balloon having a mass ‘ m ‘ is filled with gas and is held in the hands of a boy. Then suddenly it gets released and gas starts coming out of it at a constant rate. The velocities of the ejected gases are also constant at 2 m/s with respect to the balloon. Find out the velocity of the balloon when the mass of gas is reduced to half.
- l n 2
- 2 ln 4
- 2 ln 2
- None of these
Answer: 3. 2 in 2
Question 218. In the figure shown a hole of radius 2 cm is made in a semicircular disc of radius 6 π cm at a distance 8 cm from the centre C of the disc. The distance of the center of mass of this system from point C is:

- 4 cm
- 8 cm
- 6 cm
- 12 cm
Answer: 2. 8 cm
Question 219. A semicircular portion of radius ‘r’ is cut from a uniform rectangular plate as shown in the figure. The distance of the center of mass ‘C’ of the remaining plate, from point ‘O’ is :
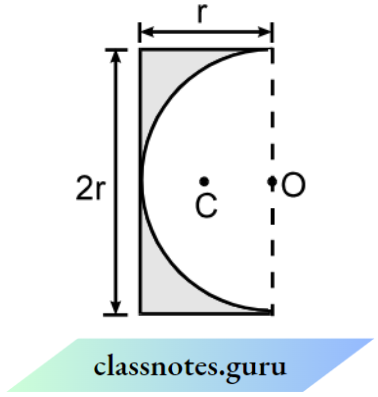
- \(\frac{2 r}{(3-\pi)}\)
- \(\frac{3 r}{2(4-\pi)}\)
- \(\frac{2 r}{(4+\pi)}\)
- \(\frac{2 r}{3(4-\pi)}\)
Answer: 4. \(\frac{2 r}{3(4-\pi)}\)
Question 220. Look at the drawing given in the figure which has been drawn with ink of uniform line-thickness. The mass of ink used to draw each of the two inner circles, and each of the two line segments is m. The mass of the ink used to draw the outer circle is 6m. The coordinates of the centers of the different parts are outer circle (0, 0), left inner circle (–a, a), right inner circle (a, a), vertical line (0, 0), and horizontal line (0, –a). The y-coordinate of the center of mass of the ink in this drawing is

- \(\frac{a}{10}\)
- \(\frac{3 r}{2(4-\pi)}\)
- \(\frac{2 r}{(4+\pi)}\)
- \(\frac{2 r}{3(4-\pi)}\)
Answer: 1. \(\frac{a}{10}\)
Question 221. Two spherical bodies of mass M and 5M and radii R and 2R respectively are released in free space with initial separation between their centres equal to 12R. If they attract each other due to gravitational force only, then the distance covered by the smaller body just before the collision is :
- 2.5R
- 4.5 R
- 7.5R
- 1.5 R
- Answer: 3. 7.5R
Question 222. A radioactive nucleus initially at rest decays by emitting an electron and neutrino at right angles to one another. The momentum of the electron is 3.2 × 10-23 kg-m/sec. and that of the neutrino is 6.4 × 10-23 kg-m/sec. The direction of the recoiling nucleus with that of the electron motion is-
- tan-1(0.5)
- tan-1
- π – tan-1
- 2π+ tan-1(2)
Answer: 3. π – tan-1
Question 223. A particle of mass 1 kg is thrown vertically upwards with a speed 100 m/s. After 5s it explodes into two parts. One part of mass 400g comes back with a speed of 25 m/s, what is the speed of the other part just after the explosion?
- 100 m/s upwards
- 600 m/s upwards
- 100 m/s downward
- 300 m/s upward
Answer: 1. 100 m/s upwards
Question 224. A mass ‘m’ moves with a velocity ‘v’ and collides inelastically with another identical mass at rest. After collision the 1st mass moves with velocity \(\frac{v}{\sqrt{3}}\) in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision:
- v
- \(\sqrt{3 v}\)
- \(\frac{2}{\sqrt{3}}\)
- \(\frac{v}{\sqrt{3}}\)
Answer: 3. \(\frac{2}{\sqrt{3}}\)
Question 225. A mass of 10 gm, moving horizontally with a velocity of 100 cm/sec, strikes the bob of a pendulum and sticks to it. The mass of the bob is also 10 gm. The maximum height to which the system can be raised is (g = 10 m/sec2)
- Zero
- 5 cm
- 2.5 cm
- 1.25 cm
Answer: 4. 1.25 cm
Question 226. A solid iron ball A of radius r collides head-on with another stationary solid iron ball B of radius 2r. The ratio of their speeds just after the collision (e = 0.5) is :
- 3
- 4
- 2
- 1
Answer: 3. 2
NEET Physics Chapter 3 Centre of Mass: MCQs for Revision and Practice
Question 227. Two balls, having linear momenta \(\overrightarrow{\mathrm{p}}_1=p \hat{\mathrm{i}} \text { and } \overrightarrow{\mathrm{p}}_2=-p \hat{\mathrm{i}} \text {, }\) undergo a collision in free space. There is no external force acting on the balls. Let \(\overrightarrow{\mathrm{p}}_1^{\prime} \text { and } \overrightarrow{\mathrm{p}}_2^{\prime}\) be their final momenta. The following option(s) is(are) Not Allowed for any non-zero value of p, a1, a2, b1, b2, c1and c2.
- \(\overrightarrow{\mathrm{p}}_1^{\prime}=\mathrm{a}_1 \hat{\mathrm{i}}+\mathrm{b}_1 \hat{\mathrm{j}}+\mathrm{c}_1 \hat{\mathrm{k}}, \overrightarrow{\mathrm{p}}_2^{\prime}=\mathrm{a}_2 \hat{\mathrm{i}}+\mathrm{b}_2 \hat{\mathrm{j}}\)
- \(\overrightarrow{\mathrm{p}}_1^{\prime}=\mathrm{c}_1 \hat{\mathrm{k}}, \overrightarrow{\mathrm{p}}_2^{\prime}=c_2 \hat{\mathrm{k}}\)
- \(\overrightarrow{\mathrm{p}}_1^{\prime}=\mathrm{a}_1 \hat{\mathrm{i}}+\mathrm{b}_1 \hat{\mathrm{j}}+\mathrm{c}_1 \hat{\mathrm{k}}, \overrightarrow{\mathrm{p}}_2^{\prime}=\mathrm{a}_2 \hat{\mathrm{i}}+\mathrm{b}_2 \hat{\mathrm{j}}-\mathrm{c}_1 \hat{\mathrm{k}}\)
- \(\overrightarrow{\mathrm{p}}_1^{\prime}=\mathrm{a}_1 \hat{\mathrm{i}}+\mathrm{b}_1 \hat{\mathrm{j}}, \overrightarrow{\mathrm{p}}_2^{\prime}=\mathrm{c}_2 \hat{\mathrm{k}}\)
Answer: 1 and 4
Question 228. An explosion blows a rock into three parts. Two parts go off at right angles of each other. These two are 1 kg first part moving with a velocity of 12 ms–1 and 2 kg second part moving with a velocity of 8 ms–1. If the third part files off with a velocity of 4 ms–1, its mass would be :
- 5 kg
- 7 kg
- 17 kg
- 3 kg
Answer: 1. 5 kg
Question 229. A ball moving with a velocity 2 m/s collides head-on with another stationary ball of double the mass. If the coefficient of restitution is 0.5, then their velocities (in m/s) after the collision will be
- 0, 1
- 1, 1
- 1, 0.5
- 0, 2
Answer: 1. 0, 1
Question 230. Two particles which are initially at rest, move towards each other under the action of their internal attraction. If their speeds are v and 2v at any instant, then the speed of the center of mass of the system will be
- 2v
- Zero
- 1.5 v
- v
Answer: 2. Zero
Question 231. A mass of m moving horizontally (along the x-axis) with velocity v collides and sticks to the mass of 3m moving vertically upward (along the y-axis) with velocity 2v. The final velocity of the combination is :
- \(\frac{1}{4} v \hat{i}+\frac{3}{2} v \hat{j}\)
- \(\frac{1}{3} v \hat{i}+\frac{2}{3} v \hat{j}\)
- \(\frac{2}{3} v \hat{i}+\frac{1}{3} v \hat{j}\)
- \(\frac{3}{2} v \hat{i}+\frac{1}{4} v \hat{j}\)
Answer: 1. \(\frac{1}{4} v \hat{i}+\frac{3}{2} v \hat{j}\)
Question 232. Two persons of masses 55 kg and 65 kg respectively, are at the opposite ends of a boat. The length of the boat is 3.0 m and weighs 100 kg. The 55 kg man walks up to the 65 kg man and sits with him. If the boat is in still water the center of mass of the system shifts by :
- 3.0 m
- 2.3 m
- Zero
- 0.75 m
Answer: 3. Zero
Question 233. Two spheres A and B of masses m1 and m2 respectively collide. A is at rest initially and B is moving with velocity v along the x-axis. After collision B has a velocity \(\frac{v}{2}\) in a direction perpendicular to the original direction. The mass A moves after collision in the direction.
- Same as that of B
- Opposite to that of B
- θ = tan-1(1/2) to the x-axis
- θ = tan-1(–1/2) to the x-axis
Answer: 4. θ = tan-1(–1/2) to the x-axis
Question 234. Three masses are placed on the x-axis: 300 g at origin, 500g at x = 40 cm and 400g at x = 70 cm. The distance of the centre of mass from the origin is :
- 40 cm
- 45 cm
- 50 cm
- 30 cm
Answer: 1. 40 cm
Question 235. An explosion breaks a rock into three parts in a horizontal plane. Two of them go off at right angles to each other. The first part of mass 1kg moves with a speed of 12 ms-1 and the second part of mass 2 kg moves with 8 ms-1 speed. If the third part flies off with 4 ms-1 speed, then its mass is :
- 5 kg
- 7 kg
- 17 kg
- 3 kg
Answer: 1. 5 kg
Question 236. A body of mass (4m) is lying in the x-y plane at rest. It suddenly explodes into three pieces. Two pieces, each of mass (m) move perpendicular to each other with equal speeds (υ). The total kinetic energy generated due to the explosion is :
- mv
- \(\frac{3}{2} m v^2\)
- 2mv2
- 4mv2
Answer: 2. \(\frac{3}{2} m v^2\)
Question 237. Two particles of masses m1, m2 move with initial velocities u1 and u2. On collision, one of the particles gets excited to a higher level, after absorbing energy ε If the final velocities of particles be v1 and v2 then we must have:
- \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2-\varepsilon\)
- \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\varepsilon=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)
- \(\frac{1}{2} m_1^2 u_1^2+\frac{1}{2} m_2^2 u_2^2+\varepsilon=\frac{1}{2} m_1^2 v_1^2+\frac{1}{2} m_2^2 v_2^2\)
- \(m_1^2 u_1+m_2^2 u_2-\varepsilon=m_1^2 v_1+m_2^2 v_2\)
Answer: 2. \(\frac{1}{2} m_1 u_1^2+\frac{1}{2} m_2 u_2^2-\varepsilon=\frac{1}{2} m_1 v_1^2+\frac{1}{2} m_2 v_2^2\)
Question 238. Two spherical bodies of mass M and 5 M and radii R and 2R are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body before a collision is:
- 4.5 R
- 7.5 R
- 1.5 R
- 2.5 R
Answer: 2. 7.5 R
Question 239. A rigid ball of mass m strikes a rigid wall at 60º and gets reflected without loss of speed as shown in the figure below. The value of impulse imparted by the wall in the ball will be

- \(\frac{\mathrm{mV}}{3}\)
- mV
- 2mV
- \(\frac{\mathrm{mV}}{2}\)
Answer: 2. mV
Question 240. A bullet of mass 10 g moving horizontally with a velocity of 400 ms–1 strike of a wooden block of mass 2 kg which is suspended by a light inextensible string of length 5 m. As a result, the center of gravity of the block is found to rise a vertical distance of 10 cm. The speed of the bullet after it emerges horizontally from the block will be
- 160 ms-1
- 100 ms-1
- 80 ms-1
- 120 m-1
Answer: 4. 120 m-1
Question 241. Two identical balls A and B having velocities of 0.5 m/s and –0.3 m/s respectively collide elastically in one dimension. The velocities of B and A after the collision respectively will be
- 0.3 m/s and 0.5 m/s
- – 0.5 m/s and 0.3 m/s
- 0.5 m/s and – 0.3 m/s
- – 0.3 m/s and 0.5 m/s
Answer: 3. 0.5 m/s and – 0.3 m/s
Question 242. A moving block having a mass of m collides with another stationary block having a mass of 4m. The lighter block comes to rest after collision. When the initial velocity of the lighter block is v, then the value of the coefficient of restitution (e) will be
- 0.5
- 0.4
- 0.8
- 0.25
Answer: 4. 0.25
Question 243. Body A of mass 4 m moving with speed u collides with another body B of mass 2 m at rest the collision is head-on and elastic in nature. After the collision, the fraction of energy lost by colliding body A is :
- \(\frac{5}{9}\)
- \(\frac{1}{9}\)
- \(\frac{8}{9}\)
- \(\frac{4}{9}\)
Answer: 3. \(\frac{8}{9}\)
Question 244. A particle of mass 5 m at rest suddenly breaks on its own into three fragments. Two fragments of mass m each move along a mutually perpendicular direction with speed v each. The energy released during the process is
- \(\frac{3}{5} m v^2\)
- \(\frac{5}{3} m v^2\)
- \(\frac{3}{2} m v^2\)
- \(\frac{4}{3} m v^2\)
Answer: 4. \(\frac{4}{3} m v^2\)
Question 245. Two small particles of equal masses start moving in opposite directions from point A in a horizontal circular orbit. Their tangential velocities are v and 2v, respectively, as shown in the figure. Between collisions, the particles move at constant speeds. After making how many elastic collisions, other than that at A, these two particles will again reach point A?

- 4
- 3
- 2
- 1
Answer: 3. 2
NEET Physics Chapter 3 Centre of Mass: MCQs for Revision and Practice
Question 246. Statement-1: Two particles moving in the same direction do not lose all their energy in a completely inelastic collision.
Statement 2: The principle of conservation of momentum holds true for all kinds of collisions.
- Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation of Statement-1.
- Statement-1 is true, Statement-2 is true; Statement-2 is not the correct explanation of Statement-1
- Statement-1 is false, Statement-2 is true.
- Statement-1 is true, Statement-2 is false.
Answer: 1. Statement-1 is true, Statement-2 is true; Statement-2 is the correct explanation of Statement-1.
Question 247. A ball of mass 0.2 kg rests on a vertical post of height 5 m. A bullet of mass 0.01 kg, traveling with a velocity of V m/s in a horizontal direction, hits the center of the ball. After the collision, the ball and bullet travel independently. The ball hits the ground at a distance of 20 m and the bullet at a distance of 100 m from the foot of the post. The initial velocity V of the bullet is

- 250 m/s
- 250\(\sqrt{2}\)m/s
- 400 m/s
- 500 m/s
Answer: 4. 500 m/s
Question 248. This question has Statement 1 and Statement 2. Of the four choices given after the Statements, choose the one that best describes the two Statements.
Statement – 1: A point particle of mass m moving with speed υ collides with stationary point particle of mass M. If the maximum energy loss possible is given as\(f\left(\frac{1}{2} m v^2\right) \text { then } f=\left(\frac{m}{M+m}\right)\)
Statement 2: Maximum energy loss occurs when the particles get stuck together as a result of the collision.
- Statement -1 is true, Statement -2 is true, and Statement -2 is the correct explanation of Statement -1.
- Statement -1 is true, Statement – 2 is true, Statment-2 is not the correct explanation of Statement – 1.
- Statement -1 is true, Statement 2 is false.
- Statement -1 is false, and Statement – 2 is true.
Answer: 4. Statement -1 is false, Statement – 2 is true.
Question 249. A particle of mass m is projected from the ground with an initial speed u0at an angle α with the horizontal. At the highest point of its trajectory, it makes a completely inelastic collision with another identical particle, which was thrown vertically upward from the ground with the same initial speed u0. The angle that the composite system makes with the horizontal immediately after the collision is :
- \(\frac{\pi}{4}\)
- \(\frac{\pi}{4}+\mathrm{a}\)
- \(\frac{\pi}{4}-\mathrm{a}\)
- \(\frac{\pi}{4}\)
Answer: 1. \(\frac{\pi}{4}\)
Question 250. A tennis ball is dropped on a horizontal smooth surface. It bounces back to its original position after hitting the surface. The force on the ball during the collision is proportional to the length of compression of the ball. Which one of the following sketches describes the variation of its kinetic energy K with time t most appropriately? The figures are only illustrative and not to the scale.

Answer: 2.
Question 251. A particle of mass m moving in the x direction with speed 2v is hit by another particle of mass 2m moving in the y direction with speed v. If the collision is perfectly inelastic, the percentage loss in the energy during the collision is close to :
- 44%
- 50%
- 56%
- 62%
Answer: 3. 56%
Question 252. The distance of the centre of mass of a solid uniform cone from its vertex is z0. If the radius of its base is R and its height is h then z0is equal to
- \(\frac{h^2}{4 R}\)
- \(\frac{3 h}{4}\)
- \(\frac{5 h}{8}\)
- \(\frac{3 h^2}{8 R}\)
Answer: 2. \(\frac{3 h}{4}\)
Question 253. It is found that if a neutron suffers an elastic collinear collision with deuterium at rest, fractional loss of its energy is pd, while for its similar collision with carbon nucleus at rest, fractional loss of energy is pc. The values of pd and pc are respectively:
- (0, 0)
- (0, 1)
- (.89, .28)
- (.28, .89)
Answer: 3. (.89, .28)
Question 254. The mass of a hydrogen molecule is 3.32 × 10-27 kg. If 1023 hydrogen molecules strike, per second, a fixed wall of area 2cm2 at an angle of 45° to the normal, and rebound elastically with a speed of 103 m/s, then the pressure on the wall is nearly :
- 2.35 × 102 N/m2
- 4.70 × 102 N/m2
- 2.35 × 103 N/m2
- 4.70 × 103 N/m2
Answer: 3. 2.35 × 103 N/m2
Question 255. In a collinear collision, a particle with an initial speed v0 strikes a stationary particle of the same mass. If the final total kinetic energy is 50% greater than the original kinetic energy, the magnitude of the relative velocity between the two particles, after collision, is :
- \(\frac{v_0}{2}\)
- \(\frac{v_0}{\sqrt{2}}\)
- \(\frac{v_0}{4}\)
- \(\sqrt{2} v_0\)
Answer: 4. \(\sqrt{2} v_0\)
Question 256. Three blocks A, B and C are lying on a smooth horizontal surface, as shown in the figure. A and B have equal masses, m which C has mass M. Block A is given an initial speed of v towards B due to which it collides with B perfectly inelastically. The combined mass collides with C, also perfectly inelastically of the initial kinetic energy is also perfectly inelastically lost in the whole process. What is the value of M/m?

- 2
- 4
- 5
- 3
Answer: 2. 4
Question 257. A piece of wood of mass 0.03 kg is dropped from the top of a 100-height building. At the same time, a bullet of mass 0.02 kg is fired vertically upwards, with a velocity of 100 ms-1 from the ground. The bullet gets embedded in the wood. Then the maximum height to which the combined system reaches above the top of the building before falling below is : (g = 10 m/s-2)
- 10 m
- 20 m
- 30 m
- 40 m
Answer: 4. 40 m
NEET Physics Class 11 Chapter 3 Centre of Mass MCQs and Answers
Question 258. A simple pendulum, made of a string of length and a bob of mass m, is released from a small angle θ0. It strikes a block of mass M, kept on a horizontal surface at its lowest point of oscillations, elastically. It bounces back and goes up to an angle θ1. Then M is given by :
- \(\mathrm{m}\left(\frac{\theta_0+\theta_1}{\theta_0-\theta_1}\right)\)
- \(\frac{\mathrm{m}}{2}\left(\frac{\theta_0-\theta_1}{\theta_0+\theta_1}\right)\)
- \(\frac{\mathrm{m}}{2}\left(\frac{\theta_0+\theta_1}{\theta_0-\theta_1}\right)\)
- \(\mathrm{m}\left(\frac{\theta_0-\theta_1}{\theta_0+\theta_1}\right)\)
Answer: 4. \(\mathrm{m}\left(\frac{\theta_0-\theta_1}{\theta_0+\theta_1}\right)\)
Question 259. The position vector of the center of mass\(\overrightarrow{\mathrm{r}}[latex]cm of an asymmetric uniform bar of the negligible area of cross-section as shown in the figure is:
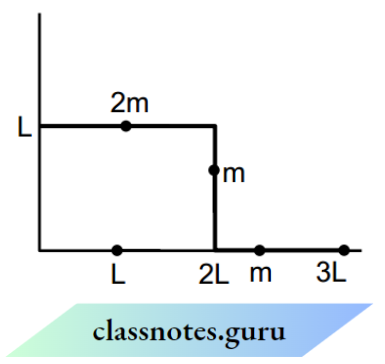
- [latex]\vec{r}_{\mathrm{cm}}=\frac{3}{8} L \hat{x}+\frac{11}{8} L \hat{y}\)
- \(\vec{r}_{c m}=\frac{11}{8} L \hat{x}+\frac{3}{8} L \hat{y}\)
- \(\vec{r}_{\mathrm{cm}}=\frac{13}{8} L \hat{x}+\frac{5}{8} L \hat{y}\)
- \(\vec{r}_{\mathrm{cm}}=\frac{5}{8} L \hat{x}+\frac{13}{8} L \hat{y}\)
Answer: 3. \(\vec{r}_{\mathrm{cm}}=\frac{13}{8} L \hat{x}+\frac{5}{8} L \hat{y}\)