pavani

NCERT Exemplar Solutions For Class 10 Maths Chapter 6  Triangles

Introduction:

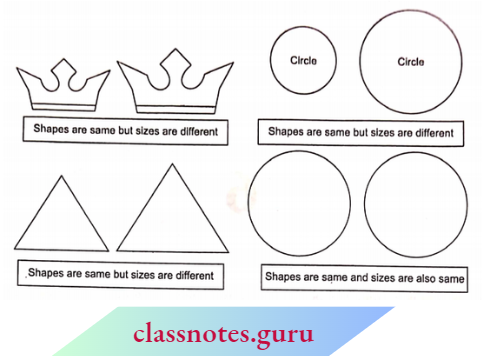
• To see the above pairs of figures, what do you think?
• Figures in a pair are alike, i.e., their shapes are the same.
• Shapes are the same but do not mean that they are necessarily equal in size.
• Shapes the same mean that their curvature is the same, i.e., figures are proportionately (not necessarily exactly) the same insides as well as angles.

NCERT Exemplar Solutions Class 10 Maths Chapter 6 Triangles

NCERT Exemplar Solutions For Class 10 Maths Chapter 6  Difference Between Proportional And Equal

1. In Terms of Sides :

⇒ \(\frac{A B}{P Q}=\frac{2 x}{2 y}=\frac{x}{y}\)

⇒ \(\frac{B C}{Q R}=\frac{3 x}{3 y}=\frac{x}{y}\)

⇒ \(\frac{A C}{P R}=\frac{4 x}{4 y}=\frac{x}{y}\)

⇒  \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}\), i.e, corresponding angles are proportional.

Read and Learn More Class 10 Maths Solutions Exemplar

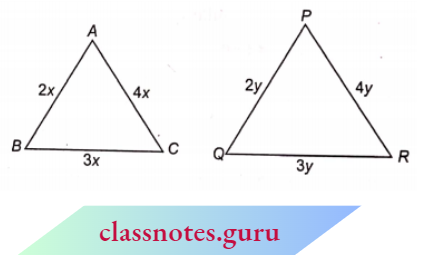
Suppose, the value of x = 2 sandy = 3.5 then the sides of the first triangle are 2 x 2, 3 x 2, 4 x 2, i.e., 4 cm, 6 cm, and 8 cm, and the sides of the second triangle are 2 x 3.5, 3 x 3.5, 4 x 3.5, i.e., 7 cm, 10.5 cm, and 14 cm. So, we can say that the corresponding sides are proportional, but that does not mean that their corresponding sides are equal.

2. In terms of Angles :

Here,\(\frac{\angle A}{\angle P}=\frac{2 x}{2 y}=\frac{x}{y}\)

⇒ \(\frac{\angle B}{\angle Q}=\frac{3 x}{3 y}=\frac{x}{y}\)

⇒ \(\frac{\angle C}{\angle R}=\frac{4 x}{4 y}=\frac{x}{y}\)

⇒ \(\frac{\angle A}{\angle P}=\frac{\angle B}{\angle Q}=\frac{\angle C}{\angle R}\)

i.e., corresponding angles are proportional.

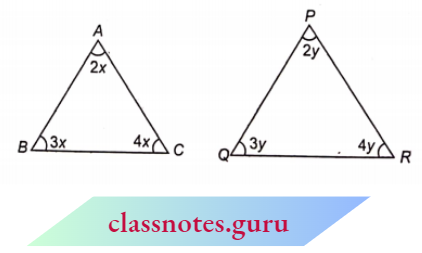
Now, see whether x and y are equal or they will be different.

We know that,

⇒ \(\angle A+\angle B+\angle C =180^{\circ}\)

⇒ \(2 r+3 x+4 r =180^{\circ}\)

⇒ \(9 x =180^{\circ} \Rightarrow x=20^{\circ}\)

⇒ \(\angle A=2 \times 20^{\circ}=40^{\circ}, \angle B =3 \times 20^{\circ}=60^{\circ}, \angle C=4 \times 20^{\circ}=80^{\circ}\)

⇒ \(\angle P+\angle Q+\angle R =180^{\circ}\)

⇒ \(2 y+3 y+4 y =180^{\circ}\)

⇒ \(9 y =180^{\circ} \Rightarrow y=20^{\circ}\)

P=2 \(\times 20^{\circ}=40^{\circ}, \angle Q =3 \times 20^{\circ}=60^{\circ}, \angle R=4 \times 20^{\circ}=80^{\circ}\)

⇒ \(\angle A=\angle P, \angle B=\angle Q\) and \(\angle C=\angle R\) .

From (1) and (2) we conclude that:

• Corresponding sides are proportional does not mean that their corresponding sides are equal.
• Corresponding angles are proportional means that their corresponding angles are necessarily equal.
• So, corresponding parts are proportional means
• Two triangles are similar if their shapes are the same.

NCERT Exemplar Solutions For Class 10 Maths Chapter 6  Definition Of Similar Triangles

Two triangles are similar if their corresponding parts are proportional.

1. their corresponding sides are proportional.
2.  their corresponding angles are equal.

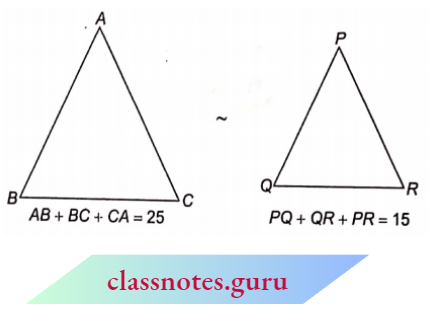
From the above figures, two triangles ABC and PQR are Bi similar, i.e.\(\triangle\)ABC ~ \(\triangle\)PQR, if any one of the following properties occurs :

(1) Their corresponding sides are proportional (or the ratio of their corresponding sides are equal)

⇒ \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}\) (SSS similarity)

(2) Their corresponding angles are equal

⇒ \(\angle A=\angle P, \angle B=\angle Q, \angle C=\angle R\) (AAA similarity)

If any two corresponding angles are equal

⇒ \(\left.\begin{array}{ll}\text { i.e., } & \angle A=\angle P \text { and } \angle B=\angle Q \\ \text { or } & \angle A=\angle P \text { and } \angle C=\angle R \\ \text { or } & \angle B=\angle Q \text { and } \angle C=\angle R\end{array}\right\}\) (AA similarity)

⇒ Any two corresponding sides are proportional and their included angles are the same i.e., or

⇒ \(\left.\begin{array}{l}
\frac{A B}{P Q}=\frac{B C}{Q R} \text { and } \angle B=\angle Q \\
\frac{A B}{P Q}=\frac{A C}{P R} \text { and } \angle A=\angle P \\
\frac{B C}{Q R}=\frac{A C}{P R} \text { and } \angle C=\angle R
\end{array}\right\}\)

The above three postulates are the postulates of the similarity of triangles

Remark:

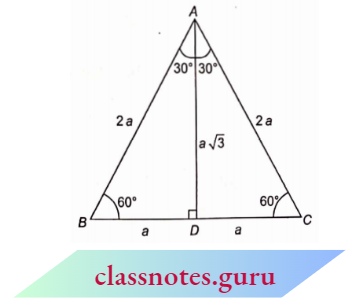
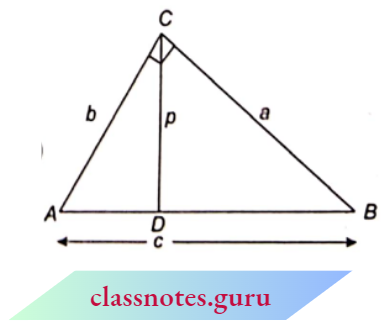
1. In an obtuse-angled triangle,

⇒  \(ar(\triangle A B C) =\frac{1}{2} \times \text { Base } \times \text { Corresponding altitude }\)[/latex]

= \(\frac{1}{2} \times B C \times A D\)

In an obtuse triangle, the perpendicular will be inside the triangle.

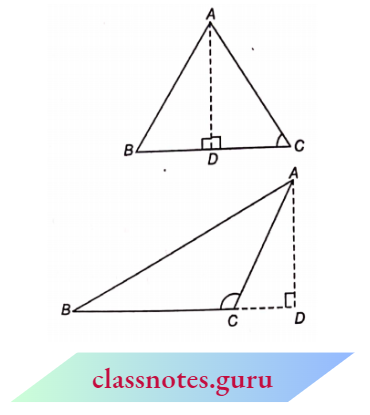
2. In an obtuse-angled triangle,

⇒ \(ar(\triangle A B C) =\frac{1}{2} \times \text { Base } \times \text { Corresponding altitude }\)

= \(\frac{1}{2} \times B C \times A D\)

In an obtuse triangle, the perpendicular will be outside the triangle.

Note: In \(\triangle\)ABC, when the base is taken as BC, then perpendicular will be drawn from the angle opposite to the base, i.e. \(\angle\)A on the base BC (whether it lies inside the BC or outside the BC).

NCERT Exemplar Solutions For Class 10 Maths Chapter 6  Difference Between Congruency And Similarity

• Two things are said to be congruent if they have the same shape as well as the same size, i.e., the two figures coincide with each other.
• Two things are said to be similar to each other if they have the same shapes but their sizes may be different.

Remark:

1. Congruent triangles are necessarily similar triangles but the converse is not always true.
2. If two triangles are similar to the third triangle, then they are similar to each other.

Basic Proportionality Theorem Or Thale’s Theorem

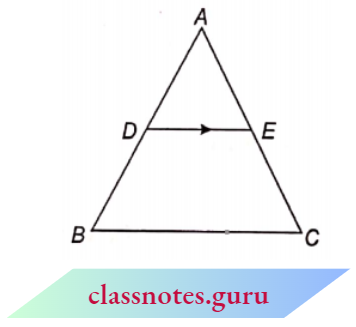
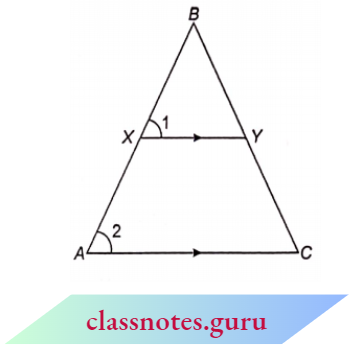
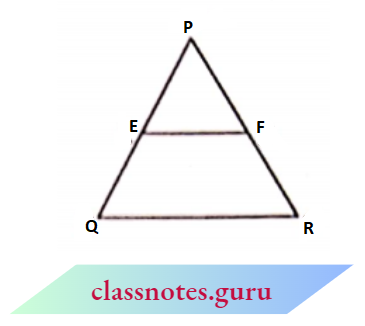
Theorem 1: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then it divides the other two sides in the same ratio.

Given: \(\triangle\)ABC in which DE || BC and DE intersects AB and AC at D and E respectively.

To Prove: \(\frac{A D}{D B}=\frac{A E}{E C}\)

Construction: Join BE and CD. Draw EL \(\perp AB\) and \(DM \perp AC\)

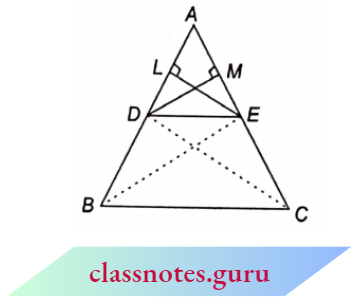
Proof:

Area of \((\triangle A D E) =\frac{1}{2} \times A D \times E L\)

Area of \((\triangle D B E) =\frac{1}{2} \times D B \times E L \)

⇒ \(\frac{{ar}(\triangle A D E)}{{ar}(\triangle D B E)} =\frac{\frac{1}{2} \times A D \times E L}{\frac{1}{2} \times D B \times E L}=\frac{A D}{D B}\)

Again Area of \(\triangle M D E =\frac{1}{2} \times A E \times D M\)

Area of \(\triangle E C D =\frac{1}{2} \times E C \times D M\)

⇒\(\frac{{ar}(\triangle A D E)}{{ar}(\triangle E C D)} =\frac{\frac{1}{2} \times A E \times D M}{\frac{1}{2} \times E C \times D M}=\frac{A E}{E C}\)

But since \(\triangle\)DBE and \(\triangle\)ECD are on the same base DE and between the same parallels DE and BC, we have

⇒ \({ar}(\triangle D B E)={ar}(\triangle E C D)\)

From (1), (2), and (3), we get \(\frac{A D}{D B}=\frac{A E}{E C}\)

Corollary: In a \(\triangle\)ABC, a line DE || BC intersects AB in D and AC in E, then prove that:

⇒ \(\frac{A B}{D B}=\frac{A C}{E C}\)

⇒ \(\frac{A D}{A B}=\frac{A E}{A C}\)

Proof: (1) From basic proportionality theorem

⇒ \(\frac{A D}{D B}=\frac{A E}{E C}\)

Adding 1 on both sides, we have

⇒ \(\frac{A D}{D B}+1 =\frac{A E}{E C}+1\)

⇒ \(\frac{A D+D B}{D B} =\frac{A E+E C}{E C} \Rightarrow \quad \frac{A B}{D B}=\frac{A C}{E C}\)

(2) From the basic proportionality theorem, we have

⇒ \(\frac{A D}{D B}=\frac{A E}{E C} \quad \Rightarrow \quad \frac{D B}{A D}=\frac{E C}{A E}\)

Adding 1 on both sides, we have

⇒ \(\frac{D B}{A D}+1 =\frac{E C}{A E}+1\)

⇒ \(\frac{D B+A D}{A D}=\frac{E C+A E}{A E}\)

⇒ \(\frac{A B}{A D}=\frac{A C}{A E} \quad \Rightarrow \quad \frac{A D}{A B}=\frac{A E}{A C}\)

Now, we can conclude

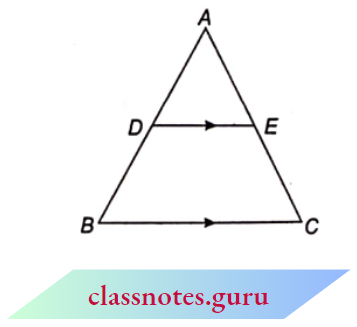
In \(\triangle A B C\) if D E || BC

1.  \(\quad \frac{A D}{D B}=\frac{A E}{E C}\) (B.P.T.)
2. \(\frac{A B}{D B}=\frac{A C}{E C}\)
3.  \(\frac{A D}{A B}=\frac{A E}{A C}\)

These Are the Same operations in R.H.S, as in the L.H.S.

NCERT Exemplar Solutions For Class 10 Maths Chapter 6  Converse of Basic Proportionality Theorem

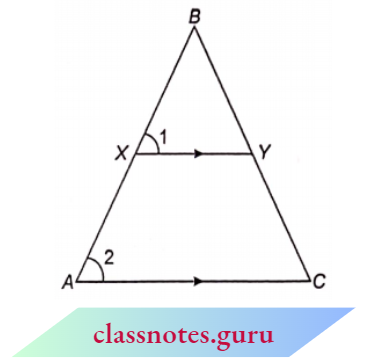
Theorem 2: If a line divides any two sides of a triangle in the same ratio then the line must be parallel to the third side.

Given: \(\triangle\)ABC in which a line l intersects AB at D and AC at E, such that 12

To Prove: DE \\BC

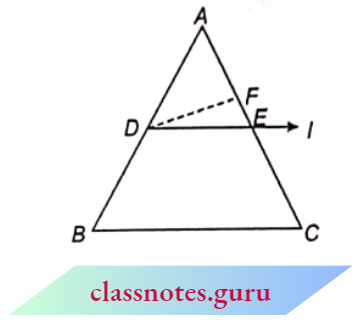
Proof: If possible, let DE is not parallel to BC, then there must be another line through D, which is parallel to BC. Let DE || BC.

Then by the basic proportionality theorem, we have

⇒ \(\frac{A D}{D B} =\frac{A F}{F C}\)

But \(\frac{A D}{D B}=\frac{A E}{E C}\)

From (1) and (2) we have \(\frac{A F}{F C}=\frac{A E}{E C}\)

Now, adding 1 on both sides

⇒ \(\frac{A F}{F C}+1=\frac{A E}{E C}+1 \quad \Rightarrow \quad \frac{A F+F C}{F C}=\frac{A E+E C}{E C}\)

⇒ \(\frac{A C}{F C}=\frac{A C}{E C} \quad \Rightarrow \quad F C=E C\)

This is possible only, when E and F coincide.

Hence D E || B C (D F || BC, by construction)

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Solved Examples

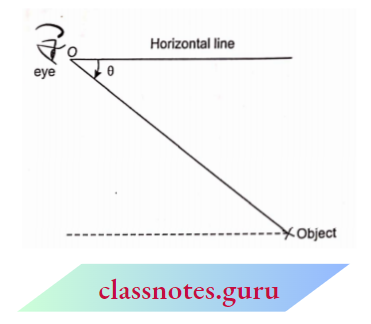
Example 1. In the adjoining figure DE || BC and D divide AB in the ratio 2 : 3. Find.

1. \(\frac{A E}{E C}\)
2. \(\frac{A E}{A C}\)

Solution:

Given

In the adjoining figure DE || BC and D divide AB in the ratio 2 : 3.

(1) Since D E || BC, hence by Thale’s theorem

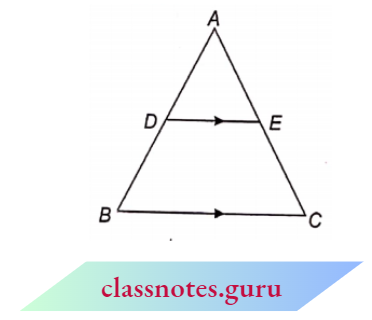
⇒ \(\frac{A D}{D B}=\frac{A E}{E C}\)

Also, \(\frac{A D}{D B}=\frac{2}{3}\) (given)

Therefore, from (1) and (2), \(\frac{A D}{D B}=\frac{A E}{E C}=\frac{2}{3}\)

(2) \(\frac{AE}{AC}\)=\(\frac{A E}{A E+E C}\)

= \(\frac{A E / E C}{A E / E C+E C / E C}\)

= \(\frac{\frac{2}{3}}{\frac{2}{3}+1}=\frac{\frac{2}{3}}{\frac{5}{3}}=\frac{2}{5}\)

Example 2. In the figure, PQ is parallel to MN, if \(\frac{K P}{P M}=\frac{4}{13}\) and KN = 20.4. Find KQ

Solution:

Given In \(\triangle\)KMN, PQ || MN

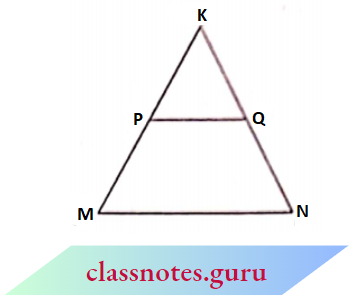
⇒ \(\frac{K P}{P M}=\frac{K Q}{Q N}\) (by B.P.T. or Thale’s theorem)

Let K Q=x, then Q N=20.4-x

Now, from (1) \(\frac{4}{13} =\frac{x}{20.4-x}\)

81.6-4 x =13 x

17 x =81.6

x =4.8 cm

Therefore K Q=4.8 cm

Example 3. In the figure, DE || BC. If DB = 10.8 cm, AE = 2.7 cm and£C =8.1 cm, find AD. DE || BC

Solution:

Given

In the figure, DE || BC. If DB = 10.8 cm, AE = 2.7 cm and£C =8.1 cm

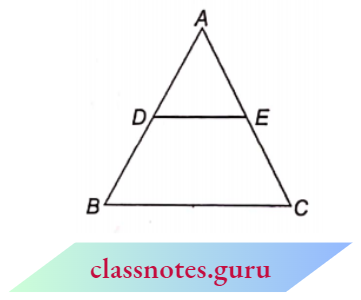
⇒ \(\frac{A D}{D B}=\frac{A E}{E C}\)

⇒ \(\frac{A D}{10.8}=\frac{2.7}{8.1}\)

AD=\(\frac{1}{3} \times 10.8 \mathrm{~cm}=3.6 \mathrm{~cm}\)

Example 4. In the given figure, in \(\triangle\)ABC, DE || BC so that AD = (4x – 3) cm, AE = (8x – 7) cm. BD = (3x – 1) cm and CE = (5x – 3) cm. Find the value of x.

Solution:

Given

In the given figure, in \(\triangle\)ABC, DE || BC so that AD = (4x – 3) cm, AE = (8x – 7) cm. BD = (3x – 1) cm and CE = (5x – 3) cm.

⇒ \(\triangle\)ABC, DE || BC

⇒ \(\frac{A D}{B D}=\frac{A E}{C E}\)

⇒ \(\frac{4 x-3}{3 x-1}=\frac{8 x-7}{5 x-3}\)

(4 x-3)(5 x-3)=(8 x-7)(3 x-1)

20 x²-27 x+9=24 x²-29 x+7

4 x²-2 x-2=0

2 x²-x-1=0

2 x²-2 x+x-1=0

2 x(x-1)+1(x-1)=0

(2 x+1)(x-1)=0

x=1 or x=-\(\frac{1}{2}\) (by Thale’s theorem)

But when x=-\(\frac{1}{2}\)

A D=\(\left[4 \times\left(-\frac{1}{2}\right)-3\right]\)=-5

Since distance cannot be negative so x \(\neq-\frac{1}{2}\)

Here X = 1

The value of x = 1

Example 5. The bisector (internal or external) of an angle of a triangle divides the opposite side (internally or externally) in the ratio of the sides containing the angle.

Solution:

Given: \(\triangle\)ABC in which the bisector AD of \(\angle\)A meets BC (or BC produced) in D.

To Prove : \(\frac{B D}{D C}=\frac{A B}{A C}\)

Construction: Draw CE || DA meeting BA (produced if necessary) in E.

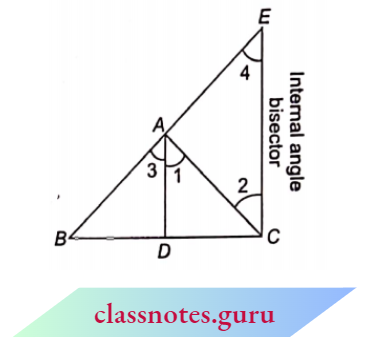
Proof: Since CE || DA

⇒ \(\angle 1=\angle 2\) (alternate angles)

and \(\angle 3 =\angle 4\) (corresponding angles) (2)

But \(\angle 1=\angle 3\) (given)…(3)

⇒ \(\angle 2=\angle 4\) [from (1), (2) and (3)]

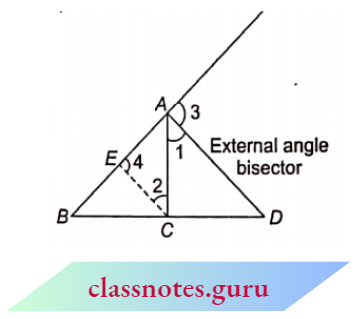
An E=A C (sides opposite to equal angles are equal) …(4)

Now, since CE || DA (construction)

⇒ \(\frac{B D}{D C}=\frac{B A}{A E}\)

⇒ \(\frac{B D}{D C}=\frac{B A}{A C}\) [from (4) and (5)]

Example 6. Prove that any line parallel to parallel sides of a trapezium divides the non-parallel sides proportionally.

Solution:

Given: A trapezium ABCD in which AB || DC.

Also a line EF || AB || DC.

To Prove: \(\frac{A E}{E D}=\frac{B F}{F C}\)

Construction: Join DB which intersects E F at G,

Proof: In \(\triangle A D B\), since E G || A B. ( E F || A B)

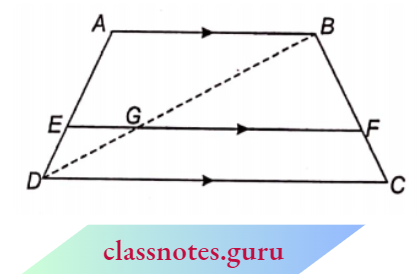
⇒ \(\frac{A E}{E D}=\frac{B G}{G D}\) (by B.P. theorem)

Also, in \(\triangle B D C, since G F || DC (E F || D C)\)

⇒ \(\frac{B F}{F C}=\frac{B G}{G D}\) (by B.P. theorem)

From (1) and (2), we have

⇒ \(\frac{A E}{E D}=\frac{B F}{F C}\)

Hence Proved.

Example 7. The side BC of a triangle ABC is bisected at D. O is any point in Al). BO and CO produced meet AC and AB at E and F respectively and AD is produced to X so that D is the mid-point of OX. Prove that AO: AX = AF: AB and show that FE || BC.

Solution:

Given

The side BC of a triangle ABC is bisected at D. O is any point in Al). BO and CO produced meet AC and AB at E and F respectively and AD is produced to X so that D is the mid-point of OX.

Join BX and CX.

Since D is the mid-point of BC (given)

BD = DC …(1)

Also, D is the mid-point of OX (given)

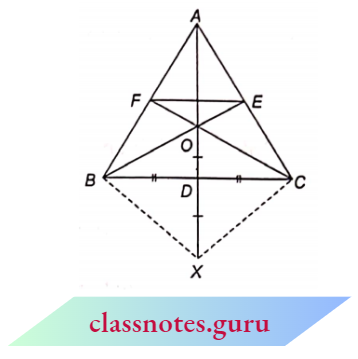
OD = DX …(2)

From (1) and (2), we have

⇒ [Square OBXC is a parallelogram (diagonals bisect each other) B

OC || BX (opposite sides of a parallelogram)

FC || BX ⇒ OE || XC

In \(\triangle A X C\),

⇒ \(\frac{A O}{O X}=\frac{A E}{E C}\) (by B.P. theorem)

From (3) and (4), we have

⇒ \(\frac{A F}{F B}=\frac{A E}{E C}\)

In \(\triangle A B C\), F E || B C. (converse of B.P. theorem)

Hence Proved.

Class 10 Maths Triangles Exemplar Solutions

Example 8. In \(\triangle\)ABC, D, and E are two points on AB such that AD = BE. If DP || BC and EQ || AC, prove that PQ || AB.

Solution:

Given: \(\triangle\)ABC in which D and E are two points such that AD = BE.

Also DP || BC and EQ || AC.

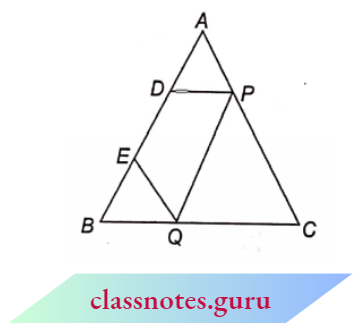
To Prove: PQ || AB

Proof: In ΔABC, Since DP || BC

⇒ \(\frac{A D}{D B}=\frac{A P}{P C}\) (by B.P. theorem) …. 1

In \(\triangle A B C\), since E Q || A C

⇒ \(\frac{B E}{E A}=\frac{B Q}{Q C}\) (by B.P. theorem) …. 2

Now, as A D = B E (given) …. 3

A D+D E=B E+D E (adding DE on both sides)

AE = BD ….. 4

From (1), (2), (3) and (4),

⇒ \(\frac{A P}{P C}=\frac{B Q}{Q C}\)

P Q || A B (by the converse of B.P. theroem)

Hence Proved.

Criteria For Similarity Of Two Triangles

• Two triangles are said to be similar if their corresponding angles are equal and corresponding sides are proportional (i.e., the ratios between the lengths of corresponding sides are equal).
• For example if in \(\triangle\)ABC and \(\triangle\)PQR
•  \(\angle A=\angle P, \angle B=\angle Q, \angle C=\angle R\)
• and, \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}\)
• then \(\triangle\)ABC is similar to \(\triangle\)PQR.
• Symbol ~ is used for “is similar to”

Conversely: If \(\triangle\)ABC is similar to \(\triangle\)PQR then

⇒ \(\angle A=\angle P, \angle B=\angle Q, \angle C=\angle R\)

⇒ \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}\)

Theorem 1 (AAA Similarity): If in two triangles the corresponding angles are equal, then their corresponding sides are proportional and hence the triangles are similar.

Given: \(\triangle\)ABC and \(\triangle\)DEF such that

⇒ \(\angle A=\angle D, \angle B=\angle E \text {, and } \angle C=\angle F\)

To Prove: \(\triangle\)ABC ~ \(\triangle\)DEF

Construction: Cut DP =AB and DQ = AC. Join PQ.

Proof: In \(\triangle\)ABC and \(\triangle\)DPQ, we have

A B =D P

A C =D Q (by construction)

⇒ \(\angle A =\angle D\)

⇒ \(\triangle A B C \cong \triangle D P Q\) (by SAS congruence)

⇒ \(\angle B =\angle P\)

But it is given that \(\angle B=\angle E\)

Therefore, \(\angle E=\angle P\)

P Q || E F

⇒ \(\frac{D P}{D E}=\frac{D Q}{D F}\)

⇒ \(\frac{A B}{D E}=\frac{C A}{F D}\)

Similarly \(\frac{A B}{D E}=\frac{B C}{E F}\)

⇒ \(\frac{A B}{D E}=\frac{B C}{E F}=\frac{C A}{F D}\)

Thus \(\angle A=\angle D, \angle B=\angle E, \angle C=\angle F\) and

⇒ \(\frac{A B}{D E}=\frac{B C}{E F}=\frac{C A}{F D}\)

Hence, \(\triangle A B C \sim \triangle D E F\).

Corollary (AA Similarity): If two angles of a triangle are respectively equal to two angles of another triangle then the two triangles are similar.

Proof: In \(\triangle A B C\) and \(\triangle D E F\) , let \(\angle A=\angle D\) and \(\angle B=\angle E\) , then 3rd \(\angle C= 3rd \angle F\)

Thus, the two triangles are equal.

Hence, the two triangles are similar.

Thus, we can see that two triangles can be proved similar if two angles of 1st triangle are equal to two angles of the other triangle respectively.

Theorem 2 (SSS Similarity): If the corresponding sides of two triangles are proportional then their corresponding angles are equal, and hence the two triangles are similar.

Given: \(\triangle\)ABC and \(\triangle\)DFF in which

To Prove: \(\triangle A B C \sim \triangle D E F\)

Construction: Let us take \(\triangle\) A B C and \(\triangle\) D E F such that

⇒ \(\frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F}\)

Cut D P=A B and D Q=A C. Join PQ

Proof: \(\frac{A B}{D E}=\frac{A C}{D F}\)

⇒ \(\frac{D P}{D E}=\frac{D Q}{D F}\)

Thus, the given triangles are equiangular and hence similar.

Theorem 3 (SAS Similarity): If one angle of a triangle is equal to one angle of the other triangle and the sides including these angles are proportional then the two triangles are similar.

Given: \(\triangle\)ABC and \(\triangle\)DPP in which

⇒ \(\angle A=\angle D and \frac{A B}{D E}=\frac{A C}{D F}\)

To Prove: \(\triangle \triangle B C \sim \triangle D E F\)

Construction: Let us take \(\triangle A B C\) and \(\triangle D E F\) such that

⇒ \(\frac{A B}{D E}=\frac{A C}{D F}\) and \(\angle A=\angle D\)

Cut D P=A B and D Q=A C. Join P Q.

Proof: In \(\triangle A B C\) and \(\triangle D P Q\)

A B=D P (by construction)

⇒ \(\angle A=\angle D\) (given)

A C=D Q (by construction)

⇒ \(\triangle A B C \cong \triangle D P Q\) (by SAS axiom)

⇒ \(\angle A=\angle D, \angle B=\angle P and \angle C=\angle Q \)

Now \(\frac{A B}{D E}=\frac{A C}{D F}\) (given)

⇒ \(\frac{D P}{D E}=\frac{D Q}{D F}\) (AB = DP and AC = DQ)

P Q || E F (by the converse of Thale’s theorem)

⇒ \(\angle P=\angle E and \angle Q=\angle F )\)

⇒ \(\angle P=\angle E\) and \(\angle Q=\angle F \)(corresponding angles)

⇒ \(\angle A=\angle D, \angle B=\angle P=\angle E \angle C=\angle Q=\angle F\)

Thus, \(\angle A=\angle D, \angle B=\angle E and \angle C=\angle F\)

So, the given triangles are equiangular and hence similar.

Some More Results

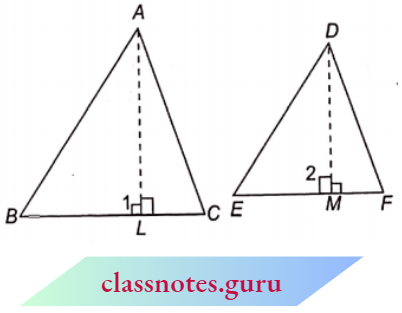
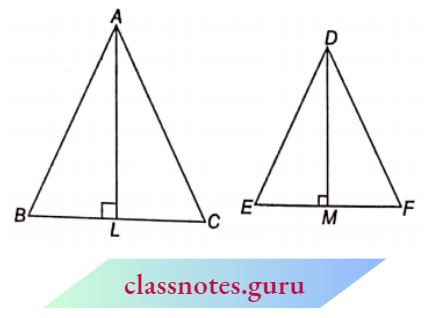
Result 1: If two triangles are equiangular, prove that the ratio of their corresponding sides is the same as the ratio of their corresponding altitudes.

Given : \(\triangle M B C\) and \(\triangle D E F \)in which \(\angle A=\angle D\), \(\angle B=\angle E\) and \(\angle C=\angle F\) and \(A L \perp B C\) and \(D M \perp E F\) :

To Prove : \(\frac{B C}{E F}=\frac{A L}{D M}\)

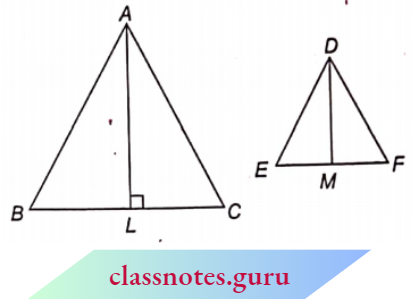
Proof : Since \(\triangle A B C\) and \(\triangle D E F\) are equiangular, therefore, \(\triangle A B C \sim \triangle D E F\)

⇒  \(\frac{A B}{D E}=\frac{B C}{E F}\)

In \(\triangle A L B\) and \(\triangle D M E\), we have

⇒ \(\angle A L B=\angle D M E=90^{\circ}\) and \(\angle B=\angle E\)

⇒ \(\triangle A L B \sim \triangle D M E\)

⇒ \(\frac{A B}{D E}=\frac{A L}{D M}\)

From (1), and (2) we get

⇒ \(\frac{B C}{E F}=\frac{A L}{D M}\)

Result 2: If two triangles are equal, prove that the ratio of their corresponding sides is the same as the ratio of the corresponding medians.

Given : \(\triangle\)ABC and \(\triangle\)DEF in which \(\angle\)A = \(\angle\)D, \(\angle\)B = \(\angle\)E and \(\angle\)C = \(\angle\)F and \(\angle\)L and \(\angle\)M are medians.

To Prove : \(\frac{B C}{E F}=\frac{A L}{D M}\)

Proof : Since \(\triangle A B C\) and \(\triangle D E F\) are equiangular, we have \(\triangle A B C \sim \triangle D E F\)

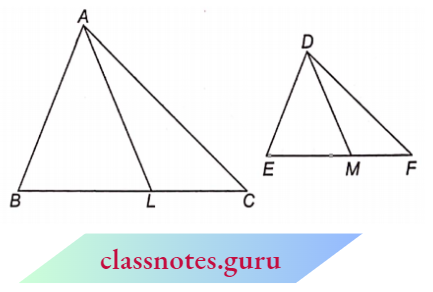
⇒ \(\frac{A B}{D E}=\frac{B C}{E F}\)

⇒ \(\frac{A B}{D E}=\frac{B C}{E F}=\frac{2 B L}{2 E M}=\frac{B L}{E M}\)

But, \(\frac{A B}{D E} =\frac{B L}{E M}\) and \(\angle B=\angle E\)

Now, in \(\triangle A B L\) and \(\triangle D E M\), we have

⇒ \(\frac{A B}{D E}=\frac{B L}{E M}\) and \(\angle B=\angle E\) (given)

⇒ \(\triangle A B L \sim \triangle D E M\) (by SAS similarity)

⇒ \(\frac{A B}{D E} =\frac{A L}{D M}\) … 2

From 1 And 2, we get

∴ \(\frac{B C}{E F}=\frac{A L}{D M}\)

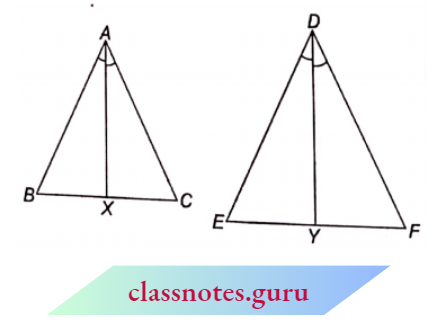
Result 3: If two triangles are equiangular, show that the ratio of the corresponding sides is the same as the ratio of the corresponding angle bisector segments.

Given : \(\triangle\)ABC and \(\triangle\)DEF in which \(\angle\)A = \(\angle\)D, \(\angle\)B = \(\angle\)E and A

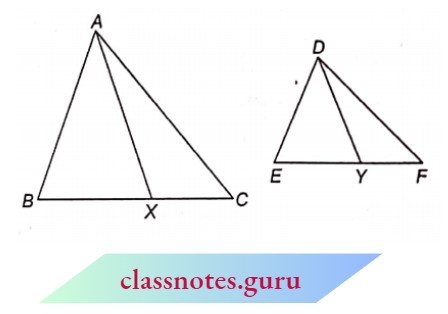
⇒ \(\angle\)C = \(\angle\)F and AX and DY are the bisectors of \(\angle\)A and \(\angle\)D
respectively.

To Prove: \(\frac{B C}{E F}=\frac{A X}{D Y}\)

Proof : Since \(\triangle\)ABC and \(\triangle\)DEF are equiangular, we have \(\triangle\)ABC ~ \(\triangle\)DEF

⇒ \(\frac{A B}{D E}=\frac{B C}{E F}\) …. 1

Now, \(\angle A=\angle D \Rightarrow \frac{1}{2} \angle A=\frac{1}{2} \angle D\)

⇒ \(\angle B A X=\angle E D Y\)

Thus in \(\triangle A B X\) and \(\triangle D E Y\), we have

⇒ \(\angle B A X =\angle E D Y\) (proved)

⇒ \(\angle B =\angle E\) (given)

⇒ \(\triangle A B X \sim \triangle D E Y\) (by AA similarity)

⇒ \(\frac{A B}{D E}=\frac{A X}{D Y}\) ….. 2

From (1) and (2), we get

⇒ \(\frac{B C}{E F}=\frac{A X}{D Y}\)

Remark:

1. If two triangles ABC and DEF are similar, then
2. \(\frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F}\)
3. \(\frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F}=\frac{A B+B C+A C}{D E+E F+D F}\) (using ratio and proportion)
4. \(\frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F}=\frac{\text { Perimeter of } \triangle A B C}{\text { Perimeter of } \triangle D E F}\)
5. Thus, if two triangles are similar, then their corresponding sides are proportional and they are proportional to the corresponding perimeters.

Triangles Class 10 Exemplar Problems with Solutions

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Traingle Importance Of Correct Namings

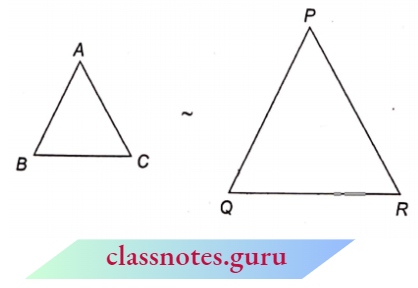
Then which of the following is correct?

•  \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}\).
• \(\frac{A B}{P R}=\frac{B C}{P Q}=\frac{A C}{Q R}\).
• \(\frac{A B}{Q R}=\frac{B C}{P Q}=\frac{A C}{P R}\)

You will say option (a) is correct, but your answer is wrong.

Until we do not know which part of one triangle is equal to which part of another triangle, how can we give the correct answer? We should give the name of the other triangle according to the first triangle. We must see the corresponding parts.

For Example,

Here , \(\angle A=\angle Q\)

⇒ \(\angle C=\angle P\)

⇒ \(\angle B=\angle R\)

Since two angles of \(\triangle\)ABC, are equal to two angles of \(\triangle\)PQR, therefore two triangles are similar to each other. For this, write the name of the first triangle say \(\triangle\)CAB. Now we have to write the name of the other triangle correspondingly, (according to \(\triangle\)CAB)

As C comes in 1st place and C = P, So  P will come in 1st place also

As A comes in 2nd place and A = Q, So Q will come in 2nd place

As the remaining place of first, A is for B so the remaining place of second A will be for R.

Corresponding sides are proportional.

⇒ \(\frac{\text { first two of } \triangle C A B}{\text { first two of } \Delta P Q R} =\frac{\text { last two of } \triangle C A B}{\text { last two of } \triangle P Q R}=\frac{\text { first and last of } \triangle C A B}{\text { first and last of } \triangle P Q R}\)

⇒ \(\frac{C A}{P Q} =\frac{A B}{Q R}=\frac{C B}{P R}\) (no need to see the figures, you can confuse there) …(1)

Also, you can write

1st angle of first \(\Delta\)=I angle of other \(\Delta\) i.e., \(\angle C=\angle P\)

2nd angle of first \(\Delta\)= 2nd angle of other \(\Delta\) i.e., \(\angle A=\angle Q \)

and 3rd angle of first \(\Delta\)= 3rd angle of other \(\Delta\) i.e. \(\angle B=\angle R\)

If we write the name of first \(\triangle\) as BCA then the name of other \(\triangle\) will be as follows (As \(\angle\)A = \(\angle\)Q => if A comes in 3rd place, so Q will also come in 3rd place and as \(\angle\)C = \(\angle\)P if C comes in 2nd places, so P will also come in 2nd place, etc.)

So, now for \(\triangle\)BCA.

(2) Then put

(3) Then finally (remaining place)

Hence, \(\triangle B C A-\triangle R P Q\)

The corresponding sides are proportional

⇒ \(\frac{\text { first two of } \triangle B C A}{\text { first two of } \triangle R P Q} =\frac{\text { last two of } \triangle B C A}{\text { last two of } \triangle R P Q}\)

= \(\frac{\text { first and last of } \triangle B C A}{\text { first and last of } \triangle R P Q}\)

B C =\(\frac{C A}{P Q}=\frac{B A}{R Q}\)

This is also the same as in (1)

Now, we shall see one example based on the above discussion

Example : D is a point on the side BC of a \(\triangle\)ABC, such that \(\angle\)ADC = \(\angle\)BAC.

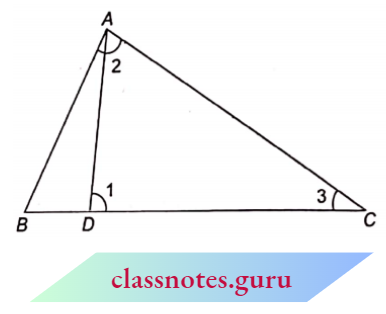
Prove that: \(\frac{C A}{C D}=\frac{C B}{C A}\)

Solution:

Don’t bother to write the correct namings of two triangles. We know that as \(\angle\)1 = \(\angle\)2 (given)

So we can take the As in which \(\angle\)1 and \(\angle\)2 occur i.e., \(tri\angle\)ADC and \(tri\angle\)ABC

Now, in \(tri\angle\)s ADC and ABC

⇒ \(\angle\)1 = \(\angle\)2

Now From We Can Write,

⇒ \(\triangle \mathrm{A} D \mathrm{~A} \sim \triangle B A C\)

Now, from this, we can write

⇒ \(\frac{\text { first two of } \triangle A D C}{\text { first two of } \triangle B A C}=\frac{\text { last two of } \triangle A D C}{\text { last two of } \triangle B A C}\)

=\(\frac{\text { first and last of } \triangle A D C}{\text { first and last of } \triangle B A C}\)

i.e., \(\frac{A D}{B A}=\underbrace{\frac{D C}{A C}=\frac{A C}{B C}}\)

or \(\frac{C A}{C D}=\frac{C B}{C A}\)

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Traingle Importance Of Correct Namings Solved Examples

Example 1. In the given figure \(\triangle\)ACB ~ \(\triangle\)APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm, AP = 2.8 cm, find C/1 and AQ.

Solution:

Given

In the given figure \(\triangle\)ACB ~ \(\triangle\)APQ. If BC = 8 cm, PQ = 4 cm, BA = 6.5 cm, AP = 2.8 cm

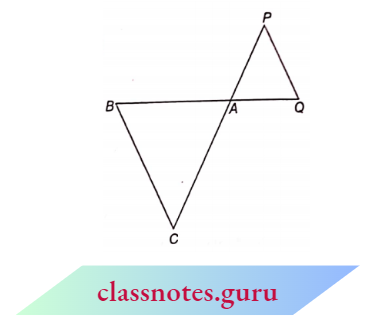
Since, \(\triangle\)ACB ~ \(\triangle\)APQ (given)

⇒ \(\frac{A C}{A P}=\frac{C B}{P Q}=\frac{A B}{A Q}\)

(don’t see the figure) write \(\frac{\text { first two }}{\text { first two }}=\frac{\text { last two }}{\text { last two }}=\frac{\text { first and last }}{\text { first and last }}\)

⇒ \(\frac{A C}{2.8}=\frac{8}{4}=\frac{6.5}{A Q}\)

Consider, \(\frac{A C}{2.8}=\frac{8}{4}\)

4 A C=8 \(\times 2.8 \quad \Rightarrow \quad A C=5.6 \mathrm{~cm}\)

Consider, \(\frac{8}{4}=\frac{6.5}{A Q}\)

2 A Q=6.5 or A Q=3.25 cm

Example 2. The triangles shown in adjoining figures are similar. Find the values of a and b.

Solution:

Given

The triangles shown in adjoining figures are similar.

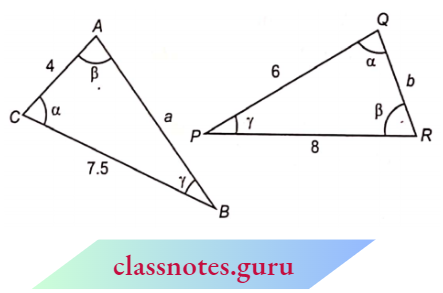
⇒ \(\angle A=\angle R, \angle B=\angle P\)and \(\angle C=\angle Q\)

⇒ \(\triangle A B C \sim \triangle R P Q\) (AAA similarity)

⇒ \(\frac{A B}{R P}\) … First Two

= \(\frac{B C}{P Q}\) ……. Last Two

= \(\frac{A C}{R Q}\) ….. First And Last

⇒ \(\frac{a}{8} =\frac{7.5}{6}=\frac{4}{b}\)

⇒ \(\frac{a}{8} =\frac{7.5}{6}\) and \(\frac{4}{b}=\frac{7.5}{6}\)

a =\(\frac{8 \times 7.5}{6}\) and \(b=\frac{4 \times 6}{7.5}\)

a =10 and b=3.2

Example 3. In the given figure if AD || BC, find the value of x.

Solution:

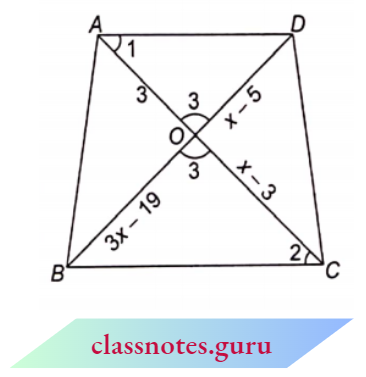
Given: AD || BC

Proof: In \(\triangle\)AOD and \(\triangle\)BOC

⇒ \(\angle 1=\angle 2\) (alternate angles)

⇒ \(\angle 3=\angle 3\) (vertically opposite angles)

i.e., \(\triangle A O D \sim \triangle C O B\) [AA corollary]

⇒ \(\frac{A O}{O C}=\frac{O D}{O B}\)

⇒ \(\frac{3}{x-3}=\frac{x-5}{3 x-19}\)

(x-3)(x-5)=3(3 x-19) \(\quad \Rightarrow \quad x^2-5 x-3 x+15=9 x-57\)

⇒ \(x^2-17 x+72=0 \quad \Rightarrow \quad x^2-9 x-8 x+72=0\)

x(x-9)-8(x-9)=0 or (x-9)(x-8)=0

x-9=0 or x=9

x-8=0 or x=8

Hence x=9,8

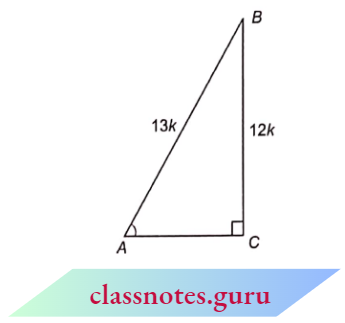
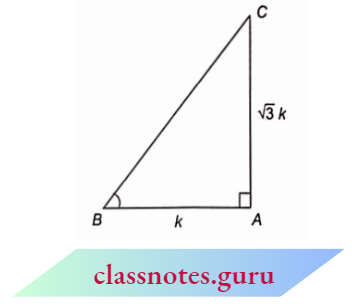
Example 4. Find ∠P in the figure below

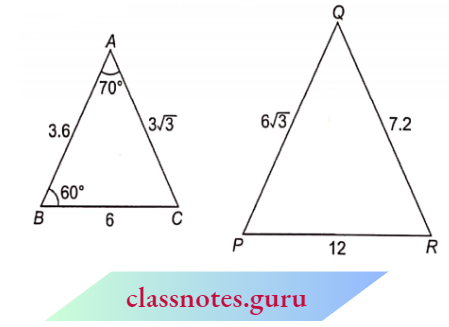
Solution:

In \(\triangle A B C\) and \(\triangle Q R P\), we have

⇒ \(\frac{A B}{Q R}=\frac{3.6}{7.2}=\frac{1}{2}, \frac{B C}{R P}=\frac{6}{12}=\frac{1}{2}\)

and \(\frac{C A}{P Q}=\frac{3 \sqrt{3}}{6 \sqrt{3}}=\frac{1}{2}\)

Thus,\(\frac{A B}{Q R}=\frac{B C}{R P}=\frac{C A}{P Q}\)

Hence, by SSS criterion,

⇒ \(\triangle A B C \sim \triangle Q R \quad\left(\quad \frac{\text { first two }}{\text { first two }}=\frac{\text { last two }}{\text { last two }}=\frac{\text { first and last }}{\text { first and last }}\right)\)

⇒ \(\angle C =\angle P\) (third angle = third angle)

But \(\angle C=180-(\angle A+\angle B)=180^{\circ}-\left(70^{\circ}+60^{\circ}\right)=50^{\circ}\)

⇒ \(\angle P=50^{\circ}\)

Example 5. In the figure AC || BD, prove that:

1. \(\triangle A C E \sim \triangle B D E\)
2. \(\frac{A E}{C E}=\frac{B E}{D E}\)

Solution:

(1) A C || B D (given)

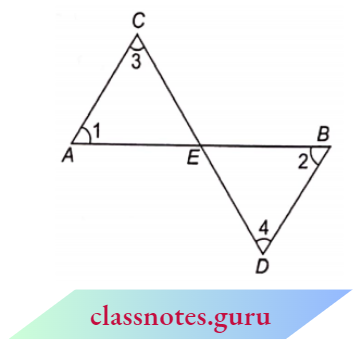
and, \(\left.\begin{array}{l}\angle 1=\angle 2 \\ \angle 3=\angle 4\end{array}\right\}\)

∴ \(\triangle \widehat{A C E \sim \triangle B D E}\) (by AA criterion)

(2) Now, since \(\triangle A C E \sim \triangle B D E\)

⇒ \(\frac{A E}{B E}=\frac{C E}{D E}\) (corresponding sides of similar \(\Delta\) s are proportional)

∴ \(\frac{A E}{C E}=\frac{B E}{D E}\) (by alternendo)

Example 6. \(\triangle\)ABC is an isosceles triangle with Ab = AC And D is a point on AC such that \(B C^2=A C \times C D\), Prove that BD = BC

Solution:

Given

\(\triangle\)ABC is an isosceles triangle with Ab = AC And D is a point on AC such that \(B C^2=A C \times C D\),

We have

⇒ \(B C^2 =A C \times C D\) and A B=A C

⇒ \(B C \times B C =A C \times C D\) and \(\angle B =\angle C\)

There may be 3 possibilities:

Possibility 1

⇒ \(\frac{B C}{A C}=\frac{C D}{B C}\)

and \(\angle C=\angle B\)

⇒ \(\triangle B \overline{D C} \sim \triangle A \overline{B C}\)

But in this case, \(\angle C \neq \angle B\)

So, the position will not suit.

Therefore, not possible.

Possibility 2.

⇒ \(\frac{B C}{C D}=\frac{A C}{B C}\)

⇒ \(\angle B=\angle C\)

⇒ \(\triangle \widehat{A B C} \sim \triangle \widehat{B D C}\)

But in this case, \(\angle B \neq \angle C\)

So, the position will not suit. Therefore, not possible.

Possibility 3.

⇒ \(\frac{B C}{A B} =\frac{C D}{B C}\)( A B=A C)

⇒ \(\angle C =\angle B \)

⇒ \(\triangle \overline{B C} D \sim \Delta \overline{A B} C\)

All positions are satisfied.

So, possible.

⇒ \(\triangle B C D \sim \triangle A B C\) (by SAS criterion)

⇒ \(\frac{B C}{A B} =\frac{C D}{B C}=\frac{B D}{A C}\)

⇒ \(\frac{B C}{A B} =\frac{B D}{A C}\)

BC =B D (A B=A C, given)

Hence Proved.

We could take directly the 3rd possibility and the solution seems to be much easier but our main aim is to make you understand why we take the 3rd one.

Example 7. In the given figure if \(\angle B=90^{\circ}\) and B D is perpendicular to A C then prove that :

1.  \(\triangle A D B \sim \triangle B D C\)
2. \(\triangle A D B \sim \triangle A B C\)
3.  \(\triangle B D C \sim \triangle A B C\)
4. \(B D^2=A D \times D C\)
5.  \(A B^2=A D \times A C\)
6. \(B C^2=C D \times A C\)
7.  \(A B^2+B C^2=A C^2\)

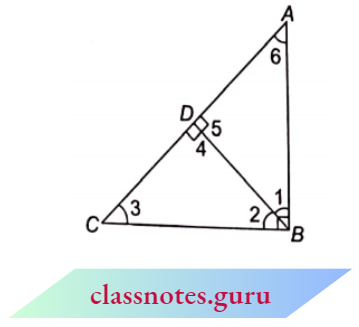
Solution:

(1) In \(\triangle A D B\) and \(\triangle B D C\),

⇒ \(\angle 5=\angle 4 (each 90^{\circ}\) )

Searching for Second Angle :

We know that \(\angle 1+\angle 2=90^{\circ}\)

Also, since \(\angle 4=90^{\circ}\)

⇒ \(\angle 2+\angle 3=90^{\circ}\) (angle sum property)

From (1) and (2), we get

⇒ \(\angle 1+\angle 2=\angle 2+\angle 3 \quad\left(\text { each } 90^{\circ}\right)\)

⇒ \(\angle 1=\angle 3\)

Now, in \(\triangle A D B\) and \(\triangle B D C\),

⇒ \(\angle 5=\angle 4\) (each \(90^{\circ}\) )

⇒ \(\angle 1=\angle 3\) (just proved)

⇒ \(\triangle A D B \sim \triangle B D C\) (AA corollary)

Hence Proved.

(2) In \(\triangle A D B\) and \(\triangle A B C\),

⇒\(\angle 5=\angle 1+\angle 2\)

\(\angle 6=\angle 6\)

⇒ \(\left(\right. each \left.90^{\circ}\right)\)

∴ \(\triangle \widehat{D B \sim \triangle A B C}\) (common)

(3) In \(\triangle B D C\) and \(\triangle A B C\),

⇒ \(\angle 4 =\angle 1+\angle 2 (each 90^{\circ} )\)

⇒ \(\angle 3 =\angle 3\) (common)

⇒ \(\triangle B D C \sim \triangle A B C\) (AA corollary)

Hence Proved.

(4) For \(B D^2=A D \times D C\), we need to prove two \(\Delta s\) similar which contain \(B D, A D\) and D C as sides.

Obviously, these are \(\triangle A B D\) and \(\triangle B D C\), we have proved these \(\triangle s\) as similar in part (1).

So, \(\Delta \underline{A \overline{D B}} \sim \Delta \underline{B} \bar{D} C\) [from part (1)]

⇒ \(\underbrace{\frac{A D}{B D}=\frac{D B}{D C}}_{\text {Taking first two }}=\frac{A B}{B C}\) (corresponding sides of similar triangles are proportional)

⇒ \(B D^2=A D \times D C\)

Hence Proved.

(5) For \(A B^2=A D \times A C\), we need to prove two triangles similar which contain AB, AD and AC as sides. Obviously, these are AABD and AABC. We have already proved these As as similar in part (2)

⇒ \(\triangle A D B \sim \triangle A B C\) [from part (2)]

⇒ \(\frac{A D}{A B}=\frac{D B}{B C}=\frac{A B}{A C}\) (corresponding sides of similar }

⇒ \(A B^2=A D \times A C\) …(1) Hence Proved.

So,\(\Delta \widehat{B D C} \sim \triangle \widehat{A B C}\) [from part (3)]

⇒ \(\frac{B D}{A B}=\frac{D C}{B C}=\frac{B C}{A C}\) (corresponding sides of similar triangles are proportional)

⇒ \(B C^2=C D \times\) A C … 2

Hence Proved.

(7) Adding results (1) and (2), we get

⇒ \(A B^2+B C^2 =A D \times A C+C D \times A C\)

= A C(A D+C D)

= \(A C \times A C=A C^2\)

Hence Proved.

Example 8. In the given figure, DEFG is a square, and ABAC = 90°. Prove that

1. \(\triangle\)AGF ~ \(\triangle\)DBG
2.  \(\triangle\)AGF-\(\triangle\)EFC
3. \(\triangle\)DBG – \(\triangle\)EFC
4. \(DE^2\) = BD x EC

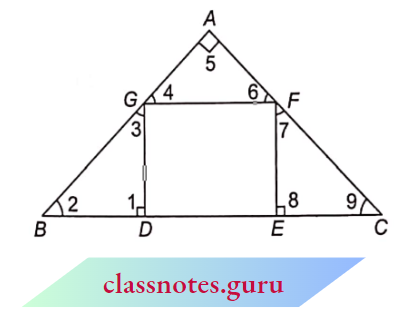
Solution:

(1) Since Square DEFG is a square

GF || BC

⇒ \(\angle 2=\angle 4\) and \(\angle 6=\angle 9\) (corresponding \(\angle s\) )

Now, in \(\triangle A G F\) and \(\triangle D B G\),

⇒ \(\angle 5\) = \(\angle 1\)

⇒ \(\angle 4 =\angle 2\)

⇒ \(\triangle A G F \sim \triangle D B G\) (each \(90^{\circ}\) )

⇒ \(\angle 5=\angle 8\)

⇒ \(\angle 4=\angle 2\) (corresponding \(\angle \mathrm{s}\) )

⇒ \(\triangle A G F \sim \triangle D B G\) (AA corollary)

Hence Proved.

(2) In \(\triangle A G F\) and \(\triangle E F C\),

⇒ \(\angle 5=\angle 8\) (each \(90^{\circ}\) )

⇒ \(\angle 6=\angle 9\) (corresponding \(\angle s\) )

⇒ \(\triangle A G F \sim \triangle E F C\)(AA corollary)

Since \(\triangle A G F \sim \triangle D B G\) [proved in (1)]

and \(\triangle A G F \sim \triangle E F C\) [proved in (2)]

⇒ \(\triangle A G F \sim \triangle D B G \sim \triangle E F C\)

Hence Proved.

(4) Now, since \(\triangle \widehat{D B G} \sim \triangle \overparen{E F C}\)

⇒ \(\frac{D B}{E F}=\frac{D G}{E C}\) (corresponding \(\Delta s\) are proportional)

DG \(\times E F=B D \times E C\)

D E \(\times D E=B D \times E C\)( DG = FE = DE being the sides of square)

⇒ \(D E^2=B D \times E C\)

If we have to prove only the fourth part i.e., prove that \(DE^2\) = BD x EC, then no need to prove the first two parts.

For \(DE^2\) = BD x EC, we need to prove two As similar which contain DE, BD, and EC.

Obviously, these are \(\triangle G B D\) and \(\triangle F E C\).

So, \(\angle I=\angle 8 (each .90^{\circ})\)

Searching for Second Angle :

As we know that \(\angle 5=90^{\circ}\)

⇒ \(\angle 2+\angle 9=90^{\circ}\) (angle sum property)

Also since \(\angle 1=90^{\circ}\)

⇒ \(\angle 2+\angle 3=90^{\circ}\) (angle sum property)

From (1) and (2),

⇒ \(\angle 2+\angle 3=\angle 2+\angle 9\)

⇒ \(\angle 3=\angle 9\)

Now, in \(\triangle G B\) and \(\triangle F E C\),

⇒ \(\angle 1=\angle 8\) (each \(90^{\circ}\) )

⇒ \(\angle 3=\angle 9\) (just proved)

⇒ \(\frac{D B}{E F}=\frac{B G}{F C}=\frac{D G}{E C}\)

Taking the first and last

⇒ \(\triangle D B G \sim \triangle E F C\) (AA corollary)

⇒ \(\frac{D B}{E F}=\frac{B G}{F C}=\frac{D G}{E C}\) (corresponding sides of similar)

⇒ \(D G \times E F=B D \times E C\)

⇒ \(D E \times D E=B D \times E C\) ( D G=E F=D E, sides of a square)

⇒ \(D E^2=B D \times E C\)

Hence Proved.

Chapter 6 Triangles NCERT Exemplar Questions

Example 9. In the adjoining Figure, if a = 18,b = 12, c = 14, and d = 8, what is the measure of x?

Solution:

Given

In the adjoining Figure, if a = 18,b = 12, c = 14, and d = 8

We have, \(\frac{P R}{Q R}=\frac{12}{18}=\frac{2}{3}\) …… 1

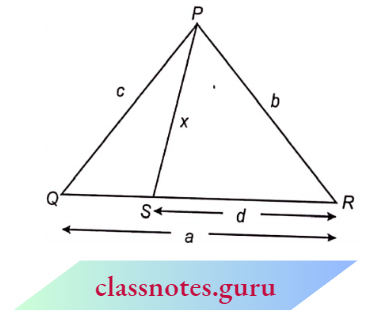
⇒ \(\frac{S R}{P R}=\frac{8}{12}=\frac{2}{3}\) …… 2

Now in \(\triangle P R S\) and \(\triangle Q R P\),

Since, \(\frac{P R}{Q R}=\frac{S R}{P R}\) [from (1) and (2)]

⇒ \(\angle R=\angle R\)

⇒ \(\Delta P \widehat{R S}-\triangle Q \overparen{R P}\) (common)

⇒ \(\frac{P R}{Q R}=\frac{S R}{P R}=\frac{P S}{Q P}\) (SAS similarity)

⇒ \(\frac{2}{3}=\frac{2}{3}=\frac{x}{14}\)

∴\(\frac{x}{14}=\frac{2}{3} \quad \Rightarrow \quad x=\frac{28}{3}\)

Example 10. In the adjoining figure, AB || CD || EF. Prove that \(\frac{1}{x}+\frac{1}{y}=\frac{1}{z}\).

Solution:

In \(triangle\) BFE and \(\triangle\) BDC

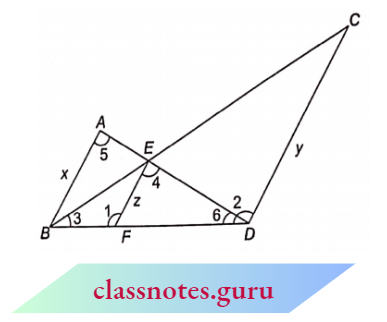
⇒ \(\angle 1=\angle 2\) (corresponding \(\angle\) s as E F || C D )

⇒ \(\angle 3=\angle 3\) (common)

⇒ \(\underline{B F E} \sim \triangle B C\) (AA corollary)

⇒ \(\frac{B F}{B D}=\frac{F E}{D C}\)

⇒ \(\frac{B F}{B D}=\frac{z}{y}\) (corresponding sides of similar triangles are proportional)

In \(\triangle D F E\) and \(\triangle D B A\),

⇒ \(\angle 4=\angle 5\) (corresponding \(\angle \)s as E F || A B )

⇒ \(\angle 6=\angle 6\) (common)

⇒ \(\triangle D F E \sim \triangle D B A\) (AA corollary)

⇒ \(\frac{D F}{D D}=\frac{F E}{D A}\) (Corresponding Sides Of Similar Triangles Are Proportional)

⇒ \(\frac{D F}{D B}=\frac{z}{x}\)

Remember, the common part in (1) and (2) should be in the denominator so that we can add easily) Adding (1) and (2), we get

⇒ \(\frac{B F}{B D}+\frac{D F}{D B} =\frac{z}{y}+\frac{z}{x}\)

⇒ \(\frac{B F+D F}{B D} =z\left(\frac{1}{y}+\frac{1}{x}\right)\)

⇒ \(\frac{B D}{B D} =z\left(\frac{1}{x}+\frac{1}{y}\right) \quad \Rightarrow \quad 1=z\left(\frac{1}{x}+\frac{1}{y}\right)\)

∴  \(\frac{1}{z} =\frac{1}{x}+\frac{1}{y}\)

Example 11. Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn, intersecting AC in L and AD produced in E. Prove that EL = 2BL.

Solution:

Given

Through the mid-point M of the side CD of a parallelogram ABCD, the line BM is drawn, intersecting AC in L and AD produced in E.

In \(\triangle\)s BMC and DME,

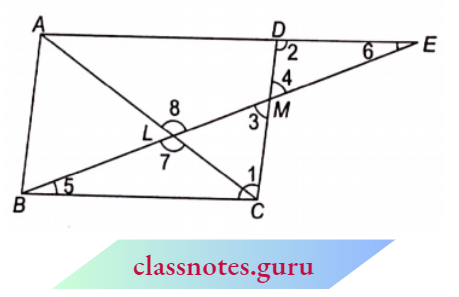
⇒ \(\angle 1 =\angle 2\) (alternate \(\angle\)s as B C || D E)

C M =D M (M is the mid-point of DC)

⇒ \(\angle 3 =\angle 4\) (vertically opposite angles)

⇒ \(\triangle B M C \simeq \triangle E M D)\)

BC = E D (corresponding parts of the congruent triangle)….. 1

But, BC = A D (opposite sides of a parallelogram)…… 2

Adding (1) and (2), we get

2 BC = D E+A D \(\Rightarrow 2 B C = A E\)

⇒ \(\frac{B C}{A E} =\frac{1}{2}\)

Now in \(\triangle B C L\) and \(\triangle E A L\)

⇒\(\angle 5 =\angle 6\)

⇒ \(\angle 7 =\angle 8\) (vertically opposite angles)

⇒ (\(\angle\)s as B C || A E )

⇒ \(\triangle B C L \sim \triangle E A L\) (AA Collary)

⇒ \(\frac{B C}{E A}=\frac{B L}{E L}\) (corresponding sides of similar triangles are proportional) ….(4)

⇒ \(\frac{1}{2}=\frac{B L}{E L}\) [ from (3) and (4)]

EL = 2BL

Hence Proved.

Example 12. The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of the first triangle is 9 cm. Find the corresponding side of the second triangle.

Solution:

Given

The perimeters of two similar triangles are 25 cm and 15 cm respectively. If one side of the first triangle is 9 cm.

Let AB = 9cm

Since \(\triangle A B C \sim \triangle P Q R\) (given)

⇒ \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}=k\) corresponding sides of similar , triangles are proportional

AB= k. PQ, BC = k. QR, AC = k. PR

⇒ \(\frac{\text { Perimeter of } \triangle A B C}{\text { Perimeter of } \triangle P Q R} =\frac{A B+B C+C A}{P Q+Q R+R P}\)

=\(\frac{k \cdot P Q+k \cdot Q R+k \cdot P R}{P Q+Q R+R P}\)

=\(\frac{k(P Q+Q R+R P)}{(P Q+Q R+R P)}\) = k

From (1) and (2), we get

⇒ \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A C}{P R}=\frac{\text { Perimeter }(\triangle A B C)}{\text { Perimeter }(\triangle P Q R)}\)

⇒ \(\frac{9}{P Q}=\frac{25}{15} \Rightarrow P Q=\frac{9 \times 15}{25}\)=5.4

Hence, the corresponding side of the second triangle is 5.4 cm.

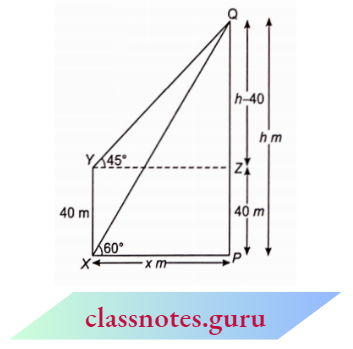
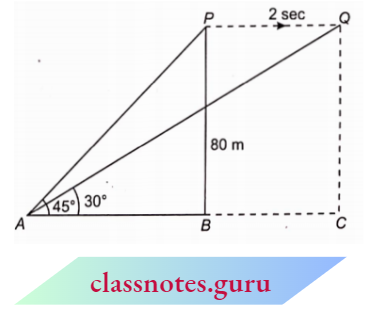
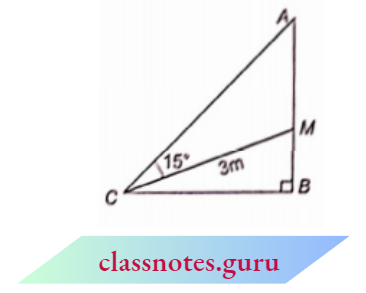
Example 13. A lamp is 3.3 m above ground. A boy I Hi em tall walks away from (be base of (bis lamp post at a speed of 0.8 m/s. Find (be the length of (be a shadow of the boy after 4 seconds.

Solution:

Given

A lamp is 3.3 m above ground. A boy I Hi em tall walks away from (be base of (bis lamp post at a speed of 0.8 m/s.

Let AB = 3.3 m be the lamp post and CD = 1.1 m be the position of the boy after 4 seconds. Also, let the shadow of the boy after 4 see = x m

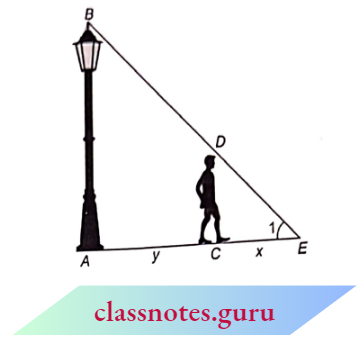
Distance travelled by boy in 4 sec =y = 0.8 x 4 = 3.2 m

Now, in \(\triangle\)AEB and \(\triangle\)CED

⇒\(\angle E A B=\angle E C D=90^{\circ}\) (obvious)

⇒ \(\angle 1=\angle 1\) (common)

⇒ \(\triangle A E B \sim \triangle C E D\) (AA corollary)

⇒ \(\triangle A E B \sim \triangle C E D\)

⇒  –\(\frac{A E}{C E}=\frac{A B}{C D}\) (corresponding sides of similar triangles are proportional)

⇒ \(\frac{x+y}{x}=\frac{3.3}{1.1}\) (110 cm =1.1 m)

x+y=3 x \(\quad \Rightarrow y=2 x\)

x=\(\frac{y}{2}=\frac{3.2}{2}=1.6\)

Hence, the length of the shadow of the boy after 4 seconds is 1.6 m

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Ratio Of The Areas Of Two Similar Triangles

Theorem: The ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.

Given : \(\triangle A B C \sim \triangle D E F\)

To Prove : \(\frac{{ar}(\triangle A B C)}{{ar}(\triangle D E F)}=\frac{A B^2}{D E^2}=\frac{A C^2}{\dot{D F}}=\frac{B C^2}{E F^2}\)

Construction : Draw A L \(\perp B C\) and D M \(\perp E F\)

Proof : Consider,\(\frac{{ar}(\triangle A B C)}{{ar}(\triangle D E F)}=\frac{\frac{1}{2} \times B C \times A L}{\frac{1}{2} \times E F \times D M}=\left(\frac{B C}{E F}\right) \cdot\left(\frac{A L}{D M}\right)\) Equation 1

Now, since \(\triangle A B C \sim \triangle D E F\)

⇒ \(\angle B=\angle E\)(corresponding angles of similar triangles are equal)

In \(\triangle A L B\) and \(\triangle D M E\),

⇒ \(\angle B=\angle E\) [ from (2)]

⇒ \(\angle 1=\angle 2\) (each \(90^{\circ}\), by construction)

⇒ \(\triangle A L B \sim \triangle D M E\)(AA corollary)

⇒ \(\frac{A B}{D E}=\frac{A L}{D M}=\frac{B L}{E M}\) (corresponding sides of similar triangles are proportional)

But \(\frac{A B}{D E}=\frac{B C}{E F}=\frac{A C}{D F}(\triangle A B C \sim \triangle D E F)\)

From (3) and (4), we have

⇒ \(\frac{A L}{D M}=\frac{B C}{E F}\)

From (1) and (5), we have

⇒ \(\frac{{ar}(\triangle A B C)}{{ar}(\triangle D E F)}=\frac{B C}{E F} \times \frac{B C}{E F}=\frac{B C^2}{E F^2}\)

=\(\frac{A B^2}{D E^2}\)

=\(\frac{A C^2}{D F^2}\) From 4

Hence, \(\frac{{ar}(\triangle A B C)}{{ar}(\triangle D E F)}=\frac{A B^2}{D E^2}=\frac{B C^2}{E F^2}=\frac{A C^2}{D F^2}\)

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Ratio Of The Areas Of Two Similar Triangles Solved Examples

Example 1. In figures \(\triangle\)ABC and \(\triangle\)DEF are similar, the areas of 4 MBC is 9 sq. cm and that of ADEF is 16 sq. cm. If EF = 4.2 cm, find BC.

Solution:

Given

In figures \(\triangle\)ABC and \(\triangle\)DEF are similar, the areas of 4 MBC is 9 sq. cm and that of ADEF is 16 sq. cm. If EF = 4.2 cm

ar(\(\triangle\)ABC) = 9 sq. cm

ar(\(\triangle\)DEF) = 16 sq. cm

EF= 4.2 cm

BC= ?

Since the ratio of areas of two similar triangles is equal to the ratio of squares on their corresponding sides

⇒ \(\frac{{ar}(\triangle A B C)}{{ar}(\triangle D E F)}=\frac{B C^2}{E F^2} \quad \Rightarrow \quad \frac{9}{16}=\left(\frac{B C}{E F}\right)^2 \)

⇒ \(\frac{B C}{4.2}=\frac{3}{4} \quad \Rightarrow \quad B C=\frac{3 \times 4.2}{4}=3.15 \mathrm{~cm}\)

Example 2. In a trapezium ABCD, O is the point of intersection of AC and BD, AB || CD, and AB = 2 x CD. If the area of \(\triangle\)AOB = 84 cm², find the area of \(\triangle\)COD.

Solution:

Given

In a trapezium ABCD, O is the point of intersection of AC and BD, AB || CD, and AB = 2 x CD. If the area of \(\triangle\)AOB = 84 cm²,

In \(\triangle AOB\) and \(\triangle COD\),

⇒ \(\angle 1 =\angle 2\) (alternate angles)

⇒ \(\angle 3 =\angle 4\) (alternate angles)

⇒ \(\Delta A O B \sim \triangle C O D\) (AA corollary)

⇒ \(\frac{{ar}(\triangle A O B)}{{ar}(\triangle C O D)} =\frac{A B^2}{C D^2}\)

(The ratio of the area of two similar triangles is equal to the ratio of the square of the corresponding sides)

= \(\frac{(2 C D)^2}{C D^2}\)

= \(\frac{4}{1}\) ( A B=2 C D, given )

∴ \(\frac{84}{{ar}(\triangle C O D)}=\frac{4}{1} \quad \Rightarrow \quad {ar}(\triangle C O D)=\frac{84}{4} \mathrm{~cm}^2=21 \mathrm{~cm}^2\)

Example 3. In the figure, DE || BC and the ratio of the areas of \(\triangle\) and trapezium BDEC is 4: 5. Find the ratio of DE: BC. If BD=2cm, Then find AD

Solution:

Given

In the figure, DE || BC and the ratio of the areas of \(\triangle\) and trapezium BDEC is 4: 5. Find the ratio of DE: BC. If BD=2cm

In \(\triangle A D E\) and \(\triangle A B C\).

⇒ \(\angle 1=\angle 2\) (corresponding angles as } \(D E \mid B C \)

⇒ \(\angle A=\angle A\) (common)

⇒ \(\triangle A D E-\triangle A B C\)

⇒ \(\frac{a r \Delta A D E}{{ar}(A B C}=\frac{A D^2}{A B^2}=\frac{D E^2}{B C^2}=\frac{A E^2}{A C^2}\) (AA corollary)(ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides)

Now;\(\frac{{ar}(\text { trapezium } B D E C)}{{ar}(\Delta+D E)}=\frac{5}{4}\)

⇒ \(\frac{{ar}(\Delta+B C)-{ar}(\Delta+D E)}{{ar}(\Delta+D E)}=\frac{5}{4}\)

⇒ \(\frac{{ar}(\Delta+B C)}{{ar}(\Delta+D E)}-1=\frac{5}{4} \quad \Rightarrow \quad \frac{{ar}(\Delta A B C)}{{ar}(\Delta A D E)}=\frac{9}{4}\)

⇒ \(\frac{{ar}(\Delta+D E)}{{ar}(\Delta+B C)}=\frac{4}{9}\)

⇒ \(\frac{D E^2}{B C^2} =\frac{4}{9}\)

⇒ \(\frac{D E}{B C} =\frac{2}{3}\)

D E: B C =2: 3 from (1) and (2)

Now, from (1) and (2), we get

⇒ \(\frac{{ar}(\Delta A D E)}{{ar}(\Delta A B C)} =\frac{A D^2}{A B^2} =\frac{4}{9}\)

⇒ \(\frac{A D}{A B} =\frac{2}{3}\Rightarrow \frac{A D}{A D+B D}=\frac{2}{3}\)

⇒ \(\frac{A D+B D}{A D} =\frac{3}{2} \Rightarrow 1+\frac{B D}{A D}=\frac{3}{2}\)

⇒ \(\frac{B D}{A D} =\frac{3}{2}-1 =\frac{1}{2}\)

∴ \(\frac{2}{A D} =\frac{1}{2} \Rightarrow A D=4 \mathrm{~cm}\)

Example 4. X and Y are points on the sides AB and BC respectively of \(\triangle\) ABC such that XY || AC and XY divides AABC into two parts equal in area. Find \(\frac{A X}{A B}\)

Solution:

Given

X and Y are points on the sides AB and BC respectively of \(\triangle\) ABC such that XY || AC and XY divides AABC into two parts equal in area.

Since X Y || A C

In \(\triangle\) BXY and \(\triangle BAC\),

⇒ \(\angle 1=\angle 2\) (corresponding angles)

⇒ \(\angle B=\angle B\) (common)

⇒ \(\triangle B X Y \sim \triangle B A C\) (AA corollary)

⇒ \(\frac{{ar}(\Delta B X Y)}{{ar}(\triangle B A C)}=\frac{B X^2}{B A^2}\) (area ratio theorem)

But \({ar}(\triangle B X Y)=\frac{1}{2} {ar}(\triangle A B C)\) (given)

⇒ \(\frac{{ar}(\triangle B X Y)}{{ar}(\triangle A B C)}=\frac{1}{2}\)

From (1) and (2), we get

⇒ \(\frac{B X^2}{A B^2}=\frac{1}{2} \Rightarrow \frac{B X}{A B}=\frac{1}{\sqrt{2}}\)

⇒ \(\frac{A B-A X}{A B}=\frac{1}{\sqrt{2}} \Rightarrow \frac{A B}{A B}-\frac{A X}{A B}=\frac{1}{\sqrt{2}}\)

⇒ \(1-\frac{A X}{A B}=\frac{1}{\sqrt{2}} \Rightarrow \frac{A X}{A B}=1-\frac{1}{\sqrt{2}}=\frac{\sqrt{2}-1}{\sqrt{2}}\)

Hence, \(\frac{A X}{A B}=\frac{2-\sqrt{2}}{2}\)

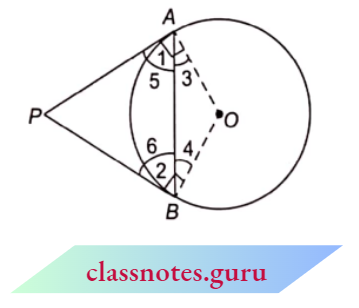
Example 5. CE and DE are equal chords of a circle with centre O. If \(\angle A O B\) = 90°, find \(\text{ar}(\triangle C E D): \text{ar}(\triangle A O B)\).

Solution:

Given

CE and DE are equal chords of a circle with centre O. If \(\angle A O B\) = 90°

Since O is the centre of the circle.

⇒ \(\angle\)E = 90° (angle in a semicircle is right angle)

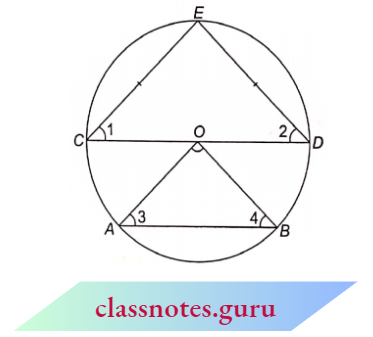
\(\angle\)I = \(\angle\)2 = 45°

(angles opposite to equal sides are equal as CE = DE)

Also, since Z\(\angle\)AOB = 90° (given)

⇒ \(\angle\)3 = \(\angle\)4 = 45°

(angles opposite to equal sides are equal as OA = OB, each radius) Now, in \(\triangle\)CED and \(\triangle\)AOB

⇒ \(\angle E =\angle A O B\)

⇒ \(\angle \mathrm{l}=\angle 3\)

⇒ \(\triangle C E D \sim \triangle A O B\)

⇒ \(\frac{\text{ar}(\triangle C E D)}{\text{ar}(\triangle A O B)}=\frac{C D^2}{A B^2}\)

= \(\frac{(2 O B)^2}{O A^2+O B^2}\)

(CD = diameter and OB = radius so, CD = 2 • OB and using Pythagoras theorem)

= \(\frac{4 O B^2}{O B^2+O B^2}\) (OA = OB, each radius)

= \(\frac{4 O B^2}{2 O B^2}=\frac{2}{1}\)

Hence, \(\frac{\text{ar}(\triangle C E D)}{\text{ar}(\triangle \triangle O B)}=\frac{2}{1}\)

Example 6. Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding altitudes.

Solution:

Given: \(\triangle A B C \sim \triangle D E F, A L \perp B C\) and \(D M \perp E F\)

To Prove: \(\frac{\text{ar}(\triangle A B C)}{\text{ar}(\triangle D E F)}=\frac{A L^2}{D M^2}\)

Proof: \(\ln \triangle A L B\) and \(\triangle D M E\),

(because the ratio of areas of two similar triangles is equal to the ratio of squares of the corresponding sides

From (1) and (2) we have \(\frac{\text{ar}(\triangle A B C)}{\text{ar}(\triangle D E F)}=\frac{A L^2}{D M^2}\)

Hence Proved.

Example 7. Prove that the ratio of the areas of two similar triangles is equal to the ratio of the squares of their corresponding angle bisector segments.
Solution:

Given: \(\triangle\)ABC ~ \(\triangle\)DEF in which AX and DY are the bisectors of \(\angle\)A and \(\angle\)D respectively.

To Prove: \(\frac{\text{ar}(\triangle A B C)}{\text{ar}(\triangle D E F)}=\frac{A B^2}{D E^2}\)

Proof: Given \(\triangle A B C \sim \triangle D E F\)

Therefore, \(\angle A =\angle D\)

⇒ \(\frac{1}{2} \angle A=\frac{1}{2} \angle D\)

⇒ \(\angle B A X=\angle E D Y\)

Now, in \(\triangle A B X\) and \(\triangle D E Y\), we have

⇒ \(\angle B A X=\angle E D Y\)

and \(\angle B =\angle E\)

⇒ \(\triangle A B X \sim \triangle D E Y\)

Hence \(\frac{A B}{D E}=\frac{A X}{D Y}\)…..(1) given

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Pythagoras Theorem

Theorem 1: In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Given: A right-angled triangle ABC in which \(\angle\)B = 90°.

To Prove: \((Hypotenuse^2=(\text { Base })^2+ Perpendicular)^2\)

i.e., \(A C^2=A B^2+B C^2\)

Construction: From B, draw \(B D \perp A C\)

Proof: In \(\triangle A D B\) and \(\triangle A B C\)

⇒ \(\angle 1=\angle 2\)

and \(\angle A =\angle A\) (common)

Hence, \(\triangle M D B \sim \triangle A B C\) (by AA corollary)

⇒ \(\frac{A D}{A B} =\frac{A B}{A C}\) (corresponding sides of similar triangle are proportional)

⇒ \(A B^2=A D \times A C\)……(1)

Now in \(\triangle B D C\) and \(\triangle A B C\)

⇒ \(\angle 5=\angle 2\) (each 90^{\circ}[/latex])

and \(\angle C=\angle C\) (common)

Hence, \(\triangle B D C \sim \triangle A B C\) (by AA corollary)

⇒ \(\frac{D C}{B C}=\frac{B C}{A C}\) (corresponding sides of similar triangles are proportional)

⇒ \(B C^2=A C \times D C\)…… (2)

Adding (1) and (2), we get

⇒ \(A B^2+B C^2=A D \times A C+A C \times D C\)

⇒ \(A B^2+B C^2=A C(A D+D C)\)

⇒ \(A B^2+B C^2=A C \times A C\)(because A D+D C=A C)

⇒ \(A B^2+B C^2=A C^2\)

Theorem 2 (Converse of Pythagoras Theorem): In a triangle, if the square of one side is equal to the sum of squares of the other two sides, then the angle opposite to the longest side is a right angle.

Given: A triangle ABC such that \(A C^2=A B^2+B C^2\)

To Prove: \(\angle\)B = 90°

Construction: Construct a triangle DEF such that DE =AB, EF = BC and \(\angle\)E = 90°. Join DF.

Proof: In right \(\triangle\)DEF

⇒ \(D F^2=D E^2+E F^2\) (by Pythagoras theorem)

⇒ \(D F^2=A B^2+B C^2\) (given DE = AB and Ef = BC)

⇒ \(D F^2=A C^2\) (given \(A C^2=A B^2+B C^2\))

DF = AC

Now, in \(\triangle A B C\) and \(\triangle D E F\)

AB = DE (by construction)

BC=EF (by construction)

AC = DF from (1)

⇒ \(\triangle A B C \cong \triangle D E F\)

Hence \(\angle E=\angle B=90^{\circ}\)

NCERT Exemplar Class 10 Maths Triangles Exercise Solutions

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Some Important Results Based Uponpythagoras Theorem

Result 1: In an obtuse-angled triangle ABC, obtuse-angled at B, if \(A D \perp C B\) (produced), prove that \(A C^2=A B^2+B C^2\) + 2BC x BD.

Given: An obtuse triangle ABC, obtuse-angled at B and AD is perpendicular to CB produced.

To Prove: \(A C^2=A B^2+B C^2\) + 2BC x BD

Proof: Since \(\triangle\)ADB is right angled triangle therefore by Pythagoras’ theorem in \(\triangle\)ADC

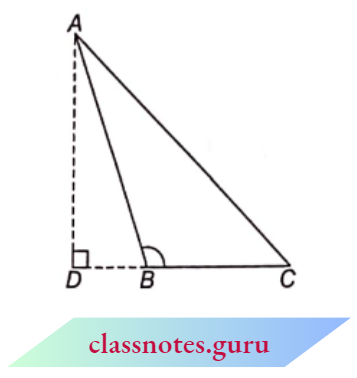
⇒ \(A C^2=A D^2+D C^2\)

⇒ \(A C^2=A D^2+(D B+B C)^2\) (because DC=D B+BC)

⇒ \(A C^2=A D^2+D B^2+B C^2+2 D B \cdot B C\)

⇒ \(A C^2=\left(A D^2+D B^2\right)+B C^2+2 B C \cdot B D\)

⇒ \(A C^2=A B^2+B C^2+2 B C \cdot B D\)

Result 2: In an acute-angled triangle ABC, if \(A D \perp B C\), prove that: \(A C^2=A B^2+B C^2-2 B C \times B D\)

Given: \(\triangle A B C\) which is an acute-angled triangle and \(A D \perp B C\)

To Prove: \(A C^2=A B^2+B C^2-2 B C \times B D\)

Proof: In \(\triangle A D C, \angle D=90^{\circ}\), hence by Pythagoras theorem

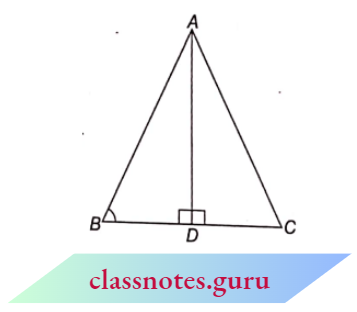
⇒ \(A C^2=A D^2+D C^2\)

⇒ \(A C^2=A D^2+(B C-B D)^2\) ( D C=B C-B D)

⇒ \(A C^2=A D^2+B C^2+B D^2-2 B C \times B D\)

⇒ \(A C^2=\left(A D^2+B D^2\right)+B C^2-2 B C \times B D\)

⇒ \(A C^2=A B^2+B C^2-2 B C \times B D\) (because \(A D^2+B D^2=A B^2\))

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Pythagoras Theorem Solved Examples

Example 1. The sides of a triangle are 5 cm, 8 cm and 11 cm respectively. Determine whether it is a right-angled triangle or not.
Solution:

Given

The sides of a triangle are 5 cm, 8 cm and 11 cm respectively.

5 = 25

8 = 64

and 11 = 121

We find that 1 = 5 + 8

Hence, it is not a right-angled triangle.

Example 2. A ladder 25 m long reaches a window of a building 20 m above the ground. Determine the distance of the foot of the ladder from the building.
Solution:

Given

A ladder 25 m long reaches a window of a building 20 m above the ground.

Let AC = 20 m be the wall of a building. A is the window and AB = 25 m be the ladder.

In right \(\triangle\)ABC

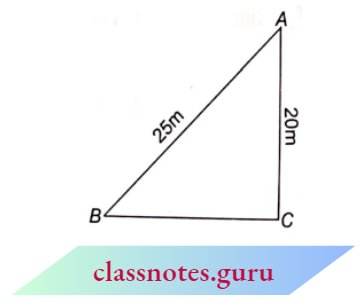
⇒ \(A B^2=B C^2+A C^2\) (by Pythagoras theorem)

⇒ \(25^2=B C^2+20^2\)

625 = \(B C^2+400\)

⇒ \(B C^2\) = 225

BC = 15

The distance of the foot of the ladder from the building = 15 cm

Example 3. P and Q are the mid-points of the sides C A and CB respectively of a \(\triangle\)ABC, oght anglers at C, prove that:

1. \(4 A Q^2=4 A C^2+B C^2\)
2. \(4 B P^2=4 B C^2+A C^2\)
3. \(4\left(A Q^2+B P^2\right)=5 A B^2\)

Solution:

Given

P and Q are the mid-points of the sides C A and CB respectively of a \(\triangle\)ABC, oght anglers at C,

1. In \(\triangle A Q C, \angle C=90^{\circ}\)

Using Pythagoras theorem. \(A Q^2=A C^2+Q C^2\)

⇒ \(A Q^2=A C^2+\left(\frac{B C}{2}\right)^2\) (because Q is the mid-point of BC)

⇒ \(A Q^2=A C^2+\frac{B C^2}{4}\)

⇒ \(4 A Q^2=4 A C^2+B C^2\)……(1) Hence proved.

2. ln \(\triangle B P C, \angle C=90^{\circ}\)

Using Pythagoras theorem, we have \(B P^2=B C^2+P C^2\)

⇒ \(B P^2=B C^2+\left(\frac{A C}{2}\right)^2\) (since P is the mid-point of AC)

⇒ \(B P^2=B C^2+\frac{A C^2}{4}\)

∴ \(4 B P^2=4 B C^2+A C^2\)……(2) Hence Proved.

3. Adding (1) and (2), we get

⇒ \(4 A Q^2+4 B P^2=4 A C^2+B C^2+4 B C^2+A C^2\)

⇒ \(4\left(A Q^2+B P^2\right)=5 A C^2+5 B C^2\)

⇒ \(4\left(A Q^2+B P^2\right)=5\left(A C^2+B C^2\right)\)

⇒ \(4\left(A Q^2+B P^2\right)=5 A B^2\) (because \(A C^2+B C^2=A B^2\))

Hence Proved.

Example 4. ABC is a right triangle, right angled at C. If p is the length of the perpendicular from C to AB and AB = c, BC = a and CA = b, then prove that

1. pc = ab
2. \(\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}\)

Solution:

Given: ABC is a right triangle, right angled at C, and p is the length of the perpendicular from C to AB.

Proof:

1. \(\text{ar}(\triangle A B C)=\frac{1}{2} \times A B \times C D\)

= \(\frac{1}{2} c p\)

Also, \(\text{ar}(\triangle M B C)=\frac{1}{2} \times \Lambda C \times B C\)

= \(\frac{1}{2} b a\)……(2)

From (1) and (2), we get, \(\frac{1}{2} p c=\frac{1}{2} a b\)

pc = ab……(3)

Hence Proved.

2. From (3) we get c = \(\frac{a b}{p}\)

In \(\triangle A B C\) \(c^2=a^2+b^2\) (by Pythagoras theorem)

⇒ \(\left(\frac{a b}{p}\right)^2=a^2+b^2 \quad \Rightarrow \quad \frac{a^2 b^2}{p^2}=a^2+b^2 \)

⇒ \(\frac{1}{p^2}=\frac{a^2+b^2}{a^2 b^2} \quad \Rightarrow \quad \frac{1}{p^2}=\frac{a^2}{a^2 b^2}+\frac{b^2}{a^2 b^2}\)

⇒ \(\frac{1}{p^2}=\frac{1}{b^2}+\frac{1}{a^2}\)

Hence Proved.

Alternative proof (Using trigonometry)

Let \(\angle C A B=\theta\)

⇒ \(\angle C B A=90^{\circ}-\theta\) (\(\angle ACB\) = 90°)

In right \(\triangle C D A\), \(\sin \theta=\frac{p}{b}\)…….(1)

In right \(\triangle C D B\), \(\sin (90-\theta)=\frac{p}{a}\)

⇒ \(\sin (90-\theta)=\frac{p}{a}\) (because \(\sin (90-\theta)=\cos \theta\))……(2)

Squaring and adding equations (1) and (2), we get \(\sin ^2 \theta+\cos ^2 \theta=\frac{p^2}{b^2}+\frac{p^2}{a^2}\)

1 = \(p^2\left(\frac{1}{a^2}+\frac{1}{b^2}\right)\)

∴ \(\frac{1}{p^2}=\frac{1}{a^2}+\frac{1}{b^2}\) (using identity \(\sin ^2 \theta+\cos ^2 \theta=1\))

Hence Proved.

Example 5. O is any point in the Interior of rectangle ABCD. Prove that \(O B^2+O D^2=O C^2+O A^2\).
Solution:

ABCD is a rectangle and O is a point interior to the rectangle. Through O, draw a line parallel to BC meeting AB and DC at F and E respectively.

Then EC = PB and DE = AF

L.H.S. = \(O B^2+O I^2\)

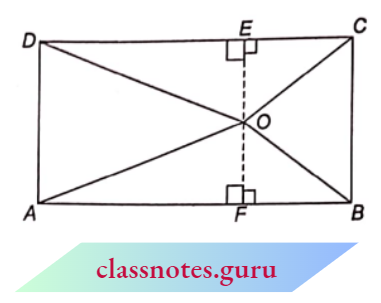
= \(\left(O F^2+F B^2\right)+\left(O E^2+D E^2\right)\)

= \(O F^2+E C^2+O E^2+A F^2\) (by Pythagoras theorem)

= \(\left(O R^2+E C^2\right)+\left(O F^2+A F^2\right)\)

= \(O C^2+O A^2\) FB and \(D E=A F\) (by Pythagoras theorem)

= R.H.S.

Hence, \(O B^2+O D^2=O C^2+O \Lambda^2\)

Hence Proved.

Example 6. In the given figure, S and T trisect QR of a right-angled triangle PQR, right-angled at Q. Prove that 8 PT2 = 3PR² + 5PS².
Solution:

Given

In the given figure, S and T trisect QR of a right-angled triangle PQR, right-angled at Q.

Let QS = ST=TR =x

Now by Pythagoras theorem Prove that \(8 P T^2=3 P R^2+5 P S^2\).

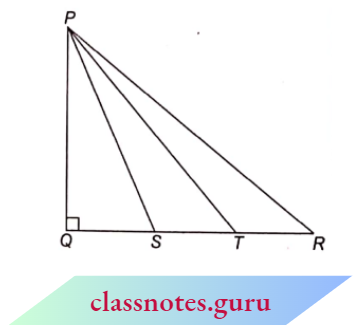
Let QS = ST = TR = x

Now by Pythagoras theorem \(P R^2=P Q^2+Q R^2=P Q^2+(3 x)^2\)

= \(P Q^2+9 x^2\)

⇒ \(3 P R^2=3 P Q^2+27 x^2\) ……(1)

Also, \(P S^2=P Q^2+Q S^2\) (by Pythagoras theorem)

= \(P Q^2+x^2\)

⇒ \(5 P S^2=5 P Q^2+5 x^2\)…..(2)

Adding (1) and (2), we get

R.H.S. = \(3 P R^2+5 P S^2=8 P Q^2+32 x^2=8(P Q^2+ Q T^2)\)

= \(8\left(P Q^2+Q T^2\right)=8 P T^2\)

= L.H.S (by Pythagoras theorem)

Hence Proved.

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Triangle Exercise 6.1

Question 1. Fill in the blanks using the correct word given in brackets:

1. All circles are……… (congruent, similar)
Solution: Similar

2. All squares are……… (similar, congruent)
Solution: Similar

3. All……..triangles are similar. (isosceles, equilateral)
Solution:  equilateral

4. Two polygons of the same number of sides are similar, if (1) their corresponding angles are … (2) their corresponding sides are
Solution: equal, proportional

Question 2. Give two different examples of

1. Similar
2. Non-similar

Solution:

1. The two circles are similar to each other.

Two squares are similar to each other.

2. A circle and a square are not similar.

A parallelogram and a rhombus are not similar.

Question 3. State whether the following quadrilaterals are similar or not
Answer:

Here the sides are proportional but the corresponding angles are not equal.

Figures are not similar

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Triangle Exercise 6.2

Question 1. In figures, (1) and (2), DE || BC. Find EC in (1) and AD in (2).
Solution:

(1) In \(\triangle A B C: D E || B C\)

⇒ \(\frac{A D}{B D}=\frac{A E}{E C}\)

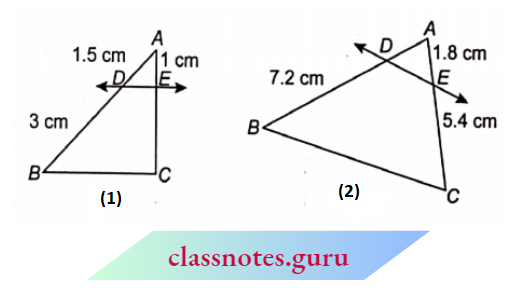
⇒ \(\frac{1.5}{3}=\frac{1}{E C}\)

EC = \(\frac{1 \times 3}{1.5}=2 \mathrm{~cm}\)

(2) ln MBC: DE || BC

⇒ \(\frac{A D}{B D}=\frac{A E}{E C} \Rightarrow \frac{A D}{7.2}=\frac{1.8}{5.4}\)

⇒ \(\frac{A D}{7.2}=\frac{1}{3} \Rightarrow A D=\frac{7.2}{3}=2.4 \mathrm{~cm}\)

Question 2. E and F are points on the sides of PQ and PR respectively of an \(\triangle\)PQR. For each of the following cases, state whether EF || QR:

1. PE = 3.9 cm. EQ = 3 cm, PF = 3.6 cm and FR = 2.4 cm
2. PE = 4 cm, QE = 4.5 cm, PF = 8 cm and RF = 9 cm
3. PQ = 1 .28 cm, PR = 2.56 cm, PE = 0.18 cm and PF = 0.36 cm

Solution:

Given

E and F are points on the sides of PQ and PR respectively of an \(\triangle\)PQR.

1. Here PE = 3.9 cm, EQ = 3 cm, PF = 3.6 cm, FR = 2.4 cm

⇒ \(\frac{P E}{E Q}=\frac{3.9}{3}=\frac{1.3}{1}\)

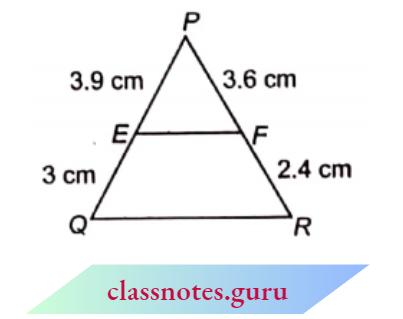
and \(\frac{P F}{F R}=\frac{3.6}{2.4}=\frac{1.5}{1}\)

because \(\frac{P E}{E Q} \neq \frac{P F}{F R}\)

EF is not parallel to QR.

2. Here PE = 4 cm, QE = 4.5 cm, PF = 8 cm, FR = 9 cm

\(\frac{P F}{E Q}=\frac{4}{4.5}=\frac{40}{45}=\frac{8}{9}=\frac{P F}{F R}\)

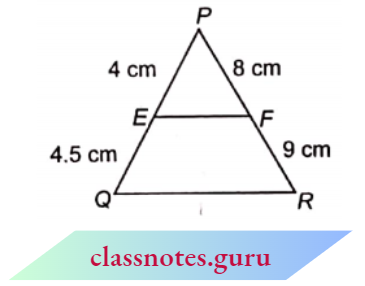
EF || QR

3. Here, PE = 0.18 cm, PQ – 1.28 cm, PF = 0.36 cm, PR = 2.56 cm

⇒ \(\frac{P E}{P Q}=\frac{0.18}{1.28}=\frac{18}{128}=\frac{9}{64}\)

and \(\frac{P F}{P R}=\frac{0.36}{2.56}=\frac{36}{256}=\frac{9}{64}\)

⇒ \(\frac{P E}{P Q}=\frac{P F}{P R}\)

EF || Q R

Question 3. in Figure, if LM || CB and LN || CD, prove that = \(\frac{A M}{A B}=\frac{A N}{A D}\)

Solution:

In \(\triangle A B C, L M \| C B\)

⇒ \(\frac{A M}{A B}=\frac{A L}{A C}\)……..(1)

In \(\triangle A C D, L N \| C D\)

⇒ \(\frac{A L}{A C}=\frac{A N}{A D}\)….(2)

From equations (1) and (2), \(\frac{A M}{A B}=\frac{A N}{A D}\)

Hence Proved.

Question 4. In the figure, DE || AC and DF || AE. Prove that \(\frac{B F}{F E}=\frac{B E}{E C}\).

Solution:

Here D E || A C

In \(\triangle A B C, \quad \frac{B E}{E C}=\frac{B D}{D A}\)……(1)

Again D F }| AE,

In \(\triangle A B E, \quad \frac{B D}{D A}=\frac{B F}{F E}\)……(2)

From equations (1) and (2), \(\frac{3 F}{E E}=\frac{B E}{E C}\)

Hence proved.

Class 10 Triangles Important Questions and Answers

Question 5. In the figure, DE || OQ and DF || OR. Show that EF || QR.

Solution:

In the figure, DE || OQ and DF || OR.

Now, from B.P.T.,

In \(\triangle P Q O\), \(\frac{P E}{E Q}=\frac{P D}{D O}\)….(1)

and, in \(\triangle P O R\), \(\frac{P F}{F R}=\frac{P D}{D O}\)…..(2)

From equations (1) and (2), \(\frac{P E}{E Q}=\frac{P F}{F R}\)

Now, in \(\triangle P Q R, \quad \frac{P E}{E Q}=\frac{P F}{F R}\)

E F || QR (from the converse of B.P.T)

Hence Proved.

Question 6. In the figure, A, B and C are points on OP, OQ and OR respectively such that AB || PQ and AC || PR. Show that BC || QR.

Solution:

In the figure, AB || PQ (given)

⇒ \(\frac{O A}{A P}=\frac{O B}{B Q}\) (from B.PT.)…..(1)

In the figure, \(A C \| P R\)(given)

⇒ \(\frac{O A}{A P}=\frac{O C}{C R}\) from B.P.T. …(2)

From equations (1) and (2), \(\frac{O B}{B Q}=\frac{O C}{C R} \Rightarrow B C \| Q R\) (from the converse of B.P.T.)

Hence Proved.

Question 7. Prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side.
Solution:

Given: \(\triangle\)ABC in which D is the mid-point of AB and DE is parallel to BC, meets AC at E

To prove: AE = EC

Proof: DE || BC

From B.P.T., \(\frac{A D}{D B}=\frac{A E}{E C}\)

but AD = D B (because D is midpoint)

⇒ \(\frac{A D}{D B}=\frac{A D}{A D}=1\)

From equations (1) and (2), \(\frac{A E}{E C}=1 \Rightarrow A E=E C\)

Hence Proved.

Question 8. Using Theorem 2, prove that the line joining the mid-points of any two sides of a triangle is parallel to the third side.
Solution:

Given: In \(\triangle\)ABC, D is the midpoint ofAB and E is the mid-point of AC.

To prove: DE || BC

Proof: D and E are the mid-points of AB and AC respectively.

AD = DB

and AE = EC

⇒ \(\frac{A D}{D B}=1\) and \(\frac{A E}{E C}=1\)

⇒ \(\frac{A D}{D B}=\frac{A E}{E C}\)

From the converse of B.P.T., DE || BC.

Hence Proved

Question 9. ABCD is a trapezium in which AB || DC and its diagonals intersect each other at the point O. Show that \(\frac{A O}{B O}=\frac{C O}{D O}\)

Solution:

ABCD is a trapezium whose diagonals intersect each other at point O.

Draw EO || AB || DC.

In \(\triangle\) ADC, EO || DC

⇒ \(\frac{A E}{E D}=\frac{A O}{O C}\)…..(1)

In \(\triangle D A B, E O \| A B\)

⇒ \(\frac{D E}{E A}=\frac{D O}{O B} \Rightarrow \frac{A E}{E D}=\frac{O B}{O D}\)……(2)

From equations (1) and (2), \(\frac{A O}{O C}=\frac{O B}{O D}\)

Hence Proved.

Question10. The diagonals of a quadrilateral ABCD intersect each other at point O such that \(\frac{A O}{B O}=\frac{C O}{D O}\). Show that ABCD is a trapezium.
Solution:

Given

The diagonals of a quadrilateral ABCD intersect each other at point O such that \(\frac{A O}{B O}=\frac{C O}{D O}\).

Draw EO || DC which meets AD at E

Now, in \(\triangle A D C, E O \| D C\)

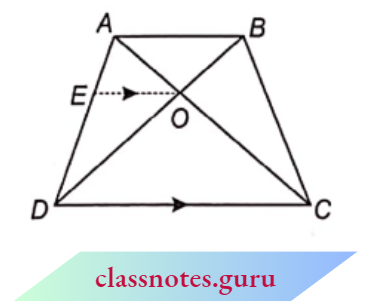
⇒ \(\frac{A E}{E D}=\frac{A O}{O C}\)…..(1)

Given, \(\frac{A O}{O C}=\frac{B O}{O D}\)…..(2)

From equations (1) and (2) \(\frac{A E}{E D}=\frac{B O}{O D} \Rightarrow E O \| A B(\ln \triangle D A B)\)

but E O || DC

AB || DC

⇒ square A B C Dis a trapezium.

Hence Proved.

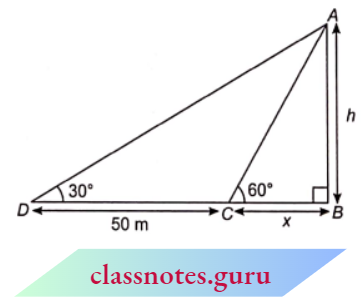
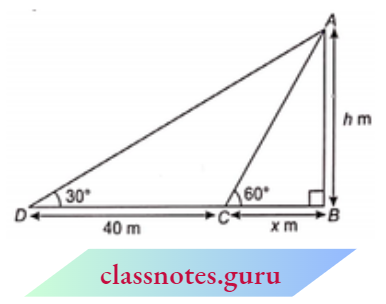
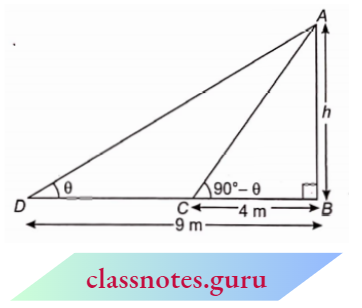
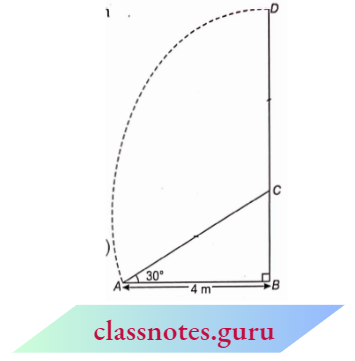
NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Triangle Exercise 6.3

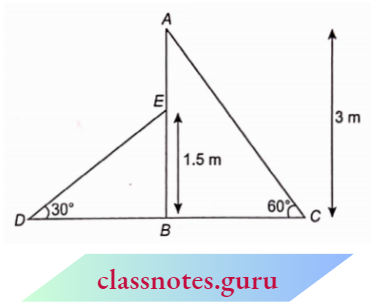
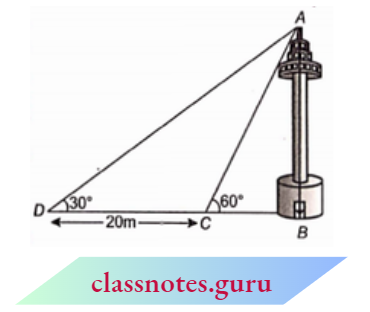
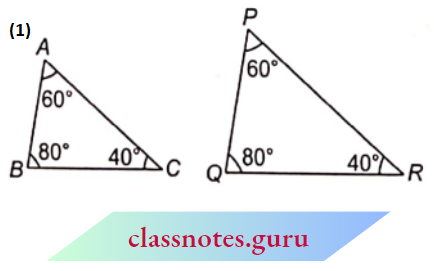
Question 1. State which pairs of triangles in figures are similar. Write the similarity criterion used by you for answering the question and also write the pairs of similar triangles in the symbolic form:

Solution:

1. In \(\triangle M B C\) and \(\triangle P Q R\),

⇒ \(\angle A=\angle P=60^{\circ}, \angle B=\angle Q=80^{\circ},\), \(\angle C=\angle R=40^{\circ}\)

⇒ \(\triangle A B C-\triangle P Q R\)

⇒ \(\triangle A B C-\triangle P Q R\) (from A.A.A. similarity)

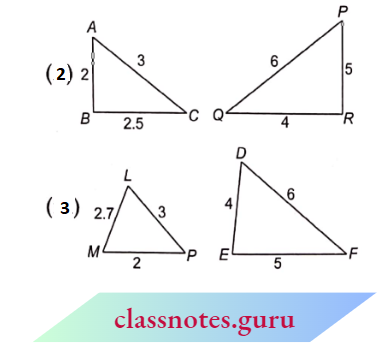
2. Here \(\frac{A B}{Q R}=\frac{2}{4}=\frac{1}{2}, \frac{B C}{R P}=\frac{2.5}{5}=\frac{1}{2}\)

and \(\frac{A C}{Q P}=\frac{3}{6}=\frac{1}{2}\)

⇒ \(\frac{A B}{Q R}=\frac{B C}{R P}=\frac{A C}{Q P}\)

⇒ \(\triangle M B C-\triangle Q R P\) (from S.S.S. similarity)

3. Here \(\frac{M P}{E D}=\frac{2}{4}=\frac{1}{2}, \frac{P L}{D F}=\frac{3}{6}=\frac{1}{2}\),

⇒ \(\frac{L M}{F E}=\frac{2.7}{5}=\frac{27}{50}\)

⇒ \(\frac{M P}{E D}=\frac{P L}{D F} \neq \frac{L M}{F E}\)

∴ \(\triangle L M P\) and \(\triangle D E F\) are not similar.

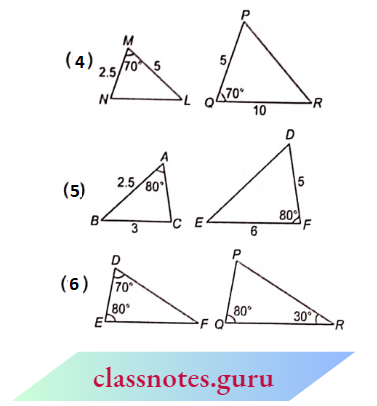
4. Here \(\frac{M P}{Q P}=\frac{2.5}{5}=\frac{1}{2}, \frac{M L}{Q R}=\frac{5}{10}=\frac{1}{2}\)

⇒ \(\frac{M P}{Q P}=\frac{M L}{Q R}\) and \(\angle M=\angle Q\)

⇒ \(\triangle M N L-\triangle Q P R\) (from S.S.A. similarity)

5.Here \(\frac{A B}{F D}=\frac{2.5}{5}=\frac{1}{2}, \angle A=\angle F=80^{\circ}\)

but AC and DE are unknown.

∴ \(\triangle A B C\) and \(\triangle D E F\) are not similar.

6. ln \(\triangle D E F\), \(\angle F=180^{\circ}-\angle D-\angle E\)

= \(180^{\circ}-70^{\circ}-80^{\circ}=30^{\circ}\)

In \(\triangle P Q R\),

⇒ \(\angle P =180^{\circ}-\angle Q-\angle R\)

= \(180^{\circ}-80^{\circ}-30^{\circ}=70^{\circ}\)

Now, \(\angle D=\angle P, \angle E=\angle Q, \angle F=\angle R\)

⇒ \(\triangle D E F \sim \triangle P Q R\) (from AAA similarity)

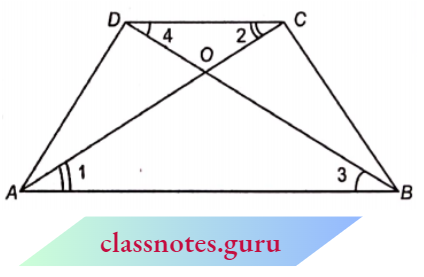
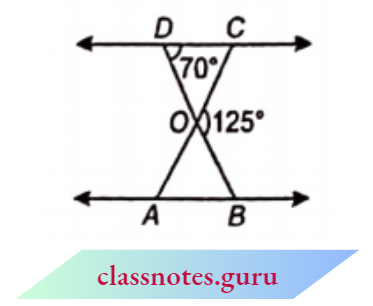
Question 2. In figure, \(\triangle O D C \sim \triangle O B A\), \(\angle B O C=125^{\circ}\) and \(\angle C D O=70^{\circ}\). Find \(\angle D O C\), \(\angle D C O\) and \(\angle O A B\).

Solution:

Here \(\angle B O C=125^{\circ}\)

and \(\angle C D O=70^{\circ}\)

⇒ \(\angle D O C+\angle B O C=180^{\circ}\) (linear pair)

⇒ \(\angle D O C=180^{\circ}-\angle B O C\)

= \(180^{\circ}-125^{\circ}=55^{\circ}\)

In \(\triangle D O C\),

⇒ \(\angle D C O=180^{\circ}-\angle C O D-\angle O D C\)

= \(180^{\circ}-55^{\circ}-70^{\circ}=55^{\circ}\)

⇒ \(\triangle O D C-\triangle O B A\)

⇒ \(\angle O C D=\angle O A B\)

∴ \(\angle O A B=55^{\circ}\)

Question 3. Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O. Using a similarity criterion for two triangles, show that \(\frac{O A}{O C}=\frac{O B}{O D}\)
Solution:

Given

Diagonals AC and BD of a trapezium ABCD with AB || DC intersect each other at the point O.

Draw EO || AB || CD

Now, in \(\triangle\)ADC,

EO || DC

⇒ \(\frac{A E}{E D}=\frac{A O}{O C}\) (from B.P.T.)…(1)

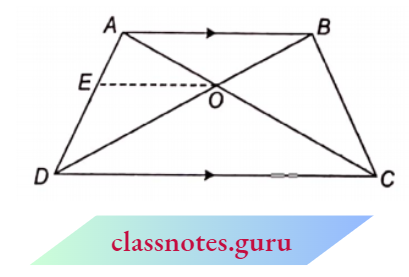
ln \(\triangle A B D\)

EO || AB

⇒ \(\frac{A E}{E D}=\frac{B O}{O D}\) (from B.P.T.)…(2)

From equations (1) and (2) \(\frac{A O}{O C}=\frac{B O}{O D}\)

Hence proved.

Class 10 Maths Chapter 6 Triangles MCQ with Answers

Question 4. In figure, \(\frac{Q R}{Q S}=\frac{Q T}{P R}\) and \(\angle 1=\angle 2\). Show that \(\triangle P Q S \sim \triangle T Q R\).

Solution:

Given

In figure, \(\frac{Q R}{Q S}=\frac{Q T}{P R}\) and \(\angle 1=\angle 2\).

In \(\triangle P Q R, \angle 1=\angle 2\) (given)

PR = PQ….(1) (sides opposite to equal angles in \(\Delta\) are equal)

Given, \(\frac{Q R}{Q S}=\frac{Q T}{P R} \Rightarrow \frac{Q R}{Q S}=\frac{Q T}{Q P}\) [from equation (1)]

⇒ \(\frac{Q S}{Q R}=\frac{Q P}{Q T}\)

In \(\triangle P Q S\) and \(\triangle T Q R\),

⇒ \(\frac{Q S}{Q R}=\frac{Q P}{Q T}\) and \(\angle S Q P=\angle R Q T\) (each \(\angle 1\))

⇒ \(\triangle P Q S \sim \triangle T Q R\) (from S.A.S. similarity)

Hence Proved.

Question 5. S and T are points on sides PR and QR of \(\triangle P Q R\) such that \(\angle P=\angle R T S\). Show that \(\triangle R P Q \sim \triangle R T S\).
Solution:

Given: \(\triangle R P Q\) and \(\triangle R T S\) in which \(\angle P=\angle R T S\)

To show: \(\triangle R P Q \sim \triangle R T S\)

Proof: \(\ln \triangle R P Q\) and \(\triangle R T S\), \(\angle 1=\angle 2\) (given)

⇒ \(\angle 3=\angle 3\) (common)

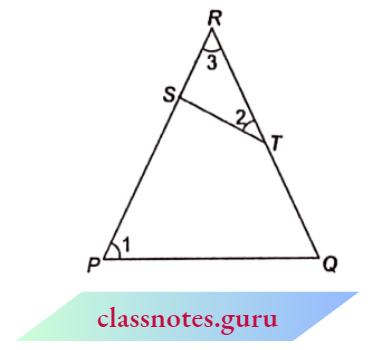
⇒ \(\triangle R P Q \sim \Delta R T S\) (from A.A. corollary)

Hence Proved.

Question 6. In the figure, if \(\triangle A B E \cong \triangle A C D\) shows that \(\triangle A D E \sim \triangle A B C\).
Solution:

Given, \(\triangle A B E \cong \triangle A C D\)

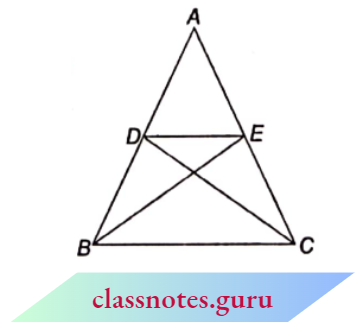
AE=AD….(1)

and AB=AC….(2)

⇒ \(\frac{A D}{A B}=\frac{A I}{A C}\) and \(\angle A=\angle A\) (common)

⇒ \(\triangle\) ADE \(\triangle\) ABC (from S.A.S. similarity)

Hence Proved.

Question 7. In the figure, altitudes AD and CE of \(\triangle\) ABC Intersect each other at the point Show that:

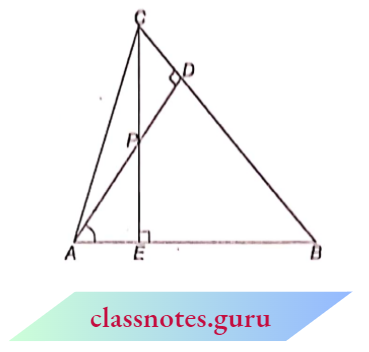
1. \(\triangle A E P-\triangle C D P\)
2. \(\triangle A B D-\triangle C B E\)
3. \(\triangle A E P \sim \triangle A D B\)
4. \(\triangle P D C-D B E C\)

Solution:

1. In the figure, \(\angle A E P=\angle C D P\) (each \(90^{\circ}\))

and \(\angle A P E=\angle C P D\) (vertically opposite angles)

⇒ \(\triangle A E P \sim \triangle C D P\) (from A.A.A. similarity)

Hence Proved.

2. In figure, \(\angle A D B=\angle C E B\) (each \(90^{\circ}\))

and \(\angle A B D=\angle C B E\) (each = \(\angle B\))

⇒ \(\triangle A B D \sim \triangle C B E\) (from A.A.A. similarity)

Hence Proved.

3.  In figure, \(\angle A E P=\angle A D B\) (each \(90^{\circ}\))

and \(\angle P A E=\angle B A D\) (common angle)

\(\triangle A E P \sim \triangle A D B\) (from A.A.A. similarity)

Hence Proved.

4. In figure, \(\angle P D C=\angle B E C\) (each \(90^{\circ}\))

and \(\angle P C D=\angle B C E\) (common angle)

⇒ \(\triangle P D C \sim \triangle B E C\) (from A.A.A. similarity)

Hence Proved.

Question 8. E is a point on the side AD produced of parallelogramABCD and BE intersects CD at F. Show that \(\triangle A B E \sim \triangle C F B\)
Solution:

Given

E is a point on the side AD produced of parallelogramABCD and BE intersects CD at F.

AE || BC and BE is a transversal.

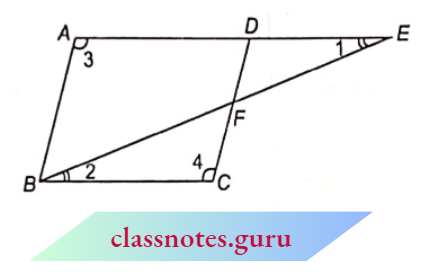
⇒ \(\angle\) 1 = \(\angle\) 2(alternate angles)

⇒ \(\angle\) 3 = \(\angle\) 4(opposite angles of parallelogram)

⇒ \(\triangle A B E \sim \triangle C F B\) (A. A similarly)

Question 9. In the figure, ABC and AMP are two right. triangles, right-angled at B and M respectively. Prove that

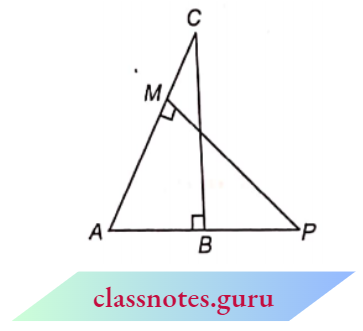
1. \(\triangle A B C \sim \triangle A M P\)
2. \(\frac{C A}{P A}=\frac{B C}{M P}\)

Solution:

Given

In the figure, ABC and AMP are two right. triangles, right-angled at B and M respectively.

1. In \(\triangle A B C\) and \(\triangle A M P\)

⇒ \(\angle A B C=\angle A M P\) (each \(90^{\circ}\))

⇒ \(\angle B A C=\angle M A P\) (common)

⇒ \(\triangle A B C \sim \triangle A M P\) (from A.A. similarity)

2. Divide (2) by (1)

⇒ \(\triangle A B C \sim \triangle A M P\)

⇒ \(\frac{C A}{P A}=\frac{B C}{M P}\) (ratio of corresponding sides)

Hence Proved.

Question 10. CD and GH are respectively the bisectors of \(\angle\) ACB and \(\angle\) EGF such that D and H lie on sides AB and FE of \(\triangle\) ABC and \(\triangle\) EFG respectively. If latex]\triangle[/latex] ABC ~ \(\triangle\) FEG.

1. \(\frac{C D}{G H}=\frac{A C}{F G}\)
2. \(\triangle D C B \sim \triangle H G E\)
3. \(\triangle D C A \sim \triangle H G F\)

Solution:

1. In \(\triangle A C D\) and \(\triangle F G H\)

⇒ \(\angle C A D=\angle G F H\)

(because \(\triangle A B C \sim \triangle F E G\))

but \(\triangle A B C \sim \triangle F E G\) (given)

⇒ \(\angle C=\angle G\)

⇒ \(\angle A C D=\angle F G H\)

From equations (1) and (2)

⇒ \(\triangle A C D \sim \triangle F G H\) (from A.A. similarity)

⇒ \(\frac{C D}{G H}=\frac{A C}{F G}\)

2. \(\triangle A B C \sim \triangle F E G\)

⇒ \(\angle A C B=\angle F G E\)

⇒ \(\frac{1}{2} \angle A C B=\frac{1}{2} \angle F G E\)

⇒ \(\angle D C B=\angle H G E\) and \(\angle D B C=\angle H E G\)

⇒ (because \(\triangle A B C \sim \triangle F E G \Rightarrow \angle B=\angle E\))

⇒ \(\triangle D C B \sim \triangle H G E\) (A.A. similarity)

3. \(\triangle A B C \sim \triangle F E G\)

⇒ \(\angle C A B=\angle G F E\)

⇒ \(\angle C A D=\angle G F H\)

⇒ \(\angle D A C=\angle H F G\)

and \(\triangle A B C \sim \triangle F E G\)

⇒ \(\angle A C B=\angle F G E\)

⇒ \(\frac{1}{2} \angle A C B=\frac{1}{2} \angle F G E\)

⇒ \(\angle D C A=\angle H G F\)

Now \(\angle D A C=\angle H F G\)

and \(\angle D C A=\angle H G F\)

⇒ \(\triangle D C A \sim \triangle H G F\) (A.A. similarity)

Hence Proved.

Question 11. In figure, E is a point on side CB produced of an isosceles triangle ABC with AB =AC. If \(A D \perp B C\) and \(E F \perp A C\), prove that \(\triangle A B D \sim \triangle E C F\).

Solution:

Given

In figure, E is a point on side CB produced of an isosceles triangle ABC with AB =AC. If \(A D \perp B C\) and \(E F \perp A C\)

⇒ \(\triangle A B C\) is isosceles in which,

AB = AC

⇒ \(\angle A C B=\angle A B C\) (angles opposite to equal sides)

⇒ \(\angle E C F=\angle A B D\)

and \(\angle E F C=\angle A D B\) (each \(90^{\circ}\))

⇒ \(\triangle E C F \sim \triangle A B D\) (from A.A. similarity)

Hence Proved.

Question 12. Sides AB and BC and median AD of a triangle ABC are respectively proportional to sides PQ and QR and median PM of \(\triangle\)PQR. Show that \(\triangle A B C \sim \triangle P Q R \text {. }\).

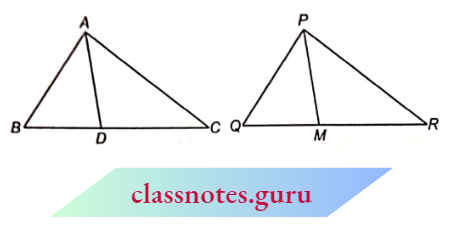
Solution:

Given: \(\triangle A B C\) and \(\triangle P Q R\), in AD \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A D}{P M}\)

To show: \(\triangle A B C \sim \triangle P Q R\)

Proof: \(\frac{A B}{P Q}=\frac{B C}{Q R}=\frac{A D}{P M}\) (given)

⇒ \(\frac{A B}{P Q}=\frac{2 B D}{2 Q M}=\frac{A D}{P M}\) (AD and PM are medians)

⇒ \(\frac{A B}{P Q}=\frac{B D}{Q M}=\frac{A D}{P M}\)

⇒ \(\triangle A B D \sim \triangle P Q M\) (from S.S.S. similarity)

⇒ \(\angle B=\angle Q\) (corresponding angles are equal of similar triangles)

Now, in \(\triangle A B C\) and \(\triangle P Q R\), \(\frac{A B}{P Q}=\frac{B C}{Q R}\) (given)

and \(\angle B=\angle Q\) (proved above)

⇒ \(\triangle A B C \sim \triangle P Q R\) (from S.A.S. similarity)

Hence Proved.

Question 13. D is a point on the side BC of a triangle ABC such that triangle ABC such that \(\angle A D C=\angle B A C\). Show that \(C A^2=C B \cdot C D\).
Solution:

Given

D is a point on the side BC of a triangle ABC such that triangle ABC such that \(\angle A D C=\angle B A C\).

In \(\triangle A B C\) and \(\triangle D A C\),

⇒ \(\angle B A C=\angle A D C\) (given)

⇒ \(\angle A C B=\angle D C A\) (common)

⇒ \(\triangle A B C \sim \triangle D A C\)

⇒ \(\frac{C D}{C A}=\frac{C A}{C B}\) (A.A. similarity)

⇒ \(C A^2=C B \times C D\)

Hence Proved.

Question 14. Sides AB and AC and median AD of a triangle ABC are respectively proportional to sides PQ and PR and median PM of another triangle PQR. Show that triangle PQR. Show that \(\triangle A B C \sim \triangle P Q R\).
Solution:

Given: \(\triangle A B C\) and \(\triangle P Q R\) in which AD and PS are the median such that

⇒ \(\frac{A B}{P Q}=\frac{A C}{P R}=\frac{A D}{P S}\)

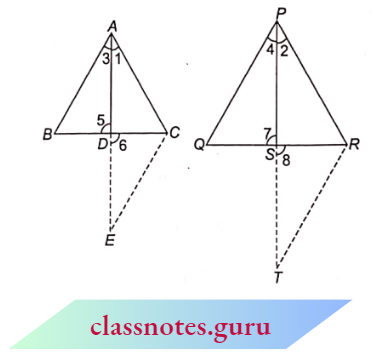
To show: \(\triangle A B C \sim \triangle P Q R\)

Construction: Produce AD to E such that AD=DE. Join EC, produce PS to T such that PS=ST.

Join TR.

Proof: In \(\triangle A B D\) and \(\triangle E C D\),

BD = DC (Dis mid-point of BC)

⇒ \(\angle\)5 = \(\angle\)6 (vertically opposite angle)

AD = DE (from construction)

⇒ \(\triangle A B D \cong \triangle E C D\) (S.A.S. congruency)

AB=EC (congruent parts of congruent triangles are equal)…(1)

Similarly, we can prove that \(\triangle P Q S \cong \triangle T R S\)

PQ=TR…..(2)

Now, \(\frac{A B}{P Q}=\frac{A C}{P R}=\frac{A D}{P S}\)

⇒ \(\frac{E C}{T R}=\frac{A C}{P R}=\frac{2 A D}{2 P S}\) (from equations (1) and (2))

⇒ \(\frac{E C}{T R}=\frac{A C}{P R}=\frac{A E}{P T}\)

⇒ \(\triangle A E C \sim \triangle P T R\) (S.S.S. similarity)

⇒ \(\angle 1=\angle 2\) (corresponding angles of similar triangles are equal)…..(3)

Similarly, we can prove that \(\angle 3=\angle 4\)…..(4)

Adding equations (3) and (4).

⇒ \(\angle 1+\angle 3=\angle 2+\angle 4 \Rightarrow \angle A=\angle P\)

Now, in \(\triangle A B C\) and \(\triangle P Q R\).

⇒ \(\frac{A B}{P Q}=\frac{A C}{P R}\) (given)

and \(\angle A=\angle P\)(proved above)

∴ \(\Delta B C-\triangle P Q R\) (S.A.S. similarity)

Question 15. A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time, a tower casts a shadow 28 m long. Find the height of the tower.
Solution:

Given

A vertical pole of length 6 m casts a shadow 4 m long on the ground and at the same time, a tower casts a shadow 28 m long.

Let MC be a pole of 6m in height and its shadow is DC = 4m. At the same time, tower AB, whose height is h metre, has its shadow BD = 28 m.

Now, \(\triangle D C M \sim \triangle D B A\)

⇒ \(\frac{D C}{D B}=\frac{C M}{B A}\)

⇒ \(\frac{4}{28}=\frac{6}{h} \quad \Rightarrow \quad h=\frac{28 \times 6}{4}=42\)

Height of tower = 42 ~m

Question 16. If AD and PM are medians of triangles ABC and PQR respectively where \(\triangle A B C – [latex]\triangle P Q R\) prove that \(\frac{A B}{P Q}=\frac{A D}{P M} \text {. }\)
Solution:

Given: AD and PM are the medians of \(\triangle A B C\) and \(\triangle P Q R\) respectively.

and \(\triangle A B C \sim \triangle P Q R\)

To prove: \(\frac{A B}{P Q}=\frac{A D}{P M}\)

Proof: In \(\triangle A B D\) and \(\triangle P Q M\),

⇒ \(\angle B=\angle Q\) (because \(\triangle A B C \sim \triangle P Q R\))

⇒ \(\frac{A B}{P Q}=\frac{\frac{1}{2} B C}{\frac{1}{2} Q R}\) (because \(\frac{A B}{P Q}=\frac{B C}{Q R}\))

⇒ \(\frac{A B}{P Q}=\frac{B D}{Q M}\)

⇒ \(\triangle A B D \sim \triangle P Q M\) (from S.A.S. similarity)

∴ \(\frac{A B}{P Q}=\frac{A D}{P M}\) Hence Proved.

NCERT Exemplar Chapter 6 Solutions with Diagrams

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Triangle Exercise 6.4

Question 1. Let \(\triangle\)ABC ~ \(\triangle\)DEF areas be, respectively, 64 cm EF = 15.4 cm, find BC.
Solution:

Given

Let \(\triangle\)ABC ~ \(\triangle\)DEF areas be, respectively, 64 cm EF = 15.4 cm

⇒ \(\triangle A B C \sim \triangle D E F\)

⇒ \(\frac{\text{ar}(\triangle A B C)}{\text{ar}(\triangle D E F)}=\frac{B C^2}{E F^2} \Rightarrow \frac{64}{121}=\frac{B C^2}{E F^2}\)

⇒ \(\frac{8}{11}=\frac{B C}{E F}\)

∴ \(BC=\frac{8}{11} \times E F=\frac{8}{11} \times 15.4=11.2 \mathrm{~cm}\)

Question 2. Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD, find the ratio of the areas of triangles AOB and COD.
Solution:

Given

Diagonals of a trapezium ABCD with AB || DC intersect each other at the point O. If AB = 2CD

In \(\triangle\)AOB and \(\triangle\)COD, \(\angle\)1 = \(\angle\)2 (vertically opposite angles)

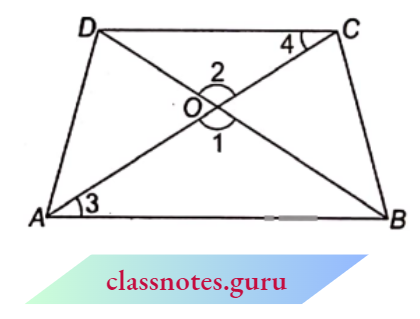
⇒  \(\angle\)3 = \(\angle\)4 (alternate angles, AB || DC)

⇒ \(\triangle A O B \sim \triangle C O D\) (A.A. corollary)

⇒ \(\frac{\text{ar}(\triangle A O B)}{\text{ar}(\triangle C O D)}=\frac{A B^2}{C D^2}\)

(because the ratio of the areas of two similar triangles is equal to the ratio of the square of their corresponding sides)

= \(\frac{(2 C D)^2}{C D^2}\) (because AB=2CD, given)

= \(\frac{4 C D^2}{C D^2}=\frac{4}{1}\)

∴ \(\text{ar}(\triangle A O B):\text{ar}(\triangle C O D)=4: 1\)

Question 3. In the figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that \(\frac{\text{ar}(A B C)}{\text{ar}(D B C)}=\frac{A O}{D O}\).

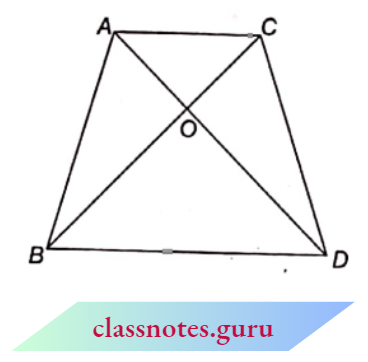
Solution:

Given

In the figure, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O

Draw \(A L \perp B C\) and \(D M \perp B C\)

In \(\triangle O L A\) and \(\triangle O M D\),

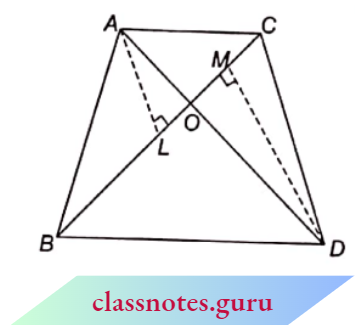
⇒ \(\angle A L O=\angle D M O=90^{\circ}\)

and \(\angle A O L=\angle D O M\) (vertically opposite angles)

⇒ \(\triangle O L A \sim \triangle O M D\) (from A.A.A. similarity)

⇒ \(\frac{A L}{D M}=\frac{A O}{D O}\)

= \(\frac{A L}{D M}=\frac{A O}{D O}\)

Now \(\frac{\text{ar}(\triangle A B C)}{\text{ar}(\triangle D B C)}=\frac{\frac{1}{2} \times(B C) \times(A L)}{\frac{1}{2} \times(B C) \times(D M)}\) [from equation (1)]

Therefore, \(\frac{\text{ar}(\triangle A B C)}{\text{ar}(\triangle D B C)}=\frac{A O}{D O}\) Hence Proved.

Question 4. If the areas of two similar triangles are equal, prove that they are congruent.
Solution:

Given, \(\triangle A B C \sim \triangle P Q R\)

⇒ \(\frac{\text{ar}(\triangle A B C)}{\text{ar}(\triangle P Q R)}=\frac{A B^2}{P Q^2}=\frac{B C^2}{Q R^2}=\frac{C A^2}{R P^2}\)

But \(\text{ar}(\triangle A B C)=\text{ar}(\triangle P Q R)\)

⇒ \(\frac{A B^2}{P Q^2}=\frac{B C^2}{Q R^2}=\frac{C A^2}{R P^2}=1\)

AB = PQ, BC = QR

CA = RP

⇒ \(\triangle A B C \cong \triangle P Q R\)(from S.S.S.)

Hence Proved.

Question 5. D, E and F are respectively the mid-points of sides AB, BC and CA of \(\triangle\) ABC. Find the ratio of the areas of \(\triangle\)DEF and \(\triangle\)ABC.
Solution:

Given: \(\triangle\)ABC in which D, E and F are the mid-points of sides BC, CA and AB respectively.

To find: The ratio of the areas of \(\triangle\)DEF and \(\triangle\)ABC.

Proof: D, E, and F are mid-points.

⇒  \(E F\| B C\) and \(E F=\frac{1}{2} B C\)

EF = BD

Similarly, \(D E=B F\) (because \(D E \| A B\) and \(\frac{1}{2} A B\))

So, \(E F B D\) is a parallelogram.

⇒ \(\angle B=\angle 1\)

Similarly, AFDE and EFDC are parallelograms.

⇒ \(\angle A=\angle 2\) and \(\angle C=\angle 3\)

i.e., \(\triangle A B C\) and \(\triangle D E F\) are equiangular.

⇒ \(\triangle D E F \sim \triangle A B C\)

⇒ \(\frac{\text{ar}(\triangle D E F)}{\text{ar}(\triangle A B C)}=\frac{D E^2}{A B^2}=\frac{F B^2}{A B^2}=\frac{(A B / 2)^2}{A B^2}=\frac{1}{4}\)

Therefore, \(\frac{\text{ar}(\triangle D E F)}{\text{ar}(\triangle A B C)}=\frac{1}{4}\)

Question 6. Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding medians.
Solution:

Given: \(\triangle\)ABC ~ \(\triangle\)DEF, AP and DQ are the medians of AABC and ADEF respectively.

To prove: \(\frac{\text{ar}(\triangle M B C)}{\text{ar}(\triangle D E F)}=\frac{A P^2}{D Q^2}\)

Proof: AP and DQ are medians.

So, BP=PC and EQ=QF

and given that \(\triangle A B C \sim \triangle D E F\)

So, \(\frac{A B}{D E}=\frac{A C}{D F}=\frac{B C}{E F}\) and \(\angle A=\angle D, \angle B=\angle E\) and \(\angle C=\angle F\)

Now, \(\frac{A B}{D E}=\frac{B C}{E F}\)

⇒ \(\frac{A B}{D E}=\frac{2 B P}{2 E Q} \Rightarrow \frac{A B}{D E}=\frac{B P}{E Q}\)

and \(\angle B=\angle E\)

⇒ \(\triangle A B P \sim \triangle D E Q\)(S.A.S. similarity)

Now, in \(\triangle A B C\) and \(\triangle D E F\), \(\frac{\text{ar}(\triangle \triangle B C)}{\text{ar}(\triangle D E F)}=\frac{A B^2}{D E^2}\)

(because the ratio of the areas of two similar triangles is equal to the ratio of the squares of its corresponding sides)

From equations (1) and (2), \(\frac{\text{ar}(\triangle A B C)}{text{ar}(\triangle D E F)}=\frac{A P^2}{D Q^2}\)

Hence Proved.

Question 7. Prove that the area of an equilateral triangle described on one side of a square is equal to half the area of the equilateral triangle described on one of its diagonals.
Solution:

Given: A square ABCD and an equilateral triangle BCE, formed on side BC and \(\triangle\) ACF formed on side AC.

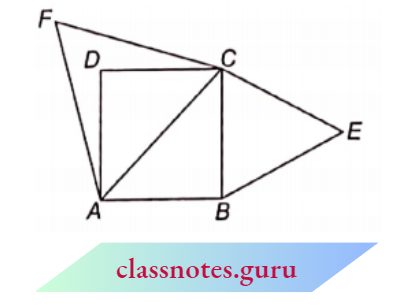
To prove: \(\text{ar}(\triangle B C E)=\frac{1}{2} \text{ar}(\triangle A C F)\)

Proof: \(\triangle B C E\) and \(\triangle A C F\) are equilateral triangles, so each angle of both is \(60^{\circ}\).

So, \(\triangle B C E \sim \triangle A C F\)

⇒ \(\frac{\text{ar}(\triangle B C E)}{\text{ar}(\triangle A C F)}=\frac{B C^2}{A C^2}=\frac{B C^2}{2(B C)^2}=\frac{1}{2}\)

Therefore, \(\text{ar}(\triangle B C E)=\frac{1}{2} \times \text{ar}(\triangle A C F)\)

Hence Proved.

Question 8. ABC and BDE are two equilateral triangles such that D is the mid-point of BC. The ratio of the areas of triangles ABC and BDE is:

1. 2: 1
2. 1: 2
3. 4: 1
4. 1: 4

Solution: 3. 4: 1

⇒ \(\triangle A B C\) and \(\triangle B D E\) are two equilateral triangles such that

BD = \(\frac{1}{2} B C\)

BD = \(\frac{1}{2} A B\) (because BC=A B)

⇒ \(\frac{A B}{B D}=\frac{2}{1}\)

⇒ \(\triangle A B C \sim \triangle B D E\)(triangles are equilateral)

⇒ \(\frac{\text{ar}(\triangle A B C)}{\text{ar}(\triangle B D E)}=\frac{A B^2}{B D^2}=\left(\frac{2}{1}\right)^2=4: 1\)

Question 9. The sides of two similar triangles are in

1. 2 : 3
2. 4: 9
3. 81: 16
4. 16: 81

Solution: 4. 16: 81

The ratio of the areas of two similar triangles = (ratio of the sides of triangles)2

= \(\left(\frac{4}{9}\right)^2=\frac{16}{81}=16: 81\)

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Triangle Exercise 6.5

Question 1. The sides of the triangles are given below. Determine which of them are right triangles. In the case of a right triangle, write the length of its hypotenuse.

1. 7 cm, 24 cm, 25 cm
2. 3 cm, 8 cm, 6 cm
3. 50 cm, 80 cm, 100 cm
4. 13 cm, 12 cm, 5 cm

Solution:

Here

1. 7² + 24² = 49 + 576 = 625 = 252

The triangle is a right-angled hypotenuse = 25 cm

2. 3² + 6² = 9 + 36 = 45 82

The triangle is not right-angled.

3. 50² + 80² = 2500 + 6400 = 8900* 1002

The triangle is not right-angled.

4. 5²+ 12² = 25 + 144= 169 = 132

∴  Triangle is right-angled

hypotenuse = 13 cm

Triangles Class 10 NCERT Exemplar Extra Questions

Question 2. PQR is a triangle right angled at P and M is a point on QR such that \(P M \perp Q R\). Show that \(P M^2=Q M \cdot M R\).
Solution:

Given

PQR is a triangle right angled at P and M is a point on QR such that \(P M \perp Q R\).

In \(\triangle P Q R, \angle P=90^{\circ}\)

and \(\angle 2+\angle 4=90^{\circ}\)

⇒ \(\angle 1+\angle 2=\angle 2+\angle 4 \Rightarrow \angle 1=\angle 4\)

Similarly, \(\angle 3=\angle 2\)

⇒ \(\triangle P Q M \sim \triangle R P M\) (from A.A. similarity)

⇒ \(\frac{Q M}{P M}=\frac{P M}{R M}\)

∴ \(P M^2=Q M \cdot M R\) Hence Proved

Question 3. In the figure, ABD is a triangle right-angled at A and AC¹ BD. Show that

1. AB² = BC • BD
2. AC² =BC- DC
3. AD = BD CD

Solution:

1. In \(\triangle A B C\) and \(\triangle D B A\),

⇒ \(\angle A B C=\angle D B A\) (common)

⇒ \(\angle A C B=\angle D A B\) (each \(90^{\circ}\))

⇒ \(\triangle A B C \sim \triangle D B A\)(A.A. similarity)

⇒ \(\frac{A B}{D B}=\frac{B C}{B A} \Rightarrow A B^2=B C \cdot B D\)

Hence Proved.

2. In \(\triangle A B C\) and \(\triangle D A C\),

⇒ \(\angle A B C=180^{\circ}-\angle A C B-\angle B A C\)

= \(180^{\circ}-90^{\circ}-\angle B A C\)

= \(90^{\circ}-\angle B A C=\angle D A C\)

and \(\angle A C B=\angle D C A\) (each \(90^{\circ}\))

⇒ \(\triangle A B C \sim \triangle D A C\) (A.A. similarity)

⇒ \(\frac{A C}{D C}=\frac{B C}{A C} \Rightarrow A C^2=B C \cdot D C\)

Hence Proved.

3.In \(\triangle D A C\) and \(\triangle D B A\),

⇒ \(\angle A D C=\angle B D A\) (common)

⇒ \(\angle D C A=\angle D A B\) (each \(90^{\circ}\))

⇒ \(\triangle D A C \sim \triangle D B A\) (A.A. similarity)

⇒ \(\frac{D A}{D B}=\frac{D C}{D A} \Rightarrow A D^2=B D \cdot C D\)

Hence Proved.

Question 4.ABC is an isosceles triangle right angled at C. Prove that \(A B^2=2 A C^2\).
Solution:

Given

ABC is an isosceles triangle right angled at C.

In \(\triangle A B C\),

AC = BC

and \(\angle C=90^{\circ}\)

⇒ \(A B^2=A C^2+B C^2\)

⇒ \(A B^2=A C^2+A C^2\) [from equation (1)]

⇒ \(A B^2=2 A C^2\)

Hence Proved.

Question 5. ABC is an isosceles triangle with AC = BC. If \(A B^2=2 A C^2\), prove that ABC is a right triangle.
Solution:

Given

ABC is an isosceles triangle with AC = BC. If \(A B^2=2 A C^2\)

In \(\triangle A B C\),

and AC = BC

⇒ \(A B^2\) =2 A C^2[/latex]

⇒ \(A B^2\) = \(A C^2+A C^2\)

⇒ \(A B^2\) and \(=A C^2+B C^2\)

⇒ \(\angle C\) and \(=90^{\circ}\) (from equation (1))

⇒ \(\angle C=90^{\circ}\)

⇒ \(\triangle A B C\) is a right-angled triangle.

Hence Proved.

Question 6. ABC is an equilateral triangle of side 2a. Find each of its altitudes.
Solution:

Given

ABC is an equilateral triangle of side 2a.

Let ABC be an equilateral triangle in which,

AB = BC = CA = 2a

AB = BC = CA = 2a

AP \(\perp\) BC

BP = \(\frac{1}{2} B C\)

= \(\frac{1}{2}(2 a)=a\)

In \(\triangle A B P\),

⇒ \(A B^2=A P^2+B P^2\)

⇒ \(A P^2=A B^2-B P^2=(2 a)^2-a^2=3 a^2\)

⇒ \(A P=a \sqrt{3}\)

Length of each altitude = \(a \sqrt{3}\) units.

Question 7. Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.
Solution:

Let ABCD be a rhombus whose side is ‘a’

The diagonals of the rhombus intersect each other at point O at right angle.

In right \(\triangle\) A O B,

⇒ \(O A^2+O B^2=a^2\) (from Pythagoras theorem)

⇒ \((\frac{1}{2} A C)^2+\left(\frac{1}{2} B D\right)^2=a^2\) (diagonals bisect each other)

⇒ \(\frac{1}{4} A C^2+\frac{1}{4} B D^2=a^2\)

⇒ \(A C^2+B D^2=4 a^2\)

⇒ \(A C^2+B D^2=a^2+a^2+a^2+a^2\)

⇒ \(A C^2+B D^2=A B^2+B C^2+C D^2+D A^2\)

Hence Proved

Question 8. In the figure, O is A a point in the interior of a triangle ABC, OD \(\perp\) BC, OE \(\perp\) AC and OF \(\perp\) AB. Show that :

1.  \(O A^2+O B^2+O C^2= O D^2-O E^2-O F^2=A F^2 +B D^2+C E^2 \)
2.  \(A F^2+B D^2+C E^2=A E^2+C D^2+B F^2\)

Solution:

Given

In the figure, O is A a point in the interior of a triangle ABC, OD \(\perp\) BC, OE \(\perp\) AC and OF \(\perp\) AB.

(1) In \(\triangle A O F\),

⇒ \(A F^2=O A^2-O F^2\)

In \(\triangle B O D\),

⇒ \(B D^2=O B^2-O D^2\)

In \(\triangle C O E\),

⇒ \(C E^2=O C^2-O E^2\)

Adding equations (1), (2) and (3),

⇒ \(A F^2 +B D^2+C E^2\)

=\(O A^2+O B^2+O C^2-O F^2-O D^2-O E^2\)

Hence Proved.

(2) From part 1

\(A F^2+B D^2+C E^2\)

= \(O A^2+O B^2+O C^2-O F^2-O D^2-O E^2\)

= \(\left(O A^2-O E^2\right)+\left(O B^2-O F^2\right)+\left(O C^2-O D^2\right)\)

=\(A E^2+B F^2+C D^2\)

Hence Proved.

Question 9. A ladder 10 m long reaches a window 8 m above the ground. Find the distance of the foot of the ladder from the base of the wall.

Solution:

Given

A ladder 10 m long reaches a window 8 m above the ground.

Let PR is a ladder of length 10 m which reaches at a window of height 8 m from the ground. The distance of the lower end of the ladder from the base of the wall is QR.

Now, \(\angle P Q R=90^{\circ}\)

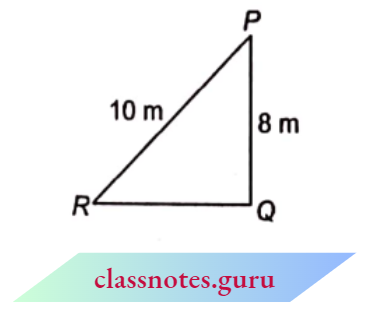
In \(\triangle P Q R\),

⇒ \(P R^2=P Q^2+Q R^2\)

⇒ \(Q R^2=P R^2-P Q^2\)

=\(10^2-8^2\)

=100-64=36

Distance of the lower end of the ladder from the base of the wall = 6 m

Question 10. A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?

Solution:

Given

A guy wire attached to a vertical pole of height 18 m is 24 m long and has a stake attached to the other end.

Let PQ be a vertical pole of height 18 m. A wire whose length is 24 m, is tied at the upper-end P of the pole. Its other end is tied at point R on the ground.

In \(\triangle P Q R\),

⇒ \(Q R^2+P Q^2 =P R^2\)

⇒ \(Q R^2 =P R^2-P Q^2=24^2-18^2\)

=576-324=252

Q R =\(\sqrt{252}=6 \sqrt{7} \mathrm{~m}\)

NCERT Exemplar Solutions Class 10 Maths Chapter 6 Triangles

Question 11. An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 same airport and flies due west at a speed of 1200 km per hour. How far apart will be the two planes after \(1 \frac{1}{2}\) hours?

Solution:

Given

An aeroplane leaves an airport and flies due north at a speed of 1000 km per hour. At the same time, another aeroplane leaves the same airport and flies due west at a speed of 1200 same airport and flies due west at a speed of 1200 km per hour.

Distance covered by aeroplane in North in 1 \(\frac{1}{2}=\frac{3}{2}\) hrs is A B=1000 \(\times \frac{3}{2}=1500 \mathrm{~km}\).

Similarly, the distance covered by aeroplane in the west in \(\frac{3}{2} \mathrm{hrs}\).

⇒ \(B C=1200 \times \frac{3}{2}=1800 \mathrm{~km}\)

In \(\triangle A B C, A C^2=A B^2+B C^2\)

=\((1500)^2+(1800)^2\)

= 2250000+3240000 = 5490000

∴ \(A C=\sqrt{5490000}=300 \sqrt{61} \mathrm{~km}\)

Question 12. Two poles of heights 6 m and 1 1 m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.

Solution :

Given

Two poles of heights 6 m and 1 1 m stand on a plane ground. If the distance between the feet of the poles is 12 m,

Let AB and CD be two vertical poles, and then

AB = 6 m, CD = 11m

and AC = 12m

Draw BE || AC, then

CE = AB = 6 m,

BE = AC = 12 m

DE = CD- CE = 11m – 6m = 5m

Now in right \(\triangle B E D\),

⇒ \(B D^2 =B E^2+D E^2\)

=\(12^2+5^2\)

=144+25

=169 \(\mathrm{~m}^2 \Rightarrow B D=13 m\)

Therefore, the distance between poles =13 m.

Question 13. D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C . Prove that \( A E^2+B D^2=A B^2+D E^2\).

Solution :

Given

D and E are points on the sides CA and CB respectively of a triangle ABC right angled at C .

In \(\triangle A C E, A E^2=A C^2+C E^2\) …..(1)

In \(\triangle A B C, \quad A B^2=A C^2+B C^2\) …. (2)

In \(\triangle C D E, \quad D E^2=C D^2+C E^2\) ….(3)

In \(\triangle D C B, \quad B D^2=C D^2+B C^2\) …..(4)

Adding equations (1) and (4),

⇒ \(A E^2+B D^2= \left(A C^2+C E^2\right)+\left(C D^2+B C^2\right)\)

= \(\left(A C^2+B C^2\right)+\left(C D^2+C E^2\right)\)

= \(A B^2+D E^2\) [from equations (2) and (3)]

Hence Proved.

Question 14. The perpendicular from A on side BC of a \(\triangle\)ABC intersects BC at D such that DB = 3 CD. Prove that 2AB² = 2AC² + BC²

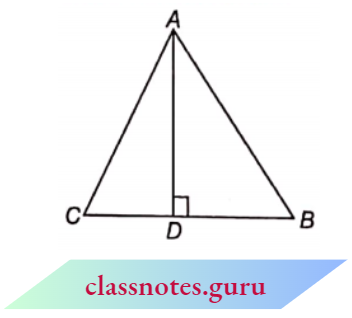
Solution:

Given, In \(\triangle A B C\), A D \(\perp B C\) and D B=3 C D

To prove : \(2 A B^2=2 A C^2+B C^2\)

Proof: \(D B=3 C D \Rightarrow \frac{D B}{C D}=\frac{3}{1}\)

Let \(D B=3 x \quad \Rightarrow \quad C D\)=x

⇒ \(\frac{D B}{B C}=\frac{3 x}{4 x}=\frac{3}{4} \quad \Rightarrow \quad D B=\frac{3}{4} B C\)

and \(\frac{D C}{B C}=\frac{x}{4 x}=\frac{1}{4} \quad \Rightarrow \quad D C=\frac{1}{4} B C\)…

Now, from Pythagoras theorem,

⇒ \(A B^2=A D^2+B D^2=\left(A C^2-D C^2\right)+B D^2\) (from Pythagoras theorem)

=\(A C^2-\frac{1}{16} B C^2+\frac{9}{16} B C^2\)

=\(A C^2+\frac{8}{16} B C^2=A C^2+\frac{1}{2} B C^2\)

⇒ \(2 A B^2=2 A C^2+B C^2\)

Hence Proved.

Question 15. In an equilateral triangle ABC, D is a point on side BC Such That B D=\(\frac{1}{3} B C\). Prove that \(9 A D^2=7 A B^2\).

Solution :

Given

In an equilateral triangle ABC, D is a point on side BC Such That B D=\(\frac{1}{3} B C\).

Let \(A B=B C=A C=6 x\)

and \(B D=\frac{1}{3} B C=\frac{1}{3} \times 6 x=2 x\)

and B E=E C=\(\frac{B C}{2}\)=3 x ( In equilateral triangle, perpendicular bisects the base)

D E=B E-B D=3 x-2 x=x

Now, from Pythagoras theorem,

⇒ \(A B^2= A E^2+B E^2\)

= \(A D^2-D E^2+B E^2\) (from Pythagoras theorem)

⇒ \((6 x)^2 =A D^2-x^2+(3 x)^2\)

⇒ \(A D^2 =36 x^2+x^2-9 x^2=28 x^2\)

⇒ \(9 A D^2= 9 \times 28 x^2=9 \times 7 \times 4 x^2\)

=\(v7 \times 36 x^2=7(A B)^2\)

⇒ \(9 A D^2 =7 A B^2\)

Hence Proved.

Question 16. In an equilateral triangle, prove that three times the square of one, side is equal to four times the square of one of its altitudes.

Solution:

Let AB=BC = CA=a

In \(\triangle\)ADB and \(\triangle\)ADC,

⇒ \({\begin{array}{lr}
A B=A C \text { (sides of equilateral triangle) } \\
\angle 1=\angle 2 & \text { (each } 90^{\circ} \text { ) } \\
A D=A D & \text { (common) }
\end{array}}. \)

⇒ \(\triangle A D B \cong \triangle A D C\) (R.H.S.)

BD = DC =\(\frac{B C}{2}=\frac{a}{2}\) (c.p.c.t.)

Now, in \(\triangle A D B\) , from Pythagoras theorem

⇒ \(A B^2=A D^2+B D^2\)

⇒ \(a^2=A D^2+\left(\frac{a}{2}\right)^2\)

⇒ \(A D^2=a^2-\frac{a^2}{4} \Rightarrow A D^2=\frac{3 a^2}{4}\)

⇒ \(4 A D^2=3 a^2\)

⇒ \(4 A D^2=3 A B^2\)

Therefore, three times the square of the side of an equilateral triangle is equal to 4 times the square of its altitude.

Hence Proved

Question 17. Tick the correct answer and justify: In \(\triangle A B C\), A B=6 \(\sqrt{3} \mathrm{~cm}\), A C=12 cm and B C=6 \cm. The angle B is :

1. \(120^{\circ}\)
2. \(60^{\circ}\)
3. \(90^{\circ}\)
4. \(45^{\circ}\)

Solution :

⇒ \(A B^2+B C^2 =(6 \sqrt{3})^2+6^2\)

=\(108+36=144=12^2=A C^2\)

⇒ \(\angle B =90^{\circ}\)

Class 10 Maths Triangles Exemplar Solutions

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Triangle Exercise 6.6

Question 1. n figure, PS is the bisector of \(\angle\)QPR of \(\triangle\)PQR. Prove that \(\frac{Q S}{S R}=\frac{P Q}{P R}\)

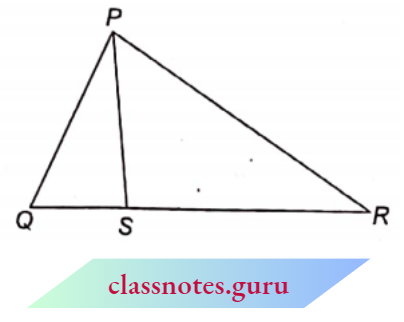
Solution:

Solution: Draw R T \\ S P which intersects the produced QP at T.

Now, R T \\ S P and R P is a transversal.

⇒ \(\angle S P R=\angle P R T\) (alternate angles) …(1)

Again, SP \\ RT and QT is a transversal.

⇒ \(\angle Q P S=\angle P T R\)

Given, \(\angle Q P S=\angle S P R \Rightarrow \angle P T R=\angle P R T\) [from equations (1) and (2)]

P R=P T

In \(\triangle Q R T\), S P \\ R T

⇒ \(\frac{Q S}{S R}=\frac{Q P}{P T} \quad \Rightarrow \quad \frac{Q S}{S R}=\frac{P Q}{P R}\) [from equation (3)]

Hence proved

Question 2. In the figure, D is a point on hypotenuse AC of \(\triangle\) ABC, such that BD \( \perp\) AC, DM \( \perp\) BC and DN \( \perp\) AB. Prove that :

1. \(D M^2=D N \cdot M C\)
2. \(D N^2=D M \cdot A N\)

Solution :

In right \(\triangle A B C\), BD is perpendicular to A-C.

⇒ \(\triangle B D C \sim \triangle A B C \sim \triangle A D B\)

(1) In \(\triangle B D C\)

⇒ \(\triangle D M \perp \sim B C\)

⇒ \(\frac{M C}{D M}=\frac{M D}{B M}\)

⇒ \(D M^2=B M \cdot M C\)

In square B M D N, \(\quad \angle D=\angle M=\angle N=90^{\circ}\)

⇒ In square B M D N is a rectangle. From equation (1),

⇒ \(D M^2=D N \cdot M C\)

Hence Proved.

(2) In \(\triangle A D B, D N \perp A B\)

In \(\triangle A N D \sim \triangle D N B, \frac{D N}{B N}=\frac{A N}{D N}\)

⇒ \(D N^2=B N \cdot A N\)

but B N=D M,

⇒ \(D N^2=D M \cdot A N\)

Hence Proved.

Question 3. Figure A B C is a triangle in which \(\angle A B C>90^{\circ}\) and \(A D \perp C B\) are produced. Prove that \(A C^2=A B^2+B C^2+2 B C \cdot B D\).

Solution :

An obtuse-angled triangle A B C in which \(\angle B\) is an obtuse angle and AD is perpendicular to produce C B,

To prove : \(A C^2=A B^2+B C^2+2 B C \times B D\)

Proof : \(\triangle A D C\) is the right triangle.

In \(\triangle A D C\), from Pythagoras theorem,

⇒ \(A C^2=A D^2+D C^2\)

⇒ \(A C^2=A D^2+(D B+B C)^2\) (D C=D B+B C)

⇒ \(A C^2=A D^2+D B^2+B C^2+2 D B \cdot B C\)

⇒ \(A C^2=\left(A D^2+D B^2\right)+B C^2+2 B C \cdot B D\)

⇒ \(A C^2=A B^2+B C^2+2 B C \cdot B D\)

Hence Proved.

Question 4. In figure, \(\triangle\)ABC is a triangle in which \(\angle\)ABC < 90° and AD \(\perp\) BC. Prove that AC² = AB² + BC² – 2BC • BD.

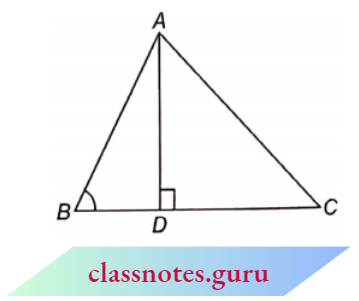
Solution:

Given: \(\triangle A B C\) is an acute-angled triangle and \(A D \perp B C\).

To prove: \(A C^2=A B^2+B C^2-2 B C \times B D\)

Proof: In \(\triangle A D C, \angle D=90^{\circ}\). So from Pythagoras theorem,

⇒ \(A C^2=\left(A D^2+B D^2\right)+B C^2-2 B C \times B D\)

⇒\(A C^2=A B^2+B C^2-2 B C \times B D\) (\(A D^2+B D^2=A B^2\))

Hence Proved.

Question 5. Figure AD is a median of a triangle ABC and AM \(\perp\) BC. Prove that

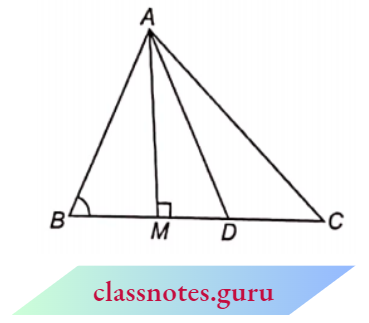
1. \(A C^2=A D^2+B C \cdot D M+\left(\frac{B C}{2}\right)^2 \)
2. \(A B^2=A D^2-B C \cdot D M+\left(\frac{B C}{2}\right)^2\)
3. \(A C^2+A B^2=2 A D^2+\frac{1}{2} B C^2\)

Solution:

⇒\(\triangle A B C\) is acute angled.

AD is a median.

B D=C D=\(\frac{1}{2} B C\)

AM is the altitude.

(1) In \(\triangle A C M\) ,

⇒ \(A C^2=A M^2+M C^2\)

⇒ \(A C^2=A M^2+(M D+C D)^2\)

= \(A M^2+M D^2+2 M D \cdot C D+C D^2\)

= \(\left(A M^2+D M^2\right)+(2 \cdot C D) \cdot D M+C D^2\)

= \(A D^2+(B C) \cdot D M+\left(\frac{1}{2} B C\right)^2\)

∴ \(A C^2=A D^2+B C \times D M+\frac{1}{4} B C^2\)

(2) In \(\triangle A B M\),

⇒ \(A B^2=A M^2+B M^2\)

= \(A M^2+(B D-D M)^2\)

= \(A M^2+B D^2+D M^2-2 B D \cdot D M\)

= \(A M^2+D M^2+\left(\frac{1}{2} B C\right)^2-B C \cdot D M\)

∴ \(A B^2 =A D^2-B C \times D M+\frac{1}{4} B C^2\)

Hence Proved.

(3) Adding equations (2) and (3),

⇒ \(A C^2+A B^2=2 A D^2+\frac{1}{2} B C^2\)

Hence Proved.

Question 6. Prove that the sum of the squares of the diagonals of a parallelogram is equal to the sum of the squares of its sides

Solution:

Draw DE \(\perp\) AB and CF perpendicular to produce AB.

In \(\triangle A E D\) and \(\triangle B F C\),

AD = B C (opposite sides of the parallelogram)

⇒ \(\angle D E A =\angle C F B\) (each \(90^{\circ}\))

D E =C F (perpendicular distance between two parallel lines)

⇒ \(\triangle A E D \cong \triangle B F C\)

An E=B F (corresponding parts of congruent triangles)

= \((A F^2+C F^2)+\left(D E^2+B E^2\right)\) (from Pythagoras theorem)

= \((A B+B F)^2+\left(B C^2-B F^2\right)+\left(A D^2-A E^2\right)+(A B-A E)\) (from Pythagoras theorem)

= \(A B^2+B F^2+2 A B \cdot B F+B C^2 -B F^2+A D^2-A E^2+A B^2+A E^2 -2 A B \cdot A E\)

= \(A B^2+2 A B \cdot A E+B C^2 +A D^2+C D^2-2 A B \cdot A E\)(A E=B F and A B=C D)

= \(A B^2+B C^2+C D^2+D A^2\)

Now, L.H.S. = \(A C^2+B D^2\)

Hence Proved.

Triangles Class 10 Exemplar Problems with Solutions

Question 7. In the figure, two chords AB and CD intersect each other at point p. Prove that :

1. \(\triangle A P C=\triangle D P B\)
2. \(A P \cdot P B=C P \cdot D P\)

Solution:

(1) In \(\triangle P^P C\) and \(\triangle D P B\),

⇒ \(\angle A P C=\angle D P B\) (vertically opposite angles)

⇒ \(\angle C A P=\angle B D P\) (angles of same segment)

⇒ \(\triangle A P C \sim \triangle D P B\) (from A.A. similarity)

Hence Proved.

(2) From part (1),

⇒ \(\triangle A P C \sim \triangle D P B \Rightarrow \frac{A P}{D P}=\frac{C P}{P B}\)

⇒ \(A P \cdot P B=C P \cdot D P\)

Hence Proved.

Question 8. In the figure, two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that

1. \(\triangle\)PAC – \(\triangle\)PDB
2. PA. PB = PC. PD

Solution:

(1) In \(\triangle P A C\) and \(\triangle P D B\),

⇒ \(\angle A P C =\angle D P B\) (common)

⇒ \(\angle P A C =180^{\circ}-\angle B A C\)

=\(\angle P D B\)

⇒ \(\Delta P A C \sim \triangle P D B\) (from A.A. similarity)

(2) \(\Delta P A C \sim \triangle P D B\)

⇒ \(\frac{A P}{D P} =\frac{P C}{P B}\)

⇒ \(P A \cdot P B =P C \cdot P D \)

Hence Proved.

Question 9. In the figure, D is a point on side BC of \(\triangle\) ABC such that \(\frac{B D}{C D}=\frac{A B}{A C}\). Prove that AD is the bisector of \(\angle\)BAC

Solution:

Produce BA to M such that

A M=A C

Join CM.

In \(\triangle M C\),

A M =A C

A C M =\(\angle A M C\) .

and \(\frac{B D}{C D}=\frac{A B}{A C}\)

⇒ \(\frac{B D}{C D}=\frac{B A}{A M}\) (given) from equation ( 1 ]

D A \\ C M

Now, \(\angle B A D=\angle A M C\) (corresponding angles)

and \(\angle D A C=\angle A C M\) (alternate angles)

From equations (2), (3) and (4)

⇒ \(\angle D A C=\angle B A D\)

A D bisects \(\angle B A C\).

Hence Proved.

Question 10. Nazima is fly Fishing in a stream. The tip of her fishing rod is 1.8 m above the surface of the water and the fly at the end of the string rests on the water 3.6 m away and 2.4 m from a point directly under the tip of the rod. Assuming that her string (from the tip of her rod to the fly) is taut, how much string does she have out (common) (see figure)? If she pulls in the string at the rate of 5 cm per second, what will be the horizontal distance of the fly from her after 12 seconds?

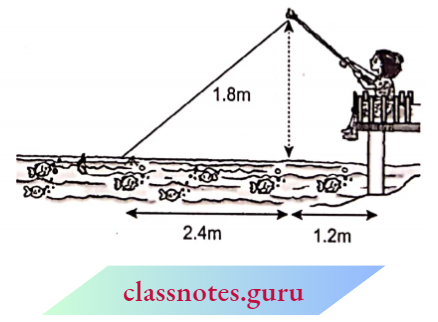
Solution:

Description of figure :

C → tip of fishing rod DC

AC string, AF → fly

The initial length of the string

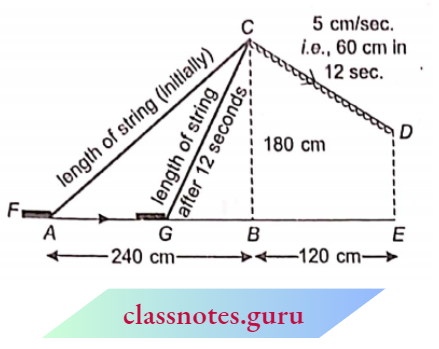
A C=\(\sqrt{(180)^2+(240)^2}\) (from Pythagoras theorem)

A C=\(\sqrt{32400+57600}\)

=300 cm

But, When Nazima pulls the string at the rate of 5 cm/sec, she pulls it 5 x 12 cm in 12 seconds.

So she pulls a 60 cm string from C to D. The remaining string CA will now CG – 300 – 60 = 240 cm because when the string pulls then its tip and fly both will move from A to G. So the horizontal distance of fly G from Nazima E will be EG.

Now, \([latex]G B^2= C G^2-C B^2\) (from Pythagoras theorem)

=\((240)^2-(180)^2\)

=57600-32400=25200

60 \(\times 2.64575\)=158.745 cm

Required distance =E G=G B+B E

=158.745+120

= 278.745 cm =2.79 m (approximately)

Chapter 6 Triangles NCERT Exemplar Questions

NCERT Exemplar Solutions For Class 10 Maths Chapter 6 Triangle Multiple Choice Question And Answers

Question 1. The length of the diagonals of a rhombus is 16 cm and 12 cm. The length of its side is :

1. 9 cm
2. 10 cm
3. 12 cm
4. 8 cm

Answer: 2. 10cm

Question 2. In \(\triangle A B C\) and \(\triangle P Q R\), \(\frac{A B}{Q R}=\frac{B C}{P R}=\frac{C A}{P Q}\), then

1. \(\triangle P Q R \sim \triangle C A B\)
2. \(\triangle P Q R \sim \triangle A B C\)
3. \(\triangle P Q R \sim \triangle C B A\)
4. \(\triangle P Q R \sim \triangle B C A\)

Answer: 1. \(\triangle P Q R \sim \triangle C A B\)

Question 3. Points D and E are on the sides AB and AC respectively of an \(\triangle\)ABC such that AD = 2 cm, BD = 3 cm, BC = 7.5 cm and DE || BC, then the length of DE is :

1. 2.5 cm
2. 3 cm
3. 5 cm
4. 6 cm

Answer: 2. 3cm

Question 4. In \(\triangle\)ABC and \(\triangle\)DEF, \(\angle\)A = \(\angle\)D, \(\angle\)F = \(\angle\)C and AB = 3DE then two triangles are :

1. congruent but not similar
2. similar but not congruent
3. neither congruent nor similar
4. congruent and similar both

Answer: 2. Similar but not congruent

Question 5. In \(\triangle\)ABC and \(\triangle\)DEF, \(\frac{A B}{D E}=\frac{B C}{F D}\)then these triangles will be similar if:

1. \(\angle B=\angle E\)
2. \(\angle A=\angle D\)
3. \(\angle B=\angle D\)
4. \(\angle A=\angle\)

Answer: 3. \(\angle B=\angle D\)

Question 6. S is a point on side PQ of \(\triangle P Q R\) such that P S=Q S=R S, then :

1. \(P Q \cdot Q R=R S^2\)
2. \(P R^2+Q R^2=P Q^2\)
3. \(Q S^2+R S^2=Q R^2\)
4. \(P S^2+R S^2=P R^2\)

Answer: 3. \(Q S^2+R S^2=Q R^2\)

Question 7. If \(\triangle\)ABC ~ \(\triangle\)PQR and BC = 5QR then ar(\(\triangle\)ABC) : ar(\(\triangle\)PQR) is :

1. 1: 25
2. 25: 1
3. 1: 5
4. 5: 1

Answer: 1. 1: 25

Question 8. The areas of two similar triangles are in the ratio 4: 9. The ratio on the sides of the triangle will be :

1. 2 : 3
2. 4: 9
3. 81: 16
4. 16: 81

Answer: 1. 2 : 3

NCERT Exemplar Class 10 Maths Triangles Exercise Solutions

Question 9. The side of an equilateral triangle is 2a. The length of each altitude will be :

1. \(a \sqrt{2}\)
2. \(2 a \sqrt{3}\)
3. \(a \sqrt{3}\)
4. 3a

Answer: 3. \(a \sqrt{3}\)

Question 10. The corresponding sides of two similar triangles are in the ratio 9:4. The ratio of the areas of these triangles will be :

1. 2 : 3
2. 4: 9
3. 81: 16
4. 16:81

Answer: 3. 81: 16

Question 11. the following figure, a line segment PQ is drawn parallel to base BC of \(\triangle\)ABC. If PQ: BC = 1 : 3 then the ratio ofAP and PB will be :

1. 1: 4
2. 1 : 3
3. 1: 2
4. 2 : 3

Answer: 3. 1: 2

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry

• Introduction: Co-ordinate geometry is the branch of mathematics in which geometry is studied algebraically, i.e., In which geometrical figures (as points, lines etc.) are studied using equations.
• Rene Descartes (1596-1665), a French mathematician was the first who introduced the Co-ordinate Geometry or Analytical Geometry or Cartesian Geometry.
• In class IX, we have studied how to locate the position of a point on a plane. Now, we will study to find the distance between two points, the section formula and the area of a triangle.

Distance Between Two Points

Let X’OX and Y’OY be coordinate axes. P and Q are two points in this cartesian plane with coordinates (X₁, Y₁) and (X₂, Y₂) respectively.

PL and QM are perpendiculars from P and Q respectively to the X-axis. PN is perpendicular from P to QM.

Now, O L =x₁, P L=y₁

O M =x₂, Q M=y₁

Coordinate Geometry Class 10 Important Questions with Solutions

Read and Learn More Class 10 Maths Solutions Exemplar

P N =L M

=O M-O L=x₂-x₁

P N=L M

and Q N =Q M-M N=Q M-P L

=y₂ – y₁

⇒ \(\triangle P Q N\) is a right-angled triangle.

⇒ \(P Q^2=P N^2+Q N^2\)

⇒ \(P Q^2=\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2\)

⇒ \(P Q=\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

Distance Between Origin And Point \(x_1, y_1\)

Distance between origin and point \(\left(x_1, y_1\right)=\sqrt{\left(x_1-0\right)^2+\left(y_1-0\right)^2}=\sqrt{x_1^2+y_1^2}\)

Condition Of Collinear Points On The Basis Of Distance

If the sum of any two distances is equal to the third distance, then the three points will be collinear.

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry Solved Examples

Example 1. Find the distance between the following points :

1. (3, 4) and (5, 2)
2. (0, 2) and (4, – 1)
3. (a, 2a) and (- a, – 2a)
4. (4, – 3) and (- 6, 5)

Solution.

(1) Distance between the points (3,4) and (5,2)

=\(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}=\sqrt{(5-3)^2+(2-4)^2}\)

=\(\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\) units

(2) Distance between the points (0,2) and (4,-1)

=\(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}=\sqrt{(4-0)^2+(-1-2)^2}\)

=\(\sqrt{(4)^2+(-3)^2}=\sqrt{16+9}=\sqrt{25}\)=5 units

(3) Distance between the points (n, 2a) and (-r,-2 a)

=\(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}=\sqrt{(-a-a)^2+(-2 a-2 a)^2}\)

=\(\sqrt{(-2 a)^2+(-4 a)^2}=\sqrt{4 a^2+16 a^2}=\sqrt{20 a^2}=2 \sqrt{5} a \)units

(4) Distance between the points (4,-3) and (-6,5)

=\(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}=\sqrt{(-6-4)^2+(5+3)^2}\)

=\(\sqrt{(-10)^2+(8)^2}=\sqrt{100+64}=\sqrt{164}=2 \sqrt{41}\)units

Example 2. Find the distance between the points (5, 8) and (- 3, 2).

Solution:

Distance between the points (5, 8) and (- 3, 2).

=\(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}=\sqrt{(-3-5)^2+(2-8)^2}\)

=\(\sqrt{(-8)^2+(-6)^2}=\sqrt{64+36}=\sqrt{100}\)=10 units

The distance between the points =10 units

Example 3. Find the distance of the point (a cos \(\theta\), a sin \(\theta\)) from the origin.

Solution:

Distance between the points {a cos \(\theta\), a sin θ) and origin (0, 0)

= \(\sqrt{(a \cos \theta-0)^2+(a \sin \theta-0)^2}\)

= \(\sqrt{a^2 \cos ^2 \theta+a^2 \sin ^2 \theta}=\sqrt{a^2\left(\cos ^2 \theta+\sin ^2 \theta\right)}\)

= \(\sqrt{a^2} (\cos ^2 \theta+\sin ^2 \theta=1)\)

= a units

The distance of the point = a units

Example 4. Find the distance of the point (3, 4) from the origin.

Solution:

Distance of the point (3, 4) to the origin

= \(\sqrt{(3-0)^2+(4-0)^2}=\sqrt{9+16}=\sqrt{25}\)=5 units

The distance of the point (3, 4) from the origin=5 units

Example 5. If the distance between the points (x, 2) and (6, 5) is 5 units, find the value of x.

Solution:

Distance between the points (x, 2) and (6, 5)

=\(\sqrt{(6-x)^2+(5-2)^2}=\sqrt{x^2-12 x+36+9}=\sqrt{x^2-12 x+45}\)

Given that, \(\sqrt{x^2-12 x+45}\)=5

⇒ \(x^2-12 x+45=25\)

⇒ \(x^2-12 x+20=0\)

⇒ \(x^2-2 x-10 x+20=0\)

x(x-2)-10(x-2)=0

(x-2)(x-10)=0

x-2=0 or x-10=0

x = 2 or x = 10

The value of x 2 or 10

Example 6. If the distances of P(x,y) from A(5, 1) and B(-1,5) are equal, then prove that 3x = 2y.

Solution:

Since P(x,y) is equidistant from A(5, 1) and B(-1, 5).

PA = PB

⇒ \(\sqrt{(x-5)^2+(y-1)^2}=\sqrt{(x+1)^2+(y-5)^2}\) (by using distance formula)

Squaring both sides, we get

⇒ \((x-5)^2+(y-1)^2=(x+1)^2+(y-5)^2\)

⇒ \(x^2-10 x+25+y^2-2 y+1=x^2+2 x+1+y^2-10 y+25\)

-10 x-2 y+26=2 x-10 y+26

-10 x-2 x=-10 y+2 y

12 x=8 y

3 x = 2 y

Hence Proved.

Example 7. Prove that the points (5, -2), (-4, 3) and (10, 7) are the vertices of an isosceles right-angled triangle.

Solution:

Given

(5, -2), (-4, 3) and (10, 7)

Let the points are A (5, – 2), B (- 4, 3) and C (10, 7).

Therefore,\(A B^2=(-4-5)^2+(3+2)^2=(-9)^2+(5)^2=81+25=106\)

⇒ \(B C^2=(10+4)^2+(7-3)^2=(14)^2+(4)^2\)=196+16=212

\(A C^2=(10-5)^2+(7+2)^2=(5)^2+(9)^2\)=25+81=106

A B=A C=\(\sqrt{106}\)

and \(A B^2+A C^2=B C^2\)

⇒ \(\triangle A B C\) is an isosceles right-angled triangle.

Hence Proved.

Example 8. Prove that the points (a, a),(-a,-a) and \((-a \sqrt{3}, a \sqrt{3})\) are the vertices of an equilateral triangle.

Solution:

Given

(a, a),(-a,-a) and \((-a \sqrt{3}, a \sqrt{3})\)

Let the points are A(a, a), B(-a,-a) and \(C(-a \sqrt{3}, a \sqrt{3})\).

A B=\(\sqrt{(-a-a)^2+(-a-a)^2}=\sqrt{(-2 a)^2+(-2 a)^2}\)

= \(\sqrt{4 a^2+4 a^2}=\sqrt{8 a^2}=2 \sqrt{2} a\)

B C=\(\sqrt{(-a \sqrt{3}+a)^2+(a \sqrt{3}+a)^2}\)

=\(\sqrt{3 a^2+a^2-2 \sqrt{3} a^2+3 a^2+a^2+2 \sqrt{3} a^2}=\sqrt{8 a^2}=2 \sqrt{2} a\)

C A=\(\sqrt{(-a \sqrt{3}-a)^2+(a \sqrt{3}-a)^2}\)

=\(\sqrt{3 a^2+a^2+2 \sqrt{3} a^2+3 a^2+a^2-2 \sqrt{3} a^2}\)

=\(\sqrt{8 a^2}=2 \sqrt{2} a\)

A B =B C = C A

∴ \(\triangle A B C\) is an equilateral triangle.

Hence Proved.

Example 9. Prove that the points (2, – 1), (4, 1), (2, 3) and (0, 1) are the vertices of a square.

Solution:

Given

(2, – 1), (4, 1), (2, 3) and (0, 1)

Let the points are A(2, – 1), B(4, 1), C(2, 3) and D(0, 1).

⇒ \(A B^2 =(4-2)^2+(1+1)^2=4+4=8\)

A B =\(\sqrt{8}=2 \sqrt{2}\)

⇒ \(B C^2 =(2-4)^2+(3-1)^2=(-2)^2+(2)^2\)=4+4=8

B C =\(\sqrt{8}=2 \sqrt{2}\)

⇒ \(C D^2 =(0-2)^2+(1-3)^2=(-2)^2+(-2)^2\)=4+4=8

C D =\(\sqrt{8}=2 \sqrt{2}\)

⇒ \(D A^2 =(2-0)^2+(-1-1)^2=(2)^2+(-2)^2\)=4+4=8

D A =\(\sqrt{8}=2 \sqrt{2}\)

Co-ordinate Geometry

⇒ \(A C^2 =(2-2)^2+(3+1)^2\)=0+16=16

A C =\(\sqrt{16}=4\)

and \(B D^2 =(0-4)^2+(1-1)^2=16+0=16\)

B D =\(\sqrt{16}=4\)

Now, A B=B C=C D=D A and A C=B D

⇒  A B C D is a square.

Example 10. Show that the points A(- 3, 3), B(7, – 2) and C(l, 1) are collinear.

Solution:

Given

A(- 3, 3), B(7, – 2) and C(l, 1)

A B =\(\sqrt{(7+3)^2+(-2-3)^2}=\sqrt{(10)^2+(-5)^2}\)

=\(\sqrt{100+25}=\sqrt{125}=5 \sqrt{5}\)

B C =\(\sqrt{(1-7)^2+(1+2)^2}=\sqrt{(-6)^2+(3)^2}\)

= \(\sqrt{36+9}=\sqrt{45}=3 \sqrt{5}\)

and \(A C =\sqrt{(1+3)^2+(1-3)^2}=\sqrt{(4)^2+(-2)^2}\)

= \(\sqrt{16+4}=\sqrt{20}=2 \sqrt{5}\)

Now, A C+B C=2 \(\sqrt{5}+3 \sqrt{5}=5 \sqrt{5}=A B\)

Points A, B and C are collinear.

Example 11. Show that the points (9, – 2), (- 5, 12) and (- 7, 10) lie on that circle whose centre is the point (1,4).

Solution:

Given

(9, – 2), (- 5, 12) and (- 7, 10)

Let the given points are A (9, -2), B (-5, 12) and C (- 7, 10),

If point‘O’is (1, 4), then

O A =\(\sqrt{(1-9)^2+(4+2)^2}=\sqrt{(-8)^2+(6)^2}\)

=\(\sqrt{64+36}=\sqrt{100}=10\)

O B =\(\sqrt{(1+5)^2+(4-12)^2}=\sqrt{(6)^2+(-8)^2}\)

= \(\sqrt{36+64}=\sqrt{100}=10\)

O C =\(\sqrt{(1+7)^2+(4-10)^2}=\sqrt{(8)^2+(-6)^2}\)

= \(\sqrt{64+36}=\sqrt{100}=10\)

OA = OB = OC

Point ‘O’ is equidistant from the points A, B and C.

Point (1,4) is the centre of that circle at which the points (9, -2), (-5, 12) and (- 7, 10) lie.

Hence Proved.

Example 12. In the given figure, \(\triangle\)ABC is an equilateral triangle of side 3 units. Find the coordinates of the other two vertices.

Solution:

Given

In the given figure, \(\triangle\)ABC is an equilateral triangle of side 3 units.

Since B is at a distance of 3 units from A on the X-axis in the positive direction, so B will be 5 units away from the origin.

So, B = (5, 0)

Let M be the mid-point of AB

⇒ \(A M=\frac{1}{2} A B=\frac{3}{2}\) units

AC = 3 Units

In right \(\triangle C M A\), by Pythagoras theorem

⇒ \(C M^2 =A C^2-\Lambda M^2\)

= \(9-\frac{9}{4}=\frac{27}{4}\)

⇒  \(C M =\sqrt{\frac{27}{4}}=\frac{3 \sqrt{3}}{2}\)

So, the coordinates of C are (O M, M C)

C=(O A+A M, M C) .

C=\(\left(2+\frac{3}{2}, \frac{3 \sqrt{3}}{2}\right)=\left(\frac{7}{2}, \frac{3 \sqrt{3}}{2}\right)\)

NCERT Exemplar Class 10 Maths Chapter 7 Solutions

Example 13. The coordinates of two vertices of an equilateral triangle are (0, 0) and (3,\(\sqrt{3}\)). Find the coordinates of the third vertex of the triangle.

Solution:

Given

The coordinates of two vertices of an equilateral triangle are (0, 0) and (3,\(\sqrt{3}\)).

Let the \(\triangle\) ABC be an equilateral triangle in which the coordinates of points B and C are (0, 0) and (3,3, \(\sqrt{3})\) respectively.

Let the coordinates of the third vertex A be (x,y).

In equilateral \(\triangle\)ABC

A B=A C=B C

⇒ \(A B^2=A C^2=B C^2\)

⇒ \(A B^2=A C^2\)

⇒ \((x-0)^2+(y-0)^2=(x-3)^2+(y-\sqrt{3})^2 \quad B(0,0)\)

⇒ \(x^2+y^2=x^2-6 x+9+y^2-2 \sqrt{3} y+3\)

⇒ \(6 x+2 \sqrt{3} y=12 \quad \Rightarrow \quad 3 x+\sqrt{3} y=6 \)

⇒ \(\sqrt{3} x+y=2 \sqrt{3} \quad y=2 \sqrt{3}-\sqrt{3} x\)

and \(A B^2=B C^2\)

⇒ \((x-0)^2+(y-0)^2=(3-0)^2+(\sqrt{3}-0)^2\)

⇒ \(x^2+y^2=9+3\)

⇒ \(x^2+(2 \sqrt{3}-\sqrt{3} x)^2=12\)

⇒ \(x^2+12+3 x^2-12 x=12\)

∴ \(4 x^2-12 x\)=0

4 x(x-3)=0

x=0 or x-3=0

x=0 or x=3

Put these values in eq. (1)

x=0, then y=2\( \sqrt{3}-0=2 \sqrt{3}\)

x=3 , y=2\( \sqrt{3}-3 \sqrt{3}=-\sqrt{3}\)

Co-ordinates of third vertex =(0,2 \(\sqrt{3}\)) or (\(3,-\sqrt{3})\)

Example 14. What point on the X-axis is equidistant from (7, 6) and (-3, 4)?

Solution:

Given

(7, 6) and (-3, 4)

We know that the y-co-ordinate of a point on the X-axis is always 0. So, let a point on the X-axis be P(x, 0) and let two given points be A(7, 6) and B(-3, 4).

According to the condition,

P A=P B

⇒ \( \sqrt{(x-7)^2+(0-6)^2}=\sqrt{(x+3)^2+(0-4)^2}\)

Squaring both sides, we have

⇒ \(x^2-14 x+49+36 =x^2+6 x+9+16\)

Required point is (3,0) 20 x =60 \(\Rightarrow x=3\)

Example 15. Find the equation of the set of all points which are twice as far from (3, 2) as from (1, 1).

Solution:

Given

(3, 2) and (1, 1)

Let P(x,y) be a point and let A(3, 2) and B = (1, 1) be two other points on the plane, such that

P A=2 P B

⇒ \(\sqrt{(x-3)^2+(y-2)^2}=2 \sqrt{(x-1)^2+(y-1)^2}\)

Squaring both sides, we have

⇒ \(x^2-6 x+9+y^2-4 y+4=4\left(x^2-2 x+1+y^2-2 y+1\right)\)

∴ \(3 x^2+3 y^2-2 x-4 y-5=0\) Which is the required equation.

Example 16. If A(2, 2), B(-2, -2), C(-2\(\sqrt{3}\),2\(\sqrt{3}\)) and D(-4 – 2\(\sqrt{3}\),4 + 2\(\sqrt{3}\)) are the co-ordinates of 4 points. What can be said about these four points?

Solution:

Given

(2, 2), B(-2, -2), C(-2\(\sqrt{3}\),2\(\sqrt{3}\)) and D(-4 – 2\(\sqrt{3}\),4 + 2\(\sqrt{3}\)) are the co-ordinates of 4 points.

A B=\(\sqrt{(-2-2)^2+(-2-2)^2}=4 \sqrt{2}\) units .

B C=\(\sqrt{(-2+2 \sqrt{3})^2+(-2-2 \sqrt{3})^2}\)

=\(\sqrt{4+12-8 \sqrt{3}+4+12+8 \sqrt{3}}=4 \sqrt{2}\) units

C D=\(\sqrt{(-2 \sqrt{3}+4+2 \sqrt{3})^2+(2 \sqrt{3}-4-2 \sqrt{3})^2}\)

= \(\sqrt{16+16}=4 \sqrt{2}\) units

A C=\(\sqrt{(2+2 \sqrt{3})^2+(2-2 \sqrt{3})^2}\)

=\(\sqrt{4+12+8 \sqrt{3}+4+12-8 \sqrt{3}}=4 \sqrt{2}\) units

A D=\(\sqrt{(2+4+2 \sqrt{3})^2+(2-4-2 \sqrt{3})^2}\)

=\(\sqrt{36+12+24 \sqrt{3}+12+4+8 \sqrt{3}}=\sqrt{64+32 \sqrt{3}}\) units

B D=\(\sqrt{(-2+4+2 \sqrt{3})^2+(-2-4-2 \sqrt{3})^2}\)

=\(\sqrt{4+12+8 \sqrt{3}+36+12+24 \sqrt{3}}=\sqrt{64+32 \sqrt{3}}\) units

Here, AB = BC = CD = AC and also, AD = BD

So, in first view, it seems to be the vertices of a square.

(But),Here, AB, BC, CD and DA are not equal, (the order of A, B, C and D must be cyclic in the case of the square).

Also, AD and BD are equal but they cannot be diagonals. So, they do not form a square. Actually, A, B and D lie on a circle with C as the centre (as CA = CB = CD i.e., C is equidistant from A, B and D).

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry – To Divide A Line Segment In a Given Ratio

Internal Division

The coordinates of a point which divides the line segment joining the points A(x₁,y₁) and B(x₂,y₂) in the ratio m: n internally are

⇒ \(\left(\frac{m x_2+n x_1}{m+n}, \frac{m y_2+n y_1}{m+n}\right)\)

Proof: Let X’OX and Y’OYare the coordinate axes and A (x₁,y₁) and B (x₂,y₂) be any two points in this cartesian plane. Let P(x,y) be any point on line segment AB which divides AB in the ratio m: n.

⇒ \(\frac{A P}{B P}=\frac{m}{n}\)

AL, PN and BM are perpendiculars from, P and B respectively on X-axis.

AH and PIC are perpendiculars from and P respectively to PN and BM.

Now, OL = x₁, OM = x₂, ON = x

AL = y₁, BM = y₂> PN =y

AH = LN = ON -OL=x-x

PH = PN – NH = PN – AL =y -y₁

Pk = NM = OM – ON =x₂-x

and BIC = BM – ICM = BM – PN =y₂ -y

Here, \(\triangle\)AHP and \(\triangle\)PKB are similar.

⇒  \(\frac{A H}{P K}=\frac{P H}{B K} =\frac{A P}{P B}\)

⇒  \(\frac{x-x_1}{x_2-x}=\frac{y-y_1}{y_2-y}=\frac{m}{n}\)

⇒  \(\frac{x-x_1}{x_2-x} =\frac{m}{n}\) and \(\frac{y-y_1}{y_2-y}=\frac{m}{n}\)

⇒  \(\frac{x-x_1}{x_2-x} =\frac{m}{n} \quad \Rightarrow \quad n x-n x_1=m x_2-m x\)

⇒  \(m x+n x =m x_2+n x_1 \quad \Rightarrow \quad(m+n) x=m x_2+n x_1\)

x =\(\frac{m x_2+n x_1}{m+n}\)

Similarly,\(\frac{y-y_1}{y_2-y}=\frac{m}{n} \quad \Rightarrow \quad n y-n y_1=m y_2-m y\)

⇒  \(m y+n y=m y_2+n y_1 \quad \Rightarrow \quad(m+n) y=m y_2+n y_1\)

y=\(\frac{m y_2+n y_1}{m+n}\)

Therefore, the co-ordinates of point P=\(\left(\frac{m x_2+m x_1}{m+n}, \frac{m y_2+m y_1}{m+n}\right)\)

Co-ordinates of the Mid-point of a Line Segment

The co-ordinates of the mid-point of the line segment joining the points A(x₁,y₁) and (x₂,y₂) are \(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

Proof: Let P (x, y) be the mid-point of the line joining the points A (x₁,y₁) and B (x₂, y₂)

Ap : PB = 1:1

x =\(\frac{1\left(x_2\right)+1\left(x_1\right)}{1+1}=\frac{x_1+x_2}{2}\)

y =\(\frac{1\left(y_2\right)+1\left(y_1\right)}{1+1}=\frac{y_1+y_2}{2}\)

Co-ordinates of point P =\(\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)\)

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry – To Divide A Line Segment In a Given Ratio Solved Examples

Example 1. Find the coordinates of a point which divides the line segment joining the points (5, 1) and (-10, 11) in the ratio 2 : 3 internally.

Solution:

Given

(5, 1) and (-10, 11)

Let the coordinates of the required point he (x,y).

Here, \(\quad\left(x_1, y_1\right)=(5,1)\) and \(\left(x_2, y_2\right)=(-10,11)\)

and \(\left(x_1, y_1\right)\) =(5,1) and \(\quad\left(x_2, y_2\right)=(-10,11)\)

m: n = 2: 3

x =\(\frac{m x_2+n x_1}{m+n}=\frac{2(-10)+3(5)}{2+3}=\frac{-20+15}{5}=\frac{-5}{5}=-1\)

y =\(\frac{m y_2+n y_1}{m+n}=\frac{2(11)+3(1)}{2+3}=\frac{22+3}{5}=\frac{25}{5}=5\)

Co-ordinates of required point =(-1,5)

Example 2. Suppose point P lies on the line segment joining points A{-3, 4) and B(- 2, – 6) such that 2AP=3BP then, find the coordinates of point P.

Solution:

A{-3, 4) and B(- 2, – 6) such that 2AP=3BP

Given That, 2 AP = 3 BP

⇒  \(\frac{A P}{B P}=\frac{3}{2}\)

m : n = 3 : 2

(x₁, y₁) = (- 3, 4) and (x₂,y₂) = (-2,- 6)

Now, let the coordinates of point P are (x,y)

x=\(\frac{3(-2)+2(-3)}{3+2}=\frac{-12}{5}\)

and y=\(\frac{3(-6)+2(4)}{3+2}=-2\)

Co-ordinates of point P=\(\left(\frac{-12}{5},-2\right)\)

Example 3. Find the co-ordinates of the mid-point of the line segment joining the points A(3, -5) and B(1, 1 )

Solution:

Co-ordinates of the mid-point of AB = \((-1 + 3 5 + (-1)^ \left(\frac{3+1}{2}, \frac{-5+1}{2}\right)=(2,-2)\)

Example 4. The coordinates of the endpoints of a diameter are (-1, 5) and (3, -1). Find the coordinates of the centre and the radius of the circle.

Solution:

Given

The coordinates of the endpoints of a diameter are (-1, 5) and (3, -1).

Let the coordinates of the end points of diameter AB be A (-1, 5) and .8 (3, -1).

Co-ordinates of the centre P = Co-ordinates of mid-point of AB

= \(\left(\frac{-1+3}{2}, \frac{5+(-1)}{2}\right)=(1,2)\)

and radius of circle = length of P A

= \(\sqrt{(1+1)^2+(2-5)^2}=\sqrt{4+9}=\sqrt{13}\) units

Example 5. The coordinates of the mid-point of the line joining the points A and B are (2, -3). If the coordinates of point A are (-3, 4), then find the coordinates of point B.

Solution:

Given

The coordinates of the mid-point of the line joining the points A and B are (2, -3). If the coordinates of point A are (-3, 4),

Let the co-ordinates of point B=\(\left(x_2, y_2\right)\)

Given that,\(\frac{-3+x_2}{2}=2 \quad \Rightarrow \quad-3+x_2=4\)

⇒ \(x_2=7\) and \(\frac{4+y_2}{2}=-3\)

4+y_2=\(-6 \quad \Rightarrow \quad y_2=-10\)

Co-ordinates of point B=(7,-10)

Example 6. Find the ratio in which the X-axis divides the line segment joining the points (8, 5) and (-3,-7).

Solution:

Let the X-axis divide the join of points (8, 5) and (- 3, – 7) in the ratio k: 1.

We know that at X-axis

y = 0

⇒ \(\frac{k \cdot y_2+1 \cdot y_1}{k+1} =0\)

⇒ \(\frac{k(-7)+1(5)}{k+1}\) =0

-7 k+5 =0

k = \(\frac{5}{7}\)

Required ratio =5: 7

Class 10 Coordinate Geometry NCERT Exemplar Book Solutions

Example 7. In what ratio does the point \(\left(\frac{24}{11}, y\right)\) divide the line segment joining the points P(2,-2) and Q(3, 7)? Also, find the value of y.

Solution:

Let \(M\left(\frac{24}{11}, y\right)\) divide the line segment joining the points.

P(2,-2) and Q(3,7) in the ratio k: 1.

⇒ \(\frac{24}{11}=\frac{k(3)+1(2)}{k+1}\) (by using section formula)

⇒ \(11(3 k+2)=24(k+1) \quad \Rightarrow \quad 33 k+22=24 k+24\)

33 k-24 k=24-22 \(\quad \Rightarrow \quad 9 k=2\)

⇒ \(k=\frac{2}{9}\)

Required ratio =k: 1

i.e.,\(\frac{2}{9}: 1\)

i.e.,2: 9 internally.

Required ratio = 2:9

Example 8. The co-ordinates of the vertices of \(\triangle\)ABC are A(3, 2), B( 1, 4) and C(-1, 0). Find the length of the median drawn from point A.

Solution:

Given

The co-ordinates of the vertices of \(\triangle\)ABC are A(3, 2), B( 1, 4) and C(-1, 0).

Let AP be the median drawn from vertex A.

The midpoint of BC is P.

Now, the coordinates of P

=\(\left(\frac{1+(-1)}{2}, \frac{4+0}{2}\right)=(0,2)\)

A P =\(\sqrt{(3-0)^2+(2-2)^2}\)

=\(\sqrt{9+0}=3 units\)

Example 9. Find the coordinates of the points of trisection of the line joining the points (3, -2) and (-3, -4).

Solution:

Let P (a, b) and Q (c, d) trisect the line joining the points A(3, -2) and B(-3, -4).

Now, point P (a, b) divides the line AB in the ratio 1:2

a =\(\frac{1(-3)+2(3)}{1+2}=\frac{3}{3}=1\)

b =\(\frac{1(-4)+2(-2)}{1+2}=-\frac{8}{3}\)

Therefore, coordinates of point P=\(\left(1,-\frac{8}{3}\right)\)

Q(c, d) divides the line A B in the ratio 2: 1.

c=\(\frac{2(-3)+1(3)}{2+1}=-1\)

d=\(\frac{2(-4)+1(-2)}{2+1}=\frac{-10}{3}\)

Therefore, co-ordinates of Q=\(\left(-1, \frac{-10}{3}\right)\)

Co-ordinates of points of trisection of A B=\(\left(1, \frac{-8}{3}\right) and \left(-1, \frac{-10}{3}\right)\)

Example 10. If two adjacent vertices of a parallelogram are (3, 2) and (-1, 0) and telagona intersect at (2, -5), then find the coordinates of the other two vertices.

Solution:

Given

Two adjacent vertices of a parallelogram are (3, 2) and (-1, 0) and telagona intersect at (2, -5)

Let two adjacent vertices of a parallelogram be A = (3, 2) and B(-1,0).

Let the coordinates of the other two vertices be C(X₁, y₁) and D(x₂, y₂)

We know that diagonals of a parallelogram bisect each other.

Mid-point of AC and the mid-point of BD are the same i.e., point O(2, -5).

⇒ \(\frac{3+x_1}{2}=2 and \frac{2+y_1}{2}\)=-5

⇒ \(x_1=1 and y_1=-12 \Rightarrow C \equiv\left(x_1, y_1\right) \equiv(1,-12)\)

Also, \(\frac{x_2-1}{2}=2 and \frac{y_2+0}{2}=-5\)

x₂=5 and y₂=-10 ⇒ D = (5,-10)

Hence, the remaining vertices are (1,-12) and (5,-10).

Example 11. The coordinates of three consecutive vertices of a parallelogram are (-1,0), (3, 1) and (2, 2). Find the coordinates of the fourth vertex of the parallelogram.

Solution:

Given

The coordinates of three consecutive vertices of a parallelogram are (-1,0), (3, 1) and (2, 2).

Let A(-1, 0), B (3, 1), C (2, 2) and D (x,y) be the vertices of a parallelogram ABCD.

We know that the diagonals of a parallelogram bisect each other.

Co-ordinates of the mid-point of AC = Co-ordinates of the mid-point of BD.

⇒  \(\left(\frac{-1+2}{2}, \frac{0+2}{2}\right)=\left(\frac{3+x}{2}, \frac{1+y}{2}\right)\)

⇒ \(\left(\frac{1}{2}, 1\right)=\left(\frac{3+x}{2}, \frac{1+y}{2}\right)\)

⇒ \(\frac{1}{2}=\frac{3+x}{2} and \quad 1=\frac{1+y}{2}\)

1=3+x and 2=1+y

x=-2 and y=1

Co-ordinates of fourth vertex =(-2,1)

Example 12. In which ratio the line y-x+2 = 0 Divides the line segment joining the points (3, -1) and (8,9)

Solution:

Let the ratio the line y-x+2 = 0 Divides the line segment joining the points (3, -1) and (8,9) in the ratio k: 1

Co-ordinates of P \(\equiv\left(\frac{8 k+3}{k+1}, \frac{9 k-1}{k+1}\right)\)

but this point P lies on the line y-x+2=0

⇒\(\frac{9 k-1}{k+1}-\frac{8 k+3}{k+1}+2\) =0

9 k-1-8 k-3+2 k+2 =0

3 k =2

k =\(\frac{2}{3}\)

Required ratio =\(\frac{2}{3}: 1=2: 3\)

Example 13. Find a point on the line through A{5, – 4) and B(-3, 2), that is, twice as far from A as from B.

Solution:

Given

A{5, – 4) and B(-3, 2)

Let P(x,y) be a point on AB such that

PA = 2PB

P A=2 P B

⇒  \(\frac{P A}{P B}=\frac{2}{1} \quad \Rightarrow \quad P A: P B=2: 1\)

So, by using the section formula for internal division,

x=\(\frac{m x_2+n x_1}{m+n}, y=\frac{m y_2+n y_1}{m+n}\)

x=\(\frac{2(-3)+1(5)}{2+1} \quad \Rightarrow \quad x=-\frac{1}{3}\)

and y=\(\frac{2(2)+1(-4)}{2+1} \Rightarrow \quad y=0\)

Required point =\(\left(-\frac{1}{3}, 0\right)\)

But, This is not the end of this question.

Think: Is it not possible that P(x, y) divides AB externally in the ratio 2: 1?

So, by using the section formula for external division,

x=\(\frac{2(-3)-1(5)}{2-1} \quad \Rightarrow x=-\frac{11}{1} \quad \Rightarrow \quad x=-11\)

and \( y=\frac{2(2)-1(-4)}{2-1} \Rightarrow y=\frac{8}{1} \quad \Rightarrow \quad y=8\)

So, the coordinates of p are (-11,8) also.

Hence, required points are \(\left(-\frac{1}{3}, 0\right)\) and (-11,8).

Example 14. Find the centroid of the triangle whose vertices are A(-1, 0), B{5, -2) and C(8, 2).

Solution:

Given

A(-1, 0), B{5, -2) and C(8, 2)

Centroid, the point where the medians of a triangle intersect, divides each median in the ratio 2: 1. Let AD be the median and G{x,y) be the centroid of \(\triangle\)ABC.

D is the mid-point of BC

D =\(\left(\frac{5+8}{2}, \frac{-2+2}{0}\right)\) (mid-point formula)

=\(\left(\frac{13}{2}, 0\right)\)

Now, G(x, y) divides the line segment joining A(-1,0) and \(D(\frac{13}{2}\), 0) internally in the ratio 2: 1.

So, by using section formula,

x=\(\frac{2\left(\frac{13}{2}\right)+1(-1)}{2+1} \quad \Rightarrow \quad x=4\)

y=\(\frac{2(0)+1(0)}{2+1} \quad \Rightarrow \quad y=0\)

and Centroid of \(\triangle A B C\)=(4,0)

Example 15. A line intersects the Y-axis and X-axis at points P and Q respectively. If (2, -5) is the mid-point of PQ, then find the coordinates of P and Q.

Solution:

Given

A line intersects the Y-axis and X-axis at points P and Q respectively. If (2, -5) is the mid-point of PQ

We know that at Y-axis, the x-coordinate is zero and at X-axis, y-coordinate is zero.

So, let P = (0,y)

and Q = (x, 0)

Since M(2, -5) is the mid-point of PQ.

By using the mid-point formula,

\(\frac{0+x}{2} =2, \quad \frac{y+0}{2}\)=-5

x =4, y=-10

P = (0,-10) and Q=(4,0)

Example 16. Point P(h, k) divides a line segment between the axes in the ratio 1: 2. Find the lengths (intercepts) on the axes made by this line segment. Also, find the area of the triangle formed by the line segment and the axes.

Solution:

Given

Point P(h, k) divides a line segment between the axes in the ratio 1: 2.

Let AB be the line segment joining A (0,y) and B(x, 0) between the axes.

P(h, k) divides the line segment in the ratio 1: 2.

Now, question arises that whether PA : PB = 1 : 2 or PB : PA = 1:2

The answer is that we always take the former part of the ratio towards the X-axis and the latter part of the ratio towards the Y-axis.

So, here we will take PB: PA = 1: 2

By using the section formula,

h=\(\frac{1(0)+2(x)}{1+2} \Rightarrow h=\frac{2 x}{3} \quad \Rightarrow \quad x=\frac{3 h}{2}\)

and k=\(\frac{1(y)+2(0)}{1+2} \Rightarrow k=\frac{y}{3} \Rightarrow y\)=3 k

So, length of intercept on the X-axis =O B=x=\(\frac{3 h t}{2}\)

and the length of intercept on the Y-axis =O A=y=3 k.

Area of \(\triangle A O B=\frac{1}{2} \times O B \times O A=\frac{1}{2} \times \frac{3 h}{2} \times 3 k=\frac{9}{4}\) hk square units

Class 10 Coordinate Geometry Extra Questions

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry -Area Of Triangle:

If the coordinates of the vertices of a triangle are [x₁,y₁), (x₂,y₂) and (x₃,y₃), then the area of a triangle (A) is given by

⇒ \(\Delta=\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]\)

or \(\Delta=\frac{1}{2}\left[\left(x_1 y_2+x_2 y_3+x_3 y_1\right)-\left(x_2 y_1+x_3 y_2+x_1 y_3\right)\right]\)

Proof: Let X’OX and Y’OY be co-ordinate axes.

Let the co-ordinates of the vertices of \(\triangle\)ABC are A (x₁,y₁), B (x₂,y₂) and C (x₃,y₃). Draw the 1 perpendicular AM, BN and CL from A, B and C. Y-axis.

□ ALMLC, □ CLNB and □ AMNB are trapezium.

Now, the Area of AABC

= Area of □ AMLC + Area of □ CLNB – Area of □ AMNB

= \(\frac{1}{2}(A M+L C) \times M L+\frac{1}{2}(C L+B N) \times L N-\frac{1}{2}(A M+B N) \times M N\)

=\(\frac{1}{2}\left(y_1+y_3\right)\left(x_3-x_1\right)+\frac{1}{2}\left(y_3+y_2\right)\left(x_2-x_3\right)-\frac{1}{2}\left(y_1+y_2\right)\left(x_2-x_1\right)\)

= \(\frac{1}{2}\left[\left(y_1+y_3\right)\left(x_3-x_1\right)+\left(y_3+y_2\right)\left(x_2-x_3\right)-\left(y_1+y_2\right)\left(x_2-x_1\right)\right]\)

=\(\frac{1}{2}\left[y_1 x_3-y_1 x_1+y_3 x_3-y_3 x_1+y_3 x_2-y_3 x_3+y_2 x_2-y_2 x_3-y_1 x_2+y_1 x_1-y_2 x_2+y_2 x_1\right] \)

=\(\frac{1}{2}\left[x_1 y_2-x_1 y_3+x_2 y_3-x_2 y_1+x_3 y_1-x_3 y_2\right]\)

=\(\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]\)

=\(\frac{1}{2}\left[\left(x_1 y_2+x_2 y_3+x_3 y_1\right)-\left(x_2 y_1+x_3 y_2+x_1 y_3\right)\right]\)

If the area of a triangle is negative then we neglect the negative sign, because the area of a triangle is always positive.

If it is given that the area of a triangle is 10 then it will be taken ± 10 for calculations to evaluate the value (s) of unknown terms.

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry – Collinear Points

Three points A (x₁, y₁ )B (x₂,y₂) and C (x₃, y₃) are collinear if Area of \(\triangle\)ABC = 0

Note: If the order of description of the boundary is anticlockwise, then the area is considered to be positive, but if the order of description is clockwise, then the area is considered to be negative.

Remark: To move from A to 6 and then from B to C, we are moving in a clockwise direction. So the above area comes out to be negative.

Now, if we take the points in an anticlockwise direction, as A(2,1), C(6,3) and B(4,5) then

area =\(\frac{1}{2}[2(3-5)+6(5-1)+4(1-3)]\)

= \(\frac{1}{2}(-4+24-8)\)=+6 square units.

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry – Collinear Points Solved Examples

Example 1. Find the area of the triangle, whose vertices are (2,1), (4,5) and (6, 3).

Solution:

Given

Vertices are (2,1), (4,5) and (6, 3)

Area of triangle = \(\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]\)

= \(\frac{1}{2}[2(5-3)+4(3-1)+6(1-5)]=\frac{1}{2}(4+8-24)\)=-6

But the area of a triangle cannot be negative

Area of triangle = 6 square units

Example 2. Find the area of a triangle, whose vertices are (2, 3), (7, 5) and (-7, -5).

Solution:

Given

Vertices are (2, 3), (7, 5) and (-7, -5)

• Area of triangle = =\(\frac{1}{2}[x_1(y_2-y_3)+x_2(y_3-y_1)+x_3(y_1-y_2)\)]
• = \(\frac{1}{2}[2(5+5)+7(-5-3)-7(3-5)]=\frac{1}{2}(20-56+14)\)=-11
• But the area of a triangle cannot be negative
• Area of triangle = 11 square units

Example 3. Find the area of the triangle, whose vertices are (a, c +a), (a,c) and (-a, c, -b).

Solution:

Given

Vertices are (a, c +a), (a,c) and (-a, c, -b)

• Area of triangle =\(\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]\)
• = \(\frac{1}{2}[a(c-c+a)+a(c-a-c-a)-a(c+a-c)]\)
• = \(\frac{1}{n}\left[a^2-2 a^2-a^2\right]=-a^2\)
• But the area of a triangle cannot be negative
• Area of triangle = \(a^2\) square units

Example 4. Prove that the points (6, 4) (4, 5) and (2, 6) are collinear.

Solution:

Given

(6, 4) (4, 5) and (2, 6)

Area of triangle = \(\frac{1}{2}\left[x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right]\)

⇒  \(\frac{1}{2}[6(5-6)+4(6-4)+2(4-5)]=\frac{1}{2}[-6+8-2]=0\)

Therefore, the given points are collinear.

Example 5. If the points A{x,y), B( 1, 4) and C(-2, 5) are collinear, then show that x + 3y = 13.

Solution:

Given points are collinear

Area of triangle = 0

⇒ \(\frac{1}{2}[x(4-5)+1(5-y)-2(y-4)]\) =0

-x+5-y-2 y+8 =0

x+3 y =13

Example 6. For what value of T, the points (k, 1), (1,-1) and (11,4) are collinear?

Solution:

The given points will be collinear if the area of the triangle = 0

⇒ \(\frac{1}{2}[k(-1-4)+1(4-1)+11(1+1)]\) =0

-5 k+3+22 =0

5 k =25

k =5

Example 7. If a \(\neq\) b \(\neq 0\), prove that the points \(\left(a, a^2\right),\left(b, b^2\right)\),(0,0) will not be collinear.

Solution:

Let the 3 points A=\(\left(a, a^2\right), B=\left(b, b^2\right)\) and C=(0,0) form a triangle ABC.

Area of triangle A B C = \(\frac{1}{2}\left|a\left(b^2-0\right)+b\left(0-a^2\right)+0\left(a^2-b^2\right)\right|\)

= \(\frac{1}{2}\left[a b^2-a^2 b\right]=\frac{1}{2} a b(b-a) \neq 0\)

Since a\((\triangle A B C) \neq 0\).

So, \(\triangle A B C\) will be formed.

Therefore 3 points A, B and C will not be collinear.

Hence Proved.

Example 8. If (x,y) is any point on the line segment joining the points (a, 0) and (0, b), then prove that \(\frac{x}{a}+\frac{y}{b}\)=1

Solution:

Given three points are collinear

Area of \(\triangle\)=0

⇒ \(\frac{1}{2}|x(0-b)+u(b-y)+0(y-0)|\)=0

-bx + ab – ay=0

Divide both sides by ab

–\(\frac{x}{a}+1-\frac{y}{b}=0 \quad \Rightarrow \quad \frac{x}{a}+\frac{y}{b}\)=1

Example 9. If P be a point equidistant from points A(3, 4) and B( 5, -2) and area \(\triangle\)PAB is 10 square units, then find the coordinates of point P.

Solution:

Let the coordinates of point P be (x,y).

Now, PA = PB

⇒ \(\sqrt{(x-3)^2+(y-4)^2}=\sqrt{(x-5)^2+(y+2)^2}\)

⇒ \(x^2+9-6 x+y^2+16-8 y=x^2+25-10 x+y^2+4+4 y^{\prime}\)

4 x-12 y=4

x-3 y=1  → Equation 1

and area of Δ=10

⇒ \(\frac{1}{2}[x(4+2)+3(-2-y)+5(y-4)]= \pm 10\)

⇒ \(6 r-6-3 y+5 y-20= \pm 20\)

6x + 2y – 26= \(\pm\) 20

6 x+2 y-26=20 or 6 x+2 y-26=-20

3 r+y=23  → Equation 2

or 3 r+y=3  →  Equation 3

From eqs. (1) and (2) From eqs. (1) and (3)

x=7, y=2 , x=1, y=0

Required co-ordinates =(7,2) or (1,0)

Coordinate Geometry Chapter Class 10 Exemplar

Example 10. The area of a triangle is 5 sq. units. Two of its vertices are (2, 1) and (3, -2). If the third vertex is \(\left(\frac{7}{2}, y\right)\), find the value of y.

Solution :

Area of a \(\triangle A B C\)=5 sq units (given)

⇒ \(\frac{1}{2}\left|2(-2-y)+3(y-1)+\frac{7}{2}(1+2)\right|=5\)

⇒ \(\left|-4-2 y+3 y-3+\frac{21}{2}\right|=10\)

⇒ \(y+\frac{7}{2}= \pm 10\)

⇒ \(y+\frac{7}{2}=10\)

y=\(10-\frac{1}{7}\)or \(y=-10-\frac{1}{7}\)

y=\(\frac{13}{2}\) or y=\(-\frac{27}{2}\)

Hence, the value of y can be \(\frac{13}{2}\) and \(-\frac{27}{2}\).

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry Miscellaneous Examples

Example 1. If the point P(k – 1, 2) is equidistant from the points A(3, K) and B(k, 5), find the values of k.

Solution:

Given that. P A=P B

⇒ \((k-1-3)^2+(2-k)^2=(k-1-k)^2+(2-5)^2\)

⇒ \((k-4)^2+(2-k)^2=(-1)^2+(-3)^2\)

⇒ \(k^2-8 k+16+4+k^2-4 k=1+9\)

⇒ \(2 k^2-12 k+10=0\)

⇒ \(k^2-6 k+5=0\)

⇒ \(k^2-5 k-k+5=0\)

⇒ \(k(k-5)-1(k-5)=0\)

(k-5)(k-1)=0

k-5=0 or k-1=0

k=5 or k=1

The values of k is 5 or 1.

Example 2. Find the point on X-axis which is equidistant from the points (5, -2) and (-3, 2).

Solution:

Let the required point on the X-axis be P(x, 0) and the given points be (5, -2) and B(—3, 2).

Now, given that

P A =P B

⇒ \(P A^2=P B^2\)

⇒ \((x-5)^2+(0+2)^2 =(x+3)^2+(0-2)^2\)

⇒ \(x^2-10 x+25+4 =x^2+6 x+9+4\)

-16 x =-\(16 \quad \Rightarrow x\)=1

The required point is (1, 0).

Example 3. Points and B(5, 7) lie on a circle uadi centre 0(2, -3y). Find the values of y. Hence, find the die radius of the die circle.

Solution:

Given

Points and B(5, 7) lie on a circle uadi centre 0(2, -3y).

Here, OA = OB (radii of a circle)

O A =O B

O A² =O B²

⇒ \((2+1)^2+(-3 y-y)^2=(2-5)^2+(-3 y-7)^2\)

⇒ \(9+16 y^2=9+9 y^2+42 y+49\)

⇒ \(7 y^2-42 y-49=0\)

⇒ \(y^2-6 y-7=0\)

⇒ \(y^2-7 y+y-7=0\)

⇒ y(y-7)+1(y-7)=0

⇒ y-7=0 or y+1=0

y=7 or y=-1

Now, the co-ordinates of centre O are either (2, -21) or (2, 3) when the centre is 0(2, -21), then radius = OB

= \(\sqrt{(2-5)^2+(-21-7)^2}\)

= \(\sqrt{9+784}=\sqrt{793}\) units

When centre is 0(2, 3), then

radius = OB

= \(\sqrt{(2-5)^2+(3-7)^2}\)

= \(\sqrt{9+16}=\sqrt{25}\)=5 units

The die radius of the die circle =5 units

Example 4. The points A(-1, 7), B{p, 3) and C(7, 3) are the vertices of a right triangle, right-angled at B. Find the value of p.

Solution:

Given

The points A(-1, 7), B{p, 3) and C(7, 3) are the vertices of a right triangle, right-angled at B.

In \(\triangle\)ABC

⇒ \(\angle\)B = 90°

⇒ \(A B^2+B C^2=A C^2\)

⇒ \((p-4)^2+(3-7)^2+(p-7)^2+(3-3)^2=(7-4)^2+(3-7)^2\)

⇒ \(p^2-8 p+16+p^2-14 p+49+0=9\)

⇒ \(2 p^2-22 p+56=0\)

⇒ \(p^2-11 p+28=0\)

⇒ \(p^2-7 p-4 p+28=0\)

⇒ \(p(p-7)-4(p-7)=0\)

⇒ \((p-7)(p-4)=0\)

p-7=0 or p-4=0

p=7 or p=4

when p=7, then the points B and C coincide and so no triangle is formed.

⇒ \(p \neq 7\)

Hence, p=4

Example 5. Find the coordinates of the point of trisection of the line segment joining the points A(-5, 6) and B(4, -3).

Solution:

Let P and Q be the points of trisection of AB, and then P divides AB in the ratio 1:2.

Co-ordinates of point P \(\equiv\left(\frac{-5 \times 2+4 \times 1}{1+2}, \frac{6 \times 2+1 \times-3}{1+2}\right) \equiv(-2,3)\) and point Q divides A B in the ratio 2: 1.

Co-ordinates of point Q=\(\left(\frac{-5 \times 1+4 \times 2}{2+1}, \frac{6 \times 1+2 \times-3}{1+2}\right)\)=(1,0)

The coordinates of the point of trisection are (-2,3) and (1,0).

Example 6. Find the ratio in which the point P(x, 2) divides the line segment joining the points. A(12, 5) and B(4, -3). Also, find the value of. v.

Solution:

Let point P(x, 2) divide AB in the ratio k: 1.

x=\(\frac{12 \times 1+k \times 4}{k+1}\) and 2=\(\frac{5 \times 1+k \times-3}{k+1}\)

Now, 2=\(\frac{5-3 k}{k+1}\)

2 k+2=\(-3 k+5 \quad \Rightarrow \quad 5 k=3\)

k=\(\frac{3}{5}\)

Required ratio =3: 5

and x=\(\frac{4 k+12}{k+1}=\frac{4 \times \frac{3}{5}+12}{\frac{3}{5}+1}=\frac{12+60}{3+5}=9\)

x=9

Example 7. Find The lengths of the medians AD and BE of \(\triangle\)ABC whose vertices are A( 7, 3),B(5, 3) and C(3, -1 ).

Solution:

Co-ordinates of mid-point D of BC

= \((\frac{3+5}{2}\), \(\frac{-1+3}{2})=(4,1)\)

Ciomodinates of mid-point E of AC :

= \(\left(\frac{3+7}{2}, \frac{-1-3}{2}\right)=(5,-2)\)

A D=\(\sqrt{(7-4)^2+(-3-1)^2}=\sqrt{9+16}=\sqrt{25}\)=5 units

and \(B E=\sqrt{(5-5)^2+(3+2)^2}=\sqrt{0+25}=\sqrt{25}=5 units\)

Example 8. If the points A(-1, -4), B(b,c) and C(5, -1) are collinear and 2b + c = 4, find the values of b and c.

Solution:

Points A(- 1, -4), B(b, c) and C(5, -1) are collinear

area of \(\triangle\)ABC = 0

-1(c + 1)+ b(-1 -2 + 4) + 5(-4-c) = 0

– c – 1 + 3b – 20 -5c = 0

3b – 6c = 21

b -2c – 7 …(1)

Given that, 2b + c = 4 (2)

from eqs. (1) and (2), we get

b = 3 and c = -2

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry Exercise 7.1

Question 1. Find the distance between the following pairs of points :

1. (2, 3), (4,1)
2. (-5, 7), (-1,3)
3. (a, b), {-a, -b)

Solution :

(1) Distance between the points (2, 3) and (4, 1)

= \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

= \(\sqrt{(4-2)^2+(1-3)^2}\)

= \(\sqrt{(2)^2+(-2)^2}\)

= \(\sqrt{(4+4)}=\sqrt{8}=2 \sqrt{2}\) units

(2) Distance between the points (-5, 7) and (-1, 3)

= \(\sqrt{(-1+5)^2+(3-7)^2}\)

= \(\sqrt{(4)^2+(-4)^2}\)

= \(\sqrt{16+16}=\sqrt{32}=4 \sqrt{2}\) units

(3) Distance between the points (a, b) and {-a, -b).

= \(\sqrt{(-a-a)^2+(-b-b)^2}\)

= \(\sqrt{(-2 a)^2+(-2 b)^2}\)

= \(\sqrt{4 a^2+4 b^2}=\sqrt{4\left(a^2+b^2\right)}\)

=2 \(\sqrt{a^2+b^2}\) units

Question 2. Find the distance between the points (0, 0) and (36, 15). Can you now find the distance between the two towns A and B where town A is located 36 km east and 15 km north of town

Solution :

Distance between the points (0, 0) and (36, 15)

= \(\sqrt{(36-0)^2+(15-0)^2}\)

= \(\sqrt{1296+225}\)

=\(\sqrt{1521}\)=39 units

We can find the distance between two cities. The coordinates of the given cities in the cartesian coordinate system are A = (0,0) and B (36, 15).

The distance between these points is AB = 39 1cm.

Question 3. Determine if the points (1, 5), (2, 3) and (- 2, -11) are collinear.

Solution :

Let the given points are A(l, 5), B{2, 3) and C(-2,-ll).

A B =\(\sqrt{(2-1)^2+(3-5)^2}\)

=\(\sqrt{1+4}=\sqrt{5}\) units

B C =\(\sqrt{(-2-2)^2+(-11-3)^2}\)

=\(\sqrt{16+196}=\sqrt{212}\) units

C A =\(\sqrt{(-2-1)^2+(-11-5)^2}\)

=\(\sqrt{9+256}=\sqrt{265}\) units

Now, AB+B C \(\neq\) C A

Given points are not collinear.

Question 4. Check whether (5, -2), (6, 4) and (7, – 2) are the vertices of an isosceles triangle.

Solution :

Let the given points are A(5, -2), B{6, 4) and C(7, -2).

Now, A B =\(\sqrt{(6-5)^2+(4+2)^2}\)

=\(\sqrt{1+36}=\sqrt{37}\) units

B C =\(\sqrt{(7-6)^2+(-2-4)^2}\)

=\(\sqrt{1+36}=\sqrt{37}\) units

In a \(\triangle\)ABC,AB = BC

⇒ \(\triangle\)ABC is an isosceles triangle.

Therefore, the given points are the vertices of an isosceles triangle.

Question 5. In a classroom, 4 friends are seated at points A, B, C and D as shown in the figure. Champa and Chameli walk into the class and after observing for a few minutes Champa asks Chameli, “Don’t you think ABCD is a square?” Chameli disagrees. Using the distance formula, find which of them is correct

Solution :

In the figure, the coordinates of A, B, C and D are (3, 4), (6, 7), (9, 4) and (6, 1) respectively.

A B =\(\sqrt{(6-3)^2+(7-4)^2}\)

= \(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2} units\)

B C =\(\sqrt{(9-6)^2+(4-7)^2}\)

=\(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\)units

C D =\(\sqrt{(6-9)^2+(1-4)^2}\)

=\(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\) units

D A =\(\sqrt{(3-6)^2+(4-1)^2}\)

=\(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\) units

A C =\(\sqrt{(9-3)^2+(4-4)^2}\)

=\(\sqrt{36+0}=\sqrt{36}=6\)units

B D =\(\sqrt{(6-6)^2+(1-7)^2}\)

=\(\sqrt{0+36}=\sqrt{36}=6 units\)

Now, AB =BC = CD = DA and AC = BD

ABCD is a square.

So, Champa is correct.

Coordinate Geometry Class 10 Exemplar Questions and Answers

Question 6. Name the type of quadrilateral formed, if any, by the following points, and give reasons for your answer:

1. (-1,-2). (1,0), (-1,2), (-3,0)
2. (-3,5). (3, 1), (0,3), (-1,-4)
3. (4, 5). (7. 6), (4, 3), (1,2)

Solution:

(1) Let points be A (-1, -2), (1,0), C (-1,2) and D (-3,0).

A B =\sqrt{(1+1)^2+(0+2)^2}

=\(\sqrt{4+4}=\sqrt{8}=2 \sqrt{2} units\)

B C =\(\sqrt{(-1-1)^2+(2-0)^2}\)

=\(\sqrt{4+4}=\sqrt{8}=2 \sqrt{2} units\)

C D =\(\sqrt{(-3+1)^2+(0-2)^2}\)

=\(\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\)units

D A =\(\sqrt{(-1+3)^2+(-2-0)^2}\)

=\(\sqrt{4+4}=\sqrt{8}=2 \sqrt{2}\) units

A C =\(\sqrt{(-1+1)^2+(2+2)^2}\)

=\(\sqrt{0+16}=\sqrt{16}\)=4 units

B D=\(\sqrt{(-3-1)^2+(0-0)^2}\)

=\(\sqrt{16+0}=\sqrt{16}\)=4 units

AB = BC = CD = DA and AC = BD

ABCD is a square.

Therefore, given points are the vertices of a square.

(2) Let given points are A(-3, 5), B(3, 1), C(0, 3) and D(-l, -4).

A B =\(\sqrt{(3+3)^2+(1-5)^2}\)

=\(\sqrt{36+16}=\sqrt{52}\)

=\(2 \sqrt{13}\)units

B C =\(\sqrt{(0-3)^2+(3-1)^2}\)

=\(\sqrt{9+4}=\sqrt{13} units\)

A C =\(\sqrt{(0+3)^2+(3-5)^2}\)

=\(\sqrt{9+4}=\sqrt{13}\) units

Now, BC + A C =\(\sqrt{13}+\sqrt{13}\)

=2 \(\sqrt{13}\)=A B

A, B and C are collinear.

Therefore, no quadrilateral will be formed from the given points.

(3) Let given points are A(4, 5), B(7, 6), C(4, 3) and D( 1,2).

A B=\(\sqrt{(7-4)^2+(6-5)^2}\)

=\(\sqrt{9+1}=\sqrt{10}\) units

B c =\(\sqrt{(4-7)^2+(3-6)^2}\)

=\(\sqrt{9+9}=\sqrt{18}=3 \sqrt{2}\) units

C D =\(\sqrt{(1-4)^2+(2-3)^2}\)

=\(\sqrt{9+1}=\sqrt{10}\) units

=\(\sqrt{(4-1)^2+(5-2)^2}\)

=\(\sqrt{9+9}=\sqrt{18}\)

=3 \(\sqrt{2}\) units

A C =\(\sqrt{(4-4)^2+(3-5)^2}\)

=\(\sqrt{0+4}=\sqrt{4}\)=2 units

B D =\(\sqrt{(1-7)^2+(2-6)^2}\)

=\(\sqrt{36+16}=\sqrt{52}\)

=2 \(\sqrt{13}units\)

AB = CD, AD = BC and AC \(\neq\) BD

ABCD is a parallelogram.

Therefore, given points are the vertices of a parallelogram.

Question 7. Find the point on the A-axis which is equidistant from (2, -5) and (-2, 9).

Solution :

Let any point of the A-axis be P(x, 0). The distance of this point from the points A(2, -5) and B(-2, 9) are equal.

PA = PB

P A^2 =P B^2

⇒ \((x-2)^2+(0+5)^2 =(x+2)^2+(0-9)^2\)

⇒ \(x^2-4 x+4+25 =x^2+4 x+4+81\)

⇒ \(x^2-4 x-x^2-4 x =4+81-4-25\)

-8x = 56

x = -7

Coordinates of required point = (-7, 0).

Question 8. Find the values of y for which the distance between the points P(2, – 3) and Q(10,jV is 10 units.

Solution :

According to the problem, PQ = 10

⇒ \(P^2=100 \)

⇒ \((10-2)^2+(y+3)^2=100\)

⇒ \(64+(y+3)^2=100\)

⇒ \((y+3)^2=100-64\)

⇒ \((v+3)^2=36\)

⇒ \((y+3)= \pm 6\)

y+3=6 or y+3=-6

y=3 or y=-9

Required values of y = 3, – 9

Question 9. If Q(0, 1) is equidistant from P(5, -3) and R(x, 6), find the values of .r. Also, find the distances QR and PR.

Solution :

Given that, Q is equidistant from P and R.

QP = QR

Q P = Q R

⇒ \(Q P^2=Q R^2\)

⇒ \((5-0)^2+(-3-1)^2=(x-0)^2+(6-1)^2\)

⇒ \(25+16=x^2+25\)

⇒ \(x^2=6 \Rightarrow x= \pm 4\)

⇒ \(Q R=\sqrt{( \pm 4-0)^2+(6-1)^2}\)

= \(\sqrt{16+25}=\sqrt{41}\) units

and P R =\(\sqrt{(5 \pm 4)^2+(-3-6)^2}\)

= \(\sqrt{(5+4)^2+81}\) or \(\sqrt{(5-4)^2+81}\)

= \(\sqrt{81+81}\) or \(\sqrt{1+81}\)

= \(\sqrt{162}\) or \(\sqrt{82}\)

P R =9 \(\sqrt{2} units\) or \(\sqrt{82} units\).

Question 10. Find a relation between x and; such that the point (x,y) is equidistant from the point (3, 6) and (- 3, 4).

Solution :

Given that, the distance of point {x,y) to (3, 6) = distance of point {x,y) to (-3, 4).

⇒ \(\sqrt{(x-3)^2+(y-6)^2}=\sqrt{(x+3)^2+(y-4)^2}\)

⇒ \((x-3)^2+(y-6)^2\)

= \((x+3)^2+(y-4)^2\)

⇒ \(x^2-6 x+9+y^2-12 y+36\)

=\(x^2+6 x+9+y^2-8 y+16\)

⇒ \(0=x^2+6 x+9+y^2-8 y+16-x^2 +6 x-9-y^2+12 y-36\)

12x- + 4y – 20 = 0

3x + y – 5 = 0

3x + y = 5

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry Co-Ordinate Geometry Exercise 7.2

Question 1. Find the coordinates of the point which divides the join of (-1, 7) and (4, -3) in the ratio 2:3.

Solution:

Let A=(-1,7),B=(4,-3)

Let p(x, y) divide AB in the ratio 2: 3.

A(-1,7), P(x, y),B(4,-3)

⇒ \((x_1, y_1)=(-1,7),(x_2, y_2)=(4,-3)\)

and m: n=2: 3

Now, x=\(\frac{m x_2+m x_1}{m+n}\)

x=\(\frac{2 \times 4+3 \times(-1)}{2+3}=\frac{8-3}{5}=\frac{5}{5}\)=1

and y=\(\frac{m y_2+n y_1}{m+n}\)

y=\(\frac{2 \times(-3)+3 \times 7}{2+3}=\frac{-6+21}{5}=\frac{15}{5}\)=3

Coordinates of required point =(1,3).

Question 2. Find the coordinates of the points of trisection of the line segment joining (4,-1) and (-2,-3).

Solution :

Given (4,-1) and (-2,-3)

Let A = (4, – 1) and B = (-2, – 3).

Let P and Q trisect the line segment AB.

AP:PB= 1:2 and

AQ:QB = 2 : 1

For point P, x=\(\frac{m x_2+n x_1}{m+n}\)

x=\(\frac{1(-2)+2(4)}{1+2}=\frac{-2+8}{3}=\frac{6}{3}=2\)

and y=\(\frac{m r_2+n y_1}{m+n}\)

⇒ \(y=\frac{1(-3)+2(-1)}{1+2}=\frac{-3-2}{3}=\frac{-5}{3}\)

Coordinates of point P \(\equiv\left(2, \frac{-5}{3}\right)\)

For point Q, \(x^{\prime}=\frac{m_1 x_2+n_1 x_1}{m_1+n_1}\)

⇒ \(x^{\prime}=\frac{2(-2)+1(4)}{2+1}=\frac{-4+4}{3}=0\)

and \(y^{\prime}=\frac{m_1 y_2+n_1 y_1}{m_1+n_1}\)

⇒ \(y^{\prime}=\frac{2(-3)+1(-1)}{2+1}=\frac{-6-1}{3}=\frac{-7}{3}\)

Coordinates of point \(Q=\left(0, \frac{-7}{3}\right)\)

Coordinate Geometry Class 10 Chapter 7 Practice Questions

Question 3. To conduct Sports Day activities, in your rectangular-shaped school ground ABCD, lines have been drawn with chalk powder at a distance of lm each. 100 flower pots have been placed at a distance of lm from each other along AD, as shown in the figure. Niharika runs \(\frac{1}{4}\)th the distance AD on the 2nd line and posts a green flag.

Preet runs \(\frac{1}{5}\) through the distance AD on the eighth line and posts a red flag. What is the distance between both flags? If Rashmi has to post a blue flag exactly halfway between the line segment joining the two flags, where should she post her flag?

Solution :

100 flower pots are placed on side AD at a distance of 1 m from each other.

AD = 100 m

Position of Niharika’s flag = distance of \(\frac{1}{4}\)th part of AD in second row

⇒ \(\left(2,100 \times \frac{1}{4}\right)=(2,25)\)

Position of Preet’s flag = distance of \(\left(\frac{1}{5}\right)\) th part of AD in eighth row

= \(\left(8,100 \times \frac{1}{5}\right)=(8,20)\)

Distance between flags

= \(\sqrt{(8-2)^2+(20-25)^2}\)

= \(\sqrt{36+25}=\sqrt{61} \mathrm{~m}\)

Coordinates of the mid-point of (2,25) and (8,20)

= \(\left(\frac{2+8}{2}, \frac{25+20}{2}\right)=\left(5, \frac{45}{2}\right)\)

So, Rashmi should post her flag in the 5th row along AD at a distance of \(\frac{45}{2} \mathrm{~m}\).

Question 4. Find the ratio in which the line segment joining the points (-3, 10) and (6, – 8) is divided by (- 1, 6).

Solution :

Given

The line segment joining the points (-3, 10) and (6, – 8) is divided by (- 1, 6)

Let the points (-1, 6) divide the line segment joining the points (-3, 10) and (6, -8) in the ratio m: 1.

⇒ \(-1=\frac{m(6)+1(-3)}{m+1}\)

and \(6=\frac{m(-8)+1(10)}{m+1}\)

⇒ \(-m-1=6 m-3 and 6 m+6=-8 m+10\)

-7 m=-2 and 14 m=4

m=\(\frac{2}{7}\) and m=\(\frac{4}{14}=\frac{2}{7}\)

Required ratio = 2: 7.

Question 5. Find the ratio in which the line segment joining A (1, -5) and (-4, 5) is divided by the Ar-axis. Also, find the coordinates of the point of division.

Solution:

Given

(1, -5) and (-4, 5)

A=\((1,-5)=\left(x_1, y_1\right)\)

and \(B=(-4,5)=\left(x_2, y_2\right)\)

Let the x-axis divide the line segment A B at point (x, 0) in the ratio m: 1.

Now, 0=\(\frac{m \cdot y_2+1 \cdot y_1}{m+1}\)

⇒ \(0=m(5)+1(-5) \Rightarrow m=1\)

m: 1=1: 1

Required ratio =1: 1

Now, \(x=\frac{m x_2+1 \cdot x_1}{m+1}=\frac{1(-4)+1(1)}{1+1}\)

= \(\frac{-4+1}{2}=\frac{-3}{2}\)

Coordinates of point of division =\(\left(-\frac{3}{2}, 0\right)\)

Question 6. If (1, 2), (4,y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order, find x and y-0

Solution:

Given

(1, 2), (4,y), (x, 6) and (3, 5) are the vertices of a parallelogram taken in order

Let the vertices of the parallelogram ABCD are A = (1, 2), B = (4, y), C = (x, 6) and D = (3, 5).

We know that the diagonals of a parallelogram bisect each other.

Coordinates of mid-point of AC = Coordinates of mid-point of BD

⇒ \(\left(\frac{1+x}{2}, \frac{2+6}{2}\right)=\left(\frac{4+3}{2}, \frac{y+5}{2}\right)\)

⇒ \(\frac{1+x}{2}=\frac{4+3}{2} and \frac{2+6}{2}=\frac{y+5}{2}\)

1+x=7 and 8=y+5

x=6 and y=3

Question 7. Find the coordinates of point A, where AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4).

Solution :

Given

AB is the diameter of a circle whose centre is (2, -3) and B is (1, 4)

Coordinates of center O = (2, -3)

Coordinates of point B = (1,4)

Let coordinates of point A = (h, k)

Now, coordinates of the mid-point of AB = coordinates of O

⇒ \(\left(\frac{h+1}{2}, \frac{k+4}{2}\right)=(2,-3)\)

⇒ \(\frac{h+1}{2}=2\) and \(\frac{k+4}{2}=-3\)

h+1=4 and k+4=-6

h=3 and k=-10

Coordinates of point A=(3,-10) .

 Question 8. If A and B are (- 2, -2) and (2, -4) respectively, find the coordinates of P such that AP = \(\frac{3}{7}\) AB and P lies on the line segment AB.

Solution :

Given

A and B are (- 2, -2) and (2, -4) respectively

A P=\(\frac{3}{7} A B\)

7 A P =3 A B\( \quad \Rightarrow \quad 7 A P=3(A P+B P)\)

7 A P =3 A P+3 BP

4 A P =3 B P \(\quad \Rightarrow \quad \frac{A P}{B P}=\frac{3}{4}\)

⇒ \(A B: B P=3: 4 \quad \Rightarrow \quad m: n=3: 4\)

and \(A A =(-2,-2)=\left(x_1, y_1\right)\)

B =\((2,-4)=\left(x_2, y_2\right)\)

Let coordinates of point P=(x, y).

x=\(\frac{m x_2+n x_1}{m+n}\)

x=\(\frac{3 \times 2+4 \times(-2)}{3+4}=\frac{6-8}{7}=\frac{-2}{7}\)

and y=\(\frac{m y_2+n y_1}{m+n}\)

⇒ \(y=\frac{3 \times(-4)+4 \times(-2)}{3+4}\)

=\(\frac{-12-8}{7}=\frac{-20}{7}\)

Coordinates of point P=\(\left(\frac{-2}{7}, \frac{-20}{7}\right)\)

Question 9. Find the coordinates of the points which divide the line segment joining A(-2, 2) and B(2, 8) into four equal parts.

Solution:

Given

A(-2, 2) and B(2, 8)

Coordinates of mid-point Q of AB

=\(\left(\frac{-2+2}{2}, \frac{2+8}{2}\right)=(0,5)\)

Coordinates of mid-point P of AQ

=\(\left(\frac{-2+0}{2}, \frac{2+5}{2}\right)=\left(-1, \frac{7}{2}\right)\)

Coordinates of mid-point R of QB

=\(\left(\frac{0+2}{2}, \frac{5+8}{2}\right)=\left(1, \frac{13}{2}\right)\)

Coordinates of the points dividing A and B into equal parts are

∴ \(\left(-1, \frac{7}{2}\right),(0,5),\left(1, \frac{13}{2}\right)\)

Question 10. Find the area of a rhombus in its vertices as (3, 0), (4, 5), (— 1, 4) and diagonals (-2.-1) taken in order. [Hint : Area of a rhombus \(\frac{1}{2}\)(product of its diagonals)]

Solution :

Given

(3, 0), (4, 5), (— 1, 4) and diagonals (-2.-1)

Let the vertices of a rhombus be in the following order :

A =(3,0), B=(4,5),

C =(-1,4), D=(-2,-1)

A C=\(\sqrt{(-1-3)^2+(4-0)^2}\)

= \(\sqrt{16+16}=\sqrt{32}=4 \sqrt{2}\) units

B D =\(\sqrt{(-2-4)^2+(-1-5)^2}\)

= \(\sqrt{36+36}=\sqrt{72}=6 \sqrt{2}\) units

Now, area of rhombus =\(\frac{1}{2} \times\) product of diagonals

= \(\frac{1}{2} \times A C \times B D\)

= \(\frac{1}{2} \times 4 \sqrt{2} \times 6 \sqrt{2}\)

=24 sq. units

The area of a rhombus =24 sq. units

Coordinate Geometry solved examples Class 10 CBSE

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry Co-Ordinate Geometry Exercise 7.3

Question 1. Find the area of the triangle whose vertices are :

1. (2, 3), (-1,0), (2,-4)
2. (-5-1), (3,-5), (5, 2)

Solution :

(1) Vertices of the given triangle are

⇒ \(\left(x_1, y_1\right)=(2,3)\),

⇒ \(\left(x_2, y_2\right)=(-1,0)\),

⇒ \(\left(x_3, y_3\right)=(2,-4)\)

Area of triangle =\(\frac{1}{2}[(x_1 y_2+x_2 y_3+x_3 y_1)\)\(-(x_2 y_1+x_3 y_2+x_1 y_3)]\)

= \(\frac{1}{2}[\{2 \times 0+(-1) \times(-4)+2 \times 3\}\)-{(-1) \times 3+2 \times 0+2 \times(-4)\}][/latex]

= \(\frac{1}{2}[(0+4+6)-(-3+0-8)]\)

= \(\frac{1}{2}(10+11)=\frac{21}{2}\)

Area of triangle =\(\frac{21}{2}\) sq. units

(2) Vertices of triangle are

⇒ \(\left(x_1, y_1\right)=(-5,-1),\left(x_2, y_2\right)=(3,-5),\left(x_3, y_3\right)=(5,2)\)

=\(\frac{1}{2}[(x_1 y_2+x_2 y_3+x_3 y_1\) \(-(x_2 y_1+x_3 y_2+x_1 y_3)]\)

=\(\frac{1}{2}[\{(-5) \times(-5)+3 \times 2+5 \times(-1)\}-\{3 \times(-1)+5 \times(-5)+(-5) \times 2\}]\)

=\(\frac{1}{2}[(25+6-5)-(-3-25-10)]\)

=\(\frac{1}{2}(26+38)=32\)

Area of triangle =32 sq. units

Question 2. In each of the following find the value of ‘k’, for which the points are collinear.

1. (7,-2), (5, 1), (3, k)
2. (8,1),(k,-4),(2,-5)

Solution :

(1) Let the given points are as follows:

A=\(\left(x_1, y_1\right)=(7,-2), \quad B=\left(x_2, y_2\right)=(5,1)C=\left(x_3, y_3\right)=(3, k)\)

A, B and C are collinear.

Area of \(\triangle A B C\)=0

⇒ \(\frac{1}{2}[(x_1 y_2+x_2 y_3+x_3 y_1) – (x_2 y_1+x_3 y_2+x_1 y_3)]\)=0

⇒ \((x_1 y_2+x_2 y_3+x_3 y_1)\)

⇒ \(-(x_2 v_1+x_2 v_2+x_1 y_3)\) =0

⇒ \({7 \times 1+5 \times k+3 \times(-2)\}-\{5 \times(-2)+3 \times 1+7 \times k}\) =0

(7+5 k-6)-(-10+3+7 k) =0

(1+5 k)-(-7+7 k) =0

1+5 k+7-7 k =0

8-2 k=0 \(\Rightarrow k =4\)

(2) Let the given points are as follows:

A \(\equiv\left(x_1, y_1\right)=(8,1), B=\left(x_2, y_2\right)=(k,-4)\),

C=\(\left(x_3, y_3\right)=(2,-5)\)

A, B and C are collinear

Area of \(\triangle A B C\)=0

⇒ \(\frac{1}{2}[(x_1 y_2+x_2 y_3+x_3 y_1)\).

⇒ \(\left.-\left(x_2 y_1+x_3 y_2+x_1 y_3\right)\right]\)=0

⇒ \(\left(x_1 y_2+x_2 y_3+x_3 y_1\right)\)

– \(\left(x_2 y_1+x_3 y_2+x_1 y_3\right)\)=0

⇒ \({8 \times(-4)+k \times(-5)+2 \times 1}\)

⇒ \({k \times 1+2 \times(-4)+8 \times(-5)}\)=0

⇒ \((-32-5 k+2)-(k-8-40)\)=0

(-30-5 k)-(k-48)=0

-30-5 k-k+48=0

-6 k+18=0 \(\Rightarrow k=3\)

Question 3. Find the area of the triangle formed by joining the mid-points of the sides of the triangle whose vertices are (0, -1), (2, 1) and (0, 3). Find the ratio of this area to the area of the given triangle.

Solution :

Given

(0, -1), (2, 1) and (0, 3)

Let vertices of \(\triangle\)ABC are

A=\(\left(x_1, y_1\right)=(0,-1), B=\left(x_2, y_2\right)=(2,1)\)

and C=\(\left(x_3, y_3\right)=(0,3)\).

Area of \(\triangle A B C\)

= \(\frac{1}{2}[(x_1 y_2+x_2 y_3+x_3 y_1\)

⇒ \(\left.-\left(x_2 y_1+x_3 y_2+x_1 y_3\right)\right\}\)

=\(\frac{1}{2}[\{0 \times 1+2 \times 3+0 \times(-1)\}\)

⇒ \(-\{2 \times(-1)+0 \times 1+0 \times 3\}]\)

=\(\frac{1}{2}[(0+6+0)-(-2+0+0)]\)

=\(\frac{1}{2}(6+2)\)=4 sq. units

Coordinates of mid-point P of AB

= \(\left(\frac{0+2}{2}, \frac{-1+1}{2}\right)=(1,0)\)

Coordinates of mid-point Q of BC

=\(\left(\frac{2+0}{2}, \frac{1+3}{2}\right)=(1,2)\)

Coordinates of mid-point R of CA

=\(\left(\frac{0+0}{2}, \frac{3-1}{2}\right)=(0,1)\)

Area of \(\triangle P Q R\)

= \(\frac{1}{2}[(1 \times 2+1 \times 1+0 \times 0) -(1 \times 0+0 \times 2+1 \times 1)]\)

= \(\frac{1}{2}[(2+1+0)-(0+0+1)\)

= \(\frac{1}{2}(3-1)\)=1 sq. unit

Now,\(\frac{\text { area of } \triangle P Q R}{\text { area of } \triangle A B C}=\frac{1}{4}\)=1: 4

Question 4. Find the area of the quadrilateral whose vertices, taken in order, are (-4, -2), (-3, -5), (3,-2) and (2,3).

Solution:

Given

(-4, -2), (-3, -5), (3,-2) and (2,3)

Let the vertices of □ ABCD in order are as follows :

A=\(\left(x_1, y_1\right)=(-4,-2)\)

B=\(\left(x_2, y_2\right)=(-3,-5)\)

C=\(\left(x_3, y_3\right)=(3,-2)\)

D=\(\left(x_4, y_4\right)=(2,3)\)

Area of  Square A B C D

= \(\frac{1}{2}\left[\left(x_1 y_2+x_2 y_3+x_3 y_4+x_4 y_1\right)\right.\)

–\((x_2 y_1+x_3 y_2+x_4 y_3+x_1 y_4)]\)

= \(\frac{1}{2}[\{(-4) \times(-5)+(-3) \times(-2)+3 \times 3 +2 \times(-2)\}-\{(-3) \times(-2)+3 \times(-5)\) +\(2 \times(-2)+(-4) \times 3\}]\)

= \(\frac{1}{2}[(20+6+9-4)-(6-15-4-12)]\)

= \(\frac{1}{2}(31+25)\)=28 sq. units

Question 5. The median of a triangle divides it into two triangles of equal areas. Verify this result for \(\triangle\)ABC whose vertices are A(4, -6), B(3, -2) and C(5, 2).

Solution:

Conlinates of mid-point D of BC’

=\(\left(\frac{3+5}{2}, \frac{-2+2}{2}\right)=(1,0)\)

Area of \(\triangle ABD\)

=\(|\begin{array}{c} \frac{1}{2}\,\{4 \times(-2)+3 \times(1)+4 \times(-6)\} -\{3 \times(-6)+4 \times(-2)+4 \times(0) \mid \end{array}\|\)

=\(\left|\frac{1}{2}\right|(-8+0-2.4)-(-18-8+(0)||\)

=\(\left|\frac{1}{2}(-32+20)\right|=|-3|\)=3 sq. units

Area of \(\triangle ACD\) е:

\( =\begin{array}{r}
\frac{1}{2}, 1(4 \times 0+4 \times 2+5 \times(-6) \mid \\
-14 \times(-6)+5 \times 0+4 \times 2) \mid
\end{array}|\)

=  \(|\frac{1}{2}(0+8-3(0)-(-24+0+8)|\)

=\( \frac{1}{2}(-22+|(0)|=|-3|\)=3sq. units

⇒ I\(\triangle ABD\)I= \(\triangle ACD\)

Therefore, the median AD divides it into two triangles of equal areas. Hence Proved.

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry Co-Ordinate Geometry Exercise 7.4

Question 1. Determine the ratio in which the line 2x + y – 4 = 0 divides the line segment joining the points A(2, – 2) and B(3, 7).

Solution :

Let the line 2x + y – 4 =0 divides the line segment joining the points A (2, -2) and P (3, 7) in the ratio m: 1 and the coordinates of the point of division are (x,y).

x=\(\frac{m(3)+1(2)}{m+1}=\frac{3 m+2}{m+1}\)

and y=\(\frac{m(7)+1(-2)}{m+1}=\frac{7 m-2}{m+1}\)

Point (x, y), lies on the line 2 x+y-4=0

⇒ \(2\left(\frac{3 m+2}{m+1}\right)+\frac{7 m-2}{m+1}-4=0\)

6 m+4+7 m-2-4(m+1)=0

13 m+2-4 m-4=0

9 m=2 \(\quad \Rightarrow \quad m=\frac{2}{9}\)

Required ratio =2: 9

Question 2. Find a relation between x and y if the points (x, y), (1,2) and (7, 0) are collinear.

Solution :

Given

Points (x, y), (1,2) and (7, 0) are collinear.

Area of \(\Delta\)=0

⇒ \(\frac{1}{2}[\{x \cdot 2+1 \cdot 0+7 \cdot y\}\)

–\(\{1 \cdot y+7 \cdot 2+0 \cdot x\}]\)=0

(2 x+7 y)-(y+14)=0

2 x+7 y-y-14=0

x+3 y-7=0

which is the required relation between x and y.

Question 3. Find the centre of a circle passing through the points (6, -6), (3, -7) and (3, 3).

Solution :

Given

(6, -6), (3, -7) and (3, 3)

Let the points A(6, -6), B(3, -7) and C(3, 3) lie on the circumference of a circle whose centre is P(h,k)

P A=P B=P C (radii of the circle )

⇒ \(P A^2=P B^2=P C^2\)

Now, vP A^2=P B^2[/latex]

Now, \(P A^2=P B^2\)

⇒ \((h-6)^2+(k+6)^2 =(h-3)^2+(k+7)^2\)

⇒ \(h^2-12 h+36+k^2 +12 k+36\)

= \(h^2-6 h+9+k^2+14 k+49\)

-12 h+6 h+12 k-14 k+72-58=0

-6 h-2 k+14=0

3 h+k=7

and \(P B^2=P^{\prime} C^2\)

⇒ \((h-3)^2+(k+7)^2=(h-3)^2+(k-3)^2\)

⇒ \((k+7)^2=(k-3)^2\)

⇒ \(k^2+14 k+49=k^2-6 k+9\)

14 k+6 k=9-49

20 k=-40

k=-2

Put the value of k in equation (1),

3 h-2 =7

h =3

Coordinates Of the centre of the circle = (3,2)

Question 4. The two opposite vertices of a MJU.UV ;uv (-1, 2) aiui (3, 2). Find the coordinates of the other two vertices.

Solution :

Given

The two opposite vertices of a MJU.UV ;uv (-1, 2) aiui (3, 2).

Let two opposite vertices of square ABCD be A(-1,2) and C(3, 2) which are known.

Let the coordinates of vertex B be (h, k).

Now, AB = BC (sides of the square)

⇒\(A B^2=B C^2\)

⇒ \((h+1)^2+(k-2)^2=(h-3)^2+(k-2)^2\)

⇒ \((h+1)^2=(h-3)^2\)

⇒ \(h^2+2 h+1=h^2-6 h+9\)

2 h+6 h=9-

8 h=8

h=1

⇒ \(Again, \quad A B^2+B C^2=A C^2 \quad\left( \angle B=90^{\circ}\right)\)

⇒ \((h+1)^2+(k-2)^2+(h-3)^2+(k-2)^2\)

=\((3+1)^2+(2-2)^2\)

⇒ \((1+1)^2+k^2-4 k+4+(1-3)^2+k^2-4 k+4\)

=16+0

⇒ \(4+2 k^2-8 k+8+4=16\)

⇒ \(2 k^2-8 k=0 \quad \Rightarrow 2 k(k-4)=0\)

k=0 or k=4

Therefore, the remaining two vertices of the square = (1,0) or (1,4)

Question 5. The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Saplings of Gulmohar are planted on the boundary at a distance of 1m from each other. There is a triangular grassy lawn in the plot as shown in the figure. The students are to sow seeds of flowering plants on the remaining area of the plot.

1. What will be the coordinates of the vertices of A BQR if C is the origin?
2. Also, calculate the areas of the triangles in these cases. What do you observe?

Solution :

(1) If A is the origin, then

P = (4. 6), Q=(3, 2), R=(6, 5)

Area of \(\triangle P Q R\)

=\(\frac{1}{2}[(4.2+3.5+6.6)-(3.6+6.2+4.5)] \)

=\(\frac{1}{2}[(8+15+36)-(18+12+20)]\)

=\(\frac{1}{2}(59-50)=\frac{9}{2}\) sq. units

(2) If C is the origin, then

P =(-12,-2), Q=(-13,-6),

R =(-10,-3)

Area of \(\triangle P Q R\)

= \(\frac{1}{2}[\{(-12)(-6)+(-13)(-3)+(-10)(-2)\}\)

–\(\{(-13)(-2)+(-10)(-6)+(-12)(-3)\}]\)

= \(\frac{1}{2}[(72+39+20)-(26+60+36)]\)

= \(\frac{1}{2}(131-122)=\frac{9}{2}\) sq. units

Area Of the Triangle is both in some cases

Class 10 Maths Coordinate Geometry chapter MCQs and Answers

Question 6. The vertices of a \(\triangle A B C\) are A (4,6), B(I, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively, such that \(\frac{A D}{A B}=\frac{A E}{A C}=\frac{1}{4}\).

Calculate the area of the \(\triangle A D E\) AB AC 4 and compare it with the area of \(\triangle A B C\).

Solution:

Given

The vertices of a \(\triangle A B C\) are A (4,6), B(I, 5) and C(7, 2). A line is drawn to intersect sides AB and AC at D and E respectively,

A=(4,6), B=(1,5), C=(7,2)

Area of \(\triangle A B C\)

= \(\frac{1}{2}[\{4.5+1.2+7.6\}\)

–\(\{1.6+7.5+4.2\}]\)

= \(\frac{1}{2}[(20+2+42) \quad \overbrace{B(1.5)}^{A(4,6)} -(6+35+8)] \)

= \(\frac{1}{2}(64-49)=\frac{15}{2}\) sq. units

Given, \(\quad \frac{A D}{A B}=\frac{1}{4} \quad \Rightarrow \quad \frac{A D}{A D+B D}=\frac{1}{4}\)

4 A D=A D+B D

3 A D=B D \(\quad \Rightarrow \quad \frac{A D}{B D}=\frac{1}{3}\)=1: 3

Point d divides B in the ratio 1 :  3. Therefore, the coordinates of point D

=\(\left(\frac{1 \times 1+3 \times 4}{1+3}, \frac{1 \times 5+3 \times 6}{1+3}\right)\)

=\(\left(\frac{1+12}{4}, \frac{5+18}{4}\right)=\left(\frac{13}{4}, \frac{23}{4}\right)\)

Again,\(\frac{A E}{A C} =\frac{1}{4} \quad \Rightarrow \quad \frac{A E}{A E+E C}=\frac{1}{4}\)

4 A E =A E+E C \(\Rightarrow 3 A E=E C\)

⇒ \(\frac{A E}{E C} =\frac{1}{3}=1: 3\)

Point E divides A-C in the ratio 1: 3. Therefore, the coordinates of point E

= \(\left(\frac{1 \times 7+3 \times 4}{1+3}, \frac{1 \times 2+3 \times 6}{1+3}\right)\)

= \(\left(\frac{7+12}{4}, \frac{2+18}{4}\right)=\left(\frac{19}{4}, 5\right)\)

Now, A = (4,6), D=\((\frac{13}{4}, \frac{23}{4}), E \equiv(\frac{19}{4}, 5\)

Area of \(\triangle A D E\)

= \(\frac{1}{2} {\left[\left\{4 \cdot \frac{23}{4}+\frac{13}{4} \cdot 5+\frac{19}{4} \cdot 6\right\}\right.}\)

–\({\frac{13}{4} \cdot 6+\frac{19}{4} \cdot \frac{23}{4}+4.5}]\)

=\(\frac{1}{2}[(23+\frac{65}{4}+\frac{114}{4})-(\frac{78}{4}+\frac{437}{16}+20)]\)

⇒ \(\frac{1}{2}\left[\frac{92+65+114}{4}-\frac{312+437+320}{16}\right] \)

= \(\frac{1}{2}\left[\frac{271}{4}-\frac{1069}{16}\right]=\frac{1}{2}\left(\frac{1084-1069}{16}\right)\)

= \(\frac{15}{32}\) square units

Now, \(\frac{\text { Area of } \triangle A D E}{\text { Area of } \triangle A B C}=\frac{15 / 32}{15 / 2}=\frac{1}{16}\)=1: 16

NCERT Exemplar Solutions for  Class 10 Maths Chapter 7 Co-Ordinate Geometry Multiple Choice Questions

Question 1. The distance of the point (3,4) from the X-axis is :

1. 3 units
2. 4 units
3. 5 units
4. 1 unit

Answer:

Question 2. The distance of the point (8, -6) from the origin is :

1. 10 units
2. 6 units
3. 8 units
4. 14 units

Answer:

Question 3.  The perimeter of a triangle with vertices (0, 0), (-3, 0) and (0, ‘1) is:

1. 14 units
2. 7 units
3. 1 unit
4. 12 Units

Answer:

Question 4. The points (-1. 0), (-1, 0) and (0, It) are the vertices of:

1. a right-angled triangle
2. an isosceles triangle
3. an equilateral triangle
4. a scalene triangle

Question 5. A(7, 0), B(4, 0) and C(S, 4) are the vertices of \(\triangle ABC\). The area of this triangle is :

1. 14
2. 28
3. 8
4. 6

Answer:

Question 6. (A-2, 3), B(6, 7) and C(8, 3) are three vertices of a parallelogram ABCD. The coordinates of vertex D are :

1. (0,1)
2. (0,-1)
3. (c) (-1, 0)
4. D(1,0)

Answer:

Question 7. The perpendicular bisector of the line segment joining the point (1,5) and (4, 6) intersects the Y-axis at point:

(0,13)

1. (0,-13)
2. (0, 12)
3. (13, 0)

Answer:

Question 8. The mid-point of line segment joining the points A(-4, 2) and B( 5, 6) is \(P\left(\frac{a}{8}, 4\right)\). Then the value of A is

1. -8
2. -4
3. 2
4. 4

Question 9. The distance of the point (-3, 5) from the Y-axis is :

1. -3
2. 2
3. 5
4. None of these

Answer:

Question 10. The distance between two points (2, 3) and (4, 1) will be :

1. 2
2. 2 \(\sqrt{3}\)
3. 2\( \sqrt{2}\)
4. 3

Answer:

Question 11. The distance between the points P(2, -3) and (3(10, y) is 10 units. The value of y will be

1. -3, 9
2. -9, 3
3. 9, 3
4. -9, 2

Answer:

Class 10 Maths Coordinate Geometry chapter MCQs and Answers

Question 12. A point on X-axis, equidistant from the points A(2, -5) and 2, 9) will be :

1. (-7, 0)
2. (-6, 0)
3. (-2, 0)
4. (2, 0)

Question 13. The distance between the points (-1, -3) and (5, 2) is :

1. \(\sqrt{61}\) units
2. \(\sqrt{37} units\)
3. \(\sqrt{17}\) units
4. 3 units

Answer: \(\sqrt{61}\) units

NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles

• Circle: A circle is a collection of all points in a plane which are at the same
• Centre: The fixed point from which all points in a plane are at the same constant distance is called the centre.
• Radius: The distance between the centre and circumference of a circle is called the radius.
• Chord: A straight line segment joining two points on a circle is called a chord of the circle.
• Secant: A straight line which intersects a circle in two distinct points is called a secant to the circle.
• Tangent: A straight line meeting a circle only at one point is called a tangent to the circle at that point.
• Point Of Contact: The point where the straight line touches (or meets at only one point) the circle is called its point of contact.
• Concentric Circles: Circles having the same centre are said to be concentric circles.

NCERT Exemplar Class 10 Maths Chapter 10 Circles

NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Theorem 1:

The tangent at any point of a circle is perpendicular to the radius through the point of contact.

Given: A circle with centre O and a tangent AB at a point P of the circle.

To Prove: OP \(\perp\) AB

Read and Learn More Class 10 Maths Solutions Exemplar

Construction: Take a point Q other than P on AB. Join OQ.

Proof: Q is a point on the tangent AB, other than the point of contact P.

Q lies outside the circle.

Let OQ interest the circle at R.

Then, OR < OQ

But, OP = OR

Therefore, OP < OQ

Thus, OP is shorter than any other line segment joining O to any point of AB.

It means OP is the shortest distance among all the lines drawn from O to. the point on the tangent other than the point of contact.

Also, we know that perpendicular distance is the shortest distance So, \(\perp\)

i.e., the radius through the point of contact is perpendicular to the tangent.

NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Theorem 2:

A line drawn through the end of a ratlins and perpendicular to it is a tangent to the circle.

Given: A circle with centre O in which OP is a radius and AB is a line through P such that OP \(\perp\) AB.

To Prove: AB is a tangent to the circle at the point P.

Construction: Take a point Q different from P, on AB. Join OQ.

Proof: We know that the perpendicular distance from a point to a line is the shortest distance between them.

• OP \(\perp\) AB
• OP is the shortest distance from O to AB.
• OP < OQ
• Q lies outside the circle.
• Thus, every point on AB other than P, lies outside the circle.
• AB meets the circle at point P only. Hence, AB is the tangent to the circle at the point P.

An Important Result of the Above Theorem

If two circles touch internally or externally, the point of contact lies in a straight line through their centres.

Given: Two circles with centre O and O’ which touch each other at P.

To Prove : P lies on the straight line 00′ i.e., the line joining the centres.

Construction: Join OP, and O’P and draw a common tangent PT to the two circles at point P.

Proof: When Circles Touch Externally :

• ∠1 = 90° …(1) (radius through the point of contact is perpendicular to the tangent)
• ∠2 = 90° (same reason) …(2)
• ∠1 + ∠2 = 90° + 90° [from (1) and (2)]
• ∠l+∠2=180°
• OPO’ is a straight line. (L.P.A.) …(3)
• When Circles Touch Internally :
• ∠OPT = ∠O’PT = 90° (radius through the point of contact is perpendicular to the tangent)
• O’OP is a straight line. (O’P, OP are both 1 to PT at the same point P and only one

∴ \(\perp\) can be drawn to a line through one point on it) …(4) From both (3) and (4), we conclude that P lies on the straight line OO’ i.e., P lies on the straight line joining the centre of the circles.

NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Theorem 3:

The lengths of tangents drawn from an external point to a circle are equal.

Given: Two tangents AP and AQ are drawn from point A to a circle with centre O.

To Prove: AP = AQ

Construction: Join OP, OQ and OA.

Proof: AP is a tangent at P and OP is the radius through P.

OP\(\perp\) AP

Similarly, OQ \(\perp\) AQ

In the right \(\triangle\) OPA and \(\triangle\) OQA

OP = OQ

OA = OA

OPA = ∠OQA

⇒ \(\triangle\) OPA = \(\triangle\) OQA

Hence, AP = AQ

Corollary : (A) If two tangents are drawn from an external point then

• They subtend equal angles at the centre, and
•  they are equally inclined to the line segment joining the centre to that point, (or, tangents are equally inclined at the centre).

Given: A circle with centre O and a point A outside it. Also, AP and AQ are the two tangents to the circle.

To Prove : \(\angle\)AOP = \(\angle\) AOQ and \(\angle\) OAP = \(\angle\) OAQ

Proof : In \(\triangle\)AOP and \(\triangle\)AOQ, we have

AP = AQ (tangents from an external point)

OP = OQ (radii of the same circle)

OA = OA (common)

⇒ \(\triangle\)AOP = \(\triangle\)AOQ (by SSS congruence)

Hence, \(\angle\)AOP = \(\angle\)AOQ and \(\angle\)OAP = \(\angle\)OAQ

(2) Prove that the tangents drawn at the endpoints of a chord of a circle make equal angles with the chord.

Given: Let AB be a chord of the given circle. PA and PB are the tangents at endpoints A and B.

To Prove : \(\angle\)5 = \(\angle\)6

Proof: Since OA and OB are the radii of a circle.

NCERT Exemplar Solutions for Circles Class 10

⇒ \(\angle\)1 = \(\angle\)2 …(1 )(each 90°, as radius through point of contact is 1 to the tangent)

Also in \(\triangle\)OAB,

Since OA = OB

⇒ \(\angle\)3 = \(\angle\)4 (angles opposite to equal sides are equal)

Subtracting equation (2) from equation (1), we get

⇒ \(\angle\)1 – \(\angle\)3 = \(\angle\)2 – \(\angle\)4

⇒ \(\angle\)5 = \(\angle\)6

Hence, tangents drawn at the endpoints of a chord of a circle make equal angles with the chord.

NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Solved Examples

Example 1. Find the length of tangent drawn to a circle of radius 6 cm, from a point at a distance of 10 cm from the centre.

Solution:

Given that

A circle of radius 6 cm, from a point at a distance of 10 cm from the centre.

Since the tangent is perpendicular to the radius through the point of contact.

• \(\angle O T P=90^{\circ}\)
• In the right triangle OTP, we have
• \(O P^2 =O T^2+P T^2\)
• \(10^2 =6^2+P T^2\)
• \(P T^2 =100-36=64\)
• P T =8 cm
• Hence, the length of the tangent is 8 cm.

The length of tangent is 8 cm.

Question 2. AP is tangent to circle O at point P. What is the length of OP?

Solution:

Given that

AP is tangent to circle O at point P.

Let the radius of the given circle be r.

OP = OB = r

OA = 2 + r, OP = r, AP =4

⇒ \(\angle OPA\) = 90° (radius through the point of contact is perpendicular to the tangent)

In right \(\triangle O P A\),

⇒ \(O A^2 =O P^2+A P^2\)

⇒ \((2+r)^2 =r^2+(4)^2\)

⇒ \(4+r^2+4 r =r^2+16\)

⇒ \(4 r =12 \quad \Rightarrow \quad r=3\)

O P = 3 cm.

The length of OP = 3 cm.

Example 3. If the angle between two tangents drawn from an external point P to a circle of radius V and centre O, is 60°, then find the length of OP.

Solution:

Given

If the angle between two tangents drawn from an external point P to a circle of radius V and centre O, is 60°,

PA and PB are two tangents from an external point P such that

⇒ \(\angle\)APB = 60°

⇒ \(\angle\)OPA = \(\angle\)OPB = 30° (tangents are equally inclined at the centre)

Also, \(\angle\)OAP = 90° (radius through the point of contact is perpendicular to the tangent)

Now in right \(\triangle\)OAP,

⇒ \(\sin 30^{\circ} =\frac{O A}{O P}\)

⇒ \(\frac{1}{2} =\frac{a}{O P} \quad \Rightarrow \quad O P\)=2 a units

The length of OP =2 a units

Example 4. In the adjoining figure, PQ is a chord of a circle and is the tangent atP such that \(\angle\)QPT = 60°. Find \(\angle\)PRQ.

Solution:

Given that

In the adjoining figure, PQ is a chord of a circle and is the tangent atP such that \(\angle\)QPT = 60°.

Join OP and OQ. Take any point S on the circumference in the alternate segment. Join SP and SQ.

Since OP \(\perp\) PT (radius through the point of contact is 1 to the tangent

⇒ \(\angle 2+\angle 1=90^{\circ}\)

⇒ \(\angle 2+60^{\circ}=90^{\circ}\)

⇒ \(\angle 2=90^{\circ}-60^{\circ}=30^{\circ}\) (given)

But O P=O Q (each radii)

⇒ \(\angle 2=\angle 3\) (angles opposite to equal sides are equal)

But O P=O Q

⇒ \(\angle 2=\angle 3\) (angles opposite to equal sides are equal)

Now in \(\triangle P O Q\),

⇒ \(\angle 2+\angle 3+\angle 4 =180^{\circ}\)

⇒ \(30^{\circ}+30^{\circ}+\angle 4 =180^{\circ}\)

⇒ \(\angle 4 =120^{\circ}\)

⇒ \(\angle 5 =\frac{1}{2} \times \angle 4\) (angle sum property) [from (1) and (2)]

(The degree measure of an area is twice the angle subtended by it in an alternate segment)

⇒ \(\angle 5=\frac{1}{2} \times 120^{\circ}\)

⇒ \(\angle 5 =60^{\circ}\)

∴ Also,\(\angle 5+\angle 6 =180^{\circ}\)

⇒ \(60^{\circ}+\angle 6 =180^{\circ}\)

∴ \(\angle 6 =\angle P R Q=120^{\circ}\)

Example 5. In the given figure two circles touch each other at point C. Prove that the common tangent to the circle at C bisects the common tangent at P and Q.

Solution:

In the given figure, PR and CR are both tangents drawn to c the same circle from an external point R

PR = CR …(1)

Also, QR and CR are both tangents drawn to the same circle from an external point R.

QR = CR -(2)

From ( 1 ) and (2) we get

PR = QR

R is the mid-point of PQ

i.e., the common tangent at C bisects the common tangents at P and Q

Example 6. Two circles of unequal radii neither touch nor intersect each other. Are the common tangents AB and CD always equal? If no, then give an explanation of it and if your answer is yes, then prove it.

Solution:

Let the two tangents AB and CD on producing meet at P.

Since PA and PC are tangents from an external point P to the circle with centre O

PA=PC

Also, PB and PD are tangents from an external point P to the circle with centre O’.

PB = PD …(2)

Subtracting (2) from (I), we get

PA – PB = PC- PD

AB = CD

So, the direct common tangents are of equal length

Example 7. In the adjoining figure, common tangents AB and CD to two circles intersect at P. Prove that AB = CD.

Solution:

Given that

In the adjoining figure, common tangents AB and CD to two circles intersect at P.

• Since PA and PC are two tangents to a circle with centre O from an external point P.
• PA =PC
• Also, since PB and PD are two tangents to a circle with centre O’ from an external point P.
• PB = PD
• Adding (2) and ( 1 ), we get
• PA + PB = PC + PD
• AB = CD (AB and CD are two straight lines)
• Hence Proved.

Example 8. In the given diagram, PQ and RS arc common tangents to the two circles with centres C and D. Find the length of PQ and hence the area of trapezium RSDC.

Solution:

Given

In the given diagram, PQ and RS arc common tangents to the two circles with centres C and D.

Draw CM//PS so that DCMSP becomes a rectangle.

Now, we have CR = 2 cm, DS = 7cm and CD = 13 cm

DM = DS- MS

= DS- CR

= 7-2 = 5 cm

In right ADMC, by Pythagoras theorem,

⇒ \(C M^2 =C D^2-D M^2\)

=\((13)^2-(5)^2=(12)^2\)

RS = 12 cm (opposite sides of the rectangle are equal)

PQ = 12 cm (length of common tangents to two circles are always same)

Now, ar(Trapezium RSDC)

= \(\frac{1}{2} \times\) h sum of parallel sides)

= \(\frac{1}{2} \times C M(C R+D S)\)

= \(\frac{1}{2} \times 12(2+7)=54 \mathrm{~cm}^2\)

The length of PQ is 12 cm.

The area of trapezium RSDC is 54 cm².

Example 9. AB is the diameter of a circle with centre O. AH and BK are perpendiculars from A and B to the tangent at a point P on the circle. Prove that AD + BK = AB.

Solution:

Given

AB is the diameter of a circle with centre O. AH and BK are perpendiculars from A and B to the tangent at a point P on the circle.

Let AH = x, BK=y and BM = z

⇒ \(\triangle M B K \sim \triangle M A H\) (AA corollary)

⇒ \(\frac{B K}{A H}=\frac{B M}{A M} \quad \Rightarrow \quad \frac{y}{x}=\frac{z}{2 r+z}\)

⇒ \(2 r y+y z=x z \quad \Rightarrow \quad z(x-y)=2 r y\)

z=\(\frac{2 r y}{x-y}\)

Similarly, \(\triangle M B K \sim \triangle M O P\)

⇒ \(\frac{B K}{O P}=\frac{B M}{O M} \quad \Rightarrow \quad \frac{y}{r}=\frac{z}{z+r}\)

y z+y r=z r

z(r-y)=y r

z=\(\frac{y r}{r-y}\)

From (1) and (2), we get

⇒ \(\frac{2 y}{x-y} =\frac{y r}{r-y} \quad \Rightarrow \quad \frac{2}{x-y}=\frac{1}{r-y}\)

2 r-2 y =x-y

x+y 2 r

A H+B K =A B

Example 10. In the given figure, if AB =AC, prove that BE = EC.

Solution:

Given

In the given figure, if AB =AC

We know that lengths of tangents from an external point are equal.

AD =AF  → Equation 1

DB=BE    → Equation 2

EC =FC  →  Equation 3

Now, it is given that

AB=AC

AD + DB =AF + FC

AD + DB = AB + E C From 1 And 3

D B = E C

B E = E C [From (2), DB = BE]

∴ Hence proved

Example 11. In the given figure ABC is a right-angled triangle with AB = 6 K cm, and BC = 8 cm. A circle with a centre O has been inscribed inside the triangle. Find the radius of the circle.

Solution:

Given

In the given figure ABC is a right-angled triangle with AB = 6 K cm, and BC = 8 cm. A circle with a centre O has been inscribed inside the triangle.

Let x be the radius of the circle. In the right triangle ABC

⇒ \(A C^2 =A B^2+B C^2\) (by Pythagoras Th.)

⇒ \(A C^2 =6^2+8^2\)

⇒ \(A C^2\) =36+64

⇒ \(A C^2\) =100

A C =10

Now in quadrilateral OPBR

⇒ \(\angle B =\angle P=\angle R=90^{\circ}\) each

⇒ \(\angle R O P =90^{\circ}\)sum of all angles of a quadrilateral is 360°) (each radii)

and also OP = OR (each radii)

Hence, OPBR is a square with each side x cm.

Therefore, CR = (8 -x) and PA = (6 -x)

BP = RB = x cm

Since the tangents from an external point to a circle are equal in length

AQ = AP = (6-x) and CQ = CR = (8 -x)

Now, AC = AQ + CQ

10 = 6 -x + 8 -x

10 = 14 – 2

2x = 4 = 2 cm

The radius of the circle = 2 cm

Chapter 10 Circles Class 10 Maths NCERT Exemplar

Example 12. A circle is touching the side BC of a \(\triangle\) ABC at the point and touching/IB and AC produced at Q and li respectively. Prove that AQ = \(\frac{1}{2}\) (perimeter of \(\triangle\) ABC).

Solution:

Given : \(\triangle ABC\) and a circle which touches BC, AB and AC in P, Q and R respectively.

Proof: Since the length of the two tangents drawn from an external
point to a circle are is equal, therefore,

AQ = AR

BQ = BP

CP = CR

Now, perimeter of \(\triangle ABC\) = AB + BC + AC

= AB +BP + PC +AC

= AB + BQ + CR + AC [from (2) and (3)]

= AQ+AR = 2AQ [from (1)]

Perimeter of \(\triangle ABC\) = \(\frac{1}{2} \times \text { (perimeter of } \triangle A B C)\)

Example 13. In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. IfPA = 12 cm, QC = QD = 3 cm, then find PC + PD.

Solution:

Given

In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. IfPA = 12 cm, QC = QD = 3 cm

Since the lengths of the two tangents drawn from an external point to a circle are equal,

PA = PB  → Equation (l)

CA = CQ  → Equation (2)

DB = DQ  →  Equation (3)

Now, PA = 12

PC + CA= 12 (given)

PC + CQ = 12  From 2

PC + 3 = 12 ⇒ PC= 9 cm  →  Equation 4

PB=PA = 12

PD +DB= 12

PD +DQ= 12

PD + 3 = 12

PD = 9 cm  → Equation 5

PC + PD = (9 + 9) cm = 18 cm [From 4 and 5]

PC + PD = 18 cm

Example 14. O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length AB.

Solution:

Given

O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E

Since, \(\angle O P T=90^{\circ}\) (radius through point of contact is \(\perp\) to the tangent)

In right \(\triangle O P T\),

⇒ \(OP^2+P T^2=O T^2\)

⇒ \(P T^2=O T^2-O P^2\)

⇒ \(P T^2=(13)^2-(5)^2=(12)^2\)

⇒ \(P T=12 \mathrm{~cm}\)

Let A P=x cm

At E=A P=x (lengths of tangents from an external point are equal)

A T=T P-A P=12-x

E T=O T-O E=13-5=8 cm

⇒ \(\angle A E T=90^{\circ}\)

Now; since \(\angle A E O=90^{\circ}\)(radius through point of contact is \(\perp\) to the tangent)

In right \(\triangle A E T\), by Pythagoras theorem,

⇒ \(A E^2+E T^2=A T^2\)

⇒ \(x^2+(8)^2=(12-x)^2\)

⇒ \(x^2+64=144+x^2-24 x \)

⇒ \(24 x=144-64=80\)

x=\(\frac{80}{24}=\frac{10}{3}\)

Similarly, B E=\(\frac{10}{3} \mathrm{~cm}\)

⇒ \(A B=A E+B E=\left(\frac{10}{3}+\frac{10}{3}\right) \mathrm{cm}=\frac{20}{3} \mathrm{~cm}\)

A B=\(\frac{20}{3} \mathrm{~cm}\)

The length AB is  \(\frac{20}{3} \mathrm{~cm}\)

Example 15. In the given figure, T is tangent to the circle with centre O such that O T=4 cm and \(\angle O T A=30^{\circ}\). Find the length of segment AT.

Solution:

Given

In the given figure, T is tangent to the circle with centre O such that O T=4 cm and \(\angle O T A=30^{\circ}\).

In right \(\triangle O A T\),

⇒ \(\cos 30^{\circ} =\frac{A T}{O T}\)

∴ \(\frac{\sqrt{3}}{2} =\frac{A T}{4} \quad A T=2 \sqrt{3} \mathrm{~cm}\)

The length of segment AT is 2√3 cm.

Example 16. In the given figure, OP is equal to the diameter of the circle. Prove that \(\triangle ABP\) is an equilateral triangle.

Solution: 

Given

In the given figure, OP is equal to the diameter of the circle.

Let, \(\angle O P A=\angle O P B=\theta\)( tangents are equally inclined at the centre) and the radius of the circle be r.

Since, \(\angle 1=90^{\circ}\) (radius through point of contact is \(\perp\) to the tangent)

In right \(\triangle O A P\),

⇒ \(\sin \theta =\frac{O A}{O P}=\frac{r}{2 r}=\frac{1}{2}=\sin 30^{\circ}\)

⇒ \(\theta \Rightarrow \quad 30^{\circ} \quad \Rightarrow A P B=2 \theta=2 \times 30^{\circ}=60^{\circ}\)

Now, since PA = PB (length of tangents from an external point are equal)

⇒ \(\angle 2=\angle 3\) (angles opposite to equal sides are equal)

In \(\triangle M P B\).

⇒ \(\angle 2+\angle 3+\angle A P B=180^{\circ}\)

⇒ \(\angle 2+\angle 2+60^{\circ}=180^{\circ}\)

⇒ \(\angle 2=\angle 3=60^{\circ}\)

⇒ \(\angle 2+\angle 3+\angle A P B =180^{\circ}\) (angle sum property)

⇒ \(\angle 2+\angle 2+60^{\circ} =180^{\circ}\) [from (1) and (2)]

2 \(\angle 2 =120^{\circ} \quad \Rightarrow \quad \angle 2=60^{\circ}\)

⇒ \(\angle 2=\angle 3=60^{\circ}\)

So, all the angles of \(\triangle A P B are 60^{\circ}\).

∴ \(\triangle A P B\) is an equilateral triangle.

Example 17. If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that \(\angle D B C=120^{\circ}\), prove that B C+B D=B O.

Solution:

Given

If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that \(\angle D B C=120^{\circ}\),

⇒ \(\angle 1+\angle 2 =120^{\circ}\)

But \(\angle 1 =\angle 2\)

⇒ \(\angle 1+\angle 1 =120^{\circ}\)

2 \(\angle 1 =120^{\circ}\)

⇒ \(\angle 1 =60^{\circ}\)

Also, \(\angle O C B =90^{\circ}\) (radius through point of contact is \(\perp\) to the tangent)

Now, in right \(\triangle O C B\),

⇒ \(\cos 60^{\circ}=\frac{B C}{O B} \quad \Rightarrow \quad \frac{1}{2}=\frac{B C}{O B}\)

O B=B C+B C

O B=2 B C \(\quad \Rightarrow \quad O B=B C+B C\)

O B=B C+B D(length of tangents from an external point are equal)

∴ Hence Proved.

Example 18. In the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.

Solution:

Given

In the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P.

Join OP, OA and OB.

Let PA = x cm and PM = y cm

P A =P B (length of tangents from an external point are equal)

P M =P M (common)

⇒ \(\angle 1 =\angle 2\) (tangents are equally inclined at the centre)

⇒ \(\triangle A M P \cong \triangle B M P\) (SAS congruency)

A M=M B=\(\frac{9.6}{2}=4.8 \mathrm{~cm}\)

and \(\angle P M A=\angle P M B\)

But \(\angle P M A+\angle P M B=180^{\circ}\)

⇒ \(\angle P M A=\angle P M B=90^{\circ}\)

Now, in right \(\triangle A M P\),

⇒ \(x^2=y^2+(4.8)^2\) (by Pythagoras theorem)

Also, in right \(x^2=y^2+(4.8)^2\)\triangle A M O\(x^2=y^2+(4.8)^2\),

⇒ \((4.8)^2+O M^2 =(6)^2\)

⇒ \(O M^2 =36-23.04=12.96\)

⇒ \(O M =\sqrt{12.96}=3.6 \mathrm{~cm}\)

Now, \(\angle O A P=90^{\circ}\) (radius through point of contact is \perp to the tangent)

In right \(\triangle M O P\),

⇒ \(O P^2 =O A^2+A P^2 \Rightarrow(y+3.6)^2=36+x^2\)

⇒ \(y^2+12.96+7.2 y =36+y^2+(4.8)^2\)

⇒ \(7.2 y =36+23.04-12.96 \quad \Rightarrow \quad 7.2 y=46.08 \)

y =\(\frac{46.08}{7.2}=6.4 \mathrm{~cm}\)

Put this value of y in equation (1),

⇒ \(x^2 =(6.4)^2+(4.8)^2=40.96+23.04=64\)

x = 8 cm

Hence, x=8 cm and y=6.4 cm

Example 19. The radii of two concentric circles are 1 3 cm and 8 cm. AB is the diameter of the bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.

Solution:

Given

The radii of two concentric circles are 1 3 cm and 8 cm. AB is the diameter of the bigger circle. BD is a tangent to the smaller circle touching it at D.

Produce BD to E which cuts the circle at E. Join AE and OD.

Since AB is the diameter of the bigger circle.

⇒  \(\angle A E B=90^{\circ}\) (angle in a semicircle is right angle)

Also, \(\angle O D B=90^{\circ}\)(radius through point of contact is \(\perp\) to the tangent)

Now, in \(\triangle B O D\) and \(\triangle B A E\)

⇒ \(\angle B =\angle B\) (common)

⇒ \(\angle O D B =\angle A E B\) (each \(90^{\circ}\) )

⇒ \(\Delta B O D =\triangle B A E\)

⇒ \(\frac{O D}{A E} =\frac{O B}{A B}\)(corresponding sides of similar triangles are proportional)

⇒ \(\frac{8}{A E}=\frac{r}{2 r} \quad \Rightarrow A E=16 \mathrm{~cm}\)

Since, \(O D \perp E B\)

D E=D B (\(\perp\) drawn from the centre to the chord bisects the chord)

In right \(\triangle O D B\),

⇒ \(D B^2 =O B^2-O D^2=(13)^2-(8)^2=169-64=105\)

D B =\(\sqrt{105} \mathrm{~cm}=E D\)

Now, in right \(\triangle A E D\), by Pythagoras theorem

⇒ \(A D^2 =A E^2+E D^2\)

⇒ \(A D^2 =(16)^2+105=256+105=361\)

∴ \(A D =\sqrt{361}\) i.e.. 19 cm

Hence, A D =19 cm.

The length AD =19 cm.

Class 10 Circles Questions with Solutions

NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles  Exercise 10.1

Question 1. How many tangents can a circle have?

Solution :

Infinitely many tangents can be drawn on a circle.

Question 2. Fill in the blanks :

1. A tangent to a circle intersects it in point (s).
2. A line intersecting a circle in two points is called a
3. A circle can have parallel tangents at the most.
4. The common point of a tangent to a circle and the circle is called

Answer :

1. one
2. secant
3. two
4.  point of contact

Question 3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm, Length PQ is :

• 12 cm
• 13 cm
• 8.5 cm
• \(\sqrt{119} \mathrm{~cm}\)

Solution : 4. \(\sqrt{119} \mathrm{~cm}\)

Here OP = 5 cm,

OQ = 12 cm In \(\triangle\)POQ

In \(\triangle P O Q \)

⇒ \(P Q^2 =O Q^2-O P^2\)

=\(12^2-5^2=119\)

P Q =\(\sqrt{119}\) cm

Question 4. Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.

Solution:

1. Let the centre of the circle be O. The line AB lies outside the circle. Draw the perpendicular OM from O to AB.
2. The perpendicular OM intersects the circle at P. Draw a line EPF from P parallel to AB.
3. EF is the required tangent of the circle.
4. Draw a line CD parallel to AB which intersects the circle at two points. It is the required secant of the circle.

NCERT Class 10 Maths Chapter 10 Extra Questions

NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Exercise 10.2

Question 1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is :

1. 7 cm
2. 12 cm
3. 15 cm
4. 24.5 cm

Answer: 1.

Here, PQ = 24 cm and OQ = 25 cm

In \(\triangle O P Q\)

⇒ \(O P^2=O Q^2-P Q^2\)(from Pythagoras theorem)

= \(25^2-24^2=625-576=49\)

OP = 7 cm

Radius of circle = 7 cm

Question 2. In the figure, if TP and TQ arc the Uvo tangents to a circle with centre O so that ZPOQ = 110°, then Z PTQ is equal to :

1. 60°
2. 70°
3. 80°
4. 90°

Answer: 2.

Here TP and TQ are the tangents to the circle.

⇒ \(\angle\)OPT = \(\angle\)OQT = 90°

In □ OPTQ,

⇒ \(\angle\)OPT + \(\angle\)PTQ + \(\angle\)OQT + \(\angle\)POQ = 360°

90° + ZPTQ + 90° + 110° = 360°

⇒ \(\angle\)PTQ = 360° -290°

∴ \(\angle\)PTQ = 70°

Question 3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°, then ∠POA is equal to :

1. 50°
2. 60°
3. 70°
4. 80°

Answer: 1. 50°

PA and PB are two tangents of the circle.

⇒ \(\angle\)PAO = \(\angle\)PBO = 90°

Given : \(\angle\)APB =80°

Now, in □PAOB,

⇒ \(\angle\)AOB + \(\angle\)PAO + \(\angle\)APB + \(\angle\)PBO = 360°

⇒ \(\angle\)AOB + 90° + 80° + 90° = 360°

⇒ \(\angle\)AOB = 360° – 260° = 100°

Now, PO bisects \(\angle\)AOB.

⇒ \(\angle\)POA = – \(\angle\)AOB = – x 100° = 50°

Question 4. Prove that the tangents drawn at the ends of the diameter of a circle are parallel.

Solution :

Let AB be the diameter of a circle with centre O. PA and PB are the tangents to the circle at A points A and B respectively.

Now Z\(\angle\)PAB = 90°

and \(\angle\)QBA = 90°

\(\angle\)PAB +QBA = 90° + 90° = 180°

PA || QB Hence Proved.

Question 5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.

Solution :

Given: A circle with centre O a tangent AQB and a perpendicular PQ is drawn from the point of contact Q to AB.

To Prove: The perpendicular PQ passes through the centre of the circle.

Proof: AQ is the tangent of the circle at point Q.

AQ will be the perpendicular to the radius of the circle.

PQ \(\perp\) AQ

The centre of the circle will lie on the line PQ.

Perpendicular PQ passes through the centre of the circle.

Hence Proved.

Question 6. The length of a tangent from point A at a distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.

Solution :

Given

The length of a tangent from point A at a distance 5 cm from the centre of the circle is 4 cm.

Let O be the centre of the circle and PQ is a tangent to the circle from point P.

Given that, PQ = 4 cm and OP = 5 cm

Now,\(\angle O Q P=90^{\circ}\)

In \(\triangle O Q P\) ,

⇒  \(O Q^2=O P^2-P Q^2\)

=\(5^2-4^2\)

= 25-16 = 9

OQ = 3 cm

Radius of circle = 3 cm

Question 7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.

Solution :

Given

Two concentric circles are of radii 5 cm and 3 cm.

Here, we draw two circles C₁ and C₂ with radii = 3 cm and r₂ = 5 cm c₂ respectively.

Now, we draw a chord AB which touches the circle C₁ at D.

O is the centre of concentric circles.

Now we draw the perpendicular from O to AB which bisects AB at D.

i.e., AD = BD

In right \(\triangle O B D\),

⇒ \(O B^2=O D^2+D B^2\) (from Pythagoras theorem)

⇒ \(5^2 =3^2+D B^2\)

⇒ \(D B^2\) =25-9=16

DB = 4 cm

Length of chord = AB = 2BD

= 2 x 4 = 8 cm

Question 8. A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD=AD + BC.

Solution :

Given

A quadrilateral ABCD is drawn to circumscribe a circle.

The sides of quadrilateral ABCD touch the circle at P, Q, R and S as shown in the figure. We know that the tangents drawn from an external point to the circle are equal.

AP = AS, BP = BQ,

CR = CQ, DR = DS

On adding, AP + BP + CR + DR

= AS + BQ + CQ + DS

⇒ AB + CD = (AS + DS) + (BQ + CQ)

⇒ AB + CD = AD + BC

Hence Proved.

Question 9. In the figure, XY and X’ Y’ are two parallel tangents to a circle with centre O and another tangent AB with the point of contact C intersecting XY at A and X’ Y’ at B. Prove that \(\angle\)AOB = 90°.

Solution :

Given

In the figure, XY and X’ Y’ are two parallel tangents to a circle with centre O and another tangent AB with the point of contact C intersecting XY at A and X’ Y’ at B.

The tangents from an external point to a circle are equal.

AP = AC

In \(\triangle A P O\) and \(\triangle A C O\),

AP = AC

AO = AO (common)

OP = OC (radii of a circle)

From S.S.S. congruency,

⇒ \(\triangle A P O \cong \triangle A C O\)

⇒ \(\angle P A O=\angle O A C\)

⇒ \(\angle P A C=2=\angle C A O\)

Similarly, we can prove that

⇒ \(\angle C B O =\angle O B Q\)

⇒ \(\angle C B Q =2 \angle C B O\)

⇒ \(Y \| X^{\prime} Y^{\prime}\)

⇒ \(\angle P A C+\angle Q B C=180^{\circ}\)

(sum of interior angles of the same side of a transversal is \(180^{\circ}\) )

2. \(\angle C A O+2 \angle C B O =180^{\circ}\)

⇒ \(\angle C A O+\angle C B O =90^{\circ}\)

In \(\triangle A O B\),

⇒  \(C A O+\angle C B O+\angle A O B=180^{\circ}\)

⇒ \(\angle C A O+\angle C B O=180^{\circ}-\angle A O B\) From equations (1) and (2)

⇒ \(180^{\circ}-\angle A O B=90^{\circ}\)

∴ \(\angle A O B=90^{\circ}\) Hence Proved.

Question 10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtends ey the line segment joining the points of contact at the centre.

Solution :

PA and PB are the tangents of the circle.

\(\angle O A P=\angle O B P=90^{\circ}\)

In O A P B

⇒  \(\Rightarrow \quad 90^{\circ}+\angle A P B+90^{\circ}+\angle A O B=360^{\circ}\)

⇒ \(\angle A P B+\angle A O B=180^{\circ}\)

⇒ \(\angle A P B\) and \(\angle A O B\) are supplementary.

Hence Proved.

Question 11. Prove that the parallelogram circumscribing a circle is a rhombus.

Solution :

Let a parallelogram ABCD is given. Let the parallelogram touch the circle at points, P, Q, R and S.

AP and AS are the tangents drawn from an -external point A to the circle.

AP = AS …(1)

Similarly, BP = BQ _ (2)

CR = CQ (3)

DR = DS (4)

Adding equations (1), (2), (3) and (4),

AP + BP + CR+DR = AS + BQ + CQ + DS

(AP + BP) + (CR + DR)

= (AS+ DS) + (BQ + CQ)

AB + CD = AD+BC

AB + AB = AD + AD {CD = AB, BC = AD, opposite sides of a parallelogram)

2 AB = 2 AD

AB = AD

So, ABCD is a rhombus. (adjacent sides of a parallelogram are equal)

Hence Proved.

Question 12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.

Solution :

Given

A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively.

Given that: CD = 6 cm,

BD = 8 cm and radius = 4 cm

Join OC, OA and OB.

We know that the tangents drawn from an external point to a circle are equal.

CD = CF = 6 cm and BD = BE = 8 cm

Let AF = AE = x cm c

In \(\triangle\)OCB,

area of triangle \(A_1 =\frac{1}{2} \times \text { base } \times \text { height }\)

= \(\frac{1}{2} \times C B \times O D\)

= \(\frac{1}{2} \times 14 \times 4=28 \mathrm{~cm}^2\)

In \(\triangle O C A\),

area of triangle

⇒ \(A_2 =\frac{1}{2} \times A C \times O F \)

=\(\frac{1}{2}(6+x) \times 4\)

=12+2 x

In \(\triangle O B A\).

area of triangle

⇒ \(A_3 =\frac{1}{2} \times A B \times O E\)

=\(\frac{1}{2}(8+x) \times 4\)

=16+2 x

Now, semiperimeter of triangle ABC,

s =\(\frac{1}{2}(A B+B C+C A)\)

s =\(\frac{1}{2}(x+6+14+8+x)\)

=14+x

Now, area of \(\triangle A B C\)

=\(A_1+A_2+A_3\)

=28+(12+2 x)+(16+2 x)

=56+4 x

From Heron’s formula,

Area of \(\triangle A B C\)

= \(\sqrt{s(s-a)(s-b)(s-c)}\)

= \(\sqrt{(14+x)(14+x-14)(14+x-x-6)} \quad(14+x-x-8)\)

= \(\sqrt{(14+x)(x)(8)(6)}\)

= \(\sqrt{(14+x) 48 x}\)

From equations (1) and (2),

⇒  \(\sqrt{(14+x) 48 x}=56+4 x\)

Squaring both sides,

⇒ \((14+x) 48 x =4^2(14+x)^2\)

3 x =14+x

⇒ \(2 x=14-\Rightarrow \quad x\) =7

A C=6+x=6+7 =13 cm

A B=8+x=8+7 =15 cm

Question 13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Solution :

We know that the tangents drawn R from an external point to a circle subtend equal angles at the centre.

⇒ \(\angle 1=\angle 2\) ,

⇒ \(\angle 3=\angle 4\) ,

⇒ \(\angle 5=\angle 6\)

and \(\angle 7=\angle 8\)

Now, \(\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6+\angle 7+\angle 8 =360^{\circ}\)

⇒ \(2 \angle 2+2 \angle 3+2 \angle 6+2 \angle 7 =360^{\circ} \)

⇒ \((\angle 2+\angle 3)+(\angle 6+\angle 7) =180^{\circ}\)

⇒ \(\angle A O B+\angle C O D =180^{\circ}\)

Similarly, \(\angle B O C+\angle A O D =180^{\circ}\)

Hence Proved.

NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Multiple Choice Questions

Question 1. If the angle between two radii of a circle is 1 10° then the angle between the tangents drawn at the ends of these radii is :

1. 110°
2. 100°
3. 90°
4. 70°

Answer: 4. 70°

Question 2. If two tangents PA and PB drawn from point P are of equal length 4 cm, then the radius of the die circle is :

1. 1 cm
2. 2 cm
3. 4 cm
4. 3 cm

Answer: 3. 4 cm

Question 3. In the adjoining figure, PA and PB are tangents to a circle with centre 0 such that \(angle\)APB = 40°. \(angle\)OAB is :

1. 20°
2. 40°
3. 30°
4. 15°

Answer: 1. 20°

Question 4. If two tangents of a circle of radius 6 cm are drawn such that the angle between them is 60 then the length of each tangent is :

1. 2 \(\sqrt{3} \mathrm{~cm}\)
2. 6 \(\sqrt{3} \mathrm{~cm}\)
3. 3 cm
4. 6 cm

Answer: 2. 6 \(\sqrt{3} \mathrm{~cm}\)

Question 5. Two tangents PQ and PR are drawn to a circle of radius 5 cm where P is 13 cm away from centre O. The area of quadrilateral PQOR is :

1. \(60 \mathrm{~cm}^2\)
2. \(30 \mathrm{~cm}^2\)
3. \(65 \mathrm{~cm}^2\)
4. \(32.5 \mathrm{~cm}^2\)

Answer: 1. \(60 \mathrm{~cm}^2\)

Class 10 Maths Circles important questions and answers

Question 6. In the adjoining figure, O is the centre of the circle, PQ is the chord and the tangent PR drawn from points on the circle makes a 50° angle from chord PQ, \(\angle\) POQ is :

1. 90°
2. 80°
3. 100°
4. 75°

Answer: 3. 100°

Question 7. The radii of two circles are 3 cm and 4 cm and both circles touch each other externally. The distance between their centres is :

1. 1 cm
2. 3 cm
3. 5 cm
4. 7 cm

Answer: 4. 7 cm