CBSE Class 12 Maths Chapter 1 Important Questions: Key Concepts and Solutions

Overview of Chapter 1 Relations And Functions

Chapter 1 of CBSE Class 12 Maths covers essential concepts such as relations and functions. Understanding these topics is crucial for solving problems effectively.

CBSE Class 12 Maths Chapter 1 Relations And Functions Important Questions

Question 1. Let set X = {1, 2, 3} and a relation R is defined in X as R = {(1, 3), (2, 2), (3,2)}, then minimum ordered pairs which should be added in relation R to make it reflexive and symmetric are:

1. {(1,1), (2. 3), (1,2)}
2. {(3, 3), (3, 1), (1,2)}
3. {(1, 1), (3, 3), (3. 1), (2, 3)}
4. {(1,1), (3, 3), (3, 1), (1,2)}

Solution: 3. {(1, 1), (3, 3), (3. 1), (2, 3)}

Given, R= {(1,3), (2,2), (3,2)} on set X = {1.2, 3}

Then: if R is reflexive and symmetric, then R= {(1, 1), (2, 2), (3, 3), (1,3), (3, 2), (3, 1), (2, 3)}

Hence: the ordered pairs to be added are: {(1, 1), (3, 3), (3, 1), (2, 3)}

Read and Learn More CBSE Class 12 Maths Important Question and Answers

CBSE Class 12 Maths Chapter 1 Important Question 2. If R = {(x, y); x, y ∈ Z, x² + y² ≤ 4} is a relation in set Z. then the domain of R is :

1. {0, 1,2}
2. {-2,-1, 0, 1,2}
3. {0,-1,-2}
4. {-1,0, 1}

Solution: 2. {-2,-1, 0, 1,2}

Given: R = {(x, y) : x, y ∈ Z, x² + y² ≤ 4} is a relation in set Z.

Hence: according to the given relation.

Domain of R= {-2, —1, 0. 1.2}

Important Questions For Class 12 Maths Chapter 1

Question 3. Let X = {x²: x ∈ N} and the function f: N →X is defined by f(x) = x², x ∈ N. Then, this function is :

1. Injective only
2. Not objective
3. Surjective only
4. Bijective

Solution: 4. Bijective

f(x) = x²; x ∈ N; f : N → X where X = {x²: x ∈ N}

Now; f(x₁) = f(x₂)

⇒ x²₁ = x²₂

⇒ (x₁ + x₂) (x₁ – x₂) = 0

Now : x₁ + x₂ ≠ 0 (x₁,x₂ ∈ N)

⇒ x₁ – x₂ = 0 ⇒ x₁ = x₂

Hence; f is one-one.

Let y = f(x) ⇒ y = x²

⇒ x = √y

∀ y ∈ X, there exists x ∈ N

Hence, every element of the co-domain has pre-images in the domain.

⇒ Range = Co-domain

∴  f is onto.

∴ The given function is bijective.

Relations And Functions Class 12 Important Questions

Question 4. A function f: R → R defined by f(x) = 2 + x² is :

1. Not one-one
2. One-one
3. Not onto
4. Neither one-one nor onto

Solution: 4. Neither one-one nor onto

f(x) = 2 + x² f: R → R

One-one: Let x₁ and x₂ ∈ R such that

f(x₁) = f(x₂) => x²₁ + 2 = x²₂ = 2

⇒ x₁ = ±x₂ ⇒  f is not one-one

Onto: Let y = f(x) ⇒ y = x² + 2 ⇒ x \(=\sqrt{y-I} \in R\)

∴ y – 2 ≥ 0 ⇒ y ≥ 2 ⇒ y ∈ R [2, ∞)

Range 5≠ co-domain

Also: f is not onto as there is no pre-image for negative real numbers.

Hence; f is neither one-one nor onto.

Question 5. Write the smallest reflexive relation on set A = {a, b, c}.

Solution:

For reflexive relation, each and every element of the given set must be related to itself, at least i.e. the smallest reflexive relation on set A will be {(a, a), (b, b), (c, c)}.

Class 12 Maths Chapter 1 Important Questions With Solutions

Question 6. If f = {(1.2), (2, 4), (3, 1), (4, k)} is a one-one function from set A to A, where A = {1, 2, 3, 4}; then find the value of k.

Solution:

In a one-on-one function, different elements must have different images. So, according to the given function, f = {(1,2), (2. 4), (3, 1), (4, k)}, the value of k must be 3.

CBSE Class 12 Maths Chapter 1 Important Question 7.

1. Check whether the relation R defined on the set {1, 2, 3, 4} as R = {(a, b); b = a + 1} is transitive. Justify your answer. Or
2. If the relation R on the set A = {x : 0 ≤ x ≤12} given by R = {(a, b): a = b} is an equivalence relation, then find the set of all elements related to 1.

Solution:

1. Given. R = ((a, b): b = a + 1} defined on the set A = {1, 2, 3, 4}

⇒ R = {(1, 2), (2, 3), (3, 4)}

By definition, for transitive relation, if a R b and b R c ⇒ a R c ∀ a, b, c ∈ A

For 1,2, 3 ∈ A; (1,2) ∈ R and (2, 3) ∈ R but (1, 3) ∉ R

Therefore, R is not transitive.

Aliter: Given; R = {(a, b): b = a + 1} defined on the set A – {1,2, 3,4}

For transitive relation: Let (a, b) ∈ R and (b, c) ∈ R ∀ a, b, c ∈ A

⇒ b = a + 1 and c = b + 1

⇒ c = a + 2

or (a, c) ∉ R

∴ R is not transitive

or

2. The elements in R that are related to 1 will be those elements from set A which are equal to 1.

Hence, the set of elements related to 1 is {1}.

Aliter: Let x ∈ A which is related to 1 by the given relation R = {(a, b): a = b}

x R 1 ⇒ (x, 1) ∈ R ⇒ x = 1

∴ [1] = {1}

Relations And Functions Important Questions For Cbse Class 12

Question 8. The relation R in the set {1.2,3} given by R = {(1, 2), (2, 1), (1, 1)} is:

1. Symmetric and transitive, but not reflexive
2. Reflexive and symmetric, but not transitive
3. Symmetric, but neither reflexive nor transitive
4. An equivalence relation

Solution: 3. Symmetric, but neither reflexive nor transitive

Let A= {1,2, 3} and R = {(1, 2), (2, 1), (1, 1)}

R is not reflexive as (2, 2) and (3,3) ∉ R.

R is a symmetric relation as (a, b) ∈ R and (b, a) ∈ R ∀ a, b ∈ A.

R is not a transitive relation because (2, 1) ∈ R and (1,2) ∈ R but (2, 2) ∉ R.

Hence; R is symmetric, but neither reflexive nor transitive.

Question 9. Let A = {1,3, 5}, Then the number of equivalence relations in A containing (1,3) is

1. 1
2. 2
3. 3
4. 4

Solution: 2. 2

R₁ = {(1, 1), (3, 3), (5, 5), (1, 3), (3, 1)}

and R₂ = {(1, 1), (3. 3), (5, 5), (1, 3), (3, 1), (1,5), (5, 1), (3, 5), (5, 3)}

Hence, the number of equivalence relations in A containing (1, 3) is 2.

CBSE Class 12 Maths Chapter 1 Extra Questions

Question 10. Check whether the relation R in the set N of natural numbers given by R = {(a, b): a is divisor of b} is reflexive, symmetric or transitive. Also, determine whether R is an equivalence relation.

Solution:

The relation R in the set N is given by:

R = {(a, b): a is divisor of b}

⇒ aRb => \(\frac{b}{a}\) = K ∈ 1 ∀ a, b ∈ N,

Reflexive; aRa ∀ a∈N (By definition)

aRa ⇒ \(\frac{a}{a}\)= 1 ∈ I which is true.

So, R is reflexive relation.

Symmetric: we have

aRb ⇒ \(\frac{b}{a}\) = K ∈ I ∀ a, b ∈ N

⇒ \(\frac{a}{b}=\frac{1}{K} \notin I\)

⇒ b K a ∀ a, b∈ N

∴ If aRb ⇒ bRa ∀ a, b ∈ N, then R is not a symmetric relation.

Transitive: If aRb ⇒ \(\frac{b}{a}=K_1\) ∈ I ∀ a, b ∈ N ….(1)

bRc ⇒ \(\frac{c}{b}=K_2\) ∈ I ∀ b, c ∈ N ….(2)

from equation (1) and (2) \(\frac{b}{a} \times \frac{c}{b}=K_1 \times K_2 \Rightarrow \frac{c}{a}-\left(K_1 K_2\right) \in I \Rightarrow a R c\)

So, R is a transitive relation

∴ R is reflexive and transitive but not symmetric

R is not an equivalence relation on N.

Question 11. Check whether the relation R defined on the set A = {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric, or transitive.

Solution:

Given, R = {(a, b): b = a + 1} is defined on the set A = {1, 2, 3, 4, 5, 6}

⇒ R= {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}

Reflexive: By definition, a R a ∀a, b ∈ A

Now, 1 ∈ A but (1, 1) ∉ R.

Therefore, R is not reflexive.

Symmetric: By definition, if a R b ⇒ b R a ∀ a, b ∈ A

For 1,2 ∈ A, It can be observed that (1,2) ∈ R but (2, 1) ∉ R.

Therefore, R is not symmetric.

Transitive: By definition, if a R b and b R c ⇒ a R c ∀ a, b, c ∈ A

For 1,2, 3 ∈ A, (1,2) ∈ R and (2, 3) ∈ R but (1, 3)  ∉ R

Therefore, R is not transitive.

Hence, R is neither reflexive nor symmetric nor transitive.

Aliter: Given; R = {(a, b): b = a + 1} defined on the set A = {1,2, 3, 4, 5, 6}

Reflexive: (a, a) ∈ R ∀ a ∈ A

⇒ a = a + 1; which is not true;

∴ R is not reflexive.

Symmetric: Let (a, b) ∈ R ∀ a, b ∈ A

⇒ b = a + 1

⇒ (b, a) ∉ R [a ≠ b + 1]

∴ R is not symmetric

Transitive: Let (a, b) ∈ R and (b, c) ∈ R ∀ a, b, c ∈ A

⇒ b = a + 1 and c = b + 1

⇒ c = a + 2 or (a, c ) ∉ R

∴ R is not transitive.

Hence; R is neither reflexive nor symmetric nor transitive.

Relations And Functions Previous Year Questions Class 12

Question 12. Let A = {x ∈ Z : 0 ≤ x ≤12}. Show that R = {(a, b): a, b ∈ A, |a – b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. Also; write the equivalence class [2]. or, Show that the function f: R → R defined by \(f(x)=\frac{x}{x^2+1}\). ∀ x ∈R is neither one-one nor onto.

Solution:

Given, R = {(a, b): a, b ∈ A, |a – b| is divisible by 4}

Reflexive: Let a ∈ A

Now, |a — a| = 0. which is divisible by 4

So, (a, a) ∈ R ∀ a ∈ A

Hence, R is reflexive.

Symmetric: Let a, b ∈ A such that (a, b) ∈ R i.e. |a — b| is divisible by 4.

⇒ |-(b – a)| = |b — a| is also divisible by 4.

Hence; (b, a) ∈ R.

So, R is symmetric.

Transitive: Let a, b, c ∈ A such that (a, b), (b, c) ∈ R

i.e. |a – b| and |b – c| is divisible by 4.

Let \(|\mathrm{a}-\mathrm{b}|=4 \mathrm{k}_1\)

⇒ \(\mathrm{~b}-\mathrm{c}|=4 \mathrm{k}_2\)

⇒ \((\mathrm{a}-\mathrm{b})= \pm 4 \mathrm{k}_1\)….(1)

⇒ \((b-c)= \pm 4 k_2\)….(2)

Adding equations (1) and (2); \((\mathrm{a}-\mathrm{b})+(\mathrm{b}-\mathrm{c})= \pm 4 \mathrm{k}_1 \pm 4 \mathrm{k}_2= \pm 4\left(\mathrm{k}_1+\mathrm{k}_2\right)\)

⇒ a – c is divisible by 4.

⇒ |a – c| is divisible by 4.

Hence; (a, c) ∈ R

So, R is transitive.

Hence; R is an equivalence relation.

Further, let (x, 1) ∈ R ∀ x ∈ A ⇒ |x  – 1| is divisible by 4

⇒ x – 1 = 0, 4, 8, 12

⇒ x= 1, 5, 9 [x = 13 ∉ A]

Equivalence class of [1] = {1,5,9}

[The set of all elements related to 1 represents its equivalence class]

Now, we will find the equivalence class of [2]

Let (x, 2) ∈ R ∀ x ∈ A

⇒ |x — 2| = 0, 4, 8, 12

⇒ x = 2, 6, 10 [x = 14 ∉ A]

∴ Equivalence class of [2] = {2, 6, 10}. or,

f : \(R \rightarrow R ; f(x)=\frac{x}{x^2+1}\)

1. One-one function: we have \(\mathrm{f}\left(\mathrm{x}_1\right)=\mathrm{f}\left(\mathrm{x}_2\right), \forall, \mathrm{x}_1, \mathrm{x}_2 \in \mathrm{R}\)

⇒ \(\frac{x_1}{x_1^2+1}=\frac{x_2}{x_2^2+1}\)

⇒ \(x_1 x_2^2+x_1=x_2 x_1^2+x_2 \quad \Rightarrow\left(x_1 x_2^2-x_2 x_1^2\right)+\left(x_1-x_2\right)=0\)

⇒ \(x_1 x_2\left(x_2-x_1\right)+\left(x_1-x_2\right)=0 \Rightarrow\left(x_1-x_2\right)\left(-x_1 x_2+1\right)=0\)

⇒ \(x_1=x_2 \text { and } x_1 x_2=1 \text { or } x_1=\frac{1}{x_2}\)

One-one function Example: Let \(\mathrm{x}_1=2 \in \mathrm{R} ; \mathrm{x}_2=1 / 2 \in \mathrm{R}\)

Then, \(f\left(x_1\right)=f(2)=2 / 5\) and \(f\left(x_2\right)=f(1 / 2)=2 / 5\)

⇒ latex]x_1 \neq x_2[/latex] but \(f\left(x_1\right)=f\left(x_2\right)\)

∴ f is not a one-on-one function

2. Onto function: Let y = f(x)

⇒ y = \(\frac{x}{x^2+1} \Rightarrow x^2 y-x+y=0\)

⇒ x = \(\frac{1 \pm \sqrt{1-4 y^2}}{2 y} \in R \text { if } 1-4 y^2 \geq 0 \text { and } y \neq 0\)

⇒ \(4 y^2-1 \leq 0 \text { or }(2 y+1)(2 y-1) \leq 0\)

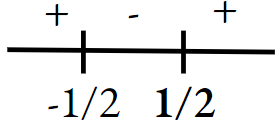
⇒ \(x \in\left[-\frac{1}{2}, 0\right) \cup\left(0, \frac{1}{2}\right]\)

Thus, every element of the Co-domain does not have its pre-image in the domain.

Hence, f: R → R is not onto.

∴ f is neither one-one nor onto.

CBSE Class 12 Maths Chapter 2 Important Questions: Key Concepts and Solutions

Overview of Chapter 2

Chapter 2 of CBSE Class 12 Maths focuses on Inverse Trigonometric Functions. Understanding these functions is crucial for solving various mathematical problems effectively.

CBSE Class 12 Maths Chapter 2 Inverse Trigonometric Functions Important Questions

Question 1. The principal value of \(\cos ^{-1}\left(\frac{1}{2}\right)+\sin ^{-1}\left(-\frac{1}{\sqrt{2}}\right)\) is

1. \(\frac{\pi}{12}\)
2. \(\pi\)
3. \(\frac{\pi}{3}\)
4. \(\frac{\pi}{6}\)

Solution: 1. \(\frac{\pi}{12}\)

⇒ \(\cos ^{-1}\left(\frac{1}{2}\right)+\sin ^{-1}\left(-\frac{1}{\sqrt{2}}\right)=\frac{\pi}{3}+\left(-\frac{\pi}{4}\right)\)

= \(\frac{4 \pi-3 \pi}{12}=\frac{\pi}{12}\)

Read and Learn More CBSE Class 12 Maths Important Question and Answers

Question 2. The principal value of \(\tan ^{-1}\left(\tan \frac{9 \pi}{8}\right)\) is:

1. \(\frac{\pi}{8}\)
2. \(\frac{3 \pi}{8}\)
3. \(-\frac{\pi}{8}\)
4. \(-\frac{3 \pi}{8}\)

Solution: 1. \(\frac{\pi}{8}\)

⇒ \(\tan ^{-1}\left[\tan \left(\frac{9 \pi}{8}\right)\right]=\tan ^{-1}\left[\tan \left(\pi+\frac{\pi}{8}\right)\right]\)

= \(\tan ^{-1}\left[\tan \left(\frac{\pi}{8}\right)\right]=\frac{\pi}{8} \in\left(-\frac{\pi}{2} \cdot \frac{\pi}{2}\right)\)

Inverse Trigonometric Functions Class 12 Important Questions

Question 3. What is the domain of the function cos^-1(2x-3)?

1. [-1, 1]
2. (1,2)
3. (-1, 1)
4. [1,2]

Solution: 4. [1,2]

For the given function: -1 ≤ 2x – 3 ≤ 1

⇒ 2 ⇒ 2x ⇒ 4

⇒ 1 ≤ x ≤ 2

Question 4. The principal value of [tan^-1 √3 – cot^-1 (-√3)] is

1. π
2. \(-\frac{\pi}{2}\)
3. 0
4. \(2 \sqrt{3}\)

Solution: 2. \(-\frac{\pi}{2}\)

⇒ \(\tan ^{-1}(\sqrt{3})-\cot ^{-1}(-\sqrt{3})=\frac{\pi}{3}-\left(\pi-\cot ^{-1}(\sqrt{3})\right)\)

=\(\frac{\pi}{3}-\left(\pi-\frac{\pi}{6}\right)=\frac{\pi}{3}-\frac{5 \pi}{6}=\frac{-3 \pi}{6}=\frac{-\pi}{2}\)

Question 5. The range or the principal valurbrance of the function y = sec^-1 x is ____

or,

The principal value of \(\cos ^{-1}\left(-\frac{1}{2}\right)\) is

Solution:

y = \(\sec ^{-1} x\) (given)

Range of \(\sec ^{-1} x\) is [0, π]-{π/2}

Or

Let \(\cos ^{-1}\left(-\frac{1}{2}\right)=y\)

⇒ \(\cos y=-\frac{1}{2} \Rightarrow \cos y=\cos \left[\pi-\frac{\pi}{3}\right]\)

⇒ \(\cos y=\cos \frac{2 \pi}{3} \Rightarrow y=\frac{2 \pi}{3} \in[0, \pi]\)

Class 12 Maths Chapter 2 Important Questions With Solutions

Question 6. Simplify \(\sec ^{-1}\left(\frac{1}{2 x^2-1}\right), 0<x<\frac{1}{\sqrt{2}} \text {. }\)

Solution:

Let y = \(\sec ^{-1}\left(\frac{1}{2 x^2-1}\right), 0<x<\frac{1}{\sqrt{2}}\)

Put x = \(\cos \theta\); then \(\theta=\cos ^{-1} x\)

y = \(\sec ^{-1}\left(\frac{1}{2 \cos ^2 \theta-1}\right)\)

= \(\sec ^{-1}\left(\frac{1}{\cos 2 \theta}\right)=\sec ^{-1}(\sec 2 \theta)=2 \theta=2 \cos ^{-1} x\)

Question 7. Prove that: \(3 \sin ^{-1} x=\sin ^{-1}\left(3 x-4 x^3\right), x \in\left[-\frac{1}{2}, \frac{1}{2}\right]\)

Solution:

To prove: \(3 \sin ^{-1} x=\sin ^{-1}\left(3 x-4 x^3\right), x \in\left[-\frac{1}{2}, \frac{1}{2}\right]\)

R.H.S = sin^-1(3x – 4x³)

Put x = sinθ :  θ = sin^-1x

⇒ R.H.S = sin^-1 (3sinθ – 4sin³θ) – sin^-1(sin3θ) = 3θ = 3sin^-1x = L.H.S

Hence, proved.

CBSE Class 12 Maths Chapter 2 Conclusion

Focusing on these important questions will enhance your preparation for CBSE Class 12 Maths Chapter 2. Regular practice will build confidence and improve your problem-solving skills.

CBSE Class 12 Maths Chapter 4 Determinates Important Questions

Question 1. Three points P(2x, x + 3), Q(0, x) and R(x + 3, x + 6) are eollinear. then x is equal to

1. 0
2. 2
3. 3
4. 1

Solution: 4. 1

As per the given condition \(\left|\begin{array}{ccc}
2 x & x+3 & 1 \\
0 & x & 1 \\
x+3 & x+6 & 1
\end{array}\right|=0\)

[ar(ΔPQR) = 0]

⇒ 2x (x – x – 6) — 0(x + 3 – x — 6) + (x + 3) {x + 3 – x} =0

or -12x + 3x + 9 = 0 => -9x = -9 => x = 1

Read and Learn More CBSE Class 12 Maths Important Question and Answers

Question 2. If C_ij denotes the cofactor of element p_ij of the matrix P = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & 2 & 4
\end{array}\right]\) , then the value of C₃₁, C₂₃ is:

1. 5
2. 24
3. -4
4. -5

Solution: 1. 5

P = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
0 & 2 & -3 \\
3 & 2 & 4
\end{array}\right]\) (given)

⇒ C₃₁, C₂₃ = (3-4), {(-1)(2+3)} = 5

Determinants Class 12 Important Questions

Question 3. The system of linear equations 5x + ky = 5; 3x + 3y = 5 will be consistent if:

1. k ≠ -3
2. k = -5
3. k = 5
4. k ≠ 5

Solution: 4. k ≠ 5

The system of linear equations is given as:

5x + ky = 5 and 3x + 3y = 5

It can be written in matrix form as \(\left[\begin{array}{ll}
5 & k \\
3 & 3
\end{array}\right]\left[\begin{array}{l}
x \\
y
\end{array}\right]=\left[\begin{array}{l}
5 \\
5
\end{array}\right]\)

or A X = B

So; the given system of linear equations is consistent if |A| ≠ 0

⇒ \(\left|\begin{array}{ll}
5 & \mathrm{k} \\
3 & 3
\end{array}\right|\) 0

⇒15 – 3 k ≠ 0

⇒ k ≠ 5

Question 4. If, for the matrix \(A=\left[\begin{array}{cc}
\alpha & -2 \\
-2 & \alpha
\end{array}\right]\),\(\left|\mathrm{A}^2\right|=125\); then the value of α is:

1. 3
2. -3
3. 1
4. 1

Solution: 1. 3

Class 12 Maths Chapter 4 Important Questions With Solutions

Given \(\left|A^3\right|=125\)

⇒ \((|A|)^3=125\)

(because \(\left|A^n\right|=|A|^n\))

⇒ \(\left(\alpha^2-4\right)^3=125\)

⇒ \(\left(\alpha^2-4\right)=5\)

⇒ \(\alpha^2=9\) or \(\alpha= \pm 3\)

Question 5. Let matrix X = [x_ij] is given by X = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 4 & -5 \\
2 & -1 & 3
\end{array}\right]\), Then, the matrix Y = [m_ij]. where m_ij = Minor of X_ij is:

1. \(\left[\begin{array}{ccc}
   7 & -5 & -3 \\
   19 & 1 & -11 \\
   -11 & 1 & 7
   \end{array}\right]\)
2. \(\left[\begin{array}{ccc}
   7 & -19 & -11 \\
   5 & -1 & -1 \\
   3 & 11 & 7
   \end{array}\right]\)
3. \(\left[\begin{array}{ccc}
   7 & 19 & -11 \\
   -3 & 11 & 7 \\
   -5 & -1 & -1
   \end{array}\right]\)
4. \(\left[\begin{array}{ccc}
   7 & 19 & -11 \\
   -1 & -1 & 1 \\
   -3 & -11 & 7
   \end{array}\right]\)

Solution: 

X = \(\left[\begin{array}{ccc}
1 & -1 & 2 \\
3 & 4 & -5 \\
2 & -1 & 3
\end{array}\right]\)

Now, Y = [m_ij]

⇒ Y = \(\left[\begin{array}{lll}
m_{11} & m_{12} & m_{13} \\
m_{21} & m_{22} & m_{23} \\
m_{31} & m_{32} & m_{33}
\end{array}\right] \Rightarrow Y=\left[\begin{array}{ccc}
7 & 19 & -11 \\
-1 & -1 & 1 \\
-3 & -11 & 7
\end{array}\right]\)

Determinants Important Questions CBSE Class 12

Question 6. If x =-4 is a root of \(\left|\begin{array}{lll}
x & 2 & 3 \\
1 & x & 1 \\
3 & 2 & x
\end{array}\right|\) = 0, then the sum of the other two roots is:

1. 4
2. -3
3. 2
4. 5

Solution: 1. 4

⇒ \(\left|\begin{array}{lll}
x & 2 & 3 \\
1 & x & 1 \\
3 & 2 & x
\end{array}\right|\) = 0 (given)

⇒ \(x\left(x^2-2\right)-2(x-3)+3(2-3 x)=0\)

⇒ \(x^3-2 x-2 x+6+6-9 x=0\)

⇒ \(x^3-13 x+12=0\)

⇒ \((x+4)\left(x^2-4 x+3\right)=0\)

(because x=-4 is a root)

⇒ \((x+4)(x-1)(x-3)=0\)

Hence; the sum of other two roots = 1 + 3 = 4

Determinants Class 12 Important Questions

Question 7. The inverse of the matrix \(X=\left[\begin{array}{lll}2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4\end{array}\right]\)

1. \(24\left[\begin{array}{ccc}1 / 2 & 0 & 0 \\ 0 & 1 / 3 & 0 \\ 0 & 0 & 1 / 4\end{array}\right]\)
2. \(\frac{1}{24}\left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right]\)
3. \(\frac{1}{24}\left[\begin{array}{lll}2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4\end{array}\right]\)
4. \(\left[\begin{array}{ccc}1 / 2 & 0 & 0 \\ 0 & 1 / 3 & 0 \\ 0 & 0 & 1 / 4\end{array}\right]\)

Solution:

Given, \(X=\left[\begin{array}{lll}2 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4\end{array}\right]\)

|X| = \(2(12)-0+0=24 \neq 0\)

⇒ \(X^{-1}\) exists

Now, adj X = \(\left[\begin{array}{ccc}12 & 0 & 0 \\ 0 & 8 & 0 \\ 0 & 0 & 6\end{array}\right]\)

⇒ \(X^{-1}=\frac{1}{|X|} \cdot \mathrm{adj} X\)

⇒ \(X^{-1}=\frac{1}{24}\left[\begin{array}{ccc}
12 & 0 & 0 \\
0 & 8 & 0 \\
0 & 0 & 6
\end{array}\right]=\left[\begin{array}{ccc}
1 / 2 & 0 & 0 \\
0 & 1 / 3 & 0 \\
0 & 0 & 1 / 4
\end{array}\right]\)

Question 8. If A is square matrix of order 3 such that A(adj A) = \(\left[\begin{array}{ccc}-2 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & -2\end{array}\right]\), then find |A|.

Solution:

Given, A (adj A) = \(\left[\begin{array}{ccc}-2 & 0 & 0 \\ 0 & -2 & 0 \\ 0 & 0 & -2\end{array}\right]\)

We know that A(adj A)= |A| I

Now, A(adj A)= \(-2\left[\begin{array}{lll}1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1\end{array}\right] = -2I = |A| I\)

⇒ |A|=-2

CBSE Class 12 Maths Chapter 4 Extra Questions

Question 9. If A is a non-singular square matrix of order 3 such that A² = 3A, then the value of |A| is?

1. -3
2. 3
3. 9
4. 27

Solution:

Given, A² = 3A, |A| ≠ 0, order of A is 3

∴ |A²| = |3A|

⇒ |A|²= 3³|A|

(|A²| = |A|² and |KA| = Kⁿ|A|)

or |A| = 27

Question 10. If A is a square matrix satisfying A’A = I, write the value of |A|.

Solution:

A’A = I (given)

⇒ \(\left|A^{\prime} A\right|=|I|\)

⇒ \(\left|A^{\prime}\right||A|=|I| \Rightarrow|A|^2=1\) (because \(\left|A^{\prime}\right|=|A|\))

⇒ \(|A|=1 \text { or }|A|=-1\)

Question 11. Given, \(A=\left[\begin{array}{cc}2 & -3 \\ -4 & 7\end{array}\right]\), compute A^-1 and show that 2A^-1 = 9I – A.

Solution:

Given, \(A=\left[\begin{array}{cc}2 & -3 \\ -4 & 7\end{array}\right]\)

|A| = \(14-(12)=2 \neq 0\)

Hence, A is invertible.

adj A = \(\left[\begin{array}{ll}
7 & 3 \\
4 & 2
\end{array}\right]\)

Hence, \(A^{-1}=\frac{1}{|A|} \cdot \mathrm{adj} \cdot(\mathrm{A})\)

⇒ \(\mathrm{A}^{-1}=\frac{1}{2}\left[\begin{array}{ll}
7 & 3 \\
4 & 2
\end{array}\right] \text { or } 2 \mathrm{~A}^{-1}=\left[\begin{array}{ll}
7 & 3 \\
4 & 2
\end{array}\right]\)….(1)

Now, R.H.S. = \(9 \mathrm{I}-\mathrm{A}\)

⇒ \(9\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]-\left[\begin{array}{cc}
2 & -3 \\
-4 & 7
\end{array}\right]=\left[\begin{array}{cc}
9 & 0 \\
0 & 9
\end{array}\right]-\left[\begin{array}{cc}
2 & -3 \\
-4 & 7
\end{array}\right]=\left[\begin{array}{ll}
7 & 3 \\
4 & 2
\end{array}\right]=2 A^{-1}\)= L.H.S. [from (1)]

Hence proved.

Question 12. If \(A=\left[\begin{array}{ccc}
3 & 4 & 2 \\
0 & 2 & -3 \\
1 & -2 & 6
\end{array}\right]\); find A^-1.

Determinants Previous Year Questions Class 12

Hence solve the following system of equations: 3x + 4y + 2z = 8; 0x + 2y + 3z = 3 and x + 2y + 6z = -2 or,

OR

If \(A^{-1}=\left[\begin{array}{ccc}3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2\end{array}\right]$ and $B=\left[\begin{array}{ccc}1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1\end{array}\right]\) find \((A B)^{-1} \text {. }\)

Solution:

Given, \(A=\left[\begin{array}{ccc}
3 & 4 & 2 \\
0 & 2 & -3 \\
1 & -2 & 6
\end{array}\right]\)

⇒ |A| = 3(12 -6)-4(0 + 3) + 2(0-2)= 18- 12-4=2*0

Hence, A^-1 exists.

Now, co-factors are given as:

C₁₁ = 6, C₁₂ = —3, C₁₃ = -2,

C₂₁=-28, C₂₂ = 16, C₂₃= 10,

C₃₁= -16, C₃₂ = 9, C₃₃ = 6

Hence adj A = \(\left[\begin{array}{ccc}6 & -3 & -2 \\ -28 & 16 & 10 \\ -16 & 9 & 6\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{ccc}6 & -28 & -16 \\ -3 & 16 & 9 \\ -2 & 10 & 6\end{array}\right]\)

⇒ \(A^{-1}=\frac{1}{|A|}(\mathrm{adj} A)=\frac{1}{2}\left[\begin{array}{ccc}
6 & -28 & -16 \\
-3 & 16 & 9 \\
-2 & 10 & 6
\end{array}\right]\)….(1)

The system of linear equations is given as:

3x + 4y + 2z = 8

0x + 2y —3 = 3

x – 2y + 6z = -2

This system is written in matrix form as

⇒ \(\left[\begin{array}{ccc}
3 & 4 & 2 \\
0 & 2 & -3 \\
1 & -2 & 6
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
8 \\
3 \\
-2
\end{array}\right]\)

⇒ AX = B

⇒ X = \(A^{-1} \cdot B\)

⇒ X = \(\frac{1}{2}\left[\begin{array}{ccc}
6 & -28 & -16 \\
-3 & 16 & 9 \\
-2 & 10 & 6
\end{array}\right] \cdot\left[\begin{array}{l}
8 \\
3 \\
-2
\end{array}\right]=\frac{1}{2}\left[\begin{array}{l}
48-84+32 \\
-24+48-18 \\
-16+30-12
\end{array}\right]\)

[from (1) and (2)]

⇒ \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\frac{1}{2}\left[\begin{array}{r}
-4 \\
6 \\
2
\end{array}\right]\)

x=-2, y=3, z=1

Or

Given, \(A^{-1}=\left[\begin{array}{ccc}3 & -1 & 1 \\ -15 & 6 & -5 \\ 5 & -2 & 2\end{array}\right]\)…(1)

and \(B=\left[\begin{array}{ccc}1 & 2 & -2 \\ -1 & 3 & 0 \\ 0 & -2 & 1\end{array}\right]\)

|B| = 1 (3 – 0) – 2(- 1 – 0) – 2(2 – 0) = 3 + 2 – 4 = 1 ≠ 0

Now, the co-factors of matrix B are given as

⇒ \(C_{11}=3, C_{12}=1, C_{13}=2\)

⇒ \(C_{21}=2, C_{22}=1, C_{23}=2,\)

⇒ \(C_{31}=6, C_{32}=2, C_{33}=5\)

∴ (adj)(B) = \(\left[\begin{array}{lll}
3 & 1 & 2 \\
2 & 1 & 2 \\
6 & 2 & 5
\end{array}\right]^1=\left[\begin{array}{lll}
3 & 2 & 6 \\
1 & 1 & 2 \\
2 & 2 & 5
\end{array}\right]\)

⇒ \(B^{-1}=\frac{1}{|B|}(\mathrm{adj} B)=\left[\begin{array}{lll}
3 & 2 & 6 \\
1 & 1 & 2 \\
2 & 2 & 5
\end{array}\right]\)….(2)

∴ (AB)^-1 = B^-1 A^-1

= \(\left[\begin{array}{lll}
3 & 2 & 6 \\
1 & 1 & 2 \\
2 & 2 & 5
\end{array}\right] \cdot\left[\begin{array}{ccc}
3 & -1 & 1 \\
-15 & 6 & -5 \\
5 & -2 & 2
\end{array}\right]\)

=\(\left[\begin{array}{ccc}
9-30+30 & -3+12-12 & 3-10+12 \\
3-15+10 & -1+6-4 & 1-5+4 \\
6-30+25 & -2+12-10 & 2-10+10
\end{array}\right]\)

⇒ \((A B)^{-1}=\left[\begin{array}{ccc}
9 & -3 & 5 \\
-2 & 1 & 0 \\
1 & 0 & 2
\end{array}\right]\)

(from (1) and (2))

⇒ \((\mathrm{AB})^{-1}=\left[\begin{array}{ccc}
9 & -3 & 5 \\
-2 & 1 & 0 \\
1 & 0 & 2
\end{array}\right]\)

Question 13. If \(A=\left[\begin{array}{ccc}5 & -1 & 4 \\ 2 & 3 & 5 \\ 5 & -2 & 6\end{array}\right]\), find A^-1 and use it to solve the following system of equations.

5x – y + 4z = 5

2x + 3y + 5z = 2

5x – 2y + 6z = -1

Solution:

Given, \(A=\left[\begin{array}{ccc}5 & -1 & 4 \\ 2 & 3 & 5 \\ 5 & -2 & 6\end{array}\right]\)

∴ |A| = \(\left|\begin{array}{ccc}
5 & -1 & 4 \\
2 & 3 & 5 \\
5 & -2 & 6
\end{array}\right|\) = 5(18+10) + (12 – 25) + 4 (-4 – 15)= 140 – 13 – 76 = 51 ≠ 0.

Hence: A^-1 exists

Now co-factors of elements of A are:

⇒ \(A_{11}=28, A_{12}=13, A_{13}=-19\)

⇒ \(A_{21}=-2, A_{22}=10, A_{23}=5\)

⇒ \(A_{31}=-17, A_{32}=-17, A_{33}=17\)

∴ adj A = \(\left[\begin{array}{ccc}
28 & 13 & -19 \\
-2 & 10 & 5 \\
-17 & -17 & 17
\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{ccc}
28 & -2 & -17 \\
13 & 10 & -17 \\
-19 & 5 & 17
\end{array}\right]\)

⇒ \(A^{-1}=\frac{1}{|A|}(\mathrm{adj} A)=\frac{1}{51}\left[\begin{array}{ccc}
28 & -2 & -17 \\
13 & 10 & -17 \\
-19 & 5 & 17
\end{array}\right]\)

Given system of equations are

5x – y + 4z = 5

2x + 3y + 5z = 2

5x – 2y + 6z = -1

This system is written in matrix form as

⇒ \({\left[\begin{array}{ccc}
5 & -1 & 4 \\
2 & 3 & 5 \\
5 & -2 & 6
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{r}
5 \\
2 \\
-1
\end{array}\right] }\)

⇒ AX = B ⇒ X=\(A^{-1}\) B

⇒ \({\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\frac{1}{51}\left[\begin{array}{ccc}
28 & -2 & -17 \\
13 & 10 & -17 \\
-19 & 5 & 17
\end{array}\right]\left[\begin{array}{r}
5 \\
2 \\
-1
\end{array}\right]}\)

or \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\frac{1}{51}\left[\begin{array}{l}
140-4+17 \\
65+20+17 \\
-95+10-17
\end{array}\right]\)

⇒ \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\frac{1}{51}\left[\begin{array}{r}
153 \\
102 \\
-102
\end{array}\right]=\left[\begin{array}{r}
3 \\
2 \\
-2
\end{array}\right]\)

⇒ x= 3, y = 2, z = -2

Question 14. Show that, for matrix A = \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
1 & 2 & -3 \\
2 & -1 & 3
\end{array}\right]\), A³-6 A²+5 A+11 I=O, Hence, find \(A^{-1}\).

Or,

Using the matrix method, solve the following system of equations:

3x – 2y + 3z = 8

2x + y – z = 1

4x – 3y + 2z = 4

Important Question for Class 12 Maths Chapter 4

Solution:

Given A = \(\left[\begin{array}{ccc}
1 & 1 & 1 \\
1 & 2 & -3 \\
2 & -1 & 3
\end{array}\right]\)

To prove: A³ – 6A² + 5A + 11 I = O

⇒ \(A^2=A \cdot A=\left[\begin{array}{rrr}
1 & 1 & 1 \\
1 & 2 & -3 \\
2 & -1 & 3
\end{array}\right] \cdot\left[\begin{array}{rrr}
1 & 1 & 1 \\
1 & 2 & -3 \\
2 & -1 & 3
\end{array}\right]=\left[\begin{array}{ccc}
1+1+2 & 1+2-1 & 1-3+3 \\
1+2-6 & 1+4+3 & 1-6-9 \\
2-1+6 & 2-2-3 & 2+3+9
\end{array}\right]\)

⇒ \(A^2=\left[\begin{array}{rrr}
4 & 2 & 1 \\
-3 & 8 & -14 \\
7 & -3 & 14
\end{array}\right]\)

and \(A^3= A^2 \cdot A=\left[\begin{array}{rrr}
4 & 2 & 1 \\
-3 & 8 & -14 \\
7 & -3 & 14
\end{array}\right] \cdot\left[\begin{array}{rrr}
1 & 1 & 1 \\
1 & 2 & -3 \\
2 & -1 & 3
\end{array}\right]\)

–\(\left[\begin{array}{rrr}
4+2+2 & 4+4-1 & 4-6+3 \\
-3+8-28 & -3+16+14 & -3-24-42 \\
7-3+28 & 7-6-14 & 7+9+42
\end{array}\right]\)

⇒ \(A³=\left[\begin{array}{ccc}
8 & 7 & 1 \\
-23 & 27 & -69 \\
32 & -13 & 58
\end{array}\right]\)

L.H.S. = \(A^3-6 A^2+5 A+11I\)

= \(\left[\begin{array}{ccc}
8 & 7 & 1 \\
-23 & 27 & -69 \\
32 & -13 & 58
\end{array}\right]-6\left[\begin{array}{ccc}
4 & 2 & 1 \\
-3 & 8 & -14 \\
7 & -3 & 14
\end{array}\right]+5\left[\begin{array}{ccc}
1 & 1 & 1 \\
1 & 2 & -3 \\
2 & -1 & 3
\end{array}\right]+11\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)

= \(\left[\begin{array}{ccc}
8-24+5+11 & 7-12+5+0 & 1-6+5+0 \\
-23+18+5+0 & 27-48+10+11 & -69+84-15+0 \\
32-42+10+0 & -13+18-5+0 & 58-84+15+11
\end{array}\right]\)

= \(\left[\begin{array}{lll}
0 & 0 & 0 \\
0 & 0 & 0 \\
0 & 0 & 0
\end{array}\right]=\mathrm{O}\) Zero matrix

Now, A³-6A²+5A+11 I = O

A³A^-1 – 6A²A ^-1+ 5AA^-1 + 11 I A^-1 = OA^-1 (Post multiplying both sides by \(A^{-1}\)

A²(AA^-1)-6A(AA^-1)+5(AA^-1)+11 I A^-1 = OA^-1

A²-6A +5I + 11A^-1 = O

because AA^-1=I and OA^-1 =O

⇒ \(A^{-1}=\frac{-1}{11} \cdot\left(A^2-6 A+5I\right)=\frac{-1}{11}\left\{\left[\begin{array}{ccc}
4 & 2 & 1 \\
-3 & 8 & -14 \\
7 & -3 & 14
\end{array}\right]-6\left[\begin{array}{ccc}
1 & 1 & 1 \\
1 & 2 & -3 \\
2 & -1 & 3
\end{array}\right]+5\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\right\}\)

⇒ \(A^{-1}=\frac{-1}{11}\left[\begin{array}{ccc}
4-6+5 & 2-6+0 & 1-6+0 \\
-3-6+0 & 8-12+5 & -14+18+0 \\
7-12+0 & -3+6+0 & 14-18+5
\end{array}\right]\)

⇒ \(A^{-1}=\left[\begin{array}{ccc}
-3 / 11 & 4 / 11 & 5 / 11 \\
9 / 11 & -1 / 11 & -4 / 11 \\
5 / 11 & -3 / 11 & -1 / 11
\end{array}\right]\)

The given system of equations are:

3x -2y + 3 z = 8

2x + y – z = 1 and

4x – 3y + 2z = 4

Determinants Class 12 Questions With Answers

By using the matrix method; the given system of equations can be written as; AX = B

where \(A=\left[\begin{array}{ccc}3 & -2 & 3 \\ 2 & 1 & -1 \\ 4 & -3 & 2\end{array}\right], X=\left[\begin{array}{l}x \\ y \\ z\end{array}\right]\) and \(B=\left[\begin{array}{l}8 \\ 1 \\ 4\end{array}\right]\)

Now; \(|A|=\left|\begin{array}{ccc}3 & -2 & 3 \\ 2 & 1 & -1 \\ 4 & -3 & 2\end{array}\right|\)=-3+16-30=-17 ≠0

Hence; \(\mathrm{A}^{-1}\) exists.

Now; \(A=\left[\begin{array}{ccc}3 & -2 & 3 \\ 2 & 1 & -1 \\ 4 & -3 & 2\end{array}\right]\)

Co-factors are given as: \(C_{11}=-1, \quad C_{12}=-8, C_{13}=-10, C_{21}=-5, C_{22}=-6, C_{23}=1, C_{31}=-1, C_{32}=9, C_{33}=7\)

Hence, (adj)(A)= \(\left[C_{i j}\right]^{\mathrm{T}}\)

adj(A)= \(\left[\begin{array}{ccc}
-1 & -5 & -1 \\
-8 & -6 & 9 \\
-10 & 1 & 7
\end{array}\right]\)

Now; AX = \(B \Rightarrow X=A^{-1} \cdot B\) = \(\frac{\mathrm{adj} A}{|A|} \cdot B\)

⇒ \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=-\frac{1}{17}\left[\begin{array}{ccc}
-1 & -5 & -1 \\
-8 & -6 & 9 \\
-10 & 1 & 7
\end{array}\right] \cdot\left[\begin{array}{l}
8 \\
1 \\
4
\end{array}\right]=-\frac{1}{17}\left[\begin{array}{c}
-8-5-4 \\
-64-6+36 \\
-80+1+28
\end{array}\right]=-\frac{1}{17}\left[\begin{array}{l}
-17 \\
-34 \\
-51
\end{array}\right]\)

⇒ \(\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\)

x=1, y=2, z=3

Question 15. If \(A=\left[\begin{array}{ccc}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\), find A^-1. Hence, using A^-1, solve the system of equations:

2x – 3y + 5z = 11,

3x + 2y – 4z = -5,

x + y -2z = -3.

Solution:

Given, \(A=\left[\begin{array}{ccc}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\)

A is invertible if |A| ≠ 0

Now. |A| = 2(-4 + 4) + 3 (-6 + 4) + 5(3 – 2)= 0 – 6 + 5 =-1≠0

Co-factors are given as :

⇒ \(C_{11}=0, C_{12}=2, C_{13}=1\)

⇒ \(C_{21}=-1, C_{22}=-9, C_{23}=-5\)

⇒ \(C_{31}=2, C_{32}=23, C_{33}=13\)

⇒ (adj) \((\mathrm{A})=\left[\mathrm{C}_{1 \mathrm{ij}}\right]^{\mathrm{T}}\)

or (adj) \((\mathrm{A})=\left[\begin{array}{ccc}
0 & 2 & 1 \\
-1 & -9 & -5 \\
2 & 23 & 13
\end{array}\right]^{\mathrm{T}}=\left[\begin{array}{ccc}
0 & -1 & 2 \\
2 & -9 & 23 \\
1 & -5 & 13
\end{array}\right]\)

⇒ \(\mathrm{A}^{-1}=\frac{\mathrm{adj}(\mathrm{A})}{|\mathrm{A}|}=\left[\begin{array}{ccc}
0 & 1 & -2 \\
-2 & 9 & -23 \\
-1 & 5 & -13
\end{array}\right]\)

Now, given equations are 2x-3y + 5z = 11; 3x + 2y -4z = -5 and x + y – 2z = -3

⇒ \({\left[\begin{array}{ccc}
2 & -3 & 5 \\
3 & 2 & -4 \\
1 & 1 & -2
\end{array}\right]\left[\begin{array}{l}
\mathrm{x} \\
\mathrm{y} \\
\mathrm{z}
\end{array}\right]=\left[\begin{array}{l}
11 \\
-5 \\
-3
\end{array}\right]}\)

⇒ \(\mathrm{AX}=\mathrm{B} \text { or } \mathrm{X}=\mathrm{A}^{-1} \mathrm{~B} \\
\Rightarrow \mathrm{X}=\left[\begin{array}{ccc}
0 & 1 & -2 \\
-2 & 9 & -23 \\
-1 & 5 & -13
\end{array}\right]\left[\begin{array}{l}
11 \\
-5 \\
-3
\end{array}\right]\)

or \(\mathrm{X}=\left[\begin{array}{c}
0 \times 11+(1) \times(-5)+(-2) \times(-3) \\
(-2) \times 11+9 \times(-5)+(-23) \times(-3) \\
(-1) \times 11+5 \times(-5)+(-13) \times(-3)
\end{array}\right] \\
\Rightarrow \quad\left[\begin{array}{l}
\mathrm{x} \\
\mathrm{y} \\
\mathrm{z}
\end{array}\right]=\left[\begin{array}{l}
1 \\
2 \\
3
\end{array}\right]\)

⇒ \(\mathrm{x}=1, \mathrm{y}=2, \mathrm{z}=3\)

CBSE Class 12 Maths Chapter 3 Matrices Important Questions

Question 1. The number of all possible matrices of order 2 x 3 with each country 1 or 2 is :

1. 16
2. 6
3. 64
4. 24

Solution: 3. 6

Required number of possible matrices

= (Number of entries)^order

= (2)^2×3 = (2)⁶ = 64

Read and Learn More CBSE Class 12 Maths Important Question and Answers

Important Questions For Class 12 Maths Chapter 3

Question 2. If a matrix A is both symmetric and skewed, symmetric. then A is necessarily a

1. Diagonal matrix
2. Zero square matrix
3. Square matrix
4. Identity matrix

Solution: 2. Zero square matrix

Given; A^T = A (symmetric matrix)

and -A^T= A (skew-symmetric matrix)

⇒ 2A = O or A = O

Hence, A is necessarily a zero-square matrix

Question 3. If \(\left[\begin{array}{cc}
3 c+6 & a-d \\
a+d & 2-3 b
\end{array}\right]=\left[\begin{array}{cc}
12 & 2 \\
-8 & -4
\end{array}\right]\), then the value of ab-cd is

1. 4
2. 16
3. -4
4. -16

Solution: 1. 4

Given: \(\left[\begin{array}{cc}
3 c+6 & a-d \\
a+d & 2-3 b
\end{array}\right]=\left[\begin{array}{cc}
12 & 2 \\
-8 & -4
\end{array}\right]\)

On comparing both sides, we get

a – d = 2 and a + d = -8

⇒  2a = -6 Or a=-3

⇒ d = -5

Also; 3c + 6 = 12, 2-3b = -4

⇒ c = 2, b = 2

Hence, ab- cd = (-3)2 – 2(-5) = -6 + 10 = 4

Question 4. For two matrices \(P=\left[\begin{array}{cc}
3 & 4 \\
-1 & 2 \\
0 & 1
\end{array}\right] \text { and } Q^{\top}=\left[\begin{array}{ccc}
-1 & 2 & 1 \\
1 & 2 & 3
\end{array}\right]\), P-Q is

1. \(\left[\begin{array}{cc}2 & 3 \\ -3 & 0 \\ 0 & -3\end{array}\right]\)
2. \(\left[\begin{array}{cc}4 & 3 \\ -3 & 0 \\ -1 & -2\end{array}\right]\)
3. \(\left[\begin{array}{cc}4 & 3 \\ 0 & -3 \\ -1 & -2\end{array}\right]\)
4. \(\left[\begin{array}{cc}2 & 3 \\ 0 & -3 \\ 0 & -3\end{array}\right]\)

Solution: 2. \(\left[\begin{array}{cc}4 & 3 \\ -3 & 0 \\ -1 & -2\end{array}\right]\)

⇒ \(Q^{\top}=\left[\begin{array}{ccc}-1 & 2 & 1 \\ 1 & 2 & 3\end{array}\right] \Rightarrow Q=\left[\begin{array}{cc}-1 & 1 \\ 2 & 2 \\ 1 & 3\end{array}\right]\)

Hence, \(P-Q=\left[\begin{array}{cc}3 & 4 \\ -1 & 2 \\ 0 & 1\end{array}\right]-\left[\begin{array}{cc}-1 & 1 \\ 2 & 2 \\ 1 & 3\end{array}\right]=\left[\begin{array}{cc}4 & 3 \\ -3 & 0 \\ -1 & -2\end{array}\right]\)

Matrices Class 12 Important Questions

Question 5. A matrix A = [a_ij]_3×3 is defined by \(a_{i j}=\left\{\begin{array}{ccc}
2 i+3 j & ; & i<j \\
5 & ; & i=j \\
3 i-2 j & ; & i>j
\end{array}\right.\), The number of elements in A, which are more than 5, is

1. 3
2. 4
3. 5
4. 6

Solution: 2. 4

Given; A = [a_ij]_3×3

where \(a_{i j}=\left\{\begin{array}{ccc}
2 i+3 j & ; & i<j \\
5 & ; & i=j \\
3 i-2 j & ; & i>j
\end{array}\right.\)

⇒ A= \(\left[\begin{array}{lll}
5 & 8 & 11 \\
4 & 5 & 13 \\
7 & 5 & 5
\end{array}\right]\)

Hence; required number =4

Question 6. For the matrix X = \(\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]\), (X²-X) is:

1. 21
2. 31
3. 1
4. 51

Solution: 1. 21

⇒ \(X^2=\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right] \cdot\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]=\left[\begin{array}{lll}
2 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 2
\end{array}\right]\)

⇒ \(X^2-X=\left[\begin{array}{lll}
2 & 1 & 1 \\
1 & 2 & 1 \\
1 & 1 & 2
\end{array}\right]-\left[\begin{array}{lll}
0 & 1 & 1 \\
1 & 0 & 1 \\
1 & 1 & 0
\end{array}\right]=\left[\begin{array}{lll}
2 & 0 & 0 \\
0 & 2 & 0 \\
0 & 0 & 2
\end{array}\right]=21\)

Question 7. Find the order of matrix A such that \(\left[\begin{array}{cc}2 & -1 \\ 1 & 0 \\ -3 & 4\end{array}\right]\), A = \(\left[\begin{array}{cc}-1 & -8 \\ 1 & -2 \\ 9 & 22\end{array}\right]\)

or,

If B = \(\left[\begin{array}{cc}
1 & -5 \\
0 & -3
\end{array}\right]\) and A+2 B = \(\left[\begin{array}{cc}
0 & 4 \\
-7 & 5
\end{array}\right]\), find matrix A.

Solution:

Let \(\mathrm{B}=\left[\begin{array}{cc}2 & -1 \\ 1 & 0 \\ -3 & 4\end{array}\right]\) and \(\mathrm{C}=\left[\begin{array}{cc}-1 & -8 \\ 1 & -2 \\ 9 & 22\end{array}\right]\)

We have \(\left[\begin{array}{cc}2 & -1 \\ 1 & 0 \\ -3 & 4\end{array}\right]_{3 \times 2} \quad A=\left[\begin{array}{cc}-1 & -8 \\ 1 & -2 \\ 9 & 22\end{array}\right]_{3 \times 2}\)

Let the order of A be m x n

BA will be possible if several columns in matrix B should be equal to several rows in matrix A ⇒ m = 2.

and the order of BA is 3 x n

Since, BA = C.

⇒ Order of BA will be the same as that of matrix C

⇒ 3 x n = 3 x 2

⇒ n = 2

Then, the order of matrix A is 2 x 2

A+2 B \(\left[\begin{array}{cc}
0 & 4 \\
-7 & 5
\end{array}\right]\) (given)

⇒ A = \(\left[\begin{array}{cc}
0 & 4 \\
-7 & 5
\end{array}\right]-2 B=\left[\begin{array}{cc}
0 & 4 \\
-7 & 5
\end{array}\right]-2\left[\begin{array}{cc}
1 & -5 \\
0 & -3
\end{array}\right]=\left[\begin{array}{cc}
0 & 4 \\
-7 & 5
\end{array}\right]-\left[\begin{array}{cc}
2 & -10 \\
0 & -6
\end{array}\right]\)

⇒ A = \(\left[\begin{array}{cc}
-2 & 14 \\
-7 & 11
\end{array}\right]\)

Question 8. If A = \(\left[\begin{array}{lll}
1 & 0 & 4
\end{array}\right]\) and B = \(\left[\begin{array}{l}
2 \\
5 \\
6
\end{array}\right]\), find AB.

Solution:

AB= \(\left[\begin{array}{lll}
1 & 0 & 4
\end{array}\right]_{1 \times 3}\left[\begin{array}{l}
2 \\
5 \\
6
\end{array}\right]_{3 \times 1}\)

= \([1 \times 2+0 \times 5+4 \times 6]_{1 \times 1}=[2+0+24]=[26]\)

Class 12 Maths Chapter 3 Important Questions With Solutions

Question 9. Given, a skew-symmetric matrix \(A = \mathrm{A}=\left[\begin{array}{ccc}
0 & \mathrm{a} & 1 \\
-1 & \mathrm{~b} & 1 \\
-1 & \mathrm{c} & 0
\end{array}\right]\), then value of (a+b+c)² is

Solution:

Given \(A = \mathrm{A}=\left[\begin{array}{ccc}
0 & \mathrm{a} & 1 \\
-1 & \mathrm{~b} & 1 \\
-1 & \mathrm{c} & 0
\end{array}\right]\)

A is a skew-symmetric matrix, A^T = -A

⇒ \(A^{\top}=\left[\begin{array}{ccc}
0 & -1 & -1 \\
a & b & c \\
1 & 1 & 0
\end{array}\right] \text { and }-A=\left[\begin{array}{ccc}
0 & -a & -1 \\
1 & -b & -1 \\
1 & -c & 0
\end{array}\right]\)

So, a = 1, b = 0 and c = -1

Now (a + b + c)² = (1 +0-1)² = 0

Question 10. If the matrices A = \(\left[\begin{array}{ccc}
0 & \mathrm{a} & -3 \\
2 & 0 & -\mathrm{t} \\
\mathrm{b} & 1 & 0
\end{array}\right]\) is skew symmetric, find the values of ‘a’ and ‘b’.

Solution:

A = \(\left[\begin{array}{ccc}
0 & \mathrm{a} & -3 \\
2 & 0 & -\mathrm{t} \\
\mathrm{b} & 1 & 0
\end{array}\right]\) (given)

A is skew-symmetric ⇒ A^T = -A

⇒ \(\left[\begin{array}{ccc}
0 & 2 & b \\
a & 0 & 1 \\
-3 & -1 & 0
\end{array}\right]=\left[\begin{array}{ccc}
0 & -a & 3 \\
-2 & 0 & 1 \\
-b & -1 & 0
\end{array}\right]\)

⇒ a=-2, b=3

Question 11. If the matrix A = \(\left[\begin{array}{cc}
0 & 6-5 x \\
x^2 & x+3
\end{array}\right]\) is symmetric, find the values of x?

Solution:

A = \(\left[\begin{array}{cc}
0 & 6-5 x \\
x^2 & x+3
\end{array}\right]\) (given)

For a symmetric matrix, A = A¹

⇒ \(\left[\begin{array}{cc}
0 & 6-5 x \\
x^2 & x+3
\end{array}\right]=\left[\begin{array}{cc}
0 & x^2 \\
6-5 x & x+3
\end{array}\right]\)….(1)

∴ 6-5x = x² [from (1)]

⇒ x² + 5x – 6 = 0

⇒ (x + 6) (x -1) = 0

⇒ x = – 6, 1

Question 12. If A = \(\left[\begin{array}{cc}
-3 & 2 \\
1 & -1
\end{array}\right] \text { and } I=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\), find scalar k such that A² + I = KA

Solution:

Given, A = \(\left[\begin{array}{cc}
-3 & 2 \\
1 & -1
\end{array}\right] \text { and } I=\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]\)

⇒ \(\left[\begin{array}{cc}
-3 & 2 \\
1 & -1
\end{array}\right]\left[\begin{array}{cc}
-3 & 2 \\
1 & -1
\end{array}\right]+\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]=K\left[\begin{array}{cc}
-3 & 2 \\
1 & -1
\end{array}\right]\)

(because \(A^2+I=K A\))

⇒ \(\left[\begin{array}{cc}
11 & -8 \\
-4 & 3
\end{array}\right]+\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]\) = \(\left[\begin{array}{cc}
-3 \mathrm{~K} & 2 \mathrm{~K} \\
\mathrm{~K} & -\mathrm{K}
\end{array}\right]\)

∴ \(\left[\begin{array}{cc}
12 & -8 \\
-4 & 4
\end{array}\right]\) = \(\left[\begin{array}{cc}
-3 \mathrm{~K} & 2 \mathrm{~K} \\
\mathrm{~K} & -\mathrm{K}
\end{array}\right]\)

⇒ K = -4 (on comparing both sides)

Matrices Subjective And Objective Questions Class 12

Question 13. If A = \(\left[\begin{array}{cc}
4 & 2 \\
-1 & 1
\end{array}\right]\) , show that (A-2I)(A-3I) = O.

Solution:

A = \(\left[\begin{array}{cc}
4 & 2 \\
-1 & 1
\end{array}\right]\) (given)

⇒ A-2I = \(\left[\begin{array}{cc}
4 & 2 \\
-1 & 1
\end{array}\right]-2\left[\begin{array}{ll}
1 & 0 \\
0 & 1
\end{array}\right]=\left[\begin{array}{cc}
2 & 2 \\
-1 & -1
\end{array}\right]\)

and A-3I = \(\left[\begin{array}{cc}
4 & 2 \\
-1 & 1
\end{array}\right]-3\left[\begin{array}{cc}
1 & 0 \\
0 & 1
\end{array}\right]=\left[\begin{array}{cc}
1 & 2 \\
-1 & -2
\end{array}\right]\)

⇒ (A-2I)(A-3I) = \(\left[\begin{array}{cc}
2 & 2 \\
-1 & -1
\end{array}\right]\left[\begin{array}{cc}
1 & 2 \\
-1 & -2
\end{array}\right]=\left[\begin{array}{cc}
2-2 & 4-4 \\
-1+1 & -2+2
\end{array}\right]=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]=O\)

CBSE Class 12 Maths Chapter 12 Linear Programming Important Questions

Question 1. A Linear programming problem is as follows: Minimize Z = 2x + y

Subject to the constraints:

• x ≥ 3, x ≤ 9, y ≥ 0,
• x-y ≥ 0, x + y ≤ 14

The feasible region has:

1. 5 corner points including (0, 0) and (9, 5)
2. 5 corner points including (7, 7) and (3, 3)
3. 5 corner points including (14, 0) and (9, 0)
4. 5 corner points including (3, 6) and (9, 5)

Solution: 2. 5 corner points including (7, 7) and (3, 3)

Given; Z = 2x + y subject to the constraints

x ≥ 3, x ≤ 9, y ≥ 0, x – y ≥ 0, x + y ≤ 14

Read and Learn More CBSE Class 12 Maths Important Question and Answers

Hence, the feasible region has 5 corner points including (7, 7) and (3, 3)

Question 2. A Linear Programming Problem is as follows: Maximise/Minimise objective function Z = 2x – y + 5

Subject to the constraints:

• 3x + 4y ≤ 60,
• x + 3y ≤ 30,
• x ≥ 0, y ≥ 0

Linear Programming Class 12 Important Questions

If the corner points of the feasible region are A(0, 10), B(12, 6), C(20, 0) and 0(0,0); then which of the following is true?

1. The maximum value of Z is 40
2. The minimum value of Z is -5
3. The difference between the maximum and minimum values of Z is 35
4. At two corner points, the value of Z is equal

Solution: 2. The minimum value of Z is -5.

Question 3. The corner points of the feasible region determined by a set of constraints (linear inequalities) are P(0, 5), Q(3, 5), R(5, 0), and S(4, 1) and the objective function is Z = ax + 2by; where a, b > 0. The condition on ‘a’ and ‘b’ such that the maximum of Z occurs at Q and S is:

1. a-5b=0
2. a-3b = 0
3. a – 2b = 0
4. a – 8b = 0

Solution: 4. a – 8b = 0

Given points arc P(0, 5), Q(3, 5), R(5, 0) and S(4, 1) and Z = ax + 2by

Since the maximum of Z occurs at Q and S;

⇒ 3a + 10b = 4a + 2b

⇒ 8b = a ⇒ a – 8b = 0

Class 12 Maths Chapter 12 Important Questions With Solutions

Question 4. For an L.P.P.. the objective function is Z = 4x + 3y and the feasible region is determined by a set of constraints (linear inequations) as shown in the graph.

Which one of the following statements is true?

1. The maximum value of Z is at R
2. The maximum value of Z is at Q
3. The value of Z at R is less than the value of P
4. The value of Z at Q is less than the value of R

Solution: 2. Maximum value of Z is at Q

Z = 4x + 3y

A maximum value of Z is at Q.

Linear Programming Important Questions CBSE

Question 5. Solve the following problem graphically: Maximize Z = 3x + 9y

Subject to the constraints:

• x + 3y ≤ 60,
• x + y ≥ 10,
• x ≤ y,
• x ≥ 0, y ≥ 0

Solution:

First of all, let us graph the feasible region of the system of linear inequalities given above. The feasible region ABCD is shown.

Note that the region is bounded. The coordinates of the comer points A, B, C, and D are (0, 10), (5, 5), (15, 15), and (0, 20) respectively.

The maximum value of Z is 180. which occurs at every point of the line segment joining the points C and D.

CBSE Class 12 Maths Chapter 13 Probability Important Questions

Question 1. If A and B are two independent events and P(A) = \(\frac{1}{3}\), P(B) = \(\frac{1}{2}\); find \(\mathrm{P}(\overline{\mathrm{A}} \mid \overline{\mathrm{B}})\).

Solution:

Given, A and B are two independent events and P(A) = \(\frac{1}{3}\), P(B) = \(\frac{1}{2}\)

⇒ P(A∩B) = P(A).P(B) = \(\frac{1}{3}\) x \(\frac{1}{2}\) = \(\frac{1}{6}\)

⇒ P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{\frac{6}{1}}{\frac{1}{2}}=\frac{1}{3}\)

⇒ \(\mathrm{P}(\overline{\mathrm{A}} / \overline{\mathrm{B}})=\mathrm{P}(\overline{\mathrm{A} / \mathrm{B}})=1-\mathrm{P}(\mathrm{A} / \mathrm{B}) \Rightarrow \mathrm{P}(\overline{\mathrm{A}} / \overline{\mathrm{B}})=1-\frac{1}{3}=\frac{2}{3}\)

Read and Learn More CBSE Class 12 Maths Important Question and Answers

Question 2. A coin is tossed once. If the head comes up, a die is thrown; blit if the tail comes up, the coin is tossed again. Find the probability of obtaining a head and number 6.

Solution:

S = {(H, 1), (H, 2), (H, 3), (H, 4), (H, 5), (H, 6), (T, H), (T, T)}

Let event A denote “obtaining head” and B denote “obtaining number 6”

⇒ P(A) = \(\frac{1}{2}\), P(B) = \(\frac{1}{6}\)

Hence, the probability of obtaining head and number 6

= P[{(H, 6)}]= P(A∩B) = P(A).P(B) = \(\frac{1}{2}\) x \(\frac{1}{6}\) = \(\frac{1}{12}\)

Probability Class 12 Important Questions

Question 3. Two cards are drawn successively with replacement from a well-shuffled pack of 52 cards. Find the probability distribution of the number of spade cards.

Solution:

Let random variable X denote the number of spade cards; then the possible values of X are 0, 1 or 2.

P(X = 0) = P(no spade and no spade) = \(\frac{39}{52} \times \frac{39}{52}=\frac{3}{4} \times \frac{3}{4}=\frac{9}{16}\)

P(X = 1) = P(spade and no spade or no spade and spade)

= \(\left(\frac{13}{52} \times \frac{39}{52}\right)+\left(\frac{39}{52} \times \frac{13}{52}\right)=\left(\frac{1}{4} \times \frac{3}{4}\right)+\left(\frac{3}{4} \times \frac{1}{4}\right)=\frac{3}{8}\)

P(X = 2) = P(spade and spade) = \(\left(\frac{13}{52} \times \frac{13}{52}\right)=\left(\frac{1}{4} \times \frac{1}{4}\right)=\frac{1}{16}\)

Hence, the probability distribution of X is:

Question 4. A pair of dice is thrown and the sum of the numbers appearing on the dice is observed to be 7. Find the probability that the number 5 has appeared on at least one die.

Or,

The probability that A hits the target is \(\frac{1}{3}\) and the probability that B hits it is \(\frac{2}{5}\). If both try to hit the target independently, find the probability that the target is hit.

Solution:

When a pair of dice is thrown, the sample space S contains 36 outcomes.

Let E: Event that number 5 has appeared on at least one die.

F: Event that the sum of the numbers on the dice is 7

⇒ E = {(5,1), (5,2), (5,3), (5, 4), (5, 5), (5,6), (1,5), (2,5), (3,5), (4,5), (6,5)}, F = {(1, 6), (2,5), (3,4), (4,3), (5,2), (6,1)}

∴ E ∩ F = {(5, 2), (2,5)}

Class 12 Maths Chapter 13 Important Questions With Solutions

Now; P(E∩F) = \(\frac{2}{36}\),P(F) = \(\frac{6}{36}\)

Hence, required probability = \(P(E / F)=\frac{P(E \cap F)}{P(F)}=\frac{(2 / 36)}{(6 / 36)}=\frac{1}{3}\)

Given; P(E₁) = \(\frac{1}{3}\), P(E2) =\(\frac{2}{5}\)

⇒ \(P\left(\overline{E_1}\right)=\frac{2}{3} \cdot P\left(\overline{E_2}\right)=\frac{3}{5}\)

⇒ Required Probability = P(target is hit)

= \(1-\mathrm{P}\left(\overline{\mathrm{E}}_1 \overline{\mathrm{E}}_2\right)=1-\mathrm{P}\left(\overline{\mathrm{E}}_1\right) \cdot \mathrm{P}\left(\overline{\mathrm{E}}_2\right)=1-\left(\frac{2}{3} \times \frac{3}{5}\right)=1-\frac{2}{5}=\frac{3}{5}\)

Or,

Let E₁: Event that A hits the target

Let E₂: Event that B hits the target

Given; \(P\left(E_1\right)=\frac{1}{3}, P\left(E_2\right)=\frac{2}{5} \Rightarrow P\left(\overline{E_1}\right)=\frac{2}{3} \cdot P\left(\overline{E_2}\right)=\frac{3}{5}\)

⇒ Required Probability = P (target is hit)

= \(1-\mathrm{P}\left(\overline{\mathrm{E}}_1 \overline{\mathrm{E}}_2\right)=1-\mathrm{P}\left(\overline{\mathrm{E}}_1\right) \cdot \mathrm{P}\left(\overline{\mathrm{E}}_2\right)=1-\left(\frac{2}{3} \times \frac{3}{5}\right)=1-\frac{2}{5}=\frac{3}{5}\)

Question 5. A random variable X has the probability distribution:

Find the value of K and P(X ≤ 2).

Solution:

We know that ∑ P(X) = 1 (for probability distribution)

⇒ 0 + K + 4K + 3K + 2K = 1

⇒ 10 K = 1

⇒ K = \(\frac{1}{10}\)…..(1)

∴ P(X ≤ 2) = P(X = 0) + P(X = 1) + P(X = 2)

= 0 + k + 4K = 5K = \(\frac{5}{10}\) = \(\frac{1}{2}\) (from (1))

Probability Important Questions CBSE

Question 6. A purse contains 3 silver and 6 copper coins and a second purse contains 4 silver and 3 copper coins. If a coin is drawn at random from one of the two purses, find the probability that it is a silver coin.

Solution:

Let E₁: Event that first purse is selected. E₂: Event that second purse is selected and A: Event that silver coin is drawn

⇒ \(P\left(E_1\right)=\frac{1}{2}, P\left(E_2\right)=\frac{1}{2}, P\left(A / E_1\right)=\frac{3}{9}, P\left(A / E_2\right)=\frac{4}{7}\)

∴ \(P(A)-P\left(E_1\right) P\left(A / E_1\right)+P\left(E_2\right) \cdot P\left(A / E_2\right)\) (by total probability theorem)

= \(\left(\frac{1}{2} \times \frac{3}{9}\right)+\left(\frac{1}{2} \times \frac{4}{7}\right)=\frac{1}{6}+\frac{2}{7}=\frac{19}{42}\)

Question 7. A coin is tossed 5 times. What is the probability of getting

1. 3 heads,
2. At most 3 heads?

Or,

Find the probability distribution of X, the number of heads in a simultaneous loss of two coins.

Solution:

1. P 3 Heads= \({ }^5 \mathrm{C}_3\left(\frac{1}{2}\right)^3\left(\frac{1}{2}\right)^2=10 \times \frac{1}{8} \times \frac{1}{4}=\frac{5}{16}\)

2. P (at most 3 Heads) =\(1-\mathrm{P}(4)-\mathrm{P}(5)\)

= \(1-{ }^3 C_4\left(\frac{1}{2}\right)^4\left(\frac{1}{2}\right)-{ }^3 C_5\left(\frac{1}{2}\right)^5=1-\frac{5}{32}-\frac{1}{32}=\frac{26}{32}=\frac{13}{16}\)

Or,

Let X denotes the number of heads in a simultaneous toss of two coins, then the possible values of X are 0, 1 or 2.

P(X=0)=P(TT)= \(\left(\frac{1}{2} \cdot \frac{1}{2}\right)=\frac{1}{4}\),

P(X=1)=P(HT)+P(T H)=\(\left(\frac{1}{2} \cdot \frac{1}{2}\right)+\left(\frac{1}{2} \cdot \frac{1}{2}\right)=\frac{2}{4}\),

P(X=2)=P(HH)=\(\left(\frac{1}{2} \cdot \frac{1}{2}\right)=\frac{1}{4}\)

Hence; the probability distribution of X is given as :

Question 8. If P(not A) = 0.7, P(B) = 0.7 and P(B/A) = 0.5, then find P( A/B)

Solution:

Given; \(\mathrm{P}(\overline{\mathrm{A}})\) = 0.7 ⇒ 1 – P(A) = 0.7 ⇒ P(A) = 0.3 and P(B) = 0.7

Also, P(B/A) = 0.5; P(A/B) = ?

We know that: P(B/A) = \(\frac{P(B \cap A)}{P(A)} \Rightarrow 0.5=\frac{P(B \cap A)}{0.3}\)

⇒ P(B ∩ A) = 0.5 x 0.3 = 0.15

Now, P(A ∩ B) = P(B ∩ A) = 0.15

⇒ P(A/B) = \(\frac{P(A \cap B)}{P(B)}=\frac{0.15}{0.70}=\frac{15}{70}=\frac{3}{14}\)

Question 9. A black and a red die are rolled together. Find the conditional probability of obtaining the sum 8, given that the red die resulted in a number less than 4.

Solution:

Let E: Event of obtaining the sum 8 on the dice.

F: Event that red die resulted in a number less than 4, and let first and second die represent the black and red die respectively.

⇒ E = {(2, 6), (3, 5), (4, 4), (5, 3), (6, 2)}

⇒ n(E) = 5,

F = {(1,1),(1,2),(1,3),(2,1),(2,2),(2,3)}(3,1),(3,2),(3,3),(4,1),(4,2),(4,3),(5,1),(5,2),(5,3),(6,1),(6,2),(6,3)}

⇒ n(F) = 18

and E ∩ F = {(5, 3), (6, 2)}

⇒ n(E ∩F) = 2

Here, \(\mathrm{P}(\mathrm{F})=\frac{18}{36}=\frac{1}{2}$ and $\mathrm{P}(\mathrm{E} \cap \mathrm{F})=\frac{2}{36}=\frac{1}{18}\)

∴ Required probability = \(P(E / F)=\frac{P(E \cap F)}{P(F)}=\frac{1 / 18}{1 / 2}=\frac{1}{9}\)

Probability Previous Year Questions Class 12

Question 10. A shopkeeper sells three types of flower seeds A₁, A₂, A₃. They are sold in the form of a mixture, where the proportions of these seeds are 4:4:2 respectively. The germination rates of the three types of seeds are 45%, 60% and 35% respectively. Based on the above information, answer the following questions

1. Calculate the probability that a randomly chosen seed will germinate.
2. Calculate the probability that the seed is of type A,, given that a randomly chosen seed germinates.

Solution:

Given, A₁: A₂: A₃ = 4 : 4 : 2

⇒ \(P\left(A_1\right)=\frac{4}{10}, P\left(A_2\right)=\frac{4}{10}\) and \(P\left(A_3\right)=\frac{2}{10}\)

Let E be the event that a seed germinates.

∴ \(P\left(\frac{E}{A_1}\right)=\frac{45}{100} \cdot P\left(\frac{E}{A_2}\right)=\frac{60}{100}\) and \(P\left(\frac{E}{A_7}\right)=\frac{35}{100}\)

1. \(\mathrm{P}(\mathrm{E})=\mathrm{P}\left(\mathrm{A}_1\right) \cdot \mathrm{P}\left(\mathrm{E} / \mathrm{A}_1\right)+\mathrm{P}\left(\mathrm{A}_2\right) \cdot \mathrm{P}\left(\mathrm{E} / \mathrm{A}_2\right)+\mathrm{P}\left(\mathrm{A}_3\right) \cdot \mathrm{P}\left(\mathrm{E} / \mathrm{A}_3\right)\)….(1)

= \(\left(\frac{4}{10} \cdot \frac{45}{100}\right)+\left(\frac{4}{10} \cdot \frac{60}{100}\right)+\left(\frac{2}{10} \cdot \frac{35}{100}\right)=\frac{490}{1000}=\frac{49}{100}=0.49\)

2. \(P\left(A_2 / E\right)=\frac{P\left(A_2\right) \cdot P\left(E / A_2\right)}{P\left(A_1\right) \cdot P\left(E / A_1\right)+P\left(A_2\right) \cdot P\left(E / A_2\right)+P\left(A_3\right) \cdot P\left(E / A_3\right)}\)

= \(\left(\frac{\frac{4}{10} \times \frac{60}{100}}{\frac{49}{100}}\right)\) (from (1))

= \(\frac{24}{49}=0.48\)

Question 11. A student either knows or guesses or copies the answer to a multiple-choice question with four choices. The probability that he makes a guess is 1/3 and the probability that he copies the answer is 1/6. The probability that his answer is correct given that he copied, is 1/8. Let E₁, E₂ and E₃ are the events that the student guesses, copies or knows the answer respectively and A is the event that the student answers correctly.

1. What is the probability that he answers correctly, given that he knows the answer?

1. 1
2. 1/2
3. 2/3
4. 1/4

2. What is the probability that he answers correctly, given that he knows the answer?

1. 1
2. 0
3. 1/4
4. 1/8

3. What is the probability that he answers correctly, given that he had made a guess?

1. 1/4
2. 0
3. 1
4. 1/8

4. What is the probability that he knew the answer to the question, given that he answered it correctly?

1. 24/29
2. 4/29
3. 1/29
4. 3/29

5. \(\sum_{k=1}^3 P\left(E_1 \mid A\right) \text { is : }\)

1. 0
2. 1/3
3. 1
4. 11/8

Solution:

Given that:

E₁ = Event that the student guesses the answer.

E₂ = Event that the student copies the answer.

E₃ = Event that the student knows the answer,

and A = event that the student answers correctly

Now, \(P\left(E_1\right)=\frac{1}{3}\) and \(P\left(E_2\right)=\frac{1}{6}\)

∴ \(P\left(E_1\right)+P\left(E_2\right)+P\left(E_3\right)=1 \Rightarrow \frac{1}{3}+\frac{1}{6}+P\left(E_3\right)=1\)

or \(P\left(E_3\right)=1-\frac{3}{6}=\frac{1}{2}\)….(1)

Also, \(\mathrm{P}\left(\mathrm{A} / \mathrm{E}_2\right)=\frac{1}{8}\) (given), \(\mathrm{P}\left(\mathrm{A} / \mathrm{E}_3\right)=1\)….(2)

(because his answer is correct, given that he knows it]

Chapter 13 Maths Class 12 Important Questions

and \(P\left(A / E_1\right)=\frac{1}{4}\)…..(3)

(his answer is correct, given that he guesses and the multiple choice question has four choices)

1. (2)Required probability = P(E₃) = 1/2 (from eq(1))

2. (1)Required probability = P( A/E₃) = 1 (from eq(2))

3. (1) Required probability = P( A/E₁) = 1/4 (from eq(3))

4. (1) Required probability = P(E₃/A)

= \(\frac{P\left(E_3\right) \cdot P\left(A / E_3\right)}{P\left(E_1\right) \cdot P\left(A / E_1\right)+P\left(E_2\right) \cdot P\left(A / E_2\right)+P\left(E_3\right) \cdot P\left(A / E_3\right)}\) (By Baye’s Theorem)

= \(\frac{\left(\frac{1}{2} \times 1\right)}{\left(\frac{1}{3} \times \frac{1}{4}\right)+\left(\frac{1}{6} \times \frac{1}{8}\right)+\left(\frac{1}{2} \times 1\right)}=\frac{\frac{1}{2}}{\left(\frac{1}{12}+\frac{1}{48}+\frac{1}{2}\right)}\)

= \(\frac{\frac{1}{2}}{\left(\frac{4+1+24}{48}\right)}=\frac{1}{2} \times \frac{48}{29}=\frac{24}{29}\)

5. (3) \(\sum_{k=1}^3 \mathrm{P}\left(\mathrm{E}_2 \mid \mathrm{A}\right)\)

= \(\mathrm{P}\left(\mathrm{E}_1 / \mathrm{A}\right)+\mathrm{P}\left(\mathrm{E}_2 / \mathrm{A}\right)+\mathrm{P}\left(\mathrm{E}_2 / \mathrm{A}\right)=\frac{\mathrm{P}\left(\mathrm{E}_1\right) \cdot \mathrm{P}\left(\mathrm{A} / \mathrm{E}_1\right)+\mathrm{P}\left(\mathrm{E}_2\right) \cdot \mathrm{P}\left(\mathrm{A} / \mathrm{E}_2\right)+\mathrm{P}\left(\mathrm{E}_3\right) \cdot \mathrm{P}\left(\mathrm{A} / \mathrm{E}_3\right)}{\mathrm{P}\left(\mathrm{E}_1\right) \cdot \mathrm{P}\left(\mathrm{A} / \mathrm{E}_1\right)+\mathrm{P}\left(\mathrm{E}_2\right) \cdot \mathrm{P}\left(\mathrm{A} / \mathrm{E}_2\right)+\mathrm{P}\left(\mathrm{E}_3\right) \cdot \mathrm{P}\left(\mathrm{A} / \mathrm{E}_3\right)}\)

[By applying Baye’s theorem and then taking L.C.M.] =1

Probability MCQ Questions Class 12

Question 12. Suppose a girl throws a die. If she gets 1 or 2, she tosses a coin three times and notes the number of tails. If she gets 3, 4. 5 or 6. she tosses a coin once and notes whether a ‘head’ or ‘tail’ is obtained. If she obtained exactly one ‘tail1, what is the probability that she threw 3, 4.. 5 or 6 with the die?

Solution:

When a die is thrown then the sample space contains 6 outcomes i.e. S= {1,2, 4, 5, 6}

Let E₁: Event that she gets 1 or 2 on the die,

E₂: Event that she gets 3, 4, 5 or 6 on the die.

A: Event that she acts exactly one tail

Here, \(\mathrm{P}\left(\mathrm{E}_1\right)=\frac{2}{6}=\frac{1}{3}, P\left(\mathrm{E}_2\right)=\frac{4}{6}=\frac{2}{3} \text { and } \mathrm{P}\left(\mathrm{A} / \mathrm{E}_1\right)=\frac{3}{8}, \mathrm{P}\left(\mathrm{A} / \mathrm{E}_2\right)=\frac{1}{2}\)

When she gets 1 or 2, then she throws a coin three times, and the outcomes are {HHH, TTT, HHT, THH, HTH, TTH, HTT, THT}

⇒ Required probability = P(E₂/A)

= \(\frac{P\left(E_2\right) \cdot P\left(A / E_2\right)}{P\left(E_1\right) P\left(A / E_1\right)+P\left(E_2\right) \cdot P\left(A / E_2\right)} \text { (Using Baye’s Theorem) } \)

= \(\frac{\frac{2}{3} \times \frac{1}{2}}{\left(\frac{1}{3} \times \frac{3}{8}\right)+\left(\frac{2}{3} \times \frac{1}{2}\right)}=\frac{\frac{1}{3}}{\left(\frac{1}{8}+\frac{1}{3}\right)}=\frac{8}{11}\)

Question 13. Two numbers are selected at random (without replacement) from the first six positive integers. Let X denote the larger of the two numbers obtained. Find the probability distribution of the random variable X. and hence find the mean of the distribution. [CBSE 2018|

Solution:

S = {1, 2, 3, 4, 5, 6}

X denotes the larger of the two numbers (given)

If X = 2, then favourable cases are {(1, 2),(2,1)}

If X = 3, then favourable cases are {(1, 3),(2, 3), (3, 1),(3, 2)}

If X = 4, then favourable cases are {(1, 4),(2, 4),(3, 4),(4, 1),(4. 2),(4, 3)}

If X = 5, then favourable cases are {(1, 5),(2, 5),(3, 5),(4, 5),(5,1),(5, 2),(5, 3),(5, 4)}

If X = 6, then favourable cases are {(1,6),(2,6),(3,6),(4,6),(5,6),(6, 1),(6,2),(6,3),(6,4),(6,5)}

⇒ Mean = \(\Sigma X . P(X)=\frac{4+12+24+40+60}{30}=\frac{140}{30}=\frac{14}{3}\)

Question 14. A bag contains 5 red and 4 black balls, a second bag contains 3 red and 6 black balls. One of the two bags is selected at random and two balls are drawn at random (without replacement), both of which are found to be red. Find the probability that the balls are drawn from the second bag.

Solution:

Let E₁: Event that first bag is selected,

E₂: Event that the second bag is selected,

E: Event that both drawn balls are red

∴ Required probability = \(\mathrm{P}\left(\mathrm{E}_2 / \mathrm{E}\right)\)

Probability Subjective And Objective Questions

= \(\frac{P\left(E_2\right) \cdot P\left(E_{/} / E_2\right)}{P\left(E_1\right) \cdot P\left(E / E_1\right)+P\left(E_2\right) \cdot P\left(E / E_2\right)}\)(Using Bayes’ Theorem)

= \(\frac{\frac{1}{2} \times \frac{1}{12}}{\frac{1}{2} \times \frac{5}{18}+\frac{1}{2} \times \frac{1}{12}}=\left(\frac{\frac{1}{12}}{\frac{5}{18}+\frac{1}{12}}\right)=\frac{3}{13}\)

CBSE Class 12 Maths Chapter 8 Application Of Integrals Important Questions

Question 1. Using integration, find the area bounded by the curve y ²= 4x, y-axis, and y = 3.

Or,

Using integration, find the region’s area bounded by the line 2y = – x + 8, x-axis. x = 2 and x = 4.

Solution:

Given curve is y² = 4x ….(1)

and given line is y = 3 …..(2)

From equations (1) and (2):

Point of intersection is B(9/4, 3)

Read and Learn More CBSE Class 12 Maths Important Question and Answers

⇒ Required Area = \(\int_0^3\) x dy

= \(\frac{1}{4} \int_0^3 y^2, d y=\frac{1}{4}\left[\frac{y^3}{3}\right]_0^3=\frac{1}{4}\left[\frac{3^3}{3}-\frac{0}{3}\right]=\left(\frac{1}{4}, \frac{27}{3}\right)=\frac{9}{4} \text { sq. units }\)

Or,

Given lines are 2y + x = 8, x = 2 and x = 4

⇒ Required area = \(\int_2^4 y \mathrm{dx}=\int_2^4\left(\frac{8-\mathrm{x}}{2}\right) \mathrm{dx}\)

= \(\int_2^4\left(4-\frac{1}{2} \mathrm{x}\right) \mathrm{dx}=\left[4 \mathrm{x}-\frac{1}{2}\left(\frac{\mathrm{x}^2}{2}\right)\right]_2^4\)

= \(\left[4 \times 4-\frac{1}{4}(4)^2\right]-\left[4 \times 2-\frac{1}{4}(2)^2\right]\)

=12-7=5

∴Required Area = 5 sq. units

Application Of Integrals Class 12 Important Questions

Question 2. Using integration, find the area bounded by the circle x² + y² = 9.

Solution:

The whole area enclosed by the given circle will be 4 times the area of the region AOBA bounded by the curve, x-axis, and the ordinates x = 0 and x = 3 [as the circle is symmetrical about both the x-axis and y-axis]

⇒ Required area = \(4 \int_0^3 y d x=4 \int_0^3 \sqrt{3^2-x^2} d x \quad\left[x^2+y^2=3^2 \text { gives } y= \pm \sqrt{3^2-x^2}\right]\)

As the region AOBA lies in the first quadrant, v is taken as positive. Integrating, we get the whole area enclosed by the given circle

⇒ Required area = \(4\left[\frac{x}{2} \sqrt{3^2-x^2}+\frac{3^2}{2} \sin ^{-1}\left(\frac{x}{3}\right)\right]_0^3\)

= \(4\left[\left(\frac{3}{2} \times 0+\frac{3^2}{2} \sin ^{-1}(1)\right)-0\right]=4\left(\frac{3^2}{2}\right)\left(\frac{\pi}{2}\right)=9 \pi \text { sq. units }\)

Question 3. Find the area of the region bounded by curve 4x²=y and the line y = 8x + 12. using integration.

Solution:

Given curve is 4x²= y….(1)

and given line is y = 8x + 12…..(2)

From equation (1) and (2), we get:

4x² – 8x – 12 = 0

⇒ x² – 2x – 3 = 0

⇒ (x-3) (x + 1) = 0 =3 x = 3, -1

From equation (1); when x = 3, y = 36 and when x = – 1 ⇒ y = 4.

So, point of intersection of the curve and line tire (3, 36) and (-1,4).

⇒ Required Area = \(\int_{-1}^3\left\{(8 x+12)-4 x^2\right\} d x=\left[\frac{8 x^2}{2}+12 x-\frac{4 x^3}{3}\right]_{-1}^3\)

= \((36+36-36)-\left(4-12+\frac{4}{3}\right)=36+\frac{20}{3}=\frac{128}{3} \text { sq. units }\)

Class 12 Maths Chapter 8 Important Questions With Solutions

Question 4. Using integration, find the area of the region bounded by the curves x² + y² = 4, x =√3y, and the x-axis lying in the first quadrant.

Solution:

Given curve x² + y² = 4 is a circle with center (0, 0) and radius 2.

And line is x = √3y

Now, for the point of intersection of the line and circle, we have:

⇒ 4y² = 4 ⇒ y = ± 1

For y = 1; x = √3

So. point C is (3, 1)

Required area = area of OACO + Area of ABCA

= \(\int_0^{\sqrt{3}} y_{\text ({line })} d x+\int_{\sqrt{3}}^2 y_{\mid \text {circle } \mid} d x=\frac{1}{\sqrt{3}} \int_0^{\sqrt{3}} x d x+\int_{\sqrt{3}}^2 \sqrt{4-x^2} d x\)

= \(\frac{1}{2 \sqrt{3}}\left[x^2\right]_0^{\sqrt{3}}+\left[\frac{x}{2} \sqrt{4-x^2}+\frac{4}{2} \sin ^{-1}\left(\frac{x}{2}\right)\right]_3^{-2}\)

= \(\frac{1}{2 \sqrt{3}}(3)+\left\{2 \sin ^{-1}(1)-\frac{\sqrt{3}}{2}-2 \sin ^{-1}\left(\frac{\sqrt{3}}{2}\right)\right\}=\frac{\sqrt{3}}{2}+\left(2 \times \frac{\pi}{2}\right)-\frac{\sqrt{3}}{2}-2 \times \frac{\pi}{3}=\frac{\pi}{3} \text { sq.units }\)

Application Of Integrals Important Questions CBSE

Question 5. Using the method of integration, find the area of the triangle ABC. coordinates of whose vertices are A(2. 0), B(4, 5) and C(6, 3).

Solution:

Vertices of ΔABC are A(2,0), B(4,5) and C (6,3)

Equation of line AB: y = 5/2(x – 2)

Equation of line BC: y = 9-x

Equation of line AC: y= 3/4(x-2)

⇒ Required Area of ΔABC = \(\int_2^4(\text { line } \mathrm{AB}) \mathrm{dx}+\int_4^6(\text { line } \mathrm{BC}) \mathrm{dx}-\int_2^6(\text { line } \mathrm{AC}) \mathrm{dx}\)

= \(\frac{5}{2} \int_2^4(x-2) d x+\int_4^6(9-x) d x-\frac{3}{4} \int_2^6(x-2) d x\)

= \(\frac{5}{2}\left[\frac{x^2}{2}-2 x\right]_2^4+\left[9 x-\frac{x^2}{2}\right]_4^6-\frac{3}{4}\left[\frac{x^2}{2}-2 x\right]_2^6\)

= \(\frac{5}{2}[(8-8)-(2-4)]+[(54-18)-(36-8)]-\frac{3}{4}[(18-12)-(2-4)]\)

= \(\left(\frac{5}{2} \times 2\right)+8-\left(\frac{3}{4} \times 8\right)=5+8-6=7 \text { sq. units }\)

Question 6. Using the method of integration, find the area of a triangle whose vertices arc (1, 0), (2, 2), and (3, 1).

Solution:

Equation of line AB is y – 0 = \(\frac{(2-0)}{(2-1)}(x-1) \Rightarrow y=2(x-1)\)

Equation of line BC is y – 2 = \(\frac{(1-2)}{(3-2)}(x-2) \Rightarrow y=(-x+1)\)

Equation of line AC is y – 0 = \(\frac{(1-0)}{(3-1)}(x-1) \Rightarrow y=1/2(x-1)\)

⇒ Required Area = \(\int_1^2(\text { line } A B) d x+\int_2^3(\text { line } B C) d x-\int_1^3(\text { line } A C) d x\)

= \(\int_1^2 2(\mathrm{x}-1) \mathrm{dx}+\int_2^3(-\mathrm{x}+4) \mathrm{dx}-\int_1^3 \frac{1}{2}(\mathrm{x}-1) \mathrm{dx}\)

= \(2\left(\frac{\mathrm{x}^2}{2}-\mathrm{x}\right)_1^2+\left(\frac{-\mathrm{x}^2}{2}+4 \mathrm{x}\right)_2^3-\frac{1}{2}\left(\frac{\mathrm{x}^2}{2}-\mathrm{x}\right)_1^3\)

= \(2\left[(2-2)-\left(\frac{1}{2}-1\right)\right]+\left[\left(\frac{-9}{2}+12\right)-(-2+8)\right]-\frac{1}{2}\left[\left(\frac{9}{2}-3\right)-\left(\frac{1}{2}-1\right)\right] \)

= \(\left(2 \times \frac{1}{2}\right)+\left(\frac{-9}{2}+6\right)-\frac{1}{2}(4-2)=1+\frac{3}{2}-1=\frac{3}{2} \text { sq. units }\)

CBSE Class 12 Maths Chapter 8 Extra Questions

Question 7. Using integration, find the region’s area in the first quadrant enclosed by the x-axis, the line y = x, and the circle x² + y² = 32.

Solution:

Given line is y = x ….(1)

and given circle is x² + y² = 32….(2)

From equations (1) and (2); we have

2x² = 32 ⇒ x = ± 4

∴ y = ± 4

Now; (4, 4) lies in 1st quadrant

⇒ Required Area  = \(\int_0^4 x d x+\int_1^{4 \sqrt{2}} \sqrt{32-x^2} d x\)

= \(\left(\frac{x^2}{2}\right)_0^4+\left[\frac{x}{2} \sqrt{32-x^2}+\frac{32}{2} \sin ^{-1}\left(\frac{x}{4 \sqrt{2}}\right)\right]_{-4}^{4 \sqrt{2}}\)

= \((8-0)+\left[\left(0+16 \times \frac{\pi}{2}\right)-\left(8+16 \times \frac{\pi}{4}\right)\right]=4 \pi \text { sq. units }\)