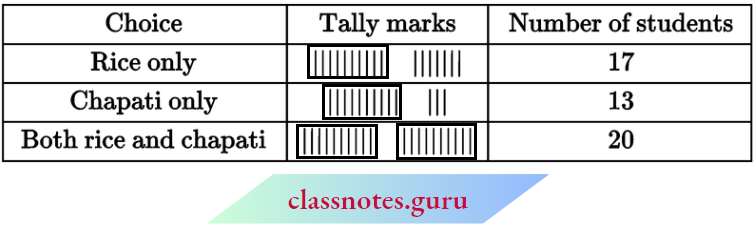
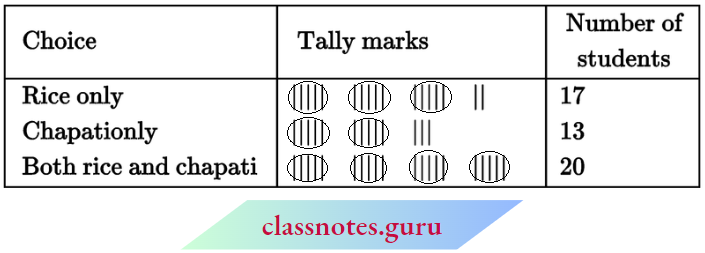
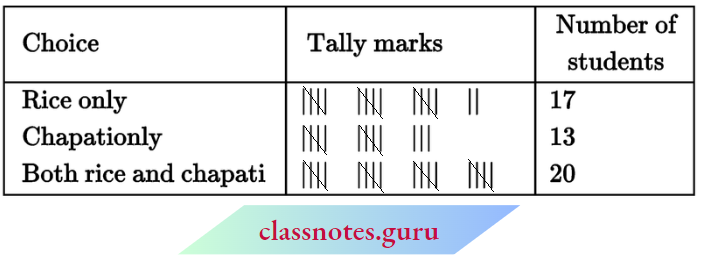
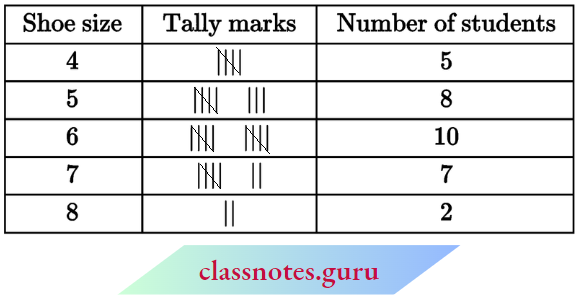
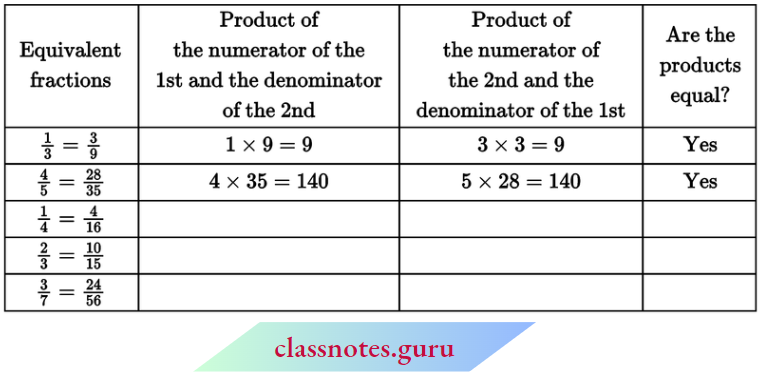
NCERT Notes For Class 6 Maths Playing With Numbers
Playing With Numbers Introduction
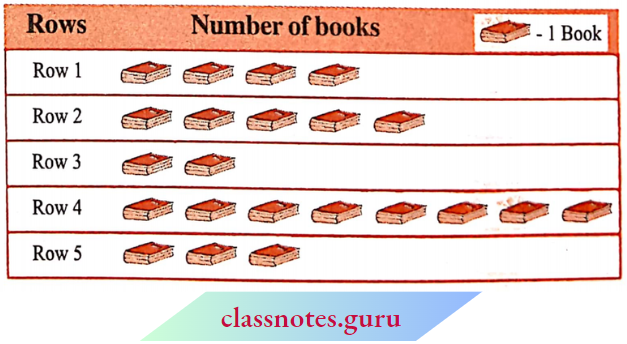
Ramesh has 6 marbles with him. He wants to arrange them in rows in such a way that each row has the same number of marbles. He arranges them in the following ways and matches the total number of marbles.
1. 1 Marble in each row
Number of rows = 6
Total number of marbles = 1 x 6 = 6.

2. 2 marbles in each row
Number of rows = 3
Read and Learn More NCERT Notes for Class 6 Maths
Total number of marbles = 2 x 3 = 6.

3. 3 marbles in each row
Number of rows = 2
Total number of marbles = 3 x 2 = 6.

4. He could not think of any arrangement in which each row had 4 marbles or 5 marbles. So, the only possible arrangement left was with all the 6 marbles in a row.
Number of rows = 1
Total number of marbles = 6 x 1 = 6

From these calculations, Ramesh observes that 6 can be written as a product of two numbers in different ways as
6 = 1 x 6; 6 = 2 x 3; 6 = 3 x 2; 6 = 6 x 1;
From 6 = 2 x 3, it can be said that 2 and 3 exactly divide 6. So, 2 and 3 are exact divisors of 6. From the other product 6 = 1 x 6, the exact divisors of 6 are found to be 1 and 6.
Thus, 1, 2, 3, and 6 are exact divisors of 6. They are called the factors of 6. found to be 1 and 6. Try arranging 18 marbles in rows and find the factors of 18.
NCERT Notes For Class 6 Maths Factors and Multiples
Mary wants to find those numbers that are exactly divided by 4. She divides 4 by numbers less than 4 this way.

She finds that the number 4 can be written as 4 = 1 x 4; 4 = 2 x 2; 4 = 4×1 and knows that the numbers 1,2 and 4 are exact divisors of 4.
These numbers are called factors of 4.
A factor of a number is an exact divisor of that number.
Observe each of the factors of 4 is less than or equal to 4.
Game-1: This is a game to be played by two persons say A and B. It is
about spotting factors.
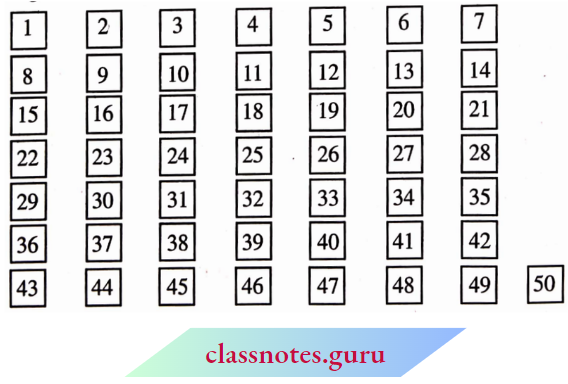
It requires 50 pieces of cards numbered 1 to 50.
Arrange the cards on the table like this.
Steps
- Decide who plays first, A or B.
- Let A play first. He picks up a card from the table and keeps it with him.
- Suppose the card has the number 28 on it.
- Player B then picks up all those cards having numbers which are factors of
the number on A’s card (i.e. 28), and puts them in a pile near him. - Player B then picks up a card from the table and keeps it with him. From the cards that are left, A picks up all those cards whose numbers are factors of the number on B’s card. A puts them on the previous card that he collected.
- The game continues like this until all the cards are used up.
- A will add up the numbers on the cards that he has collected. B too will do the same with his cards. The player with the greater sum will be the winner. The game can be made more interesting by increasing the number of cards. Play this game with your friend. Can you find some way to win the game?
When we write the number 20 as 20 = 4 x 5, we say 4 and 5 are factors of 20. We also say that 20 is a multiple of 4 and 5.
The representation 24 = 2 x 12 shows that 2 and 12 are factors of 24, whereas 24 is a multiple of 2 and 12.
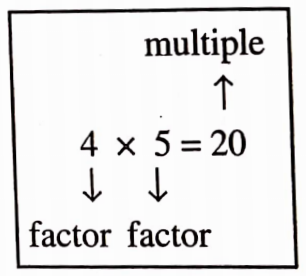
We can say that a number is a multiple of each of its factors
Let us now see some interesting facts about factors and multiples.
- Collect a number of wooden or paper strips of length 3 units each.
- Join them end to end as shown in the following figure.
The length of the strip at the top is 3 =1 x 3 units.
The length of the strip below it is 3 +3 =6 units.
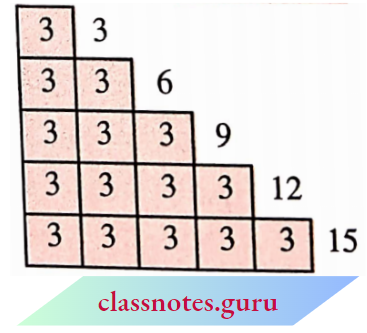
Also, 6 = 2 x 3. The length of the next strip is 3 + 3 + 3 = 9 units, and 9 = 3 x 3. Continuing this way we can express the other lengths as,
12 = 3 x 4; 15 = 5 x 3
We say that the numbers 3, 6, 9, 12, 15 are multiples of 3.
The list of multiples of 3 can be continued as 18, 21, 24, …
Each of these multiples is greater than or equal to 3.
The multiples of the number 4 are 4, 8, 12, 16, 20, 24, …
The list is endless. Each of these numbers is greater than or equal to 4
Let us see what we conclude about factors and multiples:
1. Is there any number that occurs as a factor of every number? Yes. It is 1. For example 6 = 1 x 6, 18 = 1 x 18, and so on. Check it for a few more numbers.
We say 1 is a factor of every number.
2. Can 7 be a factor of itself? Yes. You can write 7 as 7 = 7 x 1. What about 10? and 15?
You will find that every number can be expressed in this way. We say that every number is a factor of itself.
3. What are the factors of 16? They are 1, 2, 4, 8, 16. Out of these factors do you find any factor which does not divide 16? Try it for 20; 36.
You will find that every factor of a number is an exact divisor of that number.
4. What are the factors of 34? They are 1,2, 17 and 34. Out of these which is the greatest factor? It is 34 itself.
The other factors 1,2 and 17 are less than 34. Try to check this for 64, 81, and 56.
We say that every factor is less than or equal to the given number.
5. The number 76 has 5 factors. How many factors does 136 or 96 have? You will find that you are able to count the number of factors of each of these.
Even if the numbers are as large as 10576, 25642, etc., or larger, you can still count the number of factors of such numbers, (though you may find it difficult to factorize such numbers).
We say that the number of factors of a given number is finite.
6. What are the multiples of 7? Obviously, 7, 14, 21, 28,… You will find that each of these multiples is greater than or equal to 7. Will it happen with each number? Check this for the multiples of 6, 9, and 10.
We find that every multiple of a number is greater than or equal to that number.
7. Write the multiples of 5. They are 5, 10, 15, 20, … Do you think this list will end anywhere? No! The list is endless. Try it with multiples of
6, 7 etc.
We find that the number of multiples of a given number is infinite.
8. Can 7 be a multiple of itself? Yes, because 7 = 7 x 1. Will it be true for other numbers also? Try it with 3, 12 and 16.
You will find that every number is a multiple of itself.
The factors of 6 are 1, 2, 3 and 6. Also, 1 + 2 + 3 + 6 = 12 = 2 x 6. We find that the sum of the factors of 6 is twice the number 6.
All the factors of 28 are 1, 2, 4, 7, 14, and 28. Adding these we have, 1 + 2 + 4 + 7 + 14 + 28 = 56 = 2 x 28. The sum of the factors of 28 is equal to twice the number 28.
A number for which the sum of all its factors is equal to twice the number is called a perfect number. The numbers 6 and 28 are perfect numbers.
Is 10 a perfect number?
Example 1: Write all the factors of 68.
Solution :
We note that
68 = 1 x 68
68 = 2 x 34
68 = 4 x 17
68 = 17 x 4
Stop here, because 4 and 17 have occurred earlier.
Thus, all the factors of 68 are 1,2,4,17, 34 and 68.
Example 2: Find the factors of 36.
Solution:
36 = 1 x 36
36 = 2 x 18
36 = 3 x 12
36 = 4 x 9
36 = 6 x 6
Stop here, because both factors (6) are the same. Thus, the factors are 1,2, 3,4, 6, 9, 12,18 and 36.
Example 3: Write the first five multiples of 6.
Solution:
The required multiples are 6 x 1= 6, 6 x 2 = 12, 6 x 3 = 18, 6 x 4 = 24, 6 x 5 = 30 i.e. 6, 12, 18, 24, and 30.
Prime And Composite Numbers
We are now familiar with the factors of a number. Observe the number of factors of a few numbers arranged in this table.
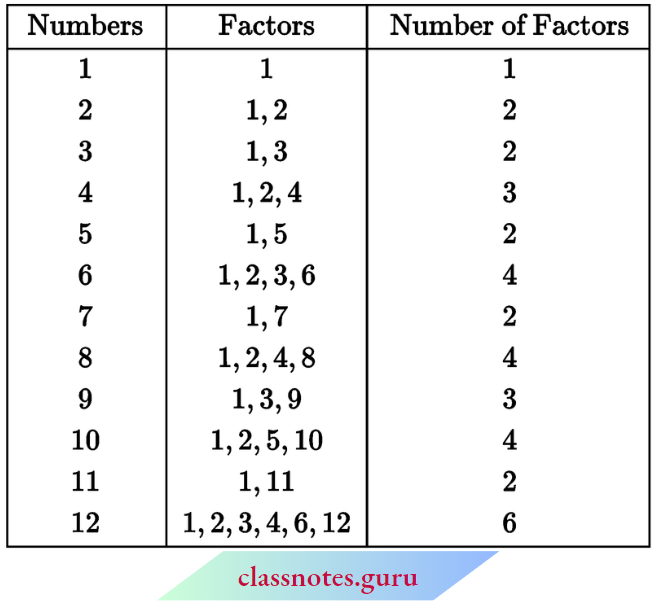
We find that
- The number 1 has only one factor (i.e. itself).
- There are numbers, having exactly two factors 1 and the number itself. Such numbers are 2,3,5,7,11 etc. These numbers are prime numbers.
- The numbers other than 1 whose only factors are 1 and the number itself are called Prime numbers.
Try to find some more prime numbers other than these.
There are numbers having more than two factors like 4,6,8,9,10 and so on. These numbers are composite numbers.
Numbers having more than two factors are called Composite numbers. Is 15 a composite number? Why? What about 18? 25?
Without actually checking the factors of a number, we can find prime numbers from 1 to 100 with an easier method.
This method was given by a Greek Mathematician Eratosthenes, in the third century B.C. Let us sec the method. List all numbers from 1 to 100, as shown below.
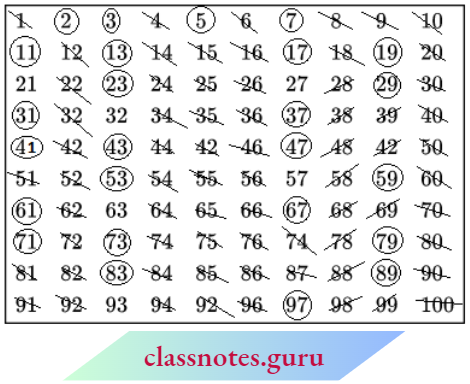
Step 1: Cross out 1 because it is not a prime number.
Step 2: Encircle 2, cross out all the multiples of 2, other than 2 itself, i.e. 4,6, 8, and so on.
Step 3: You will find that the next uncrossed number is 3. Encircle 3 and cross out all the multiples of 3, other than 3 itself.
Step 4: The next uncrossed number is 5. Encircle 5 and cross out all the multiples of 5 other than 5 itself.
Step 5: Continue this process till all the numbers in the list are either encircled or crossed out.
All the encircled numbers are prime numbers. All the crossed-out numbers, other than 1 are composite numbers.
This method is called the Sieve of Eratosthenes.
Example 4: Write all the prime numbers less than 15.
Solution :
By observing the Sieve Method, we can easily write the required prime numbers as 2,3, 5,7,11, and 13.
even and odd numbers
Do you observe any pattern in the numbers 2,4, 6, 8, 10, 12, 14,…? You will find that each of them is a multiple of 2.
These are called even numbers. The rest of the numbers 1, 3, 5, 7, 9,11,… are called odd numbers.
You can verify whether a two-digit number or a three-digit number is even or not. How will you know whether a number like 756482 is even? By dividing it by 2. Will it not be tedious?
We say that a number with 0,2,4,6, 8 at the one’s place is an even number. So, 350,4862,59246 are even numbers. The numbers 457,2359,8231 are all odd.
Let us try to find some interesting facts:
- Which is the smallest even number? It is 2. Which is the smallest prime number? It is again 2.
- Thus, 2 is the smallest prime number which is even.
- The other prime numbers are 3,5,7,11,13,… Do you find any even number in this list? Of course not, they are all odd.
Thus, we can say that every prime number except 2 is odd.
NCERT Notes For Class 6 Maths Tests For Divisibility Of Numbers
Is the number 38 divisible by 2? by 4? by 5?
By actually dividing 38 by these numbers we find that it is divisible by 2 but not by 4 and by 5.
Let us see whether we can find a pattern that can tell us whether a number is divisible by 2,3,4,5,6, 8,9,10, or 11. Do you think such patterns can be easily seen?
Divisibility by 10: Charu was looking at the multiples of 10. The multiples are 10, 20, 30,40, 50, 60,… She found something common in these numbers. Can you tell me what? J Each of these numbers has 0 in one place.
She thought of some more numbers with 0 at one place ^ like 100,1000,3200,7010. She also found that all such numbers are divisible by 10.
She finds that if a number has 0 in the ones place then it is divisible by 10. Can you find out the divisibility rule for 100?
Divisibility by 5: Mani found some interesting patterns in the numbers 5,10, 15,20,25,30,35,… Can you tell the pattern? Look at the unit’s place.
All these numbers have either 0 or 5 in their ones place. We know that these numbers are divisible by 5.
Mani took up some more numbers that are divisible by 5, like 105, 215, 6205, 3500. Again these numbers have either 0 or 5 in their places.
He tried to divide the numbers 23, 56, 97 by 5. Will he be able to do that? Check it. He observes that a number that has either 0 or 5 in its place is divisible by 5, other numbers leave a remainder. Is 1750125 divisible 5?
Divisibility by 2: Charu observes a few multiples of 2 to be 10, 12,14,16… and also numbers like 2410,4356, 1358, 2972, 5974.
She finds some patterns in the place of these numbers. Can you tell that? These numbers have only the digits 0, 2,4, 6, and 8 in one place.
She divides these numbers by 2 and gets the remainder 0. She also finds that the numbers 2467, and 4829 are not divisible by 2. These numbers do not have 0, 2, 4, 6, or 8 in their one place.
Looking at these observations she concludes that a number is divisible by 2 if it has any of the digits 0,2,4, 6, or 8 in its ones place.
Divisibility by 3: Are the numbers 21, 27, 36, 54, 219 divisible by 3? Yes, they are.
Are the numbers 25, 37, 260 divisible by 3? No.
Can you see any pattern in the one place? We cannot, because numbers with the same digit in the ones places can be divisible by 3, like 27, or may not be divisible by 3 like 17, 37.
Let us now try to add the digits of 21, 36, 54, and 219. Do you observe anything special? 2+1=3,3+6=9,5+4=9,2+1+9=12.
All these additions are divisible by 3.
Add the digits 25, 37, 260. We get 2+5=7, 3+7=10, 2+6+0 = 8.
These are not divisible by 3.
We say that if the sum of the digits is a multiple of 3, then the number is divisible by 3. Is 7221 divisible by 3?
Divisibility by 6: Can you identify a number that is divisible by both 2 and 3? One such number is 18. Will 18 be divisible by 2×3=6? Yes, it is.
Find some more numbers like 18 and check if they are divisible by 6 also.
Can you quickly think of a number that is divisible by 2 but not by 3?
Now for a number divisible by 3 but not by 2, one example is 27. Is 27 divisible by 6? No. Try to find numbers like 27.
From these observations, we conclude that if a number is divisible by 2 and 3 then it is divisible by 6 also.
Divisibility by 4: Can you quickly give five 3-digit numbers divisible by 4? One such number is 212. Think of such 4-digit numbers. One example is 1936.
Observe the number formed by the ones and tens places of 212. It is 12; which is divisible by 4. For 1936 it is 36, again divisible by 4.
Try the exercise with other such numbers, for example, 4612; 3516; 9532. Is the number 286 divisible by 4? No. Is 86 divisible by 4? No.
So, we see that a number with 3 or more digits is divisible by 4 if the number formed by its last two digits (i.e. ones and tens) is divisible by 4. Check this rule by taking ten more examples.
Divisibility for 1 or 2-digit numbers by 4 has to be checked by actual division.
Divisibility by 8: Are the numbers 1000, 2104, and 1416 divisible by 8? You can check that they are divisible by 8. Let us try to see the pattern.
Look at the digits at ones, tens, and hundreds in place of these numbers. These are 000,104 and 416 respectively. These too are divisible by 8.
Find some more numbers in which the number formed by the digits at units, tens, and hundreds place (i.e. last 3 digits) is divisible by 8.
For example, 9216,8216,7216,10216, 9995216, etc. You will find that the numbers themselves are divisible by 8.
We find that a number with 4 or more digits is divisible by 8 if the number formed by the last three digits is divisible by 8. Is 73512 divisible by 8?
The divisibility for numbers with 1,2 or 3 digits by 8 has to be checked by actual division.
Divisibility by 9: The multiples of 9 are 9, 18, 27, 36, 45, 54,… There are other numbers like 4608, and 5283 that are also divisible by 9.
Do you find any pattern when the digits of these numbers are added?
1 + 8 = 9, 2 + 7 = 9, 3 + 6 = 9, 4 + 5 = 9 4 + 6 + 0 + 8= 18,5 + 2 + 8 + 3 = 18 All these sums are also divisible by 9. Is the number 758 divisible by 9?
No. The sum of its digits 7 + 5 + 8 = 20 is also not divisible by 9.
These observations lead us to say that if the sum of the digits of a number is divisible by 9, then the number itself is divisible by 9.
Divisibility by 11: The numbers 308,1331 and 61809 are all divisible by 11. We form a table and see if the digits in these numbers lead us to some pattern.

We observe that in each case the difference is either 0 or divisible by 11. All these numbers are also divisible by 11.
For the number 5081, the difference between the digits is (5+8) – (1+0) = 12 which is not divisible by 11. The number 5081 is also not divisible by 11.
Thus, to check the divisibility of a number by 11, the rule is, to find the difference between the sum of the digits at odd places (from the right) and the sum of the digits at even places (from the right) of the number.
If the difference is either 0 or divisible by 11, then the number is divisible by 11.
NCERT Notes For Class 6 Maths Common Factors and Common Multiples
Observe the factors of some numbers taken in pairs.
1. What are the factors of 4 and 18?
The factors of 4 are 1, 2, and 4.
The factors of 18 are 1,2,3,6,9 and 18.
The numbers 1 and 2 are the factors of both 4 and 18.
They are the common factors of 4 and 18.
2. What are the common factors of 4 and 15?
These two numbers have only 1 as the common factor.
What about 7 and 16?
Two numbers having only 1 as a common factor are called co-prime numbers. Thus, 4 and 15 are co-prime numbers.
Are 7 15,12 49,18 and 23 co-prime numbers?
3. Can we find the common factors of 4,12 and 16?
Factors of 4 are 1, 2, and 4.
Factors of 12 are 1, 2, 3, 4, 6 and 12.
Factors of 16 are 1, 2, 4, 8 and 16.
Clearly, 1, 2, and 4 are the common factors of 4,12, and 16.
Find the common factors of (1) 8, 12, 20 (2) 9,15, 21.
Let us now look at the multiples of more than one number taken at a time.
1. What are the multiples of 4 and 6?
The multiples of 4 are 4, 8,12,16, 20,24,… (write a few more)
The multiples of 6 are 6,12,18, 24, 30, 36,… (write a few more)
Out of these, are there any numbers that occur in both lists?
We observe that 12,24, 36,… are multiples of both 4 and 6.
Can you write a few more?
They are called the common multiples of 4 and 6.
2. Find the common multiples of 3,5 and 6.
Multiples of 3 are 3, 6, 9,12,15, 18,21, 24, 27, 30, 33, 36,… Multiples of 5 are 5,10,15, 20, 25, 30, 35,…
Multiples of 6 are 6, 12, 18, 24, 30,…
Common multiples of 3,5 and 6 are 30, 60,…
Write a few more common multiples of 3,5 and 6.
Example 5: Find the common factors of 75,60 and 210.
Solution:
Factors of 75 are 1, 3, 5, 15, 25 and 75.
Factors of 60 are 1, 2, 3,4, 5, 6,10,12, 15, 30 and 60.
Factors of 210 are 1,2,3,5,6,7,10,14,15,21,30,35,42,70,105 and 210.
Thus, common factors of 75,60 and 210 are 1,3,5 and 15.
Example 6: Find the common multiples of 3,4 and 9.
Solution:
Multiples of 3 are 3,6,9,12,15,18, 21, 24,27,30, 33,36, 39,42, 45,48,….
Multiples of 4 are 4, 8,12,16, 20, 24, 28, 32, 36, 40,44,48,…
Multiples of 9 are 9,18, 27, 36,45, 54,63, 72, 81,…
Clearly, common multiples of 3,4, and 9 are 36,72,108,…
Prime Factorisation
When a number is expressed as a product of its factors we say that the number has been factorised. Thus, when we write 24 = 3×8, we say that 24 has been factorized. This is one of the factorizations of 24.
The others are:
24 = 2 x 12
= 2 x 2 x 6
= 2 x 2 x 2 x 3
24 = 4 x 6
= 2 x 2 x 6
= 2 x 2 x 2 x 3
24 = 3 x 8
= 3 x 2 x 2 x 2
= 2 x 2 x 2 x 3
In all the above factorisations of 24, we ultimately arrive at only one factorisation 2 x 2 x 2 x 3. In this factorization, the only factors 2 and 3 are prime numbers.
Such a factorization of a number is called a prime factorization. Let us check this for the number 36.
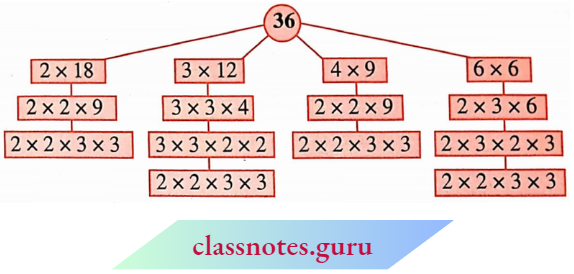
The prime factorization of 36 is 2 x 2 x 3 x 3. i.e. the only prime factorization of 36.
Example 7: Find the prime factorization of 980.
Solution:
We proceed as follows:
We divide the number 980 by 2,3,5,7 etc. in this order repeatedly so long as the quotient is divisible by that number. Thus, the prime factorization of 980 is 2 x 2 x 5 x 7 x 7.
⇒ \(\begin{array}{r|r}
2 & 980 \\
\hline 2 & 490 \\
\hline 5 & 245 \\
\hline 7 & 49 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
Highest Common Factor
We can find the common factors of any two numbers. We now try to find the highest of these common factors.
What are the common factors of 12 and 16? They are 1,2 and 4.
What is the highest of these common factors? It is 4.
What are the common factors of 20, 28 and 36? They are 1, 2 and 4 and again 4 is the highest of these common factors.
The Highest Common Factor (HCF) of two or more given numbers is the highest (or greatest) of their common factors.
It is also known as the Greatest Common Divisor (GCD).
The HCF of 20, 28, and 36 can also be found by prime factorization of these numbers as follows:
⇒ \(\begin{array}{l|l}
2 & 20 \\
\hline 2 & 10 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
⇒ \(\begin{array}{l|l}
2 & 28 \\
\hline 2 & 14 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
⇒ \(\begin{array}{l|l}
2 & 36 \\
\hline 2 & 18 \\
\hline 3 & 9 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
Thus,
20 = 2 x 2 x 5
28 = 2 x 2 x 7
36 = 2 x 3 x 3
The common factor of 20,28 and 36 is 2(occurring twice). Thus, HCF of 20, 28 and 36 is 2 x 2 = 4.
NCERT Notes For Class 6 Maths Lowest Common Multiple
What are the common multiples of 4 and 6? They are 12,24,36,… Which is the lowest of these? It is 12.
We say that the lowest common multiple of 4 and 6 is 12. It is the smallest number and both the numbers are factors of this number.
The Lowest Common Multiple (LCM) of two or more given numbers is the lowest (or smallest or least) of their common multiples. What will be the LCM of 8 and 12? 4 and 9? 6 and 9?
Example 8: Find the LCM of 12 and 18.
Solution:
We know that common multiples of 12 and 18 are 36,72,108 etc. The lowest of these is 36. Let us see another method to find the LCM of two numbers.
The prime factorizations of 12 and 18 are:
12 = 2 x 2 x 3; 18 = 2 x 3 x 3
In these prime factorizations, the maximum number of times the prime factor 2 occurs is two; this happens for 12. Similarly, the maximum number of times the factor 3 occurs is two; this happens for 18.
The LCM of the two numbers is the product of the prime factors counted the maximum number of times they occur in any of the numbers. Thus, in this case, LCM = 2 x 2 x 3 x 3 = 36.
Example 9: Find the LCM of 24 and 90.
Solution:
The prime factorizations of 24 and 90 are:
24 = 2 x 2 x 2 x 3; 90 = 2 x 3 x 3 x 5
In these prime factorizations, the maximum number of times the prime factor 2 occurs is three; this happens for 24.
Similarly, the maximum number of times the prime factor 3 occurs is two; this happens for 90. The prime factor 5 occurs only once in 90.
Thus, LCM = (2 x 2 x 2) x (3 x 3) x 5 = 360
Example 10: Find the LCM of 40, 48 and 45.
Solution:
The prime factorizations of 40,48 and 45 are;
40 = 2 x 2 x 2 x 5
48 = 2 x 2 x 2 x 2 x 3
45 = 3 x 3 x 5
The prime factor 2 appears a maximum number of four times in the prime factorization of 48, the prime factor 3 occurs a maximum number of two times in the prime factorization of 45, The prime factor 5 appears one time in the prime factorizations of 40 and 45, we take it only ponce.
Therefore, required LCM = (2 x 2 x 2 2) x (3 x 3) x 5 = 720
LCM can also be found in the following way:
Example 11: Find the LCM of 20, 25 and 30.
Solution:
We write the numbers as follows in a row:
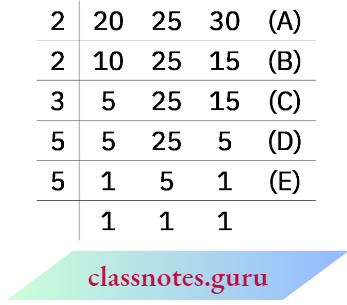
So, LCM = 2 x 2 x 3 x 5 x 5.
- Divide by the least prime number which divides at least one of the given numbers. Here, it is 2. The numbers like 25 are not divisible by 2 so they are written as such in the next row.
- Again divide by 2. Continue this till we have no multiples of 2.
- Divide by the next prime number which is 3.
- Divide by the next prime number which is 5.
- Again divide by 5.
NCERT Notes For Class 6 Maths Some Problems On HCF And LCM
We come across a number of situations in which we make use of the concepts of HCF and LCM. We explain these situations through a few examples.
Example 12: Two tankers contain 850 liters and 680 liters of kerosene oil respectively. Find the maximum capacity of a container that can measure the kerosene oil of both tankers when used an exact number of times.
Solution:
The required container has to measure both tankers in a way that the count is an exact number of times.
So its capacity must be an exact divisor of the capacities of both the tankers. Moreover, this capacity should be maximum. Thus the maximum capacity of such a container will be the HCF of 850 and 680.
⇒ \(\begin{array}{l|l}
2 & 850 \\
\hline 5 & 425 \\
\hline 5 & 85 \\
\hline 17 & 17 \\
\hline & 1
\end{array}\)
⇒ \(\begin{array}{l|l}
2 & 680 \\
\hline 2 & 340 \\
\hline 2 & 170 \\
\hline 5 & 85 \\
\hline 17 & 17 \\
\hline & 1
\end{array}\)
Hence,
850 = 2 x 5 x 5 x 17 = 2 x 5 x 17 x 5 and
680 = 2 x 2 x 2 x 5 x 17 = 2 x 5 x 17 x 2 x 2
The common factors of 850 and 680 are 2, 5 and 17.
Thus, the HCF of 850 and 680 is 2 x 5 x 17 = 170.
Therefore, the maximum capacity of the required container is 170 liters.
It will fill the first container in 5 and the second in 4 refills.
Example 13: In a morning walk, three persons step off together. Their steps measure 80 cm, 85 cm, and 90 cm respectively. What is the minimum distance each should walk so that all can cover the same distance in complete steps?
Solution:
The distance covered by each one of them is required to be the same as well as minimum. The required minimum distance each should walk would be the lowest common multiple of the measures of their steps.
Can you describe why? Thus, we find the LCM of 80, 85, and 90. The LCM of 80, 85, and 90 is 1 2240.
The required minimum distance is 12240 cm.

Example 14: Find the least number which when divided by 12, 16, 24, and 36 leaves a remainder of 7 in each case.
Solution:
We first find the LCM of 12, 16, 24, and 36 as follows:
∴ \(\begin{array}{c|cccc}
2 & 12 & 16 & 24 & 36 \\
\hline 2 & 6 & 8 & 12 & 18 \\
\hline 2 & 3 & 4 & 6 & 9 \\
\hline 2 & 3 & 2 & 3 & 9 \\
\hline 3 & 3 & 1 & 3 & 9 \\
\hline 3 & 1 & 1 & 1 & 3 \\
\hline & 1 & 1 & 1 & 1
\end{array}\)
Thus, LCM = 2 x 2 x 2 x 2 x 3 x 3 = 144
144 is the least number which when divided by the given numbers will leave the remainder 0 in each case. But we need the least number that leaves the remainder 7 in each case.
Therefore, the required number is 7 more than 144. The required least number = 144 + 7 = 151.