Class 11 Chemistry

CBSE Class 11 Chemistry Notes For Chapter 2 Structure Of Atom Discovery Of Fundamental Particles

The atomic theory of matter was first proposed by Sir John Dalton (an English scientist) in 1808. His theory, called Dalton’s atomic theory was a landmark in the history of chemistry. According to this theory, the atom is the smallest, indivisible, discrete particle of matter, which takes part in chemical reactions.

However, the researches done by eminent scientists like J. J. Thomson, Goldstein, Rutherford, Chadwick, Bohr, and others towards the end of the 19th century and in the beginning of the 20th century have conclusively proved that atoms were no longer the smallest indivisible particle. Rather, atoms are -3 composed of several smaller particles called subatomic particles. At present J. scientists have identified about 35 different subatomic particles, some of L which are stable while the others are unstable. These particles may be divided under three heads which is shown in the adjacent table.

The three subatomic particles namely electrons, protons, and neutrons are the main constituents of an atom and are regarded as the fundamental particles

Cathode rays: Discovery of electron 

William Crookes, in 1878, studied the conduction of electricity through gases. A discharge tube was filled with a gas at very low pressure (0.01 mm Hg) and the electrodes were connected to a source of high voltage \(\approx 10^4 \mathrm{~V}\).

It was observed that the glass wall behind the anode began to glow with a faint greenish light called fluorescence.

Further investigations revealed that this fluorescence was due to the bombardment of the glass wall by certain invisible rays which were emitted from the cathode surface and moved towards the anode with tremendous speed.

The rays originated from the cathode and were called the cathode ray.

CBSE Class 11 Chemistry Notes Chapter 2 Structure of Atom

Nature of cathode rays: J.J Thomson (in 1897) and others characterized these rays based on different experimental findings.

1. Cathode rays are emitted perpendicularly from the cathode surface and travel towards the anode.
2. They cast a sharp shadow on any opaque object placed in their path. So, like ordinary light, cathode rays also travel in straight lines.
3. When a light paddle wheel (made of mica) is placed in their path, the wheel begins to rotate. This indicates that cathode rays are composed of material particles and possess momentum.
4. As cathode rays possess momentum, they can penetrate thin foil metals like aluminum.

1. Cathode rays are deflected by an electric field (towards the positive plate) as well as by a magnetic field, suggesting that cathode rays consist of negatively charged particles.
2. When these rays strike a metal foil, the foil gets heated indicating that cathode rays produce a heating effect.
3. Cathode rays ionize the gas through which they pass.
4. Like ordinary light, cathode rays affect photographic plates. This is called fogging.
5. Cathode rays produce fluorescence on the glass walls of a tube or a screen coated with zinc sulfide 1 ‘(ZnS) or barium platinocyanide Ba[Pt(CN)6].
6. Cathode rays produce X-rays when they strike against the surface of hard metals like tungsten, molybdenum, etc.
7. The characteristics of cathode rays are independent of the material of the cathode nature of the gas used in the discharge tube.
8. Considering the various properties of cathode rays, J. J. Thomson concluded that cathode rays are made of material particles, cathode rays carry a negative charge.
9. He named these negatively charged particles as negatron. Later, these particles were named electrons by G. J. Stoney (in 1874).

J. J. Thomson (1897) used discharge tubes fitted with electrodes made of different metals and filled different gases in the tube. Every time he found that the ratio of charge to mass of electrons (e/m) was the same.

e/m of electron = \(\frac{\text { charge of cathode ray particle }}{\text { mass of cathode ray particle }}\)

= \(1.76 \times 10^8 \mathrm{C} \cdot \mathrm{g}^{-1}\)

= \(1.76 \times 10^{11} \mathrm{C} \cdot \mathrm{kg}^{-1}\)

R. A. Millikan (1917) with the help of his oil drop experiment, determined the charge of an electron. Charge ofan electron (e) = -1.602 x 10^–19 C (or, -4.8 x 10^–1°esu)

No other fundamental particle is known to contain a charge lower than this. This is the minimum measurable quantity of negative charge.

The quantity of electrical charge carried by all negatively charged panicles is an integral multiple of this charge.

Hence, the electronic charge is considered to be die fundamental unit of electricity and is called one unit. The mass of an electron can be calculated from the values of e and e/m.

Mass of an electron = \(\frac{e}{e / m}=\frac{1.602 \times 10^{-19} \mathrm{C}}{1.76 \times 10^8 \mathrm{C} \cdot \mathrm{g}^{-1}} \)

= \(9.11 \times 10^{-28} \mathrm{~g}=9.11 \times 10^{-31} \mathrm{~kg}\)

= 0.000548

1 u = \(1.66 \times 10^{-24}\)

Mass of an electron = \(\frac{1}{1837}\) x mass of a hydrogen atom Thus, a hydrogen atom is 1837 times heavier than an electron. The mass of an electron being very small may be considered as negligible for all practical involving chemical calculations.

Therefore, an electron may be defined as a subatomic particle having a unit negative charge (1.602 × 10^-9C) & negligible mass (9.11 × 10^-28g).

The radius of an electron = 2.8 × 10^-13cm

Electrons are universal constituents of matter:

The elm ratio of negatively charged particles constituting the cathode rays was found to be the same irrespective of the nature of the cathode and the nature of the gas used in the discharge tube, thereby showing that the electrons are the basic constituents of all atoms.

Other experiments showing the existence of electrons:

The following experiments show that the same charge-to-mass ratio exists for the electrons emitted—

1. Spontaneously from radioactive substances in the form of X-rays.
2. when ultraviolet rays are incident on the surface of active metals (Example: Na, K, etc.).
3. When certain metal filaments are heated to a very high temperature.
4. When any form of matter is exposed to X-rays.

Origin of cathode rays in discharge tube:

1. On applying high voltage, electrons are first emitted from the surface of the cathode which travel in straight lines with high speed.
2. During their passage through the gas inside the tube, more electrons are ejected due to the bombardment of the gas molecules by the high-speed electrons.
3. On increasing the voltage in the discharge tube, the speed of the electrons increases, and the electron density in the cathode ray increases.

Applications of cathode ray tube:

In picture tubes of televisions:

The picture tube of a television is a cathode ray tube. Due to fluorescence, a picture is formed on the television screen when an electron beam strikes the screen coated with a fluorescent or phosphorescent material.

In fluorescent tubes:

These types of tubes are filled with gases like argon, nitrogen, etc. along with a small amount of mercury vapor under very low pressure.

• They are cathode ray tubes with their inner walls coated with a suitable fluorescent material.
• On passing electric current, electric discharge occurs inside the tube.
• As a result, electrons from the cathode are transferred to the higher energy state due to collision with the atoms and molecules of the gases or the mercury vapor.
• On their return to the ground state photons are emitted in the form of UV rays. These rays hit the inner walls of the tube and produce visible light.

Anode rays: Discovery of proton

• Since negatively charged electrons are the essential constituents of all atoms and the atom as a whole is electrically neutral, it was thought that some positively charged particles must also be present in the atom.
• Goldstein, in 1886, performed the discharge tube experiment using a perforated cathode. On passing electric discharge at low pressure, he observed that some luminous rays were emitted from the side of the anode which passed through the holes in the cathode and produced fluorescence on the glass wall coated with zinc sulfide.
• These rays were originally called canal rays as they passed through the holes in the cathode.
• As they travel from the side of the anode towards the cathode, these rays are also called anode rays.
• These were named positive rays (since they were found to carry a positive charge) by J. J. Thomson (1907).

Characteristics of anode rays:

• Anode rays travel in straight lines but their speed is much less than that ofthe cathode rays.
• They consist of material particles.
• They are positively charged as indicated by the direction of their deflection in the electric and magnetic fields.
• From the extent of deflection in the electric field, it was proved that the particles constituting the anode rays arc are much heavier than electrons.
• The E/M value of the particles in the anode rays is much smaller than that of the cathode ray particles.
• Furthermore, the e/m value of the particles depends on the nature ofthe gas taken in the discharge tube.
• The E/M value of anode ray particles is maximum when hydrogen gas (the lightest element) is used in the discharge tube.
• The mass of the particle with this maximum e/m value is almost the same as that of an H-atom and its charge is equal to that of an electron but opposite in sign.
• It may therefore be concluded that such anode ray particles with maximum e/m value are none other than H-atoms devoid of electrons. These were called protons by Rutherford (1911).

Anode rays produced using H₂ gas in the discharge tube consist of positively charged particles:

H⁺ [highest e/m ], D⁺, H⁺, HD⁺, and D⁺ [lowest e/m].

Origin of anode rays:

• On applying high voltage between the electrodes in the discharge tube, cathode ray particles (i.e., electrons) move at a high speed toward the anode.
• In the course of their motion, they collide with the gas molecules or atoms and knock out one or more electrons to produce positively charged ions, thereby constituting anode rays.

⇒ \(\text { A (neutral gaseous atom) } \stackrel{\text { ionised }}{\longrightarrow} \mathrm{A}^{+}+e\)

• Thus, the anode rays are not emitted from the anode but produced from the gaseous substance present in the discharge tube.
• So it is clear that the e/m ratio of the ray particles depends on the gaseous substance in the discharge tube. For example, the use of hydrogen to the formation of H+ ions which constitute the orhunode rays.

⇒ \(\mathbf{H} \text { (atom) }-\boldsymbol{e} \stackrel{+}{\longrightarrow} \mathbf{H}^{+} \text {(proton) }\)

E/m of proton = +9.58× 10⁴C.g^-1

Charge of proton = + 1.602×10^-19 C (Or, +4.8 × 10^-10esu)

Mass of proton (m) = \(\frac{\text { charge of a proton }}{c / m \text { of a proton }}\)

= \(\frac{1.602 \times 10^{-19}}{9.58 \times 10^4}\)

= \(1.6725 \times 10^{-24} \mathrm{~g}\)

This mass is nearly the same as that of an H-atom. A proton Is 1836 times heavier than an electron. So, a proton carries 1 unit of +ve charge and it is 1 836 times heavier than an electron.

Radius of a proton \(\approx 1.2 \times 10^{-13} \mathrm{~cm}\)

Proton is a fundamental constituent of all atoms:

• Taking different gases in the discharge tube experiment, it was shown that the mass of anode ray particles is minimal when hydrogen is used as the gaseous substance.
• Masses of other anode ray particles produced in different experiments using different gases are always integral multiples of the mass of a proton.
• Thus a proton, like an electron, is also a fundamental constituent of all atoms.
• Apart from the electrical discharge in gases under low pressure, protons are also emitted in certain nuclear reactions

Example: The bombardment of aluminum metal with a particle

⇒ \(\left({ }_2^4 \mathrm{He}\right)\) or bombardment of nitrogen gas with neutron \(\left({ }_0^1 n\right)\)

⇒ \({ }_{13}^{27} \mathrm{Al}+{ }_2^4 \mathrm{He} \rightarrow{ }_{14}^{30} \mathrm{Si}+{ }_1^1 \mathrm{H} ; \quad{ }_7^{14} \mathrm{~N}+{ }_0^1 n \rightarrow{ }_6^{14} \mathrm{C}+{ }_1^1 \mathrm{H}\)

Differences Between Cathode And Anode Rays

Radioactivity:

After the discovery of electrons and protons, it is well established that the atoms are divisible into sub-atomic particles.

• This was further supported by the phenomenon of radioactivity, discovered by Becquerel in 1896.
• The phenomenon of spontaneous emission of active radiations by certain elements like uranium, radium, etc.
• Is called radioactivity, and the elements emitting such radiation are called radioactive elements.

On placing a sample of uranium mineral in a cavity made in a block of lead and allowing the emitted rays to pass through strong electric or magnetic fields, the radiation is resolved in three directions.

• The rays which are deflected slightly towards the negative plate and hence carry + ve charge are called α rays. The particles present in a -rays are called particles, α- rays are called α – particles, and each particle carries 2 units +ve charge and has a mass of 4u. So these are helium atoms with two units +ve charge and are represented as ₂⁴He.
• The rays that are deflected towards the positive plate to a larger extent must carry a -ve charge. These are called α-rays. The particles present in β -rays are called β -P-particles. These particles have the same charge and mass as that of the electrons and are represented as _-1⁰e.
• The rays that remain undeflected are called γ-rays. These are purely electromagnetic radiations.

Discovery Of Neutron

• According to the atomic mass scale, a proton has a mass of one unit while an electron has a negligible mass.
• If an atom comprises only electrons and protons then the mass of an atom will be almost equal to the sum of the masses of the protons present in it.
• In practice, it is found that except for ordinary hydrogen, all other atoms have masses much greater than the sum of the masses of the protons contained by diem.
• This led the scientists to search for a neutral particle having considerable mass. Rutherford, in 1920, predicted the presence of a fundamental particle within an atom, having no charge but one unit mass. This particle was termed a neutron.
• James Chadwick (a student of Rutherford), in 1932, performed some scattering experiments in which he bombarded beryllium metal with fast-moving a -particles emitted from radioactive polonium.
• He observed that new types of particles were emitted which was not deflected by the electric or magnetic field. i.e., those were neutral.
• The mass of such a particle was found to be nearly equal to that of a proton or a hydrogen atom.
• These neutral particles having a unit mass must be the same particle i.e., neutron as predicted by Rutherford. Being neutral, neutrons are more penetrating than electrons or protons.

Mass of neutron = 1.675 × 10^-24 g

⇒ \(\approx\)mass of a proton

= 1837 x mass ofan electron

e/m of neutron = [because neutron has no charge]

Atoms of all elements except hydrogen constitute three fundamental particles:

1. Electron,
2. Proton and
3. Neutron.

In each atom, the number of protons is equal to the number of electrons because an atom as a whole is electrically neutral. Ordinary hydrogen contains no neutron, it only contains one proton and one electron.

Subatomic particles other than an electron, proton, and neutron, are also known

Example: Positron \(\left({ }_{+1}^0 e\right),\); 71 -meson, neutrino (v), photon, etc.

Class 11 Chemistry Chapter 2 Structure of Atom NCERT Notes

Structure Of Atom Numerical Examples

Question 1. An atom of an element contains 2 electrons In the first shell (n – 1 ), 8 electrons in the second shell (n = 2), and 5 electrons in the third shell (n = 3).

There are 16 neutrons in the nucleus of the atom. From these data, find—

1. The atomic no. of the element,
2. the no. of s and -electrons in the atom,
3. Mass no. of the element.

Answer:

1. Atomic number = number of protons = number of electrons =2+8 + 5

= 15

2. \(\begin{array}{|c|c|c|c|}
\hline \text { Shell No. } & \begin{array}{c}
\text { Total no. of } \\
\text { electrons }
\end{array} & \begin{array}{c}
\text { No. of } \\
s \text {-electrons }
\end{array} & \begin{array}{c}
\text { No. of } \\
p \text {-electrons }
\end{array} \\
\hline 1 & 2 & 2 & 0 \\
\hline 2 & 8 & 2 & (8-2)=6 \\
\hline 3 & 5 & 2 & (5-2)=3 \\
\hline
\end{array}\)

∴ Total number of s- electron – 2 + 2+2 =6

Total number of p -electron 6 + 3 =9

3. The mass number of protons + number of neutrons = 15+16

= 31.

Question 2. Determine the number of protons present In 5.6 I16. of n sample of oxygen gas at STP, containing \({ }^{16} 0\) isotope only.
Answer:

The number of oxygen molecules present in 22.4 L of the gas = 6.022 × 10²³.

∴ 5.6 L of oxygen at STP contains = \(\frac{5.6 \times 6.022 \times 10^{23}}{22.4}\)

= 1.50055  × 10²³ Molecules

Number of O-atoms in the given volume of the gas

⇒ \(2 \times 1.50055 \times 10^{23}=3.011 \times 10^{23}\)

since oxygen is diatomic]

Now, each ¹⁶O atom contains 8 protons.

∴ Number of protons in 3.011 × 10²³ atoms of oxygen

= 8 × 3.01 1 × 10²³

= 2.4088 × 10²⁴

Question 3. Find the number of protons required to fill u sphere of 10cm3 volume. What Is the muss of those number of protons?
Answer:

The radius of a proton = 1.2 × 10¹³ cm (approx.)

∴ The approximate volume of a proton \(=\frac{4}{3} \pi r^3\)

⇒ \(\frac{4}{3} \times 3.14 \times\left(1.2 \times 10^{-13}\right)^3 \mathrm{~cm}^3=7.235 \times 10^{-39} \mathrm{~cm}^3\)

∴ The number of protons which can be accommodated in the sphere of capacity 10 cm3

⇒ \(\frac{10}{7.235 \times 10^{-39}}=1.382 \times 10^{39}\)

∴ The mass of that number of protons

1.382 × 10³⁹ × 1.672 ×10^-24 g

= 2.311 × 10¹⁵g

= 2.311 × 10¹² kg

Question 4. Determine the number of neutrons and their mass, present in 7 mg of \({ }^{14}{ }_6^{14} \mathrm{C}\) Assume that the mass of I neutron = muss of 1 H-atom.
Answer:

No. of neutrons present In a \({ }_6^{14} \mathrm{C} \text {-atom }\) atom = (14-6)= 8

Number of atoms in 1 gram morn or 14 g of carbon-containing only \({ }_6^{14} \mathrm{C}\) isotope 6.022 x 10²³

∴ In 7 mg or 0.007 g of carbon, the number of atoms \(=\frac{6.022 \times 10^{23} \times 0.007}{14}\)

∴ In 7 mg of carbon, the number of neutrons

∴ \(=\frac{6.022 \times 10^{23} \times 0.007 \times 8}{14}=24.088 \times 10^{20}\)

Again, mass of 6.022 × 10²³ atoms of hydrogen = 1.008 g

∴ Mass of 1 atom of hydrogen \(=\frac{1.008}{6.022 \times 10^{23}} \mathrm{~g}\)

= mass of 1 neutron [according to the given condition]

∴ Mass of 24.088 × 10²⁰ neutrons

⇒ \(\frac{1.008 \times 24.088 \times 10^{20}}{6.022 \times 10^{23}}=4.032 \times 10^{-3} \mathrm{~g}\)

Question 5. How many different types of HCl molecule can be produced from two natural isotopes of hydrogen ¹H = 99% and ²H = 1%) and two natural isotopes of chlorine (³CI = 76% and 37CI = 24%). Arrange the molecules obtained in the decreasing order of their availability.
Answer:

Four different types of HCl molecules can be produced.

They are

⇒ \({ }^1 \mathrm{H}^{35} \mathrm{Cl},{ }^1 \mathrm{H}^{37} \mathrm{Cl},{ }^2 \mathrm{H}^{35} \mathrm{Cl},{ }^2 \mathrm{H}^{37} \mathrm{Cl} \text {. }\)

Since the availability of XH and 35C1 are comparatively 2H and 37C1, the decreasing order of their availability

⇒ \({ }^1 \mathrm{H}^{35} \mathrm{Cl}>{ }^1 \mathrm{H}^{37} \mathrm{Cl}>{ }^2 \mathrm{H}^{35} \mathrm{Cl}>{ }^2 \mathrm{H}^{37} \mathrm{Cl}\)

Question 6. A sample of oxygen contains the isotope, 180. How many neutrons are present in 11.2L of the gas at STP?
Answer:

Atomic Number of oxygen

= 8 Number of neutrons in a 180 isotope

= 18-8

= 10

∴ Number of atoms in 22.4 L of 18O isotope at STP

= 2 × 6.022 × 10²³

∴ Number of neutrons in 22.4L of 180 isotopes at STP

= 10 × 2 × 6.022 ×10²³ [since oxygen molecule is diatomic]

∴ Number of neutrons in 11.2Lof 180 isotopes at STP

=  \(\frac{10 \times 2 \times 6.022 \times 10^{23} \times 11.2}{22.4}\)

= \(6.022 \times 10^{24}\)

Question 7. A sample contains two isotopes, 160 and 180. How many protons are present in 11.2L of the sample at STP? What would be the difference in the no. of protons, if the sample contains only one isotope?
Answer:

Each of the atoms of 160 and 180 contains 8 protons (atomic number of oxygen = 8 ) Total number of atoms is 22.41. oxygen ( 160 and 180 ) at SIT = 6.022 × 10²³×2

[since oxygen molecule is diatomic]

Number of protons in 22.4L oxygen sample at STP

= \(\frac{8 \times 2 \times 6.022 \times 10^{23} \times 11.2}{22.4}\)

∴ Number of protons in 11.2 L oxygen sample at STP

= \(4.8176 \times 10^{24}\)

If the sample contains only one isotope, then there will be no difference in the number of protons because both 16O and 180 isotopes contain 8 protons in their atoms.

Electromagnetic Radiation: Origin Of Atomic Spectra

We have already seen that Rutherford’s atomic model failed to explain the atomic spectra and stability of an atom.

• In order to investigate the reasons behind the failure of the Rutherford model, scientists felt the need to explain the nature and origin of atomic spectra.
• Atomic spectra result from the electromagnetic radiations emitted by the excited atoms.
• These electromagnetic radiations can pass through a vacuum also. According to Newton and other physicists, light is nothing but a stream of very small particles. The phenomena of reflection, refraction, etc.
• Can be successfully explained using Newton’s theory but those like dispersion, interference, etc. cannot. Thus, the particle nature of light was replaced by the wave nature of light.

Wave nature of electromagnetic radiation: Maxwell’s theory

James Maxwell (1865) studied the nature of light and concluded that light is transmitted in the form of electromagnetic waves, which are associated with oscillating electric and magnetic fields.

• The oscillating electric and magnetic fields are perpendicular to each other and are both perpendicular to the direction of propagation ofthe wave.
• The absorption or emission of radiation by a body occurs continuously.
• The radiations possessing wave character, travel with the velocity of light (3 x 108m-s_1 in vacuum).
• The color of the radiation depends on its wavelength.
• Electromagnetic waves, unlike sound waves or water waves, do not need a material medium for propagation, Electromagnetic waves can travel through a vacuum.

Some quantities related to electromagnetic radiation

Electromagnetic spectrum:

Different types of electromagnetic radiation differ only in their frequencies and hence in their wavelengths.

The order of increasing wavelengths is:

Cosmic rays <γ -rays < X-rays < UV rays (150-3800Å) < visible light (3800-7600Å) < IR-rays (7600-6 × 106Å) < Microwaves < Radio waves.

• The complete spectrum obtained by arranging these electromagnetic radiations in order of their increasing wavelengths or decreasing frequencies is called electromagnetic spectrum.
• Various types of electromagnetic radiation have different energies and are being used for different applications.

Some applications of electromagnetic waves are listed below.

Limitations of electromagnetic wave theory:

This theory successfully explains the properties of light such as interference and diffraction.

However, it failed to explain the phenomena such as

1. Black body radiation
2. Photoelectric effect line spectra of atoms
3. Variation of heat capacity of solids as a function of temperature.

Black body radiation:

An ideal body, which emits and absorbs radiations of all frequencies is called a black body and the radiation emitted by such a body is called black body radiation.

• When a substance having a high melting point is heated, viz an iron bar, it first turns red, then yellow, and then glows with a white light and finally with a blue light.
• According to electromagnetic wave theory, since the emission and absorption of energy occur continuously, the energy of an electromagnetic wave is supposed to be proportional to its intensity and independent of its frequency or wavelength.
• So according to wave theory, a body should emit radiation ofthe same colour although its intensity may vary as the heating is continued.
• We have already seen that, on applying heat, the color of a solid changes with the temperature rise.
• The color change indicates that the frequency of radiation emitted increases with the rise in temperature (since red light indicates low frequency and blue light indicates high).
• Hence, electromagnetic wave theory can’t explain black body radiation.

The variation of intensity with wavelength of radiation emitted by a black body at two different temperatures ( T₁ and T₂ ).

The intensity of the radiation emitted depends only on temperature.

At a given temperature, the intensity of radiation emitted increases with a decrease in wavelength reaches a maximum value at a certain wavelength, and then starts decreasing with a further decrease in wavelength. (Observe the variation in the plot from right to left).

Structure of Atom Class 11 Notes

Photoelectric effect:

The phenomenon of ejection of electrons from the surface of a metal when the light of a suitable wavelength falls on it, is called the photoelectric effect and the ejected electrons are called photoelectrons.

• The apparatus used for studying the photoelectric effect. In the figure, Tis an evacuated glass tube fitted with two quartz windows.
• Two metal plates, A and B, are fitted at two ends of the tube. The plate A is photosensitive and acts as the cathode.
• The plate B is the electron detector and acts as the anode. The plate electrodes are connected to a battery via a milliammeter.
• When the light of a suitable wavelength strikes plate A, photoelectrons are ejected from it The electrons are attracted by detector B and so they move toward it
• These electrons are responsible for the flow of current through the external circuit which can be measured using the milliamm.
• By measuring the strength of the current flowing through the circuit, it is possible to determine the kinetic energy ofthe electrons.

The following are a few important observations about the Velocity 3 x 108 photoelectric effect: 

• For any given metal, there exists a minimum frequency called threshold frequency (VG).
• At frequencies below the threshold frequency, no electrons are emitted, no matter how large the intensity of the incident light or how long the irradiation occurs.
• The number of photoelectrons emitted per second is proportional to the intensity ofthe incident light.
• The kinetic energy of the photoelectrons is direct radiation of a frequency of 97.8 MHz. proportional to the frequency of the incident radiation.
• With an increase in the frequency of light, the kinetic energy of the electrons increases.
• The kinetic energy ofthe photoelectrons are independent of the intensity ofthe incident radiation.

The observations cannot be explained based on electromagnetic wave theory. For instance:

• According to this theory, the absorption or emission of radiation occurs continuously. Hence, the energy of light is expected to depend on the intensity of the incident light.
• Thus, light of any frequency can be made to have sufficient energy to cause the emission of electrons, merely by increasing its intensity. However, this is not true in practice.
• According to this theory, the energy of the ejected electrons should be proportional to the intensity of the incident light, which is not the case in reality.

Numerical examples

Question 1. Yellow light emitted from a sodium lamp has a wavelength of 580 nm. Calculate the frequency and wave number of yellow light.

Answer:

⇒ \(\lambda=580 \mathrm{~nm}=580 \times 10^{-7} \mathrm{~cm}\)

Since 1nm = 10^-7 cm

⇒ \(v=\frac{c}{\lambda}=\frac{3 \times 10^{10}}{580 \times 10^{-7}}=5.17 \times 10^{14} \mathrm{~s}^{-1}\)

⇒ \(\vec{v}=\frac{1}{\lambda}=\frac{1}{580 \times 10^{-7}}=17241.37 \mathrm{~cm}^{-1}\)

Question 2. A radio station broadcasts at a frequency of 100 MH_z. How long would it take to reach a receiving system at a distance of 300 km? Calculate the wavelength and wave number of these radiations.
Answer:

Required time \(=\frac{\text { Distance }}{\text { Velocity }}=\frac{300 \times 100}{3 \times 10^8}=3 \times 10^{-3} \mathrm{~s}\)

Since the Velocity of any electromagnetic radiation = 3 ×10⁸m.s^-1

Wavelength of that radiation \(\lambda=\frac{c}{v}=\frac{3 \times 10^{\circ}}{100 \times 10^6}=3 \mathrm{~m}\)

Since 100MHz =1006 Hz]

Wave number (v) = 1/λ = 1/3

= 0.33m^-1

Question 3. Calculate the wavelength of an electromagnetic radiation of frequency of 97.8 MHz.
Answer:

Wavelength of radiation \(\lambda=\frac{c}{v}=\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{97.8 \times 10^6 \mathrm{~s}^{-1}}\)

= 3.06 m

Question 4. How long would it take a radio wave of frequency, 6.2× 10⁸s^-1 to travel from Mars to Earth, the observation distance being 8.1 × 10⁷km?
Answer:

The velocity of any electromagnetic radiation (c) 3 × 10⁸m

Required time \(\frac{\text { Distance }}{\text { Velocity }}\)

= =\(\frac{8.1 \times 10^7 \times 10^3}{3 \times 10^8}\)

= 270s

= 4min 30s

Particle nature of electromagnetic radiation: Planck’s quantum theory

The electromagnetic wave theory could successfully explain the various phenomena of light such as interference, diffraction, polarisation, etc.

• However, it failed to explain the various phenomena involving energy transfer, namely black body radiation, photoelectric effect, etc.
• The failure of the classical electromagnetic theory of radiation led Max Planck (1900) to propose a new theory known as ‘Planck’s quantum theory’.
• Later this theory was extended by Einstein (1905). The main points of this theory are— M Radiant energy is emitted or absorbed in the form of small, discrete packets of energy called ‘quanta’ (singular quantum). In the case of light, the quantum of energy is often called ‘photon’.
• The energy of each quantum of radiation does not have a fixed value. It depends on the frequency of the emitted or absorbed radiation.
• The energy possessed by each quantum of radiation is directly proportional to its frequency, i.e.,

E ∝ v or E = hv [where E = energy of each quantum or photon, v = frequency of the radiation, h = Planck’s constant (6.626 ×10^-27erg-s or 6.626 × 10^-34J-s )].

The total amount of energy emitted or absorbed by a body must be an integral multiple of a quantum, i.e., E = nhv [where n = number of photons, absorbed or emitted by a body]. This means the amount of energy emitted or absorbed by a body can be—hv, 2hv, 3hv, etc. but never 0.5 hv or 1.4 hv.

The energy possessed by one photon is called one quantum.

The energy possessed by one-mole photons is called one Einstein.

1 einstein = NO (or 6.022 × 10²³ ) quanta.

∴ 1 einstein energy (J5) = N₀hv

Explanation of black body radiation based on quantum theory:

When a solid is heated, the atoms are set into oscillations emitting radiations of frequency v.

As heating is continued the atoms absorb more energy and emit radiations of higher frequency. Since the frequency of red light is minimal, an iron rod on heating first turns red and then yellow (higher frequency than red) and further turns into white and finally blue.

Explanation of the photoelectric effect based on quantum theory:

Einstein (1905) explained different aspects of the photoelectric effect using Planck’s quantum theory, as follows

• When a light of certain frequency strikes a metal surface, photons ofthe light collide with the electrons ofthe metal. Each photon thus transfers its entire energy (hv) to each of the colliding electrons.
• Photoelectrons are emitted only if the energy of the photon is sufficient to overcome the force of attraction between the electron and the nucleus.
• In other words, electrons are emitted from the surface of metals, when irradiated with photons of a certain minimum frequency known as threshold frequency (hv₀).
• The minimum energy of a photon that causes photoelectric emission is known as the photoelectric work function (hv₀).

If the frequency of the incident radiation (v) is greater than the threshold frequency (v₀), the excess energy of the protons Is transferred to the ejected electrons ns kinetic energy;

⇒  \(\frac{1}{2} mv-W_0\).

Hence, the kinetic energy of the ejected electrons

• Increases with an Increase In the frequency of the Incident light.
• Keeping the frequency constant, If the Intensity of the incident light Is
• Increased, the number of photons striking the metal surface increases,
• This In turn Increases the number of electrons of the metal colliding with the photons, which In turn increases the strength of the photoelectric current.
• The above observations are By experimental results, A plot of the kinetic energy of emitted photoelectrons against the frequency of the absorbed photons gives a straight line with slope, h.

Keeping the frequency constant, a plot of the kinetic energy of the entitled photoelectrons against the intensity of incident radiation gives n straight line parallel to the x-axis.

Dual nature of electromagnetic radiation:

Prom the above discussion It Is clear that the properties of radiation like Interference or diffraction can be explained if the light is considered to have a wave nature whereas, other properties of light such as black body radiation, photoelectric effect, etc.

Can be explained, if the light is considered to have a particle nature. Thus, it is concluded that light behaves both as a wave and also as a stream of particles. Therefore light is said to have a dual nature.

Numerical Examples

Question 1. A Ray of habit or frequency SOA is incident on a metal surface and thus, absorbs 10^-7J of Calculate the number of photons Incident on the mental surface
Answer:

Let the number of photons incident on the metal surface = n

∴ \(n h v=10^{-7} \text { or, } \frac{n h c}{\lambda}=10^{-7}\)

Or, \(\frac{n \times 6.626 \times 10^{-34} \times 3 \times 10^8}{5000 \times 10^{-10}}=10^{-7}\)

Or, \(n=\frac{10^{-7} \times 5000 \times 10^{-10}}{6.626 \times 10^{-34} \times 3 \times 10^8}=2.51 \times 10^{11}\)

Question 2. The threshold frequency, v0 for a metal is 7.0× 10⁴s^-1. Calculate the kinetic energy of an electron emitted, when radiation of frequency, v = 1.2 × 10¹⁵s^-1, strikes this metal.
Answer:

Kinetic energy of the photoelectrorts \(\left(\frac{1}{2} m v^2\right)=h\left(v-v_0\right)\)

= \(\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right)\left(1.2 \times 10^{15} \mathrm{~s}^{-1}-7.0 \times 10^{14} \mathrm{~s}^{-1}\right)\)

= \(3.31 \times 10^{-19} \mathrm{~J}\)

Question 3. If a light with frequency 2.0 × 10¹⁶Hz emitted photo o electrons with double the kinetic energy as emitted by the light of frequency 1.25 × 10¹⁶ Hz from the same metal surface, calculate the threshold frequency of the metal
Answer:

Kinetic energy of photoelectrons \(\left(\frac{1}{2} m v^2\right)=h\left(v-v_0\right)\)

Given, h(2.0 × 10¹⁶-v₀) = h(1.25 × 10¹⁶-v₀) ×2

or, v₀ = (2.5- 2.0) × 10¹⁶ =0.5 ×10¹⁶

= 5 × l0¹⁵Hz

Question 4. When a radiation of frequency 7.5×10¹⁴ Hz strikes a metal surface, the maximum kinetic attained by the emitted electrons is 1.6 × 10^-19J. Calculate the threshold frequency of the metal.
Answer:

Kinetic energy ofemitted electrons \(\left(\frac{1}{2} m v^2\right)=h\left(v-v_0\right)\)

Given, 1.6 × 10^-19 = h(v-v₀)

Or, \(\frac{1.6 \times 10^{-19}}{6.626 \times 10^{-34}}=7.5 \times 10^{14}-v_0\)

or, v₀ = 7.5 × 10¹⁴ –  2.41 × 10¹⁴

= 5.09 ×10¹⁴ Hz

Question 5. Calculate the energy of each quantum of electromagnetic radiation having a wavelength of 6000 Å. [h = 6.624 × 10^-27erg.s]
Answer:

Energy of each quantum, \(E=h v=\frac{h c}{\lambda}\)

∴ \(E=6.624 \times 10^{-27} \times \frac{3 \times 10^{10}}{6000 \times 10^{-8}}=3.312 \times 10^{-12} \mathrm{erg}\)

[c = 3 × 10cm.s^-1

λ = 6000Å

λ = 6000 × 10^-8cm ]

NCERT Solutions Class 11 Chemistry Chapter 2 Structure of Atom

Question 6. Calculate the energy of 1 mol of photons of an electromagnetic radiation of frequency 2.6 × 10²³. [h = 6.026 × 10^-34j.s
Answer:

The energy of l mol photons = N₀hv

= 0.022 × 10²³ × 6.626 × 10^-34 × 2.5 × 10H

= 99.75 kj.mol^-`1

Question 7. How many photons of light with wavelength 400 CBM provide 1 energy? = 6.626 × 10^-34J.s
Answer:

Energy of 1 photon \(=h v=\frac{h c}{\lambda}\)

⇒ \(=\frac{6.626 \times 10^{-34} \times 3 \times 10^8}{400 \times 10^{-9}} \mathrm{~J}\)

[since 1nm= 10^-9m]

∴ No. of photons required to produce 1.0J energy

= \(\frac{1.0}{\left(6.626 \times 10^{-34} \times 3 \times 10^8\right) /\left(400 \times 10^{-9}\right)} \)

= \(\frac{400 \times 10^{-9}}{6.626 \times 10^{-34} \times 3 \times 10^8}=2.012 \times 10^{18}\).

Question 8. Find the wave number and energy of each photon present in yellow light having wavelength 580nm. (c = 3 ×10⁸ m.s^-1 and h = 6.627 × 10^-34J.s]
Answer:

Wave number \((\bar{v})=\frac{1}{\lambda}=\frac{1}{580 \times 10^{-9}} \mathrm{~m}^{-1}\)

= 1.724 ×10^-16 m^-1

∴  1nm = 10^-9m

Energy of each photon {E) = \(h v=h \times \frac{c}{\lambda}\)

⇒ \(\left(6.627 \times 10^{-34}\right) \times \frac{3 \times 10^8}{580 \times 10^{-9}}=3.428 \times 10^{-19} \mathrm{~J}\)

Question 9. Calculate the frequency of light emitted when an electron drops from a higher to lower energy level of an atom and the difference between the two energy levels is 35.64 x 10^-13erg.[h = 6.624 × 10^-27erg-s]
Answer:

E₁ and E₂ are the two energy levels, then the difference between their energies is given by, E₂-E₁ = hv or, ΔE = hv

h = Planck’s constant and

v = Frequency of light emitted

∴ \(v=\frac{\Delta E}{h}=\frac{35.64 \times 10^{-13} \mathrm{erg}}{6.624 \times 10^{-13} \mathrm{erg} \cdot \mathrm{s}}=5.3804 \times 10^{14} \mathrm{~s}^{-1}\)

Question 10. An 80 W bulb emits a monochromatic light of wavelength 480nm. Calculate the number of photons emitted per second by the bulb.
Answer:

Power of the bulb =80 W = 80.s^-1

Energy of a photon \(=h v=\frac{h c}{\lambda}\)

= \(\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right)\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{480 \times 10^{-9} \mathrm{~m}}\)

= \(4.14 \times 10^{-19} \mathrm{~J}\)

Number of emitted photons per second =  \(\frac{80 \mathrm{~J} \cdot \mathrm{s}^{-1}}{4.14 \times 10^{-19} \mathrm{~J}}\)

= \(1.932 \times 10^{20} \mathrm{~s}^{-1}\)

Question 11. Calculate the wavelength of a photon (in nm) having energy of 1 eV.
Answer:

Energy of 1 photon, E = 1 eV = \(1.609 \times 10^{-19} \mathrm{~J}\)

E = hv = \(=h \frac{c}{\lambda}\)

Or, λ = \(\frac{h c}{E}=\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{1.609 \times 10^{-19}}\)

= \(12.35 \times 10^{-7} \mathrm{~m}\)

= \(\frac{12.35 \times 10^{-7}}{10^{-9}}\)

Question 12. The iodine molecule absorbs radiation of wavelength 450nm to dissociate into iodine atoms. If each molecule of iodine absorbs 1 quantum of radiation, determine the kinetic energy of the iodine atom. (Bond energy of I₂ = 240kJ.mol^-1 )
Answer:

The energy required for the dissociation of 1 mol of iodine molecules = Bond energy of I₂ molecule = 240kJ

∴ The energy required for the dissociation of a single iodine molecule

= \(\frac{240 \times 10^3}{6.022 \times 10^{23}} \mathrm{~J}\)

= \(3.985 \times 10^{-19} \mathrm{~J}\)

Energy absorbed by each iodine molecule \(=h v=\frac{h c}{\lambda}\)

⇒ \(\frac{6.626 \times 10^{-34} \times 3 \times 10^8}{450 \times 10^{-9}} \mathrm{~J}=4.417 \times 10^{-19} \mathrm{~J}\)

∴ The surplus energy after the dissociation of each molecule of iodine =(4.417-3.985) × 10^-19J =4.32 × 10^-20J

This surplus energy imparts kinetic energy to each iodine molecule.

The surplus energy that imparts kinetic energy to each iodine atom

= \(\frac{4.32 \times 10^{-20}}{2} \mathrm{~J}\)

= \(2.16 \times 10^{-20} \mathrm{~J}\)

∴ The kinetic energy of each iodine atom = 2.16 × 10^-20J.

Question 13. Calculate the energy associated with 1 mol of photon corresponding to electromagnetic radiation having a frequency of 5 × 10^-14Hz.
Answer:

Energy associated with 1 mol of a photon is given by, E=Nhv [AT = Avogadro number, h = Planck’s constant, v = frequency of radiation]

= \(6.022 \times 10^{23} \times\left(6.626 \times 10^{-34}\right) \times\left(5 \times 10^{14}\right) \mathrm{J}\)

= \(199.51 \times 10^3\) J

= 199.51 kJ

Emission And Absorption Spectra

When light or any other electromagnetic radiation is made to pass through a spectroscope, the light separates into various components of different wavelengths, producing various colored bands.

The set of colored bands formed is called a spectrum. Spectra can be of two types —

1. Emission spectrum and
2. Absorption spectrum

Emission spectrum: When the radiation emitted from any source such as any incandescent solid, liquid, or gaseous substance (i.e., by passing an electric discharge through a gas at low pressure or by heating some substance to high temperature) is directly analyzed through a spectroscope, the spectrum obtained is called an emission spectrum.

Depending on the source of radiation, the emission spectrum can be divided into two types—

Continuous spectrum:

The spectrum produced when white light emitted from any source such as the sun, a bulb, a molten metal, or any incandescent source is passed through a spectroscope is a continuous spectrum.

• In this spectrum, the colors from red to violet are arranged sequentially continuously, without any break.
• In this spectrum, red lies at one end and violet at the other, and the rest of the colors lie between these two colors.
• The colors are so continuous that each of them appears to merge into the other.

Hence, it is known as a continuous spectrum. It contains all the wavelengths of the visible range.

For example— Solar spectrum.

The spectrum emitted from an incandescent source that contains all the wavelengths of light of the visible range is known as continuous spectrum. There are no. black lines in this spectrum.

Line spectrum or atomic spectrum:

• If a gaseous element is heated or an electric discharge is passed through the gas at low pressure and the light emitted is resolved in a spectroscope, the spectrum obtained is not continuous.
• In this case, the different colored lines obtained are separated from each other by dark bands.
• The spectrum obtained is called the line spectrum.

The excited gaseous atoms are responsible for the piotirllou of such spectrum, lunco, line spectrum Is also known as the atomic spectrum.

In a lino spectrum, each line corresponds to a particular wavelength. The line spectrum of each element consists of a group of lines with certain fixed wavelengths, Every element has Its characteristic spectrum, which is different from those of other elements.

For example, (the spectrum of sodium vapor gives two yellow lines. Hence, the line spectrum of each element characterizes the atom of that element.

Therefore, the atomic spectrum of an element can be used to identify the element and Is sometimes called the fingerprint of its atoms.

Absorption spectrum:

When white light emitted from a heated incandescent substance is passed through a liquid or a gaseous substance, radiations of certain wavelengths are absorbed.

• If the emergent radiations are resolved in a spectroscope, a few dark lines are observed, in the atoms. Otherwise continuous spectrum.
• These dark lines constitute the absorption spectrum of that absorbing substance (liquid or gas).
• The dark lines in the absorption spectrum are at the same place where colored lines are obtained in the emission spectrum for the same substance.
• This indicates that the wavelengths of radiation absorbed in the absorption spectrum are the same as those emitted in the case of the emission spectrum.

Differences between emission and absorption spectra

Emission spectrum: Line spectrum of a hydrogen atom

• To study the emission spectrum of hydrogen, the gas is taken in a discharge tube at low pressure, and an electric discharge is passed through it. ill H₂ molecules dissociate into energetically excited Hatoms and emit electromagnetic radiation.
• The emitted radiation is allowed to pass through the prism in a spectroscope.
• The resulting spectrum consists of a large number of isolated sharp lines grouped into different series, named after their discoverers. These lines constitute the line spectrum (discontinuous spectrum).
• The visible region ofthe hydrogen spectrum can be viewed even with the naked eye. It was discovered by Balmer in 1885 and hence the series of isolated spectral lines involving the visible region is called the Balmer series.
• Balmer observed four prominent lines (red, bluish-green, blue and violet) in the visible region and these were designated as Ha, Hy, and respectively.

Balmer (1885) showed that the wave numbers (inverse of wavelengths) of the spectral lines in the visible region (Balmer series) can be expressed by the empirical formula,

⇒ \(\bar{v}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right]\) ……[1]

Where R is the universal constant, known as Rydberg’s constant Its value is 1.09678 × 10⁵ cm^-1. n is an integer equal to or greater than 3 (i’.e., n = 3, 4, 5, 6 v (wave number) =i, where X – wavelength.

• Replacing n by 3, 4, 5, and 6 respectively the wave numbers of the spectral lines, Hy and can be calculated.
• Further investigation on the line spectrum of hydrogen (using an improved spectroscope) led to the discovery of five other series lines in the ultraviolet and infrared regions. These are indicated in the adjacent table.
• Rydberg (1890), showed that all series of lines in the hydrogen spectrum could be described by the following expression (similar to Balmer’s empirical formula)

⇒ \(\bar{v}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\) …..[2]

Where nx =1, 2, 3, 4,……, n2 = n1 + 1 , n1 + 2,…….

Series Of Lines In The Line Spectrum Of Hydrogen Atom 

Putting n1 = 1,2, 3, 4, 5, 6 and n2 = + 1, n1 + 2, n+3, … etc., die wave numbers of the spectral lines corresponding to Lyman, Balmer, Paschen, Brackett Pfund and Humphreys series can be calculated.

The cause of the formation of the line spectrum of hydrogen was not exactly known at that time.

However, it was believed that the line spectrum was obtained as a result of absorption and subsequent emission of energy discontinuously by the electron present in the H-atom. Hence, the line spectrum is also called an atomic spectrum.

Numerical Examples

Question 1. Calculate the wavelengths of Hff and in the emission spectrum of hydrogen. [R = 109678 cm^-1].
Answer:

Balmers equation is given by \(\bar{v}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right]\)

n=3 for H and n = 6 for H

∴ \(\bar{v}_{\mathrm{H}_a}=109678\left(\frac{1}{2^2}-\frac{1}{3^2}\right)=109678 \times \frac{5}{36} \mathrm{~cm}^{-1}\)

∴ \(\lambda_{\mathrm{H}_\alpha}=\frac{1}{\bar{v}_{\mathrm{H}_\alpha}}=\frac{36}{109678 \times 5}=6.565 \times 10^{-5} \mathrm{~cm}\)

Similarly \(\bar{v}_{\mathrm{H}_\delta}=109678\left(\frac{1}{2^2}-\frac{1}{6^2}\right)=109687 \times \frac{8}{36} \mathrm{~cm}^{-1}\)

∴ \(\lambda_{\mathrm{H}_8}=\frac{1}{\bar{v}_{\mathrm{H}_8}}=\frac{36}{109678 \times 8}=4.10 \times 10^{-5} \mathrm{~cm}\)

NCERT Class 11 Chemistry Chapter 2 Atom Structure Notes

Question 2. Identify the spectral line having a wavelength of 4.863 x 10_5cm in the emission spectra of hydrogen.
Answer:

Wave no \(\bar{v}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right]\)

[Given, lamba = 4.863 × 10^-5Cm]

∴ \(\bar{v}=\frac{1}{\lambda}=\frac{1}{4.863 \times 10^{-5}}=109678\left[\frac{1}{4}-\frac{1}{n^2}\right]\)

∴ \(\frac{1}{n^2}=\frac{1}{4}-\frac{1}{4.863 \times 10^{-5} \times 109678}=0.0625 \quad \text { or, } n=4\)

The spectral line with wavelength 4.863 × 10^-5cm is Hbeta.

Question 3. Determine the wavelength and frequency of the radiation having the longest wavelength in the Lyman series of hydrogen atoms.
Answer:

Rydberg’s equation \(\frac{1}{\lambda}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\): In case of lyman series. For the wavelength to be the longest, the difference in energies between the two energy levels should be minimal.

Hence, n₂= 2

∴ \(\frac{1}{\lambda}=109678\left(\frac{1}{1^2}-\frac{1}{2^2}\right) \quad \text { or, } \frac{1}{\lambda}=109678\left(1-\frac{1}{4}\right)\)

∴ \(\lambda=\frac{4}{3 \times 109678}=1215.67 \times 10^{-8} \mathrm{~cm}=1215.67\)

So, the X radiation109678 has the longest wavelength in the Lyman series = 1215.67×10-8 cm.

∴ Frequency of the radiation

⇒ \(v=\frac{c}{\lambda}=\frac{3 \times 10^{10}}{1215.67 \times 10^{-8}} \mathrm{~s}^{-1}\)

=\(2.467 \times 10^{15} \mathrm{~s}^{-1}\)

Question 4. The wave number of a spectral line in the Lyman series of H-atom is 82260 cm-1. Show that this line has appeared in this series due to the return of the electron from the second to the first orbit.
Answer:

Wave number \(\bar{v}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)

∴ \(\nabla=R\left[1-\frac{1}{n_2^2}\right] \text { or, } \frac{\bar{v}}{R}=1-\frac{1}{n_2^2}\)

Or, \(\frac{1}{n_2^2}=1-\frac{\bar{v}}{R}=1-\frac{82260}{109680}=\frac{27420}{109680}=\frac{1}{4}=\frac{1}{2^2}\)

∴ n2=2

This means that the electron has returned from the second to the first orbit.

Question 5. Calculate the shortest and longest wavelengths in the Lyman series of the hydrogen spectrum.
Answer:

For the Lyman series, n₁ = 1 and n₂ = 2,3,4, …..

Rydberg equation \(\vec{v}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right],\)

The difference between nx and n2 is maximum for the shortest wavelength in the Lyman series. Hence n2 = .

∴ \(\frac{1}{\lambda_{\min }}=\bar{v}_{\max }=R\left[\frac{1}{1^2}-\frac{1}{\infty^2}\right]=R=109678 \mathrm{~cm}^{-1}\)

∴ \(\lambda_{\min }=\frac{1}{109678}=9.117 \times 10^{-6} \mathrm{~cm}=911.7\)

Similarly, the difference between n₁ and n₂ is minimal for the longest wavelength in the Lyman series. Hence, n₂ = 2

∴ \(\frac{1}{\lambda_{\max }}=\bar{v}_{\min }=R\left[\frac{1}{1^2}-\frac{1}{2^2}\right]=\frac{3}{4} R\)

∴ \(\frac{1}{\lambda_{\max }}=\bar{v}_{\min }=R\left[\frac{1}{1^2}-\frac{1}{2^2}\right]=\frac{3}{4} R\)

∴ \(\lambda_{\max }=\frac{4}{3 R}=\frac{4}{3 \times 109678}\)

=\(1215.7 \times 10^{-8} \mathrm{~cm}=1215.7\)

Question 6. Show that the Balmer series appears between 3647A and 6563A in the hydrogen spectrum
Answer:

For Balmer series \(\frac{1}{\lambda}=\bar{v}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right], n=3,4,5, \cdots \infty\)

The Limits Of the Balmer Series Can Be obtained when n = 3 and n = 00 respectively

⇒ \(\frac{1}{\lambda_{\min }}=\bar{v}_{\max }=R\left[\frac{1}{2^2}-\frac{1}{\infty^2}\right]=\frac{R}{4}=\frac{109678}{4} \mathrm{~cm}^{-1}\)

∴ \(\lambda_{\min }=\frac{4}{109678} \mathrm{~cm}=3647 \times 10^{-8} \mathrm{~cm}=3647 \)

Also, \(\frac{1}{\lambda_{\max }}=\bar{v}_{\min }=R\left[\frac{1}{2^2}-\frac{1}{3^2}\right]=\frac{5 R}{36}=\frac{5 \times 109678}{36} \mathrm{~cm}^{-1}\)

∴ \(\lambda_{\max }=\frac{36}{5 \times 109678}=6564 \times 10^{-8} \mathrm{~cm}=6564 \)

Question 7. Calculate the wavelength of the spectral line with n2 = 3 in the Lyman series of hydrogen atoms.
Answer:

In Lyman series, = 1

∴ \(\bar{v}=R\left[\frac{1}{1^2}-\frac{1}{3^2}\right]=109678 \times \frac{8}{9} \mathrm{~cm}^{-1}\)

Since n₂ = 3

⇒ \(\lambda=\frac{1}{\bar{v}}=\frac{9}{109678 \times 8}=1.026 \times 10^{-5} \mathrm{~cm}\)

Bohr’s Atomic Model

In 1913, Neils Bohr, an eminent scientist successfully explained the stability of an atom and the cause of the appearance of line spectra with the help of Planck’s quantum theory.

He rectified the defects of Rutherford’s nuclear model and put forward a new atomic model for the hydrogen atom which is known as Bohr’s atomic model or Rutherford-Bohr’s atomic model.

Postulates Of Bohr’s Model Of Atom

The theory, put forward by Bohr regarding the structure of the H-atom, is based on three revolutionary postulates—

Postulate 1:

The electron in the hydrogen atom revolves around the nucleus only in certain selected circular paths (called orbits) which are associated with definite energies. The electrons revolve only in those orbits in which the angular momentum ofthe electron is a whole number multiple of \(\frac{h}{2 \pi},\) i.e., the angular momentum of the electron, \(m v r=n \times \frac{h}{2 \pi}\), Where n= 1,2,3,4 ……….etc, m = mass of the electron, v = velocity of the electron, r = radius of the orbit, h = Planck’s constant. Thus, the angular.

Postulate 2:

When an electron revolves in any selected orbit, it neither emits nor absorbs energy. The energy of an electron in a particular orbit remains constant. These orbits are, therefore, called stationary orbits although the electrons are not stationary. Electrons revolving in a stationary orbit are said to be in the stationary state.

Explanation:

Each stationary orbit is considered as the energy level. The energy of an electron revolving in a stationary orbit is supposed to be the energy of that particular orbit although the orbit has no energy of its own. The energy of the orbit increases with an increase in its distance from the nucleus.

Depending on their distance from the nucleus, these orbits are divided into seven energy levels such as K, L, M, N… etc. and these are designated respectively by the numbers 1, 2, 3, 4 . . . etc.

The numbers signifying the energy levels are known as principal quantum numbers (re). These orbits can be arranged in the increasing order of their energy as follows:

K(n = 1) < L(n = 2) < M(n = 3) < N(n = 4)… etc.

Postulate 3:

When an electron jumps from a higher stationary energy, level to a lower stationary energy level, it emits a fixed amount of energy in the form of radiation. On the other hand, when an electron absorbs a certain amount of energy, it moves to a higher energy level.

Electrons can never occupy a position in between two successive stationary energy levels.

Mathematical expression:

If the frequency of radiation emitted or absorbed is assumed to be v and the energies of the higher and lower stationary orbits as E₂ and E₁ respectively, then the difference in energy, ΔE = E₂-E₁ =hv, [where h = Planck’s constant

[Since E₂ and E₁ have fixed values, the magnitude of v is also fixed. This accounts for the existence of some definite lines in the emission spectra of hydrogen. Energy is involved in the transition of electrons.

Concept of quantization of energy:

The concept of quantization of energy can be best understood by taking the following example: When a person moves down a staircase, his energy changes discontinuously.

He can have only certain definite values of energies corresponding to those of the various steps.

Alternatively, the energy of the person is quantized. However, if he goes down a ramp, his energy changes continuously, having any value corresponding to any point on the ramp. In short, energy is not quantized.

Calculation Of Various Quantities For Hydrogen-Like Atoms Using Bohr’s Theory

The radius of ‘faith orbit:

Suppose the total quantity of positive charge in the nucleus of a hydrogen-like atom is Ze (where Z = atomic number and e = charge of a proton or an electron).

The only electron present in that atom is revolving around the nucleus in a circular orbit of radius, r with velocity, v.

According to Coulomb’s law, the attractive force of the nucleus on the electron i.e… the centripetal force = [where Ze is the total positive charge on the nucleus and e =charge of an electron].

In case of an electron revolving with velocity v, centrifugal force = \(\frac{m v^2}{r}\) [where m = mass of electron and r = radius ofthe orbit], For the stability of an atom, the centripetal force must be equal to the centrifugal force, i.e

⇒ \(\frac{Z e^2}{r^2}=\frac{m v^2}{r} \quad \text { or, } v^2=\frac{Z e^2}{m r}\)  …………………….. (1)

According to Bohr’s theory, the angular momentum of the revolving electron in a stationary orbit is an integral multiple \(\frac{h}{2 \pi} \text { i.e., } m v r=\frac{n h}{2 \pi}\)

[where, n = 1,2,3… etc., are whole numbers]

Or, \(v=\frac{n h}{2 \pi m r}\)…………………….. (2)

Or, \(v^2=\frac{n^2 h^2}{4 \pi^2 m^2 r^2}\) …………………….. (3)

Hence, from equations [1] and [3] we have,

⇒ \(\frac{Z e^2}{m r}=\frac{n^2 h^2}{4 \pi^2 m^2 r^2} \quad \text { or, } \frac{Z e^2}{m}=\frac{n^2 h^2}{4 \pi^2 m^2 r}\)

Or, \(r=\frac{n^2 h^2}{4 \pi^2 m^2} \times \frac{m}{Z e^2} \text { or, } r=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

i.e., radius of ‘n’ th orbit \(r_n=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)…………………….. (4)

Equation [4] indicates the radius of with orbit of the revolving electron.

The velocity of a revolving electron in ‘n’th orbit:

According to Bohr’s theory, the angular momentum of a revolving electron is given by, mvr \(=\frac{n h}{2 \pi} \quad \text { or, } r=\frac{n h}{2 \pi m v}\)

Again, the radius of ‘n’ th orbit, r \(=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

Comparing the above two relations we may write,

⇒ \(\frac{n h}{2 \pi m v}=\frac{n^2 h^2}{4 \pi^2 m Z e^2} \quad \text { or, } \frac{1}{v}=\frac{n h}{2 \pi Z e^2} \quad \text { or, } v=\frac{2 \pi Z e^2}{n h}\)

∴ The velocity of an electron revolving in the ‘n’th Bohr orbit is given by

⇒ \(v_n=\frac{2 \pi Z e^2}{n h}\)…………………….. (5)

Substituting the values of n = 1, 2, 3, etc., in this equation, the velocity of revolving electrons in different Bohr orbits can be determined.

The velocity of resolving electron in the ‘ n ‘th orbit of the H atom.

= \(\frac{2 \times \frac{22}{7} \times 1 \times\left(4.8 \times 10^{-10}\right)^2}{n \times\left(6.626 \times 10^{-27}\right)}=\frac{2.186 \times 10^8}{n} \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

Relation between the velocities of an electron in ‘n’th and first orbit:

Velocity of an electron revolving in the’ n ‘th orbit.

⇒ \(\left(v_n\right)=\frac{2 \pi \mathrm{Z} e^2}{n h}\) and that in the first orbit, (v1) \(=\frac{2 \pi Z e^2}{1 \times h}\)

∴ \(\frac{v_n}{v_1}=\frac{2 \pi Z e^2}{n h} \times \frac{1 \times h}{2 \pi Z e^2}=\frac{1}{n}\)

∴ \(\frac{v_n}{v_1}=\frac{2 \pi Z e^2}{n h} \times \frac{1 \times h}{2 \pi Z e^2}=\frac{1}{n}\)

or, \(v_n=v_1 \times \frac{1}{n}\)

Relation between the radius of ‘n’th orbit and the first orbit.

Radius of ‘n th orbit \(\left(r_n\right)=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\) and the radius of the first orbit \(\left(r_1\right)=\frac{1^2 \cdot h^2}{4 \pi^2 m Z e^2}=\frac{h^2}{4 \pi^2 m Z e^2}\)

∴ \(\frac{r_n}{r_1}=\frac{n^2 h^2}{4 \pi^2 m Z e^2} \times \frac{4 \pi^2 m Z e^2}{h^2}=n^2\)

or, rn = r₁ × n²

The total energy of an electron revolving in ‘n’th orbit:

The total energy of electron revolving in ‘ n ‘th orbit, En = Kinetic energy + Potential energy

E_n = Kinetic energy + Potential energy

= \(\frac{1}{2} m v^2+\left(-\frac{Z e^2}{r}\right)=\frac{1}{2} m \times \frac{Z e^2}{m r}-\frac{Z e^2}{r}\)

= \(\frac{1}{2} \frac{Z e^2}{r}-\frac{Z e^2}{r}=-\frac{Z e^2}{2 r}=-\frac{Z e^2}{2} \times \frac{1}{r}\)

∴ \(v^2=\frac{Z e^2}{m r}\)

Since \(v^2=\frac{Z e^2}{m r}\)

= \(-\frac{Z e^2}{2} \times \frac{4 \pi^2 m Z e^2}{n^2 h^2}\)

r = \(\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)…………………….. (6)

Equation [6] Indicates the energy of the electron revolving in the orbit of a Hydrogen- like

For hydrogen atom Z =1

∴ For hydrogen atom, \(E_n=-\frac{2 \pi^2 m e^4}{n^2 h^2}\)…………………….. (7)

Substituting the values of m, e, n, and R in equation number[7] we have

⇒ \(E_n=-\frac{2 \times(22 / 7)^2 \times\left(9.108 \times 10^{-28} \mathrm{~g}\right) \times\left(4.8 \times 10^{-10} \mathrm{esu}\right)^4}{n^2 \times\left(6.626 \times 10^{-27} \mathrm{erg} \cdot \mathrm{s}\right)^2}\)

= \(-\frac{2.176 \times 10^{-11}}{n^2} \mathrm{erg} \cdot \text { atom }^{-1}\)

= \(-\frac{2.176 \times 10^{-18}}{n^2} \mathrm{~J} \cdot \mathrm{atom}^{-1}=-\frac{1312}{n^2} \mathrm{~kJ} \cdot \mathrm{mol}^{-1} \quad \cdots[7 \mathrm{a}]\)

Energies E₁,  E₂, E₃, etc., are calculated by putting n – 1, 2, 3, etc. in equation [7a] and are represented schematically in.

It is observed from these values that successive energy levels are not equidistant. The energy gap between two successive levels decreases with an increase in distance from the nucleus.

When an electron is at an infinite distance from the nucleus, its potential energy is zero.

Work done to bring the electron from an infinite distance to a distance V concerning the nucleus gives the measure of its potential energy.

The force of attraction between the nucleus and the electron is I given by, F = (applying Coulomb’s law).

∴ The potential energy of the electron at a distance ‘r’ from the nucleus \(=\int_{r=\infty}^{r=\infty} \frac{Z e^2}{r^2} d r=-\frac{Z e^2}{r}\)

Electronic energy as negative energy:

When an electron is at an infinite distance (n = ∞) from the nucleus, it experiences no force of attraction from the nucleus. Hence, the energy of the electron at an infinite distance from / the nucleus is taken as zero (E_∞ = 0).

• When the electron moves towards the nucleus, it experiences a force of attraction from the nucleus.
• As a result, some energy is released and the energy of the electron becomes negative. Due to the release of energy, the stability of the electron occupying a fixed orbit in the atom is increased.
• As the electron comes closer to the nucleus, it experiences a greater force of attraction and hence more energy is released, thereby making the electronic energy more negative.

All these facts are per the expression of electronic energy,

⇒ \(E_n=-\frac{2 \pi^2 m Z^2 e^4}{n^2 h^2}\) As n decreases, the energy of the electron decreases (because it is associated with a -ve sign) and hence the stability of the electron in the atom increases.

Thus, the negative value ofthe electronic energy in an atom signifies that the stability of the electron increases as it occupies orbits closer to the nucleus.

The energy is minimal when it revolves around the nucleus occupying the first orbit (i.e., n = 1).

The ratio of the energies of an electron revolving in the V th orbit and the first orbit of the hydrogen-like atom:

⇒ \(\frac{E_n}{E_1}=\left(-\frac{2 \pi^2 m Z^2 e^4}{n^2 h^2}\right) \times \frac{1}{\left(-\frac{2 \pi^2 m Z^2 e^4}{1^2 \times h^2}\right)}=\frac{1}{n^2}\)

∴ \(E_n=E_1 \times \frac{1}{n^2}\) …………………….. (8)

The radius of the first orbit of the hydrogen atom:

From equation number [4], it is seen that the radius of the ‘ n ’ th orbit of a hydrogen-like atom, \(r_n=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

Where, h = Planck’s constant = 6.626 × 10^-27erg-s , m = mass of electron = 9.1× 10^-28g, e =charge of electron = 4.8 × 10^-10esu]

Derivation of Rydberg’s equation

When an electron of a hydrogen atom jumps from ‘ n₂ ‘th orbit to‘ ‘th orbit, let the frequency of emitted radiation be v. According to Bohr’s theory,

⇒ \(h v=E_{n_2}-E_{n_1}=\left(-\frac{2 \pi^2 m e^4}{n_2^2 h^2}\right)-\left(-\frac{2 \pi^2 m e^4}{n_1^2 h^2}\right)[\text { for } \mathrm{H}, Z=1]\)

=\(\frac{2 \pi^2 m e^4}{h^2}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

⇒ \(\frac{2 \pi^2 m e^4}{h^2}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\) …………………….. (9)

∴ \(v=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\) …………………….. (10)

or, \(\frac{c}{\lambda}=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Since \(h v=E_{n_2}-E_{n_1}=\left(-\frac{2 \pi^2 m e^4}{n_2^2 h^2}\right)-\left(-\frac{2 \pi^2 m e^4}{n_1^2 h^2}\right)\)

⇒ \(\frac{2 \pi^2 m e^4}{h^2}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

∴ \(v=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Or, \(\frac{c}{\lambda}=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Since \(v=\frac{c}{\lambda}\)

Or, \(\frac{1}{\lambda}=\frac{2 \pi^2 m e^4}{c h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Since \(\frac{1}{\lambda}=\bar{v}\) = wave Number ]

or, \(\bar{v}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\) …………………….. (11)

R is a constant known as Rydberg’s constant.

∴ Rydberg’s constant,R \(=\frac{2 \pi^2 m e^4}{c h^3}\) …………………….. (12)

Note that earlier equation in article[11]no is2.4.4.comparable with equation [2]

Equation [11] is Rydberg’s equation which is related to the line spectra of the hydrogen atom:

Expression for wave number of spectral lines involving one-electron ions is given by

⇒ \(\bar{v}=Z^2 \times R\left(\frac{1}{n^2}-\frac{1}{n_2^2}\right) \text {, where } Z=\text { atomic number. }\)

⇒  \(\bar{v}=Z^2 \times R\left(\frac{1}{n^2}-\frac{1}{n_2^2}\right) \text {, where } Z=\text { atomic number. } \)

Calculation of the value of Rydberg’s constant: Substituting the values of n, m, e, c and h in equation [12] we get,

Rydberg’s constant, \(R=\frac{2 \pi^2 m e^4}{c h^3}\)

= \(\frac{2 \times(3.14)^2 \times\left(9.108 \times 10^{-28} \mathrm{~g}\right) \times\left(4.8 \times 10^{-10} \mathrm{esu}\right)^4}{\left(2.9979 \times 10^{10} \mathrm{~cm} \cdot \mathrm{s}^{-1}\right) \times\left(6.626 \times 10^{-27} \mathrm{erg} \cdot \mathrm{s}\right)^3}\)

=109737cm^-1

The experimentally measured value of Rydberg’s constant is 109677 cm-1. This value of R agrees fairly well with that ofthe calculated value.

Wavelength of radiation emitted due to electronic transition from third to second Bohr orbit: Rydberg’s equation related to the frequency ofthe spectral lines of H -atom-

R= 109677 cm^-1

The wavelength of radiation (A) emitted due to the transition of an electron of a hydrogen atom from the third orbit (n = 3) to the second orbit (n = 2) can be calculated with the help of this equation.

⇒ \(\frac{1}{\lambda}=R\left(\frac{1}{2^2}-\frac{1}{3^2}\right)\)

Since \(\bar{v}=\frac{1}{\lambda} \text { and } n_1=2, n_2=3\)

Or, \(\frac{1}{\lambda}=109677 \times\left(\frac{9-4}{36}\right)=\frac{109677 \times 5}{36} .\)

∴ \(\lambda=\frac{36}{109677 \times 5}=6564.7 \times 10^{-8} \mathrm{~cm}=6564.7 \)

As the wavelength of visible light lies between 4000-8000 A, the line spectrum appears in the visible region. It represents the Balmer series.

Structure of Atom Chapter 2 NCERT Solutions Class 11

The ionization potential of the H-atom from Rydberg’s equation:

The ionization potential of hydrogen is defined as the energy required to transfer the electron from the first orbit (n = 1) of a hydrogen atom to an infinite distance to form an H+ ion.

Or, \(\frac{1}{\lambda}=\frac{2 \pi^2 m e^4}{c h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\left[ \bar{v}=\frac{1}{\lambda} \text { and } R=\frac{2 \pi^2 m e^4}{c h^3}\right]\)

Or, \(\frac{c}{\lambda}=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Or, \(v=\frac{2 \pi^2 m e^4}{h^3}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Since \(v=\frac{c}{\lambda}\)

Or, \(h v=\frac{2 \pi^2 m e^4}{h^2}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

Or, \(\Delta E=\frac{2 \pi^2 m e^4}{h^2}\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

[since E =Hv]

Substituting n₁ = 1 and n₂ = infinite in the equation, the value of the ionization potential of a hydrogen atom can be obtained.

∴ The ionization potential of H-atom (in CGS unit)

⇒ \(\frac{2 \times(3.14)^2 \times\left(9.108 \times 10^{-28}\right) \times\left(4.8 \times 10^{-10}\right)^4}{\left(6.626 \times 10^{-27}\right)^2} \times\left(\frac{1}{1^2}-\frac{1}{\infty^2}\right)\)

= 2170 × 10^-14 × (1 -0) =2170 × 10^-14erg-atom^-1

= 2170 × 10^-14× 6.24 × 10¹¹ eV-atom^-1

= 13.6 eV-atomr1 =13.6 x 1.6022 × 10^-19 atom^-1

= 13.6 x 1.6022 x 10-19 x 6.022 × 10-19-mol^-1

= 1312kJ-mol^-1

[since 1 erg = 6.24 × 10¹¹eV]

The ionization energy of other one-electron species is given by, \(I E=(I E)_{\mathrm{H}} \times \frac{Z^2}{n^2}, \text { where }(I E)_{\mathrm{H}}\) = Inonisation Energy Of H-atom, Z = Atmotic number,n = principal Quantum number from which the electron is removed.

Number of revolutions of an electron ptt second:

Velocity of an electron revolving in the ‘n’ th orbit \(v_n=\frac{2 \pi Z e^2}{n h}\)

Perimeter of the orbit = 2nrn \(=\frac{2 \pi n^2 h^2}{4 \pi^2 m Z e^2}=\frac{n^2 h^2}{2 \pi m Z e^2}\)

∴ Number of revolutions of an electron in the ‘ n ’th orbit per second = \(=\frac{\text { Velocity }}{\text { Perimeter }}\)

= \(\frac{2 \pi Z e^2}{n h} \div \frac{n^2 h^2}{2 \pi m Z e^2}\)

= \(\frac{2 \pi Z e^2}{n h} \times \frac{2 \pi m Z e^2}{n^2 h^2}=\frac{4 \pi^2 m Z^2 e^4}{n^3 h^3}\)

Explanation of hydrogen spectrum by Bohr’s theory

Bohr’s theory furnishes a logical explanation of the origin ground state) of six series of spectral lines in the atomic spectrum of hydrogen.

• Under ordinary conditions, the revolving electron ESS Merits Of Bohr’s atomic model in the hydrogen atom exists in the lowest energy state (n = 1 ), known as the ground state.
• If energy (Example: heat, light) is available for absorption, then the electron present in the kT-shell (n=1) absorbs the energy and moves to a higher energy level [L(n = 2), Af(n = 3), N(n = 4)…..etc.]. This state is known as the excited state.
• Since in a sample of hydrogen, there are a large number of atoms, the electrons in different H-atoms absorb different amounts of energies (quanta) and are promoted to different higher energy levels viz., n = 2, 3, 4,
• When the source of energy is removed, electrons jump back to any lower energy level by emitting energy (quanta) as radiations of different frequencies which give rise to different lines in the spectrum. When electrons from orbits n = 2,3,4, ••• jump back to orbit n = 1, a series of lines, known as the Lyman series is obtained.
• Similarly, if electrons from higher energy levels n = 3, 4, 5, 6, . . . jump back to energy level n = 2, the Balmer series will appear in the spectrum.

In the same way, when the electrons return to the third energy level (n = 3), Paschen series, to the fourth energy level (n = 4), Brackett series, to the fifth energy level (n = 5), Pfimd series and to the sixth energy level (n = 6), Humphreys series is obtained in the spectrum. The formation of six spectral series is illustrated below.

Thus, it is clear that a hydrogen atom containing only one electron can form several series of lines in its atomic spectrum.

Merits Of Bohr’s atomic model

Stability of an atom:

One of the main postulates of Bohr’s theory regarding the structure of an atom is that an electron while revolving in its stationary orbit does not emit any energy.

So, the electron moving continuously around the nucleus in a fixed orbit will never fall on the nucleus i.e., this postulate offers a reasonable explanation regarding the stability of an atom by eliminating the main defect of Rutherford’s nuclear model.

Line spectrum of H-atom:

Bohr’s atomic model can explain the discontinuous spectra formed in different one-electron systems such as H – atoms, He⁺ ion, Li²⁺ ion, etc.

The radius of the first orbit of H-atom:

From Bohr’s theory, it has been possible to estimate the value of the radius of the first orbit (n = 1) of a hydrogen atom.

Its value is 0.529 × 10^-8 cm or 0.529 Å. This value has been calculated later by other methods and found to be very close to that obtained based on Bohr’s theory.

Principal quantum number:

The idea of principal quantum numbers was first established through Bohr’s model.

The energy of an electron:

Based on Bohr’s theory, the energy of an electron revolving in any quantum level can be calculated and from this, it has also been possible to estimate the energy emitted or absorbed due to the transition of an electron from one energy level to another.

Thus, the relative positions of different lines in atomic spectra can be explained.

Rydberg’s constant and its value:

With the help of Bohr’s theory, mathematical expression as well as the value of Rydberg’s constant can be determined.

Limitations of Bohr’s atomic model

Spectra of atoms or ions having two or more electrons:

(i.e., multi-electron system) cannot be explained with the help of Bohr’s theory.

1. When spectroscopes with high resolving powers were used, it was found that each line in the spectrum was split into several closely spaced lines (called fine structure) which could not be explained by Bohr’s theory.
2. Bohr’s theory could not explain the splitting of spectral lines under the influence of magnetic field (Zeeman effect) or electric field (Stark effect) i.e., the formation of fine structure of atomic spectra.
3. Bohr’s atomic model is two-dimensional and hence, fails to give an idea about the actual three-dimensional electronic model of the atom.
4. According to de Broglie (1923), a tiny particle like an electron has dual character i.e., an electron has a particle as well as wave nature. Bohr treated the electron only as a particle, i.e., Bohr’s model ignored the dual character of the electron.
5. According to Bohr’s atomic model, an electron moves around the nucleus along a fixed circular path with a definite velocity.
6. However, according to Heisenberg’s uncertainty principle, it is impossible to simultaneously measure both the position and velocity (or momen- turn) of a subatomic particle-like electron with absolute accuracy at a particular instant.
7. Thus, Bohr’s theory directly contradicts Heisenberg’s uncertainty principle.

Sommerfeld’s modification Of Bohr’s Theory Idea Of Elliptical Orbits

To explain the fine structure of spectral lines in the hydrogen spectrum.

Sommerfeld (in 1915) extended Bohr’s theory and proposed that—

1. An electron moves around a positively charged nucleus in different elliptical orbits in addition to circular orbits.
2. When the electron moves in an elliptical orbit, the nucleus remains at one of the foci.
3. When the electron moves in a circular path, the angle of revolution changes while the distance from the nucleus remains the same.
4. However, in an elliptical motion, both the angle of revolution (or radial angle) and the distance (‘ r’ or radial distance) ofthe electron from the nucleus change.
5. In order to describe an elliptical path, Sommerfeld introduced the concept of a second quantum number, called the azimuthal quantum number, denoted by the letter ‘k’ in addition to the principal quantum number n. These two quantum numbers are related to each other by the equation,

⇒ \(\frac{n}{k}=\frac{\text { length of major axis }(a)}{\text { length of minor axis }(b)}\)

⇒ \(\frac{k}{n}=\frac{b}{a}=\sqrt{1-\epsilon^2}[\epsilon=\text { eccentricity }]\)

When n = k, i.e., length of major axis = length of major axis, the ellipse reduces to a circle. Thus, a circular orbit is a special case of the elliptical orbit.

For each value of n, k may have n different values. These are 1, 2, 3…, n. Thus for the Bohr orbit with n – 4, there are four Sommerfeld orbits (three elliptical orbits + one circular orbit) with k = 1, 2, 3, and 4. When k = 4, the elliptical orbit reduces to a circular orbit.

Sommerfeld thus introduced the concept of subshells in a principal quantum shell. The difference in energy between any two subshells is quite small.

The fine structure of the hydrogen spectrum can be explained by assuming several transitions between several subshells, each characterized by different values of k but the same value of n.

To explain the splitting of spectral lines under the influence of the electric or magnetic fields, Sommerfeld suggested that the electronic orbits may lie in different planes.

Discussion:

• Bohr’s idea of ‘electrons moving in circular ‘ orbits’ was extended by Sommerfeld by introducing the concept of elliptical orbits.
• According to Einstein’s theory of relativity, the equation expressing the relation between rest mass and mass of a moving particle is given by \(=m_0 /\left(1-\frac{v^2}{c^2}\right)^{1 / 2}\) between rest mass and mass of a moving particle is given by m- mass of the moving particle, v=velocity of the moving particle, c = velocity of light).
• According to Kepler’s law, the velocity of a body moving in an elliptical orbit is maximum at the perihelion (closest to the focus) and minimum at the aphelion (farthest from the focus).
• Therefore, the mass of an electron moving in an elliptical orbit is maximum at the perihelion and minimum at the aphelion.
• Consequently, the electron is compelled to deviate from its original orbit to a new and identical elliptical path that lies in the same plane. Thus, the elliptical path continues its precession slowly surrounding the nucleus.
• Due to this continuous precessional motion of the elliptical orbit, the energy of the electron undergoes a slight change depending on the position of the elliptical orbit.
• The fine structure of spectral lines observed in the atomic spectra actually originates from the slight difference in energy ofthe electron.

Merits of Sommerfeld’s modification

• Due to the introduction of azimuthal quantum numbers, the concept of multiple elliptical orbits corresponding to the same principal quantum number came into being.
• Due to multiple values of azimuthal quantum number for the same value of the principal quantum number, the transition of an electron can occur from one quantum level to another which may result in multiple lines in the spectrum. Thus the fine structure of the spectrum can be explained by Sommerfeld’s theory.
• The subshells belonging to the same principal energy levels have different eccentricities. The more is the eccentricity of a subshell, the more is the opportunity for the electrons residing in that subshell to be closer to the nucleus. Thus, the subshell wifi possesses more penetration power and the corresponding electrons belonging to the subshell will have more power to shield the nuclear charge.

Demerits of Sommerfeld’s Modification.

• Like Bohr’s atomic model, the atomic structure proposed by Sommerfeld is also two-dimensional. this model also fails to explain the three-dimensional model of atomic structure.
• Sommerfeld’s modification also fails to explain the spectra of multi-electron atoms.
• The relative intensities of the fines in the spectra cannot be explained by using this theory.
• Sommerfeld’s atomic model contradicts Heisenberg’s uncertainty principle because according to the latter, it is impossible to simultaneously determine the exact position and exact momentum of an electron.

Numerical Examples

Question 1. Calculate the energy associated with the fifth orbit of H-atom, if the energy associated with the first orbit is 2.17 x 1018J.atom-1
Answer:

⇒ \(E \propto \frac{1}{n^2} \text { or } E=\frac{K}{n^2}\)

∴ \(E_1=\frac{K}{1^2}(\text { for } n=1) \text { and } E_5=\frac{K}{5^2}(\text { for } n=5)\)

∴ \(\frac{E_5}{E_1}=\frac{1}{25} \quad \text { or, } E_5=\frac{E_1}{25}=\frac{-2.17 \times 10^{-18}}{25}\)

=-8.68 × 10^-20 J atom^-1

Question 2. The radius of the first orbit of the H-atom is 0.53A. Find the radius of the fifth orbit.
Answer:

⇒ \(r_n=r_1 \times n^2\)

∴ \(r_5=r_1 \times 5^2=0.53 \times 25=13.25\)

Question 3. Will there be regular variations in the energy associated with successive principal quantum numbers of hydrogen-like atoms?
Answer:

No, the variation will not be regular because, energy Associated with an element with an electron in n-th Orbit, En = \(=\frac{-2 \pi^2 m Z^2 e^4}{n^2 h^2}\)

For a hydrogen-like atom, \(\frac{-2 \pi^2 m Z^2 e^4}{n^2 h^2}\) = constant

∴ \(E_n=\frac{K}{n^2}\)

∴ \(E_1=\frac{K}{1^2}, E_2=\frac{K}{2^2}, E_3=\frac{K}{3^2}, E_4=\frac{K}{4^2}, \cdots \text { etc. }\)

From the values of the energy associated with the electrons, it is clear that the variation of energy in successive principal quantum numbers of hydrogen-like atoms is not regular. the spacing between the energy levels decreases, as we move outwards from the nucleus.

Atomic Structure Class 11 Chemistry Notes PDF

Question 4. Energy associated with the n-th orldt of 11 -atom Is I ‘l (i given by the expression, \(E_n=-\frac{13.6}{n^2}\). Show that \(E_{(n+1)}-E_n=\frac{13.6 \times 2}{n^3} \mathrm{eV} \text {, when ‘ } n \text { ‘ is very large. }\)
Answer:

⇒ \(E_{(n+1)}-E_n=\left[-\frac{13.6}{(n+1)^2}-\left(-\frac{13.6}{n^2}\right)\right]\)

= \(\left[\frac{13.6}{n^2}-\frac{13.6}{(n+1)^2}\right] \mathrm{eV}=\frac{13.6(2 n+1)}{n^2(n+1)^2} \mathrm{eV}\)

If the value of n is very large, then (2n + l)=2n and(n+l)=n

∴ \(E_{(n+1)}-E_n=\frac{13.6 \times 2 n}{n^2 \times n^2}=\frac{13.6 \times 2}{n^3} \mathrm{eV}\)

Question 5. If an electron Is promoted from the first orbit to the third orbit of a hydrogen atom, then by how many times will the radius of the orbit be increased?
Answer:

The radius ofthe n -th orbit of H -atom \(r_n=\frac{n^2 h^2}{4 \pi^2 m e^2}\)

Radius ofthe first orbit \(\left(r_1\right)=\frac{1^2 \times h^2}{4 \pi^2 m e^2}\)

Radius of the third orbit (r3) \(=\frac{3^2 \times h^2}{4 \pi^2 m e^2}\)

∴ \(\frac{r_3}{r_1}=\frac{3^2 \times h^2}{4 \pi^2 m e^2} \times \frac{4 \pi^2 m e^2}{h^2}=9 \text { i.e., } r_3=9 \times r_1 \text {. }\)

∴ The radius ofthe orbit will be increased by 9 times

Question 6. If an electron drops from the third orbit (n = 3) to the first orbit (n = 1) of the H-atom, what will be the frequency and wavelength of the radiation emitted? What would have happened if the electron jumped from the first orbit to the third orbit?
Answer: Let the frequency of the emitted radiation be v.

Then \(v=R \times c \times\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right] \mathrm{cps}\)

=\(109677 \times 3 \times 10^{10} \times\left(\frac{1}{1^2}-\frac{1}{3^2}\right)\)

=\(329031 \times 10^{10} \times\left(1-\frac{1}{9}\right)\)

Since R = 109677 cm-1 and c = 3 × 10¹⁰ em s^-1 ]

= 3.29 × 10¹⁵ × 0.889 = 2.925 ×10¹⁵  cps.

The wavelength of the emitted radiation,

⇒ \(\lambda=\frac{c}{v}=\frac{3 \times 10^{10}}{2.925 \times 10^{15}}=1.025 \times 10^{-5} \mathrm{~cm}=1025 \mathrm{~A}\)

When an electron jumps from the 1st orbit to the 3rd orbit then energy is absorbed.

The frequency and wavelength of absorbed radiation are the same i.e., the frequency and wavelength of absorbed radiation will be 2.925 x 1015 cps and 1025A respectively.

Quantities 7. Find the wavelength (in angstrom) of the photon| emitted when an electron jumps from the second Bohr orbit to the first Bohr orbit of the hydrogen atom. The ionization potential of the hydrogen atom in its ground energy state =2.17 x 10-11 erg-atom-1
Answer:

The energy of the electron in the electron in first orbit (n = 1 ) of hydrogen atom \(E_1=-\frac{2 \pi^2 m e^4}{h^2}\)

The ionization potential of hydrogen atom le., the energy required to move the electron from n = 1 energy level to an infinite distance

=2.17 × 10¹¹ erg.

∴ Energy of electron in1st (n = 1) orbit =-2.17 × 10¹¹ erg

=1221 × 10^-8 cm =1221Å

Since 1Å = 10^-8 cm]

Question 8. Determine Balmer the series wavelengths of H and H Lines in the Balmer Series [ R= 109670 cm^-1 ]
Answer:

For Balmer series:

⇒ \(\bar{v}=\frac{1}{\lambda}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)

For Balmer Series n₁ =2 And For The Line Hα, n₂ = 3

∴ \(\frac{1}{\lambda}=109670\left[\frac{1}{2^2}-\frac{1}{3^2}\right]=109670\left(\frac{1}{4}-\frac{1}{9}\right)\)

∴ \(\lambda=\frac{36}{109670 \times 5}=6.565 \times 10^{-5} \mathrm{~cm}\)

For the line H_β, n₂ = 4

⇒ \(\frac{1}{\lambda}=109670\left[\frac{1}{2^2}-\frac{1}{4^2}\right]=109670\left(\frac{1}{4}-\frac{1}{16}\right)\)

∴ \(\lambda=\frac{16}{109670 \times 3}=4.863 \times 10^{-5} \mathrm{~cm}\)

Question 9. Find the velocity of the electron revolving in the third orbit of the hydrogen atom. Also, determine the number of revolutions of the electron per second around the nucleus.
Answer:

The velocity of the electron revolving in the 3rd orbit around the nucleus of the hydrogen atom,

The radius of the n ’ th orbit of H-atom, rn \(=\frac{n^2 h^2}{4 \pi^2 m e^2}\)

∴ Radius ofthe third orbit (r³) \(=\frac{3^2 h^2}{4 \pi^2 m e^2}\)

= \(\frac{9 \times\left(6.627 \times 10^{-27}\right)^2}{4 \times(3.14)^2 \times\left(9.108 \times 10^{-28}\right) \times\left(4.8 \times 10^{-10}\right)^2}\)

= 4.77 × 10^-8 cm [m = 9.108 × 10^-28 g]

Circumference ofthe third orbit

= 27πr³ = 2 × 3.14 × 4.77 × 10^-8 =2.99 × 10^-7cm

∴ Number of revolutions of electron per second around the nucleus \(=\frac{\text { Velocity }}{\text { Circumference of the orbit }}\)

= \(\frac{7.278 \times 10^7}{2.99 \times 10^{-7}}=2.43 \times 10^{14}\)

Question 10. Prove that the velocity of an electron revolving in the 1st orbit of H-atom is nearly 10^-2 times that of light.
Answer:

According to Bohr’s theory, mvr \(=\frac{n h}{2 \pi}\)

The radius of‘ n ‘th orbit, r \(=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

From equations [1] and [2], we have \(\frac{n h}{2 \pi m \nu}=\frac{n^2 h^2}{4 \pi^2 m Z e^2}\)

⇒ \(\text { or, } \frac{1}{v}=\frac{n h}{2 \pi \mathrm{Z} e^2} \text { or, } v=\frac{2 \pi \mathrm{Z} e^2}{n h}\)

For hydrogen atom, Z = 1 ; Hence, \(\nu=\frac{2 \pi e^2}{n h}\)

For the first orbit, n = 1 , e = 4.8 x 10^-1 esu,

h = 6.627 × 10^-27 erg-s

∴ The velocity of moving electron in the first orbit

⇒ \(v=\frac{2 \times 3.14 \times\left(4.8 \times 10^{-10}\right)^2}{1 \times 6.627 \times 10^{-27}}\)

= 2.183 × 10⁸ =(2.183 × 10^-10) × 10^-2 cm-s^-1

Again, the velocity of light =3 × 10¹⁰ cm-s^-1

Hence, the velocity of an electron revolving in the first orbit of the H-atom is almost 10-2 times ofthe velocity of light.

Question 11. If the energy of the first Bohr orbit is – 13.58 eV, then what will be the energy of the third Bohr orbit?
Answer:

Energy of n -th Bohr-orbit of H-atom, En \(=-\frac{2 \pi^2 m e^4}{n^2 h^2}\)

∴ Energy first Bohr orbit, E1 \(=-\frac{2 \pi^2 m e^4}{1^2 \times h^2}\)

∴ Energy of third Bohr orbit, E3 \(=-\frac{2 \pi^2 m e^4}{3^2 \times h^2}\)

Hence \(\frac{E_3}{E_1}=\frac{2 \pi^2 m e^4}{9 \times h^2} \times \frac{h^2}{2 \pi^2 m e^4}=\frac{1}{9}\)

∴ \(E_3=\frac{1}{9} \times E_1=\frac{1}{9} \times(-13.58) \mathrm{eV}=-1.509 \mathrm{eV}\)

Question 12. The velocity of an electron revolving in a certain orbit of the H-atom is \(\frac{1}{275}\) times the velocity of light. Find the orbit in which the electron is revolving.
Answer: Let the electron is revolving in the n-th orbit.

The velocity ofthe electron in the n -th orbit, \(V_n=\frac{2 \pi Z e^2}{n h}\)

[since Z=1

e= 4.8 × 10¹⁰ esu

h = 6.626 × 10^-27erg.s]

= \(\frac{2 \times 3.14 \times\left(4.8 \times 10^{-10}\right)^2}{n \times 6.626 \times 10^{-27}}\)

Since Z = 1

e = 4.8 × 10^-10esu

h= 6.626 × 10^-27 erg.s

= \(\frac{2.18 \times 10^8}{n} \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

Given, the velocity of revolution of the electron

= \(\frac{1}{275} \times\left(3 \times 10^{10}\right) \mathrm{cm} \cdot \mathrm{s}^{-1}=1.09 \times 10^8 \mathrm{~cm} \cdot \mathrm{s}^{-1}\)

∴ \(\frac{2.18 \times 10^8}{n}=1.09 \times 10^8\)

or, \(n=\frac{2.18 \times 10^8}{1.09 \times 10^8}=2\)

∴ The electron is revolving in the 2nd orbit of H-atom.

Question 13. According to Bohr’s theory, the energy of an electron in n-th, \(E_n=-\frac{21.76 \times 10^{-19}}{n^2} \mathrm{~J}\) J. Find the longest Wavelength of radiation required to remove one electron from the 3rd orbit of He+ ion.
Answer:

The energy of the electron in n -th orbit of H-atom,

⇒ \(E_n=-\frac{2 \pi^2 m e^4}{n^2 h^2}\)

[Since Z=1]

∴ \(-\frac{2 \pi^2 m e^4}{n^2 h^2}=-\frac{21.76 \times 10^{-19}}{n^2}=21.76 \times 10^{-19}\)

Now the energy ofthe electron in’ n ‘th orbit of He+ ion.

⇒ \(E_n^{\prime}=-\frac{2 \pi^2 Z^2 m e^4}{n^2 h^2}=-\frac{2 \pi^2 \times 2^2 \times m e^4}{n^2 h^2}\)

Since Z=2.

Therefore, E’n \(=-\frac{2 \pi^2 m e^4}{n^2 h^2} \times 4\)

∴ \(E_3=-\frac{2 \pi^2 m e^4}{3^2 \times h^2} \times 4\)

Removal of an electron from the 3rd orbit means a transfer of electron from the 3rd orbit to n = infinite.

∴ Energy ofthe electron at an infinite distance

Therefore the energy required to remove the electron,

⇒ \(\Delta E=E_{\infty}-E_3=0-\left(-\frac{2 \pi^2 m e^4}{3^2 \times h^2} \times 4\right)=\frac{2 \pi^2 m e^4}{h^2} \times \frac{4}{9}\)

∴ \(\Delta E=21.76 \times 10^{-19} \times \frac{4}{9} \mathrm{~J}\)

Since \(\frac{2 \pi^2 m e^4}{h^2}=21.76 \times 10^{-19}\)

We know, AE = \(h \times \frac{c}{\lambda}\)

⇒ \(\text { or, } \quad \frac{\left(6.627 \times 10^{-34}\right) \times\left(3 \times 10^8\right)}{\lambda}=21.76 \times 10^{-19} \times \frac{4}{9}\)

[Since h = 6.627 × 10^-34j-s and c = 3 × 10⁸m-s^-1 ]

Hence \(\lambda=\frac{9 \times\left(6.627 \times 10^{-34}\right) \times\left(3 \times 10^8\right)}{21.76 \times 10^{-19} \times 4}\)

= 2056 × 10^-19m = 2056 Å

1 Å = 10^-10 m = 20556 Å

[Since 1 Å = 10-10m]

Question 14. Calculate the energy emitted when electrons of 1.0g. An og atom of hydrogen undergoes transition emitting the spectra) line of lowest energy in the visible region of Its atomic spectrum [R_H = 1.1 ×  10⁷m^-1].
Answer:

The given spectral line in the visible region corresponds to the Balmer series. For the Balmer series,

⇒ \(\vec{v}=R_M\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)

For Lowest Energy, n₁ =2 and n₂= 3.

∴ \(\frac{1}{\lambda}=R_H\left[\frac{1}{2^2}-\frac{1}{3^2}\right]=1.1 \times 10^7 \times \frac{5}{36}\)

The amount of energy emitted during the transition of an electron, E = hv \(=h \times \frac{c}{\lambda}=h \times c \times \frac{1}{\lambda}\)

= \(6.626 \times 10^{-34} \times 3 \times 10^8 \times\left(1.1 \times 10^7 \times \frac{5}{36}\right)=3.037 \times 10^{-19} \mathrm{~J}\)

∴ The energy emitted when electrons of gram-atom of hydrogen undergo transition =N0 x hv

= 6.022  ×  10²³× (3.037 × 10^-19) J = 18.28 ×  10⁴ J = 182.8 kj

Question 15. The atomic spectrum of hydrogen contains a series of four lines having wavelengths 656.5, 486.3, 434.2, and 410.3 nm. Determine the wavelength of the next line in the same series [R_H = 109678 cm^-1].
Answer:

As the given wavelengths lie in the visible region, they should belong to the Balmer series. For Balmer series, nx = 2. The value of n1=2 the shortest wavelength (410.3nm) can be determined using the equation,

⇒\(\bar{v}=\frac{1}{\lambda}=R_H\left(\frac{1}{2^2}-\frac{1}{n_2^2}\right)\)

Or, \(\frac{1}{410.3 \times 10^{-7} \mathrm{~cm}}=109678 \mathrm{~cm}^{-1}\left(\frac{1}{4}-\frac{1}{n_2^2}\right)\)

Or, \(\frac{1}{n_2^2}=\frac{1}{4}-\frac{1}{410.3 \times 10^{-7} \times 109678} \quad \text { or, } \frac{1}{n_2^2}=0.25-0.22\)

Or, \(n_2^2=\frac{1}{0.03}=33.33\)

∴ N₂ =6

Thus, the next line is obtained as a result of the transition of an electron from n₂ = 7 to = 2.

∴ \(\frac{1}{\lambda}=109678\left(\frac{1}{2^2}-\frac{1}{7^2}\right) \mathrm{cm}^{-1}=25181 \mathrm{~cm}^{-1}\)

Or, \(\lambda=\frac{1}{25181}=3.971 \times 10^{-5} \mathrm{~cm}=397.1 \mathrm{~nm}\)

Question 16. The angular momentum of an electron in a Bohr’s orbit of a hydrogen atom is 3.1655× 10³⁴kgm²s^-1. Calculate the wavelength of the spectral line emitted when an electron falls from this level to the next lower level.
Answer:

Angular momentum of an electron in ‘n-th’ Bohr orbit of H-atom, mvr \(=\frac{n h}{2 \pi}\)

Or, \(3.1655 \times 10^{-34}=\frac{n \times 6.626 \times 10^{-34}}{2 \times 3.14}\)

⇒ \(\bar{v}=\frac{1}{\lambda}=109678\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right) \mathrm{cm}^{-1}\)

= \(109678\left(\frac{1}{2^2}-\frac{1}{3^2}\right)\)

= \(\lambda=6.564 \times 10^{-5} \mathrm{~cm}\)

Since n₁ = 2, n₂ = 3

Question 17. Calculate the distance of separation between the second and third orbits of the hydrogen atom.
Answer:

The radius of the n-th orbit of the H-atom is given by \(r_n=0.529 \times n^2\)

∴ r₃– r₂ =0.529(32-22)Å

= 0.529 × 5

= 2.645 Å

Class 11 Chemistry Atom Structure Important Topics

Question 18. After absorbing an energy of 2.044¹∪10-19J, the electron of the H-atom will jump to which orbit?
Answer:

The energy of the electron in the n-th orbit of the H-atom is,

⇒ \(E_n=\frac{-2.18 \times 10^{-19}}{n^2} \mathrm{~J}\)

The energy of an electron in the ground state (n = 1) is

Ex = \(E_1=-21.8 \times 10^{-19} \mathrm{~J}\)

If tire electron absorbs an energy of 2.044 × 10—19 J, the total energy

= \(\left(-21.8 \times 10^{-19}+20.44 \times 10^{-19}\right) \mathrm{J}=-1.36 \times 10^{-19} \mathrm{~J}\)

∴ \(\frac{-21.8 \times 10^{-19}}{n^2}=-1.36 \times 10^{-19} \mathrm{~J}\)

∴ \(n=\sqrt{\frac{-21.8 \times 10^{-19}}{-1.36 \times 10^{-19}}}=4\)

Thus, the electron will jump to the fourth orbit.

Towards The Development Of Quantum Mechanical Model Of Atom

The limitations of Bohr’s model of the atom led to the development of a new improved model for atoms. Two significant concepts that led to the formulation of such a model were:

Dual nature of matter particles, Heisenberg’s uncertainty principle.

Dual Nature Of Matter Particles: De Broglie Theory

Both the scientists, Niels Bohr and Sommerfeld regarded electrons as negatively charged particles. However, the particle nature of the electron failed to explain some of its characteristics.

In 1905, Einstein suggested that light has a dual nature i.e., both wave nature as well as particle nature.

In 1924, French physicist, Louis de Broglie concluded that just like radiations, moving electrons or other such microscopic particles are associated with wave nature i.e., they exhibit wave nature as well as particle nature.

The wave associated with a particle is called a matter wave or de Broglie wave.

The wavelength associated with a moving particle is given by the de Broglie equation \(\lambda=\frac{h}{m v}=\frac{h}{p}\) [A = wavelength of the moving particle, m = mass of the particle, v = velocity of the particle, p = momentum of tire particle, h = Planck’s constant.] All the properties of electrons and other matter particles can be explained by its wave-particle duality.

From de Broglie equation, \(\lambda \propto \frac{1}{m v}\)

Since h=Constant i.e., wavelength \(\propto \frac{1}{\text { momentum }}\)

Thus, the wavelength of the wave associated with a fast-moving particle is inversely proportional to its momentum.

Derivation of de Broglie Equation:

The de Broglie equation was derived by using Planck’s quantum theory and Einstein’s equation of grass-energy equivalency. According to Planck’s quantum theory,

where, c = velocity of light, E = energy of a photon, v = frequency and A = wavelength.

According to Einstein’s equation, E = mc²

Where, m = mass ofa photon, c = velocity of a photon.

From [1] and [2] we have \(\frac{h c}{\lambda}=m c^2 \text { or, } \lambda=\frac{h}{m c} \cdots[3]\) de Broglie pointed out that equation (3) can be applied to fast-moving matter particles such as electrons.

∴ \(\lambda=\frac{h}{m v}\) [m = mass & v = velocity ofthe particle]

This is de Broglie equation.

The wave associated with fast-moving matter particles is called matter wave or de Broglie wave.

This type of wave is distinctively different from electromagnetic waves.

de Broglie equation has no significance for moving particles having large mass because in such cases the wavelength of the associated wave is too small for ordinary observation.

For example, the wavelength associated with a cricket ball of mass 200 g (0.2 kg) moving with a velocity of 1 m-s-1 is—

⇒ \(\lambda=\frac{h}{m v}=\frac{6.62 \times 10^{-34}}{0.2 \times 1} \mathrm{~m}=3.31 \times 10^{-23} \mathrm{pm}\)

Such a small value of A cannot be measured.

Application of wave nature of electrons:

The concept of the wave nature of electrons is used in electron microscopes to get images of particles as tiny as 10A and for studying the surface structure of solid substances.

Angular momentum of Bohr electron from do Broglie equation:

According to de Broglie, a tiny particle like an electron, revolving in a circular orbit must have a wave character associated with it. Thus, for the wave (associated with the moving electron) to be completely in phase, the circumference of the orbit should be an integral multiple of the wavelength, λ.

∴ 2πλ = nλ or, λ \(=\frac{2 \pi r}{n}\)

[where, r = radius of the orbit and n = an integer] From de Broglie equation \(\lambda=\frac{h}{m v}\)

[where, m = mass of electron, v = velocity of electron.]

∴ \(\frac{2 \pi r}{n}=\frac{h}{m v} \text { or, } m v r \text { (angular momentum) }=\frac{n h}{2 \pi}\)

[where, r = radius of the orbit and n = an integer] From de Broglie Equation

⇒ \(\lambda=\frac{h}{m v}\)

This is the same relation as predicted by Bohr.

Circumference of the electronic orbit and the wavelength associated with the electronic motion:

From Bohr’s theory, angular momentum of an electron revolving in a circular orbit is an integral multiple of \(\frac{h}{2 \pi} \text { i.e., } m v r=\frac{n h}{2 \pi}\) orbit is an integral multiple of \(\frac{h}{2 \pi} \text { i.e., } m v r=\frac{n h}{2 \pi}\)

or, \(m v=\frac{n h}{2 \pi r}\)

r = radius ofthe orbit, v = velocity ofelectron. From de Broglie equation, \(\lambda=\frac{h}{m v} \quad \text { or, } m v=\frac{h}{\lambda}\)

[where λ = wavelength associated with moving electron.]
From [1] and [2] we have, \(\frac{n h}{2 \pi r}=\frac{h}{\lambda} \quad \text { or, } 2 \pi r=n \lambda\) or, 2πr = nλ

So, the circumference of the electronic orbit is an integral multiple of the wavelengths associated with the motion of electrons.

The kinetic energy of a moving particle and the de Broglie wavelength associated with it:

Kinetic energy(E) of a particle (mass = m) moving with velocity v is given by,

\(E=\frac{1}{2} m v^2 \quad \text { or, } m E=\frac{1}{2} m^2 v^2 \quad \text { or, } m v=\sqrt{2 m E}\) …………………..(1)

From de Broglie equation \(\lambda=\frac{h}{m \nu} \quad \text { or, } m v=\frac{h}{\lambda}\)…………………..(2)

[λ = wavelength associated with the moving particle] From 1 and 2 we have

⇒ \(\frac{h}{\lambda}=\sqrt{2 m E} \text { or, } \lambda=\frac{h}{\sqrt{2 m E}}\) …………………..(3)

Calculation of de Broglie wavelength of the electron from the potential applied:

If an accelerating potential V is applied to an electron beam, the energy acquired by each electron

= e (charge in coulomb)×  V(potential in volt)

= eV electron – volt

This energy becomes the kinetic energy of the electron.

∴ \(\frac{1}{2} m v^2=e V \quad \text { or, } \quad v=\sqrt{\frac{2 e V}{m}}\)

Substituting the values of h, m, and e in equation [1], we get \(\lambda=\frac{1.226 \times 10^{-9}}{\sqrt{V}} \mathrm{~m}\)

In place of the electron, if any other charged particle carrying Q coulomb is accelerated under a potential difference of V volt, then kinetic energy = QV. Hence \(\lambda=\frac{h}{\sqrt{2 m Q V}}\)

Numerical Examples

Question 1. Calculate the wavelength of the de Broglie wave associated with an electron moving with a velocity of 2.05 x 107m-s-1
Answer:

From de Broglie equation:

⇒ \(\lambda=\frac{h}{m v}\)

Where λ = wavelength , m = mass ofthe electron, v = velocity of the electron,

⇒ \(\lambda=\frac{6.626 \times 10^{-34}}{\left(9.11 \times 10^{-31}\right) \times\left(2.05 \times 10^7\right)}\)

= \(3.548 \times 10^{-11} \mathrm{~m}\)

Question 2. Calculate the velocity of an electron having de Broglie wavelength of 200A \(\left[m=9.11 \times 10^{-31} \mathrm{~kg}, h=6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right]\)
Answer:

According to de Broglie equation, \(\lambda=\frac{h}{m v}\)

∴ \(v=\frac{h}{m \lambda}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{\left(9.11 \times 10^{-31} \mathrm{~kg}\right) \times\left(200 \times 10^{-10} \mathrm{~m}\right)}\)

= 3.64 ×  × 10 ^–34 m.s

[Since 1Å =10¹⁰m]

Question 3. Calculate the ratio of velocities of a moving electron to that of a proton associated with the same de Broglie wavelength. [mg = 9.11 × 10^-31 kg, mp = 1.67 × 10^-27 kg, h = 6.626 × 10^-34 J.s]
Answer:

As given in the question, Ae = Ap

∴ \(\frac{h}{m_e \nu_e}=\frac{h}{m_p \nu_p}\)

∴ \(\frac{v_e}{v_p}=\frac{m_p}{m_e}=\frac{1.67 \times 10^{-27}}{9.11 \times 10^{-31}}=1833\)

Question 4. Calculate the momentum of the particle which has a de Broglie wavelength of O.lA
Answer:

⇒ \(\lambda=\frac{h}{m v}\)

∴ \(m v=\frac{h}{\lambda}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{0.1 \times 10^{-10} \mathrm{~m}}\)

= 6.626 ×10  ^–23kg-m-s-1.

Since 1A= 10-10m]

Question 5. Calculate the de Broglie wavelength of a proton that is moving with a kinetic energy of 5 x 10-23J.
Answer:

Mass of a proton = 1.67 x 10-27kg

Kinetic energy of a proton =5 x 10 23J

∴ \(\frac{1}{2} m v^2=5 \times 10^{-23}\)

Or, \(\frac{1}{2} \times 1.67 \times 10^{-27} \times v^2=5 \times 10^{-23}\)

∴ \(v=\left(\frac{10 \times 10^{-23}}{1.67 \times 10^{-27}}\right)^{1 / 2}=244.7 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

∴ \(\lambda=\frac{h}{m \nu}=\frac{6.626 \times 10^{-34}}{1.67 \times 10^{-27} \times 244.7}=1.62 \times 10^{-9} \mathrm{~m}\)

∴ \(\lambda=\frac{h}{m \nu}=\frac{6.626 \times 10^{-34}}{1.67 \times 10^{-27} \times 244.7}=1.62 \times 10^{-9} \mathrm{~m}\)

Question 6. Calculate the de Broglie wavelength of an electron moving With A speed that is 1% of the speed of light.
Answer:

⇒ \(\lambda=\frac{h}{m v}\)

=\(\frac{6.626 \times 10^{-34}}{\left(9.11 \times 10^{-31}\right) \times\left(3 \times 10^8 \times \frac{1}{100}\right)} \)

= \(2.42 \times 10^{-10} \mathrm{~m}\)

Question 7. Calculate the kinetic energy of an a- -particle that has a de Broglie wavelength of 8 pm.
Answer:

Mass of an a -particle \(=\frac{4 \times 10^{-3}}{6.022 \times 10^{23}} \mathrm{~kg}=6.64 \times 10^{-27} \mathrm{~kg}\)

⇒ \(\lambda=\frac{h}{m v} \text { or, } v=\frac{h}{m \lambda}=\frac{6.626 \times 10^{-34}}{\left(6.64 \times 10^{-27}\right) \times\left(8 \times 10^{-12}\right)}\)

= 1.247× 10¹⁴m.s^-1

[since 1 pm = 10^-121m]

The kinetic energy of the α -particle = 1/2 mv²

=\(\frac{1}{2} \times\left(6.64 \times 10^{-27}\right) \times\left(1.247 \times 10^4\right)^2 \mathrm{~J}=5.16 \times 10^{-19} \mathrm{~J}\)

Question 8. Calculate the de Broglie wavelength of an electron accelerating in a particle accelerator through a potential difference of 110 million volt
Answer:

The kinetic energy of an electron under the potential difference of of110 million volts = llOMeV =110x 106eV

∴ \(\frac{1}{2} m v^2=110 \times 10^6 \mathrm{eV}=110 \times 10^6 \times 1.602 \times 10^{-19} \mathrm{~J}\)

Or, \(\frac{1}{2} \times 9.11 \times 10^{-31} \times v^2=110 \times 10^6 \times 1.602 \times 10^{-19}\)

∴ \(v=\left(\frac{2 \times 110 \times 10^6 \times 1.602 \times 10^{-19}}{9.11 \times 10^{-31}}\right)^{1 / 2}\)

= 6.22 × 10⁹m.s^-1

∴ \(\frac{h}{m v}=\frac{6.626 \times 10^{-34}}{\left(9.11 \times 10^{-31}\right) \times\left(6.22 \times 10^9\right)} \)

= \(1.17 \times 10^{-13} \mathrm{~m}\)

Structure of Atom Chapter 2 Class 11 Chemistry Detailed Notes

Question 9. Find de Broglie wavelength associated with a tennis ball of mass 60 g moving with a velocity of 10 m.s^-1
Answer:

de Broglie wavelength, \(\lambda=\frac{h}{m v}\)

Here, h = 6.626 × 10^-34 J.s^-1

m = 60g = 60 ×10^-3 kg = 6 × 10^-2 kg, v = 10 m.s^-1

∴ \(\lambda=\frac{6.626 \times 10^{-34}}{6 \times 10^{-2} \times 10}=1.105 \times 10^{-33} \mathrm{~m}\)

Question 10. Calculate the wavelength (in nm) associated with a beam of protons moving with a velocity of 10³m-s^-1. [Mass of proton 1.67 ×10^-27kg, h = 6.63 × 10^-34 J.s^-1]
Answer:

de Broglie wavelength \(\lambda=\frac{h}{m v}\)

= \(\frac{6.63 \times 10^{-34}}{1.67 \times 10^{-27} \times 10^3} \mathrm{~m}=0.40 \times 10^{-9} \mathrm{~m}\)

= 0.40 nm

Question 11. Calculate the wavelength of an a -particle having an energy of 6.8 × 10^-18J.
Answer:

⇒ \(\lambda=\frac{h}{\sqrt{2 m E}}=\frac{6.626 \times 10^{-34}}{\sqrt{2 \times 6.8 \times 10^{-18} \times\left(4 \times 1.67 \times 10^{-27}\right)}}\)

= 2.198 × 10^-12m

Question 12. Calculate the wavelength of the wave associated with an electron beam, if the beam is accelerated by a potential difference of 5000 volts.
Answer:

Kinetic energy ofthe electron = 5000 eV

= 5000 × 1.602 ×10^-19J

The velocity of an electron due to the applied potential difference is ms^-1. Hence, kinetic energy \(=\frac{1}{2} m v^2\)

∴ \(\frac{1}{2} m v^2=5000 \times 1.602 \times 10^{-19} \mathrm{~J}\)

= 5000 × 1.602 ×10^-19  Kg.m².s^-1

∴ \(v=\sqrt{\frac{2 \times 5000 \times 1.602 \times 10^{-19}}{9.11 \times 10^{-31}}}=4.193 \times 10^7 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

[since mass of electron = 9.11 × 10^-31kg]

From de Brogile Equation , we get, \(\lambda=\frac{h}{m v}\)

⇒ \(\frac{6.626 \times 10^{-34}}{9.11 \times 10^{-31} \times 4.193 \times 10^7}\)

= \(=0.1736 \times 10^{-10} \mathrm{~m}\)

=0.1736 Å

Question 13. The electron of 2 -atom in the ground state absorbs energy equal to 1.5 times the minimum energy, required to remove the electron from the hydrogen atom. Calculate the wavelength of the electron emitted, [mass of electron =9.11 X 10-31kg]
Answer:

The energy required to remove an electron from the ground state of H-atom = 13.6eV. Therefore, energy absorbed by the electron of H-atom = 1.5 × 13.6eV = 20.4eV

∴ Residual energy after removal ofthe electron

= (20.4- 13.6)eV = 6.8eV = 6.8 × 1.602 ×10^-19

This residual energy is converted into kinetic energy.

∴ \(\frac{1}{2} m v^2=6.8 \times 1.602 \times 10^{-19}\)

∴ \(v=\sqrt{\frac{6.8 \times 1.602 \times 10^{-19}}{9.11 \times 10^{-31}}}\)

= \(1.546 \times 10^6 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

λ = \(\frac{h}{m v}\)

=\(\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{\left(9.11 \times 10^{-31} \mathrm{~kg}\right) \times\left(1.546 \times 10^6 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}\)

= \(4.70 \times 10^{-10} \mathrm{~m}\)

Question 14. Find the velocity of an electron so that its momentum is equal to that of a photon Of Wavelength 650nm.
Answer:

⇒ \(\lambda=\frac{h}{p}\) [from de Broglie Equation]

∴ If the momentum of electron = momentum of a photon, then A of electron =A of photon = 650nm

Applying de Broglie equation to electron, \(\lambda=\frac{h}{p}=\frac{h}{m v}\)

∴v =  \(\frac{h}{m \lambda}=\frac{6.63 \times 10^{-34}}{\left(9.11 \times 10^{-31}\right)\left(650 \times 10^{-9}\right)}\)

= 118.97 m.s^-1

Question 15. The kinetic energy of a subatomic particle is 3.60 x 10_24J. Calculate the frequency of the corresponding particle wave.
Answer:

Kinetic energy \(=\frac{1}{2} m v^2=3.60 \times 10^{-24} \mathrm{~J}\)

∴ mv² = 2 × 3.60 × 10^-24J

=7.2× 10^-24J For any given wave

∴ \(=\frac{v}{v}\)

∴ \(\frac{h}{m v}=\frac{v}{v} \text { or, } v=\frac{m v^2}{h}\) \(=\frac{7.2 \times 10^{-24}}{6.626 \times 10^{-34}}=1.086 \times 10^{10} \mathrm{~s}^{-1}\)

Question 16. Calculate the mass of a photon with wavelength 3.6A.
Answer:

A = 3.2Å =3.2× 10^-10m Velocity of photons (v) = velocity of light

= 3.2× 10^-8m.s^-1

From de Broglie equation, \(\lambda=\frac{h}{m v}\)

Or, \(m=\frac{h}{\lambda v}=\frac{6.626 \times 10^{-34}}{\left(3.2 \times 10^{-10}\right) \times\left(3 \times 10^8\right)}=6.9 \times 10^{-33} \mathrm{~kg}\)

Heisenberg’s Uncertainty Principle Numerical Examples

Question 1. Calculate the uncertainty in velocity (m.s^-1 ) of a moving object of mass 25 g, if the uncertainty in its position is 10-5m. [h = 6.6 × 10^-34 J.s]
Answer:

We, know \(\Delta x \cdot \Delta p=\frac{h}{4 \pi} \text { or, } \Delta x \cdot m \Delta v=\frac{h}{4 \pi}\)

∴ \(\Delta v=\frac{6.6 \times 10^{-34}}{4 \times 3.14 \times 10^{-5} \times 0.025}\)

= \(2.099 \times 10^{-28} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

= \(\Delta x=10^{-5} \mathrm{~m}, m=25 \mathrm{~g}\)

= 0.025kg

Question 2. An electron has a velocity of 600m-s_1 [accuracy: 0.005%]. With what accuracy can we locate the position of this electron?[mass of an electron = 9.1 × 10^-31kg, h = 6.6 ×  10^-34 J.s ]
Answer:

According to uncertainty principle, \(\Delta x \cdot m \Delta v=\frac{h}{4 \pi}\)

Or, \(\frac{6.6 \times 10^{-34}}{4 \times 3.14 \times\left(9.1 \times 10^{-31}\right) \times\left(600 \times \frac{0.005}{100}\right)}\)

⇒ \(\frac{6.6 \times 10^{-34}}{4\times 3.14 \times 9.1 \times 10^{-31} \times 0.03}\)

⇒\(1.92 \times 10^{-3} \mathrm{~m}\)

Question 3. The uncertainties in position and velocity of a particle arc 10-1° in and 5.27× 10^-24 m-s^-1 respectively. Calculate the mass of the particle.
Answer:

According to uncertainty principle \(\Delta x \cdot \Delta p=\frac{h}{4 \pi}\)

or, \((\Delta p)^2=\frac{h}{4 \pi}\)

[since \(\Delta x=\Delta p\)

Therefore \(\Delta p=\sqrt{\frac{h}{4 \pi}} \quad \text { or, } m \Delta v=\sqrt{\frac{h}{4 \pi}} \text { or, } \Delta v=\frac{1}{2 m} \sqrt{\frac{h}{\pi}}\)

Question 4. If uncertainties in the position and momentum of a moving object are the same, find uncertainty in velocity
Answer:

According to uncertainly principle, \(\Delta x \cdot \Delta p=\frac{h}{4 \pi}\)

Or, \((\Delta p)^2=\frac{h}{4 \pi}\)

∴ Δx = Δp

∴ Δp =   \(\sqrt{\frac{h}{4 \pi}}\)

Or, mΔv =  \(\sqrt{\frac{h}{4 \pi}} \text { or, } \Delta v=\frac{1}{2 m} \sqrt{\frac{h}{\pi}}\)

Question 5. Calculate the uncertainty in the velocity of an electron if the uncertainty in its position is of the order ±12pm
Answer:

According to uncertainly principle, Δx.mΔv = h/4π

Δv = \(\)

Mass of electron =9.11 ×  10^-31kg

And 1pm=10^-12 m

= \(4.82 \times 10^6 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Class 11 Chemistry Structure of Atom Summary

Question 6. Calculate the minimum uncertainty in the position of a bullet of mass 2.5g having a probable velocity between 60,000,000 and 60,000,001 m.s^-1
Answer:

The maximum uncertainty in velocity

Av =60,000,001-60,000,000 =l m.s^-1

According to the uncertainty principle, Ax – mAv = h/mv

∴ \(\Delta x=\frac{h}{4 \pi m \times \Delta v}\)

= \(\frac{6.626 \times 10^{-34}}{4 \times 3.14 \times\left(2.5 \times 10^{-3}\right) \times 1}\)

= \(2.12 \times 10^{-32} \mathrm{~m}\)

Question 7. The uncertainty in the determination of the velocity of a dust particle (of mass O.lmg) is 4.5 X 10-20 m-s Calculate the least uncertainty in its position.
Answer:

⇒  \(\Delta x \times \Delta p \frac{h}{4 \pi} \text { or, } \Delta x \times m \Delta v \frac{h}{4 \pi} \text { or, } \Delta x \frac{h}{4 \pi m \times \Delta v}\)

Least uncertainty in determining its position,

Δx  = \(\frac{h}{4 \pi m \times \Delta v}=\frac{6.626 \times 10^{-5}}{4 \times 3.14 \times\left(0.1 \times 10^{-6}\right)\times\left(4.5 \times 10^{-20}\right)}\)

= \(1.172 \times 10^{-8} \mathrm{~m}\)

Question 8. If uncertainties in the measurement of the position and momentum of an electron are found to be equal in magnitude, then what is the uncertainty in the measurement of velocity? Comment on the result.
Answer:

According to uncertainty principle, \(\Delta x \times \Delta p=\frac{h}{2 \pi}\)

Given, Δx =Δp

∴ \((\Delta p)^2=\frac{h}{4 \pi} \text { or, } \Delta p=\sqrt{\frac{h}{4 \pi}}\)

Or, \(m \Delta v=\sqrt{\frac{h}{4 \pi}}, \text { or } \Delta v=\frac{1}{m} \sqrt{\frac{h}{4 \pi}}\)

= \(\frac{1}{9.11 \times 10^{-31}} \sqrt{\frac{6.626 \times 10^{-34}}{4 \times 3.14}}=7.97 \times 10^{12} \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Question 9. Calculate the product of uncertainties in the position and velocity of an electron of mass 9.1 X 10-31kg, according to Heisenberg’s uncertainty principle.
Answer:

According to uncertainty principle, \(\Delta x \cdot \Delta p=\frac{h}{4 \pi}\)

Or, \(\Delta x \cdot m \Delta v=\frac{h}{4 \pi} \quad \text { or, } \Delta x \cdot \Delta v=\frac{h}{4 \pi m}\)

=  \(\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{4 \times 3.14 \times 9.11 \times 10^{-31} \mathrm{~kg}}\)

= \(5.79 \times 10^{-5} \mathrm{~m}^2 \cdot \mathrm{s}^{-1}\)

Shapes Of Orbitals From Wave Function

It has been stated earlier that the three-dimensional space around the nucleus in which the probability of finding an electron is maximum is called an orbital.

To obtain a clear idea about the shapes of orbitals, we will first discuss the variation of—

1. The radial part of the wave function,
2. Square of the radial wave function, and
3. Radial distribution function with an increase in distance from the nucleus.

Variation Of Radial Part Of Wave Function With Distance From The Nucleus

Schrodinger wave equation for the electron in a one-electron atom (H-atom) can be solved to get different expressions for wave function \((\psi)\) for different orbitals.

The orbital wave function for an electron in an atom has no physical meaning. It is simply a mathematical function of the coordinates of the electron.

However, for different orbitals the plots of the radial part of the corresponding wave functions as a function of r (distance from the nucleus) are different. depicts such plots for Is, 2s, 2p and 3s orbitals.

For is -orbital, the radial part of the wave function [ψ(r) or R] decreases sharply with increasing distance, r, from the dying nucleus.

For 2s -orbital ψ (r) or R, decreases sharply in the beginning, becomes zero at a particular distance, and then becomes negative as r increases.

FM 3s-orbilal \(\psi\). decreases sharply in the Beginning with an Increase In r, becomes zero At A Particcular Distance, And Then Becomes negative. On Further Increases In \(r, \psi(r)\) again becomes zero and finally becomes positive.

For 2p -orbital if \(\psi(r)\) rises from zero to a maximum, then decreases with increasing distance (r) from the nucleus. On further increase in distance, ifr(r) approaches almost zero.

For 3p -orbital,\(\psi(r)\) rises from zero and attains a maximum value. On further increase in ψ(r) begins to decrease and becomes zero at a particular distance. Then it becomes negative with a further increase in r.

Characteristic features observed in the plots of r vs Ψ(r):

1. The radial part of the wave functions for 2s, 3s, 3p, etc. orbitals can be positive or negative depending upon the distance (r) from the nucleus. These are not related to the positive and negative charges.
2. For each orbital, the radial part of the wave function Ψ(r) approaches zero as r→∞.
3. For 2s, 3s, and 3p -orbitals, one common feature for the variation of wave function Ψ(r)) with distance is that Ψ(r) becomes zero at a finite distance from the nucleus. However, for different orbitals if Ψ(r) becomes zero at different distances Ψ(r).
4. The distance Ψ(r) at which becomes zero is called a nodal point radial node or simply node. At the nodal point, the radial wave function if Ψ(r) changes its sign from positive to negative or vice versa.
5. For different orbitals, the number of radial nodes =(n-1-1).
6. This indicates that the number of radial nodes is determined by the values of the principal quantum number ( n) and azimuthal quantum number (Z) of the orbital under consideration.

There is no relation between the positive and negative values of the wave function with the positive and negative charges.

Radial probability density [Ψ²(r) Or R²] graphs variation Of the square Of Radical Wave Function With Distance From The nucleus (r)

The square of the radial wave function, Ψ²(r) or R2 for an orbital gives the radial density.

According to the German physicist, Max Bom, the radial density, Ψ²(r) at a point gives the probability density of the electron at that point along a particular radial line.

The variation of Ψ²(r) as a function of r for different orbitals is given in the figure. The nature of these curves is different for different orbitals.

For Is -orbital, probability density is maximum near the nucleus (r≈0) and decreases sharply as we move from it.

For 2s -orbital the probability density is maximum near the nucleus (r≈0).

With increasing distance, Ψ2(r) first decreases sharply to zero and starts increasing again. After reaching a small maxima it decreases again and approaches zero as the value of r increases further.

The intermediate region (a spherical shell) where this probability density reduces to zero is called the nodal surface or simply node.

In general ns -orbital has (n- 1) nodes. Thus, the number of nodes for 2s -orbital is one, two for 3s and so on, i.e., the number of nodes increases with an increase of principal quantum number n.

The probability density variation for Is and 2s orbitals can be visualized in terms of charge cloud diagrams. In these diagrams, the density of the dots in a region represents the electron probability density in that region.

For 2p- Orbital Probability Density Is zero at r = 0. However, with increasing distance, it begins to increase and reaches a maximum and then decreases gradually as the distance (r) from the nucleus increases and ultimately approaches zero.

From similar plots of various orbitals, it has been found that all orbitals except s, have zero electron density at r = 0.

Radial probability distribution curve: Variation of radial distribution function (RDF) with distance from the nucleus (r)

The plot of Ψ²(r) versus r gives the probability density for the electron around the nucleus. However, in order to determine the total probability in an infinitesimally small region, we have to multiply probability density if Ψ2(r) by the volume of the region i.e., probability = Ψ²(r) x dv [where dv = volume of the region].

Since the atoms have spherical symmetry, it is more useful to discuss the probability of finding the electron in a spherical shell between the spheres of radii r and (r + dr).

The volume of such a shell of extremely small thickness, dr, is 4nr2dr. So we have, Probability = R2 x 4rrr2dr = 47tr2Ψ²(r)(r)dr [since R = Ψ²(r))].

This gives the probability of finding the electron at a particular distance (r) from the nucleus. This is called radial distribution function (RDF).

Radial distribution function (RDF) = 4πr²ψ²(r)dr

Important information obtained from the plots of RDF vs r:

1. For all orbitals, the probability is zero at the nucleus.
2. If the point r = 0 is neglected, then it can be seen that,
3. The number of radial nodes for any orbital -n-l- 1,
4. The number of maxima (peak) for any orbital =(n-l- 1) +1 = (n-/). The peak in any curve gives the distance from the nucleus to that point where the probability of finding the electron is maximum. This is called the radius of maximum probability.
5. All the s -orbitals, except the first one (Is), have a shell-like structure, rather like an onion, or a hailstone, consisting of concentric layers of electron density. Similarly, all but the first p -p-orbital (2p) and the first dorbital (3d) have shell-like structures.
6. The first s -s-orbital (Is), first p -p-p-orbital (2p) and first orbital (3d) have two important characteristics—
7. they do not contain radial nodes and contain only one maxima.
8. Examination of the plots for Is, 2s, and 3s -orbitals shows that the most probable distance of maximum probability density increases markedly as the principal quantum number increases.
9. Furthermore, by comparing the plots for 2s and 2p, or 3s, 3p, and 3d -orbitals it is seen that the most probable radius decreases slightly as the azimuthal quantum number increases.

Shapes Of Orbitals

The angular part of the wave function, A; m(6, 0), depends on the azimuthal (/) and magnetic (m) quantum numbers but is independent ofthe principal quantum number (n).

On the other hand, the radial part of the wave function, Rn t(r), depends on the principal quantum number (n).

Thus the principal quantum number ( n) determines the size, while the azimuthal (/)and magnetic (m) quantum numbers determine the shape of an orbital.

Shape of s-orbital:

From the solutions of the Schrodinger equation for s -s-orbital of H-atom, it has been known that the value of wave function ψ, or the probability of finding the electron ψ2 in space around the nucleus depends only on the distance from the nucleus but not on the direction.

• In other words, there is an equal probability of finding the electron at a given distance in all directions Around the nucleus, i.e. ψ=f(r)
• Thus all s -orbitals are spherical. For Is -orbital, RDF (the probability of finding the electron) increases as the distance from the nucleus increases and reaches a maximum value at a particular distance.
• (This distance is 0.529A for the electron in the ground state of H-atom). Then this probability begins to decrease and becomes negligible at large distances.
• Thus for Is -orbital, the probability of finding the electron is zero at r = 0 and also at r =∞

Like Is -orbital, 2s -orbital is also spherical.

However, 2s -orbital differs from Is -orbital in the fact that the probability of finding the electron is zero not only at r = 0 and r = ∞ but also at a particular distance between r = 0 and r – ∞.

• In fact, for 2s -orbital, RDF (the probability of finding the electron) increases as the distance from the nucleus increases and reaches a maximum value.
• Then it begins to decrease and becomes zero at a particular distance.
• The spherical shell of zero electron density is called a nodal surface or simply a node.
• After crossing the nodal surface the probability of finding the electron begins to increase again and reaches a second maxima.

This second maximum represents the region of the highest electron density in a 2s orbital. This is known as an antinode.

• After crossing this region of highest electron density, die probability of finding the electron again begins to decrease and approaches zero as the value of r increases further.
• Thus 2s -orbital has a shell-like structure consisting of concentric layers of electron density.
• 3s -orbital is also spherical. Its structure is similar to that of the 2s -orbital, but it differs from the 2s orbital as it has two nodal surfaces and three regions of maximum electron density.
• The probability of finding the electron at the 3rd maxima is the highest and is called the antinode in a 3s -orbital.
• Thus there are two nodes before the arrival of the highest probability region. These are pictorially represented in
• Angular wave function \(\left[\mathrm{A}_{L, m}(\theta, \phi)\right]\) for s -orbital does not depend on θ and Φ.
• It has non-zero values (with equal magnitude) in all possible directions. So s -orbital has no nodal plane.

Points to remember: Is, 2s, and 3s -orbitals are all spherical, but they differ from each other in the following respects—

Size and energy of ns -orbital increases as the magnitude of n increases. Thus, we have Is < 2s < 3s—.

Depending on the value of n, there are different numbers of nodes in ns -orbital. Thus, there are 0, 1, and 2 nodes for Is, 2s, and 3s -orbitals respectively.

Shapes of ρ-orbitals:

On solving the Schrodinger equation for 2p orbital of H-atom, it has been known that wave function depends on—

• The distance (r) from the nucleus and also the orientation of the orbital in three-dimensional space (x, y, z).
• Probability density calculation shows that each p -p-orbital consists of two sections, which are the regions of maximum electron density.
• These two sections are called lobes, which are on either side ofthe plane passing through the nucleus.
• The probability density of the electron is zero on this plane. It is called the nodal plane.
• Again, the probability density of the electron is equal in both lobes, but the wave function has opposite signs in the two lobes.

• Now, for p-orbitals, f= 1 and hence m = -1,0, +1. Thus there are three p-orbitals in any quantum level (except n = 1 ). The size, shape, and energy of the three p -orbitals are identical.
• They differ, however, in the way the lobes are oriented. Since the lobes may be considered to lie along the three axes x, y, and z, they are assigned the designations px, py, and pz respectively.
• It should be noted, however, that there is no simple relation between the values of m(-l; 0, +1) and the x, y, and z directions.

The wave functions for the three p -p-orbitals are—

⇒ \(\psi_x=f(r) \cdot f(x) ; \psi_y=f(r) \cdot f(y) ; \psi_z=f(r) \cdot f(z)\)

The three p-orbitals corresponding to a particular quantum level are said to be degenerate because they have the same energy.

• Thus there are three degenerate p-orbitals in each of the second n = 2, third n = 3, fourth n = 4, etc. quantum levels.
• Like s -s-orbitals, p -p-orbitals increase in size and energy with an increase in the principal quantum number (n). Hence the order of increasing size and energy of various p -p-orbitals is 2p< 3p < 4p < …..
• Now the number of radial nodes for 2p -orbital -n-1-1 = 2-1-1 = 0. Thus 2p -orbitals [i.e., 2px, 2py, 2pz) have no radial nodes.

The number of radial nodes for p -p-orbitals of some of the higher quantum levels is given in the following table.

For px -orbital probability density is zero in the yz -plane. So yz -plane is the nodal plane of px -orbital. Similarly zx and xy -planes are the nodal planes for py and pz orbitals respectively.

• It should be remembered that the number of nodal planes for any orbital is equal to the value of azimuthal quantum number l corresponding to that orbital.
• The number of nodal planes is, however independent of the principal quantum number ‘ n ‘.

The no. of nodal planes for s, p, d, and f-orbitals (belonging to any principal quantum level) are 0, 1, 2, and 3 respectively.

Shapes of d-orbitals:

From solutions of the Schrodinger wave equation for 3d -orbitals of H-atom it has been known that the wave function depends on the distance from the nucleus (r) and also on two different directions in space,

For example f(f)  = f(r)-f(x)-f(y) Now, for 3d -orbital, 1 = 2. Hence m = -2, -1, 0, +1, +2.

Thus there are five d -d-orbitals in the 3rd quantum level.

These d -d-orbitals have the same energy and hence they are degenerate. These orbitals are designated as dxydyzdzx>dx2-y2 and dz2- Probability density calculation shows that the orientations of these orbitals in space are different.

The shapes of the first four d -d-orbitals are similar to each other (which has four lobes) whereas that ofthe fifth dz2 is different (which has only two lobes).

The d -orbitals for which n is greater than three {viz., 4d, 5d, etc.) also have shapes similar to 3d -orbitals, but they differ in energy and size.

dxy -orbital has four lobes, lying in the xy -plane. The hatch lobe makes an angle of 45° with x and y-axes.

The wave function for d -orbital has the same sign (either + or – ) in each pair of opposite lobes, but opposite signs (+ and – ) I in adjacent lobes, relating to the symmetry of the angular wave function.

The wave function if =0 along the x, y, and z axes indicates that the xz – and yz – planes represent the nodal planes of the d -orbital.

These planes are at right angles with each other. Similarly, dyz -the orbital has four lobes lying in the yz -plane, each lobe makes an angle of 45° with the y and z axes.

The wave function dxy =0 along the three axes (x, y, and z) indicates that the xy and xz planes constitute the nodal planes of the dyz -orbital. The planes are at right angles with each other.

Similarly, dxz -the orbital has four lobes lying in the xz-plane, each lobe makes an angle of 45° with x and z-axes. The wave function ifrd =0 along the three axes (x, y, and z), indicates that xy and yz -planes constitute the nodal planes of dxz -orbital. These planes are at right angles with each other.

dx2-y2 -orbital has four lobes which lie along the x and y axes in the xy -plane. The wave function xy = ψ ax2-y2 along the z-axis indicates that this orbital has two nodal planes that pass through the origin and make angles of 45° with xz and yz -planes. These two planes are at right angles with each other.

dz² -orbital has two lobes (having the same sign which lie along the z-axis and contain an annular portion surrounding the nucleus in the xy-plane. This annular portion of the orbital is called the doughnut or belly band.

A conical surface passing through the origin constitutes the nodal plane of the dz2 -orbital.

F-Orbitals Schrodinger wave equation gives a set of solutions when the azimuthal quantum number f has the value 3. These are called f-orbitals. For l = 3, m has the values -3, -2, -1, 0, +1, +2, +3. Thus there are seven f-orbitals.

For the existence of f-orbitals, the minimum value of the principal quantum number, n, has to be 4, as the value of l cannot be greater than (n-l).

These seven orbitals have the same energy (degenerate) but they differ in their orientations in space. The seven f-orbitals are designated.

⇒ \(\text { as }-f_{x\left(x^2-y^2\right)}, f_{y\left(x^2-y^2\right)}, f_{z\left(x^2-y^2\right)}, f_{x y z}, f_{z^3}, f_{y z^2}, f_{x z^2} \text {. }\)

1. No. spherical/radial nodes in any orbital = n-1- 1
2. No. of planar or angular nodes in any orbital = Z
3. Total no. of nodes in any orbital = n-1

Structure of Atom Class 11 Notes

Rules For Filling Up Of Electrons In Different Orbitals

The correct ground state electronic configuration of an atom is obtained based on the following principles—Pauli’s exclusion principle, Hund’s rule, and the Aufbau principle.

Pauli’s exclusion principle

Principle:

The knowledge of four quantum numbers is important in assigning the exact location of the electron within an atom.

• After meticulous study of the line spectra of atoms, Wolfgang Pauli in 1925 proposed his exclusion principle which is widely known as Pauli’s exclusion principle.
• According to this principle, no two electrons in an atom will have the same values for all four quantum numbers (n, l, m, and s).
• If three of the quantum numbers of any two electrons are the same then they must differ in their fourth quantum number.
• If the quantum numbers n, l, and m of two electrons have identical values, then the value of s should be different (+i for one and for the other).
• Therefore, the corollary of this principle may be stated as—each orbital can accommodate a maximum of two electrons having an opposite spin.

With the help of Pauli’s exclusion principle, the maximum number of electrons a subshell can accommodate can be calculated. For example—

s -subshell:

In the case of s -subshell, 1 = 0. Therefore m = 0. Number of orbitals in s -subshell = 1.

According to Pauli’s exclusion principle, each orbital can hold a maximum number of two electrons. So, s -subshell can accommodate a maximum of 2 electrons.

p -subshell:

For p -subshell, 1=1 and m = —1,0, +1. The number of orbitals in the -subshell is three (px, py, and pz ).

According to Pauli’s exclusion principle, since each orbital can hold a maximum of 2 electrons, the maximum accommodating capacity of p -subshell {i.e., three p orbitals)

=3 × 2 = 6 electrons.

d -subshell:

In the case of d -subshell, 1 = 2, m = -2, -1, 0 +1, +2. Thus, m has 5 values indicating the presence of 5 orbitals. As the maximum number of electrons that each orbital can hold is 2, the maximum number of electrons that a d -d-subshell can accommodate is 5× 2 = 10.

f-subshell:

For f-subshell, l = 3, m = -3, -2, -1, 0, +1, +2, +3. Seven values of m indicate the presence of seven orbitals. Hence the maximum number of electrons that may be present in f-subshell is 7 × 2 = 14.

Pauli’s exclusion principle also permits the determination of the maximum number of electrons that can be present in a certain orbit or shell.

Example:

For L -shell (n = 2), l has two values, i.e., 1 = 0 [ssubshell] and l = 1 [p -subshell].

The s -subshell can hold 2 electrons and p -subshell can accommodate 6 electrons. Therefore, the maximum accommodating capacity for L shell =(2 + 6) = 8 electrons.

Similarly, it can be shown that, the maximum number of electrons that can be accommodated in M-shell (n = 3) = 18 and the maximum number of electrons that may be present in IVshell (n = 4) =32.

Electron accommodating capacity of K, L, M, and V-shell

Thus, it is seen that the maximum number of electrons accommodated in any electronic orbit with the principal quantum number’ n’ is 2n2.

Number of orbitals and electron accommodating capacity of different shells.

Hund’s multiplicity rule:

This rule helps decide the mode of filling of the orbitals of the same energy level with electrons.

Rule:

The pairing of electrons in the orbitals within the same subshell does not take place until the orbitals are singly filled up with electrons having parallel spin.

Discussion:

The rule implies that orbitals with the same energy are filled up first with one electron and then the additional electron occupies the singly filled orbital orbital to form paired electrons (with opposite spin).

The energy order of the orbitals, the Aufbau principle, and the electronic configuration of atoms

The German word ‘Aufbau’ means ‘to build one by one! The Aufbau principle gives the sequence of gradual filling up of the different subshells of multi-electron atoms.

Aufbau principle:

The Aufbau principle states that electrons are added progressively to the various orbitals in the order of increasing energy, starting with the orbital with the lowest energy.

Electrons never occupy the die orbital of higher energy leaving the orbital of lower energy vacant.

A study of the results of spectral analysis has led to the arrangement of the shells and subshell in the increasing order of their energies in the following sequence:

Is < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f< Sd < 6p < 7s < 5f< 6d ..

Electronic configuration always conforms to Pauli’s Exclusion Principle.

According to Hund’s rule, pairing electrons in the orbitals within the same subshell (degenerate orbitals hating the same n ) cannot occur until the orbitals are singly filled up.

The energy of the subshell increases with an increase in the value of (n + l). In a multi-electron atom, the energy of a subshell, cannot be determined only by principal quantum number (n ), in exclusion of azimuthal quantum number (Z).

The correct order of energies of various subshells is determined by the (n + 1) rule or Bohr-Bury rule.

The implication of the rule can be better understood with the help ofthe following example.

In case of 3d -subshell, (n + Z) = (3 + 2) = 5, but for 4s -subshell, (n + Z) = (4 + 0) = 4 .

From this, it is clear that the energy of the 4s -subshell is less than that of the 3d -subshell. Hence, the electron goes to the 4s subshell first, in preference to the 3d -subshell.

If Two subshells have the same value for{n + 1), then the electron enters that subshell which has a lower value of n.

For example, for 3d -subshell, (n + 1) = (3 + 2) = 5 and for 4p -subshell, (n + 1) = (4 + 1) = 5 In this case, the electron first enters the 3d -subshell which has a.lower value of n.

The sequence in which the subshells are filled with electrons.

The figure depicts the sequence of filling up of the subshells with electrons. The electronic configuration of any atom can be easily predicted from this diagram.

Exceptions to (n+1) rule:

Exceptions to the {n + Z) rule are found to occur in the case of filling up of electrons in Lanthanum (La) and Actinium (Ac).

The values of (n + 1) in the case of both the subshells 4/ and 5d (4 + 3 = 7 = 5 + 2) are found to be the same.

Similarly the values of (n +1) in the case of both the subshells 5/ and 6d (5 + 3 = 8 = 6 + 2) are equal. So, the order of energies of these subshells is 4f< 5d and 5f< 6d.

According to the (n + Z) rule, the expected electronic configuration of La (57) and Ac (89) should be [Xe]4/15d06s2 and [Rn]5/16d°7s2 respectively.

However, the electronic configuration of La and Ac are actually [Xe]4/ and [Rn]5/°6d17s2 respectively. In other words, lanthanum and actinium are exceptions to the (n + 1) rule.

Method of writing electronic configuration of an atom 1) To express the electronic configuration of an atom, the principal quantum number (n = 1, 2, 3… etc.) is written first.

The symbol ofthe subsheU(s, p, d, f, etc.) is written to the right ofthe principal quantum number. For example, s -subshell of the first shell is expressed as Is; sand subshells of the second shell are expressed as 2s and 2p respectively.

The total number of electrons present in any subshell is then written as the right superscript of the subshell symbol.

For example, the electronic configuration, ls²2s²2p⁵ suggests that the s -subshell of the first shell contains 2 electrons, and the s, and p -subshells of the second shell contain 2 electrons and 5 electrons respectively. Thus, the total number of electrons present is equal to 9.

Examples: Electronic configuration of ₁₇CL atom:

The atomic number of chlorine is 17. Number of electrons present in chlorine atom is 17.

Out of these 17 electrons, 2 electrons are present in the s -subshell of the first shell (K-shell), 2 electrons and 6 electrons in the s – and p -subshell of the second shell (L -shell) respectively, and 2 and 5 electrons are present in the s – and p -subshell of the third shell (Mshell) respectively.

Thus, the electronic configuration of the chlorine atom is ls²2s²2p63s²3p5.

Electronic configuration of ₂₆Fe atom:

The atomic number of iron is 26. Number of electrons present in an atom of iron is 26. These 26 electrons are distributed in K, L, M, and N-shells in such a way that their electronic configuration becomes ls²2s²2p⁶3s²3pe³de4s².

Here the symbol signifies an orbital and the arrow sign (↑) means an odd electron and the paired arrow sign (↓↑) stands for a pair of electrons with opposite spins.

Stability of half-filled or filled subshells The electronic configurations of some atoms have certain characteristic features.

It is seen that half-filled and filled subshells are more stable compared to nearly half-filled or nearly-filled subshells.

Hence, if the (n-1)d -subshell of any atom contains 4 or 9 electrons and the ns -subshell contains 2 electrons, then one electron from the ns -subshell gets shifted to the (n-1) d subshell, thereby making a total number of either 5 or 10 electrons in it. As a result, ns -subshell is left with 1 electron instead of 2.

The extra stability of half-filled and filled subshells can be explained in terms of the symmetrical distribution of electrons and exchange energy.

Symmetrical distribution of electrons:

The subshells with half-filled or filled electrons are found to have a more symmetrical distribution of electrons.

Consequently, they have lower energy which ultimately results in greater stability of the electronic configuration.

Electrons present in the same subshell have equal energy but their spatial distribution is different. As a result, the magnitude of the shielding effect of another is quite small and so, the electrons are more strongly attracted by the nucleus.

Interelectronic repulsion:

Two types of interactions are possible between electrons of the same subshell due to interelectronic repulsive force.

Interaction due to electronic charge:

The magnitude of the repulsive force acting between two electrons situated at n distance r from each other is inversely proportional to the square of the distance between them.

Consequently, the stability of two-electron or multi-electron ions or atoms increases with an increase in distance r. Thus, die two electrons present in the d -d-subshell prefer to be in two separate d -orbitals instead of one leading to the increased stability ofthe atom or ion.

Interaction due to rotation of electrons:

Two electrons tend to remain close to each other if they have opposite spins. On the other hand, if both the electrons have parallel spin, then they prefer to remain far from each other.

The electrons occupying degenerate orbitals (orbitals of the same energy) can exchange their positions with other electrons with the same spin. In this process, exchange energy is released.

The greater the probability of exchange, the more stable the configuration. The probability of exchange is greater in the case of a half-filled or filled subshell.

Thus, the magnitude of exchange energy is greatest for half-filled or filled subshells leading to their exceptionally high stability.

This exchange energy forms the basis of Hund’s multiplicity rule. The relative magnitude of exchange energy can be calculated by the formula,

No. of exchanges \(=\frac{n !}{2 \times(n-2) !}\)

(n = number of degenerate electrons with parallel spin.)

Number of interactions in case of d4 electronic configuration

NCERT Solutions Class 11 Chemistry Chapter 2 Structure of Atom

Total number of exchanges for d4 electronic configuration

=3+2+1=6

Number of interactions in case of d5 electronic configuration

Electronic configuration of ions

When an additional electron is added to an orbital of an atom, a negatively charged ion called an anion is formed while the removal of an electron from the orbital of an atom produces a positively charged ion called cation.

1. Electronic configuration of anions:

The total number of electrons present in an anionic species is = (Z + n) where Z = atomic number and n = number of electrons gained. The electronic configuration ofthe anion is written based on the total number of electrons present in it.

Examples: 

1. Fluoride ion (F^–): Total number of electrons present in F^– ion

= (9 + 1) = 10

Electronic configuration of F^– ion =  ls²2s²2p^6-

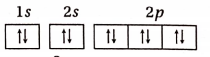
2. Nitride ion (N³¯ ): Total number of electrons present in N³¯ ion

= (7 + 3) = 10

Electronic configuration of N³¯ ion = ls²2s²2p⁶

3. Oxide ion (O²¯): Total number of electrons present in  O²¯ ion

= (8 + 2) = 10.

Electronic configuration of O²¯ ion = ls²2s²2p⁶

4. Sulphide Ion (S²¯): Total number ofelectrons present in S²¯ ion

=(1.6 + 2) = 18

Electronic configuration of S²¯ ion = ls²2s²2p⁶3s²3p⁶

2. Electronic Configuration of cations:

• A total number of electrons present in a cationic species = (Z-n) where Z = atomic number and n = number of electrons lost.
• For writing the electronic configuration of the cation, the electronic configuration of the neutral atom is written first.
• Then requisite no. of electrons is removed from the outermost shell. Electrons from the ns -subshell should be removed before removing any electron from the (n- 1)d -subshell.
• The total number of electrons present in a cationic species = (Z-n) where Z = atomic number and n = number of electrons lost.
• For writing the electronic configuration of the cation, the electronic configuration of the neutral atom is written first.
• Then requisite no. of electrons is removed from the outermost shell. Electrons from the ns -subshell should be removed before removing any electron from the (n- 1)d -subshell.

Examples:

1. Sodium ion (Na⁺):

Electronic configuration of = \({ }_{11} \mathrm{Na}: 1 s^2 2 s^2 2 p^6 3 s^1\)

⇒ \(\mathrm{Na}^{+} \text {lon: } 1 s^2 2 s^2 2 p^6\)

2. Chromium Ion (Cr³⁺):

Electronic Configuration of =   \({ }_{24} \mathrm{Cr}: 1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^5 4 s^1\)

⇒ \(\mathbf{C r}^{3+} \text { ion: } 1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^3\)

3. Manganese ion (Mn²⁺):

Electronic Configuration of = \(25^{\mathrm{Mn}}: 1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^5 4 s^2\)

⇒ \(\mathbf{M n}^{2+} \text { ion: } 1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^5\)

4. Ferrous (Fe²⁺) and Ferric (Fe³⁺) ion:

Electronic Configuration of = \({ }_{26} \mathrm{Fe}: 1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^6 4 s^2\)

⇒ Ferrous ion (Fe²⁺): =\(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^6\)

⇒ Similarly, ferric ion (Fe³⁺):

Electronic Configuration of =\(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^5\)

5. Cuprous (Cu⁺) and Cupric (Cu²⁺) ion:

⇒  Cu⁺+ ion:

Electronic Configuration of = ls²2s²2p⁶3s²3p⁶63d¹⁰

⇒ Similarly, cupric ion (Cu²⁺):

Electronic Configuration of =  ls²2s²2p⁶3s²3p⁶63d⁹

Numerical Examples

Question 1. A sample of gaseous oxygen contains only 180 isotopes. How many neutrons are present in 11.2 L of the gas at STP?
Answer:

No. of neutrons present in an atom of 180 isotope

=(18-8) = 10

∴ No. of neutrons present in 11.2L of  the gas

= \(\frac{2 \times 10 \times 6.022 \times 10^{23} \times 11.2}{22.4}=6.022 \times 10^{24}\)

Question 2. Calculate the energy required for the promotion of electrons from the 1st to 5th Bohr orbit of all the atoms present in 1 mole of H-atoms.
Answer:

Electronic energy in the n-th orbit ofH-atom

⇒ \(E_n=-\frac{1312}{n^2} \mathrm{~kJ} \cdot \mathrm{mol}^{-1}\)

∴ Total energy required

= \(\left(E_5-E_1\right)=-\frac{1312}{5^2}-\left(-\frac{1312}{1^2}\right)=1259.52 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}\)

Question 3. Calculate the velocity (cm-s-1) and frequency of revolution of electron present in the 3rd orbit of H-atom.
Answer:

Velocity of revolving electron present in the 3rd orbit of H atom

= \(\frac{2 \pi z e^2}{n h}=\frac{2 \times \pi \times 1 \times\left(4.8 \times 10^{-10}\right)^2}{3 \times 6.626 \times 10^{-27}}\)

Frequency of revolution ofthe electron

= \(\frac{v}{2 \pi r}=\frac{v}{2 \pi\left(\frac{n^2 h^2}{4 \pi^2 m z e^2}\right)}=\frac{2 \pi m v z e^2}{n^2 h^2}\)

= \(\frac{2 \times 3.14 \times\left(9.11 \times 10^{-28}\right) \times\left(7.27 \times 10^7\right) \times 1 \times\left(4.8 \times 10^{-10}\right)^2}{(3)^2 \times\left(6.626 \times 10^{-27}\right)^2}\)

= 2.4242 ×  10¹⁴

Question 4. Calculate the wavelength and frequency associated with the spectral line having the longest wavelength in the fund series of hydrogen spectra.
Answer:

In the case of the Pfund series, the spectral line with the longest wavelength is obtained when the electronic transition occurs from n2 = 6 to nl = 5. Thus

⇒ \(\bar{v}=\frac{1}{\lambda}=109678\left(\frac{1}{5^2}-\frac{1}{6^2}\right)=1340.5\)

⇒ \(\lambda=7.4 \times 10^{-4} \mathrm{~cm}\)

= \(\frac{c}{\lambda}=\frac{3 \times 10^{10}}{7.4 \times 10^{-4}}\)

v = \(\frac{c}{\lambda}=\frac{3 \times 10^{10}}{7.4 \times 10^{-4}}=4.05 \times 10^{13} \mathrm{~s}^{-1}\)

= \(4.05 \times 10^{13} \mathrm{~Hz}\)

Question 5. Calculate the energy of 1 mol of photons associated with a frequency of 5 ×10¹⁰s^-1
Answer:

E = N₀hv=  \(6.022 \times 10^{23}\left(6.626 \times 10^{-34}\right)\left(5 \times 10^{10}\right)\)

=19.95J

Question 6. The wavelength associated with a moving particle of mass 0.1 mg is 3.3× 10^-29m. Find its velocity, [h = 6.6×  10^-34 kg.m².s^-1]
Answer:

λ =  \(\frac{h}{m v}\)

v = \(\frac{h}{m \lambda}=\frac{6.6 \times 10^{-34}}{\left(0.1 \times 10^{-6}\right) \times\left(3.3 \times 10^{-29}\right)}\)

= \(200 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Question 7. Calculate the kinetic energy of a moving electron associated with a wavelength of 4.8 pm.
Answer:

v = \(\frac{h}{m \lambda}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{\left(9.11 \times 10^{-31} \mathrm{~kg}\right) \times\left(4.8 \times 10^{-12} \mathrm{~m}\right)}\)

= \(1.51 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Kinetic energy

⇒  \(=\frac{h}{m \lambda}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{\left(9.11 \times 10^{-31} \mathrm{~kg}\right) \times\left(4.8 \times 10^{-12} \mathrm{~m}\right)}\)

=\(1.038 \times 10^{-14} \mathrm{~J}\)

NCERT Class 11 Chemistry Chapter 2 Atom Structure Notes

Question 8. Calculate the frequency and wavelength of the energy emitted when the electron jumps from the 4th orbit to the 1st orbit of the H-atom.
Answer:

⇒  \(\bar{v}=\frac{1}{\lambda}=1.09678 \times 10^7 \times\left(\frac{1}{1^2}-\frac{1}{4^2}\right)=10.28 \times 10^6 \mathrm{~m}^{-1}\)

⇒  \(\text { Frequency, } v=\frac{c}{\lambda}=\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{9.73 \times 10^{-8} \mathrm{~m}}=3.1 \times 10^5 \mathrm{~s}^{-1}\)

Question 9. The wavelength of the first line in the Balmer series of H-atom is 15200 cm^-1. Calculate the wavelength of the first line in the same series of Li²⁺ ions. 10. The ionization potential of sodium is 4.946 × 102kJ.mol^-1 Calculate the wavelength of the radiation required to ionize a sodium atom

⇒  \(\bar{v}_{\mathrm{H}}=R_H\left(\frac{1}{2^2}-\frac{1}{n^2}\right)=15200 \mathrm{~cm}^{-1}\)

= \(\bar{v}_{\mathrm{Li} \mathrm{i}^{3+}}=\bar{v}_{\mathrm{H}} \times z^2=15200 \times 3^2=136800 \mathrm{~cm}^{-1}\)

Question 11. The wavelength range of the visible spectrum extends from violet (400 nm) to red (750 nm). Express these wavelengths in frequencies (Hz) (Inm = 10⁹m)
Answer:

For violet light, \(v_1=\frac{c}{\lambda_1}=\frac{3 \times 10^8}{400 \times 10^{-9}}=7.5 \times 10^{14} \mathrm{~Hz}\)

For red light, \(v_2=\frac{c}{\lambda_2}=\frac{3 \times 10^8}{750 \times 10^{-9}}=4.0 \times 10^{14} \mathrm{~Hz}\)

Thus the frequency range of visible light extends from 11.0 × 10¹⁴HZ to 7.5 × 10¹⁴ Hz.

NCERT Solutions For Class 11 Chemistry Chapter 2 Structure Of Atom Very Short Questions And Answers

Question 1. What is the value of the elm of an electron?
Answer: 1.76 × 10⁸Cg^-1

Question 2. How many times is a proton heavier than an electron?
Answer: 1837 times (approx.),

Question 3. Mention one similarity between isobar and isotone-
Answer: Atoms of different elements,

Question 4. What is wave number?
Answer: No. of waves in 1 cm,

Question 5. Arrange in order of the increasing wavelength
Answer: γ-ray

Question 6. What is meant by stationary orbit?
Answer: Orbits in which the energy of revolving electrons remains fixed

NCERT Class 11 Chemistry Chapter 2 Very Short Questions and Answers

Question 7. Who proposed the quantum theory of radiation?
Answer: M. Planck

Question 8. What is the value of Planck’s constant in the SI unit?
Answer: 6.626 × 10^-34

Question 9. What is the value of the angular momentum of an electron occupying the second orbit in an atom?
Answer: \(\frac{h}{\pi}\)

Question 10. Mention the symbol and the mass number of an element that contains two neutrons in the nucleus.
Answer: \({ }_2^4 \mathrm{He}\)

Question 11. Why is the spectrum of H⁺ not obtained?
Answer: Because H⁺ does not contain any electrons,

Question 12. How many protons & electrons are in H^–ion?  
Answer: One proton and two electrons,

Question 13. From which principal energy state, the excited electron comes down to yield spectral lines in the Balmer series?
Answer: L-shell (n = 2),

Question 14. How many neutrons are present in and ₂₀ ⁴⁰ Ca ²⁺
Answer: 20 neutrons,

Question 15. What is the nature of hydrogen spectra?
Answer: Discontinuous spectrum or line spectrum,

Question 16. Mention one ion that obeys Bohr’s theory.
Answer: He⁺,

Question 17. Write the relationship between wavelength and momentum of a moving microscopic particle. Who proposed this relationship?
Answer: \(\lambda=\frac{h}{m v}\)

Question 18. Indicate the limitation of Broglie’s equation.
Answer: Not applicable to macroscopic particles,

Question 19. Is the uncertainty principle applicable to stationary electrons?
Answer: Not applicable

Class 11 Chemistry Chapter 2 Structure of Atom Short Q&A

Question 20. Energy associated with which of the following waves is not quantized?

• Electromagnetic wave
• Matter-wave

Answer: Matter waves,

Question 21. What is an orbital according to the quantum mechanical model?
Answer: The region around the nucleus has the maximum probability of finding an electron,

Question 22. How do you specify an electron in an atom?
Answer: By using four quantum numbers (n, l, m and s),

Question 23. What is the maximum number of orbitals in the ‘j’th orbit?
Answer: n²,

Question 24. Which is the lowest energy level containing ‘g1 sub-shell?
Answer:  n = 5 (fifth shell),

Question 25. Identify the orbital with n = 4 and 1 = 0.
Answer: 4s,

Question 26. Which ‘d’-orbital does not contain four lobes?
Answer: d_z2

Question 27. Which quantum electron?
Answer: Azimuthal quantum number (l),

Question 28. Write the electronic configuration of Mn
Answer: ls²2s²2p⁵3s² 3p⁶3d⁵,

Question 29. What is the total number of nodes in 3d -orbital?
Answer:

Total no. of nodes =(n-1)

= 3- 1

= 2

Question 30. Which subshell has the lowest screening power?
Answer: f

Question 31. Which quantum number is used to distinguish between the electrons present in a single orbital?
Answer: Spin quantum number, S,

Question 32. What are the quantum numbers used to indicate the size and shape of orbitals?
Answer: Principal & azimuthal quantum numbers,

Question 33. State the condition under which electronic energy is considered to be negative.
Answer: When the electron is at an infinite distance from the nucleus ( n = ∞ )

Question 34. What are the fundamental constituents____of atom?
Answer: Electrons, protons, and neutrons are the fundamental constituents of an atom.

Question 35. Name the element containing no neutrons.
Answer: Ordinary hydrogen atom or protium:

Structure of Atom Class 11 Very Short Questions and Answers

Question 36. Name the anode ray particle with the highest value.
Answer: The e/m value of a proton (H⁺ ion) has the highest value.

Question 37. What is the consequence when cathode rays strike a hard metal surface like tungsten?
Answer: X-rays are produced.

Question 38. Why is an electron called a universal particle?
Answer: Its mass and charge are independent of its source

Question 39. What is the value of a fundamental unit of electricity?
Answer: The charge carried by one electron is said to be the fundamental unit of electricity. Its magnitude is 4.8 × 10^-19 esu or 1.602 × 10^-19 C.

Question 40. Besides electron, proton, and neutron, name two other subatomic particles.
Answer: Positron (₊₁e ⁰ ) and Neutrino (₀v⁰ ).

Question 41. Out of X-rays, γ-rays, and microwaves, which one has die highest and which one has die lowest frequency?
Answer:

Highest frequency: γ-rays

Lowest frequency: Microwave

Question 42. Arrange the given subshells in the increasing order of their energies: 3d, 4p, 4s, 5p, 4d, 6s, 4f.
Answer:

The sequence of energy of the given subshells is 4s < 3d < 4p < 4d < 5p < 6s < 4.

Question 43. What is the main difference between a wave emitted by an electric bulb and that associated with a tiny particle moving at a very high speed?
Answer: The bulb emits electromagnetic waves, while that associated with the moving particle is matter.

Question 44. At what distance from the nucleus is the radial probability maximum for the Is -orbital of the hydrogen atom? What is this distance called?
Answer: At a distance of 0.529Å, the radial probability is maximum. This distance is called the Bohr radius.

Question 45. In which shell(s), there is no existence of d -subshell?
Answer: There is no existence of ‘d’ subshell in K and L -shells

Question 46. Out of the four quantum numbers which one does not result from the solution of the Schrodinger wave equation?
Answer: Spin quantum number.

Quantum 47. The 4f-subshell of an atom contains 12 electrons. What is the maximum number of electrons having spins in the same direction?
Answer: Seven electrons have spin in the same direction.

Question 48. What is the lowest value of n that allows g-orbitals to exist?
Answer: For the existence of g-subshell, 1 should be 4. For a given orbital, the maximum value of 1 = (n-1). Thus, for 1 = 4, the minimum value of n should be 5.

Question 49. An electron is in one of the 3d orbitals. Give the possible values on n, l, and mI for this electron.
Answer:

For 3d-subshell, n = 3,1 = 2  and m₁ = -2, -1, 0, +1, +2.

Question 50. Give the number of electrons in the species ⁺H₂, H₂, and.
Answer: The number of electrons present in ⁺H₂, H₂, and ₂O⁺ is 1, 2, and 15 respectively.

Question 51. Arrange falling radiations in increasing order of frequency; radiation from microwave own amber light from traffic signal radiation from FM radio cosmic ray from outer space X-rays.
Answer: Radiation from FM radio < microwave < amber light < Xrays < cosmic rays.

Question 52.  Write the possible values of’ m ‘ for a 4/-electron. 

Answer:

For a 4f-elcctron, n = 4, l = 3. Thus, the possible value of m will be: +3, +2, +1, 0, -1, -2, -3

Question 53. How many numbers of electrons are present in one HClO₄ molecule?
Answer: In one molecule of HClO₄molecule, total number of electrons present in it = (1 + 17 + 4 ×  8) = 50

Very Short Questions for Class 11 Chemistry Chapter 2

Question 54. Explain why cathode rays are produced only at very low pressure of gas inside the discharge tube-
Answer: Gases being had conductor do not allow electricity to pass through them In discharge tube at high pressure.

Question 55. Mention two uses of cathode ray tubes in our daily life.
Answer: Television picture tube and fluorescent tube.

Question 56. Calculate the charge of 1 mol electron.
Answer: Charge Avogrado no, x Charge of 1 electron

⇒  (6.022 × 10²³) × (1,602 ×10^-19) =9.047 × 10⁴C

Question 57. What happens when high-velocity cathode rays strike a tungsten foil?
Answer: X-rays are emitted.

Question 58. Who discovered the neutron?
Answer: J. Chadwick (1932).

Question 59.  Between proton or neutron which one is heavier?
Answer: Neutron (1.675× 10^-24g) is slightly heavier than proton (1.6725× 10^-24g).

Question 60. Name the experiment that helps us to determine the number of protons in the nucleus of an atom.
Answer: Moseley’s experiment on X-rays

Question 61. What is the relation between Cl^– and S^2-?
Answer: Both have 18 electrons and hence, are isoelectronic

Question 62. Mention the most important application of the de Broglie concept.
Answer: The de-Broglie concept is utilized in the construction of an electron microscope used for the measurement of the size of very small objects.

Question 63. Identify the relation between the nuclides, ₁₄Si³⁸ & ₁₅P³¹.
Answer: The number of neutrons in the nuclides is the same. Thus, they are isotones.

Question 64. A cation M³⁺ has 23 electrons. Find the atomic no. of M.
Answer: Number of electrons present in the neutral M-atom.

Question 65. Mention any three phenomena that can be explained with the help of the wave theory of light.
Answer: Interference, diffraction, polarisation.

Question 66. Differentiate between a quantum and a photon.
Answer:

The smallest packet of energy of any electromagnetic radiation is quantum and that of light is called a photon.

Question 67. Which property of electromagnetic radiation is useful in explaining the phenomena involving energy transfer?
Answer: Particle nature of electromagnetic radiation

Question 68. An electron beam hitting a ZnS screen produces scintillations on it What do you conclude?
Answer: From this phenomenon, we can conclude that electrons have a particle nature.

Question 69. An electron beam after hitting a nickel crystal produces a diffraction pattern. What do you conclude?
Answer: From this phenomenon, we can conclude that electrons have a particle nature.

Question 70. What type of spectrum will be obtained if the electron o/Hatom approaches its nucleus inspiral pathway?
Answer: A continuous spectrum will be obtained due to the constant emission of energy.

Question 71. Name the series of spectral lines observed in the visible region of the hydrogen spectrum.
Answer: Balmer series

Question 72. Which electronic transition corresponds to the third line in the Balmer series ofthe hydrogen spectrum?
Answer: Electronic transition from the 5th orbit to the 2nd orbit.

Question 73. Name the five series in the atomic spectrum of hydrogen.
Answer: Lyman, Balmer, Paschen, Brackett and Pfund.

Question 74. What is meant by the quantization energy of an electron?
Answer: This means that the electrons in an atom have only definite values of energy

Question 75. Mint is the value of Planck’s constant in the SI unit.
Answer: h = 6.626 × 10^-34J-s

NCERT Class 11 Structure of Atom Very Short Answer Solutions

Question 76. Which theory forms the basis of Bohr’s atomic model?
Answer: Planck’s quantum theory.

Question 77. Who proposed the concept of the dual nature of electrons?
Answer: The concept was proposed by de Broglie.

Question 78. Whatare de Broglie waves?
Answer: The waves associated with matter particles in motion are called matter waves or de Broglie waves.

Question 79. Write de Broglie equation for microscopic particles.
Answer: \(\lambda=\frac{h}{p}\) wavelength p = momentum of particle (mv).

Question 80. What is the relation between wave nature and particle nature of moving particles?
Answer: Wave nature \(\propto \frac{1}{\text { particle nature }}\).

Question 81. For which particles is the uncertainty principle applicable?
Answer: Heisenberg’s uncertainty principle applies to tiny subatomic particles like electrons, protons, neutrons, etc.

Question 82. Write Schrodinger’s wave equation, indicating the significance ofthe notations used.
Answer: Schrodinger’s wave equation is based on the dual nature (wave and particle) of electrons.

Question 83. What is the basis of Schrodinger’s wave equation?
Answer: Schrodinger’s wave equation is based on the dual nature (wave and particle) of electrons.

Question 84. Schrodinger’s wave equation does not give us any idea about which quantum number.
Answer: Spin quantum number (s).

Question 85. How many nodal planes are present in 5d –orbital.
Answer: Number of nodal planes in 5d -orbital = 2

Question 86. Write the expression for radial distribution Junction.
Answer: RDF = 4π²r Ψ²

Question 87. Calculate the number of radial nodes and planar nodes in the 4d_x²-y² orbital.
Answer:

No. of radial nodes =n-l-1 = 4-2-1 = 1

No. of planar nodes = l = 2

Question 88. What will be the sign of 2Ψ along an axis on the two opposite sides ofthe nucleus?
Answer: The sign of Ψ_2p along an axis will be opposite on the two opposite sides ofthe nucleus

Question 89. What will be the values of Ψ_2px,Ψ_2py, and Ψ_2pz When the value of r=0?
Answer: When r = 0 , the value of Ψ_2px ,Ψ_2py  and Ψ_2pz, is zero (0).

Question 90. In which direction the value of Ψd_xy is zero?
Answer: Along the x,y, and z-axis

Question 91. In which direction the value of  d_x²-y² is the highest?
Answer: Along the x and y-axis.

Question 92. How many angular nodes are present in d_xy -orbital? Identify them.
Answer: Two angular nodes are present (xz -plane and yz -plane).

Question 93. In which direction is the value ofdÿ, is zero?
Answer: Along z -the z-axis.

Question 94. How many angular nodes are possible for an orbital?
Answer: ‘V number of angular nodes are possible (where Z = azimuthal quantum number).

Question 95. Does the number of angular nodes of an orbital depend on the principal quantum number?
Answer: No, it depends only on the azimuthal quantum number.

Structure of Atom Class 11 NCERT Solutions for Short Questions

Question 96. How many angular nodes are present in s -s-orbital? Indicate the subshells present in the M -M-shell. How many orbitals are present in this shell?
Answer: s -orbital does not possess any angular nodes because the value of the angular wave function cannot be zero in any direction.

Question 97. How many quantum numbers are needed to designate an orbital? Name them.
Answer: Three quantum numbers are needed to designate an orbital, namely, ‘ n ‘ l’ and ‘ m

Question 98. Write the vdltt&Wfthe magnetic quantum number for the ‘3d ’-orbitals.
Answer: For 3d orbitals, 1 = 2. Hence the values of the magnetic quantum no., ‘ m’ are +2, +1, 0, -1, -2.

Question 99.4f-subshell of an atom contains 10 electrons. How many of Write the expression for the orbital angular momentum of a revolving electron.
Answer: The orbital angular momentum of the electron, ‘U is given by: L \(\sqrt{l(l+1)} \times \frac{h}{2 \pi}\)

Question 100. Write the expression for the orbital angular momentum of arevolving electron
Answer: The orbital angular momentum of an electron, ‘U is given by: I = \(\sqrt{l(l+1)} \times \frac{h}{2 \pi}.\)

Question 101. Why does an electron pair in an orbital have an opposite spin?
Answer: If a pair of electrons with parallel spin are present in the same orbital then they will repel each other.

Question 102. Balmer series of hydrogen spectrum lies in which region?
Answer: It lies in the visible region ofthe spectrum.

Question 103. How are the frequency and wave number of electromagnetic radiation related to each other?
Answer:

⇒ v=\(\frac{c}{\lambda}=c \times \frac{1}{\lambda}=c \times \bar{v}\)wave number \(\bar{v}=\frac{1}{\lambda}\)

Question 104. An electron beam after passing through a thin foil of gold produces a diffraction pattern (consisting of several concentric rings). What do you conclude?
Answer: Electron in motion has wage character.

Question 105. What is a quantum?
Answer: The smallest packet of energy of any radiation is called a quantum.

Question 106. What happens when an electron hits a zinc sulfide screen and what does it prove?
Answer: A scintillation is produced, which in turn proves that the electron has a particle nature.

Question 107. A scintillation is produced, which in turn proves that the electron has a particle nature.
Answer: [‘ m ‘ and ‘ e ‘ represent the mass and charge of the electron]

Question 108. Is Heisenberg’s uncertainty principle applicable to a stationary electron? Explain
Answer: It is not applicable. Since the velocity of a stationary electron is ‘zero’, (v = 0), its position can be located accurately.

Question 109. Name the series of spectral lines obtained, when electrons from various energy levels jump to the first orbit in hydrogen
Answer: Lyman series

Question 110. An atom of an element contains 29 electors and 35 n = 2, 1 = 1, neutrons. Deduce the number of protons and the electronic configuration of the element.
Answer: For an electrically neutral atom, the number of protons = the number of electrons = 29.

NCERT Solutions For Class 11 Chemistry Chapter 2 Structure Of Atom Fill In The Blanks

Question 1. The cgs unit of Planck’s constant is unit is _____________
Answer: Erg-s, J.s,

Question 2. The angular momentum of an electron in the nth orbit is _____________ 2+ ion.
Answer: nh/2π

Question 3. If an α -particle and two (i -particles are emitted from a radioactive element, the element produced becomes an _____________of the parent element.
Answer: Isotope

Question 4. With the help of Bohr’s atomic model, the idea of _____________quantum number was first obtained.
Answer: Principal

Question 5. Bohr’sunitatomic of Rydberg’smodel ignored constant _____________
Answer: Three-dimensional

Question 6. The unit of Rydergs’s Constant In CGS UNit is _____________
Answer: Cm^-1

Class 11 Chemistry Structure of Atom Very Short Questions

Question 7. The range of wavelength of visible light is _____________
Answer:  4000°-8000A°

Question 8. The ionization potential of hydrogen is _____________
Answer:  Cm^-1

Question 9. Uhlenbeck and Goudsmit introduced the concept of_____________ quantum number.
Answer: 13.54eV

Question 10. The product of uncertainties in the position and momentum of an electron is always equal to or greater than_____________
Answer: Spin

Question 11. The product of uncertainties in the position and momentum of the electron is always equal to or greater than_____________
Answer: h/4n

Question 12. The number of magnetic quantum numbers required to describe the electrons of-subshell is _____________
Answer: 1. 12.5

NCERT Solutions For Class 11 Chemistry Chapter 2 Structure Of Atom Long Question And Answers

Question 1. The second line of the Lyman series of H-atom coincides with the sixth line of the Paschen series of an ionic species ‘X. Identify ‘X. (Suppose the value of the Rydberg constant, R is the same in both cases)
Answer:

For the second line of the Lyman series of H-atom,

⇒ \(\bar{v}=R\left(\frac{1}{1^2}-\frac{1}{3^2}\right)\)

For the sixth line of the Paschen series of the species ‘X with atomic number Z, v \(=R Z^2\left(\frac{1}{3^2}-\frac{1}{9^2}\right)\)

Since the Second Line Of Lyman Seriea Coincides With The Sixth Line Of the Paschen Series Of The Species X We Can equate

⇒ \(R\left(\frac{1}{1^2}-\frac{1}{3^2}\right)=R Z^2\left(\frac{1}{3^2}-\frac{1}{9^2}\right)\)

⇒ \(\frac{8}{9}=Z^2 \times \frac{8}{81} \quad \text { or, } Z^2=9\)

Z = 3

∴ The Ionic Spec ies Would Be Li²⁺

Question 2. An element of atomic weight Z consists of two isotopes of mass number (Z-1) and (Z + 2). Calculate the % of the higher isotope.
Answer:

Let the % of the higher isotope [mass number (Z + 2) ] be x.

Hence other isotope [mass number (Z- 1) ] will be (100- x)

Average atomic weight (Z) \(=\frac{x(Z+2)+(100-x)(Z-1)}{100}\)

100Z = Zx + 2x+ 100Z- 100- Zx + x

Or, 3x = 100

or, x= 33.3%

NCERT Class 11 Chemistry Chapter 2 Long Question and Answers

Question 3. Show that the sum of energies for the transition from n = 3 to n = 2 and from n = 2 to n = 1 is equals to the energy of transition from n = 3 to n = 1 in the case of an H-atom. Are wavelength and frequencies of the emitted spectrum also additive to their energies?
Answer:

⇒  \(\begin{aligned}& \Delta E_{3 \rightarrow 2}=R_H\left(\frac{1}{2^2}-\frac{1}{3^2}\right) \\& \Delta E_{2 \rightarrow 1}=R_H\left(\frac{1}{1^2}-\frac{1}{2^2}\right) \\& \Delta E_{3 \rightarrow 1}=R_H\left(\frac{1}{1^2}-\frac{1}{3^2}\right)\end{aligned}\)

From equation (1), (2) and (3) we have,

⇒ \(\Delta E_{3 \rightarrow 2}+\Delta E_{2 \rightarrow 1}=R_H\left(\frac{1}{1^2}-\frac{1}{3^2}\right)=\Delta E_{3 \rightarrow 1}\)

⇒ \(\text { Thus, } \Delta E_{3 \rightarrow 1}=\Delta E_{3 \rightarrow 2}+\Delta E_{2 \rightarrow 1}\)

Since E – hv hence frequencies are also additive but \(E=\frac{h c}{\lambda}\) and thus wavelengths are not additive

Question 4. The Schrodinger wave equation for the 2s electron of a hydrogen atom is, \(\psi_{2 s}=\frac{1}{4 \sqrt{2 \pi}}\left[\frac{1}{a_0}\right]^{3 / 2} \times\left[2-\frac{r}{a_0}\right] \times e^{-r / 2 a_0}\) Node is defined as the point where the probability of finding an electron is zero.
Answer: 

∴ \(\text { If } r=r_0, \psi_{2 s}^2=0\)

∴ \(\frac{1}{32 \pi}\left(\frac{1}{a_0}\right)^2\left(2-\frac{r_0}{a_0}\right)^2 e^{-r_0 / 2 a_0}=0\)

The only factor that can be zero in the above expression is \(\left(2-\frac{r_0}{a_0}\right)\)

∴ \(2-\frac{r_0}{a_0}=0 ; \quad \text { or, } r_0=2 a_0 \text {. }\)

Question 5. If the uncertainty in the position of a moving electron is equal to its DC Broglie wavelength, prove that Its velocity is completely uncertain.
Answer: Uncertainty in the position of the electron, Ax = λ.

λ = \(\frac{h}{p}\) [From de Broglie equation]

∴ \(p=\frac{h}{\lambda}=\frac{h}{\Delta x} \quad \text { or, } \Delta x=\frac{h}{p}\)

According to Heisenberg’s uncertainty principle

∴ \(\Delta x \cdot \Delta p  \frac{h}{4 \pi} \quad \text { or, } \frac{h}{p} \cdot \Delta p\frac{h}{4 \pi} \quad \text { or, } \quad \frac{\Delta p}{p}\frac{1}{4 \pi}\)

or, \(\frac{m \Delta v}{m v}  \frac{1}{4 \pi} \quad \text { or, } \quad \Delta v  \frac{v}{4 \pi}\)

The uncertainty in velocity is so large that its velocity Is uncertain.

Question 6. The electron revolving In the n-th orbit of the Be³⁺ ion has the same speed as that of the electron in the ground state of the hydrogen atom. Find the value of n.
Answer:

The velocity of an electron in the n-th orbit of hydrogen-like species is given by, \(v_n=\frac{Z}{n} \times v_1\)

[where v₁ = velocity of the electron in the 1st orbit of H-atom i.e., the velocity of the electron in the ground state of H-atom, and Z = Atomic number of hydrogen-like species]

Now for \(\mathrm{Be}^{3+} \text {-ion } Z=4 \text {, so } v_n=\frac{4}{n} \times v_1\)

But it is given that, v_n = v₁

∴ \(v_1=\frac{4}{n} v_1 \quad \text { or } n=4\)

Question 7. The mass number of an ion with a unit negative charge is 37. The number of neutrons present in the ion is 10.6% more than that of electrons. Identify the ion.
Answer:

Let the number of protons in the ion = x. Therefore, the number of electrons =x + 1 (y the ion contains a unit negative charge). Thus, the number of neutrons =37-x.

Number of neutrons Number of electrons

= 37- x – (x + 1) = 36-2x

Percent of excess neutrons as compared to electrons =\(\frac{(36-2 x) \times 100}{x+1}\)

Given= \(\frac{(36-2 x) \times 100}{x+1}\)

= 10.6

Or = \(\frac{36-2 x}{x+1}=\frac{106}{1000}\)

or, x = 17.04=17 [v the number of protons present in an atom or an ion cannot be a fraction]

Hence it is a chloride ion (Cl)

Class 11 Chemistry Chapter 2 NCERT Solutions Long Q&A

Question 8. Mention Heisenberg’s uncertainty principle. Calculate the uncertainty of velocity of an electron which has an uncertainty in the position of 1Å
Answer:

According to the Heisenberg uncertainty principle,

⇒ \(\Delta x \times \Delta p\frac{h}{4 \pi} \quad \text { or } \Delta x \times m \Delta v \frac{h}{4 \pi}\)

The uncertainty in position, Δx = 1Å  = 10^-10m

Thus  Δv

= \(\frac{h}{\Delta x \times m \times 4 \pi}\)

= \(\frac{6.626 \times 10^{-34}}{10^{-10} \times 9.1 \times 10^{-31} \times 4 \pi}\)

= \(5.794 \times 10^5 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

Question 9. Calculate the number of electrons which will together weigh one gram. Calculate the mass and charge of one mole of electrons.
Answer:

Mass of one electron = 9.11× 10^-31kg.

∴ 1g or 10 3 kg = \(\frac{1}{9.11 \times 10^{-31}} \times 10^{-3}\) electrons 9.11 ×10^-31 = 1.098 × 10²⁷ elctrons.

Mass of one electron = 9.11× 10^-31kg.

So, mass of one mole of elctrons = (9.11 ×10^-31kg) x (6.022 ×10²³) = 5.485 × 10^-7 kg Charge on one electron = 1.602 × 10^-31C

Thus, charge on one mole of elctrons = (1.602 × 10^-19C) × (6.022 × 10²³) = 9.65 × 10⁴C.

Question 10.

1. Calculate the total number of electrons present in one mole of methane.
2. Find
   1. The total number and
   2. The total mass of neutrons in 7 mg of 14C. (Assume that the mass of a neutron = 1.675 × 10^-27kg).
3. Find
   1. The total number and
   2. The total mass of protons in 34 mg of NH₃ at STP.

Will the answer change if the temperature and pressure are changed?
Answer:

1. 1 molecule of CH₄ contains =6 + 4 = 10 electrons. Thus, one mole or 6.022 × 10²³ molecules will contain

= 6.022 × 10²³× 10 = 6.022 × 10²⁴ electrons.

2.

1. 1 mol ¹⁴C-atom = 6.022 × 10²³

¹⁴C atoms = 14g

¹⁴C .One ¹⁴C -atom contains =14-6 = 8 neutrons.

∴ 14g or 14000 mg 14C = 8 × 6.022 × 10²³ neutrons

2.  Mass of one neutron = 1.675 × 10^-27kg.

So, the mass of 2.4088× 10^-21 k neutrons

= (2.4088 × 10²¹) × (1.675 × 10^-27) = 4.0347 × 10^-6 kg

3.

1. 1 mol NH₃  ≡ l7g NH₄ ≡ 6.022 × 10²³ molecules of NH₃.

Therefore, the number of protons present in 17g

NH₃ = (6.022 × 10²³) × (7 + 3) = 6.022 × 10²⁴

Number of protons in 34 mg or 0.034 g mass 6.022× 10²⁴

NH’₃ – Hg× 0.034g = 1.2044 × 10²²

2. Mass of a proton = 1.6725 × 10^-27kg

Mass of 1.2044 × 10²² protons

= (1.6725× 10^-27) × (1.2044 × 10²²) =2.014 × 10^-5kg

There is no effect of temperature and pressure.

Question 11. What is the number of photons of light with a wavelength of 4000 pm that provide 1J of energy?
Answer:

Wavelength of light (A) = 4000pm

= 4000 × 10^-12m = 4 × 10^-9m

According to Planck’s quantum theory, the energy of a photon

⇒ \(E=N h v=N h \frac{c}{\lambda}\)

[N= no. of photons h= 6.626 × 10^-34 J-s , c = 3.0 ×10⁸ m-s^-1]

⇒  \(N=\frac{E \times \lambda}{h \times c}\)

= \(\frac{1 \mathrm{~J} \times\left(4 \times 10^{-9} \mathrm{~m}\right)}{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right)\left(3.0 \times 10^8\mathrm{~m} \cdot \mathrm{s}^{-1}\right)}\)

= \(2.012 \times 10^{16}\)

Question 12. A photon of wavelength 4 x 10-7m strikes on the metal surface, the work function of the metal is 2.13 eV. Calculate the energy of the photon (eV) the kinetic energy of the emission, and the velocity of the photoelectron (leV = 1.6020 × 10^-19J)
Answer:

Energy of a photon (E) = ,\(h v=\frac{h c}{\lambda}\)

=  \(\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{4 \times 10^{-7} \mathrm{~m}}\)

= \(4.97 \times 10^{-19} \mathrm{~J}\)

Or, energy of a photon \(=\frac{4.97 \times 10^{-19}}{1.602 \times 10^{-19}} \mathrm{eV}=3.10 \mathrm{eV}\)

The kinetic energy of emitted electron = energy of a photon- work function of a metal.

= (4.97 × 10^-19– 2.13 × 1.602 × 10^-19)J

= 1.56 × 10^-19

J = 0.97eV

Kinetic energy of photoelctron, \(\frac{1}{2} m v^2=1.56 \times 10^{-19} \mathrm{~J}\)

⇒ \(\text { or, } v^2=\frac{2 \times 1.56 \times 10^{-19}}{m}=\frac{2 \times 1.56 \times 10^{-19}}{9.108 \times 10^{-31}}=0.34 \times 10^{12}\)

Velocity of photoelectron, v = 5.83 × 10^-5m.s^-1

Question 13. A 25-watt bulb emits monochromatic yellow light of wavelength of 0.57 pm. Calculate the rate of emission of quanta per second.
Answer:

Energy emitted by the bulb = 25 watts = 25 J-s^-1

Energy ofa photon (E) = hv \(h \frac{c}{\lambda}\)

λ = 0.57μm

c= \(0.57 \times 10^{-6} \mathrm{~m}\)

c = \(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

h = \(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\)

Substituting the values we get,

E= \(\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right)\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{0.57 \times 10^{-6} \mathrm{~m}}=3.49 \times 10^{-19} \mathrm{~J}\)

No. of quanta emitted \(=\frac{25 \mathrm{~J} \cdot \mathrm{s}^{-1}}{3.49 \times 10^{-19} \mathrm{~J}}=7.16 \times 10^{19} \mathrm{~s}^{-1}\)

Long Questions for Class 11 Chemistry Chapter 2 Structure of Atom

Question 14. What is the wavelength of light emitted when the electron in a hydrogen atom undergoes a transition from an energy level with n = 4 to an energy level with n = 2?
Answer:

According to the Rydberg equation, wave number,

⇒ \(\bar{v}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

⇒  \(\bar{v}=109677\left[\frac{1}{(2)^2}-\frac{1}{(4)^2}\right] \mathrm{cm}^{-1}\)

[R = 109677 cm^-1 and n₂ = 4, n₁ = 2]cm^-1

Or, v = 109677 × \(\frac{3}{16}\) = 20564.43cm

λ = \(\frac{1}{\bar{\nu}}=\frac{1}{20564.43} \mathrm{~cm}\)

= 4.86 × 10^-5cm = 486 × 10^-7crn

= 486 × 10^-9nm

= 486nm.

Question 15. How much energy is needed to ionize an H-atom if the electron occupies n = 5 orbit? Compare your answer with the ionization enthalpy of the H-atom (energy required to remove the electron from n = 1 orbit).
Answer:

⇒  \(E_n=-\frac{21.76 \times 10^{-19}}{n^2} \mathrm{~J}\)

⇒\(E_1=-21.76 \times 10^{-19} \mathrm{~J}\)

⇒ \(E_5=-\frac{21.76 \times 10^{-19}}{(5)^2}\)

= \(-8.704 \times 10^{-20} \mathrm{~J} \text { and } E_{\infty}=0\)

⇒  \(\frac{\Delta E}{\Delta E^{\prime}}=\frac{8.704 \times 10^{-20} \mathrm{~J}}{21.76 \times 10^{-19} \mathrm{~J}}=4 \times 10^{-2}\)

Question 16. The energy associated with the first orbit in the hydrogen atom is -2.18 ×  10^-18J. atom^-1. What is the energy associated with the fifth orbit? Calculate the radius of Bohr’s fifth orbit for the hydrogen atom.
Answer:

Energy of the first orbit (E1) = -2.18 ×  10^-18J-atom^-1

We know that the energy of n-th orbit (En) \(=E_1 \times \frac{Z^2}{n^2}\)

=\(-2.18 \times 10^{-18} \times \frac{1^2}{n^2}\)

For H-atom, Z= 1

Thus energy of 5th Orbit (e5) \(=-2.18 \times 10^{-18} \times \frac{1^2}{5^2}\)

= -8.72 × 10^-20 J atom

Bohr radius for n-th-orbit of H-atom (rn) = 0.529 × n²A

[For H-atom, Z = 1]

∴ Bohr radius of 5th orbit, r₅ = 0.529 × 5² Å

= 13.225Å

Question 17. Find the wave number for the longest wavelength transition In the Balmer series of atomic hydrogen.
Answer:

The equation used for explaining the line spectrum of hydrogen for \(\bar{v}=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\) Balmer series, n₁ = 2

As \(\bar{v}=\frac{1}{\lambda}, \lambda\) will be longest if n2 is minimum.

Thus, here n₂ = n₁ + 1

= 2+1

= 3 (R = 109677 cm^-1 )

So. \(\vec{v}=R\left(\frac{1}{2^2}-\frac{1}{3^2}\right)\)

Or, \(\bar{v}=109677\left(\frac{1}{2^2}-\frac{1}{3^2}\right) \mathrm{cm}^{-1}\)

= \(109677 \times \frac{5}{36} \mathrm{~cm}^{-1}=1.5233 \times 10^4 \mathrm{~cm}^{-1}\)

Question 18. What is the energy in joules, required to shift the electron of the hydrogen atom from the first Bohr orbit to the fifth Bohr orbit and what is the wavelength of the light emitted when the electron returns to the ground state? The ground state electron energy is -2.18 × 5^-11 erg.
Answer:

Given: energy of ground state (Ex) = -2.18 × 10¹ erg

Energy of n-th orbit, \(E_n=\frac{E_1}{n^2} \operatorname{erg}=\frac{-2.18 \times 10^{-11}}{n^2} \mathrm{erg}\)

The amount of energy required when an electron jumps from the last orbit to 5th orbit.

⇒ \(\Delta E=E_5-E_1=\frac{-2.18 \times 10^{-11}}{5^2}-\left(-2.18 \times 10^{-11}\right)\)

= \(2.18 \times 10^{-11}\left(1-\frac{1}{25}\right)\)

= 2.093 × 10¹¹ erg

=  2.093 × 10^-18 J

[1 erg = 10^-7 J ]

The amount of energy released when the electron returns from the 5th orbit to the list-orbit =2.093 × 10¹¹ erg

We know that, AE = hv \(=h \frac{c}{\lambda}\)

⇒ \(\frac{h c}{\Delta E}=\frac{\left(6.626 \times 10^{-27} \mathrm{erg} \cdot \mathrm{s}\right) \times\left(3 \times 10^{10} \mathrm{~cm} \cdot \mathrm{s}^{-1}\right)}{2.093 \times 10^{-11} \mathrm{erg}}\)

= 9.497 × 10^-6cm

=950 × 10^-8cm

= 950 Å

Question 19. The electron energy in the hydrogen atom is given by E_n = (-2.18 × 10^-18)/n²J. Calculate the energy required to remove an electron completely from the n = 2 orbit. What is the longest wavelength of light in cm that can be used to cause this transition?
Answer:

E₂ = \(-\frac{2.18 \times 10^{-18}}{(2)^2} \mathrm{~J}=-5.45 \times 10^{-19} \mathrm{~J}\)

The energy required to remove an electron completely from the orbit with

⇒ n \(n=2, \Delta E=E_{\infty 0}-E_2=0-\left(-5.45 \times 10^{-19} \mathrm{~J}\right)\)

= 5.45 × 10^-19J

⇒ \(=\frac{h c}{\Delta E}=\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{5.45 \times 10^{-19} \mathrm{~J}}\)

= \(3.647 \times 10^{-7} \mathrm{~m}=3.647 \times 10^{-5} \mathrm{~cm}\)

Question 20. Calculate the wavelength of an electron moving with a velocity of 2.05× 10^-7 m.s^-1
Answer:

The velocity of an electron ( v) = 2.05 × 10^-17 S^-1 According to de Broglie equation,

Wavelength \((\lambda)=\frac{h}{m v}\)

= \(\frac{6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}{\left(9.108 \times 10^{-31} \mathrm{~kg}\right) \times\left(2.05 \times 10^7 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}\)

Thus, the wavelength of the electron will be 3.549 × 10^-11 m

NCERT Solutions Class 11 Chemistry Chapter 2 Structure of Atom

Question 21. The mass of an electron is 9.1 x 10-31kg. If its K.E is 3.0 × 10^-25J, calculate its wavelength.
Answer:

Mass of an electron (m) = 9.1 × 10^-31 kg

⇒ \(\mathrm{KE}=\frac{1}{2} m v^2=3.0 \times 10^{-25} \mathrm{~J}\)

Velocity of an electron \((v)=\sqrt{\frac{2 \times \mathrm{KE}}{m}}=\sqrt{\frac{2 \times 3.0 \times 10^{-25}}{9.1 \times 10^{-31} \mathrm{~kg}}}\)

= 812 m.s^-1

Wavelength of the moving electron \((\lambda)=\frac{h}{m v}\)

= \(\frac{6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}{\left(9.1 \times 10^{-31} \mathrm{~kg}\right) \times\left(812 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}=8.967 \times 10^{-7} \mathrm{In}\)

Question 22.

1. Write the electronic configurations of the following ions: 

1. H^–
2. Xa^–
3. O^2-
4. F^–

2. What are the atomic numbers of elements whose outermost electrons are represented by 

1. 3s¹
2.  2p³
3. 3p⁵

3. Which atoms are indicated by the following configurations?

1. [He]2s¹
2. [Ne]3s²3p³
3. [Ar]4s²3d¹

Answer: 

1. 

1. H^–: Is²
2. Na⁺ : ls²2s²2p⁵
3. O^2--: ls²s²p⁶
4. F^–: ls²2s²2p⁶

2.

1. The configuration ofthe elementwill be ls²2s²2p⁶3s¹; its atomic numberwill be 11.
2. The configuration of the element will be 1s²2s²2p³; its atomic number will be 7.
3. The configuration of the element will be ls²2s²2p⁶3s²3p⁵; its atomic number will be 17.

3.

1. Lithium (Li), (Z = 3)
2. Phosphorous (P), (Z =15)
3. Scandium (Sc), (Z= 21).

Question 23. An atomic orbital has n = 3. What are the possible values of 1 and m1? List the quantum numbers (m{ and 1) of electrons for 3d orbital. Which of the following orbitals are possible? 1 p, 2s. 2p and 3f
Answer:

1. If n = 3 , then 1 = 0, 1, 2

When I = 0, m₁ = 0; when l = 1 , m₁ = -1, 0, +1 ;

When l = 2, m₁= -2, -1, 0, +1, +2

2. For 3d-subshell, n = 3 and 1 = 2; for l = 2, m₁= -2,-1,+1,+2

3. lp is not possible because for p-subshe,l=1. When n = 1, l cannot be 1. 2s is possible because for subshell, 1 = 0, when n = 2, 1 can be 0. 2p is possible because for p-subshell,l =1, when n = 2,l can be 1. 3f is not possible because for f-subshell, l = 3. When n = 3,   l cannot be 3.

Question 24. Calculate the energy required for the process \(\mathrm{He}^{+}(g) \rightarrow \mathrm{He}^{2+}(g)+e\) The ionization energy of the H-atom in the ground state is 2.18 ×10^-18J.atom^-1
Answer:

The energy of an electron residing in the nth-orbit of a hydrogen-like atom/ion is En \(=-\frac{2 \pi^2 m Z^2 e^4}{n^2 h^2}\)

Ionization enthalpy for h- atom = E∞ – E₁

= 0\(-\left[-\frac{2 \pi^2 m e^4 \times 1^2}{1^2 \times h^2}\right]\)

Or, \(\frac{2 \pi^2 m e^4}{h^2}=2.18 \times 10^{-18} \mathrm{~J}\)

IE = 2. 18 ×  10^-18J

Again, ionisation enthalpy of He+ ion = E∞ – E₁

= 0 \(-\left[-\frac{2 \pi^2 m e^4 \times 2^2}{1^2 \times h^2}\right]\)

Since Z = 2

= \(4 \times \frac{2 \pi^2 m e^4}{h^2}=4 \times 2.18 \times 10^{-18} \mathrm{~J}=8.72 \times 10^{-18} \mathrm{~J}\)

∴ Energy required for the process = 8.72 ×  10^-18J

Question 25. The longest wavelength doublet absorption transition is observed at 589 and 589.6 nm. Calculate the frequency of each radiation and energy difference between two excited states.
Answer:

λ₁ = 589nm = 589× 10^-9m

∴ Frequency, v1 \(=\frac{c}{\lambda_1}=\frac{3.0 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{589 \times 10^{-9} \mathrm{~m}}\)

λ₂ = 589.6nm = 589.6 × 10^-9 m

∴ Frequency (v2) \(=\frac{c}{\lambda_2}=\frac{3.0 \times 10^8}{589.6 \times 10^{-9}}=5.088 \times 10^{14} \mathrm{~s}^{-1}\)

The difference in energy (AE) = E₁-E₂ = h(v₁-v₂)

= 6.626 ×  10^-34× (5.093- 5.088) × 10¹⁴

= 3.313 ×  10^-22J

Question 26. The ejection of the photoelectron from the silver metal In the photoelectric effect experiment can be stopped by applying the voltage of 0.35 V when the radiation 256.7 nm is used. Calculate the work function for silver metal.
Answer:

The energy of incident radiation, E = hv = work function of a metal + Kinetic energy of photoelectrons.

or, \(B=h v=h \frac{c}{\lambda}=\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{\left(256.7 \times 10^{-9} \mathrm{~m}\right)}\)

Or, E = 7.74 ×  10^-19J

= 4.03eV

Since leV = 1.602 ×  10^-19J)

The potential applied provides the Kinetic energy to the electron. Thus, the kinetic energy of the electron =0.35eV. So, the work function of silver metal = (4.83- 0.35)eV

= 4.48eV.

Question 27. Emission transitions in the Paschcn series end at orbit n = 3 and start from orbit n and can be represented as v = 3.29 ×  10^-15(Hz) [1/3²-1/n²]. Calculate the value of n if the transition is observed at 1285 nm. Find the region of the spectrum.
Answer:

⇒ \(v=\frac{c}{\lambda}=\frac{3.0 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{1285 \times 10^{-9} \mathrm{~m}}=3.29 \times 10^{15}\left(\frac{1}{3^2}-\frac{1}{n^2}\right)\)

⇒ \(2.33 \times 10^{14}=3.29 \times 10^{15}\left(\frac{1}{9}-\frac{1}{n^2}\right)\)

Or = \(\quad \frac{2.33 \times 10^{14}}{3.29 \times 10^{15}}=\frac{1}{9}-\frac{1}{n^2} \text { or, } 0.071=\frac{1}{9}-\frac{1}{n^2}\)

⇒ \(\text { or, } \frac{1}{n^2}=\frac{1}{9}-0.071 \text { or, } \frac{1}{n^2}=0.040 \text { or, } n^2=25\)

or, n – 5. Therefore, radiation corresponding to 1285 nm belongs to the infrared region.

Question 28. An element with mass number 81 contains 31.7% more neutrons as compared to protons. Assign the atomic symbol.
Answer:

No. of protons + no. of neutrons = mass number = 81

Let, the number of protons present in an atom = x

Number of neutrons present \(=x+\frac{31.7}{100} \times x\)

As given in the question, x + 1.317x = 81

or, 2.317x = 81 or, x = 34.96

= 35

Thus, number of protons = 35 l.e., atomic number = 35

The element with atomic number 35 is Br

∴ The Symbol is \({ }_{35}^{81} \mathrm{Br} \text {. }\)

Question 29. Neon gas is generally used in the sign boards. If it emits strongly at 616 nm, calculate the dying frequency of emission, distance traveled by this radiation in the 30s energy of quantum, and the number of quanta present if it produces 21 of energy.
Answer:

A = 616nm = 616 ×  10^-19 m, c = 3 ×  10^-8m.s^-1

Radiation Frequency

⇒ \(v=\frac{c}{\lambda}=\frac{3 \times 10^8}{616 \times 10^{-9}}=4.87 \times 10^{14} \mathrm{~s}^{-1}\)

Distance (s) traveled by the radiation in 30 s = ext =3 x 108m-s-1 x 30 s = 9 ×  10⁹m.

Energy of quantum

E = hv = 6.626 × 10^-34 × 4.87 ×  10¹⁴

= 3.23 × 10^-19J.

Number of quanta = \(\frac{\text { total energy }}{\text { energy of each quantum }}\)

= \(\frac{2 \mathrm{~J}}{3.23 \times 10^{-19} \mathrm{~J}}=6.19 \times 10^{18}\)

Chapter 2 Structure of Atom Long Answer Solutions

Question 30. In astronomical observations, signals observed from the distant stars are generally weak. If the photon detector receives a total of 3.15 ×  10^-18J from the radiations of 600 nm, calculate the number of photons received by the detector.
Answer:

Wavelength λ= 600nm = 600 ×  10^-9m.

Energy of phyton \(=\frac{h c}{\lambda}=\frac{\left(6.626 \times 10^{-34}\right) \times\left(3 \times 10^8\right)}{600 \times 10^{-9}}\)

= 3.313 ×  10^-19 J.

Number of photons detected by the detector

= \(\frac{\text { total energy received by the detector }}{\text { energy of each photon }}\)

= \(\frac{3.15 \times 10^{-18} \mathrm{~J}}{3.313 \times 10^{-19} \mathrm{~J}}=9.15 \approx 10 \text { photons. }\)

Question 31. Lifetimes of the molecules in the excited states are often measured by using a pulsed radiantly source of duration nearly in the nano-second range. If the radiation source has a duration of 2 ns and the number of photons emitted during the pulse source is 2.5×  10¹⁵, calculate the energy of the source.
Answer:

Frequency emission (v)=  \(=\frac{1}{\text { time period }}=\frac{1}{2 \times 10^{-9} \mathrm{~s}}\)

= 0.5×  10⁹s^-1

The energy of emission =Nhv

= 2.5 × 10¹⁵ × 6.626 ×10^-34 × 0.5 × 10⁹

= 8.2825 × 10¹⁰ J.

Question 32. The work function for the cesium atom is 1.9 eV. Calculate

1. The threshold wavelength and
2. The threshold frequency of the radiation. If the cesium element is irradiated with a wavelength of 500 nm, calculate the kinetic energy and the velocity of the ejected photoelectron.

Answer:

The work function of cesium ( w₀) = h₀= 1.9eV

∴ Threshold frequency, v0 \(=\frac{1.9 \mathrm{eV}}{h}=\frac{1.9 \times 1.602 \times 10^{-19}}{6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}}\)

Or, v₀= 4.59 ×  10¹⁴ s^-1

[since leV = 1.602 × 10^-19J]

Again, threshold wavelength (A0) = c/v₀

= \(\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{4.59 \times 10^{14} \mathrm{~s}^{-1}}\)

= \(6.536 \times 10^{-7} \mathrm{~m}\)

1. Thus threshold wavelength of cesium = 6.536 × 10^-7m

= 654 × 10^-9m = 654nm

2.Threshold frequency = 4.59 × 10¹⁴s^-1Kinetic energy (KE) of the emitted electron

⇒ \(\frac{1}{2} m v^2=h v-w_0=\left(h v-h v_0\right)=h c\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)\)

Or, Kinetic energy (KE)

= \(\left(6.626 \times 10^{-34}\right)\left(3 \times 10^8\right)\left(\frac{1}{500 \times 10^{-9} \mathrm{~m}}-\frac{1}{654 \times 10^{-9} \mathrm{~m}}\right)\)

Or, KE = 9.36 × 10^-20J; So, the Kinetic energy of the emitted electron is 9.36 × 10^-20J.

Or, \(\frac{1}{2} m v^2=9.36 \times 10^{-20}\)

Or, \(v^2=\frac{9.36 \times 10^{-20} \times 2}{9.108 \times 10^{-31}} \text { or, } v=4.53 \times 10^5\)

Hence, the velocity of the emitted electron is 4.53 × 10⁵m.s^-1

Question 33. The following results are observed when sodium metal is irradiated with different wavelengths. Calculate

1. Threshold wavelength and
2. Planck’s constant.
   

λ(nm) – v × 10^-5(cm.s^-1)

1. 500 – 2.55
2. 450 – 4.35
3. 400- 5.35

Answer:

1. Let threshold wavelength = λ0nm = λ₀ × 10^-9m

Again, the Kinetic energy of the emitted electron.

⇒ \(\left(\frac{1}{2} m v^2\right)=h\left(v-v_0\right)=h c\left(\frac{1}{\lambda}-\frac{1}{\lambda_0}\right)\) …………………(1)

Putting the given values in (1) we get

⇒ \(\frac{1}{2} m\left(2.55 \times 10^5\right)^2=\frac{h c}{10^{-9}}\left(\frac{1}{500}-\frac{1}{\lambda_0}\right)\) …………………(2)

⇒ \(\frac{1}{2} m\left(4.35 \times 10^5\right)^2=\frac{h c}{10^{-9}}\left(\frac{1}{450}-\frac{1}{\lambda_0}\right)\)…………………(3)

⇒ \(\frac{1}{2} m\left(5.35 \times 10^5\right)^2=\frac{h c}{10^{-9}}\left(\frac{1}{400}-\frac{1}{\lambda_0}\right)\) …………………(4)

Dividing (3) by (2) we get \(\frac{\lambda_0-450}{450 \lambda_0} \times \frac{500 \lambda_0}{\lambda_0-500}=\left(\frac{4.35}{2.55}\right)^2\)

Or, λ₀ = 530.88=531 nm

2. Substituting the value of λ0 in (4) we have

⇒ \(\frac{1}{2} \times\left(9.108 \times 10^{-31}\right) \times\left(5.35 \times 10^5\right)^2\)

=\(\frac{h \times 3 \times 10^8}{10^{-9}}\left(\frac{1}{400}-\frac{1}{531}\right) \quad \text { or, } h=7.045 \times 10^{-34}\)

Value of Planck’s constant obtained = 7.045 ×  10^-34 J.s

Question 34. If the photon of the wavelength 150 pm strikes an atom and one of its inner bound electrons is ejected out with a velocity of 1.5× 10⁷ m.s^–1, calculate the energy with which it is bound to the nucleus.
Answer:

The energy of an incident photon

⇒\(\frac{h c}{\lambda}=\frac{\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}{\left(150 \times 10^{-12} \mathrm{~m}\right)}\)

= 1.3252 × 10^-15 J

= 13.252 × 10^-16 J

Kinetic energy of emitted  electron \(\left(\frac{1}{2} m v^2\right)\)

= \(\frac{1}{2} \times\left(9.108 \times 10^{-31} \mathrm{~kg}\right) \times\left(1.5 \times 10^7 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)^2\)

= 1.025× 10^-16 J

So, the energy with which the electron was bound to the

nucleus =(13.252 × 10^-16 – 1.025 × 10^-16 )J

= 12.227 × 10^-16 J = 7.632 ¹ 10³eV

Structure of Atom Chapter 2 Class 11 Long Answer Solutions

Question 35. Calculate the wavelength for the emission transition if it starts from the orbit having a radius of 1.3225 nm and ends at 211.6 pm. Name the series to which this transition belongs and the region of the spectrum.
Answer:

For a 1 electron system, the radius of the n-th orbit \(=\frac{52.9 n^2}{Z}\) pm

The radius of the orbit from which the transition of the electron occurs

= 1.3225nm = 1322.5pm \(=\frac{52.9 n_1^2}{Z}\)

The radius ofthe orbit to which the electron is added.

⇒ \(r_2=211.6 \mathrm{pm}=\frac{52.9 n_2^2}{Z}\)

⇒  \(\text { So, } \frac{r_1}{r_2}=\frac{1322.5}{211.6}=\frac{n_1^2}{n_2^2} \text { or, } \frac{n_1}{n_2}=2.5\)

When n₁ = 5 and n₂ = 2, the equation obtained for n1 and n2 is satisfied. Thus, the transition occurs from n = 5 to n = 2 and belongs to the Balmer series.

∴ Wave number (v) = 109677 \(\times\left(\frac{1}{2^2}-\frac{1}{5^2}\right)\)

= 2.3 × 10⁴cm^-1. and wavelength \((\lambda)=\frac{1}{\bar{v}}=\frac{1}{2.3 \times 10^4} \mathrm{~cm}\)

= 4.35 × 10^-5cm

= 435nm

Thus, it lies in the visible region.

Question 36. If the velocity of the electron in Bohr’s first orbit is 2.19 ×  10⁶m.s^-1, calculate the de Broglie wavelength associated with it.
Answer:

v = \(2.19 \times 10^6 \mathrm{~m} \cdot \mathrm{s}^{-1}\)

m = \(9.108 \times 10^{-31} \mathrm{~kg}\)

λ = \(\frac{h}{m u}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{\left(9.108 \times 10^{-31} \mathrm{~kg}\right) \times\left(2.19 \times 10^6 \mathrm{~m} \cdot \mathrm{s}^{-1}\right)}\)

= \(3.32 \times 10^{-10} \mathrm{~m}=332 \times 10^{-12} \mathrm{~m}\)

= 332pm

Question 37. The velocity associated with a proton moving in a j potential difference of 1000 V is 4.37 × 10^-3m.s^-1. If the hockey ball of mass 0.1 kg is moving with this velocity, calculate the wavelength associated with this velocity.
Answer:

Velocity of hockey ball =4.37 × 105m.s^-1 , mass = 0.1kg

∴ Wavelength (λ) = \(\frac{h}{m v}=\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{0.1 \mathrm{~kg} \times 4.37 \times 10^5 \mathrm{~m} \cdot \mathrm{s}^{-1}}\)

= \(1.52 \times 10^{-38} \mathrm{~m}\)

Question 38. If the position of the electron is measured within an accuracy of ± 0.002nm, calculate the uncertainty In the momentum of the electron. Suppose the momentum of the electron Is h/(4xm × 0.05)nm, is there any problem in defining this value?
Answer:

Given, Ax = 0.002nm = 2 x 10-3nm = 2 x 10-12m According to Heisenberg’s uncertainty principle.

⇒ \(\Delta x \times \Delta p=\frac{h}{4 \pi} \quad \text { or, } \Delta p=\frac{h}{4 \pi \Delta x}\)

= \(\frac{6.626 \times 10^{-34}}{4 \times 3.14 \times 2 \times 10^{-12}}=2.638 \times 10^{-23} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}\)

Again Momentum of the electron

= \(=\frac{1}{4 \pi \times 0.05 \mathrm{~nm}}=\frac{n}{4 \pi \times 5 \times 10^{-11} \mathrm{~m}} \)

= \(\frac{6.626 \times 10^{-34} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}}{4 \times 3.14 \times 5 \times 10^{-11} \mathrm{~m}}\)

= \(1.055 \times 10^{-24} \mathrm{~kg} \cdot \mathrm{m}^2 \cdot \mathrm{s}^{-1}\)

The value of uncertainty cannot be greater than the actual momentum. Thus the actual magnitude of momentum cannot m be defined in as reality

Question 39. The quantum numbers of six electrons are given below. Arrange them in order of increasing energy. list if any of this combinationÿ) has/ have the same energy.

• n = 4, l = 2, m₁=-2 m_s =-1/2
• n = 4, l = 2, m₁=1 m_s =+1/2
• n = 4, l = 2, m₁=0 m_s =+1/2
• n = 4, l =2, m₁=-2 m_s =-1/2
• n = 4, l = 2, m₁=-2 m_s =+1/2
• n = 4, l = 2, m₁=-2 m_s =+1/2

Answer: The orbital occupied by the electrons that are designated by the given sets of quantum numbers are,

1. 4d
2. 3d
3. 4p
4. 3d
5. 3p
6. 4p

So, increasing the order of their energies will be:

5<2<4<6=3<1

Question 40. What transition in the hydrogen spectrum would have the same wavelength as the Balmer transition n = 4 to n = 2 of the He+ spectrum?
Answer:

For Balmer transition, n = 4 to n = 2, for He+ spectrum, the Rydberg equation is,

⇒ \(\bar{v}=\frac{1}{\lambda}=R Z^2\left(\frac{1}{2^2}-\frac{1}{4^2}\right)=R \times 2^2 \times \frac{3}{16}=\frac{3 R}{4}\)

∴  He, Z=2

For Hydrogen spectrum

⇒ \(\bar{v}=\frac{1}{\lambda}=R Z^2\left(\frac{1}{n^2}-\frac{1}{n_2^2}\right)=R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)\)

According To The Question,

⇒ \(R\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)=\frac{3 R}{4}\)

or, \(\left(\frac{1}{n_1^2}-\frac{1}{n_2^2}\right)=\frac{3}{4}\)

The equation (1) will be true if n = 1 and n -2.

For hydrogen, the spectrum transition is from n = 2 to n = 1.

Class 11 Chemistry Long Questions on Structure of Atom

Question 41. Which of the following subshells have no real existence?

1. 2d
2. 3f
3. 4g
4. 5d

Answer:

In the case of d -subshell, l = 2. In the second shell ( n = 2), the values of l are 0 and 1. So there cannot be any d -d-subshell In the third shell. Therefore, we can say that there Is no real existence of a 2d subshell.

In the case of f-subshell, l = 3. In the third shell (n = 3), the values of l are 0, 1, and 2. Since there cannot be any f-subshell In this shell, there is no real existence of 3f- subshell.

ln case of g -subshell, l = 4. In the fourth shell (n = 4), the values of l are 0, 1, 2, and 3. Since there cannot be any g subshell in this shell, there is no real existence of a 4g subshell.

In the case of d -subshell, l = 2. In the fifth shell (n = 5), the values of l are 0, 1, 2, 3 and 4. Therefore 5d sub-shell has real existence.

Question 42. An electron is described by magnetic quantum no.m = +3. Indicate the lowest possible value of ‘n ’for this electron. (tv) n = 4,1=0
Answer:

For an electron having magnetic quantum number m = +3, the lowest possible value of azimuthal quantum number ‘ l’ would be 3, and for an electron having 1 = 3, the lowest possible value for ‘ n’ would be 4.

In other words, the lowest possible energy level (‘n’) that the electron would occupy is the 4th shell (n = 4).

For an electron having magnetic quantum number m = +3, the lowest possible value of azimuthal quantum number ‘ l’ would be 3, and for an electron having 1 = 3, the lowest possible value for ‘ n’ would be 4.

In other words, the lowest possible energy level (‘n’) that the electron would occupy is the 4th shell (n = 4).

NCERT Solutions For Class 11 Chemistry Chapter 3 Classification Of Elements And Periodicity In Properties Very Short Question And Answers

Question 1. Who proposed the ‘law of octaves’?
Answer: Newland

Question 2. For which of the elements, the ‘Law of octave’ is not applicable?
Answer: Heavy mental

Question 3. Identify the element predicted by Mendeleev as ekaaluminium.
Answer: Gallium

Question 4. Mention the name of the group in the periodic table, which contains solid, liquid, and gaseous elements.
Answer: Group 72 or 17

Question 5. Mention the position of the alkali metals in the periodic table.
Answer: Group 1 A or 1

Question 6. Give an example of an element whose atomic mass has been corrected by Mendeleev’s periodic table.
Answer: Be

NCERT Class 11 Chemistry Chapter 3 Very Short Questions and Answers

Question 7. Who proved that atomic number but not atomic mass is the more proper determining factor of the periodicity of elements?
Answer: Moseley

Question 8. Give an example of d -a block element which is not regarded as a transition element.
Answer: Zn

Question 9. How many rare earth elements are present in the periodic table? Give an example-
Answer: 14

Question 10. Give the common electronic configuration of d-block elements.
Answer: (n-1) s1-10 ns 1-2

Question 11. Name the transition element having the lowest atomic mass.
Answer: Se

Question 12. Which element gives brick red coloration to the flame? In which block, the element is in the periodic table?
Answer: Ca, s-block

Question 13. Mention the respective block of the elements having atomic numbers 7, 11, and 22.
Answer: p,s,d

Question 14. What do you mean by representative elements?
Answer: Elements Of S and P- block’s

Question 15. Give two terminal elements of the rare earth element series.
Answer: Ce, lu

Question 16. How will you detect the starting and ending of a period in the periodic table?
Answer: By electronic configuration.

Question 17. Which block contains inner transition elements?
Answer: F

Question 18. Give an example of a transition element, which has filled d-subshellinits ground state.
Answer: Cu

Question 19. Why the ions or atoms of the transition elements are paramagnetic?
Answer: Due to the presence of unpaired d -electrons, 20. Cations of group-1A and 2A,

Question 20. Give an example of a diamagnetic.
Answer: Cations of group-1A and 2A,

Question 21. Why and Co called ferromagnetic?
Answer: They can easily be converted into magnets.

Question 22. Which element gives golden-yellow coloration to the flame?
Answer: Na

Question 23. Why Mg cannot be identified by flame test?
Answer: They can easily be converted into magnets.

Question 24. Which are called ‘noble metals’?
Answer: Elements of 5d -series (especially Pt, Au, and Hg ),

Question 25. Give the electronic configuration of the outermost shell of lanthanides.
Answer: 4f^1-14 5d^0-16s²

Question 26. Which of the groups in the periodic table contain all the metallic elements?
Answer: Group-2A

Question 27. Give the names of the ‘noble gas’ elements present in the second and fifth periods.
Answer: Ne, Xe

Question 28. Mention the name and atomic number of the element present in group 13 of the third period.
Answer: Al.13

Question 29. Give the electronic configuration of the fifth element ofthe first transition series.
Answer: Electronic configuration of Mn

Question 30. Identify the transition element(s): K, Mn, Ca, Cs, Fe, Cu, pb.
Answer: Mn, Fe, Cu, Pb,

Question 31. Name two elements that do not give a flame test.
Answer: Be, Mg

Class 11 Chemistry Chapter 3 NCERT Very Short Questions and Answers

Question 32. Which lanthanide elements have only 1 electron in a 5dsubshell?
Answer: Lu

Question 33. Write the outermost electronic configuration of chalcogens.
Answer: ns² np⁴

Question 34. What will be the position in the periodic table of the element having electronic configuration ls²2s²2p⁴?
Answer: Second period, Grop -16

Question 35. Mention the position of the pnictogens in the long form of the periodic table.
Answer: 15

Question 37. Which element has the highest oxidizing property?
Answer: Fluorine

Question 38. Give one example of each metal, nonmetal, or metalloid presenting the p-block of the periodic table.
Answer: Pb.N.As

Question 39. Give the names of two non-metals present in s -block of the periodic table.
Answer: H₂.He

Question 40. What is the unit of electron affinity?
Answer: Kj-mol^-1

Question 41. Is the value of the electron affinity of an element zero?
Answer: Yes

Question 42. Between Fe2+ and Fe3+, which is smaller in size, and 6. Why?
Answer: Fe³⁺, Z/e ratio is higher,

Question 43. Which element of each pair has higher electron affinity?

• Br, Cl
• F, Cl
• O, S

Answer:

• Cl
• Cl
• S

Question 44. The first ionization potential of carbon is 11.2 eV. State whether the value of the first ionization potential of silicon is the same or greater or less than that of carbon
Answer: Lower

Question 45. Arrange s,p,d & f-subshells according to the screening power.
Answer: S>p>d> f

Question 46. Which element has the lowest ionization potential?
Answer: Cs

Question 47. Which element has the highest ionization potential?
Answer: He

Question 48. What is the unit of ionization potential?
Answer: eV atom^-1

Question 49. What is the change observed in the covalent character of the oxides of the elements starting from Na to Cl in the third period?
Answer: Increases

Question 50. Arrange the following in increasing order of ionic radius: Na⁺, F^–, O^2-, Al³⁺, N^3-.
Answer: Al³⁺ < Na⁺ < F^– < O^2- < N^3-

Question 51. Why does nitrogen have a higher ionization enthalpy than that of Oxygen? Arrange the following in increasing order of acidity: NO₂, Al₂O₃, SiO₂, CIO₂
Answer: Na < Al< Mg < Si

Question 52. What will be the order of, Mg, Al, and SI in terms of the first ionization enthalpy?
Answer: Mg²⁺ < Na⁺ < F^– < O^2-

Question 53. Arrange the following ions in ascending order of radius: Na⁺, F^–, O^2-, Mg²⁺.
Answer: Mg²⁺ < Na+ <F^– < O^2-

Question 54. Arrange Mg, Al, Si, and Na in the increasing order of their ionization potentials.
Answer: Na < Al < Mg < Si

Question 55. How many periods and groups are there in the present form (i.e., long form) of the periodic table?
Answer: 7 periods and 18 groups

Question 56. Which group ofthe long form of the periodic table contains solid, liquid, and gaseous elements?
Answer: Group-17.

Question 57. Identify the following as acidic, basic, or amphoteric oxides: BeO, Al₂O₃
Answer:

Acidic oxide: SiO, basic Oxide: CaO, Amphoteric oxides: BeO, Al₂O₃.

Question 58. Between XaOH and CsOH, which one is more basic and why?
Answer:

CsOH is more basic than NaOH because the electronegativity of Cs is more electropositive than Na.

Classification of Elements and Periodicity in Properties Class 11 Very Short Questions

Question 59. Write down the names ofthe coinage metals and indicate their positions in the long form ofthe periodic table.
Answer: Cu, Ag, Au (periods 4, 5, & 6 in group 11).

Question 60. Indicate the period that contains the first series of transition elements.
Answer: 4th period.

Question 61. Which block in the periodic table contains metals, nonmetals, and metalloids? Give three examples of metalloids.
Answer: p -block; Si, Ge, As

Question 62. Write the IUPAC name and symbol of the element with atomic number 135.
Answer:

IUPAC name: Untripentium; Symbol: Utp

Question 63. Arrange the following elements in decreasing order of their atomic radius: Na, H, Si, S, P, Cl
Answer: Na > Si > P > S > Cl > H

Question 64. Indicate the largest and smallest species among the following: Mg, Al, Mg²⁺, Al³⁺⁺
Answer:

Largest: Mg

Smallest: Al³⁺

Question 65. Arrange the following compounds in increasing order of their reducing: NH₃, PH₃, and AsH₃
Answer: NH₃ < pH₂< AsH₃

Question 66. Classify as basic, amphoteric, or acidic: BeO, Al₂O₃, CaO, SiO₂
Answer:

BeO, Al₂O₃: Amphoteric

CaO: Basic

SiO₂: Acidic

Question 67. Write the names ofthe smallest cation and anion.
Answer: H⁺ and H^–

Question 68. Mention the names of two noble metals and indicate their positions in the periodic table.
Answer: Pt and Au. In the periodic table, they are present in the 6th period in the 10th and 11th groups respectively.

Question 69. Based on atomic number and position in the periodic table arrange the following elements in decreasing order of their metallic character: Si, Na, Mg, P, Be.
Answer: Na > Mg > Be > Si > P

Very Short Questions for Class 11 Chemistry Chapter 3

Question 70. Arrange in increasing order of oxidizing power: F, Br, Cl, I
Answer: I < Br < Cl < F

Question 71. The atom of an element has the electronic configuration ls²2s²2p⁶3s²3p⁵. Identify a metal or non-metal.
Answer: Non-metal

Question 72. Which is most acidic: S₃, P₂O₅, ZnO, Na₂O?
Answer: SO₃ is the most acidic compound.

Question 73. Which is most basic: SiO₂, MgO, Al₂O₃, Na₂O?
Answer: Na₂O is the most basic compound

Question 74. For which elements, Newlands’ law of octaves is not applicable?
Answer: Heavier elements beyond Ca

Question 75. Which periods in Mendeleev’s periodic table (modified form) do not contain subgroups?
Answer: Periods 1, 2 and 3

Question 76. How many periods and groups are there in the present form (i.e., long form) of the periodic table?
Answer: 7 periods and 18 groups

Question 77. Write down the names ofthe coinage metals and indicate their positions in the long form ofthe periodic table.
Answer: Cu, Ag, Au (periods 4, 5, & 6in group 11).

Question 78. Mention the names of the first member of each of the first, second, and third series of transition elements.
Answer: Scandium (Sc), Yttrium (Y), and Lanthanum (La)

Question 79. Mention the names of the first and last members of the actinide series.
Answer: Thorium (Th) and Lawrencium (Lr).

Question 80. What are pnictogens and chalcogens?
Answer: Gr-15 elements: pnictogens; Gr-16 elements: chalcogens

Question 81. Elements of the same group exhibit similar chemical properties—why?
Answer: Because they have similar outer electronic configurations.

Question 82. Why are sodium (Na) and potassium (K) placed in the same group of the periodic table? Give any two reasons.
Answer: (n- l)d^1-10 ns¹,(n-2)f^1-14(n-l)d^0-1ns²

Question 83. Give general electronic configurations of 1 transition elements and 2 inner-transition elements
Answer: Due to the presence of unpaired electrons in (n-l)d subshell

Question 84. Which group ofthe long form of the periodic table contains solid, liquid, and gaseous elements?
Answer: Group-17.

Question 85. Find the atomic number of an element that belongs to the third period and group 17 in the periodic table.
Answer: The atomic number ofthe given element = 17

Question 86. An element belongs to the third period of p -block. It has five valence electrons. Predict its group.
Answer:

Group ofthe element= 10 + no. of valence electrons = 10 + 5 = 15

NCERT Class 11 Chemistry Chapter 3 Classification of Elements Very Short Q&A

Question 87. What is the reason for the strong reducing character of s-block elements?
Answer: Since they have low ionization energy.

Question 88. Which one of the following exhibits paramagnetism? Sc³⁺+, Cr³⁺, Cu⁺, Zn².
Answer: Cr³⁺ : [Ar]3d³. Due to the presence of unpaired electrons, it exhibits paramagnetism.

Question 89. Name the elements with which even and odd series of 4th, 5th, and 6th periods begin.
Answer: Even series begins with K, Rb, and Cs. The odd series begins with Cu, Ag, and Au.

Question 90. How many periods and groups are there in the modem version of Mendeleev’s table?
Answer: There are 7 periods and 9 groups of a modern version of Mendeleev’s periodic table.

Question 91. Arrange the following elements in the increasing order of their first ionization enthalpy. Li, Be, Na, Mg
Answer: Na < Li < Mg < Be

Question 92. Arrange the following elements in the decreasing order of their electro-negativity. Si, N, F, Cl
Answer:  F >Cl > N> Si

Question 93. What are the various factors due to which the ionization enthalpy of the main group elements tends to decrease down a group?
Answer: The two factors are Atomic size and screening effect.

NCERT Solutions For Class 11 Chemistry Chapter 3 Classification Of Elements And Periodicity In Properties Fill In The Blanks

Question 1. Mendeleev’s periodic law was similar to the law proposed by the scientist______________.
Answer: Lothar Meyer

Question 2. In Mendeleev’s periodic table, the______________incomplete period.
Answer: Seventh

Question 3. The starting elements of even series are K, Rb, and ______________period is an
Answer: Cs

Question 4. The starting elements of odd series are______________Au.
Answer: CU

Question 5. Meneleev’s triad elements are Ag and are the ______________ fundamental property of the element.
Answer: Transition elements

Question 6. ‘The elements from 58Ce to 71Lu are called ______________
Answer: lanthanides

Question 7. Be, Mg, Ca are called______________1L
Answer: Alkaline Earth

Question 8. Cu, Ag, Au are called______________metals.
Answer: Coinage

Question 9. S, Se, Te are called ______________
Answer: Chalcogens,

Periodicity in Properties Class 11 NCERT Short Questions and Answers

Question 10. The potential of s -s-block elements is. Except Be and______________ the s -block elements response to the flame test.
Answer: Low

Question 11. Except Be and______________the s -block elements response to the flame test.
Answer: Mg

Question 12. The s -s-block elements of the fourth, fifth, and sixth periods can form complex compounds by vacant d -orbital. in as they have ______________.
Answer: Coordinate Covalency

Question 13. Noble metals are chemically______________.
Answer: Insert

Question 14. F-block elements are _ the presence of odd electrons. block elements generally form colored in nature due to the omplex compounds.
Answer: Paramagnetic

Question 15. Block elements Generally from colored complex compounds ______________.
Answer: d

Question 16. Zn, Cd, and are not they are d-block elements.
Answer: Hg

Question 17. The element with electronic configuration ls22s22p4 is presentin group______________.
Answer: 16

Question 18. The general electronic configuration of transition
elements is______________
Answer: (n-1)d^{1- 10}-10 ns^1-2

Question 19. Effective nuclear charge = total nuclear change ______________.
Answer: Screening Constant,

NCERT Solutions for Classification of Elements Class 11 Very Short Questions

Question 20. The IUPAC name of the element having an atomic number 150 is______________
Answer: Unpentrilum

Question 21. For homonuclear diatomic molecule, covalent radius = ______________x intemuclear distance.
Answer: \(\frac{1}{2}\)

Question 22. The internuclear distance of the HCl molecule is 1.36 A and the covalent radius of the chlorine atom is 0.99 A. Thus, the covalent radius of the hydrogen atom will be______________.
Answer: 0.37

Question 23. The covalent radius of an element is ______________ der Waals radius.
Answer: Shorter

Question 24. Anionic radius is ______________ radius.
Answer: Greater

Question 25. On moving from left to right across a period, the acidic property of oxide of element______________.
Answer: Increases

Question 26. Hydrides of most of the non-metals are ______________nature.
Answer: Colvent and nonpolar

Question 27. The first ionization potential of carbon is. the second ionization potential is ______________.
Answer: Increases

Question 28. Among the halogens,______________ nature.
Answer: Idonine

Question 29. Electron affinity of Be and are ______________ almost same.
Answer: Mg

Question 30. In a particular energy Level(orbit), the Followers the orders s>p>f.
Answer: Screening effect,

Question 31. In the case of elements belonging to the same group, ionic radii with increases in atomic number ______________.
Answer: Increases

Question 32. F-,Ar,Mg²⁺,Rb⁺ are inons ______________
Answer: Isoelectronic

Chapter 3 Classification of Elements Very Short Q&A Class 11

Question 33. The ionization enthalpy of Cu and K can be explained based on______________.
Answer: Screening effect

Question 34. of the atom of any element and the first ionization enthalpy of its anion (unit -ve charge) are the same.
Answer: Electron affinity

Question 35. Atomic mass = Atomic volume x______________.
Answer: Density

Question 36. Low solubility of Li₂CO₃ and MgCO₃ in water can be explained by______________.
Answer: Diagonal relationship.

NCERT Solutions For Class 11 Chemistry Chapter 2 Structure Of Atom Short Question And Answers 

Question 1. Which one of the following is associated with λ = A Broglie wave of longer wavelength a proton or an I electron moving with the same velocity?
Answer:

λ = \(\frac{h}{m v}\)

∴ \(\frac{\lambda_p}{\lambda_e}=\frac{m_e}{m_p}\)

⇒ \(m_p>m_e\)

∴ \(\lambda_e>\lambda_p\)

Question 2. Mention the difference in angular momentum of the electron belonging to 3p and 4p -subshell.
Answer:

In the case of p -p-orbitals, the value of the azimuthal quantum number Is 1. Hut the magnitude of angular momentum of an electron present in any subshell depends on the value of l. It is Independent ofthe value of the principal quantum number n.

Orbital angular momentum= \(\sqrt{l(l+1)} \times \frac{h}{2 \pi}\)

Thus, there is no difference in angular momentum of the electrons belonging to 3p and 4p -subshells.

Question 3. Are the differences in energy between successive energy levels of a hydrogen-like atom the same? Explain.
Answer:

No, the differences are not the same. The energy of an electron revolving in ‘ n ‘th orbit, En \(=-\frac{2 \pi^2 m z^2 e^4}{n^2 h^2}\)

Hence, the difference in energy between first (n = 1) and second (n = 2) shell

⇒  \(E_1-E_2=-\frac{2 \pi^2 m z^2 e^4}{h^2}\left(\frac{1}{1^2}-\frac{1}{2^2}\right)=-\frac{2 \pi^2 m z^2 e^4}{h^2} \times \frac{3}{4}\)

Similarly \(E_2-E_3=-\frac{2 \pi^2 m z^2 e^4}{h^2}\left(\frac{1}{2^2}-\frac{1}{3^2}\right)\)

= \(-\frac{2 \pi^2 m z^2 e^4}{h^2} \times \frac{5}{36}\)

Obviously, E₁– E₂±E₂– E₃

NCERT Class 11 Chemistry Chapter 2 Short Question and Answers

Question 4. Energy by associated the expression, with the \(E_n=-\frac{13.6}{n^2} \mathrm{eV}\) orbite V of. Show-atom \(E_{(n+I)}-E_n=\frac{13.6 \times 2}{n^3} \mathrm{eV},\)
Answer:

⇒ \(E_{(n+1)}-E_n=\left[-\frac{13.6}{(n+1)^2}-\left(-\frac{13.6}{n^2}\right)\right]\)

⇒  \(\left[\frac{13.6}{n^2}-\frac{13.6}{(n+1)^2}\right] \mathrm{eV}=\frac{13.6(2 n+1)}{n^2(n+1)^2}\)

If the value of n is very large, then (2n + 1)= 2n and

⇒ \((n+1) \approx n \quad\)

∴ \(E_{(n+1)}-E_n=\frac{13.6 \times 2 n}{n^2 \times n^2}=\frac{13.6 \times 2}{n^3} \mathrm{eV}\)

Question 5. de Broglie wavelength of the wave associated with a moving electron and a proton are equal. Show the velocity of the electron is greater than that of the proton.
Answer:

According to de-Broglie’s theory applicable to microscopic particles like electron-\(\lambda=\frac{h}{m v}\)[m =maSsofthe moving particle, v = velocity ofthe moving particle].

Now if the mass and velocity of the electron are me and ve and the mass and velocity of the proton are mp and vp respectively then according to the question

⇒  \(\frac{h}{m_e v_e}=\lambda=\frac{h}{m_p v_p}\)

∴ \(m_e v_e=m_p v_p \quad \text { or, } \frac{v_e}{v_p}=\frac{m_p}{m_e}\)

But, m_p > m_e so, v_e> v_p (proved)

Question 6. Calculate the accelerating potential that must be applied on a proton beam to give it an effective wavelength of 0.005 nm.
Answer:

λ = \(\frac{h}{m v}=\frac{6.626 \times 10^{-34}}{1.67 \times 10^{-27} \times v}\)

∴ v = 7.94 × 10⁴m.s^-1

If the accelerating potential is V volts, then energy acquired by the proton =eV. This becomes the kinetic energy ofthe proton.

Hence \(e V=\frac{1}{2} m v^2\)

e V = \(\frac{1}{2} m v^2\)

∴ v = 32.8v

Question 7. Arrange the following radiations in the order of their increasing frequencies
Answer:

1. The amber light of traffic signals,
2. FM radio waves
3. X-rays
4. Cosmic rays

Answer:

2 < 1 < 3 < 4

Question 8. In the case of a 15X-atom, five valence electrons are. If the spin quantum number of B and R is +1 then find the group(s) of electrons with three of the quantum numbers the same.
Answer:

The spin quantum number of ‘R’ is given as \(+\frac{1}{2}\) and hence that of ‘P’ and ‘Q’ will also be \(+\frac{1}{2}\).

Electrons P, Q, and R are in 3p -orbital, so their n and l values i.e., principal and azimuthal quantum numbers will also be the same.

Therefore, P, Q, and R form a group having three quantum numbers the same. Both A and B belong to 3s having the value of n = 3, l = 0 and m = 0. Hence they also have values of three quantum numbers the same.

Question 9. How are the following affected by the increase in intensity ofthe incident light?

1. Threshold frequency,
2. The kinetic energy of the emitted electrons,
3. Strength photoelectric current.

Answer: No effect

1. Remains the same
2. Increases.

Question 10. Give examples of the production of Photons from electrons and electrons from photons.
Answer:

When high-velocity electrons (cathode rays) strike the surface of hard metals like tungsten, platinum, etc., X – rays are produced.

When a light of suitable frequency or any other electromagnetic radiation strikes a metal surface, electrons are ejected from it.

Question 11. Mention die factors affecting the kinetic energy of the photoelectrons. Does the maximum kinetic energy depend on the intensity of light?
Answer:

1. The frequency of the incident radiation and
2. Work function ofthe metal.
3. Maximum kinetic energy does not depend on the intensity ofthe incident light.

Question 12. Why does the photoelectric work function differently for different metals?
Answer:

1. Electrons in a metal are delocalized and move freely throughout the crystal lattice of the metal.
2. Hence each electron has to do some work to overcome the force of attraction of the metal ions.
3. The amount of energy required to eject the electrons (known as work function) depends on the metal. Hence, different metals have different work functions.

Question 13. Explain The role of threshold frequency in photoelectric effect is in agreement with the particle nature of light and in disagreement with the wave nature of light’
Answer:

According to the wave theory of light, the photoelectric effect can occur by increasing the intensity of the incident light. However, according to particle theory, there is a minimum frequency (threshold frequency), for each metal below which, the photoelectric effect is not possible (no matter how high the intensity of light).

It has been experimentally proved that the photoelectric effect depends on the frequency of the incident light but not on its intensity. The threshold frequency of each metal is unique.

Hence photoelectric effect can be successfully explained with the help of the particle nature of light.

Question 14. Mention the property of electromagnetic radiation (wave nature or particle nature or both) that can best explain the following phenomena—

1. Photoelectric effect
2. Interference
3. Black body radiation
4. Diffraction
5. Einstein’sequation (e = hv)
6. Planck’s equation{e – me2).

Answer:

1. Particle nature
2. Wave nature
3. Particle nature
4. Wave nature
5. Both wave and particle nature
6. Particle nature

Question 15. Indicate spectral regions corresponding to Lyman, Balmer, Paschen & Brackettseries in the line spectrum of hydrogen.
Answer:

1. Lyman series →Ultraviolet
2. Balmer series → Visible
3. Paschen series → Infrared
4. Brackett series → Far infrared

Class 11 Chemistry Chapter 2 NCERT Solutions Short Questions

Question 16. Give two examples of the particle nature of electromagnetic radiation.
Answer:

When light of a suitable frequency strikes a metal, photoelectrons are ejected from its surface. This phenomenon (of photoelectric effect) supports the particle nature of electromagnetic radiation.

The phenomenon of black body radiation also supports the particle nature of electromagnetic radiation.

Question 17. Give the Rydberg formula for the calculation of the wave number of various spectral lines ofthe spectrum. What is the value Rydberg constant?
Answer:

Rydberg’s formula: \(\bar{v}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right]\)

Where = 1, 2, 3, 4,…. etc;

n₂ =n₁+1. = n₁ + 2, = n₁ + 3, …………………… etc.

R = Rydberg’s constant = 109678cm^-1 ; v =wave number

Question 18. Indicate all the possible pathways (involving one or more steps)for the transition of an excited electron from the 4th orbit to the ground state.
Answer:

• n₄→ n₁
• n₄→ n₁→ n₁
• n₄→ n₃→ n₁ and
• n₄→ n₃ → n₂→ n₁

Question 19. What are the ground state and excited state of an electron?
Answer:

When the electrons in an atom are in their lowest (normal) energy state, they revolve in their respective orbits without losing energy. This state of the atom is called its ground state.

When energy is supplied to an atom by subjecting it to electric dischdt&eior high temperature, an electron in the atom may jump from its normal energy level (ground state) to some higher energy level, by absorbing a definite amount of energy. This state of the atom is called the excited state

Question 20. What do you understand by stationary states?
Answer:

According to Bohr’s theory of the hydrogen atom, electrons revolve around the nucleus in some fixed orbits, and during its motion, the electron does not lose energy. For this reason, these orbits are known as electronic orbits at stationary states.

When an electron stays in such an orbit, it does not remain stationary at all. Had it been so, the electron, being attracted by the nucleus would have fallen onto the nucleus. The electron always remains in motion to overcome the influence of nuclear attractive force

Question 21. Differentiate Itetween Rydbergformula & Balmerformula.
Answer:

The Rydberg formula is used to calculate the wave number of different series of lines of the spectrum of hydrogen or Hlike atoms. It is given by

⇒ \(\bar{v}=R\left[\frac{1}{n_1^2}-\frac{1}{n_2^2}\right] Z^2(Z=1 \text { for hydrogen })\)

Where R = Rynx = 1, 2, 3, etc, n₂ = n₁ + 1 , n₁ + 2, n₁ + 3 , etc.

When n₁ = 2 in the Rydberg formula, it is called the Balmer formula.

Balmer formula is given by \(\bar{v}=R\left[\frac{1}{2^2}-\frac{1}{n^2}\right], \text { where } n=3,4,5 \cdots \text { etc. }\)

Question 22. Prove that, the velocity of an electron revolving in the first orbit is twice that revolving in the second orbit of the H-atom.
Answer:

The velocity of the electron in the nth orbit

v = \(\frac{2 \pi e^2}{n h}\)

∴  \(m v r=\frac{n h}{2 \pi} \text { and } r=\frac{n^2 h^2}{4 \pi^2 m e^2}\)

The velocity of electron in second orbit \(v_2=\frac{2 \pi e^2}{2 \times h}\)

Therefore \(\frac{v_1}{v_2}=\frac{2 \pi e^2}{h} \times \frac{2 h}{2 \pi e^2}=2\)

therefore \(\frac{v_1}{v_2}=\frac{2 \pi e^2}{h} \times \frac{2 h}{2 \pi e^2}=2 \quad \text { or, } v_1=2 v_2\)

Question 23. Derive a relation between kinetic energy and de Broglie wavelength associated with a moving electron.
Answer:

We know, the kinetic energy (E) of the particle moving with velocity v, is given by, \(E=\frac{1}{2} m v^2\) or, 2E = mv₂

or, 2mE = m₂v₂

⇒ \(m v=\sqrt{2 m E}\)

Question 24. What happens to the de Broglie wavelength associated with a moving particle if its velocity is doubled?
Answer:

The de Broglie wavelength reduces to half its initial value

⇒ \(\text { [as } \left.\lambda=\frac{h}{m v} \text {, or } \lambda \propto \frac{1}{v}\right]\)

Question 25. A hard-struck cricket ball does not produce waves. Why?
Answer:

Due to the large size of the cricket ball, its mass is large and hence its wavelength is negligible.

Therefore \(\lambda \propto \frac{1}{m}\)

Structure of Atom Class 11 Short Q&A

Question 26. Two particles P and Q are moving with the same velocity, but the de Broglie wavelength of P is thrice that of Q. What do you conclude?
Answer:

Since \(\lambda^{\circ} \frac{1}{m}, \lambda_P \propto \frac{1}{m_P} \text { and } \lambda_Q \propto \frac{1}{m_Q}\)

⇒\(\frac{\lambda_P}{\lambda_Q}=\frac{m_Q}{m_P}, \text { or } \frac{m_Q}{m_P}=\frac{\lambda_P}{\lambda_Q}=\frac{3}{1} \text { or, } m_Q=3 \times m_P\)

∴ Mass of Q is Thrice that of P.

Question 27. Compare the wavelengths of a molecule of each 02 and C02, travelling with the same velocity.
Answer:

Since \( \lambda \propto \frac{1}{m} ; \quad \lambda_{\mathrm{O}_2} \propto \frac{1}{32 \mathrm{u}} \text { and } \lambda_{\mathrm{CO}_2} \propto \frac{1}{44 \mathrm{u}}\)

[ V Molar mass of O₂ & CO₂ are 32u & 44u respectively]

Thus, the wavelengths of a molecule of each O₂ and CO₂ traveling with the same velocity is in the ratio 11:

Question 28. Is there any significance of Heisenberg’s uncertainty principle in our daily life?
Answer:

In our daily life, we deal with objects of ordinary size. So the uncertainties in their position and momentum are very small as compared to the size and momentum of the n- n-object respectively. So, such uncertainties may be neglected. Thus, the uncertainty principle has no significance in our daily life.

Question 29. Why does Bohr’s model contradict Heisenberg’s uncertainty principle?
Answer:

According to Bohr’s theory, negatively charged particles (electrons) inside an atom revolve around the nucleus in well-defined orbits having a fixed radius.

To balance the nuclear attractive force, electrons must move with a definite velocity. However, according to the uncertainty principle, it is impossible to determine simultaneously the exact position and the momentum (or velocity) of a microscopic particle like an electron. Thus, Bohr’s model contradicts Heisenberg’s uncertainty principle.

Question 30. Explain why the uncertainty principle is significant only for subatomic particles, but not for macroscopic objects.
Answer:

The position of a subatomic particle can be located accurately by illuminating it with some electromagnetic radiation.

The energy of the photon associated with such radiation is sufficient to disturb a subatomic particle so that there is uncertainty in the measurement of the position and momentum of the subatomic particles. However, this energy is insufficient to disturb a macroscopic object.

Question 31. Why is it not possible to overcome the uncertainty of Heisenberg’s principle using devices having high precision?
Answer:

Heisenberg’s uncertainty principle has no relation with the precisions of measuring devices.

AVe knows that the subatomic particles are very tiny and thus cannot be seen measured even under a powerful microscope; To velocity or to locate the position of the subatomic particles, they are illuminated (struck, protons) with suitable electromagnetic radiation.

Hence, the precision of measuring devices is not possible in overcoming Heisenberg’s uncertainty principle.

Question 32. How many radial nodes are present in

1. 3s -orbital and 
2. 2p -orbital?

Answer:

Radial nodes of 3s -orbital =n – l -1 = 3 – 0 – 1 = 2

Radial nodes of 2p -orbital = n- l -1 = 2 – 1 – 1 = 0

Question 33. How many radial nodes and planar nodes are present in 3p -orbital?
Answer:

No. of radial nodes = n-l-1

= 3-1-1

= 2-1

= 1

No. of planar nodes =l=1

Total no. of nodes = n- 1 = 3- 1 = 2

Question 34. What do you mean by the Acceptable values of e and Corresponding wave functions that are obtained by solving the Schrodinger wave equation for h-atom?
Answer:

No, atomic orbitals do not possess a sharp boundary. This is because the electron clouds are scattered to a large distance from the nucleus. The density of electron clouds decreases with increasing distance from the nucleus but theoretically, it never becomes zero

Question 35. In which direction the value of

1. ψ_2px
2. ψ_2py
3. ψ_{2pz ,} is the highest? Px

Answer:

• At the negative and positive direction of the x -x-axis.
• At the negative and positive direction of y -y-axis.
• At the negative and positive direction of the z-axis.

Question 36. Why s -orbital does not possess directional properties?
Answer:

The angular part of the wave function of s-orbital does not depend on θ and ∅

As a result, a symmetrical distribution of electron density occurs with increasing distance from the nucleus. Thus, s -the orbital is spherically symmetrical and does not possess directional properties.

Question 37. Indicate the subshells present in the M -M-shell. How many orbitals are present in this shell?
Answer

In the case of M-shell, the principal quantum number, n = 3. The values of azimuthal quantum no. Z are’ 0 ‘, ‘ 1’, and ‘2’.

This means that the M-shell contains three subshells, namely, ‘p’ and ‘ d’. For each value of‘ Z ’, the magnetic quantum number ‘ m ’ can have 2Z + 1 values. Therefore M-shell contains 2Z+ 1 orbital.

Question 38. Write the values of the azimuthal quantum number ‘l’ in the third energy level and(it) 3d -subshell of an atom.
Answer:

In the third energy level, the principal quantum number n = 3

Values of azimuthal quantum no., ‘ Z ’ are 0, 1, and 2.

For any d -subshell, 1 = 2.

Question 39. What is the maximum number of electrons that can be accommodated in the subshell with 1 = 3?
Answer:

For every value of’ Z ‘, ‘ m ’ can have 2Z + 1 values.

Since For Z = 3, m can have 2Z+ 1 values, i.e., 2 × 3 + 1 = 7 values. Therefore, the number of orbitals in the given shell = 7.

The maximum number of electrons that can be accommodated in these orbitals = 2×7 = 14 [v each orbital can accommodate a maximum of 2 electrons].

Question 40. What is the maximum number of electrons that can be accommodated in an orbital with m = +3?
Answer:

Each value of the magnetic quantum number ‘m’ indicates only one orbital and each orbital can accommodate a maximum of 2 electrons.

This means that the orbital Indicated by m = +3 can accommodate a maximum of 2 electrons.

Question 41. When Be is bombarded with a -particles, a new element viz carbon Is formed whereas, when gold is bombarded with a -particles, no new elements are formed. Explain.
Answer:

There are 79 protons in the nucleus of a gold (_7gAu) atom, while α -particles are helium nuclei with 2 unit positive charges.

The approaching α -particles are repelled strongly due to high positive charges of Au nuclei and thus suffer deflection.

On the other hand, there are only 4 protons in the nucleus of the beryllium (₄Be) atom are very weak compared to those between the gold nuclei and o – particles, due to the low positive charge of the Be nucleus. Thus, the fast-moving a -particles collide with Be nuclei and cause splitting

⇒  \({ }_4^9 \mathrm{Be}+{ }_2^4 \mathrm{He} \longrightarrow{ }_6^{12} \mathrm{C}+{ }_0^1 n\)

NCERT Solutions Class 11 Chemistry Chapter 2 Short Questions

Question 42. Why are atomic spectra not continuous?
Answer:

Each electron in an atom is associated with a definite energy corresponding to different energy levels. These electrons absorb energy from various external sources (like heat, light, etc.) and are promoted to higher energy levels. These excited electrons radiate different amounts of energy and return to the ground state.

Since the difference between any two energy levels is fixed, the atomic spectra obtained are discontinuous line spectra having fixed wavelengths. The spectrum so obtained consists of a few bright lines but does not contain all the possible spectral lines corresponding to a range of given wavelengths. Thus, atomic spectra are not continuous.

Question 43. With the help of Bohr’s theory, how will you determine the kinetic energy of hydrogen or hydrogen-like atoms?
Answer:

Let the no. of positive charges in the nucleus of a given atom or ion be Z.e (Z = atomic no., e = charge of a proton). According to Bohr’s theory, the electron present in that atom or ion revolves around the nucleus only in stationary orbits.

Let the radius ofthe stationary orbit be ‘r’ For the stability of the atom, the coulombic force must be equal to the centrifugal force of the electron moving with a velocity

⇒  \(\frac{Z e^2}{r^2}=\frac{m v^2}{r} \text { or } \frac{1}{2} m v^2=\frac{Z e^2}{2 r}\)

Question 44. What is the precessional motion of the orbit?
Answer:

According to Sommerfeld’s relativistic correction of the atomic model, an electron revolves in an elliptical orbit around the nucleus, which is located at the focus of the ellipse.

• This results in a continual change in the mass and velocity of the electron. The mass of the moving electron increases with its velocity.
• The velocity of this electron is maximum when closest to the focus of the ellipse (perihelion) and minimum when farthest from the focus (aphelion). Because of its increased mass at the perihelion, the electron experiences a stronger force of attraction from the nucleus.
• This compels the electron to deviate from its original orbit to a new and identical orbit, which lies in the same plane. The perihelion moves each time the electron completes a revolution.
• Thus the entire electron orbit moves about an axis passing through the nucleus. This phenomenon is known as Sommerfeld’s precession or precessional motion of the orbit.

Question 45. Name the noble gas and give its atomic number if the number of d -d-electrons present in this atom is equal to the difference in the no. of electrons present in the p and s- s-subshells
Answer:

The noble gas is krypton (Kr). Its atomic number = 36

Electronic configuration: ls²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶

• Number of s -electrons = 2 + 2 + 2 + 2 = 8
• Number of p -electrons = 6 + 6 + 6 = 18
• Number of d -electrons = 10

∴ Number of p -electrons number of s -electrons =18-8 = 10= number of d -electrons

Question 46. There is a wavelength limit beyond which the spectrum of any given series of the H-atom becomes continuous. Why?
Answer:

The energy difference between the first and second orbits is maximum. With the increase in the value of the principal quantum number (n), the energy difference between two successive orbits decreases. Consequently, after a particular value of n, the energy levels become very closely spaced and as a result, they seem to be continuous.

Question 47. How will you prove that electrons are negatively charged particles with a definite mass?
Answer:

Under the influence of an electric field the cathode rays as well as the electron beam, are deflected towards the positive plate of the electric field. Cathode rays also neutralize the gold leaf ‘ electroscope, charged with positive electricity.

Thus it can be proved that electrons are negatively charged. A light paddle wheel placed in the path of cathode rays, begins to rotate, showing that cathode rays are made of matter particles.

Question 48. Calculate the number of particles present in 0.1 g electron.
Answer:

Number of electrons = \(\frac{\text { Total mass of electrons }}{\text { Mass of Celestron }}\)

= \(\frac{0.1 \mathrm{~g}}{9.11 \times 10^{-28} \mathrm{~g}}\)

=\(1.0977 \times 10^{26}\)

Question 49. The charge-to-mass ratio of an electron is 1836 times greater than that ofa proton. Establish a mathematical relation to compare their masses.
Answer:

Given \(\frac{e}{m_e}=1836 \times \frac{e}{m_p}\) However the charge on 1 electron Is the same as that of 1 proton

⇒ \(\frac{1}{m_e}=\frac{1836}{m_p}\)

or, m_p = 1836 x m_e

Question 50. Two discharge tubes containing H₂ and O₂ gas respectively are subjected to electrical discharge at low pressure. Will there be any difference like cathode rays and anode formed inside the tube?
Answer:

In both cases, cathode rays with identical properties are produced, because these rays are independent of the nature of the material of the cathode and the gas used in the discharge tube. However, in these two cases, anode rays with different properties are produced since these rays depend on the nature of the gas used in the discharge tube.

Question 51. Explain the generation ofthe positively charged particles in the discharge tube when hydrogen gas is used.
Answer:

Due to the high voltage in the discharge tube, H₂ and D₂ are dissociated into H and D atoms.

Due to the knockout of electrons from atoms or molecules present in the discharge tube by cathode rays, H⁺₂, D⁺₂, H⁺, and D⁺ ions are produced.

Similarly, HD+ ions are also produced by the knockout of electrons from a few HD molecules (produced by a combination of H and D atoms)

Question 52. How many protons will be needed to fill a spherical vessel of volume 10cm3? Also, calculate the mass of these protons.
Answer:

Volume of proton \(=\frac{4}{3} \pi r^3=\frac{4}{3} \times 3.14 \times\left(1.2 \times 10^{-13}\right)^3 \mathrm{~cm}^3\)

⇒ \(\frac{\text { Volume of a sphere }}{\text { Volume of a proton }}\)

= \(\frac{10}{\frac{4}{3} \times 3.14 \times\left(1.2 \times 10^{-13}\right)^3}\)

Mass of protons = No. of protons × Mass of a proton

= (1.382 × 10³⁹)× (1.6725× 10^-24)g =2.311 × 10¹⁵g.

Question 53. An element has an isotope with a mass number of 14. It contains 8 neutrons. Identify the element.
Answer:

Mass number = No. of protons+ No. of neutrons.

Number of protons =14 – 8 =6

The atomic number ofthe element = 6, which means, the element is ‘Carbon’.

Question 54. Why was it necessary to consider the existence of neutrons in the nucleus of an atom?
Answer:

The actual mass of an atom of an element, except hydrogen, Is greater than the sum of the masses of protons and electrons present in that atom. Hence, Rutherford in 1920, proposed the existence of an uncharged particle in an atom having unit mass. This particle was called the neutron.

Question 55. Identify the subshells denoted by the following:

n = 4,l = 2

n = 5, l = 3

 n = 6, l = 4

Answer:

1. 4d
2. 5f
3. 6g
4. 4s

Question 56. Which quantum number is to be mentioned to distinguish between the electrons present in the -K-shell? 
Answer:

For k-shell (n = 1), l = 0 and m = 0. This indicates that K-shell has only one orbital and this orbital can accommodate a maximum of 2 electrons having spin quantum no., ‘s’ with values +1/2 and -1/2.

So, to distinguish between the two electrons in the K-shell, it is important to indicate their spin quantum numbers.

Question 57. Write the values of n, l, and m for 3p -subshell.
Answer:

For 3p -orbitals, n = 3 , l = 1 and m = +1 , 0, -1 . Hence, 3p -subshell has 3 orbitals.

The values of and ‘ m ‘ for these orbitals are as follows:

1. n = 3, l = 1 , m = +1
2. n = 3,  l = l, m = 0
3. n = 3, l = 1 , m =-1

Question 58. Which of the following two orbitals is associated with a higher energy?

1. n = 3, l = 2, m = +1
2. n = 4, l = 0, m = 0

Answer: The algebraic sum of n and / determines the energy of a given subshell. The higher the value of (n + l), of an orbital, the higher its energy. Thus, the orbital with n = 3, l= 2 is associated with a higher energy.

Short Questions and Answers for Class 11 Chemistry Chapter 2

Question 59. Is there any difference between the angular momentum of 3p and 4p -electrons?
Answer:

For any p -subshell, 1=1. The angular momentum of an electron depends on the values of all and is independent of the values of Angular momentum, \(L=\sqrt{l(l+1)} \frac{h}{2 \pi}.\).

Since 1=1 for both the p -subshells (3p and 4p), there is no difference in the angular momentum ofthe electrons occupying those subshells

Question 60. Mention the sequence in which the following orbitals are filled up by electrons: 3d and 4p.
Answer:

The energy of a given subshell is determined by the algebraic sum of’ and ‘Vue., n + 1.

11 the ‘n +l’ values of any two subshells are equal, then the electron enters the one with lower’ n ’. In the 3d -subshell, n = 3 , l = 2 n + l = 3 + 2 = 5 In the 4p -subshell, n = 4, 1=1

B +1 =4 +1 = 5 Since for the 3d -subshell, n = 3 which is lower than that of 4p where n = 4, the electron first enters the 3d -subshell.

Question 61. What is the maximum number of Ad -electrons with spin quantum number s =?
Answer:

For a 4d -subshell, n = 4, 1 = 2 and m = +2, +1,0, -1,-2. This implies that 5 orbitals in this sub-shell can accommodate a maximum of 10 electrons.

5 of these electrons have s = +| and the remaining 5 have -i . Hence maximum number of 4d -electrons with 2 i spin quantum no., s = -1/2 is 5.

Question 62. Is it possible for atoms with even atomic numbers to contain unpaired electrons?
Answer:

Atoms with even atomic numbers can have unpaired electrons. This is by Hund’s rule which states that the orbitals within the same subshell are at first filled up singly with electrons having parallel spin before pairing takes place.

For instance, in the case of a carbon atom (atomic number 6 and electronic configuration: ls²2s²2p_x¹2p_y¹2p_z⁰ ), there are two unpaired electrons

Question 63. Write the electronic configurations of Cu and Cr -atoms.
Answer:

Electronic configuration of ₂₉Cu

ls²2s²2p⁶3s²3p²3d¹⁰4s¹

Electronic configuration of ₂₄Cr :

ls²2s²2p²⁶3s²3p⁶3d⁵4s¹

Question 64. Write the electronic configurations of Fe²⁺ and Cu⁺ ions.
Answer:

Electronic configuration of Fe²⁺ (atomic number =26):

ls²2s²2p⁶3s²3p⁶3d²⁶

Electronic configuration of Cu⁺ (atomic number = 29 ):

1s²2s²2p⁶3s²3p⁶3d¹⁰

Question 65. Which of the following has a maximum number of unpaired electrons? (1) Mn²⁺Fe2+Cu2+ Cr
Answer:

The following are the electronic configurations of the given ions and atoms:

Mn2+: ls²2s²2p⁶3s²3p⁶3d⁵

Fe²⁺: ls²2s²2p⁶3s²3p⁶3d⁹

Cu²-: ls²2s²2p⁶3s²3p⁶3d⁹

Cr: ls²2s²2p⁶3s²3p⁶3d⁵4s¹

Question 66. Calculate the number of unpaired electrons in the N -atom.
Answer:

Electronic configuration of (atomic no. =7): ls²2s²2p³

According to Hund’s rule, the 3 electrons in the 2psubshell occupy the three p -p-orbitals (px, py, pz) singly.

Hence, the no. of unpaired electrons present in N = 3.

Question 67. How many electrons of the Ne -atom have clockwise spin?
Answer:

Electronic configuration of Ne (atomic number = 10)

Each of the pair of electrons present in each ofthe Is, 2s, 2px, 2py, and 2pz orbitals have a clockwise spin and the other, an anti-clockwise spin. Therefore no. of electrons of Ne-atom having clockwise spin = 5.

Question 68. Write the names and symbols of an atom, a cation, and an anion with the electronic configuration Is2.
Answer:

Atom: Helium (He);

Cation: Lithium-ion (Li⁺),

Anion: Hydride ion (H^– ).

Question 69. How many nodes are there in 3s -orbital?
Answer:

The node is the spherical shell (or region) inside the s -s-orbital where electron density is zero. In the case of 3s orbital, there are two such spherical shells where the electron density is zero.

So 3s -orbital has two radial nodes but no angular node (1 = 0). So the total no. of nodes is 2. [No. of nodal surfaces =n- 1, where n is the principal quantum number]

Question 70. How many nodal points are there in 3p -orbital?
Answer:

In a p -orbital the electron density, at the point where the two lobes meet is zero.

This point is called the nodal point of the p-orbital. So each of the three 3p -orbitals (viz., px, py, and pz ) has only one nodal point.

Question 71. Indicate principal and azimuthal quantum numbers for the subshells:

1. 4s
2. 5d
3. 2p
4. 6

Answer:

1. n = 4, 1 = 0
2. n = 5,1 =2
3. n = 2, 1=1
4. n = 6, 1 = 3

Question 72. An element (symbol M) has 26 protons in the nucleus. Write the electronic configuration of M²⁺ and M³⁺.
Answer:

₂₆M: ls²2s²2p⁶3s²3p⁶3d⁶4s²

₂₆M²⁺: ls²2s²2p⁶3s²3p⁶3d⁶

₂₆M³⁺ : ls²2s²2p⁶3s²3p⁶3d⁵

Question 73. There are 8 electrons in the 3d -subshell of an atom. Among these, what will be the maximum number of electrons with similar spin? What is the number of odd electrons?
Answer:

1. Electronic configuration of 3d -subshell
2. Maximum number of electrons with the same spin = 5.
3. Number of odd electrons in that atom = 2.

Question 74. Among the following pairs of orbitals which orbital will experience the larger effective nuclear charge?

1. 2s and
2. 3s,
3. 4d and
4. 4f,
5. 3d and
6. 3p

Answer:

1. 2s
2. 4d
3. 3p

Question 75. Indicate the number of impaired electrons in:

1. P
2. Si
3. Cr
4. Fe and
5. kr

Answer:

1. ₁₅P = ls²2s²2p⁶3s²3p_x¹3p_y¹3p_z¹ ; number of unpaired electrons = 3.
2. ₁₄Si = ls²2s²2p⁶3s²3p_x¹3p_y¹ number of unpaired electrons = 2.
3. ₂₄Cr = ls²2s²2p⁶3s²3p⁶3d⁵4s¹; number of paired electrons = 6 (5 in d-subshell &1 in s-subshell).
4. ₂₆Fe = ls²2s²2p⁶3s²3p⁶3d⁶4s²; number of unpaired electrons in d-subshell = 4.
5. ₃₆Kr = ls²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁶; number of unpaired electrons = 0.

Question 76. How many subshells are associated with n =4? How many electrons will be present in the subshells having ms value of \(-\frac{1}{2}\) for n = 4?
Answer:

For n = 4, l = 0, 1, 2, 3. Thus, the energy level with n = 4 contains four subshell (4s, 4p, 4d and 4f).

For n = 4, the number of orbitals (n)2 = (4)2 = 16.

Each orbital will have only one electron with ms = Hence, for n = 4, 16 electrons will be present in the subshells with the value of ms \(=-\frac{1}{2}.\)

Question 77. Write the complete symbol for the atom with the h = 6.626 × 10^-34J.s, c = 3.0× 10⁸m-s^-1 ] given atomic number (Z) and atomic mass (A)

1. Z = 17, A = 35
2. Z= 92, A=233
3. Z = 4, A = 9

Answer:

⇒ \({ }_{17}^{35} \mathrm{Cl}\)

⇒  \({ }_{92}^{233} \mathrm{U}\)

⇒  \({ }_4^9 \mathrm{Be}\)

Question 78. Yellow light emitted from a sodium lamp has a wavelength (A) of 580 nm. Calculate the frequency (v) and wave number (v) of the yellow light.
Answer:

Wavelength, A =580nm =580 × 10^-9m =5.80 ×10^-7m.

Frequency of yellow light.

v = \(\frac{c}{\lambda}=\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{5.80 \times 10^{-7} \mathrm{~m}}=5.17 \times 10^{14} \mathrm{~s}^{-1}\)

Speed of light, c = 3 × 10⁸ m.s^-1  and wave number,

⇒ \(\bar{v}=\frac{1}{\lambda}=\frac{1}{5.80 \times 10^{-7} \mathrm{~m}}\)

= 1.72 × 10⁸ m.s^-1

Structure of Atom Chapter 2 Short Answer Solutions Class 11

Question 79. Find the energy of each of the photons which corresponds to light of frequency 3 × × 10¹⁵ Hz. Have a wavelength of 0.50A
Answer:

⇒ \(=h v=\left(6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s}\right) \times\left(3 \times 10^{15} \mathrm{~s}^{-1}\right)\)

=1.988× 10^-18J

E =  \(h v=\frac{h c}{\lambda}\)

= \(\frac{6.626 \times 10^{-34} \mathrm{~J} \cdot \mathrm{s} \times 3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{0.50 \times 10^{-10} \mathrm{~m}}\)

= 3.978 × 10^-15J

Question 80. Calculate the wavelength, frequency, and wavenumber of a light wave whose period is 2.0 × 10^-10s.
Answer:

⇒ \(\text { Frequency }(v)=\frac{1}{\text { period }}=\frac{1}{2.0 \times 10^{-10} \mathrm{~s}}=5 \times 10^9 \mathrm{~s}^{-1}\)

⇒ \(\text { Wavelength }(\lambda)=\frac{c}{\lambda}=\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{5 \times 10^9 \mathrm{~s}^{-1}}=6 \times 10^{-2} \mathrm{~m}\)

And wavelength \((\bar{v})=\frac{1}{\lambda}=\frac{1}{6 \times 10^{-2} \mathrm{~m}}=16.66 \mathrm{~m}^{-1}\)

Question 81. Electromagnetic radiation of wavelength 242 is just sufficient to ionize the sodium atom. Calculate the ionization energy of sodium in kJ.mol^-1
Answer:

Ionisation energy ofsodium (E) = Nhv \(=N h \frac{c}{\lambda}\)

E = \(\frac{\left(6.022 \times 10^{23}\right) \times\left(6.626 \times 10^{-34}\right) \times\left(3 \times 10^8\right)}{242 \times 10^{-9}}\)

= 4.946  ×  10⁵ J.mol^-1

= 494.6 kJ-mol^-1

Question 82. Electrons are emitted with zero velocity from a metal surface when it is exposed to radiation of wavelength 6800 A. Calculate threshold frequency (vQ) and work function (W0) of the meta
Answer:

Threshold frequency \(v_0=\frac{c}{\lambda_0}=\frac{3 \times 10^8 \mathrm{~m} \cdot \mathrm{s}^{-1}}{6800 \times 10^{-10} \mathrm{~m}}\)

= 4.41 ×  10¹⁴ s^-1

And the work function of the metal ( wQ) = hv0

= (6.626 × 10³⁴ J.s) ×  (4.41 × 10^-14.s^-1) =2.92 ×10^-19J

Question 83. Which of the following are isoelectronic species i.e., those having the same number of electrons? Na⁺,K⁺,Mg²⁺, Ca²⁺, S^2-,Ar
Answer:

The number of electrons present in

Na⁺=(11 – 1) =10

K⁺=( 19 – 1) =18

Mg²⁺ =(12 – 2) = 10

Ca²⁺ =(20 – 2)=18

S^2- =(1 6+ 2) =18

Ar = 18.

Elance, Na⁺, and Mg²⁺ are isoelectronic because they contain 10 electrons each. K⁺, Ca²⁺, S^2-, and Ar are isoelectronic because they contain 18 electrons each.

Question 84.

1. What is the orbital angular momentum of a p -electron in \(\frac{h}{2 \pi}\) unit?
2. The atomic numbers of two elements X and Y are 15 and 27 respectively. Write down the electronic configuration of X^3- and Y³⁺ ions.
   

Answer:

1. The orbital angular momentum in \(\frac{h}{2 \pi}\) unit is given by \(\sqrt{l(l+1)}\) where l = azimuthal quantum number.

For p -orbital , l = 1.

∴ The orbital angular momentum of p -orbital in \(\frac{h}{2 \pi}\) unit

= \( \sqrt{l(l+1)}=\sqrt{1(1+1)}=\sqrt{2} .\)

2. ₁₅X^3- : ls²2s²2p⁶3s²3p⁶

₂₇Y³⁺ : ls²2s²2p⁶3s²3p⁶3d⁶

Question 85.

1. The electronic configuration of an atom is \([Z](n-2) f^{14}(n-1) d^1 n s^2\). What is the minimum position of the atom in the periodic table and correspondingly what is the atomic number of Z?
2. Find the number of impaired electrons in the atom of the element having atomic number 16
3. Which of the following ions does not obey Bohr’s atomic theory? He²⁺+,Li²⁺,B³⁺,Be³⁺
   

Answer:

Electronic configuration of the given atom:

1. (n-2)f^1-14-14(n-1)d^0-1 ns². So, it can be stated that the given atom belongs f-block. Hence, the element is of group IIIB and its electronic configuration is identical to ₇₁Lu of the lanthanoids and Lu of the actinoids. The lowest position available to the atom ofthe element is the 6th period and group-IIlB(3). Thus, it belongs to the lanthanoids and has atomic number 71.

2. The electronic configuration of an atom ofthe element with atomic number 16 is 1s²2s²2p⁶3s²3p_x²3p_y¹ 3p_z¹. Thus, number of unpaired electrons is two.

3.  Be³⁺does not obey Bohr’s atomic theory because it is 2- an electron system

Question 86. Using s, p, and d notations, describe the orbital with the following quantum numbers.

• n- 1,
• 1=0;
• n = 3;
• 1 = 1
• n = 4;
• 1 = 2;
• n = 4;
• l = 3

Answer:

• 1s
• 2s
• 4d
• 4f

Question 87. Explain, giving reasons, which of the following sets of quantum numbers are not possible

• n = 0, l = 0, m₁ = 0, m_s = \(+\frac{1}{2}\)
• n = 1, l = 0, m₁ = 0, m_s = \(-\frac{1}{2}\)
• n = 1, l =1, m₁ = 0, m_s = \(+\frac{1}{2}\)
• n = 2, l = 1, m₁ = 0, m_s = \(-\frac{1}{2}\)
• n = 3, l = 3, m₁ = -3, m_s = \(+\frac{1}{2}\)
• n = 3, l = 1, m₁ = 0, m_s = \(+\frac{1}{2}\)

Answer: This is not possible because n cannot be zero. and are not possible because the value of n cannot be equal to 1.

Question 88. How many electrons in an atom may have the following quantum numbers?

1. n = 4,
2. m_s = \(+\frac{1}{2}\)
3. n = 3, l = 0

Answer: For n = 4, the total number of electron

= 2n² = 2 × 4² = 32 . Among these 32 electrons, half,16 electrons will have s or m_s = \(+\frac{1}{2}\) and the other 16 electrons will have ms = \(-\frac{1}{2}\)

n = 3 , l = 0 means 3s -subshell. The maximum number of electrons in this subshell is two.

NCERT Class 11 Chemistry Chapter 2 Structure of Atom Short Q&A

Question 89. Show that the circumference of the Bohr orbit for the hydrogen atom is an integral multiple of the de Broglie wavelength associated with the electron revolving around the orbit.
Answer:

According to Bohr’s postulate, angular momentum \(m v r=\frac{n h}{2 \pi}\) [n = principle quantum number = 1, 2, 3, 4 …………..

Again, according to the de Broglie equation, for a revolving electron, wavelength \((\lambda)=\frac{h}{m v}\)

Substituting the value of A from (2) in (1) we have, 2pi r = n lambda (n = 1,2, 3, 4….)

Thus, the circumference of the Bohr orbit is an integral multiple ofthe de Broglie wavelength ofthe revolving electron.

Question 90. An ion with mass number 37 possesses one unit of negative charge. If the ion contains 11.1% more neutrons than electrons, find the symbol of the ion
Answer:

As the ion contains one unit of negative charge, the ion has one electron more than the number of protons. Total number of electrons and neutrons =37 + 1 = 38. Let the number of electrons in the ion = x.

Hence, number of neutron \(=x+\frac{11.1}{100} \times x=1.111 x\)

Again, x+ 1. 111 x = 38 or, x = 18

Thus, the number of electrons present in the ion = 18.

Thus, the number of protons present in the ion =18-1 = 17

So, the element’s atomic number is 17 i.e., the atom is chlorine. its symbol ,\({ }_{17}^{37} \mathrm{Cl}^{-}\)

Question 91. An ion with mass number 56 contains 3 units of positive charge and 30.4% more neutrons than electrons. Assign the symbol to this ion.
Answer:

The ion contains three units of positive charge. Thus, the number of electrons in the ion is three less than that of the number of protons. Number of protons + number of neutrons mass number =56. let, the number of electrons in the ion be x.

Number of neutrons present in the ion \(=x+\frac{30.4}{100} \times x=1.304 x\)

Again, the total number of electrons and neutrons = 53. x + 1.304x = 53 or, 2.304x = 53 Thus, number of electrons present in the ion = 23 and the number of protons =  23 + 3 = 26 .

The element with atomic number 26 is Fe and their symbol will be \({ }_{26}^{56} \mathrm{Fe}^{3+}\).

Question 92. Nitrogen laser produces radiation at a ‘wavelength of 337.1 nm. If the die number of photons emitted is 5.6 × 10²⁴, calculate the power of this laser.
Answer:

⇒ \(E=N h v=N h \frac{c}{\lambda}\)

= \(\frac{\left(5.6 \times 10^{24}\right) \times\left(6.626 \times 10^{-34}\right) \times\left(3.0 \times 10^8\right)}{\left(337.1 \times 10^{-9}\right)}\)

= 33 × 10⁶J

Question 93. The dual behavior of matter proposed by de Broglie led to = 1.52 × 10^-38, the discovery of an electron microscope often used for the highly magnified images of biological molecules and another type of material. If the velocity of the electron in this microscope is 1.6 × 10⁶m.s^-1, calculate the de Broglie wavelength associated with this electron.
Answer:

Velocity of an electron (y) = 1.6 ×10⁶m.s^-1 and mass of an electron (m) = 9.108 × 10^-31 kg

∴ de Broglie wavelength \((\lambda)=\frac{h}{m v}\)

= \(\frac{6.626 \times 10^{-34}}{9.108 \times 10^{-31} \times 1.6 \times 10^6}\)

= \(4.55 \times 10^{-10} \mathrm{~m}=455 \mathrm{pm}\)

Question 94. Similar to electron diffraction, a neutron diffraction microscope is also used for the determination of the structure of molecules. If the wavelength used here is 800 pm, calculate the characteristic velocity associated with the neutron.
Answer:

Mass of neutron (m) = 1.675 × 10²⁷kg

According to de Broglie equation, wavelength \((\lambda)=\frac{h}{m v}\)

∴ Velocity ofa neutron \(v=\frac{h}{m \lambda}\)

Or, \(v=\frac{6.626 \times 10^{-34}}{1.675 \times 10^{-27} \times 800 \times 10^{-12}}\)

or, v = 494m.s^-1

Question 95. The bromine atom possesses 35 electrons. It contains 6 electrons in a 2p orbital. 6 electrons in 3p orbital and 5 electron in 4p orbital. Which of these electrons experiences the lowest effective nuclear charge?
Answer:

The value of n for the 4p electrons is highest and hence they are the furthest from the nucleus and thus experience the lowest effective nuclear charge.

In a given orbit, for the same type of subshells, the higher the value of n, the lower the value of effective nuclear charge.

Short Questions for Class 11 Chemistry Chapter 2 NCERT

Question 96. In Rutherford’s experiment, generally, the thin foil of heavy atoms, like gold, platinum, etc. have been used to be bombarded by the a -particles. What difference would be observed from the above results if the thin foil of light atoms like aluminum etc. is used?
Answer:

The nucleus of heavy atoms contains a large amount of chlorine. positive charge. Thus, the a -particles that move towards the nucleus are deflected back due to strong repulsion by the nucleus. Those particles which pass through the region closer to the nucleus are deflected in different directions. On the other hand, the nucleus of light atoms contains a small amount of positive charge. Hence, a negligible number of particles are deflected back or are deflected by small angles.

Question 97. Symbol \({ }_{35}^{79} \mathrm{Br}\) and \({ }^{79} \mathrm{Br}\) symbol \({ }_{35}^{79} \mathrm{Br}\) and \({ }^{35} \mathrm{Br}\) are not acceptable. Answer briefly.
Answer:

⇒ \({ }_{35}^{79} \mathrm{Br}\) is not acceptable because mass number should be written as superscript and atomic number as subscript. ₃₅Br is not acceptable because the atomic number of an element is fixed but the mass number is not fixed. It depends on the isotopes. Thus, an indication of mass number is essential.

Question 98. Why is the line spectrum of an element known as the fingerprint of its atoms?
Answer:

The line spectrum of any element consists of several lines having different wavelengths. It is observed that each element has its characteristic spectrum, different from those of all other elements.

The spectra of any two elements can never be identical. Hence, the line spectrum of an element is known as the fingerprint of its atoms

Question 99. Does atomic orbitals possess a sharp boundary? Explain.
Answer:

No, atomic orbitals do not possess a sharp boundary. This is because the electron clouds are scattered to a large distance from the nucleus.

The density of electron clouds decreases with increasing distance from the nucleus but theoretically, it never becomes zero

Question 100. Why do we consider each stationary state as an energy level with a definite value?
Answer:

Electrons in a particular orbit do not lose or gain energy. In other words, the energy of an electron in a particular orbit remains constant. Hence, these orbits or stationary states are known as energy levels having definite values.

Question 101. There are nine electrons in the 5f-orbital of an atom of an element Mention the maximum number of electrons that have the same spin and number of impaired electrons.
Answer:

Element Mention the maximum number of electrons that have the same spin and number of impaired electrons-

Thus, the maximum number of electrons with the same spin will be 7, and several unpaired electrons will be 5.

Question 102. Explain whether 3f-orbital is present in P-atom. State the rule
Answer:

Electronic configuration: 1s²2s²2p⁶3s²3p¹_x3p_y¹3_z¹

Pliosphorous atom does not contain 3f- subshell.

For 3f-subshell, n = 3 . Hence, the maximum value of f = (n- l) = 2 i.e., d -subshell.

Question 103.

1. What are the quantum numbers by which an electron In an atom can be designated?
2. What Is the maximum number of quantum numbers that may be the same or two electrons of an atom?

Answer:

1. Principal quantum number (n), azimuthal quantum number (Z), magnetic quantum number (m), and spin quantum number (s) are required to designate an electron in an atom.
2. The maximum number of quantum numbers that may be the same for two electrons of an atom is 3.

NCERT Class 11 Structure of Atom Short Answer Questions

NCERT Solutions For Class 11 Chemistry Chapter 2 Structure Of Atom Warm-Up Exercise Question And Answers

Question 1.  If the energy of the first Bohr’s orbit is -13.58 eV of a hydrogen atom, calculate the energy of the third Bohr’s orbit of that atom.
Answer:

According to Bohr’s theory

⇒ \(E_n=-13.58 \times \frac{Z^2}{n^2} \mathrm{eV}=-13.58 \times \frac{1^2}{3^2} \mathrm{eV}=-1.5089 \mathrm{eV}\)

Question 2. Which quantum numbers specify the size and the shape of electronic orbital?
Answer:

The size of an electronic orbital is determined by the principal quantum number (n) and the azimuthal quantum number (f) determines the shape of an electronic orbital.

Question 3. Write down the values of the quantum numbers of the electron in the outermost shell of sodium.
Answer:

The electron present in the outermost shell of sodium is identified as 3s. Its principal quantum number n = 3, azimuthal quantum number 1 = 0, magnetic quantum number, m = 0 and spin quantum number, s = +1/2.

Question 4. Which is the lowest principal energy level that permits the existence of off-subshell?
Answer:

For f-subshell, the value of the azimuthal quantum number Z is 3. So the lowest principal energy level that permits the existence of an f -subshell is the fourth shell (i.e, N -N-shell)

Question 5. The unpaired electrons in A1 and Si are present in the 3p orbital. Which electrons will experience a more effective nuclear charge from the nucleus?
Answer:

The nuclear charge of silicon (+14) is greater than that of aluminum (+13). Hence the impaired 3p -electron of silicon will experience a more effective nuclear charge.

Question 6. Mention the most important application of the de Broglie concept.
Answer:

The de-Broglie concept is utilized in the construction of an electron microscope used for the measurement of the size of very small objects.

Question 7. What is the physical significance of Ψ and Ψ²?
Answer:

The wave function has no physical significance, while Ψ² gives the probability density i.e., the probability of finding the electron at any point around the nucleus.

Question 8. Write Schrodinger’s wave equation in the briefest possible form.
Answer:

The briefest form of Schrodinger’s wave equation is, \(\widehat{\mathrm{H}} \psi=E \psi\), where H is known as the Hamiltonian operator.

Question 9. What do you mean by ‘doughnut’?
Answer:

The two lobes of d -the orbital are distributed along the z-axis and a sphere is situated with the nucleus at its center. This sphere is called a ‘doughnut’

Question 10. How many angular nodes are present in dÿ Identify them.
Answer:

Two angular nodes are present (they pass through the origin and lie at an angle of 45° with the xz and zipline and themselves lie perpendicular to each other)

Question 11. Why do p-orbitals possess directional properties?
Answer:

The angular part of the wave function of p -p-orbital depends on the value of 6 and <p. Thus, p -p-orbitals possess directional properties.

Question 12. Why is the de Broglie wave termed a matter wave?
Answer:

Since the de Broglie wave is associated with fast-moving tiny material particles, it is also known as matter wave. The wavelength of such waves depends on the mass and velocity of the particles.

Question 13. Write the mathematical expression for Heisenberg’s uncertainty principle-
Answer:

⇒ \(\Delta x \cdot \Delta p \frac{h}{4 \pi},\) where Ax and Ap are uncertainties in the determination of exact position and momentum respectively.

Question 14. How many photons are emitted in the transition of the electron from the first to the first energy level of the H-atom?
Answer:

There is only one electron in the H-atom. Hence, during the transition of electrons from the fourth to the first energy level, only one photon is emitted.

Question 15. How is the radius of an electronic orbit related to the principal quantum number?
Answer:

The relation between the radius (r) ofthe electronic orbit and the principal quantum number (n) is given by, Therefore, the radius of the orbit is directly proportional to the square ofthe principal quantum number.

Question 16. How would you obtain the line spectrum of hydrogen?
Answer:

When hydrogen gas at low pressure is taken in the discharge tube and the light emitted on passing electric discharge is resolved in a spectroscope, the spectrum obtained is the line spectrum of hydrogen.

Question 17. Explain why Rutherford did not mention the presence of neutrons in the proposed nuclear model of the atom.
Answer:

In the year 1911, when Rutherford proposed the nuclear model of the atom, the existence of neutrons was still not known (In fact, neutrons were discovered in 1932). Hence, Rutherford did not mention the presence of neutrons.

Question 18. From this experiment, it was concluded that the entire mass and positive ‘charge is present at the center of an atom.
Answer:

From Rutherford’s -particle scattering experiment, it was concluded that the entire mass and positive charge are present at the center of an atom.

Question 19. What is the nuclear model of the atom?
Answer:

The atomic model which describes the rotation of electrons in different orbitals around the positively charged nucleus is called the nuclear model of the atom.

Question 20. Identify the isotopes and isobars from the following list of atoms with a given number of protons and neutrons.
Answer:

A and B have the same number of protons but different numbers of neutrons. Hence, A and B are isotopes. C and D have different numbers of protons, but the sum of the protons and neutrons, in both cases, are the same. Hence, C and D are isobars.

Question 21. Find the total number of electrons present in l mol methane.
Answer:

1 methane (CH₄) molecules 1 C-atom + 4 H- atoms Number of electrons in CH₄ molecule =1  6 + 4 × 1

= 10. Therefore, the total number of electrons in l mol of CH4 = 6.022 × 10²³ × 10 = 6.022 × 10²⁴

Chapter 2 Structure of Atom Short Questions and Answers Class 11

Question 22. What are electromagnetic radiations? What is their velocity in a vacuum?
Answer:

Electromagnetic waves with wavelength ranging between 0.003 and 0.3m are known as microwaves. As these waves collectively travel in the same direction over a long distance, they are used in radars.

Question 23. State the principle of the formation of electromagnetic radiation.
Answer:

Electromagnetic waves with wavelengths ranging between 0.003 and 0.3m are known as microwaves. As these waves collectively travel in the same direction over a long distance, they are used in radars.

Question 24. What are microwaves? Why are they used in radars?
Answer:

Electromagnetic waves with wavelength ranging between 0.003-0.3m is known as microwaves. As these waves collectively travel in the same direction over a long distance, they are used in radars.

Question 25. Arrange the various types of radiations constituting the electromagnetic spectrum, in the decreasing order of their frequencies.
Answer:

The various radiations in the electromagnetic spectrum in decreasing order of their frequencies are as follows:

Cosmic rays > γ-rays> X-rays> UV-rays > visible rays > microwaves > radio waves.

Question 26. What is black body radiation Out of red and blue light, which one is associated with photons possessing higher energy?
Answer:

Blue light has a higher frequency (v) than red light. The energy of each photon = hv. Consequently, the photons associated with blue light have higher energy.

Question 27. Energy associated with X-rays is higher than that of visible light— explain.
Answer:

The energy of electromagnetic radiation refers to the energy of its photons (hv).

Since, ν_x-ray > ν_{visible light} -hence, hν_x-ray > hν_{visible light}  Thus, the energy of X-rays is higher than that of visible light.

Question 28. State the Pauli exclusion principle. Write the electronic configurations of ₂₄Cr³⁺ and ₂₇CO³⁺
Answer:

₂₄Cr³⁺: ls²2s²2p⁶3s²3p⁶3d³

₂₇CO³⁺: ls²2s²2p⁶3s²3p⁶3d⁶

Question 29. What is the maximum number of emission lines when the excited electron of the H atom in n = 6 drops to the ground state?
Answer:

The number of lines produced in a spectrum when an electron returns from the nth energy state to the ground state

= ∑(n₂-n₁) =∑(6- 1)

= ∑(5) = 5 + 4 + 3 + 2+1

= 15.

Question 30. A certain particle carries 2.5 = 1.602 × 10^-19 of static electric charge. Find the no. electrons present in It.
Answer:

Charge of electron = 1.602 × 10^-19 C (excluding -ye sign

∴ No. electrons contained in \(=\frac{2.5 \times 10^{-16} \mathrm{C}}{1.602 \times 10^{-19} \mathrm{C}}=1560\)

Question 31. Calculate the mass of 1 mol electron.
Answer:

Mass = Avogrado number x Mass of one electron

= (6.022 × 10²³) x (9.11 × 10^-28)

= 0.5486 mg

Question 32. A discharge tube containing H2 gas at low pressure is subjected to high voltage. Will there be er Ission of protons from the anode?
Answer:

In a discharge tube, anode rays are not emitted from the anode. Therefore protons are not emitted from the anode. However, they are produced from H2gas, by the knockout of the electrons by high-speed cathode rays.

Question 33. Write the nuclear reaction for the emission of neutrons. Indicate the e/m value of the neutron.
Answer:

When beryllium foil is bombarded with or -particles, it undergoes a nuclear reaction which primarily leads to the emission of chargeless particles called the neutron.

⇒ \({ }_4^9 \mathrm{Be}+{ }_2^4 \mathrm{He} \longrightarrow{ }_6^{12} \mathrm{C}+{ }_0^1 n\)

Question 34. Mention the symbol, charge, and names of the discoverers of positron, -meson, and neutrino.
Answer:

When beryllium foil is bombarded with or -particles, it undergoes a nuclear reaction which primarily leads to the emission of chargeless particles called neutrons.

Question 35. Write the symbols of two anions isoelectronic with K⁺ 
Answer:

K⁺ion: ls²2s²2p⁶3s²3p⁶.

Two anions that are isoelectronic with K⁺ -ion are S^2- and Cl^–

Question 36.

1. What is the stationary energy level of an electron? 
2. Write the electronic configurations of CO²⁺ and As³⁺ ions. (Atomic number of Co is 27 and As is 33).

Answer:

According to Bohr’s theory, the energy level in which an electron emits no energy is known as the stationary energy level of that electron.

₂₇CO²⁺ : ls²2s²2p⁶3s²3p⁶3d⁷

₃₃AS³⁺ : ls²2s²2p⁶3s²3p⁶3d¹⁰4s

Question 37. State the Heisenberg’s uncertainty principle. Calculate the de Broglie wavelength associated with an electron moving with a velocity of 1.0 × 10⁷ m/s. (Mass of an electron: 9.1 x 10-31kg
Answer:

Wavelength \(\lambda=\frac{h}{m v}\) [h = Planck’s constant, m = mass of an electron, v = velocity of an electron]

λ = \(\frac{6.626 \times 10^{-34}}{9.1 \times 10^{-31} \times 1.0 \times 10^7}=7.281 \times 10^{-11} \mathrm{~m}\)

Question 38. Write down the electronic configuration of 14Si and 25Mn stating the underlying principle. Which of the following orbitals is not possible? 1 p, 2d, 3s, 3f
Answer:

First Part: The underlying principle is ‘The Aufbau principle! For electronic configuration see article no. 2.10.3.

Second Part: Ip, 2d, and 3f orbitals are not possible.

Question 39. When an electron jumps down from the 5th Bohr orbit to the 3rd Bohr orbit in the H atom, how many numbers of spectral lines will be formed?
Answer:

When an electron jumps down from the 5th Bohr orbit to the 3rd Bohr orbit in an H atom it can jump directly or it can jump to the 4th Bohr orbit first and from it, jump to the 3rd Bohr orbit. Thus, we get 3 spectral lines for these 3 transitions.

Question 40. Write the values of the four quantum numbers of the electron(s) in the outermost shell of the Cr-atom.
Answer:

According to the electronic configuration of b 24Cr(ls²2s²2p⁶3s²3p⁶3d⁵4s¹), the outermost shell configuration of the Cr-atom is: 4s¹. therefore Quantum numbers for 4s¹: n = 4, l = 0, m = 0 , s= \(+\frac{1}{2}\)

Question 41. Which is most paramagnetic among Cu²⁺, and Fe²⁺, and why?
Answer:

From the electronic configurations it is observed that the number of unpaired electrons in Cu²⁺, Fe²⁺, and Cr³⁺, ions are 1, 4, and 3 respectively. So Fe²⁺, ion, containing the highest number of unpaired electrons, will be most paramagnetic.

NCERT Class 11 Chemistry Chapter 2 Short Question and Answers

Question 42. Why splitting of spectral lines is observed when the source producing the atomic spectrum is placed in a magnetic field?
Answer:

In the presence of a magnetic field, the orbitals present in a sub-shell (which were originally degenerate) take up different orientations and hence their degeneracy is lost.

Electronic configuration: ls²2s²2p⁶3s²3p⁶3d¹⁰4s¹.

Question 43. Write two differences between orbit and orbital. Two sets of four quantum numbers of an electron are (n = 4, 1 = 3, m = 3, s = -) and n = 3, 1 = 2, 2 m = -2, s = 0). Which one of these sets is not correct and why?
Answer:

The second set is incorrect because the value of s can be either \(\frac{1}{2} \text { or }-\frac{1}{2}\) but can never be zero.

Question 44. Write the electronic configuration of Cu⁺ and Cr²⁺ ions (Atomic numbers of Cu and Cr are 29 and 24 respectively).
Answer:

Cu⁺: ls²2s²2p⁶3s²3p⁶3d¹⁰

Cr²⁺: 1s²2s²2p⁶3s²3p⁶3d⁴

Question 45. A cation M³⁺ has 23 electrons. What is the atomic number of M?
Answer:

Number of electrons present in the neutral M atom = 23 + 3 = 26. So, die number of protons in the nucleus = 26. Hence, the atomic number of M is 26.

Question 46. What is the unit of Planck’s constant in S.I.? What other physical quantity has the same unit?
Answer:

The SI unit of Planck’s constant ‘h’ =kg-m².s^–1

The SI unit of angular momentum (mvr) is also kg-m².s^–1

Question 47. Do atomic orbitals have sharp boundaries?
Answer:

No, atomic orbitals do not have sharp boundaries because the probability of finding an electron even at a large distance is never zero, although it may be very small.

NCERT Class 11 Chemistry Short Answer Questions

• Chapter 7 Equilibrium Short Question And Answers
• Chapter 8 Redox Reactions Short Question And Answers
• Chapter 10 S Block Elements

• Chapter 11 Some P Block Elements
• Chapter 12 Organic Chemistry Basic Principles And Techniques
• Chapter 14 Environmental Chemistry Short Answer Questions

• NCERT Class 11 Chemistry Chapter 5 States Of Matter Gases And Liquids Very Short Question And Answers
• NCERT Class 11 Chemistry Chapter 6 Chemical Thermodynamics Very Short Question And Answers
• NCERT Class 11 Chemistry Chapter 8 Redox Reactions Very Short Questions And Answers

NCERT Class 11 Chemistry Chapter 10 S Block Elements Very Short Answer Questions

• NCERT Class 11 Chemistry Chapter 11 Some P Block Elements Very Short Answer Questions
• NCERT Class 11 Chemistry Chapter 12 Organic Chemistry Basic Principles And Techniques Very Short Question And Answers
• NCERT Class 11 Chemistry Chapter 14 Environmental Chemistry Very Short Answer Questions
• NCERT Class 11 Chemistry Equilibrium Very Short Answer Questions

• NCERT Class 11 Chemistry Chapter 10 S Block Elements
• NCERT Class 11 Chemistry Chapter 11 Some P Block Elements
• NCERT Class 11 Chemistry Chapter 12 Organic Chemistry Basic Principles And Techniques
• NCERT Class 11 Chemistry Chapter 8 Redox Reactions

• NCERT Class 11 Chemistry Chemical Thermodynamics
• NCERT Class 11 Chemistry Equilibrium
• NCERT Class 11 Chemistry Chapter 14 Environmental Chemistry

• Chapter 1 Equilibrium Multiple Choice Questions
• Chapter 2 Structure Of Atom Multiple Choice Questions
• Chapter 8 Redox Reactions Multiple Choice Questions
• Chapter 10 S Block Elements Multiple Choice Questions
• Chapter 11 Some P Block Elements Multiple Choice Questions

• Chapter 12 Organic Chemistry Basic Principles And Techniques Multiple Choice Questions
• Chapter 14 Environmental Chemistry Multiple Choice Questions
• Chapter 13 Hydrocarbons Multiple Choice Questions
• Chemical Thermodynamics Multiple Choice Questions

CBSE Class 11 Chemistry Notes For Chapter 8 Redox Reactions Introduction

Chemical reactions, according to their nature, are divided into different classes, such as combination reactions, decomposition reactions, elimination reactions, polymerisation reactions and many other types.

Oxidation-reduction or redox-reaction is a class of chemical reactions in which oxidation and reduction occur simultaneously. A large number of chemical and biological reactions belong to this class. Some processes that are associated with oxidation-reduction reactions are the rusting of iron, the production of caustic soda and chlorine by electrochemical method, the production of glucose by photosynthesis, the generation of electric power by battery, fuel cell, etc.

Redox Concept Reactions According To Electronic

Oxidation reaction:

A chemical reaction in which an atom, an ion or a molecule loses one or more electrons is called an oxidation reaction. An atom, ion or molecule is oxidised by loss of electron (s).

Examples: Oxidation reactions involving—

Loss of electron(s) by an atom:

Generally atoms of metallic elements such as Na, K, Ca, etc., undergo oxidation by losing electron(s), thereby producing positive ions.

⇒ \(\mathrm{Na} \longrightarrow \mathrm{Na}^{+}+e ; \mathrm{K} \longrightarrow \mathrm{K}^{+}+e ; \mathrm{Ca} \longrightarrow \mathrm{Ca}^{2+}+2 e\)

Read and Learn More CBSE Class 11 Chemistry Notes

Loss of electron(s) by a cation:

Some cations such as Fe²⁺, Sn²⁺, Cu⁺, etc., undergo oxidation by losing one or more electrons, thereby forming higher charges.

Fe²⁺→ Fe³⁺ + e; Sn²⁺ → Sn⁴⁺+ 2e

Cu²⁺ → Cu²⁺ + e

Loss of electron(s) by an anion:

Anions such as I^– and Br^– ions oxidise to neutral atoms or molecules by losing electron(s).

I₂^– →I₂ + 2e;2Br^– — Br₂ + 2e

Loss of electron(s) by a molecule:

Neutral molecules such as H₂, H₂O₂ and H₂O oxidise to cations by losing one or more electrons

H₂ → 2H+ + 2e;  H₂O₂→ O₂ + 2H⁺ + 2e

H₂O→ ½ O₂ + 2H⁺+ 2e

CBSE Class 11 Chemistry Notes Chapter 8 Redox Reactions

Reduction reaction:

A chemical reaction in which an atom, an ion or a molecule gains one or more electrons is called a reduction reaction. An atom, ion or molecule is reduced by the gain of electron(s).

Examples: Reduction reactions involving—

Gain of electron(s) by an atom:

Atoms of different elements in particular, such as, atoms of chlorine, bromine, oxygen and other non-metals are reduced to anions by gaining electron(s).

Cl + e → Cl^–

Br+ e→ Br^–

O+ 2e — O^2-

Gain of electron(s) by a cation:

Cations such as H⁺, Fe²⁺, Fe³⁺, Cu²⁺ etc., are reduced to neutral atoms or cations with lower charges by accepting electron(s)

H⁺+ e → H;  Fe²⁺+2e → Fe

Fe³⁺+ e → Fe²⁺ ; Fe³⁺+ 3e  → Fe

Cu²⁺+ 2e →Cu ; Cu²⁺+ e  → Cu⁺

Gain of electron(s) by a molecule:

Neutral molecules such as Cl₂, O₂, H₂O₂ etc., are reduced by gaining one or more electrons.

Cl₂ + 2e → 2CF ; O₂  + 4H⁺ + 4e→2H₂ O

H₂O₂ + 2H+ + 2e →  2H₂ O

Oxidant and reductant in light of electronic concept

Oxidant:

In a redox reaction, the species that itself gets reduced by accepting electron(s) but oxidises other substances is called an oxidant or oxidising agent. So, an oxidising agent is an electron acceptor. The greater the tendency of a substance to accept electrons, the greater the oxidising power it possesses.

Examples:

Oxygen (O₂), hydrogen peroxide (H₂O₂), halogens (F₂, Cl₂, Br₂, I₂), nitric acid (HNO₃), potassium permanganate (KMnO₄), potassium dichromate (K₂Cr₂O₇), sulphuric acid (H₂SO₄), etc.

Reductant:

In a redox reaction, the species that itself gets oxidised by losing electron(s) but reduces other substances is called a reductant or a reducing agent. So, a reducing agent is an electron donor.

The substance has a high tendency to lose electrons and acts as a strong reducing agent. Alkali metals (Na, K, Rb, Cs, etc.,) of group-IA of the periodic table show a strong tendency to lose electrons and hence behave as powerful reducing agents.

Examples: Hydrogen (H₂), hydrogen sulphide (H₂S), carbon (C), some metals (Na. K, Fe. Al, etc.), stannous chloride (SnCl₂), sulphur dioxide (SO₂), oxalic add (H₂C₂O₄), sodium thiosulphate (Na₂S₂O₂), etc.

According to an electronic concept;

• Oxidation involves the loss of one or more electrons. Reduction involves the gain of one or more electrons.
• Oxidants are electron acceptors. Reductants are electron donors.

Identification of oxidants and reductants with the help of electronic concept

Reaction: 2KI(aq) + Br₂(l)→2KBr(aq) + l₂(s)

The reaction can be represented in ionic form as

2K⁺ (aq) + 2I (aq) + Br₂(l)→ 2K^+- (aq)+ 2Br^–(aq) + I₂(s)……………………..(1)

This equation shows that in the reaction, the K⁺ ion does not undergo any change. The only function that it does In the reaction is to balance the charge. So, the K⁺ ion only acts as a spectator ion in the reaction.

Redox Reactions Class 11 Chemistry Notes

Hence, the net ionic equation of the reaction is-

2I(aq) + Br₂(l)→ I₂(s) + 2Br^–(aq)

Equation(2) shows that the I^– ion produces I₂ by losing electrons, while Br₂ forms Br^– ions by gaining electrons. 1 lenco, In this reaction, the conversion of I^– into

[2l^–(aq) → l₂(s) + 2e] is an oxidation reaction. On the other hand, the conversion of Br₂ into Br^– →2Br (l)] is a reduction reaction. Thus, in this reaction, ion, i.e., Kl is the reductant and Br₂ is the oxidant.

Oxidation-reduction occur simultaneously

Neither an oxidation reaction nor a reduction reaction can occur alone. Oxidation and reduction reactions are complementary to each other. In a reaction system, if a reactant loses an electron, then there must be another reactant In the system that will gain the lost electron. Thus, oxidation and reduction reactions must occur together.

In a redox reaction, the reducing agent gets oxidised by losing electron(s), while the oxidising agent gets reduced by accepting the lost electron(s). For example, Metallic zinc reacts with copper sulphate in a solution to form metallic copper and zinc sulphate.

⇒ \(\mathrm{Zn}(s)+\mathrm{CuSO}_4(a q) \rightarrow \mathrm{ZnSO}_4(a q)+\mathrm{Cu}(s) \downarrow\)

In an aqueous solution, CuSO₄ and ZnSO₄ exist almost completely In dissociated state. So, the reaction can be expressed in the form of an ionic equation as

⇒ \(\mathrm{Zn}(s)+\mathrm{Cu}^{2+}(a q) \rightarrow \mathrm{Zn}^{2+}(a q)+\mathrm{Cu}(s)\)

In this reaction, the Zn atom loses two electrons, forming the Zn^2- ion (oxidation). On the other hand, the Cu²⁺ ion accepts these two lost electrons to produce Cu^– atom (reduction)

In this reaction, the Zn-atom can lose electrons only because the Cu²⁺ ion present in the reaction system accepts those lost electrons. Alternatively, the Cu²⁺ ion can get reduced by accepting electrons only because the Zn-atom present in the reaction system lose electrons.

So, in a reaction, when a substance undergoes oxidation, another substance present in the reaction system undergoes reduction. Tints it can be said that oxidation and reduction occur simultaneously.

Half-reaction

Any redox reaction consists of two half-reactions, one is for an oxidation reaction and the other is for a reduction reaction Both of these reactions are called a half-reaction.

In a redox reaction, the half-reaction Involving oxidation Is called oxidation half-reaction, and the half-reaction involving reduction is called reduction half-reaction.

Redox reaction = Oxidation half-reaction Reduction half-reaction

Reaction 1:

Reaction 2:

Reaction 3:

Oxidation State And Oxidation Number

According to electronic theory, redox reactions can be explained in terms of electron transfer. The electronic theory can be applied in the case of ionic compounds because, in the formation of ionic compounds, one reactant gives up the electron(s) and another reactant accepts those electron(s).

However, this theory cannot be applied in the case of a redox reaction involving covalent compounds due to the absence of cations or anions in such compounds. Thus this theory is unable to Identify the oxidant and reductant in such types of reactions.

To overcome this problem, the concept of oxidation number has been introduced. All types of redox reactions can be explained based on oxidation number. Each constituent element of any compound has a definite valency. Similarly, it can be assumed that each atom of any element has a definite oxidation number.

Oxidation state

An atom of an element converts into an ion when it loses or gains an electron. The loss of one or more electrons by an atom results in the formation of a cation, while the gain of one or more electrons produces an anion.

Cation is the oxidised state and anion is the reduced state of an element For example, the Na+ ion is the oxidised state of the Na atom and the Cl- ion represents the reduced state of the Cl -atom. The state of oxidation or reduction of an element presenting a compound is called the oxidation state of that element.

Oxidation state Definition:

The state of oxidation or reduction in which an atom of an element exists in a compound is called the oxidation state of the element in that compound.

From the element charge of the compound ion of an element present in an ionic compound, the oxidation state of that element can be easily determined. If the element exists as a cation in the compound, the element is said to be in the oxidised state. On the other hand, if the element exists as an anion in the compound, then the element is said to be in a reduced state.

Example:

In the formation of the compound ZnCl₂, the Zn atom loses two electrons to produce a Zn²⁺ ion and two CIatoms accept two electrons, one electron each to yield two Cl- ions. Zn²⁺ ion combines with two Cl- ions to form a ZnCl₂ molecule.

Thus, in ZnCl₂, the Zn -atom exists in the oxidised state, while the Cl -atom exists in the reduced state. Cations or anions derived from the same element may exist in different oxidation states in different compounds. For example, in CuCl₂, Cu exists as Cu²⁺, while in CuCl, it exists as Cu⁺ ion. Thus, the oxidation state of Cu in CuCl₂ is higher than that in CuCl.

Oxidation number

Oxidation number Definition:

The oxidation number of an element in a compound is a definite number, which indicates the extent of oxidation or reduction to convert an atom of the element from its free state to its bonded state in the compound.

If oxidation is necessary to effect such a change, then the oxidation number will be positive. The oxidation number will be negative when such a change requires reduction. The oxidation number of an atom or molecule in its free state is considered to be zero (0).

The number expressing the die oxidation state of the atom of an element in a compound denotes the oxidation number of the elements in the compound.

The oxidation number of elements in electrovalent compounds:

The charge that an atom of an element In the molecule of an electrovalent compound carries, is equal to the oxidation number of the element In a compound, According to the nature (positive or negative) of the charge, the oxidation number may be positive or negative. The number of electrons (s) lost or gained by an atom during the formation of an Ionic compound determines the oxidation number of the clement in that compound.

Examples:

ln NaCl, sodium and chlorine exist ns Na⁺ and (11- ions, respectively. So the oxidation numbers of sodium and chlorine are +1 and – 1, respectively. In FeCI₂> Iron and chlorine are present as Fe²⁺ and Cl^– Ions, so the oxidation numbers of iron and chlorine are +2 and -1, respectively.

The oxidation number of elements in covalent compounds:

The formation of a covalent compound does not involve the direct transfer of electron(s) between the participating atoms; instead, a covalent bond Is formed by the sharing of electrons.

When two atoms of different electronegativities form a covalent bond(s) through the sharing of one or more electron pairs, they do not get an equal share of the electrons.

The more electronegative atom acquires a greater possession of the shared electron pair (s) than the less electronegative atom.

As a result, the more electronegative atom acquires a partial negative charge. It Is assumed that the atom of the more electronegative element has gained electron(s) i.e. it has been reduced and the less electronegative atom has lost electron(s) i.e., It has been oxidised.

The oxidation number of an atom In a covalent compound is considered to be equal to the number of electron pair(s) the atom shares with one or more atoms of different electronegativities in the compound, If the atom concerned is of higher electronegativity, then Its oxidation number is taken as negative, and if It is of lower electronegativity, its oxidation number is taken as positive.

In the case of a molecule of an element, such as H₂, N₂, O₂, Cl₂ etc., the two atoms of the same electronegativity are covalently linked by sharing electron pair (s) between them. Hence, these two atoms use the electron pair(s) equally and none of the atoms acquire a positive or negative charge. Therefore, the oxidation number of the atoms In the molecule of these elements is regarded as zero.

Example:

1. In hydrogen chloride molecule (HCl) one electron pair exists between H and Cl-atoms, As the electronegativity of chlorine is more than that of hydrogen, the oxidation number of H^–  +1 and that of Cl =-1,

2. In water (H₂O) molecule, the O -atom shares two electron palms, one each with two separate H -atoms. As oxygen is more electronegative than hydrogen, the oxidation number of H -atom +l and that of O -atom =-2.

3. In a carbon dioxide molecule (CO₂), a carbon atom shares four electron pairs, to each with two separate O atoms. As oxygen has higher electronegativity than carbon, in CO₂ molecule, the oxidation number of C = + 4 and that of O =-2

4. In the ethylene (C₂H₄) molecule, two equivalent carbon atoms share two C=C electron pairs between themselves, Since these two electron pairs are equally shared by two C -atoms, they have no role in determining the oxidation number of C.

Again, each carbon atom shares two electron pairs with two separate H -atoms. As carbon is more electronegative than hydrogen, the oxidation number of each H -atom = + 1 and the oxidation number of each C -atom =-2.

Rules For Calculating the Oxidation Number Of An Element

The following rules are to be followed in determining the oxidation number of an element in a compound.

The oxidation number of an element in its free or elementary state is taken as zero (0).

Example:

⇒ \(\stackrel{0}{\mathrm{Z}} \mathrm{n}, \stackrel{0}{\mathrm{Cu}}, \stackrel{0}{\mathrm{C}} \mathrm{L}_2, \stackrel{\ominus}{\mathrm{P}}_4, \stackrel{0}{\mathrm{~S}}_8 \text {, etc. }\) Etc.,

The oxidation number of a monoatomic ion in an ionic compound is equal to its charge.

Example:

In FeCl₂, iron and chlorine exist as Fe²⁺ and Cl^–. So, in i.e., Cl₂, the oxidation number of Fe and Cl are +2 and -1 respectively.

In the case of a polyatomic ion, the sum of the oxidation numbers of all the atoms present in it is equal to the charge of the Ion.

Examples:

The sum of oxidation numbers of all the atoms presenting [Fe(CN)₈]4- =-1.0 The sum of the oxidation numbers of the atoms Cr₂O₇ ^2- ion =-2.

Determination of the oxidation numbers of the atoms in covalent compounds has been discussed in

The algebraic sum ofthe oxidation numbers of all atoms in a neutral molecule is zero(O).

Example: In the FeCl₃ molecule, the oxidation number of Fe is +3 and the oxidation number of Cl is -1. So, the total oxidation number of the atoms in the FeCl₃ molecule =(+3) + 3 × (- 1) = 0.

NCERT Solutions for Class 11 Chemistry Chapter 8 Redox Reactions

The oxidation number of hydrogen:

In metallic hydride, it is always

In all hydrogen-containing compounds except for metallic hydrides, it is +1.

Example:

The oxidation number of oxygen in its compounds:

The oxidation number of oxygen in most compounds=-2

Example:

• In peroxide compounds (H₂O₂ Na₂O₂), the oxidation number of oxygen =-1.
• In superoxides (Example; KO₂), the oxidation number of oxygen =-1/2.
• Since fluorine is more electronegative than oxygen, the oxidation number of oxygen in F₂O = +2.
• In all fluorine-containing compounds, the oxidation number of fluorine =- 1.
• There are some elements which always show, fixed oxidation numbers in their compounds.

Example:

Alkali metals (Li, Na, K, Rb, Cs) always show a +1 oxidation state in their compounds. The oxidation number of alkaline earth metals (Be, Mg, Ca, Sr, Ba, Ra ) is +2 in their compounds. The oxidation number of Zn in its compounds is +2 and the oxidation number of Al in its compounds is +3.

The maxim oxidation1 number of an element cannot exceed its group numbering in the periodic table.

The following always have definite oxidation numbers in their compound

Calculation of oxidation number in some compounds

The oxidation number of an element in a compound can be calculated if the oxidation numbers of other elements in the compound are known.

The oxidation number of S in H₂SO₄:

Suppose, the oxidation number of S in H₂SO₄ = x.

The total oxidation number of two H-atoms in the H₂SO₄ molecule = 2 × (+1) = +2.

Total oxidation number of four O -atoms in H₂SO₄ molecule = 4 × (-2) =-8 .% Total oxidation number of all atoms in a H₂SO₄ molecule = +2 + x + (-8) = x- 6.

Now, the sum of the oxidation numbers of all atoms in a molecule = 0.

Therefore, x – 6 = 0 or, x = +6

∴ The oxidation number of S in H₂SO₄ = +6

The oxidation number of Cl in KClO₄:

If the oxidation number of Cl = x, then the total oxidation number of all the atoms in the KClO₄ molecule

=+1+x+ 4 × (-2) = x- 7

The sum of oxidation numbers for all the atoms present in a molecule = 0.

∴ x-7 = 0 or, x = +7

Hence, the oxidation number of Cl in KClO₄ =

The oxidation number of N in NH₄NO₃:

NH₄NO₃ is an ionic compound in which NH₄ and NO-₃ are the cation and anion, respectively.

Let the oxidation no. of in NH⁺₄ ion be x. Then the total oxidation no. of the atoms present in this ion = x + 4.

For a polyatomic ion, the oxidation no. of the ion is equal to its charge i.e., the oxidation number of the NH₄ ion

= +1. x + 4

= +1 or, x = -3.

Again, if the oxidation number of N in NO₃ is y, then y + 3 × (-2) = -1 or, y = +5.

Hence, in NH₄NO₃ the oxidation number of one Natom is -3 and that of another N -atom is +5.

The oxidation number of Cl in Ca(OCl)Cl:

In this compound. The Cl -atom in OCl^– is linked with the O-atom, and another Cl atom exists as the Cl^– ion. The oxidation number of the Cl -atom that exists as Cl^– ion =-1.

Let the oxidation number of the Cl atom in OCP be x.

∴ – 2+ x =-1 or, x =+l

So, in Ca(.OCDCl, the oxidation number of one Cl atom is 1 and that of another Cl^– atom is +1.

The oxidation number of Mn in KMnO₄: Suppose, the oxidation number ofMn.in KMn04 = x.

Total oxidation number ofthe atoms in KMnO₄ =+1 + x+ 4 × (-2) = x-7

∴ x-7 = 0 or, x = +7

Hence, the oxidation number of in KMnO₄ =+7

The oxidation number of P in H₄P₂O₇:

Let the oxidation number of P in H₄P₂O₇ be x. Hence, the total oxidation number of P-atom in the H₄P₂O₇ molecule

= 4 × (+1) -+2 × x + 7(-2)

= 4-+2x -14

= 2x- 10

2x- 10 = 0

Or, x = 5

Therefore, the oxidation number of P in H₄P₂O₇ = +5

Class 11 Chemistry Redox Reactions Notes

The oxidation number of Fe in Fe(CO)₅:

CO is a neutral ligand (molecule) and its oxidation number = 0. So, the oxidation number of Fein Fe(CO)- is zero (0).

The oxidation number of Fe in K₄[Fe(CN)₆]:

Suppose, the oxidation number of Fe in K4[Fe(CN)₆] =x. Hence, 4 × (+1) + x+ 6 × (-1) = 0

The oxidation number of an element in 3 compounds may be zero(0):

In compounds like C₆H₁₂O₆, HCHO, CH₂C₁₂ etc., the oxidation number of carbon is zero (0). Suppose, the oxidation number ofCin C₆H₁₂O₆ = x. So, 6x+ 12x(+1) + 6x(-2) = 0

∴ x = 0

Some exceptions regarding the determination of oxidation number

The anomaly fractional oxidation state:

Since electrons can not be transferred fractionally, the fractional oxidation state of an element seems to be a hypothetical case. But in compounds like Fe₃O_{4, and} NaS₄O6 the oxidation states of Fe, and S are \(+\frac{8}{3}\) and +2.5, respectively.

The fractional oxidation state is only the average oxidation state of an element when two or more of its atoms with different oxidation states are present in a compound. For such compounds, the actual oxidation state can be determined by knowing the structure of the compound.

1. The oxidation number of Cr in CrO₅:

According to the usual method, the oxidation number of Cr in the CrO₅ molecule would be +10.

However, the oxidation number of Cr can never exceed 6 because the total number of electrons in its 3d and 4s orbitals is 6. From the chemical structure of CrO₅, it can be shown that the oxidation number of Cr in CrO₅ is, in fact, +6.

Let the oxidation number of Cr in the CrO₅ molecule be x.

x +  1 × (-2) (for O )+ 4 × (-1)(for O-atoms linked in O – O bond ) = 0

x = +6.

Hence, the oxidation number of Cr in CrO₅ = +6.

2. The oxidation number of S in H₂SO₅:

According to the tyre .usual method, the oxidation number of sulphur in the H₂SO₆ molecule is +8

The oxidation number of sulphur can never exceed + 6. The chemical structure of H₉SO₆ shows that the oxidation number of sulphur in H₂SO₅ is

Suppose, the oxidation number of S in H₂SO₅ = x

2 × (+1)( For H-atoms) + x + 2 × (-1) ( (For O-atoms held by O—O bond + 3 × (-2) ( For other- O-atoms)

x = + 6

Hence, the oxidation number of the S -atom in H₂SO₅ = +6

3. The oxidation number of S in Na₂S₂O₃:

According to the usual method, the average value of oxidation numbers of S in Na₂S₂O₃ molecule = +2

However the reaction of Na₂S₂O₃ with dilute H₂SO₄, one of the two S -atoms in Na₂S₂O₃ is precipitated as sulphur and the other is oxidised to SO₂.

Therefore, the two S -atoms in the Na₂S₂O₃ molecule are not identical. Consequently, their oxidation numbers cannot be the same. The chemical structure of the Na₂S₂O₃ molecule indicates that the two sulphur atoms in it are linked by a coordinate bond.

The oxidation number of the S -atom accepting the electron pair in the coordinate bond is considered to have an oxidation number of -2. If the oxidation number ofthe other S -atom is taken as .x, then.

2 × (+1)( For Na-atoms)  + 3 × (-2) ( (For O-atoms) + x × 1 + 1 × (-2) = 0 ( (For S-atom by coordinate bond)

∴ x = +6

Therefore, in the Na₂S₂O₃ molecule, the oxidation number of one S -atom is -2 and that of the other is +6

Redox Reactions Chapter 8 NCERT Notes

4. The oxidation number of S in Na₂S₄O₆:

According to the usual method, the average value of oxidation numbers of S in Na₂S₄O₆ molecule would be + 2.5

In atoms, this molecule is covalently oxidationlinkednumberis zero. If of the two oxidation sulphur numbers of each ofthe remaining two S -atoms is x, the

x × 2 (For S)+ 2× 0 (For S-S)+ 6 ×(-2)(For O) ×  2×  (+1) (For Na)= 0

Or 2x- 12 +12 = 0, x =+5

Therefore, the oxidation number of each of the two remaining S -atoms in Na₂S₄O₆ is +5

Explanation Of Oxidation-Reduction In Terms Of Oxidation Number

According to the concept of oxidation number, oxidation is a chemical reaction in which the oxidation number of atoms increases and reduction is a chemical reaction in which the oxidation number of an atom decreases.

So, oxidation means an increase in oxidation number, whereas reduction means a decrease in oxidation number. Examples of oxidation and reduction are as follows.

Explanation of oxidation-reduction reaction

Consider the reaction of HNO₃ with H₂S, forming nitric oxide (NO) and sulphur. In this reaction, the oxidation number of N decreases from +5 in HNO₂ to +2 in NO and the oxidation number of S increases from -2 in H₂S to 0 in S. So, the reaction brings about a reduction of HN03 and oxidation of H₂S.

In a redox reaction, all the atoms of a participating reactant do not change their oxidation number. Only one atom of the reactant changes oxidation number. This element is called an effective or reactive element.

In the previous example, only the N -atom of HNO₃ changes oxidation number. The oxidation numbers of hydrogen or oxygen remain the same before and after the reaction.

The reaction of FeSO₄ with KMnO4 acidified with dilute H₂SO₄ results in K₂SO₄, MnSO₄, FeSO₄ and H₂O.

In this reaction, the oxidation number of Mn decreases (+ 7→ + 2) and the oxidation number of Fe increases (+2 → + 3). Therefore, in the reaction, KMnO₄ is reduced and FeSO₄ is oxidised

CBSE Class 11 Redox Reactions Chapter 8 Notes

Identification of oxidant and reductant based on oxidation number

In redox reactions, the substance that gets oxidised is the reducing agent and the substance that gets reduced is the oxidising agent. Based on oxidation number, it can be stated that in a redox reaction, the substance in which the oxidation number of an atom increases is the producing agent and the substance in which the oxidation number of an atom decreases is the oxidising agent.

Example:

In presence of H₂SO₄, K₂Cr₂O₇ reacts with KI to form I₂ and chromic sulphate [Cr₂(SO₄)₃]

Here, the oxidation number of Cr decreases from +6 to +3 and the oxidation number of 1- increases from -1 to 0. Therefore, K₂Cr₂O₇ acts as an oxidising agent and KI acts as a reducing agent.

How a redox reaction is identified:

At first oxidation number of each of the constituent elements of the participating substances is assigned. If the oxidation numbers of the elements change, then the reaction is identified as a redox reaction. If none of the elements shows any change in oxidation number, then the reaction is not a redox reaction.

Example: Identify whether the given two reactions are redox reactions or not

In this reaction, the oxidation numbers of all the atoms of the participating substances remain the same. Hence, it is not a redox reaction.

In this reaction, the oxidation number of N increases 0) and the oxidation number of oxygen decreases (0 →2). Hence, it is a redox reaction.

Auto Oxidation-Reduction Reactions

There are some redox reactions in which the same substance gets partially oxidised and reduced. This type of reaction is termed an auto oxidation-reduction reaction.

Example: Potassium chlorate (KCLO₃) on heating decomposes to produce KCl and O₂ gas:

In this reaction, the oxidation number of Cl decreases from +5 to -1 and the oxidation number of oxygen increases from- 2 to 0. So, in this reaction of KClO₃, one atom (O) is oxidised and the other (Cl) is reduced.

Lead nitrate undergoes thermal decomposition to produce PbO, NO gas and 02 gas:

In this reaction, the oxidation number of the N -atom reduces from +5 to +4 and the oxidation number of the O -atom increases from -2 to zero (0 ). Hence, in the reaction, the N atom is reduced and the O -atom is oxidised. So, Pb(NO₃)₃ in its thermal decomposition undergoes oxidation and reduction simultaneously.

Ammonium nitrate (NH₄NO₃) on heating decomposes to produce water vapour, N₂ gas and O₂ gas

NFI₄NO₃ is an ionic compound, consisting of ammonium cation (NH⁺₄) and nitrate anion (NO₃). The oxidation numbers of the N -atom in NH₄⁺  and NO₂ ions are -3 and 5 respectively.

In this reaction, the oxidation number of N in the NH₄ ion increases (-3 → 0) and the oxidation number of N in NO₃ decreases (+ 5 → 0). Therefore, NH₄NO₃ undergoes oxidation and t In this reaction, reduction at die same time.

Disproportionation And Comproportionation Reactions

Disproportionation reaction in which an element of a reactant undergoes oxidation and reduction simultaneously, resulting in two substances in which one of the elements exists in a higher oxidation state and the other exists in a lower oxidation state

Examples:

In the reaction of chlorine with cold and dilute NaOH solution, sodium hypochlorite (NaOCl) and sodium chloride are formed. In this reaction oxidation number of chlorine decreases (0→ -1) and increases (0→ +1) at the same time. thus, chlorine is simultaneously oxidised and reduced in the reaction.

Therefore, this reaction is an example of a disproportionation reaction.

When white phosphorus is heated with a caustic soda solution, phosphine (PH₄) and sodium hypophosphite (NaH₂PO₂) and produced.

Here P. undergoes oxidation and reduction simultaneously. In one of the products (PH₄), P exists in a lower oxidation state (-3) and the other product (NaH₄PO₂), it exists in a higher oxidation state (+1). Hence, the tills reaction is an example of a disproportionation reaction.

NCERT Class 11 Chemistry Redox Reactions Chapter 8

Comproportionation Reaction:

It is a reaction in which two reactants containing a particular element but in two different oxidation states react with each other to produce a substance in which the said element exists in an intermediate oxidation state.

Therefore, a comproportionation reaction is the opposite of a disproportionation reaction.

Example: KBrO₃ reacts with KBr in an acidic medium to produce Br₂.

In this reaction, the oxidation number of one Br-torn decreases (from +5 to. 0) and that of another Br-atom increases (from -1 to 0 ). Br₂ is formed by the oxidation of KBrO₃ and the reduction of KBr. The oxidation number of Br₂ is zero, which is intermediate between the oxidation numbers of Br atoms in KBrO, (+5 ) and KBr (-1 ). Therefore, it is a comproportionation reaction.

Equivalent Mass Of Oxidant And Reductant

The equivalent mass of oxidants and reductants is calculated by following two different methods. In one method, the calculation is done in terms of several electron (s) gained by an oxidant or the number of electrons (s) lost by a reductant. The other method takes into account the change in the oxidation number of an element present in the oxidising and reducing agents.

Oxidation number method:

The equivalent mass of an oxidant or reductant denotes the number obtained by dividing the molecular mass of the oxidant or reductant with the change in oxidation number of an element in the oxidant or reductant in their respective reduction or oxidation reaction.

⇒ \(\begin{aligned}
& \text { Equivalent mass of the oxidant }
\end{aligned}=\frac{\text { Molecular or formula mass of oxidant }}{\begin{array}{c}
\text { Total change in oxidation number } \\
\text { of an element present in a molecule } \\
\text { of the oxidant during its reduction }
\end{array}}\)

⇒ \(\begin{aligned}
& \text { Equivalent mass of the reductant }
\end{aligned}=\frac{\text { Molecular or formula mass of reductant }}{\begin{array}{c}
\text { Total change in oxidation number } \\
\text { of an element present in a molecule } \\
\text { of the reductant during its reduction }
\end{array}}\)

Determination of equivalent mass of oxidants 

Determination of equivalent mass of reductants

Electronic method: Equivalent mass of an oxidant or reductant is a number obtained by dividing the molecuslar mass or formula mass of an oxidant or reductant by the number ofelectron(s) gained or lost by a molecule of that oxidant or reductant during reduction or oxidation ofthe respective compound.

The equivalent mass of an oxidant or a reductant is formulated  as:

Equivalent mass ofthe oxidant = \(\frac{\text { Molecular or formula mass of oxidant }}{\text { Number of electron(s) gained by each molecule of oxidant during reduction }}\)

Equivalent mass bf the reductant = \(\frac{\text { Molecular mass or formula mass of a reductant }}{\text { Number of electron(s) lost by each molecule of reductant during oxidation }}\)

Class 11 Chemistry Redox Reactions Example Solutions

Determination of equivalent mass of oxidants

Determination of equivalent mass of reductants