Sainavle

Change In Entropy And Spontaneity Of A Process

We have seen that there are many spontaneous processes (like the melting of ice above 0°C and 1 atm) in which the entropy ofthe system increases (ASurr > 0). Again, there are some spontaneous processes (such as the transformation of water into ice below 0°C and 1 atm) in which the entropy of the system decreases (Δ < 0).

Hence, the change in entropy of the system alone cannot predict the spontaneity of a process; instead, we must consider the change in entropy of the system as well as that of the surroundings. In a process, if the change in entropy of the system and its surroundings are AS and ASsurr respectively, then the total change in entropy in the process

⇒ \(\Delta S_{\text {total }}=\Delta S_{\text {sys }}+\Delta S_{\text {surr }}\)

The system and its surroundings constitute the universe. So,

⇒  \(\Delta S_{\text {total }}=\Delta S_{\text {univ }}=\Delta S_{s y s}+\Delta S_{\text {surr }}\)

All spontaneous processes occur irreversibly, and in any irreversible process, the entropy of the universe increases. So, for a spontaneous process,

⇒ \(\Delta S_{\text {univ }}=\left(\Delta S_{\text {sys }}+\Delta S_{\text {surr }}\right)>0\)

In a reversible process, any change in the entropy of the system is exactly balanced by the entropy change in the surroundings. Therefore, in a reversible process.

⇒ \(\Delta S_{\text {sys }}=-\Delta S_{\text {surr }} \text { or, }-\Delta S_{\text {sys }}=\Delta S_{\text {surr }}\)

Read and Learn More CBSE Class 11 Chemistry Notes

So, for a reversible process,

⇒ \(\Delta S_{u n i v}=\Delta S_{s y s}+\Delta S_{s u r r}=0\) When the spontaneous process reaches equilibrium, the value of

⇒ \(\Delta S_{u n i v}\left(=\Delta S_{s y s}+\Delta S_{\text {surr }}\right)=0.\).

For any spontaneous process,

⇒ \(\Delta S_{u n i v}\left(=\Delta S_{s y s}+\Delta S_{s u r r}\right)>0\)

For any reversible process, \(\Delta S_{u n i v}\left(=\Delta S_{s y s}+\Delta S_{s u r r}\right)>0\)

At equilibrium ofa process, \(\Delta S_{u n i v}\left(=\Delta S_{s y s}+\Delta S_{s u r r}\right)=0\)

At normal atmospheric pressure, water spontaneously converts into ice below o°C although the entropy change of the system (ΔSsys) in v.n is negative:

H₂O molecules in ice are held orderly at fixed positions, which makes them unable to move about within ice. On the other hand, H₂O molecules in water are not held at fixed positions as in ice and are capable of moving throughout the water.

Therefore, the molecular randomness in water is quite greater than that in ice. Thus entropy ofthe system decreases when water transforms into ice. So, in this process, Δ< 0.

As this transformation is an exothermic process, the heat released by the system is absorbed by the surroundings. As a result, the randomness as well as the entropy ofthe surroundings increases. So, ΔSys> 0.

CBSE Class 11 Chemistry Notes Entropy and Spontaneity

However, in this process, the increase in entropy of the surroundings is greater than the decrease in entropy of the system. Consequently, the total change in entropy or the entropy ofthe universe (ASuntv) becomes positive. This favors the spontaneous conversion of water into ice below 0°C temperature and at normal atmospheric pressure.

Change in entropy and condition of spontaneity of a process in an isolated system

As an isolated system does not interact with its surroundings the total energy of such a system always remains constant is any process in it.

Therefore, the driving force for any spontaneous process in an isolated system is the change in entropy of the system. In such type of system, since surroundings remain unchanged, \(\Delta S_{\text {surr }}=0\) hence for any spontaneous process occurring in an isolated system,

⇒ \(\Delta S_{s y s}+\Delta S_{s u r r}>0 \text { or }, \Delta S_{s y s}\)

With the progress of a spontaneous process occurring in an isolated system, the entropy of the system gradually increases. When the process reaches equilibrium, the entropy
ofthe system gets maximized, and no further change in its value takes place.

Hence, at equilibrium, of a process occurring in an isolated system,

⇒  \(S_{\text {sys }}=\text { constant or, } d S_{\text {sys }}=0 \text { or, } \Delta S_{\text {sys }}=0 \text {. }\).

Change in entropy and spontaneity of exothermic and endothermic reactions

Change in entropy and spontaneity of an exothermic reaction:

In an exothermic reaction, heat is released by the reaction system. The released heat is absorbed by the surroundings, causing the randomness as well as the entropy of the surroundings to increase. Thus, ASsurr is always positive for exothermic reactions. However, the entropy of the system may decrease or increase for such type of reactions.

If the total entropy ofthe products is greater than the total entropy of the reactants in an exothermic reaction, then \(\Delta S_{s y s}>0\) In this case the value \(\Delta S_{u n i v}\) is greater or less than \(\Delta S_{\text {surr }}\). As a result, the reaction occurs sponataneouslty.

In an exothermic reaction if the total entropy of the reactants is greater than the total entropy of the products then

⇒ \(\Delta S_{s y s}<0\). Such type of reactions will be spontaneous if the numerical value of \(\Delta S_{\text {surr }}\) is greater than \(\Delta S_{s y s}\) because only in this condition \(\Delta S_{\text {univ }}>0\).

Change in entropy and spontaneity of an endothermic reaction: In an endothermic reaction, the heat is absorbed by the system from its surroundings. Causing the randomness as well as the entropy of the surroundings to decrease. So, in an endothermic reaction,

ΔS_surr < 0. Hence, an endothermic reaction will be spontaneous only when \(\Delta S_{s y s}\) is +ve and its magnitude is greater than that of \(\Delta S_{\text {surr }}\)

Entropy and the second law of thermodynamic

The second law of thermodynamics is expressed in various ways. One statement of this law is—”All spontaneous processes occur irreversibly and proceed in a definite direction We know that, for any spontaneous or natural changes, the total change in entropy of the system and the surroundings is positive, i.e., for any spontaneous change

⇒  \(\Delta S_{s y s}+\Delta S_{s u r r}>0.\).

Therefore, in all natural or spontaneous processes, the entropy of the universe continuously increases In other words all natural or spontaneous processes move in that direction which leads to the increase in entropy of the universe. Conversely, any process, which does not increase the entropy ofthe universe, will not occur spontaneously.

Second law of thermodynamics gives entropy For all the natural processes, the entropy of the universe is gradually increasing and approaching a maximum.

Processes occurring in nature are spontaneous. In all these processes, energy may be transformed into different forms although the total energy of the universe remains constant the entropy of the universe does not remain constant It is always increasing due to natural processes.

Entropy and Spontaneity in Thermodynamics Class 11 Notes

Entropy and Spontaneity in Law of Thermodynamics Numerical Examples

Question 1. The latent heat of fusion of ice at 0°C is 6025.24 J-mol-1 Calculate molar entropy of the process at 0°C.
Answer:

The change in entropy due to melting of lmol of ice

= \(\frac{\text { Molar latent heat (or enthalpy) of fusion of ice }}{\text { Melting point of ice }}\)

⇒ \(=\frac{6025.24 \mathrm{~J} \cdot \mathrm{mol}^{-1}}{(273+0) \mathrm{K}}=22.07 \mathrm{~J} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1}\)

Question 2. The enthalpy change for the transformation of water into vapor at the standard boiling point is 40.8 kl. mol^-1. Calculate the entropy change for the process.
Answer:

Change in entropy for the process

⇒ \(\frac{\text { Molar enthalpy of vaporisation of water }}{\text { Boiling point of water }}\)

= \(\frac{40.8 \times 10^3 \mathrm{~J} \cdot \mathrm{mol}^{-1}}{(273+100) \mathrm{K}}\)

⇒ \(109.38 \mathrm{~J} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1}\)

Question 3. The enthalpy of vaporization of benzene at 80°C (boiling point) is 31-mol^-1. What will be the change in entropy for the transformation of 31.2 g of benzene vapor into liquid benzene at 80°C?
Answer:

⇒  \(31.2 \mathrm{~g} \text { benzene }=\frac{31.2}{78}=0.4 \mathrm{~mol}[\text { Molar mass }=78] .\)

Enthalpy of condensation for lmol benzene vapor =(-)x enthalpy of vaporization of lmol liquid benzene =-31 kj. Therefore, the enthalpy of condensation of 0.4 mol of benzene =-31 × 0.4

=-12.4 kj.

∴ The change in entropy for the transformation of0.4 mol of benzene vapor into liquid benzene at 80°C,

⇒ \(\Delta S=-\frac{12.4 \times 10^3 \mathrm{~J}}{(273+80) \mathrm{K}}=-35.127 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

Question 4. 1 mol or on Ideal gas If. expanded from lu Initial: volume of II, lo (lie Hind volume of 1(H) t, ul 25C. What will be changed In enthalpy for this process?
Answer:

⇒ \(\Delta S=2.303 n R \log \frac{V_2}{V_1}\)

⇒ \(=2.303 \times 8.314 \log \frac{100}{1}=38.29 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

So, the change in entropy for this process = +398.29j

Question 5. The pressure of 1 mol of an Ideal gas confined In a cylinder fitted with a piston is 50 atm. The gas is expanded reversibly when the cylinder Is kept in contact with a thermostat at 25°C. During expansion, the pressure of the gas is decreased from 90 to 9 atm. Calculate the change in entropy in (Ids process, ff the heat absorbed by the gas during expansion he 5705 f, then calculate the change in entropy of the surroundings?
Answer:

We know \(\Delta S=2.303 n R \log \frac{p_1}{p_2}\)

Given, Px = 50 atm, P2 – 5 atm and n = 1

∴ The change in entropy of the system (i.e., gas)

⇒ \(\Delta S=2.303 \times 8.314 \log \frac{50}{5}=19.15 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

Here surroundings are at a fixed temperature (25°C). During expansion, the heat absorbed by the gas from the surroundings = 5705 J.

Therefore, at 25’C, the heat released by the surroundings =-5705 j.

∴ Change in entropy of the surroundings,

⇒ \(\Delta S_{\text {surr }}=-\frac{5705}{(273+25)} \mathrm{J} \cdot \mathrm{K}^{-1}=-19.14 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

Law of Thermodynamics Entropy and Spontaneity Class 11 Notes

Question 6. At 1 atm and 298 K, entropy change of the reaction, \(4 \mathrm{Fe}(s)+3 \mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{Fe}_2 \mathrm{O}_3(s) \text { is }-549.4 \mathrm{~J} \cdot \mathrm{K}^{-1} \text {. }\) In this reaction, if A// = -1648 kj, then predict whether the reaction is spontaneous or not.
Answer:

As the reaction enthalpy is negative the reaction is exothermic. Therefore, the heat released by the given reaction will be equal to the heat absorbed by the surroundings Consequently the entropy of the surroundings will increase. Heat absorbed by the surroundings =(-) x heat released by the system

=-ΔH = -(-1648)kJ

= +1648 kj.

∴ Change in entropy of the surroundings

⇒ \(\Delta S_{\text {surr }}=-\frac{\Delta H}{T}=\frac{1648 \times 10^3}{298} \mathrm{~J} \cdot \mathrm{K}^{-1}=5530.2 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

Thus, in this reaction \(\Delta S_{\text {untv }}=\Delta S_{\text {sys }}+\Delta S_{\text {surr }}\)

= (-549.4 + 5530.2)J.K^-1= +4980.8 J.K^-1

Since \(\Delta S_{u n I v}>0\) the reaction will occur spontaneously.

Question 7. At 1 atm and 298 K, ΔH° value for the reaction \(2 \mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightarrow 2 \mathrm{H}_2 \mathrm{O}(l) \text { is }-572 \mathrm{~kJ}\) . Calculate the change in entropy ofthe system and surroundings for this reaction. Is this reaction spontaneous at that temperature and pressure? Given: Standard molar entropies of H₂(g), O₂(g) & H₂O(f) at 298K are 130.6, 205.0, and 69.90 J. K^-1. mol^-1 respectively
Answer:

The change in entropy of the given reaction

Δ = \(\left[2 S^0\left(\mathrm{H}_2 \mathrm{O}, l\right)\right]-\left[2 \times S^0\left(\mathrm{H}_2, g\right)+S^0\left(\mathrm{O}_2, g\right)\right]\)

=\( 2 \times 69.9-(2 \times 130.6+205)] \mathrm{J} \cdot \mathrm{K}^{-1}\)

= \(-326.4 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

Change in entropy of the surroundings in the reaction

⇒ \(\Delta S_{\text {surr }}\)=\(-\frac{\Delta H^0}{298}\)

= \(\frac{572 \times 10^3}{298} \mathrm{~J} \cdot \mathrm{K}^{-1}\)

=\(+1919.4 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

∴ Total change in entropy,

⇒ \(\Delta S_{\text {univ }}\)= \(\Delta S_{\text {sys }}+\Delta S_{\text {surr }}\)

= -326.4+1919.4

= \(+1593 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

Since \(\Delta S_{u n i v}>0,\) then the reaction will occur spontaneously at 298 K and 1 atm.

CBSE Class 11 Entropy and Spontaneity in Thermodynamics

Question 8. The molar enthalpy of fusion and the molar entropy of fusion for ice at 0°C and 1 atm are 6.01 kj- mol^-1 and 22.0 J K^-1.mol^-1 respectively. Assuming ΔH and ΔS are independent of temperature, show that the inciting of ice at 1 atm is not spontaneous, while the reverse process is spontaneous.
Answer:

A process is spontaneous when the change in entropy of the universe \(\left(\Delta S_{u n i v}=\Delta S_{s y s}+\Delta S_{s u r r}\right)\) is positive. The transformation of the office into water involves the process.

⇒ \(\mathrm{H}_2 \mathrm{O}(s)\rightarrow \mathrm{H}_2 \mathrm{O}(l)\)

⇒  \(\Delta H =6.01 \mathrm{~kJ} \cdot \mathrm{mol}^{-1} ; \Delta S=22.0 \mathrm{~J} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1}\)

Now , \(\Delta S_{\text {sys }}=22.0 \mathrm{~J} \cdot \mathrm{mol}^{-1}\)

⇒ \(\Delta S_{\text {surr }}=\frac{\Delta H}{T}=\frac{-6010}{271}\)

=\(-22.17 \mathrm{~J} \cdot \mathrm{mol}^{-1}\)

Thus,  \(\Delta S_{\text {univ }}=\Delta S_{\text {sys }}+\Delta S_{\text {surr }}=22.0+(-22.17) \mathrm{J} \cdot \mathrm{mol}^{-1}\)

= \(-0.17 \mathrm{~J} \cdot \mathrm{mol}^{-1}\)

Hence, the total entropy change in the process is negative at 271 K. Therefore, the transformation of ice into water at -2°C is not spontaneous. The reverse process i.e., the conversion of water to ice at -2°C is spontaneous. This is because at -2°C and atm pressure the overall entropy (ΔSuniv) is +0.17 J . mol^-1

Gibbs Free Energy Or Free Energy

In the previous section, we have seen that entropy can be used as a criterion for the spontaneity of a process. In an isolated system, a process will be spontaneous if ΔSis positive during this process.

But natural processes seldom occur in isolated systems. In other systems, a process will be spontaneous if

⇒ \(\Delta S_{\text {universe }}\left(=\Delta S_{s y s}+\Delta S_{s u r t}\right)\) is positive. Many are quite inconvenient.

It is, thus, very useful to reformulate the spontaneity criterion in such a way that only the system is to be considered. For our purpose, J. ‘Willard Gibbs introduced a new thermodynamic function called Gibbs free energy” or free energy, denoted by‘ G  immerse processes in which determination of ΔSt.

At constant temperature and pressure, the spontaneity ofa process can be determined from the value ofthe change in Gibbs free energy of the system.

As most of the physical or chemical changes occur at constant pressure, it is convenient to use the concept of free energy to determine the spontaneity of that change.

Definition Of Gibbis free energy:

It is the thermodynamic property of a system, whose decrease in a spontaneous process at constant temperature and pressure, measures the maximum useful energy obtainable in the form of work from the process.

In any spontaneous process occurring at constant temperature and pressure, the decrease in Gibbs free energy (-ΔG) = maximum useful or network performed by the system on the surroundings.

Read and Learn More CBSE Class 11 Chemistry Notes

Mathematical form of Gibbs free energy:

The total energy of a system, one part is free for doing useful work, and another part is unavailable, and cannot be converted into work. If the value of entropy of a system is S at T K, then the amount of unavailable energy of the system is TxS.

Therefore, the total energy of the system = G (free energy) + TS (unavailable energy) Generally enthalpy (H) is considered as the total energy of the system.

Thus, H = G+TS or, G = H-TS…………….(1)

Where G, H, and S are Gibbs free energy, enthalpy, and entropy ofthe system respectively. T is the temperature of the system in the Kelvin scale. Equation [1] is the mathematical form of Gibbs free energy or free energy.

CBSE Class 11 Chemistry Notes Gibbs Free Energy

Gibbs free energy is a state function:

Gibbs free energy (G), enthalpy (H), and entropy (S) of a system are related by the equation, G = H-TS. As H. S and T are state functions, Gibbs free energy (G) is also a state function.

Thus, the value of Gibbs free energy (G) of any system depends only on the present state of the system and not on how the system has reached its present state. Hence, the change in Gibbs free energy (AG) of any process doesn’t depend upon the nature of the process but depends only on the initial and final states of the process.

Gibbs free energy is an extensive property:

Enthalpy (H) and the product of entropy and absolute temperature (fxS) of the system depend on the amount of the substance present in the system.

With increasing amounts of the substance, values of these quantities are increased. Hence Gibbs free energy (G = H- TS) depends on the amount of the substance present in the system. Therefore, Gibbs free energy (G) is an extensive property of the system.

Change in Gibbs free energy in a process occurring at constant temperature and pressure: The change in Gibbs free energy in a process occurring at a constant temperature and pressure,

ΔG = Δ(H-TS) = ΔH-Δ(TS)

∴ ΔG = (ΔH- TAS) [Δ(TS) = TΔS as T = constant]

The above equation represents the relation between the entropy change (AS), enthalpy change (AH), and absolute temperature (T) for a physical or chemical change occurring at a particular temperature and pressure. Using this equation, it is possible to predict the spontaneity of a process at constant temperature and pressure.

Change in Gibbs free energy for a physical or chemical change and process

At a particular temperature (T) and pressure (P), if the change in enthalpy and change in entropy for a physical or chemical process are AH and AS, respectively, then the change in Gibbs free energy,

ΔG = ΔH -TAS……………….(1)

If ΔS_sys and ΔS_surr are the changes in entropies of the system and its surroundings, respectively, then the total change in entropy for the process

⇒  \(\Delta S_{\text {total }}=\Delta S_{\text {univ }}=\Delta S_{\text {sys }}+\Delta S_{\text {surr }}\) The heat gained by the system at fixed pressure and temperature, qsys= change in enthalpy (ΔH). So sys=ΔH

Therefore, the heat lost by the surroundings at a fixed pressure and temperature \(\left(q_{\text {surr }}\right)=-q_{\text {sys }}=-\Delta H.\)

So, the change in entropy of the surroundings for a physical or chemical change at a particular temperature and pressure,

⇒ \(\Delta S_{\text {surr }}=\frac{q_{\text {surr }}}{T}=-\frac{\Delta H}{T}\)

And the total change in entropy at a particular temperature and pressure,

⇒ \(\Delta S_{\text {total }}=\Delta S_{\text {sys }}+\Delta S_{\text {surt }}=\Delta S-\frac{\Delta H}{T} \quad\left[\text { where } \Delta S=\Delta S_{\text {sys }}\right]\)

Or, \(T \Delta S_{\text {total }}=T \Delta S-\Delta H \text { or, } \Delta H^{\prime}-T \Delta S=-T \Delta S_{\text {total }}\) ……………………….(2)

Comparing equations (1) and (2) \(\Delta G=-T \Delta S_{\text {total }}\)…………………….(3)

Equation (3) represents the relation between changes in Gibbs free energy (AG) for a physical or chemical change at a fixed temperature and pressure and the total change in entropy of the system and surroundings \(\left(\Delta S_{\text {total }}\right)\) for that process.

We know that a process will be spontaneous if the total change in entropy of the system and surrounding in the process is positive; i.e.,

⇒ \(\Delta S_{\text {total }}\left(=\Delta S_{\text {sys }}+\Delta S_{\text {surr }}\right)>0.\) According to

equation [3], \(\text { if } \Delta S_{\text {total }}>0 \text {, then } \Delta G<0 \text {. }\)

Thus, a physical or chemical change at a fixed temperature and pressure will be spontaneous ifthe change in Gibbs free energy (AG) is negative i.e., ΔG < 0.

If in a process, the total change in entropy ofthe system and its surroundings is -ve, i.e.,

⇒ \(\Delta S_{\text {total }}\left(=\Delta S_{s v s}+\Delta S_{s u r r}\right)<0,\) then the process will be non-spontaneous, but the reverse the process will be spontaneous. From equation [3], if

⇒ \(\Delta S_{\text {total }}<0 \text {, then } \Delta G>0\text {. }\)

Thus, for a physical or chemical change at a fixed pressure and temperature, if the Gibbs free change is positive (ΔG > 0), then the process will be nonspontaneous but the reverse one will be spontaneous.

The total change in entropy of the system and surroundings will be zero, i.e.,

⇒  \(\Delta S_{\text {total }}\left(=\Delta S_{\text {sys }}+\Delta S_{\text {surr }}\right)=0\) for a process at equilibrium. According to equation [3], if

⇒  \(\Delta S_{\text {total }}=0 \text { then } \Delta G=0\).

Therefore, the Gibbs free energy change will be zero, i.e., ΔG = 0 for a physical change or chemical reaction at equilibrium under the condition ofa fixed pressure and temperature.

Reaction; A→ B (at constant and pressure)

If &G(=GB- GA) <0 at a fixed temperature and pressure; then the transformation of A to B will be spontaneous.

If ΔG(= GB- Ga) > 0 at a fixed temperature and pressure; then the transformation of A to B will be non-spontaneous. But the transformation of B to A will be spontaneous as GB > GA and for the reverse process the value of ΔG(= GA- GB) is negative.

If ΔG(=Gb- Ga) = 0, then A and B will be in equilibrium. In this condition, the rate of transformation of B into A or A into B will be the same. So no net change will occur either in the forward or in the reverse direction.

NCERT Solutions Class 11 Chemistry Gibbs Free Energy

Effect of ΔH and ΔS on the value of ΔG for any physical change or chemical reaction:

Effect of temperature on the change in Gibbs free energy and the spontaneity of a process

We know that ΔG = ΔH- TΔS. In this relation, the values of both ΔH and ΔS may be either positive or negative, but the temperature (in the Kelvin scale) is always positive. Again TΔS is a temperature-dependent quantity.

With the increase or decrease in temperature, the magnitude of TΔS increases or decreases, and the value of ΔH almost remains unchanged. So, ΔG depends on temperature. From the signs of ΔH and ΔS, we can predict the effect of temperature on ΔG.

The different possibilities have been discussed in the following table:

Numerical Examples

Question 1. \(\mathrm{Br}_2(l)+\mathrm{Cl}_2(\mathrm{~g}) \rightarrow 2 \mathrm{BrCl}(\mathrm{g})\); Whether the reaction is spontaneous or not at a certain pressure & 298 K ? [Aff=29.3 kJ.mol^-1, ΔS=104.1 J. K^-1.mol^-1]
Answer:

We know, ΔG = ΔH- ΔTS

∴ ΔG =29.3 ×10³ -(298× 104.1)

=-1721.8 J- mol^-1

As ΔG is negative, this process is spontaneous.

Question 2. At a certain pressure and 27°C, the values of ΔG and ΔH ofa the process are- 400 kj and 50 kj respectively. Is the process exothermic? Is it spontaneous? Determine the entropy change of the process.
Answer:

As per given data ΔH = 50 kj. As the value of ΔH is positive, it is not an exothermic process.

For the process ΔG =-400 kj at a certain pressure and 27°C. As ΔG is negative, it is a spontaneous process.

ΔG = ΔH- TΔS

∴ -400 = 50-300 × ΔS

or, ΔS =1.5kJ.K^-1

=1500 kJ.k^-1

Question 3. Values of ΔH to ΔS for the given reaction are -95.4kJ and -198.3 J.K^-1 respectively: \(\mathrm{N}_2(g)+3 \mathrm{H}_2(g) \rightarrow 2 \mathrm{NH}_3(g)\) State whether the reaction will be spontaneous at 500 K or not. Consider AH and AS are independent of temperature.
Answer:

We know, ΔG = ΔH- TΔS

Given, ΔH = -95.4 kj , ΔS = -198.3 J.K^-1 and T = 500 K.

∴ ΔG= [-95.4 ×10³- 500 × (-198.3)]J

= 3750 J

= 3.75 kJ

As the value of ΔG is positive at constant pressure and 500 K temperature, it is not a spontaneous process.

Gibbs Free Energy and Spontaneity Class 11 Chemistry

Question 4. In and the ASreaction,= + 35 JA(s). K^-1+. State B(g)-C(g)whether+ D(g)the reaction, ΔH =31 will k^-1 be spontaneous at 100°C and 1100°C or not? Consider ΔH and ΔS are independent of temperature.
Answer:

We know, ΔG = ΔH- TΔS. Now at 100°C,

ΔG = ΔH-TΔS = 31 × 10³- (273 + 100) × 35

=+ 17945J

∴ At 1100°C, = 31 × 10³-(273 + 1100) × 35

=-17055 J

At 100°C, AG for the given reaction is positive, so the reaction will be non-spontaneous. On the contrary, at 1100°C, AG for the given reaction is negative, so it will be spontaneous.

Question 5. Is the vaporization of water at 50°C and 1 atm spontaneous? Given: For vaporization of water at that temperature and pressure, ΔH = 40.67 kj.mol^-1 and ΔS = 108.79 J.K^-1.mol^-1.
Answer:

We know, ΔG = ΔH- TΔS

∴ ΔG=ΔH- TΔS = 40.67 × 10³- (323 × 108.79)

= + 5530.83 J.mol^-1

As ΔG = +ve, so vaporization will be non-spontaneous.

Question 6. At 25°C and 1 atm, the heat of formation of 1 mol of water is -285.8 kj. mol^-1. State whether the formation reaction will be spontaneous at that temperature and pressure or not. Given: The molar entropies of H₂(g) ,O₂ (g) & H₂O(Z) at 25°C and 1 atm are 130.5, 205.0 and 69.9 J.K^-1.mol^-1 respectively.
Answer:

The equation for the formation reaction of water:

⇒ \(\mathrm{H}_2(g)+\frac{1}{2} \mathrm{O}_2(g) \rightarrow \mathrm{H}_2 \mathrm{O}(l) ; \Delta H=-285.8 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}\)

The change in entropy for this reaction, \(\Delta S=S_{\mathrm{H}_2 \mathrm{O}(l)}-\left(S_{\mathrm{H}_2(g)}+\frac{1}{2} S_{\mathrm{O}_2(g)}\right)\)

= \(\left[69.9-130.5-\left(\frac{1}{2} \times 205\right)\right] \mathrm{J} \cdot \mathrm{K}^{-1}=-163.1 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

Therefore, the change in Gibbs free energy at 25°C and 1 atm for the formation of1 mol of H₂O(Z) from 1 mol of H₂(g) and

⇒ \(\text { and } \frac{1}{2} \mathrm{~mol} \text { of } \mathrm{O}_2(\mathrm{~g}), \Delta G=\Delta H-\mathrm{T} \Delta S\)

= -285.8¹ 103- 298 × (-163.1) =-237.196 kJ

As ΔG is negative at 25°C and 1 atm, so the formation of water at this temperature and pressure will be spontaneous.

Determination of temperature at which equilibrium is established in a physical or chemical change

We know that at a given temperature and pressure the change in free energy (AG) for a reaction is zero when the reaction is at equilibrium. Therefore, at equilibrium,

⇒ \(\Delta G=\Delta H-T \Delta S=0 \text { or, } \mathbf{T}=\frac{\Delta \boldsymbol{H}}{\Delta S}\)……………………………..(1)

Applying equation no.(1), we can determine the temperature at which equilibrium is established in a physical or chemical change.

Example: The values of the enthalpy and entropy changes ofthe system are + 40.7 kj- mol^-1 and 109.1 J. K^-1mol^-1respectively for the process, H₂O(Z) H₂O(g) at 1 atm pressure. At which temperature equilibrium will be established between water and water vapor?
Answer:

At equilibrium ΔG = 0 and T \(=\frac{\Delta H}{\Delta S} .\)

Given: ΔH = 40.7 kj.mol-1 = 40.7 ×103 J.mol-1 and AS = 109.11 -K-1- mol-1

∴ \(T=\frac{40.7 \times 10^3 \mathrm{~J} \cdot \mathrm{mol}^{-1}}{109.1 \mathrm{~J} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1}}=373 \mathrm{~K}\)

373 K (100°C) is the normal boiling point of water. So, at 1 atm and 100°C, water and its vapor will remain in equilibrium.

The temperature at which a physical or chemical change becomes spontaneous We have seen. that in any physical or chemical change, if the signs of AH and AS are the same (either + or – ), then the sign of AG as well as the spontaneity of that change depends on temperature.

Suppose, for a physical or chemical change at a particular temperature and pressure, ΔH > Δ and ΔS > Δ. According to the relation, ΔG = ΔH- TΔS the process is spontaneous because when TΔS > ΔH, ΔG<Δ This means that

ΔH- TΔS < 0 or TΔS > ΔH thus,

⇒  \(T>\frac{\Delta H}{\Delta S}\)

Hence, the process will be spontaneous when \(T>\frac{\Delta H}{\Delta S}\), if \(T<\frac{\Delta H}{\Delta S}\)

ΔS the process will be non-spontaneous, but the reverse process will be spontaneous. For a physical or chemical change if ΔH < 0 and ΔS < 0, then it can be shown that the process will be spontaneous when

⇒\(T<\frac{\Delta H}{\Delta S}. \text { If } T>\frac{\Delta H}{\Delta S}\)

The process will be non-spontaneous, but the reverse process will be spontaneous.

Question 1. In the reaction, A-B+ C, ΔH = 25 kj. mol^-1and ΔS = 62.5 J.K^-1. At which temperature the reaction will occur spontaneously at constant Pressure?
Answer:

The condition for the spontaneity of a reaction at a given temperature & pressure is ΔG < 0.

We know ΔG = ΔH- TΔS For a spontaneous reaction,

ΔH- TΔS < 0 or, \(\Delta H<T \Delta S \quad \text { or, } T \Delta S>\Delta H \quad \text { or, } T>\frac{\Delta H}{\Delta S}\)

Given: ΔH = 25 × 103 J and ΔS = 62.5 J . K^-1

Therefore \(T>\frac{25 \times 10^3 \mathrm{~J}}{62.5 \mathrm{~J} \cdot \mathrm{K}^{-1}} \quad \text { or, } T>400 \mathrm{~K} \text {. }\)

Question 2. H₂O(g) H₂O(l) ; Δh = -40.4 kj.mol^-1 ΔS = -108.3 J.K^-1.mol^-1. At which temperature the process will be spontaneous at a constant 1 atm?
Answer:

In this process ΔH<0 and ΔS <0. For such type of process, the temperature at which the reaction will occur spontaneously \(T<\frac{\Delta H}{\Delta S}\)

Given: ΔH=-40.4 × 10³ J mol-1, ΔS=-108.3 J.K^-1.mol^-1

∴ \(T<\frac{\Delta H}{\Delta S} \quad \text { or, } T<\frac{40.4 \times 10^3}{108.3} \quad \text { or, } T<373 \mathrm{~K}\)

∴ The process will be spontaneous below 373 K (100°C).

Question 3. H₂(g)+Br(Z)-+2HBr(g); ΔH=-72.8kJ (1 atm, 25°C) If molar enterpoies of H₂(g), Br₂(l),HBr(g) are 130.5, 152.3 and 198.3j.k^-1.mol^-1 respectively then at which temperature the reaction will be spontaneous?
Answer:

Change in entropy for the given reaction,

⇒ \(\Delta S=2 S_{\mathrm{HBr}(g)}-\left[S_{\mathrm{H}_2(g)}+S_{\mathrm{Br}_2(l)}\right] \)

=\([2 \times 198.3-(130.5+152.3)] \mathrm{J} \cdot \mathrm{K}^{-1}=113.8 \mathrm{~J} \cdot \mathrm{K}^{-1}\)

As ΔH < 0 and ΔS > 0 for the given reaction, the reaction will be spontaneous at any temperature.

Gibbs Free Energy Formula Class 11 Chemistry Notes

Question 4. For the reaction A(g) + B(g)→ C(s) +D(l); ΔH =-233.5 kj and ΔS = -466.1 J. K^-1 At what temperature, equilibrium will be established? In which directions the reaction will proceed above and below that temperature?
Answer:

At constant temperature and pressure, the equilibrium temperature ofa reaction \(T=\frac{\Delta H}{\Delta S}.\)

Given:ΔH = -233.5 × 10³ J and ΔS = -466.1 J .K^-1

Therefore \(T=\frac{233.5 \times 10^3}{466.1} \mathrm{~K}=500.9 \mathrm{~K}=227.9^{\circ} \mathrm{C}\)

∴ At 227.9°C, the reaction will attain equilibrium.

When T > 500.9 K, the magnitude of TΔS is greater than that of ΔH. Then according to the equation, ΔG = ΔH- TΔS, the value of AG will be positive. So the reaction will be non-spontaneous above 500.9 K.

When T < 500.9 K, the magnitude of TΔS is less than that of ΔH. According to the equation, ΔG = ΔH- TΔS, ΔG will be negative. Therefore, the reaction will be spontaneous below 500.9 K

The standard free energy of formation of a substance and the standard free energy change in a chemical reaction

Standard free energy of formation:

The standard free energy of the formation of a compound is denoted by \(\Delta G_f^0\) and its unit is kj.mol-1 (or kcal-mol^-1).

Definition:

The free energy change associated with the formation of 1 mol of a pure compound from its constituent elements present at standard state is termed as the standard free energy of formation of that compound.

The value of standard free energy of formation of any element at 25°C and 1 atm pressure is taken as zero. For the elements having different allotropic forms, the standard free energy of formation of the most stable allotrope at 25°C and 1 atm pressure is taken as zero.

For example,\(\left(\Delta G_f^0\right)\) [C (graphite)] = 0 but \(\left(\Delta G_f^0\right)\) [C dimond] ≠0.

Standard free energy of formation (G_f°) of some elements and compounds at 25°C:

Standard free energy change in a chemical reaction:

In any reaction, the change in free energy (ΔG) depends on temperature, pressure, and concentration. Thus to compare the ΔG of different reactions, the standard free energy change is calculated.

Definition:

It is defined as the change in free energy when the specified number of moles of reactions (indicated by the balanced chemical equation] in their standard states are completely converted to the products in their standard states.

It is expressed by ΔG°. At a particular temperature, the standard free energy change in a reaction is calculated from the standard free energy of formation ofthe reactants and products at that temperature.

The change in standard free energy in a reaction, ΔG° =

The sum of the standard ‘free energy of formation of the products – the sum of the standard free energy of formation of the reactants \(\)

Or,\(\Delta G^0=\sum n_1 \Delta G_{f, 1}^0-\sum n_j \Delta G_{f, j}^0\)

Where n₁ and n₂ to are the number of moles of i -th product and j-th reactant In the balanced chemical equation whereas ΔG °_f,t, and ΔG °_f,j are the standard free energy of formation of the j -th product and j-th reactantrespectively

Example: in the case of the reaction aS+bB-cC+dD:

⇒ \(\Delta G^0=\left[c \times \Delta G_f^0(C)+d \times \Delta G_f^0(D)\right]\)

⇒  –\(\left[a \times \Delta G_f^0(A)+b \times \Delta G_f^0(B)\right]\)

The standard free energy change (ΔG°) in a reaction can also be determined from the values of the standard change enthalpy (ΔH0) and standard change in entropy (ΔS0), using the following equation,

⇒ \(\Delta G^0=\Delta H^0-T \Delta S^0\)

ΔG° =ΔH° TΔS° ……………………………(1)

ΔG° and the spontaneity of a physical or chemical change:

If ΔG° < 0 for any physical or chemical change, then the process will be spontaneous under standard conditions.

If the value of ΔG° > 0 for any physical or chemical change, then the process will be nonspontaneous under standard conditions. However, the reverse process will be spontaneous under standard conditions.

Free energy change in a chemical reaction, reaction equilibrium, and equilibrium constant

ΔG° in a reaction can be determined either from the values of the standard free energies of formation of the participating reactants and products or from the equation,

ΔG°=  ΔH°- TΔS°. But if a reaction occurs in a condition other than standard condition then the free energy change of the reaction can be calculated using the following relation.

⇒ \(\Delta G=\Delta G^0+R T \ln Q\)…………………………..(1)

Where Q = reaction quotient [a detailed discussion on reaction quotient has been made, T = temperature in Kelvin scale, R = the universal gas constant, ΔGs the free energy change in a reaction at constant pressure and a constant temperature TK, ΔG°= the standard free energy change in the reaction at TK

Relation between standard free energy change (AG°) and equilibrium constant (K  The relation between ΔG° and K can be derived from the above equation [1] For a reaction at equilibrium, ΔG = 0 at constant temperature and pressure. Also at equilibrium, the reaction quotient (Q) = equilibrium constant (JC). Therefore, according to the equation [1], at equilibrium

∴ 0 = ΔG° +RT in K°

or, ΔG-RT in k………………………..(2)

Or, ΔG° = -2.03 RT Log K………………………..(3)

Equations (2) and (3) show the relationship between the standard free energy change in a reaction (ΔG0) and the equilibrium constant (K) of the reaction at a particular temperature (T).

Hence, using these equations [2 and 3], he value of the equilibrium constant (K) of a reaction at a particular temperature (F) can be determined from the value of the standard free energy change of the reaction (ΔG°) at the same temperature (T).

Alternatively, the value of ΔG° can be determined from the value of K by using equations [2] and [3]. According to equation [2] (or [3]);

1. If ΔG° is negative, then In K (or logic) will be positive. Thus K > 1
2. If ΔG° is positive, then In K (or logic) will be negative Thus K < 1.
3. If ΔG° is equal to zero, then In K (or logic) will be equal to zero. Thus K = 1.

Class 11 Chemistry Gibbs Free Energy Thermodynamics

Numerical Examples

Question 1. In the given reaction, calculate the standard free energy change at 25°C: \(\mathrm{N}_2(g)+3 \mathrm{H}_2(g) \rightarrow 2 \mathrm{NH}_3\) [Given that, ΔH° = -91.8 kJ and ΔS° = -198 J. K^-1]
Answer:

We know, ΔG° = ΔH°- TΔS°

ΔH° = -91.8 kJ , ΔS°=-198 J.K-1 , F

= (273 +25) = 298K

ΔG° =-91.8 ×  10³- 298 × (-198)

=-32796J

=-32.796kJ

Question 2. In the given reaction, calculate standard free energy change at 25°C: 2NO(g) + 0,(g) 2NO₂(g). Is the reaction spontaneous under standard conditions?\(\left[\right. Given: At 25^{\circ} \mathrm{C}, \Delta G_f^0[\mathrm{NO}(\mathrm{g})]=86.57 \mathrm{~kJ} \cdot \mathrm{mol}^{-1} and \Delta G_f^0\left[\mathrm{NO}_2(g)\right]=51.30 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}.\)
Answer:

⇒  \(\left.\Delta G^0=\sum \Delta G_f^0 \text { (products }\right)-\sum \Delta G_f^0(\text { reactants })\)

In the given case,

⇒ \(\Delta G^0=2 \Delta G_f^0\left[\mathrm{NO}_2(g)\right]-2 \Delta G_f^0[\mathrm{NO}(g)]-\Delta G_f^0\left[\mathrm{O}_2(g)\right]\)

⇒ \(\text { Given: } \left.\Delta G_f^0[\mathrm{NO}(g)]=86.57 \mathrm{k}\right] \cdot \mathrm{mol}^{-1}\)

⇒ \(\Delta G_f^0\left[\mathrm{O}_2(\mathrm{~g})\right]=0 \text { and } \Delta G_f^0\left[\mathrm{NO}_2(\mathrm{~g})\right]=51.30 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}\)

[∴ Standard free energy of formation of an element =0]

Since the value of ΔG° is negative, so the reaction will be spontaneous under standard conditions.

Question 3. At 25°C, the standard free energy change for a reaction is 5.4 kJ. Calculate the value of the equilibrium constant of the reaction at that temperature.
Answer:

We know, ΔG° = -RTlnK.

∴ We have, ΔG° = 5.4 kJ

= 5.4 × 10³ J and T

= 298 K

Or, log k = 0.95

∴ K= 0.113

Therefore, at 25°C the value of the equilibrium constant for the given reaction will be 0.113.

Question 4. The equilibrium constant for a reaction is 1.6 × 10^-6at 298K. Calculate the standard free energy change (ΔG°) and standard entropy change (ΔS°) of the reaction at that temperature. Given, at 298 K, ΔH° = 25.34 kJ
Answer:

We know. ΔG° = -RTinK

∴ ΔG° =-8.314 × 298 ln(1.6 × 10^-6)

= 33064J = 33.064 kJ

∴ The standard free energy change at 298 K = + 33.064 kJ

Again we know, ΔG°=ΔH°- TΔS°

Here, ΔH°=25.34 kJ

∴ +33.064 = 25.34- 298 × ΔS°

So, the standard entropy change for the reaction = 25.9j. k^-1

Question 5. At 298 K, the standard free energy of formation of H₂O(l) = 23.7 kJ.mol^-1 calculates the value of equilibrium constant temperature for the following reaction:

⇒\(2 \mathrm{H}_2 \mathrm{O}(t) \rightarrow 2 \mathrm{H}_2(g)+\mathrm{O}_2(g)\)

Answer:

Standard free energy change for the given reaction,

⇒ \(\Delta G^0=2 \Delta G^0\left[\mathrm{H}_2(g)\right]+\Delta G^9\left[\mathrm{O}_2(g)\right]-2 \Delta G^9\left\{\left[\mathrm{H}_2 \mathrm{O}(l)\right]\right.\)

The standard free energy of the formation of an element Is
taken as zero, so

⇒ \(\Delta G_f^0\left[\mathrm{O}_2(g)\right]=0 \text { and } \Delta G_j^9\left[\mathrm{H}_2(g)\right]=0 \text {. }\)

Therefore \(\left.\left.\Delta G^0=[0+0-2 \times(-237.13)] \mathrm{k}\right]=+474.25 \mathrm{k}\right]\)

∴ +474.26 × 10³ =-8.314 ×  298 in k or k

= -191.42

∴ K= 7.36 ×  10^-84

So, the equilibrium constant for the reaction = 7.36 ×  10^-84

NCERT Class 11 Chemistry Gibbs Free Energy Explanation

The Third Law Of Thermodynamics

Statement of the third law of thermodynamics:

The entropy of a pure and perfectly crystalline substance at 0 K temperature is equal to zero.

Explanation:

In a perfect crystalline solid, all the constituent particles are perfectly arranged in a well-ordered manner. Defects like point defects, line defects, etc., that can generally be observed in crystal lattices, are found to be absent in a perfect crystal.

The constituent particles become motionless and attain the lowest energy in such as substance at absolute zero. As a result, the randomness of those constituent particles becomes zero. For this reason, the value of entropy of a pure and perfectly crystalline substance is zero.

Explanation of thermodynamic probability:

A system can achieve a particular thermodynamic state in various ways or configurations. The number of ways in which a particular state can be achieved is called thermodynamic probability and is designated by the symbol ‘W’.

With increasing thermodynamic probability the randomness as well as the entropy of the system increases. So we can expect that there exists a relationship between the two quantities S and W. Lauding Boltzmann introduced a relation between S and W. The relation is S = k InW; where k- Boltzmann constant.

At absolute zero, all the constituent particles would occupy the minimum energy state, and hence there is only one way of arranging the constituent particles in different energy levels i.e., W = 1. This gives S = 0. So, for a pure and perfect crystalline substance, the value of entropy is zero at zero kelvin. This is the statement of the third law of thermodynamics.

Application of the third law of thermodynamics: The absolute value of entropy can be determined by making use of this law. If the increase in entropy of a substance is ΔS due to an increase in temperature from OK to TK then ΔS = ST- SQ; where, ST and SQ are the entropies of that substance at TK, and 0 K, respectively. According to the third law of thermodynamics, SQ = 0. Therefore, S = ST. So by measuring ΔS, it is possible to determine the absolute value of entropy of a substance at T K.

Class 11 Chemistry Gibbs Free Energy and Entropy

Heat or enthalpy of neutralization

Heat or enthalpy of neutralization Definition:

The change in enthalpy that occurs when 1 gram equivalent of an acid is completely neutralized by 1 gram equivalent of a base or vice-versa in a dilute solution at a particular temperature is called the enthalpy (or heat) of neutralization.

The change in enthalpy that occurs when 1 mol of H⁺ ions reacts completely with mol of OH^– ions in a dilute solution to form 1 mol water at a particular temperature is known as the Enthalpy (or heat) of neutralization.

The enthalpy of neutralization is denoted as ΔHN, where subscript TV ‘indicates ‘neutralization’.

Neutralization of strong acid and strong base:

If both the acid and base are strong, then the value of heat of neutralization constant is found to be almost and this value is ~57.3 kj.

Le Chateuer’s Principle

Equilibrium of a chemical reaction is established under some conditions such as pressure, temperature, Concentration, etc. Le Chatelier, a celebrated French chemist studied the effect of such conditions on a large number of chemical equilibria.

He summed up his observations regarding the effect of these factors on equilibrium in the form of generalization which is commonly known as Le Chatelier’s principle.

Le Chateuer’s Principle:

If a system under equilibrium Is subjected to a change In pressure, temperature, or concentration then the equilibrium will shift Itself in such a way as to reduce the effect of that change.

The effect of the change in the various conditions of the chemical reactions at equilibrium is discussed below based on Le Chatelier’s principle.

Effect of change in concentration of reactant or product at equilibrium of a reaction

According to Le Chatelier’s principle, at a constant temperature, keeping the volume fixed, if the concentration of reactant or product at equilibrium is changed, the equilibrium will shift in the direction in which the effect of change in concentration is reduced as far as possible.

With the help of the following general reaction, let us discuss how the change in concentration of reactant or product affects the equilibrium of a chemical reaction: A + B⇌ C+D

Read and Learn More CBSE Class 11 Chemistry Notes

Effect of addition of reactant to the reaction system at equilibrium at constant volume and temperature

Reaction: A+B⇌C+D

1. At constant temperature, keeping the volume un¬ changed, if a certain amount of reactant (A or J3) is added to the system at equilibrium, the concentration of that reactant will increase.
2. As a result, the reaction will no longer remain in the state of equilibrium.
3. According to Le Chatelier’s principle, the system will arrange itself in such a manner so that the effect of increased concentration of that reactant is reduced as far as possible. Naturally, the equilibrium will tend to shift in a direction that causes a decrease in the concentration of the added reactant.
4. Since the concentrations of the reactants reduce in the forward direction, the net reaction will occur in this direction until a new equilibrium is established when the rates of both the forward and reverse reactions become the same.
5. Therefore, the addition of reactant to the reaction system at equilibrium causes the equilibrium to shift to the right. As a result, the yields of the products (C and D) increase.

CBSE Class 11 Chemistry Notes Le Chatelier’s Principle

Conclusion:

At constant volume and temperature, when some quantity of reactant is added to a reaction system at equilibrium, the equilibrium shifts to the right, and the yield of product (s) increases.

Example: Reaction: N₂(g) + 3H₂(g) 2NH₃(g)

At constant temperature, keeping the volume fixed, if some quantity of H₂(g) is added to the above system at equilibrium, the net reaction will occur In the forward direction until a new equilibrium is established.

This means that the addition of some H₂(g) to the reaction system at equilibrium causes the equilibrium to shift to the tire right. As a result, the yield of NH₃(g) will increase.

Effect of addition of the product to the reaction system at equilibrium at constant volume and temperature:

Reaction: A+B ⇌C+D

At constant temperature, keeping the volume fixed, when some quantity of the product (C or D) is added to the system at equilibrium, the concentration of that product increases.

• As a result, the reaction will no longer remain in the state of equilibrium.
• According to Le Chatelier’s principle, the system will adjust itself in such a way that the effect of an increase in concentration of that product is reduced as far as possible. Naturally, the equilibrium of the system will try to shift in a direction that reduces the concentration of the added product.
• Since the concentrations of the product decrease in the reverse direction, the net reaction will occur in this direction until a new equilibrium is established when the rates of both the forward and reverse reactions become identical.
• Therefore, the addition of aproduct to the reaction system at equilibrium makes the equilibrium shift to the left. As a result, the concentrations of the reactants (4 and B) increase.

Conclusion:

At constant volume and temperature, if some quantity of product is added to a reaction system remaining at equilibrium, then the equilibrium will shift to the left. As a result, the concentration of product(s) decreases, whereas that of the reactant(s) increases.

Effect of removal of reactant from the reaction system at equilibrium at constant volume and temperature:

Reaction: A+B⇌C+D

At constant temperature without changing the volume If some amount of reactant (4 orB) is removed from the system at equilibrium, the concentration of that reactant decreases.

• As a result, the reaction will no longer exist in the state of equilibrium.
• According to Le Chatelier’s principle, the system will adjust itself in such a manner so that the effect of a decrease in concentration of that reactant is reduced as far as possible. Naturally, the equilibrium of the system will shift in a direction that increases the concentration of that reactant.
• Since the concentration of the reactants increases in the reverse direction, the net reaction will occur in this direction until a new equilibrium is established when both the forward and reverse reactions take place at equal rates.
• Therefore, the removal of a reactant from the reaction system results in shifting the equilibrium position to the left. As a result, the yield of the products (C and D) will decrease and that of the reactants (A and B) will increase.

Conclusion:

At constant volume and temperature, if some quantity of reactant(s) is removed from the reaction system at equilibrium, the equilibrium will shift to the left. As a result, the yield of product(s) decreases, whereas that of the reactant(s) increases

Effect of removal of the product from the reaction system at equilibrium at constant volume and temperature:

Reaction: A+B⇌C+D

At fixed temperature, keeping the volume unaltered, when some quantity of product (C or D) is removed from the system at equilibrium, the concentration of that product will decrease.

• As a result, the reaction will no longer remain in the equilibrium state.
• According to Le Chatelier’s principle, the system will adjust itself in such a manner, so that the effect of a decrease in the concentration ofthatproduct is reduced as far as possible. Hence, the equilibrium will shift in a direction that increases the concentrations of that removed product.
• Since the concentration of the products increases in the forward direction, the net reaction will occur in this direction until a new equilibrium is established.
• Therefore, the removal of a product from the reaction system results in shifting the equilibrium position to the right. As a result, the yields of products( C or D) increase.

Conclusion:

At constant volume and temperature, if some quantity of a product is removed from the reaction system at equilibrium, the equilibrium will shift to the right. As a result, the yield of product(s) increases and that of the reactant(s)

Explanation of the effect of addition or removal of reactant or product on equilibrium in terms of reaction quotient: Let us suppose, at a given temperature, the following reaction Is at equilibrium: A+B ⇌ C+D

Le Chatelier’s Principle Class 11 Chemistry Notes

Equilibrium constant:

⇒ \(K_c=\frac{[C]_{e q} \times[D]_{e q}}{[A]_{e q} \times[B]_{e q}}\) ……………………………..(1)

Where (A)_eq,(B)_eq, (C)_eq and [D]eq are equilibrium molar concentrations of A, B, C, and D respectively.

Effect of addition of the reactant:

Suppose, keeping the temperature and volume fixed, some amount of A is added to the reaction system at equilibrium. Consequently, the concentration of A in the mixture will increase.

Let the concentration of A increase from [A]eq to [A]. At this condition, the reaction quotient will be—

⇒ \(Q_c=\frac{[C]_{e q} \times[D]_{e q}}{[A] \times[B]_{e q}}\) …………………………………(2)

Since,[(A)>(A)_eq , Q_c<K_c. Thus, the reaction is not in equilibrium now (because at equilibrium, Q_c = K_c). Due to the increase in concentration of A, the forward reaction will take place to a greater extent compared to the reverse reaction. As a result, the value of the numerator in equation (2) increases and that of the denominator decreases, leading to a net increase in the value of Q_c.

A time comes when Q_c = K_c and the equilibrium is re-established. Therefore, the addition of reactant (A) to the above reaction system at equilibrium will result in a shift of the equilibrium to the right. As a result, the yields of the products (C and D) increase.

Effect of addition of the product:

At constant temperature and volume, if some amount of C is added to the reaction at equilibrium, then the concentration of C in the reaction mixture will increase. Suppose, the concentration of C increases from (c). at this condition, the reaction quotient Will Be-

⇒ \(Q_c=\frac{[C] \times[D]_{e q}}{[A]_{e q} \times[B]_{e q}}\)

Since,(C)>[C]_eq ,Q_c>K_c. As Q_c≠K_c, the reaction is no longer at equilibrium. Re-establishing of the equilibrium occurs when Q_c = K_c

This is possible if the shifting of equilibrium occurs to the left because this will cause the numerator to decrease and the denominator to increase in the equation (3). As a result of the shifting of equilibrium to the left, the yields of the products decrease.

Effect Of Removal Of The Reactant:

Keeping the temperature and volume fixed, let some amount of A be removed from the reaction system at equilibrium.

Consequently, the concentration of A in the reaction mixture will be reduced and eventually, the equilibrium will be disturbed. At this condition, Q_c will be greater than Kc i.e., Q_c > K_c. This will cause the equilibrium to shift to (lie left. As u result, the yields of the products (C and I) decrease.

Effect of removal of the product:

At constant temperature and volume, If some amount of product C is removed from the reaction system, the equilibrium will be disturbed because of a decrease in the concentration of C in the reaction mixture.

At this condition, Q_c < K_c. As a result, equilibrium will shift to the right. Consequently, the yields of the products ( C and D) increase.

Some examples from everyday life:

Drying of clothes:

Clothes dry quicker when there is a breeze or we keep on shaking them. This is because water vapor of the nearby air is removed and cloth loses more water vapor to re-establish equilibrium with the surrounding air.

Transport of O₂ by hemoglobin in blood:

Oxygen breathed in combines with the hemoglobin in the lungs according to equilibrium, Hb(s) + O₂(g) HbO₂(s). In the tissue the pressure of oxygen is low. To re-establish equilibrium oxyhemoglobin gives up oxygen. But in the lungs, more oxyhemoglobin is formed due to the high pressure of oxygen.

Removal of CO₂ from tissues by blood: This equilibrium

⇒ \(\mathrm{CO}_2(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \rightleftharpoons \mathrm{H}_2 \mathrm{CO}_3(a q)\) ⇌ \(\mathrm{H}^{+}(a q)+\mathrm{HCO}_3^{-}(a q)\)

In tissue, partial pressure of CO₂ is high thus, CO₂ dissolves in the blood. In the lungs, the partial pressure of CO₂ is low, it is released from the blood.

NCERT Solutions Class 11 Chemistry Le Chatelier’s Principle

Tooth decay by sweets:

Our teeth are coated with an enamel of insoluble substance known as hydroxylapatite,

If we do not brush our teeth after eating sweets, the sugar gets fermented on the teeth and produces H ions which combine with the OH ions shifting the above equilibrium in the forward direction thereby causing tooth decay.

Effect of pressure on equilibrium at constant temperature

The effect of change in pressure at equilibrium is observed only for those chemical reactions whose reactants and products are in a gaseous state and have different numbers of moles.

The effect of change in pressure is not significant for the chemical reactions occurring in a solid or liquid state because the volume of a liquid or a solid does not undergo any appreciable change with the variation of pressure.

Effect of increase in pressure:

• At constant temperature, a reaction exists at equilibrium under a definite pressure. Keeping the temperature constant, if the pressure on the system at equilibrium is increased, then the reaction will no longer exist at equilibrium.
• According to Le Chatelier’s principle, the system will tend to adjust itself in such a way as to minimize the effect of the increased pressure as far as possible.
• At constant temperature, the only way to counteract the effect of the increase in pressure is to decrease the volume or to reduce the number of moles (or molecules).
• Hence, at a constant temperature, if the pressure on the system at equilibrium is increased, then the net reaction will take place in a direction that is accompanied by a decrease in volume or several moles (or molecules).

Effect Of decrease in pressure:

• At constant temperature, if the pressure of a reaction system at equilibrium is decreased, then the reaction will no longer remain at equilibrium.
• According to Le Chatelier’s principle, the net reaction will tend to occur in a direction that is associated with an increase in the volume or number of molecules.
• So, at a constant temperature, the decrease in pressure at the equilibrium of a reaction will result in a shifting of equilibrium in a direction that is accompanied by an increase in volume or an increase in the number of molecules (or moles).

Example:

Let, at a constant temperature, the following reaction is at equilibrium: N₂(g) + 3H₂(g) 2NH₃(g). In the reaction, the number of moles of the product is fewer than that of the reactants. So, the forward reaction is accompanied by a decrease in volume.

Effect of increase in pressure at equilibrium:

At constant temperature, if the pressure of the reaction system at equilibrium is increased, then according to Le Chatelier’s principle, the equilibrium of the reaction will shift to the right i.e., the forward reaction will occur to a greater extent compared to the reverse reaction.

So the yield of NH₃(g) will increase. Effect of decrease in pressure at equilibrium: Keeping the temperature constant, if the pressure of the reaction system at equilibrium is decreased, then according to Le Chatelier’s principle, the equilibrium will shift to the left i.e., the backward reaction will occur to a greater extent, leading to a reduction in the yield of NH₃.

For gaseous reactions in which the total number of mole of reactants is equal to that of the products (i.e.,Δn = 0), equilibrium is unaffected by the change in pressure.

This is because these types of reactions are not accompanied by any volume change. Some examples are:

⇒ \(\mathrm{H}_2(g)+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(g) ; \quad \mathrm{N}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})\)

⇒ \( \text { and } \mathrm{H}_2(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HCl}(\mathrm{g}) \text {. }\)

Effect of pressure on the equilibrium of some chemical reactions at constant temperature:

Effect of temperature on equilibrium

Chemical reactions are usually associated with the evolution or absorption of heat. A reaction in which heat is evolved is called an exothermic reaction, while a reaction in which heat is absorbed is called an endothermic reaction.

In a reversible reaction, if the reaction in any one direction is endothermic, then the reaction in the reverse direction will be exothermic. The temperature of a system at equilibrium can be increased by supplying heat from an external source while the temperature of the system can be lowered by cooling.

Class 11 Chemistry Le Chatelier’s Principle NCERT Notes

Effect of increase in temperature:

At equilibrium, if the temperature of a system is increased, then according to Le Chatelier’s principle, the system will try to offset the effect of the increase in temperature as far as possible. As a result, when the temperature of a reaction system at equilibrium is raised, equilibrium will shift in a direction in which heat is absorbed because it is possible to neutralize the effect of an increase in temperature through the absorption of heat.

Effect of increase In temperature in case of endothermic reactions:

If the temperature is increased at the equilibrium of an endothermic reaction, the forward reaction will take place to a greater extent compared to the reverse reaction until a new equilibrium is established when both the forward and backward reaction occur at equal rates. As a result, equilibrium shills to the right, and the yields of products Increase.

Effect of Increase In Temperature In the case of exothermic reactions:

The temperature Is Increased at the equilibrium of an exothermic reaction, and then the reverse reaction will occur to a greater extent than the forward reaction until a new equilibrium is established when both the forward and backward reactions take place at equal rates. This makes the equilibrium of the reaction shift to the left, resulting In decreased yields of the products.

Effect of decrease in temperature:

According to I.C. Chntolicr’s principle, when the temperature of any system at equilibrium is decreased, the system will try to offset the effect of a decrease in temperature as far as possible.

Therefore, when the temperature is decreased at equilibrium, the equilibrium will shift in a direction in which heat is evolved because it is possible to neutralize the effect of a decrease in temperature through the evolution of heat.

Effect of decrease in temperature In case of endothermic reactions:

As heat is absorbed in an endothermic reaction, a decrease in temperature at equilibrium of such a reaction causes the backward reaction to take place to a greater extent compared to the forward reaction until a new equilibrium is established. As a result, the equilibrium shifts to the left, and the yields of products decrease.

Effect of decrease in temperature in case of exothermic reactions:

If the temperature is decreased at the equilibrium of an exothermic reaction, the forward reaction will take place to a greater extent compared to the reverse reaction until a new equilibrium is established. As a result, shifts to the right, and the yields of products increase.

Example: Manufacturing of ammonia (NH₃) by Haber’s process is an example of an exothermic reaction:

N₂(g) + 3H₂(g) ?=± 2NH₃(g); AH = -22kcl. In this case, the forward reaction is exothermic.

Hence, the backward reaction is endothermic. Effect of increase in temperature at equilibrium:

If the temperature is increased at the equilibrium of the reaction, then according to Le Chatelier’s principle, the backward reaction will take place to a greater extent compared to the forward reaction’ until a new equilibrium is formed. Hence, the equilibrium will shift to the left, causing a decrease in the yield of NH₃.

Effect of decrease In temperature at equilibrium:

If the temperature  Is decreased at the equilibrium of the reaction, then according to i.e., Cliuteller’sprinciple, the equilibrium will be In (the direction In which heat Is generated ie., in ibis case, the forward reaction will be favored, and consequently the yield of N 1 L, will be higher.

Formation of NO(g) from N₂(g) and O₂(g) Is an endothermic reaction:

N₂(g) + O₂(g) ⇌ 2NO(g); ΔH = + 44 kcal Here the forward reaction is endothermic. Hence, the backward reaction Is exothermic.

Effect of increase In temperature on equilibrium:

If the temperature is Increased at the equilibrium of the reaction, then according to Lc Cliatelier’s principle, the forward reaction will take place to a greater extent compared to the backward reaction until a new equilibrium is formed. Hence, the equilibrium will shift to the right, leading to a higher NO.

Effect of decrease in temperature on equilibrium:

If the temperature is decreased at the equilibrium of the reaction, then according to Le Cliatelier’s principle, the equilibrium will shift in the direction in which heat is generated i.e., in this case, the backward reaction will be favored over the forward reaction. Consequently, the yield of NO will be reduced.

Le Chatelier’s Principle in Chemical Equilibrium Class 11

Effect Of Catalyst On Equilibrium

A catalyst has no role in the equilibrium of a reaction. At a given temperature, when a reaction is conducted separately in the presence and the absence of a catalyst, the composition of the equilibrium mixture formed in either case remains the same. This is because the catalyst increases the rates of the forward and backward reactions equally.

The catalyst functions to make the attainment of equilibrium faster by accelerating the rates of both the forward and reverse reactions to the same extent. The yield of product in a reaction cannot be increased with the use of a catalyst.

Effect of addition of inert gas on equilibrium

At constant temperature, adding an inert gas (He, Ne, Ar, etc.) to an equilibrium reaction system can be done at constant volume or pressure.

Effect of addition of inert gas at constant volume:

At constant temperature, keeping the volume fixed, when an inert gas is added to a reaction system at equilibrium, the total number of molecules (or moles) in the system increases. So, the total pressure of the system increases, but the partial pressure of the components does not change. Hence, the equilibrium of the system remains undisturbed.

Effect of addition of inert gas at constant pressure:

Keeping both temperature & pressure fixed, the addition of inert gas to a reaction system at equilibrium causes an increase in the volume of the system (because the total number of moles in the system increases) with a consequent decrease in partial pressures of the components.

So, the sum of the partial pressures of the reactants and the products also decreases. In this situation, equilibrium will shift in a direction that increases the volume of the reaction system i.e., the number of molecules in the reaction system.

Depending on An, three situations may arise—

Numerical Examples

Question 1. At 986°C, 3 mol of H₂O(g) and 1 mol of CO(g) react with each other according to the reaction, CO(g) + H₂O(g)⇌CO₂(g) + H₂(g). At equilibrium, the total pressure of the reaction mixture is found to be 2.0 atm. If Kc = 0.63 (at 986°C), then at equilibrium find O the number of moles of H₂(g), 0 the partial pressure of each of the gases.
Answer:

Let, a decrease in several moles of H₂O(g) be x after the reaction attains equilibrium. Consequently, number of moles of CO also decreases by x. According to the reaction, each of CO₂(g) and H₂(g) increases by x number of moles.

Therefore, number of moles of different substances will be as follows:

So, the total number of moles of different substances at equilibrium =1 – x + 3 – x + x + x = 4

Partial pressures of different substances at equilibrium:

⇒ \(p_{\mathrm{CO}}=\frac{(1-x)}{4} \times 2=\frac{1}{2}(1-x)\)

⇒ \(p_{\mathrm{H}_2 \mathrm{O}}=\left(\frac{3-x}{4}\right) \times 2=\frac{1}{2}(3-x)\)

⇒ \(p_{\mathrm{CO}_2}=\left(\frac{x}{4}\right) \times 2=\frac{x}{2}\)

⇒ \(p_{\mathrm{H}_2}=\left(\frac{x}{4}\right) \times 2=\frac{x}{2}\)

⇒ \(p_{\mathrm{CO}_2}=\left(\frac{x}{4}\right) \times 2=\frac{x}{2} ; p_{\mathrm{H}_2}=\left(\frac{x}{4}\right) \times 2=\frac{x}{2}\)

In the given reaction, Δn = 0.

Therefore, K_p – K_c = 0.63.

In the given, ,K_p=\(\frac{p_{\mathrm{CO}_2} \times p_{\mathrm{H}_2}}{p_{\mathrm{CO}} \times p_{\mathrm{H}_2 \mathrm{O}}}\)

⇒ \(\text { So, } 0.63=\frac{\left(\frac{x}{2}\right) \times\left(\frac{x}{2}\right)}{\left(\frac{1-x}{2}\right) \times\left(\frac{3-x}{2}\right)}=\frac{x^2}{(1-x) \times(3-x)}\)

or, x²= 0.63x²- 2.52x+ 1.89

or, x² + 6.81x- 5.108 = 0

∴ x = 0.681

∴ At equilibrium, the number of moles of H2(g) = 0.68

∴ At equilibrium \(p_{\mathrm{CO}}=\frac{1}{2}(1-0.681)=0.1595 \mathrm{~atm}\)

⇒ \(p_{\mathrm{H}_2 \mathrm{O}}=\frac{1}{2}(3-0.681)=1.1595 \mathrm{~atm}\)

⇒ \(p_{\mathrm{CO}_2}=p_{\mathrm{H}_2}=\frac{0.681}{2}=0.3405 \mathrm{~atm}\)

NCERT Class 11 Chemistry Le Chatelier’s Principle Explanation

Question 2. For the reaction, N₂O₄(g), and – 2NO₄(g) occurring in a closed vessel at 300K, the partial pressures of N₂O₄(g) and NO₂(g) at equilibrium are 0.28 atm and 1.1 atm respectively. What will be the partial pressures of these gases if the volume of the reaction system is doubled keeping the temperature constant?
Answer:

Equilibrium constant,

⇒  \(K_p=\frac{\left(p_{\mathrm{NO}_2}\right)^2}{p_{\mathrm{N}_2 \mathrm{O}_4}}=\frac{(1.1)^2}{0.28}=4.32\)

If the volume of the reaction system is doubled at constant temperature, then partial pressures of N₂O₄ and NO₂ will decrease to half of their initial values. Therefore, partial pressures of N₂O₄ and NO₂ will be 0.14 and 0.55 atm respectively.

So, the equilibrium of the reaction will be disturbed. Now, according to Le Chaterlier’s principle, a reaction will attain a new equilibrium by shifting to the right because in such a case the number of moles as well as the volume will increase.

Let, at the new equilibrium, the partial pressure of N₂O₄(g) decreases to p atm. According to the equation, the partial pressure of NO₂(g) will increase to 2p atm. Therefore, at a new equilibrium,

The partial pressure of each of the component gases will be:

⇒ \(K_p=\frac{\left(p_{\mathrm{NO}_2}\right)^2}{p_{\mathrm{N}_2 \mathrm{O}_4}}=\frac{(0.55+2 p)^2}{(0.14-p)}=4.32\)

Or, 4p² + 2.2p + 0.3025 = 4.32(0.14-p) = 0.6048-4.32p

or, p² + 1.63p- 0.0755 = 0

∴ p = 0.045 atm

So, at new equilibrium, partial pressure of N₂O₄(g) = (0.14-0.045) atm = 0.095 atm and partial pressure of

NO₂ = (0.55 + 2 × 0.045) atm = 0.64 atm

Question 3. PCl₅(g)⇌PCl₃(g) + Cl₂(g); K_p =1.8 At 250°C if 50% of PCl₅ dissociates at equilibrium then what should be the pressure of the reaction system?
Answer:

Let the initial number of moles of PCl₅g) be a. At equilibrium, 50% dissociation of PCl₅(g) will occur if the pressure of the reaction system = P atm. After 50% dissociation of PCl₅(g), the number of moles of PCl₅(g) decreases by an amount of 0.5a, and for PCl₃(g) and Cl₂(g) it increases by 0.5a.

So at equilibrium:

At equilibrium, total no. moles = 0.5a + 0.5a + 0.5a = 1.5a

∴ At equilibrium, partial pressure of different components

⇒ \(\text { are, } p_{\mathrm{PCl}_5}=\frac{(0.5 a)}{(1.5 a)} P=\frac{P}{3} ; p_{\mathrm{PCl}_3}=\frac{P}{3} \text { and } p_{\mathrm{Cl}_2}=\frac{P}{3}\)

Equilibrium constant of the reaction \(K_p=\frac{p_{\mathrm{PCl}_3} \times p_{\mathrm{Cl}_2}}{p_{\mathrm{PCl}_5}}\)

So at 5.4 atm pressure, 50% of PCl₅(g) will be dissociated at 250°C.

Question 4. At a particular temperature and 0.50 aim pressure, NH) Ami some amount of .solid NH₄HS arc present In a rinsed container. Solid NH₃(g) dissociates to give NH₄(g) and H₂S(g). At equilibrium, the total pressure of (ho reaction-mixture Is found to be 0.8 1 atm. Hud the value of the equilibrium constant of this reaction at that temperature.
Answer:

Reaction: NH₄H(s) ⇌ NH₃(g) + H₂S(g)

From the reaction, it is dear that, ) mol NH₄HS(s) dissociation produces 1 mol NH₃(g) and 1 mol H₂S(g). So, at a particular temperature and volume, the partial pressure of NHa(g) and I H₂S(g) will be the same and independent of the amount of NH₄HS(s).

Le Chatelier’s Principle Class 11 Chemistry Summary

Let, partial pressure of H₂S(g) at equilibrium =p atm. Therefore, partial pressure of NH₃(g) and H₂S(g) at Initial stage and at equilibrium arc as follows:

∴ 0.5 + 2p = 0.04 or, p = 0.17 atm

∴ At equilibrium, partial pressure of NH₃,

PNH₃ = (0.5 + 0.17) atm =0.67 atm and partial pressure of

H₂S,PH₂S = 0.17 atm

So, the equilibrium constant of the reaction, K_p = PNH₃ × PH₂O

= 0.67 ×  0.17 = 0.1139 atm²

Acids And Bases

Acids and bases according to Arrhenius’s theory

Acids:’

Hydrogen-containing compounds that ionize in an aqueous solution to produce H+ ions are called acids.

Example:

The hydrogen-containing compounds such as HCl, HNO₃, H₂SO₄, CH₃COOH, etc., ionize in aqueous solutions to form H⁺ ions. Thus, these compounds are acids according to Arrhenius’s theory.

Bases A compound that ionizes in an aqueous solution to produce hydroxyl ions (OH-) is called a base.

Example: The compounds such as NaOH, KOH, Ca(OH)₂ NH₄OH, etc., ionize in aqueous solution to produce OH’ ions and hence are termed as bases according to Arrhenius theory.

1. NaOH(ag) Na⁺(ag) + OH^–(aq)
2. KOH(ag)→ K⁺(aq) + OH^–(aq)
3. Ca(OH)2(aq)→ Ca²⁺(aq) + 2OH^–(aq)
4. NH4OH(aq)→ NH⁺(aq) + OH^–(aq)

Read and Learn More CBSE Class 11 Chemistry Notes

Limitations of Arrhenius theory: Arrhenius theory is useful for defining acids and bases. It explains the acid-base neutralization reaction by the simple equation:

H₃O+(aq) + OH-(aq)→2H₂O(Z). However, there are certain limitations of this theory.

According to this theory, the presence of water is essential for a compound to exhibit its acidic or basic properties. However, the fact that acidic or basic property of a compound is its characteristic property, which is independent of the presence of water.

• The acidic or basic properties of a substance that is insoluble in water cannot be explained by this theory.
• The acidity or basicity of any compound in non-aqueous solvents cannot be explained by Arrhenius’s theory. For example, the acidity of NH₄C1 orbasicity of NaNH₂ in liquid
  ammonia cannot be explained by this theory.
• According to Arrhenius’s theory, compounds containing only hydroxyl ions are considered as bases. Consequently, the basicity of ammonia (NH₃), methylamine (CH₃NH₂), aniline (C₆H₅NH₂), etc., cannot be explained by this theory.
• According to Arrhenius’s theory, only the hydrogen-containing compounds that ionize in aqueous solution to produce H+ ions are considered acids. Consequently, the acidity of compounds such as PC1₅, BF₃, and A1C1₃ cannot be explained by this theory.

CBSE Class 11 Chemistry Notes Acids and Bases

Acids And Bases According To Bronsted Lowry Concept (Protonic Theory)

Definitions of acids and- bases according to the theory proposed by J.N. Bronsted and T.M. Lowry are given below:

1. Acid: An acid is a substance that can donate a proton (or H+ ion)
2. Base: A base is a substance that can accept a proton (or J+ ions)

So, according to this theory, an acid is a proton donor and a base is a proton acceptor.

Example: HCl(aq) + H₂O(aq)→H₃O⁺(aq) + Cl^–(aq)

In this reaction, HC1 donates one proton, behaving as acid, while H20 accepts a proton, behaving as a base.

According to this theory, apart from the mill compounds (HCI, HNO₃, CH₃COOH, etc cations example;

NH⁴⁺, C₆H₅NH₃⁺,[Fe(H₂O)₆]³⁺, [A](H₂O)₆]3⁺, etc.) and anions (example HSO^–₄, HCO^–₃, HC₂O^–₄ etc.] and The acidic properties of these three types of substances are shown by the following reactions ;

CH₃COOOH(aq)+ H₂O(l) ⇌ H₃O⁺(aq)+CH₃COO^–(aq)

H₂SO₄(aq) + 2H₂O(l)⇌ 2H₃O⁺(aq)+SO₄^2-(aq)

NH₄⁺(aq) + H₂O(l)⇌ H₃O⁺(aq) +NH₃(aq)

[Fe(H₂O)₆]³⁺ (aq) + H₂O(l) ⇌ [Fe(H₂O)₅OH]²⁺(aq)+ H₃O⁺(aq)

H₂PO₄^–(aq) + H₂O(l) ⇌ H₃O⁺(aq)+HPO₄^2-(aq)

Similarly, apart from the neutral compounds (e.g., NH₃, C₆H5NH₂, H₂O, etc.), a large number of unions

Example: OH^–, CH₃COO^–, CO₃^2-, etc.) can act as a base,

The following reactions indicate the basic properties of these two lands of substances:

1. CH₃COO^–(aq) + H₂O(l)⇌ CH₃COOH(aq) + OH^–(aq)
2. NH₃(aq) +H₂O(l)⇌NH⁺4(aq) + OH^–(aq)
3. HPO₄^2--(aq) + H₂O(l)⇌ (aq) + OH^–(aq)

Concept of conjugate acid-base pair:

Concept of conjugate acid-base pair Definition:

Apair of species (a neutral compound and the Ion produced from it or, an ion and a neutral compound formed from it or, an ion and the other ion produced from it) having a difference of one proton is called a conjugate acid-base pair.

Examples: (H₂O, H₃O⁺), (H₂PO₄^–, HPO₄^2-), (CH₃COO^–, CH₃COOH ), etc., are some examples of conjugate acid-base pairs.

Explanation:

To get an idea about conjugate acid-base pair, let us consider the ionization of CH₃COOH in an aqueous solution:

CH₃CO₂H(aq) + H₂O(l) ⇌CH₃CO₂ (aq) + H₃O+(aq)

Since CH3COOH is a weak acid, it undergoes partial ionization in the solution, and the above equilibrium is tints established. In the forward reaction, the CH₃COOH molecule donates a proton (H+ion) which is accepted by the H₂O molecule.

Therefore, according to the Bronsted-Lowry concept, CH₂COOH is an acid and H₂O is a base. In the reverse reaction, the H₃O⁺ ion donates a proton which is accepted by a CH₃COO^– ion. Therefore, in the reverse reaction, H₃O⁺ ion acts as an acid and CH₃COO^– as a base.

⇒ \(\underset{\text { acid }}{\mathrm{CH}_3 \mathrm{CO}_2 \mathrm{H}}(a q)+\underset{\text { base }}{\mathrm{H}_2 \mathrm{O}}(l) \underset{\text { base }}{\mathrm{CH}_3 \mathrm{CO}_2^{-}(a q)}+\underset{3}{\mathrm{H}_3 \mathrm{O}^{+}}(a q)\) ………………….(1)

In equation (1), CH₃COO^– ion is the conjugate base of CH₆COOH and CH₃COOH is the conjugate acid of CH₃COO^– ion. Hence, (CH₃COOH, and CH₃COO^–) constitute a conjugate acid-base pair.

Similarly, in equation (1), H₂O is the conjugate base of the H₃O⁺ ion and the H₃O⁺ion is the conjugate acid of H₂O. Therefore, (H₃O⁺, H₂O ) constitutes a conjugate acid-base pair.

An acid donates a proton to produce a conjugate base and a base accepts a proton to produce a conjugate acid. The conjugate base of an acid has one fewer proton than the acid. On the other hand, the conjugate acid of the base has one more proton than the base

Acid -conjugate base:

Acids and Bases Class 11 Chemistry Notes

Base-conjugate base:

Strength of conjugate acid-base pair or Bronsted acid-base pair in aqueous solution:

The stronger an acid, the greater its ability to donate a proton. Similarly, a base with greater proton-accepting ability exhibits stronger basicity.

• The acids HCL, HNO₃, H₂SO₄, etc., undergo complete ionization in aqueous solution to form H₃O⁺ ions and the corresponding conjugate bases. Hence, these are considered strong acids in an aqueous solution. In an aqueous solution, the conjugate base produced from a strong acid has less tendency than H₂O to accept a proton. Therefore in an aqueous solution, the conjugate base of a strong acid is found to be very weak.
• The acids HF, HCN, CH₆COOH, HCOOH, etc., undergo slight ionization in an aqueous solution to produce H₂O+ions and the corresponding conjugate bases. As these acids have little tendency to donate protons in aqueous solution, they are called weak acids.
• In an aqueous solution, the conjugate base produced from a weak acid has more tendency’ than H₂O to accept a proton. Therefore, in aqueous solution, the conjugate base of a weak add is found to be stronger than H₂O.
• In aqueous solution, strong bases like NH₂, O₂^–, H⁺ etc., react completely with water to form their corresponding conjugate adds and OH^– ions. These conjugate acids are later than H₂O. Hence, in aqueous solution, the conjugate acid of a strong base is very weak.

On the other hand, in an aqueous solution, weak bases like NH₃, CH₃NH₂, etc., react partially with water to produce the corresponding conjugate acids and OH^– ions. These conjugate acids are stronger than H₂O. Therefore, in an aqueous solution, the conjugate acid of a weak base is strong.

The conjugate acid of a strong base has little tendency to accept protons. On the other hand, the conjugate acid of a weak base has a high tendency to accept protons.

Acid-base neutralization reactions according to Bronstedlowry concept:

According to the Bronsted-Lowry concept, in an acid-base neutralization reaction, a proton from an acid molecule gets transferred to a molecule of a base.

As a result, the acid converts to its conjugate base, and the base changes to its conjugate acid by accepting a proton.

Example:

Strength of Acids and Bases Class 11 Chemistry Notes

Limitations of Bronsted-Lowry concept:

With the help of this theory, the reaction of an acid with a base is explained in terms of the gain or loss of proton(s). However, there are many acid-base reactions in which the exchange of proton(s) does not take place. Such types of acid-base reactions cannot be explained by this theory.

The acidic properties of many non-metallic oxides (for example; CO₂, SO₂ ) and basic properties of many metallic oxides (for example; CaO, BaO) cannot be explained with the help of the Bronsted-Lowry concept. Also, the acidic properties of BF₃, AlCl₂, SnCl₂, etc., cannot be explained with the help of this theory.

Lewis’s Concept Of Acids And Bases

On the electronic theory of valency, scientist Gilbert N. Lewis proposed the following definitions of acids and bases.

Acid: An acid is a substance which can accept a pair of electrons

Examples:

The compounds that have a central atom with incomplete octets can act as Lewis acids, such as BF₃ BCl₃, AlCl₃, etc.

In some compounds due to the presence of vacant orbitals in the central atom, the octet can be expanded. These compounds can also behave as Lewis acids, such as PCl₃, SnCl₃, SiF₄, etc.

SiF₄ (Lewis acid) + 2F^– (Lewis base) → [SiF₆]^2-

Cations like H⁺, Ag⁺, Cu²⁺, Fe³⁺, Al³⁺, etc., behave as Lewis acids.

NCERT Solutions Class 11 Chemistry Acids and Bases

Molecules containing multiple bonds between two atoms of different electronegativities behave as Lewis acids, such as CO₂, SO₂, etc.

Base: A base Is a Substance that can donate a pair of electrons

Example: Compounds that contain an atom having one or more lone pairs of electrons behave as Lewis bases, such as NH₃, H₂O: CH₃OH, etc.

Anions like NH^–, Cl^–, I^–, OH^–, CN^– etc., are considered as Lewis bases.

• A Lewis add is an acceptor of a pair of electrons and forms a coordinate bond with a Lewis base.
• A Lewis base is a donor of a pair of electrons and forms a coordinate bond with Lewis acid.

Limitations of Lewis’s concept:

• This concept provides no idea regarding the relative strengths of acids and bases.
• This theory contradicts the general concept of acids by considering BF₃ AlCl₃, and simple cations as acids.
• The behaviour ofprotonic adds such as HCl, H₂SO₄ etc., cannot be explained by this concept. These acids do not form coordinate bonds with bases which is the primary requirement Lewis concept.
• Normally, the formation of coordination compounds is slow, therefore acid-base reactions should also be slow, but acid-base reactions are extremely fast, this cannot be explained by the Lewis concept.

Degree Of Ionisation And Ionisation Constant Of Weak Electrolyte

Weak electrolytes partially dissociate into ions in solutions and there always exists a dynamic equilibrium involving the dissociated ions and the undissociated molecules.

This state of equilibrium is called an ionic equilibrium. The equilibrium constant associated with an ionic equilibrium is known as the ionization or dissociation constant of the weak electrolyte.

Degree Of Ionisation

During the ionization of a solution of a weak electrolyte, the fraction of its total number of molecules that get dissociated at equilibrium is called the degree of ionization or dissociation of the electrolyte.

Degree of ionization of an electrolyte (α)

Number of dissociated molecules of the electrolyte at equilibrium/ Total number of molecules of the electrolyte.

Suppose, a fixed volume of solution contains 0.5 mol of a dissolved electrolyte. If 0.2 mol of this electrolyte gets dissociated at equilibrium, then the degree of dissociation (a) O₂ of the electrolyte

⇒  \(\frac{0.2}{0.5}=0.4\), i.e., 40 % of the electrolyte exists in an ionized state in the solution.

As strong electrolytes dissociate completely in solutions, their degree of dissociation (a)= 1 but, the degree of dissociation of weak electrolytes is always less than 1.

Read and Learn More CBSE Class 11 Chemistry Notes

Ionization or dissociation constant of weak electrolytes:

Let us consider the following equilibrium which is established by a weak AB because of its partial ionization in water

⇒ \(\mathrm{AB}(a q) \rightleftharpoons \mathrm{A}^{+}(a q)+\mathrm{B}^{-}(a q)\)

Applying the law of mass action to the equilibrium we have the equilibrium constant, K,

⇒ K= \(\frac{\left[\mathrm{A}^{+}\right]\left[\mathrm{B}^{-}\right]}{[\mathrm{AB}]}\)

Where [A⁺, [B^–], and [AB] is the molar concentrations (mol L^-1) of A⁺, B^–, and AB, respectively at equilibrium.

K represents the ionization or dissociation constant of the weak electrolyte AB.

The value of equilibrium constant (K) changes well with a variation of temperature,  at a constant uimporniure, It has a fixed value.

Oslwald’s dilution law

Let the initial concentration (before dissociation) of an aqueous solution of a weak electrolyte AB c mol^-1,

CBSE Class 11 Chemistry Notes Degree of Ionisation

The following equilibrium Is established due to the partial dissociation of ΔH in an aqueous solution:

AB(aq) ⇌  A⁺+ (aq)+ B^–(aq)

Suppose, at equilibrium, the degree of ionization or dissociation of ΔH is a. So, a mol of ΔH on Its ionization will result In a mol of Δ1 Ion and a mol of H- Ions. The number of moles of AB that remain unlonloniscd is (1 — α).

Hence at equilibrium, the molar concentrations of different species will be as follows:

By applying the law of mass action to this equilibrium, we get an equilibrium constant

⇒ \((K)=\frac{\left[\mathrm{A}^{+}\right] \times\left[\mathrm{B}^{-}\right]}{[\mathrm{AB}]}=\frac{\alpha c \times \alpha c}{c(1-\alpha)}=\frac{\alpha^2 c}{1-\alpha}\) ……………………..(1)

Equation (1) represents the mathematical expression of Ostwald’s dilution law. The equilibrium constant (K) is called the Ionisation constant of the weak electrolyte, AB. At ordinary concentration, the value of the degree of dissociation (a) of a weak electrolyte is generally very small. So, (1 – α)≈1

.With this approximation equation (1) can be written as,

K = \(\alpha^2 c \quad \text { or, } \quad \alpha=\sqrt{\frac{K}{\boldsymbol{c}}}\)……………………..(2)

Equation (2) is the simplified mathematical expression of Ostwald’s dilution law Conclusion,’ From equation (2), it can be concluded that—

The degree of dissociation (or) of a weak electrolyte in a solution is inversely proportional to the square root of the concentration of the solution (since at constant temperature, K has a definite value).

So, at a fixed temperature, the degree of dissociation of a weak electrolyte in its solution increases with the decrease in the concentration of the solution and decreases with the caraway in the concentration of the solution, It roof of weak electrolyte remains dissolved In 6, of the solution, then the molar concentration of the solution,

c=  \(\frac{1}{V}.\) Substituting

c= \(\frac{1}{V} .\) In equation (2),

we have an α = √KV Thin equation showing that when v Increases (as happens when the solution Is diluted), the degree of dissociation of the electrolyte also Increases.

Ostwald’s dilution law:

At a certain temperature, the degree of Ionisation of a weak electrolyte in a solution Is Inversely proportional to the square root of the molar concentration of the solution.

Or, At a certain temperature, the degree of ionization of a weak electrolyte In a solution is directly proportional to the square root of the volume of the solution containing mol of the electrolyte.

Limitation of Ostwald’s dilution law:

Ostwald’s dilution law applies to weak electrolytes only. As strong electrolytes ionize almost completely at all concentrations, this law does not apply to them.

Ionization or dissociation constant of a weak acid and concentration of H30+ ions in its aqueous solution

Weak acids partially dissociate into ions in aqueous solutions, and there always exists a dynamic equilibrium involving the dissociated ions and the undissociated molecules. Like any other equilibrium, such type of equilibrium also has an equilibrium constant, known as the ionization or dissociation constant of the corresponding weak acid.

The ionization constant of a weak acid is designated by the Ionisation constant of a weak monobasic acid:

Let HA be a weak monobasic acid which on partial ionization in an aqueous solution forms the following equilibrium

HA(aq) + H₂O(l) ⇌H₃O⁺(aq) + A^–(aq)

Using the law of mass action to the above equilibrium, we get equilibrium contract

⇒ \(K=\frac{\left[\mathrm{H}_3\mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]\left[\mathrm{H}_2 \mathrm{O}\right]}\)

where [H₃O⁺], [A^–], [HA], and [H₂O] represent the molar concentrations (mol-L^-1) of H₃O⁺, A⁺, HA, and H₂O, respectively, at equilibrium in solution.

In the solution, the concentration of H₂O is much higher than that of HA and its concentration does not change significantly due to partial ionization of HA.

The concentration of H₂O, therefore, remains constant.

So, \(K \times\left[\mathrm{H}_2 \mathrm{O}\right]=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\)

Since [H₂O] = constant, the K ×  (H₂O] constant is known as the ionization or dissociation constant of the weak acid and Is designated by ‘Ka’.

∴ \(K_a=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+} \| \mathrm{A}^{-}\right]}{[\mathrm{II} \mathrm{A}]}\)

Significance of ionization constant of a weak acid:

Like any other equilibrium constant, the value of the ionization constant (Ka) of a weak acid is constant at a fixed temperature.

The higher the tendency of a weak acid HA to donate proton in water, the higher the concentration of H₃O⁺ and A^– ions at equilibrium in the solution.

Hence from equation (1), it can be said that the stronger the acid, the larger the value of its ionization constant.

If the solutions of two monobasic acids have the same molar concentration, then the solution containing the acid with a larger value of Ka will have a higher concentration of H30+ ions than the other solution.

Ionization constants (Ka) of some weak monobasic acids at 25°C [in water]

The concentration of H₃O⁺ ions in an aqueous solution of a weak monobasic acid:

Let a weak acid HA on its partial ionization water form the following equilibrium:

HA(aq) + H₂O(l)⇌ H₃O⁺(aq) + A^–(aq)

If the initial concentration of HA in its aqueous solution is C mol.L^-1 and the degree of ionization of HA

At equilibrium is then the concentrations of different species at equilibrium will be as follows:

(During ionization of a weak acid, the concentration of H20 remains unchanged.) Therefore, the Ionisation constant of the weak add HA,

⇒ \(K_a=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \times\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}=\frac{c \alpha \times c \alpha}{c(1-\alpha)}=\frac{\alpha^2 c}{1-\alpha}\)

At ordinary concentration, the degree of dissociation (a) of a weak acid is negligible. So, (1 – α)≈1

⇒ \(\text { Hence, } K_a=\alpha^2 c \text { or, } \alpha=\sqrt{\frac{K_a}{c}}\)

Therefore, if the concentration (c) of a weak monobasic acid and its ionization constant (Ka) are known, then the degree of ionization (a) of the acid can be calculated by using the equation (1)

Concentration of H₃O⁺ ion [H₃O⁺] = αc…………………………(2)

⇒ \(\text { or, }\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\alpha c=\sqrt{\frac{K_a}{c}} \times c=\sqrt{c \times K_a}\)

In an aqueous solution of a weak acid, if the concentration of the acid and its degree of ionization (or) are known, then the concentration of H₃O+ ions in the solution can be calculated by using equation (2)

Alternatively, if the concentration (c) of the acid and its ionization constant (Ka) is known, then the concentration of H₃O⁺ ions can be calculated by using the equation (3).

Degree of Ionisation Class 11 Chemistry Notes

Relative strengths of two weak monobasic acids:

Let us consider the aqueous solutions of two weak acids HA and HA-, each with the same molar concentration of cool-L^–

At a given temperature, if the ionization constants of HA and HA’ are K_a and K’_a respectively and a and a are their degrees of ionization in their respective solutions, then

⇒ \(\alpha=\sqrt{\frac{K_a}{c}} \quad \text { and } \quad \alpha^{\prime}=\sqrt{\frac{K_a^{\prime}}{c}}\)

∴ \(\frac{\alpha}{\alpha^{\prime}}=\sqrt{\frac{K_a}{K_a^{\prime}}}\)

Therefore, at a particular temperature, if the molar concentrations of the solutions of two weak monobasic acids are the same, then the acid having a larger ionization constant will have a higher degree of ionization than the other.

The degree of dissociation (a) of a weak acid in its solution of a given concentration is a measure of its strength (or proton donating tendency). The higher the degree of dissociation of an acid in its solution, the stronger the acid.

It means that the strength of an acid in its solution is proportional to its degree of dissociation in the solution.

Hence, at a particular temperature, for a definite molar concentration

⇒ \(\frac{\text { Strength of acid } \mathrm{HA}}{\text { Strength of acid } \mathrm{HA}^{\prime}}=\sqrt{\frac{K_a}{K_a^{\prime}}}\)

Ionization constant of weak polybasic acids:

An acid with more than one replaceable H-atom is called a polybasic acid,

Example:

H₂CO₃, H₃PO₄, and H₂S. H₃SO₄ and H₂S are dibasic acids as they have two replaceable H-atoms, whereas H₃PO₄ is a tribasic acid as it has three replaceable hydrogen atoms.

These acids dissociate in a series of steps, each of which attains an equilibrium and has its characteristic equilibrium constant.

Example: Ionisation of H₃PO₄ in water:

In water, H₃PO₄ ionizes in the following three steps as it contains three replaceable hydrogen atoms:

1. H₃PO₄(aq) + H₂O ⇌ H₃O⁺(aq) + H₂PO₄^–  (aq)

Ionization constant,

Ka₁ = \(\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \times\left[\mathrm{H}_2 \mathrm{PO}_4^{-}\right]}{\left[\mathrm{H}_3 \mathrm{PO}_4\right]}\)

2. H₂PO₄^–(aq) + H₂O ⇌ H₃O⁺(aq) + HPO₄^2- (aq)

Ionization constant

Ka₂ = \(\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \times\left[\mathrm{HPO}_4^{2-}\right]}{\left[\mathrm{H}_2 \mathrm{PO}_4^{-}\right]}\)

H₂PO₄^2-  + H₂O ⇌ H₃O⁺(aq) +PO₄^3- (aq)

Ionization constant,

Ka₃= \(\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \times\left[\mathrm{PO}_4^{3-}\right]}{\left[\mathrm{HPO}_4^{2-}\right]}\)

Overall ionization constant, K_a = Ka₁ × Ka₂ × Ka₃

At constant temperature, Ka₁ > Ka₂ > Ka₃ for a weak tribasic acid. Due to the electrostatic force of attraction, a singly charged anion (for example- HS^– or H₂PO^–4) has less tendency to lose a proton than a neutral molecule (for example H₂S ).

Similarly, it is more difficult for a doubly charged anion (For example:  HPO₄^2- ) to lose a proton than a singly charged anion.

Ionization or dissociation constant of a weak base and concentration of OH^– ions in its aqueous solution

When a weak base is dissolved in water, it reacts with water to form its conjugate acid and OH- ions. Eventually, an equilibrium involving the conjugate acid and unreacted base is established. Such an equilibrium has its characteristic equilibrium constant known as the ionization constant of the weak base. The ionization constant of weak basis is denoted by.

Ionisation Constant of a weak monoacid lc base:

Let us consider an aqueous solution of a weak monoacidic base B. Since B is a weak base, a small nili fiber of molecules reacts with an equal number of H₂O molecules to form the conjugate acid, BH⁺, and OH^– ions.

A dynamic equilibrium is thus established between BH⁺, OH^– and unionized molecules as follows:

⇒ \(\mathrm{B}(a q)+\mathrm{H}_2 \mathrm{O}(l) \rightleftharpoons \mathrm{BH}^{+}(a q)+\mathrm{OH}^{-}(a q)\)

Applying the law of mass action to the above equilibrium, we have, an equilibrium constant

⇒  \(K=\frac{\left[\mathrm{BH}^{+}\right]\left[\mathrm{OH}^{-}\right]}{[\mathrm{B}]\left[\mathrm{H}_2 \mathrm{O}\right]}\)

Where [BH⁺], [OH^–], [B], and [H₂O] represent the molar concentrations of BH⁺, OH⁺, B, and H₂O respectively, at equilibrium. In an aqueous solution, the concentration of H₂O is much higher than that of B. Thus, any change in concentration that occurs because of the reaction of H₂O with B can be neglected. So, [H₂O] remains essentially constant.

So, \(K \times\left[\mathrm{H}_2 \mathrm{O}\right]=\frac{\left[\mathrm{BH}^{+}\right]\left[\mathrm{OH}^{-}\right]}{[\mathrm{B}]}\)

Since [H₂O] = constant, K × [H₂O] = constant This constant is known as the ionization constant of the weak base B and is denotedby’Kb ‘

Therefore \(K_b=\frac{\left[\mathrm{BH}^{+}\right]\left[\mathrm{OH}^{-}\right]}{[\mathrm{B}]}\)

Equation (1) expresses the ionization constant for the weak monoacidic base, B.

Significance of ionization constant of a weak base:

As in the case of other equilibrium constants, the ionization constant of a weak base (Kb) has a definite value at a particular temperature.

If the weak base, B, has a high tendency to accept protons in water, it reacts with water to a greater extent. This results in high concentrations of BH⁺ and OH^– in the solution and gives rise to a large value of Kb for the base. Therefore, the larger the value of Kb for a weak base, the stronger the base.

At a certain temperature, if the aqueous solution of two weak bases has some molar concentration, then the solution containing the base with a larger value of Kb will have a higher concentration of OH” ions at equilibrium in the solution.

Ionization constants (kb) of some weak mono-acidic bases at 25 °C :

The concentration of OH^– in an aqueous solution of a weak monoacidic base: Let a weak base, B on partial ionization in an aqueous solution form the following equilibrium:

B(aq) + H₂O(l) ⇌ BH⁺(aq) + OH^–(aq)

Let the initial concentration of B in the aqueous solution be c mol.L^-1. According to the above equation, at equilibrium, if the concentration of OH^– is x mol.L^-1, then the concentrations of BH⁺ & B will be × mol.L^-1and (c-x) mol.L^-1 respectively because according to the given equation, 1 molecule of B and 1 molecule of H20 react to form one BH⁺ and one OH^– ion.

Therefore, ionization constant ofthe weak base, B is:

⇒ \(K_b=\frac{\left[\mathrm{BH}^{+}\right] \times\left[\mathrm{OH}^{-}\right]}{[\mathrm{B}]}=\frac{x \times x}{\mathrm{c}-x}=\frac{x^2}{c-x}\)

Since the base is weak, a very small amount of it reacts with water. So, x is negligible in comparison to c, and hence c-xx.

⇒ \(K_b=\frac{x^2}{c} \quad \text { or, } x=\sqrt{K_b \times c}\)

Therefore, in an aqueous solution of the weak base, B

⇒ \(\left[\mathrm{OH}^{-}\right]=\sqrt{K_b \times c}\)

If the ionization constant (Kb) of a monoacidic weak base and the concentration (c) of its aqueous solution are known, then the concentration of OH⁺ ions in the solution can be determined with the help of equation (1)

Determination of [H₃O⁺] in a solution of strong acid and [OH-] in a solution of a strong base

Strong acids (For example HCl, HBr, HClO₄, HNOs, H₂SO₂) and strong bases [e.g., NaOH, KOH, Ca(OH)₂] completely ionize in their aqueous solutions. Hence, the concentration of H₃O⁺ ions (or, OH^– ions) in the aqueous solution of a strong acid (or a strong base) can be calculated from the initial concentration of the acid (or base) in the solution.

When the concentration of the solution is in ‘molar’ unit:

Suppose, the molarity of an aqueous solution of a strong acid (or base) is M. If each acid (or base) molecule in the solution produces × H₃O⁺ (or OH^–) ions, then in the case of solution of an acid, [H₃O⁺] = x M and in the case of solution of a base [OH^–] = x x M.

Examples:

1. 1 molecule of strong monobasic acid on its ionization (HCl, HBr, HClO₄, HNO₃, etc.) gives an H₃O⁺ ion. Hence, in such a solution, the molar concentration of H₃O⁺ ions = the molar concentration of the acid solution.

For example, the molar concentration of H₃O⁺ ions in 0.1(M) HCl or HNO₃ solution = 0.1(M).

2. Each molecule of a strong dibasic acid (for example H₂SO₄) on its ionization produces two H₃O⁺ ions.

Therefore, in such a solution, [HsO⁺] =2x molar concentration of the solution. For example, in 0.1(M) H₂SO₄ solution, [H₃O⁺] =2 × 0.1

= 0.2(M).

3.Similarly, in 0.1(M) NaOH solution, [OH^–] =0.1(M) and in O.l(M) Ca(OH)₂ solution, [OH^–] =2 × 0.1

= 0.2(M).

NCERT Solutions Class 11 Chemistry Degree of Ionisation

When the concentration of the solution is in ‘normal unit:

If the concentration of a solution of strong acid (or base) is given in the ‘normal’ unit, then the concentration of H₃O⁺ (or OH^– ) ion in that solution will be equal to the normal concentration of the solution.

Example:

1. If The concentration of H₃O⁺ ionizing.l(N) H₂SO₄ solution= 0.1(N). Since the H₃O+ ion is monovalent, the molar concentration of the H₂O+ ion in 0.1(N) H₂SO₄ solution is 0.1(M).

The concentration of OH^– ion in 0.1(N) Ca(OH)₂ solution= 0.1(N). Since OH^– is monovalent, the molar concentration of OH^– ion in 0.1(N) Ca(OH)₂ solution= 0.1(M) Normality of a solution =nx Molarity; where n= basicity in case of an acid; acidity in case of a base; total valency location (or anion) per formula unit in case of a salt.

Examples:

1. 0.1  (M) HCl = 0.1(N) HCl solution.

∵ Basicity of HCl =1

2. 0.1(M) H₂SO₄ = 2 × 0.1 = 0.2 (N)H₂SO₄ solution.

∵  Basicity Of H₂SO₄ =2

3. 0.1(M) H₂SO₄ = 2 × 0.1 = 0.2 (N)H₂SO₄ solution.

∵  Acidity Of CO(OH₂)=2

4. 0.1(M) Ca₂+ = 2 × 0.1= 0.2 (N) Ca₂⁺

∵ Valency Of Ca²⁺ in its salt =2

5. 0.1(M)Al₂(SO₄)₃ solution = 6 × 0.1 = 0.6(N) Al₂(SO₄)₃ solution

∵ In each molecule of Al₂(SO₄)₃,

Total valency of cation (Al³⁺) or anion (SO₄^2-) = Number of ions of Al³⁺or SO₄^2- x Valency of Al³⁺ or SO₄^2- =6]

Degree Of Ionisation Numerical Examples

Question 1. At 25°C temperature, the molar concentrations of NH₃, NH+4 and OH- at equlibrium are 9.6 × 10^-3(M), 4.0 × 10^-4(M) and 4.0 × 10^-4(M) respectively. Determine the ionization constant of NH₃ at that temperature.
Answer:

In the aqueous solution of NH₃, the following equilibrium is established

⇒  NH₃(aq) + H₂O(l) ⇌  NH₄⁺(aq) + OH^– (aq)

∴ Ionisation Constant Of NH₃, Kb = \(=\frac{\left[\mathrm{NH}_4^{+}\right] \times\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{NH}_3\right]}\)

As [NH₃] = 9.6 × 10^-3+(m),

[NH₄⁺] = 4.0 × 10^-4(M)

[OH^–] = 4.0 × 10^-4(M)

⇒ \(K_b=\frac{\left(4 \times 10^{-4}\right) \times\left(4 \times 10^{-4}\right)}{9.6 \times 10^{-3}}=1.67 \times 10^{-5}\)

Question 2. A 0.1(M) solution of acetic acid is 1.34% ionized at 25°C Calculate the ionization constant of the acid.
Answer:

We know, the ionization constant of a weak monobasic acid example CH₃COOH is

⇒ \(K_a=\frac{\alpha^2 c}{1-\alpha}\) where- a = degree of ionization and c = initial concentration of the acid solution.

As \(\alpha=\frac{1.34}{100}=1.34 \times 10^{-2} \text { and } c=0.1(\mathrm{M})\)

⇒ \(K_a=\frac{\alpha^2 c}{1-\alpha}=\frac{\left(1.34 \times 10^{-2}\right)^2 \times 0.1}{\left(1-1.34 \times 10^{-2}\right)}=1.82 \times 10^{-5}\)

∴ At 25°C, ionisation constant of CH₃COOH = 1.82 × 10^-5

Question 3. In a 0.01(M) acetic acid solution, the degree of ionization of acetic acid is 4.2%. Determine the concentration of HgO+ ions in that solution
Answer:

Acetic acid is a weak monobasic acid. In such a solution, [H30+] = ac; where, c and a are the initial concentration of the acid and its degree of ionization respectively.

⇒ \(\text { As } \alpha=\frac{4.2}{100}=4.2 \times 10^{-2} \text { and } c=0.01(\mathrm{M}) \text {, }\) in 0.01(M) acetic acid solution.

[H₃O⁺] =ac = 4.2 × 10^-2 ×  0.01

= 4.2 × 10^-4 (M)

Question 4. The value of the ionization constant of pyridine (C₆H₆N) at 25°C is 1.6 × 10^-9. what is the concentration of OH^– ions in a 0.1(M) aqueous solution of pyridine at that temperature
Answer:

Pyridine is a monoacidic base. In aqueous solutions of such bases

⇒ \(\left[\mathrm{OH}^{-}\right]=\sqrt{c \times K_b}\)

Where c = initial concentration of the base and K_b = ionization constant of the weak base.

As c = 0.1(M) and Kb = 1.6 × 10^-9 in 0.1(M)

Aqueous pyridine solution,

⇒ \(\left[\mathrm{OH}^{-}\right]=\sqrt{0.1 \times 1.6 \times 10^{-9}}=1.26 \times 10^{-5}(\mathrm{M}) .\)

Degree of Ionisation NCERT Notes Class 11

Question 5. At 25°C, the value of the ionization constant of a weak monobasic acid, HA is 1.6 × 10^-4 What is the degree of ionization of HA in its 0.1(M) aqueous solution?
Answer:

Degree of ionization of weak monobasic acid (a) \(=\sqrt{\frac{K_a}{c}}.\)

Given, c = 0.1(M) and Ka = 1.6 × 10-4

The degree of ionization of HA in its 0.1(M) aqueous solution

= \(\sqrt{\frac{K_a}{c}}=\sqrt{\frac{1.6 \times 10^{-4}}{0.1}}=0.04\)

∴ Degree of ionisation of HA in its 0.1(M) aqueous solution = 0.04 x 100%= 4%

Question 6. The ionization constant of ammonia is 1.8 × 10^-5at 25°C. Calculate the degree of ionization of ammonia in its 0.1(M) aqueous solution at that temperature.
Answer:

NH₃ is a weak monoacidic base. In aqueous solutions degree of ionization (a) of such base

⇒ \(\sqrt{\frac{\kappa_b}{c}}.\)

As c = 0.1(M) and k_b = 1.8 × 10^-5 tire degree of ionisation of NH₆ in its 0.1(M) aqueous solution

⇒ \(\sqrt{\frac{1.8 \times 10^{-5}}{0.1}}=0.0134=0.0134 \times 100 \%=1.34 \%\)

Ionic Product Of Water

Pure water is a very poor conductor of electricity, indicating its very low ionization. Due to the die self-ionization of pure water, H⁺ and OH^– ions are formed and the following dynamic equilibrium involving H⁺, OH^–ions, and unionized water molecules is established:

H₂O(l) + H₂O ⇌  H₃O⁺(aq) + OH^–(aq)

Applying the mass action to this equilibrium, we get

⇒ \(K_d=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \times\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{H}_2 \mathrm{O}^2\right.}\)

where [H₃O⁺], [OH^– ], and [H₂O] are the molar concentrations of H₃O+ OH (aq) and H₂O(l) at equilibrium, respectively, and Kd is the ionization or dissociation constant of water.

As the degree of ionization of water Is very small, its equilibrium concentration is almost the same as Its concentration before Ionisation. Thus, at equilibrium, [H₂O]2 = constant.

From equation(1)  we have, kd[H₂O)² = [H₃O⁺] × [OH^–]

Since, [H₂O]² = constant, Kd × [H₂O]² = constant. This constant is called the Ionic product of water & is denoted by K_w.

Therefore K_w=[H₃O⁺] × [OH^–]

Degree of Ionisation Formula and Examples Class 11

Concentrations of H₃O⁺ and OH^– in aqueous solution

Any aqueous solution, whether it is acidic or basic, always contains both H₃O⁺ and OH ions. A concentrated acid solution also contains OH^– ions although its concentration is much lower compared to H₃O⁺ ions. Likewise, a concentrated alkali solution also contains H₃O⁺ ions but with a much lower concentration than OH^– ions.

On the other hand, in a neutral solution, the concentrations of H₃O+ and OH ions are always the same. At a particular temperature, if the ionic product of water Kw, then for

⇒ \(\text { a neutral solution: }\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]=\sqrt{K_w}\)

⇒ \(\text { an acidic solution: }\left[\mathrm{H}_3 \mathrm{O}^{+}\right]>\sqrt{K_w} \text { and }\left[\mathrm{OH}^{-}\right]<\sqrt{K_w}\)

⇒ \(\text { a basic solution: }\left[\mathrm{H}_3 \mathrm{O}^{+}\right]<\sqrt{K_w} \text { and }\left[\mathrm{OH}^{-}\right]>\sqrt{K_w}\)

At 25°C, Kw = 10’14. So, at this temperature, in the case of

an acidic solution: [H₃O⁺] > 10^-7 mol.L^-1 and [OH^-1] < 10^-7 mol.L^-1

a basic solution: [OH^–] > 10^-7 mol.L^-1 and [H₃O⁺] < 10^-7 mol.L^-1

Determination of [H₂O₄] and [OH-] in aqueous solution:

At a particular temperature, if the value of and any one of [H₃O+] or [OH-] are known, then the other can be determined using either of the following equations:

⇒ \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\frac{K_w}{\left[\mathrm{OH}^{-}\right]} \text {or, }\left[\mathrm{OH}^{-}\right]=\frac{K_w}{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}\)

For example, in an aqueous solution at 25°C if [H₃O⁺] = 10^-4(M),

⇒ \(\text { then }\left[\mathrm{OH}^{-}\right]=\frac{10^{-14}}{10^{-4}}=10^{-10}(\mathrm{M})\)

[since K_w(25°C)=10^-14]

PK_w = pK_w = -log10K_w At 25°C,K_w=10^-14

Therefore, at 25°C, pK_w = -log₁₀ ( 10^-14) = 14.

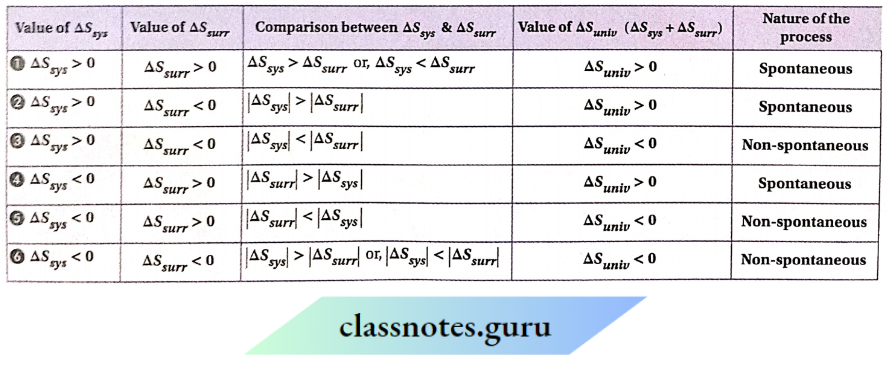
Concept Of PH And PH Scale

In the case dilute solution of an acid or a base, the concentration of H30+ or OH’ ions Is generally expressed in terms of the negative power of 10.

For instance, the concentration of H₃O⁺ negative power of 10. For instance, the concentration of H₃O⁺ concentration of OH^– ions In 0.0002(M) NaOH solution is 2 x 10^-4 mol. L^-1 . However, it is very inconvenient to express the concentration of H₃O⁺ or OH^– ions in terms of such negative power.

To overcome such difficulty encountered in the case of dilute solutions, Sorensen introduced the system of expressing the concentration of H₃O⁺ ions by pH (pH stands for Potein of hydrogen ion; the German word ‘Potenz’ means ‘power’).

PH Scale Definition:

The ph of a solution is defined as the negative i logarithm to the 10 of Its H30′ Ion concentration In mol^-1

Therefore, pH=-log 10[H₃O⁺]

Example:

If the concentration of If. O^– Ions In a solution is 10-3(M), then all of the solution  = -log 10 (10^-3) =3

Read and Learn More CBSE Class 11 Chemistry Notes

Important points to remember about all of the solutions:

1. pH – log10[H₃O⁺] . According to this equation, If (the concentration of Ions in a solution Increases, then the of the solution decreases, and vice-versa. Thus, the higher the value for a solution, [H₃O⁺] lower the pH of the solution. Conversely, the lower the value for a solution, the higher the pH of the solution.

Example:

If [H₃O⁺] = 10^-3 (M) In an aqueous solution, then all of the solution = 3. Now, If the solution Is diluted such that [H₃O⁺ ] = 10^-5 =  (M), then the pH of that solution increases and becomes 5.

2. If the pH of an aqueous solution is increased or decreased by one unit, then the concentration of H₈O+ Ions In the solution undergoes a ten-fold decrease or increase in its value.

CBSE Class 11 Chemistry Notes Concept of pH and pH Scale

Example:

Let the pH of an aqueous solution be 3. So, [H₃O⁺] in the solution = 10^-pH= 10^-3(M). Now, by diluting the solution, If the pH of (lie solution Is made 4, then, the concentration of H₃O+ ions i.e., H₃O+ will be =10^-pH= 10-1 (M).

Hence, when the pH of (lie solution is increased by one unit, the concentration of H₃O4 Ions In the solution decreases by a factor of ten. Similarly, the decrease In pH by one unit corresponds to a ten-fold Increase In [H₃O⁺.] The acidity of a solution Increases with a decrease In pH and decreases with an Increase In pH.

The POH of a solution Is defined as the negative logarithm to the base 10 of Its OH- Ion concentration In mol. L^-1.

Therefore POH = – log₁₀ [OH^–]

Important points about the pH of a solution:

1. With a decrease or Increase In (lie concentration of OH- ions In the solution, the pOH of the solution Increases or decreases respectively
2. The basicity of a solution increases with a decrease in pOH and decreases with an increase in pOH.

Relation holen pH, pOH, and pK_w

At a fixed temperature, for pure water or an aqueous solution,

⇒ \(\left|\mathrm{H}_3 \mathrm{O}^{+}\right| \times\left[\mathrm{OH}^{-} \mid=K_w\right.\)

Taking negative logarithms on both sides, we get

-log₁₀[H₃O⁺]-log₁₀[OH^–]= – log₁₀ K_w

Or,  p+HpOH =PK_w

Therefore, at a fixed temperature, for pure water or an aqueous solution, pH+POH= pk

At 25C, pKw = J 4. Hence, at 25°C, for pure water or any aqueous solution pH+POH =14

Values of pH and pOH for pure water:

Pure water is neutral. Hence, in pure water [H₃O⁺] = [OH^–]

⇒ \(\text { or, }-\log _{10}\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=-\log _{10}\left[\mathrm{OH}^{-}\right] \text {or, } p \mathrm{HOH}\)

From the relation, pH + pOH = pKw, we have 2pH= 2pOH = p K_w

Or \(p H=p O H=\frac{1}{2} p K_w\)

At 25 °C, pK_w= 14 . Hence, in the case of pure water at 25 °C,

⇒ \(p H=p O H=\frac{1}{2} \times 14=7\)

At 100°C, pKw = 1 2.26. Hence, in the case of pure water at 100 °C,

⇒ \(p H=p O H=\frac{1}{2} \times 12.26=6.13\)

pH of pure water at 100 °C is lower than that at 25 °C. Hence, at 100 °C, the molar concentration of H₂O+ ions is higher than that at 25°C. However, this does not mean that pure water is acidic at 100 C. Because the concentration of H₂O⁺ and OH^– ions are always the same in pure water, it Is always neutral irrespective of temperature

pH of a basic solution

To calculate the pH of a basic solution, the equation pH + pOH = pK w is used. If the temperature is 25°C, then pKw = 14. Therefore, at 25°C, if the pOH of an aqueous solution lies at 3, then,

pH = 14 -pOH =14-3 = 11.

PH -scale

PH -scale Definition: The scale in terms of which the acidity or basicity of any aqueous solution is expressed by its pH value is called the pH scale.

Range of pH-scale at 25°C:

Generally in dilute solution, the concentration of H₃O⁺ or OH^– ions is not more than 1mol.L^-1. If in the solution, [H₃O⁺] = 1 mol.L^-1, then pH = —log 10- = 0.

If in the solution, [OH^–] = 1 mol.L^-1, then [H₃O⁺] = 10^-14 mol.L^-1 [since At 25°C, Kw = 10^-14]. Hence, for a dilute solution.

pH = -log 10^-14

=1 4

Therefore, at 25 °C, the pH of a dilute aqueous solution ranges from 0 to 14.

Range of pW-scale vs. temperature:

The value of pKw of water determines the range of pH -scale. Since the value of pKw varies with the temperature change, the range of pH -scale also changes with the temperature change.

The range of the pH -scale can generally be expressed in the following way:

The value of pKw decreases with an increase in temperature. As a result, the range of pH -scale also decreases. For instance, at 25°C, pK_w = 14. Hence, at this temperature, the pH scale extends from 0 to 14. On the other hand, at 100°C, pK_w = 12.26. Thus, at this temperature pH scale extends from 0 to 12.26. For a neutral aqueous solution at 25°C, pH = 7, and at 100°C, pH =6.13.

a pH of neutral, acidic, and basic solutions at 25’C:

pH of neutral aqueous solution:

In the case of a neutral aqueous solution at 25°C,

[H3O⁺]=[OH^–] =, O^-14

= 10^-7mol.L^-1. Hence, for a neutral solution at 25°C, pH =-Iog₁₀ [H₃O⁺] =log₁₀10^-7 = 7.

pH of aqueous acidic solution:

In the case of an aqueous acidic solution at 25 °C, [H₃O⁺] > 10^-7 mol.L^-1 or, -log₁₀ [H₃O⁺]<7 or, pH < 7.

pH of aqueous basic solution:

For an aqueous basic solution at 25 °C, [H₂O⁺] < 10^-7 mol.L^-1 or, -log₁₀[H₃O+] >7 or, pH> 7.

At 25 °C, Forneutralaqueoussolution: pH = 7

For acidic aqueous solution: pH< 7

The pH of a solution of a weak acid and that of a weak base

Weak acids or weak bases ionize partially in their aqueous solutions. So, the concentration of H₃O⁺ or OH^– ions in an aqueous solution of a weak acid or a weak base cannot be determined directly from their initial concentrations.

To determine the pH (or pOH) of a weak acid (or weak base), the initial concentration of the acid (or base) as well as the degree. of ionization of the add (or base) or ionization constant of the acid (or base) should be known.

pH and pH Scale Class 11 Chemistry Notes

Determination of a solution of a weak monobasic acid:

Let a weak monobasic acid be HA. In an aqueous solution,

Hapartiallyionises to establish the given equilibrium:

HA(aq) + H₂O(l) ⇌  H₃O+(aq) + A^– (aq)

If the initial concentration of HA = c (M), its degree of ionization at equilibrium = a and its ionization constant

⇒ \(=K_a \text {, then }\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=\alpha c=\sqrt{\frac{K_a}{c}} \times c=\sqrt{c \times K_a}\)

∴ For HA, pH = -log₁₀[H₂O+] = -log₁₀(αc)……………………………….(1)

⇒ \(\text { or, } p H=-\log _{10}\left(c \times K_a\right)^{1 / 2}=-\frac{1}{2} \log _{10} K_a-\frac{1}{2} \log c\)

∴ \(p H=\frac{1}{2} p K_a-\frac{1}{2} \log c\) ……………………………….(2)

Thus, if the initial concentration (c) of the solution and the degree of ionization (α) of the acid are known, the pH of the solution can be determined by applying equation (1) Or, from the knowledge of the initial concentration (c) of the solution and the ionization constant (K_a) of the acid at the experimental temperature, it is possible to determine the of that solution with the help of equation (2)

Since the ionization constant of a weak acid (or base) is very small similar to the concentration of H₃O⁺ (or OH^–) ions in very dilute solutions, the ionization constant can also be expressed in terms of ‘p’ pKa = -log₁₀K_a  and pK_b = -log₁₀K_b.

So, a smaller value of Ka (or Kb) corresponds to a large value of pK_a (or pK_b) and vice-versa. The stronger an acid, the larger its Ka, and hence the smaller its pK_a.

For this reason, between two weak acids, the one with a smaller value of pKa is stronger than the other in water. Similarly, between two weak bases, the one with a small value of pKb is stronger than the other in water.

Determination of pH of a solution of a weak monoacidic base:

Let B be a weak monoacidic base. In an aqueous solution, B reacts with water and forms the following equilibrium.

⇒ \(\mathrm{B}(a q)+\mathrm{H}_2 \mathrm{O}(l) \rightleftharpoons \mathrm{BH}^{+}(a q)+\mathrm{OH}^{-}(a q)\)

In aqueous solution \(\left[\mathrm{OH}^{-}\right]=\sqrt{c \times K_b}\)

∴ \(-\log _{10}\left[\mathrm{OH}^{-}\right]=-\log _{10}\left(c \times K_b\right)^{1 / 2}\)

⇒ \(\text { or, } p O H=-\frac{1}{2} \log _{10} K_b-\frac{1}{2} \log c\)

∴ \(p O H=\frac{1}{2} p K_b-\frac{1}{2} \log c\)

Hence, if we know the initial concentration (c) of the weak monoacidic base in the solution and its ionization constant (Kb) at the experimental temperature, then we can calculate the pOH of the solution by applying equation (1).

Now, pH+ pOH = 14 [at 25°C]

∴ For a solution of weak monoacidic base,

⇒ \(p H=14-p O H=14-\left(\frac{1}{2} p K_b-\frac{1}{2} \log c\right)\)

∴ \(p H=14-\frac{1}{2} p K_b+\frac{1}{2} \log c\)

Therefore, by putting the values of pKb and concentration (c) of the solution in equation (2), the pH of the solution can be determined.

pH (or pOH) of an aqueous solution of acid (or base) having concentration <10-7(m)

It is apparent that for an aqueous solution of 10-7(M)HCl, pH = 7,

And an aqueous solution of 0-8(M) NaOH, pOH = and i.e., pH = 14 -pOH

= 14-8

= 6.

However, these values are not acceptable because the pH of an acidic solution and the pOH of a basic solution are always less than 7. Similarly, the pOH of an acidic solution and the pH of a basic solution are always greater than 7.

1. Generally, in the calculation of the pH or pOH of an aqueous acidic or basic solution, the concentration of H₃O⁺ or OH^– ions produced by the ionization of water is considered to be negligible. However, we cannot neglect them when the concentration of the acidic or basic solutions is very small [≤10^-7 (M)].

2. The total concentration of HgO+ ions in a very dilute aqueous acid solution = the concentration of H₆O+ ions produced by the ionization of acid + the concentration of H₆O⁺ ions produced by ionization of water. If the acid solution is calculated by using this total concentration of H₃O⁺, then the value of pH is always found to be less than 7.

The total concentration of OH^– ions in a very dilute aqueous base solution is the concentration of OH^– ions produced by the ionization of base + the concentration of OH- ions produced by the ionization of water.

If pOH of the baste solution is calculated by using this total concentration of OH-, then the value of pOH is always found to be less than 7.

NCERT Solutions Class 11 Chemistry pH and pH Scale

Numerical Examples

Determine the pH of the following solutions:

1. 0.01(N)HCl
2. 0 0.05(M) H₂SO₄
3. 0 0.001(N) H₂SO₄.

Answer:

1. 0.01(N) HCl = 0.01(M)I-HCl solution HCl is a monobasic acid] In 0.01(M) [since HCl is a monobasic acid]

[since 1 molecule of HCl ionizes to give a single H₃O⁺ ion] In case of an aqueous 0.01(M) HCl solution, pH = -log₁₀[H₃O⁺]

= -log₁₀(0.01) = 2.0

2. In 0.05(M) H₂SO₄ solution, [H₃O⁺]= 2 × 0.05= 0.1(M)

Since Each H₂SO₄ molecule ionises to give two H₃0+ ions] For an aqueous 0.05(M)H2S04 solution,

pH = -log10[H₃O⁺] = -log10(0.1) = 1.0

3. In 0.001(N) H₂SO4 solution, [H₃O+] = 0.001(M) In case of an aqueous 0.001(N) H₂SO₄ solution,

pH = -log₁₀[H₃O⁺] = -log₁₀(0.001)

= 3.0

Question 2. Determine the pH of the following solutions:

1. 0.1(N)NaOH
2. 0 0.005(M)
3. Ca(OH)₂

Answer:

1. 0.1(N)NaOH = 0.1(M)NaOH [NaOH is amino acid base]

In 0.1(M)NaOH solution, [OH^– ] = 0.1(M)

∴ For an aqueous 0.1(M)NaOH solution pOH = -log₁₀[OH^–]

= -log₁₀(0.1)

= 1.0

∴ pH = 14- pOH

= 14-1

= 13

2. In case of 0.005(M) Ca(OH)₂ solution, [OH-] = 2 × 0.005 = 0.01(M)

Since Each Ca(OH)₂ molecule ionizes to give 2 OH^– ions]

∴ In case of 0.005(M) Ca(OH)₂ solution,

pOH = -log₁₀[OH^–]

= -log10(0.01) = 2

∴ pH = 14- pOH

= 14- 2

= 12

Question 3. Calculate the concentrations of HaO⁺ and OH^– ions in the solutions with the following pH values at 25 °C. 0

1. pH = 5.0
2. pH = 12

Answer:

1. In the case of a solution with pH = 5,

[H₃O⁺] = 10^-PH(M) = 10^-5(M)

∴ In this solution,

⇒ \(\left[\mathrm{OH}^{-}\right]=\frac{10^{-14}}{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}=\frac{10^{-14}}{10^{-5}}(\mathrm{M})=10^{-9}(\mathrm{M})\)

2. In case of a solution with pH = 12

[H₃O⁺] = 10^-pH (M)

= 10^-12 (M)

∴ In the solution

⇒ \(\left[\mathrm{OH}^{-}\right]=\frac{10^{-14}}{\left[\mathrm{H}_3 \mathrm{O}^{+}\right]}\)

= \(\frac{10^{-14}}{10^{-12}}(\mathrm{M})=10^{-2}(\mathrm{M})\)

Question 4. Calculate the amount of Ca(OH)₂ required to be dissolved to prepare 250mL aqueous solution of pH = 12.
Answer:

As given in the question, the pH of the solution =12.

∴ pOH = 14- 12 = 2

∴ In the solution, [OH^–] = 10^-pOH

= 10^-2(M)

Common Ion Effect On The Ionisation Of Weak Acids And Weak Bases

In a solution of two electrolytes, the ion which is common to both electrolytes, is called the common ion.

Example:

Acetic acid on its partial ionization forms CH₃COO^–(aq) and H₃O⁺(aq), and sodium acetate on its complete ionization forms CH₃COO^–(aq) and Na⁺(aq). As the CH₃COO^– (aq) ion is common to both CH₃COOH and CH₃COONa, it is a common ion in this system.

Common Ion:

Effect When a strong electrolyte is added to a solution of a weak electrolyte having an ion common with a strong electrolyte, the extent of ionization of the weak electrolyte decreases. This phenomenon is called the common ion effect.

Common ion effect on ionization of a weak acid:

Effect of common anion:

Acetic acid is a weak acid. It partially ionizes in its aqueous solution, forming the following equilibrium

CH₃COOH(aq) + H₂O(l) ⇌ H₃O⁺(aq) + CH₃COO^–(aq)

If CH₃COONa is added to this solution, then CH₃COONa, being a strong electrolyte, ionizes almost completely into Na⁺ and CH₃COO^– ions (common ion) in the solution. Consequently, the equilibrium involved in the ionization of acetic acid gets disturbed.

So, according to Le Chatelier’s principle, some of the CH₃COO^– ions combine with an equal number of H₃O⁺ ions to form the unionized CH₃COOH and H₂O molecules, thereby causing the equilibrium to shift to the left.

As a result, the degree of ionization of CH₃COOH and the concentration of H₃O⁺ ions in the solution decreases. This leads to increased pH of the solution.

Effect of common cation:

When a strong acid such as HCl is added to a solution of acetic acid, it almost completely ionizes into H₃O⁺ and Cl^– ions. The complete dissociation of HCl increases the concentration of H₃O⁺ (ag) ions (common ion) in the solution. As a result, the equilibrium formed by the ionization of CH₆COOH gets disturbed.

According to Le principle, some of the H₃O⁺ ions combine with an equal number of CH₆COO- ions to form unionized CH₆COOH and H₂O molecules. As a result, the equilibrium shifts to the left, causing a decrease in the degree of ionization of CH₃COOH.

Common ion effect on ionization of a weak base:

Effect of common cation: Ammonia (NH₃) is a weak base. In aqueous solution, NH₃ reacts with water to establish the following equilibrium:

NH₃(aq) + H₂O(l)  ⇌ NH+(aq) + OH^– (aq)

If a strong electrolyte such as, NH₄Cl is added to this solution, it almost completely ionizes to form NH₄⁺(aq) and Cl^– (aq). The complete ionization of NH₄Cl gives rise to a high concentration of NH₃(aq) ions (common ions) in the solution. As a result, the equilibrium involved in the ionization of NH₃(aq) gets disturbed.

According to Le Chatelier’s principle, some NH₃(aq) ions combine with an equal number of OH^– ions to form unionized NH₃ and H₂O molecules and thereby cause the equilibrium to shift to the left. Consequently, the degree of ionization of NH3 as well as the concentration of OH^– ions in the solution decreases. This results in a decrease in the pH of the solution.

Effect of common anion:

When NaOH (a strong base) is added to an aqueous solution of NH₃, it almost completely ionizes into Na⁺ and OH^– ions. This increases the concentration of OH^– ions (common ions) in the solution.

As a result, the equilibrium involved in the ionization of NH₃ gets disturbed. According to Le Chatelier’s principle, some OH^– ions combine with an equal number of NH^– ions to form unionized NH₃ and H₂O molecules, thereby causing the equilibrium to shift to the left. This results in a decrease in the degree of ionization of NH₃.

Hydrolysis Of Salts

A normal salt (Example; NaCl, KCl, Na₂SO₄ CH₃COONa, NH₄Cl ) does not contain any ionizable H-atom or OH- ion. The solutions of normal salts are therefore expected to be neutral as they are formed by the complete neutralization of an acid. and a base. However, the aqueous solutions of many normal salts are found to be acidic or basic.

Example:

Aqueous solutions of NH₄Cl, FeCl₃, AlCl₃, etc., acidic, and those of CH₆COONa, NaF, and KCN are basic. This is because the cations or the anions produced by the dissociation of these salts react partially with water to produce an H₃O⁺ or OH^– ions solution. This increases the concentration of H₃O⁺ or OH^– ions in the solution. As a result, the solutions become acidic or basic. Such a phenomenon is known as hydrolysis.

Hydrolysis Definition

The process in which the cations or the anions or both of a normal salt in its aqueous solution react with water to furnish H₃O⁺ or OH^– ions, thus making the solution acidic or alkaline is known as hydrolysis of the salt.

Types of normal salts that undergo hydrolysis

A salt forms due to the reaction of an acid with a base. An acid or a base may be strong or weak. Four different normal salts are possible depending upon the nature of acids and bases involved in their formations.

Among these salts, those produced by reactions of strong acids and strong bases do not undergo hydrolysis. So, if the acid and the base that react to form a salt are weak or one of them is weak, then the salt formed will undergo hydrolysis.

Consequently, aqueous solutions of these salts are either acidic (pH < 7) or basic (pH > 7).On the other hand, an aqueous solution of a salt strong acid, and strong base is always neutral (pH = 7).

Hydrolysis of salts obtained from strong acids and strong bases

A salt of this type does not undergo hydrolysis in its aqueous solution because neither its cation nor its anion reacts with water.

As a result, the concentration of H⁺ ions or OH^– ions in the solution is not affected; that is, the equality of their concentrations is not disturbed. This is why an aqueous solution of a salt derived from a strong acid and a strong base is neutral (pH = 7).

Concept of pH and pH Scale Chapter 11 NCERT Notes

Explanation:

NaCl is a salt of strong acid (HCl) and strong base (NaOH).

1. NaCl dissociates almost completely In aqueous solution to produce Na⁺ (aq) and Cl (aq) ions

[NaCl(aq) → Na+(aq) + Cl^–(aq)].

Water also ionizes slightly to produce an equal number of

H₃O⁺ (aq) and OH^–(aq) ions

[2H₂O(l) ⇌ H₃O⁺(aq) + OH^–(aq)].

2. Na⁺ (aq) is a very weak Bronsted acid and it is unable to react with H₂O to produce a proton:

3. On the other hand, Cl^– ion is the conjugate base of strong acid HCl. Hence, it is a very weak Bronsted base. For this reason, Cl^– is unable to react with water to produce a proton:

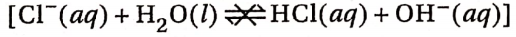
4. Thus, an aqueous solution of NaCl contains H₃O⁺ and OH^– ions in equal concentration. As a result, the aqueous solution of NaCl is neutral. For the same reason, other salts obtained from strong acids and strong bases form neutral aqueous solutions.

Hydrolysis of salts obtained from weak acids and strong bases

A salt of this type undergoes hydrolysis in its aqueous solution as its anion reacts with water to form OH^– ions. As a result, the concentration of OH^– in the solution becomes higher than that of H₃O⁺, thereby making the solution basic (pH > 7). Since anion of such a salt takes part in hydrolysis, this type of hydrolysis is called anionic hydrolysis.

Explanation: KCN is a salt-weak acid (HCN) and strong base (KOH)

1. It dissociates almost completely in its aqueous solution and produces K⁺(aq) and CN^–(aq) ions

[KCN(aq)⇌ K⁺(ag) + CN^–(ag)].

Water also ionizes slightly to produce an equal number of H₃O⁺(aq) and OH^–(aq)

2H₂O(l) ⇌ H₃O⁺(aq) + OH^–(aq)

2. K⁺(aq) is a very weak Bronsted acid. So, it cannot react with to produce a proton:

3. On the other hand, CN^– ion is the conjugate base of a weak acid (HCN). Hence, it has sufficient basic character to abstract a proton from an H₂O molecule to form OH^–ions:

4. The formation of OH^– ions increases the concentration of OH^– ions in the solution and makes the solution basic (pH > 7). For the same reason, other salts obtained from weak acids and strong bases form basic aqueous solutions.

Hydrolysis of salts obtained from strong acids and weak bases

A salt of this type undergoes hydrolysis in its aqueous solution because its cation reacts with water to form H₃O⁺  ions. As a result, the concentration of H₃O⁺ ions in the solution becomes higher than that of OH^– ions. This makes the solution acidic (pH < 7). Since the cation of such a salt takes part in hydrolysis, this type of hydrolysis is called cationic hydrolysis.

Hydrolysis of salts obtained from strong acids and weak bases Explanation:

Ammonium chloride (NH₄Cl) is formed by the reaction of HCl (a strong acid) with NH₃ (a weak base).

1. NH₄Cl almost completely dissociates in its aqueous solution to produce,

NH₄ ⁺(aq) and Cl^–(aq) ions

[NH₄Cl(aq)→NH₄⁺(aq) + Cl^– (aq)]. H₂O also ionislightly to produce equal number of

2H₂O(l) ⇌  H₃O⁺(aq) + OH^–(aq)

2. Cl^– ion is the conjugate. the base of strong acid :

So, Cl^– ions fail and hence, is a very weak Bronsted base. So, Cl- ion fails to react with H₂O to produce OH^– ions

Class 11 Chemistry pH and pH Scale Summary

3. NH₄⁺ ion is the conjugate acid of a weak base, NH₃, and has sufficient acidic character to donate a proton to H₂O molecules. Thus, NH₄⁺ ion reacts with water to form unionised molecules of NH₃ and H₃O⁺ ions

NH₄⁺(aq) + H₂O(l) ⇌  NH₃(aq) + H₃O⁺(aq)]

4. The formation of HaO⁺ ions increases the concentration of H₃O⁺ ions in the solution and makes the solution acidic (pH < 7). For the same reason, other salts obtained from strong acids & weak bases form acidic aqueous solutions.

Aqueous solution of FeCI₃ [or Fe(NO₂)g] is acidic:

Being a strong electrolyte, FeCl₃ undergoes complete dissociation in the solution to form

[Fe(H₂O)g]³⁺(aq) & Cl^–(aq):

FeCl₃(aq) + 6H₂O(l) →  [Fe(H₂O)₆]³⁺(aq) + 3Cl^–

Water also ionises slightly to produce equal number of H₃O⁺ ions and OH^–(aq) ions

2H₂O(l) ⇌  H₃O⁺(aq) + OH^–(aq)] . Cl^– ion is the conjugate base of strong acid (HCl).

Hence, it is a very weak Bronsted base and fails { to react with water in aqueous solution. Due to the small size and higher charge of Fe³⁺ ion, its charge density is very high. As a result, the H₂O molecules bonded to the Fe³⁺ ion are polarised and their O—H bonds become very weak.

These O—H bonds are easily dissociated to produce H+ ions, which are accepted by H₂O molecules to form H₃O+ ions.

Fe(H₂O)₆]³⁺(aq) +H₂O⇌ Fe(H₂O)₅OH]²⁺(aq) +H₃O⁺(aq)

Among the H₂O molecules attached to the Fe3+ ion,

The one which releases proton finally gets attached to the Fe3+ ion as OH- ion. For the same reason, aqueous solutions of AICl₃, CuSO₃, etc., are acidic.

AlCl₃(aq) + 6H₂O(l) → [Al(H₂O)₆]³⁺(aq) + 3Cl^–(aq)

[Al(H₂O)₆]³⁺(aq) + H₂O(l) ⇌  [Al(H₂O)₅ OH]²⁺+H₃O⁺(aq)

Hydrolysis of salts obtained from weak acids and weak bases

In the case of a salt of this type, both the cation and anion react with water. In reaction with water, the cation forms H₃O⁺ ions, and the anion forms OH^– ions. Aqueous solutions of such a salPipay be acidic, basic, or neutral, depending upon the relative acid strength of the cation and base strength of anion. If the strengths of the cation and anions are the same, the solution will be neutral.

On the other hand, if the strength of the cation is greater or less than that of the anion, then the solution will be acidic or basic.

When the aqueous solution of the salt is neutral:

CH₃COONH₄ is a salt of weak acid, CH₃COOH, and a weak base, NH₃.

Explanation:

1. Being a strong electrolyte, CH₃COONH₄ dissociates almost completely in aqueous solution to produce NH₄ and CH₃COO^–(aq) ions:

CH₃COONH₄O(aq)  →  CH₃COO^–  (aq) + NH₄^– (aq).H₂O  weak electrolyte, also ionizes slightly in solution to produce an equal number of H₃O⁺(aq) and OH^–  (aq) ions

[2H₂O(l) ⇌ H₃O+(aq) + OH^– (aq)].

2. NH₄⁺ion is the conjugate acid of a weak base (NH₃) and CH₃COO^– is the conjugate base of a weak acid, (CH₃COOH). In an aqueous solution, both NH₄ and CH₃COO^– are stronger than H₂O (which can act both as a weak Bronsted acid and base). As a result, CH₃COO^– and NH₃ ions react with water to establish the following equilibria:

NH⁺(aq) + H₂O(l) ⇌  NH₃(aq) + H₃O+(aq)

CH₃COO^– (aq) + H₂O(l) ⇌ CH₃COOH(aq) + OH^–(aq)

3. At ordinary temperature, both CH₃COO^– and NH₃ ions have the same value of dissociation constants. As a result, they get hydrolyzed to the same extent in aqueous solution.

Therefore, the aqueous solution of CH₃COONH₄ contains equal concentrations of H₃O⁺ (produced by the hydrolysis of NH₄ ions) and OH^– (produced by the hydrolysis of CH₃COO^– ions), and hence, the solution is neutral.

When the aqueous solution of the salt is acidic:

Ammonium formate (HCOONH₄ strong electrolyte) is a salt of weak acid, HCOOH, and weakbase, NH₃.

Explanation:

1. HCOONH₄ dissociates almost completely in its aqueous solution to form HCOO and NH

[HCOONH₄(aq) H → HCOO^–(aq) + NH₄⁺ (aq)]

H₂O, a weak electrolyte, also ionizes slightly to form an equal number of H₃O+{aq) and OH-(aq) ions. NH₄ and HCOO^– react with water to form the given equilibria:

NH₄⁺(aq) + H₂O(l)  ⇌ NH₃(aq) + H₃O⁺ (aq)

HCOO^– (aq) +H₂O(l) ⇌  HCOOH(aq) + OH^–(aq)

2. At ordinary temperature, Ka for NH₄⁺ is larger than K_b for HCOO^– i.e., in aqueous solution NH^–  hydrolyses to a greater extent than HCOO^–. The concentration of H₃O⁺ is more than that of OH^–. So, the aqueous solution of HCOONH₄ is acidic.

When the aqueous solution of the salt is basic:

Ammonium bicarbonate, NH₄HCO₃ is a salt of a weak acid, HCO₃, and weak base, NH₃.

Explanation:

1. Strong electrolyte, NH₄HCO₃ dissociates almost completely solution to form NH+ and HCO₃ ions:,

⇒ \(\left[\mathrm{NH}_4 \mathrm{HCO}_3(a q) \rightarrow \mathrm{NH}_4^{+}(a q)+\mathrm{HCO}_3^{-}(a q)\right] \cdot \mathrm{H}_2 \mathrm{O}\)

A weak electrolyte, also Ionises slightly to form an equal number of H₃O⁺ (aq) and OH^– ) ions

[2H₂O(l)x ⇌ H₃O⁺+ OH(aq) ]. NH₃ and HCO₃^–ions react with water to establish die following equilibria.

⇒ \(\\mathrm{NH}_4^{+}(a q)+\mathrm{H}_2 \mathrm{O}(l)\rightleftharpoons \mathrm{NH}_3(a q)+\mathrm{H}_3 \mathrm{O}^{+}(a q)\)

⇒ \(\mathrm{HCO}_3^{-}(a q)+\mathrm{H}_2 \mathrm{O}(l)\rightleftharpoons \mathrm{H}_2 \mathrm{CO}_3(a q)+\mathrm{OH}^{-}(a q)\)

2. At ordinary temperature, K_b for HCO₃^– Is much greater than K_afor NH₄⁺ This means that in an aqueous solution, HCO₃^– ions hydrolyze to a greater extent than NH₄⁺ ions. So, the concentration of OH^– ions is more than that of H₃O⁺  ions in an aqueous solution of NH₄HCO₃. Thus, the aqueous solution of NH₄HCO₃, Is music in nature.

Hydrolysis constant, degree of hydrolysis, and pH of an aqueous solution of a salt

Hydrolysis constant:

In the hydrolysis of a salt, u dynamic equilibrium is established Involving the unhydrolyzed salt and the species formed by hydrolysis. The equilibrium constant corresponding to this equilibrium Is called the hydrolysis constant.

Degree of hydrolysis:

The degree of hydrolysis (ft) of a salt may be defined as the fraction of the total number of moles of that salt hydrolyzed in its aqueous solution at equilibrium. In an aqueous solution, the degree of hydrolysis of salt is ft— it means that out of 1 mol of the salt dissolved in the solution, ft mol undergoes hydrolysis.

Relation Between Ionisation Constants Of Conjugate Acid-Base

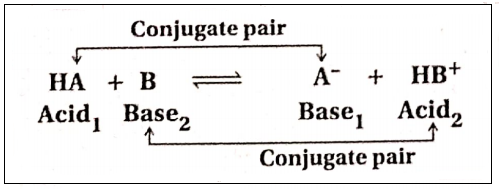
Let’s consider a weak acid, HA. The conjugate base of this acid is A^–. Hence, the conjugate acid-base pair is (HA, A^–).

In an aqueous solution, HA and A^– form the following equilibrium:

⇒ \(\mathrm{HA}(a q)+\mathrm{H}_2 \mathrm{O}(l) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(a q)+\mathrm{A}^{-}(a q)\)

The ionisation constant of HA,

K_a = \(\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \times\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\) ………………………….(1)

pH and pH Scale in Acids and Bases Class 11 Chemistry Notes

In aqueous solution, the base A- reacts with water to form the following equilibrium:

A-(aq) + H₂O(l)⇌ HA(aq) + OH-(aq)

The ionisation constant of

⇒  \(\mathrm{A}^{-}, K_b=\frac{[\mathrm{HA}] \times\left[\mathrm{OH}^{-}\right]}{\left[\mathrm{A}^{-}\right]}\) ………………………….(2)

Multiplying equations (1) and (2), we have,

K_a × K_b= [H₃O⁺]’× [OH^–]

Again, Kw = [H₃O⁺] ×  [OH^–]

∴ K_a × K_b = K_w

Equation (3) represents the relation between ionization constants of a conjugate acid-base. This equation applies to any conjugate acid-base pair in aqueous solutions

at 25°C,K_w = 10^-14

Therefore, at this temperature, K_a × K_b = 10^-14

Therefore, at a given temperature, we know the value of Kw and the ionization constant of any one member of the conjugate acid-base pair, then the ionization constant of the other can be determined by applying equation (4)

Examples:

1. At 25°C, Ka (CH₃COOH) = 1.8 × 10^-5

So, at 25°C, Kb (CH₃COO^– ) \(=\frac{10^{-14}}{K_a}\)

=\(\frac{10^{-14}}{1.8 \times 10^{-5}}\)

2. At 25°C, K_b  (NH₃) = 1.8 ×10^-5

⇒ \(\text { So, at } 25^{\circ} \mathrm{C}, K_a\left(\mathrm{NH}_4^{+}\right)=\frac{10^{-14}}{K_a}\)

=\(\frac{10^{-14}}{1.8 \times 10^{-5}}=5.5 \times 10^{-10}\)

pH Scale and Its Calculation Class 11 Chemistry Notes

Derivation of the relation, pK_a + pK_b = pK _w:

We know that, K_a × K_b = K_w. Taking negative logarithms on both sides

we have, -log10 (K_a × K_b) = -log₁₀ K_w

or, -log₁₀ K_a– log₁₀  Kb = -log₁₀ K_w

∴ PK_a+PK_b = PK_w

At 25°C, pK_w = 14.

So, at 25°C, pK_a + pK_b = 14

Hence, if the pKa of the acid (or pKb of the base) in a conjugate acid-base pair is known, then the pKb of the base (or pKa of the acid) can be determined by using equation (5)

Buffer Solutions

At ordinary temperature, the pH of pure water is 7. Now, when 1 mL of (M) HCl solution is added to 100 mL of pure water, it is observed that the value of pH decreases from 7 to 2.

Again, if 1 mL of 1 (M) NaOH solution is added to 100 mL of pure water the value of the pH of the solution increases from 7 to 2. However, many solutions resist the change in pH even when a small quantity of acid or base is added to them. Such solutions are called buffer solutions.

Buffer Solutions Definition:

A buffer solution may be defined as a solution that resists the change in its pH when a small amount of acid or base is added to it.

Various types of buffer solutions depending on the nature of the acid/base and the salt:

1. Solution of a weak acid and its salt

An aqueous solution of a weak acid and its salt acts as a buffer solution.

Example:

Aqueous solutions of CH₃COOH and CH₃COONa, H₂CO₃ and NaHCO₃, citric acid and sodium citrate, boric acid, and sodium borate, etc.

Read and Learn More CBSE Class 11 Chemistry Notes

2. Solution of a weak base and its salt

An aqueous solution of a weak base and its salt acts as a buffer solution.

Example: Aqueous solutions of NH₃ and NH₄Cl, aniline and anilinium hydrochloride, etc.

3. Solution of two salts of a polybasic acid

An aqueous solution containing two salts of a polybasic acid can act as a buffer solution.

CBSE Class 11 Chemistry Notes Buffer Solutions

Example:

Aqueous solutions of Na₂CO₃ and NaHCO₃ (NaHCO₃ is a weak acid and Na₂CO₃ is its salt), NaIT₂PO₄ and Na₂HPO₄ etc.

4. Solution of a salt derived from a weak acid and a weak base

An aqueous solution of a salt formed by a weak acid and a weak base can function as a buffer solution.

Example:

CH₃COONH₄ is a salt of weak acid (CH₃COOH) and weak base (NH₄OH). A solution of this salt acts as a buffer solution.

Types of buffer solutions depending on their pH values: Depending on pH values, buffer solutions are of two types—

1. Acidic buffer

Buffer solutions with a pH lower than 7 are called acidic buffers. Aqueous solutions of CH₃COOH and CH₃COONa, aqueous solutions of lactic acid and sodium lactate, etc., are some common examples of acidic buffer solutions.

2. Basic buffer

Buffer solutions with a pH higher than 7 are called basic buffers. An aqueous solution of NH₄OH and NH₄Cl is an example of a basic buffer solution.

Mechanism of buffer action

Mechanism of buffer action Definition:

The ability of a buffer solution to resist the change of its pH value on the addition of a small amount of an acid or a base to it is called buffer action.

Mechanism of action of an acidic buffer

To understand the mechanism of buffer action of an acidic buffer, let us consider an acidic buffer solution that consists of CH₃COOH and CH₃COONa.

In the solution, CH₃COONa almost completely dissociates into CH₃COO^–(aq) and Na⁺ ions, whereas acetic acid, being a weak electrolyte, partially dissociates into CH₃COO-(aq) and H₃O⁺(aq).

The partial dissociation of acetic acid leads to the formation of the following equilibrium.

CH₃COOH(aq) + H₂O (l) ⇌  CH₃COC^–(aq) + H₃O⁺(aq)

As CH₃COOH ionizes partially and CH₃COONa ionizes almost completely, the solution consists of high concentrations of CH₃COOH and CH₃COO^–ions

Addition of a small amount of strong acid:

If a small amount of strong acid (example: HCl ) is added to this buffer solution, H₃O⁺ ions produced from the strong acid combine with an equal number of CH₃COO- ions present in the solution to form unionized CH₃COOH molecules:

CH₃COO^–(aq)+ H₃O⁺(l)→CH₃COOH(aq) + H₂O(l)

This causes the equilibrium involved in the ionization of CH₃COOH (equation 1) to shift to the left. As a result, the concentration of H₃O⁺ Ionsin in the solution virtually remains the same, i.e., the pH of the solution remains almost unchanged.

Buffer Solutions Class 11 Chemistry Notes

Addition of a small amount of strong base:

When a small amount of a strong base like NaOH, OH, etc., is added to this buffer solution, the OH^– ions obtained from the strong base combine with an equal number of H₄, and  ions (which results mainly from the dissociation of CH₃COOH ) present in the solution, producing unionized water molecules.

Consequently, the equilibrium associated with the ionization of CH₃COOH [eqn. (1)] gets disturbed. So, according to Le Chatcller’s principle, some molecules of CH₃COOH ionize to produce H₃O^– ions, and the equilibrium, shifts towards the right. Therefore, the addition of a small quantity of a strong base with almost no change in are to the solution causes the concentration of either OH^– ions or H₂O⁺ ions, and consequently pH of the solution remains almost unaltered.

Mechanism of action of basic buffer:

Let us consider a basic buffer solution consisting of a weak base NH₃ and its salt, NH₄Cl. Being a strong electrolyte, ammonium chloride (NH₄Cl) dissociates almost completely in solution:

NH₄Cl(aq)→ NH₄^–(aq) + Cl^–(aq).

However, NH₃, being a weak base, reacts partially with water and forms the following equilibrium solution.

⇒ \(\mathrm{NH}_3(a q)+\mathrm{H}_2 \mathrm{O}(l) \rightleftharpoons \mathrm{NH}_4^{+}(a q)+\mathrm{OH}^{-}(a q)\) …………………………………………..(1)

As NH₃ reacts partially with water and NH₄Cl gets completely dissociated, the concentration of NH₃ and NH₃ in the solution is sufficient.

Addition of a small amount of strong acid:

If a small quantity of strong acid (for example HCl, H₂SO₄) is added to this buffer solution, H₃O⁺ ions obtained from the strong acid react almost completely with an equal number of OH- ions (which results mainly from the reactions of NH₃ with water) present in the solution and produce unionized water molecules.

As a result, the equilibrium [eqn. (1)] gets disturbed. According to Le Chatelier’s principle, some NH₃ molecules react with water to form OH^– ions. As a result, the equilibrium [eqn. (1)] shifts to the right. So, the addition of a small amount of a strong acid to the buffer solution causes almost no change in concentration of either OH^– ions or H₃O⁺ ions, i.e., the pH of the solution remains unchanged.

Addition of a small amount of strong base:

When a small quantity of a strong base (for example NaOH, KOH is added to the buffer solution, OH- ions produced by the strong base react almost completely with an equal number of NHJ ions present in the solution and form unionized

NH₃ molecules [NH⁺(aq) + OH^– (aq) →NH₃ (aq) + H₂O(l)].

As a result the equilibrium [eqn. (1)] shifts to the left. Consequently, the concentration of OH- ions in the solution virtually remains the same, and hence pH of dissolution remains unchanged.

Buffer action of two salts of polybasic acid (in solution):

Let us consider the buffer solution comprising of two salts NaH₂PO₄ and Na₂HPO₄ (which are the salts of polybasic acid, H₃PO₄ ). In this solution, NaH₂PO₄ acts as an acid while Na₂HPO₄ as a salt, and both of them undergo complete dissociation as given below:

NaH₂PO₄(aq) → Na+(aq) + H₂PO₄^– (aq)

Na₂HPO₄(aq)→ 2Na⁺(aq) + HPO₄^2-(aq)

H₂PO₄ itself is a weak acid and due to a common ion (HPO₄^2-), it undergoes slight ionization in the solution forming the following equilibrium:

⇒ \(\mathrm{H}_2 \mathrm{PO}_4^{-}(a q)+\mathrm{H}_2 \mathrm{O}(l) \rightleftharpoons \mathrm{HPO}_4^{2-}(a q)+\mathrm{H}_3 \mathrm{O}^{+}(a q)\) ……………………(1)

As H₂PO₄ undergoes slight ionization and Na₂HPO₄ gets completely ionized, the concentration of H₂PO₄ and HPO₄^– in the solution is sufficient.

Addition of a small amount of strong acid:

When a small quantity of a strong acid is added to this buffer solution, H₃O⁺ ions produced by the strong acid react almost completely with an equal number of HPO^– ions, and form unionized H₂PO₄ ions

⇒ \(\mathrm{HPO}_4^{2-}(a q)+\mathrm{H}_3 \mathrm{O}^{+}(a q) \rightarrow \mathrm{H}_2 \mathrm{PO}_4^{-}(a q)+\mathrm{H}_2 \mathrm{O}(l)\)

As a result, the equilibrium [eqn. (1)] shifts towards the left. Hence, the effect of the addition of a small amount of strong acid is neutralized. Thus, the pH of the solution remains unchanged.

Addition of a small amount of strong base:

When a small quantity of a strong base is added to the buffer solution, OH^– ions from the added base almost completely react with an equal number of H₃O⁺ ions (which results mainly from the ionization of H₂PO₄ ) present in the solution and form unionized water molecules, This disturbs the ionization equilibrium of NaH₂PO₄.

As a result, according to Le Chatelier’s principle, some molecules of NaH₂PO₄ ionize to form H₃O⁺ ions and cause the equilibrium to shift towards the right. Therefore, the addition of a small quantity of a strong base makes no change in the concentration of either OH^– ions or H₃O⁺ ions, and consequently, the pH of the solution remains almost unchanged.

NCERT Solutions Class 11 Chemistry Buffer Solutions

Determination of pH of a buffer solution: Henderson’s equation

Let us consider a buffer solution consisting of a weak acid (HA) and its salt (MA). In the solution, MA dissociates completely, forming M⁺(aq) and A^–(aq) ions, while the weak acid, HA, because of its partial ionization, forms the following equilibrium

⇒ \(\mathrm{HA}(a q)+\mathrm{H}_2 \mathrm{O}(l) \rightleftharpoons \mathrm{H}_3 \mathrm{O}^{+}(a q)+\mathrm{A}+(a q)\)

Applying the law of mass action to the abbveÿequilibrium, we have the ionization constant of HA

⇒ \(K_a=\frac{\left[\mathrm{H}_3 \mathrm{O}^{+}\right] \times\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]},\)

Where, [H₃O⁺], [A^–], and [HA] are the molar concentrations of H₃O⁺, A^–, and HA respectively at equilibrium.

∴ \(\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=K_a \times \frac{[\mathrm{HA}]}{\left[\mathrm{A}^{-}\right]}\)

Taking negative logarithms on both sides we get,

⇒ \(-\log _{10}\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=-\log _{10} K_a-\log _{10} \frac{[\mathrm{HA}]}{\left[\mathrm{A}^{-}\right]}\)

⇒ \(-\log _{10}\left[\mathrm{H}_3 \mathrm{O}^{+}\right]=-\log _{10} K_a-\log _{10} \frac{[\mathrm{HA}]}{\left[\mathrm{A}^{-}\right]}\)

Or, ,\(p H=p K_a+\log _{10} \frac{\left[\mathrm{A}^{-}\right]}{[\mathrm{HA}]}\)………………(1)

As HA is a weak acid, its ionization in the solution is very small, which gets further decreased in the presence ofthe common ion, A^–. Therefore, the molar concentration of unionized HA can be considered to be the same as the initial molar concentration of HA.

Again, the molar concentration of A^– ions produced by complete dissociation of MA is much higher than that of A^– ions produced by partial ionization of HA. Therefore, the total molar concentration of A^– ions in the solution is almost the same as the initial molar concentration of MA in the solution.

∴ From equation (1) \(p H=p K_a+\log \frac{[\text { salt }]}{[\text { acid }]}\)  ………………(2)

Where Ka is the ionization constant of the weak acid; [acid] and [salt] are the initial molar concentrations of acid and salt respectively the buffer solution. Equation [2] is called the Henderson’s equation.

It is used to determine the pH of a buffer solution consisting of a weak acid and its salt. Similarly, the equation for determining the pOH of a buffer solution consisting of a weak base and its salt is-

⇒  \(p O H=p K_b+\log \frac{[\text { salt] }}{\text { [base] }}\)

Where, K, b is the ionization constant of the weak base; [salt] and [base] represent the initial molar concentrations of salt and base respectively. The above equation can be rewritten as,

⇒ \(p H=14-p O H=14-p K_b-\log \frac{[\text { salt] }}{\text { [base] }}\)

At a fixed temperature, the value of pK_a of a weak acid is fixed. Hence, at a fixed temperature, the pH of a buffer solution consisting of a weak add and its salt depends upon the die value of the pKa of the weak acid as well as the ratio of the molar concentrations of the salt to the molar concentration of the acid.

Similarly, at a particular temperature, the pH of a buffer solution consisting of a weak base and its salt depends on the value of pK_b of the weak base and the ratio of molar concentrations of the salt to the base.

Applications of Henderson’s equation:

If the molar concentrations of a weak acid (or base) and its salt present in a buffer solution as well as the dissociation constant of that acid (or base) are known, then that solution can be determined by using Henderson’s equation.

If in an acidic or basic buffer solution, the molar concentrations of the weak acid (or base) and its salt and pH of that solution are known, then the dissociation constant of the weak acid (or base) can be calculated with the help of Henderson’s equation.

For the preparation of a buffer solution with a desired value of pH, the ratio of the weak acid and its salt (or weak base and its salt) in the solution can be determined by Henderson’s equation.

Buffer Solutions and their Types Class 11 NCERT Notes

Buffer Capacity

Buffer Capacity Definition:

The buffer capacity of a buffer solution is defined as the number of moles of a strong base or an acid required to change the pH of 1L of that buffer solution by unity.

When an acid is added to a buffer solution, its pH value decreases, whereas when a base is added to a buffer solution, its pH value increases.

Mathematical explanation:

When the pH of 1 L of solution increases by d(pH) due to the addition of db mol of any strong base, then the buffer capacity of that buffer solution

⇒  \(\beta=\frac{d b}{d(p H)}\)

Similarly, when the pH of 1L of buffer solution decreases by d(pH) due to the addition of da mol of any acid, then the buffer capacity of that buffer solution \(\beta=\frac{d a}{d(p H)}\)

Some important facts regarding buffer capacity:

• If the buffer capacity of any buffer solution is high, then a greater amount of a strong add or base will be required to bring about any change in the pH of that solution.
• Between two buffer solutions having the same components, the buffer capacity of that solution will be higher when the concentrations of the components are
  higher.
• In a buffer solution, if the difference in molar concentration of die components is small, then the addition of a small amount of strong acid or base causes a small change in molar concentrations of die components.

Consequently, the change in pH of the die solution also becomes small. For this reason, the die buffer capacity of a buffer solution becomes maximum when the molar concentrations ofthe components are the same.

1. The buffer capacity of a buffer solution consisting of a weak acid and its salt becomes maximum when die molar concentrations of the weak acid and its salt become equal. Under this condition, the pH of the buffer solution = pK_a of the weak acid

Example: The buffer capacity of CH₃COOH/CH₃COONa solution will be maximum when its pH = 4.74 (since, pKa of CH₃COOH =4.74).

2. For the same reason, the buffer capacity of a buffer solution consisting of a weak base and its salt becomes maximum when the pOH of the buffer becomes equal to the pKb of the weak base. For example, the buffer capacity of NH₃/NH₄Cl solution will be maximum when its pOH = 4.74 (since, pKb of NH₃ = 4.74)

pH range of buffer capacity:

A buffer solution consisting of a weak acid and its salt will work properly only when the ratio of the molar concentration of the salt to the acid lies between 0.1 to 10. Therefore, according to Henderson’s equation, the pH -range for the buffer capacity of such a buffer will vary from (pK_a – 1) to (pK_b + 1). 0 Similarly the range of pOH for buffer capacity of a buffer consisting of a weak base and its salt will vary from (pK_b – 1) to (pK_b+ 1).

pH of Buffer Solutions Class 11 Chemistry

Importance of butter solutions

1. The pH of human blood lies between 7.35 to 7.45, i.e., human blood is slightly alkaline. In spite, ofthe presence of acidic or basic substances produced due to various metabolic processes, the pH of human blood remains almost constant because ofthe presence of different buffer systems like bicarbonate-carbonic acid buffer (HCO^–₃ / H₂CO₃), phosphate buffer (HPO₄^2- /H₄PO₄^–), etc.

Excess acid in the blood is neutralized by the reaction:

HCO₃^– + H₃O⁺⇌ H₂CO₃ +H₂O. H₂CO₃ formed decomposes into CO₂ and water.

The produced CO₂ is exhaled out through the lungs. Again, if any base (OH^–) from an external source enters the blood, it gets neutralized by the reaction:

H₂CO₃ + OH^– ⇌  HCO₃^– +H₂O.

2. Buffers find extensive use in analytical works as well as in chemical industries. In these cases, a buffer solution is used to maintain pH at a certain value. For instance, in qualitative analysis, in electroplating, tanning of hides and skins, fermentation, manufacture of paper, ink, paints, and dyes, etc., pH is strictly maintained. Buffer solution is also used for the preservation of fruits & products derived from fruits.

Solubility And Solubility Product

The terms ‘solubility’ and ‘solubility product’ are often used in the context of the dissolution of a solute in a liquid. It is important to note that these two terms do not have the same meaning and therefore cannot be used interchangeably.

Comparison between solubility and solubility product:

• The term solubility applies to all kinds of solutes (ionic, neutral, sparingly soluble, or highly soluble) whereas the term solubility product is mainly used for sparingly soluble compounds.
• The solubility of a solute in a solution may change due to common ion effects or formation of complex salt but its solubility product remains constant at a fixed temperature.
• Both solubility and solubility products of a solute in a liquid change with the temperature variation.

Solubility products of sparingly soluble salts

Salts having solubilities less than 0.01 mol-L^-1 at ordinary temperature are commonly known as sparingly soluble salts. Some examples of such salts are AgCl, BaSO₄, CaSO₄, etc. A salt of this type in its saturated aqueous solution remains virtually insoluble and only a small part of it gets dissolved but the dissolved portion of the salt, however small it may be, gets completely dissociated.

Read and Learn More CBSE Class 11 Chemistry Notes

Solubility Product:

The Solubility Product of A sparingly soluble salt at a given temperature is defined as the product of the molar concentrations of the constituent ions in its saturated solution, each concentration term raised to a power representing the number of ions of that type produced by dissociation of one formula unit of the salt.

CBSE Class 11 Chemistry Notes Solubility and Solubility Product

Characteristics of solubility product:

• At a particular temperature, the solubility product of a sparingly soluble salt has a fixed value. Its value changes with temperature variation.
• At a particular temperature, the solubility product of a sparingly soluble salt in its saturated solution remains unaltered if the concentrations of the constituent ions are changed. It remains fixed even in the presence of other ions in the solution.

Equation of solubility product:

Let’s consider the equilibrium that exists in a saturated solution of the sparingly soluble salt, AxBy. In this solution, undissolved AxBy remains in equilibrium with the ions (A+ and B- ) produced from the dissociation of dissolved A_xB_y.

⇒ \(\mathrm{A}_x \mathrm{~B}_y(s \text {, undissolved }) \rightleftharpoons x \mathrm{~A}^{y+}(a q)+y \mathrm{~B}^{x-}(a q)\)

Applying the law of mass action we have, an equilibrium constant,

⇒ \(K=\frac{\left[\mathrm{A}^{y+}\right]^x \times\left[\mathrm{B}^{x-}\right]^y}{\left[\mathrm{~A}_x \mathrm{~B}_y(s)\right]}\)

Where, [A^y+], [B^x-], and [A_x B_y(s)] are the molar concentrations of A^y+,B^+-– and A_xB_y(s) respectively, at equilibrium.

Now, the molar concentration of pure solid at a particular temperature is constant. Again, at a given temperature, the equilibrium constant, K is also constant.

So, at a given temperature, K  ×  [A_x × B_y(s)] = constant.

∴ K ×  [A_x × B_y(s)]=[A^y+]^x ×  [B^x-]^y

Or K_sp = [A^y+] × [B^x-]^y [ sp = solubility product ]

Where, K_sp = K ×  [A_x B_y(s)] = constant.

K_sp is called the solubility product or solubility product constant of the sparingly soluble salt, A_xB_y.

Relation between solubility and solubility product

In case of a sparingly soluble salt of the type AB: Equilibrium formed by a sparingly soluble salt of the type AB in its saturated aqueous solution:

AB(s) ⇌ A⁺ (aq) + B^–(aq)

∴ The solubility product of, Ksp = [A⁺] × [B⁺]

Let the solubility of the salt, AB, in its saturated aqueous solution at a given temperature be S mol.L^-1

Hence, in the solution, the molar concentration of A⁺ ions [A⁺] = S mol.L^-1 and that of B^– ions, [B-] = S mol.L^-1 [v one formula unit of AB on dissociation gives one A+ and one B^– ion].

∴ K_sp = [A⁺][B^–] = S ×  S = S²

∴ K_sp  = s² ……………………….. (1)

and S = \(\sqrt{K_{s p}}\)……………………… (2)

Equation (1) is the relation between the solubility the and solubility product of a sparingly soluble salt of the type AB.

Equation (2) indicates that the solubility of a sparingly soluble salt, AB is equal to the square root of its solubilityproduct.

Example: AgCl is a sparingly soluble salt. In a saturated solution of AgCl, the following equilibrium is formed:

⇒ \(\mathrm{AgCl}(s) \rightleftharpoons \mathrm{Ag}^{+}(a q)+\mathrm{Cl}^{-}(a q)\)

So, the solubility product of AgCl, K_sp = [Ag²⁺] × [Cl^–]

Suppose, at a certain temperature, the solubility of AgCl in its saturated aqueous solution = S mol.L^-1. Hence, in the solution,

[Ag⁺] tS mol.L^-1 and [Cl^–] = S mol.L^-1

∴ K_sp  = [Ag+] × [Cl^–] = S × S = S²

Similarly, in the case of other sparingly soluble salts ofthe type AB (CaSO₄, BaSO₄, AgBr, etc.), K_sp = S²

In the case of a sparingly soluble salt of type AB₂:

The following equilibrium exists in a saturated aqueous solution of a sparingly soluble salt of the type AB₂:

⇒ \(\mathrm{AB}_2(s) \rightleftharpoons \mathrm{A}^{2+}(a q)+2 \mathrm{~B}^{-}(a q)\)

∴ The solubility product of AB₂, K_sp = [A²⁺] × [B^–]²

Let the solubility of AB₂ in its saturated solution at a given temperature be S mol.L-1. Therefore, in the solution, [A²⁺] = S mol-L^-1, [B^–] = 2S mol.L^-1 formula unit of AB₂ dissociates into one A²⁺ ion and two B_ ions].

∴ K_sp = [A²⁺] × [B^–]² = S ×  (2S)² = 4S³

∴ K_sp = 4S³ …………………………..(1)

Equation (1) represents the relation between the solubility and the solubility product of the sparingly soluble salt AB₂.

Example:

In a saturated aqueous solution of CaF₂, the following equilibrium exist:

CaF₂(s) ⇌  Ca²⁺(aq) + 2F^–(aq)

The solubility product of CaF₂, K_sp = [Ca²⁺] [F^–]² Let the solubility of CaF2 in its saturated aqueous solution at a certain temperature = S mol.L-1. So, in the saturated solution,

[Ca²⁺] = S mol.L^-1 and [F^–] =2S mol.L^-1

K_sp = [Ca²⁺ ] ×  [F^–]² = S ×  (2S)² = 4S³

Similarly, in the case of other sparingly soluble salts ofthe type

AB₂ (BaF2, PbCl₂, etc.), K_sp= 4S³

In case sparingly soluble salt of the type A_xB_y :

In a saturated aqueous solution of a salt of the type A_xB_y, the following equilibrium is established:

A_xB_y (s) ⇌ xA^y+(aq) + y B^x-(aq)

∴ The solubility product of A_xB_y,

K_sp = [A^y+]^x×  [B^x-]y

Suppose, the solubility of its saturated solution is = S mol.L^-1

Hence, in the solution, [A^y+] = xS mol-L^-1 and [B^x- ] = yS mol.L^-1

Since one formula unit of AxBy dissociates into x number of A^y+ and y number of B^x- ions]

∴ K_sp = [A^y+]^x×  [B^x-]y

= (xS)^x × (yS)^y=(x^x y^y) S^x+y

∴ K_sp = x^x y^y(S)^x+y

Solubility and Solubility Product Class 11 Chemistry Notes

Equation [1] represents the relation between the solubility and the solubility product of sparingly soluble salt A_xB_y

Relation between solubility (s) and solubility product (k) of some sparingly soluble salts:

Values of solubility  products (Ksp) of some sparingly soluble salt at 25 °C:

Common Ion Effect On The Solubility Of A Sparingly Soluble Salt 

In a saturated solution of a sparingly soluble salt, if a strong electrolyte having a common ion is added, then the solubility of the sparingly soluble salt decreases.

Hence, the solubility of a sparingly soluble salt in an aqueous solution of a salt having a common ion is less than its solubility m pure water.

Example:

The solubility of AgCl in an aqueous 0.1(M) KCl solution is less than its solubility in pure water. Here, the communion is Cl^– ion

Explanation:

 The following equilibrium is established in the saturated aqueous solution of, AgCl

The solubility product of AgCl, K_sp = [Ag⁺] × [Cl^–]. At a certain temperature, the value of K_sp is constant. Hence, the product of molar concentrations [Ag⁺] × [Cl^–] ) of

Ag⁺ and Cl are always constant at a particular temperature.

Therefore, if the molar concentration of one of the ions between Ag⁺ and Cl^– is increased, then the molar concentration of the other will be decreased to maintain a constant value of K_sp.

Let strong electrolyte KCl (having common ion Cl^– ) be added to the saturated solution AgCl. This will increase the molar concentration of the common ion (Cl^–) in the solution.

According to Le Chatelier’s principle, to maintain the constancy of K_sp some of the Cl^– ions combine with an equal number of Ag⁺ ions to form solid AgCl. This causes the equilibrium to shift to the left. As a result, the solubility of AgCl in the solution decreases.

At the new equilibrium, [Cl^–] << [Ag⁺], and the solubility of AgCl becomes equal to [Ag⁺]. If an aqueous AgNO₃ solution instead of KCl is added to the saturated solution of AgCl, then the solubility of AgCl will also decrease because of the communion (Ag⁺) effect.

NCERT Solutions Class 11 Chemistry Solubility and Solubility Product

Increase in solubility due to the presence of common ion:

AgCN is a sparingly soluble salt and its solubility increases when KCN is added to its aqueous solution. However, this increase in solubility does not contradict the principle of solubility product.

KCN reacts with sparingly soluble AgCN, and forms a water-soluble complex, K [Ag(CN)₂]. Thus, the solubility of AgCN increases.

KCN(aq) + AgCN(aq) K [Ag(CN)₂] (aq) A similar phenomenon is observed in the case of mercuric iodide (Hgl₂).

It shows greater solubility in an aqueous KI solution due to the formation of a water-soluble complex, 2KI[HgI₄].

2KI(aq) + Hgl₂ (aq) ⇌  K₂ [HgI₄](aq)

Effect of pH on solubility

The solubility of salts of weak acids like phosphate increases at lower pH. This is because, at a lower pH, the concentration of the anion decreases due to its protonation. This in mm increases the solubility of that salt.

Example: Consider the solubility equilibrium:

CaF₂(s) ⇌ Ca²⁺+(aq) + 2F^–(aq)……………….(1)

If the solution is made more acidic, it results in the protonation of some ofthe fluoride ions.

⇒ \(\mathrm{H}_3 \mathrm{O}^{+}(a q)+\mathrm{F}^{-}(a q) \rightleftharpoons \mathrm{HF}(a q)+\mathrm{H}_2 \mathrm{O}(l)\)

As acid is added, the concentration of F^– ion decreases due to the reaction(2).

This causes the equilibrium [1] to shift to the right, thereby increasing the concentration of Ca²⁺ ions. Thus, more CaF₂ dissolves in a more acidic solution.

Principle of solubility product and precipitation of sparingly soluble salts

Principle of solubility product:

At a particular temperature, the precipitation of salt from its solution or its dissolution in the solution depends on the value ofthe solubility product of the salt at that temperature.

If the product of the molar concentrations of the constituent ions, with suitable powers, of the salt in the solution exceeds the value of the solubility product of the salt at that temperature, then the salt will be precipitated from the solution.

If this value does not exceed the solubility product of that salt, then the salt will not be precipitated. This principle is known as the principle of solubility product. This principle is extensively used in different chemical analysis and industrial processes.

Explanation:

At 25°C, the solubility product of AgCl is 1.8 × 10^-10. Hence, in the saturated solution of AgCl at 25°C, the highest value of the product of molar concentrations of Ag+ and Cl- ions is 1.8× 10^-10

If the product of molar concentrations of Ag+ and Cl^– ions is less than, then the solution will be unsaturated. Under this condition, AgCl will be dissolved in the solution to increase the concentration of Ag+ and Cl^– ions and this will continue until the product of ofmolar concentrations of Ag⁺ and Cl^– becomes equal to.

If the product of molar concentrations of Ag⁺ and Cl^– is greater than K_sp(AgCl), then AgCl will be precipitated and this will continue unless the product ofmolar concentrations of Ag⁺ and Cl^– becomes equal to K_sp (AgCl).

Applications of solubility product

Application-1:

At a certain temperature, if the solubility product of a sparingly soluble salt is known, then the solubility of the salt, as well as the molar concentrations of the constituent ions of the salt in its saturated solution, can be determined.

Conditions for precipitation:

In the solution, if the product of the molar concentrations (with appropriate powers) of the constituent cation and anion of the salt at a particular temperature.

Is greater than the solubility product of the salt at that temperature, then the salt will be precipitated, Is less than the solubility product of the salt at that temperature, then the salt will remain dissolved in the solution, Is equal to the solubility product of the salt at that temperature.

Then the solution will just be saturated. In this case, the dissolved portion of the salt remains in equilibrium with the undissolved part.

NCERT Class 11 Chemistry Solubility Product Formula and Examples

Applications of solubility product principle

Preparation of pure NaCl from impure NaCl:

Pure sodium chloride can be prepared from impure sodium chloride by applying this principle. When dry HCl gas is introduced into the saturated aqueous solution of impure sodium chloride, the concentration of Cl- ions increases to a great extent and the ionic product of Na⁺ and Cl^–, i.e., [Na⁺] × [Cl^–] exceeds the solubility product of NaCl. Consequently, sodium chloride gets separated as pure crystals.

During this precipitation, impurities like MgCl₂, CaCl₂, etc., do not precipitate out as the values of the ionic product of the constituent ions of these impurities do not exceed their respective solubility products.

Separation of NaHCO₃ by Solvay process:

In this process, a saturated solution of sodium chloride is added to a solution of NH₄HCO₃.

The reaction concerned is:

⇒  \(\mathrm{NH}_4 \mathrm{HCO}_3(a q)+\mathrm{NaCl}(a q) \rightarrow \mathrm{NaHCO}_3(a q)+\mathrm{NH}_4 \mathrm{Cl}(a q)\)

Among the compounds participating in the reaction, NaHCO₃ has the least value of solubility product. The product of the molar concentrations of Na+ and HCO₃^– ions present in the solution can easily exceed the solubility product of NaHCO₃, and hence NaHCO₃. gets precipitated.

[KHCO₃ cannot be prepared by the Solvay process because the solubility product of KHCO₃ Is very high.]

Manufacture of soaps:

Soap consists of sodium or potassium salts of organic fatty acids of high molecular mass, such as stearic acid, oleic acid, etc. During the manufacturing of soaps, some amount of soap remains in a colloidal state in the mother liquor. If some NaCl is added to this solution, then the concentration of Na⁺ ions increases, thereby decreasing the solubility of soap. As a result, soap gets precipitated.

Application in analytical chemistry:

The principle of solubility product is extremely helpful in the qualitative analysis of basic radicals. Based on the values of the solubility product, the basic radicals of inorganic salts are divided into different groups.

Group 1:

Basic radicals \(\mathbf{A g}^{+}, \mathbf{P b}^{2+}, \mathbf{H g}_2^{2+}(\text { ous })\)

Group reagent:  6(N) HCl

As the values of the solubility product of chlorides of group-1 metals are sufficiently low [At 25°C, K_sp(AgCl)

= 1.8 × 10^-10, K_sp(Hg₂Cl₂)

= 1.2 × 10 K_sp(PbCl₂)

= 1.7 × 10^-18],

In addition to (N)HCI, the solubility products of these chlorides are exceeded by the products of the molar concentration of the corresponding ions. So, these chlorides get precipitated.

On the other hand, the chlorides of other groups have higher values of solubility product and thus are not precipitated.

[The solubility product of PbCl₂ is much higher than that of both AgCl and Hg₂Cl₂. So, Pb²⁺. ions are not completely precipitated as PbCl₂ in group 1. Pb²⁺. ions left in the solution are separated as precipitate in group 2.

Group 2:

Basic radicals: Cu²⁺+, Pb²⁺, Cd²⁺, Hg²⁺ (i.e ), Bi³⁺, As³⁺, Sb³⁺, Sn²⁺.

Group reagent:

H₂S gas in the presence of dilute HCl In an aqueous solution, H₂S ionizes partially to produce S^2- ions, which precipitate the basic radicals of this group as their corresponding sulfides (CuS, PbS, CdS, etc.).

The solubility product ofthe metallic sulphides of group-2

[K_sp(CuS) = 8.0 × 10^-37, K_sp (PbS) = 3.0 × 10^-28,

K_sp(CdS) = 1.0 × 10^-27 ,K_sp(HgS) = 2 × 10^-53

K_sp (Bi₂S₃) = 1.6 × 10^-72]  are much smaller as compared to those of the sulfides of the subsequent groups.

So, when H₂S gas is passed through the solution consisting of different basic radicals in the presence of HCl, the product of molar concentrations of the corresponding ions of each of the sulfides of this group exceeds its corresponding solubility product. Hence, only the sulfides of this group are precipitated.

It is important to note that the degree of ionization of weak acid H₂S in the presence of HCl decreases due to the common ion (H⁺) effect. As a result, except for group- 2, the solubility products of sulfides of the subsequent groups are not exceeded. Therefore, except for the sulfide salts of group 2, sulfides of all other groups are not precipitated.

Another notable point is that among the sulfides of group-2, the solubility products of CdS and PbS are sufficiently high. So, as a result of the common ion effect, if the concentration of S^2-ions decreases to a large extent, CdS and PbS are not precipitated. It has been experimentally proved that if H₂S gas is passed through the solution using 0.3(N) HCl solution, then all the sulfides of this group are completely precipitated, but the precipitation of the sulfides of other groups does not occur.

Solubility Product and Ksp Class 11 Chemistry Notes

Group 3A Basic radicals: Fe³⁺ , Al³⁺ , Cr³⁺ Group reagent:

NH4OH solutions presence of NH₄Cl The basic radicals of this group are precipitated as their corresponding hydroxides [Fe(OH)₃, Al(OH)₃, Cr(OH₃) ]. The solubility products of the hydroxides of the basic radicals of group 3A are much smaller than those of the hydroxides belonging to the subsequent groups.

So, when NH₄OH is added to the solution of different basic radicals in the presence of NH₄Cl, only the solubility products of the hydroxides of group-3A are exceeded, resulting in the preferential precipitation of the hydroxides of group-3A basic radicals. The hydroxides of the basic radicals of subsequent groups are not removed by this way of precipitation

Here, it is to be noted that the degree of ionization of weak base NH₃ in the presence of NH₄Cl is decreased due to the common ion (NH₄⁺) effect. As a result, the concentration of OH ions decreases to such an extent that except for group-3A, the solubility product of metallic hydroxides of the subsequent groups is not exceeded. Therefore, except for group-3A, metallic hydroxides of other groups are not precipitated.

Group 3 Basic radicals: Co²⁺, Ni²⁺, Mn²⁺, Zn²⁺

Group reagent:

H₂S in the presence of NH3 For precipitation of the basic radicals of this group as their corresponding sulfides [CoS, ZnS, MnS, NiS], H₂S gas is passed through the test solution in the presence of NH3.

In the presence of OH^– ions produced by the dissociation of NH₄OH, the equilibrium involving the dissociation of the weak acid H2S gets shifted to the right, forming sulfide ions (S^2-) to a greater extent

[H₂S(aq) + 2H₂O ⇌  2H₃O⁺(aq) + S^2-(aq)].

Due to a sufficient increase in the concentration of S^2- ions, the solubility products of the sulfides of group-3B are exceeded. Hence, the basic radicals of this group are precipitated as sulfides.

• Thermodynamic Process and Their Types
• Chemical Properties Of Group-13 Elements
• Enthalpy
• First Law Of Thermodynamics
• Quantum Number
• Some P Block Elements Group-14 Elements
• Aliphatic Hydrocarbons Alkanes

• Classification Of Organic Compounds On The Basis of Functional Group
• Fundamental Concepts Of Organic Reaction Mechanism
• Organic Chemistry Basic Principles And Techniques
• States Of Matter Gases And Liquids States Of Matter Gases And Liquids
• Purification And Analysis Of Organic Compounds
• Qualitative and Quantitative Analysis Of Organic Compounds
• Periodic Trends In Properties Of The Elements
• Position Of Hydrogen And Inert Gases In The Periodic Table
• Valency
• Long Form Of Periodic Table
• Mendeleev’s Periodic Table