NCERT Solutions For Class 8 Chemistry
- Chapter 1 Matter Notes
- Chapter 2 Physical And Chemical Changes Notes
- Chapter 3 Elements, Compounds And Mixtures Notes
- Chapter 4 The Structure Of The Atom

Question 1. “Indian road transportation is confronted with problems”. Justify the statement.
Answer:
Road transportation is economical for the transportation of smaller amounts of goods and few passengers over short and medium distances.
Though they are relatively cheap and easy to construct and maintain, road transportation in India is confronted with a number of problems.

Question 2. Discuss the importance of tourism in India.
Answer:
Tourism has great importance in the economy and cultural development of India. It promotes national integration. It makes us aware of the beauty and rich cultural heritage of our nation.
It promotes inter-regional relationships. Tourism encourages cultural pursuits and provides support to local handicrafts. It helps in the development of international understanding. Tourism is considered to be an invincible trade.
India’s natural beauty, diversity, and glorious past attract innumerable visitors to India every year. Overseas holidayers and travelers have awarded India the fourth rank among the best holiday destinations in the world.
Over 2.6 million foreign tourists visit India every year. Foreign tourists visit India for heritage tourism, cultured tourism, ecotourism, adventure tourism, medical tourism, and business tourism. Tourism in India has grown substantially over the last three decades.
Foreign tourists’ arrivals in the country witnessed an increase of 23.5% during the year 2004 as against the year 2005. Thus, tourism has contributed ₹ 21,828 crore of foreign exchange.
The trend is towards the increase of foreign tourism and foreign exchange. Tourism also plays a major role in employment generation.
More than 15 million people are directly engaged in the tourism industry and many more are indirectly connected to it. There is a bright future for the Tourism Industry in India.
Lifelines of National Economy Class 10
Question 3. Write a short note on:
Answer:
Question 4. Why is Road Transport more useful than Rail Transport in India?
Or
“Road transport is considered more useful as compared to rail transport”. Give reasons.
Answer:
Road transport is more useful than Railways on account of the following reasons:
Class 10 Geography Chapter 7 Solutions
Question 5. How do physical and economic factors influence the distribution pattern of the Indian railways network? Explain with suitable examples.
Answer:
The distribution pattern ofthe railway network in India has been greatly influenced by physical and economic factors.
Question 6. What are the merits of pipeline transport in India?
Answer:
pipelines are used for the transportation of crude oil, petroleum products, and Natural gas. The merits of pipeline transportation in India are as follows:
Question 7. Explain why is air transport preferred in the north-eastern States of India.
Or
Why is air travel preferred in northeastern states?
Answer:
The air transport is preferred in the north-eastern regions of India because of the following reasons:
So, the airways are also within the financial reach of the common people in this region. On account of all these factors, airways are the preferred mode of transportation in the northeastern states of India.
NCERT Solutions for Class 10 Geography Chapter 7
Question 8. “Rail transport is the most convenient means of transportation”. Why?
Answer:
Railways can transport a large number of goods and passengers over long distances at an economical cost. Hence, Railways are the most convenient means of transport in the vast Northern Plains of India.
The flat terrain, dense population, rich agricultural resources, and greater industrial activity have favored the development of railways in the Northern Plains of India.
Therefore, this region has transport networks. Railways have accelerated the development of industry and agriculture in this region by providing quick availability of raw materials and distributing the finished products to the market.
Question 9. Discuss the significance of National Highways and Border Roads.
Answer:
Question 10. What social values are promoted by tourism?
Answer:
Tourism not only is helpful in developing the economy of a region but also promotes social values like support for local handicrafts, cultural pursuits, and national integration.
It generates care, and concern about the environment, culture, and heritage. Tourism also develops love and concern for fellow countrymen and international understanding.
Lifelines of National Economy NCERT Solutions
Question 11. Outline the values that the means of transport and communication help in developing among the people.
Answer:
The means of transport and communication help in developing the following values among the people:
Question 12. What values among users will help in the maintenance of railway property?
Answer:
Take care of national property.
Sense of collective responsibility
Geometry has a long and rich history. The term ‘Geometry’ is the English equivalent of the Greek word ‘Geometron’. ‘Geo’ means Earth and ‘metron’ means Measurement.
According to historians, geometrical ideas were shaped in ancient times, probably due to the need for art, architecture, and measurement.
These include occasions when the boundaries of cultivated lands had to be marked without giving room for complaints. Construction of magnificent palaces, temples, lakes, dams, and cities, art, and architecture propped up these ideas.

Even today geometrical ideas are reflected in all forms of art, measurements, architecture, engineering, cloth designing, etc. You observe and use different objects like boxes, tables, books, the tiffin box you carry to your school for lunch, the ball with which you play, and so on.
Read and Learn More NCERT Notes for Class 6 Maths
All such objects have different shapes. The ruler which you use, and the pencil with which you write are straight. The pictures of a bangle, the one rupee coin, or a ball appear round.
Here, you will learn some interesting facts that will help you know more about the shapes around you.

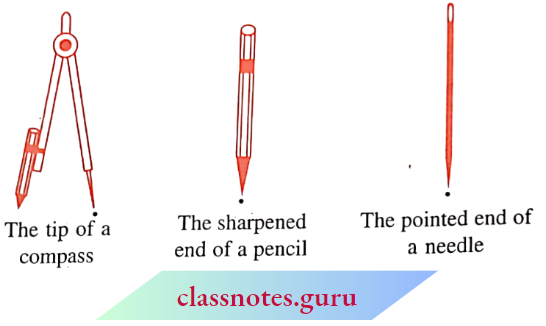
With the sharp tip of the pencil, mark a dot on the paper. The sharper the tip, the thinner will be the dot. This almost invisible tiny dot will give you an idea of a point.
A point determines a location.
These are some models for a point:
If you mark three points on a paper, you will be required to distinguish them. For this, they are denoted by a single capital letter like A, B, C.
These points will be read as point A, point B, and point C.
Of course, the dots have to be invisibly thin.
Fold a piece of paper and unfold it. Do you see a fold? This gives the idea of a line segment. It has two end points A and B.
Take a thin thread. Hold its two ends and stretch it without a slack. It represents a line segment. The ends held by hands are the end B points of the line segment.

The following are some models for a line segment:
Try to find more examples of line segments from your surroundings.
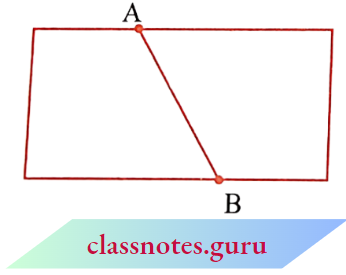
Mark any two points A and B on a sheet of paper. Try to connect A to B by all possible routes.

What is the shortest route from A to B?
This shortest join of points A to B (including A and B) shown here is a line segment. It is denoted by \(\overrightarrow{A B}\) or \(\overrightarrow{B A}\) . Points A and B are called the endpoints of the segment.
Imagine that the line segment from A to B (i.e. \(\overrightarrow{A B}\) ) is extended beyond A in one direction and beyond B in the other direction without any end (see figure). You now get a model for a line.

Do you think you can draw a complete picture of a line? No. (Why?)
A line through two points A and B is written as \(\overrightarrow{A B}\)• It extends indefinitely in both directions. So it contains a countless number of points. (Think about this).
Two points are enough to fix a line. We say ‘Two points determine a line’.
The adjacent diagram is that of a line PQ written as \(\overrightarrow{P Q}\). Sometimes a line is denoted by a letter like l, m.
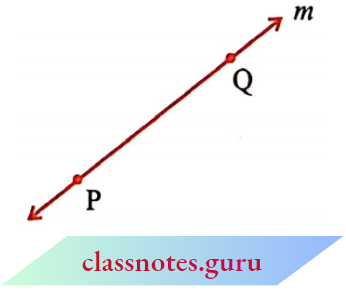
Look at the diagram. Two lines l1 and l2 are shown. Both the lines pass through point P.
We say l1 and l2 intersect at P. If two lines have one common point, they are called intersecting lines.
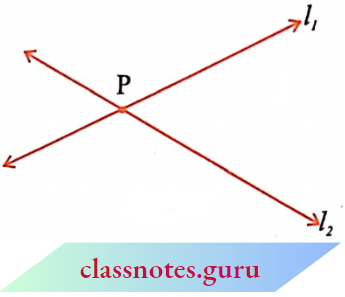
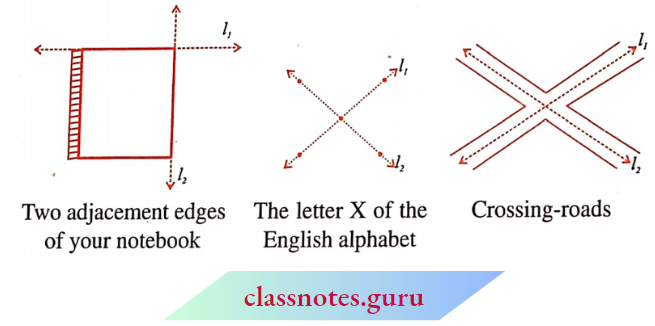
The following are some models of a pair of intersecting lines:
Try to find some more models for a pair of intersecting lines.
Let us look at this table. The top ABCD is flat. Are you able to see some points and line segments?
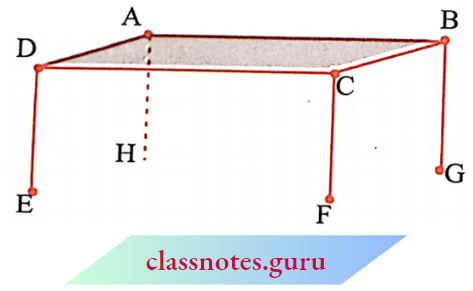
Are there intersecting line segments?
Yes, AS and BQ intersect at the point B.
Which fine segments intersect at A? at C? or at D?
Do the lines AD and CD intersect?
Do the lines \(\overrightarrow{A D}\) and \(\overrightarrow{B C}\) intersect?
You find that on the table’s surface, there are line segments that will not meet, however far they are extended. \(\overrightarrow{A D}\) and \(\overrightarrow{B C}\) form one such pair. Can you identify one more such pair of lines (which do not meet) on the top of the table?
Lines like these that do not meet are said to be parallel and are called parallel lines.
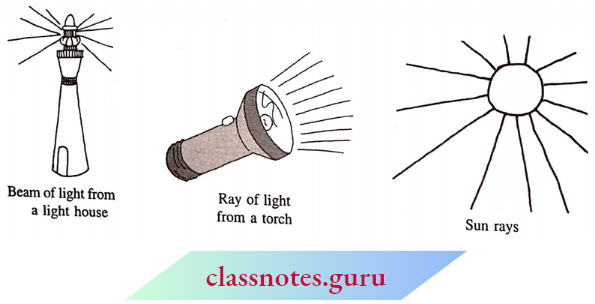
The following are some models of a ray:
A ray is a portion of a line. It starts at one point (called the starting point or initial point) and goes endlessly in a direction.
Look at the diagram of the ray shown here. Two points are shown on the ray.
They are
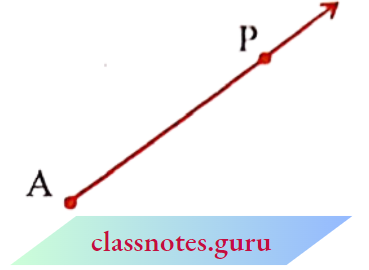
We denote it by \(\overrightarrow{\mathrm{AP}}\)
You can draw some of these drawings without lifting the pencil from the paper and without die use of a ruler. These are all curves.
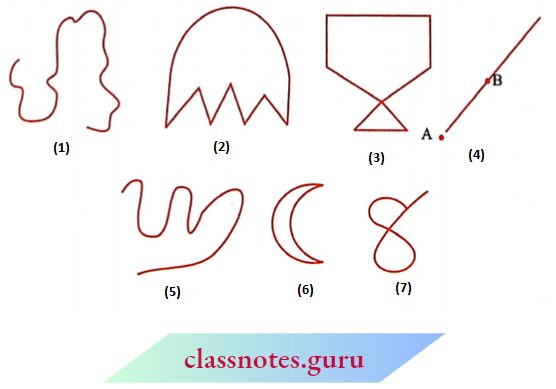
‘Curve’ in everyday usage means “not straight’’. In Mathematics, a curve can be straight like the one shown.
Observe that curves (3) and (4) in Figure cross themselves, whereas curves (1), (2), (5), and (6) do not. If a curve does not cross itself, then it is called a simple curve.
Draw five more simple curves and five curves that are not simple.
Consider these now.
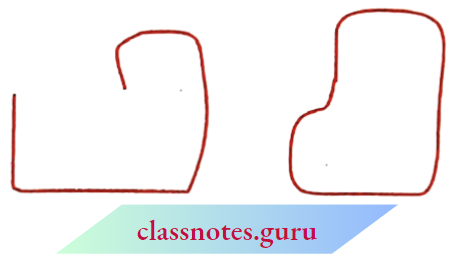
What is the difference between these two? The first i.e. (1) is an open curve and the second i.e. (2) is a closed curve. Can you identify some closed and open curves from the above? Draw five curves each that are open and closed.
Position in a figure
A court line in a tennis court is divided into three parts: inside the line, on the line, and outside the line. You cannot enter inside without crossing the line.
A compound wall separates your house from the road. You talk about ‘inside’ the compound, ‘on’ the boundary of the compound, and ‘outside’ the compound.
In a closed curve, thus, there are three parts.
The below is in the interior, C is in the exterior and B is on the curve.
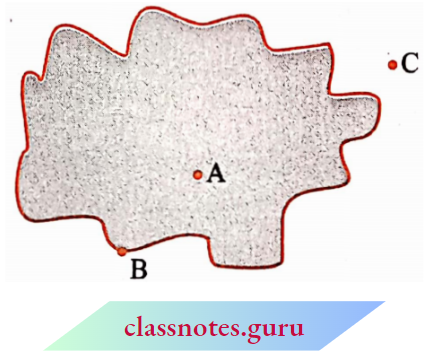
The interior of a curve together with its boundary is called its “region”.
Look at these below (1), (2), (3), (4), (5) and (6).
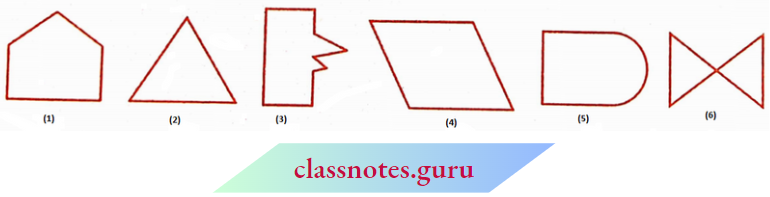
What can you say? Are they closed? How does each one of them differ from die other? (1), (2), (3), (4), and (5) are special because they are made up entirely of line segments.
Out of these (1), (2), (3), and (4) are also simple closed curves. They are called polygons.
So, a figure is a polygon if it is a simple closed figure made up entirely of line segments. Draw ten differently shaped polygons.
Sides, vertices, and diagonals
Examine the figure given here. Give justification to call it a polygon.
The line segments forming a polygon are called its sides.
What are the sides of polygon ABCDE? (Note how the comers are named in order.)
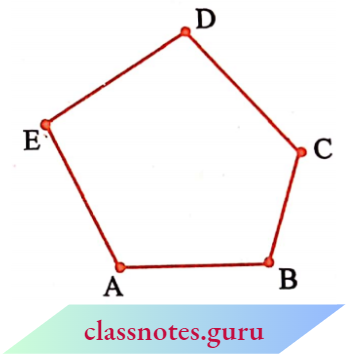
Sides are \(\overline{\mathrm{AB}}\), \(\overline{\mathrm{BC}}\), \(\overline{\mathrm{CD}}\), \(\overline{\mathrm{DE}} \text { and } \overline{\mathrm{EA}}\).
The meeting point of a pair of sides is called its vertex.
Sides \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{ED}}\) meet at E, so E is a vertex of the polygon ABCDE. Points B and C are its other vertices. Can you name the sides that meet at these points? Can you name the other vertices of the above polygon ABCDE?
Any two sides with a common endpoint are called the adjacent sides of the polygon.
Are the sides \(\overline{\mathrm{AB}}\) and \(\overline{\mathrm{BC}}\) adjacent? How about \(\overline{\mathrm{AE}}\) and \(\overline{\mathrm{DC}}\)? The endpoints of the same side of a polygon are called the adjacent vertices.
Vertices E and D are adjacent, whereas vertices A and D are not adjacent vertices. Do you see why?
Consider the pairs of vertices which are not adjacent. The joins of these vertices are called the diagonals of the polygon.
In the given \(\overline{\mathrm{AC}}, \overline{\mathrm{AD}}, \overline{\mathrm{BD}}, \overline{\mathrm{BE}} \text { and } \overline{\mathrm{CE}}\) are diagonals. Is \(\overline{\mathrm{BC}}\) a diagonal, Why or why not?

If you try to join adjacent vertices, will the result be a diagonal?
Name all the aides, adjacent aides, and adjacent vertices of the figure ABCDE.
Draw q polygon ABCDEFGH and name all the aides, adjacent sides, and vertices as well as the diagonals of the polygon.
Angles are made when comers are formed.
Here is a picture where the top of a box is like a hinged lid. The edges AD of the box and AP of the door can be imagined as two rays \(\overrightarrow{\mathrm{AD}}\) and \(\overrightarrow{\mathrm{AD}}\).
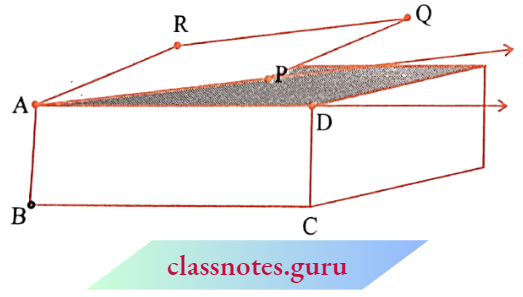
These two rays have a common initial point A. The two rays here together are said to form an angle.
An angle is made up of two rays starting from a common initial point. The two rays forming the angle are called the arms or sides of the angle. The common initial point is the vertex of the angle.
This is an angle formed by rays \(\overrightarrow{\mathrm{OP}} \text { and } \overline{\mathrm{OQ}}\). To show this we use a small curve at the vertex. 0 is the vertex. What are the sides? Are they not \(\overrightarrow{\mathrm{OP}} \text { and } \overline{\mathrm{OQ}}\)?
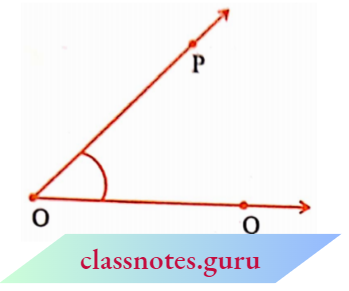
How can we name this angle? We can simply say that is an angle at O. To be more specific we identify two points, one on each side and the vertex to; tame the angle. Angle POQ is thus a better way of naming the angle. We denote this by ∠POQ.
Take any angle, say ∠ABC.
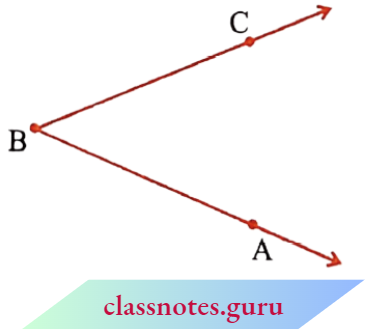
Shade that portion of the paper bordering \(\overrightarrow{\mathrm{BA}}\) and where \(\overrightarrow{\mathrm{BC}}\) lies.
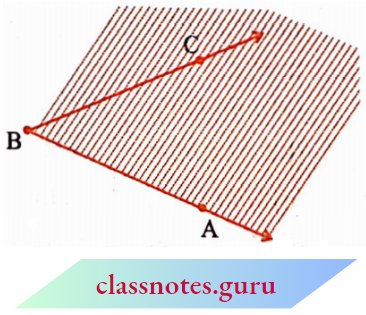
Now shade in a different color the portion of the paper bordering \(\overrightarrow{\mathrm{BC}}\) and where \(\overrightarrow{\mathrm{AB}}\) lies.
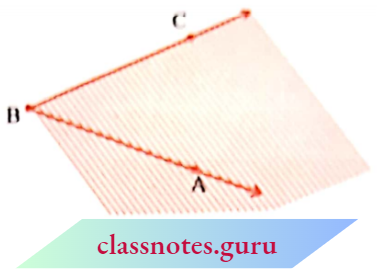
The portion common to both shadings is called the interior of ABC. (Note that the interior is not a restricted area; it extends indefinitely since the two sides extend indefinitely).
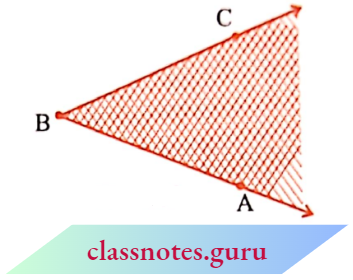
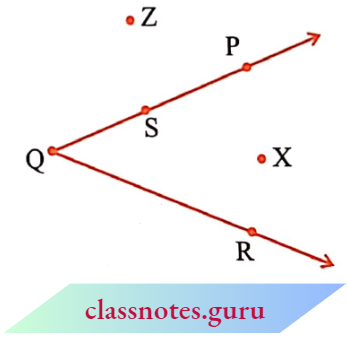
In this diagram, X is in the interior of the angle, Z is not in the interior but in the exterior of the angle, and S is on the ∠PQR. Thus, the angle also has three parts associated with it.
Understanding Elementary Shapes Introduction
All the shapes we see around us are formed using curves or lines. We can see comers, edges, planes, open curves, and closed curves in our surroundings.
We organize them into line segments, angles, triangles, polygons, and circles. We find that they have different sizes and measures. Let us now try to develop tools to compare their sizes.
We have drawn and seen so many line segments. A triangle is made of three, and a quadrilateral of four line segments. A line segment is a fixed portion of a line.
This makes it possible to measure a line segment. This measure of each line segment is a unique number called its “length”. We use this idea to compare line segments.
To compare any two line segments, we find a relation between their lengths. This can be done in several ways.
Read and Learn More NCERT Notes for Class 6 Maths
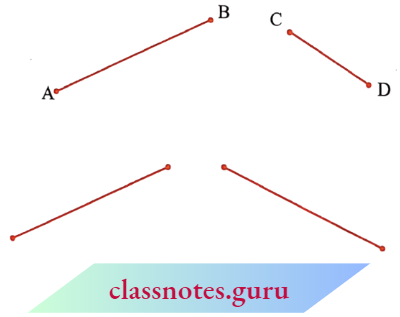
1. Comparison by observation:
By just looking at them can you tell which one is longer?
You can see that \(\overline{\mathrm{AB}}\) is longer.
But you cannot always be sure about your usual judgment.
For example, look at the adjoining segments:
The difference in lengths between these two may not be obvious. This makes other ways of comparing necessary.

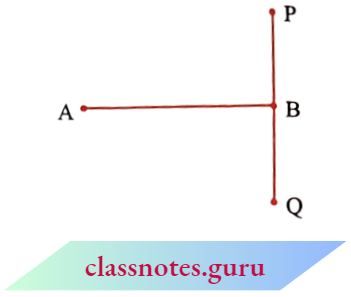
In this adjacent figure, \(\overline{\mathrm{AB}} \text { and } \overline{\mathrm{PQ}}\) have the same lengths. This is not quite obvious.
So, we need better methods of comparing line A segments.
2. comparison by tracing

To compare \(\overline{\mathrm{AB}} \text { and } \overline{\mathrm{CD}}\), we use a tracing paper, trace \(\overline{\mathrm{CD}}\), and place the traced segment on AB.
Can you decide now which one among \(\overline{\mathrm{AB}} \text { and } \overline{\mathrm{CD}}\), is longer?
The method depends upon the accuracy of tracing the line segment. Moreover, if you want to compare with another length, you have to trace another line segment.
This is difficult and you cannot trace the lengths every time you want to compare them.
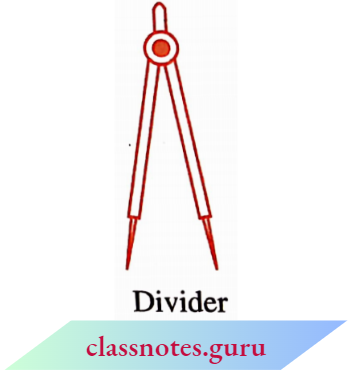
3. Comparison Using Ruler and a Divider
Have you seen or can you recognize all the instruments in your instrument box? Among other things, you have a miler and a divider.

Note how the meter is marked along one of its edges. It is divided into 15 parts. Each of these 15 parts is 1cm in length. Each centimeter is divided into subparts. Each subpart of the division of a cm is 1mm.
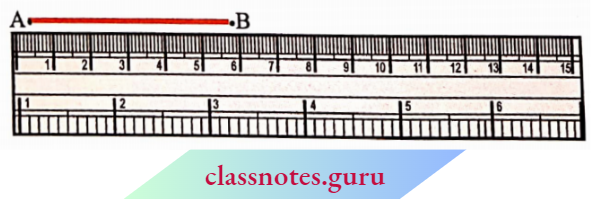
How many millimeters make one centimeter? Since 1cm = 10 mm, how will we write 2 cm? 3mm? What do we mean by 7.7 cm?
Place the zero mark of the meter at A.
Read the mark against. This gives the length of \(\overline{\mathrm{AB}}\). Suppose the length is 5.8 cm, we may write, Length AB = 5.8 cm or more simply as AB = 5.8 cm.
There is room for errors even in this procedure. The thickness of the meter may cause difficulties in reading off the marks on it.
Let us use the divider to measure length.
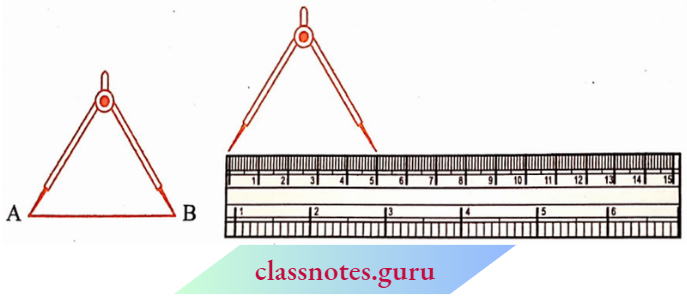
Open the divider. Place the end point of one of its arms at A and the end point of the second arm at B.
Taking care that the opening ofthe divider is not disturbed, lift the divider and place it on the ruler. Ensure that one endpoint is at the zero mark of the ruler. Now read the mark against the other endpoint.
You have heard of directions in Geography. We know that China is to the north of India, and Sri Lanka is to the south. We also know that the Sun rises in the east and sets in the west. There are four main directions.
They are North (N), South (S), East (E) and West (W). Do you know which direction is opposite to the north? Which direction is opposite to the west? Just recollect what you know already.
We now use this knowledge to learn a few properties about angles. Stand facing north.
Turn clockwise to the east.
We say you have turned through a right angle. Follow this with a ‘right-angle-tum’, clockwise.
You now face south. If you turn by a right angle in the anti-clockwise direction, which direction will you face? It is east again! (Why?) Study the following positions
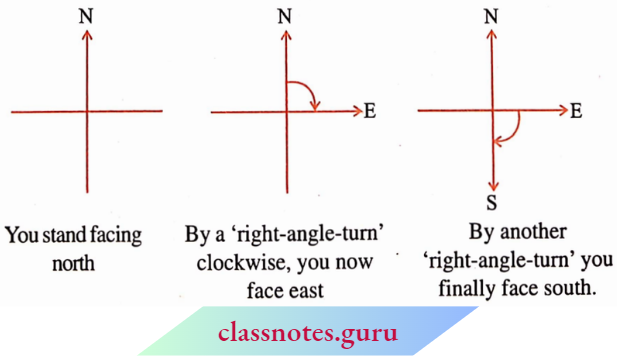
From facing north to facing south, you have turned by two right angles. Is not this the same as a single turn by two right angles? The turn from north to east is at a right angle.
The turn from north to south is by two right angles; it is called a straight angle. (NS is a straight line) Stand facing south.
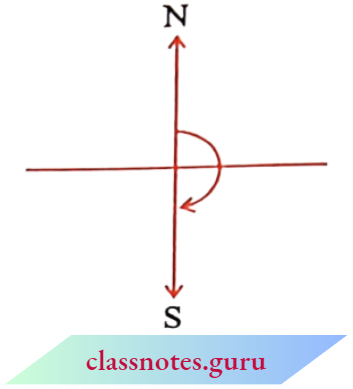
Turn by a straight angle. Which direction do you face now? You face north! To turn from north to south, you took a straight-angle turn, again to turn from south to north.
You took another straight-angle turn in the same direction. Thus, turning by two straight angles you reach your original position.
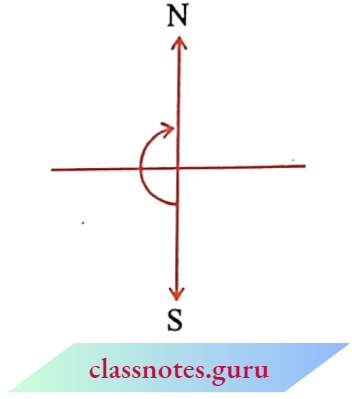
By how many right, angles should you turn in the same direction to reach your original position? Turning by two straight angles (or four right angles) in the same direction makes a full turn.
This one complete turn is called one revolution. The angle for one revolution is a complete angle. We can see such revolutions on clock faces.
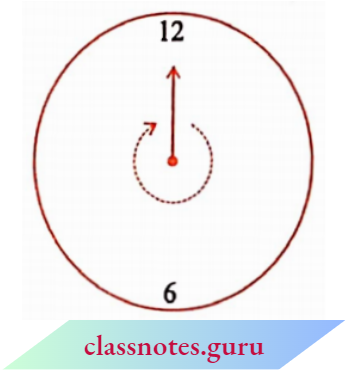
When the hand of a clock moves from one position to another, it turns through an angle.
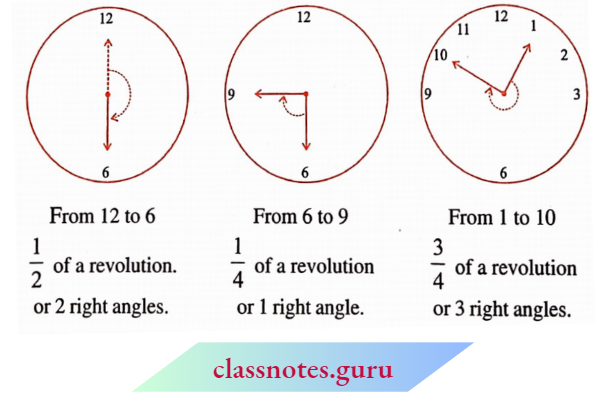
Suppose the hand of a clock starts at 12 and goes round until it reaches 12 again. Has it not made one revolution? So, how many right angles has it moved? Consider these examples
We saw what we mean by a right angle and a straight angle. However, not all the angles we come across are one of these two kinds.
The angle made by a ladder with the wall (or with the floor) is neither a right angle nor a straight angle.
Are there angles smaller than a right angle? Are there angles greater than a right angle? Have you seen a carpenter’s square? It looks like the letter “L” of the English alphabet.
He uses it to check right angles. Let us also make a similar ‘tester’ for a right angle.

Other Names
1. An angle smaller than a right angle is called an acute angle. These are acute angles

Do you see that each one of them is less than one-fourth of a revolution? Examine them with your RA tester.
2. If an angle is larger than a right angle but less than a straight angle, it is called an obtuse angle. These are obtuse angles.
Do you see that each one of them is greater than one-fourth of a revolution but less than half a revolution? Your RA tester may help to examine.
Identify the obtuse angles in the previous examples too.
3. A reflex angle is larger than a straight angle. It looks like this. (See the angle mark) Were there any reflex angles in the shapes you made earlier? How would you check for them?

The improvised ‘Right-angle tester’ we made is helpful to compare angles with a right angle. We were able to classify the angles as acute, obtuse, or reflex.
But this does not give a precise comparison. It cannot find which one of the two obtuse angles is greater. So in order to be more precise in comparison, we need to ‘measure’ the angles. We can do it with a ‘protractor’.
The measure of angle
We call our measure, ‘degree measure’. One complete revolution is divided into 360 equal parts. Each part is a degree. We write 360° to say ‘three hundred sixty degrees’.
The Protractor
You can find a readymade protractor in your ‘instrument box’. The curved edge is divided into 180 equal parts.
Each part is equal to a ‘degree’. The markings start from 0° on the right side and end at 180° on the left side, and vice versa.
Suppose you want to measure an angle ABC.
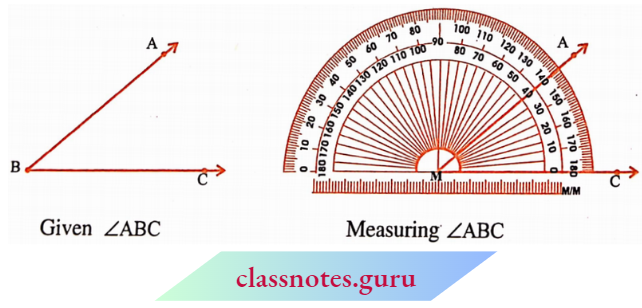
We write m ∠ABC= 40°, or simply ∠ABC= 40°.
When two lines intersect and the angle between them is a right angle, then the lines are said to be perpendicular. If a line AB is perpendicular to CD, we write \(A B \perp C D \text {. }\) .
If \(A B \perp C D\), then should we say that \(\mathrm{CD} \perp \mathrm{AB}\) also?
Perpendiculars around us!
You can give plenty of examples from things around you for perpendicular lines (or line segments). The English alphabet T is one. Is there any other alphabet that illustrates perpendicularity?
Consider the edges of a postcard. Are the edges perpendicular?
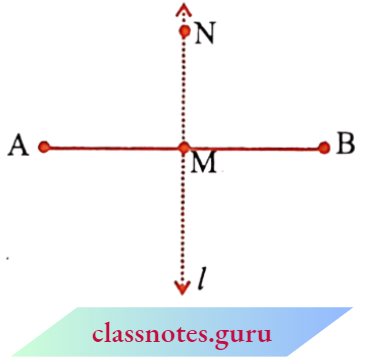
Let \(\overline{\mathrm{AB}}\) be a line segment. Mark its midpoint as M. Let MN be a line perpendicular to \(\overline{\mathrm{AB}}\) through M.
Does MN divide \(\overline{\mathrm{AB}}\) into two equal parts? MN bisects \(\overline{\mathrm{AB}}\) (that is, divides \(\overline{\mathrm{AB}}\) into two equal parts) and is also perpendicular to \(\overline{\mathrm{AB}}\).
So we say MN is the perpendicular bisector of \(\overline{\mathrm{AB}}\). You will learn to construct it later.
Quadrilaterals
A quadrilateral, if you remember, is a polygon that has four sides.
So far you studied polygons of 3 o r4 sides (known as triangles and quadrilaterals respectively). We now try to extend the idea of polygon to figures with more sides. We may classify polygons according to the number of their sides.
image-
You can find many of these shapes in everyday life. Windows, doors, walls, almirahs, blackboards, notebooks are all usually rectanglular in shape. Floor tiles are rectangles. The sturdy nature of a triangle makes it the most useful shape in engineering constructions.
Ramesh has 6 marbles with him. He wants to arrange them in rows in such a way that each row has the same number of marbles. He arranges them in the following ways and matches the total number of marbles.
1. 1 Marble in each row
Number of rows = 6
Total number of marbles = 1 x 6 = 6.

2. 2 marbles in each row
Number of rows = 3
Read and Learn More NCERT Notes for Class 6 Maths
Total number of marbles = 2 x 3 = 6.

3. 3 marbles in each row
Number of rows = 2
Total number of marbles = 3 x 2 = 6.

4. He could not think of any arrangement in which each row had 4 marbles or 5 marbles. So, the only possible arrangement left was with all the 6 marbles in a row.
Number of rows = 1
Total number of marbles = 6 x 1 = 6

From these calculations, Ramesh observes that 6 can be written as a product of two numbers in different ways as
6 = 1 x 6; 6 = 2 x 3; 6 = 3 x 2; 6 = 6 x 1;
From 6 = 2 x 3, it can be said that 2 and 3 exactly divide 6. So, 2 and 3 are exact divisors of 6. From the other product 6 = 1 x 6, the exact divisors of 6 are found to be 1 and 6.
Thus, 1, 2, 3, and 6 are exact divisors of 6. They are called the factors of 6. found to be 1 and 6. Try arranging 18 marbles in rows and find the factors of 18.
Mary wants to find those numbers that are exactly divided by 4. She divides 4 by numbers less than 4 this way.

She finds that the number 4 can be written as 4 = 1 x 4; 4 = 2 x 2; 4 = 4×1 and knows that the numbers 1,2 and 4 are exact divisors of 4.
These numbers are called factors of 4.
A factor of a number is an exact divisor of that number.
Observe each of the factors of 4 is less than or equal to 4.
Game-1: This is a game to be played by two persons say A and B. It is
about spotting factors.
It requires 50 pieces of cards numbered 1 to 50.
Arrange the cards on the table like this.
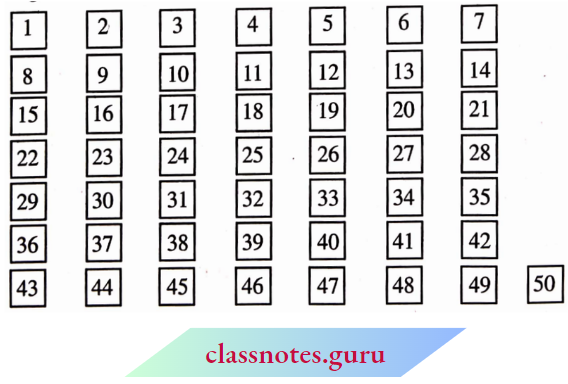
Steps
When we write the number 20 as 20 = 4 x 5, we say 4 and 5 are factors of 20. We also say that 20 is a multiple of 4 and 5.
The representation 24 = 2 x 12 shows that 2 and 12 are factors of 24, whereas 24 is a multiple of 2 and 12.
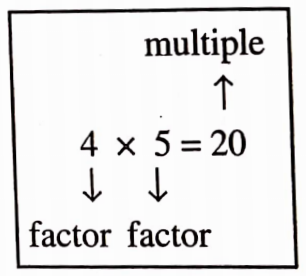
We can say that a number is a multiple of each of its factors
Let us now see some interesting facts about factors and multiples.
The length of the strip at the top is 3 =1 x 3 units.
The length of the strip below it is 3 +3 =6 units.
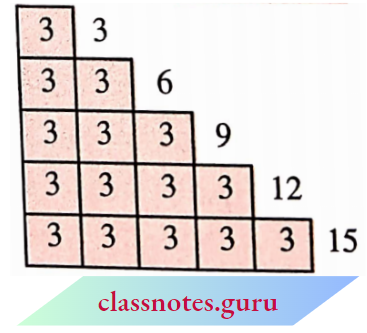
Also, 6 = 2 x 3. The length of the next strip is 3 + 3 + 3 = 9 units, and 9 = 3 x 3. Continuing this way we can express the other lengths as,
12 = 3 x 4; 15 = 5 x 3
We say that the numbers 3, 6, 9, 12, 15 are multiples of 3.
The list of multiples of 3 can be continued as 18, 21, 24, …
Each of these multiples is greater than or equal to 3.
The multiples of the number 4 are 4, 8, 12, 16, 20, 24, …
The list is endless. Each of these numbers is greater than or equal to 4
Let us see what we conclude about factors and multiples:
1. Is there any number that occurs as a factor of every number? Yes. It is 1. For example 6 = 1 x 6, 18 = 1 x 18, and so on. Check it for a few more numbers.
We say 1 is a factor of every number.
2. Can 7 be a factor of itself? Yes. You can write 7 as 7 = 7 x 1. What about 10? and 15?
You will find that every number can be expressed in this way. We say that every number is a factor of itself.
3. What are the factors of 16? They are 1, 2, 4, 8, 16. Out of these factors do you find any factor which does not divide 16? Try it for 20; 36.
You will find that every factor of a number is an exact divisor of that number.
4. What are the factors of 34? They are 1,2, 17 and 34. Out of these which is the greatest factor? It is 34 itself.
The other factors 1,2 and 17 are less than 34. Try to check this for 64, 81, and 56.
We say that every factor is less than or equal to the given number.
5. The number 76 has 5 factors. How many factors does 136 or 96 have? You will find that you are able to count the number of factors of each of these.
Even if the numbers are as large as 10576, 25642, etc., or larger, you can still count the number of factors of such numbers, (though you may find it difficult to factorize such numbers).
We say that the number of factors of a given number is finite.
6. What are the multiples of 7? Obviously, 7, 14, 21, 28,… You will find that each of these multiples is greater than or equal to 7. Will it happen with each number? Check this for the multiples of 6, 9, and 10.
We find that every multiple of a number is greater than or equal to that number.
7. Write the multiples of 5. They are 5, 10, 15, 20, … Do you think this list will end anywhere? No! The list is endless. Try it with multiples of
6, 7 etc.
We find that the number of multiples of a given number is infinite.
8. Can 7 be a multiple of itself? Yes, because 7 = 7 x 1. Will it be true for other numbers also? Try it with 3, 12 and 16.
You will find that every number is a multiple of itself.
The factors of 6 are 1, 2, 3 and 6. Also, 1 + 2 + 3 + 6 = 12 = 2 x 6. We find that the sum of the factors of 6 is twice the number 6.
All the factors of 28 are 1, 2, 4, 7, 14, and 28. Adding these we have, 1 + 2 + 4 + 7 + 14 + 28 = 56 = 2 x 28. The sum of the factors of 28 is equal to twice the number 28.
A number for which the sum of all its factors is equal to twice the number is called a perfect number. The numbers 6 and 28 are perfect numbers.
Is 10 a perfect number?
Example 1: Write all the factors of 68.
Solution :
We note that
68 = 1 x 68
68 = 2 x 34
68 = 4 x 17
68 = 17 x 4
Stop here, because 4 and 17 have occurred earlier.
Thus, all the factors of 68 are 1,2,4,17, 34 and 68.
Example 2: Find the factors of 36.
Solution:
36 = 1 x 36
36 = 2 x 18
36 = 3 x 12
36 = 4 x 9
36 = 6 x 6
Stop here, because both factors (6) are the same. Thus, the factors are 1,2, 3,4, 6, 9, 12,18 and 36.
Example 3: Write the first five multiples of 6.
Solution:
The required multiples are 6 x 1= 6, 6 x 2 = 12, 6 x 3 = 18, 6 x 4 = 24, 6 x 5 = 30 i.e. 6, 12, 18, 24, and 30.
We are now familiar with the factors of a number. Observe the number of factors of a few numbers arranged in this table.
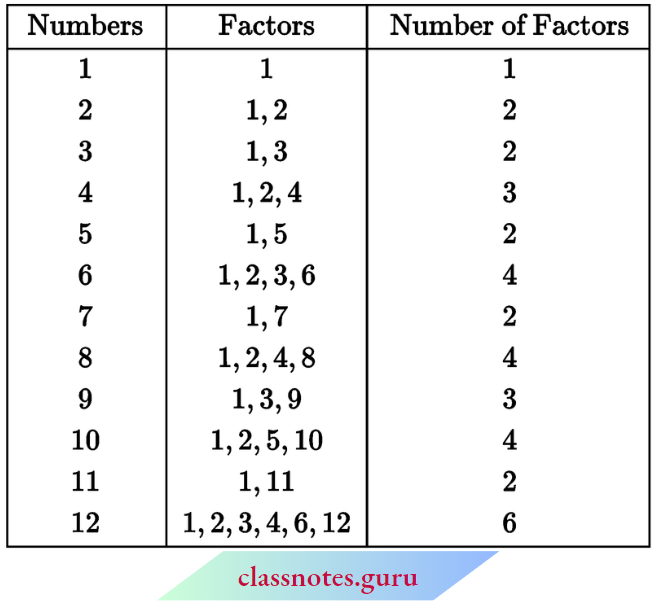
We find that
Try to find some more prime numbers other than these.
There are numbers having more than two factors like 4,6,8,9,10 and so on. These numbers are composite numbers.
Numbers having more than two factors are called Composite numbers. Is 15 a composite number? Why? What about 18? 25?
Without actually checking the factors of a number, we can find prime numbers from 1 to 100 with an easier method.
This method was given by a Greek Mathematician Eratosthenes, in the third century B.C. Let us sec the method. List all numbers from 1 to 100, as shown below.
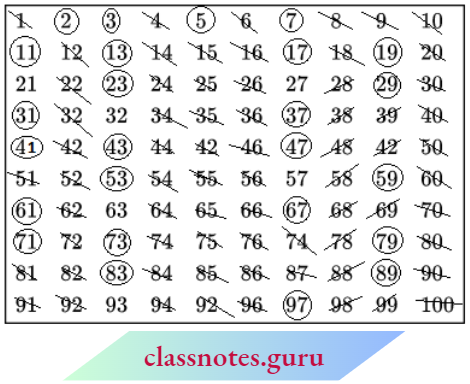
Step 1: Cross out 1 because it is not a prime number.
Step 2: Encircle 2, cross out all the multiples of 2, other than 2 itself, i.e. 4,6, 8, and so on.
Step 3: You will find that the next uncrossed number is 3. Encircle 3 and cross out all the multiples of 3, other than 3 itself.
Step 4: The next uncrossed number is 5. Encircle 5 and cross out all the multiples of 5 other than 5 itself.
Step 5: Continue this process till all the numbers in the list are either encircled or crossed out.
All the encircled numbers are prime numbers. All the crossed-out numbers, other than 1 are composite numbers.
This method is called the Sieve of Eratosthenes.
Example 4: Write all the prime numbers less than 15.
Solution :
By observing the Sieve Method, we can easily write the required prime numbers as 2,3, 5,7,11, and 13.
even and odd numbers
Do you observe any pattern in the numbers 2,4, 6, 8, 10, 12, 14,…? You will find that each of them is a multiple of 2.
These are called even numbers. The rest of the numbers 1, 3, 5, 7, 9,11,… are called odd numbers.
You can verify whether a two-digit number or a three-digit number is even or not. How will you know whether a number like 756482 is even? By dividing it by 2. Will it not be tedious?
We say that a number with 0,2,4,6, 8 at the one’s place is an even number. So, 350,4862,59246 are even numbers. The numbers 457,2359,8231 are all odd.
Let us try to find some interesting facts:
Thus, we can say that every prime number except 2 is odd.
Is the number 38 divisible by 2? by 4? by 5?
By actually dividing 38 by these numbers we find that it is divisible by 2 but not by 4 and by 5.
Let us see whether we can find a pattern that can tell us whether a number is divisible by 2,3,4,5,6, 8,9,10, or 11. Do you think such patterns can be easily seen?
Divisibility by 10: Charu was looking at the multiples of 10. The multiples are 10, 20, 30,40, 50, 60,… She found something common in these numbers. Can you tell me what? J Each of these numbers has 0 in one place.
She thought of some more numbers with 0 at one place ^ like 100,1000,3200,7010. She also found that all such numbers are divisible by 10.
She finds that if a number has 0 in the ones place then it is divisible by 10. Can you find out the divisibility rule for 100?
Divisibility by 5: Mani found some interesting patterns in the numbers 5,10, 15,20,25,30,35,… Can you tell the pattern? Look at the unit’s place.
All these numbers have either 0 or 5 in their ones place. We know that these numbers are divisible by 5.
Mani took up some more numbers that are divisible by 5, like 105, 215, 6205, 3500. Again these numbers have either 0 or 5 in their places.
He tried to divide the numbers 23, 56, 97 by 5. Will he be able to do that? Check it. He observes that a number that has either 0 or 5 in its place is divisible by 5, other numbers leave a remainder. Is 1750125 divisible 5?
Divisibility by 2: Charu observes a few multiples of 2 to be 10, 12,14,16… and also numbers like 2410,4356, 1358, 2972, 5974.
She finds some patterns in the place of these numbers. Can you tell that? These numbers have only the digits 0, 2,4, 6, and 8 in one place.
She divides these numbers by 2 and gets the remainder 0. She also finds that the numbers 2467, and 4829 are not divisible by 2. These numbers do not have 0, 2, 4, 6, or 8 in their one place.
Looking at these observations she concludes that a number is divisible by 2 if it has any of the digits 0,2,4, 6, or 8 in its ones place.
Divisibility by 3: Are the numbers 21, 27, 36, 54, 219 divisible by 3? Yes, they are.
Are the numbers 25, 37, 260 divisible by 3? No.
Can you see any pattern in the one place? We cannot, because numbers with the same digit in the ones places can be divisible by 3, like 27, or may not be divisible by 3 like 17, 37.
Let us now try to add the digits of 21, 36, 54, and 219. Do you observe anything special? 2+1=3,3+6=9,5+4=9,2+1+9=12.
All these additions are divisible by 3.
Add the digits 25, 37, 260. We get 2+5=7, 3+7=10, 2+6+0 = 8.
These are not divisible by 3.
We say that if the sum of the digits is a multiple of 3, then the number is divisible by 3. Is 7221 divisible by 3?
Divisibility by 6: Can you identify a number that is divisible by both 2 and 3? One such number is 18. Will 18 be divisible by 2×3=6? Yes, it is.
Find some more numbers like 18 and check if they are divisible by 6 also.
Can you quickly think of a number that is divisible by 2 but not by 3?
Now for a number divisible by 3 but not by 2, one example is 27. Is 27 divisible by 6? No. Try to find numbers like 27.
From these observations, we conclude that if a number is divisible by 2 and 3 then it is divisible by 6 also.
Divisibility by 4: Can you quickly give five 3-digit numbers divisible by 4? One such number is 212. Think of such 4-digit numbers. One example is 1936.
Observe the number formed by the ones and tens places of 212. It is 12; which is divisible by 4. For 1936 it is 36, again divisible by 4.
Try the exercise with other such numbers, for example, 4612; 3516; 9532. Is the number 286 divisible by 4? No. Is 86 divisible by 4? No.
So, we see that a number with 3 or more digits is divisible by 4 if the number formed by its last two digits (i.e. ones and tens) is divisible by 4. Check this rule by taking ten more examples.
Divisibility for 1 or 2-digit numbers by 4 has to be checked by actual division.
Divisibility by 8: Are the numbers 1000, 2104, and 1416 divisible by 8? You can check that they are divisible by 8. Let us try to see the pattern.
Look at the digits at ones, tens, and hundreds in place of these numbers. These are 000,104 and 416 respectively. These too are divisible by 8.
Find some more numbers in which the number formed by the digits at units, tens, and hundreds place (i.e. last 3 digits) is divisible by 8.
For example, 9216,8216,7216,10216, 9995216, etc. You will find that the numbers themselves are divisible by 8.
We find that a number with 4 or more digits is divisible by 8 if the number formed by the last three digits is divisible by 8. Is 73512 divisible by 8?
The divisibility for numbers with 1,2 or 3 digits by 8 has to be checked by actual division.
Divisibility by 9: The multiples of 9 are 9, 18, 27, 36, 45, 54,… There are other numbers like 4608, and 5283 that are also divisible by 9.
Do you find any pattern when the digits of these numbers are added?
1 + 8 = 9, 2 + 7 = 9, 3 + 6 = 9, 4 + 5 = 9 4 + 6 + 0 + 8= 18,5 + 2 + 8 + 3 = 18 All these sums are also divisible by 9. Is the number 758 divisible by 9?
No. The sum of its digits 7 + 5 + 8 = 20 is also not divisible by 9.
These observations lead us to say that if the sum of the digits of a number is divisible by 9, then the number itself is divisible by 9.
Divisibility by 11: The numbers 308,1331 and 61809 are all divisible by 11. We form a table and see if the digits in these numbers lead us to some pattern.

We observe that in each case the difference is either 0 or divisible by 11. All these numbers are also divisible by 11.
For the number 5081, the difference between the digits is (5+8) – (1+0) = 12 which is not divisible by 11. The number 5081 is also not divisible by 11.
Thus, to check the divisibility of a number by 11, the rule is, to find the difference between the sum of the digits at odd places (from the right) and the sum of the digits at even places (from the right) of the number.
If the difference is either 0 or divisible by 11, then the number is divisible by 11.
Observe the factors of some numbers taken in pairs.
1. What are the factors of 4 and 18?
The factors of 4 are 1, 2, and 4.
The factors of 18 are 1,2,3,6,9 and 18.
The numbers 1 and 2 are the factors of both 4 and 18.
They are the common factors of 4 and 18.
2. What are the common factors of 4 and 15?
These two numbers have only 1 as the common factor.
What about 7 and 16?
Two numbers having only 1 as a common factor are called co-prime numbers. Thus, 4 and 15 are co-prime numbers.
Are 7 15,12 49,18 and 23 co-prime numbers?
3. Can we find the common factors of 4,12 and 16?
Factors of 4 are 1, 2, and 4.
Factors of 12 are 1, 2, 3, 4, 6 and 12.
Factors of 16 are 1, 2, 4, 8 and 16.
Clearly, 1, 2, and 4 are the common factors of 4,12, and 16.
Find the common factors of (1) 8, 12, 20 (2) 9,15, 21.
Let us now look at the multiples of more than one number taken at a time.
1. What are the multiples of 4 and 6?
The multiples of 4 are 4, 8,12,16, 20,24,… (write a few more)
The multiples of 6 are 6,12,18, 24, 30, 36,… (write a few more)
Out of these, are there any numbers that occur in both lists?
We observe that 12,24, 36,… are multiples of both 4 and 6.
Can you write a few more?
They are called the common multiples of 4 and 6.
2. Find the common multiples of 3,5 and 6.
Multiples of 3 are 3, 6, 9,12,15, 18,21, 24, 27, 30, 33, 36,… Multiples of 5 are 5,10,15, 20, 25, 30, 35,…
Multiples of 6 are 6, 12, 18, 24, 30,…
Common multiples of 3,5 and 6 are 30, 60,…
Write a few more common multiples of 3,5 and 6.
Example 5: Find the common factors of 75,60 and 210.
Solution:
Factors of 75 are 1, 3, 5, 15, 25 and 75.
Factors of 60 are 1, 2, 3,4, 5, 6,10,12, 15, 30 and 60.
Factors of 210 are 1,2,3,5,6,7,10,14,15,21,30,35,42,70,105 and 210.
Thus, common factors of 75,60 and 210 are 1,3,5 and 15.
Example 6: Find the common multiples of 3,4 and 9.
Solution:
Multiples of 3 are 3,6,9,12,15,18, 21, 24,27,30, 33,36, 39,42, 45,48,….
Multiples of 4 are 4, 8,12,16, 20, 24, 28, 32, 36, 40,44,48,…
Multiples of 9 are 9,18, 27, 36,45, 54,63, 72, 81,…
Clearly, common multiples of 3,4, and 9 are 36,72,108,…
When a number is expressed as a product of its factors we say that the number has been factorised. Thus, when we write 24 = 3×8, we say that 24 has been factorized. This is one of the factorizations of 24.
The others are:
24 = 2 x 12
= 2 x 2 x 6
= 2 x 2 x 2 x 3
24 = 4 x 6
= 2 x 2 x 6
= 2 x 2 x 2 x 3
24 = 3 x 8
= 3 x 2 x 2 x 2
= 2 x 2 x 2 x 3
In all the above factorisations of 24, we ultimately arrive at only one factorisation 2 x 2 x 2 x 3. In this factorization, the only factors 2 and 3 are prime numbers.
Such a factorization of a number is called a prime factorization. Let us check this for the number 36.
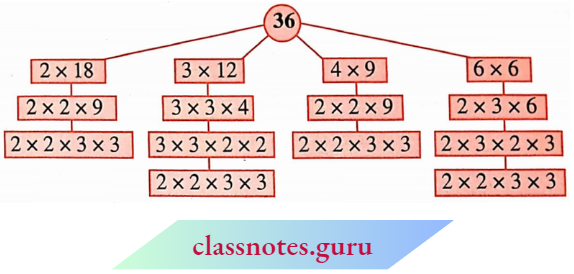
The prime factorization of 36 is 2 x 2 x 3 x 3. i.e. the only prime factorization of 36.
Example 7: Find the prime factorization of 980.
Solution:
We proceed as follows:
We divide the number 980 by 2,3,5,7 etc. in this order repeatedly so long as the quotient is divisible by that number. Thus, the prime factorization of 980 is 2 x 2 x 5 x 7 x 7.
⇒ \(\begin{array}{r|r}
2 & 980 \\
\hline 2 & 490 \\
\hline 5 & 245 \\
\hline 7 & 49 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
We can find the common factors of any two numbers. We now try to find the highest of these common factors.
What are the common factors of 12 and 16? They are 1,2 and 4.
What is the highest of these common factors? It is 4.
What are the common factors of 20, 28 and 36? They are 1, 2 and 4 and again 4 is the highest of these common factors.
The Highest Common Factor (HCF) of two or more given numbers is the highest (or greatest) of their common factors.
It is also known as the Greatest Common Divisor (GCD).
The HCF of 20, 28, and 36 can also be found by prime factorization of these numbers as follows:
⇒ \(\begin{array}{l|l}
2 & 20 \\
\hline 2 & 10 \\
\hline 5 & 5 \\
\hline & 1
\end{array}\)
⇒ \(\begin{array}{l|l}
2 & 28 \\
\hline 2 & 14 \\
\hline 7 & 7 \\
\hline & 1
\end{array}\)
⇒ \(\begin{array}{l|l}
2 & 36 \\
\hline 2 & 18 \\
\hline 3 & 9 \\
\hline 3 & 3 \\
\hline & 1
\end{array}\)
Thus,
20 = 2 x 2 x 5
28 = 2 x 2 x 7
36 = 2 x 3 x 3
The common factor of 20,28 and 36 is 2(occurring twice). Thus, HCF of 20, 28 and 36 is 2 x 2 = 4.
What are the common multiples of 4 and 6? They are 12,24,36,… Which is the lowest of these? It is 12.
We say that the lowest common multiple of 4 and 6 is 12. It is the smallest number and both the numbers are factors of this number.
The Lowest Common Multiple (LCM) of two or more given numbers is the lowest (or smallest or least) of their common multiples. What will be the LCM of 8 and 12? 4 and 9? 6 and 9?
Example 8: Find the LCM of 12 and 18.
Solution:
We know that common multiples of 12 and 18 are 36,72,108 etc. The lowest of these is 36. Let us see another method to find the LCM of two numbers.
The prime factorizations of 12 and 18 are:
12 = 2 x 2 x 3; 18 = 2 x 3 x 3
In these prime factorizations, the maximum number of times the prime factor 2 occurs is two; this happens for 12. Similarly, the maximum number of times the factor 3 occurs is two; this happens for 18.
The LCM of the two numbers is the product of the prime factors counted the maximum number of times they occur in any of the numbers. Thus, in this case, LCM = 2 x 2 x 3 x 3 = 36.
Example 9: Find the LCM of 24 and 90.
Solution:
The prime factorizations of 24 and 90 are:
24 = 2 x 2 x 2 x 3; 90 = 2 x 3 x 3 x 5
In these prime factorizations, the maximum number of times the prime factor 2 occurs is three; this happens for 24.
Similarly, the maximum number of times the prime factor 3 occurs is two; this happens for 90. The prime factor 5 occurs only once in 90.
Thus, LCM = (2 x 2 x 2) x (3 x 3) x 5 = 360
Example 10: Find the LCM of 40, 48 and 45.
Solution:
The prime factorizations of 40,48 and 45 are;
40 = 2 x 2 x 2 x 5
48 = 2 x 2 x 2 x 2 x 3
45 = 3 x 3 x 5
The prime factor 2 appears a maximum number of four times in the prime factorization of 48, the prime factor 3 occurs a maximum number of two times in the prime factorization of 45, The prime factor 5 appears one time in the prime factorizations of 40 and 45, we take it only ponce.
Therefore, required LCM = (2 x 2 x 2 2) x (3 x 3) x 5 = 720
LCM can also be found in the following way:
Example 11: Find the LCM of 20, 25 and 30.
Solution:
We write the numbers as follows in a row:
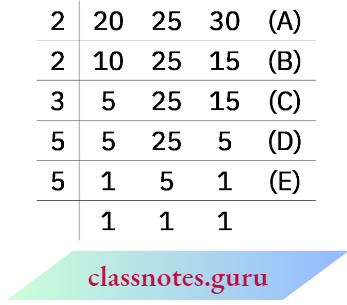
So, LCM = 2 x 2 x 3 x 5 x 5.
We come across a number of situations in which we make use of the concepts of HCF and LCM. We explain these situations through a few examples.
Example 12: Two tankers contain 850 liters and 680 liters of kerosene oil respectively. Find the maximum capacity of a container that can measure the kerosene oil of both tankers when used an exact number of times.
Solution:
The required container has to measure both tankers in a way that the count is an exact number of times.
So its capacity must be an exact divisor of the capacities of both the tankers. Moreover, this capacity should be maximum. Thus the maximum capacity of such a container will be the HCF of 850 and 680.
⇒ \(\begin{array}{l|l}
2 & 850 \\
\hline 5 & 425 \\
\hline 5 & 85 \\
\hline 17 & 17 \\
\hline & 1
\end{array}\)
⇒ \(\begin{array}{l|l}
2 & 680 \\
\hline 2 & 340 \\
\hline 2 & 170 \\
\hline 5 & 85 \\
\hline 17 & 17 \\
\hline & 1
\end{array}\)
Hence,
850 = 2 x 5 x 5 x 17 = 2 x 5 x 17 x 5 and
680 = 2 x 2 x 2 x 5 x 17 = 2 x 5 x 17 x 2 x 2
The common factors of 850 and 680 are 2, 5 and 17.
Thus, the HCF of 850 and 680 is 2 x 5 x 17 = 170.
Therefore, the maximum capacity of the required container is 170 liters.
It will fill the first container in 5 and the second in 4 refills.
Example 13: In a morning walk, three persons step off together. Their steps measure 80 cm, 85 cm, and 90 cm respectively. What is the minimum distance each should walk so that all can cover the same distance in complete steps?
Solution:
The distance covered by each one of them is required to be the same as well as minimum. The required minimum distance each should walk would be the lowest common multiple of the measures of their steps.
Can you describe why? Thus, we find the LCM of 80, 85, and 90. The LCM of 80, 85, and 90 is 1 2240.
The required minimum distance is 12240 cm.

Example 14: Find the least number which when divided by 12, 16, 24, and 36 leaves a remainder of 7 in each case.
Solution:
We first find the LCM of 12, 16, 24, and 36 as follows:
∴ \(\begin{array}{c|cccc}
2 & 12 & 16 & 24 & 36 \\
\hline 2 & 6 & 8 & 12 & 18 \\
\hline 2 & 3 & 4 & 6 & 9 \\
\hline 2 & 3 & 2 & 3 & 9 \\
\hline 3 & 3 & 1 & 3 & 9 \\
\hline 3 & 1 & 1 & 1 & 3 \\
\hline & 1 & 1 & 1 & 1
\end{array}\)
Thus, LCM = 2 x 2 x 2 x 2 x 3 x 3 = 144
144 is the least number which when divided by the given numbers will leave the remainder 0 in each case. But we need the least number that leaves the remainder 7 in each case.
Therefore, the required number is 7 more than 144. The required least number = 144 + 7 = 151.
As we know, we use 1, 2, 3, 4,… when we begin to count. They come naturally when Westart is counting. Hence, Mathematically call the counting numbers Natural numbers.
Predecessor And Successor
Given any natural number, you can add 1 to that number and get the next number i.e. you get its successor.
The successor of 16 is 16 + 1 = 17, that of 19 is 19 +1 = 20 and so on.
The number 16 comes before 17, we say that the predecessor of 17 is 17-1=16, the predecessor of 20 is 20 – 1 = 19, and so on.
The number 3 has a predecessor and a successor. What about 2? The successor is 3 and the predecessor is 1. Does 1 have both a successor and a predecessor?
We can count the number of children in our school; we can also count the number of people in a city; we can count the number of people in India. The number of people in India.
the number of people in the whole world can also be counted. We may not be able to count the number of stars in the sky or the number of hair on our head but if we are able, there would be a number for them also.

We can then add one more to such a number and get a larger number. In that case, we can even write the number of hair on two heads taken together.
It is now perhaps obvious that there is no largest number. Apart from these questions shared above, there are many others that can come to our mind when we work with natural numbers.
Read and Learn More NCERT Notes for Class 6 Maths
You can think of a few such questions and discuss them with your friends. You may not clearly know the answers to many of them!
We have seen that the number 1 has no predecessor in natural numbers. To the
collection of natural numbers we add zero as the predecessor for 1.
The natural numbers along with zero form the collection of whole numbers.
In your previous classes, you have learnt to perform all the basic operations like addition, subtraction, multiplication and division of numbers.
You also know how to apply them to problems. Let us try them on a number line. Before we proceed, let us find out what a number line is!
Draw a line. Mark a point on it. Label it 0. Mark a second point to the right of 0. Label it 1.
The distance between these points labelled as 0 and 1 is called unit distance.
On this line, mark a point to the right of 1 and at a unit distance from 1 and label it 2. In this way go on labelling points at unit distances as 3, 4, 5,… on the line. You can go to any whole number on the right in this manner.
This is a number line for all numbers.

What is the distance between the points 2 and 4? Certainly, it is 2 units. Can you tell the distance between the points 2 and 6, between 2 and 7?
On the number line, you will see that the number 7 is on the right of 4. his number 7 is greater than 4, i.e. 7 > 4. The number 8 lies on the right of 6 and 8 > 6.
These observations help us to say that, out of any two whole
numbers, the number on the right of the other number is the greater number.
We can also say that the whole number on the left is the smaller number.
For example, 4 < 9; 4 is on the left of 9. Similarly, 12 > 5; 12 is to the
right of 5.
What can you say about 10 and 20?
Mark 30, 12, and 18 on the number line. Which number is at the farthest left? Can you say which number from 1005 and 9756 would be on the right relative to the other number?
Place the successor of 12 and the predecessor of 7 on the number line.
Addition on the number line
The addition of whole numbers can be shown on the number line. Let us see the addition of 3 and 4.
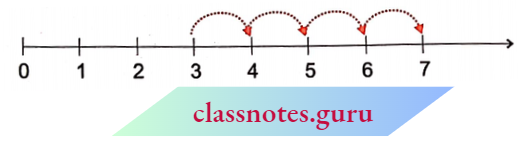
Start from 3. Since we add 4 to this number we make 4 jumps to the right; from 3 to 4, 4 to 5, 5 to 6 and 6 to 7 as shown above. The tip of the last arrow in the fourth jump is at 7.
The sum of 3 and 4 is 7, i.e. 3 + 4 = 7.
Subtraction on the number line
The subtraction of two whole numbers can also be shown on the number line.
Let us find 7-5.
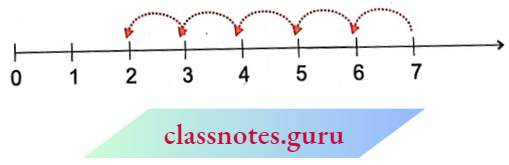
Start from 7. Since 5 is being subtracted, so move towards left with 1 jump of 1 unit. Make 5 such jumps. We reach the point 2. We get 7- 5 = 2.
Multiplication on the number line
We now see the multiplication of whole numbers on the number line.
Let us find 4 x 3.
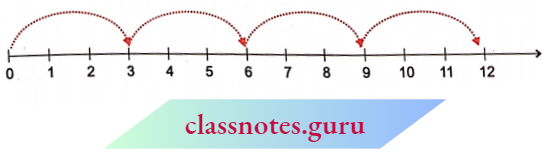
Start from 0, move 3 units at a time to the right, and make such 4 moves. Where do you reach? You will reach 12. So, we say, 3 x 4 = 12.
Counting things is easy for us now. We can count objects in large numbers, for example, the number of students in the school, and represent them through numerals. We can also communicate large numbers using suitable number names.
It is not as if we always knew how to convey large quantities in conversation or through symbols. Many thousands of years ago, people knew only small numbers. Gradually, they learned how to handle larger numbers.
They also learned how to express large numbers in symbols. All this came through the collective efforts of human beings. Their path was not easy, they struggled all along the way.
The development of the whole of Mathematics can be understood this way. As human beings progressed, there was a greater need for the development of Mathematics and as a result, Mathematics grew further and faster.
We use numbers and know many things about them. Numbers help us count concrete objects. They help us to say which collection of objects is bigger and arrange them for example, first, second, etc.
Read and Learn More NCERT Notes for Class 6 Maths
Numbers are used in many different contexts and in many ways. Think about various situations where we use numbers. List five distinct situations in which
numbers are used.
We enjoyed working with numbers in our previous classes. We have added, subtracted, multiplied, and divided them. We also looked for patterns in number sequences and did many other interesting things with numbers.
In this chapter, we shall move forward on such interesting things with a bit of review and revision as well.

As we have done quite a lot of this earlier, let us see if we remember which is the greatest among these:
1. 92, 392, 4456, 89742
89742 I am the greatest
2. 1902, 1920, 9201, 9021, 9210
9210 I am the greatest
So, we know the answer
We just looked at the number of digits and found the answer. The greatest number has the most thousands and the smallest is only in hundreds or in tens.
Make five more problems of this kind and give them to your friends to solve.
Now, how do we compare 4875 and 3542?
This is also not very difficult. These two numbers have the same number of digits. They are both in thousands. But the digit at the thousands place in 4875 is greater than that in 3542. Therefore, 4875 is greater than 3542.
Next tell me which is greater, 4875 or 4542? Here too the numbers have the same number of digits. Further, the digits at the thousands place are the same in both.
What do we do then? We move to the next digit, that is to the digit at the hundreds place. The digit at the hundreds place is greater in 4875 than in 4542. Therefore, 4875 is greater than 4542.
If the digits at the hundreds place are also the same in the two numbers, then what do we do?
Compare 4875 and 4889; Also compare 4875 and 4879.
How Many Numbers Can You Make?
Suppose, we have four digits 7, 8, 3, 5. Using these digits we want to make different 4-digit numbers in such a way that no digit is repeated in them. Thus, 7835 is allowed, but 7735 is not. Make as many 4-digit numbers as you can.
Which is the greatest number you can get? Which is the smallest number?
The greatest number is 8753 and the smallest is 3578.
Think about the arrangement of the digits in both. Can you say how the largest number is formed? Write down your procedure.
Shifting Digits
Have you thought how fun it would be if the digits in a number could shift (move^frpm from one place to the other?
Thinlq about what would happen to 182. It could become as large as 821 and as small as 128. Try this with 391 as well.
Now think about this. Take any 3-digit number and exchange the digit at the hundreds place with the digit at the one’s place.
Write the numbers formed in both ascending and descending order.
Before 7 9 5
Exchanging the 1st and the 3rd tiles.
After 5 9 7
If you exchange the 1st and the 3rd tiles (i.e. digits), in which case does the number become greater? In which case does it become smaller?
Try this with a 4-digit number.
Introducing 10,000
We know that beyond 99 there is no 2-digit number. 99 is the greatest 2-digit number. Similarly, the greatest 3-digit number is 999 and the greatest 4-digit number is 9999. What shall we get if we add 1 to 9999?
Look at the pattern:
9 + 1 = 10 = 10 x 1
99 + 1 = 100 = 10 x 10
999 + 1 = 1000 = 10 x 100
We observe that
Greatest single digit number + 1 = smallest 2-digit number
Greatest 2-digit number + 1 = smallest 3-digit number
Greatest 3-digit number + 1 = smallest 4-digit number
We should then expect that on adding 1 to the greatest 4-digit number, we would get the smallest 5-digit number, that is 9999 + 1 = 10000.
The new number which comes next to 9999 is 10000. It is called ten thousand. Further, 10000 = 10 x 1000.
Revisiting Place Value
You have done this quite earlier, and you will certainly remember the expansion of a 2-digit number like 78 as 78 = 70 + 8 = 7 x 10 + 8
Similarly, you will remember the expansion of a 3-digit number like 278 as 278 = 200 + 70 + 8 = 2 x 100 + 7 x 10 + 8
We say, here, 8 is at one place, 7 is at the tens place, and 2 at the hundreds place.
Later on, we extended this idea to 4-digit numbers.
For example, the expansion of 5278 is 5278 = 5000 + 200 + 70 + 8
= 5 x 1000 + 2 x 100 + 7 x 10 + 8
Here, 8 is at one place, 7 is at the tens place, 2 is at the hundreds place and 5 is at the thousands place.
With the number 10000 known to us, we may extend the idea further. We may write 5-digit numbers like 45278 = 4 x 10000 + 5 x 1000 + 2 x 100 + 7 x 10 + 8
We say that here 8 is at one place, 7 at the tens place, 2 at the hundreds place, 5 at the thousands place, and 4 at ten thousand places.
The number is read as forty-five thousand, two hundred seventy-eight. Can you now write the smallest and the greatest 5-digit numbers?
Introducing 1,00,000
Which is the greatest 5-digit number?
Adding 1 to the greatest 5-digit number should give the smallest 6-digit number: 99,999 + 1 = 1,00,000
This number is named one lakh. One lakh comes next to 99,999.
10 x 10,000 = 1,00,000
We may now write 6-digit numbers in the expanded form as
2,46,853 = 2 x 1,00,000 + 4x 10,000 + 6 x 1,000 + 8 x 100 + 5 x 10 + 3 x 1
This number is 3 in one place, 5 in the tens place, 8 in the hundreds place, 6 in the thousands place, 4 in ten thousand places, and 2 in lakh place. Its number name is two lakh forty-six thousand eight hundred fifty three.
Larger numbers
If we add one more to the greatest 6-digit number we get the smallest 7-digit number. It is called ten lakh.
Write down the greatest 6-digit number and the smallest 7-digit number. Write the greatest 7-digit number and the smallest 8-digit number. The smallest 8-digit number is called one crore.
Complete The Pattern:
Remember
1 hundred =10 tens
1 thousand = 10 hundreds = 100 tens
1 lakh = 100 thousands = 1000 hundreds
1 crore =100 lakhs = 10,000 thousands
9 + 1 = 10
99 + 1 = 100
999 + 1 = 1,000
9.999 + 1 = 10,000
99.999 + 1 = 1,00,000
9.99.999 + 1 = 10,00,000
99.99.999 + 1 = 1,00,00,000
We come across large numbers in many different situations. For example, while the number of children in your class would be a 2-digit number, the number of children in your school, would be a 3 or 4-digit number.
The number of people in the nearby town would be much larger.
You must have noticed that in writing large numbers in the sections above, we have often used commas.
Commas help us in reading and writing large numbers. In our Indian System of Numeration, we use ones, tens, hundreds, thousands, and then lakhs and crores.
Commas are used to mark thousands, lakhs, and crores. The first comma comes after hundreds place (three digits from the right) and marks thousands. The second comma comes two digits later (five digits from the right).
It comes after ten thousand places and marks lakh. The third comma comes after another two digits (seven digits from the right). It comes after ten lakh place and marks crore.
For example,
5,08,01,592
3,32,40,781
7,27,05,062
Try reading the numbers given above. Write five more numbers in this form and read them.
International System of Numeration
In the International System of Numeration, as it is being used we have ones, tens, hundreds, thousands, and then millions. One million is a thousand thousand. Commas are used to mark thousands and millions.
It comes after every three digits from the right. The first comma marks thousands and the next comma marks millions. For example, the number 50,801,592 is read in the International System as fifty million eight hundred one thousand five hundred ninety-two.
In the Indian System, it is five crore eight lakh one thousand five hundred ninety-two.
How many lakhs make a million?
How many millions make a crore?
Take three large numbers. Express them in both Indian and International Numeration systems.
Interesting Fact:
To express numbers larger than a million, a billion is used in the International System of Numeration: 1 billion = 1000 million.
In earlier classes, we learned that we use centimeters (cm) as a unit of length. For measuring the length of a pencil, the width of a book or notebook, etc., we use centimeters. Our ruler has marks on each centimeter.
However, we find centimeters too big when measuring the thickness of a pencil. We use millimeters (mm) to show the thickness of a pencil.
1. 10 millimetres = 1 centimetre
To measure the length of the classroom or the school building, we shall find a centimeter too small. We use meters for this purpose.
2. 1 metre =100 centimetres = 1000 millimetres
Even meter is too small when we have to state distances between cities, say, Delhi and Mumbai, or Chennai and Kolkata. For this, we need kilometers (km).
3. 1 kilometre = 1000 metres
How many millimeters make 1 kilometer?
Since 1 m = 1000 mm
1 km = 1000 m = 1000 x 1000 mm = 10,00,000 mm
We go to the market to buy rice or wheat; we buy it in kilograms (kg). But items like ginger or chilies which we do not need in large quantities, we buy in grams (g). We know 1 kilogram = 1000 grams.
Have you noticed the weight of the medicine tablets given to the sick? It is very small. It is in milligrams (mg)
1 gram = 1000 milligrams.
What is the capacity of a bucket for holding water? It is usually 20 liters (l). Capacity is given in liters. But sometimes we need a smaller unit, the milliliters. A bottle of hair oil, a cleaning liquid, or a soft drink has labels that give the quantity of liquid inside in milliliters (ml).
1 litre = 1000 millilitres.
Note that in all these units we have some words in common like kilo, milli, and centi. You should remember that among these kilo is the greatest and milli is the smallest; the kilo shows 1000 times greater, and the milli shows 1000 times smaller, i.e. 1 kilogram = 1000 grams, 1 gram = 1000 milligrams.
Similarly, centi shows 100 times smaller, i.e. 1 metre = 100 centimetres.
We have done a lot of problems that have addition, subtraction, multiplication, and division. We will try solving some more here. Before starting, look at these examples and follow the methods used.
Example 1. The population of Sundamagar was 2,35,471 in the year 1991. In the year 2001, it was found to be increased by 72,958. What was the population of the city in 2001?
Solution:
Population of the city in 2001
= Population of the city in 1991 + Increase in population = 2,35,471 + 72,958
Now, \(\begin{array}{r}
235471 \\
+72958 \\
\hline 308429 \\
\hline
\end{array}\)
Salma added them by writing 235471 as 200000 + 35000 + 471 and 72958 as 72000+958. She got the addition as 200000 +107000 +1429 = 308429. Mary added it as 200000 + 35000 + 400 + 71 + 72000 + 900 + 58 = 308429
Answer: The population of the city in 2001 was 3,08,429
All three methods are correct.
Example 2. In one state, the number of bicycles sold in the year 2002-2003 was 7,43,000. In the year 2003-2004, the number of bicycles sold was 8,00,100. In which year were more bicycles sold? and how many more?
Solution:
Clearly, 8,00,100 is more than 7,43,000. So, in that state, more bicycles were sold in the year 2003-2004 than in 2002-2003.
Now, \(\begin{array}{r}
800100 \\
-743000 \\
\hline 057100 \\
\hline
\end{array}\)
Check the answer by adding \(\begin{array}{r}
743000 \\
+57100 \\
\hline 800100 \\
\hline
\end{array}\) (the answer is right)

Can you think of alternative ways of solving this problem?
Answer: 57,100 more bicycles were sold in the year 2003-2004.
Example 3. The town newspaper is published every day. One copy has 12 pages, every day 11,980 copies are printed. How many total pages are printed every day?
Solution:
Each copy has 12 pages. Hence, 11,980 copies. will have 12 x 11,980 pages. What would this number be? More than 1,00,000 or lesser.
Try to estimate.
Now, \(\begin{array}{r}
11980 \\
\times 12 \\
\hline 23960 \\
+\quad 119800 \\
\hline 143760 \\
\hline
\end{array}\)

Answer: Every day 1,43,760 pages are printed.
Example 4. The number of sheets of paper available for making notebooks is 75,000. Each sheet makes 8 pages of a notebook. Each notebook:(contains 200 pages. How many notebooks can be made from the paper available?
Solution:
Each sheet makes 8 pages.
Hence, 75,000 sheets make 8 x 75,000 pages,
Now, \(\begin{array}{r}
75000 \\
\times 8 \\
\hline 600000 \\
\hline
\end{array}\)

Thus, 6,00,000 pages are available for making notebooks.
Now, 200 pages make 1 notebook.
Hence, 6,00,000 pages make 6,00,000 -r 200 notebooks.
Now,
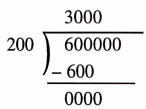
The answer is 3,000 notebooks.
An average is which represents the large number of observations in a concise or single numerical data. It is a representative value around which all the values of the variable concentrate. It is called the measure of central tendency.
The word ‘average’ has been defined differently by various authors. According to Dr. Bowley, “Statistics is the science of averages.”
According to Gorton and Cowden, “An average is a single value within the range of the data used to represent all the values in the series.”
It is clear from the above definitions that an average is a single value that represents a group of values.
Read and Learn More Class 10 Maths Solutions Exemplar

NCERT Exemplar Solutions Class 10 Maths Chapter 14 Statistics
Objectives Of Statistical Averages
The statistical average has the following objectives:
Properties Of Statistical Averages
Good averages should possess the following properties:
Types Of Averages
There are different types:
Mean is that value that can be calculated by dividing the sum of all terms of the series by the number of terms of the series.
Characteristics of Mean
For example, the average of 5, 9, and 10 is \(\frac{5+9+10}{3}=8\) which is not an observation in the series. Now, we shall discuss the mean of grouped data.
Direct Method for the Mean of a Grouped Frequency Distribution
Step 1: Find the class mark xi for each class: \(x_i=\frac{\text { lower limit }+ \text { upper limit }}{2}\)
Step 2: Find xi for each i.
Step 3 : Find the mean using the formula, mean = \(\frac{\Sigma f_i x_i}{\Sigma f_i}\)
Direct Method For The Mean Of A Grouped Frequency Distribution Solved Examples
Question 1. Find the mean of the following frequency distribution by direct method:

Solution:
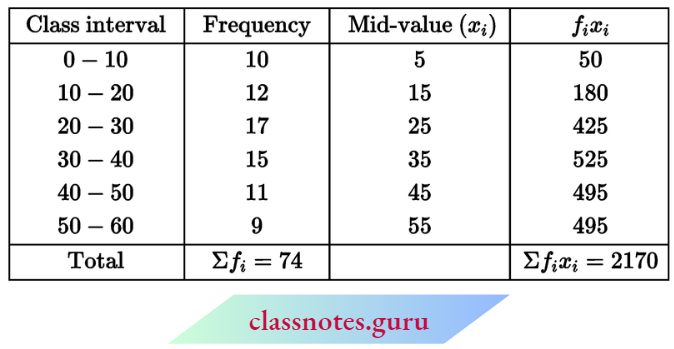
Now, \(\text { mean } \bar{x}=\frac{\Sigma f_i x_i}{\Sigma f_i}=\frac{2170}{74}=29.32\)
Question 2. If the mean of the following data is 26, then find the value of p:

Solution:
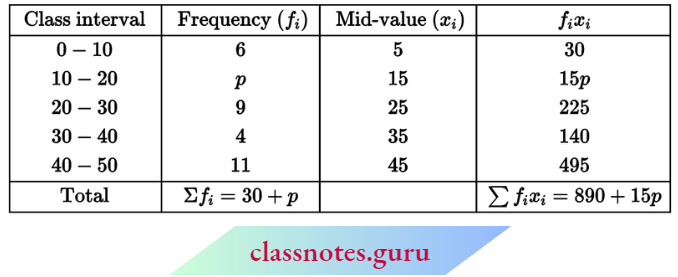
Now, arithmetic mean \(\bar{x}=\frac{\Sigma f_i x_i}{\Sigma f_i}\)
⇒ \(26=\frac{890+15 p}{30+p}\)
⇒ 780 + 26p = 890 + 15p
⇒ 11p = 110
⇒ p = 10
The value of p = 10
Question 3. Find the mean from the following data:

Solution:
First, we will convert the given table into a table containing class intervals and corresponding frequencies:
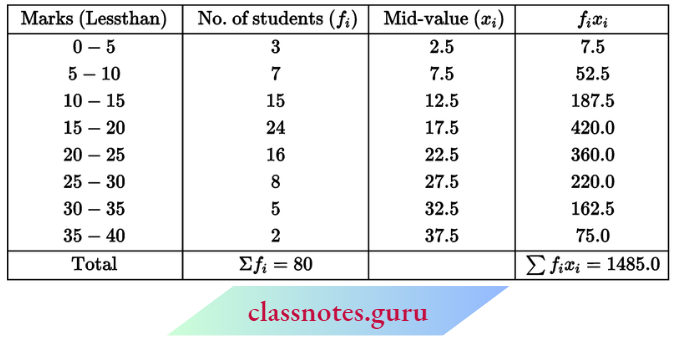
Now, \(\text { mean } \bar{x}=\frac{\Sigma f_i x_i}{\Sigma f_i}=\frac{1485}{80}=18.5625\)
Assumed-Mean Method for the Mean of Grouped Frequency Distribution
Step 1: Find the class marks xi for each class interval: \(x_i=\frac{\text { lower limit }+ \text { upper limit }}{2}\)
Step 2: Choose a suitable value of xi from the middle values as the assumed mean and represent it by ‘a’.
Step 3: Find the deviations di =Xi – a for each i.
Step 4: Fin didi for each i.
Step 5: Find the mean using the formula: \(\bar{x}=a+\frac{\Sigma f_i d_i}{\Sigma f_i}\)
Question 4. Find the mean for the following distribution table by shortcut method:

Solution:
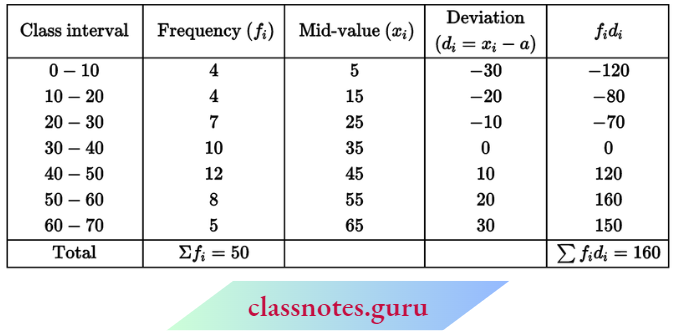
Let assumed mean a = 35
⇒ \(\text { mean } \bar{x}=a+\frac{\Sigma f_i d_i}{\Sigma f_i}=35+\frac{160}{50}=35+3.2=38.2\)
Question 5. The height of 84 trees is given in the following table. Find their arithmetic mean by shortcut method:

Solution:
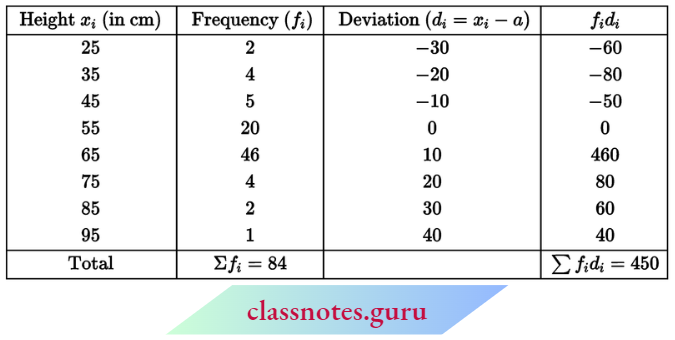
Let assumed mean a = 55
∴ \(\text { mean } \bar{x}=a+\frac{\Sigma f_i d_i}{\Sigma f_i}=55+\frac{450}{84}=55+5.36=60.36 \mathrm{~cm}\)
Step Deviation Method for the Mean of Grouped Frequency Distribution
Step 1: Find the class marks xi for each class. \(x_i=\frac{\text { lower limit }+ \text { upper limit }}{2}\)
Step 2: Choose a suitable value of xi from the middle values as the assumed mean and represent it by ‘a’.
Step 3: Find h = upper limit – a lower limit which is the same for all the classes.
Step 4: Calculate \(u_i=\frac{x_i-A}{h}\) for each i.
Step 5: Calculate fiμi for each i.
Step 6: Find the mean using the formula \(\bar{x}=a+\frac{\Sigma f_i u_i}{\sum f_i} \times h\).
An Important Result
First, we should know the meanings of step and deviation (used in the step-deviation method for finding the mean).
Deviation
All xi’s are deviated (displaced) from their places by adding or subtracting the same non-zero quantity from each value. This is called the deviation.
Step
Big jump or fall in all xi’s in multiples i.e., all xi’s are deviated from their places by multiplying or by dividing with the same number.
But if we divide by only 1, then the step-deviation method and assumed method are the same.
So, if a student is asked to find the mean by step-deviation method and he solves this by assumed mean method then there is no harm.
Question 6. Find the mean of the following table by step deviation method:
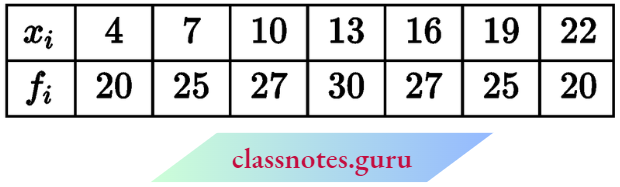
Solution:
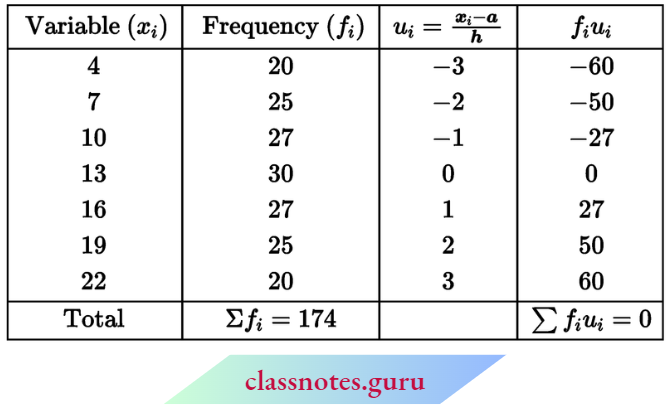
Here, h = 3
Let assumed mean a = 13
∴ \(\text { mean } \bar{x}=a+\frac{\Sigma f_i \cdot u_i}{\Sigma f_i} \times h=13+\frac{0}{174} \times 3=13\)
Question 7. The marks obtained by 30 students are given in the following table. Find their mean-by-step deviation method:

Solution:
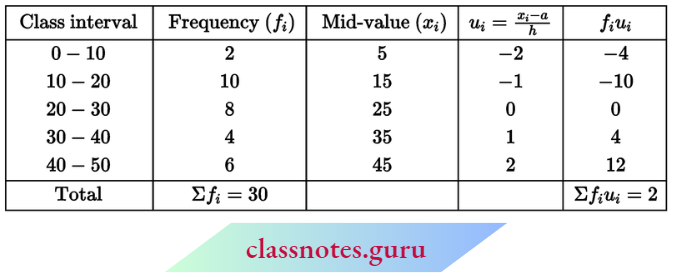
Class 10 Statistics NCERT Exemplar
Let assumed mean a = 25
Here, h = 10
∴ \(\text { mean } \bar{x}=a+\frac{\Sigma f_i u_i}{\Sigma f_i} \times h=25+\frac{2}{30} \times 10=25.67\)
Question 8. Find the mean for the following data by step-deviation method:
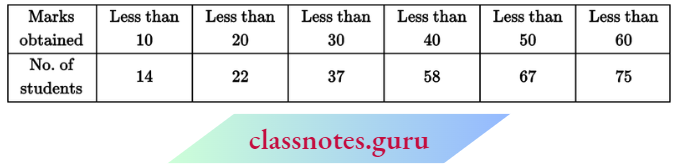
Solution:
The given data can be written in the following form:

Now, \(\text { mean }=a+\frac{\Sigma f_i u_i}{\Sigma f_i} \times h=35+\frac{-48 \times 10}{75}=28.6\)
Question 9. Find the mean for the following distribution:

Solution:
First, we will convert the given table into the exclusive form:
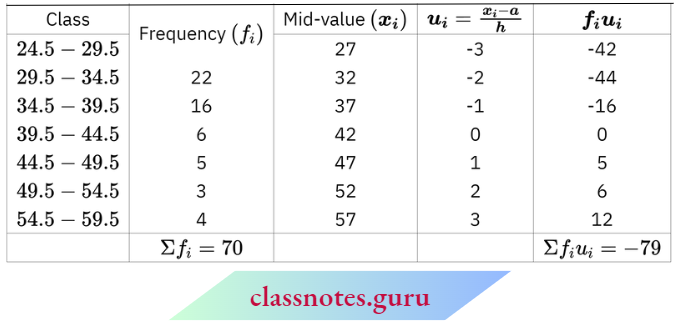
Here, h = 5
Let assumed mean a = 42
Now, \(\text { meàn }=a+\frac{\Sigma f_i u_i}{\Sigma f_i} \times h=42+\frac{(-79) \times 5}{70}=36.36\)
Question 10. Find the class limits corresponding to each frequency if the mean of the following distribution is 33 and the assumed mean is 35:

Solution:
Here, we are given \(\bar{x}=33 \text { and } a=35\)
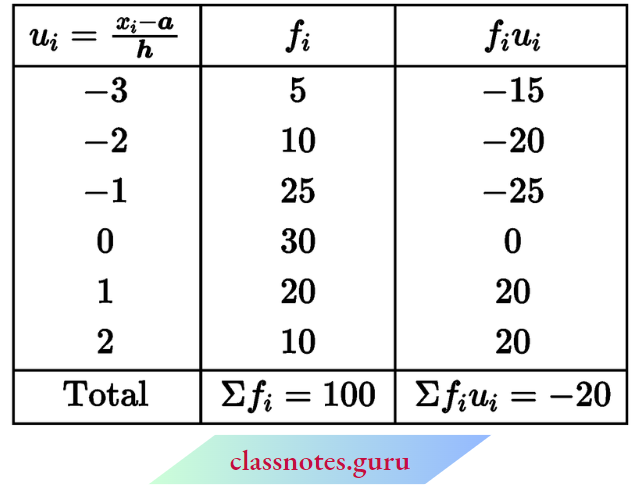
Now, \(\text { mean } \bar{x}=a+\frac{\Sigma f_i u_i}{\Sigma f_i} \times h\)
⇒ \(33=35+\frac{-20}{100} \times h\)
⇒ -200 = -20 h ⇒ h = 10
Now, if \(u_i=-3 \Rightarrow \frac{x_i-35}{10}=-3 \Rightarrow x_i-35=-30 \Rightarrow x_i=5\) and width i.e., h = 10, So, class limits of the first group is 0-10. (subtract and add \(\frac{h}{2}\) from lower and upper boundaries) if \(u_i=-2 ⇒ \frac{x_i-35}{10}=-2 ⇒ x_i-35=-20 x_i=15\) and width i.e., h = 10. So class limits of the second group are 10-20 (subtract and add \(\frac{h}{2}\) from lower and upper boundaries). Similarly, the class limits of other groups are 20-30, 30-40, 40-50 and 50-60.
The median is the value of the variable which divides the group into two equal parts, one part comprising all values greater and the other all values less than the median.
or
The median of a series is the value of that actual or estimated when a series is arranged in ascending or descending order which divides the distribution into two equal parts.
Properties acre Merits of Median
Demerits of Median
Median for Ungrouped Data
Method: Arrange the data in ascending or descending order of their magnitudes. Let the total number of observations be N.
Median for Grouped Data
Method: We make the cumulative frequency table for the grouped data. Now we will find that class interval by dividing the total number of frequencies by 2 in which the median lies. This class interval is called the median class. Now we will use the following result to find the median:
Median \(M=l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)
where l1 = lower limit of the median class
l2 = upper limit of median class
i = l2 – l1
f = frequency of median class
N = sum of frequencies
C = cumulative frequency of the class preceding (just before) the median class
Remark:
If an inclusive (discontinuous) series is given then first of all we will prepare an exclusive series from the given inclusive series. To make it we subtract and add the same number i.e.,
⇒ \(\frac{\text { Lower limit of a class – Upper limit of previous class }}{2}\)
Question 1. Find the median from the following table:

Solution:
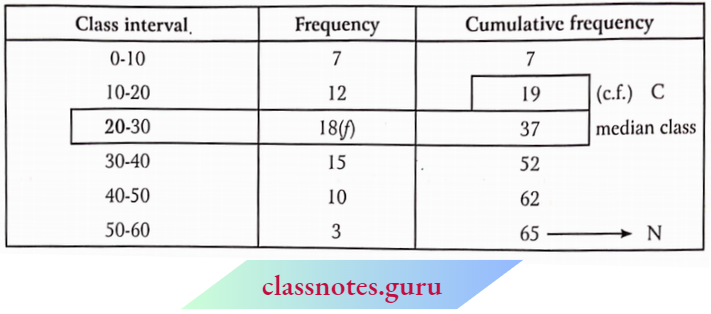
Here, N = 65
∴ For median class \(\frac{N}{2}=\frac{65}{2}=32.5\)
∴ Median class = 20-30
Here l1=20, l2 = 30
⇒ i = 30-20= 10,
f= 18, C= 19
∴ Median \(M=l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i=20+\frac{(32.5-19)}{18} \times 10=20+\frac{135}{18}=27.5\)
Question 2. Find the median from the following table:

Solution:

Here, N = 100
⇒ \(\frac{N}{2}=\frac{100}{2}=50\)
Median class = 40-55
Here l1 = 40, l2 = 55
⇒ i = 55 – 40 = 15, f = 44, C = 26
Now, Median \(M=l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i=40+\frac{(50-26)}{44} \times 15\)
= \(40+\frac{15 \times 24}{44}=40+8.18=48.18\)
Question 3. Find the median from the following data:

Solution:
Converting into a simple frequency table :
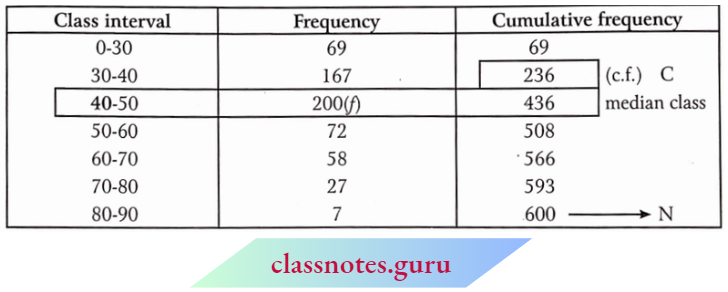
Here, N = 600
⇒ \(\frac{N}{2}=\frac{600}{2}=300\)
∴ Median class = 40-50
and l1 = 40, l2 = 50, i = 50 – 40 = 10, f = 200, C = 236
Now, median \(M=l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i=40+\frac{(300-236)}{200} \times 10\)
= \(40+\frac{10 \times 64}{200}=40+3.2=43.2\)
Question 4. Find the median for the following frequency distribution:

Solution:
First, we will convert the given data into exclusive form:

Here, N = 400
⇒ \(\frac{N}{2}=\frac{400}{2}=200\)
Median class is 165.5 – 168.5
Now, l1 = 165.5, l2 = 168.5, i = 1 68.5 – 165.5 = 3, f= 136, C = 132
and median \(M=l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)
= \(165.5+\frac{(200-132)}{136} \times 3\)
= \(=165.5+\frac{3 \times 68}{136}=167\)
Question 5. Find the median for the following data:

Solution:
Construct the following table from the given data:
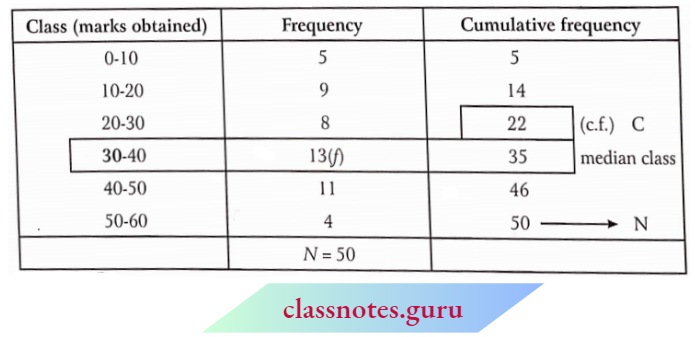
Here, N = 50
⇒ \(\frac{N}{2}=\frac{50}{2}=25\)
The median class is 30 – 40
Now, l1= 30, l2 = 40, i = 40 – 30 = 10, f = 13, C = 22
and median \(M=l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)
= \(30+\frac{(25-22)}{13} \times 10=32.31\)
Question 6. Find the missing frequency if the median for the given distribution is 24:

Solution:

Here, N = 62 + p
⇒ Median = 24
⇒ The median class is 20-30
∴ l1 = 20, l2 = 30 ⇒ i = 30- 20 = 10
f = 25, C = 30
Now, Median \(M=l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)
⇒ \(24=20+\frac{\left(\frac{62+p}{2}-30\right)}{25} \times 10\)
⇒ \(4=\frac{10}{25}\left(\frac{62+p-60}{2}\right)\)
20 = p + 2 ⇒ p = 18
Mode is the value of a variable that occurs most often, i.e., the value of the observation having the maximum frequency (most frequent item of the group).
Modal Class
The class having maximum frequency is called the modal class.
Computation of Mode for a Continuous Frequency Distribution
The formula for Calculating Mode:
Mode = \(l+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)
Where, l = lower limit of modal class
l = frequency of modal class
h = width of the modal class
f0 = frequency of the class preceding the modal class
f2 = frequency of the class following the modal class
Step 1: Determine the class of maximum frequency.
Step 2: Obtain all values required in the formula.
Step 3: Substitute values in the formula and solve.
Question 1. Compute the mode for the following frequency distribution:

Solution:
The modal class is 20-30 as it has the maximum frequency.
∴ I = 20, f1 = 28, f0 = 16, f2 = 20
and h = 10
Mode \(M=l+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)
Mode \(M=20+\frac{28-16}{2 \times 28-16-20} \times 10\)
= \(20+\frac{12}{56-16-20} \times 10=20+\frac{12}{20} \times 10=26 \)
Hence, mode = 26
Question 2. Calculate the value of mode for the following frequency distribution:

Solution:
The given data is in inclusive form. So, we convert it into exclusive form, as given below:

The modal class is 12.5 – 16.5 as it has the maximum frequency.
l =12.5, f1 = 15, f0 = 12, f2 = 14, h = 4
Mode = \(l+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)
Mode = \(12.5+\frac{15-12}{2 \times 15-12-14} \times 4\)
= \(12.5+\frac{3}{4} \times 4=12.5+3=15.5\)
Hence, mode = 15.5
Question 3. The mode of the following series is 17.3. Find the missing frequency:

Solution:
15-20 is the modal class as mode 17.3 lies in this class.
Here, l = 15, f1 = 24, f0=x (say), f2 = 17 and h = 5 and mode = 17.3
∴ Mode(M) = \(l+\frac{f_1-f_0}{2 f_1-f_0-f_2} \times h\)
⇒ \(17.3=15+\frac{24-x}{2 \times 24-x-17} \times 5\)
⇒ \(17.3=15+\frac{24-x}{31-x} \times 5\)
⇒ 2.3 (31 – x) = 120-5x
⇒ 2.3 x 31 – 2.3 x = 120 – 5x
⇒ 5x – 2.3 x = 120 – 71.3
⇒ 2.7 x = 48.7
∴ \(x=\frac{48.7}{2.7}=18.03\)
Hence, the missing frequency is 18.
Question 4. A survey regarding the heights (in cm) of 50 girls in class 10 of a school was conducted and the following data was obtained:

Find the mean, median, and mode of the above data.
Solution:
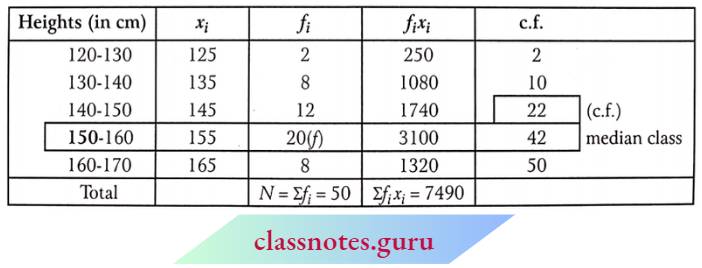
1. Mean: Mean = \(\frac{\Sigma f_i x_i}{\Sigma f_i}=\frac{7490}{50}=149.80\)
2. Median: Here, \(\frac{N}{2}=\frac{50}{2}=25\)
∴ The median class is 150 – 160
∴ Median = \(l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)
= \(150+\frac{25-22}{20} \times 10\)
= 150 + 1.5 = 151.5
3. Mode: The modal class is 150-160 as it has the maximum frequency.
∴ Mode = \(\text { Mode }=l+\left(\frac{f_1-f_0}{2 f_1-f_0-f_2}\right) \times h\)
= \(150+\left(\frac{20-12}{40-12-8}\right) \times 10\)
= \(150+\frac{8}{20} \times 10\)
= 150 + 4 = 154.
Hence, the mean height of the girls = 149.80 cm
the median height = 15 1.5 cm
Empirical Relationship Between Three Measures of Central Tendency
The relationship between mean, median, and mode is.
Mode = 3(Median) – 2(Mean)
and the modal height = 154 cm
Statistics Class 10 Exemplar Questions with Solutions
Question 1. Find the mean and median of the following frequency distribution:

Also, find the mode of the following data.
Solution:
We have
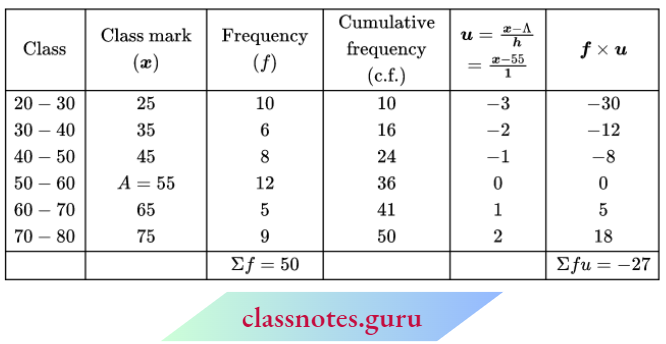
Let assumed mean A = 55, h= 10, Σf= 50 and Σfu = -27
Mean \(\bar{x}=A+\left[h \times \frac{\Sigma(f u)}{\Sigma f}\right]\)
⇒ \(\bar{x}=55+\left(10 \times \frac{-27}{50}\right)\)
⇒ \(\bar{x}=55-5.4\)
⇒ \(\bar{x}=49.6\)
Here, N = 50 \(\frac{N}{2}=\frac{50}{2}=25\)
Cumulative frequency greater than 25 is 36 and the corresponding class is 50-60.
∴ l1=50,/= 12, l2 = 60, C = 24, i = 60-50= 10
Now, \(\text { median }(M)=l_1+\frac{\left(\frac{N}{2}-C\right)}{f} \times i\)
= \(50+\frac{10}{12}(25-24)=50+\frac{10}{12}\)
= 50 + 0.83 = 50.83
Mode = 3(Median) – 2(Mean)
Mode = 3 x 50.83- 2 x 49.60
= 152.49-99.20 = 53.29
Mode = 53.29
An ogive is a freehold graph showing the curve of a cumulative frequency distribution.
If we plot the points talcing the upper limit of the class intervals as x coordinates and their corresponding cumulative frequencies asy coordinates and then join these points by a free hand curve, the curve so obtained is called the cumulative frequency curve.
We may follow the following steps:
Less Than Series
When we mark the upper-class limits along the X-axis and corresponding cumulative frequency polygon along the 7-axis, then the obtained curve is called cumulative frequency curve or ogive for less than series.
Greater Than Series
When we mark the lower class limits along the X-axis and corresponding cumulative frequency polygon along the Y-axis, then the curve so obtained is called cumulative frequency curve or ogive for greater than series.
To Obtain Median From Cumulative Frequency Curve
Method-1
Step 1: Draw a cumulative frequency curve for the given frequency distribution.
Step 2: Locate \(\frac{N}{2}\) on the Y-axis. Let it be M.
Step 3: From point M draw a line parallel to X-axis cutting the curve at point N.
Step 4: From N, draw NP perpendicular to the X-axis cutting the X-axis at P.
The value of P is the median of the data.
Method-2
Step 1: Draw both ogives (less than series and more than series) on the same axis.
Step 2: From the point of intersection of these curves draw perpendicular X-axis. Let it meet the X-axis at point M. Value of M is the required median.
Question 1. Draw a less than cumulative frequency curve (ogive) for the following distribution:

Solution:
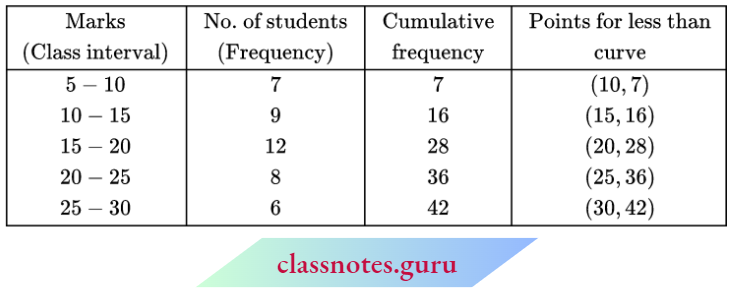
Taking upper-class limits along the X-axis and corresponding cumulative frequencies along the Y-axis mark the points (10, 7) (15, 16), (20, 28), (25, 36), and (30, 42).
Join the points marked by a free-hand curve.
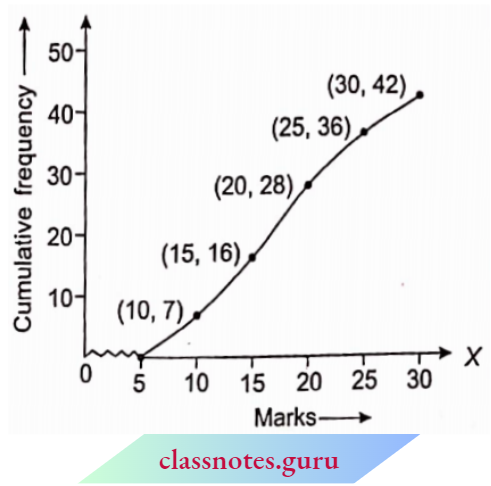
Remark:
Students are advised to leave some points (one on two) without joining, which do not lie on the curve. It is not necessary to join all the points.
This will not affect the median. You can imagine that the given information is not correct, but you have to make a free-hand curve.
Question 2. In a study of the cases of diabetes the following data was obtained:

Draw a less than ogive for the above data.
Solution:
The given frequency distribution is discontinuous, to convert it into a continuous distribution, we subtract 0.5 from the lower limit and add 0.5 to the upper limit respectively. So, the continuous cumulative frequency distribution table is as follows:
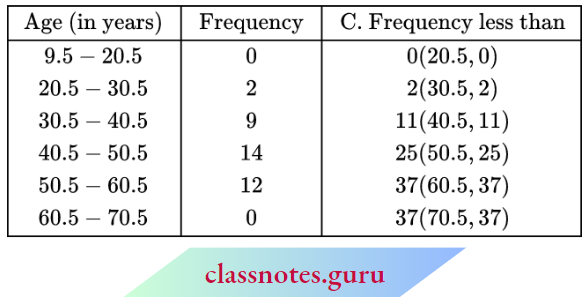
Required ogive is given below:
Question 3. Construct a less than ogive and a more than ogive from the following data:

Solution:
Cumulative frequency distribution table according to ages (in years) less than and more than are:

Question 4. During the medical checkup of 35 students of a class, their weights were recorded as follows:

Draw a less than type and a more than type ogive from the given data. Hence obtain the median weight from the graph.
Solution:
1. Less than Series:
We may prepare the less-than series as follows:
Scale:\(\left\{\begin{array}{l}
\text { Along the } X \text {-axis, } 5 \text { small div. }=1 \mathrm{~kg} . \\
\text { Along the } Y \text {-axis, } 10 \text { small div. }=5 \mathrm{~kg} .
\end{array}\right.\)
We plot the points A(40, 3), B(42, 5), C(44, 9), D(46, 14), E(48, 28), F(50, 32) and G(52, 35).
Join AB, BC, CD, DE, EF, and FG with a free hand to get the curve representing ‘Less than series’.
2. More than Series:
We may prepare more than one series as follows:
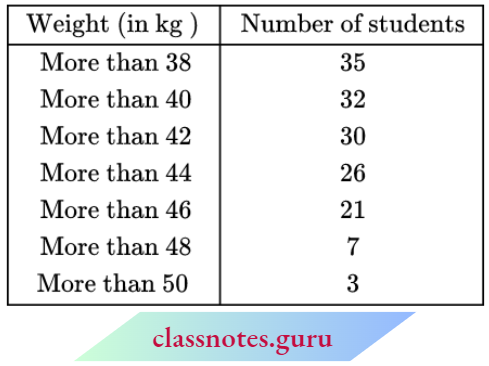
On the same graph-paper as above we plot the points E(38, 35), Q(40, 32), R(42, 30), S(44, 26), 7(46, 21); (7(48, 7) and 7(50, 3). Join EQ, QR, RS, ST, TV, and UV with a free hand to get the curve representing ‘More than series’.
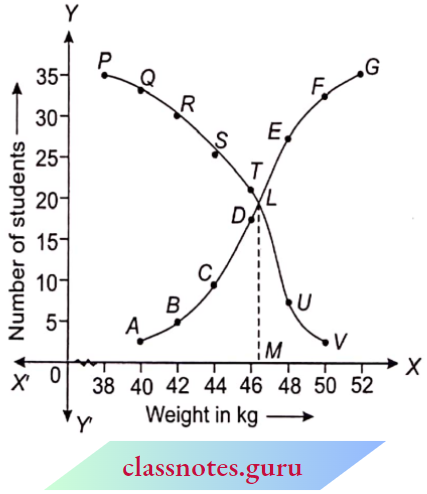
Scale:\(\left\{\begin{array}{l}
\text { Along the } X \text {-axis, } 5 \text { small div. }=1 \mathrm{~kg} \\
\text { Along the } Y \text {-axis, } 10 \text { small div. }=5 \text { students }
\end{array}\right.\)
The two curves intersect at point L. Draw LM ⊥ OX.
∴ Median weight = OM = 46.5 kg
Question 5. Find the median for the following distribution:

Solution:
Using the given data, first of all, construct a cumulative frequency table and then draw ogive (cumulative frequency curve).
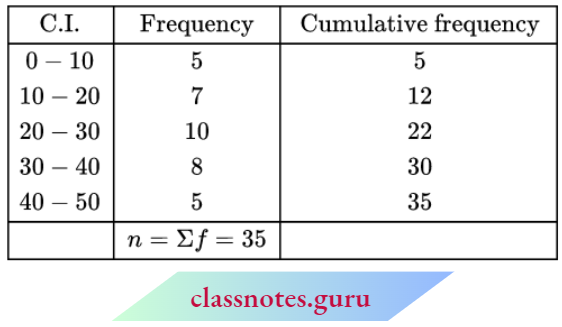
Since, the no. of terms, n = 35
∴ Median = \(\left(\frac{n+1}{2}\right) \text { th term }\)
= \(\left(\frac{35+1}{2}\right) \text { th term }=18 \text { th term }\)
Through mark 18 on the Y-axis, draw a horizontal line that meets the curve at point A.
Through point A, on the curve, the draw meets the X-axis at point B. The value of point B on the X-axis is the median.
It is clear from the cumulative frequency curve drawn that the die median is 26.
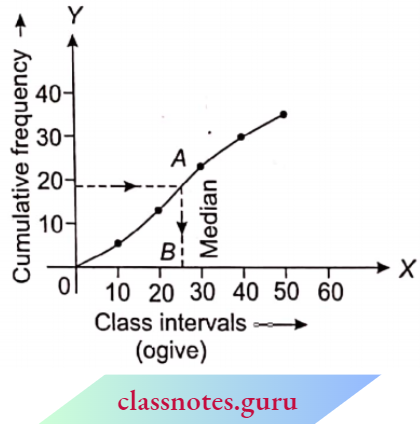
Class 10 Maths Chapter 14 Solutions
Question 1. A survey was conducted by a group of students as a part of their environment awareness program, in which they collected the following data regarding the number of plants in 20 houses in a locality. Find the mean number of plants per house.

Which method did you use for finding the mean, and why?
Solution:
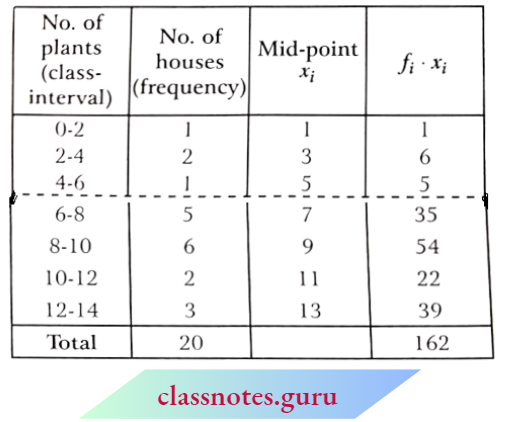
Mean \(\bar{x}=\frac{\sum f_i \cdot x_i}{\sum f_i}=\frac{162}{20}=8.1\)
∴ The mean number of plants per house = 8.1.
The direct method is used here because the values of Xi and fi are very small.
Question 2. Consider the following distribution of daily wages of 50 workers of a factory.
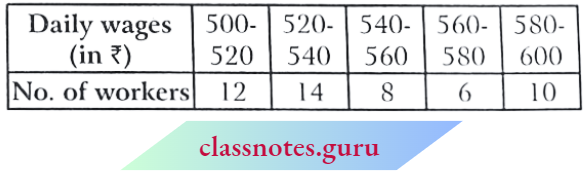
Find the mean daily wages of the workers of the factory by using an appropriate method.
Solution:
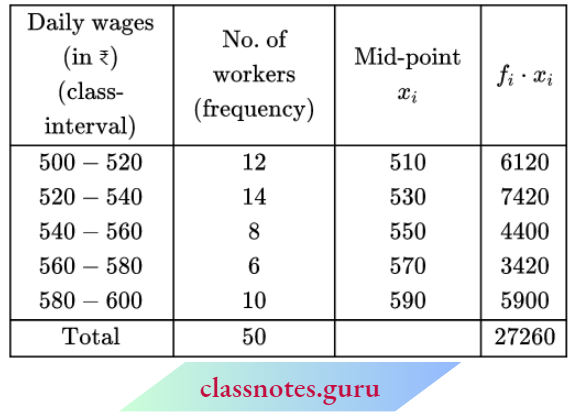
Mean \(\bar{x}=\frac{\sum f_i \cdot x_i}{\sum f_i}=\frac{27260}{50}=545.20\)
∴ Mean wages of workers = ₹ 545.20
Question 3. The following distribution shows the daily pocket allowance of children of a locality. The mean pocket allowance is ₹ 18. Find the missing frequency f:

Solution:
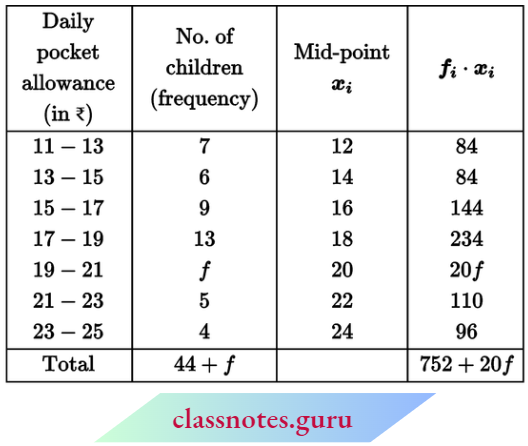
Now, mean pocket allowance = \(\frac{\sum f_i \cdot x_i}{\sum f_i}\)
⇒ \(18=\frac{752+20 f}{44+f}\)
⇒ 792 + 18f = 752 + 20f
⇒ 792 – 752 = 20f – 18f
⇒ 40 = 2f ⇒ f = 20
The missing frequency f = 20
Question 4. Thirty women were examined in a hospital by a doctor and the number of heartbeats per minute were recorded and summarised as follows. Find the mean heartbeats per minute for these women, choosing a suitable method.
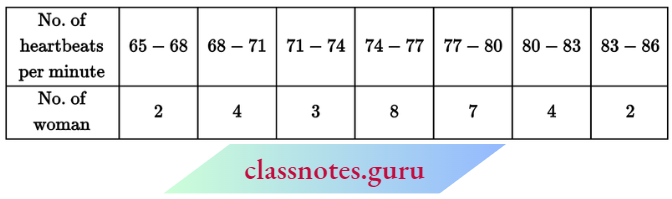
Solution:
Let assumed mean A = 75.6
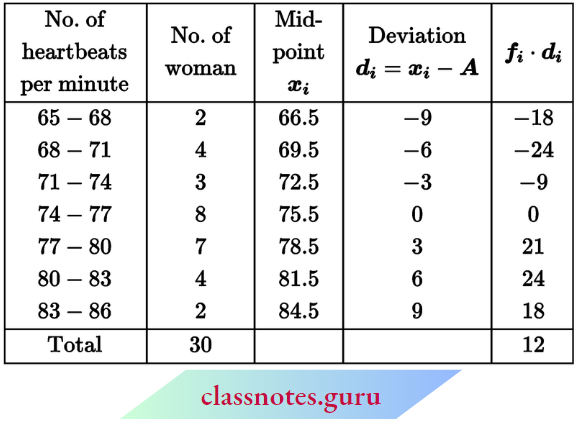
∴ Mean heartbeats per minute
⇒ \(\bar{x}=A+\frac{\sum f_i \cdot d_i}{\sum f_i}=75.5+\frac{12}{30}\)
= 75.5 + 0.4 = 75.9
The mean heartbeats per minute for these women = 75.9
Question 5. In a retail market, fruit vendors were selling mangoes kept in packing boxes. These boxes contained varying numbers of mangoes. The following was the distribution of mangoes according to the number of boxes:
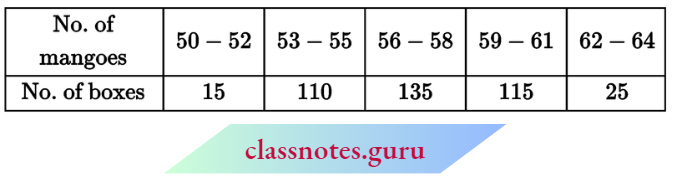
Find the mean number of mangoes kept in a packing box. Which method of finding the mean did you choose?
Solution:
Here, h = 3
Let assumed mean A = 57

∴ Mean \(\bar{x}=A+h \cdot \frac{\sum f_i \cdot u_i}{\sum f_i}\)
= \(57+\frac{3 \times 25}{400}=57+0.1875\)
= 57.1875
∴ Mean number of mangoes = 57.1875
≈ 57.19
Here, the assumed mean method is used.
Question 6. The table below shows the daily expenditure on food of 25 households in a locality.

Find the mean daily expenditure on food by a suitable method.
Solution:
Here, h = 50
Let assumed mean A = ₹ 225
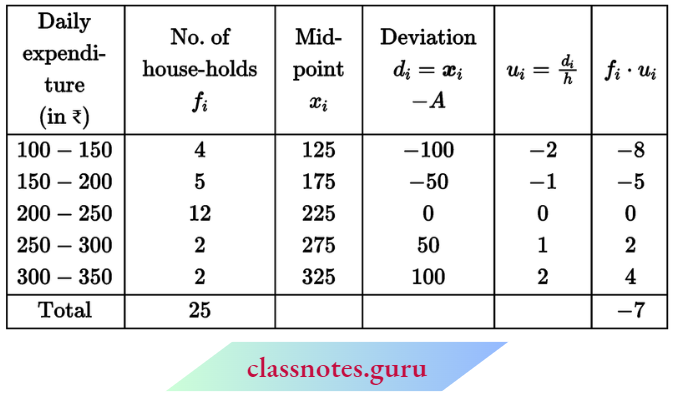
∴ Mean \(\bar{x}=A+h \cdot \frac{\sum f_i \cdot u_i}{\sum f_i}\)
= \(225+50 \times \frac{(-7)}{25}\)
= 225 – 14 = ₹ 221
Therefore, the mean daily expenditure on food per family = ₹ 211.
Question 7. To find out the concentration of SO2 in the air (in parts per million, i.e., ppm), the data was collected for 30 localities in a certain city and is presented below:
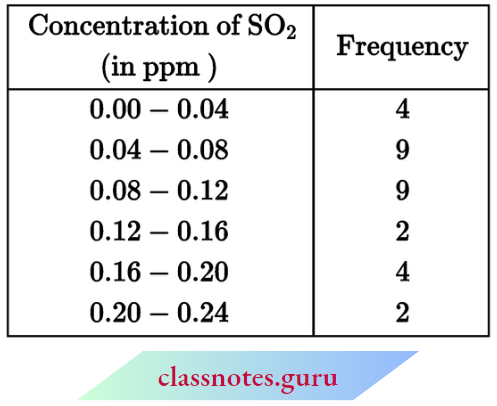
Find the mean concentration of SO2 in the air.
Solution:
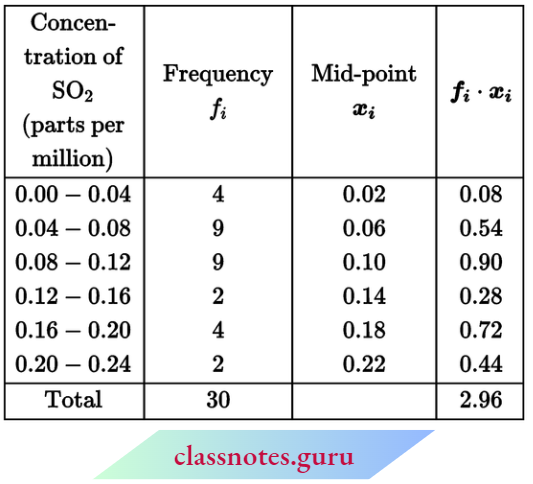
∴ Mean \(\bar{x}=\frac{\sum f_i \cdot x_i}{\sum f_i}=\frac{2}{30}\)
= 0.0986 parts per million.
The mean concentration of SO2 in the air = 0.0986 parts per million.
Question 8. A class teacher has the following absentee record of 40 students of a class for the whole term. Find the mean number of days a student was absent.

Solution:
Mean \(\bar{x}=\frac{\sum f_i \cdot x_i}{\sum f_i}=\frac{499}{40}=12.475\)
∴ The mean number of absences of students = 12.475 days per student
Question 9. The following table gives the literacy rate (in percentage) of 35 cities. Find the mean literacy rate.
Solution:
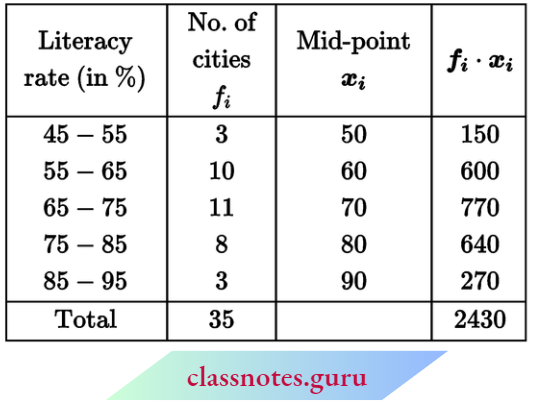
Mean \(\bar{x}=\frac{\sum f_i \cdot x_i}{\sum f_i}=\frac{2430}{35}=69.43\)
∴ The mean percentage rate of literacy = 69.43
Question 1. The following table shows the ages of the patients admitted to a hospital during a year:

Find the mode and the mean of the data given above. Compare and interpret the two measures of central tendency.
Solution:
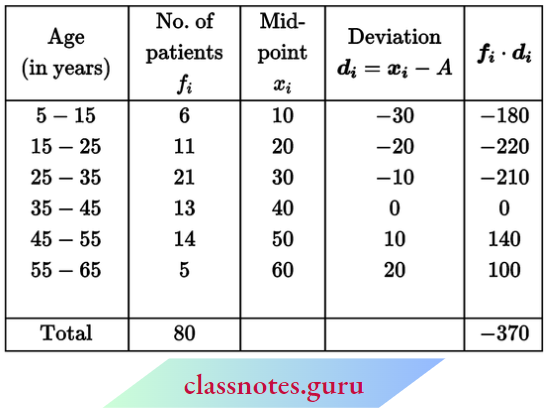
Lot assumed mean A = 40
∴ Mean \(\bar{x}=A+\frac{\sum f_1 \cdot d_i}{\sum f_i}=40+\frac{(-370)}{80}\)
= 40 – 4.625
= 35.375 years
For more,
Highest frequency = 23
∴ Modal class: 35 – 45
Now, l1= 35, l2 = 45
f = 23, f1 =21, f2 = 14
and mode = \(l_1+\frac{\left(f-f_1\right)\left(l_2-l_1\right)}{2 f-f_1-f_2}\)
= \(35+\frac{(23-21)(45-35)}{46-21-14}\)
= \(35+\frac{2 \times 10}{11}\)
= 35. 1.8 = 36.8 years.
Mode = 36.8 years.
Question 2. The following data gives information on the observed lifetimes (in hours) of 225 electrical components:

Determine the modal lifetime of the components.
Solution:
Highest frequency = 61
∴ Modal class: 60 – 80
Now, l1 = 60, l2 = 80
f = 61, f1 = 52, f2 = 38
and mode = \(l_1+\frac{\left(f-f_1\right)\left(l_2-l_1\right)}{2 f-f_1-f_2}\)
= \(60+\frac{(61-52)(80-60)}{2 \times 61-52-38}\)
= \(\begin{equation}
60+\frac{9 \times 20}{32}=60+5.625
\end{equation}\)
= 65.625 hours
Question 3. The following data gives the distribution of the total monthly household expenditure of 200 families in a village. Find the modal monthly expenditure of the families. Also, find the mean monthly expenditure:
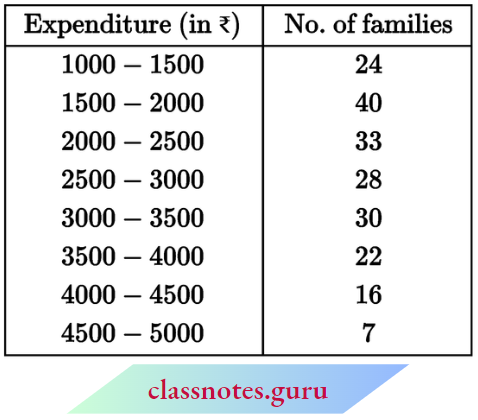
Solution:
Highest frequency = 40
∴ Modal class: 1500-2000
Now, l1 = 1500, l2 = 2000
f = 40, f1 = 24, f2= 33
and mode = \(l_1+\frac{\left(f-f_1\right)\left(l_2-l_1\right)}{2 f-f_1-f_2}\)
= \(1500+\frac{(40-24)(2000-1500)}{2 \times 40-24-33}\)
= \(1500+\frac{16 \times 500}{23}\)
= 1500 + 347.83 = ₹ 1847.83
Let assumed A = ₹ 2750
Here, h = 500
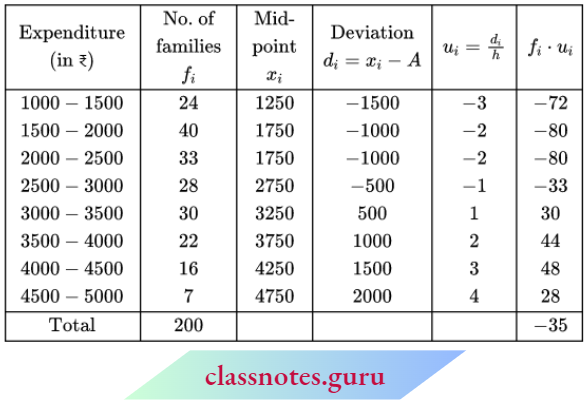
Mean Monthly expenditure
⇒ \(\bar{x}=A+h \cdot \frac{\sum f_i \cdot u_i}{\sum f_i}\)
⇒ \(2750+\frac{500 \times(-35)}{200}\)
= 2750 – 87.50 = ₹ 2662.50
Mean Monthly expenditure = ₹ 2662.50
Question 4. The following distribution gives the state-wise teacher-student ratio in higher secondary schools in India. Find the mode and mean of this data. Interpret the two measures.
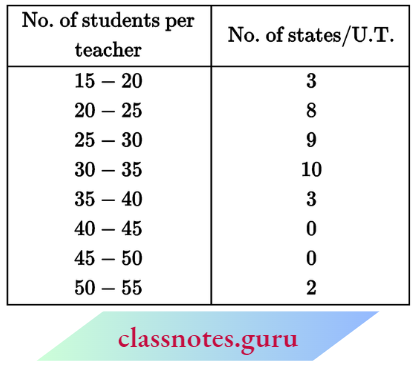
Solution:
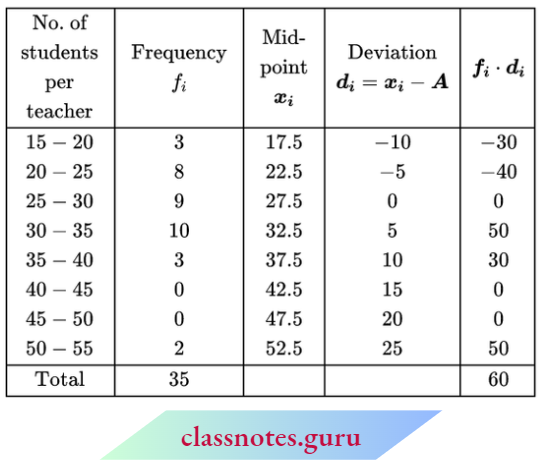
Here, maximum frequency = 10
∴ Model class: 30-35
Now, l1 = 30, l2 = 35
f = 10, f1 = 9, fi2 = 3
and mode = \(l_1+\frac{\left(f-f_1\right)\left(l_2-l_1\right)}{2 f-f_1-f_2}\)
= \(30+\frac{(10-9)(35-30)}{2 \times 10-9-3}\)
= \(30+\frac{5}{8}=30+0.625\)
= 30.625 students per teacher
For mean,
let assumed mean A = 27.5
Now, mean = \(A+\frac{\sum f_i \cdot d_i}{\sum f_i}=27.5+\frac{60}{35}\)
= 27.5 + 1.7
= 29.2 students per teacher
So, in the higher secondary schools of India, the mean number of students per teacher is 29.2 states while the number of students per teacher in maximum states is 30.625.
Question 5. The given distribution shows the number of runs scored by some top batsmen of the world in one-day international cricket matches.
Find the mode of the data.
Solution:
Here, maximum frequency = 18
∴ Modal class: 4000 – 5000
Now, l1 = 4000, l2 = 5000
f = 18, f1 = 4, f2 = 9
and mode = \(l_1+\frac{\left(f-f_1\right)\left(l_2-l_1\right)}{2 f-f_1-f_2}\)
= \(4000+\frac{(18-4)(5000-4000)}{2 \times 18-4-9}\)
= \(4000+\frac{14 \times 1000}{23}\)
= 4000 + 608.7 = 4608.7
≈ 4608 run (approximately)
The mode of the data = 4608 run (approximately)
NCERT Exemplar Statistics Class 10 Exercise Solutions
Question 6. A student noted the number of cars passing through a spot on the road for 100 periods each of 3 minutes and summarised it in the table given below. Find the mode of the data:

Solution:
Here, maximum frequency = 20
∴ Model class: 40-50
Now, l1 = 40, l2 = 50
f = 20, f1 = 12, f2 = 11
and mode = \(l_1+\frac{\left(f-f_1\right)\left(l_2-l_1\right)}{2 f-f_1-f_2}\)
= \(40+\frac{(20-12)(50-40)}{2 \times 20-12-11}\)
= \(40+\frac{8 \times 10}{17}=40+4.7\)
= 44.7
The mode of the data = 44.7
Question 1. The following frequency distribution gives the monthly consumption of electricity of 68 consumers of a locality. Find the median, mean, and mode of the data and compare them.
Solution:
Let assumed mean A = 115
Here, h = 20
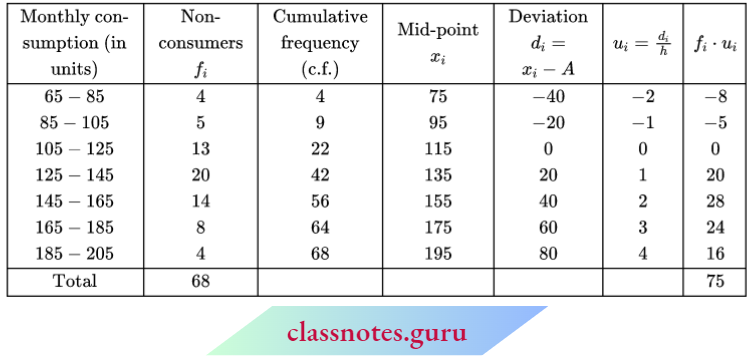
Here, N = 68
⇒ \(\frac{N+1}{2}=\frac{68+1}{2}=34.5\)
∴ Median class = 125 – 145
Now, l1 = 125, l2 = 145
f = 20, C = 22
and median (M) = \(l_1+\frac{\left(\frac{N}{2}-C\right)\left(l_2-l_1\right)}{f}\)
= \(125+\frac{\left(\frac{68}{2}-22\right)(145-125)}{20}\)
= \(125+\frac{12 \times 20}{20}\)
= 125 + 12 = 137
Mean \(\bar{x}=A+h \cdot \frac{\sum f_i \cdot d_i}{\sum f_i}\)
= \(115+\frac{20 \times 75}{68}\)
= 115 + 22.06 = 137.06
Again, maximum frequency = 20
∴ Modal class: 125-145
Now, l1 = 125, l2= 145
f = 20, f1 = 13, f2 = 14
∴ Mode = \(l_1+\frac{\left(f-f_1\right)\left(l_2-l_1\right)}{2 f-f_1-f_2}\)
= \(125+\frac{(20-13)(145-125)}{2 \times 20-13-14}\)
= \(125+\frac{7 \times 20}{13}\)
= 125 + 10.77 = 135.77
The values of median, mean and mode are equal approximately.
Question 2. If the median of the distribution given below is 28.5. find the value of x and y:
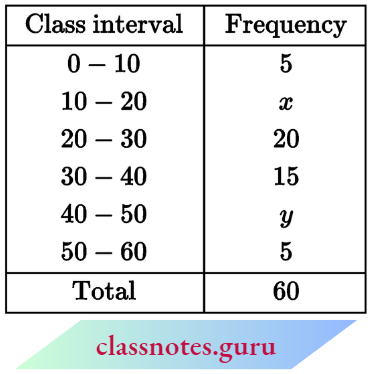
Solution:
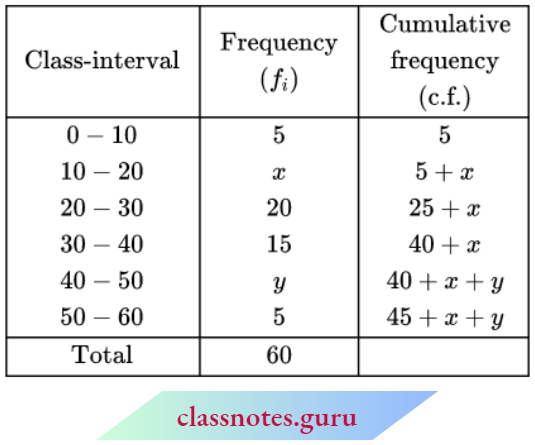
Now, 45 + x + y = 60
⇒ x + y = 15 → (1)
Given that, median = 28.5
∴ Median class: 20 – 30
Now, l1 = 20, l2 = 30
f = 20, c = 5 + x, N = 60
Median = \(l_1+\frac{\left(\frac{N}{2}-C\right)\left(l_2-l_1\right)}{f}\)
⇒ \(28.5=20+\frac{\left(\frac{60}{2}-5-x\right)(30-20)}{20}\)
⇒ \(28.5-20=\frac{(25-x)(10)}{20}\)
⇒ \(8.5=\frac{25-x}{2} \quad ⇒ \quad 17=25-x\)
⇒ x = 25 – 17 = 8
From equation (1),
8 + y = 15
⇒ y = 15 – 8 = 7
∴ x = 8, y = 7
The value of x and y is 8 and 7.
Question 3. A life insurance agent found the following data for the distribution of ages of 100 policyholders. Calculate the median age, if policies are given only to persons aged 18 years onwards but less than 60 years.
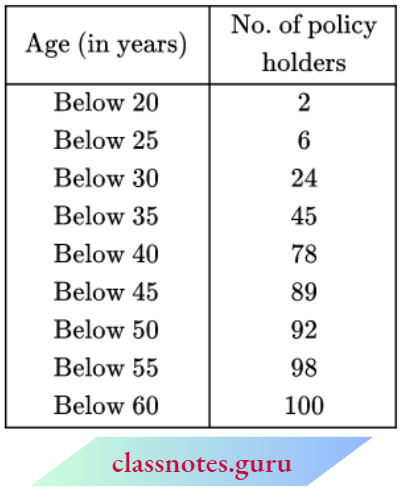
Solution:
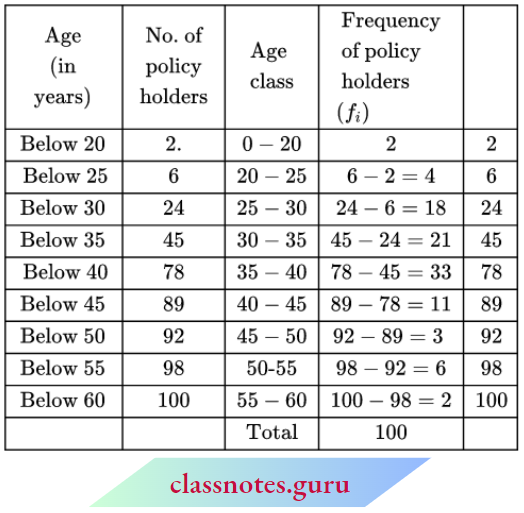
N = 100
∴ \(\frac{N+1}{2}=\frac{100+1}{2}=50.5\)
⇒ Median class: 35 – 40
∴ l1 = 35, l2 = 40
f = 33, C = 45
Median = \(l_1+\frac{\left(\frac{N}{2}-C\right)\left(l_2-l_1\right)}{f}\)
= \(35+\frac{\left(\frac{100}{2}-45\right)(40-35)}{33}\)
= \(35+\frac{5 \times 5}{33}=35+0.76\)
= 35.76 years.
Median = 35.76 years.
Class 10 Statistics Problems and Solutions NCERT Exemplar
Question 4. The lengths of40 the leaves of a plant are measured correctly to the nearest millimeter and the data obtained is represented in the following table:
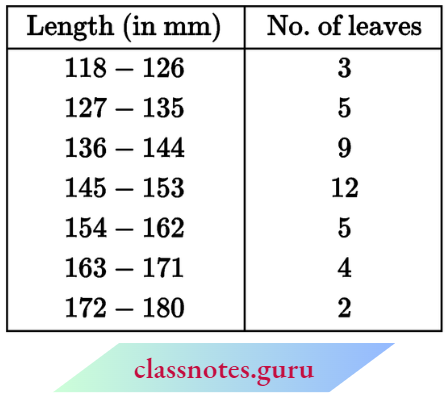
Find the median length of the leaves.
[Hint: The data needs to be converted to continuous classes for finding the median since the formula assumes continuous classes. The classes then change to 117.5-126.5, 126.5-135.5, …, 171.5 – 180.5.]
Solution:
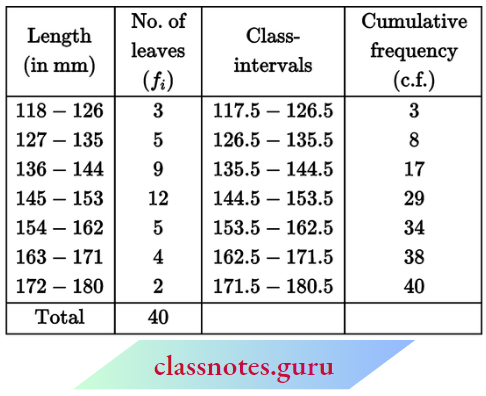
∴ \(N=40 \Rightarrow \frac{N+1}{2}=\frac{40+1}{2}=20.5\)
⇒ Median class: 144.5 – 153.5
l1 = 144.5, l2 = 153.5
f = 12, C = 17
and median = \(l_1+\frac{\left(\frac{N}{2}-C\right)\left(l_2-l_1\right)}{f}\)
= \(144.5+\frac{\left(\frac{40}{2}-17\right)(153.5-144.5)}{12}\)
= \(144.5+\frac{3 \times 9}{12}=144.5+2.25\)
= 146.75 mm
Therefore, the median length of leaves = 146.75 mm
Question 5. The following table gives the distribution of the lifetime of 400 neon lamps:
Find the median lifetime of a lamp.
Solution:
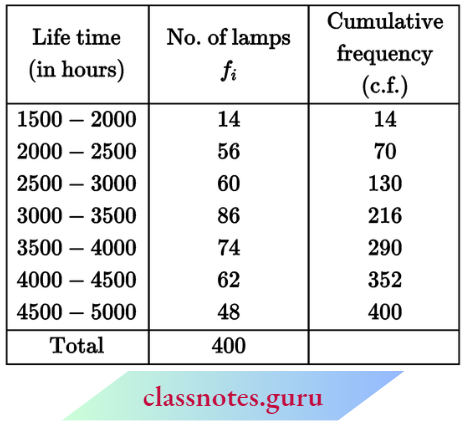
Here, N = 400
∴ \(\frac{N+1}{2}=\frac{400+1}{2}=200.5\)
Median class: 3000 – 3500
Now, l1 = 3000, l2 = 3500
f = 86, C = 130
and median = \(=l_1+\frac{\left(\frac{N}{2}-C\right)\left(l_2-l_1\right)}{f}\)
= \(=3000+\frac{\left(\frac{400}{2}-130\right)(3500-3000)}{86}\)
= \(3000+\frac{70 \times 500}{86}\)
= 3000 + 406.98 = 3406.98 hours
Therefore, the mean lifetime of lamps = 3406.98 hours.
Question 6. 100 surnames were randomly picked up from a local telephone directory and the frequency distribution of the number of letters in the English alphabets in the surnames was obtained as follows:

Determine the median number of letters in the surnames. Find the mean number of letters in the surnames. Also, find the modal size of the surnames.
Solution:
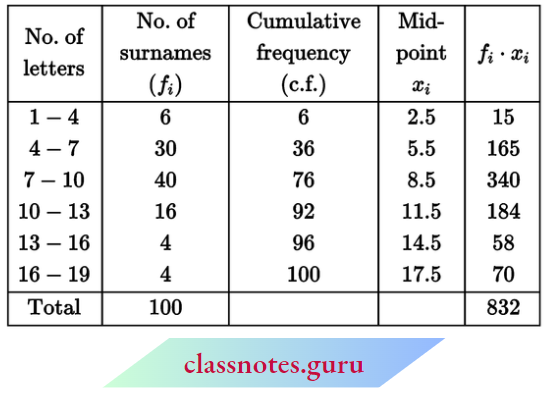
N = 100
∴ \(\frac{N+1}{2}=\frac{100+1}{2}=50.5\)
⇒ Median class: 7 – 10
Now, l1 = 7, l2 = 10
f = 40, C = 36
∴ Median = \(l_1+\frac{\left(\frac{N}{2}-C\right)\left(l_2-l_1\right)}{f}\)
= \(7+\frac{\left(\frac{100}{2}-36\right)(10-7)}{40}\)
= \(7+\frac{14 \times 3}{40}\)
= 7 + 1.05 = 8.05
Mean = \(\frac{\sum f_i \cdot x_i}{\sum f_i}=\frac{832}{100}=8.32\)
Fir mode,
Maximum frequency = 40
∴ Modal class 7 – 10
Now, l1 = 7, l2 = 10
f = 40, f1 = 30, f2 = 16
and mode = \(l_1+\frac{\left(f-f_1\right)\left(l_2-l_1\right)}{2 f-f_1-f_2}\)
= \(7+\frac{(40-30)(10-7)}{2 \times 40-30-16}\)
= \(7+\frac{10 \times 3}{34}\)
= 7 + 0.88 = 7.88
Mode = 7.88
Question 7. The distribution below gives the weights of 30 students in a class. Find the median weight of the students.

Solution:
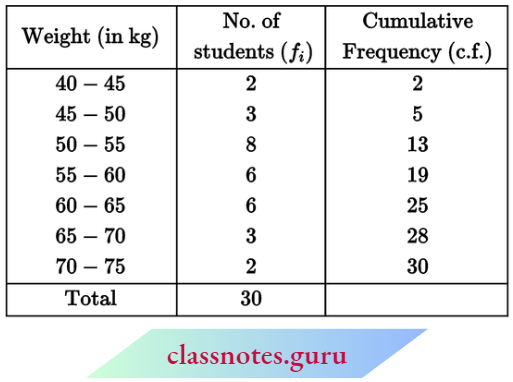
Here, N = 30
∴ \(\frac{N+1}{2}=\frac{30+1}{2}=15.5\)
⇒ Median class: 55 – 60
Now, l1 = 55, l2 = 60, f = 6, C= 13
and median = \(l_1+\frac{\left(\frac{N}{2}-C\right)\left(l_2-l_1\right)}{f}\)
= \(55+\frac{\left(\frac{30}{2}-13\right)(60-55)}{6}\)
= \(55+\frac{2 \times 5}{6}\)
= 55 + 1.67
= 56.67 kg
Question 1. The following distribution gives the daily income of 50 workers of a factory.

Convert the distribution above to a less type cumulative frequency distribution, and draw its ogive.
Solution:
Cumulative frequency curve (ogive)
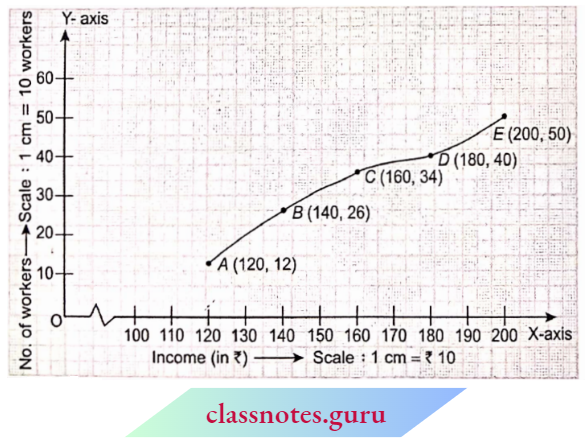
NCERT Exemplar Class 10 Statistics Chapter 14 Important Questions
Question 2. During the medical check-up of 35 students of a class, their weights were recorded as follows:
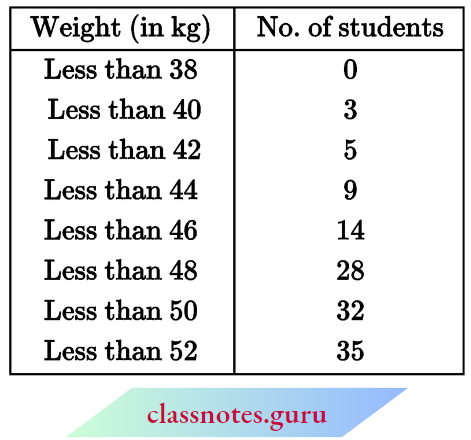
Draw a less than type ogive for the given data. Hence obtain the median weight from the graph and verify the result by using the formula.
Solution:
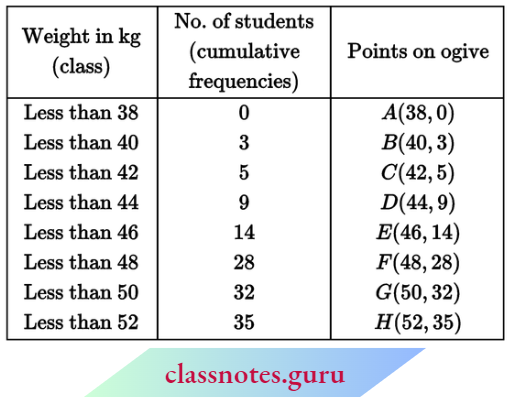
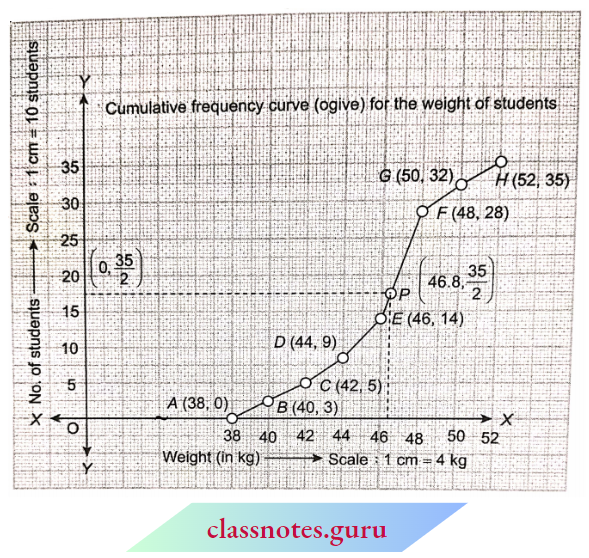
To find the median:
Question 3. The following table gives the production yield per hectare of the heat of wheat of 100 farms in a village.

Change the distribution to a more than type distribution, and draw its ogive.
Solution:
Convert the given distribution to the ‘more than’ type distribution.

Distribution of “More than” type
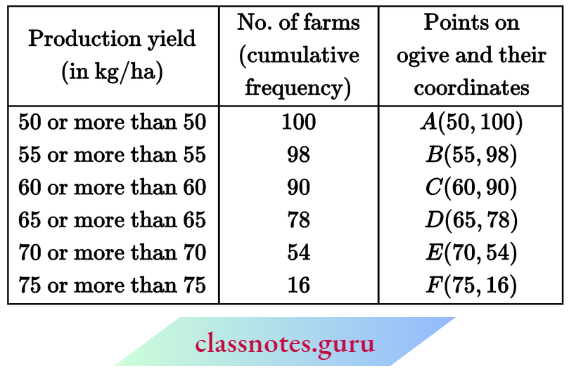
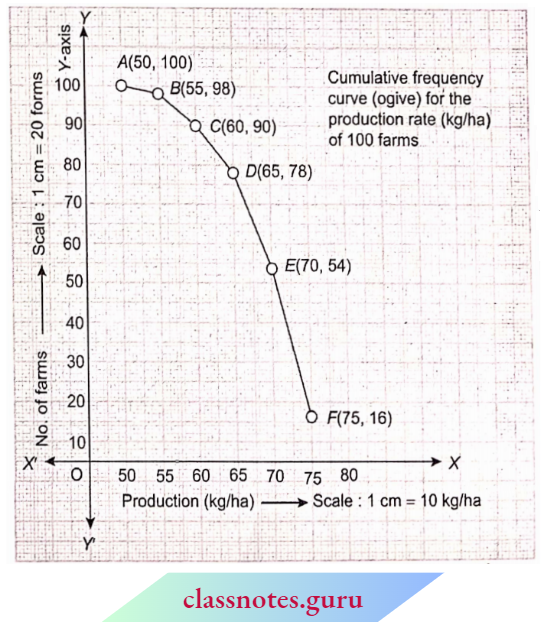
Question 1. In the formula \(\bar{x}=a+\frac{\Sigma f_i d_i}{\Sigma f_i}\) to determine the mean of grouped data, di is the deviation from and the following:
Answer: 3. Mid-point of classes
Question 2. If xi is the mid-points of class intervals of grouped data and fi are their corresponding frequencies, then the value of Σ(fi – xi – \(\bar{x}\)) is:
Answer: 2. 0
Question 3. For the distribution

the sum of the upper limits of the median class and modal class is:
Answer: 1. 70
Question 4. The abscissa of the point of intersection of cumulative frequency curves of ‘less than type’ and ‘more than type’ gives the ______ of the data:
Answer: 2. Median
Question 5. A cumulative frequency curve is necessary in
Answer: 2. Median
Question 6. For the distribution

the upper limit of the median class is:
Answer: 4. 29.5
Question 7. In the distribution

the modal class is:
Answer: 3. 40 – 50
Question 8. The modal class of the following frequency distribution will be

Answer: 2. 3 – 5
Question 9. The arithmetic mean of 3, 4, 6, and x is 5. The value of x will be:
Answer: 3. 7
Statistics NCERT Exemplar Class 10 Sample Paper Questions
Question 10. The arithmetic mean of positive even numbers from 1 to 10 will be:
Solution: 3. 6
Question 11. 1 hejnean ol n observations is \(\bar{x}\). If each observation is increased by a, then the new mean will be:
Answer: 1. \(\bar{x}\)+ a
Question 12. For a frequency distribution, the relation between mean, median, and mode is:
Answer: 3. Mode = 3 median – 2 mean
Question 13. The mean of natural number from 1 to 9 will be:
Answer: 2. 5
Question 14. For a frequency distribution, the mean is 20.5 and the median is 20. Its mode will be:
Answer: 3. 19
In our daily lives, we come across some situations, for which we do not have any definite answer, although we know what the possible results (outcomes) are.
Probability For Example :
Read and Learn More Class 10 Maths Solutions Exemplar

NCERT exemplar class 10 maths chapter 15 solutions
An operation which gives some outcomes (results) under some given conditions is known as the ‘experiment’.
For Example:
Probability Trial
Experimenting repeatedly under similar conditions is called a trial.
The set (collection) of all possible outcomes of usually denoted by S.
For Example:
(1). In tossing a coin ← experiment
Sample space denoted by S=\(\left\{\begin{array}{cc}
H & T \\
(\text { Head ) } & \text { (Tail) }
\end{array}\right\}\)
(2). In throwing a die ← experiment
S = {1,2, 3, 4, 5, 6}
(3). In tossing a coin 3 times ← experiment
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
(4). In throwing two dice simultaneously ← experiment
S=\(\left\{\begin{array}{l}
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6) \\
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6) \\
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6) \\
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6) \\
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6) \\
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)
\end{array}\right\}\)
Any outcome or combination of some outcomes constitutes an event. Each event is a subset (part) of the sample space.
For Example:
(1). Let S = {1, 2, 3, 4, 5, 6}, when a die is thrown and let E1 is the event of “getting an odd number”.
∴ E1 = {1, 3, 5}
(2). Let E2 be the event of “getting an even number”.
∴ E2 = {2, 4, 6}
(3) Let E3 be the event of “getting a prime number”.
∴ E3 = {2,3, 5}
All above events are part of a subset of a sample space.
Remark: Total number of elements in a sample space = (Number of outcomes of an event)No‘of times
For Example:
(1). In tossing a coin 3 times,
The total number of elements in a sample space denoted by
n(S) = (2)3 → No.of times
Possible outcomes of a coin = 8
(2). In throwing 2 dice,
n(S) = (6)2 → No.of times
Possible outcomes of an experiment = 36
An event is called a simple event if it contains only one element. In terms of set, it is a singleton set.
For Example:
(1) In “tossing a coin”, sample space S = {H, T}
Let A = event of getting a head = {H} and B = event of getting a tail = {T}
Here A and B are simple events.
(2). In “tossing a coin 2 times”, S = {(H, H), (H, T), (T, H), (T, T)}
Let A = event of getting a head on the first coin and getting a tail on the second coin = {(H, T)}
B = event of getting a head on the first coin = {(H, H), (H, T)}
Here, A is a simple event but B is not a simple event as B has two sample points.
To understand the experiment, sample space and event, are given below.

It is necessary that event is a part of the sample space
About the Playing Cards
1. A pack of playing cards has 52 cards in all.
2. It has 2 Colours – [Red (26 cards); Black (26 cards)]
3. It has 4 suites
Numbering on each card of each suit as :

Actually, A, J, Q and IC are written in place of 1, 11, 12 and 13.
So, in a pack of 52 cards, 4 cards of the same number are there.
Note: Kings, Queens and Jacks are called the face cards while the aces together with face cards are called the honour cards.
For Example: Number 2 will be in spade, club, heart as well as in diamond. Similarly, the number IC will be in spade, dub, heart and diamond also.
class 10 maths probability exemplar solutions
The events are said to be equally likely when we have no reason to believe that one is more likely to occur than the other. Each of the possible outcomes has an equal chance of occurring.
For Example:
Now, let us try to understand the meaning of probability.
(Probability: probable, perhaps, possibly, chances etc.)
For this, first, we see some experiments.
(1 ). In tossing a coin, S = {H, T}
What are the chances of getting a head—only {H}?
You will say 50% or fifty-fifty—Correct.
∴ \(50 \% \text { means } \frac{50}{100}, \text { i.e., } \frac{1}{2}=\frac{n(\text { favourable cases })}{n(S)}\)
Our favourable case is getting a head ⇒ n(E) = 1
and the total number of outcomes in a sample space ⇒ n(S)= 2
(2). In throwing a die, S = {l, 2, 3, 4, 5, 6}
What are the chances of getting an even number, i.e., {2,4, 6}?
Again, you will say 50% or fifty-fifty—Correct.
∴ Probability of an event =\(\frac{\text { Number of favourable cases }}{\text { Total number of cases }}\)
Now, tell me O’ girl!
What is the probability of getting a head exactly 2 times when we toss a coin 3 times simultaneously?
Now, you see example (1) of sample space and give the correct answer.
Yes! Your answer is correct. It is \(\frac{3}{8}\)
Now, you can make understand to your friend easily that
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
In these 8 outcomes, only 3 underlined contain exactly two heads.
∴ Our favourable cases = 3 and total number of outcomes = 8
∴ Required probability = \(\frac{3}{8}\)
The value of the probability of any event always lies between 0 and 1. When the probability of an event is 0, it is said to be an impossible event and when the probability of an event is l, it is said to be a sure event.
Explanation: We know that a set (collection) of favourable outcomes is a part of the whole sample space.
∴ Number of favourable cases \(\leq\) Total number of cases.
⇒ \(\frac{\text { Number of favourable cases }}{\text { Total number of cases }} \leq 1\) → (1)
Now, see the following example :
“In throwing a die numbered l to 6”, find the probability of getting a number greater than 6”.
Here there is no such possibility to get a number which is greater than 6.
Favourable number of cases ≥ 0
So. always a number of favourable cases \(\leq\) 0
∴ \(\frac{\text { Number of favourable cases }}{\text { Total number of cases }} \leq 0\)
Combining Eqs. (1) and (2), we get
∴0 \(\leq\) Probability of an event \(\leq\) 1
Remember: In each experiment, we assume that the chance of each outcome is the same.
If an event £ can happen in any one of the n different ways with the probabilities P1, P2, P3 …. respectively, then the probability for the event £ is equal to the sum of the individual probabilities P1, P2, P3, …Pn
For Example:
When a die is rolled, then any one of the numbers,1,2, 3, 4, 5 or 6 can be shown up.
Total number of outcomes = 6
Number of even numbers (2, 4 or 6)= 3
∴ Probability of getting an even number = \(\frac{\text { Favourable outcomes }}{\text { Total number of outcomes }}=\frac{3}{6}=\frac{1}{2}\)
Also, Probability of getting 2 = \(\frac{1}{6}\)
Probability of getting 4 = \(\frac{1}{6}\)
Probability of getting 6 = \(\frac{1}{6}\)
∴ Probability of getting an even number = \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{1}{2}\)
If E is an event, then the event ‘not £’ is a complementary event of E.
For Example:
When we throw a die, let E be the event getting a number less than or equal to 2, then the event ‘not E’, i.e., getting a number greater than 2 is a complementary event of E. Complementary of E is denoted by E or \((\bar{E})\)
∴ \(P(E)+P(\bar{E})\)=1
Let E be an event, then the number of outcomes favourable to E is greater than or equal to zero and is less than or equal to the total number of outcomes. It follows than
∴ \(0 \leq P(E) \leq 1\).
All the possible outcomes of any trial taken together are called exhaustive events.
For Example:
From a group of 2 boys and 3 girls, two children are selected at random. Describe the events:
S = {B1B2, B1G1, B1G2, B2G2, B2G1,B2G2, B2G2, G1G2, G2G3, G1G3}
E1 = event that both the selected children are girls
= {G1G2, G2G3, G1G3}
E2 = event that the selected children consist of 1 boy and 1 girl
= {B1G1, B1G2, B1G3, B2G1, B2G2, B2G2}
E3 = event that at least one boy is selected
= {B1B2, B1G1, B1G2, B1G3, B2G1, B2G2, B2G3}
Here E1 and E2 together do not constitute S.
∴ E1 and E2 are not exhaustive events,
and E2 and E3 also do not form the whole sample space S.
∴ E2 and E3 are not exhaustive events.
But E1 and E3 together form a whole sample space.
∴ E1 and E3 are exhaustive events.
Question 1. In any situation that has only two possible outcomes, each outcome will have probability \(\frac{1}{2}\). Find whether it is true or false.
Solution:
False,
The probability of each outcome will be \(\frac{1}{2}\) only when the two outcomes are equally likely.
For Example:
On the eve of Deepawali, we are lighting the candles in night on the roof.
The candles may be “lightening off due to heavy rain” or “they may not be lightening off” are not equally likely events because they do have not equal chances of occurring.
The possibility of falling rain at the time of the festival Deepawali is very less.
Question 2. A marble is chosen at random from 6 marbles numbered 1 to 6. Find the probability of getting a marble having number 2 and 6 on it.
Solution:
Given
A marble is chosen at random from 6 marbles numbered 1 to 6.
The favourable case is to get a marble on which both numbers 2 and 6 are written. But there is no such marble.
So, n(E) = 0 and n(S) = 6
∴ Required probability =\(\frac{n(E)}{n(S)}=\frac{0}{6}\)=0
Question 3. A marble is chosen at random from 6 marbles numbered 1 to 6. Find the probability of getting a marble having the number 2 or 6 on it.
Solution:
Given
A marble is chosen at random from 6 marbles numbered 1 to 6.
Here n(E) = 2 [either 2 or 6]
and n(S) = 6
∴ Required probability = \(\frac{2}{6}=\frac{1}{3}\)
Question 4. A fair coin is tossed
Solution:
(1). When a fair coin is tossed, there are two possible outcomes. Either the head appears on the uppermost face or the tail appears on the uppermost face.
S = {H, T}; n {S} = 2
(2). \(P(\text { tail })=\frac{\text { No. of favourable outcomes }}{\text { No. of possible outcomes }}=\frac{1}{2}\)
NCERT exemplar class 10 probability questions with answers
Question 5. A fair die is tossed. List the sample space. State the probability of the event :
Solution:
When a fair die is tossed, the number of possible outcomes is 1, 2, 3, 4, 5 and 6.
Sample space S = {1,2, 3,.4, 5, 6); n (S) = 6
(1). Let A be the event which denotes “a number less than 3 appears”.
A= {1,2}, n(A) = 2;
⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{2}{6}=\frac{1}{3}\)
(2). Let E be the event which denotes “a number greater than 3” appears.
E= {4,5,6}; n{E) =3
⇒ P(E)=\(\frac{n(E)}{n(S)}=\frac{3}{6}=\frac{1}{2}\)
(3). Let B be the event in which “a number greater than or equal to 3” appears.
B = {3, 4, 5, 6}; n(B) = 4
⇒ P(B)=\(\frac{n(B)}{n(S)}=\frac{4}{6}=\frac{2}{3}\)
Question 6. Two dice are thrown simultaneously. Find the probability of getting:
Solution:
Elementary events associated with the random experiment of throwing two dice are :
{1,1} {1,2} {1,3} {1,4} {1,5} {1,6}
{2,1} {2,2} {2,3} {2,4} {2,5} {2,6} .
{3,1} {3,2} {3,3} {3,4} {3,5} {3,6}
{4,1} {4,2} {4,3} {4,4} {4,5} {4,6}
{5,1} {5,2} {5,3} {5,4} {5,5} {5,6}
{6,1} {6,2} {6,3} {6,4} ‘{6,5} {6,6}
∴ Total number of elementary events = 6 x 6 = 36.
(1). Let A be the event of getting an even number as the sum, i.e., 2, 4, 6, 8, 10, 12.
The sum is even.
∴ Sum may be 2 or 4 or 6 or 8 10 or 12.
So, elementary events favourable to events are (1,1), (1,3), (3,1),(2,2), (1,5), (5, 1), (2, 4), (4, 2),'(3, 3), (2, 6), (6, 2), (4, 4), (5, 3), (3, 5), (5, 5), (6, 4), (4, 6) and (6, 6). C
clearly, a favourable number of outcomes =18
Hence, required probability = \(\frac{18}{36}=\frac{1}{2}\)
(2). Let B be the event of getting an even number as the product, i.e., 2, 4, 6, 8, 10, 12, 16, 18,20,24,30,36.
∴ Elementary events favourable to event £ are : (1, 2), (2, 1), (1, 4), (4, 1), (2, 2), (1, 6), (6, 1), (2, 3), (3, 2), (2, 4), (4, 2), (2, 5), (5, 2), (2, 6), (6, 2), (3, 4), (4, 3), (4, 4), (3, 6), (6, 3), (4, 5), (5, 4), (4, 6), (6, 4), (5, 6), (6, 5), (6, 6).
∴ Favourable number of outcomes = 27
Hence, required probability = \(\frac{27}{36}=\frac{3}{4}\)
(3). Let C be the event of getting the sum as a prime number, i.e., 2, 3, 5, 7, 11.
Elementary events favourable to event C are :(1, 1), (1 2), (2, 1),(1, 4), (4, 1), (2, 3), (3, 2), (1, 6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3), (6, 5), (5, 6)
∴ Favourable number of outcomes =15
Hence, required probability = \(\frac{15}{36}=\frac{5}{12}\)
(4). Let D be the event of getting a total of at least 10, i.e., 10, 11, 12.
Then, the elementary events favourable to D are (6, 4), (4, 6), (5, 5), (6, 5), (5, 6) and (6, 6).
∴ Favourable number of outcomes = 6
Hence, required probability = \(\frac{6}{36}=\frac{1}{6}\)
(5). Let E be the event of getting a Doublet, i.e., (1,1), (2,2), (3,3), (4, 4), (5,5), (6,6).
Clearly, a favourable number of outcomes = 6
∴ \(P(E)=\frac{6}{36}=\frac{1}{6}\)
Question 7.
Solution:
1. As a die is rolled once, therefore there are six possible outcomes, i.c., 1,2,3, 4, 5, 6.
(1). Let A be an event “getting a prime number”.
Favourable cases for a prime number are 2, 3, 5,
i.e., n(A) = 3
Hence, P(A)=\(\frac{n(A)}{n(S)}=\frac{3}{6}=\frac{1}{2}\)
(2). Let A be an event “getting a number between 3 and 6”.
Favourable cases for events A are 4 or 5.
i.e., n(A) = 2
⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{2}{6}=\frac{1}{3}\)
(3). Let A be an event “a number greater than 4”.
Favourable cases for events A are 5 and 6.
i.e., n(A) = 2
⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{2}{6}=\frac{1}{3}\)
(4). Let A be the event of getting a number at most 4.
∴ A = {1,2, 3, 4} ⇒ n(A) = 4, n(S) = 6
∴ Required probability = \(\frac{n(A)}{n(S)}=\frac{4}{6}=\frac{2}{3}\)
(5). Let A be the event of getting a factor of 6.
∴ A = {1,2, 3, 6} r ⇒ n(A) = 4, n(S) = 6
∴ Required probability = \(\frac{n(A)}{n(S)}=\frac{4}{6}=\frac{2}{3}\)
2. Since a pair of dice is thrown once, so there are 36 possible outcomes.
i.e., n(S) = 36
(1). Let A be an event “a total 6”. Favourable cases for a total of 6 are (2, 4), (4, 2), (3, 3),(5, 1), (1,5).
i.e., n(A) = 5
Hence, P(A)=\(\frac{n(A)}{n(S)}=\frac{5}{36}\)
(2). Let A be an event “a total of 10”. Favourable cases for a total of 10 are (6, 4), (4, 6),(5,5).
i.e., n(A) = 3
⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{3}{36}=\frac{1}{12}\)
(3). Let A be an event “the same number of both the dice”. Favourable cases for the same number on both the dice are (1, 2), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6).
i.e.. n(A)= 6
⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)
(4). Let A be an event “of getting a total of 9”. Favourable cases for a total of 9 are (3,6), (6,3), (4,5), (5,4). ”
i.e., n(A) = 4
⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{4}{36}=\frac{1}{9}\)
3. We have, n(S) = 36
(1). Let A be an event “a sum less than 7” i.e., 2, 3, 4, 5, 6.
Favourable cases for a sum less than 7 are : (1, 1), (1, 2), (2, l),(l,3), (3, 1), (2, 2), (1,4), (4, 1), (2, 3), (3, 2), (1,5), (5, 1), (2, 4), (4, 2), (3, 3)
i.e., n(A) = 15
⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{15}{36}=\frac{5}{12}\)
(2). Let/1 be an event “product less than 16” i.e., 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15.
Favourable cases for a product less than 16 are : (1, 1), (1, 2), (2, 1),(1, 3), (3, 1), (1, 4), (4, 1), (2, 2), (1, 5), (5, 1), (1, 6), (6, 1), (2, 3), (3, 2), (2, 4), (4, 2), (3, 3), (2, 5),(5, 2), (2, 6), (6, 2), (3, 4), (4, 3), (3, 5), (5, 3).
n(A) = 25
Hence, P(A)=\(\frac{n(A)}{n(S)}=\frac{25}{36}\)
(3). Let A be an event “a doublet of odd numbers”.
Favourable cases for a doublet of odd numbers are (1, 1), (3, 3), (5, 5)
i.e., n(A) = 3
Hence P(A)=\(\frac{n(A)}{n(S)}=\frac{3}{36}=\frac{1}{12}\)
Question 8. A standard deck of 52 cards is shuffled. Ritu draws a single card from the deck at random. What is the probability that the card is a jack?
Solution:
Given
A standard deck of 52 cards is shuffled. Ritu draws a single card from the deck at random.
S = Sample space of all possible outcomes, or 52 cards.
Thus, n(S) = 52
E = Event of selecting a jack. There are four jacks in the deck; jack of hearts, of diamonds, of spades, and of clubs.
Thus n(E) = 4 .
∴ P(E)=\(\frac{\text { Number of possible jacks }}{\text { Total number of possible cards }}=\frac{4}{52}=\frac{1}{13}\)
Hence, the probability that the card is jack is \(\frac{1}{13}\)
Question 9. A bag contains 5 black, 7 red and 3 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is:
Solution:
Given
A bag contains 5 black, 7 red and 3 white balls. A ball is drawn from the bag at random.
Total number of balls = 5 + 7 + 3= 15
1. Number of red balls = 7
∴ P(drawing a red ball) = \(\frac{7}{15}\)
2. Number of black or white balls = 5 + 3 = 8
∴ P(drawing a black or white ball) =\(\frac{8}{15}\)
3. Number of balls which are not black =15-5 = 10
∴ P(drawing a ball that is not black) = \(\frac{10}{15}\) = \(\frac{2}{3}\)
Hence, the probability of getting a red ball, a black or white ball and not a black ball are \(\frac{7}{15}, \frac{8}{15}\) and \(\frac{2}{3}\) respectively.
Question 10. The probability of selecting a rotten apple randomly from a heap of 900 apples is 0.18. What is the number of rotten apples in the heap?
Solution:
Given
The probability of selecting a rotten apple randomly from a heap of 900 apples is 0.18
Total number of apples in a heap = 900
Let the number of rotten apples in a heap = x
Number of rotten apples = \(\frac{\text { Number of rotten apples }}{\text { Total number of apples in a heap }}\)
Now, probability (rotten apple) = \(0.18=\frac{x}{900}\)
∴ x = 900 x 0.18 = 162
∴ Number of rotten apples in a heap of apples =162
Question 11. One card is drawn from a well-shuffled deck of 52 cards. Find the probability of drawing:
Solution:
1. The number of possible outcomes of drawing an ace is 4 as the number of aces in the deck is 4.
The total number of outcomes relating to drawing a card from a deck of 52 cards is 52.
∴ P(drawing an ace) = \(\frac{4}{52}=\frac{1}{13}\)
2. As there is only one card ‘2’ of spades, there is one favourable outcome only.
∴ Probability of drawing ‘2’ of spades = \(\frac{1}{52}\)
3. Since, there are two cards of TO’ of a black suit, one 10 of spade and the other 10 of the club, the probability of drawing 10 of a black suit = \(\frac{2}{52}=\frac{1}{26}\)
Question 12. A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears
Solution:
Given
A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box
We have, n(S) = 90
(1) Let A be the event of getting “a two-digit number”.
∴ Favourable cases are 10, 11, 12, 13, 14, …, 90.
∴ n(A)=81
∴ P(A)=\(\frac{n(A)}{n(S)}=\frac{81}{90}=\frac{9}{10}\)
(2) Let B be the event of getting “a number divisible by 5 “.
∴ Favourable cases are 10,15,20,25,30, …, 90.
Let there be n in numbers.
Tn =90
∴ 10+(n-1) 5 =90 [\(a_n\) of A.P.=a+(n-1)d]
⇒ (n-1) 5 =80 ⇒ n-1 = 16 ⇒ n=17
∴ n(B) =17
∴ P(B) =\(\frac{n(B)}{n(S)}=\frac{17}{90}\)
NCERT class 10 maths chapter 15 exemplar solutions
Question 13. A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to all of the numbers 1,2, 3, …,12. What is the probability that it will point to
Solution:
Given
A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to all of the numbers 1,2, 3, …,12.
n(S) = Total number of elementary events = 12.
1. Favourable number of elementary events that point to 10 = 1
∴ Required probability = \(\frac{1}{12}\)
2. Let A be the event “point of the arrowhead towards an odd number”
∴ n(A) = {1,3, 5, 7, 9, 11} = 6
∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{12}=\frac{1}{2}\)
3. Let E be the event “pointing towards a number which is a multiple of 3”
∴ n(E) = {3, 6, 9, 12} = 4
∴ P(E) = \(\frac{n(A)}{n(S)}=\frac{4}{12}=\frac{1}{3}\)
Question 14. A bag contains 15 white balls and some black balls. If the probability of drawing a black ball is thrice that of a white ball, find the number of black balls in the bag.
Solution:
Given
A bag contains 15 white balls and some black balls. If the probability of drawing a black ball is thrice that of a white ball
Number of white balls in a bag =15
Suppose the number of black balls in the bag = x
Total number of balls in the bag = 15 + x
P(white ball) =\(\frac{15}{15+x}\)
P(black ball) =\(\frac{x}{15+x}\)
Now, P(black ball ) =3 P( white ball )
⇒ \(\frac{x}{15+x} =3 \times \frac{15}{15+x} \quad \Rightarrow \quad x=45\)
Therefore, the number of black balls in the bag is 45
Question 15. Find the probability of having 53 Tuesdays in a:
Solution:
1. A non-leap year contains 365 days. So, by dividing it by 7, we get 52 weeks and 1 more day.
So, since 52 weeks are there, it means 52 Tuesdays will also be there necessarily with probability 1 and 1 more day may be either Sun. or Mon. or Tue. or Wed. or Thur. or Fri. or Sat.
So, to get 53 Tuesdays, we have to select one more Tuesday from these 7 possibilities with probability \({1}{7}\)
Therefore, probability of having 53 Tuesdays in a non-leap year = \(1 \times \frac{1}{7}=\frac{1}{7}\)
2. In a leap year, there are 366 days and 364 days make 52 weeks and therefore 52 Tuesdays. So, the probability of getting 52 Tuesdays till now is l(sure event). The remaining two days can be
Sunday – Monday
Monday – Tuesday
Tuesday – Wednesday
Wednesday – Thursday
Thursday – Friday
Friday – Saturday
Saturday – Sunday
Hence, favourable outcomes = 2 and total outcomes = 7.
Therefore, the probability of having 53 Tuesdays in a leap year is \(1 \times \frac{2}{7}=\frac{2}{7}\)
Question16. It is known that a box of 600 electric bulbs contains 12 defective bulbs. One bulb is taken out at random from this box. What is the probability that it is a non-defective bulb?
Solution:
Given
It is known that a box of 600 electric bulbs contains 12 defective bulbs. One bulb is taken out at random from this box.
The number of non-defective bulbs in the box = 600 – 12 = 588
So, probability of taking out a non-defective bulb = \(\frac{588}{600}=\frac{49}{50}\)=0.98
Question 17. Two customers are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on
Solution:
Given
Two customers are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any day as on another day.
1. Both the customers visit the shop on the same day, i.e., there are 6 days (Monday to Saturday) and each is equally likely.
∴ Probability of both will visit on the same day
= First will go on Monday and the other will also go on Monday or the first will go on Tuesday and the other will go on Tuesday:
or first will go on Saturday and other will also go on Saturday
=\(\frac{1}{6} \times \frac{1}{6}+\frac{1}{6} \times \frac{1}{6}+\ldots+\frac{1}{6} \times \frac{1}{6}=6 \times \frac{1}{6} \times \frac{1}{6}=\frac{1}{6}\)
Alternative Method:
The first person will definitely go to the market on any of the six days with probability 1 (sure event). If both go to the market the same day then the second person has only 1 choice (only that 1 day when the first goes). So, its probability of going to the market = \(\frac{1}{6}\)
∴ Required probability = \(1 \times \frac{1}{6}=\frac{1}{6}\)
2. The first person will definitely go to the market on any of the six days with probability 1 (sure event). Since both will not go on the same day, so second person has now only 5 choices (except this 1 day when first go to the market). So, the probability of the second man go to the other day = \(\frac{5}{6}\)
∴ Required probability = \(1 \times \frac{5}{6}=\frac{5}{6}\)
3. There are 5 consecutive days, i.e., Monday Tuesday, Tuesday Wednesday, Wednesday Thursday, Thursday Friday, Friday Saturday.
∴ Required probability = 5 \times \frac{1}{6} \times \frac{1}{6}=\frac{5}{36}
Question 18. Find the probability of getting 52 Sundays in a leap year.
Solution:
A leap year has 366 days, so by dividing it by 7, we get 52 weeks and 2 days more. 52 weeks means 52 Sundays surely. Now, what will you say?
Perhaps you will say that the probability of getting 52 Sundays in a leap year is 1. Your answer is not correct. Why?
Think about the two remaining days. If from the remaining 2 days, 1 day is the Sunday, then there are 53 Sundays in a leap year.
So, the question does not end at the stage that probability is 1. We have to consider necessarily the two remaining days.
The remaining 2 days may be (Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday).
For only 52 Sundays we want the combination of (Sunday, and Monday) or (Saturday, and Sunday not to occur. So, to get the required probability.
= (52 Sundays with probability 1) and (5 other possibilities out of 7 with probability \(\left(\frac{5}{7}\right)\))
= \(1 \times \frac{5}{7}=\frac{5}{7}\)
Question 19. If a number x is chosen at random from the numbers -2, -1, 0, 1, 2. What is the probability that \(x^2<2\)?
Solution:
We are presenting a table for x and x.

Clearly, x can take any one of the five values.
∴ Total number of cases = 5
Now, x3 < 2 when x = -1 or 0 or 1
∴ Favourable cases = 3
∴ Required probability =\(\frac{\text { Number of favourable cases }}{\text { Total number of cases }}=\frac{3}{5}\)
NCERT exemplar solutions for class 10 maths probability chapter
Question 20. A circle with a radius of 10 cm is drawn somewhere on a rectangular piece of paper of dimensions 10 cm x 30 cm, This paper is kept horizontally on the tabletop and a point is marked on the rectangular paper without seeing It. bind the probability that it will marked outside the circle. {Take \(\pi=\frac{22}{7}\)
Solution:
Given
A circle with a radius of 10 cm is drawn somewhere on a rectangular piece of paper of dimensions 10 cm x 30 cm, This paper is kept horizontally on the tabletop and a point is marked on the rectangular paper without seeing It.
Area of rectangle =40 \(\times 30 \mathrm{~cm}^2=1200 \mathrm{~cm}^2 \)
Area of circle =\(\pi(10)^2=100 \pi \mathrm{cm}^2\)
∴ Area of remaining portion =(1200-100 \(\pi) \mathrm{cm}^2\)
∴ Required probability =\(\frac{\text { Favourable portion }}{\text { Total portion }}=\frac{100(12-\pi)}{1200}\)
= \(\frac{12-\frac{22}{7}}{12}=\frac{84-22}{7 \times 12}=\frac{62}{7 \times 12}=\frac{31}{42}\)
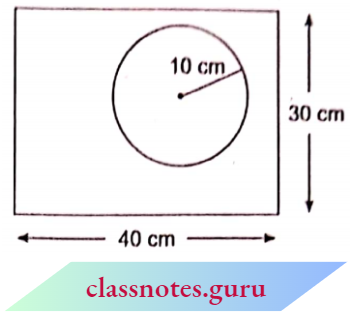
Question 21. A square dart board is placed in the first quadrant from x = 0 to,x = 6 and = 0 to x = 6. A triangular region on the dartboard is enclosed y = 2, x = 6 and y = x. Find the probability that a dart that randomly hits the dartboard will land in the triangular region formed by the three lines.
Solution:
Given
A square dart board is placed in the first quadrant from x = 0 to,x = 6 and = 0 to x = 6. A triangular region on the dartboard is enclosed y = 2, x = 6 and y = x.
Area of square board =\((6)^2=36 \mathrm{sq}\). units
Now, DE = 6 – 2 = 4 units
BD = 6 – 2 = 4 units
∴ Area of \(\triangle B D E =\frac{1}{2} \times D E \times B D=\frac{1}{2} \times 4 \times 4\)
= 8 sq units
Hence, required probability =\(\frac{Area of \triangle B D E}{{ Area of square } O A B C}\)
= \(\frac{8}{6 \times 6}=\frac{2}{9}\)
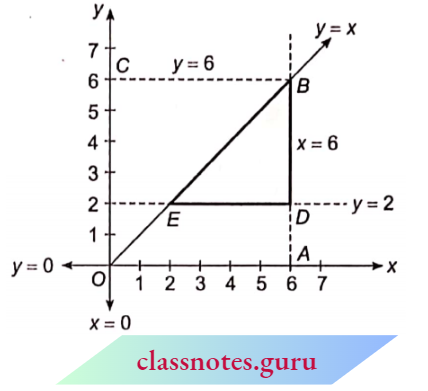
Question 1. Complete the following statements:
Solution:
Question 2. Which of the following experiments have equally likely outcomes? Explain.
Solution:
Question 3. Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of a football game?
Solution:
Tossing a coin is considered to be a fair way because the coin is symmetric and the possibilities of getting head or tail are equal.
Question 4. Which of the following cannot be the probability of an event?
Solution: 2. -1.5
Because the probability of an event cannot be smaller than zero.
chapter 15 probability NCERT exemplar solutions step by step
Question 5. If P(E) = 0.05, what is the probability of ‘not E’?
Solution :
P(E) = 0.05
Probability of ‘E-not’ = 1 – P(E)
= 1 – 0.05 = 0.95
Question 6. A bag contains lemon-flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out:
Solution :
There are only lemon-flavoured candies in the bag.
If a candy is drawn at random from the bag, then
1. The probability of drawing an orange-flavoured candy = 0.
So. the probability of drawing an orange-flavoured candy = 0.
2. The event of drawing a lemon-flavoured candle is a certain event.
So. the probability of drawing a lemon-flavoured candy = 1
Question 7. It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
Solution:
The probability of 2 students not having the same birthday = 0.992
∴ The probability of 2 students having the same birthday = 1 – 0.992 = 0.008
Question 8. A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is
Solution:
Total balls 3 + 5 = 8
Total possible outcomes of drawing a ball at random from the bag = 8
1. Favourable outcomes of drawing a red ball = 3
∴ The probability of drawing a red ball
Favourable outcomes of = \(\frac{\text { drawing a red ball }}{\text { Total possible outcomes }}\)
=\(\frac{3}{8}\)
2. Probability that the ball drawn is not red = 1 – probability that the ball drawn is red.
Question 9. A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be
Solution:
Total marbles = 5 + 8 + 4=17 Total possible outcomes of drawing a marble at random from the box = 17
1. Favourable outcomes of drawing a red marble = 5.
∴ The probability that the marble drawn is red
Favourable outcomes of = \(\frac{\text { drawing a red ball }}{\text { Total possible outcomes }}\)
=\(\frac{5}{17}\)
2. Favourable outcomes of drawing a white marble = S
∴ Possibility of drawing a white marble
Favourable outcomes of \(\frac{\text { drawing a red ball }}{\text { Total possible outcomes }}\)
= \(\frac{8}{17}\)
3. Favourable outcomes of drawing a green marble = 4
⇒ Favourable outcomes that the marble drawn is not green = 17 – 4 =13
∴ The probability that the marble drawn is not green
Favourable outcomes = \(\frac{\text { marble drawn is not green }}{\text { Total possible outcomes }}\)
= \(\frac{13}{17}\)
Question 10. A piggy bank contains a hundred 50 p coins, fifty ₹ 1 coins, twenty ₹ 2 coins and ten ₹ 5 coins. If it is equally likely that one of the tyre coins will fall out when the bank is turned upside down, what is the probability that the coin?
Solution:
No. of coins of 50 paise =100
No. of coins of ₹ 1 =50
No. of coins of ₹ 2 =20
No. of coins of ₹ 5 = 10
Total coins = 100 + 50 + 20 + 10 = 180
Total outcomes that one coin will fall out = 180
1. The favourable outcomes that the coin fall out is 50 paise = 100
∴ Probability that coin fall out is of 50 paise =\(\frac{100}{180}=\frac{5}{9}\)
2. The favourable outcome that the coin falls out is ₹ 5 = 10
∴ Probability that coin fall out is of Rs 5 = =\(\frac{10}{180}=\frac{1}{18}\)
Therefore, the probability that the coin falls out is not ₹ 5
= \(1-\frac{1}{18}=\frac{17}{18}\)
Question 11. Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish. What is the probability that the fish taken out is a male fish?
Solution :
Total no. of fish = 5 + 8 = 13
Total possible outcomes of taking a fish = 13
Favourable outcomes of taking a male fish = 5
Probability of a male fish
Favourable outcomes
= \(\frac{\text { drawing a male fish }}{\text { Total no. of possible outcomes of drawing a fish }}\)
= \(\frac{5}{3}\)
Question 12. A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2,3,4,5,6,7,8. and these are equally likely outcomes.
What is the probability that it will point at:
Solution :
Total no. of outcomes of pointing by an arrow =8
1. Favourable outcomes that the arrow indicates the number 8 = 1
∴ Probability of this event = \(\frac{1}{8}\)
Favourable outcomes that the arrow indicates an odd number = {1,3,5, 7} = 4
∴ Probability of this event = \(\frac{4}{8}=\frac{1}{2}\)
3. Favourable outcomes that the arrow indicates a number greater than 2 = {3,4,5,6,7,8} = 6
∴ Probability of this event = \(\frac{6}{8}\) =\(\frac{3}{4}\)
4. Favourable outcomes that the arrow indicates a number less than 9. = {1,2, 3, 4, 5, 6, 7, 8} = 8
∴ Probability of this event = \(\frac{8}{8}\)=1
Question 13. A die is thrown once. Find the probability of getting:
Solution:
Possible outcomes in one throw of a die = {1,2,3,4,5,6}
Total possible outcomes = 6
1. Prime numbers = {2, 3, 5} = 3
∴ Probability of getting a prime number = \(\frac{3}{6}=\frac{1}{2}\)
2. Numbers lying between 2 to 6 = {3,4,5} = 3
∴ Probability of this event = \(\frac{3}{6}=\frac{1}{2}\)
3. Odd numbers = {1, 3, 5} = 3
∴ Probability of this event =\(\frac{3}{6}=\frac{1}{2}\)
Question 14. One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting:
Solution:
Total possible outcomes of drawing a card from the pack of cards = 52.
1. Favourable outcomes of getting a king of red colour = 2.
∴ Probability of drawing a icing of red colour = =\(\frac{2}{52}=\frac{1}{26}\) .
2. Favourable outcomes of getting a face card = 12
∴ Probability of drawing a face card = \(\frac{12}{52}=\frac{3}{13}\)
3. Favourable outcomes of getting a face card of red colour = 6
∴ Probability of drawing a face card of red colour =\(\frac{6}{52}=\frac{3}{26}\)
4. Favourable outcomes of drawing a jack of heart = 1
∴ Probability of drawing a jack of heart = \(\frac{1}{52}\)
5. Favourable outcomes of drawing a card of spade = 13
∴ Probability of drawing a card of spade = \(\frac{13}{52}={1}{4}\)
6. Favourable outcomes of drawing a queen of diamonds = 1
∴ Probability of drawing a queen of diamond = \(\frac{1}{52}\)
Question 15. Five cards—the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random.
Solution:
Total favourable outcomes of drawing a card from the five playing cards = 5
1. Favourable outcomes of drawing a queen = 1
∴ Probability of drawing a queen = \(\frac{1}{5}\)
2. Remaining cards when ‘queen’ is drawn and put aside = 4
(1). Favourable outcomes of drawing a card of ace = 1
∴ Probability of drawing the second card ace = \(\frac{1}{4}\)
(2). Favourable outcomes of drawing a queen = 0
∴ Probability of drawing the second card of queen = \(\frac{0}{4}\)=0
class 10 maths chapter 15 probability important questions
Question 16. 12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.
Solution :
No. of good pens = 132
No. of defective pens = 12
Total pens = 132 + 12 = 144
Total favourable outcomes of drawing a pen = 144
Favourable outcomes of drawing a good pen = 132
∴ Probability of drawing a good pen = \(\frac{132}{144}\) = \(\frac{11}{12}\)
Question 17.
Solution:
Total bulbs = 20
Defective bulbs = 4
1. If a bulb is drawn at random then total possible outcomes = 20
Favourable outcomes of a defective bulb = 4.
∴ Probability of a defective bulb = \(\frac{4}{20}=\frac{1}{5}\)
2. If the bulb drawn is not defective and it is not replaced. Now a bulb is drawn then
Total possible outcomes =19
Favourable outcomes of a defective bulb = 4
∴ Probability of a defective bulb = \(\frac{4}{19}\)
⇒ Probability of a non-defective bulb =\(1-\frac{4}{19}=\frac{15}{19}\)
Question 18. A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears
Solution:
Total no. of discs = 90
Possible outcomes of drawing a disc = 90
1. Two digit numbers = {10, 11, 12, …90}
Favourable outcomes of drawing a two’ digit number = 81
Now, the probability of getting a two-digit number on the disc =\(\frac{81}{90}=\frac{9}{10}\)
2. Perfect square numbers in given numbers
= {1,4, 9, …,81}
⇒ Favourable outcomes of drawing a perfect square number = 9
Now, the probability that the number marked on the disc is a perfect square =\(\frac{9}{90}=\frac{1}{10}\)
3. Numbers divisible by 5 in the given numbers = (5, 10, 15,…, 90}
⇒ Favourable outcomes of a number drawn divisible by 5 = 18
Now, the probability that the number marked on the disc is divisible by 5 = \(\frac{18}{90}=\frac{1}{5}\)
Question 19. A child has a die whose six faces show the letters as given below:
A B C D E A
The die is thrown once. What is the probability of getting
Solution:
Total possible outcomes in a throw of die = 6
1. Favourable outcome of getting A = 2
∴ Probability of getting A = \(\frac{2}{6}=\frac{1}{3}\)
2. Favourable outcomes of getting D = 1
∴ Probability of getting D = \(\frac{1}{6}\)
Question 20. Suppose you drop a die at random on the rectangular region shown. What is the probability that it will land inside the circle with a diameter of 1 m?
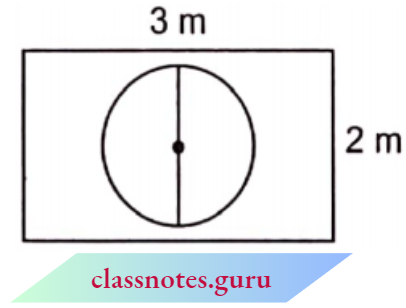
Solution:
Area of rectangle = \(3 \times 2=6 \mathrm{~m}^2\)
Diameter of circle =1 m
⇒ Radius of circle =\(\frac{1}{2} \mathrm{~m}\)
⇒ Area of circle =\(\pi\left(\frac{1}{2}\right)^2=\frac{\pi}{4} \mathrm{~m}^2\)
Now, the probability that in one throw of a die, the die lands inside the circle
= \(\frac{\text { Area of circle }}{\text { Area of rectangle }}\)
= \(\frac{\pi / 4}{6}=\frac{\pi}{4 \times 6}=\frac{\pi}{24}\)
Question 21. A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that:
Solution:
Total number of ball pens = 144
No. of defective ball pens = 20
∴ No. of good ball pens = 144 – 20 = 124
No. of favourable outcomes of drawing a pen randomly = 144
1. To buy the pen, it must be a good one.
∴ Favourable outcomes of drawing a good ball pen=124
⇒ Probability of buying a good ball pen =\(\frac{124}{144}=\frac{31}{36}\)
2. If the ball pen is defective then she will not buy it.
∴ Favourable outcomes of drawing a defective ball pen = 20
⇒ Probability of drawing a defective ball pen =\(\frac{20}{144}=\frac{5}{36}\)
Question 22. Two dice, one blue and one grey, are thrown at the same time,
1. Complete the following table:
2. A student argues that ‘there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability \(\frac{1}{11}\). Do you agree with this argument? Justify your answer.
Solution :
1. In a throw of two dice, possible outcomes are
⇒ \(\left\{\begin{array}{llllll}
(1,1), & (1,2), & (1,3), & (1,4), & (1,5), & (1,6) \\
(2,1), & (2,2), & (2,3), & (2,4), & (2,5), & (2,6) \\
(3,1), & (3,2), & (3,3), & (3,4), & (3,5), & (3,6) \\
(4,1), & (4,2), & (4,3), & (4,4), & (4,5), & (4,6) \\
(5,1), & (5,2), & (5,3), & (5,4), & (5,5), & (5,6) \\
(6,1), & (6,2), & (6,3), & (6,4), & (6,5), & (6,6)
\end{array}\right\}\)
Total possible outcomes = 36
Outcome of getting the sum 2 = (1, 1)
Favourable outcomes of getting a sum 2 = 1
∴ Probability of getting the sum 2 = \(\frac{1}{36}\)
Outcomes of getting the sum 3 = (1, 2), (2, 1)
Favourable outcomes of getting the sum 3 = 2
∴ Probability of getting the sum 3 = \(\frac{2}{36}={1}{18}\)
Outcomes of getting the sum 4 = (1,3), (2, 2), (3, 1)
Favourable outcomes of getting the sum 4 = 3
∴ Probability of getting the sum 4 = \(\frac{3}{36}={1}{12}\)
Outcomes of getting the sum 5 = (1,4), (2, 3), (3, 2), (4, 1)
Favourable outcomes of getting the sum 5=4
∴ Probability of getting the sum 5 = \(\frac{4}{36}={1}{9}\)
Outcomes of getting the sum 6 = (1,5), (2, 4), (3, 3), (4, 2), (5, 1)
Favourable outcomes of getting the sum 6 = 5
∴ Probability of getting the sum 6 = \(\frac{5}{36}\)
Outcomes of getting the sum 7 = (1,6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)
Favourable outcomes of getting the sum 7 = 6
∴ Probability of getting the sum 7 = \(\frac{6}{36}={1}{6}\)
Outcomes of getting the sum 8 = (2, 6), (3, 5), (4, 4), (5, 3), (6, 2)
Favourable outcomes of getting the sum 8 = 5
∴ Probability of getting the sum 8 = \(\frac{5}{36}\)
Outcomes of getting the sum 9 = (3,6), (4, 5), (5, 4), (6, 3)
Favourable outcomes of getting the sum 9 = 4
∴ Probability of getting the sum 9 = \(\frac{4}{36}={1}{9}\)
Outcomes of getting the sum 10 = (4, 6),(5, 5), (6, 4)
Favourable outcomes of getting the sum 10 = 3
∴ Probability of getting the sum 10 = \(\frac{3}{36}={1}{12}\)
Outcomes of getting the sum 11 = (5, 6), (6, 5)
Favourable outcomes of getting the sum 11 = 2
∴ Probability of getting the sum 11= \(\frac{2}{36}={1}{18}\)
Outcomes of getting the sum 12 = (6, 6)
Favourable outcomes of getting the sum 12 = 1
∴ Probability of getting the sum 12 = \(\frac{1}{36}\)
Now, the given table will be as follows:
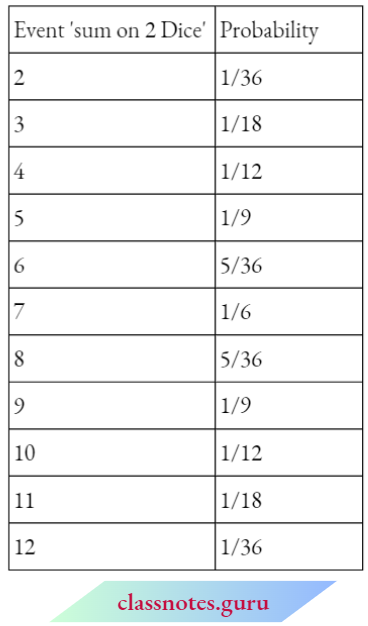
2. The student’s argument is wrong because the favourable outcomes of every event are different.
Probability chapter exemplar questions with detailed solutions
Question 23. A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hanifwins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Solution :
Given
A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hanifwins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise.
All possible outcomes in three throws of a coin of ₹ 1.
HHH, HHT, HTH, THH, HTT, THT, TTH,
TTT → Total possible outcomes = 8
Favourable outcomes of 3 heads = 1
Favourable outcomes of 3 tails = 1
∴ Favourable outcomes to win = 2
Now, favourable outcomes to lose = 8 – 2 = 6
Therefore, the probability to lose
= \(\frac{\text { Favourable outcomes to lose }}{\text { Total possible outcomes }}\)
= \(\frac{6}{8}=\frac{3}{4}\)
Question 24. A die is thrown twice. What is the probability that:
[Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment]
Solution:
In two throws of a die, the all possible outcomes are :
(1.1), (1,2), (1,3), (1,4), (1,5), (1,6)
(2.1), (2,2), (2,3), (2,4), (2,5), (2,6)
(3.1), (3,2), (3,3), (3,4), (3,5), (3,6)
(4.1), (4,2), (4,3), (4,4), (4,5), (4,6)
(5.1), (5,2), (5,3), (5,4), (5,5), (5,6)
(6.1), (6,2), (6,3), (6,4), (6,5), (6,6)
Total possible outcomes = 36
Outcomes in which 5 comes up = 11
Outcomes in which 5 does not come up = 36 – 11 = 25
1. Favourable outcomes that 5 does not come up = 25
∴ Probability of not getting 5 = \(\frac{25}{36}\)
2. Favourable outcomes that 5 will come up at least once = 11
∴ Probability that 5 will come up at least once = \(\frac{11}{36}\)
Question 25. Which of the following arguments are correct and which are not correct? Clive reasons for your answer.
Solution:
1. When two coins are tossed together, then there are not three outcomes, but the following four outcomes are obtained:
HH, HT, TH, TT
So, the .ugumom of the student is false.
2. In one throw of a die
All possible outcomes {1, 2, 3, 4, 5, 6} 6
Outcomes of getting an even number = {2. 4, 6} = 3
Outcomes of gelling an odd number = (1,3,5} =3
∴ Possibility of getting an odd number= \(\frac{3}{6}=\frac{1}{2}\)
Therefore, the argument of the student is true.
Question 1. Two customers Shvam and Ehta visit a particular shop in the same week (Tuesday to Saturday), Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on
Solution:
Hence, the total possible outcomes are as follows:
Toral possible outcomes = 25
1. Outcomes that both customers visit on the same day
= (T. T), (W, W), (Th. Th), (F, F), (S, S)
Total favourable outcomes = 5
So. is probability Drat Bodi will visit on the same day
= \(\frac{5}{25}=\frac{1}{5}\)
2. Outcomes that both customers visit on consecutive days
= (T, W), (W; Th), (Th, F), (F, S), (W, T), (Th, W), (F, Th), (S, F)
Total favourable outcomes = 8
So, the probability that both visit on consecutive days the shop
= \(\frac{8}{25}\)
3. Probability that both visit the shop on the same day = \(\frac{1}{5}\) [from part (1)]
∴ The probability that both visit the shop on different days
1= \(\frac{1}{5}= {4}{5}\)
Question 2. A die is numbered in such a way that its faces show the numbers 1,2,2, 3, 3, 6. It is thrown two times and the total score in two throws is noted. Complete the following table which gives a tew values of the total score on the two throws:
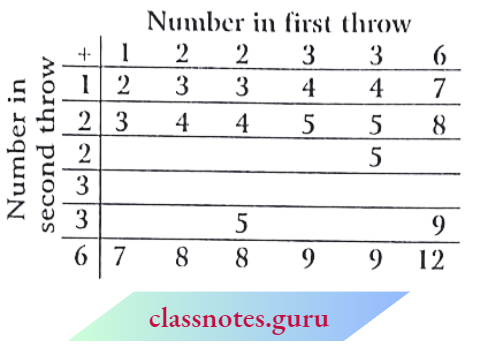
Number in the first throw What is the probability that the total score is
Solution:
Total possible outcomes = 36
1. Favourable outcomes of getting the sum as an even number = 18
∴ Probability of getting the sum as even number = \(\frac{18}{36}=\frac{1}{2}\)
2. Favourable outcomes of getting a sum 6 = 4
∴ Probability of getting a sum 6= \(\frac{4}{36}=\frac{1}{9}\)
3. Favourable outcomes of getting a sum less than 6=15.
∴ Probability of getting a sum less than 6 =\(\frac{15}{36}=\frac{5}{12}\)
Question 3. A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.
Solution:
Given
A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball
Let the number of blue balls =x
Given, the number of red balls = 5
Total balls = x + 5
∴ The probability of drawing a blue ball
⇒ P(B)=\(\frac{x}{x+5}\)
and the probability of drawing a red ball
⇒ P(R)=\(\frac{5}{x+5}\)
Given that, P(B) =2 \(\times P(R)\)
⇒ \(\frac{x}{x+5} =\frac{2 \times 5}{x+5}\)
⇒ x =10
⇒ Number of blue balls =10
Question 4. A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball?
If 6 more black balls are put in the box, the probability of drawing a black ball is now double of what it was before. Find x.
Solution:
Given
A box contains 12 balls out of which x are black. If one ball is drawn at random from the box,
Total balls in the box = 12
Black balls = x
∴ Probability of drawing a black ball = \(\frac{x}{12}\)
On putting 6 more black balls in the box, Total balls = 12 + 6= 18 Black balls = x + 6
Now, probability of drawing a black ball = \(\frac{x+6}{12}\)
Given that, \(\frac{x+6}{18} =2 \times \frac{x}{12}\)
⇒ \(\frac{x+6}{18} =\frac{x}{6}\)
⇒ x + 6 = 3 x
⇒ 2 x = 6 ⇒ x = 3
Question 5. A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green 2 is \(\frac{2}{3}\). Find the number of blue balls in the jar.
Solution:
Given
A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green 2 is \(\frac{2}{3}\).
Total marbles in jar = 24
Let green marbles in jar = x
∴ Probability of drawing 1 green marble from jar = \(\frac{x}{24}\)
Given that, \(\frac{x}{24}=\frac{2}{3}\)
x = \(\frac{2}{3} \times 24\)
⇒ x = 16
∴ Green marbles = 16
⇒ Blue marbles = 24 – 16 = 8
MCQs and subjective questions in class 10 probability exemplar
Question 1. The probability of a sure event is:
Answer: 2. 1
Question 2. The sum of the probabilities ofan event and its complementary event is:
Answer: 3. 1
Question 3. The probability of winning a match by Ravi is \(\frac{2}{5}\). The probability of his losing the match is
Answer: 1. \(\frac{3}{5}\)
Question 4. If P(A) represents the probability of an event, A, then:
Answer: 3. 0 ≤ P(A) ≤1
Question 5. When a dice is thrown, the probability of getting an even number less than 3, is:
Answer: 4. \(\frac{1}{6}\)
CBSE class 10 maths probability exemplar chapter explanation
Question 6. The probability of selecting a prime number from the numbers 1 to 20, is:
Answer: 2. \(\frac{2}{5}\)
Question 7. In a year, which is not a leap year, the probability of 53 Monday is:
Answer: 4. \(\frac{1}{7}\)
The objects which occupy space have three dimensions) arc called solids.

A cuboid is a rectangular solid having six faces all of which are rectangles. The cuboid has six faces. The opposite faces are all congruent. Two adjacent faces meet in a line.
This line is called the edge of the cuboid. There are 12 edges of a cuboid. The point where three adjacent edges meet is called the vertex of the cuboid. There are 8 vertices of a cuboid.
The three edges that meet on the vertex of a cuboid are called its length, breadth and height. A cube is a cuboid in which all the edges are of equal length and every one of the six faces is a square.
NCERT Exemplar Solutions for Class 10 Maths Chapter 13
Read and Learn More Class 10 Maths Solutions Exemplar
Total Surface (Surface Area) of a Cuboid and a Cube
The sum of the area of the faces of the cuboid is called its surface. The areas of opposite faces are equal, so the total surface of the A cuboid is
2lb + 2bh + 2hl = 2 (bh+ hl +lb)
For a cube, l = b = h = a (say)
Surface of a cube = 2(a.a + a.a + a.a) = 6a2
The Length of the Diagonal of a Cuboid and a Cube
Diagonal of a floor \(D^{\prime} B^{\prime}=\sqrt{l^2+b^2}\). So, if we want to find the length of the longest rod DB’, then we make a new right-angled A treating, DB’ as hypotenuse, base as D’B’ and height as DD’ which is h. So, the length of the diagonal of a cuboid DB’.
= \(\sqrt{\left(D^{\prime} B^{\prime}\right)^2+\left(D D^{\prime}\right)^2}=\sqrt{l^2+b^2+h^2}\)
For a cube, l = b = h = a (say)
∴ The length of the diagonal of a cube = \(\sqrt{a^2+a^2+a^2}=a \sqrt{3}\)
Lateral Surface Area of a Cuboid and a Cube
The volume of a Cuboid and a Cube
The volume of any solid figure is the amount of space enclosed within its bounding faces.
The volume of a cuboid of length l units, breadth b units and height h units are lbh cubic units.
= (length x breadth x height) cubic units
= (area of the base x height) cubic units.
For a cube,
Volume of cube = a3 cubic units,
where, the length of the edge of the cube is a unit.
Note: The measurements of volume are as follows:
1 cm3 = 103 cubic mm
1 m3 = 1000 litre = 1 kl
If a rectangle is revolved about one of its sides as its axis, the solid so formed is called a right circular cylinder.
The side AD about which the rectangle ABCD revolves is called the height of the cylinder.
The line CD is called the generating line because when it revolves round AB, it generates the cylinder.
If you cut the hollow cylinder along AD and spread the piece, it becomes a rectangle whose one side is AD and the other side is AB which is equal to the circumference of a circle whose radius is the radius of the cylinder.
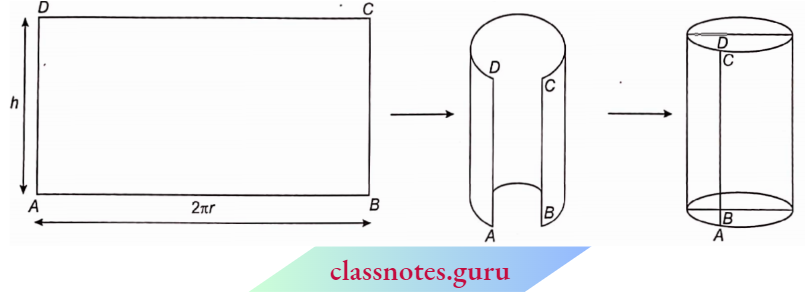
Hence, Side AB = 2πr
If h is the height of the cylinder, the area of ABCD
= AB x AD = 2πrh
Thus, the area of the curved surface of the cylinder
= 2πrh = perimeter of base x height
Whole Surface of a Cylinder
The whole surface area of a cylinder
= Curved surface + Area of the base + Area of the top
= 2πrh + πr2 + nr2 = 2πrh + 2πr2 = 2πr(h + r)
Volume of a Cylinder
The volume of a cylinder = Area of the base x Height
= nr2 x h = nr2h
Note: If the top and bottom are removed from the total surface area, then only the curved surface area remains.
Solids like iron pipes, rubber tubes, etc., are in the shape of hollow cylinders.
For a hollow cylinder of height h and with external and internal radii R and r respectively, we have
Volume of the material = Exterior volume- Interior volume
= πR2h- πr2h = πh (R2– r2)
The curved surface of the hollow cylinder
= External surface + Internal surface = 2πRh + 2πrh = 2πh(R + r)
The total surface area of the hollow cylinder
= Curved surface + 2(Area of base rings)
= (2πRh + 2πrh) + 2(πR2– πr2) = 2πh(R + r) + 2π(R2 – r2)
= 2π(R + r) (h+R-r)
A right circular cone is a solid generated by the revolution of a right-angled triangle about sides containing the right angle as the axis.
Let CAB be a right-angled triangle, right-angled at A. The hypotenuse CB revolves around the side CA as the fixed axis. The hypotenuse CB will generate the curved surface of a cone.
The radius of the circular base is called the radius of the cone. It is usually denoted by ‘r’.
The point C is called the vertex of the cone.
The length CA of the axis is called the height of the cone. It is usually ‘denoted by ‘h’.
The hypotenuse CB is called the generating line of the cone and its length is called the slant height. It is usually denoted by l.
The volume of Right Circular Cone
Volume of a cone = \(\frac{1}{3}\) (area of the base) x height’
i.e., \(V=\frac{1}{3} \pi r^2 h\)
where r = radius of the base and h = height.
Slant height of right circular cone = \(l=\sqrt{h^2+r^2}\)
The curved surface of the Right Circular Cone
Curved surface of a cone = \(\pi r l=\pi r \sqrt{h^2+r^2}\)
where r = radius of the base, l = slant height of the cone.
Total Surface of Right Circular Cone
Total surface of the cone = Area of the base + Area of the curved surface
i.e., total surface of the cone = πr2 + πrl = πr(r + l).
Surface Areas and Volumes Class 10 Exemplar Solutions
When a circle is revolved about its diameter, the solid thus formed is a sphere. Let AB be the diameter of a circle ADB and 0 be its centre.
If the circle ADB revolves around AB, point D takes different positions and a closed solid is formed.
A sphere may also be defined as a solid bounded by a closed surface, all points on which are at a constant distance from a fixed point.
Curved Surface Area and Volume of a Sphere
The curved surface area of a sphere = 4πr2, where r is the radius of the sphere.
The volume of sphere = \(\frac{4}{3} \pi r^3\)
A plane through the centre of a sphere divides the sphere into two equal parts. Each part is called a hemisphere.
If r is the radius of the hemisphere, then
Volume of hemisphere = \(\frac{2}{3} \pi r^3\)
Curved surface area = 2πr2
Total surface area = 2πr2 + πr2 = 3πr2.
A spherical shell having external radius R and internal radius r, then we have
Volume of material = \(\frac{4}{3} \pi R^3-\frac{4}{3} \pi r^3=\frac{4}{3} \pi\left(R^3-r^3\right)\)
Volume And Surface Area Of Solids Solved Examples
Question 1. A tent of cloth is cylindrical upto 1 m in height and conical above it of the same radius of base. If the diameter of the tent is 6 m and the slant height of the conical part is 5 m, find the cloth required to make this tent.
Solution:
Given
A tent of cloth is cylindrical upto 1 m in height and conical above it of the same radius of base. If the diameter of the tent is 6 m and the slant height of the conical part is 5 m,
Diameter of base 2r = 6 m
⇒ \(r=\frac{6}{2}=3 \mathrm{~m}\)
Height of cylindrical path h = 1 m
The slant height of conical part l = 5 m
Cloth required in tent = 2πrh + πrl
= πr (2h + l)
= \(\frac{22}{7} \times 3(2 \times 1+5)=66 \mathrm{~m}^2\)
The cloth required to make this tent =66 m²
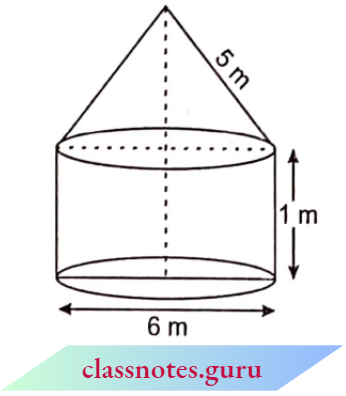
Question 2. The base and top of a right circular cylindrical drum are hemispherical. The diameter of the cylindrical part is 14 cm and the total height is 30 cm. Find the total surface area of the drum.
Solution:
Given
The base and top of a right circular cylindrical drum are hemispherical. The diameter of the cylindrical part is 14 cm and the total height is 30 cm.
Here 2r = 14
⇒ r = 7 cm
Height of cylindrical part h = 30 – 2 x 7 = 16 cm
The total surface area of the drum = 2 x the Curved surface of the hemisphere + the Curved surface of the cylinder
= 2 x 2πr2 + 2πrh
= 2πr(2r + h)
= \(2 \times \frac{22}{7} \times 7(2 \times 7+16)\)
= 44 x 30 = 1320 cm2
The total surface area of the drum = 1320 cm2
Volume and Surface Area Class 10 Exemplar Questions
Question 3. Three cubes, each with an 8 cm edge, are joined end to end. Find the total surface area of the resulting cuboid.
Solution:
Given
Three cubes, each with an 8 cm edge, are joined end to end.
As is clear from the adjoining figure;
the length of the resulting cuboid = 3 x 8 cm = 24 cm
Its width = 8 cm and its height = 8 cm
i.e., l = 24 cm, b = 8 cm and h = 8 cm
∴ The total surface area of the resulting cuboid
= 2(1 x b + b x h + h x l)
= 2 (24 x 8 + 8 x 8 + 8 x 24) cm2 = 896 cm2
The total surface area of the resulting cuboid = 896 cm2
Question 4. A rectangular sheet of tin 58 cm x 44 cm is to be made into an open box by cutting off equal squares from the corners and folding up the flaps. What should be the volume of box if the surface area of box is 2452 cm2?
Solution:
Given
A rectangular sheet of tin 58 cm x 44 cm is to be made into an open box by cutting off equal squares from the corners and folding up the flaps.
Let a square of x cm from each corner be removed from a rectangular sheet.
So, length of box = (58 – 2x) cm
breadth of box = (44 – 2x) cm
and height of box = x cm
∴ Surface area of open box = 2 (lb + bh + hl)- lb
⇒ 2[(58 – 2x) (44 – 2x) + x (44 – 2x) + x (58 – 2x)]- (58 – 2x)(44 – lx) = 2452
⇒ (58- 2x) (44- 2x) + 2x(44- 2x) + 2x (58 – 2x) = 2452
⇒ (29 – x) (22 – x) + x (22 – x) + x (29 – x) = 613
⇒ 638 – 51x + x2 + 22x – x2 + 29x – x2 = 613
⇒ x2 = 25
⇒ x = 5 cm (x = – 5 is not admissible)
∴ Volume of box = x(58 – 2x) (44- 2x) = 5(58- 10)(44 – 10)
= 5 x 48 x 34 cm3 = 8160 cm3
The volume of box = 8160 cm3
Question 5. The radii of two right circular cylinders are in the ratio 2 : 3 and their heights are in the ratio 5:4. Calculate the ratio of their curved surface areas and also the ratio of their volumes.
Solution:
Given
The radii of two right circular cylinders are in the ratio 2 : 3 and their heights are in the ratio 5:4.
Let the radii of the two cylinders be 2r and 3r respectively and their heights be 5h and 4h.
∴ \(\frac{\text { Curved surface area of 1st cylinder }\left(S_1\right)}{\text { Curved surface area of 2nd cylinder }\left(S_2\right)}=\frac{2 \pi \times 2 r \times 5 h}{2 \pi \times 3 r \times 4 h}\)
i.e., \(\frac{S_1}{S_2}=\frac{5}{6}\) or S1: S2 = 5:6
⇒ \(\frac{\text { Volume of 1st cylinder }\left(V_1\right)}{\text { Volume of 2nd cylinder }\left(V_2\right)}=\frac{\pi \times(2 r)^2 \times 5 h}{\pi \times(3 r)^2 \times 4 h}\)
i.e., \(\frac{V_1}{V_2}=\frac{5}{9}\) or V1:V2= 5:9
The ratio of their volumes = 5:9
Question 6. The volume and surface area of a solid hemisphere are numerically equal. What is the diameter of the hemisphere?
Solution:
Given
The volume and surface area of a solid hemisphere are numerically equal.
We have,
Volume of hemisphere = Surface area of hemisphere
⇒ \(\frac{2}{3} \pi r^3=3 \pi r^2\) = 2r = 9
Hence, the diameter of the hemisphere = 9 units
Question 7. The curved surface area of a cone of height 8 m is 1 88.4 m2. Find the volume of a cone.
Solution:
Given
The curved surface area of a cone of height 8 m is 1 88.4 m2.
πrl = 188.4
⇒ \(r l=\frac{188.4}{3.14}=60\)
⇒ r2l2 = 3600
⇒ r2(h2 + r2) = 3600
⇒ r2(64 + r2) = 3600
⇒ r4 + 64r2 – 3600 = 0
⇒ (r2+ 100) (r2– 36) = 0
∴ r2 = -100 or r2 = 36
⇒ r = 6 (∵ r2 = -100 is not possible)
∴ Volume of a cone = \(\frac{1}{3} \pi r^2 h=\frac{1}{3} \times 3.14 \times 36 \times 8=301.44 \mathrm{~m}^3\)
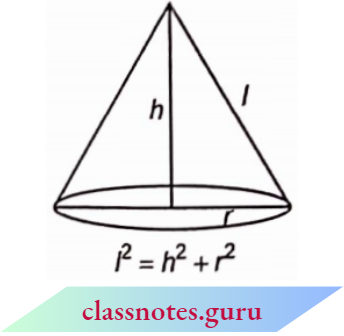
Question 8. A conical tent is required to accommodate 157 persons, each person must have 2 m2 of space on the ground and 15 m3 of air to breathe. Find the height of the tent; also calculate the slant height.
Solution:
Given
A conical tent is required to accommodate 157 persons, each person must have 2 m2 of space on the ground and 15 m3 of air to breathe.
1 person needs 2 m2 of space.
∴ 157 persons needs 2 x 157 m space on the ground
∴ r2 = 2 x 157
∴ \(r^2=\frac{2 \times 157}{3.14}=100\) = r = 100
Also, 1 person needs 15 m of air.
∴ 157 persons need 15 x 157 m3 of air.
∴ \(\frac{1}{3} \pi r^2 h=15 \times 157\)
⇒ \(h=\frac{15 \times 157 \times 3}{3.14 \times 100}=22.5 \mathrm{~m}\)
∴ l2 =h2 + r2 = (22.5)2 + (10)2 = 606.25
∴ \(l=\sqrt{606.25}=24.62 \mathrm{~m}\)
The height of the tent =22.5 m
The slant height= 24.62 m

Question 9. The radius and height of a solid right circular cone are in the ratio of 5:12. If its volume is 314 cm find its total surface area. [Take π = 3.14]
Solution:
Given
The radius and height of a solid right circular cone are in the ratio of 5:12. If its volume is 314 cm
Let the radius of the cone = 5x
∴ Height of cone = 12r
∴ l2 = (5r)2 + (12x)2 = 169 x2
∴ \(l=\sqrt{169 x^2}=13 x\)
It is given that volume = 314 cm2
∴ \(\frac{1}{3} \pi(5 x)^2(12 x)=314\)
⇒ \(\frac{1}{3} \times 3.14 \times 25 \times 12 \times x^3=314\)
⇒ \(x^3=\frac{314 \times 3}{3.14 \times 25 \times 12}=1\)
∴ x = 1
∴ Radius r = 5 x 1 = 5 cm
Height h = 1 2 x 1 = 1 2 cm
and slant height l= 13 x I = 13 cm
Now, total surface area of cone = πr(l + r) = 3.14 x 5 (13 + 5) = 3.14 x 5 x 18
= 282.60 cm2
Hence, the total surface area of a cone is 282.60 cm.
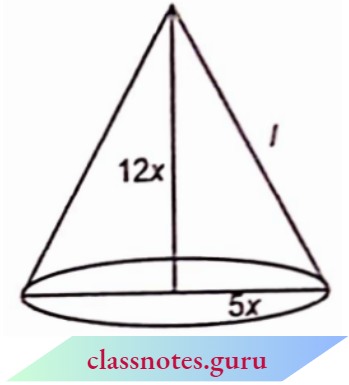
Question 10. If h, C, and V respectively are the height, the curved surface area and the volume of a cone. Prove that 3πVh3 – C2h2 + 9V2 = 0.
Solution:
Given
h, C, and V respectively are the height, the curved surface area and the volume of a cone.
⇒ \(C=\pi r l, V=\frac{1}{3} \pi r^2 h, l^2=h^2+r^2\)
L.H.S. = 3πVh3 – C2h2 + 9V2
= \(3 \pi\left(\frac{1}{3} \pi r^2 h\right) h^3-(\pi r l)^2 h^2+9\left(\frac{1}{3} \pi r^2 h\right)^2\)
= \(\pi^2 r^2 h^4-\pi^2 r^2 h^2\left(h^2+r^2\right)+9 \times \frac{1}{9} \pi^2 r^4 h^2\)
= π2r2h4 – π2r2h4 – π2r4h2 + π2r4h2 = 0 = R.H.S. Hence Proved.
Question 11. A cone of equal height and equal base is cut off from a cylinder of height 24 cm and base radius 7 cm. Find the total surface and volume of the remaining solid.
Solution:
Given
A cone of equal height and equal base is cut off from a cylinder of height 24 cm and base radius 7 cm.
Here r = 7 cm, h = 24 cm
The volume of remaining solid = Volume of the cylinder – Volume of a cone
= \(\pi r^2 h-\frac{1}{3} \pi r^2 h=\frac{2}{3} \pi r^2 h\)
= \(\frac{2}{3} \times \frac{22}{7} \times 7 \times 7 \times 24=2464 \mathrm{~cm}^3\)
Now, l2 = h2 + r2 = (24)2 + (7)2
= 576 + 49 = 625
⇒ l = 25 cm
∴ Total surface area of remaining solid
= Curved surface of cylinder + Curved surface of cone + Area of top
= 2πrh +πrI + πr2
= πr(2h + l + r)
= \(\frac{22}{7} \times 7(2 \times 24+25+7)=22 \times 80=1760 \mathrm{~cm}^2\)
Total surface area of remaining solid = 1760 cm²
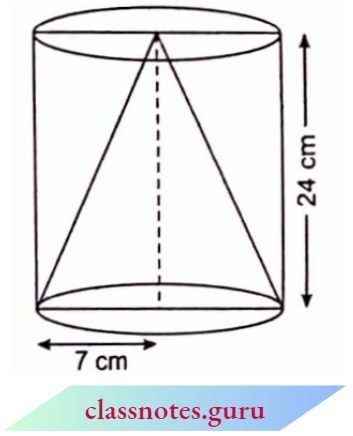
Question 12: From a wooden cubical block of edge 7 cm, the largest possible right conical piece is cut out whose base is on one of the faces of the cube. Calculate:
Solution:
Initial volume of the block = a3 = 73 cm3
The base of the largest cone will touch the sides of the base of the cube, and the height will be equal to the length of the edge of the cube.
∴ For the cone, r = 3.5 cm and h = 7 cm.
1. The volume of the cone = \(\frac{1}{3} \pi r^2 h=\frac{\pi}{3} \cdot\left(\frac{7}{2}\right)^2 \cdot 7 \mathrm{~cm}^3\)
∴ volume of the wood left = \(\left\{7^3-\frac{1}{3} \cdot \frac{22}{7} \cdot\left(\frac{7}{2}\right)^2 \cdot 7\right\} \mathrm{cm}^3\)
= \(\left(7^3-\frac{11 \times 7^2}{3 \times 2}\right) \mathrm{cm}^3=7^2\left(7-\frac{11}{6}\right) \mathrm{cm}^3\)
= \(\frac{49 \times 31}{6} \mathrm{~cm}^3=\frac{1519}{6} \mathrm{~cm}^3=253 \frac{1}{6} \mathrm{~cm}^3\)
2. The total surface area of the wood left
= Total surface area of the cube- Area of the base of the cone + Curved surface area of the cone.
= 6a2 – πr2 + πrl
= \(\left\{6 \times 7^2-\frac{22}{7} \cdot\left(\frac{7}{2}\right)^2+\frac{22}{7} \cdot \frac{7}{2} \cdot \sqrt{7^2+\left(\frac{7}{2}\right)^2}\right\} \mathrm{cm}^2\)
= \(\left(6 \times 49-\frac{11 \times 7}{2}+11 \cdot 7 \cdot \frac{\sqrt{5}}{2}\right) \mathrm{cm}^2=\left\{294+\frac{77}{2}(\sqrt{5}-1)\right\} \mathrm{cm}^2\)
= \(\left(294+\frac{77}{2} \times 1.24\right) \mathrm{cm}^2=341.74 \mathrm{~cm}^2\)
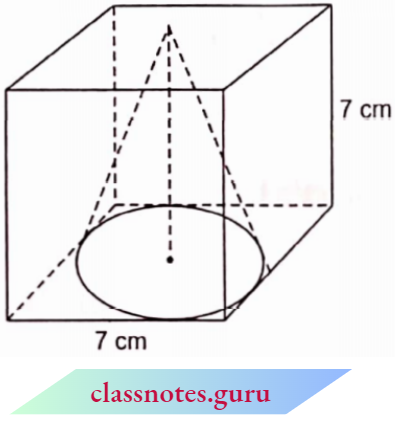
Question 13. A sphere is inscribed in a cylinder such that the sphere touches the cylinder. Show that the curved surface is equal to the curved surface of the cylinder.
Solution:
Given
A sphere is inscribed in a cylinder such that the sphere touches the cylinder.
A cylinder circumscribed a sphere is shown.
Here, the radius of the sphere = radius of the cylinder = r
Height of cylinder h = 2r
Now, the curved surface of the sphere = 4πr2
and the curved surface of sphere of cylinder = 2πrh = 2πr(2r) = 4πr2
Therefore, the curved surface of the sphere and the curved surface of the cylinder are equal.
Hence proved.

Question 14. The largest possible cube Is made from a wooden sphere of radius 6√3 cm. Find the surface area of the cube.
Solution:
Given
The largest possible cube Is made from a wooden sphere of radius 6√3 cm
Here, a diagonal of the cube will be the diameter of the sphere
∴ length of a diagonal of the cube = 2 x 6√3 cm = 12√3 cm
If an edge of the cube is a then a diagonal of the cube = √3 a
= 12√3 cm
∴ a = 12 cm.
∴ The surface area of the cube = 6a2 = 6.(12)2 cm2 = 864 cm2
Question 15. A hemisphere is inscribed in a cylinder and a cone is inscribed in the hemisphere. The cone vertex lies in the centre of the upper circular part of the cylinder. Show that: \(\frac{1}{3}\) x Volume of cylinder = \(\frac{1}{2}\)x Volume of hemisphere = Volume of cone
Solution:
Given
A hemisphere is inscribed in a cylinder and a cone is inscribed in the hemisphere. The cone vertex lies in the centre of the upper circular part of the cylinder.
Let radius of cone = radius of cylinder = radius of hemisphere = r
∴ Height of cone = Height of cylinder = r
Now, the volume of cone = \(\frac{1}{3} \pi r^2 \cdot(r)=\frac{1}{3} \pi r^3\) → (1)
Volume of hemisphere = \(\frac{2}{3} \pi r^3\)
⇒ \(\frac{1}{2}\)x Volume of hemisphere = \(\frac{1}{3} \pi r^3\) → (2)
and Volume of cylinder = πr2(r) = r3
⇒ \(\frac{1}{3}\) x Volume of cylinder = \(\frac{1}{3} \pi r^3\) → (3)
From equations (1), (2) and (3)
⇒ \(\frac{1}{3}\) x Volume of cylinder = \(\frac{1}{2}\)x Volume of hemisphere
= Volume of cone
Hence proved.
Question 16. Water in a canal, 5.4 m wide and 1.8 m deep is flowing at a speed of 25 km/hr. How much area can it irrigate in 40 minutes, if 10 cm of standing water is required for irrigation?
Solution:
Given
Water in a canal, 5.4 m wide and 1.8 m deep is flowing at a speed of 25 km/hr.
Width of canal = 5.4 m
Height of canal = 1.8 m
In one hour, water is moving upto 25 km = 25000 m
∴ We treat it as the length of the canal.
∴ Volume of water in canal in 1 hour = (25000 x 5.4 x 1.8)m3
⇒ Volume of water in the canal in 40 minutes = 243000 m3
∴ Volume of water in canal in 60 minutes = \(\frac{243000}{60} \times 40 \mathrm{~m}^3\)
= 162000 m3
This water can irrigate a field upto the height of 10 cm = 0. 1 m
∴ Volume = Area = Area x height
⇒ 162000 = Area x 0.1
⇒ Area of field = \(\frac{162000}{0.1} \mathrm{~m}^2=1620000 \mathrm{~m}^2\) (∵Note: 1 Hectare = 1000 m)
= \(\frac{1620000}{10000} \text { hectare }\)
= 162 hectare.
So, 162 hectare area can be irrigated.
When a solid is converted into another without any loss of material then its volume remains the same.
If a larger solid is converted into smaller solids then the number of smaller solids
= \(\frac{\text { Volume of larger solid }}{\text { Volume of } 1 \text { smaller solid }}\)
Conversion Of Solid Form One Shape To Another And Mixed Problems Solved Examples
Question 1. A solid metallic cuboid of dimensions 9 m x 8 m x 2 m is melted and recast into solid cubes of edge 2m. Find the number of cubes so formed.
Solution:
Given
A solid metallic cuboid of dimensions 9 m x 8 m x 2 m is melted and recast into solid cubes of edge 2m.
Let x cubes each of edge 2 m are formed to melt a cuboid of dimensions 9 x 8 x 2.
So, \(\text { number of cubes }=\frac{\text { Volume of cuboid }}{\text { Volume of } 1 \text { cube }}\)
∴ \(x=\frac{9 \times 8 \times 2}{2}=72\)
So, 72 cubes will be formed
Question 2. Three cubes of metal whose edges are in the ratio 3:4 are melted down into a single cube whose diagonal is 12√3 cm, Find the edges of the three cubes.
Solution:
Given
Three cubes of metal whose edges are in the ratio 3:4 are melted down into a single cube whose diagonal is 12√3 cm,
The ratio in the edges = 3:4:5
Let edges be 3x, 4x and 5x respectively.
∴ Volumes of three cubes will be 27x3, 64x3 and 125x3 in cm3 respectively.
Now, sum of the volumes of these three cubes = 27x3 + 64x3 + 125 x3 = 216 x3 cm3
Let the edge of the new cube be a cm.
Diagonal of new cube = a√3 cm
a√3 = 12√3
Volume of new cube = (12)3 = 1728 cm3
Now by the given condition
216x3 = 1728
⇒ x3 = 8
⇒ x = 2
∴ \(\left.\begin{array}{rl}
\text { Edge of 1 cube } & =3 \times 2=6 \mathrm{~cm} \\
\text { Edge of 2 cube } & =4 \times 2=8 \mathrm{~cm} \\
\text { Edge of 3 cube } & =5 \times 2=10 \mathrm{~cm}
\end{array}\right\}\).
Question 3. A cube of metal with a 2.5 cm edge is melted and cast into a rectangular solid whose base is 1.25 cm by 0.25 cm. Assuming no loss in melting find the height of the solid. Also, find the gain in the surface area.
Solution:
Given
A cube of metal with a 2.5 cm edge is melted and cast into a rectangular solid whose base is 1.25 cm by 0.25 cm.
The volume of the cube = (edge)3 = (2.5)3 cu. cm
Area of the base of rectangular solid = 1 .25 x 0.25 sq. cm
∴ Height of solid = \(\frac{\text { Volume }}{\text { Area of base }}=\frac{(2.5)^3}{1.25 \times 0.25}=50 \mathrm{~cm}\)
Surface area of the cube = 6 x (edge)2 = 6 x (2.5)2 = 37.5 sq. cm
Surface area of the solid = 2(lb + bh + hl) = 2(50 x 1.25 + 1.25 x 0.25 + 50 x 0.25)
= 2(62.5 + 0.3125 + 12.5) = 150.625 sq. cm
∴ Gain in surface area = 150.625 – 37.50 = 113.125 sq. cm
Question 4. A granary is in the shape of a cuboid of size 8m x 6m x 3m. If a bag of grain occupies a space of 0.65 m3, how many bags can be stored in the granary?
Solution:
Given
A granary is in the shape of a cuboid of size 8m x 6m x 3m. If a bag of grain occupies a space of 0.65 m³
The size of the granary is 8 m x 6 m x 3 m,
Volume of granary = 8 x 6 x 3 = 144m3
The volume of one bag of grain = 0.65 m3
The number of bags which can be stored in the granary
= \(\frac{\text { Volume of granary }}{\text { Volume of each bag }}=\frac{144}{0.65}=221.54 \text { or } 221 \text { bags. }\)
Class 10 Surface Area and Volume Important Questions
Question 5. A cylinderical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide. Find the height of the water level in the tank.
Solution:
Given
A cylinderical bucket 28 cm in diameter and 72 cm high is full of water. The water is emptied into a rectangular tank 66 cm long and 28 cm wide.
Let the height of the water level in the tank = x m,
then according to the problem
πr2h = l x b x x
or \(\frac{22}{7} \times 14 \times 14 \times 72=66 \times 28 \times x\)
or \(x=\frac{\frac{22}{7} \times 14 \times 14 \times 72}{66 \times 28}=24 \mathrm{~cm}\)
Question 6. A rectangular container whose base is a square of side 15 cm stands on a horizontal table and holds water upto 3 cm from the top. When a cube is placed in the water and is completely submerged, the water rises to the top and 54 cm of water overflows. Calculate the volume of the cube and its surface area.
Solution:
Given
A rectangular container whose base is a square of side 15 cm stands on a horizontal table and holds water upto 3 cm from the top. When a cube is placed in the water and is completely submerged, the water rises to the top and 54 cm of water overflows.
Volume of the cube submerged = Volume of water that fills 3 cm height of the container + Volume of water that overflows
= 15 x 15 x 3 + 54 = 729 cm3
If the side of the cube submerged = x cm
Its volume = x3 cm3
∴ x3 = 729 = 9 x 9 x 9
⇒ x = 9 cm.
∴ The side of the cube = 9 cm
And its surface area = 6 x (side) =6 x 9 x 9 = 486 cm2
Question 7. A solid spherical ball of iron with a radius of 6 cm is melted and recast into three solid spherical balls. The radii of the two of balls are 3 cm and 4 cm respectively, determine the diameter of the third ball.
Solution:
Given
A solid spherical ball of iron with a radius of 6 cm is melted and recast into three solid spherical balls. The radii of the two of balls are 3 cm and 4 cm respectively,
Let the radius of the third ball = r cm
∴ The volume of three balls formed = Volume of the ball melted
⇒ \(\frac{4}{3} \pi(3)^3+\frac{4}{3} \pi(4)^3+\frac{4}{3} \pi(r)^3=\frac{4}{3} \pi(6)^3\)
⇒ 27 + 64 + r3 = 216
⇒ r3 = 125, i.e., r = 5 cm
∴ The diameter of the third ball = 2 x 5 cm = 10 cm
Question 8. 50 circular plates each of radius 7 cm and thickness 0.5 cm are placed one above the other to form a solid right circular cylinder. Find
Solution:
The height of the cylinder formed by placing 50 plates = 50 x 0.5 = 25 cm
Radius of cylinder formed = Radius of plate = 7 cm
1. Total surface area of cylinder = 2πrh + 2πr2
= \(\left[2 \times \frac{22}{7} \times 7 \times 25+2 \times \frac{22}{7} \times(7)^2\right] \mathrm{cm}^2\)
= (1100 + 308) cm2 = 1408 cm2
2. Volume of cylinder = \(\pi r^2 h=\frac{22}{7} \times(7)^2 \times 25=3850 \mathrm{~cm}^3\)
Question 9. A rectangular paper of 22 cm x 12 cm is folded in two different ways and forms two cylinders.
Solution:
When the paper is folded along a 12 cm side,
then height of cylinder h1 = 22 cm and 2πr1 = 12
⇒ \(r_1=\frac{12}{2 \pi}=\frac{6}{\pi} \mathrm{cm}\)
∴ Volume = \(V_1=\pi r_1^2 h_1=\pi \times\left(\frac{6}{\pi}\right)^2 \times 22=\frac{792}{\pi}=\frac{792 \times 7}{22}=252 \mathrm{~cm}^3\)
When the paper is folded along a 22 cm side,
then height of cylinder h2 = 12 cm and 2πr2 = 22
⇒ \(2 \times \frac{22}{7} \times r_2=22\)
⇒ \(r_2=\frac{7}{2} \mathrm{~cm}\)
∴ Volume V2 = r22h2
= \(\frac{22}{7} \times\left(\frac{7}{2}\right)^2 \times 12\)
= \(\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 12=462 \mathrm{~cm}^3\)
Question 10. A semicircle of radius 17.5 cm is rotated about its diameter. Find the curved surface of the generated solid.
Solution:
Given
A semicircle of radius 17.5 cm is rotated about its diameter.
The solid generated by a circle rotated about its diameter is a sphere.
Now, the radius of the sphere r = 17.5 cm.
and its curved surface = \(4 \pi r^2=4 \times \frac{22}{7} \times 17.5 \times 17.5=3850 \mathrm{~cm}^2\)
Question 11. A sphere of radius 6 cm is melted and recast into a cone of height 6 cm. Find the radius of the cone.
Solution:
Given
A sphere of radius 6 cm is melted and recast into a cone of height 6 cm.
Radius of sphere = 6 cm
∴ Volume of sphere = \(\frac{4}{3} \pi(6)^3=288 \pi \mathrm{cm}^3\)
Let the radius of cone = r
Height of cone = 6 cm
∴ Volume of cone = \(\frac{1}{3} \pi r^2 h=\frac{1}{3} \pi r^2 \times 6=2 \pi r^2\)
Given that, Volume of cone = Volume of a sphere
⇒ 2nr2 – 288 7r
⇒ r2= 144
⇒ r = 12
Therefore, the radius of the cone = 12 cm
Question 12. The height and radius of the base of a metallic cone are 27 cm and 16 cm respectively. It is melted and recast into a sphere. Find the radius and curved surface of the sphere.
Solution:
Given
The height and radius of the base of a metallic cone are 27 cm and 16 cm respectively. It is melted and recast into a sphere.
Height of cone h = 27 cm
The radius of cone r = 16 cm
∴ Volume of cone = \(\frac{1}{3} \pi r^2 h=\frac{1}{3} \pi(16)^2 \times 27 \mathrm{~cm}^3\)
Let the radius of the sphere = R
∴ Volume of sphere = \(\frac{4}{3} \pi R^3\)
Now, Volume of sphere = Volume of cone
⇒ \(\frac{4}{3} \pi R^3=\frac{1}{3} \pi(16)^2 \times 27\)
⇒ \(R^3=\frac{16^2 \times 27}{4}=4^3 \times 3^3\)
R = 4 x 3 = 12cm
and curved surface of sphere = 4R2 = 4(12)2 = 576 cm2
Question 13. The radius of a metallic sphere is 60 mm. It is melted and recast into a wire of diameter 0.8 mm. Find the length of the wire.
Solution:
Given
The radius of a metallic sphere is 60 mm. It is melted and recast into a wire of diameter 0.8 mm.
Radius of sphere = 60 mm = 6 cm
∴ Volume of sphere = \(\frac{4}{3} \pi(6)^3=288 \pi \mathrm{cm}^3\)
Let, the length of wire = l cm
Radius of wire \(r=\frac{0.8}{2} \mathrm{~mm}=0.4 \mathrm{~mm}=\frac{0.4}{10} \mathrm{~cm}=\frac{4}{100} \mathrm{~cm}\)
∴ Volume of wire = \(\pi r^2 l=\pi\left(\frac{4}{100}\right)^2 \cdot l\)
Now, Volume of wire = Volume of a sphere
⇒ \(\pi \times \frac{4}{100} \times \frac{4}{100} \times l=288 \pi\)
⇒ \(l=\frac{288 \times 100 \times 100}{4 \times 4}=180000 \mathrm{~cm}=1800 \mathrm{~m}\)
Question 14. A wire of diameter 3 mm is wound around a cylinder whose height is 1 2 cm and radius 5 cm so as to cover the curved surface of the cylinder completely. Find
Solution:
Given
A wire of diameter 3 mm is wound around a cylinder whose height is 1 2 cm and radius 5 cm so as to cover the curved surface of the cylinder completely.
1. Let the wire wounded around the cylinder complete n revolutions.
Diameter (width) of wire = 3 m- 0.3 cm
So, the whole height of the cylinder = 0.3 n cm
But the whole height of the cylinder = 12 cm
∴ \(0.3 n=12 \Rightarrow n=\frac{12}{0.3}=\frac{120}{3}=40\)
So, 40 revolutions are completed to wound the wire completely on the cylinder.
In 1 revolution, the length of the wire = 2 πr
∴ In 40 revolutions, the length of the wire = 40 x 2πr
= \(80 \times \frac{22}{7} \times 5 \mathrm{~cm}=1257.14 \mathrm{~cm}\)
= 12.57 m.
2. Now, radius of wire = \(\frac{0.3}{2}=0.15 \mathrm{~cm}\)
Volume of wire = area of cross section x length of wire
= π(0.15)2 x 1257.14 = 88.898 cm3
∴ Mass of wire = volume x density
= 88.898 x 8.88 g= 789.41 g
Hence, the length of the wire = 12.57 m
and mass of wire = 789.41 g
Question 15. A metallic cylinder of diameter 16 cm and height 9 cm is melted and recast into a sphere of diameter 6 cm. How many such spheres can be formed?
Solution:
Given
A metallic cylinder of diameter 16 cm and height 9 cm is melted and recast into a sphere of diameter 6 cm.
For the cylinder,
Radius = \(\frac{16}{2} = 8cm[latex]
Height = 9cm
∴ Volume of cylinder = JI(8)2(9) = 576K cm3
Diameter of sphere = 6 cm
∴ Radius of sphere = [latex]\frac{6}{2}=3 cm\)
Now, volume of one sphere = \(\frac{4}{3} \pi(3)^3=36 \pi \mathrm{cm}^3\)
∴ Number of spheres formed = \(\frac{\text { Volume of cylinder }}{\text { Volume of one sphere }}=\frac{576 \pi}{36 \pi}=16\)
Question 16. A solid metallic right circular cone of height 6.75 cm and radius of the base 12 cm is melted and two solid spheres formed from it. If the volume of one of the spheres is 8 times that of the other, find the radius of the smaller sphere.
Solution:
Given
A solid metallic right circular cone of height 6.75 cm and radius of the base 12 cm is melted and two solid spheres formed from it. If the volume of one of the spheres is 8 times that of the other
Let the radius of the smaller sphere be r and the radius of the larger sphere be R.
image
So, \(\frac{1}{3} \pi(12)^2 \times 6.75=\frac{4}{3} \pi r^3+\frac{4}{3} \pi R^3\)
⇒ (12)2 x 6.75 = 4(r3 + R3) → (1)
Now, the volume of the larger sphere = 8 x the Volume of the smaller sphere
⇒ \(\frac{4}{3} \pi R^3=8 \times \frac{4}{3} \pi r^3\)
R3 = 8r3 = R = 2r → (2)
From equations (1) and (2), we get
12 x 12 x 6.75 = 4(r3 + 8r3)
⇒ \(9 r^3=\frac{12 \times 12 \times 6.75}{4}\)
⇒ \(r^3=\frac{12 \times 12 \times 6.15}{4 \times 9}=27=(3)^3\)
r = 3 cm.
Hence, the radius of a smaller sphere = 3 cm.
Question 17. Water is flowing at the rate of 3 km an hour through a circular pipe of 20 cm internal diameter into a circular cistern of diameter 10 m and depth 2m. In how much time will the cistern be filled?
Solution:
Given
Water is flowing at the rate of 3 km an hour through a circular pipe of 20 cm internal diameter into a circular cistern of diameter 10 m and depth 2m.
Internal diameter of pipe = 20 cm
∴ Internal radius of pipe = 10 cm = \(\frac{1}{10}m\)
Rate of flow of water = 3 km/h
⇒ Rate of flow of water = \(\frac{3 \times 1000}{60 \times 60} \mathrm{~m} / \mathrm{sec}\)
Diameter of cistern = 10 m
Radius of cistern = 5 m
Height of cistern = 2 m
Water discharge by pipe in 1 sec
= π x r2 x flow of water
= \(\pi \times\left(\frac{1}{10}\right)^2 \times \frac{3 \times 1000}{60 \times 60} \mathrm{~m}^3 / \mathrm{sec}\)
Volume of cistern = π x 52 x 2 m3
Time taken to fill the cistern = \(\frac{\text { Volume of cistern }}{\text { Volume of water discharge in }1 \mathrm{sec}}\)
= \(\frac{\pi \times 25 \times 2}{\pi \times \frac{1}{100} \times \frac{3 \times 1000}{60 \times 60}} \mathrm{sec}=\frac{25 \times 2 \times 100 \times 60 \times 60}{3 \times 1000} \mathrm{sec}\)
= \(\frac{5 \times 60 \times 60}{3} \sec =\frac{5 \times 60 \times 60}{3 \times 60 \times 60} \text { hours }=\frac{5}{3} \text { hours }\)
Time taken to fill the cistern =\(\frac{5}{3} \text { hours }\)
Chapter 13 Class 10 Maths NCERT Exemplar with solutions
Question 18. The volume of a sphere is 288 π cm3. 27 small spheres can be formed with this sphere. Find the radius of a small sphere.
Solution:
Given
The volume of a sphere is 288 π cm3. 27 small spheres can be formed with this sphere.
Volume of 27 small spheres = Volume of one big sphere = 288π
Volume of 1 small sphere = \(\frac{288}{27} \pi\)
\(\frac{4}{3} \pi r^3=\frac{32}{3} \pi\) where r = radius of small sphere
r3 = 8
r = 2 cm
The radius of a small sphere = 2 cm
Question 19. Find:
Solution:
1. Curved surface area = \(2 \pi r h=2 \times \frac{22}{7} \times \frac{4.2}{2} \times 4.5=59.4 \mathrm{~m}^2\)
2. Total steel used = Total surface area (Assuming thickness = 0 m)
= 2πr(r + h)
= \(2 \times \frac{22}{7} \times \frac{4.2}{2}\left(\frac{4.2}{2}+4.5\right)\)
= \(\frac{44}{7} \times 2.1 \times \frac{13.2}{2}=22 \times 0.3 \times 13.2=87.12 \mathrm{~m}^2\)
Let the actual steel used be x m2
= \(\frac{11}{12} x=87.12\)
= \(x=\frac{87.12 \times 12}{11}=95.04 \mathrm{~m}^2\)
Question 20. In one fortnight (15 days) of a given month, there was a rainfall of 11.10 cm in a river valley. If the area of the valley is 97280 km2, show that the total rainfall of a day was approximately equivalent to the addition (sum) to the normal water of three rivers earth 1072 km long, 7.5 m wide and 3m deep. (Round off the volumes upto one place of decimal).
Solution:
Given
In one fortnight (15 days) of a given month, there was a rainfall of 11.10 cm in a river valley. If the area of the valley is 97280 km2
Area of the valley = 97280 km2 = 9.728 x 104 km2
= 9.728 x 1010 m2
∴ Volume (amount) of rainfall in the valley in one fortnight (15 days)
= \(9.728 \times 10^{10} \times \frac{11.10}{100} \mathrm{~m}^3=107.98 \times 10^8 \mathrm{~m}^3\)
∴ Amount of rainfall in 1 day = \(\frac{107.98 \times 10^8}{15} \mathrm{~m}^3\)
= 7.198 x 108 m3 = 7.2 x 108m3 → (1)
Now, length of each river = 1072 km = 1072000 m
breadth of each river = 75 m
and depth of each river = 3 m
∴ Amount (volume) of water in each river = 1072000 x 75 x 3 m3
∴ Volume of water in 3 such rivers = 3 x 1.072 x 106 x 75 x 3 m3
= 7.236 x 108 m3 = 7.2 x 108 m3 → (2)
From (1 ) and (2), we can say that total rainfall in a day is approximately the same as the volume of 3 rivers.
Question 21. The dimensions of a solid iron cuboid are 4.4 m x 2.6 m x 1.0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness of 5 cm. Find the length of the pipe.
Answer:
Given
The dimensions of a solid iron cuboid are 4.4 m x 2.6 m x 1.0 m. It is melted and recast into a hollow cylindrical pipe of 30 cm inner radius and thickness of 5 cm.
Length of solid iron cuboid = 4.4 m
Breadth of solid iron cuboid = 2.6 m
Height of solid iron cuboid = 1.0 m
∴ Volume of solid cuboid = 4.4 x 2.6 x 1 = 11.44 m3
= 11.44 x 100 x 100 x 100 cm3
This cuboid is melted and recast into a hollow cylinder.
∴ The volume of a cuboid = Volume of a hollow cylinder
⇒ 11.44 x 106 = πR2h – πr2h
⇒ 11.44 x 106 = πh(R2– r2) [∵ r = 30 cm, width = 5 cm, R = 35 cm]
⇒ \(11.44 \times 10^6=\frac{22}{7} \times h(R-r)(R+r)\)
⇒ 11 .44 x 106 x 7 = 22 x h (35 – 30) (35 + 30)
⇒ \(h=\frac{11.44 \times 10^6 \times 7}{22 \times 5 \times 65} \mathrm{~cm}=\frac{11440000 \times 7}{22 \times 5 \times 65} \mathrm{~cm}\)
= 11200 cm = 112 m
Hence, the length of the pipe = 112 m
Question 22. A tank measures 2 m long, 1.6 m wide and 1 m depth. Water is there upto 0.4 m in height. Brides measuring 25 cm x 14 cm x 10 cm are put into the tank so that water may come upto the top. Each brick absorbs water equal \(\frac{1}{7} \text { th }\) to that of its own volume. How many bricks will be needed?
Solution:
Let x bricks be needed
∴ Volume of x bricks = x X 0.25 X 0.1 4 X 0.1 m3
The volume of water absorbed by bricks
= \(=\frac{1}{7} x \times 0.25 \times 0.14 \times 0.1\)
∴ Remaining water in the tank = \(2 \times 1.6 \times 0.4-\frac{1}{7} \times x \times 0.25 \times 0.14 \times 0.1\)
Now, the Volume of water in the tank + Volume of x bricks
= Volume of tank
⇒ \(\left(2 \times 1.6 \times 0.4-\frac{x}{7} \times 0.25 \times 0.14 \times 0.1\right)+x \times 0.25 \times 0.14 \times 0.1\) = 2 x 1.6 x 1
⇒ \(\frac{6 x}{7} \times 0.25 \times 0.14 \times 0.1=2 \times 1.6 \times 0.6\)
⇒ \(x=\frac{2 \times 1.6 \times 0.6 \times 7}{6 \times 0.25 \times 0.14 \times 0.1}=\frac{2 \times 16 \times 6 \times 7 \times 1000}{6 \times 25 \times 14 \times 1}=640\)

Question 23. A metallic solid sphere of radius 10.5 cm is melted and recast into smaller solid cones, each of radius 3.5 cm and height 3 cm. How many cones will be made?
Solution:
Given
A metallic solid sphere of radius 10.5 cm is melted and recast into smaller solid cones, each of radius 3.5 cm and height 3 cm.
Let n cones be recast from the sphere.
∴ The sum of volumes of n cones = volume of a sphere
⇒ \(n\left[\frac{1}{3} \pi(3.5)^2 \times 3\right]=\frac{4}{3} \pi(10.5)^3\)
⇒ \(n=\frac{4 \times 10.5 \times 10.5 \times 10.5}{3.5 \times 3.5 \times 3}=126\)
Hence, 126 cones will be made.
Frustum: If a right circular cone is cut by a plane parallel to the base of the cone then the portion between the plane and base is called the frustum of the cone.
How To Find The Volume And Surface Area Of A Bucket
Let a bucket of height h and radii of upper and lower ends be r1 and r2 respectively.
Now we shall find three parts:
Proof :
1. Let the slant height of the bucket be l
Now, draw DC ⊥ AB
l2=h2 + (r1 – r2)2
⇒ \(l=\sqrt{h^2+\left(r_1-r_2\right)^2}\)
2. Let EO = H and DO = L
ΔABO ~ ΔDEO
∴ \(\frac{A B}{D E}=\frac{B O}{E O}=\frac{A O}{D O}\)
⇒ \(\frac{r_1}{r_2}=\frac{h+H}{H}=\frac{l+L}{L}\)
⇒ \(\frac{r_1}{r_2}=\frac{h+H}{H} \quad \text { and } \quad \frac{r_1}{r_2}=\frac{l+L}{L}\)
⇒ Hr1 = hr2 + Hr2 and Lr1 = lr2 + Lr2
⇒ H(r1– r2) = hr2 ⇒ L(r1 – r2) = lr2
⇒ \(H=\frac{h r_2}{r_1-r_2} \quad \text { and } \quad L=\frac{l r_2}{r_1-r_2}\)
Curved surface area of bucket = C.S.A of larger cone- C.S.A of smaller cone
= \(\pi r_1(L+l)-\pi r_2 L=\pi r_1\left[\frac{l r_2}{r_1-r_2}+l\right]-\pi r_2\left(\frac{l r_2}{r_1-r_2}\right)\)
= \(\pi r_1 l\left(\frac{r_2+r_1-r_2}{r_1-r_2}\right)-\frac{\pi r_2^2 l}{r_1-r_2}\)
= \(\frac{\pi l}{r_1-r_2}\left(r_1^2-r_2^2\right)=\frac{\pi l\left(r_1+r_2\right)\left(r_1-r_2\right)}{\left(r_1-r_2\right)}\)
= \(\pi l\left(r_1+r_2\right) \text { where } l=\sqrt{h^2+\left(r_1-r_2\right)^2}\)
Total surface area = C.S.A. of bucket + Area of the smaller circle
= πl(r1 + r2) + πr22
3. Volume of bucket = Volume of larger cone – Volume of smaller cone
= \(\frac{1}{3} \pi l_l\left(r_1^2+r_1 r_2+r_2^2\right)\)
= \(\frac{1}{3} \pi r_1^2(H+h)-\frac{1}{3} \pi r_2^2 \cdot H\)
= \(\frac{1}{3} \pi r_1^2\left[\frac{h r_2}{r_1-r_2}+h\right]-\frac{1}{3} \pi r_2^2\left(\frac{h r_2}{r_1-r_2}\right)\)
= \(\frac{1}{3} \pi r_1^2 h\left(\frac{r_2+r_1-r_2}{r_1-r_2}\right)-\frac{1}{3} \frac{\pi h r_2^3}{r_1-r_2}\)
= \(\frac{1}{3} \frac{\pi h}{r_1-r_2}\left(r_1^3-r_2^3\right)\)
= \(\frac{1}{3} \frac{\pi h}{r_1-r_2}\left(r_1-r_2\right)\left(r_1^2+r_1 r_2+r_2^2\right)\)
= \(\frac{1}{3} \pi h\left(r_1^2+r_2^2+r_1 r_2\right)\)
Note: Actually, the bucket is a frustum cone made of cutting the bucket by a plane parallel to the base.
Question 1. A cone is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base, Compare the volume of the two parts.
Solution:
Given
A cone is divided into two parts by drawing a plane through the mid-point of its axis, parallel to its base
We can solve this using similarity.
Let r and li be the radius and height of a cone OAB
Let OE = \(\frac{h}{2}\)
As OED and OFB are similar
∴ \(\frac{O E}{O F}=\frac{E D}{F B} \frac{h / 2}{h}=\frac{E D}{r}\)
⇒ \(E D=\frac{r}{2}\)
Now volume of cone OCD = \(\frac{1}{3} \pi r^2 h=\frac{1}{3} \times \pi \times\left(\frac{r}{2}\right)^2 \times \frac{h}{2}=\frac{\pi r^2 h}{24}\)
and Volume of cone OAB = \(\frac{1}{3} \times \pi \times r^2 \times h=\frac{\pi r^2 h}{3}\)
∴ \(\frac{\text { Volume of part } O C D}{\text { Volume of part } C D A B}=\frac{\frac{\pi r^2 h}{24}}{\frac{\pi r^2 h}{3}-\frac{\pi r^2 h}{24}}=\frac{\frac{1}{24}}{\frac{1}{3}-\frac{1}{24}}=\frac{\frac{1}{24}}{\frac{8-1}{24}}=\frac{1}{7}\)
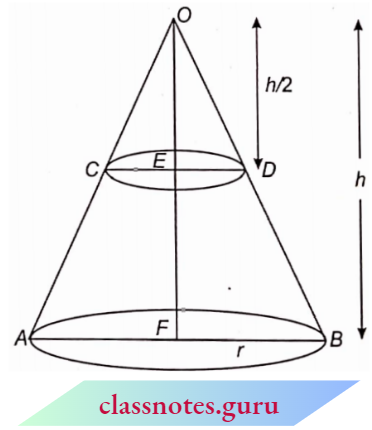
Question 2. The height of a right circular cone is trisected by two planes drawn parallel to the base. Show that the ratio of volumes of the three portions starting from the top is in the ratio 1:7:19.
Solution:
Given
The height of a right circular cone is trisected by two planes drawn parallel to the base.
Since height is trisected, therefore by basic proportionality theorem, base radii of three cones VCD, VA’B’ and VAB are also in the ratio 1: 2 : 3.
( ∵ VL : VM : VN = r2 : r1 : r = 1:2:3)
Let volume of cone VCD = V = \(\frac{1}{3} \pi r_2{ }^2 h\)
∴ Volume of cone VA’B’ = \(\frac{1}{3} \pi r_1^2(2 h)=\frac{1}{3} \pi\left(2 r_2\right)^2(2 h)=8 \times \frac{1}{3} \pi r_2{ }^2 h=8 V\)
and volume of cone VAB = \(\frac{1}{3} \pi r^2(3 h)=\frac{1}{3} \pi\left(3 r_2\right)^2(3 h)=27 \times \frac{1}{3} \pi r_2^2 h=27 \mathrm{~V}\)
∴ Ratio of volumes of 3 portions
= Volume(VCD) : Volume(CD£’A’) : Volume(A’B’BA)
= V: 8V – V: 27V – 8V = 1: 7: 19
Hence Proved.
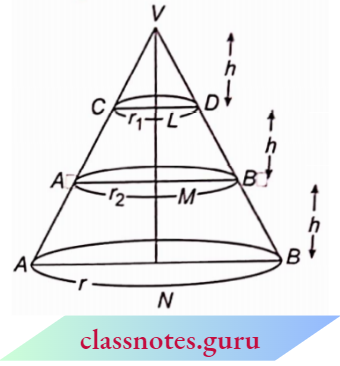
Question 3. The radii of the faces of a frustum of a cone are 3 cm and 4 cm and its height is 5cm. Find its volume.
Solution:
Given
The radii of the faces of a frustum of a cone are 3 cm and 4 cm and its height is 5cm.
Here r = 3 cm, R = 4 cm and h = 5 cm
Volume of frustum of cone = \(\frac{1}{3} \pi l\left(R^2+r^2+R r\right) \text { cu. units }\)
= \(\frac{1}{3} \times \frac{22}{7} \times 5\left(4^2+3^2+4 \times 3\right)\)
= \(\frac{1}{3} \times \frac{110}{7}(16+9+12)\)
= \(\frac{110}{21} \times 37=\frac{4070}{21} \mathrm{~cm}^3\)
Volume of frustum of cone =\(\frac{4070}{21} \mathrm{~cm}^3\)
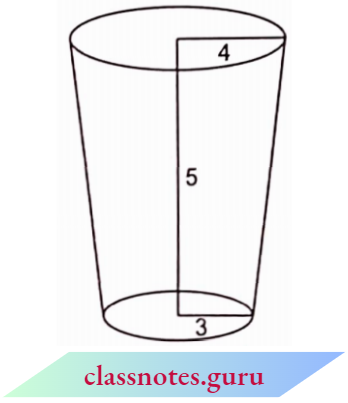
Question 4. The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume is \(\frac{1}{27}\) of the volume of the given cone, at what height above the base, the section has been made?
Solution:
Given
The height of a cone is 30 cm. A small cone is cut off at the top by a plane parallel to the base. If its volume is \(\frac{1}{27}\) of the volume of the given cone
Let OA – h ⇒ AB = 30- h
and let AC = r, BD = R
ΔOAC ~ ΔOBD,
∴ \(\frac{h}{30}=\frac{r}{R} \Rightarrow r=\frac{h R}{30}\)
Now, Volume of smaller cone = \(\frac{1}{27}\) x Volume of larger cone
⇒ \(\frac{1}{3} \pi r^2 h=\frac{1}{27} \times \frac{1}{3} \pi R^2 \times 30\)
⇒ \(\frac{1}{3} \pi\left(\frac{h R}{30}\right)^2 \cdot h=\frac{1}{27} \times \frac{1}{3} \pi R^2 \times 30\)
⇒ \(\frac{h^3}{30^2}=\frac{30}{27} \Rightarrow h^3=\frac{30^3}{3^3} \Rightarrow h=10\)
∴ Reqired height = 30 – 10 = 20 cm.
1 kl = 1 m3
1000 l = 100 x 100 x 100 cm3
1 litre = 1000 cm3
= \(1 \mathrm{~cm}^3=\frac{1}{1000} \text { litre }\)

Question 5. The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm. Find its capacity in litres and the amount of sheets required to make this bucket. (\(\text { Take } \pi=\frac{22}{7}\))
Solution:
Given
The radii of the ends of a bucket 30 cm high are 21 cm and 7 cm.
Although we can solve this problem by using similar triangles, here we are using the direct formula.
Volume of bucket = \(\frac{1}{3} \pi h\left(r_1^2+r_1 r_2+r_2^2\right)\)
= \(\frac{1}{3} \times \frac{22}{7} \times 30\left(21^2+21 \times 7+7^2\right)\)
= \(\frac{1}{3} \times \frac{22}{7} \times 30 \times 637=20020 \mathrm{~cm}^3=\frac{20020}{1000} \text { lit. }\)
⇒ Capacity = 20.02 lit
Area of sheet = C.S.A. of bucket + Area of base
= πl(r1 + r2) + r22 = π[l(r1 + r2) + r22 (∵ \(l=\sqrt{h^2+\left(n_1-r_2\right)^2}\) = \(\sqrt{900+14^2}\) = \(\sqrt{1096}\) = 33.106)
= \(\frac{22}{7}[33.106(28)+49]\)
= 3067.32 = 3067cm2 (approx.)
Area of sheet = 3067cm2 (approx.)
Question 6. A bucket is 32 cm in diameter at the top and 20 cm in diameter at the bottom. Find the capacity of the bucket in litres if it is 21 cm deep. Also, find the cost of the tin sheet used in making the bucket at the rate of ₹ 1.50 per sq dm.
Solution:
Given
A bucket is 32 cm in diameter at the top and 20 cm in diameter at the bottom.
Here R = 16 cm, r = 10 cm and h = 21 cm
Volume of frustum of a cone = \(\frac{\pi h}{3}\left(R^2+r^2+R r\right)\)
= \(\frac{22}{7} \times \frac{1}{3} \times 21\left(16^2+10^2+16 \times 10\right)\)
= 22(256 + 100 + 160)
= 22 x 516 = 11352cm3
= \(\frac{11352}{1000} \text { litres }=11.352 \text { litres }\)
Now for slant height l of frustum
l2 = h2 + (R-r)2
l2 = 212 + (16 – 10)2
l2 = 441 + 36
l2 = 477
∴ \(l=\sqrt{477}=21.84 \mathrm{~cm}\)
Now S.A of bucket = πl(R + r) + πr2
= \(\frac{22}{7} \times 21.84 \times(16+10)+\frac{22}{7} \times 10^2\)
= \(\frac{22}{7}(21.84 \times 26+100)\)
= \(\frac{22}{7} \times 667.84=2098.92 \mathrm{~cm}^2=20.99 \mathrm{dm}^2\)
Cost of sheet @ ₹ 1 .50 per sq. dm. = 20.99 x 1.50 = ₹ 31.49
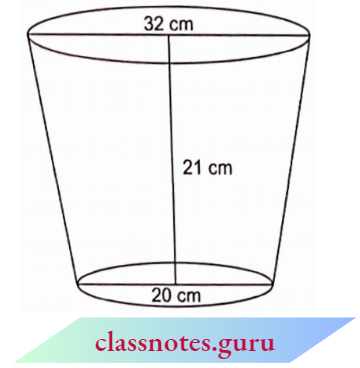
CBSE Class 10 Maths Chapter 13 Exemplar problems
Question 1. 2 cubes each of volume 64 cm3 are joined end to end. Find the surface area of the resulting cuboid.
Solution:
Given,
volume of cube = 64 cm3
(side)3 = 64
(side)3 = 43
side = 4 cm
Side of cube = 4 cm
A cuboid is formed by joining two cubes together as shown.
∴ For cuboid
length l = 4 + 4 = 8 cm
height h = 4 cm
Now, the total surface area of a cuboid
= 2(l.b + b.h + l.h)
= 2 (8 x 4 + 4 x 4 + 8 x 4)
= 2 (32 + 16 + 32) = 160 cm2
The surface area of the resulting cuboid = 160 cm2
Question 2. A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm. Find the inner surface area of the vessel.
Solution:
Given
A vessel is in the form of a hollow hemisphere mounted by a hollow cylinder. The diameter of the hemisphere is 14 cm and the total height of the vessel is 13 cm.
In the adjoining figure, a cylinder is surmounted on the hemisphere.
Diameter of hemisphere 2r = 14 cm
⇒ Radius of hemisphere r = 7 cm
The radius of cylinder r = 1 cm
Now, the total height of the vessel = 13 cm
⇒ h + r = 13 cm
⇒ h = 13 – 7 = 6 cm
Height of cylinder, h = 6 cm
The inner surface area of the cylinder = 2πrh
Inner curved surface area of hemisphere = 2πr2
Inner surface area of vessel = 2πrh + 2πr2
= 2πr(h + r)
= \(2 \times \frac{22}{7} \times 7 \times(6+7)\)
= 44 x 13 = 572 cm2
The inner surface area of the vessel = 572 cm2
Question 3. A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of the same radius. The total height of the toy is 15.5 cm. Find the total surface area of the toy.
Solution:
Given
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of the same radius. The total height of the toy is 15.5 cm.
In the adjoining figure, a cone of the same cross-section is surmounted on the hemisphere.
The radius of base of cone r = 3.5 cm
⇒ Radius of hemisphere r = 3.5 cm
Total height of toy = 15.5 cm
⇒ h + r = 15.5
⇒ h = 15.5 – 3.5 = 12 cm
∴ Height of cone h = 12 cm
Now, from l2 = h2 + r2
l2 = (12)2 + (3.5)2
= 144 + 12.25
= 156.25
⇒ \(l=\sqrt{156.25}=12.5 \mathrm{~cm}\)
∴ The curved surface area of the cone = πrl
and curved surface area of hemisphere = 2πr2
So, the total surface area of the toy = πrl + 2πr2
= πr (l + 2r)
= \(\frac{22}{7} \times 3.5 \times(12.5+2 \times 3.5)\)
= 11 x 19.5 = 214.5cm2
The total surface area of the toy = 214.5cm2
Question 4. A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid.
Solution:
Given
A cubical block of side 7 cm is surmounted by a hemisphere.
The base of the hemisphere is on the upper face of a cube of edge 7 cm,
∴ Maximum diameter of hemisphere = edge of the cube
= 7 cm
⇒ 2r = 7 ⇒ \(r=\frac{7}{2} \mathrm{~cm}\)
Now, the total surface area of the solid
= total surface area of cube + curved surface of the hemisphere – an area of the base of the hemisphere
= 6 x (side)2 + 2πr2– πr2
= 6 x (side)2 + πr2
= \(=6 \times 7 \times 7+\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\)
= 294 + 38.5 = 332.5 cm2
The total surface area of the solid = 332.5 cm2
Question 5. A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube. Determine the surface area of the remaining solid.
Solution:
Given
A hemispherical depression is cut out from one face of a cubical wooden block such that the diameter l of the hemisphere is equal to the edge of the cube.
Let the side of the cube = a
Diameter of hemisphere = side of the cube
⇒ 2r = a = \(r=\frac{a}{2}\)
Now, the surface area of remaining solid = total surface of the hemisphere – an area of the base of the hemisphere
= 6a2 + 2πr2– πr2
= 6a2 + πr2
= \(6 a^2+\pi\left(\frac{a}{2}\right)^2=\frac{24 a^2+\pi a^2}{4}\)
= \(\frac{a^2(24+\pi)}{4} \text { square units }\)
The surface area of the remaining solid = \(\frac{a^2(24+\pi)}{4} \text { square units }\)
Question 6. A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm. Find its surface area.
Solution:
Given
A medicine capsule is in the shape of a cylinder with two hemispheres stuck to each of its ends. The length of the entire capsule is 14 mm and the diameter of the capsule is 5 mm
Diameter of capsule = 5 mm
2r = 5 mm
r = 2.5 mm
∴ The radius of the cylindrical part = radius of the hemisphere = 2.5 mm
Length of capsule = 14 mm
⇒ h + 2r = 14 mm
⇒ h = 14 – 2r = 14 – 5 = 9 mm
Now the surface area of the capsule = 2 x curved surface of hemisphere + curved surface of the cylinder
= 2 x 2πr2 + 2πrh = 2πr (2r + h)
= \(2 \times \frac{22}{7} \times 2.5 \times(5+9)\)
= \(\frac{110}{7} \times 14=220 \mathrm{~mm}^2\)
The surface area of the capsule = 220 mm²
Question 7. A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m, find the area of the canvas used for making the tent. Also, find the cost of the canvas of the tent at the rate of ₹ 500 per m2.
Solution:
Given
A tent is in the shape of a cylinder surmounted by a conical top. If the height and diameter of the cylindrical part are 2.1 m and 4 m respectively, and the slant height of the top is 2.8 m,
In the adjoining, a tent is shown in which a cone is surmounted by a cylinder.
Diameter of cylindrical part 2r = 2. 1 m
⇒ \(r=\frac{2.1}{2} \mathrm{~m}\)
Height of cylindrical part h = 4 m
Radius of conical part \(r=\frac{2.1}{2} \mathrm{~m}\)
The slant height of conical part l = 2.8 m
Now, the area of canvas required to form a tent = curved surface of the cylindrical part + curved surface of the conical part
= 2πrh + πrl
= πr (2h + l)
= \(\frac{22}{7} \times \frac{2.1}{2} \times(2 \times 4+2.8)\)
= 3.3 x 10.8 = 35.64 m2
the area of canvas required to form a tent
Class 10 Maths Chapter 13 Important Questions with answers
Question 8. From a solid cylinder whose height is 2.4 cm and diameter is 1.4 cm, a conical cavity of the same height and same diameter is hollowed out. Find the total surface area of the remaining solid to the nearest cm2.
Solution:
Diameter of cylinder 2r = 1.4 cm
⇒ r = 0.7 cm
∴ The radius of the cylinder = radius of the cone = r = 0.7 cm
Height of cylinder = height of cone = h = 2.4 cm
If the slant height of the cone is l, then
l2 = h2 + r2= (2.4)2 + (0.7)2
= 5.76 + 0.49 = 6.25
⇒ \(l=\sqrt{6.25}=2.5 \mathrm{~cm}\)
Surface area of remaining solid
= area of base of cylinder + curved surface of cylinder + curved surface of cone
= πr2 + 2πrh + πrl
= πr (r + 2h + l)
= \(\frac{22}{7} \times 0.7 \times(0.7+2 \times 2.4+2.5)\)
= 2.2 x 8 = 17.6 cm2
Question 9. A wooden article was made by scooping out a hemisphere from each end of a solid cylinder, as shown. If the height of the cylinder is 10 cm, and its base is of radius 3.5 cm, find the total surface area of the article.
Solution:
The total surface area of the article
= curved surface of cylinder + 2 x curved surface of a hemisphere
= 2πrh + 2 x 2πr2
= 2πr (h+2r)
= \(2 \times \frac{22}{7} \times 3.5 \times(10+2 \times 3.5)\)
= 22 x 17 = 374 cm2

Question 1. A solid is in the shape of a cone standing on a hemisphere with both their radii being equal to 1 cm and the height of the cone is equal to its radius. Find the volume of the solid in terms of π.
Solution:
Radius of hemisphere = radius of cone = r = 1 cm
Height of cone h = radius of cone = 1 cm
Volume of hemisphere = \(\frac{2}{3} \pi r^3\)
Volume of cone = \(\frac{1}{3} \pi r^2 h\)
∴ The volume of solid = volume of hemisphere + volume of a cone
= \(\frac{2}{3} \pi r^3+\frac{1}{3} \pi r^2 h\)
= \(\frac{2}{3} \pi(1)^3+\frac{1}{3} \pi(1)^2(1)\)
= \(\frac{2}{3} \pi+\frac{1}{3} \pi=\pi \mathrm{cm}^3\)
Question 2. Rachel, an engineering student, was asked to make a model shaped like a cylinder with two cones attached at its two ends by using a thin aluminium sheet. The diameter of the model is 3 cm and its length is 12 cm. If each cone has a height of 2 cm, find the volume of air contained in the model that Rachel made. (Assume the outer and inner dimensions of the model to be nearly the same.)
Solution:
The model is shown in the given below.
Diameter 2r = 3 cm
⇒ \(r=\frac{3}{2} \mathrm{~cm}\)
Height of each cone h = 2 cm
Let the height of the cylinder = H
∴ H + h + h = 12 cm
⇒ H + 2 + 2 = 12
⇒ H = 12 – 4 = 8 cm
The volume of model = volume of cylinder + 2 x volume of a cone
= \(\pi r^2 H+2 \times \frac{1}{3} \pi r^2 h\)
= \(\pi r^2\left(H+\frac{2 h}{3}\right)\)
= \(\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times\left(8+\frac{2 \times 2}{3}\right)\)
= \(\frac{22}{7} \times \frac{3}{2} \times \frac{3}{2} \times \frac{28}{3}=66 \mathrm{~cm}^3\)
Air contained in model = 66 cm3
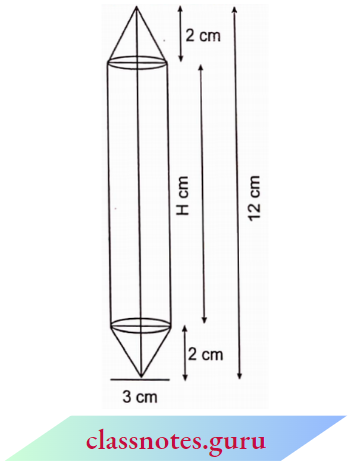
Question 3. A gulab jamun contains sugar syrup up to about 30% of its volume. Find approximately how much syrup would be found in 45 gulab jamuns, each shaped like a cylinder with two hemispherical ends with a length of 5 cm and a diameter of 2.8 cm.
Solution:
For one gulab jamun,
Diameter 2r = 2.8 cm
⇒ r = 1.4 cm
Height of cylindrical part h = 5 – r – r
= 5-1.4 – 1.4 = 2.2 cm
Volume of one gulab jamun
= volume of cylindrical part + 2 x volume of hemispherical part
= \(\pi r^2 h+2 \times \frac{2}{3} \pi r^3\)
= \(\pi r^2\left(h+\frac{4 r}{3}\right)\)
= \(\frac{22}{7} \times 1.4 \times 1.4 \times\left(2.2+\frac{4 \times 1.4}{3}\right)\)
= 25.051 cm3
⇒ Volume of 45 gulab jamuns = 45 x 25.051
= 1127.295 cm3
Volume of sugar syrup in 45 gulab jamuns
= 30% of 1127.295
= \(1127.295 \times \frac{30}{100} \mathrm{~cm}^3\)
= 338.1885 cm3 ≈ 338 cm3
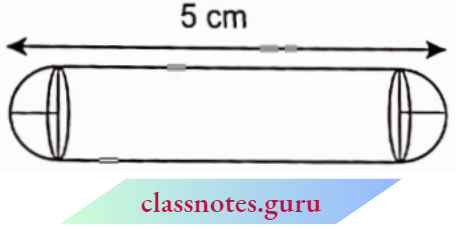
Question 4. A pen stand made of wood is in the shape of a cuboid with four conical depressions to hold pens. The dimensions of the cuboid are 15 cm by 10 cm by 3.5 cm. The radius of each of the depressions is 0.5 cm and the depth is 1.4 cm. Find the volume of wood in the entire stand.
Solution:
Volume of cuboid = 15 x 10 x 3.5 cm3
= 525 cm3
For conical depression
r = 0.5 cm and h = 1.4 cm
∴ The volume of one cavity
= \(\frac{1}{3} \pi r^2 h=\frac{1}{3} \times \frac{22}{7} \times 0.5 \times 0.5 \times 1.4\)
= \(\frac{1.1}{3} \mathrm{~cm}^3\)
⇒ Volume of four depression= \(4 \times \frac{1.1}{3} \mathrm{~cm}^3\)
= 1.467 cm3
Now, the volume of wood used in the pen stand
= volume of cuboid – volume of four depression
= (525 – 1 .467) cm3 = 523.533 cm3
Question 5. A vessel is in the form of an inverted cone. Its height is 8 cm and the radius of its top, which is open, is 5 cm. It is filled with water up to the brim. When lead shots, each of which is a sphere of radius 0.5 cm are dropped into the vessel, one-fourth of the water flows out. Find the number of lead shots dropped in the vessel.
Solution:
The radius of cone r = 5 cm
and height h = 8 cm
⇒ Volume of cone = \(\frac{1}{3} \pi r^2 h\)
The volume of water filled in the cone
= \(\frac{1}{3} \pi r^2 h=\frac{1}{3} \pi \times(5)^2 \times 8\)
= \(\frac{200}{3} \pi \mathrm{cm}^3\)
The volume of water flows out on dropping lead shots in it.
= \(\frac{1}{4} \times \frac{200 \pi}{3}=\frac{50 \pi}{3} \mathrm{~cm}^3\)
The radius of shot R = 0.5 cm
Volume of one lead shot = \(\frac{4}{3} \pi R^3=\frac{4}{3} \pi(0.5)^3 \mathrm{~cm}^3\)
= \(\frac{\pi}{6} \mathrm{~cm}^3\)
Now, number of shots
= \(\frac{\text { volume of water flows out }}{\text { volume of one shot }}\)
= \(\frac{50 \pi / 3}{\pi / 6}=\frac{50 \pi}{3} \times \frac{6}{\pi}=100\)
NCERT Exemplar Problems and Solutions for Surface Areas and Volumes
Question 6. A solid iron pole consists of a cylinder of height 220 cm and base diameter 24 cm, which is surmounted by another cylinder of height 60 cm and radius 8 cm. Find the mass of the pole, given that 1 cm3 of iron has approximately 8g mass. (Use π = 3.14)
Solution:
For the first cylinder,
Diameter 2r = 24 cm
⇒ r = 12 cm
Height h = 220 cm
∴ Volume = πr2h = π x 12 x 12 x 220 cm3
= 31680 π cm3
For the second cylinder,
Radius R = 8 cm
Height H = 60 cm
Volume = πr2H = π x 8 x 8 x 60
= 3840π cm3
Volume of the pole = (31680π + 3840π) cm3
= 35520π cm3
∴ Weight of pole = 35520π x 8 g
= 35520 x 3.14 x 8 g
= 892262.4 g = 892.2624 kg
= 892.26 kg
Question 7. A solid consisting of a right circular cone of height 120 cm and radius 60 cm standing on a hemisphere of radius 60 cm is placed upright in a right circular cylinder full of water such that it touches the bottom. Find the volume of water left in the cylinder, if the radius of the cylinder is 60 cm and its height is 180 cm.
Solution:
The radius of cylinder r = 60 cm and
height h = 1 80 cm
∴ Volume of cylinder = πr2h
= π x 60 x 60 x 180 cm3
= 648000π cm3
The radius of cone R = 60 cm
and height H = 120 cm
∴ Volume of cone = \(\frac{1}{3} \pi R^2 H\)
= \(\frac{1}{3} \pi \times 60 \times 60 \times 120 \mathrm{~cm}^3\)
= 144000 cm3
The volume of solid formed from the cone and hemisphere
= (144000π + 144000π) cm3
= 288000π cm3
⇒ Volume of water displaced by this solid
= 288000π cm3
∴ The volume of the remaining water in a cylinder
= (648000π – 288000π) cm3
= 360000π cm3
= \(360000 \times \frac{22}{7} \mathrm{~cm}^3\)
= \(1131428.57 \mathrm{~cm}^3=\frac{1131428.57}{1000000} \mathrm{~m}^3\)
= 1.131 m3 (approx.)
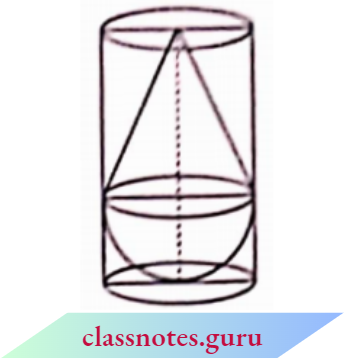
Question 8. A spherical glass vessel has a cylindrical neck 8 cm long, and 2 cm in diameter; the diameter of the spherical part is 8.5 cm. By measuring the amount of water it holds, a child finds its volume to be 345 cm3. Check whether she is correct, taking the above as the inside measurements, and π = 3.14.
Solution:
Radius of cylindrical part \(r=\frac{2}{2}=1 \mathrm{~cm}\)
and height h = 8 cm
∴ The volume of the cylindrical part = nr2h
= π(1)2(8) = 8πcm3
Radius of spherical part, \(R=\frac{8.5}{2}=\frac{17}{4} \mathrm{~cm}\)
∴ The volume of the spherical part,
= \(\frac{4}{3} \pi R^3=\frac{4 \pi}{3} \times \frac{17}{4} \times \frac{17}{4} \times \frac{17}{4} \mathrm{~cm}^3\)
= \(\frac{4913}{48} \pi \mathrm{cm}^3\)
∴ Volume of cylinder = \(\left(8 \pi+\frac{4913 \pi}{48}\right) \mathrm{cm}^3\)
= \(\frac{384 \pi+4913 \pi}{48} \mathrm{~cm}^3[/latex
= [latex]\frac{5297 \pi}{48} \mathrm{~cm}^3=\frac{5297}{48} \times 3.14 \mathrm{~cm}^3\)
= 346.51 cm3
So the answer 345 cm3 of a child is not correct.
∴ Correct volume of cylinder = 346.51 cm3
Question 1. A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm. Find the height of the cylinder.
Solution:
Given
A metallic sphere of radius 4.2 cm is melted and recast into the shape of a cylinder of radius 6 cm.
The radius of sphere R = 4.2 cm
The radius of cylinder r = 6 cm
Let the height of the cylinder = h
Now, the volume of the cylinder = volume of a sphere
⇒ \(\pi r^2 h=\frac{4}{3} \pi R^3\)
⇒ \(h=\frac{4 R^3}{3 r^2}=\frac{4 \times 4.2 \times 4.2 \times 4.2}{3 \times 6 \times 6} \mathrm{~cm}\)
= 2.744 cm
∴ Height of cylinder = 27.44 cm
Question 2. Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere. Find the radius of the resulting sphere.
Solution:
Given
Metallic spheres of radii 6 cm, 8 cm and 10 cm, respectively, are melted to form a single solid sphere.
Let r1 = 6 cm, r2 = 8 cm and r3 = 10 cm
Let the radius of a bigger solid sphere = R
The volume of a bigger solid volume
= sum of volumes of three given spheres
⇒ \(\frac{4}{3} \pi R^3=\frac{4}{3} \pi r_1^3+\frac{4}{3} \pi r_2^3+\frac{4}{3} \pi r_3^3\)
⇒ \(R^3=r_1^3+r_2^3+r_3^3\)
= 63 + 83+ 102
= 216 + 512 + 1000 = 1728 = 122
⇒ R = 12 cm
∴ The radius of the new solid sphere = 12 cm
Question 3. A 20 m deep well with a diameter of 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m. Find the height of the platform.
Solution:
Given
A 20 m deep well with a diameter of 7 m is dug and the earth from digging is evenly spread out to form a platform 22 m by 14 m.
Radius of well, \(r=\frac{7}{2} m\)
and depth h = 20 m
Let the height of the platform be H metre.
∴ The volume of the platform = the volume of the well.
⇒ 22 x 14 x H = πr2h
⇒ \(22 \times 14 \times H=\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 20\)
⇒ \(H=\frac{22 \times 7 \times 7 \times 20}{7 \times 2 \times 2 \times 22 \times 14}=2.5 \mathrm{~m}\)
∴ Height of platform = 2.5 m
Question 4. A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment. Find the height of the embankment.
Solution:
Given
A well of diameter 3 m is dug 14 m deep. The earth taken out of it has been spread evenly all around it in the shape of a circular ring of width 4 m to form an embankment.
Diameter of well 2r = 3 m
⇒ \(r=\frac{3}{2}=1.5 \mathrm{~m}\)
and depth h = 14 m
∴ The volume of earth taken out from the well = nr2h
= \(\frac{22}{7} \times 1.5 \times 1.5 \times 14=99 \mathrm{~m}^3\)
Now, the outer radius of the well, R = 1.5 + 4 = 5.5m
∴ Area of the ring of platform = π (R2 – r2)
= \(\frac{22}{7}\left[(5.5)^2-(1.5)^2\right]\)
= \(\frac{22}{7} \times 7 \times 4=88 \mathrm{~m}^2\)
Let the height of the embankment = H
∴ 88 x H = 99
⇒ \(H=\frac{99}{88}=\frac{9}{8}=1.125 \mathrm{~m}\)
Height of embankment = 1.1 25 m
Class 10 Maths Chapter 13 surface area of solid shapes
Question 5. A container shaped like a right circular cylinder having a diameter of 12 cm and a height of 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice cream.
Answer:
Given
A container shaped like a right circular cylinder having a diameter of 12 cm and a height of 15 cm is full of ice cream. The ice cream is to be filled into cones of height 12 cm and diameter 6 cm, having a hemispherical shape on the top.
The radius of the cylindrical container
∴ \(r=\frac{12}{2} \mathrm{~cm}=6 \mathrm{~cm}\)
and height h= 15 cm
∴ Volume = πr2h = 71 x 6 x 6 x 15
= 540 π cm3
⇒ The total volume of ice cream = 540cm3
The radius of cone = radius of hemisphere = R
⇒ \(R=\frac{6}{2}=3 \mathrm{~cm}\)
Height of cone, H = 12 cm
The volume of ice cream in one cone + hemisphere
= \(\frac{1}{3} \pi R^2 H+\frac{2}{3} \pi R^3=\frac{1}{3} \pi R^2(H+2 R)\)
= \(\frac{1}{3} \pi \times 3 \times 3 \times(12+2 \times 3)=54 \pi\)
Now, number of cones = \(\frac{\text { Total volume of ice cream }}{\text { Volume of ice cream in one cone }}\)
= \(\frac{540 \pi}{54 \pi}=10\)
Question 6. How many silver coins, 1.75 cm in diameter and of thickness 2 mm, must be melted to form a cuboid of dimensions 5.5 cm x 10 cm x 3.5 cm?
Solution:
Let the number of silver coins = n
Radius of coin \(r=\frac{1.75}{2} \mathrm{~cm}=\frac{7}{8} \mathrm{~cm}\)
Height h = 2 mm = \(\frac{2}{10} \mathrm{~cm}=\frac{1}{5} \mathrm{~cm}\)
The volume of one coin = πr2h
= \(\frac{22}{7} \times \frac{7}{8} \times \frac{7}{8} \times \frac{1}{5}=\frac{77}{160} \mathrm{~cm}^3\)
∴ Volume of n coins = \(\frac{77 n}{160} \mathrm{~cm}^3\)
Volume of cuboid = 5.5 x 10 x 3.5 = 192.5 cm3
Now, the volume of n coins = volume of a cuboid
⇒ \(\frac{77 n}{160}=192.5 \Rightarrow n=\frac{192.5 \times 160}{77}\)
⇒ n = 400
∴ Number of silver coins = 400
Question 7. A cylinder bucket, 32 cm high and with radius of base of 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm, find the radius and slant height of the heap.
Solution:
Given
A cylinder bucket, 32 cm high and with radius of base of 18 cm, is filled with sand. This bucket is emptied on the ground and a conical heap of sand is formed. If the height of the conical heap is 24 cm
For cylindrical buckets,
Radius r = 18 cm
Height h = 32 cm
∴ The volume of sand = volume of the bucket
= πr2h = π x 18 x 18 x 32 cm3
= 10368π cm3
For conical heap,
Let Raidus = R
Height H = 24 cm
∴ Volume of conical heap = \(\frac{1}{3} \pi R^2 H=\frac{1}{3} \pi R^2 \times 24=8 \pi R^2\)
Now, the volume of conical heap = volume of sand
⇒ 8πR2 = 10368π ⇒ R2 = 1296
⇒ R = 36 cm
∴ l2 = H2 + R2 = 242 + 362
= 576 + 1296 = 1872
⇒ \(l=\sqrt{1872}=12 \sqrt{13} \mathrm{~cm}\)
Question 8. Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h. How much area will it irrigate in 30 minutes, if 8 cm of standing water is needed?
Solution:
Given
Water in a canal, 6 m wide and 1.5 m deep, is flowing with a speed of 10 km/h.
Speed of water in canal = 10 km/h
= \(\frac{10 \times 1000}{60} \mathrm{~m} / \mathrm{min}\)
= \(\frac{500}{3} \mathrm{~m} / \mathrm{min}\)
Width of canal = 6 m and depth = 1.5 m
Now, the canal will transfer the water equal to the volume of a cuboid of dimensions.
⇒ \(6 \mathrm{~m} \times 1.5 \mathrm{~m} \times \frac{500}{3} m\) in 1 minute.
∴ Volume of water transfer in 30 minutes
= \(30 \times 6 \times 1.5 \times \frac{500}{3}=45000 \mathrm{~m}^3\)
If the depth of the irrigating region = 8 cm
= \(\frac{8}{100} \mathrm{~m}\) then
area x depth = 45000
⇒ \({Area} \times \frac{8}{100}=45000\)
⇒ \(\text { Area }=\frac{45000 \times 100}{8}=562500 \mathrm{~m}^2\)
Therefore, the area of the region irrigated by the canal in 30 minutes = 562500 m2
Question 9. A farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h, in how much time will the tank be filled?
Solution:
Given
farmer connects a pipe of internal diameter 20 cm from a canal into a cylindrical tank in her field, which is 10 m in diameter and 2 m deep. If water flows through the pipe at the rate of 3 km/h
Diameter of tank 2r = 10 m
⇒ r = 5 m
and depth h = 2m
∴ Volume of tank = r2h = (5)2 x 2 = 50 m3
Again, diameter of pipe = 2R = 20 cm
⇒ \(R=10 \mathrm{~cm}=\frac{10}{100} \mathrm{~m}=\frac{1}{10} \mathrm{~m}\)
Speed of water in pipe = 3 km/h
= \(\frac{3 \times 1000}{60} \mathrm{~m} / \mathrm{min}\)
= 50m/min
Now the pipe will transfer the water into the tank in 1 minute equal to the volume of a cylinder of radius \(\frac{1}{10}\) m and length 50 m.
∴ Time taken to fill the tank = \(\frac{\text { volume of cylindrical tank }}{\text { volume of water transfer in tank in 1 minute }}\)
= \(\frac{50 \pi}{\pi \times\left(\frac{1}{10}\right)^2 \times 50}=100 \text { minutes }\)
∴ Time taken to fill the tank completely = 100 minutes
Surface Area and Volume problems Class 10 with answers
Question 1. A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm. Find the capacity of the glass.
Solution:
Given
A drinking glass is in the shape of a frustum of a cone of height 14 cm. The diameters of its two circular ends are 4 cm and 2 cm.
The diameters of the frustum of the cone are 4 cm and 2 cm.
∴ Radius r1 = 2 cm and r2 = 1 cm
∴ Height of glass h = 14 cm
∴ The volume of a glass of the shape of a frustum of a cone
= \(\frac{1}{3} \pi h\left(r_1^2+r_1 r_2+r_2^2\right)\)
= \(\frac{1}{3} \times \frac{22}{7} \times 14\left[(2)^2+2 \times 1+(1)^2\right]\)
= \(\frac{44}{3}[4+2+1]\)
= \(\frac{44 \times 7}{3}=\frac{308}{3} \mathrm{~cm}^3\)
= \(=102 \frac{2}{3} \mathrm{~cm}^3\)
So, capacity of glass = = \(102 \frac{2}{3} \mathrm{~cm}^3\)
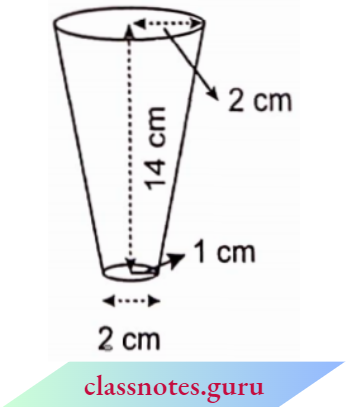
Question 2. The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm. Find the curved surface area of the frustum.
Solution :
Given
The slant height of a frustum of a cone is 4 cm and the perimeters (circumference) of its circular ends are 18 cm and 6 cm.
The slant height of the frustum of cone l = 4 cm.
Circumference of one end 2πr1 = 18 cm
∴ πr1 = 9 cm
Circumference of other ends 2πr2 = 6 cm
∴ πr2 = 3 cm
Curved surface area of frustum = π(r1 + r2) l
= (πr1 + πr2) l
= (9 + 3) x 4
= 48 cm2
Therefore, the curved surface area of the frustum of the cone = 48 cm2.
Question 3. A fez, tire cap used by the Turks, is shaped like the frustum of a cone. If its radius on the open side is 10 cm, its radius at the upper base is 4 cm and its slant height is 15 cm, find the area of material used for making it.
Solution:
Given
A fez, tire cap used by the Turks, is shaped like the frustum of a cone. If its radius on the open side is 10 cm, its radius at the upper base is 4 cm and its slant height is 15 cm
The cap is in the form of a frustum of a cone whose slant height is l = 15 cm.
Radius r1 = 10 cm and radius r2= 4 cm
∴ Curved surface of cap = π(r1 + r2) l
= \(\frac{22}{7}(10+4) \times 15=660 \mathrm{~cm}^2\)
Area of the closed end of the cap
= \(\pi r_2^2=\frac{22}{7} \times(4)^2 \mathrm{~cm}^2\)
= \(\frac{352}{7} \mathrm{~cm}^2=50 \frac{2}{7} \mathrm{~cm}^2\)
∴ Total canvas used in cap = Curved surface of cap + area of closed-end
= \(\left(660+50 \frac{2}{7}\right) \mathrm{cm}^2\)
= \(710 \frac{2}{7} \mathrm{~cm}^2\)
Therefore, the area of material used for making cap
∴ \(710 \frac{2}{7} \mathrm{~cm}^2\)
Question 4. A container, opened from the top and made up of a metal sheet, is in the form of a frustum of a cone of height 1 6 cm with radii of its lower arid upper ends as 8 cm and 20 cm, respectively. Find the cost of the milk which can completely fill the container, at the rate of ₹ 20 per litre. Also find the cost of the metal sheet used to make the container, if it costs ₹ 8 per 100 cm2. (Take π = 3.14)
Solution:
The vessel is in the shape of a frustum of a cone whose height is h = 16 cm.
And radius of upper end r1 = 20 cm and radius of lower end r2 = 8 cm
Then, the volume of the vessel = volume of the frustum
= \(\frac{1}{3} \pi h\left(r_1^2+r_1 r_2+r_2^2\right)\)
= \(\frac{1}{3} \pi \times 16 \times\left[(20)^2+20 \times 8+(8)^2\right]\)
= \(\frac{16}{3} \pi \times 624 \mathrm{~cm}^3=3328 \pi \mathrm{cm}^3\)
= 3328 x 3.14 cm3 = 10449.92 cm3 [∴ π = 3.14]
The milk required to fill the vessel is 10449.92 cm3 or 10.450 litre.
Then, cost of milk at ₹ 20 per litre = 20 x ₹ 10.45 = ₹ 209
The sheet will be used to make the curved surface and base of the vessel.
Then, the area of the base of the vessel = nr22
= 3.14 x (8)2 = 3.14 x 64 = 200.96 cm2
The slant height of the vessel
⇒ \(l=\sqrt{h^2+\left(r_1-r_2\right)^2}=\sqrt{(16)^2+(20-8)^2}\)
= \(\sqrt{256+144}=\sqrt{400}=20 \mathrm{~cm}\)
Then, curved surface of vessel = π (r1 + r2) l
= 3.14 (20 + 8) x 20 cm2
= 3.14 x 28 x 20 cm2
= 1758.4 cm2
∴ Area of sheet used in vessel
= (1758.4 + 200.96) cm2
= 1959.36 cm2
Cost of the sheet at the rate of ₹ 8 per 1 00 cm2
= \(₹ \frac{8}{100} \times ₹ 1959.36=₹ 156.7488\)
= ₹ 156.75
∴ Cost of milk = ₹ 209
and cost of sheet = ₹ 156.75
Question 5. A metallic right circular cone 20 cm high and whose vertical angle is 60° is cut into two parts at the middle of its height by a plane parallel to its base. If the frustum so obtained be drawn into a wire of diameter \({1}{16}\) cm, find the length of the wire.
Solution:
In the given, the diameter of the base of the cone is A’OA and the vertex is V. The angle of the vertex is A’VA = 60°, and then the semi-vertical angle of the cone is α = 30°.
Height of cone = 20 cm
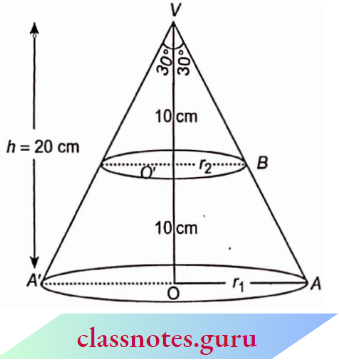
Then, in right ΔOAV,
⇒ \(\tan \alpha=\frac{O A}{O V} \Rightarrow \tan 30^{\circ}=\frac{r_1}{20} \Rightarrow \frac{1}{\sqrt{3}}=\frac{r_1}{20}\)
⇒ \(r_1=\frac{20}{\sqrt{3}} \mathrm{~cm}\)
∵ ΔVO’B and ΔVOA are similar.
∴ \(\frac{V O^{\prime}}{V O}=\frac{O^{\prime} B}{O A} \Rightarrow \frac{10}{20}=\frac{r_2}{r_1} \Rightarrow \frac{r_2}{r_1}=\frac{1}{2}\)
⇒ \(r_1=2 r_2 \Rightarrow r_2=\frac{1}{2} r_1=\frac{1}{2} \times \frac{20}{\sqrt{3}}=\frac{10}{\sqrt{3}} \mathrm{~cm}\)
and height of frustum \(\dot{h}=\frac{1}{2}\) x height of cone
= 10 cm
Then, volume of frustum = \(\frac{1}{3} \pi h\left(r_1^2+r_1 r_2+r_2^2\right)\)
⇒ \(\frac{1}{3} \pi(10)\left[\left(\frac{20}{\sqrt{3}}\right)^2+\frac{20}{\sqrt{3}} \times \frac{10}{\sqrt{3}}+\left(\frac{10}{\sqrt{3}}\right)^2\right]\)
⇒ \(\frac{1}{3} \pi 10\left[\frac{400}{3}+\frac{200}{3}+\frac{100}{3}\right]\)
⇒ \(\frac{7000}{9} \pi \mathrm{cm}^3\)
Diameter of cylindrical wire = \(\frac{1}{16}\) cm
Radius of wire \(r=\frac{1}{32} \mathrm{~cm}\) cm
Let the length of the wire drawn be l cm.
Then, the volume of wire = πr2l
⇒ \(\pi \times \frac{1}{32} \times \frac{1}{32} \times l=\frac{\pi}{1024} l \mathrm{~cm}^3\)
∵ The wire is drawn from the frustum of the cone.
∴ The volume of wire = volume of the frustum
⇒ \(\frac{\pi}{1024} l=\frac{7000}{9} \pi\)
⇒ \(l=\frac{7000 \pi}{9} \times \frac{1024}{\pi} \mathrm{cm}^3\)
= \(\frac{70}{9} \times 1024 \mathrm{~m}\)
= \(\frac{71680}{9} \mathrm{~m}=7964.44 \mathrm{~m}\)
Therefore, the length of the wire = 7964.44 m
Exemplar Class 10 Maths Chapter 13 CBSE practice questions
Question 1. A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, to cover the curved surface of the cylinder. Find the length and mass of the wire, assuming the density of copper to be 8.88 g per cm3.
Solution:
Given
A copper wire, 3 mm in diameter, is wound about a cylinder whose length is 12 cm, and diameter 10 cm, to cover the curved surface of the cylinder.
The diameter of the cylinder = 10 cm and
height of cylinder = 12 cm
∴ Circumference of cylinder
= π x diameter = π x 10 = 10π cm
∴ Length of wire used in one round about a cylinder
= 10 cm
∵ The length of the cylinder is 12 cm or 120 mm. When one round of wire is wound on the cylinder then it covers 3mm length of the cylinder.
When two rounds of wire are wound on the cylinder then it covers the (2 x 3) mm length of the cylinder.
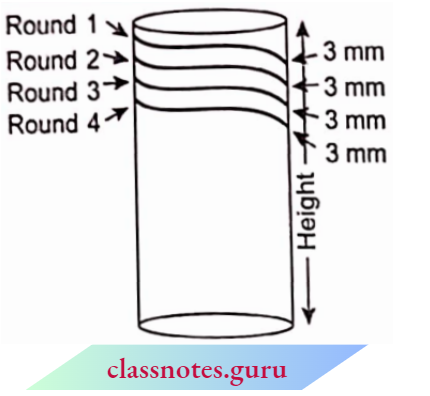
When three rounds of wire are wound on the cylinder then it covers (3×3) mm length of the cylinder.
When four rounds of wire are wound on the cylinder then it covers the (4×3) mm length of the cylinder.
The number of wounds of wire to cover the cylinder = \(\frac{120}{3} = 40\)
Length of required wire to wound 40 rounds on cylinder
= 40 x 10 π = 400 π cm
= 400 x 3.14 cm = 1256 cm(approx.)
= 12.56 m
So, the required length of wire = 12.56 m
The volume of wire = length x area of the wire
= \(1256 \times \pi \frac{d^2}{4} \quad\left[d=3 \mathrm{~mm}=\frac{3}{10} \mathrm{~cm}\right]\)
= \(1256 \times 3.14 \times \frac{9}{100 \times 4}\)
= \(\frac{314 \times 3.14 \times 9}{100}=88.74 \mathrm{~cm}^3\)
and mass of wire = 88.74 x 8.88 g
= 788.01 g = 0.788 kg
Question 2. A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. (Choose the value of π as found appropriate.)
Solution:
Given
A right triangle, whose sides are 3 cm and 4 cm (other than hypotenuse) is made to revolve about its hypotenuse.
In right ΔABC, ∠B = 90°, AB = 4 cm,
BC = 3 cm
Then, area of \(\triangle A B C=\frac{3 \times 4}{2}=6 \mathrm{~cm}^2\)
Hypotenuse \(A C=\sqrt{A B^2+B C^2}\)
= \(\sqrt{(4)^2+(3)^2}=\sqrt{25}=5\)
BOB’ is perpendicular to AC, if BO = r, then area of \(\triangle A B C=\frac{A C \times B O}{2}=\frac{5}{2} B O=\frac{5}{2} r\)
Then, \(\triangle A B C=\frac{A C \times B O}{2}=\frac{5}{2} B O=\frac{5}{2} r\)
Then, \(\frac{5}{2} r=6\) (∵\(\frac{5}{2} r\)and 6 both are area of AABC)
∴ \(r=\frac{6 \times 2}{5}=2.4 \mathrm{~cm}\)
Now, the radius r = 2.4 cm of the double cone formed by rotating the right ΔABC.
Then, volume of double cone (two cones) = volume of cone (A, BB’) + volume of cone (C, BB’)
= \(\frac{1}{3} \pi r^2(A O)+\frac{1}{3} \pi r^2(O C)\)
= \(\frac{1}{3} \pi r^2(A O+O C)\)
= \(\frac{1}{3} \pi r^2(A C)\) [ AO + OC = AC]
= \(\frac{1}{3} \pi \times(2.4)^2 \times 5=9.6 \pi \mathrm{cm}^3\)
= 9.6 x 3.14 cm3 (π = 3.14)
= 30.144 cm3
and surface area of the double cone (both cones)
= curved surface of the cone (A, BB’) + curved surface of the cone (C, BB’)
= πr (AB) + πr (BC) = nr (AB +BC)
= 3.14 x 2.4 x (4 +3) =3.14 x 2.4 x 7
= 52.75 cm2
Therefore, the volume of the double cone = 30.144 cm3 and surface area = 52.75 .cm2 (approximately).

Question 3. A cistern, internally measuring 150cm x 120cm x 110cm, has 129600 cm3 of water in it. Porous bricks are placed in the water until the cistern is full to the brim. Each brick absorbs one-seventeenth of its own volume of water. How many bricks can be put in without overflowing the water, each brick being 22.5 cm x 7.5 cm x 6.5 cm?
Solution:
Volume of cistern
= 150 x 120 x 110 cm3
= 1980000 cm3
The volume of water filled in cistern = 129600 cm3
Volume of each brick = 22.5 x 7.5 x 6.5 cm3
= 1096.875 cm3
Let on placing x bricks, the water rises upto the brim in the cistern.
Then, volume of x bricks = 1096.875 x cm3
Then, volume of absorbs water by bricks = \(1096.875 x \times \frac{1}{17}=\frac{1096.875 x}{17} \mathrm{~cm}^3\)
Then, the volume of remaining water in cistern = \(\left(129600-\frac{1096.875 x}{17}\right) \mathrm{cm}^3\)
Now, volume of x bricks + volume of water in cistern = volume of cistern
∴ \(1096.875 x+129600-\frac{1096.875 x}{17}\) = 1980000
or \(1096.875 x-\frac{1096.875 x}{17}\) = 1980000 – 129600
or \(1096.875 x\left(1-\frac{1}{17}\right)=1850400\)
or \(1096.875 x=\frac{1850400 \times 17}{16}\)
or \(x=\frac{1850400 \times 17}{16 \times 1096.875}\)
= 1792.4 = 1792 (approximately)
Therefore, the number of bricks placed in the cistern is 1792 (approximately).
Question 4. In one fortnight of a given month, there was a rainfall of 10 cm in a river valley. If the area of the valley is 7280 km2, show that the total rainfall was approximately equivalent to the addition to the normal water of three rivers each 1072 km long, 75 m wide and 3 m deep.
Solution:
The volume of each river
= 10721cm x 75 m x 3 m
= 1072 x 75 x 3 x 1000 m3
= 241200000 m3
∴ The volume of total water in three rivers
= 3 x 241200000 m3
∴ Total water of rivers = 723600000 m3
∴ Area of valley = 7280 km2
= 7280 x (1000)2 m2
= 7280000000 m
∴ Volume of rainwater
= \(7280000000 \times \frac{10}{100} \mathrm{~m}^3\) (∵\(10 \mathrm{~cm}=\frac{10}{100} \mathrm{~m}\))
= 728000000 m3
These two volumes are not equal.
So, it is clear that the given data given in the question are incorrect.
Question 5. An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attached to a frustum of a cone. If the total height is 22 cm, the diameter of the cylindrical portion is 8 cm and the diameter portion is 8 cm and the diameter of the top of the funnel is 18 cm, find the area of the tin sheet required to make the funnel.
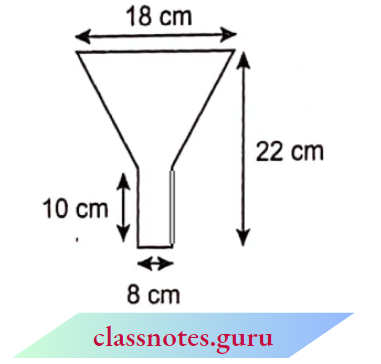
Solution:
Height of cylindrical part h = 10 cm
Total height of funnel = 22 cm
∴ Height of frustum of cone (H) = 22 – 10 = 12 cm
Upper radius of frustum of cone = \(R_1=\frac{18}{2}=9 \mathrm{~cm}\)
Lower radius of frustum of cone = \(R_2=\frac{8}{2}=4 \mathrm{~cm}\)
The radius of cylindrical part r = 4 cm
The curved surface of the cylindrical part = 2 πrh
= 2π x 4 x 10 = 80 π cm2
The slant height of the frustum of a cone
⇒ \(l=\sqrt{H^2+\left(R_1-R_2\right)^2}\)
= \(\sqrt{(12)^2+(9-4)^2}=\sqrt{144+25}\)
= \(\sqrt{169}=13 \mathrm{~cm}\)
So, the total surface area of the funnel
∴ The curved surface of the frustum of a cone
= π (R1+ R2) l
= π (9 + 4) x 13 = 169 π cm2
∴ The curved surface area of the cylindrical part + curved surface area of the frustum of a cone
= 80 π + 169π = 249π cm2
= \(249 \times \frac{22}{7} \mathrm{~cm}^2\)
= \(\frac{5478}{7}=782 \frac{4}{7} \mathrm{~cm}^2\)
Therefore, area of tin sheet used in funnel = \(782 \frac{4}{7} \mathrm{~cm}^2\)
Volume and surface area formulas Class 10 NCERT Exemplar
Question 6. Derive the formula for the curved surface area and total surface area of the frustum of a cone.
Solution:
Let for the (V, AB), V is the vertex, r2 the base radius and l2 the slant height. A cone (V, CD) is cut off from this cone from a point O’ below h1 from the vertex V of this cone, parallel to the base whose’ radius is r1 and slant height is l1.
Draw the perpendicular DE from point D to the base.
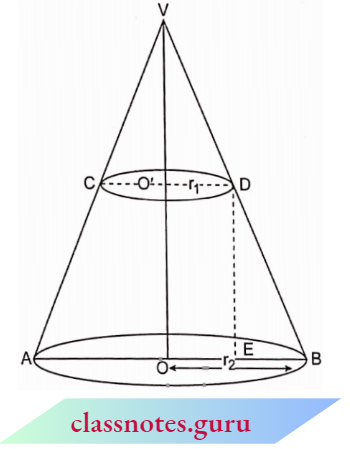
In ΔVO’D and ΔDEB,
∠VO’D = ∠DEB (VO and DE both are perpendicular to the base)
∠VDO’ = ∠DBE (the bases of two cones are parallel to each other)
∴ ΔVO’D and ΔDEB are similar
\(\frac{V D}{B D}=\frac{O^{\prime} D}{E B}\)or \(\frac{l_1}{l}=\frac{O^{\prime} D}{O B-O E}=\frac{O^{\prime} D}{O B-O^{\prime} D}\)
while BD = l = slant height of the frustum
⇒ \(\frac{l_1}{l}=\frac{r_1}{r_2-r_1} \Rightarrow l_1=\left(\frac{r_1}{r_2-r_1}\right) l\) → (1)
The curved surface area of a frustum
= curved surface area of cone (V, AB) – curved surface area of cone ( V, CD)
= πr2l2 -πr1l1 = πr2(l1 + BD) – πr1l1
= πr2l1 +πr2 (BD) – πr1l1
= π(r2-r1) l1 + πr2 l
= \(\pi\left(r_2-r_1\right)\left(\frac{r_1}{r_2-r_1}\right) l+\pi r_2 l\) [from eqn. (1)]
= π r1l + πr2l
So, curved surface area of frustum = π (r1 + r2) l
Hence Proved
And total surface area of a frustum
= curved surface + area of first end + area of second end
= π(r1 + r2) / + πr12 + πr22
= π(r1 + r2)l + π (r12 + r22)
Hence Proved.
Question 7. Derive the formula for the volume of the frustum of a cone.
Solution:
From the last question, for the cone (V, AB), height = h2 and radius = r2
∴ Volume of cone (V, AB) = \(\frac{1}{3} \pi r_2^2 h_2\)
and volume of cone (V, CD) = \(\frac{1}{3} \pi r_1^2 h_1\)
∴ Volume of frustum = volume of cone (V, AB) – volume of cone (V, CD)
∴ Volume of frustum (V)
= \(\frac{1}{3} \pi r_2^2 h_2-\frac{1}{3} \pi r_1^2 h_1\) → (1)
∴ h2 = VO’= VO’ + O’O = h1 + h
∴ Put h2 = h1 +h in eqn. (1),
Volume of frustum V = \(\frac{1}{3} \pi r_2^2\left(h_1+h\right)-\frac{1}{3} \pi r_1^2 h_1\)
Volume of frustum V = \(\frac{1}{3} \pi\left(r_2^2-r_1^2\right) h_1+\frac{1}{3} \pi r_2^2 h\) → (2)
In similar ΔVO’D and ΔDEB,
\(\frac{h_1}{h}=\frac{r_1}{r_2-r_1} \quad \Rightarrow \quad h_1=\left(\frac{r_1}{r_2-r_1}\right) h\)Put \(h_1=\left(\frac{r_1}{r_2-r_1}\right) h\) in eqn. (2),
⇒ \(V=\frac{1}{3} \pi\left(r_2^2-r_1^2\right) \frac{\eta_1}{\left(r_2-r_1\right)} h+\frac{1}{3} \pi r_2^2 h\)
= \(\frac{1}{3} \pi\left(r_2+r_1\right) r_1 h+\frac{1}{3} \pi r_2^2 h\)
= \(\frac{1}{3} \pi\left(r_1^2+r_1 r_2\right) h+\frac{1}{3} \pi r_2^2 h\)
= \(\frac{1}{3} \pi\left(r_1^2+r_1 r_2+r_2^2\right) h\)
Therefore, the volume of the frustum of the cone
= \(\frac{1}{3} \pi\left(r_1^2+r_1 r_2+r_2^2\right) h\) Hence Proved.
Question 1. A surah is a combination of:
Answer: 1. A sphere and a cylinder
Question 2. A glass is generally of the shape of:
Answer: 2. A frustum of a cone
Question 3. A plummet is a combination of:
Answer: 2. A hemisphere and a cone
NCERT Exemplar Surface Area Volume Solved Questions
Question 4. An iron piece in the shape of a cuboid of dimensions 49 cm x 33 cm x 24 cm is melted and recast into a solid sphere. The radius of the sphere is:
Answer: 1. 21 cm
Question 5. While converting a shape of a solid into another shape, the volume of the new shape:
Answer: 3. Remains same
Question 6. The ratio of the surface of two spheres is 16:9. The ratio of their volumes is:
Answer: 2. 64: 27
Question 7. The diameter of a sphere exactly inscribed in a right circular cylinder of radius r cm and height h cm (h > 2r) is:
Answer: 2. 2r cm