Sainavle

• Calorimetry
• Calorimetry And Thermal Expansion
• Thermal Expansion
• Mathematical Tools

• Algebra
• Double Differentiation
• Multiplication Of Vectors
• Rules For Differentiation
• Rules For Integration
• Trigonometry
• Vector

NEET Physics Class 11 Chapter 10 Mathematical Tools – Algebra

Quadratic Equation And Its Solution:

An algebraic equation of second order (the highest power of the variable is equal to 2) is called a quadratic equation. Equation ax² + bx + c = 0 is the general quadratic equation.

The general solution of the above quadratic equation or value of variable x

⇒ \(x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}\)

⇒ \(x_1=\frac{-b+\sqrt{b^2-4 a c}}{2 a}\)

and \(x_2=\frac{-b-\sqrt{b^2-4 a c}}{2 a}\)

Sum of roots = x₁ + x₂ = – \(\frac{\mathrm{b}}{\mathrm{a}}\) and product of roots = x₁ + x₂ = \(\frac{\mathrm{c}}{\mathrm{a}}\)

For real roots b²– 4ac ≥ 0 and for imaginary roots b² – 4ac < 0.

Algebra in Mathematical Tools NEET Physics Class 11 Solutions

Question 1. find roots of f (x) = x² – 4x + 3, f (x) = – x² + 3x – 5 Every quadratic equation has 2 roots (x₁ x₂) such that f (x₁) and f (x₂) is zero.

Graph of quadratic Equation: ax² + bx + c

Graph of a quadratic equation is of parabolic nature.

Points where the graph cuts the x-axis are roots of a quadratic equation.

Binomial Expression: An algebraic expression containing two terms is called a binomial expression.

For example (a + b), (a + b)³, (2x – 3y)^-1, \(\left(x+\frac{1}{y}\right)\),etc are binomial theorem

Binomial Theorem

⇒ \((a+b)^n=a^n+n a^{n-1} b^1+\frac{n(n-1)}{2 \times 1} a^{n-2} b^2+\ldots \ldots \ldots \ldots,(1+x)^n\)

⇒ \(1+n x+\frac{n(n-1)}{2 \times 1} x^2+\ldots \ldots \ldots\)

Binomial Approximation

If x is very small, then terms containing higher powers of x can be neglected so (1 + x)n = 1 + nx

Logarithm Definition: Every positive real number N can be expressed in exponential form as

N = a^x…… (1)for example.,  49 = 7²

where ‘a’ is also a positive real different than unity and is called the base and ‘x’ is called the exponent. We can write the relation (1) in logarithmic form as

loga N = x ……..  (2)

Hence the two relations and

NEET Class 11 Algebra in Mathematical Tools: Problems and Solutions

are identical where N > 0, a > 0, a ≠ 1

Hence logarithm of a number to some base is the exponent by which the base must be raised to get that number.

The logarithm of zero does not exist and the logarithm of (–) ve reals is not defined in the system of real numbers. a is raised what power to get N

Question 2. Find value of

1. \(\log _{81} 27\)
2. \(\log _{10} 100\)
3. \(\log 9 \sqrt{3}\)

Answer:

1. \(\log _{81} 27\)

⇒ \(3^3=3^{4 x}\)

gives x = 3/4

2. \(\log _{10} 100\)

⇒ \(10^2=10^x\)

gives x = 2

3. \(\log 9 \sqrt{3}\)

⇒ \(9 \sqrt{3}\left(\frac{1}{3}\right)^x\)

⇒ \(3^{5 / 2}=3^{-x}\)

gives x = -5/2

Note:

Unity has been excluded from the base of the logarithm as in this case, log1N will not be possible, and if N = 1 then log11 will have infinitely many solutions and will not be unique which is necessary in the functional notation.

a N log N a = is an identify for all N > 0 and a > 0, a ≠ 1 for example.,  \(2^{\log _2 5}\) = 5

The number N in (2) is called the antilog of ‘x’ to the base ‘a’. Hence If log₂512 is 9 then antilog₂9 is equal to 2² = 512

Using the basic definition of log we have 3 important deductions :

log_NN = 1 i.e. logarithm of the number to the same base is 1.

⇒ \(\log _{\frac{1}{N}}\) =–1 i.e. logarithm of a number to its reciprocal is –1.

log_a 1 = 0 i.e. logarithm of unity to any base is zero. (basic constraints on number and base must be observed.)

⇒ \(\log ^{\log _a n}\)= n is an identify for all N > 0 and a > 0; a ≠ 1 for example., \(\log ^{\log _a n}\)

Algebraic Methods in NEET Physics Class 11 Mathematical Tools

Whenever the number and base are on the same side of unity then the logarithm of that number to the base is (+ve), however, if the number and base are located on different sides of unity then the logarithm of that number to the base is (–ve) for example.,

log₁₀ 100 = 2

log_1/10 100 =– 2

For a non negative number ‘a’ and \(n \geq 2, n \in N \sqrt[n]{a}=a^{1 / n}\)

NEET Physics Chapter 10 Algebra: Study Notes and Solutions

Componend And Dividend Rule

If \(\frac{p}{q}=\frac{a}{b}\) then \(\frac{p+q}{p-q}=\frac{a+b}{a-b}\)

Arithmetic Progression (AP)

General from: a, a + d, a + 2d, ……………a + (n – 1)d

Here a = first term, d = common difference

Sum of n terms \(S_n=\frac{n}{2}[a+a+(n-1) d]=\frac{n}{2}\left[I^{\text {st }} \text { term }+n^{\text {th }} \text { term }\right]\)

NEET Physics Class 11 Chapter 10 Mathematical Tools – Trigonometry

Measurement Of Angle And Relationship Between Degrees And Radian

In navigation and astronomy, angles are measured in degrees, but in calculus, it is best to use units called radians because they simplify later calculations.

Let ACB be a central angle in a circle of radius r, as in the figure. Then the angle ACB or θ is defined in radius as –

θ = \(\frac{\text { Arc length }}{\text { Radius }}\)

θ = \(\frac{\widehat{A B}}{r}\)

If r = 1 then θ = AB

The radian measure for a circle of unit radius of angle ACB is defined as the length of the circular arc AB. Since the circumference of the circle is 2π and one complete revolution of a circle is 360º, the relation between radians and degrees is given by: π radians = 180º

Trigonometry Solutions for NEET Physics Class 11 Chapter 10

Angle Conversion Formulas

1 degree = \(\frac{\pi}{180}\) (≈ 0.02) radian

Degrees to radians: multiply by \(\frac{\pi}{180}\)

1 radian ≈ 57 degrees

Radians to degrees : multiply by \(\frac{180}{\pi}\)

Question 1.

1. Convert 45º to radians.
2. Convert \(\frac{\pi}{6}\) rad to degrees.

Answer:

1. \(\text { 45 – } \frac{\pi}{180}=\frac{\pi}{4} \mathrm{rad}\)
2. \(\frac{\pi}{6} \cdot \frac{180}{\pi}=30^{\circ}\)

Question 2. Convert 30º to radians.

Answer:

⇒ \(30^{\circ} \times \frac{\pi}{180}\)

⇒ \(\frac{\pi}{6} \mathrm{rad}\)

Question 3. Convert \(\frac{\pi}{3}\) rad to degrees.

Answer:

⇒ \(\frac{\pi}{3} \times \frac{180}{\pi}\)= 60º

Standard values

1. \(30^{\circ}=\frac{\pi}{6} \mathrm{rad}\)
2. \(45^{\circ}=\frac{\pi}{4} \mathrm{rad}\)
3. \(60^{\circ}=\frac{\pi}{3} \mathrm{rad}\)
4. \(90^{\circ}=\frac{\pi}{2} \mathrm{rad}\)
5. \(120^{\circ}=\frac{2 \pi}{3} \mathrm{rad}\)
6. \(135^{\circ}=\frac{3 \pi}{4} \mathrm{rad}\)
7. \(150^{\circ}=\frac{5 \pi}{6} \mathrm{rad}\)
8. \(180^{\circ}=\pi \mathrm{rad}\)
9. \(360^{\circ}=2 \pi \mathrm{rad}\)

(Check these values yourself to see that they satisfy the conversion formulae)

NEET Physics Class 11 Chapter 10 Mathematical Tools – Measurement Of Positive And Negative Angles

An angle in the xy-plane is said to be in standard position if its vertex lies at the origin and its initial ray lies along the positive x-axis.

Angles measured counterclockwise from the positive x-axis are assigned positive measures; angles measured clockwise are assigned negative measures.

NEET Physics Class 11 Chapter 10 Trigonometry: Problems and Solutions

NEET Physics Class 11 Chapter 10 Mathematical Tools – Six Basic Trigonometric Functions

The trigonometric function of a general angle θ is defined in terms of x, y, and r.

Sine: sinθ = \(\frac{\text { opp }}{\text { hyp }}=\frac{\mathrm{y}}{\mathrm{r}}\)

Cosecant: cosecθ = \(\frac{\text { hyp }}{\text { opp }}=\frac{\mathrm{r}}{\mathrm{y}}\)

Cosine: cosθ = \(\frac{\text { adj }}{\text { hyp }}=\frac{x}{r}\)

Secant: secθ = \(\frac{\text { hyp }}{\text { adj }}=\frac{r}{x}\)

Tangent: tanθ = \(\frac{\text { opp }}{\text { adj }}=\frac{y}{x}\)

Cotangent: cotθ = \(\frac{\text { adj }}{\text { opp }}=\frac{x}{y}\)

Values Of Trigonometric Functions

If the circle has radius r = 1, the equations defining sinθ and cos θ become Cos θ = x, sinθ = y

We can then calculate the values of the cosine and sine directly from the coordinates of P.

Question 1. Find the six trigonometric ratios from the given figure

Answer:

sinθ = \(\frac{\text { opp }}{\text { hyp }}=\frac{4}{5}\)

cosθ = \(\frac{\text { adj }}{\text { hyp }}=\frac{3}{5}\)

tan θ = \(\frac{\text { opp }}{\text { adj }}=\frac{4}{3}\)

cosec θ = \(\frac{\text { hyp }}{\text { opp }}=\frac{5}{4}\)

sec θ = \(\frac{\text { hyp }}{\text { adj }}=\frac{5}{3}\)

cotθ = \(\frac{\text { adj }}{\text { opp }}=\frac{3}{4}\)

Question 2. Find the sine and cosine of angle θ shown in the unit circle if the coordinates of point p are as shown.

Answer:

cos θ = x-coordinate of P = – \(\frac{1}{2}\)

2sin θ = y-coordinate of P = \(\frac{\sqrt{3}}{2}\)

Mathematical Tools – Trigonometry Solutions NEET Physics Class 11

NEET Physics Class 11 Chapter 10 Mathematical Tools – Rules For Finding Trigonometric Ratio Of Angles Greater Than 90°

Step 1 → Identify the quadrant in which the angle lies.

Step 2 → If angle = (nπ ± θ) where n is an integer. Then trigonometric function of (nπ ± θ)= same trigonometric function of θ and the sign will be decided by the CAST Rule.

If angle = \(\left[(2 n+1) \frac{\pi}{2} \pm \theta\right]\) where n is an integer. Then the trigonometric function of \(\left[(2 n+1) \frac{\pi}{2} \pm \theta\right]\)= complimentary trigonometric function of θ and sign will be decided by CAST Rule.

Values of sin θ, cos θ, and tan θ for some standard angles.

Question 1. Evaluate sin 120°

Answer:

sin 120°

= sin (90° + 30°)

= cos 30°

⇒ \(\frac{\sqrt{3}}{2}\)

Aliter sin 120°

= sin (180° – 60°)

= sin 60°

⇒ \(\frac{\sqrt{3}}{2}\)

Question 2. Evaluate cos 135°

Answer:

cos 135°

= cos (90° + 45°)

= – sin 45°

⇒ \(-\frac{1}{\sqrt{2}}\)

Question 3. Evaluate cos 210°

Answer:

cos 210°

= cos (180° + 30°)

= – cos30°

⇒ \(-\frac{\sqrt{3}}{2}\)

Trigonometry for NEET Physics Class 11: Formulas and Solutions

Question 4. Evaluate tan 210°

Answer:

tan 210°

= tan (180° + 30°)

= tan 30°

= \(\frac{1}{\sqrt{3}}\)

NEET Physics Class 11 Chapter 10 Mathematical Tools – General Trigonometric Formulas

Question 1. \(\cos ^2 \theta+\sin ^2 \theta=1\)

Answer:

⇒ \(1+\tan ^2 \theta=\sec ^2 \theta\)

⇒ \(1+\cot ^2 \theta={cosec}^2 \theta\)

Question 2. cos(A + B) = cos A cos B – sin A sin B

Answer:

sin( A + B) = sin A cos B + cos A sin B

⇒ \(\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B}\)

NEET Class 11 Mathematical Tools – Trigonometry: Problems and Solutions

Question 3. sin 2θ = 2 sin θ cos θ; cos 2θ = cos² θ – sin²θ = 2cos² θ – 1 = 1 – 2sin² θ

Answer:

⇒ \(\cos ^2 \theta=\frac{1+\cos 2 \theta}{2}\)

⇒ \(\sin ^2 \theta=\frac{1-\cos 2 \theta}{2}\)

Question 4.

In Δ ABC, the sine rule

Answer:

ΔABC need not be right-angled, \(\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}\)

Question 5. Cosine Rule:

Answer:

cosA = \(\frac{\mathrm{b}^2+\mathrm{C}^2-\mathrm{a}^2}{2 \mathrm{bc}}\)

cosB = \(\frac{a^2+C^2-b^2}{2 a c}\)

cosC = \(\frac{a^2+b^2-c^2}{2 a b}\)

NEET Physics Class 11 Chapter 10 Mathematical Tools – Coordinate Geometry

To specify the position of a point in space, we use a right-handed rectangular axes coordinate system. This system consists of

1. Origin
2. Axis or axes.

If a point is known to be on a given line or in a particular direction only one coordinate is necessary to specify its position, if it is in a plane, two coordinates are required, if it is in space three coordinates are needed.

Origin

This is any fixed point that is convenient to you. All measurements are taken w.r.t. this fixed point.

Axis or Axes

Any fixed direction passing through the origin and convenient to you can be taken as an axis.

• If the position of a point or the position of all the points under consideration always happens to be in a particular direction, then only one axis is required. This is generally called the x-axis.
• If the positions of all the points under consideration are always in a plane, two perpendicular axes are required.
• These are generally called the x and y-axis. If the points are distributed in space, three perpendicular axes are taken which are called the x, y, and z-axis.

Position Of A Point In xy Plane

The position of a point is specified by its distances from the origin along (or parallel to) the x and y-axis as shown in the figure.

Here x-coordinate and y-coordinate are called abscissa and ordinate respectively.

Distance Formula

The distance between two points (x₁, y₁) and (x₂, y₂) is given by

d = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

Note: In space d = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2+\left(z_2-z_1\right)^2}\)

Slope Of A Line

The slope of a line joining two points A(x₁, y₁) and B(x₂, y₂) is denoted by
m and is given by

m = \(\frac{\Delta \mathrm{y}}{\Delta \mathrm{x}}=\frac{\mathrm{y}_2-\mathrm{y}_1}{\mathrm{x}_2-\mathrm{x}_1}=\tan \theta\) [If both axes have identical scales]

Here θ is the angle made by a line with a positive x-axis. The slope of a line is a quantitative measure of inclination.

Question 1. For points (2, 14) find abscissa and ordinate. Also, find the distance from the y and x-axis.

Answer:

Abscissa = x-coordinate = 2 = distance from y-axis.

Ordinate = y-coordinate = 14 = distance from the x-axis.

NEET Physics Chapter 10 Mathematical Tools: Trigonometry Solutions

Question 2. Find the value of a if distances between the points (–9 cm, a cm) and (3 cm, 3cm) is 13 cm.

Answer:

By using distance formula d = \(\sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2}\)

⇒ \(13 \sqrt{[3-(-9)]^2+[3-a]^2}\)

⇒ 13² = 12² + (3 – a)²

⇒ (3 – a)² = 13² – 12² = 5²

⇒ (3 – a) = ± 5

⇒ a = 2 cm or 8 cm

Question 3. A dog wants to catch a cat. The dog follows the path whose equation is y-x = 0 while the cat follows the path whose equation is x² + y² = 8. The coordinates of possible points for catching the cat are.

1. (2, – 2)
2. (2, 2)
3. (–2, 2)
4. (–2, 2)
5. (2, 4)

Answer:

Let catching point be (x¹, y¹) then, y¹ – x¹ = 0 and x¹² + y¹² = 8

Therefore, 2x¹² = 8

⇒ x¹² = 4

⇒ x¹ = ± 2;

so possible ae (2, 2) and (–2, –2).

NEET Physics Class 11 Chapter 10 Mathematical Tools – Rules For Differentiation

Derivative Of A Constant:

The first rule of differentiation is that the derivative of every constant function is zero. If c is constant, then \(\frac{\mathrm{d}}{\mathrm{dx}} \mathrm{c}\) = 0

⇒ \(\frac{d}{d x}(8)=0\)

⇒ \(\frac{d}{d x}\left(-\frac{1}{2}\right)=0\)

Power Rule:

If n is a real number, then \(\frac{d}{d x} x^n=n x^{n-1}\)

To apply the power Rule, we subtract 1 from the original exponent (n) and multiply the result by n.

⇒ \(\begin{array}{l|l|l|l|l|l}\mathrm{f} & \mathrm{x} & \mathrm{x}^2 & x^3 & x^4 & \ldots \\\hline f^{\prime} & 1 & 2 x & 3 x^2 & 4 x^3 & \ldots\end{array}\)

Question 1. 

1. \(\frac{d}{d x}\left(\frac{1}{x}\right)\)

⇒ \(\frac{d}{d x}\left(x^{-1}\right)\)

⇒ \((-1) x^{-2}\)

⇒ \(-\frac{1}{x^2}\)

2. \(\frac{d}{d x}\left(\frac{4}{x^3}\right)\)

⇒ \(4 \frac{d}{d x} \quad\left(x^{-3}\right)\)

⇒ \(4(-3) x^{-4}\)

⇒ \(-\frac{12}{x^4}\)

The Constant Multiple Rule:

If u is a differentiable function of x, and c is a constant, then \(\frac{d}{d x}(c u)=c \frac{d u}{d x}\)

In particular, if n is a positive integer, then \(\frac{d}{d x}\left(c x^n\right)=c n x^{n-1}\)

Rules for Differentiation NEET Physics Class 11 Chapter 10

Question 2. The derivative formula

⇒ \(\frac{\mathrm{d}}{\mathrm{dx}}\left(3 \mathrm{x}^2\right)\)

= 3(2x)

= 6x

says that if we rescale the graph of y = x² by multiplying each y-coordinate by 3, then we multiply the slope at each point by 3.

Question 3. A useful special case

The derivative of the negative of a differentiable function is the negative of the function’s derivative. Rule 3 with c = –1 gives.

⇒ \(\frac{d}{d x}(-u)=\frac{d}{d x}(-1 \cdot u)=-1 \quad \frac{d}{d x}(u)=-\frac{d}{d x}\)

The Sum Rule

The derivative of the sum of two differentiable functions is the sum of their derivatives. If u and v are differentiable functions of x, then their sum u + v is differentiable at every point where u and v are both differentiable functions in their derivatives.

⇒ \(\frac{d}{d x}(u-v)=\frac{d}{d x}[u+(-1) v]\)

⇒ \(\frac{d u}{d x}+(-1) \frac{d v}{d x}=\frac{d u}{d x}-\frac{d v}{d x}\)

The Sum Rule also extends to sums of more than two functions, as long as there are only finitely many functions in the sum. If u₁, u₂,………u_n are differentiable at x, then so is u₁+ u₂+ ……..+ u_n, and

⇒ \(\frac{d}{d x}\left(u_1+u_2+\ldots . .+u_n\right)\)

⇒ \(\frac{d u_1}{d x}+\frac{d u_2}{d x}+\ldots \ldots .+\frac{d u_n}{d x}\)

Question 4.

1. \(y= x^4+12 x \\\)

⇒ \(\frac{d y}{d x}=\frac{d}{d x}\left(x^4\right)+\frac{d}{d x}(12 x)\)

⇒ \(4 x^3+12\)

2. \(y =x^3+\frac{4}{3} x^2-5 x+1\)

⇒ \(\frac{d y}{d x} =\frac{d}{d x}\left(x^3\right)+\frac{d}{d x}\left(\frac{4}{3} x^2\right)-\frac{d}{d x}(5 x)+\frac{d}{d x}(1)\)

⇒ \(3 x^2+\frac{4}{3} \cdot 2 x-5+0\)

⇒ \(3 x^2+\frac{8}{3} x-5\)

Notice that we can differentiate any polynomial term by term, the way we differentiated the polynomials in the above example.

The Product Rule

If u and v are differentiable at x, then so is their product uv, and \(\frac{d}{d x}(u v)=u \frac{d v}{d x}+v \frac{d u}{d x}\)

The derivative of the product uv is u times the derivative of v plus v times the derivative of u. In prime notation (uv)’ = uv’ + vu’.

While the derivative of the sum of two functions is the sum of their derivatives, the derivative of the product of two functions is not the product of their derivatives. For instance,

⇒ \(\frac{d}{d x}(x . x)=\frac{d}{d x}\left(x^2\right)=2 x,\),

while \(\frac{\mathrm{d}}{\mathrm{dx}} \text { (x) } \frac{\mathrm{d}}{\mathrm{dx}} \text {.(x) }\)= 1.1 = 1.

NEET Physics Class 11 Chapter 10 Differentiation Problems and Solutions

Question 5. Find the derivatives of y = (x² + 1) (x³ + 3).

Answer:

From the product Rule with u = x² + 1 and v = x³ + 3, we find

⇒ \(\frac{d}{d x}\left[\left(x^2+1\right)\left(x^3+3\right)\right]\)

= (x² + 1) (3x²) + (x³ + 3) (2x)

= 3x⁴ + 3x² + 2x⁴ + 6x

= 5x⁴ + 3x² + 6x.

For example can be done as well (perhaps better) by multiplying out the original expression for y and differentiating the resulting polynomial. We now check :

y=(x² + 1)(x³ + 3)=x⁵ +x³+3x² + 3

⇒ \(\frac{d y}{d x}=5 x^4+3 x^2+6 x\)

This is in agreement with our first calculation.

There are times, however, when the product Rule must be used. In the following examples. We have only numerical values to work with.

Question 6. Let y = uv be the product of the functions u and v. Find y’ (2)if u’(2)= 3, u’(2)= –4, v(2)= 1, and v’(2)= 2.

Answer:

From the Product Rule, in the form

y’ = (uv)’ = uv’ + vu’

we have y’(2) = u(2) vs(2) + v(2) up(2)

= (3)(2)+(1) (–4)

= 6 – 4 = 2.

The Quotient Rule

If u and v are differentiable at x, and v(x) ≠ 0, then the quotient u/v is differentiable at x, and

⇒ \(\frac{d}{d x}\left(\frac{u}{v}\right)=\frac{v \frac{d u}{d x}-u \frac{d v}{d x}}{v^2}\)

Just as the derivative of the product of two differentiable functions is not the product of their derivatives, the derivative of the quotient of two functions is not the quotient of their derivatives.

Question 7. Find the derivative of y = \(\frac{t^2-1}{t^2+1}\)

Answer: We apply the Quotient Rule with u = t² – 1 and v = t² + 1:

⇒ \(\frac{d y}{d t}=\frac{\left(t^2+1\right) \cdot 2 t-\left(t^2-1\right) \cdot 2 t}{\left(t^2+1\right)^2}\)

⇒ \(\frac{\mathrm{d}}{\mathrm{dt}}\left(\frac{\mathrm{u}}{\mathrm{v}}\right)=\frac{\mathrm{v}(\mathrm{du} / \mathrm{dt})-\mathrm{u}(\mathrm{dv} / \mathrm{dt})}{\mathrm{v}^2}\)

⇒ \(\frac{2 t^3+2 t-2 t^3+2 t}{\left(t^2+1\right)^2}=\frac{4 t}{\left(t^2+1\right)^2}\)

Derivative Of Sine Function

⇒ \(\frac{\mathrm{d}}{\mathrm{dx}}\)(sinx) cos x

Question 8.

1. y = x² – sin x :

⇒ \(\frac{d y}{d x}=2 x-\frac{d}{d x}(\sin x)\) Difference Rule

= 2x -cos x

2. y = x² sin x :

⇒ \(\frac{d y}{d x}=x^2 \frac{d}{d x}(\sin x)+2 x \sin x\)Product Rule

⇒ \(x^2 \cos x+2 x \sin x\)

3. y = \(\frac{\sin x}{x}\)

⇒ \(\frac{d y}{d x}=\frac{x \cdot \frac{d}{d x}(\sin x)-\sin x .1}{x^2}\) Quotient rule

⇒ \(\frac{x \cos x-\sin x}{x^2}\)

Derivative Of Cosine Function

⇒ \(\frac{\mathrm{d}}{\mathrm{dx}}\)(cosx)= – sinx

Question 9.

1. y = 5x + cos x

⇒ \(\frac{d y}{d x}=\frac{d}{d x}(5 x)+\frac{d}{d x}(\cos x)\) Sum Rule

= 5 – sin x

2. y = sinx cosx

⇒ \(\frac{d y}{d x}=\sin x \frac{d}{d x}(\cos x)+\cos x \frac{d}{d x}(\sin x)\) Product Rule

= sinx (– sinx) + cosx (cosx)

= cos² x – sin² x

Derivatives Of Other Trigonometric Functions

Because sin x and cos x are differentiable functions of x, the related functions

tan x = \(\frac{\sin x}{\cos x}\)

cot x = \(\frac{\cos x}{\sin x}\)

sec x = \(\frac{1}{\cos x}\)

cosec x = \(\frac{1}{\sin x}\)

are differentiable at every value of x at which they are defined. There derivatives. Calculated from the Quotient Rule, are given by the following formulas.

⇒ \(\frac{d}{d x}\)(tan x) = sec² x ;

⇒ \(\frac{d}{d x}\)(sec x) = sec x tan

⇒ \(\frac{d}{d x}\)(cot x) = – cosec² x ;

⇒ \(\frac{d}{d x}\)(cosec x) = – cosec x cot x

Question 10. Find dy / dx if y = tan x.

Answer:

⇒ \(\frac{d}{d x}(\tan x)\)

⇒ \(\frac{d}{d x}\left(\frac{\sin x}{\cos x}\right)\)

⇒ \(\frac{\cos x \frac{d}{d x}(\sin x)-\sin x \frac{d}{d x}(\cos x)}{\cos ^2 x}\)

⇒ \(\frac{\cos x \cos x-\sin x(-\sin x)}{\cos ^2 x}\)

⇒ \(\frac{\cos ^2 x+\sin ^2 x}{\cos ^2 x}\)

⇒ \(\frac{1}{\cos ^2 x}=\sec ^2 x\)

Mathematical Tools – Differentiation Rules NEET Physics Class 11

Question 11.

1. \(\frac{d}{d x}(3 x+\cot x)\)

⇒ \(3+\frac{d}{d x}(\cot x)\)

⇒ \(3-{cosec}^2 x\)

2. \(\frac{d}{d x}\left(\frac{2}{\sin x}\right)\)

⇒ \(\frac{d}{d x}(2{cosec} x)\)

⇒ \(2 \frac{d}{d x}({cosec} x)\)

= 2 (–cosec x cot x)

= – 2 cosec x cot x

Derivative Of Logarithm And Exponential Functions

⇒ \(\frac{d}{d x}\left(\log _e x\right)=\frac{1}{x}\)

⇒ \(\frac{d}{d x}\left(e^x\right)=e^x\)

Question 12. y=\(e^x \cdot \log _e(x)\)

Answer:

⇒ \(\frac{d y}{d x}=\frac{d}{d x}\left(e^x\right) \cdot \log (x)+\frac{d}{d x}\left[\log _e(x)\right] e^x\)

⇒ \(\frac{d y}{d x}=e^x \cdot \log _e(x)+\frac{e^x}{x}\)

Question 13. \(\frac{d}{d t}\)

Answer: ω cos ωt

Question 14. \(\frac{d}{d t}\)(cos t)

Answer: −ω sin ωt

Question 15.

1. \(\frac{d}{d x} \cos 3 x \quad\)

⇒ \(-\sin 3 x \frac{d}{d x} 3 x\)

= – sin 3x

2. \(\frac{d}{d x} \sin 2 x \quad\)

⇒ \(\cos 2 x \frac{d}{d x}(2 x)\)= cos 2x.2

= 2 cos 2x

3. \(\frac{d}{d t}\)(A sin (ωt + φ)

= A cos (ωt + φ)\(\frac{d}{d t}\)(ωt + φ)

= A cos (ωt + φ). ω.

= A ω cos (ωt + φ)

Question 16. \(\frac{d}{d x}\left(\frac{1}{3 x-2}\right)\)

Answer:

⇒ \(\frac{d}{d x}(3 x-2)^{-1} \quad\)

⇒ \(-1(3 x-2)^{-2} \frac{d}{d x}(3 x-2)\)

⇒ \(-1(3 x-2)^{-2}(3)\)

⇒ \(-\frac{3}{(3 x-2)^2}\)

NEET Class 11 Differentiation Rules: Formulas and Solutions

Question 17. \(\frac{d}{d t}[A \cos (\omega t+\varphi)]\)

Answer:

= –Aω sin (ωt + φ)

Chain Rule

If f (x) is given as function of g(x) i.e., y = f(g(x)) and we are required to find \(\frac{d y}{d x}\) assume dx g(x)= u

⇒ y = f

⇒ \(\frac{d y}{d u}=f^{\prime}(4)\)

⇒ \(\frac{d u}{d x}=g^{\prime}(x)\)

Example: y = sin (x²)

y = log(x² + 5x)

y = sin (cos x)

y = A sin (ωt + φ), A,ω,φ, are constant

Radian Vs. Degrees

⇒ \(\frac{d}{d x} \sin \left(x^{\circ}\right)=\frac{d}{d x} \sin \left(\frac{\pi x}{180}\right)\)

⇒ \(\frac{\pi}{180} \cos \left(\frac{\pi x}{180}\right)=\frac{\pi}{180} \cos \left(x^{\circ}\right)\)

Rules For Integration

Constant Multiple Rule

A function is an antiderivative of a constant multiple of of a function f if and only if it is k times an antiderivative of f. ∫ k f(x)dx k = ∫f(x)dx; where k is a constant 

Question 1. \(\int 5 x^2 d x\)

Answer: \(\frac{5 x^3}{3}+C\)

Question 2. \(\int \frac{7}{x^2} d x\)

Answer:

⇒ \(\int 7 x^{-2} d x\)

⇒ \(-\frac{7 x^{-1}}{1}+C\)

⇒ \(\frac{-7}{x}+C\)

NEET Physics Class 11 Integration Problems and Solutions

Question 3. \(\int \frac{t}{\sqrt{t}} d t\)

⇒ \(\int t^{1 / 2} d t=\frac{t^{3 / 2}}{3 / 2}+C\)

⇒ \(\frac{2}{3} t^{3 / 2}+C\)

Sum And Difference Rule

A function is an antiderivative of a sum or difference f ± g if and only if it is the sum or difference of an antiderivative of f or an antiderivative of g.

⇒ \(\int[f(x) \pm g(x)] d x=\int f(x) d x \pm \int g(x) d x\)

Question 4. Term–by–term integration. Evaluate : ∫(x² – 2x + 5) dx.

Answer:

If we recognize that (x³ /3) – x² + 5x is an antiderivative of x² – 2x + 5, we can evaluate the integral as

If we do not recognize the antiderivative right away, we can generate it term by term with the sum and difference Rule:

⇒ \(\int\left(x^2-2 x+5\right) d x\)

⇒ \(\int x^2 d x-\int 2 x d x+\int 5 d x\)

⇒ \(\frac{x^3}{3}+C_1-x^2+C_2+5 x+C_3\)

This formula is more complicated than it needs to be. If we combine C₁,C₂ and C₃ into a single constant C = C₁+ C₂+ C₃, the formula simplifies to

⇒ \(\frac{x^3}{3}-x^2+5 x+C\)

and still gives all the antiderivatives there are. For this reason, we recommend that you go right to the final form even if you elect to integrate term by term. Write

⇒ \(\int\left(x^2-2 x+5\right) d x\)

⇒ \(\int x^2 d x-\int 2 x d x+\int 5 d x\)

⇒ \(\frac{x^3}{3}-x^2+5 x+C\)

Find the simplest antiderivative you can for each part and add the constant at the end.

Integration Rules NEET Physics Class 11 Chapter 10 Solutions

Question 5. Find a body’s velocity from its acceleration and initial velocity. The acceleration of gravity near the surface of the earth is 9.8 m/sec². This means that the velocity v of a body falling freely in a vacuum changes at the rate of \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 9.8 m/sec². If the body is dropped from rest, what will its velocity be t seconds after it is released?

Answer:

In mathematical terms, we want to solve the initial value problem that consists of

The differential condition: \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 9.8

The initial condition: v = 0 when t = 0 ( abbreviated as v (0) = 0 )

We first solve the differential equation by integrating both sides concerning t:

⇒ \(\frac{\mathrm{dv}}{\mathrm{dt}}\) = 9.8 The differential equation

⇒ \(\int \frac{d v}{d t} d t=\int 9.8 d t\) Integrate with respect to t.

v + C₁ = 9.8t + C₂ Integrals evaluated

v = 9.8t + C. Constants combined as one

This last equation tells us that the body’s velocity t seconds into the fall is 9.8t + C m/sec. For value of C: What value? We find out from the initial condition:

v = 9.8t + C

0 = 9.8(0) + C v( 0) = 0

C = 0.

Conclusion: The body’s velocity t seconds into the fall is

v = 9.8t + 0 = 9.8t m/sec.

• The indefinite integral F(x) + C of the function f(x) gives the general solution y = F(x) + C of the differential equation dy/dx = f(x).
• The general solution gives all the solutions of the equation (there are infinitely many, one for each value of C).
• We solve the differential equation by finding its general solution We then solve the initial value problem by finding the particular solution that satisfies the initial condition y(x_o) = y_o( y has the value yo when x = x_o.).

Definite Integration Or Integration With Limits

⇒ \(\int_a^b f(x) d x=[g(x)]_a^b=g(b)-g(a)\)

where g(x) is the antiderivative of f(x) i.e. g´(x) = f(x)

Question 6. \(\int_{-1}^4 3 d x\)

Answer:

⇒ \(3 \int_{-1}^4 d x\)

⇒ \(3[x]_{-1}^4\)

⇒ \(3[4-(-1)]\)

= (3)(5)=15

⇒ \(\int_0^{\pi / 2} \sin x d x\)

⇒ \([-\cos x]_0^{\pi / 2}\)

⇒ \(-\cos \left(\frac{\pi}{2}\right)+\cos (0)\)

= –0 + 1 = 1

NEET Physics Class 11 Chapter 10 Integration Techniques and Solutions

Application Of Definite Integral: Calculation Of Area Of A Curve

From the graph shown in the figure if we divide the whole area into infinitely small strips of dx width. We take a strip at x position of dx width.

A small area of this strip dA = f(x) dx

So, the total area between the curve and x-axis = sum of area of all strips = \(\int_a^b f(x) d x\)

Let f(x) ≥ 0 be continuous on [a,b]. The area of the region between the graph of f and the x-axis is

A = \(\int_a^b f(x) d x\)

Integration Methods for NEET Physics Class 11: Formulas and Solutions

Question 7. Find the area under the curve of y = x from x = 0 to x = a

Answer:

Multiplication Of Vectors

1. The Scalar Product:

The scalar product or dot product of any two vectors \(\vec{A} \text { and } \vec{B}\), denoted as \(\vec{A} \cdot \vec{B}\)(read \(\vec{A}\).\(\vec{B}\)) is defined as the product of their magnitude with cosine of angle between them. Thus, \(\overrightarrow{\mathrm{A}}\). \(\vec{B}\) = AB cos θ {here θ is the angle between the vectors}

The Scalar Product Properties:

It is always a scalar which is positive if the angle between the vectors is acute (i.e. < 90º) and negative if the angle between them is obtuse (i.e. 90º < θ ≤ 180º)

It is commutative, i.e., \(\vec{A} \cdot \vec{B}=\vec{A} \cdot \vec{B}\)

It is distributive, i.e., \(\vec{A} \cdot(\vec{B}+\vec{C})=\vec{A} \cdot \vec{B}+\vec{A} \cdot \vec{C}\)

As by definition \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\)= AB cos θ.

The angle between the vectors θ = \(\cos ^{-1}\left[\frac{\vec{A} \cdot \vec{B}}{A B}\right]\)

⇒ \(\vec{A}.\vec{B}\) = A (B cos θ) = B (A cos θ)

Geometrically, B cos θ is the projection of \(\vec{B} \text { onto } \vec{A}\), and A cos θ is the projection of \(\vec{A} \text { onto } \vec{B}\) shown. So \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\) is the product of the magnitude of \(\overrightarrow{\mathrm{A}}\) and the component of \(\overrightarrow{\mathrm{B}}\) along \(\overrightarrow{\mathrm{A}}\) and vice versa.

Component of \(\vec{B} \text { along } \overrightarrow{\mathrm{A}}\) = B cosθ = \(\frac{\vec{A} \cdot \vec{B}}{A}=\vec{A} \cdot \vec{B}\)

Component of \(\vec{A} \text { along } \overrightarrow{\mathrm{B}}\) along = \(\frac{\vec{A} \cdot \vec{B}}{B}=\vec{A} \cdot \vec{B}\)

Scalar product of two vectors will be maximum when cos θ = max = 1, i.e., θ = 0º, i.e., vectors are parallel

⇒ \((\vec{A} \cdot \vec{B})_{\max }=A B\)

If the scalar product of two nonzero vectors vanishes then the vectors are perpendicular. The scalar product of a vector by itself is termed as self dot product and is given by

⇒ \((\vec{A})^2=\vec{A} \cdot \vec{A}=A A \cos \theta=A A \cos 0^{\circ}=A^2\)

⇒ \(A=\sqrt{\vec{A} \cdot \vec{A}}\)

In case of unit vector \(\hat{n}\)

⇒ \(\hat{n} . \hat{n}=1 \times 1 \times \cos 0^{\circ}=1\)

⇒ \(\hat{n} \cdot \hat{n}=\hat{i} \cdot \hat{i}=\hat{j} \cdot \hat{j}=\hat{k} \cdot \hat{k}=1\)

In case of orthogonal unit vectors \(\hat{\mathrm{i}}, \hat{\mathrm{j}} \text { and } \hat{\mathrm{k}}\); \(\hat{i} \cdot \hat{j}=\hat{j} \cdot \hat{k}=\hat{k} \cdot \hat{i}=0\)

⇒ \(\vec{A} \cdot=\left(\hat{i} A_x+\hat{j} A_y+\hat{k} A_z\right) \cdot\left(\hat{i} B_x+\hat{j} B_y+\hat{k} B_z\right)\)

⇒ \(\left[A_x B_x+A_y B_y+A_z B_z\right]\)

Multiplication of Vectors NEET Physics Class 11 Solutions

Question 1. If the Vectors \(\vec{P}=a \hat{i}+a \hat{j}+3 \hat{k} \text { and } \vec{Q}=a \hat{i}-2 \hat{j}-\hat{k}\) are perpendicular to each other. Find the value of a?

Answer:

If vectors \(\vec{P} \text { and } \vec{Q}\) are perpendicular

⇒ \(\vec{P} \cdot \vec{Q}=0\)

⇒ \((a \hat{i}+a \hat{j}+3 \hat{k}) \cdot(a \hat{i}-2 \hat{j}-\hat{k})=0\)

⇒ \(a^2-2 a-3=0\)

⇒ \(a^2-3 a+a-3=0\)

⇒  a(a-3)+1(a-3) = 0

⇒ (a + 1)(a – 3) = 0

⇒ a + 1 = 0  or  a – 3 = 0

⇒ a = -1 or a = 3

⇒ a = -1,3

Question 2. Find the component of \(3 \hat{i}+4 \hat{j} \text { along } \hat{i}+\hat{j}\)?

Answer:

Component of \(\overrightarrow{\mathrm{A}}\)along \(\overrightarrow{\mathrm{B}}\) is given by \(\frac{\vec{A} \cdot \vec{B}}{B}\) hence required component

⇒ \(\frac{(3 \hat{i}+4 \hat{j}) \cdot(\hat{i}+\hat{j})}{\sqrt{2}}\)

⇒ \(\frac{7}{\sqrt{2}}\)

Question 3. Find angle between \(\vec{A}=3 \hat{i}+4 \hat{j} \text { and } \vec{B}=12 \hat{i}+5 \hat{j}\)

Answer:

We have cos θ = \(\frac{\vec{A} \cdot \vec{B}}{A B}\)

⇒ \(\frac{(3 \hat{i}+4 \hat{j}) \cdot(12 \hat{i}+5 \hat{j})}{\sqrt{3^2+4^2} \sqrt{12^2+5^2}}\)

⇒ \(\cos \theta=\frac{36+20}{5 \times 13}=\frac{56}{65}\)

⇒ \(\theta=\cos ^{-1} \frac{56}{65}\)

2. Vector Product

The vector product or cross product of any two vectors \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) A and B, denoted as \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}(\text { read } \overrightarrow{\mathrm{A}} \text { cross } \overrightarrow{\mathrm{B}})\) is defined as:

⇒ \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}=\mathrm{AB} \sin \theta \hat{n}\)

Here θ is the angle between the vectors and the direction \(\hat{n}\) is given by the right-hand-thumb rule.

Vector Multiplication Methods in NEET Physics Class 11

Right-Hand-Thumb Rule:

To find the direction of \(\hat{n}\) draw the two vectors \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) with both the tails coinciding.

Now place your stretched right palm perpendicular to the plane of \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) in such a way that the fingers are along the vector \(\overrightarrow{\mathrm{A}}\) and when the fingers are closed they go towards \(\overrightarrow{\mathrm{B}}\). The direction of the thumb gives the direction of \(\hat{n}\)

Vector Product Properties

The vector product of two vectors is always a vector perpendicular to the plane containing the two vectors i.e. orthogonal to both vectors.

A and B, though the vectors \(\vec{A} \text { and } \vec{B}\) though the vector \(\vec{A} \text { and } \vec{B}\) may or may not be orthogonal.

Vector product of two vectors is not commutative i.e. \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}} \neq \overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{A}}\)

But \(|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|=|\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{A}}|\) = AB sin θ

The vector product is distributive when the order of the vectors is strictly maintained i.e.

⇒ \(\mathrm{A} \times(\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{C}})=\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{C}}\)

The magnitude of the vector product of two vectors will be maximum when sinθ = max = 1, i.e, θ = 90º

⇒ \(|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|_{\max }=\mathrm{AB}\) i.e., the magnitude of the vector product is maximum if the vectors are orthogonal.

The magnitude of the vector product of two non–zero vectors will be minimum when |sinθ| = minimum = 0,i.e., θ = 0º or 180º, and vectors are collinear.
min | A B | 0 × =i.e., if the vector product of two non–zero vectors vanishes, the vectors are collinear.

Note: When θ = 0º then vectors may be called like vectors or parallel vectors and when θ = 180º then vectors may be called unlike vectors or antiparallel vectors.

The self-cross product i.e. product of a vector by itself vanishes i.e. is a null vector.

Note: Null vector or zero vector: A vector of zero magnitude is called a zero vector. The direction of a zero vector is determinate (unspecified).

⇒ \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{A}}=\mathrm{AA} \sin 0^{\circ} \hat{\mathrm{n}}=\overrightarrow{0}\)

Note: Geometrical meaning of vector product of two vectors

1. Consider two vectors \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) which are represented by \(\overrightarrow{\mathrm{OP}} \text { and } \overrightarrow{\mathrm{QP}} \text { and } \angle \mathrm{POQ}=\theta\)
2. Complete the parallelogram OPRQ. Join P with Q. Here OP = A and OQ = B. Draw QN ⊥OP
3. Magnitude of the cross product of \(\vec{A} \text { and } \vec{B}\)

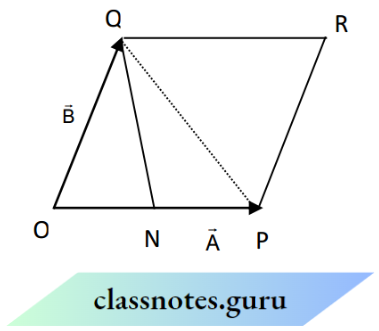
⇒ \(|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|=\mathrm{AB} \sin \theta\)

= (OP)(OQ sin θ)

= (OP)(NQ) (∵ NQ = OQ sin θ)

= base × height

= Area of parallelogram OPRQ

Area of ΔPOQ = ΔPOQ = \(\frac{\text { base } \times \text { height }}{2}=\frac{(\mathrm{OP})(\mathrm{NQ})}{2}\)

⇒ \(\frac{1}{2}|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|\)

∴ Area of parallelogram OPRQ = 2 [area of Δ OPQ] = \(|\vec{A} \times \vec{B}|\)

Formulae to find Area

If \(\vec{A} \text { and } \vec{B}\) are two adjacent sides of a triangle, then its area = \(\frac{1}{2}|\vec{A} \times \vec{B}|\)

If \(\vec{A} \text { and } \vec{B}\) are two adjacent sides of a parallelogram, then its area = \(|\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}|\)

If \(\vec{A} \text { and } \vec{B}\) are diagonals of a parallelogram then its area = \(\frac{1}{2}|\vec{A} \times \vec{B}|\)

In case of unit vector \(\hat{n}, \quad \hat{n} \times \hat{n}=\overrightarrow{0} \Rightarrow \hat{i} \times \hat{i}=\hat{j} \times \hat{j}=\hat{k} \times \hat{k}=\overrightarrow{0}\)

In case of orthogonal unit vectors \(\hat{i}, \hat{j} \text { and } \hat{k}\) in accordance with right-hand-thumb-rule,

In terms of compound, \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}\)

⇒ \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
A_x & A_y & A_z \\
B_x & B_y & B_z
\end{array}\right|=\hat{i}\left|\begin{array}{cc}
A_y & A_z \\
B_y & B_z
\end{array}\right|-\hat{j}\left|\begin{array}{cc}
A_x & A_z \\
B_x & B_z
\end{array}\right|+\hat{k}\left|\begin{array}{cc}
A_x & A_y \\
B_x & B_y
\end{array}\right|\)

The magnitude of the area of the parallelogram formed by the adjacent sides of vectors \(\vec{A} \text { and } \vec{B}\) equal to

NEET Class 11 Chapter 10 Vector Multiplication: Cross and Dot Products

Question 4. \(\overrightarrow{\mathrm{A}}\) is Eastwards and \(\overrightarrow{\mathrm{B}}\) is downwards. Find the direction of \(\overrightarrow{\mathrm{A}} \times \vec{B}\)?

Answer:

Applying the right-hand thumb rule we find that \(\overrightarrow{\mathrm{A}} \times \vec{B}\) is along North.

Question 5. If \(\vec{A} \cdot \vec{B}=|\vec{A} \times \vec{B}|\), find angle between \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\)

Answer:

⇒ \(\vec{A} \cdot \vec{B}=|\vec{A} \times \vec{B}|\)

AB cos θ = AB sin θ

tan θ = 1

⇒ θ = 45º

Question 6. Two vectors \(\vec{A} \text { and } \vec{B}\) are inclined to each other at an angle θ. Find a unit vector that is perpendicular to both \(\vec{A} \text { and } \vec{B}\)

Answer:

⇒ \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}=\mathrm{AB} \sin \theta \hat{n}\)

⇒ \(\hat{n}=\frac{\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}}{\mathrm{AB} \sin \theta}\) here \(\hat{n}\) is perpendicular to both \(\vec{A} \text { and } \vec{B}\)

Question 7. Find \(\vec{A} \times \vec{B}\) if \(\vec{A}=\hat{i}-2 \hat{j}+4 \hat{k}\) and \(\vec{B}=2 \hat{i}-\hat{j}+2 \hat{k}\)

Answer:

⇒ \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}\)

⇒ \(\left|\begin{array}{ccc}
\hat{i} & \hat{j} & \hat{k} \\
1 & -2 & 4 \\
3 & -1 & 2
\end{array}\right|\)

⇒ \(\hat{i}(-4-\hat{j}(-4))-(2-12)+\hat{k}(-1-(-6))=10 \hat{j}+5 \hat{k}\)

Question 8. Find the value of

1. sin (− θ)
2. cos (− θ)
3. tan (− θ)
4. cos (\(\frac{\pi}{2}\)− θ)
5. sin (\(\frac{\pi}{2}\)+ θ)
6. cos (\(\frac{\pi}{2}\)+ θ) 2
7. sin (π − θ)
8. cos (π − θ)
9. sin (\(\frac{3 \pi}{2}\)− θ)
10. cos (\(\frac{3 \pi}{2}\)− θ)
11. sin (\(\frac{3 \pi}{2}\)+ θ)
12. cos (\(\frac{3 \pi}{2}\)+ θ)
13. tan (\(\frac{\pi}{2}\)− θ)
14. cot (\(\frac{\pi}{2}\)− θ) 2

Answers :

1. – sin θ
2. cos θ
3. – tan θ
4. sin θ
5. cos θ
6. – sin θ
7. sin θ
8. – cos θ
9. – cos θ
10. – sin θ
11. – cos θ
12. sin θ
13. cot θ
14. tan θ

Multiplication of Vectors for NEET Physics Class 11

Question 9.

1. For what value of m the vector \(\vec{A}=2 \hat{i}+3 \hat{j}-6 \hat{k}\) is perpendicular to \(\vec{B}=3 \hat{i}-m \hat{j}+6 \hat{k}\)
2. Find the components of vector \(\vec{A}=2 \hat{i}+3 \hat{j}\) along the direction of \(\hat{i}+\hat{j}\)?

Answers :

1. m = –10
2. \(\frac{5}{\sqrt{2}}\)

Question 10.

1. \(\overrightarrow{\mathrm{A}}\) is North–East and \(\overrightarrow{\mathrm{B}}\) is downwards, find the direction of \(\vec{A} \times \vec{B}\)
2. Find \(\vec{B} \times \vec{A} \text { if } \vec{A}=3 \hat{i}-2 \hat{j}+6 \hat{k}\) and \(\vec{B}=\hat{i}-\hat{j}+\hat{k}\)

Answers :

1. North-West.
2. \(-4 \hat{i}-3 \hat{j}+\hat{k}\)

NEET Physics Class 11 Chapter 10 Mathematical Tools Multiple Choice Question And Answers

Question 1. The surface area of a sphere as a function of its radius is A(r) = 4πr₂ the value of A(10) will be :

1. 1358 m²
2. 324 m²
3. 314 m²
4. 1256 m²

Answer: 4. 1256 m²

Question 2. If f (x) = x² –1

1. 5
2. 6
3. 7
4. 8

Answer: 4. 8

Question 3. If f(x) = \(x+\frac{1}{x}\), then the value of f(1) will be

1. 2
2. – 2
3. 1
4. – 1

Answer: 1. 2

NEET Physics Class 11 Chapter 10 Mathematical Tools MCQs

Question 4. Find v (0), where v (t) = 3 + 2t

1. 5
2. 6
3. 3
4. None

Answer: 3. 3

Question 5. If f(θ) = sin θ, find \(f\left(\frac{\pi}{6}\right)\)

1. \(\frac{\pi}{6}\)
2. \(\frac{1}{2}\)
3. 2
4. \(\frac{\pi}{3}\)

Answer: 2. \(\frac{1}{2}\)

Question 6. If f (x) = 5, then the value of f (10) will be

1. 10
2. 5
3. 15
4. None

Answer: 2. 5

Question 7. tan15° is equivalent to :

1. \((2-\sqrt{3})\)
2. \((5+\sqrt{3})\)
3. \(\left(\frac{5-\sqrt{3}}{2}\right)\)
4. \(\left(\frac{5+\sqrt{3}}{2}\right)\)

Answer: 1. \((2-\sqrt{3})\)

Question 8. sin²θ is equivalent to:

1. \(\left(\frac{1+\cos \theta}{2}\right)\)
2. \(\left(\frac{1+\cos 2 \theta}{2}\right)\)
3. \(\left(\frac{1-\cos 2 \theta}{2}\right)\)
4. \(\left(\frac{\cos 2 \theta-1}{2}\right)\)

Answer: 3. \(\left(\frac{1-\cos 2 \theta}{2}\right)\)

Question 9. sinA. sin(A + B) is equal to

1. cos²A . cosB + sinA sin²B
2. \(\sin ^2 A \cdot \cos B+\frac{1}{2} \cos 2 A \cdot \sin B\)
3. \(\sin ^2 A \cdot \cos B+\frac{1}{2} \sin 2 A \cdot \sin B\)
4. sin²A . sinB + cosA cos²B

Answer: 3. \(\sin ^2 A \cdot \cos B+\frac{1}{2} \sin 2 A \cdot \sin B\)

Question 10. –sinθ is equivalent to :

1. \(\cos \left(\frac{\pi}{2}+\theta\right)\)
2. \(\cos \left(\frac{\pi}{2}-\theta\right)\)
3. \(\sin (\theta-\pi)\)
4. \(\sin (\pi+\theta)\)

Answer: (1,2,4)

Question 11. θ is the angle between the side CA and CB of a triangle, shown in the figure then θ is given by :

1. \(\cos \theta=\frac{2}{3}\)
2. \(\sin \theta=\frac{\sqrt{5}}{3}\)
3. \(\tan \theta=\frac{\sqrt{5}}{2}\)
4. \(\tan \theta=\frac{2}{3}\)

Answer: 2. \(\sin \theta=\frac{\sqrt{5}}{3}\)

Question 12. If tan θ = \(\frac{1}{\sqrt{5}}\) and θ lies in the first quadrant, the value of cos θ is :

1. \(\sqrt{\frac{5}{6}}\)
2. \(-\sqrt{\frac{5}{6}}\)
3. \(\frac{1}{\sqrt{6}}\)
4. \(-\frac{1}{\sqrt{6}}\)

Answer: 1. \(\sqrt{\frac{5}{6}}\)

Question 13. Calculate the slope of a shown line

1. 2/3
2. – 2/3
3. 3/2
4. –3/2

Answer: 2. – 2/3

NEET Physics Class 11 Chapter 10 Mathematical Tools MCQs Practice

Question 14. The speed (v) of a particle moving along a straight line is given by v = t² + 3t – 4 where v is in m/s and t in second. Find a time t at which the particle will momentarily come to rest.

1. 3
2. 4
3. 2
4. 1

Answer: 4. 1

Find the derivative of given functions w.r.t. corresponding independent variable.

Question 15. y = x² + x + 8

1. \(\frac{d y}{d x}=2 x+1\)
2. \(\frac{d y}{d x}=2+1\)
3. \(\frac{d y}{d x}=2 x-1\)
4. \(\frac{d y}{d x}=x+1\)

Answer: 1. \(\frac{d y}{d x}=2 x+1\)

Question 16. y = tan x + cot x

1. tan² x + cosec² x
2. cot² x – sin² x
3. sec² x – cosec² x
4. sec x + cosec x 2

Answer: 3. sec2 x – cosec2 x

Question 17. y = lnx + ex, then \(\frac{d^2 y}{d x^2}\) is equal to

1. \(\frac{1}{x^2}-e^x\)
2. \(\frac{1}{\mathrm{x}^2}+\mathrm{e}^{\mathrm{x}}\)
3. \(\frac{1}{x}+e^x\)
4. \(-\frac{1}{x^2}+e^x\)

Answer: 4. \(-\frac{1}{x^2}+e^x\)

Question 18. y = \(\mathrm{e}^{\mathrm{x}} \ell \mathrm{n} \mathrm{x}\)

1. \(\mathrm{e}^{\mathrm{x}} \ell \mathrm{n} x+\frac{\mathrm{e}^{\mathrm{x}}}{\mathrm{x}}\)
2. \(e^x \ell n x-\frac{e^x}{x}\)
3. \(\mathrm{e}^{\mathrm{x}} \ln x-\frac{e}{\mathrm{x}} \)
4. None of these

Answer: 1. \(\mathrm{e}^{\mathrm{x}} \ell \mathrm{n} x+\frac{\mathrm{e}^{\mathrm{x}}}{\mathrm{x}}\)

Question 19. y = sin 5 x

1. 5 cos 5 x
2. 3 cos 3 x
3. 5 cos 5x
4. 2 cos 2x

Answer: 1. 5 cos 5 x

Question 20. (x + y)² = 4

1. \(\frac{d y}{d x}=+1\)
2. \(\frac{d y}{d x}=-1\)
3. \(\frac{d}{d x}=-1\)
4. \(\frac{d y}{d}=-1\)

Answer: 2. \(\frac{d y}{d x}=-1\)

Question 21. y = 2u³, u = 8x – 1

1. \(\frac{d y}{d x}=48(8 x-1)^2\)
2. \(\frac{d y}{d x}=58(5 x-1)^2\)
3. \(\frac{d y}{d x}=48(8 x-1)^2\)
4. \(\frac{d y}{d x}=28(8 x-1)\)

Answer: 1. \(\frac{d y}{d x}=48(8 x-1)^2\)

Question 22. Given s = t² + 5t + 3, find \(\frac{\mathrm{ds}}{\mathrm{dt}}\) at t = 1

1. 7
2. 9
3. 12
4. 15

Answer: 1. 7

Question 23. If s = ut + \(s=u t+\frac{1}{2} a t^2\), where u and a are constants. Obtain the value of \(\frac{\mathrm{ds}}{\mathrm{dt}}\)

1. u – at
2. u + at
3. 2u + at
4. None of these

Answer: 2. u + at

Question 24. The minimum value of y = 5x² – 2x + 1 is

1. \(\frac{1}{5}\)
2. \(\frac{2}{5}\)
3. \(\frac{4}{5}\)
4. \(\frac{3}{5}\)

Answer: 3. \(\frac{4}{5}\)

Question 25. y = \(\frac{2 x+5}{3 x-2}\)

1. \(y^{\prime}=\frac{-19}{(3 x-2)^2}\)
2. \(y^{\prime}=\frac{19}{(3 x-2)}\)
3. \(y^{\prime}=\frac{-19}{(3 x+2)}\)
4. \(y^{\prime}=\frac{-19}{(3 x+2)^2}\)

Answer: 4. \(y^{\prime}=\frac{-19}{(3 x+2)^2}\)

Question 26. A uniform metallic solid sphere is heated uniformly. Due to thermal expansion, its radius increases at the rate of 0.05 mm/second. Find its rate of change of volume concerning the time when its radius becomes 10 mm. (take p = 3.14)

1. 31.4 mm³/second
2. 62.8 mm³/second
3. 3.14 mm³/second
4. 6.28 mm³/second

Answer: 2. 62.8 mm³/second

Question 27. If y = 3t² – 4t; then the minima of y will be at :

1. 3/2
2. 3/4
3. 2/3
4. 4/3

Answer: 3. 2/3

Question 28. If y = sin(t²) ,then \(\frac{d^2 y}{d t^2}\) will be –

1. 2t cos(t²)
2. 2 cos (t²) – 4t² sin (t²)
3. 4t² sin (t²)
4. 2 cos (t²)

Answer: 2. 2 cos (t²) – 4t² sin (t²)

Class 11 NEET Physics Chapter 10 Mathematical Tools MCQs

Question 29. The displacement of a body at any time t after starting is given by s = 15t – 0.4t². The velocity of the body will be 7 ms^-1 after time :

1. 20 s
2. 15 s
3. 10 s
4. 5 s

Answer: 3. 10 s

Question 30. For the previous question, the acceleration of the particle at any time t is :

1. –0.8 m/s²
2. 0.8 m/s²
3. –0.6 m/s²
4. 0.5 m/s²

Answer: 1. –0.8 m/s²

Question 31. If the velocity of a particle is given by v = 2t⁴ then its acceleration (dv/dt) at any time t will be given by :

1. 8t³
2. 8t
3. –8t³
4. t²

Answer: 1. 8t³

Question 32. The maximum value of xy subject to x + y = 8, is :

1. 8
2. 16
3. 20
4. 24

Answer: 2. 16

Question 33. If y = 3t² – 4t; then the minima of y will be at :

1. 3/2
2. 3/4
3. 2/3
4. 4/3

Answer: 3. 2/3

Question 34. The slope of the graph as shown in the figure at points 1, 2 and is m₁, m₂, and m₃ respectively then

1. m₁ > m₂ > m₃
2. m₁ < m₂ < m₃
3. m₁ = m₂ = m₃
4. m₁ = m₂ > m₃

Answer: 2. m₁ < m₂ < m₃

Question 35. The magnitude of the slope of the shown graph.

1. First increases then decreases
2. First decrease then increases
3. Increase
4. Decrease

Answer: 2. First decrease then increases

Question 36. y = – x² + 3

1. \(\frac{d y}{d x}=-2 x, \frac{d^2 y}{d x^2}=-2\)
2. \(\frac{d y}{d x}=2 x, \frac{d^2 y}{d x^2}=-2\)
3. \(\frac{d y}{d x}=-2 x, \frac{d^2 y}{d x^2}=2\)
4. None of these

Answer: 1. \(\frac{d y}{d x}=-2 x, \frac{d^2 y}{d x^2}=-2\)

Question 37. y = \(\frac{x^3}{3}+\frac{x^3}{2}+\frac{x}{4}\)

1. \(\frac{d y}{d x}=x^2-x+\frac{1}{4}, \frac{d^2 y}{d x^2}=2 x+3\)
2. \(\frac{d y}{d x}=x^2+x-\frac{1}{4}, \frac{d^2 y}{d x^2}=2 x+1\)
3. \(\frac{d y}{d x}=x^2+x+\frac{1}{4}, \frac{d^2 y}{d x^2}=2 x+1\)
4. \(\frac{d y}{d x}=x^2+x+\frac{1}{4}, \frac{d^2 y}{d x^2}=2 x-1\)

Answer: 3. \(\frac{d y}{d x}=x^2+x+\frac{1}{4}, \frac{d^2 y}{d x^2}=2 x+1\)

Question 38. y = 4 – 2x – x^-3

1. \(\frac{d y}{d x}=2+3 x^{-4}, \frac{d^2 y}{d x^2}=-12 x^{-5}\)
2. \(\frac{d y}{d x}=-2+3 x^{-4}, \frac{d^2 y}{d x^2}=-12 x^{-5}\)
3. \(\frac{d y}{d x}=-2+3 x^{-4}, \frac{d^2 y}{d x^2}=12 x^{-5}\)
4. \(\frac{d y}{d x}=-2-3 x^{-4}, \frac{d^2 y}{d x^2}=-12 x^{-5}\)

Answer: 2. \(\frac{d y}{d x}=-2+3 x^{-4}, \frac{d^2 y}{d x^2}=-12 x^{-5}\)

Question 39. y = – 10x + 3 cos x

1. 10 – 3 sin x
2. – 10 + 3 sin x
3. – 10 + 5 sin x
4. – 10 – 3 sin x

Answer: 4. – 10 – 3 sin x

Question 40. y = \(\frac{3}{x}+5 \sin x\)

1. \(-\frac{3}{x^2}+5 \cos x\)
2. \(\frac{3}{x^2}+5 \cos \mathrm{x}\)
3. \(-\frac{3}{x^2}-\cos x\)
4. \(-\frac{3}{x^2}-5 \cos x\)

Answer: 1. \(-\frac{3}{x^2}+5 \cos x\)

Question 41. y = cosec \(x-4 \sqrt{x}+7\)

1. \(-\csc x \cot x-\frac{2}{\sqrt{x}}\)
2. \(\csc x \cot x+\frac{2}{\sqrt{x}}\)
3. \(-\csc x \cot x+\frac{2}{\sqrt{x}}\)
4. \(\csc x \cot x+\frac{2}{\sqrt{x}}\)

Find \(\frac{\mathrm{ds}}{\mathrm{dt}}\)

Answer: 1. \(-\csc x \cot x-\frac{2}{\sqrt{x}}\)

Question 42. s = tan t – t

1. sec²t + t
2. sec²t
3. sec t – 1
4. sec²t – 1

Answer: 4. sec²t – 1

Question 43. s = t² – sec t + t

1. 2t + sec t tan t + 1
2. 2t – sec t tan t + 1
3. 2t – sec t tan t –1
4. 2t + sec²tan t – 1

Answer: 2. 2t – sec t tan t + 1

Question 44. p = \(5+\frac{1}{\cot q}\) find \(\frac{d p}{d q}\)

1. sec² q
2. sec³ q
3. sec q
4. tan² q

Answer: 1. sec² q

Question 45. p = (1 + cosec q) cos q, find \(\frac{d p}{d q}\)

1. sin q – cosec² q
2. – sin q – cosec² q
3. – sin q – cos² q
4. sec q – cosec² q

Answer: 2. – sin q – cosec² q

Question 46. y = sin³ x , find the \(\frac{d y}{d x}\)

1. 3 sin² x (cosx)
2. 3 sin³ x (cosx)
3. 3 sin x (cos x)²
4. sin x (cos x)

Answer: 1. 3 sin² x (cosx)

Question 47. y = 5 cos^-4 x, find \(\frac{d y}{d x}\)

1. 20 in x cos^-5 x
2. 10 in x cos^-5 x
3. 20 in x cos^-3 x
4. 20 in x sin^-5 x

Answer: 1. 20 sin x cos^-5 x

Find the derivatives of the functions

Question 48. s = \(\frac{4}{3 \pi} \sin 3 t+\frac{4}{5 \pi} \cos 5 t\)

1. \(\frac{4}{\pi}\)(cos 3t – sin 5t)
2. \(\frac{4}{\pi}\) 4(cos 3t + sin 5t)
3. \(\frac{4}{\pi}\)(cos t – sin t)
4. \(\frac{4}{\pi}\)(cot 3t – sec 5t)

Answer: 1. \(\frac{4}{\pi}\)(cos 3t – sin 5t)

Question 49. s = \(\sin \left(\frac{3 \pi t}{2}\right)+\cos \left(\frac{3 \pi t}{2}\right)\)

1. \(\frac{3 \pi}{2}\left[\cos \left(\frac{3 \pi t}{2}\right)-\sin \left(\frac{3 \pi t}{2}\right)\right]\)
2. \(\frac{3 \pi}{2}\left[\cos \left(\frac{3 \pi t}{2}\right)+\sin \left(\frac{3 \pi t}{2}\right)\right]\)
3. \(\frac{3 \pi}{2}\left[\cot \left(\frac{3 \pi t}{2}\right)+\sin \left(\frac{3 \pi t}{2}\right)\right]\)
4. None of these

Answer: 1. \(\frac{3 \pi}{2}\left[\cos \left(\frac{3 \pi t}{2}\right)-\sin \left(\frac{3 \pi t}{2}\right)\right]\)

Find integrals of given functions

Question 50. \(\int\left(x^2-2 x+1\right) d x\)

1. \(\frac{x^3}{3}+x^2-x-c\)
2. \(\frac{x^3}{3}+x+x+c\)
3. \(\frac{x}{3}+x^2+x-c\)
4. \(\frac{x^3}{3}-x^2+x+c\)

Answer: 4. \(\frac{x^3}{3}-x^2+x+c\)

Question 51. \(\int\left(\sqrt{x}+\frac{1}{\sqrt{x}}\right) d x\)

1. \(\frac{2 \sqrt{x}}{3}+2 \sqrt{x}-c\)
2. \(\frac{2 \sqrt{x^2}}{3}-2 \sqrt{x}+c\)
3. \(\frac{2 \sqrt{x^3}}{3}+2 \sqrt{x}+c\)
4. \(\frac{2 \sqrt{x}}{2}+2 \sqrt{x}-c\)

Answer: 3. \(\frac{2 \sqrt{x^3}}{3}+2 \sqrt{x}+c\)

Question 52. \(\int \frac{1}{3 x} d x\)

1. \(\frac{1}{3} \ln x+x\)
2. \(\frac{1}{3} \ln x\)
3. \(\frac{1}{2} \ln x+x\)
4. \(\frac{1}{3} \ln x+x\)

Answer: 4. \(\frac{1}{3} \ln x+x\)

Question 53. \(\int x \sin \left(2 x^2\right) d x\), (use,u = 2x²)

1. \(-\frac{1}{4} \cos \left(2 x^2\right)+C\)
2. \(\frac{1}{4} \cos \left(2 x^2\right)+C\)
3. \(-\frac{1}{2} \cos (2 x)+C\)
4. \(-\frac{1}{3} \cos \left(3 x^2\right)+C\)

Answer: 1. \(-\frac{1}{4} \cos \left(2 x^2\right)+C\)

Question 54. \(\int \frac{3}{(2-x)^2} d x\)

1. \(\frac{3}{2-x}+C\)
2. \(\frac{2}{2-x}+C\)
3. \(\frac{3}{2-x}+C\)
4. \(\frac{3}{2+x}+C\)

Answer: 1. \(\frac{3}{2-x}+C\)

NEET Physics Class 11 Mathematical Tools Multiple Choice Questions

Question 55. \(\int_{-4}^{-1} \frac{\pi}{2} d \theta\)

1. \(\frac{3 \pi}{3}\)
2. \(\frac{3 \pi}{2}\)
3. \(\frac{2 \pi}{3}\)
4. \(\frac{\pi}{2}\)

Answer: 1. \(\frac{3 \pi}{3}\)

Question 56. \(\int_0^1 e^x d x\)

1. e – 1 m
2. e + 1
3. e – 2
4. None of these

Answer: 1. e – 1 m

Question 57. y = 2x, the area under the curve from x = 0 to x = b will be

1. b²/2 units
2. b² units
3. 2b² units
4. b/2 units

Answer: 2. b2 units

Question58. y = \(\int_0^\pi \sin x d x\)

1. 2 units
2. 3 units
3. 4 units
4. 5 units

Answer: 1. 2 units

Question 59. The integral \(\int_1^5 x^2 d x\) is equal to

1. \(\frac{125}{3}\)
2. \(\frac{124}{3}\)
3. \(\frac{1}{3}\)
4. 45

Answer: 2. \(\frac{124}{3}\)

Question 60. \(\int x^{-\frac{3}{2}} d x\) is equal to :

1. \(\frac{-2}{\sqrt{x}}+C\)
2. \(\frac{2}{\sqrt{x}}+C\)
3. \(2 \sqrt{x}+C\)
4. \(-2 \sqrt{x}+C\)

Answer: 1. \(\frac{-2}{\sqrt{x}}+C\)

Question 61. \(\int x^{-\frac{5}{3}} d x\) is equal to :

1. \(\frac{3}{2} x^{\frac{2}{3}}+C\)
2. \(-\frac{3}{2} x^{\frac{2}{3}}+C\)
3. \(\frac{3}{2} x^{-\frac{2}{3}}+C\)
4. \(-\frac{3}{2} x^{-\frac{2}{3}}+C\)

Answer: 4. \(-\frac{3}{2} x^{-\frac{2}{3}}+C\)

Question 62. \(\int x^{2019} d x\) dx ∫is equal to :

1. \(\frac{x^{2020}}{2020}+C\)
2. \(\frac{x^{2018}}{2018}+C\)
3. \(2019 \mathrm{X}^{2018}+\mathrm{C}\)
4. \(-2012 X^{2011}+C\)

Answer: 1. \(\frac{x^{2020}}{2020}+C\)

Question 63. ∫2sin(x)dx is equal to :

1. –2cos x + C
2. 2 cosx + C
3. –2 cos x
4. 2 cox

Answer: 1. –2cos x + C

Question 64. \(\int(\sin x+\cos x) d x\) is equal to :

1. –cox + sinx
2. – cox + sinx + C
3. cosx – sinx + C
4. – cosx – sinx + C

Answer: 2. – cost + sinx + C

Question 65. \(\int\left(x+x^2+x^3+x^4\right) d x\) is equal to :

1. 1+2x+3x²+4x³ + C
2. 1+2x+3x²+4x³
3. \(\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+\frac{x^5}{5}+C\)
4. \(\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+\frac{x^5}{5}\)

Answer: 3. \(\frac{x^2}{2}+\frac{x^3}{3}+\frac{x^4}{4}+\frac{x^5}{5}+C\)

Question 66. If y = sin(ax+b), ∫y dx will be :

1. \(\frac{\cos (a x+b)}{a}+C\)
2. \(-\frac{\cos (a x+b)}{a}+c\)
3. a cos(ax+b)+C
4. – a cos(ax+b)+C

Answer: 2. \(-\frac{\cos (a x+b)}{a}+c\)

Question 67. If y = x²sin(x³), then ∫y dx will be :

1. \(-\cos \left(x^3\right)+C\)
2. \(\left(-\frac{\cos x^3}{3}\right)+C\)
3. \(\cos \left(x^3\right)+C\)
4. \(\frac{\cos x^3}{3}+C\)

Answer: 2. \(\left(-\frac{\cos x^3}{3}\right)+C\)

Question 68. If y = x², then area of curve y v/s x from x = 0 to 2 will be :

1. 1/3
2. 8/3
3. 4/3
4. 2/3

Answer: 2. 8/3

Question 69. If y = t sin (t²) then ∫ydt will be : 

1. \(\frac{\cos \left(\mathrm{t}^2\right)}{2}+\mathrm{c}\)
2. \(\frac{\cos \left(\mathrm{t}^2\right)}{2}+\mathrm{c}\)
3. \(\frac{-\cos \left(\mathrm{t}^2\right)}{2}+\mathrm{c}\)
4. \(\cos \left(t^2\right)\)

Answer: 3. \(\frac{-\cos \left(\mathrm{t}^2\right)}{2}+\mathrm{c}\)

Question 70. If x = (6y + 4) (3y² + 4y + 3) then ∫x day will be :

1. \(\frac{1}{3 y^2+4 y+3}\)
2. \(\frac{\left(3 y^2+4 y+3\right)^2}{2}+C\)
3. \(\left(3 y^2+4 y+3\right)\)
4. \(\frac{(6 y+4)}{\left(3 y^2+4 y+3\right)}\)

Answer: 2. \(\frac{\left(3 y^2+4 y+3\right)^2}{2}+C\)

Question 71. Value of \(\int_0^{\pi / 2} \cos 3 t\) it is

1. \(\frac{2}{3}\)
2. \(-\frac{1}{3}\)
3. \(-\frac{2}{3}\)
4. \(\frac{1}{3}\)

Answer: 2. \(-\frac{1}{3}\)

Question 72. \(\int_0^1\left(t^2+9 t+c\right) d t=\frac{9}{2}\). Then the value of ‘c’.

1. \(\frac{2}{3}\)
2. \(-\frac{1}{3}\)
3. \(-\frac{2}{3}\)
4. \(\frac{1}{3}\)

Answer: 2. \(-\frac{1}{3}\)

Question 73. Find the value of the following integration. \(\int_0^{2 \pi} \sin ^2 \theta d \theta\) Here c,a are constants.

1. π
2. 2π
3. 3 π
4. 4 π

Answer: 1. π

NEET Physics Chapter 10: Mathematical Tools MCQs and Solutions

Question 74. If y = \(\frac{1}{a x+b}\), then ∫y dx will be :

1. \(\frac{1}{(a x+b)^2}+C\)
2. \(a x+b+C\)
3. \(a \ln (a x+b)+C\)
4. \(\frac{\ln (a x+b)}{a}+C\)

Answer: 4. \(\frac{\ln (a x+b)}{a}+C\)

Question 75. \(\int_\pi^{2 \pi} \theta d \theta\)

1. \(\frac{3 \pi^2}{2}\)
2. \(\frac{3 \pi^3}{2}\)
3. \(\frac{\pi^3}{2}\)
4. π

Answer: 1. \(\frac{3 \pi^2}{2}\)

Question 76. \(\int_0^{\sqrt[3]{7}} x^2 d x\)

1. \(\frac{7}{3}\)
2. \(\frac{7}{4}\)
3. \(\frac{5}{4}\)
4. 0

Answer: 1. \(\frac{7}{3}\)

Question 77. \(\int_0^1 \frac{d x}{3 x+2}\)

1. \(\ln \left(\frac{5}{2}\right)^{1 / 3}\)
2. \(\ln \left(\frac{5}{2}\right)^{1 / 2}\)
3. \(\ln \left(\frac{5}{2}\right)^{1 / 4}\)
4. None of these

Answer: 1. \(\ln \left(\frac{5}{2}\right)^{1 / 3}\)

Question 78. \(\int(x+1) d x\)

1. \(\frac{x^2}{2}+2 x-C\)
2. \(\frac{x^2}{2}+x+C\)
3. \(\frac{x^2}{2}-x+C\)
4. \(\frac{x^2}{2}-x-C\)

Answer: 2. \(\frac{x^2}{2}+2 x-C\)

Question 79. ∫ (5–6x) dx

1. 5x – x² + C
2. x – 3x²– C
3. 5x + 3x² + C
4. 5x – 3x² + C

Answer: 4. 5x – 3x² + C

Question 80. \(\int\left(3 t^2+\frac{t}{2}\right) d t\)

1. \(t^2+\frac{t^2}{4}-C\)
2. \(t^2+\frac{t^2}{4}+C\)
3. \(t^3-\frac{t^2}{4}-C\)
4. \(\frac{t^3}{6}+t^4+C\)

Answer: 2. \(t^2+\frac{t^2}{4}+C\)

Question 81. \(\int\left(\frac{t^2}{2}+4 t^3\right) d t\)

1. \(\frac{t^3}{6}+t^2+C\)
2. \(\frac{t^3}{6}+t+C\)
3. \(\frac{t^3}{6}-t+C\)
4. \(\frac{t^3}{6}+t^4+C\)

Answer: 4. \(\frac{t^3}{6}+t^4+C\)

Question 82. \(\int x^{-1 / 3} d x\)

1. \(\frac{3}{2} x^{2 / 3}+C\)
2. \(\frac{3}{2} x^{2 / 5}+C\)
3. \(\frac{3}{2} x^{1 / 3}+C\)
4. \(\frac{3}{2} x^{2 / 7}+C\)

Answer: 1. \(\frac{3}{2} x^{2 / 3}+C\)

Question 83. \(\int\left(\frac{\sqrt{x}}{2}+\frac{2}{\sqrt{x}}\right) d x\)

1. \(\frac{x^{3 / 2}}{3}+4 x^{1 / 2}+C\)
2. \(\frac{x^{3 / 2}}{3}+x^{1 / 2}+C\)
3. \(\frac{x^{3 / 2}}{3}+4 x^{2 / 5}+C\)
4. \(\frac{x^{3 / 2}}{3}+4 x^2+C\)

Answer: 1. \(\frac{x^{3 / 2}}{3}+4 x^{1 / 2}+C\)

Question 84. \(\int\left(8 y-\frac{2}{y^{1 / 4}}\right) d y\)

1. \(4 y^2-\frac{8}{3} y^{3 / 4}+C\)
2. \(4 y^2+\frac{8}{3} y^{3 / 4}+C\)
3. \(y^2-\frac{8}{3} y^{3 / 4}+C\)
4. \(4 y^2-\frac{8}{3} y^{1 / 3}+C\)

Answer: 1. \(4 y^2-\frac{8}{3} y^{3 / 4}+C\)

Question 85. \(\int 2 x\left(1-x^{-3}\right) d x\)

1. \(x+\frac{2}{x}-C\)
2. \(x^2+\frac{2}{x}+C\)
3. \(2 x^2+\frac{2}{x}+C\)
4. \(5 x^2+\frac{2}{x}+C\)

Answer: 2. \(x^2+\frac{2}{x}+C\)

Question 86. ∫(– 2cost) dt

1. – 2 sin t + C
2. – 3 sin t + C
3. – 5 sin t + C
4. – 7 sin t + C

Answer: 1. – 2 sin t + C

Question 87. ∫(– 5 sint) dt

1. 5 cos t + C
2. 2 cos t – C
3. 5 cosec t + C
4. 5 tan t + C

Answer: 1. 5 cos t + C

Question 88. \(\int 7 \sin \frac{\theta}{3} d \theta\)

1. \(-21 \cos \frac{\theta}{3}+\mathrm{C}\)
2. \(-14 \cos \frac{\theta}{3}+C\)
3. \(-42 \cos \frac{\theta}{3}\)
4. \(-7 \cos \frac{\theta}{3}+C\)

Answer: 1. \(-21 \cos \frac{\theta}{3}+\mathrm{C}\)

Question 89. ∫3cos 5θ+C

1. \(\frac{3}{5} \sin 5 \theta+C\)
2. \(\frac{3}{5} \sin 3 \theta+C\)
3. \(\frac{3}{5} \cos 5 \theta+C\)
4. \(\frac{3}{5} \sec 5 \theta+C\)

Answer: 1. \(\frac{3}{5} \sin 5 \theta+C\)

Question 90. \(\int\left(-3 \csc ^2 x\right) d x\) dx

1. 3 cot x + C
2. cot x + C
3. 3 tan x + C
4. 5 cot x + C

Answer: 1. 3 cot x + C

Question 91. \(\int\left(-\frac{\sec ^2 x}{3}\right) d x\)

1. \(\frac{-\tan x}{3}+x\)
2. \(\frac{-\tan x}{3}+C\)
3. \(\frac{-\tan x}{3}+C\)
4. None

Answer: 2. \(\frac{-\tan x}{3}+C\)

Question 92. \(\int \frac{\csc \theta \cot \theta}{2} d \theta\)

1. \(-\frac{1}{2} \csc \theta+C\)
2. \(-\frac{1}{2} \tan \theta+C\)
3. \(-\frac{1}{2} \cot \theta+C\)
4. \(-\frac{1}{2} \sec \theta+C\)

Answer: 1. \(-\frac{1}{2} \csc \theta+C\)

NEET Physics Mathematical Tools MCQs for Chapter 10

Question 93. \(\int \frac{2}{5} \sec \theta \tan \theta \mathrm{d} \theta\)

1. \(\frac{2}{5} \sec \theta+C\)
2. \(\frac{2}{5} \cos \theta+\mathrm{C}\)
3. \(\frac{2}{5} \tan \theta+C\)
4. \(\frac{2}{5}{cosec} \theta+C\)

Answer: 1. \(\frac{2}{5} \sec \theta+C\)

Question 94. \(\int\left(4 \sec x \tan -2 \sec ^2 x\right) d x\)

1. 4 sec x – 2 tan x + C
2. 2 sec x – 2 tan x + C
3. 4 sec x – 3 tan x + C
4. 4 sec x–5 tan x + C

Answer: 1. 4 sec x – 2 tan x + C

Question 95. \(\int \frac{1}{2}\left(\csc ^2 x-{cxc} x \cot x\right) d x\)

1. \(-\frac{1}{2} \cot x+\frac{1}{2} \csc x+C\)
2. \(\frac{1}{2} \tan x+\frac{1}{2} \csc x+C\)
3. \(-\frac{1}{2} \sec x+\frac{1}{2} \csc x+C\)
4. \(-\frac{1}{2} \sin x+\frac{1}{2} \csc x+C\)

Answer: 1. \(-\frac{1}{2} \cot x+\frac{1}{2} \csc x+C\)

Question 96. \(\int\left(\sin 2 x-\csc ^2 x\right) d x\)

1. \(-\frac{1}{2} \cos 2 x-\cot \mathrm{x}+C\)
2. \(-\frac{1}{2} \cos 2 x+\cot \mathrm{x}+\mathrm{C}\)
3. \(-\frac{1}{2} \cos 3 x-\cot x+C\)
4. \(-\frac{1}{2} \cos 2 x+\tan x+C\)

Answer: 2. \(-\frac{1}{2} \cos 2 x+\cot \mathrm{x}+\mathrm{C}\)

Question 97. \(\int(2 \cos 2 x-3 \sin 3 x) d x\)

1. sin 2x + cos 3x + C
2. sin 2x + cos 5x + C
3. sin 2x + cot 3x + C
4. sin 3x + cos 3x + C

Answer: 1. sin 2x + cos 3x + C

Question 98. \(\int \frac{1+\cos 4 t}{2} d t\)

1. \(\frac{t}{2}+\frac{\sin 4 t}{8}+C\)
2. \(\frac{t}{2}-\frac{\sin 4 t}{8}-C\)
3. \(\frac{t}{3}+\frac{\sin 4 t}{8}+C\)
4. All of these

Answer: 1. \(\frac{t}{2}+\frac{\sin 4 t}{8}+C\)

Question 99. \(\int \frac{1-\cos 6 \mathrm{t}}{2} \mathrm{dt}\)

1. \(\frac{t}{2}+\frac{\sin 6 t}{12}+C\)
2. \(\frac{t}{2}-\frac{\sin 6 t}{12}+C\)
3. \(2 \times \frac{t}{2}-\frac{\sin 6 t}{12}+C\)
4. \(\frac{t}{2}-\frac{\sin 6 t}{12}+C\)

Answer: 2. \(\frac{t}{2}-\frac{\sin 6 t}{12}+C\)

Question 100. \(\int\left(1+\tan ^2 \theta\right) d \theta\)

1. tan θ + C
2. cot θ + C
3. sec θ + C
4. cosec θ + C

Answer: 1. tan θ + C

Question 101. \(\int_{1 / 2}^{3 / 2}(-2 x+4) d x\)

1. 2 square units
2. 4 square units
3. 6 square units
4. 8 square units

Answer: 1. 2 square units

Evaluate definite integrals of the following functions

Question 102. \(\int_0^{\pi / 2} \theta^2 d \theta\)

1. \(\frac{\pi^3}{24}\)
2. \(\frac{\pi^2}{24}\)
3. \(\frac{\pi^2}{36}\)
4. \(\frac{\pi^2}{48}\)

Answer: 1. \(\frac{\pi^3}{24}\)

Question 103. \(\int_0^{3 b} x^2 d x\)

1. 9b³
2. 3b³
3. 27b³
4. 81 b³

Answer: 1. 9b³

Question 104. The forces, each numerically equal to 5N, are acting as shown in the Figure. Find the angle between forces.

1. 90º
2. 180º
3. 120º
4. 160º

Answer: 3. 120º

Question 105. The vector joining the points A (1, 1, –1) and B (2, –3, 4) and pointing from A to B is –

1. \(-\hat{i}+4 \hat{j}-5 \hat{k}\)
2. \(\hat{i}+4 \hat{j}+5 \hat{k}\)
3. \(\hat{i}-4 \hat{j}+5 \hat{k}\)
4. \(-\hat{i}-4 \hat{j}-5 \hat{k}\)

Answer: 4. \(-\hat{i}-4 \hat{j}-5 \hat{k}\)

Question 106. A vector of magnitude 30 and direction eastwards is added with another vector of magnitude 40 and direction Northwards. Find the magnitude and direction of the resultant with the east.

1. 45, 50º with East
2. 53, 75 with East
3. 53, 50º with East
4. 50, 53º with East

Answer: 4. 50, 53º with East

Question 107. The vector sum of the forces of 10 N and 6 N can be

1. 2 N
2. 8 N
3. 18 N
4. 20 N.

Answer: 2. 8 N

NEET Physics Class 11 Chapter 10: Key Concepts and MCQs

Question 108. The vector sum of two forces P and Q is minimum when the angle θ between their positive directions, is

1. \(\frac{\pi}{4}\)
2. \(\frac{\pi}{3}\)
3. \(\frac{\pi}{2}\)
4. \(\pi\)

Answer: 4. \(\pi\)

Question 109. The vector sum of two vectors \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) is maximum, then the angle θ between two vectors is –

1. 0º
2. 30°
3. 45°
4. 60°

Answer: 1. 0º

Question 110. Find the magnitude of \(3 \hat{i}+2 \hat{j}+\hat{k}\)?

1. \(\sqrt{10}\)
2. \(\sqrt{11}\)
3. \(\sqrt{13}\)
4. \(\sqrt{14}\)

Answer: 4. \(\sqrt{14}\)

Question 111. If \(\overrightarrow{\mathrm{A}}=3 \hat{\mathrm{i}}+4 \hat{\mathrm{j}}\) then find \(\hat{A}\)

1. \(\frac{3 \hat{i}+4 \hat{j}}{5}\)
2. \(\frac{2 \hat{i}+3 \hat{j}}{5}\)
3. \(\frac{2 \hat{i}+4 \hat{j}}{5}\)
4. \(\frac{3 \hat{i}-2 \hat{j}}{5}\)

Answer: 1. \(\frac{3 \hat{i}+4 \hat{j}}{5}\)

Question 112. One of the rectangular components of a velocity of 60 km h–1 is 30 km h–1. Find another rectangular component.

1. \(30 \sqrt{3} \mathrm{~km} \mathrm{~h}^{-1}\)
2. \(20 \sqrt{3} \mathrm{~km} \mathrm{~h}^{-1}\)
3. \(30 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}\)
4. \(30 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}\)

Answer: 1. \(30 \sqrt{3} \mathrm{~km} \mathrm{~h}^{-1}\)

Question 113. The x and y components of a force are 2 N and – 3N. The force is

1. \(2 \hat{i}-3 \hat{j}\)
2. \(2 \hat{i}+3 \hat{j}\)
3. \(-2 \hat{i}-3 \hat{j}\)
4. \(3 \hat{i}+2 \hat{j}\)

Answer: 1. \(2 \hat{i}-3 \hat{j}\)

Question 114. A force of 30 N is inclined at an angle θ to the horizontal. If its vertical component is 18 N, find the horizontal component & the value of θ

1. 24 N ; 370 approx
2. 20 N ; 470 approx
3. 25 N ; 350 approx
4. 37 N ; 240 approx

Answer: 1. 24 N; 370 approx

Question 115. The angle θ between directions of forces \(\vec{A} \text { and } \vec{B}\) is 90º where A = 8 dyne and B = 6 dyne. If the resultant \(\vec{R}\) makes an angle α with \(\vec{A}\) then find the value of ‘α’?

1. 47º
2. 37º
3. 75º
4. 120º

Answer: 2. 37º

Question 116. If \(\vec{A}=3 \hat{i}+4 \hat{j} \text { and } \vec{B}=\hat{i}+\hat{j}+2 \hat{k}\) then find out unit vector along \(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\)

1. \(\frac{4 \hat{i}+5 \hat{j}-2 \hat{k}}{\sqrt{45}}\)
2. \(\frac{2 \hat{i}-5 \hat{j}-2 \hat{k}}{\sqrt{45}}\)
3. \(\frac{4 \hat{i}-2 \hat{j}+2 \hat{k}}{\sqrt{45}}\)
4. \(\frac{4 \hat{i}+5 \hat{j}+2 \hat{k}}{\sqrt{45}}\)

Answer: 4. \(\frac{4 \hat{i}+5 \hat{j}+2 \hat{k}}{\sqrt{45}}\)

Question 117. The x and y components of the vector \(\overrightarrow{\mathrm{A}}\) are 4m and 6m respectively. The x,y components of vector are \(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\) 10m and 9m respectively. Find the length of \(\overrightarrow{\mathrm{B}}\) and the angle that \(\overrightarrow{\mathrm{B}}\) makes with the x-axis.

1. \(3 \sqrt{3}, \tan ^{-1} \frac{1}{2}\)
2. \(3 \sqrt{5}, \tan ^{-1} \frac{1}{2}\)
3. \(3 \sqrt{5}, \tan \frac{1}{3}\)
4. \(2 \sqrt{3}, \tan ^{-1} \frac{1}{2}\)

Answer: 2. \(3 \sqrt{5}, \tan ^{-1} \frac{1}{2}\)

Question 118. A vector is not changed if

1. It is displaced parallel to itself
2. It is rotated through an arbitrary angle
3. It is cross-multiplied by a unit vector
4. It is multiplied by an arbitrary scalar.

Answer: 1. It is displaced parallel to itself

Question 119. If the angle between two forces increases, the magnitude of their resultant

1. Decreases
2. Increases
3. Remains unchanged
4. First decreases and then increases

Answer: 1. Decreases

Question 120. Which of the following sets of displacements might be capable of bringing a car to its returning point?

1. 5, 10, 30 and 50 km
2. 5, 9, 9 and 16 km
3. 40, 40, 90 and 200 km
4. 10, 20, 40 and 90 km

Answer: 21. 5, 9, 9 and 16 km

Question 121. When two vectors \(\overrightarrow{\mathrm{a}} \text { and } \overrightarrow{\mathrm{b}}\) are added, the magnitude of the resultant vector is always

1. Greater than (a + b)
2. Less than or equal to (a + b)
3. Less than (a + b)
4. Equal to (a + b)

Answer: 2. Less than or equal to (a + b)

Question 122. If \(|\vec{A}+\vec{B}|=|\vec{A}|=|\vec{B}|\), then the angle between \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) is

1. 0º
2. 60º
3. 90º
4. 120º

Answer: 4. 120º

Question 123. Vector \(\overrightarrow{\mathrm{A}}\) is of length 2 cm and is 60º above the x-axis in the first quadrant. Vector \(\overrightarrow{\mathrm{B}}\) is of length 2 cm and 60º below the x-axis in the fourth quadrant. The sum \(\) is a vector of magnitude –

1. 2 along + y-axis
2. 2 along + x-axis
3. 1 along – x-axis
4. 2 along – x-axis

Answer: 2. 2 along + x-axis

Question 124. Which of the following is a true statement?

1. A vector cannot be divided by another vector
2. Angular displacement can either be a scalar or a vector.
3. Since the addition of vectors is commutative therefore vector subtraction is also commutative.
4. The resultant of two equal forces of magnitude F acting at a point is F if the angle between the two forces is 120º.

Answer: 1. A vector cannot be divided by another vector

Question 125. In the Figure which of the ways indicated for combining the x and y components of vector a is proper to determine that vector?

Answer: 1

Question 126. Two vectors having an equal magnitude of 5 units have an angle of 60º between them. Find the magnitude of their resultant vector and its angle from one of the vectors.

1. 5, 20º
2. \(5 \sqrt{3}\), 30º
3. 3, 40º
4. 3, 50º

Answer: 2. \(5 \sqrt{3}\), 30º

Mathematical Tools MCQs for NEET Physics Chapter 10

Question 127. Two forces each numerically equal to 10 dynes are acting as shown in the figure, then find the resultant of these two vectors.

1. 5 dyne
2. 10 dyne
3. 15 dyne
4. 25 dyne

Answer: 2. 10 dyne

Question 128. The magnitude of pairs of displacement vectors is given. Which pairs of displacement vectors cannot be added to give a resultant vector of magnitude 13 cm?

1. 4 cm, 16 cm
2. 20 cm, 7 cm
3. 1 cm, 15 cm
4. 6 cm, 8 cm

Answer: 3. 1 cm, 15 cm

Question 129. If \(\overrightarrow{\mathrm{A}}=3 \hat{\mathrm{i}}+2 \hat{\mathrm{i}} \text { and } \overrightarrow{\mathrm{B}}=2 \hat{\mathrm{i}}+3 \hat{\mathrm{i}}-\hat{\mathrm{k}}\), then find a unit vector along \((\vec{A}-\vec{B})\)

1. \(\frac{\hat{\mathrm{i}}+\hat{\mathrm{j}}-\hat{\mathrm{k}}}{\sqrt{3}}\)
2. \(\frac{\hat{i}-\hat{j}-\hat{k}}{\sqrt{3}}\)
3. \(\frac{\hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}}{\sqrt{3}}\)
4. \(\frac{\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}}}{\sqrt{3}}\)

Answer: 3. \(\frac{\hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}}{\sqrt{3}}\)

Question 130. If \(\hat{n}\) is a unit vector in the direction of the vector \(\overrightarrow{\mathrm{A}}\), then –

1. \(\hat{n}=\frac{\vec{A}}{|A|}\)
2. \(\hat{n}=\vec{A}|\vec{A}|\)
3. \(\hat{n}=\frac{|\vec{A}|}{\vec{A}}\)
4. \(\hat{n}=\hat{n} \times \vec{A}\)

Answer: 1. \(\hat{n}=\frac{\vec{A}}{|A|}\)

Question 131. The resultant of \(\vec{A} \text { and } \vec{B}\) makes an angle α with \(\vec{A} \text { and } \vec{B}\), then :

1. α < β
2. α < β
3. α < β if A > B
4. α < β if A = B

Answer: 3. α < β if A > B

Question 132. If \(\vec{P}+\vec{Q}=\vec{P}-\vec{Q}\) and θ is the angle between \(\overrightarrow{\mathrm{P}} \text { and } \overrightarrow{\mathrm{Q}}\), then

1. θ = 0º
2. θ = 90º
3. P =0
4. Q = 0

Answer: 4. Q = 0

Question 133. The magnitudes of the sum and difference of two vectors are the same, then the angle between them is

1. 90º
2. 40º
3. 45º
4. 60º

Answer: 1. 90º

Question 134. The projection of a vector \(3 \hat{i}+4 \hat{k}\) on the y-axis is:

1. 5
2. 4
3. 3
4. 3

Answer: 4. 3

Question 135. Two forces of 12N and 8N act up the n body. The resultant force on the body has a maximum value of-

1. 4N
2. 0N
3. 20 N
4. 8 N

Answer: 3. 20 N

Question 136. In figure, \(\vec{E}\) equals

1. \(\vec{A}\)
2. \(\vec{B}\)
3. \(\vec{A}+\vec{B}\)
4. \(-(\vec{A}+\vec{B})\)

Answer: 4. \(-(\vec{A}+\vec{B})\)

Question 137. In figure, \(\overrightarrow{\mathrm{D}}-\overrightarrow{\mathrm{C}}\) equals

1. \(\vec{A}\)
2. \(-\overrightarrow{\mathrm{A}}\)
3. \(\vec{B}\)
4. \(-\vec{B}\)

Answer: 1. \(\vec{A}\)

Question 138. In the figure, \(\vec{E}+\vec{D}-\vec{C}\) equals

1. \(\vec{A}\)
2. \(-\overrightarrow{\mathrm{A}}\)
3. \(\vec{B}\)
4. \(-\vec{B}\)

Answer: 4. \(-\vec{B}\)

Question 139. Forces proportional to AB, BC, and 2CA act along the sides of triangle ABC in order. They’re resultant represented in magnitude and direction as

1. CA
2. AC
3. BC
4. CB

Answer: 1. CA

Question 140. A given force is resolved into components P and Q equally inclined to it. Then :

1. P = 2Q
2. 2P = Q
3. P = Q
4. None of these

Answer: 3. P = Q

Question 141. A particle starting from the origin (0,0) moves in a straight line in the (x, y) plane. Its coordinates at a later time are (\(\sqrt{3}\), 3). The path of the particle makes with the x-axis an angle of :

1. 30º
2. 45º
3. 60º
4. 0º

Answer: 3. 60º

Question 142. If \(\overrightarrow{\mathrm{A}}=\hat{\mathrm{i}}+\hat{\mathrm{J}}+\hat{\mathrm{k}} \text { and } \overrightarrow{\mathrm{B}}=2 \hat{\mathrm{i}}+\hat{\mathrm{J}}\) find (a) \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\) (b) \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}\)

1. 3 and \(-\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-\hat{\mathrm{k}}\)
2. 5 and \(-\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-\hat{\mathrm{k}}\)
3. 1 and \(-\hat{i}+2 \hat{j}+\hat{k}\)
4. 3 and \(-\hat{\mathrm{i}}-2 \hat{\mathrm{j}}+\hat{\mathrm{k}}\)

Answer: 1. 3 and \(-\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-\hat{\mathrm{k}}\)

Question 143. If \(|\vec{A}|=4,|\vec{B}|\) = 3 and θ = 60º in figure, Find (a) \(\overrightarrow{\mathrm{A}} \cdot \overrightarrow{\mathrm{B}}\) (b) \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}\)

1. 3 and \(6 \sqrt{3}\)
2. 6 and \(3 \sqrt{3}\)
3. 6 and \(3 \sqrt{6}\)
4. 6 and \(6 \sqrt{3}\)

Answer: 4. 6 and \(6 \sqrt{3}\)

NEET Class 11 Physics Chapter 10 Mathematical Tools MCQs with Answers

Question 144. Three non zero vector \(\overrightarrow{\mathrm{A}}, \overrightarrow{\mathrm{B}} and \overrightarrow{\mathrm{C}}\) satisfy the relation \(\vec{A} \cdot \vec{B}=0 \text { and } \vec{A}. \vec{C}=0\). Then \(\overrightarrow{\mathrm{A}}\)= 0 can be parallel to :

1. \(\vec{B}\)
2. \(\overrightarrow{\mathrm{C}}\)
3. \(\vec{B} \cdot \vec{C}\)
4. \(\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{C}}\)

Answer: 4. \(\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{C}}\)

Question 145. If \(\vec{A}=4 \hat{i}+n \hat{J}-2 \hat{k} \text { and } \vec{B}=2 \hat{i}+3 \hat{j}+\hat{k}\), then find the value of n so that \(\overrightarrow{\mathrm{A}} \perp \overrightarrow{\mathrm{B}}\)

1. n = 2
2. n = – 1
3. n + 1
4. n = – 2

Answer: 4. n = – 2

Question 146. If \(\vec{F}=(4 \hat{i}-10 \hat{j}) \text { and } \vec{r}=(5 \hat{i}-3 \hat{j})\), then calculate torque \((\vec{\tau}=\vec{r} \times \vec{F})\)

1. \(-38 \hat{k}\)
2. \(-35 \hat{k}\)
3. \(-55 \hat{k}\)
4. \(-28 \hat{k}\)

Answer: 1. \(-38 \hat{k}\)

Question 147. Find a unit vector perpendicular to both the vectors) \((2 \hat{i}+3 \hat{j}+\hat{k}) \text { and }(\hat{i}-\hat{j}+2 \hat{k})\)

1. \(\hat{n}= \pm \frac{1}{\sqrt{83}}(7 \hat{i}+3 \hat{j}+5 \hat{k})\)
2. \(\hat{n}= \pm \frac{1}{\sqrt{83}}(-7 \hat{i}-3 \hat{j}+5 \hat{k})\)
3. \(\hat{n}= \pm \frac{1}{\sqrt{83}}(7 \hat{i}-3 \hat{j}-5 \hat{k})\)
4. \(\hat{n}= \pm \frac{1}{\sqrt{58}}(7 \hat{i}-3 \hat{j}-5 \hat{k})\)

Answer: 3. \(\hat{n}= \pm \frac{1}{\sqrt{83}}(7 \hat{i}-3 \hat{j}-5 \hat{k})\)

Question 148. Which of the following vector identities is false?

1. \(\vec{P}+\vec{Q}=\vec{Q}+\vec{P}\)
2. \(\vec{P}+\vec{Q}=\vec{Q} \times \vec{P}\)
3. \(\vec{P} \cdot \vec{Q}=\vec{Q} \cdot \vec{P}\)
4. \(\vec{P} \times \vec{Q} \neq \vec{Q} \times \vec{P}\)

Answer: 2. \(\vec{P}+\vec{Q}=\vec{Q} \times \vec{P}\)

Question 149. The area of a parallelogram, whose diagonals are \(\) will be

1. 14 unit
2. \(5 \sqrt{3}\)
3. \(10 \sqrt{3}\)
4. \(20 \sqrt{3}\)

Answer: 3. \(10 \sqrt{3}\)

Question 150. If \(\overrightarrow{\mathrm{A}}=\hat{\mathrm{i}}+\hat{\mathrm{j}} \) and \(\overrightarrow{\mathrm{B}}=\hat{\mathrm{i}}-\hat{\mathrm{j}}\) The value of \((\vec{A}+\vec{B}) \cdot(\vec{A}-\vec{B})\) is :

1. \(\sqrt{2}\)
2. 0
3. \(\frac{1}{2}\)
4. 2

Answer: 2. 0

Question 151. Vectors \(\vec{A}=\hat{i}+\hat{j}-2 \hat{k} \text { and } \vec{B}=3 \hat{i}+3 \hat{j}-6 \hat{k}\) are:

1. Parallel
2. Antiparallel
3. Perpendicular
4. At acute angle with each other

Answer: 3. Perpendicular

Question 152. If two vectors are given as : \(\overrightarrow{\mathrm{A}}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-\hat{\mathrm{k}}\) and \( \overrightarrow{\mathrm{B}}=-\hat{\mathrm{i}}-\hat{\mathrm{j}}+\hat{\mathrm{k}}\) then the vector is not perpendicular to \(\) is:

1. \(-2 \hat{i}+4 \hat{j}+2 \hat{k}\)
2. \(\hat{i}+\hat{j}+\hat{k}\)
3. \(25 \hat{i}-625 \hat{j}-25 \hat{k}\)
4. \(3 \hat{i}-2 \hat{j}-3 \hat{k}\)

Answer: 1. \(-2 \hat{i}+4 \hat{j}+2 \hat{k}\)

Question 153. If a vector \(2 \hat{i}+3 \hat{j}+8 \hat{k}\) is perpendicular to the vector \(4 \hat{i}-4 \hat{j}+\alpha \hat{k}\), then the value of α is :

1. –1
2. \(\frac{1}{2}\)
3. \(-\frac{1}{2}\)
4. 1

Answer: 3. \(-\frac{1}{2}\)

Question 154. If the angle between the vectors \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\)is θ, the value of the product \((\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{A}}) \cdot \overrightarrow{\mathrm{A}}\) is equal to :

1. BA² cos θ
2. BA² sin θ
3. BA² sin θ cos θ
4. Zero

Answer: 4. Zero

Question 155. \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) are two vectors and θ is the angle between them, if \(|\vec{A} \times \vec{B}|=\sqrt{3}(\vec{A} \cdot \vec{B})\) the value of θ is :

1. 60º
2. 45º
3. 30º
4. 90º

Answer: 1. 60º

Question 156. Two forces P and Q acting at a point are such that if P is reversed, the direction of the resultant is turned through 90º. Then

1. P = Q
2. P =2Q
3. P = \(\frac{Q}{2}\)
4. No relation between P and Q

Answer: 1. P = Q

Question 157. The vector sum of two forces is perpendicular to their vector differences. In that case, the forces :

1. Are not equal to each other in magnitude
2. Cannot be predicted
3. Are equal to each other
4. Are equal to each other in magnitude

Answer: 4. Are equal to each other in magnitude

Question 158. If \(|\vec{A} \times \vec{B}|=\sqrt{3} \cdot \vec{A}, \vec{B}\) then the value of \(|\vec{A}+\vec{B}|\) is :

1. \(\left(\mathrm{A}^2+\mathrm{B}^2+\mathrm{AB}\right)^{1 / 2}\)
2. \(\left(A^2+B^2+\frac{A B}{\sqrt{3}}\right)^{1 / 2}\)
3. \(A+B\)
4. \(\left(\mathrm{A}^2+\mathrm{B}^2+\sqrt{3} A B\right)^{1 / 2}\)

Answer: 1. \(\left(\mathrm{A}^2+\mathrm{B}^2+\mathrm{AB}\right)^{1 / 2}\)

Question 159. Velocity as a function of time is V(t) = sin²t – cos(2t). Then the value of \(\left(\frac{\pi}{3}\right)\) will be :

1. \(\frac{2}{3}\)
2. \(\frac{1}{4}\)
3. \(\frac{1}{4}\)
4. \(\frac{5}{4}\)

Answer: 4. \(\frac{5}{4}\)

Question 160. If f = \(2 \pi \frac{x^3 y^5}{\sqrt{z}}\) then log f is equal to :

1. \(\log 2 \pi+3 \log x+5 \log y+\frac{1}{2} \log z\)
2. \(\log 2 \pi+3 \log x+5 \log y-\frac{1}{2} \log z\)
3. \(\log 2 \pi-3 \log x+5 \log y+\frac{1}{2} \log z\)
4. \(\log 2 \pi+3 \log x+5 \log y+\log z\)

Answer: 2. \(\log 2 \pi+3 \log x+5 \log y-\frac{1}{2} \log z\)

Question 161. Which of the following is true

1. sin37° + cos37° = sin53° + cos53°
2. sin37° – cos37° = cos53° – sin53°
3. tan37° + 1 = tan 53° – 1
4. tan37° × tan53° = 1

Answer: 1. sin37° + cos37° = sin53° + cos53°

Question 162. If y₁ = A sinθ₁ and y₂ = A sin θ₂ then

1. \(y_1+y_2=2 A \sin \left(\frac{\theta_1+\theta_2}{2}\right) \cos \left(\frac{\theta_1-\theta_2}{2}\right)\)
2. \(y_1+y_2=2 A \sin \theta_1 \sin \theta_1\)
3. \(y_1-y_2=2 A \sin \left(\frac{\theta_1-\theta_2}{2}\right) \cos \left(\frac{\theta_1+\theta_2}{2}\right)\)
4. \(y_1, y_2=-2 A^2 \cos \left(\frac{\pi}{2}+\theta_1\right) \cdot \cos \left(\frac{\pi}{2}-\theta_2\right)\)

Answer: (1,3)

Question 163. If R² = A² + B² + 2AB cosθ , if |A| = |B| then value of magnitude of R is equivalent to :

1. 2Acosθ
2. \(A \cos \frac{\theta}{2}\)
3. \(2 A \cos \frac{\theta}{2}\)
4. \(2 B \cos \frac{\theta}{2}\)

Answer: (3,4)

Question 164. A particle starting from the origin (0, 0) moves in a straight line in the (x, y) plane. Its coordinates at a later time are (\(\sqrt{3}\), 3). The path of the particle makes with the x-axis an angle of :

1. 30º
2. 45º
3. 60º
4. 0º

Answer: 3. 60º

Question 165. Find the value of an if the distance between the point (–9cm, a cm) and (3cm, 3 cm) is 13 cm.

1. 6 cm
2. 8 cm
3. 10 cm
4. 12 cm

Answer: 2. 8 cm

Question 166. y = lnx² + sin x

1. \(\frac{d y}{d x}=\frac{2}{x}+\cos x, \frac{d^2 y}{d x^2}=\frac{-2}{x^2}-\sin x\)
2. \(\frac{d y}{d x}=\frac{2}{x}-\cos x, \frac{d^2 y}{d x^2}=\frac{-2}{x^2}+\sin x\)
3. \(\frac{d y}{d x}=-\frac{2}{x}+\cos x, \frac{d^2 y}{d x^2}=\frac{-2}{x^2}-\sin x\)
4. \(\frac{d y}{d x}=-\frac{2}{x}-\cos x, \frac{d^2 y}{d x^2}=\frac{2}{x^2}-\sin x\)

Answer: 1. \(\frac{d y}{d x}=\frac{2}{x}+\cos x, \frac{d^2 y}{d x^2}=\frac{-2}{x^2}-\sin x\)

Question 167. y = \(\sqrt[7]{x}+\tan x\)

1. \(\frac{d y}{d x}=-\frac{x^{-\frac{6}{7}}}{7}+\sec ^2 x, \frac{d^2 y}{d x^2}=\frac{-6}{49} x^{\frac{-13}{7}}-2 \tan x \sec ^2 x\)
2. \(\frac{d y}{d x}=\frac{x^{-\frac{6}{7}}}{7}+\sec ^2 x, \frac{d^2 y}{d x^2}=\frac{-6}{49} x^{\frac{-13}{7}}+2 \tan x \sec ^2 x\)
3. \(\frac{d y}{d x}=\frac{x^{-\frac{6}{7}}}{7}-\sec ^2 x, \frac{d^2 y}{d x^2}=\frac{-6}{49} x^{\frac{-13}{7}}-2 \tan x \sec ^2 x\)
4. \(\frac{d y}{d x}=\frac{x^{-\frac{6}{7}}}{7}+\sec ^2 x, \frac{d^2 y}{d x^2}=\frac{6}{49} x^{\frac{-13}{7}}+2 \tan x \sec ^2 x\)

Answer: 2. \(\frac{d y}{d x}=\frac{x^{-\frac{6}{7}}}{7}+\sec ^2 x, \frac{d^2 y}{d x^2}=\frac{-6}{49} x^{\frac{-13}{7}}+2 \tan x \sec ^2 x\)

NEET Physics Chapter 10: Mathematical Tools MCQs and Solutions

Find the derivative of given functions w.r.t. the corresponding independent variable.

Question 168. y = \(\left(x+\frac{1}{x}\right)\left(x-\frac{1}{x}+1\right)\)

1. \(\frac{d y}{d x}=1+2 x+\frac{2}{x^3}-\frac{1}{x^2}\)
2. \(\frac{d y}{d x}=1+2 x-\frac{2}{x^3}-\frac{1}{x^2}\)
3. \(\frac{d y}{d x}=1+2 x+\frac{2}{x^3}-\frac{1}{x^2}\)
4. \(\frac{d y}{d x}=1+2 x+\frac{2}{x^3}+\frac{1}{x^2}\)

Answer: 3. \(\frac{d y}{d x}=1+2 x+\frac{2}{x^3}-\frac{1}{x^2}\)

Question 169. r = (1 + sec θ) sin θ, r′ is

1. \(\frac{d r}{d \theta}=\cos \theta+\sec ^2 \theta\)
2. \(\frac{d r}{d \theta}=\cos \theta-\sec ^2 \theta\)
3. \(\frac{d r}{d \theta}=\cos \theta+\tan ^2 \theta\)
4. \(\frac{d r}{d \theta}=\cos \theta+\sec ^2 \theta\)

Answer: 1. \(\frac{d r}{d \theta}=\cos \theta+\sec ^2 \theta\)

Question 170. q = \(\sqrt{2 r-r^2}\), find \(\frac{\mathrm{dq}}{\mathrm{dr}}\)

1. \(\frac{1-r}{\sqrt{2 r-r^2}}\)
2. \(\frac{1+r}{\sqrt{2 r+r^2}}\)
3. \(\frac{1-r}{\sqrt{3 r+r}}\)
4. \(\frac{1-r}{\sqrt{2 r-r^2}}\)

Answer: 1. \(\frac{1-r}{\sqrt{2 r-r^2}}\)

Find \(\frac{d y}{d x}\)

Question 171. y = \(\frac{\cot x}{1+\cot x}\)

1. \(\frac{-\csc ^2 x}{(1+\cot x)^2}\)
2. \(\frac{-\csc ^2 x}{(1-\cot x)^2}\)
3. \(\frac{-\csc ^2 x}{(1+\cot x)^2}\)
4. \(\frac{-\csc ^2 x}{(1+\tan x)^2}\)

Answer: 1. \(\frac{-\csc ^2 x}{(1+\cot x)^2}\)

Question 172. y = \(\frac{\ell \mathrm{nx}+\mathrm{e}^{\mathrm{x}}}{\tan \mathrm{x}}\), then \(\frac{d y}{d x}\) is

1. \(\frac{\tan x\left(e^x+\frac{1}{x}\right)+\sec ^2 x\left(e^x+\ell \ln x\right)}{\tan ^2 x}\)
2. \(\frac{\tan x\left(e^x+\frac{1}{x}\right)-\sec ^2 x\left(e^x+\ell \ln x\right)}{\tan ^2 x}\)
3. \(\frac{\tan x\left(e^x-\frac{1}{x}\right)-\sec ^2 x\left(e^x+\ell n x\right)}{\tan ^2 x}\)
4. \(\frac{\tan x\left(e^x+\frac{1}{x}\right)-\sec ^2 x\left(e^x-\ell n x\right)}{\tan ^2 x}\)

Answer: 1. \(\frac{\tan x\left(e^x+\frac{1}{x}\right)+\sec ^2 x\left(e^x+\ell \ln x\right)}{\tan ^2 x}\)

Find \(\frac{\mathrm{dy}}{\mathrm{dx}}\) as a function of x

Question 173. x³ + y³ = 18 xy

1. \(\frac{d y}{d x}=\frac{18 y+3 x^2}{3 y^2+18 x}\)
2. \(\frac{d y}{d x}=\frac{15 y+3 x^2}{3 y^2-18 x}\)
3. \(\frac{d y}{d x}=\frac{18 y-3 x^2}{3 y^2-18 x}\)
4. \(\frac{d y}{d x}=\frac{18 y-3 x^2}{3 y^2+12 x}\)

Answer: 3. \(\frac{d y}{d x}=\frac{18 y-3 x^2}{3 y^2-18 x}\)

Question 174. Find two positive numbers x & y such that x + y = 60 and xy is maximum –

1. 15, 45
2. 30, 30
3. 20, 40
4. 10, 50

Answer: 2. 30, 30

Find integrals of given functions.

Question 175. \(\int x^{-3}(x+1) d x\)

1. \(-\frac{1}{x}-\frac{1}{2 x^2}+C\)
2. \(\frac{1}{x}+\frac{1}{2 x^2}+C\)
3. \(3-\frac{1}{2 x^2}+C\)
4. \(-\frac{1}{x}+\frac{1}{2 x^2}+C\)

Answer: 1. \(-\frac{1}{x}-\frac{1}{2 x^2}+C\)

Question 176. \(\int\left(1-\cot ^2 x\right) d x\)

1. 2x + cot x + C
2. x + cot x + C
3. 2x – cot x + C
4. 2x + tan x + C

Answer: 1. 2x + cot x + C

Question 177. ∫cos (tanθ + secθ)dθ

1. – cos θ + θ + C
2. – cos θ – θ + C
3. – cosec θ + θ + C
4. – 2cos θ + θ + C

Answer: 1. – cos θ + θ + C

Question 178. \(\int \sqrt{3-2 s} d s\)

1. \(-\frac{1}{3}(3-2 s)^{2 / 3}+C\)
2. \(-\frac{1}{3}(3-2 s)^{3 / 2}+C\)
3. \(-\frac{1}{3}(3+2 s)^{3 / 2}+C\)
4. None of these

Answer: 2. \(-\frac{1}{3}(3-2 s)^{3 / 2}+C\)

Question 179. \(\int \frac{d x}{\sqrt{5 x+8}}\)

1. \(\left[\frac{2}{5} \sqrt{5 x+8}\right]+C\)
2. \(\left[\frac{2}{5} \sqrt{3 x-8}\right]+C\)
3. \(\left[\frac{2}{5} \sqrt{5 x-4}\right]-C\)
4. \(\left[\frac{2}{5} \sqrt{5 x-4}\right]\)

Answer: 1. \(\left[\frac{2}{5} \sqrt{5 x+8}\right]+C\)

Question 180. \(\int_0^{\sqrt{\pi}} x \sin x^2 d x\)

1. 1
2. 2
3. 3
4. 1

Answer: 1. 1

Use a definite integral to find the area of the region between the given curve and the x-axis on the interval [0,b],

Question 181. y = 3x²

1. b³
2. b²
3. b
4. b⁵

Answer: 1. b³

NEET Physics Mathematical Tools MCQs for Chapter 10

Question 182. Two vectors \(\overrightarrow{\mathrm{a}} \text { and } \overrightarrow{\mathrm{b}}\) inclined at an angle θ w.r.t. each other have a resultant \(\overrightarrow{\mathrm{c}}\) which makes an angle β with \(\overrightarrow{\mathrm{a}}\). If the directions of \(\overrightarrow{\mathrm{a}} \text { and } \overrightarrow{\mathrm{b}}\) are interchanged, then the resultant will have the same

1. Magnitude
2. Direction
3. Magnitude as well as direction
4. Neither magnitude nor direction.

Answer: 1. Magnitude

Question 183. Two vectors \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) lie in a plane. Another vector \(\overrightarrow{\mathrm{C}}\) lies outside this plane. The resultant \(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{C}}\) of these three vectors

1. Can be zero
2. Cannot be zero
3. Lies in the plane of \(\vec{A} and \vec{B}\)
4. Lies in the plane of \(\overrightarrow{\mathrm{A}} and \overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\)

Answer: 2. Cannot be zero

Question 184. The rectangular components of a vector are (2, 2). The corresponding rectangular components of another vector are (1, \(\sqrt{3}\)). Find the angle between the two vectors

1. 10º
2. 15º
3. 20º
4. 25º

Answer: 2. 15º

Question 185. Given : \(\vec{a}+\vec{b}+\vec{c}\)= 0. Out of the three vectors \(\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}} \text { and } \overrightarrow{\mathrm{c}}\) two are equal in magnitude. The magnitude of the vector \(\sqrt{2}\) times that of either of the two having equal magnitude. The angles between vectors are:

1. 90º, 135º,. 135º
2. 30º, 60º, 90º
3. 45º, 45º, 90º
4. 45º, 60º, 90º

Answer: 1. 90º, 135º,. 135º

Question 186. Let \(\vec{a} \text { and } \vec{b}\) be two non-null vectors such that \(|\vec{a}+\vec{b}|=|\vec{a}-2 \vec{b}|\). Then the value of \(\frac{|\vec{a}|}{|\vec{b}|}\) may be :

1. \(\frac{1}{4}\)
2. \(\frac{1}{8}\)
3. 1
4. 2

Answer: (3,4)

Question 187. A truck traveling due north at 20 ms^-1 turns west and travels with the same speed. What is the change in velocity?

1. \(20 \sqrt{2} \mathrm{~ms}^{-1}\) south-west
2. \(40 \mathrm{~ms}^{-1}\) south-west
3. \(20 \sqrt{2} \mathrm{~ms}^{-1}\) north-west
4. \(40 \mathrm{~ms}^{-1}\) north-west

Answer: 1. \(20 \sqrt{2} \mathrm{~ms}^{-1}\) south-west

Question 188. Determine that vector which when added to the resultant of \(\overrightarrow{\mathrm{P}}=2 \hat{\mathrm{i}}+7 \hat{\mathrm{j}}-10 \hat{\mathrm{k}}\) and \(\vec{Q}=\hat{i}+2 \hat{j}+3 \hat{k}\) a unit vector along X-axis.

1. \(-2 \hat{i}-9 \hat{j}+7 \hat{k}\)
2. \(+2 \hat{i}+9 \hat{j}-7 \hat{k}\)
3. \(-2 \hat{i}+7 \hat{j}+9 \hat{k}\)
4. \(+2 \hat{i}-5 \hat{j}+3 \hat{k}\)

Answer: 1. \(-2 \hat{i}-9 \hat{j}+7 \hat{k}\)

Question 189. Two vectors acting in opposite directions have a resultant of 10 units. If they act at right angles to each other, then the result is 50 units. Calculate the magnitude of two vectors.

1. P = 40 ; Q = 30
2. P = 30 ; Q = 40
3. P = 80 ; Q = 50
4. P = 30 ; Q = 40

Answer: 1. P = 40 ; Q = 30

Question 160. Find the resultant of the three vectors \(\overrightarrow{\mathrm{OA}}, \overrightarrow{\mathrm{OB}} \text { and } \overrightarrow{\mathrm{OC}}\) each of magnitude r as shown in the figure?

1. \(r(1+\sqrt{2})\)
2. \(r(1-\sqrt{2})\)
3. \((1+\sqrt{2})\)
4. \(r(1+\sqrt{2})^2\)

Answer: 1. \(r(1+\sqrt{2})\)

Question 161. A car is moving on a straight road due north with a uniform speed of 50 km h^-1 when it turns left through 90º. If the speed remains unchanged after turning, the change in the velocity of the car in the turning process is

1. Zero
2. \(50 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}\) S-W direction
3. \(50 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}\) N-W direction
4. 50 km h^-1 due west.

Answer: 2. \(50 \sqrt{2} \mathrm{~km} \mathrm{~h}^{-1}\) S-W direction

Question 162. Six forces, 9.81 N each, acting at a point are coplanar. If the angles between neighboring forces are equal, then the resultant is

1. 0 N
2. 9.81 N
3. 2 × 9.81 N
4. 3 × 9.81 N.

Answer: 1. 0 N

Question 163. At what angle must the two forces (x + y) and (x – y) act so that the resultant may be \(\sqrt{\left(x^2+y^2\right)}\)?

1. \(\cos ^{-1}\left[\frac{-\left(x^2+y^2\right)}{2\left(x^2-y^2\right)}\right]\)
2. \(\cos ^{-1}\left[\frac{-2\left(x^2-y^2\right)}{x^2+y^2}\right]\)
3. \(\cos ^{-1}\left[\frac{-\left(x^2+y^2\right)}{x^2-y^2}\right]\)
4. \(\cos ^{-1}\left[\frac{\left(x^2-y^2\right)}{x^2+y^2}\right]\)

Answer: 1. \(\cos ^{-1}\left[\frac{-\left(x^2+y^2\right)}{2\left(x^2-y^2\right)}\right]\)

Question 164. The magnitude of the scalar product of two vectors is 8 and that of the vector product is \(8 \sqrt{3}\). The angle between them is :

1. 30º
2. 60º
3. 120º
4. 150º

Answer: (2,3)

Question 165. A vector \(\vec{A}\) points vertically downward and \(\vec{B}\) points towards the east, then the vector product \(\overrightarrow{\mathrm{A}} \times \overrightarrow{\mathrm{B}}\) is

1. Along west
2. Along east
3. Zero
4. Along south

Answer: 4. Along south

Question 166. Which of the arrangement of axes in a figure? can be labeled “right-handed coordinate system”? As usual, each axis label indicates the positive side of the axis.

1. (1), (2)
2. (3), (4)
3. (6)
4. (5)

Answer: (1,2,3)

NEET Physics Mathematical Tools MCQs for Chapter 10

Question 167. The unit vector perpendicular to each of the vectors \(3 \hat{i}+\hat{j}+2 \hat{k}\) and \(2 \hat{i}-2 \hat{j}+\hat{k}\) is given by

1. \(\frac{1}{\sqrt{3}}(\hat{i}-\hat{j}-\hat{k})\)
2. \(\frac{1}{\sqrt{3}}(\hat{\mathbf{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}})\)
3. \(\frac{5 \hat{i}+\hat{j}+4 \hat{k}}{\sqrt{46}}\)
4. \(\pm \frac{5 \hat{i}+\hat{j}-4 \hat{k}}{\sqrt{42}}\)

Answer: 4. \(\pm \frac{5 \hat{i}+\hat{j}-4 \hat{k}}{\sqrt{42}}\)

Question 168. Three vectors \(\overrightarrow{\mathrm{A}}, \overrightarrow{\mathrm{B}} \text { and } \overrightarrow{\mathrm{C}}\) are such that \(\overrightarrow{\mathrm{A}}=\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{C}}\) and their magnitudes are in ratio 5: 4 : 3 respectively. Find the angle between vector \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{C}}\)

1. 35º
2. 53º
3. 60º
4. 75º

Answer: 2. 53º

Question 169. A car travels 6 km towards the north at an angle of 45° to the east and then travels a distance of 4 km towards the north at an angle of 135° to the east. How far is the point from the starting point? What angle does the straight line joining its initial and final position make with the east?

1. \(\sqrt{50} \mathrm{~km} and \tan ^{-1}(5)\)
2. \(10 \mathrm{~km} and \tan ^{-1}(\sqrt{5})\)
3. \(\sqrt{52} \mathrm{~km} and \tan ^{-1}(5)\)
4. \(\sqrt{52} \mathrm{~km} and \tan ^{-1}(\sqrt{5})\)

Answer: 3. \(\sqrt{52} \mathrm{~km} and \tan ^{-1}(5)\)

Question 170. The vectors \(\vec{A} \text { and } \vec{B}\) are such that: 

⇒\(|\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}|=|\overrightarrow{\mathrm{A}}-\overrightarrow{\mathrm{B}}|\)

The angle between the two vectors is :

1. 90°
2. 60°
3. 75°
4. 45°

Answer: 1. 90°

Question 171. Six vectors, \(\vec{a}\) through \(\vec{f}\) have the magnitudes and directions indicated in figure e. Which of the following statements is true?

1. \(\vec{b}+\vec{c}=\vec{f}\)
2. \(\vec{d}+\vec{c}=\vec{f}\)
3. \(\vec{d}+\vec{e}=\vec{f}\)
4. \(\vec{b}+\vec{e}=\vec{f}\)

Answer: 3. \(\vec{d}+\vec{e}=\vec{f}\)

Question 172. If dimensions of critical velocity υc of a liquid flowing through a tube are expressed as \(\left[\eta^{\mathrm{x}} \rho^{\mathrm{y}} \mathrm{r}^{\mathrm{x}}\right]\), where η, ρ, and r are the coefficient of viscosity of the liquid, density of a liquid, and radius of the tube respectively, then the values of x, y, and z are given by :

1. –1, –1, 1
2. –1, –1, –1
3. 1,1,1
4. 1, –1, –1

Answer: 4. 1, –1, –1

Question 173. If vectors \(\vec{A}=\cos \omega t \hat{i}+\sin \omega t \hat{j} \text { and } \vec{B}=\cos \frac{\omega t}{2} \hat{i}+\sin \frac{\omega t}{2} \hat{j}\) are functions of time, then the value of t at which they are orthogonal to each other is :

1. \(t=\frac{\pi}{2 \omega}\)
2. \(t=\frac{\pi}{\omega}\)
3. \(t=0\)
4. \(t=\frac{\pi}{4 \omega}\)

Answer: 2. \(t=\frac{\pi}{\omega}\)

Question 174. If the magnitude of the sum of two vectors is equal to the magnitude of the difference of the two vectors, the angle between these vectors is :

1. 180°
2. 0°
3. 90°
4. 45°

Answer: 3. 90°

Question 175. A particle moves so that its position vector is given by \(\overrightarrow{\mathrm{r}}=\cos \omega t \hat{x}+\sin \omega t \hat{y}\). Where ω is a constant. Which of the following is true?

1. Velocity and acceleration both are perpendicular to \(\overrightarrow{\mathrm{r}}\)
2. Velocity and acceleration both are parallel to \(\overrightarrow{\mathrm{r}}\)
3. Velocity is perpendicular to \(\overrightarrow{\mathrm{r}}\) and acceleration is directed towards the origin
4. Velocity is perpendicular to \(\overrightarrow{\mathrm{r}}\) and acceleration is directed away from the origin

Answer: 3. Velocity is perpendicular to \(\overrightarrow{\mathrm{r}}\) and acceleration is directed towards the origin

Question 176. The x and y coordinates of the particles at any time are x = 5t -2t² and y = 10t respectively, where x and y are in meters and t in seconds. The acceleration of the particle at t = 2s is

1. 5m/s²
2. -4 m/s²
3. – 8 m/s²
4. 0

Answer: 2. -4 m/s²

Question 177. The moment of the force, \(\overrightarrow{\mathrm{F}}=4 \hat{\mathrm{i}}+5 \hat{\mathrm{j}}-6 \hat{\mathrm{k}}\) at (2, 0, –3), about the point (2, –2, –2), is given by

1. \(-8 \hat{\mathrm{i}}-4 \hat{\mathrm{j}}-7 \hat{\mathrm{k}}\)
2. \(-4 \hat{\mathrm{i}}-\hat{\mathrm{j}}-8 \hat{\mathrm{k}}\)
3. \(-7 \hat{i}-4 \hat{j}-8 \hat{k}\)
4. \(-7 \hat{i}-8 \hat{j}-4 \hat{k}\)

Answer: 3. \(-7 \hat{i}-4 \hat{j}-8 \hat{k}\)

Question 178. In the cube of side ‘as shown in the figure, the vector from the central point of the face ABOD to the central point of the face BEFO will be :

1. \(\frac{1}{2} a(\hat{j}-\hat{k})\)
2. \(\frac{1}{2} a(\hat{j}-\hat{i})\)
3. \(\frac{1}{2} \mathrm{a}(\hat{\mathrm{k}}-\hat{\mathrm{i}})\)
4. \(\frac{1}{2} a(\hat{i}-\hat{k})\)

Answer: 2. \(\frac{1}{2} a(\hat{j}-\hat{i})\)

NEET Physics Class 11 Chapter 10 Mathematical Tools MCQs Practice

Question 179. Two forces P and Q, of magnitude 2F and 3F, respectively are at an angle θ with each other. If the force Q is doubled, then their resultant also gets doubled. Then, the angle θ is :

1. 30°
2. 60°
3. 90°
4. 120°

Answer: 4. 120°

Question 180. Two vectors \(\vec{A} \text { and } \vec{B}\) have equal magnitudes. The magnitude of \((\vec{A}+\vec{B})\) is ‘n’ times the magnitude of \((\vec{A}-\vec{B})\). The angle between \(\vec{A} \text { and } \vec{B}\) is

1. \(\sin ^{-1}\left[\frac{n-1}{n+1}\right]\)
2. \(\cos ^{-1}\left[\frac{n^2-1}{n^2+1}\right]\)
3. \(\sin ^{-1}\left[\frac{n^2-1}{n^2+1}\right]\)
4. \(\cos ^{-1}\left[\frac{n-1}{n+1}\right]\)

Answer: 2. \(\cos ^{-1}\left[\frac{n^2-1}{n^2+1}\right]\)

NEET Physics Solutions For Class 11 Chapter 10  Vector

In physics we deal with two types of physical quantity one is scalar and the other is a vector. Each scalar quantity has magnitude.

The magnitude of a physical quantity means a product of numerical value and unit of that physical quantity. For example mass = 4 kg

Magnitude of mass = 4 kg

and unit of mass = kg

Examples of scalar quantities: are mass, speed, distance, etc.

Scalar quantities can be added, subtracted, and multiplied by simple laws of algebra.

1. Definition Of Vector

If a physical quantity in addition to magnitude –

1. Has a specified direction.
2. It should obey the commutative law of additions
   1. \(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{A}}\)
3. Obeys the law of parallelogram of addition, then and then only it is said to be a vector. If any of the above conditions is not satisfied the physical quantity cannot be a vector.

If a physical quantity is a vector it has a direction, but the converse may or may not be true, i.e. if a physical quantity has a direction, it may or may not a be vector. e.g. time, pressure, surface tension current, etc. have directions but are not vectors because they do not obey the parallelogram law of addition.

The magnitude of a vector \((\overrightarrow{\mathrm{A}})\) is the absolute value of a vector and is indicated by \(|\vec{A}|\) or A.

Examples of vector quantity are displacement, velocity, acceleration, force, etc.

Vector Solutions for NEET Physics Class 11 Chapter 10

Representation Of Vector: Geometrically, the vector is represented by a line with an arrow indicating the direction of the vector as

Mathematically, vector is represented by \(\overrightarrow{\mathrm{A}}\)

Sometimes it is represented by the bold letter A.

Important Points: If a vector is displaced parallel to itself it does not change

If a vector is rotated through an angle other than a multiple of 2π (or 360º) it changes.

If the frame of reference is translated or rotated the vector does not change (though its components may change).

Two vectors are called equal if their magnitudes and directions are the same,
and they represent values of the same physical quantity.

The angle between two vectors means the smaller of the two angles between the vectors when they are placed tail to tail by displacing either of the vectors parallel to itself (i.e. 0 ≤ θ ≤ π).

2. Unit Vector

A unit vector is a vector that has a unit magnitude and points in a particular direction. Any vector \((\overrightarrow{\mathrm{A}})\) can be written as the product of unit vector \((\hat{A})\) in that direction and magnitude of the given vector.

⇒ \(\overrightarrow{\mathrm{A}}=\mathrm{A} \hat{\mathrm{A}} \text { or } \hat{\mathrm{A}}=\frac{\vec{A}}{\mathrm{~A}}\)

A unit vector has no dimensions or units. Unit vectors along the positive x-, y- and z-axes of a rectangular coordinate system are denoted by

⇒ \(\hat{\mathrm{i}}, \hat{\mathrm{j}} \text { and } \hat{\mathrm{k}}\) and respectively such that

⇒ \(|\hat{\mathrm{i}}|=|\hat{\mathrm{j}}|=|\hat{\mathrm{k}}|\) = 1

NEET Physics Chapter 10 Vector Mathematical Tools Solutions

Question 1. Three vectors \(\overrightarrow{\mathrm{A}}, \overrightarrow{\mathrm{B}}, \overrightarrow{\mathrm{C}}\) are shown in the figure. Find angle between

1. \(\overrightarrow{\mathrm{A}} \text { and } \vec{B}\),
2. \(\overrightarrow{\mathrm{B}} \text { and } \vec{C}\)
3. \(\overrightarrow{\mathrm{A}} \text { and } \vec{C}\).

Answer:

To find the angle between two vectors we connect the tails of the two vectors. We can shift \(\overrightarrow{\mathrm{B}}\) such that tails of \(\overrightarrow{\mathrm{A}}, \overrightarrow{\mathrm{B}} \text { and } \overrightarrow{\mathrm{C}}\) are connected as shown in figure.

Now we can easily observe that angle between \(\vec{A} \text { and } \vec{B}\) is 60º, \(\vec{B} \text { and } \vec{C}\) is 15º and between \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{C}}\)is 75º.

Question 2. A unit vector along East is defined as \(\hat{\mathbf{i}}\). A force of 10⁵ dynes acts westwards. Represent the force in terms of \(\hat{\mathbf{i}}\)

Answer:

⇒ \(\overrightarrow{\mathrm{F}}=-10^5 \hat{\mathrm{i}}\) dynes

3. Multiplication Of A Vector By A Scalar

Multiplying a vector \(\overrightarrow{\mathrm{A}}\) with a positive number λ gives a vector \(\vec{B}(=\lambda \overrightarrow{\mathrm{A}})\) whose magnitude is changed by the factor λ but the direction is the same as that of \(\overrightarrow{\mathrm{A}}\).

Multiplying a vector \(\overrightarrow{\mathrm{A}}\) by a negative number λ gives a vector \(\overrightarrow{\mathrm{B}}\) whose direction is opposite to the direction of \(\overrightarrow{\mathrm{A}}\) and whose magnitude is − λ times \(|\vec{A}|\)

Question 3. A physical quantity (m = 3kg) is multiplied by a vector \(\overrightarrow{\mathrm{a}}\) such that \(\overrightarrow{\mathrm{F}}=\mathrm{m} \overrightarrow{\mathrm{a}}\). Find the magnitude and direction of \(\overrightarrow{\mathrm{F}}\) if

1. \(\overrightarrow{\mathrm{a}}=3 \mathrm{~m} / \mathrm{s}^2\) Eastwards
2. \(\overrightarrow{\mathrm{a}}=-4 \mathrm{~m} / \mathrm{s}^2\) Northwards

Answer:

1. \(\overrightarrow{\mathrm{F}}=\mathrm{m} \overrightarrow{\mathrm{a}}=3 \times 3 \mathrm{~ms}^{-2}\) East wards = 9 N Eastwards
2. \(\overrightarrow{\mathrm{F}}=\mathrm{m} \vec{a}=3 \times(-4)\) Northwards

= – 12 N North wards = 12 N Southwards

4. Addition Of Vectors

The addition of vectors is done by parallelogram law or the triangle law :

Parallelogram Law Of Addition Of Vectors: If two vectors \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) are represented by two adjacent sides of a parallelogram both pointing outwards (and their tails coinciding) as shown. Then the diagonal drawn through the intersection of the two vectors represents the resultant (i.e., the vector sum of \(\vec{A} \text { and } \vec{B}\)).

R = \(\sqrt{A^2+B^2+2 A B \cos \theta}\)

The direction of resultant vector \(\overrightarrow{\mathrm{R}} \text { from } \overrightarrow{\mathrm{A}}\) given by

⇒ \(\tan \phi=\frac{\mathrm{MN}}{\mathrm{PN}}\)

⇒ \(\frac{\mathrm{MN}}{\mathrm{PQ}+\mathrm{QN}}\)

⇒ \(\frac{\mathrm{B} \sin \theta}{\mathrm{A}+\mathrm{B} \cos \theta}\)

⇒ \(\varphi=\tan ^{-1}\left(\frac{B \sin \theta}{A+B \cos \theta}\right)\)

Triangle law of addition of vectors: To add two vectors \(\vec{A} \text { and } \vec{B}\) shift any of the two vectors parallel to itself until the tail of \(\vec{B}\) is at the head of \(\vec{A}\).

The sum \(\vec{A}+\vec{B}\) is a vector \(\vec{R}\) drawn from the tail of \(\vec{A}\)to the head of \(\vec{B}\), i.e.,\(\vec{A}+\vec{B}=\vec{R}\). As the figure formed is a triangle, this method is called the ‘ triangle method’ of the addition of vectors.

If the ‘triangle method’ is extended to add any number of vectors in one operation as shown. Then the figure formed is a polygon and hence the name Polygon Law of addition of vectors is given to such type of addition.

Important Points:

To a vector only a vector of the same type can be added that represents the same physical quantity and the resultant is a vector of the same type.

As R = [A² + B² + 2AB cosθ]^1/2 so R will be maximum when, cos θ = max = 1, i.e., θ = 0º, i.e. vectors are like or parallel and R_max= A + B.

The resultant will be minimum if, cos θ = min = -1, i.e., θ = 180º, i.e. vectors are antiparallel, and R_min = A ~ B.

If the vectors A and B are orthogonal, i.e., θ = 90º, R = \(\sqrt{A^2+B^2}\)

As previously mentioned the resultant of two vectors can have any value from (A ~ B) to (A + B) depending on the angle between them and the magnitude of the resultant decreases as θ increases from 0º to 180º

The minimum number of unequal coplanar vectors whose sum can be zero is three.

The resultant of three non-coplanar vectors can never be zero, or a minimum number of noncoplanar vectors whose sum can be zero is four.

Subtraction of a vector from a vector is the addition of a negative vector, i.e.,

⇒ \(\vec{A}-\vec{B}=\vec{A}+(-\vec{B})\)

From figure it is clear that \(\vec{A}-\vec{B}\) is equal to addition of \(\overrightarrow{\mathrm{A}}\) with reverse of \(\overrightarrow{\mathrm{B}}\)

⇒ \(|\vec{A}-\vec{B}|=\left[(A)^2+\left(B^2\right)+2 A B \cos \left(180^{\circ}-\theta\right)\right]^{1 / 2}\)

⇒ \(|\vec{A}-\vec{B}|=\sqrt{A^2+B^2-2 A B \cos \theta}\)

Change in a vector’s physical quantity means subtraction of the initial vector from the final vector.

Question 4. Find the resultant of two forces each having magnitude F₀, and the angle between them is θ.

Answer:

⇒ \(F_{\text {Resultant }}^2=F_0^2+F_0^2+2 F_0^2 \cos \theta\)

⇒ \(2 F_0^2(1+\cos \theta)\)

⇒ \(2 F_0^2\left(1+2 \cos ^2 \frac{\theta}{2}-1\right)\)

⇒ \(2 \times 2 F_0^2 \cos ^2 \frac{\theta}{2}\)

⇒ \(\mathrm{F}_{\text {resultant }}=2 \mathrm{~F}_0 \cos \frac{\theta}{2}\)

Class 11 NEET Physics Vector Problems and Solutions

Question 5. Two non zero vectors \(\vec{A} \text { and } \vec{B}\) are such that \(|\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}|=|\overrightarrow{\mathrm{A}}-\overrightarrow{\mathrm{B}}|\). Find angle between \(\overrightarrow{\mathrm{A}}\)and \(\overrightarrow{\mathrm{B}}\)

Answer:

⇒ \(|\vec{A}+\vec{B}|=|\vec{A}-\vec{B}|\)

⇒ A² + B² + 2AB cos θ

= A² + B² – 2AB cos θ

⇒ 4AB cos θ = 0

⇒ cos θ = 0

⇒ θ = \(\frac{\pi}{2}\)

Question 6. If the sum of two unit vectors is also a unit vector. Find the magnitude of their difference.

Answer:

Let \(\hat{A} \text { and } \hat{B}\) are the given unit vectors and \(\hat{R}\) is their resultant then

⇒ \(|\hat{R}|=|\hat{A}+\hat{B}|\)

⇒ \(1=\sqrt{(\hat{A})^2+(\hat{B})^2+2|\hat{A} \| \hat{B}| \cos \theta}\)

1 = 1 + 1 + 2 cos θ

⇒ cos θ = \(-\frac{1}{2}\)

⇒ \(|\hat{A}-\hat{B}|=\sqrt{(\hat{A})^2+(\hat{B})^2-2|\hat{A}||\hat{B}| \cos \theta}\)

⇒ \(\sqrt{1+1-2 \times 1 \times 1\left(-\frac{1}{2}\right)}\)

⇒ \(\sqrt{3}\)

5. Resolution Of Vectors

If \(\vec{a} \text { and } \vec{b}\) be any two nonzero vectors in a plane with different directions and \(\overrightarrow{\mathrm{A}}\)be another vector in the same plane.

⇒ \(\overrightarrow{\mathrm{A}}\) can be expressed as a sum of two vectors – one obtained by multiplying \(\overrightarrow{\mathrm{a}}\) by a real number and the other obtained by multiplying

⇒ \(\overrightarrow{\mathrm{b}}\) by another real number.

⇒ \(\overrightarrow{\mathrm{A}}=\lambda \overrightarrow{\mathrm{a}}+\mu \overrightarrow{\mathrm{b}}\) (where λ and μ are real numbers)

We say that \(\overrightarrow{\mathrm{A}}\) has been resolved into two component vectors namely

⇒ \(\lambda \vec{a} \text { and } \mu \vec{b}\)

λ \(\vec{a} \text { and } \mu \vec{b}\) along \(\overrightarrow{\mathrm{a}} \text { and } \overrightarrow{\mathrm{b}}\) respectively. Hence one can resolve a given vector into two component vectors along a set of two vectors − all three lie in the same plane.

Resolution Along Rectangular Component:

It is convenient to resolve a general vector along the axes of a rectangular coordinate system using vectors of unit magnitude, which we call unit vectors. \(\hat{\mathrm{i}}, \hat{\mathrm{j}}, \hat{\mathrm{k}}\) are unit vector along x,y and z-axis as shown in figure below:

Resolution in two Dimension

Consider a vector \(\overrightarrow{\mathrm{A}}\) that lies in xy plane as shown in figure,

⇒\(\overrightarrow{\mathrm{A}}=\overrightarrow{\mathrm{A}}_1+\overrightarrow{\mathrm{A}}_2\)

⇒ \(\vec{A}_1=A_x \hat{i}, \quad \vec{A}_2=A_y \hat{j}\)

⇒ \(\vec{A}=A_x \hat{i}+A_y \hat{j}\)

The quantities A_x and A_y are called x- and y- components of the vector \(\overrightarrow{\mathrm{A}}\)

A_x is itself not a vector but \(A_x \hat{i}\) is a vector and so is \(A_y \hat{j}\)

A_x= A cos θ and A_y= A sin θ

It’s clear from the above equation that a component of a vector can be positive, negative, or zero depending on the value of θ. A vector \(\overrightarrow{\mathrm{A}}\) can be specified in a plane by two ways:

Its magnitude A and the direction θ it makes with the x-axis; or

Its components are A_x and A_y.

A = \(A=\sqrt{A_x^2+A_y^2}, \theta=\tan ^{-1} \frac{A_y}{A_x}\)

Note: If A = Ax ⇒ Ay = 0 and if A = Ay ⇒ Ax= 0 i.e. components of a vector perpendicular to itself is always zero.

The rectangular components of each vector and those of the

sum

⇒\(\overrightarrow{\mathrm{C}}=\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\) are shown in the figure. We saw that

⇒\(\overrightarrow{\mathrm{C}}=\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\) is equivalent to both

C_x = A_x+ B_x

and C_y = A_y+ B_y

Resolution In Three Dimensions: A vector \(\overrightarrow{\mathrm{A}}\) in components along x-, y- and z-axis can be written as:

⇒\(\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{BP}}=\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{BP}}\)

⇒\(\vec{A}=\vec{A}_z+\vec{A}_x+\vec{A}_y=\vec{A}_x+\vec{A}_y+\vec{A}_z\)

⇒ \(A_x \hat{i}+A_y \hat{j}+A_z \hat{k}\)

A = \(\sqrt{A_x^2+A_y^2+A_z^2}\)

⇒ \(A_x=A \cos \alpha, A_y=A \cos \beta, A_z=A \cos \gamma\)

where cos α, cos β, and cos γ are termed as Direction Cosines of a given vector \(\overrightarrow{\mathrm{A}}\).

cos² α + cos² β + cos² γ = 1

Mathematical Tools in Physics: Vector Solutions for NEET Class 11

Question 7. A mass of 2 kg lies on an inclined plane as shown in the figure. Resolve its weight along and perpendicular to the plane.(Assumeg=10m/s²)

Answer:

Component along the plane = 20 sin 30 = 10 N

component perpendicular to the plane = 20 cos 30 = \(10 \sqrt{3} \mathrm{~N}\)

Question 8. A vector makes an angle of 30º with the horizontal. If a horizontal component of the vector is 250. Find the magnitude of a vector and its vertical component.

Answer: Let vector is \(\overrightarrow{\mathrm{A}}\)

⇒ \(A_x=A \cos 30^{\circ}\) = 250

⇒ \(\frac{A \sqrt{3}}{2}\)

A= \(\frac{500}{\sqrt{3}}\)

⇒ \(A_y=A \sin 30^{\circ}\)

⇒ \(\frac{500}{\sqrt{3}} \times \frac{1}{2}\)

⇒ \(\frac{250}{\sqrt{3}}\)

Question 9. A = \(\overrightarrow{\mathrm{A}}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-3 \hat{k}\), when a vector \(\overrightarrow{\mathrm{B}}\) is added to \(\overrightarrow{\mathrm{A}}\), we get a unit vector along x-axis. Find the value of \(\overrightarrow{\mathrm{B}}\)? Also, find its magnitude

Answer:

⇒\(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}=\hat{\mathrm{i}}\)

⇒ \(\vec{B}=\hat{i}-\vec{A}=\hat{i}-(\hat{i}+2 \hat{j}-3 \hat{k})=-2 \hat{j}+3 \hat{k}\)

⇒ \(|\vec{B}|=\sqrt{(2)^2+(3)^2}=\sqrt{13}\)

Question 10. In the above question find a unit vector along \(\vec{B}\).

Answer:

⇒ \(\vec{B}=\frac{\vec{B}}{B}=\frac{-2 \hat{j}+3 \hat{k}}{\sqrt{13}}\)

Question 11. Vector \(\overrightarrow{\mathrm{A}}, \overrightarrow{\mathrm{B}} \text { and } \overrightarrow{\mathrm{C}}\) have magnitude 5, \(5 \sqrt{2}\) and 5 respectively, direction of \(\overrightarrow{\mathrm{A}}, \overrightarrow{\mathrm{B}} \text { and } \overrightarrow{\mathrm{C}}\) are towards east, North-East and North respectively. If \(\hat{i} \text { and } \hat{j}\) and are unit vectors along East and North respectively. Express the sum \(\vec{A}+\vec{B}+\vec{C}\) in terms of \(\hat{i}, \hat{j}\). Also, Find the magnitude and direction of the resultant.

Answer:

⇒ \(\overrightarrow{\mathrm{A}}=5 \hat{i}\)

⇒ \(\overrightarrow{\mathrm{C}}=5 \hat{j}\)

⇒ \(\vec{B}=5 \sqrt{2} \cos 45 \hat{i}+5 \sqrt{2} \sin 45 \hat{j} \quad=5 \hat{i}+5 \hat{j}\)

⇒ \(\vec{A}+\vec{B}+\vec{C}=5 \hat{i}+5 \hat{i}+5 \hat{j}+5 \hat{j} \quad=10 \hat{i}+10 \hat{j}\)

⇒ \(|\vec{A}+\vec{B}+\vec{C}|\)

⇒ \(\sqrt{(10)^2+(10)^2}=10 \sqrt{2}\)

⇒ \(\tan \theta=\frac{10}{10}=1\)

θ = 45º from East

Key Concepts of Vector Mathematics in NEET Physics Class 11

Question 12. You walk 3 Km west and then 4 Km headed 60° north of east. Find your resultant displacement

1. Graphically and
2. Using vector components.

Answer:

Picture the Problem: The triangle formed by the three vectors is not a right triangle, so the magnitudes of the vectors are not related by the Pythagoras theorem. We find the resultant graphically by drawing each of the displacements to scale and measuring the resultant displacement.

If we draw the first displacement vector 3 cm long and the second one 4 cm long, we find the resultant vector to be about 3.5 cm long.

Thus the magnitude of the resultant displacement is 3.5 Km. The angle θ made between the resultant displacement and the west direction can then be measured with a protractor. It is about 75°.

Let \(\overrightarrow{\mathrm{A}}\) be the first displacement and choose the x-axis to be in the easterly direction. Compute \(A_x \text { and } A_y, A_x=-3, A_y=0\)

Similarly, compute the components of the second displacement \(\vec{B}, B_x=4 \cos 60^{\circ}=2, B_y=4\) sin 60° = \(2 \sqrt{3}\)

The components of the resultant displacement = \(\vec{A}+\vec{B}\) are found by addition,

⇒ \(\overrightarrow{\mathrm{C}}=(-3+2) \hat{i}+(2 \sqrt{3}) \hat{j}=-\hat{i}+2 \sqrt{3} \hat{j}\)

The Pythagorean theorem gives the magnitude of \(\overrightarrow{\mathrm{C}}\)

⇒ \(C=\sqrt{1^2+(2 \sqrt{3})^2}\)

⇒ \(\sqrt{13}\)

⇒ 3.6

The ratio of C_y to C_x gives the tangent of the angle θ between \(\overrightarrow{\mathrm{C}}\) and the x-axis.

⇒ tan θ = \(2 \sqrt{3}\)/(-1)

⇒ \(\theta=-74^{\circ}\)

Remark: Since the displacement (which is a vector) was asked for, the answer must include either the magnitude and direction, or both components. In (2) we could have stopped at step 3 because the x and y components completely define the displacement vector.

• We converted the magnitude and direction to compare with the answer to part (1). Note that in step 5 of (2), a calculator gives the angle as –74°. However, the calculator can’t distinguish whether the x or y components are negative.
• We noted in the figure that the resultant displacement makes an angle of about 75° with the negative x-axis and an angle of about 105° with the positive x-axis. This agrees with the results in (a) within the accuracy of our measurement.

NEET Physics Class 11 Chapter 10 Mathematical Tools – Double Differentiation

If f is a differentiable function, then its derivative f’ is also a function, so f’ may have a derivative of its own, denoted by (f’)’ = f’’.

This new function f’’ is called the second derivative of f because it is the derivative of the derivative of f. Using Leibniz notation, we write the second derivative of y = f (x) as

⇒ \(\frac{d}{d x}\left(\frac{d y}{d x}\right)=\frac{d^2 y}{d x^2}\)

Another notation is f ’’ (x) = D₂ f (x) = D²f(x)

NEET Physics Class 11 Double Differentiation Key Concepts and Solutions

Interpretation Of Double Derivative

We can interpret f ’’ (x) as the slope of the curve y = f ’(x) at the point (x, f ’(x)). In other words, it is the rate of change of the slope of the original curve y = f (x).

• In general, we can interpret a second derivative as a rate of change of a rate of change. The most familiar example of this is acceleration, which we define as follows.
• If s = s(t) is the position function of an object that moves in a straight line, we know that its first derivative represents the velocity v(t) of the object as a function of time:

v(t) = s’(t) = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)

• The instantaneous rate of change of velocity concerning time is called the acceleration a(t) of the object.
• Thus, the acceleration function is the derivative of the velocity function and is therefore the second derivative of the position function:

a (t) = v’(t) = s’’(t)

or in Leibniz notation, a = \(\frac{d v}{d t}=\frac{d^2 s}{d t^2}\)

Double Differentiation NEET Physics Class 11 Chapter 10 Solutions

Question 1. If f (x) = x cos x, find f ’’ (x).

Answer:

Using the Product Rule, we have

f’ (x) = \(x \frac{d}{d x}(\cos x)+\cos x \frac{d}{d x}(x)\)

= – x sin x + cos x

To find f’’ (x) we differentiate f’(x):

f’’(x) = \(\frac{d}{d x}\) (–x sin x + cos x)

⇒ \(-x \frac{d}{d x}(\sin x)+\sin x \frac{d}{d x}(-x)+\frac{d}{d x}(\cos x)\)

= – x cos x – sin x – sin x

= – x cos x – 2 sin x

Question 2. The position of a particle is given by the equation s = f (t) = t³ – 6t² + 9t. where t is measured in seconds and s in meters. Find the acceleration at time t. What is the acceleration after 4s?

Answer:

The velocity function is the derivative of the position function :

s = f (t) = t³ – 6t² + 9t

⇒ v(t) = \(\frac{d s}{d t}=3 t^2-12 t+9\)

The acceleration is the derivative of the velocity function :

⇒ \(a(t)=\frac{d^2 s}{d t^2}=\frac{d v}{d t}=6 t-12\)

⇒ \(a(4)=6(4)-12=12 \mathrm{~m} / \mathrm{s}^2\)

Application Of Derivatives

Differentiation As A Rate Of Change

⇒ \(\frac{d y}{d x}\) is rate of change of ‘y’ with respect to ‘x’ :

For examples:

1. v =\(\frac{d x}{d t}\) This means velocity ‘v’ is the rate of change of displacement ‘x’ concerning time ‘t’
2. a = \(\frac{d v}{d t}\) This means acceleration ‘a’ is the rate of change of velocity ‘v’ concerning time ‘t’.
3. F = \(\frac{d p}{d t}\) This means force ‘F’ is the rate of change of momentum ‘p’ concerning time ‘t’.
4. τ = \(\frac{d L}{d t}\) This means torque ‘τ ’ is the rate of change of angular momentum ‘L’ concerning time ‘t’
5. Power = \(\frac{d W}{d t}\) This means power ‘P’ is the rate of change of work ‘W’ concerning time ‘t’
6. Ι = \(\frac{d q}{d t}\) This means current ‘Ι’ is the rate of flow of charge ‘q’ concerning time ‘t’

NEET Class 11 Physics Chapter 10 Double Differentiation Problems and Solutions

Question 1. The area A of a circle is related to its diameter by the equation A = \(\frac{\pi}{4} D^2\). How fast is the area changing concerning the diameter when the diameter is 10 m?

Answer:

The (instantaneous) rate of change of the area concerning the diameter is

⇒ \(\frac{\mathrm{dA}}{\mathrm{dD}}=\frac{\pi}{4} 2 \mathrm{D}=\frac{\pi \mathrm{D}}{2}\)

When D = 10 m, the area is changing at a rate (π/2) 10 = 5π m²/m. This means that a small change

ΔD m in the diameter would result in a change of about 5π ΔD m² in the area of the circle.

Question 2. Experimental and theoretical investigations revealed that the distance a body released from rest falls in time t is proportional to the square of the amount of time it has fallen. We express this by saying that

s = \(\frac{1}{2} \mathrm{gt}^2\)

Double Differentiation Practice Problems for NEET Physics Class 11

where s is distance and g is the acceleration due to Earth’s gravity. This equation holds in a vacuum, where there is no air resistance, but it closely models the fall of dense, heavy objects in air. The figure shows the free fall of a heavy ball bearing released from rest at time t = 0 sec.

1. How many meters does the ball fall in the first 2 sec?
2. What is its velocity, speed, and acceleration then?

Answer:

1. The free–fall equation is s = 4.9 t².

During the first 2 sec. the ball falls

s= 4.9(2)² = 19.6 m,

2. At any time t, velocity is derivative of displacement:

v(t) = s’(t) = \(\frac{d}{d t}\)(4.9t²) = 9.8 t.

At t = 2, the velocity is v= 19.6 m/sec in the downward (increasing s) direction. The speed at t = 2 is

speed = |v(2)| = 19.6 m/sec.

a = \(\frac{\mathrm{d}^2 \mathrm{~s}}{\mathrm{dt}^2}\)

= 9.8m/s²

Double Differentiation Techniques in NEET Physics Class 11

Maxima And Minima:

Suppose a quantity y depends on another quantity x in a manner shown in the figure. It becomes maximum at x₁ and minimum at x₂. At these points, the tangent to the curve is parallel to the x−axis, and hence its slope is tan θ = 0. Thus, at a maximum or a minimum,

slope = \(\frac{d y}{d x}=0\)

Application Of Derivatives Maxima:

Just before the maximum, the slope is positive, at the maximum, it is zero and just after the maximum, it is negative. Thus, \(\frac{d y}{d x}\) decreases at a maximum and hence the rate of change of \(\frac{d y}{d x}\) is negative at a maximum i.e. \(\frac{d}{d x}\left(\frac{d y}{d x}\right)\) < 0 at maximum.

The quantity \(\frac{d}{d x}\left(\frac{d y}{d x}\right)\) is the rate of change of the slope. It is written as \(\frac{d^2 y}{d x^2}\)

Conditions for maxima are: \(\frac{d y}{d x}=0\)

⇒ \(\frac{d^2 y}{d x^2}<0\)

Application Of Derivatives Minima:

Similarly, at a minimum the slope changes from negative to positive. Hence with the increases of x., the slope is increasing which means the rate of change of slope concerning x is positive

hence \(\frac{d}{d x}\left(\frac{d y}{d x}\right)>0\)

Conditions for minima are: \(\frac{d y}{d x}=0\)

⇒ \(\frac{d^2 y}{d x^2}>0\)

Quite often it is known from the physical situation whether the quantity is a maximum or a minimum.

The test on \(\frac{d^2 y}{d x^2}\) may then be omitted.

NEET Physics Class 11 Chapter 10: Mathematical Tools – Double Differentiation Formulas and Solutions

Question 3. Find minimum value of y = 1 + x² – 2x

⇒ \(\frac{d y}{d x}=2 x-2\) for minima \(\frac{d y}{d x}=0\)

2x-2 = 0

x = 1

⇒ \(\frac{d^2 y}{d x^2}=2\)

⇒ \(\frac{d^2 y}{d x^2}>0\)

at x =1, there are minima

for a minimum value of y

y_minima = 1 + 1 – 2 = 0

Calorimetry And Thermal Expansion Multiple Choice Question And Answers

Question 31. A block of ice at -10ºC is slowly heated and converted to steam at 100ºC. Which of the following curves represent the phenomenon qualitatively:

Answer: 1.

Question 32. 540 g of ice at 0°C is mixed with 540g of water at 80°C. What is the final temperature of the mixture?

1. 0°C
2. 40°C
3. 80°C
4. 0°C

Answer: 1. 0°C

Question 33. The thermal capacity of anybody is :

1. A measure of its capacity to absorb heat
2. A measure of its capacity to provide heat
3. The quantity of heat required to raise its temperature by a unit degree
4. The quantity of heat required to raise the temperature of a unit mass of the body by a unit degree

Answer: 3. The quantity of heat required to raise its temperature by a unit degree

NEET Physics Class 11 Calorimetry and Thermal Expansion MCQs

Question 34. The figure shows the pressure-temperature phase diagram for water, the curves corresponding to sublimation, fusion, and vaporization respectively are

1. AO, OB, and OC
2. BO, OC, and AO
3. OC, BO, and AO
4. AO, OC, and BO

Answer: 1. AO, OB and OC

Question 35. An electric kettle takes a 4A current at 220V. How much time will it take to boil 1 kg of water at a temperature of 20°C? The temperature of boiling water is 100°C:

1. 6.3 min
2. 8.4 min
3. 12.6 min
4. 4.2 min

Answer: 1. 6.3 min

Question 36. The time taken by an 836 W heater to heat one liter of water from 10ºC to 40ºC is :

1. 50 s
2. 100 s
3. 150 s
4. 200 s

Answer: 3. 150 s

Question 37. 2 liters of water at 27°C is heated by a 1 kW heater in an open container. On average heat is lost to surroundings at the rate of 160 J/s. The time required for the temperature to reach 77°C is

1. 8 min 20 sec
2. 10 min
3. 7 min
4. 14 min

Answer: 1. 8 min 20 sec

Question 38. A piece of ice (heat capacity = 2100 J kg^-1ºC^-1 and latent heat = 3.36 × 105 J kg^-1) of mass m grams is at –5 ºC at atmospheric pressure. It is given 420 J of heat so that the ice starts melting. Finally, when the ice-water mixture is in equilibrium, it is found that 1 gm of ice has melted. Assuming there is no other heat exchange in the process, the value of m is:

1. 8 gm
2. 5 gm
3. 6 gm
4. 10 gm

Answer: 1. 8 gm

Question 39. Two large holes are cut in a metal sheet. If this is heated, distances AB and BC, (as shown) 

1. Both will increase
2. Both will decrease
3. AB increases, BC decreases
4. AB decreases, BC increases

Answer: 1. Both will increase

Question 40. A steel scale is to be prepared such that the millimeter intervals are to be accurate within 6 ×10^-5 mm. The maximum temperature variation from the temperature of calibration during the reading of the millimeter marks is (α = 12 × 10^-6 k^-1)

1. 4.0°C
2. 4.5°C
3. 5.0°C
4. 5.5°C

Answer: 3. 5.0°C

Question 41. Expansion during heating –

1. Occurs only in a solid
2. Increases the density of the material
3. Decreases the density of the material
4. Occurs at the same rate for all liquids and solids.

Answer: 3. Decreases the density of the material

Calorimetry and Thermal Expansion MCQs for NEET Physics Class 11

Question 42. If a bimetallic strip is heated, it will.

1. Bend towards the metal with a lower thermal expansion coefficient.
2. Bend towards the metal with a higher thermal expansion coefficient.
3. Twist itself into a helix.
4. Have no bending.

Answer: 1. Bend towards the metal with a lower thermal expansion coefficient.

Question 43. Two holes of unequal diameters d₁ and d₂(d₁ > d₂) are cut in a metal sheet. If the sheet is heated-

1. Both d₁and d₂ will decrease
2. Both d₁ and d₂ will increase
3. d₁ will increase d₂ will decrease
4. d₁ will decrease, d₂ will increase

Answer: 2. Both d₁ and d₂ will increase

Question 44. Two bars of copper having the same length but unequal diameter are heated to the same temperature. The change in length will be –

1. More in thinner bar
2. More in thicker bar
3. Same for both the bars
4. Determined by the ratio of length and diameter of the bars

Answer: 3. Same for both the bars

Question 45. A metallic bar is heated from 0ºC to 100ºC. The coefficient of linear expansion is 10^-5K^-1. What will be the percentage increase in length

1. 0.01%
2. 0.1%
3. 1%
4. 10%

Answer: 2. 0.1%

Question 46. A pendulum clock has an iron pendulum 1m long (α_iron = 10^-5/ºC). If the temperature rises by 10ºC, the clock-

1. Will lose 8 seconds per day
2. Will lose 4.32 seconds per day
3. Will gain 8 seconds per day
4. Will gain 4.32 seconds per day

Answer: 2. Will lose 4.32 seconds per day

Question 47. Two rods of lengths l₁and l₂ are made of materials whose coefficient of linear expansions is α₁ are α₂. If the difference between two lengths is independent of temperature –

1. \(\frac{\ell_1}{\ell_2}=\frac{\alpha_1}{\alpha_2}\)
2. \(\frac{\ell_1}{\ell_2}=\frac{\alpha_2}{\alpha_1}\)
3. \(\ell_2^2 \alpha_1=\ell_1^2 \alpha_2\)
4. \(\frac{\alpha_1^2}{\ell_1}=\frac{\alpha_2^2}{\ell_2}\)

Answer: 2. \(\frac{\ell_1}{\ell_2}=\frac{\alpha_2}{\alpha_1}\)

Question 48. If α, β, γ are respectively the linear, superficial and cubical expansivity of a homogeneous solid, then –

1. α : β : γ = 1 : 2 : 3
2. α : β : γ = 3 : 2 : 1
3. α : β : γ = 2 : 3 : 1
4. α : β : γ = 3 : 1 : 3

Answer: 1. α : β : γ = 1 : 2 : 3

Question 49. The coefficient of linear expansion of steel and brass are 11 × 10^-6/ºC and 19 × 10^-6/ºC respectively. If their difference in lengths at all temperatures has to be kept constant at 30cm, their lengths at 0ºC should be –

1. 71.25 cm and 41.25 cm
2. 82 cm and 52 cm
3. 92 cm and 62 cm
4. 62.25 cm and 32.25 cm

Answer: 1. 71.25 cm and 41.25 cm

Question 50. A solid ball of metal has a spherical cavity inside it. If the ball is heated, the volume of the cavity will –

1. Increase
2. Decrease
3. Remains unchanged
4. Have its shape changed

Answer: 1. Increase

Question 51. If the length of a cylinder on heating increases by 2%, the area of its base will increase by

1. 0.5%
2. 2%
3. 1%
4. 4%

Answer: 4. 4%

Question 52. A uniform metal rod is used as a bar pendulum. If the room temperature rises by 10ºC, and the coefficient of linear expansion of the metal of the rod is 2 × 10^-6 perºC, the period of the pendulum will have a percentage increase of –

1. – 2 × 10^-3
2. – 1 × 10^-3
3. 2 × 10^-3
4. 1 × 10^-3

Answer: 4. 1 × 10^-3

Question 53. The volume of a solid decreases by 0.6% when it is cooled to 50ºC. Its coefficient of linear expansion is –

1. 4 × 10^-6K
2. 5 × 10^-5K
3. 6 × 10⁴K
4. 4 × 10^-5K

Answer: 4. 4 × 10^-5K

Question 54. Which of the following graphs represents variation in density of water with temperature best –

Answer: 4.

Question 55. A rectangular block is heated from 0ºC to 100ºC. The percentage increase in its length is 0.10% What will be the percentage increase in its volume?

1. 0.03 %
2. 0.10%
3. 0.30%
4. None of these

Answer: 3. 0.30%

NEET Physics Class 11 Multiple Choice Questions on Calorimetry

Question 56. A thin copper wire of length l increases in length by 1% when heated from 0ºC to 100ºC. If a then cooper plate of area 2l × l is heated from 0ºC to 100ºC, the percentage increase in its area will be

1. 1%
2. 2%
3. 3%
4. 4%

Answer: 2. 2%

Question 57. If Ι is the moment of inertia of a solid body having α -coefficient of linear expansion then the change in Ι corresponding to a small change in temperature ΔT is

1. \(\frac{1}{2}\) α Ι ΔT
2. 2α Ι ΔT
3. 2 α Ι ΔT
4. 3 α Ι ΔT

Answer: 3. 2 α Ι ΔT

Question 58. A liquid with a coefficient of volume expansion γ is filled in a container of a material having the coefficient of linear expansion α .Ιf the liquid overflows on heating, then.

1. γ > 3α
2. γ < 3α
3. γ = 3α
4. None of these

Answer: 1. γ > 3α

Question 59. Two rods having lengths l₁ and l₂, made of materials with the linear expansion coefficient α₁ and α₂, were soldered together. The equivalent coefficients of linear expansion for the obtained rod:-

⇒ \(\frac{\ell_1 \alpha_2+\ell_2 \alpha_1}{\ell_1+\ell_2}\)

⇒ \(\frac{\alpha_1 \alpha_2}{\alpha_1+\alpha_2}\)

⇒ \(\frac{\ell_1 \alpha_1+\ell_2 \alpha_2}{\ell_1+\ell_2}\)

⇒ \(\frac{\left(\alpha_1+\alpha_2\right)}{2}\)

Answer: 3. \(\frac{\ell_1 \alpha_1+\ell_2 \alpha_2}{\ell_1+\ell_2}\)

Question 60. The volume thermal expansion coefficient of an ideal gas at constant pressure and temperature TK is

1. T
2. T²
3. \(\frac{1}{\mathrm{~T}}\)
4. \(\frac{1}{\mathrm{~T}^2}\)

Answer: 3. 1T

Question 61. A metallic ball and a highly stretched spring are made of the same material and have the same mass. They are heated so that they melt, the latent heat required

1. Are the same for both
2. Is greater for the ball
3. Is greater for the spring
4. The two may or may not be the same depending on the metal

Answer: 1. Are the same for both

Question 62. The coefficients of linear expansions of brass and steel are α₁ and α₂ respectively. When we take a brass rod of length l₁ and a steel rod of length l₂ at 0°C, then the difference in their lengths (l₂– l₁) will remain the same at all temperatures if :

1. α₁l₁= α₂l₂
2. α₁l₂= α₂l₁
3. α₁₂l₂= α_2²l₁
4. α₁l_2² = α₂ l_1²

Answer: 1. α₁l₁= α₂l₂

Question 63. If on heating liquid through 80ºC, the mass expelled is (1/100) th of mass still remaining, the coefficient of apparent expansion of liquid is:

1. 1.25 × 10^-4/ºC
2. 12.5 × 10^-4/ºC
3. 1.25 × 10^-5/ºC
4. None of these

Answer: 1. 1.25 × 10^-4/ºC

Question 64. An iron bar of length l and having a cross-section A is heated from 0 to 100ºC. If this bar is so held that it is not permitted to expand or bend, the force that is developed is:

1. Inversely proportional to the cross-sectional area of the bar
2. Independent of the length of the bar
3. Inversely proportional to the length of the bar
4. Directly proportional to the length of the bar

Answer: 2. Independent of the length of the bar

Thermal Expansion and Calorimetry MCQs for NEET Physics Class 11

Question 65. If the sphere of iron is heated, then its

1. Density increases
2. Volume increases
3. Radius decreases
4. None of these

Answer: 2. Volume increases

Question 66. Two rods, one of aluminum of length l₁ having a coefficient of linear expansion αaand the other of steel having a coefficient of linear expansion α_s and length l₂ are joined end to end. The expansion in both the rods is the same for the same variation of temperature. Then the value of \(\frac{\ell_1}{\ell_1+\ell_2}\)
Answer:

1. \(\frac{\alpha_{\mathrm{s}}}{\alpha_{\mathrm{a}}}\)
2. \(\frac{\alpha_{\mathrm{a}}}{\alpha_{\mathrm{s}}}\)
3. \(\frac{\alpha_s}{\alpha_a+\alpha_s}\)
4. \(\frac{\alpha_a}{\alpha_a+\alpha_s}\)

Answer: 3. \(\frac{\alpha_s}{\alpha_a+\alpha_s}\)

Question 67. A difference in temperature of 25º C is equivalent to a difference in franchise:

1. 45º F
2. 72º F
3. 32º F
4. 25º F

Answer: 1. 45º F

Question 68. What is the temperature at which we get the same reading on both the centigrade and Fahrenheit scales?

1. – 40ºC or – 40ºF
2. – 30ºC or – 30º F
3. – 30ºC or – 40ºF
4. – 10ºC or – 10ºF

Answer: 1. – 40ºC or – 40ºF

Question 69. Absolute temperature can be calculated by

1. Mean square velocity of molecules
2. Motion of the molecule
3. Both (a) and (b)
4. None of the above

Answer: 1. Mean square velocity of molecules

Question 70. The absolute zero is the temperature at which

1. Water freezes
2. All substances exist in a solid state
3. Molecular motion ceases
4. None of the above

Answer: 3. Molecular motion ceases

Question 71. Absolute zero (0K) is the temperature at which

1. Matter ceases to exist
2. Ice melts and water freezes
3. The volume and pressure of a gas become zero
4. None to these

Answer: 3. The Volume and pressure of gas become zero

Question 72. The temperature on the Celsius scale is 25°C. What is the corresponding temperature on the Fahrenheit scale

1. 40°F
2. 77°F
3. 50°F
4. 45°F

Answer: 2. 77°F

Question 73. Two thermometers are used to record the temperature of a room. If the bulb of one is wrapped in a wet hanky

1. The temperature recorded by both will be the same
2. The temperature recorded by the wet-bulb thermometer will be greater than that recorded by the other
3. The temperature recorded by the dry-bulb thermometer will be greater than that recorded by the other
4. None of the above

Answer: 3. The temperature recorded by dry-bulb thermometer will be greater than that recorded by the other

Question 74. A centigrade and a Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit thermometer registers 140°F. What is the fall in temperature as registered by the Centigrade thermometer

1. 30°
2. 40°
3. 60°
4. 80°

Answer: 2. 40°

NEET Physics Class 11 Calorimetry: MCQs and Answers

Question 75. A 5°C rise in temperature is observed in a conductor by passing a current. When the current has doubled the rise in temperature will be approximately:

1. 16°C
2. 10°C
3. 20°C
4. 12°C

Answer: 3. 20°C

Question 76. Value of – 40ºC in Fahrenheit scale is:

1. –40º F
2. 32°F
3. –32ºF
4. 40ºC

Answer: 1. –40º F

Question 77. If temperature of an object is 140º F, then its temperature in centrigrade is :

1. 105ºC
2. 32ºC
3. 140°C
4. 60ºC

Answer: 4. 60ºC

Question 78. The color of a star indicates its :

1. Temperature
2. Distance
3. Velocity
4. Size

Answer: 1. Temperature

Question 79. The temperature of a body on a kelvin scale is found to be x K. When it is measured by Fahrenheit thermometer, it is found to be x°F, then the value of x is:

1. 30
2. 313
3. 574.25
4. 301.25

Answer: 3. 574.25

Question 80. A constant pressure thermometer when immersed in ice-cooled water gives a volume reading of 47.5 units and when immersed in boiling liquid, it gives a reading of 67 units. What is the boiling point of the liquid?

1. 135°C
2. 125°C
3. 112°C
4. 100°C

Answer: 3. 112°C

Question 81. A beaker is completely filled with water at 4°C. The water will overflow if it is :

1. Warmed to a temperature greater than 4°C
2. Cooled to a temperature less than 4°C
3. and both
4. None of the above

Answer: 3. and both

Question 82. On a new scale of temperature (which is linear) called the W scale, the freezing and boiling points of water are 39°W and 239°W respectively. What will be the temperature on the new scale, corresponding to a temperature of 39°C on the Celsius scale?

1. 78°C
2. 117°W
3. 200°W
4. 139°W

Answer: 2. 117°W

Question 83. A thermally isolated vessel contains 100 g of water at 0ºC. When air above the water is pumped out, some of the water freezes and some evaporates at 0ºC itself. Then the mass of the ice formed if no water is left in the vessel. Latent heat of vaporization of water at 0ºC = 2.10 × 10⁶ J/kg and latent heat of fusion of ice = 3.36 × 10⁵J/kg.

1. 86.2 g
2. 13.8 g
3. 76.2 g
4. 65.6 g

Answer: 1. 86.2 g

Question 84. 2 kg ice at – 20 ºC is mixed with 5 kg water at 20 ºC. The final amount of water in the mixture would be : Given: specific heat of ice = 0.5 cal/g ºC, specific heat of water = 1 cal/g ºC, latent heat of fusion of ice = 80 cal/gm ]

1. 6 kg
2. 7 kg
3. 3.5 kg
4. 5 kg

Answer: 1. 6 kg

Question 85. In an insulated vessel, 0.05 kg of steam at 373 K and 0.45 kg of ice at 253 K are mixed. Find the final temperature of the mixture (in Kelvin).

Given, L_fusion = 80 cal/gm = 336 J/gm, L_vaporization = 540 cal/gm = 2268 J/gm,

S_ice = 2100 J/kg K = 0.5 cal/gm K and S_water = 4200 J/kg K = 1 cal/gmK

1. 273 K.
2. 373 K
3. 300 K
4. 253 K

Answer: 1. 273 K.

Question 86. The weight of a person is 60 kg. If he gets 105 calories heated through food and the efficiency of his body is 28%, then upto how much height he can climb when he user entire energy gained is climbing

1. 100 m
2. 200 m
3. 400 m
4. 1000 m

Answer: 2. 200 m

Question 87. When a block of iron floats in mercury at 0°C a fraction k₁ of its volume is submerged, while at the temperature 60ºC, a fraction k₂ is seen to be submerged. If the coefficient of volume expansion of iron is γFe, then the ratio \(\frac{k_1}{k_2}\)

1. \(\frac{1+60 \gamma_{\mathrm{Fe}}}{1+60 \gamma_{\mathrm{Hg}}}\)
2. \(\frac{1-60 \gamma_{\mathrm{Fe}}}{1+60 \gamma_{\mathrm{Hg}}}\)
3. \(\frac{1+60 \gamma_{\mathrm{Fe}}}{1-60 \gamma_{\mathrm{Hg}}}\)
4. \(\frac{1+60 \gamma_{\mathrm{Hg}}}{1+60 \gamma_{\mathrm{Fe}}}\)

Answer: 1. \(\frac{1+60 \gamma_{\mathrm{Fe}}}{1+60 \gamma_{\mathrm{Hg}}}\)

Question 88. A hot wire of copper is stretched at a temperature of 150ºC between two fixed walls. At what temperature will the wire break when it is cooled? The breaking stress of copper is 2.45 × 10⁸ N/m² Young’s modulus of copper = 11.8 × 10¹⁰ N/m², coefficient of linear expansion of copper = 1.6 ×10^-5/ºC.

1. 20.2ºC
2. 43.2ºC
3. 64.9ºC
4. 70.2ºC

Answer: 1. 20.2ºC

Calorimetry and Thermal Expansion Questions for NEET Physics Class 11

Question 89. Liquid oxygen at 50K is heated to 300 K at a constant pressure of 1 atm. The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time?

Answer: 1.

Question 90. Steam at 1000C is passed into 20g of water at 100C. When water acquires a temperature of 800C, the mass of water present will be:

[Take specific heat of water = 1 cal g^-1 °C^-1 and latent heat of steam = 540 cal g^-1]

1. 24 g
2. 31.5 g
3. 42.5 g
4. 22.5 g

Answer: 4. 22.5 g

Question 91. The value of the coefficient of volume expansion of glycerin is 5 × 10^-4 K^-1. The fractional change in the density of glycerin for a rise of 40°C in its temperature, is:

1. 0.020
2. 0.025
3. 0.010
4. 0.015

Answer: 1. 0.020

Question 92. a piece of ice falls from a height h so that it melts completely. Only one-quarter of the heat produced is absorbed by the ice and all energy of ice gets converted in to heat during its fall. The value of h is :

[Latent heat of ice is 3.4 × 10⁵ J/Kg and g = 10 N/kg]

1. 68 km
2. 34 km
3. 544 km
4. 136 km

Answer: 4. 136 km

Question 93. A sample of 0.1 g of water at 100ºC and normal pressure (1.013 × 105 Nm^-2) requires 54 cal of heat energy to convert to stream at 100ºC. If the volume of the steam produced is 167.1 cc, the change in internal energy of the sample is:

1. 104.3 J
2. 84.5 J
3. 42.2 J
4. 208.7 J

Answer: 4. 208.7 J

Question 94. A metal rod of Young’s modulus Y and coefficient of thermal expansion α is held at its two ends such that its length remains invariant. If its temperature is raised by tºC, the linear stress developed in its is:

1. \(\frac{Y}{\alpha t}\)
2. \(Y \alpha t\)
3. \(\frac{1}{(Y \alpha t)}\)
4. \(\frac{\alpha t}{Y}\)

Answer: 2. \(Y \alpha t\)

Question 95. An aluminum sphere of 20 cm diameter is heated from 0ºC to 100ºC. Its volume changes by (given that coefficient of linear expansion for aluminum α_Al = 23 × 10^-6/ºC)

1. 2.89 cc
2. 9.28 cc
3. 49.8 cc
4. 28.9 cc

Answer: 4. 28.9 cc

Question 96. A wooden wheel of radius R is made of two semicircular parts (see figure). The two parts are held together by a ring made of a metal strip of cross-sectional area S and length L. L is slightly less than 30 2πR. To fit the ring on the wheel, it is heated so that its temperature rises by ΔT and it just steps over the wheel. As it cools down to the surrounding temperature, it presses the semicircular parts together. If the coefficient of linear expansion of the metal is α, and its Young’s modulus is Y, the force that one part of the wheel applies on the other part is:

1. 2πSYαΔT
2. SYαΔT
3. π SYαΔT
4. 2SYαΔT

Answer: 4. 2SYαΔT

Question 97. A pendulum clock loses 12 s a day if the temperature is 40°C and gains 4 s a day if the temperature is 20°C. The temperature at which the clock will show the correct time, and the coefficient of linear expansion (α) of the metal of the pendulum shaft are respectively:

1. 60°C ; α = 1.85 × 10^-4/°C
2. 30°C ; α = 1.85 × 10^-3/°C
3. 55°C ; α = 1.85 × 10^-2/°C
4. 25°C ; α = 1.85 × 10^-5/°C

Answer: 4. 25°C ; α = 1.85 × 10^-4/°C

NEET Physics Class 11 Thermal Expansion and Heat MCQs

Question 98. A copper ball of mass 100 gm is at a temperature T. It is dropped in a copper calorimeter of mass 100 gm, and filled with 170 gm of water at room temperature. Subsequently, the temperature of the system is found to be 75º C. T is given by : (Given: room temperature = 30ºC, specific heat of copper = 0.1 cal/gmºC)

1. 825º C
2. 800ºC
3. 885ºC
4. 1250ºC

Answer: 3. 885ºC

Question 99. An external pressure P is applied on a cube at 0°C so that it is equally compressed from all sides. K is the bulk modulus of the material of the cube and α is its coefficient of linear expansion. Suppose we want to bring the cube to its original size by heating it. The temperature should be raised by:

1. \(3 P K \alpha\)
2. \(\frac{\mathrm{P}}{3 \alpha \mathrm{K}}\)
3. \(\frac{\mathrm{P}}{\alpha \mathrm{K}}\)
4. \(\frac{3 \alpha}{\mathrm{PK}}\)

Answer: 2. \(\frac{\mathrm{P}}{3 \alpha \mathrm{K}}\)

Question 100. An unknown metal of mass 192 g heated to a temperature of 100°C was immersed into a brass calorimeter of mass 128 g containing 240 g of water at a temperature of 8.4°C. Calculate the specific heat of the unknown metal if the water temperature stabilizes at 21.5°C. (Specific heat of brass is 394 J kg^-1 K^-1)

1. 916 J kg^-1 K^-1
2. 458 J kg^-1 K^-1
3. 1232 J kg^-1 K^-1
4. 654 J kg^-1 K^-1

Answer: 1. 916 J kg^-1 K^-1

Question 101. A metal ball of mass 0.1 kg is heated upto 500°C and dropped into a vessel of heat capacity 800 JK^-1 containing 0.5 kg water. The initial temperature of the water and vessel is 30°C. What is the approximate percentage increment in the temperature of the water? [Specific Heat Capacities of water and metal are, respectively, 4200 Jkg^-1K^-1 and 400Jkg^-1K^-1]

1. 30%
2. 25%
3. 15%
4. 20%

Answer: 4. 20%

Question 102. Two rods A and B of identical dimensions are at a temperature of 30°C. If A is heated upto 180°C and B upto T°C, then the new lengths are the same. If the ratio of the coefficients of linear expansion of A and B is 4 : 3, then the value of T is :

1. 270°C
2. 200°C
3. 230°C
4. 250°C

Answer: 3. 230°C

Calorimetry and Thermal Expansion MCQ Practice for NEET Physics

Question 103. Ice at -20°C is added to 50 g of water at 40 °C. When the temperature of the mixture reaches 0°C, it is found that 20 g of ice is still unmelted. The amount of ice added to the water was close to (Specific heat of water = 4.2J/g/°C Specific heat of Ice = 2.1 J/g/°C. Heat of fusion of water at 0°C = 334 J/g

1. 100 g
2. 40 g
3. C60 g
4. 50 g

Answer: 2. 40 g