NCERT Notes For Class 6 Maths Chapter 1 Knowing Our Numbers
Knowing Our Numbers Introduction
Counting things is easy for us now. We can count objects in large numbers, for example, the number of students in the school, and represent them through numerals. We can also communicate large numbers using suitable number names.
It is not as if we always knew how to convey large quantities in conversation or through symbols. Many thousands of years ago, people knew only small numbers. Gradually, they learned how to handle larger numbers.
They also learned how to express large numbers in symbols. All this came through the collective efforts of human beings. Their path was not easy, they struggled all along the way.
The development of the whole of Mathematics can be understood this way. As human beings progressed, there was a greater need for the development of Mathematics and as a result, Mathematics grew further and faster.
We use numbers and know many things about them. Numbers help us count concrete objects. They help us to say which collection of objects is bigger and arrange them for example, first, second, etc.
Read and Learn More NCERT Notes for Class 6 Maths
Numbers are used in many different contexts and in many ways. Think about various situations where we use numbers. List five distinct situations in which
numbers are used.
We enjoyed working with numbers in our previous classes. We have added, subtracted, multiplied, and divided them. We also looked for patterns in number sequences and did many other interesting things with numbers.
In this chapter, we shall move forward on such interesting things with a bit of review and revision as well.

Comparing Numbers
As we have done quite a lot of this earlier, let us see if we remember which is the greatest among these:
1. 92, 392, 4456, 89742
89742 I am the greatest
2. 1902, 1920, 9201, 9021, 9210
9210 I am the greatest
So, we know the answer
We just looked at the number of digits and found the answer. The greatest number has the most thousands and the smallest is only in hundreds or in tens.
Make five more problems of this kind and give them to your friends to solve.
Now, how do we compare 4875 and 3542?
This is also not very difficult. These two numbers have the same number of digits. They are both in thousands. But the digit at the thousands place in 4875 is greater than that in 3542. Therefore, 4875 is greater than 3542.
Next tell me which is greater, 4875 or 4542? Here too the numbers have the same number of digits. Further, the digits at the thousands place are the same in both.
What do we do then? We move to the next digit, that is to the digit at the hundreds place. The digit at the hundreds place is greater in 4875 than in 4542. Therefore, 4875 is greater than 4542.
If the digits at the hundreds place are also the same in the two numbers, then what do we do?
Compare 4875 and 4889; Also compare 4875 and 4879.
How Many Numbers Can You Make?
Suppose, we have four digits 7, 8, 3, 5. Using these digits we want to make different 4-digit numbers in such a way that no digit is repeated in them. Thus, 7835 is allowed, but 7735 is not. Make as many 4-digit numbers as you can.
Which is the greatest number you can get? Which is the smallest number?
The greatest number is 8753 and the smallest is 3578.
Think about the arrangement of the digits in both. Can you say how the largest number is formed? Write down your procedure.
Shifting Digits
Have you thought how fun it would be if the digits in a number could shift (move^frpm from one place to the other?
Thinlq about what would happen to 182. It could become as large as 821 and as small as 128. Try this with 391 as well.
Now think about this. Take any 3-digit number and exchange the digit at the hundreds place with the digit at the one’s place.
- Is the new number greater than the former one?
- Is the new number smaller than the former number?
Write the numbers formed in both ascending and descending order.
Before 7 9 5
Exchanging the 1st and the 3rd tiles.
After 5 9 7
If you exchange the 1st and the 3rd tiles (i.e. digits), in which case does the number become greater? In which case does it become smaller?
Try this with a 4-digit number.
Introducing 10,000
We know that beyond 99 there is no 2-digit number. 99 is the greatest 2-digit number. Similarly, the greatest 3-digit number is 999 and the greatest 4-digit number is 9999. What shall we get if we add 1 to 9999?
Look at the pattern:
9 + 1 = 10 = 10 x 1
99 + 1 = 100 = 10 x 10
999 + 1 = 1000 = 10 x 100
We observe that
Greatest single digit number + 1 = smallest 2-digit number
Greatest 2-digit number + 1 = smallest 3-digit number
Greatest 3-digit number + 1 = smallest 4-digit number
We should then expect that on adding 1 to the greatest 4-digit number, we would get the smallest 5-digit number, that is 9999 + 1 = 10000.
The new number which comes next to 9999 is 10000. It is called ten thousand. Further, 10000 = 10 x 1000.
Revisiting Place Value
You have done this quite earlier, and you will certainly remember the expansion of a 2-digit number like 78 as 78 = 70 + 8 = 7 x 10 + 8
Similarly, you will remember the expansion of a 3-digit number like 278 as 278 = 200 + 70 + 8 = 2 x 100 + 7 x 10 + 8
We say, here, 8 is at one place, 7 is at the tens place, and 2 at the hundreds place.
Later on, we extended this idea to 4-digit numbers.
For example, the expansion of 5278 is 5278 = 5000 + 200 + 70 + 8
= 5 x 1000 + 2 x 100 + 7 x 10 + 8
Here, 8 is at one place, 7 is at the tens place, 2 is at the hundreds place and 5 is at the thousands place.
With the number 10000 known to us, we may extend the idea further. We may write 5-digit numbers like 45278 = 4 x 10000 + 5 x 1000 + 2 x 100 + 7 x 10 + 8
We say that here 8 is at one place, 7 at the tens place, 2 at the hundreds place, 5 at the thousands place, and 4 at ten thousand places.
The number is read as forty-five thousand, two hundred seventy-eight. Can you now write the smallest and the greatest 5-digit numbers?
Introducing 1,00,000
Which is the greatest 5-digit number?
Adding 1 to the greatest 5-digit number should give the smallest 6-digit number: 99,999 + 1 = 1,00,000
This number is named one lakh. One lakh comes next to 99,999.
10 x 10,000 = 1,00,000
We may now write 6-digit numbers in the expanded form as
2,46,853 = 2 x 1,00,000 + 4x 10,000 + 6 x 1,000 + 8 x 100 + 5 x 10 + 3 x 1
This number is 3 in one place, 5 in the tens place, 8 in the hundreds place, 6 in the thousands place, 4 in ten thousand places, and 2 in lakh place. Its number name is two lakh forty-six thousand eight hundred fifty three.
Larger numbers
If we add one more to the greatest 6-digit number we get the smallest 7-digit number. It is called ten lakh.
Write down the greatest 6-digit number and the smallest 7-digit number. Write the greatest 7-digit number and the smallest 8-digit number. The smallest 8-digit number is called one crore.
Complete The Pattern:
Remember
1 hundred =10 tens
1 thousand = 10 hundreds = 100 tens
1 lakh = 100 thousands = 1000 hundreds
1 crore =100 lakhs = 10,000 thousands
9 + 1 = 10
99 + 1 = 100
999 + 1 = 1,000
9.999 + 1 = 10,000
99.999 + 1 = 1,00,000
9.99.999 + 1 = 10,00,000
99.99.999 + 1 = 1,00,00,000
We come across large numbers in many different situations. For example, while the number of children in your class would be a 2-digit number, the number of children in your school, would be a 3 or 4-digit number.
The number of people in the nearby town would be much larger.
NCERT Notes For Class 6 Maths Use Of Commas
You must have noticed that in writing large numbers in the sections above, we have often used commas.
Commas help us in reading and writing large numbers. In our Indian System of Numeration, we use ones, tens, hundreds, thousands, and then lakhs and crores.
Commas are used to mark thousands, lakhs, and crores. The first comma comes after hundreds place (three digits from the right) and marks thousands. The second comma comes two digits later (five digits from the right).
It comes after ten thousand places and marks lakh. The third comma comes after another two digits (seven digits from the right). It comes after ten lakh place and marks crore.
For example,
5,08,01,592
3,32,40,781
7,27,05,062
Try reading the numbers given above. Write five more numbers in this form and read them.
International System of Numeration
In the International System of Numeration, as it is being used we have ones, tens, hundreds, thousands, and then millions. One million is a thousand thousand. Commas are used to mark thousands and millions.
It comes after every three digits from the right. The first comma marks thousands and the next comma marks millions. For example, the number 50,801,592 is read in the International System as fifty million eight hundred one thousand five hundred ninety-two.
In the Indian System, it is five crore eight lakh one thousand five hundred ninety-two.
How many lakhs make a million?
How many millions make a crore?
Take three large numbers. Express them in both Indian and International Numeration systems.
Interesting Fact:
To express numbers larger than a million, a billion is used in the International System of Numeration: 1 billion = 1000 million.
NCERT Notes For Class 6 Maths Large Numbers In Practice
In earlier classes, we learned that we use centimeters (cm) as a unit of length. For measuring the length of a pencil, the width of a book or notebook, etc., we use centimeters. Our ruler has marks on each centimeter.
However, we find centimeters too big when measuring the thickness of a pencil. We use millimeters (mm) to show the thickness of a pencil.
1. 10 millimetres = 1 centimetre
To measure the length of the classroom or the school building, we shall find a centimeter too small. We use meters for this purpose.
2. 1 metre =100 centimetres = 1000 millimetres
Even meter is too small when we have to state distances between cities, say, Delhi and Mumbai, or Chennai and Kolkata. For this, we need kilometers (km).
3. 1 kilometre = 1000 metres
How many millimeters make 1 kilometer?
Since 1 m = 1000 mm
1 km = 1000 m = 1000 x 1000 mm = 10,00,000 mm
We go to the market to buy rice or wheat; we buy it in kilograms (kg). But items like ginger or chilies which we do not need in large quantities, we buy in grams (g). We know 1 kilogram = 1000 grams.
Have you noticed the weight of the medicine tablets given to the sick? It is very small. It is in milligrams (mg)
1 gram = 1000 milligrams.
What is the capacity of a bucket for holding water? It is usually 20 liters (l). Capacity is given in liters. But sometimes we need a smaller unit, the milliliters. A bottle of hair oil, a cleaning liquid, or a soft drink has labels that give the quantity of liquid inside in milliliters (ml).
1 litre = 1000 millilitres.
Note that in all these units we have some words in common like kilo, milli, and centi. You should remember that among these kilo is the greatest and milli is the smallest; the kilo shows 1000 times greater, and the milli shows 1000 times smaller, i.e. 1 kilogram = 1000 grams, 1 gram = 1000 milligrams.
Similarly, centi shows 100 times smaller, i.e. 1 metre = 100 centimetres.
We have done a lot of problems that have addition, subtraction, multiplication, and division. We will try solving some more here. Before starting, look at these examples and follow the methods used.
Example 1. The population of Sundamagar was 2,35,471 in the year 1991. In the year 2001, it was found to be increased by 72,958. What was the population of the city in 2001?
Solution:
Population of the city in 2001
= Population of the city in 1991 + Increase in population = 2,35,471 + 72,958
Now, \(\begin{array}{r}
235471 \\
+72958 \\
\hline 308429 \\
\hline
\end{array}\)
Salma added them by writing 235471 as 200000 + 35000 + 471 and 72958 as 72000+958. She got the addition as 200000 +107000 +1429 = 308429. Mary added it as 200000 + 35000 + 400 + 71 + 72000 + 900 + 58 = 308429
Answer: The population of the city in 2001 was 3,08,429
All three methods are correct.
Example 2. In one state, the number of bicycles sold in the year 2002-2003 was 7,43,000. In the year 2003-2004, the number of bicycles sold was 8,00,100. In which year were more bicycles sold? and how many more?
Solution:
Clearly, 8,00,100 is more than 7,43,000. So, in that state, more bicycles were sold in the year 2003-2004 than in 2002-2003.
Now, \(\begin{array}{r}
800100 \\
-743000 \\
\hline 057100 \\
\hline
\end{array}\)
Check the answer by adding \(\begin{array}{r}
743000 \\
+57100 \\
\hline 800100 \\
\hline
\end{array}\) (the answer is right)

Can you think of alternative ways of solving this problem?
Answer: 57,100 more bicycles were sold in the year 2003-2004.
Example 3. The town newspaper is published every day. One copy has 12 pages, every day 11,980 copies are printed. How many total pages are printed every day?
Solution:
Each copy has 12 pages. Hence, 11,980 copies. will have 12 x 11,980 pages. What would this number be? More than 1,00,000 or lesser.
Try to estimate.
Now, \(\begin{array}{r}
11980 \\
\times 12 \\
\hline 23960 \\
+\quad 119800 \\
\hline 143760 \\
\hline
\end{array}\)

Answer: Every day 1,43,760 pages are printed.
Example 4. The number of sheets of paper available for making notebooks is 75,000. Each sheet makes 8 pages of a notebook. Each notebook:(contains 200 pages. How many notebooks can be made from the paper available?
Solution:
Each sheet makes 8 pages.
Hence, 75,000 sheets make 8 x 75,000 pages,
Now, \(\begin{array}{r}
75000 \\
\times 8 \\
\hline 600000 \\
\hline
\end{array}\)

Thus, 6,00,000 pages are available for making notebooks.
Now, 200 pages make 1 notebook.
Hence, 6,00,000 pages make 6,00,000 -r 200 notebooks.
Now,
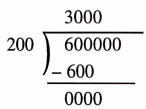
The answer is 3,000 notebooks.
