NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials

NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials

An Expression of the form p(x)= a₀+a₀x+a₀x₀…..+a₀xⁿ

For example.,

5x+1 is a polynomial of degree in x. Here, a0,a1,a2,…..an are real numbers.

2x²-x-1 is apolynomial in x of degree 2.

y³-2y²+y+5 is a polynomial in y of degree 3.

5z⁴-3z+1 is a polynomial in z of degree 4.

Constant Polynomial

A polynomial of degree zero is called a constant polynomial.

For example., p(x) = -3, q(x) = 2,f(x) = \(\sqrt{2}\) etc., are constant polynomials. (These are independent of variable)

Zero Polynomial

It is also a constant polynomial with a particular constant value of 0.

So,f(x) = 0 is a zero polynomial. Its degree is not defined, as we cannot say definitely about its degree. Forms of zero polynomial may be

Read and Learn More Class 10 Maths Solutions Exemplar

f(x) = 0 = 0 . x² – 0 .x + 0 = 0 . x⁵ – 0 . x²= 0 . J-5 + 0. x⁹ + 0. x⁴ – 0 . x² + 0., etc.

So, we cannot say anything about the degree of a zero polynomial.

Linear Polynomial

A polynomial of degree 1 is called a linear polynomial.

It is of the form

p(x) = ax + b,

where a ≠ 0

For example., 3x + 5, 5 – 2x, etc.

Quadratic Polynomial

A polynomial of degree 2 is called a quadratic polynomial. It is of the form

p(x) = ax² +bx + c, where a ≠ 0

x² + 5x + 1, 3x² – x + 1, 5 – x² etc.

Cubic Polynomial

A polynomial of degree 3 is called a cubic polynomial.

It is of the form

p(x) = ax³ +bx² +cx + d, where a ≠ 0

For example., x³ – x + 1, 5x² – 4x² – 2x + 1 etc.

Bi-quadratic Polynomial (or Quartic)

A polynomial of degree 4 is called a biquadratic polynomial.

It is of the form

p(x) = ax⁴ + bx³ + cx² + dx + e, a ≠ 0

For example., 2x⁴ -x² + 1, 2- 3x +x² + 4x² -x⁴ etc.

Note

Some other names for polynomials are:

NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials – Value Of A Polynomial At A Given Point

Let p(x) be a polynomial in x and a is any real number. Then the value obtained by putting x = a in the polynomial p(x) is called the value of the polynomial p(x) at x = a.

This value is denoted by p(a).

P(x) = x² +x- 1,

then p(5) = 5²+5-1= 25+5 = 29

NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials – Zeroes Of A Polynomial

A really a is called a zero of a polynomial P(x), if P(α) = 0

or, in other words,

zero of a polynomial is the real value of a variable that vanishes the whole polynomial i.e., the value of a variable that makes the whole polynomial zero.

For example., if P(x) = x²-3x+2

p(2) = 2²-3×2+2 = 4-6+2 = 0

∴ 2 is a zero of p(x)

To find the zero/es of a polynomial p(x), put the polynomial equation p(x) = 0.

For example,

Find the zeroes of polynomial p(x) = x² – 5x – 6

We know that zero of a polynomial is the value of a variable by which p(x) = 0.

⇒ x² – 5x – 6 = 0 ⇒ (x – 6) (x + 1) = 0

∴ either x – 6 = 0 or x+1=0

⇒ x = 6 or x= -1

So, 6 and -1 are two values of x which make the value of polynomial zero. (You can check on putting these values directly They will make p(x) = 0

Hence, 6 and -1 are the zeroes of the given polynomial.

2. Find the zeroes of polynomial p(x) = x² – 4x + 4

For zeroes, p(x) = 0

⇒ x²-4x +4 = 0

⇒ (x – 2)² = 0x – 2 = 0

⇒ x = 2

or x²-4x + 4 = 0 ⇒ (x – 2)(x – 2) = 0

⇒ x = 2, 2

It means, in this case, we get the repeated zeroes. But, we shall say the zero of this polynomial is 2 not the 2 and 2. To say 2 and 2 has no sense. So, if a polynomial has 2 or 3 or more repeated zeroes, we will say only one zero it has.

3. Find the zeros of polynomial p(x)_ = ax²+bx+c, a≠0

To find the zeroes, we put p(x) = 0

∴ \(a x^2+b x+c=0\)

⇒ \(x^2+\frac{b x}{a}+\frac{c}{a}=0\)  (dividing both sides by a)

⇒ \(x^2+\frac{b}{a} x+\underbrace{\frac{b^2}{4 a^2}-\frac{b^2}{4 a^2}}_{\begin{array}{c}
\text { Adding and subtracting } \\
\text { the same quantity }
\end{array}}+\frac{c}{a}=0\)

⇒ \(\left[\text { adding and subtracting }\left(\frac{\text { coff. of } x}{2}\right)^2\right]\)

⇒ \( \left(x+\frac{b}{2 a}\right)^2-\left(\frac{b^2}{4 a^2}-\frac{c}{a}\right)=0 \)

⇒ \(\left(x+\frac{b}{2 a}\right)^2-\left(\frac{b^2-4 a c}{4 a^2}\right)=0\)

⇒ \(\left(x+\frac{b}{2 a}\right)^2-\left(\frac{\sqrt{b^2-4 a c}}{2 a}\right)^2=0\)

(every number is the square of its square root)

⇒ \(\left(x+\frac{b}{2 a}+\frac{\sqrt{b^2-4 a c}}{2 a}\right)\left(x+\frac{b}{2 a}-\frac{\sqrt{b^2-4 a c}}{2 a}\right)=0\left[a^2-b^2=(a+b)(a-b)\right]\)

⇒ \(x=\frac{-b-\sqrt{b^2-4 a c}}{2 a} \text { or } x=\frac{-b+\sqrt{b^2-4 a c}}{2 a}\)

There are two zeroes of a given polynomial.

From the above 3 examples, we observe some very special points :

Zeroes are the values of x when p(x) orj; = 0. It means for example (6, 0) and (-1, 0) must be the points on the polynomial as well as on the x-axis (because the y-coordinate is zero) i.e., the intersection point of the polynomial and x-axis.

Conversely, we can say that if we draw the graph of a polynomial then the x-coordinate or abscissa of the intersection point of the curve and x-axis will give us the zeroes of the polynomial.

From the example, we notice that repeated zeroes will occur only when the polynomial is a perfect square. We still say it as only one zero. We also get only one zero from a linear polynomial, then what is the difference between linear polynomial and quadratic polynomial when we get only one zero in both cases?

So, our conclusion in this case is that a linear polynomial will be a straight line that will cut the x-axis at one point, and the x-coordinate of that point is the zero of that polynomial while a quadratic polynomial in this case of repeated zeroes will not cut the x-axis but it will touch the x-axis and turns thereafter. This is the basic difference between both types of polynomials in the case of one zero.

For example, we see that if x = 6 is a zero of the polynomial then, (x – 6) is one factor of the polynomial. If x = -1 is a zero of the polynomial then (x+ 1) is also one factor of polynomial.

So, if x = α and x = β are the zeroes of a polynomial then, necessarily (x – α) and (x – β) are the factors of that polynomial.

So, if α and β are the zeroes of a polynomial then the polynomial will be In the form (x-α) (x-β). Is it correct 100%? Perhaps, not, Why?

If we find the zeroes of x²-5x-6, we get 6 and -1 as zeros, if we find the zeros of 2x²-10x-12 i.e., 2(x²-5x-6) we also get 6 and -1 as zeros. If we find zeros of 3x²-15x-18 i.e., 3(x²-5x-6). we also get 6 and -1 as the zeroes. If we find the zero of

⇒ \(-\frac{1}{3} x^2+\frac{5}{3} x+2 \text { i.e… }-\frac{1}{3}\left(x^2-5 x-6\right)\)

also get the zeroes as 6 and -1.

Then, if it is given that a and |3 arc the zeroes of a quadratic polynomial then the quadratic polynomial will be k (x – α) (x – β), where k may be any non-zero real number.

Now, let us study the curves (polynomials) graphically.

NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials – Geometrical Meaning Of Zeroes Of A Polynomial

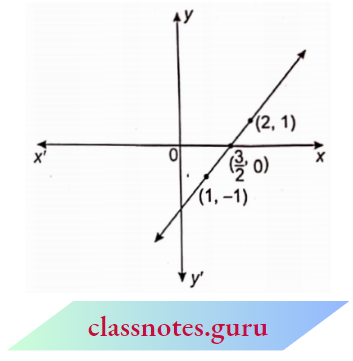
Case 1: Consider the first-degree polynomial p(x) = ax + b, a≠0. We know that the graph of y = ax + b is a straight line for example., consider the equation y = 2x – 3. This line passes through the point (1, -1) and (2, 1). Draw the graph of this line as shown. It crosses the x-axis at a point this linear equation has exactly one zero namely \(\frac{3}{2}\).

Thus, for the polynomial p(x) = ax + b, (a≠0) zero of p(x) is \(x=-\frac{b}{a}\)

Case 2: Consider the second-degree polynomial p(x) = ax + bx + c, a ≠ 0.

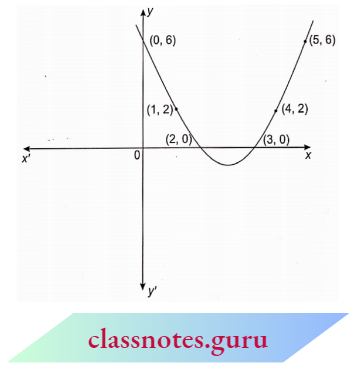
Consider an example say p(x) = x² – 5x + 6. Let us see the graph of y = x² -5x + 6.

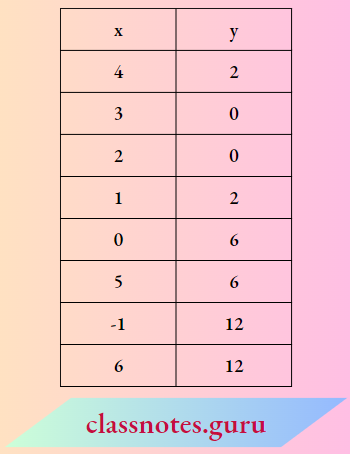
Draw the graph of this line as shown.

This graph intersects the j-axis at two points namely (2, 0) and (3, 0). In fact the graph of y = ax² + bx + c, a ≠ 0 has one of the two shapes either open upwards like when a > 0 or open downward like A when a < 0. These curves are called parabolas.

1. When the graph cuts the x-axis at two points A and A’.

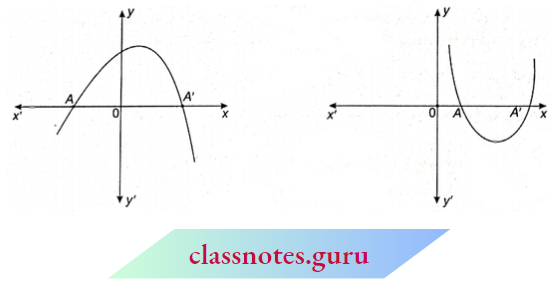
Here, the x coordinates of A and A’ are two zeroes of the quadratic polynomial.

2. When the graph cuts the x-axis at one point i.e., at two coincident points.

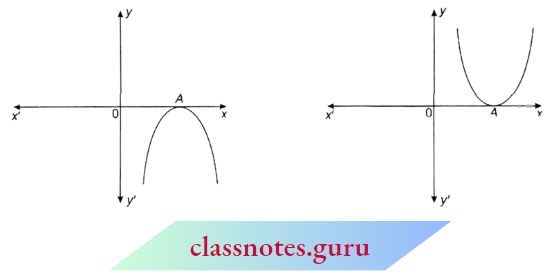
The x coordinate of A is the only zero of the quadratic polynomial.

3. When the graph is either completely above the x-axis or completely below the x-axis i.e., it does not cut the x-axis at any point.

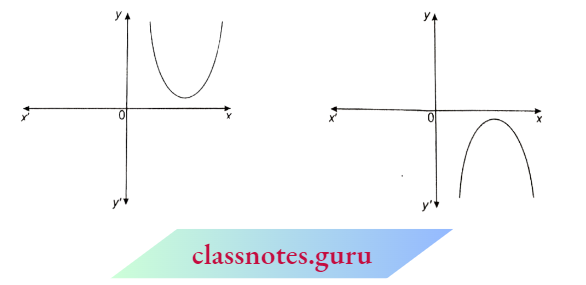
The quadratic polynomial has no zero in this case.

Case 3: Consider the third-degree polynomial p(x) = ax³ + bx² + cx + d, a ≠ 0.

It can have at most 3

zeroes, depending upon the point of intersection of y = ax³ +bx²+cx+d and x-axis.

NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials – Relation Between Zeroes And Coefficients Of A Quadratic Polynomial

Consider the quadratic polynomial

p(x) – ax² +bx + c, a ≠ 0

Let α, and β be the zeroes of p(x), then (x – α) and (x – β) will be the factors of p(x).

ax² + bx + c = k(x – α) (x – β), k ≠ 0

= k [x² – (α + β)x + αβ]

= kx² – k(α + β)x + Kαβ

On comparing the coefficients of like powers on both sides, we get

k = a

⇒ \(-k(\alpha+\beta)=b \Rightarrow-a(\alpha+\beta)=b \Rightarrow \alpha+\beta=\frac{-b}{a}\)

⇒ \(k \alpha \beta=c \Rightarrow \quad a \alpha \beta=c \Rightarrow \alpha \beta=\frac{c}{a}\)

∴ \(\text { sum of zeroes }=-\frac{\text { coefficient of } x}{\text { coefficient of } x^2},\)

⇒ \(\text { product of zeroes }=\frac{\text { constant term }}{\text { coefficient of } x^2}\)

If a and p are the zeroes of a quadratic polynomial p(x), then

p(x) = k[x² – (α + β)x + αβ], k ≠ 0

NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials – Quadratic Polynomial Solved Examples

Question 1. Find zeroes of the polynomial x – 3x + 2 and verify the relation between its zeroes and coefficients.
Solution:

Given x – 3x + 2

Let p(x) =x²-3x + 2 = x²-2x-x + 2

= x(x-2)-1 (x-2) = (x-2) (x- 1)

∴ P(x) = 0

⇒ (x- 2)(x – 1) = 0

⇒ x – 2 = 0 or x – 1 = 0

⇒ x = 2 or x – 1

∴ Zeroes of p(x) are 2 and 1

Now, Sum of zeroes = 2 + 1 = 3 = \(-\frac{-3}{1}=-\frac{\text { coefficient of } x}{\text { coefficient of } x^2}\)

and product of zeroes = (2) (1) = 2 = \(\frac{2}{1}=\frac{\text { constant term }}{\text { coefficient of } x^2}\)

Question 2. Find zeroes of the quadratic \(\sqrt{3} x^2-8 x+4 \sqrt{3}\) and verify the relation between the zeroes and coefficients.
Solution:

Given \(\sqrt{3} x^2-8 x+4 \sqrt{3}\)

Let p(x) = \(\sqrt{3} x^2-8 x+4 \sqrt{3}=\sqrt{3} x^2-6 x-2 x+4 \sqrt{3}\)

\(\sqrt{3} x(x-2 \sqrt{3})-2(x-2 \sqrt{3})=(x-2 \sqrt{3})(\sqrt{3} x-2)\)

∴ p(x) = 0

⇒ \((x-2 \sqrt{3})(\sqrt{3} x-2)\) = 0

⇒ \(x-2 \sqrt{3}=0\)

or \(\sqrt{3} x-2=0\)

⇒ \(x=2 \sqrt{3}\)

or \(x=\frac{2}{\sqrt{3}}\)

∴ Zeroes of p(x) are \(2 \sqrt{3} \text { and } \frac{2}{\sqrt{3}}\)

Now, sum of zeros = \(=2 \sqrt{3}+\frac{2}{\sqrt{3}}\)

⇒ \(\frac{6+2}{\sqrt{3}}\)

⇒ \(\frac{8}{\sqrt{3}}\)

⇒ \(-\frac{(-8)}{\sqrt{3}}\)

⇒ \(-\frac{\text { coefficient of } x}{\text { coefficient of } x^2}\)

and product of zeros = \((2 \sqrt{3})\left(\frac{2}{\sqrt{3}}\right)=4\)

⇒ \(\frac{4 \sqrt{3}}{\sqrt{3}}\)

⇒ \(\frac{\text { constant term }}{\text { coefficient of } x^2}\)

Question 3. Find zeroes of the polynomial x2 – 4 and verify the relation between /crocs and coefficients.
Solution:

Given x² – 4

Let p(x) = x² – 4 = x² – 2² = (x – 2) (x + 2)

∴ p(x) = 0

(x-2)(x + 2) = 0

x – 2 = 0 or x + 2 = 0

x = 2 or x = -2

∴ Zeroes of p(x) are 2 and -2

Now, sum of zeroes = 2 + (-2) = 0 = \(-\frac{0}{1}=-\frac{\text { coefficient of } x}{\text { coefficient of } x^2}\)

and product of zeroes = (2) (-2) = -4 = \(\frac{-4}{1}=\frac{\text { constant term }}{\text { coefficient of } x^2}\)

Question 4. Find a quadratic polynomial, the sum of whose zeroes is 5 and their product is 6. Hence, find the zeroes of the polynomial.
Solution:

Given

The sum of whose zeroes is 5 and their product is 6

Let a and (3 be the zeroes of the polynomial p(x).

Given that α + β = 5 and αβ = 6

Now, p(x) – x² – (α + β)x + αβ = x² – 5x ÷ 6 = x² – 3x – 2x ÷ 6

= x(x – 3) – 2 (x – 3) = (x – 3) (x – 2)

There may be so many different polynomials which satisfy the given condition. Actually the general quadratic polynomial will be k(x² – 5x + 6), where k = 0

∴ p(x) = 0

⇒ (x – 2)(x – 3) = 0

⇒ (x – 2) = 0 or (x – 3) = 0

⇒ x = 2 or x = 3

Zeroes are 2 and 3

zeroes of the polynomial 2 and 3.

Question 5. If the product of zeroes of the polynomial (ax² – 6x – 6) is 4. find the value of a.
Solution:

Given polynomial = ax² – 6x – 6

product of zeroes = \(\frac{\text { constant term }}{\text { coefficient of } x^2}\)

⇒ \(4=\frac{-6}{a}\)

4a = -6

⇒ \(a=-\frac{6}{4}\)

⇒ \(=-\frac{3}{2}\)

The value of a =\( -\frac{3}{2}\)

Question 6. If x = \(\frac{2}{3}\) and .v = -3 are zeroes of the quadratic polynomial ax2+7x+b, then find the values of a and b.
Solution:

Given

x = \(\frac{2}{3}\) and .v = -3 are zeroes of the quadratic polynomial ax2+7x+b

Let p(x) = ax² + 7x + b

∵ \(x=\frac{2}{3}\) and x = -3 are zeroes of p(x)

⇒ \(p\left(\frac{2}{3}\right)=0\)

⇒ \(a\left(\frac{2}{3}\right)^2+7\left(\frac{2}{3}\right)+b=0\)

⇒ \(\frac{4 a}{9}+\frac{14}{3}+b=0\)

⇒ \(b=-\frac{4 a}{9}-\frac{14}{3}\)

and p(-3) = 0

⇒ a(-3)²+7(-3)+b = 0

⇒ \( 9 a-21-\frac{4 a}{9}-\frac{14}{3}=0\)

⇒ \(\frac{81 a-4 a}{9}=\frac{14}{3}+21=\frac{14+63}{3}\)

⇒ \(\frac{77 a}{9}=\frac{77}{3}\)

a=3

For equation (1)

⇒ \(b=\frac{-4 \times 3}{9}-\frac{-14}{3}=-6\)

a=3, b=-6

The values of a and b are 3 and -6.

Question 7. If one zero of the polynomial (a² + 9)x² + 13x+6a is reciprocal of the other, find the value of a.
Solution:

Given

one zero of the polynomial (a² + 9)x² + 13x+6a is reciprocal of the other

Let p(x) = (a² + 9)x² +13x+ 6a

Let α and \(\frac{1}{\alpha}\) be zeroes of p(x) then,

product of zeroes = \(\frac{\text { constant term }}{\text { coefficient of } x^2}\)

⇒ \(\alpha \cdot \frac{1}{\alpha}=\frac{6 a}{a^2+9}\)

⇒ \(I=\frac{6 a}{a^2+9}\)

⇒ a²+9 = 6a

⇒ a²-6a+9 = 0

⇒ (a-3)² = 0

⇒ a-3 = 0

a = 3

The value of a is 3.

NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials – Relation Between Zeroes And Coefficients Of A Cubic Polynomial

Consider a cubic polynomial.

p(x) = ax³ + bx² + cx + d, a ≠ 0

Let α, β, γ be zeroes of p(x), then (x – α), (x – β), (x – γ) will be the factors of p(x).

∴ ax³ + bx² + cx + d = k(x – α)(x- β)(x – γ)

Comparing, we get

k = a

⇒ \(-k(\alpha+\beta+\gamma)=b \quad \Rightarrow \quad \alpha+\beta+\gamma=-\frac{b}{a}\)

(k=a)

⇒ \(k(\alpha \beta+\beta \gamma+\gamma \alpha)=c \quad \Rightarrow \quad \alpha \beta+\beta \gamma+\gamma \alpha=\frac{c}{a}\)

⇒ \(-k \alpha \beta \gamma=d \quad \Rightarrow \quad \alpha \beta \gamma=-\frac{d}{a}\)

p(x) = \(x^3-(\alpha+\beta+\gamma) x^2+(\alpha \beta+\beta \gamma+\gamma \alpha) x-\alpha \beta \gamma .\)

NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials – Division Algorithm For Polynomials

If(x) and g(x) are two polynomials with g(x) ≠ 0, then we can find polynomials q(x) and r(x), such that

f(x) = q{x) x g(x) + r(x).

where r(x) = 0 or deg {r(A)} < deg {g(x)}.

NCERT Exemplar Solutions for Class 10 Maths Chapter 2 Polynomials – Division Algorithm Solved Examples

Question 1. Verify that 1,2,3 is the zeros of the cubic polynomial p(x) = x³-6x²+11x-6 and verify the relation between its zeroes and coefficients.
Solution:

Given p(x) = x³-6x²+11x-6

Here,

p(x)=\(x^3-6 x^2+11 x-6\)

p(1)=\(1^3-6(1)^2+11(1)-6=1-6+11-6=0\)

p(2)=\(=2^3-6(2)^2+11(2)-6=8-24+22-6=0\)

p(3)=\(=3^3-6(3)^2+11(3)-6=27-54+33-6=0\)

and

∴ 1,2 and 3 are zeroes of p(x).

Now, \(\alpha+\beta+\gamma\)

⇒ \(1+2+3=6\)

⇒ \(-\frac{-6}{1}\)

⇒ \(-\frac{\text { coefficient of } x^2}{\text { coefficient of } x^3}\)

αβ + βγ+ γα = (1 )(2) + (2)(3) + (3)(1) = 2 + 6 + 3= 11

⇒ \(\frac{11}{1}\)

⇒ \(\frac{\text { coefficient of } x}{\text { coefficient of } x^3}\)

⇒ \(\text { and } \alpha \beta y=(1)(2)(3)=6=-\frac{-6}{1}=-\frac{\text { constant term }}{\text { coefficient of } x^3}\)

Question 2. Find a cubic polynomial whose zeroes are \(\frac{1}{2},-\frac{3}{2}\) and 2
Solution:

Given

a cubic polynomial whose zeroes are \(\frac{1}{2},-\frac{3}{2}\) and 2

Let \(\alpha=\frac{1}{2}, \beta=-\frac{3}{2} \text { and } \gamma=2\)

∴ \(\alpha+\beta+\gamma=\frac{1}{2}-\frac{3}{2}+2=1\)

⇒ \(\alpha \beta+\beta \gamma+\gamma \alpha=\left(\frac{1}{2}\right)\left(-\frac{3}{2}\right)+\left(-\frac{3}{2}\right)(2)+\left(\frac{1}{2}\right)(2)=\frac{-3}{4}-3+1=-\frac{11}{4}\)

⇒ \(\alpha \beta \gamma=\left(\frac{1}{2}\right)\left(-\frac{3}{2}\right)(2)=-\frac{3}{2}\)

Cubic polynomial = \(x^3-(\alpha+\beta+\gamma) x^2+(\alpha \beta+\beta \gamma+\gamma \alpha) x-\alpha \beta \gamma\)

⇒ \(x^3-x^2-\frac{11}{4} x-\frac{3}{2} \approx 4 x^3-4 x^2-11 x-6\)

The cubic polynomial is \(x^3-x^2-\frac{11}{4} x-\frac{3}{2} \approx 4 x^3-4 x^2-11 x-6\)

Question 3. Divide 2x²+x-5 by x + 2 and verify the division algorithm.
Solution:

Given  2x²+x-5 and x + 2

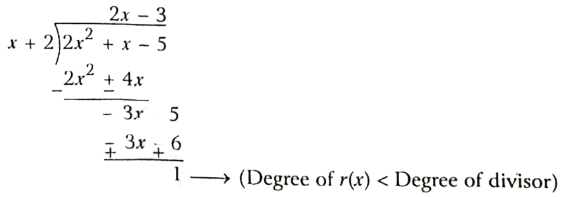
Now, quotient = 2x- 3, remainder = 1

dividend = 2x² + x- 5 and divisor = x+ 2

and quotient x division + remainder = (2x-3)(x+2) +1

\(2 x^2+4 x-3 x-6+1=2 x^2+x-5\)

= division

Question 4. If the polynomial \(\left(x^4+2 x^3+8 x^2+12 x+18\right)\) is divided by another polynomial (x2+5), the remainder comes out to be (px+q). Find the values of p and q.
Solution:

Given \(\left(x^4+2 x^3+8 x^2+12 x+18\right)\) is divided by another polynomial (x2+5)

Let f(x) = \(x^4+2 x^3+8 x^2+12 x+18\) and g(x) = x²+5

On dividing f(x) by g(x)

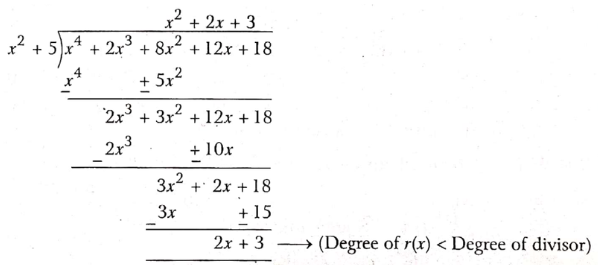
∵ the remainder is given px+q.

∴ p=2 and q=3

The values of p and q 2 and 3.

Question 5. What real number should be subtracted from the polynomial (3x³ + 10x² – 14x + 9) so that (3x- 2) divides it exactly?
Solution:

Given (3x³ + 10x² – 14x + 9)

On dividing (3x³ + 10x² – 14x + 9) by (3x- 2)

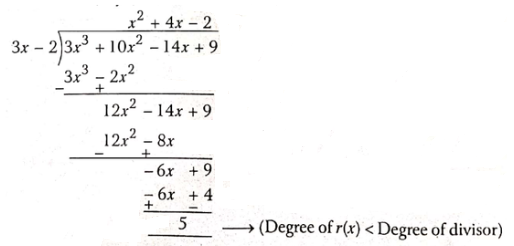
∵ the remainder = 5

∴ required number = 5

The real number should be subtracted from the polynomial is 5.

Question 6. If 2 is a zero of the polynomial x³-2x²-x+2, then find its other zeroes.
Solution:

Given

2 is a zero of the polynomial x³-2x²-x+2

Let p(x) = x³-3x³-x+2

∵ x=2 is a zero of p(x)

(x-2) is a factor of p(x)

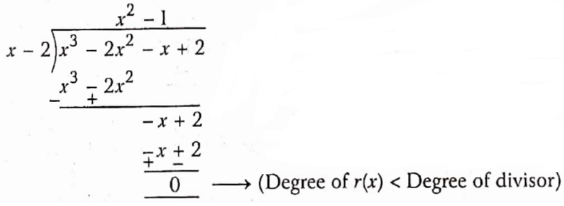
∴ p(x) = \(x^3-2 x^2-x \div 2=(x-2)\left(x^2-1\right)=(x-2)\left(x^2-1^2\right)\)

= (x-2)(x-1)(x 1)

Now, p(x) = 0

⇒ (x-2)(x-1)(x 1) = 0

⇒ x-2 = 0 or x-1 = 0  or x  1 =0

⇒ x=2 or x=1 or x=-1

Hence, other zeroes are 1 and -1.

Question 7. Obtain all other zeroes of (x⁴ + 4x³– 2x²– 20x- 15) if two of its zeroes are \(\sqrt{5} \text { and }-\sqrt{5}\)
Solution:

Given

(x⁴ + 4x³– 2x²– 20x- 15) if two of its zeroes are \(\sqrt{5} \text { and }-\sqrt{5}\)

Let p(x) = x⁴ + 4x³– 2x⁴– 20x- 15

∵ \(\sqrt{5} \text { and }-\sqrt{5}\) are zeroes of p(x)

∴ \(x-\sqrt{5} \text { and } x+\sqrt{5}\) are factors of p(x).

So, \((x-\sqrt{5})(x+\sqrt{5})=x^2-5\) is a factor of p(x)

∴ p(x) = \(x^4+4 x^3-2 x^2-20 x-15=\left(x^2-5\right)\left(x^2+4 x+3\right)\)

⇒ \(\left(x^2-5\right)\left[x^2+x+3 x+3\right]=\left(x^2-5\right)[x(x+1)+3(x+1)]\)

⇒ \(\left(x^2-5\right)(x+1)(x+3)\)

∴ The other zeroes are given by

x+1 = 0 or x+3 = 0

⇒ x = -1 or x = -3

Hence, other zeroes are -1 and -3

Question 8. Find zeroes of the polynomial p(x) = x³ – 9x² + 26x – 24, if it is given that the product of its two zeroes is 8.
Solution:

Given polynomial p(x) = x³ – 9x² + 26x – 24

Let α, β, γ be zeroes of the given polynomial p(x), such that αβ = 8 …….(1)

⇒ \(\alpha+\beta+\gamma=-\frac{(-9)}{1}=9\) ……….(2)

⇒ \(\alpha \beta+\beta \gamma+\gamma \alpha=\frac{26}{1}=26\) …..(3)

⇒ \(\alpha \beta \gamma=-\frac{(-24)}{1}=24\) ………..(4)

From (1) and (4)

8γ = 24

γ = 3

Put γ = 3 in (2), we get α+β = 6 ……..(5)

⇒ \((\alpha-\beta)^2=(\alpha+\beta)^2-4 \alpha \beta\)

⇒ \(=(6)^2-4(8)\)

⇒ \(=36-32\)

⇒ \(=4\)

⇒ \(\alpha-\beta= \pm 2\) …..(6)

Solving (5) and (6), we get

a= 4, b = 2  or a=2, b = 4 and r = 3

So, zeroes are 2,3 and 4

Question 9. Find the common zeroes of the polynomials x³ +x²– 2x- 2 and x³– x² – 2x + 2.
Solution:

Given x³ +x²– 2x- 2 and x³– x² – 2x + 2

For the common zeroes, first, we find the H.C.F. of given polynomials by Euclid’s division method (long division method)

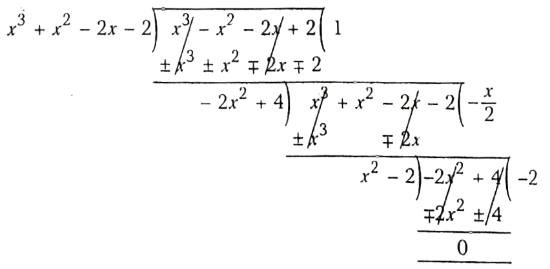
Hence, the H.C.F. of the given polynomials is (x² – 2). Thus, the common zeroes of the given polynomials are the zeroes of x²– 2 i.e. \((x+\sqrt{2})(x-\sqrt{2})\)

So, zeroes of \(\sqrt{2} \text { and }-\sqrt{2}\).

NCERT Exemplar Solutions for Class 10 Maths Chapter 2  Polynomials Exercise 2.1

Question 1. The graphs o(y = p(x) are given below, for some polynomials p{x). Find the number of zeroes of p(x), in each case.

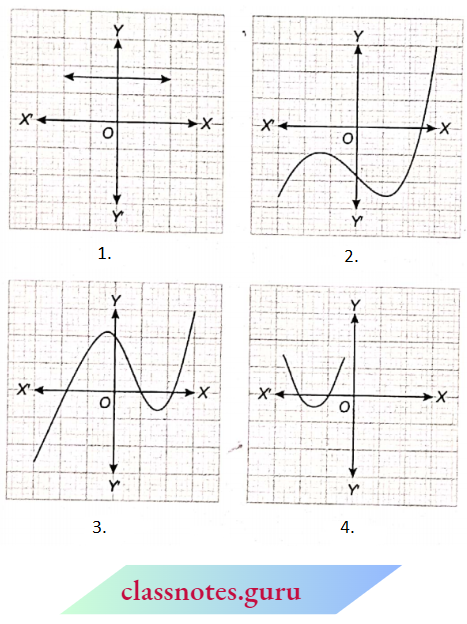
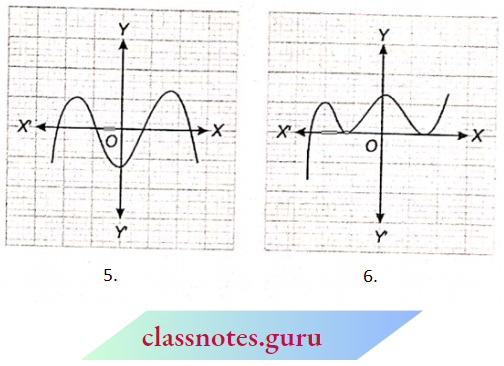
Solution:

1. The graph of the polynomial p(x) does not intersect the x-axis at any point.

∴ Number of its zeroes is zero.

2. The graph of the polynomial p(x) intersects the x-axis at one point.

∴ Number of its zeroes is one.

3. The graph of the polynomial p(x) intersects the x-axis at three points.

∴ Number of its zeroes is 3.

4. The graph of the polynomial p(x) intersects the x-axis at two points.

∴ Number of its zeroes is 2

5. The graph of the polynomial p(x) intersects the x-axis at four points.

∴ Number of its zeroes is 4.

6. The graph of the polynomial p(x) intersects the x-axis at three points.

∴ Number of its zeroes is 3.

NCERT Exemplar Solutions for Class 10 Maths Chapter 2  Polynomials Exercise 2.2

Question 1. Find the zeroes of the following quadratic polynomials and verify the relationship between the zeroes and the coefficients:

1. x² – 2x- 8
2. 4s² – 4s + 1
3. 6x² – 3 – 7x
4. 4u² + 8u
5. t²– 15
6. 3x² -x- 4

Solution:

Let p(x) =x² – 2x- 8

= x²-4x + 2x-8

= x(x- 4) + 2(x- 4)

= (x- 4)(x + 2)

The zeroes of p(x) will be given by x- 4 = 0 and x + 2 = 0.

x- 4 = 0 ⇒ x = 4

x + 2 = 0 ⇒ x = -2

∴ Zeroes of p(x) = 4,-2

Now, from p(x) = x² – 2x- 8

a = 1 , b = -2, c = -8

∴ \(-\frac{b}{a}=-\frac{(-2)}{1}=2\)

= 4+(-2) = sum of zeroes

and \(\frac{c}{a}=\frac{-8}{1}=-8\)

= 4(-2) = product of zeroes

∴ Relations between the zeroes of polynomial and the coefficients are true.

2. Let p(s) = 4s² – 4s +1 = 4s²-2s-2s +1

= 2s(2s-1) -1 (2s-1)

= (2s-1)(2s-1)

The zeroes ofp(s) will be given by 2s -1 = 0 and 2s – 1 = 0.

∴ 2s – 1 = 0 \(s=\frac{1}{2}\)

Therefore, zeroes of p(s) = \(\frac{1}{2}, \frac{1}{2}\)

Now, from p(s) = 4s2 – 4s + 1

a = 4, b =-4, c = 1

⇒ \(-\frac{b}{a}=-\frac{(-4)}{4}=1\)

⇒ \(\frac{1}{2}+\frac{1}{2}\)

=  sum of zeroes

and \(\frac{c}{a}=\frac{1}{4}=\frac{1}{2} \times \frac{1}{2}\) = Product zeroes.

Relations between the zeroes of polynomial and the coefficients are true.

3. Let p(x) = 6x² – 3 -7x = 6x² – 7x- 3

= 6x²– 9x + 2x- 3

= 3x(2x-3) + 1(2x- 3)

= (2r- 3)(3x+ 1)

The zeroes of p(x) will be given by 2x- 3 = 0 and 3x+ 1=0.

∴ 2x-3 = 0 ⇒ \(x=\frac{3}{2}\)

and 3x + 1 = 0 ⇒ \(x=-\frac{1}{3}\)

Therefore, zeroes of p(x) = \(\frac{3}{2},-\frac{1}{3}\)

Now, from p(x) =  6×2- 7x- 3

a = 6, b=-7, c = -3

⇒ \(-\frac{b}{a}=-\frac{(-7)}{6}=\frac{7}{6}=\frac{3}{2}+\left(-\frac{1}{3}\right)\)

= sum of zeroes.

⇒ \(\frac{c}{a}=\frac{-3}{6}=-\frac{1}{2}=\frac{3}{2} \times\left(-\frac{1}{3}\right)\)

= product of zeroes.

Therefore, the relations between the zeroes of the polynomials and the coefficients are true.

4. Let p(u)= 4u² + 8u = 4u(u + 2) Zeroes of p(u) will be given by 4u = 0 and u + 2 = 0.

∴ 4u = 0 ⇒ u = 0

and u + 2 = 0  ⇒ u = -2

Therefore, zeroes of p(u) = 0, -2.

Now, from p(u) = 4u² + 8u, a = 4, b = 8, c = 0

∴ \(-\frac{b}{a}=-\frac{8}{4}=-2=0+(-2)=\text { sum of zeroes. }\)

and \(\frac{c}{a}=\frac{0}{4}=0=0(-2)=\text { product of zeroes. }\)

Therefore, the relations between the zeroes of the polynomials and the coefficients are true.

5.  Let p(t) = t² – 15

⇒ \(t^2-(\sqrt{15})^2=(t-\sqrt{15})(t+\sqrt{15})\)

The zeroes of p{t) will be given by

⇒ \(t-\sqrt{15}=0\) and \(t-\sqrt{15}=0\)

Now, \(t-\sqrt{15}=0\) \(\Rightarrow \quad t=\sqrt{15}\)

and \(t-\sqrt{15}=0\) \(\Rightarrow t=-\sqrt{15}\)

Zeroes of p(t) = \(\sqrt{15} \text { and }-\sqrt{15}\)

From p(t) = t² – 15

a = 1, b = 0, c =-l5

⇒ \(-\frac{b}{a}=-\frac{0}{1}=0=\sqrt{15}+(-\sqrt{15})\)

= sum of zeroes.

and \(\frac{c}{a}=\frac{-15}{1}=-15=(\sqrt{15})(-\sqrt{15})\)

= product of zeroes.

Therefore, the relations between the zeroes of the polynomials and the coefficients are true.

6.  Let p(x)  = \(3 x^2-x-4=3 x^2-4 x+3 x-4\)

⇒ \(x(3 x-4)+1(3 x-4)\)

⇒ \((3 x-4)(x+1)\)

The zeroes of p(x) will be given by 3x – 4 = 0 and x + 1 = 0.

Now, 3x- 4 = 0 ⇒ \(x=\frac{4}{3}\)

and x+ 1 = 0 ⇒ A =-l

Zeroes of p(x) = \(\frac{4}{3}\) and -1

From p(x) = 3x²-x-4

a = 3, b = -1, c = -4

⇒ \(-\frac{b}{a}=-\frac{(-1)}{3}=\frac{1}{3}=\frac{4}{3}+(-1)\)

= sum of zeroes.

and \(\frac{c}{a}=\frac{-4}{3}=\frac{4}{3} \times(-1)=\text { sum of product. }\)

Therefore, the relations between the zeroes of the polynomials and the coefficients are true.

Question 2. Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively:

1. \(\frac{1}{4},-1\)
2. \(\sqrt{2}, \frac{1}{3}\)
3. \(0, \sqrt{5}\)
4. 1,1
5. \(-\frac{1}{4}, \frac{1}{4}\)
6. 4,1

Solution:

1. Let the zeroes of the polynomial be α and β.

∴ \(\alpha+\beta=\frac{1}{4} \text { and } \alpha \beta=-1\)

∴ quadratic polynomial = (x- α) (x- β)

= x² – (α+ β)x + αβ

= \(x^2-\frac{1}{4} x-1=\frac{1}{4}\left(4 x^2-x-4\right)\)

∴ Required polynomial = 4x² – x- 4.

2. Let the zeroes of the polynomial be a and p.

∴ \(\alpha+\beta=\sqrt{2} \quad \text { and } \quad \alpha \beta=\frac{1}{3}\)

∴ quadratic polynomial = (x – α)(x – β)

⇒ \(x^2-(\alpha+\beta) x+\alpha \beta=x^2-\sqrt{2} x+\frac{1}{3}\)

⇒ \(\frac{1}{3}\left(3 x^2-3 \sqrt{2} x+1\right)\)

∴ Required polynomial = \(3 x^2-3 \sqrt{2} x+1\)

3. Let the zeroes of the polynormal be a and p

∴ \(\alpha+\beta=0 \text { and } \alpha \beta=\sqrt{5}\)

∴ quadratic polynomial = (x – α)(x – β)

⇒ \(x^2-(\alpha+\beta) x+\alpha \beta\)

⇒ \(x^2-0(x)+\sqrt{5}=x^2+\sqrt{5}\)

4.  Let the zeroes of the polynomial be a and p.

α + β = 1 and αβ = 1

∴ quadratic polynomial = (x- a)(x- P)

= x² – (α + β)x + αβ

x²– x + 1

5.  Let the zeroes of the polynomial be a and p.

∴ \(\alpha+\beta=-\frac{1}{4} \text { and } \alpha \beta=\frac{1}{4}\)

Now, quadratic polynomial = (x – α)(x – β)

x² – (α + β)x + αβ

⇒ \(\alpha+\beta=-\frac{1}{4} \text { and } \alpha \beta=\frac{1}{4}\)

Therefore, required polynomial = 4x² + x + 1

6. Let the zeroes of the polynomial be α and β.

∴ α + β = 4 and αβ = 1

Now, quadratic polynomial = (x- α)(x- β)

= x² — (α + β)x + αβ

= x²-4x+ 1.

NCERT Exemplar Solutions for Class 10 Maths Chapter 2  Polynomials Exercise 2.3

Question 1. Divide the polynomial p(x) by the polynomial g(x) and find the quotient and remainder in each of the following :

1. p(x) =x³– 3x² + 5x-3, g(x) =x²-2
2. p(x) = x⁴ – 3x² + 4x + 5, g(x) =x²+1 -x
3. p(x) = x⁴ – 5A + 6, g(x) = 2 -x²

Solution:

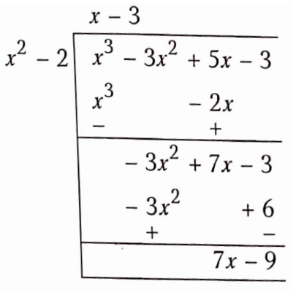
Now, P(x) = g(x). q(x) + r(x)

∴ quotient q(x) = x- 3

and remainder r(x) = 7x- 9

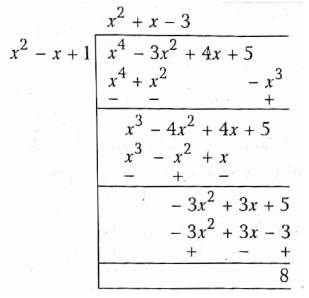
Now, P(x) = g(x) f(x) + r(x)

∴ quotient q(x) = x² +x-3

and remainder r(x) = 8

Now, p(x) = g(x) q(x) + r(x)

∴ quotient q(x) = -x² – 2

and remainder r(x)= -5x + 10

Question 2. Check whether the first polynomial is a factor of the second polynomial by dividing the second polynomial by the first polynomial:

1. t²-3, 2t⁴ + 3t³– 2t²– 9t- 12
2. x² + 3x + 1, 3x⁴ + 5x³– 7x² + 2x + 2
3. x³– 3x + 1, x⁵ – 4x³ + x² + 3x +1

Solution:

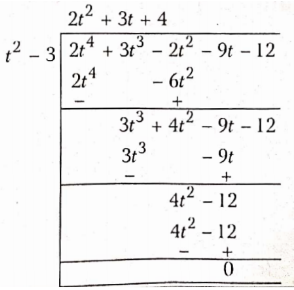
Now, p(t) g(t) + (t) + r(t)

∴ quotient q(t) = 2t² + 3t + 4 and remainder r(x)= 0.

∵ The remainder is zero.

∴ t² – 3 is a factor of 2t⁴ + 3t³ -2t² – 9t – 12.

Now, p= g(x) q(x) + r(x)

∴ quotient q(x) = 3x² – 4x + 2 and remainder r(x) = 0

∵ The remainder is zero.

∴ x² + 3x + 1 is a factor of 3x⁴ + 5x³– 7x² + 2x + 2.

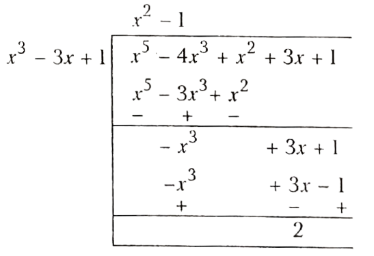
Now, P(x) = g(x) q(x) + r(A)

∴ quotient q(x) = x²– 1 and remainder r(x) = 2.

∵ The remainder is not zero.

∴ x²– 3x + 1 is not a factor x⁵ – 4x³ + x² + 3x + 1 .

Question 3. Obtain all other zeroes of 3×4 + 6×3 – 2×2 – 10x – 5 if two of its zeroes are \(\sqrt{\frac{5}{3}} \text { and }-\sqrt{\frac{5}{3}}\)
Solution:

Given 3x⁴ + 6x³ – 2x² – 10x – 5

Two of its zeroes are \(\sqrt{\frac{5}{3}} \text { and }-\sqrt{\frac{5}{3}}\)

Let the remaining two zeroes be α and β.

Given zeroes are \(\sqrt{\frac{5}{3}} \text { and }-\sqrt{\frac{5}{3}}\)

Quadratic polynomial from zeroes.

⇒ \(\left(x-\sqrt{\frac{5}{3}}\right)\left(x+\sqrt{\frac{5}{3}}\right)\)

⇒ \(x^2-\frac{5}{3}=\frac{1}{3}\left(3 x^2-5\right)\)

∴ quadratic polynomial = 3x² – 5

Now, (x- α)(x- β)(3x² – 5)

⇒ \(3 x^4+6 x^3-2 x^2-10 x-5\)

⇒ \((x-\alpha)(x-\beta)=\frac{3 x^4+6 x^3-2 x^2-10 x-5}{3 x^2-5}\)

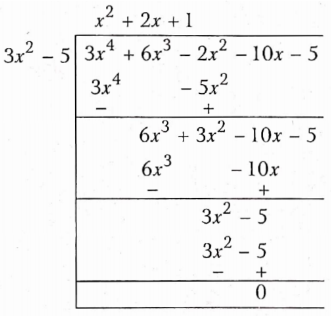
∴ (x- α)(x- β) = x² + 2x + 1

= (x+ 1)(x + 1)

∴ α = -1, β =-1

⇒ Remaining zeroes =-1,-1.

Question 4. On dividing x³ – 3x² + x + 2 by a polynomial g(x), the quotient and remainder were x- 2 and -2x + 4, respectively. Find g(x).
Solution:

Given

x³ – 3x² + x + 2

Let p(x) = x³ – 3x² + x + 2

quotient q(x) =x – 2 and remainder r(x)= -2x + 4

Now, p(x) = g(x) . q(x) + r(x)

⇒ g(x)-q(x) = p(x)- r(x)

= (x³ – 3x² + x + 2) – (-2x + 4)

= x³ – 3x² + x + 2 + 2x- 4

= x³ – 3x² + 3x- 2

⇒ g(x) = \(\frac{x^3-3 x^2+3 x-2}{x-2}\) (∵ q (x) = x-2)

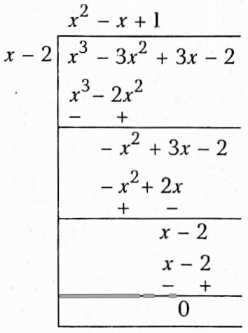
Therefore, g(x) = x²-x+1

Question 5. Give examples of polynomials p(x), g(A), q(x) and r(x), which satisfy the division algorithm and

1. Deg P(x) = deg q(x)
2. Deg q(x) = deg r(x)
3. Deg r(x) = 0

Solution:

1. deg p(x) = deg q(x)

We know that

p(x) = g(x) q(x) + r(x)

∴ degree of g(x) = zero

Let p(x) = 2x³ + 6x² + 2x- 1

and g(x) = 2

∴ q(x) = x³ + 3x² + x and r(x) = -1

So, p(x) = 2x³ + 6x² + 2x- 1, = 2,

q(x) = x³ + 3x² + x, r(x) = -1

degree q(x) = degree r(x)

We know that

p(x) = q(x) +r(x)

If q(x) and r(x) are polynomials of the first degree then a degree of p(x) must be 1 more than the degree: of g(x)

Let p(x) =  x³ + 3x² + 2x + 5 and g(x) = x² – 1

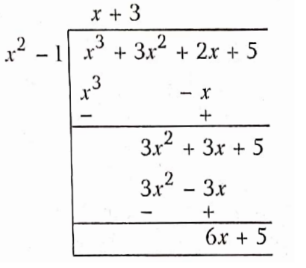
∴ q(x) = x + 3 and r(x) = 6x + 5

so, p(x) = x³ + 3x² + 2x + 5, g(x) =x²-1

q(x) = x + 3, r(x) = 6x + 5

3. degree r(x) = 0

For this, the degree of g(x) must be 1.

Let p(x) = 2x³ – 3×2 +x+ 4 and g(x) = x- 1 .

∴ q(x) = 2x² – x and r(x) = 4

Therefore, p(x) = 2x³ – 3x² + x + 4, g(x) = x- 1,

q(x) = 2x² – x, r(x) = 4

NCERT Exemplar Solutions for Class 10 Maths Chapter 2  Polynomials Exercise 2.4 (Optional)

Question 1. Verify that the numbers given alongside of the cubic polynomials below are their zeroes. Also verify the relationship between the zeroes and the coefficients in each case :

1. \(2 x^3+x^2-5 x+2 ; \frac{1}{2}, 1,-2\)
2. \(x^3-4 x^2+5 x-2 ; 2,1,1\)

Solution:

1. Let p(x) = \(2 x^3+x^2-5 x+2\)

∴ \(p\left(\frac{1}{2}\right)=2\left(\frac{1}{2}\right)^3+\left(\frac{1}{2}\right)^2-5\left(\frac{1}{2}\right)+2\)

⇒ \(\frac{1}{4}+\frac{1}{4}-\frac{5}{2}+2=0\)

⇒ \(\frac{1}{2}\)is a zero of p(x).

Again ,p(1) = 2(1)³ + (1)² – 5(1) + 2

=2 + 1 – 5 + 2 = 0

⇒ 1 is a zero of p(A).

Again p(-2) = 2(-2)³ + (-2)² – 5(-2) + 2

= -16 + 4+10 + 2 = 0

⇒ -2 is a zero of p(x)

Now, in p(x) = 2x³ +x² -5x + 2

a = 2,b = 1 ,c = -5, d = 2

⇒ \(-\frac{b}{a}=-\frac{1}{2}=\frac{1}{2}+1+(-2)=\text { sum of zeroes }\)

⇒ \(\frac{c}{a}=\frac{-5}{2}=\frac{1}{2} \times 1+1 \times(-2)+\frac{1}{2} \times(-2)\)

= sum of the product of zeroes taken two at a time.

and \(-\frac{d}{a}=\frac{-2}{2}=-1\)

⇒ \(\frac{1}{2} \times 1 \times(-2)=\text { product of zeroes}\)

Therefore the relations between the zeroes of the polynomial and the coefficients are true.

2. Let p(x) = x³ – 4x² + 5x -2

p(2) = (2)³ – 4(2)² + 5(2)-2

= 8-16+10-2 = 0

⇒ 2 is a zero of p(x).

Again P(1) = (1)³ – 4(1)² + 5(1)-2

= 1-4 + 5- 2 = 0

= 1 is a zero of p(x).

Now, for p(x) = x³ – 4x² + 5x- 2

a= 1, b =-4, c = 5, d = -2

∴ \(-\frac{b}{a}=-\frac{(-4)}{1}=4=2+1+1=\text { sum of zeroes. }\)

⇒ \(\frac{c}{a}=\frac{5}{1}=5=2 \times 1+1 \times 1+1 \times 2\)

= sum of the product of zeroes taken two at a time.

and \(-\frac{d}{a}=-\frac{(-2)}{1}=2=2 \times 1 \times 1\)

= product of zeroes.

Therefore the relations between the zeroes of the polynomial and the coefficients are true.

Question 2. Find a cubic polynomial with the sum, the sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, and -14 respectively.
Solution:

Given

The sum of the product of its zeroes taken two at a time, and the product of its zeroes as 2, -7, and -14 respectively

Let the zeroes be α, β, and γ.

∴ α + β + γ = 2

αβ + βγ + γα = -7 and αβγ = -14

∴ Cubic polynomial = (x-α)(x-β)(x-γ)

= x³ – (α+ β + γ)x2+ (αβ + βγ + γα)x- αβPγ

= x³-2x²-7x+ 14

Question 3. If the zeroes of the polynomial x³ – 3x² + x + 1 are a – b, a, a + b, find a and b.
Solution:

Given

x³ – 3x² + x + 1

a – b, a, a + b, are zeroes of polynomial.

Let p(x) = x² – 3x² +x + 1

⇒ A= 1, B =-3, C = 1,D = 1

sum of zeroes = \(-\frac{B}{A}\)

a-b + a + a + b = \(-\frac{(-3)}{1}\)

3a = 3

a= 1

and product of zeroes = \(-\frac{D}{A}\)

⇒ \((a-b) \cdot a \cdot(a+b)=-\frac{1}{1}\)

⇒ \(a\left(a^2-b^2\right)=-1\)

⇒ \(1-b^2=-1\)

⇒ \(b^2=2\)

⇒ \(b= \pm \sqrt{2}\)

∴ \(a=1, b= \pm \sqrt{2}\)

Question 4. If two zeroes of the polynomial x⁴ – 6x³ – 26x² + 138x- 35 are \(2 \pm \sqrt{3}\) , find other zeroes.
Solution:

Given

x⁴ – 6x³ – 26x² + 138x- 35

Two zeroes of a polynomial are \(2+\sqrt{3} \text { and } 2-\sqrt{3} \text {. }\)

Let the remaining two zeroes be a and p

∴ \((x-\alpha)(x-\beta)(x-2-\sqrt{3})(x-2+\sqrt{3})\)

⇒ \(x^4-6 x^3-26 x^2+138 x-35\)

⇒ \(\quad(x-\alpha)(x-\beta)\left[(x-2)^2-(\sqrt{3})^2\right]\)

⇒ \(x^4-6 x^3-26 x^2+138 x-35\)

⇒ \(\quad(x-\alpha)(x-\beta)\left(x^2-4 x+4-3\right)\)

⇒ \(x^4-6 x^3-26 x^2+138 x-35\)

⇒ \(\quad(x-\alpha)(x-\beta)\)

⇒ \(\quad\frac{x^4-6 x^3-26 x^2+138 x-35}{x^2-4 x+1}\)

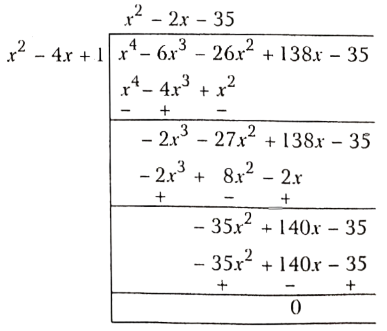
∴ (x -α) (x- β) = x² – 2x- 35 = x²– 7x + 5x- 35

= x(x- 7) + 5(x- 7)

= (x- 7)(x + 5)

The other zeroes are α = 7, β = -5

Question 5. If the polynomial x⁴ – 6x³ + 16x²-25x+10 is divided by another polynomial x²-2x + k. the remainder comes out to be x + a, find k and a.
Solution:

Given

x⁴ – 6x³ + 16x²-25x+10 and x²-2x + k

Let p(x) = x⁴ – 6x³ + 16x² – 25x + 10 divisor g(x) = x² -2x + k and remainder r(x) = x + a

According to the problem,

(2k – 9)x +(10-8k + k²) = x + a Comparing the coefficient of x

2k-9= 1

⇒ 2k = 1 + 9= 10

⇒ k = 5

Comparing the constant terms

10 – Sk + k² = a

⇒ 10-40 + 25 = a  (put K = 5)

⇒ a = -5

So, k = 5 and a =-5

NCERT Exemplar Solutions for Class 10 Maths Chapter 2  Polynomials Multiple Choice Questions

Question 1. If one zero of the polynomial 3x² + x- k is 3 then the value of k is :

1. -30
2. -24
3. 30
4. 24

Answer: 3. 30

Question 2. A polynomial with zeroes 2 and -3 is:

1. x² -x- 6
2. x² + x- 6
3. x² – 6
4. x² + 6

Answer: 2. x² + x- 6

Question 3. The number of polynomials with zeroes 4 and 3, is :

1. 1
2. 2
3. 3
4. Infinite

Answer: 4. Infinite

Question 4. The zeroes of x² + 6a + 5 are:

1. Both positive
2. Both negative
3. Both equal
4. One zero is zero

Answer: 2. Both negative

Question 5. If two zeroes of the polynomial ax³ + bx² + cx + d are zero, then third zero is :

1. \(-\frac{b}{a}\)
2. \(\frac{b}{a}\)
3. \(\frac{c}{a}\)
4. \(-\frac{c}{a}\)

Answer: 1. \(-\frac{b}{a}\)

Question 6. If x⁶– 1 is divided by a polynomial of third degree, the maximum degree of the remainder can be:

1. 0
2. 1
3. 2
4. 3

Answer: 3. 2

Question 7.  The product of zeros of ax² + bx + c, a≠0 is:

1. \(-\frac{b}{a}\)
2. \(\frac{b}{a}\)
3. \(-\frac{c}{a}\)
4. \(\frac{c}{a}\)

Answer: 4. \(\frac{c}{a}\)