NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles
- Circle: A circle is a collection of all points in a plane which are at the same
- Centre: The fixed point from which all points in a plane are at the same constant distance is called the centre.
- Radius: The distance between the centre and circumference of a circle is called the radius.
- Chord: A straight line segment joining two points on a circle is called a chord of the circle.
- Secant: A straight line which intersects a circle in two distinct points is called a secant to the circle.
- Tangent: A straight line meeting a circle only at one point is called a tangent to the circle at that point.
- Point Of Contact: The point where the straight line touches (or meets at only one point) the circle is called its point of contact.
- Concentric Circles: Circles having the same centre are said to be concentric circles.

NCERT Exemplar Class 10 Maths Chapter 10 Circles
NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Theorem 1:
The tangent at any point of a circle is perpendicular to the radius through the point of contact.
Given: A circle with centre O and a tangent AB at a point P of the circle.
To Prove: OP \(\perp\) AB
Read and Learn More Class 10 Maths Solutions Exemplar
Construction: Take a point Q other than P on AB. Join OQ.
Proof: Q is a point on the tangent AB, other than the point of contact P.
Q lies outside the circle.
Let OQ interest the circle at R.
Then, OR < OQ
But, OP = OR
Therefore, OP < OQ
Thus, OP is shorter than any other line segment joining O to any point of AB.
It means OP is the shortest distance among all the lines drawn from O to. the point on the tangent other than the point of contact.
Also, we know that perpendicular distance is the shortest distance So, \(\perp\)
i.e., the radius through the point of contact is perpendicular to the tangent.
NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Theorem 2:
A line drawn through the end of a ratlins and perpendicular to it is a tangent to the circle.
Given: A circle with centre O in which OP is a radius and AB is a line through P such that OP \(\perp\) AB.
To Prove: AB is a tangent to the circle at the point P.
Construction: Take a point Q different from P, on AB. Join OQ.
Proof: We know that the perpendicular distance from a point to a line is the shortest distance between them.
- OP \(\perp\) AB
- OP is the shortest distance from O to AB.
- OP < OQ
- Q lies outside the circle.
- Thus, every point on AB other than P, lies outside the circle.
- AB meets the circle at point P only. Hence, AB is the tangent to the circle at the point P.
An Important Result of the Above Theorem
If two circles touch internally or externally, the point of contact lies in a straight line through their centres.
Given: Two circles with centre O and O’ which touch each other at P.
To Prove : P lies on the straight line 00′ i.e., the line joining the centres.
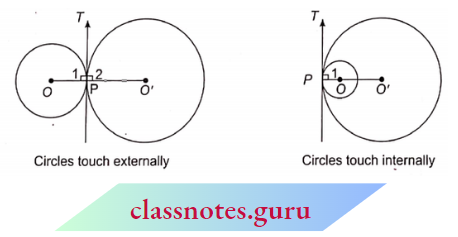
Construction: Join OP, and O’P and draw a common tangent PT to the two circles at point P.
Proof: When Circles Touch Externally :
- ∠1 = 90° …(1) (radius through the point of contact is perpendicular to the tangent)
- ∠2 = 90° (same reason) …(2)
- ∠1 + ∠2 = 90° + 90° [from (1) and (2)]
- ∠l+∠2=180°
- OPO’ is a straight line. (L.P.A.) …(3)
- When Circles Touch Internally :
- ∠OPT = ∠O’PT = 90° (radius through the point of contact is perpendicular to the tangent)
- O’OP is a straight line. (O’P, OP are both 1 to PT at the same point P and only one
∴ \(\perp\) can be drawn to a line through one point on it) …(4) From both (3) and (4), we conclude that P lies on the straight line OO’ i.e., P lies on the straight line joining the centre of the circles.
NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Theorem 3:
The lengths of tangents drawn from an external point to a circle are equal.
Given: Two tangents AP and AQ are drawn from point A to a circle with centre O.
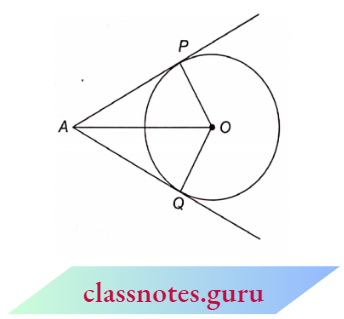
To Prove: AP = AQ
Construction: Join OP, OQ and OA.
Proof: AP is a tangent at P and OP is the radius through P.
OP\(\perp\) AP
Similarly, OQ \(\perp\) AQ
In the right \(\triangle\) OPA and \(\triangle\) OQA
OP = OQ
OA = OA
OPA = ∠OQA
⇒ \(\triangle\) OPA = \(\triangle\) OQA
Hence, AP = AQ
Corollary : (A) If two tangents are drawn from an external point then
- They subtend equal angles at the centre, and
- they are equally inclined to the line segment joining the centre to that point, (or, tangents are equally inclined at the centre).
Given: A circle with centre O and a point A outside it. Also, AP and AQ are the two tangents to the circle.
To Prove : \(\angle\)AOP = \(\angle\) AOQ and \(\angle\) OAP = \(\angle\) OAQ
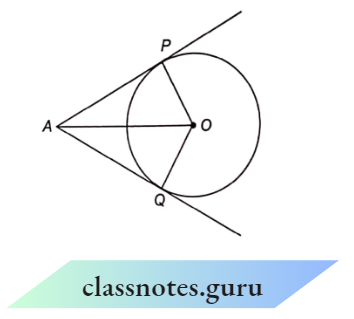
Proof : In \(\triangle\)AOP and \(\triangle\)AOQ, we have
AP = AQ (tangents from an external point)
OP = OQ (radii of the same circle)
OA = OA (common)
⇒ \(\triangle\)AOP = \(\triangle\)AOQ (by SSS congruence)
Hence, \(\angle\)AOP = \(\angle\)AOQ and \(\angle\)OAP = \(\angle\)OAQ
(2) Prove that the tangents drawn at the endpoints of a chord of a circle make equal angles with the chord.
Given: Let AB be a chord of the given circle. PA and PB are the tangents at endpoints A and B.
To Prove : \(\angle\)5 = \(\angle\)6
Proof: Since OA and OB are the radii of a circle.
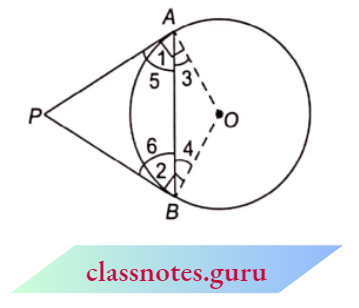
NCERT Exemplar Solutions for Circles Class 10
⇒ \(\angle\)1 = \(\angle\)2 …(1 )(each 90°, as radius through point of contact is 1 to the tangent)
Also in \(\triangle\)OAB,
Since OA = OB
⇒ \(\angle\)3 = \(\angle\)4 (angles opposite to equal sides are equal)
Subtracting equation (2) from equation (1), we get
⇒ \(\angle\)1 – \(\angle\)3 = \(\angle\)2 – \(\angle\)4
⇒ \(\angle\)5 = \(\angle\)6
Hence, tangents drawn at the endpoints of a chord of a circle make equal angles with the chord.
NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Solved Examples
Example 1. Find the length of tangent drawn to a circle of radius 6 cm, from a point at a distance of 10 cm from the centre.
Solution:
Given that
A circle of radius 6 cm, from a point at a distance of 10 cm from the centre.
Since the tangent is perpendicular to the radius through the point of contact.
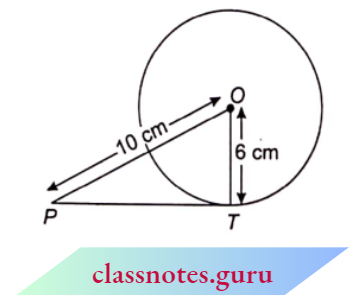
- \(\angle O T P=90^{\circ}\)
- In the right triangle OTP, we have
- \(O P^2 =O T^2+P T^2\)
- \(10^2 =6^2+P T^2\)
- \(P T^2 =100-36=64\)
- P T =8 cm
- Hence, the length of the tangent is 8 cm.
The length of tangent is 8 cm.
Question 2. AP is tangent to circle O at point P. What is the length of OP?
Solution:
Given that
AP is tangent to circle O at point P.
Let the radius of the given circle be r.
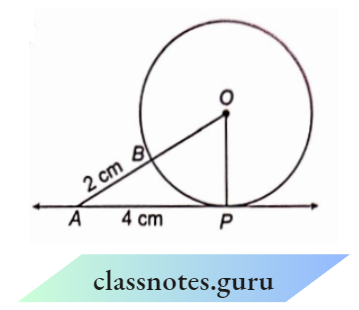
OP = OB = r
OA = 2 + r, OP = r, AP =4
⇒ \(\angle OPA\) = 90° (radius through the point of contact is perpendicular to the tangent)
In right \(\triangle O P A\),
⇒ \(O A^2 =O P^2+A P^2\)
⇒ \((2+r)^2 =r^2+(4)^2\)
⇒ \(4+r^2+4 r =r^2+16\)
⇒ \(4 r =12 \quad \Rightarrow \quad r=3\)
O P = 3 cm.
The length of OP = 3 cm.
Example 3. If the angle between two tangents drawn from an external point P to a circle of radius V and centre O, is 60°, then find the length of OP.
Solution:
Given
If the angle between two tangents drawn from an external point P to a circle of radius V and centre O, is 60°,
PA and PB are two tangents from an external point P such that
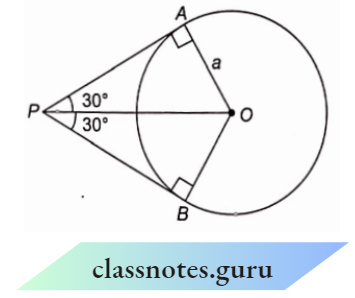
⇒ \(\angle\)APB = 60°
⇒ \(\angle\)OPA = \(\angle\)OPB = 30° (tangents are equally inclined at the centre)
Also, \(\angle\)OAP = 90° (radius through the point of contact is perpendicular to the tangent)
Now in right \(\triangle\)OAP,
⇒ \(\sin 30^{\circ} =\frac{O A}{O P}\)
⇒ \(\frac{1}{2} =\frac{a}{O P} \quad \Rightarrow \quad O P\)=2 a units
The length of OP =2 a units
Example 4. In the adjoining figure, PQ is a chord of a circle and is the tangent atP such that \(\angle\)QPT = 60°. Find \(\angle\)PRQ.
Solution:
Given that
In the adjoining figure, PQ is a chord of a circle and is the tangent atP such that \(\angle\)QPT = 60°.
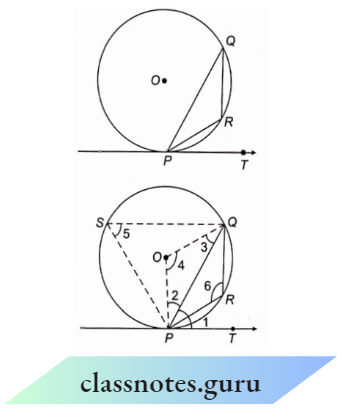
Join OP and OQ. Take any point S on the circumference in the alternate segment. Join SP and SQ.
Since OP \(\perp\) PT (radius through the point of contact is 1 to the tangent
⇒ \(\angle 2+\angle 1=90^{\circ}\)
⇒ \(\angle 2+60^{\circ}=90^{\circ}\)
⇒ \(\angle 2=90^{\circ}-60^{\circ}=30^{\circ}\) (given)
But O P=O Q (each radii)
⇒ \(\angle 2=\angle 3\) (angles opposite to equal sides are equal)
But O P=O Q
⇒ \(\angle 2=\angle 3\) (angles opposite to equal sides are equal)
Now in \(\triangle P O Q\),
⇒ \(\angle 2+\angle 3+\angle 4 =180^{\circ}\)
⇒ \(30^{\circ}+30^{\circ}+\angle 4 =180^{\circ}\)
⇒ \(\angle 4 =120^{\circ}\)
⇒ \(\angle 5 =\frac{1}{2} \times \angle 4\) (angle sum property) [from (1) and (2)]
(The degree measure of an area is twice the angle subtended by it in an alternate segment)
⇒ \(\angle 5=\frac{1}{2} \times 120^{\circ}\)
⇒ \(\angle 5 =60^{\circ}\)
∴ Also,\(\angle 5+\angle 6 =180^{\circ}\)
⇒ \(60^{\circ}+\angle 6 =180^{\circ}\)
∴ \(\angle 6 =\angle P R Q=120^{\circ}\)
Example 5. In the given figure two circles touch each other at point C. Prove that the common tangent to the circle at C bisects the common tangent at P and Q.
Solution:
In the given figure, PR and CR are both tangents drawn to c the same circle from an external point R
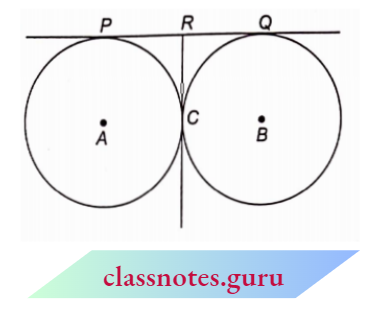
PR = CR …(1)
Also, QR and CR are both tangents drawn to the same circle from an external point R.
QR = CR -(2)
From ( 1 ) and (2) we get
PR = QR
R is the mid-point of PQ
i.e., the common tangent at C bisects the common tangents at P and Q
Example 6. Two circles of unequal radii neither touch nor intersect each other. Are the common tangents AB and CD always equal? If no, then give an explanation of it and if your answer is yes, then prove it.
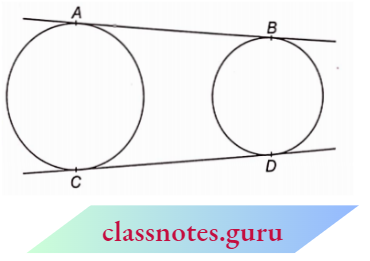
Solution:
Let the two tangents AB and CD on producing meet at P.
Since PA and PC are tangents from an external point P to the circle with centre O
PA=PC
Also, PB and PD are tangents from an external point P to the circle with centre O’.
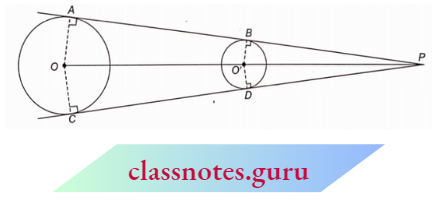
PB = PD …(2)
Subtracting (2) from (I), we get
PA – PB = PC- PD
AB = CD
So, the direct common tangents are of equal length
Example 7. In the adjoining figure, common tangents AB and CD to two circles intersect at P. Prove that AB = CD.
Solution:
Given that
In the adjoining figure, common tangents AB and CD to two circles intersect at P.
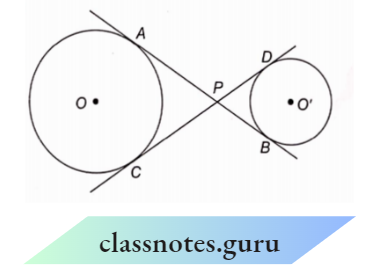
- Since PA and PC are two tangents to a circle with centre O from an external point P.
- PA =PC
- Also, since PB and PD are two tangents to a circle with centre O’ from an external point P.
- PB = PD
- Adding (2) and ( 1 ), we get
- PA + PB = PC + PD
- AB = CD (AB and CD are two straight lines)
- Hence Proved.
Example 8. In the given diagram, PQ and RS arc common tangents to the two circles with centres C and D. Find the length of PQ and hence the area of trapezium RSDC.
Solution:
Given
In the given diagram, PQ and RS arc common tangents to the two circles with centres C and D.
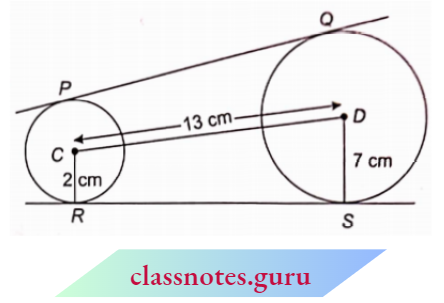
Draw CM//PS so that DCMSP becomes a rectangle.
Now, we have CR = 2 cm, DS = 7cm and CD = 13 cm
DM = DS- MS
= DS- CR
= 7-2 = 5 cm
In right ADMC, by Pythagoras theorem,
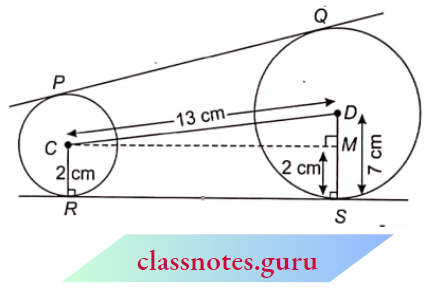
⇒ \(C M^2 =C D^2-D M^2\)
=\((13)^2-(5)^2=(12)^2\)
RS = 12 cm (opposite sides of the rectangle are equal)
PQ = 12 cm (length of common tangents to two circles are always same)
Now, ar(Trapezium RSDC)
= \(\frac{1}{2} \times\) h sum of parallel sides)
= \(\frac{1}{2} \times C M(C R+D S)\)
= \(\frac{1}{2} \times 12(2+7)=54 \mathrm{~cm}^2\)
The length of PQ is 12 cm.
The area of trapezium RSDC is 54 cm².
Example 9. AB is the diameter of a circle with centre O. AH and BK are perpendiculars from A and B to the tangent at a point P on the circle. Prove that AD + BK = AB.
Solution:
Given
AB is the diameter of a circle with centre O. AH and BK are perpendiculars from A and B to the tangent at a point P on the circle.
Let AH = x, BK=y and BM = z
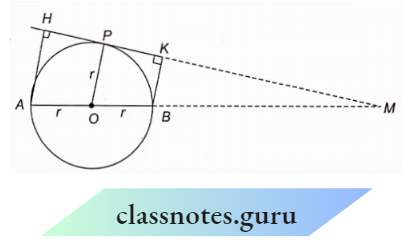
⇒ \(\triangle M B K \sim \triangle M A H\) (AA corollary)
⇒ \(\frac{B K}{A H}=\frac{B M}{A M} \quad \Rightarrow \quad \frac{y}{x}=\frac{z}{2 r+z}\)
⇒ \(2 r y+y z=x z \quad \Rightarrow \quad z(x-y)=2 r y\)
z=\(\frac{2 r y}{x-y}\)
Similarly, \(\triangle M B K \sim \triangle M O P\)
⇒ \(\frac{B K}{O P}=\frac{B M}{O M} \quad \Rightarrow \quad \frac{y}{r}=\frac{z}{z+r}\)
y z+y r=z r
z(r-y)=y r
z=\(\frac{y r}{r-y}\)
From (1) and (2), we get
⇒ \(\frac{2 y}{x-y} =\frac{y r}{r-y} \quad \Rightarrow \quad \frac{2}{x-y}=\frac{1}{r-y}\)
2 r-2 y =x-y
x+y 2 r
A H+B K =A B
Example 10. In the given figure, if AB =AC, prove that BE = EC.
Solution:
Given
In the given figure, if AB =AC
We know that lengths of tangents from an external point are equal.
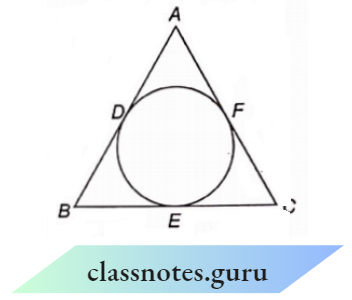
AD =AF → Equation 1
DB=BE → Equation 2
EC =FC → Equation 3
Now, it is given that
AB=AC
AD + DB =AF + FC
AD + DB = AB + E C From 1 And 3
D B = E C
B E = E C [From (2), DB = BE]
∴ Hence proved
Example 11. In the given figure ABC is a right-angled triangle with AB = 6 K cm, and BC = 8 cm. A circle with a centre O has been inscribed inside the triangle. Find the radius of the circle.
Solution:
Given
In the given figure ABC is a right-angled triangle with AB = 6 K cm, and BC = 8 cm. A circle with a centre O has been inscribed inside the triangle.
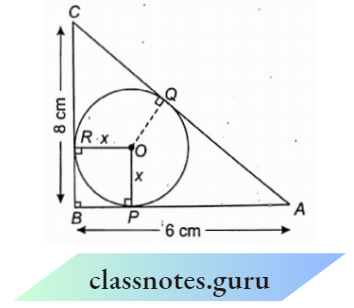
Let x be the radius of the circle. In the right triangle ABC
⇒ \(A C^2 =A B^2+B C^2\) (by Pythagoras Th.)
⇒ \(A C^2 =6^2+8^2\)
⇒ \(A C^2\) =36+64
⇒ \(A C^2\) =100
A C =10
Now in quadrilateral OPBR
⇒ \(\angle B =\angle P=\angle R=90^{\circ}\) each
⇒ \(\angle R O P =90^{\circ}\)sum of all angles of a quadrilateral is 360°) (each radii)
and also OP = OR (each radii)
Hence, OPBR is a square with each side x cm.
Therefore, CR = (8 -x) and PA = (6 -x)
BP = RB = x cm
Since the tangents from an external point to a circle are equal in length
AQ = AP = (6-x) and CQ = CR = (8 -x)
Now, AC = AQ + CQ
10 = 6 -x + 8 -x
10 = 14 – 2
2x = 4 = 2 cm
The radius of the circle = 2 cm
Chapter 10 Circles Class 10 Maths NCERT Exemplar
Example 12. A circle is touching the side BC of a \(\triangle\) ABC at the point and touching/IB and AC produced at Q and li respectively. Prove that AQ = \(\frac{1}{2}\) (perimeter of \(\triangle\) ABC).
Solution:
Given : \(\triangle ABC\) and a circle which touches BC, AB and AC in P, Q and R respectively.
Proof: Since the length of the two tangents drawn from an external
point to a circle are is equal, therefore,
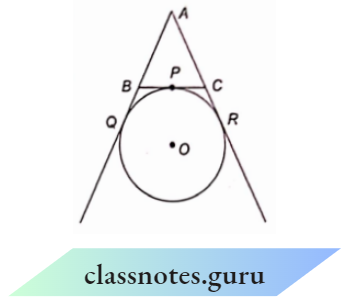
AQ = AR
BQ = BP
CP = CR
Now, perimeter of \(\triangle ABC\) = AB + BC + AC
= AB +BP + PC +AC
= AB + BQ + CR + AC [from (2) and (3)]
= AQ+AR = 2AQ [from (1)]
Perimeter of \(\triangle ABC\) = \(\frac{1}{2} \times \text { (perimeter of } \triangle A B C)\)
Example 13. In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. IfPA = 12 cm, QC = QD = 3 cm, then find PC + PD.
Solution:
Given
In the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. IfPA = 12 cm, QC = QD = 3 cm
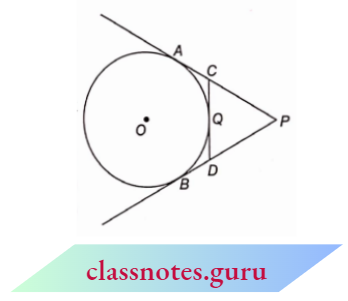
Since the lengths of the two tangents drawn from an external point to a circle are equal,
PA = PB → Equation (l)
CA = CQ → Equation (2)
DB = DQ → Equation (3)
Now, PA = 12
PC + CA= 12 (given)
PC + CQ = 12 From 2
PC + 3 = 12 ⇒ PC= 9 cm → Equation 4
PB=PA = 12
PD +DB= 12
PD +DQ= 12
PD + 3 = 12
PD = 9 cm → Equation 5
PC + PD = (9 + 9) cm = 18 cm [From 4 and 5]
PC + PD = 18 cm
Example 14. O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E, find the length AB.
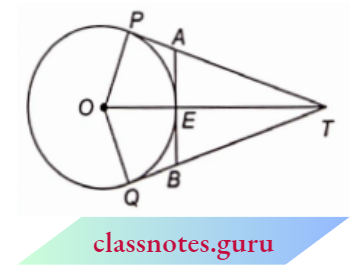
Solution:
Given
O is the centre of a circle of radius 5 cm. T is a point such that OT = 13 cm and OT intersects the circle at E. If AB is the tangent to the circle at E
Since, \(\angle O P T=90^{\circ}\) (radius through point of contact is \(\perp\) to the tangent)
In right \(\triangle O P T\),
⇒ \(OP^2+P T^2=O T^2\)
⇒ \(P T^2=O T^2-O P^2\)
⇒ \(P T^2=(13)^2-(5)^2=(12)^2\)
⇒ \(P T=12 \mathrm{~cm}\)
Let A P=x cm
At E=A P=x (lengths of tangents from an external point are equal)
A T=T P-A P=12-x
E T=O T-O E=13-5=8 cm
⇒ \(\angle A E T=90^{\circ}\)
Now; since \(\angle A E O=90^{\circ}\)(radius through point of contact is \(\perp\) to the tangent)
In right \(\triangle A E T\), by Pythagoras theorem,
⇒ \(A E^2+E T^2=A T^2\)
⇒ \(x^2+(8)^2=(12-x)^2\)
⇒ \(x^2+64=144+x^2-24 x \)
⇒ \(24 x=144-64=80\)
x=\(\frac{80}{24}=\frac{10}{3}\)
Similarly, B E=\(\frac{10}{3} \mathrm{~cm}\)
⇒ \(A B=A E+B E=\left(\frac{10}{3}+\frac{10}{3}\right) \mathrm{cm}=\frac{20}{3} \mathrm{~cm}\)
A B=\(\frac{20}{3} \mathrm{~cm}\)
The length AB is \(\frac{20}{3} \mathrm{~cm}\)
Example 15. In the given figure, T is tangent to the circle with centre O such that O T=4 cm and \(\angle O T A=30^{\circ}\). Find the length of segment AT.
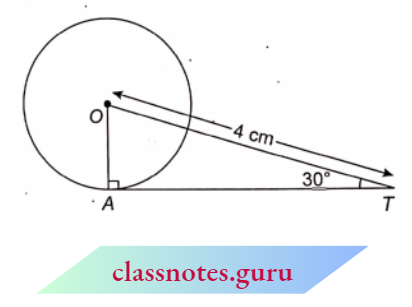
Solution:
Given
In the given figure, T is tangent to the circle with centre O such that O T=4 cm and \(\angle O T A=30^{\circ}\).
In right \(\triangle O A T\),
⇒ \(\cos 30^{\circ} =\frac{A T}{O T}\)
∴ \(\frac{\sqrt{3}}{2} =\frac{A T}{4} \quad A T=2 \sqrt{3} \mathrm{~cm}\)
The length of segment AT is 2√3 cm.
Example 16. In the given figure, OP is equal to the diameter of the circle. Prove that \(\triangle ABP\) is an equilateral triangle.
Solution:
Given
In the given figure, OP is equal to the diameter of the circle.
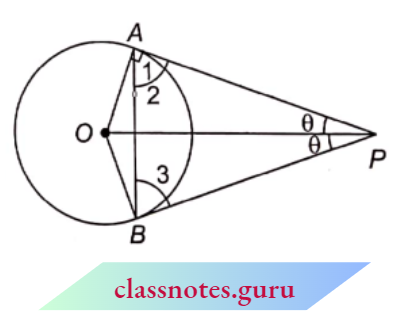
Let, \(\angle O P A=\angle O P B=\theta\)( tangents are equally inclined at the centre) and the radius of the circle be r.
Since, \(\angle 1=90^{\circ}\) (radius through point of contact is \(\perp\) to the tangent)
In right \(\triangle O A P\),
⇒ \(\sin \theta =\frac{O A}{O P}=\frac{r}{2 r}=\frac{1}{2}=\sin 30^{\circ}\)
⇒ \(\theta \Rightarrow \quad 30^{\circ} \quad \Rightarrow A P B=2 \theta=2 \times 30^{\circ}=60^{\circ}\)
Now, since PA = PB (length of tangents from an external point are equal)
⇒ \(\angle 2=\angle 3\) (angles opposite to equal sides are equal)
In \(\triangle M P B\).
⇒ \(\angle 2+\angle 3+\angle A P B=180^{\circ}\)
⇒ \(\angle 2+\angle 2+60^{\circ}=180^{\circ}\)
⇒ \(\angle 2=\angle 3=60^{\circ}\)
⇒ \(\angle 2+\angle 3+\angle A P B =180^{\circ}\) (angle sum property)
⇒ \(\angle 2+\angle 2+60^{\circ} =180^{\circ}\) [from (1) and (2)]
2 \(\angle 2 =120^{\circ} \quad \Rightarrow \quad \angle 2=60^{\circ}\)
⇒ \(\angle 2=\angle 3=60^{\circ}\)
So, all the angles of \(\triangle A P B are 60^{\circ}\).
∴ \(\triangle A P B\) is an equilateral triangle.
Example 17. If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that \(\angle D B C=120^{\circ}\), prove that B C+B D=B O.
Solution:
Given
If from an external point B of a circle with centre O, two tangents BC and BD are drawn such that \(\angle D B C=120^{\circ}\),
⇒ \(\angle 1+\angle 2 =120^{\circ}\)
But \(\angle 1 =\angle 2\)
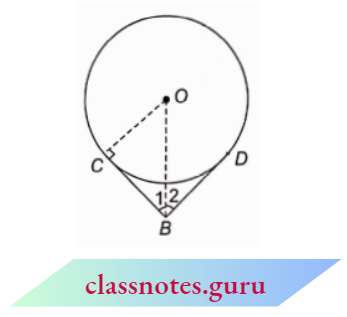
⇒ \(\angle 1+\angle 1 =120^{\circ}\)
2 \(\angle 1 =120^{\circ}\)
⇒ \(\angle 1 =60^{\circ}\)
Also, \(\angle O C B =90^{\circ}\) (radius through point of contact is \(\perp\) to the tangent)
Now, in right \(\triangle O C B\),
⇒ \(\cos 60^{\circ}=\frac{B C}{O B} \quad \Rightarrow \quad \frac{1}{2}=\frac{B C}{O B}\)
O B=B C+B C
O B=2 B C \(\quad \Rightarrow \quad O B=B C+B C\)
O B=B C+B D(length of tangents from an external point are equal)
∴ Hence Proved.
Example 18. In the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P. Find the length of PA.
Solution:
Given
In the adjoining figure, AB is a chord of length 9.6 cm of a circle with centre O and radius 6 cm. The tangents at A and B intersect at P.
Join OP, OA and OB.
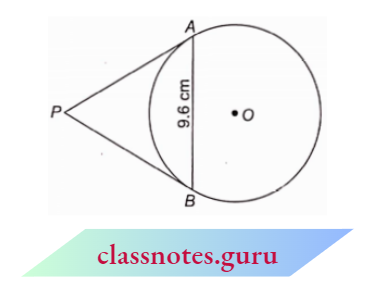
Let PA = x cm and PM = y cm
P A =P B (length of tangents from an external point are equal)
P M =P M (common)
⇒ \(\angle 1 =\angle 2\) (tangents are equally inclined at the centre)
⇒ \(\triangle A M P \cong \triangle B M P\) (SAS congruency)
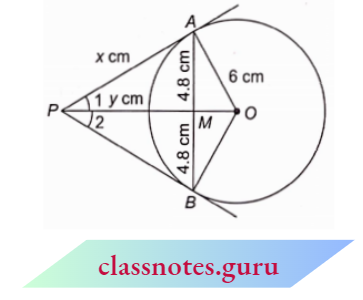
A M=M B=\(\frac{9.6}{2}=4.8 \mathrm{~cm}\)
and \(\angle P M A=\angle P M B\)
But \(\angle P M A+\angle P M B=180^{\circ}\)
⇒ \(\angle P M A=\angle P M B=90^{\circ}\)
Now, in right \(\triangle A M P\),
⇒ \(x^2=y^2+(4.8)^2\) (by Pythagoras theorem)
Also, in right \(x^2=y^2+(4.8)^2\)\triangle A M O\(x^2=y^2+(4.8)^2\),
⇒ \((4.8)^2+O M^2 =(6)^2\)
⇒ \(O M^2 =36-23.04=12.96\)
⇒ \(O M =\sqrt{12.96}=3.6 \mathrm{~cm}\)
Now, \(\angle O A P=90^{\circ}\) (radius through point of contact is \perp to the tangent)
In right \(\triangle M O P\),
⇒ \(O P^2 =O A^2+A P^2 \Rightarrow(y+3.6)^2=36+x^2\)
⇒ \(y^2+12.96+7.2 y =36+y^2+(4.8)^2\)
⇒ \(7.2 y =36+23.04-12.96 \quad \Rightarrow \quad 7.2 y=46.08 \)
y =\(\frac{46.08}{7.2}=6.4 \mathrm{~cm}\)
Put this value of y in equation (1),
⇒ \(x^2 =(6.4)^2+(4.8)^2=40.96+23.04=64\)
x = 8 cm
Hence, x=8 cm and y=6.4 cm
Example 19. The radii of two concentric circles are 1 3 cm and 8 cm. AB is the diameter of the bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD.
Solution:
Given
The radii of two concentric circles are 1 3 cm and 8 cm. AB is the diameter of the bigger circle. BD is a tangent to the smaller circle touching it at D.
Produce BD to E which cuts the circle at E. Join AE and OD.
Since AB is the diameter of the bigger circle.
⇒ \(\angle A E B=90^{\circ}\) (angle in a semicircle is right angle)
Also, \(\angle O D B=90^{\circ}\)(radius through point of contact is \(\perp\) to the tangent)
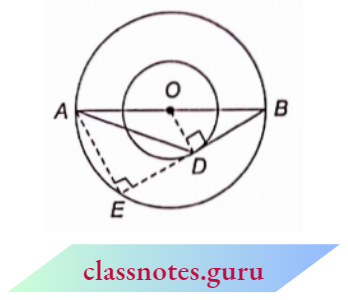
Now, in \(\triangle B O D\) and \(\triangle B A E\)
⇒ \(\angle B =\angle B\) (common)
⇒ \(\angle O D B =\angle A E B\) (each \(90^{\circ}\) )
⇒ \(\Delta B O D =\triangle B A E\)
⇒ \(\frac{O D}{A E} =\frac{O B}{A B}\)(corresponding sides of similar triangles are proportional)
⇒ \(\frac{8}{A E}=\frac{r}{2 r} \quad \Rightarrow A E=16 \mathrm{~cm}\)
Since, \(O D \perp E B\)
D E=D B (\(\perp\) drawn from the centre to the chord bisects the chord)
In right \(\triangle O D B\),
⇒ \(D B^2 =O B^2-O D^2=(13)^2-(8)^2=169-64=105\)
D B =\(\sqrt{105} \mathrm{~cm}=E D\)
Now, in right \(\triangle A E D\), by Pythagoras theorem
⇒ \(A D^2 =A E^2+E D^2\)
⇒ \(A D^2 =(16)^2+105=256+105=361\)
∴ \(A D =\sqrt{361}\) i.e.. 19 cm
Hence, A D =19 cm.
The length AD =19 cm.
Class 10 Circles Questions with Solutions
NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Exercise 10.1
Question 1. How many tangents can a circle have?
Solution :
Infinitely many tangents can be drawn on a circle.
Question 2. Fill in the blanks :
- A tangent to a circle intersects it in point (s).
- A line intersecting a circle in two points is called a
- A circle can have parallel tangents at the most.
- The common point of a tangent to a circle and the circle is called
Answer :
- one
- secant
- two
- point of contact
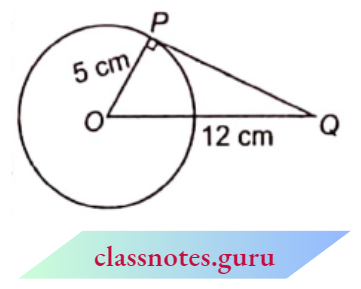
Question 3. A tangent PQ at a point P of a circle of radius 5 cm meets a line through the centre O at a point Q so that OQ = 12 cm, Length PQ is :
- 12 cm
- 13 cm
- 8.5 cm
- \(\sqrt{119} \mathrm{~cm}\)
Solution : 4. \(\sqrt{119} \mathrm{~cm}\)
Here OP = 5 cm,
OQ = 12 cm In \(\triangle\)POQ
In \(\triangle P O Q \)
⇒ \(P Q^2 =O Q^2-O P^2\)
=\(12^2-5^2=119\)
P Q =\(\sqrt{119}\) cm
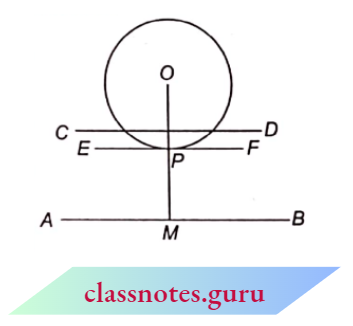
Question 4. Draw a circle and two lines parallel to a given line such that one is a tangent and the other, a secant to the circle.
Solution:
- Let the centre of the circle be O. The line AB lies outside the circle. Draw the perpendicular OM from O to AB.
- The perpendicular OM intersects the circle at P. Draw a line EPF from P parallel to AB.
- EF is the required tangent of the circle.
- Draw a line CD parallel to AB which intersects the circle at two points. It is the required secant of the circle.
NCERT Class 10 Maths Chapter 10 Extra Questions
NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Exercise 10.2
Question 1. From a point Q, the length of the tangent to a circle is 24 cm and the distance of Q from the centre is 25 cm. The radius of the circle is :
- 7 cm
- 12 cm
- 15 cm
- 24.5 cm
Answer: 1.
Here, PQ = 24 cm and OQ = 25 cm
In \(\triangle O P Q\)
⇒ \(O P^2=O Q^2-P Q^2\)(from Pythagoras theorem)
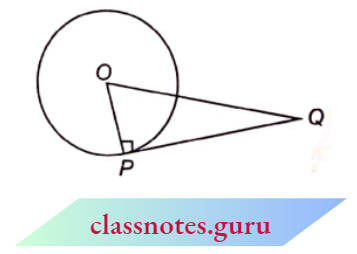
= \(25^2-24^2=625-576=49\)
OP = 7 cm
Radius of circle = 7 cm
Question 2. In the figure, if TP and TQ arc the Uvo tangents to a circle with centre O so that ZPOQ = 110°, then Z PTQ is equal to :
- 60°
- 70°
- 80°
- 90°
Answer: 2.
Here TP and TQ are the tangents to the circle.
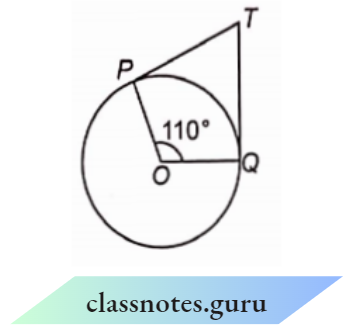
⇒ \(\angle\)OPT = \(\angle\)OQT = 90°
In □ OPTQ,
⇒ \(\angle\)OPT + \(\angle\)PTQ + \(\angle\)OQT + \(\angle\)POQ = 360°
90° + ZPTQ + 90° + 110° = 360°
⇒ \(\angle\)PTQ = 360° -290°
∴ \(\angle\)PTQ = 70°
Question 3. If tangents PA and PB from a point P to a circle with centre O are inclined to each other at an angle of 80°, then ∠POA is equal to :
- 50°
- 60°
- 70°
- 80°
Answer: 1. 50°
PA and PB are two tangents of the circle.
⇒ \(\angle\)PAO = \(\angle\)PBO = 90°
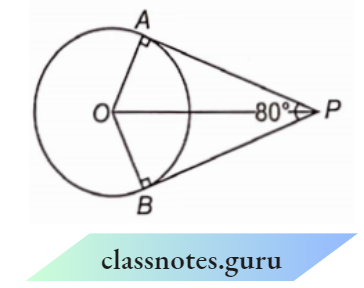
Given : \(\angle\)APB =80°
Now, in □PAOB,
⇒ \(\angle\)AOB + \(\angle\)PAO + \(\angle\)APB + \(\angle\)PBO = 360°
⇒ \(\angle\)AOB + 90° + 80° + 90° = 360°
⇒ \(\angle\)AOB = 360° – 260° = 100°
Now, PO bisects \(\angle\)AOB.
⇒ \(\angle\)POA = – \(\angle\)AOB = – x 100° = 50°
Question 4. Prove that the tangents drawn at the ends of the diameter of a circle are parallel.
Solution :
Let AB be the diameter of a circle with centre O. PA and PB are the tangents to the circle at A points A and B respectively.
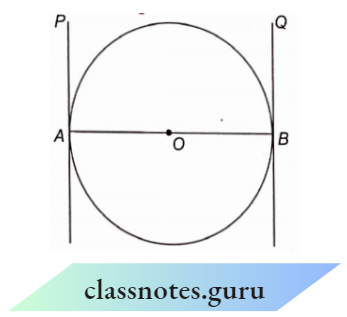
Now Z\(\angle\)PAB = 90°
and \(\angle\)QBA = 90°
\(\angle\)PAB +QBA = 90° + 90° = 180°
PA || QB Hence Proved.
Question 5. Prove that the perpendicular at the point of contact to the tangent to a circle passes through the centre.
Solution :
Given: A circle with centre O a tangent AQB and a perpendicular PQ is drawn from the point of contact Q to AB.
To Prove: The perpendicular PQ passes through the centre of the circle.
Proof: AQ is the tangent of the circle at point Q.
AQ will be the perpendicular to the radius of the circle.
PQ \(\perp\) AQ
The centre of the circle will lie on the line PQ.
Perpendicular PQ passes through the centre of the circle.
Hence Proved.
Question 6. The length of a tangent from point A at a distance 5 cm from the centre of the circle is 4 cm. Find the radius of the circle.
Solution :
Given
The length of a tangent from point A at a distance 5 cm from the centre of the circle is 4 cm.
Let O be the centre of the circle and PQ is a tangent to the circle from point P.
Given that, PQ = 4 cm and OP = 5 cm
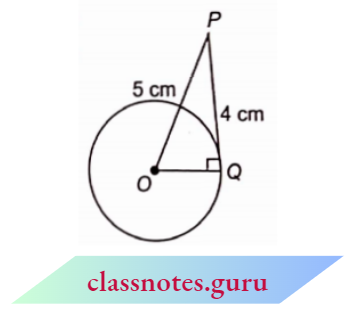
Now,\(\angle O Q P=90^{\circ}\)
In \(\triangle O Q P\) ,
⇒ \(O Q^2=O P^2-P Q^2\)
=\(5^2-4^2\)
= 25-16 = 9
OQ = 3 cm
Radius of circle = 3 cm
Question 7. Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle.
Solution :
Given
Two concentric circles are of radii 5 cm and 3 cm.
Here, we draw two circles C1 and C2 with radii = 3 cm and r2 = 5 cm c2 respectively.
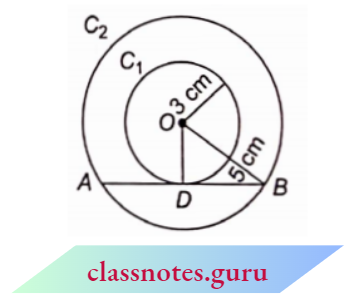
Now, we draw a chord AB which touches the circle C1 at D.
O is the centre of concentric circles.
Now we draw the perpendicular from O to AB which bisects AB at D.
i.e., AD = BD
In right \(\triangle O B D\),
⇒ \(O B^2=O D^2+D B^2\) (from Pythagoras theorem)
⇒ \(5^2 =3^2+D B^2\)
⇒ \(D B^2\) =25-9=16
DB = 4 cm
Length of chord = AB = 2BD
= 2 x 4 = 8 cm
Question 8. A quadrilateral ABCD is drawn to circumscribe a circle. Prove that AB + CD=AD + BC.
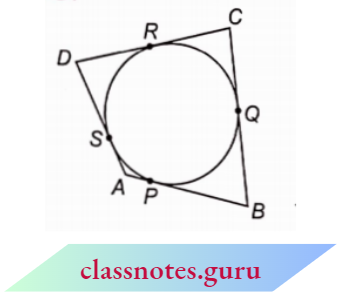
Solution :
Given
A quadrilateral ABCD is drawn to circumscribe a circle.
The sides of quadrilateral ABCD touch the circle at P, Q, R and S as shown in the figure. We know that the tangents drawn from an external point to the circle are equal.
AP = AS, BP = BQ,
CR = CQ, DR = DS
On adding, AP + BP + CR + DR
= AS + BQ + CQ + DS
⇒ AB + CD = (AS + DS) + (BQ + CQ)
⇒ AB + CD = AD + BC
Hence Proved.
Question 9. In the figure, XY and X’ Y’ are two parallel tangents to a circle with centre O and another tangent AB with the point of contact C intersecting XY at A and X’ Y’ at B. Prove that \(\angle\)AOB = 90°.
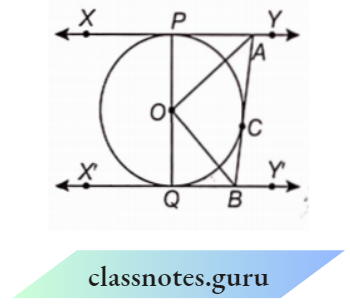
Solution :
Given
In the figure, XY and X’ Y’ are two parallel tangents to a circle with centre O and another tangent AB with the point of contact C intersecting XY at A and X’ Y’ at B.
The tangents from an external point to a circle are equal.
AP = AC
In \(\triangle A P O\) and \(\triangle A C O\),
AP = AC
AO = AO (common)
OP = OC (radii of a circle)
From S.S.S. congruency,
⇒ \(\triangle A P O \cong \triangle A C O\)
⇒ \(\angle P A O=\angle O A C\)
⇒ \(\angle P A C=2=\angle C A O\)
Similarly, we can prove that
⇒ \(\angle C B O =\angle O B Q\)
⇒ \(\angle C B Q =2 \angle C B O\)
⇒ \(Y \| X^{\prime} Y^{\prime}\)
⇒ \(\angle P A C+\angle Q B C=180^{\circ}\)
(sum of interior angles of the same side of a transversal is \(180^{\circ}\) )
2. \(\angle C A O+2 \angle C B O =180^{\circ}\)
⇒ \(\angle C A O+\angle C B O =90^{\circ}\)
In \(\triangle A O B\),
⇒ \(C A O+\angle C B O+\angle A O B=180^{\circ}\)
⇒ \(\angle C A O+\angle C B O=180^{\circ}-\angle A O B\) From equations (1) and (2)
⇒ \(180^{\circ}-\angle A O B=90^{\circ}\)
∴ \(\angle A O B=90^{\circ}\) Hence Proved.
Question 10. Prove that the angle between the two tangents drawn from an external point to a circle is supplementary to the angle subtends ey the line segment joining the points of contact at the centre.
Solution :
PA and PB are the tangents of the circle.
\(\angle O A P=\angle O B P=90^{\circ}\)In O A P B
⇒ \(\Rightarrow \quad 90^{\circ}+\angle A P B+90^{\circ}+\angle A O B=360^{\circ}\)
⇒ \(\angle A P B+\angle A O B=180^{\circ}\)
⇒ \(\angle A P B\) and \(\angle A O B\) are supplementary.
Hence Proved.
Question 11. Prove that the parallelogram circumscribing a circle is a rhombus.
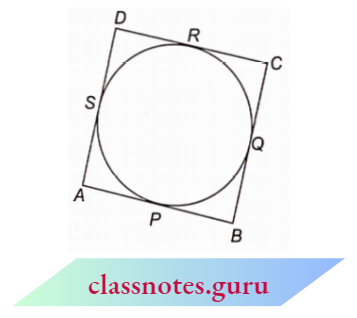
Solution :
Let a parallelogram ABCD is given. Let the parallelogram touch the circle at points, P, Q, R and S.
AP and AS are the tangents drawn from an -external point A to the circle.
AP = AS …(1)
Similarly, BP = BQ _ (2)
CR = CQ (3)
DR = DS (4)
Adding equations (1), (2), (3) and (4),
AP + BP + CR+DR = AS + BQ + CQ + DS
(AP + BP) + (CR + DR)
= (AS+ DS) + (BQ + CQ)
AB + CD = AD+BC
AB + AB = AD + AD {CD = AB, BC = AD, opposite sides of a parallelogram)
2 AB = 2 AD
AB = AD
So, ABCD is a rhombus. (adjacent sides of a parallelogram are equal)
Hence Proved.
Question 12. A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively. Find the sides AB and AC.
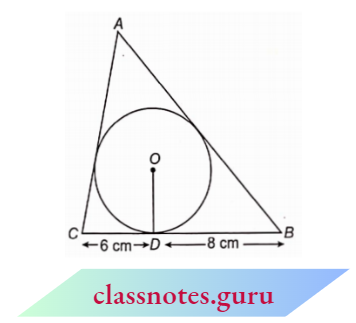
Solution :
Given
A triangle ABC is drawn to circumscribe a circle of radius 4 cm such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 8 cm and 6 cm respectively.
Given that: CD = 6 cm,
BD = 8 cm and radius = 4 cm
Join OC, OA and OB.
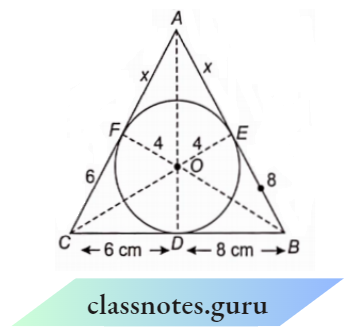
We know that the tangents drawn from an external point to a circle are equal.
CD = CF = 6 cm and BD = BE = 8 cm
Let AF = AE = x cm c
In \(\triangle\)OCB,
area of triangle \(A_1 =\frac{1}{2} \times \text { base } \times \text { height }\)
= \(\frac{1}{2} \times C B \times O D\)
= \(\frac{1}{2} \times 14 \times 4=28 \mathrm{~cm}^2\)
In \(\triangle O C A\),
area of triangle
⇒ \(A_2 =\frac{1}{2} \times A C \times O F \)
=\(\frac{1}{2}(6+x) \times 4\)
=12+2 x
In \(\triangle O B A\).
area of triangle
⇒ \(A_3 =\frac{1}{2} \times A B \times O E\)
=\(\frac{1}{2}(8+x) \times 4\)
=16+2 x
Now, semiperimeter of triangle ABC,
s =\(\frac{1}{2}(A B+B C+C A)\)
s =\(\frac{1}{2}(x+6+14+8+x)\)
=14+x
Now, area of \(\triangle A B C\)
=\(A_1+A_2+A_3\)
=28+(12+2 x)+(16+2 x)
=56+4 x
From Heron’s formula,
Area of \(\triangle A B C\)
= \(\sqrt{s(s-a)(s-b)(s-c)}\)
= \(\sqrt{(14+x)(14+x-14)(14+x-x-6)} \quad(14+x-x-8)\)
= \(\sqrt{(14+x)(x)(8)(6)}\)
= \(\sqrt{(14+x) 48 x}\)
From equations (1) and (2),
⇒ \(\sqrt{(14+x) 48 x}=56+4 x\)
Squaring both sides,
⇒ \((14+x) 48 x =4^2(14+x)^2\)
3 x =14+x
⇒ \(2 x=14-\Rightarrow \quad x\) =7
A C=6+x=6+7 =13 cm
A B=8+x=8+7 =15 cm
Question 13. Prove that opposite sides of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.
Solution :
We know that the tangents drawn R from an external point to a circle subtend equal angles at the centre.
⇒ \(\angle 1=\angle 2\) ,
⇒ \(\angle 3=\angle 4\) ,
⇒ \(\angle 5=\angle 6\)
and \(\angle 7=\angle 8\)
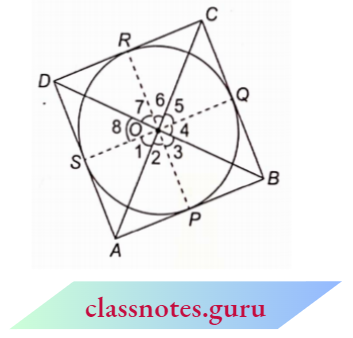
Now, \(\angle 1+\angle 2+\angle 3+\angle 4+\angle 5+\angle 6+\angle 7+\angle 8 =360^{\circ}\)
⇒ \(2 \angle 2+2 \angle 3+2 \angle 6+2 \angle 7 =360^{\circ} \)
⇒ \((\angle 2+\angle 3)+(\angle 6+\angle 7) =180^{\circ}\)
⇒ \(\angle A O B+\angle C O D =180^{\circ}\)
Similarly, \(\angle B O C+\angle A O D =180^{\circ}\)
Hence Proved.
NCERT Exemplar Solutions For Class 10 Maths Chapter 10 Circles Multiple Choice Questions
Question 1. If the angle between two radii of a circle is 1 10° then the angle between the tangents drawn at the ends of these radii is :
- 110°
- 100°
- 90°
- 70°
Answer: 4. 70°
Question 2. If two tangents PA and PB drawn from point P are of equal length 4 cm, then the radius of the die circle is :
- 1 cm
- 2 cm
- 4 cm
- 3 cm
Answer: 3. 4 cm
Question 3. In the adjoining figure, PA and PB are tangents to a circle with centre 0 such that \(angle\)APB = 40°. \(angle\)OAB is :
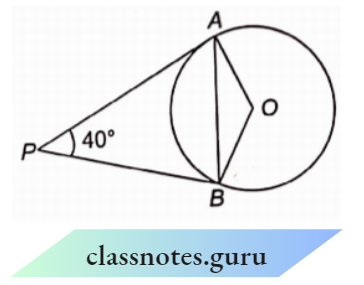
- 20°
- 40°
- 30°
- 15°
Answer: 1. 20°
Question 4. If two tangents of a circle of radius 6 cm are drawn such that the angle between them is 60 then the length of each tangent is :
- 2 \(\sqrt{3} \mathrm{~cm}\)
- 6 \(\sqrt{3} \mathrm{~cm}\)
- 3 cm
- 6 cm
Answer: 2. 6 \(\sqrt{3} \mathrm{~cm}\)
Question 5. Two tangents PQ and PR are drawn to a circle of radius 5 cm where P is 13 cm away from centre O. The area of quadrilateral PQOR is :
- \(60 \mathrm{~cm}^2\)
- \(30 \mathrm{~cm}^2\)
- \(65 \mathrm{~cm}^2\)
- \(32.5 \mathrm{~cm}^2\)
Answer: 1. \(60 \mathrm{~cm}^2\)
Class 10 Maths Circles important questions and answers
Question 6. In the adjoining figure, O is the centre of the circle, PQ is the chord and the tangent PR drawn from points on the circle makes a 50° angle from chord PQ, \(\angle\) POQ is :
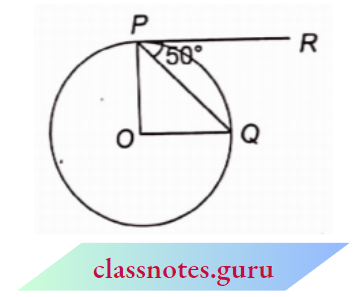
- 90°
- 80°
- 100°
- 75°
Answer: 3. 100°
Question 7. The radii of two circles are 3 cm and 4 cm and both circles touch each other externally. The distance between their centres is :
- 1 cm
- 3 cm
- 5 cm
- 7 cm
Answer: 4. 7 cm
