NCERT Exemplar For Class 10 Maths Chapter 9 Some Applications Of Trigonometry
Practical Use Of Trigonometry
The main purpose of studying trigonometry is to determine the height of buildings, towers, telephone poles, trees, the width of the river, the distance of the ship from the lighthouse etc. Although it is not easy to measure them, we can determine these things by using knowledge of trigonometric ratios, before doing so, let us first discuss some necessary definitions.

Line Of Sight: When an observer looks at an object then the line joining the observer’s eye to the object is called the line of sight.
Angle Of Elevation: When an observer sees an object situated in an upward direction, the angle formed by the line of sight with a horizontal line is called an angle of elevation.
NCERT Exemplar Class 10 Maths Chapter 9
Read and Learn More Class 10 Maths Solutions Exemplar
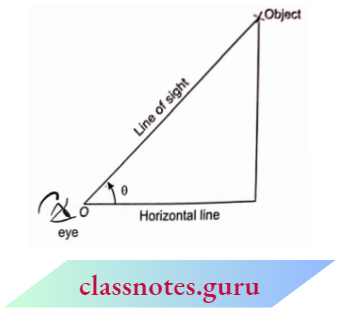
Angle Of Depression: When an observer sees an object .situated in a downward direction, the angle formed by the line of sight with a horizontal line is called an angle of depression.
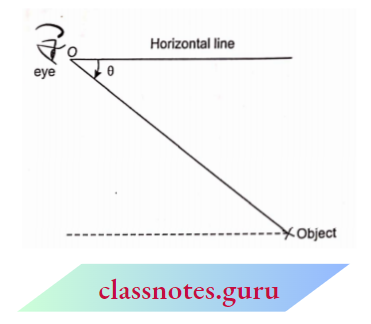
In the adjoining above given, θ is the angle of depression of the object as seen from O.
NCERT Exemplar For Class 10 Maths Chapter 9 Some Applications Of Trigonometry Solved Examples
Example 1. The length of the shadow of a vertical pole is \(\frac{1}{\sqrt{3}}\) times its height. Show that the angle of elevation of the sun is 60°.
Solution:
Given:
The length of the shadow of a vertical pole is \(\frac{1}{\sqrt{3}}\) times its height.
Let PQ be a vertical pole whose height is \(\frac{h}{\sqrt{3}}\). Its shadow is OQ whose height is.
Let the angle of elevation of the sun be \(\angle\)POQ = 0
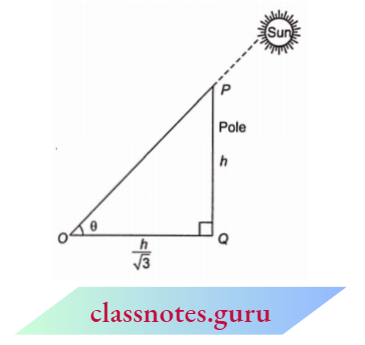
In \(\triangle\)POQ,
⇒ \(\tan \theta =\frac{P Q}{O Q}=\frac{h}{h / \sqrt{3}}=\sqrt{3}=\tan 60^{\circ}\)
⇒ \(\theta =60^{\circ}\)
The angle of elevation of the sun = 60°.
Example 2. If a tower 30 m high, casts a shadow 10 \(\sqrt{3}\) m long on the ground, then what is the angle of elevation of the sun?
Solution:
It is given that AB = 30 m be the height of the tower and BC = \(\sqrt{3}\) m its shadow on the ground.
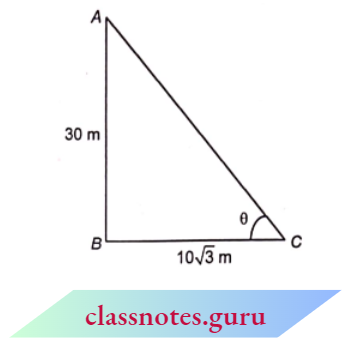
Let \(\theta\) be the angle of elevation.
In a right triangle,
⇒ \(\tan \theta =\frac{A B}{B C}\)
= \(\frac{30}{10 \sqrt{3}}=\frac{3}{\sqrt{3}}=\sqrt{3}\)
= \(\tan 60^{\circ}\)
⇒ \(\theta =60^{\circ}\)
Hence, the angle of elevation of the sun= 60°
Example 3. A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall, find the height of the wall.
Solution:
Given:
A ladder 15 metres long just reaches the top of a vertical wall. If the ladder makes an angle of 60° with the wall
Let PR be a ladder of length 15 m and QR, a wall of height h.
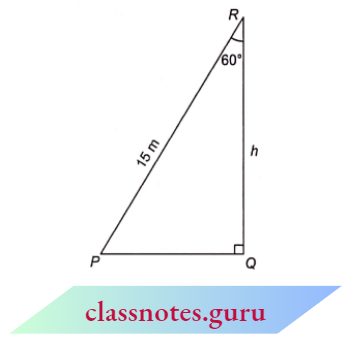
Given that \(\angle\)PRQ = 60°
In \(\triangle P Q R\),
⇒ \(\cos 60^{\circ} =\frac{h}{P R} \quad \Rightarrow \quad \frac{1}{2}=\frac{h}{15}\)
⇒ \(\Rightarrow \quad h =\frac{15}{2} \mathrm{~m}\)
Height of the wall =\(\frac{15}{2} \mathrm{~m}=7.5 \mathrm{~m}\)
Question 4. The shadow of a tower standing on a level plane is found to be 50 m longer when the sun’s elevation is 30° than when it is 60°. Find the height of the tower.
Solution:
Given
The shadow of a tower standing on a level plane is found to be 50 m longer when the sun’s elevation is 30° than when it is 60°.
Let AB be a tower of height ‘h’ metres and BD and BC be its shadows when the angles of elevation of the sun are 30° and 60° respectively.
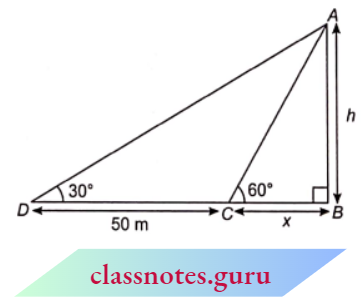
⇒ \(\angle A D B=30^{\circ}, \angle A C B=60^{\circ} \text { and } C D=50 \mathrm{~m}\)
Let BC = x metres.
In \(\triangle A B C\)
⇒ \(\tan 60^{\circ} =\frac{A B}{B C} \quad \Rightarrow \quad \sqrt{3}=\frac{h}{x}\)
⇒ \( x =\frac{h}{\sqrt{3}}\)
In \(\triangle A B D\)
⇒ \(\tan 30^{\circ}=\frac{A B}{B D} \Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{x+50}\)
⇒ \(\sqrt{3} h=x+50 \Rightarrow \sqrt{3} h=\frac{h}{\sqrt{3}}+50\)
⇒ \(h=h+50 \sqrt{3} \quad \Rightarrow \quad 2 h=50 \sqrt{3} \quad \Rightarrow \quad h=25 \sqrt{3}\)
Height of the tower =\(25 \sqrt{3} \mathrm{~m}\)
Question 5. The angle of elevation of the top of a tower from a point on the ground is 30°. After walking 40 m towards the tower, the angle of elevation becomes 60°. Find the height of the tower.
Solution:
Given
The angle of elevation of the top of a tower from a point on the ground is 30°. After walking 40 m towards the tower, the angle of elevation becomes 60°.
Let AB be a tower of height 7i’ metres. From points D and C on the ground, the angle of elevation of top A of the tower is 30° and 60° respectively.
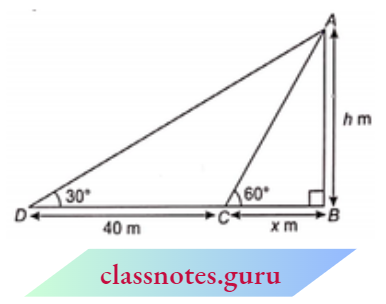
Given that CD = 40 m
Let BC = x metres
In \(\triangle A B C\)
⇒ \(\tan 60^{\circ} =\frac{A B}{B C} \quad \Rightarrow \quad \sqrt{3}=\frac{h}{x}\)
x =\(\frac{h}{\sqrt{3}}\)
In \(\triangle A B D\)
⇒ \(\tan 30^{\circ} =\frac{A B}{B D} \Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{40+x}\)
⇒ \(\sqrt{3} h =40+x \Rightarrow \sqrt{3} h=40+\frac{h}{\sqrt{3}}\)
⇒ \(3 h =40 \sqrt{3}+h \Rightarrow 2 h=40 \sqrt{3}\)
⇒ \(h =20 \sqrt{3}\)
Height of the tower =\(20 \sqrt{3} \mathrm{~m}\)
Question 6. The angle of elevation of the top of a tower from two points distant ‘s’ and ‘t’ from its foot are complementary. Prove that the height of the tower is \(\sqrt{st}\) .
Answer:
Given
The angle of elevation of the top of a tower from two points distant ‘s’ and ‘t’ from its foot are complementary.
Let BC be a tower of height ‘h’. Let AC = s and DC = t.
From points A and D, the angle of elevation of top B of the tower is complementary.
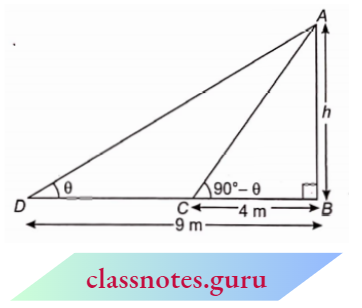
Let \(\angle B A C=\theta\)
⇒ \(\angle B D C=90^{\circ}-\theta\)
In \(\triangle B A C\)
⇒ \(\tan \theta=\frac{B C}{A C}=\frac{h}{s}\)
In \(\triangle B D C\)
⇒ \(\tan \left(90^{\circ}-\theta\right) =\frac{B C}{C D} \Rightarrow \cot \theta=\frac{h}{t}\)
⇒ \(\Rightarrow\frac{1}{\tan \theta} =\frac{h}{t} \quad \Rightarrow \frac{s}{h}=\frac{h}{t}\)
⇒ \(h^2 =s t \Rightarrow h=\sqrt{s t}\)
height of the tower =\(\sqrt{s t}\)
Example 7. A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance of 4 m from the root. Find the height of the tree before broken.
Solution:
Given
A tree is broken by the wind. The top struck the ground at an angle of 30° and at a distance of 4 m from the root.
Given that A B=4 m and \(\angle\) B A C=\(30^{\circ}\). Also C D=C A In \(\triangle \)A B C,
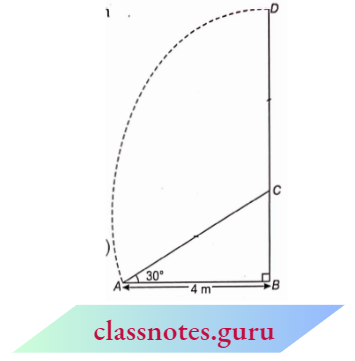
⇒ \(\tan 30^{\circ}=\frac{B C}{A B} \quad \Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{B C}{4}\)
B C=\(\frac{4}{\sqrt{3}} \mathrm{~m}\)
and \(\quad \cos 30^{\circ}=\frac{A B}{A C} \quad \Rightarrow \quad \frac{\sqrt{3}}{2}=\frac{4}{A C}\)
A C=\(\frac{8}{\sqrt{3}} \mathrm{~m} \Rightarrow C D=\frac{8}{\sqrt{3}} \mathrm{~m}( A C=C D)\)
Now the total height of the tree =B C+C D
= \(\frac{4}{\sqrt{3}}+\frac{8}{\sqrt{3}}=\frac{12}{\sqrt{3}}=4 \sqrt{3} \mathrm{~m}\)
The height of the tree before broken = \(4 \sqrt{3} \mathrm{~m}\)
Applications of Trigonometry Class 10 Exemplar
Example 8. From the top of a tower 71 m high, the angles of depression of two objects, which are in line with the foot of the tower are \(\alpha\) and \(\beta(\beta>\alpha)\). Find the distance between the two objects.
Solution:
Given
From the top of a tower 71 m high, the angles of depression of two objects, which are in line with the foot of the tower are \(\alpha\) and \(\beta(\beta>\alpha)\).
Let AB be a tower of height ‘h’m. From the top A’ of the tower, the angle of depression of two objects D and C are ‘ \(\beta\) And \(\alpha\) respectively.
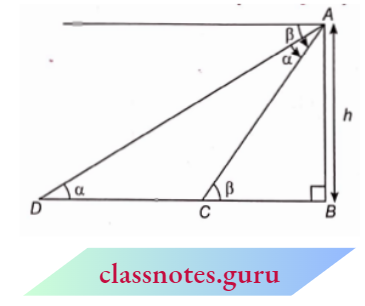
In \(\triangle A B C\)
⇒ \(\tan \beta=\frac{A B}{B C} =\frac{h}{B C}\)
B C =\(\frac{h}{\tan \beta}=h \cot \beta\)
In \(\triangle A B D\)
⇒ \(\tan \alpha =\frac{A B}{B D}=\frac{h}{B D}\)
B D =\(\frac{h}{\tan \alpha}=h \cot \alpha\)
Subtract equation (1) from (2), we get
⇒ \(B D-B C=h \cot \alpha-h \cot \beta\)
⇒ \(C D=h(\cot \alpha-\cot \beta)\)
⇒ \(C D=h(\cot \alpha-\cot \beta)\)
The distance between the objects =\(h(\cot \alpha-\cot \beta) \mathrm{m}\).
Example 9. Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 60°. If the height of the tower is 150 m, find the distance between the two men.
Solution:
Given
Two men are on opposite sides of a tower. They measure the angles of elevation of the top of the tower as 30° and 60°. If the height of the tower is 150 m
Lot CD bo a tower of height 1 50 m. Two men A and B are on the opposite sides of the tower.
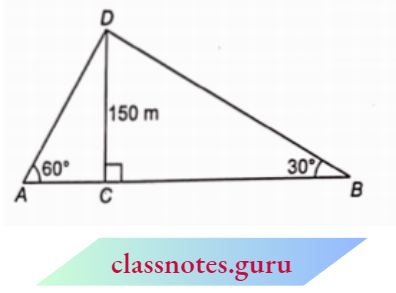
Given that, \(\angle D A C=60^{\circ}\) and \(\angle D B C=30^{\circ}\)
In \(\triangle D A C\)
⇒ \(\tan 60^{\circ} =\frac{D C}{A C} \quad \Rightarrow \quad \sqrt{3}=\frac{150}{A C}\)
⇒ \(A C =\frac{150}{\sqrt{3}}=50 \sqrt{3} \mathrm{~m}\)
In \(\triangle B C D\)
⇒ \(\tan 30^{\circ} =\frac{D C}{B C} \Rightarrow \frac{1}{\sqrt{3}}=\frac{150}{B C} \Rightarrow B C=150 \sqrt{3} \mathrm{~m}\)
A B = A C+B C
= \((50 \sqrt{3}+150 \sqrt{3}) \mathrm{m}=200 \sqrt{3} \mathrm{~m}\)
Therefore the distance between two \(\mathrm{men}=200 \sqrt{3} \mathrm{~m}\)
Example 10. A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h, At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are a and p respectively. Prove that the height of the tower is \(\left(\frac{h \tan \alpha}{\tan \beta-\tan \alpha}\right)\)
Solution:
Given:
A vertical tower stands on a horizontal plane and is surmounted by a vertical flagstaff of height h, At a point on the plane, the angles of elevation of the bottom and the top of the flagstaff are a and p respectively.
Let AB be a tower and BC be the flagstaff.
Let O be the observer.
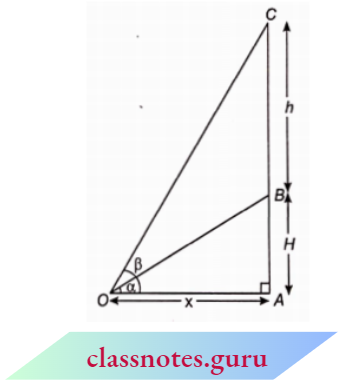
Now, \(\angle A O B=\alpha\), \(\angle A O C=\beta\) and B C=h
Let A B = H and O A = x
In \(\triangle O A B\)
\(\tan \alpha=\frac{A B}{O A}=\frac{H}{x} \quad \Rightarrow \quad x=\frac{H}{\tan \alpha}\) → Equation 1
In \(\triangle O A C\)
⇒ \(\tan \beta=\frac{A C}{O A}=\frac{H+h}{x} \Rightarrow x=\frac{H+h}{\tan \beta}\) → Equation 2
From equations (1) and (2), we get
⇒ \(\frac{H}{\tan \alpha} =\frac{H+h}{\tan \beta}\)
⇒ \(H \tan \beta =H \tan \alpha+h \tan \alpha\)
⇒ \(H(\tan \beta-\tan \alpha) =h \tan \alpha\)
H =\(\frac{h \tan \alpha}{\tan \beta-\tan \alpha}\)
Height of the tower =\(\frac{h \tan \alpha}{\tan \beta-\tan \alpha}\)
Example 11. The angle of elevation of the top of a vertical lower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 47′. Find the height of the tower.
Solution:
Given
The angle of elevation of the top of a vertical lower from a point on the ground is 60°. From another point 10 m vertically above the first, its angle of elevation is 47′.
Let All he a vertical lower. From point C, the angle of elevation of the top of the tower is 60° and from point) as shown, the angle of elevation of the tower is 45°.
⇒ \(\angle A C B=60^{\circ}, \angle A D E=45^{\circ}\) and \(D C=10 \mathrm{~m}\)
In \(\triangle D E\),
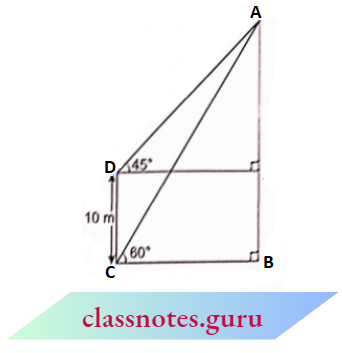
⇒ \(\tan 45^{\circ}=\frac{A E}{D E} \quad \Rightarrow \quad A E=D E \ldots(1)\left( \tan 45^{\circ}=1\right)\)
In \(\triangle A B C\),
⇒ \(\tan 60^{\circ} =\frac{A B}{B C} \quad \Rightarrow \quad \sqrt{3}=\frac{A B}{D E} \quad( B C=D E)\)
\(A B =\sqrt{3} D E\)A E+B E =\(\sqrt{3} A E\)
⇒ \(B E =A E(\sqrt{3}-1)\)
A E =\(\frac{B E}{\sqrt{3}-1}=\frac{10}{\sqrt{3}-1} \times \frac{\sqrt{3}+1}{\sqrt{3}+1}\)
⇒ \(\frac{10(1.732+1)}{3-1}=5 \times 2.732=13.66\)
Now, A B =A E+B E=A E+C D
= \((13.66+10) \mathrm{m}=23.66 \mathrm{~m}\)
Height of the tower =23.66 m
Example 12. The angle of elevation of the top Q of a vertical towerPQ from a point Y- on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of the tower is 45°. Find the height of the tower PQ and the distance PX. (Use \(\sqrt{3}\)=1.73)
Solution:
Given
The angle of elevation of the top Q of a vertical towerPQ from a point Y- on the ground is 60°. From a point Y, 40 m vertically above X, the angle of elevation of the top Q of the tower is 45°.
Let height of tower PQ be h m and let P X = x m
Since, X Y=40=P Z
Q Z=P Q-P Z=h-40.
In right \(\triangle Q Z Y\),
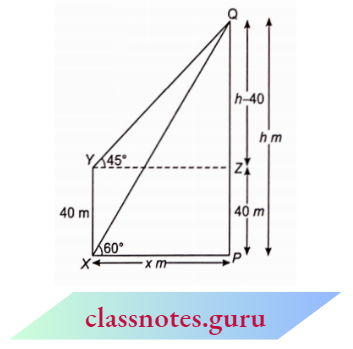
⇒ \(\tan 45^{\circ}=\frac{h-40}{x} \Rightarrow 1=\frac{h-40}{x}\)
⇒ \(h-40=x \Rightarrow x=h-40\)
In right \(\triangle Q P X\),
⇒ \(\tan 60^{\circ}=\frac{h}{x} \quad \Rightarrow \quad \sqrt{3}=\frac{h}{x}\)
x=\(\frac{h}{\sqrt{3}}\)
From equations (1) and (2), we get
h-40=\(\frac{h}{\sqrt{3}} \quad \Rightarrow h \sqrt{3}-40 \sqrt{3}=h\)
⇒ \(h(\sqrt{3}-1)=40 \sqrt{3} \Rightarrow h=\frac{40 \sqrt{3}}{\sqrt{3}-1}\)
h= \(\frac{40 \sqrt{3}(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=20(3+\sqrt{3})\)
h = \(20(3+1.73)=20 \times 4.73=94.6 \mathrm{~m}\)
x =h-40
=94.6-40=54.6 m
Hence, the height of tower PQ is 94.6 m and the distance P X is 54.6 m.
Example 13. As observed from the top of a lighthouse, 100 m high above sea level, the angles of depression of a ship, sailing directly towards it, change from 30° to 60°. Find the distance travelled by the ship during the period of observation.(Use \(\sqrt{3}\)=1.73)
Solution:
Given
As observed from the top of a lighthouse, 100 m high above sea level, the angles of depression of a ship, sailing directly towards it, change from 30° to 60°.
Let the height of the lighthouse be A B=100 m and let D be the ship which is sailing towards it. Also, let D C=x m.
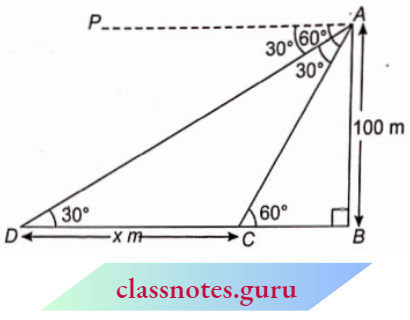
Here, \(\angle C A D =60^{\circ}-30^{\circ}=30^{\circ}\)
⇒ \(\angle C D A =\angle C A D\)
D C=A C=x (angles opposite to equal sides are equal)
Now, in right \(\triangle A B C\),
⇒ \(\sin 60^{\circ}=\frac{A B}{A C} \quad \Rightarrow \quad \frac{\sqrt{3}}{2}=\frac{100}{D C}\)
⇒ \(D C=\frac{200}{\sqrt{3}}=\frac{200 \sqrt{3}}{3}=\frac{200 \times 1.73}{3}\)
⇒ \(D C=\frac{346}{3}\)=115.3 m
Hence, the distance travelled by ship is 115.3 m.
Question 14. An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively. Find the width of the river. (Use \(\sqrt{3}\)=1.73)
Solution:
Given
An aeroplane is flying at a height of 300 m above the ground. Flying at this height, the angles of depression from the aeroplane of two points on both banks of a river in opposite directions are 45° and 60° respectively.
Let an aeroplane P fly at a height of 300 m above the x-ground
PM = 300m
Depression angles are \(\angle X P A=45^{\circ}\) and \(\angle Y P B=60^{\circ}\).
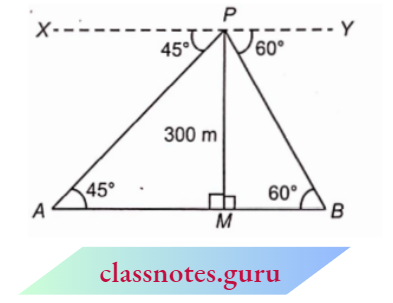
Now, in right \(\triangle P M A\),(alternate angles)
⇒ \(\tan 45^{\circ}=\frac{P M}{A M} \quad \Rightarrow \quad 1=\frac{300}{A M} . \quad \Rightarrow \quad A M=300 \mathrm{~m}\)
In right \(\triangle P M B\),
⇒ \(\tan 60^{\circ}=\frac{P M}{M B} \quad \Rightarrow \quad \sqrt{3}=\frac{300}{M B} \quad \Rightarrow \quad M B=\frac{300}{\sqrt{3}}=100 \sqrt{3}\)
Width of river =A M+M B
= \((300+100 \sqrt{3}) \mathrm{m}=(300+100 \times 1.732) \mathrm{m}\)
=(300+173.2) m=473.20 m
Hence, the width of the river = 473.20 m
Example 15. A man observes a car from the top of a tower, which is moving towards the tower at a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes, find the time taken by the car now to reach the tower.
Solution:
Given
5. A man observes a car from the top of a tower, which is moving towards the tower at a uniform speed. If the angle of depression of the car changes from 30° to 45° in 12 minutes
Let AB = h m be the height of the tower.
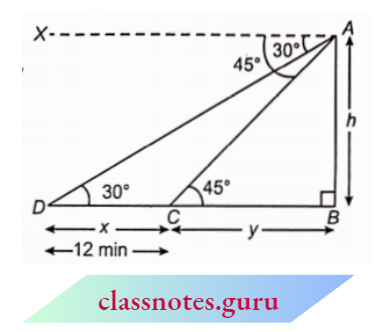
Since the depression angle changes from 30° to 45° in 12 minutes, therefore, time taken from D to C = 12 min.
Let DC = x m and CB -y m
Now, in right \(\triangle A B C\),
⇒ \(\tan 45^{\circ}=\frac{h}{y} \Rightarrow 1=\frac{h}{y} \Rightarrow h=y\)
In right \(\triangle A B D\),
⇒ \(\tan 30^{\circ} =\frac{h}{x+y} \quad \Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{h}{x+y}\)
⇒ \(x+y =h \sqrt{3}\)
x+y =y \(\sqrt{3}\)
⇒ \(y(\sqrt{3}-1) =x\)
Now time taken by car in moving \(x \mathrm{~m}=12 \mathrm{~min}\)
Time taken by car in moving \(y(\sqrt{3}-1) \mathrm{m}=12 \mathrm{~min}\)
Time taken by car in moving \(y \mathrm{~m}=\frac{12}{\sqrt{3}-1} \mathrm{~min}\)
= \(\frac{12(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)} \min =\frac{12(1.732+1)}{2}\)
=6 \(\times 2.732=16.39 \mathrm{~min}\)
Hence, required time =16.39 minutes.
The time taken by the car now to reach the tower =16.39 minutes.
Example 16. A bird is sitting on the top of an 80 m-high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such a way that it remains at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°. Find the speed of flying of the bird.(Take, \(\sqrt{3}\)=1.73)
Solution:
Given
A bird is sitting on the top of an 80 m-high tree. From a point on the ground, the angle of elevation of the bird is 45°. The bird flies away horizontally in such a way that it remains at a constant height from the ground. After 2 seconds, the angle of elevation of the bird from the same point is 30°.
Let P be the position of a bird at the height of 80 m with the angle of elevation 45° from A.
Let after 2 seconds, it reaches Q from where its elevation angle is 30°.
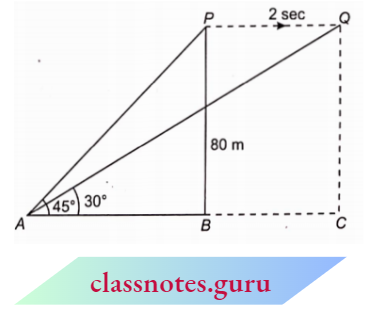
Now, in right \(\triangle P B A\),
⇒ \(\tan 45^{\circ} =\frac{P B}{A B} \quad \Rightarrow \quad 1=\frac{80}{A B}\)
A B = 80 m
In right \(\triangle Q C A\),
⇒ \(\tan 30^{\circ} =\frac{Q C}{A C} \Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{80}{A C}\)
⇒ \(A C =80 \sqrt{3} \mathrm{~m}\)
BC =A C-A B
=80 \(\sqrt{3}-80 \quad=80(\sqrt{3}-1)\)
= \(80(1.732-1)=80 \times 0.732=58.56 \mathrm{~m}\)
Now, speed of bird =\(\frac{\text { Distance }}{\text { time }}=\frac{58.56}{2} \mathrm{~m} / \mathrm{sec}=29.28 \mathrm{~m} / \mathrm{sec}\) .
The speed of flying of the bird =\( 29.28 \mathrm{~m} / \mathrm{sec}\) .
Example 17. The angle of elevation of a cloud from a point 7z’ metres above a lake is a and the angle of depression of its reflection in the lake is p. Prove that the distance of the cloud from the point of observation is \(\frac{2 h \sec \alpha}{\tan \beta-\tan \alpha}\)
Solution:
Given:
The angle of elevation of a cloud from a point 7z’ metres above a lake is a and the angle of depression of its reflection in the lake is p.
Let AB be a lake. The angle of elevation of cloud P at point A on height TP from the lake is a and the angle of depression of the reflection F of cloud is \(\beta\).
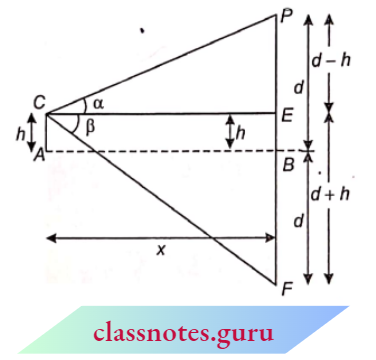
⇒ \(\angle P C E=\alpha and \angle F C E=\beta\)
Let B P=F B=d
P E=B P-E B
P E=B P-A C=d-h
and F E=F B+B E=F B+A C=d+h
Let C E = x
In \(\triangle C E F\),
⇒ \(\tan \beta=\frac{E F}{C E} \quad \Rightarrow \quad \tan \beta=\frac{d+h}{x}\) → Equation 1
In \(\triangle P E C\),
⇒ \(\tan \alpha=\frac{P E}{C E} \quad \Rightarrow \quad \tan \alpha=\frac{d-h}{x}\) → Equation 2
Subtract equation (2) from equation (1), we get
⇒ \(\tan \beta-\tan \alpha=\frac{d+h}{x}-\frac{d-h}{x}=\frac{2 h}{x} \quad \Rightarrow \quad x=\frac{2 h}{\tan \beta-\tan \alpha}\)
In \(\triangle P E C\),
⇒ \(\cos \alpha=\frac{C E}{P C}=\frac{x}{P C} \quad \Rightarrow \quad P C=\frac{x}{\cos \alpha}=x \sec \alpha\) Equation 3
PC = \(\frac{2 h \sec \alpha}{\tan \beta-\tan \alpha}\)
Hence, the distance of the cloud from the point of observation =\(\frac{2 h \sec \alpha}{\tan \beta-\tan \alpha}\)
Class 10 Trigonometry height and distance solutions
Example 18. A man standing on the deck of a ship which is 14 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Find the distance of the hill from the ship and the height of the hill.
Solution:
Given
A man standing on the deck of a ship which is 14 m above water level, observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°.
Let the height of the hill AB = h m and let the position of man at 14 m above the sea level is D.
Let B C=x \(\mathrm{~m} \Rightarrow D E=x \mathrm{~m}\)
In right \(\triangle D C B\),
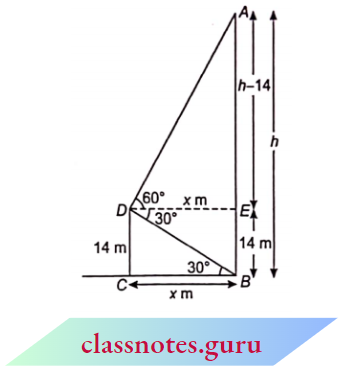
⇒ \(\tan 30^{\circ}=\frac{D C}{B C} \quad \Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{14}{x} \quad \Rightarrow \quad x=14 \sqrt{3} \mathrm{~m}\)
In right \(\triangle A E D\),
⇒ \(\tan 60^{\circ} =\frac{A E}{D E} \quad \Rightarrow \quad \sqrt{3}=\frac{h-14}{x}\)
⇒ \(x \sqrt{3} =h-14 \quad \Rightarrow \quad 14 \sqrt{3} \times \sqrt{3}\)=h-14 [ from (1) ]
h =42+14=56 m
Hence, the die distance of the hill from the ship is x i.e., \(14 \sqrt{3} m\) and the height of the hill is 56 m.
NCERT Exemplar For Class 10 Maths Chapter 9 Some Applications Of Trigonometry Exercise 9.1
Question 1. A circus artist is climbing a 20 m-long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.
Solution :
Given:
A circus artist is climbing a 20 m-long rope, which is tightly stretched and tied from the top of a vertical pole to the ground.
In \(\triangle A B C\),
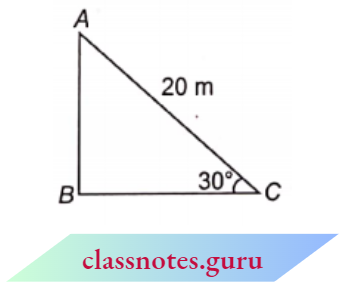
⇒ \(\sin 30^{\circ} =\frac{A B}{A C}\)
⇒ \(\frac{1}{2}=\frac{A B}{20}\)
B =10
Height of pole = 10 m
Question 2. A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m. Find the height of the tree.
Solution :
Given
A tree breaks due to a storm and the broken part bends so that the top of the tree touches the ground making an angle of 30° with it. The distance between the foot of the tree to the point where the top touches the ground is 8 m.
Let the part CD of the tree BD break in the air and touch the ground at point A.

According to the problem,
AB = 8 m and \(\angle\) BAC = 30°
In \(\triangle A B C\),
⇒ \(\tan 30^{\circ} =\frac{B C}{A B} \quad \stackrel{A 0^{\circ}}{\longleftrightarrow} \mathrm{m}_8\)
⇒ \(\frac{1}{\sqrt{3}} =\frac{B C}{8}\)
⇒ \(B C =\frac{8}{\sqrt{3}} \mathrm{~m}\)
and \(\cos 30^{\circ} =\frac{A B}{A C} \Rightarrow \frac{\sqrt{3}}{2}=\frac{8}{A C}\)
⇒ \(A C =\frac{16}{\sqrt{3}} \mathrm{~m}\)
C D =\(\frac{16}{\sqrt{3}} \mathrm{~m}\) (A C=C D)
Now, the height of the tree = BC + CD
=\(\frac{8}{\sqrt{3}}+\frac{16}{\sqrt{3}}=\frac{24}{\sqrt{3}}=8 \sqrt{3} \mathrm{~m}\)
The height of the tree =\( 8 \sqrt{3} \mathrm{~m}\)
Question 3. A contractor plans to install two slides for the children to play in a park. For children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground. What should be the length of the slide in each case?
Solution :
Given
A contractor plans to install two slides for the children to play in a park. For children below the age of 5 years, she prefers to have a slide whose top is at a height of 1.5 m and is inclined at an angle of 30° to the ground, whereas for elder children, she wants to have a steep slide at a height of 3m, and inclined at an angle of 60° to the ground.
Let the slide for elder children be AC and for younger children be DE.
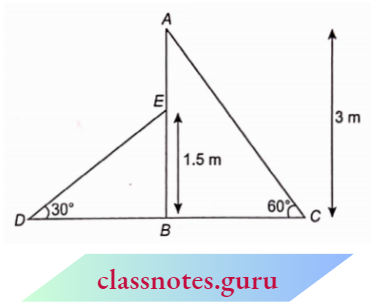
In \(\triangle A B C\),
⇒ \(\angle A B C=90^{\circ}\)
A B=3 m
⇒ \(\sin 60^{\circ}=\frac{A B}{A C} \Rightarrow \frac{\sqrt{3}}{2}=\frac{3}{A C}\)
A C=\(\frac{6}{\sqrt{3}}=2 \sqrt{3} \mathrm{~m}\)
In \(\triangle B D E\),
⇒ \(\angle D B E =90^{\circ}\)
B E=1.5 m
⇒ \(\sin 30^{\circ} =\frac{B D}{D E}\)
⇒ \(\frac{1}{2} =\frac{1.5}{D E} \Rightarrow D E\) =3 m
Length of slide for elder children
=2\( \sqrt{3} \mathrm{~m}\)
and length of slide for younger children =3 m
Question 4. The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower, is 30°. Find the height of the tower.
Solution :
Let AB be the tower.
The angle of elevation of the top of the tower from point C, 30m away from A is 30°.
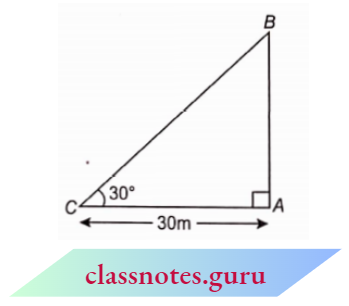
In \(\triangle B A C\),
⇒ \(\tan 30^{\circ}=\frac{A B}{A C}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{A B}{30}\)
⇒ \(A B=\frac{30}{\sqrt{3}}=10 \sqrt{3} \mathrm{~m}\)
Height of the tower =\(10 \sqrt{3} \mathrm{~m}\)
Question 5. A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°. Find the length of the string, assuming that there is no slack in the string.
Solution:
Given
A kite is flying at a height of 60 m above the ground. The string attached to the kite is temporarily tied to a point on the ground. The inclination of the string with the ground is 60°.
Let the height of kite A from the ground is 60 m and AC is the string.
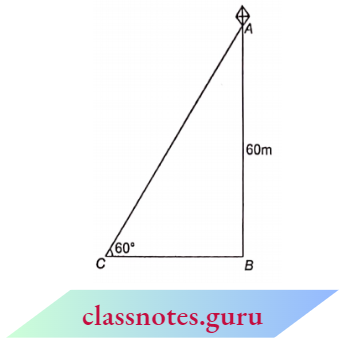
Given : \(\angle A C B=60^{\circ}\)
In \(\triangle A B C\),
⇒ \(\sin 60^{\circ}=\frac{60}{A C}\)
⇒ \(\frac{\sqrt{3}}{2}=\frac{60}{A C}\)
A C=\(\frac{120}{\sqrt{3}}=40 \sqrt{3} \mathrm{~m}\)
Length of string =40 \(\sqrt{3}\) m
Question 6. A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building. Find the distance he walked towards the building
Solution:
Given
A 1.5 m tall boy is standing at some distance from a 30 m tall building. The angle of elevation from his eyes to the top of the building increases from 30° to 60° as he walks towards the building.
Let, the height of building AN = 30 m
Here, BM = height of boy = 1.5 m
DN = BM = 1.5 m
AD = AN -AD = 30- 1.5 = 28.5 m
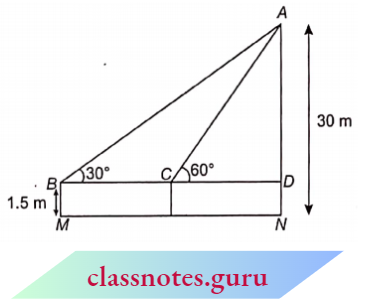
In \(\triangle A C D\),
⇒ \(\tan 60^{\circ} =\frac{A D}{C D} \quad \Rightarrow \quad \sqrt{3}=\frac{28.5}{C D}\)
⇒ \(C D =\frac{28.5}{\sqrt{3}}=9.5 \sqrt{3} \mathrm{~m}\)
In \(\triangle A B D\),
⇒ \(\tan 30^{\circ}=\frac{A D}{B D} \Rightarrow \frac{1}{\sqrt{3}}=\frac{28.5}{B D}\)
⇒ \(B D=28.5 \sqrt{3} \mathrm{~m}\)
Now, \(B C=B D-C D\)
=28.5 \(\sqrt{3}-9.5 \sqrt{3}=19 \sqrt{3} \mathrm{~m}\)
Distance walked by boy towards the building \(19 \sqrt{3} \mathrm{~m}\)
Question 7. From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively. Find the height of the tower.
Solution:
Given
From a point on the ground, the angles of elevation of the bottom and the top of a transmission tower fixed at the top of a 20 m high building are 45° and 60° respectively.
Let, CD be the height of the transmission tower.
Here, the height of the building
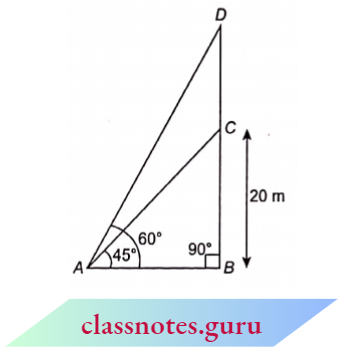
BC = 20 m
In \(\triangle A B C\),
⇒ \(\tan 45^{\circ} =\frac{B C}{A B}\)
=\(\frac{20}{A B}\)
A B =20 m
In \(\triangle A B D\),
⇒ \(\tan 60^{\circ}=\frac{B D}{A B} \quad \Rightarrow \sqrt{3}=\frac{B D}{20}\)
B D=20 \(\sqrt{3} m\)
B C+C D=20 \(\sqrt{3}\)
20+C D=20 \(\sqrt{3}\)
C D=20\((\sqrt{3}-1) \mathrm{m}\)
Height of transmission tower =20\((\sqrt{3}-1) \mathrm{m}\)
Trigonometry Exemplar Solutions Class 10
Question 8. A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°. Find the height of the pedestal.
Solution:
Given
A statue, 1.6 m tall, stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60° and from the same point, the angle of elevation of the top of the pedestal is 45°.
Let AB be the statue of height 1.6 m at the top of pedestal BC.
⇒ \(\angle B D C =45^{\circ}\)
and \(\angle A D C =60^{\circ}\)
Let C D =x
and BC =h
In \(\triangle B C D\),
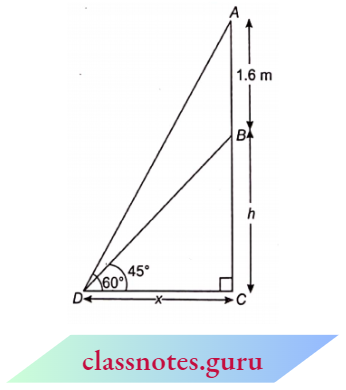
⇒ \(\tan 45^{\circ} =\frac{B C}{C D}\)
1 =\(\frac{h}{x}\)
h =x (1)
In ACD.
⇒ \(\tan 60^{\circ} =\frac{A C}{C D}\)
⇒ \(\sqrt{3} =\frac{h+1.6}{x}\)
⇒ \(\sqrt{3} =\frac{h+1.6}{h}\) [from eqn. (1)]
⇒ \(\sqrt{3} h\) =h+1.6
h\((\sqrt{3}-1)\) =1.6
h =\(\frac{1.6}{\sqrt{3}-1}=\frac{1.6 \times(\sqrt{3}+1)}{3-1}\)
=0.8(1.732+1)=2.1856
Height of pedestal \(\approx 2.18 \mathrm{~m}\)
Question 9. The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high, find the height of the building
Solution:
Given
The angle of elevation of the top of a building from the foot of the tower is 30° and the angle of elevation of the top of the tower from the foot of the building is 60°. If the tower is 50 m high
Let AB be the tower and CD be the building.
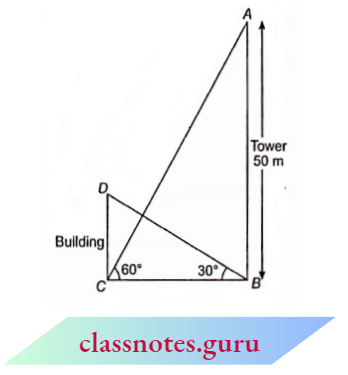
Here, the height of Tower AB is 50 m
⇒ \(\angle A C B=60^{\circ}\),
⇒ \(\angle D B C=30^{\circ}\)
In \(\triangle A B C\),
⇒ \(\sqrt{3}=\frac{50}{B C}\)
⇒ \(\tan 60^{\circ}=\frac{A B}{B C}\)
B C=\(\frac{50}{\sqrt{3}}\)
In \(\triangle B C D\),
⇒ \(\tan 30^{\circ}=\frac{C D}{B C} \quad \Rightarrow \quad \frac{1}{\sqrt{3}}=\frac{C D}{B C}\)
C D=\(\frac{B C}{\sqrt{3}}=\frac{50}{\sqrt{3} \times \sqrt{3}}=\frac{50}{3}\)
C D=16.67 m
Height of building =16.67 m
Question 10. Two poles of equal height are standing opposite each other on either side of the road, which is 80 m wide. them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively. Find the height of the poles and the distances of the points from the poles.
Solution:
Given:
Two poles of equal height are standing opposite each other on either side of the road, which is 80 m wide. them on the road, the angles of elevation of the top of the poles are 60° and 30°, respectively.
Let two poles AB and CD of equal heights ‘h’ be on either side of a road 80 m broad.
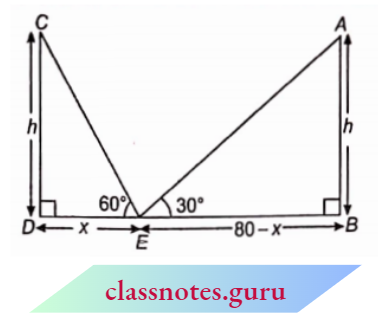
At point E,
Given : \(\angle C E D=60^{\circ}\) and \(\angle A E B=30^{\circ}\)
Let D E=x
B E = 80-x
In \(\triangle C D E\),
⇒ \(\tan 60^{\circ} =\frac{C D}{D E} \quad \Rightarrow \quad \sqrt{3}=\frac{h}{x}\)
h = \(x\sqrt{3}\) Equation (1)
In \(\triangle A B E\)
⇒ \(\tan 30^{\circ}=\frac{A B}{B E} \quad \Rightarrow \frac{1}{\sqrt{3}}=\frac{h}{80-x}\)
⇒ \(\frac{1}{\sqrt{3}}=\frac{x \sqrt{3}}{80-x}\) [from Equation (1)]
3 \(\mathrm{r}=80-x \Rightarrow 4 x=80\)
x = 20
80-x=80-20=60 and h=20 \(\sqrt{3}\)
Height of each pole =20 \(\sqrt{3} \mathrm{~m}\)
Distance of two poles from point E=20 m and 60 m.
Question 11. A TV tower stands vertically on the bank of an A canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point D 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°. Find the height of the tower and the width of the canal.
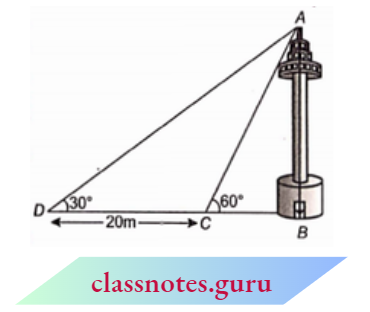
Solution:
Given
A TV tower stands vertically on the bank of an A canal. From a point on the other bank directly opposite the tower, the angle of elevation of the top of the tower is 60°. From another point D 20 m away from this point on the line joining this point to the foot of the tower, the angle of elevation of the top of the tower is 30°.
In \(\triangle B C\).
⇒ \(\tan 60^{\circ} =\frac{A B}{B C}\)
⇒ \(\sqrt{3} =\frac{A B}{B C}\)
⇒ \(A B =\sqrt{3} \cdot B C\)
In \(\triangle A B D\),
⇒ \(\tan 30^{\circ} =\frac{A B}{B D}\)
⇒ \(\frac{1}{\sqrt{3}} =\frac{\sqrt{3} B C}{B C+C D}\)
3 BC =B C+C D
2 BC =20
BC =10
Put in equation (1),
A B =\(10 \sqrt{3} \mathrm{~m}\)
Height of tower =10 \(\sqrt{3} \mathrm{~m}\)
and width of canal =10 m
Question 12. From the top of a 7 m high building, the angle of elevation of the top of a cable tower is 60° and the angle of depression of its foot is 45°. Determine the height of the tower.
Solution :
Let CD be a building of height 7m and AB be a cable tower.
Given :
⇒ \(\angle A D E=60^{\circ}\) and \(\angle D B C=45^{\circ}\)
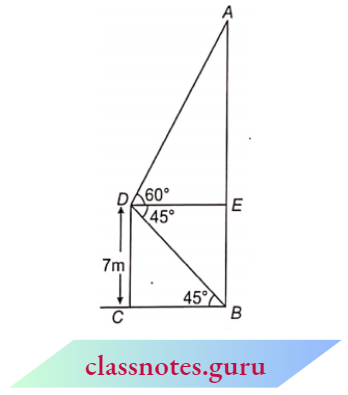
In \(\triangle B C D\),
⇒ \(\tan 45^{\circ} =\frac{D C}{B C} \Rightarrow 1=\frac{7}{B C}\)
B C = 7 m
In \(\triangle A D E\),
⇒ \(\tan 60^{\circ}=\frac{A E}{D E} \Rightarrow \sqrt{3}=\frac{A E}{B C} \quad(D E=B C)\)
⇒ \(A E=\sqrt{3} B C=1.732 \times 7=12.124 \mathrm{~m}\)
⇒ \(A B=A E+B E=12.124+7=19.124 \mathrm{~m}\)
Height of tower =19.124 m
Question 13. As observed from the top of a 75 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse, find the distance between the two ships
Solution :
Given
As observed from the top of a 75 m high lighthouse from the sea level, the angles of depression of the two ships are 30° and 45°. If one ship is exactly behind the other on the same side of the lighthouse
Let AB be a lighthouse whose height is 75 m. The position of the two ships is at C and D.

In \(\triangle A B C\),
⇒ \(\tan 45^{\circ} =\frac{A B}{A C}\)
1 =\(\frac{75}{A C} \Rightarrow A C=75 \mathrm{~m}\)
In \(\triangle A B D\),
⇒ \(\tan 30^{\circ}=\frac{A B}{A D} \Rightarrow \frac{1}{\sqrt{3}}=\frac{75}{A D}\)
⇒ \(A D=75 \sqrt{3} \Rightarrow C D+A C=75 \sqrt{3}\)
⇒ \(C D=75 \sqrt{3}-75=75(\sqrt{3}-1)\)
Distance between two ships =\(75(\sqrt{3}-1)\) m
Question 14. A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After elevation reduces to 30°. Find the distance travelled by the balloon during the interval.
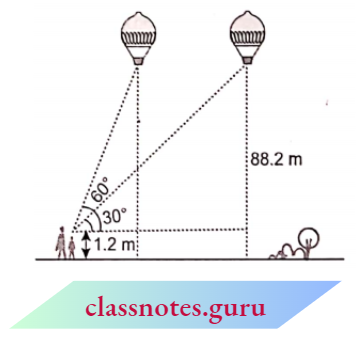
Solution:
Given
A 1.2 m tall girl spots a balloon moving with the wind in a horizontal line at a height of 88.2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 60°. After elevation reduces to 30°.
Let C be the position of the girl. The two positions of the balloon are A and P.
PD = AB = 88.2 – 1.2 = 87 m
In right \(\triangle A B C\),
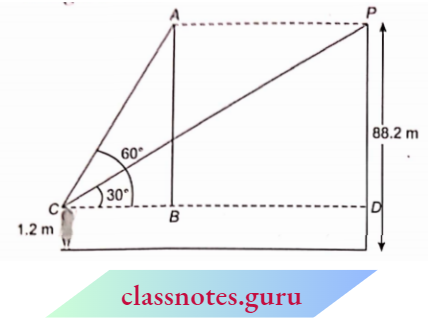
⇒ \(\tan 60^{\circ} =\frac{A B}{B C}\)
⇒ \(\sqrt{3}=\frac{87}{B C} \quad \Rightarrow B C=\frac{87}{\sqrt{3}}\) → Equation 1
In right \(\triangle PDC\),
⇒ \(\tan 30^{\circ}=\frac{P D}{C D}\)
⇒ \(\frac{1}{\sqrt{3}} =\frac{87}{C D} \quad \Rightarrow C D=87 \sqrt{3}\)
Now, BD = C D – B C = 87
⇒ \(\sqrt{3}-\frac{87}{\sqrt{3}}=87\left(\sqrt{3}-\frac{1}{\sqrt{3}}\right)\)
=87 \(\times \frac{3-1}{\sqrt{3}}=\frac{2 \times 87}{\sqrt{3}} \mathrm{~m}\)
= \(\frac{2 \times 87}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}}=\frac{2 \times 87 \times \sqrt{3}}{3}\)
= 58 \(\sqrt{3} \mathrm{~m}\)
Therefore, distance between two positions of balloons =58 \(\sqrt{3} m\)
Question 15. Question 15. A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°. Find the time taken by the car to reach the foot of the tower from this point.
Solution :
Given
A straight highway leads to the foot of a tower. A man standing at the top of the tower observes a car at an angle of depression of 30°, which is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 60°.
Let the height of the tower be AB and the two positions of the car be C and D.
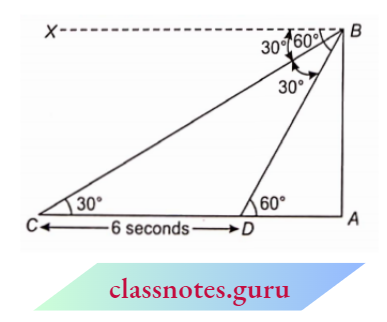
⇒ \(\angle D B C=\angle D B X-\angle C B X=60^{\circ}-30^{\circ}=30^{\circ}\)
In \(\triangle B D C\),
⇒ \(\angle D B C =\angle D C B\)
C D =B D
⇒ \(\left({cach} 30^{\circ}\right)\)
(the sides opposite to equal angles are equal) In right \(\triangle B A D\),
⇒ \(\cos 60^{\circ}=\frac{A D}{D B} \Rightarrow \frac{1}{2}=\frac{A D}{D B} \Rightarrow D B=2 A D\)
CD = 2 AD
Now, time taken to cover distance CD = 6 sec.
Time taken to cover distance 2AD = 6 sec.
Time is taken to cover distance AD = 3 sec.
Class 10 Trigonometry Word Problems with Answers
Question 16. The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6 m.
Solution :
Given
The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m from the base of the tower and in the same straight line with it are complementary.
Let AB be a tower of height h. Two points C and D are at 4 m and 9 m distances respectively from B.
Let, \(\angle A D C=\theta\)
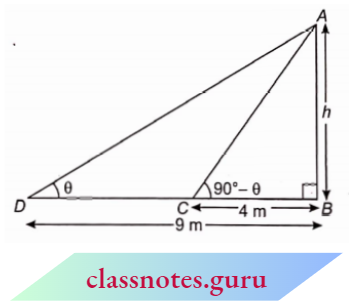
⇒ \(\angle A C B=90^{\circ}-\theta\)
In \(\triangle A B D\),
⇒ \(\tan \theta=\frac{A B}{B D}=\frac{h}{9}\) → Equation 1
In \(\triangle A B C\),
⇒ \(\tan \left(90^{\circ}-\theta\right)=\frac{A B}{B C}\)
⇒ \(\cot \theta=\frac{h}{4}\)
⇒ \(\frac{1}{\tan \theta}=\frac{h}{4} \quad \Rightarrow \frac{9}{h}=\frac{h}{4}\) [from equation 1 ]
⇒ \(h^2=36 \quad \Rightarrow h=6\)
Height of tower =6 m
Hence Proved.
