NCERT Exemplar For Class 10 Maths Chapter 8 Introduction To Trigonometry

NCERT Exemplar For Class 10 Maths Chapter 8  Introduction To Trigonometry

The word ‘trigonometry’ is derived from the Greek words: trigonon and metron. The word trigonon means a figure formed by three sides i.e., triangle, and metron means a measure. So, we can say that in trigonometry we solve the problems related to the sides and angles of a triangle.

NCERT Exemplar For Class 10 Maths Chapter 8  Identity

1. An equation is a statement of equality between two expressions that is true for all values of the variable involved (taking into consideration the domain i.e., limitations of the variable), and is called an identity.
2. An equation that involves trigonometric ratios of an angle and is true for all values of the angle is called a trigonometric identity.

Read and Learn More Class 10 Maths Solutions Exemplar

NCERT Exemplar For Class 10 Maths Chapter 8  Angle

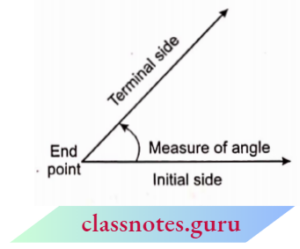
An angle is considered as a figure obtained by rotating a given ray about its endpoint. The measure of an angle is the amount of rotation from its initial side to the terminal side. If the ray rotates in an anticlockwise direction then the angle will be positive. If the ray rotates in a clockwise direction then the angle will be negative.

NCERT Exemplar For Class 10 Maths Chapter 8  Trigonometric Ratios

The ratio of any two sides of a right-angled triangle is called trigonometric ratio. In the adjoining figure, \(\angle\)YAX = 0 is an acute angle. Consider a point C on ray AY. Draw perpendicular CB from C to AX.

⇒ \(\triangle\) ABC is a right-angled triangle in which

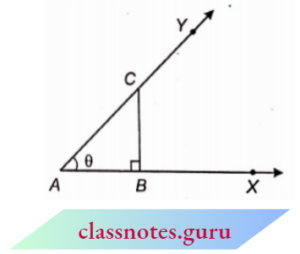
⇒ \(\angle\)ABC = 90°

In \(\triangle\) ABC, let \(\angle\)BAC = 0

For \(\angle\)BAC = \(\theta\),

perpendicular P = BC

base B = AB

And hypotenuse H = AC

The ratio \(\frac{\text { perpendicular }}{\text { hypotenuse }}\) is called the sine of \(\theta\) and is written as \(\sin \theta\).

⇒ \(\sin \theta=\frac{P}{H}=\frac{B C}{A C}\)

The ratio \(\frac{\text { base }}{\text { hypotenuse }}\) is called the cosine of \(\theta\) and is written as \(\cos \theta\).

⇒ \(\cos \theta=\frac{B}{H}=\frac{A B}{A C}\)

The ratio \(\frac{\text { perpendicular }}{\text { base }}\) is called the tangent of \(\theta\) and is written as \(\tan \theta\).

∴ \(\tan \theta=\frac{P}{B}=\frac{B C}{A B}\)

Introduction to Trigonometry

The ratio \(\frac{\text { base }}{\text { perpendicular }}\) is called the cotangent of \(\theta\) and is written as \(\cot \theta\).

⇒ \(\cot \theta=\frac{B}{P}=\frac{A B}{B C}\)

The ratio \(\frac{\text { hypotenuse }}{\text { base }}\) is called the secant of \(\theta\) and is written as \(\sec \theta\).

⇒ \(\sec \theta=\frac{H}{B}=\frac{A C}{A B}\)

The ratio \(\frac{\text { hypotenuse }}{\text { perpendicular }}\) is called the cosecant of \(\theta\) and is written as \(cosec\theta\).

cosec \(\theta=\frac{H}{P}=\frac{A C}{B C}\)

Therefore, \(\sin \theta=\frac{1}{{cosec} \theta}=\frac{\text { perpendicular }}{\text { hypotenuse }}\), cosec \(\theta=\frac{1}{\sin \theta}=\frac{\text { hypotenuse }}{\text { perpendicular }}\)

⇒ \(\cos \theta=\frac{1}{\sec \theta}=\frac{\text { base }}{\text { hypotenuse }}\), \(\sec \theta=\frac{1}{\cos \theta}=\frac{\text { hypotenuse }}{\text { base }}\)

⇒ \(\tan \theta=\frac{1}{\cot \theta}=\frac{\sin \theta}{\cos \theta}=\frac{\text { perpendicular }}{\text { base }}\), \(\cot \theta=\frac{1}{\tan \theta}=\frac{\cos \theta}{\sin \theta}=\frac{\text { base }}{\text { perpendicular }}\)

Remember :

•  \(\sin \theta \neq \sin \times \theta\)
• \(\cos \theta \neq \cos \times \theta\)
• \(\sin ^2 \theta =(\sin \theta)^2 \neq \sin ^2 \theta^2 \neq \sin ^2\)
• \(cosec \theta =\frac{1}{\sin \theta}=(\sin \theta)^{-1} \neq \sin ^{-1} \theta\)

NCERT Exemplar For Class 10 Maths Chapter 8  Perpendicular, Base, And Hypotenuse In A Right-Angled Triangle

See carefully the following right-angled triangles :

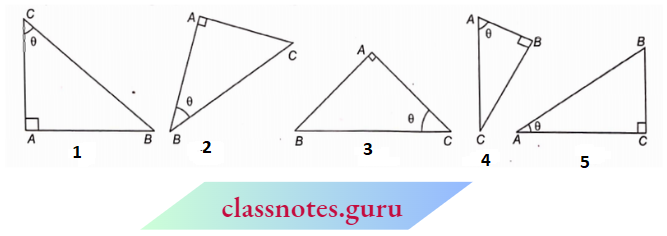
Let us see the values of trigonometric ratios in the different figures in terms of AB, BC, and AC.

Remember:

1. The side of the triangle at which the right angle (90°) and the given angle lie, is called the base.
2.  The side opposite to the 90° angle is called the hypotenuse.
3. The third remaining side is called the perpendicular.

Now,

In (1). \(\sin \theta=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{A B}{B C}\)

In (2). \(\tan \theta=\frac{\text { perpendicular }}{\text { base }}=\frac{A C}{A B}\)

In (3). \(\sec \theta=\frac{\text { hypotenuse }}{\text { base }}=\frac{B C}{A C}\)

In (4). cosec \(\theta=\frac{\text { hypotenuse }}{\text { perpendicular }}=\frac{A C}{B C}\)

In (5). \(\cos \theta=\frac{\text { base }}{\text { hypotenuse }}=\frac{A C}{A B}\)

NCERT Exemplar For Class 10 Maths Chapter 8  Solved Examples

Example 1. In \(\triangle\) ABC, \(\angle\) B = 90°, if AB = 5 cm, BC = 12 cm, then find the values of the following :

1. sin A
2. cos A
3. cot A
4. cosec C
5. sec C
6. tan C

Solution.

In \(\triangle\) A B C, from Pythagoras theorem

⇒ \(A C^2=A B^2+B C^2 =5^2+12^2\)

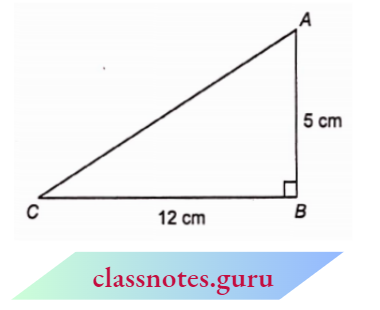
=25+144=169

A C=13 cm

For \(\angle\) A, the base is AB, perpendicular is BC. For \(\angle C\), the base is BC, the perpendicular is AB, while the hypotenuse is the same i.e., AC for both angles.

1. \(\sin A=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{B C}{A C}=\frac{12}{13}\)
2. \(\cos A=\frac{\text { base }}{\text { hypotenuse }}=\frac{A B}{A C}=\frac{5}{13}\)
3. \(\cot A=\frac{\text { base }}{\text { perpendicular }}=\frac{A B}{B C}=\frac{5}{12}\)
4. cosec C=\(\frac{\text { hypotenuse }}{\text { perpendicular }}=\frac{A C}{A B}=\frac{13}{5}\)
5. \(\sec C=\frac{\text { hypotenuse }}{\text { base }}=\frac{A C}{B C}=\frac{13}{12}\)
6.  \(\tan C=\frac{\text { perpendicular }}{\text { base }}=\frac{A B}{B C}=\frac{5}{12}\)

Question 2. In \(\triangle\) ABC, \(\angle B=90^{\circ}\) and \(\sin A=\frac{4}{5}\), then find the values of all other trigonometric ratios for \(\angle\) A.

Solution:

We know that, \(\sin A=\frac{4}{5}=\frac{\text { perpendicular }}{\text { hypotenuse }}\)

Now construct a \(\triangle\) A B C in which

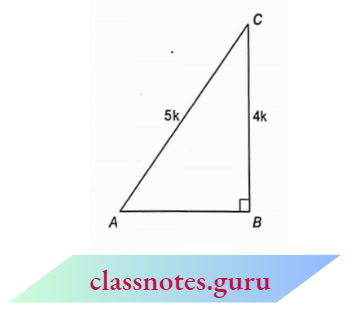
⇒ \(\angle B=90^{\circ}\), B C=4 k and A C=5 k .

In \(\triangle\) A B C, from Pythagoras theorem

⇒ \(A B^2+B C^2=A C^2\)

⇒ \(A B^2=A C^2-B C^2=(5 k)^2-(4 k)^2\)

=25 \(k^2-16 k^2=9 k^2\)

AB = 3k

Now,\(\cos A=\frac{\text { base }}{\text { hypotenuse }}=\frac{A B}{A C}=\frac{3 k}{5 k}=\frac{3}{5}\)

⇒ \(\tan A=\frac{\text { perpendicular }}{\text { base }}=\frac{B C}{A B}=\frac{4 k}{3 k}=\frac{4}{3}\)

cosec A=\(\frac{\text { hypotenuse }}{\text { perpendicular }}=\frac{A C}{B C}=\frac{5 k}{4 k}=\frac{5}{4}\)

⇒ \(\sec A=\frac{\text { hypotenuse }}{\text { base }}=\frac{A C}{A B}=\frac{5 k}{3 k}=\frac{5}{3}\)

∴ \(\cot A=\frac{\text { base }}{\text { perpendicular }}=\frac{A B}{B C}=\frac{3 k}{4 k}=\frac{3}{4}\)

Example 3. In \(\triangle\) PQR, \(\angle R=90^{\circ}\) and \(\tan \theta=\frac{5}{12}\) where \(\angle\) QPR = \(\theta\). Find the values of all other trigonometric ratios for \(\angle \theta\).

Solution:

We know that,

⇒ \(\tan \theta=\frac{\text { perpendicular }}{\text { base }}=\frac{5}{12}\)

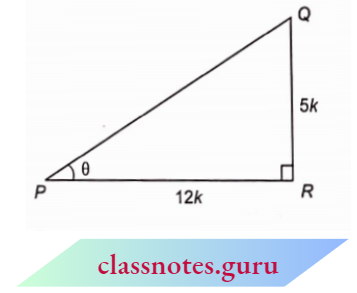
Now, construct a \(\triangle P Q R\) in which

P R=12 k, Q R=5 k and \(\angle Q R P=90^{=}\). }

Let \(\angle Q P R=\theta\)

In \(\triangle\) PQR,

From Pythagoras theorem

⇒ \(P Q^2=P R^2+Q R^2=(12 k)^2+(5 k)^2=144 k^2+25 k^2=169 k^2\)

PQ = 13k

Now,\(\sin \theta=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{Q R}{P Q}=\frac{5 k}{13 k}=\frac{5}{13}\)

⇒ \(\cos \theta=\frac{\text { base }}{\text { hypotenuse }}=\frac{P R}{P Q}=\frac{12 k}{13 k}=\frac{12}{13}\)

⇒ \(cosec 0 =\frac{\text { hypotenuse }}{\text { perpendicular }}=\frac{P(2}{Q R}=\frac{13 k}{5 k}=\frac{13}{5}\)

⇒ \(\sec \theta =\frac{\text { hypotenuse }}{\text { base }}=\frac{P Q}{P R}=\frac{13 k}{12 k}=\frac{13}{12}\)

⇒ \(\cot \theta =\frac{\text { basse }}{\text { perpendicular }}=\frac{P R}{Q R}=\frac{12 k}{5 k}=\frac{12}{5}\)

Example 4. In \(\triangle A B C\), \(\angle C=90^{\circ}\) and cosec A=\(\frac{13}{12}\) find the values of all other trigonometric ratios for \(\angle A\).

Solution:

We know that,

cosec A=\(\frac{\text { hypotenuse }}{\text { perpendicular }}=\frac{13}{12}\)

Now, construct a \(\triangle A B C\) in which A B=13 k, B C=12 k and \(\angle A C B=90^{\circ}\).

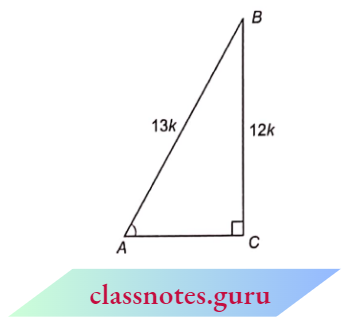
In \(\triangle A B C\), from Pythagoras theorem

⇒ \(A C^2+B C^2 =A B^2\)

⇒ \(A C^2 =A B^2-B C^2=(13 k)^2-(12 k)^2\)

=\(169 k^2-144 k^2=25 k^2\)

AC = 5 k

Now, \(\sin A=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{B C}{A B}=\frac{12 k}{13 k}=\frac{12}{13}\)

⇒ \(\cos A=\frac{\text { base }}{\text { hypotenuse }}=\frac{A C}{A B}=\frac{5 k}{13 k}=\frac{5}{13}\)

⇒ \(\tan A=\frac{\text { perpendicular }}{\text { base }}=\frac{B C}{A C}=\frac{12 k}{5 k}=\frac{12}{5}\)

⇒ \(\sec A=\frac{\text { hypotenuse }}{\text { base }}=\frac{A B}{A C}=\frac{13 k}{5 k}=\frac{13}{5}\)

∴ \(\cot A=\frac{\text { base }}{\text { perpendicular }}=\frac{A C}{B C}=\frac{5 k}{12 k}=\frac{5}{12}\)

Example 5. If cos A=\(\frac{1}{3}\), then find the values of sin A and tan A

Solution:

Construct a right-angled triangle ABC in which cos A=\(\frac{1}{3}=\frac{\text { base }}{\text { hypotenuse }}=\frac{A B}{A C}\)

Let AB = k and AC = 3 k

From Pythagoras theorem,

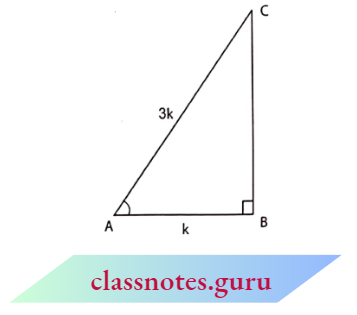
From Pythagoras theorem, \(B C^2+A B^2 =A C^2\)

⇒ \(B C^2 =A C^2-A B^2=(3 k)^2-(k)^2\)

= \(9 k^2-k^2=8 k^2\)

BC = \(\sqrt{8 k^2}=2 \sqrt{2} k\)

The values of sin A and tan A are

⇒ \(\sin A=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{B C}{A C}=\frac{2 \sqrt{2} k}{3 k}=\frac{2 \sqrt{2}}{3}\)

and \(\tan A=\frac{\text { perpendicular }}{\text { base }}=\frac{B C}{A B}=\frac{2 \sqrt{2} k}{k}=2 \sqrt{2}\)

Example 6. In \(\triangle A B C\), \(\tan B=\sqrt{3}\) find the values of cosec B and cos B.

Solution:

Construct a right-angled triangle ABC in which

⇒ \(\tan B=\sqrt{3}=\frac{\sqrt{3}}{1}=\frac{\text { perpendicular }}{\text { base }}=\frac{A C}{A B}\)

Let \(A C=\sqrt{3}\) k and AB = k

From Pythagoras theorem

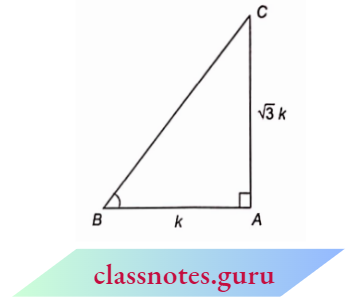
⇒ \(B C^2 =A B^2+A C^2\)

=\((k)^2+(\sqrt{3} k)^2\)

⇒ \(B C^2 =k^2+3 k^2=4 k^2\)

BC =2 k

The values of cosec B and cos B are

⇒ \(cosec B =\frac{\text { hypotenuse }}{\text { perpendicular }}=\frac{B C}{A C}=\frac{2 k}{\sqrt{3} k}=\frac{2}{\sqrt{3}}\)

and \(\cos B =\frac{\text { base }}{\text { hypotenuse }}=\frac{A B}{B C}=\frac{k}{2 k}=\frac{1}{2}\)

Example 7. If \(\cos \theta=\frac{4}{5}\), then find the value of \(\left(\sin \theta \cos \theta+\tan ^2 \theta\right) \)

Solution:

Given that, \(\cos \theta=\frac{4}{5}\)

Construct a right-angled \(\triangle A B C\) in which \(\angle B A C=90^{\circ}\), AC = 4 k and BC = 5k.

In \(\triangle ABC\),

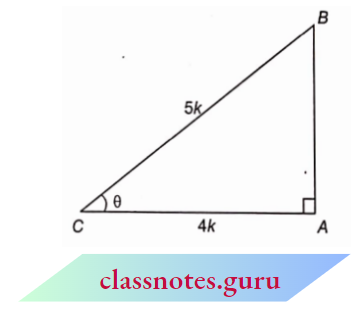
From Pythagoras theorem

⇒ \(A B^2+A C^2 =B C^2\)

⇒ \(A B^2 =B C^2-A C^2=(5 k)^2-(4 k)^2\)

= \(25 k^2-16 k^2=9 k^2\)

AB = 3k

and \(\sin \theta =\frac{A B}{B C}=\frac{3 k}{5 k}=\frac{3}{5}\)

⇒ \(\tan \theta =\frac{A B}{A C}=\frac{3 k}{4 k}=\frac{3}{4}\)

Now, \(\sin \theta \cos \theta+\tan ^2 \theta=\frac{3}{5} \cdot \frac{4}{5}+\left(\frac{3}{4}\right)^2=\frac{12}{25}+\frac{9}{16}\)

= \(\frac{192+225}{400}=\frac{417}{400}\)

The value of \(\left(\sin \theta \cos \theta+\tan ^2 \theta\right) \)= 417/400.

Example 8. If sec A=2, then find the value of \(\frac{1}{\cot A}+\frac{\cos A}{1+\sin A}\).

Solution:

Given that, \(\sec A=2=\frac{2}{1}\)

Construct a right-angled \(\triangle A B C\) in which

⇒ \(\angle A B C=90^{\circ}\), AB = k and AC = 2k .

In \(\triangle A B C\),

From Pythagoras theorem

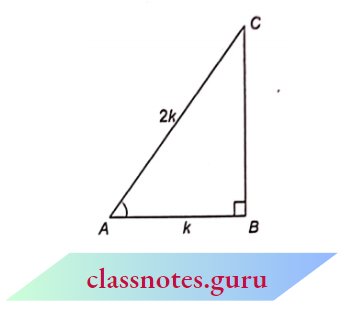
⇒ \(A B^2+B C^2 = A C^2\)

⇒ \(B C^2 =A C^2-A B^2=(2 k)^2-(k)^2=4 k^2-k^2=3 k^2\)

⇒ \(B C=\sqrt{3} k\)

Now, \(\cot A=\frac{A B}{B C}=\frac{k}{\sqrt{3} k}=\frac{1}{\sqrt{3}}\)

⇒ \(\sin A=\frac{B C}{A C}=\frac{\sqrt{3} k}{2 k} =\frac{\sqrt{3}}{2}\) and \(\cos A=\frac{A B}{A C}=\frac{k}{2 k}=\frac{1}{2}\)

⇒ \(\frac{1}{\cot A}+\frac{\cos A}{1+\sin A}=\frac{1}{\frac{1}{\sqrt{3}}}+\frac{\frac{1}{2}}{1+\frac{\sqrt{3}}{2}}=\sqrt{3}+\frac{\frac{1}{2}}{\frac{2+\sqrt{3}}{2}}\)

= \(\sqrt{3}+\frac{1 \times(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})}=\sqrt{3}+\frac{2-\sqrt{3}}{4-3}\)

= \(\sqrt{3}+2-\sqrt{3}=2\)

The value of \(\frac{1}{\cot A}+\frac{\cos A}{1+\sin A}\) = 2

Example 9. If \(\cot A=\frac{b}{a}\), then prove that:

Solution:

⇒ \(\frac{a \sin A-b \cos A}{a \sin A+b \cos A}=\frac{a^2-b^2}{a^2+b^2}\)

We have,

L.H.S. =\(\frac{a \sin A-b \cos A}{a \sin A+b \cos A} =\frac{a \frac{\sin A}{\sin A}-b \frac{\cos A}{\sin A}}{a \frac{\sin A}{\sin A}+b \frac{\cos A}{\sin A}}\)

=\(\frac{a-b \cot A}{a+b \cot A}=\frac{a-b \times \frac{b}{a}}{a+b \times \frac{b}{a}}\) (dividing Nr. and Dr. by sin A ) (\(\cot A=\frac{b}{a}\))

=\(\frac{\frac{a^2-b^2}{a}}{\frac{a^2+b^2}{a}}=\frac{a^2-b^2}{a^2+b^2}\)= R.H.S

Hence Proved.

Example 10. In the adjoining figure, AM = BM and \(\angle B=90^{\circ}\). If \(\angle B C M=\theta\), then find the values of the following :

1. sin θ
2. tan θ
3. sec θ

Solution:

In \(\triangle A B C\),

From Pythagoras theorem

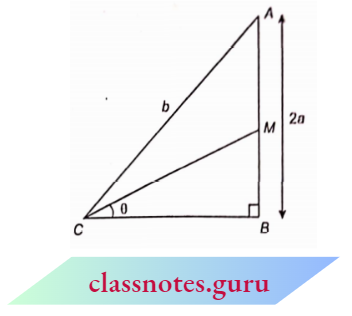
⇒ \(B C^2 =A C^2-A B^2=b^2-(2 a)^2=b^2-4 a^2\)

⇒ \(B C =\sqrt{b^2-4 a^2}\)

Now, \(B M=\frac{A B}{2}=a\)

In \(\triangle B C M\),

From Pythagoras theorem

⇒ \(C M^2 =B C^2+B M^2=\left(b^2-4 a^2\right)+a^2=b^2-3 a^2\)

⇒ \(C M =\sqrt{b^2-3 a^2}\)

⇒ \(\sin \theta=\frac{B M}{C M}=\frac{a}{\sqrt{b^2-3 a^2}}\)

⇒ \(\tan \theta=\frac{B M}{B C}=\frac{a}{\sqrt{b^2-4 a^2}}\)

∴ \(\sec \theta=\frac{C M}{B C}=\frac{\sqrt{b^2-3 a^2}}{\sqrt{b^2-4 a^2}}\)

Example 11. In the adjoining figure, \(\angle B C D=\angle A D B(each 90^{\circ} )\). If B C=3 cm and the length of the side opposite \(\angle C\) in \(\triangle B C D\) is 5 cm, then find the square root of the length of the side opposite to \(\angle D\) in MDB.

Solution:

Draw DE \(\perp A B\)

In right \(\triangle B C D\), by Pythagoras theorem,

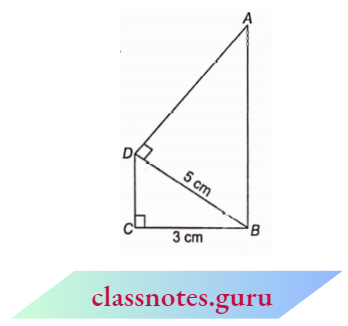
In right \(\triangle A E D\), by Pythagoras theorem,

⇒ \(A D^2=A E^2+D E^2\)

⇒ \(y^2=x^2+9\)

In right \(\triangle A D B\), by Pythagoras theorem,

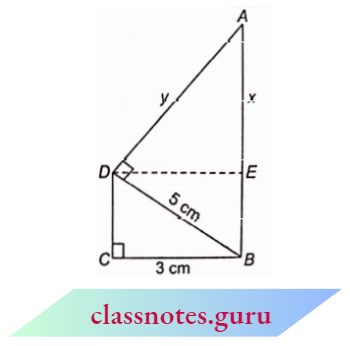
⇒ \(A B^2=A D^2+D B^2\)

⇒ \((x+4)^2=y^2+25\)

⇒\(x^2+8 x+16=\left(x^2+9\right)+25\)

8 x=18

x=\(\frac{18}{8}=2.25 \mathrm{~cm}\)

⇒\(A B=x+4=2.25+4=6.25 \mathrm{~cm}\)

⇒\(\sqrt{A B}=\sqrt{6.25}=2.5 \mathrm{~cm}\)

NCERT Exemplar For Class 10 Maths Chapter 8  Signs Of The Trigonometric Ratios

Let a rotating line rotate \(\angle XOA\) = \(\theta\) in an anticlockwise direction, starting from its initial position OX. Here, PM is perpendicular from P to OX where P is a point on side OA.

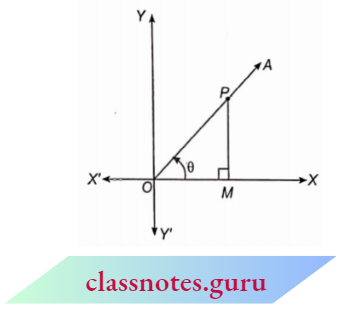
In the first quadrant, 0 is the acute angle.

Here, OM > 0, PM > 0, OP > 0

Now,

⇒ \(\sin \theta=\frac{P M}{O P}>0\) ,\(\cos \theta=\frac{O M}{O P}>0\)

⇒ \(\tan \theta=\frac{P M}{O M}>0\) ,\(\cot \theta=\frac{O M}{P M}>0\)

⇒ \(\sec \theta=\frac{O P}{O M}>0 , cosec \theta=\frac{O P}{P M}>0\)

Therefore, all trigonometric ratios for all angles in the first quadrant are positive.

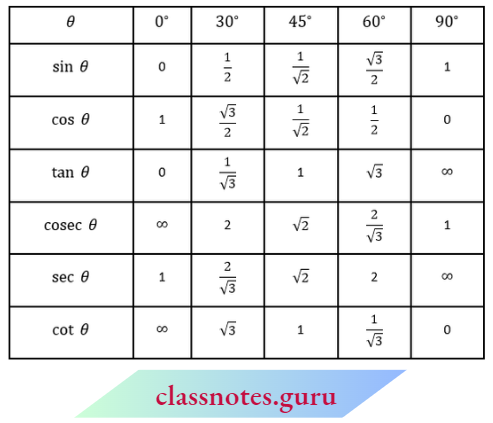
Trigonometric Ratios Of Specific Angles

1. Trigonometric Ratios for 30° and 60°

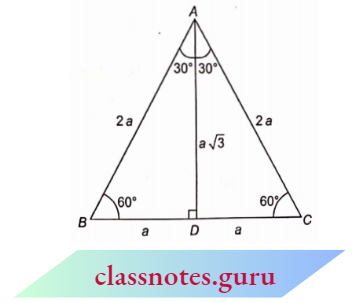
⇒ \(\triangle ABC\) is an equilateral triangle whose side is ‘2a’.

⇒ \(\triangle A B C\) is an equilateral triangle whose side is ‘ 2 a ‘.

⇒ \(\angle A B C=\angle A C B=\angle B A C=60^{\circ}\)

AD is perpendicular from A to BC.

and \(\angle BAD =\angle C A D=30^{\circ}\)

B D = CD = a.

In \(\triangle A B D\), from Pythagoras theorem

⇒ \(A D^2+B D^2=A B^2\)

⇒ \(A D^2+a^2 =(2 n)^2\)

⇒ \(A D^2 =3 a^2\)

A D =a \(\sqrt{3}\)

For \(30^{\circ}\), in \(\triangle A B D\)

Base AD = a \(\sqrt{3}\), perpendicular B D= a and hypotenuse AB = 2a

⇒ \(\sin 30^{\circ}=\frac{B D}{A B}=\frac{a}{2 a}=\frac{1}{2}\)

⇒ \(cosec 30^{\circ}=\frac{A B}{B D}=\frac{2 a}{a}=2\)

⇒ \(\cos 30^{\circ}=\frac{A D}{A B}=\frac{a \sqrt{3}}{2 a}=\frac{\sqrt{3}}{2}\)

⇒ \(\sec 30^{\circ}=\frac{A B}{A D}=\frac{2 a}{a \sqrt{3}}=\frac{2}{\sqrt{3}}\)

⇒ \(\tan 30^{\circ}=\frac{B D}{A D}=\frac{a}{a \sqrt{3}}=\frac{1}{\sqrt{3}}\)

⇒ \(\cot 30^{\circ}=\frac{A D}{B D}=\frac{a \sqrt{3}}{a}=\sqrt{3}\)

For \(60^{\circ}\), in \(\triangle A B D\)

⇒ \(\sin 60^{\circ}=\frac{A D}{A B}=\frac{a \sqrt{3}}{2 a}=\frac{\sqrt{3}}{2}\)

⇒ \(\cos 60^{\circ}=\frac{B D}{A B}=\frac{a}{2 a}=\frac{1}{2}\)

⇒ \(\tan 60^{\circ}=\frac{A D}{B D}=\frac{a \sqrt{3}}{a}=\sqrt{3}\)

⇒ \(cosec 60^{\circ}=\frac{A B}{A D}=\frac{2 a}{a \sqrt{3}}=\frac{2}{\sqrt{3}}\)

⇒ \(\sec 60^{\circ}=\frac{A B}{B D}=\frac{2 a}{a}=2\)

⇒ \(\cot 60^{\circ}=\frac{B D}{A D}=\frac{a}{a \sqrt{3}}=\frac{1}{\sqrt{3}}\)

2. Trigonometric Ratios for 450

In \(\triangle\)ABC, \(\angle\)ABC = 90° and \(\angle\)BAC = 45°.

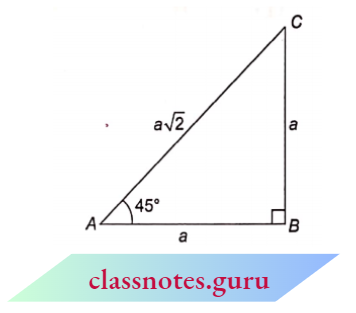
Therefore, \(\angle\)ACB = 45°

Let AB = BC = a

From Pythagoras theorem

In \(\triangle A B C\), \(\angle A B C=90^{\circ}\) and \(\angle B A C=45^{\circ}\). Therefore, \(\angle A C B=45^{\circ}\)

Let AB = BC = a

From Pythagoras theorem

⇒ \(A C^2 =A B^2+B C^2\)

=\( a^2+a^2=2 a^2\)

A C =a \(\sqrt{2}\)

For A=\(45^{\circ}\),

⇒ \(\sin 45^{\circ}=\frac{B C}{A C}=\frac{a}{a \sqrt{2}}=\frac{1}{\sqrt{2}}\)

⇒ \(cosec 45^{\circ}=\frac{A C}{B C}=\frac{a \sqrt{2}}{a}=\sqrt{2}\)

⇒ \(\cos 45^{\circ}=\frac{A B}{A C}=\frac{a}{a \sqrt{2}}=\frac{1}{\sqrt{2}}\)

⇒ \(\sec 45^{\circ}=\frac{A C}{A B}=\frac{a \sqrt{2}}{a}=\sqrt{2}\)

⇒ \(\tan 45^{\circ}=\frac{B C}{A B}=\frac{a}{a}\)=1

⇒ \(\cot 45^{\circ}=\frac{A B}{B C}=\frac{a}{a}=1\)

3. Trigonometric Ratios for 0°

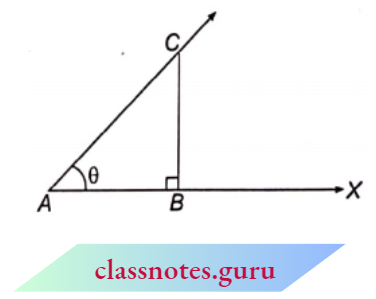
In \(\triangle \)ABC, \(\angle\)BAC = 0 and \(\angle\)ABC = 90°.

For angle \(\theta\), base = AB, perpendicular = BC and hypotenuse = AC.

In \(\triangle\)ABC, it is clear that as the value of ‘\(\theta\)’ decreases, the length of BC decreases, and for 0 = 0°, BC = 0 and AC = AB. Therefore,

Introduction to Trigonometry

⇒ \(\sin 0^{\circ}=\frac{B C}{A C}=\frac{0}{A C}=0\)

⇒ \(cosec 0^{\circ}=\frac{A C}{B C}=\frac{A C}{0}=\infty\)

⇒ \(\cos 0^{\circ}=\frac{A B}{A C}=\frac{A B}{A B}=1\)

⇒ \(\sec 0^{\circ}=\frac{A C}{A B}=\frac{A B}{A B}=1\)

⇒ \(\tan 0^{\circ}=\frac{B C}{A B}=\frac{0}{A B}=0\)

⇒ \(\cot 0^{\circ}=\frac{A B}{B C}=\frac{A B}{0}=\infty\)

4. Trigonometric Ratios for 90°

In \(\triangle\)ABC, it is clear that as the value of ‘0’ increases, the length of AB decreases, and for 0 = 90°, AB = 0 and AC = BC.

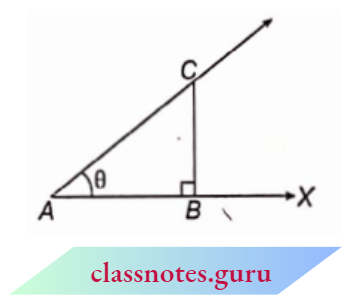
Therefore, \(\sin 90^{\circ}=\frac{B C}{A C}=\frac{A C}{A C}=1\)

⇒ \(cosec 90^{\circ}=\frac{A C}{B C}=\frac{B C}{B C}=1\)

⇒ \(\cos 90^{\circ}=\frac{A B}{A C}=\frac{0}{A C}=0 \sec 90^{\circ}=\frac{A C}{A B}=\frac{A C}{0}=\infty\)

∴ \(\tan 90^{\circ}=\frac{B C}{A B}=\frac{B C}{0}=\infty \cot 90^{\circ}=\frac{A B}{B C}=\frac{0}{B C}=0\)

NCERT Exemplar For Class 10 Maths Chapter 8  Trigonometry Solved Examples

Example 1. Evaluate : \(\sin ^2 60^{\circ} \tan 45^{\circ}-\cos ^2 45^{\circ} \sec 60^{\circ}\)

Solution:

We know that,

⇒ \(\sin 60^{\circ}=\frac{\sqrt{3}}{2}, \tan 45^{\circ}=1, \cos 45^{\circ}=\frac{1}{\sqrt{2}}, \sec 60^{\circ}=2\)

⇒ \(\sin ^2 60^{\circ} \tan 45^{\circ} -\cos ^2 45^{\circ} \sec 60^{\circ} \)

= \(\left(\frac{\sqrt{3}}{2}\right)^2(1)-\left(\frac{1}{\sqrt{2}}\right)^2(2)=\frac{3}{4}-\frac{1}{2} \times 2=\frac{3}{4}-1=\frac{3-4}{4}=-\frac{1}{4}\)

\(\sin ^2 60^{\circ} \tan 45^{\circ}-\cos ^2 45^{\circ} \sec 60^{\circ}\) = -1/4.

Example 2. Evaluate : \(\cos 60^{\circ} \cos 30^{\circ}+\sin 60^{\circ} \sin 30^{\circ}\)

Solution:

We know that,

⇒ \(\cos 60^{\circ} =\frac{1}{2}, \cos 30^{\circ}=\frac{\sqrt{3}}{2}, \sin 60^{\circ}=\frac{\sqrt{3}}{2}, \sin 30^{\circ}=\frac{1}{2}\)

⇒ \(\cos 60^{\circ} \cos 30^{\circ}+ \sin 60^{\circ} \sin 30^{\circ}\)

= \(\frac{1}{2} \times \frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2} \times \frac{1}{2}=\frac{\sqrt{3}+\sqrt{3}}{4}=\frac{2 \sqrt{3}}{4}=\frac{\sqrt{3}}{2}\)

\(\cos 60^{\circ} \cos 30^{\circ}+\sin 60^{\circ} \sin 30^{\circ}\) = 1/2

Example 3. Show that : \(\cos 60^{\circ}=2 \cos ^2 30^{\circ}-1\)

Solution:

L.H.S. =\(\cos 60^{\circ}=\frac{1}{2}\)

R.H.S. = \(2 \cos ^230^{\circ}-1=2\left(\frac{\sqrt{3}}{2}\right)^2-1=2\left(\frac{3}{4}\right)-1=\frac{3}{2}-1\)

=\(\frac{3-2}{2}=\frac{1}{2}\)

L.H.S. = R.H.S. Hence Proved

Example 4. If \(A=15^{\circ}\), then find the value of \(\sec 2 A\).

Solution: 

A =\(15^{\circ} \Rightarrow 2 A=2 \times 15^{\circ}=30^{\circ} \)

⇒ \(\sec 2 A =\sec 30^{\circ}=\frac{2}{\sqrt{3}}\)

The value of \(\sec 2 A\) =\( \frac{2}{\sqrt{3}}\)

Example 5. If \(\sin x=1\), then find the value of \(\tan \frac{x}{3}\).

Solution:

⇒ \(\sin x =1\)

⇒ \(\sin x =\sin 90^{\circ} \Rightarrow x =90^{\circ}\)

⇒ \(\frac{x}{3} =\frac{90^{\circ}}{3}=30^{\circ}\)

∴ \(\tan \frac{x}{3}=\tan 30^{\circ}=\frac{1}{\sqrt{3}}\)

The value of \(\tan \frac{x}{3}\) =[latec]\frac{1}{\sqrt{3}}[/latex]

Example 6. If \(\sin (A+B)=\frac{\sqrt{3}}{2}\) and \(\cos (A-B)=\frac{\sqrt{3}}{2}\), then find the values of A and B Given that, \(\sin (A+B)=\frac{\sqrt{3}}{2}\)

Solution:

⇒ \(\sin (A+B)=\sin 60^{\circ} \quad \Rightarrow \quad A+B=60^{\circ}\) Equation 1

and \(\cos (A-B)=\frac{\sqrt{3}}{2}\)

⇒ \(\cos (A-B)=\cos 30^{\circ} \quad \Rightarrow \quad A-B=30^{\circ}\) Equation 2

Adding equations (1) and (2)

⇒ \(A+B =60^{\circ}\)

2 A =\(90^{\circ} \quad\Rightarrow \quad A-B =30^{\circ} \)

A = \(45^{\circ}\)

Put A=\(60^{\circ}\) in equation (1)

⇒ \(45^{\circ}+B=60^{\circ} \quad \Rightarrow \quad B=60^{\circ}-45^{\circ}=15^{\circ}\)

The values of A and B are

⇒ \(A=45^{\circ}\) and \(B=15^{\circ}\)

Example 7.  In an acute-angled AABC, if tan (A + B – C) = 1 and see (B + C – A) = 2, then find the value of cos (45 – 3A).

Solution:

Solution. We have.

tan (A + B – C) = 1 = tan 45°

=* A + B- C = 45° …(1)

Also sec (B + C – A) = 2 = sec 60°

B + C – A = 60° …(2)

Adding equations (1) and (2), we get

25 = 105° ⇒ 5 = 52.5° …(3)

Subtracting equation (1) from equation (2), we get

2C – 2A = 15° ⇒ C-A = 7.5° …(4)

We know that A + 5 + C = 180°

⇒ A + C = 180° – 52.5° [from (3)]

⇒ A + C= 127.5° …(5)

⇒ -A + C = 7.5° …(4)

Adding equations (4) and (5), we get

2C = 135° ⇒ C = 67.5°

A = 127.5°-67.5° = 60°

cos (45 – 3A) = cos (4 x 52.5° – 3 x 60°) = cos (210° – 180°) = cos 30° = \(\frac{\sqrt{3}}{2}\)

The value of cos (45 – 3A) = \(\frac{\sqrt{3}}{2}\)

Example 8. If sin A= cos A, then evaluate \(\tan A+\sin ^2 A+1\).

Solution:

We know that, in A = cos A, then

Now, A =\(45^{\circ}\)

⇒ \(\tan A+\sin ^2 A+1 =\tan 45^{\circ}+\sin ^2 45^{\circ}+1\)

= \(1+\left(\frac{1}{\sqrt{2}}\right)^2+1=2+\frac{1}{2}=\frac{5}{2}\)

\(\tan A+\sin ^2 A+1\) = \(\frac{5}{2}\)

Example 9. Find the value of \(\left(\theta_1+\theta_2\right)\) if

Solution:

⇒ \(\tan \left(\theta_1+\theta_2\right)=\frac{\tan \theta_1+\tan \theta_2}{1-\tan \theta_1 \cdot \tan \theta_2}\)

where, \(\tan \theta_1=\frac{1}{2}\) and \(\tan \theta_2=\frac{1}{3}\).

⇒ \(\tan \left(\theta_1+\theta_2\right) =\frac{\tan \theta_1+\tan \theta_2}{1-\tan \theta_1 \cdot \tan \theta_2}=\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{2} \times \frac{1}{3}}\)

= \(\frac{\frac{3+2}{6}}{1-\frac{1}{6}}=\frac{\frac{5}{6}}{\frac{5}{6}}=1=\tan 45^{\circ}\)

∴ \(\theta_1+\theta_2 =45^{\circ}\)

The value of \(\left(\theta_1+\theta_2\right)\) = 45°

Example 10. Evaluate : cos 1° cos 2° cos 3° … cos 179°

Solution:

cos 90° whose value is zero lies in between cos 1° cos 2° cos 3°.., cos 179°

cos 1° cos 2° cos 3°… cos 179°

= cos 1° cos 2° cos 3° …. cos 90° cos 179°

= cos 1° cos 2° cos 3° …. X 0 X cos 179°

= 0 (0 x finite number = 0)

cos 1° cos 2° cos 3° … cos 179° = 0

Question 11. In the adjoining figure, a right-angled triangle $A B C$ is shown in which AM = CM = 3 m. If \(\angle A C M=15^{\circ}\), then find A C:

Solution:

Here, AM = CM

⇒ \(\angle A C M = \angle C A M\) (opposite angles of equal sides)

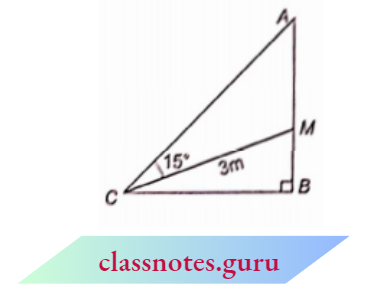
⇒ \(\angle C A M=15^{\circ}\)

⇒ \(\angle A C B=90^{\circ}-15^{\circ}=75^{\circ}\)

and \(\angle B C M=\angle A C B-\angle A C M=75^{\circ}-15^{\circ}=60^{\circ}\)

In \(\triangle B C M\),

⇒ \(\cos (\angle B C M)=\frac{B C}{C M}\)

⇒ \(\cos 60^{\circ}=\frac{B C}{3}\)

⇒ \(\frac{1}{2}=\frac{B C}{3}\)

⇒ \(B C=\frac{3}{2} \mathrm{~m}\)

and \(\sin (\angle B C M)=\frac{B M}{C M}\)

⇒ \(\sin 60^{\circ}=\frac{B M}{3}\)

⇒ \(\frac{\sqrt{3}}{2}=\frac{B M}{3}\)

⇒ \(B M=\frac{3 \sqrt{3}}{2} \mathrm{~m}\)

⇒ \(A B=A M+B M=\left(3+\frac{3 \sqrt{3}}{2}\right) \mathrm{m}\)

Now, in \(\triangle A B C\), from Pythagoras theorem

⇒ \(A C^2 =A B^2+B C^2=\left(3+\frac{3 \sqrt{3}}{2}\right)^2+\left(\frac{3}{2}\right)^2=9+\frac{27}{4}+9 \sqrt{3}+\frac{9}{4}\)

= \(18+9 \sqrt{3}=9(2+\sqrt{3})=\frac{9}{2}(4+2 \sqrt{3})\)

AC =\(\sqrt{\frac{9(4+2 \sqrt{3})}{2}}=\frac{3(\sqrt{3}+1)}{\sqrt{2}} \mathrm{~m}\)

NCERT Exemplar For Class 10 Maths Chapter 8  Relation Between Trigonometric Ratios

1. \(\sin \theta \times cosec\theta=1\)

• \(\sin \theta=\frac{1} {cosec \theta}\)
• \(cosec \theta=\frac{1}{\sin \theta}\)

2. \(\cos \theta \times \sec \theta=1\)

•  \(\cos \theta=\frac{1}{\sec \theta}\)
•  \(\sec \theta=\frac{1}{\cos \theta}\)

3. \(\tan \theta \times \cot \theta=1\)

• \(\tan \theta=\frac{1}{\cot \theta}\)
•  \(\cot \theta=\frac{1}{\tan \theta}\)

4. \(\tan \theta=\frac{\sin \theta}{\cos \theta}\)

5. \(\cot \theta=\frac{\cos \theta}{\sin \theta}\)

If the value of a trigonometric function is known, then we can find the values of other trigonometric functions. We can use Pythagoras’ theorem and the above results for it.

NCERT Exemplar For Class 10 Maths Chapter 8  Trigonometric Identities

We know about the algebraic equations.

The algebraic equation satisfies a particular value of the variable but in trigonometry, the equation can satisfy all values of the variable, such equations are called trigonometric identities.

1.  \(\sin ^2 \theta+\cos ^2 \theta=1\)
2.  \(\sec ^2 \theta=1+\tan ^2 \theta\)
3. \(cosec^2 \theta=1+\cot ^2 \theta\)

Identity 1. \(\sin ^2 \theta+\cos ^2 \theta\)=1

Proof : Let \(\triangle\)ABC is a right-angled triangle in which \(\angle\)ABC = 90°

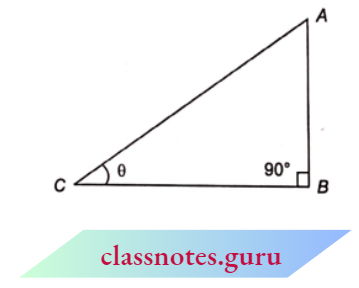
Let \(\angle\)ACB = \(\theta\)

For this angle ‘\(\theta\)’

AB = perpendicular

BC = base

AC = hypotenuse

From Pythagoras theorem,

⇒ \(A B^2+B C^2=A C^2\)

Now,\(\sin \theta=\frac{A B}{A C}\) and \(\cos \theta=\frac{B C}{A C}\)

Divide each term in equation (1) by A C^2

⇒ \(\frac{A B^2}{A C^2}+\frac{B C^2}{A C^2}=\frac{A C^2}{A C^2}\)

⇒ \(\left(\frac{A B}{A C}\right)^2+\left(\frac{B C}{A C}\right)^2=1 \quad \Rightarrow \quad \sin ^2 \theta+\cos ^2 \theta\)=1

Identity 2. \(\sec ^2 \theta=1+\tan ^2 \theta\)

Proof: In \(\triangle M B C\),

⇒ \(A B^2+B C^2=A C^2\)

Now,\(\tan \theta=\frac{A B}{B C}\) and \(\sec \theta=\frac{A C}{B C}\)

Divide each term by \(B C^2\) in equation (1)

⇒ \(\frac{A B^2}{B C^2}+\frac{B C^2}{B C^2}=\frac{A C^2}{B C^2}\)

⇒ \(\left(\frac{A B}{B C}\right)^2+1=\left(\frac{A C}{B C}\right)^2 \Rightarrow \tan ^2 \theta+1=\sec ^2 \theta\)

Identity 3. \(cosec^2 \theta=1+\cot ^2 \theta\)

Proof : In \(\triangle A B C\),

⇒ \(A B^2+B C^2=A C^2\)

Now,\(\cot \theta=\frac{B C}{A B}\) and \(cosec \theta=\frac{A C}{A B}\)

Divide each term in equation (1) by \(A B^2\)

⇒ \(\frac{A B^2}{A B^2}+\frac{B C^2}{A B^2}=\frac{A C^2}{A B^2} \)

⇒ \(1+\left(\frac{B C}{A B}\right)^2=\left(\frac{A C}{A B}\right)^2 \Rightarrow 1+\cot ^2 \theta={cosec}^2 \theta\)

Alternate Proof: Identity (2) \(\sec ^2 \theta=1+\tan ^2 \theta\) and (3)\(cosec^2 \theta=1+\cot ^2 \theta\) can be proved with the help of identity (1) \(\sin ^2 \theta+\cos ^2 \theta\)=1.

Proof of \(\sec ^2 \theta=1+\tan ^2 \theta\) :

From identity (1)

⇒ \(\sin ^2 \theta+\cos ^2 \theta\)=1

Divide each term by \(\cos ^2 \theta\)

⇒ \(\frac{\sin ^2 \theta}{\cos ^2 \theta}+\frac{\cos ^2 \theta}{\cos ^2 \theta}=\frac{1}{\cos ^2 \theta}\)

⇒ \(left(\frac{\sin \theta}{\cos \theta})^2+1=\left(\frac{1}{\cos \theta}\right)^2\)

⇒ \(\tan ^2 \theta+1 =\sec ^2 \theta \Rightarrow \sec ^2 \theta=1+\tan ^2 \theta\)

Proof of \(cosec^2 \theta=1+\cot ^2 \theta\) :

From identity ( 1 ) \(\sin ^2 \theta+\cos ^2 \theta\)=1

Divide each term by \(\sin ^2 \theta\)

⇒ \(\frac{\sin ^2 \theta}{\sin ^2 \theta}+\frac{\cos ^2 \theta}{\sin ^2 \theta}=\frac{1}{\sin ^2 \theta}\)

⇒ \(1+\left(\frac{\cos \theta}{\sin \theta}\right)^2=\left(\frac{1}{\sin \theta}\right)^2\)

⇒ \(1+\cot ^2 \theta= cosec^2 \theta\)

∴ \(cosec^2 \theta=1+\cot ^2 \theta\)

Other Form of the Above Identities :

1. \(\sin ^2 \theta+\cos ^2 \theta=1\)

• \(\cos ^2 \theta=1-\sin ^2 \theta\)
•  \(\sin ^2 \theta=1-\cos ^2 \theta\)

2. \(\sec ^2 \theta=1+\tan ^2 \theta\)

• \(\tan ^2 \theta=\sec ^2 \theta-1\)
• \(\sec ^2 \theta-\tan ^2 \theta=1\)

3. \(cosec^2 \theta=1+\cot ^2 \theta\)

•  \(\cot ^2 \theta= cosec^2 \theta-1\)
•  \(cosec^2 \theta-\cot ^2 \theta\)=1

NCERT Exemplar For Class 10 Maths Chapter 8  Trigonometric Solved Examples

Example 1. Simplify : \(\left(1+\tan ^2 \theta\right)(1-\sin \theta)(1+\sin \theta)\)

Solution:

⇒ \(\left(1+\tan ^2 \theta\right)(1-\sin \theta)(1+\sin \theta) \)

⇒ \(=\left(1+\tan ^2 \theta\right)\left[(1)^2-(\sin \theta)^2\right]=\left(1+\tan ^2 \theta\right)\left(1-\sin ^2 \theta\right)\)

= \(\sec ^2 \theta \cdot \cos ^2 \theta \quad \text { (using the identities } \sec ^2 \theta=1+\tan ^2 \theta \text { and } \sin ^2 \theta+\cos ^2 \theta=1 \text { ) }\)

= \(\frac{1}{\cos ^2 \theta} \cdot \cos ^2 \theta\)=1

\(\left(1+\tan ^2 \theta\right)(1-\sin \theta)(1+\sin \theta)\) = 1

Example 2. Prove that : \(\cos ^2 \theta \cdot cosec\theta+\sin \theta= cosec \theta\)

Solution:

L.H.S. =\(\cos ^2 \theta \cdot cosec \theta+\sin \theta=\cos ^2 \theta \cdot \frac{1}{\sin \theta}+\sin \theta\)

= \(\frac{\cos ^2 \theta}{\sin \theta}+\frac{\sin \theta}{1}=\frac{\cos ^2 \theta+\sin ^2 \theta}{\sin \theta}=\frac{1}{\sin \theta}\)

= cosec \(\theta\)= R.H.S.

\(\cos ^2 \theta \cdot cosec\theta+\sin \theta= cosec \theta\)

Question 3. Prove that : \(\sec ^4 \theta-\tan ^4 \theta=1+2 \tan ^2 \theta\)

Solution:

L.H.S. =\(\sec ^4 \theta-\tan ^4 \theta=\left(\sec ^2 \theta\right)^2-\left(\tan ^2 \theta\right)^2\)

=\(\left(\sec ^2 \theta+\tan ^2 \theta\right)\left(\sec ^2 \theta-\tan ^2 \theta\right)=\left(1+\tan ^2 \theta+\tan ^2 \theta\right)\left(1+\tan ^2 \theta-\tan ^2 \theta\right)\)

=\(\left(1+2 \tan ^2 \theta\right)(1)=1+2 \tan ^2 \theta= R.H.S\).

Hence Proved

\(\sec ^4 \theta-\tan ^4 \theta=1+2 \tan ^2 \theta\)

Question 4. Prove that : \(\frac{1+\cos \theta-\sin ^2 \theta}{\sin \theta+\sin \theta \cos \theta}=\cot \theta\)

Answer:

L.H.S. =\(\frac{1+\cos \theta-\sin ^2 \theta}{\sin \theta+\sin \theta \cos \theta}=\frac{\left(1-\sin ^2 \theta\right)+\cos \theta}{\sin \theta(1+\cos \theta)}=\frac{\cos ^2 \theta+\cos \theta}{\sin \theta(1+\cos \theta)}\)

=\(\frac{\cos \theta(\cos \theta+1)}{\sin \theta(1+\cos \theta)}=\frac{\cos \theta}{\sin \theta}=\cot \theta\)= R.H.S.

\(\frac{1+\cos \theta-\sin ^2 \theta}{\sin \theta+\sin \theta \cos \theta}=\cot \theta\)

Example 5. If \(\tan \theta=\frac{4}{3}\) , then find the value of \(\frac{3 \sin \theta-2 \cos \theta}{3 \sin \theta+5 \cos \theta}\) .

Solution:

⇒ \(\frac{3 \sin \theta-2 \cos \theta}{3 \sin \theta+5 \cos \theta}=\frac{3 \frac{\sin \theta}{\cos \theta}-2 \frac{\cos \theta}{\cos \theta}}{3 \frac{\sin \theta}{\cos \theta}+5 \frac{\cos \theta}{\cos \theta}}\)

=\(\frac{3 \tan \theta-2}{3 \tan \theta+5}=\frac{3 \times \frac{4}{3}-2}{3 \times \frac{4}{3}+5}=\frac{4-2}{4+5}=\frac{2}{9}\)

The value of \(\frac{3 \sin \theta-2 \cos \theta}{3 \sin \theta+5 \cos \theta}\) =\( \frac{2}{9}\)

Example 6. Prove that : \((\sec A+\tan A)(1-\sin A)=\cos A\)

Solution:

L.H.S. =\((\sec A+\tan A)(1-\sin A)\)

= \(\left(\frac{1}{\cos A}+\frac{\sin A}{\cos A}\right)(1-\sin A)=\frac{(1+\sin A)}{\cos A}(1-\sin A)\)

= \(\frac{1-\sin ^2 A}{\cos A}=\frac{\cos ^2 A}{\cos A}=\cos A\) = R.H.S.

\((\sec A+\tan A)(1-\sin A)=\cos A\)

Example 7. Prove that : \({cosec A-\cot A=\frac{1}{cosec} A+\cot A}\)

Solution:

L.H.S. = \(cosec A-\cot A=(cosec A-\cot A) \cdot \frac{(cosec A+\cot A)}{(cosec A+\cot A)}\)

= \(\frac{cosec^2 A-\cot ^2 A}{cosec A+\cot A}=\frac{1}{cosec A+\cot A}\)= R.H.S.

Hence Proved.

\({cosec A-\cot A=\frac{1}{cosec} A+\cot A}\)

Example 8. Prove that: \(\frac{\sec A+1}{\tan A}=\frac{\tan A}{\sec A-1}\)

Solution:

L.H.S. =\(\frac{\sec A+1}{\tan A}=\frac{\sec A+1}{\tan A} \times \frac{\sec A-1}{\sec A-1}\)

[divide numerator and denominator by (sec A-1)]

= \(\frac{\sec ^2 A-1}{\tan A(\sec A-1)}=\frac{\tan ^2 A}{\tan A(\sec A-1)}\)

= \(\frac{\tan A}{\sec A-1}\)= R.H.S.

Hence Proved.

\(\frac{\sec A+1}{\tan A}=\frac{\tan A}{\sec A-1}\)

Example 9. Prove that : \(\sin \theta(1+\tan \theta)+\cos \theta(1+\cot \theta)= cosec \theta+\sec \theta\)

Solution:

L.H.S. =\(\sin \theta(1+\tan \theta)+\cos \theta(1+\cot \theta)\)

=\(\sin \theta(1+\tan \theta)+\cos \theta\left(1+\frac{1}{\tan \theta}\right)\)

= \(\sin \theta(1+\tan \theta)+\cos \theta\left(\frac{\tan \theta+1}{\tan \theta}\right)\)

=\((1+\tan \theta)\left[\sin \theta+\frac{\cos \theta}{\left(\frac{\sin \theta}{\cos \theta}\right)}\right]=(1+\tan \theta)\left(\sin \theta+\frac{\cos ^2 \theta}{\sin \theta}\right)\)

=\(\left(1+\frac{\sin \theta}{\cos \theta}\right)\left(\frac{\sin ^2 \theta+\cos ^2 \theta}{\sin \theta}\right)=\left(1+\frac{\sin \theta}{\cos \theta}\right)\left(\frac{1}{\sin \theta}\right)\)

⇒ \(=\frac{1}{\sin \theta}+\frac{\sin \theta}{\cos \theta} \times \frac{1}{\sin \theta}\)

= \(cosec \theta+\sec \theta\)= R.H.S.

\(\sin \theta(1+\tan \theta)+\cos \theta(1+\cot \theta)= cosec \theta+\sec \theta\)

Example 10. If \(\sec \theta+\tan \theta=p\),then prove that : \(\frac{p^2-1}{p^2+1}=\sin \theta\)

Solution:

L.H.S. =\(\frac{p^2-1}{p^2+1}=\frac{(\sec \theta+\tan \theta)^2-1}{(\sec \theta+\tan \theta)^2+1}=\frac{\sec ^2 \theta+\tan ^2 \theta+2 \sec \theta \tan \theta-1}{\sec ^2 \theta+\tan ^2 \theta+2 \sec \theta \tan \theta+1}\)

= \(\frac{\left(\sec ^2 \theta-1\right)+\tan ^2 \theta+2 \sec \theta \tan \theta}{\sec ^2 \theta+\left(\tan ^2 \theta+1\right)+2 \sec \theta \tan \theta}\)

= \(\frac{\tan ^2 \theta+\tan ^2 \theta+2 \sec \theta \tan \theta}{\sec ^2 \theta+\sec ^2 \theta+2 \sec \theta \tan \theta}\)

= \(\frac{2 \tan ^2 \theta+2 \sec \theta \tan \theta}{2 \sec ^2 \theta+2 \sec \theta \tan \theta}=\frac{2 \tan \theta(\tan \theta+\sec \theta)}{2 \sec \theta(\sec \theta+\tan \theta)}\)

= \(\frac{\tan \theta}{\sec \theta}=\frac{\sin \theta}{\cos \theta} \times \frac{\cos \theta}{1}\)

= \(\sin \theta\) = R.H.S.

Hence Proved

\(\frac{p^2-1}{p^2+1}=\sin \theta\)

Alternative Method : We have \(\sec \theta+\tan \theta=p\)

⇒ \(\frac{1}{\cos \theta}+\frac{\sin \theta}{\cos \theta}=\frac{p}{1}\Rightarrow \quad \frac{1+\sin \theta}{\cos \theta}=\frac{p}{1}\)

Squaring both sides, we get

⇒ \(\frac{(1+\sin \theta)^2}{\cos ^2 \theta}=\frac{p^2}{1}\)

⇒ \(\frac{(1+\sin \theta)^2}{1-\sin ^2 \theta}=\frac{p^2}{1}\){ (using identity } \(\sin ^2 \theta+\cos ^2 \theta=1 \text { ) }\)

⇒ \(\frac{(1+\sin \theta)^2}{(1+\sin \theta)(1-\sin \theta)}=\frac{p^2}{1} \quad \Rightarrow \quad \frac{1+\sin \theta}{1-\sin \theta}=\frac{p^2}{1}\)

Applying componendo and dividends, we get

⇒ \(\frac{2}{2 \sin \theta}=\frac{p^2+1}{p^2-1}\)

∴ \(\frac{1}{\sin \theta}=\frac{p^2+1}{p^2-1} \Rightarrow \quad \sin \theta=\frac{p^2-1}{p^2+1}\)

Example 11. Prove that : \(\frac{\sec \theta+1-\tan \theta}{\tan \theta+1-\sec \theta}=\frac{\sin \theta}{1-\cos \theta}\)

Solution:

Note: In such type of questions, it is better to write \(\sec ^2 \theta-\tan ^2 \theta or cosec^2 \theta-\cot ^2 \theta\) in only numerator.

If in R.H.S. the single term in either numerator or denominator is \(sin \theta\) then convert the question in cosec \(\theta\) and cot \(\theta\) and if the single term is cos \(\theta\) then convert the question in see \(\theta\) and tan \(\theta\).

As in this question in R.H.S. single term \(sin \theta\) is in the numerator so we will use \(cosec^2 \theta-\cot ^2 \theta\) for 1.

(dividing Nr and Dr by \(\sin \theta\) to convert it in } \(cosec \theta and \cot \theta \text { ) }\)

= \(\frac{{cosec} \theta+\cot \theta-1}{1+\cot \theta-{cosec} \theta}=\frac{{cosec} \theta+\cot \theta-\left({cosec}^2 \theta-\cot ^2 \theta\right)}{1+\cot \theta-{cosec} \theta}\)

= \(\frac{({cosec} \theta+\cot \theta)-({cosec} \theta+\cot \theta)({cosec} \theta-\cot \theta)}{1+\cot \theta-{cosec} \theta} \)

= \(\frac{({cosec} \theta+\cot \theta)[1-{cosec} \theta+\cot \theta]}{1+\cot \theta-{cosec} \theta}={cosec} \theta+\cot \theta \)

= \(\frac{1}{\sin \theta}+\frac{\cos \theta}{\sin \theta}=\frac{(1+\cos \theta)}{\sin \theta}=\frac{(1+\cos \theta)(1-\cos \theta)}{\sin \theta(1-\cos \theta)}\)

= \(\frac{1-\cos ^2 \theta}{\sin \theta(1-\cos \theta)}=\frac{\sin ^2 \theta}{\sin \theta(1-\cos \theta)}=\frac{\sin \theta}{1-\cos \theta}=\text { R.H.S. }\)

Hence Proved.

\(\frac{\sec \theta+1-\tan \theta}{\tan \theta+1-\sec \theta}=\frac{\sin \theta}{1-\cos \theta}\)

Example 12. If x=r \(\sin A \cos C\), y=r \(\sin A \sin C\) and z=r \(\cos A\), then prove that :

⇒ \(r^2=x^2+y^2+z^2\)

Solution:

Here, x=r sin A cos C, y=r sin A sin C and z=r cos A

Now, R.H.S. = \(x^2+y^2+z^2\)

= \((r \sin A \cos C)^2+(r \sin A \sin C)^2+(r \cos A)^2\)

= \(r^2 \sin ^2 A \cos ^2 C+r^2 \sin ^2 A \sin ^2 C+r^2 \cos ^2 A\)

= \(r^2 \sin ^2 A\left(\cos ^2 C+\sin ^2 C\right)+r^2 \cos ^2 A \quad\left(\cos ^2 C+\sin ^2 C=1\right)\)

= \(r^2 \sin ^2 A+r^2 \cos ^2 A\)

= \(r^2\left(\sin ^2 A+\cos ^2 A\right)\)

= \(r^2\) =L.H.S.

\(r^2=x^2+y^2+z^2\)

Hence Proved.

NCERT Exemplar For Class 10 Maths Chapter 8  Identities And Equations

Identities are special + type of equations that are true for all values of the variable while equations are true for some particular values of the variable.

NCERT Exemplar For Class 10 Maths Chapter 8  Solved Examples

Example 1. Check whether the equation \(\frac{\tan \phi+\sin \phi}{\tan \phi-\sin \phi}=\frac{\sec \phi+1}{\sec \phi-1}\) is an identity or not?

Solution:

L.H.S. = \(\frac{\tan \phi+\sin \phi}{\tan \phi-\sin \phi}=\frac{\frac{\sin \phi}{\cos \phi}+\sin \phi}{\frac{\sin \phi}{\cos \phi}-\sin \phi}\)

= \(\frac{\sin \phi \sec \phi+\sin \phi}{\sin \phi \sec \phi-\sin \phi}=\frac{\sin \phi(\sec \phi+1)}{\sin \phi(\sec \phi-1)}=\frac{\sec \phi+1}{\sec \phi-1}\)= R.H.S.

L.H.S. = R.H.S.

And this equation is true for all values of \phi.

The given equation is an identity.

Example 2. Check whether the following equation \(\tan ^4 \theta+\tan ^6 \theta=\tan ^3 \theta \sec ^2 \theta\) is an identity or not?

Solution:

Given equation,

⇒ \(\tan ^4 \theta+\tan ^6 \theta =\tan ^3 \theta \sec ^2 \theta\)

⇒ \(\tan ^4 \theta\left(1+\tan ^2 \theta\right) =\tan ^3 \theta \sec ^2 \theta\)

⇒ \(\tan ^4 \theta \sec ^2 \theta =\tan ^3 \theta \sec ^2 \theta\)

L.H.S. \(\neq\) R.H.S.

It is not an identity.

Again, \(\tan ^4 \theta \sec ^2 \theta-\tan ^3 \theta \sec ^2 \theta=0\)

⇒ \(\tan ^3 \theta \sec ^2 \theta(\tan \theta-1)\) =0

⇒ \(\tan ^3 \theta\)=0 or \(\sec ^2 \theta=0\) or \(\tan \theta-1\)=0

Therefore, given equation satisfies only for \(\theta=0^{\circ}\) and \(\theta=45^{\circ}\).

The given equation is not an identity.

Alternate Method : For \(\theta=60^{\circ}\)

L.H.S. =\(\tan ^4 60^{\circ}+\tan ^6 60^{\circ}\)

= \((\sqrt{3})^4+(\sqrt{3})^6=9+27=36\)

and R.H.S. =\(\tan ^3 60^{\circ} \cdot \sec ^2 60^{\circ}\)

= \((\sqrt{3})^3(2)^2=12 \sqrt{3}\)

L.H.S. \(\neq\) R.H.S.

The given equation is not an identity.

Example 3. Solve : \(2 \sin ^2 \theta=\frac{1}{2}, 0^{\circ}<\theta<90^{\circ}\)

Solution:

⇒ \(2 \sin ^2 \theta =\frac{1}{2}\)

⇒ \(\sin ^2 \theta =\frac{1}{2 \times 2}=\frac{1}{4}\)

⇒ \(\sin \theta =\sqrt{\frac{1}{4}}=\frac{1}{2}\)

⇒ \(\sin \theta =\sin 30^{\circ}\)

∴ \(\theta =30^{\circ}\)

Example 4. Find the value of \(\theta if 2 \cos 3 \theta=1\) and \(0^{\circ}<\theta<90^{\circ}\).

Solution:

2 \(\cos 3 \theta\) =1

⇒ \(\cos 3 \theta =\frac{1}{2}\)

⇒ \(\cos 3 \theta =\cos 60^{\circ}\)

3 \(\theta =60^{\circ}\)

∴ \(\theta =20^{\circ}\)

The Value of θ = 20°

Example 5. Find the value of \(\theta\) if \(\sec ^2 \theta+\tan ^2 \theta=\frac{5}{3}\) and θ lies in first quadrant.

Solution:

⇒ \(\sec ^2 \theta+\tan ^2 \theta =\frac{5}{3}\)

⇒ \(1+\tan ^2 \theta+\tan ^2 \theta =\frac{5}{3} \quad \Rightarrow \quad 2 \tan ^2 \theta=\frac{5}{3}-1=\frac{2}{3}\)

⇒ \(\tan ^2 \theta=\frac{1}{3} \quad \Rightarrow \quad \tan ^2 \theta=\left(\frac{1}{\sqrt{3}}\right)^2\)

⇒ \(\tan \theta=\frac{1}{\sqrt{3}}\) (talking positive sign only)

⇒ \(\tan \theta=\tan 30^{\circ} \Rightarrow \theta=30^{\circ}\)

The value of \(\theta\) if \(\sec ^2 \theta+\tan ^2 \theta=\frac{5}{3}\) = 30°

Example 6. If \(0^{\circ}<\alpha<90^{\circ}\), then solve the equation \(\frac{\sin \alpha}{1-\cos \alpha}+\frac{\sin \alpha}{1+\cos \alpha}=4\).

solution:

⇒ \(\frac{\sin \alpha}{1-\cos \alpha}+\frac{\sin \alpha}{1+\cos \alpha} =4\)

⇒ \(\frac{\sin \alpha(1+\cos \alpha)+\sin \alpha(1-\cos \alpha)}{(1-\cos \alpha)(1+\cos \alpha)}=4\)

⇒ \(\frac{\sin \alpha+\sin \alpha \cos \alpha+\sin \alpha-\sin \alpha \cos \alpha}{1-\cos ^2 \alpha}\) =4

⇒ \(\frac{2 \sin \alpha}{\sin ^2 \alpha}\)=4

⇒ \(\frac{2}{\sin \alpha}\)=4

⇒ \(\sin \alpha =\frac{1}{2}=\sin 30^{\circ}\)

⇒ \(\alpha=30^{\circ}\)

Example 7. If \(0^{\circ}<\theta<90^{\circ}\), then find the value of \(\theta\) from the equation \(\frac{\cos ^2 \theta}{\cot ^2 \theta-\cos ^2 \theta}=3\)

Solution:

⇒ \(\frac{\cos ^2 \theta}{\cot ^2 \theta-\cos ^2 \theta}=3\)

⇒ \(\frac{\cos ^2 \theta}{\frac{\cos ^2 \theta}{\sin ^2 \theta}-\cos ^2 \theta}=3 \Rightarrow \frac{\cos ^2 \theta}{\cos ^2 \theta\left(\frac{1}{\sin ^2 \theta}-1\right)}=3\)

⇒ \(\frac{1}{\frac{1}{\sin ^2 \theta}-1}=3 \quad \Rightarrow \quad \frac{1}{\frac{1-\sin ^2 \theta}{\sin ^2 \theta}}=3\)

⇒ \(\frac{\sin ^2 \theta}{1-\sin ^2 \theta}=3 \quad \Rightarrow \quad \frac{\sin ^2 \theta}{\cos ^2 \theta}=3\)

⇒ \(\tan ^2 \theta=(\sqrt{3})^2\)

⇒ \(\tan \theta=\sqrt{3}\) (taking positive sign only)

⇒ \(\tan \theta=\tan 60^{\circ}\)

∴ \(\theta=60^{\circ}\)

The Value of θ = 60°

NCERT Exemplar For Class 10 Maths Chapter 8  Complementary Angles

Two angles are said to be complementary angles if their sum is 90°.

\(\theta\) and (90°- \(\theta\)) are complementary angles.

NCERT Exemplar For Class 10 Maths Chapter 8  Trigonometric Ratios Of Complementary Angles

Let a rotating ray rotate 90° in an anticlockwise direction from the initial position OX and reach OY and after this, it rotates ‘9’ angle in a clockwise direction and reaches the OA position.

⇒ \(\angle\)XOA = 90° – \(\theta\).

Now, P is a point on side OA. PM and PN are perpendiculars from P to OX and OY respectively.

⇒ \(\sin \left(90^{\circ}-\theta\right)=\frac{P M}{O P}=\frac{O N}{O P}=\cos \theta\)

⇒ \(\cos \left(90^{\circ}-\theta\right)=\frac{O M}{O P}=\frac{P N}{O P}=\sin \theta\)

⇒ \(\tan \left(90^{\circ}-\theta\right)=\frac{P M}{O M}=\frac{O N}{P N}=\cot \theta\)

⇒ \(\cot \left(90^{\circ}-\theta\right)=\frac{O M}{P M}=\frac{P N}{O N}=\tan \theta\)

⇒ \(\sec \left(90^{\circ}-\theta\right)=\frac{O P}{O M}=\frac{O P}{P N}= cosec \theta\)

⇒ \({cosec}\left(90^{\circ}-\theta\right)=\frac{O P}{P M}=\frac{O P}{O N}=\sec \theta\)

⇒ \(\sin \left(90^{\circ}-\theta\right)=\cos \theta\)

⇒ \(\cos \left(90^{\circ}-\theta\right)=\sin \theta\)

⇒ \(\tan \left(90^{\circ}-\theta\right)=\cot \theta\)

⇒ \(\cot \left(90^{\circ}-\theta\right)=\tan \theta\)

⇒ \(\sec \left(90^{\circ}-\theta\right)={cosec} \theta\)

⇒ \({cosec}\left(90^{\circ}-\theta\right)=\sec \theta\)

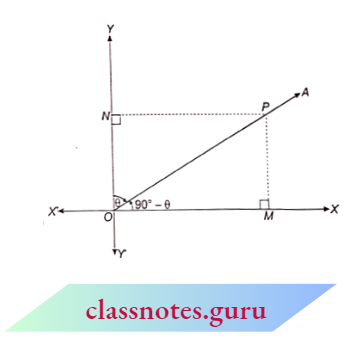
NCERT Exemplar For Class 10 Maths Chapter 8  Summary :

⇒ \(\sin \left(90^{\circ}-\theta\right)=\cos \theta\)

⇒ \(\cos \left(90^{\circ}-\theta\right)=\sin \theta\)

⇒ \(\tan \left(90^{\circ}-\theta\right)=\cot \theta\)

⇒ \(\cot \left(90^{\circ}-\theta\right)=\tan \theta\)

⇒ \(\sec \left(90^{\circ}-\theta\right)= cosec \theta\)

cosec\(\left(90^{\circ}-\theta\right)=\sec \theta\)

NCERT Exemplar For Class 10 Maths Chapter 8  Solved Examples

Example 1. Evaluate the following :

1. \(\frac{\sin 58^{\circ}}{\cos 32^{\circ}}\)
2.  \(\frac{\sec 42^{\circ}}{{cosec} 48^{\circ}}\)

Solution:

1.  \(\frac{\sin 58^{\circ}}{\cos 32^{\circ}}=\frac{\sin \left(90^{\circ}-32^{\circ}\right)}{\cos 32^{\circ}}=\frac{\cos 32^{\circ}}{\cos 32^{\circ}}\)=1
2. \(\frac{\sec 42^{\circ}}{{cosec} 48^{\circ}}=\frac{\sec \left(90^{\circ}-48^{\circ}\right)}{{cosec} 48^{\circ}}=\frac{{cosec} 48^{\circ}}{{cosec} 48^{\circ}}\)=1

Example 2. Evaluate:

1. \(\tan 42^{\circ}-\cot 48^{\circ}\)
2. \(\sec 36^{\circ}- cosec 54^{\circ}\)

Solution:

(1)\(\tan 42^{\circ}-\cot 48^{\circ} =\tan 42^{\circ}-\cot \left(90^{\circ}-42^{\circ}\right)\)

=\(\tan 42^{\circ}-\tan 42^{\circ}\)=0

(2) \(\sec 36^{\circ}- cosec 54^{\circ}=\sec 36^{\circ}- cosec\left(90^{\circ}-36^{\circ}\right)\)

=\(\sec 36^{\circ}-\sec 36^{\circ}\)=0

Example 3. Prove that :

1. \(\sin 42^{\circ} \cos 48^{\circ}+\sin 48^{\circ} \cos 42^{\circ}=1\)
2.  \(\cos 70^{\circ} \cos 20^{\circ}-\sin 70^{\circ} \sin 20^{\circ}=0\)

Solution:

(1) L.H.S. =\(\sin 42^{\circ} \cos 48^{\circ}+\sin 48^{\circ} \cos 42^{\circ}\)

=\(\sin 42^{\circ} \cos \left(90^{\circ}-42^{\circ}\right)+\sin \left(90^{\circ}-42^{\circ}\right) \cos 42^{\circ}\)

= \(\sin 42^{\circ} \sin 42^{\circ}+\cos 42^{\circ} \cos 42^{\circ}\)

= \(\sin ^2 42^{\circ}+\cos ^2 42^{\circ}\)

= 1 = R.H.S.

Hence Proved.

(2) L.H.S. = cos 70° cos 20° – sin 70° sin 20°

= cos 70° cos 20° – sin (90° – 20°) sin(90° – 70°)

= cos 70° cos 20° – cos 20° cos 70°

= 0 = R.H.S.

Example 4. Without using trigonometric tables, evaluate :

⇒ \(\left(\frac{\tan 20^{\circ}}{{cosec} 70^{\circ}}\right)^2+\left(\frac{\cot 20^{\circ}}{\sec 70^{\circ}}\right)^2+2 \tan 15^{\circ} \tan 37^{\circ} \tan 53^{\circ} \tan 60^{\circ} \tan 75^{\circ}\)

Solutions:

⇒ \(\left(\frac{\tan 20^{\circ}}{{cosec} 70^{\circ}}\right)^2+\left(\frac{\cot 20^{\circ}}{\sec 70^{\circ}}\right)^2+2 \tan 15^{\circ} \tan 37^{\circ} \tan 53^{\circ} \tan 60^{\circ} \tan 75^{\circ}\)

= \(\left\{\frac{\tan 20^{\circ}}{{cosec}\left(90^{\circ}-20^{\circ}\right)}\right\}^2+\left\{\frac{\cot 20^{\circ}}{\sec \left(90^{\circ}-20^{\circ}\right)}\right\}^2\)

+2 \(\tan 15^{\circ} \tan 37^{\circ} \tan \left(90^{\circ}-37^{\circ}\right) \cdot(\sqrt{3}) \tan \left(90^{\circ}-15^{\circ}\right)\)

⇒ \(+2 \tan 15^{\circ} \tan 37^{\circ} \tan \left(90^{\circ}-37^{\circ}\right) \cdot(\sqrt{3}) \tan \left(90^{\circ}-15^{\circ}\right)\)

= \(\left(\frac{\tan 20^{\circ}}{\sec 20^{\circ}}\right)^2+\left(\frac{\cot 20^{\circ}}{{cosec} 20^{\circ}}\right)^2+2 \tan 15^{\circ} \tan 37^{\circ} \cot 37^{\circ} \cdot(\sqrt{3}) \cot 15^{\circ}\)

= \(\left(\frac{\sin 20^{\circ} / \cos 20^{\circ}}{1 / \cos 20^{\circ}}\right)^2+\left(\frac{\cos 20^{\circ} / \sin 20^{\circ}}{1 / \sin 20^{\circ}}\right)^2+2 \sqrt{3} \tan 15^{\circ} \tan 37^{\circ} \cdot \frac{1}{\tan 37^{\circ}} \cdot \frac{1}{\tan 15^{\circ}}\)

= \(\sin ^2 20^{\circ}+\cos ^2 20^{\circ}+2 \sqrt{3}=1+2 \sqrt{3}\)

Example 5. Without using trigonometric tables, evaluate the following :

⇒ \(\frac{{cosec}^2\left(90^{\circ}-\theta\right)-\tan ^2 \theta}{4\left(\cos ^2 48^{\circ}+\cos ^2 42^{\circ}\right)}-\frac{2 \tan ^2 30^{\circ} \sec ^2 52^{\circ} \sin ^2 38^{\circ}}{\left({cosec}^2 70^{\circ}-\tan ^2 20^{\circ}\right)}\)

Solution:

⇒ \(\frac{{cosec}^2\left(90^{\circ}-\theta\right)-\tan ^2 \theta}{4\left(\cos ^2 48^{\circ}+\cos ^2 42^{\circ}\right)}-\frac{2 \tan ^2 30^{\circ} \sec ^2 52^{\circ} \sin ^2 38^{\circ}}{\left({cosec}^2 70^{\circ}-\tan ^2 20^{\circ}\right)}\)

= \(\frac{\sec ^2 \theta-\tan ^2 \theta}{4\left\{\cos ^2\left(90^{\circ}-42^{\circ}\right)+\cos ^2 42^{\circ}\right)}-\frac{2\left(\frac{1}{\sqrt{3}}\right)^2 \sec ^2\left(90^{\circ}-38^{\circ}\right) \sin ^2 38^{\circ}}{{cosec}^2\left(90^{\circ}-20^{\circ}\right)-\tan ^2 20^{\circ}}\)

= \(\frac{1}{4\left(\sin ^2 42^{\circ}+\cos ^2 42^{\circ}\right)}-\frac{2{cosec}^2 38^{\circ} \cdot \sin ^2 38^{\circ}}{3\left(\sec ^2 20^{\circ}-\tan ^2 20^{\circ}\right)}\)

= \(\frac{1}{4}-\frac{2{cosec}^2 38^{\circ} \times \frac{1}{{cosec}^2 38^{\circ}}}{3}=\frac{1}{4}-\frac{2}{3}=\frac{-5}{12}\)

Example 6. Prove that :

1. \(\sin \left(40^{\circ}-\theta\right)-\cos \left(50^{\circ}+\theta\right)\)=0
2. \(\sec \left(65^{\circ}+\theta\right)-{cosec}\left(25^{\circ}-\theta\right)\)=0

Solution:

(1) L.H.S. =\(\sin \left(40^{\circ}-\theta\right)-\cos \left(50^{\circ}+\theta\right)\)

=\(\sin \left\{90^{\circ}-\left(50^{\circ}+\theta\right)\right\}-\cos \left(50^{\circ}+\theta\right)\)

=\(\cos \left(50^{\circ}+\theta\right)-\cos \left(50^{\circ}+\theta\right)\)=0= R.H.S.

(2) L.H.S. =\(\sec \left(65^{\circ}+0\right)- {cosec}\left(25^{\circ}-\theta\right)\)

=\(\sec \left\{90^{\circ}-\left(25^{\circ}-0\right)\right\}-{cosec}\left(25^{\circ}-\theta\right)\)

=\({cosec}\left(25^{\circ}-\theta\right)- {cosec}\left(25^{\circ}-\theta\right)\)=0= R.H.S.

Example 7. Express each of the following in terms of trigonometric ratios of angles between 0° and 45°.

1. sin 70° + sec 70°
2.  tan 65° + cosec 65°
3. cos 81° + cot 80°

Solution:

1. sin 70° + sec 70° = sin (90° – 20°) + sec (90° – 20°) = cos 20° + cosec 20°
2. tan 65° + cosec 65° = tan (90° – 25°) + cosec (90° – 25°) = cot 25° + sec 25°
3. cos 81° + cot 80° = cos (90° – 9°) + cot (90° -10°) = sin 9° + tan 10°

Example 8. If sin 3A = cos (A – 26°) where 3A is an acute angle, then find the value of A

Solution:

Given that,

sin 3A = cos (A – 26°).

cos (90° – 3A) = cos (A – 26°) ⇒ 90° – 3A =A – 26°

⇒ -471=-116° ⇒ A =29°

The value of A =29°

Example 9. If sin (\(\theta\)+ 24°) = cos \(\theta\) and \(\theta\) + 24° is an acute angle, then find the value of \(\theta\).

Solution:

Given that,

sin (\(\theta\)+ 24°) = cos \(\theta\)

⇒ sin (\(\theta\) + 24°) = sin (90° – \(\theta\))

⇒ \(\theta\) + 24° = 90° – \(\theta\)

⇒ 2\(\theta\) = 66°

∴ \(\theta\)= 33°

The value of θ = 33°

Example 10. If A, B, C are the angles of \(\triangle\) M B C, show that \(\sin \frac{B+C}{2}=\cos \frac{A}{2}\).

Solution:

In \(\triangle\) A B C,

A+B+C=\(180^{\circ}\)

B+C=\(180^{\circ}-A\)

⇒ \(\frac{B+C}{2}=90^{\circ}-\frac{A}{2}\)

⇒ \(\sin \frac{B+C}{2}=\sin \left(90^{\circ}-\frac{A}{2}\right)\)

⇒ \(\sin \frac{B+C}{2}=\cos \frac{A}{2}\)

Example 11. If \(\sin 36^{\circ}\)=p, then find \(\sin 54^{\circ}\) in terms of p.

Solution: 

We have, \(\sin 36^{\circ}\)=p

⇒ \(\sin ^2 36^{\circ}=p^2 \quad \Rightarrow \quad 1-\cos ^2 36^{\circ}=p^2\)

⇒ \(\cos ^2 36^{\circ}=1-p^2 \quad \Rightarrow \quad \cos ^2\left(90^{\circ}-54^{\circ}\right)=1-p^2\)

⇒ \(\sin ^2 54^{\circ}=1-p^2\)

∴ \(\sin 54^{\circ}=\sqrt{1-p^2}\)(taking only positive sign as \(54^{\circ}\) lies in 1 quadrant)

Example 12. If \(\tan 1^{\circ} \tan 2^{\circ} \tan 3^{\circ} \tan 4^{\circ} \ldots \tan 89^{\circ}=x^2-8\), then find the value of x .

Solution:

⇒ \(x^2-8=\left(\tan 1^{\prime \prime} \tan 89^{\circ}\right)\left(\tan 2^{\prime \prime} \tan 88^{\circ}\right)\left(\tan 3^{\circ} \tan 87^{\circ}\right) \ldots\left(\tan 44^{\circ} \tan 46^{\circ}\right) \tan 45^{\circ}\)

⇒ \(\left.=\left[\tan 1^{\circ} \tan \left(90^{\circ}-1^{\circ}\right)|| \tan 2^{\circ \prime} \tan \left(90^{\circ}-2^{\circ}\right)\right] \mid \tan 3^{\circ} \tan \left(90^{\circ}-3^{\circ}\right)\right]\) … \(\left|\tan 44^{\circ} \tan \left(90^{\circ}-44^{\circ}\right)\right| \times 1\)

=\(\left(\tan 1^{\prime \prime} \cot 1^{\circ}\right)\left(\tan 2^{\circ} \cot 2^{\circ}\right)\left(\tan 3^{\circ} \cot 3^{\circ}\right) \ldots\left(\tan 44^{\circ} \cot 44^{\circ}\right)\)

=\(1 \times 1 \times 1 \times \ldots \times 1 \quad(\tan x \cdot \cot x=\tan x \cdot \frac{1}{\tan x}=1). \)

⇒ \(x^2-8\)=1

⇒ \(x^2=9 \quad \Rightarrow \quad x= \pm 3\)

The value of  \( \quad x= \pm 3\)

NCERT Exemplar For Class 10 Maths Chapter 8  Introduction Of Trigonometry Exercise 8.1

Question 1. In \(\triangle A B C\), right-angled at B, AB = 24 cm, BC = 7 cm. Determine :

1. sin A, cos A
2. sin C, cos C

Solution :

In \(\triangle A B C\),

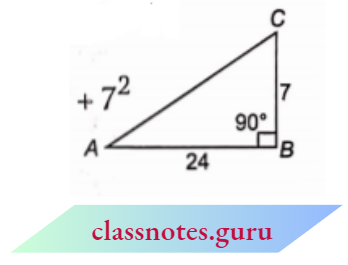
AB = 24 cm, BC = 7 cm and \(\angle B=90^{\circ}\)

From Pythagoras theorem,

⇒ \(A C^2 =A B^2+B C^2=24^2+7^2\)

=576+49=625

AC = 25 cm

(1) \(\sin A=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{B C}{A C}=\frac{7}{25}\)

⇒ \(\cos A=\frac{\text { base }}{\text { hypotenuse }}=\frac{A B}{A C}=\frac{24}{25}\)

(2) \(\sin C=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{A B}{A C}=\frac{24}{25}\).

⇒ \(\cos C=\frac{\text { base }}{\text { hypotenuse }}=\frac{B C}{A C}=\frac{7}{25}\).

Question 2. In figure, find \(\tan P-\cot R\),

Solution :

In \(\triangle\) PQR,

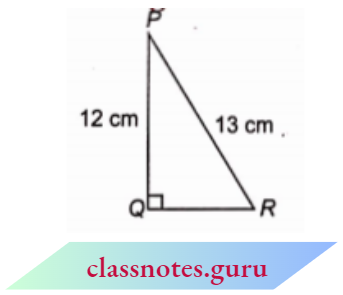
⇒ \(P Q^2+Q R^2 =P R^2\)

⇒ \(Q R^2 =P R^2-P Q^2\)

⇒ \(Q R^2 =(13)^2-(12)^2\)

=169-144=25 \(\Rightarrow Q R=5 \mathrm{~cm}\)

Now, \(\tan P=\frac{\text { perpendicular }}{\text { base }}=\frac{5}{12}\)

⇒ \(\cot R=\frac{\text { base }}{\text { perpendicular }}=\frac{5}{12}\)

∴ \(\tan P-\cot R=\frac{5}{12}-\frac{5}{12}=0\)

\(\tan P-\cot R\) = 0

Question 3. If \(\sin A=\frac{3}{4}\), calculate cos A and tan A.

Solution :

⇒ \(\sin A=\frac{3}{4}\)

In \(\triangle A B C\),

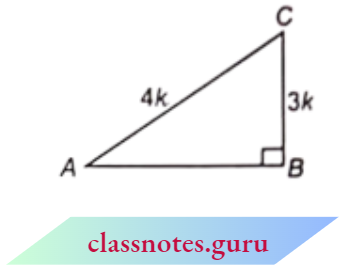
Let BC = 3k

and AC = 4k

⇒ \(A B^2+B C^2 =A C^2\)

⇒ \(A B^2 =A C^2-B C^2\)

⇒ \(A C^2 =(4 k)^2-(3 k)^2\)

= \(16 k^2-9 k^2=7 k^2\)

A B = \(\sqrt{7} k\)

Now, \(\cos A=\frac{\text { base }}{\text { hypotenuse }}=\frac{\sqrt{7} k}{4 k}=\frac{\sqrt{7}}{4}\)and \(\tan A=\frac{\text { perpendicular }}{\text { base }}=\frac{3 k}{\sqrt{7} k}=\frac{3}{\sqrt{7}}\)

Question 4. Given 15 cotA = 8, find sin A and Sec A.

Solution :

⇒ \(15 \cot A=8 \Rightarrow \cot A=\frac{8}{15}\)

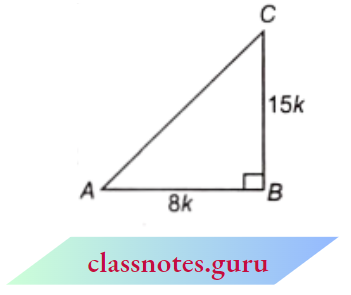
Let base =8 k=A B

and Perpendicular =15 k=B C

In \(\triangle A B C\),

⇒ \(A C^2=A B^2+B C^2\)

= \((8 k)^2+(15 k)^2\)

= \(64 k^2+225 k^2=289 k_A^2\)

AC = 17 k

Now, \(\sin A=\frac{\text { perpendicular }}{\text { hypotenuse }}\)

= \(\frac{B C}{A C}=\frac{15 k}{17 k}=\frac{15}{17}\)

and \(\sec A=\frac{\text { hypotenuse }}{\text { base }}\)

= \(\frac{A C}{A B}=\frac{17 k}{8 k}=\frac{17}{8}\)

Question 5. Given \(\sec \theta=\frac{13}{12}\), calculate all other trigonometric ratios.

Solution :

⇒ \(\sec \theta=\frac{13}{12}\)

Introduction to Trigonometry

⇒ \(\sec \theta=\frac{\text { hypotenuse }}{\text { base }}=\frac{13}{12}\)

Let, in \(\triangle A B C\), \(\angle B=90^{\circ}\) and \(\angle A=\theta\)

Let, A C=13 k and A B=12 k

Now, \(A B^2+B C^2=A C^2\)

⇒ \(B C^2 =A C^2-A B^2=(13 k)^2-(12 k)^2\)

= \(169 k^2-144 k^2=25 k^2\)

BC = 5 k

Now, \(\sin \theta=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{5 k}{13 k}=\frac{5}{13}\)

⇒ \(\cos \theta=\frac{\text { base }}{\text { hypotenuse }}=\frac{12 k}{13 k}=\frac{12}{13}\)

⇒ \(\tan \theta=\frac{\text { perpendicular }}{\text { base }}=\frac{5 k}{12 k}=\frac{5}{12}\)

cosec \(\theta=\frac{\text { hypotenuse }}{\text { perpendicular }}=\frac{13 k}{5 k}=\frac{13}{5}\)

∴ \(\cot \theta=\frac{\text { base }}{\text { perpendicular }}=\frac{12 k}{5 k}=\frac{12}{5}\)

Question 6. If \(\angle A\) and \(\angle B\) are acute angles such that \(\cos A=\cos B\), then show that \(\angle A=\angle B\).

Solution :

Let, in \(\triangle A B C, \angle C=90^{\circ}\)

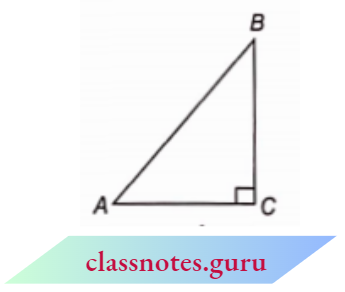
⇒ \(\angle A\) and \(\angle B\) are acute angles.

Given,\(\cos A=\cos B\)

Question 7. If \(\cot \theta=\frac{7}{8}\), evaluate :

1.  \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\),
2. \(\cot ^2 \theta\)

Solution :

⇒ \(\cot \theta=\frac{7}{8}\)

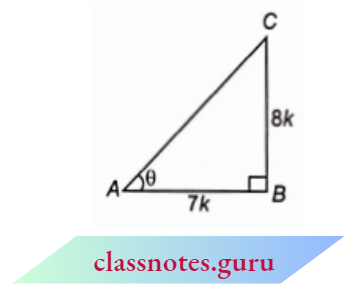
⇒ \(\cot \theta=\frac{\text { base }}{\text { perpendicular }}=\frac{7}{8}\)

Let, in \(\triangle A B C\), \(\angle B=90^{\circ}\) and \(\angle A=\theta\)

Let base AB = 7k

and perpendicular BC = 8k

Now, \(A C^2=A B^2+B C^2\)

=\((7 k)^2+(8 k)^2\)

=\(49 k^2+64 k^2=113 k^2\)

A C =\(\sqrt{113} k\)

Now, \(\sin \theta=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{B C}{A C}\)

=\(\frac{8 k}{\sqrt{113 k}}=\frac{8}{\sqrt{113}}\)

and \(\cos \theta=\frac{\text { base }}{\text { hypotenuse }}=\frac{A B}{A C}\)

= \(\frac{7 k}{\sqrt{113 k}}=\frac{7}{\sqrt{113}}\)

(1) \(\frac{(1+\sin \theta)(1-\sin \theta)}{(1+\cos \theta)(1-\cos \theta)}\)

= \(\frac{\left(1+\frac{8}{\sqrt{113}}\right)\left(1-\frac{8}{\sqrt{113}}\right)}{\left(1+\frac{7}{\sqrt{113}}\right)\left(1-\frac{7}{\sqrt{113}}\right)}\)

= \(\frac{(1)^2-\left(\frac{8}{\sqrt{113}}\right)^2}{(1)^2-\left(\frac{7}{\sqrt{113}}\right)^2}=\frac{1-\frac{64}{113}}{1-\frac{49}{113}}\)

= \(\frac{113-64}{113-49}=\frac{49}{64}\)

(2) \(\cot ^2 \theta=\left(\frac{7}{8}\right)^2=\frac{49}{64}\)

Question 8. If \(3 \cot A=4\), check whether \(\frac{\left(1-\tan ^2 A\right)}{\left(1+\tan ^2 A\right)}=\cos ^2 A-\sin ^2 A\) or not.

Solution :

3 cot A=4

⇒ \(\cot A=\frac{4}{3}\)

Now, \(\cot A=\frac{\text { base }}{\text { perpendicular }}=\frac{4}{3}\)

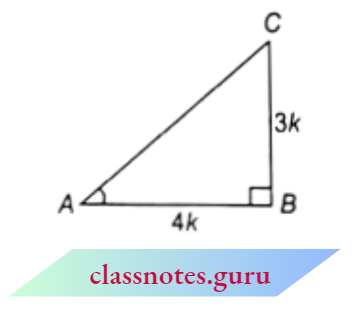
In \(\triangle A B C, \angle B =90^{\circ}\)

base A B =4 k, perpendicular B C = 3 k

⇒ \(A C^2 =A B^2+B C^2=(4 k)^2+(3 k)^2\)

= \(16 k^2+9 k^2=25 k^2\)

A C = 5 k

Now, \(\tan A=\frac{\text { perpendicular }}{\text { base }}=\frac{B C}{A B}=\frac{3 k}{4 k}=\frac{3}{4}\)

⇒ \(\cos A=\frac{\text { base }}{\text { hypotenuse }}=\frac{A B}{A C}=\frac{4 k}{5 k}=\frac{4}{5}\)

⇒ \(\sin A=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{B C}{A C}=\frac{3 k}{5 k}=\frac{3}{5}\)

Now, \( \frac{1-\tan ^2 A}{1+\tan ^2 A}=\frac{1-\left(\frac{3}{4}\right)^2}{1+\left(\frac{3}{4}\right)^2}\)

= \(\frac{1-\frac{9}{16}}{1+\frac{9}{16}}=\frac{16-9}{16+9}=\frac{7}{25}\)

and \(\cos ^2 A-\sin ^2 A=\left(\frac{4}{5}\right)^2-\left(\frac{3}{5}\right)^2\)

=\(\frac{16}{25}-\frac{9}{25}=\frac{16-9}{25}=\frac{7}{25}\)

∴ \(\frac{1-\tan ^2 A}{1+\tan ^2 A}=\cos ^2 A-\sin ^2 A\)

Question 9. In triangle ABC, right-angled at B, if \(\tan A=\frac{1}{\sqrt{3}}\), find the value of:

1. \(\sin A \cos C+\cos A \sin C\)
2.  \(\cos A \cos C-\sin A \sin C\)

Solution :

In \(\triangle A B C, \angle B=90^{\circ}\)

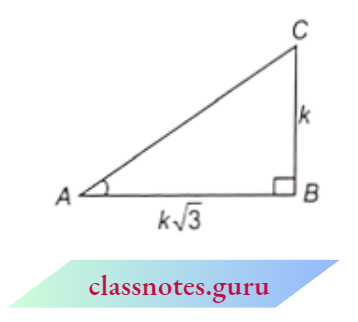
⇒ \(\tan A=\frac{1}{\sqrt{3}}\)

⇒ \(\tan A =\frac{\text { perpendicular }}{\text { base }}\)

= \(\frac{1}{\sqrt{3}}\)

Let perpendicular B C = k and base \(A B=k \sqrt{3}\)

Now, \(A C^2 =A B^2+B C^2=(k \sqrt{3})^2+k^2\)

= \(3 k^2+k^2=4 k^2\)

A C = 2 k

Now, \(\sin A=\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{B C}{A C}=\frac{k}{2 k}=\frac{1}{2}\)

⇒ \(\cos A =\frac{\text { base }}{\text { hypotenuse }}=\frac{A B}{A C}=\frac{k \sqrt{3}}{2 k}=\frac{\sqrt{3}}{2}\)

⇒ \(\sin C =\frac{\text { perpendicular }}{\text { hypotenuse }}=\frac{A B}{A C}\)

= \(\frac{k \sqrt{3}}{2 k}=\frac{\sqrt{3}}{2}\)

⇒ \(\cos C=\frac{\text { base }}{\text { hypotenuse }}=\frac{B C}{A C}=\frac{k}{2 k}=\frac{1}{2}\)

(1) \(\sin A \cos C+\cos A \sin C =\frac{1}{2} \times \frac{1}{2}+\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}\)

= \(\frac{1}{4}+\frac{3}{4}=1\)

(2) \(\cos A \cos C-\sin A \sin C=\frac{\sqrt{3}}{2} \times \frac{1}{2}-\frac{1}{2} \times \frac{\sqrt{3}}{2}=0\)

Question 10. In \(\triangle\) PQR, right-angled at Q, PR + QR = 25 cm and PQ = 5 cm. Determine the values of sin P, cos P, and tan P.

Solution :

In \(\triangle P Q R\), \(\angle Q=90^{\circ}\)

and P Q =5 cm

P R+Q R =25  → Equation 1

Now, \(P R^2=P Q^2+Q R^2\)

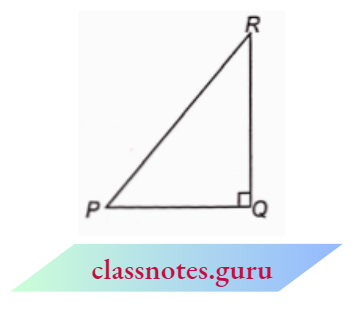
⇒ \(P R^2-Q R^2=P Q^2\)

⇒ \((P R-Q R)(P R+Q R) =5^2\)

⇒ \((P R-Q R) \times 25 =2\)

P R-Q R =1  → Equation 2

Adding equations (1) and (2),

2 \(\cdot P R=26 \quad \Rightarrow \quad P R=13\)

From equation (1)

Now, Q R =25-P R=25-13=12

⇒ \(\sin P =\frac{Q R}{P R}=\frac{12}{13}\)

⇒ \(\cos P =\frac{P Q}{P R}=\frac{5}{13}\)

∴ \(\tan P =\frac{Q R}{P Q}=\frac{12}{5}\)

Question 11. State whether the following are true or false. Justify your answer.

1. The value of tan A is always less than 1.
2.  sec A = \(\frac{12}{5}\) for some value of angle A.
3. cos A is the abbreviation used for the cosecant of angle A.
4. cot A is the product of cot and A.
5. \(\sin \theta=\frac{4}{3}\) for some angle \(\theta\).

Solution :

(1) False, \(\tan A=\frac{\text { perpendicular }}{\text { base }}\)

tan A < l is possible only when the perpendicular is smaller the base but it is not always necessary, hypotenuse

(2) True, sec A=\(\frac{\text { hypotenuse }}{\text { base }}\)

Hypotenuse is always greater than the base.

Therefore, sec A = \(\frac{12}{5}\), is true tor some angle A

(3) False, cos A, is the brief form of the cosine of \(\angle\)A

NCERT Exemplar For Class 10 Maths Chapter 8  Introduction To Trigonometry Exercise 8.2

Question 1. Evaluate the following :

1.  \(\sin 60^{\circ} \cos 30^{\circ}+\sin 30^{\circ} \cos 60^{\circ}\)
2.  \(2 \tan ^2 45^{\circ}+\cos ^2 30^{\circ}-\sin ^2 60^{\circ}\)
3. \(\frac{\cos 45^{\circ}}{\sec 30^{\circ}+{cosec} 30^{\circ}}\)
4.  \(\frac{\sin 30^{\circ}+\tan 45^{\circ}-{cosec} 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}\)
5. \(\frac{5 \cos ^2 60^{\circ}+4 \sec ^2 30^{\circ}-\tan ^2 45^{\circ}}{\sin ^2 30^{\circ}+\cos ^2 30^{\circ}}\)

Solution :

(1) \(\sin 60^{\circ} \cos 30^{\circ}+\sin 30^{\circ} \cos 60^{\circ}\)

=\(\frac{\sqrt{3}}{2} \times \frac{\sqrt{3}}{2}+\frac{1}{2} \times \frac{1}{2}\)

=\(\frac{3}{4}+\frac{1}{4}=\frac{4}{4}=1\)

(2) \(2 \tan ^2 45^{\circ}+\cos ^2 30^{\circ}-\sin ^2 60^{\circ}\)

=\(2(1)^2+\left(\frac{\sqrt{3}}{2}\right)^2-\left(\frac{\sqrt{3}}{2}\right)^2\)

=\(2+\frac{3}{4}-\frac{3}{4}=2\)

(3) \(\frac{\cos 45^{\circ}}{\sec 30^{\circ}+{cosec} 30^{\circ}}\)

=\(\frac{1 / \sqrt{2}}{\frac{2}{\sqrt{3}}+\frac{2}{1}}\)

⇒ \(=\frac{1}{\sqrt{2}\left(\frac{2+2 \sqrt{3}}{\sqrt{3}}\right)}\)

⇒ \(=\frac{\sqrt{3}}{2 \sqrt{2}(\sqrt{3}+1)}\)

= \(\frac{\sqrt{3} \cdot \sqrt{2}(\sqrt{3}-1)}{2 \sqrt{2}(\sqrt{3}+1) \cdot \sqrt{2}(\sqrt{3}-1)}\)

= \(\frac{\sqrt{2}(3-\sqrt{3})}{2 \cdot 2(3-1)}=\frac{3 \sqrt{2}-\sqrt{6}}{8}\)

(4) \(\frac{\sin 30^{\circ}+\tan 45^{\circ}-{cosec} 60^{\circ}}{\sec 30^{\circ}+\cos 60^{\circ}+\cot 45^{\circ}}\)

= \(\frac{\frac{1}{2}+1-\frac{2}{\sqrt{3}}}{\frac{2}{\sqrt{3}}+\frac{1}{2}+1}\)

= \(\frac{\frac{\sqrt{3}+2 \sqrt{3}-4}{2 \sqrt{3}}}{\frac{4+\sqrt{3}+2 \sqrt{3}}{2 \sqrt{3}}}=\frac{3 \sqrt{3}-4}{3 \sqrt{3}+4}\)

= \(\frac{3 \sqrt{3}-4}{3 \sqrt{3}+4} \times \frac{3 \sqrt{3}-4}{3 \sqrt{3}-4}\)

= \(\frac{27+16-24 \sqrt{3}}{(3 \sqrt{3})^2-(4)^2}\)

= \(\frac{43-24 \sqrt{3}}{27-16}\)

= \(\frac{43-24 \sqrt{3}}{11}\)

(5) \(\frac{5 \cos ^2 60^{\circ}+4 \sec ^2 30^{\circ}-\tan ^2 45^{\circ}}{\sin ^2 30^{\circ}+\cos ^2 30^{\circ}}\)

=\(\frac{5\left(\frac{1}{2}\right)^2+4\left(\frac{2}{\sqrt{3}}\right)^2-(1)^2}{\left(\frac{1}{2}\right)^2+\left(\frac{\sqrt{3}}{2}\right)^2}\)

=\(\frac{\frac{5}{4}+4 \times \frac{4}{3}-1}{\frac{1}{4}+\frac{3}{4}}=\frac{\frac{15+64-12}{12}}{1}=\frac{67}{12}\)

Question 2. Choose the correct option and justify your choice :

(1) \(\frac{2 \tan 30^{\circ}}{1+\tan ^2 30^{\circ}}\)= ?

1. \(\sin 60^{\circ}\)
2. \(\cos 60^{\circ}\)
3. \(\tan 60^{\circ}\)
4. \(\sin 30^{\circ}\)

(2) \(\frac{1-\tan ^2 45^{\circ}}{1+\tan ^2 45^{\circ}}=\) ?

1. \(\tan 90^{\circ}\)
2. 1
3. \(\sin 45^{\circ}\)
4. 0

(3) \(\sin 2 A=2 \sin A\) is true when A=

1. \(0^{\circ}\)
2. \(30^{\circ}\)
3. \(45^{\circ}\)
4. \(60^{\circ}\)

(4) \(\frac{2 \tan 30^{\circ}}{1-\tan ^2 30^{\circ}}\)=

1. \(\cos 60^{\circ}\)
2. \(\sin 60^{\circ}\)
3. \(\tan 60^{\circ}\)
4. \(\sin 30^{\circ}\)

Solution:

(1) 1

⇒ \(\frac{2 \tan 30^{\circ}}{1+\tan ^2 30^{\circ}}=\frac{2 \times \frac{1}{\sqrt{3}}}{1+\left(\frac{1}{\sqrt{3}}\right)^2}\)

= \(\frac{\frac{2}{\sqrt{3}}}{1+\frac{1}{3}}=\frac{\frac{2}{\sqrt{3}}}{\frac{4}{3}}=\frac{2}{\sqrt{3}} \times \frac{3}{4}=\frac{\sqrt{3}}{2}=\sin 60^{\circ}\)

(2) 4

⇒ \(\frac{1-\tan ^2 45^{\circ}}{1+\tan ^2 45^{\circ}}=\frac{1-(1)^2}{1+(1)^2}=\frac{1-1}{1+1}=\frac{0}{2}=0\)

(3) 1

If A =\(0^{\circ}\)then \(2 A=0^{\circ}\)

⇒ \(\sin 2 A =\sin 0^{\circ}=0\)

and \(2 \sin A =2 \sin 0^{\circ}\)

=2 \(\times 0=0\)

So, for \(A=0^{\circ}, \sin 2 A=2 \sin A\)

(4) 3

⇒ \(\frac{2 \tan 30^{\circ}}{1-\tan ^2 30^{\circ}} =\frac{2 \times \frac{1}{\sqrt{3}}}{1-\left(\frac{1}{\sqrt{3}}\right)^2}=\frac{2 / \sqrt{3}}{1-\frac{1}{3}}=\frac{2 / \sqrt{3}}{2 / 3}\)

= \(\frac{2}{\sqrt{3}} \times \frac{3}{2}=\sqrt{3}=\tan 60^{\circ}\)

Question 3. If \(\tan (A+B)=\sqrt{3}\) and \(\tan (A-B)=\frac{1}{\sqrt{3}}\) ; \(0^{\circ}<A+B \leq 90^{\circ}\) ; A>B, find A and B.

Solution :

⇒ \(\tan (A+B)=\sqrt{3}\)

⇒ \(\tan (A+B)=\tan 60^{\circ}\)

⇒ \(A+B=60^{\circ}\)

and \(tan (A-B)=\frac{1}{\sqrt{3}}\)

⇒ \(\tan (A-B)=\tan 30^{\circ} \Rightarrow A-B=30^{\circ}\)

Adding equations (1) and (2)

⇒ \(A+B=60^{\circ}\)

⇒ \(A-B=30^{\circ}\)

⇒ \( 2 A=90^{\circ}\)

⇒ \(A \quad A=45^{\circ}\)

Put the value of A in equation (1),

⇒ \(45^{\circ}+B=60^{\circ} \Rightarrow \quad B\)

A=\(45^{\circ}\) and B=\(15^{\circ} \quad 45^{\circ}=15^{\circ}\)

Question 4. State whether the following are true or false. Justify your answer.

1. \(\sin (A+B)=\sin A+\sin B\)
2. The value of \(\sin \theta\) increases as \(\theta\) increases.
3.  The value of \(\cos \theta\) increases as \(\theta\) increases.
4. \(\sin \theta=\cos \theta\) for all values of θ.
5.  cot A is not defined for A=\(0^{\circ}\)

Solution :

(1) False,

Let A=\(30^{\circ}\) and B=\(60^{\circ}\)

⇒ \(\sin (A+B)=\sin \left(30^{\circ}+60^{\circ}\right)=\sin 90^{\circ}=1\)

and \(\sin A+\sin B=\sin 30^{\circ}+\sin 60^{\circ}\)

= \(\frac{1}{2}+\frac{\sqrt{3}}{2}=\frac{\sqrt{3}+1}{2} \neq 1 \)

⇒ \(\sin (A+B) \neq \sin A+\sin B\)

(2) True, as the value of \(\theta\) varies from \(\theta^{\circ}\) to \(90^{\circ}\) then the value of \(\sin \theta\) varies from 0 to 1 .

(3) False, as the value of \(\theta\) varies front 0° to 90° then the value of cos \(\theta\) varies from 1 to 0,

i.e, the value of cos \(\theta\) decreases.

(4) False,

⇒ \(\theta\) = 0° then sin \(\theta\) = sin 0° = 0

and \(\cos 0=\cos \theta^{\circ}=1\)

⇒ \(\sin 0 \times \cos 0\), if \(\theta=0^{\circ}\)

(5) True,

⇒ \(A=0^{\circ}\) than \(\cot A=\cot 0^{\circ}\) which is not defined.

NCERT Exemplar For Class 10 Maths Chapter 8  Exercise 8.3

Question 1. Evaluate :

1. \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\)
2. \(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\)
3. \(\cos 48^{\circ}-\sin 42^{\circ}\)
4. \(cosec 31^{\circ}-\sec 59^{\circ}\)

Solution :

(1) \(\frac{\sin 18^{\circ}}{\cos 72^{\circ}} =\frac{\sin \left(90^{\circ}-72^{\circ}\right)}{\cos 72^{\circ}}\)

=\(\frac{\cos 72^{\circ}}{\cos 72^{\circ}}=1\)

\(\frac{\sin 18^{\circ}}{\cos 72^{\circ}}\) = 1

(2)\(\frac{\tan 26^{\circ}}{\cot 64^{\circ}} =\frac{\tan \left(90^{\circ}-64^{\circ}\right)}{\cot 64^{\circ}}\)

=\(\frac{\cot 64^{\circ}}{\cot 64^{\circ}}=1\)

\(\frac{\tan 26^{\circ}}{\cot 64^{\circ}}\) =1

(3)\(\cos 48^{\circ}-\sin 42^{\circ} =\cos \left(90^{\circ}-42^{\circ}\right)-\sin 42^{\circ}\)

=\(\sin 42^{\circ}-\sin 42^{\circ}=0\)

\(\cos 48^{\circ}-\sin 42^{\circ}\) =0

(4) \({cosec} 31^{\circ}-\sec 59^{\circ}\)

= \({cosec}\left(90^{\circ}-59^{\circ}\right)-\sec 59^{\circ}\)

=\(\sec 59^{\circ}-\sec 59^{\circ}=0\)

\(cosec 31^{\circ}-\sec 59^{\circ}\)= 0

Question 2. Show that:

1. \(\tan 48^{\circ} \tan 23^{\circ} \tan 42^{\circ} \tan 67^{\circ}=1\)
2. \(\cos 38^{\circ} \cos 52^{\circ}-\sin 38^{\circ} \sin 52^{\circ}=0\)

Solution :

(1) L.H.S. =\(\tan 48^{\circ} \tan 23^{\circ} \tan 42^{\circ} \tan 67^{\circ}\)

=\(\tan 48^{\circ} \cdot \tan 23^{\circ} \cdot \tan \left(90^{\circ}-48^{\circ}\right)\)

⇒ \(\cdot \tan \left(90^{\circ}-23^{\circ}\right)\)

= \(\tan 48^{\circ} \cdot \tan 23^{\circ} \cdot \cot 48^{\circ} \cdot \cot 23^{\circ}\)

= \(\tan 48^{\circ} \cdot \tan 23^{\circ} \cdot \frac{1}{\tan 48^{\circ}} \cdot \frac{1}{\tan 23^{\circ}}\)

= 1 = R.H.S.

Hence Proved.

(2) L.H.S.=\(\cos 38^{\circ} \cos 52^{\circ}-\sin 38^{\circ}+\sin 52^{\circ}\)

=\(\cos \left(90^{\circ}-52^{\circ}\right) \cdot \cos \left(90^{\circ}-38^{\circ}\right)\)

⇒ \(-\sin 38^{\circ} \cdot \sin 52^{\circ}\)

=\(\sin 52^{\circ} \cdot \sin 38^{\circ}-\sin 38^{\circ} \cdot \sin 52^{\circ}\)

= 0 = R.H.S

Hence Proved.

Question 3. If \(\tan 2 A=\cot \left(A-18^{\circ}\right)\), where 2 A is an acute angle, find the value of A.

Solution:

⇒ \(\tan 2 A =\cot \left(A-18^{\circ}\right)\)

⇒ \(\cot \left(90^{\circ}-2 A\right) =\cot \left(A-18^{\circ}\right)\)

⇒ \(90^{\circ}-2 A =A-18^{\circ}\)

⇒ \(90^{\circ}+18^{\circ} =A+2 A\)

⇒ \(3 A =108^{\circ}\)

A =\(36^{\circ}\)

The value of A =\(36^{\circ}\)

Question 4. If \(\tan A=\cot B\), prove that

A+B=\(90^{\circ}\).

Solution :

⇒ \(\tan A=\cot B\)

⇒ \(\tan A=\tan \left(90^{\circ}-B\right)\)

⇒ \(A=90^{\circ}-B\)

⇒ \(A+B=90^{\circ}\)

Hence Proved.

Question 5. If \(\sec 4 A={cosec}\left(A-20^{\circ}\right)\), where 4 A is an acute angle, find the value of A.

Solution :

⇒ \(\sec 4 A = cosec \left(A-20^{\circ}\right)\)

cosec\(\left(90^{\circ}-4 A\right) = cosec\left(A-20^{\circ}\right)\)

⇒ \(90^{\circ}-4 A =A-20^{\circ}\)

⇒ \(90^{\circ}+20^{\circ} =A+4 A\)

⇒ \(5 A =110^{\circ}\)

A =\(22^{\circ}\)

The value of A =\(22^{\circ}\)

Question 6. If A, B and C are interior angles of a triangle A B C, then show that \(\sin \left(\frac{B+C}{2}\right)=\cos \frac{A}{2}\)

Solution :

In \(\triangle A B C\)

⇒ \(A+B+C=180^{\circ}\)

⇒ \(B+C=180^{\circ}-A\)

⇒ \(\frac{B+C}{2}=\frac{180^{\circ}-A}{2}\)

= \(\frac{180^{\circ}}{2}-\frac{A}{2}=90^{\circ}-\frac{A}{2}\)

⇒ \(\sin \left(\frac{B+C}{2}\right)=\sin \left(90^{\circ}-\frac{A}{2}\right)\)

⇒ \(\sin \left(\frac{B+C}{2}\right)=\cos \frac{A}{2}\)

Hence Proved.

NCERT Exemplar For Class 10 Maths Chapter 8  Exercise 8.4

Question 1. Express the trigonometric ratios \(\sin A, \sec A\) and \(\tan A\) in terms of \(\cot A\).

Solution :

⇒ \(\sin A=\frac{1}{cosec^2 A}\)

⇒ \(\sin A=\frac{1}{\sqrt{{cosec}^2 A}}\)

⇒ \(\sin A=\frac{1}{\sqrt{1+\cot ^2 A}}\)

⇒ \(\sec A=\sqrt{\sec ^2 A}\)

⇒ \(\sec A=\sqrt{1+\tan ^2 A}\)

⇒ \(\sec A=\sqrt{1+\left(\frac{1}{\cot A}\right)^2}\)

⇒ \(\sec A=\sqrt{1+\frac{1}{\cot ^2 A}}=\sqrt{\frac{\cot ^2 A+1}{\cot ^2 A}}\)

and \(\tan A=\frac{1}{\cot A}\)

Question 2. Write all the other trigonometric ratios of \(\angle A\) in terms of \sec A.

Solution :

⇒ \(\sin A=\sqrt{\sin ^2 A} =\sqrt{1-\cos ^2 A}\)

= \(\sqrt{1-\frac{1}{\sec ^2 A}}=\sqrt{\frac{\sec ^2 A-1}{\sec ^2 A}}\)

⇒ \(\sin A =\frac{\sqrt{\sec ^2 A-1}}{\sec A}\)

cos A =\(\frac{1}{\sec A}\)

tan A =\(\sqrt{\tan ^2 A}\)

⇒ \(\tan A =\sqrt{\sec ^2 A-1}\)

⇒ \(\cot A =\frac{1}{\tan A}=\frac{1}{\sqrt{\tan ^2 A}}\)

⇒ \(\cot A=\frac{1}{\sqrt{\sec ^2 A-1}}\)

⇒ \(cosec A=\sqrt{{cosec}^2 A}=\sqrt{1+\cot ^2 A}\)

= \(\sqrt{1+\frac{1}{\tan ^2 A}}\)

= \(\sqrt{\frac{1+\tan ^2 A}{\tan ^2 A}}=\sqrt{\frac{\sec ^2 A}{\sec ^2 A-1}}\)

cosec A=\(\frac{\sec A}{\sqrt{\sec ^2 A-1}}\)

Question 3. Evaluate:

1. \(\frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}}\)
2. \(\sin 25^{\circ} \cos 65^{\circ}+\cos 25^{\circ} \sin 65^{\circ}\)

Solution:

(1) \(\frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}}\)

=\(\frac{\sin ^2\left(90^{\circ}-27^{\circ}\right)+\sin ^2 27^{\circ}}{\cos ^2\left(90^{\circ}-73^{\circ}\right)+\cos ^2 73^{\circ}}\)

=\(\frac{\cos ^2 27^{\circ}+\sin ^2 27^{\circ}}{\sin ^2 73^{\circ}+\cos ^2 73^{\circ}}=\frac{1}{1}=1\)

1. \(\frac{\sin ^2 63^{\circ}+\sin ^2 27^{\circ}}{\cos ^2 17^{\circ}+\cos ^2 73^{\circ}}\)=1

(2) \(\sin 25^{\circ} \cdot \cos 65^{\circ}+\cos 25^{\circ} \sin 65^{\circ}\)

= \(\sin 25^{\circ} \cdot \cos \left(90^{\circ}-25^{\circ}\right)\)

⇒ \(+\cos 25 \sin \left(90^{\circ}-25^{\circ}\right)\)

= \(\sin 25^{\circ} \cdot \sin 25^{\circ}+\cos 25^{\circ} \cdot \cos 25^{\circ}\)

= \(\sin ^2 25^{\circ}+\cos ^2 25^{\circ}=1\)

\(\sin 25^{\circ} \cos 65^{\circ}+\cos 25^{\circ} \sin 65^{\circ}\) = 1

Question 4. Choose the correct option. Justify your choice.

(1) 9 \(\sec ^2 A-9 \tan ^2 A\)=

1. 1
2. 9
3. 8
4. 0

(2) \((1+\tan \theta+\sec \theta)\)

1. \((1+\cot \theta- cosec \theta)\)=
2. 0
3. 1
4. 2

(3) \((\sec A+\tan A)(1-\sin A)=\)

1. sec A
2. sin A
3. cosec A
4. cos A

(4) \(\frac{1+\tan ^2 A}{1+\cot ^2 A}\)=

1. \(\sec ^2 A\)
2. -1
3. \(\cot ^2 A\)
4. \(\tan ^2 A\)

Solution :

(1) Answer. (2)

⇒ \(9 \sec ^2 A-9 \tan ^2 A=9\left(\sec ^2 A-\tan ^2 A\right)\)

=9 \(\times \)1=9

9 \(\sec ^2 A-9 \tan ^2 A\)= 9

(2) Answer. (3)

⇒ \((1+\tan \theta+\sec \theta)(1+\cot \theta-{cosec} \theta)\)

=\(1+\cot \theta-{cosec} \theta+\tan \theta+\tan \theta \cdot \cot \theta\)

⇒ –\(\tan \theta \cdot {cosec} \theta+\sec \theta+\sec \theta \cdot \cot \theta-\sec \theta \cdot{cosec} \theta\)

= \(1+\cot \theta-{cosec} \theta+\tan \theta +\frac{\sin \theta}{\cos \theta} \cdot \frac{\cos \theta}{\sin \theta}-\frac{\sin \theta}{\cos \theta} \cdot \frac{1}{\sin \theta}+\sec \theta\)

⇒ \(+\frac{1}{\cos \theta} \cdot \frac{\cos \theta}{\sin \theta}-\sec \theta {cosec} \theta\)

=\(1+(\cot \theta+\tan \theta)-{cosec} \theta\)

⇒ \(+1-\sec \theta+\sec \theta+ cosec \theta\)

⇒ \(-\sec \theta cose \theta\)

= \(2+\left(\frac{\cos \theta}{\sin \theta}+\frac{\sin \theta}{\cos \theta}\right)-\sec \theta {cosec} \theta\)

= \(2+\frac{\cos { }^2 \theta+\sin ^2 \theta}{\sin \theta \cdot \cos \theta}-\sec \theta{cosec} \theta\)

= \(2+\frac{1}{\sin \theta \cos \theta}-\frac{1}{\cos \theta \sin \theta}=2\) .

\((1+\tan \theta+\sec \theta)\) =1

(3) Answer. (4)

⇒ \((\sec A+\tan A)(1-\sin A)\)

= \(\left(\frac{1}{\cos A}+\frac{\sin A}{\cos A}\right)(1-\sin A)\)

= \(\left(\frac{1+\sin A}{\cos A}\right)(1-\sin A)\)

= \(\frac{1-\sin ^2 A}{\cos A}=\frac{\cos ^2 A}{\cos A}=\cos A \)

\((\sec A+\tan A)(1-\sin A)=\) =cos A

(4) Answer. (4)

⇒ \(\frac{1+\tan ^2 A}{1+\cot ^2 A} =\frac{1+\tan ^2 A}{1+\frac{1}{\tan ^2 A}}=\frac{1+\tan ^2 A}{\frac{\tan ^2 A+1}{\tan ^2 A}}\)

=\(\tan ^2 A\)

\(\frac{1+\tan ^2 A}{1+\cot ^2 A}\)= \(\tan ^2 A\)

NCERT Exemplar For Class 10 Maths Chapter 8  Trigonometry Multiple-Choice Questions

Question 1. The value of \(\sin 45^{\circ}+\cos 45^{\circ}\) is :

1. 2
2. \(\sqrt{2}\)
3. \(\frac{\sqrt{3}}{2}\)
4. 1

Answer: 2. \(\sqrt{2}\)

The value of \(\sin 45^{\circ}+\cos 45^{\circ}\) is \(\sqrt{2}\)

Question 2. If \(\sin A=\frac{3}{2}\) then the value of tan A is:

1. \(\frac{5}{3}\)
2. \(\frac{4}{3}\)
3. \(\frac{3}{4}\)
4. \(\frac{3}{5}\)

Answer: 3. \(\frac{3}{4}\)

The value of tan A is \(\frac{3}{4}\)

Question 3. If \(\sin A+\sin ^2 A=1\) then the value of \(\left(\cos ^2 A+\cos ^4 A\right)\) is :

1. 1
2. \(\frac{1}{2}\)
3. 2
4. \(\frac{1}{3}\)

Answer: 1. 1

The value of \(\left(\cos ^2 A+\cos ^4 A\right)\) is 1.

Question 4. If \(\cos 8 \alpha=\sin \alpha\) and \(8 \alpha<90^{\circ}\) then the value of \(\tan 3 \alpha\) is :

1. 0
2. 1
3. \(\sqrt{3}\)
4. \(\frac{1}{\sqrt{3}}\)

Answer: 4. \(\frac{1}{\sqrt{3}}\)

The value of \(\tan 3 \alpha\) is  \(\frac{1}{\sqrt{3}}\)

Question 5. In \(\triangle A B C\), \(\angle C=90^{\circ}\). The value of \(\cos (A+B)\) is :

1. 1
2. 0
3. -1
4. \(\frac{1}{2}\)

Answer: 2.  0

The value of \(\cos (A+B)\) is 0

Question 6. If \(4 \tan \theta=3\) then the value of \(\frac{4 \sin \theta-3 \cos \theta}{\sin \theta+\cos \theta}\) is :

1. \(-\frac{16}{25}\)
2. \(\frac{16}{25}\)
3. 0
4. 4

Answer: 3.  0

Question 7. The value of \(\sin \left(60^{\circ}+\theta\right)-\cot \left(30^{\circ}-\theta\right)\) is :

1. 0
2. 2 \(\tan \theta\)
3. \(2 \cot \theta\)
4. \(2 \sqrt{3}\)

Answer: 1.  0

Question 8. If \(\cos \theta=\sin \theta, 0 \leq \theta<90^{\circ}\), then angle \(\theta\) is equal to :

1. \(0^{\circ}\)
2. \(30^{\circ}\)
3. \(45^{\circ}\)
4. \(60^{\circ}\)

Answer: 3. \(45^{\circ}\)

\(\theta\) is equal to \(45^{\circ}\)

Question 9. If \(\sin A=\frac{3}{5}\) then the value of \(\cos A\) is:

1. \(\frac{5}{4}\)
2. \(\frac{4}{5}\)
3. \(\frac{5}{3}\)
4. \(\frac{4}{3}\)

Answer: 2. \(\frac{4}{5}\)

The value of \(\cos A\) is \(\frac{4}{5}\)

Question 10. If \(\sec \theta=2\) then the value of \(\theta\) is:

1. \(30^{\circ}\)
2. \(45^{\circ}\)
3. \(60^{\circ}\)
4. \(90^{\circ}\)

Answer: 3. \(60^{\circ}\)

The value of \(\theta\) is \(60^{\circ}\)

Question 11. If \(\cos ^2 \theta=\frac{1}{2}\) then the value of \(\sin ^2 \theta\) is:

1. \(\frac{1}{4}\)
2. \(\frac{\sqrt{3}}{2}\)
3. \(\frac{1}{\sqrt{2}}\)
4. \(\frac{1}{2}\)

Answer: 4. \(\frac{1}{2}\)

The value of \(\sin ^2 \theta\) is \(\frac{1}{2}\)

Question 12. If \(\tan \theta=\frac{2 a b}{a^2-b^2}\) then the value of \(\cos \theta\) is:

1. 1
2. \(\frac{a^2-b^2}{a^2+b^2}\)
3. \(\frac{a^2+b^2}{a^2-b^2}\)
4. \(\frac{2 a b}{a^2+b^2}\)

Answer: 2.  \(\frac{a^2-b^2}{a^2+b^2}\)

The value of \(\cos \theta\) is \(\frac{a^2-b^2}{a^2+b^2}\)

Question 13. If cosec A= A, \(0^{\circ} \leq A \leq 90^{\circ}\) then \(\angle A\) is equal to :

1. \(120^{\circ}\)
2. \(60^{\circ}\)
3. \(45^{\circ}\)
4. \(30^{\circ}\)

Answer: 3. \(45^{\circ}\)

Question 14. If \(3 \cot A=4\) then the value of \(\sec A\) is :

1. \(\frac{3}{4}\)
2. \(\frac{5}{4}\)
3. \(\frac{2}{3}\)
4. \(\frac{3}{2}\)

Answer: 2. \(\frac{5}{4}\)

The value of \(\sec A\) is \(\frac{5}{4}\)