Important Questions For CBSE Class 12 Maths Chapter 1 Relations And Functions

CBSE Class 12 Maths Chapter 1 Relations And Functions Important Questions

Question 1. Let set X = {1, 2, 3} and a relation R is defined in X as R = {(1, 3), (2, 2), (3,2)}, then minimum ordered pairs which should be added in relation R to make it reflexive and symmetric are:

1. {(1,1), (2. 3), (1,2)}
2. {(3, 3), (3, 1), (1,2)}
3. {(1, 1), (3, 3), (3. 1), (2, 3)}
4. {(1,1), (3, 3), (3, 1), (1,2)}

Solution: 3. {(1, 1), (3, 3), (3. 1), (2, 3)}

Given, R= {(1,3), (2,2), (3,2)} on set X = {1.2, 3}

Then: if R is reflexive and symmetric, then R= {(1, 1), (2, 2), (3, 3), (1,3), (3, 2), (3, 1), (2, 3)}

Hence: the ordered pairs to be added are: {(1, 1), (3, 3), (3, 1), (2, 3)}

Read and Learn More CBSE Class 12 Maths Important Question and Answers

Question 2. If R = {(x, y); x, y ∈ Z, x² + y² ≤ 4} is a relation in set Z. then the domain of R is :

1. {0, 1,2}
2. {-2,-1, 0, 1,2}
3. {0,-1,-2}
4. {-1,0, 1}

Solution: 2. {-2,-1, 0, 1,2}

Given: R = {(x, y) : x, y ∈ Z, x² + y² ≤ 4} is a relation in set Z.

Hence: according to the given relation.

Domain of R= {-2, —1, 0. 1.2}

Question 3. Let X = {x²: x ∈ N} and the function f: N →X is defined by f(x) = x², x ∈ N. Then, this function is :

1. Injective only
2. Not objective
3. Surjective only
4. Bijective

Solution: 4. Bijective

f(x) = x²; x ∈ N; f : N → X where X = {x²: x ∈ N}

Now; f(x₁) = f(x₂)

⇒ x²₁ = x²₂

⇒ (x₁ + x₂) (x₁ – x₂) = 0

Now : x₁ + x₂ ≠ 0 (x₁,x₂ ∈ N)

⇒ x₁ – x₂ = 0 ⇒ x₁ = x₂

Hence; f is one-one.

Let y = f(x) ⇒ y = x²

⇒ x = √y

∀ y ∈ X, there exists x ∈ N

Hence, every element of the co-domain has pre-images in the domain.

⇒ Range = Co-domain

∴  f is onto.

∴ The given function is bijective.

Question 4. A function f: R → R defined by f(x) = 2 + x² is :

1. Not one-one
2. One-one
3. Not onto
4. Neither one-one nor onto

Solution: 4. Neither one-one nor onto

f(x) = 2 + x² f: R → R

One-one: Let x₁ and x₂ ∈ R such that

f(x₁) = f(x₂) => x²₁ + 2 = x²₂ = 2

⇒ x₁ = ±x₂ ⇒  f is not one-one

Onto: Let y = f(x) ⇒ y = x² + 2 ⇒ x \(=\sqrt{y-I} \in R\)

∴ y – 2 ≥ 0 ⇒ y ≥ 2 ⇒ y ∈ R [2, ∞)

Range 5≠ co-domain

Also: f is not onto as there is no pre-image for negative real numbers.

Hence; f is neither one-one nor onto.

Question 5. Write the smallest reflexive relation on set A = {a, b, c}.
Solution:

For reflexive relation, each and every element of the given set must be related to itself, at least i.e. the smallest reflexive relation on set A will be {(a, a), (b, b), (c, c)}.

Question 6. If f = {(1.2), (2, 4), (3, 1), (4, k)} is a one-one function from set A to A, where A = {1, 2, 3, 4}; then find the value of k.
Solution:

In a one-on-one function, different elements must have different images. So, according to the given function, f = {(1,2), (2. 4), (3, 1), (4, k)}, the value of k must be 3.

Question 7.

1. Check whether the relation R defined on the set {1, 2, 3, 4} as R = {(a, b); b = a + 1} is transitive. Justify your answer. Or
2. If the relation R on the set A = {x : 0 ≤ x ≤12} given by R = {(a, b): a = b} is an equivalence relation, then find the set of all elements related to 1.

Solution:

1. Given. R = ((a, b): b = a + 1} defined on the set A = {1, 2, 3, 4}

⇒ R = {(1, 2), (2, 3), (3, 4)}

By definition, for transitive relation, if a R b and b R c ⇒ a R c ∀ a, b, c ∈ A

For 1,2, 3 ∈ A; (1,2) ∈ R and (2, 3) ∈ R but (1, 3) ∉ R

Therefore, R is not transitive.

Aliter: Given; R = {(a, b): b = a + 1} defined on the set A – {1,2, 3,4}

For transitive relation: Let (a, b) ∈ R and (b, c) ∈ R ∀ a, b, c ∈ A

⇒ b = a + 1 and c = b + 1

⇒ c = a + 2

or (a, c) ∉ R

∴ R is not transitive

or

2. The elements in R that are related to 1 will be those elements from set A which are equal to 1.

Hence, the set of elements related to 1 is {1}.

Aliter: Let x ∈ A which is related to 1 by the given relation R = {(a, b): a = b}

x R 1 ⇒ (x, 1) ∈ R ⇒ x = 1

∴ [1] = {1}

Question 8. The relation R in the set {1.2,3} given by R = {(1, 2), (2, 1), (1, 1)} is:

1. Symmetric and transitive, but not reflexive
2. Reflexive and symmetric, but not transitive
3. Symmetric, but neither reflexive nor transitive
4. An equivalence relation

Solution: 3. Symmetric, but neither reflexive nor transitive

Let A= {1,2, 3} and R = {(1, 2), (2, 1), (1, 1)}

R is not reflexive as (2, 2) and (3,3) ∉ R.

R is a symmetric relation as (a, b) ∈ R and (b, a) ∈ R ∀ a, b ∈ A.

R is not a transitive relation because (2, 1) ∈ R and (1,2) ∈ R but (2, 2) ∉ R.

Hence; R is symmetric, but neither reflexive nor transitive.

Question 9. Let A = {1,3, 5}, Then the number of equivalence relations in A containing (1,3) is

1. 1
2. 2
3. 3
4. 4

Solution: 2. 2

R₁ = {(1, 1), (3, 3), (5, 5), (1, 3), (3, 1)}

and R₂ = {(1, 1), (3. 3), (5, 5), (1, 3), (3, 1), (1,5), (5, 1), (3, 5), (5, 3)}

Hence, the number of equivalence relations in A containing (1, 3) is 2.

Question 10. Check whether the relation R in the set N of natural numbers given by R = {(a, b): a is divisor of b} is reflexive, symmetric or transitive. Also, determine whether R is an equivalence relation.
Solution:

The relation R in the set N is given by:

R = {(a, b): a is divisor of b}

⇒ aRb => \(\frac{b}{a}\) = K ∈ 1 ∀ a, b ∈ N,

Reflexive; aRa ∀ a∈N (By definition)

aRa ⇒ \(\frac{a}{a}\)= 1 ∈ I which is true.

So, R is reflexive relation.

Symmetric: we have

aRb ⇒ \(\frac{b}{a}\) = K ∈ I ∀ a, b ∈ N

⇒ \(\frac{a}{b}=\frac{1}{K} \notin I\)

⇒ b K a ∀ a, b∈ N

∴ If aRb ⇒ bRa ∀ a, b ∈ N, then R is not a symmetric relation.

Transitive: If aRb ⇒ \(\frac{b}{a}=K_1\) ∈ I ∀ a, b ∈ N ….(1)

bRc ⇒ \(\frac{c}{b}=K_2\) ∈ I ∀ b, c ∈ N ….(2)

from equation (1) and (2) \(\frac{b}{a} \times \frac{c}{b}=K_1 \times K_2 \Rightarrow \frac{c}{a}-\left(K_1 K_2\right) \in I \Rightarrow a R c\)

So, R is a transitive relation

∴ R is reflexive and transitive but not symmetric

R is not an equivalence relation on N.

Question 11. Check whether the relation R defined on the set A = {1, 2, 3, 4, 5, 6} as R = {(a, b): b = a + 1} is reflexive, symmetric, or transitive.
Solution:

Given, R = {(a, b): b = a + 1} is defined on the set A = {1, 2, 3, 4, 5, 6}

⇒ R= {(1, 2), (2, 3), (3, 4), (4, 5), (5, 6)}

Reflexive: By definition, a R a ∀a, b ∈ A

Now, 1 ∈ A but (1, 1) ∉ R.

Therefore, R is not reflexive.

Symmetric: By definition, if a R b ⇒ b R a ∀ a, b ∈ A

For 1,2 ∈ A, It can be observed that (1,2) ∈ R but (2, 1) ∉ R.

Therefore, R is not symmetric.

Transitive: By definition, if a R b and b R c ⇒ a R c ∀ a, b, c ∈ A

For 1,2, 3 ∈ A, (1,2) ∈ R and (2, 3) ∈ R but (1, 3)  ∉ R

Therefore, R is not transitive.

Hence, R is neither reflexive nor symmetric nor transitive.

Aliter: Given; R = {(a, b): b = a + 1} defined on the set A = {1,2, 3, 4, 5, 6}

Reflexive: (a, a) ∈ R ∀ a ∈ A

⇒ a = a + 1; which is not true;

∴ R is not reflexive.

Symmetric: Let (a, b) ∈ R ∀ a, b ∈ A

⇒ b = a + 1

⇒ (b, a) ∉ R [a ≠ b + 1]

∴ R is not symmetric

Transitive: Let (a, b) ∈ R and (b, c) ∈ R ∀ a, b, c ∈ A

⇒ b = a + 1 and c = b + 1

⇒ c = a + 2 or (a, c ) ∉ R

∴ R is not transitive.

Hence; R is neither reflexive nor symmetric nor transitive.

Question 12. Let A = {x ∈ Z : 0 ≤ x ≤12}. Show that R = {(a, b): a, b ∈ A, |a – b| is divisible by 4} is an equivalence relation. Find the set of all elements related to 1. Also; write the equivalence class [2]. or, Show that the function f: R → R defined by \(f(x)=\frac{x}{x^2+1}\). ∀ x ∈R is neither one-one nor onto.
Solution:

Given, R = {(a, b): a, b ∈ A, |a – b| is divisible by 4}

Reflexive: Let a ∈ A

Now, |a — a| = 0. which is divisible by 4

So, (a, a) ∈ R ∀ a ∈ A

Hence, R is reflexive.

Symmetric: Let a, b ∈ A such that (a, b) ∈ R i.e. |a — b| is divisible by 4.

⇒ |-(b – a)| = |b — a| is also divisible by 4.

Hence; (b, a) ∈ R.

So, R is symmetric.

Transitive: Let a, b, c ∈ A such that (a, b), (b, c) ∈ R

i.e. |a – b| and |b – c| is divisible by 4.

Let \(|\mathrm{a}-\mathrm{b}|=4 \mathrm{k}_1\)

⇒ \(\mathrm{~b}-\mathrm{c}|=4 \mathrm{k}_2\)

⇒ \((\mathrm{a}-\mathrm{b})= \pm 4 \mathrm{k}_1\)….(1)

⇒ \((b-c)= \pm 4 k_2\)….(2)

Adding equations (1) and (2); \((\mathrm{a}-\mathrm{b})+(\mathrm{b}-\mathrm{c})= \pm 4 \mathrm{k}_1 \pm 4 \mathrm{k}_2= \pm 4\left(\mathrm{k}_1+\mathrm{k}_2\right)\)

⇒ a – c is divisible by 4.

⇒ |a – c| is divisible by 4.

Hence; (a, c) ∈ R

So, R is transitive.

Hence; R is an equivalence relation.

Further, let (x, 1) ∈ R ∀ x ∈ A ⇒ |x  – 1| is divisible by 4

⇒ x – 1 = 0, 4, 8, 12

⇒ x= 1, 5, 9 [x = 13 ∉ A]

Equivalence class of [1] = {1,5,9}

[The set of all elements related to 1 represents its equivalence class]

Now, we will find the equivalence class of [2]

Let (x, 2) ∈ R ∀ x ∈ A

⇒ |x — 2| = 0, 4, 8, 12

⇒ x = 2, 6, 10 [x = 14 ∉ A]

∴ Equivalence class of [2] = {2, 6, 10}. or,

f : \(R \rightarrow R ; f(x)=\frac{x}{x^2+1}\)

1. One-one function: we have \(\mathrm{f}\left(\mathrm{x}_1\right)=\mathrm{f}\left(\mathrm{x}_2\right), \forall, \mathrm{x}_1, \mathrm{x}_2 \in \mathrm{R}\)

⇒ \(\frac{x_1}{x_1^2+1}=\frac{x_2}{x_2^2+1}\)

⇒ \(x_1 x_2^2+x_1=x_2 x_1^2+x_2 \quad \Rightarrow\left(x_1 x_2^2-x_2 x_1^2\right)+\left(x_1-x_2\right)=0\)

⇒ \(x_1 x_2\left(x_2-x_1\right)+\left(x_1-x_2\right)=0 \Rightarrow\left(x_1-x_2\right)\left(-x_1 x_2+1\right)=0\)

⇒ \(x_1=x_2 \text { and } x_1 x_2=1 \text { or } x_1=\frac{1}{x_2}\)

One-one function Example: Let \(\mathrm{x}_1=2 \in \mathrm{R} ; \mathrm{x}_2=1 / 2 \in \mathrm{R}\)

Then, \(f\left(x_1\right)=f(2)=2 / 5\) and \(f\left(x_2\right)=f(1 / 2)=2 / 5\)

⇒ latex]x_1 \neq x_2[/latex] but \(f\left(x_1\right)=f\left(x_2\right)\)

∴ f is not a one-on-one function

2. Onto function: Let y = f(x)

⇒ y = \(\frac{x}{x^2+1} \Rightarrow x^2 y-x+y=0\)

⇒ x = \(\frac{1 \pm \sqrt{1-4 y^2}}{2 y} \in R \text { if } 1-4 y^2 \geq 0 \text { and } y \neq 0\)

⇒ \(4 y^2-1 \leq 0 \text { or }(2 y+1)(2 y-1) \leq 0\)

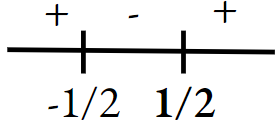
⇒ \(x \in\left[-\frac{1}{2}, 0\right) \cup\left(0, \frac{1}{2}\right]\)

Thus, every element of the Co-domain does not have its pre-image in the domain.

Hence, f: R → R is not onto.

∴ f is neither one-one nor onto.