NEET Physics Class 11

NEET Physics Solutions For Class 11 Chapter 10  Vector

In physics we deal with two types of physical quantity one is scalar and the other is a vector. Each scalar quantity has magnitude.

The magnitude of a physical quantity means a product of numerical value and unit of that physical quantity. For example mass = 4 kg

Magnitude of mass = 4 kg

and unit of mass = kg

Examples of scalar quantities: are mass, speed, distance, etc.

Scalar quantities can be added, subtracted, and multiplied by simple laws of algebra.

1. Definition Of Vector

If a physical quantity in addition to magnitude –

1. Has a specified direction.
2. It should obey the commutative law of additions
   1. \(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}=\overrightarrow{\mathrm{B}}+\overrightarrow{\mathrm{A}}\)
3. Obeys the law of parallelogram of addition, then and then only it is said to be a vector. If any of the above conditions is not satisfied the physical quantity cannot be a vector.

If a physical quantity is a vector it has a direction, but the converse may or may not be true, i.e. if a physical quantity has a direction, it may or may not a be vector. e.g. time, pressure, surface tension current, etc. have directions but are not vectors because they do not obey the parallelogram law of addition.

The magnitude of a vector \((\overrightarrow{\mathrm{A}})\) is the absolute value of a vector and is indicated by \(|\vec{A}|\) or A.

Examples of vector quantity are displacement, velocity, acceleration, force, etc.

Vector Solutions for NEET Physics Class 11 Chapter 10

Representation Of Vector: Geometrically, the vector is represented by a line with an arrow indicating the direction of the vector as

Mathematically, vector is represented by \(\overrightarrow{\mathrm{A}}\)

Sometimes it is represented by the bold letter A.

Important Points: If a vector is displaced parallel to itself it does not change

If a vector is rotated through an angle other than a multiple of 2π (or 360º) it changes.

If the frame of reference is translated or rotated the vector does not change (though its components may change).

Two vectors are called equal if their magnitudes and directions are the same,
and they represent values of the same physical quantity.

The angle between two vectors means the smaller of the two angles between the vectors when they are placed tail to tail by displacing either of the vectors parallel to itself (i.e. 0 ≤ θ ≤ π).

2. Unit Vector

A unit vector is a vector that has a unit magnitude and points in a particular direction. Any vector \((\overrightarrow{\mathrm{A}})\) can be written as the product of unit vector \((\hat{A})\) in that direction and magnitude of the given vector.

⇒ \(\overrightarrow{\mathrm{A}}=\mathrm{A} \hat{\mathrm{A}} \text { or } \hat{\mathrm{A}}=\frac{\vec{A}}{\mathrm{~A}}\)

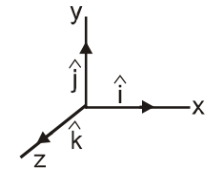
A unit vector has no dimensions or units. Unit vectors along the positive x-, y- and z-axes of a rectangular coordinate system are denoted by

⇒ \(\hat{\mathrm{i}}, \hat{\mathrm{j}} \text { and } \hat{\mathrm{k}}\) and respectively such that

⇒ \(|\hat{\mathrm{i}}|=|\hat{\mathrm{j}}|=|\hat{\mathrm{k}}|\) = 1

NEET Physics Chapter 10 Vector Mathematical Tools Solutions

Question 1. Three vectors \(\overrightarrow{\mathrm{A}}, \overrightarrow{\mathrm{B}}, \overrightarrow{\mathrm{C}}\) are shown in the figure. Find angle between

1. \(\overrightarrow{\mathrm{A}} \text { and } \vec{B}\),
2. \(\overrightarrow{\mathrm{B}} \text { and } \vec{C}\)
3. \(\overrightarrow{\mathrm{A}} \text { and } \vec{C}\).

Answer:

To find the angle between two vectors we connect the tails of the two vectors. We can shift \(\overrightarrow{\mathrm{B}}\) such that tails of \(\overrightarrow{\mathrm{A}}, \overrightarrow{\mathrm{B}} \text { and } \overrightarrow{\mathrm{C}}\) are connected as shown in figure.

Now we can easily observe that angle between \(\vec{A} \text { and } \vec{B}\) is 60º, \(\vec{B} \text { and } \vec{C}\) is 15º and between \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{C}}\)is 75º.

Question 2. A unit vector along East is defined as \(\hat{\mathbf{i}}\). A force of 10⁵ dynes acts westwards. Represent the force in terms of \(\hat{\mathbf{i}}\)

Answer:

⇒ \(\overrightarrow{\mathrm{F}}=-10^5 \hat{\mathrm{i}}\) dynes

3. Multiplication Of A Vector By A Scalar

Multiplying a vector \(\overrightarrow{\mathrm{A}}\) with a positive number λ gives a vector \(\vec{B}(=\lambda \overrightarrow{\mathrm{A}})\) whose magnitude is changed by the factor λ but the direction is the same as that of \(\overrightarrow{\mathrm{A}}\).

Multiplying a vector \(\overrightarrow{\mathrm{A}}\) by a negative number λ gives a vector \(\overrightarrow{\mathrm{B}}\) whose direction is opposite to the direction of \(\overrightarrow{\mathrm{A}}\) and whose magnitude is − λ times \(|\vec{A}|\)

Question 3. A physical quantity (m = 3kg) is multiplied by a vector \(\overrightarrow{\mathrm{a}}\) such that \(\overrightarrow{\mathrm{F}}=\mathrm{m} \overrightarrow{\mathrm{a}}\). Find the magnitude and direction of \(\overrightarrow{\mathrm{F}}\) if

1. \(\overrightarrow{\mathrm{a}}=3 \mathrm{~m} / \mathrm{s}^2\) Eastwards
2. \(\overrightarrow{\mathrm{a}}=-4 \mathrm{~m} / \mathrm{s}^2\) Northwards

Answer:

1. \(\overrightarrow{\mathrm{F}}=\mathrm{m} \overrightarrow{\mathrm{a}}=3 \times 3 \mathrm{~ms}^{-2}\) East wards = 9 N Eastwards
2. \(\overrightarrow{\mathrm{F}}=\mathrm{m} \vec{a}=3 \times(-4)\) Northwards

= – 12 N North wards = 12 N Southwards

4. Addition Of Vectors

The addition of vectors is done by parallelogram law or the triangle law :

Parallelogram Law Of Addition Of Vectors: If two vectors \(\overrightarrow{\mathrm{A}} \text { and } \overrightarrow{\mathrm{B}}\) are represented by two adjacent sides of a parallelogram both pointing outwards (and their tails coinciding) as shown. Then the diagonal drawn through the intersection of the two vectors represents the resultant (i.e., the vector sum of \(\vec{A} \text { and } \vec{B}\)).

R = \(\sqrt{A^2+B^2+2 A B \cos \theta}\)

The direction of resultant vector \(\overrightarrow{\mathrm{R}} \text { from } \overrightarrow{\mathrm{A}}\) given by

⇒ \(\tan \phi=\frac{\mathrm{MN}}{\mathrm{PN}}\)

⇒ \(\frac{\mathrm{MN}}{\mathrm{PQ}+\mathrm{QN}}\)

⇒ \(\frac{\mathrm{B} \sin \theta}{\mathrm{A}+\mathrm{B} \cos \theta}\)

⇒ \(\varphi=\tan ^{-1}\left(\frac{B \sin \theta}{A+B \cos \theta}\right)\)

Triangle law of addition of vectors: To add two vectors \(\vec{A} \text { and } \vec{B}\) shift any of the two vectors parallel to itself until the tail of \(\vec{B}\) is at the head of \(\vec{A}\).

The sum \(\vec{A}+\vec{B}\) is a vector \(\vec{R}\) drawn from the tail of \(\vec{A}\)to the head of \(\vec{B}\), i.e.,\(\vec{A}+\vec{B}=\vec{R}\). As the figure formed is a triangle, this method is called the ‘ triangle method’ of the addition of vectors.

If the ‘triangle method’ is extended to add any number of vectors in one operation as shown. Then the figure formed is a polygon and hence the name Polygon Law of addition of vectors is given to such type of addition.

Important Points:

To a vector only a vector of the same type can be added that represents the same physical quantity and the resultant is a vector of the same type.

As R = [A² + B² + 2AB cosθ]^1/2 so R will be maximum when, cos θ = max = 1, i.e., θ = 0º, i.e. vectors are like or parallel and R_max= A + B.

The resultant will be minimum if, cos θ = min = -1, i.e., θ = 180º, i.e. vectors are antiparallel, and R_min = A ~ B.

If the vectors A and B are orthogonal, i.e., θ = 90º, R = \(\sqrt{A^2+B^2}\)

As previously mentioned the resultant of two vectors can have any value from (A ~ B) to (A + B) depending on the angle between them and the magnitude of the resultant decreases as θ increases from 0º to 180º

The minimum number of unequal coplanar vectors whose sum can be zero is three.

The resultant of three non-coplanar vectors can never be zero, or a minimum number of noncoplanar vectors whose sum can be zero is four.

Subtraction of a vector from a vector is the addition of a negative vector, i.e.,

⇒ \(\vec{A}-\vec{B}=\vec{A}+(-\vec{B})\)

From figure it is clear that \(\vec{A}-\vec{B}\) is equal to addition of \(\overrightarrow{\mathrm{A}}\) with reverse of \(\overrightarrow{\mathrm{B}}\)

⇒ \(|\vec{A}-\vec{B}|=\left[(A)^2+\left(B^2\right)+2 A B \cos \left(180^{\circ}-\theta\right)\right]^{1 / 2}\)

⇒ \(|\vec{A}-\vec{B}|=\sqrt{A^2+B^2-2 A B \cos \theta}\)

Change in a vector’s physical quantity means subtraction of the initial vector from the final vector.

Question 4. Find the resultant of two forces each having magnitude F₀, and the angle between them is θ.

Answer:

⇒ \(F_{\text {Resultant }}^2=F_0^2+F_0^2+2 F_0^2 \cos \theta\)

⇒ \(2 F_0^2(1+\cos \theta)\)

⇒ \(2 F_0^2\left(1+2 \cos ^2 \frac{\theta}{2}-1\right)\)

⇒ \(2 \times 2 F_0^2 \cos ^2 \frac{\theta}{2}\)

⇒ \(\mathrm{F}_{\text {resultant }}=2 \mathrm{~F}_0 \cos \frac{\theta}{2}\)

Class 11 NEET Physics Vector Problems and Solutions

Question 5. Two non zero vectors \(\vec{A} \text { and } \vec{B}\) are such that \(|\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}|=|\overrightarrow{\mathrm{A}}-\overrightarrow{\mathrm{B}}|\). Find angle between \(\overrightarrow{\mathrm{A}}\)and \(\overrightarrow{\mathrm{B}}\)

Answer:

⇒ \(|\vec{A}+\vec{B}|=|\vec{A}-\vec{B}|\)

⇒ A² + B² + 2AB cos θ

= A² + B² – 2AB cos θ

⇒ 4AB cos θ = 0

⇒ cos θ = 0

⇒ θ = \(\frac{\pi}{2}\)

Question 6. If the sum of two unit vectors is also a unit vector. Find the magnitude of their difference.

Answer:

Let \(\hat{A} \text { and } \hat{B}\) are the given unit vectors and \(\hat{R}\) is their resultant then

⇒ \(|\hat{R}|=|\hat{A}+\hat{B}|\)

⇒ \(1=\sqrt{(\hat{A})^2+(\hat{B})^2+2|\hat{A} \| \hat{B}| \cos \theta}\)

1 = 1 + 1 + 2 cos θ

⇒ cos θ = \(-\frac{1}{2}\)

⇒ \(|\hat{A}-\hat{B}|=\sqrt{(\hat{A})^2+(\hat{B})^2-2|\hat{A}||\hat{B}| \cos \theta}\)

⇒ \(\sqrt{1+1-2 \times 1 \times 1\left(-\frac{1}{2}\right)}\)

⇒ \(\sqrt{3}\)

5. Resolution Of Vectors

If \(\vec{a} \text { and } \vec{b}\) be any two nonzero vectors in a plane with different directions and \(\overrightarrow{\mathrm{A}}\)be another vector in the same plane.

⇒ \(\overrightarrow{\mathrm{A}}\) can be expressed as a sum of two vectors – one obtained by multiplying \(\overrightarrow{\mathrm{a}}\) by a real number and the other obtained by multiplying

⇒ \(\overrightarrow{\mathrm{b}}\) by another real number.

⇒ \(\overrightarrow{\mathrm{A}}=\lambda \overrightarrow{\mathrm{a}}+\mu \overrightarrow{\mathrm{b}}\) (where λ and μ are real numbers)

We say that \(\overrightarrow{\mathrm{A}}\) has been resolved into two component vectors namely

⇒ \(\lambda \vec{a} \text { and } \mu \vec{b}\)

λ \(\vec{a} \text { and } \mu \vec{b}\) along \(\overrightarrow{\mathrm{a}} \text { and } \overrightarrow{\mathrm{b}}\) respectively. Hence one can resolve a given vector into two component vectors along a set of two vectors − all three lie in the same plane.

Resolution Along Rectangular Component:

It is convenient to resolve a general vector along the axes of a rectangular coordinate system using vectors of unit magnitude, which we call unit vectors. \(\hat{\mathrm{i}}, \hat{\mathrm{j}}, \hat{\mathrm{k}}\) are unit vector along x,y and z-axis as shown in figure below:

Resolution in two Dimension

Consider a vector \(\overrightarrow{\mathrm{A}}\) that lies in xy plane as shown in figure,

⇒\(\overrightarrow{\mathrm{A}}=\overrightarrow{\mathrm{A}}_1+\overrightarrow{\mathrm{A}}_2\)

⇒ \(\vec{A}_1=A_x \hat{i}, \quad \vec{A}_2=A_y \hat{j}\)

⇒ \(\vec{A}=A_x \hat{i}+A_y \hat{j}\)

The quantities A_x and A_y are called x- and y- components of the vector \(\overrightarrow{\mathrm{A}}\)

A_x is itself not a vector but \(A_x \hat{i}\) is a vector and so is \(A_y \hat{j}\)

A_x= A cos θ and A_y= A sin θ

It’s clear from the above equation that a component of a vector can be positive, negative, or zero depending on the value of θ. A vector \(\overrightarrow{\mathrm{A}}\) can be specified in a plane by two ways:

Its magnitude A and the direction θ it makes with the x-axis; or

Its components are A_x and A_y.

A = \(A=\sqrt{A_x^2+A_y^2}, \theta=\tan ^{-1} \frac{A_y}{A_x}\)

Note: If A = Ax ⇒ Ay = 0 and if A = Ay ⇒ Ax= 0 i.e. components of a vector perpendicular to itself is always zero.

The rectangular components of each vector and those of the

sum

⇒\(\overrightarrow{\mathrm{C}}=\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\) are shown in the figure. We saw that

⇒\(\overrightarrow{\mathrm{C}}=\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}\) is equivalent to both

C_x = A_x+ B_x

and C_y = A_y+ B_y

Resolution In Three Dimensions: A vector \(\overrightarrow{\mathrm{A}}\) in components along x-, y- and z-axis can be written as:

⇒\(\overrightarrow{\mathrm{OP}}=\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{BP}}=\overrightarrow{\mathrm{OC}}+\overrightarrow{\mathrm{CB}}+\overrightarrow{\mathrm{BP}}\)

⇒\(\vec{A}=\vec{A}_z+\vec{A}_x+\vec{A}_y=\vec{A}_x+\vec{A}_y+\vec{A}_z\)

⇒ \(A_x \hat{i}+A_y \hat{j}+A_z \hat{k}\)

A = \(\sqrt{A_x^2+A_y^2+A_z^2}\)

⇒ \(A_x=A \cos \alpha, A_y=A \cos \beta, A_z=A \cos \gamma\)

where cos α, cos β, and cos γ are termed as Direction Cosines of a given vector \(\overrightarrow{\mathrm{A}}\).

cos² α + cos² β + cos² γ = 1

Mathematical Tools in Physics: Vector Solutions for NEET Class 11

Question 7. A mass of 2 kg lies on an inclined plane as shown in the figure. Resolve its weight along and perpendicular to the plane.(Assumeg=10m/s²)

Answer:

Component along the plane = 20 sin 30 = 10 N

component perpendicular to the plane = 20 cos 30 = \(10 \sqrt{3} \mathrm{~N}\)

Question 8. A vector makes an angle of 30º with the horizontal. If a horizontal component of the vector is 250. Find the magnitude of a vector and its vertical component.

Answer: Let vector is \(\overrightarrow{\mathrm{A}}\)

⇒ \(A_x=A \cos 30^{\circ}\) = 250

⇒ \(\frac{A \sqrt{3}}{2}\)

A= \(\frac{500}{\sqrt{3}}\)

⇒ \(A_y=A \sin 30^{\circ}\)

⇒ \(\frac{500}{\sqrt{3}} \times \frac{1}{2}\)

⇒ \(\frac{250}{\sqrt{3}}\)

Question 9. A = \(\overrightarrow{\mathrm{A}}=\hat{\mathrm{i}}+2 \hat{\mathrm{j}}-3 \hat{k}\), when a vector \(\overrightarrow{\mathrm{B}}\) is added to \(\overrightarrow{\mathrm{A}}\), we get a unit vector along x-axis. Find the value of \(\overrightarrow{\mathrm{B}}\)? Also, find its magnitude

Answer:

⇒\(\overrightarrow{\mathrm{A}}+\overrightarrow{\mathrm{B}}=\hat{\mathrm{i}}\)

⇒ \(\vec{B}=\hat{i}-\vec{A}=\hat{i}-(\hat{i}+2 \hat{j}-3 \hat{k})=-2 \hat{j}+3 \hat{k}\)

⇒ \(|\vec{B}|=\sqrt{(2)^2+(3)^2}=\sqrt{13}\)

Question 10. In the above question find a unit vector along \(\vec{B}\).

Answer:

⇒ \(\vec{B}=\frac{\vec{B}}{B}=\frac{-2 \hat{j}+3 \hat{k}}{\sqrt{13}}\)

Question 11. Vector \(\overrightarrow{\mathrm{A}}, \overrightarrow{\mathrm{B}} \text { and } \overrightarrow{\mathrm{C}}\) have magnitude 5, \(5 \sqrt{2}\) and 5 respectively, direction of \(\overrightarrow{\mathrm{A}}, \overrightarrow{\mathrm{B}} \text { and } \overrightarrow{\mathrm{C}}\) are towards east, North-East and North respectively. If \(\hat{i} \text { and } \hat{j}\) and are unit vectors along East and North respectively. Express the sum \(\vec{A}+\vec{B}+\vec{C}\) in terms of \(\hat{i}, \hat{j}\). Also, Find the magnitude and direction of the resultant.

Answer:

⇒ \(\overrightarrow{\mathrm{A}}=5 \hat{i}\)

⇒ \(\overrightarrow{\mathrm{C}}=5 \hat{j}\)

⇒ \(\vec{B}=5 \sqrt{2} \cos 45 \hat{i}+5 \sqrt{2} \sin 45 \hat{j} \quad=5 \hat{i}+5 \hat{j}\)

⇒ \(\vec{A}+\vec{B}+\vec{C}=5 \hat{i}+5 \hat{i}+5 \hat{j}+5 \hat{j} \quad=10 \hat{i}+10 \hat{j}\)

⇒ \(|\vec{A}+\vec{B}+\vec{C}|\)

⇒ \(\sqrt{(10)^2+(10)^2}=10 \sqrt{2}\)

⇒ \(\tan \theta=\frac{10}{10}=1\)

θ = 45º from East

Key Concepts of Vector Mathematics in NEET Physics Class 11

Question 12. You walk 3 Km west and then 4 Km headed 60° north of east. Find your resultant displacement

1. Graphically and
2. Using vector components.

Answer:

Picture the Problem: The triangle formed by the three vectors is not a right triangle, so the magnitudes of the vectors are not related by the Pythagoras theorem. We find the resultant graphically by drawing each of the displacements to scale and measuring the resultant displacement.

If we draw the first displacement vector 3 cm long and the second one 4 cm long, we find the resultant vector to be about 3.5 cm long.

Thus the magnitude of the resultant displacement is 3.5 Km. The angle θ made between the resultant displacement and the west direction can then be measured with a protractor. It is about 75°.

Let \(\overrightarrow{\mathrm{A}}\) be the first displacement and choose the x-axis to be in the easterly direction. Compute \(A_x \text { and } A_y, A_x=-3, A_y=0\)

Similarly, compute the components of the second displacement \(\vec{B}, B_x=4 \cos 60^{\circ}=2, B_y=4\) sin 60° = \(2 \sqrt{3}\)

The components of the resultant displacement = \(\vec{A}+\vec{B}\) are found by addition,

⇒ \(\overrightarrow{\mathrm{C}}=(-3+2) \hat{i}+(2 \sqrt{3}) \hat{j}=-\hat{i}+2 \sqrt{3} \hat{j}\)

The Pythagorean theorem gives the magnitude of \(\overrightarrow{\mathrm{C}}\)

⇒ \(C=\sqrt{1^2+(2 \sqrt{3})^2}\)

⇒ \(\sqrt{13}\)

⇒ 3.6

The ratio of C_y to C_x gives the tangent of the angle θ between \(\overrightarrow{\mathrm{C}}\) and the x-axis.

⇒ tan θ = \(2 \sqrt{3}\)/(-1)

⇒ \(\theta=-74^{\circ}\)

Remark: Since the displacement (which is a vector) was asked for, the answer must include either the magnitude and direction, or both components. In (2) we could have stopped at step 3 because the x and y components completely define the displacement vector.

• We converted the magnitude and direction to compare with the answer to part (1). Note that in step 5 of (2), a calculator gives the angle as –74°. However, the calculator can’t distinguish whether the x or y components are negative.
• We noted in the figure that the resultant displacement makes an angle of about 75° with the negative x-axis and an angle of about 105° with the positive x-axis. This agrees with the results in (a) within the accuracy of our measurement.

NEET Physics Class 11 Chapter 10 Mathematical Tools – Double Differentiation

If f is a differentiable function, then its derivative f’ is also a function, so f’ may have a derivative of its own, denoted by (f’)’ = f’’.

This new function f’’ is called the second derivative of f because it is the derivative of the derivative of f. Using Leibniz notation, we write the second derivative of y = f (x) as

⇒ \(\frac{d}{d x}\left(\frac{d y}{d x}\right)=\frac{d^2 y}{d x^2}\)

Another notation is f ’’ (x) = D₂ f (x) = D²f(x)

NEET Physics Class 11 Double Differentiation Key Concepts and Solutions

Interpretation Of Double Derivative

We can interpret f ’’ (x) as the slope of the curve y = f ’(x) at the point (x, f ’(x)). In other words, it is the rate of change of the slope of the original curve y = f (x).

• In general, we can interpret a second derivative as a rate of change of a rate of change. The most familiar example of this is acceleration, which we define as follows.
• If s = s(t) is the position function of an object that moves in a straight line, we know that its first derivative represents the velocity v(t) of the object as a function of time:

v(t) = s’(t) = \(\frac{\mathrm{ds}}{\mathrm{dt}}\)

• The instantaneous rate of change of velocity concerning time is called the acceleration a(t) of the object.
• Thus, the acceleration function is the derivative of the velocity function and is therefore the second derivative of the position function:

a (t) = v’(t) = s’’(t)

or in Leibniz notation, a = \(\frac{d v}{d t}=\frac{d^2 s}{d t^2}\)

Double Differentiation NEET Physics Class 11 Chapter 10 Solutions

Question 1. If f (x) = x cos x, find f ’’ (x).

Answer:

Using the Product Rule, we have

f’ (x) = \(x \frac{d}{d x}(\cos x)+\cos x \frac{d}{d x}(x)\)

= – x sin x + cos x

To find f’’ (x) we differentiate f’(x):

f’’(x) = \(\frac{d}{d x}\) (–x sin x + cos x)

⇒ \(-x \frac{d}{d x}(\sin x)+\sin x \frac{d}{d x}(-x)+\frac{d}{d x}(\cos x)\)

= – x cos x – sin x – sin x

= – x cos x – 2 sin x

Question 2. The position of a particle is given by the equation s = f (t) = t³ – 6t² + 9t. where t is measured in seconds and s in meters. Find the acceleration at time t. What is the acceleration after 4s?

Answer:

The velocity function is the derivative of the position function :

s = f (t) = t³ – 6t² + 9t

⇒ v(t) = \(\frac{d s}{d t}=3 t^2-12 t+9\)

The acceleration is the derivative of the velocity function :

⇒ \(a(t)=\frac{d^2 s}{d t^2}=\frac{d v}{d t}=6 t-12\)

⇒ \(a(4)=6(4)-12=12 \mathrm{~m} / \mathrm{s}^2\)

Application Of Derivatives

Differentiation As A Rate Of Change

⇒ \(\frac{d y}{d x}\) is rate of change of ‘y’ with respect to ‘x’ :

For examples:

1. v =\(\frac{d x}{d t}\) This means velocity ‘v’ is the rate of change of displacement ‘x’ concerning time ‘t’
2. a = \(\frac{d v}{d t}\) This means acceleration ‘a’ is the rate of change of velocity ‘v’ concerning time ‘t’.
3. F = \(\frac{d p}{d t}\) This means force ‘F’ is the rate of change of momentum ‘p’ concerning time ‘t’.
4. τ = \(\frac{d L}{d t}\) This means torque ‘τ ’ is the rate of change of angular momentum ‘L’ concerning time ‘t’
5. Power = \(\frac{d W}{d t}\) This means power ‘P’ is the rate of change of work ‘W’ concerning time ‘t’
6. Ι = \(\frac{d q}{d t}\) This means current ‘Ι’ is the rate of flow of charge ‘q’ concerning time ‘t’

NEET Class 11 Physics Chapter 10 Double Differentiation Problems and Solutions

Question 1. The area A of a circle is related to its diameter by the equation A = \(\frac{\pi}{4} D^2\). How fast is the area changing concerning the diameter when the diameter is 10 m?

Answer:

The (instantaneous) rate of change of the area concerning the diameter is

⇒ \(\frac{\mathrm{dA}}{\mathrm{dD}}=\frac{\pi}{4} 2 \mathrm{D}=\frac{\pi \mathrm{D}}{2}\)

When D = 10 m, the area is changing at a rate (π/2) 10 = 5π m²/m. This means that a small change

ΔD m in the diameter would result in a change of about 5π ΔD m² in the area of the circle.

Question 2. Experimental and theoretical investigations revealed that the distance a body released from rest falls in time t is proportional to the square of the amount of time it has fallen. We express this by saying that

s = \(\frac{1}{2} \mathrm{gt}^2\)

Double Differentiation Practice Problems for NEET Physics Class 11

where s is distance and g is the acceleration due to Earth’s gravity. This equation holds in a vacuum, where there is no air resistance, but it closely models the fall of dense, heavy objects in air. The figure shows the free fall of a heavy ball bearing released from rest at time t = 0 sec.

1. How many meters does the ball fall in the first 2 sec?
2. What is its velocity, speed, and acceleration then?

Answer:

1. The free–fall equation is s = 4.9 t².

During the first 2 sec. the ball falls

s= 4.9(2)² = 19.6 m,

2. At any time t, velocity is derivative of displacement:

v(t) = s’(t) = \(\frac{d}{d t}\)(4.9t²) = 9.8 t.

At t = 2, the velocity is v= 19.6 m/sec in the downward (increasing s) direction. The speed at t = 2 is

speed = |v(2)| = 19.6 m/sec.

a = \(\frac{\mathrm{d}^2 \mathrm{~s}}{\mathrm{dt}^2}\)

= 9.8m/s²

Double Differentiation Techniques in NEET Physics Class 11

Maxima And Minima:

Suppose a quantity y depends on another quantity x in a manner shown in the figure. It becomes maximum at x₁ and minimum at x₂. At these points, the tangent to the curve is parallel to the x−axis, and hence its slope is tan θ = 0. Thus, at a maximum or a minimum,

slope = \(\frac{d y}{d x}=0\)

Application Of Derivatives Maxima:

Just before the maximum, the slope is positive, at the maximum, it is zero and just after the maximum, it is negative. Thus, \(\frac{d y}{d x}\) decreases at a maximum and hence the rate of change of \(\frac{d y}{d x}\) is negative at a maximum i.e. \(\frac{d}{d x}\left(\frac{d y}{d x}\right)\) < 0 at maximum.

The quantity \(\frac{d}{d x}\left(\frac{d y}{d x}\right)\) is the rate of change of the slope. It is written as \(\frac{d^2 y}{d x^2}\)

Conditions for maxima are: \(\frac{d y}{d x}=0\)

⇒ \(\frac{d^2 y}{d x^2}<0\)

Application Of Derivatives Minima:

Similarly, at a minimum the slope changes from negative to positive. Hence with the increases of x., the slope is increasing which means the rate of change of slope concerning x is positive

hence \(\frac{d}{d x}\left(\frac{d y}{d x}\right)>0\)

Conditions for minima are: \(\frac{d y}{d x}=0\)

⇒ \(\frac{d^2 y}{d x^2}>0\)

Quite often it is known from the physical situation whether the quantity is a maximum or a minimum.

The test on \(\frac{d^2 y}{d x^2}\) may then be omitted.

NEET Physics Class 11 Chapter 10: Mathematical Tools – Double Differentiation Formulas and Solutions

Question 3. Find minimum value of y = 1 + x² – 2x

⇒ \(\frac{d y}{d x}=2 x-2\) for minima \(\frac{d y}{d x}=0\)

2x-2 = 0

x = 1

⇒ \(\frac{d^2 y}{d x^2}=2\)

⇒ \(\frac{d^2 y}{d x^2}>0\)

at x =1, there are minima

for a minimum value of y

y_minima = 1 + 1 – 2 = 0

NEET Physics Class 11 Chapter 1 Calorimetry And Thermal Expansion Heat

The energy that is being transferred between two bodies or between adjacent parts of a body as a result of temperature difference is called heat. Thus, heat is a form of energy.

• It is energy in transit whenever temperature differences exist. Once it is transferred, it becomes the internal energy of the receiving body.
• It should be clearly understood that the word “heat” is meaningful only as long as the energy is being transferred.
• Thus, expressions like “heat in a body” or “heat of a body” are meaningless. Heat transfer from a body at high temperature to low temperature.

When we say that a body is heated it means that its molecules begin to move with greater kinetic energy. So, it is the energy of molecular motions.

S.Ι. unit of heat energy is joule (J). Another practical unit of heat energy is calorie (cal).

1 calorie = 4.18 joules.

1 calorie: The amount of heat needed to increase the temperature of 1 gm of water from 14.5 to 15.5 ºC at one atmospheric pressure is 1 calorie.

Mechanical Equivalent of Heat

In the early days, the heat was not recognized as a form of energy. The heat was supposed to be something needed to raise the temperature of a body or to change its phase. The calorie was defined as the unit of heat.

• A number of experiments were performed to show that the temperature may also be increased by doing mechanical work on the system.
• These experiments established that heat is equivalent to mechanical energy and measured how much mechanical energy is equivalent to a calorie. If mechanical work W produces the same temperature change as heat H, we write,

W = JH

where J is called the mechanical equivalent of heat. J is expressed in joule/calorie. The value of J gives how many joules of mechanical work is needed to raise the temperature of 1 g of water by 1°C. It is a conversion factor and not a physical quantity.

Calorimetry and Thermal Expansion NEET Physics Class 11 Solutions

Question 1. What is the change in potential energy (in calories) of a 10 kg mass when it falls through 10 m?

Solution: Change in potential energy

Mass = 10 kg

Gravitation = 10

Height = 10 m

ΔU = mgh = 10 × 10 × 10 = 1000 J

⇒ \(\frac{1000}{4.186} \text { cal }\)

NEET Physics Class 11 Chapter 1 Specific Heat

The specific heat of a substance is equal to the heat gained or released by that substance to raise or fall its temperature by 1ºC for a unit mass of a substance.

When a body is heated, it gains heat. On the other hand, heat is lost when the body is cooled. The gain or loss of heat is directly proportional to:

1. The mass of the body ΔQ ∝ m
2. Rise or fall of temperature of the body ΔQ ∝ Δ T

ΔQ ∝ m Δ T or ΔQ = m s Δ T

or dQ = m s d T or Q = m ∫s d T.

where s is a constant and is known as the specific heat of the body s = \(\frac{Q}{m \Delta T}\) joule/kg-kelvin and C.G.S. unit is cal./gm °C.

Qm TΔ. S.Ι. unit of s is

Specific heat of water : S = 4200 J/kgºC = 1000 cal/kgºC = 1 Kcal/kgºC = 1 cal/gmºC

Specific heat of steam = half of specific heat of water = specific heat of ice

Question 1. Calculate the heat required to increase the temperate of 1 kg water by 20ºC

Solution :

Heat required = ΔQ = msΔθ

∵ S = 1 cal/gmºC = 1 Kcal/kgºC

= 1 × 20 = 20 Kcal.

Heat capacity or Thermal capacity: The heat capacity of a body is defined as the amount of heat required to raise the temperature of that body by 1°. If ‘m’ is the mass and ‘s’ the specific heat of the body, then

Heat capacity = m s.

Units of heat capacity in the CGS system is, cal ºC^-1; the SI unit is, JK^-1

Important Points:

1. We know, s = \(\frac{Q}{m \Delta T}\), if the substance undergoes the change of state which occurs at constant temperature (Isothermal ΔT = 0), then s = Q/0 = ∞. Thus the specific heat of a substance when it melts or boils at constant temperature is infinite.
2. If the temperature of the substance changes without the transfer of heat adiabatic (Q = 0) then s = \(\frac{Q}{m \Delta T}\) = 0. Thus when liquid in the thermos flask is shaken, its temperature increases without the transfer of heat, and hence the specific heat of liquid in the thermos flask is zero.
3. To raise the temperature of saturated water vapors, heat (Q) is withdrawn. Hence, the specific heat of saturated water vapors is negative. (This is for your information only and not in the course)
4. The slight variation of specific heat of water with temperature is shown in the graph at 1-atmosphere pressure. Its variation is less than 1% over the interval from 0 to 100ºC.

Relation between Specific heat and Water equivalent: It is the amount of water that requires the same amount of heat for the same temperature rise as that of the object

ms ΔT = m_W S_W ΔT ⇒ mW = \(\frac{\mathrm{ms}}{\mathrm{s}_{\mathrm{W}}}\)

In calorie s_W = 1

∴ m_W = ms

m_W is also represented by W

So, W = ms.

Phase change: Heat required for the change of phase or state,

Q = mL, L = latent heat.

Latent heat (L): The heat supplied to a substance that changes its state at constant temperature is called latent heat of the body.

Latent heat of Fusion (L_f ): The heat supplied to a substance which changes it from solid to liquid state at its melting point and 1 atm. pressure is called latent heat of fusion. The latent heat of the fusion of ice is 80 kcal/kg

Latent heat of vaporization (L_v): The heat supplied to a substance that changes it from liquid to vapor state at its boiling point and 1 atm. pressure is called latent heat of vaporization. The latent heat of vaporization of water is 540 kcal kg^-1.

If in question latent heat of ice or steam is not mentioned and to solve the problem, it is required to assume them, we should consider the following values.

Latent heat of ice: L = 80 cal/gm = 80 Kcal/kg = 4200 × 80 J/kg

Latent heat of steam: L = 540 cal/gm = 540 Kcal/kg = 4200 × 540 J/kg

The given behavior of a solid substance when it is continuously heated is shown. Various parts show.

OA − solid state, AB − solid + liquid state (Phase change)

BC − liquid state, CD − liquid + vapor state (Phase change)

DE − vapor state

When there is no change of state for example., OA, BC, DE

Slope, \(\frac{\Delta T}{\Delta \mathrm{Q}}=\frac{1}{\mathrm{~ms}} \quad \Rightarrow \quad \frac{\Delta \mathrm{T}}{\Delta \mathrm{Q}} \propto \frac{1}{\mathrm{~s}}\)

The mass (m) of a substance is constant. So, the slope of T – Q graph is inversely proportional to specific heat. In the given diagram.

(slope) OA > (slope) DE

then (s)_OA < (s)_DE

when there is a change of state for example., AB and CD

ΔQ = mL

If (length of AB) > (length of CD)

then (latent heat of AB) > (latent heat of CD)

Question 2. Find the amount of heat released when 1 kg steam at 200ºC is converted into –20ºC ice.

Answer:

Heat required ΔQ = heat release to convert steam at 200 ºC into 100ºC steam + heat release to convert 100ºC steam into 100ºC water + heat release to convert 100º water into 0ºC water + heat release to convert 0 ºC water into 0ºC ice + 0ºC ice converted to – 20ºC ice.

⇒ \(\Delta Q=1 \times \frac{1}{2} \times 100+540 \times 1+1 \times 1 \times 100+1 \times 80+1 \times \frac{1}{2}=780(\mathrm{Kcal})\)

NEET Physics Chapter 1 Calorimetry and Thermal Expansion Problems and Solutions

NEET Physics Class 11 Chapter 1 Superficial Or Areal Expansion

When a solid is heated and its area increases, then the thermal expansion is called superficial or areal expansion. Consider a solid plate of area A0. When it is heated, the change in the area of the plate is directly proportional to the original area A₀ and the change in temperature ΔT.

dA = βA₀dT or ΔA = β A₀ Δ T; β is called real expansion

β = \(\frac{\Delta \mathrm{A}}{\mathrm{A}_0 \Delta \mathrm{T}}\) Unit of β is ºC^-1 or K^-1.

A = A₀(1 + β Δ T)

Where A is an area of the plate after heating.

it follows that β = 2α.

Question 1. A plane lamina has an area of 2m² at 10ºC then what is its area at 110ºC Its superficial expansion is 2 × 10^-5/C

Answer:

Area of plane lamina = 2m²

Superficial expansion = 2 × 10^-5/C

A = A₀ ( 1 + β Δ θ ) = 2 {1 + 2 × 10⁵ × (110 – 10)}

= 2 × {1 + 2 × 10^-3} m²

NEET Physics Class 11 Chapter 1 Volume Or Cubical Expansion

When a solid is heated and its volume increases, then the expansion is called volume expansion or cubical expansion. Let us consider a solid or liquid whose original volume is V₀. When it is heated to a new volume, then the change ΔV

dV = γV₀dT or ΔV = γ V₀ Δ T

⇒ \(\gamma=\frac{\Delta V}{V_0 \Delta T}\) Unit of γ is ºC^-1 or K^-1.

V = V₀(1 + γ Δ T)

where V is the volume of the body after heating.

It can be shown easily that γ = 3α for isotropic solids.

Question 1. The volume of the glass vessel is 1000 cc at 20°C. What volume of mercury should be poured into it at this temperature so that the volume of the remaining space does not change with temperature? The coefficient of cubical expansion of mercury and glass is 1.8 × 10^-4/°C and 9.0 × 10^-6/°C respectively.

Answer:

Let the volume of the glass vessel at 20ºC be Vgand volume of mercury at 20ºC be Vm so the volume of remaining space is = V_g– V_m

It is given constant so that

V_g– V_m= V_g’ – V’_m

where V₀‘ and V_m‘ are final volumes.

V_g– V_m= V_g{1 + γ_g Δθ} – V_m{1 + γ_Hg Δθ} ⇒ V_gγ_g= V_mγ_Hg

⇒ V_m = \(V_m=\frac{100 \times 9 \times 10^{-6}}{1.8 \times 10^{-4}} V_m=50 \mathrm{cc}\)

Relation Between α, β And γ

1. For isotropic solids: α : β : γ = 1 : 2 : 3 or \(\frac{\alpha}{1}=\frac{\beta}{2}=\frac{\gamma}{3}\)
2. For non-isotropic solid β = α₁+ α₂ and γ = α₁+ α₂+ α₃. Here α₁, α_2, and α₃ are coefficients of linear expansion in the X, Y, and Z direction.

Question 1. If the percentage change in length is 1% with the change in temperature of a cuboid object (l × 2l × 3l) then what is the percentage change in its area and volume?

Answer:

Percentage change in length with change in temperature = %l

⇒ \(\frac{\Delta \ell}{\ell} \times 100=\alpha \Delta \theta \times 100=1\)

change in area ⇒ % A = \(\frac{\Delta \mathrm{A}}{\mathrm{A}} \times 100=\beta \Delta \theta \times 100\)

⇒ 2 (α Δ θ × 100) % A = 2%

Change in volume

% V = \(\) × 100 = V Δ θ × 100 = 3 (α Δ θ × 100) % V = 3 %

NEET Physics Class 11 Chapter 1 Variation Of Density With Temperature

As we know mass = volume × density.

The mass of a substance does not change with a change in temperature so with an increase in temperature, volume increases so density decreases and vice-versa.

d = \(\frac{d_0}{(1+\gamma \Delta T)}\)

For solids values of γ are generally small so we can write d = d₀(1 − γ ΔT) (using binomial expansion).

Note:

1. γ for liquids is of the order of 10−3.
2. Anomalous expansion of water:

For water density increases from 0 ºC to 4 ºC so γ is negative and for 4 ºC to higher temperature γ is positive. At 4 ºC density is maximum. This anomalous behavior of water is due to the presence of three types of molecules i.e. H₂O, (H₂O)₂and (H₂O)₃ having different volumes/masses at different temperatures.

This anomalous behavior of water causes ice to form first at the surface of a lake in cold weather. As winter approaches, the water temperature decreases initially at the surface. The water there sinks because of its increased density.

Consequently, the surface reaches 00C first and the lake becomes covered with ice. Aquatic life is able to survive the cold winter as the lake bottom remains unfrozen at a temperature of about 4°C.

Question 1. The densities of wood and benzene at 0°C are 880 kg/m³ and 900 kg/m³ respectively. The coefficients of volume expansion are 1.2 × 10^-3/°C for wood and 1.5 × 10^-3/°C for benzene. At what temperature will a piece of wood just sink in benzene?

Answer:

At just sink gravitation force = up thrust force

⇒ mg = F_B

⇒ Vp₁g = Vp₂g

⇒ p₁= p₂

⇒ \(\frac{880}{1+1.2 \times 10^{-3} \theta}=\frac{900}{1+1.5 \times 10^{-3} \theta}\)

⇒ θ = 83º C

NEET Physics Class 11 Chapter 1 Apparent Expansion Of A Liquid In A Container

Initially container was full. When temperature increases by ΔT,

volume of liquid V_L= V₀(1 + γ_L Δ T)

volume of container V_C= V₀(1 + γ_C Δ T)

So overflow volume of liquid relative to the container

ΔV = V_L− V_C ΔV = V₀(γ_L− γ_C) ΔT

So, the coefficient of apparent expansion of liquid w.r.t. Container

γ_apparent = γ_L− γ_C.

In case of expansion of liquid + container system:

if γ_L> γ_C ⎯→ level of liquid rise

if γ_L< γ_C ⎯→ level of liquid fall

Increase in height of liquid level in a tube when the bulb was initially completely filled

h = \(h=\frac{\text { volume of liquid }}{\text { area of tube }}=\frac{V_0\left(1+\gamma_L \Delta T\right)}{A_0\left(1+2 \alpha_S \Delta T\right)}=h_0\left\{1+\left(\gamma_L-2 \alpha_S\right) \Delta T\right\}\)

h = h₀{ 1 + ( γ_L– 2α_S) ΔT}

where h₀= original height of liquid in a container

α_S= linear coefficient of expansion of container.

Calorimetry and Thermal Expansion in NEET Physics Class 11

Question 1. A glass vessel of volume 100 cm³ is filled with mercury and is heated from 25°C to 75°C. What volume of mercury will overflow? The coefficient of linear expansion of glass = 1.8 × 10^-6/°C and the coefficient of volume expansion of mercury is 1.8 × 10^-4/°C.

Answer:

ΔV = V₀(γ_L– γ_C) ΔT = 100 × {1.8 × 10^-4 – 3 × 1.8 × 10^-6} × 50

ΔV = 0.87 cm³

Variation Of Force Of Buoyancy With Temperature

If the body is submerged completely inside the liquid

For solid, Buoyancy force F_B= V₀ dL g

V₀= Volume of the solid inside the liquid,

d_L= density of liquid

Volume of body after increase its temperature V = V₀[1 + γ_S Δθ],

Density of body after increase its temperature d′_L = \(\frac{d_{\mathrm{L}}}{\left[1+\gamma_{\mathrm{L}} \Delta \theta\right]}\)

Buoyancy force of body after increasing its temperature, \(F_B^{\prime}=V d_L^{\prime} g \quad \Rightarrow \frac{F_B^{\prime}}{F_B}=\frac{\left[1+\gamma_S \Delta \theta\right]}{\left[1+\gamma_L \Delta \theta\right]}\)

If γ_S< γ_L then F′_B< F_B

(Buoyant force decreases) or apparent weight of the body in liquid gets increased

[W − F′_B> W − F_B].

Question 1. A body is floating on the liquid if we increase temperature then what changes occur in buoyancy force? (Assume the body is always in floating condition)

Answer:

The body is in equilibrium

So, mg = B (Boyant Force)

The gravitational force does not change with a change in temperature. So buoyancy force remains constant.

By increasing temperature density of the liquid decreases so the volume of the body inside the liquid increases to keep the Buoyance force constant and equal to the gravitational force)

Question 1. In the previous question discuss the case when the body move downward, upwards and remains at same position when we increases temperature.

Answer:

Let f = fraction of volume of body submerged in liquid

⇒ \(\mathrm{f}=\frac{\text { volume of body submerged in liquid }}{\text { total volume of body }}\)

⇒ \(f_1=\frac{v_1}{v_0} \text { at } \theta_1{ }^{\circ} \mathrm{C}\)

⇒ \(f_2=\frac{v_2}{v_0\left(1+3 \alpha_S \Delta \theta\right)}\) at θ2ºC

for equilibrium mg = B = v1d1g = v2d2g. d

so v₂ = \(\frac{v_1 d_1}{d_2}\)

⇒ \(d_2=\frac{d_1}{1+\gamma_L \Delta \theta}=v_1\left(1+\gamma_L \Delta \theta\right)\)

⇒ \(f_2=\frac{v_1\left(1+\gamma_L \Delta \theta\right)}{v_0\left(1+3 \alpha_s \Delta \theta\right)}\)

where Δθ = θ₂– θ₁

Case 1: Body move downward if f₂> f₁

means γ_L> 3α_S

Case 2: Body moves upwards if f₂< f₁

means γ_L< 3α_S

Case 3: The body remains in the same position

if f₂= f₁

means γ_L= 3α_S

NEET Physics Class 11 Chapter 1 Calorimetry and Thermal Expansion Solutions

Bimetallic Strip

Two strips of different metals are welded together to form a bimetallic strip, when heated uniformly it bends in the form of an arc, and the metal with a greater coefficient of linear expansion lies on the convex side. The radius of the arc is thus formed by bimetal:

⇒ \(\ell_0\left(1+\alpha_1 \Delta \theta\right)=\left(\mathrm{R}-\frac{\mathrm{d}}{2}\right) \theta\)

⇒ \(\ell_0\left(1+\alpha_2 \Delta \theta\right)=\left(R+\frac{d}{2}\right) \theta\)

⇒ \(\frac{1+\alpha_2 \Delta \theta}{1+\alpha_1 \Delta \theta}=\frac{R+\frac{d}{2}}{R-\frac{d}{2}}\)

⇒ \(R=\frac{d}{\left(\alpha_2-\alpha_1\right) \Delta \theta}\)

⇒ \(\Delta \theta=\text { change in temperature }=\theta_2-\theta_1\)

• A bimetallic strip, consisting of a strip of brass and a strip of steel welded together as shown in figure (3). At temperature T₀ in figure and figure  (2). The strip bends as shown at temperatures above the reference temperature.
• Below the reference temperature, the strip bends the other way. Many thermostats operate on this principle, making and breaking an electrical constant as the temperature rises and falls as shown in Figure (2).

Key Concepts and Solutions for Calorimetry and Thermal Expansion NEET

Applications Of Thermal Expansion

1. A small gap is left between two iron rails of the railway.
2. Iron rings are slipped on the wooden wheels by heating the iron rings
3. The stopper of a glass bottle jammed in its neck can be taken out by heating the neck.
4. The pendulum of a clock is made of invar [an alloy of zinc and copper].

Temperature

Temperature may be defined as the degree of hotness or coldness of a body. Heat energy flows from a body at a higher temperature to that at a lower temperature until their temperatures become equal. At this stage, the bodies are said to be in thermal equilibrium.

Measurement of Temperature: The branch of thermodynamics which deals with the measurement of temperature is called thermometry.

• A thermometer is a device used to measure the temperature of a body.
• The substances like liquids and gases that are used in the thermometer are called thermometric substances. Suppose a physical quantity X varies linearly with temperature then

⇒ \(X_t=X_0(1+\alpha \mathrm{t}) \Rightarrow \quad t=\frac{X_t-X_0}{X_0 \alpha}\)

α is constant and X0 is the value of X at the reference temperature set at 0º. In the case of absolute scale

⇒ \(\frac{X_T}{X_0}=\frac{T}{T_0} \quad \Rightarrow \quad T=T_0 \frac{X_T}{X_0}=273.16 \frac{X_T}{X_0} K\)

Different Scales of Temperature: A thermometer can be graduated into the following scales.

1. The Centigrade or Celsius scale (ºC)
2. The Fahrenheit scale (ºF)
3. The Reaumer scale (ºR)
4. Kelvin scale of temperature (K)

Comparison Between Different Temperature Scales:

The formula for the conversion between different temperature scales is:

⇒ \(\frac{\mathrm{K}-273}{100}=\frac{\mathrm{C}}{100}=\frac{\mathrm{F}-32}{180}=\frac{\mathrm{R}}{80}\)

A general formula for the conversion of temperature from one scale to another:

⇒ \(=\frac{\text { Temp. on other scale }\left(\mathrm{S}_1\right) \text {-Lower fixed point }\left(\mathrm{S}_1\right)}{\text { Upper fixed point }\left(\mathrm{S}_2\right) \text {-Lower fixed point }\left(\mathrm{S}_1\right)}\)

⇒ \(=\frac{\text { Temp. on other scale }\left(\mathrm{S}_2\right) \text {-Lower fixed point }\left(\mathrm{S}_2\right)}{\text { Upper fixed point }\left(\mathrm{S}_2\right) \text {-Lower fixed point }\left(\mathrm{S}_2\right)}\)

Thermometers: Thermometers are devices that are used to measure temperatures. All thermometers are based on the principle that some physical property of a system changes as the system temperature changes.

Required properties of good thermometric substance.

1. Non-sticky (absence of adhesive force)
2. Low melting point (in comparison with room temperature)
3. High boiling temperature
4. The coefficient of volumetric expansion should be high (to increase accuracy in measurement).
5. Heat capacity should be low.
6. Conductivity should be high Mercury (Hg) suitably exhibits the above properties.

NEET Physics Chapter 1 Calorimetry and Thermal Expansion: Revision Notes

Types Of Thermometers

The Constant-volume Gas Thermometer: The standard thermometer, against which all other thermometers are calibrated, is based on the pressure of a gas in a fixed volume.

The figure shows such a constant volume gas thermometer; it consists of a gas-filled bulb connected by a tube to a mercury manometer.

T = \((273.16 \mathrm{~K})\left(\lim _{{gas} \rightarrow 0} \frac{p}{p_3}\right)\)

P = Pressure at the temperature being measured,

P₃ = pressure when the bulb is in a triple point cell.

Question 1. The readings of a thermometer at 0ºC and 100ºC are 50 cm and 75 cm of mercury column respectively. Find the temperature at which its reading is 80 cm of mercury column.

Answer:

By using formula

⇒ \(\frac{80-50}{75-50}=\frac{T-0}{100-0}\)

⇒ T = 120ºC

Question 2. A bullet of mass 10 gm in moving with speed 400m/s. Find its kinetic energy in calories.

Answer:

⇒ \(\Delta k=\frac{1}{2} \times \frac{10}{1000} \times 400 \times 400=800\)

⇒ \(\frac{800}{4.2}=\mathrm{Cal}\) = 191.11 Cal.

NEET Class 11 Calorimetry and Thermal Expansion Study Materials

Question 3. Calculate the amount of heat required to convert 1 kg steam from 100ºC to 200ºC steam.

Answer:

Heat req. = 1 × \(\frac{1}{2}\)× 100 = 50 kcal

Question 4. Calculate the heat required to raise the temperature of 1 g of water through 1ºC.

Answer:

Heat req. = 1 × 10^-3 × 1 × 1 = 1 × 10^-3 kcal

Question 5. 420 J of energy supplied to 10 g of water will raise its temperature by

Answer:

⇒ \(\frac{420 \times 10^{-3}}{4.20}=10 \times 10^{-3} \times 1 \times \Delta \mathrm{t}=10^{\circ} \mathrm{C}\)

Question 6. The ratio of the densities of the two bodies is 3: 4 and the ratio of specific heats is 4 : 3 . Find the ratio of their thermal capacities for unit volume.

Answer:

⇒ \(\frac{\rho_1}{\rho_2}=\frac{3}{4}, \frac{s_1}{s_2}=\frac{4}{3}\)

⇒ \(\theta=\frac{\mathrm{m} \times \mathrm{s}}{\mathrm{m} / \mathrm{\rho}}\)

⇒ \(\frac{\theta_1}{\theta_2}=\frac{s_1}{s_2} \times \frac{\rho_1}{\rho_2}=1: 1\)

Question 7. Heat is released by 1 kg steam at 150ºC if it converts into 1 kg water at 50ºC.

Answer:

H = 1 ×\(\frac{1}{2}\)× 50 + 1 × 540 + 1 × 1 × 50

= 540+75 = 615

Heat release = 615 Kcal.

Question 8. 200 gm water is filled in calorimetry of negligible heat capacity. It is heated till its temperature is increased by 20ºC. Find the heat supplied to the water.

Answer:

H = 200 × 10^-3 × 1 × 20 = 4 Kcal.

Heat supplied = 4000 cal = 4 Kcal

Question 9. A bullet of mass 5 gm is moving with a speed of 400 m/s. strike a target and energy. Then calculate the rise of the temperature of the bullet. Assuming all the loss in kinetic energy is converted into heat energy of the bullet if its specific heat is. 500J/kgºC.

Answer:

Kinetic energy = 12× 5 × 10^-3 × 400 × 400 = 5 × 10^-3 × 500 × ΔT

ΔT = 160º C

The rise in temperature is 160 ºC

Question 10. 1 kg ice at –10ºC is mixed with 1 kg water at 100ºC. Then find the equilibrium temperature and mixture content.

Answer:

Heat gained by 1 kg ice at – 10ºC to convert into 0ºC ice = 1 × \(\frac{1}{2}\)x10 = 5Kcal = 5000 cal

In the thermal equilibrium

5 + 1 × 80 + 1 × T = 1 × (100 – T)

85 = 100 – 2T ⇒ 2T = 15

⇒ \(\theta=\frac{15}{2}\) = 7.5 ºC, water, entire ice melts.

Question 11. 1 kg ice at –10º is mixed with 1kg water at 50ºC. Then find the equilibrium temperature and mixture content.

Answer:

The heat required by ice at –10ºC to convert it into 0ºC water

1 × \(\frac{1}{2}\)× 10 + 1 × 50 = 55 Kcal

The heat released by 1 kg of water to reduce its temperature from

50ºC to 0ºC = 1 × 1 × 50 = 50 kcal

Heat required > Heat released so, ice will not completely melt. Let m g ice melt then for equilibrium.

1 × \(\frac{1}{2}\) × 10 + 80 m = 50 m ⇒ 80 m = 45 ⇒ m = \(\frac{45}{80}\)

⇒ \(\text { Content of mixture }\left\{\begin{array}{ll}
\text { water } & \left(1+\frac{45}{80}\right) \mathrm{kg} \\
\text { ice } & \left(1-\frac{45}{80}\right) \mathrm{kg}
\end{array}\right\} \text { and temperature is } 0^{\circ} \mathrm{C}\)

Calorimetry and Thermal Expansion: Important Problems for NEET Physics Class 11

Question 12. A small ring having a small gap is shown in the figure on heating what will happen to the size of the gap?

Answer:

The gap will also increase. The reason is the same as in the above example.

Question 13. A concrete slab has a length of 10 m on a winter night when the temperature is 0°C. Find the length of the slab on a summer day when the temperature is 35°C. The coefficient of linear expansion of concrete is 1.0 × 10^-5/°C.

Answer:

l1= 10(1 + 1 × 10^-5× 35) = 10.0035 m

Question 14. A steel rod is clamped at its two ends and rests on a fixed horizontal base. The rod is unstrained at 20°C. Find the longitudinal strain developed in the rod if the temperature rises to 50°C. Coefficient of linear expansion of steel = 1.2 × 10^-5/°C.
Δ αΔt

Answer:

⇒ \(\frac{\Delta \ell}{\ell}=\frac{\ell_0 \alpha \Delta t}{\ell_0}\)= – 3.6 × 10^-4

Question 15. If the rod is initially compressed by Δl length then what is the strain on the rod when the temperature

1. Is increased by Δθ
2. Is decreased by Δθ.

Answer:

1. Strain = \(\frac{\Delta \ell}{\ell}+\alpha \Delta \theta\)
2. Strain = \(\left|\frac{\Delta \ell}{\ell}-\alpha \Delta \theta\right|\)

Question 16. A pendulum clock with having copper rod keeps the correct time at 20°C. It gains 15 seconds per day if cooled to 0°C. Calculate the coefficient of linear expansion of copper.

Answer:

⇒ \(\frac{15}{24 \times 60 \times 60}=\frac{1}{2} \alpha \times 20\)

⇒ \(\alpha=\frac{1}{16 \times 3600}=1.7 \times 10^{-5} /{ }^{\circ} \mathrm{C}\)

Question 17. A meter scale made of steel is calibrated at 20°C to give the correct reading. Find the distance between the 50 cm mark and the 51 cm mark if the scale is used at 10°C. The coefficient of linear expansion of steel is 1.1 × 10^-5/°C.

Answer:

lt = 1 (1 – 1.1 × 10^-5 × 10) = 0.99989 cm

Question 18. A uniform solid brass sphere rotates with an angular speed ω₀ about a diameter. If its temperature is now increased by 100ºC. What will be its new angular speed? (Given α_B = 2.0 × 10^-5 perºC)

1. \(\frac{\omega_0}{1-0.002}\)
2. \(\frac{\omega_0}{1+0.002}\)
3. \(\frac{\omega_0}{1+0.004}\)
4. \(\frac{\omega_0}{1-0.004}\)

Answer:

⇒ \(\mathrm{I}_0 \omega_0=\mathrm{I}_{\mathrm{t}} \omega \mathrm{t}\)

⇒ \(M r_0{ }^2 \omega_0={Mr}_0{ }^2(1+2 \alpha \Delta \mathrm{T}) \omega_{\mathrm{t}}\)

⇒ \(\omega_t=\frac{\omega_0}{1+0.004}\)

Question 19. The volume occupied by a thin-wall brass vessel and the volume of a solid brass sphere is the same and equal to 1,000 cm³ at 0ºC. How much will the volume of the vessel and that of the sphere change upon heating to 20ºC? The coefficient of linear expansion of brass is α = 1.9 × 10^-5.

Answer:

V = V₀(1 + 3α ΔT) = 1.14 cm³ ⇒ 1.14 cm³ for both

NEET Physics Class 11 Calorimetry and Thermal Expansion Key Formulas

Question 20. A thin copper wire of length L increases in length by 1%, when heated from temperature T₁ to T₂. What is the percentage change in area when a thin copper plate having dimensions 2L × L is heated from T₁ to T₂?

1. 1%
2. 3%
3. 4%
4. 2%

Answer: \(\ell_{\mathrm{f}}=\mathrm{L}(1+\alpha \Delta \mathrm{t})=\frac{\mathrm{L}_{\mathrm{f}}}{\mathrm{L}} \times 100=(1+\alpha \Delta t) \times 100=1 \%\)

⇒ \(A=2 L \times L(1+2 \alpha \Delta t)=\frac{A_f}{2 L \times L} \times 100=(1+2 \alpha \Delta t) \times 100=2 \%\)

Question 21. The density of water at 0°C is 0.998 g/cm³ and at 4°C is 1.000 g/cm³. Calculate the average coefficient of volume expansion of water in the temperature range of 0 to 4°C.

Answer: \(d_t=\frac{d_0}{1+\gamma \Delta t}\)

⇒ \(1=\frac{0.998}{1+\gamma \times 4}\)

= – 5 × 10^-4/°C

Question 22. A glass vessel measures exactly 10 cm × 10 cm × 10 cm at 0°C. it is filled completely with mercury at this temperature. When the temperature is raised to 10°C, 1.6 cm³ of mercury overflows. Calculate the coefficient of volume expansion of mercury. Coefficient of linear expansion of glass = 6.5 × 10^-6/°C

Answer:

ΔV = V_Hg – V_V

1.6 = 10³(γ_L× 10 – 10³ × 3 × 6.5 × 10^-6 × 10

γ_L = (1.6 + 0.195) × 10^-4 = 1.795 × 10^-4/°C

Question 23. A metal ball immersed in alcohol weighs W₁ at 00C and W₂ at 500C. The coefficient of cubical expansion of the metal is less than alcohol. Assuming that the density of the metal is large compared to that of the alcohol, find which of W₁ and W₂ is greater.

Answer:

⇒ \(\gamma_{\mathrm{M}}<\gamma_{\ell} \text { so, } \frac{F_{\mathrm{B}}^{\prime}}{F_{\mathrm{B}}}=\frac{\left[1+\gamma_{\mathrm{S}} \Delta \theta\right]}{\left[1+\gamma_{\ell} \Delta \theta\right]} F_{\mathrm{B}}^{\prime}<F_{\mathrm{B}}\)

So Apprent weight increased so, W₂> W₁

Question 24. In the figure strip brass or steel have a higher coefficient of linear expansion.

Answer:

Brass Strip; a strip of higher α is on the convex side.

Question 25. The upper and lower fixed points of a faulty thermometer are 5ºC and 105º C. If the thermometer reads 25ºC, what is the actual temperature?

Answer:

⇒ \(\frac{25-5}{100}=\frac{C-0}{100}\)

C = 20ºC

Question 26. At what temperature is the Fahrenheit scale reading equal to twice Celsius?

Answer:

⇒ \(\frac{F-32}{180}=\frac{C-0}{100}=\)

⇒ \(\frac{C-0}{100}\)

1 × -160 = 9x

x = 160º

Calorimetry and Thermal Expansion Solutions for NEET Physics Class 11

Question 27. The temperature of a patient is 40º C. Find the temperature on a Fahrenheit scale.

Answer:

⇒ \(\frac{F-32}{180}\)

⇒ \(\frac{40-0}{100}\)

F = 104ºC

Calorimetry And Thermal Expansion Multiple Choice Question And Answers

Question 31. A block of ice at -10ºC is slowly heated and converted to steam at 100ºC. Which of the following curves represent the phenomenon qualitatively:

Answer: 1.

Question 32. 540 g of ice at 0°C is mixed with 540g of water at 80°C. What is the final temperature of the mixture?

1. 0°C
2. 40°C
3. 80°C
4. 0°C

Answer: 1. 0°C

Question 33. The thermal capacity of anybody is :

1. A measure of its capacity to absorb heat
2. A measure of its capacity to provide heat
3. The quantity of heat required to raise its temperature by a unit degree
4. The quantity of heat required to raise the temperature of a unit mass of the body by a unit degree

Answer: 3. The quantity of heat required to raise its temperature by a unit degree

NEET Physics Class 11 Calorimetry and Thermal Expansion MCQs

Question 34. The figure shows the pressure-temperature phase diagram for water, the curves corresponding to sublimation, fusion, and vaporization respectively are

1. AO, OB, and OC
2. BO, OC, and AO
3. OC, BO, and AO
4. AO, OC, and BO

Answer: 1. AO, OB and OC

Question 35. An electric kettle takes a 4A current at 220V. How much time will it take to boil 1 kg of water at a temperature of 20°C? The temperature of boiling water is 100°C:

1. 6.3 min
2. 8.4 min
3. 12.6 min
4. 4.2 min

Answer: 1. 6.3 min

Question 36. The time taken by an 836 W heater to heat one liter of water from 10ºC to 40ºC is :

1. 50 s
2. 100 s
3. 150 s
4. 200 s

Answer: 3. 150 s

Question 37. 2 liters of water at 27°C is heated by a 1 kW heater in an open container. On average heat is lost to surroundings at the rate of 160 J/s. The time required for the temperature to reach 77°C is

1. 8 min 20 sec
2. 10 min
3. 7 min
4. 14 min

Answer: 1. 8 min 20 sec

Question 38. A piece of ice (heat capacity = 2100 J kg^-1ºC^-1 and latent heat = 3.36 × 105 J kg^-1) of mass m grams is at –5 ºC at atmospheric pressure. It is given 420 J of heat so that the ice starts melting. Finally, when the ice-water mixture is in equilibrium, it is found that 1 gm of ice has melted. Assuming there is no other heat exchange in the process, the value of m is:

1. 8 gm
2. 5 gm
3. 6 gm
4. 10 gm

Answer: 1. 8 gm

Question 39. Two large holes are cut in a metal sheet. If this is heated, distances AB and BC, (as shown) 

1. Both will increase
2. Both will decrease
3. AB increases, BC decreases
4. AB decreases, BC increases

Answer: 1. Both will increase

Question 40. A steel scale is to be prepared such that the millimeter intervals are to be accurate within 6 ×10^-5 mm. The maximum temperature variation from the temperature of calibration during the reading of the millimeter marks is (α = 12 × 10^-6 k^-1)

1. 4.0°C
2. 4.5°C
3. 5.0°C
4. 5.5°C

Answer: 3. 5.0°C

Question 41. Expansion during heating –

1. Occurs only in a solid
2. Increases the density of the material
3. Decreases the density of the material
4. Occurs at the same rate for all liquids and solids.

Answer: 3. Decreases the density of the material

Calorimetry and Thermal Expansion MCQs for NEET Physics Class 11

Question 42. If a bimetallic strip is heated, it will.

1. Bend towards the metal with a lower thermal expansion coefficient.
2. Bend towards the metal with a higher thermal expansion coefficient.
3. Twist itself into a helix.
4. Have no bending.

Answer: 1. Bend towards the metal with a lower thermal expansion coefficient.

Question 43. Two holes of unequal diameters d₁ and d₂(d₁ > d₂) are cut in a metal sheet. If the sheet is heated-

1. Both d₁and d₂ will decrease
2. Both d₁ and d₂ will increase
3. d₁ will increase d₂ will decrease
4. d₁ will decrease, d₂ will increase

Answer: 2. Both d₁ and d₂ will increase

Question 44. Two bars of copper having the same length but unequal diameter are heated to the same temperature. The change in length will be –

1. More in thinner bar
2. More in thicker bar
3. Same for both the bars
4. Determined by the ratio of length and diameter of the bars

Answer: 3. Same for both the bars

Question 45. A metallic bar is heated from 0ºC to 100ºC. The coefficient of linear expansion is 10^-5K^-1. What will be the percentage increase in length

1. 0.01%
2. 0.1%
3. 1%
4. 10%

Answer: 2. 0.1%

Question 46. A pendulum clock has an iron pendulum 1m long (α_iron = 10^-5/ºC). If the temperature rises by 10ºC, the clock-

1. Will lose 8 seconds per day
2. Will lose 4.32 seconds per day
3. Will gain 8 seconds per day
4. Will gain 4.32 seconds per day

Answer: 2. Will lose 4.32 seconds per day

Question 47. Two rods of lengths l₁and l₂ are made of materials whose coefficient of linear expansions is α₁ are α₂. If the difference between two lengths is independent of temperature –

1. \(\frac{\ell_1}{\ell_2}=\frac{\alpha_1}{\alpha_2}\)
2. \(\frac{\ell_1}{\ell_2}=\frac{\alpha_2}{\alpha_1}\)
3. \(\ell_2^2 \alpha_1=\ell_1^2 \alpha_2\)
4. \(\frac{\alpha_1^2}{\ell_1}=\frac{\alpha_2^2}{\ell_2}\)

Answer: 2. \(\frac{\ell_1}{\ell_2}=\frac{\alpha_2}{\alpha_1}\)

Question 48. If α, β, γ are respectively the linear, superficial and cubical expansivity of a homogeneous solid, then –

1. α : β : γ = 1 : 2 : 3
2. α : β : γ = 3 : 2 : 1
3. α : β : γ = 2 : 3 : 1
4. α : β : γ = 3 : 1 : 3

Answer: 1. α : β : γ = 1 : 2 : 3

Question 49. The coefficient of linear expansion of steel and brass are 11 × 10^-6/ºC and 19 × 10^-6/ºC respectively. If their difference in lengths at all temperatures has to be kept constant at 30cm, their lengths at 0ºC should be –

1. 71.25 cm and 41.25 cm
2. 82 cm and 52 cm
3. 92 cm and 62 cm
4. 62.25 cm and 32.25 cm

Answer: 1. 71.25 cm and 41.25 cm

Question 50. A solid ball of metal has a spherical cavity inside it. If the ball is heated, the volume of the cavity will –

1. Increase
2. Decrease
3. Remains unchanged
4. Have its shape changed

Answer: 1. Increase

Question 51. If the length of a cylinder on heating increases by 2%, the area of its base will increase by

1. 0.5%
2. 2%
3. 1%
4. 4%

Answer: 4. 4%

Question 52. A uniform metal rod is used as a bar pendulum. If the room temperature rises by 10ºC, and the coefficient of linear expansion of the metal of the rod is 2 × 10^-6 perºC, the period of the pendulum will have a percentage increase of –

1. – 2 × 10^-3
2. – 1 × 10^-3
3. 2 × 10^-3
4. 1 × 10^-3

Answer: 4. 1 × 10^-3

Question 53. The volume of a solid decreases by 0.6% when it is cooled to 50ºC. Its coefficient of linear expansion is –

1. 4 × 10^-6K
2. 5 × 10^-5K
3. 6 × 10⁴K
4. 4 × 10^-5K

Answer: 4. 4 × 10^-5K

Question 54. Which of the following graphs represents variation in density of water with temperature best –

Answer: 4.

Question 55. A rectangular block is heated from 0ºC to 100ºC. The percentage increase in its length is 0.10% What will be the percentage increase in its volume?

1. 0.03 %
2. 0.10%
3. 0.30%
4. None of these

Answer: 3. 0.30%

NEET Physics Class 11 Multiple Choice Questions on Calorimetry

Question 56. A thin copper wire of length l increases in length by 1% when heated from 0ºC to 100ºC. If a then cooper plate of area 2l × l is heated from 0ºC to 100ºC, the percentage increase in its area will be

1. 1%
2. 2%
3. 3%
4. 4%

Answer: 2. 2%

Question 57. If Ι is the moment of inertia of a solid body having α -coefficient of linear expansion then the change in Ι corresponding to a small change in temperature ΔT is

1. \(\frac{1}{2}\) α Ι ΔT
2. 2α Ι ΔT
3. 2 α Ι ΔT
4. 3 α Ι ΔT

Answer: 3. 2 α Ι ΔT

Question 58. A liquid with a coefficient of volume expansion γ is filled in a container of a material having the coefficient of linear expansion α .Ιf the liquid overflows on heating, then.

1. γ > 3α
2. γ < 3α
3. γ = 3α
4. None of these

Answer: 1. γ > 3α

Question 59. Two rods having lengths l₁ and l₂, made of materials with the linear expansion coefficient α₁ and α₂, were soldered together. The equivalent coefficients of linear expansion for the obtained rod:-

⇒ \(\frac{\ell_1 \alpha_2+\ell_2 \alpha_1}{\ell_1+\ell_2}\)

⇒ \(\frac{\alpha_1 \alpha_2}{\alpha_1+\alpha_2}\)

⇒ \(\frac{\ell_1 \alpha_1+\ell_2 \alpha_2}{\ell_1+\ell_2}\)

⇒ \(\frac{\left(\alpha_1+\alpha_2\right)}{2}\)

Answer: 3. \(\frac{\ell_1 \alpha_1+\ell_2 \alpha_2}{\ell_1+\ell_2}\)

Question 60. The volume thermal expansion coefficient of an ideal gas at constant pressure and temperature TK is

1. T
2. T²
3. \(\frac{1}{\mathrm{~T}}\)
4. \(\frac{1}{\mathrm{~T}^2}\)

Answer: 3. 1T

Question 61. A metallic ball and a highly stretched spring are made of the same material and have the same mass. They are heated so that they melt, the latent heat required

1. Are the same for both
2. Is greater for the ball
3. Is greater for the spring
4. The two may or may not be the same depending on the metal

Answer: 1. Are the same for both

Question 62. The coefficients of linear expansions of brass and steel are α₁ and α₂ respectively. When we take a brass rod of length l₁ and a steel rod of length l₂ at 0°C, then the difference in their lengths (l₂– l₁) will remain the same at all temperatures if :

1. α₁l₁= α₂l₂
2. α₁l₂= α₂l₁
3. α₁₂l₂= α_2²l₁
4. α₁l_2² = α₂ l_1²

Answer: 1. α₁l₁= α₂l₂

Question 63. If on heating liquid through 80ºC, the mass expelled is (1/100) th of mass still remaining, the coefficient of apparent expansion of liquid is:

1. 1.25 × 10^-4/ºC
2. 12.5 × 10^-4/ºC
3. 1.25 × 10^-5/ºC
4. None of these

Answer: 1. 1.25 × 10^-4/ºC

Question 64. An iron bar of length l and having a cross-section A is heated from 0 to 100ºC. If this bar is so held that it is not permitted to expand or bend, the force that is developed is:

1. Inversely proportional to the cross-sectional area of the bar
2. Independent of the length of the bar
3. Inversely proportional to the length of the bar
4. Directly proportional to the length of the bar

Answer: 2. Independent of the length of the bar

Thermal Expansion and Calorimetry MCQs for NEET Physics Class 11

Question 65. If the sphere of iron is heated, then its

1. Density increases
2. Volume increases
3. Radius decreases
4. None of these

Answer: 2. Volume increases

Question 66. Two rods, one of aluminum of length l₁ having a coefficient of linear expansion αaand the other of steel having a coefficient of linear expansion α_s and length l₂ are joined end to end. The expansion in both the rods is the same for the same variation of temperature. Then the value of \(\frac{\ell_1}{\ell_1+\ell_2}\)
Answer:

1. \(\frac{\alpha_{\mathrm{s}}}{\alpha_{\mathrm{a}}}\)
2. \(\frac{\alpha_{\mathrm{a}}}{\alpha_{\mathrm{s}}}\)
3. \(\frac{\alpha_s}{\alpha_a+\alpha_s}\)
4. \(\frac{\alpha_a}{\alpha_a+\alpha_s}\)

Answer: 3. \(\frac{\alpha_s}{\alpha_a+\alpha_s}\)

Question 67. A difference in temperature of 25º C is equivalent to a difference in franchise:

1. 45º F
2. 72º F
3. 32º F
4. 25º F

Answer: 1. 45º F

Question 68. What is the temperature at which we get the same reading on both the centigrade and Fahrenheit scales?

1. – 40ºC or – 40ºF
2. – 30ºC or – 30º F
3. – 30ºC or – 40ºF
4. – 10ºC or – 10ºF

Answer: 1. – 40ºC or – 40ºF

Question 69. Absolute temperature can be calculated by

1. Mean square velocity of molecules
2. Motion of the molecule
3. Both (a) and (b)
4. None of the above

Answer: 1. Mean square velocity of molecules

Question 70. The absolute zero is the temperature at which

1. Water freezes
2. All substances exist in a solid state
3. Molecular motion ceases
4. None of the above

Answer: 3. Molecular motion ceases

Question 71. Absolute zero (0K) is the temperature at which

1. Matter ceases to exist
2. Ice melts and water freezes
3. The volume and pressure of a gas become zero
4. None to these

Answer: 3. The Volume and pressure of gas become zero

Question 72. The temperature on the Celsius scale is 25°C. What is the corresponding temperature on the Fahrenheit scale

1. 40°F
2. 77°F
3. 50°F
4. 45°F

Answer: 2. 77°F

Question 73. Two thermometers are used to record the temperature of a room. If the bulb of one is wrapped in a wet hanky

1. The temperature recorded by both will be the same
2. The temperature recorded by the wet-bulb thermometer will be greater than that recorded by the other
3. The temperature recorded by the dry-bulb thermometer will be greater than that recorded by the other
4. None of the above

Answer: 3. The temperature recorded by dry-bulb thermometer will be greater than that recorded by the other

Question 74. A centigrade and a Fahrenheit thermometer are dipped in boiling water. The water temperature is lowered until the Fahrenheit thermometer registers 140°F. What is the fall in temperature as registered by the Centigrade thermometer

1. 30°
2. 40°
3. 60°
4. 80°

Answer: 2. 40°

NEET Physics Class 11 Calorimetry: MCQs and Answers

Question 75. A 5°C rise in temperature is observed in a conductor by passing a current. When the current has doubled the rise in temperature will be approximately:

1. 16°C
2. 10°C
3. 20°C
4. 12°C

Answer: 3. 20°C

Question 76. Value of – 40ºC in Fahrenheit scale is:

1. –40º F
2. 32°F
3. –32ºF
4. 40ºC

Answer: 1. –40º F

Question 77. If temperature of an object is 140º F, then its temperature in centrigrade is :

1. 105ºC
2. 32ºC
3. 140°C
4. 60ºC

Answer: 4. 60ºC

Question 78. The color of a star indicates its :

1. Temperature
2. Distance
3. Velocity
4. Size

Answer: 1. Temperature

Question 79. The temperature of a body on a kelvin scale is found to be x K. When it is measured by Fahrenheit thermometer, it is found to be x°F, then the value of x is:

1. 30
2. 313
3. 574.25
4. 301.25

Answer: 3. 574.25

Question 80. A constant pressure thermometer when immersed in ice-cooled water gives a volume reading of 47.5 units and when immersed in boiling liquid, it gives a reading of 67 units. What is the boiling point of the liquid?

1. 135°C
2. 125°C
3. 112°C
4. 100°C

Answer: 3. 112°C

Question 81. A beaker is completely filled with water at 4°C. The water will overflow if it is :

1. Warmed to a temperature greater than 4°C
2. Cooled to a temperature less than 4°C
3. and both
4. None of the above

Answer: 3. and both

Question 82. On a new scale of temperature (which is linear) called the W scale, the freezing and boiling points of water are 39°W and 239°W respectively. What will be the temperature on the new scale, corresponding to a temperature of 39°C on the Celsius scale?

1. 78°C
2. 117°W
3. 200°W
4. 139°W

Answer: 2. 117°W

Question 83. A thermally isolated vessel contains 100 g of water at 0ºC. When air above the water is pumped out, some of the water freezes and some evaporates at 0ºC itself. Then the mass of the ice formed if no water is left in the vessel. Latent heat of vaporization of water at 0ºC = 2.10 × 10⁶ J/kg and latent heat of fusion of ice = 3.36 × 10⁵J/kg.

1. 86.2 g
2. 13.8 g
3. 76.2 g
4. 65.6 g

Answer: 1. 86.2 g

Question 84. 2 kg ice at – 20 ºC is mixed with 5 kg water at 20 ºC. The final amount of water in the mixture would be : Given: specific heat of ice = 0.5 cal/g ºC, specific heat of water = 1 cal/g ºC, latent heat of fusion of ice = 80 cal/gm ]

1. 6 kg
2. 7 kg
3. 3.5 kg
4. 5 kg

Answer: 1. 6 kg

Question 85. In an insulated vessel, 0.05 kg of steam at 373 K and 0.45 kg of ice at 253 K are mixed. Find the final temperature of the mixture (in Kelvin).

Given, L_fusion = 80 cal/gm = 336 J/gm, L_vaporization = 540 cal/gm = 2268 J/gm,

S_ice = 2100 J/kg K = 0.5 cal/gm K and S_water = 4200 J/kg K = 1 cal/gmK

1. 273 K.
2. 373 K
3. 300 K
4. 253 K

Answer: 1. 273 K.

Question 86. The weight of a person is 60 kg. If he gets 105 calories heated through food and the efficiency of his body is 28%, then upto how much height he can climb when he user entire energy gained is climbing

1. 100 m
2. 200 m
3. 400 m
4. 1000 m

Answer: 2. 200 m

Question 87. When a block of iron floats in mercury at 0°C a fraction k₁ of its volume is submerged, while at the temperature 60ºC, a fraction k₂ is seen to be submerged. If the coefficient of volume expansion of iron is γFe, then the ratio \(\frac{k_1}{k_2}\)

1. \(\frac{1+60 \gamma_{\mathrm{Fe}}}{1+60 \gamma_{\mathrm{Hg}}}\)
2. \(\frac{1-60 \gamma_{\mathrm{Fe}}}{1+60 \gamma_{\mathrm{Hg}}}\)
3. \(\frac{1+60 \gamma_{\mathrm{Fe}}}{1-60 \gamma_{\mathrm{Hg}}}\)
4. \(\frac{1+60 \gamma_{\mathrm{Hg}}}{1+60 \gamma_{\mathrm{Fe}}}\)

Answer: 1. \(\frac{1+60 \gamma_{\mathrm{Fe}}}{1+60 \gamma_{\mathrm{Hg}}}\)

Question 88. A hot wire of copper is stretched at a temperature of 150ºC between two fixed walls. At what temperature will the wire break when it is cooled? The breaking stress of copper is 2.45 × 10⁸ N/m² Young’s modulus of copper = 11.8 × 10¹⁰ N/m², coefficient of linear expansion of copper = 1.6 ×10^-5/ºC.

1. 20.2ºC
2. 43.2ºC
3. 64.9ºC
4. 70.2ºC

Answer: 1. 20.2ºC

Calorimetry and Thermal Expansion Questions for NEET Physics Class 11

Question 89. Liquid oxygen at 50K is heated to 300 K at a constant pressure of 1 atm. The rate of heating is constant. Which one of the following graphs represents the variation of temperature with time?

Answer: 1.

Question 90. Steam at 1000C is passed into 20g of water at 100C. When water acquires a temperature of 800C, the mass of water present will be:

[Take specific heat of water = 1 cal g^-1 °C^-1 and latent heat of steam = 540 cal g^-1]

1. 24 g
2. 31.5 g
3. 42.5 g
4. 22.5 g

Answer: 4. 22.5 g

Question 91. The value of the coefficient of volume expansion of glycerin is 5 × 10^-4 K^-1. The fractional change in the density of glycerin for a rise of 40°C in its temperature, is:

1. 0.020
2. 0.025
3. 0.010
4. 0.015

Answer: 1. 0.020

Question 92. a piece of ice falls from a height h so that it melts completely. Only one-quarter of the heat produced is absorbed by the ice and all energy of ice gets converted in to heat during its fall. The value of h is :

[Latent heat of ice is 3.4 × 10⁵ J/Kg and g = 10 N/kg]

1. 68 km
2. 34 km
3. 544 km
4. 136 km

Answer: 4. 136 km

Question 93. A sample of 0.1 g of water at 100ºC and normal pressure (1.013 × 105 Nm^-2) requires 54 cal of heat energy to convert to stream at 100ºC. If the volume of the steam produced is 167.1 cc, the change in internal energy of the sample is:

1. 104.3 J
2. 84.5 J
3. 42.2 J
4. 208.7 J

Answer: 4. 208.7 J

Question 94. A metal rod of Young’s modulus Y and coefficient of thermal expansion α is held at its two ends such that its length remains invariant. If its temperature is raised by tºC, the linear stress developed in its is:

1. \(\frac{Y}{\alpha t}\)
2. \(Y \alpha t\)
3. \(\frac{1}{(Y \alpha t)}\)
4. \(\frac{\alpha t}{Y}\)

Answer: 2. \(Y \alpha t\)

Question 95. An aluminum sphere of 20 cm diameter is heated from 0ºC to 100ºC. Its volume changes by (given that coefficient of linear expansion for aluminum α_Al = 23 × 10^-6/ºC)

1. 2.89 cc
2. 9.28 cc
3. 49.8 cc
4. 28.9 cc

Answer: 4. 28.9 cc

Question 96. A wooden wheel of radius R is made of two semicircular parts (see figure). The two parts are held together by a ring made of a metal strip of cross-sectional area S and length L. L is slightly less than 30 2πR. To fit the ring on the wheel, it is heated so that its temperature rises by ΔT and it just steps over the wheel. As it cools down to the surrounding temperature, it presses the semicircular parts together. If the coefficient of linear expansion of the metal is α, and its Young’s modulus is Y, the force that one part of the wheel applies on the other part is:

1. 2πSYαΔT
2. SYαΔT
3. π SYαΔT
4. 2SYαΔT

Answer: 4. 2SYαΔT

Question 97. A pendulum clock loses 12 s a day if the temperature is 40°C and gains 4 s a day if the temperature is 20°C. The temperature at which the clock will show the correct time, and the coefficient of linear expansion (α) of the metal of the pendulum shaft are respectively:

1. 60°C ; α = 1.85 × 10^-4/°C
2. 30°C ; α = 1.85 × 10^-3/°C
3. 55°C ; α = 1.85 × 10^-2/°C
4. 25°C ; α = 1.85 × 10^-5/°C

Answer: 4. 25°C ; α = 1.85 × 10^-4/°C

NEET Physics Class 11 Thermal Expansion and Heat MCQs

Question 98. A copper ball of mass 100 gm is at a temperature T. It is dropped in a copper calorimeter of mass 100 gm, and filled with 170 gm of water at room temperature. Subsequently, the temperature of the system is found to be 75º C. T is given by : (Given: room temperature = 30ºC, specific heat of copper = 0.1 cal/gmºC)

1. 825º C
2. 800ºC
3. 885ºC
4. 1250ºC

Answer: 3. 885ºC

Question 99. An external pressure P is applied on a cube at 0°C so that it is equally compressed from all sides. K is the bulk modulus of the material of the cube and α is its coefficient of linear expansion. Suppose we want to bring the cube to its original size by heating it. The temperature should be raised by:

1. \(3 P K \alpha\)
2. \(\frac{\mathrm{P}}{3 \alpha \mathrm{K}}\)
3. \(\frac{\mathrm{P}}{\alpha \mathrm{K}}\)
4. \(\frac{3 \alpha}{\mathrm{PK}}\)

Answer: 2. \(\frac{\mathrm{P}}{3 \alpha \mathrm{K}}\)

Question 100. An unknown metal of mass 192 g heated to a temperature of 100°C was immersed into a brass calorimeter of mass 128 g containing 240 g of water at a temperature of 8.4°C. Calculate the specific heat of the unknown metal if the water temperature stabilizes at 21.5°C. (Specific heat of brass is 394 J kg^-1 K^-1)

1. 916 J kg^-1 K^-1
2. 458 J kg^-1 K^-1
3. 1232 J kg^-1 K^-1
4. 654 J kg^-1 K^-1

Answer: 1. 916 J kg^-1 K^-1

Question 101. A metal ball of mass 0.1 kg is heated upto 500°C and dropped into a vessel of heat capacity 800 JK^-1 containing 0.5 kg water. The initial temperature of the water and vessel is 30°C. What is the approximate percentage increment in the temperature of the water? [Specific Heat Capacities of water and metal are, respectively, 4200 Jkg^-1K^-1 and 400Jkg^-1K^-1]

1. 30%
2. 25%
3. 15%
4. 20%

Answer: 4. 20%

Question 102. Two rods A and B of identical dimensions are at a temperature of 30°C. If A is heated upto 180°C and B upto T°C, then the new lengths are the same. If the ratio of the coefficients of linear expansion of A and B is 4 : 3, then the value of T is :

1. 270°C
2. 200°C
3. 230°C
4. 250°C

Answer: 3. 230°C

Calorimetry and Thermal Expansion MCQ Practice for NEET Physics

Question 103. Ice at -20°C is added to 50 g of water at 40 °C. When the temperature of the mixture reaches 0°C, it is found that 20 g of ice is still unmelted. The amount of ice added to the water was close to (Specific heat of water = 4.2J/g/°C Specific heat of Ice = 2.1 J/g/°C. Heat of fusion of water at 0°C = 334 J/g

1. 100 g
2. 40 g
3. C60 g
4. 50 g

Answer: 2. 40 g

NEET Physics Class 11 Chapter 1 Calorimetry

The branch of thermodynamics which deals with the measurement of heat is called calorimetry.

• A simple calorimeter is a vessel generally made of copper with a stirrer of the same material. The vessel is kept in a wooden box to isolate it thermally from the surroundings. A thermometer is used to measure the temperature of the contents of the calorimeter.
• Objects at different temperatures are made to come in contact with each other in the calorimeter.
• As a result, heat is exchanged between the object as well as with the calorimeter. Neglecting any heat exchange with the surrounding, the total height is conserved i.e. heat given by one is equal to that taken by the other.

Calorimetry Concepts and Solutions for NEET Physics Class 11

Law of Mixture:

When two substances at different temperatures are mixed together, the exchange of heat continues to take place till their temperatures become equal. This temperature is then called the final temperature of the mixture. Here, Heat taken by one substance = Heat given by another substance.

⇒ m₁s₁(T₁− T_m) = m₂ s₂(T_m− T₂)

Calorimetry NEET Physics Class 11 Solutions

Question 1. An iron block of mass 2 kg, falls from a height of 10 m. After colliding with the ground it loses 25% energy to its surroundings. Then find the temperature rise of the block. (Take sp. heat of iron 470 J/kg ºC)

Solution:

⇒ \(\mathrm{ms} \Delta \theta=\frac{4}{4} \mathrm{mgh}\)

= \(\Delta \theta=\frac{3 \times 10 \times 10}{4 \times 470}=0.159^{\circ} \mathrm{C}\)

Note: If specific heat is given as calorie / kgºC, it is to be converted to J/kgºC by multiplying with 4.18

Zeroth law of thermodynamics:

If objects A and B are separately in thermal equilibrium with a third object C, then objects A and B are also in thermal equilibrium with each other.

Question 2. The temperature of equal masses of three different liquids A, B, and C are 10ºC 15ºC, and 20ºC respectively. The temperature when A and B are mixed is 13ºC and when B and C are mixed, it is 16ºC. What will be the temperature when A and C are mixed?

Solution:

when A and B are mixed

ms₁ × (13 – 10) = m × s₂× (15 – 13)

3s₁= 2s₂….. (1)

when B and C are mixed

s_s × 1 = s_s× 4 …… (2)

when C and A are mixed

s₁(θ – 10) = s₃× (20 – θ) ….(3)

by using equation (1), (2) and (3)

we get θ = \(\frac{140}{11}^{\circ} \mathrm{C} \)

NEET Physics Chapter 1 Calorimetry: Solutions and Explanations

Question 3. If three different liquids of different masses specific heat and temperature are mixed with each other then what is the temperature mixture at thermal equilibrium?

1. m₁, s₁, T₁ → specification for liquid
2. m₂, s₂, T₂ → specification for liquid.
3. m₃, s₃, T₃ → specification for liquid.

Solution:

Total heat lost or gained by all substances is equal to zero

ΔQ = 0

m₁s₁(T – T₁) + m₂s₂(T – T₂) + m₃s₃(T – T₃) = 0

So, T = \(\frac{m_1 s_1 T_1+m_2 s_2 T_2+m_3 s_3 T_3}{m_1 s_1+m_2 s_2+m_3 s_3}\)

Question 4. The following equation calculates the value of H 1kg ice at –20ºC = H + 1 Kg water at 100ºC, here H means heat required to change the state of a substance.

Solution:

The heat required to convert 1 kg ice at – 20ºC into 1 kg water at 100ºC

ΔQ (Kcal) = 1 kg ice at – 20ºC to 1 kg ice at 0ºC ice + 1 kg water

at 0ºC + 1 kg water at 0ºC to 1 kg water at 100ºC

= 1 ×\(\frac{1}{2}\)× 20 + 1 × 80 + 1 × 100 = 190 Kcal.

So H = – 190 Kcal

The negative sign indicates that 190 Kcal heat is withdrawn from 1 kg water at 100ºC to convert it into 1 kg ice at – 20ºC

NEET Physics Class 11 Calorimetry Problems and Solutions

Question 5. 1 kg ice at –20ºC is mixed with 1 kg steam at 200ºC. Then find the equilibrium temperature and mixture content.

Solution:

Let equilibrium temperature is 100 ºC heat required to convert 1 kg ice at –20ºC to 1 kg water at 100ºC is equal to

H₁= 1 ×\(\frac{1}{2}\)× 20 + 1 × 80 + 1 × 1 × 100 = 190 Kcal

The heat released by steam to convert 1 kg steam at 200ºC to 1 kg water at 100ºC is equal to

H₂= 1 ×\(\frac{1}{2}\)× 100 + 1 × 540 = 590 Kcal

1 kg ice at – 20ºC = H₁+ 1kg water at 100ºC …… (1)

1 kg steam at 200ºC = H₂ + 1kg water at 100ºC ……. (2)

by adding equation (1) and (2)

1 kg ice at –20ºC + 1 kg steam at 200ºC = H1+ H2+ 2 kg water at 100ºC.

Here heat required to ice is less than the heat supplied by steam so the mixture equilibrium temperature is 100ºC then steam is not completely converted into water.

So the mixture has water and steam which is possible only at 100ºC

mass of steam which converted into water is equal to

m = \(\frac{190-1 \times \frac{1}{2} \times 100}{540}=\frac{7}{27} \mathrm{~kg}\)

so mixture content mass of steam = \(1-\frac{7}{27}=\frac{20}{27} \mathrm{~kg}\)

mass of water = \(1+\frac{7}{27}=\frac{34}{27} \mathrm{~kg}\)

NEET Physics Class 11 Chapter 1 Thermal Expansion

Most materials expand when their temperature is increased. Railway roads tracks, and bridges all have some means of compensating for thermal expansion.

• When a homogeneous object expands, the distance between any two points on the object increases. Figure 5 shows a block of metal with a hole in it.
• The expanded object is like a photographic enlargement. In the hole expands in the same proportion as the metal, it does not get smaller

Thermal Expansion NEET Physics Class 11 Solutions

• At the atomic level, thermal expansion may be understood by considering how the potential energy of the atoms varies with distance.
• The equilibrium position of an atom will be at the minimum of the potential energy well if the well is symmetric. At a given temperature each atom vibrates about its equilibrium position and its average remains at the minimum point.
• If the shape of the well is not symmetrical the average position of an atom will not be at the minimum point.
• When the temperature is raised the amplitude of the vibrations increases and the average position is located at a greater interatomic separation. This increased separation is manifested as expansion of the material as shown in figure 6.
• Almost all solids and liquids expand as their temperature increases. If allowed. Solids can change in length, area, or volume, while liquids change in their volume.

Question 1. A rectangular plate has a circular cavity as shown in the figure. If we increase its temperature then which dimension will increase in the following figure?

Answer:

Distance between any two points on an object increases with an increase in temperature. So, all dimensions a, b, c, and d will increase

NEET Physics Class 11 Chapter 1 Thermal Expansion Solutions

Question 2. In the given figure, when temperature is increased then which of the following increases

1. R₁
2. R₂
3. R₂– R₁
4. None of these

Answer: All of the above

– – – – – represents expanded Boundary

——— represents the original Boundary

As the intermolecular distance between atoms increases on heating hence the inner and outer perimeter increases. Also if the atomic arrangement in radial direction is observed then we can say that it also increases hence all A, B, C are true.

NEET Physics Chapter 1 Thermal Expansion: Solutions and Explanations

NEET Physics Class 11 Chapter 1 Linear Expansion

When the rod is heated, its increase in length ΔL is proportional to its original length L₀ and change in temperature ΔT where ΔT is in ºC or K.

dL = αL₀dT ⇒ ΔL = α L₀ Δ T If α ΔT << 1

⇒ \(\alpha=\frac{\Delta L}{L_0 \Delta T}\) where α is called the coefficient of linear expansion whose unit is ºC−1 or K−1.

L = L₀(1 + α Δ T). Where L is the length after heating the rod.

Variation of a with temperature and distance

If α varies with distance, α = ax + b.

The total expansion = ∫(ax + b) ΔT dx.

If α varies with temperature, α = f (T). Then ΔL = ∫α L0dT

Note: Actually thermal expansion is always 3-D expansion. When the other two dimensions of an object are negligible with respect to one, then observations are significant only in one dimension and it is known as linear expansion.

Thermal Expansion Problems and Solutions for NEET Physics Class 11

Question 1. What is the percentage change in length of a 1m iron rod if its temperature changes by 100ºC? α for iron is 2 × 10–5/ºC.

Answer:

percentage change in length due to temperature change

⇒ \(\% \Delta \ell=\frac{\Delta \ell}{\ell}\)× 100 = αΔθ × 100 = 2 × 10–5 × 100 × 100 = 0.2%

Thermal Stress Of A Material: If a rod is free to expand then there will be no stress and strain.

• Stress and strain is produced only when an object is restricted to expand or contract according to change in temperature.
• When the temperature of the rod is decreased or increased under constrained condition , compressive or tensile stresses are developed in the rod. These stresses are known as thermal stresses.

Strain = \(\frac{\Delta \mathrm{L}}{\mathrm{L}_0}=\frac{\text { final length }- \text { original length }}{\text { original length }}=\alpha \Delta \mathrm{T}\)

Note: Original and final length should be at the same temperature.

Consider a rod of length l₀ which is fixed between two rigid supports separated at a distance l₀ now if the temperature of the rod is increased by Δθ then the strain produced

strain = \(
$$
=\frac{\text { length of the rod at new temperature- natural length of the rod at new temperature }}{\text { natural length of the rod at new temperature }}
$$\)

⇒ \(\frac{\ell_0-\ell_0(1+\alpha \Delta \theta)}{\ell_0(1+\alpha \Delta \theta)}=\frac{-\ell_0 \alpha \Delta \theta}{\ell_0(1+\alpha \Delta \theta)}\)

∵α is very small. So, Δθ << 1

strain = – α Δ θ (negative sign in the answer represents that the length of the rod is less than the natural length which means is compressed at the ends.)

Question 2. In the given figure a rod is free at one end and the other end is fixed. When we change the temperature of a rod by Δθ, the strain produced in the rod will be

1. αΔθ
2. \(\frac{1}{2}\)αΔθ
3. Zero
4. Information incomplete

Answer: 3. Zero

Here rod is free to expand from one side so by changing temperature no strain will be produced in the rod. Hence ans. is (3)

Thermal Expansion NEET Physics Class 11 Solutions and Explanation

Question 3. An iron ring measuring 15.00 cm in diameter is to be shrunk on a pulley which is 15.05 cm in diameter. All measurements refer to the room temperature 20°C. To what minimum temperature should the ring be heated to make the job possible? Calculate the strain developed in the ring when it comes to room temperature. Coefficient of linear expansion of iron = 12 × 10^-6/°C.

Answer:

The ring should be heated to increase its diameter from 15.00 cm to 15.05 cm.

Using l2= l1(1 + α Δθ), ⇒ Δθ = \(\Delta \theta=\frac{\left(\ell_2-\ell_1\right)}{\ell_1 \alpha}\)

⇒ \(\frac{0.05 \mathrm{~cm}}{15.00 \mathrm{~cm} \times 12 \times 10^{-6} /{ }^{\circ} \mathrm{C}}=278^{\circ} \mathrm{C}\)

The temperature = 20°C + 278°C = 298°C.

The strain developed = \(\frac{\ell_2-\ell_1}{\ell_1}\) = 3.33 × 10–3

NEET Class 11 Thermal Expansion Study Notes and Solutions

Question 4. A steel rod of length 1m rests on a smooth horizontal base. If it is heated from 0°C to 100°C, what is the longitudinal strain developed?

Answer: In the absence of external force no strain or stress will be created hear rod is free to move. 9

Question 5. A steel rod is clamped at its two ends and rests on a fixed horizontal base. The rod is in natural length at 20°C. Find the longitudinal strain developed in the rod if the temperature rises to 50°C. Coefficient of linear expansion of steel = 1.2 × 10^-5/°C.

Answer:  As we know strain

strain = \(\frac{\text { change in length }}{\text { original length }}=\frac{\Delta \ell}{\ell_0}\)

∴ Strain = αΔθ

= 1.2 × 10^-5 × (50 – 20) = 3.6 × 10^-4

here strain is compressive strain because the final length is smaller than the initial length.

Question 6. A steel wire of a cross-sectional area of 0.5 mm² is held between two fixed supports. If the wire is just taut at 20°C, determine the tension when the temperature falls to 0°C. The coefficient of linear expansion of steel is 1.2 × 10^-5/°C and Young’s modulus is 2.0 × 10¹¹N/m².

Answer:

here final length is more than the original length so that strain is tensile and tensile force is given by

F = AY α Δ t = 0.5 × 10^-6 × 2 × 10¹¹ × 1.2 × 10^-5 × 20 = 24 N

Variation Of Time Period Of Pendulum Clocks:

The time represented by the clock hands of a pendulum clock depends on the number of oscillations performed by the pendulum every time it reaches its extreme position the second hand of the clock advances by one second that means second hand moves by two seconds when one oscillation incomplete

Let T = \(2 \pi \sqrt{\frac{L_0}{g}}\) at temperature θ0 and T′ = \(2 \pi \sqrt{\frac{L}{g}}\) at temperature θ.

⇒ \(\frac{\mathrm{T}^{\prime}}{\mathrm{T}}=\sqrt{\frac{\mathrm{L}^{\prime}}{\mathrm{L}}}=\sqrt{\frac{\mathrm{L}[1+\alpha \Delta \theta]}{\mathrm{L}}}\) = 1+\(\frac{1}{2}\)2α Δ θ (Binomial approximation is used)

Therefore change (loss or gain) in time per unit time lapsed is

⇒ \(\frac{\mathrm{T}^{\prime}-\mathrm{T}}{\mathrm{T}}=\frac{1}{2} \alpha \Delta \theta\)

gain or loss in time in duration of ‘t’ in

Δt = \(\frac{1}{2}\)α Δθ t, if T is the correct time then 2

1. θ < θ0, T′ < T clock becomes fast and gains time
2. θ > θ0, T′ > T clock becomes slow and loses time

NEET Physics Class 11 Thermal Expansion: Conceptual Solutions

Question 7. A pendulum clock consists of an iron rod connected to a small, heavy bob. If it is designed to keep the correct time at 20°C, how fast or slow will it go in 24 hours at 40°C? Coefficient of linear expansion of iron = 1.2 × 10^-6 /°C.

Answer:

The time difference that occurred in 24 hours (86400 seconds) is given by

Linear Expansion of iron = 1.2 x 10^-6 /°C.

Δt = \(\frac{1}{2}\) 2α Δθ t

= \(\frac{1}{2}\)× 1.2 × 10^-6 × 20 × 86400 = 1.04 sec.

This is a loss of time as θ is greater than θ₀. As the temperature increases, the time period also increases. Thus, the clock goes slow.

Measurement of length by metallic scale:

Case 1

When an object is expanded only (figure 9a)

l₂= l₁{1 + α₀(θ₂– θ₁)

l₁= actual length of object at θ₁ºC = measure length of object at θ₁ºC.

l₂= actual length of object at θ₂ºC = measure length of object at θ₂ºC.

α₀= linear expansion coefficient of an object.

Case 2

When only the measuring instrument is expanded actual length of the object will not change but a measured value (MV) decreases.

MV = l₁{ 1 – α_s(θ₂– θ₁)}

α_s= linear expansion coefficient of measuring instrument.

at θ₁ C MV = 3

at θ₁ C MV = 2.2

Case 3

If both expanded simultaneously

MV = {1 + (α₀– α_s) (θ₂– θ₁)

1. If α₀> α_s, then the measured value is more the actual value at θ₁ºC
2. If α₀< α_s, then the measured value is less the actual value at θ₁ºC

at θ₁ºC MV = 3.4

θ₂ºC MV = 4.1

Measured value = calibrated value × {1 + α Δ θ}

where α = α₀– α_s

α₀= coefficient of linear expansion of object material, α_s = coefficient of linear expansion of scale material.

Δθ = θ − θ_C

θ = temperature at the time of measurement θ_C= temperature at the time of calibration. For scale, true measurement = scale reading [1 + α (θ − θ₀)]

If θ > θ₁ true measurement > scale reading

θ < θ₀ true measurement < scale reading

NEET Physics Chapter 1 Thermal Expansion: Key Solutions

Question 8. A bar measured with a vernier caliper is found to be 180mm long. The temperature during the measurement is 10ºC. The measurement error will be if the scale of the vernier caliper has been graduated at a temperature of 20ºC : (α = 1.1 × 10-5°C^-1. Assume that the length of the bar does not change.)

1. 1.98 × 10^-1 mm
2. 1.98 × 10^-2 mm
3. 1.98 × 10^-3 mm
4. 1.98 × 10^-4 mm

Answer: True measurement = scale reading [1 + α (θ − θ₀)]

= 180 × {1+ (10 – 20) × (–1.1 × 10^-5) }

measurement error = true measurement – scale reading

= 180 × {1+ (10 – 20) × (–1.1 × 10^-5) } – 180

= 1.98 × 10^-2 mm