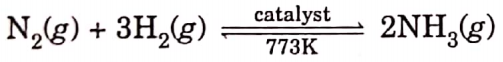NCERT Solutions For Class 10 Science Chapter 3 Metals And Non-Metals Long Question And Answers
Question 1. Explain the process by which the metal is obtained from its molten chloride.
Answer:
Sodium
4Na + O2 → 2Na2O
Na2O+ H2O → 2NaOH
Sodium is obtained from sodium chloride by the process of electrolytic reduction.
Reactions: At cathode: Na+ + e → Na
At anode: 2Cl–→ Cl2 + 2e ̄
Metals and Non-Metals NCERT Class 10 Science Solutions
Read and Learn More Class 10 Science Solutions
Question 2.
In the formation of a compound between two atoms A and B, A loses two electrons and B gains one electron. What is the nature of the bond between A and B?
- Suggest the formula of the compound formed between A and B.
- On similar lines explain the formation of the MgCl2, molecule.
- Common salt conducts electricity only in the molten state. Why?
- Why is the melting point of NaCl high?
Answer:
1.
1. Ionic Bond
2.

2. Mg → Mg+ + 2e–
2Cl + 2e → 2CH–

3. Na+ and Cl– are free to move in the molten state but not in a solid state.
4. It is due to the strong force of attraction between Na+ and Cl–.

Question 3. Seema cooks and sometimes overcooks food to make it tender irrespective of the fact that it destroys some nutrients. She adds spices, sugar and/or salt to make it tastier and enjoyable.
Geeta uses plant roots and fruits which have enough sugar. She uses food of a vegetable origin which is better than animal origin. Seema enjoys spicy food but also takes one tablet for heartburn, one for digestion and another to release constipation.
She uses stale food or the food repeatedly warmed which loses its nutritive value. She uses frozen and preserved food which has a shelf life, after which it is inedible.
- Why should we prefer food from vegetable origin and not from animal origin?
- Why should we not take spicy food?
- Why should we not overcook food?
- Why should we not take frozen and preserved food and always prefer fresh food?
- What values are possessed by Geeta?
Answer:
1. Food of vegetable origin is less complex and easily digestible as compared to food of animal origin.
2. It leads to indigestion and sometimes constipation and heartburn.
3. It will lead to loss of nutrients.
4. It has a shelf life and is not fit for use and after sometimes it becomes stale. Fresh food is rich in nutrients.
5. Geeta has good eating habits and she keeps her family healthy.
Question 4.
- An ore on treatment with dilute hydrochloric acid produces brisk effervescence. What step will be required to obtain metal from the enriched ore?
- Copper coin is kept immersed in silver nitrate solution for some time. What change will take place in the coin and the colour of the solution? Write a balanced chemical equation of the reaction involved.
Answer:
1. Carbonate ore
Steps
1. Calcination: Carbonate ore is heated in a limited supply of air and oxide is obtained,
Example:
ZnCO(s) → (Heat) → ZnO(s) +CO(g)
Reduction with carbon: Oxide ore is heated with carbon
ZnO(s) + C(s) → Zn(s) + CO(g)
2. Copper, being more reactive than silver will displace silver from the silver nitrate solution and there will be deposition of silver on a copper coin. The colour of the solution will turn to blue.
Example:
Cu(s) + 2AgNO3(aq) → Cu(NO3)2(aq) + 2Ag(s)
NCERT Class 10 Science Chapter 3: Metals and Non-Metals Summary
Question 5.
1. List two differences between calcination and roasting in tabular form.
2. Which method will you use to reduce the following? Explain by giving a suitable example.
- Oxides of less reactive metals.
- Oxides of moderately reactive metals.
- Oxides of highly reactive metals.
Answer:
1.

2.
1. Self-reduction (In the presence of heat).
2HgO → (Heat) → 2Hg+O
2Cu2O+Cu2S → (Heat) → 6Cu +SO2
2. Reduction using carbon.
ZnO + C→ Zn + CO
Sometimes, some highly reactive metals are used as reducing agents.
Example:
3MnO2 + 4Al→ 3Mn + 2Al2O3 + Heat
Or Fe2O3 + 2Al → 2Fe + Al2O3 + Heat
3. Electrolytic reduction.
Example: Na, Mg, and Ca are obtained by electrolysis of their molten chlorides.
Question 6. Write a chemical equation when zinc granules react with:
- Sulphuric acid
- Hydrochloric acid
- Aluminium chloride
- Sodium hydroxide
⇒ \(\mathrm{Zn}+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \mathrm{ZnSO}_4+\mathrm{H}_2\)
⇒ \(\mathrm{Zn}+2 \mathrm{HCl} \longrightarrow \mathrm{ZnCl}_2+\mathrm{H}_2\)
⇒ \(\mathrm{Zn}+\mathrm{AlCl}_3 \longrightarrow \text { No reaction }\)
⇒ \(\mathrm{Zn}+2 \mathrm{NaOH} \longrightarrow \mathrm{Na}_2 \mathrm{ZnO}_2+\mathrm{H}_2\)
⇒ \(\mathrm{Zn}+4 \mathrm{HNO}_3 \longrightarrow \mathrm{Zn}\left(\mathrm{NO}_3\right)_2+2 \mathrm{NO}_2+2 \mathrm{H}_2 \mathrm{O}\)
Question 7. State reason why
- Ionic compounds have high melting and boiling points.
- Ionic compounds are soluble in water.
- Ionic compounds are solid and somewhat hard.
- Ionic compounds conduct electricity in a molten state.
- The metals tend to lose electrons.
Answer:
- Ionic compounds have high melting and boiling points because a considerable amount of energy is required to break the strong inter-ionic attraction.
- Ionic compounds are soluble in water because their oppositely charged ions break by the opposite pole of water molecules.
- They are solids and are somewhat hard because of the strong force of attraction between the positive and the negative ions.
- Ionic compounds conduct electricity in a molten state because the electrostatic forces of attraction between the oppositely charged ions are overcome due to heat.
- Metals lose electrons as a tendency to attain a filled valence shell.
Question 8. Here are some general statements. Give one exception for each statement.
- Metals are lustrous.
- Metals are solids at room temperature.
- Metals have a high melting point.
- Non-metals are non-lustrous.
- Non-metals are insulators or non-conductors of electricity.
Answer:
- Sodium
- Mercury
- Gallium
- Iodine
- Carbon
NCERT Solutions Chapter 3: Metals and Non-Metals Questions and Answers
Question 9.
1. Write two differences between calcination and roasting.
2. No reaction occurs when granules of solid ‘A’ are mixed with a powder of solid ‘B’: However when the mixture is heated, a reaction starts with the evolution of much heat.
Product ‘C’ of the reaction settles down as a liquid metal and solid product ‘D’ keeps floating over the liquid ‘C’. This reaction is sometimes used to make metals for ready use in odd places.
- Based on this information, make assumptions about ‘A’ and ‘B’ and corresponding deductions about ‘C’ and ‘D’ and write a balanced chemical equation for the reaction. Include in the chemical equation the physical states of the reactants and products, the need for heating to start the reaction, and the exothermic reaction.
- Name two types of chemical reactions to which this reaction can belong.
Answer:
1.

1. ‘A’ is aluminium, and ‘B’ is a ferric oxide (Iron (3) oxide).
2.

This reaction is a displacement reaction because ‘Al’ is displacing ‘Fe’. It is also a redox reaction because ‘Al’ is a reducing agent and Fe2O3 is an oxidising agent.
Question 10. Define activity series of metals. Arrange the metals gold, copper, iron and magnesium in order of their increase in reactivity.
- What will you observe when:
- Some zinc pieces are put in a copper sulphate solution.
- Some silver pieces are put into a green-coloured ferrous sulphate solution.
Answer:
The series of metals in which metals are arranged in decreasing order of their reactivity.
Au < Cu < Fe < Mg is increasing order of reactivity.
The blue solution will become colourless and reddish-brown copper metal will be deposited.
⇒ \(\mathrm{Zn}(s)+\underset{\text { Blue }}{\mathrm{CuSO}_4(a q)} \longrightarrow \underset{\text { Colourless }}{\mathrm{ZnSO}_4(a q)}+\underset{\text { (reddish brown) }}{\mathrm{Cu}(s)}\)
Ag(s) + FeSO4(aq) → No reaction
The reaction will not take place because ‘Ag’ is less reactive than iron.
Question 11. An ore on heating in the air, gives sulphur dioxide gas. Name the method in each metallurgical step, that will be required to extract this metal from its ore.
State which of the following reactions will take place or not, giving the suitable reason for each.
Zn(s) + CuSO4(aq) → ZnSO4(aq) + Cu(s)
Fe(s) + ZnSO4(aq) → FeSO4(aq) + Zn(s)
Answer:
As the ore gives SO2 on heating, it is sulphide ore.
Steps of metallurgy:
Concentration of ore by froth floatation process.
Conversion of sulphide ore into oxide by roasting.
Conversion of metal oxide to metal either by heating along or by reduction with carbon.
Zn(s) + CuSO4(aq) → ZnSO4(aq) + Cu(s)
Yes, because Zn is more reactive than copper so will displace copper from the copper sulphate solution.
Fe(s) + ZnSO4(aq) →FeSO4(aq) + Zn(s)
No, because Fe is less reactive than Zn.
Question 12. How is the method of extraction of metals high up in the reactivity series different from that for metals in the middle? Why the same process cannot be applied to them? Explain giving equations, the extraction of sodium.
Answer:
Metals high up in the series are obtained by electrolytic reduction because these metals are strong reducing agents and therefore cannot be obtained by chemical reduction.
Metals in the middle of the series are less reactive and can be obtained by chemical reduction. The same process can’t be used for both of them as highly reactive metals can’t be obtained by chemical reduction.
Extraction of sodium is done by electrolysis of molten sodium chloride.
2 NaCl →(Electrolysis) → 2Na(s)+Cl2(g)
Question 13.
- Differentiate between roasting and calcination. Explain the two with the help of suitable chemical equations. How is zinc extracted from its ore?
- Name two metals that can be used to reduce metal oxides to metals.
Answer:
1.
Roasting: It is a process in which sulphide ore is heated in the presence of oxygen to convert it into oxide.
2ZnS+ 3O2→ 2ZnO + 2SO2
Calcination: It is a process in which carbonate ore is heated in the absence of air to form oxide.
ZnCO2(s) → (heat) → ZnO(s) + CO2(g)
By reduction process, Zn can be extracted from its ore.
Reduction. ZnO+C → Zn + CO2
2. Aluminium, Magnesium.
Metals and Non-Metals: NCERT Class 10 Science Key Concepts
Question 14.
- State two methods to prevent the rusting of iron.
- Name the ores of the following metals
- Mercury, and
- Zinc
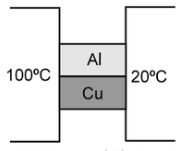
- Explain with the help of a diagram, how copper metal can be refined. Label the important arrangements in the experimental set-up.
Answer:
1.
- Painting
- Galvanisation
2.
- Cinnabar
- Zinc Blende
3. Impure copper is taken as an anode whereas pure copper is taken as a cathode. Copper sulphate solution (CuSO4) is taken as an electrolyte. When an electric current is passed, impure copper changes to ions which gain electrons at the cathode and change into pure copper. Impurities are left behind as anode mud.

At anode: Cu(s) → Cu2+ (aq) + 2e– Impure →
At cathode: Cu2+ (aq) + 2e– → Cu(s)(Pure)
Question 15.
1. What are amphoteric oxides? Give two examples.
2. State reasons for the following:
- Silver and copper lose their shine when they are exposed to air. Name the substance formed on their surface in each case.
- Tarnished copper vessels are cleaned with tamarind juice.
- Aluminium is more reactive than iron yet there is less corrosion of aluminium as compared to iron when both are exposed to air.
Answer:
Those oxides react with both acid as well as base to produce salt and water
Example: Al2O3, and ZnO.
- These metals get corroded. Silver forms black Ag2S (silver sulphide) and copper forms a greenish layer of basic copper carbonate CuCO3.Cu(OH)2.
- Tamarind contains acid which reacts with basic copper carbonate and the product gets dissolved and removed from the copper vessel.
- Aluminium forms an oxide layer on its surface which does not further react with air.
Question 16. Samples of four metals A, B, C, and D were taken and added to the following solution one by one. The results obtained have been tabulated as follows.

NCERT Solutions for Chapter 3: Metals and Non-Metals Detailed Explanation
Use the Table above to answer the following questions about metals A, B, C, and D.
- Which is the most reactive metal?
- What would you observe if B is added to a solution of Copper (II) sulphate?
- Arrange the metals A, B, C, and D in the order of decreasing reactivity.
Answer:
1. B is the most reactive metal. From the table, B can displace iron from its solution, but others cannot.
2. B is more reactive than iron which is more reactive than copper. Hence B is more reactive than copper and displaces copper from its solution.
3. Thus, one will observe that the blue colour of copper sulphate fades away and red-brown particles of copper settle at the bottom of the container.
B > A > C > D.
Question 17.
- Write the electron-dot structures for sodium, oxygen and magnesium.
- Show the formation of Na2O and MgO by the transfer of electrons.
- What are the ions present in these compounds?
Answer:
1. Electron-dot structures of sodium, oxygen and magnesium:

2.
Formation Of Na2O by The Transfer of electron:

Formation Of MgO by The Transfer of electron:

3.
- Sodium (Na) and Oxide ion (O2-) are present in Na, O.
- Magnesium ion (Mg2+) and Oxide ion (O2-)) are present in MgO.
Question 18. Define the terms:
- Mineral
- Ore
- Gangue
Answer:
1. Mineral:
The naturally occurring compounds of metals which are generally mixed with other matter such as soil, rocks and limestone are called minerals.
2. Ore:
The minerals which contain a high percentage of the metal and the metal can be extracted profitably, i.e., with low cost and minimum effort, are called ores.
3. Gangue:
The impurity of sand, rocking materials and other contaminations present in the ore is called gangue.
Question 19. What chemical process is used to obtain a metal from its oxide?
Answer:
A chemical process called reduction is used to obtain a metal from its oxide. Zinc oxide is reduced to metallic zinc by heating with carbon.
⇒ \(\mathrm{ZnO}(\mathrm{s})+\mathrm{C}(\mathrm{s}) \longrightarrow \mathrm{Zn}(\mathrm{s})+\mathrm{CO}(\mathrm{g})\)
Sometimes displacement processes can also be used. Highly reactive metals like sodium, calcium, aluminium, etc., are used as reducing agents because these displace metals of low reactivity from their compounds,
Example:
2Al(s) + Fe2O3(s) → (Heat)→ Fe(s) + Al2O3(S).
Question 20. Metallic oxides of zinc, magnesium and copper were heated with the following metals:

Answer:

Class 10 Science Chapter 3: Metals and Non-Metals Practice Questions
Question 21. Give reasons
- Platinum, gold and silver are used to make jewellery.
- Sodium, potassium and lithium are stored under oil.
- Aluminium is a highly reactive metal, yet it is used to make utensils for cooking.
- Carbonate and sulphide ores are usually converted into oxides during the process of extraction.
Answer:
- Because Pt, Au and Ag do not react with SO2, CO2 and H2S gas present in the air and hence their glow is retained.
- Sodium, potassium and lithium are stored under oil because they vigorously react with oxygen in the air and even catch fire.
- Yes, aluminium is a reactive metal, still, it is being used to make utensils for cooking. This is because aluminium forms a non-reactive layer of aluminium oxide which resists spoiling any food material.
- Carbonate and sulphide ores are usually converted into oxides during the process of extraction because it is easier to obtain a metal from its oxide as compared to its carbonates and sulphides.
Question 22. Differentiate between metal and non-metal based on their chemical properties.
Answer:
Difference between metals and non-metals based on chemical properties.

Question 23.
- Show the formation of MgO by the transfer of electrons.
- Name the cation and the anion.
- Write three properties of ionic compounds.
Answer:
1.

2.
- Cation is positively charged [Mg2+]
- Anion is negatively charged (O2-).
3. A solution of ionic compounds contains ions since electricity conduction requires the movement of charged particles that conduct electricity.
- Soluble in water.
- Good conductor of electricity in a molten state and aqueous solution.
- High melting and boiling points.
Question 24. Differentiate between roasting and calcination.
Answer:
Differentiate between roasting and calcination

Question 25. Name the ore of mercury. How is mercury extracted from its ore?
Answer:
HgS-Cinnabar.
First, HgS is converted into HgO.

Then, HgO is reduced to mercury on further heating.

Question 26. State reasons for the following
- Metals conduct electricity.
- Non-metals in general do not displace hydrogen from dilute acids.
- Aluminium easily combines with oxygen but still it can be used for making kitchen utensils.
Answer:
1. Metals have electrons which are free to move.
2. A non-metal is an electron acceptor. It cannot supply electrons to H+ ions. Hydrogen can only be displaced from dilute acids if electrons are supplied to the H+ ions of the acid. The layer of aluminium oxide formed prevents the metal from further oxidation.
Question 27. A metal ‘X’ acquires a green colour coating on its surface on exposure to air.
- Identify the metal ‘X’ and name the process responsible for this change.
- Name and write the chemical formula of the green coating formed on the metal.
- List two important methods to prevent the process.
Answer:
Metal is copper. The process is corrosion.
Basic copper carbonate [CuCO3.Cu(OH)2]
It should be coated with tin.
It should be mixed with other metals to form alloys.
Question 28. Differentiate between metals and non-metals based on their chemical properties.
Answer:
Differentiate between metals and non-metals based on their chemical properties

NCERT Class 10 Science Chapter 3: Metals and Non-Metals Review
Question 29. Write balanced chemical equations for the following reactions:
- Dilute sulphuric acid reacts with aluminium powder.
- Dilute hydrochloric acid reacts with sodium carbonate.
- Carbon dioxide is passed through lime water.
Answer:
⇒ \(2 \mathrm{Al}(s)+3 \mathrm{H}_2 \mathrm{SO}_4(\text { dil. }) \longrightarrow \mathrm{Al}_2\left(\mathrm{SO}_4\right)_3(a q)+3 \mathrm{H}_2(\mathrm{~g})\)
⇒ \(\mathrm{Na}_2 \mathrm{CO}_3(\mathrm{~s})+2 \mathrm{HCl}(\text { dil. }) \longrightarrow 2 \mathrm{NaCl}(a q)+\mathrm{H}_2 \mathrm{O}(l)+\mathrm{CO}_2(g)\)
⇒ \(\underset{\text { Lime water }}{\mathrm{Ca}(\mathrm{OH})_2(a q)}+\mathrm{CO}_2(\mathrm{~g}) \longrightarrow \underset{\text { (White ppt.) }}{\mathrm{CaCO}_3(\mathrm{~s})}+\mathrm{H}_2 \mathrm{O}(l)\)
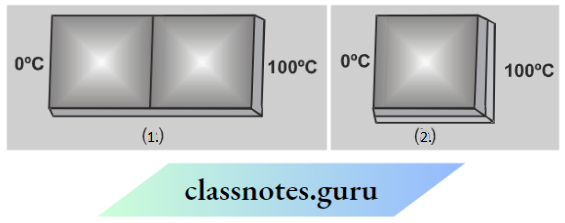
Question 30. Observe the two test tubes A and B in the diagram given below and answer the following questions

- In which test tube will the reaction take place?
- Write a balanced equation for the reaction.
- Name the type of reaction.
Answer:
In the first test tube, the reaction will take place.
Fe(s) + CuSO4(aq) → FeSO4(aq) + Cu(s)
Displacement reaction
Question 31. What is meant by the reactivity series of metals? State which of the following chemical reactions will take place giving the suitable reason for each.
- Zn(s) + CuSO4(aq) → ZnSO4(aq) + Cu(s)
- Fe(s) + ZnSO4(aq) → FeSO4(aq) + Zn(s)
- Zn(s) + FeSO4(aq) → ZnSO4(aq) + Fe(s)
Answer:
- A reactivity series is a series of metals arranged in the order of their decreasing reactivities (activities).
- The reaction will take place because Zn is above Cu in the activity series and is more reactive than Cu.
- The reaction will not take place as Fe is below Zn in the activity series and cannot displace Zn from its solution.
- The reaction will take place because Zn is more reactive than Fe.
Question 32. Iqbal treated a lustrous, divalent element M with sodium hydroxide. He observed the formation of bubbles in the reaction mixture. He made the same observations when this element was treated with hydrochloric acid. Suggest how can he identify the produced gas. Write chemical equations for both reactions.
Answer:
As the element is lustrous, it must be a metal. As it is divalent and reacts with NaOH with the formation of bubbles of a gas (H2 gas), it must be zinc. Further, zinc also reacts with HCl acid with the evolution of the same gas H2.
The gas can be identified by bringing a lighted candle near it when it burns with a popping sound. The reactions taking place are as follows:
⇒ \(\underset{\text { Zinc }}{\mathrm{Zn}}+\underset{\text { Sodium hydroxide }}{2 \mathrm{NaOH}} \longrightarrow \underset{\text { Sodium zincate }}{\mathrm{Na}_2 \mathrm{ZnO}_2}+\underset{\text { Hydrogen gas }}{\mathrm{H}_2}\)
⇒ \(\underset{\text { Zinc }}{\mathrm{Zn}}+\underset{\text { Hydrochloric acid }}{2 \mathrm{HCl}} \longrightarrow \underset{\text { Zinc chloride }}{\mathrm{ZnCl}_2}+\underset{\text { Hydrogen gas }}{\mathrm{H}_2}\)
Question 33. You are given a hammer, a battery, a bulb, wires and a switch.
- How could you use them to distinguish between samples of metals and non-metals?
- Assess the usefulness of these tests in distinguishing between metals and non-metals.
Answer:
1.
- On hammering the metals and non-metals, metals would give thin sheets whereas non-metals would break down into pieces.
- Using a bulb, a battery, wires a switch, etc., given, an arrangement of the type shown in the figure will be made.

When the sample of metals and non-metals is inserted one by one between the clips and switch is made on. The bulb will glow when the metal is inserted, whereas the bulb will not glow in the case of non-metal.
2. Method A seems to be quite authentic in making a difference between metals and non-metals.
Question 34. An alkali metal A gives a compound B (molecular mass = 40) on reacting with water. The compound B gives a soluble compound C on treatment with aluminium oxide. Identify A, B, and C and give the reaction involved.
Answer:
⇒ \(\underset{\begin{array}{c}
\text { Sodium } \\
\text { (Alkalimetal) }
\end{array}}{2 \mathrm{Na}}+\underset{\text { (B) }}{2 \mathrm{H}_2 \mathrm{O}} \longrightarrow \underset{\begin{array}{c}
\text { Sodium hydroxide } \\
\text { (Mol. mass }=40 \text { ) }
\end{array}}{2 \mathrm{NaOH}}+\mathrm{H}_2\)
⇒ \(\underset{(\mathrm{B})}{2 \mathrm{NaOH}}+\underset{\begin{array}{c}
\text { Aluminium } \\
\text { oxide }
\end{array}}{\mathrm{Al}_2 \mathrm{O}_3} \longrightarrow \underset{\begin{array}{c}
\text { Sodium aluminate } \\
\text { (Soluble in water) }
\end{array}}{2 \mathrm{NaAlO}_2(a q)}+\mathrm{H}_2 \mathrm{O}(l)\)
Question 35. Give the reaction involved during the extraction of zinc from its ore by
- Roasting of zinc ore
- Calcination of zinc ore
Answer:
1. \(\underset{\text { Zinc sulphide }}{2 \mathrm{ZnS}(\mathrm{s})}+\underset{\text { From air }}{3 \mathrm{O}_2(\mathrm{~g})} \frac{\text { Heat }}{\begin{array}{c}
\text { Presence of excess } \\
\text { of air }
\end{array}} \underset{\text { Zinc oxide }}{2 \mathrm{ZnO}(\mathrm{s})}+\underset{\text { Sulphur dioxide }}{2 \mathrm{SO}_2(\mathrm{~g})}\)
2. \(\underset{\text { Zinc carbonate }}{\mathrm{ZnCO}_3(s)} \frac{\text { Heat }}{\text { Absence of air }} \underset{\text { Zinc oxide }}{\mathrm{ZnO}(s)}+\underset{\text { Carbon dioxide }}{\mathrm{CO}_2(g) \uparrow}\)
NCERT Class 10 Science: Metals and Non-Metals – Important Notes
Question 36. A non-metal A which is the largest constituent of air, when heated with H2 in a 1:3 ratio in the presence of catalyst (Fe) gives a gas B. On heating with O, it gives an oxide C. If this oxide is passed into water in the presence of air it gives an acid D which acts as a strong oxidising agent.
- Identify A, B, C, and D
- To which group of the periodic table does this non-metal belong?
Answer:
A = N2 (Nitrogen)
B = NH3 (ammonia)
C = NO (Nitrogen oxide)
D = HNO3 (Nitric acid)
Element A belongs to group 15 of the periodic table.
Question 37. Give the steps involved in the extraction of metals of low and medium reactivity from their respective sulphide ores.
Answer:

Question 38. Explain the following
- The reactivity of Al decreases if it is dipped in HNO3
- Carbon cannot reduce the oxides of Na or Mg
- NaCl is not a conductor of electricity in a solid state whereas it does conduct electricity in an aqueous solution as well as in a molten state
- Iron articles are galvanised
- Metals like Na, K, Ca and Mg are never found in their free state in nature
Answer:
- Due to the formation of a layer of oxide i.e., Al2O3.
- Na or Mg are more reactive metals as compared to carbon.
- In solid NaCl, the movement of ions is not possible due to its rigid structure but in aqueous solution or molten state, the ions can move freely.
- To protect from corrosion
- They are highly reactive
Question 39.
1. Given below are the steps for the extraction of copper from its ore. Write the reactions involved.
- Roasting of copper sulphide(l)
- Reduction of copper oxide with copper(1) sulphide(l)
- Electrolytic refining
2. Draw a neat and well-labelled diagram for electrolytic refining of copper.
Answer:
1.
1. Roasting of sulphide ore
2. 2Cu2S(s) + 3O2(S) → (Heat)→ 2Cu2O(S) + 2SO2(g)
2Cu2O+ CuS → (Heat)→ 6Cu(s) + SO2(g)
This reaction is known as auto-reduction.
3. Reaction for electrolytic refining
At cathode: \(\mathrm{Cu}^{2+}(a q)+2 \mathrm{e}^{-} \longrightarrow \mathrm{Cu}(s)\)
At anode: \(\mathrm{Cu}(s) \longrightarrow \mathrm{Cu}^{2+}(a q)+2 e^{-}:\)
2. Diagram for electrolytic refining of copper

Question 40. Two ores A and B were taken. On heating ore A gives CO2, whereas, ore B gives SO What steps will you take to convert them into metals?
Answer:
Ore A is the carbonate of any metal (MCO). It can be converted into metal by calcination followed by smelting or electrolytic reduction depending upon the nature of a metal.
MCO(s) → (Heat)→ MO(s)+CO↑ (Calcination)
MO(s)+C → (Heat)→ M(s)+CO↑ (Reduction)
Ore of B is any metal sulphate. To obtain the metal from this ore, first roasting then reduction is done.
Reduction
Reaction → 2MS (s) + 3O2(g) → 2MO (s) + 2SO2 (g)
MO (s) + C (s) M (s) → CO (g)
Question 41. Explain the following
- The reactivity of Al decreases if it is dipped in HNO3.
- Carbon cannot reduce the oxides of Na or Mg.
- NaCl is not a conductor of electricity in a solid state whereas it does conduct electricity in an aqueous solution as well as in a molten state.
- Iron articles are galvanized.
Answer:
When Al metal reacts with HNO3, Al2O3 is formed which further gets deposited on aluminium metal. Hence, more Al metal is not available for the reaction because the Al2O3 layer is passive.
Na and Mg both metals are very reactive. These metals have more affinity towards oxygen than carbon. Hence, carbon cannot reduce the oxides of these metals.
In NaCl, ions are responsible for the conduction of electricity. In a solid state, ions are strongly held by the electrostatic force of attraction and are not free to move. In an aqueous state or molten state, ions are free to move so conduction of electricity takes place.
Galvanization is a process to protect the iron from rusting. Iron articles get rusted when come in contact with air and moisture.
Question 42. A non-metal A is an important constituent of our food and forms two oxides B and C. Oxide B is toxic whereas C causes global warming.
- Identify A, B, and C.
- To which group of the periodic table does A belong?
Answer:
As per the given information, non-metal A is carbon. It is an important constituent of our food (like carbohydrates, fat, protein). It forms two oxides-carbon monoxide which is toxic and carbon dioxide which in excess causes global warming.
A = Carbon (C)
B = Carbon monoxide (CO)
C = Carbon dioxide (CO2)
A belongs to 14 groups of the periodic table
6C = 2.4
Group Number = Valence e+ 10 (for non-metals) = 4 + 10 = 14
Question 43. Nidhi and Nishi were visiting Qutub Minar along with their classmates. After seeing Qutub Minar, they went to see an iron pillar nearby. Nidhi said to Nishi, “Look this pillar was made around 400 BC as history says. But this has not rusted. What could be the technology behind this?” Nishi replied, “Yes this is amazing. Let us ask madam, how could the technicians of that era make such a wonder.”
- What possibly was stated by Madam to the queries of Nidhi and Nishi?
- How do the electrical conductivity and melting point of metals change when they are mixed to form an alloy?
Answer:
A thin layer of magnetic oxide was formed on the surface as a result of the finishing treatment given to the pillar. The pillar was painted with a mixture of different salts and then heated and quenched.
The electrical conductivity and melting point decrease on alloying the metals.
Question 44. Pratyush took sulphur powder on a spatula and heated it. He collected the gas evolved by inverting a test tube over it, as shown in the figure.

1. What will be the action of gas on
- Dry litmus paper?
- Moist litmus paper?
2. Write a balanced chemical equation for the reaction taking place.
Answer:
1.
- No action on dry litmus paper.
- Moist litmus paper becomes red as the gas is acidic.
2. The balanced equation for the reaction taking place:
⇒ \(\underset{\text { Sulphur }}{\mathrm{S}}+\underset{\text { Oxygen }}{\mathrm{O}_2(g)} \longrightarrow \underset{\begin{array}{c}
\text { Sulphur } \\
\text { dioxide }
\end{array}}{\mathrm{SO}_2}\)
Question 45. A jeweller made jewellery of 22-carat gold and also charged his customers the rate of
- Why can’t we make jewellery out of 24-carat gold?
- Name two metals that can be added to make gold jewellery.
- What value of the jeweller is seen in the above act?
Answer:
- Pure 24-carat gold is very soft and cannot retain the shape and design given to it while making the jewellery. Hence it is not advised to make use of 24-carat gold jewellery.
- Copper and silver can be added to gold to make it strong and use it for making jewellery designs.
- Jeweller is showing the value of honesty and faithfulness.
NCERT Solutions for Metals and Non-Metals: Chemical Properties and Applications
Question 46. A group of students presented a speech in the school assembly on “How to minimize the use of heavy metals?” They told how mercury thermometers when broken and thrown away in the garbage lead to soil and underground water pollution. They also showed how cadmium and lead also cause dangerous health problems.
- Name two heavy metals that are present in the mobile batteries.
- Name the disease caused due to mercury entering into our food chain.
- What value of the group of students is reflected above?
Answer:
- Lead and cadmium are used in the mobile batteries.
- Mercury causes Minamata disease.
- The students showed the value of group work, cooperative learning, concern for nature and responsible behaviour.
Question 47. The use of aluminium foil occurs during lunch breaks. Eco-club suggests minimising the use of foils and rests all ensured to put it into dustbin for recycling.
- Why is aluminium metal used for making foils?
- Give one more use of aluminium metal with its quality being utilised in that use.
- What values did eco-club members show?
Answer:
- Aluminium metal is a very malleable metal and can be drawn into thin sheets. It also forms a protective layer of aluminium oxide which does not allow the foil to react with food.
- Aluminium is a good conductor of electricity and is very ductile metal, it can be drawn into thin wires.
- Eco-club members showed the value of group work, collaborative approach and aware and responsible citizens.