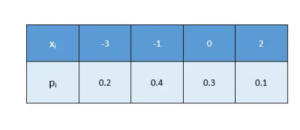
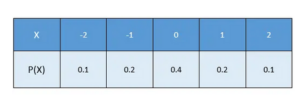
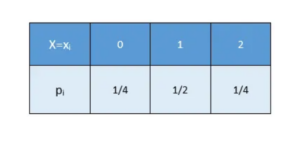
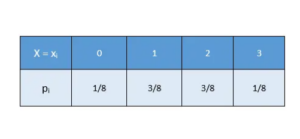
Relations And Functions
Relations And Functions Exercise 1A Review Of Facts And Formulae
1. A relation R in a set A is a subset of A x A
If (a, b) ∈ R, then a R b.
If (a, b) ∉ R, then a is not related to b.
Domain (R) = {a: (a, b) ∈ R] and Range (R) = {b: (a, b) ∈ R}.
2. Let R be a relation on a non-empty set A. Then, R is said to be:
1. Reflexive, if (a, a) ∈ R for each a ∈ A
i.e., if a R a for each a ∈ R.
2. Symmetric, if (a, b) ∈ R ⇒ (b, a) ∈ R
i.e., a R b ⇒ b Ra
3. Transitive, if (a, b) e R and (b, c)e R ⇒ (a, c) ∈ R
Read and Learn More WBCHSE Solutions For Class 12 Maths
i.e., a R b, b R c ⇒ a R c.
3. A relation R on a set A is said to be an equivalence relation if it is reflexive, symmetric, and transitive.
4. Equivalence class, determined by an element a is defined as a
⇒ [a] = [b ∈ A : (a, b) ∈ R}
Relations And Functions Exercise 1A Multiple Choice Questions
Question 1. Let A = {1, 2, 3} and let R = {(1, 1), (2, 2), (3, 3), (1, 3), (3, 2), (1, 2)}. Then, R is
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- Symmetric and transitive but not reflexive
- An equivalence relation
Answer: 2. Reflexive and transitive but not symmetric
R is reflexive and transitive but not symmetric
Question 2. Let A = {a, b, c} and let R= {(a, a), (a, b), (b, a)}. Then, Ris
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- Symmetric and transitive but not reflexive
- An equivalence relation
Answer: 3. Symmetric and transitive but not reflexive
R is symmetric and transitive but not reflexive
Question 3. Let A = {1,2, 3} and let R= {(1,1), (2, 2), (3, 3), (1, 2), (2, 1), (2, 3), (3, 2)}. Then, R is
- Reflexive and symmetric but not transitive
- Symmetric and transitive but not reflexive
- Reflexive and transitive but not symmetric
- An equivalence relation
Answer: 1. Reflexive and symmetric but not transitive
(1,2)∈ R and (2,3) ∈ R, But, (1,3) ∉ R So, R is not transitive.
Question 4. Let S be the set of all straight lines in a plane. Let R be a relation on S Defined by a R b ⇔ a ⊥ b. Then, R is
- Reflexive but neither symmetric nor transitive
- Symmetric but neither reflexive nor transitive
- Transitive but neither reflexive nor symmetric
- An equivalence relation
Answer: 2. Symmetric but neither reflexive nor transitive
a ⊥ b is not true. So R is not reflexive
a ⊥ b and b ⇒ b ⊥ a is always true.
Question 5. Let S be the set of all straight lines in a plane. Let R be a relation on S Defined by a R b ⇔ a || b. Then, R is
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- Symmetric and transitive but not reflexive
- An equivalence relation
Answer: 4. An equivalence relation
Question 6. Let Z be the set of all integers and let R be a relation on Z defined by a R b o (a-b) is divisible by 3. Then, R is
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- Symmetric and transitive but not reflexive
- An equivalence relation
Answer: 4. An equivalence relation
Question 7. Let R be a relation on the set N of all natural numbers, defined by a R b ⇔ a is a factor of b. Then, R is
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- Symmetric and transitive but not reflexive
- An equivalence relation
Answer: 2. Reflexive and transitive but not symmetric
Question 8. Let Z be the set of all integers and let R be a relation on Z defined by a R b ⇔ a>b. Then, R is
- Symmetric and transitive but not reflexive
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- An equivalence relation
Answer: 3. Reflexive and transitive but not symmetric
Question 9. Let S be the set of all real numbers and let R be a relation on S defined by a R b ⇔ IaI ≤ b. Then, R is
- Reflexive but neither symmetric nor transitive
- Symmetric but neither reflexive nor transitive
- Transitive but neither reflexive nor symmetric
- None of these
Answer: 3. Transitive but neither reflexive nor symmetric
⇒ I-3I ≤ -3 is not true. So, R is not reflexive.
⇒ I-1I ≤ 1 ⇒ (-1) R1. But I-1I ≤ 1 is not true.
∴ R is not symmetric
3. a R b, b R c ⇒ IaI ≤ b and IbI ≤ c ⇒ IaI ≤ c.
Question 10. Let S be the set of all real numbers and let R be a relation on S, defined by a R b ⇔ Ia-bI ≤ 1. Then, R is
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- Symmetric and transitive but not reflexive
- An equivalence relation
Answer: 1. Reflexive and symmetric but not transitive
⇒ Ia- aI = 0 ≤ 1 is always true.
⇒ a R b ⇒ Ia- b I≤1 ⇒ I-(a-b)I<1 ⇒ Ib-aI <1 ⇒ b R a.
⇒ 2 R 1 and 1 R \(\frac{1}{2}\).
But, 2 is not related to \(\frac{1}{2}\). So, R is not transitive.
Question 11. Let S be the set of all real numbers and let R be a relation on S, defined by a R b ⇔(1 + ab) > 0. Then, R is
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- Symmetric and transitive but not reflexive
- None of these
Answer: 1. Reflexive and symmetric but not transitive
a R a, since (1 + a2) > 0.
a R b ⇒ (1 + ab) > 0 ⇒ (1 + ba) > 0 ⇒b R a.
Let a = \(\frac{-1}{2}\), b = \(\frac{-1}{2}\) and c = R.
Then, a R b and b R c. But, a is not related to c.
Question 12. Let S be the set of all triangles in a plane and let R be a relation on S defined by Δ1S Δ2 ⇔ Δ1 ≡ Δ2. Then, R is
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- Symmetric and transitive but not reflexive
- An equivalence relation
Answer: 4. An equivalence relation
Question 13. Let S be the set of all real numbers and let R be a relation on S defined by a R b ⇔ a2 + b2 = 1. Then, R is
- Symmetric but neither reflexive nor transitive
- Reflexive but neither symmetric nor transitive
- Transitive but neither reflexive nor symmetric
- None of these
Answer: 1. Symmetric but neither reflexive nor transitive
(l2 + 12) ≠ 1. So,1 R 1 is not true.
a R b ⇒ a2+ b2 =1 ⇒ b2 + a2 =1 ⇒ b R a.
1 R 0 and 0 R 1. But,1 is not related to 1.
Question 14. Let JR be a relation on N x N, defined by (a, b) R (c, d)⇔ a+d= b+ c. Then, R is
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- Symmetric and transitive but not reflexive
- An equivalence relation
Answer: 4. An equivalence relation
Question 15. Let A be the set of all points in a plane and let O be the origin. Let R = {(P, Q): OP= OQ}. Then, R is
- Reflexive and symmetric but not transitive
- Reflexive and transitive but not symmetric
- Symmetric and transitive but not reflexive
- An equivalence relation
Answer: 4. An equivalence relation
Question 16. Let Q be the set of all rational numbers and * be the binary operation, defined by a * b = a + 2b, then
- * is commutative but not associative
- * is associative but not commutative
- * is neither commutative nor associative
- * is both commutative and associative
Answer: 3. * is neither commutative nor associative
Question 17. Let a * b = a + ab for all a, b ∈ Q. Then,
- * Is not a binary composition
- * Is not commutative
- * Is commutative but not associative
- * Is both commutative and associative
Answer: 2. * Is not commutative
Question 18. Let Q+ be the set of all positive rationals. Then, the operation * on Q+ defined by a * b \(=\frac{a b}{2}\) for all a, b ∈ Q+ is
- Commutative but not associative
- Associative but not commutative
- Neither commutative nor associative
- Both commutative and associative
Answer: 4. Both commutative and associative
Question 19. Let Z be the set of all integers and let a*b = a – b + ab. Then, * is
- Commutative but not associative
- Associative but not commutative
- Neither commutative nor associative
- Both commutative and associative
Answer: 3. Neither commutative nor associative
Question 20. Let Z be the set of all integers. Then, the operation * on Z defined by a*b= a + b – ab is
- Commutative but not associative
- Associative but not commutative
- Neither commutative nor associative
- Both commutative and associative
Answer: 4. Both commutative and associative
Question 21. Let Z+be the set of all positive integers. Then, the operation * on Z+ defined by a * b = ab is
- Commutative but not associative
- Associative but not commutative
- Neither commutative nor associative
- Both commutative and associative
Answer: 3. Neither commutative nor associative
Question 22. Define * on Q- {-1} by a * a+ b+ ab. Then, * on Q- {-1} is
- Commutative but not associative
- Associative but not commutative
- Neither commutative nor associative
- Both commutative and associative
Answer: 4. Both commutative and associative
Relations And Functions Exercise 1B Review Of Facts And Formulae
1. Function: Let A and B be two non-empty sets. Then, a rule / which associates to each x e A, a unique element fix) of B, is called a function from A to B, and we write, \(f\): A → B.
Dom (f) = {x ∈ A :f(x) ∈ B}, range (f)= {f(x): x ⇒ A}.
2. Let f: A→ B. Then
⇒ f is one-one ⇔ {f(x1) =f(x2) ⇒ x1 = x2}
⇒ f is onto ⇔ range (f) = B.
3. Two functions/ and g are said to be equal if they have the same domain and f(x)=g(x) ∀ x.
4. Invertible functions: A function is said to be invertible if/is one-one and
onto.f{x) = y ⇒ f-1(y) = x.
5. Composite of two functions:
⇒ Let/: A → B and g: B→ C, then g o f: A → C is called the composite of f and g.
⇒ Dom (g o f) = dom (f)
g o f is defined only when range (f) ⊆ dom (g)
⇒ Dom (f o g) = dom(g).
f o g is defined only when range (g) ⊆ dom (f)
Relations And Functions Exercise 1B Multiple Choice Questions
Question 1. f : N → N : f(x) = 2x is
- One-one and onto
- One-one and into
- Many-one and onto
- Many-one and into
Answer: 2. One-one and into
⇒ 2x = 3
⇒ x = \(\frac{3}{2}\)
∴ f is into.
Question 2. f : N → N : f(x) = x2+ x+1 is
- One-one and onto
- One-one and into
- Many-one and onto
- Many-one and into
Answer: 2. One-one and into
⇒ f(x1) = f(x2)
= x21+x1 +1
= x22+x2 +1
= (x21– x22) + (x1-x2) = 0
⇒ (x1-x2)(x1+x2+1) = 0
= x1– x2= 0
= x1 = x2.
∴ f is one-one.
f(x) =1 ⇒ x2+ x+1 =1 ⇒ x(x+ 1) = 0 ⇒ x= 0 or x=-1.
And, none of 0 and -1 is in N. So, f is into.
Question 3. f: R→ R : f(x) = x2 is
- One-one and onto
- One-one and into
- Many-one and onto
- Many-one and into
Answer: 4. Many-one and into
Question 4. f: R→ R : f(x) = x3 is
- One-one and onto
- One-one and into
- Many-one and onto
- Many-one and into
Answer: 1. Many-one and into
Question 5. f : R+→+R+: f(x) = ex is
- Many-one and into
- Many-one and onto
- One-one and into
- One-one and onto
Answer: 4. One-one and onto
⇒ f(x1) = f(x2) => ex1 = ex2
⇒ x1 = x2
∴ f is one-one.
For each x ∈ R+ ∃ log x ∈ R+ s.t. f(log x)= x.
So,/is onto.
Question 6. \(f:\left[\frac{-\pi}{2}, \frac{\pi}{2}\right] \rightarrow[-1,1]: \) f(x) = sin x is
- One-one and into
- One-one and onto
- Many-one and into
- Many-one and onto
Answer: 2. One-one and onto
Question 7. f : R → R :f(x) = cos x is
- One-one and into
- One-one and onto
- Many-one and into
- Many-one and onto
Answer: 3. Many-one and into
Cos (2π- θ) = cos θ ⇒ f is Many-one.
Range (f) = [-1, 1] ⊂ R => f is into.
Question 8. f : C→ R : f(z) = IzI is
- One-one and into
- One-one and onto
- Many-one and into
- Many-one and onto
Answer: 3. Many-one and into
i ≠-i. But f(i) = f(-i)=1. So, fis many-one.
-1 ∈ R having no pre-image in C. So, fis into.
Question 9. Let A = R- {3} and B =R- {1}. Then f: A → B : f(x) = \(\frac{(x-2)}{(x-3)}\) is
- One-one and into
- One-one and onto
- Many-one and into
- Many-one and onto
Answer: 2. One-one and onto
⇒ f(x1)= f(x2)
⇒ \(\frac{\left(x_1-2\right)}{\left(x_1-3\right)}=\frac{\left(x_2-2\right)}{\left(x_3-3\right)}\)
⇒ x1= x2, So f is one one.
Let \(\frac{x-2}{x-3}\). Then, x\(=\frac{3 y-2}{y-1}\). Clearly y ≠1 and x≠3
Question 10. Let f: N → N: f(n)=
\(\frac{1}{2}\)(n+1) when n is odd
\(\frac{n}{2}\),when n is even
- One-one and into
- One-one and onto
- Many-one and onto
- Many-one and into
Answer: 4. Many-one and into
f (1) = f(2) shows that/is many-one.
If n is odd, then (2n- 1) is odd, and f(2n- 1) =n.
If n is even, then 2n is even, and f (2n) = n.
∴ f is onto.
Question 11. Let A and B be two non-empty sets and let f: (A x B) → (B x A): f(a, b) = (b, a). Then, f is
- One-one and onto
- One-one and into
- Many-one and onto
- Many-one and into
Answer: 1. One-one and onto
Question 12. Let f: Q→ Q: f(x) = (2x + 3). Then,f-1(y) = ?
- (2y- 3)
- \(\\)
- \(\frac{1}{2}\)(y-3)
- None of these
Answer: 3. \(\frac{1}{2}\)(y-3)
y = 2x+3
x = \(\frac{1}{2}(y-3)\)
⇒ \(f^{-1}(y)=\frac{4 y}{(4-3 y)}\)
Question 13.\(\text { Let } f: R-\left\{\frac{-4}{3}\right\} \rightarrow R-\left\{\frac{4}{3}\right\}: f(x)=\frac{4 x}{(3 x+4)} \text {. Then, } f^{-1}(y)=\text { ? }\)
- \(\frac{4 y}{(4-3 y)}\)
- \(\frac{4 y}{(4+3 y)}\)
- \(\frac{4 y}{(3 y-4)}\)
- None of these
Answer: 1. \(\frac{4 y}{(4-3 y)}\)
⇒ \(y\frac{4 x}{3 x+4}\)
⇒ \(x\frac{4 y}{(4-3 y)}\)
⇒ \(f^{-1}(y)=\frac{4 y}{(4-3 y)}\)
Question 14. Let f : N→X : f(x) = 4x2 + 12x+ 15. Then f-1(y) =?
- \(\frac{1}{2}(\sqrt{y-4}+3)\)
- \(\frac{1}{2}(\sqrt{y-6}-3)\)
- \(\frac{1}{2}(\sqrt{y-4}+5)\)
- None of these
Answer: 2. \(\frac{1}{2}(\sqrt{y-6}-3)\)
y = 4x2 +12x+15
= (2x+3)2 +6
⇒ \(x\frac{1}{2}(\sqrt{y-6}-3)\)
⇒ \(f^{-1}(y)=\frac{1}{2}(\sqrt{y-6}-3)\)
Question 15. \(\text { If } f(x)=\frac{(4 x+3)}{(6 x-4)}, x \neq \frac{2}{3} ; \text { then }(f \circ f)(x)=\text { ? }\)
- x
- (2x-3)
- \(\frac{4 x-6}{3 x+4}\)
- None of these
Answer: 1. x
f(x)= \(\frac{4 x+3}{6 x-4}\) = y(say)
Then f(y)= \(\frac{4 y+3}{6 y-4}\)
= \(=\frac{4\left(\frac{4 x+3}{6 x-4}\right)+3}{6\left(\frac{4 x+3}{6 x-4}\right)-4}\)
= \(=\frac{34 x}{34}\)
= x
⇒ f[f(x)] = x ⇒ (f o f) (x) = x
Question 16. If f(x) = (x2 — 1) and g(x) = (2x + 3), then (g o f)(x) = ?
- (2X2+ 3)
- (3X2 + 2)
- (2x2 + 1)
- None of these
Answer: 3. (2x2+ 1)
(g o f )(x) = g [f(x)] = g(x2-1)
= 2(x2-1)+3 = (2x2+1)
Question 17. \(\text { If } f\left(x+\frac{1}{x}\right)=x^2+\frac{1}{x^2}, \text { then } f(x)=?\)
- x2
- x-1
- x-2
- None of these
Answer: 3. x-2
Let \(x+\frac{1}{x}\)= z Then,
f(z) = \(f\left(x+\frac{1}{x}\right)=\left(x^2+\frac{1}{x^2}\right)=\left(x+\frac{1}{x}\right)^2-2\)= (z-2)
f(z)= (x2-2)
Question 18. \(\text { If } f(x)=\frac{1}{(1-x)^{\prime}} \text {, then }(f \circ f \circ f)(x)=\text { ? }\)
- \(\frac{1}{(1-3 x)}\)
- \(\frac{x}{(1+3 x)}\)
- x
- None of these
Answer: 3. x
(f o f)(x) = f{f(x)}
= \(f\left(\frac{1}{1-x}\right)=\frac{1}{\left(1-\frac{1}{1-x}\right)}\)
= \(\frac{1-x}{-x}=\frac{x-1}{x}\)
{f o(f o f)}(x) ={f o(f o f)(x)}]= \(=f\left(\frac{x-1}{x}\right)=\frac{1}{1-\frac{x-1}{x}}=x1/3\)
Question 19. \(\text { If } f(x)=\sqrt[3]{3-x^3}, \text { then }(f \circ f)(x)=\text { ? }\)
- x1/3
- x
- (1-x1/3)
- None of these
Answer: 2. x
(fof)(x) =f{f(x)}- {(3- x3) 1/3} = f/(y), where y= (3- x3) 1/3
= (3- y3)1/3= [3- {3- x3}]1/3= (x3)1/3= x
Question 20. If f(x) = x2– 3x + 2, then (f o f)(x) = ?
- x
- x4-6x3
- x4– 6x3+10x2
- None of these
Answer: 4. None of these
(fof)(x) =f{f(x)} =f{x2– 3x + 2) =f(y), where y= (x2– 3x+ 2)
= y2– 3y+ 2= (x2– 3x+ 2)2– 3(x2– 3x+ 2) + 2= (x4– 6x3 + 10x2– 3x).
Question 21. If f(x) = 8x3 and g(x) = x1/3, then (g o f)(x) = ?
- x
- 2x
- \(\frac{x}{2}\)
- 3×2
Answer: 2. 2x
(g of)(x) = g{f(x)] = g(8x3) = (8x3)1/3= 2x.
Question 22. If f (x) = x2, g(x) = tan x and h(x) = log x, then {ho(gof}}\(\left(\sqrt{\frac{\pi}{4}}\right)\)
- 0
- 1
- \(\frac{1}{x}\)
- \(\frac{1}{2} \log \frac{\pi}{4}\)
Answer: 1. 0
{ho(g o f)}(x) = (ho g){f(x)} = (h o g)(x2)
= h{g(x2)} = h(tan x2) = log(tan x2)
∴ \(\{h \circ(g \circ f)\} \sqrt{\frac{\pi}{4}}=\log \left(\tan \frac{\pi}{4}\right)\)
= log 1
= 0
Question 23. If/= {(1, 2), (3, 5), (4, 1)} andg= {(2, 3), (5, 1), (1, 3)}, then (g o f) = ?
- {(3,1), (1,3), (3, 4)}
- {(1,3), (3, 1), (4, 3)}
- {(3,1), (1,3), (3, 4)}
- {(2, 5), (5, 2), (1,5)}
Answer: 2. {(1,3), (3, 1), (4, 3)}
⇒ Dom (gof) = Dom (f) = {1, 3, 4}
⇒ (g o f )(l) =g{f(l)} = g(2) = 3,(g of)(3) =g{f(3)} =g(5) =1
⇒ (g o f)(4) = g[f(4)) =g(1) = 3
⇒ g o f= {(1/3), (3, 1), (4, 3)}.
Question 24. Let/(x) = \(\sqrt{9-x^2}\). Then, dom (f) =?
- [-3, 3]
- (-∞, -3]
- [3, ∞)
- (-∞, -3] u (4, ∞)
Answer: 1. [-3, 3]
f(x) is defined only when 9- x2 > 0 => x2 <9 =» -3 < x < 3.
∴ Dom (f) = [-3, 3].
Question 25. Let f(x) \(\sqrt{\frac{x-1}{x-4}}\). Then, dom (f) = ?
- [1,4)
- [1,4]
- (-∞,4]
- (-∞,1]∪ (4,∞)
Answer: 4. (-∞,1]∪ (4,∞)
f(x) is defined when-4≠ 0 and \(\frac{x-1}{x-4}\)
⇒ x ≠ 4 and (x ≥ 4 or x<l) => (x>4 or x<l)
⇒ Dom (f) = (-∞, 1]u (4, ∞).
Question 26. Let f(x) \(f(x)=e^{\sqrt{x^2-1}}\). Then, dom (f) =?
- (∞-,1]
- [-1,∞)
- (1,∞)
- (-∞,-1](1,∞)
Answer: 3. (1,∞)
f(x) is defined only when (x2-1) > 0 and (x- 1) > 0
⇒ (x – l)(x+ 1) ≥ 0 and (x- 1) > 0 => x+1 > 0 and x-1 > 0⇒ x >1
∴ dom (f) = (1, ∞).
Question 27. Let f(x) = \(\frac{x}{\left(x^2-1\right)}\) . Then, dom (f) =?
- R
- R-1
- R- {-1}
- R- {-1,1}
Answer: 4. R- {-1,1}
f(x) is not defined when (x- 1) = 0, i.e., when (x- l)(x+ 1) = 0,
i.e., when x=1 or x= -1.
dom (f) = R—{1, -1}.
Question 28. Let f(x)= \(\). Then ,dom(f) = ?
- (-1,1)
- [-1/ 1]
- [-l, 1]- {0}
- None of these
Answer: 3. [-l, 1]- {0}
⇒ \(\frac{\sin ^{-1} x}{x}\) is defined only when x≠ 0 and x ∈ [-1,1].
∴ dom (f)= [-1,1]- {0}.
Question 29. Let f(x) = cos-12x. then, dom (f) =?
- [-1,1]
- \(\left[\frac{-1}{2}, \frac{1}{2}\right]\)
- \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
- \(\left[\frac{-\pi}{4}, \frac{\pi}{4}\right]\)
Answer: 2. \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
sin-12x is defined only when 2x ∈ [-1, 1] => x \(\left[\frac{-1}{2}, \frac{1}{2}\right]\)
Question 30. Let f(x) = Cos-1(3x-1) . Then, dom (f) =?
- \(\left(0, \frac{2}{3}\right)\)
- \(\left[0, \frac{2}{3}\right]\)
- \(\left[\frac{-2}{3}, \frac{2}{3}\right]\)
- None of these
Answer: 2. \(\left[0, \frac{2}{3}\right]\)
cos-1 (3x- 1) is defined only when (3x-1) ∈ [-1, 1]
⇒ 3x ∈ [0, 2] => x ∈ \(\left[0, \frac{2}{3}\right]\)
⇒ dom(f)= \(\left[0, \frac{2}{3}\right]\)
Question 31. Let f(x)= \(\sqrt{\cos x}\). Then, dom (f) = ?
- \(\left[0, \frac{\pi}{2}\right]\)
- \(\left[\frac{3 \pi}{2}, 2 \pi\right]\)
- \(\left[0, \frac{\pi}{2}\right] \cup\left[\frac{3 \pi}{2}, 2 \pi\right]\)
- None of These
Answer: 3. \(\left[0, \frac{\pi}{2}\right] \cup\left[\frac{3 \pi}{2}, 2 \pi\right]\)
f(x) is defined only when cos x > 0.
⇒ x liesin 1st or 4th quadrant.
⇒ \(=\left[0, \frac{\pi}{2}\right] \cup\left[\frac{3 \pi}{2}, 2 \pi\right]\)
Question 32. Let f(x) = \(\sqrt{\log \left(2 x-x^2\right)}\). then, dom (f) = ?
- (0,2)
- [1,2]
- (-,1)
- None of these
Answer: 4. None of these
f (x) is defined only when log (2x- x2) > 0
⇒ (2x- x2) >1 => (1 + x2– 2x) < 0
⇒ (1- x)2 < 0
⇒ (1- x) = 0
⇒ x=1.
⇒ dom (f) = {1}.
Question 33. Let f(x) = x2. Then, dom (/) and range (/) are respectively
- R and R
- R+ and R+
- R and R+
- R and R- {0}
Answer: 3. R and R+
f(x) = x2 is clearly defined for each x ∈ R.
So, dom (f)=R. y= x2 x=± \(x= \pm \sqrt{ } y .\)
When y < 0, there is no real value of x. So, y ≥ 0.
∴Range (f) = R.
Question 34. Let f(x) = x3. Then, dom (f) and range (f) are respectively.
- R and R
- R+ and R+
- R and R+
- R+ and R
Answer: 1. R and R
f (x) = x3 is defined for each x ∈ R.
So, dom (f)=R.
For each y∈ R,y1/3 ∈ R and so x= is real.
∴ range (f) =R.
Question 35. Let f(x)= \(\log (1-x)+\sqrt{x^2-1}\).Then ,dom(f) = ?
- (1,∞)
- (-∞,-1)
- [-1,1]
- (0,1)
Answer: 2. (-∞,-1)
Let f (x) = g{x) + h(x), where g(x) = log (1- x) and h(x) = \(\sqrt{x^2-1}\)
g(x) is defined only whenl-x>0 => x<l.So, dom (g) = (∞, 1)
h(x) is defined only when x2-1 > 0 => x >1 or x <-1
∴ dom (h) = (-∞, -1]∪[1, ∞)
∴ dom (f) = dom (g)∩ dom(h) = (-∞, -1].
Question 36. Let \(=\frac{1}{\left(1-x^2\right)}\). Then ,range(f)= ?
- [-∞,1)
- [1,∞)
- [-1,1]
- None of these
Answer: 2. [0,1)
y = \(\frac{1}{\left(1-x^2\right)}\)
x = \(\sqrt{1-\frac{1}{y}}\)
Clearly, x is not defined when y = 0 or 1\(-\frac{1}{y}\) < 0, i.e., y = 0 or y < 1.
∴ range (f) = [1, ∞).
Question 37. Let f(x)\(=\frac{x^2}{\left(1+x^2\right)}\)
- [1,∞]
- [0,1)
- [-1,1]
- (0,1)
Answer: 2. [0,1)
y = \(\frac{x^2}{\left(1+x^2\right)} \Rightarrow x=\sqrt{\frac{y}{1-y}}\)
Clearly, x is defined only when \(\frac{y}{(1-y)}\) and(1-y)≠ 0, i.e., when 0 ≤ y ≤ 1.
So, range (f) = [0, 1).
Question 38. The range of f(x) = \(x+\frac{1}{x}\) is
- [-2,2]
- [2,∞)
- (-∞,-2)
- None of these
Answer: 4. None of these
y\(=\frac{x^2+1}{x}\)
⇒ x2– xy + 1= 0
x= \(\frac{y \pm \sqrt{y^2-4}}{2}\)
Question 39. The range of f(x) = ax, Where a> 0 is
- ]-∞,0]
- ]∞-,0)
- [0,∞)
- (0,∞)
Answer: 4. (0,∞)
Clearly, ax> 0 whatever may be the value of x.
∴ Range (f) = (0, ∞)
Relations And Functions Exercise 1C Results At A Glance
1. sin-1x = θ => x = sin θ
cos-1x = θ => x = cos θ
tan-1x = θ =» x = tan θ
2. Domain and range of inverse functions

3. sin (sin-1x) = x, if-1 ≤ x ≤ 1
cos (cos-1x) = x, if-1 ≤ x ≤ 1
tan (tan-1x) = x, if ∞ < x < ∞
4.
sin-1(sin x) = x, if x ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
cos -1(cos x) = x, if x ∈ [0, π]
tan-1(tan x) = x, if x ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
5.
sin-1x = cosec-1\(\left(\frac{1}{x}\right)\) , x≠0
cos-1x = sec-1\(\left(\frac{1}{x}\right)\) , x≠0
tan-1x= cot-1\(\left(\frac{1}{x}\right)\) , x≠0
cosec-1x= sin-1 \(\left(\frac{1}{x}\right)\),(x ≤ -1 or x ≥ 1)
sec-1x= cos-1\(\left(\frac{1}{x}\right)\), when (x ≤1 or x ≥ 1)
cot-1x = tan-1\(\left(\frac{1}{x}\right)\), when x > 0
6. sin-1(-x) = -sin-1x
cos-1(-x) = 7i- cos-1x
tan-1(-x) = -tan-1x
cot-1(-x) =n- cot-1x
sec-1(-x) =n- sec-1x
cosec-1(-x) = -cosec-1x
7. sin-1-x + cos-1-x =\(\frac{\pi}{2}\) -1 ≤ x ≤1
tan-1-x + cot-1-x = \(\frac{\pi}{2}\) , x ≠ 0
sec -1x + cosec -1x = \(\frac{\pi}{2}\), (x ≤ -1 or x ≥ 1)
8.
1. For 0 <x< 1, we have
sin-1-x= \(\cos ^{-1} \sqrt{1-x^2}\)
= \(\tan ^{-1} \frac{x}{\sqrt{1-x^2}}=\cot ^{-1} \frac{\sqrt{1-x^2}}{x}\)
= \(\sec ^{-1} \frac{1}{\sqrt{1-x^2}}\)
= cosec-1 \(\frac{1}{x}\)
2. Cos-1-x= \(\sin ^{-1} \sqrt{1-x^2}\)
= \(\tan ^{-1} \frac{\sqrt{1-x^2}}{x}\)
= \(\cot ^{-1} \frac{x}{\sqrt{1-x^2}}\)
= \(\sec ^{-1} \frac{1}{x}\)
= cosec-1 \(\frac{1}{\sqrt{1-x^2}}\)
3. For x>0, We Have
tan-1x= \(\sin ^{-1} \frac{x}{\sqrt{1+x^2}}\)
= \(\cos ^{-1} \frac{1}{\sqrt{1+x^2}}=\cot ^{-1} \frac{1}{x}\)
= \(\sec ^{-1} \sqrt{1+x^2}\)
= cosec-1 \(\frac{\sqrt{1+x^2}}{x}\)
9.
2sin-1x = sin-1(\(2 x \sqrt{1-x^2}\)) = cos-1 (1- 2x2)
2cos-1x = cos-1(2x2– 1) = sin -1\(\left(2 x \sqrt{1-x^2}\right.\))
2tan-1x= tan-1\(\left(\frac{2 x}{1-x^2}\right)\) = cos-1\(\left(\frac{1-x^2}{1+x^2}\right)\)
10.
3sin-1x = sin-1(3x- 4x3)
3cos-1x = cos-1(4x3– 3x)
3tan-1x = tan-1\(\left(\frac{3 x-x^3}{1-3 x^2}\right)\)
11.
When x > 0, y > 0 and xy < 1, we have
tan-1x + tan y-1 = tan-1\(\left(\frac{x+y}{1-x y}\right)\)
When x > 0, y > 0 and xy > 1, we have
tan-1x + tan y-1 = π + tan-1\(\left(\frac{x+y}{1-x y}\right)\)
12.
sin–1x + sin–1y = sin–1(\(x \sqrt{1-y^2}+y \sqrt{1-x^2}\))
sin–1x – sin–1y = sin–1(\(x \sqrt{1-y^2}-y \sqrt{1-x^2}\))
cos–1x + cos–1y= cos–1(\(x y-\sqrt{1-x^2} \cdot \sqrt{1-y^2}\))
cos–1x – cos–1y = cos–1(\(x y+\sqrt{1-x^2} \cdot \sqrt{1-y^2}\))
cot –1x+ cot –1x= cot–1\(\left(\frac{x y-1}{x+y}\right)\)
cot –1x- cot –1y = cot–1\(\left(\frac{x y+1}{x-y}\right)\)
Relations And Functions Exercise 1C Multiple Choice Questions
Question 1. The principal value of \(\cos ^{-1}\left(\frac{\sqrt{3}}{2}\right)\)
- \(\frac{\pi}{6}\frac{\pi}{6}\)
- \(\frac{5 \pi}{6}\)
- \(\frac{7 \pi}{6}\)
- None of these
Answer: 1. \(\frac{\pi}{6}\frac{\pi}{6}\)
1. Let cos-1\(\left(\frac{\sqrt{3}}{2}\right)\), where x ∈ [0, π].
Then, cos x=\(\frac{\sqrt{3}}{2}\)= cos\(\frac{\pi}{6}\)
⇒ x= \(\frac{\pi}{6}\)
Question 2. The principal value of cosec-1(2) is
- \(\frac{\pi}{3}\)
- \(\frac{\pi}{6}\)
- \(\frac{2 \pi}{3}\)
- \(\frac{5 \pi}{6}\)
Answer: 2. \(\frac{\pi}{6}\)
Let cosec-1(2) = x, where x ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)-{0}
Then, cosec x= 2cosec \(\frac{\pi}{6}\)
⇒ x= \(\frac{\pi}{6}\)
Question 3. The principal value of \(\cos ^{-1}\left(\frac{-1}{\sqrt{2}}\right)\)
- \(\frac{-\pi}{4}\)
- \(\frac{\pi}{4}\)
- \(\frac{3 \pi}{4}\)
- \(\frac{5 \pi}{4}\)
Answer: 3. \(\frac{3 \pi}{4}\)
Let cos-1 \(\left(\frac{-1}{\sqrt{2}}\right)\) = x, where x∈ [0,π]
Then,cos x = \(\frac{-1}{\sqrt{2}}\)
= \(-\cos \frac{\pi}{4}=\cos \left(\pi-\frac{\pi}{4}\right)\)
= \(\cos \frac{3 \pi}{4} \Rightarrow x=\frac{3 \pi}{4}\)
Question 4. The principal value of \(\sin ^{-1}\left(\frac{-1}{2}\right)\) is
- \(\frac{-\pi}{6}\)
- \(\frac{5 \pi}{6}\)
- \(\frac{7 \pi}{6}\)
- None of these
Answer: 1. \(\frac{-\pi}{6}\)
Let sin-1 \(\left(\frac{-1}{2}\right)\) = x where x∈\(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
Then, sin x = \(\frac1{-1}{2}\)
= \(-\sin \frac{\pi}{6}=\sin \left(\frac{-\pi}{6}\right)\)
⇒ x= \(frac{-\pi}{6}\)
Question 5. The principal value of \(\cos ^{-1}\left(\frac{-1}{2}\right)\) is
- \(\frac{-\pi}{3}\)
- \(\frac{2 \pi}{3}\)
- \(\frac{4 \pi}{3}\)
- \(\frac{\pi}{3}\)
Answer: 2. \(\frac{2 \pi}{3}\)
Let cos-1 \(\frac{-1}{2}\) = x where x∈[0,π]
Then, cos x = \(\frac{-1}{2}\)
= \(-\cos \frac{\pi}{3}\)
= \(\cos \left(\pi-\frac{\pi}{3}\right)=\cos \frac{2 \pi}{3}\)
x = \(\frac{2 \pi}{3}\)
Question 6. The principal value of tan \(\tan ^{-1}(-\sqrt{3})\)
- \(\frac{2 \pi}{3}\)
- \(\frac{4 \pi}{3}\)
- \(\frac{-\pi}{3}\)
- None of these
Answer: 3. \(\frac{-\pi}{3}\)
Let tan-1\(-\sqrt{3}\)= x, where x ∈\(\left(\frac{-\pi}{2},\frac{\pi}{2}\right)\)
Then, tan x= \(-\sqrt{3}\)
= \(-\tan \frac{\pi}{3}=\tan \left(\frac{-\pi}{3}\right)\)
⇒ \(x=\frac{-\pi}{3}\)
Question 7. The principal value of cot-1(-1) is
- \(\frac{-\pi}{4}\)
- \(\frac{\pi}{4}\)
- \(\frac{5 \pi}{4}\)
- \(\frac{3 \pi}{4}\)
Answer: 4. \(\frac{3 \pi}{4}\)
Let co-1(-1) = x, where x ∈ [0, π].
Then, cot x=-1
= \(-\cot \frac{\pi}{4}=\cot \left(\pi-\frac{\pi}{4}\right)\)
= \(\cot \frac{3 \pi}{4}\)
⇒ x= \(\frac{-\pi}{3}\)

Question 9. The principal value of cosec-1 \((-\sqrt{2})\) is
- \(\frac{-\pi}{4}\)
- \(\frac{3 \pi}{4}\)
- \(\frac{5 \pi}{4}\)
- None of these
Answer: 1. \(\frac{-\pi}{4}\)
Let cosec\((-\sqrt{2})\)= x, where x ∈\(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)– {0}
Then , cosec x \(-\sqrt{2}\)
= cosec \(\frac{-\pi}{4}\)
= cosec \(\frac{-\pi}{4}\)
x = \(\frac{-\pi}{4}\)
Question 10. The principal value of \(\cot ^{-1}(-\sqrt{3})\)
- \(\frac{-\pi}{6}\)
- \(\frac{-\pi}{6}\)
- \(\frac{7 \pi}{6}\)
- \(\frac{5 \pi}{6}\)
Answer: 4. \(\frac{5 \pi}{6}\)
Let cot\((-\sqrt{3})\)= x, where x [0,π]
Then , cot x \(-\sqrt{3}\)
= -cot \(\frac{\pi}{6}\)
\(=\cot \left(\pi-\frac{\pi}{6}\right)=\cot \frac{5 \pi}{6}\)
x= \(\frac{5 \pi}{6}\)
Question 11. The value of \(\sin ^{-1}\left(\sin \frac{2 \pi}{3}\right)\)
- \(\frac{2 \pi}{3}\)
- \(\frac{5 \pi}{3}\)
- \(\frac{\pi}{3}\)
- None of these
Answer: 3. \(\frac{\pi}{3}\)
Let sin-1\(\left(\sin \frac{2 \pi}{3}\right)\) = x , where x ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
Then,sin x = \(\sin \frac{2 \pi}{3}=\sin \left(\pi-\frac{\pi}{3}\right)=\sin \frac{\pi}{3}\)
x= \(\frac{\pi}{3}\)
Question 12. The value of \(\cos ^{-1}\left(\cos \frac{13 \pi}{6}\right)\)
- \(\frac{13 \pi}{6}\)
- \(\frac{7 \pi}{6}\)
- \(\frac{5 \pi}{6}\)
- \(\frac{\pi}{6}\)
Answer: 4. \(\frac{\pi}{6}\)
Let cos \(\left(\cos \frac{13 \pi}{6}\right)\)= x, where x [0,]
Then,cos x = \(\cos \frac{13 \pi}{6}=\cos \left(2 \pi+\frac{\pi}{6}\right)\)
x= \(\frac{\pi}{6}\)
Question 13. The value of \(\tan ^{-1}\left(\tan \frac{7 \pi}{6}\right)\)
- \(\frac{7 \pi}{6}\)
- \(\frac{5 \pi}{6}\)
- \(\frac{\pi}{6}\)
- None of these
Answer: 3. \(\frac{\pi}{6}\)
Let tan-1\(\left(\tan \frac{7 \pi}{6}\right)\) = x,where x ∈ \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
Then, tan x = tan \(\left(\tan \frac{7 \pi}{6}\right)\)
= tan \(\left(\pi+\frac{\pi}{6}\right)=\tan \frac{\pi}{6}\)
x= \(\frac{\pi}{6}\)
Question 14. The value of \(\cot ^{-1}\left(\cot \frac{5 \pi}{4}\right)\)
- \(\frac{\pi}{4}\)
- \(\frac{-\pi}{4}\)
- \(\frac{3 \pi}{4}\)
- None of these
Answer: 1. \(\frac{\pi}{4}\)
Let cos-1\(\left(\cot \frac{5 \pi}{4}\right)\) = x, where x [0,π]
Then ,cot x = cot \(\frac{5 \pi}{4}\)
= \(\cot \frac{5 \pi}{4}=\cot \left(\pi+\frac{\pi}{4}\right)\)
x\(=\frac{\pi}{4}\)
Question 15. The value of \(\sec ^{-1}\left(\sec \frac{8 \pi}{5}\right)\)
- \(\frac{2 \pi}{5}\)
- \(\frac{3 \pi}{5}\)
- \(\frac{8 \pi}{5}\)
- None of these
Answer: 1. \(\frac{2 \pi}{5}\)
Let sec-1\(\left(\sec \frac{8 \pi}{5}\right)\)= x where x∈[0,π]- \(\left\{\frac{\pi}{2}\right\}\)
Then, sec x \(\frac{8 \pi}{5}\)
= sec \(\sec \left(2 \pi-\frac{2 \pi}{5}\right)=\sec \frac{2 \pi}{5}\)
x = \(\frac{2 \pi}{5}\)
Question 16. The value of cosec-1 (cosec\(\frac{4 \pi}{3}\)) is
- \(\frac{\pi}{3}\)
- \(\frac{-\pi}{3}\)
- \(\frac{2 \pi}{3}\)
- None of these
Answer: 2. \(\frac{-\pi}{3}\)
Let cosec-1 \(\frac{4 \pi}{3}\)= x where x ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]-\{0\}\)
Then,cosec x= cosec \(\frac{4 \pi}{3}\)
= cosec\(\left(\pi+\frac{\pi}{3}\right)\)
=- cosec \(\frac{\pi}{3}\)
=cosec \(\frac{-\pi}{3}\)
x =\(\frac{-\pi}{3}\)
Question 17. The value of \(\tan ^{-1}\left(\tan \frac{3 \pi}{4}\right)\)
- \(\frac{3 \pi}{4}\)
- \(\frac{\pi}{4}\)
- \(\frac{-\pi}{4}\)
- None of these
Answer: 3. \(\frac{-\pi}{4}\)
Let tan-1\(\left(\tan \frac{3 \pi}{4}\right)\)= x, where x ∈ \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
Then,tan x= \(\tan \frac{3 \pi}{4}\)
= tan\(\left(\pi-\frac{\pi}{4}\right)=\tan \left(\frac{-\pi}{4}\right)\)
x = \(\frac{-\pi}{4}\)
Question 18. \(\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\)
- 0
- \(\frac{2 \pi}{3}\)
- \(\frac{\pi}{2}\)
- π
Answer: 3. \(\frac{\pi}{2}\)
Let ,sin-1 x= \(\left(\frac{-1}{2}\right)\)= x, where x ∈ \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
Then , sin x = \(-\frac{1}{2}\)
-sin = \(\frac{\pi}{6}=\sin \left(\frac{-\pi}{6}\right)\)
x= \(\frac{-\pi}{6}\)
Given example = \(\frac{\pi}{3}-\left(\frac{-\pi}{6}\right)=\left(\frac{\pi}{3}+\frac{\pi}{6}\right)\) Question
= \(\frac{3 \pi}{6}=\frac{\pi}{2}\)
Question 19. If x ≠ 0, then cos (tan-1x+ cot-1x)
- -1
- 1
- 0
- None of these
Answer: 3. 0
⇒ \(\cos \left(\tan ^{-1}+\cot ^{-1} x\right)\)
= \(\cos \frac{\pi}{2}\)
= 0
Question 20. The value of sin \(\sin \left(\cos ^{-1} \frac{3}{5}\right)\)
- \(\frac{2}{5}\)
- \(\frac{4}{5}\)
- \(\frac{-2}{5}\)
- None of these
Answer: 2. \(\frac{4}{5}\)
cos-1 x \(=\sin ^{-1} \sqrt{1-x^2}\)
= \(\cos ^{-1} \frac{3}{5}=\sin ^{-1} \sqrt{1-\frac{9}{25}}\)
= \(\sin ^{-1} \frac{4}{5}\)
∴ \(\sin \left(\cos ^{-1} \frac{3}{5}\right)=\sin \left(\sin ^{-1} \frac{4}{5}\right)=\frac{4}{5}\)
Question 21. \(\cos ^{-1}\left(\cos \frac{2 \pi}{3}\right)+\sin ^{-1}\left(\sin \frac{2 \pi}{3}\right)\)
- \(\frac{4 \pi}{3}\)
- \(\frac{\pi}{2}\)
- \(\frac{3 \pi}{4}\)
- π
Answer: 4. \(\frac{3 \pi}{4}\)
cos-1 \(\left(\cos \frac{2 \pi}{3}\right)=\sin ^{-1}\left(\sin \frac{2 \pi}{3}\right)\)
= \(=\cos ^{-1}\left\{\cos \left(\pi-\frac{\pi}{3}\right)\right\}+\sin ^{-1}\left\{\sin \left(\pi-\frac{\pi}{3}\right)\right\}\)
= \(\cos ^{-1}\left(-\cos \frac{\pi}{3}\right)+\sin ^{-1}\left\{\sin \frac{\pi}{3}\right\}=\cos ^{-1}\left(\frac{-1}{2}\right)+\frac{\pi}{3}\)
= \(\left(\frac{2 \pi}{3}+\frac{\pi}{3}\right)=\pi\)
Question 22. \(\tan ^{-1}(\sqrt{3})-\sec ^{-1}(-2)\)
- \(\frac{\pi}{3}\)\(\frac{-\pi}{3}\)
- \(\frac{5 \pi}{3}\)
- None of these
Answer: 2. \(\frac{-\pi}{3}\)
⇒ \(\tan ^{-1} \sqrt{3}-\sec ^{-1}(-2)\)
= \(\tan ^{-1} \sqrt{3}-\left(\pi-\sec ^{-1} 2\right)\)
= \(\frac{\pi}{3}-\pi+\frac{\pi}{3}=\frac{-\pi}{3}\)
Question 23. \(\cos ^{-1} \frac{1}{2}+2 \sin ^{-1} \frac{1}{2}\)
- \(\frac{2 \pi}{3}\)
- \(\frac{3 \pi}{2}\)
- 2π
- None of these
Answer: 1. \(\frac{2 \pi}{3}\)
= \(\cos ^{-1} \frac{1}{2}+2 \sin ^{-1} \frac{1}{2}\)
= \(\frac{\pi}{3}+\left(2 \times \frac{\pi}{6}\right)=\left(\frac{\pi}{3}+\frac{\pi}{3}\right)\)
= \(\frac{2 \pi}{3}\)
Question 24. \(\tan ^{-1} 1+\cos ^{-1}\left(\frac{-1}{2}\right)+\sin ^{-1}\left(\frac{-1}{2}\right)\)
- π
- \(\frac{2 \pi}{3}\frac{2 \pi}{3}\)
- \(\frac{3 \pi}{4}\)
- \(\frac{\pi}{2}\)
Answer: 3. \(\frac{3 \pi}{4}\)
⇒ \(\tan ^{-1} 1+\cos ^{-1}\left(\frac{-1}{2}\right)+\sin ^{-1}\left(\frac{-1}{2}\right)\)
= \(\frac{\pi}{4}+\left(\pi-\cos ^{-1} \frac{1}{2}\right)-\sin ^{-1} \frac{1}{2}\)
= \(\left(\frac{\pi}{4}+\pi-\frac{\pi}{3}-\frac{\pi}{6}\right)\)
= \(\frac{3 \pi}{4}\)
Question 25. tan[2 tan-1\(\frac{1}{5}-\frac{\pi}{4}\)]= ?
- \(\frac{7}{17}\)
- \(\frac{-7}{17}\)
- \(\frac{7}{12}\)
- \(\frac{-7}{12}\)
Answer: 2. \(\frac{-7}{17}\)
Let 2\(\tan ^{-1} \frac{1}{5}=\theta\) .
Then \(\tan ^{-1} \frac{1}{5}=\frac{1}{2} \theta \Rightarrow \tan \frac{1}{2} \theta=\frac{1}{5}\)
∴ \(\tan \theta=\frac{2 \tan \frac{1}{2} \theta}{1-\tan ^2 \frac{1}{2} \theta}=\frac{\left(2 \times \frac{1}{5}\right)}{\left(1-\frac{1}{25}\right)}\)
= \(\left(\frac{2}{5} \times \frac{25}{24}\right)=\frac{5}{12}\)
∴ \(\tan \left[2 \tan ^{-1} \frac{1}{5}-\frac{\pi}{4}\right]=\tan \left(\theta-\frac{\pi}{4}\right)=\frac{\tan \theta-\tan \frac{\pi}{4}}{1+\tan \theta \cdot \tan \frac{\pi}{4}}\)
= \(\frac{\left(\frac{5}{12}-1\right)}{\left(1+\frac{5}{12} \times 1\right)}=\frac{\left(\frac{-7}{12}\right)}{\left(\frac{17}{12}\right)}=\frac{-7}{17}\)
Question 26. \(\tan \frac{1}{2}\left(\cos ^{-1} \frac{\sqrt{5}}{3}\right)\)= ?
- \(\frac{(3-\sqrt{5})}{2}\)
- \(\frac{(3+\sqrt{5})}{2}\)
- \(\frac{(5-\sqrt{3})}{2}\)
- \(\frac{(5+\sqrt{3})}{2}\)
Answer: 1. \(\frac{(3+\sqrt{5})}{2}\)
Let \(\cos ^{-1} \frac{\sqrt{5}}{3}=\theta\).Then,cos \(\cos \theta=\frac{\sqrt{5}}{3}\)
⇒ \(\tan \frac{1}{2}\left(\cos ^{-1} \frac{\sqrt{5}}{3}\right)=\tan \frac{1}{2} \theta=\frac{\sin (\theta / 2)}{\cos (\theta / 2)}\)
⇒ \(\sqrt{\frac{1-\cos \theta}{1+\cos \theta}}=\left\{\frac{\left(1-\frac{\sqrt{5}}{3}\right)}{\left(1+\frac{\sqrt{5}}{3}\right)}\right\}^{1 / 2}\)
= \(\left(\frac{3-\sqrt{5}}{3+\sqrt{5}}\right)^{1 / 2}=\left\{3-\frac{\sqrt{5}}{3+\sqrt{5}} \times \frac{3-\sqrt{5}}{3+\sqrt{5}}\right\}^{1 / 2}\)
= \(\frac{(3-\sqrt{5})}{2}\)
Question 27. \(\sin \left(\cos ^{-1} \frac{3}{5}\right)\)
- \(\frac{3}{4}\)
- \(\frac{4}{5}\)
- \(\frac{3}{5}\)
- None of these
Answer: 2. \(\frac{4}{5}\)
Let cos-1 \(\frac{3}{5}\)= x ∈ where [0,π] .Then ,cos x= \(\frac{3}{5}\)
∴ Since x[0,π],sinx > 0
∴ Since x\(\sqrt{1-\frac{9}{25}}\)
= \(\sqrt{\frac{16}{25}}=\frac{4}{5}\)
⇒ \(\sin \left(\cos ^{-1} \frac{3}{5}\right)=\frac{4}{5}\)
Question 28. \(\cos \left(\tan ^{-1} \frac{3}{4}\right)\)
- \(\frac{3}{5}\)
- \(\frac{4}{5}\)
- \(\frac{4}{9}\)
- None of these
Answer: 2. \(\frac{4}{5}\)
Let \(\tan ^{-1} \frac{3}{4}\) = x where x ∈ \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
∴tan x= \(\frac{3}{4}\) and since x ∈ \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\),we have cos x>0
∴cos x = \(\frac{1}{\sec x}=\frac{1}{\sqrt{1+\tan ^2 x}}\)
= \(\frac{1}{\sqrt{1+\frac{9}{16}}}=\frac{4}{5}\)
= \(\cos \left(\tan ^{-1} \frac{3}{4}\right)\)
cos x=\(\frac{4}{5}\)
Question 29. \(\sin \left\{\frac{\pi}{3}-\sin ^{-1}\left(\frac{-1}{2}\right)\right\}\)
- 1
- 0
- \(\frac{-1}{2}\)
- None of these
Answer: 1. 1
⇒ \(\sin \left\{\frac{\pi}{3}-\sin ^{-3}\left(\frac{-1}{2}\right)\right\}=\sin \left\{\frac{\pi}{3}+\sin ^{-1} \frac{1}{2}\right\}\)
sin = \( \left(\frac{\pi}{3}+\frac{\pi}{6}\right)=\sin \frac{\pi}{2}\)
= 1
Question 30. \(\sin \left(\frac{1}{2} \cos ^{-1} \frac{4}{5}\right)\)
- \(\frac{1}{\sqrt{5}}\)
- \(\frac{2}{\sqrt{5}}\)
- \(\frac{1}{\sqrt{10}}\)
- \(\frac{2}{\sqrt{10}}\)
Answer: 3. \(\frac{1}{\sqrt{10}}\)
Let \(\cos ^{-1} \frac{4}{5}=\) = x where x∈ [0,π].
Then cos x= \(\frac{4}{5}\)
Since x∈ [0,π] ⇒ \(\frac{1}{2} x \in\left[0, \frac{\pi}{2}\right] \Rightarrow \sin \frac{1}{2} x>0\)
sin = \( \left(\frac{1}{2} \cos ^{-1} \frac{4}{5}\right)=\sin \frac{1}{2} x\)
= \(\sqrt{\frac{1-\cos x}{2}}=\sqrt{\frac{\left(1-\frac{4}{5}\right)}{2}}=\)
= \(\frac{1}{\sqrt{10}}\)
Question 31. \(\tan ^{-1}\left\{2 \cos \left(2 \sin ^{-1} \frac{1}{2}\right)\right\}\)
- \(\frac{\pi}{3}\)
- \(\frac{\pi}{4}\)
- \(\frac{3 \pi}{4}\)
- \(\frac{2 \pi}{3}\)
Answer: 2. \(\frac{\pi}{4}\)
⇒ \(\tan ^{-1}\left\{2 \cos \left(2 \sin ^{-1} \frac{1}{2}\right)\right\}\)
= \(\tan ^{-1}\left\{2 \cos \left(2 \times \frac{\pi}{6}\right)\right\}\)
= \(\tan ^{-1}\left\{2 \times \frac{1}{2}\right\}\)
tan-1 1= \(\frac{\pi}{4}\)
Question 32. \(\text { If } \cot ^{-1}\left(\frac{-1}{5}\right)=x, \text { then } \sin x=?\)
- \(\frac{1}{\sqrt{26}}\)
- \(\frac{5}{\sqrt{26}}\)
- \(\frac{1}{\sqrt{24}}\)
- None of these
Answer: 2. \(\frac{5}{\sqrt{26}}\)
cot-1\(\left(\frac{-1}{5}\right)\)
cot x= \(\left(\frac{-1}{5}\right)\),where x∈ (0,π)
sin x>0 in (0,π)
sin x= 1/ cosecx
= \(\frac{1}{\sqrt{1+\cot ^2 x}}\)
⇒\(\frac{1}{\sqrt{1+\frac{1}{25}}}=\frac{5}{\sqrt{26}}\)
Question 33. \(\sin ^{-1}\left(\frac{-1}{2}\right)+2 \cos ^{-1}\left(\frac{-\sqrt{3}}{2}\right)=?\)
- \(\frac{\pi}{2}\)
- π
- \(\frac{3 \pi}{2}\)
- None of these
Answer: 3. \(\frac{3 \pi}{2}\)
Range of \(\cos ^{-1} \text { is }\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
cos-1= \(\left(\frac{-\sqrt{3}}{2}\right)\)
x = \(\frac{-\sqrt{3}}{2}\)
– cos = \(\frac{\pi}{6}=\cos \left(\pi-\frac{\pi}{6}\right)=\cos \frac{5 \pi}{6}\)
x= \(\frac{5 \pi}{6}\)
sin-1= \(\left(\frac{-1}{2}\right)+2 \cos ^{-1}\left(\frac{-\sqrt{3}}{2}\right)\)=
= \(-\sin ^{-1} \frac{1}{2}+2 \times \frac{5 \pi}{6}\)
= \(-\frac{\pi}{6}+\frac{5 \pi}{3}=\frac{4 \pi}{6}\)
=\(\frac{3 \pi}{2}\)
Question 34. \(\tan ^{-1}(-1)+\cos ^{-1}\left(\frac{-1}{\sqrt{ } 2}\right)=?\)
- \(\frac{\pi}{2}\)
- π
- \(\frac{3 \pi}{2}\)
- \(\frac{2 \pi}{2}\)
Answer: 1. \(\frac{\pi}{2}\)
Range of \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
⇒ \(\tan ^{-1}(-1)=x \Rightarrow \tan x=-1\)
= – \(\tan \frac{\pi}{4}=\tan \left(\frac{-\pi}{4}\right) \Rightarrow\)
= \(x\frac{-\pi}{4}\)
The range of cos-1 is [0,π]
= \(\cos ^{-1}\left(\frac{-1}{\sqrt{2}}\right)\) = y
cos y = \(\frac{-1}{\sqrt{2}}\)
= \(-\cos \frac{\pi}{4}=\cos \left(\pi-\frac{\pi}{4}\right)=\cos \frac{3 \pi}{4}\)
y = \(\frac{3 \pi}{4}\)
Given example = \(-\frac{\pi}{4}+\frac{3 \pi}{4}=\frac{2 \pi}{4}=\frac{\pi}{2}\)
Question 35. \(\cot \left(\tan ^{-1} x+\cot ^{-1} x\right)=?\)
- 1
- \(\frac{1}{2}\)
- 0
- None of these
Answer: 3. 0
Given example = \(\cot \frac{\pi}{2}\)= 0
Question 36. \(\tan ^{-1} 1+\tan ^{-1} \frac{1}{3}=?\)
- \(\tan ^{-1} \frac{4}{3}\)
- \(\tan ^{-1} \frac{2}{3}\)
- \(\tan ^{-1} 2\)
- \(\tan ^{-1} 3\)
Answer: 3. \(\tan ^{-1} 2\)
⇒ \(\tan ^{-1} 1+\tan ^{-1} \frac{1}{3}\)
\(=\tan ^{-1}\left\{\frac{1+\frac{1}{3}}{1-\frac{1}{3}}\right\}\)
= \(\tan ^{-1} 2\)
Question 37. \(\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}=?\)
- \(\frac{\pi}{3}\)
- \(\frac{\pi}{4}\)
- \(\frac{\pi}{2}\)
- \(\frac{2 \pi}{3}\)
Answer: 2. \(\frac{\pi}{4}\)
⇒ \(\tan ^{-1} \frac{1}{2}+\tan ^{-1} \frac{1}{3}\)
tan-1\(\left\{\frac{\frac{1}{2}+\frac{1}{3}}{1-\frac{1}{6}}\right\}\)
tan-1\(=\frac{\pi}{4}\)
Question 38. \(2 \tan ^{-1} \frac{1}{3}=?\)
- \(\tan ^{-1} \frac{3}{2}\)
- \(\tan ^{-1} \frac{3}{4}\)
- \(\tan ^{-1} \frac{4}{3}\)
- None of these
Answer: 2. \(\tan ^{-1} \frac{3}{4}\)
Use \(2 \tan ^{-1} x=\tan ^{-1}\left(\frac{2 x}{1-x^2}\right)\)
Question 39. \(\cos \left(2 \tan ^{-1} \frac{1}{2}\right)=?\)
- \(\frac{3}{5}\)
- \(\frac{4\frac{3}{5}[}{5}\)
- \(\frac{7}{8}\)
- [None of these
Answer: 1. \(\frac{3}{5}\)
Use \(2 \tan ^{-1} x=\cos ^{-1}\left(\frac{1-x^2}{1+x^2}\right)\)
Question 40. \(\sin \left[2 \sin ^{-1} \frac{4}{5}\right]\)
- \(\frac{12}{25}\)
- \(\frac{80}{89}\)
- \(\frac{75}{128}\)
- None of these
Answer: 2. \(\frac{80}{89}\)
Use \(2 \tan ^{-1} x=\sin ^{-1}\left(\frac{2 x}{1+x^2}\right)\)
Question 41. \(\sin \left[2 \sin ^{-1} \frac{4}{5}\right]\)
- \(\frac{2}{25}\)
- \(\frac{16}{25}\)
- \(\frac{24}{25}\)
- None of these
Answer: 3. \(\frac{16}{25}\)
Use \(2 \sin ^{-1} x=\sin ^{-1}\left[2 x \sqrt{1-x^2}\right]\)
Question 42. \(\text { If } \tan ^{-1} x=\frac{\pi}{4}-\tan ^{-1} \frac{1}{3} \text {, then } x=?\)
- \(\frac{1}{2}\)
- \(\frac{1}{4}\)
- \(\frac{1}{6}\)
- None of these
Answer: 1. \(\frac{1}{2}\)
\(\frac{\pi}{4}-\tan ^{-1} \frac{1}{3}=\tan ^{-1} 1-\tan ^1 \frac{1}{3}\)
\(\tan ^{-1}\left\{\frac{\left(1-\frac{1}{3}\right)}{\left(1+\frac{1}{3}\right)}\right\}=\tan ^{-1} \frac{1}{2}\)
= \(\frac{1}{2}\)
Question 43. \(\text { If } \tan ^{-1}(1+x)+\tan ^{-1}(1-x)=\frac{\pi}{2} \text {, then } x=\text { ? }\)
- 1
- -1
- 0
- \(\frac{1}{2}\)
Answer: 3. 0
We know that \(\tan ^{-1} x+\cot ^{-1} x=\frac{\pi}{2}\)
= \(\tan ^{-1} x+\tan ^{-1} \frac{1}{x}=\frac{\pi}{2}\)
= \(\tan ^{-1}(1+x)+\tan ^{-1}(1-x)=\frac{\pi}{2}\)
(1-x)= \(\frac{1}{(1+x)}\)(1-x) = 1
x= 0
Question 44. \(\text { If } \sin ^{-1} x+\sin ^{-1} y=\frac{2 \pi}{3}, \text { then }\left(\cos ^{-1} x+\cos ^{-1} y\right)=?\)
- \(\frac{\pi}{6}\)
- \(\frac{\pi}{3}\)
- \(\pi\)
- \(\frac{2 \pi}{3}\)
Answer: 2. \(\frac{\pi}{3}\)
⇒ \(\sin ^{-1} x+\sin ^{-1} y=\frac{2 \pi}{3}\)
∴ \(\left(\frac{\pi}{2}-\cos ^{-1} x\right)+\left(\frac{\pi}{2}-\cos ^{-1} y\right)=\frac{2 \pi}{3}\)
⇒ \(\cos ^{-1} x+\cos ^{-1} y=\left(\pi-\frac{2 \pi}{3}\right)=\frac{\pi}{3}\)
Question 45. \(\left(\tan ^{-1} 2+\tan ^{-1} 3\right)=?\)
- \(\frac{-\pi}{4}\)
- \(\frac{\pi}{4}\)
- \(\frac{3 \pi}{4}\)
- \(\pi\)
Answer: 3. \(\frac{3 \pi}{4}\)
( x = 2,y = 3) = xy>1
∴ \(\pi+\tan ^{-1}\left(\frac{2+3}{1-2 \times 3}\right)=\pi+\tan ^{-1}(-1)\)
= \(\pi-\tan (1)=\left(\pi-\frac{\pi}{4}\right)\)
= \(\frac{3 \pi}{4}\)
Question 46. \(\text { If } \tan ^{-1} x+\tan ^{-1} 3=\tan ^{-1} 8, \text { then } x=\text { ? }\)
- \(\frac{1}{3}\)
- \(\frac{1}{5}\)
- 3
- 5
Answer: 2. \(\frac{1}{5}\)
⇒ \(\tan ^{-1} x+\tan ^{-1} 3=\tan ^{-1} 8\)
= \(\frac{3+x}{1-3 x}\)= 8
3+x = 8-24x
x= \(\frac{1}{5}\)
Question 47. \(\text { If } \tan ^{-1} 3 x+\tan ^{-1} 2 x=\frac{\pi}{4} \text {, then } x=\text { ? }\)
- \(\frac{1}{2} \text { or }-2\)
- \(\frac{1}{3} \text { or }-3\)
- \(\frac{1}{4} \text { or }-2\)
- \(\frac{1}{6} \text { or }-1\)
Answer: 4. \(\frac{1}{6} \text { or }-1\)
⇒ \(\tan ^{-1}\left(\frac{3 x+2 x}{1-6 x^2}\right)=\frac{\pi}{4}\)
∴ \(\frac{5 x}{1-6 x^2}=\tan \frac{\pi}{4}=1\)
= \(\frac{5 x}{1-6 x^2}=\tan \frac{\pi}{4}\)= 1
⇒ 6x2+5x-1 = 0
(x+1)(6x-1)= 0
x= -1 or x= \(\frac{1}{6}\)
Question 48. \(\tan \left\{\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{2}{3}\right\}=?\)
- \(\frac{13}{6}\)
- \(\frac{17}{6}\)
- \(\frac{19}{6}\)
- \(\frac{23}{6}\)
Answer: 2. \(\frac{17}{6}\)
cos-1 x= \(\frac{\sqrt{1-x^2}}{x}\)
cos-1\(\frac{4}{5}\) = tan-1\(\frac{\sqrt{1-\frac{16}{25}}}{(4 / 5)}\)
tan-1 = \(\frac{3}{4}\)
∴ \(\cos ^{-1} \frac{4}{5}+\tan ^{-1} \frac{2}{3}=\tan ^{-1} \frac{3}{4}+\tan ^{-1} \frac{2}{3}\)
tan-1 = \(\frac{\left(\frac{3}{4}+\frac{2}{3}\right)}{\left(1-\frac{3}{4} \times \frac{2}{3}\right)}\)
tan-1 = \(\frac{17}{6}\)
\(\cos ^{-1} \frac{4}{5}=\tan ^{-1} \frac{\sqrt{1-\frac{16}{25}}}{(4 / 5)}=\tan ^{-1} \frac{3}{4} \)
∴ Given example = \(\tan \left\{\tan ^{-1} \frac{17}{6}\right\}=\frac{17}{6}\)
Question 49. cot-1 + cosec-1\(\frac{\sqrt{41}}{4}\)
- \(\frac{\pi}{6}\)
- \(\frac{\pi}{4}\)
- \(\frac{\pi}{3}\)
- \(\frac{3 \pi}{4}\)
Answer: 2. \(\frac{\pi}{4}\)
cosec x-1 = \(\cot ^{-1} \sqrt{x^2-1}\)
cosec x-1 = \(\frac{\sqrt{41}}{4}\)
cot-1 = \(\frac{\sqrt{41}}{4}\) -1
cot-1 = \(\frac{5}{4}\)
= \(\cot ^{-1} 9+\cot ^{-1} \frac{5}{4}\)
= \(\tan ^{-1} \frac{1}{9}+\tan ^{-1} \frac{4}{5}\)
Question 50. Range of sin-1x is
- \(\left[0, \frac{\pi}{2}\right]\)
- [0, π]
- \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
- None of these
Answer: 3. \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
Question 51. The range of cos-1x is
- [0, π]
- \(\left[0, \frac{\pi}{2}\right]\)
- \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
- None of these
Answer: 1. [0, π]
Question 52. The range of tan-1x is
- \(\left(0, \frac{\pi}{2}\right)\)
- \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
- \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
- None of these
Answer: 2. \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
Question 53. The range of sec-1x is
- \(\left[0, \frac{\pi}{2}\right]\)
- [0, π]
- \([0, \pi]-\left\{\frac{\pi}{2}\right\}\)
- None of these
Answer: 3. \([0, \pi]-\left\{\frac{\pi}{2}\right\}\)
Question 54. Range of cosec-1x is
- \(\left(\frac{-\pi}{2}, \frac{\pi}{2}\right)\)
- \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]\)
- \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]-\{0\}\)
- None of these
Answer: 3. \(\left[\frac{-\pi}{2}, \frac{\pi}{2}\right]-\{0\}\)
Question 55. Domain of cos-1x is
- [0,1]
- [-1,1]
- [-1,0]
- None of these
Answer: 2. [-1,1]
Question 56. Domain of sec-1 x is
- [-1,1]
- R- {0}
- R- [-1,1]
- R- {-1,1}
Answer: 3. R- [-1,1]









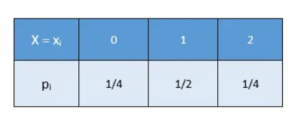
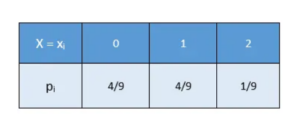
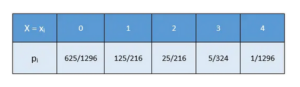
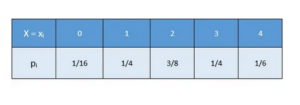
 Conditions for the Applicability of a Binomial Distribution
Conditions for the Applicability of a Binomial Distribution