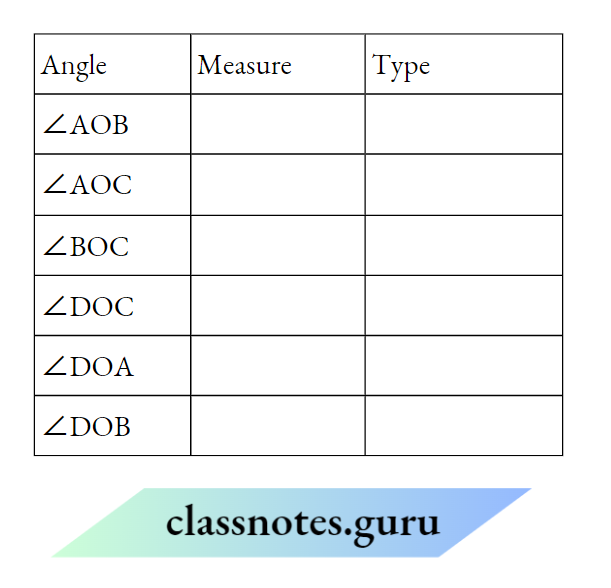
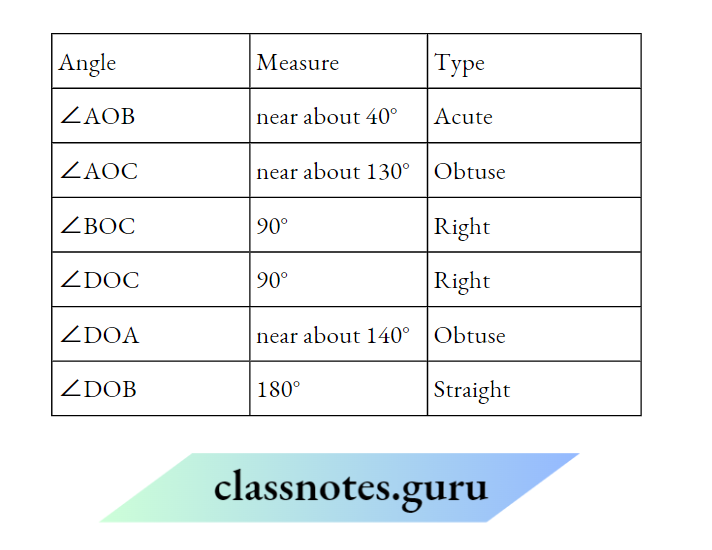
NCERT Class 7 History Chapter 1 What Does The Term Pan Regional Empire Mean
In the study of history, especially within the NCERT Class 7 curriculum, the term “pan-regional empire” pops up quite a bit. But what does it really mean? Essentially, it refers to empires that extend their influence and control over multiple regions, impacting various cultures, economies, and political systems. Understanding this concept helps us grasp the dynamics of historical power and its lasting effects on the world today.
The Term Pan Regional Empire Mean
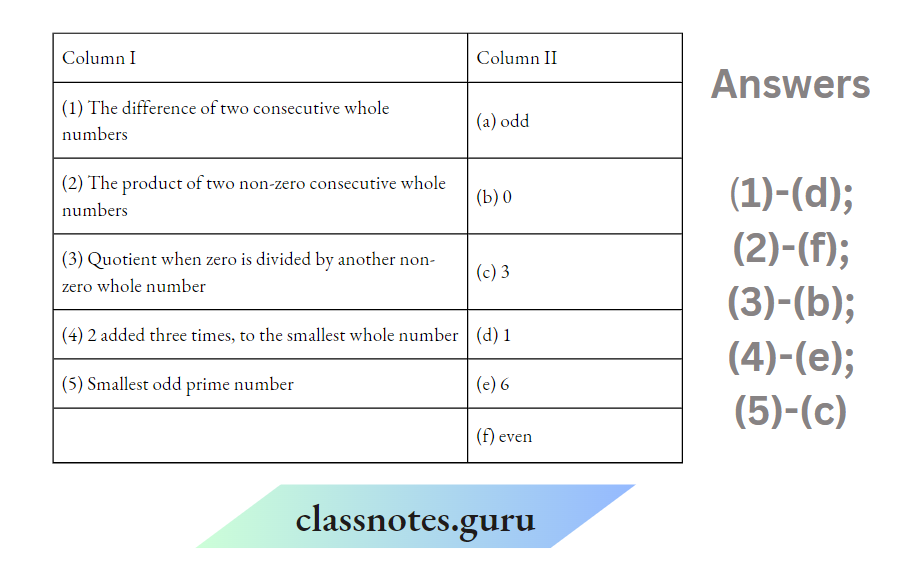
- Pan-regional empires span across multiple regions, not limited to a single territory.
- These empires influence politics, culture, and economy in the regions they control.
- Historical examples include the Mughals, Cholas, and Tughluqs, showcasing diverse impacts.
- Cultural exchange is a hallmark of pan-regional empires, blending traditions and practices.
- Studying these empires helps us understand the foundations of modern nation-states.
Defining Pan-Regional Empires
So, what exactly is a pan-regional empire? It’s a term you’ll run into in history, especially when studying empires that weren’t just local big shots, but had influence way beyond their immediate area. Think of it as an empire that’s gone global… well, ‘global’ for its time, anyway.
Characteristics Of Pan-Regional Empires
Okay, so how do you spot one of these pan-regional empires? Here are a few things to look for:
- Large Territory: They control a big chunk of land, often made up of different regions with their own cultures and histories.
- Strong Central Government: They need a solid government to keep everything together and enforce their rules across such a large area.
- Economic Influence: They usually have a strong economy that affects other states around them, whether through trade, resources, or even just being a big market.
It’s important to remember that these empires weren’t always about conquering and controlling. Sometimes, their influence came from being a center of trade or culture, which drew other regions into their orbit.
Class 7 History Chapter 1 NCERT Solutions
Historical Examples of Pan-Regional Empires
When we talk about pan-regional empires, a few names pop up pretty quickly. The Mughal Empire is a classic example, but there are others too. Think about the Roman Empire, or even the Mongol Empire. They all had a huge impact on multiple regions, not just their own backyard.
Here’s A Quick Comparison:
The Role of Culture in Pan-Regional Empires
Culture plays a big role in these empires. It’s not just about armies and taxes. Often, they spread their culture – their art, language, religion – to the regions they influence. This can happen through trade, migration, or even just the prestige of being part of a powerful empire. This cultural exchange can leave a lasting mark, even after the empire itself is gone.
The Significance of Pan-Regional Empires

Political Influence Across Regions
Pan-regional empires weren’t just about land; they were about power. Their influence extended far beyond their borders, shaping the political landscape of entire regions. They could dictate terms of trade, influence succession in neighboring states, and even redraw political boundaries.
Think of it like a giant chess game, with the empire making all the moves. This influence wasn’t always direct control, but rather a web of alliances, dependencies, and sometimes, just plain intimidation.
The ripple effects of their decisions could be felt for generations.
Economic Impact on Neighboring States
These empires weren’t just political behemoths; they were economic powerhouses too. Their vast resources and control over trade routes meant they could significantly impact the economies of neighboring states.
They could create economic dependencies, where smaller states relied on the empire for trade, resources, or even protection. This could lead to prosperity for some, but also exploitation and economic stagnation for others. It’s a complex relationship, with winners and losers.
Here’s a simple example of how trade might have been structured:
Cultural Exchange And Integration
Pan-regional empires were melting pots of culture. As they expanded, they brought together diverse populations, leading to a fascinating exchange of ideas, customs, and traditions.
This wasn’t always a peaceful process, but it often resulted in the integration of different cultures, creating new hybrid forms. Think of the spread of language, religion, and art. This cultural exchange could enrich the lives of people across the empire, but it could also lead to the suppression of local cultures in favor of the dominant one. The Mughals as a Pan-Regional Empire are a great example of this.
The legacy of these empires is complex. They left behind a mix of achievements and failures, prosperity and exploitation, cultural integration and suppression. Understanding their impact requires a nuanced perspective, recognizing both the positive and negative consequences of their rule.
Here are some common elements of cultural exchange:
- Language
- Religion
- Art and Architecture
- Cuisine
The Mughals As A Pan-Regional Empire

The Mughal Empire stands out as a prime example of a pan-regional empire in Indian history. Their influence stretched across a vast territory, impacting various aspects of life from politics to culture. It’s a great case study when trying to understand what this term really means.
Expansion Of The Mughal Empire
The Mughals didn’t just pop up overnight; their empire was built through strategic military campaigns and alliances. Starting from a relatively small area, they gradually expanded their control, incorporating diverse regions and people.
This expansion wasn’t always smooth, of course, and involved plenty of conflict and negotiation. By the time of emperors like Akbar, the empire was huge, encompassing much of the Indian subcontinent.
Cultural Contributions Of The Mughals
One of the most lasting legacies of the Mughals is their contribution to Indian culture. They weren’t just conquerors; they were also patrons of the arts, architecture, and literature. The fusion of Persian, Central Asian, and Indian styles resulted in a unique and vibrant cultural synthesis.
Think about the Taj Mahal, for example, or the development of Urdu as a new language. These are just a couple of examples of how the Mughals shaped the cultural landscape.
NCERT Solutions for Class 7 History Chapter 1
Administrative Innovations In The Mughal Era
The Mughals were also known for their administrative skills. They implemented a centralized system of governance, dividing the empire into provinces and establishing a uniform system of taxation. This wasn’t always popular, but it did help to create a more stable and efficient state. They also introduced new technologies and agricultural practices, which helped to boost the economy. It’s interesting to see how these administrative structures influenced later systems of governance in India.
The Mughal Empire’s success wasn’t just about military might; it was also about their ability to integrate diverse cultures and create a sense of shared identity. This is a key aspect of what makes them a pan-regional empire, rather than just a large kingdom.
Comparing Pan-Regional Empires
Differences Between Regional And Pan-Regional Empires
Okay, so what really sets a pan-regional empire apart from just a regular, run-of-the-mill regional one? Well, it’s all about scale and influence. A regional empire typically dominates a specific geographic area, maybe a river valley or a peninsula.
Think local. A pan-regional empire, on the other hand, stretches across multiple distinct regions, impacting diverse cultures and economies. It’s like comparing a local coffee shop to a massive, international chain. Here’s a quick breakdown:
- Scope: Regional empires are localized; pan-regional empires are widespread.
- Influence: Regional empires have limited impact beyond their borders; pan-regional empires exert broad influence.
- Complexity: Pan-regional empires face greater administrative and logistical challenges.
Similarities Among Various Pan-Regional Empires
Even though empires like the Mughals, the Romans, and the Mongols existed in different times and places, they shared some surprising similarities. They all needed strong leadership, efficient administration, and a powerful military to maintain control.
They also tended to promote some level of cultural or economic integration to unify their vast territories. Think about it – you can’t rule a huge area if everyone’s fighting each other all the time. Some common threads include:
- Centralized power structures.
- Infrastructure development (roads, communication systems).
- Standardized legal or administrative systems.
- Promotion of trade and economic activity.
Lessons From Historical Pan-Regional Empires
What can we learn from these old empires? Quite a bit, actually. Studying their rise and fall can give us insights into things like governance, cultural exchange, and the challenges of managing diversity. For example, the problem of two emperors highlights the complexities of power dynamics.
It’s a reminder that even the most powerful empires are not invincible. They often collapse due to internal strife, economic problems, or external pressures. Understanding these patterns can help us better understand current global dynamics.
Pan-regional empires teach us that long-term success requires more than just military might. It demands effective governance, economic stability, and the ability to integrate diverse populations into a cohesive whole. Ignoring these factors often leads to decline and eventual collapse.
The Legacy of Pan-Regional Empires
Influence on Modern Nation-States
Pan-regional empires, though relics of the past, continue to shape the world we live in. Their influence is evident in the borders, political systems, and cultural landscapes of many modern nation-states. For example, the administrative structures and legal frameworks established by empires like the Romans or the Mughals often served as models for subsequent governments.
The concept of centralized authority, standardized laws, and efficient bureaucracy can be traced back to these historical entities. The lasting impact is undeniable.
Cultural Heritage And Identity
These empires weren’t just about political control; they were melting pots of culture. Think about the spread of languages, religions, and artistic styles across vast territories. This cultural exchange has left an indelible mark on the identities of people living in those regions today.
Many traditions, customs, and even culinary practices can be traced back to the era of pan-regional empires. It’s pretty wild to think about how much of our daily lives is influenced by things that happened centuries ago.
Continuing Impact On Global Relations
The dynamics of power and influence established by pan-regional empires still resonate in today’s global relations. The relationships between countries, the formation of alliances, and even the sources of conflict can often be understood in the context of historical imperial legacies.
For instance, the borders drawn by colonial powers continue to be a source of tension in some parts of the world. Understanding these historical roots is key to understanding current geopolitical realities.
The echoes of pan-regional empires are all around us, shaping our world in ways we might not always realize. From the food we eat to the laws we follow, their influence is woven into the fabric of modern society.
It’s a reminder that history is not just something that happened in the past; it’s an ongoing process that continues to shape our present and future.
Challenges Faced by Pan-Regional Empires
Internal Conflicts And Governance Issues
Running a huge empire isn’t easy, and pan-regional empires often struggled with keeping everyone happy. Think about it: different regions, different cultures, and different ideas about how things should be run. This could lead to a lot of infighting. One of the biggest challenges was balancing the needs of the central government with the desires of local leaders.
- Succession struggles: Who takes over when the leader dies?
- Religious differences: Keeping the peace between different faiths.
- Regional autonomy: How much power should local areas have?
Trying to manage all of this while also dealing with corruption and inefficiency? It’s a recipe for disaster. It’s like trying to juggle flaming torches while riding a unicycle – impressive if you can pull it off, but most of the time, something’s going to fall.
What Does The Term Pan Regional Empire Mean Class 7
Resistance From Local Powers
Not everyone is thrilled about being part of a big empire. Local rulers often didn’t want to give up their power, and people didn’t always like being told what to do by some far-off emperor. This led to rebellions and resistance movements. Maintaining control required constant vigilance and often brutal suppression of dissent. The struggle against foreign oppression was a common theme.
- Guerilla warfare: Small-scale attacks that wear down the empire.
- Popular uprisings: People rising up against the government.
- Alliance building: Local powers joining together to fight the empire.
Economic Strain And Resource Management
Empires need money to run, and pan-regional empires were no exception. Maintaining a large army, building infrastructure, and keeping the government running all cost a lot. Sometimes, the empire would overspend, leading to economic problems. Resource management was key, but often poorly executed.
Plus, think about the logistics of moving resources around such a vast area. It’s not like they had Amazon Prime back then! Getting food, materials, and money where they needed to be was a huge challenge. And if there was a famine or some other disaster? Things could get really bad, really fast.
Understanding The Concept In NCERT Class 7 History
Key Themes in NCERT Class 7 History
NCERT Class 7 History introduces young students to the medieval period of India, a time of significant change and the rise of various kingdoms. A key theme is understanding how empires expanded and interacted with different regions.
The textbook covers topics like the Delhi Sultanate, the Mughal Empire, and regional cultures, providing a foundation for understanding India’s diverse past. It also touches upon social and economic life, religious developments, and artistic achievements during this period.
How Pan-Regional Empires Are Presented
The concept of pan-regional empires is introduced through the study of empires like the Mughals. The textbook explains how these empires extended their influence over vast territories, integrating diverse cultures and administrative systems.
It highlights the strategies they used for expansion, governance, and maintaining control over their territories. The focus is on illustrating how these empires were not just about military conquest but also about establishing systems that could manage and benefit from the resources and cultures of different regions.
Importance of Studying Pan-Regional Empires
Studying pan-regional empires is important for several reasons:
- It helps students understand the interconnectedness of different regions in India’s history.
- It shows how political and economic systems evolved over time.
- It provides insights into the cultural exchange and integration that occurred under these empires.
Understanding the rise and fall of pan-regional empires gives students a broader perspective on the forces that have shaped India’s identity and its place in the world. It encourages critical thinking about the legacies of these empires and their relevance to contemporary issues.
Our Look at Pan-Regional Empires
In summary, understanding pan-regional empires gives us a clearer picture of how power and culture spread across different areas. These empires, like the Mughals, didn’t just stick to one place; they reached out to influence many regions.
This kind of expansion often led to a mix of traditions, languages, and governance styles. It’s fascinating to see how these connections shaped societies and left lasting impacts. So, next time you hear about a pan-regional empire, think about the wide-reaching effects it had on the world around it.
Frequently Asked Questions
What Is A Pan-Regional Empire?
A pan-regional empire is a large empire that has influence over multiple regions or areas. It connects different cultures and people under one rule.
What Are Some Features Of Pan-Regional Empires?
Pan-regional empires often have a strong central government, a diverse population, and a mix of cultures. They also usually control trade routes and have significant military power.
Can You Name Some Historical Examples Of Pan-Regional Empires?
Yes! Some well-known examples include the Roman Empire, the Mughal Empire, and the Ottoman Empire. Each of these empires ruled over a wide area and influenced many cultures.
What Role Does Culture Play In Pan-Regional Empires?
Culture is very important in pan-regional empires. They often spread their own culture while also adopting elements from the regions they control, leading to a rich mix of traditions.
How Do Pan-Regional Empires Impact Neighboring Regions?
Pan-regional empires can greatly influence neighboring regions politically, economically, and culturally. They often create trade connections and promote cultural exchanges.
Why Is It Important To Study Pan-Regional Empires In History?
Studying pan-regional empires helps us understand how different cultures interact and how power dynamics work. It also shows us the impact of these empires on modern nations.