NCERT Solutions For Class 8 Maths Chapter 6 Cubes And Cube Roots

NCERT Solutions For Class 8 Maths Chapter 6 Cubes And Cube Roots Introduction

Hardy – Ramanujan Number

Look at the following relations :

1729 = 1728 + 1 = 12³ + 1³

1729 = 1000 + 729 = 10³ + 9³

1729 is the smallest Hardy – Ramanujan Number (a number expressed as a sum of two cubes in two different ways is known as a Hardy- Ramanujan Number). There are infinitely many such numbers.

Few are 4104 (2, 16; 9, 15), 13832 (18, 20; 2, 24

Q. Check it with the numbers given in the brackets. 4104 (2, 16; 9, 15) and 13832 (18, 20; 2, 24)

2³ + 16³  = 8 + 4096 = 4104

9³ + 15³ = 729 + 3375 = 4104

18³ + 20³ = 5832 + 8 000 = 13832

2³ + 24³ = 8 + 13824 = 13832

Read and Learn More NCERT Solutions For Class 8 Maths

Cubes

Numbers obtained when a number is multiplied by itself three times are known as cube numbers or perfect cubes.

For example: 1, 8, 27,

The cube of a natural number m is denoted by m3 and is expressed as

m³ = m x m x m.

Thus, 1³ = 1 x 1 x 1 = 1

2³ = 2 × 2× 2 = 8

3³ = 3 ×  3 × 3 = 27, and so on

Question 1. How many cubes of side? 1 cm will \ make a cube of side 2 cm?
Solution:

2 × 2 × 2 = 8 cubes of side 1 cm will make a cube of side 2 cm.

Question 2. How many cubes of side 1 cm will make a cube of side 3 cm?
Solution:

3 × 3 × 3 = 27 cubes of side 1 cm will make a cube of side 3 cm

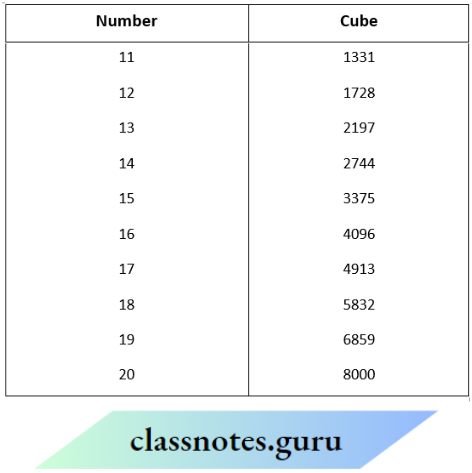
Question 3. Following are the cubes of the numbers from 11 to 20
Solution:

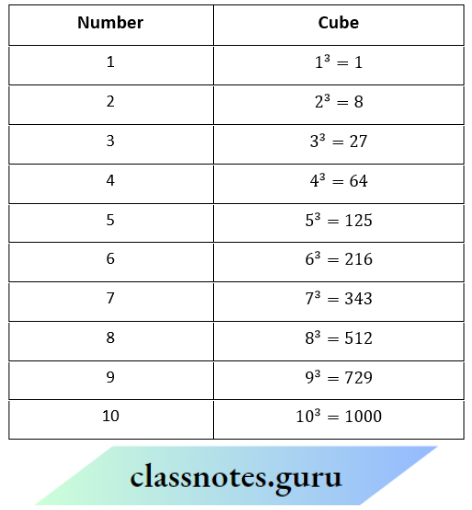
Question 4. Complete the following cubes of numbers  From 1 to 10

Solution:

Question 5. Are there only ten perfect cubes from 1 to 1000?
Solution:
Yes :

There are only ten perfect cubes from 1 to 1000.

These are: 1, 8, 27, 64, 126, 216, 343, 512, 729 and 1000

Question 6. How many perfect cubes are there from 1 to 100?
Solution:

There are only four perfect cubes from 1 to 100.

 These are: 1, 8, 27, and 64.

Question 7. Observe the cubes of even numbers. Are they all even? What can you say about the cubes of odd numbers?
Solution:

1. The cubes of even numbers are all even.
2. The cubes of odd numbers are all odd.

Question 8. Consider a few numbers having 1 as the one’s digit (or unit’s). Find the cube of each of them. What can you say about the one digit of the cube of a number having 1 as the one’s digit? Similarly, explore the one’s digit of cubes of numbers ending in 2, 3, 4,
Solution:

We observe that the one digit of the cube of a number having 1 as the one’s digit is 1. Similarly, the one’s digit of cubes of numbers ending in 0, 2, 3, 4, 5, 6, 7, 8, 9 are 0, 8, 7, 4, 5, 6, 3, 2, 9 respectively

Question 9. Find the one digit ofthe cube ofeach of the following numbers.

1. 3331
2. 8888
3. 149
4. 1005
5. 1024
6. 77
7. 5022
8. 53

Solution:

1. 3331

Unit digit of the number = 1

Unit digit of the cube of the number = 1

∴  1 × 1 × 1 = \(\underline{1}\)

2.  8888

Unit digit of the number = 8

Unit digit of the cube of the number = 2.

∴  8 × 8 × 8 = 51\(\underline{2}\)

3.  149

Unit digit of the number = 9

Unit digit of the cube of the number = 9

∴  9 × 9 × 9 = 72\(\underline{9}\)

4.  1005

Unit digit of the number = 5

Unit digit of the cube of the number = 5.

∴  5 × 5 × 5 = 12\(\underline{5}\)

5. 1024

Unit digit of the number = 4

Unit digit of the cube of the number = 4

∴  4 × 4 × 4 × 4 = 6\(\underline{4}\)

4. 77

Unit digit of the number = 7

Unit digit of the cube of the number = 3.

∴  7 × 7 × 7 = 34\(\underline{3}\)

8. 5022

Unit digit of the number = 2

Unit digit of the cube of the number = 8

∴  2 × 2 × 2 = \(\underline{8}\)

8. 53

Unit digit of the number = 3

Unit digit of the cube of the number = 7

∴  3 × 3 × 3 = 2\(\underline{7}\)

Some Interesting Patterns

If in the prime factorization of any number, each prime factor appears three times, then the number is a perfect cube.

For example, 216 =\(\underline{2 \times 2 \times 2} \times \underline{3 \times 3 \times 3} \times \underline{3 \times 3} \times \underline{5 \times 5}\)

= 2³ ×  3³ = (2× 3)³ = 6³ which is a perfect cube.

Question 1. How many consecutive odd numbers will be needed to obtain the sum as 10³?
Solution:  Ten.

Question 2. Express the following numbers as the sum of odd numbers using the above pattern.

1. 6³
2. 8³
3. 7³

Solution: 

1. 6³

Here, n = 6

∴ (n – 1) = 5

We start with n × (n – 1) + 1

= 6× 5 +1

= 31

6³ = 31 + 33 + 35 + 37+ 39 + 41

2. 8³

Here, n = 8

∴ (n – 1) = 7

We start with n × (n – 1) + 1

= 8 × 7  + 1

=  56+1

=  57

8³ = 57 + 59 + 61 + 63 + 65 + 67 + 69 + 71

3. 7³

Here, n = 7

(n -1) = 6

We start with n × (n – 1) + 1,

7 × 6 + 1,

= 42+1

= 43

7³ = 43 + 45 + 47 + 49 + 51 + 53 + 55

Question 3. Consider the following pattern.

1. 2³ – 1³ = 1 + 2 × 1 × 3
2. 3³ – 2³ = 1 + 3 × 2 × 3
3. 4³ – 3³= 1 + 4 × 3 × 3

Using the above pattern, find the value of the following:

1. 7³ – 6³
2. 12³ – 11³
3. 20³ – 19³
4. 51³  – 50³ 

Sol.

1. 7³ – 6³ 

= 1 + 7 × 6 ×3

=1+126

= 127

2. 12³ – 11³

= 1 + 12 × 11 × 3

=1 + 396

= 397

3.  20³- 19³

T = 1 + 20 × 19 × 3

= 1 + 1140

= 1141

4.  51³ – 50³

1 + 51 × 50 × 3

= 1 + 7650

= 7651

Question 4. Which of the. following are perfect cubes

1. 400
2. 3375
3. 8000
4. 15625
5. 90000
6. 6859
7. 2025
8. 10648

1.  400

By prime factorisation,

Grouping the factors in triplets

400 = \(\underline{2 \times 2 \times 2} \times\)  2× 5 × 5.

= 2³ × 2× 5× 5

Bylaws of exponents

In the above factorization, 2 and 5 × 5 remain after grouping 2’s in triplets.

∴ 400 is not a perfect cube

2.33375

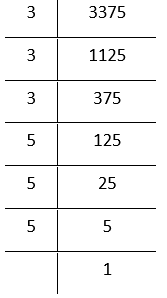
Therefore, 400 is not a perfect cube

By prime factorisation,

3375 = \(\underline{3 \times 3 \times 3} \times \underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 3³× 5³

Bylaws of exponents

= (3 × 5)³

= 15³, which is a perfect cube.

∴  3375 is a perfect cube.

3. 80000

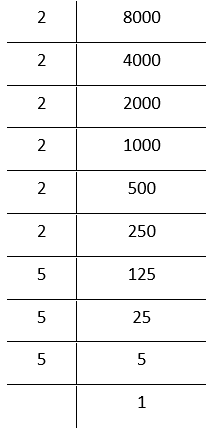
By prime factorisation,

8000 =  \(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2} \times \underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 2³× 2³ × 5³

Bylaws of exponents

= (2 × 2 ×5)³

= 20³, which is a perfect cube.

∴   8000 is a perfect cube

4.15625

By prime factorisation,

15625 = \(\underline{5 \times 5 \times 5} \times \underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 5³× 5³

Bylaws of exponents

= (5 × 5)³

Bylaws of exponents

25³, which is a perfect cube.

∴  15625 is a perfect cube

5. 9000

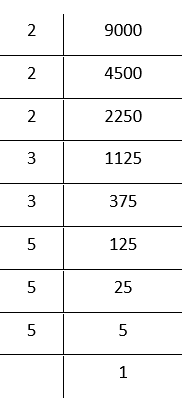
By prime factorisation,

9000 = \(\underline{2 \times 2 \times 2} \times\) 3× 3 × \(\underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

In the above factorization, 3×3 remains after grouping 2’s and 5’s in triplets.

∴  9000 is not a perfect cube.

6. 6859

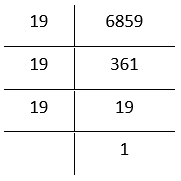
By prime factorisation

6859 = \(\underline{19 \times 19 \times 19}\)

Grouping the factors in triplets

= 19³

Bylaws of exponents which is a perfect cube

∴  6859 is a perfect cube

7. 2025

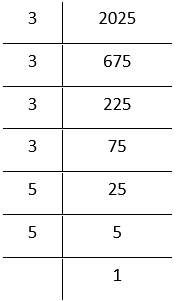
By prime factorisation,

2025  = \(\underline{3 \times 3 \times 3} \times\) 3 × 5 × 5

Grouping the factors in triplets

= 3³ × 3 × 5 × 5

Bylaws of exponents

In the above factorization, 3 and 5 ×  5 remain after grouping 3’s in triplets.

∴ 2025 is not a perfect cube

8. 10648

By prime factorisation

10648 = \(\underline{2 \times 2 \times 2} \times \underline{11 \times 11 \times 11} \times \)

Grouping the factors in triplets

= 2³ × 11³

Bylaws of exponents

= (2 × 11)³

Bylaws of exponents

= 22³, which is a perfect cube.

∴  10648 is a perfect cube

Smallest Multiple That Is A Perfect Cube

Sometimes we have to find the smallest natural number by which a number is multiplied or divided to make it a perfect cube

Question 1. Check which of the following are perfect cubes

1. 2700
2. 6000
3. 64000
4. 500
5. 125000
6. 50000
7. 21600
8. 10000
9. 27000000
10. 1000

What pattern do you observe in these perfect cubes
Solution:

1. 2700

By prime factorisation,

2700 = 2× 2× \(\underline{3 \times 3 \times 3}\)×  5 ×  5

Grouping the factors in triplets

= 2  × 2 × 3³× 5× 5

Bylaws of exponents

In the above factorization, 2 × 2 and

5× 5 remain after grouping 3’s in triplets.

∴ 2700 is not a perfect cube

2. 16000

By prime factorisation,

16000 = \(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2}\)  × 2 × \(\underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 2³ × 2³ × 2 ×  5³

Bylaws of exponents

In the above factorization, 2 remains after grouping 2’s and 5’s in triplets.

∴ 16000 is not a perfect cube

3. 64000

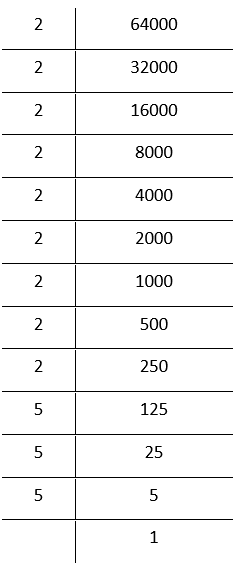
By prime factorisation,

64000 = \(\underline{2 \times 2 \times 2 } \times \underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2} \times \underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 2³ ×2³ × 2³× 5³

By laws of exponents

= (2 × 2 × 2 ×5)³

= 40³, which is a perfect cube.

∴  64000 is a perfect cube

4.  900

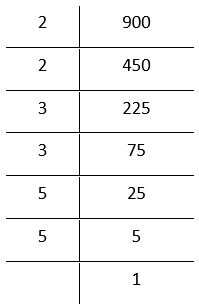
By prime factorisation,

900 = 2 ×2 × 3 × 3 × 5 × 5

In the above factorization, 2 × 2, 3 × 3, and 5 × 5 remain when we try to group the factors in triplets.

∴ 900 is not a perfect cube.

5. 125000

By prime factorisation,

125000 = \(\underline{2 \times 2 \times 2 } \times \underline{5 \times 5 \times 5} \times \underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 2³ × 5³ × 5³

Bylaws of exponents

= (2 × 5 × 5)³

= 50³, which is a perfect cube.

∴  125000 is a perfect cube.

6. 36000

By prime factorisation,

3600 = \(\underline{2 \times 2 \times 2 } \times \underline{2 \times 2 } \times \underline{3 \times 3} \times \underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 2³ × 2 × 2 × 3 × 3 × 5³

Bylaws of exponents

In the above factorization, 2 × 2 and 3 ×3 remain after grouping 2’s and 5’s in  triplets

∴  36000 is not a perfect cube.

7. 21600

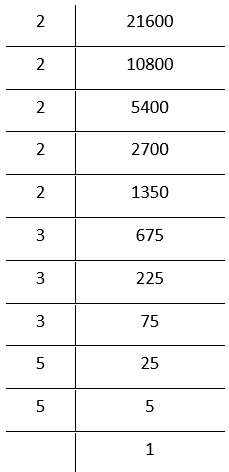
By prime factorisation

21600 = \(\underline{2 \times 2 \times 2 }\) × 2 × 2 ×  \(\underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 2³ × 2 × 2×3³×5 × 5

Bylaws of exponents

In the above factorization, 2×2 and 5×5 remain after grouping 2’s and 3’s in triplets

∴  21600 is not a perfect cube.

8. 10000

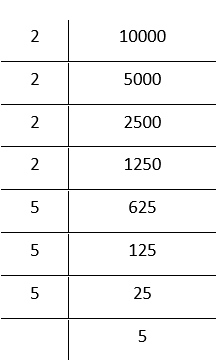
By prime factorisation,

1000 =\(\underline{2 \times 2 \times 2}\) ×  2 × \(\underline{5 \times 5 \times 5}\) × 5

Grouping the factors in triplets

= 2³ × 2 × 5³ × 5

Bylaws of exponents

In the above factorization, 2 and 5 remain after grouping 2’s and 5’s in triplets.

∴ 10000 is not a perfect cube

9. 27000000

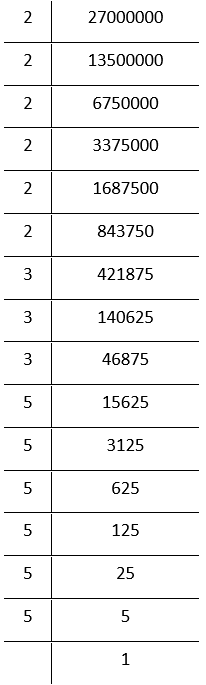
By prime factorisation,

27000000

=\(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2} \times \underline{3 \times 3 \times 3} \times \underline{5 \times 5 \times 5}\times \underline{5 \times 5 \times 5}\)

Grouping the factors in triplet

= 2³×2³ × 3³× 5³ × 5³

Bylaws of exponents

= 300³, which is a perfect cube.

∴  27000000 is a perfect cube.

10. 1000

By prime factorization,

1000 = \( \underline{2 \times 2 \times 2} \times \underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 2³ × 5³

Bylaws of exponents

= (2 × 5)³ I By laws of exponents

= 10³, which is a perfect cube.

Therefore, 1000 is a perfect cube.

We observe the following pattern in these perfect cubes:

1. If in the end of a number, the number of zeros is not 3 or a multiple of 3, then that number cannot be a perfect cube
2. If in the end of a number, the number £ of zeros is 3 or a multiple of 3, then JJJ that number may be a perfect cube.
3. Thus, the number of zero at the end of a perfect cube (if it is so) must essentially be 3 or a multiple of3, failing which the number cannot be a perfect cube.

NCERT Solutions For Class 8 Maths Chapter 6 Cubes And Cube Roots Exercise 6.1

Question 1. Which of the following numbers are not perfect cubes?

1. 216
2. 129
3. 1000
4. 100
5. 46656

Solution:

1. 216

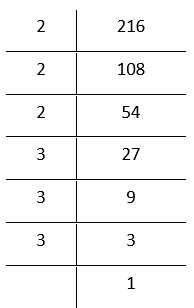
By prime factorisation

216 =  \(\underline{2 \times 2 \times 2}\times \underline{3 \times 3 \times 3}\)

Grouping the factors in triplets

= 2³ × 3³

Bylaws of exponents

= (2 × 3)³

= 6³ which is a perfect cube.

∴  216 is a perfect cube

2. 128

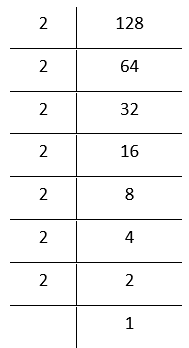
By prime factorisation

128 = \(\underline{2 \times 2 \times 2}\times \underline{2 \times 2 \times 2}\) × 2

Grouping the factors in triplets

= 2³ × 2³ × 2

Bylaws of exponents

In the above factorization,2remainsafter grouping the 2 ‘s in triplets

∴ 128 is not a perfect cube

3. 1000

By prime factorisation

= \(\underline{2 \times 2 \times 2}\times \underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 2³× 5³

Bylaws of exponents

= (2 × 5)³ = 10³

Bylaws of exponents

Which is a perfect cube.

∴ 1000 is a perfect cube

4. 100

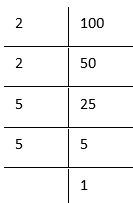
By prime factorisation

100 =  \(\underline{2 \times 2 \times }\times \underline{5 \times 5}\)

In (he above factorization, 2 × 2,5  × 5 remains when we try to group the factors in triplets

Therefore, 100 is not a perfect, cube.

5.46656

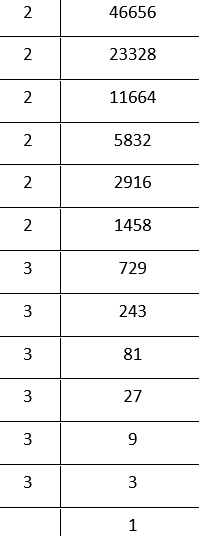
By prime factorisation,

46656 = \(\underline{2 \times 2 \times 2 \times 2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3} \times \underline{3 \times 3 \times 3}\).

Grouping the factors in triplets

= 2³ × 2³×3³ × 3³

Bylaws of exponents

= (2 ×2 × 3 × 3)³

Bylaws of exponents

= 36³, which is a perfect cube.

∴  46656 is a perfect cube

Question 2. Find the smallest number by which each of the following numbers must be multi¬ plied to obtain, a perfect cube

1. 243
2. 256
3. 72
4. 675
5. 100

Solution:

1. 243

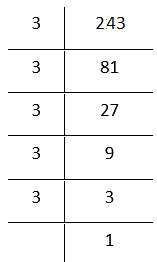
By prime factorisation

243 =\(\underline{3 \times 3 \times 3}\) × 3 × 3

Grouping the factors in triplets

The prime factor 3 does not appear in a group of three.

Therefore, 243 is not a perfect cube.   To make it a cube, we need one more 3. In that case

243 = \(\underline{3 \times 3 \times 3} \times \underline{3 \times 3 \times 3}\)

= \(3^3 \times 3^3\)

= (3×3)³

729, which is a perfect cube.

Hence, the smallest number by which 243 should be multiplied to obtain a perfect cube is 3.

The resulting perfect cube is 3.

2. 256

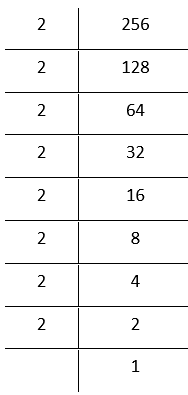
By prime factorisation

256 =\(\underline{2 \times 2 \times 2}\underline{2 \times 2 \times 2}\) 2 x 2

Grouping the factors in triplets

In the above factorisation 2× 2  after grouping 2‘s in Iriplols. Therefore, 128 is not a perfect cube. To make it a perfect, cube, we need one 2 more. In that, case

256× 2 = \(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2} \times 2 \times 2\)

= 2³×2³× 2³

Bylaws of exponents

= (2×2×2)³

Bylaws of exponents

8³ = 512, which is a perfect cube.

Hence, the smallest number by which 256 must be multiplied to obtain a perfect cube is 2

The resulting perfect cube is 512 (= 8³)

3. 72

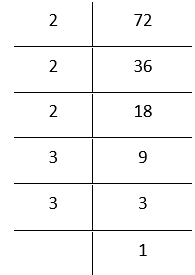
By prime factorisation,

72 = 2 × 2 × 2 × 3 × 3

Grouping the factors in triplets

The prime factor 3 does not appear in a group of three.

Therefore, 72 is not a perfect cube. To make it a perfect cube, we need one more 3. In that case,

72 × 3 = \(\underline{2 \times 2 \times 2} \times \underline{3 \times 3 \times 3}\)

= 2³ ×3³

Bylaws of exponent

= (2 × 3)³

Bylaws of exponents

6³ = 216 which is a perfect cube.

Hence, the smallest number by which 72 must be multiplied to obtain a perfect cube is 3.

The resulting perfect cube is 216 (= 6³)

4. 675

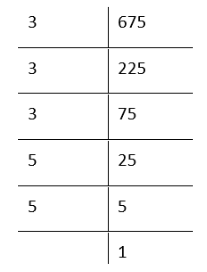
By prime factorisation,

675 = 5 × 3 × 3 × 5 × 5

Grouping the factors in triplets

The prime factor 5 does not appear in a group of three. Therefore, 675 is not a perfect cube.

To make it a perfect cube, we need one more 5. In that case

675 ×  5 = \(\underline{3 \times 3 \times 3} \times \underline{5 \times 5 \times 5} \)

= 3³× 5³

Bylaws of exponents

= (3×5)³

Bylaws of exponents

= 15³

∴ 3375 which is a perfect cube.

Hence, the smallest number by which 675 must be multiplied to obtain a perfect cube is 5.

The resulting perfect cube is 3375 (= 15³)

5. 100

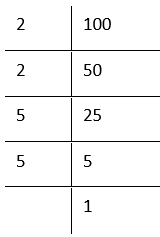
By prime factorisation,

100 = 2 × 2 × 5 × 5

Grouping the factors in triplets

The prime factors 2 and 5 do not appear in a group of three. Therefore, 100 is not a perfect cube.

To make it a perfect cube, we need one 2 and one 5 more. In that case,

100 × 2 × 5 = \(\underline{2 \times 2 \times 2} \times \underline{5 \times 5 \times 5} \)

= 2³ × 5³

Bylaws of exponents 2

= (2 × 5)³

Bylaws of exponents

= 10³

∴ 1000 which is a perfect cube.

Hence, the smallest number by which 100 must be multiplied to obtain a perfect cube is 2× 5 = 10

The resulting perfect is 1000 (= 10³ )

Question 3. Find the smallest number by which each of the following numbers must be divided to obtain a perfect cube.

1. 81
2. 128
3. 135
4. 192
5. 704

Solution:

1. 81

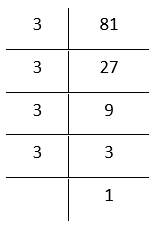
By prime factorisation

81 =\(\underline{3 \times 3 \times 3}\times\) 3

Grouping the factors in triplets

In the above factorization, 3 remains after grouping the 3’s in triplets. Therefore,

81 is not a perfect cube. If we divide the number by 3, then in the prime factorization of the quotient, this 3 will not remain. In that case,

81 ÷ 3  = \(\underline{3 \times 3 \times 3}\)

= 3³

Bylaws of exponents which is a perfect cube

Hence, the smallest whole number by which 81 must be divided to obtain a perfect cube is 3.

The resulting ideal cube is 27 (= 3³)

2. 128

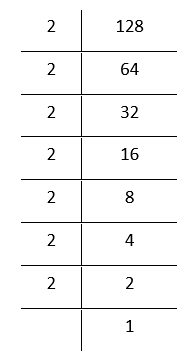
By prime factorisation,

128 = \(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2}\)

Grouping the factors in triplets

In the above factorization, 2 remains after grouping’ the 2’s in triplets.

Therefore, 128 is not a perfect cube. If we divide the number by 2, then in the prime factorization ofthe quotient, this 2 will not remain. In that case,

128 ÷ 2 = \(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2}\)

= 2³ × 2³

= (2 × 2)³

Bylaws of exponents

= 4³, which is a perfect cube.

Hence, the smallest whole number by  which 128 must be divided to obtain a perfect cube is 2

The resulting ideal cube is 64 (= 4³)

3. 135

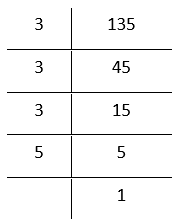
By prime factorisation,

135 = \(\underline{3 \times 3 \times 3} \times 5\)

Grouping the factors in triplets.

The prime factor 5 does not appear in a group of three. So 135 is not a perfect cube

In the factorisation 5 appears only once. If we (u) 704 divide 135 by 5, then the prime factorization of the quotient, will not contain 5.

In that case

135 ÷ 5 = \(\underline{3 \times 3 \times 3}\)

Grouping the factors in triplets

= 27

Bylaws of exponents, which is a perfect cube.

Hence, the smallest whole number by  which 135 must be divided to obtain a perfect cube is 5

The resulting perfect cube is 27 (= 33)

4. 192

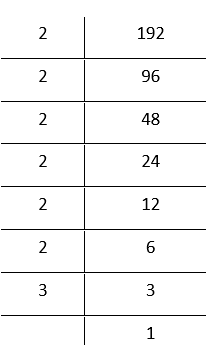
By prime factorisation,

192  = \(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2} \) × 3

Grouping the factors in triplets

The prime factor 3 does not appear in a group of three. So 192 is not a perfect cube. In the factorization of 192, 3 appears only once. So if we divide the number by 3, then the prime factorization of the quotient will not contain 3.

.In that case,

192 ÷ 3 = \(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2} \) × 3

= 2³ × 2³

= (2 × 2)³

Bylaws of exponents

= 4³ = 64

Which is a perfect cube.

Hence, the smallest whole number by which 192 must be divided to obtain a perfect cube is 3.

The resulting perfect cube is 64 (= 4³)

5. 704

By prime factorisation,

704  =  \(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2} \) × 11

Grouping the factors in triplets

The prime factor 11 does not appear in the group of three.

So, 704 is not a perfect cube.

In the factorization 11 appears only one time.

So if we divide 704 by 11, then the prime factorization of the quotient will not contain 11. In that case

704 ÷ 11 = 2 × 2 × 2 × 2 × 2 × 2

Grouping the factors in triplets

2³ × 2³

Bylaws of exponents

= (2 × 2)³

= 4³

= 64

Which is a perfect cube.

Hence, the smallest whole number by which 704 must be divided to obtain a perfect cube is 11.

The resulting perfect cube is 64 (= 4³).

Question 4. Parikshit makes a cuboid of plasticine of sides 5 cm, 2  How many such cuboids will he need to form a cube? cm, 5 cm.
Solution:

Volume of a cuboid

= 5 × 2 × 5 cm³

Since there is only one 2 and only two 5’s in the prime factorization, so, we need 2 × 2 × 5, i.e.t 20 to make a perfect cube.

Therefore, we need 20 such cuboids to make a cube.

Cube Roots

The cube root is the inverse operation of finding a cube.

2³ = 8 ⇒  2 is the cube root of 8.

The symbol denotes the cube root. Thus,\(\sqrt[3]{8}=2\)

Cube Root Through Prime Factorisation Method

We express the given number into product of its prime factors and make triplets (groups of three) of similar factors. Then, we take one factor from each triplet and multiply. The product so obtained gives the cube root of the given number.

Question 1. State true or false: for any integer m, m²< m³. Why?
Solution:

False, if m is a negative integer.

True, if m is a positive integer (natural number).

Verification. Let us take a negative integer m =-1. Then,

m²= (- 1)2 = (- 1)² ×  (-1) = 1

m³ = (_ 1)3 = (- 1)³ × (-1) × (-1)

= – 1

Clearly, m² > m³

Hence, the given statement is false if m is a negative integer.

We get the same inference for m = – 2, -3,-4, etc.

Again, let us take a positive integer(natural number) m = 2. Then,

m² = (2)² = 2 × 2 = 4

m³ = (2)³ = 2 × 2 × 2 = 8

Clearly, m² < m³

Hence, the given statement is true if m is a positive integer (natural number).

We get the same inference for m = 3, 4,5… etc

Cube Root of a Cube Number Steps

1. Obtain the given number. Start making groups of three digits starting from the rightmost digit of the number.
2. The first group will give one’s (unit’s) digit of the required cube root.
3.  Then, take another group. Find the two closest cube numbers between which this group lies. Take the one’s place of the smaller number as the ten’s place of the required cube root

NCERT Solutions For Class 8 Maths Chapter 6 Cubes And Cube Roots Exercise 6.2

Question 1. Find the cubit root of each of the foUouiu# numbers by prime factorization method :

1. 64
2. 512
3. 10648
4. 27000
5. 15625
6. 13824
7. 110592
8. 46656
9. 175616
10. 91125

Solution:

1. 64

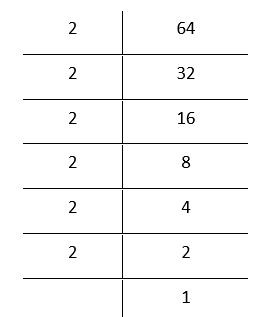
The prime factorization of 64 is

= \(\underline{2 \times 2 \times 2} \times \underline {2\times 2 \times 2}\)

Grouping the factors in triplets

= 2³× 2³

= (2 × 2)³

= 4³

Bylaws of exponents

∴ \(\sqrt[3]{64}\) = 2 × 2

2.512

The prime factorisation of 512 is

⇒ \(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2}\)

Grouping the factors in triplets

= 2³× 2³ × 2³

= (2 × 2 ×2)³

= 8³

Bylaws of exponents

∴ \(\sqrt[3]{512}\) = 2 × 2 ×2

= 8³

3. 10648

Prime factorization of 10648 is

⇒ [late]\underline{2 \times 2 \times 2} \times \underline{11 \times 11 \times 11} [/latex]

Grouping the factors in triplets

= 2³ x 11³

= (2 × 11)³

∴ \(\sqrt[3]{10648}\) = 2 × 11

= 22³

4. 27000

Prime factorisation of 27000 is

⇒ \(\underline{2 \times 2 \times 2} \times \underline{3 \times 3  \times 3 } \times \underline{5 \times 5 \times 5 } \times \underline{5 \times 5}\)

Grouping the factors in triplets

= 2³ × 3³ × 5³

= (2 × 3 × 5)³

Bylaws of exponents

= 30³

∴ \(\sqrt[3]{27000}\) = 2×3 × 5

= 30

5. 15625

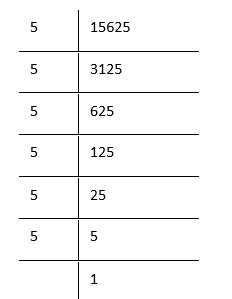
The prime factorization of 15625 is

⇒ \(\underline{5 \times 5 \times 5} \times \underline{5 \times 5  \times 5 }\)

Grouping the factors in triplets

= 5³ × 5³

= (5 × 5)³

Bylaws of  exponents

= 25³

∴ \(\sqrt[3]{15625}\) = 5 × 5

= 25

6. 13824

Prime factorization of 13824 is

⇒  \(\underline{2 \times 2 \times 2}\times \underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2} \times \underline{3 \times 3 \times 3}\)

Grouping the factors in triplets

= 2³ × 2³× 2³ × 3³

=(2× 2 × 2 × 3)³

Bylaws of exponents

= 24³

∴ \(\sqrt[3]{13824}\)  = 2× 2 × 2 × 3

= 24

7. 1110592

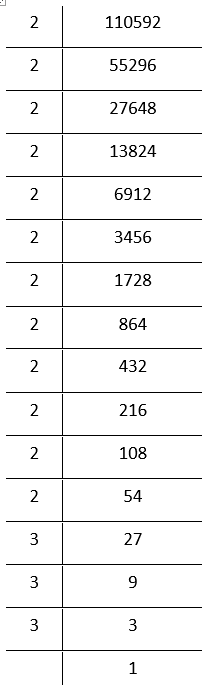
Prime factorisation of 110592 is

⇒  \(\underline{2 \times 2 \times 2}\)× \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{2 \times 2 \times 2}\) × \(\underline{3 \times 3 \times 3}\)

Grouping the factors into triplets

= 2³ × 2³ × 2³ × 2³ × 3

= (2 × 2 × 2 × 2 ×3)³

Bylaws of exponents

= 48³

∴ \(\sqrt[3]{110592}\) =2 × 2 × 2 × 2 ×3

8. 46656

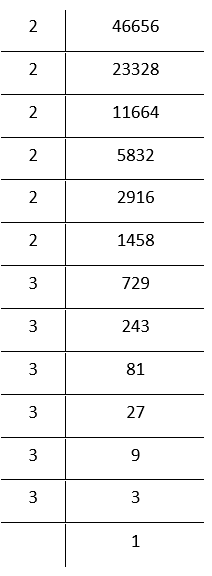
Prime factorization of 46656 is

⇒ \(\underline{2 \times 2 \times 2} \times \underline{2 \times 2 \times 2} \times \underline{3 \times 3 \times 3} \times \underline{3 \times 3 \times 3}\)

Grouping the factors in triplets

= 2³× 2³ × 3³ × 3³

= (2 × 2 × 3 × 3)³

Bylaws of exponents

= 36³

∴ \(\sqrt[3]{46656}\) = 2 × 2 × 3 × 3

=36

9. 175616

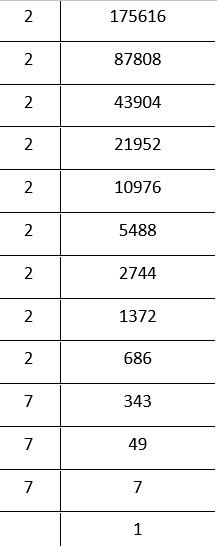
Prime factorisation of 175616 is

⇒  \(\underline{2 \times 2 \times 2 \times} \times \underline{2 \times 2 \times 2 \times} \times \underline{2 \times 2 \times 2 \times} \times \underline{7 \times 7 \times 7}\)

Grouping the factors in triplets

= 2³ × 2³ × 2³ × 7³

= (2 × 2 × 2 × 7)³

Bylaws of exponents

= 56³

∴ \(\sqrt[3]{175616}\) = 2 × 2 × 2 × 7

= 56

10. 91125

Prime factorization of 91125 is

⇒ \(\underline{3 \times 3 \times 3 \times} \times \underline{3 \times 3 \times 3 \times} \times \underline{5 \times 5 \times 5}\)

Grouping the factors in triplets

= 3³ ×3³ × 5³

= (3 × 3× 5)³

Bylaws of exponents

= 45³

∴ \(\sqrt[3]{91125}\) =3 × 3× 5

= 45

NCERT Solutions For Class 8 Maths Chapter 6 Cubes And Cube Roots Multiple Choice Questions

Question 1. Which of the following numbers is a perfect cube?

1. 125
2. 36
3. 75
4. 100

Solution: 1. 125

125 = 5 × 5 × 5 = 5³

Question 2. Which of the following numbers is a cube number?

1. 1000
2. 400
3. 100
4. 600.

Solution: 1.1000

1000 = 10 × 10 × 10 = 10³

Question 3. Which of the following numbers is not a perfect cube?

1. 1331
2. 512
3. 343
4. 100

Solution: 4. 100

100 = 2 ×2 × 5 ×5

= 2² × 5².

Question 4. Which of the following numbers is not a cube number?

1. 10000
2. 3375
3. 64
4. 729.

Solution: 1. 10000

10000 = 2 × 2 ×2 × 2 ×5 ×5× 5 ×5

= 2⁴ × 5⁴

= 2³× 2 × 5³ × 5

Question 5. The cube of an odd natural number is

1. Even
2. Odd
3. Maybe even, maybe odd
4. Prime number.

Solution: 2. Odd

3 × 3 × 3 = 27 (odd)

Question 6. The cube of an even natural number is

1. Even
2. Odd
3. Maybe even, maybe odd
4. Prime number.
5. Solution: 1. Even

6 × 6 × 6 = 216 (even)

Question Question 7. The one digit of the cube of the number 111 is

1. 1
2. 2
3. 3
4. 9.

Solution: 1. 1

1 × 1 × 1 =  1

Question 8. The one digit of the cube of the number 242 is

1. 2
2. 4
3. 6
4. 8.

Solution: 4. 8

2 × 2 × 2= 8.

Question 9. The one digit of the cube of the number 123 is

1. 3
2. 6
3. 9
4. 7

Solution: 4. 7

3 × 3 × 3 =2\(\underline{7}\)

Question 10. The one’s digit of the cube of the number 144 is

1. 1
2. 2
3. 3
4. 4.

Solution: 4. 4

4 × 4 ×4 = 6\(\underline{4}\)

Question 11. The one’s digit of the cube of the number 50 is

1. 1
2. 0
3. 5
4. 4

Solution: 2. 0

0 × 0 × 0 = 0

Question 12. The one digit of the cube of the number 326 is

1. 2
2. 3
3. 6
4. 4

Solution: 3. 3

6 × 6 × 6 = 21\(\underline{6}\)

Question 13. The one digit of the cube of the number 325 is

1. 2
2. 5
3. 3
4. 6.

Solution: 2. 5

5× 5× 5= 12\(\underline{5}\)

Question 14. The one digit of the cube of the number 347 is

1. 3
2. 4
3. 7
4. 1

Solution: 1. 3

7×7×7 = 34\(\underline{3}\)

Question 15. The one digit of the cube of the number 68 is

1. 1
2. 2
3. 6
4. 8

Solution: 2. 2

8× 8 ×8 = 51\(\underline{2}\)

Question 16. The one digit of the cube of the number 249 is

1. 2
2. 4
3. 9
4. 1

Solution: 3. 9

9 × 9 × 9 = 72\(\underline{9}\)

Question 17. What is the one’s digit in the cube root of the cube number 1331?

1. 1
2. 2
3. 3
4. 4

Solution: 1. 1

1 × 1 × 1 = 1

Question 18. What is the one digit in the cube root of the cube number 1000000?

1. 0
2. 1
3. 2
4. 9

Solution: 1. 0

0 ×0 × 0 = 0

Question 19. What is the one’s digit in the cube root of the cube number 1728?

1. 1
2. 2
3. 3
4. 9

Solution: 2. 2

2 × 2 × 2 = \(\underline{8}\)

Question 20. What is the one’s digit in the cube root, of the cube number 2197′?

1. 1
2. 2
3. 3
4. 7

Solution: 3. 3

3× 3 × 3 = 2\(\underline{7}\)

Question 21. What is t lie one’s digit, in the cube root, of the cube number 2744?

1. 1
2. 2
3. 3
4. 4

Solution: 4. 4

4 × 4 × 4 = 6\(\underline{4}\)

Question 22. What is the one’s digit in the cube root of the cube number 3375?

1. 2
2. 3
3. 5
4. 4

Solution: 3. 5

5 × 5 × 5 = 12\(\underline{5}\)

Question 23. What is the one’s digit in the cube root of the cube number 4096? 

1. 2
2. 6
3. 4
4. 9.

Solution: 2. 6

6 × 6 × 6 = 21\(\underline{6}\).

Question 24. What is the one’s digit in the cube root of the cube number 4913?

1. 7
2. 9
3. 3
4. 6

Solution: 1. 7

7 × 7 ×7 = 34\(\underline{3}\)

Question 25. What is the one’s digit in the cube root of the cube number 5832?

1. 2
2. 4
3. 6
4. 8

Solution: 4. 8

8 × 8 × 8 = 51\(\underline{2}\)

Question 26. What is the one’s digit in the cube root of the cube number 6859?

1. 7
2. 8
3. 9
4. 6

Solution: 3. 9

8 × 8 × 8 = 51\(\underline{2}\)

Question 27. What, is the one’s digit in the cube root of the cube number 8000 ?

1. 0
2. 2
3. 4
4. 8

Solution: 1. 0

0 × 0 × 0 = 0.

Question 28. The number of zeroes at the end of the cube of the number 20 is

1. 1
2. 2
3. 3
4. 6

Solution: 3. 3

Number of zeroes at the end of the number 20 = 1

Number of zeroes at the end of its cube = 3 × 1 = 3

Question 29. The number of zeroes at the end of the cube root of the cube number 1000 is

1. 1
2. 2
3. 3
4. 4

Solution: 1. 1

The number of zeroes at the end of the cube = 3

Number of zeroes at the end of the cube root = \(\frac{3}{3}\)

= 1

Question 30. The number of zeroes at the end of the cube of the number 100 is

1. 1
2. 2
3. 4
4. 6

Solution: 4. 6

Number of zeroes at the end of the number 100 = 2

Number of zeroes at the end of its cube = 3 × 2

= 6

Question 31. The number of zeroes at the end of the cube root Of the cube number 8000000 in

1. 1
2. 2
3. 3
4. 6

Solution: 2. 2

The number of zeroes at the end of the cube = 6

Number of zeroes at the end of the cube root =\(\frac{6}{3}\)

= 2

Question 32. Find the smallest number by which the number 108 must be multiplied to obtain a perfect, cube. ,

1. 2
2. 3
3. 4
4. 5

Solution: 1. 2

108 = 2 × 2 × 3 × 3 × 3

= 2 × 2 × 3³

Question 33. Find the smallest number by which the number 250 must be divided to obtain a perfect cube.

1. 2
2. 3
3. 4
4. 5

Solution: 1. 3

250 = 5 ×5 × 5 × 2 = 5³ × 2

Question 34. Find the smallest number by which the number 72 must be multiplied to obtain a perfect cube.

1. 2
2. 3
3. 4
4. 6

Solution: 2. 3

72 = 2 × 2 × 2 × 3 × 3

= 2³ × 3 × 3

Question 35. Find the smallest number by which the number 375 must be divided to obtain a perfect cube.

1. 2
2. 3
3. 5
4. 4.

Solution: 2. 3

375 = 3 × 5 × 5 × 5

= 3× 5³.

Question 36. Find the smallest number by which the number 100 must be multiplied to obtain a perfect cube.

1. 5
2. 2
3. 4
4. 10

Solution: 4. 10

100 = 2 × 2 ×5 × 5.

Question 37. Find the smallest number by which the number 10000 must be divided to obtain a perfect cube.

1. 2
2. 5
3. 10
4. 100.

Solution: 3. 10

10000 = 2 × 2 × 2 × 2 ×5×5 × 5 × 5

= 2³ × 2 × 5³× 5

Question 38. Find the smallest number by which the number 200 must be multiplied to obtain a perfect cube.

1. 2
2. 10
3. 5
4. 100

Solution: 3. 5

200 =2 × 2 × 2 × 5 × 5

= 2³ ×5 × 5

Question 39. Find the smallest number by which the number 625 must be divided to obtain a perfect cube.

1. 3
2. 5
3. 25
4. 125

Solution: 2. 5

625 = 5 × 5 × 5 ×5

= 5³ × 5.

Question 40. Kind the smallest number by which (bo number 128 must the multiplied to obtain a perfect cube.

1. 2
2. 4
3. 3
4. 8

Solution: 2. 4

128 =2 × 2 × 2 × 2 × 2 × 2 × 2

= 2³ ×2³ × 2

Question 41. Find the smallest number bv which the number 250 must be divided to obtain a perfect cube.

1. 2
2. 4
3. 8
4. 16

Solution: 2. 4

256 = 2 × 2× 2× 2 × 2× 2 ×  2×2

= 2³ × 2³ × 2 × 2.

Question 42. Find the smallest number by which the number 30 must be multiplied to obtain a perfect cube.

1. 6
2. 2
3. 3
4. 4

Solution: 1. 6

36 = 2 × 2 × 3 × 3

Question 43. Find the smallest number by which the number 1290 must be divided to obtain a perfect cube.

1. 6
2. 2
3. 4
4. 3

Solution: 1. 6

1296 = 2 × 2× 2 × 2 × 3 × 3

=  2³× 2 ×3³× 3

Question 44. Find the smallest number by which the number 392 must be multiplied to obtain a perfect cube.

1. 3
2. 5
3.  7
4. 6

Solution: 3.  7

392 = 2 × 2 × 2 × 7× 7

Question 45. Find the smallest number by which the number 2401 must be divided to obtain a perfect cube.

1. 1
2. 0
3. 5
4. 9.

Solution: 1. 1

2401 = 7 × 7 × 7 × 7

= 7³ × 7

Question 46. Find the smallest number by which the number 121 must be multiplied to obtain a perfect cube.

1. 1
2. 9
3. 11
4. 5

Solution: 3.11

121 = 11× 11

Question 47. Find the smallest number by which the number 88 must be divided to obtain a perfect cube.

1. 11
2. 5
3. 7
4. 9

Solution: 1.11

88 = 2 × 2 ×2 × 11

= 2³ ×11

Question 48. The volume of a cube is 64 cm3. The edge of the cube is

1. 4 cm
2. 8 cm
3. 16 cm
4. 6 cm

Solution: 1. 4 cm

Edge = \(\sqrt[3]{64}=\sqrt[3]{2 \times 2 \times 2 \times 2 \times 2 \times 2}\)

= \(\sqrt[3]{2^3 \times 2^3}\)

= 2 × 2

= 4.

Question 49. Apala makes a cuboid of plasticine with sides 5 cm, 4 cm, 2 cm. How many such cuboids will be needed to form a cube?

1. 20
2. 25
3. 10
4. 16

Solution: 2. 25

Volume = 5 × 4 × 2

= 5 × 2× 2 × 2

= 5 ×2³

Question 50. Which of the following is false?

1. A Cube of any odd number is odd
2. A perfect cube does not end with two zeroes
3. The cube of a single-digit number may be a single-digit number
4. There is no perfect cube that ends with 8.

Solution: 4.   There is no perfect cube that ends with 8.

1728 = 12 × 12  × 12

= 12³

NCERT Solutions For Class 8 Maths Chapter 6 Cubes And Cube RootsTrue Or False

There are four perfect cubes between 1 and 100 – False

2. Ifa2 ends in 9, then a3 ends in 9  – False

3. Ifa2 ends in 5, then a3 ends in 25  – False

4. 999 is not a perfect cube  – True

5. Cube roots of 1 are + 1 and -1   – False

6. Cube of any odd number is even – False

7. A perfect cube does not end with two zeros – True

8. If the square of a number ends with 5, then its cube ends with 25. – False

⇒  15² = 225, 15³= 3375

9. There is no perfect cube that ends – False

⇒   12³ = 1728

10. The cube of a two-digit number may be a three-digit number – False 

⇒   10³ = 1000, 99³= 970299

11. The cube of a two-digit number may have seven or more digits -False 

⇒  10³ = 1000, 99³ = 970299

12. The cube of a single-digit number may be a single-digit number – True

⇒  1³ = 1; 2³ = 8

NCERT Solutions For Class 8 Maths Chapter 6 Cubes And Cube Roots Fill In The Blanks

1. \(\sqrt[3]{x}\)represents the Cube  root of the number x

2. 1 cm³  10³ mm³

3. The cube of a number ending in 9 will end in the digit → 9

4. The cube of 100 will have zeros 6 at the end

5. There are  8 perfect cubes between 1 and 1000.

6. Find the value of \(\sqrt[3]{125} \times \sqrt[3]{-64}\) → 20

7. Find the least number by which 72 should be multiplied to make it a perfect cube → 3

8. Find the least number by which 72 should be divided to make it a perfect cube → 9

9. Find(1.1)³→ 1.331

10. Find the number whose cube is 64000 →  40