NCERT Solutions For Class 8 Maths Chapter 1 Rational Numbers

NCERT Solutions For Class 8 Maths Chapter 1 Rational Numbers Introduction

• The counting numbers 1, 2, 3, 4,………… are called natural numbers.
• The smallest natural number is 1. There is no greatest natural number.
• If we add 0 to the collection of natural numbers, what we get is called the collection of whole numbers. are called natural numbers. are whole numbers.
• Every natural number is a whole number but every whole number is not a natural number, e.g., 0 is a whole number but not a natural number.
• The positive integers are the same as natural numbers.
• We get negative integers if we put a negative sign before each positive integer. Thus, – 1, – 2, – 3, – 4,
• The smallest positive integer is 1. The greatest negative integer is -1.
• The number ‘O’ is neither positive nor negative. It is greater than every negative integer and smaller than every positive integer. It is simply an integer.
• Thus, 0, 1, 2, 3, and 4, are negative integers.÷
• Several p/q where p and q are integers and q ≠ 0 is called a rational number.
• All the above types of numbers are needed to solve various kinds of simple algebraic equations  

Read and Learn More NCERT Solutions For Class 8 Maths

Properties Of Rational Numbers

The list of properties of rational Numbers can be given as follows :

1. Closure
2. Commutativity
3. Associativity
4. The role of zero
5. The role of 1
6. Negative (or additive inverse) of a number
7. Reciprocal (or multiplicative inverse)
8. Distributivity of multiplication over addition for rational numbers

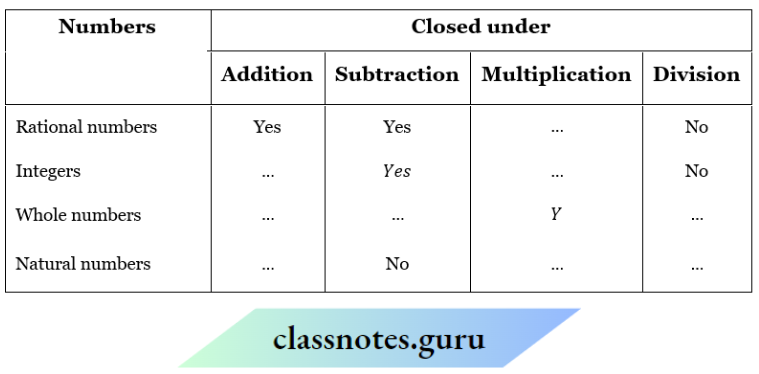
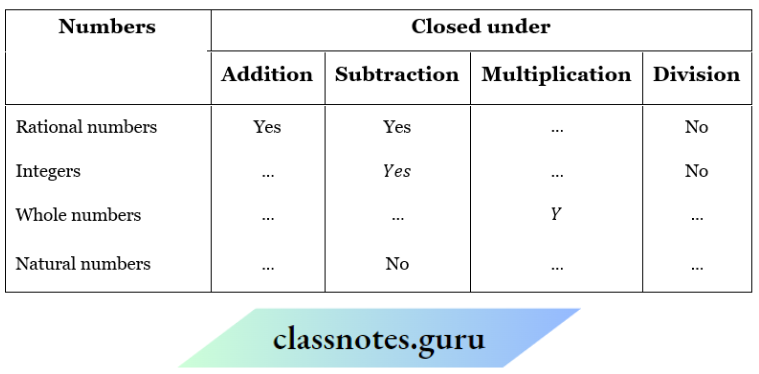
Closure

Whole numbers

Question 1. 4+7 =________________ Is it a whole number
Solution:

4 + 7=11

Yes, It is a whole number.

Question 2. 3×7 = _______________Is it a whole number?
Solution:

3 × 7 = 21

Yes, It is a whole number

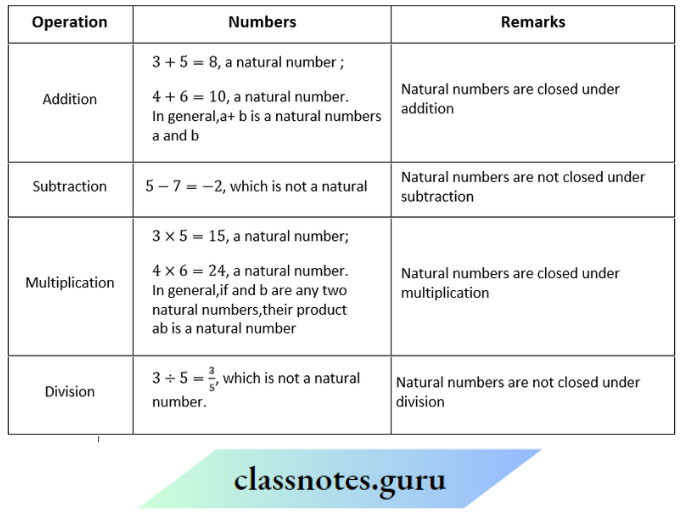
Question 3. Check for closure property under all four operations for natural numbers
Solution:

Integers

Question 1. Is – 7 + (- 5) an integer?
Solution:

– 7 + (- 5)

– 7 + (- 5) = – 12

Yes,  Which is an integer.

Question 2. Is 8 + 5 an integer?
Solution:

8 + 5

8 + 5 = 13

Yes,  Which is an integer

Question 3. Is 5 – 7 an integer?
Solution:

5 – 7

5 – 7 = -2

Yes, Which is an integer.

Question 4. Is 8 – (- 6) an integer?
Solution:

8 – (- 6)

8 – (- 6) = 8 + 6

= 14,

Yes, Which is an integer.

Question 5. Is – 5 × 8= do integer?
Solution:

– 5 × 8

– 5 × 8= – 40

Yes,  Which is an integer

Rational numbers

Question 1.\(\frac{-3}{8}+\frac{(-4)}{5}\)= ________ Is it a rational number ?
Solution:

⇒ \(\frac{-3}{8}+\frac{(-4)}{5}\)

=\(\frac{-15+(-32)}{40}\)

= \(\frac{-47}{40}\)

Yes, It is a rational number

Question 2. \(\frac{5}{8}-\frac{4}{5}=\frac{25-32}{40}\) = _________________ it is a ralional number?
Solution:

⇒ \(\frac{5}{8}-\frac{4}{5}\)

= \(\frac{25-32}{40}\)

= \(\frac{-7}{40}\)

Yes, It is a rational number.

Question 3. \(\frac{-5}{9}+\frac{(-7)}{6}\) _______________ Is it a rational number?
Solution:

⇒ \(\frac{3}{7}-\left(\frac{-8}{5}\right)=\frac{3}{7}+\frac{8}{5}\)

= \(\frac{15+56}{35}\)

=\(\frac{71}{35}\) .

Yes, It is a rational number.

Question 4. \(\frac{4}{7}+\frac{6}{11}\) Is it a rational number ?
Solution:

⇒  \(\frac{4}{7}+\frac{6}{11}\)

= \(\frac{44+42}{77}=\frac{86}{77}\)

Yes, It is a rational number

Question 5. \({4}{5} \times \frac{-6}{11}\)___________Is it a rational number?
Solution:

⇒ \(\frac{4}{5} \times \frac{-6}{11}\)

= \(\frac{24}{55}\)

Yes, It is a rational number.

Question 6. \(\frac{2}{7}+\frac{5}{3}\)= _______________Is it a rational number?
Solution:

⇒ \(\frac{2}{7} \div \frac{5}{3}\)

=\(\frac{2}{7} \times \frac{3}{5}\)

= \(\frac{6}{35}\)

Yes, It is a rational number

Question 7. \(\frac{-3}{8}+\frac{-2}{9}\)= ______________ It is a rational numbers
Solution:

⇒ \(\frac{-3}{8} \div \frac{-2}{9}\)

= \(\frac{-3}{8} \times \frac{-9}{2}\)

= \(\frac{27}{16}\)

Yes, it is a rational number.

Question 8. Check it for a few more pairs of rational numbers

1. \(\frac{3}{5}+\frac{7}{13}\)
Solution: 

⇒ \(\frac{3}{5}+\frac{7}{13}\)

= \(\frac{39+35}{65}\)

= \(\frac{74}{65}\)

Rational number

2. \(\frac{3}{7}+\frac{(-4)}{9}\)
Solution:

⇒ \(\frac{3}{7}+\frac{(-4)}{9}\)

= \(\frac{27+(-28)}{63}\)

Rational number

3. \(\frac{-5}{9}+\frac{(-7)}{6}\)
Solution:

⇒ \(\frac{-5}{9}+\frac{(-7)}{6}\)

= \(\frac{-10+(-21)}{18}\)

Rational number

Question 9. Try this for some more pairs of rational numbers

1. \(\frac{-3}{8}-\frac{4}{5}\)
Solution:

⇒ \(\frac{-3}{8}-\frac{4}{5}\)

= \(\frac{-15-32}{40}\)

=\(\frac{-47}{40}\)

Rational number

2. \(\frac{2}{9}-\frac{3}{7}\)
Solution:

⇒ \(\frac{2}{9}-\frac{3}{7}\)

= \(\frac{14-27}{63}\)

= –\(\frac{13}{63}\)

Rational number

3. \(\frac{-3}{4} \times \frac{7}{8}\)
Solution:

⇒ \(\frac{-3}{4} \times \frac{7}{8}\)

= –\(\frac{21}{32}\)

Rational number

4. \(\frac{5}{8} \times \frac{3}{7}\)
Solution:

⇒ \(\frac{5}{8} \times \frac{3}{7}\)

= \(\frac{15}{56}\)

Rational number

Question 10. Fill in the blanks in the following table

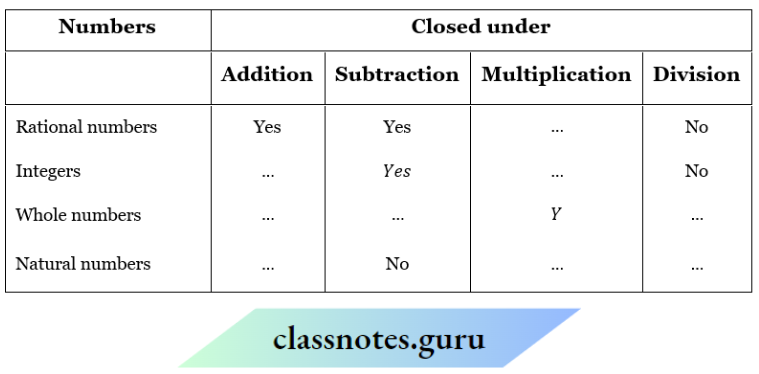
Solution:

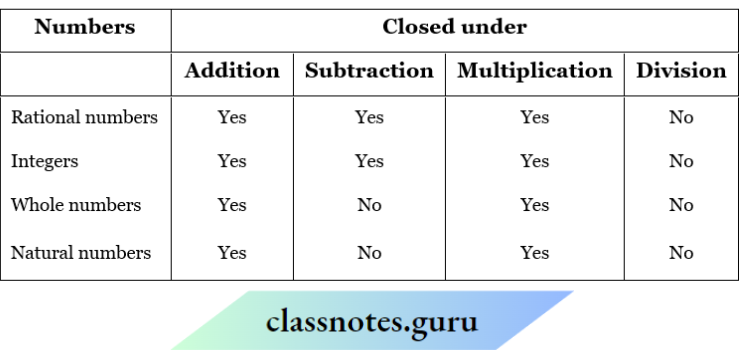
Commutativity

Whole numbers

Question 1. Recall the commutativity of different operations for whole numbers by filling the following table.

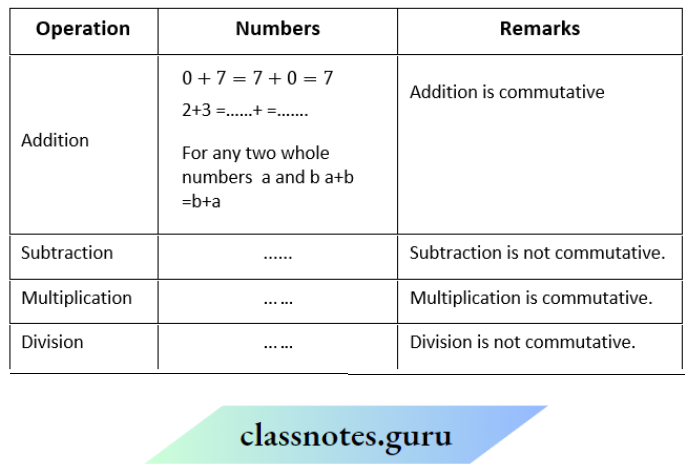
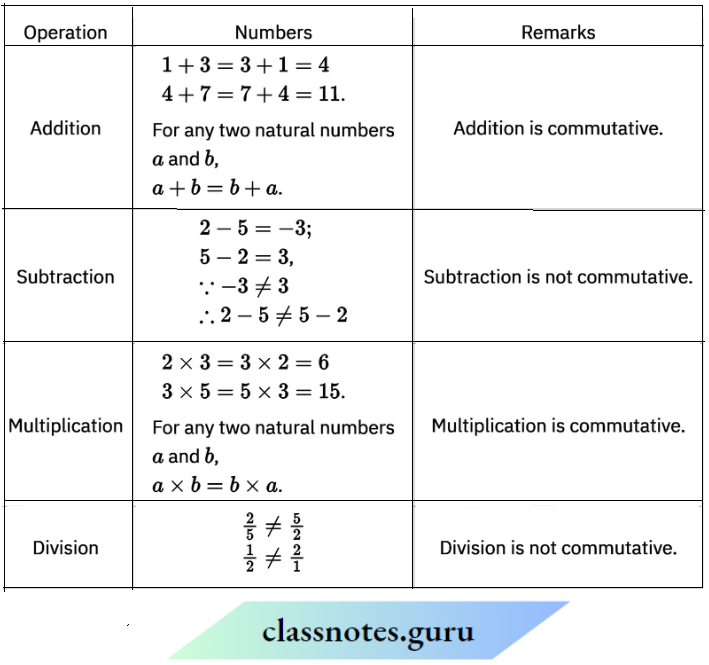
Check whether the commutativity of the. operations hold for natural numbers also.
Solution:

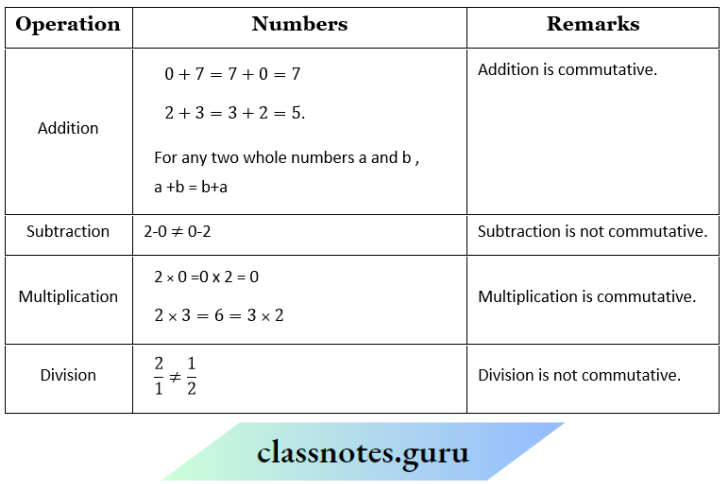
Commutativity of the operations for natural numbers also.

Integers

Question 1.  Fill in the following table and check the commutativity of different operations for integers:

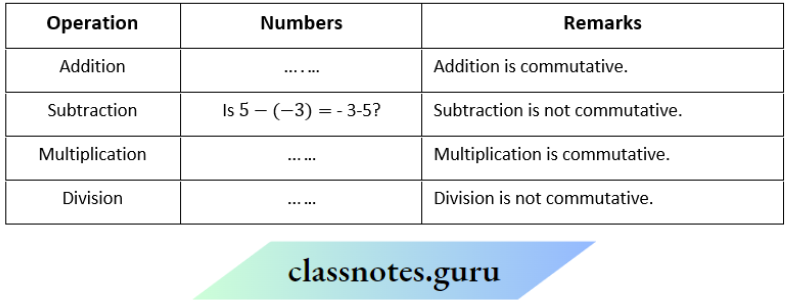
Solution:

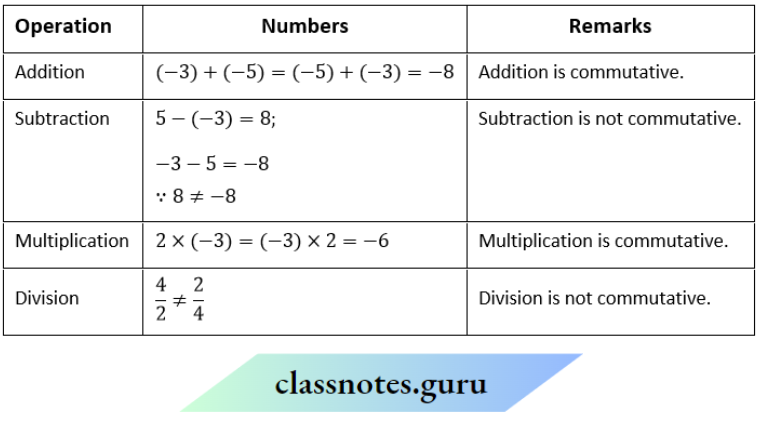
Rational numbers

Question 1. \(\frac{-6}{5}+\left(\frac{-8}{3}\right)\) = \(\ldots \ldots \text { and } \frac{-8}{3}+\left(\frac{-6}{5}\right)=\ldots\) Is \(\frac{-6}{5}+\left(\frac{-8}{3}\right) \)= \(\left(\frac{-8}{3}\right)+\left(\frac{-6}{5}\right) \)
Solution:

⇒ \(\frac{-6}{5}+\left(\frac{-8}{3}\right)\)

= \( \frac{-18+(-40)}{15}=\frac{-58}{15}\)

= \(\frac{-8}{3}+\left(\frac{-6}{5}\right)\)

= \(\frac{-40+(-18)}{15}=\frac{-58}{15}\)

So, \(\frac{-6}{5}+\left(\frac{-8}{3}\right)=\left(\frac{-8}{3}\right)+\left(\frac{-6}{5}\right)\)

Question 2. Is \(\frac{3}{8}+\frac{1}{7}=\frac{1}{7}+\left(\frac{-3}{8}\right)\)?
Solution.

⇒ \(\frac{-3}{8}+\frac{1}{7}=\frac{-21+8}{56} \)

= \(\frac{-13}{56}\)

= \(\frac{1}{7}+\left(\frac{-3}{8}\right)=\frac{8+(-21)}{56}\)

= \(\frac{-13}{56}\)

So, \(\frac{-3}{8}+\frac{1}{7}=\frac{1}{7}+\left(\frac{-3}{8}\right)\).

Question 3. Is \(\frac{2}{3}-\frac{5}{4}=\frac{5}{4}-\frac{2}{3}\)
Solution:

⇒ \(\frac{2}{3}-\frac{5}{4}=\frac{8-15}{12}=\frac{-7}{12} \)

⇒ \(\frac{5}{4}-\frac{2}{3}=\frac{15-8}{12}=\frac{7}{12}\)

⇒  \(\frac{-7}{12} \neq \frac{7}{12} \)

∴ \(\frac{2}{3}-\frac{5}{4} \neq \frac{5}{4}-\frac{2}{3} \)

⇒  \(\frac{1}{2}-\frac{3}{5}=\frac{3}{5}-\frac{1}{2} \)

⇒  \(\frac{1}{2}-\frac{3}{5}=\frac{5-6}{10}=\frac{-1}{10} \)

⇒  \(\frac{3}{5}-\frac{1}{2}=\frac{6-5}{10}=\frac{1}{10} \)

⇒  \(\frac{-1}{10} \neq \frac{1}{10} \)

⇒  \(\frac{1}{2}-\frac{3}{5} \neq \frac{3}{5}-\frac{1}{2}\)

Question 4. \(\frac{-8}{9} \times\left(\frac{-4}{7}\right)=\frac{32}{63} \)
Solution:

⇒ \(\frac{-4}{7} \times\left(\frac{-8}{9}\right)=\frac{32}{63}\)

So, \(\frac{-8}{9} \times\left(\frac{-4}{7}\right)=\frac{-4}{7} \times\left(\frac{-8}{9}\right)\)

Question 5. \(\frac{-5}{9} \times \frac{7}{8}\)
Solution:

= \(\frac{7}{8} \times\left(\frac{-5}{9}\right)\)

= \(\frac{-35}{72}\)

Question 6. \(\frac{-6}{11} \times\left(\frac{-3}{5}\right)\)
Solution:

⇒ \(\frac{-6}{11} \times\left(\frac{-3}{5}\right)\)

=\(\frac{-3}{5} \times\left(\frac{-6}{11}\right)\)

= \(\frac{18}{55}\)

⇒ \(\frac{2}{3} \times \frac{4}{7}=\frac{4}{7} \times \frac{2}{3}=\frac{8}{21}\)

Question 7. Is \(\frac{-5}{4} \div \frac{3}{7}=\frac{3}{7}\div\left(\frac{-5}{4}\right)\)
Solution:

⇒ \(\frac{-5}{4} \div \frac{3}{7}=\frac{3}{7} \div\left(\frac{-5}{4}\right)\)

= \(\frac{-35}{12}\)

And \(\frac{3}{7} \div \frac{-5}{4}=\frac{3}{7} \times\left(\frac{-4}{5}\right) \)

=  \(\frac{-12}{35}\)

Since \(\frac{-35}{12} \neq \frac{-12}{35} \)

∴ \(\frac{-5}{4} \div \frac{3}{7} \neq \frac{3}{7} \div\left(\frac{-5}{4}\right)\)

Question 8. Complete the following table:

Solution: 

Associativity

Whole numbers

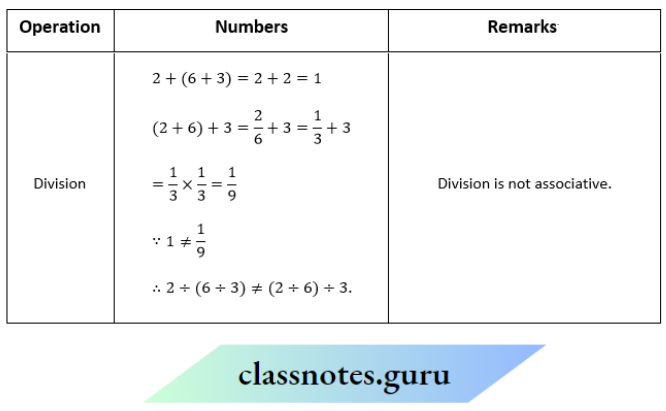
Question 1. Recall the associativity of the four operations for whole numbers through this table

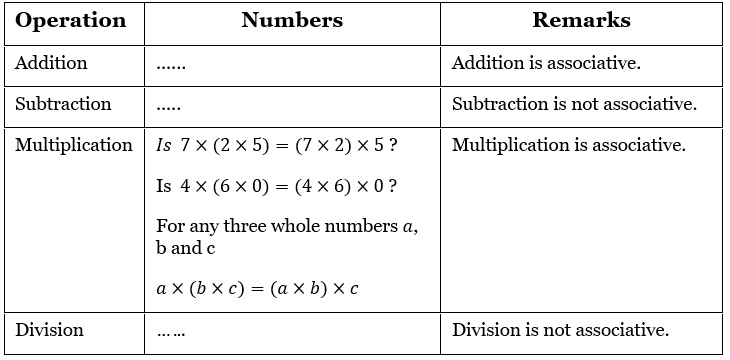
Fill in this table and. verify the remarks given in the last column. Check for yourself the associativity of different operations for natural numbers
Solution:

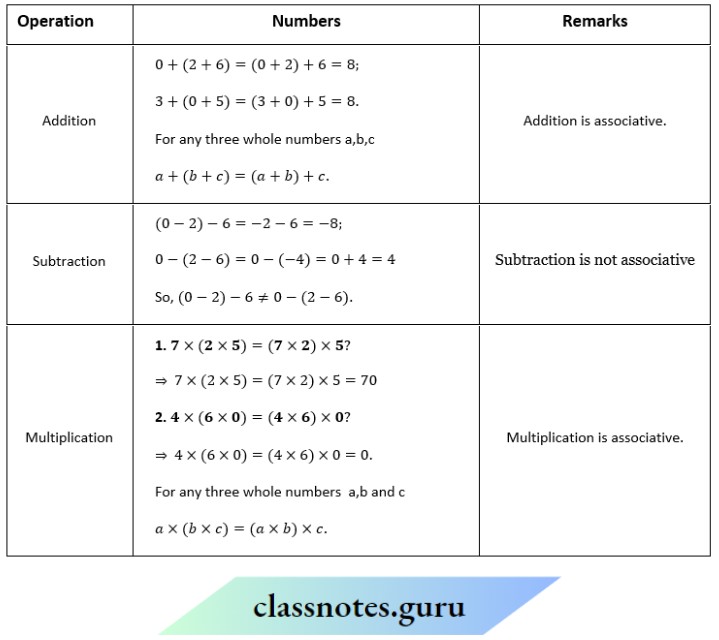
Integers

Question 1. Is (-2) + [3 + (-4)] = [(-2) + 3] + (-4)?
Solution:

Yes; (-2) + [3 + (-4)]

= [(-2) + 3] + (-4)

= -3.

Addition is associative

Question 2. -Is (-6) +[(-4) +(-5)] = (-6) + (-4)] + (-5)?
Solution:

Yes; (-6) + [(-4) + (-5)]

= [(-6) + (-4)] + (-5)

= -15

Addition is associative

Question 3. Is 5 – (7 – 3) = (5 – 7) – 3?
Solution:

5 – (7 – 3) = 5 – 4

= 1

(5 – 7) – 3 = -2 – 3

= -5

1 ≠ – 5

∴  No; 5 – (7 – 3) ≠ (5 – 7) – 3.

Subtraction is not associative

Question 4. Is 5× [(- 7) × (-8)] = [5× (- 7)] × (- 8) ?
Solution:

Yes; 5 × [(-7) × (-8)]

= [5× (-7)] ×(-8)

= 280.

Multiplication is associative

Question 5. Is (- 4) × [(- 8)×(- 5)]= (-4) x (-8)]× (-5)
Solution:

Yes; (-4) × [(-8) × (-5)]

= [(-4) × (-8)] × (-5)

= -160

Multiplication is associative

Question 6.  Is [(-10) ÷ 2] ÷ (- 5)= (-10) ÷[2 ÷ (-5)]?
Solution:

[(-10) ÷ 2] ÷ (-5)= (-5) ÷ (-5) = 1

(-10) ÷ [2 ÷ (-5)]= (-10) ÷ \(\frac{-2}{5}\)

= (-10) ×\(\frac{-5}{2}\)

= 25

∴ 1 ≠ 25

∴ No; [(-10) ÷ 2] ÷ (-5)≠ (-10) ÷ [2 ÷ (-5)]

The division is not associative

Rational numbers

Question 1. Find \(\frac{-1}{2}+\left[\frac{3}{7}+\left(\frac{-4}{3}\right)\right]\) and \(\left[\frac{-1}{2}+\frac{3}{7}\right]+\left(\frac{-4}{3}\right) \text {. }\) Are the two sums equal?
Solution:

⇒ \(\frac{-1}{2}+\left[\frac{3}{7}+\left(\frac{-4}{3}\right)\right]\)

= \(\frac{-1}{2}+\frac{9+(-28)}{21}=\frac{-1}{2}+\left(\frac{-19}{21}\right)\)

= \(\frac{-21+(-38)}{42}=\frac{-59}{42}\)

And \( {\left[\frac{-1}{2}+\frac{3}{7}\right]+\left(\frac{-4}{3}\right)}\)

= \(\frac{-7+6}{14}+\left(\frac{-4}{3}\right)=\frac{-1}{14}+\left(\frac{-4}{3}\right)\)

= \(\frac{-3+(-56)}{42}=\frac{-59}{42}\)

= \(\frac{-1}{2}+\left[\frac{3}{7}+\left(\frac{-4}{3}\right)\right] \)

= \(\left[\frac{-1}{2}+\frac{3}{7}\right]+\left(\frac{-4}{3}\right)\)

= \(\left[\frac{-1}{2}+\frac{3}{7}\right]+\left(\frac{-4}{3}\right)\)

Question 2. \(\frac{-3}{4}+\left[\frac{2}{3}+\left(\frac{-6}{7}\right)\right]\)
Solution:

⇒ \(\frac{-3}{4}+\left[\frac{2}{3}+\left(\frac{-6}{7}\right)\right]\)

= \(\frac{-3}{4}+\frac{14+(-18)}{21}=\frac{-3}{4}+\left(\frac{-4}{21}\right)\)

= \(\frac{-63+(-16)}{84}=\frac{-79}{84} \)

= \(\left[\frac{-3}{4}+\frac{2}{3}\right]+\left(\frac{-6}{7}\right) \)

= \(\frac{-9+(8)}{12}+\left(\frac{-6}{7}\right)=\frac{-1}{12}+\left(\frac{-6}{7}\right) \)

= \(\frac{-7+(-72)}{84}=\frac{-79}{84}\)

So,yes \(\frac{-3}{4}+\left[\frac{2}{3}+\left(\frac{-6}{7}\right)\right]\)

= \(\left[\frac{-3}{4}+\frac{2}{3}\right]+\left(\frac{-6}{7}\right) \)

Question 3. \( \frac{-1}{4}+\left[\frac{2}{9}\right.\left.+\left(\frac{-5}{11}\right)\right] \)
Solution:

⇒  \( \frac{-1}{4}+\left[\frac{2}{9}\right.\left.+\left(\frac{-5}{11}\right)\right] \)

= \(\frac{-1}{4}+\left(\frac{22-(45)}{99}\right) \)

= \(\frac{-1}{4}+\left(\frac{-23}{99}\right) \)

⇒ \(\left[\frac{-1}{4}\right.\left.+\frac{2}{9}\right]+\left(\frac{-5}{11}\right)\)

= \(\frac{-99+(-92)}{396}=\frac{-191}{396}\)

= \(\frac{-9+8}{36}+\left(\frac{-5}{11}\right)\)

= \(\frac{-1}{36}+\left(\frac{-5}{11}\right)=\frac{-11+(-180)}{396}\)

= \(\frac{-191}{396} \)

⇒ \(\frac{-1}{4}+\left[\frac{2}{9}+\left(\frac{-5}{11}\right)\right] \)

= \(\left[\frac{-1}{4}+\frac{2}{9}\right]+\left(\frac{-5}{11}\right)\)

Question 4. \(\frac{-2}{3}-\left[\frac{-4}{5}-\frac{1}{2}\right]\) Check for yourself
Solution:

= \(\left[\frac{-2}{3}-\left(\frac{-4}{5}\right)\right]-\frac{1}{2}\)

= \(\frac{-2}{3}-\left[\frac{-4}{5}-\frac{1}{2}\right]\)

= \(\frac{-2}{3}-\left(\frac{-8-5}{10}\right)=\frac{-2}{3}-\left(\frac{-13}{10}\right)\)

= \(\frac{-2}{3}+\frac{13}{10}=\frac{-20+39}{30}=\frac{19}{30}\)

And \({\left[\frac{-2}{3}-\left(\frac{-4}{5}\right)\right]-\frac{1}{2}=\left[\frac{-2}{3}+\frac{4}{5}\right]-\frac{1}{2}} \)

= \(\left[\frac{-10+12}{15}\right]-\frac{1}{2}=\frac{2}{15}-\frac{1}{2} \)

= \(\frac{4-15}{30}=\frac{-11}{30}\)

So, No ; \(\frac{-2}{3}-\left[\frac{-4}{5}-\frac{1}{2}\right]\)≠ \(\frac{-2}{3}\)– (\(\frac{-4}{5}\)) – \(\frac{1}{2}\)

Question 5. \(\left(\frac{-7}{3} \times \frac{5}{4}\right) \times \frac{2}{9}\)___________
Solution:

⇒\(\left(\frac{-7}{3} \times \frac{5}{4}\right) \times \frac{2}{9}=\frac{-35}{12} \times \frac{2}{9}\)

=\(\frac{-35}{54}\)

So, Yes ;

Question 6. Is \(\frac{2}{3} \times\left(\frac{-6}{7} \times \frac{4}{5}\right)=\left(\frac{2}{3} \times \frac{-6}{7}\right) \times \frac{4}{5} \)
Solution:

⇒ \(\frac{2}{3} \times\left(\frac{-6}{7} \times \frac{4}{5}\right)\)

= \(\frac{2}{3} \times \frac{-24}{35}=\frac{-48}{105}\)________ (1)

=  \(\frac{2}{3}\)× \(\frac{-6}{7}\)× \(\frac{4}{5}\)

= \(\frac{-12}{21} \times \frac{4}{5}=\frac{-48}{105}\)________ (2)

So, Yes; A = B

Question 7. \(\frac{-6}{5} \times\left(\frac{2}{3} \times \frac{1}{8}\right)\)
Solution:

⇒ \(\frac{-6}{5} \times\left(\frac{2}{3} \times \frac{1}{8}\right)=\frac{-6}{5} \times \frac{1}{12}\)

=\(\frac{-1}{10}\)

And  \(\left(\frac{-6}{5} \times \frac{2}{3}\right) \times \frac{1}{8}=\frac{-4}{5} \times \frac{1}{8}=\frac{-1}{10}\)

So, Yes

⇒ \(\frac{-6}{5} \times\left(\frac{2}{3} \times \frac{1}{8}\right)=\left(\frac{-6}{5} \times \frac{2}{3}\right) \times \frac{1}{8}\)

Question 8. \(\frac{2}{7} \times\left(\frac{-5}{9} \times \frac{2}{3}\right) \)
Solution:

⇒ \(\frac{2}{7} \times\left(\frac{-5}{9} \times \frac{2}{3}\right) \)

=\(\frac{2}{7} \times\left(\frac{-10}{27}\right)=\frac{-20}{189} \)

= \(\left(\frac{2}{7} \times \frac{-5}{9}\right) \times \frac{2}{3}=\frac{-10}{63} \times \frac{2}{3}\)

=\(\frac{-20}{189}\)

So, Yes; A=B

Question 9. \(\frac{1}{2}+\left[\frac{-1}{3}+\frac{2}{5}\right]=\left[\frac{1}{2}+\left(\frac{-1}{3}\right)\right]+\frac{2}{5}\),Is L.H.S. =R.H.S. ? Check for yourself
Solution:

L.H.S.\(\frac{1}{2}+\left(\frac{-1}{3}+\frac{2}{5}\right)\)

= \(\frac{1}{2} \div\left(\frac{-1}{3} \times \frac{5}{2}\right)\)

= \(\frac{2}{5} is \frac{5}{2}\)

= \(\frac{1}{2}+\left(-\frac{5}{6}\right) \)

= \(\frac{1}{2} \times \frac{-6}{5}=\frac{-3}{5} \)

R.H.S= \(\left[\frac{1}{2}+\left(\frac{-1}{3}\right)\right]+\frac{2}{5}\)

= \(\left(\frac{1}{2} \times \frac{-3}{1}\right) \div \frac{2}{5}=\frac{-3}{2}+\frac{2}{5} \)

= \(\frac{-3}{2} \times \frac{5}{2}=\frac{-15}{4}\)

So, No; L.H.S ≠R. H.S.

Question 10. Complete the following table:

Solution:

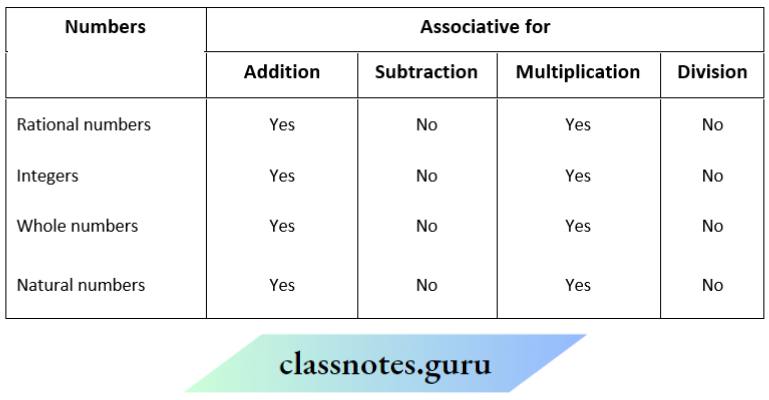
Question 11. Do you think the properties commutativity and associativity made the calculations
Sol.

Yes! The properties of commutativity and associativity made the calculations easier

The Rolie Of Zero (0)

Question 1. \(-5+0=\ldots \ldots. \ldots \ldots .=-5\)
Solution:

-5+0=0+(-5)=-5

Question 2.  \(\frac{-2}{7}+\ldots \ldots .=0+\left(\frac{-2}{7}\right)=\frac{-2}{7}\)

⇒ \(\frac{-2}{7}+0=0+\left(\frac{-2}{7}\right)=\frac{-2}{7}\)

Question 3. Do a few more such additions. What do you observe?
Solution:

1. 3 + 0 = 0 + 3 = 3

2. -9 +0 = 0 + (-9) = -9

3.\(\frac{-3}{4}+0=0+\left(\frac{-3}{4}\right)=\frac{-3}{4}\)

We observe that when we add 0 to a whole number, the sum is again that whole number. This happens for integers and rational numbers also.

The Role Of 1

Question 1. \(\frac{-2}{7} \times 1=\ldots \ldots . . \times \ldots . .=\frac{-2}{7}\)
Solution:

– \(\frac{2}{7} \times 1=1 \times \frac{-2}{7}=\frac{-2}{7}\)

Question 2. \(\frac{3}{8} \times \ldots \ldots=1 \times \frac{3}{8}=\frac{3}{8}\)
Solution:

⇒ \(\frac{3}{8} \times 1=1 \times \frac{3}{8}\)

= \(\frac{3}{8}\)

Question 3.  What do you find?
Solution:

We find that when we multiply any rational number by 1, we get back the same rational number as the product

Question 4. Check for a few more rational numbers

1. 7 × 1
Solution:

7 × 1 = 7 = 1 × 7

2.\(\frac{-3}{5} \times 1\)
Solution:

⇒ \(\frac{-3}{5} \times 1\)

=\(1 \times \frac{-3}{5}=\frac{-3}{5}\)

3. \(\frac{7}{9} \times 1\)
Solution:

⇒ \(\frac{7}{9} \times 1\)

= \(1 \times \frac{7}{9}=\frac{7}{9}\)

Question 5. Is 1 the multiplicative identity for integers? For whole numbers?
Solution:

Yes, 1 is the multiplicative identity for integers as well as for whole numbers.

Question 6. If a property holds for rational numbers, will it also hold for integers?

1. For whole numbers?
2. Which will?
3. Which will not?

Solution:

1. Except for the following property, the properties of the rational numbers will also hold good for integers :

If a and b are rational numbers, then a÷b is also a rational number if b ≠ 0 but a÷ b is not necessarily an integer where a and b are integers

Eample: \(\frac{4}{5}\)is a rational number. Here 4 and 5 are integers, while \(\frac{4}{5}\) is not an integer

2. Except for the following properties, the properties of the rational numbers will also hold good for whole numbers:

If a and b are rational numbers, then, a- b is also a rational number. But if a and b are whole numbers, then A b is not necessarily a whole number

Let 4 and 5 be whole numbers, but 4 – 5 = -1 is not a whole number.

2. If a and b are rational numbers, then, a + b is a rational number if b  but if a and b are whole numbers, then a + b is not necessarily a whole number.

Example: 4 and 5 are whole numbers but \(\frac{4}{5}\) is not a whole number

Disberstivity Of Multiplication Over Addition For Rational

For all rational numbers a, b, and c,

a(b + c) = ab + ac.

a(b-c) = ab – ac

Question 1. \(\left\{\frac{7}{5} \times\left(\frac{-3}{12}\right)\right\}+\left\{\frac{7}{5} \times \frac{5}{12}\right\}\)
Solution:

⇒ \(\left\{\frac{7}{\mathbf{5}} \times\left(\frac{-3}{12}\right)\right\}+\left\{\frac{7}{5} \times \frac{\mathbf{5}}{\mathbf{1 2}}\right\}\)

= \(\frac{7}{5} \times\left\{\left(\frac{-3}{12}\right)+\frac{5}{12}\right\} \)

= \(\frac{7}{5} \times\left\{\frac{(-3)+5}{12}\right\}=\frac{7}{5} \times \frac{2}{12} \)

= \(\frac{7}{5} \times \frac{1}{6}=\frac{7}{30} \)

Question 2. \(\left\{\frac{9}{16} \times \frac{4}{12}\right\}+\left\{\frac{9}{16} \times \frac{-3}{9}\right\}\)
Solution:

⇒ \(\left\{\frac{9}{16} \times \frac{4}{12}\right\}+\left\{\frac{9}{16} \times \frac{-3}{9}\right\} \)

= \(\frac{9}{16} \times\left\{\frac{4}{12}+\left(\frac{-3}{9}\right)\right\}\)

= \(\frac{9}{16} \times\left\{\frac{1}{3}+\left(\frac{-1}{3}\right)\right\} \)

= \(\frac{9}{16} \times\left\{\frac{1-1}{3}\right\}=\frac{9}{16} \times 0=0 .\)

NCERT Solutions For Class 8 Maths Chapter 1 Rational Numbers Exercise 1.1

Question 1.  Name the property under multiplication used in each of the following

1. \( \frac{-4}{5} \times 1=1 \times \frac{-4}{5}=-\frac{4}{5} \)

2. \(\frac{13}{17} \times \frac{-2}{7}=\frac{-2}{7} \times \frac{-13}{17}\)

3. \(\frac{-19}{29} \times \frac{29}{-19}=1\)

Solution:

1.1 is the multiplicative identity

2. Commutativity of multiplication

3. Multiplicative inverse.

Question 2. Tell what property allows you tocompute :\(\frac{1}{3} \times\left(6 \times \frac{4}{3}\right) \text { as }\left(\frac{1}{3} \times 6\right) \times \frac{4}{3} \text {. }\)
Solution:

Associativity of multiplication

Question 3. The product of two rational numbers is always a
Solution:

The product of two rational numbers is always a rational number.

NCERT Solutions For Class 8 Maths Chapter 1 Rational Numbers Multiple Choice Questions

Question 1. Which of the following statements is false?

1. Natural numbers are closed under addition
2. Whole numbers are closed under the addition
3. Integers are closed under the addition
4. Rational numbers are not closed under addition.

Solution: 4. Rational numbers are not closed under addition.

Question 2. Which of the following statements is false?

1. Natural numbers are closed under subtraction
2. Whole numbers are not closed under subtraction
3. Integers are closed under subtraction
4. Rational numbers are closed under subtraction.

Solution: 1. Natural numbers are closed under subtraction

Question 3. Which of the following statements is true?

1. Natural numbers are closed under multiplication
2. Whole numbers are not closed under multiplication
3. Integers are not closed under multiplication
4. Rational numbers are not closed under multiplication.

Solution: 1. Natural numbers are closed under multiplication

Question 4. Which of the following statements is true?

1. Natural numbers are closed under the division
2. Whole numbers are not closed under the division
3. Integers are closed under the division
4. Rational numbers are closed under division.

Solution: 2.  Whole numbers are not closed under the division

Question 5. Which of the following statements is false?

1. Natural numbers are commutative for addition
2. Whole numbers are commutative for addition
3. Integers are not commutative for addition
4. Rational numbers are commutative for addition.

Solution: 3. Integers are not commutative for addition

Question 6. Which of the following statements is true?

1. Natural numbers are commutative for subtraction
2. Whole numbers are commutative for subtraction
3. Integers are commutative for subtraction
4. Rational numbers are not commutative for subtraction.

Solution: 4. Rational numbers are not commutative for subtraction.

Question 7. Which of the following statements is false?

1. Natural numbers are commutative for multiplication
2. Whole numbers are commutative for multiplication
3. Integers are not commutative for multiplication
4. Rational numbers are commutative for multiplication.

Solution: 3. Integers are not commutative for multiplication

Question 8. Which of the following statements is true?

1. Natural numbers are commutative for division
2. Whole numbers are not commutative for division
3. Integers are commutative for division
4. Rational numbers are commutative for division.

Solution: 2. Whole numbers are not commutative for division

Question 9. Which of the following statements is true?

1. Natural numbers are associative for addition
2. Whole numbers are not associative for addition
3. Integers are not associative for addition
4. Rational numbers are not associative for addition.

Solution: 1. Natural numbers are associative for addition

Question 10. Which of the following statements is true?

1. Natural numbers are associative for subtraction
2. Whole numbers are not associative for subtraction
3. Integers are associative for subtraction
4. Rational numbers are associative for subtraction

Solution: 2. Whole numbers are not associative for subtraction

Question 11. Which of the following statements is true?

1. Natural numbers are not associative for multiplication
2. Whole numbers are not associative for multiplication
3. Integers are associative for multiplication
4. Rational numbers are not associative for multiplication.

Solution: 3. Integers are associative for multiplication

Question 12. Which of the following statements is true?

1. Natural numbers are associative for division
2. Whole numbers are associative for division
3. Integers are associative for division
4. Rational numbers are not associative for division

Solution: 4. Rational numbers are not associative for division

Question 13. 0 is not

1. A natural number
2. A whole number
3. An integer
4. A rational number.

Solution: 1. A natural number

Question 14. ½ is

1. A natural number
2. A whole number
3. A n integer
4. A rational number.

Solution: 4.  A rational number.

Question 15. a + 6 = 6 + a is called

1. Commutative law of addition
2. Associative law of addition
3. Distributive law of addition
4. None of these.

Solution: 1. Commutative law of addition

Question 16. a × b = b × a is called

1. Commutative law for addition
2. Commutative law for multiplication
3. Associative law for addition
4. Associative law for multiplication.

Solution: 2. Commutative law for multiplication

Question 17. (a + b) + c = a + (b + c) is called

1. Commutative law for multiplication
2. Commutative law for
3. Additionassociative law for addition
4. Associative law for multiplication.

Solution: 3. Additionassociative law for addition

Question 18. a × (b × c) = (a × b) × c is called

1. Associative law for addition
2. Associative law for multiplication
3. Commutative law for addition
4. Commutative law for multiplication.

Solution: 2. Associative law for multiplication

Question 19. a (6 + c) = ab + ac is called

1. Commutative law
2. Associative law
3. Distributive law
4. None of these

Solution: 3. Distributive law

Question 20. The additive identity for rational numbers is

1. 1
2. -1
3. 0
4. None of these.

Solution: 3. 0

Question 21. The multiplicative identity for rational numbers is

1. -1
2. 1
3. 0
4. None of these

Solution: 2. 1

Question 22. How many rational numbers are there between any two given rational numbers?

1. Only one
2. Only two
3. Countless
4. Nothing can be said.

Solution: 3. Countless

Question 23. If a and 6 are two continuous rational numbers, then

1. \(\frac{a+b}{2}<a\)
2. \(\frac{a+b}{2}<b\)
3. \(\frac{a+b}{2}=a\)
4. \(\frac{a+b}{2}>b\)

Solution: 2.  \(\frac{a+b}{2}<b\)

NCERT Solutions For Class 8 Maths Chapter 1 Rational Numbers True Or False

1. a – 0 and 0 – a represent the same rational number where a ≠ 0. – False

2. 0 is a rational number – True

3. Between any two given rational numbers, there are countless rational numbers – True

NCERT Solutions For Class 8 Maths Chapter 1 Rational Numbers Fill In The Blanks

1. A number of the form p/q, where p and q are integers and q ≠0 is called a → Rational number

2. Write the number 0 reduced by 1 → (-1)

3. Are the two rational numbers p/q and q≠0 equivalent    →Yes

4. In the rational number p/q, why q≠0  → Since division by zero is not defined

5. Which rational number on the number line is equidistant from 0 and -1  → (\(\frac{-1}{2}\)).