NCERT Exemplar Solutions for Class 10 Maths Chapter 3 Linear Equations In Two Variables

Linear Equations In Two Variables Introduction

First of all we shall understand the meaning of terms used in the name of the chapter “Linear equations in two variables”.

Consider the following equations:

⇒ \(3 x-8 y=21,2 x+5 y=14, \frac{7}{4} x+\frac{9}{5} y=\frac{5}{6}\)

Each of these equations contains two variables over R (real numbers). An equation of the form an ax + by + c = 0, where a, b, c are real numbers (a ≠ 0, b ≠ 0) is called a linear equation in two variables x and b, where a is the coefficient of x, b is the coefficient of y and c is a constant term.

Solution Of The Simultaneous Linear Equations

Any pair of values of x and y which satisfies the equation is called the solution of the equation. It means a solution of two equations is the point (x, y) of the intersection of two straight lines or any two curves. This point will lie on both the equations (curves).

If the equation contains only one variable, the graph of such type of equation will be a straight line parallel to the x-axis or y-axis according to a form of equation as ay = b or ax = b, where a ≠ 0. The graph of a linear equation in two variables is also a straight line.

The general form of a pair of linear equations in two variables x and y is

a₁x +b₁y +c₁ = 0

a₂x + b₂y + c₂ = 0

where a₁,b₁,C₁,a₂,b₂ and C₂ are all real numbers.

A system of linear equations will have either a unique solution or infinitely many solutions or no solution. If a system of simultaneous linear equations has a solution (either unique or infinitely many), then the system is said to be consistent otherwise it is said to be an inconsistent system.

Consistent System: A system of simultaneous linear equations is said to be consistent if it has at least one solution.

In-consistent System: A system of simultaneous linear equations is said to be inconsistent if it has no solution.

Graphical Method To Solve The Simultaneous Linear Equations

Let the given system of linear equations be

a₁x +b₁y +c₁ = 0 ……(1)

a₂x + b₂y + c₂ = 0 ……(2)

A pair of linear equations in two variables will be represented by two straight lines, both to be considered together. The following three possibilities can happen:

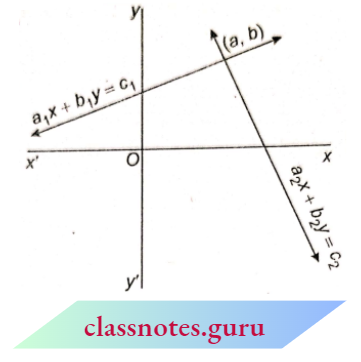
1. The two lines intersect at exactly one point. Let the coordinates of a point of intersection be (a, b).
Solution:

Given

The two lines intersect at exactly one point. Let the coordinates of a point of intersection be (a, b)

Then, x = a and y = b are the unique solutions of the given system of equations.

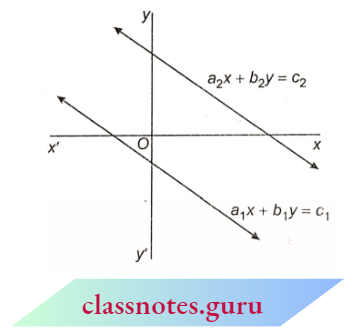
2. The two lines are parallel to each other.
Solution:

Then there is no common solution to the given system of equations. Thus, in this case, the given system is inconsistent.

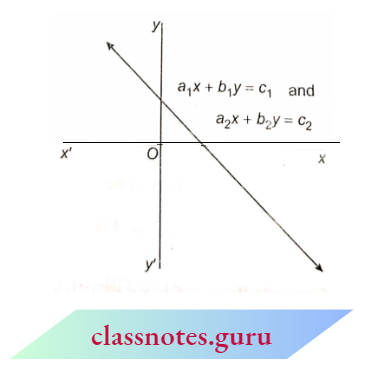
3. One line overlaps the other i.e., the two lines are coincident.
Solution:

Then the given system of equations has infinitely many solutions.

Simultaneous Linear Equations Solved Examples

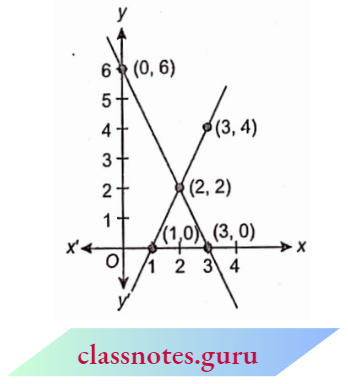
Question 1. Solve graphically the system of linear equations x +y =10 and x-y = 4.
Solution:

Given

x +y =10 and x-y = 4

For x +y= 10, it can be written as y = 10- x

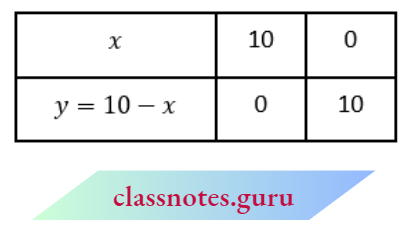
For equation x-y = 4, it can be written as y = x- 4

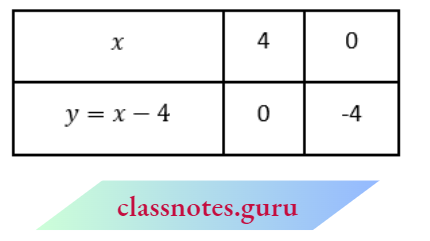
Now we plot the points A(10, 0), B(0, 10) and P(4, 0), Q(0, -4)

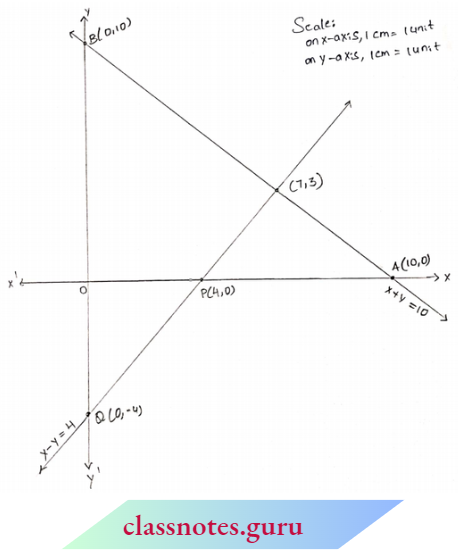
We observe that the two lines representing the two equations intersect at points (7, and 3). Hence, \(\left.\begin{array}{l}
x=7 \\
y=3
\end{array}\right\}\) is a solution of given equation.

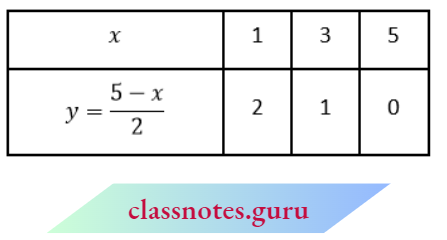
Question 2. Show graphically that the system of equations 2x + 4y = 10 and 3x + 6y = 12 has no solution.
Solution:

The given equation is

2x + 4y = 1 0

4y = 1 0 – 2x

⇒ \(y=\frac{5-x}{2}\)

Now for equation 3x + 6y – 12

6y = 12-3x

⇒ \(y=\frac{4-x}{2}\)

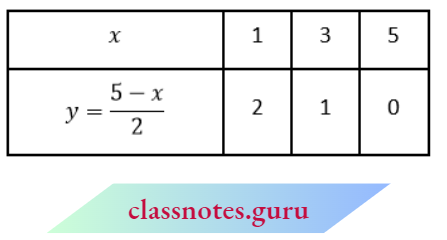
Now plot the points 2l(1, 2), B(3, 1), C(5, 0) and P(2, 1), Q(0, 2), R(4, 0) on the same graph paper.

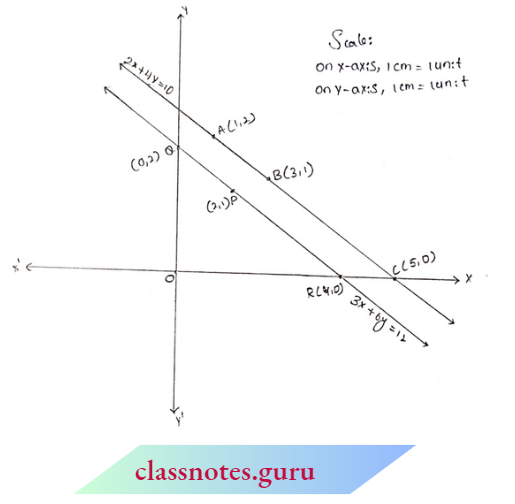
We observe from the graph that the two lines are parallel to each other i.e., they do not intersect each other at any point. Hence, the given system of equations has no solution.

Question 3. Show graphically that the system of equations 3x -y=2, 9x-3y = 6 has an infinite = number of solutions. When this system has infinitely many solutions, then find any two solutions. Also, find the y-intercept made by this line.
Solution:

For equation 3x -y = 2

y = 3x-2 ……..(1)

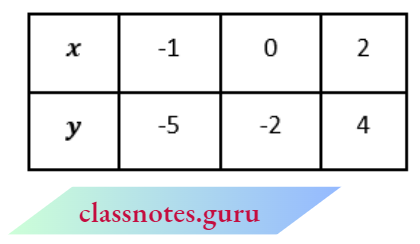
and for equation 9x- 3y = 6

3y = 9x- 6

y = \(\frac{9 x-6}{3}\)

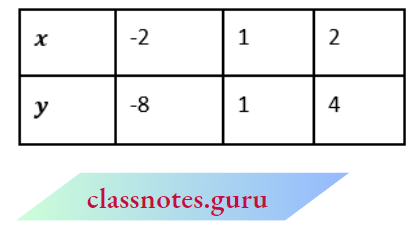
Now, plot the points A(-1, -5), B(0, -2), C(2, 4) and P(-2, -8), Q(1, 1), R(2, 4) on the graph paper. We observe from the graph that the two lines coincide. Hence, a given system of equations has an infinite number of solutions.

For any two solutions, Put x = 0 in equation (1), we get = -2 If we put x = 1 in the equation (1), we get = 1

So, two solutions are \(\left.\left.\begin{array}{l}
x=0 \\
y=-2
\end{array}\right\} \text { and } \begin{array}{l}
x=1 \\
y=1
\end{array}\right\}\)

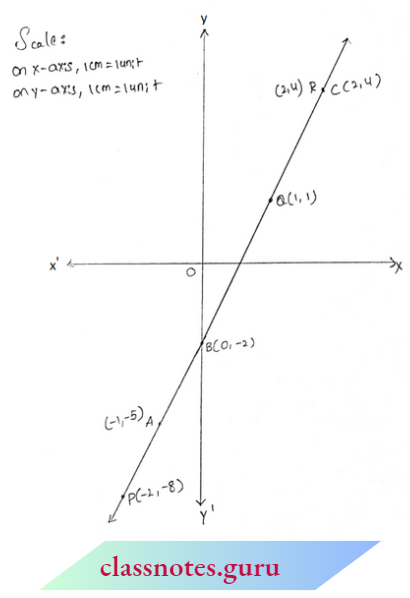
This line (both lines are the same) cuts the y-axis at 2 units below the origin. So, its y-intercept (part) is -2

Algebraic Methods Of Solving Simultaneous Linear Equations In Two Variables

Elimination by “Substitution” Method (or Simply “Substitution Method”)

Step 1: From any of the given two equations, find the value of one variable in terms of other.

Step 2: Substitute the value of the variable obtained in step 1 in the other equation. In this way, have eliminated one variable with the help of substitution. So the name fell as “elimination by substitution”. Now, solve it to get the value of one variable.]

Step 3: Substituting the value of the variable obtained in step 2 in the result of step 1 get the value of the remaining unknown variable.

Algebraic Methods Solved Examples

Question 1. Solve x +y = 7 and 3x- 2y = 11.
Solution:

Given x +y = 7 …(1)

and 3x-2y= 11 …(2)

From equation (1) we get y = 7 -x …(3)

Substituting the value of y from equation (3) in (2), we get

3x-2 (7-x) = 11

3x- 14 + 2r= 11

5x- 14= 11

5x = 25 or x = 5

Substituting the value of x in equation (3), we get

y = 7 – 5 ⇒ y = 2

∴ Solution is \(\left.\begin{array}{l}
x=5 \\
y=2
\end{array}\right\}\)

Question 2. Solve 15x- 8y = 29 and 17x + 12y = 75.
Solution:

Given equations are 15x- 8y = 29 ….(1)

and 17x + 12y = 75 …….(2)

From equation (1), we get

⇒ \(x=\frac{29+8 y}{15}\) …..(3)

Substituting the value of x from equation (3) in (2), we get

⇒ \(17\left(\frac{29+8 y}{15}\right)+12 y=75\)

⇒ 493 + 136y + 180y = 1125

⇒ 316y= 1125-493

⇒ 316y = 632

⇒ y = 2

Substituting the value of y in equation (3) we get

⇒ \(x=\frac{29+8 \times 2}{15}\)

⇒ \(x=\frac{45}{15}\)

⇒ x = 3

Hence, the solution is \(\left.\begin{array}{l}
x=3 \\
y=2
\end{array}\right\}\)

Elimination by Equating the Coefficients (Elimination Method)

Step 1: Multiply both the equations by a suitable number, so that the coefficients of x or the coefficients of y in both the equations become equal.

Step 2: If these coefficients are of the same sign then subtract the new equations otherwise add them.

Step 3: Solve the resulting equation to find the value of unknown. In this process, you will see that we have eliminated one variable. So, the name fell as “elimination by equating the coefficients”.

Step 4: Substitute this value in any of the two equations given and find the value of the other unknown.

Example 3. Solve 3x- 4y = 20 and x + 2y = 5.
Solution:

The given equations are 3x- 4y = 20 ….(1)

and x+2y=5 …..(2)

Multiplying equation (1) by 1 and (2) by 2, we get

3x- 4y = 20 ……(3)

2x+4y = 10 ……(4)

Adding these equations, we get

5x = 30

x=6

Substituting x = 6 in equation (1), we get

3 × 6- 4y = 20

18 -4y = 20

-4y = 2

y = \(-\frac{1}{2}\)

Hence, the solution is \(\left.\begin{array}{l}
x=6 \\
y=-\frac{1}{2}
\end{array}\right\}\)

Question 4. Solve 3x – 17y = 23 and \(\frac{x}{3}+\frac{y}{4}=4 .\)
Solution:

The given equations are 3x-y = 23 ….(1)

and \(\frac{x}{3}+\frac{y}{4}=4\)

4x + 3y = 48 ….(2)

Multiplying equation (1) by 3 and (2) by 1, we get

9x-3y = 69 …..(3)

4x + 3y = 48 …..(4)

Adding equations (3) and (4), we get

13x = 117

⇒ x = 9

Substituting x = 9 in equation (1), we get

3 x 9-y = 23

⇒ 27 -y = 23

⇒ -y =-4

⇒ y = 4

Hence, the solution is \(\left.\begin{array}{l}
x=9 \\
y=4
\end{array}\right\}\)

Question 5. Solve \(4 x+\frac{6}{y}=15 \text { and } 6 x-\frac{8}{y}=14 \text {. }\)
Solution:

The given equation are \(4 x+\frac{6}{y}=15\)…(1)

and \(6 x-\frac{8}{y}=14\)

Multiplying equation (1) by 4 and (2) by 3, we get

⇒ \(16 x+\frac{24}{y}=60\) …..(3)

⇒ \(18 x-\frac{24}{y}=42\) …..(4)

Adding equations (3) and (4), we get

34x = 102 ⇒ x = 3

Substituting x = 3 in equation (1), we get

⇒ \(4 \times 3+\frac{6}{y}=15\)

⇒ \(\frac{6}{y}=15-12\)

⇒ \(\frac{6}{y}=3\)

⇒ 3y = 6

or y = 2

Hence, the solution is \(\left.\begin{array}{l}
x=3 \\
y=2
\end{array}\right\}\)

Question 6. Solve for x and y, \(\frac{1}{2 x}-\frac{1}{y}=-1 \text { and } \frac{1}{x}+\frac{1}{2 y}=8 \text {. }\)
Solution:

The given equations are \(\frac{1}{2 x}-\frac{1}{y}=-1\) ….(1)

and \(\frac{1}{x}+\frac{1}{2 y}=8\) …..(2)

Let \(\frac{1}{x}=u \text { and } \frac{1}{y}=v\) then equations (1) and (2) can be written as

⇒ \(\frac{n}{2}-v=-1\)

⇒ u – 2v = -2 …….(3)

and \(u+\frac{v}{2}=8\)

⇒ 2u + v = 16 …….(4)

Multiplying equation (3) by 1 and (4) by 2, we get

⇒ u – 2v = -2 ….(5)

⇒ 4u + 2v = 32 ….(6)

Adding equations (5) and (6), we get

⇒ 5u = 30

⇒ u = 6

Substituting u = 6 in equation (3), we get

⇒ 6-2v = -2

⇒ -2v = -8

⇒ v = 4

Now, \(\frac{1}{x}=u\)

⇒ \(\frac{1}{x}=6\)

⇒ \(x=\frac{1}{6}\)

and \(\frac{1}{y}=v\)

⇒\(\frac{1}{y}=4\)

⇒\(x=\frac{1}{4}\)

Hence, the solution is \(\left.\begin{array}{l}
x=\frac{1}{6} \\
y=\frac{1}{6}
\end{array}\right\}\)

Question 7. Solve \(\frac{20}{x+y}+\frac{3}{x-y}=7 \text { and } \frac{8}{x-y}-\frac{15}{x+y}=5\)
Solution:

Given equations are

⇒ \(\frac{20}{x+y}+\frac{3}{x-y}=7\) ……..(1)

and \(\frac{8}{x-y}-\frac{15}{x+y}=5\) ……(2)

Let \(\) then equation (1) and (2) can be written as

20a + 3b = 7 ……(3)

and -15a + 8b = 5 …….(4)

Multiplying equation (3) by 8 and (4) by 3, we get

160a + 24b = 56 ……(5)

-45a + 24b = 15 ……(6)

Subtracting equation (6) from equation (5), we get

205a = 41

⇒ \(a=\frac{1}{5}\)

Substituting \(a=\frac{1}{5}\) in equation (3), we get

⇒ \(20 \times \frac{1}{5}+3 b=7\)

⇒ 32b = 3

⇒ b = 1

Now, \(\frac{1}{x+y}=a \quad \Rightarrow \quad \frac{1}{x+y}=\frac{1}{5} \quad \Rightarrow x+y=5\) ……(7)

and \(\frac{1}{x-y}=b \quad \Rightarrow \quad \frac{1}{x-y}=1 \quad \Rightarrow x-y=1\) …..(8)

Adding equations (7) and (8), we get

2x= 6

x = 3

Substituting x = 3 in equation (7), we get

3 +y = 5

⇒ y = 2

Hence, the solution is \(\left.\begin{array}{l}
x=3 \\
y=2
\end{array}\right\}\)

Question 8.

1. Solve 8x- 3y = 5xy and 6x-5y = -2xy. How many solutions, does this system of equations have?
2. Solve for x and y, by reducing the following equations in a pair of linear equations: 2x + 3y = 5xy and 3x-2y=xy.

Solution:

Given equations are 8x-3y = 5xy

and 6x- 5y- -2xy

The given equations are not linear in the variables x and y. These can be reduced into linear equations.

If we put x = 0 in either of the equations, we get y = 0. Hence, x = 0 and y = 0 is a solution of these equations.

To find another solution, divide each of the given equations by xy

So, \(\frac{8}{y}-\frac{3}{x}=5\) ……(1)

and \(\frac{6}{y}-\frac{5}{x}=-2\) …..(2)

Let \(\frac{1}{y}=a \text { and } \frac{1}{x}=b\) then from equations (1) and (2), we get

⇒ \(\left.\begin{array}{l}
8 a-3 b=5 \\
6 a-5 b=-2
\end{array}\right\} \text { linear equations }\) …….(3)and (4)

Multiplying equation (3) by 5 and (4) by 3, we get

40a -15b = 25 ……(5)

18a – 15b = -6 ……(6)

Subtracting equation (6) from (5), we get

22a = 31

⇒ \(a=\frac{31}{22}\)

Putting a = \(\frac{31}{22}\) in equation (3), we get

⇒ \(8 \times \frac{31}{22}-3 b=5\)

⇒ \(\frac{124}{11}-3 b=5\Rightarrow-3 b=5-\frac{124}{11}\)

⇒ \(-3 b=-\frac{69}{11}\Rightarrow=\frac{23}{11}\)

Now, \(\frac{1}{y}=a \quad \Rightarrow \quad \frac{1}{y}=\frac{31}{22} \quad \Rightarrow \quad y=\frac{22}{31}\)

and \(\frac{1}{x}=b \quad \Rightarrow \quad \frac{1}{x}=\frac{23}{11} \quad \Rightarrow \quad x=\frac{11}{23}\)

Hence, the solution of the given two equations are \(\left.\left.\begin{array}{l}
x=0 \\
y=0
\end{array}\right\} \text { and } \quad \begin{array}{l}
x=\frac{11}{23} \\
y=\frac{22}{31}
\end{array}\right\}\)

So, the given system of equations has two solutions.

Note:

In the above example 10,

1. If it is given that x ≠ 0, y ≠ 0 or reduce the given equations in a pair of linear equations, then we have a right to divide both the equations by xy. In this way, we get only one solution i.e., \(x=\frac{11}{23}, y=\frac{22}{31}\) only. When no condition is given to the equations then we get the two solutions of this system of equations i.e.,

⇒ \(\left.\left.\begin{array}{l}
x=0 \\
y=0
\end{array}\right\} \text { and } \begin{array}{r}
x=\frac{11}{23} \\
y=\frac{22}{31}
\end{array}\right\}\) (for more details, see “Gold coins” at the end of this chapter).

2. We have,

2x + 3y = 5xy ……(1)

3x-2y=xy …..(2)

Dividing equations (1) and (2) by xy, we get

⇒ \(\frac{2 x}{x y}+\frac{3 y}{x y}=\frac{5 x y}{x y}\Rightarrow \frac{2}{y}+\frac{3}{x}=5\) …..(3)

and \(\frac{3 x}{x y}-\frac{2 y}{x y}=\frac{x y}{x y}\Rightarrow \frac{3}{y}-\frac{2}{x}=1\) …….(4)

Let \(\frac{1}{x}=u \text { and } \frac{1}{y}=v\)

∴ Equations (3) and (4) become,

2v + 3u = 5 ….(5)

3v- 2u = 1 ….(6)

Now this is a pair of linear equations, multiplying equation (5) by 2 and equation (6) by 3, we get

4v + 6u = 10 …(7)

9v – 6u = 3 …..(8)

On adding equations (7) and (8), we get

13v = 13

⇒ v = 1

Putting v = 1 in equation (5), we get

2(1) + 3u = 5

3u = 3

u=1

Now, u = 1 ⇒ \(\frac{1}{x}=1\) => x =1

and v = 1 ⇒ \(\frac{1}{y}=1\) => y =l

Hence, the required solution is \(\left.\begin{array}{l}
x=1 \\
y=1
\end{array}\right\}\)

Question 9. Solve \(\frac{1}{2(2 x+3 y)}+\frac{12}{7(3 x-2 y)}=\frac{1}{2} \text { and } \frac{7}{2 x+3 y}+\frac{4}{3 x-2 y}=2,\) by reducing them into a pair of linear equations.
Solution:

The given equations

⇒ \(\frac{1}{2(2 x+3 y)}+\frac{12}{7(3 x-2 y)}=\frac{1}{2}\) ….(1)

and \(\frac{7}{2 x+3 y}+\frac{4}{3 x-2 y}=2\) ….(2)

are not linear equations. So, first of all, we shall make these as a pair of linear equations, by putting

⇒ \(\frac{1}{2 x+3 y}=a \text { and } \frac{1}{3 x-2 y}=b\)

Therefore, equations (1) and (2) become,

⇒ \(\frac{1}{2} a+\frac{12}{7} b=\frac{1}{2}\) ….(3)

and 7a + 4b = 2 …….(4)

Multiplying equation (3) by 14, we get

7a + 24b = 7 ……(5)

Subtracting equation (5) from (4), we get

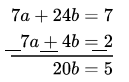
b = \(\frac{1}{4}\)

Putting b = \(\frac{1}{4}\) in equation (4), we get

⇒ \(7 a+4\left(\frac{1}{4}\right)=2 \quad \Rightarrow 7 a=2-1 \quad \Rightarrow a=\frac{1}{7}\)

since, \(a=\frac{1}{7} \quad \Rightarrow \frac{1}{2 x+3 y}=\frac{1}{7} \quad \Rightarrow 2 x+3 y=7\) ……..(6)

and \(b=\frac{1}{4} \quad \Rightarrow \frac{1}{3 x-2 y}=\frac{1}{4} \quad \Rightarrow 3 x-2 y=4\) ……….(7)

Multiplying equation (6) by 2 and equation (7) by 3, we get

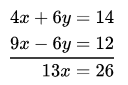
⇒ x = 2

On adding, we get

Putting x = 2 in equation (8), we get,

4(2) + 6y= 14

6y = 14- 8

y = 1

Hence, the solution is \(\left.\begin{array}{r}
x=2 \\
y=1
\end{array}\right\}\)

Question 10. Solve 41x + 53y = 135 and 53x + 41y = 147
Solution:

Given equations are 41x + 53y = 135 ……..(1)

53x + 41y = 147 ……..(2)

On adding equations (1) and (2) we get

94x + 94y = 282

⇒ x+y = 3 ………(3)

On subtracting equation (2) from (1), we get

-12x+ 12y = -12

⇒ x-y- 1 …………(4)

Adding equations (3) and (4), we get

2x= 4  ⇒ x = 2

Putting x = 2 in equation (3)

2 + y = 3 ⇒ y = 1

Hence, the solution is \(\left.\begin{array}{r}
x=2 \\
y=1
\end{array}\right\}\)

Question 11. Solve (a – b)x + (a+b)y = a²– 2ab – b² and (a + b)(x +y) = a² + b².
Solution:

Given equations are (a- b)x + (a + b]y = a² – 2ab – b² ….(1)

and (a + b)(x+y) – a² +b²

or (a + b)x + (a +b)y = a² + b² …….(2)

On subtracting equation (2) from (1), we get

(a – b)k- [a + b)x = a² – 2ab- b² – a² – b²

⇒  x(a -b -a -b) = -2b² – 2ab

⇒ -2bx = -2b(b + a)

⇒ x = a +b

Putting x= (a + b) in equation (1), we get

(a – b)(a + b) + (a + b)y = a²– 2ab- b²

a² -b² + (a +b)y = a² – 2ab – b²

(a +b)y = -2ab

⇒ \(y=\frac{-2 a b}{a+b}\)

Hence, the solution is \(\left.\begin{array}{l}
x=a+b \\
y=\frac{-2 a b}{a+b}
\end{array}\right\}\)

Method of Cross Multiplication

Theorem : If a₁x+b₁y +c₁ =0 and a₂x +b₂y + c₂ = 0 be a system of simultaneous linear equations in two variables x and y such that \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2} \text { i.e., } a_1 b_2-a_2 b_1 \neq 0\).

Then the system has a unique solution given by

⇒ \(x=\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1} \text { and } y=\frac{c_1 a_2-c_2 a_1}{a_1 b_2-a_2 b_1}\)

Proof: The given equations are

a₁x +b₁y + c₁ = 0

a₂x +b₂y + c₂ = 0

Multiplying equation (1) by b₂ and (2) by b₁ and subtracting we get

⇒ \(\left(a_1 b_2-a_2 b_1\right) x=\left(b_1 c_2-b_2 c_1\right)\)

⇒ \(x=\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1}\)

Again multiplying equation (1) by a2, (2) by A J and subtracting we get

⇒ \(y\left(a_2 b_1-a_1 b_2\right)=c_2 a_1-c_1 a_2\)

⇒ \(y=\frac{c_1 a_2-c_2 a_1}{a_1 b_2-a_2 b_1}\)

Hence, x = \(\frac{b_1 c_2-b_2 c_1}{a_1 b_2-a_2 b_1} \text { and } y=\frac{c_1 a_2-c_2 a_1}{a_1 b_2-a_2 b_1} \text {. }\)

⇒ \(y=\frac{c_1 a_2-c_2 a_1}{a_1 b_2-c_2 b_1}\)

Solved Examples

Question 1. Solve the following system of equations by using the method of cross multiplication 2x+3y = 7 and 6x + 5y = 11.
Solution:

Given

2x+3y = 7 and 6x + 5y = 11

The given equations can be written as 2x + 3y- 7 = 0

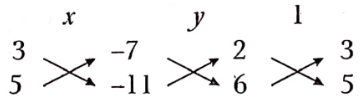
⇒ \(\frac{x}{3 \times(-11)-5 \times(-7)}=\frac{y}{-7 \times 6-(-11) \times 2}=\frac{1}{2 \times 5-6 \times 3}\)

⇒ \(\frac{x}{-33+35}=\frac{y}{-42+22}=\frac{1}{10-18}\)

⇒ \(\frac{x}{2}=\frac{y}{-20}=\frac{1}{-8}\)

when \(\frac{x}{2}=-\frac{1}{8} \quad \text { or } \quad x=-\frac{1}{4}\)

and \(\frac{y}{-20}=-\frac{1}{8} \quad \text { or } \quad y=\frac{20}{8}=\frac{5}{2}\)

Hence, \(\left.\begin{array}{l}
x=-\frac{1}{4} \\
y=\frac{5}{2}
\end{array}\right\}\) is the required solution.

Question 2. Solve the following system of equations bx + ay = 2ab and ax -by- a² – b².

Solution:

Given

bx + ay = 2ab and ax -by- a² – b²

Given equations can be written as

bx + ay- 2ab = 0 and ax- by – a² + b² = 0

By cross multiplication method, we have

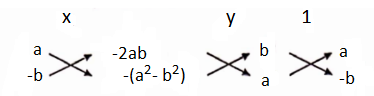
⇒ \(\frac{x}{a \times\left[-\left(a^2-b^2\right)\right]-(-b) \times(-2 a b)}=\frac{y}{(-2 a b) \times a-\left[-\left(a^2-b^2\right)\right] \times b}=\frac{1}{b \times(-b)-a \times a}\)

⇒ \(\frac{x}{a\left(-a^2+b^2-2 b^2\right)}=\frac{y}{-2 a^2 b+a^2 b-b^3}=\frac{1}{-b^2-a^2}\)

⇒ \(\frac{x}{a\left(-a^2-b^2\right)}=\frac{y}{-a^2 b-b^3}=\frac{1}{-b^2-a^2}\)

⇒ \(\frac{x}{a\left(-a^2-b^2\right)}=\frac{1}{-b^2-a^2}\)

⇒ \(x=\frac{-a\left(a^2+b^2\right)}{-1\left(b^2+a^2\right)}\) or x = a

⇒ \(\frac{y}{-a^2 b-b^3}=\frac{1}{-b^2-a^2}\)

⇒ \(y=\frac{-b\left(a^2+b^2\right)}{-1\left(b^2+a^2\right)}\) or y = b

Hence, \(\left.\begin{array}{l}
x=a \\
y=b
\end{array}\right\}\) is the required solution.

Question 3. Solve the following system of equations for x and y, a(x +y) + b(x -y) = a² – ab + b² and a(x +y) -b(x -y) = a² + ab + b².
Solution:

Given

a(x +y) + b(x -y) = a² – ab + b² and a(x +y) -b(x -y) = a² + ab + b²

Given equations can be written as

⇒ ax + ay +bx -by = a² – ab + b²

⇒ (a + b)x + (a -b)y = a² – ab + b²

and ax+ ay -bx + by =a² +ab +b² ….(1)

⇒ (a – b)x + (a + b)y = a² + ab + b² …..(2)

For equations (1) and (2) by cross multiplication method, we have

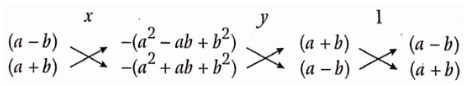
⇒ \(\frac{y}{\left[-\left(a^2-a b+b^2\right)\right] \times(a-b)-\left[-\left(a^2+a b+b^2\right) \times(a+b)\right]}=\frac{1}{(a+b)(a+b)-(a-b)(a-b)}\)

⇒ \(\frac{x}{-\left(a^3-b^3\right)+\left(a^3+b^3\right)}\)

⇒ \(\frac{y}{-\left(a^3-a^2 b+a b^2-a^2 b+a b^2-b^3\right)+\left(a^3+a^2 b+a b^2+a^2 b+a b^2+b^3\right)}=\frac{1}{(a+b)^2-(a-b)^2}\)

⇒ \(\frac{x}{2 b^3}=\frac{y}{2 a^2 b-2 a b^2+b^3+2 a^2 b+2 a b^2+b^3}=\frac{1}{4 a b}\)

⇒ \(\frac{x}{2 b^3}=\frac{y}{4 a^2 b+2 b^3}=\frac{1}{4 a b}\)

⇒ \(\frac{x}{2 b^3}=\frac{y}{2 b\left(2 a^2+b^2\right)}=\frac{1}{4 a b}\)

when \(\frac{x}{2 b^3}=\frac{1}{4 a b} \quad \Rightarrow \quad x=\frac{2 b^3}{4 a b} \quad \Rightarrow \quad x=\frac{b^2}{2 a}\)

and \(\frac{y}{2 b\left(2 a^2+b^2\right)}=\frac{1}{4 a b} \Rightarrow y=\frac{2 b\left(2 a^2+b^2\right)}{4 a b} \Rightarrow y=\frac{2 a^2+b^2}{2 a}\)

Hence, \(\left.\begin{array}{rl}
x=\frac{b^2}{2 a} \\
y=\frac{2 a^2+b^2}{2 a}
\end{array}\right\}\) is the required solution.

Condition For Solvability Of Linear Equations

Consistent and In-consistent System: When a system of equations a₁ x + b₁ y = c₁ and a₂x + b₂y = c₂ has a solution, the system is said to be consistent. A consistent system has one or more solutions. When a system has no solution, the system is said to be inconsistent.

Conditions for Solvability

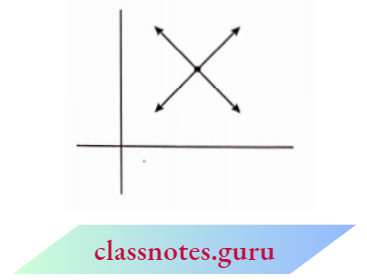
1. If \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2},\) then the given system of equations has a unique solution and thus it is consistent.
Solution:

In this case, the two lines intersect at exactly one point.

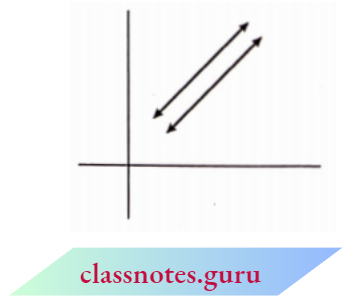
2. If \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) then there is no solution and system is in-consistent.
Solution:

In this case, the two lines are parallel to each other. They will not meet at any point.

3. If \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\) then the system has infinitely many solutions; s and thus the system is consistent and the given pair of linear equal.
Solution:

In this case, the two lines coincide each other, i.e., the two lines are the same. So, we say such lines as coincident lines.

Remark:

If c₁ and c₂ are both equal to zero, the solution can be found more easily as follows:

1. When \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2} ，\) then only solution is x = y = 0
2. When \(\frac{a_1}{a_2}=\frac{b_1}{b_2}\) then there are infinite number of non-zero solution.

Linear Equations Solved Examples

Question 1. Show that the following system of equations has a unique solution:

1. 7x – 2y = 3
   22x – 3y = 16
2. 3x + y = 17
   8x + 11y = 37

and also solve the system of equations in each case.

Solution:

Given equations are 7x- 2y = 3 …….(1)

22x- 3y = 16 …….(2)

Here, a₁ = 7, b₁ = -2 and c₁ = 3

a₂ = 22, b₂ = -3 and c₂= 16

Now, \(\frac{a_1}{a_2}=\frac{7}{22} \text { and } \frac{b_1}{b_2}=\frac{-2}{-3}=\frac{2}{3}\)

Since, \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\) Hence, the given system has a unique solution.

By cross multiplication method, we have

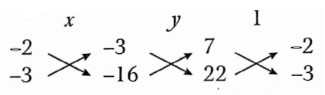
⇒ \(\frac{x}{(-2) \times(-16)-(-3) \times(-3)}=\frac{y}{(-3) \times 22-(-16) \times 7}=\frac{1}{7 \times(-3)-22 \times(-2)}\)

⇒ \(\frac{x}{32-9}=\frac{y}{-66+112}=\frac{1}{-21+44}\)

⇒ \(\frac{x}{23}=\frac{y}{46}=\frac{1}{23}\)

when \(\frac{x}{23}=\frac{1}{23}\)

x = 1 and \(\frac{y}{46}=\frac{1}{23}\) y = 2

Hence, \(\left.\begin{array}{l}
x=1 \\
y=2
\end{array}\right\}\) is the required solution.

The given system of equations is 3x + y = 17 ……..(1)

8x + 11y = 37 ……..(2)

Here a₁ = 3, b₁ =1 and c₁ = 17

a₂ = 8, b₂ = 11 and c₂ = 37

Now, \(\frac{a_1}{a_2}=\frac{3}{8}, \frac{b_1}{b_2}=\frac{1}{11}\)

Since \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\). Hence, the given system has a unique solution.

We can write the equations as

3x+y- 17 = 0 and 8r + 1ly- 37 = 0

By cross multiplication method, we have

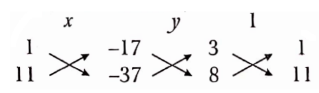
⇒ \(\frac{x}{1 \times(-37)-11 \times(-17)}=\frac{y}{(-17) \times 8-(-37) \times 3}=\frac{1}{3 \times 11-8 \times 1}\)

⇒ \(\frac{x}{-37+187}=\frac{y}{-136+111}=\frac{1}{33-8}\)

⇒ \(\frac{x}{150}=\frac{y}{-25}=\frac{1}{25}\)

When \(\frac{x}{150}=\frac{1}{25}\) = x = 6 and \(\frac{y}{-25}=\frac{1}{25}\) = y = -1

Hence, \(\left.\begin{array}{l}
x=6 \\
y=-1
\end{array}\right\}\) is the required solution

Question 2. Find the value of k for which the system of equations 2x + ky = 1 and 3x- 5y = 7 has a unique solution.
Solution:

The given system of equations is

2x +ky = 1 ……..(1)

and 3x- 5y = 7 ……..(2)

Here, a₁ =2, b₁=k and c₁ = 1

a₂ = 3, b₂ = -5 and c₂ = 7

The system has unique solution if \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

⇒ \(\frac{2}{3} \neq \frac{k}{-5} \quad \text { or } \quad k \neq \frac{-10}{3}\)

So, k can take any real value except \(\frac{-10}{3}\)

Question 3. Find the value of k for which the system of equations x + 2y = 5, 3x + ky – 1 5 = 0 has no solution.
Solution:

The given system of equations is

x + 2y- 5 = 0 ………(1)

3x + ky- 15 = 0 ……..(2)

Here, a₁ = 1, b₁ = 2, c₁ =-5

a₂ = 3, b₂ = k, c₂ = -15

If the equations have no solution then

⇒ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

⇒ \(\frac{1}{3}=\frac{2}{k} \neq \frac{-5}{-15} \Rightarrow \frac{1}{3}=\frac{2}{k} \quad \text { and } \quad \frac{2}{k} \neq \frac{-5}{-15}\)

k = 6 and k ≠ 6 which is impossible.

Hence, there is no such value of k for which the given system has no solution.

Question 4. For what value(s) of a will the system of linear equations αx + 3y = α – 3 and 12x + αy = a have a unique solution?
Solution:

The given equations are

αx + 3y = α – 3

12x + αy = α

Here a₁ = α, b₁ = 3 and c₁ = α- 3

a₂ = 12, b₂ = α and c₂ = α

The system has a unique solution if \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

⇒ \(\frac{\alpha}{12} \neq \frac{3}{\alpha}\)

⇒ a² ≠  36

⇒ a ≠ ± 6

i.e., a ≠ 6 and a ≠ -6

So, α can take any real value except -6 and 6

Question 5. Find the value(s) of k for which the system of equations 5x + 2y = k and 10x + 4y = 3 has infinitely many solutions.
Solution:

The given system of equations is

5x + 2y – k = 0 and 10k + 4y- 3 = 0

Here a₁ = 5, b₁ = 2 and c₁ = k

a₂= 10, b₂ = 4 and c₂ = -3

The system has infinitely many solutions if

⇒ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

⇒ \(\frac{5}{10}=\frac{2}{4}=\frac{-k}{-3}\)

Hence, for k = \(\frac{3}{2}\), the given system of equations will have infinitely many solutions.

Question 6. Find the values of p and q for which the following system of equations has an infinite number of solutions: 2x + 3y = 7 and (p+q)x+(2p-q)y = 21.
Solution:

The given system of equations is

2x + 3y = 7

(p + q)x + (2p- q)y = 21

Here a₁ = 2, b₁ = 3,

a₂ =P + q, b₂ = q and c₂ = 21

The given system will have an infinite number of solutions if

⇒ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

⇒ \(\frac{2}{p+q}=\frac{3}{2 p-q}=\frac{7}{21}\)

Taking the first two and last two expressions

⇒ \(\frac{2}{p+q}=\frac{1}{3} \quad \text { and } \quad \frac{3}{2 p-q}=\frac{1}{3}\)

p + q = 6 and 2p-q = 9

Solving p + q = 6 and 2p- q = 9, we get

p = 5 and q = 1

Hence, the given system of equations will have infinitely many solutions, if p = 5 and q = 1.

Question 7. For which value(s) of A, will the pair of equations represent coincident lines k x + 3y – (k + 3) = 0 and 12x + ky + k = 0?
Solution:

Comparing the given equations with

a₁x + b₁y + c₁ = 0

a₂x+ b₂y + c₂ = 0

We have

⇒ \(\frac{a_1}{a_2}=\frac{k}{12}, \frac{b_1}{b_2}=\frac{3}{k} \text { and } \frac{c_1}{c_2}=\frac{-(k+3)}{k}\)

Now, for coincident lines

⇒ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

⇒ \(\frac{k}{12}=\frac{3}{k}=-\frac{(k+3)}{k}\)

Taking the first two expressions, we get

⇒ \(\frac{k}{12}=\frac{3}{k}\)….(1)

k² = 36

k = +6

Taking the last two expressions, we get

⇒ \(\frac{3}{k}=-\frac{(k+3)}{k}\) …..(2)

3k = -k² – 3k

k² + 6k = 0

k(k + 6) = 0

∴ k = 0 or k = -6

But k = -6 is a value which satisfies both the equations (1) and (2).

∴ k = -6

Linear Equations Solved Examples

Question 1. The sum of the two numbers is 85. If the larger number exceeds four times the smaller one by 5. Find the numbers.
Solution:

Given

The sum of the two numbers is 85. If the larger number exceeds four times the smaller one by 5.

Let the two numbers x andy, and x > y.

According to question, x + y = 85 ……(1)

and x – 4y = 5 …..(2)

Subtracting equation (2) from (1), we get

5y = 80

⇒ y = 16

Putting, y = 16 in equation (1), we get

x+ 16 = 85

⇒ x = 69

Hence, the required numbers are 69 and 16.

Question 2. The sum of the two numbers is 18. The sum of their reciprocals is \(\frac{1}{4}\) Find the numbers.
Solution:

Given

The sum of the two numbers is 18. The sum of their reciprocals is \(\frac{1}{4}\)

Let the two numbers be x and y.

∴ According to the condition,

x + y = 18 …….(1)

According to the 2 condition, \(\frac{1}{x}+\frac{1}{y}=\frac{1}{4}\) ……(2)

⇒ \(\frac{y+x}{x y}=\frac{1}{4}\)

⇒ xy = 4(x+y)

⇒ xy = 4 × 18

⇒ xy = 72

Now, we know that

(x-y)² = (x+y)²-4xy

⇒ (x -y)² = (18)² – 4(72) = 324 – 288 = 36

∴ x-y = ± 6

If x-y = 6 ….(3)

Now, from equations (3) and (1),

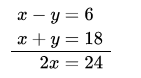
∴ x= 12

∴ y = 18-12

= 6

∴ Two numbers are 12 and 6 in both cases.

If x – y = -6 …….(4)

Now, from equations (4) and (1),

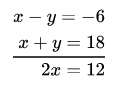
∴ x= 6

∴ y = 18-6

= 12

Question 3. Five years hence father’s age will he three times the age of his son. Five years ago, the father was seven times as old as his son. Find their present ages.
Solution:

Given

Five years hence father’s age will he three times the age of his son. Five years ago, the father was seven times as old as his son.

Let the present age of the son be x years and the present age of the father by years.

Five years hence, the age of son = x + 5

and the age of father = y + 5

Using given information

3(x + 5)=y + 5

⇒ 3x-y = -10 …….(1)

Five years ago, age of son = (x- 5) years

age of father = (y- 5) years

∴ 7(x-5)=y-5

7x -y = 30 ………(2)

Subtracting equation (1) from (2), we get

4x = 40

⇒ x = 10

On substituting x = 10 in equation (1)

3 × 10 – y = -10

⇒ 30 -y =-10

⇒ -y = -40

⇒ y = 40

Hence, the present age of the son is 10 years and the present age of a father is 40 years.

Question 4. The sum of the digits of a two-digit number is 9. The number obtained by reversing the order of the digits of the given number exceeds the given number by 27. Find the given number.
Solution:

Given

The sum of the digits of a two-digit number is 9. The number obtained by reversing the order of the digits of the given number exceeds the given number by 27.

Let the digit at the unit’s place be x and the ten’s place be y.

∴ Number = 10y +x

On reversing the digits, the new number = 10x+y

According to the given conditions,

x+y = 9 …..(1)

10x+y = 21 + (10y +x)

9x-9y = 21

x-y = 3 …….(2)

Adding equations (1) and (2), we get

2x= 12

x = 6

Putting x= 6 in equation (1), we get

6+y = 9

y = 3

Hence, the required number = 10y +x= 10 x 3 + 6 = 36

Question 5. If 2 is added to the numerator of a fraction it reduces to \(\frac{1}{2}\) and if 1 is subtracted from the denominator, it reduces to \(\frac{1}{3}\) Find the fraction.
Solution:

Given

If 2 is added to the numerator of a fraction it reduces to \(\frac{1}{2}\) and if 1 is subtracted from the denominator, it reduces to \(\frac{1}{3}\)

Let the fraction be \(\frac{x}{y}\), where the numerator is x and the denominator is y.

According to 1 condition, \(\frac{x+2}{y}=\frac{1}{2}\)

2x+ 4 = y

⇒ 2x-y = -4 ……(1)

According to 2 condition, \(\frac{x}{y-1}=\frac{1}{3}\)

⇒ 3x=y- 1

⇒ 3x -y = -1 …..(2)

Subtracting equation (2) from (1), we get

-x = -3

⇒ x = 3

Substituting x = 3 in equation (1), we get

2 x 3 -y = -4

⇒ -y = -10

⇒ y = 10

Hence, the required fraction is \(\frac{x}{y}=\frac{3}{10}\)

Question 6. A man sold a chair and table together for ₹760 thereby making a profit of 25% on chairs and 10% on tables. By selling them together for ₹767.50, he would have made a profit of 1 0% on a chair and 25% on the table. Find the cost price of each.
Solution:

Given

A man sold a chair and table together for ₹760 thereby making a profit of 25% on chairs and 10% on tables. By selling them together for ₹767.50, he would have made a profit of 1 0% on a chair and 25% on the table.

Let the cost price of the chair = ₹x and the cost price of the table = ₹y

Now, two cases arise:

Case 1: 25% profit on chair and 10% profit on table

Selling price of chair = \(₹\left(x+\frac{25 x}{100}\right)=₹ \frac{125 x}{100}\)

Selling price of table = \(₹\left(y+\frac{10 y}{100}\right)=₹ \frac{110 y}{100}\)

But total S.P = ₹760

⇒ \(\frac{125 x}{100}+\frac{110 y}{100}=760 \quad \Rightarrow 125 x+110 y=76000\)

∴ 25x + 22y = 15200 ……(1)

Case 2: 10% profit on chair and 25% profit on table

Selling price of chair = \(₹\left(x+\frac{10 x}{100}\right)=₹ \frac{110 x}{100}\)

Selling price of table = \(₹\left(y+\frac{25 y}{100}\right)=₹ \frac{125 y}{100}\)

But total S.P. = ₹767.50

∴ \(\frac{110 x}{100}+\frac{125 y}{100}=767.50\)

⇒ 110x + 125y = 76750

⇒ 22x + 25y = 15350 ……(2)

To solve equations (1) and (2), adding equations (1) and (2), we get

47x + 47y = 30550

⇒ x + y = 650 …….(3)

Subtracting equation (2) from (1), we get

3x- 3y = -150

⇒ x-y = -50 ….(4)

On adding equations (3) and (4), we get

2x = 600

⇒ x = 300

Putting x = 300 in equation (3), we get

300 +y = 650

⇒ y = 650- 300 = 350

Cost of chair = ₹300 and cost of table = ₹350

Question 7. A lady has 25 paise and 50 paise coins in her purse. If in all she has 40 coins and the value of her money is ₹12.75, how many coins of each type does she have?
Solution:

Given

A lady has 25 paise and 50 paise coins in her purse. If in all she has 40 coins and the value of her money is ₹12.75,

Let a number of 25 paise coins be x and a number of 50 paise coins be y.

According to the given conditions, we have

x + y = 40 ….(1)

and 25x + 50y= 1275 …..(2)

Multiplying equation (1) by 50, we get

50x+50y = 2000

Subtracting equation (3) from (2), we get

-25x = -725

⇒ x = 29

Substituting x = 29 in equation (1), we get

29 + y = 40

⇒ y = 11

Hence, the number of 25 paise coins = 29 and the number of 50 paise coins = 11.

Question 8. 2 men and 7 boys can finish a work in 4 days, while 4 men and 4 boys can finish the same work in 3 days. How long would it take one man or one boy to do it?
Solution:

Given

2 men and 7 boys can finish a work in 4 days, while 4 men and 4 boys can finish the same work in 3 days.

Let 1 man can do a piece of work in* days while a boy can do a piece of work in y ways.

∴ One man’s one day work = \(\frac{1}{x}\)

and one boy’s one day work = \(\frac{1}{y}\)

According to the given conditions,

⇒ \(\frac{2}{x}+\frac{7}{y}=\frac{1}{4}\) ……(1)

and \(\frac{4}{x}+\frac{4}{y}=\frac{1}{3}\) …….(2)

Multiplying equation (1) by 2 and (2) by 1, we get

⇒ \(\frac{4}{x}+\frac{14}{y}=\frac{1}{2}\) ……..(3)

⇒ \(\frac{4}{x}+\frac{4}{y}=\frac{1}{3}\) ……..(4)

Subtracting equation (4) from (3), we get

⇒ \(\frac{14}{y}-\frac{4}{y}=\frac{1}{2}-\frac{1}{3} \Rightarrow \frac{10}{y}=\frac{1}{6}\)

⇒ y = 60

Substituting y = 60 in equation (1), we get

⇒ \(\frac{2}{x}+\frac{7}{60}=\frac{1}{4} \quad \Rightarrow \quad \frac{2}{x}=\frac{1}{4}-\frac{7}{60}\)

⇒ \(\frac{2}{x}=\frac{8}{60}\)

⇒ 8x= 120 or x = 15

Hence, one man would do the work in 15 days and one boy in 60 days.

Question 9. A boat goes 301km upstream and 44 km downstream in 10 hours. In 1 3 hours it can go 40 1cm upstream and 55 km downstream. Determine the speed of the stream and that of the boat in still water.
Solution:

Given

A boat goes 301km upstream and 44 km downstream in 10 hours. In 1 3 hours it can go 40 1cm upstream and 55 km downstream.

Let the speed of the boat in still water is x km/hr and the speed of the stream is y km/hr.

∴ speed of boat upstream = (x-y) km/hr

and speed of boat downstream = (x +y) km/hr

We know that, speed = \(\frac{\text { distance }}{\text { time }}\)

According to the given conditions,

Time taken in going 30 km upstream = \(\frac{30}{x-y} \mathrm{hr}\)

Time taken in 44 lem downstream = \(\frac{40}{x+y} \mathrm{hr}\)

∴ \(\frac{30}{x-y}+\frac{44}{x+y}=10\)

Similarly in the second condition,

⇒ \(\frac{40}{x-y}+\frac{55}{x+y}=13\)

Let \(\frac{1}{x-y}=a \text { and } \frac{1}{x+y}=b,\), we get

30a + 44b = 10

and 40a + 55b =13

Multiplying equation (3) by 4 and (4) by 3, we get

120a+ 1766 = 40

120a+ 1656 = 39

Subtracting equation (6) from (5), we get

11b = 1

⇒ b = \(\frac{1}{11}\)

Putting b = \(\frac{1}{11}\) inequation (3), we get

⇒ \(30 a+44 \times \frac{1}{11}=10\)

30a = 6

⇒ \(a=\frac{1}{5}\)

⇒ \(\frac{1}{x-y}=\frac{1}{5}\text { or }x-y=5\) ……(7)

and \(\frac{1}{x+y}=11\text { or }x+y=11\) …….(8)

Solving equations (7) and (8), we get

x = 8 and y = 3

Hence, the speed of a boat in still water = 8 km/hr and the speed of the water stream = 3 km/hr.

Question 10. A boat which travels at the rate of 10.5 km/hr downstream takes 3 times as long time to go to a certain distance up a river as to go the same distance down. Find the rate at which the stream flows.
Solution:

Given

A boat which travels at the rate of 10.5 km/hr downstream takes 3 times as long time to go to a certain distance up a river as to go the same distance down.

Let the speed of the stream = x km/hr

and the speed of the boat in still water = y km/hr

∴ Speed of boat downstream = (x +y) km/hr

and speed of boat upstream = (y- x) km/hr

Let the distance be D km.

∴ According to the problem,

x+y = 10.5 ……(1)

Also, time taken by boat upstream = 3 x time taken by boat downstream

⇒ \(\frac{D}{y-x}=3 \times \frac{D}{10.5}\)

y – x = 3.5 ……(2)

Adding equations (1) and (2), we get

2y= 14 ⇒ y = 7

Putting y = 7 in equation (1), we get

x+7 = 10.5 ⇒ x= 3.5

Hence, speed of stream = 3.5 km/hr

Linear Equations In Two Variables Exercise 3.1

Question 1. Aftab tells his daughter, “Seven years ago, 1 was seven times as old as you were then. Also, three years from now, 1 shall be three times as old as you will be.” (Isn’t this interesting?) Represent this situation algebraically and graphically.
Solution:

Given

Aftab tells his daughter, “Seven years ago, 1 was seven times as old as you were then. Also, three years from now, 1 shall be three times as old as you will be.”

Let the present age of Aftab be x years and the present age of his daughter be x years.

7 years ago,

age of Aftab = (x- 7) years

age of his daughter = (y- 7) years

According to the problem,

x-7 = 7(y -7)

⇒ x-7 = 7y- 49

⇒ x-7y = -42

3 years later,

age of Aftab = (x + 3) years

age of his daughter = (y + 3) years

According to the problem,

x + 3 = 3(y + 3)

⇒ x + 3 = 3y + 9

⇒ x- 3y = 6

∴ The algebraic form of the given problem is as follows:

x- 7y = -42 and x- 3y = 6

Now, x-7y = -42

x = 7y – 42

y = 5 then x=7 × 5-42=-7

y = 6 then x-7 × 6 – 42 = 0

y = 7 then A=7 × 7-42 = 7

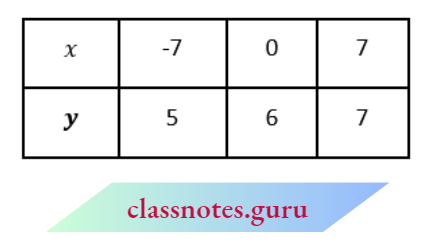
and x- 3y = 6 ⇒ x = 3y + 6

y = -1 then x = 3 × -1 +6 = 3

y = 0 then x = 3 × 0 + 6 = 6

y = -2 then x = 3 × -2 + 6 = 0

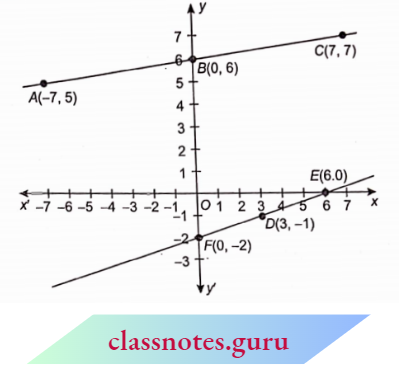
Mark and join the given points in the two tables. It is the graphical form of the given problem.

Question 2. The coach of a cricket team buys 3 bats and 6 balls for ₹3900. Later, she buys another bat and 3 more balls of the same kind for ₹1300. Represent this situation algebraically and geometrically.
Solution:

Given

The coach of a cricket team buys 3 bats and 6 balls for ₹3900. Later, she buys another bat and 3 more balls of the same kind for ₹1300.

Let the cost of a bat = ₹x

and cost of a ball = ₹y

According to the problem,

3x + 6y = 3900

x + 2y= 1300 ……….(1)

x + 3y = 1300 ……….(2)

Equations (1 ) and (2) represent the algebraic form of the given problem.

From equation (1),

x = 1300 -2y

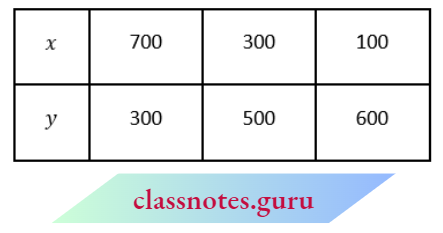
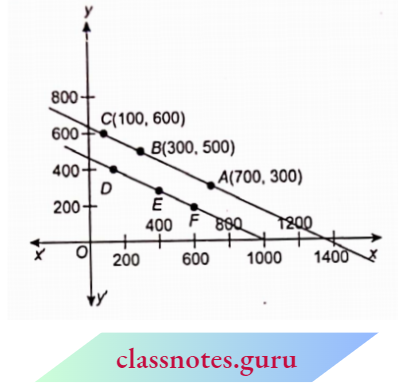
Mark the points A(700, 300), B(300, 500), C(100, 600) and join them.

From equation (2), x- 1300- 3y

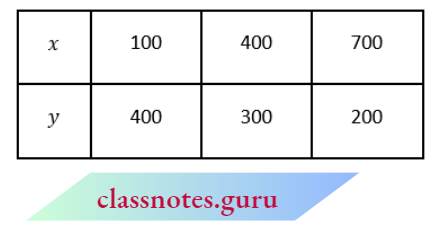
Mark the points D = (100, 400), E = (400, 300), E(700, 200) and join them.

It is the geometric form of the given problem.

Question 3. The cost of 2 kg of apples and I kg of grapes in a day was found to be ‘ 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ‘ 300. Represent the situation algebraically and geometrically.
Solution:

Given

The cost of 2 kg of apples and I kg of grapes in a day was found to be ‘ 160. After a month, the cost of 4 kg of apples and 2 kg of grapes is ‘ 300.

Let the cost of 1 kg apple = ₹x

and cost of 1kg grapes = ₹y

According to the problem,

2x+y = 160 ……(1)

4x + 2y = 300

2x+y = 150 ……(2)

Equation (1) and equation (2) is the algebraic form of the given problem.

From equation (1),y = 160- 2x

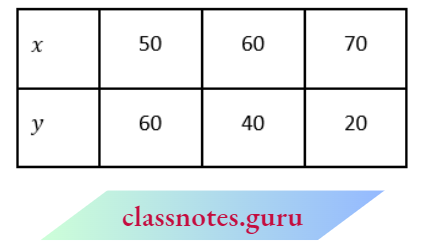
Mark the points A(50, 60), B(60, 40) and C(70, 20) and join them.

From equation (2), y = 150-2x

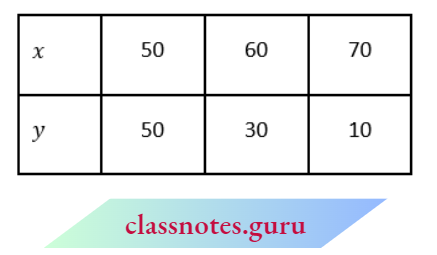
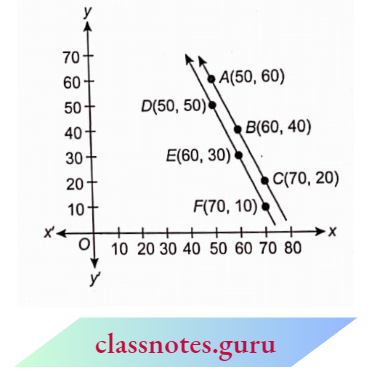
Mark the points D(50, 50), E(60, 30) and F(70, 10) and join them.

The lines shown in the graph represent the geometric form of the given problem.

Linear Equations In Two Variables Exercise 3.2

Question 1. Form the pair of linear equations in the following problems and find their solutions graphically.

1. 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.
2. 5 pencils and 7 pens together cost ₹50, whereas 7 pencils and 5 pens together cost ₹ 46. Find the cost of one pencil and that of one pen.

Solution:

1. Let many boys = x and a number of girls =y.

According to the problem,

x +y = 10 ……(1)

y – x + 4 …….(2)

From equation (1), x +y = 10 ⇒ y = 10 – x

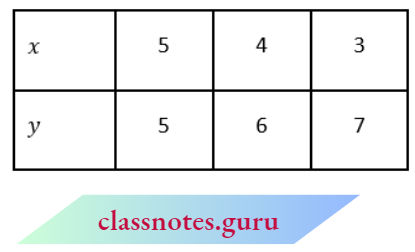
Mark the points A(5, 5), B(4, 6) and C(3, 7) and join them.

From equation (2), y = x + 4

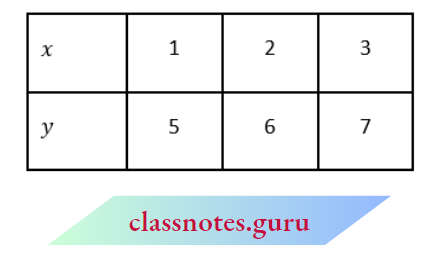
Mark the points D(1, 5), E(2, 6) and C(3, 7) and join them.

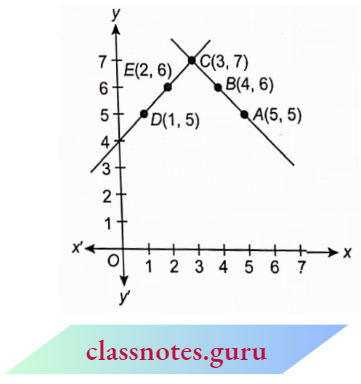
Both lines intersect at points C(3, 7).

∴ x = 3, y = 7

⇒ Number of boys = 3 and number of girls = 7

2. Let the cost of 1 pencil = ₹x

and the cost of 1 pen = ₹y

According to the problem,

5x + 7y = 50

⇒ \(x=\frac{50-7 y}{5}\)

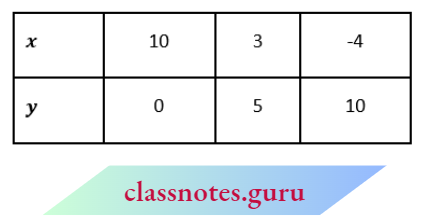
Mark the points A(10, 0), B(3, 5) and C(-4, 10) and join them

And 7x + 5y – 46 ⇒ \(x=\frac{46-5 y}{7}\)

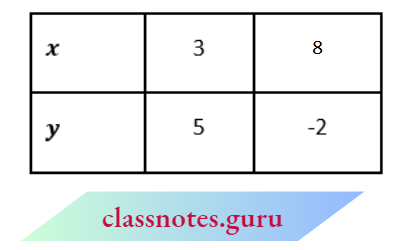
Mark the points B(3, 5) and E(8, -3) and join them.

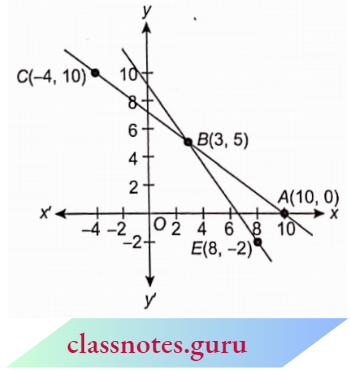
Two lines intersect at point (3,5).

∴ x = 3,y = 5

∴ Cost of 1 pencil= ₹3

and cost of 1 pen = ₹5.

Question 2. On comparing the ratios \(\frac{a_1}{a_2}, \frac{b_1}{b_2} \text { and } \frac{c_1}{c_2}\), find representing the following pairs of linear equations intersect at a point, are parallel or coincident :

1. 5x- 4y + 8 = 0
   7x + by- 9 = 0
2.  9x + 3y+12 = 0
   18r + 6y + 24 = 0
3. 6x-3y+ 10 = 0
   2x-y + 9 = 0

Solution:

1. Given equations, 5x- 4y + 8 = 0 and 7x + 6y – 9 = 0

Here, a₁ = 5, b₁ = -4, c₁ = 8

a₂ = 7, b₂ = 6, c₂ = -9

Now, \(\frac{a_1}{a_2}=\frac{5}{7}, \frac{b_1}{b_2}=\frac{-4}{6}=\frac{-2}{3}, \frac{c_1}{c_2}=\frac{8}{-9}\)

∵ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

∴ Two lines intersect at a point.

2. Given equations, 9x + 3y+ 12 = 0 and 18x + 6y + 24 =0

Here,

a₁ = 9, b₁ = 3, c₁ = 12

a₂ = 18, b₂ = 6, c₂ = 24

Now \(\frac{a_1}{a_2}=\frac{9}{18}=\frac{1}{2}, \frac{b_1}{b_2}=\frac{3}{6}=\frac{1}{2}\)

and \(\frac{c_1}{c_2}=\frac{12}{24}=\frac{1}{2}\)

∵ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

∴ Two lines are coincident

3. Given equations, 6x- 3y + 10 = 0 and 2x-y + 9 =0

Here, a₁ = 6, b₁ = -3, c₁ = 10

a₂ = 2, b₂=-1, c₂ = 9

Now \(\frac{a_1}{a_2}=\frac{6}{2}=\frac{3}{1}, \frac{b_1}{b_2}=\frac{-3}{-1}=\frac{3}{1}\)

and \(\frac{c_1}{c_2}=\frac{10}{9}\)

∵ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

∴ Two lines are parallel.

Question 3. On comparing the ratios, \(\frac{a_1}{a_2}, \frac{b_1}{b_2} \text { and } \frac{c_1}{c_2}\), find out whether the following pair of linear equations are consistent, or inconsistent.

1. 3x + 2y = 5; 2x- 3y = 7
2. 2x- 3y = 8; 4x- 6y = 9
3. \(\frac{3}{2} x+\frac{5}{3} y=7 ; 9 x-10 y=14\)
4. 5x-3y = 11;-10x+6y = -22
5. \(\frac{4}{3} x+2 y=8 ; 2 x+3 y=12\)

Solution:

1. Given equations,

3x + 2y = 5 ⇒ 3x + 2y – 5 = 0

and 2x- 3y = 7 ⇒ 2x- 3y- 7 = 0

Here, a₁ =3, b₁ = 2, c₁ = -5

a₂ = 2, b₂ =-3, c₂ = -7

Now, \(\frac{a_1}{a_2}=\frac{3}{2}, \frac{b_1}{b_2}=\frac{2}{-3} \text { and } \frac{c_1}{c_2}=\frac{-5}{-7}=\frac{5}{7}\)

∵ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

∴ Given equations have a unique solution.

⇒ Given pair of equations is consistent.

2. Given equations,

2x-3y = 8 ⇒ 2x-3y-8 = 0

and 4x- 6y= 9 ⇒ 4r-6y-9 = 0

Here, a₁= 2, b₁ = -3, c₁ = -8

a₂ = 4, b₂ = -6, c₂ = -9

Now, \(\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}, \frac{b_1}{b_2}=\frac{-3}{-6}=\frac{1}{2}\)

and \(\frac{c_1}{c_2}=\frac{-8}{-9}=\frac{8}{9}\)

∵ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

∴ Given equations have no solution.

⇒  Given pair of equations is inconsistent.

3. Given equations, \(\frac{3}{2} x+\frac{5}{3} y=7 \Rightarrow \frac{3}{2} x+\frac{5}{3} y-7=0\)

and 9x- 10y = 14 ⇒ 9x- 10y- 14 = 0

Here, \(a_1=\frac{3}{2}, b_1=\frac{5}{3}, c_1=-7\)

and \(a_2=9, b_2=-10, c_2=-14\)

Now, \(\frac{a_1}{a_2}=\frac{3 / 2}{9}=\frac{1}{6}, \frac{b_1}{b_2}=\frac{5 / 3}{-10}=-\frac{1}{6}\)

and \(\frac{c_1}{c_2}=\frac{-7}{-14}=\frac{1}{2}\)

∵ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

∴ Given equations have a unique solution.

⇒ Given pair of equations is consistent.

4. Given equations,

5x-3y =11 ⇒ 5x- 3y – 11 = 0

and -10x + 6y = -22 ⇒ -10x + 6y + 22 = 0

Here, a₁ = 5, b₁ -3, c₁ = -11

a₂ = -10, b₂ = 6, c₂ = 22

Now, \(\frac{a_1}{a_2}=\frac{5}{-10}=-\frac{1}{2}, \frac{b_1}{b_2}=\frac{-3}{6}=-\frac{1}{2}\)

and \(\frac{c_1}{c_2}=\frac{-11}{22}=\frac{-1}{2}\)

∵ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

∴ Two lines are coincident i.e., they will have infinitely many solutions.

⇒ Given pair of equations is consistent.

5. Given equations, \(\frac{4}{3} x+2 y=8\)

⇒ \(\frac{4}{3} x+2 y-8=0\)

and 2x + 3y = 12

⇒ 2x + 3y – 12 = 0

Here, \(a_1=\frac{4}{3}, b_1=2, c_1=-8\)

a₂ = 2, b₂ = 3, c₂ =-12

Now, \(\frac{a_1}{a_2}=\frac{4 / 3}{2}=\frac{2}{3}, \frac{b_1}{b_2}=\frac{2}{3}, \frac{c_1}{c_2}=\frac{-8}{-12}=\frac{2}{3}\)

∵ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

∴ Two lines are coincident i.e., they will have infinitely many solutions.

⇒ Given pair of equations is consistent.

Question 4. Which of the following pairs of linear equations are consistent/inconsistent? If consistent, obtain the solution graphically:

1. x + y = 5, 2x + 2y = 10
2. x-y = 8, 3x- 3y = 16
3. 2x+y-6 = 0, 4x- 2y – 4 = 0
4. 2x-2y-2 = 0, 4x-4y-5 = 0

Solution:

1. Given equations,

x+y = 5 ⇒ x+y-5 = 0

and 2x + 2y = 10 ⇒ 2x + 2y – 10 = 0

Here, a₁ = 1, b₁ = 1, c₁ = -5

a₂ = 2, b₂ = 2, c₂ = -10

Now, \(\frac{a_1}{a_2}=\frac{1}{2}, \frac{b_1}{b_2}=\frac{1}{2} \text { and } \frac{c_1}{c_2}=\frac{-5}{-10}=\frac{1}{2}\)

∵ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

∴ Given equations have infinitely many solutions.

⇒ Given pair of equations is consistent.

Now, x + y = 5 ⇒ y = 5-x

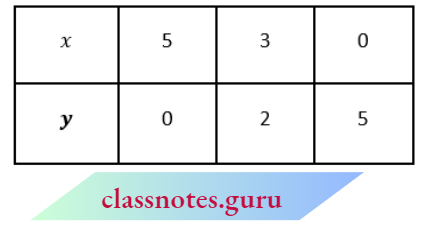
Mark the points (5, 0), (3, 2) and (0, 5) and join them.

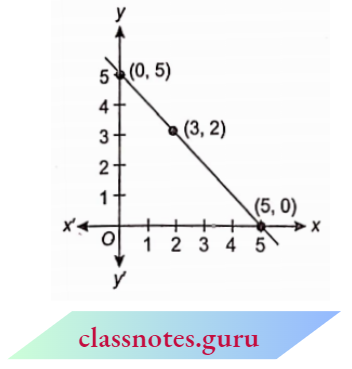
It is the required solution of given equations.

2. Given equations,

x-y = 8 ⇒ x -y- 8 = 0

3x-3y = 16 ⇒ 3x- 3y – 16 = 0

a₁ = 1, b₁ =-1, c₁ =-8

a₂= 3, b₂ = -3, c₂= -16

Now, \(\frac{a_1}{a_2}=\frac{1}{3}, \frac{b_1}{b_2}=\frac{-1}{-3}=\frac{1}{3} \text { and } \frac{c_1}{c_2}=\frac{-8}{-16}=\frac{1}{2}\)

∵ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

∴ Given system of equations has no solution

⇒ Given pair of equations is inconsistent.

3. Given equations,

2x+y – 6 =0 and 4x-2y -4 = 0

Here, a₁ = 2, b₁ = 1, c₁ = -6

a₂ = 4, b₂= -2, c₂ = -4

Now, \(\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}, \frac{b_1}{b_2}=\frac{1}{-2}=-\frac{1}{2}\)

∵ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

∴ Given equations have a unique solution.

⇒ Given pair of equations is consistent.

From the first equation,

2x +y- 6 =0 ⇒ y = 6- 2x

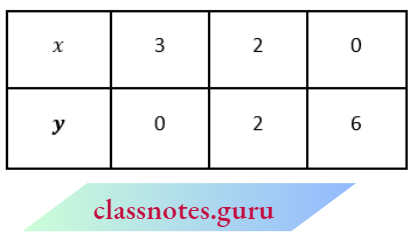
Mark the points (3, 0), (2, 2) and (.0, 6) and join them.

From the second equation,

4x- 2y- 4 = 0 ⇒ 2x -y – 2 = 0

y = 2x-2

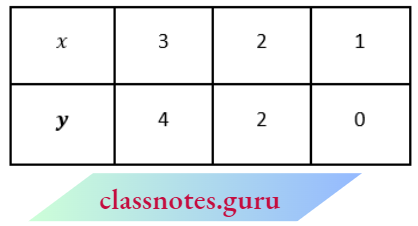
Mark the points (3, 4), (2, 2) and (1,0) and join them.

Two lines intersect at point (2, 2).

∴ Solution of given pair of equations: x = 2, y = 2

4. Given equations,

2x- 2y – 2 = 0 and 4x- 4y- 5 = 0

Here, a₁ = 2, b₁ = -2, c₁ = -2

a₂ = 4, b₂ = -4, c₂ = -5

Now \(\frac{a_1}{a_2}=\frac{2}{4}=\frac{1}{2}, \frac{b_1}{b_2}=\frac{-2}{-4}=\frac{1}{2}, \frac{c_1}{c_2}=\frac{-2}{-5}=\frac{2}{5}\)

∵ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

∴ Given system of equations has no solution.

⇒ Given pair of equations is inconsistent.

Question5. Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m. Find the dimensions of the garden.
Solution:

Given

Half the perimeter of a rectangular garden, whose length is 4 m more than its width, is 36 m.

Let the length of the garden = x metre

and breadth =y metre.

∴ The perimeter of a rectangular garden

= 2(length + breadth)

= 2(x+y)

So, half the perimeter = x+y

but it is given that, half the perimeter = 36 m

∴ x+y = 36 ….(1)

and x=y + 4 i.e., x-y = 4 …(2)

To solve the equations (1) and (2) we get x=20, y = 16

Therefore, length = 20 m and breadth = 16 m.

Question 6. Given the linear equation 2x + 3y- 8 = 0, write another linear equation in two variables such that the geometrical representation of the pair so formed is:

1. Intersecting lines
2. Parallel lines
3. Coincident lines

Solution: Given a linear equation,

2x+ 3y- 8 = 0

Here, a₁ = 2, b₁ = 3, c₁ =-8

1. We know that, intersecting lines

⇒ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

∴ Taking a₂ = 3, b₂ = 4 and c₂ = 2

Required equation, 3x + 4y + 2 = 0

2. We know that, for parallel lines,

⇒ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

∴ Taking = 4, = 6 and = 5

Required equation, 4x + 6y + 5 = 0

3. We know that, for coincident lines,

⇒ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

∴ Taking a₂ = 4, b₂ = 6, c₂ = -16

Required equation, 4x+ 6y- 16 = 0

Question 7. Draw the graphs of the equations x -y +1=0 and 3x + 2y – 12 = 0. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis, and shade the triangular region.
Solution:

x-y =-1 ⇒ x=y – 1

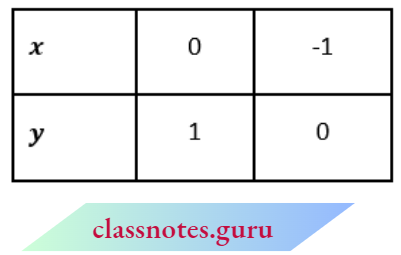
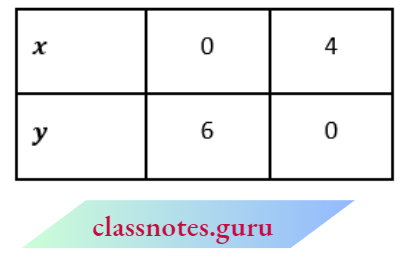
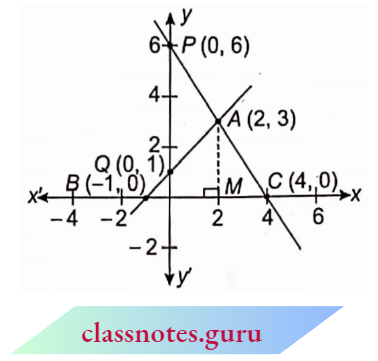
3x + 2y =12 ⇒ \(x=\frac{12-2 y}{3}\)

Mark the points Q(0, 1),B(-1, 0), P(0, 6) and C(4, 0).

Obtain the graph of the given lines on the graph paper by joining BQ and PC.

Two lines intersect at point A(2, 3).

∴ x = 2, y = 3

Lines intersect x-axis at points B(-l, 0) and C(4, 0).

Draw the perpendicular AM from A to BC

∴ Area of ΔABC = \(\frac{1}{2} \times B C \times A M\)

⇒ \(\frac{1}{2} \times 5 \times 3\)

= 7.5 square units.

Linear Equations In Two Variables Exercise 3.3

Question 1. Solve the following pair of linear equations by the substitution method :

1. x+y= 14, x-y = 4
2. s-t = 3, \(\frac{s}{3}+\frac{t}{2}=6\)
3. 3x-y = 3, 9x-3y = 9
4. 0.2x + 0.3y = 1.3, 0.4x + 0.5y = 2.3
5. \(\sqrt{2} x+\sqrt{3} y=0\), \(\sqrt{3} x-\sqrt{8} y=0\)
6. \(\frac{3 x}{2}-\frac{5 y}{3}=-2\), \(\frac{1}{2 x}+\frac{1}{3 y}=2\)

Solution:

1. x+y = 14 …..(1)

x-y = 4 ……(2)

From equation (1),

x+y =14 ⇒ x= 14 -y

Put this value of x in equation (2),

14 -y -y = 4

⇒ -2y = 4-14 =-10

⇒ y = 5

Put the value of y in equation (3),

x = 14-5 = 9

∴ x = 9, y = 5

2. s-t = 3 …..(1)

⇒ \(\frac{s}{3}+\frac{t}{2}=6\) …….(2)

From equation (1)

s-t =3 ⇒ s = 3 + t ……(3)

Put the value of s from equation (3) to equation (2),

⇒ \(\frac{3+t}{3}+\frac{t}{2}=6 \Rightarrow \frac{6+2 t+3 t}{6}=6\)

⇒ 6+5t = 36

⇒ 5t = 36-6 = 30

⇒ t = 6

Put this value of t in equation (3),

s = 3 + t = 3 + 6 = 9

s =9, t = 6

3. 3x -y = 3 …….(1)

9x- 3y = 9 ……(2)

From equation (1),

3x-y=3 ⇒ y = 3x-3 ,..(3)

Put the value of y from equation (3) to equation (2),

9x- 3(3x- 3) = 9

⇒ 9x- 9x + 9 =9

⇒ 9 = 9

From here, we do not obtain the values of x and y.

∴ Given equations have infinitely many solutions.

4. 0.2x + 0.3y = 1.3 + 3y = 13 …….(1)

and 0.4r + 0.5y = 2.3 => 4x + 5y = 23 …..(2)

From equation (1),

2x + 3y = 13 => 2x = 13-3y-

⇒ \(x=\frac{13-3 y}{2}\)…….(3)

Put the value of x from equation (3) to equation (2)

⇒ \(\frac{4(13-3 y)}{2}+5 y=23\)

⇒ 2(13 -3y) + 5y = 23

⇒ 26 – 6y + 5y = 23

⇒ -y = 23 – 26 =-3

⇒ y = 3

Put the value of y in equation (3)

⇒ \(x=\frac{13-3 \times 3}{2}\)

⇒ \(x=\frac{13-9}{2}=2\)

∴ x = 2,y = 3

5. \(\sqrt{2} x+\sqrt{3} y=0\) …….(1)

⇒ \(\sqrt{3} x-\sqrt{8} y=0\) ……(2)

From equation (2),

⇒ \(\sqrt{3} x=\sqrt{8} y\)

⇒ \(x=\frac{\sqrt{8}}{\sqrt{3}} y\) ……..(3)

Put the value of x from equation (3) to equation (1),

⇒ \(\sqrt{2} \cdot \frac{\sqrt{8}}{\sqrt{3}} y+\sqrt{3} y=0 \Rightarrow \frac{4 y+3 y}{\sqrt{3}}=0\)

⇒ 7y = 0

⇒ y = 0

Put this value of y in equation (3),

⇒ \(x=\frac{\sqrt{8}}{\sqrt{3}} \times 0=0\)

∴ x = 0,y = 0

6. \(\frac{3 x}{2}-\frac{5 y}{3}=-2\) ……(1)

⇒ \(\frac{x}{3}+\frac{y}{2}=\frac{13}{6}\) …..(2)

From equation (1)

⇒ \(\frac{3 x}{2}=-2+\frac{5 y}{3}=\frac{-6+5 y}{3}\)

⇒ \(x=\frac{10 y-12}{9}\) ………(3)

Put the value of x from equation (3) to equation (2),

⇒ \(\frac{1}{3} \cdot\left(\frac{10 y-12}{9}\right)+\frac{y}{2}=\frac{13}{6}\)

⇒ \(\frac{20 y-24+27 y}{-54}=\frac{13}{6}\)

⇒ \(47 y-24=\frac{13}{6} \times 54=117\)

⇒ 47y = 117 + 24= 141

⇒ y = 3

Put this value of/ in equation (3),

⇒ x = \(\frac{10 \times 3-12}{9}=2\)

∴ x = 2, y = 3

Question 2. Solve 2x + 3y = 11 and 2x -4y = -24 and hence find the value of ‘m’ for which y = mx + 3.
Solution:

Here, 2x + 3y= 11 ……(1)

2x- 4y = -24 …….(2)

From equation (2), 4y = 2x+ 24

y = \(\frac{x+12}{2}\) …….(3)

Put the value of y from equation (3) to equation (1),

⇒ \(2 x+3\left(\frac{x+12}{2}\right)=11\)

⇒ 4x + 3(x + 12)= 11 x 2

⇒ 4x + 3x + 36 = 22

⇒ 4x = 22- 36

⇒ 7x = -14

⇒ x = -2

Put x = -2 in equation (3),

⇒ \(y=\frac{-2+12}{2} \Rightarrow y=\frac{10}{2}=5\)

Put x =-2 andy = 5 in the equation, y = mx + 3

⇒ 5 = m x (-2) + 3

⇒ 5 = -2m + 3

⇒ 2m = 3-5=-2

⇒ m = -1

The value of ‘m’ = -1

Question 3. Form the pair of linear equations for the following problems and find their solution by substitution method :

1. The difference between two numbers is 26 and one number is three times the other. Find them.
2. The larger of two supplementary angles exceeds the smaller by 18 degrees. Find them.
3. The coach of a cricket team buys 7 bats and 6 balls for ₹3800. Later, she buys 3 bats and 5 balls for ₹1750. Find the cost of each bat and each ball.
4. The taxi charges in a city consist of a fixed charge together with the charge for the distance covered. For a distance of 10 km, the charge paid is ?₹105 and for a journey of 15 km, the charge paid is ₹155. What are the fixed charges and the charge per km? How much does a person have to pay for travelling a distance of 25 km?
5. A fraction becomes \(\frac{9}{11}\) if 2 is added to both the numerator and the denominator. If 3 is added to both the numerator and the denominator it becomes \(\frac{5}{6}\) Find the fraction.
6. Five years hence, the age of Jacob will be three times that of his son. Five years ago, Jacob’s age was seven times that of his son. What are their present ages?

Solution:

1. Let two numbers be x and y. According to the problem,

x-y = 26

⇒ x = 26 +y ……(1)

and x = 3y …..(2)

⇒ 26 +y = 3y

Put the value of x from equation (1),

⇒ 3y -y= 26

⇒ 2y = 26

⇒ y= 13

From equation (2),

x = 3 x 13 = 39

Therefore numbers =39 and 13

2. Let two angles are x and y According to the problem,

x+y = 180°

⇒ x = 180° -y ……(1)

and x =y+ 18° …..(2)

⇒ 180° -y =y+ 18°

Put the value of x from equation (1)

⇒ -y – y = 18°- 180°

⇒ -2y = -162°

⇒ y = 81°

From equation (2),

x = 81°+ 18° = 99°

∴ Required angle= 99° and 81°

3. Let the cost of one bat = ₹x

and the cost of one ball = ₹y

According to the question,

⇒ 7x + 6y = 3800

⇒ 7x = 3800 – 6y

⇒ \(x=\frac{3800-6 y}{7}\) …….(1)

and 3x+5y = 1750 …….(2)

Put the value of x from equation (1),

⇒ \(\frac{11400-18 y+35 y}{7}=1750\)

11400+ 17y = 12250

⇒ 17y= 12250- 11400 = 850

⇒ y = 50

Put the value of y in equation (1),

⇒ \(x=\frac{3800-6 \times 50}{7}=\frac{3500}{7}=500\)

∴ Cost of 1 bat = ₹500

and Cost of 1 ball = ₹50

4. Let fixed charge = ₹x

and the fare for each lem = ₹y

According to the problem,

x+10y = 105

⇒ x = 105 – 10y …..(1)

and x+15y = 155

⇒ 105 – 10y + 15y = 155

Put the value of x from equation (1),

⇒ 5y = 155- 105 = 50

⇒ y = 10

Put the value of y in equation (1),

x = 105- 10 x 10 = 5

∴ Fixed charge = ₹5

and the fare of each km = ₹10

Fare for travelling 25 km

= x + 25y = 5 + 25 x 10

= 5 + 250 = ₹255

5. Let fraction \(\frac{x}{y}\)

According to the problem,

⇒ \(\frac{x+2}{y+2}=\frac{9}{11}\)

⇒ 11x + 22 = 9y + 18

⇒ 11x = 9y-4

⇒ x = \(\frac{9 y-4}{11}\) ……(1)

and \(\frac{x+3}{y+3}=\frac{5}{6}\)

6x + 18 = 5y + 15

6x = 5y- 3

⇒ \(\frac{6(9 y-4)}{11}=5 y-3\)

Put the value of* from equation (1),

⇒ 54y – 24 = 55y- 33

⇒ 54y- 55y = -33 + 24

⇒ -y = -9 ⇒ y = 9

Put the value of y in equation (1)

⇒ \(x=\frac{9 \times 9-4}{11}=7\)

∴ Fraction = \(\frac{x}{y}=\frac{7}{9}\)

6. Let the present age of Jacob = x years

and present age of son = y years

After 5 years,

Jacob’s age = (x + 5) years

son’s age = (y + 5) years

According to the problem,

x + 5 = 3(y + 5)

⇒ x = 3y+ 10 …….(1)

Five years ago,

Jacob’s age = (x- 5) years

son’s age = (y- 5) years

According to the problem, x- 5 = 7(y-5)

⇒ 3y+10-5 = 7y – 35

Put the value of x from equation (1),

⇒ 3y-7y = -35-5 ⇒ -4y =-40

⇒ y = 10

Put the value of y in equation (1),

⇒ x = 3 x 10+10 = 40

∴ The present age of Jacob = 40 years

Present age of son = 10 years

Linear Equations In Two Variables Exercise 3.4

Question 1. Solve the following pair of linear equations bv the elimination method and the substitution method:

1. x +y = 5 and 2x- 3y = 4
2. 3a + 4y = 10 and 2x- 2y = 2
3. 3x- 5y -4 = 0 and 9x = 2y + 7
4. \(\frac{x}{2}+\frac{2 y}{3}=-1 \text { and } x-\frac{y}{3}=3\)

Solution:

1. x +y = 5 ……(1)

2x-3y = 4 …….(2)

Elimination method

Multiply equation (1) by 3 and adding in equation (2),

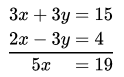
⇒ \(x=\frac{19}{5}\)

Put this value of or in equation (1),

⇒ \(\frac{19}{5}+y=5\)

⇒ \(y=5-\frac{19}{5}=\frac{6}{5}\)

∴ \(x=\frac{19}{5}, y=\frac{6}{5}\)

Substitution method

From equation (1),

⇒ x + y = 5 ⇒ x = 5 -y ……(3)

Put the value of x from equation (3) to equation (2)

⇒ 2(5 -y) -3y = 4 ⇒ 10 -2y- 3y = 4

⇒ -5y = 4-10 = -6

⇒ \(y=\frac{6}{5}\)

Put this value of y in equation (3),

⇒ \(x=5-\frac{6}{5}=\frac{25-6}{5}=\frac{19}{5}\)

∴ \(x=\frac{19}{5}, y=\frac{6}{5}\)

Here both methods are appropriate.

2. 3x + 4y = 10 …….(1)

2x-2y = 2 ……(2)

Elimination method

Multiply equation (2) by 2 and adding in equation (1),

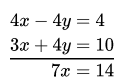
x = 2

Put the value of x in equation (1)

3×2+4y = 10

⇒ 4y = 10-6 = 4

⇒ y = 1

∴ x = 2, y = 1

Substitution method

From equation (2),

2x- 2y = 2 ⇒ x-y = 1

⇒ x = 1+y ……(3)

Put the value of x from equation (3) to equation (1),

3(1+y) + 4y = 10

⇒ 3 + 3y + 4y = 10

⇒ 7y = 10- 3 = 7

⇒ y = 1

Put this value of y in equation (1),

x = 1+y

⇒ x = 1+1=2

∴ x = 2, y = 1

Here both methods are appropriate.

3. 3x- 5y- 4 = 0

⇒ 3x- 5y = 4 …(1)

9a = 2y + 7

⇒ 9x-2y= 7 …(2)

Elimination method

Multiply equation (1) by 3 and subtracting from equation (2),

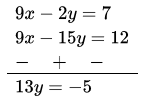
⇒ \(y=\frac{-5}{13}\)

Put this value of y in equation (1),

⇒ \(3 x-5\left(\frac{-5}{13}\right)=4\)

⇒ \(3 x=4-\frac{25}{13}=\frac{52-25}{13}=\frac{27}{13}\)

⇒ \(x=\frac{9}{13}\)

⇒ \(x=\frac{9}{13}\), \(x=\frac{-5}{13}\)

Substitution method

From equation (1),

3x- 5y = 4 ⇒ 3x = 4 + 5y

⇒ \(x=\frac{4+5 y}{3}\) ….(3)

Put the value of x from equation (3) to equation (2),

⇒ \(\frac{9(4+5 y)}{3}-2 y=7\)

3(4 + 5y) – 2y = 7k

⇒ 12 + 15y- 2y = 7

⇒ 13y = 7 – 12= -5 ⇒ \(y=\frac{-5}{13}\)

Put this value of y in equation (3),

⇒ \(x=\frac{4+5\left(\frac{-5}{13}\right)}{3}=\frac{52-25}{3 \times 13}=\frac{27}{3 \times 13}=\frac{9}{13}\)

⇒ \(x=\frac{9}{13}, y=\frac{-5}{13}\)

Here both methods are appropriate.

4. \(\frac{x}{2}+\frac{2 y}{3}=-1 \Rightarrow 3 x+4 y=-6\) …..(1)

⇒ \(x-\frac{y}{3}=3 \quad \Rightarrow 3 x-y=9\) => 3x-y = 9 …..(2)

Elimination method

Subtracting equation (2) from (1),

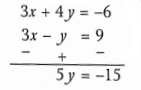
y = -3

Put the value of y in equation (2),

3x- (-3) = 9

⇒ 3x = 9-3 = 6 ⇒ x = 2

x = 2, y- -3

Substitution method

From equation (2),

3x-y= 9

y = 3x- 9 …..(3)

Put this value of y in equation (1)

⇒ 3x + 4(3x- 9) = -6

⇒ 3x + 12x- 36 = -6

⇒ 15x = -6 + 36 = 30

⇒ x = 2

Put this value of x in equation (3),

y = 3×2-9 = -3

∴ x = 2, y = -3

Here both methods are appropriate.

Question 2. Form the pair of linear equations in the following problems, and find their solutions (if they exist) by the elimination method :

1. If we add 1 to the numerator and subtract 1 from the denominator, a fraction reduces to 1. It becomes \(\frac{1}{2}\) if we only add 1 to the denominator. What is the fraction?
2. Five years ago, Nuri was thrice as old as Sonu. Ten years later, Nuri will be twice as old as Sonu. How old are Nuri and Sonu?
3. The sum of the digits of a two-digit number is 9. Also, nine times this number is twice the number obtained by reversing the order of the digits. Find the number.
4. Meena went to a bank to withdraw ₹2000. She asked the cashier to give her ₹50 and ₹100 notes only. Meena got 25 notes in all. Find how many notes of ₹50 and ₹100 she received.
5. A lending library has a fixed charge for the first three days and an additional charge for each day thereafter. Saritha paid ₹27 for a book kept for seven days, while Susy paid ₹21 for a book she kept for five days. Find the fixed charge and the charge for each extra day.

Solution:

1. Let fraction = \(\frac{x}{y}\)

According to the problem,

⇒ \(\frac{x+1}{y-1}=1\)

⇒ x + 1 = y- 1

⇒ x-y = -2 …..(1)

and \(\frac{x}{y+1}=\frac{1}{2}\)

⇒ 2x = y + 1

⇒ 2x-y = 1 ……(2)

Subtracting equation (1) from equation (2),

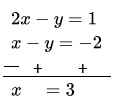
Put this value of x in equation (1),

3 -y = -2 ⇒ y = 3 + 2 = 5

∴ Fraction = \(\frac{x}{y}=\frac{3}{5}\)

2. Let present age of Noori = A years and present age of Sonu =y years 5 years ago,

the age of Noori = (x- 5) years

the age of Sonu = (y – 5) years

According to the problem,

(x-5) =3(y-5)

⇒ x- 5 = 3y – 15

⇒ x-3y = -10 ……(1)

After 10 years,

the age of Noori = (x + 10) years

the age of Sonu = (y + 10) years

According to the problem,

(x + 10) = 2(y + 10)

⇒ x+ 10 = 2y + 20

⇒ x- 2y = 10 …..(2)

Subtracting equation (2) from equation (1),

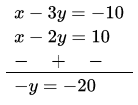
⇒ y = 20

Put the value of y in equation (2),

⇒ x- 2 × 20 = 10

⇒ x = 10 + 40 = 50

∴ The present age of Noori = 50 years

and present age of Sonu = 20 years

3. Let two digit number = 10x +y

According to the problem,

x+y = 9 ….(1)

and 9(10x +y) = 2 x number formed by reversing the digits.

= 2(10 +x)

⇒ 90x+ 9y = 20y + 2x

⇒ 88x- 11y = 0

⇒ 8x -y = 0 …..(2)

Adding equations (1) and (2),

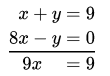
⇒ x = 1

Put the value of A in equation (2),

8×1 -y – 0 ⇒ y = 8

∴ Number = 10A +y = 10 x 1 + 8 = 18

4. Let ₹50 note = x

and ₹100 note = y

According to the problem,

x+y = 25

and ₹100 note =y

According to the problem,

⇒ x+y = 25 …..(1)

and 50x + 100y = 2000

⇒ x + 2y= 40 …..(2)

Subtracting equation (1) from equation (2),

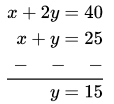
Put this value of y in equation (1),

x + 15 = 25

x = 10

∴ ₹50 note =10

and ₹100 note = 15 …(2)

5. Let the fixed charges for the first 3 days = ₹x

and the charge per day after it = ₹y

According to the problem,

charges for 7 days = ? 27

⇒ x+ (7 – 3)y = 27 ⇒ x + 4y = 27 …(1)

and charges for 5 days = ₹21

⇒ x+ (5 – 2)y = 21

⇒ x + 2y = 21 …..(2)

Subtracting equation (2) from equation (1)

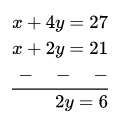
⇒ y = 3

Put this value of y in equation (l),

⇒ x + 4×3 = 27 ⇒  x = 27 – 12 = 15

Fixed charges = ₹15

and charges per day after the first 3 days = ₹3

Linear Equations In Two Variables Exercise 3.5

Question 1. Which of the following pairs of linear equations has a unique solution, no solution, or infinitely many solutions? In case there is a unique solution, find it by using cross multiplication method.

1. x- 3y – 3 = 0, 3x- 9y -2 = 0
2. 2x + y = 5, 3x + 2y = 8
3. 3x- 5y = 20, 6x- 10y = 40
4. x- 3y -7 = 0, 3x-3y- 15 = 0

Solution:

1. x-3y-3 = 0

3x- 9y- 2 = 0

Here, a₁ = 1, b₁ = -3, c₁ =-3

a₂ = 3, b₂ = -9, c₂ = -2

∴ \(\frac{a_1}{a_2}=\frac{1}{3}, \frac{b_1}{b_2}=\frac{-3}{-9}=\frac{1}{3} \text { and } \frac{c_1}{c_2}=\frac{-3}{-2}=\frac{3}{2}\)

∵ \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\)

∴ Given pair of equations has no solution.

2. 2x +y = 5 ⇒ 2x +y – 5 = 0

3x + 2y =8 ⇒ 3x + 2y – 8 = 0

Here, a₁ = 2, b₁ = 1, c₁ = -5

a₂ = 3, b₂ = 2, c₂ = -8

∴ \(\frac{a_1}{a_2}=\frac{2}{3}, \frac{b_1}{b_2}=\frac{1}{2}\)

∵ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

∴ Given pairofequations has a unique solution.

From the cross-multiplication method,

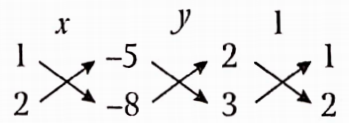
⇒ \(\frac{x}{-8-(-10)}=\frac{y}{-15-(-16)}=\frac{1}{4-3}\)

⇒ \(\frac{x}{2}=\frac{y}{1}=\frac{1}{1} \quad \Rightarrow x=2, y=1\)

3. 3x- 5y = 20 ⇒ 3x-5y- 20 = 0

6x- 10y = 40 ⇒ 6x- 10y- 40 = 0

Here, a₁ =3, b₁, =-5, c₁, =-20

a₂ = 6, b₂ =-10 c₂ = -40

∴ \(\frac{a_1}{a_2}=\frac{3}{6}=\frac{1}{2}, \frac{b_1}{b_2}=\frac{-5}{-10}=\frac{1}{2}, \frac{c_1}{c_2}=\frac{-20}{-40}=\frac{1}{2}\)

∵ \(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\)

∴ Given pair of equations has infinitely many solutions.

4. x-3y – 7 = 0

3x-3y- 15 = 0

Here, a₁ = 1, b₁ = -3, c₁ = -7

a₂ = 3, b₂ = -3, c₂ = -15

∴ \(\frac{a_1}{a_2}=\frac{1}{3}, \frac{b_1}{b_2}=\frac{-3}{-3}=1\)

∵ \(\frac{a_1}{a_2} \neq \frac{b_1}{b_2}\)

∴ Given pair ofequations has aunique solution.

Now, from the cross-multiplication method,

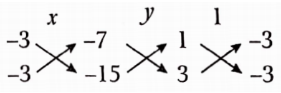
⇒ \(\frac{x}{45-21}=\frac{y}{-21+15}=\frac{1}{-3+9}\)

⇒ \(\frac{x}{24}=\frac{y}{-6}=\frac{1}{6}\)

⇒ \(\frac{x}{4}=\frac{y}{-1}=\frac{1}{1}\)

⇒ x = 4, y = -1

Question 2.

1. For which values of a and b does the following pair of linear equations have an infinite number of solutions? 2x + 3y = 7, (a-b)x+(a+b)y = 3a+b-2
2. For which value of k will the following pair of linear equations have no solution? 3x- +y = 1, (2k-1)x+(k-1)y = 2k+1

Solution:

1. Here, 2x + 3y – 7 = 0

and (a – b)x + (a + b)y – (3a + b – 2) = 0

Now, a₁ = 2, b₁ = 3, c₁ = -7,

a₂= a – b, b₂ = a + b, c₂ =- (3a +b- 2)

For infinitely many solutions,

⇒ \(\frac{2}{a-b}=\frac{3}{a+b}=\frac{-7}{-(3 a+b-2)}\)

⇒ \(\left(\frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2}\right)\)

⇒ \(\frac{a-b}{2}=\frac{a+b}{3}=\frac{3 a+b-2}{7}\)

From the first and second expressions,

⇒ \(\frac{a-b}{2}=\frac{a+b}{3}\)

⇒ 3a-3b = 2a + 2b

⇒ a = 5b …(1)

From the second and third expressions,

⇒ \(\frac{a+b}{3}=\frac{3 a+b-2}{7}\)

⇒ 7a + 7b = 9a + 3b – 6

⇒ 4b = 2a -6

⇒ 2b = a-3 …(2)

From equations (1) and (2),

2b = 5b -3 ⇒ 6 = 1

Put 6= 1 in equation (1),

a = 5 x 1 ⇒ a = 5

2. Here, 3x+y- 1 =0 …..(1)

and (2k- 1)x + (k- l)y- (2k + 1) = 0 …(2)

Here, a₁ =3, b₁ = 1, c₁ = -1,

a₂ =2k-1, b₂ = k-1, c₂ = -(2k+1)

⇒ \(\frac{a_1}{a_2}=\frac{3}{2 k-1}, \frac{b_1}{b_2}=\frac{1}{k-1}, \frac{c_1}{c_2}=\frac{1}{2 k+1}\)

For no solution, \(\frac{a_1}{a_2}=\frac{b_1}{b_2} \neq \frac{c_1}{c_2}\) i.e., \(\frac{3}{2 k-1}=\frac{1}{k-1} \neq \frac{1}{2 k+1}\)

⇒ \(\frac{3}{2 k-1}=\frac{1}{k-1} \neq \frac{1}{2 k+1}\)

⇒ 3(k-1) = 2k-1 and k-1 = 2k+1

⇒ 3k-3 = 2k-1 and k = -2

⇒ k = 2 and k = -2

Therefore, the given system will have no solution when k = 2

Question 3. Solve the following pair of linear equations by the substitution and cross-multiplication methods. 8x + 5y = 9, 3x + 2y = 4
Solution:

Given equations

8x + 5y = 9 …….(1)

3x- + 2y = 4 ……(2)

Substitution method

From equation (1),

⇒ 8x = 9 – 5y

⇒ \(x=\frac{9-3 y}{8}\) ……(3)

Put this value of x in equation (2),

⇒ \(\frac{3(9-5 y)}{8}+2 y=4\)

⇒ \(\frac{27-15 y+16 y}{8}=4\)

⇒ 27 +y = 32 = 5

Put the value of/ in equation (3)

⇒ \(x=\frac{9-5 \times 5}{8}=\frac{9-25}{8}=-2\)

⇒ x = -2, y = 5

From the cross-multiplication method,

8x + 5y- 9 = 0

3x + 2y- 4 = 0

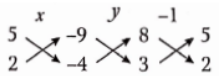
⇒ \(\frac{x}{-20+18}=\frac{y}{-27+32}=\frac{1}{16-15}\)

⇒ \(\frac{x}{-2}=\frac{y}{5}=\frac{1}{1}\)

⇒ x = -2, y = 5

Here, both methods are appropriate.

Question 4. Form the pair of linear equations in the following problems and find their solutions (if they exist) by any algebraic method :

1. A part of monthly hostel charges are fixed and the remaining depends on the number of days one has taken food in the mess. When student A takes food for 20 days she has to pay ₹1000 as hostel charges whereas student B, who takes food for 26 days, pays ₹1180 as hostel charges. Find the fixed charges and the cost of food per day.
2. A fraction becomes when \(\frac{1}{3}\) is subtracted from the numerator and it becomes \(\frac{1}{4}\) when 8 is added to its denominator. Find the fraction.
3. Yash scored 40 marks on a test, getting 3 marks for each right answer and losing 1 mark for each wrong answer. Had 4 marks been awarded for each correct answer and 2 marks been deducted for each incorrect answer, then Yash would have scored 50 marks. How many questions were there in the test?
4. Places’ A’ and B are 100 1cm apart on a highway. One car starts from A and another from B at the same time. If the cars travel in the same direction at different speeds, they meet in 5 hours. If they travel towards each other, they meet in 1 hour. What are the speeds of the two cars?
5. The area of a rectangle gets reduced by 9 square units, if its length is reduced by 5 units and breadth is increased by 3 units. If we increase the length by 3 units and the breadth by 2 units, the area increases by 67 square units. Find the dimensions of the rectangle.

Solution:

Let fixed charge = ₹x

and the cost of food per day = ₹y

∴ x + 20y = 1000 ………(1)

and x + 26y = 1180 ………(2)

Subtracting equation (1) from equation (2),

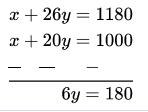
⇒ y = 30

From equation (1),

x + 20×30 = 1000

⇒ x = 1000-600 = 400

∴ Fixed charge = ₹400

and cost of food per day = ₹30

2. Let, fraction = \(\frac{x}{y}\)

According to the problem,

⇒ \(\frac{x-1}{y}=\frac{1}{3}\)

⇒ 3x-3=y

⇒ 3x-y = 3 …….(1)

and \(\frac{x}{y+8}=\frac{1}{4}\)

⇒ 4x =y + 8 ….(2)

⇒ 4x -y = 8

Subtracting equation (2) from equation (1),

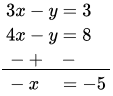
Put the value of x in equation (2),

4×5-y = 8 ⇒ y = 20-8 = 12

∴ Fraction = \(\frac{x}{y}=\frac{5}{12}\)

3. Let number of correct answers = x and number of incorrect answers =7.

According to the first condition,

3x -7 = 40 ……..(1)

According to the second condition,

4x-2y =50 ⇒ 2x -7 = 25 ……..(2)

Subtracting equation (2) from equation (1),

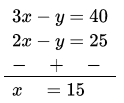
Put the value of x in equation (2),

⇒ 2(15) -7 = 25

⇒ 30 -7 = 25 ⇒ y = 30 – 25 = 5

Total number of questions in a test

= x +7 =15 + 5= 20

4. Let the speed of the car starting from A =xkm/hr and the speed of the car starting from B =                       7 km/hr

Case 1: When they move in the same direction:

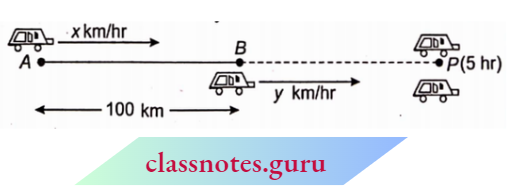
Distance covered by car A = AP= x × 5 Km ( ∵ distance = speed x time)

Distance covered by carB = BP = y × 5 km

⇒ but AB = 100 km

⇒ AP-BP = 100

⇒ 5x -5y = 100 ⇒ x-y=20 …….(1)

Case 2: When they move in opposite directions :

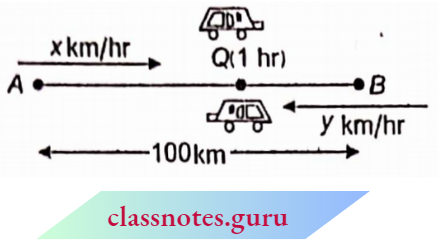
Distance covered by car A = AQ=x × 1 km

Distance covered by carB = BQ =y × 1 km

AB = 100 km

AQ + BQ = 100 ⇒ x +y = 100 …(2)

Adding equations (1) and (2),

2x = 1 20 ⇒ x = 60 km/hr

Put x = 60 in equation (2)

y = 100 – 60 = 40 km/hr

∴ Speed Of car A = 60 km/hr and speed of cal- B = 40 km/hr.

5. Let the length of the rectangle be x and breadth y units.

∴ Area of rectangle = xy square units

According to the given conditions,

⇒ (x-5)(y + 3) =xy-9

⇒ xy+ 3x-5y- 15 = xy- 9

⇒ 3x- 5y = 6 …….(1)

and (x + 3)(y + 2) = xy + 67

⇒ xy + 2x + 3y + 6= xy + 67

⇒ 2x + 3y =61 ……..(2)

Multiplying equation (1) by 3 and equation (2) by 5

9x- 15y = 18 …(3)

10x + 15y = 305

Adding equations (3) and (4)

19x = 323 ⇒ x = 17

Put x = 17 in equations (1)

3 x 17 – 5y = 6

⇒ 51-5y = 6

⇒ -5y = -45 ⇒ y = 9

Therefore, the length of the rectangle = 17 units and the breadth = 9 units.

Linear Equations In Two Variables Exercise 3.6

Question 1. Solve the following pairs of equations by reducing them to a pair of linear equations :

1. \(\frac{1}{2 x}+\frac{1}{3 y}=2 \quad \frac{1}{3 x}+\frac{1}{2 y}=\frac{13}{6}\)
2. \(\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}=2 \quad \frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}=-1\)
3. \(\frac{4}{x}+3 y=14 \quad \frac{3}{x}-4 y=23\)
4. \(\frac{5}{x-1}+\frac{1}{y-2}=2 \quad \frac{6}{x-1}-\frac{3}{y-2}=1\)
5. \(\frac{7 x-2 y}{x y}=5 \quad \cdot \quad \frac{8 x+7 y}{x y}=15\)
6. 6x + 3y = 6xy, 2x + 4y = 5xy
7. \(\frac{10}{x+y}+\frac{2}{x-y}=4\),\(\frac{15}{x+y}-\frac{5}{x-y}=-2\)
8. \(\frac{1}{3 x+y}+\frac{1}{3 x-y}=\frac{3}{4}\), \(\frac{1}{2(3 x+y)}-\frac{1}{2(3 x-y)}=\frac{-1}{8}\)

Solution:

1. Given equations, \(\frac{1}{2 x}+\frac{1}{3 y}=2,\)

⇒ \(\frac{1}{3 x}+\frac{1}{2 y}=\frac{13}{6}\)

Let, \(\frac{1}{x}=a \text { and } \frac{1}{y}=b\)

∴ Given equations, \(\frac{a}{2}+\frac{b}{3}=2\)

⇒ 3a + 2b = 12 …….(1)

and \(\frac{a}{3}+\frac{b}{2}=\frac{13}{6}\)

⇒ 2a+3b = 13 ……….(2)

Multiplying equation (1) by 2 and equation (2) by 3 and subtracting,

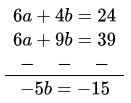
⇒ b = 3

Put the value of b in equation (1),

⇒ 3a + 2 × 3 = 12

⇒ 3a = 12-6 = 6

⇒ a = 2

Now, \(\frac{1}{x}=a \quad \Rightarrow \quad x=\frac{1}{a}=\frac{1}{2}\)

and \(\frac{1}{y}=b \quad \Rightarrow \quad y=\frac{1}{b}=\frac{1}{3}\)

∴ \(x=\frac{1}{2}, y=\frac{1}{3}\)

2. Given equations, \(\frac{2}{\sqrt{x}}+\frac{3}{\sqrt{y}}=2\)

⇒ \(\frac{4}{\sqrt{x}}-\frac{9}{\sqrt{y}}=-1\)

Let \(\frac{1}{\sqrt{x}}=A \text { and } \frac{1}{\sqrt{y}}=B\)

∴ Given equations, 2A + 3B =2 …(1)

4A-9B = -1 ……(2)

Multiplying equation (1) by 3 and adding in equation (2),

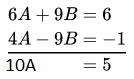
⇒ \(A=\frac{1}{2}\)

Put the value of A in equation (1),

⇒ \(2 \times \frac{1}{2}+3 B=2\)

35 = 2-1 = 1 = B = \(\frac{1}{3}\)

Now, \(\frac{1}{\sqrt{x}}=A \quad \Rightarrow \sqrt{x}=\frac{1}{A}\)

⇒ \(x=\frac{1}{A^2}=\frac{1}{\left(\frac{1}{2}\right)^2}=4\)

and \(\frac{1}{\sqrt{y}}=B \Rightarrow \sqrt{y}=\frac{1}{B}\)

⇒ \(y=\frac{1}{B^2}=\frac{1}{\left(\frac{1}{3}\right)^2}=9\)

∴ x = 4, y = 9

3. Given equations, \(\frac{4}{x}+3 y=14, \frac{3}{x}-4 y=23\)

Let \(\frac{1}{x}=A\)

∴ Given equations, 4A + 3y = 14 ………(1)

3A – 4y = 23 ………(2)

Multiplying equation (1) by 4 and equation (2) by 3 and adding

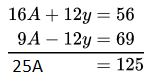
⇒ A = 5

Put the value of A in equation (1),

4 × 5 + 3y = 14

⇒ 3y = 14 – 20 = -6

⇒ y = -2

Now, \(\frac{1}{x}=A \Rightarrow x=\frac{1}{A}=\frac{1}{5}\)

⇒ \(x=\frac{1}{5}, y=-2\)

4. Given equations, \(\frac{5}{x-1}+\frac{1}{y-2}=2\)

and \(\frac{6}{x-1}-\frac{3}{y-2}=1\)

Let \(\frac{1}{x-1}=A \text { and } \frac{1}{y-2}=B\)

∴ Given equations, 5A + B = 2 …..(1)

6A-3B = 1 ……(2)

Multiplying equation (1) by 3 and adding in equation (2),

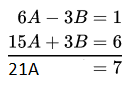
⇒ \(A=\frac{7}{21}=\frac{1}{3}\)

Put the value of A in equation (1),

⇒ \(5 \times \frac{1}{3}+B=2 \quad \Rightarrow B=2-\frac{5}{3}=\frac{1}{3}\)

Now, \(\frac{1}{x-1}=A\)

⇒ \(x-1=\frac{1}{A}=\frac{1}{1 / 3}=3\)

⇒ x = 4

and \(\frac{1}{y-2}=B\)

⇒ \(y-2=\frac{1}{B}=\frac{1}{1 / 3}=3\)

⇒ y = 5

∴ x = 4, y = 5

5. Given equations, \(\frac{7 x-2 y}{x y}=5\)

⇒ \(\frac{7 x}{x y}-\frac{2 y}{x y}=5\)

⇒ \(\frac{7}{y}-\frac{2}{x}=5\) …..(1)

and \(\frac{8 x+7 y}{x y}=15 \Rightarrow \frac{8 x}{x y}+\frac{7 y}{x y}=15\)

⇒ \(\frac{8}{y}+\frac{7}{x}=15\) ……(2)

Let \(\frac{1}{y}=A \quad \text { and } \quad \frac{1}{x}=B\)

∴ From equation (1), 7A-2B =5 …(3

From equation (2), 8A + 7B = 15 …(4)

Multiplying equation (3) by 7 and equation (4) by 2 and adding,

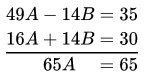
⇒ A = 1

Put the value of A in equation (4),

8 × 1 + 7B = 15

⇒ 7B = 15 – 8 = 7

⇒ B = 1

Now, \(\frac{1}{x}=B \Rightarrow x=\frac{1}{B}=\frac{1}{1}=1\)

and \(\frac{1}{y}=A \Rightarrow y=\frac{1}{A}=\frac{1}{1}=1\)

∴ x = 1, y =1

6. Given equations, 6x+3y = 6xy

⇒ \(\frac{6 x}{3 x y}+\frac{3 y}{3 x y}=\frac{6 x y}{3 x y} \Rightarrow \frac{2}{y}+\frac{1}{x}=2\) …….(1)

and 2x + 4y = 5xy

⇒ \(\frac{2 x}{x y}+\frac{4 y}{x y}=\frac{5 x y}{x y} \Rightarrow \frac{2}{y}+\frac{4}{x}=5\) ……..(2)

Let \(\frac{1}{y}=A \quad \text { and } \quad \frac{1}{x}=B\)

∴ From equation (1), 2A + B = 2 …..(3)

From equation (2), 2A + 4B = 5 …..(4)

Subtracting equation (3) from equation (4),

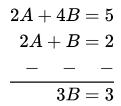
B=1

Put the value of B in equation’ (3),

2A + 1 = 2 ⇒ 2A = 2-1 = 1

⇒ \(A=\frac{1}{2}\)

Now, \(\frac{1}{y}=A\)

⇒ \(y=\frac{1}{A}=\frac{1}{1 / 2}=2\)

⇒ \(\frac{1}{x}=B \quad \Rightarrow x=\frac{1}{B}=\frac{1}{1}=1\)

∴ x = 1, y = 2

7. Given equations,

⇒ \(\frac{10}{x+y}+\frac{2}{x-y}=4\) …..(1)

⇒ \(\frac{15}{x+y}-\frac{5}{x-y}=-2\) ….(2)

Let \(\frac{1}{x+y}=A \text { and } \frac{1}{x-y}=B\)

∴ From equation (1), 10A + 25 = 4

From equation (2), 15A – 55 = -2

Multiplying equations (3) by 5 and equation (4) by 2 and adding,

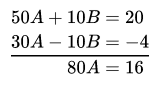
⇒ \(A=\frac{16}{80}=\frac{1}{5}\)

Put the value of A in equation (3),

⇒ \(10 \times \frac{1}{5}+2 B=4 \Rightarrow 2+2 B=4\)

2B = 4-2 = 2 ⇒ B = 1

Now \(\frac{1}{x+y}=A=\frac{1}{5}\)

⇒ x+y = 5 …..(5)

and \(\frac{1}{x-y}=B=1\)

⇒ x-y = 1 …..(6)

Adding equation (5) and equation (6)

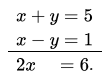
⇒ x= 3

Put the value of x in equation (5)

3 + = 5 ⇒ y = 2

∴ x = 3, y = 2

8. Given equations, \(\frac{1}{3 x+y}+\frac{1}{3 x-y}=\frac{3}{4}\) …….(1)

and \(\frac{1}{2(3 x+y)}-\frac{1}{2(3 x-y)}=-\frac{1}{8}\) ….(2)

Let \(\frac{1}{3 x+y}=A \text { and } \frac{1}{3 x-y}=B\)

From equation (1)

⇒ \(\frac{1}{3 x+y}+\frac{1}{3 x-y}=\frac{3}{4}\) ……(1)

and \(\frac{1}{2(3 x+y)}-\frac{1}{2(3 x-y)}=-\frac{1}{8}\) …..(2)

Let \(\frac{1}{3 x+y}=A \text { and } \frac{1}{3 x-y}=B\)

From equation (1), \(A+B=\frac{3}{4}\) ……(3)

From equation (2), \(\frac{A}{2}-\frac{B}{2}=-\frac{1}{8}\)

⇒ \(A-B=-\frac{2}{8} \Rightarrow A-B=-\frac{1}{4}\) ……(4)

Adding equations (3) and (4)

A = \(\frac{1}{4}\)

Put the value of A in equation (3),

⇒ \(\frac{1}{4}+B=\frac{3}{4}\)

⇒ \(B=\frac{3}{4}-\frac{1}{4}=\frac{2}{4}=\frac{1}{2}\)

Now \(\frac{1}{3 x+y}=A=\frac{1}{4}\)

⇒ 3x-y= 4 ….(5)

and \(\frac{1}{3 x-y}=B=\frac{1}{2}\)

⇒ 3x-y= 2 ….(6)

Adding equations (5) and (6),

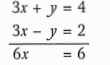
⇒ x= 1

Put the value of x in equation (5),

⇒ 3 × 1 +y = 4

⇒ y = 4-3=1

∴ x = 1, y = 1

Question 2. Formulate the following problems as a pair of equations, and hence find their solutions:

1. Ritu can row downstream 20 km in 2 hours, and upstream 4 km in 2 hours. Find her speed of rowing in still water and the speed of the current.
2. 2 women and 5 men can together finish an embroidery work in 4 days, while 3 women and 6 men can finish it in 3 days. Find the time taken by 1 woman alone to finish the work, and also that taken by 1 man alone.
3. Roohi travels 300 km to her home partly by train and partly by bus. She takes 4 hours if she travels 60 km by train and the remaining by bus. If she travels 100 km by train and the remaining by bus, she takes 10 minutes longer. Find the speed of the train and the bus separately.

Solution:

1. Let the speed of Ritu in still water = x km/hr

and speed of current =y km/hr

∴ speed in downstream = (x +y) km/hr

and speed in upstream = (x -y) km/hr

Now from \(\text { time }=\frac{\text { distance }}{\text { speed }}\)

⇒ \(\frac{20}{x+y}=2 \text { and } \frac{4}{x-y}=2\)

⇒ x + y = 10 …..(1)

and x-y = 2 ….(2)

Adding equations (1) and (2),

2x = 12 ⇒ x= 6

Put x = 6 in equation (1),

6 +y = 10 ⇒ y = 4

∴ Speed of Ritu in still water = 6 km/hr

and speed of current = 4 km/hr

2. Let 1 woman can finish the work in x days and 1 man can finish the work in y days.

∴ 1 day work of 1 woman = \(\frac{1}{x}\)

1 day work of 1 man = \(\frac{1}{y}\)

1-day work of 2 women and 5 men \(\frac{2}{x}+\frac{5}{y}=\frac{5 x+2 y}{x y}\)

∴ Time taken to finish the work = \(\frac{x y}{5 x+2 y}\)

Given that, \(\frac{x y}{5 x+2 y}=4\)

Similarly in second case, \(\frac{x y}{6 x+3 y}=3\)

Then, \(\frac{5 x+2 y}{x y}=\frac{1}{4} \text { and } \frac{6 x+3 y}{x y}=\frac{1}{3}\)

⇒ \(\frac{20}{y}+\frac{8}{x}=1 \text { and } \frac{18}{y}+\frac{9}{x}=1\)

Let \(\frac{1}{x}=u \text { and } \frac{1}{y}=v\)

∴ 20v + 8u = 1 …..(1)

and 18v+9u = 1 ….(2)

Multiplying equation (1) by 9 and equation (2) by 8,

180v-144v = 9-8

⇒ 36v = 1

⇒ v = \(\frac{1}{36}\)

Put v = \(\frac{1}{36}\) in equation (2),

⇒ \(18 \times \frac{1}{36}+9 u=1\)

⇒ 9u = \(1-\frac{1}{2}\)

⇒ 9u = \(\frac{1}{2}\)

⇒ u = \(\frac{1}{18}\)

Now, \(u=\frac{1}{18} \quad \text { and } \quad v=\frac{1}{36}\)

⇒ \(\frac{1}{x}=\frac{1}{18} \text { and } \frac{1}{y}=\frac{1}{36}\)

⇒ x= 18 and y = 36

Therefore, 1 woman can finish the work alone in 18 days and 1 man can finish the work alone in 36 days.

3. Let the speed of train = x km/hr and speed of bus =y km/hr

In the first case, Ruhi goes 60 km from the train and 240 km from a bus in 4 hours.

⇒ \(\frac{60}{x}+\frac{240}{y}=4\)

⇒ \(\frac{15}{x}+\frac{60}{y}=1\) …..(1)

Similarly in the second case, she goes 100 km from the train and 200 km from a bus in \(4 \frac{1}{6}\) hours.

⇒ \(\frac{100}{x}+\frac{200}{y}=4+\frac{1}{6}\) ,\(\left(10 \text { minutes }=\frac{1}{6} \mathrm{hr}\right)\)

⇒ \(\frac{100}{x}+\frac{200}{y}=\frac{25}{6}\)

⇒ \(\frac{24}{x}+\frac{48}{y}=1\) ….(2)

Let \(\frac{1}{x}=u \text { and } \frac{1}{y}=v\)

⇒ 15u + 60v = 1 ……(3)

and 24u + 48v = 1 …..(4)

Multiplying equation (3) by 24 and equation (4) by 15 and subtracting,

24(15u + 60v)- 15(24u + 48v) =24-15

⇒ 440v – 720v = 9

⇒ 20v = 9

⇒ v = \(\frac{9}{720}=\frac{1}{80}\)

Put v = \(\frac{1}{80}\)

⇒ \(15 u+60 \times \frac{1}{80}=1\)

⇒ \(15 u=1-\frac{3}{4}=\frac{1}{4}\)

⇒ u = \(\frac{1}{60}\)

Now, u = \(\frac{1}{60}\) and v = \(\frac{1}{80}\)

⇒ \(\frac{1}{x}=\frac{1}{60} \text { and } \frac{1}{y}=\frac{1}{80}\)

⇒ x = 60 and y = 80

Therefore, the speed of the train = 60 km/hr and speed of bus = 80 km/hr.

Linear Equations In Two Variables Exercise 3.7 (Optional)

Question 1. The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years. Find the ages of Ani and Biju.
Solution:

Given

The ages of two friends Ani and Biju differ by 3 years. Ani’s father Dharam is twice as old as Ani and Biju is twice as old as his sister Cathy. The ages of Cathy and Dharam differ by 30 years.

For convenience, let their ages be according to their names.

Now, A – B = ± 3 ……(1) (As we don’t know who is older)

and \(\left.\begin{array}{rl}
D=2 A \\
B=2 C \Rightarrow C=\frac{B}{2}
\end{array}\right\}\)

and D – C = 30

But we don’t know who is older, so D-C= ±30

⇒ \(2 A-\frac{B}{2}= \pm 30 \Rightarrow 4 A-B= \pm 60\) ……..(2)

Now from equations (1) and (2), four cases are possible:

Question 2. One says, “Give me a hundred, friend! f shall then become twice as rich as you”. The other replies, “If you give me ten, I shall be six times as rich as you”. Tell me what is the amount of their (respective) capital? [From the Bijaganita of Bhaskara 2]

[Hint : x + 100 = 2(y- 100),y + 10 = 6(x- 10)].

Solution:

Let them have ₹x and ₹y respectively.

∴ According to the given condition,

⇒ x+ 100 = 2 (y- 100)

⇒ x – 2y = -300 …..(1)

and 6(x- 10) = + 10 ⇒ 6x-y = 70 …(2)

Multiplying equation (2) by 2 and subtracting from equation (1),

x- 12x = -300 – 140 ⇒ -11x = -440

x = ₹40

Put in c(|untion (1),

40 – 2y = -300

2y – 340 ⇒ y = ₹170

So, they have ₹40 and ₹170 respectively.

Question 8. A train covered a certain distance at a uniform speed. If the train would have been 10 km/h faster, it would have taken 2 hours less than the scheduled time. And, if the train were slower by 10 km/h; it would have taken 3 hours more than the scheduled time. Find the distance covered by the train.
Solution:

Let speed of train = x km/hr and distance covered = y km

Time taken at this speed = \(\frac{y}{x} \text { hours }\)

If speed = (x + 10) km/hr

then time taken = \(\frac{y}{x+10} \text { hours }\)

∴ \(\frac{y}{x+10}=\frac{y}{x}-2 \Rightarrow \frac{y}{x+10}=\frac{y-2 x}{x}\)

⇒ xy = (x+10)(y-2x)

⇒ xy = xy-2x²+10y-20x

⇒ -2x²+ 10y-20x = 0 …(1)

If speed = (x- 10) km/hr

then time taken = \(\frac{y}{x-10} \mathrm{hr}\)

∴\(\frac{y}{x-10}=\frac{y}{x}+3\)

⇒ \(\frac{y}{x-10}=\frac{y+3 x}{x}\)

⇒ xy = (x-10)(y+3x)

⇒ xy = xy + 3x²-10y-30x

⇒ 3x²– 10y-30x = 0 ……(2)

Adding equations (1) and (2),

x² – 50x = 0 ⇒ x(x-50) = 0

⇒ x = 0 or x-50 = 0

⇒ x = 0 or x = 50

x = 0 is not possible

∴ x = 50 km/hr

Put the value of x in equation (1),

-2(50)² + 10y- 20×50 = 0

⇒ -5000+ 10y- 1000 = 0

⇒ 10y = 6000

⇒ y = 6000km

∴ Distance covered = 600 km

Question 4. ‘The students of a class are made to stand in rows. If 3 students arc extra in a row, there would be 1 row. If 3 students are less in a and there would be 2 rows more. Find the number of students in the class.
Solution:

Given

‘The students of a class are made to stand in rows. If 3 students arc extra in a row, there would be 1 row. If 3 students are less in a and there would be 2 rows more.

Let the number of rows = x

and number of students in each row = y

Total number of students in the class = xy

According to the first condition,

(y + 3) (x- 1) = xy

⇒ xy-y + 3xr3 = xy

⇒ 3x-y = 3 …(1)

According to the second condition,

(y-3)(x + 2)=xy

⇒ xy + 2y-3x- 6 = xy

⇒ 3x-2y = -6 ……(2)

Subtracting equation (2) from equation (1),

y = 9

Put y = 9 in equation (1),

3x- 9 =3

⇒ 3x= 12

⇒ x = 4

∴ Total number of students in the class = xy = 4 x 9 = 36

Question 5. In ΔABC, ∠C = 3∠B = 2(∠A+∠B). Find the three angles.
Solution:

Given

In ΔABC, ∠C = 3∠B = 2(∠A+∠B).

Let ∠A=x° and ∠B=y°

∴ ∠C = 3∠B ⇒ ∠C = 3y°

and ∠C = 2(∠A + ∠B)

⇒ 3y° = 2(x° +y°)

⇒ 2x + 2y-3y =0

⇒ 2x-y = 0 ……(1)

∵ ∠A + ∠B + ∠C = 180° (sum of three angles of Δ)

⇒ x+y + 3y = 180

⇒ x + 4y = 180 …..(2)

Multiplying equation (2) by 2

2x+ 8y = 360 …….(3)

Subtracting equation (3) from (1),

-9y = -360 ⇒ y = 40°

Put y = 40° in equation (1),

2x- 40 = 0

⇒ 2x = 40 ⇒ x = 20°

So, ∠A = 20°, ∠B = 40°

and ∠C = 3 × 40° = 120°

Question 6. Draw the graphs of the equations 5x-y = 5 and 3x – y = 3. Determine the coordinates of the vertices of the triangle formed by these lines and the x-axis.
Solution:

5x-y = 5 y ⇒ 5x-5

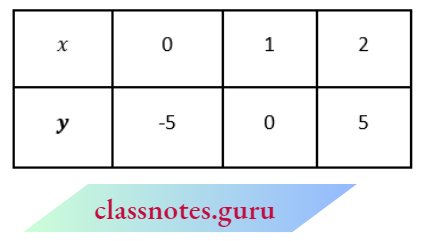
Mark the points A(0, -5), B( 1, 0) and C(2, 5) and join them.

Again, 3x -y = 3 ⇒ y= 3x-3

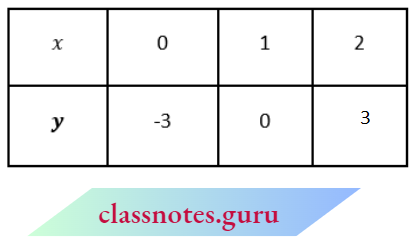
Mark the points D(0, -3), B( 1, 0) and E(2, 3) and join them.

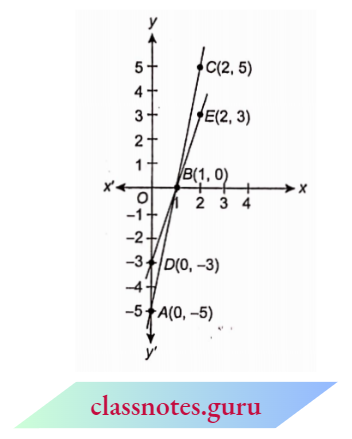
The coordinates of the vertices of ΔBDA formed by two lines and the y-axis are as follows :

B( 1, 0), A(0, -5) and D(0, -3)

Now area of ΔBAD = \(\frac{1}{2} \times A D \times B O\)

⇒ \(\frac{1}{2} \times 2 \times 1\)

= 1 sq. units

Question 7. Solve the following pair of linear equations :

1. px + qy -p – q , qx-py = p + q
2. ax + by = c, bx + ay = 1 + c
3. \(\), ax + by = a2 +b2
4. (a – b)x + (a + b)y = a2 – 2ab – b2, (a + b)(x +y) =a2 +b2
5. 152x – 378y = -74, -378x + 152y = -604

Solution:

1. Given equation,

px + qy = p-q ….(1)

and qx – py = p+q

Multiplying equation (1) by p and equation (2) by q and adding,

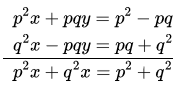
⇒ \(\left(p^2+q^2\right) x=p^2+q^2\)

⇒ x = 1

Put the value of x in equation (1),

p×1+qy = p-q

⇒ qy = -q

⇒ y = -1

∴ x = 1, y = -1

2. ax + by = c

⇒ ax + by -c = 0

⇒ bx + ay = 1 +c ⇒ bx + ay- (1+ c) = 0

Now,

∴ \(\frac{x}{-b(1+c)+a c}=\frac{y}{-b c+a(1+c)}=\frac{1}{a^2-b^2}\)

⇒ \(\frac{x}{a c-b-b c^y}=\frac{1}{a^2-b^2}\)

⇒ \(\frac{y}{-b c+a+a c}=\frac{1}{a^2-b^2}\)

⇒ \(x=\frac{a c-b-b c}{a^2-b^2}\)

⇒ \(y=\frac{a+a c-b c}{a^2-b^2}\)

3. \(\frac{x}{a}-\frac{y}{b}=0 \quad \Rightarrow b x-a y+0=0\)

⇒ ax+by = a²+b²

⇒ ax+by-(a²+b²) = 0

Now

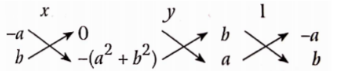
∴ \(\frac{x}{a\left(a^2+b^2\right)-0}=\frac{y}{0+b\left(a^2+b^2\right)}=\frac{1}{b^2+a^2}\)

⇒ \(\frac{x}{a\left(a^2+b^2\right)}=\frac{y}{b\left(a^2+b^2\right)}=\frac{1}{a^2+b^2}\)

⇒ \(\frac{x}{a}=\frac{y}{b}=1\)

⇒ \(\frac{x}{a}=1 \text { and } \frac{y}{b}=1\)

⇒ x = a and y = b

4. (a-b)x+(a+b)y = a²-2ab-b²

⇒ (a-b)x+(a+b)y – (a² – 2ab -b²) = 0

(a + b) (x+y) = a² + b²

⇒ (a-b)x+(a+b)y – (a²-b²) = 0

Now x

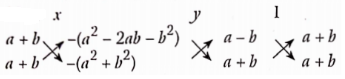
⇒ \(\frac{x}{-(a+b)\left(a^2+b^2\right)+(a+b)\left(a^2-2 a b-b^2\right)}\)

⇒ \(\frac{y}{-(a+b)\left(a^2-2 a b-b^2\right)+(a-b)\left(a^2+b^2\right)}\)

⇒ \(\frac{1}{(a-b)(a+b)-(a+b)^2}\)

⇒ \(\frac{x}{(a+b)\left(-a^2-b^2+a^2-2 a b-b^2\right)}\)

⇒ \(\begin{gathered}\frac{y}{-\left(a^3-a^2 b-3 a b^2-b^3\right)} \\+\left(a^3-a^2 b+a b^2-b^3\right)\end{gathered}\)

⇒ \(\frac{1}{(a+b)(a-b-a-b)}\)

\(\frac{x}{(a+b)\left(-2 a b-2 b^2\right)}=\frac{y}{4 a b^2}=\frac{1}{(a+b)(-2 b)}\)

⇒ \(\frac{x}{-2 b(a+b)^2}=\frac{1}{-2 b(a+b)}\)

and \(\frac{y}{4 a b^2}=\frac{1}{-2 b(a+b)}\)

⇒ x = a + b and y = \(\frac{-2 a b}{a+b}\)

5. 152x-378y = -74 ….(1)

-378A + 152y = -604 …..(2)

Adding equations (1) and (2),

-226A- 226y = -678 ⇒ x+y= 3 ….(3)

Subtracting equation (2) from equation (1),

530x – 530y = 530 ⇒ x-y = 1 …(4)

Adding equation (3) and (4),

⇒ 2x = 4

⇒ x = 2

Put x = 2 in equation (3),

⇒ 2+y =3

⇒ y = 1

∴ x = 2, y = 1

Question 8. ABCD is a cyclic quadrilateral. Find the angles of the cyclic quadrilateral.
Solution:

Given

ABCD is a cyclic quadrilateral.

We know that the sum of opposite angles of a cyclic quadrilateral is 180°.

∴ ∠A + ∠C = 180°

⇒ 4y + 20+ (-4A) = 180°

⇒ -4x + 4y = 1 80°- 20° = 160°

⇒ -x+y = 40°…(1)

and ∠B + ∠D = 180°

⇒ (3y-5)+(-7x + 5) = 180°

⇒ -7x + 3y = 1 80° …..(2)

Multiplying equation (1) by 3 and subtracting from equation (2),

⇒ x = -15°

Put the value of A in equation (1),

⇒ -(-15°) +y = 40°

⇒ y = 40°- 15° = 25°

Now, ∠A = 4y + 20° = 4 × 25° + 20°

= 120°

∠B = 3y- 5

= 3 × 25°- 5° = 70°

∠C = -4A = -4(-15°)

= 60°

∠D = -7A + 5° =-7(-15°) + 5°

= 110°

Linear Equations In Two Variables Multiple Choice Questions

Question 1. The pair of equations 5x- 15y = 16 and 3x – 9y = \(\frac{48}{5}\) has/have :

1. One solution
2. No solution
3. Infinitely many solutions
4. None of these

Answer: 3. Infinitely many solutions

Question 2. If any pair of linear equations is consistent then the lines of their graphs will be :

1. Coincident or intersecting
2. Parallel
3. Always coincident
4. Always intersecting

Answer: 1. Coincident or intersecting

Question 3. The pair of equations x = 2,y = 3 represents those lines which are graphically:

1. Parallel
2. Coincident
3. Intersecting at (2, 3)
4. Intersecting at (3, 2)

Answer: 2. Coincident

Question 4. The sum of digits of a number of two digits is 9. If 9 is added to it, the digits of this number are reversed. The number is :

1. 27
2. 36
3. 45
4. 54

Answer: 3. 45

Question 5. If x + 3y = 8 and k x + 6y-16 = 0isa pair of coincident lines then the value of k is:

1. 1
2. 2
3. 3
4. 4

Answer: 2. 2

Question 6. If 3x + ky = 6 and 2x + 5y = 0 are parallel lines then the value of k is:

1. 7.5
2. -7.5
3. 2.5
4. -2.5

Answer: 1. 7.5

Question 7. Shyam has 25 coins of ₹5 and ₹10. If the total amount is ₹175, then the number of coins is:

1. 5
2. 10
3. 15
4. 20

Answer: 3. 15

Question 8. The solution of the equations x-y = 2 and x+y = 2 will be:

1. x = 0, y = 2
2. x = 2, y = 0
3. x = 4, y = 2
4. x = -2,y- 0

Answer: 2. x = 2, y = 0