NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Introduction

In our daily lives, we come across some situations, for which we do not have any definite answer, although we know what the possible results (outcomes) are.

Probability For Example :

1. When a coin is tossed, it is certain that it will come down but it may turn up a head or may not turn up a head.
2. When a die is thrown, it may turn up a particular number 3 or not.
3. It may rain today.
4. The above situations predict die uncertainty (chance), therefore all are referred to a phenomenon which may or may not occur. The probability estimates the degree of uncertainty regarding the happening of a given phenomenon.

Read and Learn More Class 10 Maths Solutions Exemplar

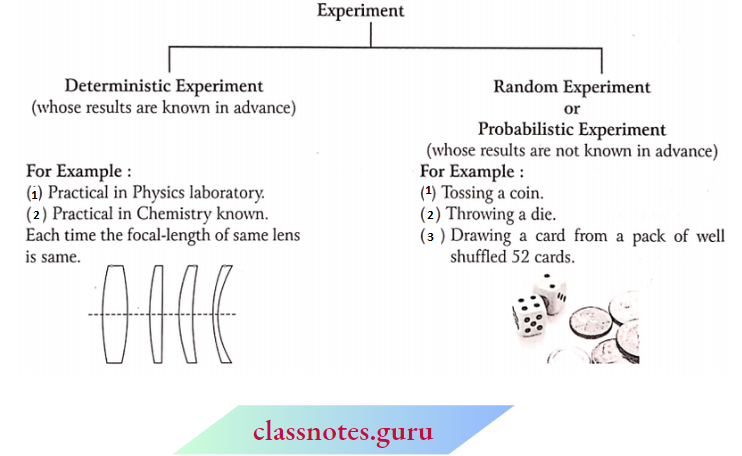
NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Experiment

An operation which gives some outcomes (results) under some given conditions is known as the ‘experiment’.

For Example:

1. “Tossing a coin” is an experiment with two outcomes: head and tail.
2. “Throwing a die” is an experiment with six outcomes: 1,2, 3, 4, 5 and 6. The plural of die is dice.

Probability Trial

Experimenting repeatedly under similar conditions is called a trial.

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Sample Space

The set (collection) of all possible outcomes of usually denoted by S.

For Example:

(1). In tossing a coin ← experiment

Sample space denoted by S=\(\left\{\begin{array}{cc}
H & T \\
(\text { Head ) } & \text { (Tail) }
\end{array}\right\}\)

(2). In throwing a die ← experiment

S = {1,2, 3, 4, 5, 6}

(3). In tossing a coin 3 times ← experiment

S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

(4). In throwing two dice simultaneously ← experiment

S=\(\left\{\begin{array}{l}
(1,1),(1,2),(1,3),(1,4),(1,5),(1,6) \\
(2,1),(2,2),(2,3),(2,4),(2,5),(2,6) \\
(3,1),(3,2),(3,3),(3,4),(3,5),(3,6) \\
(4,1),(4,2),(4,3),(4,4),(4,5),(4,6) \\
(5,1),(5,2),(5,3),(5,4),(5,5),(5,6) \\
(6,1),(6,2),(6,3),(6,4),(6,5),(6,6)
\end{array}\right\}\)

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Event

Any outcome or combination of some outcomes constitutes an event. Each event is a subset (part) of the sample space.

For Example:

(1). Let S = {1, 2, 3, 4, 5, 6}, when a die is thrown and let E₁ is the event of “getting an odd number”.

∴ E₁ = {1, 3, 5}

(2). Let E₂ be the event of “getting an even number”.

∴ E₂ = {2, 4, 6}

(3) Let E₃ be the event of “getting a prime number”.

∴ E₃ = {2,3, 5}

All above events are part of a subset of a sample space.

Remark: Total number of elements in a sample space = (Number of outcomes of an event)No‘of times

For Example:

(1). In tossing a coin 3 times,

The total number of elements in a sample space denoted by

n(S) = (2)^{3 → No.of times}

Possible outcomes of a coin = 8

(2). In throwing 2 dice,

n(S) = (6)^{2 → No.of times}

Possible outcomes of an experiment = 36

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Simple Event Or Elementary Event

An event is called a simple event if it contains only one element. In terms of set, it is a singleton set.

For Example:

(1) In “tossing a coin”, sample space S = {H, T}

Let A = event of getting a head = {H} and B = event of getting a tail = {T}

Here A and B are simple events.

(2). In “tossing a coin 2 times”, S = {(H, H), (H, T), (T, H), (T, T)}

Let A = event of getting a head on the first coin and getting a tail on the second coin = {(H, T)}

B = event of getting a head on the first coin = {(H, H), (H, T)}

Here, A is a simple event but B is not a simple event as B has two sample points.

To understand the experiment, sample space and event, are given below.

It is necessary that event is a part of the sample space

About the Playing Cards

1. A pack of playing cards has 52 cards in all.

2. It has 2 Colours – [Red (26 cards); Black (26 cards)]

3. It has 4 suites

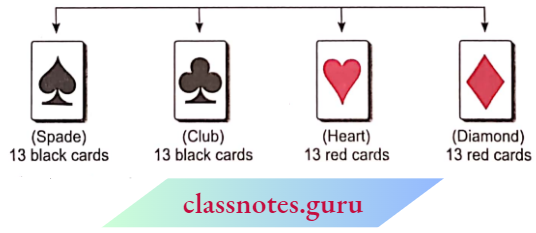
Numbering on each card of each suit as :

Actually, A, J, Q and IC are written in place of 1, 11, 12 and 13.

So, in a pack of 52 cards, 4 cards of the same number are there.

Note: Kings, Queens and Jacks are called the face cards while the aces together with face cards are called the honour cards.

For Example: Number 2 will be in spade, club, heart as well as in diamond. Similarly, the number IC will be in spade, dub, heart and diamond also.

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Equally Likely Events

The events are said to be equally likely when we have no reason to believe that one is more likely to occur than the other. Each of the possible outcomes has an equal chance of occurring.

For Example:

1. In “rolling a die”. There are six possible outcomes in the sample space, each is equally likely to occur.
2. In “tossing a coin”, getting a tail or a head are equally likely events.

Now, let us try to understand the meaning of probability.

(Probability: probable, perhaps, possibly, chances etc.)

For this, first, we see some experiments.

(1 ). In tossing a coin, S = {H, T}

What are the chances of getting a head—only {H}?

You will say 50% or fifty-fifty—Correct.

∴ \(50 \% \text { means } \frac{50}{100}, \text { i.e., } \frac{1}{2}=\frac{n(\text { favourable cases })}{n(S)}\)

Our favourable case is getting a head ⇒ n(E) = 1

and the total number of outcomes in a sample space ⇒ n(S)= 2

(2). In throwing a die, S = {l, 2, 3, 4, 5, 6}

What are the chances of getting an even number, i.e., {2,4, 6}?

Again, you will say 50% or fifty-fifty—Correct.

∴ Probability of an event =\(\frac{\text { Number of favourable cases }}{\text { Total number of cases }}\)

Now, tell me O’ girl!

What is the probability of getting a head exactly 2 times when we toss a coin 3 times simultaneously?

Now, you see example (1) of sample space and give the correct answer.

Yes! Your answer is correct. It is \(\frac{3}{8}\)

Now, you can make understand to your friend easily that
S = {HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

In these 8 outcomes, only 3 underlined contain exactly two heads.

∴ Our favourable cases = 3 and total number of outcomes = 8

∴ Required probability = \(\frac{3}{8}\)

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Minimum And Maximum Values Of Probability Of An Event

The value of the probability of any event always lies between 0 and 1. When the probability of an event is 0, it is said to be an impossible event and when the probability of an event is l, it is said to be a sure event.

Explanation: We know that a set (collection) of favourable outcomes is a part of the whole sample space.

∴ Number of favourable cases \(\leq\) Total number of cases.

⇒ \(\frac{\text { Number of favourable cases }}{\text { Total number of cases }} \leq 1\) → (1)

Now, see the following example :

“In throwing a die numbered l to 6”, find the probability of getting a number greater than 6”.

Here there is no such possibility to get a number which is greater than 6.

Favourable number of cases ≥ 0

So. always a number of favourable cases \(\leq\) 0

∴ \(\frac{\text { Number of favourable cases }}{\text { Total number of cases }} \leq 0\)

Combining Eqs. (1) and (2), we get

∴0 \(\leq\) Probability of an event \(\leq\) 1

Remember: In each experiment, we assume that the chance of each outcome is the same.

• Die or die must be fair.
• The coin must be unbiased (We do not consider the possibility that the coin can land on its side). We will consider that coin will land on any one of its faces, i.e., either head or tail.

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Theorems Of Addition Of Probabilities

If an event £ can happen in any one of the n different ways with the probabilities P₁, P₂, P₃ …. respectively, then the probability for the event £ is equal to the sum of the individual probabilities P₁, P₂, P₃, …Pn

For Example:

When a die is rolled, then any one of the numbers,1,2, 3, 4, 5 or 6 can be shown up.

Total number of outcomes = 6

Number of even numbers (2, 4 or 6)= 3

∴ Probability of getting an even number = \(\frac{\text { Favourable outcomes }}{\text { Total number of outcomes }}=\frac{3}{6}=\frac{1}{2}\)

Also, Probability of getting 2 = \(\frac{1}{6}\)

Probability of getting 4 = \(\frac{1}{6}\)

Probability of getting 6 = \(\frac{1}{6}\)

∴ Probability of getting an even number = \(\frac{1}{6}\) + \(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{1}{2}\)

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Complementary Events

If E is an event, then the event ‘not £’ is a complementary event of E.

For Example:

When we throw a die, let E be the event getting a number less than or equal to 2, then the event ‘not E’, i.e., getting a number greater than 2 is a complementary event of E. Complementary of E is denoted by E or \((\bar{E})\)

∴ \(P(E)+P(\bar{E})\)=1

Let E be an event, then the number of outcomes favourable to E is greater than or equal to zero and is less than or equal to the total number of outcomes. It follows than

∴ \(0 \leq P(E) \leq 1\).

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Exhaustive Events

All the possible outcomes of any trial taken together are called exhaustive events.

For Example:

From a group of 2 boys and 3 girls, two children are selected at random. Describe the events:

S = {B₁B₂, B₁G₁, B₁G₂, B₂G₂, B₂G₁,B₂G₂, B₂G₂, G₁G₂, G₂G₃, G₁G₃}

E₁ = event that both the selected children are girls

= {G₁G₂, G₂G₃, G₁G₃}

E₂ = event that the selected children consist of 1 boy and 1 girl

= {B₁G₁, B₁G₂, B₁G₃, B₂G₁, B₂G₂, B₂G₂}

E₃ = event that at least one boy is selected

= {B₁B₂, B₁G₁, B₁G₂, B₁G₃, B₂G₁, B₂G₂, B₂G₃}

Here E₁ and E₂ together do not constitute S.

∴ E₁ and E₂ are not exhaustive events,

and E₂ and E₃ also do not form the whole sample space S.

∴ E₂ and E₃ are not exhaustive events.

But E₁ and E₃ together form a whole sample space.

∴ E₁ and E₃ are exhaustive events.

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Solved Examples

Question 1. In any situation that has only two possible outcomes, each outcome will have probability \(\frac{1}{2}\). Find whether it is true or false.

Solution:

False,

The probability of each outcome will be \(\frac{1}{2}\) only when the two outcomes are equally likely.

For Example:

On the eve of Deepawali, we are lighting the candles in night on the roof.

The candles may be “lightening off due to heavy rain” or “they may not be lightening off” are not equally likely events because they do have not equal chances of occurring.

The possibility of falling rain at the time of the festival Deepawali is very less.

Question 2. A marble is chosen at random from 6 marbles numbered 1 to 6. Find the probability of getting a marble having number 2 and 6 on it.

Solution:

Given

A marble is chosen at random from 6 marbles numbered 1 to 6.

The favourable case is to get a marble on which both numbers 2 and 6 are written. But there is no such marble.

So, n(E) = 0 and n(S) = 6

∴ Required probability =\(\frac{n(E)}{n(S)}=\frac{0}{6}\)=0

Question 3. A marble is chosen at random from 6 marbles numbered 1 to 6. Find the probability of getting a marble having the number 2 or 6 on it.

Solution:

Given

A marble is chosen at random from 6 marbles numbered 1 to 6.

Here n(E) = 2   [either 2 or 6]

and n(S) = 6

∴ Required probability = \(\frac{2}{6}=\frac{1}{3}\)

Question 4. A fair coin is tossed

1. List the sample space.
2. What is P(tail)?

Solution:

(1). When a fair coin is tossed, there are two possible outcomes. Either the head appears on the uppermost face or the tail appears on the uppermost face.

S = {H, T}; n {S} = 2

(2). \(P(\text { tail })=\frac{\text { No. of favourable outcomes }}{\text { No. of possible outcomes }}=\frac{1}{2}\)

Question 5. A fair die is tossed. List the sample space. State the probability of the event :

1. A number less than 3 appears
2. A number greater than 3 appears
3. A number greater than or equal to 3 appears

Solution:

When a fair die is tossed, the number of possible outcomes is 1, 2, 3, 4, 5 and 6.

Sample space S = {1,2, 3,.4, 5, 6); n (S) = 6

(1). Let A be the event which denotes “a number less than 3 appears”.

A= {1,2}, n(A) = 2;

⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{2}{6}=\frac{1}{3}\)

(2). Let E be the event which denotes “a number greater than 3” appears.

E= {4,5,6}; n{E) =3

⇒ P(E)=\(\frac{n(E)}{n(S)}=\frac{3}{6}=\frac{1}{2}\)

(3). Let B be the event in which “a number greater than or equal to 3” appears.

B = {3, 4, 5, 6}; n(B) = 4

⇒ P(B)=\(\frac{n(B)}{n(S)}=\frac{4}{6}=\frac{2}{3}\)

Question 6. Two dice are thrown simultaneously. Find the probability of getting:

1. An even number is the sum
2. An even number as the product
3. The sum as a prime number
4. A total of at least 10
5. A doublet.

Solution:

Elementary events associated with the random experiment of throwing two dice are :

{1,1} {1,2} {1,3} {1,4} {1,5} {1,6}

{2,1} {2,2} {2,3} {2,4} {2,5} {2,6} .

{3,1} {3,2} {3,3} {3,4} {3,5} {3,6}

{4,1} {4,2} {4,3} {4,4} {4,5} {4,6}

{5,1} {5,2} {5,3} {5,4} {5,5} {5,6}

{6,1} {6,2} {6,3} {6,4} ‘{6,5} {6,6}

∴ Total number of elementary events = 6 x 6 = 36.

(1). Let A be the event of getting an even number as the sum, i.e., 2, 4, 6, 8, 10, 12.

The sum is even.

∴ Sum may be 2 or 4 or 6 or 8 10 or 12.

So, elementary events favourable to events are (1,1), (1,3), (3,1),(2,2), (1,5), (5, 1), (2, 4), (4, 2),'(3, 3), (2, 6), (6, 2), (4, 4), (5, 3), (3, 5), (5, 5), (6, 4), (4, 6) and (6, 6). C

clearly, a favourable number of outcomes =18

Hence, required probability = \(\frac{18}{36}=\frac{1}{2}\)

(2). Let B be the event of getting an even number as the product, i.e., 2, 4, 6, 8, 10, 12, 16, 18,20,24,30,36.

∴ Elementary events favourable to event £ are : (1, 2), (2, 1), (1, 4), (4, 1), (2, 2), (1, 6), (6, 1), (2, 3), (3, 2), (2, 4), (4, 2), (2, 5), (5, 2), (2, 6), (6, 2), (3, 4), (4, 3), (4, 4), (3, 6), (6, 3), (4, 5), (5, 4), (4, 6), (6, 4), (5, 6), (6, 5), (6, 6).

∴ Favourable number of outcomes = 27

Hence, required probability = \(\frac{27}{36}=\frac{3}{4}\)

(3). Let C be the event of getting the sum as a prime number, i.e., 2, 3, 5, 7, 11.

Elementary events favourable to event C are :(1, 1), (1 2), (2, 1),(1, 4), (4, 1), (2, 3), (3, 2), (1, 6), (6, 1), (2, 5), (5, 2), (3, 4), (4, 3), (6, 5), (5, 6)

∴ Favourable number of outcomes =15

Hence, required probability = \(\frac{15}{36}=\frac{5}{12}\)

(4). Let D be the event of getting a total of at least 10, i.e., 10, 11, 12.

Then, the elementary events favourable to D are (6, 4), (4, 6), (5, 5), (6, 5), (5, 6) and (6, 6).

∴ Favourable number of outcomes = 6

Hence, required probability = \(\frac{6}{36}=\frac{1}{6}\)

(5). Let E be the event of getting a Doublet, i.e., (1,1), (2,2), (3,3), (4, 4), (5,5), (6,6).

Clearly, a favourable number of outcomes = 6

∴ \(P(E)=\frac{6}{36}=\frac{1}{6}\)

Question 7.

• A die is thrown once. Find the probability of getting :
  1. A prime number
  2. A number between 3 and 6
  3. A number greater than 4
  4. A number at most 4
  5. A factor of 6.
• When two dice are thrown find the probability of obtaining :
  1. A total of 6
  2. A total of 10
  3. Same number on both dice
  4. A total of 9.
• Two different dice are thrown together. Find the probability that the numbers obtained :
  1. Have a sum of less than 7
  2. Have a product of less than 16
  3. Is a doublet of odd numbers.

Solution:

1. As a die is rolled once, therefore there are six possible outcomes, i.c., 1,2,3, 4, 5, 6.

(1). Let A be an event “getting a prime number”.

Favourable cases for a prime number are 2, 3, 5,

i.e., n(A) = 3

Hence, P(A)=\(\frac{n(A)}{n(S)}=\frac{3}{6}=\frac{1}{2}\)

(2). Let A be an event “getting a number between 3 and 6”.
Favourable cases for events A are 4 or 5.

i.e., n(A) = 2

⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{2}{6}=\frac{1}{3}\)

(3). Let A be an event “a number greater than 4”.

Favourable cases for events A are 5 and 6.

i.e., n(A) = 2

⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{2}{6}=\frac{1}{3}\)

(4). Let A be the event of getting a number at most 4.

∴ A = {1,2, 3, 4} ⇒ n(A) = 4, n(S) = 6

∴ Required probability = \(\frac{n(A)}{n(S)}=\frac{4}{6}=\frac{2}{3}\)

(5). Let A be the event of getting a factor of 6.

∴ A = {1,2, 3, 6} r ⇒ n(A) = 4, n(S) = 6

∴ Required probability = \(\frac{n(A)}{n(S)}=\frac{4}{6}=\frac{2}{3}\)

2. Since a pair of dice is thrown once, so there are 36 possible outcomes.

i.e., n(S) = 36

(1). Let A be an event “a total 6”. Favourable cases for a total of 6 are (2, 4), (4, 2), (3, 3),(5, 1), (1,5).

i.e., n(A) = 5

Hence, P(A)=\(\frac{n(A)}{n(S)}=\frac{5}{36}\)

(2). Let A be an event “a total of 10”. Favourable cases for a total of 10 are (6, 4), (4, 6),(5,5).

i.e., n(A) = 3

⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{3}{36}=\frac{1}{12}\)

(3). Let A be an event “the same number of both the dice”. Favourable cases for the same number on both the dice are (1, 2), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6).

i.e.. n(A)= 6

⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{6}{36}=\frac{1}{6}\)

(4). Let A be an event “of getting a total of 9”. Favourable cases for a total of 9 are (3,6), (6,3), (4,5), (5,4). ”

i.e., n(A) = 4

⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{4}{36}=\frac{1}{9}\)

3. We have, n(S) = 36

(1). Let A be an event “a sum less than 7” i.e., 2, 3, 4, 5, 6.

Favourable cases for a sum less than 7 are : (1, 1), (1, 2), (2, l),(l,3), (3, 1), (2, 2), (1,4), (4, 1), (2, 3), (3, 2), (1,5), (5, 1), (2, 4), (4, 2), (3, 3)

i.e., n(A) = 15

⇒ P(A)=\(\frac{n(A)}{n(S)}=\frac{15}{36}=\frac{5}{12}\)

(2). Let/1 be an event “product less than 16” i.e., 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15.

Favourable cases for a product less than 16 are : (1, 1), (1, 2), (2, 1),(1, 3), (3, 1), (1, 4), (4, 1), (2, 2), (1, 5), (5, 1), (1, 6), (6, 1), (2, 3), (3, 2), (2, 4), (4, 2), (3, 3), (2, 5),(5, 2), (2, 6), (6, 2), (3, 4), (4, 3), (3, 5), (5, 3).

n(A) = 25

Hence, P(A)=\(\frac{n(A)}{n(S)}=\frac{25}{36}\)

(3). Let A be an event “a doublet of odd numbers”.

Favourable cases for a doublet of odd numbers are (1, 1), (3, 3), (5, 5)

i.e., n(A) = 3

Hence P(A)=\(\frac{n(A)}{n(S)}=\frac{3}{36}=\frac{1}{12}\)

Question 8. A standard deck of 52 cards is shuffled. Ritu draws a single card from the deck at random. What is the probability that the card is a jack?

Solution:

Given

A standard deck of 52 cards is shuffled. Ritu draws a single card from the deck at random.

S = Sample space of all possible outcomes, or 52 cards.

Thus, n(S) = 52

E = Event of selecting a jack. There are four jacks in the deck; jack of hearts, of diamonds, of spades, and of clubs.

Thus n(E) = 4 .

∴ P(E)=\(\frac{\text { Number of possible jacks }}{\text { Total number of possible cards }}=\frac{4}{52}=\frac{1}{13}\)

Hence, the probability that the card is jack is \(\frac{1}{13}\)

Question 9. A bag contains 5 black, 7 red and 3 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is:

1. Red
2. Black or white
3. Not black.

Solution:

Given

A bag contains 5 black, 7 red and 3 white balls. A ball is drawn from the bag at random.

Total number of balls = 5 + 7 + 3= 15

1. Number of red balls = 7

∴ P(drawing a red ball) = \(\frac{7}{15}\)

2. Number of black or white balls = 5 + 3 = 8

∴ P(drawing a black or white ball) =\(\frac{8}{15}\)

3. Number of balls which are not black =15-5 = 10

∴ P(drawing a ball that is not black) = \(\frac{10}{15}\) = \(\frac{2}{3}\)

Hence, the probability of getting a red ball, a black or white ball and not a black ball are \(\frac{7}{15}, \frac{8}{15}\) and \(\frac{2}{3}\) respectively.

Question 10. The probability of selecting a rotten apple randomly from a heap of 900 apples is 0.18. What is the number of rotten apples in the heap?

Solution:

Given

The probability of selecting a rotten apple randomly from a heap of 900 apples is 0.18

Total number of apples in a heap = 900

Let the number of rotten apples in a heap = x

Number of rotten apples = \(\frac{\text { Number of rotten apples }}{\text { Total number of apples in a heap }}\)

Now, probability (rotten apple) = \(0.18=\frac{x}{900}\)

∴ x = 900 x 0.18 = 162

∴ Number of rotten apples in a heap of apples =162

Question 11. One card is drawn from a well-shuffled deck of 52 cards. Find the probability of drawing:

1. An ace
2. ‘2’ of spades
3. ‘10’ of a black suit.

Solution:

1. The number of possible outcomes of drawing an ace is 4 as the number of aces in the deck is 4.

The total number of outcomes relating to drawing a card from a deck of 52 cards is 52.

∴ P(drawing an ace) = \(\frac{4}{52}=\frac{1}{13}\)

2. As there is only one card ‘2’ of spades, there is one favourable outcome only.

∴ Probability of drawing ‘2’ of spades = \(\frac{1}{52}\)

3. Since, there are two cards of TO’ of a black suit, one 10 of spade and the other 10 of the club, the probability of drawing 10 of a black suit = \(\frac{2}{52}=\frac{1}{26}\)

Question 12. A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears

1. A two-digit number,
2. A number divisible by 5.

Solution:

Given

A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box

We have, n(S) = 90

(1) Let A be the event of getting “a two-digit number”.

∴ Favourable cases are 10, 11, 12, 13, 14, …, 90.

∴ n(A)=81

∴ P(A)=\(\frac{n(A)}{n(S)}=\frac{81}{90}=\frac{9}{10}\)

(2) Let B be the event of getting “a number divisible by 5 “.

∴ Favourable cases are 10,15,20,25,30, …, 90.

Let there be n in numbers.

T_n =90

∴ 10+(n-1) 5 =90 [\(a_n\) of A.P.=a+(n-1)d]

⇒ (n-1) 5 =80 ⇒ n-1 = 16 ⇒ n=17

∴ n(B) =17

∴ P(B) =\(\frac{n(B)}{n(S)}=\frac{17}{90}\)

Question 13. A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to all of the numbers 1,2, 3, …,12. What is the probability that it will point to

1. 10
2. An odd number
3. A number which is a multiple of 3?

Solution:

Given

A game of chance consists of spinning an arrow which is equally likely to come to rest pointing to all of the numbers 1,2, 3, …,12.

n(S) = Total number of elementary events = 12.

1. Favourable number of elementary events that point to 10 = 1

∴ Required probability = \(\frac{1}{12}\)

2. Let A be the event “point of the arrowhead towards an odd number”

∴ n(A) = {1,3, 5, 7, 9, 11} = 6

∴ P(A) = \(\frac{n(A)}{n(S)}=\frac{6}{12}=\frac{1}{2}\)

3. Let E be the event “pointing towards a number which is a multiple of 3”

∴ n(E) = {3, 6, 9, 12} = 4

∴ P(E) = \(\frac{n(A)}{n(S)}=\frac{4}{12}=\frac{1}{3}\)

Question 14. A bag contains 15 white balls and some black balls. If the probability of drawing a black ball is thrice that of a white ball, find the number of black balls in the bag.

Solution:

Given

A bag contains 15 white balls and some black balls. If the probability of drawing a black ball is thrice that of a white ball

Number of white balls in a bag =15

Suppose the number of black balls in the bag = x

Total number of balls in the bag = 15 + x

P(white ball) =\(\frac{15}{15+x}\)

P(black ball) =\(\frac{x}{15+x}\)

Now, P(black ball ) =3 P( white ball )

⇒ \(\frac{x}{15+x} =3 \times \frac{15}{15+x} \quad \Rightarrow \quad x=45\)

Therefore, the number of black balls in the bag is 45

Question 15. Find the probability of having 53 Tuesdays in a:

1. Non-leap year
2. Leap year.

Solution:

1. A non-leap year contains 365 days. So, by dividing it by 7, we get 52 weeks and 1 more day.

So, since 52 weeks are there, it means 52 Tuesdays will also be there necessarily with probability 1 and 1 more day may be either Sun. or Mon. or Tue. or Wed. or Thur. or Fri. or Sat.

So, to get 53 Tuesdays, we have to select one more Tuesday from these 7 possibilities with probability \({1}{7}\)

Therefore, probability of having 53 Tuesdays in a non-leap year = \(1 \times \frac{1}{7}=\frac{1}{7}\)

2. In a leap year, there are 366 days and 364 days make 52 weeks and therefore 52 Tuesdays. So, the probability of getting 52 Tuesdays till now is l(sure event). The remaining two days can be

Sunday – Monday
Monday – Tuesday
Tuesday – Wednesday
Wednesday – Thursday
Thursday – Friday
Friday – Saturday
Saturday – Sunday

Hence, favourable outcomes = 2 and total outcomes = 7.

Therefore, the probability of having 53 Tuesdays in a leap year is \(1 \times \frac{2}{7}=\frac{2}{7}\)

Question16. It is known that a box of 600 electric bulbs contains 12 defective bulbs. One bulb is taken out at random from this box. What is the probability that it is a non-defective bulb?

Solution:

Given

It is known that a box of 600 electric bulbs contains 12 defective bulbs. One bulb is taken out at random from this box.

The number of non-defective bulbs in the box = 600 – 12 = 588

So, probability of taking out a non-defective bulb = \(\frac{588}{600}=\frac{49}{50}\)=0.98

Question 17. Two customers are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on

1. The same day
2. Different days
3. Consecutive days?

Solution:

Given

Two customers are visiting a particular shop in the same week (Monday to Saturday). Each is equally likely to visit the shop on any day as on another day.

1. Both the customers visit the shop on the same day, i.e., there are 6 days (Monday to Saturday) and each is equally likely.

∴ Probability of both will visit on the same day

= First will go on Monday and the other will also go on Monday or the first will go on Tuesday and the other will go on Tuesday:

or first will go on Saturday and other will also go on Saturday

=\(\frac{1}{6} \times \frac{1}{6}+\frac{1}{6} \times \frac{1}{6}+\ldots+\frac{1}{6} \times \frac{1}{6}=6 \times \frac{1}{6} \times \frac{1}{6}=\frac{1}{6}\)

Alternative Method:

The first person will definitely go to the market on any of the six days with probability 1 (sure event). If both go to the market the same day then the second person has only 1 choice (only that 1 day when the first goes). So, its probability of going to the market = \(\frac{1}{6}\)

∴ Required probability = \(1 \times \frac{1}{6}=\frac{1}{6}\)

2. The first person will definitely go to the market on any of the six days with probability 1 (sure event). Since both will not go on the same day, so second person has now only 5 choices (except this 1 day when first go to the market). So, the probability of the second man go to the other day = \(\frac{5}{6}\)

∴ Required probability = \(1 \times \frac{5}{6}=\frac{5}{6}\)

3. There are 5 consecutive days, i.e., Monday Tuesday, Tuesday Wednesday, Wednesday Thursday, Thursday Friday, Friday Saturday.

∴ Required probability = 5 \times \frac{1}{6} \times \frac{1}{6}=\frac{5}{36}

Question 18. Find the probability of getting 52 Sundays in a leap year.

Solution:

A leap year has 366 days, so by dividing it by 7, we get 52 weeks and 2 days more. 52 weeks means 52 Sundays surely. Now, what will you say?

Perhaps you will say that the probability of getting 52 Sundays in a leap year is 1. Your answer is not correct. Why?

Think about the two remaining days. If from the remaining 2 days, 1 day is the Sunday, then there are 53 Sundays in a leap year.

So, the question does not end at the stage that probability is 1. We have to consider necessarily the two remaining days.

The remaining 2 days may be (Sunday, Monday), (Monday, Tuesday), (Tuesday, Wednesday), (Wednesday, Thursday), (Thursday, Friday), (Friday, Saturday), (Saturday, Sunday).

For only 52 Sundays we want the combination of (Sunday, and Monday) or (Saturday, and Sunday not to occur. So, to get the required probability.

= (52 Sundays with probability 1) and (5 other possibilities out of 7 with probability \(\left(\frac{5}{7}\right)\))

= \(1 \times \frac{5}{7}=\frac{5}{7}\)

Question 19. If a number x is chosen at random from the numbers -2, -1, 0, 1, 2. What is the probability that \(x^2<2\)?

Solution:

We are presenting a table for x and x.

Clearly, x can take any one of the five values.

∴ Total number of cases = 5

Now, x³ < 2 when x = -1 or 0 or 1

∴ Favourable cases = 3

∴ Required probability =\(\frac{\text { Number of favourable cases }}{\text { Total number of cases }}=\frac{3}{5}\)

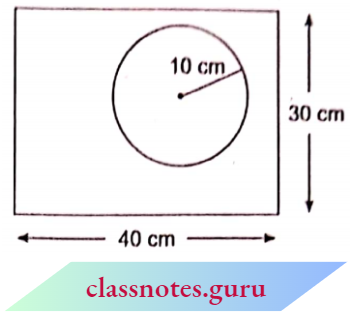
Question 20. A circle with a radius of 10 cm is drawn somewhere on a rectangular piece of paper of dimensions 10 cm x 30 cm, This paper is kept horizontally on the tabletop and a point is marked on the rectangular paper without seeing It. bind the probability that it will marked outside the circle. {Take \(\pi=\frac{22}{7}\)

Solution:

Given

A circle with a radius of 10 cm is drawn somewhere on a rectangular piece of paper of dimensions 10 cm x 30 cm, This paper is kept horizontally on the tabletop and a point is marked on the rectangular paper without seeing It.

Area of rectangle =40 \(\times 30 \mathrm{~cm}^2=1200 \mathrm{~cm}^2 \)

Area of circle =\(\pi(10)^2=100 \pi \mathrm{cm}^2\)

∴ Area of remaining portion =(1200-100 \(\pi) \mathrm{cm}^2\)

∴ Required probability =\(\frac{\text { Favourable portion }}{\text { Total portion }}=\frac{100(12-\pi)}{1200}\)

= \(\frac{12-\frac{22}{7}}{12}=\frac{84-22}{7 \times 12}=\frac{62}{7 \times 12}=\frac{31}{42}\)

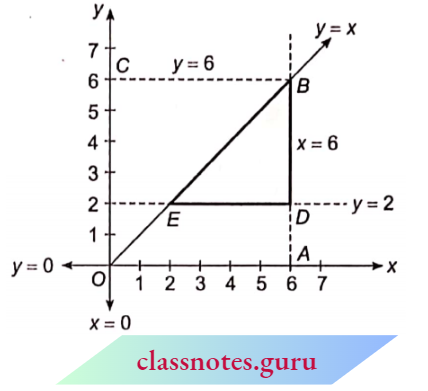
Question 21. A square dart board is placed in the first quadrant from x = 0 to,x = 6 and = 0 to x = 6. A triangular region on the dartboard is enclosed y = 2, x = 6 and y = x. Find the probability that a dart that randomly hits the dartboard will land in the triangular region formed by the three lines.

Solution:

Given

A square dart board is placed in the first quadrant from x = 0 to,x = 6 and = 0 to x = 6. A triangular region on the dartboard is enclosed y = 2, x = 6 and y = x.

Area of square board =\((6)^2=36 \mathrm{sq}\). units

Now, DE = 6 – 2 = 4 units

BD = 6 – 2 = 4 units

∴ Area of \(\triangle B D E =\frac{1}{2} \times D E \times B D=\frac{1}{2} \times 4 \times 4\)

= 8 sq units

Hence, required probability =\(\frac{Area of \triangle B D E}{{ Area of square } O A B C}\)

= \(\frac{8}{6 \times 6}=\frac{2}{9}\)

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Exercise 15.1

Question 1. Complete the following statements:

1. Probability of an event E + Probability of the event ‘not E’ = ________.
2. The probability of an event that cannot happen is ________ Such an event is called ___________.
3. The probability of an event that is certain to happen is _______ Such an event is called _______.
4. The sum of the probabilities of all the elementary events of an experiment is _________.
5. The probability of an event is greater than or equal to _______ and less than or equal to ________.

Solution:

1. Probability of an event E + Probability of the event ‘not F = 1.
2. The probability of an event that cannot happen is zero. Such an event is called an impossible event.
3. The probability of an event that is certain to happen is 1. Such an event is called a certain event.
4. The sum of the probabilities of all the elementary events of an experiment is 1.
5. The probability of an event is greater than or equal to zero and less than or equal to one.

Question 2. Which of the following experiments have equally likely outcomes? Explain.

1. A driver attempts to start a car. The car starts or does not start.
2. A player attempts to shoot a basketball. She/he shoots or misses the shot.
3. A trial is made to answer a true-false question. The answer is right or wrong.
4. A baby is born. It is a boy or a girl?

Solution:

1. A driver attempts to start a car. Here the possibility of starting a car is more than that of not starting the car. So this experiment is not equally likely.
2. A player attempts to shoot a basketball.
   • In the same condition, the possibilities of shoots or misses the shoots are not the same. So this experiment is not equally likely.
3. A trial is made to answer a true-false question. The possibilities of right or wrong answers are the same. So this experiment is equally likely.
4. A baby is born. The possibilities of this baby being a boy or a girl are equal. So this experiment is equally likely.

Question 3. Why is tossing a coin considered to be a fair way of deciding which team should get the ball at the beginning of a football game?

Solution:

Tossing a coin is considered to be a fair way because the coin is symmetric and the possibilities of getting head or tail are equal.

Question 4. Which of the following cannot be the probability of an event?

1. \(frac{2}{3}\)
2. -1.5
3. 15%
4. 0.7

Solution: 2. -1.5

Because the probability of an event cannot be smaller than zero.

Question 5. If P(E) = 0.05, what is the probability of ‘not E’?

Solution :

P(E) = 0.05

Probability of ‘E-not’ = 1 – P(E)

= 1 – 0.05 = 0.95

Question 6. A bag contains lemon-flavoured candies only. Malini takes out one candy without looking into the bag. What is the probability that she takes out:

1. An orange-flavoured candy?
2. A lemon-flavoured candy?

Solution :

There are only lemon-flavoured candies in the bag.

If a candy is drawn at random from the bag, then

1. The probability of drawing an orange-flavoured candy = 0.

So. the probability of drawing an orange-flavoured candy = 0.

2. The event of drawing a lemon-flavoured candle is a certain event.

So. the probability of drawing a lemon-flavoured candy = 1

Question 7. It is given that in a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?

Solution:

The probability of 2 students not having the same birthday = 0.992

∴ The probability of 2 students having the same birthday = 1 – 0.992 = 0.008

Question 8. A bag contains 3 red balls and 5 black balls. A ball is drawn at random from the bag. What is the probability that the ball drawn is

1. Red?
2. Not red?

Solution:

Total balls 3 + 5 = 8

Total possible outcomes of drawing a ball at random from the bag = 8

1. Favourable outcomes of drawing a red ball = 3

∴ The probability of drawing a red ball

Favourable outcomes of = \(\frac{\text { drawing a red ball }}{\text { Total possible outcomes }}\)

=\(\frac{3}{8}\)

2. Probability that the ball drawn is not red = 1 – probability that the ball drawn is red.

Question 9. A box contains 5 red marbles, 8 white marbles and 4 green marbles. One marble is taken out of the box at random. What is the probability that the marble taken out will be

1. Red?
2. White?
3. Not green?

Solution:

Total marbles = 5 + 8 + 4=17 Total possible outcomes of drawing a marble at random from the box = 17

1. Favourable outcomes of drawing a red marble = 5.

∴ The probability that the marble drawn is red

Favourable outcomes of = \(\frac{\text { drawing a red ball }}{\text { Total possible outcomes }}\)

=\(\frac{5}{17}\)

2. Favourable outcomes of drawing a white marble = S

∴ Possibility of drawing a white marble

Favourable outcomes of \(\frac{\text { drawing a red ball }}{\text { Total possible outcomes }}\)

= \(\frac{8}{17}\)

3. Favourable outcomes of drawing a green marble = 4

⇒ Favourable outcomes that the marble drawn is not green = 17 – 4 =13

∴ The probability that the marble drawn is not green

Favourable outcomes = \(\frac{\text { marble drawn is not green }}{\text { Total possible outcomes }}\)

= \(\frac{13}{17}\)

Question 10. A piggy bank contains a hundred 50 p coins, fifty ₹ 1 coins, twenty ₹ 2 coins and ten ₹ 5 coins. If it is equally likely that one of the tyre coins will fall out when the bank is turned upside down, what is the probability that the coin?

1. Will be a 50 p coin?
2. Will not be a ₹ 5 coin?

Solution:

No. of coins of 50 paise =100

No. of coins of ₹ 1 =50

No. of coins of ₹ 2 =20

No. of coins of ₹ 5 = 10

Total coins = 100 + 50 + 20 + 10 = 180

Total outcomes that one coin will fall out = 180

1. The favourable outcomes that the coin fall out is 50 paise = 100

∴ Probability that coin fall out is of 50 paise =\(\frac{100}{180}=\frac{5}{9}\)

2. The favourable outcome that the coin falls out is ₹ 5 = 10

∴ Probability that coin fall out is of Rs 5 = =\(\frac{10}{180}=\frac{1}{18}\)

Therefore, the probability that the coin falls out is not ₹ 5

= \(1-\frac{1}{18}=\frac{17}{18}\)

Question 11. Gopi buys a fish from a shop for his aquarium. The shopkeeper takes out one fish at random from a tank containing 5 male fish and 8 female fish. What is the probability that the fish taken out is a male fish?

Solution :

Total no. of fish = 5 + 8 = 13

Total possible outcomes of taking a fish = 13

Favourable outcomes of taking a male fish = 5

Probability of a male fish

Favourable outcomes

= \(\frac{\text { drawing a male fish }}{\text { Total no. of possible outcomes of drawing a fish }}\)

= \(\frac{5}{3}\)

Question 12. A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1,2,3,4,5,6,7,8. and these are equally likely outcomes.

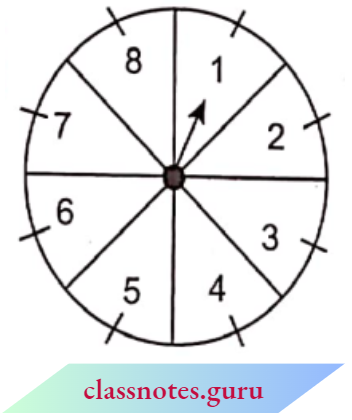
What is the probability that it will point at:

1. 8?
2. An odd number?
3. A number greater than 2?
4. A number less than 9?

Solution :

Total no. of outcomes of pointing by an arrow =8

1. Favourable outcomes that the arrow indicates the number 8 = 1

∴ Probability of this event = \(\frac{1}{8}\)

Favourable outcomes that the arrow indicates an odd number = {1,3,5, 7} = 4

∴ Probability of this event = \(\frac{4}{8}=\frac{1}{2}\)

3. Favourable outcomes that the arrow indicates a number greater than 2 = {3,4,5,6,7,8} = 6

∴ Probability of this event = \(\frac{6}{8}\) =\(\frac{3}{4}\)

4. Favourable outcomes that the arrow indicates a number less than 9. = {1,2, 3, 4, 5, 6, 7, 8} = 8

∴ Probability of this event = \(\frac{8}{8}\)=1

Question 13. A die is thrown once. Find the probability of getting:

1. A prime number
2. A number lying between 2 and 6
3. An odd number.

Solution:

Possible outcomes in one throw of a die = {1,2,3,4,5,6}

Total possible outcomes = 6

1. Prime numbers = {2, 3, 5} = 3

∴ Probability of getting a prime number = \(\frac{3}{6}=\frac{1}{2}\)

2. Numbers lying between 2 to 6 = {3,4,5} = 3

∴ Probability of this event = \(\frac{3}{6}=\frac{1}{2}\)

3. Odd numbers = {1, 3, 5} = 3

∴ Probability of this event =\(\frac{3}{6}=\frac{1}{2}\)

Question 14. One card is drawn from a well-shuffled deck of 52 cards. Find the probability of getting:

1. A king of red colour
2. A face card
3. A red-face card
4. The jack of hearts
5. A spade
6. The Queen of diamonds

Solution:

Total possible outcomes of drawing a card from the pack of cards = 52.

1. Favourable outcomes of getting a king of red colour = 2.

∴ Probability of drawing a icing of red colour = =\(\frac{2}{52}=\frac{1}{26}\) .

2. Favourable outcomes of getting a face card = 12

∴ Probability of drawing a face card = \(\frac{12}{52}=\frac{3}{13}\)

3. Favourable outcomes of getting a face card of red colour = 6

∴ Probability of drawing a face card of red colour =\(\frac{6}{52}=\frac{3}{26}\)

4. Favourable outcomes of drawing a jack of heart = 1

∴ Probability of drawing a jack of heart = \(\frac{1}{52}\)

5. Favourable outcomes of drawing a card of spade = 13

∴ Probability of drawing a card of spade = \(\frac{13}{52}={1}{4}\)

6. Favourable outcomes of drawing a queen of diamonds = 1

∴ Probability of drawing a queen of diamond = \(\frac{1}{52}\)

Question 15. Five cards—the ten, jack, queen, king and ace of diamonds, are well-shuffled with their face downwards. One card is then picked up at random.

1. What is the probability that the card is the queen?
2. If the queen is drawn and put aside, what is the probability that the second card picked up is
   1. An ace?
   2. A queen?

Solution:

Total favourable outcomes of drawing a card from the five playing cards = 5

1. Favourable outcomes of drawing a queen = 1

∴ Probability of drawing a queen = \(\frac{1}{5}\)

2. Remaining cards when ‘queen’ is drawn and put aside = 4

(1). Favourable outcomes of drawing a card of ace = 1

∴ Probability of drawing the second card ace = \(\frac{1}{4}\)

(2). Favourable outcomes of drawing a queen = 0

∴ Probability of drawing the second card of queen = \(\frac{0}{4}\)=0

Question 16. 12 defective pens are accidentally mixed with 132 good ones. It is not possible to just look at a pen and tell whether or not it is defective. One pen is taken out at random from this lot. Determine the probability that the pen taken out is a good one.

Solution :

No. of good pens = 132

No. of defective pens = 12

Total pens = 132 + 12 = 144

Total favourable outcomes of drawing a pen = 144

Favourable outcomes of drawing a good pen = 132

∴ Probability of drawing a good pen = \(\frac{132}{144}\) = \(\frac{11}{12}\)

Question 17.

1. A lot of 20 bulbs contain 4 defective ones. One bulb is drawn at random from the lot. What is the probability that this bulb is defective?
2. Suppose the bulb drawn in (1) is not defective and is not replaced. Now one bulb is drawn at random from the rest. What is the probability that this bulb is not defective?

Solution:

Total bulbs = 20

Defective bulbs = 4

1. If a bulb is drawn at random then total possible outcomes = 20

Favourable outcomes of a defective bulb = 4.

∴ Probability of a defective bulb = \(\frac{4}{20}=\frac{1}{5}\)

2. If the bulb drawn is not defective and it is not replaced. Now a bulb is drawn then

Total possible outcomes =19

Favourable outcomes of a defective bulb = 4

∴ Probability of a defective bulb = \(\frac{4}{19}\)

⇒ Probability of a non-defective bulb =\(1-\frac{4}{19}=\frac{15}{19}\)

Question 18. A box contains 90 discs which are numbered from 1 to 90. If one disc is drawn at random from the box, find the probability that it bears

1. A two-digit number
2. A perfect square number
3. A number divisible by 5.

Solution:

Total no. of discs = 90

Possible outcomes of drawing a disc = 90

1. Two digit numbers = {10, 11, 12, …90}

Favourable outcomes of drawing a two’ digit number = 81

Now, the probability of getting a two-digit number on the disc =\(\frac{81}{90}=\frac{9}{10}\)

2. Perfect square numbers in given numbers
= {1,4, 9, …,81}

⇒ Favourable outcomes of drawing a perfect square number = 9

Now, the probability that the number marked on the disc is a perfect square =\(\frac{9}{90}=\frac{1}{10}\)

3. Numbers divisible by 5 in the given numbers = (5, 10, 15,…, 90}

⇒ Favourable outcomes of a number drawn divisible by 5 = 18

Now, the probability that the number marked on the disc is divisible by 5 = \(\frac{18}{90}=\frac{1}{5}\)

Question 19. A child has a die whose six faces show the letters as given below:

A B C D E A

The die is thrown once. What is the probability of getting

1. A?
2. D?

Solution:

Total possible outcomes in a throw of die = 6

1. Favourable outcome of getting A = 2

∴ Probability of getting A = \(\frac{2}{6}=\frac{1}{3}\)

2. Favourable outcomes of getting D = 1

∴ Probability of getting D = \(\frac{1}{6}\)

Question 20. Suppose you drop a die at random on the rectangular region shown. What is the probability that it will land inside the circle with a diameter of 1 m?

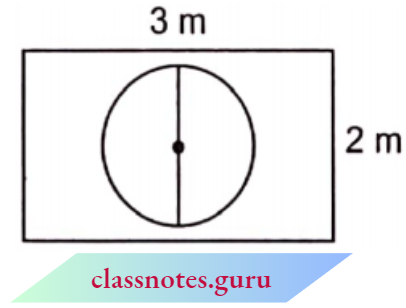
Solution:

Area of rectangle = \(3 \times 2=6 \mathrm{~m}^2\)

Diameter of circle =1 m

⇒ Radius of circle =\(\frac{1}{2} \mathrm{~m}\)

⇒ Area of circle =\(\pi\left(\frac{1}{2}\right)^2=\frac{\pi}{4} \mathrm{~m}^2\)

Now, the probability that in one throw of a die, the die lands inside the circle

= \(\frac{\text { Area of circle }}{\text { Area of rectangle }}\)

= \(\frac{\pi / 4}{6}=\frac{\pi}{4 \times 6}=\frac{\pi}{24}\)

Question 21. A lot consists of 144 ball pens of which 20 are defective and the others are good. Nuri will buy a pen if it is good, but will not buy if it is defective. The shopkeeper draws one pen at random and gives it to her. What is the probability that:

1. She will buy it?
2. She will not buy it?

Solution:

Total number of ball pens = 144

No. of defective ball pens = 20

∴ No. of good ball pens = 144 – 20 = 124

No. of favourable outcomes of drawing a pen randomly = 144

1. To buy the pen, it must be a good one.

∴ Favourable outcomes of drawing a good ball pen=124

⇒ Probability of buying a good ball pen =\(\frac{124}{144}=\frac{31}{36}\)

2. If the ball pen is defective then she will not buy it.

∴ Favourable outcomes of drawing a defective ball pen = 20

⇒ Probability of drawing a defective ball pen =\(\frac{20}{144}=\frac{5}{36}\)

Question 22. Two dice, one blue and one grey, are thrown at the same time,

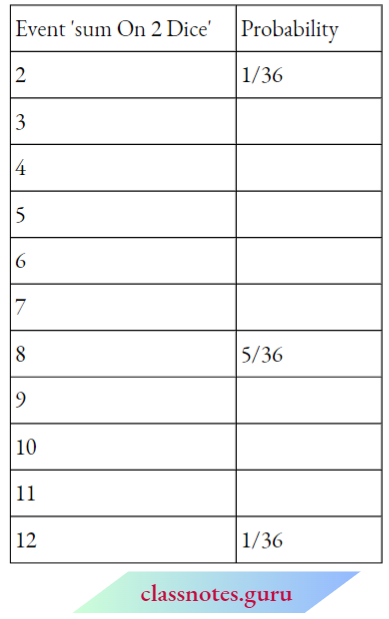
1. Complete the following table:

2. A student argues that ‘there are 11 possible outcomes 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 and 12. Therefore, each of them has a probability \(\frac{1}{11}\). Do you agree with this argument? Justify your answer.

Solution :

1. In a throw of two dice, possible outcomes are

⇒ \(\left\{\begin{array}{llllll}
(1,1), & (1,2), & (1,3), & (1,4), & (1,5), & (1,6) \\
(2,1), & (2,2), & (2,3), & (2,4), & (2,5), & (2,6) \\
(3,1), & (3,2), & (3,3), & (3,4), & (3,5), & (3,6) \\
(4,1), & (4,2), & (4,3), & (4,4), & (4,5), & (4,6) \\
(5,1), & (5,2), & (5,3), & (5,4), & (5,5), & (5,6) \\
(6,1), & (6,2), & (6,3), & (6,4), & (6,5), & (6,6)
\end{array}\right\}\)

Total possible outcomes = 36

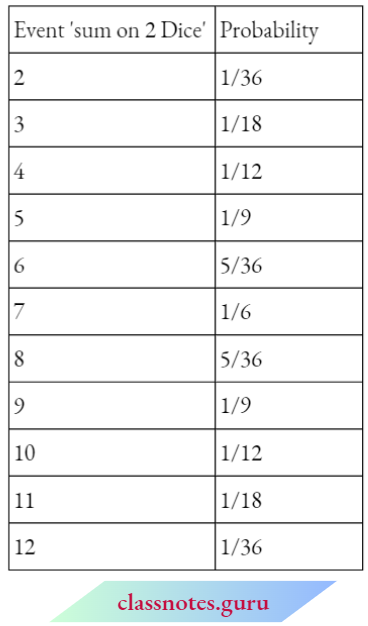
Outcome of getting the sum 2 = (1, 1)

Favourable outcomes of getting a sum 2 = 1

∴ Probability of getting the sum 2 = \(\frac{1}{36}\)

Outcomes of getting the sum 3 = (1, 2), (2, 1)

Favourable outcomes of getting the sum 3 = 2

∴ Probability of getting the sum 3 = \(\frac{2}{36}={1}{18}\)

Outcomes of getting the sum 4 = (1,3), (2, 2), (3, 1)

Favourable outcomes of getting the sum 4 = 3

∴ Probability of getting the sum 4 = \(\frac{3}{36}={1}{12}\)

Outcomes of getting the sum 5 = (1,4), (2, 3), (3, 2), (4, 1)

Favourable outcomes of getting the sum 5=4

∴ Probability of getting the sum 5 = \(\frac{4}{36}={1}{9}\)

Outcomes of getting the sum 6 = (1,5), (2, 4), (3, 3), (4, 2), (5, 1)

Favourable outcomes of getting the sum 6 = 5

∴ Probability of getting the sum 6 = \(\frac{5}{36}\)

Outcomes of getting the sum 7 = (1,6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)

Favourable outcomes of getting the sum 7 = 6

∴ Probability of getting the sum 7 = \(\frac{6}{36}={1}{6}\)

Outcomes of getting the sum 8 = (2, 6), (3, 5), (4, 4), (5, 3), (6, 2)

Favourable outcomes of getting the sum 8 = 5

∴ Probability of getting the sum 8 = \(\frac{5}{36}\)

Outcomes of getting the sum 9 = (3,6), (4, 5), (5, 4), (6, 3)

Favourable outcomes of getting the sum 9 = 4

∴ Probability of getting the sum 9 = \(\frac{4}{36}={1}{9}\)

Outcomes of getting the sum 10 = (4, 6),(5, 5), (6, 4)

Favourable outcomes of getting the sum 10 = 3

∴ Probability of getting the sum 10 = \(\frac{3}{36}={1}{12}\)

Outcomes of getting the sum 11 = (5, 6), (6, 5)

Favourable outcomes of getting the sum 11 = 2

∴ Probability of getting the sum 11= \(\frac{2}{36}={1}{18}\)

Outcomes of getting the sum 12 = (6, 6)

Favourable outcomes of getting the sum 12 = 1

∴ Probability of getting the sum 12 = \(\frac{1}{36}\)

Now, the given table will be as follows:

2. The student’s argument is wrong because the favourable outcomes of every event are different.

Question 23. A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hanifwins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.

Solution :

Given

A game consists of tossing a one rupee coin 3 times and noting its outcome each time. Hanifwins if all the tosses give the same result i.e., three heads or three tails, and loses otherwise.

All possible outcomes in three throws of a coin of ₹ 1.

HHH, HHT, HTH, THH, HTT, THT, TTH,

TTT → Total possible outcomes = 8

Favourable outcomes of 3 heads = 1

Favourable outcomes of 3 tails = 1

∴ Favourable outcomes to win = 2

Now, favourable outcomes to lose = 8 – 2 = 6

Therefore, the probability to lose

= \(\frac{\text { Favourable outcomes to lose }}{\text { Total possible outcomes }}\)

= [/latex]\frac{6}{8}=\frac{3}{4}[/latex]

Question 24. A die is thrown twice. What is the probability that:

1. 5 will not come up either time?
2. 5 will come up at least once?

[Hint: Throwing a die twice and throwing two dice simultaneously are treated as the same experiment]

Solution:

In two throws of a die, the all possible outcomes are :

(1.1), (1,2), (1,3), (1,4), (1,5), (1,6)

(2.1), (2,2), (2,3), (2,4), (2,5), (2,6)

(3.1), (3,2), (3,3), (3,4), (3,5), (3,6)

(4.1), (4,2), (4,3), (4,4), (4,5), (4,6)

(5.1), (5,2), (5,3), (5,4), (5,5), (5,6)

(6.1), (6,2), (6,3), (6,4), (6,5), (6,6)

Total possible outcomes = 36

Outcomes in which 5 comes up = 11

Outcomes in which 5 does not come up = 36 – 11 = 25

1. Favourable outcomes that 5 does not come up = 25

∴ Probability of not getting 5 = \(\frac{25}{36}\)

2. Favourable outcomes that 5 will come up at least once = 11

∴ Probability that 5 will come up at least once = \(\frac{11}{36}\)

Question 25. Which of the following arguments are correct and which are not correct? Clive reasons for your answer.

1. If two coins are tossed simultaneously there are three possible outcomes—two heads, two tails or one of each. Therefore, for each of these outcomes, the probability is \(\frac{1}{3}\)
2. If a die is thrown, there are two possible outcomes—an odd number or an even number. Therefore, the probability of getting an odd number is \(\frac{1}{2}\)

Solution:

1. When two coins are tossed together, then there are not three outcomes, but the following four outcomes are obtained:

HH, HT, TH, TT

So, the .ugumom of the student is false.

2. In one throw of a die

All possible outcomes {1, 2, 3, 4, 5, 6} 6

Outcomes of getting an even number = {2. 4, 6} = 3

Outcomes of gelling an odd number = (1,3,5} =3

∴ Possibility of getting an odd number= \(\frac{3}{6}=\frac{1}{2}\)

Therefore, the argument of the student is true.

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Exercise 15.2

Question 1. Two customers Shvam and Ehta visit a particular shop in the same week (Tuesday to Saturday), Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on

1. The same day?
2. Consecutive days?
3. Different days?

Solution:

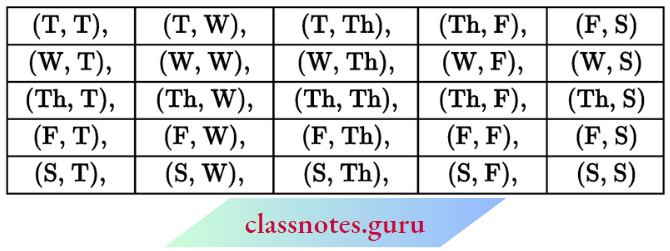
Hence, the total possible outcomes are as follows:

Toral possible outcomes = 25

1. Outcomes that both customers visit on the same day

= (T. T), (W, W), (Th. Th), (F, F), (S, S)

Total favourable outcomes = 5

So. is probability Drat Bodi will visit on the same day

= \(\frac{5}{25}=\frac{1}{5}\)

2. Outcomes that both customers visit on consecutive days

= (T, W), (W; Th), (Th, F), (F, S), (W, T), (Th, W), (F, Th), (S, F)

Total favourable outcomes = 8

So, the probability that both visit on consecutive days the shop

= \(\frac{8}{25}\)

3. Probability that both visit the shop on the same day = \(\frac{1}{5}\) [from part (1)]

∴ The probability that both visit the shop on different days

1= \(\frac{1}{5}= {4}{5}\)

Question 2. A die is numbered in such a way that its faces show the numbers 1,2,2, 3, 3, 6. It is thrown two times and the total score in two throws is noted. Complete the following table which gives a tew values of the total score on the two throws:

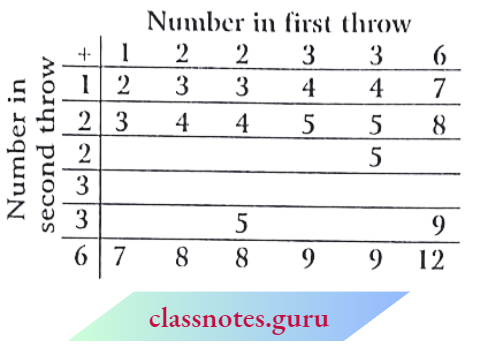
Number in the first throw What is the probability that the total score is

1. Even?
2. 6?
3. At least 6?

Solution:

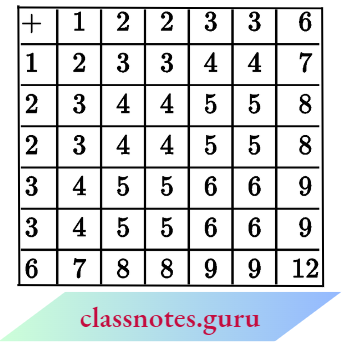
Total possible outcomes = 36

1. Favourable outcomes of getting the sum as an even number = 18

∴ Probability of getting the sum as even number = \(\frac{18}{36}=\frac{1}{2}\)

2. Favourable outcomes of getting a sum 6 = 4

∴ Probability of getting a sum 6= \(\frac{4}{36}=\frac{1}{9}\)

3. Favourable outcomes of getting a sum less than 6=15.

∴ Probability of getting a sum less than 6 =\(\frac{15}{36}=\frac{5}{12}\)

Question 3. A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball, determine the number of blue balls in the bag.

Solution:

Given

A bag contains 5 red balls and some blue balls. If the probability of drawing a blue ball is double that of a red ball

Let the number of blue balls =x

Given, the number of red balls = 5

Total balls = x + 5

∴ The probability of drawing a blue ball

⇒ P(B)=\(\frac{x}{x+5}\)

and the probability of drawing a red ball

⇒ P(R)=\(\frac{5}{x+5}\)

Given that, P(B) =2 \(\times P(R)\)

⇒ \(\frac{x}{x+5} =\frac{2 \times 5}{x+5}\)

⇒ x =10

⇒ Number of blue balls =10

Question 4. A box contains 12 balls out of which x are black. If one ball is drawn at random from the box, what is the probability that it will be a black ball?

If 6 more black balls are put in the box, the probability of drawing a black ball is now double of what it was before. Find x.

Solution:

Given

A box contains 12 balls out of which x are black. If one ball is drawn at random from the box,

Total balls in the box = 12

Black balls = x

∴ Probability of drawing a black ball = \(\frac{x}{12}\)

On putting 6 more black balls in the box, Total balls = 12 + 6= 18 Black balls = x + 6

Now, probability of drawing a black ball = \(\frac{x+6}{12}\)

Given that, \(\frac{x+6}{18} =2 \times \frac{x}{12}\)

⇒ \(\frac{x+6}{18} =\frac{x}{6}\)

⇒ x + 6 = 3 x

⇒ 2 x = 6 ⇒ x = 3

Question 5. A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green 2 is \(\frac{2}{3}\). Find the number of blue balls in the jar.

Solution:

Given

A jar contains 24 marbles, some are green and others are blue. If a marble is drawn at random from the jar, the probability that it is green 2 is \(\frac{2}{3}\).

Total marbles in jar = 24

Let green marbles in jar = x

∴ Probability of drawing 1 green marble from jar = \(\frac{x}{24}\)

Given that, \(\frac{x}{24}=\frac{2}{3}\)

x = \(\frac{2}{3} \times 24\)

⇒ x = 16

∴ Green marbles = 16

⇒ Blue marbles = 24 – 16 = 8

NCERT Exemplar Solutions for Class 10 Maths Chapter 15 Probability Multiple Choice Question And Answers

Question 1. The probability of a sure event is:

1. 0
2. 1
3. -l
4. \(\frac{1}{2}\)

Answer: 2. 1

Question 2. The sum of the probabilities ofan event and its complementary event is:

1. -1
2. 0
3. 1
4. None of these

Answer: 3. 1

Question 3. The probability of winning a match by Ravi is \(\frac{2}{5}\). The probability of his losing the match is

1. \(\frac{3}{5}\)
2. \(\frac{2}{5}\)
3. 1
4. 0

Answer: 1. \(\frac{3}{5}\)

Question 4. If P(A) represents the probability of an event, A, then:

1. P(A)<0
2. P(A)>1
3. 0 ≤ P(A) ≤1
4. -1 ≤ P(A)≤ 1

Answer: 3. 0 ≤ P(A) ≤1

Question 5. When a dice is thrown, the probability of getting an even number less than 3, is:

1. 0
2. \(\frac{1}{2}\)
3. \(\frac{1}{3}\)
4. \(\frac{1}{6}\)

Answer: 4. \(\frac{1}{6}\)

Question 6. The probability of selecting a prime number from the numbers 1 to 20, is:

1. \(\frac{7}{20}\)
2. \(\frac{2}{5}\)
3. \(\frac{9}{20}\)
4. \(\frac{1}{2}\)

Answer: 2. \(\frac{2}{5}\)

Question 7. In a year, which is not a leap year, the probability of 53 Monday is:

1. \(\frac{6}{7}\)
2. \(\frac{3}{7}\)
3. \(\frac{2}{7}\)
4. \(\frac{1}{7}\)

Answer: 4. \(\frac{1}{7}\)