CBSE Class 12 Maths Model Question Paper 2022-2023

CBSE Class 12 Maths Multiple Choice Questions And Answers

Question 1. If \(\mathrm{A}=\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\), then A is equal to

1. \(\left[\begin{array}{ll}0 & 1 \\ 0 & 0\end{array}\right]\)
2. \(\left[\begin{array}{cc}0 & 2023 \\ 0 & 0\end{array}\right]\)
3. \(\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right]\)
4. \(\left[\begin{array}{cc}2023 & 0 \\ 0 & 2023\end{array}\right]\)

Solution: 3. \(\left[\begin{array}{ll}0 & 0 \\ 0 & 0\end{array}\right]\)

⇒ \(\mathrm{A}=\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\)

⇒ \(\mathrm{A}^2=\mathrm{A} \times \mathrm{A}=\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\left[\begin{array}{ll}
0 & 1 \\
0 & 0
\end{array}\right]\)

= \(\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)

⇒ \(\mathrm{A}^{2023} = [latex]\mathrm{A}^2 \times \mathrm{A}^{2021}=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right] \cdot \mathrm{A}^{2021}=\left[\begin{array}{ll}
0 & 0 \\
0 & 0
\end{array}\right]\)

Question 2. If \(\left[\begin{array}{ll}
2 & 0 \\
5 & 4
\end{array}\right]\)= P + Q, where P is symmetric and Q is a skew-symmetric matrix, then Q is equal to

1. \(\left[\begin{array}{cc}2 & 5 / 2 \\ 5 / 2 & 4\end{array}\right]\)
2. \(\left[\begin{array}{cc}0 & -5 / 2 \\ 5 / 2 & 0\end{array}\right]\)
3. \(\left[\begin{array}{cc}0 & 5 / 2 \\ -5 / 2 & 0\end{array}\right]\)
4. \(\left[\begin{array}{cc}2 & -5 / 2 \\ 5 / 2 & 4\end{array}\right]\)

Solution: 2. \(\left[\begin{array}{cc}0 & -5 / 2 \\ 5 / 2 & 0\end{array}\right]\)

⇒ \(\left[\begin{array}{ll}
2 & 0 \\
5 & 4
\end{array}\right]=\mathrm{P}+\mathrm{Q}\)

Let \(\mathrm{A}=\left[\begin{array}{ll}
2 & 0 \\
5 & 4
\end{array}\right]\)

A = \(\mathrm{P}+\mathrm{Q} \Rightarrow \mathrm{A}=\frac{1}{2}\left(\mathrm{~A}+\mathrm{A}^{\prime}\right)+\frac{1}{2}\left(\mathrm{~A}-\mathrm{A}^{\prime}\right)\)

∴ Q = \(\frac{1}{2}\left(\mathrm{~A}-\mathrm{A}^{\prime}\right)\)

= \(\frac{1}{2}\left\{\left[\begin{array}{ll}
2 & 0 \\
5 & 4
\end{array}\right]-\left[\begin{array}{ll}
2 & 5 \\
0 & 4
\end{array}\right]\right\}=\frac{1}{2}\left[\begin{array}{cc}
0 & -5 \\
5 & 0
\end{array}\right]=\left[\begin{array}{cc}
0 & -5 / 2 \\
5 / 2 & 0
\end{array}\right]\)

Question 3. If \(\left[\begin{array}{lll}
1 & 2 & 1 \\
2 & 3 & 1 \\
3 & a & 1
\end{array}\right]\) is a non-singular matrix and a ∈ A, then the set A is

1. R
2. {0}
3. {4}
4. R-{4}

Solution: 4. R-{4}

For non-singular matrix Δ ≠ 0

⇒ \(\left|\begin{array}{lll}
1 & 2 & 1 \\
2 & 3 & 1 \\
3 & a & 1
\end{array}\right| \neq 0 \Rightarrow a-4 \neq 0 \Rightarrow a \neq 4 \Rightarrow A=R-\{4\}\) (because a ∈ A)

Question 4. If |A| = |k A|, where A is a square matrix of order 2, then the sum of all possible values of k is

1. 1
2. -1
3. 2
4. 0

Solution: 4. 0

|A|=|k A|

|A| = \(k^2|A|\)

⇒ \(k^2=1 \Rightarrow k= \pm 1\)

The sum of all possible values of k is 1+(-1)=0

Question 5. If \(\frac{d}{dx}\) [f(0)] = 0, then f(x) is equal to

1. \(a+b\)
2. \(\frac{a x^2}{2}+b x\)
3. \(\frac{a x^2}{2}+b x+c\)
4. \(b\)

Solution: 2. \(\frac{a x^2}{2}+b x\)

⇒ \(\frac{d}{d x}[f(x)]=a x+b\)

f(x) = \(\int(a x+b) d x\)

f(x) = \(\frac{a x^2}{2}+b x+C\)

f(0)=C=0

⇒ f(x) = \(\frac{a x^2}{2}+b x\)

Question 6. Degree of the differential equation \(\sin x+\cos \left(\frac{d y}{d x}\right)=y^2\) is

1. 2
2. 1
3. Not Defined
4. 0

Solution: 2. 1

⇒ \(\sin x+\cos \left(\frac{d y}{d x}\right)=y^2 \Rightarrow \cos \left(\frac{d y}{d x}\right)=y^2-\sin x \Rightarrow \frac{d y}{d x}\)

= \(\cos ^{-1}\left(y^2-\sin x\right)\)

∴ Degree =1

Question 7. The integrating factor of the differential equation \(\left(1-y^2\right) \frac{d x}{d y}+y x=a y \cdot(-1<y<1)\) is

1. \(\frac{1}{y^2-1}\)
2. \(\frac{1}{\sqrt{y^2-1}}\)
3. \(\frac{1}{1-y^2}\)
4. \(\frac{1}{\sqrt{1-y^2}}\)

Solution: 4. \(\frac{1}{\sqrt{1-y^2}}\)

⇒ \(\left(1-y^2\right) \frac{d x}{d y}+y x=a y,-1<y<1\)

⇒ \(\frac{d x}{d y}+x \cdot \frac{y}{1-y^2}=\frac{\text { ay }}{1-y^2}\)

This is a linear differential equation of the form, \(\frac{d x}{d y}+P x=Q\), where \(P=\frac{y}{1-y^2}\) and \(Q=\frac{a y}{1-y^2}\)

I.F. =\(\mathrm{e}^{\int \mathrm{p} \cdot \mathrm{dy}}=\mathrm{e}^{\int \frac{\mathrm{y}}{1-y^2} \mathrm{dy}}\)

Put \(1-\mathrm{y}^2=\mathrm{t} \Rightarrow-2 \mathrm{dy}=\mathrm{dt} \Rightarrow \mathrm{ydy}=-\frac{1}{2} \mathrm{dt}\)

I.F = \(\mathrm{e}^{-\frac{1}{2} \int \frac{\mathrm{d}}{1}}=\mathrm{e}^{-\frac{1}{2} \log \mathrm{t}}=\mathrm{e}^{\log \left(\mathrm{t}^{-122}\right.}\)

∴ I.F. = \(\frac{1}{\sqrt{t}}=\frac{1}{\sqrt{1-y^2}}\)

Question 8. Unit vector along \(\overline{\mathrm{PQ}}\), where coordinates of P and Q respectively are (2, 1,-1) and (4, 4, -7), is

1. \(2 \hat{i}+3 \hat{j}-6 \hat{k}\)
2. \(-2 \hat{i}-3 \hat{j}+6 \hat{k}\)
3. \(\frac{-2 \hat{i}}{7}-\frac{3 \hat{j}}{7}+\frac{6 \hat{k}}{7}\)
4. \(\frac{2 \hat{\mathrm{i}}}{7}+\frac{3 \hat{\mathrm{j}}}{7}-\frac{6 \hat{\mathrm{k}}}{7}\)

Solution: 4. \(\frac{2 \hat{\mathrm{i}}}{7}+\frac{3 \hat{\mathrm{j}}}{7}-\frac{6 \hat{\mathrm{k}}}{7}\)

⇒ PQ = \(\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}}\)

⇒ PQ = \((4 \hat{i}+4 \hat{j}-7 \hat{k})-(2 \hat{i}+\hat{j}-\hat{k}) \Rightarrow P Q=2 \hat{i}+3 \hat{j}-6 \hat{k}\)

Unit vector along \(\overrightarrow{P Q}=\frac{\overrightarrow{P Q}}{\overrightarrow{|P Q|}}=\frac{2 \hat{i}+3 \hat{j}-6 \hat{k}}{\sqrt{49}}=\frac{2 \hat{i}}{7}+\frac{3 \hat{j}}{7}-\frac{6 \hat{k}}{7}\)

Question 9. The position vector of the mid-point of line segment AB is \(3 \hat{i}+2 \hat{j}-3 \hat{k}\). If the position vector of point A is \(2 \hat{i}+3 \hat{j}-4 \hat{k}\). then the position vector of the point B is

1. \(\frac{5 \hat{\mathrm{i}}}{2}+\frac{5 \hat{\mathrm{j}}}{2}-\frac{7 \hat{\mathrm{k}}}{2}\)
2. \(4 \hat{i}+\hat{j}-2 \hat{k}\)
3. \(5 \hat{\mathrm{i}}+5 \hat{\mathrm{j}}-7 \hat{\mathrm{k}}\)
4. \(\frac{\hat{\mathrm{i}}}{2}-\frac{\hat{\mathrm{j}}}{2}+\frac{\hat{\mathrm{k}}}{2}\)

Solution: 2. \(4 \hat{i}+\hat{j}-2 \hat{k}\)

⇒ \(\overrightarrow{\mathrm{OC}}=\frac{\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}}}{2}\)

⇒ 2 \(\overrightarrow{\mathrm{OC}}=\overrightarrow{\mathrm{OA}}+\overrightarrow{\mathrm{OB}} \)

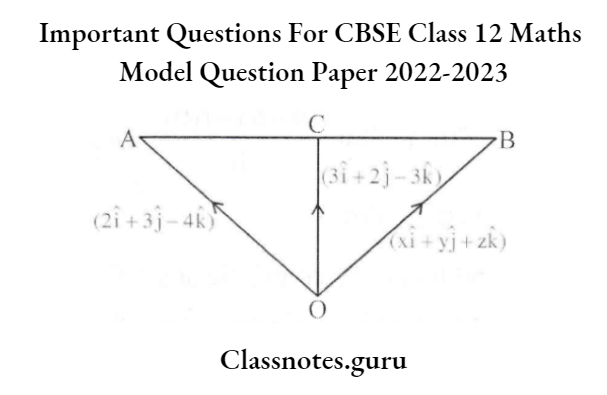
⇒ \(\overrightarrow{\mathrm{OB}}=2 \overrightarrow{\mathrm{OC}}-\overrightarrow{\mathrm{OA}} \)

= \(2(3 \hat{\mathrm{i}}+2 \hat{\mathrm{j}}-3 \hat{\mathrm{k}})-(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}-4 \hat{\mathrm{k}})\)

= \(4 \hat{\mathrm{i}}+\hat{\mathrm{j}}-2 \hat{\mathrm{k}}\)

Question 10. Projection of vector \(2 \hat{\mathrm{i}}+3 \hat{\mathrm{j}}\) on the vector \(3 \hat{\mathrm{i}}-2 \hat{\mathrm{j}}\) is

1. 0
2. 12
3. \(\frac{12}{\sqrt{13}}\)
4. \(\frac{-12}{\sqrt{13}}\)

Solution: 1. 0

Let \(\vec{a}=2 \hat{i}+3 \hat{j}\) and \(\vec{b}=3 \hat{i}-2 \hat{j}\)

Projection \(\overrightarrow{\mathrm{a}}\) and \(\overrightarrow{\mathrm{b}}=\frac{\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}}{|\overrightarrow{\mathrm{b}}|}=\frac{6-6}{\sqrt{9+4}}=\frac{0}{\sqrt{13}}=0\)

Question 11. The equation of a line passing through the point (1, 1, 1) and parallel to the z-axis is

1. \(\frac{x}{1}=\frac{y}{1}=\frac{z}{1}\)
2. \(\frac{x-1}{1}=\frac{y-1}{1}=\frac{z-1}{1}\)
3. \(\frac{x}{0}=\frac{y}{0}=\frac{z-1}{1}\)
4. \(\frac{x-1}{0}=\frac{y-1}{0}=\frac{z-1}{1}\)

Solution: 4. \(\frac{x-1}{0}=\frac{y-1}{0}=\frac{z-1}{1}\)

Equation of the line passing through (1, 1, 1) and parallel to the z-axis is \(\frac{x-1}{0}=\frac{y-1}{0}=\frac{z-1}{1}\) (Dr’s of line parallel to z-axis are 0, 0, 1)

Question 12. If the sum of numbers obtained on throwing a pair of dice is 9, then the probability that the number obtained on one of the dice is 4, is

1. 1/9
2. 4/9
3. 1/18
4. 1/2

Solution: 4. 1/2

Let E: The number obtained on one of the dice is 4.

E = {(1,4), (2, 4), (3, 4), (5, 4), (6, 4), (4, 1), (4, 2), (4, 3), (4, 5), (4, 6)}

F: Sum of numbers a pair of dice is 9 F: {(6, 3), (3, 6), (5, 4), (4, 5)}

E∩F = {(5, 4). (4, 5)}

P(E/F) = \(\frac{\mathrm{P}(\mathrm{E} \cap \mathrm{F})}{\mathrm{P}(\mathrm{F})}=\frac{\frac{2}{36}}{\frac{4}{36}}=\frac{1}{2}\)

Question 13. Anti-derivative of \(\frac{\tan x-1}{\tan x+1}\) with respect to x is

1. \(\sec ^2\left(\frac{\pi}{4}-x\right)+c\)
2. \(-\sec ^2\left(\frac{\pi}{4}-x\right)+c\)
3. \(\log \left|\sec \left(\frac{\pi}{4}-x\right)\right|+c\)
4. \(-\log \left|\sec \left(\frac{\pi}{4}-x\right)\right|+c\)

Solution: 3. \(\log \left|\sec \left(\frac{\pi}{4}-x\right)\right|+c\)

Let I = \(\int \frac{\tan x-1}{\tan x+1} d x=-\int \frac{1-\tan x}{1+\tan x} d x=-\int \tan \left(\frac{\pi}{4}-x\right) d x\)

= \(\frac{-\log \left|\sec \left(\frac{\pi}{4}-x\right)\right|}{-1}+C=\log \left|\sec \left(\frac{\pi}{4}-x\right)\right|+C\)

Question 14. If (a, b), (c, d), and (e, f) are the vertices of ΔABC and Δ denotes the area of ΔABC, then \(\left|\begin{array}{lll}
\mathrm{a} & \mathrm{c} & \mathrm{e} \\
\mathrm{b} & \mathrm{d} & \mathrm{f} \\
\mathrm{l} & \mathrm{l} & 1
\end{array}\right|\) is equal to

1. 2Δ²
2. 4Δ²
3. 2Δ
4. 4Δ

Solution: 2. 4Δ²

⇒ \(\Delta=\frac{1}{2}\left|\begin{array}{lll}
\mathrm{a} & \mathrm{b} & 1 \\
\mathrm{c} & \mathrm{d} & 1 \\
\mathrm{e} & \mathrm{f} & 1
\end{array}\right|\)

⇒ \(\left|\begin{array}{lll}
\mathrm{a} & \mathrm{b} & 1 \\
\mathrm{c} & \mathrm{d} & 1 \\
\mathrm{c} & \mathrm{f} & 1
\end{array}\right|=2 \Delta\)

⇒ \(\left|\begin{array}{lll}
\mathrm{a} & \mathrm{c} & \mathrm{c} \\
\mathrm{b} & \mathrm{d} & \mathrm{f} \\
1 & 1 & 1
\end{array}\right|=2 \Delta\)

[because |\(\mathrm{A}^{\prime}\)|= |A|]

⇒ \(\left|\begin{array}{lll}
\mathrm{a} & \mathrm{c} & \mathrm{e} \\
\mathrm{b} & \mathrm{d} & \mathrm{f} \\
\mathrm{l} & \mathrm{l} & 1
\end{array}\right|=4 \Delta^2\)

Question 15. The function f(x) = x |x| is

1. Continuous and differentiable at x = 0.
2. Continuous but not differentiable at x = 0.
3. Differentiable but not continuous at x = 0.
4. Neither differentiable nor continuous at x = 0.

Solution: 1. Continuous and differentiable at x = 0.

f(x) = \(x|x|=\left\{\begin{array}{cc}
x^2 ; x \geq 0 \\
-x^2 ; x<0
\end{array}\right.\)

⇒ \(f^{\prime}\left(0^{-}\right)=\lim _{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}=\lim _{h \rightarrow 0} \frac{h^2-0}{h}=0 \in R\)

⇒ \(f^{\prime}\left(0^{-}\right)=\lim _{h \rightarrow 0} \frac{f(0-h)-f(0)}{-h}=\lim _{h \rightarrow 0} \frac{-h^2-0}{-h}=0 \in R\)

∴ \(f^{\prime}\left(0^{+}\right)=f^{\prime}\left(0^{-}\right)\)

So f(x) is differentiable at x=0.

Also \(\mathrm{f}(\mathrm{x})\) is continuous at x=0

Question 16. If \(\tan \left(\frac{x+y}{x-y}\right)=k\), then \(\frac{d y}{d x}\) is equal to

1. \(\frac{-y}{x}\)
2. \(\frac{y}{x}\)
3. \(\sec ^2\left(\frac{y}{x}\right)\)
4. \(-\sec ^2\left(\frac{y}{x}\right)\)

Solution: 2. \(\frac{y}{x}\)

⇒ \(\tan \left(\frac{x+y}{x-y}\right)=k \Rightarrow \frac{x+y}{x-y}=\tan ^{-1} k\)

Differentiate with respect to x, (x-y)\(\left[1+\frac{d y}{d x}\right]-(x+y)\left[1-\frac{d y}{d x}\right]=0\)

⇒ \(\frac{d y}{d x}[(x-y)+(x+y)]=(x+y)-(x-y) \Rightarrow \frac{d y}{d x}=\frac{2 y}{2 x}=\frac{y}{x}\)

Question 17. The objective function Z = ax + by of an LPP has a maximum value of 42 at (4, 6) and a minimum value of 19 at (3, 2). Which of the following is true?

1. a = 9, b = 1
2. a = 5, b = 2
3. a = 3, b = 5
4. a = 5, b = 3

Solution: 3. a = 3, b = 5

Z=ax+by

Let A(4,6), B(3,2)

∵ \(Z_A=42, Z_1=19\)

⇒ 4 a+6 b=42….(1)

and 3 a+2 b=19……(2)

from Equation (1) and (2)

∴ a=3, b=5

Question 18. The corner points of the feasible region of a linear programming problem are (0, 4), (8, 0) and \(\left(\frac{20}{3}, \frac{4}{3}\right)\). If Z = 30x + 24y is the objective function, then (maximum value of Z – minimum value of Z) is equal to

1. 40
2. 96
3. 120
4. 136

Solution: Bonus

Z_max – Z_min = 240- 96 = 144

Statement of Assertion (A) is followed by a statement of Reason (R).

1. Both (A) and (R) are true and (R) is the correct explanation of (A).
2. (B) Both (A) and (R) are true, but (R) is not the correct explanation of (A).
3. (A) is true but (R) is false.
4. (A) is false but (R) is true.

Question 19. Assertion (A): Maximum value of (cos^-1 x)² is π².

Reason (R): Range of the principal value branch of \(\cos ^{-1} \mathrm{x} \text { is }\left[\frac{-\pi}{2}, \frac{\pi}{2}\right] \text {. }\)

Solution: 3. (A) is true but (R) is false.

Assertion : \(\cos ^{-1} x \in[0, \pi], \forall x \in[-1,1]\)

max. of \(\cos ^{-1} x\) is \(\pi\)

∴ max of \(v\left(\cos ^{-1} x\right)^2=\pi^2\)

Hence, Assertion is true.

Reason: The range of the principal value branch of \(\cos ^{-1} \mathrm{x}\) is \([0, \pi]\).

The reason is false.

Question 20. Assertion (A): If a line makes angle α, β, γ with the positive direction of the coordinate axes, then sin²α + sin²β + sin²β = 2

Reason (R): The sum of squares of the direction cosines of a line is 1.

Solution: 1. Both (A) and (R) are true and (R) is the correct explanation of (A).

Assertion: \(l=\cos \alpha \cdot m=\cos \beta \cdot n=\cos \gamma\)

∵ \(l^2+m^2+n^2=1\)

∴ \(\cos ^2 \alpha+\cos ^2 \beta+\cos ^2 \gamma=1\)

⇒ \(\left(1-\sin ^2 \alpha\right)+\left(1-\sin ^2 \beta\right)+\left(1-\sin ^2 \gamma\right)=1\)

⇒ \(\sin ^2 \alpha+\sin ^2 \beta+\sin ^2 \gamma=2\)

The assertion is true.

Reason: Reason is also true as \(l^2+m^2+n^2=1\).

Both (A) and (R) are true and R is the correct explanation of A.

Very Short Answer Type Questions And Answers

Question 1. Evaluate \(\sin ^{-1}\left(\sin \frac{3 \pi}{4}\right)+\cos ^{-1}(\cos \pi)+\tan ^{-1}(1) \text {. }\)

Or,

Draw the graph of cos x, where x [0, 1]. Also, write its range.

Solution:

sin \(^{-1}\left(\sin \frac{3 \pi}{4}\right)+\cos ^{-1}(\cos \pi)+\tan ^{-1}(1)\)

= \(\sin \left(\sin \left(\pi-\frac{\pi}{4}\right)\right)+\cos ^{-1}(\cos \pi)+\tan ^{-1}(1)\) (because Range of \(\sin ^{-1} x\) is \(\frac{-\pi}{2}\), \(\frac{\pi}{2}\)

= \(\sin \left(\sin \frac{\pi}{4}\right)+\cos ^{-1}(\cos \pi)+\tan ^{-1}(1)=\frac{\pi}{4}+\pi+\frac{\pi}{4}=\frac{3 \pi}{2}\)

Or,

Let f(x) = cos^-1 x, where x ∈ [-1, 0]

Range of f(x) is (\(\frac{\pi}{\pi}\))

Question 2. A particle moves along the curve 3y = ax’ + 1 such that at a point with x-coordinate 1, the y-coordinate is changing twice as fast at x-coordinate. Find the value of a.
Solution:

Given cure, \(3 y=a x^3+1, x=1\) and \(\frac{d y}{d t}=2 \frac{d x}{d t} \Rightarrow \frac{d y}{d x}=2\)

Now, differentiating \(3 \mathrm{y}=\mathrm{ax}^3+1\) with respect to x \(\frac{3 \mathrm{dy}}{\mathrm{dx}}=3 \mathrm{ax}^2\)

3 x 2= \(3 \mathrm{a}(1)^2\) (because x=1)

6 = 3a

∴ a = 2

Question 3. If \(\vec{a}, \vec{b}, \vec{c}\) are three non-zero unequal vectors such that \(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{b}}=\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{c}}\), yhen find the angle between \(\vec{a}\) and \(\vec{b}\) – \(\vec{c}\).
Solution:

Given that, \(\vec{a} \cdot \vec{b}=\vec{a} \cdot \vec{c}\)….(1)

Let angle between \(\vec{a}\) and \(\vec{b}-\vec{c}\) be \(\theta\) then \(\cos \theta=\frac{\vec{a} \cdot(\vec{b}-\vec{c})}{|\vec{a}||\vec{b}-\vec{c}|}\)

⇒ \(\cos \theta=\frac{\vec{a} \cdot \vec{b}-\vec{a} \cdot \vec{c}}{|\vec{a}||\vec{b}-\vec{c}|}\)

∵ \(\overrightarrow{\mathrm{a}}, \overrightarrow{\mathrm{b}}, \overrightarrow{\mathrm{c}} \neq \overrightarrow{0} \text { and } \overrightarrow{\mathrm{b}} \neq \overrightarrow{\mathrm{c}}\)

⇒ \(\cos \theta=0=\cos \frac{\pi}{2}\) (from equation (1))

⇒ \(\theta=\frac{\pi}{2}\)

Aliter: Given that, \(\vec{a} \cdot \vec{b}=\vec{a} \cdot \vec{c}\)

⇒ \(\vec{a} \cdot(\vec{b}-\vec{c})=0\)

Since \(\vec{a}, \vec{b}, \vec{c}\) are non-zero unequal vectors

∴ \(\vec{a} \perp(\vec{b}-\vec{c})\)

Hence angle between \(\vec{a}\) and \((\vec{b}-\vec{c})\) is \(\frac{\pi}{2}\).

Question 4. Find the coordinates of points on line \(\frac{x}{1}=\frac{y-1}{2}=\frac{z+1}{2}\) which are at a distance of √11 units from the origin.
Solution:

Given line is \(\frac{x}{1}=\frac{y-1}{2}=\frac{z+1}{2}=\lambda\) (let)

Let arbitrary point on line is \(\mathrm{P}(\lambda, 2 \lambda+1,2 \lambda-1)\)

According to question \(\mathrm{OP}=\sqrt{11}\)

⇒ \(\sqrt{(\lambda-0)^2+(2 \lambda+1-0)^2+(2 \lambda-1-0)^2}=\sqrt{11}\)

⇒ \(\lambda^2+4 \lambda^2+4 \lambda+1+4 \lambda^2-4 \lambda+1=11 \Rightarrow 9 \lambda^2=9 \Rightarrow \lambda= \pm 1\)

Hence required points are (1,3,1)and (-1,-1,-3)

Question 5. If \(y=\sqrt{a x+b} \text {, prove that } y\left(\frac{d^2 y}{d x^2}\right)+\left(\frac{d y}{d x}\right)^2=0\)

Or,

If \(f(x)=\left\{\begin{array}{l}a x+b: 0<x \leq 1 \\ 2 x^2-x: 1<x<2\end{array}\right.\) is a differentiable function in (0, 2) then find the value of a and b.

Solution:

Given that, \(y=\sqrt{a x+b}\)….(1)

Differentiating with respect to x, \(\frac{d y}{d x}=\frac{1}{2 \sqrt{a x+b}} \times a=\frac{a}{2 y}\) [From eq.(1)]

⇒ \(2 y \frac{d y}{d x}=a \Rightarrow 2\left(\frac{d y}{d x}\right)^2+2 y \frac{d^2 y}{d x^2}=0\) [Again differentiating with respect to x]

⇒ \(y \frac{d^2 y}{d x^2}+\left(\frac{d y}{d x}\right)^2=0\)

Or,

Method-1: Given that. \(f(x)=\left\{\begin{array}{l}a x+b: 0<x \leq 1 \\ 2 x^2-x: 1<x<2\end{array}\right.\)

Every differentiable function is always continuous.

If f(x) is continuous at \(\mathrm{x}=1\) then \(\mathrm{RHL}=\mathrm{LHL}=\mathrm{f}(1)\)

R.H.L. \(\lim _{x \rightarrow 1} 2 x^2-x=1\)

f(1)=a+b

∴ a+b=1….(1)

Now, f(x) is differentiable at x=1

So, RHD = LHD

⇒ \(\left[\frac{\mathrm{d}}{\mathrm{dx}}\left(2 \mathrm{x}^2-\mathrm{x}\right)\right]_{\mathrm{x}=1}=\left[\frac{\mathrm{d}}{\mathrm{dx}}(\mathrm{ax}+\mathrm{b})\right]_{\mathrm{x}=1}\)

⇒ \((4 \mathrm{x}-1)_{\mathrm{x}=1}=\mathrm{a} \Rightarrow 4-1=\mathrm{a} \Rightarrow \mathrm{a}=3\)

3 + b = 1 [from eq.(1)]

∴ b = -2

Method-2: Given that, \(f(x)= \begin{cases}a x+b & ; 0<x \leq 1 \\ 2 x^2-x: & 1<x<2\end{cases}\)

Every differentiable function is always continuous. If f(x) is continuous at x=1 then RHL = LHL = f(1)

R.H.L. \(\lim _{x \rightarrow 1} 2 x^2-x=1\)

f(1)=a+b

∴ a+b=1….(1)

Now, f(x) is differentiable at x=1

∴ \(f^{\prime}\left(1^{-}\right)=f^{\prime}\left(1^{-}\right)\)

⇒ \(\lim _{h \rightarrow 0} \frac{f(1+h)-f(1)}{h}=\lim _{h \rightarrow 0} \frac{f(1-h)-f(1)}{-h}\)

⇒ \(\lim _{h \rightarrow 0} \frac{\left\{2(1+h)^2-(1+h)\right\}-(a+b)}{h}=\lim _{h \rightarrow 0} \frac{a(1-h)+b-(a+b)}{-h}\)

⇒ \(\lim _{h \rightarrow 0} \frac{2 h^2+3 h+(1-a-b)}{h}=\lim _{h \rightarrow 0} \frac{-a h}{-h}\)

⇒ \(\lim _{h \rightarrow 0} \frac{h(2 h+3)+(1-a-b)}{h}=a \Rightarrow \lim _{h \rightarrow 0}(2 h+3)+\lim _{h \rightarrow 0} \frac{1-a-b}{h}=a\)

⇒ \(\lim _{h \rightarrow 0}(2 h+3)+\lim _{h \rightarrow 0} \frac{1-1}{h}=a\) [From eq.(1)]

⇒ 3 + 0 = a

⇒ a = 3 and b = -2 [From eq.(1)]

Short Answer Type Questions And Answers

Question 1. Evaluate \(\int_0^{\pi / 4}\) log(1+tan x) dx

Or,

Find \(\int \frac{d x}{\sqrt{\sin ^3 x \cos (x-\alpha)}}\)

Solution:

Let I \(=\int_0^{\frac{\pi}{4}} \log (1+\tan x) d x\)….(1)

⇒ I = \(\int_0^{\frac{\pi}{4}} \log \left[1+\tan \left(\frac{\pi}{4}-x\right)\right] d x \quad\left(\int_0^a f(x) d x=\int_0^a f(a-x) d x\right)\)

⇒ I = \(\int_0^{\frac{\pi}{4}} \log \left\{1+\frac{\tan \frac{\pi}{4}-\tan x}{1+\tan \frac{\pi}{4} \tan x}\right\} d x\)

⇒ I = \(\int_0^{\frac{\pi}{4}} \log \left\{1+\frac{1-\tan x}{1+\tan x}\right\} d x\)

⇒ I = \(\int_0^{\frac{\pi}{1}}\left\{\log \frac{2}{(1+\tan x)}\right\} d x\)

⇒ I \(=\int_0^{\frac{\pi}{4}} \log 2 d x-\int_0^{\frac{\pi}{4}} \log (1+\tan x) d x\)

⇒ \(\mathrm{I}=\int_0^{\frac{\pi}{4}} \log 2 \mathrm{dx}-\mathrm{I}\) (From (1))

⇒ \(2 \mathrm{I}=[\mathrm{x} \log 2]_9^{\frac{\pi}{4}}\)

⇒ \(2 \mathrm{I}=\frac{\pi}{4} \log 2 \Rightarrow \mathrm{I}=\frac{\pi}{8} \log 2\)

Or,

Let \(I=\int \frac{d x}{\sqrt{\sin ^3 x \cos (x-\alpha)}} \Rightarrow I=\int \frac{d x}{\sqrt{\sin ^3 x(\cos x \cdot \cos \alpha+\sin x \cdot \sin \alpha)}}\)

⇒ I = \(\int \frac{d x}{\sqrt{\sin ^4 x(\cot x \cdot \cos \alpha+\sin \alpha)}} \Rightarrow I=\int \frac{\mathrm{cosec}^2 x d x}{\sqrt{\cot x \cdot \cos \alpha+\sin \alpha}}\)

Put \(\cot x \cdot \cos \alpha+\sin \alpha=t^2 \Rightarrow-\mathrm{cosec}^2 x \cdot \cos \alpha d x=2 t d t \Rightarrow \mathrm{cosec}^2 x d x=\frac{-2 t d t}{\cos \alpha}\)

∴ I = \(-\frac{1}{\cos \alpha} \int \frac{2 \mathrm{t} d \mathrm{t}}{\sqrt{\mathrm{t}^2}} \Rightarrow \mathrm{I}=-\frac{2}{\cos \alpha} \int \mathrm{dt}=-\frac{2 \mathrm{t}}{\cos \alpha}+\mathrm{c}\)

I = \(-\frac{2}{\cos \alpha} \sqrt{\cot x \cos \alpha+\sin \alpha}+\mathrm{c} \Rightarrow \mathrm{I}=-\frac{2}{\cos \alpha} \sqrt{\frac{\cos x \cos \alpha+\sin \mathrm{x} \sin \alpha}{\sin x}}+\mathrm{c}\)

I = \(-\frac{2}{\cos \alpha} \sqrt{\frac{\cos (\mathrm{x}-\alpha)}{\sin x}}+\mathrm{c}\)

Question 2. Find \(\int e^{\cot ^{-1} x}\left(\frac{1-x+x^2}{1+x^2}\right) d x\)
Solution:

I = \(\int_{\log \sqrt{2}}^{\log \sqrt{5}} \frac{1}{\left(e^x+e^{-x}\right)\left(e^x-e^{-x}\right)} d x\)

I = \(\int_{\log \sqrt{2}}^{\log \sqrt{3}} \frac{e^{2 x}}{\left(e^{2 x}+1\right)\left(e^{2 x}-1\right)} d x\)

I = \(\int_{\log \sqrt{2}}^{\log \sqrt{3}} \frac{e^{2 x}}{\left(e^{2 x}\right)^2-1} d x\)

Put \(\mathrm{e}^{2 \mathrm{x}}=1 \Rightarrow \mathrm{e}^{2 \mathrm{x}} \mathrm{dx}=\frac{1}{2} \mathrm{dt}\); when \(\mathrm{x}=\log \sqrt{3}\) then t =3; when \(\mathrm{x}=\log \sqrt{2}\) then t=2

Now, \(I=\frac{1}{2} \int_2^3 \frac{d t}{t^2-1}\)

Question 4. Find the general solution of the differential equation (xy-x²)dy = y² dx

Or,

Find the general solution of the differential equation \(\left(x^2+1\right) \frac{d y}{d x}+2 x y=\sqrt{x^2+4}\)

Solution:

Given (xy-x²)dy = y² dx

⇒ \(\frac{d y}{d x}=\frac{y^2}{x y-x^2}\)

Put y = vx and \(\frac{d y}{d x}=v+x \frac{d v}{d x}\)

⇒ v+x \(\frac{d v}{d x}=\frac{v^2 x^2}{v x^2-x^2}\)

⇒ \(v+x \frac{d v}{d x}=\frac{v^2}{v-1}\)

⇒ \(x \frac{d v}{d x}=\frac{v^2}{v-1}-v\)

⇒ \(x \frac{d v}{d x}=\frac{v^2-v^2+v}{v-1}\)

⇒ \(x \frac{d v}{d x}=\frac{v}{v-1} \Rightarrow \frac{v-1}{v} d v=\frac{d x}{x}\)

On integrals both sides,

⇒ \(\int \frac{v-1}{v} d v=\int \frac{d x}{x} \Rightarrow \int\left(1-\frac{1}{v}\right) d v=\int \frac{d x}{x}\)

⇒ \(v-\log v=\log x+\log C\)

⇒ \(\frac{y}{x}-\log \frac{y}{x}=\log x+\log C\) (because y = vx)

⇒ \(\frac{y}{x}=\log \frac{y}{x}+\log x+\log C \Rightarrow \frac{y}{x}=\log C y\)

⇒ \(C y=e^{y / x} \Rightarrow y=C^{\prime} e^{y / x}\) (because \(\frac{1}{C}=C^{\prime}\))

Or,

Given differential equation is \(\left(x^2+1\right) \frac{d y}{d x}+2 x y=\sqrt{x^2+4}\)

⇒ \(\frac{d y}{d x}+\frac{2 x y}{1+x^2}=\frac{\sqrt{x^2+4}}{1+x^2}\)

This is a linear differential equation of the form \(\frac{d y}{d x}+P y=Q\).

where P = \(\frac{2 x}{1+x^2}\) and \(Q=\frac{\sqrt{x^2+4}}{1+x^2}\)

Now. I.F. = \(\mathrm{e}^{\int \mid {p dx}}=\mathrm{e}^{\int \frac{2 \mathrm{x}}{1+\mathrm{x}^2} \mathrm{dx}}=\mathrm{e}^{\left.\log x 1+\mathrm{x}^2\right)}\)

I.F. =1+x²

The solution of a given differential equation is given by

y (I.F.) = \(\int Q \cdot(\text { I.F. }) d x \Rightarrow y\left(1+x^2\right)=\int \frac{\sqrt{x^2+4}}{1+x^2}\left(1+x^2\right) d x\)

⇒ \(y\left(1+x^2\right)=\int \sqrt{x^2+4} d x\)

⇒ \(y\left(1+x^2\right)=\frac{x}{2} \int \sqrt{x^2+4}+2 \log \left|x+\sqrt{x^2+4}\right|+C\)

Question 5. Two balls are drawn at random one by one with replacements from an urn containing an equal number of red balls and green balls. Find the probability distribution of a number of red balls. Also, find the mean of the random variable.

Or,

A and B throw a die alternately till one of them gets a ‘6’ and wins the game. Find their respective probabilities of winning, if A starts the game first.

Solution:

Let X = number of reed balls, X = 0, 1, or 2

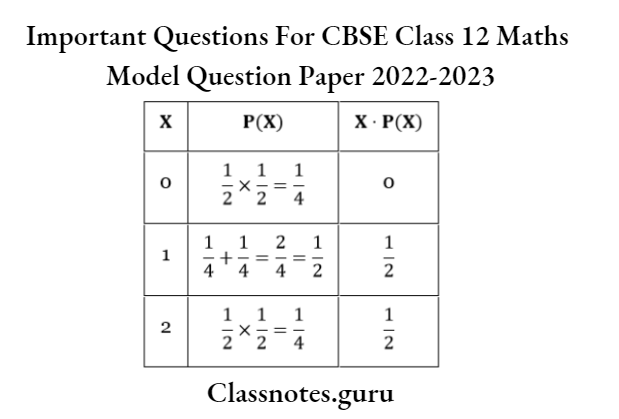
Mean = E(X) = ∑(X) P(X) = 1/2 + 1/2 = 1

Or,

Let S denote the success (getting a ‘6’) and F denote the failure (not getting a’6′)

∴ P(S) = 1/6, P(F) = 5/6

P(A wins in the first throw) = P(S) = 1/6

A gets the third throw, when the first throw by A and the second thrown by B result in failures.

i.e., P(A wins in third throw) = P(FFS) = P(F).P(F).P(S) = \(\frac{5}{6} \times \frac{5}{6}=\frac{1}{6}=\left(\frac{5}{6}\right)^2 \times \frac{1}{6}\)

Similarly P(A wins in the fifth throw) = P(FFFFS) = P(F) P(F) P(F) P(F) P(S)

= \(\left(\frac{5}{6}\right)^4\left(\frac{1}{6}\right)\) and so on

P(A wins) = \(\frac{1}{6}+\left(\frac{5}{6}\right)^2\left(\frac{1}{6}\right)+\left(\frac{5}{6}\right)^4\left(\frac{1}{6}\right)+\ldots \ldots . .=\frac{\frac{1}{6}}{1-\left(\frac{5}{6}\right)^{-2}}=\frac{\frac{1}{6}}{1-\frac{25}{36}}=\frac{\frac{1}{6}}{\frac{11}{36}}=\frac{6}{11}\)

P(B wins) = 1-P(A wins) = \(1-\frac{6}{11}=\frac{5}{11}\)

Question 6. Solve the following linear programming problem graphically. Minimize: Z = 5x + 10y

Subject to constraints:

• x + 2y ≤ 120
• x + y ≥ 60, x – 2y ≥ 0
• x ≥ 0, y ≥ 0

Solution:

Minimize Z = 5x + 10y

Subject to constraints x + 2y ≤120, x + y ≥ 60, x 0, x -2y ≥ 0

So, the feasible region lies in the first quadrant.

∴ The feasible region is ABCDA.

On solving equations x-2y = 0andx + y = 60. we get D(40,20)

And on solving equations x-2y = 0 and x + 2y = 120, we get C(60,30)

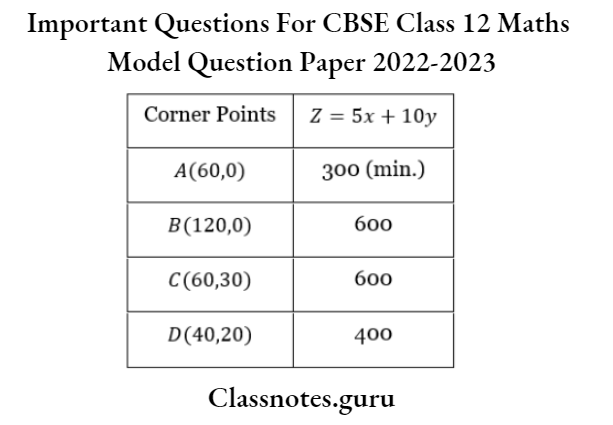
The corner points of the feasible region are. A(60,0), E(120,0) ,C(60,30)and D(40,20).

The values of Z at these points are as follows;

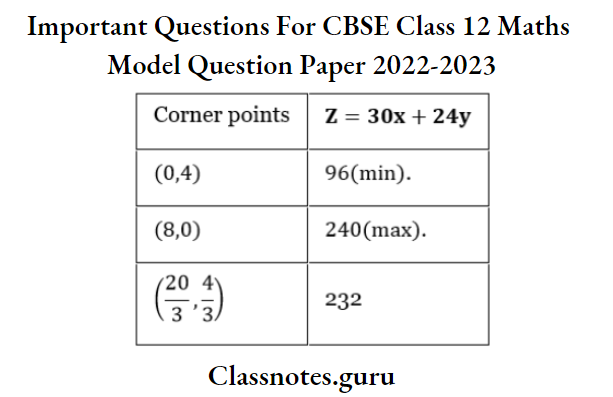
The minimum value of Z is 300 at A(60,0)

Long Answer Type Questions And Answers

Question 1. If \(A=\left[\begin{array}{ccc}-3 & -2 & -4 \\ 2 & 1 & 2 \\ 2 & 1 & 3\end{array}\right], B=\left[\begin{array}{ccc}1 & 2 & 0 \\ -2 & -1 & -2 \\ 0 & -1 & 1\end{array}\right]\), then find AB and use it to solve the following system of equations: x – 2y = 3, 2x – y – z = 2, and -2y + z = 3

Or,

If \(f(\alpha)=\left[\begin{array}{ccc}
\cos \alpha & -\sin \alpha & 0 \\
\sin \alpha & \cos \alpha & 0 \\
0 & 0 & 1
\end{array}\right]\), prove that f(α), f(-β) = f(α-β).

Solution:

Given, \(A=\left[\begin{array}{ccc}-3 & -2 & -4 \\ 2 & 1 & 2 \\ 2 & 1 & 3\end{array}\right], B=\left[\begin{array}{ccc}1 & 2 & 0 \\ -2 & -1 & -2 \\ 0 & -1 & 1\end{array}\right]\)

AB = \(\left[\begin{array}{ccc}
-3 & -2 & -4 \\
2 & 1 & 2 \\
2 & 1 & 3
\end{array}\right]\left[\begin{array}{ccc}
1 & 2 & 0 \\
-2 & -1 & -2 \\
0 & -1 & 1
\end{array}\right]\)

= \(\left[\begin{array}{lll}
1 & 0 & 0 \\
0 & 1 & 0 \\
0 & 0 & 1
\end{array}\right]\)

⇒ AB = \(\mathrm{I}\)

i.e. \(\mathrm{A}=\mathrm{B^-1}\)….(1)

Now, given system of equations, is

x-2y=3

2x-y-z=2

-2y+z=3

This system can be written in matrix equation form as

⇒ \({\left[\begin{array}{ccc}
1 & -2 & 0 \\
2 & -1 & -1 \\
0 & -2 & 1
\end{array}\right]\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{l}
3 \\
2 \\
3
\end{array}\right] }\)

B^T X=C

⇒ X = (B^T)^-1 C = (B^-1)^T C

[(A^T)^-1 = (A^-1)^T]

⇒ X = A^T C

⇒ \({\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{lll}
-3 & 2 & 2 \\
-2 & 1 & 1 \\
-4 & 2 & 3
\end{array}\right]\left[\begin{array}{l}
3 \\
2 \\
3
\end{array}\right] \Rightarrow\left[\begin{array}{l}
x \\
y \\
z
\end{array}\right]=\left[\begin{array}{c}
1 \\
-1 \\
1
\end{array}\right] }\)

∴ x=1, y=-1, z=1

Or,

Given, \(f(\alpha)=\left[\begin{array}{ccc}
\cos \alpha & -\sin \alpha & 0 \\
\sin \alpha & \cos \alpha & 0 \\
0 & 0 & 1
\end{array}\right]\)

f\((-\beta)=\left[\begin{array}{ccc}
\cos (-\beta) & -\sin (-\beta) & 0 \\
\sin (-\beta) & \cos (-\beta) & 0 \\
0 & 0 & 1
\end{array}\right]=\left[\begin{array}{ccc}
\cos \beta & \sin \beta & 0 \\
-\sin \beta & \cos \beta & 0 \\
0 & 0 & 1
\end{array}\right]\)

∴ \(f(\alpha) \cdot f(-\beta)=\left[\begin{array}{ccc}
\cos \alpha & -\sin \alpha & 0 \\
\sin \alpha & \cos \alpha & 0 \\
0 & 0 & 1
\end{array}\right]\left[\begin{array}{ccc}
\cos \beta & \sin \beta & 0 \\
-\sin \beta & \cos \beta & 0 \\
0 & 0 & 1
\end{array}\right]\)

⇒ f\((\alpha) \cdot f(-\beta)=\left[\begin{array}{ccc}
\cos \alpha \cos \beta+\sin \alpha \sin \beta & \cos \alpha \sin \beta-\sin \alpha \cos \beta & 0 \\
\sin \alpha \cos \beta-\cos \alpha \sin \beta & \sin \alpha \sin \beta+\cos \alpha \cos \beta & 0 \\
0 & 0 & 1
\end{array}\right]\)

⇒ f\((\alpha) \cdot f(-\beta)=\left[\begin{array}{ccc}
\cos (\alpha-\beta) & -\sin (\alpha-\beta) & 0 \\
\sin (\alpha-\beta) & \cos (\alpha-\beta) & 0 \\
0 & 0 & 1
\end{array}\right]\)

∴ \(f(\alpha), f(-\beta)=f(\alpha-\beta)\)

Question 2. Find the equations of the diagonals of the parallelogram PQRS whose vertices are P(4, 2, -6), Q(5, -3,1), R(12, 4, 5) and S(11, 9, -2). Use these equations to find the point of intersection of diagonals.

Or,

A-line l passes through point (-1, 3, -2) and is perpendicular to both the lines \(\frac{x}{1}\) = \(\frac{y}{2}\) = \(\frac{z}{3}\) and \(\frac{x+2}{-3}=\frac{y-1}{2}=\frac{z+1}{5}\). Find the vector equation of the line l. Hence obtain its distance from the origin.

Solution:

Given, the vertices of parallelogram PQRS are P(4, 2, -6), Q(5, -3,1), R(12, 4, 5) and S(11,9, -2).

Equation of diagonal PR is \(\frac{x-4}{12-4}=\frac{y-2}{4-2}=\frac{z+6}{5+6}\) i.e. \(\frac{x-4}{8}=\frac{y-2}{2}=\frac{z+6}{11}\)

Equation of diagonal QS is \(\frac{x-5}{11-5}=\frac{y+3}{9+3}=\frac{z-1}{-2-1}\) i.e. \(\frac{x-5}{6}=\frac{y+3}{12}=\frac{z-1}{-3}\)

Now, the coordinates of any point on diagonal PR is T(8λ + 4, 2λ+ 2, 11λ,- 6)

if point T also lies on the diagonal QS. then \(\frac{(8 \lambda+4)-5}{6}=\frac{(2 \lambda+2)+3}{12}=\frac{(11 \lambda-6)-1}{-3} \Rightarrow \frac{8 \lambda-1}{6}=\frac{2 \lambda+5}{12}=\frac{11 \lambda-7}{-3}\)

On solving, we get: λ = 1/2

Hence, the point of intersection of diagonals PR and QR is \(\mathrm{T}\left(8 \times \frac{1}{2}+4,2 \times \frac{1}{2}+2,11 \times \frac{1}{2}-6\right) \text { i.e. T }\left(8,3, \frac{-1}{2}\right)\)

Or,

Equation of a line l passes through point (-1, 3, 2 ) is \(\frac{x+1}{a}=\frac{y-3}{b}=\frac{z+2}{c}\)….(1)

If line l is perpendicular to lines \(\frac{x}{1}=\frac{y}{2}=\frac{z}{3}\) and \(\frac{x+2}{-3}=\frac{y-1}{2}=\frac{z+1}{5}\) both, then a + 2b + 3c = 0 ……(2)

and -3a + 2b + 5c = 0 ….(2)

From equation (2) and (3) \(\frac{a}{10-6}=\frac{b}{-9-5}=\frac{c}{2+6} \text { i.c. } \frac{a}{4}=\frac{b}{-14}=\frac{c}{8}\)

So, Dr’s offline l are 4, – 14, 8 i.e. 2, -7, 4

Equation of line l in cartesian does is \(\frac{x+1}{2}=\frac{y-3}{-7}=\frac{z+2}{4}\)

Equation of line l in vector form is \(\vec{r}=(-\hat{i}+3 \hat{j}-2 \hat{k})+\lambda(2 \hat{i}-7 \hat{j}+4 \hat{k})\)

The coordinates of any point on the line l are P(2λ, -1, + 3, 4λ – 2)

dr’s of line OP are 2λ-1, -7λ + 3, 4λ -2

Since. OP ⊥ l

2(2λ – 1) -7 (-7λ + 3) + 4(4λ – 2) = 0

⇒ 69λ = 31

∴ λ = 31/69

So, the coordinates of point P are P\(\left(\frac{-7}{69}, \frac{-10}{69} \cdot \frac{-14}{69}\right)\)

Now, the distance of line l from the origin is

OP = \(\sqrt{\left(\frac{-7}{69}\right)^2+\left(\frac{-10}{69}\right)^2+\left(\frac{-14}{69}\right)^2}\)

= \(\sqrt{\frac{49+100+196}{(69)^2}}=\sqrt{\frac{345}{(69)^2}}=\sqrt{\frac{5}{69}} \text { units }\)

Aliter:

Distance of line (l) from the origin (0, 0, 0) is D = \(\frac{\left|\vec{b} \times\left(\vec{a}_2-\vec{a}_1\right)\right|}{|\vec{b}|}\)

⇒ D = \(\frac{|(2 \hat{i}-7 \hat{j}+4 \hat{k}) \times[(-\hat{i}+3 \hat{j}-2 \hat{k})-(0 \hat{i}+0 \hat{j}+0 \hat{k})]|}{|2 \hat{i}-7 \hat{j}+4 \hat{k}|}\)

⇒ D = \(\frac{|-2 \hat{i}+\hat{k}|}{|2 \hat{i}-7 \hat{j}+4 \hat{k}|}=\frac{\sqrt{5}}{\sqrt{69}} \text { units }\)

Question 3. Using integration, find the area of the region bounded by line y =√3x, the curve \(y=\sqrt{4-x^2}\), and the y-axis in the first quadrant.
Solution:

Given, line y = A√3X…..(1)

curve y = \(y=\sqrt{4-x^2}\)….(2)

from equation (1) and (2) \(y=\sqrt{4-x^2}\) = 3x

⇒ 4 -X²= 3X²

⇒ x² = 1

⇒ x = 1

from equation (1) when x = 1 ⇒ y = √3

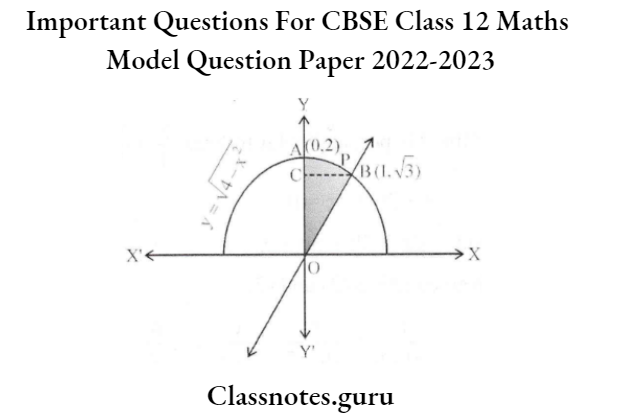
The point of intersection of line (1) and curve (2) is B( 1, √3 )

Required Area = Area of the region APBOA

= Area of the region CBOC + area of the region APBCA

= \(\int_0^{\sqrt{3}} \frac{y}{\sqrt{3}} d y+\int_{\sqrt{3}}^2 \sqrt{4-y^2} d y=\left[\frac{y^2}{2 \sqrt{3}}\right]_0^{\sqrt{3}}+\left[\frac{y}{2} \sqrt{4-y^2}+\frac{4}{2} \sin ^{-1} \frac{y}{2}\right]_{\sqrt{3}}^2\)

= \(\left(\frac{\sqrt{3}}{2}-0\right)+\left[2 \cdot \frac{\pi}{2}-\left\{\frac{\sqrt{3}}{2}+2 \cdot \frac{\pi}{3}\right\}\right]=\frac{\sqrt{3}}{2}+\left[\pi-\frac{\sqrt{3}}{2}-\frac{2 \pi}{3}\right]=\frac{\pi}{3} \text { sq. units }\)

Question 4. A function f : [- 4, 4] → [O. 4] is given by f(x) = \(\sqrt{16-x^2}\) . Show that f is an onto function but not a one-one function. Further, find all possible values of ‘a’ for which f(a) =√7
Solution:

Given, function f:[-4,4] → [0,4] is given by \(f(x)=\sqrt{16-x^2}\)

One-one: f(-4) = \(\sqrt{16-(-4)^2}=0\)

f(4) = \(\sqrt{16-(4)^2}=0\)

⇒ \(f(-4)=f(4) \text { but }-4 \neq 4\)

Since different elements of the domain have the same image in the codomain.

So function f is not a one-to-one function.

Onto: Let \(y \in\lceil 0,4]\) such that \(f(x)=y=\sqrt{16-x^2} ; y \geq 0\)

⇒ x = \(\pm \sqrt{16-\mathrm{y}^2}\)

Here, \(16-y^2 \geq 0\)

⇒ (4-y)(4+y) \(\geq 0\)

⇒  (y-4)(y+4) \(\leq 0\)

⇒  \(-4 \leq y \leq 4 \text { and } y \geq 0\)

So, \(y \in[0,4]\)

Therefore the range of f=[0,4]= codomain of f.

So, function f is onto function.

if f(x)=\(\sqrt{7}\)

⇒ \(\sqrt{16-a^2}=\sqrt{7} \Rightarrow 16-a^2=7 \Rightarrow a^2=9 \Rightarrow a \pm 3\)

Assessment Questions And Answers

Question 1. Engine displacement is the measure of the cylinder volume swept by all the pistons of a piston engine. The piston moves inside the cylinder bore

The cylinder bore in the form of a circular cylinder open at the top is to be made from a metal sheet of area 75 π cm².

Based on the above information, answer the following questions:

1. If the radius of the cylinder is r cm and the height is h cm. then write the volume V of the cylinder in terms of radius r.
2. Find \(\frac{dV}{dr}\)
3. Find the radius of the cylinder when its volume is maximum.

Or,

For maximum volume, h > r. State true or false and justify.

Solution:

Given \(\mathrm{r}\) and \(\mathrm{h}\) be the radius and height of the cylinder bore open at the top.

Then, \(\pi \mathrm{r}^2+2 \pi \mathrm{rh}=75 \pi \mathrm{cm}^2\) (given)

⇒ \(\mathrm{r}^2+2 \mathrm{rh}=75 \Rightarrow \mathrm{h}=\frac{75-\mathrm{r}^2}{2 \mathrm{r}}\)

(1) \(\mathrm{V}=\pi \mathrm{r}^2 \mathrm{~h}\)

V = \(\pi r^2\left(\frac{75-r^2}{2 r}\right)=\frac{\pi}{2}\left[75 r-r^3\right]\) [from equation (1)]

(2) Differential equation (2) with respect to \(\frac{\mathrm{dV}}{\mathrm{dr}}=\frac{\pi}{2}\left[75-3 \mathrm{r}^2\right]\)

(3) For maximum volume \(\frac{\mathrm{dV}}{\mathrm{dr}}=0 \Rightarrow \frac{\pi}{2}\left[75-3 \mathrm{r}^2\right]=0 \Rightarrow \mathrm{r}^2=25 \Rightarrow \mathrm{r}=5\)

Now, \(\frac{d^2 V}{d r^2}=\frac{\pi}{2}[-6 r] \Rightarrow \frac{d^2 V}{d r^2})_{r=5}=-\frac{\pi}{2} \times 30<0\)

Hence, volume is maximum at r=5

Question 37. Recent studies suggest that roughly 12% of the world’s population is left-handed.

Depending on the parents, the chances of having a left-handed child are as follows :

• A: When both father and mother are left-handed: The chances of a left-handed child is 24%.
• B: When the father is right-handed and the mother is left-handed: The chances of a left-handed child is 22%.
• C: When the father is left-handed and the mother is right-handed: The chances of a left-handed child is 17%.
• D: When both father and mother are right-handed: The chances of a left-handed child is 9%.

Assuming that P(A) = P(B) = P(C) = P(D) = 1/4 and L denotes the event that the child is left-handed.

Based on the above information, answer the following questions:

1. Find P(L/C)
2. Find P(L/A)
3. Find P(A/L)

Or,

Find the probability that a randomly selected child is left-handed given that exactly one of the parents is left-handed.

Solution:

Given events are

• A: When both father and mother are left-handed: The chances of a left-handed child is 24%.
• B: When the father is right-handed and the mother is left-handed: The chances of left-handed children is 22%.
• C: When the father is left-handed and the mother is right-handed: The chances of a left-handed child is 17%.
• D: When both father and mother are right-handed: The chances of a left-handed child is 9%.

P(A) = P(B) = P(C) = P(D) = 1/4 and L: Child is left-handed.

Now, \(\mathrm{P}(\mathrm{L} / \mathrm{A})=\frac{24}{100}, \mathrm{P}(\mathrm{L} / \mathrm{B})=\frac{22}{100}, \mathrm{P}(\mathrm{L} / \mathrm{C})=\frac{17}{100}, \mathrm{P}(\mathrm{L} / \mathrm{D})=\frac{9}{100}\)

(1) \(\mathrm{P}(\mathrm{L} / \mathrm{C})=17 \%=\frac{17}{100}\)

(2) \(\mathrm{P}(\overline{\mathrm{L}} / \Lambda)=1-\mathrm{P}(\mathrm{L} / \mathrm{\Lambda})=1-\frac{24}{100}=\frac{76}{100}\)

(3) P(A/L)= \(\frac{P(A) \cdot P(L / A)}{P(A) \cdot P(L / A)+P(B) \cdot P(L / B)+P(C) \cdot P(L / C)+P(D) \cdot P(L / D)}\)

⇒ \(P(A / L)=\frac{\frac{1}{4} \times \frac{24}{100}}{\frac{1}{4} \times \frac{24}{100}+\frac{1}{4} \times \frac{22}{100}+\frac{1}{4} \times \frac{17}{100}+\frac{1}{4} \times \frac{9}{100}}=\frac{24}{24+22+17+9}=\frac{24}{72}=\frac{1}{3}\)

Or

Required probability = \(\mathrm{P}(\mathrm{L} / \mathrm{B} \cup \mathrm{C})=\frac{22}{100}+\frac{17}{100}=\frac{39}{100}\)

Question 3. The use of electric vehicles will curb air pollution in the long run.

The use of electric vehicles is increasing every year and the estimated electric vehicles in use at any time t is given by the function V: V(t) = 1/5 t³ — 5/2 t² + 25t-2 where t represents the time and t = 1, 2, 3 …. corresponds to years 2001, 2002, and 2003 respectively.

Based on the above information, answer the following questions

1. Can the above function be used to estimate the number of vehicles in the year 2000? Justify.
2. Prove that the function V(t) is an increasing function.

Solution:

Given that, \(V(t)=\frac{1}{5} t^3-\frac{5}{2} t^2+25 t-2\)….(1)

where t represents the time and t=1,2,3 \(\ldots\) corresponds to years 2001, 2002, 2003 ….respectively.

1. When \(\mathrm{t}=0\), then \(\mathrm{V}(0)=-2\) that means there is no vehicles are used in the year 2000.
2. Differentiating equation (1) concerning \(V^{\prime}(t)=\frac{3}{5} t^2-5 t+25=\frac{3}{5}\left(t^2-\frac{25}{3} t+\frac{125}{3}\right)\)

⇒ \(V^{\prime}(t)=\frac{3}{5}\left(t^2-\frac{25}{3} t+\left(\frac{25}{6}\right)^2-\left(\frac{25}{6}\right)^2+\frac{125}{3}\right)=\frac{3}{5}\left[\left(t-\frac{25}{6}\right)^2+\frac{875}{36}\right]\)

⇒ \(V^{\prime}(t)>0 \forall t \in 1,2,3 \ldots \ldots .\)

Hence, V(t) is increasing function.