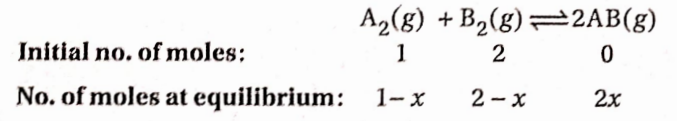CBSE Class 11 Chemistry Notes For Chapter 7 Equilibrium Introduction
Under a given set of experimental conditions, a system is said to be at equilibrium if the macroscopic properties of the system, such as temperature, pressure, concentration, etc. do not show any change with time.
There are two types of equilibria:
Static equilibrium and Dynamic equilibrium. Equilibrium involving physical and chemical changes is dynamic.
A dynamic equilibrium is established when two or more opposing processes occur in a system at the same rate. For example, if the decomposition of hydrogen iodide [2HI(g)⇌ H2(g) +I2(g)] is carried out in a closed vessel, it is found that the reaction is never complete.
At the onset of the reaction, the system contains only hydrogen iodide (reactant) molecules. With time, the concentration of molecules gradually decreases.
In contrast, the concentrations of H2 and I2 (product) molecules gradually increase till a stage is reached at which no further change in concentrations of either the reactants or the products takes place.
At this stage, the reaction appears to have stopped. This state of the system at which no further change occurs is called a state of equilibrium. This state of equilibrium is not static, but it is dynamic because the forward and backward reactions are still going on at the same rate.
Due to this dynamic nature of equilibrium, no change in concentration and other properties of the system occurs at the equilibrium state.
CBSE Class 11 Chemistry Notes Chapter 7 Equilibrium
Read and Learn More CBSE Class 11 Chemistry Notes
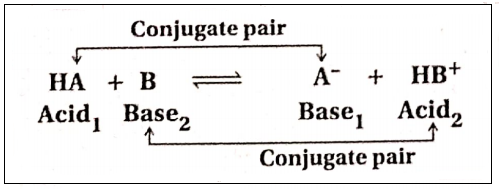
Equilibrium involving chemical reaction (i.e., chemical equilibrium) is represented as:
Reactants; F=± Products The double half arrows indicate that the reactions in both directions are going on simultaneously.
The mixture consisting of reactants and products in the equilibrium state is called an equilibrium mixture. Dynamic equilibrium is also observed in case of physical changes, particularly during the transition of state example melting of solids, vaporization of liquids, etc.
CBSE Class 11 Chemistry Notes For Physical Equilibrium
Equilibrium involving physical processes is called physical equilibrium. Thus, the equilibria attained during the dissolution of a salt, the evaporation of a liquid, etc., are examples of physical equilibria. Different types of physical equilibria are briefly discussed in the following section.
Solid-liquid Equilibrium
At the melting point (or freezing point) of a pure substance, both its solid and liquid phases co-exist and a dynamic equilibrium develops between the two phases:
Solid-liquid When the system with the above equilibrium mixture is heated, the temperature of the system remains constant until the whole solid transforms into liquid. Similarly, if heat is withdrawn from this system, the temperature of the system remains constant until the whole liquid transforms into a solid.
Melting point Or freezing point
At Normal atmospheric pressure, the temperature at which the solid and the liquid states of a pure substance remain in equilibrium is called the normal melting point (or normal freezing point) of the substance.
When the solid and liquid phases of a pure substance are kept in contact with each other at its melting point in a closed insulated container, no exchange of heat takes place between the system and its surroundings.
However, a state of dynamic equilibrium is established between the solid and the liquid phases inside the container. It is also observed that the masses of solid and liquid phases do not change with time and the temperature of the system remains constant.
Example: Let us take some ice cubes together with some water inside a thermos flask at 0°C and 1 atm pressure and leave the mixture undisturbed. After some time it will be seen that the masses of ice and water are not changing with time and also the temperature remains unchanged. This represents an equilibrium between ice and water
Equilibrium: H2O (s)⇌H2O(l)
- Although we observed apparent change inside the thermos flask, a careful examination shows that some activity is still going on between the two phases of water.
- Some molecules of ice convert into water, while at the same time, the same number of molecules of water convert into ice.
- However, as the masses of ice and water remain unchanged, it can be concluded that the two opposite processes (i.e., melting of ice and freezing of water) occur at the same rate.
The rate of melting of ice = The rate of freezing of water
Thus, the equilibrium that is established in the solid-liquid system is dynamic.
Liquid-vapour equilibrium
- The equilibrium between a liquid and its vapor can be better understood if we consider the vaporization of water in a closed vessel. Let us take a closed vessel connected to a manometer and a vacuum pump as shown in
- The closed vessel is first evacuated. The levels of mercury are the same in both the limbs of the manometer.
- Then some pure water is introduced into the vessel and the whole apparatus is kept at room temperature (or any desired temperature by placing it in a thermostat).
- After some time it is seen that the level of mercury in the left limb begins to fall and the right begins to rise and eventually the levels of mercury in both limbs become fixed at two different levels. Under this condition, the system is said to have attained equilibrium

Equilibrium: H2O(Z) ⇌H2O(g)
Class 11 Chemistry Chapter 7 Equilibrium NCERT Notes
Molecular interpretation:
At the initial stage of the experiment, as more and more water changes into vapor (by evaporation), the pressure inside the vessel gradually increases. This is indicated by the fall in mercury level in the left limb of the manometer.
- The molecules of water vapor, so produced, collide among themselves, with the walls of the vessel and also with the surface of the water.
- Water vapor molecules with lower kinetic energy get converted into liquid states when they come in contact with the surface of water. This is called condensation.
- At the beginning of the experiment, the rate of evaporation of water is greater than the rate of condensation of its vapor. However, with time, the rate of condensation increases, and that of evaporation decreases.
- After some time, the rates of evaporation and condensation become equal. It is said that a dynamic equilibrium is established between water and its vapor

At equilibrium: The rate of evaporation = The rate of condensation
- The difference in the levels of mercury in the two limbs gives a measure of the equilibrium vapor pressure or saturated vapor pressure of water at the experimental temperature.
- At a fixed temperature, if a liquid remains in equilibrium with its vapor, then the pressure exerted by the vapor is called the vapor pressure of the liquid at that temperature.
- An equilibrium between a liquid and its vapor is established only in a closed vessel. If the liquid is placed in an open vessel, then its vapor diffuses into the air. Consequently, no equilibrium is established between a liquid and its vapor in an open container.
Solid Vapour equilibrium
In general, solid substances have verylow vapor pressure compared with liquid substances at the same temperature.
- However, some substances, e.g., iodine, camphor, solid CO2, naphthalene, etc. have high vapor pressure even at ordinary temperatures.
- Such substances can convert directly from the solid to the vapor state without passing through the liquid state.
- In this process of transformation of a solid directly to the When sublimation of volatile solids done in a closed vessel, equilibrium is established between the solid and its vapor.
- Example: If we take some solid iodine [I2(s)] in a closed vessel and heat it below its melting point (113.6°C), it is found that the vessel gets filled with violet vapor of iodine.
- Initially the intensity of color increases and eventually it becomes constant. Under this condition, the rate of sublimation of solid iodine is equal to the rate of condensation of iodine vapor. This results in a state of dynamic equilibrium as below,
Equilibrium: I2(s)⇌ I2(g)
Other substances showing this kind of equilibrium are:
- NH4Cl(s)⇌NH4Cl(g)
- Camphor (s)⇌ Camphor (g)
Equilibrium involving dissolution of solid in liquid
- Suppose, at a fixed temperature, an excess amount of a solid substance, say sugar (solute), is added to a definite volume of a suitable solvent (say water) taken in a beaker and then the mixture is stirred well with a glass rod.
- The particles (i.e., molecules in case of non-electrolytes and ions in case of electrolytes) of solute gradually pass into the solvent, thereby increasing the concentration of the solute in the solution. This process is called dissolution of solute.
- Then a stage comes when no more solute dissolves in the solvent. Instead, the solute settles down at the bottom of the beaker i.e., a saturated solution is obtained.
- During the process of dissolution of solute, the reverse process also occurs simultaneously, i.e., the solute particles from the solution get deposited on the surface of the undissolved solute (a process called crystallization).
- Initially, the rate of dissolution of the solid solute is higher than the rate of crystallization of the dissolved solute.
- However, with time, as the solution becomes more and more concentrated, the rate of dissolution decreases, and that of crystallization increases. Finally, the rate of dissolution becomes equal to that of crystallization.
- Under this condition, a state of equilibrium is established between the dissolved solute particles and the undissolved solid solute. The equilibrium can be represented as,
Solute (solid)⇌Solute (in solution)

This state of equilibrium is said to be dynamic because the process of dissolution and crystallization continues as long as the temperature and other external conditions remain unchanged.
The solution obtained at equilibrium is called a saturated solution. The concentration of the saturated solution depends on the temperature.
Equilibrium involving the dissolution of gas in liquid
- The solubility of a gas in a given liquid depends on the experimental temperature and pressure and also on the nature of the liquid and the gas under consideration.
- When a gas (say CO2) comes in contact with a liquid, the molecules of the gas begin to collide with the surface of the liquid. Consequently, some of the gas molecules get attracted by the molecules of the liquid and ultimately pass into the liquid phase.
- % At a fixed temperature and pressure, if a gas is passed continuously through a fixed amount of a liquid kept in a closed vessel, gas molecules get dissolved in the liquid, and eventually, a saturated solution of the gas in the liquid is obtained.
- In this solution, a dynamic equilibrium is established between the dissolved gas and the gas over the liquid surface.
- Under this condition, the rate of dissolution of the gas molecules in the liquid is equal to the rate at which the dissolved gas molecules escape from the solution.
- Thus, it is a dynamic equilibrium; Liquid + Gas Dissolved gas.
Taking CO2 as the gaseous substance it can be represented as:

At a fixed temperature, the amount of gas dissolved in a liquid depends upon the pressure of the gas over the liquid. The concentration of the dissolved gas increases with the increase in the pressure of the gas. Henry’s law demonstrates how the solubility of a gas in a liquid varies with pressure at a given temperature.
Henry’s law:
The mass (or mole fraction) of a gas dissolved in a given mass of a solvent at a given temperature is directly proportional to the pressure of the gas over the solvent.
In a fixed amount of a liquid, if a gas with a pressure of p dissolves by an amount of w, then according to Henry’s law, wp or, w = kp [k is the proportionality constant]
The reason for fizzing out of CO2 gas when a soda water uc is exposed:
In a sealed soda water bottle, CO2 remains dissolved in liquid under high pressure, and an equilibrium exists between the dissolved CO2 and CO2 gas present over the liquid.
- As soon as the bottle is opened, the pressure of CO2 gas over the liquid decreases and becomes equal to the atmospheric pressure.
- Since the solubility of a gas in a liquid is proportional to the pressure of the gas, the solubility decreases considerably because of the lowering of pressure.
- As a result, a large amount of dissolved CO2 escapes from the solution until a new equilibrium is established.
This phenomenon of escaping CO2 gas is associated with a fizzing sound. This is also the reason why a soda water bottle turns flat when left open in the air for some time.

CBSE Class 11 Chemistry Notes For Irrversible And Reversible Reactions
Irreversible reactions
A reaction in which the products formed do not react together to revert to the reactants despite the changes in reaction conditions is called an irreversible reaction.
Examples: When potassium chlorate (KClO3) is heated in an open vessel, potassium chloride (KCl) and oxygen (O2) are produced.
However, KCl and O2 do not react with each other to regenerate KClO3. So, the thermal decomposition of KClO2 is an example of an irreversible reaction.
Most of the ionic reactions are irreversible. For example, when an aqueous solution of KCl is treated with an aqueous AgNO3 solution, a curdy white precipitate of AgCl and KNO3 is produced, but the precipitated AgCl and KNO3 do not react back to AgNO3 and KCl.
⇒ \(\mathrm{AgNO}_3(a q)+\mathrm{KCl}(a q) \rightarrow \mathrm{AgCl}(s) \downarrow+\mathrm{KNO}_3(a q)\)
Characteristics of an irreversible rea
ction:
- The products in an irreversible reaction do not show any tendency to react together. So, the reaction in the opposite direction can never happen. For this reason, an irreversible reaction attains completion in course of time.
- Since an irreversible reaction undergoes completion, the reactants participating in the reaction in equivalent amounts are completely exhausted.
- Irreversible reactions are accompanied by a decrease in Gibbs free energy (i.e., ΔG<0).
Reversible reactions
A Reaction in which the products formed react together to regenerate the reactants, and an equilibrium is established between the reactants and products under the condition of the reaction is called a reversible reaction.
Example: The thermal decomposition of NH4Cl vapor in a closed vessel is a reversible reaction.
⇒ \(\mathrm{NH}_4 \mathrm{Cl}(\text { vapour }) \rightleftharpoons \mathrm{NH}_3(g)+\mathrm{HCl}(g)\)
Explanation:
When NH4Cl(vapor) is heated in a closed vessel at 350°C, it undergoes thermal decomposition, producing NH3 and HCl gases. However, even after a long time, it is observed that the reaction mixture contains not only NH3 and HCl but also NH4Cl vapor.
This proves that the decomposition of NH4Cl vapor in a closed container never gets completed. In another closed vessel, if an equimolar mixture of NH3 and HCl gases is heated at 350°C for a long time, the vessel is found to contain NH4Cl vapor along with NH3 and HCl gases.
This means that the reaction between NH3 and HCl in a closed vessel never gets completed. Thus, it can be concluded that on heating NH4Cl vapor, it decomposes to produce NH3 and HCl gases which again react partially to form NH4Cl vapor.
Hence, the thermal decomposition of NH4Cl vapor is a reversible reaction. The following reactions show reversibility when carried out in a closed vessel.
⇒ \(\mathrm{N}_2(g)+3 \mathrm{H}_2(g) \rightleftharpoons 2 \mathrm{NH}_3(g) ; \mathrm{H}_2(g)+\mathrm{I}_2(g) \rightleftharpoons 2 \mathrm{HI}(g)\)
⇒ \(\mathrm{PCl}_5(g) \rightleftharpoons \mathrm{PCl}_3(g)+\mathrm{Cl}_2(g) ; \mathrm{N}_2 \mathrm{O}_4(g) \rightleftharpoons 2 \mathrm{NO}_2(g)\)
Characteristics of reversible reaction:
In a reversible reaction, both the forward and the backward reactions occur simultaneously. In the forward reaction, the reactants react together to yield the products, while the products react together to produce the reactants in the backward reaction.
NCERT Solutions Class 11 Chemistry Chapter 7 Equilibrium
For example, when an equimolecular mixture of H2 gas and I2 vapor is heated in a closed container, the following reaction takes place—
⇒ \(\mathrm{H}_2(g)+\mathrm{I}_2(g) \rightleftharpoons 2 \mathrm{HI}(g) .\)
Here, the forward reaction is: H2(g) + I2(g) →2HI(g) and the backward reaction is: 2HI(g)→H2(g) + I2(g)
Since a reversible reaction is not complete, the reactants are not completely consumed in such reactions. Instead, a mixture containing both the reactants and the products is obtained.
- Such reactions achieve an equilibrium state when the rate of the forward reaction becomes equal to that of the backwaed reaction.
- At a given temperature and pressure, when a reversible reaction reaches equilibrum, the gibbs free energy change becomes zero i.e., ΔGp, T=0
- Reversibility and irreversibility of chemical reactions when carried out in open and closed containers
- Many chemical reactions that are found to be irreversible when carried out in open containers become reversible when they are carried outin closed containers.
- Different results are obtained when solid calcium carbonate (CaCO3) is heated separately in a closed container and in an open container.
Explanation: On strong heating solid CaCO2 decomposes to solid CaO and CO2 gas. If CaCO3 is decomposed in an open container, CO2 gas escapes from the container into the air, and only solid CaO remains as residue. As the reactant (solid CaCO3) in this reaction gets converted into products completely, the reaction is considered as an irreversible reaction.
H2(g) +I2(g) ⇌ 2HI(g).
If the same quantity of CaCO3 is decomposed in a closed container, some quantity of CaCO3 is still found to remain undecomposed. This is because CO2 produced in the reaction cannot escape from the container.
As a result, a portion of CO2 gas reacts with an equivalent amount of CaO to form CaCO3 again. Hence, in the closed vessel, the reaction occurs reversibly. Consequently, a mixture of CaCO3, CaO, and CO2 is found to be present in the reaction vessel.
⇒ \(\mathrm{CaCO}_3(\mathrm{~s}) \stackrel{\Delta}{\rightleftharpoons} \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})\)
When steam is passed over the red-hot iron, ferrosoferric oxide (Fe3O4) and H2 gas are produced.
Explanation: If the reaction is carried out in an open vessel, the H2 gas produced diffuses into the air. So, Fe3O4 resulting from the reaction cannot have hydrogen gas to react with.
Consequently, the reverse reaction cannot take place. For this reason, at the end of the reaction, only Fe3O4 is left behind as residue in the reaction vessel.
⇒ \(3 \mathrm{Fe}(s)+4 \mathrm{H}_2 \mathrm{O}(\mathrm{g}) \longrightarrow \mathrm{Fe}_3 \mathrm{O}_4(s)+4 \mathrm{H}_2(\mathrm{~g}) \uparrow\)
However, if the reaction is carried out in a closed vessel, the H2 gas produced cannot escape from the container. As a result, a certain amounts of H2 gas and Fe3O4 together and regenerate Fe and H2O.
Hence, in a closed vessel, the reaction occurs both in the forward and reserve. directions, giving a mixture of Fe(s), H2O(g), Fe3O4(s) and H2(g).
⇒ \(3 \mathrm{Fe}(s)+4 \mathrm{H}_2 \mathrm{O}(g) \rightleftharpoons \mathrm{Fe}_3 \mathrm{O}_4(s)+4 \mathrm{H}_2(g)\)
CBSE Class 11 Chemistry Notes For Chemical Equilibrium
Let us consider a hypothetical reversible reaction A +B⇌C+D, Which is started with 1 mol of A and lmol of B in a closed container at a given temperature.
1. At the beginning, the reaction system does not contain C and D (products). It contains only A and B (reactants). So, the reaction occurs only in the forward direction (A + B→C+ D).
2. At the outset of the reaction, since the concentrations of the reactants are maximum, the rate of the forward reaction is also maximum. This is because the rate of a reaction is directly proportional to the concentrations of the reactants.
3. As there are no C and D molecules at the start, the backward reaction (C+D→A + B) does not occur. However, the backward reaction starts occurring with the formation of A and B in the forward reaction. As C and D accumulate is the reaction system, they begin to react together to form A and B.
4. With time, the concentrations of C and D increase, while the concentrations of A and B decrease. As a result, the rate of the backward reaction increases, while that of the forward reaction decreases.
5. Eventually, a moment comes when the rate of the forward reaction becomes equal to the rate ofthe backward reaction.

6. When the rate of the forward reaction is equal to that of the reverse reaction, the reaction is said to have reached the state of equilibrium. However, at equilibrium, the reaction does not stop; instead, both the forward and backward reactions occur simultaneously at the same rate

7. The mixture of reactants and products at the equilibrium of a reaction is called the equilibrium mixture. The concentrations of the reactants and products in the equilibrium mixture are called their equilibrium concentrations. If the conditions {i.e., temperature, pressure, etc.) of the reaction remain undisturbed the relative concentrations of the reactants and products in the equilibrium mixture do not change with time.
Chemical equilibrium
The state of a reversible chemical reaction at a given temperature and pressure when the rates of the forward and reverse reactions become the same, and the concentrations of the reactants and products remain constant with time then the particular state is called the state of chemical equilibrium.
Chemical equilibrium is a dynamic
After the attainment of equilibrium of a reversible chemical reaction, if the reaction system is left undisturbed for an indefinite period at constant temperature and pressure,
- Then the relative amounts of the reactants and the products are found to remain unaltered.
- This observation leads to the impression that a reaction stops completely at equilibrium. However, it has been proved experimentally that the reaction does not cease rather both the forward and the backward reactions continue at the same rate. This is the reason why chemical equilibrium is designated as a dynamic equilibrium.
- Experimental proof of the dynamic nature of chemical equilibrium:
- When some quantity of pure CaCO3 is heated strongly above 827°Cin a closed vessel (A), it decomposes into CaO and CO2, and an equilibrium is established
⇒ \(\mathrm{CaCO}_3(\mathrm{~s}) \rightleftharpoons \mathrm{CaO}(\mathrm{s})+\mathrm{CO}_2(\mathrm{~g})\)
At equilibrium, the temperature and pressure of the reaction vessel remain unaltered with time.
- Now this vessel is connected with another closed vessel 14 containing CO2 at the equilibrium pressure and temperature in such a way that there will be no effect on the equilibrium of the reaction occurring in vessel (A).
- After some time, a small quantity of solid is collected from the vessel (A) and analyzed. The analytical data indicates the presence of 14C in CaCO3.
- This is possible only if some amount of 14CO2 and CaO combine to form Ca14CO3 at equilibrium. At the same time, some quantity of CaCO3 decomposes to produce CaO and CO2.
- So, the pressure on the reaction vessel remains constant. Thus, this experiment proves that even after the attainment of equilibrium, the reactions do not cease, both the forward and the reverse reactions proceed simultaneously at the same rate.
Characteristics of chemical equilibrium
Permanency of chemical equilibrium:
As long as the conditions under which a reaction attains equilibrium remain unaltered, no further change in equilibrium takes place, that is to say, the composition of the equilibrium mixture and other properties of it remains the same with time.
Dynamic nature of equilibrium:
Even after the attainment of equilibrium, a chemical reaction does not cease; both the forward and the reverse reactions continue at equal rates.
Incompleteness of the reaction at equilibrium:
At the equilibrium of a reaction, both the forward and reverse reactions take place simultaneously at the same rate. If any one of these reactions goes to completion, then the term equilibrium becomes irrelevant. Hence, for the equilibrium to exist, the reactions of both directions will have to be incomplete.
Approachability of equilibrium from either direction:
Under a given set of conditions, a reversible reaction attains the same equilibrium state irrespective of whether the reaction is started with its reactants or products.
Example: H2 gas and I2 vapor are allowed to react with each other in a closed vessel at 445°C. Eventually, the following equilibrium is established,
⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{I}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{HI}(\mathrm{g})\)
The equilibrium mixture is found to contain H1, H2, and I2 with mole percents of 80%, 10%, and 10%, respectively. In a separate container with the same volume, if 2 moles of H1 gas are heated at 445°C, then H1 gas decomposes to H2 and I2 gases, and eventually, the following equilibrium is established, 2HI(g) H2(g) + I2(g).
Here also, the equilibrium consists of H1, H2, and I2 with mole percents of 80%, 10%, and 10%, respectively. Thus, the same equilibrium mixture is obtained, no matter whether we start the reaction with HI(g) or H2(g) and l2(g).
Chemical Equilibrium Class 11 Chemistry Notes
A catalyst cannot alter the state of equilibrium:
A catalyst is a substance that enhances the rate of a reaction without being used up in the reaction. A catalyst does not affect the position of equilibrium in a reaction. Its only function is to reduce the time that a reaction takes to reach an equilibrium state.
In the presence of a catalyst, the forward and reverse reactions of a reversible reaction are speeded up to the same extent. Under a given set of conditions, if a reaction is carried out in the presence or absence of a catalyst, then the same equilibrium mixture is obtained. That is, in both cases, the concentrations of the reactants and products are found to be the same.
Homogeneous and heterogeneous equilibria
Homogeneous equilibrium:
An equilibrium in which all the substances, Z.e., reactants, and products, are in the same phase is known as homogeneous equilibrium.
Examples 1. N2(g) + 3H2(g)⇌ 2NH3(g)
2SO2(g) + O2(g) ⇌2SO3(g)
CH3COOH(Z) + C2H5OH(l) ⇌CH3COOC2H5(Z) + H20(l)
Heterogeneous equilibrium:
An equilibrium in which the reactants and products are in different phases is known as heterogeneous equilibrium.
Examples CaCO3(s) ⇌CaO(s) + CO2(g)
2HgO(s)⇌ 2Hg(l) + O2(g)
CBSE Class 11 Chemistry Notes For The Law Of Mass Action
In 1864, C.W. Guldberg and P. Waage formulated a law regarding the dependence of the reaction rate on the concentration of the reactant. This law is known as the law of mass action.
At a constant temperature, the rate of a chemical reaction at any instant during the reaction is directly proportional to the active mass of each of the reactants at that instant.
So, the rate of a reaction increases with the increase in active masses of the reactants, while it decreases with the decrease in active masses of the reactants.
Active mass:
The active mass of a substance is generally considered as the same as its molar concentration. The active mass is expressed in different ways.
- In case of a dissolved substance is a solution, the active mass of the substance is taken to be the same as its molar concentration.
- If a VL solution contains n mol of a substance, then the active mass (or molar concentration) of the substance is n/v .
- In the case of a component gas in a gas mixture, the active mass of the component can be expressed either in terms of its molar concentration or partial pressure in the mixture.
- This is because the partial pressure of a component gas in a gas mixture is directly proportional to its molar concentration.
For a pure solid or liquid, the active mass is always taken as unity (1).
The molar concentration of a pure solid or liquid is directly proportional to its density:
⇒ \(\frac{\text { number of moles of the substance }}{\text { volume of the substance (in } \mathrm{L})}\)
= \(\frac{\text { mass of the substance }}{\text { molar mass of the substance }} \times \frac{1}{\text { volume of the substance (in L) }}\)
= \(\frac{\text { mass of the substance }}{\text { volume of the substance (in } \mathrm{L})} \times \frac{1}{\text { molar mass of the substance }}\)
= \(\frac{\text { density of the substance }}{\text { molar mass of the substance }}\)
As the molar mass of a pure substance is a fixed quantity, the molar concentration of a pure solid or liquid is directly proportional to its density. The density of a pure solid or liquid is constant at a given temperature, so its molar concentration.
Mathematical expression of the law of mass action: Let us consider the following simple chemical reaction in which one mole of A reacts with one mole of B, forming one:
Mole of C: A + B→C According to the law of mass action, at a particular moment during the reaction, the rate of the reaction, or, r = k(A) (B) Where (A) and (B) are the active masses or molar concentration + of A and B, respectively at that moment, and k is proportionality constant, known as the rate constant of the reaction. Equation (1) represents the rate equation of the said reaction. Here is a table is which some reactions and their rate equations are given.

General statement of the law of mass action:
At constant temperature, the rate of a chemical reaction at any instant is directly proportional to the product of molar concentrations (active masses) of the reactants at that instant, each concentration (active mass) term being raised to a power which appears as a stoichiometric coefficient of the species in the balanced chemical equation of the reaction.
Mathematical Form Of The Law Of Mass Action For A Reversible Reaction
Suppose, a reaction is started with ‘ a’ mol of A and ‘b 1 mol of B, and the reaction of A with B leads to the formation of C and D.
Let the reaction occur according to the following equation and form an equilibrium:
aA + bB cC + dD According to the law of mass action, at equilibrium, the rate of forward reaction
(rf)=kf [A]a × [B]b
Or rf = Kf
And that of backward reaction
(rb)∝[D]d × [E]e
Or, rb= kb [D]d× [E]e
Where k and kb are the rate constants of the forward and the backward reactions respectively. (A), (B), (D), and (E) are the respective molar concentrations or active masses (mol.L-1) of A, B, D, and E at equilibrium.
At equilibrium, the rate of the forward reaction (ry) = the rate of the backward reaction (rb).
⇒ \(\text { So, } k_f[A]^a \times[B]^b=k_b[D]^d \times[E]^e\)
⇒ \(\text { or, } \frac{k_f}{k_b}=\frac{[D]^d \times[E]^e}{[A]^a \times[B]^b} \text { or, } \boldsymbol{K}=\frac{[\boldsymbol{D}]^d \times[E]^e}{[A]^a \times[B]^b}\)
The ratio of the two rate constants (fcy and kb) is a constant quantity at a given temperature.
So, K is a constant. The constant ‘K’ is called the equilibrium constant of the said reversible reaction. Equation (1) expresses the mathematical form of the law of mass action of the given reversible reaction.
In the expression of the equilibrium constant, the reaction. concentration terms of the reactants and the products represent their respective molar concentrations at equilibrium. They do not denote their initial concentrations
At constant temperature, the equilibrium constant (K) of a chemical reaction has a definite value. The value of K changes with temperature. This is because the changes of values of kJ- and kJ with the temperature change do not occur to the same extent.
Equilibrium constant
The equilibrium constant of a reaction is the ratio of the product of the active masses of products at equilibrium to the product of the active masses of reactants at equilibrium, with each active mass term raised to a power equal to its stoichiometric coefficient in the balanced equation of the reaction.
The equilibrium constant is also represented as Kc, Kp or Kx depending on whether the active mass is expressed in terms of molar concentrations partial pressure, or mole fraction.
Different kinds of equilibrium constants:

The law of chemical equilibrium:
This law states that when a reversible chemical reaction reaches equilibrium at a particular temperature, the ratio of the product of active masses of the products to that of the reactants, with each active mass term raised to a power equal to its stoichiometric coefficient in the balanced chemical equation is constant.
The mathematical expression for the law of chemical equilibrium can be obtained by applying the law of mass action to a reversible reaction at equilibrium. For a general reversible reaction, aA + bB dD + cE; the mathematical expression can be written as, (constant at a particular temperature) [A]n[B];’
⇒ \(\frac{[D]^d[E]^e}{[\mathrm{~A}]^a[B]^b}=K\) = K (constant at a particular temperature
Expression of the equilibrium constant in case of a heterogeneous equilibrium
At a given temperature, the active mass or molar concentration of a pure solid or liquid is always taken as unity (1). For this reason, in the case of a heterogeneous equilibrium, the active mass or molar concentration term of a pure solid or liquid does not appear in the expression of the equilibrium constant.
Examples: The thermal decomposition of solid CaCO3 in a closed container leads to the following equilibrium:
CaCO3(s) ⇌ CaO(s) + CO2(g)
⇒\(K_c=\frac{[\mathrm{CaO}(\mathrm{s})]\left[\mathrm{CO}_2(\mathrm{~g})\right]}{\left[\mathrm{CaCO}_3(\mathrm{~s})\right]}=\left[\mathrm{CO}_2(\mathrm{~g})\right]\)
[CaCO3(s)] = 1, [CaO(s)] = 1 ] and Kp = PCO2(g)
As the value of Kc or Kp is constant of a given temperature, the molar concentration or the partial pressure of CO2(g) at the equilibrium formed on the decomposition of solid CaC03 at a given temperature is always constant.
The following equilibrium is established during the vaporization of water in a closed vessel:
H2O(l) ⇌ H2O(g)
Here, the equilibrium constant
⇒ \(K_c=\frac{\left[\mathrm{H}_2 \mathrm{O}(\mathrm{g})\right]}{\left[\mathrm{H}_2 \mathrm{O}(l)\right]}=\left[\mathrm{H}_2 \mathrm{O}(\mathrm{g})\right]\)
Therefore, the molar concentration or the partial pressure of water vapor remaining in equilibrium with pure water at a particular temperature is always constant.
Expression of equilibrium constants of some chemical reactions:


Relation Between Different Equilibrium Constants
Relation between Kp and Kc
Let the following reversible gaseous reaction is at equiUbriumin a closed container at a certain temperature
aA(g) + bB(g);=± dD(g) + eE(g) If the molar concentrations of A(g), B(g), D(g) and E(g) at equilibrium be [A], [B], [D] and [£] respectively, and the partial pressures of A(g), B(g), D(g) and E(g) at equilibrium be pA, PiB pD and pp respectively, then
⇒ \(K_c=\frac{[D]^d \times[E]^G}{[A]^a \times[B]^b}\) ……………………(1)
⇒ \(K_p=\frac{p_D^d \times p_E^e}{p_A^a \times p_B^b}\) ……………………(2)
If the reaction mixture behaves as an ideal gas, then the ideal gas equation can be applied to each of the species present in the mixture.
If the pressure, temperature, and volume of n mole of an ideal gas are P, T, and V respectively,
Then \(P V=n R T \quad \text { or, } P=\left(\frac{n}{V}\right) R T=C R T\)
C= Molar concentration
Now by applying this equation to each species of the reaction mixture, we get
⇒ \(p_A=[A] R T, p_B=[B] R T, p_D=[D] R T \text { and } p_E=[E] R T \text {. }\)
Putting the values of pA, pB, PD, and pE into equation (2), we have
⇒ \(K_p=\frac{\{[D] R T\}^d \times\{[E] R T\}^e}{\{[A] R T\}^a \times\{[B] R T\}^b}\)
=\(\frac{[\mathrm{D}]^d \times[E]^e}{[A]^a \times[B]^b}(R T)^{(d+e)-(a+b)}\)
Or, \(K_p=K_c(R T)^{\Delta n}\)
Where, Δn = (d+ e)-(a + b) = the total number of moles of gaseous products – the total number of moles of gaseous reactants.
⇒ \(K_p=K_c(R T)^{\Delta n}\) ………………….(3)
Inequation (3), the value of Δn may be +ve, -ve, or zero. When the number of moles of the gaseous products is greater than, less than, or equal to the number of moles of the gaseous reactants, then the values of Δn become positive, negative, or zero, respectively.
If An is positive, Kp is greater than Kc. If Δn is negative, then the value of Kp is smaller than Kc. If Δn = 0, then Kp and Kc have the same value.
Relation between KP and Kc in case of some chemical and physical changes:

Relation between KP and Kx
Let, at a constant temperature, the following reversible gaseous reaction is at equilibrium in a closed vessel:
⇒ \(a A(g)+b B(g) \rightleftharpoons d D(g)+e E(g)\)
⇒ \(K_p=\frac{p_D^d \times p_E^e}{p_A^a \times p_B^b}\)……………….(1)
⇒ \(K_x=\frac{x_D^d \times x_E^e}{x_A^a \times x_B^b}\)……………….(2)
Where, PA, PB, PD, and PE are the partial pressures of A, B, D, and E respectively, at equilibrium, and xA, xB, xD and xE are their respective mole fractions at equilibrium. The partial pressure of a component gas in a gas mixture is its mole fraction times the total pressure of the mixture.
Hence, the relation between the partial pressures and mole fractions of the different components in the said gas mixture is
PA = xA xP, PB = xB xP, PD = xD xP, and PE = xE x P where P is the total pressure of the gas mixture at equilibrium.
Putting the values of PA, PB ,PD, and PE into equation (1), we have
⇒ \(K_p=\frac{\left(x_D \times P\right)^d \times\left(x_E \times P\right)^e}{\left(x_A \times P\right)^a \times\left(x_B \times P\right)^b}\)
= \(\frac{x_D^d \times x_E^e}{x_A^a \times x_B^b} \times(P)^{(d+e)-(a+b)}\)
= \(K_x \times(P)^{(d+e)-(a+b)}\)
∴ \(K_p=K_x \times P^{\Delta n}\) ……………….(3)
Here Δn = the total number of moles of gaseous products – the total number of moles of gaseous reactants. Equation (3) denotes the relation between Kp and Kx.
Relation between Kc and Kx
Let the following reversible gaseous reaction be at equilibrium at a temperature T and pressure P in a closed vessel
aA(g) + bB{g) ⇌ dD(g) + eE(g)
For this reaction, the relation between Kp and Kc is,
Kp = Kc (RT)Δn………………………..(1)
And the relation between Kp and Kx is
, Kp = Kx (P)Δn………………………..(2)
Where Δn = total number of moles of the gaseous products- total number of moles of the gaseous reactants. From equations (1) and (2), we have, Kc(RT)ÿn = Kx(P)ÿn
∴ , Kc = \(K_x\left(\frac{P}{R T}\right)^{\Delta n}\)………………………(3)
Equation (3) gives the relation between KP and Kk.
Relation Between KP, Kc & Kx
KP = Kc(RT)Δn = KX(P)Δn When Δn = 0 for a reaction
Example: H2(g) +I2(g) ⇌ 2HI(g)
Or, N2(g) + O2(g) 2NO(g)], ⇌ then, KP= Kc = Kx
Characteristics of the equilibrium constant
At constant temperature, the value of the equilibrium constant for each chemical reaction has a definite value. Temperature change brings about an increase or decrease in the value equilibrium constant.
- In the case of an endothermic reaction, the value of the equilibrium constant increases with the rise in temperature, while in the case of an exothermic reaction, the value of the equilibrium constant decreases with the rise in temperature
- The values of KP and Kc are not influenced by pressure. If the temperature remains constant, the increase or decrease in pressure does not alter the values of KP and KP. However, except for a reaction for which Δn = 0, the value of depends upon pressure.
- The value of the equilibrium constant for any reaction neither increases nor decreases in the presence of a catalyst because the rate of both the forward and the backward reactions increase equally.
- The value of the equilibrium constant of a chemical reaction at a given temperature does not depend on the initial concentration of the reactants.
Example:
PCl5(g)⇌ PCl3(g) + Cl2(g)
In this reaction, Kp at 450°C is 0.19. At 450°C, if the reaction is started with PCl5(g) at any concentration, the value of Kp for the reaction is always 0.19.
The value of the equilibrium constant of any reaction depends on how the balanced equation for the reaction is written.
Consider the reaction in which NH3(g) is synthesized from N2 and H2 gases. The balanced equation for this reaction is:
N5(g) + 3H2(g) ⇌ 2NH3(g)
One can also write the equation as
⇒ \(\frac{1}{2} \mathrm{~N}_2(\mathrm{~g})+\frac{3}{2} \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons \mathrm{NH}_3(\mathrm{~g})\)
In case of(1), equilibrium constant
⇒ \(K_{c_1}=\frac{\left[\mathrm{NH}_3\right]^2}{\left[\mathrm{~N}_2\right]\left[\mathrm{H}_2\right]^3},\)
While in case of (2), equilibrium constant, \(K_{c_2}=\frac{\left[\mathrm{NH}_3\right]}{\left[\mathrm{N}_2\right]^{1 / 2}\left[\mathrm{H}_2\right]^{3 / 2}}\)
Thus, the values of Kcl and Kc are not the same. Comparingÿ andÿ gives =
⇒ \(K_{c_1}=K_{c_2}^2 \text {, i.e., } K_{c_2}=\sqrt{K_{c_1}}\)
Suppose, the equilibrium constant of the reaction,
aA + bB dD+eE is K.
NCERT Class 11 Chemistry Chapter 7 Equilibrium Important Topics
If the coefficients of the reactants and products are multiplied by then the equation becomes:
maA + mbB mdD + meE For this equation, the equilibrium constant, K = Km. Again, if the coefficients of the reactants and products are divided by m then the equation becomes:
⇒ \(\frac{1}{m} a A+\frac{1}{m} b B \rightleftharpoons \frac{1}{m} d D+\frac{1}{m} e E\)
For this equation, the equilibrium constant, K” = K1/m
For any reversible chemical reaction, the values of ΔT equilibrium constants for the forward and the reverse reactions are reciprocal to each other.
Example:
⇒ \(\mathrm{N}_2(g)+3 \mathrm{H}_2(g) \rightleftharpoons 2 \mathrm{NH}_3(g)\) for this reaction equilibrium constant
⇒ \(K_c=\frac{\left[\mathrm{NH}_3\right]^2}{\left[\mathrm{~N}_2\right] \times\left[\mathrm{H}_2\right]^3}\)……………………(1)
If the reaction is started with NH3 gas (product), then the reaction is:
2NH3(g) ⇌ N2(g) + 3H2(g)
= \(\frac{\left[\mathrm{N}_2\right] \times\left[\mathrm{H}_2\right]^3}{\left[\mathrm{NH}_3\right]^2}\) ……………………(2)
From equations (1) and (2), we get \(K_c=\frac{1}{K_c{ }^{\prime}}\)
if a given reaction is expressed as the sum of two or more individual reactions, then the equilibrium constant of the given reaction equals the product of the equilibrium constants of the individual reactions.
If reaction (3) =reaction (2) + reaction (1), then equilibrium constant of reaction [3] = equilibrium constant of reaction [2] x equilibrium constant of reaction [1].
Example:
Reaction 1: \(A+B \rightleftharpoons C ; K_1=\frac{[C]}{[A][B]}\)
Reaction 2: \(C \rightleftharpoons D ; K_2=\frac{[D]}{[C]}\)
Reaction 3. \(A+B \rightleftharpoons D ; K_3=\frac{|D|}{[A][B]} .\)
Reaction 1+ reaction 2: \(A+B \rightleftharpoons D\)
∴ \(K_1 \times K_2=\frac{[C]}{[A][B]} \times \frac{[D]}{[C]}=\frac{[D]}{[A][B]}=K_3\)
Unit of the equilibrium constant
The unit of equilibrium constant depends on the difference between the sum of the exponents of the concentration (or partial pressure) terms in the numerator and that is the denominator of the equilibrium constant expression. Suppose, this difference is Δx. If Cl Δx = 0, then neither Kc nor Kp has a unit
Δx = 0, then both Kp and Kc have units.
Kp and Kc for different values of Δx

Values of Δx and the unit of equilibrium constant for some reactions:

The equilibrium constant is unitless:
The term ‘active mass’ mentioned in the law of mass action is unitless. Consequently, Kp or Kc is also unitless. With the help of thermodynamics, it can be shown that the partial pressure of any species present in the expression of Kp is the ratio of measured pressure (P0) of that species at equilibrium to its standard pressure (P0). Since (P/P0) is unitless, Kp is also unitless.
In the case of a pure gas, standard pressure (P0) is taken as 1 atm. Similarly, the concentration of any species present in the expression of Kc is the ratio of the measured concentration (C) of that constituent at equilibrium to its standard concentration (C0). Since (C/C0) is unitless, Kc Is also unitless. The standard concentration (C0) of a solute dissolved in a solution is taken as 1(M) or 1 mol. L-1
Graphical representations of some reversible reactions
1. Reaction: H2(g) +I2 (g) ⇌ 2 HI(g)
Initialconcn.(mol.L-1): 1.0 + 1.0 ⇌ 0
The equilibrium concentration of H2(g) = 0.22mol.L-1

2. Reaction: 2HI(g)+ ⇌ H2(g) +I2 (g)
Initialconcn.(mol.L-1): 2.0 ⇌ 0+ 0
The equilibrium concentration of HI(g) = 1.56 mol. L-1

3. Reaction: N2(g) +3H2(g) ⇌ 2NH3(g)
Initialconcn.(mol.L-1): 1.0 + 3.0 ⇌ 0
The equilibrium concentration of NH3(g) = 1.56 mol. L-1

4. Reaction: H2(g) + CO2(g) ⇌ H2O(g) + CO(g)
Initialconcn.(mol.L-1): 2.0 + 1.0 ⇌ 0 + 0
The equilibrium concentration of H2(g)= 1.6 mol. L-1

Class 11 Chemistry Chapter 7 Equilibrium Summary
Numerical Examples
Question 1. At a particular temperature, the values of rate constants of forward and backward reactions are 1.5× 10-2 L -mol-1 .s-1 and 1.8 × 10-3 L-mol-1.s-1 respectively for the reaction A + B — C + D. Determine the equilibrium constant of the reaction at that temperature
Answer:
Equilibrium constant,
⇒ \(K=\frac{\text { Rate constant of forward reaction }}{\text { Rate constant of backward reaction }}\)
⇒ \(=\frac{1.5 \times 10^{-2} \mathrm{~L} \cdot \mathrm{mol}^{-1} \cdot \mathrm{s}^{-1}}{1.8 \times 10^{-3} \mathrm{~L} \cdot \mathrm{mol}^{-1} \cdot \mathrm{s}^{-1}}=8.33\)
Question 2. At a particular temperature, the equilibrium constant of the reaction 2A + B 2C is 8.0 × 10 L-mol-1. If the rate constant of the reverse reaction is 1.24 L.mol-1 .s-1, then find the value of the rate constant of the forward reaction at that temperature.
Answer:
Equilibrium constant
⇒ \(K=\frac{\text { Rate constant of forward reaction }}{\text { Rate constant of reverse reaction }}\)
∴ The rate constant of the forward reaction = K x rate constant of the reverse reaction =
8 × 104 ×1.24 L-2.mol-2.s-1
= 9. 92 × 104 L-2.mol-2.s-1
Question 3. For the reaction 2SO2(g) +O2(g)⇌ 2SO3(g), Kp = 3×1024 at 25°C. Find the value of ICc.
Answer:
For the given reaction, Δn = 2-(2 + 1) = -1
As given, Kp = 3 × 1024, T = (273 + 25) = 298K and
R = 0.0821 L-atm-mol-1.K-1
We know Kp = Kc(RT)n
Or, 3 × 1024 = Kc(0.0821 × 298)-1
Kc = 3 × 1024 × 0.0821 × 298
= 7.34 × 1025
Question 4. At 1500 K, Kc = 2.6 × 10-9 for the reaction 2BrFg(g) Br2(g) + 5F2(g). Determine the Kp of the reaction at that temperature.
Answer:
For the given reaction, Δn = (1+5)-2 = +4.
As per given data,
Kc = 2.6 × 10-9
T = 1500K
Using R = 0.0821 L-atm-mol-1.K-1
In the equation Kp = Kc{RT)Δn,
Kp = 2.6 × 10-9× (0.0821 × 1500)4
= 0.598
Question 5. Find the temperature at which the numerical values of Kp and Kc will be equal to each other for the reaction \(\frac{1}{2} \mathrm{~N}_2(\mathrm{~g})+\frac{3}{2} \mathrm{H}_2(\mathrm{~g}) \rightleftharpoons \mathrm{NH}_3(\mathrm{~g})\)
Answer:
In the case of the given reaction,
⇒ \(\Delta n=1-\left(\frac{1}{2}+\frac{3}{2}\right)=-1\).
If the numerical values of Kp and Kc be x, then for the above reaction, Kp = x atm-1 and = x(mol. L-1)-1=x L-mol-1
Therefore, Kp = Kc(RT)-1
Or, \(x \mathrm{~atm}^{-1}=x \mathrm{~L} \cdot \mathrm{mol}^{-1} \times \frac{1}{0.0821 \mathrm{~L} \cdot \mathrm{atm} \cdot \mathrm{mol}^{-1} \cdot \mathrm{K}^{-1} \times T}\)
∴ T=12.18K
∴ The numerical values of Kp and Kc for the given reaction will be equal to 12.18K.
Question 6. At 400°C, H2(g) and I2(g) are allowed to react in a closed vessel of 5 L capacity to produce in HI(g). At equilibrium, the mixture in the flask Is found to consist of 0.6 mol H2(g), 0.6 mol I2(g), and 3.5 mol I2(g). Determine the value of Kc of the reaction.
Answer: Equilibrium of the reaction is:
H2(g) + I2(g)⇒2HI(g)
⇒ \(\text { Therefore, } K_c=\frac{[\mathrm{HI}]^2}{\left[\mathrm{H}_2\right] \times\left[\mathrm{I}_2\right]}\)
The capacity of the vessel = 5 L.
Hence, molar concentrations of H2, I2 and HI are:
⇒ \(\left[\mathrm{H}_2\right]=\frac{0.6}{5}=0.12 \mathrm{~mol} \cdot \mathrm{L}^{-1} ;\)
⇒ \(\left[\mathrm{I}_2\right]=\frac{0.6}{5}=0.12 \mathrm{~mol} \cdot \mathrm{L}^{-1} \text { and }[\mathrm{HI}]=\frac{3.5}{5}=0.7 \mathrm{~mol} \cdot \mathrm{L}^{-1}\)
∴ \(K_c=\frac{(0.7)^2}{(0.12) \times(0.12)}=34.03\)
Question 7. At a particular temperature, CO(g) reacts with Cl2(g) in a closed container to produce COCI2(g). In the equilibrium mixture, partial pressures of CO(g), Cl2(g), and COCl2(g) are found to be 0.12, 1.2, and 0.58 atm respectively. Find the value of Kp of the reaction, \(\mathrm{CO}(g)+\mathrm{Cl}_2(\mathrm{~g}) \rightleftharpoons \mathrm{COCl}_2(\mathrm{~g}).\)
Answer:
For the given equilibrium \(K_p=\frac{p_{\mathrm{COCl}_2}}{p_{\mathrm{CO}} \times p_{\mathrm{Cl}_2}}\)
As given, PCO =o 0.12 atm,PCl2= 1.2 atm, and
PCOCl = 0.58 atm at equilibrium.
∴ \(K_p=\frac{0.58}{0.12 \times 1.2}\)
= 4.03
Question 8. In a closed vessel of 1 dm3 capacity, 1 mol N2(g) and 2 mol H2(g) interact to produce 0.8 mol NH3(g) in the equilibrium mixture. What is the concentration of H2(g) in the equilibrium mixture?
Answer:
Equation of the equilibrium reaction:
⇒ \(\mathrm{N}_2(g)+3 \mathrm{H}_2(g) \rightleftharpoons 2 \mathrm{NH}_3(g)\)
It is observed from the reaction that 1 mol N2(g) and 3 mol H2(g) are necessary for the production of 2 mol NH3(g).
Therefore, for the production of 0.8 mol NH3(g), the number of moles of H2(g) required \(=\frac{3}{2} \times 0.8=1.2 \mathrm{~mol}\)
Hence, the number of moles of H2(g) remaining in the equilibrium mixture
= 2-1.2 = 0.8
And its molar concentration =0.8 mol.L-1
Since 1 dm3=1L
Question 9. At 20°C, 0.258mol A(g) and 0.592 mol 5(g) are mixed in a closed vessel of capacity to conduct the following reaction: A(g) + 2B(g) C(g). If 0.035 mol C(g) remains in the equilibrium mixture, then determine the partial pressure of each constituent at equilibrium.
Answer:
According to the equation, 1 mol A(g) reacts with 2 mol 5(g) to produce 1 mol C(g).
Hence, 0.035 mol A(g) and 2 × 0.035 = 0.07 mol 5(g) are required to produce 0.035 mol C(g).
Therefore, equilibrium molar concentrations of different constituents will be as follows:

As given, T = (273 + 20) K = 293 K
∴ At equilibrium,
PA = [A]BT =0.0446 × 0.0821 × 293 = 1.072 atm
PB = [B]5T = 0.1044 × 0.0821 × 293 = 2.511 atm
PC = [C]5T = 7 × 10-3× 0.0821 × 293 = 0.168 atm
Equilibrium Chapter 7 NCERT Solutions for Class 11
Question 10. 2 mol of were heated in a sealed tube at 440°C until the equilibrium was reached. HI was found to be 22% dissociated. Calculate the equilibrium constant for the reaction
2HI(g) ⇌ H2(g) +I2(g)
Answer:
For the given reaction \(K_c=\frac{\left[\mathrm{H}_2\right] \times\left[\mathrm{I}_2\right]}{[\mathrm{HI}]^2}\)
As given in the question, HI(g) undergoes 22% dissociation. Hence, out of 2 mol HI(g),
2 × 0.22 = 0.44 mol HI(g) dissociates.
As obtained from the equation, 2 mol HI(g) dissociates to produce 1 mol H2(g) and 1 mol I2(g). Therefore, 0.44 mol HI(g) dissociates to form 0.22mol of each of H2(g) and I2(g).
If the volume of the container is V L, then the equilibrium molar concentrations of different constituents will be as follows:

= 1.56 /V
∴ \(K_c=\frac{\left[\mathrm{H}_2\right] \times\left[\mathrm{I}_2\right]}{[\mathrm{HI}]^2}=\frac{\frac{0.22}{V} \times \frac{0.22}{V}}{\left(\frac{1.56}{V}\right)^2}\)
= 0.0198
Question 11. 1 mol PCl5(g) is heated in a closed container of 2-litre capacity. If at equilibrium, the quantity of PCl5g) is 0.2 mol then calculate the value of the equilibrium constant for the given reaction
⇒ \(\mathrm{PCl}_5(g)\rightleftharpoons\mathrm{PCl}_3(g)+\mathrm{Cl}_2(g)\)
Answer:
For the above reaction \(K_c=\frac{\left[\mathrm{PCl}_3\right] \times\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}\)
As per the given data, the number of moles of PCl5(g) at equilibrium =0.2. Hence, number of moles of PCl5(g) dissociated =(1- 0.2)
= 0.8.
According to the equation, 1 mol PCl5(g) dissociates to produce 1 mol of each of PCl3(g) and Cl2(g). Therefore, 0.8 mol PCl5(g) will dissociate to give 0.8 mol of each ofPCl3(g) and Cl2(g).
As given, the volume of the container = 2 L. So, the equilibrium concentrations of different constituents are as follows:

∴ \(K_c=\frac{\left[\mathrm{PCl}_3\right] \times\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}=\frac{0.4 \times 0.4}{0.1}\)
=1.6
Question 12. The following reaction is carried out at a particular temperature in a closed vessel of definite volume: CO2(g) +H2(g)s=± CO(g) + H2O(g). Initially, partial pressures of CO2(g) and H2(g) are 2 atm and 1 atm respectively and that of CO2(g) at equilibrium is 1.4 atm. Calculate the equilibrium constant of the reaction.
Answer:
For the given reaction \(K_p=\frac{p_{\mathrm{CO}} \times p_{\mathrm{H}_2 \mathrm{O}}}{p_{\mathrm{CO}_2} \times p_{\mathrm{H}_2}}\)
As given, partial pressure of CO2(g) at equilibrium (Pco2) = 1-4 atm. Hence, decrease in pressure of CO2(g) until the equilibrium is reached =(2- 1.4)atm = 0.6atm According to the equation, 1 mol CO2(g) reacts with 1 mol H2(g) to form 1 mol CO(g) and 1 mol H2O(g).
Therefore, if the pressure of CO2(g) is reduced by 0.6 atm, then the pressure of H2(g) will also be reduced by 0.6 atm and the pressure of each of CO(g) and H2O(g) will be 0.6 atm Hence, partial pressures of different constituents at equilibrium will be as follows:

∴ \(K_p=\frac{p_{\mathrm{CO}} \times p_{\mathrm{H}_2 \mathrm{O}}}{p_{\mathrm{CO}_2} \times p_{\mathrm{H}_2}}\)
= \(\frac{0.6 \times 0.6}{1.4 \times 0.4}\)
= 0.64
Question 13. B(g) + C(g) ⇌ A(g). At constant temperature, a mixture of 1 mol A(g), 2 mol E(g), and 3 mol C(g) is left to stand in a closed vessel of 1 L capacity. The equilibrium mixture is found to contain B(g) of 0.175 molar concentration (mol.L-1). Find the value of the equilibrium constant at that temperature.
Answer:
For the above reaction \(K_c=\frac{[A]}{[B] \times[C]}\)
As given, at equili-brium, [B] =0.175 mol.L-1.
So, 2-0.175=1.825 mol.L-1 of B participated in the reaction.
Now according to the equation, 1 mol B and 1 mol C combine to form 1 mol A. So, 1.825 mol of B and 1.825 mol of C combine to produce 1.825 mol of A. Thus at equilibrium, the concentration of A, B, and C will be

Since the volume of the container = 1L
∴ \(K_c=\frac{[A]}{[B] \times[C]}=\frac{2.825}{0.175 \times 1.175}=13.74\)
Reaction Quotient, Q
The reaction quotient of a reaction has the same form as the equilibrium constant expression. However, the values of molar concentrations (or partial pressures) in the expression of the reaction quotient are the values at any instant of the reaction, whereas these values in the equilibrium constant expression represent the equilibrium values.
Hence, at a particular temperature, the value of the equilibrium constant of a reaction is fixed but that of the reaction quotient is not.
Reaction Quotient:
At constant temperature, the reaction quotient of a reaction at any instant may be defined as the ratio of the product of molar concentrations (or partial pressures) of the products to that of the reactants, with each concentration (or partial pressure) term raised to a power equal to its stoichiometric coefficient in the balanced chemical equation.
The reaction quotient is denoted by Q. When the reaction quotient is expressed in terms of the molar concentration of the reactants and the products, then it is represented by Qc.
The reaction quotient expressed by the partial pressures of the reactants and the products is represented by QP.
- At the start of the reaction, only reactants are present in the reaction system. So, the value of the numerator in the expression of Q (reaction quotient) is zero, and consequently Q = 0.
- If a reaction goes to completion, then only the products are present in the reaction system. So, the value of the denominator in the expression of Q is zero, and hence Q→∞.
If the reaction system contains both the reactants and products, then Q assumes a value in between zero and ∞.
1. For the reaction, aA + bB ⇌ dD + eE, the reaction quotient at any moment
⇒ \(Q_c=\frac{[D]^d \times[E]^e}{[A]^a \times[B]^b}\).
Where (A), (B), (D), and (E) are molar concentrations of A, B, D, and E respectively, at that moment.
For the same reaction, the expression of Kc:
⇒ \(K_c=\frac{[D]_{e q}^d \times[E]_{e q}^e}{[A]_{e q}^a \times[B]_{e q}^b}\)
Where [A]eq, [B]eq, [D]eq, and [E]eq are the molar concentrations of A, B, D, and E respectively, at equilibrium.
2. For the reaction, aA(g) + bB(g) ⇌ dD(g) + eE(g)
The reaction quotient at any instant,
⇒ \(Q_p=\frac{p_D^d \times p_E^e}{p_A^a \times p_B^b}\)
PA, PB, PD, and PE are the partial pressures of A, B, D, and E respectively, at that instant.
For the same reaction, the expression of Kp:
⇒ \(K_p=\frac{\left(p_D\right)_{e q}^d \times\left(p_E\right)_{e q}^e}{\left(p_A\right)_{e q}^a \times\left(p_B\right)_{e q}^b}\)
Where (PA)eq, (PB)eq, (PC)eq, and (Pp)eq are the partial pressures of, B, D, and E, respectively, at equilibrium.
Significance of reaction quotient:
At a particular temperature, by comparing the values of the reaction quotient (Q) of a chemical reaction at any instant and the equilibrium constant (K) of the reaction at that temperature, one can predict the extent to which the reaction has proceeded.
From the values of Q and AT, it is possible to predict whether the reaction has already reached or will reach the state of equilibrium. If equilibrium is not attained, then it can also be predicted whether the reaction will proceed in the forward or backward direction to achieve equilibrium.
Predicting the direction of reaction from the values of Qc and KP


Example: At 700 K, for the following reaction which is carried out in a closed vessel: H2(g) + I2(g) ⇌ 2HI(g). Kc = 55.0 at 700K.
Analysis of the reaction mixture at a given moment during the reaction shows that the molar concentrations of H2(g), I2(g), and HI(g) are 1.8, 2.8, and 0.4 mol-L-1, respectively. Is the reaction at equilibrium at that moment? If not, in which direction will we proceed to attain equilibrium?
Answer:
For the given reaction, \(Q_c=\frac{[\mathrm{HI}]^2}{\left[\mathrm{H}_2\right] \times\left[\mathrm{I}_2\right]}\)
At the moment of analysis \(Q_c=\frac{(0.4)^2}{1.8 \times 2.8}=0.0317\)
Hence, Qc< Kc. Therefore, the reaction is not at equilibrium. To attain equilibrium, the value of Qc will increase until it becomes equal to Kc.
Again, the value of Qc will increase if, in its expression, the value of the Numerator increases and that of the denominator decreases. This is possible if the forward reaction occurs to a greater extent Therefore, the reaction will proceed more in the forward direction to attain equilibrium.
Applications Of Equilibrium Constant
Application-1:
At a given temperature, the value of the equilibrium constant indicates the extent to which a reaction has proceeded before it attains equilibrium.
Explanation:
In the expression equilibrium constant (K) of a reaction, the concentrations of the products appear in the numerator, while that of the reactants appears in the denominator.
Hence, a larger value of equilibrium constant (K) for any reversible reaction signifies higher concentrations of the products than reactants in the equilibrium mixture. This means reactants convert into products to a large extent before attaining equilibrium. Hence, the position of equilibrium lies far to the right.
Example:

Application 2: If the value of the equilibrium constant of a reaction at a given temperature is known, then the concentrations of the reactants and products at equilibrium can be calculated from the known initial concentrations of the reactants
Question 1. At 550 K, the value of the equilibrium constant (K£) is 0.08 for the given
PCl5(g)⇌ PCl3(g)+Cl2(g) occurring in a closed container.
If the equilibrium concentration of PClg(g) and Cl2(g) are 0.75 and 0.32 mol-L-1 respectively, then find the concentration of PCl3(g).
Answer:
For the given reaction \(K_c=\frac{\left[\mathrm{PCl}_3\right] \times\left[\mathrm{Cl}_2\right]}{\left[\mathrm{PCl}_5\right]}\)
As given, [PCl5] = 0.75mol.L-1
[Cl5] = 0.32 mol.L-1 and KC = 0.08.
∴ \(\left[\mathrm{PCl}_3\right]=K_c \times \frac{\left[\mathrm{PCl}_5\right]}{\left[\mathrm{Cl}_2\right]}\)
= \(0.08 \times \frac{0.75}{0.32}=0.187 \mathrm{~mol} \cdot \mathrm{L}^{-1}\)
∴ The equilibrium concentration of PCl3 = 0.187mol.L-1.
CBSE Class 11 Equilibrium Chapter 7 Key Points
Question 2. At a given temperature, Kp is 0.36 for the reaction, 2SO2(g) + O2(g)⇌ 2SO3(g) occurring in a closed vessel. If at equilibrium, the partial pressures of SO2(g) & O2(g) are 0.15 atm & 0.8 atm respectively, then calculate the partial pressure of SO3(g).
Answer:
For the given reaction, Kp \(K_p\)
= \(\frac{\left(p_{\mathrm{SO}_3}\right)^2}{\left(p_{\mathrm{SO}_2}\right)^2 \times p_{\mathrm{O}_2}}\)
As Given Kp =0.36, PSO2= 0.15 atm and Po2= 0.8 atm
∴ (PSO3)2 = Kp ×(PSO2×2 ×Po2 = 036 × (0.15)2 × (0.8)
= 6.48 × 10-3. atm or PSO3= 0.08 atm
Question 3. For the reaction, A2(g)+B2(G) ⇌ 2AB (g), the value of the equilibrium constant is 50 at 100°C. If a flask of 1 L capacity containing 1 mol A2 is connected with another flask of 2 L capacity containing 2 mol B2, then calculate the number of moles of AB at equilibrium.
Answer:
Equilibrium constant, \(K_c=\frac{[\mathrm{AB}]^2}{\left[\mathrm{~A}_2\right] \times\left[\mathrm{B}_2\right]}\)
The equation of the reaction shows that the reduction of x mol of A2 leads to the reduction of x mol of B2 and the formation of 2x mol of AB. Hence, the number of moles of A2, B2, and AB at equilibrium will be as follows.
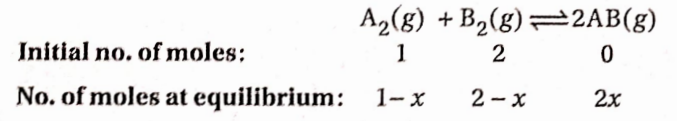
Now if the two flasks are connected, then the total volume of the reaction system becomes (1 + 2)L = 3L.
Hence, at equilibrium \(\left[\mathrm{A}_2\right]=\left(\frac{1-x}{3}\right) \mathrm{mol} \cdot \mathrm{L}^{-1}\)
⇒ \([B]=\left(\frac{2-x}{3}\right) \mathrm{mol}^{-1} \mathrm{~L}^{-1} \text { and }[\mathrm{AB}]=\left(\frac{2 x}{3}\right) \mathrm{mol} \cdot \mathrm{L}^{-1} \text {. }\)
Therefore,
⇒ \(K_c=\frac{\left(\frac{2 x}{3}\right)^2}{\left(\frac{1-x}{3}\right) \times\left(\frac{2-x}{3}\right)}=50 \text { or, } \frac{4 x^2}{(1-x)(2-x)}=50\)
or, 4x2 = 50x2– 1 50x + 100
Or, 46x2– 150x+ 100 = 0
Or, \(x=\frac{150 \pm \sqrt{(150)^2-4 \times 46 \times 100}}{2 \times 46}=2.32 \text { or, } 0.934\)
∴ 2x = 4.64 or, 1.868
By the Initial number of moles of A2 and B2, the number of moles of AB cannot be 4.64. Therefore, the number of moles of AB at equilibrium = 1 .868.
Question 4. At a particular temperature, the value of Kp is 100 for the reaction, \(2 \mathrm{NO}(g) \rightleftharpoons \mathrm{N}_2(g)+\mathrm{O}_2(g)\)occurringin a closed container. If the initial pressure of NO(g) is 25 atm then calculate the partial pressures of NO, N2, and O2 at equilibrium.
Answer:
For the given reaction \(K_p=\frac{p_{\mathrm{N}_2} \times p_{\mathrm{O}_2}}{\left(p_{\mathrm{NO}}\right)^2}\)
After the attainment of equilibrium, if the reduction in pressure of (g) is p atm, then partial pressures of different constituents at equilibrium will be as follows:

[The equation shows that at constant temperature and pressure if the pressure reduction of NO(g) is p atm then the increase in pressure of each of N2(g) and O2(g) will be P/2 atm.
⇒ \(\text { Hence, } K_p=\frac{\left(\frac{p}{2}\right) \times\left(\frac{p}{2}\right)}{(25-p)^2}=100 \text { or, }\left(\frac{p}{25-p}\right)^2=400\) \(\text { or, } \frac{p}{25-p}=20 \text { or, } 21 p=25 \times 20\) ∴ P= 23.8 atm
Therefore, at equilibrium, partial pressure of NO(g) = (25- 23.8) atm = 1.2 atm andpartial pressure of N2(g) = partial pressure Of
⇒ \(\mathrm{O}_2(\mathrm{~g})=\frac{23.8}{2}=11.9 \mathrm{~atm}\)
Application-3: If the value of the equilibrium constant of any reaction at a constant temperature is known, then it is possible to predict whether the mixture of reactants and products is in equilibrium and if not, in which direction the reaction will proceed Formore discussion, to attains equilibrium article number at that 7.6. temperature.
Free Energy Change (ΔG) Of A Reaction and Equilibrium Constant
Suppose, at a temperature of TK, A and B react together to produce D and E according to the following equation: \(a A+b B \rightleftharpoons d D+e E\)
⇒ \(K=\frac{[D]_{e q}^d \times[E]_{e q}^e}{[A]_{e q}^a \times[B]_{e q}^b}[e q=\text { equilibrium }]\)…………………………..(1)
Where (A)eq, (B)eq, (D) eq, and (E )eq are the molar concentrations of A, B, D, and E respectively, at equilibrium.
If ΔG is the from the energy of the system, then with the help of can show that
⇒ \(\Delta G=\Delta G^0+N T \ln \frac{[D]^a \times[B]^b}{[A]^a \times[B]^b}\)
or, ΔG = ΔG0+RT in Q…………………………..(2)
Where,
⇒ \(Q=\frac{[D]^d \times[B]^c}{[A]^a \times[B]^b}\) and (A),(B),(D ), and (E)
Represent the active masses or molar concentrations of A, B, I) and respectively at a given moment during the reaction. Is the reaction quotient.
ΔG° Is the standard free energy change of the reaction. If In a reaction, (lie molar concentration of each of the reactants and products. If unity, then the free energy change of the reaction is called (IK; standard free energy change (ΔG0).
For a reaction at constant temperature and pressure, if—
- ΔG is negative, the reaction is spontaneous as written.
- ΔG is positive, the reaction Is non-spontane O us as written.
- ΔG is zero, the reaction Is at equilibrium.
Now, at the equilibrium of a reaction, ΔG = 0 and
⇒ \(Q=\frac{[D]_{e q}^a \times[B]_{e q}^e}{[A]_{e q}^a \times[B]_{e q}^b}=K \text { [equilibrium constant] }\)
Hence, from equation (2) we get, 0 = ΔG° + RTlnK or, ΔG° = -RTlnK …………………………..(3)
Or,ΔG° = -2.303RTlogK …………………………..(4)
Or, K= e-ΔG0/Rt…………………………..(5)
Equations (3), (4), and (5) represent the relation between equilibrium constant {K) and the standard free energy change (ΔG°) of a reaction at a given temperature.
From equations (2) and (3), we get, ΔG = -RTlnK +RTlnQ
or ΔG = RT In \(\frac{Q}{K}\) …………………………..(6)
Equation (6) is called reaction isotherm.
If the equilibrium constant expression of a reaction is written in terms of the molar concentrations of reactants and products then K=Ke. This gives
⇒ \(\Delta G^0=-R T \ln K_c \text { or, } K_c=e^{-\Delta G^0 / R T}\)
For gaseous reactions, equilibrium constant expression is written in terms of the partial pressures of reactants and products. So, for such reactions K=K and AG° = -RTlnK p or, Kp = e-ΔG0/RT.
In the equation, reactant products taken the standards I molstatel, of 1, the equation the; -RT in K p, the standard state of each reactant and products Is considered to be 1 atm.
Significance Of the reaction ΔG°=-RT in K
- At a particular temperature If the value of AG° is known, then the value of the equilibrium constant (K) can be calculated by using this equation. Similarly, If the equilibrium constant of a reaction at a given temperature is known, then the value of A <7° can be determined by using this reaction.
- If ΔG° < 0, i.e., ΔG° = – ve, then K will be greater than [K> 1]. Under such conditions, the amount of products will be relatively more than that of the reactants present in the equilibrium mixture, i.e., the forward reaction predominates.
- If ΔG° >0, i.e., ΔG = + ve, then K will be less than 1 [K < 1]. In such cases, the concentration of the reactants is greater than that of the products, i.e., the backward reaction predominates.
CBSE Class 11 Chemistry Notes For Free Energy Change (ΔG) Of A Reaction and Equilibrium Constant Numerical Examples
Question 1. For the reaction A(g) + 2B(g) ⇌ 2D(g), ΔG0– 2kJ.mol-1 at 500 K. What is the value of Kp for the reaction ½A(g) + B(g) ⇌ D(g) at that temperature?
Answer:
From the equation ΔG0 = -RTlnKp, we get
⇒ \(\ln K_p=-\frac{\Delta G^0}{R T}=-\frac{2000 \mathrm{~J} \cdot \mathrm{mol}^{-1}}{8.314 \mathrm{~J} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1} \times 500 \mathrm{~K}}\)
=-0.4811
∴ Kp= 0.6181
∴ For the given reaction \(K_p=\frac{\left(p_D\right)^2}{p_A \times\left(p_B\right)^2}\)
If the equilibrium constant for the reaction
⇒ \(\frac{1}{2} A(g)+B(g) \rightleftharpoons D(g) \text { be } K_p^{\prime} \text {, then } K_p^{\prime}=\frac{p_D}{p_A^{1 / 2} \times p_B}\)
∴ \(K_p^{\prime}=\sqrt{K_p} \quad K_p^{\prime}=\sqrt{0.6181}=0.7862\).
Question 2. Find the value of ΔG0 and ICc for the following reaction at 298K. \(\mathrm{NO}(g)+\frac{1}{2} \mathrm{O}_2(g) \rightleftharpoons \mathrm{NO}_2(g)\) Given: standard free energy of formation (ΔG) of NO2 and NO are 52.0 and 87.0 kj.mol-1 respectively.
Answer:
ΔG° of a reaction = ∑ΔGf0 of products -∑ΔGf0 of reactants. For the given reaction,
⇒ \(\Delta G^0=\Delta G_f^0\left(\mathrm{NO}_2\right)-\Delta G_f^0(\mathrm{NO})-\frac{1}{2} \Delta G_f^0\left(\mathrm{O}_2\right)\)
= 52.0- 87.0- 0.0 = -35.0 kl -mol-1
We know that, ΔG0=-RT In Kc
Or, -35 × 103 J-mol-1
= – 8.314 K-1 mol-1 × 298K ln Kc
or; lnKc = 14.126
∴ Kc = 1.365 × 106
CBSE Class 11 Equilibrium Chapter 7 Key Points
Question 3. At 298K, for the attainment of equilibrium of the reaction N2O4(g) ⇌ 2NO25mol of each of the constituents is taken. Due to this, the total pressure of the mixture turns 20 atm. If ΔGf0 (N2O4)= 100 kJ-mol-1 and ΔGf0 (NO2) = 50 k(J-moI_1) then
- Give the value of ΔG of the reaction.
- In which direction will the reaction proceed to equilibrium?
Answer:
For the reaction,
⇒ \(\Delta G^0 & =2 \Delta G_f^0\left(\mathrm{NO}_2\right)-\Delta G_f^0\left(\mathrm{~N}_2 \mathrm{O}_4\right)\)
= \((2 \times 50-100)=0 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}\)
Total number of moles in the reaction mixture =5 + 5 =10
⇒ \(\text { So, } p_{\mathrm{N}_2 \mathrm{O}_4}=\frac{5}{10} \times 20=10 \mathrm{~atm} \& p_{\mathrm{NO}_2}\)
= \(\frac{5}{10} \times 20=10 \mathrm{~atm}\)
Therefore, the Qp of the reaction
⇒ \(\frac{\left(p_{\mathrm{NO}_2}\right)^2}{p_{\mathrm{N}_2 \mathrm{O}_4}}=\frac{(10)^2}{10}=10\)
1. We know, ΔG = ΔG0 + RT]nQp
∴ ΔG =0 + 8.314 × 298 In 10 = 5.706 kJ
Since ΔG0 =0
Again, ΔG0 =-RT In Kp;
So, 0 = -RT In Kp [since ΔG0 = 0]
or, Kp = 1
Since, Qp > Kp, the reaction wall proceeds more toward the left to attain equilibrium.
CBSE Class 11 Chemistry Notes For Determination Of Equilibrium Constants Of Some Reactions
Esterification of alcohol:
CH3COOH(I) + C2H5OH(I) ⇌ CH3COOC2H5(Z) + H2O(Z)
Let at a particular temperature, a mol of acetic acid (CH3COOH) reacts with b mol of ethyl alcohol (C2H5OH) to produce x mol of ethyl acetate (CH3COOC2H5) and x mol of water (H2O) at equilibrium.
According to the balanced equation, for the formation of x mol of ester and x mol of H2O, x mol of CH3COOH and x mol of C2H5OH are required. If the volume of the reaction mixture is by V L, the die concentration of the different species at equilibrium as well as
The expression of the equilibrium constant will be as given in the following table:

Formation of NO(g) from N2(g) and O2(g): For the reaction:
⇒ \(\mathrm{N}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \rightleftharpoons 2 \mathrm{NO}(\mathrm{g})\);
Let us assume, at a constant temperature a mol of N2 reacts with b mol of O2 in a closed container of VL to produce 2xmol of NO at equilibrium.
According to the equation,ifx mol of N2 and O2 reacts with each other, then 2x mol of NO are formed.
Let, the total pressure of the reaction mixture at equilibrium = P. The molar concentrations and partial pressures of the reactants and products at equilibrium and
The expressions of Kp and Kc are given in the table:

Dissociation of PCl5 gas: For the reaction:
PCl5(g)⇌PCl3(g) + Cl2(g);
Let us assume, at a particular temperature, 1 mol of PCl5 gas is heated in a closed vessel of V L capacity so that x mol of PCI5 gets dissociated at equilibrium.
According to the given equation, x mol of PCl5 on dissociation produces x mol of PCl3 and x mol of Cl2.
1. Let us assume that die total pressure of the reaction mixture at equilibrium is P. Hence, the molar concentrations and partial pressures of the reactant and products at equilibrium
The expression equilibrium constants are given in the following table:

Formation of NH3 from N2 and H2:
For the reaction: N2(g) + 3H2(g) v=± 2NH3(g);
Let us assume, at a particular temperature, 1 mol of N2(g) is allowed to react with 3 mol of H2(g) in a closed vessel of V L capacity. After the attainment of equilibrium, if 2x mol of NH3(g) is produced, then according to the equation x mol of N2(g) and 3x mol of H2(g) would be consumed.
Let, the total pressure of the reaction mixture be at equilibrium. Therefore, the molar concentrations and partial pressures of the reactants and product at equilibrium and the expression of equilibrium constants are given in the following table

Thermal decomposition of ammonium carbamate:
Reaction:
⇒\(\mathrm{NH}_2 \mathrm{CO}_2 \mathrm{NH}_4(\mathrm{~s}) \Rightarrow 2 \mathrm{NH}_3(\mathrm{~g})+\mathrm{CO}_2(\mathrm{~g})\).
Let us assume, the l mol of NH2CO2NH4(s) is heated at a particular temperature in a closed vessel of volume VL.
At equilibrium, if x mol of NH2CO2NH4(g) undergoes decomposition, then, according to the equation, 2x mol of NH3 and x mol of CO2, will be produced.
The total pressure of the reaction mixture at equilibrium = P, then the molar concentrations and partial pressures of products and the expression of equilibrium constants are given in the table:

CBSE Class 11 Chemistry Notes For Relation Between Degree Of Dissociation And Degree Of Association With Vapour Density
When a compound undergoes incomplete dissociation, an equilibrium is established between the undissociated molecules of the die compound with the species formed on dissociation.
The extent of dissociation of a compound is usually quantized in terms of the degree of dissociation. It is defined as the ratio of the number of moles of the compound that dissociates to the initial number of moles of the compound.
Similarly, if a compound undergoes association, its extent of association is quantized in terms of degree of association. It is defined as the ratio of the number of moles of die compound associates to the initial number of moles of the compound.
Relation between the vapor density and degree of dissociation
Suppose, each molecule of gas A2 on dissociation forms n molecules of gas B. If the reaction is initiated with 1 mol of gas A in a closed vessel of volume V at constant temperature and pressure, then the die number of moles of A2 and B at equilibrium are as follows-

Where = the degree of dissociation of A2
∴Total number of moles of the mixture at equilibrium =1- α + nα =1 + α(n- 1) mol
At constant temperature and pressure, the total volume of [1 + o(n- 1)] mol of the gas mixture is [1 + α(n- 1)× V].
Let the actual density and vapor density of gas A2 before dissociation be d and D, respectively. Since the volume of the system increases on the dissociation of gas A2 the density and vapour density of the gas mixture at equilibrium will be different from the actual values of these two quantities for gas A2.
Suppose, the observed density and vapor density of the gas mixture at equilibrium be d’ and D’, respectively.
Since the mass of the system remains the same, we can write
d × V = d’ × V[1 + α(n- 1)]
Or, \(\frac{d}{d^{\prime}}=1+\alpha(n-1)\)……………………………….(1)
\(\frac{D}{D!}=1+\alpha(n-1)\)……………………………….(1)
∴ \(\frac{d}{d^{\prime}}=\frac{D}{D^{\prime}}\)
From equation (1) we get \(\alpha=\frac{d-d^{\prime}}{d^{\prime}(n-1)}\)
From equation (2) we get \(\alpha=\frac{d-d^{\prime}}{d^{\prime}(n-1)}\)
Relation between the vapor density and degree of association
Let us consider n mol of gas A associated to form 1 mol of gas B. If the reaction is initiated with 1 mol of gas A in a closed vessel of volume V at constant temperature and pressure,
Then the number of moles of A and B at equilibrium are as follows:

where a = the degree of association of A
∴ Total number of moles of the mixture at equilibrium
⇒ \(=1-\alpha+\frac{\alpha}{n}=1-\alpha\left(1-\frac{1}{n}\right) \mathrm{mol}\)
At constant temperature and pressure, the total volume of
⇒ \(\left[1-\alpha\left(1-\frac{1}{n}\right)\right]\) mol gas
⇒ \(\left[1-\alpha\left(1-\frac{1}{n}\right) \times v\right]\)
Now, let actual density and vapor density of gas A before association be d and D respectively.
Chemical Equilibrium Class 11 NCERT Solutions
If the observed density and vapor density of the gas mixture at equilibrium are d’ and D’, respectively, then—
⇒ \(d \times V=d^{\prime} \times V\left[1-\alpha\left(1-\frac{1}{n}\right)\right]\)
Or, \(\frac{d}{d^{\prime}}=1-\alpha\left(1-\frac{1}{n}\right)\)…………………………(1)
⇒ \(\frac{D}{D^{\prime}}=1-\alpha\left(1-\frac{1}{n}\right)\) …………………………(2)
Since ⇒ \(\frac{d}{d^{\prime}}=\frac{D}{D^{\prime}}\)
From equation (1) we get
⇒ \(\alpha=\frac{d^{\prime}-d}{d^{\prime}\left(1-\frac{1}{n}\right)}\)
From equation (2) we get
⇒ \(\alpha=\frac{D^{\prime}-D}{D^{\prime}\left(1-\frac{1}{n}\right)}\)
CBSE Class 11 Chemistry Notes For Chapter 7 Equilibrium Ionic Equilibrium Introduction
The compounds that conduct electricity in a molten state or solution and dissociate chemically into new substances are called electrolytes.
Various acids Example: HCl, HNO3, H2SO4),
Bases Example: NaOH, KOH)
Salts Example: NaCl, KCl, CuSO4, AgNO3)
Dissolve in water to conduct electricity. Hence, these are electrolytes.
On the both er hand, substances that are unable to conduct electricity either in a molten state or in solution are known as non-electrolytes. Glucose, sugar, alcohol, benzene, etc., are examples of non-electrolytes. In an aqueous solution (or in a molten state), electrolytes undergo spontaneous dissociation or ionization to produce positively and negatively charged particles or ions.
This is known as electrolytic dissociation or ionization. The ions can conduct electricity in the solution. In a particular solvent and at a certain temperature and concentration, the degree of dissociation or ionization of any electrolytic substance depends on the nature of that substance. The fraction of the total amount of dissolved electrolyte that exists in a dissociated or ionized state is called the degree of dissociation or ionization.
Depending on the degree of ionization in an aqueous solution, electrolytes can be classified into two categories Strong electrolytes and Weak electrolytes. The electrolytes which dissociate almost completely in aqueous solution at all concentrations are called strong electrolytes.
Strong acids Example: HCl, HNO3, H2SO4 ),
Strong bases Example: NaOH, KOH
Most of the salts Example: NaCl, KC1, NH4Cl, CuSO4 )
Are strong electrolytes. Electrolytes that dissociate partially aqueous solution are called weak electrolytes.
Some salts Example: BaSO4, HgCl2
Most of the organic acids Example: HCOOH, CHgCOOH
A few in organic bases Example: Fe(OH)3, NH3 ),
Some inorganic acids Example: HCN, and H2CO3 ) are weak electrolytes. In aqueous solutions, strong electrolytes undergo almost complete ionization.
Hence, such ionisations are represented by a single arrow(→)
For example:
NaCl(aq)→ Na+(aq) + Cl–(aq); HCl(aq)→H+(aq) + Cl– (aq).
On the other hand, weak electrolytes undergo partial ionization in aqueous solution. Hence, such ionisations are reversible. Consequently, in an aqueous solution of weak electrolytes, a dynamic equilibrium exists between the dissociated ions and unionized molecules. This is known as ionic equilibrium.
Due to its irreversible nature, such ionisations are represented by double arrows(→).
For example:
HCN(aq) ⇌ H+(ag) + CN–(aq); CH3COOH(aq) ⇌ CH3COO–(aq) + H+(aq)