vijayad

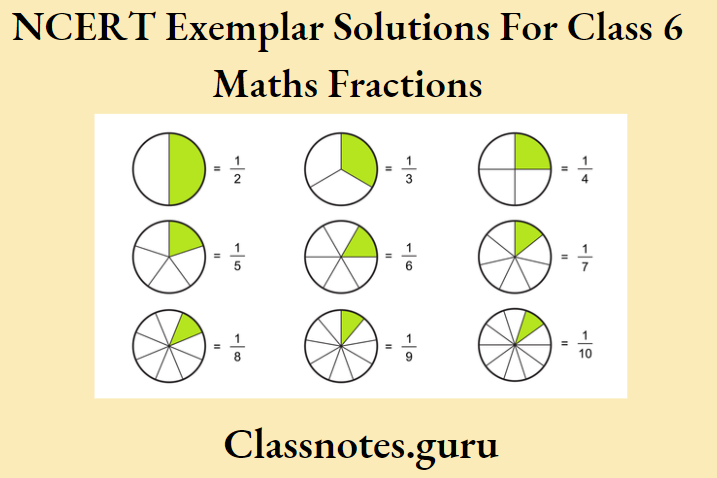
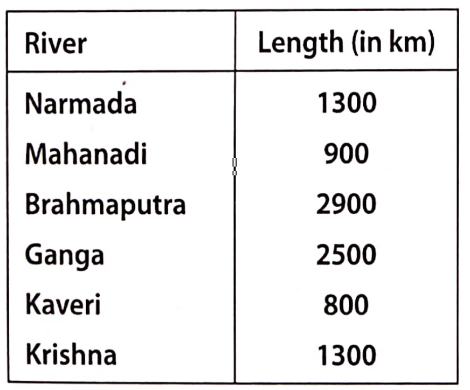
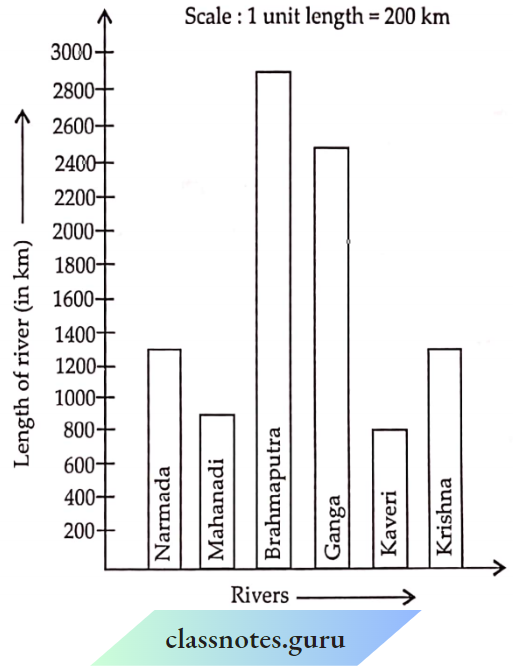
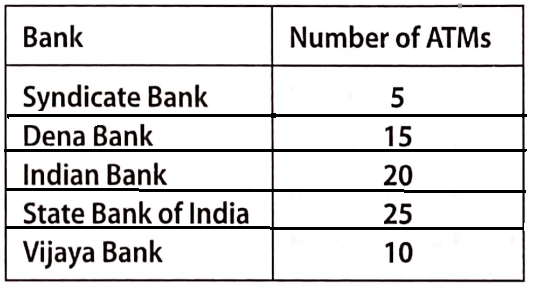
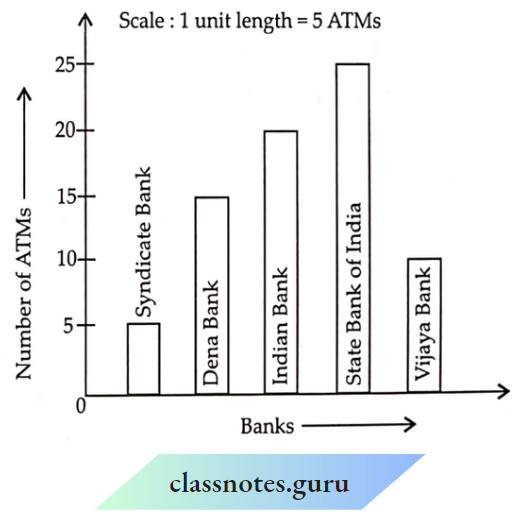
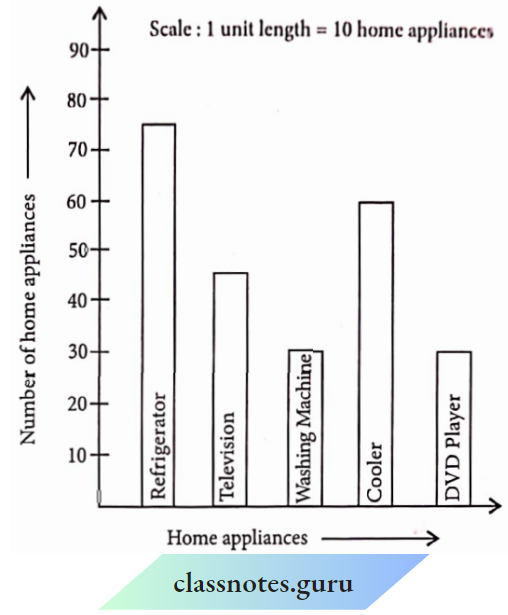
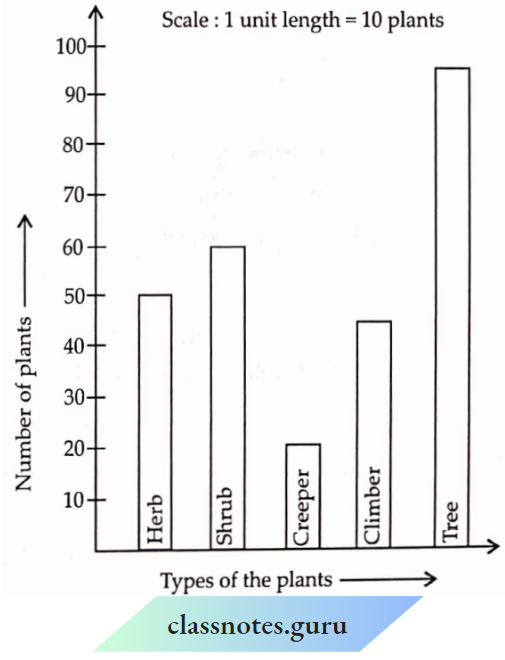
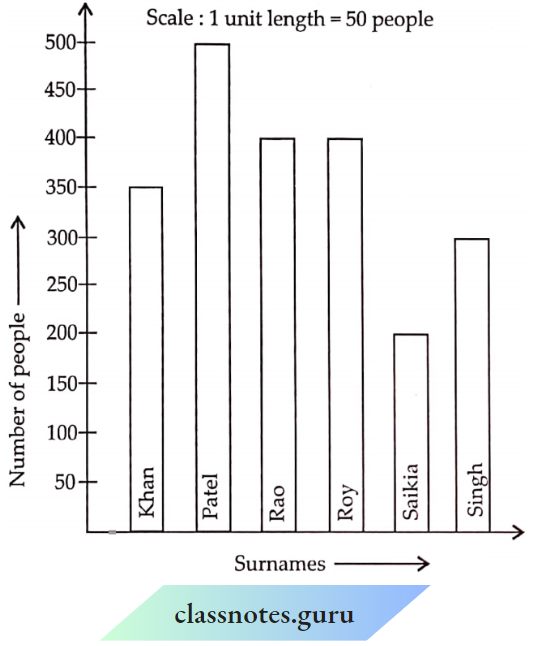
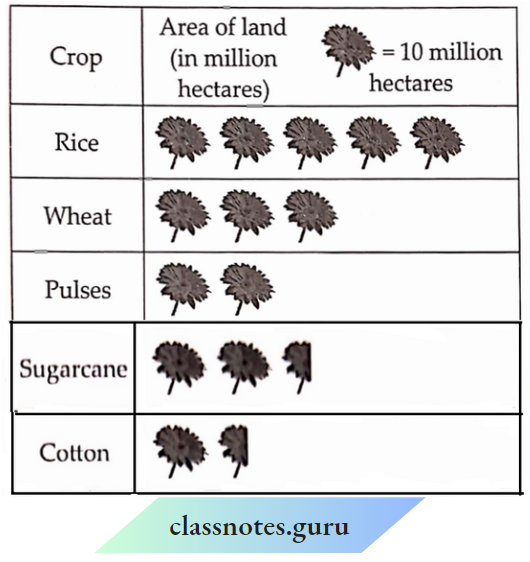
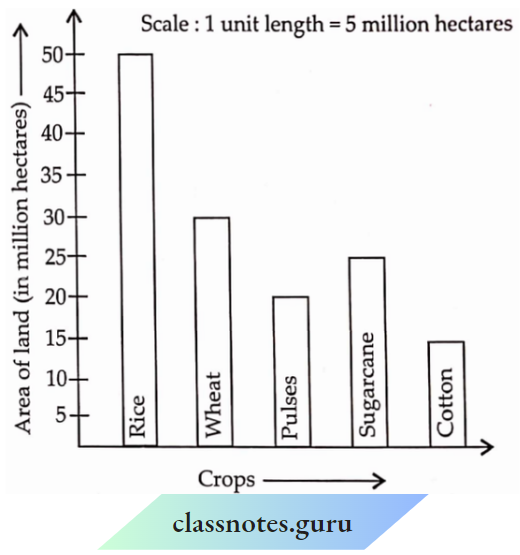
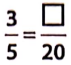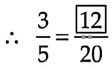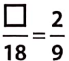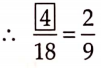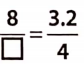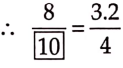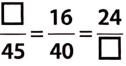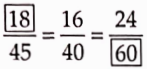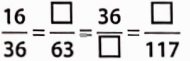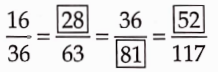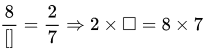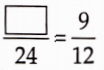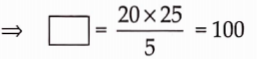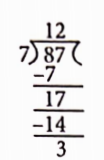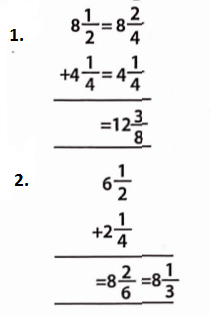Introduction To Graphs Introduction

The purpose of the graph is to show numerical facts in visual form for their better and quicker understanding. It is especially very useful when there is a trend or comparison to be shown.

A Line Graph

It is a graph which displays data that changes continuously over periods.

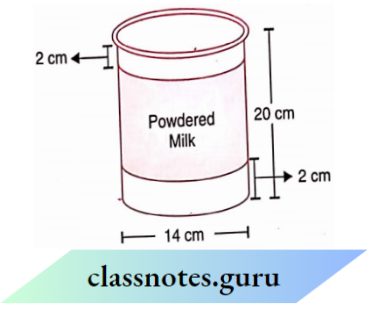
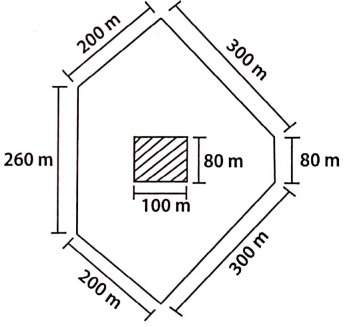
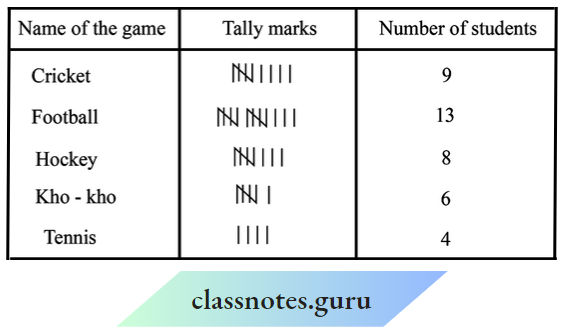
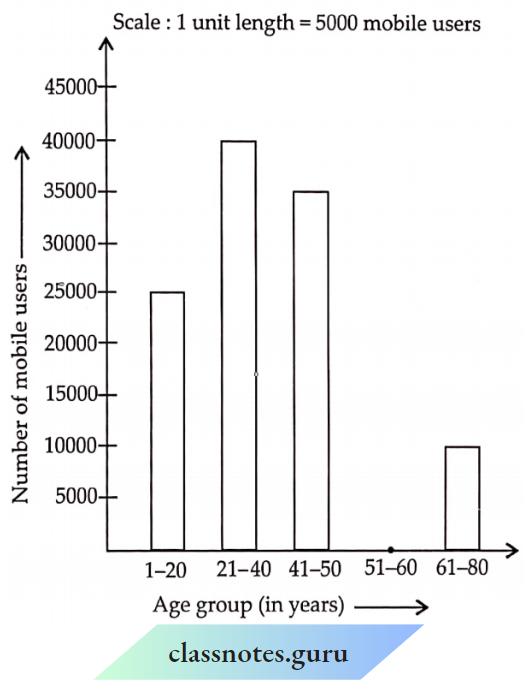
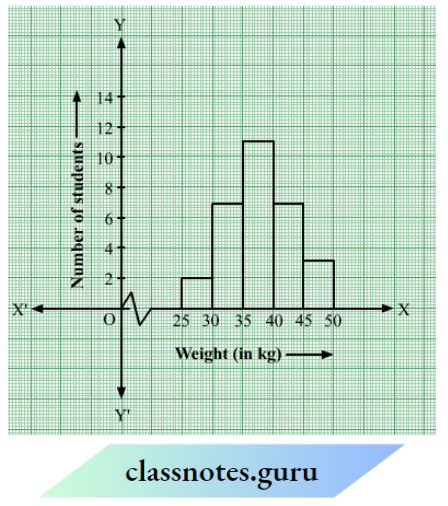
Question What is the information that you gather from the given histogram? Try to list them out.
Solution:

This histogram illustrates the distribution of weights (in kg) of 40 persons in a locality. The information that we gather from this histogram is as follows :

A maximum number of persons in the locality have their weights (in kg) in the interval 50-55.

The minimum number of persons in the locality have their weights (in kg) in the interval 40- 45

NCERT Solutions for Class 8 Maths Chapter 13 Introduction to Graphs

Read and Learn More NCERT Solutions For Class 8 Maths

Introduction To Graphs Exercise 13.1

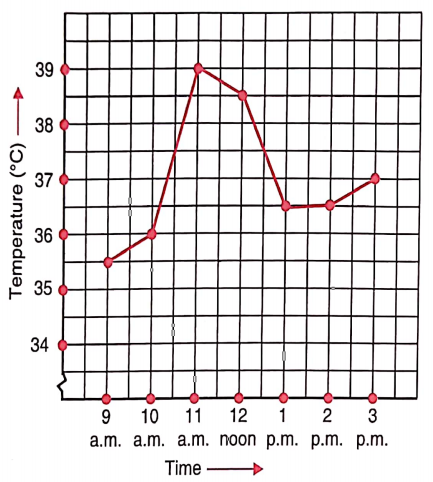
Question 1. The following graph shows a patient’s temperature in a hospital, recorded every hour.

1. What was the patient’s temperature at 1 p.m.?
2. When was the patient’s temperature 38.5°C?
3. The patient’s temperature was the same two times during the period given. What were these two times?
4. What was the temperature at 1.30 p.m.? How did you arrive at your answer?
5. During which period did the patient’s temperature show an upward trend?

Solution:

The patient’s temperature at 1 p.m. was 36.5°C.

The patient’s temperature was 38.5°C at 12 noon

The two times when the patient’s temperature was the same were 1 p.m. and 2 p.m.

The temperature at 1.30 p.m. was 36.5°C.

From the graph, we see that the temperature was constant from 1 p.m. to 2 p.m. Since 1.30 p.m. comes in between 1 p.m. and 2 p.m., therefore we arrived at our answer.

The patient’s temperature showed an upward trend during the periods 9 a.m. to 10 a.m., 10 a.m. to 11 a.m. and 2 p.m. to 3 p.m.

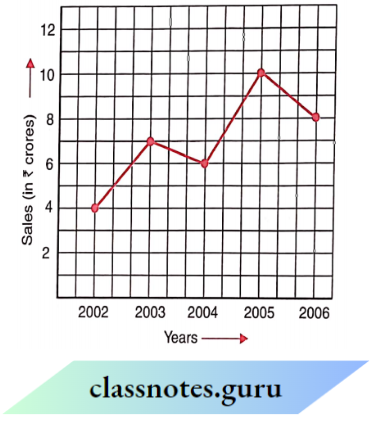
Question 2. The following line graph shows the yearly sales figures for a manufacturing company.

1. What were the sales in
   1. 2002
   2. 2006?
2. What were the sales in
   1. 2003
   2. 2005?
3. Compute the difference between the y sales in 2002and 2006.
4. In which year was the greatest difference between the sales compared to the previous year?

Solution:

The sales in

1. 2002 were ₹ 4 crores and in
2. 2006 were ₹ 8 crores.

The sales in

1. 2003 were ₹ 7 crores and in
2. 2005 were ₹ 10 crores.

The difference between the sales in 2002 and 2006 = ₹ 8 crores – ₹ 4 crores = ₹ 4 crores

The difference between the sales in 2002 and 2003 =₹ 7 crores – ? 4 crores =₹ 3 crores

The difference between the sales in 2003 and 2004=₹ 7 crores – ₹ 6 crores = ₹ 1 crore

The difference between the sales in 2004 and 2005 =₹ crores – ₹ 6 crores = ₹ 4 crores

The difference between the sales in 2005 and 2006

= ₹ 10 crores – ₹ 8 crores = ₹ 2 crores

Therefore, in the year 2005, the difference between the sales as compared to the previous year was the greatest.

Question 3. For an experiment in Botany, two different plants, plant A and plant B were grown under similar laboratory conditions. Their heights were measured at the end of each week for 3 weeks. The results are shown in the following graph.

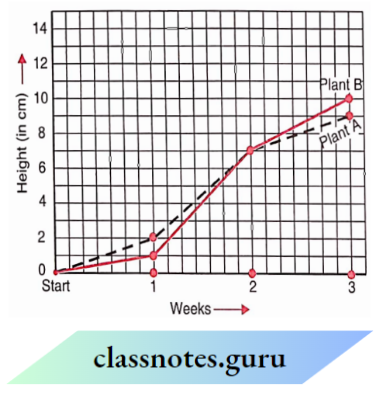
1. How high was Plant A after
   1. 2 weeks
   2. 3 weeks?
2. (b) How high was Plant B after
   1. 2 weeks
   2. 3 weeks?
3. How much did Plant A grow during the 3rd week?
4. How much did Plant B grow from the end of the 2nd week to the end of the 3rd?
5. During which week did Plant. A grow most?
6. During which week did the Plant grow the least?
7. Were the two plants of the same height during any week shown here? Specify.

Solution:

1.  The height of Plant A

1. after 2 weeks was 7 cm high and
2. after 3 weeks it was 9 cm high.

2.  The height of Plant B

1. after 2 weeks it was 7 cm high and
2. after 3 weeks it was 10 cm high.

3. Plant A grew 9 cm – 7 cm = 2 cm during the 3rd week.

4.  From the end of the 2nd week to the end of the 3rd week, Plant B grew = 10 cm – 7 cm = 3 cm.

5.  The Plant A grew in 1st week = 2 cm – 0 cm = 2 cm

The Plant A grew in 2nd week = 7 cm – 2 cm = 5 cm

The Plant A grew in 3rd week = 9 cm – 7 cm = 2 cm

Therefore, the Plant A grew mostly in Weeks second week

6.  The Plant B grew in 1st week = 1 cm – 0 cm = 1cm

The Plant B grew in 2nd week = 7 cm – 1 cm = 6 cm

The Plant B grew in 3rd week = 10 cm – 7 cm = 3 cm

Therefore, Plant B grew the least in the first week.

7.  At the end of the week, the two plants shown here were of the same height.

Question 4. The following shows the temperature forecast and the actual temperature for each day of the week:

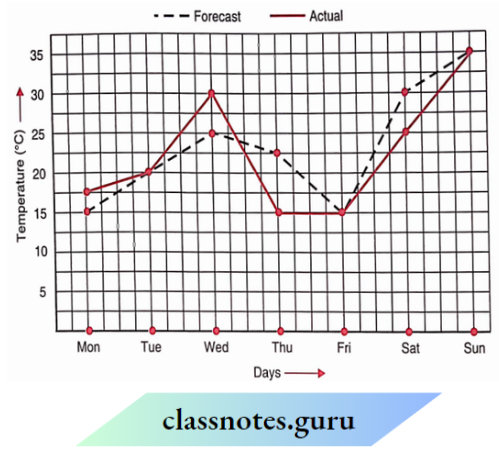
1. On which days was the forecast temperature the same as the actual temperature?
2. What was the maximum forecast temperature during the week?
3. What was the minimum actual temperature during the week?
4. On which day did the actual temperature differ the most from the forecast temperature?

Solution:

1. The forecast temperature was the same as the actual temperature on Tuesday, Friday and Sunday. This is indicated by the points where the two graphs intersect.
2. The maximum forecast temperature during the week was 35°C.
3. The minimum actual temperature during the week was 15°C.

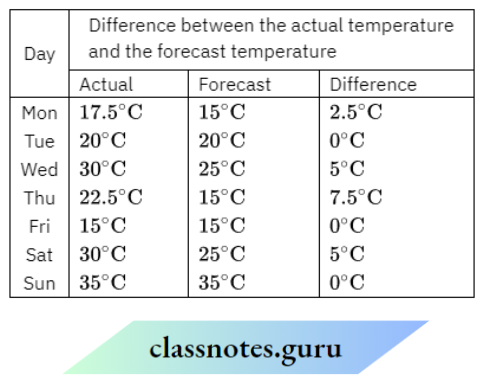
Since the maximum temperature difference is 7.5°C, therefore, the actual temperature filtered the most from the forecast temperature on Thursday.

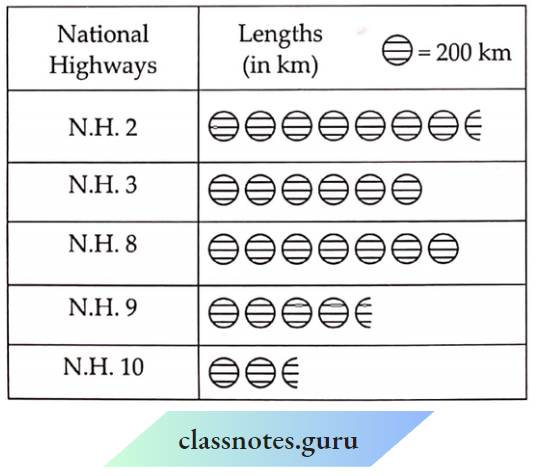
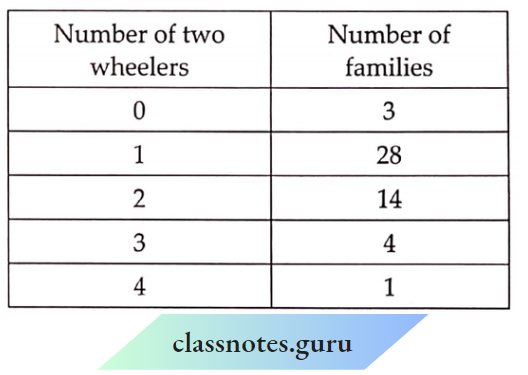
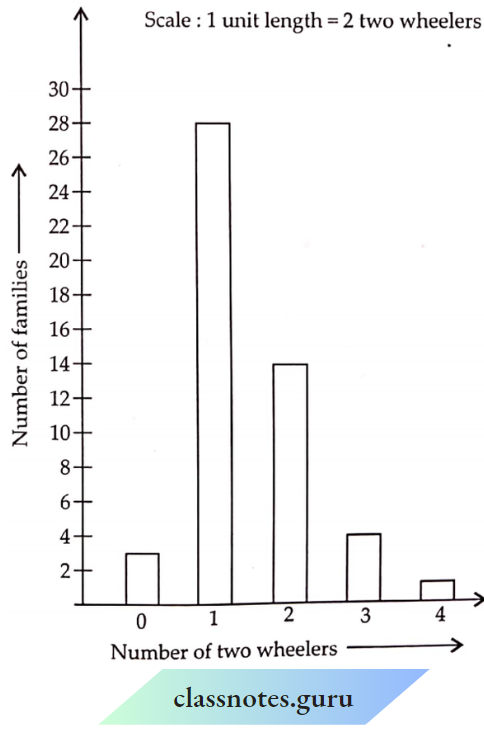
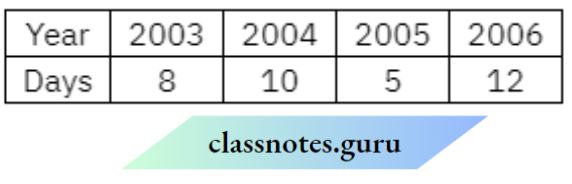
Question 5. Use the tables below to draw linear graphs.

The number of days a hillside city received snow in different years

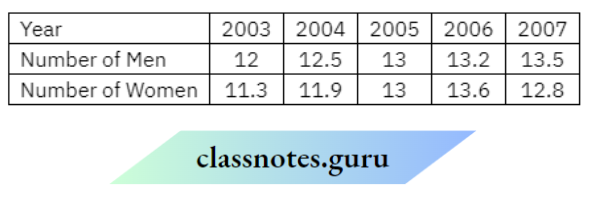
Population (in thousands) of men and women in a village in different years

Solution:

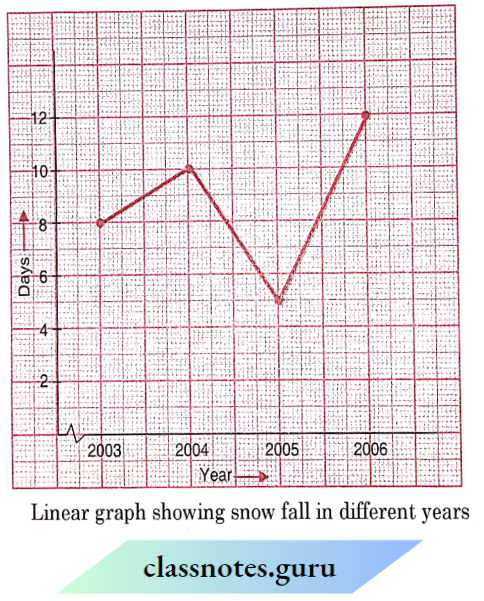
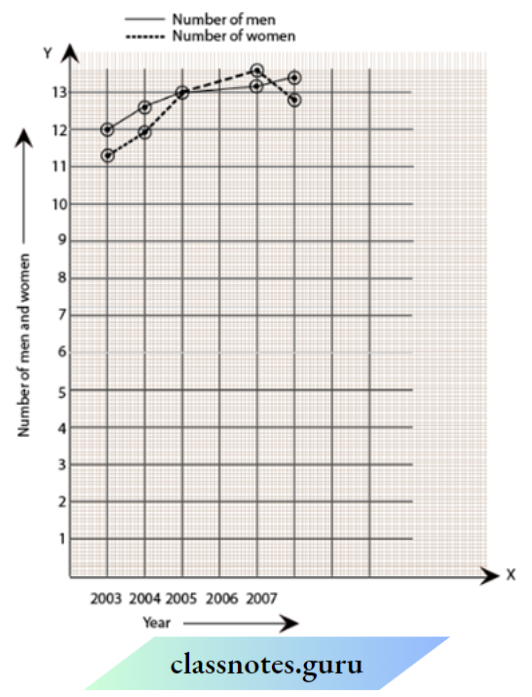
Class 8 Maths Chapter 13 Introduction to Graphs Solutions

Question 6. A courier person cycles from a town to a neighbouring suburban area to deliver a parcel to a merchant. His distance from the town at different times is shown in the following graph.

1. What is the scale taken for the time xis?
2. How much time did the person take 4 for the trave?
3. Flow far is the place of the merchant from the tow?
4. Did the person slop on his way? Explain.
5. During which period did he ride fast?

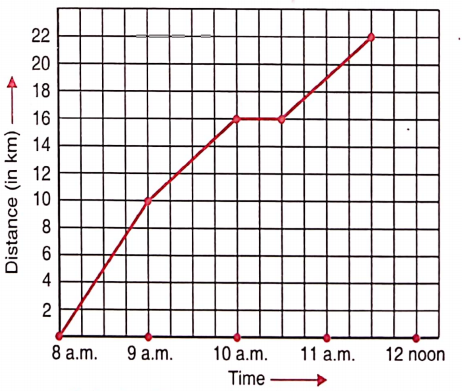
Solution:

1.  The scale taken for the time axis (i.e., along the x-axis) is 4 units = 1 hour.

2.  Time of the start of the travel = 8 a.m.

Time of the end of the travel = 11.30 a.m.

The time taken by the person for the travel = Difference between 8 a.m. and 11.30 a.m. = 31/2 hours.

3.  The place of the merchant from the town is 22 km.

4.  Yes. This is indicated by the horizontal part of the graph (10 a.m. -10.30 a.m.)

Distance covered by the person between 8 a.m. and 9 a.m. = (10 – 0) km = 10 km

Distance covered by the person between 9 a.m. and 10 a.m. = (16- 10)=6 km

covered by km the person between 10 a.m. and 10: 30 a.m. = (16 – 16) km = 0 km

Distance covered by the person between 10.30 a.m. and 11.30 a.m. = (22 – 16) km = 6 km

He rides fastest between 8 a.m. and 9 a.m

Question 7. Can there be a time-temperature graph as follows? Justify your answer.

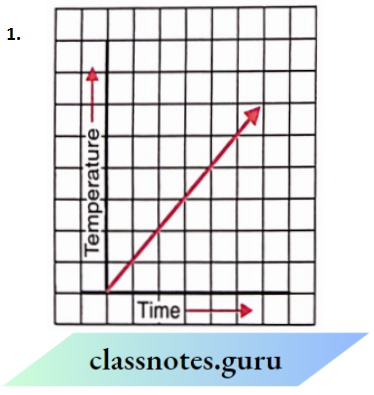
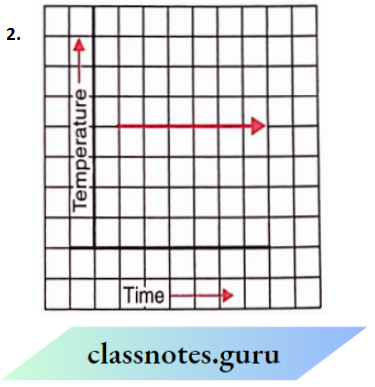
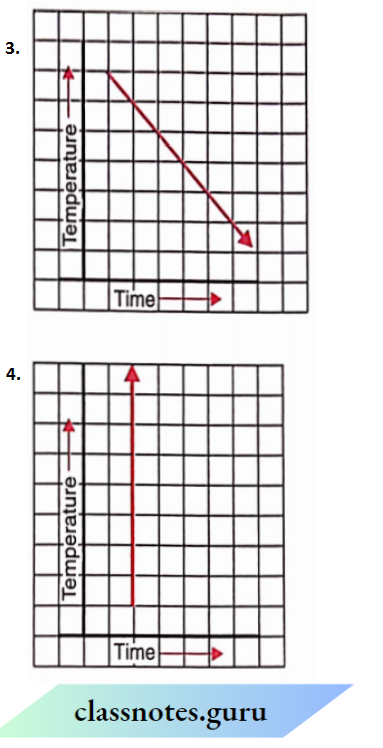
Solution:

1. Yes, it can be It is a time-temperature graph because it shows an increase in temperature with an increase in time. Yes, it can be
2. it is a time-temperature graph because it shows a decrease in temperature with an increase in time.
3. It cannot be a time-temperature graph because it shows infinitely many different temperatures at one particular time which is not possible.
4. Yes, it can be It is a time-temperature graph because it shows a fixed temperature at different times (or increasing times)

Some Applications

In our daily life, we observe two quantities that are interrelated i.e., the change in one quantity is accompanied by a change in the other quantity, for example: the more the number of days a labourer works, the more the wages he gets. More the sugar we purchase, more the amount we have to pay.

In the first, case, the number of days is called the independent variable (or control variable) and the wages are called the dependent variable. Similarly, in the second case, the amount of sugar is the independent variable whereas the money paid is the dependent variable.

Thus, an independent variable is a variable which can take values freely i.e., whose value is not dependent on any other variable whereas a dependent variable is a variable where value depends upon the other variable, i.e., independent variable.

The relation between the independent and dependent variables can be shown by a graph.

Question 1. The number of litres of petrol you buy to fill a car’s petrol tank will decide the amount you have to pay. Which is the independent variable here? Think about it

Solution:

The independent variable here is the amount of petrol we buy to fill a car’s petrol tank.

Question 2. In the given example use the graph to find how much petrol can be purchased for 800.

Solution:

Mark the point representing 800 the on y-axis. From this point, draw a line, parallel to the line graph at point, draw a line parallel to OY to ow cut OX at a point This point represents litres on the x-axis Hence, 16 litres of petrol can be purchased for 800

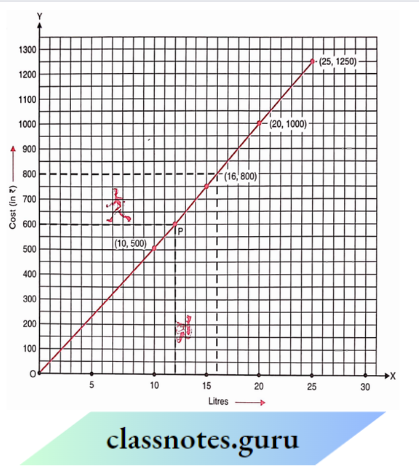
Question Is Example a case of direct variation?

Solution:

It is a case of direct variation as

⇒  \(\frac{100}{10}=\frac{200}{20}=\frac{300}{30}=\frac{500}{50}=\frac{1000}{100}\) = 10 (constant)

Exercise 13.2

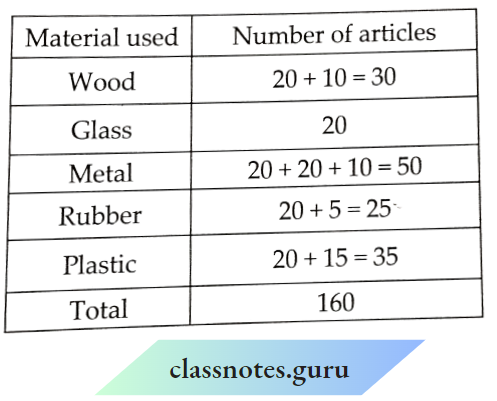
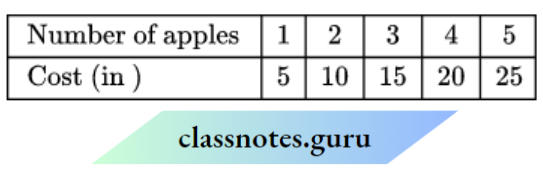
Question 1. Draw the graph for the following tables of values, with suitable scales on the axes.

1.  Cost of apples

2.  Distance travelled by car

1. How much distance did the car cover during the period 7.30 a.m. to 8 a.m.?
2. What was the time when the car had covered a distance of 1000 km since its star?

3.  Interest on deposits for a year

1. Does the graph pass through the origin?
2. Use the graph to find the interest on 72500 for a year.
3. To get an interest of f280 per year, how much money should be deposited?

Solution:

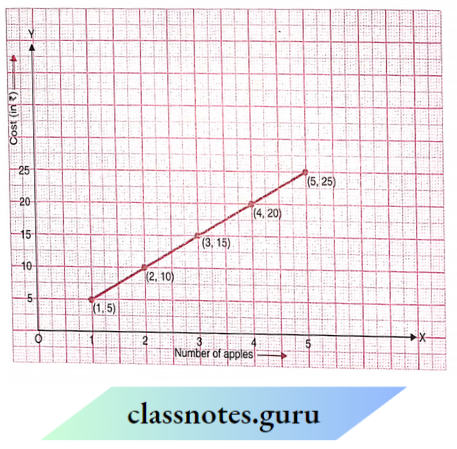
Scale:

On the horizontal axis: 2 units = 1 apple

On the  vertical axis: 1 unit = ? 5

Mark the number of apples on the horizontal axis.

Mark cost (in ?)the on vertical axis.

Plot, the points: (1, 5), (2, 10), (3, 15), (4, 20) and (5, 25).

Join the points.

We get a linear graph.

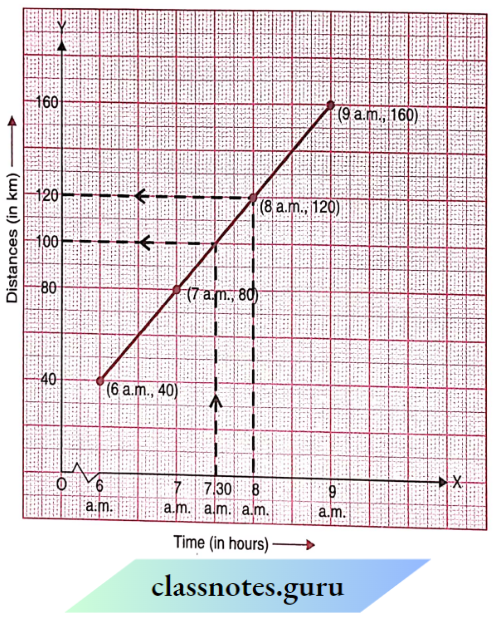
Scale :

On the  horizontal axis: 2 units = 1 hour

On the  vertical axis: 2 units = 40 km

Mark time (in hours)the on horizontal axis.

Mark distances (in km)the on vertical axis.

Plot the points (6 a.m., 40), (7 a.m., 80), (8 a.m., 120) and (9 a.m. 160).

Join the points.

We get a linear graph.

Distance covered during 7.30 a.m. to 8 a.m. = 120 km – 100 km = 20 km

The time when the car had covered a distance of 100 k Since its start was 7.30 a.m.

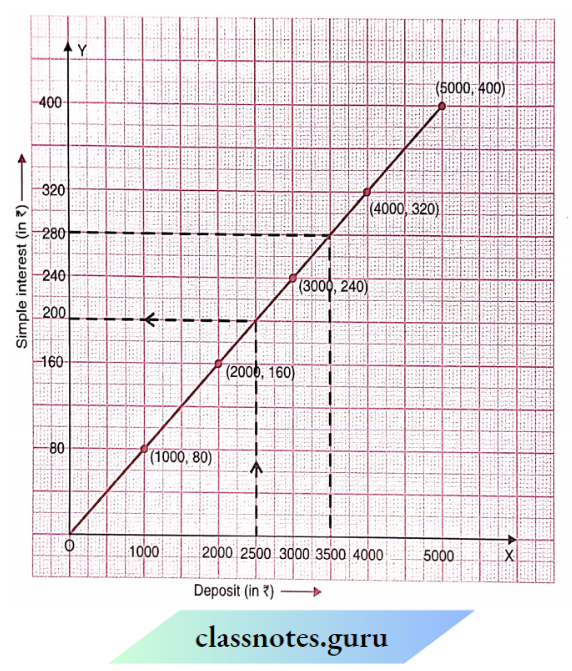
Scale :

On the horizontal axis: 2 units? 1000

On the vertical axis: 2 units  80

Mark deposit (in ?) on the horizontal axis.

Mark simple interest (in ?) on the vertical axis.

Plot the points (1000, 80), (2000, 160), (3000, 240), (4000, 320) and (5000, 400).

Join the points.

We get a linear graph.

Yes, The graph passes through the origin.

Interest o ? 2500 for a year = ? 200

To get an interest of? 280 per year? 3500 should be deposited.

Question 2. Draw a graph for the following:

Is it a linear graph?

Is it a linear graph?

Solution:

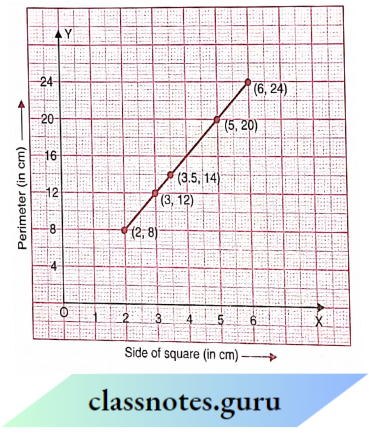
Scale:

On the  horizontal axis : 1 unit = 1 cmOn thee  vertical axi : 1 unit = 4 cm

Mark the  side of the square (in cm) on the  horizontal axis

Mark the  perimeter (in cm) on vertical

Plot the points (2, 8), (3,12), (3.5, 14), (5, 20) and (6, 24).

Join the points.

Yes, It is a linear graph.

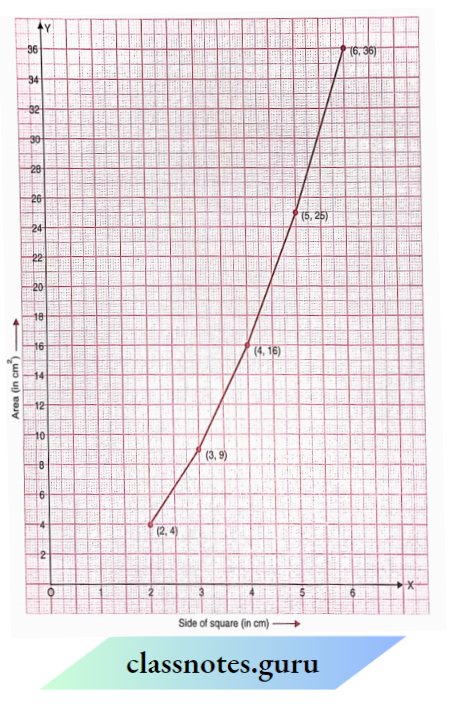
Scale :

On the horizontal axis: 2 units = 2 cm

On the vertical axis: 1 unit = 2 cm

Mark the side of the square (in cm) on the horizontal axis.

Mark the area (in cm2) on the vertical axis.

Plot the points (2, 4), (3, 9), (4, 16), (5, 25) and (6, 36).

Join the points.

The graph we get is not linear.

Introduction to Graphs Class 8 NCERT Solutions

Multiple-Choice Questions and Solutions

Observe the following bar graph and answer the related questions:

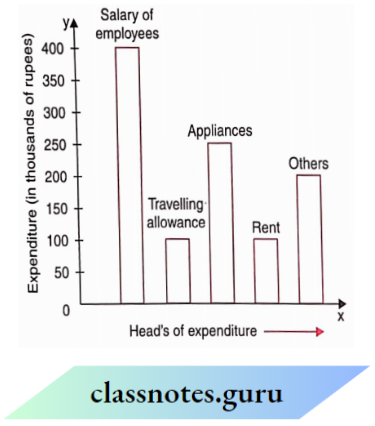
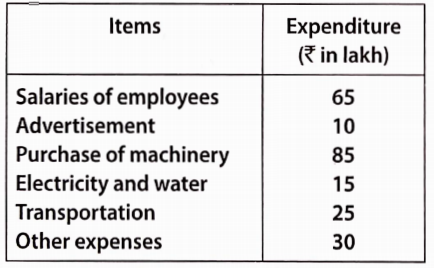
Question 1. On which head, is the expenditure maximum?

1. Travelling allowance
2. Rent
3. Appliances
4. Salary of employees.

Solution: 4. Salary of employees.

Question 2. On which head or head, is the expenditure minimum?

1. Travelling allowance or rent
2. Appliances
3. Salary of employees
4. Others.

Solution: 1. Travelling allowance or rent

Question 3. On which two heads, is the expenditure the same?

1. Salary of employees and others
2. Travelling allowance and rent
3. Appliances and rent
4. Appliances and others

Solution: 2. Travelling allowance and rent

Question 4. What is the difference in expenditure (in thousands of rupees) between the salary of employees and rent?

1. 100
2. 200
3. 300
4. 400

Solution: 3. 300

Question 5. What is the sum of the expenditures (in thousands of rupees) on travelling allowance and rent?

1. 100
2. 200
3. 300
4. 400

Solution: 2. 200

Observe the following circle graph and answer the related questions:

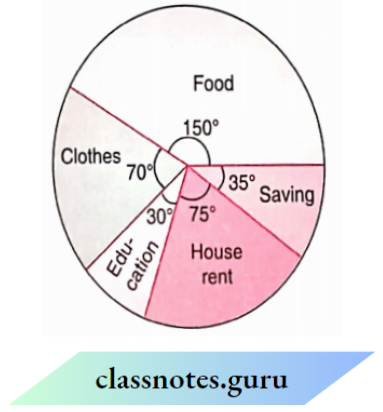
Question 6. On which head is the expenditure maximum?

1. Food
2. Clothes
3. House rent
4. Education.

Solution: 1. Food

Question 7. On which head is the expenditure minimum

1. Education
2. Food
3. House rent
4. Clothes.

Solution: 1. Education

Question 8. If the budget of the family is ₹ 10800, what is the savings?

1. ₹ 1050
2. ₹ 950
3. ₹ 1000
4. ₹ 1200.

Solution: 1. ₹ 1050

Question 9. What is the difference in spending on clothes and education the budget of the family is ₹ 1000.

1. ₹ 1200
2. ₹ 800
3. ₹ 1000
4. ₹ 1500.

Solution: 1. ₹ 1200

Question 10. What is the sum of the expenditures on food and education if the budget of the family is ₹ 1080?

1. ₹ 5000
2. ₹ 5400
3. ₹ 8000
4. ₹ 6000

Solution: 3. ₹ 8000

Observe the following circle graph and answer the related questions:

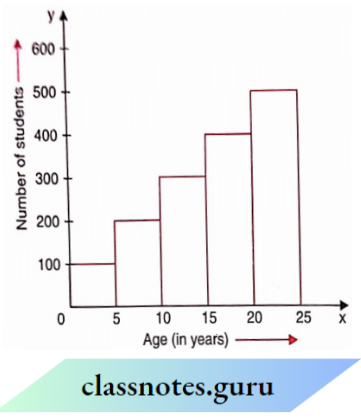
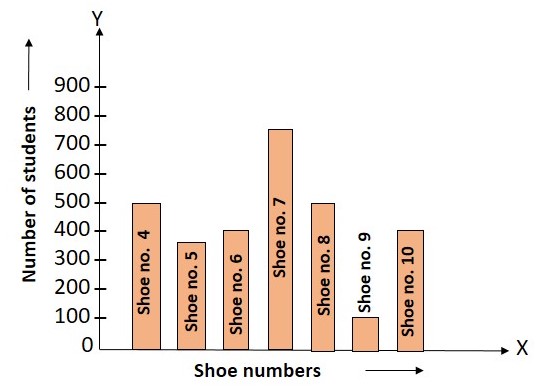
Question 11. In which class intervals, are the maximum number of students?

1. 0-5
2. 5-10
3. 20-25
4. 15-20

Solution: 3. 20-25

Question 12. In which class intervals, are the minimum number of students?

1. 0-5
2. 5-10
3. 10-15
4. 15-20

Solution: 1. 0-5

Question 13. In which class intervals, is the number of students 200?

1. 0-5
2. 5-10
3. 20-25
4. 15-20

Solution: 1. 0-5

NCERT Class 8 Maths Chapter 13 Exercise Solutions

Question 14. The difference in the number of students in class intervals 0-5 and 5- 10 is

1. 100
2. 200
3. 300
4. 400

Solution: 1. 100

Question 15. The sum of the number of students in the class intervals 10-15 and 20-25 is

1. 800
2. 900
3. 600
4. 400

Solution: 1. 800

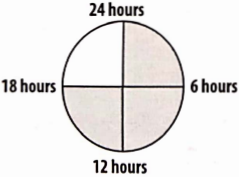
Observe the following temperature-timeline graph and answer the related questions:

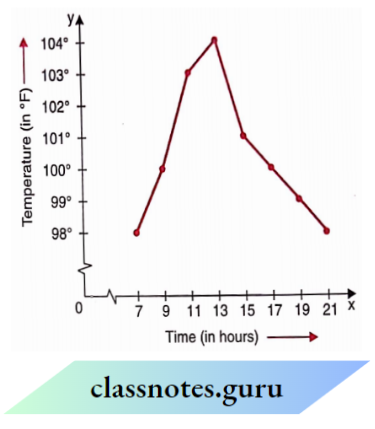
Question 16. At what time is the temperature maximum?

1. 13 hours
2. 15 hours
3. 11 hours
4. 19 hours

Solution: 1. 13 hours

Question 17. At what time(s) is the temperature minimum?

1. 7 hours and 21 hours
2. 9 hours
3. 11 hours
4. 13 hours.

Solution: 1. 7 hours and 21 hours

Question 18. 103°F temperature is the time

1. 11 hours
2. 13 hours
3. 15 hours
4. 21 hours.

Solution: 1. 11 hours

Question 19. What is the difference of temperatures at 7 hours and 21 hours?

1. 0°F
2. 1°F
3. 2°F
4. 3°F

Solution: 1. 0°F

Question 20. What is the rise in temperature from 11 hours to 13 hours?

1. 1°F
2. 2°F
3. 3°F
4. 4°F

Solution: 1. 1°F

Question 21. What is the fall in temperature from 13 hours to 21 hours?

1. 2°F
2. 3°F
3. 4°F
4. 6°F

Solution: 1. 2°F

Class 8 Maths Chapter 13 Question Answer

Question 22. The coordinates of the origin are

1. (0,0)
2. (1,0)
3. (0,1)
4. (1,1)

Solution: 1. (0,0)

Question 23. What are the coordinates of a point whose .v-coordinate is 3 andy-coordinate is 4?

1. (3,3)
2. (3,4)
3. (4,3)
4. (4,3)

Solution: 2. (3,4)

Question 24. What are the coordinates of a point whose x-coordinate is 1 and y-coordinate is 0?

1. (1,0)
2. (0,0)
3. (0,1)
4. (1,1)

Solution: 1. (1,0)

Question 25. What are the coordinates of a point whose v-coordinate is 0 and whose y-coordinate is?

1. (0,1)
2. (0,0)
3. (1,0)
4. (1,1).

Solution: 1. (0,1)

Observe the following velocity-lime graph and answer the related questions:

Question 26. At what time is the velocity maximum?

1. 7
2. 8
3. 9
4. 10

Solution: 1. 6

Question 27. At what time is the velocity minimum?

1. 8
2. 9
3. 10
4. 11

Solution: 4. 11

Question 28. At what times are the velocities equal?

1. 8 and 12
2. 9 and 11
3. 7 and 12
4. 11 and 13.

Solution: 1. 8 and 12

Question 29. What is the fall in velocity from 7 to 1 1?

1. 80 km/hour
2. 90 km/hour
3. 100 km/hour
4. 20 km/hour.

Solution: 1. 80 km/hour

Question 30. What is the rise in velocity from 11 to 12?

1. 10 km/hour
2. 20 km/hour
3. 30 km/hour
4. 60 km/hour.

Solution: 4. 60 km/hour.

Observe the following runs-over graph and answer the related questions:

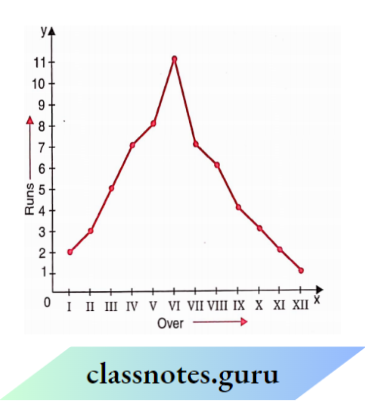
Question 31. In which over is the maximum scoreboard scored?

1. 2
2. 4
3. 5
4. 6

Solution: 4. 6

Question 32. In which over are the maximum runs scored?

1. 10
2. 11
3. 12
4. 9

Solution: 3. 12

Question 33. What is the difference in runs scored in IV and V overs?

1. 1
2. 2
3. 3
4. 4

Solution: 1. 1

Question 34. What is the sum of runs scored in I and XII overs?

1. 1
2. 2
3. 3
4. 4

Solution: 1. 1

Question 35. 3 runs are scored in which over?

1. 2 and 10
2. 1 and 5
3. 7 and 8
4. 10 and 12

Solution: 3. 7 and 8

Class 8 Maths NCERT Chapter 13 Graph Questions

Read the graph and answer the related questions:

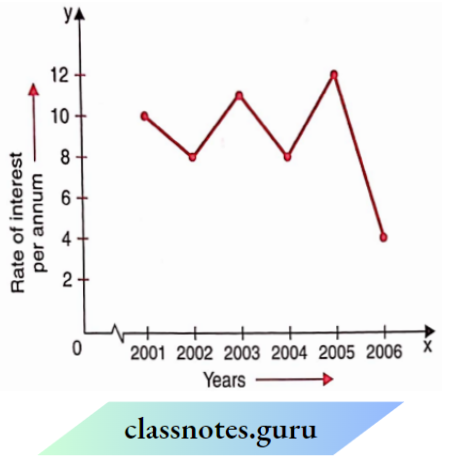
Question 36. In which year was the rate of interest maximum?

1. 2005
2. 2003
3. 2006
4. 2002.

Solution: 1. 2005

Question 37. In which year was the rate of interest minimum 

1. 2006
2. 2004
3. 2001
4. 2005.

Solution: 1. 2006

Question 38. The difference in the maximum and minimum rates of interests

1. 2%
2. 4%
3. 6%
4. 8%.

Solution: 4. 8%.

Question 39. The rise in interest from 2004 to 2005 was

1. 2%
2. 4%
3. 6%
4. 8%.

Solution: 2. 4%

Question 40. The fall in interest from 2001 to 2002 was

1. l%
2. 2%
3. 3%
4. 4%.

Solution: 2. 2%

Read the graph and answer the related questions :

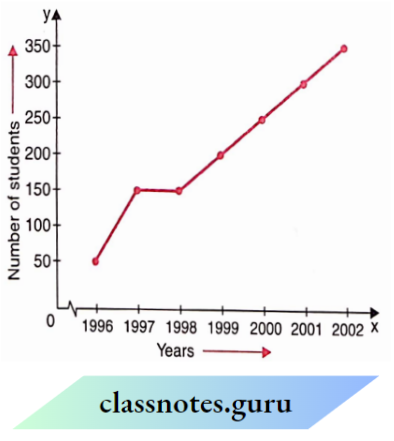
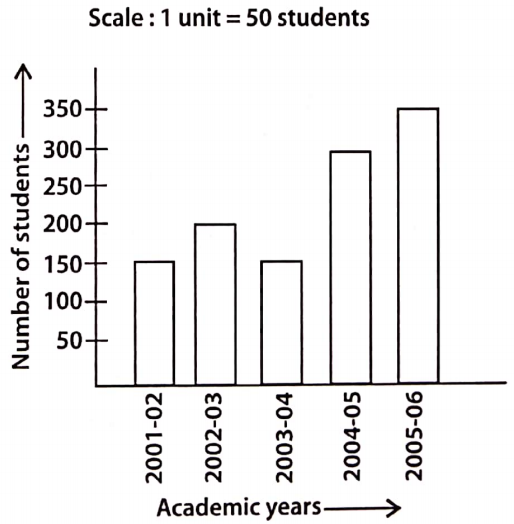
Question 41. How many students appeared in the year 2000?

1. 200
2. 250
3. 300
4. 350.

Solution: 2. 250

Question 42. In which year did 50 students appear? 

1. 1998
2. 2001
3. 1997
4. 1996.

Solution: 4. 1996.

Question 43. In which year did the maximum number of students appear?

1. 2002
2. 2000
3. 2001
4. 1999.

Solution: 1. 2002

Question 44. What is the maximum number of students that appeared in any year?

1. 350
2. 300
3. 250
4. 300.

Solution: 1. 350

Question 45. In which two years was the number of students appearing the same?

1. 1997 and 1998
2. 1998 and 1999
3. 1999 and 2000
4. 2000 and 2001.

Solution: 1. 1997 and 1998

Introduction to Graphs Class 8 Chapter Explanation and Solutions

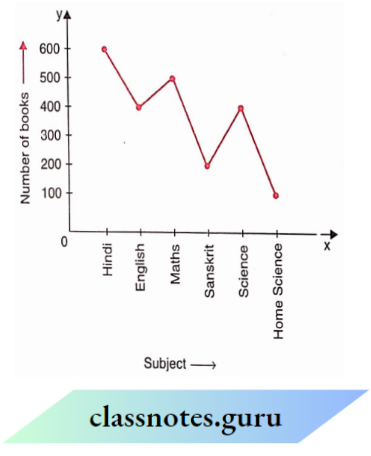
Read the graph and answer the related questions:

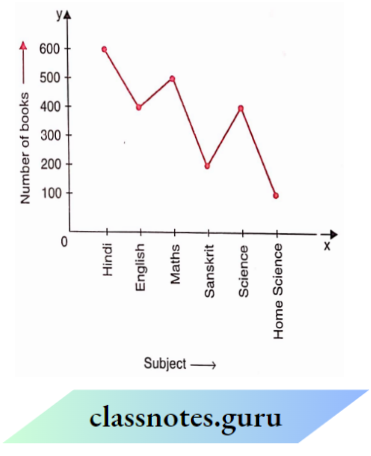
Question 46. The maximum books are of which subject?

1. Hindi
2. Science
3. English
4. Sanskrit.

Solution: 1. Hindi

Question 47. The minimum books are of which subject

1. Home Science
2. Sanskrit
3. Science
4. English.

Solution: 1. Home Science

Question 18. 500 books are of which subject 

1. English
2. Science
3. Hindi
4. Maths.

Solution: 4. Maths.

Question 49. How many books are on the subject of Home Science?

1. 100
2. 200
3. 300
4. 400

Solution: 1. 100

Question 50. How many books are there in Sanskrit and Home Science taken together?

1. 100
2. 200
3. 300
4. 400

Solution: 3. 300

Read the graph and answer the related questions:

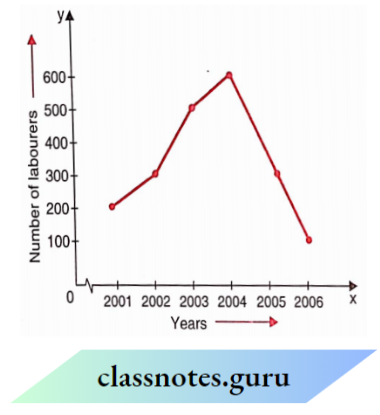
Question 51. In which year was the number of labourers maximum?

1. 2001
2. 2002
3. 2003
4. 2004

Solution: 4. 2004

Question 52. In which year was the number of labourers minimum?

1. 2003
2. 2004
3. 2005
4. 2006

Solution: 4. 2006

Question 53. What was the difference in the number of labourers in the years 2002 and 203?

1. 100
2. 200
3. 300
4. 400

Solution: 2. 200

Question 54. Find the rise in the number of labourers from 2001 to 2004.

1. 200
2. 300
3. 400
4. 500

Solution: 3. 400

NCERT Solutions for Class 8 Maths Chapter 13 Introduction to Graphs with Examples

Question 55. Find the sum of the number of labourers in the years 2004 and 2006.

1. 700
2. 600
3. 200
4. 500

Solution: 1. 700

Read the circle graph and answer the related questions:

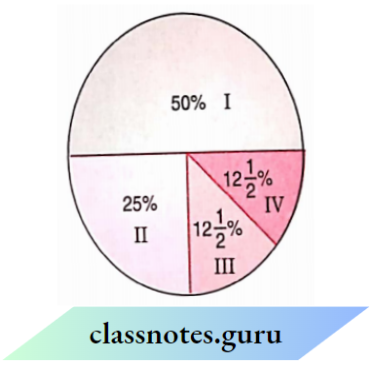
Question 56. There are in all 101000 students a school. The number of students in the class I are

1. 500
2. 250
3. 125
4. None of these

Solution: 1. 500

Question 57. The number of students in class II is

1. 500
2. 250
3. 125
4. 100

Solution: 2. 250

Question 58. In which two classes is the number of students the sesame 

1. 1 and 2
2. 1 and 3
3. 3 and 4
4. 1 and 4

Solution: 3. 3 and 4

Question 59. The minimum number of students in any class is

1. 125
2. 250
3. 500
4. 1000

Solution: 1. 125

Question 60. The sum of the number of students in class 3 and class 4 is

1. 500
2. 1000
3. 50
4. 250

Solution: 4. 250

True-False

Write whether the following statements are ‘D ue or False:

1. The coordinates of the origin are (0, 0): True

2. The .v-coordinate of a point is its distance from r-the axis: False

3. For fixing a point on the graph sheet, we need two coordinates: True

4. The relation between the pendent variable and the dependent variable is shown through a graph: True

Class 8 Chapter 13 Graphs Questions and Answers Step-by-Step

Fill in the Blanks

1. Comparison of parts of a whole can be done by_____: pie chart

2. A point which lies on both these is_____: (0,0)

3. The r-coordinate of every point lying on the y-axis is_____: 0

4. The process of fixing a point with the help of x and y coordinates is called_____of the point: Plotting

5. What will you get after joining the points (-1, -1), (0, 0) and (3, 3): A straight line passing through the origin

6. What will you get after joining the points (1, 0), (1, 1) and (1, -1): A straight line not passing through the origin

7. What is the distance of the point (3, 4) from s-axis: 4

8. In the following graph, what are the coordinates of P: (3,2)

Graph Plotting and Interpretation Class 8 Maths Chapter 13 Solutions

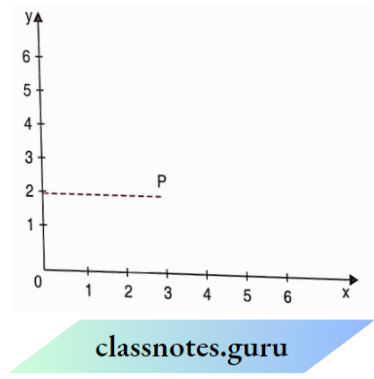
9. In the following graph, which letter indicates (the point (3, 0): A

Exponents And Powers

Exponents And Powers Introduction

If a is any non-zero integer and n is a positive integer, then

x a (n times) is written as a”,

i.e., a” is the continued product of a multiplied by itself n times.

Here, ‘o’ is called the base, and V is called the ‘exponent’ or ‘index’.

The number a” is read as a raised to the power of or simply as ‘nth power of o’.

The notation a” is called the exponential or power notation.

We can write large numbers more conveniently using exponents.

For example :

10000 = 104; 243 = 35; 128 = 27, etc.

Now, we shall learn about negative exponents

Read and Learn More NCERT Solutions For Class 8 Maths

Powers With Negative Exponents

If a is any non-zero integer and m is a positive integer, then

⇒ \(a^{-m}=\frac{1}{a^m}\)

Note: a m is called the multiplicative inverse of am as a-m x am = 1

Am and a ~m are multiplicative inverses of each other.

Note 2: \(a^m=\frac{1}{a^{-m}}\)

Question: What is 10 ~10 equal to?

Solution: \(10^{-10}=\frac{1}{10^{10}}\)

NCERT solutions for class 8 maths chapter 10

Question 1. Find the multiplicative inverse of the following:

1. 2-4
2. 10-5
3. 7-2
4. 5-3
5. 10-100

Solution:

The multiplicative inverse is \(2^{-4}=\left(\frac{1}{2^{-4}}\right) \text { is } 2^4\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

The multiplicative inverse of \(10^{-5}=\left(\frac{1}{10^{-5}}\right) \text { is } 10^5\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

The multiplicative inverse of \(7^{-2}=\left(\frac{1}{7^{-2}}\right) \text { is } 7^2\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

The multiplicative inverse \(5^{-3}=\left(\frac{1}{5^{-3}}\right) \text { is } 5^3\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

The multiplicative inverse\(10^{-100}=\left(\frac{1}{10^{-100}}\right) \text { is } 10^{100}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

Question 2. Expand the following numbers using exponents :

1. 1025.63
2. 1256.249

Solution:

1025.63

1 x 1000 + 0 x 100 + 2 x 10 + 5 x 1 + 6 x\(\frac{1}{10}+3 \times \frac{1}{100}\)

= 1 x 103 + 0 x 102 + 2 x 101 + 5 x 10° + 6 x 10-1 + 3 x 10-2

1256.249

= 1 x 1000 + 2 x 100 + 5 x 10

+ 6x 1+ 2 x \( \frac{1}{10}+4 \times \frac{1}{100}+9 \times \frac{1}{1000}\)

= 1 X 103 + 2 X 102 + 5 X 101 + 6 x 10° + 2 x 10-1 + 4 x 10-2 + 9 x lO-3

Laws Of Exponents

If a, b are non-zero integers and m, n are any integers, then

1. am x an = am+ n
2. \(\frac{a^m}{a^n}=a^{m-n}\)
3. (am)n = amn
4. am x bm = (ab)m
5. \(\frac{a^m}{b^m}=\left(\frac{a}{b}\right)^m\)
6. a° = 1
7. \(\left(\frac{a^{-m}}{b^{-n}}\right)=\frac{b^n}{a^m}\)
8. \(\left(\frac{a}{b}\right)^{-m}=\left(\frac{b}{a}\right)^m\)

Remember

an” = 1 = n = 0

1n = 1 where n is any integer.

(- 1)n = 1 where n is any even integer.

(-1)n =-1 where n is any odd integer.

Q. Simplify and write in exponential form:

(-2)-3X (-2)-4

p3 x p -I0

32 x 3-5 x 36

Solution:

(-2)~3 x (-2)-4 = (- 2)(“3) + (-4>

am x an = am +n

= (-2)-7 = {(-1) x 2} -7

⇒ \(\frac{1}{\{(-1) \times 2\}^7}= \frac{1}{(-1)^7 \times(2)^7}\)

(ab)m = am bm

⇒ \(\frac{1}{(-1) \times 2^7}=-\frac{1}{2^7}\)

⇒ \(\mid(-1)^{\text {odd integer }}=-1\)

⇒ \(p^3 \times p^{-10}=p^{3+(-10)}=p^{-7}=\frac{1}{p^7}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

32 x 3-5 x 36 = 32 + (-5) + 6 = 33

Exponents And Powers Exercise 10.1

Question 1. Evaluate:

1. 3-2
2. (-4)-2
3. \(\left(\frac{1}{2}\right)^{-5}\)

Solution:

⇒ \(3^{-2}=\frac{1}{3^2}=\frac{1}{9}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

⇒ \((-4)^{-2}=\frac{1}{(-4)^2}=\frac{1}{16}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

⇒ \(\left(\frac{1}{2}\right)^{-5}=\left(\frac{2}{1}\right)^5\)

⇒ \( a^{-m}=\frac{1}{a^m}\)

⇒ \(\frac{2^5}{1^5}\)

⇒ \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)

⇒ \(\frac{32}{1}=32\)

1n = 1 where n is an integer

Exponents and powers class 8 solutions

Question 2. Simplify and express the result in power notation with a positive exponent

1. \((-4)^5 \div(-4)^8\)
2. \(\left(\frac{1}{2^3}\right)^2\)
3. \((-3)^4 \times\left(\frac{5}{3}\right)^4\)
4. (3-7 – 3-10) x 3-5
5. 2-3 x (-7) -3

Solution:

1. (-4)6 ÷ (-4)8

⇒ \(\frac{(-4)^5}{(-4)^8}\)

⇒ \((-4)^{5-8}\)

⇒ \((-4)^{-3}\frac{a^m}{a^n}=a^{m-n}\)

⇒ \(=\frac{1}{(-4)^3}  a^{-m}=\frac{1}{a^m}\)

which is the required form.

2. \(\left(\frac{1}{2^3}\right)^2 =\frac{1^2}{\left(2^3\right)^2}\)

⇒ \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)

⇒ \(\frac{1}{2^{3 \times 2}} \)

⇒ \( \mid\left(a^m\right)^n=a^m\)

⇒ \(\frac{1}{2^6}\)

which is the required form

3. \((-3)^4 \times\left(\frac{5}{3}\right)^4=\{(-1) \times 3\}^4 \times \frac{5^4}{3^4} \)

⇒ \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)

⇒ \((-1)^4(3)^4 \times \frac{5^4}{3^4}\)

I (ab)m = am bm

= (- 1)4 x 54

= 1 x 54

(-1) even integer = 1

= 54

which is the required form.

4. (3-7 / 3-10) x 3-5

⇒ \(=\frac{3^{-7}}{3^{-10}} \times \frac{1}{3^5}\)

⇒ \( a^{-m}=\frac{1}{a^m}\)

⇒ \(3^{-7-(-10)} \times \frac{1}{3^5}\)

⇒ \(\frac{a^m}{a^n}=a^{m-n}\)

⇒ \(3^3 \times \frac{1}{3^5} \)

⇒ \(\frac{a^m}{a^n}=a^{m-n}\)

⇒ \(3^{3-5} \)

⇒ \(3^{-2} \)

⇒ \(a^{-m}=\frac{1}{a^m}\)

which is the required form.

5. \(2^{-3} \times(-7)^{-3}\)

⇒ \(\frac{1}{2^3} \times \frac{1}{(-7)^3}\)

⇒ \(\frac{1}{[2 \times(-7)]^3}=\frac{1}{a^m}\)

(ab)m = amb

⇒ \(\frac{1}{(-14)^3}\)

which is the required form.

Question 3. Find the value of:

(3° + 4 -1) x 22

(2-1 x 4-1)/2 -2

⇒ \(\left(\frac{1}{2}\right)^{-2}+\left(\frac{1}{3}\right)^{-2}+\left(\frac{1}{4}\right)^{-2}\)

⇒ \(\left(3^{-1}+4^{-1}+5^{-1}\right)^0\)

⇒ \(\left\{\left(\frac{-2}{3}\right)^{-2}\right\}^2.\)

Solution:

1. (3° + 4-1) x 22

⇒ \(\left(1+\frac{1}{4}\right) \times 4\)

⇒ \(a^{-m}=\frac{1}{a^m}, \quad a^0=1\)

⇒ \(\frac{5}{4} \times 4=5\)

(2-1 x 4-1) + 2″2

= {2 -l x (22)-1} + 2 -2

= {2-1 x 22x(-1>} -f2-2

(am)n = amn

= (2-’X2-2)T2-2 = 2(-1)+(-2) 2-2

am x a” = am+”

= 2-3 4- 2″2

⇒ \(\frac{2^{-3}}{2^{-2}}=2^{-3-(-2)} \)

⇒ \(\frac{a^m}{a^n}=a^{m-n}\)

⇒ \(2^{-1}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

⇒ \(\frac{1}{2}\)

3.\(\left(\frac{1}{2}\right)^{-2}+\left(\frac{1}{3}\right)^{-2}+\left(\frac{1}{4}\right)^{-2}\)

⇒ \(\frac{1^{-2}}{2^{-2}}+\frac{1^{-2}}{3^{-2}}+\frac{1^{-2}}{4^{-2}}\)

⇒ \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)

⇒ \(\frac{2^2}{1^2}+\frac{3^2}{1^2}+\frac{4^2}{1^2}\)

⇒ \(\frac{4}{1}+\frac{9}{1}+\frac{16}{1}\)

= 4 + 9 + 16 = 29

4. [3-1 + 4-1 + 5-1]0

⇒ \({\left[\frac{1}{3}+\frac{1}{4}+\frac{1}{5}\right]^0 }\)

⇒ \(\left(\frac{20+15+12}{60}\right)^0\)

⇒ \(\quad \text { | LCM }(3,4,5)=60\)

⇒ \(\left(\frac{47}{60}\right)^0=1\)

Aliter

(3-1 + 4-1 +5-1)° = 1

a°= 1

5. \(\left\{\left(\frac{-2}{3}\right)^{-2}\right\}^2\)

⇒ \(\left(\frac{-2}{3}\right)^{(-2) \times 2}\)

⇒ \(\mid\left(a^m\right)^n=a^{m n}\)

⇒ \(\left(\frac{-2}{3}\right)^{-4}\)

⇒ \(\left(\frac{3}{-2}\right)^4 \)

⇒ \( \left(\frac{a}{b}\right)^{-m}=\left(\frac{b}{a}\right)^m\)

⇒ \(\frac{3^4}{(-2)^4}=\frac{3^4}{(-1 \times 2)^4}\)

⇒ \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)

⇒ \(\frac{3^4}{(-1)^4(2)^4}\)

⇒ \((a b)^m=a^m b^m\)

⇒ \(\frac{3^4}{1 \times 2^4} \)

⇒ \((-1)^{\text {even integer }}=1\)

⇒ \(\frac{3^4}{2^4}\)

⇒ \(\frac{3 \times 3 \times 3 \times 3}{2 \times 2 \times 2 \times 2}=\frac{81}{16}\)

Class 8 maths chapter 10 question answer

Question 4. Evaluate:

1.  \(\frac{8^{-1} \times 5^3}{2^{-4}}\)
2.  \(\left(5^{-1} \times 2^{-I}\right) \times 6^{-1}\)

Solution:

1. \(\frac{8^{-1} \times 5^3}{2^{-4}}\)

⇒ \(\frac{2^4 \times 5^3}{8^1}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

⇒ \(\frac{16 \times 125}{8}=250\)

2. \(\left(5^{-1} \times 2^{-1}\right) \times 6^{-1}=\left(\frac{1}{5} \times \frac{1}{2}\right) \times \frac{1}{6}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

⇒ \(\frac{1}{10} \times \frac{1}{6}=\frac{1}{60}\)

Question 5. Find the value of m for which 5m + 5-3 = 55

Solution:

5m + 5-3 = 55

⇒ \(\frac{5^m}{5^{-3}} =5^5\)

⇒ \(5^{m-(-3)} =5^5\)

⇒ \(\frac{a^m}{a^n}=a^{m-n}\)

⇒ \(5^{m+3} =5^5\)

bases are equal exponents are equal

m + 3 = 5

m = 5-3

m = 2

Question 6. Evaluate:

1. \(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)
2. \(\left(\frac{5}{8}\right)^{-7} \times\left(\frac{8}{5}\right)^{-4}.\)

Solution:

⇒ \(\left\{\left(\frac{1}{3}\right)^{-1}-\left(\frac{1}{4}\right)^{-1}\right\}^{-1}\)

⇒ \(\left(\frac{1^{-1}}{3^{-1}}-\frac{1^{-1}}{4^{-1}}\right)^{-1}\)

⇒ \(\left(\frac{a}{b}\right)^m=\frac{a^m}{b^m}\)

⇒ \(\left\{\frac{\frac{1}{1^1}}{\frac{1}{3^1}}-\frac{\frac{1}{1^1}}{\frac{1}{4^1}}\right\}^{-1}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

⇒ \(\left(\frac{3^1}{1^1}-\frac{4^1}{1^1}\right)^{-1}\)

⇒ \(a^1=a\)

⇒ \(\left(\frac{3}{1}-\frac{4}{1}\right)^{-1}\)

⇒ \( (3-4)^{-1}\)

⇒ \((-1)^{-1}=\frac{1}{(-1)^1}\)

⇒ \(| a^{-m}=\frac{1}{a^m}\)

⇒ \(\frac{1}{(-1)}\)

\((-1)^{\text {odd integer }}=-1\)= -1

⇒ \(\left(\frac{5}{8}\right)^{-7} \times\left(\frac{8}{5}\right)^{-4}=\frac{5^{-7}}{8^{-7}} \times \frac{8^{-4}}{5^{-4}}\)

⇒ \(\frac{5^{-7}}{5^{-4}} \times \frac{8^{-4}}{8^{-7}}\)

⇒ \(=5^{(-7)-(-4)} \times 8^m=\frac{a^m}{b^m}\)

⇒ \(\frac{a^m}{a^n}=a^{m-n}\)

⇒ \(5^{-7+4} \times 8^{-4}+7 \)

⇒ \(\frac{1}{5^3} \times 8^3=\frac{8^3}{5^3}\)

⇒ \(\frac{8 \times 8 \times 8}{5 \times 5 \times 5}=\frac{512}{125}\)

Question 7. Simplify:

1. \(\frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}} \quad(t \neq 0)\)
2. \(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\)

Solution:

1. \(\frac{25 \times t^{-4}}{5^{-3} \times 10 \times t^{-8}}\)

⇒ \(\frac{25 \times 5^3}{10} \times \frac{t^8}{t^4}\)

⇒ \(\frac{625}{2} \times \frac{t^8}{t^4}\)

⇒ \(\frac{625 t^4}{2}\)

⇒ \(\frac{3^{-5} \times 10^{-5} \times 125}{5^{-7} \times 6^{-5}}\)

⇒ \(\frac{3^{-5} \times(2 \times 5)^{-5} \times(5 \times 5 \times 5)}{5^{-7} \times(2 \times 3)^{-5}}\)

⇒ \(\frac{3^{-5} \times 2^{-5} \times 5^{-5} \times 5^3}{5^{-7} \times 2^{-5} \times 3^{-5}} \)

⇒ \(\quad(a b)^m=a^m b^m\)

⇒ \(\frac{5^{-5} \times 5^3}{5^{-7}}=\frac{5^{(-5)+3}}{5^{-7}}\)

⇒ \(\mid a^m \times a^n=a^{m+n}\)

⇒ \(\frac{5^{-2}}{5^{-7}}=5^{(-2)-(-7)}\)

⇒ \(5^{-2+7}=5^5\)

Use Of Exponents To Express Small Numbers In Standard Form

A number is said to be in standard form if expressed in the form K x 10″ where 1 < K < 10 and n is an integer. A number written in standard form is said to be expressed in scientific notation.

Tiny numbers can be expressed in standard form using negative exponents.

1. To express a large number, we move the decimal point to the left such that only one digit is left to the left side of the decimal point and multiply the resulting number by 10n where n is the number of places to which the decimal point has been moved to the left.

For example : 270,000,000,000 = 2.7 x 1011

(Decimal point has have been moved to the left for11 places)

2. To express a number (< 1), we move the decimal point to the right such that only one digit is left to the left side of the decimal point and multiply the resulting number by 10~’1 where n is the number of places to which the decimal point has been shifted to the right.

For example : 0.000 0009 = 9 x 10^-7

(Decimal point has have been shifted to the right for 7 places.)

Question 1. Identify huge and very small numbers from the above facts and write them in the following table:

Solution:

Question 2. Write the following numbers in standard form:

1. 0.000000564
2. 0.0000021
3. 21600000
4. 15240000

Solution:

1.  0.000000564

= 5.64 x 10^-7

Moving decimal 7 places to the right

2.  0.0000021

0.0000021 = 2.1 x 10^-6

Moving decimal 6 places to the right

3.  21600000

21600000 = 2.16 x 10⁷

Moving decimal 7 places to the left

4.  15240000

15240000 = 1.524 x 10⁷

Moving decimal 7 places to the left

Question 2. Write all the facts given in the standard form.

Solution:

(1) The distance from the Earth to the Sun is 1.496 x 10¹¹ m

149, 600,000,000 = 1.496 x 10¹¹.

Moving the decimal 11 places to the left

(2) The speed of light is 3 x 10⁸ m/sec.

300, 000, 000 = 3 x10⁸.

Moving decimal 8 places to the left

The thickness of the Class VII Mathematics book is 2 x 10¹ mm.

20 = 2 x 10 = 2 x 10¹

The average diameter of a Red Blood Cell is 7 x 10 6 mm.

0.00 0007 = 7 x 10^-6

Moving decimal 6 places to the right

The thickness of human hair is in the range of 5 x 10 -3 cm to 1 x I0″2cm

⇒ \(0.005=\frac{5}{1000}=\frac{5}{10^3}=5 \times 10^{-3}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

⇒ \(0.01=\frac{1}{100}=\frac{1}{10^2}=1 \times 10^{-2}\)

The distance of the moon from the Earth is 3.84467 x 10⁸m

384,467,000 = 3.84467 x 10⁸

I Moved the decimal 8 places to the left

(7) The size of a plant cell is 1.275 x 10^-5m

0.00001275 = 1.275 x 10⁵

Moving decimal 5 places to the right

The average radius of the Sun is 6.95 x10⁵km

695000 = 695 x 1000 = 695 x 10³ = 6.95 x 10⁵

(9) Mass of fuel in a space shuttle

solid rocket booster is 5.036 x 10⁵ kg

503600

= 5036 x 100 = 5036 x 10²

= 5.036 x 10³ x 10²

= 5.036 x 10³⁺²

a^m x aⁿ = a^m+n

= 5.036 x 10⁵

(10) Thickness of a piece of paper is 1.6 x10^-3 cm

0.0016 = 1.6 x 10^-3

Moving decimal 3 places to the right

The diameter of wire on a computer chip is 3 x 10^-6 m

is 3 x 10^-6

0.000003 = 3 x 01³

Moving decimal 6 places to the right

(12) The height of Mount Everest is 8.848 x 10³  m.

8848 = 8.848 x 1000 = 8.848 x 10³

Class 8 chapter 10 exponents and powers

Exponents And Powers Exercise 10.2

Question 1. Express the following numbers in standard form:

1. 0.0000000000085
2. 0.00000000000942
3. 6020000000000000
4. 0.00000000837
5. 31860000000.

Solution:

1. 0.0000000000085

0.0000000000085 = 8.5 x 10^-12

Moving the decimal 12 places to the right

2. 0.00000000000942

0.00000000000942 = 9.42 x 10^-15

Moving the decimal 12 places to the right

3. 6020000000000000

6020000000000000 = 6.02 x 10¹⁵

Moving the decimal 15 places to the left

4. 0.00000000837

0.00000000837 = 8.37 x 10^-9

Moving decimal 9 places to the right

5. 31860000000

31860000000 = 3.186 x 10¹⁰

Moving decimal 10 places to the left

Question 2. Express the following numbers in the usual form:

1. 3.02 x 10^-6
2. 4.5 x 10⁴
3. 3 x 10^-8
4. 1.0001 x 10⁹
5. 5.8 x 10¹²
6. 3.61492 x 10⁶

Solution:

⇒ \(3 \times 10^{-8}=\frac{3}{10^8}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

⇒ \(=\frac{3.02}{1000000}\)

⇒ 0.00000302

2. 4.5 x 10⁴ = 4.5 x 10000 = 45000

3.  \(3.02 \times 10^{-6}=\frac{3.02}{10^6}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

⇒ \(\frac{3}{100000000}\)

=0.00000003

4. 1.0001 X 10⁹

= 1.0001 X 1000,000,000

= 1,000,100,000

5. 5.8 X 10¹²

= 5.8 X 1,000,000,000,000

= 5,800,000,000,000

6. 3.61492 x 10⁶

= 3.61492 x 1,000,000

= 3,614,920

Question 3. Express the number appearing in the following statements in standard form:

1. 1 micron is equal to \(\frac{1}{1000000} m\)
2. The charge of an electron is 0. 000, 000,000,000,000,000,1 6 coulomb.
3. The size of bacteria is 0. 0000005 m
4. The size of a plant cell is 0. 00001 275 m
5. The thickness of thick paper is 0.07 mm.

Solution:

1.  \(\frac{1}{1000000} \mathrm{~m}= \frac{1}{10^6}\)

⇒ \(1 \times 10^{-6} \mathrm{~m}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

which is the required standard form.

2.  0.000,000,000,000,000,000,16 coulomb

⇒ \(\frac{16}{100,000,000,000,000,000,000} \text { coulomb }\)

⇒ \(frac{16}{10^{20}} \text { coulomb }\)

⇒ \(\frac{1.6 \times 10}{10^{20}} \text { coulomb }\)

⇒ \(\frac{1.6 \times 10^1}{10^{20}} \text { coulomb } \quad \mid a^1=a\)

⇒ \(1.6 \times 10^{1-20} \text { coulomb } \frac{a^m}{a^n}=a^{m-n}\)

⇒ \(1.6 \times 10^{-19} \text { coulomb }\)

which is the required standard form.

3. 0.0000005 m

⇒ \(\frac{5}{10000000} \mathrm{~m} \)

⇒ \(\frac{5}{10^7} \mathrm{~m}\)

⇒ \(5 \times 10^{-7} \mathrm{~m}\)

which is the required standard form.

4.  \(0.00001275 \mathrm{~m} =\frac{1275}{100,000,000} \mathrm{~m}\)

⇒ \(\frac{1275}{10^8} \mathrm{~m}\)

⇒ \(\frac{1275}{10^3 \times 10^5} \mathrm{~m}\)

| am x a” = am + n

⇒ \(\frac{1275}{10^3} \times 10^{-5} \mathrm{~m}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

⇒ \(1.275 \times 10^{-5} \mathrm{~m}\)

which is the required standard form.

5. \( 0.07 \mathrm{~mm} =\frac{7}{100}\)

⇒ \(\frac{7}{10^2}=7 \times 10^{-2} \mathrm{~mm}\)

⇒ \(a^{-m}=\frac{1}{a^m}\)

which is the required standard form

NCERT class 8 maths chapter 10 solutions PDF

Question 4. In a stack, there are 5 books each of thickness 20 mm, and 5 paper sheets each of thickness 0. 016mm. What is the total thickness of the stack?

Solution:

Total thickness of books = 5 x 20 mm = 100 mm

Total thickness of paper sheets = 5 x 0.016 mm = 0.080 mm

Total thickness of the stack

= Total thickness of books + Total thickness of paper sheets

= 100 mm + 0.080 mm

= (100 + 0.080) mm

= 100.080 mm

= 1.0008 x 10² mm.

Moving decimal 2 places to the left

Hence, the total thickness of the stack is 1.0008 x IQ2 mm.

Exponents And Powers Multiple-Choice Question And Solutions

Question 1. a^m x aⁿ is equal to

1. a^m+n
2. a^m-n
3. a^mn
4. a^n-m

Solution: 1. a^m+n

Question 2. a^m ÷ a^m is equal to

1. a^m+n
2. a^m-n
3. a^mn
4. a^n-m

Solution: 1. a^m+n

Question 3. (a^m)is equal to

1. a^m+n
2. a^m-n
3. a^mn
4. a^n-m

Solution: 3. a^mn

Question 4. Am x is equal to

1. (ab)^m
2. (ab)^-m
3. a^mb
4. ab^m

Solution: 1. (ab)^m

Question 5. a0 is equal to

1. 0
2. 1
3. -1
4. a

Solution: 2. 1

Question 6. \(\frac{a^m}{b^m}\) is equal to

1. \(\left(\frac{a}{b}\right)^m\)
2. \(\left(\frac{b}{a}\right)^m\)
3. \(\frac{a^m}{b}\)
4. \(\frac{a}{b^m}\)

Solution: 1. \(\left(\frac{a}{b}\right)^m\)

Question 7. 2 x 2 x 2 x 2 x 2 is equal to

1. 24
2. 23
3. 22
4. 25

Solution: 4. 25

Question 8. In 102, the exponents

1. l
2. 2
3. 10
4. 1

Solution: 2. 2

Question 9. In 102, the base is

1. 1
2. 0
3. 10
4. 100

Solution: 3. \(\frac{1}{10}\)

Exponents and powers class 8 extra questions

Question 10. 10^-1 is equal to

1. 10
2. -1
3. \(\frac{1}{10}\)
4. \(-\frac{1}{10} \text {. }\)

Solution: 3. \(\frac{1}{10}\)

Question 11. The multiplicative inverse of 2^-3 is

1. 2
2. 3
3. -3
4. 2³

Solution: 4. 2³

Question 12. The multiplicative inverse of 10⁵ is

1. 5
2. 10
3. 10^-5
4. 10⁵

Solution: 3. 10^-5

Question 13. The multiplicative inverse of \( \frac{1}{2^2}\)

1. 2^-2
2. 2²
3. 2
4. 1

Solution: 2. 22

Question 14. The multiplicative inverse of 10 “10 is

1. 10
2. \(\frac{1}{10}\)
3. 10^-10
4. 10¹⁰

Solution: 4. 10¹⁰

Question 15. The multiplicative inverse of a^m is

1. a
2. m
3. a^m
4. a^-m

Solution: 5. a^-m

Question 16. 5³ x 5^-1 is equal to

1. 5
2. 5³
3. 5^-1
4. 5²

Solution: 4. 5²

Question 17. (-2)⁵ x (- 2)⁶ is equal to

1. 2
2. -2
3. -5
4. 6

Solution: 2. -2

Question 18. 3² x 3^-4 x 3⁵ is equal to

1. 3
2. 3²
3. 3³
4. 3⁵

Solution: 3. 3³

19. (- 2) 2 is equal to

1. \(\frac{1}{4}\)
2. \(\frac{1}{2}\)
3. \(-\frac{1}{2}\)
4. \(-\frac{1}{4}\)

Solution: 1. \(\frac{1}{4}\)

Question 20. \(\left(\frac{1}{2}\right)^{-4}\) is equal to

1. 2
2. 2⁴
3. 1
4. 2^-4

Solution: 2. 2⁴

Class 8 maths exponents and powers worksheet

Question 21. (2⁰ + 4^-1) x 22 is equal to

1. 2
2. 3
3. 4
4. 5

Solution: 4. 5

Question 22. (2^-1 + 3^-1 + 5^-1)⁰ is equal to

1. 2
2. 3
3. 5
4. 1

Solution: 4. 1

Question 23. 3^m÷ 3^-3 = 3⁵ ⇒ m is equal to

1. 1
2. 2
3. 3
4. 4

Solution: 2. 2

Question 24. (-2)^m+1 x (-2)⁴ = (- 2)⁶ ⇒ m =

1. 0
2. 1
3. -1
4. none of these

Solution: 2. 1

Question 25. (-1)⁶⁰ is equal to

1. -1
2. 1
3. 50
4. -50

Solution: 2. 1

Question 26. (-1)⁵¹ is equal to

1. -1
2. 1
3. 51
4. -51

Solution: 1. -1

Question 27. 149600000000 is equal to

1. 1.496 x 10¹¹
2. 1.496 x lO¹⁰
3. 1.496 x 10¹²
4. 1.496 x 10⁵

Solution: 1. 1.496 x 10¹¹

Question 28. 300000000 is equal to

1. 3 x 10⁸
2. 3 x 10⁷
3. 3 x 10⁶
4. 3 x 10⁹

Solution: 1. 3 x 10⁸

Question 29. 0.000007 is equal to

1. 7 x 10^-6
2. 7 x 10^-6
3. 7 x 10^-4
4. 7 x 10^-3

Solution: 1. 7 x 10^-6

NCERT maths class 8 chapter 10 explanation

Question 30. 384467000 is equal to

1. 3.84467 x 1o⁸
2. 3.84467 x 10³
3. 3.84467 x 10⁷
4. 3.84467 x 10⁶

Solution: 1. 3.84467 x 10⁸

Question 31. 0.00001275 is equal to

1. 1.275 x 10^-6
2. 1.275 x 10^-3
3. 1.275 x 10⁴
4. 1.275 x 10³

Solution: 1. 1.275 x 10^-6

Question 32. 695000 is equal to

1. 6.95 x 10⁵
2. 6.95 x 10³
3. 6.95 x 10⁶
4. 6.95 x 10⁴

Solution: 1. 6.95 x 10⁵

Question 33. 503600 is equal to

1. 5.036 x 10⁵
2. 5.036 x 10⁶
3. 5.036 x 10⁴
4. 5.036 x 10⁷

Solution: 1. 5.036 x 10⁵

Question 34. 0.0016is equal to

1. 1.6 x 10 ^-3
2. 1.6 x 10^-2
3. 1.6 x 10 ^-4
4. 1.6 x lO^-5

Solution: 1. 1.6 x 10^-3

Question 35. 0.000003 is equal to

1. 3 x 10^-6
2. 3 x 10⁶
3. 3 x 10⁵
4. 3 x 10^-5

Solution: 1. 3 x 10^-6

Question 36. 8848 is equal to

1. 8.848 x 10³
2. 8.848 x 10²
3. 8.848 x 10
4. 8.848 x 10⁴

Solution: 1. 8.848 x 10³

Question 37. 1.5 x 10¹¹ is equal to

1. 150000000000
2. 15000000000
3. 1500000000
4. 1500000000000

Solution: 1. 150000000000

Question 38. 2.1 x 10^-6 is equal to

1. 0.0000021
2. 0.000021
3. 0.00021
4. 0.0021.

Solution: 1. 0.0000021

Exponents and powers class 8 important questions

Question 39. 2.5 x 10⁴ is equal to

1. 25
2. 250
3. 2500
4. 25000

Solution: 4. 25000

Question 40. 0.07 x 1O¹⁰is equal to

1. 700000000
2. 7000000
3. 7000
4. 7

Solution: 1. 700000000

Exponents And Powers True-False

Write whether the following statements are True or False:

1. The value of \(\left\{(-1)^{-1}\right\}^{-1}\) is 1: False

2. The reciprocal of \(\left(\frac{4}{3}\right)^0\) is 1: True

3. The standard form of \(\frac{1}{1000000}\) is 1.0 x 10 -6: True

4. If 6m + 6 “3 = 66, then the value of m is 3: True

5. 2345.6 = 2 x 1000 + 3 x 100 + 4 x 10 + 5 x 1 + 6 x 10 – 1: True

Class 8 maths chapter 10 solved exercises

Exponents And Powers Fill in the Blanks

1. (1000)° = 1

2. The standard form of 1,234,500,000,000 is: 1.2345 x 1012

3. The multiplicative inverse of(-3) ~2 is: (-3)2

4. (- 9)4 -5- (- 9)10 is equal to (-9)-6

5. The value of (2 -1 + 3 -1 + 4 -1)° is : 1

6. Write 1.0002 x 109 in the usual form: 1000200000

7. Write the reciprocal of 10 _1: 10

8. Find the value of*if* “3 = (100)1-4 + (100)°: 100

9. By what number should (-8) -1 be divided, so that the quotient may be equal to (-8) -1: 1

10. If = \(\frac{5^m \times 5^2 \times 5^{-3}}{5^{-5}}=5^4\) then find the value of m: 0

Mensuration

Mensuration Introduction

We know that the perimeter of a closed figure is the distance around its boundary. Also, the area of a closed figure is the measurement of the region covered by it.

• Moreover, the volume of a solid is the amount of space occupied by it. We know how to find the areas and perimeters of various plane figures such as triangles, parallelograms, rectangles, rhombuses, squares, circles, pathways, and borders in rectangular shapes, etc.
• Here, we shall learn to solve the problems related to perimeters and areas of general quadrilaterals and trapeziums.
• We shall also learn to solve the problems related to areas of polygons (regular and irregular) by using the formula for the area of a triangle and that for the area of a trapezium.
• Moreover, we shall also learn to find out the surface areas, and volumes of cubes, cuboids, and cylinders.

Area Of A Polygon

We use the method of triangulation which means splitting into triangles.

Read and Learn More NCERT Solutions For Class 8 Maths

Question 1.  Divide the following polygon (Figures) into parts (triangles and trapezium) to find out its area.

Solution:

NCERT Solutions for Class 8 Maths Chapter 9 Mensuration

2. Polygon ABODE is divided into parts as shown below. Find its area ifAD = 8 cm, AH = 6 cm, AG = 4 cm, AF = 3 cm, and perpendiculars BF = 2 cm, CH = 3 cm, EG = 2.5 cm.

Solution:

Area of polygon ABCDE = Area of A AFB + Area of trapezium FBCH + Area of A CHD + Area of A ADE …..(1)

Area of Δ AFB = (I) =\(\frac{1}{2}\) x AF x BF = \(\frac{1}{2}\) x 3 x 2 = 3 cml²

Area of trapezium FBCH = (2) = FH x \(\frac{(\mathrm{BF}+\mathrm{CH})}{2}=3 \times \frac{(2+3)}{2}=7.5 \mathrm{~cm}^2\)

FH = AH-AF = 6- 3 = 3

Area of Δ CHD = (3) = \(\frac{1}{2} \times \mathrm{HD} \times \mathrm{CH}=\frac{2 \times 3}{2}=3 \mathrm{~cm}^2\)

HD = AD -AH = 8 – 6 = 2cm

Area of Δ ADE = (4) \(\frac{1}{2} \times \mathrm{AD} \times \mathrm{GE}=\frac{1}{2}\) x 8 x 2.5 = 10 cm2

From (1),

Area of polygon ABCDE = Area [(1) + (2) + (3) + (4)]

= 3 + 7.5 + 3 + 10 = 23.5 cml²

3. Find the area of polygon MNOPQR (Figure), if

MP = 9 cm, MD = 7 cm, MC = 6 cm, MB – 4 cm, MA = 2 cm, NA, OC, QD, and RB are perpendicular to diagonal MP.

Solution:

Area of polygon MNOPQR

= Area of A MAN + Area of trapezium ACON + Area of A OOP + AreaofAPDQ + Area of trapezium DBRQ + AreaofARBM …(1)

Given:

MP = 9 cm, MD = 7 cm, MC = 6 cm, MB = 4 cm MA = 2 cm

Area of A MAN = (1) = \(\frac{\mathrm{MA} \times \mathrm{AN}}{2}=\frac{2 \times 2.5}{2}=2.5 \mathrm{~cm}^2\)

Area of trapezium ACON = (2) = \(\frac{(\mathrm{AN}+\mathrm{CO}) \times \mathrm{AC}}{2}=\frac{(\mathrm{AN}+\mathrm{CO}) \times(\mathrm{MC}-\mathrm{MA})}{2}\)

Area of A 0CP = (3) = \(\frac{\mathrm{CP} \times \mathrm{OC}}{2}=\frac{(\mathrm{MP}-\mathrm{MC}) \times \mathrm{OC}}{2}=\frac{(9-6) \times 3}{2}\) = 4.5 cml²

AreaofAPDQ = (4) = \(\frac{\mathrm{PD} \times \mathrm{DQ}}{2}=\frac{(\mathrm{MP}-\mathrm{MD}) \times \mathrm{DQ}}{2}=\frac{(9-7) \times 2}{2}\) = 2cm2

Area of trapezium DBRQ = (5) \(\frac{(\mathrm{DQ}+\mathrm{BR}) \times \mathrm{BD}}{2}=\frac{(2+2.5) \times(\mathrm{MD}-\mathrm{MB})}{2}\)

⇒  \(\frac{(2+2.5) \times(7-4)}{2}=6.75 \mathrm{~cm}^2\)

Area of ARBM= (6) =\(\frac{\mathrm{MB} \times \mathrm{RB}}{2}=\frac{4 \times 2.5}{2}=5 \mathrm{~cm}^2\)

From (1),

Area of polygon MNOPQR

= Area [(1) + (2) + (3)+ (4)+ (5) + (6)]

= 2.5 cml² + 11cml² + 4.5 cml² + 2 cml² + 6.75 cml² + 5 cml²

= 31.75 cml²

Mensuration Exercise 9.1

Question 1. The shape of the top surface of a table is a trapezium. Find its area if its parallel sides are 1 m and 1.2 m and the perpendicular distance between them is 0.8 m.

Solution:

Area of the top surface of the table

⇒  \(\frac{1}{2} h(a+b)\)

⇒  \(\frac{1}{2} \times 0.8 \times(1.2+1)\)

⇒  \(0.88 \mathrm{~m}^2\)

Class 8 Chapter 9 Maths NCERT Solutions PDF

Question 2. The area of the trapezium is 34 cm2, and the length of one of the parallel sides is 10 cm and its height is 4 cm. Find the length of the other parallel side.

Solution:

Let the length of the other parallel side be b cm

Area of trapezium = \(\frac{1}{2} h(a+b)\)

⇒  \(34 =\frac{1}{2} \times 4 \times(10+b)\)

⇒  \(34 =2 \times(10+b)\)

⇒  \(10+b =\frac{34}{2}\)

10 + b = 17

b = 17 – 10

b = 7cm

Hence, the length of another parallel side is 7cm

Question 3. The length of the fence of a trapezium-shaped field ABCD is 120 m. If BC = 48 m, CD = 17 m, and AD = 40 m, find the area of this field. Side AB is perpendicular to the parallel sides AD and BC.

Solution:

The fence of the trapezium-shaped field

ABCD = 120 m

AB + BC + CD + DA = 120

AB + 48 + 17 + 40 = 120

AB + 105 = 120

AB = 120 – 105

AB = 15 m

Area of the field

⇒  \(\frac{(B C+A D) \times A B}{2}\)

⇒  \(\frac{(48+40) \times 15}{2}=660 \mathrm{~m}^2 .\)

Hence, the area of the trapezium-shaped field is 660 ml²

Question 4. The diagonal of a quadrilateral-shaped field is 24 m and the perpendiculars dropped on it. from the remaining opposite vertices are 8 m and 13 m. Find the area, of the field

Solution: Area of the field

⇒  \(\frac{1}{2} d\left(h_1+h_2\right)\)

⇒  \(\frac{24 \times(8+13)}{2}=\frac{24 \times 21}{2}\)

= 12 x 21 = 252 ml².

Hence, the area of the quadrilateral-shaped field is 252 ml².

Question 5. The diagonals of a rhombus are 7.5 cm and 12 cm. Find its area.

Solution:

Area of the rhombus

⇒  \(\frac{1}{2} \times d_1 \times d_2=\frac{1}{2} \times 7.5 \times 12\)

= 45cml²

Hence, the area of the rhombus is 45cml²

Question 6. Find the area of a rhombus whose side is 5 cm. and whose altitude is 4.8 cm. If one of its diagonals is 8 cm long, find the length of the other diagonal.

Solution:

Area of the rhombus

= base (b) x altitude (h)

= 5 x 4.8 = 24 cml²

Area of the rhombus

⇒  \(\frac{1}{2} \times d_1 \times d_2\)

⇒  \(24 =\frac{1}{2} \times 8 \times d_2\)

⇒  \(24 =4 d_2\)

⇒  \(d_2 =\frac{24}{4}=6 \mathrm{~cm}\)

Hence, the length of the other diagonal of a rhombus is 6 cm.

Mensuration Class 8 NCERT Question Answer

Question 7. The floor of a building consists of 3,000 tiles which are rhombus shaped and each of its diagonals are 45 cm and 30 cm in length. Find the total cost of polishing the floor if the cost per m2 is 4.

Solution:

Area of a tile = \(=\frac{1}{2} \times d_1 \times d_2=\frac{1}{2} \times 45 \times 30\)

= 675 cm2

Area of the floor = 675 x 3,000 cm2 = 20,25,000 cm²

⇒  \(\frac{20,25,000}{100 \times 100} \mathrm{~m}^2\)

lm² = 100 X 100 cml²

202.50 ml²

The cost of polishing per ml² = 4

Total cost of polishing the floor

= 202.50 x 4

= $ 810.

Hence, the total cost of polishing the floor is? 810

Question 8. Mohan wants to buy a trapezium field. Its side along the river is parallel to and twice the side along the road. If the area of this field is 10,500 m2 and the perpendicular distance between the two parallel sides is 100 m., find the length of the side along the river.

Solution:

Let the length of the side along the road be m. Then, the length of the side along the river is 2x m.

Area of the field = 10,500square meters

⇒ \(\frac{1}{2} h(a+b)=10500\)

⇒ \(\frac{100 \times(2 x+x)}{2}=10,500\)

⇒ \(150 x =10,500\)

⇒ \(x =\frac{10,500}{150}\)

x= 70

2x = 2 x 70 = 140m

Hence, the length of the side along the river is 140 m.

Question 9. The top surface of the raised platform is in the shape of a regular octagon as shown in the figure. Find the area of the octagonal surface.

Solution:

Area of the octagonal surface

= Area of rectangular surface + 2(Area of trapezoidal surface)

Since the octagon is regular, therefore, the two trapeziums will be congruent.

Hence, their surface area of 111 will be equal.

⇒ \(11 \times 5+2 \times\left[\frac{(5+11) \times 4}{2}\right] \mathrm{m}^2\)

55 + 64 m2 = 119 ml²

Question 10. There is a pentagonal-shaped park as shown in the figure. ForfindingitsareaJyoti and Kavita divided it into two different ways

Find the area of this park using both ways. Can you suggest some other way offind¬ ing its area?

Solution: Jyoti’s diagram

Here, the pentagonal shape is split into two congruent trapeziums.

Area of the park

⇒ \(2 \times\left[\frac{(15+30)}{2} \times \frac{15}{2}\right]\)

⇒ \(\frac{675}{2}\)

= 337.5 m2

Kavita’s diagram:

Here, the pentagonal shape is split into a square and a triangle.

Area of the park

= Area of square + Area of triangle

⇒ \(=15 \times 15 \mathrm{~m}^2+\frac{15 \times(30-15)}{2} \mathrm{~m}^2\)

⇒ \(=225 \mathrm{~m}^2+\frac{225}{2} \mathrm{~m}^2\)

= 225 m2 + 112.5 ml²

= 337.5 ml²

Another way of finding the area

Here, the pentagonal shape is split into three triangles, out of which two triangles are congruent.

Area of the park \(=\frac{15 \times(30-15)}{2} \mathrm{~m}^2 +2 \times\left[\frac{15 \times 15}{2}\right] \mathrm{m}^2 \)

Class 8 Maths Chapter 9 Solutions with Explanation

Question 11. The diagram of the adjacent picture frame has outer dimensions = 24 cm x 28 cm and inner dimensions 16 cm x 20 cm. Find the area of each section of the frame, if the width of each section is the same

Solution:

Area of the right section of the frame

⇒ \(\frac{28+20}{2} \times \frac{24-16}{2} \mathrm{~cm}^2\)

⇒ \(\frac{48}{2} \times \frac{8}{2}=24 \times 4=96 \mathrm{~cm}^2\)

The section is a trapezium

Similarly, the area of the left section of the frame = 96 cm2

The area of the upper section of the frame

⇒ \(\frac{24+16}{2} \times \frac{28-20}{2} \mathrm{~cm}^2\)

⇒ \(\frac{40}{2} \times \frac{8}{2}=20 \times 4 \mathrm{~cm}^2\)

= 80 cml²

Similarly, the area of the lower section of the frame

= 80 cml²

Solid Shapes

Two-dimensional figures are the faces of three-dimensional shapes. If two faces of a shape are identical, then they are called congruent faces.

Surface Area Of Cube, Cuboid, And Cylinder

The surface area of a solid is the sum of the areas of its faces.

Mensuration Cuboid

Total surface area of a cuboid = 2 (lb + bh + hl)

where l, b, and h are the length, width, and height of the cuboid, respectively

Question: Find the total surface area of the following cuboids (Figure):

Solution:

The total surface area of the first cuboid

= 2(lb + bh + hi)

= 2(6 x 4 + 4 x 2 + 2 x 6)

= 2(24 + 8 + 12) = 88 cml²

The total surface area of the second cuboid

= 2(lb+ bh + hi)

= 2(4 x 4 + 4 x 10 + 10 x 4)

= 2(16 + 40 + 40) = 192 cml²

Class 8 Mensuration Exercise-wise Solutions

Question 1 . Cover the lateral surface of a cuboidal duster (which your teacher uses in the classroom) using a strip of brown sheet of paper, such that it just fits around the surface. Remove the paper. Measure the area of the paper. Is it the lateral surface area of the duster?

Solution:

(i) Yes, we can say that the area of this strip of brown sheet paper is equal to the lateral surface area of the duster.

Question 2. Measure the length, width, and height of your classroom and find

1. The total surface area of the room, ignoring the area of windows and doors.
2. The lateral surface area of this room.
3. The total area of the room which is to be white-washed.

Solution:

2.  Please find yourself

Question 3. Can we say that the total surface area of a cuboid

= lateral surface area + 2 x area of base?

Question 4. If we interchange the lengths of the base and the height of a cuboid to get another cuboid, will its lateral surface area change?

Solution:

1. Yes, we can say that the total surface area of a cuboid

= lateral surface area + 2 x area of base.

2. Lateral surface area of cuboid (i) = 2(1 + b) h

The lateral surface area of the cuboid (ii)

= 2(h + b) l. These results are different.

Hence, yes; the lateral surface area will change if we interchange the length of the base and the height of a cuboid

Mensuration Cube

The total surface area of a cube = 6l², where l is the side of the cube. The lateral surface area of a cube = 4l², where l is the side of the cube.

Question: Draw the pattern shown on a squared paper and cut it out. (You know that this pattern is a net of a cube). Fold it along the lines and tape the edges to form a cube.

1. What is the length, width, and height of the cube? Observe that all the faces of a cube are square. This makes the length, height, and width of a cube equal.
2. Write the area of each of the faces. Are they equal?
3. Write the total surface area of this cube
4. If each side of the cube is l, what will be the area of each face?
5. Can we say that the total surface area of a cube of side l is 6l²?

Solution:

(a) Length of the cube

= Width of the cube

= Length of the cube of side s

Area of each face = l x l = l².

Yes, they are equal.

(c) Total surface area of this cube = 6l².

Area of each face = l².

Yes, we can say that the total surface area of a cube of side l is 6l²

10. Find the surface area of Cube A and the lateral surface area of Cube B.

Solution:

The surface area of the cube (A)

= 6l²

= 6(10)2cm²

= 600 cm²

The lateral surface area of the cube (B)

= 4l²

= 4 x 8 x 8cm²

= 256 cm²

Question .1 Two cubes each with side b are joined to form a cuboid (Figure). What is the surface area, of this cuboid?

How will you arrange 12 cubes of equal length to form a cuboid of the smallest surface area?

After the surface area of a cube is painted, the cube is cut into 64 smaller cubes of the same dimensions (Figure).

How many have no face painted? 1 face painted? 2faces painted? 3faces painted?

Solution:

By joining two cubes on each side b,

we get a cuboid whose

length (L) = b + b = 2b units

breadth (B) = b units

and height (H) = b units

The surface area of this cuboid

= 2(L x B + B x H + H x L)

= 2[2b x b + b x b + b x 2b] sq. units

= 2[2b² + b² + 2b² sq. units

= 10b² sq. units

≠ 12b². (No, it is not equal to 1262)

Again, by joining three cubes, each with ® side b, we get a cuboid whose

length (L) = 6 + 6 + 6 = 36 units

breadth (B) = 6 units

height (H) = 6 units

The surface area of the cuboid formed by joining the three cubes

= 2 (L x B + B x H + H x L)

= 2 x [3b x b + b x b + b x 3b] sq. units

= 2 x [3b² + b² + 3b²] sq. units

= 14b² sq. units

≠186²(No, it is not equal to 18b²)

(ii) In the first arrangement,

L = 66, B = 26, H = 26

Surface area

= 2 x (6b x 2b + 2b x 2b + 2b x 6b)

= 2 x (12b² + 4b² + 12b²)

= 56b²

In the second arrangement,

L = 4b

B = 6

H = 3b

Surface area

= 2 x (4b x b + b x 3b + 3b x 4b)

= 2 x (4b² + 3b² + 12b²)

= 38b²

Hence, for the smallest surface area, the second arrangement must be made.

(Hi) 16 cubes have no faces painted.

24 cubes have 1 face painted.

16 cubes have 2 faces painted.

8 cubes have 3 faces painted.

CBSE Class 8 Maths Chapter 9 Solutions

Mensuration Cylinders

Formulae :

The lateral (curved) surface area of a cylinder = 2kvh

Total surface area of a cylinder = 2nr (h + r)

where r is the radius of the base and h is the height of the cylinder.

We take n to be \(\frac{22}{7}\) unless otherwise stated

Question .1  Find the total surface area of the following cylinders.

Solution:

For the First Cylinder

r = 14 cm

h = 8 cm

Total surface area of the cylinder = 2nr(r + h)

= 2 x 22 x 2 x 22 = 88 x 22

= 1936 cm²

For the Second Cylinder

h = 2 m

The total surface area of the cylinder

= 2πr (r + h)

⇒ \(2 \times \frac{22}{7} \times 1 \times(1+2) \mathrm{m}^2\)

⇒ \(\frac{132}{7} \mathrm{~m}^2=18 \frac{6}{7} \mathrm{~m}^2\)

Question 2.  Note that the lateral surface area of a cylinder is the circumference of the base x the height of the cylinder. Can. We write the lateral surface area of the cuboid as the perimeter of the base x height of the cuboid.

Solution:

Lateral surface area

= 2 x [(l x h) + (b x h)]

= 2 (l + b) x h

= Perimeter of base b x height of the cuboid

Yes, we can write the surface area of a cuboid as

perimeter of base x height of the cuboid

Mensuration Exercise 9.2

Question 1. There are two cuboidal boxes as shown in the adjoining figure. Which box requires a lesser amount of material to make?

Solution:

First Cuboidal Box

l = 60 cm, b = 40 cm, h = 50 cm

Total surface area

= 2(lb + bh + hl)

= 2(60 x 40 + 40 x 50 + 50 x 60) cm²

= 2(2400 + 2000 + 3000) cm²

= 2(7400) cm²

= 14800 cm²

Second Cuboidal Box

l = 50 cm, b = 50 cm, h = 50 cm

Total surface area

= 2(lb + bh + hl)

= 2(50 x 50 + 50 x 50 + 50×50) cm²

= 2(2500 + 2500 + 2500) cm²

= 2(7500) cm²

= 15000 cm²

Since the total surface area of the first cuboidal box is less than the total surface area of the second cuboidal box, therefore, box (a) requires a lesser amount of material to make.

NCERT Class 8 Mensuration Chapter Questions

Question 2. A suitcase with measures 80 cm x 48 cm x 24 cm is to be covered with a tarpaulin cloth. How many meters of tarpaulin of width 96 cm are required to cover 100 such suitcases?

Solution:

Here,

Length of the suitcase (l) = 80 cm

The breadth of the suitcase (b) = 48 cm

Height of the suitcase (h) = 24 cm

The total surface area of the suitcase

= 2(lb + bh + hl)

= 2(80 x 48 + 48 x 24 + 24 x 80) cm2

= 2(3840 + 1152 + 1920) cm²

= 2(6912) cm²

= 13824 cm²

Width of tarpaulin = 96 cm

Length of tarpaulin required to cover 1 suitcase

⇒ \(\frac{\text { Total surface area of the suitcase }}{\text { Width of tarpaulin }}\)

⇒ \(=\frac{13824}{96}=144 \mathrm{~cm}\)

Length of tarpaulin required to cover 100 such suitcases

= 144 x 100 cm = 14400 cm

⇒ \(\frac{14400}{100} \mathrm{~m}=144 \mathrm{~m}\)

Hence, 144 m of tarpaulin is required.

Question 3. Find the side of a cube whose surface area is 600 cm2.

Solution:

Let the side of the cube be a cm. Then, the total surface area of the cube

= 6a² cm²

According to the question,6a² = 600

⇒ \(a^2=\frac{600}{6}\)

a²= 100

a = √1oo

a = 10 cm

Hence, the side of the cube is 10 cm.

Question 4. Rukhsar painted the outside of the cabinet measuring 1 m x 2 m x 1.5 m. How much surface area did she cover if she painted all except the bottom of the cabinet?

Solution:

I = 2m 7 cm

b = 1 m

h = 1.5 m

Required area

= 2[2 x 1 + 1 x 1.6 + 1.5 x 2] -2xl

= 2[2 +1.5 + 3] – 2

= 13 m²-2 m²

= 11 m²

Hence, she covered 11 m² of surface area.

Question 5. Daniel is painting the walls and ceiling of the cuboidal hall with a length, breadth, and height of 15 m, 10 m, and 1 m, respectively. From each can of paint, 100 m² of area is painted. How many cans of paint will she need to paint the room?

Solution:

Z = 15 m

b = 10 m

h = 7 m

Surface area to be painted

= 2(1 x 6 + b x h + h x l) – l x b

= 2 (15 x 10 + 10 x 7 + 7 x 15) m² – (15 x 10) m²

= 2(150 + 70 + 105) m² – 150 m²

= 2(325) m² – 150 m²

= 650 m² – 150 m²

= 500 m²

Number of cans needed \(=\frac{\text { Surface area to be painted }}{\text { Area painted by } 1 \text { can }}\)

⇒ \(=\frac{500}{100}=5\)

Hence, she will need 5 cans of paint to paint the room.

Question 6. Describe how the two figures (below) are alike and how they are different. Which box has a larger lateral surface area?

Solution:

Likeness→ Both have the same height.

Difference → One is a cylinder, the other is a cube;

The cylinder is a solid obtained by revolving a rectangular area about one side.

A cube is a solid enclosed by six square faces.

A cylinder has two circular faces, whereas a cube has six square faces

For First Box

Diameter = 7 cm

Radius (r) =\(\frac{\text { Diameter }}{2}=\frac{7}{2} \mathrm{~cm}\)

Height (h) = 7 cm

Lateral surface area = 2nrh

⇒ \(2 \times \frac{22}{7} \times \frac{7}{2} \times 7\) = 154 cm²

For the Second Box

l = 7 cm

b = 7 cm

h = 7 cm

Lateral surface area

= 4 = 4 x (7)2

= 196cm2

Hence, the second box has a larger lateral surface area

Class 8 Chapter 9 Surface Area and Volume

Question 7. A closed cylindrical tank of radius 7 m and height 3 m is made from a sheet of metal. How much sheet of metal is required?

Solution:

r = 7 m

h = 3 m

Total surface area

= 2πr(r + h)

⇒ \(2 \times \frac{22}{7} \times 7 \times(7+3)\) = 440 m²

Hence, 440 m² of metal sheet is required.

Question  8. The lateral surface area of a hollow cylinder is 4224 cm². It is cut along its height and forms a rectangular sheet of width 33 cm. Find the perimeter of the rectangular sheet.
Solution:

The lateral surface area of the hollow

cylinder = 4224 cm²

The area of the rectangular sheet = 4224 cm2

Length x width = 4224 cm²

Length x 33 = 4224

Length = \(\frac{4224}{33}\)

Length = 128 cm

The perimeter of the rectangular sheet

= 2(Length + Breadth)

= 2(128 + 33) cm

= 2(161) cm

= 322 cm

Hence, the perimeter of the rectangular sheet is 322 cm.

Question 9. A road roller takes 750 complete revolutions to move once over to level a road. Find the area of the road if the diameter of a road roller is 84 cm and the length is 1 m.

Solution:

The diameter of the road roller = 84 cm

Radius (r) of the road roller \(\frac{84}{2} \mathrm{~cm}=42 \mathrm{~cm}\)

Length (h) of the road roller = 1 m = 100 cm

The lateral surface area of the road roller = 2πrh

⇒ \(2 \times \frac{22}{7} \times 42 \times 100\)

= 26,400 cm2

The area of the road is covered in 1 complete revolution

= 26,400 cm²

The area of the road covered 750 complete revolutions

= 26,400 x 750 cm²

= 1,98,00,000 cm²

⇒ \(\frac{1,98,00,000}{100 \times 100} \mathrm{~m}^2\)

= 1,980 m²

Question 10. A company packages its milk powder in a cylindrical container whose base has a diameter of 14 cm and a height of 20 cm. The company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from the top and bottom, what is the area of the label

Solution:

For a cylindrical container

The diameter of the base = 14 cm

Radius of the base (r) =\(\frac{14}{2} \mathrm{~cm}\)

= 7 cm

Height (h) = 20 cm

The curved surface area of the container = 2πrh

⇒ \(=2 \times \frac{22}{7} \times 7 \times 20\)

= 880 cm²

Surface area of the label

= 880 cm²

⇒ \(-2\left(2 \times \frac{22}{7} \times 7 \times 2\right) \mathrm{cm}^2\)

= 880 cm2 – 176 cm²

= 704 cm²

Hence, the surface area of the label is 704 cm².

Aliter:

The label is in the form of a cylinder for which

radius (R) =\(\frac{14}{2}=7 \mathrm{~cm}\)

height (H) = 20 – (2 + 2) = 16 cm

Area of the label = 2πRH

⇒ \(=2 \cdot \frac{22}{7} \cdot 7 \cdot 16=704 \mathrm{~cm}^2\)

Hence, the surface area of the label is 1704 cm².

Class 8 Mensuration Worksheet with Answers

Volume Of Cube, Cuboid, And Cylinder

The volume of a three-dimensional object is the amount of space occupied by it. Volume is measured in cubic units.

Question 1 cubic cm

= 1 cm x 1 cm x 1 cm

= 1 cm³

= 10 mm x 10 mm x 10 mm

= mm³

1 cubic m

= lm x lm x lm = lm3

1 cubic mm

= 1 mm x l mm x 1 mm 1 cubic mm

= 1 mm³

= 0.1 cm x 0.1 cm x 0.1 cm

cm³

1 cubic mm

= 1 mm x l mm x 1 mm 1 cubic mm

= 1 mm³

= 0.1 cm x 0.1 cm x 0.1 cm

=100cm³

1 cubic mm

= 1 mm x l mm x 1 mm 1 cubic mm

= 1 mm³

= 0.1 cm x 0.1 cm x 0.1 cm

cm³

Cuboid Formula

Volume of cuboid = Ibh

where l, b, and h are the length, width, and height of the cuboid, respectively.
OR

The volume of the cuboid = area of the base x height cuboid.

YouTakecan36arrangecubes of the qualm size many(ie., ways.lengthObserveofeachthecubefollowingis same. table Arrange and fill the min the to blank torn a

We have the following observations:

Since then, we have used 36 cubes of equal size to form these 36 cubic units. Also, the volume of each cuboid is the height of the cuboid. From the above example ese cuboids, the volume of each cuboid = l x b x h

Since l x b is the area of its b

The volume of a cuboid = Area of base x Therefore, we can also say that,

Question 1.  Can you think of such objects whose

Solution: The volume of Godow reservoirs, etc., can be found by this method.

Question: Find the volume of the following cuboids (Figure).

Solution:

(i) Volume of the cuboid

= l x b x h

= (8x3x2) cm³

= 48 cm³

(ii) Volume of the cuboid

= Area of Base x Height

⇒ \(24 \times \frac{3}{100}\)

⇒ \(\frac{72}{100}=0.72 \mathrm{~m}^3\)

Cube

The volume of the cube = 1³, where l is the side of the cube.

Question 1.  Find the volume of the following cubes.

1. with a side of 4 cm
2. with a side of 1.5 m

Solution:

Volume of the cube = (Side)³

= 4 x 4 x 4 cm³

= 64 cm³

(b) Volume of the cube = (Side)³

= 1.5 x 1.5 x 1.5 m³

= 3.375 m³

NCERT Solutions for Class 8 Maths Chapter 9 Mensuration

Question 2.  Arrange 64 cubes of equal size in as many ways as you can to form a cuboid. Find the surface area of each arrangement. Can solid shapes of the same volume have the same surface area?

Solution:

Some arrangements are as follows :

The surface area in the arrangement

(1) = 2 x (64 x l + i x l + l x 64)

258 square units

2 x (32 x 2 + 2 x l + i x 32)

= 196 square units

= 2 x (16 x 2 + 2 x 2 + 2 x 16)

= 136 square units

= 2 x (16 x 4 + 4 x 1 + 1x 16)

= 168 square units

=2 x (8 x 4 + 4 x 2 + 2 x 8) = 112 square units

= 2 x (4 x 4 + 4 x 4 + 4 x 4)

= 96 square units, etc.

Also, the volume of the cuboid obtained in each case is 64 cubic units. So, No, we cannot say that solid shapes of the same volume need to have the same surface area.

Question 3. The company sells biscuits. For packing purposes, they are using cuboidal boxes :

box A → 3 cm x 8 cm x 20 cm,

box B → 4 cm x 12 cm x 10 cm.

1. What size of the box will be economical for the company? Why?
2. Can you suggest any other size (dimensions) that has the same volume but is more economical than these?

Solution:

Box A: Total surface area

= 2 x (3 x 8 + 8 x 20 + 20 x 3) cm²

= 2 x (24 +160 + 60) cm²

= 2 x 244 cm² = 488 cm²

Box B: Total surface area

= 2 x (4 x 12 + 12 x 10 + 10 x 4) cm²

= 2 x (48 + 120 + 40) cm²

= 2 x208 cm2 = 416 cm².

-Since the total surface area of box B is lesser than the total surface area of box A, therefore, the size of 4 cm x 12 cm x 10 cm of the

The box will be economical for the company to use for packing purposes.

(The volume of both the boxes are same as given below)

Again, the volume of the cuboidal box A

= 3 x 8 x 20

= 480 cm³ and, volume of the cuboidal box B

= 4 x 12 x 10

= 480 cm³

Yes, we can suggest another size (dimensions) which has the same volume but is more economical than these. It is 10 m x 6 m x 8 m.

Volume = 10 x 6 x 8 = 480 cm³

Total surface area = 2 x (10 x 6 + 6 x 8 + 8 x 10) cm2 = 376 cm².

This size (dimensions) has the same volume, but it is more economical than boxes A and B.

Cylinder Formula:

Volume of cylinder = πr²h

where r is the radius of the base and h is the height of the cylinder

Question 1.   Find the volume of the following cylinders :

Solution:

r = 7 cm, h = 10 cm

The volume of the cylinder = πr²h

⇒ \(=\frac{22}{7} \times 7^2 \times 10\)

⇒ \(=\frac{22}{7} \times 7 \times 7 \times 10\)

= 1540 cm³

The Volume of the cylinder

= Area of base x height

= (250 x 2) m³

= 500 m³

Volume And Capacity

There is not much difference between these two words.

Volume refers to the amount of space occupied by an object.

Capacity refers to the quantity that a container holds.

Note: If a water tin holds 100 cm³ of water, then the capacity of the water tin is 100 cm³.

Capacity is also measured in terms of liters.

The relation between liter and cm³ is,

1 mL = 1 cm³, 1 L = 1000 cm³.

lm3 = 10,00,000 cm³= 1000 L.

Mensuration Exercise 9.3

Question 1. Given a cylindrical tank, in which situation will you find the surface area, and in which situation is volume?

1. To find how much it can hold,
2. The number of cement bags required to plaster it.
3. To find the number of smaller tanks that can be filled with water from it.

Solution:

Volume

Surface area

Volume.

Question 2. The diameter of cylinder A is 7 cm, and the height is 14 cm. The diameter of cylinder B is 14 cm, and the height is 7cm. Without doing any calculations, can you suggest whose volume is greater? Verify it by finding the volume of both cylinders. Check whether the cylinder with greater volume also has a greater surface area.

Solution:

The volume of cylinder B is greater.

For Cylinder A

⇒ \(r=\frac{7}{2} \mathrm{~cm}\)

h = 14 cm

Volume = nr²h

⇒ \(=\frac{22}{7} \times \frac{7}{2} \times \frac{7}{2} \times 14\)

= 539 cm³

For Cylinder B

⇒ \(r=\frac{14}{2} \mathrm{~cm}=7 \mathrm{~cm}\)

h = 7 cm

Volume = nr2h

⇒ \(\frac{22}{7} \times 7 \times 7 \times 7\)

= 1078 cm³.

By actual calculation of volumes of both the cylinders, it is verified that the volume of cylinder B is greater

Surface Area

For Cylinder A

Surface area = 2jir (r + h)

⇒ \(2 \times \frac{22}{7} \times \frac{7}{2} \times\left(\frac{7}{2}+14\right)\)

⇒ \(2 \times \frac{22}{7} \times \frac{7}{2} \times \frac{35}{2}\)

= 385 cm²

For Cylinder B

Surface area

=27tr(r + h)

⇒ \(2 \times \frac{22}{7} \times 7 \times(7+7)\)

⇒ \(2 \times \frac{22}{7} \times 7 \times 14\)

By actual calculation of the surface area of both cylinders, we observe that the cylinder with greater volume (Cylinder B) has a greater surface area.

Class 8 Maths Mensuration Chapter Solutions

Question 3. Find the height of a cuboid whose base area is 180 cm² and volume is 900 cm³.

Solution:

Height of the cuboid = \(=\frac{\text { Volume of the cuboid }}{\text { Base area of the cuboid }}\)

⇒ \(=\frac{900}{180}\) = 5 cm

Question 4. A cuboid is of dimensions 60 cm x 54 cm x 30 cm. How many small cubes with sides 6 cm can be placed in the given cuboid?

Solution:

Volume of the cuboid = 60 x 54 x 30 cm³

= 97200 cm³

The volume of a small cube

= 6 x 6 x 6 cm³

= 216 cm³

Number of small cubes that can be placed in the given cuboid

⇒ \(\frac{\text { Volume of the cuboid }}{\text { Volume of a small cube }}\)

⇒ \(\frac{97200}{216}=450\)

Hence, 450 small cubes can be placed in the given cuboid.

Question 5. Find the height of the cylinder whose volume is 1.54 m² and whose diameter of the base is 140 cm.
Solution:

The diameter of the base = 140 cm

Radius of the base (r)= \(=\frac{140}{2} \mathrm{~cm}=70 \mathrm{~cm}\)

Area of the base = nr²

⇒ \(=\frac{22}{7} \times 70 \times 70\)

= 15400 cm²

The volume of the cylinder

= 1.54 m³

= 1.54 x 100 x 100 x 100 cm³

= 15,40,000 cm³

Height of the cylinder

⇒ \(\frac{\text { Volume of the cylinder }}{\text { Area of the base of the cylinder }}\)

⇒ \(\frac{(2)}{(1)}\)

⇒ \(=\frac{15,40,000}{15400}\)

= 100 cm

= 1 m

Hence, the height of the cylinder is 1 m.

Question 6. A milk tank is in the form of a cylinder whose radius is 1.5 m and length is 7 m. Find the quantity of milk in liters that can be stored in the tank

solution:

For milk tank

r = 1.5 m

h = 7 m

Capacity = nFh

⇒ \(=\frac{22}{7} \times 1.5 \times 1.5 \times 7\)

⇒ \(=\frac{22}{7} \times \frac{15}{10} \times \frac{15}{10} \times 7\)

= 49.5 m³ I

= 49.5 x 1000 L I

[lm³ = 1000 L]

= 49500 L.

Hence, the quantity of milk that can be stored in the tank is 49500 litres.

Question 7. If each edge of a cube is doubled,

1. how many times will its surface area increase?
2. how many times will its volume increase?

Solution:

Let the original edge of the cube be a cm.

Then, its new edge = 2a cm

The original surface area of the cube = 6a² cm²

The new surface area of the cube

= 6(2a)² cm²

= 24a² cm²

= 4 (6a² cm²)

= 4 original surface area,

Hence, its surface area will increase 4 times.

Originalvolume ofthe cube = a³ cm³

A new volume of the cube

= (2a)³ cm³

= 8a³ cm³

= 8 x the original volume of the cube.

Hence, its volume will increase 8 times

Question 8. Water is poured into a cuboidal g reservoir at the rate of 60 liters per minute. If the volume of the reservoir is 108 m3, find the BL number of hours it will take to fill the reservoir

Solution:

Volume of reservoir

= 108 m³

= 108 x 1000 L

[1 m³ = 1000 L]

= 108000 L

Water poured per minute = 60 L

Time taken to fill the reservoir

⇒ \(\frac{\text { Volume of the reservoir }}{\text { Water poured per minute }}\)

⇒ \(\frac{108000}{60} \mathrm{~m}\)

⇒ \(\frac{108000}{60 \times 60} \text { hours }\)

= 30 hours

Hence, the number of hours it will take to fill the reservoir is 30

Mensuration Class 8 NCERT Question Answer

Mensuration Multiple-Choice Questions and Solutions

Question 1. 1 cm³ =

1. 1000 mm³
2. 100 mm³
3. 10 mm³
4. \(\frac{1}{1000} \mathrm{~mm}^3 .\)

Solution: 1. 1000 mm³

Question 2. 1 m³ =

1. 1000000 cm³
2. 100 cm³
3. 10 cm³
4. \(\frac{1}{1000} \mathrm{~cm}^3 .\)

Solution: 1. 1000000 cm³

Question 3. 1 mm³ =

1. 0.001 cm³
2. 0.01cm³
3. 0.1 cm³
4. 100 cm³

Solution: 1. 0.001 cm³

Question 4. 1 cm³ =

1. 0.000001m³
2. 0.01m³
3. 0.1m³
4. 1000m³

Solution: 1. 0.000001m³

Question 5. The surface area of a cuboid of length l, breadth b, and height h is

1. lbs
2. lb + bh + hl
3. 2 (lb + bh + hi)
4. 2 (l+ b)h.

Solution: 3. 2 (lb + bh + hi)

Question 6. The surface area of a cube of edge a is

1. 4a²
2. 6a²
3. 3a²
4. a²

Solution: 2. 6a²

Question 7. The total surface area of a cylinder of base radius r and height h is

1. 2πr (r + h)
2. πr (r + h)
3. 2πrh
4. 2πr²

Solution: 1. 2πr (r + h)

Question 8. The volume of a cuboid of length l, breadth b, and height h is

1. lbh
2. lb + bh + hl
3. 2 (lb + bh + hl)
4. 2(l + b)h.

Solution: 1. lb

Question 9. The volume of a cube of edge a is

1. a²
2. a³
3. a⁴
4. 6a²

Solution: 2. a³

Question 10. The volume of a cylinder of base radius and height his

1. 2πrh
2. πr²h
3. 2πr (r + h)
4. \(\frac{1}{3} \pi r^2 h .\)

Solution: 2. nr2h

Question 11. 1 L =

1. 10 cm³
2. 100 cm³
3. 1000 cm³
4. 10000 cm³

Solution: 3. 1000 cm³

Question 12. 1 m³ =

1. 1L
2. 10 L
3. 100L
4. 1000 L

Solution: 4. 1000 L

Question 13. The area ofthe trapezium

1. 9 cm²
2. 6 cm²
3. 7 cm²
4. 24 cm²

Solution: 1. 9 cm²

Area \(=\frac{(4+2) 3}{2}=9 \mathrm{~cm}^2\)

Mensuration Class 8 NCERT Question Answer

Question 14. The area of the trapezium

1. 6 cm²
2. 4 cm²
3. 3 cm²
4. 9 cm²

Solution: 1. 6 cm²

Area \(=\frac{(3+1) 3}{2}=6 \mathrm{~cm}^2\)

Question 15. The perimeter of the trapezium

1. 12 cm
2. 24 cm
3. 6 cm
4. 18 cm.

Solution: 1. 12 cm

Perimeter = 3+ 3 + 2 + 4 = 12 cm

Question 16. The area of a rhombus is 60 cm². One diagonal is 10 cm. The other diagonal is

1. 6 cm
2. 12 cm
3. 3 cm
4. 24 cm.

Solution: 2. 12 cm

⇒ \(\frac{1}{2}\)x 10 X = d260 => d2 = 12cm

Question 17. The area of a trapezium is 40 cm². Its parallel sides are 12 cm and 8 cm. The distance between the parallel sides is

1. 1cm
2. 2cm
3. 3cm
4. 4cm

Solution: 4. 4cm

⇒ \(\frac{(12+8) d}{2}=\) – 40 =» d = 4cm

Question 18. 8 persons can stay in a cubical room. Each person requires 27 m³ of air. The side of the cube is

1. 6m
2. 4m
3. 3m
4. 2m

Solution: 1. 6m

Volume = 8 x 27 = 216 m3.

Side = 216 = 6 m

Question 19. If the height of the cuboid becomes zero, it will take the shape of a

1. cube
2. parallelogram
3. circle
4. rectangle

Solution: 4. rectangle

Height = \(\frac{80}{20}=4 \mathrm{~m} .\)

Question 20. The volume of a room is 80 m³. The area of the floor is 20 m². The height of the 1 room is

1. 1m
2. 2m
3. 3m
4. 4m

Solution: 4. 4m

Question 21. The floor of a room is a square of side 6 m. Its height is 4 m. The volume of the room is

1. 140 m³
2. 142 m³
3. 144 m³
4. 145 m³

Solution: 3. 144 m³

Volume = 6x6x4 = 144 m³

Question 22. The base radius and height of a right circular cylinder are 14 cm and 5 cm, respectively. Its curved surface is

1. 220 cm²
2. 440 cm²
3. 1232 cm²
4. 2π x 14 x (14 + 5) cm²

Solution: 2. 440 cm²

Curved surface =\(2 \times \frac{22}{7} \times 14 \times 5\)

= 440 cm².

Question 23. The heights of the two right circular cylinders are the same. Their volumes are respectively 16πm³  and 8lπm³. The ratio of their base radius

1. 16:81
2. 4:9
3. 2: 3
4. 9: 4.

Solution: 2. 4:9

⇒ \(\frac{\pi r_1^2 h}{\pi \pi_2^2 h}=\frac{16 \pi}{81 \pi} \Rightarrow \frac{r_1}{r_2}=\frac{4}{9}\)

Question 24. The ratio of the radii of two right circular cylinders is 1 : 2 and the ratio of their heights is 4 : 1. The ratio of their volumes is

1. 1:1
2. 1:2
3. 2:1
4. 4:1

Solution: 1. 1:1

⇒ \(\frac{r_1}{r_2}=\frac{\pi(1)^2 4}{\pi(2)^2 1}=1: 1 \text {. }\)

Class 8 Maths Chapter 9 Solutions with Explanation

Question 25. A glass in the form of a right circular cylinder is half full of water. Its base radius is 3 cm and its height is 8 cm. The volume of water is

1. 18π cm³
2. 36π cm³
3. 9π cm³
4. 36π cm³

Solution: 2. 36πcm³

Volume = \(\frac{1}{2} \pi \times 3 \times 3 \times 8=36 \pi \mathrm{cm}^3 .\)

Question 26. The base area of the right circular cylinder is 16ft cm³. Its height is 5 cm. Its curved surface area is

1. 40π cm²
2. 30π cm²
3. 20π cm²
4. 10π cm²

Solution: 1. 40π cm²

πr² = 16π => r = 4 cm

Curved surface area = 2xπX4x5 = 40π cm²

Question 27. The base radius and height of a right circular cylinder are 5 cm and 10 Its total surface area is

1. 150ft cm²
2. 150 cm²
3. 300ft cm²
4. 300n cm²

Solution: 1.150π cm²

Total surface area = 2πr (h + r)

= 2π5 (10 + 5) = 150π cm².

Mensuration True-False

Write whether the following statements are True or False:

1. The volume of a solid is the measurement of the space occupied by it: True

2. The areas of any two faces of a cuboid are equal:  False

3. Two cuboids with equal volumes essentially have equal surface areas: False

4. The radii of two cylinders having the same volume are in the ratio 1 : 3. Then, the ratio of their heights is 9: 1: True

5. The volume of a cube is 216 cm³. Its surface area is 216 cm3: True

Mensuration Fill In The Blanks

1. The areas of any two faces of a cube are_______: Equal

2. The total surface area of a cube, whose volume is 1 cm³, is_____:   1cm²

3. 1 litre = _______cm³:  1000

4. 1 mm =_______ m : \(\frac{1}{1000} \mathrm{~m}\)

5. The ratio of radii of two cylinders is 1: 2 and heights are in the ratio 4: 5. Find the ratio of their volumes:  1:5

6. A metal sheet 64 cm long, 27 cm broad, and 8 cm thick is melted into a cube. Find the side of the cube:  24 cm

7. A cube of side 2 cm is cut into 1 cm cubes. What is the percentage increase in the volume after such a cutting:   0%

8. Find the area of the following figure: 10 cm²

Algebraic Expressions And Identities Addition And Subtraction Of Algebraic Expressions

While adding (or subtracting) polynomials, first look for like terms and add (or subtract) them; then handle the unlike terms. Note that the sum of x number of like terms is another like term whose coefficient is the sum of the coefficients of the like terms being added.

Addition And Subtraction Of Algebraic Expressions Exercise 8.1

Question 1. Add the following.

xb – bc, bc – cx, cx – xb

x – b + xb, b – c + be, c – x + xc

2p²q² – 3pq + 4, 5 + 7pq – 3p²q²

l² + m², m² + n² n² + l², 2lm + 2mn + 2nl

Read and Learn More NCERT Solutions For Class 8 Maths

Solution: 1. xb – bc, bc – cx, cx – xb

Thus, the sum of the given expressions is 0.

2. x-b + xb, b-c + bc, c-x+xc

Class 8 Maths Algebraic Expressions and Identities

Thus, the sum of the given expressions is ab + bc + cx

3. 2p²q² – 3pq + 4, 5 + 7pq – 3p²q²

4. l² + m², m² + n², n² + l², 2lm + 2mn + 2nl

Thus, the sum of the given expressions is 2(l² + m² + n² + Im + mn + nl).

Question 2.

1. Subtract 4x – 7xb + 3b + 12 from 12x – 9xb + 5b – 3
2. Subtract 3xy + 5yz – 7zx from 5xy – 2yz – 2zx + lOxyz
3. Subtract 4p²q – 3pq + 5pq² – 8p + 7q – 10 from IS – 3p – 11q + 5pq – 2pq² + 5p²q

Solution:

Thus, the required answer is 8a – 2ab + 26- 15

Thus, the required answer is 28 + bp- 18q + 8pq- Ipq² + p²q

Algebraic Expressions Class 8 Solutions

8.2 Multiplication Of Algebraic Expressions: Introduction

There exist x number of situations when we need to multiply algebraic expressions. For example, in finding the xerox of x rectangle whose sides are given xs expressions

Question 1. Can you think of two more such situations, where we may need to multiply algebraic expressions?

[Hint: Think of speed and time; Think of interest to be paid, the principal and the rate of simple interest; etc.].

Solution:

Distance = Speed x Time

Simple Interest

Principal x Rate of simple interest

⇒ \(=\frac{\text { per annum } \times \text { Time in years }}{100}\)

Multiplying A Monomial By A Monomial

A monomial multiplied by an x monomial always gives an x monomial.

Multiplying Two Monomials

In the product of two monomials

Coefficient = coefficient of first monomial x coefficient of second monomial

Algebraic factor – algebraic factor of first monomial x algebraic factor of second monomial

Multiplying Three Or More Monomixls

We first multiply the first two monomials and then multiply the resulting monomial by the third monomial. This method can be extended to the product of any number of monomials.

Rules Of Signs

(1) The product of two factors is positive or negative accordingly xs the two factors have like signs or unlike signs. Note that

1. (+) x (+) = +
2. (+) X (-) = –
3. (-) x (+) = –
4. (-) x (-) = +

(2) If x is x vxrixble xnd p, q xre positive inteqers, then

x^p x x^q = x^p+q

Class 8 Maths Chapter 8 Question Answer

Question 1. Find 4x x 5y x 7z. First, find 4x x 5y and. multiply it by 7z; or first, find 5y x 7z and multiply it by 4x. Is the result the same? What do you observe? Does the order in which you carry out the multiplication matter?

Solution:

4x x 5y x 7z

4x x 5y = (4 x 5) x (x x y)

= 20 x (xy) = 20 xy

(4x x 5y) x 7z = 20xy x lz

= (20 x 7) x (xy x z)

= 140 x (XYZ)

= 140xyz …(1)

OR

5y x 7z = (5 x 7) x (y x z)

– 35 X (yz) = 35yz

4x X (5y X 7z) = 4x X 35yz

= (4 x 35) x (x x yz)

= 140 x (xyz)

= I40xyz…..(2)

We observe from Eqns. (1) and (2) that the result is the same. It shows that the product of monomials is associative, i.e., the order in which we multiply monomials does not matter.

Addition And Subtraction Of Algebraic Expressions Exercise 8.2

Question 1. Find the product of the following pairs of monomials:

1. 4, 7p
2. -4p, 7p
3. -4p, 7pq
4. 4p³, -3p
5. 4p, 0.

Solution:

(1)  4, 7p

4 x 7p = (4 x 7) x p

= 28 x p

= 28p

(2)  – 4p, Ip

(-4p)x(7p) = {(-4) x 7} x (P x P)

= (-28) x p2

= -28p2

(3)  -4p, 7pq

(- 4p) x (Ipq) = {(- 4) x 7} x (p x (pq)}

= (-28) x (p x p x q)

= (-28) x p²

= -28p²q

(4)  4p², – 3p

(4p³) x ( -3p) = {4 x (_ 3)} x (p³ Xp)

= (-12) X p⁴

= – 12p⁴

(5)  4p, 0

(4p) x 0 = (4×0) x p

0 x p = 0

Class 8 Maths Chapter 8 Exercise Solutions

Question 2. Find the press of rectangles with the following pairs of monomials xs their lengths and breadths respectively:

(p, q) ; (10m, 5n); (20x² 5y²); (4x, 3.x²); (3mn, 4np).

Solution:

1.  (p, q)

Length = p

Brexdth = q

Area of the rectangle

= Length x Brexdth

= P x q

= pq

2.  (10m, 5n)

Length = 10 m

Brexdth = 5 n

Area of the rectangle

= Length x Brexdth

= (10m) x (5n)

= (10 x 5) x (m x n)

= 50 x (mn)

= 50 mn

3. (2Ox² , 5y²)

Length = 20X²

Brexdth = 5y²

Area of the rectangle

= Length x Brexdth

= (20x²) x (5y²)

= (20 x 5) x (x² x y²)

= 100 x (x2/)

= 100x²y²

4.  (4x,3x²)

Length = 4x

Brexdth = 3X²

Area of the rectangle

= Length x Brexdth

= (4x) x (3x²)

= (4 x 3) x (x x x²)

= 12 x x³ = 12X³

CBSE Class 8 Algebraic Expressions and Identities

5.  (3mn, 4np)

Length = 3mn

Brexdth = 4np

Area of the rectangle

= Length x Brexdth

= (Smn) x (4np)

= (3×4) x (mn) x (np)

= 12 x m x (n x n)xp

= 12 mn²p.

Question 3. Complete the table of products.

Solution:

We have.

1. 2x x -5y = {2 x (- 5)} x (x x y) = – lOxy

2x x 3X² = (2 x 3) x (x x x²) = 6X³

2x x (- 4xy) = {2 x (-4)} x x x (xy)

= -8 X (x X x) X y

= – 8 x²y

2x X 7x²y = (2 X 7) X (x X x²) x y = 14x²y

2x x (-9X²y²) = {2 x (-9)> x (x x x²) Xy²

= – 18x³y²

2. (-5y)x(2x)

= {(-5) x 2} X (y X x)

= – 10 xy

(- 5y) x (- 5p)

= {(-5) x (-5)} x y xy

= 25 y²

(~5y) x 3X2

= {(-5) x 3} x yx2

= – 15.x²y

(-5y) x ( – 430’)

= {(-5) X (- 4)} x XX (y X y)

= 20 xy²

(-5y) x (7x²y)

= {(-5) X 7} X x² X (yXy)

= -35 x²y²

(~5y) x (-qx2ÿ)

= {(-5) x (- 9)} x x2x(yxy2)

= 45 x²y³

Algebraic Identities Class 8 Explanation

3. 3x² x 2x = (3 x 2) x (x2 x x) = 6X²

3X² x 3x² = (3 x 3) x (x² x x²) = 9 x⁴

3x⁴ x (- 4 xy) = 3 x (- 4)} x (x2 x x) x y = – 12x³y

3x² x 7x²y

= (3 x 7) x (x² x x1) xy

= 21×4

3x² x (- 9X² y²)

= {3 x (- 9)} x (x² x x²)xy²

= – 27xy

4. (-4xy) x 2x

= {(_4) x 2} x {x x x) xy

= -8x²y

(-4xy) x (-5y)

= {(- 4) x (- 5)} X X x (y x y)

= 20xy²

(-4x²y) x 3X²

= {(- 4) x 3} x (ix x²) x y

= – 12x²y

(-430) x (- 4xy)

= {(-4) X (_4)}x (ixi)x(y Xy)

= 16x²y²

(-4xy) X Ixÿy

= {(-4) X 7} X (x X X²) X (y X y)

= -28x³y²

(- 4xy) X (- 9X²)

={(-4) x (-9)} X (x X x²) X (y X y²)

= 36x³y³

5. 7x²y x 2x

= (7 x 2) x (x2 x x) x y

= 14x²y

7x²y x (- 5y)

= {7 x (-5)} x x² X (y Xy)

= – 35x²y²

7x²y X(3x²)

– (7 x 3) X (*2 x x2) Xy = 21x4y

7x²y x (- 4 xy)

= {7 X (-4)} X (x² x x) X (y X y)

= -28x³y²

7x2y x 7x2p

= (7 x 7) X (x² X X²) x (y X y)

= 49x⁴y²

7-X²y X (_ 9x²ÿ2)

= {7X(-9)} X (x²X X²) X (y x y²)

= -63x⁴y³

(- 9x²,y²) x 2x

= {(-9) x 2} x x( x x) x y2

= -18x³y²

(-9xV) x (-5y)

= {(-9) x (-5)} x x² x x² (y²x y)

– 45x²y³

(- 9x2y²) x (3X²)

= {(- 9) x 3} x (x² x x²) x y2

= – 27x⁴ y²

(- 9x²y) x (- 4xy)

= {(-9) x (-4)} x (x² x X) x (y2 x y)

= 36 x⁴

(~9x2y2) x (7x2y)

= {(-9)x7}x(x2Xx2)X(y2xy)

= – 63 xy

(-9x2y²) x (- 9xY)

= {(-9) x (-9)}x ft? xÿ x (y2 x y2)

= 81 x⁴y⁴

Class 8 Maths Chapter 8 Examples with Solutions

Question 4. Obtain the volume of rectangular boxes with the following length, breadth, and height respectively:

1. 5x, 3x², 7x.4
2. 2p, 4q, 8r
3. xy, 2x²y, 2xy²
4. x, 2b, 3c.

Solution:

1.  5x, 3x², 7×4

Length = 5x

Brexdth = 3x²

Height = 7×4

Volume of the rectangular box

= Lenqth x Breadth x Heiqht

= (5x) x (3x²) x (7×4)

= (5 x 3 x 7) x (x x x² x x4)

= 105×7

2.   2p, xq, 8r

Lenqth = 2p

Brexdth = xq

Heiqht = 8r

Volume of the rectxnqulxr box

= Lenqth x Brexdth x Heiqht

= (2p) x (xq) x (8r)

= (2 x 4 x 8) x (p x q x r)

= 64 pqr

3.  xy, 2x²y, 2xy²

Length = xy

Brexdth = 2x²y

Height = 2xy²

The volume of the rectangular box

= Length x Breadth x Height

= (xy) x (2x²y) x (2xy²)

= (2 x 2) x (x x x² x x) x (yxyxy²)

= 4x4y4

4.  x, 2b, 3c

Length = x

Brexdth = 2b

Height = 3c

The volume of the rectangular box

= Length x Breadth x Height

= (x) x (2b) x (3c)

= (2 x 3) x (x x b x c)

= 6xbc

Question 5. Obtain the product of

1. xy, yz, zx
2. x, -x², x3
3. 2, 4y, 8y2, 16y³
4. x, 2b, 3c,6xbc
5. m, -mn, mn

Solution:

1.  xy, yz, zx

Required product

= (xy) x (yz) x (zx)

= (x x X) X (y X y) X (Z X z)

= x² x x ²z²

= x2²y²z²

2.  x, -x², x³

Required product

= (x) x (-x²) x (x²)

= – (x x x² x x³)

= -x⁶

3.  2, 4y, 8y² 16y³

Required product

= (2) x (4y) x (8y²) x (16y³)

= (2 x 4 x 8 x 16) x (y x y2 x y3)

= 1024y⁶

4.  x, 2b, 3c, 6xbc

Required product

= (x) x (26) x (3c) x (6xbc)

= (2 x 3 x 6) x (x x x) x (6 x 6) x(c x c)

= 36 x²b²c²

5.  m, – mn, mn

Required product

= (m) x (-mn) x (mnp)

= (- 1) x (m x m x m) x (n xn) xp

= -m²n²p

NCERT Solutions for Class 8 Maths Chapter 8

Multiplying A Monomial By A Polynomial

While multiplying x polynomial by x monomial, we multiply every term in the polynomial by the monomial.

Using the distributive law, we carry out the multiplication term by term.
It states that if P, Q, and R are three monomials, then

1. P x (Q + R) = (P x Q) + (p x R)
2.  (Q + R) x p = (Q x P) + (R x P)

Question. Find the product:

1.  2x(3x + 5xy) (H)x,2 (2xb – 5c).

Solution:

1.  2x (3x + 5ry)

2x (3x + 5xy) = (2x) x (3x) + (2x) x (5xy)

= (2 x 3) x(xxx) + (2 x 5) x (x x x) x y

= 6x² + 10 x2y

2.  a² (2xb-5c)

x2(2xb – 5c) = (x2) x (2xb) – (x2) x (5C)

= (1 x 2) x (x2 x x) X b -(1 X 5) X x2 X c

= 2a³b – 5a²c

8.4.2 Multiplying A Monomial By A Trinomial

By using the distributive law, we carry out the multiplication term by term

Question. Find the product: (4p² + 5p + 7) x 3p.

Solution:

(4p² + 5p + 7) x 3p.

= (4p²x 3p) + (5p x 3p)+ (7 x 3p)

= (4 x 3) x (p² x P) + (5 x 3) x (p x p) + (7 x 3) x p

= 12p3+ 15p² + 21p

Addition And Subtraction Of Algebraic Expressions Exercise 8.3

Question 1. Carry out the. multiplication of the expressions in exch for the following pairs:

1. 4p, q + r
2. ab, a – b
3. a + b, 7a²b²
4. a²-9, 4a
5. PQ + qr + rp, 0

Solution:

1.   4p, q + r

(4p) x (q+ r) = (dp) x (q) + (4 p) x (r)

By distributive law

= (4 x 1) x p x q + (4 x 1) x p x r

= 4pq + 4pr

(2) xb, x-b

(ab) x (a-b) = (ab) x (a) – (ab) x (b)

By distributive law

= (1 x 1) x (a x a) xb

– (1 x 1) a x (b x b)

= a²b – ab²

3.  a+b, 7a²b²

(x +b) x (7a²b²)

= x x 7a² b² + 5 x 7×2 b2

By distributive law

= (1 x 7) x (a x x²) x b² + (1 x 7) x a² x (a x b2)

= 7a³b² + 7a²b³

a²– 9, 4a

(a²– 9) x (4a)

= a²x 4a – 9 x 4a

By distributive law

= ( 1 x 4) x (a² x a) – (9 x 4) x a

= 4a³-36a

PQ + qr + rp, 0

(PQ + qr+ rp) x (0)

= (pq) x 0 + (qr) x 0 + (rp) x 0.

By distributive law

= 0 + 0 + 0 = 0.

Class 8 Chapter 8 Maths NCERT Solutions PDF

Question 2. Complete the table:

Solution:

We have,

(1) a x (b + c + d)

= a x b + a x c + a x d

= ab + ac + ad

(2) (X + y – 5) x 5xy

= pC x 5pc_y + y x 5*y + (-5) x 5xy

= (1 X 5) X (x x X) X y

+ (1 x 5) X X X (y X y)

+ {(-5) x 5}x xy

= 5x²y + 5xy² – 25xy

(3) p x (6p² – 7p + 5)

= p x 6p² + p x (- 7p) + p x 5

= (1 x 6) x (p xp²)

+ {1 x (- 7)} x (p x p) + 5 x p

= 6p³ – 7p² + 5p

(4) 4p²q² x (p² – q²)

= 4p²q² x p² + 4p²q² x (-q²)

= (4 x 1) x (p² x p²) x q²

+ {4 X (- 1)} X p² X (q² X q²)

= 4p⁴ q² – 4p² q⁴.

(5)(a + b + c) x abc

= a x abc + b x abc + c x abc

= (ax a) x b x c

+ a x (b x b) x c

+ a x b x (c x c)

= a² bc + ab² c + abc²

Question 3. Find the product:

(a²) x(2a²²) x (4a²⁶)

⇒ \(\left(\frac{2}{3} x y\right) \times\left(\frac{-9}{10} x^2 y^2\right)\)

⇒ \(\left(-\frac{10}{3} p q^3\right) \times\left(\frac{6}{5} p^3 q\right)\)

x x x² x x³x x⁴

Solution. (1) (x²) x (2x²²) x (4x²⁶)

= (1 x 2 x 4) x (x² x x²² x x²⁶)

= 8 X a^2+22+26

By laws of exponents

= 8 x a⁵⁰ = 8 x 50

⇒ \(\left(\frac{2}{3} x y\right) \times\left(-\frac{9}{10} x^2 y^2\right)\)

⇒ \(\left\{\frac{2}{3} \times\left(-\frac{9}{10}\right)\right\} \times\left(x \times x^2\right) \times\left(y \times y^2\right)\)

⇒ \(-\frac{3}{5} x^3 y^3\) I by laws of exponents

3.   \(\left(-\frac{10}{3} p q^3\right) \times\left(\frac{6}{5} p^3 q\right)\)

⇒ \(=\left\{\left(-\frac{10}{3}\right) \times \frac{6}{5}\right\} \times\left(p \times p^3\right) \times\left(q^3 \times q\right)\)

= -4p⁴q⁴.    By laws of exponents

(4) X x x² X x³ X x⁴

X x x² x x³ X x⁴ = (1 X 1 X 1 X 1) X X¹ X x² X x³ X x⁴

= (1) X x ^1+2+3+4

= X10.

By laws of exponents

Question 4. (a) Simplify: 3x (4x -5) +3 and find us values for (1) x = 3, (2) x =\(\frac{1}{2}\)

(b) Simplify: x(x² + x + 1) + 5 xnd find its value for

(1) x = 0, (2) x = 1 and (3) x = -1.

Solution :

1.  3x (4x-5) + 3

= (3x) (xx) – (3x) (5) + 3

= (3 x 4) x (x x x) – (3 x 5) x x + 3

= 12x² – 15x + 3

(i) When x = 3,

12x² – 15.x + 3

= 12(3)² – 15(3) + 3

= 12 x 9 – 45 + 3

= 108 – 45 + 3 = 66

2.  When x =\(\frac{1}{2}\)

12X² – 15.x + 3

⇒ \(12\left(\frac{1}{2}\right)^2-15\left(\frac{1}{2}\right)+3\)

⇒ \(12\left(\frac{1}{4}\right)-\frac{15}{2}+3\)

⇒ \(3-\frac{15}{2}+3\)

⇒ \(6-\frac{15}{2}\)

⇒ \(\frac{12-15}{2}\)

⇒ \(-\frac{3}{2}\)

(b) a(a² + x + 1) + 5

a x a² + a x a + (a x 1 + 5 )

= a³ + a² + a+ 5

1.  When a = 0

a³ + a²+ a + 5 = (0)3 + (0)2 + (0) + 5

=0+0+0+5=5

2.  When a =1

a³ + a² + a+ 5 = (l)3 + (l)2 + (1) + 5

=l+l+l+5=8

3.  When a=-l

a³ +a² + a+ 5

= (- 1)3 + (- l)2 + (- 1) + 5

= —1 + 1 — 1 + 5 = 4

Class 8 Maths Algebraic Expressions and Identities

Question  5.

1. add : p(p – q), q(q – r) and r(r-p)
2. add: 2x(z – x – y)and 2y (z -y- x)
3. Subtract: 31 (l – 4m. + 5n) from 41 (10n-3m + 21)
4. Subtract: 3x(x +b+c)-2b(x-b+c) from 4c(- x + b+ c).

Solution:

(1) First expression

= p(p-q)=pxp-pxq

= p² – pq

Second expression

= q(q-r)

= q x q – q x r

= q² – qr

Third expression

= r(r – p)

=r x r – r x p

= r² – rp

adding the three expressions,

image

First expression

= 2x (z – x – y)

= (2x) X (2)-(2x) X (x) – (2x) X (y)

= 2xz -2x² – 2xy

Second expression

= 2y(z-y-x)

= (2y) x (z) – (2y) x (y) – (2y)x(x)

= 2yz – 2y² – 2yx

adding the two expressions,

image

First expression

= 31(1 – 4m + 5n)

= (31) x (l) – (31) x (4m) + (31) x (bn)

= 312 – 12lm + 15In

Second expression

= 41 (10n – 3m + 2l)

= (41) x (10n) – (4l) x (3m) + (4l) x (2l)

= 40ln – 12lm + 8l²

Subtracting,

image

First expression

= 3x (x + 6 + c) – 26 (x – 6 + c)

= [(3x) x (x) + (3x) x (6) + (3x) x (c)]

-[(26) x (x) + (26) x (6) – (26) x (c)]

= [3a² + 3ab + 3ac]- [2ab- 2b² + 2bc]

= 3a² + 2b² + 3ab – 2ab- 2bc + 3ac

– 3a² + 2b² + ab- 2bc + 3ac

Second expression

= 4c (- x + 6 + c)

= 4c x (-x) + 4c x 6 + 4c x c

= -4xc + 46c + 4c2

Subtracting

image

8.5 Multiplying A Polynomial By A Polynomial

We multiply the term of one polynomial by each term of the other polynomial. Also, we combine the like terms in the product.

Multiplying A Binomial By A Binomial

We use distributive law and multiply each of the two terms of one binomial by exchanging the two terms of the other binomial and combining like terms in the product.

Thus, if P, Q, R, and S are four monomials, then

(P + Q) x (R + S) = P x (R + S) +Qx(R + S)

= (P x R + P x S) + (QXR + QXS)

= PR + PS + QR + QS.

8.5.2 Multiplying A Binomial By A Trinomial

We use distributive law and multiply each of the three terms in the trinomial by exchanging the two terms in the binomial and combining like terms in the product.

Addition And Subtraction Of Algebraic Expressions Exercise 8.4

Question 1. Multiply the binomial:

1. (2x + 5) and (4x – 3)
2. (y – 8) and (3y – 4)
3. (2.51 – 0.5 m) and (2.51 + 0.5m)
4. (x + 3b) and (x + 5)
5. (2pq + 3q²) and (3pq – 2q²)
6. \(\left(\frac{3}{4} x^2+3 b^2\right) \text { and } 4\left(x^2-\frac{2}{3} b^2\right)\)

Solution:

(i) (2x + 5) xnd (4x – 3)

(2x + 5) x (4x – 3)

= (2x) x (4x – 3) + 5 x (4x – 3) by distributive law

= (2x) x (4x) – (2x) x (3) + (5) x (4x) – (5) x (3)

= 8x² – 6x + 20x – 15

= 8x² + (20x – 6x) – 15 Combining like terms

= 8x² + 14x – 15

2. (y – 8) and (3y – 4) by distributive law

(y – 8) x (3y – 4)

= y x (3y – 4) – 8 x (3y – 4) – (8) x (3y) + 8 x 4

= (y) x (3y) – (y) x (4)

= 3y² – 4y -24y + 32 Combining like terms

3. (2.5 l – 0.5 m) xnd (2.5 l + 0.5 m)

(2.5 l – 0.5 m) x (2.5 l + 0.5 m)

= (2.5 l) x (2.5 l + 0.5 m) – (0.5 m) x (2.5 l + 0.5 m) by distributive law

= (2.5 Z) x (2.5 Z) + (2.5 l) x (0.5 m) – (0.5 m) x (2.5 l) – (0.5 m) x (0.5 m)

= 6.25 12 + 1.25 Zm – 1.25 m/- 0.25 m² Combining like terms

= 6.25 l² + (1.25 lm – 1.25 lm) – 0.25 m²

= 6.25 l² – 0.25 m²

4. (x + 3 b) and (x + 5)

(a + 35) x (x + 5)

= a x (c +5) + (3b) x (x + 5) by distributive law

= (a) x (x) + (a) x (5) + (3b) x (x) + (3b) x (5)

= ax + 5a + 3bx + 15b

5.  (2pq + 3q²) and (3pq – 2q²)

(2pq + 3q²) x (3pq – 2q²)

= (2pq) x (3pq – 2q²) + (3q²) x (3pq – 2q²) by distributive law

= (2pq) x (3pq) – (2pq) x (2q²) + (3q²) x (3pq) – (3q²) x (2q²)

= 6p2q2 – 4pq³ + 9pq³ – Qqi

= 6p²q² + (9pq³ – 4pq³) – 6q⁴ Combining like terms

= 6p²q² + 5pqz – 6q⁴

⇒ \(\left(\frac{3}{4} x^2+3 b^2\right) \text { and } 4\left(x^2-\frac{2}{3} b^2\right)\)

⇒ \(\left(\frac{3}{4} x^2+3 b^2\right) \times 4\left(x^2-\frac{2}{3} b^2\right)=\left(\frac{3}{4} x^2+3 b^2\right) \times\left(4 x^2-\frac{8}{3} b^2\right)\)

⇒ \(\frac{3}{4} x^2 \times\left(4 x^2-\frac{8}{3} b^2\right)+3 b^2 \times\left(4 x^2-\frac{8}{3} b^2\right)\) by distributive law

⇒ \(\left(\frac{3}{4} x^2\right) \times\left(4 x^2\right)-\left(\frac{3}{4} x^2\right) \times\left(\frxc{8}{3} b^2\right)+\left(3 b^2\right) \times\left(4 x^2\right)-\left(3 b^2\right) \times\left(\frac{8}{3} b^2\right)\)

= 3a⁴ – 2a²b² + 12b²a² – 8b⁴

= 3a⁴ + (12a²b² -2a²b²) -8b⁴

= 3a⁴ + 10a²b² – 8b⁴Combining like terms

Question 2. Find the product:

1. (5 – 2x) (3 + x)
2. (x + 7y) (7x-y)
3. (x² + b) (x + b²)
4. (p² – q²) (2p + q)

Solution:

(i) (5 – 2x) (3 + x)

= (5) x (3 + x) – (2x) x (3 + x)

= (5) x (3) + (5) x (x) – (2x) X (3) – (2x) X (X)

= 15 + 5x – 6x – 2x²

= 15 – x – 2x²

2.  (x + 7y) (7x – y)

= (x) x (7x – y) + (7y) x (7x – y)

= (x) x (7x) – (x) x (y) + (7y) x (7x) – (7y) x (y)

= 7x² – xy + 49yx – 7y²

= 7x² + 48xy – 7y²

3.  (a² + b) (a + b²)

= a² x (a+ b²) + b x (a + b²)

= (a²) x (a) + (a²) x (b²) + (b) x (a) + (b) x (b²)

= a³ + a²b² + ab + b³

= a³ + a²b² + ab + b³

4.  (p² – q²) (2p + q)

= p² x (2p + q) – q² x (2p + q)

= (p²) x (2p) + (p²) x (q) – (q²) x (2p)- (q²) x (q)

= 2p³+ p²q – 2q²p – q³

= 2p³ + p²q – 2pq² – q³

Class 8 Maths Chapter 8 Question Answer

Question 3. Simplify :

1. (x² – 5) (x+ 5) + 25
2. (x² + 5) (b³ + 3) + 5
3. (l + s²) (l² – s)
4. (x + b)(c – d) + (x – 6) (c + d)+ 2 (xc + bd)
5. (x + y) (2x + y) + (x + 2y)(x – y)
6.  (x + y) (x² – xy + y²)
7. (1.5x – 4y)(1.5x + 4y + 3)- 4.5x + I2y
8. (x + b + c) (x. + b – c).

Solution:

1.   (x² – 5) (x + 5) + 25

= x²(x + 5) – 5(x + 5) + 25

= (x² x X) + (x² x 5) – (5 x X) – (5 x 5) + 25

= x³ + 5X² – 5x – 25 + 25

= x³ + 5×2 – 5x

2.  (a² + 5) (b³ + 3) + 5

= a²(b³ + 3) + 5(b³ + 3) + 5

= (a² x b³) + (a² x 3) + (5 x b³) +(5a³) + 5

= a²b³ + 3a² + 5b³ + 15 + 5

= a²b³ + 3a² + 5b³ + 20

3.  (t + s²) (t² – s)

= t(t² – s) + s²(t² – s)

= (tx t²) – (t X s) + (s² X t²) – (s² X s)

= t² -ts + s²t² – s³

4.  (a + b) (c – d) + (a – b) (c + d) + 2(ac + bd)

= a(c – d) + b(c – d) + a(c + d) – b(c + d) + 2(oc + bd)

= ac – ad + be – bd + ac + ad – be – bd + 2ac + 2bd by distributive law

= (ac + ac + 2ac) + (ad- ad) + (be- be) + (2bd – bd – bd)

= 4ac combines the like terms

5.  (x + y) (2x + y) + (x + 2y) (x – y)

= x(2x + y) + y(2x + y) + x(x – y) + 2y(x – y)

= (X X 2x) + (x X y) + (y X 2x) + (y x y) + (x x x) – (x X y) (2y x x)- (2y x y

By distributive law

– 2×2 + xy + 2xy + y² + x2 – xy + 2xy – 2y²

= (2x² + x²) + (xy + 2xy – xy + 2xy) + (y2 – 2y²)

= 3x² + 4xy – y²

6.  (x + y) (x² – xy + y²)

x(x² – xy + y²)= y(x² – xy + y²)

(x x x²) – (x x xy) + (x x y²) + (y x x²) – (y x xy) + (y x y² ) | by distributive law

x³ – x²y + xy² + x²y – xy² + y3

= x^-3 + x²y – x²y) + (xy² – xy²) + y3   combining the like terms

= x^–3 + y²

7.  (1.5x – 43-) (1.5x + 4y + 3) – 4.5x + 12y

= 1.5x (1.5x + 4y + 3)- 4y (1.5x + 4y + 3) – 4.5x + 12y | by distributive law

= (1.5x x 1.5x) + (1.5x x 4y) + (1.5x X 3) – (4y x 1.5x) – (4y x 4y) – (4y x 3) – 4.5x + 12y | by distributive law

2.25x² + 6xy + 4.5x – 6xy – 16y2 – 12y – 4.5x + 12y

= 2.25x² + (6xy – 6xy) – 16y² + (4.5x – 4.5x) + (12y – 12y) I combining the like terms

= 2.25x² – 16y²

8.  (a + b + c) (a + b – c)

= a(a + b-c) + b(a + b-c) + c(a + 6-c) I by distributive law

= a2 + ab – ac + ab + b² – be + ae + be – c²    I by distributive law

= a²+ (ab + ab) + (ac – ac) + b² + (be – be) – c² combining the like terms

= a² + 2ab + b2 – c²

Addition And Subtraction Of Algebraic Expressions Multiple-Choice Questions And Solutions

Question 1. The expression x + 3 is in

1. one variable
2. two variables
3. no variable
4. none of these.

Solution: 1. one variable

Question 2. The expression 4xy + 7 is in

1. one variable
2. two variables
3. no variable
4. none of these.

Solution: 2. two variables

Algebraic Identities Class 8 Explanation

Question 3. The expression x + y + z is in

1. one variable
2. no variable
3. three variables
4. two variables.

Solution: 3. three variables

Question 4. The value of 5x when x = 5 is

1. 5
2. 10
3. 25
4. -5.

Solution: 3. 25

Question 5. The value of x² – 2x + 1 when x = 1 is

1. l
2. 2
3. -2
4. 0.

Solution: 4. 0

Question 6. The value of x² + y2 when x = 1, y = 2 is

1. l
2. 2
3. 4
4. 5.

Solution: 4. 5

Question 7. The value of x² – 2yx + y2 when x = 1, y = 2 is

1. l
2. -l
3. 2
4. -2.

Solution: 1. 1

Question 8. The value of x² – xy + y2 when x = 0, y = 1 is

1. 0
2. -l
3. l
4. none of these.

Solution: 3. 1

Question 9. The sum of lx, lOx, and 12x is

1. 17x
2. 22x
3. 19x
4. 29x.

Solution: 4. 29x.

Question 10. The sum of 8pq and -17pq is

1. pg
2. 9pqr
3. -9pq
4. -pg.

Solution: 3.-9pq

Question 11. The sum of 5x², -7X², 8x², 11x² and -9x² is

1. 2x²
2. 4x²
3. 6x²
4. 8x²

Solution: 4. 8x².

Question 12. The sum ofx² y²-z² and z²-x² is

1. 0
2. 3x²
3. 3y²
4. 3z²

Solution: 1. 0

Question 13. What do you get when you subtract – 3xy from 5xy?

1. 3xy
2. 5xy
3. 8xy
4. xy.

Solution: 3. 8xy

Question 14. The result of the subtraction of law from 0 is 4

1. 0
2. 7x
3. -7x
4. x

Solution: 3. -7x

Class 8 Maths Chapter 8 Examples with Solutions

Question 15. The result of subtraction of 3x from – 4x is

1. -7x
2. 7x
3. x
4. -x.

Solution: 1. -7x

Question 16. The product of 4mn and 0 is

1. 0
2. 1
3. mn
4. 4mn.

Solution: 1. 0

Question 17. The product of 5x and 2y is

1. xy
2. 2×7
3. 5xy
4. 10xy.

Solution: 4. 10xy.

Question 18. The product of lx and -12x is

1. 84x²
2. -84x²
3. x²
4. -x².

Solution: 2. -84x²

Question 19. The area of a rectangle whose length and breadth are 9 and 4y respectively is

1. 4y³
2. 9y³
3. 36y³
4. 13y³

Solution: 3. 36y³

Question 20. The area of a rectangle with length 2l2m and breadth 3Im? is

1. 6l3m³
2. l3m³
3. 2l3m³
4. 4l3m³

Solution: 1. 6l3m³

Question 21. The volume of a cube of side 2a is

1. 4a³
2. 2a
3. 8a³
4. 8.

Solution: 3. 8a³

Question 22. The volume of a cuboid of dimensions a, 6, c is

1. abc
2. a2b2c2
3. a3b3c3
4. none of these.

Solution: 1. abc

Question 23. The product of x², – x³, – x⁴ is

1. x⁹
2. x⁵
3. x⁷
4. x⁶

Solution: 1. x⁹

Class 8 Maths Chapter 8 Exercise Solutions

Addition And Subtraction Of Algebraic Expressions True-False

Write whether the following statements are True or False:

1. In a polynomial, the exponents of the variables are always non-negative integers:   True

2. a (b + c) = ab + ae is called the distributive property : True

3. a² – b² is the product of (a – b) and (a + b): True

Addition And Subtraction Of Algebraic Expressions Fill in the Blanks

1. The value of, when 92 -72 = 8p, is___________ : 4

2. On subtracting -a²b² from 2ab², we get___________:  2a²b²

3. The difference between the squares of two consecutive natural numbers is their_______: Sum

4. Area of a rectangle with length 3 ab² and breadth 4 ac² is_______:  12a²b²c²

5. Write the product of the monomials -12a, -15a², a²b:  180 a³b³

6. Add a² + b² – c²  b²  + c² – a²  and c²  + a² – b² :  a² + b² + c²

7. Find the value of, if 1000y = (981)² – (19)²:  962