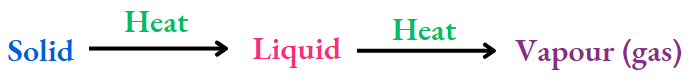Marksparks

NCERT Class 8 Chemistry Chapter 8 Water Notes

Life would not have been possible on Earth without water. Water is the most abundant compound on our planet, covering three-fourths of the Earth’s surface. It constitutes about seven tenths of our bodies and more than nine tenths of fruits and vegetables.

Water can dissolve many substances —solids, liquids and gases alike. It controls the temperature of the atmosphere and also our bodies.

Read And Lean More Class 8 Chemistry

We need water for:

• Domestic purposes: Like cooking, drinking, washing and bathing;
• Agricultural purposes: Like irrigation, jute processing and dairy farming; and
• Industrial purposes: It is used as a solvent, reactant and coolant.

NCERT Solutions for Water Class 8

The sources of water are surface water bodies like ponds, rivers, lakes, seas and oceans, and groundwater. Both surface water and groundwater are replenished by the rain. In this chapter, we will discuss the properties of water as a solvent and also the types of natural water (i.e., hard and soft water).

Water—A Universal Solvent

Water is called a universal solvent as it dissolves a larger number of substances than any other.

It is this property of water that helps a river dissolve many minerals from the soil and finally discharge them into the sea. Thus, a sea or an ocean is a vast store of minerals and other soluble substances.

How a Solute Dissolves in Water

A solute, when mixed with water or any other solvent, separates into molecules. And these molecules hide themselves in the intermolecular space of water or the solvent and appear to have disappeared.

As the solute molecules occupy the intermolecular space of the solvent, the volume of the solvent does not change when a solute dissolves in it.

Water is Superior to Other Solvents

Water is superior to other solvents as it helps the solute fragment into molecules or radicals. A water molecule is electrically neutral.

• But there is a slight positive charge on the hydrogen atoms and an equivalent amount of negative charge on the oxygen atom, so that the opposite charges cancel each other.
• Such a molecule is called a polar molecule and thus water is a polar solvent.
• Due to polarity, water molecules experience a coulomb attraction (i.e., an electrostatic force of attraction) for polar solutes, including those containing radicals.
• When such a solute is stirred in water, the water molecules cling to the solute molecules or radicals. And take them away in a cage-like structure. Thus, the solute seems to disappear.
• All salts are made up of radicals. For example, sodium chloride (NaCl) is made up of Na⁺ and Cl^– radicals, sodium sulphate (Na₂SO₄) of Na⁺ and SO^2-₄ radicals, magnesium sulphate (MgSO₄) of Mg²⁺ and SO^2-₄ radicals, copper(H) sulphate (CuSO₄) of Cu²⁺ and SO^2-₄ radicals and ammonium nitrate (NH₄NO₃) of NH₄⁺ and NO^–₃ radicals.
• Hence, most salts are soluble in water. No wonder the sea is a vast store of salts.
• A large number of bases [i.e., NaOH, KOH, Ca(OH)₂ and NH₄OH] are also soluble in water as they too are made up of radicals. And so are acids

Example: HCl, HNO₃, H₂SO₄ and H₃PO₄) as they are polar.

Apart from these, a big number of organic compounds

Example: Methyl alcohol, ethyl alcohol, acetone, formaldehyde, formic acid, acetic acid, glucose, fructose, sucrose and vitamins) They are soluble as they are also polar

Solutions, Suspensions and Colloids

Solutions, suspensions and colloids are important types of mixtures. Let us discuss them now

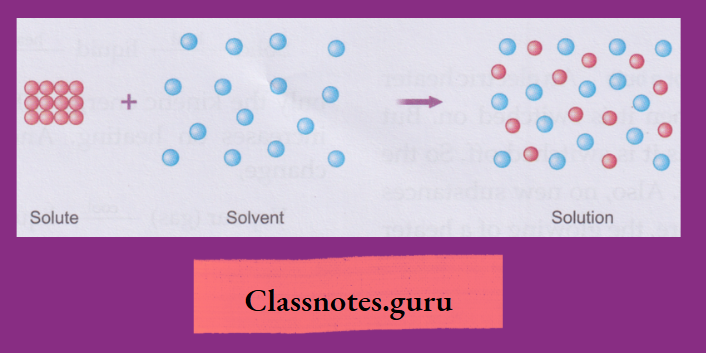
Solutions:

• A solution is a homogeneous mixture of one or more solutes with a solvent
• Common examples of solutions are the homogeneous mixtures of common salt, sugar, copper(II) sulphate, calcium chloride, potassium nitrate, potassium permanganate and ammonium chloride with water.

A solution has the important characteristics of:

• Being transparent and
• Passing through a filter paper or a membrane.

The size of the solute particles must be very small—1 nm (i.e., 10^-9 m or a millionth of a millimetre) or less in diameter.

The terms solute and solvent are used in respect of a solution. They are replaced by the terms dispersed phase and dispersion (or continuous) medium, respectively, for a suspension as well as a colloid.

Suspensions

A suspension is a heterogeneous mixture of one or more dispersed phases in a dispersion medium

Muddy water is a common example of a suspension. Here, soil is the dispersed phase and water, the dispersion medium. Similarly, chalk (CaCO₃) or gypsum (CaSO₄.2H₂O; blackboard chalk), when stirred in water, gives a suspension.

NCERT Class 8 Chemistry Chapter 8 Water

For a suspension, it is not necessary that the dispersed phase be a solid and the dispersion medium a liquid. The suspensions of

• A liquid in a liquid, called an emulsion
  • Example: An oil-water emulsion
• A liquid in a gas, called fog
  • Example: Water in air
• A solid in a gas, called smoke
  • Example: Carbon in the air is also quite common.

The size of a dispersed particle in a suspension is much larger than that of a solute in a solution. It is 10^-6 m (i.e., a millionth of a metre) or more in diameter.

A suspension is not transparent. And the dispersed particles slowly settle down because, being large, they are heavy too. You must have seen that the soil settles down from muddy water in a glass.

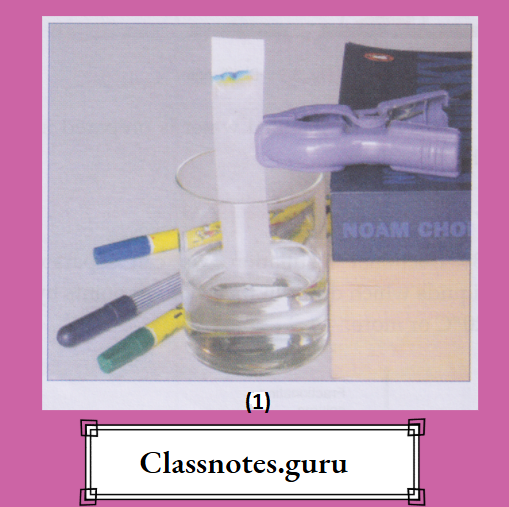
Colloids

A colloid is a homogeneous mixture of one or more dispersed phases in a dispersion medium. Milk is the most common example of a colloid —butterfat globules dispersed in water. Jam, jelly, whipped cream and gelatin are also common examples of a colloid.

Colloids are not transparent. And the dispersed particles do not settle down. The size of a dispersed particle is in between those of a solute in a solution and a dispersed particle in a suspension, i.e., between 10^-9 m and 10^-6m (or greater than 1 nm and smaller than 1000 nm). The characteristics of a solution,s uspension and colloid are given in Table

Characteristics of a solution, suspension and colloid:

Solutions

For preparing a solution, you generally add the solute in instalments (or bit by bit) to the solvent, stirring the mixture all the time. A stage comes when the mixture refuses to take in more solute. And whatever solute you add afterwards remains undissolved and settles down at the bottom.

• Now, if you heat the mixture, the undissolved solute will also dissolve. This happens because the capability of a solvent to dissolve a solute generally increases with temperature.
• In other words, the higher the temperature, the larger is the amount of a solute that can dissolve in a given amount of a solvent
• Thus, the extra amount of solute at a higher temperature should separate from the solution when the latter is cooled.
• But in most cases, the extra solute does not separate, i.e., it remains dissolved. Hasn’t the solvent retained more solute than it can dissolve at that temperature? Yes, it has.

This usually happens with those salts (as solutes) which crystallise as hydrates,

Example: Copper(II) sulphate, which crystallises as CuSO₄.5H₂O and iron (II) sulphate, which does so as FeSO₄.7H₂O. Depending on the solute content of the solution,

Water Class 8 NCERT Notes

We find that there are three kinds of solutions:

1. Unsaturated
2. Saturated
3. Supersaturated

These are:

1. Unsaturated: A solution capable of dissolving more solute at a given temperature is called an unsaturated solution.
2. Saturated: A solution containing the maximum amount of solute that can be dissolved in it at a given temperature is called a saturated solution.
3. Supersaturated: A solution containing more solute than the given amount of the solvent is capable of dissolving at that temperature is called a supersaturated solution

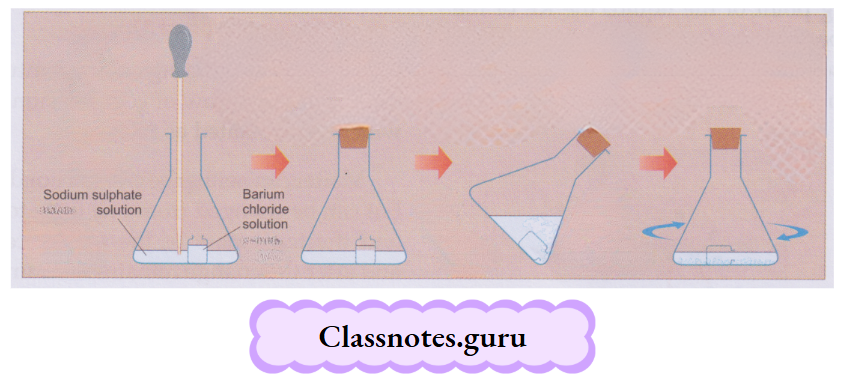
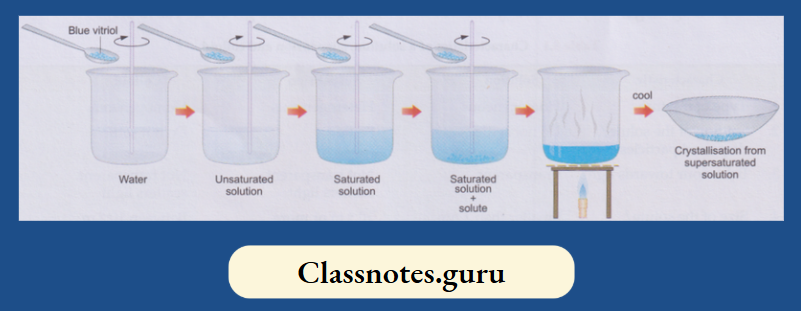
Activity:

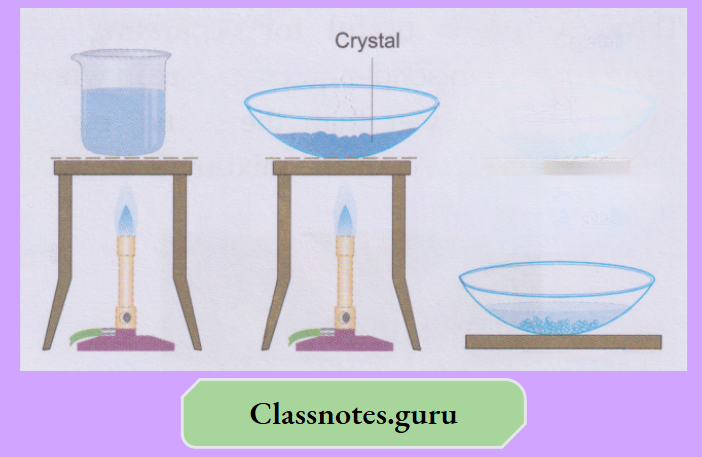
Take about 50 mL of water in a beaker and dissolve some blue vitriol crystals (CuSO₄.5H₂O) in it. Use a glass rod for stirring the mixture. Again, add a bit of the crystals and stir.

• That will also dissolve. You will find that if you keep adding the blue vitriol crystals to the water in small instalments and stirring, the crystals dissolve. But after a few instalments, the crystals will not dissolve any more.
• That is a saturated solution at the temperature you have prepared it. And, before that, when more and more crystals dissolved, the solution was unsaturated
• The crystals added to the saturated solution will settle down. Now heat the mixture, and you will find that the extra solute will also dissolve. Leave the solution to cool.

Nothing separates, and that solution is supersaturated. Transfer the solution to a china dish, evaporate a bit of it and leave it for a few hours (preferably overnight). Beautiful crystals of blue vitriol are obtained.

Hydrates

It has been found that whenever copper(II) sulphate is crystallised from an aqueous solution, the crystals have the formula CuSO₄.5H₂O.

• Similarly, iron(II) sulphate crystallises from an aqueous solution as FeSO₄.7H₂O.
• These water molecules appear in the same number every time and are called the water of crystallisation of a substance. A
• nd the substances (generally salts) containing such water molecules are called hydrates.
• The water molecules associated with a substance in a crystal and forming a part of the crystalline structure are referred to together as water of crystallisation.
• A substance containing water of crystallisation is called a hydrate.

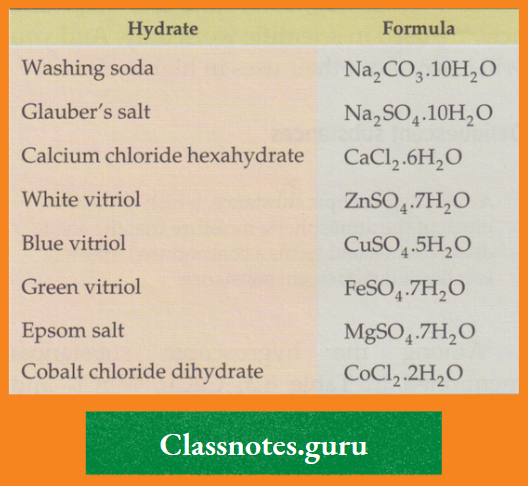
Some examples are mentioned in the Table

Some common hydrates:

The Loss of Water of Crystallisation on Heating

A hydrate, on being heated, loses its water of crystallisation. And it has been observed that it loses its crystalline structure too. You can find this for yourself by doing the following activity

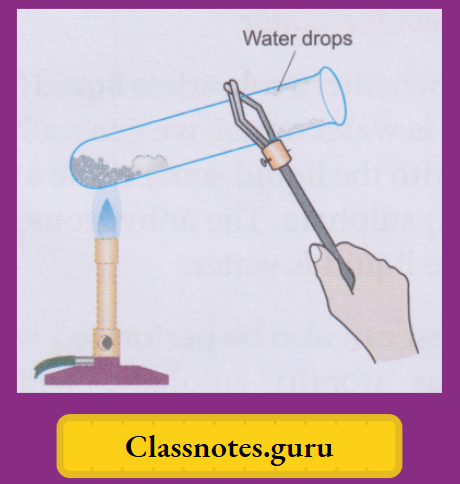
Activity:

Take a few crystals of blue vitriol in a dry test tube and heat gently. You will observe that

• The salt will slowly lose its blue colour, turning white,
• The crystals will crumble down to a powdery substance, and
• Some colourless liquid drops will collect in the colder part of the test tube.
• (Tests, which we will describe soon, indicate that these are water drops.)

Cool the white powdery substance and moisten it with a drop of water. The solid turns blue again.

Water and its Properties Class 8

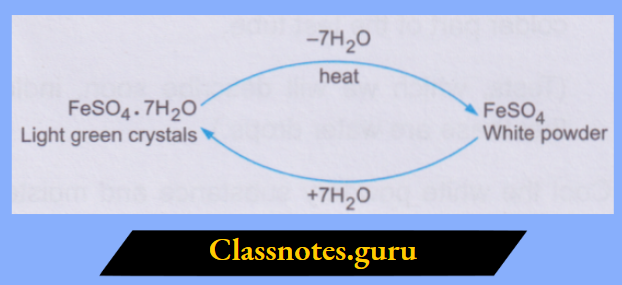
What happens during these changes can be summarised as follows.

1. The blue copper(II) sulphate pentahydrate, on being heated, loses the water molecules and changes to the white anhydrous (meaning without water) copper(II) sulphate. And, on treatment with water, the anhydrous salt changes back to the hydrated salt.

2. The crystalline structure of the hydrated salt is lost when it loses the water molecules. Thus, the water of crystallisation is a part of the crystalline structure. You can repeat the activity with the crystals of green vitriol, i.e., FeSO₄.7H₂O. By losing the water of crystallisation on being heated, the light green crystals change to a white, powdery solid (the anhydrous salt).

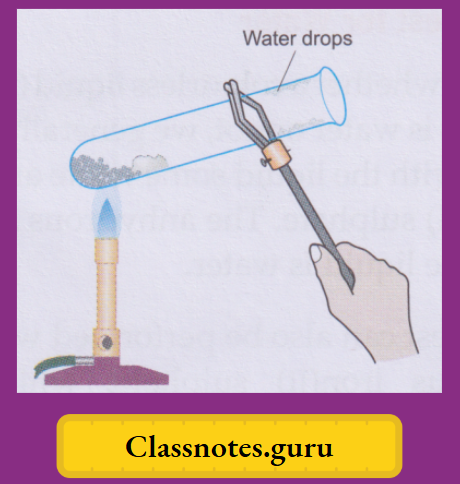
How to Test for Water

To know whether a colourless liquid (in bulk or in drops) is water or not, we generally bring in contact with the liquid some white anhydrous copper(II) sulphate. The anhydrous salt turns blue if the liquid is water. The test can also be performed with white anhydrous iron(II) sulphate, which turns green on treatment with water.

The above-mentioned anhydrous salts can be prepared by slowly heating the hydrated salts.

Hygroscopic Substances

A substance that absorbs moisture from the atmosphere is called a hygroscopic substance.

Some examples are given in the Table

Importance of Water Class 8

Some common hygroscopic substances:

They are generally used as drying agents. You might have seen a small cloth bag, containing a solid, inside a box of medicine, thermoflask or a camera. The bag contains silica gel—a common drying agent—which keeps the air inside the box dry. Other drying agents like calcium chloride, sodium hydroxide, soda lime and sulphuric acid are used in scientific work only. And you will learn about their uses in higher classes.

Deliquescent substances

A solid hygroscopic substance, which absorbs so much of the atmospheric moisture that the solid dissolves in it and forms a concentrated solution, is called a deliquescent substance.

• Among the hygroscopic substances mentioned in Table CaCl₂, MgCl₂ and NaOH are deliquescent. You must have observed that rock salt or crude common salt, when left in the open in the rainy season, appears to have melted.
• It does not melt at ordinary temperature. In fact, it contains highly deliquescent substances— CaCl₂ and MgCl₂—as impurities. So, it absorbs so much moisture from the atmosphere in the rainy season that it gets dissolved and appears to have melted.
• However, refined table salt does not show this property as it does not contain CaCl₂ or MgCl₂. Similarly, solid NaOH kept open in a beaker starts looking watery within a few minutes. (Remember that after a long time, NaOH reacts with atmospheric CO₂ also.)

The Action Of Metals And Metal Oxides On Water

Many metals and metal oxides react with water. To understand these reactions, we need to have an idea about the activity series. Metals along with hydrogen, have been arranged according to their activity in this series. The series consisting of some common metals is given here.

The Action of Metals on Water

Whenever a metal reacts with water, it does so with a view to displacing hydrogen from water. Obviously, only those metals can displace hydrogen from water which are more active than hydrogen, i.e., higher than hydrogen in the activity series. We can also understand that the more active the metal (i.e., the higher the metal in the activity series), the more vigorous is its reaction with water

We will discuss here the action of potassium (K), sodium (Na), calcium (Ca), magnesium (Mg) and iron (Fe) on water. We should remember that though tin (Sn) and lead (Pb) are higher than hydrogen in the activity series, they do not act on water

Water Cycle Class 8 Chemistry

Action of potassium and sodium on water:

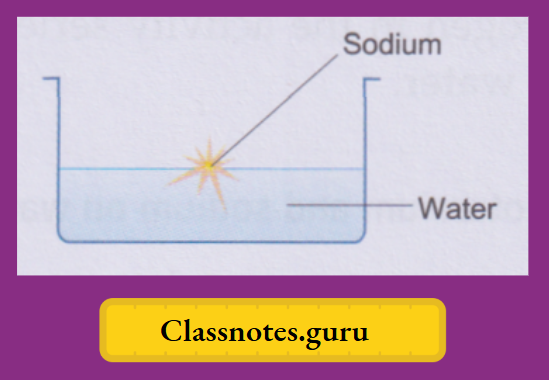
Among the common metals, potassium and sodium are the most active ones. They are soft and get quickly affected by the moisture (and also oxygen) of the air and are, therefore, preserved in kerosene. A small piece of the metal is cut with a knife, dried by pressing between the folds of a filter paper and dropped into a trough of water. We make the following observations about the two metals

Sodium:

The metal soon changes into a silvery white globule that does not sink but darts around on the surface. A hissing sound is constantly heard. And a yellow spark flies intermittently with a ‘pop’.

The resulting solution turns red litmus blue, and so it is alkaline. We infer that sodium reacts vigorously with water to form sodium hydroxide and liberate hydrogen. At the same time, the reaction is highly exothermic, and so the metal melts to form a globule.

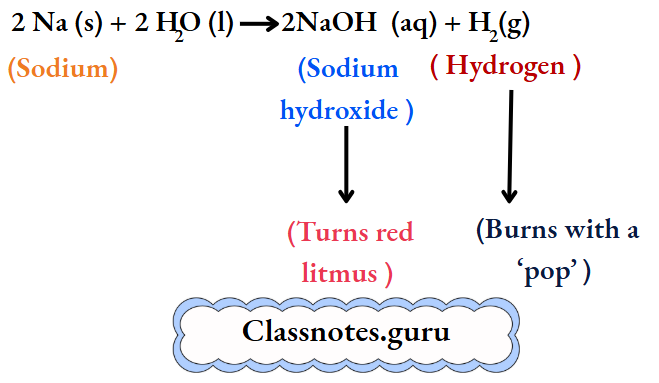
The hydrogen burns with a ‘pop’. And yellow sparks are produced by small particles of sodium. (Sodium imparts a yellow colour to a flame. Throw some common salt, i.e., sodium chloride, into the flame of a kitchen stove, and watch the colour imparted to the flame. It is yellow. Also, doesn’t a sodium vapour lamp have a yellow light?)

Potassium:

Potassium also reacts vigorously and exothermically with water to form potassium hydroxide and liberate hydrogen.

• Due to the potassium hydroxide formed, the resulting solution is alkaline and therefore turns red litmus blue.
• The only difference from the reaction of sodium is that the hydrogen liberated burns with a violet flame.
• Potassium imparts the violet colour to the flame

2K(s)(potassium)+ 2HO(l) → 2KOH(aq)(Potassium hydroxide) + H₂(g)

The action of calcium on the water ribbon

Calcium is heavier than water and a piece of the metal sinks in it. The evolution ofhydrogen starts briskly but slows down soon as the lime produced forms a coating on the metal. Calcium hydroxide (slaked lime) is much less soluble than sodium hydroxide or potassium hydroxide and makes the solution turbid. The solution is alkaline, turning red litmus blue.

Ca(s)(calcium) + 2HOH(l) → Ca(OH)₂ (aq) (calcium hydroxide (alkaline) + H₂(g)

The action of magnesium on water

Magnesium, being less active than calcium, displaces hydrogen from water very slowly at room temperature. However, the reaction is fast with steam.

⇒ \(\mathrm{Mg}+\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{MgO}+\mathrm{H}_2\)

When magnesium powder is mixed with water, the evolution of hydrogen starts slowly and stops soon because the MgO forms a coating over the metal particles. But you can verify for yourself how fast the reaction with steam is

Activity:

Boil some water in a conical flask to replace the air inside with water vapour. Continue boiling and introduce a burning piece of magnesium ribbon into the mouth of the conical flask.

• The ribbon continues to burn in steam/water vapour, though the nature of the flame changes.
• In air, magnesium burns with a dazzling white flame, but in steam, it gives a smaller, orange flame due to the burning of the liberated hydrogen

The particles of magnesium oxide falling into the water make it alkaline —the solution or the mixture turns red litmus blue.

Water Purification Class 8 Chemistry

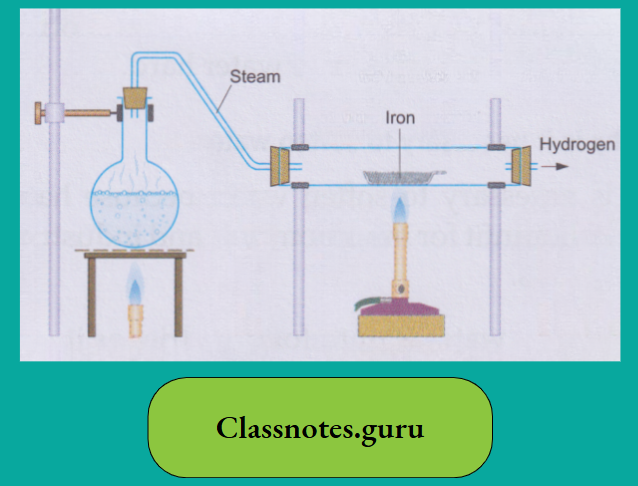
The action of iron on water

Though iron is above hydrogen in the activity series, it is much less active than magnesium. Iron displaces hydrogen from water only when steam is passed over the red-hot metal. A black oxide triiron tetroxide(Fe₃O₄), also called ferrosoferric oxide, is formed.

3 Fe (iron)+ 4H₂O(steam) → Fe₃O₄ (Triiron tetroxide) (black) + 4H₂ (hydrogen)

(Triiron tetroxide is considered a mixed oxide of iron(II) and iron(III), i.e., FeO. Fe₂O₃.)

The Action of Water on Metal Oxides

The oxide of the highly active metal, like K, Na and Ca, reacts vigorously and exothermically with water to form the hydroxide of the metal.

K₂O + H₂O→ 2KOH

Na₂O + H₂O→ 2NaOH

CaO + H₂O → Ca(OH)₂

You know that these hydroxides are alkalis.

However, as we move down the activity series, the reactivity of the metal oxide with water sharply decreases. For example, MgO reacts with water to form Mg (OH)₂ to a small extent and Al₂O₃, ZnO and Fe₂O₃, etc., to a still smaller extent.

Hard Water And Soft Water

You may have noticed that the water of some places forms lather easily with soap whereas that of other places does not lather easily.

• Water that lathers easily with soap is called soft water
• Water that does not lather easily with soap is called hard water.

What Makes Water Hard?

The presence of soluble salts (like hydrogen-carbonates, sulphates or chlorides) of calcium and magnesium in a sample of water makes it hard

Soap contains sodium salts of fatty acids. (Fatty acids are organic acids containing a large number of carbon atoms.) These salts produce lather with water. However, the calcium and magnesium salts of these fatty acids are insoluble. So, when a soap is treated with hard water, the calcium and magnesium salts of the fatty acids precipitate in the form of a scum. As a result, the soap is consumed, but no lather is produced

2Na (Ft) ( sodium salt of the fatty acid)  + Ca (HCO₃)₂(calcium hydrogencarbonate)  → 2 NaHCO₃ (sodium hydrogencarbonate) + Ca(Ft)₂ ↓ (calcium salt of the fatty acid)

Precipitation over clothes leaves dirty stains, and that over your body irritates the skin.

The hardness of water increases with the amount of dissolved calcium and magnesium salts. But remember that dissolved sodium or potassium salts

Example: NaCl, K₂SO₄, etc.) do not make water hard. This is because the sodium and potassium salts of fatty acids do not precipitate. And water containing sodium and potassium salts does lather with soap.

Temporarily and Permanently Hard Water

The hardness of some water samples can be removed by boiling, but not of all. On this basis, hard water is classified into two types.

• If the hardness ofa watersample can be removed by boiling, it is called temporarily hard water.
• If the hardness of a water sample cannot be removed by boiling, it is called permanently hard water

Temporary hardness is caused by the dissolved hydrogencarbonates of calcium and magnesium carbonates. Permanent hardness is caused by the dissolved sulphates and chlorides of calcium and magnesium.

Softening of Water

If the hardness of water is removed, soft water is produced, and the process is called softening of water.

Physical and Chemical Properties of Water Class 8

The following methods are used to soften water:

1. Boiling:

Temporarily hard water can be softened by boiling it. When such water is heated, the hydrogencarbonates of calcium and magnesium are decomposed to the carbonates. Being insoluble, the carbonates precipitate out

Ca(HCO₃)₂ (calcium hydrogencarbonate)→ CaCO₃ + CO₂↑ + H₂O

2. Treating with washing soda. Permanent hardness of water is removed by treating with washing soda (Na₂CO₃.10H₂O). A solution of washing soda is added to the water, and the carbonates of calcium and magnesium are precipitated

CaSO₄(calcium sulphate) + Na₂CO₃ (sodium carbonate) → CaCO₃ ↓ (calcium carbonate) + Na₂SO₄ (sodium sulphate) (in solution)

CaCl₂(calcium chloride)+ Na₂CO₃ (sodium carbonate) → CaCO₃ (calcium carbonate)  + 2 NaCl (sodium chloride) (in solution)

The sodium sulphate and sodium chloride formed will not make the water hard

Water Resources and Conservation Class 8

Why is it necessary to soften water?

It is necessary to soften water because hard water is unfit for most domestic and industrial purposes.

1.  Hard water is unfit for laundries as it
   • Consumes too much soap, and
   • Leaves dirty stains of calcium and magnesium salts of fatty acids on the cloth.
2. Hard water is not very suitable for bathing. The precipitates of calcium and magnesium salts of fatty acids, formed on reaction with soap, irritate the skin.
3.  It is not possible to properly cook hard foodstuffs, like pulses, in hard water.
4. Though not injurious to health, hard water does not have an agreeable taste.
5.  When used for industrial purposes (mainly in boilers), hard water produces white deposits of insoluble substances, called scales.
6. The scales consist mainly of CaCO₃, MgCO₃ and CaSO₄. They deposit on the walls of the boiler and do not allow proper conduction of heat.
7. They also block the pipes, which may cause serious accidents.

Chapter 4 The Structure Of The Atom

As you know, everything is ultimately made of atoms. It was earlier thought that atoms are indivisible but now we know that they are made up of subatomic particles—electrons, protons and neutrons. This idea has brought about a revolution in science.

How The Idea Of Atoms Emerged

The Views of Kanad

Way back in the sixth century BC, the Indian philosopher Kanad came up with the following idea.

Read And Lean More Class 8 Chemistry

• Not continuous, and
• Made up of tiny particles, named paramanus. .

(In Sanskrit, param means final or ultimate, and anu means particle.)

Kanad further said that two or more paramanus combine to form bigger particles.

NCERT Class 8 Chemistry Chapter 4 Structure of the Atom

The Views of Democritus and Leucippus

In the fifth century BC, the Greek philosophers Democritus and Leukiposs came up with a similar idea. They thought that on dividing a piece of a substance, one would ultimately get a particle that could not be divided further. They gave the name atomos (in Greek, atomos means indivisible) to these ultimate particles

Dalton’s Theory

The theories of Kanad as well as of Democritus and Leukiposs remained forgotten for more than two thousand years. But when experimental chemistry developed, it became necessary to explain observed facts. In 1803, English chemist John Dalton put forward his atomic theory,

Which can be summarised as follows:

• Elements are made up of very small particles of matter, called atoms (derived from the Greek word atomos).
• Atoms are indivisible.
• The atoms of an element have the same weight.
• The atoms of different elements have different weights.
• It is the atoms of elements that take part in a chemical reaction.
• The atoms of an element combine in a simple numerical ratio with those of other elements (s) to form a compound.

An atom is defined as the smallest part of an element that takes part in a chemical reaction

The Subatomic Particles

In the late nineteenth century, however, it was proved that atoms are divisible. And it was later found that atoms are made up of subatomic (or fundamental) particles— electrons, protons and neutrons. 35

The Electron

Under ordinary conditions, gases are bad conductors of electricity. But a gas becomes a good conductor of electricity if

1. The pressure of the gas is very low (say, 10 mm of mercury or lower), and
2. The voltage applied is very high (say, 10,000 V).

These conditions are achieved in what is called a discharge tube.

Cathode rays:

A discharge tube is a long glass tube at the two ends of which are sealed two metal plates.

• These plates can be connected to a high-voltage source and are called electrodes.
• The electrode connected to the negative terminal of the source is called the cathode, and the one connected to the positive terminal is called the anode.
• There is also a side tube which can be connected to an exhaust pump, used for lowering the pressure of the gas inside the discharge tube.
• When a high voltage is applied across the terminals, and the pressure inside the tube is 0.01-0.001 mm of mercury, the end of the tube opposite the cathode starts glowing.
• This phenomenon is called fluorescence.

Investigations have shown that some invisible rays, starting from the cathode, fall on the opposite wall of the tube, causing fluorescence. These rays were named cathode rays.

The characteristics of cathode rays:

Sir J J Thomson and others found that cathode rays have the following characteristics.

Atomic Structure NCERT Notes

1. They originate at the cathode and travel in straight lines:

When an object is placed in the path of cathode rays, a shadow of the object falls on the wall opposite the cathode. A shadow can be formed only when the rays travel in straight lines.

2. Cathode rays are a stream of particles:

A light paddle wheel, placed in the path of the cathode rays, rotates. This shows that some particles strike the plates of the wheel

3. The particles constituting cathode rays are negatively charged:

This is proved by the fact that the cathode rays bend towards the positive plate in an electric field.

4. The particles constituting cathode rays are O O all alike. They do not change with the gas, the electrodes and the kind of glass used for making the tube

Thus, Sir J J Thomson concluded that the particles constituting cathode rays are a universal constituent of all atoms. These particles were named electrons in 1897

Relative charge and mass:

The charge on an electron is taken as the unit of negative charge. So an electron is said to have a charge of -1 unit. The mass of an electron is about 1/1840th of a hydrogen atom, and so it is treated as negligible.

The Proton

An atom is electrically neutral. But the electrons present in it are negatively charged particles. Hence, the atom must also contain some positively charged particles so that the overall charge on it becomes zero. These particles should be found in the discharge tube itself, when cathode rays are formed.

NCERT Solutions for The Structure of the Atom

Anode rays:

Goldstein repeated the cathode-ray experiment using a perforated cathode.

• He observed that there was a red glow on the wall opposite the anode.
• So, some rays must have travelled in the direction opposite to that of the cathode rays, i.e., from the anode towards the cathode.
• These rays were called anode rays or canal rays (as they moved through the perforations, or canals, in the cathode).

It was found that these rays contained positively charged particles, and so J J Thomson called them positive rays

The characteristics of anode rays

The characteristics of anode rays were found by carrying out experiments similar to those with cathode rays.

The following features distinguish anode rays from cathode rays:

1. Anode rays are a stream of positively charged particles (because they bend towards the negative plate in an electric field).
2. The particles constituting anode rays differ with the gas used in the discharge tube.

What constitutes anode rays?

The electrons constituting the cathode rays must come from the atoms of the gas inside the discharge tube. Electrons are negatively charged particles, so the atoms must be left with an equivalent amount of positive charge. It is these positively charged particles that constitute the anode rays.

The Structure of the Atom Class 8 NCERT Notes

As an electron has a negligible mass, the particle A+ will have the same mass as A. So, the particles constituting anode rays will differ from gas to gas. When hydrogen, the lightest element, is taken in the discharge tube, the particles constituting the anode rays are called protons

The relative charge and mass of a proton

Charge:

The charge on a proton is the same as that on an electron, but with opposite sign. It is taken as a unit of positive charge. So, a proton has a unit positive charge, i.e., +1. The mass of a proton is the same as that of a hydrogen atom, i.e., 1 u (u stands for unified mass, which is the unit of atomic mass). A proton is about 1840 times heavier than an electron

The Neutron

The Discovery of the Nucleus Till now, we have learnt of only one particle that can account for the mass of an atom —the proton.

• The electron has negligible mass. But, except in the case of hydrogen, it was found that the mass of an atom is greater than that of the protons in it.
• Further, the unaccounted mass (i.e., the actual mass of the atom minus the mass of the protons) is either equal to or a multiple of the mass of a proton.

This suggested that an atom must contain one more kind of particle, which should have

• The same mass as a proton, but
• No electrical charge on it.

These particles were named neutrons as they should be electrically neutral. Experimentally, however, the neutron was observed much later in what is called a nuclear reaction. In 1932, James Chadwick bombarded the element beryllium with α-particles.

(α-particles are helium ions with a double positive charge, He²⁺. We will discuss this later in the chapter.) He observed that beryllium changes to carbon and that neutrons are emitted in the reaction.

Beryllium + α – particle → carbon + neutron

You will learn in higher classes that nuclear reactions are very different from chemical reactions. In a nuclear reaction, an atom can change altogether whereas in a chemical reaction, it will only rearrange itself but will not change.

Charge and mass of the subatomic particles:

The Discovery of the Nucleus

The concept of the nucleus was given by Ernest Rutherford in 1911. The idea was based on the results of his famous experiment, known as the α-particle scattering experiment.

Rutherford’s α-Particle Scattering Experiment

Rutherford bombarded a thin gold foil with α-particles. Alpha particles are emitted by radioactive substances like radium and polonium. (You will learn about radioactivity in higher classes.)

His observations and conclusions are described below:

• Most of the α-particles went straight through the foil. This is explained by the fact that they were not attracted to or repelled by any particle. In other words, the atom is mostly empty.
• Some of these particles deviated slightly from their path. This showed that they were repelled to a small extent by a positive charge.
• Very few of the particles, the ones at the centre, almost retraced their path. This meant they were strongly repelled by a small positively charged body at the centre of the atom. This positively charged body is called the nucleus.
• Since the electron has negligible mass, the mass of the atom is concentrated in the nucleus.
• Rutherford also theorised that electrons revolve around the nucleus at large distances from it.

The Atom and its Structure Class 8

Thus emerged the nuclear model of the atom from Rutherford’s α-particle scattering experiment

How Are the Subatomic Particles Placed in the Atom?

As we have just said, the mass of an atom is concentrated in its nucleus.

• The mass of an electron is negligible, but that of a proton or a neutron is lu.
• So, protons and neutrons must reside in the nucleus. Remember that the nucleus of a hydrogen atom contains only a proton and no neutrons.
• The nucleus of an atom is positively charged due to the presence of proton(s) in it.

In 1913, Niels Bohr presented the atomic model. According to it, electrons revolve around the nucleus in their orbits, just as planets do in the solar system.

Number Of Subatomic Particles In An Atom

Atomic Number and Mass Number

To know the numbers of subatomic particles in an atom, one needs to know the atomic or proton number (Z) and the mass number (A) of the atom.

• The atomic number, or the proton number, of an element is the number of protons present in the nucleus of an atom of the element.
• The sum of the numbers of protons and neutrons in an atom is known as the mass number of the atom.
• As an atom is electrically neutral, the number of electrons must be equal to the number of protons. So, in an atom,

The number of electrons = Z,

The number of protons = Z, and

The number of neutrons

= mass number- number of protons

= mass number- atomic number

= A-Z

Atomic Models NCERT Notes

Nuclide symbol

The nuclide symbol of an atom is the symbol of the element with its atomic number as the subscript and mass number as the superscript, which are set to the left of the symbol of the element

The numbers of electrons, protons and neutrons in some atoms:

The nuclide symbol is expressed as X.

For example:

• The nuclide symbol 17 CI represents a chlorine atom, whose atomic number is 17 and mass number is 35.
• You can immediately guess that there are 17 electrons, 17 protons and 35- 17 (= 18) neutrons in the atom
• The number of fundamental particles in atoms with atomic numbers 1 to 20 is given in the table

How Electrons Are Arranged

According to the Bohr model, the electrons revolve around the nucleus in shells, called K, L, M, N, … shells. They are named in this order, starting from the innermost shell. The first shell is called the K shell, the second is called the L shell, and so on. The numbers of electrons in these shells follow a set of rules. You will learn about the arrangement of electrons in detail in higher classes.

Let us now look into the structures of the atoms of some common elements.

Electron, Proton, Neutron Class 8 Chemistry

1. Hydrogen (¹ H ₁)

The number of electrons

Nucleus

The number of protons

= Z = 1

The number of neutrons = A- Z

= 1-1

= 0

2. Carbon (¹² C ₆)

The number of electrons = Z = 6.

The number of protons = Z = 6.

The number of neutrons = A-Z

=12 – 6

= 6

3. Nitrogen (¹² N ₇)

The number of electrons = Z = 7.

The number of protons = Z = 7.

The number of neutrons = A- Z

= 14-7

= 7.

4. Oxygen (¹⁶ O ₈)

The number of electrons = Z = 8.

The number of protons = Z = 8.

The number of neutrons = A- Z

= 16 – 8

= 8.

5. Sodium (²³Na₁₁)

The number of electrons = Z = 11.

The number of protons = Z = 11.

The number of neutrons = A-Z

= 23-11

= 12.

Atomic Number and Mass Number Class 8

6. Chlorine (³⁵Cl₁₇)

The number of electrons = Z = 17.

The number of protons = Z = 17.

The number of neutrons = A- Z

= 35 – 17

= 18.

Ions

An atom is electrically neutral because the charge of the protons is balanced by that of the electrons. But what happens when an atom loses or gains an electron? If an atom loses an electron, the number of protons exceeds that of electrons. So the atom gets positively charged.

For example:

• A sodium atom has 11 protons and 11 electrons. On losing an electron, it would have 10 electrons and 11 protons.
• The greater number of protons causes the sodium atom to have a positive charge. Therefore, we say that a Na⁺ ion is formed.
• On the other hand, if an atom gains an electron, the number of electrons exceeds that of protons.

So, the atom becomes negatively charged.

NCERT Class 8 Atomic Structure Concepts

For example:

A chlorine atom contains 17 protons and 17 electrons. If it gains an electron, there are 18 electrons as against 17 protons.

• So, the chlorine atom gets a negative charge on it, i.e., a Cl^– ion is formed.
• And what if the electron lost by sodium is gained by chlorine? The ions Na⁺ and Cl^– will be formed, which, being oppositely charged, will remain together. In other words, the compound NaCl will be formed.
• Thus, it appears that electrons play a great role in the formation of compounds. You will learn about all this in higher classes.

Chapter 3 Elements, Compounds And Mixtures Notes

As you know, substances are classified as elements, compounds and mixtures. This classification is of great interest to chemists as it helps describe the kind of matter anything contains

Elements

An element cannot be split into simpler substances by chemical means. For example, hydrogen, nitrogen, oxygen, carbon, sulphur, phosphorus, iron, copper, silver and gold are elements as they cannot be split into simpler substances by chemical means.

Read And Lean More Class 8 Chemistry

• Remember that a chemical means is much more powerful than a physical means like filtration, sublimation or distillation.
• Thus, a substance which cannot be split by a chemical means will not be broken down by filtration, sublimation or distillation either.
• A substance that cannot be split into simpler substances, by a physical means like filtration, sublimation or distillation a pure substance

NCERT Solutions For Elements Compounds And Mixtures

So, an element is a pure substance.

Symbols represent elements

• A one-letter or a two-letter symbol represents an element.
• The one-letter symbols are used for elements like hydrogen (H), boron (B), carbon (C), nitrogen (N), oxygen (O), fluorine (F), sulphur (S), phosphorus (P) and iodine (I).
• These symbols are the first letters of the English names of the elements.
• Two-letter symbols were introduced to distinguish between those elements whose names start with the same letter of the alphabet

Examples:

• Hydrogen/helium, carbon/ cobalt, chromium/copper, nitrogen/nickel, iodine/indium, magnesium/manganese, etc..
• Such a symbol is made up of the first and one more letter of the English or Latin name of the element.

Elements And Compounds NCERT Notes

Some examples are given below:

Compounds

• A compound is a substance that can be split into simpler substances by chemical means.
• A compound can be split into simpler substances only by a chemical means, and not by a physical means like filtration, sublimation or distillation.
• A compound is formed by the combination of two or more elements.

For example, the compound:

• Water is formed by the combination of hydrogen and oxygen,
• Carbon dioxide, by that of carbon and oxygen,
• Sulphur dioxide, by that of sulphur and oxygen,
• Calcium carbonate, by the use of calcium, carbon and oxygen, and
• Sugar, by the way of carbon, hydrogen and oxygen

Splitting of a Compound into Simpler Substances

As we have just said, a compound can be split into simpler substances by chemical means. Some examples are given below.

NCERT Class 8 Chemistry Chapter 3 Elements, Compounds, And Mixtures

Electrolysis of Water:

Electrolysis is chemical decomposition brought about by passing an electric current through a liquid or a solution.

• Pure water is a bad conductor of electricity, i.e., it does not allow an electric current to pass through it.
• But water mixed with a small amount of an acid (hydrochloric or sulphuric acid)—called acidulated water—is a good conductor of electricity.
• When an electric current is passed through acidulated water using a setup of this kind, water decomposes to give hydrogen at the negative electrode (cathode) and oxygen at the positive electrode (anode).

Thermal decomposition:

The splitting of a substance into simpler substances by the action of heat on it is called thermal decomposition.

For example:

Chalk, i.e., calcium carbonate (which contains calcium, carbon and oxygen), on being heated, gives calcium oxide (containing calcium and oxygen) and carbon dioxide (containing carbon and oxygen).

Both products are simpler than calcium carbonate, and so the latter is a compound.

There are other examples too:

Compounds are Represented by Formulae

A compound is represented by a formula, which shows how many atoms of which element constitute a molecule of the compound.

Elements, Compounds And Mixtures NCERT Notes

For example:

Water is represented by the formula H₂O, indicating that two atoms of hydrogen and one of oxygen constitute a molecule of it. You can derive similar information from the formulae of the following compounds.

Important Characteristics of a Compound

You should remember some important characteristics of a compound.

1. A compound can be split into its constituent elements only by chemical means and not by physical means like filtration, sublimation and distillation.

For example:

Water cannot be split into hydrogen and oxygen by any of the physical means mentioned above.

But it can be split by a chemical means like electrolysis. Hydrogen can also be obtained from water by the chemical action of an active metal like sodium on water.

⇒ \(\begin{aligned}\text { Sodium }+ \text { water } \rightarrow \text { sodium hydroxide + hydrogen} \uparrow\end{aligned}\)

Similarly, hydrogen can be obtained from an acid (like hydrochloric or sulphuric acid) by the action of a metal like magnesium, zinc or iron on the acid.

Magnesium + Hydrochloric acid( dilute) → MAgnesium chloride + Hydrogen ↑

Zinc + Sulphuric acid(dilute) → Zinc sulphate + Hydrogen ↑

2. The properties of a compound are entirely different from those of the constituent elements.

For example:

Hydrogen (a combustible gas) reacts with oxygen (a supporter of combustion) to form water (which is neither combustible nor a supporter of combustion).

You can also compare the properties of carbon dioxide with those of its constituent elements, carbon and oxygen.

• Again, the bright yellow compound mercurous iodide is a product of two constituent elements—mercury and iodine. Mercury is a silver-white liquid metal and iodine, a violet-black solid.
• The constituent elements of copper(II) sulphate pentahydrate (CuSO₄.5H₂O—a blue solid) are the red metal copper, yellow solid sulphur and colourless gases hydrogen and oxygen.

3. Elements combine in a fixed proportion of atoms to form a compound.

For example:

2 atoms of hydrogen combine with 1 atom of oxygen to form

Atomic ratio of elements in some compounds:

1 molecule of water. And the atomic ratio of hydrogen to oxygen in any sample of water will be 2:1.

• Thus, 10 billion hydrogen atoms will require 5 billion oxygen atoms to form 5 billion molecules of water.
• The atomic ratios of elements in some compounds are given in Table 3.1, from which you can easily guess the formulae of the compounds.

4. A compound contains the constituent elements in a fixed proportion of mass.

For example:

By mass, water contains 1 part of hydrogen and 8 parts of oxygen.

• So, the mass ratio of H to O in water is 1 : 8. Can you guess how many grams of water will be formed by 1 g of hydrogen and 8 g of oxygen?
• The law of conservation of mass gives you the answer.
• It is 9 g (1 g + 8 g) as matter is neither created nor destroyed.
• Also, the mass ratio of C and O in CO₂ is 3:8. This suggests that every 11 g (3g + 8g) of carbon dioxide will contain 3 g of carbon and 8 g of oxygen.

You will learn in higher classes how to calculate the mass ratios of elements in a compound

Elements Compounds Mixtures Class 8

Mixture

Elements and compounds are pure substances, but rarely are they found in the pure state in nature.

• They are generally mixed with other elements, compounds or both. For example, air contains
• The elements nitrogen, oxygen and the noble gases (mainly argon), and
• The compounds are carbon dioxide and water.
• And natural water contains
• Dissolved air, and

Some salts (chlorides, sulphates, hydrogencarbonates, etc.) of metals like magnesium and calcium are dissolved in it.

Similarly, sea water contains so many dissolved substances that it is unfit for industrial, agricultural or domestic purposes.

• Thus, these substances are impure and are called mixtures. The different pure substances, which a mixture is made up of, are called the components of the mixture.
• These components can be separated by simple physical means
• A mixture is a substance which can be split into two or more pure substances by a physical means such as filtration, sublimation and distillation.

Examples of Mixtures

Most substances we come across in nature are mixtures. Fluman beings have also made many useful mixtures. Some examples are given below.

1. Air is the most commonly found mixture in nature. It contains nitrogen, oxygen, noble gases, carbon dioxide and moisture. We can separate the components by the physical means mentioned above.

2. Natural water is a mixture containing water, dissolved air and some salts which can be separated by physical means.

3. Foodstuffs

Example: Rice, wheat, pulses, vegetables, fruits, milk, butter, meat, and fish are all mixtures. They contain substances like starch, proteins, vitamins, salts, sugars and water in different proportions.

4. Medicines are mixtures containing some active ingredients in minute quantities (generally in milligrams) mixed with some other substances.

• The purpose of adding some other substances is to lessen the harshness of the chemical activity of the active ingredients.
• At the same time, the bulk increases, and it becomes easier to dispense the medicine.

5. Alloys are very common examples of mixtures. It has been found that a metal, when alloyed with other metal(s) or nonmetal(s), is generally more useful than the original metal.

For example:

Steel (containing iron, carbon and manganese) or stainless steel (containing iron, chromium and nickel) is more useful than iron. And so are brass (containing copper and zinc) and bronze (containing copper and tin) more useful than copper. Also, gold is generally mixed with silver and copper—the alloy is tougher.

6. Industrial materials like cement and glass are mixtures of silicates of metals. Cement is a mixture of calcium silicate and aluminium silicate, and glass, that of sodium silicate, potassium silicate and lead silicate.

7. All minerals are mixtures

Characteristics of a Mixture

A mixture has the following characteristics.

1. The components of a mixture may be present in any proportion

For example:

Regardless of whether you dissolve one or two spoons of sugar in a glass of water, the resulting solution will be a sugar-water mixture.

• Again, air—a gaseous mixture—contains more carbon dioxide in cities than in the countryside.
• Also, the moisture content of air is greater during the rains than in the dry season.

2. The components of a mixture coexist without chemically reacting with one another.

Types Of Mixtures Class 8 Chemistry

For example:

• Nitrogen, oxygen, carbon dioxide, noble gases and moisture coexist in air as they are and do not react among themselves to form any new substances.
• Similarly, water does not react with the soil in mud or with sugar in a sweet drink.

3. The components of a mixture retain their properties. The constituent elements of a compound do not retain their properties, but the components of a mixture do.

For example:

Hydrogen and oxygen do not show their properties in water, but water and sugar do in a sugar solution. Isn’t a sugar solution as sweet as well as watery?

4. The components of a mixture can be separated by simple physical means. By simple physical means, we mean here methods like filtration, sublimation, distillation, etc. We will discuss these methods soon

Types of Mixtures

Mixtures are usually classified based on the state of their components.

• A mixture containing two or more solids is called a solid mixture, two or more liquids, a liquid mixture, and two or more gases, a gaseous mixture.
• Besides, we can have solid-liquid, solid-gas and liquid-gas mixtures too.
• Further, a mixture can be homogeneous or heterogeneous, as described below.
• A mixture which has the same composition and properties throughout is said to be homogeneous.
• A mixture which has different compositions and properties in different parts of it is said to be heterogeneous.

One can see separately or distinguish between the different components of a heterogeneous mixture, but not ofa homogeneous mixture.

Thus, a fizzy drink that contains carbon dioxide, water and a sweetener in the same proportion throughout is a homogeneous mixture. But an oil-water mixture is a heterogeneous mixture.

Lists various kinds of mixtures, along with examples:

Types of mixtures with examples:

Separating The Components Of Mixtures

To obtain a pure substance, we often need to separate the components of a mixture.

It is only by doing so that we obtain

• Common salt from seawater,
• Drinking water from ordinary water,
• Petrol, diesel and kerosene from crude oil.

Principles of Separation

For separating the components of a mixture, we take advantage of the property of the components in which they differ the most. Such a distinguishing property can be the state, size, magnetic behaviour, solubility, melting point, boiling point or adsorbability.

Thus, it will be easy to separate

• A solid from a liquid or a gas, and a liquid from a gas,
• Smaller particles from larger ones,
• An amagnetic substance from a nonmagnetic substance,
• A soluble substance from an insoluble one
• A high-melting solid from a low-melting one
• A high-boiling liquid from a low-boiling liquid, and
• A strongly adsorbing substance from a weakly adsorbing substance.
• We will see how the methods of separation are based on these principles

Difference Between Elements and Compounds

Methods of Separation

Scientists use varied methods of separation, from simple to sophisticated. But here we will discuss some simple ones only.

Separating the Components of Mixtures

1. Sieving:

This method is based on the difference in the particle size of the components.

• When a solid mixture is stirred or shaken on a mesh, called a sieve, the particles smaller than the holes of the mesh pass through.
• And the larger ones remain on the mesh
• Fine sieves are used in the kitchen to separate bran from flour, and bigger ones at construction sites to separate stones from sand.
• Thus, sieves of different sizes are used for different solid mixtures

2. Magnetic separation:

This method is used to separate a magnetic substance from a nonmagnetic substance.

• You have learnt in the previous classes that iron, being magnetic, can be separated from sulphur or chalk, which is nonmagnetic, by moving a magnet through the mixture.
• The method, in a modified form, is highly useful in separating magnetic minerals from nonmagnetic ones. The mixture is placed on a conveyor belt moving around a magnetic wheel.
• While falling from the belt, the mixture gets separated into two heaps.

The outer heap consists of the nonmagnetic component and the inner heap, of the magnetic component (as it is attracted by the pole).

3. Sedimentation and decantation:

This method is useful for separating the components of a solid-liquid mixture in which the solid is heavier than the liquid.

Example:

• A sand-water mixture. If the mixture is allowed 3. Sedimentation and decantation.
• This method is useful for separating the components of a solid-liquid mixture in which the solid is heavier than the liquid.

Example:  A sand-water mixture. If the mixture is allowed.

The process can be used to separate immiscible liquids from one another.

However, it is not suitable for the separation of the components of a solid-liquid mixture in which the solid is lighter than the liquid, as in a husk-water mixture

4. Filtration:

If you want to separate a liquid from an insoluble solid, filtration is a better method than decantation.

You have learnt how a filter paper cone is prepared and fitted to a funnel.

• The apparatus is set up as shown.
• The solid-liquid mixture is allowed to stand for some time.
• The supernatant liquid is poured along a glass rod into the funnel.
• The liquid passes through, and the solid collects on the filter paper.
• The clear liquid thus obtained is called the filtrate.

You can easily separate sand or chalk from water by filtration.

5. Dissolution followed by evaporation or crystallisation:

This method is useful for a solid mixture of which one component is soluble in a chosen solvent but the other is not.

Example: A mixture containing

• Salt or sugar (soluble in water) and sand, chalk or sawdust (insoluble in water), or
• Sulphur (soluble in carbon disulfide) and iron filings (insoluble in carbon disulfide).

Stir a salt-sand mixture in water and warm so that the salt dissolves. Filter the mixture. The salt passes into the filtrate, and the sand remains as residue.

• The residue is washed with warm water to make the sand free of salt.
• The filtrate, along with the washings, is slowly heated in a dish, and the water evaporates, and the salt behind.
• Prepare a concentrated solution of copper (II) sulphate in a beaker by dissolving as much of the salt as possible.

Heat the mixture occasionally to dissolve more and more salt. Filter and evaporate the solution in a basin till a crust is observed at the surface of the liquid.

Mixtures And Their Types Class 8

• Stop heating and allow the solution to cool. Beautiful blue crystals of copper(II) sulphate pentahydrate will appear slowly and will grow in size with time.
• A purer sample of the salt can be obtained by crystallisation from the filtrate.
• The filtrate is heated to obtain a concentrated solution (i.e., a solution containing a smaller proportion of the solvent than usual).
• When the concentrated solution is left to cool slowly, the white crystals of the salt separate.
• Remember that a purer solid is obtained from a solution by crystallisation rather than by evaporation to dryness.
• Crystallisation sets in better and faster if the concentrated solution is seeded with a small crystal of the pure solid. For seeding, you may simply have to add the solid to the concentrated solution while cooling.
• You have learnt in the previous class how crystals of candy can be obtained from a concentrated solution of sugar.
• Here you can try to obtain the crystals of copper(II) sulphate pentahydrate (CuS04.5H20), also called blue vitriol

Experiment:

Prepare a concentrated solution of copper (II) sulphate in a beaker by dissolving as much of the salt as possible.

• Heat the mixture occasionally to dissolve more and more salt.
• Filter and evaporate the solution in a basin till a crust is observed at the surface of the liquid.
• Stop heating and allow the solution to cool.

Beautiful blue crystals of copper(II) sulphate pentahydrate will appear slowly and will grow in size with time.

Similarly, sulphur can be separated from iron filings by stirring the mixture with carbon disulfide. The sulphur comes out with the solvent. Iron is filtered, and the filtrate gives sulphur on evaporation or crystallisation.

6. Distillation:

By distillation, we can separate a solid-liquid mixture—homogeneous

Example: A solution of salt in water) or heterogeneous

Example: A sandwater or a chalk-water mixture.

The apparatus is set up as shown. The mixture is boiled in a distillation flask.

The vapours coming out condense while passing through a Liebig condenser in which they are cooled by the water circulating in the outer jacket.

• The pure liquid (Example: Water) is collected in a receiver.
• The solid—soluble (Example: Salt) or
• Insoluble (Example: Sand or chalk) remains in the distillation flask.

This is how distilled water is prepared in the laboratory

7. Fractional distillation:

By fractional distillation, we can separate liquids which differ in their boiling points by 20°C or more

The liquid mixture is boiled in the distillation flask fitted with a fractionating column and a Liebig condenser

• The mixed vapours enter the fractionating column, where the vapours of the higher¬ boiling (i.e., less volatile) liquid condense and trickle back into the distillation flask.
• The vapours of the lower-boiling (i.e., more volatile) liquid, however, pass into the Liebig condenser, where they condense; the liquid is collected in the receiver
• The temperature of the boiling mixture remains constant till the lower-boiling liquid distils completely.
• Then the temperature again rises till the higher-boiling liquid starts distilling.
• The receiver is quickly changed to collect the higher-boiling liquid.
• The liquids obtained by boiling a mixture at different temperatures are called fractions, and the method of fractional distillation is also called fractionation

By this method, we can separate

• Benzene (boiling point 80°C) is from toluene (boiling point 110°C),
• Ethyl alcohol (boiling point 78°C) from water (boiling point 100°C), and
• Petrol, diesel and kerosene from crude oil.

8. Using a separating funnel:

A separating funnel is used to separate two or more immiscible liquids.

• The mixture is placed in a separating funnel and allowed to stand.
• The different immiscible liquids form separate layers, which can be collected in different vessels one after the other.
• By this method, we can separate an oil, benzene, toluene or ether from water.

9. Sublimation:

Using this method, we can separate a substance that sublimes

Example: Ammonium chloride, camphor or iodine)

From one that does not (Example: Salt, sand or chalk).

A funnel is inverted over the mixture placed in a china dish. A dry test tube is also inverted over the outlet of the funnel. The outlet of the funnel is loosely plugged with cotton. The mixture is heated.

The sublimable component vapourises and the vapours solidify in the test tube and on the cooler part of the funnel.

10. Chromatography:

By chromatography, we can separate two or more solids from one another, provided they are soluble in the same solvent.

The solvent may be a pure liquid like water, alcohol or acetone, or a mixture of two or more of these.

The method works on the principle of adsorption.

• One should understand the difference between adsorption and absorption.
• In absorption, a substance gets equally distributed over the entire bulk of another substance, like dissolved air in natural water or carbon dioxide in a fizzy drink.
• Adsorption, however, is a surface phenomenon in which a substance is held at the surface of another by a weak force.

An example is a dye held on the surface of a fibre.

The substance that is adsorbed

(Example: A dye) is called the adsorbate, and the surface on which it is adsorbed

(Example:  A fibre), The adsorbent.

In chromatography, we generally use cellulose, silica or alumina as an adsorbent.

• Cellulose is conveniently used in the form of blotting paper, filter paper (generally Whatman 41) or specially made chromatographic paper. We will now discuss the technique of paper chromatography.
• You must have observed that blotting paper soaks up a liquid that spreads fast over the paper.
• The liquid moves even against gravity, i.e., upwards on a vertically placed blotting paper.
• A long strip of chromatographic paper or a good-quality filter paper is cut out.
• A drop of a solution of the mixture (say the ink of a green sketch pen) is placed about a centimetre from one end of the strip and dried.
• A very small amount of the solvent is taken in a jar.
• The paper strip is suspended in the jar such that the end near which the mixture is placed just touches the solvent.
• The whole set-up is left undisturbed. After some time, one can observe that the green-ink spot has moved up the strip and separated into two colours— blue and yellow.
• (In fact, the blue and yellow make up the green.)

This happens because the different dyes (pigments), i.e., the different colouring substances, are held (i.e., adsorbed) by the adsorbent with different forces—some by stronger and some by weaker forces.

• The one that is held less strongly is driven faster by the solvent than that held more strongly by the adsorbent.
• As a result, the different pigments move with different speeds over the adsorbent surface under the influence of the solvent. And so they get separated.

The array of colours on a chromatographic paper is called a chromatogram.

• One can take a mixture of inks of different colours to have a more colourful chromatogram.
• The smaller strips of different colours are now cut out from the main strip.
• And the colouring matter can be obtained from each strip by dissolving it out in the solvent and evaporating the solvent.

In chromatography, the adsorbent part is called the stationary phase, and the things that move, i.e., the solvent and the solution, are collectively known as the mobile phase.

• Different types of chromatographic techniques have been developed and named based on the types of phases.
• Column chromatography is a commonly used technique in which the stationary phase is a column of adsorbent, i.e., the adsorbent is packed in a vertically placed wide tube.
• Other well-known types are gas-liquid chromatography (GLC) and high-performance liquid chromatography (HPLC)

Separation Methods: A Summary

A summary of the methods ofseparationofthe components of mixtures is given in Table 3.3.

Methods of separating the components of different types of mixtures:

Separation of mixtures—a few examples

Through the following examples, you will learn how to choose a method for separating the components of a given mixture.

1. A sand-water mixture:

Sand can be separated from water by filtration or distillation. In distillation, the water distils out, leaving the sand as residue.

2. A salt solution:

By distillation, the water can be obtained as the distillate and the salt as the residue. (By evaporation to dryness, the salt can be obtained, but the water will be lost.)

3. A salt-sand mixture:

The salt can be dissolved in water, and the sand filtered out. The filtrate, on evaporation to dryness, yields the salt.

4. A sugar-chalk mixture:

Sugar is soluble in water, but chalk is not. So, the sugar can be dissolved in water, leaving the chalk behind. The mixture, on filtration, will give the chalk as the residue and the filtrate, on evaporation or crystallisation, will yield the sugar.

5. An iron filings-sawdust mixture:

As iron is magnetic and sawdust is not, magnetic separation will be a convenient method to separate them.

6. An iron filings—sulphur mixture:

Two methods can be used.

• Magnetic separation (Iron is magnetic, but sulphur is not.)
• Dissolution of the sulphur in carbon disulfide, followed by the recovery of the sulphur from the solution by evaporation or crystallisation.

7. A carbon-sulphur mixture:

Knowing that sulphur is soluble in carbon disulfide but carbon is not, you can suggest the method.

8. A water-oil mixture.:

As water and oil are immiscible, they will form separate layers and can, therefore, be separated by using a separating funnel.

• Remember that, like oil, chloroform, carbon tetrachloride, and ether are also immiscible with water.
• So, the method will be useful for a mixture containing water and any of these liquids.

9. A benzene-toluene mixture:

As the difference in the boiling points of benzene (80°C) and toluene (110°C) is more than 20°C, the two miscible liquids can be conveniently separated by fractional distillation.

10. An ink mixture: By paper chromatography.

11. A salt-sand-sulphur mixture:

Among the three components, only sulphur is soluble in carbon disulphide and only salt in water, but sand in either of the two solvents.

• So, the sulphur can be dissolved in carbon disulfide. From the residue containing salt and sand, the salt can be dissolved out in water, leaving the sand behind.
• The sulphur and salt can be recovered from their solutions by evaporating the solvents.
• Alternatively, first the salt canbe dissolved out in water and then sulphur in carbon disulfide.

12. A carbon-sulphur-nitre mixture (gunpowder):

Gunpowder is an explosive containing carbon, sulphur and potassium nitrate (nitre). Only sulphur is soluble in carbon disulphide, and only nitre in water.

• So, the sulphur and nitre can be dissolved out successively in carbon disulfide and water, and recovered from the solutions by evaporating the solvents or by crystallisation.
• After the final dissolution, carbon will be left as the residue.
• Alternatively, the nitre can be dissolved out first and then the sulphur.

Difference between a Mixture and a Compound.

We can now conclude that a mixture differs from a compound, as shown in Table

How a mixture differs from a compound:

Chapter 2 Physical And Chemical Changes Notes

Changes occur every moment around us. They are an integral part of nature. In this chapter, we will see how changes are classified and study physical and chemical changes systematically.

How Changes Are Classified

Let us now discuss some ways in which changes are classified

Reversible and Irreversible Changes

A change is said to be reversible when the opposite change can be brought about by reversing the conditions.

Read And Lean More Class 8 Chemistry

Changes in state of matter are the most common examples of reversible change

A solid melts on being heated and the melt solidifies (i.e., freezes) on being cooled. So, the melting of a solid and also the freezing of a liquid are reversible changes.

And so are the vaporisation of a liquid (on being heated) and the condensation of vapours (on being cooled). Also, the heating and cooling of the coil of an electric heater when the heater is switched on and off, respectively, are reversible changes

NCERT Solutions For Physical And Chemical Changes

A change is said to be irreversible when the opposite change cannot be brought about by reversing the conditions

For example:

Sugar, when heated, swells to form a brown substance which finally gets charred, i.e., forms a black mass. But the charred mass, on being cooled, does not give back sugar.

Similarly, milk can be changed into cottage cheese by boiling it with some lemon juice added to it. But cottage cheese, or paneer, cannot be changed into milk. Thus, the charring of sugar and the curdling of milk are irreversible changes. And so are the growth of plants and animals, digestion, photosynthesis, and the burning of a fuel

Activities:

1. With the help of an adult, place some sugar crystals in a china dish. Heat the solid slowly and observe the changes. It swells and becomes brown and finally black. The black mass is carbon.

2. Add a few drops of lemon juice to the milk and boil the mixture. In a short while, a thick white substance, called curd, is formed. This is called the curdling of milk. Curd is entirely different from milk. You will not be able to reverse this change.

Periodic and Nonperiodic Changes

Periodic changes are those which take place at fixed intervals of time.

• You may have seen a clock with a pendulum. The pendulum moves from side to side, or to and fro, continuously, at fixed intervals of time.
• The motion of the pendulum is an example of periodic change.
• As you know, the moon changes phase gradually from full moon to new moon and then again to full moon.
• This change takes place over 28 days. The same change is repeated over the next 28 days. So, the phases of the moon are an example of periodic change.

NCERT Class 8 Chemistry Chapter 2 Physical And Chemical Changes

• Nonperiodic changes are those which do not take place at fixed intervals of time.
• The melting of ice, vaporisation of water, curdling of milk and charring of sugar do not repeat themselves at fixed intervals of time.
• So, they are non-periodic changes.

Desirable and Undesirable Changes

The changes that are useful to us are called desirable changes whereas those that are harmful are called undesirable changes.

• Thus, the digestion of food, the ripening of fruit, the growth of living beings and the changes involved in cooking are desirable changes.
• But the rusting of iron and the spoiling of food are undesirable changes.
• Earthquakes, cyclones and volcanic eruptions are such undesirable changes that cause damage on a large scale.

Physical And Chemical Changes

Chemists are very interested in the classification of changes into physical and chemical changes. Therefore, we will study physical and chemical changes separately.

Physical Changes

A change in which no new substances are formed and which can be reversed by reversing the conditions is called a physical change. We will now discuss some examples of physical change.

Physical And Chemical Changes NCERT Notes

The glowing of a heater or a bulb:

An electric heater or a bulb glows when it is switched on.

• But the glow vanishes as it is switched off. So the change is reversible. Also, no new substances are formed.
• Therefore, the glowing of a heater or a bulb is a physical change.

Thermal expansion of a substance:

On being heated, a substance expands but on being cooled, it contracts. Also, no new substances are formed, and so the change is physical.

• You must have observed that an inflated balloon often bursts on its own at a birthday party.
• Why so? Because the air inside the balloon expands when the latter remains near a hot bulb for a while.

Changes in state of matter:

You have learnt that any change in the state of matter is reversible. And also that the kind of matter remains the same in any change in state of matter, be it solid-liquid or liquid-vapour (gas) interconversion.

For example:

The melting of ice is reversed by the freezing of water, and the vaporisation of water is reversed by the condensation of water vapour.

At the same time, the substances in the three states are the same, i.e., water (H₂O). This is true for other substances too.

Example: Sulphur, sodium, iron, copper and zinc.

The kinetic theory of matter tells us that in the change

Physical vs Chemical Changes Class 8

Only the kinetic energy (KE) of the molecules increases when heating. And in the opposite case,

The KE of the molecules decreases on cooling.

Sublimation:

This is also an example of state change. Insublimation, a solid like ammonium chloride, naphthalene, camphor or iodine directly forms vapours, without melting. And when cooled, the vapours are directly converted into the solid. Thus, the change is reversible. No new substances are formed either. So, sublimation is a physical change.

The dissolving of a substance in a liquid:

You know that a solid like sugar, salt, or glucose dissolves in water.

• The substance that dissolves is called thesoluteand the liquid in which the substance dissolves is called the solvent.
• Thus, a solute dissolves in a solvent to form a solution.
• As the solute can be obtained back from the solution by evaporating the solvent, dissolution is a physical change.
• While dissolving in a liquid, a solid breaks up into molecules inside the liquid.
• And these molecules hide themselves in the intermolecular space of the liquid.
• So the volume of a liquid does not change if II I something is dissolved in it

Chemical Changes

• A change in which new substances are formed and which cannot be reversed by reversing the conditions is called a chemical change.
• Some examples of chemical change are mentioned below.

Types Of Changes In Matter Class 8

Burning:

When lighted, a combustible substance (Example: Hydrogen, coal, wood, paper, kerosene, diesel, petrol, LPG, CNG, spirit) burns in air.

• You have learnt that burning is a fast reaction between the combustible substance and the oxygen of the air.
• When kindled, hydrogen burns in air to form a new substance, water. On being cooled, water does not give back hydrogen, so the change is irreversible.
• Thus, the burning of hydrogen is a chemical change.
• Coal contains mainly carbon. When burnt, the carbon of the coal combines with the oxygen of air to form a new substance, carbon dioxide. Carbon dioxide is a gas and is liberated into the air.

This change is irreversible —on being cooled, carbon dioxide does not give back carbon and oxygen. Hence, the burning of coal is a chemical change.

Wood or paper, when burnt, combines with the oxygen of the air and forms new substances —carbon dioxide and water vapour.

• On being cooled, carbon dioxide and water vapour do not give back to the wood or paper. Thus, the burning of wood or paper is a chemical change.
• Kerosene, diesel, petrol, LPG (liquefied petroleum gas) and CNG (compressed natural gas) are all hydrocarbons, i.e., they are made up of carbon and hydrogen only.
• When lit, they burn in air to form the new substances, carbon dioxide and water vapour.

The changes are irreversible, too. So, the burning of these fuels is a chemical change

Ethanol (i.e., ethyl alcohol, commonly called alcohol) is a compound containing carbon, hydrogen and oxygen. It is a liquid that catches fire when near a flame and burns to give carbon dioxide and water vapour. This is also a chemical change.

Physical And Chemical Changes Examples

Rusting

Iron rusts in moist air, forming a red-brown solid, called rust. The rust formed cannot be changed back to iron by reversing the condition, i.e., the change is irreversible. Thus, rusting is a chemical change.

The cooking of food

The taste of vegetables and pulses changes when they are cooked because new substances are formed in the process. Also, we cannot obtain green vegetables from a vegetable curry or grains from cooked pulses. So, the cooking of food is a chemical change.

The curdling of milk:

• Once milk is curdled
• A new substance (curd) is formed, and
• Milk cannot be obtained back from the curd, i.e., the change is irreversible. Thus, the curdling of milk is a chemical change.

The charring of sugar:

Sugar belongs to a class of compounds called carbohydrates. A carbohydrate contains carbon and the elements of water. So, when sugar is heated, water gets loosened and vaporised, and the black residue of carbon is left behind. You have learnt that the change is also irreversible and is, therefore, a chemical change.

Digestion

Food, on being digested inside our body, is changed into several different things—some of which are taken up and some expelled by the body. The change cannot be reversed either. Thus, digestion is a chemical change.

Fermentation

Fermentation is a process employed for preparing alcohol from fruits containing sugar. In the presence of enzymes, a sugar solution changes into alcohol, liberating carbon dioxide.

• As a result, a froth is formed, and the liquid appears as if it were boiling.
• The process is known as fermentation (derived from the Latin word fervere, meaning ‘to boil’).
• It is an irreversible process in which new substances are formed. Therefore, it is a chemical change

Photosynthesis:

Green plants prepare their food (glucose) from carbon dioxide and water in the presence of chlorophyll in sunlight

New substances (glucose and oxygen) are formed in the process. Also, the change is irreversible. So, photosynthesis is a chemical change.

Chemical Reactions NCERT Notes

Respiration:

In respiration, the glucose (a carbohydrate) formed by a living being combines with oxygen of the air, forming the new substances carbon dioxide and water. Energy is also released in the process, and the change is irreversible. So, respiration is a chemical change

Conservation of mass in a chemical change

The mass of the individual substance(s) undergoing a chemical change is altered. But the total mass of the reactants is the same as that of the products.

For example:

When carbon is burnt in air, the mass of carbon is reduced, and finally, the carbon vanishes.

• All the carbon gets converted to carbon dioxide.
• But the mass of the carbon used plus the mass of the oxygen taken up from the air is the same as that of the carbon dioxide formed

The mass of an iron nail increases when the nail rusts. But the mass of the original nail plus that of the oxygen and moisture taken up from the air is the same as that of the rusted nail.

Thus, a chemical change obeys the law of conservation of mass.

Comparison between physical and chemical changes:

Chemical Change NCERT Notes

Can Physical and Chemical Changes Occur Together?

Yes, they can. Let us examine the changes that occur when a candle burns.

1. The wax under the wick melts. The molten wax flows down and solidifies. These are changes in state and, therefore, physical changes

A part of the molten wax that vaporises burns to form carbon dioxide and water vapour. The burning of wax is a chemical change

Physical and Chemical Changes Involve Energy Change

There is a change in energy when a physical or chemical change occurs. Energy, usually in the form of heat, is either taken in (i.e., absorbed) or given out (i.e., evolved) by a substance undergoing a change

• A change during which heat is given out (i.e., evolved) is called an exothermic change.
• A change during which heat is taken in (i.e., absorbed) is called an endothermic change

There are many changes which are neither exothermic nor endothermic. The formation of a heterogeneous mixture is a common example of this type of change. When sand is mixed with salt or water, no heat is given out or taken in.

Energy change in a physical change

State changes:

• Energy changes take place during a state change. A solid absorbs heat to melt, and a liquid absorbs heat to change into a vapour. Thus, these are endothermic changes.
• On being cooled, gases and vapours condense and liquids freeze. Heat is given out in these processes. So, these are exothermic changes.

Activity:

Take a little water in a steel or glass bowl. Pour boiling water into a mug. Hold the bowl over the mug. Steam coming out of the mug will condense as it comes in contact with the bowl. After some time, you will find that the water in the bowl has become warmer than before.

On being boiled, water changes into water vapour. The water vapour condenses, transferring heat to the cold water in the bowl. So, the water in the bowl becomes warm.

Why an energy change in a change of state:

This happens because the kinetic energy possessed by the molecules of a substance is different in different states.

• It is the lowest in the solid state, higher in the liquid state and the highest in the gaseous state.
• So, energy (heat) will be absorbed by a solid to melt and a liquid to boil or vaporise. And heat will be evolved by vapours to condense and a liquid to freeze.
• Dissolution. Many substances evolve heat, whereas some others absorb heat while dissolving in a solvent. You can test this by doing the following activity.

NCERT Class 8 Physical And Chemical Changes

Activity:

Hold a glass in your hand. Pour some water into the glass and stir it after adding a couple of spoons of glucose. The glass will become slightly colder. Thus, the dissolution of glucose in water is an endothermic change. You can get back the glucose by evaporating the water.

When you put some glucose on your tongue, your tongue feels cool. While dissolving in the moisture of the tongue, glucose absorbs heat from it. So, your tongue feels the cooling effect. On the other hand, if you add bathroom acid (concentrated hydrochloric acid) to water, heat is evolved.

Why an energy change in dissolution:

During dissolution, the solute particles break up from the main bulk and hide themselves in the intermolecular space of the solvent.

• This affects the motion and so the KE of the molecules. The KE ofthe particles is dependent on temperature.
• And so, a change in the KE will result in the absorption or evolution of heat.

Energy change in a chemical change

All chemical changes involve a change in energy.

Burning:

You know that both heat and light are emitted when anything burns

Photosynthesis:

In photosynthesis, chlorophyll —the green pigment of leaves—absorbs sunlight (energy), and helps the plant produce glucose and oxygen from water and carbon dioxide.

Slaking of lime. You have learned that the slaking of lime is a highly exothermic reaction. So much heat is evolved when water is added to quicklime that the water boils during the reaction.

Quicklime + water→slaked lime + heat

Why an energy change in a chemical change:

A chemical change involves a rearrangement of atoms. The reactant molecules break up, and the product molecules are formed.

• These processes are not only opposite but also involve different amounts of energy.
• So, in the overall process, there is either a surplus or a deficit of energy.
• If there is a surplus, energy will be given out, and if there is a deficit, energy will be taken in. So, there is a change in energy in a chemical change.

Energy Requirement for the Completion of a Change

The energy requirements are different for the completion of the two kinds of change: endothermic and exothermic

Endothermic change:

You know that energy is absorbed in an endothermic change. In other words, a substance essentially requires energy from outside to undergo an endothermic change. Hence, an endothermic change continues only till energy is pumped in.

For example:

A solid melts or a liquid boils only when it is heated. And the reaction between nitrogen and oxygen forming nitric oxide (NO)—a highly endothermic reaction—takes place only in the presence of an electric spark. So, the reaction takes place in the sky only when there is lightning

Exothermic change:

Heat is evolved in an exothermic change. So, at first instance, it appears that no energy should be required from outside by the substance undergoing such a change. And actually, there are many exothermic changes—especially the exothermic physical changes—which do not need energy from outside at any stage of the change.

A common example is the condensation of vapour or the freezing of a liquid. Similarly, when dilute hydrochloric acid is added to a solution of sodium hydroxide, an instant reaction takes place (forming sodium chloride and water), liberating heat.

However, many exothermic reactions do not take place without being initiated by heating, igniting, illumination and sparking. But once initiated, exothermic reactions go to completion on their own.

NCERT Class 8 Physical And Chemical Changes

Some examples are given below:

1. Hydrogen does not react with oxygen when the two are only mixed, but it reacts explosively when the mixture is kindled or sparked. This is a highly exothermic reaction.
2. A piece of coal, wood or paper (in fact, any combustible substance) does not burn unless lit. But once the substance starts burning, it burns out completely.
3. The reaction between iron and sulphur, forming iron(II) sulphide, is an exothermic process.
4. When iron filings and sulphur are mixed in the mass ratio 7 : 4, nothing happens. But once the mixture is heated in a hard-glass test tube for a short while, it begins to glow, showing that a reaction has started.
5. Now you can stop heating, but you will find that the solid continues to glow, and the glow spreads throughout the mass.
6. After the glow dies out and the test tube cools down, you will find that a greyish black solid is formed, different from the original mixture. This is a compound, iron(II) sulphide.

Thus, we can conclude that an exothermic reaction, once initiated, continues. The heat evolved is more than enough to sustain it.

Chapter 1 Matter Notes

You know that matter is made up of tiny particles called molecules. Molecules are held together by a force of attraction called an intermolecular force. There is also a space between the particles called the intermolecular space.

Matter And Its Properties

The force of attraction and the space between the particles (i.e., molecules) differ from substance to substance. But for any substance,

Read And Lean More Class 8 Chemistry

• The stronger the intermolecular force, the smaller is the intermolecular space, and
• The weaker the intermolecular force, the larger is the intermolecular space

States Of Matter

You have learnt earlier that matter exists in three states

1. Solid
2. Liquid
3. Gaseous

For example:

NCERT Solutions For Matter Class 8

Water exists in three states— ice (solid), water (liquid), and water vapour (gaseous). Here we must understand that the kind of matter, i.e., the molecules constituting ice, water, or water vapour, is the same, i.e., water (H₂O).

What Causes the Difference in States

For any substance, the molecules making up the substance do not change in the three states.

• Then why is it that the substance exists in three states? It is, in fact, the force and the space between the molecules that determine the state of matter.
• The intermolecular force is the strongest in the solid state, weaker in the liquid state, and weakest in the gaseous state.

And so, the intermolecular space is the smallest in the solid state, larger in the liquid state, and the largest in the gaseous state

Thus, the molecules are most tightly held in solids, loosely held in liquids, and almost independent of each other in gases. This explains the general behaviour of solids, liquids, and gases.

Interconversion of States of Matter

As you know,

• On heating, ice turns into water and water into steam, and
• On cooling, steam turns into water and water into ice.

NCERT Class 8 Chemistry Chapter 1 Matter

Such a change in state may be brought about in other substances too, without a change in the composition

This is called the interconversion of states of matter.

• The constant temperature at which a solid turns into the corresponding liquid is called the melting point of the solid.
• The constant temperature at which a liquid freezes, i.e., turns into the corresponding solid, is called the freezing point of the liquid.
• Ordinarily, the freezing point of a liquid is the same as the melting point of the corresponding solid.

For example:

• Water freezes as well as ice melts at 0°C.
• Also, the constant temperature at which a liquid boils is called the boiling point of the liquid.

For example:

• The boiling point of water is 100°C.
• It is the temperature at which steam will condense.

States Of Matter NCERT Notes

The Kinetic Theory of Matter

The kinetic theory of matter explains the behaviour of the three states of matter.

It is summarised below.

1. All matter is made up of very tiny particles called molecules.
2. In the solid state, the particles are rigidly held in positions, about which they can only vibrate.
3. In the liquid state, the particles are in continuous motion, but are not completely separated from each other. While in motion, they collide among themselves.
   • In the gaseous state, the particles are in continuous random motion, almost independent of each other.
   • The particles in a gas travel much longer distances than in a liquid before they collide with other particles or with the walls of the vessel.
   • The collision of the particles with the walls of the vessel gives rise to the pressure of the gas
4. The particles possess some energy due to their motion. This energy is called kinetic energy (KE).
5. The KE possessed by the particles is dependent on temperature. The higher the temperature, the higher the KE, and the lower the temperature, the lower the KE

How Kinetic Theory Explains the Interconversion of States of Matter

1. Solid-liquid interconversion

Solid to liquid:

• The particles constituting a solid only vibrate about their mean positions.
• As a solid is heated, the KE of the particles increases. With rising temperature, the particles vibrate more and more vigorously till they move away from their fixed positions at a particular temperature, called the melting point of the solid.
• Thus, a solid becomes a liquid.

Liquid to solid:

• As a liquid is cooled, the KE of the particles decreases.
• The particles move shorter and shorter distances as the temperature is lowered.
• At the freezing point, the translational motion (i.e., from one point to another) of the particles ceases, and the particles get rigidly fixed. This is how a liquid changes into a solid.
• However, the particles in a solid continue to vibrate about their mean positions

Types Of Matter Class 8

2. Liquid-gas (vapour) interconversion

Liquid to gas:

The particles in a liquid are in continuous motion, during which they collide among themselves.

• If they collide strongly, some of the particles may overcome the attractive force and escape.
• A liquid evaporates in this manner. As the temperature is raised, the KE of the particles increases, and the particles collide more strongly. This leads to faster evaporation of the liquid.
• At the boiling point of the liquid, the KE of the particles becomes so great that all the particles tend to escape.
• Thus, at the boiling point, the entire liquid may turn into vapour.

Gas (vapour) to liquid:

In the gaseous state, the particles move very fast, independently of each other. As the temperature is lowered, the KE of the particles is also lowered. When low-energy gaseous particles collide with each other, they may form bigger lumps or clusters, and the gas may condense into a liquid.

Solid Liquid Gas NCERT Notes

The Conditions of Change of State Differ from Substance to Substance

A liquid freezing at 0°C and boiling at 100 °C is water.

• One boiling at 78°C is ethanol.
• The melting and boiling points are characteristic of a substance, and you can identify the substance by determining these points.
• In other words, the conditions of change of state differ from substance to substance.
• This is because the intermolecular force and the intermolecular space differ from one substance to another

Conservation Of Mass

You know that only a rearrangement of atoms or molecules takes place when a change occurs. And as the atoms or molecules of a substance have fixed masses, the total mass of the substances involved in a change should remain the same.

Law of Conservation of Mass

Lavoisier, in the late eighteenth century, gave a law, called the law of conservation of mass, which can be stated as follows.

• Matter can neither be created nor destroyed, but can be changed from one form to another, and the total mass of the substances before and after the change remains the same.
• The law of conservation of mass is true for physical as well as chemical changes.
• In a nutshell, the total mass of the substances before and after the change is the same.

Conservation of Mass Physical changes:

It is easily understood that there is no change in the mass of a substance when it undergoes a physical change.

Properties Of Matter Class 8

For example:

The mass of an electric bulb does not change after it remains lit for some time.

• Similarly, a given mass of ice, on melting, gives the same mass of water.
• And a given mass of water, on boiling, gives the same mass of water vapour.

Conservation of Mass Chemical changes:

According to the law of conservation of mass, in a chemical change, the sum of the masses of the reactants is the same as that of the products.

We must look at the total mass of the substances before and after the reaction.

Mass of the reactants = Mass of the products

Matter Science Notes

Let us consider the burning of a piece of paper. During the process, it appears that there is a loss of mass.

• But that is not the case.
• While burning, the paper takes up oxygen from the air and forms some ash, plus carbon dioxide and water vapour.
• So, we have to see whether the mass of paper plus oxygen taken from the air is equal to that of the ash plus carbon dioxide and water vapour formed.
• A detailed experiment shows that the two masses are equal.

Mass of paper + oxygen = Mass of ash + carbon dioxide + water vapour

You can verify the law with the help of a simpler experiment, as described below.

Experiment:

Put a small tube or bottle containing a solution of barium chloride into a conical flask.

NCERT Chemistry Matter Chapter

• Place some sodium sulphate solution in the flask with the help of a dropper, carefully, ensuring that the two substances do not come in contact with each other.
• Close the mouth of the flask with a cork and weigh the flask. Tilt the flask and swirl it slowly.
• A white precipitate is formed. Leave the flask for some time and weigh it again.
• You will find that there is no change in the weight of the flask.

Chapter 7 Hydrogen

Hydrogen is the lightest element known. It was first prepared by Robert Boyle by diluting sulphuric acid on iron nails. Cavendish studied the gas and called it inflammable air, as the gas burns when kindled

Occurrence And Preparation

The occurrence of Hydrogen Stars (including our sun) is mainly composed of hydrogen. Hydrogen is the most abundant element in the universe. On the earth, however, hydrogen occurs in very small amounts in the free state —in the air, in volcanic gases and the earth’s crust.

Read And Lean More Class 8 Chemistry

But there is plenty of hydrogen on Earth in combination with other elements, i.e., as part of compounds. Water is an important source of hydrogen. Every nine parts by mass of water contains one part of hydrogen. In combination with carbon, hydrogen is present in natural gas and petroleum as well as in all living things. Acids and alkalis also contain hydrogen.

Preparation of Hydrogen

Hydrogen can be obtained by the following methods.

1. By displacement reactions:

Since hydrogen is available in the combined state, it can be obtained by displacement reactions. You have learnt earlier that

• Metals, along with hydrogen,n are arranged in order of their activity in the activity series, and
• A more active metal displaces a less active one (including hydrogen) from its compounds.

Thus, metals above hydrogenin the activity series can displace hydrogen from water and acids. However, remember that tin and lead do not undergo this reaction with water and nor does lead with acids.

NCERT Solutions for Hydrogen Class 8

From water:

Highly active metals like sodium and calcium vigorously react with water, displacing hydrogen from it even in cold conditions.

2 Na + 2H₂O → 2NaOH (sodium hydroxide) + H₂↑

Ca + 2H₂O → Ca₂  (OH)(Calcium hydroxide) + H₂↑

A less active metal, like magnesium, does so when steam is passed over it.

⇒ \(\mathrm{Mg}+\underset{\text { (steam) }}{\mathrm{H}_2 \mathrm{O}} \quad \rightarrow \underset{\text { magnesium oxide }}{\mathrm{MgO}}+\mathrm{H}_2 \uparrow\)

A still less active metal like iron, when steam is passed over the red-hot metal.

3 Fe + 4H₂O(steam) ⇌ Fe₃O₄ (ferrosoferric oxide)  +4H₂ ↑

From an acid:

All metals above hydrogen (except lead) in the activity series displace hydrogen from acid, like dilute hydrochloric or sulphuric acid. (We do not consider nitric acid for this reaction because it gives the oxides of nitrogen.)

⇒ \(\left.\begin{array}{c}
2 \mathrm{Na}+2 \mathrm{HCl} \longrightarrow 2 \mathrm{NaCl}+\mathrm{H}_2 \dagger \\
\mathrm{Mg}+2 \mathrm{HCl} \longrightarrow \mathrm{MgCl}_2+\mathrm{H}_2 \uparrow
\end{array}\right] \text { Vigorous }\)

⇒  \(\left.\begin{array}{l}
\mathrm{Zn}+\mathrm{H}_2 \mathrm{SO}_4 \rightarrow \underset{\text { zinc sulphate }}{\mathrm{ZnSO}_4}+\mathrm{H}_2 \uparrow \\
\mathrm{Fe}+\mathrm{H}_2 \mathrm{SO}_4 \rightarrow \underset{\text { iron(II) sulphate }}{\mathrm{FeSO}_4}+\mathrm{H}_2 \uparrow
\end{array}\right] \text { Moderate }\)

2. By the electrolysis of water:

You have learnt earlier that acidulated water decomposes into hydrogen and oxygen when an electric current is passed through it

• The decomposition of a substance in the molten are forms. state or in solution, when an electric current is passed through it is called electrolysis.
• The substance taken in the molten state or solution is called the electrolyte. And the terminals—made of metals or graphite— through which the current enters or leaves the electrolyte are known as electrodes.
• The electrode connected to the negative pole of the battery is called the cathode, and the one connected to the positive pole of the battery, the anode. The vessel in which electrolysis is carried out is called an electrolytic cell
• An electric current passes through a compound in the molten state or solution only when the liquid contains ions. So, only such substances will act as electrolytes which are made up of ions

Example:

NaCl, which is made of Na⁺ and Cl^– ions) or form ions in solution. Pure water does not allow an electric current to pass through it. But water acidulated with (a very small amount of) dilute hydrochloric or sulphuric acid does because it dissociates.

NCERT Class 8 Chemistry Chapter 7 Hydrogen

⇒ \(\mathrm{H}_2 \mathrm{O} \rightleftharpoons \mathrm{H}^{+}+\mathrm{OH}^{-}\)

During electrolysis, the H⁺ ions move towards the negative electrode, i.e., the cathode, and get discharged (lose their charge) there by the negative charge of the electrode. And the OH” ions move to the positive electrode, i.e., the anode, and get discharged to give oxygen

You will learn in higher classes that, instead of the H⁺ ion, it is the H₃O⁺ ion (i.e., H⁺+ H₂O), called the hydronium ion, that exists in an aqueous solution

The laboratory method

Principle:

Hydrogen is prepared in the laboratory by the action of dilute hydrochloric or sulphuric acid on granulated zinc. We do not use nitric acid, as the oxides of nitrogen are formed

⇒ \(\mathrm{Zn}+2 \mathrm{HCl} \longrightarrow \mathrm{ZnCl}_2+\mathrm{H}_2 \uparrow\)

⇒ \(\mathrm{Zn}+\mathrm{H}_2 \mathrm{SO}_4 \longrightarrow \mathrm{ZnSO}_4+\mathrm{H}_2 \uparrow\)

As the gas is almost insoluble in water, it is collected by the displacement of water.

Procedure:

A conical flask is fitted with a thistle funnel and a delivery tube. The other end of the delivery tube passes through a beehive shelf placed in a water trough. A gas jar full of water is inverted over the beehive shelf. Some granulated zinc is placed in the conical flask.

Dilute hydrochloric or sulphuric acid is added through the thistle funnel till the lower end of the funnel dips in the liquid. Hydrogen then begins to evolve.

The gas is collected by the downward displacement of water. It is not collected by the downward displacement of air since a mixture of hydrogen and air is explosive.

Initially, the air inside the flask and the delivery tube is driven out. So, whatever is collected in the first one or two jars is air, and is rejected. The gas collected afterwards is hydrogen.

Why we prefer zinc to other metals

In the above method, we could have used any metal more active than hydrogen (except lead). We do not use highly active metals like sodium, calcium and magnesium because the reactions of these metals with an acid are too vigorous to control and these metals are expensive too.

The moderately active metals—zinc and iron, which are also cheaper—should be more suitable. We do not use iron either, because it forms some foul-smelling poisonous gases of silicon, sulphur and phosphorus present in it as impurities. So, we prefer zinc to other metals.

Hydrogen Class 8 NCERT Notes

Large-scale preparation

Hydrogen is prepared on a large scale, i.e., in the industry, by the following methods.

1. The electrolytic method
2. The Bosch method

Let us discuss the principles of the Bosch method.

The Bosch method:

When steam is passed over red-hot coke, what is known as water gas is formed. Water gas is a mixture of mainly carbon monoxide (CO) and hydrogen (H₂), containing some carbon dioxide (CO₂).

⇒ \(\underset{\text { (steam) }}{\mathrm{H}_2 \mathrm{O}}+\underset{\text { (red hot) }}{\mathrm{C}} \longrightarrow \underbrace{\mathrm{CO}+\mathrm{H}_2}_{\text {water gas }}\)

The water gas is mixed with excess steam and heated to 450 °C. The mixture is passed over a catalyst consisting of iron(III) oxide (Fe₂ O₃) mixed with some chromium(III) oxide (Cr₂O₃). The CO abstracts oxygen from Thistle funnel H₂O to form CO₂ and releases more H₂

⇒ \(\underbrace{\mathrm{CO}+\mathrm{H}_2}_{\text {water gas }}+\underset{\text { (steam) }}{\mathrm{H}_2 \mathrm{O}} \frac{450^{\circ} \mathrm{C}}{\mathrm{Fe}_2 \mathrm{O}_3 \text { catalyst }} \mathrm{CO}_2+2 \mathrm{H}_2\)

The CO₂ is removed from the mixture by dissolving it in water under pressure. (Remember that ordinarily, CO₂  is only slightly soluble in water but highly soluble under pressure.)

Properties

Physical Properties

1. Hydrogen is a colourless and odourless (having no smell) gas.
2. It is the lightest element and the lightest gas known. It is 14.6 times lighter than air.
3. It is almost insoluble in water

Chemical Properties

1. Reaction with oxygen (or air):

When kindled, hydrogen bums in air or oxygen to form water

⇒ \(2 \mathrm{H}_2+\mathrm{O}_2 \rightarrow 2 \mathrm{H}_2 \mathrm{O}\)

A large amount of heat is produced in this reaction. So, a mixture of hydrogen and oxygen may explode.

2. Reaction with chlorine:

When kindled, hydrogen burns in chlorine to form hydrogen chloride gas. Also, a mixture of hydrogen and chlorine, when placed in sunlight, explodes to form the same product

⇒ \(\mathrm{H}_2+\mathrm{Cl}_2 \longrightarrow \underset{\text { hydrogen chloride gas }}{2 \mathrm{HCl} \uparrow}\)

Hydrogen chloride gas can be dissolved in water to obtain hydrochloric acid.

Properties of Hydrogen Class 8

3. Reaction with sulphur:

Hydrogen reacts with molten sulphur to give hydrogen sulphide gas, which smells like rotten eggs.

⇒ \(\mathrm{H}_2+\underset{\text { (molten) }}{\mathrm{S}} \longrightarrow \underset{\text { hydrogen sulphide }}{\mathrm{H}_2 \mathrm{~S} \uparrow}\)

4. Reaction with nitrogen:

Hydrogen reacts with nitrogen only under special conditions to form an appreciable amount of ammonia.

The ammonia gas formed, in turn, decomposes back to hydrogen and nitrogen. So, this reaction occurs both ways. Such reactions are called reversible reactions.

5. Reactions with some metal oxides:

When passed over some hot metal oxides like zinc oxide, iron oxide and copper oxide, hydrogen gas converts them into the corresponding metals.

The oxides of metals like potassium, calcium, sodium and magnesium are not converted into the metals.

Hydrogen is a reducing agent. The addition of hydrogen to or the removal of oxygen from a substance is called reduction.

On the other hand, the addition of oxygen to or the removal of hydrogen from a substance is called’ oxidation. Also, a substance causing reduction is known as a reducing agent, and one causing oxidation is called an oxidising agent.

You have just seen that hydrogen

• Adds itself to oxygen, chlorine, sulphur and nitrogen, and
• Removes oxygen from some metal oxides.

Thus, hydrogen is a reducing agent. It reduces

By adding H:

1. O to H₂O
2. Cl to HCl
3. S to H₂S
4. N to NH₃

By removing O:

1. ZnO to Zn
2. PbO to Pb
3. CuO to Cu
4. FeO to Fe
5. Fe₂O₃ to Fe

Hydrogen as a Fuel Class 8

Test

Hydrogen burns with a characteristic sound, or ‘pop’. This property is used as a test for hydrogen

Uses

1. For manufacturing ammonia:

Hydrogen is used in large quantities to manufacture ammonia.

• When a mixture of hydrogen and nitrogen is passed over an iron catalyst at 500 °C and 200 atm, ammonia is formed.
• (A catalyst is an element or a compound that hastens a reaction without taking part in it.)
• This process is known as the Haber process. Ammonia is used in large quantities in the manufacture of nitrogenous fertilisers.

2. For the hydrogenation of oils:

Vegetable oils react with hydrogen in the presence of a catalyst (like nickel) to form solid fats. Such addition of hydrogen is called hydrogenation.

3. As a fuel: 

On the combustion of hydrogen, i.e., when hydrogen is burnt, heat is produced along with water

So, hydrogen can be used as a fuel. The product of the reaction is water, which does not pollute the environment. Hence, hydrogen is a clean fuel.

Hydrogen produces the maximum heat among all the known fuels. Liquid hydrogen is used as rocket fuel. However, it is difficult to handle and store.

4. The oxyhydrogen flame:

Hydrogen is used to produce an oxyhydrogen flame, which is employed for welding and cutting metals. The two gases—oxygen and hydrogen—passing through different pipes, mix at a point where the mixture is kindled. A high-temperature (2800 °C) flame, called an oxyhydrogen flame, is produced. The metal melts at this temperature, enabling it to be cut or welded.

5. As a reducing agent:

Hydrogen is used as a reducing agent in the burning laboratory and industry

6. For filling balloons:

As hydrogen is lighter than air, a balloon filled with hydrogen rises in the air and drifts in the wind. If a weather instrument is placed in it, the balloon can be used for studying weather conditions.

There was a time when such weather balloons were much in use. But the practice was stopped as such weather balloons often caught fire due to the inflammability of hydrogen. As helium, the next lightest gas, is available in plenty, it is preferred to hydrogen. Helium does not catch fire.

Hydrogen and its Compounds Class 8

Weather balloons:

Fill balloons:

In the 1930s, airships using hydrogen to float were used for transport. But they were discontinued after the airship Hindenburg caught fire in 1937, killing 36 people.

Chapter 6 Chemical Reactions

We have discussed a large number of chemical reactions. Some are accompanied by a change in colour, some by the evolution of a gas, some by the formation of a precipitate, and so on. At the molecular level, different types of changes occur. In some reactions, smaller parts add up to form bigger entities, whereas in some others, bigger entities break into smaller ones.

Again, in some reactions, one element displaces another from a compound whereas in some others, compounds exchange radicals among themselves. For a systematic study, therefore, it is essential that we classify the reactions into different types.

NCERT Solutions for Chemical Reactions Class 8

Read And Lean More Class 8 Chemistry

However, we will discuss first the change in energy in chemical reactions, which is common to all types

Change In Energy In A Reaction

All reactions are accompanied by a change in energy. Energy (in the form of heat or light) is either given out or taken in during a chemical reaction.

• A chemical reaction in which heat or light is evolved is called an exothermic reaction.
• A chemical reaction in which heat or light is absorbed is called an endothermic reaction.
• In an exothermic process, heat or light is given out to the surroundings. That is why you feel hot when you accidentally touch anything burning.
• On the other hand, in an endothermic process, heat or light is taken in, i.e., absorbed from the surroundings. That is why a cube of ice is cold to the touch.
• The ice tends to melt when you touch it. The melting of ice is an endothermic process, and the heat required for it is drawn from your hand.
• And so the cold feeling. Remember that the melting of ice is a physical change, not a chemical reaction

Why A Change In Energy In A Reaction

As we know, any two atoms in a molecule are held together by a force of attraction called a chemical bond. And also that a chemical bond is much stronger than an intermolecular force. We also know that it is the atoms that take part in a chemical reaction.

Thus, we can consider a chemical reaction to be a result of the following phenomena.

• The breaking of bonds of the reactant molecules to set the atoms free for a new combination. (Energy is absorbed in the process.)
• The formation of fresh bonds between the new partners so in the product molecules. (Energy is given out in the process.)

The energy required for the breaking of the bonds of the reactant molecules is not the same as that given out in the formation of the bonds between the new partners.

• When the energy given out in the formation of the bonds is more than that used for the breaking of the bonds, the surplus energy is evolved and the process is exothermic.

However, when the energy required for the breaking of the bonds is greater than that given out in the formation of the bonds, the difference in energy has to be compensated for from outside.

In other words, energy will be absorbed from the surroundings for the reaction to happen, and the process will be endothermic.

NCERT Class 8 Chemistry Chapter 6 Chemical Reactions

Examples of Exothermic Reactions

We will now discuss some common exothermic reactions

1. Burning:

The burning of a substance is exothermic. It is the exothermicity of burning that makes a combustible substance a fuel. For example, hydrogen, carbon (coal), CNG(CH₄), and LPG(C₄H₁₀) are fuels.

2. How some active metals react with water:

The reaction of a highly active metal like K, Na or Ca is vigorous and exothermic. Hydrogen is liberated, and the metal hydroxide is formed in the reaction.

2K(s) (potassium) + 2H₂O(l) → 2 KOH(aq)(Potassium hydroxide) + H₂(g)

2Na(s) + 2H₂O(l) → 2NaOH(aq)(sodiumhydroxide) + H₂(g)

Ca(s) + 2H₂O(l) → Ca (OH)₂(calcium hydroxide)(aq) + H₂(g)

3. The dissolution of metal oxides (bases) in water:

Bases like sodium oxide and calcium oxide vigorously react with water to form their hydroxides, releasing a large amount of heat.

The hydroxides dissolve in an excess of water. The reaction of calcium oxide (CaO, commercially known as quicklime) with water, giving calcium hydroxide [Ca(OH)₂, commercially known as slaked lime] is called the slaking of lime.

4. The dissolution of nonmetal oxides (acidic) in water:

The oxides of nonmetals are acidic and many of them dissolve in water to form acids exothermically.

⇒ \(\begin{aligned}
&\mathrm{CO}_2(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \mathrm{H}_2 \mathrm{CO}_3(\mathrm{aq}){ carbonic acid }\\\end{aligned}\)

⇒ \(\begin{aligned}
&\mathrm{SO}_2(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \mathrm{H}_2 \mathrm{SO}_3(\mathrm{aq})sulphurous acid \\\end{aligned}\)

⇒ \(\underset{\text { sulphur trioxide }}{\mathrm{SO}_3(\mathrm{l})}+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \underset{\text { sulphuric acid }}{\mathrm{H}_2 \mathrm{SO}_4(\mathrm{aq})}\)

5. The reaction between a basic and an acidic oxide:

A basic oxide reacts with an acidic oxide, forming a salt and evolving heat

⇒ \(\begin{aligned}
&\mathrm{Na}_2 \mathrm{O}(\mathrm{~s})+\mathrm{CO}_2(\mathrm{~g}) \longrightarrow \mathrm{Na}_2 \mathrm{CO}_3(\mathrm{~s})(sodium carbonate)\\
&\text { }
\end{aligned}\)

⇒ \(\mathrm{CaO}(\mathrm{~s})+\mathrm{CO}_2(\mathrm{~g}) \longrightarrow \underset{\substack{\text { calcium carbonate } \\ \text { (limestone) }}}{\mathrm{CaCO}_3(\mathrm{~s})}\)

6. Neutralisation reactions:

In a neutralisation reaction, an acid reacts with a base, forming a salt and water. All such reactions are exothermic

⇒ \(\text { Base }+ \text { acid } \longrightarrow \text { salt + water }\)

⇒ \(\mathrm{NaOH}(\mathrm{aq})+\mathrm{HCl}(\mathrm{aq}) \longrightarrow \mathrm{NaCl}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

⇒ \(\mathrm{KOH}(\mathrm{aq})+\mathrm{H}_2 \mathrm{SO}_4(\mathrm{aq}) \longrightarrow \mathrm{K}_2 \mathrm{SO}_4(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

Chemical Reactions Class 8 NCERT Notes

7. Reaction of an acid with a metal carbonate:

By performing a similar activity as above, you can conclude that heat is evolved when an acid acts on a carbonate or a hydrogencarbonate, producing CO₂

⇒ \(\mathrm{Na}_2 \mathrm{CO}_3(\mathrm{~s})+2 \mathrm{HCl}(\mathrm{aq})\) → \(2 \mathrm{NaCl}(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{CO}_2(\mathrm{~g})\)

⇒ \(\mathrm{CaCO}_3(\mathrm{~s})+2 \mathrm{HCl}(\mathrm{aq}) \longrightarrow\)\(\mathrm{CaCl}_2(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})+\mathrm{CO}_2(\mathrm{~g})\)

8. Respiration:

You know that, in respiration, the glucose formed in plants and animals combines with the oxygen of the air to give C02 and H20. The reaction, being exothermic, provides living beings with the energy to sustain their life processes.

⇒ \(\begin{aligned}
&\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6(\mathrm{aq})+6 \mathrm{O}_2(\mathrm{~g}) \longrightarrow 6 \mathrm{CO}_2(\mathrm{~g})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l})\\
&\text { glucose }
\end{aligned}\)

9. Rusting

In rusting, iron slowly combines with oxygen (air) in the presence of moisture to form the brownish red hydrated iron(III) oxide, called rust

⇒ \(4 \mathrm{Fe}(\mathrm{~s})+3 \mathrm{O}_2(\mathrm{~g})+2 x \mathrm{H}_2 \mathrm{O}(\mathrm{~g}) \longrightarrow\) \(\underset{\text { rust }}{2\left[\mathrm{Fe}_2 \mathrm{O}_3 \cdot x \mathrm{H}_2 \mathrm{O}\right](\mathrm{s})}\)

The reaction is exothermic, but too slow to let you feel its heat at any point in time.

Examples of Endothermic Reactions

Endothermic reactions are much fewer in number than exothermic ones. Some examples are given below

1. Combination of nitrogen with oxygen:

Nitrogen combines with oxygenforming nitric oxide (NO) when an electric spark is passed through a mixture of the two gases (as during lightning). The reaction is endothermic.

⇒ \(\mathrm{N}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \xrightarrow[\text { spark }]{\text { electric }} 2 \mathrm{NO}(\mathrm{~g})\)

2. Thermal decomposition of metal carbonates:

The breaking down of a substance into simpler substances on being heated is called thermal decomposition. The carbonates of many metals decompose on being heated to give the metal oxides and carbon dioxide. These are endothermic reactions. Remember that, among the common carbonates, sodium carbonate (Na2C03) and potassium carbonate (K2C03) do not undergo such a reaction

⇒ \(\mathrm{CaCO}_3(\mathrm{~s}) \xrightarrow{\text { heat }} \mathrm{CaO}(\mathrm{~s})+\mathrm{CO}_2(\mathrm{~g})\)

⇒ \(\mathrm{MgCO}_3(\mathrm{~s}) \xrightarrow{\text { heat }} \mathrm{MgO}(\mathrm{~s})+\mathrm{CO}_2(\mathrm{~g})\)

3. Photosynthesis:

We know that a plant prepares its food, glucose, from atmospheric C02 and soilmoisture in the presence of chlorophyll by absorbing sunlight.

The reaction is endothermic

⇒ \(6 \mathrm{CO}_2(\mathrm{~g})+6 \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \xrightarrow[\text { chlorophyll }]{\text { sunlight }}\) \(\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6(\mathrm{aq})+6 \mathrm{O}_2(\mathrm{~g})\)

Endothermic physical processes:

Many physical processes are endothermic. We have learnt that the melting of ice requires heat from outside and so does the boiling of water.

• Water gets converted to steam at 100 °C, but we have to heat it all along, i.e., until it is converted into steam.
• The dissolution of ammonium chloride (NH₄Cl), ammonium nitrate (NH₄NO₃) or glucose in water is also a common example of such a process. Stir any of these substances in a glass of water and hold the glass in your palm. You will feel that it has become cold

Some common observations:

Chemical reactions have the following general characteristics.

1. Exothermic reactions are more common than endothermic reactions:

This is because exothermic reactions do not need energy from the surroundings.

Types of Chemical Reactions Class 8

2. Once they begin, exothermic reactions continue on their own but endothermic reactions do not:

This is because some heat is required to keep a reaction going. And that heat is generated on its own during an exothermic reaction.

For example:

When you light a combustible substance, it burns on its own.

• When it starts rusting, a piece of iron continues to do so, though slowly, till all the iron is eaten up.
• However, this does not happen in an endothermic reaction because such a reaction does not generate any heat.
• So, the reaction goes on only as long as energy is supplied from outside.

For example:

Nitrogen combines with oxygen to form nitric oxide (NO) only as long as an electric spark is passed through a mixture of nitrogen and oxygen. The reaction stops in the absence of a spark

⇒ \(\mathrm{N}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \xrightarrow[\text { spark }]{\text { electric }} 2 \mathrm{NO}(\mathrm{~g})\)

Also, photosynthesis takes place in the presence of sunlight. Does it ever happen in the dark?

3. Most exothermic reactions too have to be initiated:

• A reaction, even exothermic, does not generally start simply when the reactants are mixed.
• Quite often, it has to be initiated by heating the reactants, igniting them, passing an electric spark through them, exposing them to UV light, etc.

For example:

A substance burns when ignited, hydrogen reacts with oxygen when ignited, and so on. You will learn the reason for this in higher classes.

Types Of Chemical Reactions

Among the different types of chemical reactions, combination, decomposition, displacement, double displacement and neutralization reactions are the ones we commonly come across. We will discuss them here.

Combination Reactions

In a combination reaction (synthesis), two or more reactants combine to form a product. Some examples are given below. The burning of some elements Elements like H, C, S, P, Ca and Mg, on being burnt in air, form their oxides

By direct combination:

1. \(2 \mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \xrightarrow{\text { burn }} 2 \mathrm{H}_2 \mathrm{O}(\mathrm{~g})\)

2.\(\mathrm{C}(\mathrm{~s})+\mathrm{O}_2(\mathrm{~g})  \xrightarrow{\text { burn }} \mathrm{CO}_2(\mathrm{~g}) \\\)

3. \(\mathrm{S}(\mathrm{~s}) +\mathrm{O}_2(\mathrm{~g}) \xrightarrow{\text { burn }} \mathrm{SO}_2(\mathrm{~g}) \\\)

4. \(2 \mathrm{Ca}(\mathrm{~s})+\mathrm{O}_2(\mathrm{~g}) \xrightarrow{\text { burn }} 2 \mathrm{CaO}(\mathrm{~s})\\\)

5. \(2 \mathrm{Mg}(\mathrm{~s})+\mathrm{O}_2(\mathrm{~g}) \xrightarrow{\text { burn }} 2 \mathrm{MgO}(\mathrm{~s})\)

The burning of carbon:

Burn some charcoal (carbon) in a deflagrating spoon. Introduce the spoon into an open gas jar near the mouth of the jar so that the burning charcoal gets a clear supply of air.

• Close the mouth of the jar with a lid when all the carbon has burned.
• Invert the jar and place it in a trough containing clear limewater and open its mouth inside the liquid.
• The limewater rises in the jar and becomes milky. This proves that carbon dioxide is formed

The burning of magnesium:

When ignited in air, say in an open gas jar, it burns with a dazzling white flame. The magnesium oxide formed deposits as a white, smoky solid on the walls of the jar

Chemical Reactions and Equations NCERT Notes

Rusting

A piece of iron, when left in moist air, slowly gets a crust of a brown-red solid called rust. Rust —a hydrated iron(III) oxide product of the direct combination of iron with the oxygen and moisture of the air.

4Fe(s) + 3O₂(g) + Moisture → 2[Fe₂O₃. xH₂O](s)(rust brown- red)

(x can vary).

The combination of elements with chlorine

Chlorine is a very active nonmetal—a greenish-yellow gas. Most metals and some nonmetals combine with chlorine to form their chlorides

⇒\(2 \mathrm{Na}(\mathrm{~s})+\mathrm{Cl}_2(\mathrm{~g}) \longrightarrow \underset{\text { sodium chlorid }}{2 \mathrm{NaCl}(\mathrm{~s})}\)

⇒ \(2 \mathrm{Fe}(\mathrm{~s})+3 \mathrm{Cl}_2(\mathrm{~g}) \xrightarrow{\text { heat }} \underset{\text { iron }(\text { III }) \text { chloride }}{2 \mathrm{FeCl}_3(\mathrm{~s})}\)

⇒ \(\mathrm{H}_2(\mathrm{~g})+\mathrm{Cl}_2(\mathrm{~g}) \xrightarrow{\text { ignite }} \underset{\text { hydrogen chloride }}{2 \mathrm{HCl}(\mathrm{~g})}\)

⇒ \(\underset{\text { phosphorus }}{\mathrm{P}_4(\mathrm{~s})}+10 \mathrm{Cl}_2(\mathrm{~g}) \xrightarrow{\text { burn }} \underset{\begin{array}{c}
\text { phosphorus } \\
\text { pentachloride }
\end{array}}{4 \mathrm{PCl}_5(\mathrm{~s})}\)

The combination of iron with sulphur

You have already learnt that iron combines with sulphur, when heated, to form iron(II) sulphide.

⇒  \(\underset{\substack{\text { iron } \\ \text { (grey) }}}{\mathrm{Fe}}+\underset{\substack{\text { sulphur } \\ \text { (yellow) }}}{\mathrm{S}} \xrightarrow{\text { heat }} \underset{\substack{\text { iron(II) sulphide } \\ \text { (greyish black) }}}{\mathrm{FeS}}\)

The combination of oxides with water

The oxide of a nonmetal generally dissolves in water to form an acid.

⇒  \(\begin{aligned}
&\mathrm{CO}_2+\mathrm{H}_2 \mathrm{O} \longrightarrow \mathrm{H}_2 \mathrm{CO}_3 (carbonic acid )\\
&\text { }
\end{aligned}\)

⇒  \(\begin{aligned}
&\mathrm{SO}_2+\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{H}_2 \mathrm{SO}_3( sulphurous acid)\\
&\text { }
\end{aligned}\)

Balancing Chemical Reactions Class 8

And the oxides of many metals combine with water to form the basic hydroxides.

⇒  \(\underset{\text { sodium oxide }}{\mathrm{Na}_2 \mathrm{O}}+\mathrm{H}_2 \mathrm{O} \longrightarrow \underset{\text { sodium hydroxide }}{2 \mathrm{NaOH}}\)

⇒  \(\underset{\text { calcium oxide }}{\mathrm{CaO}}+\mathrm{H}_2 \mathrm{O} \longrightarrow \underset{\text { calcium hydroxide }}{\mathrm{Ca}(\mathrm{OH})_2}\)

When carbon dioxide is passed through water for some time, the water turns blue litmus wine red, showing that it contains an acid.

• At the same time, limewater, which is prepared by adding water to quicklime (CaO), is a solution of Ca(OH)2 and turns red litmus blue. Thus, Ca(OH)2 is basic.
• Remember that acidic substances turn blue litmus red and basic substances turn red litmus blue

Decomposition Reactions

In a decomposition reaction, one substance breaks down into two or more simpler substances.

Some examples are given below:

Decomposition of water on electrolysis Electrolysis is a process in which a substance is decomposed, or broken down into simpler substances, by passing an electric current through it

Water mixed with a very small amount of an acid breaks down into hydrogen and oxygen on electrolysis

⇒  \(\underset{\text { water }}{\mathrm{H}_2 \mathrm{O}} \xrightarrow{\text { electrolysis }} \underset{\substack{\text { hydrogen } \\
\text { (negative } \\
\text { electrode) }}}{2 \mathrm{H}_2}+\underset{\begin{array}{c}
\text { oxygen } \\
\text { (positive } \\
\text { electrode) }
\end{array}}{\mathrm{O}_2}\)

Take some water, mixed with a few drops of dilute sulphuric acid, in a beaker. Invert two test tubes full of water into it. Remove the insulation from the ends of two thick wires. Introduce them into the test tubes as shown in. Connect the wires to a battery and pass current for some time. Gases start collecting in the test tubes. You will observe that the volume of the gas collected over the negative electrode is twice that of the gas collected over the positive electrode.

Stop passing current when there is enough gas in the test tubes. Cork the test tubes inside the water and take them out. Perform the following experiments.

The gas collected at the negative electrode:

Bring a lighted match near the mouth of the tube and open its mouth. The gas burns with a ‘pop’, and so it is hydrogen.

The gas collected at the positive electrode:

Bring a glowing matchstick near the mouth of the test tube and remove the cork. The matchstick gets lighted. So, the gas is oxygen

The experiment also shows that the volume ratio of hydrogen and oxygen in water is 2:1

Chemical Reactions and Their Types Class 8

The decomposition of baking soda

Sodium hydrogencarbonate (NaHC03) is called baking soda. On strong heating, baking soda decomposes into sodium carbonate, water (vapour) and carbon dioxide.

⇒  \(\underset{\begin{array}{c}
\text { sodium } \\
\text { hydrogencarbonate }
\end{array}}{2 \mathrm{NaHCO}_3(\mathrm{~s})} \xrightarrow{\text { heat }} \underset{\begin{array}{c}
\text { sodium } \\
\text { carbonate }
\end{array}}{\mathrm{Na}_2 \mathrm{CO}_3(\mathrm{~s})}+\underset{\begin{array}{c}
\text { water } \\
\text { vapour }
\end{array}}{\mathrm{H}_2 \mathrm{O}(\mathrm{~g})}\)

The decomposition of potassium chlorate

When strongly heated, potassium chlorate gives potassium chloride and oxygen.

⇒  \(\underset{\begin{array}{c}
\text { potassium } \\
\text { chlorate }
\end{array}}{2 \mathrm{KClO}_3(\mathrm{~s})} \xrightarrow{\text { heat }} \underset{\begin{array}{c}
\text { potassium } \\
\text { chloride }
\end{array}}{2 \mathrm{KCl}(\mathrm{~s})}+\underset{\text { oxygen }}{3 \mathrm{O}_2(\mathrm{~g})}\)

Displacement Reactions

In a displacement reaction, one element displaces another from its compound and takes its place therein.

Displacement reactions are best studied using the activity series. In the activity series, metals, along with hydrogen, are arranged in order of their activity. The higher an element is placed in the series, the more active it is. Thus, you can easily find out the relative activity of the metals along with hydrogen by consulting the series. For example, Na is more active than M,g and Mg is more active than Fe and so they fall in the following order of activity:

Na > Mg > Fe.

Could you say in what order will the activity of copper, silver, magnesium, iron and aluminium decrease? It has been observed that a more active metal displaces a less active one from its compounds.

Some common examples are given below.

The displacement of hydrogen from water by a metal:

An active metal like potassium (K), sodium (Na) or calcium (Ca) reacts with water, displacing hydrogen even in cold conditions.

2K(s) + 2H₂O(1) — 2KOH(aq) + H₂(g)

2Na(s) + 2H₂O(1) — 2NaOH(aq) + H₂(g)

Ca(s) + 2H₂O(1) — Ca(OH)₂(aq) + H₂ (g)

Magnesium, which is less active than the above-mentioned metals, reacts only at high temperatures.

When placed in steam, a burning magnesium ribbon continues to bum, forming magnesium oxide and hydrogen.

⇒ \(\underset{\text { magnesium }}{\mathrm{Mg}(\mathrm{~s})}+\underset{\text { water }(\text { steam })}{\mathrm{H}_2 \mathrm{O}(\mathrm{~g})} \longrightarrow \underset{\text { magnesium oxide }}{\mathrm{MgO}(\mathrm{~s})}+\underset{\text { hydrogen }}{\mathrm{H}_2(\mathrm{~g})}\)

In this reaction, a magnesium atom displaces two hydrogen atoms and takes their place

A less active metal like magnesium, zinc or iron easily displaces hydrogen from dilute hydrochloric or sulphuric acid.

⇒ \(\underset{\text { zinc }}{\mathrm{Zn}(\mathrm{~s})}+2 \mathrm{HCl}(\mathrm{aq}) \longrightarrow \underset{\text { zinc chloride }}{\mathrm{ZnCl}}(\mathrm{aq})+\mathrm{H}_2(\mathrm{~g})\)

⇒ \(\underset{\substack{\text { iron }}}{\mathrm{Fe}(\mathrm{~s})}+\mathrm{H}_2 \mathrm{SO}_4(\mathrm{aq}) \longrightarrow \underset{\text { iron(II) sulphate }}{\mathrm{FeSO}_4(\mathrm{aq})}+\mathrm{H}_2(\mathrm{~g})\)

The displacement of copper from copper sulphate by iron or zinc:

When an iron knife or nail is placed in a copper sulphate solution, there is a brown-red deposit of copper over the iron object

After some time, the blue colour of the solution changes to green, owing to the formation of iron(II) sulphate

⇒ \(\underset{\substack{\text { iron } \\ \text { igrey) }}}{\mathrm{Fe}(\mathrm{~s})}+\underset{\substack{\text { copper sulphate } \\ \text { (blue) }}}{\mathrm{CuSO}_4(\mathrm{aq})} \longrightarrow \underset{\text { copper }}{\text { (brown-red) }} \underset{\text { cuper }}{\mathrm{Cu}(\mathrm{~s})}+\underset{\text { (iron(I) sulphate }}{\mathrm{FeSO}_4}(\mathrm{aq})\)

Reactants and Products Class 8 Chemistry

Also, zinc displaces copper from copper sulphate, but the resultant solution is colourless. You can use a piece of granulated zinc in place of iron and it will be coated by copper

⇒ \(\underset{\substack{\text { zinc } \\ \text { (white) }}}{\mathrm{Zn}(\mathrm{~s})}+\underset{\substack{\text { copper sulphate } \\ \text { (blue) }}}{\mathrm{CuSO}_4(\mathrm{aq})} \rightarrow \underset{\substack{\text { copper } \\ \text { (brown-red) }}}{\mathrm{Cu}(\mathrm{~s})}+\underset{\substack{\text { zinc sulphate } \\ \text { (colourless) }}}{\mathrm{ZnSO}_4(\mathrm{aq})}\)

Double Displacement Reactions

In a double displacement reaction, the positive and negative radicals of two reactants are exchanged, leading to the precipitation of a product.

• Double displacement reactions are very fast, and the precipitate is formed as soon as the reactants come in contact.
• Quite often, the colour of the precipitate is different from that of the reactants. The following are some common examples
• The reaction between silver nitrate and sodium chloride
• When an aqueous solution of silver nitrate is mixed with that of sodium chloride, a white precipitate of silver chloride is formed. The sodium nitrate formed remains in solution.

AgNO₃ (aq) silver nitrate (colourless) + NaCl(aq) sodium chloride (colourless) → AgCl(s) + NaNO₃ (aq)

The reaction between barium chloride and sodium sulphate:

When a solution of barium chloride is mixed with that of sodium sulphate, a white precipitate of barium sulphate is formed along with a solution of sodium chloride.

The solution initially appears white but gradually becomes colourless as the precipitate settles down

\(\underset{\substack{\text { barium chloride } \\ \text { solution } \\ \text { (colourless) }}}{\mathrm{BaCl}_2(\mathrm{aq})}+\underset{\substack{\text { sodium sulphate } \\ \text { (colution } \\ \text { (colourless) }}}{\mathrm{Na}_2 \mathrm{SO}_4(\mathrm{aq})}\) → \(\underset{\substack{\text { barium sulphate } \\ \text { precipitate } \\ \text { (white) }}}{\mathrm{BaSO}_4(\mathrm{~s})}+\underset{\substack{\text { sodium chloride } \\ \text { solution } \\ \text { (colourless) }}}{2 \mathrm{NaCl}(\mathrm{aq})}\)

Neutralisation Reactions

In a neutralisation reaction, an acid reacts with a base, forming a salt and water. The acid as well as the base lose their properties to form a salt and water, which are neither acidic nor basic, i.e., they are neutral. So, the reaction is called a neutralisation reaction.

Some examples are given below:

Acid + Base  →  Salt+ Water

HCl(aq) + NaOH(aq)- NaCl(aq) + H₂O(I)

H₂SO₄(aq) + 2KOH(aq)→ K₂SO₄(aq) + 2H₂O(I)

H₂SO₄(aq) + 2NaOH(aq)→ Na₂SO₄(aq) + 2H₂O(I)

2HCl(aq) + Ca(OH)₂(aq)→CaCl₂(aq) + 2H₂O(I)

3HCl(aq) + Al(OH)₃(aq) → AlCl₃(aq) + 3H₂O(I)

Activity:

Take about 5 ml of dilute sodium hydroxide in a conical flask and dilute it with a test tube of water. Swirl the flask to ensure thorough mixing. Add a drop of phenolphthalein solution to it.

The contents of the flask turn pink. (Phenolphthalein is an indicator which turns red in a basic solution and colourless in a neutral or acidic solution.)

Add dilute hydrochloric acid dropwise with the help of a long dropper and swirl the contents after each addition. Add the acid till the pink colour just vanishes. The solution in the flask is neutral —neither acidic nor basic —and the reaction is neutralisation.’

Chemical Reactions in Everyday Life Class 8

Oxides And Their Nature

Oxides are an important class of compounds. We know that the two simple oxides, water (H₂O) and carbon dioxide (CO₂), play important roles in our life processes, agriculture and industry. Let us discuss the preparation and the acid-base nature of oxides in general.

Preparation

They can be prepared by the following processes.

By direct combination:

An element generally forms its oxide when heated or burned in air or oxygen. The reaction is exothermic and hence continues on its own when initiated.

Nonmetals:

⇒ \(2 \mathrm{H}_2(\mathrm{~g})+\mathrm{O}_2(\mathrm{~g}) \xrightarrow{\text { ignite }} 2 \mathrm{H}_2 \mathrm{O}(\mathrm{~g})\)

⇒ \(\mathrm{C}(\mathrm{~s})+\mathrm{O}_2(\mathrm{~g}) \xrightarrow{\text { burn }} \mathrm{CO}_2(\mathrm{~g}) \\\)

⇒ \(\mathrm{S}(\mathrm{~s})+\mathrm{O}_2(\mathrm{~g}) \xrightarrow{\text { burn }} \mathrm{SO}_2(\mathrm{~g})\)

Metals:

⇒ \(2 \mathrm{Mg}(\mathrm{~s})+\mathrm{O}_2(\mathrm{~g}) \xrightarrow{\text { ignite }} 2 \mathrm{MgO}(\mathrm{~s}) \\\)

⇒ \(2 \mathrm{Ca}(\mathrm{~s})+\mathrm{O}_2(\mathrm{~g}) \xrightarrow{\text { ignite }} 2 \mathrm{CaO}(\mathrm{~s})\)

By the thermal decomposition of some compounds

The oxides of both metals and nonmetals are formed when the hydroxides, carbonates, sulphates and nitrates of metals are strongly heated

1. Hydroxides:

1. \(\mathrm{Zn}(\mathrm{OH})_2(\mathrm{~s}) \xrightarrow{\text { heat }} \mathrm{ZnO}(\mathrm{~s})+\mathrm{H}_2 \mathrm{O}(\mathrm{~g}) \\\)

2. \({\text {(bluish white) }}{\mathrm{Cu}(\mathrm{OH})_2(\mathrm{~s}) \xrightarrow{\text { heat }} \underset{\text { (black) }}{\mathrm{CuO}(\mathrm{~s})}+\mathrm{H}_2 \mathrm{O}(\mathrm{~g})}\)

2. Carbonates:

1.\(\underset{\text { (white) }}{\mathrm{CaCO}_3(\mathrm{~s})} \xrightarrow{\text { heat }} \underset{\text { (white) }}{\mathrm{CaO}(\mathrm{~s})}+\mathrm{CO}_2(\mathrm{~g}) \\\)

2.\(\underset{\text { (white) }}{\mathrm{ZnCO}_3(\mathrm{~s})} \xrightarrow{\text { heat }} \underset{\text { (white) }}{\mathrm{ZnO}(\mathrm{~s})}+\mathrm{CO}_2(\mathrm{~g}) \\\)

3.\(\underset{\text { (white) }}{\mathrm{PbCO}_3(\mathrm{~s})} \xrightarrow{\text { heat }} \underset{\text { (yellow) }}{\mathrm{PbO}(\mathrm{~s})}+\mathrm{CO}_2(\mathrm{~g}) \\\)

4.\( \mathrm{CuCO}_3(\mathrm{~s}) \xrightarrow[\text { (green) }]{\text { heat }} \underset{\text { (black) }}{\mathrm{CuO}(\mathrm{~s})}+\mathrm{CO}_2 \text { (s) }\)

Exceptions: Na₂CO₃ and K₂CO₃

3. Sulphates:

1.\(\mathrm{Fe}_2\left(\mathrm{SO}_4\right)_3(\mathrm{~s}) \xrightarrow{\text{heat}}\mathrm{Fe}_2\mathrm{O}_3(\mathrm{~s})+3 \mathrm{SO}_3(\mathrm{~g}) \\\)

2. \(\underset{\text { (white) }}{\mathrm{CuSO}_4(\mathrm{~s})} \xrightarrow{\text { heat }} \underset{\text { (black) }}{\mathrm{CuO}(\mathrm{~s})}+\mathrm{SO}_3(\mathrm{~g})\)

Exceptions: Na₂SO₄, K₂SO₄, CaSO₄ and many others

4. Nitrates:

1. \(\begin{aligned}\mathrm{Ca}\left(\mathrm{NO}_3\right)_2(\mathrm{~s}) \xrightarrow{\text { heat }} 2 \mathrm{CaO}(\mathrm{~s})+4 \mathrm{NO}_2(\mathrm{~g})&\text {(brown) }+\mathrm{O}_2(\mathrm{~g})\\\end{aligned}\)

2.\(\underset{\text { (colourless) }}{2 \mathrm{~Pb}\left(\mathrm{NO}_3\right)_2(\mathrm{~s})} \xrightarrow[\text {}]{\text { (heat) }} \underset{\text { (yellow) }}{2 \mathrm{PbO}(\mathrm{~s})}+\underset{(brown)}{4 \mathrm{NO}_2(\mathrm{~g})}+\mathrm{O}_2(\mathrm{~g})\)

Exceptions:

NaNO₃ and KNO₃, on being heated, decompose to form sodium nitrite (NaNO₂) and potassium nitrite (KNO₂), respectively, plus oxygen.

It is left to you to write the chemical equations for the reactions.

Types of Reactions: Combination, Decomposition, and Displacement

Classification

Oxides have been classified in many ways. Here we will take up a classification based on their acid-base character

Neutral oxides:

Neutral oxides, which are only four in number, are neither acidic nor basic. They are:

• Water (H₂O)
• Carbon monoxide (CO)
• Nitrous oxide (N₂O), and
• Nitric oxide (NO)

They do not change the character of an acid or a base.

Acidic oxides:

The oxides of nonmetals, in general, are acidic. Reaction with water They dissolve in water to form acids, which neutralise bases to form salts and water.

⇒ \(\mathrm{CO}_2(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \underset{\text { Carbonic acid }}{\mathrm{H}_2 \mathrm{CO}_3(\mathrm{aq})}\)

⇒  \(\mathrm{SO}_2(\mathrm{~g})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \underset{\text { Sulphurous acid }}{\mathrm{H}_2 \mathrm{SO}_3(\mathrm{aq})}\)

⇒  \(\underset{\substack{\text { sulphur } \\ \text { trioxide }}}{\mathrm{SO}_3(\mathrm{l})}+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \underset{\text { sulphuric acid }}{\mathrm{H}_2 \mathrm{SO}_4(\mathrm{aq})}\)

⇒  \(\underset{\text { dinitric pentoxide }}{\mathrm{N}_2 \mathrm{O}_5(\mathrm{~s})}+\underset{\text { }}{\text { }} \mathrm{H}_2 \mathrm{O}(\mathrm{l}) \longrightarrow \underset{\text { }}{2 \mathrm{HNO}_3(\mathrm{aq})}\)

A compound that is obtained by removing the elements of water from an acid is called the anhydride of the acid. In other words, the anhydride of an acid is the compound which adds water to form the acid. Thus, these oxides are acid anhydrides

You know that an acid turns blue litmus red. Acidic oxides turn moistened blue litmus paper red—they first add up water (moisture of the litmus paper) to form the acids. Else you can use a solution of blue litmus.

Reaction with bases: They directly react with bases to form salts.

⇒  \(\mathrm{CO}_2(\mathrm{~g})+\mathrm{Na}_2 \mathrm{O}(\mathrm{~s}) \longrightarrow \underset{\text { Sodium carbonate}}{\mathrm{Na}_2 \mathrm{CO}_3(\mathrm{~s})}\)

⇒ \(\mathrm{SO}_2(\mathrm{~g})+2 \mathrm{KOH}(\mathrm{~s}) \longrightarrow \underset{\substack{\text { potassium } \\ \text { sulphite }}}{\mathrm{K}_2 \mathrm{SO}_3(\mathrm{~s})}+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

Basic oxides

The oxides of metals are generally basic and react with acids to form salts and water. They also react with acidic oxides to form salts.

⇒ \(\mathrm{Na}_2 \mathrm{O}(\mathrm{~s})+\mathrm{H}_2 \mathrm{SO}_4(\mathrm{aq}) \longrightarrow \mathrm{Na}_2 \mathrm{SO}_4(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l}) \\\)

⇒ \(\mathrm{MgO}(\mathrm{~s})+2 \mathrm{HCl}(\mathrm{aq}) \longrightarrow \mathrm{MgCl}_2(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

⇒ \(\mathrm{CaO}(\mathrm{~s})+\mathrm{CO}_2(\mathrm{~g}) \longrightarrow \mathrm{CaCO}_3(\mathrm{~s})\)

Basic oxides which are soluble at least to some extent turn moistened red litmus paper blue. Thus, a freely soluble metal oxide like Na₂O, a less soluble oxide like CaO and an only slightly soluble oxide like MgO turn moistened red litmus paper blue, but the insoluble CuO does not. All these are bases

Amphoteric oxides

An amphoteric oxide is one which behaves like a base in the presence of an acid and like an acid in the presence of a base. These are metal oxides like Al₂O₃, ZnO and PbO. (Remember that the corresponding hydroxides are also amphoteric.)

An amphoteric oxide reacts with an acid as well as with a base, forming a salt and water.

⇒ \(\text { Base }+ \text { acid } \rightarrow \text { salt }+ \text { water }\)

⇒ \(\mathrm{ZnO}(\mathrm{~s})+\mathrm{H}_2 \mathrm{SO}_4(\mathrm{aq}) \rightarrow \underset{\text { zinc sulphate }}{\mathrm{ZnSO}_4(\mathrm{aq})}+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

⇒ \(\mathrm{PbO}(\mathrm{~s})+2 \mathrm{HNO}_3(\mathrm{l}) \rightarrow \underset{\text { lead nitrate }}{\mathrm{Pb}\left(\mathrm{NO}_3\right)_2(\mathrm{aq})}+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

⇒ \(\text { Base }+ \text { acid } \rightarrow \text { salt }+ \text { water }\)

⇒ \(2 \mathrm{NaOH}(\mathrm{aq})+\mathrm{ZnO}(\mathrm{~s}) \rightarrow \underset{\text { sodium zincate }}{\mathrm{Na}_2 \mathrm{ZnO}_2(\mathrm{aq})}+\mathrm{H}_2 \mathrm{O}(\mathrm{l})\)

⇒ \(2 \mathrm{NaOH}(\mathrm{aq})+\mathrm{PbO}(\mathrm{~s}) \rightarrow \underset{\text { sodium plumbite }}{\mathrm{Na}_2 \mathrm{PbO}_2(\mathrm{aq})+\mathrm{H}_2 \mathrm{O}(\mathrm{l})}\)

Activities:

1 . Take about 3-5 g of zinc carbonate (ZnCO₃) in a dry test tube. Heat it strongly on a flame till the white solid turns yellow. Cool the solid and it will turn white again. This colour change can be observed again and again on heating and cooling. This is the special property of zinc oxide (ZnO). On being strongly heated, ZnCO₃ decomposes into Zno (and CO₂).

Now, divide the residue of ZnO into two parts and treat them as follows.

2. Add some dilute sulphuric acid (or dilute hydrochloric acid) to one part. The solid quickly dissolves (to form the soluble salt ZnSO₄)

Add some dilute sodium hydroxide solution to the other part and shake well. The solid will dissolve (forming the soluble salt Na₂ZnO₂).

2. Heat, as above, about 3-5 g of PbCO₃. This time, the residue is the yellow PbO yellow in hot as well as cold conditions. Divide the residue into two parts and treat them as follows

Add dilute nitric acid to one part. The yellow solid dissolves to form a colourless solution of Pb(NO₃)₂. Do not use dilute HCI or H₂SO₄, because the salts PbCI₂ or PbSO₄ would be formed, which, being insoluble, would form a crust over the solid PbO, preventing it from reacting

Add some dilute NaOH solution to the other part and shake well. The solid will dissolve to form a colourless solution of sodium plumbite, Na₂PbO₂.

Chapter 5 The Language Of Chemistry

The language of chemistry is different from 3. One or two letters of the Latin name of an element in ordinary language. Instead of using words and sentences, we use symbols, formulae (formulas) and chemical equations to represent substances and the changes they undergo.

Read And Lean More Class 8 Chemistry

Berzelius laid the foundation of this language in the early nineteenth century. And this language gradually developed into its present form.

Symbols

Symbols of different elements have been derived in three ways.

NCERT Solutions for The Language of Chemistry

1. The first letter (in capital) of the English name of an element:

2. The first letter, along with one more letter of the English name of an element:

3. One or two letters of the Latin name of an element:

What Does a Symbol Represent?

The symbol of an element represents the following.

1. An element in particular:

As you know, the symbol of sodium is Na, and that of chlorine is Cl. Instead of saying that the compound common salt is made up of the elements sodium and chlorine, you can say that it is made up of Na and Cl. You can also say that Cu is red-brown, whereas Au is yellow, and that Ca is a metal, whereas Cl is a nonmetal

2. An atom of an element:

In formulae and equations, a symbol represents one atom of an element. A numerical subscript shows more than one atom in a molecule. This is explained in the next section

Formulae

The formula of a molecule gives the number(s) of atoms of the same or different elements present in the molecule. In other words, it tells us how many atoms of which elements have combined to form the molecule.

NCERT Class 8 Chemistry Chapter 5 Language of Chemistry

Formulae of Elements

When an atom of an element combines with another atom(s) of the same element, a molecule of the element is formed. The number of atoms contained in a molecule is called the atomicity of the molecule

Molecules of nitrogen, oxygen, fluorine and chlorine contain two atoms of the element, so they are represented as N₂, O₂, F₂ and Cl_2, respectively and are said to be diatomic. A common example of a triatomic gas is ozone(O₃).

An atom of a noble-gas element,

Example:

Helium (He), neon (Ne), argon (Ar), etc., are highly inactive and do not combine with other atoms.

Hence, a molecule of a noble gas contains only one atom of the element. In other words, noble gases are monoatomic. The atomicity of phosphorus is 4(P₄) and that of sulphur is 8(S₈).

The Valency of an Element

The combining capacity of an element with other elements is known as its valency.

• It is given by the number of hydrogen atoms that one atom of the element combines with or displaces from a compound.
• One atom of Cl combines with one atom of H to form one molecule of hydrogen chloride. So, the valency of Cl is 1.
• But one atom each of O, N and C combines with two, three and four atoms of H to form a molecule of water, ammonia and methane, respectively.
• Hence, the valencies of O, N and C are 2, 3 and 4, respectively. On the other hand, the anion of Na, Mg and Al displaces one, two and three atoms of H, respectively, from an acid.
• So, the valencies of Na, Mg and Al are 1, 2, and 3, respectively.
• Elements with valencies 1, 2, 3, etc., are said to be monovalent, divalent, trivalent, and so on.
• The valencies of the first twenty elements, i.e., those having atomic numbers 1 to 20, are given in the Table.

Valencies of the first twenty elements:

When elements are arranged in increasing order of atomic number, we find that their valencies are also arranged in order,

The Valency of an Element below:

• The valency gradually rises from 1 to 4 and then falls to 1 and finally to 0.
• The elements in a column have the same valence. For example, Li, Na, and K, as well as F and Cl, have the valency
• Similarly, Be, Mg and Ca, as well as O and ,S have the valency
• The elements He, Ne and Ar do not combine with other elements and are, therefore, assigned the valency 0 (zero). They are called noble-gas elements.

You will later learn that the above kind of trend in a property is known as the periodic nature or the periodicity of the property. The term periodic means appearing at certain intervals. Don’t you find that valency has a periodic nature?

Language of Chemistry NCERT Notes

Formulae of Compounds

You have learnt earlier that the formula of a binary compound (i.e., a compound formed by only two elements) is obtained by transposing the valencies. Thus, the formula of the compound formed by the elements A (valency y) and B (valency x) is A_xB_y

The numeral subscripts are divided by a common factor, if any.

For example:

1. \(\stackrel{4}{\mathrm{C}} \stackrel{2}{\mathrm{O}} \Rightarrow \mathrm{C}_2 \mathrm{O}_4 \Rightarrow \mathrm{CO}_2\)

2.  \(\stackrel{2}{\mathrm{Ca}}{\stackrel{2}{\mathrm{O}} \Rightarrow \mathrm{Ca}_2 \mathrm{O}_2 \Rightarrow \mathrm{CaO}}\)

3. \(\stackrel{3}{\mathrm{Al}} \stackrel{3}{\mathrm{~N}} \Rightarrow \mathrm{Al}_3 \mathrm{~N}_3 \Rightarrow \mathrm{AlN}\)

There are some exceptions

Example:

H₂O (hydrogen peroxide), C₂H₂ (acetylene) and C₄H₁₀ (butane).

In which the numeral subscripts are not divided by a common factor. You will learn the reason in higher classes.

Symbols and Formulae in Chemistry Class 8

Variable valency

Some elements show variable valency,

Example:

Cu (1, 2), iron (2, 3), phosphorus (3, 5) and sulphur (2, 4, 6).

The valency of such an element in a compound is often indicated in Roman numerals in the name of the compound, as shown below

1. \(\stackrel{1}{\mathrm{Cu}}{\stackrel{2}{\mathrm{O}} \Rightarrow \mathrm{Cu}_2 \mathrm{O} \text { copper(I) oxide }}\)

2. \(\stackrel{2}{\mathrm{Cu}} \stackrel{2}{\mathrm{O}} \Rightarrow \mathrm{CuO} \text { copper(II) oxide }\)

3. \(\stackrel{2}{\mathrm{Fe}} \stackrel{2}{\mathrm{O}} \Rightarrow \mathrm{FeO} \text { iron(II) oxide }\)

4. \(\stackrel{3}{\mathrm{Fe}} \stackrel{2}{\mathrm{O}} \Rightarrow \mathrm{Fe}_2 \mathrm{O}_3 \text { iron(III) oxide }\)

As an exercise, you can guess the valencies of P in PCl₃ and PCl₅, and those of S in H₂S, SO₃ and SO₃

Compounds containing radicals

You remember that a radical is a kind of entity that can be an atom with a charge on it or a group of atoms behaving as a single atom with a charge on the group.

It has a valency which is the same as its charge (without sign).

Positive radicals Examples:

Na⁺, K⁺, NH⁺₄, Mg²⁺, Ca²⁺, Cu²⁺, Fe²⁺, Fe³⁺and Al³⁺)

Combine with Negative radicals. Examples:

Cl^–, OH^– , NO^–₃ , HCO^–₃ , CO^2-₃, SO^2-₄ , O^2- , S^2- and PO^3-₄) to form compounds.

Chemical Symbols and Formulae Class 8

The formula of such a compound can again be obtained by transposing the valencies (i.e., charges without sign) of the radicals and dividing the numbers of radicals by a common factor, if any.

Some examples are given below:

Radicals carry a charge over them, but the compounds they form do not. The compounds are electrically neutral. Hence, the positive and negative radicals must be present in a compound in such numbers that the opposite charges cancel each other.

For example:

In Al₂ (SO₄)₃, the total positive charge is 2 × 3 = 6 for two Al³⁺ ions, and the total negative charge is 3 × 2 = 6 for three SO^2-₄ ions. You can understand this by using valency cards, also given in below.

Chemical Equation

A chemical change, i.e., a chemical reaction, is represented by a chemical equation. You know that in a chemical reaction, the substances we start with are called reactants, and those we end up with are called products. In an equation, we mention the reactants on the left-hand side and the products on the right-hand side, with an arrow in between.

Reactants → Products

In the previous class, you have learnt about the word equations in which we mention the reactants and products by name. Here, we will learn to write equations using symbols and formulae instead of words

Equations Using Symbols and Formulae

Such equations are quantitative and much more informative than word equations. They are written in the following three steps.

1. Writing the skeleton:

The skeleton of an equation is first written by noting the symbols and formulae of the reactants on the left side and those of the products on the right side, with an arrow in between.

For example:

Carbon, when burnt in a sufficient supply of air, forms carbon dioxide. The skeleton of the equation is written as follows.

C + O₂ → CO₂

But carbon, when burnt in an insufficient supply of air, forms carbon monoxide. And the skeleton for the equation is

2C + O₂ → 2CO

Some more examples are given below:

2. Balancing a chemical equation:

According to the law of conservation of matter, matter can neither be created nor destroyed.

• Thus, nor can be atoms.
• As no atoms are lost or gained in a chemical reaction, the number of atoms of each element on the reactant side must be equal to that on the product side.
• A chemical equation in which the number of atoms of each element on the reactant side is the same as that on the product side is called a balanced chemical equation.
• Balanced chemical equations are of great importance in chemistry.

Understanding Chemical Language Class 8

After writing the skeleton, you should proceed as follows:

Step 1:

Count the atoms of each element on both sides of the arrow. If they tally, the equation is balanced. If not, proceed to step 2.

Step 2:

Make the number of atoms of each element equal on the both sides by using proper coefficients. (If O or N appears in the equation, balancing it first makes the task easier.)

From the examples discussed below, it will be clear that some of the skeletons written above are already balanced chemical equations and some others are not.

Example 1: Is thefollowing equation balanced? C + O₂ → CO₂
Solution:

Yes, because the number of atoms of C and O is equal on both sides of it.

Example 2: Is thefollowing equation balanced? CO₂+H₂O →H₂CO₃
Solution:

Yes, because the atom counts of C, H and O are the same on both sides of the equation

Example 3: Balance the equation C + O₂ → CO
Solution:

Follow the following steps.

Step 1: 

The atom count shows that the equation is not balanced.

Step 2:

To balance O, place the coefficient 2 before the product

C + O₂ → 2CO

Step 3:

Now, the atom count is as follows.

Chemical Formulas NCERT Class 8

Step 4:

Balance C by placing the coefficient 2 before C on the LHS.

2C + O₂ → 2CO

Step 5:

The atom count is now as follows

As the atom count of the elements on both sides is the same, the balanced equation is

2C + O₂ → 2CO

Example 4: Is the following equation balanced? If it is not, balance it.
H₂ + Cl₂ → 2HCl
Solution:

Follow the following steps.

Step 1:

The atom count shows that the equation is not balanced.

Step 2:

Place the coefficient 2 before the product

H₂ + Cl₂ → 2HCl

Step 3:

The number of atoms on the two sides is now as follows.

The numbers tally.

Therefore, the balanced chemical equation for the given reaction is

H₂ + Cl₂ → 2HCl

Example 5: Balance the following equation. H₂ +O₂ → H₂O
Solution:

Follow the following steps

Step 1:

Count the number of atoms of each element on both sides.

The atom count shows that the equation is not balanced.

Step 2:

To balance the number of oxygen atoms on both sides, place the coefficient 2 before H₂O.

H₂ +O₂ → 2H₂O

Step 3:

Again, count the atoms ofeach element on both sides.

The atom count shows that the equation is not balanced.

Step 4:

To balance the number of oxygen atoms on both sides, place the coefficient 2 before H₂O.

2H₂ +O₂ → 2H₂O

Step 5:

Tally the number of atoms of each element on both sides.

The numbers tally. Therefore, the balanced chemical equation for the reaction is

2H₂ +O₂ → 2H₂O

Example 6: The numbers tally. Therefore, the balanced chemical equation for the reaction is.
Solution:

Let us now see if we can balance a chemical equation without writing the steps so elaborately. The reactants and the product may be written as follows.

Mg +O₂ → MgO

Balance O: Mg + O₂ → 2MgO

Balance Mg: 2Mg + O₂ → 2MgO

Therefore, the balanced chemical equation for the reaction is

2Mg + O₂ → 2MgO

Molecules and Their Representations Class 8

Example 7: On being strongly heated, potassium chlorate (KClO₃ ) gives potassium chloride and oxygen. Write a balanced chemical equation for the reaction
Solution:

The reactant and the products can be written as follows.

KCIO₃→ KCI+O₂

Balance O:

2KCIO₃→ KCI + 3O₂

Balance K and Cl:

2KClO₃ → 2KCl + 3O₂

Hence, the balanced chemical equation is

2KClO₃ → 2KCl + 3O₂

Example: 8 Balance the equation

N₂ +H₂ →  NH₃

Solution:

Balance N: N₂ + H₂ → 2 NH₃

Balance H: N₂ + 3H₂→2NH₃

Thus, the balanced equation is

N₂ + 3H₂ → 2NH₃

Atoms and Molecules in NCERT Class 8

Example 9: Is the following equation balanced? If not, balance it
Na₂CO₃ + HCl → NaCl + H₂O + CO₂
Solution:

The equation is not balanced as the atom counts of Na, H and Cl on the two sides do not tally.

Balance Na: Na₂CO₃ + HCl→ 2NaCl + H₂O + C₂O

Balance H and Cl: Na₂CO₃ + 2HCl → 2NaCl + H₂O + CO₂

Hence, the balanced chemical equation is

Na₂CO₃+ 2HCl → 2NaCl + H₂O+ CO₂

Making a Chemical Equation More Informative

A balanced chemical equation tells us how many atoms and molecules of which reactants give how many atoms of which products. Had you known the masses of the atoms of different elements, you could have calculated the quantities of these substances. Keeping such calculations aside for higher classes, let us learn here how to make a chemical equation more informative.

Mentioning the conditions and catalysts:

The conditions under which a reaction takes place and the catalysts needed, if any, are mentioned at the arrow —generally, the conditions above and the catalyst below the arrow.

• You have learnt earlier that
• A catalyst is a substance that generally speeds up a reaction without itself undergoing any change.
• Sometimes, the symbol or formula is mentioned in square brackets at the arrow to indicate a catalyst.

Mentioning the states of the reactants and products:

The state of each reactant and product is mentioned along with it, using the following symbols:

(s) for the solid state

(l) for the liquid state

(g) for the gaseous state, and

(aq) for an aqueous solution

When these symbols are used, a downward arrow (↓) for a precipitate and an upward arrow ( ↑ ) for a gas on the product side are not used. Instead, we use (s) for (↓) and (g) for ( ↑ ).

Mentioning the name and colour of a substance, if needed:

The name and/or colour of a substance is mentioned, if needed, below the symbol or formula of the substance in the equation—the name outside and the colour within brackets

Examples

The following examples will show how informative a chemical equation becomes when we include the points mentioned above.

1. Hydrogen reacts with chlorine in the presence of light to form hydrogen chloride gas.

2. When ignited, a mixture of hydrogen and oxygen (in the volume ratio 2:1) explodes to form water vapour

3. Solid potassium chlorate, when heated at 200-300 °C in the presence of manganese dioxide as a catalyst, gives oxygen, leaving behind a residue of potassium chloride.

4. Carbon dioxide turns limewater milky.

(Lime water) Ca(OH)₂(aq) + CO₂(g) → CaCO₃ (s) (Milky)+ H₂O (I)

5. A burning piece of magnesium continues to burn in a jar of carbon dioxide, forming white, smoky magnesium oxide with some black carbon particles.

Chapter 9 Carbon

Present in every living being, carbon is a very important element. It has many uses. The food we eat has compounds of carbon. Coal and hydrocarbons are widely used as fuels. Carbon compounds are also used in medicines. The clothes we wear have compounds of carbon. In the form of a diamond, carbon is used as a gemstone.

In the form of graphite, carbon finds a wide application in the industry. And you will learn in higher classes that in the form of carbon nanotubes, it plays a great role in nanotechnology.

Read And Lean More Class 8 Chemistry

In one form or another, carbon forms a significant part of the mineral world.

Carbon Occurrence

In the free or combined state, carbon is widely distributed on earth.

In the Free State

Carbon exists in the free state in coal, diamond and graphite.

1. Coal:

Coal is a decomposition product of plants buried millions of years ago due to some natural phenomena. Plants contain carbon compounds, slowly converted their buried remains into carbon. The conversion of a carbon compound into carbon is called carbonisation.

2. Diamond and graphite:

Diamond and graphite are the crystalline forms of carbon found in nature. Graphite is more abundant than diamond

In the Combined State

Carbon is widely distributed in the combined state.

1. Carbon dioxide:

Air contains about 0.03% carbon dioxide (CO₂).

2. Living organisms:

All living organisms—plants and animals— have carbon compounds. Hence, everything we eat, which is derived from plants and animals, contains carbon compounds. The essential ingredients of food—carbohydrates, proteins, fats and vitamins—are compounds of carbon.

3. Minerals:

All carbonate minerals contain carbon. For example, limestone, calcite and marble are calcium carbonate (CaCO₃), and dolomite is a mixed carbonate of magnesium and calcium (MgCO₃CaCO₃).

4. Natural gas and petroleum

Natural gas and petroleum contain mainly hydrocarbons, i.e., compounds which have only carbon and hydrogen. Natural gas is mostly methane (CH₄), and petroleum is a mixture of various hydrocarbons containing a large number of carbon atoms.

Some common compounds which have carbon:

Common Compounds Which Have Carbon

Compounds containing carbon are of two types

1. Organic
2. Inorganic

All carbon-containing compounds, except carbon monoxide, carbon dioxide, carbonates and hydrogencarbonates, are called organic compounds.

And all noncarbon compounds, along with carbon monoxide, carbon dioxide, carbonates and hydrogencarbonates, are called inorganic compounds

Some examples of organic and inorganic compounds are given in Table

Carbon Allotropy

Before we take up allotropy, let us learn about crystalline and amorphous solids.

Crystalline and Amorphous Solids

Solids are divided into two classes:

1. Crystalline or true solids
2. Amorphous solids or pseudosolids.

1. Characteristics of crystalline solids:

1. The particles constituting a crystalline solid are arranged in an ordered manner in three dimensions.

2. When crystalline solids are broken or cut with a sharp knife, we get pieces with sharp edges and plane faces.

2.  Characteristics of amorphous solids:

1. The particles constituting an amorphous solid are not arranged in an ordered manner.

2. When amorphous solids are broken or cut with a sharp knife, we get pieces with curved faces.

What is Allotropy?

The phenomenon of some elements existing in different forms is called allotropy

The term allotropy has been derived from the Greek words alios (meaning ‘other’) and tropos (meaning ‘form’).

The different forms of an element are known as allotropes or allotropic modifications. The allotropes of an element are chemically the same but different from each other in structure, atomicity or both.

Carbon, oxygen, phosphorus and sulphur are some common elements that show allotropy. Diamond, graphite, the fullerenes etc., are allotropes of carbon. Dioxygen (O₂) and ozone (O₃) are allotropes of oxygen. You will learn about the allotropy of other elements in higher classes.

The allotropes of an element differ in physical properties. And though they are chemically the same, they differ in some chemical properties too.

For example:

Graphite is a good conductor of heat and electricity, whereas diamond is not. And, though both of them are chemically carbon, graphite burns in air to give carbon dioxide at 700°C, whereas diamond does so at 900 °C. Again, ozone (O₃) absorbs UV rays, whereas dioxygen (02) does not. And though both of them are oxygen, ozone is a much stronger oxidising agent than dioxygen.

Allotropy of Carbon

Carbon exists in crystalline as well as amorphous forms.

• Diamond, graphite and the fullerenes are the crystalline forms.
• And charcoals, lampblack, coke and gas carbon are the amorphous forms.
• The amorphous forms of carbon are found to contain extremely small crystals of graphite, and hence they are also called microcrystalline forms

The crystalline forms of carbon:

In its crystalline forms, a carbon atom is bonded to three or four other carbon atoms. These atoms, in turn, are bonded to other carbon atoms. In the different crystalline forms of carbon such as diamond and graphite, the atoms are arranged in a different manner.

1. Diamond:

Diamond is the costliest gemstone and the hardest natural substance known. It is so hard that it can only be cut by another diamond.

• Diamonds are formed at the high temperature and pressure that exist over
• 100 km below the Earth’s surface. They are brought to the surface along with the carrier rock —kimberlite—by volcanic action.
• They form only one part in over 15,000,000 (i.e., 15 million) parts of the rock.
• Diamonds are found mainly in Australia, Botswana and South Africa
• Diamond is artificially produced by heating graphite at a high temperature (say, 5000 °C) and pressure (say, 100,000 atmospheres).
• Diamond is generally colourless. However, the coloured varieties —yellow, brown, red, green, blue, grey or even black—are also found in nature.

The colour arises due to metallic impurities. The less costly varieties—grey and black —have no use as gemstones, and are used for cutting glass and drilling rocks

Diamond Properties:

1. Diamond is the hardest solid known.

2. It has a density of 3.51 g/cm3.

3. A properly cut diamond bends back a great percentage of the light falling on it. That is why it sparkles.The ability of a substance to bend light depends upon a property called refractive index. Diamond has a very high refractive index.

4. It has a very high melting point—3930 °C.

5. It is a bad conductor of electricity, i.e., it does not allow electric current to pass through it.

6. When ignited, it burns in air at 900 °C and in oxygen at 700 °C to give carbon dioxide

Diamond Structure:

In diamond, each carbon atom is bonded to four other carbon atoms. As shown in, the central carbon atom is bonded to four carbon atoms placed at the vertices of a tetrahedron. The other carbon atoms, in turn, are also tetrahedrally bonded to four carbon atoms each.

This kind of bonding results in the formation of a giant molecule, in which the carbon atoms are packed closely. The fact that the carbon atoms are so closely packed in diamond accounts for its high density and hardness. The strong chemical bonding between the atoms gives diamond its high melting point.

Diamond:

2. Graphite

Graphite is a black, opaque solid, found in large deposits in many countries like China, South Korea and India It is artificially prepared by strongly heating coke with silica in an electric furnace.

Graphite Properties:

• Graphite has a density of 2.2 g/cm3.
• Unlike diamond, it is very soft.
• Graphite melts at 3700°C.
•  It is a good conductor of heat andelectricity.
• It bums in air at 700 °C to give carbon dioxide

Graphite Structure:

Graphite contains layers of hexagonal rings of carbon atoms, joined together.

• Each carbon atom is shared by three rings.
• These rings occur in different planes, arranged parallel to each other.
• Each layer is held by the adjacent layer with weak forces.
• So, the adjacent carbon layers can slide over one another.
• As you can see, graphite and diamond have different structures. This accounts for the difference in their properties.

You will learn more about this in higher classes.

Graphite Uses:

•  Graphite electrodes are widely used.
• It is used as a solid lubricant for machines that work at high temperatures,
  • Example: The internal combustion engine of a motor vehicle.
• Graphite leaves a mark on paper. The ‘lead’ of a pencil is graphite mixed with clay. Being very soft, graphite has to be mixed with clay. The greater the proportion of graphite, the softer the pencil. The term graphite is derived from the Greek word grapho, meaning ‘I write’.
•  It is used for making crucibles for casting metals.
• A mixture of graphite and linseed oil is used for painting things made of iron
• It is used in nuclear reactors.

Fullerenes and carbon nanotubes

• Fullerenes and carbon nanotubes are crystalline forms of carbon.
• Nanotubes have played a great role in the development of an altogether new technology known as nanotechnology.
• You will leam about these allotropes in higher classes

The amorphous forms of carbon:

Unlike the crystalline form, the amorphous form of a substance contains loosely held particles.

• These particles easily separate and make available a large surface area.
• When a piece of a substance breaks into two, two new surfaces are created . If the pieces keep on breaking, newer surfaces appear. So, the more powdery a substance, the larger is the surface area.
• Because of its larger surface area, the amorphous form of a substance is generally more active than the crystalline form

The charcoals:

Charcoals are prepared by a process known as destructive distillation or pyrolysis. In destructive distillation, a substance is heated in the absence of air with a view to breaking larger molecules into smaller ones. During the process, certain substances distil out, and may be collected.

Wood charcoal:

Wood charcoal is prepared by the destructive distillation of wood. A mixture of gases and vapours evolves, and charcoal is left as a residue.

The mixture of gases (CO₂, CO, CH₄ and H₂) is combustible, and is known as wood gas. On being condensed, the vapours separate into a tar and a liquid. The liquid, called pyroligneous acid, contains some organic compounds.

The destructive distillation of wood can be carried out on a small scale in the laboratory.

Activity:

You can make wood charcoal at home, too. Put some wood shavings in a can, and cover it with a lid.

• Make a hole in the lid, and heat the can on a stove.
• Hold a lighted match to the mixture of gases emerging from the hole. It should burn with a steady flame
• Place a can full of ice near the hole.
• Substances in the mixture that have a low melting point will condense around this can. Turn off the stove when the gases stop evolving. Examine the cans after they have cooled.
• The wood shavings would have converted to charcoal. And there will be tar on the surface of the second can as well as on the inside surfaces of the first.

Being a form of carbon, wood charcoal shows the general properties of carbon, which we will study soon.

Activated charcoal:

Activated charcoal is prepared by heating wood charcoal at 900°C in a limited supply of air or steam.

• Any tar in the wood charcoal is removed, and the surface area of the charcoal increases greatly.
• 1 kg of activated charcoal in powder form has a surface area of 1 km².
• Hence, activated charcoal is much more active than simple wood charcoal.

Bone, or animal, charcoal:

Animal bones are first boiled with water to remove fatty substances and then subjected to destructive distillation in a retort.

The solid product in the retort is washed thoroughly with hydrochloric acid. The residual substance is bone charcoal.

Sugar charcoal:

Sugar charcoal is the purest form of carbon. It is prepared by the destructive distillation of cane sugar or by the dehydration of sugar with concentrated sulphuric acid

⇒ \(\begin{aligned}
&\mathrm{C}_{12} \mathrm{H}_{22} \mathrm{O}_{11} \rightarrow 12 \mathrm{C}+11 \mathrm{H}_2 \mathrm{O}\\
&\text { cane sugar }
\end{aligned}\)

Lampblack (soot):

When substances like oil and wax burn, soot is given out.

Activity:

You can prepare lampblack at home by burning mustard oil with the help of a wick and collecting the soot on a dish. The soot is used for preparing kajal and printer’s ink.

Coke:

Coke is obtained when coal is heated strongly in the absence of air. Coke is more porous and, therefore, more active than coal.

Gas carbon:

Gas Carbon deposits on the walls of a retort when a hydrocarbon is heated in it in the absence of air. Carbon is a good conductor of electricity and is, therefore, used as an electrode.

Some Useful Properties Of Carbon

We have already discussed some properties and uses of the different forms of carbon. Let us talk about a few more of its properties and uses.

Adsorption—A Physical Property

You have learnt that in adsorption, a thin layer of a substance is formed on the surface of another substance.

• A substance on the surface of which adsorption takes place is called an adsorbent.
• Adsorption is a surface phenomenon in which a thin layer of the adsorbed substance is formed only at the surface of the adsorbent.
  • For example: Moisture is adsorbed at any solid surface that is exposed to moist air. The formation of a thin film of oil over the surface of water is another example of adsorption.
• Being a surface phenomenon, adsorption is dependent on surface area.
• It is found that the larger the surface area of the adsorbent, the greater is the adsorption.

Adsorption by charcoals

As charcoals have a large surface area in powder form, they are good adsorbents.

The following uses of charcoals are based on this property:

• Wood charcoal is a good adsorbent of gases. It is, therefore, used in gas masks to remove poisonous gases. An active form of charcoal prepared from coconut shells is especially suitable for gas masks.
•  Bone charcoal (or animal charcoal) is used to remove the brown impurities from unrefined sugar.
• Many impurities of water are removed by filtration through charcoal. This is done in municipal water-treatment plants as well as in domestic UV purifiers.
• Activated coconut charcoal is used for separating a mixture of noble gases (helium, neon, argon, krypton and xenon). The different noble gases are adsorbed by the charcoal at different temperatures.
• Activated charcoal facilitates certain chemical reactions and is, therefore, used as a catalyst. For example, chlorine adsorbed on activated charcoal readily combines with hydrogen in the dark.

The reaction between chlorine and hydrogen in the dark is otherwise extremely slow

Chemical Properties and Their Uses

1. Reaction with oxygen or air:

On being lit, carbon burns in an excess of oxygen or air to form carbon dioxide

C + O₂ → CO₂+ heat

In an insufficient supply of air, carbon monoxide is formed.

2C + O₂ → 2CO + heat

Carbon monoxide also burns in air to form carbon dioxide

2CO + O₂ → 2CO₂ + heat

The heat produced in these reactions makes carbon a good fuel.

2. Reducing properties:

Carbon has a great affinity for oxygen. So, it combines with the oxygen present in many compounds, and thus acts as a reducing agent.

Reduction of metal oxides. When heated with coke or charcoal, the oxides of metals below aluminium in the activity series (e.g., zinc, iron, tin, lead and copper) are reduced to the corresponding metals

1. \(\underset{\text { zinc(II) oxide }}{\mathrm{ZnO}}+\mathrm{C} \xrightarrow{\text { heat }} \underset{\text { zinc }}{\mathrm{Zn}}+\mathrm{CO} \uparrow\)

2. \(\underset{\text { iron(III) oxide }}{\mathrm{Fe}_2 \mathrm{O}_3}+3 \mathrm{C} \xrightarrow{\text { heat }} \underset{\text { iron }}{2 \mathrm{Fe}}+3 \mathrm{CO} \uparrow\)

3. \(\underset{\text { tinc(I) oxxide }}{\mathrm{SnO}_2}+2 \mathrm{C} \xrightarrow[\text { heat }]{\mathrm{Sn}}+2 \mathrm{CO} \uparrow\)

4. \(\underset{\text { copper(II) oxide }}{\mathrm{CuO}}+\mathrm{C} \xrightarrow{\text { heat }} \underset{\text { copper }}{\mathrm{Cu}}+\mathrm{CO} \uparrow\)

This kind of reduction, called carbon reduction, is of great importance in metallurgy, i.e., the science of extracting metals from their ores and modifying them for use.

Reduction of water:

When steam is passed over red-hot coke, a mixture of carbon monoxide and hydrogen is formed. This mixture is called water gas

⇒ \(\underset{\text { lead(II) oxide }}{\mathrm{PbO}}+\mathrm{C} \xrightarrow{\text { heat }} \underset{\text { lead }}{\mathrm{Pb}}+\mathrm{CO} \uparrow\)

⇒  \(\underset{\text { copper(II) oxide }}{\mathrm{CuO}}+\mathrm{C} \xrightarrow{\text { heat }} \underset{\text { copper }}{\mathrm{Cu}}+\mathrm{CO} \uparrow\)

Water gas is of great industrial importance

Carbon Dioxide (CO₂)

Carbon dioxide is present in the air (-0.03%), and its amount is greater in cities than in the countryside.

Carbon dioxide is used by plants for photosynthesis and given out by plants and animals during respiration. It is present in the form of carbonates in minerals like limestone or marble (CaCO₃), dolomite (MgCO₃.CaCO₃), calamine (ZnCO₃), etc.

Obtaining CO₂

Carbon dioxide is formed in the following reactions

1. Burning of C and C-based fuels:

CO₂ is formed when C is burnt in an excess of air or oxygen

⇒ \(\mathrm{C}+\underset{\text { (excess) }}{\mathrm{O}_2} \xrightarrow{\text { burn }} \mathrm{CO}_2\)

In an insufficient supply of air, carbon monoxide is formed, which is a poisonous gas

⇒ \(2 \mathrm{C}+\mathrm{O}_2 \xrightarrow{\text { burn }} \mathrm{CO}\)

Carbon-based fuels like CNG (compressed natural gas, which is mainly methane) and LPG (liquefied petroleum gas, which is mainly butane) burn smoothly to form CO₂ and H₂O (vapour).

⇒ \(\underset{\substack{\text { methane } \\(\mathrm{CNG})}}{\mathrm{CH}_4}+2 \mathrm{O}_2 \xrightarrow{\text { burn }} \mathrm{CO}_2+2 \mathrm{H}_2 \mathrm{O}\)

⇒ \(\underset{\substack{\text { butane } \\ \text { (LPG) }}}{2 \mathrm{C}_4 \mathrm{H}_{10}}+13 \mathrm{O}_2 \xrightarrow{\text { burn }} 8 \mathrm{CO}_2+10 \mathrm{H}_2 \mathrm{O}\)

Fuels like petrol, kerosene and diesel are mixtures of hydrocarbons containing larger numbers of C atoms. They also burn to give CO₂ and H₂O

2. Thermal decomposition of carbonates:

The thermal decomposition of metal carbonates (except a few like Na₂CO₃ and K₂CO₃) gives CO₂

1. \(\underset{\begin{array}{c}
\text { magnesium } \\
\text { carbonate }
\end{array}}{\mathrm{MgCO}_3} \xrightarrow{\text { heat }} \underset{\substack{\text { magnenium } \\
\text { oxide }}}{\mathrm{MgO}}+\mathrm{CO}_2\)

2. \(\underset{\text { limestone }}{\mathrm{CaCCO}_3} \xrightarrow{\text { heat }} \underset{\text { quicklime }}{\mathrm{CaO}}+\mathrm{CO}_2\)

3. Action of an acid on a carbonate or a hydrogencarbonate:

When a carbonate or a hydrogencarbonate is treated with an acid, CO₂ is evolved with effervescence

1. \(\underset{\substack{\text { sodium } \\ \text { carbonate }}}{\mathrm{Na}_2 \mathrm{CO}_3}+\underset{\substack{\text { sulphuric } \\ \text { acid }}}{\mathrm{H}_2 \mathrm{SO}_4} \rightarrow \underset{\substack{\text { sodium } \\ \text { sulphate }}}{\mathrm{Na}_2 \mathrm{SO}_4}+\mathrm{CO}_2 \uparrow+\mathrm{H}_2 \mathrm{O}\)

2. \(\underset{\substack{\text { sodium } \\ \text { ndrogencarbonate }}}{\mathrm{NaHCO}_3}+\underset{\substack{\text { hydrochloric } \\ \text { acid }}}{\mathrm{HCl}} \underset{\mathrm{NaCl}}{ }+\mathrm{CO}_2 \uparrow\)

4. Fermentation of a sugar:

CO₂ is evolved during the fermentation of a sugar (in the presence of yeast), a process in which alcohol is formed. (This is how ethanol —an alcohol—is manufactured from the molasses obtained from the sugar industry.)

⇒ \(\underset{\text { (from the molasses) }}{\mathrm{C}_6 \mathrm{H}_{12} \mathrm{O}_6} \xrightarrow{\text { yeast }} \underset{\text { ethanol }}{2 \mathrm{C}_2 \mathrm{H}_5 \mathrm{OH}}+2 \mathrm{CO}_2\)

Laboratory preparation

Principle CO₂ is prepared in the laboratory by the action of dilute hydrochloric acid on marble (CaCO₃) chips.

⇒ \(\underset{\substack{\text { calcium carbonate marble } \\ \text { } \\ \text { }}}{\mathrm{CaCO}_3}+\underset{\substack{\text { hydrochloric acid (dilute) } \\ \text { } \\ \text { }}}{2 \mathrm{HCl}} \rightarrow \underset{\substack{\text { calcium chloride} \\ \text { }}}{\mathrm{CaCl}_2}+\mathrm{CO}_2 \mathrm{}+\mathrm{H}_2 \mathrm{O}\)

As the gas is heavier than air (~1.6 times), it is collected by the upward displacement of air.

Procedure:

Some marble chips are placed in a conical flask and covered by water. The flask is fitted with a thistle funnel and a delivery tube bent at 90° .

Dilute HCl is poured through the thistle funnel into the flask. A brisk reaction takes place. The gas evolved displaces the air inside the flask and the delivery tube first, and then collects in the gas jar by displacing the air upwards.

To test whether the jar is filled with CO₂, a lighted matchstick is brought near its mouth from time to time. When the flame gets extinguished, we infer that the jar is filled with CO₂. The delivery tube is taken out and the jar is closed by putting the lid in place.

(You could use sodium carbonate in place of marble chips and then dilute H₂SO₄ in place of dilute HCI. The reaction with marble is, however, smoother.)

Could we use H₂SO₄ instead of HCI with marble?

No, because calcium sulphate (CaSO₄) would be formed then. And the salt, being insoluble, would deposit on the chips , preventing them from coming in contact with the acid.

⇒ \(\mathrm{CaCO}_3+\mathrm{H}_2 \mathrm{SO}_4 \rightarrow \underset{\text { (insoluble) }}{\mathrm{CaSO}_4}+\mathrm{CO}_2 \uparrow+\mathrm{H}_2 \mathrm{O}\)

How about using H₂SO₄ with Na₂CO₃?

This is all right because the salt Na₂SO₄ formed is soluble.

Does the action of dilute HCI on marble chips give pure CO₂ ?

No, the gas is contaminated with HCI as the latter gets volatilised by the evolving CO₂. The gas can be freed from HCI vapours by passing it through a small amount of water before collection. Water dissolves its own volume of CO_2, but large volumes of HCl.

Properties of CO₂

Na₂CO₃ CO₂ has the following properties

Physical properties:

•  It is a colourless, odourless gas—1.67 times heavier than air
• At atmosphere pressure, the gas directly solidifies at-78.5 °C. The solid is called dry ice as it sublimes at this temperature (i.e., vaporises without turning into liquid).
• Under ordinary conditions, water dissolves its own volume of the gas. But under high pressures, the gas is highly soluble in water —the property that is used in making soda water or a fizzy drink. The dissolved CO₂ bubbles out vigorously when the pressure is released.

Chemical properties:

1. Combustion CO₂ is neither combustible nor a supporter of combustion. So, it is used in extinguishing a fire. Being heavier than air, the gas displaces air from the vicinity, and the fire gets extinguished. You can easily understand this by doing the following activity.

Activity:

Take a spoonful of baking powder in glass A and add some vinegarto it.

• CO₂ is evolved with effervescence (1).
• Let the effervescence subside (2).
• Hold glass A almost horizontally above glass B for a short while, taking care that no liquid flows from A to B (3) .Now, hold glass B in a ‘pouring mode’ over a lighted candle kept in a bowl.
• The flame is extinguished (4).

This shows that CO₂ is heavier than air. And so it can be ‘poured’ from one glass to another and then over the flame, which gets extinguished.

2. Reaction with active metals:

An active metal like Na, K or Mg abstracts oxygen from CO₂ (setting C free) when burnt in the gas.

Experiment:

• Take a gas jar full of CO₂ and introduce a burning piece of magnesium into it.
• The metal continues to bum in the gas. As a result, white smoky scales of magnesium oxide (MgO) are deposited on the inner walls of the jar.

In the reaction, some black carbon particles are also formed, which can be seen more clearly if the smoky scales of MgO are dissolved in dilute HCl.

3. Action on litmus:

The aqueous solution of the gas is weakly acidic and turns blue litmus wine-red. The acidic nature of the gas is generally tested by placing a moist blue litmus paper in the gas. An aqueous solution of C02 contains carbonic acid

⇒ \(\mathrm{CO}_2+\mathrm{H}_2 \mathrm{O} \rightleftharpoons \underset{\text { carbonic acid }}{\mathrm{H}_2 \mathrm{CO}_3}\)

4. Reaction with metal oxides:

Metal oxides are generally basic in nature, and CO₂ is acidic. So, CO₂ slowly reacts with metal oxides to form the metal carbonates, which are salts.

1. \(\underset{\substack{\text { sodium } \\ \text { oxide }}}{\mathrm{Na}_2 \mathrm{O}}+\mathrm{CO}_2 \rightarrow \underset{\substack{\text { sodium } \\ \text { carbonate }}}{\mathrm{Na}_2 \mathrm{CO}_3}\)

2. \(\underset{\substack{\text { magnesium } \\ \text { oxide }}}{\mathrm{MgO}}+\mathrm{CO}_2 \longrightarrow \underset{\substack{\text { magnesium } \\ \text { carbonate }}}{\mathrm{MgCO}_3}\)

3. \(\underset{\substack{\text { calcium } \\ \text { carbonate }}}{\mathrm{CaOClcium}}+\mathrm{CO}_2 \rightarrow \underset{\text { oxide }}{\mathrm{CaCO}_3}\)

5. Reaction with limewater:

Limewater is a dilute solution of calcium hydroxide. The reaction of CO₂ with limewater may be studied in three parts.

1. The clear limewater turns milky when CO₂ is passed through it. This is because the insoluble, white substance calcium carbonate is formed.

⇒ \(\underset{\text { limewater }}{\mathrm{Ca}(\mathrm{OH})_2}+\mathrm{CO}_2 \longrightarrow \underset{\substack{\text { calcium } \\ \text { carbonate } \\ \text { (causing milkiness) }}}{\mathrm{CaCO}_3 \downarrow}+\mathrm{H}_2 \mathrm{O}\)

2. The milkiness disappears when an excess of CO₂ is passed through the liquid. This is because the soluble, colourless compound calcium hydrogencarbonate is formed.

⇒ \(\mathrm{CaCO}_3+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2 \rightarrow \underset{\substack{\text { calcium hydrogencarbonate } \\ \text { (soluble) }}}{\mathrm{Ca}\left(\mathrm{HCO}_3\right)_2}\)

3. The milkiness reappears when the above solution is boiled. This is because the hydrogencarbonate, on being heated, decomposes back to give the carbonate, causing the milkiness.

⇒ \(\mathrm{Ca}\left(\mathrm{HCO}_3\right)_2 \xrightarrow{\text { heat }} \mathrm{CaCO}_3 \downarrow+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2 \dagger\)

Carbon Dioxide and the Environment

In low concentrations in the air, CO₂ is essential for life but in high concentrations, it is a cause of great concern. Let us see how.

1. Photosynthesis:

We know that green plants use C02 for photosynthesis and manufacture their food glucose in the process

Thus, life seems to have originated on this planet from C02 and moisture.

2. The greenhouse effect:

A greenhouse is a glasshouse inside which we can grow plants. During the day, the rays enter the glasshouse and keep the plants warm. But the glass traps a part of the heat of the rays and keeps on radiating it back, even during the night, keeping the plants warm

The carbon dioxide present in the Earth’s atmosphere plays the same role as the glass in a greenhouse. The CO₂ traps the heat of the rays and keeps radiating it back so that the warmth of the Earth is retained. The rays heat the Earth directly, but a large portion of the rays are reflected back. So, without the warmth provided by the C02 of the atmosphere, the Earth would have been much colder during the nights.

A gas that traps heat in the environment and keeps the surroundings warm is known as a greenhouse gas and the whole effect as the greenhouse effect. Thus, CO₂ is a greenhouse gas and other such gases in our environment are mainly methane (emitted by cattle dung) and flurocarbons (used as coolants in fridges and air conditioners).

Global warming

What will happen if the concentration of CO₂ increases in our environment?

• If this happens
• The average temperature of the Earth will increase
• The polar ice caps and the glaciers will melt,
• The sea level will be raised, submerging several islands and coastal cities, and
• There will be drastic climatic changes.

All this will happen due to a rise in Earth’s average temperature, i.e., due to global warming.

Afforestation can bring down the dangers of global warming by using up the increased CO₂ in photosynthesis. But the opposite activity, i.e., deforestation, is on the increase due to increased population.

With increasing deforestation as well as industrialisation, the proportion of CO₂ in our environment has increased a lot. And we are already facing the dangers of global warming. The world community is making all-out efforts to bring the proportion of CO₂ down to permissible levels.

3. Action on natural water

Natural water is slightly acidic to slightly alkaline (ph 6.5-8.5). pH is a measure of the acidic or alkaline nature of a dilute solution. It is measured with the help of a pH-meter or a pH paper.

Pure water is neutral, i.e., neither acidic nor alkaline and has pH 7.0. Acidic solutions have pH < 7, and alkaline solutions, pH > 7. You know that, on dissolving in water, CO₂ forms the weak acid H₂CO₃.

So, the gas tends to bring down the pH of water that is open to the atmosphere. For drinking purposes, slightly acidic water is better than alkaline water. Acidic water (pH 6.5) is soft and palatable but alkaline water (pH 8) is hard and unpalatable. Also, the pH inside our digestive system is acidic.

On the other hand, marine organisms thrive better in alkaline water than in acidic water. And it has been found that the increasing proportion of dissolved CO₂ is lowering the pH of seawater. This is posing a threat to marine life

Uses of CO₂

1. CO₂ is used in the industry for the manufacture of

• Metal carbonates and hydrogencarbonates,
• Example: Soda ash (Na₂ CO₃), washing soda (Na₂ CO₃. 10H₂ O), potassium and baking soda, i.e., sodium hydrogencarbonate (NaHCO₃);
• Urea, CO(NH₂ )₂ ; and
• Ethanol, C₂ H₅ OH.

2. It is used in fire extinguishers.

3. It is extensively used for making soda water and fizzy drinks

4. In welding, CO₂ is used to prevent the oxidation of the metal by air.

5. In the form of dry ice, CO₂ is used as a coolant and for depicting smoke in plays, movies, and so on.

How a fire extinguisher works

Common fire extinguishers produce carbon dioxide by the action of sulphuric acid on a solution of sodium carbonate or sodium hydrogencarbonate.

⇒ \(\mathrm{Na}_2 \mathrm{CO}_3+\mathrm{H}_2 \mathrm{SO}_4 \rightarrow \mathrm{Na}_2 \mathrm{SO}_4+\mathrm{H}_2 \mathrm{O}+\mathrm{CO}_2\)

⇒ \(2 \mathrm{NaHCO}_3+\mathrm{H}_2 \mathrm{SO}_4 \rightarrow \mathrm{Na}_2 \mathrm{SO}_4+\underbrace{2 \mathrm{H}_2 \mathrm{O}+2 \mathrm{CO}_2}_{\text {gushes out }}\)

A solution of sodium carbonate or sodium hydrogencarbonate is placed in a fire extinguisher. A sealed bottle containing sulphuric acid is also placed there. In case of fire, the acid bottle is broken by striking the plunger against a hard surface.

The acid reacts with the sodium carbonate or sodium hydrogencarbonate, and carbon dioxide is formed. A mixture of water and carbon dioxide gushes out, which is directed towards the burning object. Carbon dioxide, being heavier than air, surrounds the burning object and cuts off the supply of air. As a result, the fire is put out

Carbon Monoxide

Carbon monoxide (CO) is a common product of the combustion of carbon-based fuels. Being a poisonous gas, it pollutes air. But, at the same time, the gas is used for many industrial purposes too.

So, we will look into both these aspects of the gas here

Poisonous Nature of CO:

Let us see how the gas affects us and how we can get rid of its effects.

Concentration of CO:

The concentration of a substance, expected to be present in very small quantities in a mixture, is often expressed in parts per million (ppm). This tells us the number of parts of a substance present in 1 million (1,000,000) parts of the mixture.

The concentration of CO in air is also expressed in ppm.

For example:

• A CO level of 100 ppm in a congested city indicates that 100 litres of CO is present in1 million litres of air in that city.
• The CO level in cities generally varies from 5 to 100 ppm.

How does CO affect us?

As you know, blood transports oxygen in our body. When we inhale air, the oxygen of the air combines with haemoglobin of the blood to form oxyhaemoglobin.

• Oxyhaemoglobin runs through blood vessels and gives up its oxygen to cells, which use it for respiration.
• But CO displaces oxygen from oxyhaemoglobin to form carboxyhaemoglobin.
• The affinity of CO for haemoglobin is 325 times greater than that of oxygen. So, the displacement takes place easily.
• The formation of carboxyhaemoglobin cuts off oxygen supply to cells, and adverse effects are seen. The severity of the symptoms depends on the amount of CO in the blood.
• Inhaling air with a high CO level may even be fatal. A person may die of asphyxia in an environment of CO. So, one should not sleep in a closed room heated by a coal fire

Effects of CO poisoning:

Curing CO poisoning

Carboxyhaemoglobin slowly loses CO on being exposed to an excess of oxygen, and oxyhaemoglobin is again formed. So, a person suffering from CO poisoning should be kept on oxygen till he or she recovers

Industrial Uses of CO

Carbon monoxide is an industrial gas. Some important uses of this gas are given below.

1. Itis usedasa reducingagentin metallurgy. It can abstract the oxygen from many metal oxides and set the metal free.

⇒ \(\underset{\text { metal oxide }}{\mathrm{MO}}+\mathrm{CO} \xrightarrow{\text { heat }} \underset{\text { metal }}{\mathrm{M}}+\mathrm{CO}_2\)

For example:

The mineral bauxite (which contains Fe203) is reduced by CO in a blast furnace to give iron.

⇒ \(\underset{\text { iron(III) oxide }}{\mathrm{Fe}_2 \mathrm{O}_3}+\mathrm{CO} \xrightarrow[\text {}]{\text { heat }} \underset{\text {iron oxide }}{2 \mathrm{FeO}}+\mathrm{CO}_2\)

⇒  \(\mathrm{FeO}+\mathrm{CO} \xrightarrow{\text { heat }} \underset{\text { iron }}{\mathrm{Fe}}+\mathrm{CO}_2\)

2. Carbon monoxide is also used in metallurgy for the refining of nickel.

3. It is used on a large scale in the industrial preparation of several organic compounds such as

• Methanol
• Acetic acid
• Hydrocarbons, and

Phosgene (COCl₂, used in the synthesis of some polymers)

Fuels

We know that heat (usually accompanied by light) is produced when a substance burns. A substance that is burnt to obtain heat or light from it is called a fuel. Thus, wood, cow-dung cakes, coal, petrol, diesel, kerosene, CNG and LPG are fuels.

Hydrogen is also a good fuel, but it is difficult to handle due to its explosive nature. These fuels (except hydrogen) contain carbon.

Calorific Value of a Fuel:

The amount of heat given out by 1 g of a fuel in air or oxygen is known as the calorific value of the fuel. It is expressed in kj/g.

The calorific value of hydrogen is the highest, and that of common fuels, much lower

The calorific values of some fuels:

That the calorific value of LPG is much higher than that of the traditional fuels can be realised by doing the following activity with the help of an adult.

Activity:

Take the same volume of water in two similar vessels. Heat one of them on an LPG stove and the other on burning cow-dung cakes. You will find that the water boils on the LPG stove much sooner than that on the burning cow-dung cakes.

(You could use thermometers to observe the rate at which the temperature of water increases in the two vessels).

Thus, attaining the cooking temperature on an LPG stove will be faster than on a conventional fire as that of cow-dung cakes

Of the C-based fuels, CNG is mainly methane (CH₄ ) and LPG, butane (C₄ H₁₀ ). Methane and butane contain only hydrogen and carbon, so they belong to a class of compounds known as hydrocarbons. Hydrocarbons burn to give CO₂ and H₂O.

• Petrol, kerosene and diesel are also mixtures of hydrocarbons containing higher numbers (7 and above) of carbon atoms. Sufficient oxygen for complete combustion of the fuel may not be available from the surroundings, and so some CO and soot are also formed.
• Besides, some oxides of nitrogen and sulphur are also formed on the burning of the impurities in them. These gases and soot pollute the air.
• A good-quality coal contains about 90% and a poor-quality one, about 55% carbon. Coal is used as a fuel, but the products of combustion (CO₂ , CO, NO₂ , SO₂ , SO₃ and soot) are undesirable.
• When wood or dung cake is burnt, we get CO₂, H₂O and some CO along with a small amount of the oxides of nitrogen.
• Coal and petroleum are known as fossil fuels as they are formed by a biochemical process called fossilisation.
• Natural gas is a decay product of marine organisms and collects over petroleum in petroleum wells. Petroleum gas is obtained by the cracking (i.e., the breaking of bigger molecules into smaller ones) of petroleum.

Promoting Cleaner Fuels

The use of fuels like wood, cow-dung cake and coal for cooking and of petrol and diesel in motor vehicles is accompanied by the emission of pollutants like

• Carbon monoxide,
• Oxides of sulphur and nitrogen, and
• Soot.

CNG and LPG are considered to be much cleaner fuels than those mentioned above because, on complete burning, they form C02 and H20 only.

• These days, CNG is fast replacing petrol and diesel in motor vehicles, especially the commercial ones.
• LPG is highly recommended for use as a fuel in the kitchen. Extremely poor people can’t afford it.
• On the other hand, a large number of premature deaths occur every year on account of the use of conventional fuels.
• So, in 2016 the Government of India launched a welfare scheme to reach out to the BPL families (i.e., those who are below the poverty line) with free LPG connection. The scheme is known as the Pradhan Mantri Ujjwala Yojana.
• It aims at giving free LPG connections to 50 million women from BPL families —most living in remote rural areas. This will also help keep our environment clean.

NCERT Solutions For Class 11 Chemistry Chapter 3 Classification Of Elements And Periodicity In Properties Long Question And Answers

Question 1. Arrange according to the instructions given in the bracket:

• O, Te, Se, S (Increasing order of electronegativity)
• Na, Cu, Zn (Increasing order of electropositive character)
• I, F, Br, CI (Increasing order of metallic character)
• I, F, Br, Cl (Decreasing order of electron affinity)
• Na, K, F, Cl, Br (Increasing order of atomic radius)
• Mg, AI, Si, Na (Increasing order of ionization potential)
• PbO, MgO, ZnO (increasing order of basic character)
• Na+, Mg²⁺, Al³⁺ (Decreasing order of size)
• Cu, S, C (graphite) (Increasing order of electrical conductivity)
• Be, C, B, N, O (Increasing order of electron affinity)
• Cl, Mg, C, S (Increasing order of electronegativity)
• A1₂O₃, P₂O₅, Cl₂O₇, SO₃ (Increasing order of acidic property)
• MgO, ZnO, CaO, Na₂O, CuO (Increasing order of basic property)
• Na⁺, F-, O^2-, Mg²⁺, N^3- (Increasing order of ionic radii)
• B —Cl, Ba—Cl, Br —Cl, Cl —Cl (Increasing order of bond polarity)
• Br, F, Cl, I (Increasing order of oxidizing property)
• Na, Cs, K, Rb, Li (Increasing order of atomic volume)
• Sb₂O₃, N₂Og, AS₂O₃ (Increasing order of acidic property)

Answer:

• Te < Se < S < O
• Cu< Zn< Na
• F < Cl < Br <I
• Cl > F > Br >I
• F < Cl < Br < Na < K
• Na<Al<Mg<Si
• ZnO < PbO < MgO
• Na⁺ > Mg²⁺ > Al³⁺
• S < C(graphite) <Cu
• Be<N<B<C<0
• Mg < C = S < Cl
• Al₂O₃ < P₂O₅ < SO₃ < Cl₂O₇
• CuO < ZnO < MgO < CaO < Na20
• Mg²⁺ < Na⁺ < F^– < O^2-– < N^3-
• Ba —Cl > B —Cl > Br —Cl > Cl —Cl
• I < Br < Cl < F
• Li < Na < K < Kb < Cs
• Sb₂O₃ < AS₂O₃ < N₂O₅

Question 2. The atomic numbers of elements A, B, and C are 10, 13, & 17 respectively.

1. Write their electronic configurations.
2. Which one of them will form a cation and which one an anion?
3. Mention their valencies.

Answer:

1. Electronic configuration of ₁₀A: ls²2s²2p⁶

Electronic configuration of ₁₃B: ls²2s²2p⁶3s³3p¹

Electronic configuration of ₁₇C: ls²2s²2p⁶3s²3p⁵

2. The element, A belonging to group 18, is an inert gas.

So it will form neither a cation nor an anion. The element B, belonging to group 13, is a metal. It will readily form a cation by the loss of 3 electrons from its valence shell (3rd shell). The element C will readily gain one electron in its outermost 3rd shell to attain inert gas electronic configuration (Is²……3s²3p⁶). So, C will form an anion.

3. Valency of A = 0 (it has a complete octet of electrons in the outermost shell). Valency of B = 3 (by the loss of 3 electrons from the 3rd shell it will attain stable inert gas electronic configuration). Valency of C = 1 (because by the gain of the electron, it can attain stable inert gas configuration).

NCERT Solutions Chapter 3 Class 11 Chemistry

Question 3. A, B, and C are three elements with atomic numbers group (8 + 2) = 10. 17, 18, and 20 respectively. Write their electronic configuration. Which one of them is a metal and which one is a non-metal? What will be the formula of the compound formed by the union of A and C? What may be the nature of valency involved in the formation of the above compound?
Answer:

Electronic configuration of ₁₇A: ls²2s²2p⁶3s²3p⁵

Electronic configuration of ₁₀B: ls²2s²2p⁶3s²3p⁶

Electronic configuration of ₂₀C: ls²2s²2p⁶3s²3p⁶4s²

Element C is a metal as it can easily form a dipositive ion by the loss of two electrons from 4s -orbital. ElementA is an anon-metal as it can achieve inert gas configuration by accepting one electron in a 3p- subshell.

As already mentioned, the element C can easily, form a dipositive cation (C²⁺), while the element A readily forms a uninegative anion (A^–).

So the elements A and C can combine to form the compound CA₃.

The above-mentioned compound is electrovalent because it will be formed by the union of two A^– ions with one C²⁺ ion.

Question 4. Outer electronic configuration of 4 elements is as follows: 3d°4s1 3s²3p⁵ 4s²4p⁶ Electronic configuration of 10A: ls²2s²2p⁶ 3d⁸4s². Find their positions in the periodic table
Answer:

This element (3d°4s1) is an s -block element. So it is an element of period group 1.

This element (3s²3p⁵) is a p -p-block element containing (2 + 5) or 7 electrons in the valence shell (n = 3). Soitis an element ofthe 3rd periodin group (10 + 2 + 5) = 17.

This element (4s²4p⁶) is a p -p-block element containing (2 + 6) or 8 electrons in the valence shell (n = 4). So it is an element of the 4thperiodin group (10 + 2 + 6) = 18.

This element (3d⁸4s²) is a d-block element containing 8 electrons in the d – d-orbital of the penultimate shell (n = 3) and 2 electrons in the s – s-orbital of the valence shell (n = 4). So, it is an element of the 4th period in group (8+2)=10

Question 5. Write the electronic configuration of the element with atomic number 35. What will be the stable oxidation states of the element?
Answer:

Electronic configuration: ls²2s²2p⁶3s²3p⁶3d¹⁰4s²4p⁵. The most stable oxidation state is -1 because it can accept one electron to achieve inert gas configuration (Is²… 3d¹⁰4s²4p⁶).

Again in an excited state, it can also exhibit oxidation number +3 or +5 by forming a covalent bond by using its 3 or 5 odd electrons in its outermost shell.

Question 6. The ionization potential of O is less than that of N—explain.
Answer:

The reason for such a difference may be explained based on their electronic configurations filled, its electronic configuration is highly stable.

So, a large amount of energy is required to form N+ ion by removal of 2pelectron.

On the other hand, the formation of 0+ ion by removal of one electron from a partially filled 2p -orbital requires less energy, since the 2p -orbital of 0+ion is half-filled, the electronic configuration assumes stability. Hence, oxygen has a lower ionization potential than nitrogen.

Question 7. Explain why the ionization potentials of inert gas are very high while that of alkali metals are very low. ses are
Answer:

Outermost shells of inert gases contain octets of electrons. Besides this, each of the inner shells of inert gas elements is filled.

• Such configuration is exceptionally staMe conversion of a neutral inert gas atom into its ions try removal of an electron from the outermost shell requires large energy.
• As a result, they have high ionization potentials.
• The configuration of the outermost and penultimate shell of alkali metals is (n-1)s²(n-1)p⁶nsl (except Li ).
• Thus loss of 1 electron from their outermost shell brings about a stable configuration of inert gases.
• Hence, the conversion of alkali metals to their ions requires comparatively less amount of energy. As a result, alkali metals have low values of ionization potential.

Question 8. Which member in each of the following pairs has a lower value of ionization potential? F, Cl S, Cl Ar, K O Kr, Xe Na, Na⁺.
Answer:

Cl has lower ionization enthalpy than F because electrons of 2p-orbital are more strongly attracted by the nucleus than the 3p-electrons in Cl.

• (Note that effective nuclear charge on the outermost electrons is nearly the same for both and Cl).
• S has lower ionization enthalpy than Cl because the size of S is greater than that of Cl and also the nuclear charge of is less than that of Cl
• K has a lower ionization potential than Ar as the outermost shell is filled with electrons in Ar. On the other hand, K can attain a stable configuration like the inert gas Ar by the loss of only 1 electron.
• Xe has lower ionization enthalpy than Kr because ionization enthalpy decreases on moving down a group in the periodic table.
• Na (ls²2s²2p²⁶3s¹) has lower ionization enthalpy’ than Na⁺(ls²2s²2p⁶), because the former can attain inert gas-like electronic configuration by loss of 1 electron from its outermost shell, whereas the latter attains unstable electronic configuration (Is²2s²2p⁵) by loss of one electron from its outermost shell.

Question 9. A, B, C, and D are four elements of the same period, of which A and B belong to s -block. B and D react together to form B+D^–. C and D unite together to produce a covalent compound, CD₂.

1. What is the formula of the compound formed by A and D?
2. What is the nature of that compound?
3. What will be the formula and nature of the compound formed by the union of B and C

Answer:

Since A and B are s-block elements of the same period, one of them is an alkali metal group-1A while the other is an alkaline earth metal of group-2A. B and D react to form anionic compound B+D.^– Therefore, B is a monovalent alkali metal of group 1A, and D is a monovalent electronegative element of group 4A.

Hence, the other element A of the s -the block is a bivalent alkaline earth metal of group-2A. C and D combine to produce the covalent compound CD₂. Hence, C is a bivalent electronegative element belonging to group 6A.

1. The formula of the compound formed by the combination of electropositive bivalent element A with electronegative monovalent element D is AD₂
2. The compound is ionic or electrovalent.
3. A compound formed by reactions of electropositive monovalent element B with electronegative bivalent element C will have the formula B₂C. It is an electrovalent or ionic compound.

NCERT Solutions for Class 11 Chemistry Chapter 3 Long Questions

Question 10. What changes in the following properties are observed while moving from left to right along a period & from top to bottom in a group? Atomic volume, Valency, Electronegativity, Oxidising, and reducing powers.
Answer:

On moving from left to right across a period, atomic volume first decreases and then increases. In a group, atomic volume increases with an increase in atomic number down a group.

1. Oxygen-based valency goes on increasing from left to right over a period but does not suffer any change down a group.
2. Electronegativity increases gradually from left to right across a period while it decreases down a group with an increase in atomic number.
3. Oxidizing power increases from left to right across a period and decreases from top to bottom in a group.
4. On the other hand, reducing power decreases from left to right in a period but it increases from top to bottom in a group

Question 11. Which property did Medeleev use to classify the elements in his periodic table? Did he stick to that?
Answer:

Mendeleev classified th<? elements based on their increasing atomic weights in the periodic table. He arranged almost 63 elements in order of their increasing atomic weights placing together elements with similar properties in a vertical column

• He observed that while classifying elements in the periodic table according to increasing atomic weight, certain elements had different properties than those elements belonging to the same group.
• For such cases, Mendeleev prioritized the properties of the element over its atomic weight.
• So, he placed an element with a higher atomic weight before an element with a lower atomic weight.
• For example, iodine [I (126.91)] with a lower atomic weight than tellurium [Te (127.61)] is placed after tellurium in group VII along with elements like fluorine, chlorine, etc., due to similarities in properties with these elements.
• Thus, Mendeleev did not stick to his idea of classifying elements only according to the increasing atomic weights.

Question 12. What is the basic difference in approach between Mendeleev’s Periodic Law & Modern Periodic Law?
Answer:

According to Mendeleev’s periodic law, the physical and chemical properties of elements are a periodic function of their atomic weights.

• On the other hand, the modern periodic table states that the physical and chemical properties of the elements are a periodic function of their atomic numbers.
• Thus the basic difference in approach between Medeleev’s periodic law and modern periodic law is the change in the basis of the classification of elements from atomic weight to atomic number.
• Based on quantum numbers, justify that the sixth period of the periodic table should have 32 elements. In the modern periodic table, each period begins with the filling of a new principle energy level. Therefore, the sixth period starts with the filling of the principal quantum number, n = 6.
• In the sixth period elements, the electron first enters the 6s -orbital, and then from left to right across a period the electrons enter the 4f, 5d, and 6p orbitals of the elements.

Filling of electrons in orbitals in the case of6th period continues till a new principal energy level of quantum number, n = 7 begins, i.e., for elements of the sixth period, electrons fill up the 6s, 4f, 5d, and 6p orbitals a total number of orbitals in this case =1 + 7 + 5 + 3 = 16. Since each orbital can accommodate a maximum of two electrons, there can be 16 × 2 or 32 elements in the sixth period.

Question 13. What is the significance of the terms—’ isolated gaseous atom’ and ‘ground state’ while defining the ionization enthalpy and electron-gain enthalpy?
[Hint: Requirements for comparison purposes]
Answer:

The ionization energy of an element is defined as the minimum amount of energy required to remove the most loosely bound electron from the valence shell of an isolated gaseous atom existing in its ground state to form a cation in the gaseous state.

• Electron-gain enthalpy is defined as the enthalpy change involved when an electron is added to an isolated gaseous atom in its lowest energy state (ground state) to form a gaseous ion carrying a unit negative charge.
• The force with which an electron gets attracted by the nucleus of an atom is influenced by the presence of other atoms in the molecule or the neighborhood.
• Thus, to determine the ionization enthalpy, the interatomic forces should be minimal. Interatomic forces are minimal in the case of the gaseous state as the atoms are far apart from each other.
• Consequently, the value of ionization enthalpy is less affected by the surroundings. Similarly, for electron affinity, the interatomic forces of attraction should be minimal for the corresponding atom.
• Tor Tills reason, the term ‘Isolated gaseous atom’ Is used while defining Ionisation enthalpy and electron-gain enthalpy.
• Ground state means the state at which the atom exists In Its most stable state. If the atom Is In the excited state, then the amount of heat applied to remove an electron or the amount of heat liberated due to the addition of an electron is low.
• So, for comparison, the term ‘ground state’ Is used while defining ionization enthalpy and electron-gain enthalpy.

Question 14. The energy of an electron in the ground state of the Hatom is -2.18× 10^-18J. Calculate the ionization enthalpy of atomic hydrogen in terms of J . mol^-1. [Hint: Apply the idea of the mole concept.]
Answer:

Amount of energy required to remove an electron from a hydrogen atom at the ground state

= E_∞-E₁= 0 – E₁

= -(-2.18 ×10^-18)J

= 2.18 × 10^-8 J

Ionization enthalpy atomic hydrogen per mole = 2.18 × 10^-18 × 6.022 × 10²³

= 1312.8 × 10³ J.mol^-1 .

Question 15. How would you explain the fact that the first ionization enthalpy of sodium is lower than that of magnesium but its second ionization enthalpy is higher than that of magnesium?
Answer:

Evident that in both atoms, the valence electrons enter the 3s orbital. However, the nuclear charge of the Mg atom (+12) is greater than that of the Na atom (+11).

Again, the 3s orbital of the Mg atom being filled is more stable than half-filled.

• 3s -orbital of Na atom. Thus, the first ionization enthalpy of sodium is lower than that of magnesium.
• On the other hand, the removal of one electron from the valence shell of the Na atom leads to the formation of the Na⁺ ion whose electronic configuration is highly stable (similar to inert gas, neon).
• So high amount of energy is required to remove the second electron because it disturbs the stable electronic configuration. However, the electronic configuration of Mg⁺ is not as stable as that of Na⁺, but the electronic configuration of Mg²⁺ is more stable as it is similar to the electronic configuration of the inert gas, neon.
• So, less amount of energy is required to remove an electron from Mg⁺. Thus, the second ionization enthalpy of sodium is higher than that of magnesium.

Question 16. First ionisation enthalpy values (in kjmol^-1) of group-13 elements are: B = 801, Al = 577, Ga = 579, In = 558 and Tl = 589. How would you explain this deviation from the general trend?
Answer:

On moving down group-13 from B to Al, ionization enthalpy decreases due to an increase in atomic size and shielding effect which jointly overcome the effect of an increase in nuclear charge.

• However, ionization enthalpy increases slightly on moving from Al to Ga (2 kj.mol^-1).
• This is because due to poor shielding of valence electrons by 3d -electrons effective nuclear charge on Ga is slightly more than Al.
• On moving from Ga to In, the shielding effect of all the inner electrons overcomes the effect of the increase in nuclear charge. Thus, the ionization enthalpy of In is lower than Ga.
• Again, on moving from Into Tl, there is a further increase in nuclear charge which overcomes the shielding effect of all electrons present in the inner shells including those of 4f- and 5d -orbitals. So, the ionization enthalpy of Tl is higher than In.

Question 17. Which of the given pairs would have a more negative electron-gain enthalpy: O or F F or Cl?
Answer:

O and F both belong to the second period. As one moves from O to F, atomic size decreases and nuclear charge increases.

• Due to these factors, the incoming electron when enters the valence shell, and the amount of energy liberated in the case of F is more than that of O.
• Again, Fatom (ls²2s²2p⁵) accepts one electron to form F^– ion (ls²2s²2p⁶) which has a stable configuration similar to neon.
• However, O-atom when converted to O- does not attain any stable configuration.
• Thus energy released is much higher going from F to F^– than in going from O to O^–.
• So, the electron-gain enthalpy of is much more negative than that of O

Question 18. Would you expect the second electron-gain enthalpy of 0 as positive, more negative, or less negative than the first? Justify your answer.
Answer:

There are several valence electrons in oxygen and it requires two more electrons to complete its octet. So, the O^– atom accepts one electron to convert into an O^– an ion and in the process liberates energy. Thus, the first electron-gain enthalpy of oxygen is negative.

⇒ \(\mathrm{O}(g)+e \rightarrow \mathrm{O}^{-}(g)+141 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}\left(\Delta_i H_1=-v e\right)\)

However, when another electron is added to O^– to form an O^-2-ion, energy is absorbed to overcome the strong electrostatic repulsion between the negatively charged O ion and the second incoming electron. Thus, the second electron-gain enthalpy of oxygen is positive.

⇒ \(\mathrm{O}^{-}(\mathrm{g})+e \rightarrow \mathrm{O}^{2-}(\mathrm{g})-\left(780 \mathrm{~kJ} \cdot \mathrm{mol}^{-1}\right)\left(\Delta_i H_2=+v e\right)\)

Question 19. Use the periodic table to answer the given questions. Identify an element with 5 electrons in the outer subshell. Identify an element that would tend to lose 2 electrons. Identify an element that would tend to gain 2 electrons. Identify the group having metal, non-metal, liquid, and gas at room temperature
Answer:

Fluorine. Its configuration is ls²2s²2p⁵

• Magnesium. Its configuration is ls2²s2²p⁶3s². So, Mg loses 2 electrons from its outermost shell to form Mg²⁺ and attains a stable configuration.
• Oxygen. Its configuration is ls²2s²2p⁴ So, O agains 2 electrons to form O^2- and attains stable configuration.
• Group-17. The metallic character of astatine (At) is much greater than its non-metallic character and its melting point is very high (302°C).
• So, astatine is considered as a metal. So in group-17 there is a metal (At), non-metals (F₂, Cl₂, Br₂, I₂), liquid (Br₂) and gas (F₂, Cl₂).

Question 20. The order of reactivity of group-1 LI < Na < K < Rb < Cs whereas that of group-17 elements Is F > Cl > Br >I. Explain.
Answer:

There is only one electron in the valence shell of the elements of group 1.

• Thus, they have a strong tendency to lose this single electron.
• The tendency to lose electrons depends on the ionization enthalpy.
• As ionization enthalpy decreases down the group, the correct order of increasing reactivity of group 1 elements is Li < Na < K < Rb < Cs.
• On the other hand, there are 7 electrons in the valence shell of the elements of group-17.
• Thus, they have a strong tendency to gain a single electron. The tendency to gain electrons depends on the electrode potentials of the elements.
• As the electrode potential of elements decreases down the group, the correct order of activity is F > Cl > Br >I.

Alternate explanation:

In the case of halogens, their reactivity increases with the increase in electron-gain enthalpy.

Order of electron-gain enthalpy:

F < Cl > Br >I. As electron gain enthalpy decreases from Cl to, the order of reactivity also follows this sequence. However, fluorine is the most reactive halogen as its bond dissociation energy is very low.

Question 21. Assign the position of the element having outer electronic configuration:

1. ns²np⁴ for n = 3, 
2. (n-1)d²ns² for n = 4
3. (n-2)f⁷(n-1)d¹ns² for n = 6, in the periodic table.

Answer:

1. As n= 3, the element belongs to the period. Since the last electron enters the p-orbital, the given element is a p-block element.

For p-block elements, group no. of the element = 10+no. of electrons in the valence shell.

• The element is in the (10+6) = 16th period.

2. As n = 4, the element belongs to the fourth period. Since is present in the element, it is a block element. For d-block elements, group no. of the element = no. of ns electrons + no. of(n-1) f electrons = 2+2 = 4. Therefore, the element is in the 4th period.

3. As n – 6, the element belongs to the sixth period. Since the last electron enters the f-orbital, the element is a f-block element. All f-block elements are situated in the third group of the periodic table.

Class 11 Chemistry Chapter 3 NCERT Solutions Long Question and Answers

Question 22. The first (Δ_iH₁) and second (Δ_iH₂)) ionization enthalpies (klmol^-1) and the (Δ_cgH)electron gain enthalpy (in kj.mol^-1 ) of a few elements are given below:

Which of the above elements is likely to be:

1. The least reactive clement?
2. The most reactive metal.
3. The most reactive non-metal.
4. The least reactive non-metal.
5. The metal can form a stable binary halide of the formula MX₂(X = halogen).
6. The metal that can form a predominantly stable covalent halide of the formula MX (X = halogen)?

Answer:

⇒ \(\begin{array}{|c|c|c|c|}
\hline \text { Elements } & \left(\Delta H_1\right) & \left(\Delta H_2\right) & \left(\Delta_{c g} H\right) \\
\hline \text { 1 } & 520 & 7300 & -60 \\
\hline \text { 2 } & 419 & 3051 & -48 \\
\hline \text { 3 } & 1681 & 3374 & -328 \\
\hline \text { 4 } & 1008 & 1846 & -295 \\
\hline \text { 5 } & 2372 & 5251 & +48 \\
\hline \text {6 } & 738 & 1451 & -40 \\
\hline
\end{array}\)

1. Element 5: Element 5 is the least reactive metal as it has the highest first ionization enthalpy & positive electron-gain enthalpy.
2.  Element 2: Element 2 is the most reactive metal as it has lowest first ionization enthalpy & low negative electron-gain enthalpy.
3. Element 3: Element 3  is the most reactive non-metal because it has very high first ionization enthalpy and very high negative electron-gain enthalpy.
4. Element 4: Element 4  is the least reactive non-metal because it has a high negative electron-gain enthalpy but not so high first ionization enthalpy.
5. Element 6: Element 6 has low first and second ionization enthalpy. Again, the first ionization enthalpy of this element is higher than those ofthe alkali metals. Thus, the given element is an alkaline earth metal and can form a stable binary halide ofthe formula MX2.
6. The first ionization enthalpy of elements is low but its second ionization enthalpy is high. So, it is an alkali metal and can form a stable covalent halide (MX)

Question 23. Predict the formulas of the stable binary compounds that would be formed by given pairs of elements:

1. Li and O
2. Mg and N
3. Al and I
4. Si and O, P and F
5. Element with atomic numbers 71 and F.

Answer:

Question 24. What will be the name (IUPAC) and symbol if the element with atomic number 119 is discovered? Write its electronic configuration. Also, write the formulas of the stable chloride and oxide of this element.
Answer:

IUPAC name : Ununennium, Symbol: Uue

Atomic number ofthe element =119 = 87 + 32

• It is known that the element with atomic number 87 is francium (Fr). Fr belongs to group 1 in the 7th period of the periodic table.
• So, the element with atomic number 119 will take its position in group 1 and 8th period just below francium(Fr).
• The electronic configuration of this element will be [UuojBs1, (where Uuo = Ununoctium, Z = 118). It will be an alkali metal with valency=1
• If the symbol ofthe element is ‘M’ then the formulas of its stable chloride and oxide will be MCI and M₂O respectively.

Question 25. Elements A, B, and C have atomic numbers (Z- 2), Z, and (Z +1) respectively. Of these, B is an inert gas. Which one of these has the highest electronegativity? Which one of these has the highest ionization potential? What is the formula of the compound formed by the combination of A and C? What is the nature of the bond in this compound?
Answer:

Since element B (atomic no =Z) is an inert gas, the element ‘A’ with atomic number (Z- 2) is included in group 6A.

On the other hand, the element C, having an atomic number (Z + 1) must belong to groups (alkali metal). Hence, the electronegativity of the element A is maximum.

• The element B, being an inert gas, has the highest value of ionization potential.
• The valency of the element A, belonging to group (8- 6) = 2, and that ofthe element C, being an element of group IA, is 1.
• Therefore, the formula of the compound formed by A and C will be C₂A.
• Being a strongly electronegative element and C being a strongly electropositive element complete their octet through gain and loss of electrons respectively.
• So, the nature of the bond formed between C and A in C₂A isionic or electrovalent bond.

Question 26. The atomic radius of ₁₀Ne is more than that of ₉F —why?
Answer:

Fluorine forms diatomic molecules, thus the atomic radius of fluorine is a measure of half of the internuclear distance in its molecule (i.e., half of the covalent bond length of an F₂ molecule) but neon being an inert gas, its atoms are incapable of forming covalent bonds by mutual combination amongst themselves.

• The only force that comes into play between the atoms is the weak van der Waals force.
• So a measure of the atomic radius of Ne is equal to its van der Waals radius but the van der Waals radius is always greater than the covalent radius.
• Thus, the atomic radius of neon is larger than that of fluorine.
• Furthermore, due to an increase in the number of electrons in the outermost 2p -orbital of Ne, there occurs an increase in electron-electron repulsion.
• So 2p-orbital of Ne suffers expansion leading to its increased atomic radius.

Question 27. The first electron affinity of oxygen is negative but the second electron affinity is positive—explain.
Answer:

• When an electron is added to the valence shell of an isolated gaseous O-atom in its ground state to form a negative ion, energy is released.
• Because a neutral oxygen atom tends to complete its octet with electrons. So, the electron affinity of oxygen is an exothermic process and its value is negative.
• When an extra electron is added to an O- ion, that second electron experiences a force of repulsion exerted by the negative charge ofthe anion. So, first, this process requires a supply of energy from an external source.
• This accounts for the endothermic nature of second electron affinity and has a positive value.

Question 28. The electron affinity of sodium is negative but magnesium has a positive value—why?
Answer:

Electronic configuration of ₁₁Na: ls²2s²2p⁶3s¹

Electronic configuration of ₁₂Mg: ls²2s²2p⁶3s²

• The addition of one electron to the 3s -orbital of Na leads to a comparatively stable electronic configuration with a fulfilled orbital.
• So, this process of the addition of electrons to Na is an exothermic, process. So, the electron affinity of Na is negative. On the other hand, Mg has fulfilled 3s orbital and has a stable electronic configuration.
• So the addition of an electron to the 3p -orbital destabilizes the electronic configuration of Mg.
• Additional energy is required for the addition of electrons to the outermost shell of Mg i.e., this process is endothermic and thus the value of electron affinity ofMg is positive.

Question 29. If the electron affinity of chlorine is 350 kJ. moI^-1, then what is the amount of energy liberated to convert 1.775 g of chlorine (existing at atomic state) to chloride ions completely (in a gaseous state)
Answer:

Atomic mass of chlorine = 35.5 g .mol^-1

The energy liberated in the conversion of 35.5 g of Cl to Cl^– ion =350 kj

Energyliberatedin the conversion of1.775 g of Cl to Cl^–

⇒ \(\text { ion }=\frac{350}{35.5} \times 1.775=17.5 \mathrm{~kJ}\)

Question 30. The second ionization enthalpy of Mg is sufficiently high and the second electron-gain enthalpy of O has a positive value. How do you explain the existence of Mg²⁺ O^2- rather than Mg⁺O^– ?
Answer:

The lattice energy of an ionic crystal depends on the force of attraction between the cations and anions

⇒ \(\left(F \propto \frac{q_1 q_2}{r^2}\right)\)

So, the magnitude of lattice energy increases as the charges on the cation and anion increase. Consequently, the lattice energy of Mg²⁺ O^2- is very much greater than that of Mg⁺ O^–.

The lattice energy of Mg²⁺ O^2- is so high that it exceeds the unfavorable effects of the second ionization enthalpy of Mg and the second electron-gain enthalpy of 0.

So, Mg²⁺ O^2- is a stable ionic compound, and its formation is favored over Mg⁺ O^–.

Question 31. The atomic numbers of some elements are given below. Classify them into three groups so that the two elements in each group exhibit identical chemical behavior: 9, 12, 16, 34, 53, 56.
Answer:

Atomic Number →  Electronic configuration

9 → \(1 s^2 2 s^2 2 p^5\)

12 → \(1 s^2 2 s^2 2 p^6 3 s^2\)

16 → \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^4\)

34 → \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^{10} 4 s^2 4 p^4 \)

53 → \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^{10} 4 s^2 4 p^6 4 d^{10} 5 s^2 5 p^5\)

56 → \(1 s^2 2 s^2 2 p^6 3 s^2 3 p^6 3 d^{10} 4 s^2 4 p^6 4 d^{10} 5 s^2 5 p^6 6 s^2\)

Elements with atomic numbers 9 and 53 belong to the -block and they have similar outer electronic configurations (ns²np⁵). So they will exhibit similar chemical properties. Their group number = (10 + 2 + 5) = 17. Elements with atomic numbers 12 and 56 belong to s -block and they have similar outer electronic configurations (ns²).

So they will exhibit similar chemical properties. Their group number = 2. Elements with atomic numbers 16 and 34 belong to the -block and they have similar outer electronic configurations (ns²np²).

So, they will exhibit similar chemical properties. Their group number = (10 + 2 + 4) = 16. So, based on similarity in chemical properties, the given elements are divided into three groups :

Group-2 → 12,56 (Atomic number)

Group-16 → 16,34 (Atomic number)

Group-17→ 9,53 (Atomic number)

Question 32. Though the nuclear charge of sulfur is more than that of phosphorus, yet the ionization potential of phosphorus is relatively high”—why?
Answer:

1. \({15} \mathrm{P}: 1 s^2 2 s^2 2 p^6 3 s^2 3 p_x^1 3 p_y^1 3 p_z^1\)

2. \({16} \mathrm{~S}: 1 s^2 2 s^2 2 p^6 3 s^2 3 p_x^2 3 p_y^1 3 p_z^1\)

3p -orbital of the outermost shell of the P -atom being half filled, this electronic configuration is very stable. So, the removal of one 3p -electron to produce a P+ ion requires a sufficiently high amount of energy.

On the other hand, the amount of energy required for removing one electron from a partially filled 3p -orbital of the S -atom to yield an S⁺ ion is relatively less, since the half-filled 3p -orbital of S+ assumes the extra stability due to the loss of this electron. This accounts for the higher value of ionization potential of phosphorus, relative to sulfur.

Question 33. Mg has relatively higher ionization enthalpy than A1 although the atomic number of the latter is more than the former—explain why.
Answer:

Electronic configuration of ₁₂Mg \(: 1 s^2 2 s^2 2 p^6 3 s^2\)

Electronic Configuration of \({ }_{13} \mathrm{Al}: 1 s^2 2 s^2 2 p^6 3 s^2 3 p^1\)

The penetration effect of the s-electron is greater than that of the electron. So it is easier to remove the 3p-electron from the outermost shell of Al.

Furthermore, the removal of this electron gives Al+, which has filled 3s-orbital (stable electronic configuration) in the outermost shell. On the other hand, Mgatom has filled 3s-orbital (stable electronic configuration) in its ground state.

Removal of one electron from the 3s-orbital of Mg-atom will require a large amount of energy because the resulting Mg⁺ ion will have a less stable electronic configuration (ls²2s²2p⁶3s¹). Furthermore, it is rather difficult to remove an electron from the s-orbital having a greater penetration effect. So ionization enthalpy of Mg is greater than that of A.

Question 34. Why are electron-gain enthalpy of Be and N positive?
Answer:

The fact that Be and N have positive electron-gain enthalpy values can be explained by considering the given electron-gain processes.

It is observed that the stable electronic configuration of both Be and N -atoms is disturbed by the addition of an electron to each of them.

Consequently, such electron addition processes involve the absorption of energy and hence, both Be and N have positive electron-gain enthalpy values.

Question 35. The electron affinity of lithium is negative but the electron affinity of beryllium is positive”—why?
Answer:

Electronic configuration of ₃Li: ls²2s¹

Electronic configuration of ₄Be: ls²2s²

In addition of an electron to Li-atom, the 2s -orbital of Li becomes filled with electrons, and consequently, that electronic configuration attains stability.

• This process is accompanied by the liberation of energy. On the other hand, Be has a stable electronic configuration with a frilly-filled 2s subshell.
• When an electron is added to Be-atomic occupies 2p -subshell causing destabilization ofthe stable electronic configuration.
• This process is accompanied by the absorption of heat. Naturally electron affinity of Li is negative but the electron affinity ofBe is positive.

Question 36. Which of the following statements related to the modern periodic table is incorrect?

• p -p-block has 6 columns because a maximum of 6 electrons can occupy all the orbitals in a p-shell.
• d -block has 8 columns, as a maximum of 8 electrons can occupy all the orbitals in a d -subshell.
• Each block contains many columns equal to the number of electrons that can occupy that subshell.
• Block indicates the value of azimuthal quantum number (l) for the last subshell that received electrons in building up electronic configuration

Answer: The statement is incorrect because d -the block has 10 columns because a maximum of ten electrons can occupy all the orbitals in a d -subshell.

Periodicity in Properties and Classification of Elements Class 11

Question 37. Anything that influences the valence electrons will affect the chemistry of the element. Which one of the following factors does not affect the valence shell?

1. Valence principal quantum number (n)
2. Nuclear charge (Z)
3. Nuclear mass
4. Number of core electrons.
5. Nuclear mass does not affect the valence shell electrons (such as, and H have similar chemical properties.
6. The size of isoelectronic species F-, Ne, Na+ is affected by: nuclear charge (Z)
7. valence principal quantum number (n)

Question 38. What do you mean by isoelectronic species? Name a species that will be isoelectronic with each of the given atoms or ions:

1.  F^–
2. Ar,
3. Mg²⁺
4.  Rb⁺

Answer:

Electronic ions are ions of different elements that have the same number of electrons but different magnitudes of nuclear charge.

1. There are (9 + 1) or 10 electrons in F^–.

Isoelectronic species of F^– are :

• Nitride (N^3-) ion [7 + 3]
• Oxide (O^–₂) ion [8 + 2]
• Neon (Ne) atom [10]
• Sodium (Na⁺) ion [11-1],
• Magnesium (Mg²⁺) ion [12-2]
• Aluminum (Al³⁺) ion [13-3].

2. There are =18 electrons in Ar.

Isoelectronic species are:

• Phosphide (P^3-) ion [15 + 3]
• Sulfide (S^2-) ion [16 + 2]
• Chloride (Cl^– ion [17 + 1]
• Potassium (K⁺) ion [19 -1], and
• Calcium (Ca²⁺) ion [20-2 ].

3. There are (12-2) = 10 electrons in Mg²⁺

Isoelectronic species are: 

• Nitride (N^3-) ton [7 + 3]
• Oxide (O^2-) ion [8 + 2]
• Fluoride (F^–)ion [9+1]
• Sodium (Na+) ion [11-1].

4. There are (37-1)= 36 electrons In Kb.

Isoelectronic species are:

• Rb+ is bromide (Br^–) Ion [35 + 1],
• Krypton (Kr) atom [36]
• Strontium (Sr^2-) Ion [30^2-].

Question 39. The atomic numbers of three elements A, B, and C are 9, 13, and 17 respectively.

1. Write their electronic configuration.
2. Ascertain their positions in the periodic table.
3. Which one is most electropositive and which one is most electronegative?

Answer:

1. Electronic configurations of

₉A: ls²2s²2p⁵

₁₃B: ls²2s²2p⁶3s²3p¹

₁₇C: ls²2s²2p⁶3s²3p⁵

2. All three elements are p -p-block elements. Hence, their group and period numbers are as follows

Element → Period number → Group number

A → 2 → 10 + 2 + 5 = 17

B→ 3→ 10 + 2 + 1 = 13

c→ 3→ 10 + 2 + 5 = 17

3. Element B can easily donate 3 electrons from its outermost shell to attain a stable inert gas configuration. So, it is the most electropositive element

Elements A and C are electronegative because they can accept one electron to attain a stable inert gas electronic configuration. These elements (A and C) have similar outer electronic configurations
(ns²np⁵) but the size of A is smaller than that of C. So, the electronegativity of A is greater than that of C. Hence, A is the most electronegative element.