Kristensmith

NCERT Exemplar Solutions for Class 10 Maths Chapter 12  Area Related To Circles

Area Related To Circles Introduction

We are familiar with the shape of a circle. The circumference of the wheels of cars, and coins appears as a circle.

A circle can be defined as “A figure with an outline, every point on this outline is at the same constant distance from a certain point inside the figure, which is called the centre”.

NCERT Exemplar Class 10 Maths Chapter 12

NCERT Exemplar Solutions for Class 10 Maths Chapter 12  Area Related To Circles Area And Circumference Of A Circle

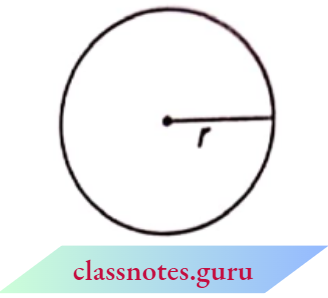
Let r be the radius of the circle. The distance travelled once around a circle is its perimeter, usually called its circumference. Now

Area of circle = πr²

Circumference of circle = 2πr

Read and Learn More Class 10 Maths Solutions Exemplar

π(pi) is a fixed irrational number whose approximate value is \(3.1416 \text { as } \frac{22}{7} \text { or } \frac{355}{113}\) (sometimes)

Diameter: A chord of a circle passing through its centre is called the diameter of the circle.

Diameter = 2 x radius

NCERT Exemplar Solutions for Class 10 Maths Chapter 12  Area Related To Circles Formulae Of Circle

1. Area of circle = πr²
2. Circumference of a circle = 2πr

3. Area of semicircle = \(\frac{1}{2} \pi r^2\)

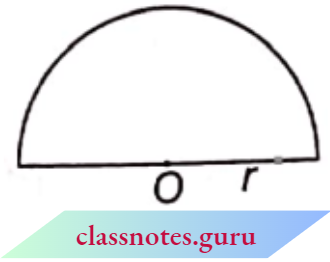
4. Perimeter of semicircle = (πr + 2r)

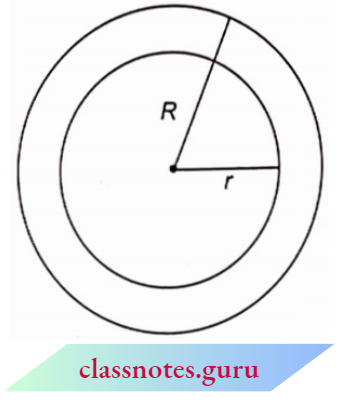
5. For a ring having outer radius = R and inner radius = r
Area of ring = π(R² – r²)

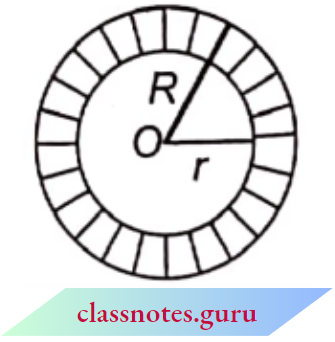
6. For rotation of the hands of a clock

1. Angle described by minute hand in 60 minutes = 360°
2. Angle described by hour hand in 12 hours = 360°

7. For rotating wheels

1. Distance moved by a wheel in 1 rotation = its circumference
2. Number of rotation in unit time = \(\frac{\text { distance moved in unit time }}{\text { circumference }}\)

NCERT Exemplar Solutions for Class 10 Maths Chapter 12  Area Related To Circles Solved Examples

Question 1. The circumference of a field is 220 m. Find

1. Its radius
2. Its area.

Solution:

Circumference of circle = 220 m

2πr = 220

⇒ \(r=\frac{220 \times 7}{2 \times 22}=35 \mathrm{~m}\)

Area of circle = \(\pi r^2=\frac{22}{7} \times 35 \times 35=3850 \mathrm{~m}^2\)

Question 2. Find the area of a circular park whose radius is 4.5 m.

Solution:

Area of circular park = r²

⇒ Area = \(\text { Area }=\frac{22}{7} \times 4.5 \times 4.5\)

Area = 63.63 m²

The area of a circular park = 63.63 m²

Question 3. The area of a circular plot is 346.5 m². Calculate the cost of fencing the plot at the rate of ₹ 6 per metre.

Solution:

Area of plot = 346.5 m²

⇒ πr² = 346.5 m² ⇒ \(r^2=\frac{346.5 \times 7}{22}\)

⇒ r² = 110.25 ⇒ r = 10.5 m

Circumference of plot = \(2 \pi r=2 \times \frac{22}{7} \times 10.5=66 \mathrm{~m}\)

Cost of fencing = Circumference x Cost of fencing per metre

= ₹ 66 x 6 = ₹ 396

The cost of fencing the plot at the rate of ₹ 6 per metre = ₹ 396

Question 4. The diameter of a cycle wheel is 28 cm. How many revolutions will it make in moving 13.21cm?

Solution:

Given

The diameter of a cycle wheel is 28 cm.

Distance travelled by the wheel in one revolution = \(2 \pi r=\frac{22}{7} \times 28=88 \mathrm{~cm}\)

Total distance travelled by the wheel = 13.2 x 1000 x 100 cm

Number, of revolutions made by the wheel = \(\frac{\text { total distance }}{\text { circumference }}\)

= \(\frac{13.2 \times 1000 \times 100}{88}=15000 \text { revolutions }\)

15000 revolutions will it make in moving 13.21cm.

Question 5. The circumference of a circle exceeds the diameter by 16.8 cm. Find the radius of the circle.

Solution:

Given

The circumference of a circle exceeds the diameter by 16.8 cm.

Let the radius of the circle be r.

Diameter = 2r

Circumference of circle = 2πr

Using the given information, we have

2πr = 2r + 16.8

⇒ \(2 \times \frac{22}{7} \times r=2 r+16.8\)

⇒ 44r = 14r + 16.8 x 7

⇒ 30r = 117.6

∴ \(r=\frac{117.6}{30}=3.92 \mathrm{~cm}\)

The radius of the circle =3.92 cm

Question 6. Find the area of a ring whose outer and inner radii are respectively 20cm and 1 5cm.

Solution:

Outer radius R = 20 cm

Inner radius r = 15 cm

∴ Area of ring = π(R² – r²)

⇒ Area of ring = \(\frac{22}{7}\left[(20)^2-(15)^2\right]=\frac{22}{7}(400-225)=\frac{22}{7} \times 175 \mathrm{~cm}^2\)

= 22 x 25 = 550 cm².

The area of a ring = 550 cm².

Question 7. A race track is in the form of a ring whose inner circumference is 352 m and the outer circumference is 396 m. Find the width of the track.

Solution:

Given

A race track is in the form of a ring whose inner circumference is 352 m and the outer circumference is 396 m.

Let R and r be the outer and inner radii of the circle.

The width of the track = (R – r) cm

Now, 2πr = 352 ⇒ \(2 \times \frac{22}{7} \times r=352\)

⇒ \(r=\frac{352 \times 7}{2 \times 22}=7 \times 8=56 \mathrm{~m}\)

Again, 2πR = 396 ⇒ \(2 \times \frac{22}{7} \times R=396\)

⇒ \(R=\frac{396 \times 7}{2 \times 22}=7 \times 9=63 \mathrm{~m}\)

∴ R = 63 m, r = 56 m

Width of the track = (R- r) m = (63 – 56) m = 7 m.

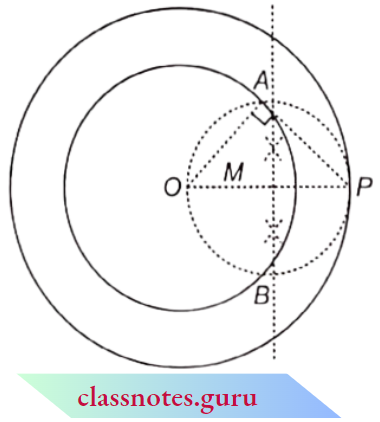
Question 8. Two circles touch internally. The sum of their areas is 116π cm² and the distance between their centres is 6 cm. Find the radii of the circles.

Solution:

Given

Two circles touch internally. The sum of their areas is 116π cm² and the distance between their centres is 6 cm.

Let two circles with centres O’ and O having radii R and respectively touch each other at P.

It is given that OO’ = 6

R – r = 6 ⇒ R = 6 + r → (1)

Also, πR² + πr² = 116π (given)

π(R² + r²) = 116π

⇒ R² + r²= 116 → (2)

∴ From equations (1) and (2), we get

(6 + r)² + r² = 116

⇒ 36 + r² + 12r + r²= 116 ⇒ 2r² + 12r – 80 = 0

⇒ r² + 6r – 40 = 0 = (r + 10) (r – 4) = 0

∴ r = -10 or r = 4

But the radius cannot be negative. So, we reject r = -10

∴ r = 4 cm

∴ R = 6 + 4 = 10cm [from(1)]

Hence, the radii of the two circles are 4 cm and 10 cm.

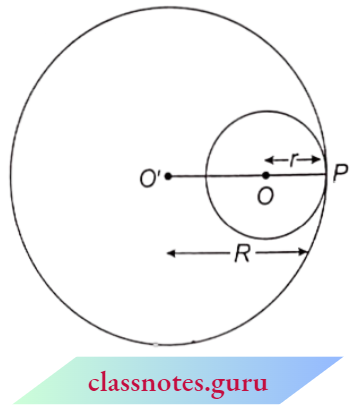
Area Related to Circles Class 10 Exemplar Solutions

Question 9. The radius of a wheel of a bus is 45 cm. Determine its speed in kilometres per hour, when its wheel makes 315 revolutions per minute.

Solution:

Given

The radius of the wheel of the bus = 45 cm

∴ Circumference of the wheel = 2ar

= \(2 \times \frac{22}{7} \times 45=\frac{1980}{7} \mathrm{~cm}\)

∴ Distance covered by the wheel in one revolution = \(\frac{1980}{7} \mathrm{~cm}\)

Distance covered by the wheel in 315 revolutions = \(315 \times \frac{1980}{7}\)

= 45 x 1 980 = 89 100 cm

= \(\frac{89100}{1000 \times 100} \mathrm{~km}=\frac{891}{1000} \mathrm{~km}\)

∴ Distance covered in 60 minutes or 1 hr =\(\frac{891}{1000} \times 60=\frac{5346}{100}=53.46 \mathrm{~km}\)

Hence, speed of bus = 53.46 km/hr

Question 10. Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the adjoining figure. Find the area of the shaded region.

Solution:

Given

Three semicircles each of diameter 3 cm, a circle of diameter 4.5 cm and a semicircle of radius 4.5 cm are drawn in the adjoining figure.

Required area = (area of larger semicircle with radius 4.5 cm) – (area of two smaller semicircles with radius of each \(\frac{3}{2}\) cm and a circle with radius \(\frac{4.5}{2}\) cm + (area of smaller semicircle with radius \(\frac{3}{2}\) cm)

= \(\frac{1}{2} \pi(4.5)^2-\left[2 \times \frac{1}{2} \pi\left(\frac{3}{2}\right)^2+\pi\left(\frac{4.5}{2}\right)^2\right]+\left[\frac{1}{2} \pi\left(\frac{3}{2}\right)^2\right]\)

= \(\frac{1}{2} \pi(4.5)^2-\pi\left(\frac{3}{2}\right)^2-\pi\left(\frac{4.5}{2}\right)^2+\frac{1}{2} \pi\left(\frac{3}{2}\right)^2\)

= \(\frac{1}{4} \pi\left[2 \times(4.5)^2-9-(4.5)^2+\frac{9}{2}\right]=\frac{1}{4} \pi \times 4.5[2 \times 4.5-2-4.5+1]\)

= \(\frac{1}{4} \pi \times 4.5(3.5)=\frac{1}{4} \times \frac{22}{7} \times 4.5 \times 3.5=12.375 \mathrm{~cm}^2\).

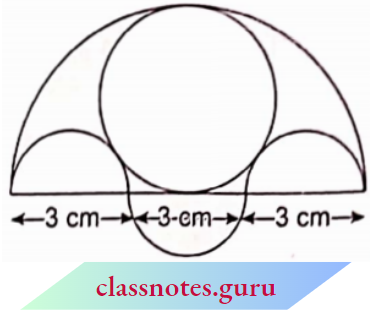
The area of the shaded region =12.375 cm².

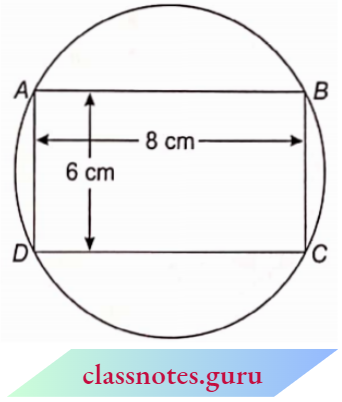
Question 11. In the adjoining figure, find the area of the shaded region. (Use π = 3.14)

Solution:

Diameter BD = \(\sqrt{6^2+8^2}=\sqrt{36+64}=\sqrt{100}=10 \mathrm{~cm}\)

Radius = \(]frac {10}{2}\) = 5 cm

Area of circle = πr² = 3. 1 4 x 52 = 3. 14 x 25 = 78.50 cm²

Area of rectangle ABCD = 8 x 6 = 48 cm²

Hence, area of shaded region = 78.50- 48 = 30.5 cm²

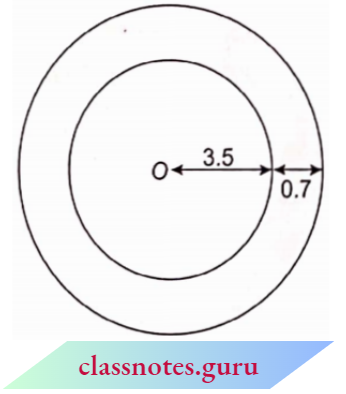
Question 12. A park is of the shape of a circle of diameter 7 m. It is surrounded by a path of width 0.7 m. Find the expenditure of cementing the path, if its cost is ₹ 110 per sq. m.

Solution:

Given

A park is of the shape of a circle of diameter 7 m. It is surrounded by a path of width 0.7 m

The radius of the circular park = 3.5 m

There is a path of width 0.7 m.

So, the radius of the external circle R = 3.5 + 0.7

⇒ R = 4.2 cm

Area of path = πR² – πr² = n(R- r) (R + r)

= \(\frac{22}{7}(4.2-3.5)(4.2+3.5)\)

= \(\frac{22}{7} \times 0.7 \times 7.7=16.94 \mathrm{~m}^2\)

Now, the cost of cementing 1 m² of path = ₹ 110

Cost of cementing 16.94 m² of path = ₹ ( 110 x 16.94) = ₹ 1863.40

Question 13. Find the area of the region between the two concentric circles, if the length of a chord of the outer circle just touching the inner circle at a particular point on it is 10 cm. \(Take, \pi=\frac{22}{7}\)

Solution:

Let the chord AB touch the inner circle at C and let 0 be the centre of both the circles, then

OC = r, OA = R and AB = 10 cm

Now, since OC ⊥ AB (∵ radius through the point of contact is perpendicular to the tangent)

∴ C is the mid-point of AB (∵ ⊥ drawn from the centre to the chord, bisects the chord)

⇒ \(A C=\frac{1}{2} A B=\frac{1}{2} \times 10=5 \mathrm{~cm}\)

Now, in right ΔOCA,

OA² = OC² +AC² (by Pythagoras theorem)

R² – r² = 25 → (1)

The required area of the region between two concentric circles

= πR² – πr² = π(R²– r²) – 25π [from(1)]

= \(25 \times \frac{22}{7}=78.57 \mathrm{~cm}^2\)

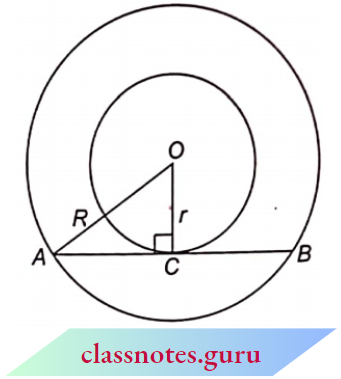
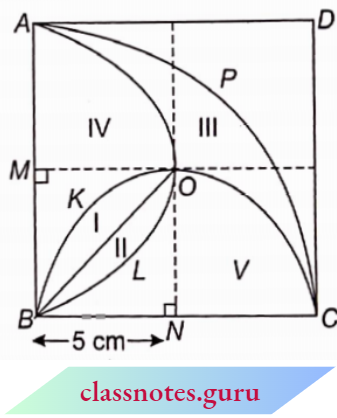
Question 14. In the adjoining figure, CM = 5 cm, RB = 9 cm, CD ⊥ AB, O is the centre of the larger circle and K is the centre of the smaller circle. Find the area of the shaded region.

Solution:

Let the radius of the larger circle be R and the radius of the smaller circle is r.

Since, CM = 5 cm

∴ MO = R – 5

Also OB = R and RB = 9

∴ OR = R – 9

In ΔAOM,

∠1 + ∠2 = 90° → (1)

In ΔAMR,

∠2 + ∠3 = 90° (the angle in a semicircle is the right angle) → (2)

From eqs. (1) and (2), we get

∠1 + ∠2 = ∠2 + ∠3

⇒ ∠1 = ∠3

In Δs AMO and MOR

∠1 = ∠3 (just proved)

∠4 = ∠5 (each 90°)

∴ ΔAMO ~ ΔMRO (AA corollary)

∴ \(\frac{M O}{R O}=\frac{A O}{M O}\)

⇒ \(\frac{R-5}{R-9}=\frac{R}{R-5}\)

⇒ (R – 5)² = R (R-9) = R² + 25 – 10R = R² – 9R

⇒ R = 25 cm

Now, 2R – 9 = 2r ⇒ 2r = 41

⇒ r = 20.5 cm

Required area = πR² – πr² = π(R + r) (R – r)

= \(\frac{22}{7} \times 45.5 \times 4.5 = 643.5 \mathrm{~cm}^2\)

Question 15. A square of the largest area is cut out of a circle. What % of the area of the circle is lost as trimmings?

Solution:

Let the radius of the circle be r units.

∴ Area of circle = πr² sq. units

Let ABCD be the largest square.

∴ Length of diagonal = 2r = side √2

side = \(\frac{2 r}{\sqrt{2}}=\sqrt{2} r\)

∴ Area (square ABCD) = (side)² = (√2r)² = 2r²

∴ Area of circle lost by cutting out of a square of largest area = 2r²

∴ Required percentage of the area of circle lost = \(\frac{2 r^2}{\pi r^2} \times 100=\frac{200}{\pi} \%\).

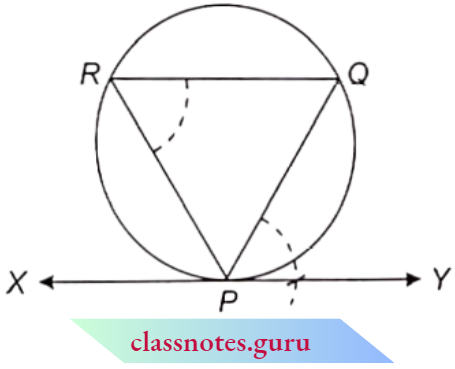
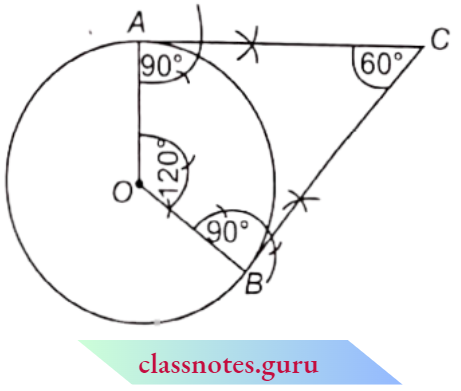
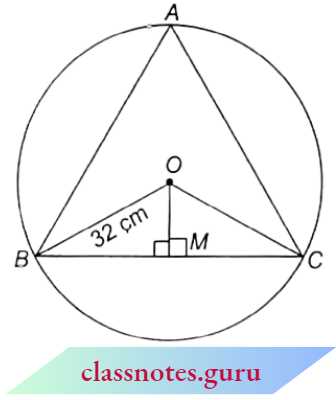
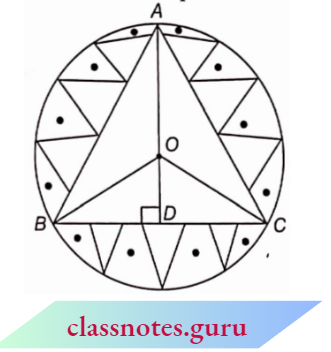
Question 16. In a circular table covering of radius 32 cm, a design (shade) is formed leaving an equilateral triangle ABC in the middle as shown in the adjacent figure. Find the area of the shaded region.

Solution:

Since ABC is an equilateral triangle.

∴ ∠A = 60°

⇒ ∠BOC = 2 x ∠BAC = 2 x 60° = 120° (degree measure of an arc is twice the angle subtended by it in an alternate segment)

Draw OM ⊥ BC

So, we can prove

ΔOMB ≅ ΔOMC (R.H.S. congruency)

∴ ∠BOM = ∠COM = 60° (c.p.c.t.)

In the right ΔOMB, we have

⇒ \(\sin 60^{\circ}=\frac{B M}{O B}\)

∴ \(\frac{\sqrt{3}}{2}=\frac{B M}{32} \quad = \quad B M=16 \sqrt{3} \mathrm{~cm}\)

∴ BC = 2 x 16√3 = 32√3 cm

∴ Area of shaded region = Area of circle- ar(AABC)

= \(\pi r^2-\frac{(\text { side })^2 \sqrt{3}}{4}=\pi \times(32)^2-(32 \sqrt{3})^2 \times \frac{\sqrt{3}}{4}\)

= \((32)^2\left(\frac{22}{7}-\frac{3 \sqrt{3}}{4}\right)=1024\left(\frac{22}{7}-\frac{3 \sqrt{3}}{4}\right) \mathrm{cm}^2\)

NCERT Exemplar Solutions for Class 10 Maths Chapter 12  Area Of Sector And Segment Of A Circle

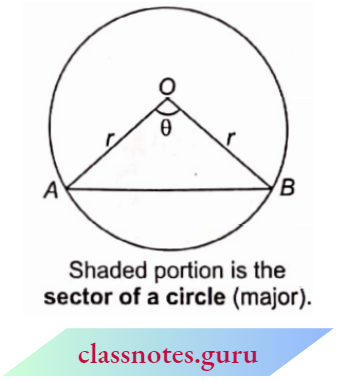
Sector: The shaded region (shown in the figure) OAXB is called a sector of the circle. Its boundary consists of arc AXB and two radii OA and OB. This sector has an angle θ, subtended at the centre of the circle by the arc AXB.

The region bounded by two radii of a circle and intercepted by them is called a sector of the circle.

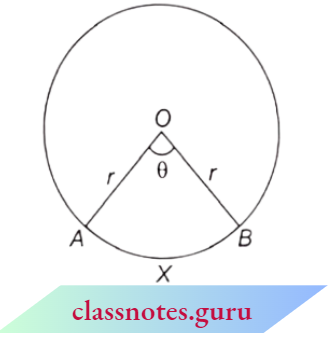
When θ < 180°, arc AB is a minor arc and when θ > 180°, arc AB is a major arc.

Now for sector AOB with ∠AOB = θ°, then the length of minor arc AB \(2 \pi r \times \frac{\theta}{360^{\circ}} \text { i.e., } \frac{\pi r \theta}{180^{\circ}}\)

(Actually, 2πr is the distance covered in travelling the whole circumference in which an angle of 360 is formed at the centre. But for the length of the arc AXB, we do not rotate 360°, here we needed only 0 part of 360°)

∴ \(l=\frac{2 \pi r \theta}{360}\)

and the area of sector is \(\pi r^2 \times \frac{\theta}{360^{\circ}}\)

∴ \(A=\frac{\pi r^2 \theta}{360^{\circ}}\)

Relation between Length of Arc and Area of Sector

Area of sector \(A=\pi r^2 \times \frac{\theta}{360^{\circ}}\)

= \(\pi r \times \frac{\theta}{360^{\circ}} \times r=\frac{1}{2} \times 2 \pi r \times \frac{\theta}{360} \times r=\frac{1}{2} l r\)

Segment of a Circle: A segment of a circle is defined as the part of a circle bounded by a chord and the circumference. The segment containing the major arc is the major segment while the segment containing the minor arc is a minor segment.

Area of minor segment = Area of the sector- an area of ΔOAB.

= \(\left(\frac{\pi r^2 \theta}{360^{\circ}}-\frac{1}{2} r^2 \sin \theta\right) \text { sq. unit }\)

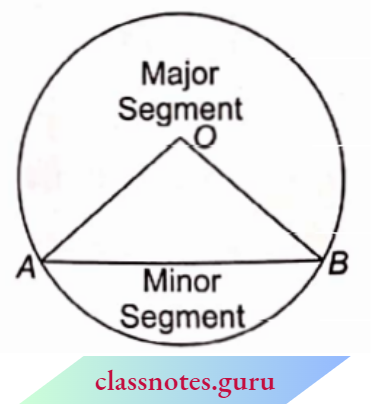
Area of major segment = Area of circle- Area of minor segment

Perimeter of sector = \(\frac{\pi r \theta}{180^{\circ}}+2 r\)

Perimeter of minor segment = \(\frac{\pi r \theta}{180^{\circ}}\) + Length of chord AB

Area of semicircle = \(\frac{\pi r^2}{2}\)

Perimeter of semicircle = \(\pi r+2 r\)

Area of quarter circle = \(\frac{\pi r^2}{4}\)

Perimeter of quarter circle = \(\frac{\pi r}{2}+2 r\)

NCERT Exemplar Solutions for Chapter 12 Class 10

NCERT Exemplar Solutions for Class 10 Maths Chapter 12  Area Related To Circles Solved Questions And Answers

Question 1. The perimeter of a semi-circular protractor is 32.4 cm. Calculate:

1. The radius of the protractor in cm,
2. the arc of the protractor in cm².

Solution:

Let the radius of the protractor be r cm.

Perimeter of semicircle protractor = (πr + 2r)cm

∴ r(π + 2) = 32.4

⇒ \(r\left(\frac{22}{7}+2\right)=32.4\)

⇒ \(r \times \frac{36}{7}=32.4 \quad ⇒ \quad r=\frac{32.4 \times 7}{36} ⇒ r=6.3 \mathrm{~cm}\)

Hence, the radius of the protractor = 6.3 cm

Area of semi-circular protractor = \(\frac{1}{2} \pi r^2\)

= \(\frac{1}{2} \times \frac{22}{7} \times 6.3 \times 6.3=62.37 \mathrm{~cm}^2\)

Hence, the area of the protractor = 62.37 cm²

Question 2. The minute hand of a clock is √2I cm long. Find the area described by the minute hand on the face of the clock between 6 a.m. and 6.05 a.m.

Solution:

In 60 minutes, the minute hand of a clock move through an angle of 360°.

∴ In 5 minutes hand will move through an angle = \(\frac{360^{\circ}}{60} \times 5=30^{\circ}\)

Now, r = √21 cm and θ = 30°

The area of sector described by the minute hand between 6 a.m. and 6.05 a.m.

= \(\frac{\pi r^2 \theta}{360^{\circ}}=\frac{22}{7} \times(\sqrt{21})^2 \times 30^{\circ} \times \frac{1}{360^{\circ}}=5.5 \mathrm{~cm}^2\)

Question 3. In the adjoining figure, calculate:

1. The length of minor arc ACB
2. Area of the shaded sector.

Solution:

Here, θ = 150°, r = 14 cm

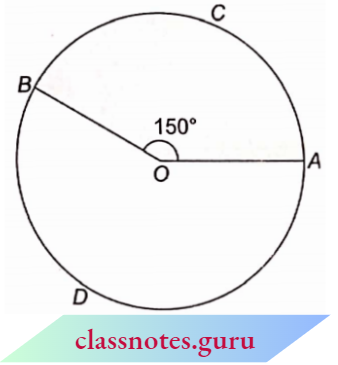
1. Length of minor arc = \(\frac{\pi r \theta}{180^{\circ}}\)

= \(\frac{22}{7} \times 14 \times 150^{\circ} \times \frac{1}{360^{\circ}}\)

= 36.67 cm

2. Area of shaded sector = \(\frac{\pi r^2 \theta}{360^{\circ}}=\frac{22}{7} \times(14)^2 \times 150^{\circ} \times \frac{1}{360^{\circ}}=256.67 \mathrm{~cm}^2\)

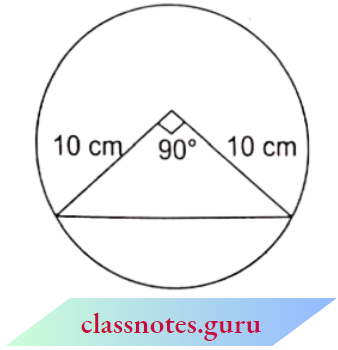
Question 4. A chord AB of a circle of radius 10 cm makes a right angle at the centre of the circle. Find the area of the major and minor segments. (Use π = 3.14).

Solution:

Area of sector OAB = \(\frac{\pi r^2 \theta}{360^{\circ}}=3.14 \times 10^2 \times \frac{90^{\circ}}{360^{\circ}}=78.5 \mathrm{~cm}^2\)

Now, area of \(\triangle A O B=\frac{1}{2} \times(10)^2=50 \mathrm{~cm}^2\)

Area of the minor segment = (78.5 – 50) cm² = 28.5 cm²

Area of the major segment = Area of the circle – Area of the minor segment

= (3.14 x 10² – 28.5) cm² = (314 – 28.5) cm² = 285.5 cm²

Question 5. In the adjoining figure, the side of the square is 28 cm and the radius of each circle is half of the length of the side of the square where O and O’ are the centres of the circle. Find the area of the shaded region.

Answer:

Side of square = 28 cm

and the radius of each circle = 14 cm

Required area = area of square excluding the two sectors + area of two circles

= \((28)^2-2\left[\pi(14)^2 \times \frac{90^{\circ}}{360^{\circ}}\right]+2\left[\pi(14)^2\right]\)

= \((28)^2-2 \times \frac{22}{7} \times 14 \times 14 \times \frac{1}{4}+2 \times \frac{22}{7} \times 14 \times 14\)

= 784 – 308 + 1232 = 1708 cm²

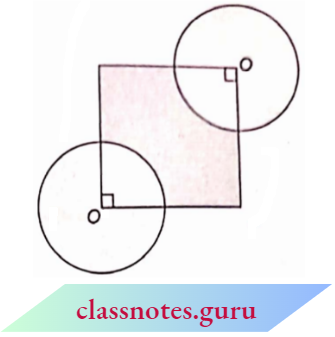
Question 6. In the adjoining figure, ABCD is a trapezium with AB || DC, AB = 18 cm, DC = 32 cm and the distance between AB and DC is 14 cm. If arcs of equal radii 7 cm taking A, B, C and D as centres, have been drawn, then find the area of the shaded region.

Solution:

Area of the shaded region

= area of trapezium – area of four sectors

= \(\begin{aligned}
\frac{1}{2} \times 14(32+18)-\left[\pi(7)^2 \times \frac{\angle A}{360^{\circ}}+\right. & \pi(7)^2 \times \frac{\angle B}{360^{\circ}} \left.+\pi(7)^2 \times \frac{\angle C}{360^{\circ}}+\pi(7)^2 \times \frac{\angle D}{360^{\circ}}\right]
\end{aligned}\)

= \(=7 \times 50-\frac{\pi \times(7)^2}{360^{\circ}}(\angle A+\angle B+\angle C+\angle D)\)

= \(=350-\frac{22}{7} \times \frac{7 \times 7}{360^{\circ}} \times 360^{\circ}\) (∵ sum of all the four angles of a quad. is 360°)

= 350 – 154 = 196 cm²

Hence, the area of the shaded region is 196 cm².

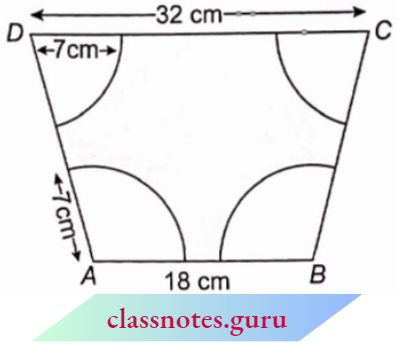
Question 7. In the adjoining figure, two circular flower beds have been shown on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection O of the diagonals of the square lawn, find the sum of areas of the lawn and the flower beds.

Solution:

We know that the diagonals of a square bisect each other perpendicularly.

∴ ∠DOC = 90°

Also diagonal BD = side √2 = 56√2m

∴ \(O D=\frac{1}{2} \times B D=28 \sqrt{2} \mathrm{~m}\)

∴ Area of \(\triangle D O C=\frac{1}{2} \times 28 \sqrt{2} \times 28 \sqrt{2}=(28)^2 m^2\)

Area of sector ODCO = \(\pi(O D)^2 \times \frac{\theta}{360^{\circ}}\)

= \(\pi(28 \sqrt{2})^2 \times \frac{90^{\circ}}{360^{\circ}}=\frac{11 \times 28 \times 28}{7} \mathrm{~m}^2\)

= 1232 m²

∴ Area of 1 flower bed = Area of sector- Area of A

= 1232 -(28)² = 448 m²

∴ Area of 2 flowers beds = 2 x 448 = 896 m²

Area of square lawn = (56)² = 3136 m²

∴ Required area = 896 + 3136 = 4032 m²

Question 8. In the adjoining, ABCD is a square of side 10 cm and two A semicircles with side of the square as diameter. A quarter circle is also seen with a side of the square as a radius. Find the area of the square region excluding the shaded part (Deepak).(Takeπ = 3.14)

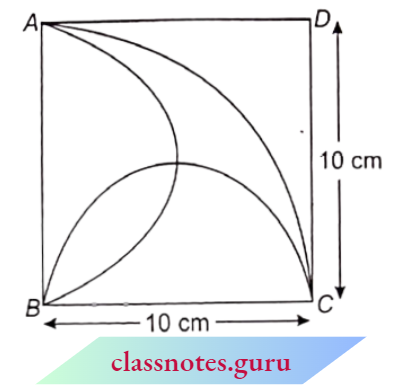
Solution:

First of all, we will find the area of 1 and 2 i.e., Batti of Deepak, draw OM ⊥ AB and ON ⊥ BC.

ar(1) = ar(sector NBKO) – ar(ABNO)

= \(\pi(5)^2 \times \frac{90^{\circ}}{360^{\circ}}-\frac{1}{2} \times 5 \times 5\)

ar (2) = ar (1)

⇒ \(\operatorname{ar}(\mathrm{1}+\mathrm{2})=2\left(\frac{25 \pi}{4}-\frac{25}{2}\right)=\frac{25}{2}(\pi-2)\)

∴ \(\frac{25}{2}(3.14-2)=14.25 \mathrm{~cm}^2\)

Now, area of deepak = ar(quadrant APCB) – [ar(semicircle 4 + 1 + 2) + ar(semicircle 5 + 1 + 2) – 2 x ar (1 + 2)]

= \(\pi(10)^2 \times \frac{90}{360}-\left[2 \times \frac{\pi(5)^2}{2}-2 \times 14.25\right]\)

25π – (25π – 28.5) = 28.5 cm²

Area of unshaded portion = Area of the square- Area of deepak

= (10)²– 28.5 = 100 – 28.5 = 71.5 cm²

The area of the square region excluding the shaded part = 71.5 cm²

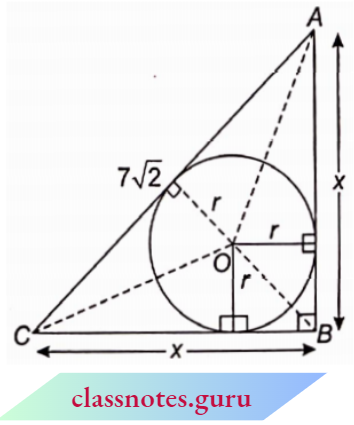
Question 9. If the hypotenuse of an isosceles right triangle is 7√2 cm, find the area of the circle inscribed in it.

Solution:

Let AB = BC = x cm

∴ In right ΔABC, by Pythagoras theorem

x² + y² = (7√2)²

⇒ 2x² = 98 = x² = 49 ⇒ x = 7 cm

∴ ar(ABC) = ar(AOB)+ ar(BOC) + ar(COA)

⇒ \(\frac{1}{2} \times x \times x=\frac{1}{2} \times x \times r+\frac{1}{2} \times x \times r+\frac{1}{2} \times 7 \sqrt{2} \times r\)

⇒\(r=\frac{7}{2+\sqrt{2}} \times \frac{2-\sqrt{2}}{2-\sqrt{2}}=\frac{7(2-\sqrt{2})}{2}\)

⇒ \(7 \times 7=7 \times r+7 \times r+7 \sqrt{2} \times r \Rightarrow r=\frac{7}{2+\sqrt{2}}\)

Area of circle = πr²

= \(\frac{22}{7} \times \frac{49(2-\sqrt{2})^2}{4}=\frac{77}{2} \times(4+2-4 \sqrt{2})\)

= 77(3 – 2√2) cm²

The area of the circle inscribed in it = 77(3 – 2√2) cm²

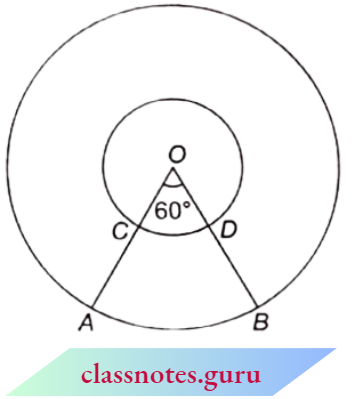
Question 10. In the adjoining figure, two concentric circles with centre O have radii of 21 cm and 42 cm. If ∠AOB = 60°, find the area of the shaded region. (\(\text { Use } \pi=\frac{22}{7}\))

Solution:

Required area = area of a larger circle with a radius of 42 cm – an area of a smaller circle with a radius of 21 cm – (area of unshaded portion CDBA)

= π(42)² – π(21 )² – [(area of the larger sector with radius 42 cm) – (area of the smaller sector with radius 21 cm)]

= \(\pi(42)^2-\pi(21)^2-\left[\pi(42)^2 \times \frac{60}{360}-\pi(21)^2 \times \frac{60}{360}\right]\)

= \(\pi(42)^2-\pi(21)^2-\frac{1}{6} \pi(42)^2+\frac{1}{6} \pi(21)^2=\frac{5}{6} \pi(42)^2-\frac{5}{6} \pi(21)^2\)

= \(\frac{5}{6} \pi \times(21)^2[4-1]=\frac{5}{6} \times \frac{22}{7} \times 21 \times 21 \times 3=3465 \mathrm{~cm}^2\)

The area of the shaded region =3465 cm²

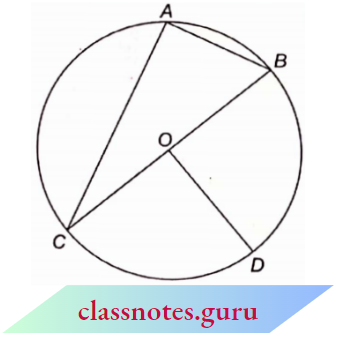
Question 11. In the adjoining figure, O is the centre of the circle with AC = 24 cm, AB = 7 cm and ∠BOD = 90°. Find the area of the shaded region.

Solution:

Since O is the centre of the circle.

∴ BC is the diameter of the circle.

∴ ∠CAB = 90° (angle in a semicircle is a right angle)

Now in right ΔACB, by Pythagoras Theorem,

BC² = AC² + AB² = (24)² + (7)² = 576 + 49 = 625

∴ BC = = 25 m

∴ Diameter of circle = 25 m

∴ Radius of circle = \(\frac{25}{2}\) = 12.5 m

∴ OC = OD = 12.5 m (each radii)

∴ Area of shaded region = area of circle – ar (ΔABC) – ar (sector COD)

= \(\pi(12.5)^2-\frac{1}{2} \times A C \times A B-\pi(O C)^2 \times \frac{90^{\circ}}{360^{\circ}}\)

= \(\frac{22}{7} \times 12.5 \times 12.5-\frac{1}{2} \times 24 \times 7-\frac{22}{7} \times 12.5 \times 12.5 \times \frac{1}{4}\)

= 491.07 – 84 – 122.768 = 284.302 = 284.30 m² (approx.)

The area of the shaded region = 284.30 m² (approx.)

Class 10 Maths Chapter 12 Area Related to Circles

NCERT Exemplar Solutions for Class 10 Maths Chapter 12  Area Related To Circles Exercise 12.1

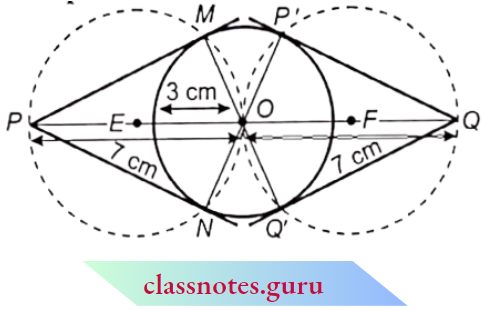
Question 1. The radii of the two circles are 19 cm and 9 cm respectively. Find the radius of the circle which has a circumference equal to the sum of the circumferences of the two circles.

Solution:

Here, r₁ = 19 cm and r₂ = 9cm

Let the radius of the new circle = R cm

Given that,

Circumference of new circle = sum of the circumference of given two circles

2πR = 2πr₁ + 2πr₂

R = r₁ + r₂ = 19 + 9 = 28 cm.

The radius of the circle = 28 cm.

Question 2. The radii of the two circles are 8 cm and 6 cm respectively. Find the radius of the circle having an area equal to the sum of the areas of the two circles.

Solution:

Here, r₁ = 8 cm and r₂ = 6 cm

Let the radius of the new circle = R cm

Given that,

Area of new circle = sum of areas of given circles

⇒ πR² = πr² + πr²

⇒ R² = r²₁ + r²₂ = 82 + 62

= 64 + 36 = 100

⇒ R = 10 cm

The radius of the circle = 10 cm

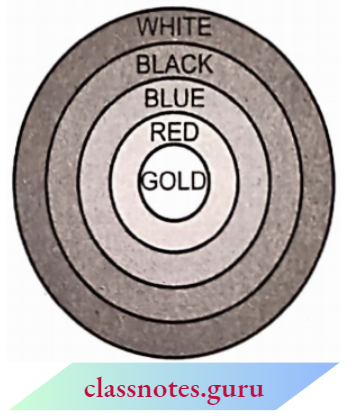
Question 3. The depicts an archery target marked with its five scoring regions from the centre outwards as Gold, Red, Blue, Black and White. The diameter of the region representing the Gold score is 21cm and each of the other bands is 10.5 cm wide. Find the area of each of the five scoring regions.

Solution:

The diameter of the Gold circle = 21 cm

∴ Radius of Gold circle = 10.5 cm

Now, the area of the Gold Circle

= \(\frac{22}{7} \times 10.5 \times 10.5 \mathrm{~cm}^2\)

= 346.5 cm²

Given, the width of each band = 10.5 cm

∴ Radius of Red circle = (10.5 + 10.5) = 21cm

Now, area of Red ring = [(external radius)² – (internal radius)²]

= \(\frac{22}{7}\left[(21)^2-(10.5)^2\right]\)

= \(\frac{22}{7} \times(441-110.25)\)

= \(\frac{22}{7} \times 330.75\)

= 1039.5 cm²

Again, radius of Blue circle = (21 + 10.5)cm = 31.5 cm

∴ Area of Blue ring

= \(\frac{22}{7}\left(31.5^2-21^2\right)\)

= \(\frac{22}{7} \times(992.25-441)\)

= \(\frac{22}{7} \times 551.25\)

= 1732.5 cm²

Again, the radius of the Black Circle

= (31.5 + 10.5)cm

= 42cm

∴ Area of Black circle

= \(\frac{22}{7} \times\left(42^2-31.5^2\right)\)

= \(\frac{22}{7} \times(1764-992.25)\)

= \(\frac{22}{7} \times 771.75=2425.5 \mathrm{~cm}^2\)

Again, radius of white circle = (42 + 10.5) cm

∴ Area of White circle

= \(=\frac{22}{7} \times\left(52.5^2-42^2\right)\)

= \(\frac{22}{7} \times(2756.25-1764)\)

= \(\frac{22}{7} \times 992.25=3118.5 \mathrm{~cm}^2\)

Question 4. The wheels of a car are of diameter 80 cm each. How many complete revolutions does each wheel make in 10 minutes when the car is travelling at a speed of 66 km per hour?

Solution:

The diameter of the wheel of a car, 2r= 80 cm

⇒ r = 40 cm

∴ Distance covered in one revolution

= circumference

= \(2 \pi r=2 \times \frac{22}{7} \times 40=\frac{1760}{7} \mathrm{~cm}\)

Now, speed of car = 66 km/hr

= \(\frac{66 \times 1000 \times 100}{60} \mathrm{~cm} / \mathrm{min}\)

∴ Distance covered in 10 minutes

= \(\frac{66 \times 1000 \times 100}{60} \times 10 \mathrm{~cm}\)

= 11 x 1000 x 100 cm

Now, the number of revolutions made by the wheel

= \(\frac{\text { Total distance covered }}{\text { Distance covered by wheel in 1 revolution }}\)

= \(\frac{11 \times 1000 \times 100}{1760 / 7}\)

= \(=\frac{11 \times 1000 \times 100 \times 7}{1760}=4375 \text { Ans }\)

Question 5. Tick the correct answer in the following and justify your choice: if the perimeter and the area of a circle are numerically equal, then the radius of the circle is:

1. 2 units
2. units
3. 4 units
4. 7 units

Solution:

1. 2 units

Let r be the radius of the circle.

Given that, in numerical form, area of circle = perimeter of circle

⇒ πr² = 2πr ⇒ r = 2 units

NCERT Exemplar Class 10 Maths Area Related to Circles with solutions

NCERT Exemplar Solutions for Class 10 Maths Chapter 12  Area Related To Circles Exercise 12.2

Question 1. Find the area of a sector of a circle with a radius of 6 cm if the angle of the sector is 60°.

Solution:

Here, the radius of the circle, r = 6 cm

The angle of the sector, θ= 60°

∴ Area of sector = \(\frac{\theta}{360^{\circ}} \times \pi r^2\)

= \(\frac{60^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 6 \times 6 \mathrm{~cm}^2\)

= \(\frac{132}{7} \mathrm{~cm}^2 \text { or } 18.86 \mathrm{~cm}^2\)

The area of a sector of a circle is 18.86 cm²

Question 2. Find the area of a quadrant of a circle whose circumference is 22 cm.

Solution:

Circumference of the circle, 2πr = 22

⇒ \(2 \times \frac{22}{7} \times r=22 \quad \Rightarrow \quad r=\frac{7}{2} \mathrm{~cm}\)

Now, the area of the quadrant of a circle

⇒ \(\frac{1}{4} \pi r^2=\frac{1}{4} \times \frac{22}{7} \times \frac{7}{2} \times \frac{7}{2}\)

∴ \(\frac{77}{8} \mathrm{~cm}^2\)

The area of a quadrant of a circle = \(\frac{77}{8} \mathrm{~cm}^2\)

Question 3. The length of the minute hand of a clock is 14 cm. Find the area swept by the minute hand in 5 minutes.

Solution:

Length of minute hand of clock = 14 cm

∴ The radius of the circle, r = 14 cm

∵ The angle subtended by minute hand in 60 min = 360°

∴ Angle subtended by minute hand in 1 minute = \(\frac{360^{\circ}}{60^{\circ}}=6^{\circ}\)

∴ The angle subtended by minute hand in 5 minutes = 30°

∴ From the formula,

area of sector of circle = \(\frac{\theta \pi r^2}{360^{\circ}}\)

= \(30^{\circ} \times \frac{22 \times(14)^2}{7 \times 360^{\circ}}\)

= \(\frac{22 \times 14 \times 2}{12}\)

= \(\frac{616}{12}=\frac{154}{3} \mathrm{~cm}^2\)

The area swept by the minute hand in 5 minutes =\(\frac{154}{3} \mathrm{~cm}^2\)

Question 4. A chord of a circle of radius 10 cm subtends a right angle at the centre. Find the area of the corresponding:

1. Minor segment
2. Major sector

Solution:

Given, the radius of the circle, AO = 10 cm.

The perpendicular is drawn from the centre of the circle to the chord of the circle which bisects this chord.

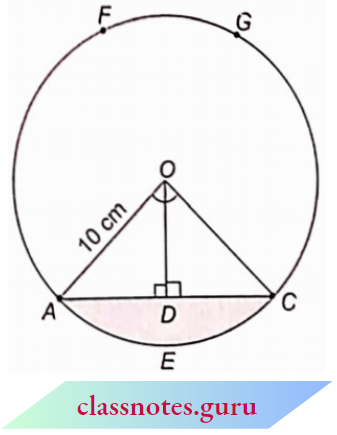
AD = DC

And ∠AOD = ∠COD

= 45°

∴ ∠AOC = ∠AOD + ∠COD

= 45° + 45° = 90°

In the right ΔAOD,

⇒ \(\sin 45^{\circ}=\frac{A D}{A O} \quad \Rightarrow \quad \frac{1}{\sqrt{2}}=\frac{A D}{10}\)

AD = 5√2 cm

and \(\cos 45^{\circ}=\frac{O D}{A O} \Rightarrow \frac{1}{\sqrt{2}}=\frac{O D}{10}\)

⇒ OD = 5√2 cm

Now, AC = 2AD

2 x 5√2 = 10√2 cm

Now, the area of ΔAOC

= \(\frac{1}{2} A C \times O D\)

= \(\frac{1}{2} \times 10 \sqrt{2} \times 5 \sqrt{2}=50 \mathrm{~cm}^2\)

Now the area of the sector

= \(\frac{\theta \pi r^2}{360^{\circ}}=\frac{90^{\circ}}{360^{\circ}} \times 3.14 \times(10)^2\)

= \(\frac{314}{4}=78.5 \mathrm{~cm}^2\)

1. Area of minor segment AEC

= area of sector OAEC – area of AOC

= 78.5 – 50 = 28.5 cm²

2. Area of major sector OAFGCO

= area of circle- area of sector OAEC

= πr²– 78.5 = 3.14 x (10)² – 78.5

314 – 78.5 = 235.5cm²

Question 5. In a circle of radius 21 cm, an arc subtends an angle of 60° at the centre. Find:

1. The length of the arc
2. The area of the sector formed by the arc
3. The area of the segment is formed by the corresponding chord.

Solution:

Here, the radius of circle r = 21 cm

The angle subtended by are at the centre, θ = 60°

1. Length of arc

= \(l=\frac{\theta}{360^{\circ}} \times 2 \pi r\)

= \(\frac{60^{\circ}}{360^{\circ}} \times 2 \times \frac{22}{7} \times 21=22 \mathrm{~cm}\)

2. Area of sector formed by the arc

= \(\frac{\theta}{360^{\circ}} \times \pi r^2\)

= \(\frac{60^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 21 \times 21\)

= 231 cm²

3. Area of segment formed by the corresponding chord

= \(\frac{\pi r^2 \theta}{360^{\circ}}-\frac{1}{2} r^2 \sin \theta\)

= \(231-\frac{1}{2} \times 21 \times 21 \times \sin 60^{\circ}\)

= \(\left(231-\frac{441 \sqrt{3}}{4}\right) \mathrm{cm}^2\)

Question 6. A chord of a circle of radius 15 cm subtends an angle of 60° at the centre. Find the areas of the corresponding minor and major segments of the circle.

(Use π = 3.14 and √3 = 1.73)

Solution:

Given

A chord of a circle of radius 15 cm subtends an angle of 60° at the centre.

Here, the radius of the circle, r = 15 cm

The angle subtended by a chord at the centre, θ = 60°

∴ Area of the corresponding minor segment

= \(\frac{\pi r^2 \theta}{360^{\circ}}-\frac{1}{2} r^2 \sin \theta\)

= \(r^2\left(\frac{\pi \theta}{360^{\circ}}-\frac{1}{2} \sin \theta\right)\)

= \(15 \times 15\left(\frac{3.14 \times 60^{\circ}}{360^{\circ}}-\frac{1}{2} \sin 60^{\circ}\right)\)

= \(225\left(\frac{3.14}{6}-\frac{1}{2} \times \frac{\sqrt{3}}{2}\right)\)

= \(225\left(\frac{3.14}{6}-\frac{1.73}{4}\right)=20.4375 \mathrm{~cm}^2\)

Now, the area of the circle = πr²

= 3.14 x 15 x 15 = 706.5 cm²

∴ Area of major segment = area of circle – an area of the minor segment

= (706.5 – 20.4375) cm²

= 686.0625 cm².

The areas of the corresponding minor and major segments of the circle = 686.0625 cm².

Question 7. A chord of a circle of radius 12 cm subtends an angle of 120° at the centre. Find the area of the corresponding segment of the circle.
(Use π = 3.14 and √3 = 1.73)

Solution:

Given

A chord of a circle of radius 12 cm subtends an angle of 120° at the centre.

Here, the radius of the circle, r = 12 cm

The angle subtended by the chord at the centre, θ = 120°

Area of the corresponding minor segment

= \(\frac{\pi r^2 \theta}{360^{\circ}}-\frac{1}{2} r^2 \sin \theta\)

= \(r^2\left(\frac{\pi \theta}{360^{\circ}}-\frac{1}{2} \sin \theta\right)\)

= \(12 \times 12 \times\left(\frac{3.14 \times 120^{\circ}}{360^{\circ}}-\frac{1}{2} \times \sin 120^{\circ}\right)\)

= \(144\left(\frac{3.14}{3}-\frac{1}{2} \times \frac{\sqrt{3}}{2}\right)\)

= \(144\left(\frac{3.14}{3}-\frac{1.73}{4}\right)\)

= 88. 44 cm²

The area of the corresponding segment of the circle = 88. 44 cm²

Question 8. A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 5 m long rope. Find:

1. The area of that part of the field in which the horse can graze.
2. The increase in the grazing area, if the rope were 10 m long instead of 5m. (Use π = 3.14)

Solution:

Given

A horse is tied to a peg at one corner of a square-shaped grass field of side 15 m by means of a 5 m long rope.

Side of square field = 15 m

The radius of the circle, r = 5m

The angle formed by chord, θ = 90°

1. Area of that part of the field where the horse can graze the grass

= \(\frac{\theta}{360^{\circ}} \times \pi r^2=\frac{90^{\circ}}{360^{\circ}} \times 3.14 \times 5^2\)

= 19.625 m²

Area of that part of the field where the horse can graze the grass = 19.625 m²

2. If the length of the rope is 10 m then the increase in the area of grazing.

= \(\frac{90^{\circ}}{360^{\circ}} \times 3.14 \times\left(10^2-5^2\right)\)

= \(\frac{1}{4} \times 3.14 \times 75\)

= 58.875 m².

If the length of the rope is 10 m then the increase in the area of grazing = 58.875 m².

Area Related to Circles problems and solutions Class 10

Question 9. A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown. Find:

1. The total length of the silver wire required.
2. The area of each sector of the brooch.

Solution:

Given

A brooch is made with silver wire in the form of a circle with a diameter of 35 mm. The wire is also used in making 5 diameters which divide the circle into 10 equal sectors as shown.

1. Diameter of circular brooch,

2r = 35 mm

= \(r=\frac{35}{2} \mathrm{~mm}\)

Length of required silver wire = 2πr

= \(2 \times \frac{22}{7} \times \frac{35}{2} \mathrm{~mm}=110 \mathrm{~mm}\)

Now, the length of 5 diameters = 5 x 2r

= \(5 \times 2 \times \frac{35}{2}=175 \mathrm{~mm}\)

Length of total wire = (110 + 175) mm

= 285 mm

The total length of the silver wire required = 285 mm

2. For each sector,

angle, \(\theta=\frac{360^{\circ}}{10^{\circ}}=36^{\circ}\)

∴ Area = \(\frac{\theta}{360^{\circ}} \times \pi r^2\)

= \(\frac{36^{\circ}}{360^{\circ}} \times \frac{22}{7} \times \frac{35}{2} \times \frac{35}{2}\)

= \(\frac{385}{4} \mathrm{~cm}^2\)

The area of each sector of the brooch = \(\frac{385}{4} \mathrm{~cm}^2\)

Question 10. An umbrella has 8 ribs which are equally spaced. Assuming an umbrella to be a flat circle of radius 45 cm, find the area between the two consecutive ribs of the umbrella.

Solution:

Given

An umbrella has 8 ribs which are equally spaced. Assuming an umbrella to be a flat circle of radius 45 cm

The radius of the umbrella,

r = length of ribs of umbrella = 45 cm

Here, number of sectors = 8

∴ Angle of sector = \(\theta=\frac{360^{\circ}}{8}=45^{\circ}\)

Now, the area between two ribs = area of the sector

= \(\frac{\theta}{360^{\circ}} \times \pi r^2\)

= \(\frac{45^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 45 \times 45 \mathrm{~cm}^2\)

= \(\frac{22275}{28} \mathrm{~cm}^2\)

The area between the two consecutive ribs of the umbrella = \(\frac{22275}{28} \mathrm{~cm}^2\)

Question 11. A car has two wipers which do not overlap. Each wiper has a blade of length 25 cm sweeping through an angle of 115°. Find the total area cleaned at each sweep of the blades.

Solution:

Given, the length of the wiper blade

r = 25 cm = r(say)

The angle formed by this blade, θ =115°

∴ Area cleaned by a blade = area of sector formed by blade

= \(\frac{\theta \pi r^2}{360^{\circ}}=115^{\circ} \times \frac{22}{7 \times 360^{\circ}} \times(25)^2\)

= \(\frac{23 \times 22}{7 \times 72} \times 625=\frac{23 \times 11 \times 625}{7 \times 36}\)

= \(\frac{158125}{252} \mathrm{~cm}^2\)

∴ Total area cleaned by two blades

= 2 x area cleaned by a blade

= \(\frac{2 \times 158125}{252}=\frac{158125}{126} \mathrm{~cm}^2\)

The total area cleaned at each sweep of the blades =\(\frac{158125}{126} \mathrm{~cm}^2\)

Question 12. To warn ships of underwater rocks, a lighthouse spreads a red-coloured light over a sector of angle 80° to a distance of 16.51cm. Find the area of the sea over which the ships are warned. (Use π = 3.14)

Solution:

Given, the angle of the sector, θ = 80°

And distance or radius, r = 16.5 km

Area of sector

= \(\frac{\theta \pi r^2}{360^{\circ}}=\frac{80^{\circ} \times 3.14 \times(16.5)^2}{360^{\circ}}\)

= \(\frac{2 \times 3.14 \times 272.25}{9}=\frac{1709.73}{9}=189.97 \mathrm{~km}^2\) which is the area of the sea over which the ships are warned.

Question 13. A round table cover has six equal designs as shown. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of ₹ 0.35 per cm². (Use √3 = 1.7)

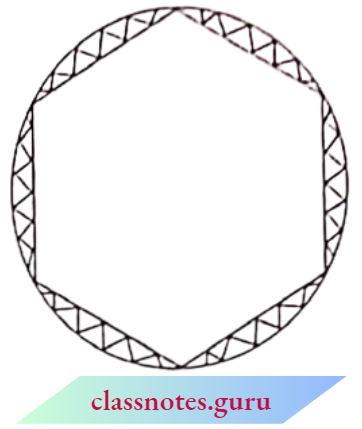
Solution:

Given

A round table cover has six equal designs as shown. If the radius of the cover is 28 cm

The radius of the table cover, r = 28 cm

Number of designs formed on table cover = 6

∴ The angle formed by each chord at the centre

= \(\frac{360^{\circ}}{6}=60^{\circ}\)

Now, the area of segment

= \(\frac{\pi r^2 \theta}{360^{\circ}}-\frac{1}{2} r^2 \sin \theta\)

= \(r^2\left(\frac{\pi}{360^{\circ}}-\frac{1}{2} \sin \theta\right)\)

⇒ Area of 6 segments

= \(6 r^2\left(\frac{\pi}{360^{\circ}}-\frac{1}{2} \sin \theta\right)\)

= \(6 \times 28 \times 28\left(\frac{60^{\circ}}{360^{\circ}} \times \frac{22}{7}-\frac{1}{2}-\sin 60^{\circ}\right)\)

= \(6 \times 28 \times 28\left(\frac{11}{21}-\frac{1}{2} \times \frac{\sqrt{3}}{2}\right)\)

= \(=6 \times 28 \times 28\left(\frac{11}{21}-\frac{1.73}{4}\right)=464.8 \mathrm{~cm}^2\)

Now, the total cost of making the design

= ₹ 0.35 x 464.8 = ₹ 162.68

The total cost of making the design = ₹ 162.68

Question 14. The area of a sector of angle p (in degrees) of a circle with radius R is

1. \(\frac{p}{180} \times 2 \pi R\)
2. \(\frac{p}{180} \times \pi R^2\)
3. \(\frac{p}{360} \times 2 \pi R\)
4. \(\frac{p}{720} \times 2 \pi R^2\)

Solution:

4. \(\frac{p}{720} \times 2 \pi R^2\)

Area of sector = \(\frac{\theta}{360^{\circ}} \times \pi r^2\)

= \(\frac{p}{360^{\circ}} \times \pi R^2=\frac{p}{720} \times 2 \pi R^2\)

NCERT Exemplar Solutions for Class 10 Maths Chapter 12  Area Related To Circles Exercise 12.3

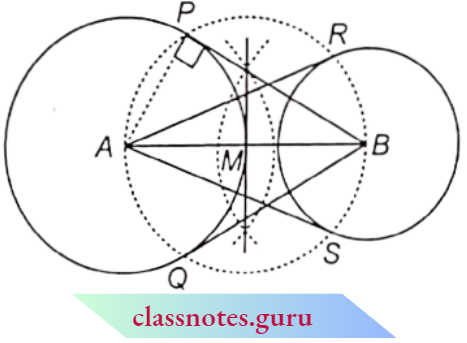
Question 1. Find the area of the shaded region in the figure, if PQ= 24 cm, PR = 7 cm and O is the centre of the circle.

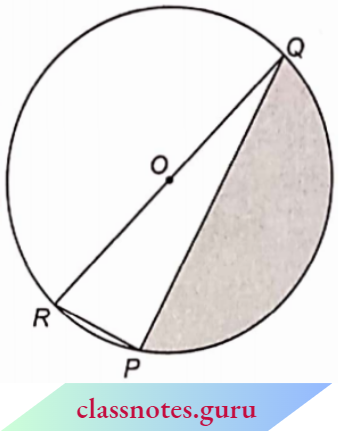
Solution:

Here, PQ = 24 cm and PR = 7 cm

∵ The angle in a semicircle is a right angle.

∴ ∠QPR = 90°

In ΔPQR,

QR² = PQ² + PR² = 24² + 7² = 625

QR = 25 cm

If r is the radius of the circle, then

2r = 25 cm

= \(r=\frac{25}{2} \mathrm{~cm}\)

Area of shaded region = area of semicircle – area of ΔPQR

= \(\frac{1}{2} \pi r^2-\frac{1}{2} \times P Q \times P R\)

= \(\frac{1}{2} \times \frac{22}{7} \times \frac{25}{2} \times \frac{25}{2}-\frac{1}{2} \times 24 \times 7\)

= \(\frac{6875}{28}-84=\frac{4523}{28} \mathrm{~cm}^2\)

The area of the shaded region =\(\frac{4523}{28} \mathrm{~cm}^2\)

Question 2. Find the area of the shaded region, if the radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.

Solution:

Given

The radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC = 40°.

Here, OA = 14 cm and OB = 7 cm

The angle of the sector, θ = 40°

∴ Area of the shaded portion

= \(\frac{\theta}{360^{\circ}} \times \pi \times\left(O B-O A^2\right)\)

= \(\frac{40^{\circ}}{360^{\circ}} \times \frac{22}{7} \times\left(14^2-7^2\right)\)

= \(\frac{1}{9} \times \frac{22}{7} \times 147=51.33 \mathrm{~cm}^2\)

The area of the shaded region =51.33 cm².

Question 3. Find the area of the shaded region, if ABCD is a square of side 14 cm and APD and BPC are semicircles.

Solution:

Given

ABCD is a square of side 14 cm and APD and BPC are semicircles.

Side of square = 14

Area of square = 14 x 14 cm² = 196 cm²

Diameter of each semicircle 2r = side of square = 14 cm

⇒ r = 7 cm

Area of one semicircle = \(\frac{1}{2} \pi r^2\)

Area of two semicircles = \(2 \times \frac{1}{2} \pi r^2=\pi r^2\)

= \(\frac{22}{7} \times 7 \times 7=154 \mathrm{~cm}^2\)

Area of shaded portion = area of the square – the sum of areas of two semicircles

= (196 – 154) cm² = 42 cm²

The area of the shaded region = 42 cm²

Question 4. Find the area of the shaded region given, where a circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as the centre.

Solution:

Given

A circular arc of radius 6 cm has been drawn with vertex O of an equilateral triangle OAB of side 12 cm as the centre.

Each side of the equilateral triangle = 12 cm

and each angle = 60°

Now, the area of an equilateral triangle

= \(\frac{\sqrt{3}}{4} \times(\text { side })^2=\frac{\sqrt{3}}{4} \times 12 \times 12 \mathrm{~cm}^2\)

= 36√3 cm²

The radius of the circle, r = 6 cm

Angle of major sector, 0 = 360° – 60° = 300°

∴ Area of major sector

= \(\frac{\theta}{360^{\circ}} \times \pi r^2\)

= \(\frac{300^{\circ}}{360^{\circ}} \times \frac{22}{7} \times 6 \times 6=\frac{660}{7} \mathrm{~cm}^2\)

Now, the area of the shaded region = area of the equilateral triangle + area of a major sector.

= \(\left(36 \sqrt{3}+\frac{660}{7}\right) \mathrm{cm}^2\)

The area of the shaded region = \(\left(36 \sqrt{3}+\frac{660}{7}\right) \mathrm{cm}^2\)

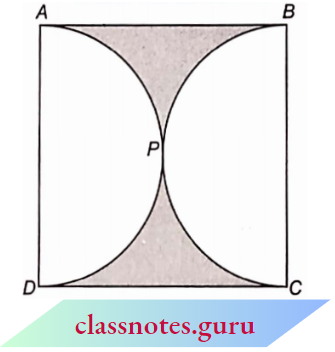
Question 5. From each A corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown. Find the area of the remaining portion of the square.

Solution:

Given

From each A corner of a square of side 4 cm a quadrant of a circle of radius 1 cm is cut and also a circle of diameter 2 cm is cut as shown.

Side of square = 4 cm

∴ Area of square = (side)² = 4² = 16 cm²

The radius of a quadrant of a circle, r = 1 cm

∴ Area of four quadrants

= \(4 \times \frac{1}{4} \pi r^2\)

= \(\frac{22}{7} \times 1 \times 1=\frac{22}{7} \mathrm{~cm}^2\)

For the circle inside the square diameter, 2R = 2 cm ⇒ R = 1 cm

Area of this circle = \(\pi R^2=\frac{22}{7} \times 1 \times 1=\frac{22}{7} \mathrm{~cm}^2\)

Now, area of shaded portion = \(16-\left(\frac{22}{7}+\frac{22}{7}\right)=\frac{68}{7} \mathrm{~cm}^2\).

Question 6. In a circular table covered of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown. Find the area of the design.

Solution:

Given

In a circular table covered of radius 32 cm, a design is formed leaving an equilateral triangle ABC in the middle as shown.

ΔABC is an equilateral triangle.

∴ ∠A = ∠B = ∠C = 60°

AD is perpendicular to BC.

∴ OA, OB, and OC are the radii of the circle.

Given that,

OA = OB = OC = 32 cm

∠BOC = 2

∠BAC = 2 x 60° = 120°

∴ \(\angle B O D=\frac{1}{2} \times 120^{\circ}=60^{\circ}\)

In ΔBOD

⇒ \(\sin 60^{\circ}=\frac{B D}{O B} ⇒ \frac{\sqrt{3}}{2}=\frac{B D}{32}\)

BD = 16√3 cm

BC = 2 BD = 32√3 cm

Area of ΔABC = \(\frac{\sqrt{3}}{4} \times B C^2\)

= \(\frac{\sqrt{3}}{4} \times(32 \sqrt{3})^2=768 \sqrt{3} \mathrm{~cm}^2\)

Area of circle = π(OB)²

= \(\frac{22}{7} \times 32 \times 32=\frac{22528}{7} \mathrm{~cm}^2\)

Now, the area of the shaded portion

= area of a circle – an area of ΔABC

= \(\left(\frac{22528}{7}-768 \sqrt{3}\right) \mathrm{cm}^2\).

The area of the shaded portion = \(\left(\frac{22528}{7}-768 \sqrt{3}\right) \mathrm{cm}^2\).

Important questions for Class 10 Maths Chapter 12 with solutions

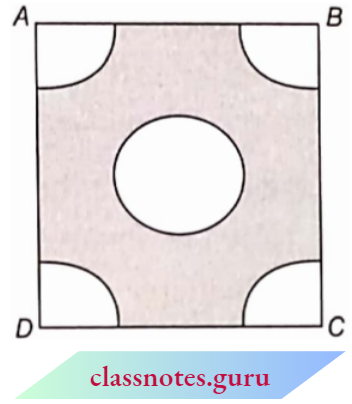
Question 7. In the ABCD is a square of side 14 cm. With centres A. B. C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.

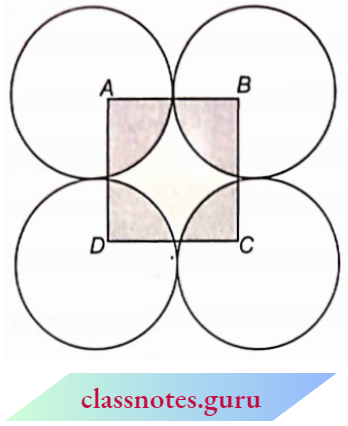
Solution:

Side of square ABCD = 14 cm

∴ Area of square = (14)² =196 cm²

Radius of first quadrant \(r=\frac{14}{2}=7 \mathrm{~cm}\)

∴ The sum of area’s four quadrants

= \(4 \times \frac{1}{4} \pi r^2=\pi r^2\)

= \(\frac{22}{7} \times 7 \times 7=154 \mathrm{~cm}^2\)

Now, the area of the shaded portion = area of the square – the sum of areas of four quadrants

= 196 = 154 = 42 cm²

The area of the shaded region = 42 cm²

Question 8. depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60 m and they are each 106 m long. If the track is 10 m wide, find:

1. The distance around the track along its inner edge.
2. The area of the track.

Solution:

Hence OB O’C = \(\frac{60}{2}=30 \mathrm{~m}\)

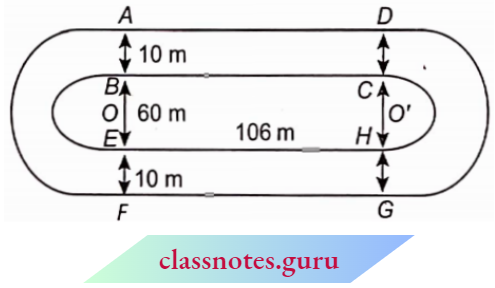
AB = CD = 10m

∴ OA = O’D = (30 + 10) m = 40 m

1. Distance covered in one round along the inner edges of the path.

= BC + EH + 2 x circumference of semicircle

= \(106+106+2 \times \frac{1}{2} \times 2 \pi \times 30\)

= \(212+2 \times \frac{22}{7} \times 30=\frac{2804}{7} \mathrm{~m}\)

2. Inner radius r = OB = 30 m

Outer radius R = OA = 40 m

Area of path = 2 x area of ABCD + 2 x area of semicircular rings

= \(=2 \times 106 \times 10+\frac{1}{2} \times \pi\left(R^2-r^2\right)\)

= \(2120+\frac{22}{7} \times\left(40^2-30^2\right)\)

= 2120 + 2200 = 4320 m²

Area of path is 4320 m²

Question 9. In the figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm, find the area of the shaded region.

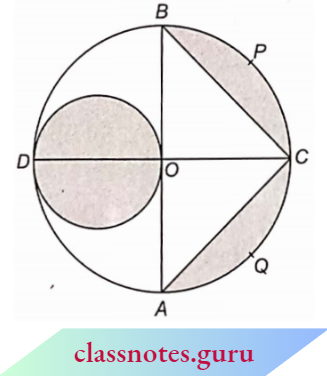
Solution:

Given

In the figure, AB and CD are two diameters of a circle (with centre O) perpendicular to each other and OD is the diameter of the smaller circle. If OA = 7 cm

The diameter of the smaller circle

OD = OA = 7 cm

∴ Radius r = \(\frac{7}{2}=3.5 \mathrm{~cm}\)

∴ Area of smaller circle = nr2

= \(\frac{22}{7} \times 3.5 \times 3.5 \mathrm{~cm}^2=38.5 \mathrm{~cm}^2\)

Area of semicircle OAQCPBO

= \(\frac{1}{2} \pi(O A)^2\)

= \(\frac{1}{2} \times \frac{22}{7} \times 7 \times 7=77 \mathrm{~cm}^2\)

Area of ΔABC = = \(\frac{1}{2} \times A B \times O C\)

= \(\frac{1}{2} \times 14 \times 7=49 \mathrm{~cm}^2\)

Now the area of the shaded portion = area of the smaller circle + area of OAQCPBO – an area of ABC

= 38.5 + 77 –  49 = 66. cm²

The area of the shaded region = 66. cm²

Question 10. The area of an equilateral triangle 11 ABC is 17320.5 cm². With each vertex of the triangle as the centre, a circle is drawn with a radius equal to half the length of the side of the triangle. Find the area of the shaded region. (Use π= 3.24 and √3 = 1.73205).

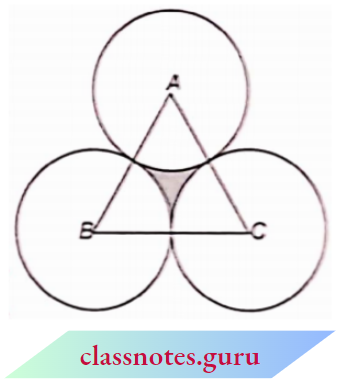
Solution:

Given

The area of an equilateral triangle 11 ABC is 17320.5 cm². With each vertex of the triangle as the centre, a circle is drawn with a radius equal to half the length of the side of the triangle.

Let the radius of each circle = r

Side of equilateral triangle = r + r = 2r

Now, area of equilateral triangle = \(\)

Given that, √3r² = 17320.5 ⇒ 1.73205r² = 17320.5

⇒ r² = 10000 ⇒ r = 100 cm

Each angle of an equilateral triangle, θ = 60° Now, the area of sectors of three circles

= \(3 \times \frac{\theta}{360^{\circ}} \times \pi r^2\)

= \(3 \times \frac{60^8}{360^{\circ}} \times 3.14 \times(100)^2\)

= 15700 cm²

Area of shaded region = area of equilateral ABD = area of three sectors

= (17320.5 – 15700) cm²

= 1620.5 cm²

The area of the shaded region = 1620.5 cm².

Question 11. On a square handkerchief, nine circular designs each of a radius of 7 cm are made. Find the area of the remaining portion of the handkerchief.

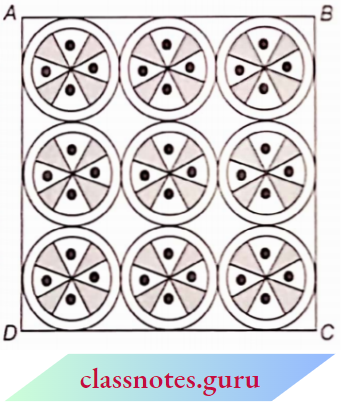
Solution:

Given, the radius of each circle, r = 7 cm

Diameter of circle, d = 14 cm = 42 cm (∵ diameter = 2 x radius)

Three horizontal circles touch each other.

Length of square = 3 x 14 cm = 42 cm

Now area of a circle = πr² = (7)²

= \(\frac{22}{7} \times(7)^2=154 \mathrm{~cm}^2\)

∴ Area of 9 circles = 9 x 154 = 1386 cm²

Now, area of square ABCD = (side)²

= (42)² = 1764 cm²

∴ Area of the remaining part of the handkerchief

= 1764 – 1386 = 378 cm²

The area of the remaining portion of the handkerchief = 378 cm²

Question 12. The OACB is a quadrant of a circle with centre O and a radius of 3.5 cm. If OD = 2 cm. find the area of the

1. Quadrant OACB
2. Shaded region.

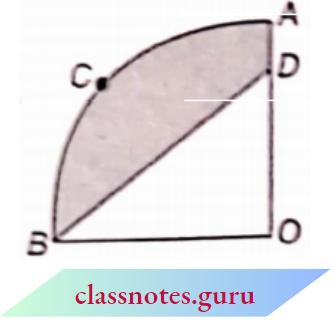
Solution:

Given

The OACB is a quadrant of a circle with centre O and a radius of 3.5 cm. If OD = 2 cm

Radius of quadrant AOB. r= 3.5 cm

1. Area of quadrant OACB

= \(\frac{1}{4} \pi^2\)

= \(\frac{1}{4} \times \frac{22}{7} \times 3.5 \times 3.5=\frac{77}{8} \mathrm{~cm}^2\)

2. Area of ΔOBD

= \(\frac{1}{2} \times O B \times O D\)

= \(\frac{1}{2} \times 3.5 \times 2=3.5 \mathrm{~cm}^2=\frac{7}{2} \mathrm{~cm}^2\)

Area of the shaded portion

= area of quadrant OACB – area of OBD

= \(\left(\frac{77}{8}-\frac{7}{2}\right) \mathrm{cm}^2=\frac{49}{8} \mathrm{~cm}^2\)

Area of the shaded portion =\(\frac{49}{8} \mathrm{~cm}^2\)

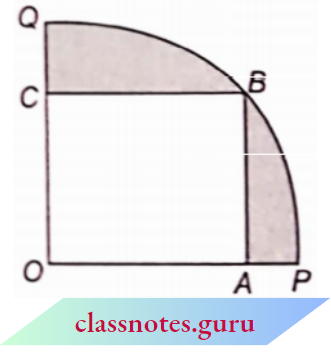
Question 13. In the square O.ABC is inscribed in a quadrant OPBQ. If OA = 20 cm, find the area of the shaded region. (Use π = 3.14)

Solution:

Given

In the square O.ABC is inscribed in a quadrant OPBQ. If OA = 20 cm

Each side of square OABC = 20 cm

∴ Area of OABC = (20)² = 400 cm²

Area of OABC = (20)² = 400 cm²

In ΔOAB,

OB² = OA² ~ AB² = 20² + 20² = 800

⇒ OB = 20√2cm

which is the radius of quadrant OPBQ.

Area of quadrant OPBQ

= \(\frac{1}{4} \pi(O B)^2=\frac{1}{4} \times 3.14 \times(20 \sqrt{2})^2\)

= 628 cm²

Now, the area of the shaded portion

= area of quadrant OPBD – area of square OABC

= (628 – 400) cm2 = 228 cm²

The area of the shaded region = 228 cm²

Question 14. AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O . If ∠AOB = 30°, find the area of the shaded region.

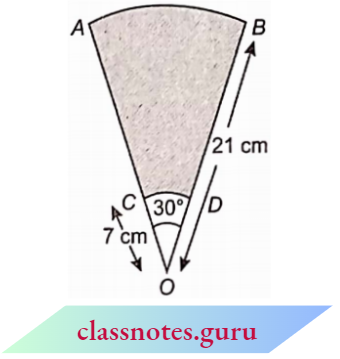
Solution:

Given

AB and CD are respectively arcs of two concentric circles of radii 21 cm and 7 cm and centre O . If ∠AOB = 30°

Here Q = 30°

Area of the shaded portion

= Area of sector OAB – area of sector OCD

= \(\frac{\theta}{360^{\circ}} \times \pi(O B)^2-\frac{\theta}{360^{\circ}} \times \pi(O C)^2\)

= \(\frac{\theta}{360^{\circ}} \times \pi\left[(O B)^2-(O C)^2\right]\)

= \(\frac{30^{\circ}}{360^{\circ}} \times \frac{22}{7} \times\left(21^2-7^2\right)\)

= \(\frac{1}{12} \times \frac{22}{7} \times 392 \mathrm{~cm}^2=\frac{308}{3} \mathrm{~cm}^2\)

Area of the shaded portion \(\frac{308}{3} \mathrm{~cm}^2\)

CBSE Class 10 Maths Area Related to Circles exemplar question answers

Question 15. The ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter. Find the area of the shaded region.

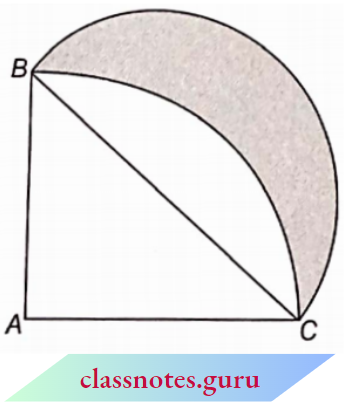
Solution:

Given

The ABC is a quadrant of a circle of radius 14 cm and a semicircle is drawn with BC as diameter.

For the quadrant ABC,

Radius r = 1 4 cm

∴ Area of quadrant ABC

= \(\frac{1}{4} \pi r^2\)

= \(\frac{1}{4} \times \frac{22}{7} \times 14 \times 14=154 \mathrm{~cm}^2\)

Area of \(\triangle A B C=\frac{1}{2} \times A B \times A C\)

= \(\frac{1}{2} \times 14 \times 14=98 \mathrm{~cm}^2\)

In right ABC,

BC² = AC² + AB² = 14² + 14² = 392

BC = 14√2 cm

∴ For the semicircle formed on BC

Radius \(R=\frac{B C}{2}=\frac{14 \sqrt{2}}{2}=7 \sqrt{2} \mathrm{~cm}\)

and area of semicircle

= \(\frac{1}{2} \pi R^2\)

= \(\frac{1}{2} \times \frac{22}{7} \times(7 \sqrt{2})^2=154 \mathrm{~cm}^2\)

Now, the area of the shaded portion

= area of ΔABC + area of semicircle – area of quadrant ABC

= (98 + 154 – 154) cm² = 98 cm²

The area of the shaded region = 98 cm²

Question 16. Calculate the area of the designed region in the figure common between the two quadrants of circles of radius 8 cm each.

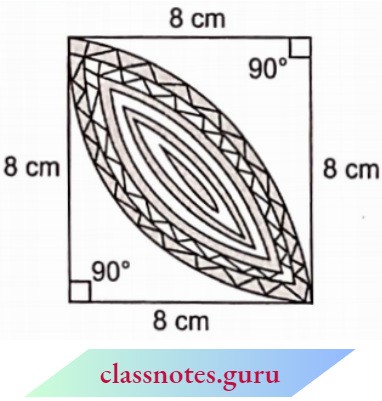
Solution:

The radius of each of quadrants ABMD and BNDC, r = 8 cm

∴ Area of two quadrants

= \(2 \times \frac{1}{4} \pi r^2\)

= \(2 \times \frac{1}{4} \times \frac{22}{7} \times 8 \times 8\)

= \(\frac{704}{7} \mathrm{~cm}^2\)

and area of square ABCD = AB² = 8² = 64 cm²

Now, the area of the shaded portion

= area of two quadrants – area of square ABCD

= \(\left(\frac{704}{7}-64\right) \mathrm{cm}^2\)

= \(\frac{256}{7} \mathrm{~cm}^2\)

The area of the designed region = \(\frac{256}{7} \mathrm{~cm}^2\)

NCERT Exemplar Solutions for Class 10 Maths Chapter 12  Area Related To Circles Multiple Choice Questions And Answers

Question 1. If the sum of the circumference of two circles of radii R₁ and R₂is equal to the circumference of a circle of radius R, then:

1. R₁ + R₂ = R
2. R₁ + R₂ > R
3. R₁ + R₂ < R
4. None of these

Answer: 1. R₁ + R₂ = R

Question 2. If the sum of the areas of two circles of radii and R₁ and R₂ is equal to the area of a circle of radius R, then:

1. R₁ + R₂ = R
2. R1 + R2 < R
3. R_1² + R_2² = R²
4. R_1² + R_2² < R²

Answer: 3. R_1² + R_2² = R²

Question 3. If the area of a circle is 154 cm², then its circumference is:

1. 11 cm
2. 22 cm
3. 44 cm
4. 66 cm

Answer: 3. 44 cm

Question 4. The area of the largest triangle inscribed in a semicircle of radius r is:

1. r²
2. \(\frac{1}{2} r^2\)
3. 2r²
4. r²√2

Answer: 1. r²

Question 5. The area of the largest square inscribed in a circle of radius 8 cm is:

1. 256 cm²
2. 64 cm²
3. 128 cm²
4. 32 cm²

Answer: 3. 128 cm²

NCERT Class 10 Area of Circle and Sector problems

Question 6. The area largest circle inscribed in a square of side 4 cm is:

1. 16π cm²
2. 8π cm²
3. 6π cm²
4. 4π cm²

Answer: 2. 8ir cm²

Question 7. If the circumference of a circle and the perimeter of a square are equal, then the ratio of their areas is:

1. 22:7
2. 14:11
3. 7:22
4. 11:14

Answer: 2. 14:11

Question 8. In the adjoining figure, the perimeter of sector OAB is:

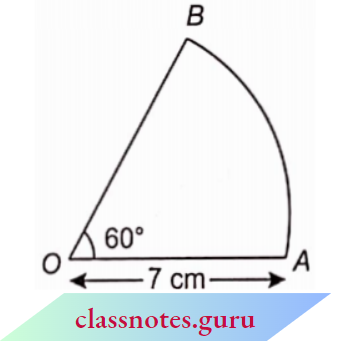
1. \(\frac{64}{3} \mathrm{~cm}\)
2. 26 cm
3. \(\frac{64}{5} \mathrm{~cm}\)
4. 19 cm

Answer: 1. \(\frac{64}{3} \mathrm{~cm}\)

Question 9. The length of the minute hand of a clock is 14 cm. The area swept by hand in one minute will be:

1. 10.26 cm²
2. 10.50 cm²
3. 10.75 cm²
4. 11.0 cm²

Answer: 1. 10.26 cm²

NCERT Exemplar For Class 10 Maths Chapter 11 Constructions Division Of A Line Segment

To divide a line segment (internally) in a given ratio m: n

Working Rule: (Internal division)

Draw a line segment AB of a given length.

Draw a ray AX making an acute angle XAB with AB.

Mark (m + n) points A₁, A₂, A₃, …, A_m+n on AX such that AA₁ = A₁A₂ = A₂A₃ = … = A_m+n-1 A_m+n.

Join A_m+n B.

Through A_m, draw A_mY || A_m+n B (if m: n) meeting AB at Y. So, Y divides AB internally in the ratio m: n.

Read and Learn More Class 10 Maths Solutions Exemplar

NCERT Exemplar Class 10 Maths Chapter 11 Constructions

Through A_n, draw A_n1Z || A_m+n B (if n: m) meeting AB at Z. So, Z divides AB internally in the ratio n: m.

In Short:

Sum (m +n) endpoint

first (m) Parallel (Y)  (say)

NCERT Exemplar For Class 10 Maths Chapter 11 Constructions Solved Problems

Question 1. Determine a point which divides a line segment 7 cm long, internally in the ratio 2:3.

Solution:

Steps of Construction:

1. Draw a line segment AB = 7 cm by using a ruler.
2. Draw any ray malting an acute ZBAC with AB.
3. Along AC, mark off (2 + 3) = 5 points A₁, A₂, A₃, A₄ and A₅ such that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅.
4. Join BA₅
5. Through A₂ draw a line A₂P parallel to A₅B by making an angle equal to \(\angle A A_5 B\) at A₂ intersecting AB at A point P.

The point P so obtained is the required point.

Justification: In ΔA₅B,

A₂P || A₅B (Construction)

∴ \(\frac{A A_2}{A_2 A_5}=\frac{A P}{P B}\) (by B.P theorem)

⇒ \(\frac{2}{3}=\frac{A P}{P B}\) (Construction)

⇒ AP : PB = 2: 3

i.e., P divides AB internally in the ratio 2 : 3.

Alternate Method:

Draw the line segment AB = 7 cm.

Draw any ray AC making an acute angle ∠BAC with AB.

Draw a ray BD parallel to Ac by making ∠ABC equal to angle ∠BAC.

Mark off 2 points A₁ and A₂ on AC and 3 points B₁, B₂, B₃ on AD such that AA₁ = A₁A₂ = BB₁ = B₁B₂ = B₂B₃

Join B₃A₂, suppose it intersects AB at point P. Then, P is the required point.

To Divide a Line Segment (Externally) in a Given Ratio m: n

Working Rule: (External Division)

Question 2. Determine a point which divides a line segment 6 cm long externally in the ratio 5 : 3.

Solution:

Steps of Construction:

1. Draw a line segment AB = 6 cm.
2. Draw any ray making an acute ∠BAX with AB.
3. Along AX, mark off (larger among the ratios) 5 points A₁, A₂, A₃, A₄, A₅ such that AA₁ = A₁A₂ = A₂A₃ = A₃A₄ = A₄A₅.
4. Join the point A₂ (5-3) with end point B.
5. Draw a line parallel to A₂B from A₅ (larger among the ratios) which meets AB produced at P.

The point P, so obtained is the required point such that AP: BP = 5 : 3.

Justification: In AA₅P,

Since A₂B || A₅P, (Construction)

∴ \(\frac{A P}{B P}=\frac{A A_5}{A_2 A_5}\) (by B.P theorem)

⇒ \(\frac{A P}{B P}=\frac{5}{3}\) (Construction)

Question 3. Determine a point which divides a line segment 6 cm long externally in the ratio 3:5.

Solution:

Steps of Construction:

1. Draw a line segment AB = 6 cm.
2. Draw any ray making an acute ∠ABX with AB.
3. Along BX, mark off (larger among the ratios) 5 points B₁, B₂, B₃, B₄ and B₅ such that BB₁ =B₁B₂ = B₂B₃ — B₃B₄ = B₄B₅.
4. Join the point B₂ (5 – 3) with endpoint A
5. Draw a line parallel to B₂A from B₅ (larger among the ratios) which meets BA produced at P.

The point P so obtained is the required point such that AP: BP = 3:5.

Justification: In ΔPBB₅,

Since, B₂A || B₅P (Construction)

∴ \(\frac{B_2 B_5}{B B_5}=\frac{A P}{B P}\) (by B.P theorem)

⇒ \(\frac{3}{5}=\frac{A P}{B P}\) (Construction)

i.e., P divides AB externally in the ratio of 3:5

Class 10 Maths Constructions Exemplar Solutions

NCERT Exemplar For Class 10 Maths Chapter 11 Constructions To Construct A Triangle Similar To A Given Triangle

Question 1. Construct a triangle similar to a given triangle ABC such that each of its sides is \(\frac{2}{3} \mathrm{rd}\) of the corresponding sides of the triangle ABC. It is given that AB = 4 cm, BC = 5 cm and AC = 6 cm.

Solution:

Given

It is given that AB = 4 cm, BC = 5 cm and AC = 6 cm.

Steps of construction:

1. Take BC = 5cm and Construct ΔABC with BA = 4cm and CA = 6cm.
2. Divide BC into three equal parts.
3. Let C be a point on BC such that \(B C^{\prime}=\frac{2}{3} B C\)
4. Draw A’C parallel to AC through C” intersecting BA at A’. ΔA’BC” is the required triangle.

Question 2. Construct an isosceles triangle whose base is 6 cm and altitude 4 cm. Then construct another triangle whose sides are \(\frac{3}{4}\) times the corresponding sides of the first triangle.

Solution:

Steps to Construction:

1. Draw a line segment BC = 6 cm.
2. Draw a perpendicular bisector of BC.
3. From mid-point D of BC on perpendicular bisector mark DA = 4 cm, join AB and AC.
4. Below BC make an acute angle ∠CBZ.
5. Along BZ mark off four points B₁, B₂, B₃ and B₄ such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄.
6. Join B₄C.
7. From B₃ draw B₃E parallel to B₄C meeting BC at E.
8. From E draw EF || CA meeting BA at F. Then, ΔFBE is the required triangle.

Question 3. Construct a quadrilateral ABCD with AB = 3 cm, AD = 2.7 cm, DB = 3.6 cm, ∠B =110° and BC = 4.2 cm. Construct another quadrilateral A’BC’D’ similar to quadrilateral ABCD so that diagonal BD’ = 4.8 cm.

Solutions:

Steps to construction:

1. Draw a line segment BC = 4.2 cm
2. At B, construct angle YBC = 110°
3. With centre B and a radius equal to 3 cm, draw an arc-cutting BT at A.
4. With centre A and a radius equal to 2.7 cm, draw an arc.
5. With centre B and radius equal to 3.6 cm, draw another arc cutting the previous arc at D.
6. Join AD, CD and BD. Then, ABCD is the required quadrilateral.
7. Produce BD to D’ such that BD’ = 4.8 cm.
8. From D’, draw a line parallel to DA which cuts BY at A’.
9. From D’, draw a line parallel to DC which cuts BC produced at D’.

Then, A’BC’D’ is the required quadrilateral similar to ABCD.

Question 4. Construct a cyclic quadrilateral ABCD in which AB = 4.2 cm, BC = 5.5 cm, CA = 4.6 cm and AD = 3 cm. Also, construct a quadrilateral similar to ABCD whose sides are 1 .5 times the corresponding sides of ABCD.

Solution:

Steps to construction:

1. Draw a line segment AB = 4.2 cm.
2. With centre A and a radius equal to 4.6 cm, draw an arc.
3. With centre B and radius equal to 5.5 cm, draw another arc cutting the previous arc at C.
4. Join AC and BC.
5. Draw the perpendicular bisectors of any two sides say AB and BC respectively of ΔABC. Let them intersect each other at O.
6. Taking O as the centre and radius as OA or OB or OC, draw a circle. This is the circumcircle of ΔABC.
7. With centre A and radius equal to 3 cm, cut an arc on the opposite side of B, to cut the circle at D.
8. Join AD and CD. Then, ABCD is the required cyclic quadrilateral.
9. Produce Ac to C’ such that \(A C^{\prime}=1.5 \times A C \text { i.e., }\left(1+\frac{1}{2}\right) A C \Rightarrow A C+\frac{1}{2} \times 4.6\) i.e., 2.3cm more.
10. From C’, draw a line parallel to CD which meets AD produced at D’.
11. From C’, draw a line parallel to CB which meets AB produced at B’. Then, AB’C’D’ is the required quadrilateral similar to cyclic quadrilateral ABCD.

NCERT Exemplar For Class 10 Maths Chapter 11 Constructions Of Tangents To A Circle

Question 1. Take a point O on the plane of the paper. With O as the centre draw a circle of radius 4 cm. Take a point on this circle and draw a tangent at P.

Solution:

Steps of Construction:

1. Take a point O on the plane of the paper and draw a circle of a given radius of 4 cm.
2. Take a point P on the circle and join OP.
3. Construct ∠OPT = 90°.
4. Produce TP to T’ to obtain the required tangent TPT’.

Question 2. Draw a circle of radius 3 cm. Take a point P on it. Without using the centre of the circle, draw a tangent to the circle at point P.

Solution:

Steps of construction:

1. Draw any chord PQ through the given point P on the circle.
2. Take a point R on the circle and join P and Q to a point R.
3. Construct ∠QPY = ∠PRQ and on the opposite side of the chord PQ.
4. Produce YP to X to get YPX as the required tangent.

Question 3. Draw a circle of radius 2.5 cm. Take a point at a distance of 5 cm from the centre of the circle. From point P, draw two tangents to the circle.

Solution:

Steps of Construction:

1. Take a point O in the plane of the paper and draw a circle of radius 2.5 cm.
2. Mark a point P at a distance of 5.0 cm from the centre O and, join OP.
3. Draw the right bisector of OP, intersecting OP at Q.
4. Taking Q as a centre and OQ = PQ as the radius, draw a circle to intersect the given circle at T and T.
5. Join PT and PT’ to get the required tangents.

Question 4. Draw a pair of tangents to a circle of radius 5 cm inclined to each other at an angle of 60°.

Solution:

Steps of Construction:

1. Take a point O on the plane of the paper and draw a circle with centre O and radius OA = 5 cm.
2. At O construct radii OA and OB such that ∠AOB equals 120° i.e., supplement of the angle between the tangents.
3. Draw perpendiculars to OA and OB at A and B respectively suppose these perpendiculars intersect at P. Then, PA and PB are required tangents.

Question 5. Draw a circle of radius 4 cm. Take a point P outside the circle. Without using the centre of the circle, draw two tangents to the circle from point P.

Solution:

Steps of Construction:

1. Draw a line segment of 4 cm.
2. Take a point P outside the circle and draw a second PAB, intersecting the circle at A and B.
3. Produce AP to C such that AP = CP.
4. Draw a semi-circle with CB as the diameter.
5. Draw PD ⊥ CB, intersecting the semi-circle at D.
6. Widi P as centre and PD as radius draw arcs to intersect the given circle at T and T’.
7. Join PT and PT’. Then, PT and PT’ are the required tangents.

NCERT Exemplar Solutions for Constructions Class 10

NCERT Exemplar For Class 10 Maths Chapter 11 Constructions Exercise 11.1

Question 1. Draw a line segment of length 7.6 cm and divide it in the ratio 5:8. Measure the two parts.

Solution:

Steps of construction :

1. Draw a line segment AB = 7.6 cm.
2. Draw a ray AX which forms an acute angle from AB.
3. Cut (8 + 5) = 13 equal marks on ray AX and mark them X₁, X₂, X₃, X₄, …, X₁₃.
4. Join X₁₃ to B.
5. Draw X₅C || X₁₃ B from X₅ which meets AB at C.

So, point C divides the line segment AB in the ratio 5:8.

On measuring two line segments, we get AC = 4.7 cm, BC = 2.9 cm

Verification: In ΔABX₁₃ and ΔACX₅, CX₅ || BX₁₃

∴ \(\frac{A C}{C B}=\frac{A X_5}{X_5 X_{13}}=\frac{5}{8}\)

⇒ AC: AB = 5:8

Question 2. Construct a triangle of sides 4 cm, 5 cm and 6 cm and then a triangle similar to it whose sides are \(\frac{2}{3}\) of the corresponding sides of the first triangle.

Solution:

Steps of construction:

1. Construct a ΔABC such that BC = 6 cm, AC = 5 cm and AB = 4 cm.
2. Draw a ray BX such that ∠CBX is at an acute angle.
3. Mark three points X₁, X₂ and X₃ on BX such that BX₁ = X₁X₂ = X₂X₃.
4. Join X₃ and C.
5. Draw a line parallel to line X₃C from X₂ which intersects BC at C’.
6. Draw a line parallel to line CA from C which meets BA at A’.

So, ΔA’B C’ is the required triangle.

Verification: By construction

X₃C || X₂C’  ⇒ \(\frac{B X_2}{X_2 X_3}=\frac{B C^{\prime}}{C^{\prime} C}\)

but \(\frac{B X_2}{X_2 X_3}=\frac{1}{2} \quad ⇒ \quad \frac{B C^{\prime}}{C^{\prime} C}=\frac{2}{1}\)

⇒ \(\frac{C^{\prime} C}{B C^{\prime}}=\frac{1}{2}\)

Adding 1 on both sides,

⇒ \(\frac{C^{\prime} C}{B C^{\prime}}+1=\frac{1}{2}+1\)

⇒ \(\frac{C^{\prime} C+B C^{\prime}}{B C^{\prime}}=\frac{1+2}{2} = \frac{B C}{B C^{\prime}}=\frac{3}{2}\)

Now, in ΔBC’A’ and ΔBCA,

CA || C’A’

from A.A. similarity, ΔBC’A’ ∼ ΔBCA

⇒ \(\frac{A^{\prime} B}{A B}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B C^{\prime}}{B C} \quad\left[\text { each }=\frac{2}{3}\right]\)

Question 3. Construct a triangle with sides 5 cm, 6 cm and 7 cm and then another triangle whose sides are \(\frac{7}{5}\) of the corresponding sides of the first triangle.

Solution:

Steps of construction:

1. Draw a line segment BC = 5 cm
2. Draw two arcs with centres B and C of radii 7 cm and 6 cm respectively which intersect each other at A.
3. Join BA and CA. ΔABC is the required triangle.
4. Draw a ray BX from B downwards, making an acute angle ∠CBX.
5. Mark seven points B₁, B₂, B₃, B₄, B₅, B₆ and B₇ on B₈ such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅ = B₅B₆ = B₆B₇
6. Join B5C and draw B₇M || B₅C from B₇, which intersects the produced BC at M.
7. Draw MN || CA from point M which intersects the produced BA at N.

Now ΔNBM is the required triangle whose sides are \(\frac{7}{5}\) of the sides of ΔABC.

Justification:

By construction,

B₇M || B₅C

∴ \(\frac{B C}{C M}=\frac{5}{2}\)

Now, \(\frac{B M}{B C}=\frac{B C+C M}{B C}\)

= \(1+\frac{C M}{B C}=1+\frac{2}{5}=\frac{7}{5}\)

∴ \(\frac{B M}{B C}=\frac{7}{5}\)

and, MN || CA

∴ ΔABC ∼ ΔNBM

and \(\frac{N B}{A B}=\frac{B M}{B C}=\frac{M N}{C A}=\frac{7}{5}\)

Question 4. Construct an isosceles triangle whose base is 8 cm and altitude 4 cm and then another triangle whose sides are \(1 \frac{1}{2}\) times the corresponding sides of the isosceles triangle.

Solution:

Steps of construction:

1. Draw the line segment BC = 8cm.
2. Draw the perpendicular bisector OQ of BC which intersects BC at P.
3. Take PA = 4 cm along PO.
4. Join BA and CA. Now ΔABC is the required isosceles triangle.
5. Draw a ray BX from B making acute angle ∠CBX.
6. Mark three points B₁, B₂ and B₃ on BX such that BB₁ = B₁B₂ = B₂B₃
7. Join B₂C and draw B₃N || B₂C from B₃ which intersects the Produced BC at N.
8. Draw NM || CA from point N which intersects the produced BA at M.

Then ΔMBN is the required rectangle.

Justification:

∵ B₃ || B₂C (by construction)

∴ \(\frac{B C}{C N}=\frac{2}{1}\)

Now \(\frac{B N}{B C}=\frac{B C+C N}{B C}=1+\frac{C N}{B C}=1+\frac{1}{2}=1 \frac{1}{2}\)

Question 5. Draw a triangle ABC with side BC = 6 cm, AB = 5 cm and ABC = 60°. Then construct a triangle whose sides are \(\frac{4}{3}\) of the corresponding sides of the triangle ABC.

Solution:

Steps of construction:

1. Construct a triangle ABC such that BC = 6 cm, AB = 5 cm and ∠ABC = 60°.
2. Draw a ray \(\overrightarrow{B X}\) such that CBX is an acute angle.
3. Mark four points X₁, X₂, X₃, and X₄ on BX such that BX₁ = X₁X₂ = X₂X₃ = X₃X₄.
4. Join X₄C.
5. Draw X₃C’ || X₄C which intersects BC at C.
6. Draw a line from C, parallel to CA which intersects BC at A’.

So, ΔA’BC’ is the required triangle.

Verification: By construction

X₄C || X₃C’ [from B.P.T.]

∴ \(\frac{B X_3}{B X_4}=\frac{B C^{\prime}}{B C} \text { but } \frac{B X_3}{B X_4}=\frac{3}{4}\) (by construction)

⇒ \(\frac{B C^{\prime}}{B C}=\frac{3}{4}\) → (1)

Now, CA || C’A’ (by construction)

ΔBC’A’ BCA [from A.A. similarity]

⇒ \(\frac{A^{\prime} B}{A B}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B C^{\prime}}{B C}=\frac{3}{4}\) [from (1)].

Chapter 11 Constructions Class 10 Maths Exemplar

Question 6. Draw a triangle ABC with side BC = 7 cm, ∠B = 45°, ∠A = 105°. Then, construct a triangle whose sides are \(\frac{4}{3}\) times the corresponding sides of ΔABC.

Solution:

Steps of construction:

1. Construct a ΔABC such that BC = 7 cm, ∠B = 45° and ∠A = 105°.
2. Draw a ray BX such that ∠CBX is at an acute angle.
3. Mark four points X₁, X₂, X₃ and X₄ on BX such that:
   Bx₁ = X₁X₂ = X₂X₃ = X₃X₄.
4. Draw a line from X4 parallel to X₃C which intersects BC produced at C’.
5. Draw a line from C parallel to CA, that intersects BA produced at A’.
6. Thus, ΔA’BC’ is the required triangle.

Verification: By construction,

C’A’ || CA [from A.A. similarity]

ΔABC ∼ ΔA’BC’

⇒ \(\frac{A^{\prime} B}{A B}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B C^{\prime}}{B C}\) → (1)

Again, by construction

X₄C’ || X₃C

∴ BX₄C’ BX₃C

⇒ \(\frac{B C^{\prime}}{B C}=\frac{B X_4}{B X_3}\)

but \(\frac{B X_4}{B X_3}=\frac{4}{3} \Rightarrow \frac{B C^{\prime}}{B C}=\frac{4}{3}\) → (2)

from (1) and (2),

∴ \(\frac{A^{\prime} B}{A B}=\frac{A^{\prime} C^{\prime}}{A C}=\frac{B C^{\prime}}{B C}=\frac{4}{3}\).

Question 7. Draw a right triangle in which the sides (other than hypotenuse) are of lengths 4 cm and 3 cm. Then construct another triangle whose sides are \(\frac{5}{3}\) times the corresponding sides of the given triangle.

Solution:

Steps of construction:

1. Draw a line segment BC = 4 cm.
2. Draw a line segment AB = 3 cm from B which makes a 90° angle from BC.]
3. Join AC. ΔABC is the given right-angled triangle.
4. Draw an acute angle ∠CBY from B downwards.
5. Mark 5 points B₁, B₂, B₃, B₄ and B₅ on BY such that BB₁ = B₁B₂ = B₂B₃ = B₃B₄ = B₄B₅.
6. Join B₃C.
7. Draw B₅C’ || B₃ C from B₅, which meets the produced BC at C.
8. Draw C’A’ || CA from C’ which meets the produced BA at A’

So, ΔA’BC’ is the required triangle.

Justification:

By construction, B₅C’ || B₃C

∴ \(\frac{B C}{C C^{\prime}}=\frac{3}{2}\)

Now, \(\frac{B C^{\prime}}{B C}=\frac{B C+C C^{\prime}}{B C}=1+\frac{C C^{\prime}}{B C}\)

= \(1+\frac{2}{3}=\frac{5}{3}\)

and, C’A’ = CA

∴ ΔABC ∼ ΔA’BC’

and \(\frac{A^{\prime} B}{A B}=\frac{B C^{\prime}}{B C}=\frac{A^{\prime} C^{\prime}}{C A}=\frac{5}{3}\)

NCERT Exemplar For Class 10 Maths Chapter 11 Constructions Exercise 11.2

Question 1. Question 1. Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths.

Solution:

Steps of construction:

1. Mark a point O.
2. Draw a circle with centre O and a radius of 6 cm.
3. Mark a point P at a distance of 10 cm from the centre.
4. Join O and P
5. Bisects OP at point M.
6. With the centre at point M, draw a circle with a radius MO or MP which intersects the given circle at A and B.
7. Join PA and PB. So, PA and PB are two required tangents. On measuring PA = PB = 9.6 cm.

Verification: Join OA and OB. Since OP is a diameter.

∠OAP = 90º; ∠OBP = 90º [angle in semicircle]

Again OA and OB are the radii of a circle.

⇒ PA and PB are tangents to the circle.

Class 10 Constructions Questions with Solutions

Question 2. Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also, verify the measurement by actual calculation.

Solution:

Steps of construction:

1. Draw two circles of radii 4 cm and 6 cm with a centre O.
2. Mark a point P on a larger circle.
3. Join O and P.
4. Find the point M of the perpendicular bisector of.OP.
5. With centre M and radius OM or PM draw a circle which intersects the smaller circle at A and B.
6. Join A and P.

So, PA is the required tangent. On measuring PA = 4.5 cm.

Verification: Join O and A.

∠PAO = 90° [angle in semcircle]

PA ⊥ OA

∵ OA is the radius of the small circle.

∴ PA is a tangent of the smaller circle

Question 3. Draw a circle of radius 3 cm. Take two points P and Q on one of its extended diameters each at a distance of 7 cm from its centre. Draw tangents to the circle from these two points P and Q.

Solution:

Given : P and Q are two points on a diameter of the circle of radius 3 cm.

and OP = OQ = 7cm

We have to construct the tangents to the circle from P and Q.

Steps of construction:

1. Draw a circle of radius 3 cm with centre O.
2. Produce its diameter on both sides and take two points P and Q on it such that OP = OQ = 7 cm.
3. Bisect OP and OQ. Let E and F be the mid-points of OP and OQ respectively.
4. Draw a circle with centre E and radius OE, which intersects the given circle (0, 3) at M and N. Again draw a circle with centre F and radius OF which intersects the given circle at P’ and Q’.
5. Join PM, PN, QP’ and QQ’. These are the required tangents from P and Q to the circle (0, 3).

Justification:

Join OM and ON. ∠OMP lies in the semicircle, so ∠OMP = 90°. OM is the radius of the circle, so MP is the tangent to the circle. Similarly PN, QP’ and OQ’ are also the tangents to the circle.

Question 4. Draw a pair of tangents to a circle of radius 5 cm inclined to each other at an angle of 60°.

Solution:

Steps of construction:

1. Construct a circle with centre O and radius = 5 cm.
2. Draw ∠AOB = 120°.
3. Draw a perpendicular on OA from point A.
4. Draw a perpendicular on OB from B.
5. Both perpendiculars intersect each other at point C.

So, CA and CB are the required tangents to the circle, inclined at a 60° angle.

Verification:

In quadrilateral OACB, from angle sum property.

⇒ 120° + 90° + 90° + ∠ACB = 360°

⇒ 300° + ∠ACB = 360°

⇒ ∠ACB = 360°- 300° = 60°

Question 5. Draw a line segment AB of length S cm. Taking A as the centre, draw a circle of radius 4 cm and taking B as the centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.

Solution:

Steps of construction:

1. Draw a line segment AB = 8 cm.
2. Draw a circle of radius 4 cm taking A as the centre.
3. Draw another circle of radius 3 cm talcing B as the centre.
4. Draw the perpendicular bisector of AB and find the mid-point M of AB.
5. Draw the circle with centre M and radius MA or MB which intersects the circle with centre A at P and Q and the circle with centre F at R and S.
6. Join BP and FQ. So, BP and FQ are the required tangents on a circle with centre A from B.
7. Now join RA and SA.

So, RA and SA are the tangents on a circle with centre B from A.

Verification: Join A and P.

∠APB = 90° => BP ⊥ AP

but AP is the radius of a circle with centre A.

⇒ AP is a tangent of the circle with centre A.

Similarly, BQ is also a tangent of the circle with centre A. Similarly AR and AS are the tangents of the circle with centre B.

NCERT Exemplar problems and solutions for Class 10 Constructions

Question 6. Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and B = 90° BD is the perpendicular from b on AC. The circle through B, C, and D is drawn. Construct the tangents from A to this circle.

Solution:

Given

Let ABC be a right triangle in which AB = 6 cm, BC = 8 cm and B = 90° BD is the perpendicular from b on AC. The circle through B, C, and D is drawn.

Steps of construction:

1. Draw line segments AB = 6 cm and BC= 8 cm perpendicular to each other. Join AC. Now ΔABC is a right-angled triangle.
2. Taking the mid-point F of BC as the centre and radius of 4 cm, draw a circle which passes through points B, C and D.
3. Join AF and bisects A it. Let O be the midpoint of AF.
4. The circle drawn with f centre O and radius OA intersects the given circle at B and M.
5. Join AB and AM, which are the required tangents.

Justification:

Join FM and FB. Now ∠AMF lies in a semicircle,

so ∠AMF = 90° ⇒ FM ⊥ AM

∵ FM is the radius of the circle, so AM is the tangent to the circle and F is the centre.

Similarly, AB is also the tangent to the circle with centre F.

Class 10 Maths Chapter 11 Constructions solved questions

Question 7. Draw a circle with the help of a bangle Take a point outside the circle. Construct the pair of tangents from this point to the circle.

Solution:

Steps of construction:

1. Draw a circle using a bangle.
2. Draw two chords AP and MT. The perpendicular bisectors of AP and MT intersect each other at O, which is the centre of the circle.
3. Take a point R outside the circle. Join OR and bisect it.
4. Let Q be the mid-point of OR. The circle drawn with centre Q and radius OQ intersects the given circle at S and N.
5. Join RS and RN, so RS and RN are the required tangents from R.

Justification:

Join OS and ON. ∠OSR lies in a semicircle, so

∠OSR = 90° ⇒ OS || SR

∵ OS is the radius of a circle with a centre of O, so SR is the centre of that circle whose centre is O. Similarly, RN is also the tangent to the circle with a centre of O.