Joankessler

Chapter 1 Magnetic Field Multiple Choice Questions Section (A): Magnet And Magnetic Field Due To A Moving Charge

Question 1. The charge on a particle is 100 times that of the electron. It is revolving in a circular path of radius 0.8 m at a frequency of 1011 revolutions per second. The magnetic field at the centre of the path will be 

1. \(10^{-7} \mu_0\)
2. \(\frac{10^{-7}}{\mu_0}\)
3. \(10^{-17} \mu_0\)
4. \(10^{-6} \mu_{}\)

Answer: 4. \(10^{-6} \mu_{}\)

Question 2. Gauss is the unit of –

1. Magnetic induction
2. Intensity of magnetization
3. dipole moment
4. None of these

Answer: 1. Magnetic induction

Question 3. A ring of radius r is uniformly charged with charge q. If the ring is rotated about its axis with angular frequency ω, then the magnetic induction at its centre will be –

1. \(10^{-7} \times \frac{\omega}{q r}\)
2. \(10^{-7} \times \frac{q}{\omega r}\)
3. \(10^{-7} \times \frac{r}{q \omega}\)
4. \(10^{-7} \times \frac{r}{q \omega}\)

Answer: 3. \(10^{-7} \times \frac{r}{q \omega}\)

Magnetic Field MCQs for NEET Physics Class 12

Question 4. If an electron revolves in the path of a circle of radius of 0.5 × 10–10 m at a frequency of 5 × 1015 cycles/s, the equivalent electric current in the circle is (charge of an electron 1.6 × 10 –19 C)

1. 0.4mA
2. 0.8mA
3. 1.2mA
4. 1.6mA

Answer: 4. 1.2mA

Question 5. A charged particle moves through a magnetic field in a direction perpendicular to it. Then the :

1. Acceleration remains unchanged
2. Velocity remains unchanged
3. The speed of the particle remains unchanged
4. The direction of the particle remains unchanged

Answer: 3. Speed of the particle remains unchanged

Question 6. A particle mass m, charge Q and kinetic energy T enter a transverse uniform magnetic field of B induction. After 3 s the kinetic energy of the particle will be

1. 3T
2. 2T
3. T
4. 4T

Answer: 3. T

Question 7. If a current is passed through a spring then the spring will :

1. Expand
2. Compress
3. Remain same
4. None of these

Answer: 2. Compress

Question 8. At a specific instant emission of radioactive compound is deflected in a magnetic field. The compound can emit:

1. Electrons
2. Protons
3. He2+
4. Neutrons

The emission at the instant can be 1, 2, 3

1. 1, 2, 3,4
2. 4
3. 2,3

Answer: 1. 1, 2, 3

Chapter 1 Magnetic Field Multiple Choice Questions Section B: Magnetic Field Due To A Straight Wire

Question 1. A thin wire is bent to form a square loop ABCD. A battery of e.m.f 2V is connected between points A and C. The magnetic induction due to the current in the loop at centre O will-

1. Be zero
2. Point away from the plane of paper
3. point along the plane of the paper
4. Point into the plane of paper

Answer: 1. Be zero

Question 2. A small linear segment of an electric circuit is lying on the x-axis extending from \(x=-\frac{a}{2} \text { to } x=\frac{a}{2}\) and a current i is flowing in it. The magnetic induction due to the segment at a point x = a on the x-axis will be

1. α a
2. zero
3. α a2
4. \(\propto \frac{1}{\mathrm{a}}\)

Answer: 2. zero

Question 3. A current i is flowing in a straight conductor of length L. The magnetic induction at a point distant \(\frac{\mathrm{L}}{4}\) from its centre will be

1. \(\frac{4 \mu_0 \mathrm{i}}{\sqrt{5} \pi \mathrm{L}}\)
2. \(\frac{\mu_0 i}{2 \pi L}\)
3. \(\frac{\mu_0 \mathrm{i}}{\sqrt{2} \mathrm{~L}}\)
4. Zero

Answer: 1. \(\frac{4 \mu_0 \mathrm{i}}{\sqrt{5} \pi \mathrm{L}}\)

Question 4. Two insulated wires of infinite length are lying mutually at right angles to each other as shown in. Currents of 2A and 1.5A respectively are flowing in them. The value of magnetic induction at point P will be

1. \(2 \times 10^{-3} \mathrm{~N} / \mathrm{A}-\mathrm{m}\)
2. \(2 \times 10^{-5} \mathrm{~N} / \mathrm{A}-\mathrm{m}\)
3. \(1.5 \times 10^{-5} \text { tesla }\)
4. \(2 \times 10^{-4} \mathrm{~N} / \mathrm{A}-\mathrm{m}\)

Answer: 3. \(1.5 \times 10^{-5} \text { tesla }\)

Question 5. A current of I ampere is flowing in an equilateral triangle of side a. The magnetic induction at the centroid will be

1. \(\frac{\mu_0 \mathrm{i}}{3 \sqrt{3} \pi a}\)
2. \(\frac{3 \mu_0 \mathrm{i}}{2 \pi \mathrm{a}}\)
3. \(\frac{5 \sqrt{2} \mu_0 i}{3 \pi a}\)
4. \(\frac{9 \mu_0 i}{2 \pi a}\)

Answer: 4. \(\frac{9 \mu_0 i}{2 \pi a}\)

Question 6. A current is flowing in a hexagonal coil of side a (Fig.). The magnetic induction at the centre of the coil will be

1. \(\frac{3 \sqrt{3} \mu_0 \mathrm{i}}{\pi a}\)
2. \(\frac{\mu_0 i}{3 \sqrt{3} \pi a}\)
3. \(\frac{\mu_0 i}{\sqrt{3} \pi a}\)
4. \(\frac{\sqrt{3} \mu_0 \mathrm{i}}{\pi a}\)

Answer: 4. \(\frac{\sqrt{3} \mu_0 \mathrm{i}}{\pi a}\)

Question 7. A straight wire of diameter 0.5 mm carrying a current of 1A is replaced by another wire of diameter 1 mm carrying the same current. The strength of the magnetic field far away is:

1. Twice the earlier value
2. One-half of the earlier value
3. One-quarter of the earlier value
4. Same as the earlier value

Answer: 4. Same as earlier value

Question 8. Two long parallel wires P and Q are held at a distance of 5m between them. If P and Q carry current of 2.5 amp and 5 amp respectively in the same direction, then the magnetic field at a point halfway between the wires is

1. \(\frac{\mu_0}{\pi}\)
2. \(\frac{\sqrt{3} \mu_0}{2 \pi}\)
3. \(\frac{\mu_0}{2 \pi}\)
4. \(\frac{3 \mu_0}{2 \pi}\)

Answer: 3. \(\frac{\mu_0}{2 \pi}\)

Question 9. A long straight wire carries an electric current of 2 A. The magnetic induction at a perpendicular distance of 5m from the wire will be

1. 4 × 10–8 T
2. 8 × 10–8 T
3. 12 × 10–8 T
4. 16 × 10–8 T

Answer: 2. 8 × 10–8 T

Question 10. The strength of the magnetic field at a point distant r near a long straight current-carrying wire is B. The field at a distance of r/2 will be

1. B/2
2. B/4
3. 4B
4. 2B

Answer: 4. 2B

Question 11. A wire in the form of a square of side ‘a’ carries a current ‘i’. Then the magnetic induction at the centre of the square wire is (Magnetic permeability of free space = u0)

1. \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{a}}\)
2. \(\frac{\mu_{\mathrm{o}} \mathrm{i} \sqrt{2}}{\pi \mathrm{a}}\)
3. \(\frac{2 \sqrt{2} \mu_0 i}{\pi a}\)
4. \(\frac{\mu_0 \mathrm{i}}{\sqrt{2} \pi a}\)

Answer: 3. \(\frac{2 \sqrt{2} \mu_0 i}{\pi a}\)

Question 12. The vector form of Biot-Savart’s law for a current carrying element is

1. \(\mathrm{d} \overrightarrow{\mathrm{B}}=\frac{\mu_0}{4 \pi} \frac{\mathrm{Id} \vec{I} \sin \phi}{\mathrm{r}^2}\)
2. \(\mathrm{d} \vec{B}=\frac{\mu_0}{4 \pi} \frac{I d / \times \hat{r}}{r^2}\)
3. \(\mathrm{d} \overrightarrow{\mathrm{B}}=\frac{\mu_0}{4 \pi} \frac{\mathrm{Id} \vec{I} \times \hat{\mathrm{r}}}{\mathrm{r}^3}\)
4. \(\mathrm{d} \overrightarrow{\mathrm{B}}=\frac{\mu_0}{4 \pi} \frac{\mathrm{Id} \vec{l} \times \hat{\mathrm{r}}}{\mathrm{r}^2}\)

Answer: 4. \(\mathrm{d} \overrightarrow{\mathrm{B}}=\frac{\mu_0}{4 \pi} \frac{\mathrm{Id} \vec{l} \times \hat{\mathrm{r}}}{\mathrm{r}^2}\)

Question 13. Two long straight wires are kept parallel. A current of 1 ampere is flowing in each wire in the same direction. The distance between them is 2r. The intensity of the magnetic field at the midpoint between them :

1. \(\frac{\mu_0 \mathrm{i}}{\mathrm{r}}\)
2. \(\frac{4 \mu_0 \mathrm{i}}{\mathrm{r}}\)
3. 0
4. \(\frac{\mu_0 i}{4 r}\)

Answer: 3. 0

Question 14. Two infinitely long, thin, insulated, straight wires lie in the x-y plane along the x and y-axis respectively. Each wire carries a current I, respectively in the positive x-direction and positive y-direction. The magnetic field will be zero at all points on the straight line:

1. y=x
2. y=-x
3. y=x-1
4. y=-x+1

Answer: 1. y=x

NEET Physics Chapter 1 Magnetic Field MCQs

Question 15. Two parallel, long wires carry currents i 1 and i2 with i1 > i2. When the current is in the same direction, the magnetic field at a point midway between the wire is 10uT. If the direction of i 2 is reversed, the field becomes 30T. The ratio i1/i2 is

1. 4
2. 3
3. 2
4. 1

Answer: 3. 2

Question 16. Two long parallel wires are at a distance 2d apart. They carry steady equal currents flowing out of the plane of the paper, as shown. The variation of the magnetic field B along the XX’ is given by

Answer: 2.

Question 17. Wires 1 and 2 carrying currents i1 and i2 respectively are inclined at an angle to each other. What is the force on a small element dl of wire 2 at distance r from wire 1 (as shown in the figure) due to the magnetic field of wire 1?

1. \(\frac{\mu_0}{2 \pi \mathrm{r}} \mathrm{i}_1 \mathrm{i}_2 \mathrm{dl} \tan \theta\)
2. \(\frac{\mu_0}{2 \pi \mathrm{r}} \mathrm{i}_1 \mathrm{i}_2 \mathrm{dl} \sin \theta\)
3. \(\frac{\mu_0}{4 \pi r} i_1 i_2 \mathrm{dl}(\cos \theta+1)\)
4. \(\frac{\mu_0}{4 \pi \mathrm{r}} \mathrm{i}_1 \mathrm{i}_2 \mathrm{dl} \sin \theta\)

Answer: 3. \(\frac{\mu_0}{4 \pi r} i_1 i_2 \mathrm{dl}(\cos \theta+1)\)

Question 18. A current i ampere flows along an infinitely long straight thin-walled tube, then the magnetic induction at any point inside the tube is:

1. Infinite
2. zero
3. \(\frac{\mu_0}{4 \pi}, \frac{2 i}{r} \text { tesla }\)
4. \(\frac{2 i}{r} \text { tesla }\)

Answer: 2. zero

Question 19. A long straight wire of radius a carries a steady current i. The current is uniformly distributed across its cross-section. The ratio of the magnetic field at \(\frac{a}{2}\) and 2a from axis is

1. 1/4
2. 4
3. 1
4. 1/2

Answer: 3. 1

Question 20. A current flows along the length of an infinitely long, straight, thin-walled pipe. Then :

1. The magnetic field is zero only on the axis of the pipe
2. The magnetic field is different at different points inside the pipe
3. The magnetic field at any point inside the pipe is zero
4. The magnetic field at all points inside the pipe is the same, but not zero

Answer: 3. The magnetic field at any point inside the pipe is zero

Question 21. Two identical conducting wires AOB and COD are placed at right angles to each other. The wire AOB carries an electric current I2 and COD carries a current O. The magnetic field on a point lying at a distance d from O, in a direction perpendicular to the plane of the wires AOB and COD, will be given by

1. \(\frac{\mu_0}{2 \pi}\left(\frac{I_1+I_2}{d}\right)^{1 / 2}\)
2. \(\frac{\mu_0}{2 \pi \mathrm{d}}\left(\mathrm{I}_1^2+\mathrm{I}_2^2\right)^{1 / 2}\)
3. \(\frac{\mu_0}{2 \pi \mathrm{d}}\left(\mathrm{I}_1+\mathrm{I}_2\right)\)
4. \(\frac{\mu_0}{2 \pi \mathrm{d}}\left(\mathrm{I}_1^2+\mathrm{I}_2^2\right)\)

Answer: 2. \(\frac{\mu_0}{2 \pi \mathrm{d}}\left(\mathrm{I}_1^2+\mathrm{I}_2^2\right)^{1 / 2}\)

Chapter 1 Magnetic Field Multiple Choice Questions Section C: Magnetic Field Due To A Circular Loop

Question 1. An electric current i is flowing in a circular coil of radius a. At what distance from the center on the axis of the coil will the magnetic field be 1/8th of its value at the center?

1. 3a
2. \(\sqrt{3} a\)
3. \(\frac{a}{3}\)
4. \(\frac{a}{\sqrt{3}}\)

Answer: 2. 3a

Question 2. The ratio of magnetic inductions at the center of a circular coil of radius a and on its axis at a distance equal to its radius will be

1. \(\frac{1}{\sqrt{2}}\)
2. \(\frac{\sqrt{2}}{1}\)
3. \(\frac{1}{2 \sqrt{2}}\)
4. \(\frac{2 \sqrt{2}}{1}\)

Answer: 1. \(\frac{1}{\sqrt{2}}\)

Question 3. A wire loop PQRSP is constructed by joining two semi-circular coils of radii r1 and r2 respectively as shown in Fig. Current i is flowing in the loop. The magnetic induction at point O will be

1. \(\frac{\mu_0 i}{4}\left[\frac{1}{r_1}-\frac{1}{r_2}\right]\)
2. \(\frac{\mu_0 \mathrm{i}}{4}\left[\frac{1}{r_1}+\frac{1}{r_2}\right]\)
3. \(\frac{\mu_0 i}{2}\left[\frac{1}{r_1}-\frac{1}{r_2}\right]\)
4. \(\frac{\mu_0 \mathrm{i}}{2}\left[\frac{1}{r_1}+\frac{1}{r_2}\right]\)

Answer: 3. \(\frac{\mu_0 i}{2}\left[\frac{1}{r_1}-\frac{1}{r_2}\right]\)

Question 4. The magnetic field on the axis of a current-carrying circular coil of radius at a distance 2a from its centre will be

1. \(\frac{\mu_0 i}{2}\)
2. \(\frac{\mu_0 i}{10 \sqrt{5} a}\)
3. \(\frac{\mu_0 \mathrm{i}}{4 \mathrm{a}}\)
4. \(\mu_0 i\)

Answer: 2. \(\frac{\mu_0 i}{10 \sqrt{5} a}\)

Question 5. The use of Helmholtz coils is to produce –

1. Uniform magnetic field
2. Non-uniform magnetic field
3. Varying magnetic field
4. Zero magnetic field

Answer: 1. Uniform magnetic field

Question 6. Two similar coils of radius R and several turns N are lying concentrically with their planes at right 3 angles to each other. The currents flowing in them are I and I respectively. The resultant magnetic induction at the centre will be (in Wb/m2).

1. \(\frac{\mu_0 \mathrm{NI}}{2 \mathrm{R}}\)
2. \(\frac{\mu_0 \mathrm{NI}}{\mathrm{R}}\)
3. \(\sqrt{3} \mu_0 \frac{\mathrm{NI}}{2 \mathrm{R}}\)
4. \(\sqrt{5} \frac{\mu_0 \mathrm{NI}}{2 \mathrm{R}}\)

Answer: 2. \(\frac{\mu_0 \mathrm{NI}}{\mathrm{R}}\)

Question 7. Two similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field through both coils, if the same current is flown:

1. \(1: \sqrt{2}\)
2. 1:2
3. 1:3
4. \(\sqrt{3}: 1\)

Answer: 1. \(1: \sqrt{2}\)

Question 8. A coil of one turn is made of a wire of a certain length and then from the same length a coil of two turns is made. If the same current is passed in both cases, then the ratio of the magnetic induction at their centres will be

1. 2:1
2. 1:4
3. 4:1
4. 1:2

Answer: 2. 1:4

Question 9. Magnetic field due to 0.1A current flowing through a circular coil of radius 0.1 m and 1000 turns at the centre of the coil is

1. 0.2T
2. 2 ×10–4 T
3. 6.28 ×10–4 T
4. 9.8 ×10–4 T

Answer: 3. 6.28 ×10–4 T

Question 10. Magnetic field due to a ring having n turns at a distance x from the centre on its axis is proportional to (if r = radius of the ring)

1. \(\frac{r}{\left(x^2+r^2\right)}\)
2. \(\frac{r^2}{\left(x^2+r^2\right)^{3 / 2}}\)
3. \(\frac{n r^2}{\left(x^2+r^2\right)^{3 / 2}}\)
4. \(\frac{n^2 r^2}{\left(x^2+r^2\right)^{3 / 2}}\)

Answer: 3. \(\frac{n r^2}{\left(x^2+r^2\right)^{3 / 2}}\)

Question 11. A circular arc of wire subtends an angle \(\frac{\pi}{2}\) at the centre. If it carries a current I and its radius of curvature is R, then the magnetic field at the centre of the arc is

1. \(\frac{\mu_0 I}{8 R}\)
2. \(\frac{\mu_0 \mathrm{I}}{\mathrm{R}}\)
3. \(\frac{\mu_0 I}{2 R}\)
4. \(\frac{\mu_0 I}{4 R}\)

Answer: 1. \(\frac{\mu_0 I}{8 R}\)

Question 12. The magnetic field of a given length of wire carrying a current for a single-turn circular coil at the centre is B, then its value for two turns for the same wire, when the same current passes through it, is

1. \(\frac{B}{4}\)
2. \(\frac{B}{2}\)
3. 2B
4. 4B

Answer: 4. 4B

Question 13. If in a circular coil A of radius R, current i is flowing and in another coil B of radius 2R a current 2i is flowing, then the ratio of the magnetic fields, BA and BB produced at the centre by them will be :

1. 1
2. 2
3. 1/2
4. 4

Answer: 1. 1

Question 14. A long wire carries a steady current. It is bent into a circle of one turn and the magnetic field at the centre of the coil is B. It is then bent into a circular loop of n turns. The magnetic field at the centre of the coil will be:

1. nB
2. n2B
3. 2nB
4. 2n2B

Answer: 2. n2B

Question 15. The magnetic field due to a current carrying circular loop of radius 3 cm at a point on the axis at a distance of 4 cm from the centre is 54 T. What will be its value at the centre of the loop?

1. 250 μT
2. 150 μT
3. 125 μT
4. 75μT

Answer: 1. 250 μT

Question 16. A long solenoid has 200 turns per cm and carries a current i. The magnetic field at its centre is 6.28×10–2 Weber/m2. Another long solenoid has 100 turns per cm and it carries a current i/3. The value of the magnetic field at its centre is

1. 1.05 × 10–4 Weber/m2
2. 1.05 × 10–2 Weber/m2
3. 1.05 × 10–5 Weber/m2
4. 1.05 × 1010–3 Weber/m2

Answer: 2. 1.05 × 10–2 Weber/m2

Chapter 1 Magnetic Field Multiple Choice Questions Section D: Magnetic Field Due To A Straight Wire And Circular Arc

Question 1. The magnetic induction at center O due to the arrangement shown in fig.–

1. \(\frac{\mu_0 i}{4 \pi r}(1+\pi)\)
2. \(\frac{\mu_0 i}{4 \pi r}\)
3. \(\frac{\mu_0 i}{4 \pi r}(1-\pi)\)
4. \(\frac{\mu_0 i}{r}\)

Answer: 1. \(\frac{\mu_0 i}{4 \pi r}(1+\pi)\)

Question 2. A current of 30 amp. is flowing in a conductor as shown in Fig. The magnetic induction at point O will be

1. 1.5 tesla
2. 1.5π × 10–4 Tesla
3. zero
4. O.15 Tesla

Answer: 2. 1.5π × 10–4 Tesla

Question 3. The magnetic induction at centre O in the following figure will be

1. \(\frac{\mu_0 i \alpha}{4 \pi}\left(\frac{1}{r_1}-\frac{1}{r_2}\right) \odot\)
2. \(\frac{\mu_0 i \alpha}{4 \pi}\left(\frac{1}{r_1}+\frac{1}{r_2}\right) \odot\)
3. \(\frac{\mu_0 i \alpha}{2 \pi}\left[\frac{1}{r_1}-\frac{1}{r_2}\right] \otimes\)
4. \(\frac{\mu_0 i \alpha}{2 \pi}\left[\frac{1}{r_1}+\frac{1}{r_2}\right]\)

Answer: 1. \(\frac{\mu_0 i \alpha}{4 \pi}\left(\frac{1}{r_1}-\frac{1}{r_2}\right) \odot\)

Question 4. Two circular coils 1 and 2 are made from the same wire but the radius of the 1st coil is twice that of the 2nd coil. What is the ratio of the potential difference applied across them so that the magnetic field at their centres is the same:

1. 3
2. 4
3. 6
4. 2

Answer: 2. 4

Chapter 1 Magnetic Field Multiple Choice Questions Section (E): Magnetic Field Due To A Cylinder, Large Sheet, Solenoid, Toroid And Ampere’s Law

Question 1. When the number of turns in a toroidal coil is doubled, then the value of magnetic flux density will become-

1. Four times
2. Eight times
3. Half
4. Double

Answer: 2. Eight times

Question 2. The length of a solenoid is 0.1 m and its diameter is very small. A wire is wound over it in two layers. The number of turns in the inner layer is 50 and that on the outer layer is 40. The strength of the current flowing in two layers is in the same direction and is 3 ampere. The magnetic induction in the middle of the solenoid will be

1. 3.4 × 10–3 Tesla
2. 3.4 × 10–3 Gauss
3. 3.4 × 103 Tesla
4. 3.4 × 103 Gauss

Answer: 4. 3.4 × 103 Gauss

Question 3. The magnetic field inside a long solenoid is –

1. Infinite
2. Zero
3. Uniform
4. Non-uniform

Answer: 1. Infinite

Question 4. The correct curve between the magnetic induction along the axis of a long solenoid due to current flow I in it and distance x from one end is

Answer: 2.

Question 5. A long solenoid has 200 turns per cm and carries a current of 2.5 amp. The magnetic field at its centre is μ0 = 4π × 10–7 weber/amp-m]:

1. 3.14 × 10–2 weber/m²
2. 6.28 × 10–2 weber/m²
3. 9.42 × 10–2 weber/m²
4. 12.56 × 10–2 weber/m²

Answer: 1. 3.14 × 10–2 weber/m²

Question 6. In a coaxial, straight cable, the central conductor and the outer conductor carry equal currents in opposite directions. The magnetic field is zero.

1. Outside the cable
2. Inside the inner conductor
3. Inside the outer conductor
4. In between the two conductors.

Answer: 2. Inside the inner conductor

Question 7. A wire is wound on a long rod of material of relative permeability r = 4000 to make a solenoid. If the current through the wire is 5 A and the number of turns per unit length is 1000 per metre, then the magnetic field inside the solenoid is:

1. 25.12 mT
2. 12.56 m T
3. 12.56 T
4. 25.12 T

Answer: 1. 25.12 mT

Question 8. A cylindrical wire of radius R carries current I uniformly distributed over its cross-section. If a circular \(\int \vec{B} \cdot \vec{d}\) loop of radius ‘ r ‘ is taken as a campervan loop, then the variation value over this loop with radius ‘ r ‘ of the loop will be best represented by

Answer: 2.

Question 9. A current flows along the length of an infinitely long, straight, thin-walled pipe. Then

1. The magnetic field at all points inside the pipe is the same, but not zero
2. The magnetic field at any point inside the pipe is zero
3. The magnetic field is zero only on the axis of the pipe
4. The magnetic field is different at different points inside the pipe.

Answer: 3. The magnetic field is zero only on the axis of the pipe

Question 10. A long solenoid carrying a current produces a magnetic field B along its axis. If the current is doubled and the number of turns per cm is halved, the new value of the magnetic field is:

1. 2B
2. 4B
3. B/2
4. B

Answer: 3. B/2

Question 11. A long, thick straight conductor of radius R carries current I uniformly distributed in its cross-section area. The ratio of the energy density of the magnetic field at a distance R/2 from the surface inside the conductor and outside the conductor is:

1. 1: 16
2. 1: 1
3. 1: 4
4. 9/16

Answer: 4. 9/16

Question 12. A coaxial cable is made up of two conductors. The inner conductor is solid and is of radius R1 & the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of the magnetic field with distance from the axis is best plotted as:

Answer: 3.

Chapter 1 Magnetic Field Multiple Choice Questions Section (F): Magnetic Force On A Charge

Question 1. When a charged particle moves at right angles to a magnetic field then which of the following quantities changes-

1. Energy
2. Momentum
3. Speed
4. All Of Above

Answer: 2. Momentum

Question 2. A proton, a neutron, and an α-particle are accelerated through the same potential difference and then they enter a uniform normal magnetic field. If the radius of the circular path of the proton is 8 cm then the radius of the circular path of the deuteron will be –

1. 11.31 cm
2. 22 cm
3. 5 cm
4. 2.5 cm

Answer: 1. 11.31 cm

Question 3. A proton and an α-particle enter a uniform magnetic field at right angles to it with the same velocity. The period of α the particle as compared to that of the proton, will be

1. Four Times
2. Two Times
3. Half
4. One Fourth

Answer: 2. Four Times

Question 4. A charged particle with charge q is moving in a uniform magnetic field. If this particle makes some angle (0 < θ < 180º) with the magnetic field then its path will be –

1. Circular
2. Straight Line
3. Helical
4. Parabolic

Answer: 3. Helical

Question 5. If a positively charged particle is moving as shown in the fig., then it will get deflected due to the magnetic field towards

1. +x direction
2. +y direction
3. –x direction
4. +z direction

Answer: 4. +z direction

Question 6. Which of the following particles will experience maximum magnetic force (magnitude) when projected with the same velocity perpendicular to a magnetic field?

1. Electron
2. Proton
3. He+
4. Li++

Answer: 4. Li++

Question 7. An electric current enters and leaves a uniform circular wire of radius through diametrically opposite points. A charged particle q moving along the axis of the circular wire passes through its center at speed υ. The magnetic force acting on the particle when it passes through the center has a magnitude.

1. \(q v \frac{\mu_0 i}{2 a}\)
2. \(\mathrm{q} v \frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{a}}\) m
3. \(q v \frac{\mu_0 i}{a}\)
4. Zero

Answer: 4. Zero

Question 8. A charged particle is moved along a magnetic field line. The magnetic force on the particle is

1. Along its velocity
2. Opposite to its velocity
3. Perpendicular to its velocity
4. Zero.

Answer: 4. Zero.

Question 9. Two particles X and Y having equal charges, after being accelerated through the same potential difference, enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the masses of X to that of Y.

1. \(\left(\frac{R_1}{R_2}\right)^{1 / 2}\)
2. \(\frac{R_2}{R_1}\)
3. \(\left(\frac{R_1}{R_2}\right)^2\)
4. \(\frac{R_1}{R_2}\)

Answer: 3. \(\left(\frac{R_1}{R_2}\right)^2\)

Question 10. A negatively charged particle falling freely under gravity enters a region having a uniform horizontal magnetic field pointing toward the north. The particle will be deflected towards

1. East
2. West
3. North
4. South

Answer: 2. West

Question 11. A proton of mass m and charge q enters a magnetic field B with a velocity v at an angle θ with the direction of B. The radius of curvature of the resulting path is

1. \(\frac{m v}{q B}\)
2. \(\frac{m v \sin \theta}{q B}\)
3. \(\frac{\mathrm{mv}}{\mathrm{qB} \sin \theta}\)
4. \(\frac{m v \cos \theta}{q B}\)

Answer: 3. \(\frac{\mathrm{mv}}{\mathrm{qB} \sin \theta}\)

Question 12. Two particles A and B of masses m A and mB respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vA and v B respectively and the trajectories are as shown in the figure. Then

1. mAvA < mBvB
2. mAvA > mBvB
3. mA < mB and vA < vB
4. mA = mB and vA = vB

Answer: 2. mAvA > mBvB

Question 13. A charged particle is released from rest in a region of steady and uniform electric and magnetic fields that are parallel to each other. The particle will move in a

1. Straight line
2. Circle
3. Helix
4. Cycloid

Answer: 1. Straight line

Question 14. A particle of mass M and charge Q moving with velocity describes a circular path of radius R when subjected to a uniform transverse magnetic field of induction B. The work done by the field when the particle completes one full circle is

1. \(\left(\frac{m v^2}{R}\right) 2 \pi R\)
2. Zero
3. BQ.2πR
4. BQv.2πR

Answer: 2. Zero

Question 15. An electron moves with a velocity of 1 × 103 m/s in a magnetic field of induction 0.3 T at an angle of 30°. If em of electron is 1.76 × 1011 C/kg, the radius of the path is nearly:

1. 10–9 meter
2. 2 × 10–8 meter
3. 10–8 meter
4. 10–10 meter

Answer: 3. 10–8 meter

Question 16. A charged particle of charge q and mass m enters perpendicularly in a magnetic field. The kinetic energy of the particle is E; then the frequency of rotation is :

1. \(\frac{q B}{m \pi}\)
2. \(\frac{q B}{2 \pi m}\)
3. \(\frac{\mathrm{qBE}}{2 \pi \mathrm{m}}\)
4. \(\frac{\mathrm{qB}}{2 \pi \mathrm{E}}\)

Answer: 2. \(\frac{q B}{2 \pi m}\)

Question 17. A Beam Of Particles With a Specific Charge of 108 C/Kg Is Entering With Velocity 3 × 105 M/S By Making An Angle Of 30° With The Uniform Magnetic Field Of 0.3 Tesla. Radius Of Curvature Of Path Of Particle Is

1. 0.5 Cm
2. 0.02 Cm
3. 1.25 Cm
4. 2 Cm

Answer: 4. 0.02 Cm

Question 18. If An Electron Enters A Magnetic Field With Its Velocity Pointing In The Same Direction As The Magnetic Field, Then:

1. The Electron Will Turn To Its Right
2. The Electron Will Turn To Its Left
3. The Velocity Of The Electron Will Increase
4. The Velocity Of The Electron Will Remain Unchanged

Answer: 4. The Velocity Of The Electron Will Remain Unchanged

Question 19. A Charge Of 1c Is Moving In A Perpendicular Magnetic Field Of 0.5 Tesla With A Velocity Of 10 M/Sec. Force Experienced Is:

1. 5 N
2. 10 N
3. 0.5 N
4. 0 N

Answer: 1. 5 N

Question 20. An Electron Accelerated By 200 V, Enters A Magnetic Field. If Its Velocity Is 8.4 × 10 6 M/Sec. Then (E/M) For It Will Be : (In C/Kg)

1. 1.75 × 1010
2. 1.75 × 1011
3. 1.75 × 109
4. 1.75 × 106

Answer: 2. 1.75 × 1011

Question 21. A Charge Q Is Moving In A Uniform Magnetic Field. The Magnetic Force Acting On It Does Not Depend Upon

1. Charge
2. Mass
3. Velocity
4. Magnetic Field

Answer: 2. Mass

Question 22. An Electron Is Travelling In the East Direction And A Magnetic Field Is Applied In an Upward Direction, the electron Will Deflect Towards

1. South
2. North
3. West
4. East

Answer: 2. North

Question 23. A Proton Enters A Magnetic Field With Velocity Parallel To The Magnetic Field. The Path Followed By The Proton Is A

1. Circle
2. Parabola
3. Helix
4. Straight Line

Answer: 4. Straight Line

Question 24. An electron (mass = 9.0 × 10–31 kg and charge = 1.6 × 10–19 coulomb) is moving in a circular orbit in a magnetic field of 1.0 × 10–4 Weber/m2. Its period of revolution is:

1. 3.5 × 10–7 second
2. 7.0 × 10–7 seconds
3. 1.05 × 10–6 seconds
4. 2.1 × 10—6 second

Answer: 1. 3.5 × 10–7 second

Question 25. A particle of mass 0.6 g and having a charge of 25 nC is moving horizontally with a uniform velocity of 1.2 × 104 ms–1 in a uniform magnetic field, then the value of the minimum magnetic induction is (g = 10ms–2)

1. Zero
2. 10 T
3. 20 T
4. 200 T

Answer: 3. 20 T

Question 26. An electron is moving with velocity in the direction of the magnetic field, then the force acting on the electron is:-

1. Zero
2. \(\mathrm{e}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})\)
3. \(\mathrm{e}(\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{v}})\)
4. 200 Joule

Answer: 1. \(\mathrm{e}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})\)

Question 27. A Vertical Wire Carries A Current In an Upward Direction. An Electron Beam Sent Horizontally Towards The Wire Will Be Deflected (Gravity Free Space)

1. Towards Right
2. Towards Left
3. Upwards
4. Downwards

Answer: 3. Upwards

Question 28. If An Electron And A Proton Having the Same Momentum Enter Perpendicularly To A Magnetic Field, Then :

1. Curved Path Of Electron And Proton Will Be Same (Ignoring The Sense Of Revolution)
2. They Will Move Undeflected
3. Curved Path Of Electron Is More Curved Than That Of Proton
4. Path Of Proton Is More Curved

Answer: 1. The Curved Path Of the Electron And Proton Will Be the Same (Ignoring The Sense Of Revolution)

Question 29. A Magnetic Needle Is Kept In A Non-Uniform Magnetic Field. It Experiences :

1. A Torque But Not A Force
2. Neither A Force Nor A Torque
3. A Force And A Torque
4. A Force But Not A Torque

Answer: 3. A Force And A Torque

Question 30. Two thin, long, parallel wires, separated by a distance ‘d’ carry a current of ‘i’ A in the same direction. They will:

1. Attract each other with a force of \(\frac{\mu_0 i^2}{(2 \pi d)}\)
2. Repel, each other with a force of \(\frac{\mu_0 i^2}{(2 \pi d)}\)
3. Attract each other with a force of \(\frac{\mu_0 i^2}{\left(2 \pi d^2\right)}\)
4. Repel each other with a force of \(\frac{\mu_0 i^2}{\left(2 \pi d^2\right)}\)

Answer: 1. Attract each other with a force of \(\frac{\mu_0 i^2}{(2 \pi d)}\)

Question 31. A uniform electric field and a uniform magnetic field are acting along the same direction in a certain region. If an electron is projected along the direction of the fields with a certain velocity, then :

1. Its velocity will decrease
2. Its velocity will increase
3. It will turn toward the right of direction of motion
4. It will turn towards the left of the direction of motion.

Answer: 1. Its velocity will decrease

Question 32. A charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time taken by the particle to complete one revolution is:

1. \(\frac{2 \pi m q}{B}\)
2. \(\frac{2 \pi q^2 B}{B}\)
3. \(\frac{2 \pi q B}{m}\)
4. \(\frac{2 \pi m}{q B}\)

Answer: 4. \(\frac{2 \pi m}{q B}\)

Question 33. In a region, steady and uniform electric and magnetic fields are present. These two fields are parallel to each other. A charged particle is released from rest in this region. The path of the particle will be a:

1. Circle
2. Helix
3. Straight line
4. Ellipse

Answer: 3. Straight line

Question 34. A charged particle with charge q enters a region of constant, uniform, and mutually orthogonal fields B E B v and with a velocity perpendicular to both and, and comes out without any change in v magnitude or direction of. Then :

1. \(\overrightarrow{\mathrm{v}}=\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{B}} / \mathrm{B}^2\)
2. \(\vec{v}=\vec{E} \times \vec{E} / B^2\)
3. \(\overrightarrow{\mathrm{V}}=\overrightarrow{\mathrm{B}} \times \overrightarrow{\mathrm{E}} / \mathrm{E}^2\)

Answer: 1. \(\overrightarrow{\mathrm{v}}=\overrightarrow{\mathrm{E}} \times \overrightarrow{\mathrm{B}} / \mathrm{B}^2\)

Question 35. A charged particle moves through a magnetic field perpendicular to its direction. Then :

1. The momentum changes but the kinetic energy is constant
2. Both momentum and kinetic energy of the particle are not constant
3. Both, the momentum and kinetic energy of the particle are constant
4. Kinetic energy changes but the momentum is constant

Answer: 1. The momentum changes but the kinetic energy is constant

Question 36. A α particle is accelerated by a potential difference of 10 4V. Find the change in its direction of motion, if it enters normally in a region of thickness 0.1 m having transverse magnetic induction of 0.1 Tesla. (Given: mass of -particle is equal to 6.4 × 10–27 kg) 

1. 15º
2. 30º
3. 45º
4. 60º

Answer: 2. 15º

Question 37. The figure shows a convex lens of focal length 10 cm lying in a uniform magnetic field B of magnitude 1.2 T parallel to its principal axis. A particle having a charge of 2.0 × 10 –3 C and a mass of 2.0 × 10–5 kg is projected perpendicular to the plane of the diagram with a speed of 4.8 m/s.

The particle moves along a circle with its center on the principal axis at a distance of 15 cm from the lens. The axis of the lens and the circle are the same. Show that the image of the particle goes along a circle and find the radius of that circle.

1. 8 cm
2. 16 cm
3. 32 cm
4. 64 cm

Answer: 1. 8 cm

Class 12 NEET Physics Magnetic Field Multiple Choice Questions

Chapter 1 Magnetic Field Multiple Choice Questions Section (G): Electric And Magnetic Force On A Charge

Question 1. Uniform electric and magnetic fields are produced in the same direction. An electron moves in such a way that its velocity remains in the direction of the electric field. The electron will –

1. Turn towards left
2. Turn towards right
3. Get decelerated
4. Get accelerated

Answer: 2. Turn towards right

Question 2. In the following fig., three paths of ∝ particles crossing a nucleus N are shown. The correct path is

1. a and c
2. a and b
3. a, b and c
4. only a

Answer: 1. a and c

Question 3. The distance between the plates of a parallel plate condenser is 4 mm and the potential difference between them is 200V. The condenser is placed in a magnetic field B. An electron is projected vertically upwards parallel to the plates with a velocity of 106 m/s. The electron passes undeviated through the space between the plates. The magnitude and direction of magnetic field B will be –

1. 0.05T
2. 0.02T
3. 0.05 T Outward
4. 0.02T Outward

Answer: 1. 0.05T

Question 4. A beam of protons enters a uniform magnetic field of 0.3T with a velocity of 4 × 10 5m/s in a direction making an angle of 60º with the direction of the magnetic field. The path of motion of the particle will be

1. Circular
2. Straight Line
3. Spiral
4. Helical

Answer: 4. Helical

Question 5. In the above question, the radius of the path of the particle will be

1. 12.0m
2. 1.2m
3. 0.12m
4. 0.012m

Answer: 4. 0.012m

Question 6. In the above question, the pitch of the helix will be

1. 4.37 m
2. 0.437 m
3. 0.0437 m
4. 0.00437 m

Answer: 3. 0.0437 m

Question 7. In a certain region of space electric field and magnetic field are perpendicular to each other and in B E an electron enters in region perpendicular to the direction of both and moves undeflected, The velocity of the electron is:

1. \(\frac{|\vec{E}|}{|\vec{B}|}\)
2. \(\vec{E} \times \vec{B}\)
3. \(\frac{|\vec{B}|}{|\vec{E}|}\)
4. \(\frac{|\vec{B}|}{|\vec{E}|}\)

Answer: 1. \(\frac{|\vec{E}|}{|\vec{B}|}\)

Question 8. A charged particle with velocity 2 × 103 m/s passed undeflected through an electric and perpendicular magnetic field. The magnetic field is 1.5 Tesla. Find electric field intensity.

1. 2 × 103 N/C
2. 1.5 × 103 N/C
3. 3 × 103 N/C
4. 4/3 × 10–3 N/C

Answer: 3. 3 × 103 N/C

Question 9. A charged particle moves in a region having a uniform magnetic field and a parallel, uniform electric field. At some instant, the velocity of the particle is perpendicular to the field direction. The path of the particle will be

1. A Straight Line
2. A Circle
3. A Helix With Uniform Pitch
4. A Helix With Nonuniform Pitch.

Answer: 4. A Helix With Nonuniform Pitch.

Question 10. In a mass spectrometer used for measuring the masses of ions, the ions are initially accelerated by an electric potential V and then made to describe semicircular paths of radius R using a magnetic field B. If the charge on the ions V and B are kept constant, the ratio mass of the ion will be proportional to:

1. \(\frac{1}{R}\)
2. \(\frac{1}{\mathrm{R}^2}\)
3. R2
4. R

Answer: 2. \(\frac{1}{\mathrm{R}^2}\)

Question 11. A charge ‘q’ moves in a region where the electric field and magnetic field both exit, then the force on it is:

1. \(\frac{1}{R}\)
2. \(\frac{1}{R^2}\)
3. R2
4. R

Answer: 2. \(\frac{1}{R^2}\)

Question 12. A very long straight wire carries a current I. At the instant when a charge +Q at point P has velocity, as shown, the force on the charge is:-

1. Opposite To Ox
2. Along Ox
3. Opposite To Oy
4. Along Oy

Answer: 4. Along Oy

Question 13. An electron moves in a circular orbit with a uniform speed v. It produces a magnetic field B at the center of the circle. The radius of the circle is proportional to :

1. \(\frac{B}{v}\)
2. \(\frac{v}{B}\)
3. \(\sqrt{\frac{v}{B}}\)
4. \(\sqrt{\frac{B}{v}}\)

Answer: 3. \(\sqrt{\frac{v}{B}}\)

Question 14. When a charged particle moving with velocity is subjected to a magnetic field of induction, the force on it is non-zero. This implies that:

1. Angle Between And Is Necessarily 90°
2. Angle Between And Can Have Any Value Other Than 90°
3. Angle Between And Can Have Any Value Other Than Zero And 180°
4. Angle Between And Is Either Zero Or 180°

Answer: 3. Angle Between And Can Have Any Value Other Than Zero And 180°

Question 15. Under the influence of a uniform magnetic field a charged particle is moving in a circle of radius R with constant speed v. The period of the motion :

1. Depends On V And Not On R
2. Depends On Both R And V
3. Is Independent Of Both R And V
4. Depends On R And Not On V

Answer: 3. Is Independent Of Both R And V

Question 16. In a mass spectrometer used for measuring the masses of ions, the ions are initially accelerated by an electric potential V and then made to describe semicircular paths of radius R using a describe semicircular paths of radius R using a magnetic field B. If V and B are kept constant, the ratio. \(\left(\frac{\text { charge on the ion }}{\text { mass of the ion }}\right)\) will be proportional to:

1. \(\frac{1}{R}\)
2. \(\frac{1}{R^2}\)
3. R2
4. R

Answer: 2. \(\frac{1}{R^2}\)

Question 17. A beam of electrons passes undeflected through mutually perpendicular electric and magnetic fields. If the electric field is switched off, and the same magnetic field is maintained, the electrons move:

1. In an elliptical orbit
2. In a circular orbit
3. Along a parabolic path
4. Along a straight line

Answer: 2. In a circular orbit

Question 18. A magnetic line of force inside a bar magnet:

1. Are From North-Pole To South-Pole Of The Magnet
2. Do Not Exist
3. Depend Upon The Area Of Cross-Section Of The Bar Magnet
4. Are From South-Pole To North-Pole Of The Magnet

Answer: 4. Are From South-Pole To North-Pole Of The Magnet

Question 19. An experimenter’s diary reads as follows; “a charged particle is projected in a magnetic field of \((7.0 \hat{i}-3.0 \hat{j}) \times 10^{-3} \mathrm{~T}\). The acceleration of the particle is found to be \((x \hat{i}+7.0 \hat{j}) \times 10^{-6} \mathrm{~m} / \mathrm{s}^2\). Find the value of x.

1. 2
2. 4
3. 3
4. 1

Answer: 3. 3

Chapter 1 Magnetic Field Multiple Choice Questions Section (H): Magnetic Force On A Current Carrying Wire

Question 1. A 0.5 m long straight wire in which a current of 1.2 A is flowing is kept a right angle to a uniform magnetic field of 2.0 tesla. The force acting on the wire will be –

1. 2N
2. 2.4 N
3. 1.2 N
4. 3 N

Answer: 3. 1.2 N

Question 2. Two parallel wires P and Q carry electric currents of 10 A and 2A respectively in mutually opposite directions. The distance between the wires is 10 cm. If the wire P is of infinite length and wire Q is 2m long, then the force acting Q will be –

1. 4 × 10–5 N
2. 8 × 10–5 N
3. 4 × 105 N
4. 0 N

Answer: 1. 4 × 10–5 N

Question 3. A current of 2A is flowing in a wire of length 50 cm. If this wire is lying in a uniform magnetic field of 5 × 10–4 N/A-m making an angle of 60º with the field, then the force acting on the wire will be –

1. 4.33 × 10–4 N
2. 4N
3. 4 dyne
4. zero

Answer: 1. 4.33 × 10–4 N

Question 4. A current-carrying, straight wire is kept along the axis of a circular loop carrying a current. The straight wire

1. Will Exert An Inward Force On The Circular Loop
2. Will Exert An Outward Force On The Circular Loop
3. Will Not Exert Any Force On The Circular Loop
4. Will Exert A Force On The Circular Loop Parallel To Itself.

Answer: 4. Will Exert A Force On The Circular Loop Parallel To Itself.

Question 5. A proton beam is going from north to south and an electron beam is going from south to north. Neglecting the earth’s magnetic field, the electron beam will be deflected.

1. Towards The Proton Beam
2. Away From The Proton Beam
3. Away From The Electron Beam
4. None Of These

Answer: 1. Towards The Proton Beam

Question 6. Two parallel wires carrying currents in the same direction attract each other because of

1. Potential Difference Between Them
2. Mutual Inductance Between Them
3. Electric Force Between Them
4. Magnetic Force Between Them

Answer: 4. Magnetic Force Between Them

Question 7. A conducting loop carrying a current I is placed in a uniform magnetic field pointing into the plane of the paper as shown. The loop will tend to.

1. Move Along The Positive X Direction
2. Move Along The Negative X Direction
3. Contract
4. Expand

Answer: 4. Expand

Question 8. A thin flexible wire of length L is connected to two adjacent fixed points and carries a current in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle.

1. IBL
2. \(\frac{\mathrm{IBL}}{\pi}\)
3. \(\frac{\mathrm{IBL}}{2 \pi}\)
4. \(\frac{\mathrm{IBL}}{4 \pi}\)

Answer: 3. \(\frac{\mathrm{IBL}}{4 \pi}\)

Question 9. A rectangular loop carrying a current i is situated near a long straight wire such that the wire is parallel to one of the sides of the loop and the plane of the loop is same as the left wire. If a steady current I is established in the wire as shown in the (fig) the loop will –

1. Rotate About An Axis Parallel To The Wire
2. Move Away From The Wire
3. Move Towards The Wire
4. Remain Stationary.

Answer: 3. Move Towards The Wire

Question 10. Select the correct alternative(s): Two thin long parallel wires separated by a distance ‘b’ are carrying a current ‘i’ ampere each. The magnitude of the force per unit length exerted by one wire on the other is

1. \(\frac{\mu_0 i^2}{b^2}\)
2. \(\frac{\mu_0 i^2}{2 \pi b}\)
3. \(\frac{\mu_0 \mathrm{i}}{2 \pi \mathrm{b}^2}\)

Answer: 2. \(\frac{\mu_0 i^2}{2 \pi b}\)

Question 11. Two parallel wires carry currents of 20 A and 40 A in opposite directions. Another wire carrying a current antiparallel to 20 A is placed midway between the two wires. The magnetic force on it will be

1. Towards 20 a
2. Towards 40 a
3. Zero
4. Perpendicular to the plane of the currents

Answer: 2. Towards 40 a

Question 12. A closed-loop PQRS carrying a current is placed in a uniform magnetic field. if the magnetic forces on segments PS, SR, and RQ are F1, F2, and F3 respectively, and are in the plane of the paper and along the directions shown the directions shown, the force on the segment QP is Two long conductors, separated by a distance d carry currents I 1 and I 2 in the same direction.

1. F3 – F1 – F2
2. \(\sqrt{\left(F_3-F_1\right)^2+F_2^2}\)
3. \(\sqrt{\left(F_3-F_1\right)^2-F_2^2}\)
4. F3 – F1 + F2

Answer: 2. \(\sqrt{\left(F_3-F_1\right)^2+F_2^2}\)

Question 13. They exert a force F on each other. Now the current in one of them is increased to two times and its direction is reversed. The distance is also increased to 3d. The new value of the force between them is :

1. –2 F
2. F/3
3. –2F/3
4. – F/3

Answer: 3. –2F/3

Chapter 1 Magnetic Field Multiple Choice Questions Section (I): Magnetic Force And Torque On A Current Carrying Loop And Magnetic Dipole Moment

Question 1. If the angular momentum of the electron is then its magnetic moment will be eJ (1)

1. \(\frac{\mathrm{eJ}}{\mathrm{m}}\)
2. \(\frac{e J}{2 m}\)
3. eJ2m
4. \(\frac{2 m}{e J}\)

Answer: 2. \(\frac{\mathrm{eJ}}{\mathrm{m}}\)

Question 2. A coil of 100 turns is lying in a magnetic field of 1T as shown in the figure. A current of 1A is flowing in this coil. The torque acting on the coil will be

1. 1N–m
2. 2N–m
3. 3N–m
4. 4N–m

Answer: 2. 2N–m

Question 3. Four wires of equal length are bent in the form of four loops P, Q, R, and S. These are suspended in a uniform magnetic field and the same current is passed in them. The maximum torque will act on.

1. P
2. Q
3. R
4. S

Answer: 4. S

Question 4. A bar magnet has a magnetic moment of 2.5 JT–1 and is placed in a magnetic field of 0.2 T. Work was done in turning the magnet from a parallel to an antiparallel position relative to the field direction.

1. 0.5 J
2. 1 J
3. 2.0 J
4. Zero

Answer: 2. 1 J

Question 5. A circular loop of area 1 cm 2, carrying a current of 10 A, is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is

1. Zero
2. 10-4 N-M
3. 10–2 N-M
4. 1 N-M

Answer: 1. Zero

Question 6. A toroid of mean radius ‘a’, cross-section radius ‘r’, and a total number of turns N. It carries a current ‘i’. The torque experienced by the toroid if a uniform magnetic field of strength B is applied :

1. Is zero
2. Is binπ r²
3. Is binπa²
4. Depends on the direction of the magnetic field.

Answer: 3. Is binπa²

Question 7. A bar magnet of magnetic moment is placed in a magnetic field of induction. The torque exerted on it is :

1. \(\overrightarrow{\mathrm{M}} \vec{B}\)
2. \(\overrightarrow{\mathrm{M}} \vec{B}\)
3. \(\vec{M} \times \vec{B}\)
4. \(-\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}\)

Answer: 3. \(\vec{M} \times \vec{B}\)

Question 8. Current is flowing in a coil of area A and number of turns N, then magnetic moment of the coil M is equal to:

1. NiA
2. \(\frac{\mathrm{Ni}}{\mathrm{A}}\)
3. \(\frac{\mathrm{Ni}}{\sqrt{\mathrm{A}}}\)
4. N2Ai

Answer: 1. NiA

Question 9. A circular loop has a radius of 5 cm and it carries a current of 0.1 amp. Its magnetic moment is:

1. 1.32 × 10–4 amp. – m²
2. 2.62 × 10–4 amp. – m²
3. 5.25 × 10–4 amp. – m²
4. 7.85 × 10–4 amp. – m²

Answer: 4. 7.85 × 10–4 amp. – m²

Question 10. The dipole moment of a current loop is independent of

1. Current In The Loop
2. Number Of Turns
3. Area Of The Loop
4. Magnetic Field In Which It Is Situated

Answer: 4. Magnetic Field In Which It Is Situated

Question 11. Current I is carried in a wire of length L. If the wire is formed into a circular coil, the maximum magnitude of torque in a given magnetic field B will be:

1. \(\frac{\text { LIB }}{4 \pi}\)
2. \(\frac{\mathrm{L}^2 \mathrm{IB}}{4 \pi}\)
3. \(\frac{\mathrm{L}^2 \mathrm{IB}}{2}\)
4. \(\frac{\mathrm{LIB}^2}{2}\)

Answer: 2. \(\frac{\mathrm{L}^2 \mathrm{IB}}{4 \pi}\)

NEET Physics Magnetic Field MCQs with Answers

Question 12. Due to the flow of current in a circular loop of radius R, the magnetic induction produced at the center of the loop is B. The magnetic moment of the loop is = Permeability constant]:

1. BR3/ 2πμ0
2. 2πBR3μ0
3. BR2/ 2μ0
4. 2πBR2/μ0

Answer: 2. 2πBR3μ0

Question 13. The magnetic moment of a circular coil carrying current is:

1. Directly proportional to the length of the wire in the coil
2. Inversely proportional to the length of the wire in the coil
3. Directly proportional to the square of the length of the wire in the coil
4. Inversely proportional to the square of the length of the wire in the coil

Answer: 3. Directly proportional to the square of the length of the wire in the coil

Question 14. To double the torque acting on a rectangular coil of n turns when placed in a magnetic field.

1. The area of the coil and the magnetic induction should be doubled
2. The area or current through the coil should be doubled
3. Only the area of the coil should be doubled
4. The number of turns is to be halved

Answer: 2. Area or current through the coil should be doubled

Question 15. The magnetic dipole moment of a rectangular loop is

1. Inversely proportional to the current in the loop
2. Inversely proportional to the area of the loop
3. Parallel to the plane of the loop and proportional to the area of the loop
4. Perpendicular to the plane of the loop and proportional to the area of the loop

Answer: 4. Perpendicular to the plane of the loop and proportional to the area of the loop

Question 16. Two bar magnets having the same geometry with magnetic moments M and 2M are firstly placed in such a way that their similar poles are same side then their period of osculation is T1. Now the polarity of one of the magnets is reversed the period of oscillation is T1. The period of oscillations will be:-

1. T₁ < T₂
2. T₁ > T₂
3. T₁ = T₂
4. T₂ = ∞

Answer: 2. T₁ > T₂

Question 17. A charged particle (charge q) is moving in a circle of radius R with uniform speed v. The associated magnetic moment μ is given by :

1. \(\frac{\mathrm{qvR}}{2}d\)
2. qvR²
3. \(\frac{\mathrm{qvR}^2}{2}\)
4. qvR

Answer: 1. \(\frac{\mathrm{qvR}}{2}\)

Question 18. A magnetic needle lying parallel to a magnetic field requires W units of work to turn it through 60º. The torque needed to maintain the needle in this position will be:

1. \(\sqrt{3} W\)
2. W
3. \((\sqrt{3} / 2) W\)
4. 2W

Answer: 1. \(\sqrt{3} W\)

Question 19. Two particles, each of mass m and charge q, are attached to the two ends of a light rigid rod of length 2 R. The rod is rotated at constant angular speed about a perpendicular axis passing through its center. The ratio of the magnitudes of the magnetic moment of the system and its angular momentum about the center of the rod is:

1. \(\frac{\mathrm{q}}{2 \mathrm{~m}}\)
2. \(\frac{q}{m}\)
3. \(\frac{2 q}{m}\)
4. \(\frac{q}{\pi m}\)

Answer: 1. \(\frac{\mathrm{q}}{2 \mathrm{~m}}\)

Question 20. A current-carrying loop is placed in a uniform magnetic field towards the right in four different orientations, arranged in the decreasing order of Potential Energy.

1. 1,3,2,4
2. 1,2,3,4
3. 1,4,2,3
4. 3,4,1,2

Answer: 1. 1,3,2,4

Question 21. A circular coil of diameter 2.0 cm has 500 turns in it and carries a current of 1.0 A. Its axis makes an angle of 30º with the uniform magnetic field of magnitude 0.40 T that exists in the space. Find the torque acting on the coil.

1. π × 10^-8 N – m
2. π × 10^-4 N – m
3. π × 10^-6 N – m
4. π× 10^-2 N – m

Answer: 4. π× 10^-2 N – m

Chapter 1 Magnetic Field Multiple Choice Questions Section (J): Magnetic Field Due To A Magnet And Earth

Question 1. When a current of 1 ampere is passed in a coil lying in the magnetic meridian then a magnetic needle 8 at its center gives some deflection. If the current in the coil is increased to ampere then at what distance from the center of the coil will the deflection of the needle remain unchanged?

1. 2R
2. 4R
3. 8R
4. R

Answer: 4. 2R

Question 2. Tangent galvanometer measures:

1. Capacitance
2. Current
3. Resistance
4. Potential difference

Answer: 2. Current

Chapter 1 Magnetic Field Multiple Choice Questions Section (k): properties of magnetic material

Question 1. When a small magnetizing field h is applied to a magnetic material, the intensity of magnetization is proportional to:

1. H‾²
2. H^1/2
3. H
4. H²

Answer: 3. H

Question 2. How does the magnetic susceptibility x of a paramagnetic material change with absolute temperature t?

1. χ ∝ T
2. χ ∝ T ¯¹
3. χ = Constant
4. χ ∝ e^T

Answer: 2. χ ∝ T ¯¹

Question 3. Consider the following statements for a paramagnetic substance kept in a magnetic field:

1. If the magnetic field increases, the magnetization increases.
2. If the temperature rises, the magnetization increases.
3. Both (a) and (b) are true (a) is true but (b) is false
4. Is true but (a) is false both (a) and (b) are false

Answer: 2. If the temperature rises, the magnetization increases.

Question 4. Which of the following relations is not correct?

1. B = μ₀ (H+I)
2. B = μ₀ (H+χm)
3. μ0 = μ₀ (1+χm)
4. μr = 1 + χm

Answer: 3. μ0 = μ₀ (1+χm)

Question 5. The hysteresis loop for the material of a permanent magnet is:

1. Short and wide
2. Tall and narrow
3. Tall and wide
4. Short and narrow

Answer: 1. Short and wide

Question 6. Select the incorrect alternative (s): when a ferromagnetic material goes through a complete cycle of magnetization, the magnetic susceptibility:

1. Has a fixed value
2. May be zero
3. May be infinite
4. May be negative

Answer: 1. Has a fixed value

Question 7. The material for making permanent magnets should have :

1. High retentivity, high coercivity
2. High retentivity, low coercivity
3. Low retentivity, high coercivity
4. Low retentivity, low coercivity

Answer: 1. High retentivity, high coercivity

Question 8. (A) soft iron is a conductor of electricity. (B) it is a magnetic material. (C) it is an alloy of iron. (D) It is used for making permanent magnets. State whether :

1. A and c are true
2. A and b are true
3. C and d are true
4. B and d are true

Answer: 2. A and b are true

Question 9. Soft iron is used in many electrical machines for :

1. Low hysteresis loss and low permeability
2. Low hysteresis loss and high permeability
3. High hysteresis loss and low permeability
4. High hysteresis loss and high permeability

Answer: 2. Low hysteresis loss and high permeability

Question 10. For protecting sensitive equipment from the external magnetic field, it should be :

1. Placed inside an aluminum can
2. Placed inside an iron can
3. Wrapped with insulation around it when passing current through it
4. Surrounded by fine copper sheet

Answer: 2. Placed inside an iron can

Question 11. If a long hollow copper pipe carries a current, then a magnetic field is produced :

1. Inside the pipe only
2. Outside the pipe only
3. Both inside and outside the pipe
4. Nowhere

Answer: 2. Outside the pipe only

Question 12. The materials suitable for making electromagnets should have

1. High retentivity and high coercivity
2. Low retentivity and low coercivity
3. High retentivity and low coercivity
4. Low retentivity and high coercivity

Answer: 3. High retentivity and low coercivity

Question 13. Needles n 1, n 2, and n 3 are made of a ferromagnetic, a paramagnetic, and a diamagnetic substance respectively. A magnet when brought close to them will:

1. Attract all three of them
2. Attract n 1 and n2 strongly but repel n3
3. Attract n 1 strongly, n2 weakly, and repel n3 weakly
4. Attract n 1 strongly, but repel n 2 and n3 weakly

Answer: 3. Attract n1 strongly, n2 weakly and repel n3 weakly

Chapter 1 Magnetic Field Multiple Choice Questions Exercise 2

Question 1. Two identical magnetic dipoles of magnetic moments 1.0 A-m2 each, placed at a separation of 2 m with their axes perpendicular to each other. The resultant magnetic field at a point midway between the dipole is:

1. 5 × 10–7 T
2. × 10–7 T
3. 10–7 T
4. 2 × 10–7 T

Answer: 2. × 10–7 T

Question 2. A moving charge produces

1. Electric field only
2. Magnetic filed only
3. Both of them
4. None of these

Answer: 3. Both of them

Question 3. Consider a long, straight wire of cross-section area A carrying a current i. Let there be n free electrons per unit volume. An observer places himself on a trolley moving in the direction opposite to the current with a speed v = (i/nAe) and separated from the wire by a distance r. The magnetic field seen by the observer is

1. \(\frac{\mu_0 i}{2 \pi r}\)
2. Zero
3. \(\frac{\mu_0 i}{\pi r}\)
4. \(\frac{\mu_0 i}{\pi r}\)

Answer: 1. \(\frac{\mu_0 i}{2 \pi r}\)

Question 4. An infinitely long conductor PQR is bent to form a right angle as shown. A current flows through PQR. The magnetic field due to this current at the point M is H 1. Now, another infinitely long straight conductor QS is connected at Q so that the current in PQ remains unchanged. The magnetic field at M is now H

1. 1/2
2. 1
3. 2/3
4. 2

Answer: 3. 2/3

Question 5. A non-planer loop of conducting wire carrying a current I is placed as shown in the figure. Each of the straight sections of the loop is of length 2a. The magnetic field due to this loop at the point P(a, 0, a) points in the direction.

1. \(\frac{1}{\sqrt{2}}(-\hat{j}+\hat{k})\)
2. \(\frac{1}{\sqrt{3}}(-\hat{j}+\hat{k}+\hat{i})\)
3. \(\frac{1}{\sqrt{3}}(\hat{i}+\hat{j}+\hat{k})\)
4. \(\frac{1}{\sqrt{3}}(\hat{i}+\hat{j}+\hat{k})\)

Answer: 4. \(\frac{1}{\sqrt{3}}(\hat{i}+\hat{j}+\hat{k})\)

Question 6. The figure shows an amperian path ABCDA. Part ABC is in vertical plane PSTU while part CDA is in horizontal plane PQRS. The direction of circulation along the path is shown by an arrow near point B and this path according to Ampere’s law will be:

1. (i1 – i2 + i3) μ0
2. (– i1 + i2) μ0
3. i3 μ0
4. (i1 + i2) μ0

Answer: 4. (i1 + i2) μ0

Question 7. A proton, a deuteron, and an α-particle having the same kinetic energy are moving in circular trajectories in a constant magnetic field. If r p, rd, and r denote respectively the radii of the trajectories of these particles then

1. rα = rp < rd
2. rα > rd > rp
3. rα = rd > rp
4. rp = rd = rα

Answer: 1. rα = rp < rd

Question 8. Two very long, straight, parallel wires carry steady currents I and – I respectively. The distance between the wires is d. At a certain instant of time, a point charge q is at a point equidistant from the v two wires, in the plane of the wires. Its instantaneous velocity is perpendicular to this plane. The magnitude of the force due to the magnetic field acting on the charge at this instant is

1. \(\frac{\mu_0 \text { Iqv }}{2 \pi d}\)
2. \(\frac{\mu_0 \text { Iqv }}{\pi d}\)
3. \(\frac{2 \mu_0 \text { Iqv }}{\pi d}\)
4. 0

Answer: 4. 0

Question 9. An ionized gas contains both positive and negative ions. If it is subjected simultaneously to an electric field along the + x direction and a magnetic field along the +z direction, then

1. Positive ions deflect toward the +y direction
2. All ions deflect toward the +y direction
3. All ions deflect toward the –y direction
4. Positive ions deflect towards –y direction and negative ions towards +y direction

Answer: 3. All ions deflect toward the –y direction

Question 10. A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of the loop. The magnetic force acting on the loop is

1. ir B
2. 2π r i B
3. zero
4. π r i B

Answer: 3. zero

Question 11. In the figure shown a current I1 is established in the long straight wire AB. Another wire CD carrying the current CD is placed in the plane of the paper. The line joining the ends of this wire is perpendicular to the wire AB. The resultant force on the wire CD is:

1. Towards negative x-axis
2. Towards positive y-axis
3. Somewhere between –x-axis and + y-axis
4. Somewhere between the +x axis and + y-axis

Answer: 4. Somewhere between the +x axis and + y-axis

Question 12. A steady current ‘l’ flows in a small square loop of wire of side L in a horizontal plane. The loop is now 2 1 folded about its middle such that half of it lies in a vertical plane. Let and respectively denote the magnetic moments of the current loop before and after folding. Then :

1. A is feebly repelled
2. B is feebly attached
3. C is strongly attracted
4. D remains unaffected

Which one of the following is true?

1. B is of a paramagnetic material
2. C is of a diamagnetic material
3. D is of a ferromagnetic material
4. A is of a non–magnetic material

Answer: 3. D is of a ferromagnetic material

Question 13. A particle of charge q and mass m moves in a circular orbit of radius r with angular speed w. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on

1. w and q
2. w, q and m
3. q and m
4. w and m

Answer: 3. q and m

Magnetic Field NEET Class 12 Chapter 1 Practice MCQs

Question 14. A power line lies along the east-west direction and carries a current of 10 amperes. The force per meter due to the earth’s magnetic field of 10–4 T is

1. 10–5 N
2. 10–4 N
3. 10–3 N
4. 10–2 N

Answer: 3. 10–3 N

Question 15. A circular coil of radius 20 cm and 20 turns of wire is mounted vertically with its plane in a magnetic meridian. A small magnetic needle (free to rotate about a vertical axis) is placed at the center of the coil. It is deflected through 45° when a current is passed through the coil in equilibrium Horizontal component of the earth’s field is 0.34 × 10–4 T. The current in the coil is:

1. \(\frac{17}{10 \pi} \mathrm{A}\)
2. 6A
3. 6×10-3A
4. \(\frac{3}{50} \mathrm{~A}\)

Answer: 1. \(\frac{17}{10 \pi} \mathrm{A}\)

Question 16. The magnetic materials having negative magnetic susceptibility are:

1. Nonmagnetic
2. Para magnetic
3. Diamagnetic
4. Ferromagnetic

Answer: 3. Diamagnetic

Question 17. A loop carrying current I lies in the x-y plane as shown in the figure. the unit vector is coming out of the plane of the paper. the magnetic moment of the current loop is :

1. \(a^2 \mathrm{I} \hat{k}\)
2. \(\left(\frac{\pi}{2}+1\right) a^2 I \hat{k}\)
3. \(-\left(\frac{\pi}{2}+1\right) a^2 I \hat{k}\)
4. \((2 \pi+1) \mathrm{a}^2 \mathrm{I} \hat{\mathrm{k}}\)

Answer: 2. \(\left(\frac{\pi}{2}+1\right) a^2 I \hat{k}\)

Question 18. An infinitely long hollow conducting cylinder with inner radius R/2 and outer radius R carries a uniform B current density along its length. The magnitude of the magnetic field, as a function of the radial distance r from the axis is best represented by:

Answer: 4.

Question 19. If a long horizontal wire is bent as shown in the figure and current i is passed through it, then the magnitude and direction of the magnetic field produced at the center of the circular part will be.

1. \(\frac{\mu_0 i}{r}, \otimes\)
2. \(\frac{\mu_0 i}{2 r}\left(1-\frac{1}{\pi}\right), \otimes\)
3. \(\frac{\mu_0 \mathrm{i}}{2 \mathrm{i}}\left[1+\frac{1}{\pi}\right] \otimes\)
4. \(\frac{\mu_0 i}{r}\left(1-\frac{1}{\pi}\right), \otimes\)

Answer: 2. \(\frac{\mu_0 i}{2 r}\left(1-\frac{1}{\pi}\right), \otimes\)

Question 20. The cosmic rays falling are deflected towards

1. East
2. West
3. Directly come down
4. None of the above

Answer: 1. East

Question 21. If A 1 = 24 and q1 = e and A0 = 22 and q 2 = 2e ions enter a uniform perpendicular magnetic field with the same speed, the ratio of the radius of their circular paths will be

1. 12/11
2. 24/11
3. 11/12
4. 11/24

Answer: 1. 12/11

Question 22. Which one of the following is ferromagnetic?

1. Co
2. Zn
3. Hg
4. Pt

Answer: 1. Co

Question 23. Sometimes positively charged particle comes from space toward earth with high velocity. Its deviation due to the magnetic field of Earth will be:

1. Towards north
2. Towards south
3. Towards west
4. Towards east

Answer: 4. Towards east

Question 24. For paramagnetic materials magnetic susceptibility is related to temperature as

1. χ ∝ T²
2. χ ∝ T¹
3. χ ∝ T¯¹
4. χ ∝ T²

Answer: 3. χ ∝ T¯¹

Question 25. Current I is flowing in a conducting circular loop of radius R. It is kept in a uniform magnetic field B. Find the magnetic force acting on the loop.

1. IRB
2. 2πIRB
3. Zero
4. πIRB

Answer: 3. Zero

Question 26. The magnetic field at the center of the semi-circular wire carrying current i is

1. \(\frac{\mu_0 i}{2 r}\)
2. \(\frac{\mu_0 i}{4 r}\)
3. \(\frac{\mu_0 i}{r}\)
4. \(\frac{\mu_0 i}{2 \pi r}\)

Answer: 3. \(\frac{\mu_0 i}{r}\)

Question 27. A wire EF carrying current i1 is placed near a current-carrying rectangular loop ABCD as shown. Then the wire EF

1. Remains unaffected
2. Is attracted towards the loop
3. Is repelled away from the loop
4. First attracted and then repelled

Answer: 3. Is repelled away from the loop

Question 28. If a current of I amp is flowing in the winding of the solenoid and n is the number of turns per unit length, then the magnetic field at the center of the solenoid is

1. μ0n1
2. \(\frac{\mu_0 n i}{2}\)
3. \(\frac{\mu_0 \mathrm{i}}{2 \mathrm{n}}\)
4. \(\frac{\mu_0 i}{n}\)

Answer: 1. μ0n1

Question 29. On a magnetic needle placed in a uniform magnetic field:

1. F ≠0, τ ≠ 0
2. F ≠0, τ= 0
3. F =0, τ ≠ 0
4. F =0, τ = 0

Answer: 3. F =0, τ ≠ 0

Question 30. An electron moves at a right angle to a magnetic field of 1.5 × 10 –2 T with a 6 × 107 m/s speed. If the specific charge of the electron is 1.7 × 1011 C/kg. The radius of the circular path will be:

1. 2.9 cm
2. 3.9 cm
3. 2.35 cm
4. 2 cm

Answer: 3. 2.35 cm

NEET Physics Magnetic Field: MCQ Practice Test

Question 31. A bar magnet of magnetic moment is placed in the magnetic field. The torque acting on the magnet is:

1. \(\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}\)
2. \(\vec{M}-\vec{B}\)
3. \(\frac{1}{2} \vec{M} \times \vec{B}\)
4. \(\overrightarrow{\mathrm{M}}+\overrightarrow{\mathrm{B}}\)

Answer: 1. \(\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}\)

Question 32. An electron and proton enter a magnetic field perpendicularly. Both have the same kinetic energy. Which of the following is true?

1. The trajectory of the electron is less curved
2. The trajectory of the proton is less curved
3. Both trajectories are equally curved
4. Both move on a straight-line path

Answer: 2. Trajectory of the proton is less curved

Question 33. A small circular flexible loop of wire of radius r carries a current I. It is placed in a uniform magnetic field B. The tension in the loop will be doubled if :

1. I is halved
2. B is halved
3. r is doubled
4. both B and I are doubled

Answer: 3. r is doubled

Question 34. Two concentric circular coils of ten turns each are situated in the same plane. Their radii are 20 cm and 40 cm and carry respectively 0.2A and 0.3A currents in opposite directions. The magnetic field in Tesla at the center is

1. \(\frac{35 \mu_0}{4}\)
2. \(\frac{\mu_0}{80}\)
3. \(\frac{7 \mu_0}{80}\)
4. \(\frac{5 \mu_0}{4}\)

Answer: 4. \(\frac{5 \mu_0}{4}\)

Question 35. A hydrogen atom is paramagnetic. A hydrogen molecule is-

1. Diamagnetic
2. Paramagnetic
3. Ferromagnetic
4. None of these

Answer: 1. Diamagnetic

Question 36. Under the influence of a uniform magnetic field a charged particle is moving in a circle of radius R with constant speed v. The period of the motion

1. Depends on v and not on r
2. Depends on both r and v
3. Is independent of both r and v
4. Depends on r and not on v

Answer: 3. Is independent of both r and v

Question 37. A charged particle (charge q) is moving in a circle of radius R with uniform speed v. The associated magnetic moment μ is given by :

1. \(\frac{\mathrm{qvR}}{2}\)
2. qvR2
3. \(\frac{\mathrm{qvR}^2}{2}\)
4. qvR

Answer: 1. \(\frac{\mathrm{qvR}}{2}\)

Question 38. The charge on a particle Y is double the charge on particle X. These two particles X and Y after being accelerated through the same potential difference enter a region of uniform magnetic field and describe circular paths of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is:

1. (2R1 / R2)2
2. (R1 / 2R2)2
3. R1 2 / 2R22
4. 2R1 / R2

Answer: 3. R1 2 / 2R22

Question 39. The magnetic needle of a tangent galvanometer is deflected by an angle 30°due to a magnet. The horizontal component of Earth’s magnetic field is 0.34 × 10 –4 T along the plane of the coil. The intensity of the magnetic field of the magnet is:

1. 1.96 × 10–4 T
2. 1.96 × 10–5 T
3. 1.96 × 104 T
4. 1.96 × 105 T

Answer: 2. 1.96 × 10–5 T

Question 40. There are 50 turns of a wire in every cm length of a long solenoid. If 4A currents are flowing in the solenoid, the approximate value of the magnetic field along its axis at an internal point and one end will be respectively:

1. 12.6 × 10–3 Wb/m2 , 6.3 × 10–3 Wb/m2
2. 12.6 × 10–3 Wb/m2, 25.1 × 10–3 Wb/m2
3. 25.1 × 10–3 Wb/m2, 12.6 × 10–3 Wb/m2
4. 25.1 × 10–5 Wb/m2, 12.6 × 10–5 Wb/m2

Answer: 3. 25.1 × 10–3 Wb/m2, 12.6 × 10–3 Wb/m2

Question 41. A particle of charge –16 × 10–18 C moving with velocity 10ms–1 along the x-axis enters a region where a magnetic field of induction B is along the y-axis and an electric field of magnitude 104V/m is along the negative z-axis. If the charged particle continues moving along the x-axis, the magnitude of B is

1. 1016 Wb/m2
2. 105 Wb/m2
3. 103 Wb/m2
4. 10–3 Web/m2

Answer: 3. 103 Wb/m2

Question 42. Before using the tangent galvanometer, its coil is set up in:

1. Magnetic Meridian
2. Perpendicular To Magnetic Meridian
3. At Angle Of 45° To Magnetic Meridian
4. It Does Not Require Any Setting

Answer: 1. Magnetic Meridian

Question 43. Two magnets are kept in a vibration magnetometer and vibrate in Earth’s magnetic field. There are 12 vibrations per minute when like poles are kept together, but only 4 vibrations per minute when opposite poles are kept together then the ratio of magnetic moments will be:

1. 3: 1
2. 1 : 3
3. 3: 5
4. 5: 4

Answer: 4. 3: 1

Question 44. In a hydrogen atom, an electron revolves around the nucleus 6.6 × 10 15 revolutions per second in a radius of 0.53 Å. The value of the magnetic field at the center of the orbit will be:

1. 0.125 V/m2
2. 1.25 V/m2
3. 12.5 V/m2
4. 125 V/m2 a

Answer: 3. 12.5 V/m2

Question 45. Properties related to diamagnetism are given below, select the wrong statement.

1. Diamagnetic material does not have a permanent magnetic moment.
2. Diamagnetism is explained in terms of electromagnetic induction.
3. Diamagnetic substances have small positive magnetic susceptibility.
4. Magnetic moments of different electrons cancel each other.

Answer: 3. Diamagnetic substances have small positive magnetic susceptibility.

Question 46. In a moving coil, the galvenometer number of turns is 48, and the area of the coil is 4 × 10 –2 m2. If the intensity of the magnetic field is 0.2 then how many turns in it are required to increase its sensitivity by 25% while area (A) and magnetic field (B) are constant?

1. 24
2. 36
3. 60
4. 54

Answer: 3. 60

Question 47. A magnet is parallel to a uniform magnetic field work done to rotate it by 60° is 0.8 joule. Then rotate it by 30° again will be:

1. 0.8 × 107 Ag
2. 4.0 Ag
3. 8 Ag
4. 0.8 Ag

Answer: 1. 0.8 × 107 Ag

Question 48. The charge on particle Y is double the charge on particle X. These two particles X and Y after being accelerated through the same potential difference enter the region of uniform magnetic field and describe circular parts of radii R1 and R2 respectively. The ratio of the mass of X to that of Y is

1. (2R1/R2)2
2. (R1/2R2)2
3. \(\frac{R_1^2}{2 R_2^2}\)
4. 2R1/R2

Answer: 3. \(\frac{R_1^2}{2 R_2^2}\)

Question 49. A proton and a deuteron are accelerated with the same potential difference and enter perpendicularly in a region of magnetic field B. If r p and r d are the radii of circular paths taken by proton and deuteron d respectively, the ratio p r would be

1. \(2 \sqrt{2}\)
2. \(\frac{1}{\sqrt{2}}\)
3. \(\frac{R_1^2}{2 R_2^2}\)
4. 2

Answer: .(Bonus/2)

Question 50. A particle of charge ‘q’ and mass ‘m’ move in a circular orbit of radius ‘r’ with frequency ‘v’. The ratio of the magnetic moment to angular momentum is

1. \(\frac{2 q v}{m}\)
2. \(\frac{q v}{2 m}\)
3. \(\frac{\mathrm{q}}{2 \mathrm{mr}}\)
4. \(\frac{q}{2 m}\)

Answer: 4. \(\frac{q}{2 m}\)

Question 51. A rectangular loop of length 20 cm, along y -the axis and breadth 10 cm along the z-axis carries a current of \((0.3 \hat{i}+0.4 \hat{j})\). If a uniform magnetic field (0.3 + 0.4 ) acts on the loop, the torque acting on it is

1. 9.6 × 10–4 Nm along x-axis
2. 9.6 × 10–3 Nm along the y-axis
3. 9.6 × 10–2 Nm along the z-axis
4. 9.6 × 10–3 Nm along the z-axis

Answer: 3. 9.6 × 10–2 Nm along z-axis

Question 52. The length of a magnet is large compared to its width and breadth. The period of its oscillation in a vibration magnetometer is 2s. The magnet is cut perpendicular to its length into three equal parts and three parts are then placed on each other with their like poles together. The period of this combination will be:

1. 2s
2. 2/3s
3. \(2 \sqrt{3} \mathrm{~s}\)
4. \(2 / \sqrt{3} \mathrm{~s}\)

Answer: 2. 2/3s

Question 53. Two concentric coils each of radius equal to 2π cm are placed at right angles to each other. 3 ampere and 4 ampere are the currents flowing in each coil respectively. The magnetic induction in weber/m 2 at the centre of the coils will be (μ0 = 4π × 10–7 Wb/A.m):

1. 12 × 10^-5
2. 10^-5
3. 5 × 10^-5
4. 7 × 10^-5

Answer: 3. 5 × 10^-5

Question 54. The relative permittivity and permeability of a material are r and r, respectively. Which of the following values of these quantities are allowed for a diamagnetic material?

1. εr = 1.5 , μr = 0.5
2. εr = 0.5 , μr = 0.5
3. εr = 1.5 ,μr = 1.5
4. εr = 0.5 , μr = 1.5

Answer: 1. εr = 1.5 ,μr = 0.5

Question 55. A horizontal overhead powerline is at a height of 4 m from the ground and carries a current of 100 A from east to west. The magnetic field directly below it on the ground is (μ0 = 4π × 10–7 T mA–1):

1. 5 × 10^-6T northward
2. 5 × 10^-6 T southward
3. 2.5 × 10^-7 T northward
4. 2.5 × 10^-7 T southward

Answer: 2. 5 × 10–6 T southward

Chapter 1 Magnetic Field Multiple Choice Questions Exercise-3

Question 1. A uniform electric field and uniform magnetic field are acting along the same direction in a certain region. If an electron is projected in the region such that its velocity is pointed along the direction of fields, then the electron:

1. Will turn towards the right of direction of motion
2. Speed will decrease
3. Speed will increase
4. Will turn towards the left direction of motion

Answer: 2. Speed will decrease

Question 2. A square loop, carrying a steady current I1 is placed in a horizontal plane near a long straight conductor carrying a steady current I1 at a distance d from the conductor as shown in the figure. The loop will experience :

1. A net repulsive force away from the conductor
2. A net torque acting upward perpendicular to the horizontal plane
3. A net torque acting downward normally to the horizontal plane
4. A net attractive force toward the conductor

Answer: 4. A net attractive force towards the conductor

Question 3. Charge q is uniformly spread on a thin ring of radius R. The ring rotates about its axis with a uniform frequency of f Hz. The magnitude of magnetic induction at the center of the ring is

1. \(\frac{\mu_0 q f}{2 R}\)
2. \(\frac{\mu_0 q}{2 f R}\)
3. \(\frac{\mu_0 q}{2 \pi f R}\)
4. \(\frac{\mu_0 \mathrm{qf}}{2 \pi R}\)

Answer: 1. \(\frac{\mu_0 q f}{2 R}\)

Question 4. A short bar magnet of magnetic moment 0.4J T–1 is placed in a uniform magnetic field of 0.16 T. The magnet is in stable equilibrium when the potential energy is:

1. –0.064 J
2. zero
3. – 0.082 J
4. 0.064

Answer: 1. –0.064 J

NEET Physics Magnetic Field Questions: Chapter 1 MCQs

Question 5. A compass needle which is allowed to move in a horizontal plane is taken to a geomagnetic pole. It:

1. Will become rigid showing no movement
2. Will stay in any position
3. Will stay in north-south direction only
4. Will stay in east-west direction only

Answer: 2. Will stay in any position

Question 6. An alternating electric field, of frequency v, is applied across the dees (radius = R) of a cyclotron that is being used to accelerate protons (mass = m). The operating magnetic field (B) used in the cyclotron and the kinetic energy (K) of the proton beam, produced by it, are given by :

1. \(B=\frac{m v}{e} \text { and } K=2 m \pi^2 v^2 R^2\)
2. \(B=\frac{2 \pi m v}{e} \text { and } K=m^2 \pi v R^2\)
3. \(B=\frac{2 \pi m v}{e} \text { and } K=2 m \pi^2 v^2 R^2\)
4. \(B=\frac{2 \pi m v}{e} \text { and } K=2 m \pi^2 v^2 R^2\)

Answer: 3. \(B=\frac{2 \pi m v}{e} \text { and } K=2 m \pi^2 v^2 R^2\)

Question 7. Two similar coils of radius R are lying concentrically with their planes at right angles to each other. The currents flowing in them are a 2 I, respectively. The resultant magnetic field induction at the center will be:

1. \(\frac{\sqrt{5} \mu_0 I}{2 R}\)
2. \(\frac{3 \mu_0 I}{2 R}\)
3. \(\frac{\mu_0 I}{2 R}\)
4. \(\frac{\mu_0 I}{R}\)

Answer: 1. \(\frac{\sqrt{5} \mu_0 I}{2 R}\)

Question 8. A proton carrying 1 MeV kinetic energy is moving in a circular path of radius R in a uniform magnetic field. What should be the energy of an α- particle to describe a circle of the same radius in the same field?

1. 2 MeV
2. 1 MeV
3. 0.5 MeV
4. 4 MeV

Answer: 2. 1 MeV

Question 9. A magnetic needle suspended parallel to a magnetic field requires J of work to turn it through 60°. The torque needed to maintain the needle in this position will be :

1. \(2 \sqrt{3} \mathrm{~J}\)
2. 3J
3. \(\sqrt{3} \mathrm{~J}\)
4. \(\frac{3}{2} \mathrm{~J}\)

Answer: 2. \(2 \sqrt{3} \mathrm{~J}\)

Question 10. A bar magnet of length ‘I’ and magnetic dipole moment ‘M’ is bent in the form of an arc as shown in the figure. The new magnetic dipole moment will be :

1. \(\frac{3}{\pi} \mathrm{M}\)
2. \(\frac{2}{\pi} \mathrm{M}\)
3. \(\frac{M}{2}\)
4. M

Answer: 1. \(\frac{3}{\pi} \mathrm{M}\)

Question 11. A current loop in a magnetic field:

1. Can be in equilibrium in one orientation
2. Can be in equilibrium in two orientations, both equilibrium states are unstable
3. Can be in equilibrium in two orientations, one stable while the other is unstable
4. Experiences a torque whether the field is uniform or nonuniform in all orientations

Answer: 3. Can be in equilibrium in two orientations, one stable while the other is unstable

Question 24. When a proton is released from rest in a room, it starts with an initial acceleration a0 towards the west. When it is projected towards the north with a speed of v0 it moves with an initial acceleration of 3a0 toward the west. The electric and magnetic fields in the room are :

1. \(\frac{\mathrm{ma}_0}{\mathrm{e}} \text { west, } \frac{2 \mathrm{ma}_0}{\mathrm{ev}_0} \text { down }\)
2. \(\frac{\mathrm{ma}_0}{\mathrm{e}} \text { east, } \frac{3 \mathrm{ma}_0}{\mathrm{ev}_0} \text { up }\)
3. \(\frac{\mathrm{ma}_0}{\mathrm{e}} \text { east, } \frac{3 \mathrm{ma}_0}{\mathrm{ev}_0} \text { down }\)
4. \(\frac{\mathrm{ma}_0}{\mathrm{e}} \text { west, } \frac{2 \mathrm{ma}_0}{\mathrm{ev}_0} \text { up }\)

Answer: 1. \(\frac{\mathrm{ma}_0}{\mathrm{e}} \text { west, } \frac{2 \mathrm{ma}_0}{\mathrm{ev}_0} \text { down }\)

Question 12. The following figures show the arrangement of bar magnets in different configurations. Each magnet has m magnetic dipole. Which configuration has the highest net magnetic dipole moment?

1. 1
2. 2
3. 3
4. 4

Answer: 3. 3

Question 13. Two identical long conducting wires AOB and COD are placed at a right angle to each other, with one above the other such that ‘O’ is the common point for the two. The wires carry I1 and O2 currents, respectively. Point ‘O’ is lying at a distance ‘d’ from ‘O’ along a direction perpendicular to the plane containing the wires. The magnetic field at the point ‘P’ will be :

1. \(\frac{\mu_0}{2 \pi d}\left(\frac{I_1}{I_2}\right)\)
2. \(\frac{\mu_0}{2 \pi d}\left(I_1+I_2\right)\)
3. \(\frac{\mu_0}{2 \pi d}\left(I_1^2-I_2^2\right)\)
4. \(\frac{\mu_0}{2 \pi \mathrm{d}}\left(\mathrm{I}_1^2+\mathrm{I}_2^2\right)^{1 / 2}\)

Answer: 4. \(\frac{\mu_0}{2 \pi \mathrm{d}}\left(\mathrm{I}_1^2+\mathrm{I}_2^2\right)^{1 / 2}\)

Question 14. An electron moving in a circular orbit of radius r makes n rotations per second. The magnetic field produced at the center has magnitude:

1. Zero
2. \(\frac{\mu_0 n^2 e}{r}\)
3. \(\frac{\mu_0 n e}{2 r}\)
4. \(\frac{\mu_0 n e}{2 \pi r}\)

Answer: 3. \(\frac{\mu_0 n e}{2 r}\)

Question 15. A wire-carrying current I has the shape as shown in the adjoining figure. Linear parts of the wire are very long and parallel to the X-axis while a semicircular portion of radius R is lying in the Y-Z plane. The magnetic field at point O is

1. \(\vec{B}=-\frac{\mu_0}{4 \pi} \frac{I}{R}(\mu \hat{i} \times 2 \hat{k})\)
2. \(\vec{B}=-\frac{\mu_0}{4 \pi} \frac{1}{R}(\pi \hat{i}+2 \hat{k})\)
3. \(\overrightarrow{\mathrm{B}}=\frac{\mu_0}{4 \pi} \frac{\mathrm{I}}{\mathrm{R}}(\pi \hat{\mathrm{i}}-2 \hat{\mathrm{k}})\)
4. \(\vec{B}=\frac{\mu_0}{4 \pi} \frac{I}{R}(\pi \hat{i}+2 \hat{k})\)

Answer: 2. \(\vec{B}=-\frac{\mu_0}{4 \pi} \frac{1}{R}(\pi \hat{i}+2 \hat{k})\)

Question 16. A long straight wire of radius carries a steady current I. The current is uniformly distributed over its cross-section. The ratio of the magnetic fields B and B, at radial distances a/2 and 2a respectively, from the axis of the wire is:

1. 4
2. 1/4
3. 1/2
4. 1

Answer: 4. 1

Question 17. The magnetic susceptibility is negative for

1. Paramagnetic and ferromagnetic materials
2. Diamagnetic material only
3. Paramagnetic material only
4. Ferromagnetic material only

Answer: 2. Diamagnetic material only

Question 18. A square loop ABCD carrying a current i is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be

1. \(\frac{\mu_0 \mathrm{IIL}}{2 \pi}\)
2. \(\frac{2 \mu_0 \mathrm{II}}{3 \pi}\)
3. \(\frac{\mu_0 \mathrm{Ii}}{2 \pi}\)
4. \(\frac{2 \mu_0 \mathrm{IiL}}{3 \pi}\)

Answer: 2. \(\frac{2 \mu_0 \mathrm{II}}{3 \pi}\)

Question 19. A long solenoid has 1000 turns. When a current of 4A flows through it, the magnetic flux linked with each turn of the solenoid is 4 × 10–3 Wb. The self-inductance of the solenoid is

1. 1H
2. 4H
3. 3 H
4. 2H

Answer: 1. 1H

Question 20. A long wire carrying a steady current is bent into a circular loop of one turn. The magnetic field at the center of the loop is B. It is then bent into a circular coil of n turns. The magnetic field at the center of this coil of n turns will be:

1. 2n2 B
2. nB
3. n2B
4. 2nB

Answer: 3. n2B

Question 21. An electron is moving in a circular path under the influence of a transverse magnetic field of 3.57 × 10–2 T. If the value of e/m is 1.76 × 1011 C/kg, the frequency of revolution of the electron is.

1. 6.82MHz
2. 1 GHz
3. 100 MHz
4. 62.8MHz

Answer: 2. 1 GHz

Question 22. A metallic rod of mass per unit length 0.5 kg m –1 is lying horizontally on a smooth inclined plane which makes an angle of 30º with the horizontal. The rod is not allowed to slide down by flowing a current through it when a magnetic field of induction 0.25 T is acting on it in the vertical direction. The current flowing in the rod to keep it stationary is:

1. 7.14 A
2. 11.32 A
3. 14.76 A
4. 5.98 A

Answer: 2. 11.32 A

Question 23. A cylindrical conductor of radius R carries constant current. The plot of the magnitude of the magnetic field, B with the distance, d from the center of the conductor, is correctly represented by the figure:

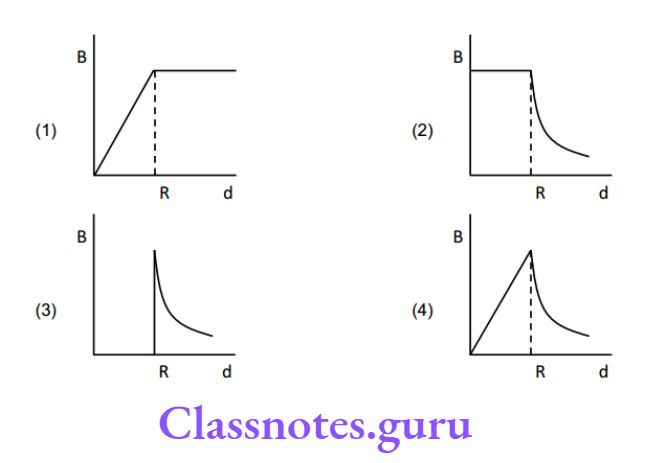
Answer: 4.

Question 24. At point A on the earth’s surface of the angle of dip, δ= +25º. At point B on the earth’s surface the angle of dip, δ= –25º. We can interpret that:

1. A and B are both located in the southern hemisphere.
2. A and B are both located in the northern hemisphere.
3. A is located in the southern hemisphere and B is located in the northern hemisphere.
4. A is located in the northern hemisphere and B is located in the southern hemisphere.

Answer: 3. A is located in the southern hemisphere and B is located in the northern hemisphere.

Question 25. Ionized hydrogen atoms and α-particle with momenta enter perpendicular to a constant magnetic field, B. The ratio of the radii of their paths rH: rα will be :

1. 1: 4
2. 2: 1
3. 1: 2
4. 4: 1

Answer: 2. 2: 1

Question 26. Two toroids 1 and 2 have total no. of turns 200 and 100 respectively with average radii 40 cm and 20 cm. If they carry the same current I, the ratio of the magnetic fields along the two loops is

1. 1: 1
2. 4: 1
3. 2: 1
4. 1: 2

Answer: 1. 1: 1

Question 27. A straight conductor carrying current I splits into two parts as shown in the figure. The radius of the circular loop is R. The total magnetic field at the center P of the loop is,

1. Zero
2. 3μ0i / 32R, outward
3. 3μ0i / 32R, inward
4. \(\frac{\mu_0 \mathrm{i}}{2 \mathrm{R}} \text {, inward }\)

Answer: 1. Zero

Question 28. The variation of EMF with time for four types of generators is shown in the figures. Which amongst them can be called AC?

1. (a) and (d)
2. (a), (b), (c), (d)
3. (a) and (b)
4. only (a)

Answer: 2. (a), (b), (c),

Question 29. A long solenoid of 50 cm in length having 100 turns carries a current of 2.5 A. The magnetic field at the center of the solenoid is \(\left(\mu_0=4 \pi \times 10^{-7} \mathrm{Tm} \mathrm{A}^{-1}\right)\)

1. 3.14×10-5T
2. 6.28×10-4T
3. 3.14×10-4T
4. 6.28×10-5T

Answer: 2. 6.28×10-4T

Question 30. An infinitely long straight conductor carries a current of 5A as shown. An electron is moving with a speed of 10 m/s parallel to the conductor. The perpendicular distance between the electron and the conductor is 20 cm at an instant. Calculate the magnitude of the force experienced by the electron at that instant.

1. 8×10-20N
2. 4×10-20N
3. 8×10-20N
4. 4×10-20N

Answer: 3. 8×10-20N

Question 31. A thick current-carrying cable of radius ‘R’ carries current ‘I’ uniformly distributed across its cross-section. The variation of magnetic field BI due to the cable with the distance ‘r’ from the axis of the cable i Represented By

Answer: 2.

Question 32. In the product \(\overrightarrow{\mathrm{F}}=\mathrm{q}(\overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}})=\mathrm{q} \overrightarrow{\mathrm{v}} \times\left(\overrightarrow{\mathrm{i}} \times \overrightarrow{\mathrm{j}}+\mathrm{B}_0 \overrightarrow{\mathrm{k}}\right)\)

For q = 1 and \(\overrightarrow{\mathrm{v}}=2 \overrightarrow{\mathrm{i}}+4 \overrightarrow{\mathrm{j}}+6 \overrightarrow{\mathrm{k}} \text { and } \overrightarrow{\mathrm{F}}=4 \overrightarrow{\mathrm{i}}-20 \overrightarrow{\mathrm{j}}+12 \overrightarrow{\mathrm{k}}\)

What will be the complete expression for \(\overrightarrow{\mathrm{B}}\)

1. \(-6 \overrightarrow{\mathrm{i}}-6 \overrightarrow{\mathrm{j}}-8 \overrightarrow{\mathrm{k}}\)
2. \(8 \overrightarrow{\mathrm{i}}+8 \overrightarrow{\mathrm{j}}-6 \overrightarrow{\mathrm{k}}\)
3. \(6 \vec{i}+6 \vec{j}-8 \vec{k}\)
4. \(-8 \overrightarrow{\mathrm{i}}-8 \overrightarrow{\mathrm{j}}-6 \overrightarrow{\mathrm{k}}\)

Answer: 1. \(-6 \overrightarrow{\mathrm{i}}-6 \overrightarrow{\mathrm{j}}-8 \overrightarrow{\mathrm{k}}\)

Question 33. A uniform conducting wire of length 12a and resistance ‘R’ is wound up as a current-carrying coil in the shape of

1. An equilateral triangle of side ‘a’
2. A square of side ‘a’

The magnetic dipole moments of the coil in each case respectively are

1. 3Ia2 and Ia2
2. 3Ia2 and 4Ia2
3. 4Ia2 and 3Ia2
4. \(\sqrt{3} \mathrm{la}^2 \text { and } 3 \mathrm{la}^3\)

Answer: 4. \(\sqrt{3} \mathrm{la}^2 \text { and } 3 \mathrm{la}^3\)

Question 34. The relations amongst the three elements of earth’s magnetic field, namely horizontal component H, vertical  component V, and dip are, (BE = total magnetic field)

1. V = BE tan , H = BE
2. V = BE sin , H = BE cos
3. V = BE cos, H = BE sin d
4. V = BE, H = BE tan

Answer: 2. V = BE sin , H = BE cos

Question 35. A wire of length L meter carrying a current of I ampere is bent in the form of a circle. Its magnetic moment is,

1. I L2/4 A m2
2. I L2 /4 A m2
3. 2 I L2 / A m2
4. I L2 /4 A m

Answer: 4. I L2 /4 A m

Question 36. An iron rod of susceptibility 599 is subjected to a magnetizing field of 1200 A m -1. The permeability of the material of the rod is \(\left(\mu_0=4 \pi \times 10^{-7} \mathrm{Tm} A^{-1}\right)\)

1. \(2.4 \pi \times 10^{-7} \mathrm{TmA^{-1 }}\)
2. \(2.4 \pi \times 10^{-4} \mathrm{Tm} \mathrm{m}^{-1}\)
3. \(8.0 \pi \times 10^{-5} \mathrm{~T} \mathrm{~m} \mathrm{~A} A^{-1}\)
4. \(2.4 \pi \times 10^{-5} T m A^{-1}\)

Answer: 2. 7 1 4 1T m A 1) 2)

Chapter 1 Magnetic Field Multiple Choice Questions Part- II: Jee (Main) / Air Problems (Previous Years)

Question 1. Two long parallel wires are at a distance 2d apart. They carry steady equal currents flowing out of the plane of the paper as shown. The variation of magnetic field B along the line XX´ is given by

Answer: 1.

Question 2. A current I flows in an infinitely long wire with a cross-section in the form of a semicircular ring of radius R. The magnitude of the magnetic induction along its axis is:

1. \(\frac{\mu_0 I}{\pi^2 R}\)
2. \(\frac{\mu_0 I}{2 \pi^2 R}\)
3. \(\frac{\mu_0 I}{2 \pi R}\)
4. \(\frac{\mu_0 I}{4 \pi R}\)

Answer: 1. \(\frac{\mu_0 I}{\pi^2 R}\)

Question 3. An electric charge +q moves with velocity \(\vec{v}=3 \hat{i}+4 \hat{j}-3 \hat{k}\) in an electromagnetic field given by: \(\vec{E}=3 \hat{i}+\hat{j}+2 \hat{k} \text { and } \vec{B}=\hat{i}+\hat{j}+3 \hat{k}\) The y – component of the force experienced by + q is :

1. 11q
2. 5q
3. 3q
4. 2q

Answer: 1. 11q

Question 4. A thin circular disk of radius R is uniformly charged with density  > 0 per unit area. The disk rotates about its axis with a uniform angular speed . The magnetic moment of the disk is :

1. \(\pi R^4 \sigma \omega\)
2. \(\frac{\pi \mathrm{R}^4}{2} \sigma \omega\)
3. \(\frac{\pi R^4}{4} \sigma \omega\)
4. \(2 \pi R^4 \sigma \omega\)

Answer: 3. \(\frac{\pi R^4}{4} \sigma \omega\)

Question 5. A charge Q is uniformly distributed over the surface of the non-conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passes through its center with an angular velocity ω. As a result of this rotation, a magnetic field of induction B is obtained at the center of the disc. if we keep both the amount of charge placed on the disc and its angular velocity constant and vary the radius of the disc then the variation of the magnetic induction at the center of the disc will be represented by the figure

Answer: 1.

Question 6. Proton, Deuteron and alpha particles of the same kinetic energy are moving in circular trajectories in a constant magnetic field. The radii of the proton, deuteron, and alpha particle are respectively r p, r d, and rα. Which one of the following relations is correct?

1. \(r_\alpha=r_p=r_d\)
2. \(r_\alpha=r_p<r_d\)
3. \(r_\alpha>r_d>r_p\)
4. \(r_a=r_d>r_p\)

Answer: 2. \(r_\alpha=r_p<r_d\)

Question 7. Two short bar magnets of length 1 cm each have magnetic moments 1.20 Am2 and 1.00 Am2 respectively. They are placed on a horizontal table parallel to each other with their N poles pointing toward the South. They have a common magnetic equator and are separated by a distance of 20.0 cm. The value of the resultant horizontal magnetic induction at the mid-point O of the line joining their centers is close to (Horizontal component of earth’s magnetic induction is 3.6× 10 –5 Wb/m2)

1. 3.6 × 10^–5 Wb/m²
2. 2.56 × 10^–4 Wb/m²
3. 3.50 × 10^–4 Wb/m²
4. 5.80 × 10^–4 Wb/m²

Answer: 2. 2.56 × 10^–4 Wb/m²

Question 8. The coercivity of a small magnet where the ferromagnet gets demagnetized is 3 × 10 3 Am–1. The current required to be passed in a solenoid of length 20 cm and several turns 100, so that the magnetic gets demagnetized when inside the solenoid, is:

1. 30 mA
2. 60 mA
3. 3 A
4. 6 A

Answer: 4. 6 A

NEET Class 12 Physics Magnetic Field: Key MCQs for Revision

Question 9. Two coaxial ideal and long solenoids of different radii carry current I in the same direction. Let be F2 the magnetic force on the inner solenoid due to the outer one and be the magnetic force on the outer solenoid due to the inner one. Then

1. \(\vec{F}_1=\vec{F}_2=0\)
2. \(\vec{F}_1 \text { is radially inwards and } \vec{F}_2 \text { is radially outwards }\)
3. \(\vec{F}_1 \text { is radially inwards and } \vec{F}_2=0\)
4. \(\vec{F}_1 \text { is radially outwards and } \vec{F}_2=0\)

Answer: 1. \(\vec{F}_1=\vec{F}_2=0\)

Question 10. Two long current-carrying thin wires, both with current L, are held by insulating threads of length L and are in equilibrium as shown in the figure, with threads making an angle ‘’ with the vertical. If wires have a mass per unit length then the value  I is : (g = gravitational acceleration)

1. \(\sin \theta \sqrt{\frac{\pi \lambda g L}{\mu_0 \cos \theta}}\)
2. \(2 \sin \theta \sqrt{\frac{\pi \lambda \mathrm{gL}}{\mu_0 \cos \theta}}\)
3. \(2 \sqrt{\frac{\pi g L}{\mu_0} \tan \theta}\)
4. \(\sqrt{\frac{\pi \lambda \mathrm{gL}}{\mu_0} \tan \theta}\)

Answer: 2. \(2 \sin \theta \sqrt{\frac{\pi \lambda \mathrm{gL}}{\mu_0 \cos \theta}}\)

Question 11. A rectangular loop of sides 10 cm and 5 cm carrying a current I of 12 A is placed in different orientations as shown in the figures below:

If there is a uniform magnetic field of 0.3 T in the positive z direction, in which orientations the loop would be in stable equilibrium and (ii) unstable equilibrium?

1. (a) and (b), respectively
2. (a) and (c), respectively
3. (b) and (d), respectively
4. (b) and (c), respectively

Answer: 3. (b) and (d), respectively

Question 12. Two identical wires A and B, each of length l, carry the same current l. Wire A is bent into a circle of radius R and wire B is bent to form a square of side ‘a’. If B A and BB are the values of a magnetic field at the centers of the circle and square respectively, then the ratio \(\frac{\mathrm{B}_{\mathrm{A}}}{\mathrm{B}_{\mathrm{B}}}\) is

1. \(\frac{\pi^2}{16 \sqrt{2}}\)
2. \(\frac{\pi^2}{16}\)
3. \(\frac{\pi^2}{8 \sqrt{2}}\)
4. \(\frac{\pi^2}{8}\)

Answer: 3. \(\frac{\pi^2}{8 \sqrt{2}}\)

Question 13. Hysteresis loops for two magnetic materials A and B are given below :

These materials are used to make magnets for electric generators, transformer cores, and electromagnet cores. Then it is proper to use:

1. A for electromagnets and B for electric generators.
2. A for transformers and B for electric generators.
3. B for electromagnets and transformers.
4. A for electric generators and transformers.

Answer: 3. B for electromagnets and transformers.

Question 14. A magnetic needle of magnetic moment 6.7 × 10–2 Am2 and moment of inertia 7.5 × 10–6 kg m2 is performing simple harmonic oscillations in a magnetic field of 0.01 T. Time taken for 10 complete oscillations is

1. 8.76s
2. 6.65s
3. 8.89s
4. 6.98s

Answer: 2. 6.65s

Question 15. The dipole moment of a circular loop carrying a current is m and the magnetic field at the center of the loop is B1. When the dipole moment is doubled by keeping the current constant, the magnetic field at the center of the loop is B2. The ratio \(\frac{\mathrm{B}_1}{\mathrm{~B}_2}\)

1. \(\sqrt{2}\)
2. \(\frac{1}{\sqrt{2}}\)
3. \(\sqrt{3}\)

Answer: 1. \(\sqrt{2}\)

Question 16. An electron, a proton, and an alpha particle having the same kinetic energy are moving in circular orbits of radii re, rp, and rα respectively in uniform magnetic field B. The relation between re, rp, and rα is

1. re < rp< rα
2. re < rα< rp
3. re > rp = rα
4. re < rp = rα

Answer: 4. re < rp = rα

Question 17. An infinitely long, current-carrying wire and a small current-carrying loop are in the plane of the paper as shown. The radius of the loop is a and the distance of its center from the wire is d(d ≫ a). If the loop applies a force F on the wire then:

1. F=0
2. \(F \propto\left(\frac{a}{d}\right)^2\)
3. \(F \propto\left(\frac{a^2}{d^3}\right)\)
4. \(F \propto\left(\frac{a}{d}\right)\)

Answer: 2. \(F \propto\left(\frac{a}{d}\right)^2\)

Question 18. A current loop, having two circular arcs joined by two radial lines is shown in the figure. It carries a current of 10 A. The magnetic field at point O will be close to :

1. 1.5 × 10-5 T
2. 1.0 × 10-7 T
3. 1.0 × 10-5 T
4. 1.5 × 10-7 T

Answer: 3. 1.0 × 10-5 T

Question 19. A bar magnet is demagnetized by inserting it inside a solenoid of length 0.2 m, 100 turns, and carrying a current of 5.2 A. The coercivity of the bar magnet is :

1. 285 A/m
2. 520 A/m
3. 1200 A/m
4. 2600 A/m

Answer: 4. 2600 A/m

Question 20. One of the two identical conducting wires of length L is bent in the form of a circular loop and the other one is into a circular coil of N identical turns. If the same current is passed in both, the ratio of the magnetic field at the central of the loop (BL) to that at the center of the coil \(\frac{\mathrm{B}_{\mathrm{L}}}{\mathrm{B}_{\mathrm{C}}}\) will be:

1. \(\frac{1}{N}\)
2. \(\frac{1}{\mathrm{~N}^2}\)
3. N2
4. N

Answer: 2. \(\frac{1}{\mathrm{~N}^2}\)

Question 21. A particle having the same charge as of electron moves in a circular path of radius 0.5 cm under the influence of a magnetic field of 0.5 T. If an electric field of 100 V/m makes it move in a straight path, then the mass of the particle is (Given charge of electron = 1.6 × 10–19 C)

1. 2.0×10-24kg
2. 1.6×10-27kg
3. 9.1×10-31kg
4. 1.6×10-19 kg

Answer: 1. 2.0×10-24kg

Question 22. A magnet of total magnetic moment A–m2 is placed in a time-varying magnetic field where B = 1 Tesla and ω= 0.125 rad/s. The work done for reversing the direction of the magnetic moment at t = 1 second is:

1. 0.014 J
2. 0.01 J
3. 0.028 J
4. 0.007 J

Answer: (Bonus) The correct answer is 0.02 J

Question 23. An insulating thin rod of length l has a linear charge density \(\rho(x)=\rho_0 \frac{x}{\ell}\) on it. The rod is rotated about an axis passing through the origin (x = 0) and perpendicular to the rod. If the rod makes n rotations per second, then the time-averaged magnetic moment of the rod is

1. \(\frac{\pi}{4} n \rho \ell^3\)
2. \(\pi \mathrm{n} \rho \ell^3\)
3. \(\frac{\pi}{3} n \rho \ell^3\)
4. \(n \rho \ell^3\)

Answer: 1. \(\frac{\pi}{4} n \rho \ell^3\)

Question 24. At some locations on earth, the horizontal component of Earth’s magnetic field is 18 × 10 –16T. At this location, a magnetic needle of length 0.12 m and pole strength 1.8 Am is suspended from its mid-point using a thread, it makes a 45° angle with horizontal equilibrium. To keep this needle horizontal, the vertical force that should be applied at one of its ends is

1. 6.5 x 10-5 n
2. 3.6 x 10-5N
3. 1.3×10-5N
4. 1.8×10-5N

Answer: 1. 6.5 x 10-5 n

Question 25. A paramagnetic substance in the form of a cube with sides 1 cm has a magnetic dipole moment of 20× 10–6J/T when a magnetic intensity of 60 × 103 A/m is applied. Its magnetic susceptibility is-

1. 4.3×10-2
2. 2.3×10-2
3. 3.3×10-4
4. 3.3×10-2

Answer: 3. 3.3×10-4

Question 26. A paramagnetic material has 1028 atoms/m3. Its magnetic susceptibility at temperature 350 K is 2.8 × 10–4. Its susceptibility at 300 K is :

1. 3.726 × 10–4
2. 3.672 × 10–4
3. 3.267 × 10–4
4. 2.672 × 10–4

Answer: 3. 3.267 × 10–4

Question 27. The mean intensity of radiation on the surface of the Sun is about 108 W/m2. The rms value of the corresponding magnetic field is closest to :

1. 102 T
2. 1 T
3. 10–2 T
4. 10–4 T

Answer: 4. 10–4 T

Question 28. A proton and an α-particle (with their masses in the ratio of 1: 4 and charges in the ratio of 1: 2) are accelerated from rest through a potential difference V. If a uniform magnetic field (B) is set up perpendicular to their velocities, the ratio of the radii rp : r of the circular paths described by them will be:

1. 1:3
2. \(1: \sqrt{3}\)
3. \(1: \sqrt{2}\)
4. 1: 2

Answer: 3. \(1: \sqrt{2}\)

Chapter 1 Magnetic Field Multiple Choice Questions Self Practice Paper

Question 1. Four infinitely long ‘L’ shaped wires, each carrying a current have been arranged as shown in the figure. Obtain the magnetic field strength at the point ‘O’ equidistant from all four corners.

1. 0
2. \(\frac{\mu_0 i}{2 \pi a}\)
3. \(\frac{2 \mu_0 i}{\pi a}\)
4. \(\frac{\mu_0 i}{\pi a}\)

Answer: 1. 0

Question 2. Find the magnetic field B at the center of a square loop of side ‘a’, carrying a current i.

1. \(\frac{2 \sqrt{2} \mu_0 i}{\pi a}\)
2. \(\frac{\sqrt{2} \mu_0 i}{\pi a}\)
3. \(\frac{2 \mu_0 i}{\pi a}\)
4. \(\frac{\mu_0 i}{2 \pi a}\)

Answer: 1. \(\frac{2 \sqrt{2} \mu_0 i}{\pi a}\)

Question 3. Each of the batteries shown in the figure has an emf equal to 10 V. Find the magnetic field B at the point p.

1. 0T
2. 2T
3. 3T
4. 5T

Answer: 1. 0T

NEET Physics Class 12 Chapter 1 Magnetic Field Multiple Choice Questions

Question 4. A charged particle is accelerated through a potential difference of 24 kV and acquires a speed of 2×10 6 m/s. It is then injected perpendicularly into a magnetic field of strength 0.2 T. Find the radius of the circle described by it.

1. 12 cm
2. 10 cm
3. 6 cm
4. 4 cm

Answer: 1. 12 cm

Question 5. In the formula X = 3 YZ2, the quantities X and Z have the dimensions of capacitance and magnetic induction respectively. The dimensions of Y in the MKS system are…………..

1. M–3 L–2 T4 Q4
2. M –3 L–2 T2 Q4
3. M –2 L–2 T4 Q4
4. M –3 L–4 T4 Q4

Answer: 1. M–3 L–2 T4 Q4

Question 6. A particle having a charge of 2.0 × 10–8 C and a mass of 2.0 × 10–10 g is projected with a speed of 2.0 × 103 m/s in a region having a uniform magnetic field (B = 0.1 T). Find the radius of the circle formed by the particle and also the frequency.

1. \(20 \mathrm{~cm}, \frac{5}{\pi} \times 10^3 \mathrm{~s}^{-1}\)
2. \(20 \mathrm{~cm}, \frac{5}{\pi} \times 10^3 \mathrm{~s}^{-1}\)
3. \(20 \mathrm{~cm}, \frac{2}{\pi} \times 10^3 \mathrm{~s}^{-1}\)
4. \(20 \mathrm{~cm}, \frac{4}{\pi} \times 10^3 \mathrm{~s}^{-1}\)

Answer: 1. \(20 \mathrm{~cm}, \frac{5}{\pi} \times 10^3 \mathrm{~s}^{-1}\)

Question 7. A proton describes a circle of radius 1 cm in a magnetic field of strength 0.10 T. What would be the radius of the circle described by a deuterium moving with the same speed in the same magnetic field?

1. 2 cm
2. 4 cm
3. 6 cm
4. 8 cm

Answer: 1. 2 cm

Question 8. A proton is projected with a velocity of 3 × 106 m/s perpendicular to a uniform magnetic field of 0.6T. Find the acceleration of the proton mass of a proton

1. \(\frac{864}{5} \times 10^{11} \mathrm{~m} / \mathrm{s}^2\)
2. \(\frac{864}{5} \times 10^{10} \mathrm{~m} / \mathrm{s}^2\)
3. \(\frac{864}{5} \times 10^{14} \mathrm{~m} / \mathrm{s}^2\)
4. \(\frac{864}{5} \times 10^{12} \mathrm{~m} / \mathrm{s}^2\)

Answer: 4. \(\frac{864}{5} \times 10^{12} \mathrm{~m} / \mathrm{s}^2\)

Question 9. A particle having a charge of 5.0 uC and a mass of 5.0 × 10–12 kg is projected with a speed of 1.0 km/s in a magnetic field of magnitude 5.0 mT. The angle between the magnetic field vector and the velocity vector is sin–1 (0.90). Show that the path of the particle will be a helix. Find the diameter of the helix and its pitch.

1. 47 cm, 67 cm
2. 36 cm, 56 cm
3. 56 cm, 67 cm
4. 57 cm, 58 cm

Answer: 2. 36 cm, 56 cm

Question 10. A proton projected in a magnetic field of 0.04 T travels along a helical path of radius 5.0 cm and pitch 20 cm. Find the components of the velocity of the proton along and perpendicular to the magnetic field. Take the mass of the proton = 1.6 × 10–27 kg.

1. \(\frac{4}{\pi} \times 10^5 \mathrm{~m} / \mathrm{s}, 2 \times 10^5 \mathrm{~m} / \mathrm{s}\)
2. \(\frac{2}{\pi} \times 10^5 \mathrm{~m} / \mathrm{s}, 2 \times 10^5 \mathrm{~m} / \mathrm{s}\)
3. \(\frac{4}{\pi} \times 10^5 \mathrm{~m} / \mathrm{s}, 4 \times 10^5 \mathrm{~m} / \mathrm{s}\)
4. \(\frac{2}{\pi} \times 10^5 \mathrm{~m} / \mathrm{s}, 4 \times 10^5 \mathrm{~m} / \mathrm{s}\)

Answer: \(\frac{2}{\pi} \times 10^5 \mathrm{~m} / \mathrm{s}, 2 \times 10^5 \mathrm{~m} / \mathrm{s}\)

Question 11. A particle moves in a circle of radius 1.0 cm under the action of a magnetic field of 0.40 T. An electric field of 200 V/m makes the path straight. Find the charge/mass ratio of the particle.

1. \(\frac{5}{4} \times 10^5 \mathrm{C} / \mathrm{kg}\)
2. \(\frac{5}{3} \times 10^5 \mathrm{C} / \mathrm{kg}\)
3. \(\frac{5}{8} \times 10^5 \mathrm{C} / \mathrm{kg}\)
4. \(\frac{8}{5} \times 10^5 \mathrm{C} / \mathrm{kg}\)

Answer: 1. \(\frac{5}{4} \times 10^5 \mathrm{C} / \mathrm{kg}\)

Question 12. A proton goes undeflected in a crossed electric and magnetic field (the fields are perpendicular to each other) at a speed of 10 5 m/s. The velocity is perpendicular to both the fields. When the electric field is switched off, the proton moves along a circle of radius 2 cm. Find the magnitudes of the electric and magnetic fields. Take the mass of the proton = 1.6 × 10 –27 kg.

1. 2 × 10 3 N/C. 5 × 10–2 T
2. 5 × 10 3 N/C. 5 × 10–1 T
3. 5 × 10 3 N/C. 5 × 10–2 T
4. 5 × 10 3 N/C. 5 × 10–3 T

Answer: 3. 5 × 10 3 N/C. 5 × 10–2 T

Question 13. A particle having mass m and charge q is released from the origin in a region in which electric field and B \(\vec{B}=+B_0 \hat{j} \text { and } \vec{E}=+E_0 \hat{i}\) magnetic field are given by and . Find the speed of the particle as a function of its X coordinate

1. \(\sqrt{\frac{2 q E_0 x}{m}}\)
2. \(\sqrt{\frac{q E_0 x}{2 m}}\)
3. \(\sqrt{\frac{q E_0 x}{4 m}}\)
4. \(\sqrt{\frac{q E_0 x}{m}}\)

Answer: 1. \(\sqrt{\frac{2 q E_0 x}{m}}\)

Question 14. Consider a 10 cm long portion of a straight wire carrying a current of 10 A placed in a magnetic field of 0.1 T making an angle of 37º with the wire. What magnetic force does the wire experience?

1. 6 × 10–1 N
2. 6 × 10–2 N
3. 6 × 10–3 N
4. 6 × 10–4 N

Answer: 2. 6 × 10–2 N

Question 15. A current of 2 A enters at the corner d of a square frame abcd of side 10 cm and leaves at the opposite corner b. A magnetic field B = 0.1 T exists in the space in a direction perpendicular to the plane of the frame as shown in the figure. Find the magnitude of the resultant magnetic force on the four sides of the frame.

1. 1 × 10–2 N
2. 2 × 10–2 N
3. \(\sqrt{2} \times 10^{-2} \mathrm{~N}\)
4. \(2 \sqrt{2} \times 10^{-2} \mathrm{~N}\)

Answer: 4. \(2 \sqrt{2} \times 10^{-2} \mathrm{~N}\)

Question 16. A magnetic field of strength 1.0 T is produced by a strong electromagnet in a cylindrical region of diameter 4.0 cm as shown in the figure. A wire, carrying a current of 2.0 A, is placed perpendicular to and intersecting the axis of the cylindrical region. Find the magnitude of the force acting on the wire.

1. 4 × 10–2 N
2. 16 × 10–2 N
3. 32 × 10–2 N
4. 8 × 10–2 N

Answer: 4. 8 × 10–2 N

Question 17. A wire of length l carries a current i along the y-axis. A magnetic field exists which is given as
\(\vec{B}=B_0(\hat{i}+\hat{j}+\hat{k}) T .\) Find the magnitude of the magnetic force acting on the wire.

1. \(\sqrt{2} \mathrm{~B}_0 \mathrm{i} \ell\)
2. \(2 \sqrt{2} \mathrm{~B}_0 \mathrm{i} \ell\)
3. \(3 \sqrt{2} \mathrm{~B}_0 \mathrm{i} \ell\)
4. \(4 \sqrt{2} \mathrm{~B}_0 \mathrm{i} \ell\)

Answer: 1. \(\sqrt{2} \mathrm{~B}_0 \mathrm{i} \ell\)

Question 18. A straight, long wire carries a current of 20 A. Another wire carrying an equal current is placed parallel to it. If the force acting on the unit length of the second wire is 2.0 × 10–4 N, what is the separation between them?

1. 20cm
2. 40cm
3. 60cm
4. 80cm

Answer: 2. 40cm

Question 19. A circular coil of 100 turns has an effective radius of 0.05 m and carries a current of 0.1 amp. How much work is required to turn it in an external magnetic field of 1.5 wb/m2 through 1800 about an axis perpendicular to the magnetic field? The plane of the coil is initially perpendicular to the magnetic field.

1. \(\pm 50 \pi \times 10^{-3} \mathrm{~J}\)
2. \(\pm 75 \pi \times 10^{-3} \mathrm{~J}\)
3. \(\pm 45 \pi \times 10^{-3} \mathrm{~J}\)
4. \(\pm 35 \pi \times 10^{-3} \mathrm{~J}\)

Answer: 2. \(\pm 75 \pi \times 10^{-3} \mathrm{~J}\)

Question 20. A rectangular coil of 100 turns has a length of 4 cm and a width of 5 cm. It is placed with its plane parallel to a uniform magnetic field and a current of 2A is sent through the coil. Find the magnitude of the magnetic field B, if the torque acting on the coil is 0.2 N-m.

1. \(\frac{1}{2} \mathrm{~T}\)
2. \(\frac{1}{4} \mathrm{~T}\)
3. \(\frac{1}{8} T\)
4. \(\frac{1}{3} T\)

Answer: 1. \(\frac{1}{2} \mathrm{~T}\)

Question 21. A point charge is moving in a circle with constant speed. Consider the magnetic field produced by the charge at a fixed point P (not the center of the circle) on the axis of the circle.

1. It is constant in magnitude only
2. It is constant in direction only
3. It is constant in direction and magnitude both
4. It is not constant in magnitude and direction both.

Answer: It is constant in magnitude only

Question 22. A current-carrying wire is placed in the grooves of an insulating semi-circular disc of radius ‘R’, as shown. The current enters at point A and leaves from point B. Determine the magnetic field at the point

1. \(\frac{\mu_0 I}{8 \pi R \sqrt{3}}\)
2. \(\frac{\mu_0 I}{4 \pi R \sqrt{3}}\)
3. \(\frac{\sqrt{3} \mu_0 I}{4 \pi R}\)
4. No of these

Answer: 2. \(\frac{\mu_0 I}{4 \pi R \sqrt{3}}\)

Question 23. The Axis of a solid cylinder of infinite length and radius R lies along the y-axis it carries a uniformly R R, y, distributed current ‘ i ’ along the +y direction. Magnetic field at a point

1. \(\left(\frac{R}{2}, y, \frac{R}{2}\right)\)
2. \(\frac{\mu_0 i}{2 \pi R}(\hat{j}-\hat{k})\)
3. \(\frac{\mu_0 i}{4 \pi R} \hat{j}\)
4. \(\frac{\mu_0 \mathrm{i}}{4 \pi R}(\hat{\mathbf{i}}+\hat{\mathrm{k}})\)

Answer: 1. \(\left(\frac{R}{2}, y, \frac{R}{2}\right)\)

Question 24. A long, straight wire carries a current along the Z-axis. One can not find two points in the X-Y plane such that

1. The magnetic fields are equal in magnitude and same in direction
2. The directions of the magnetic fields are the same
3. The magnitudes of the magnetic fields are equal
4. The field at one point is opposite to that at the other point.

Answer: 1. The magnetic fields are equal in magnitude and same in direction

Question 25. A uniform magnetic field \(\vec{B}=(3 \hat{i}+4 \hat{j}+\hat{k})\) exists in region of space. A semicircular wire of radius 1 m carrying current 1 A having its center at (2, 2, 0) is placed in an x-y plane as shown in Fig. The force on the semicircular wire will be

1. \(\sqrt{2}(\hat{i}+\hat{j}+\hat{k})\)
2. \(\sqrt{2}(\hat{i}-\hat{j}+\hat{k})\)
3. \(\sqrt{2}(\hat{i}+\hat{j}-\hat{k})\)
4. \(\sqrt{2}(-\hat{\mathrm{i}}+\hat{\mathrm{j}}+\hat{\mathrm{k}})\)

Answer: 2. \(\sqrt{2}(\hat{i}-\hat{j}+\hat{k})\)

Question 26. A proton of mass 1.67 × 10–27 kg and charge 1.6 × 10–19 C is projected with a speed of 2 × 106 m/s at an angle of 60° to the x-axis. If a uniform magnetic field of 0.104 T is applied along the y-axis, the path of the proton is:

1. A circle of radius 0.2 m and period π× 10–7 s
2. A circle of radius 0.1 m and period 2π × 10–7 s
3. A helix of radius 0.1 m and period 2π × 10–7 s
4. A helix of radius 0.2 m and period 4π × 10–7 s

Answer: 3. A circle of radius 0.1 m and period 2π × 10–7 s

Question 27. An electron traveling with a speed u along the positive x-axis enters into a region of magnetic field where B = –B 0 ˆk (x > 0). It comes out of the region with speed v then

1. v = u at y > 0
2. v = u at y < 0
3. v > u at y > 0
4. v > u at y < 0

Answer: 2. v = u at y < 0

NEET Physics Class 12 Chapter 1 Magnetic Field Multiple Choice Questions

Question 28. Which of the following statements is correct in the given figure?

1. Net Force On The Loop Is Non-Zero
2. Net Torque On The Loop Is Zero
3. Loop Will Rotate Clockwise About Axis Oo’ When Seen From O
4. Loop Will Rotate Anticlockwise About Oo’ When Seen From O

Answer: 3. Loop Will Rotate Clockwise About Axis Oo’ When Seen From O

Question 29. A magnetic field \(\vec{B}=B_0 \hat{j}\) exists in the region \(\mathrm{a}<\mathrm{x}<2 \mathrm{a} \text { and } \overrightarrow{\mathrm{B}}=-\mathrm{B}_0 \hat{\mathrm{j}}\) and , in the region 2a < x < 3a, where B V v i= 0ˆ 0 is a positive constant. A positive point charge moving with a velocity, \(\vec{V}=v_0 \hat{i},\) where v0 is a positive constant, enters the magnetic field at x = a. The trajectory of the charge in this region can be like this.

Answer: 1.

Question 30. A particle of mass M and positive charge Q, moving with a constant velocity \(\overrightarrow{\mathrm{u}}_1=4 \hat{\mathrm{i}} \mathrm{ms}^{-1} \text {, }\) enters a
region of uniform static magnetic field normal to the x-y plane. The region of the magnetic field extends
from x = 0 to x = L for all values of y. After passing through this region, the particle emerges on the
other side after 10 milliseconds with a velocity \(\overrightarrow{\mathrm{u}}_2=2(\sqrt{3} \hat{\mathrm{i}}+\hat{\mathrm{j}}) \mathrm{ms}^{-1}\) The correct statement(s) is (are):

1. The direction of the magnetic field is the –x direction.
2. The direction of the magnetic field is +z direction
3. The magnitude of the magnetic field \(\frac{50 \pi M}{3 Q}\) units
4. The magnitude of the magnetic field is \(\frac{100 \pi M}{3 Q}\) units.

Answer: 3. The magnitude of the magnetic field \(\frac{50 \pi M}{3 Q}\) units

Question 31. A conductor (shown in the figure) carrying constant current I is kept in the x-y plane in a uniform B magnetic field. IF F is the magnitude of the total magnetic force acting on the conductor, then the incorrect statement is:

1. \(\text { If } \vec{B} \text { is along } \hat{z}, F \propto(L+R)\)
2. \(\text { If } \vec{B} \text { is along } \hat{x}, F=0\)
3. \(\text { If } \vec{B} \text { is along } \hat{y}, F \propto(L+R)\)
4. \(\text { If } \vec{B} \text { is along } \hat{z}, F=\)

Answer: 4. \(\text { If } \vec{B} \text { is along } \hat{z}, F=\)

Magnetic Effect Of Current And Magnetic Force On Charge Or Current

Magnet:

Even after being neutral (showing no electric interaction), two bodies may attract/repel strongly if they have a special property. This property is known as magnetism. This force is called magnetic force.

Those bodies are called magnets. Later on, we will see that it is due to circulating currents inside the atoms. Magnets are found in different shapes, but a bar magnet is frequently used for many experimental purposes.

When a bar magnet is suspended at its middle, as shown, and it is free to rotate in the horizontal plane it always comes to equilibrium in a fixed direction.

One end of the magnet (say A) is directed approximately towards the north and the other (say B) approximately towards the south. This observation is made everywhere on the earth.

Due to this reason the end A, which points towards the north direction is called NORTH POLE and the other end which points towards the south direction is called the SOUTH POLE. They can be marked as ‘N’ and ‘S’ on the magnet.

This property can be used to determine the north or south direction anywhere on the earth and indirectly east and west also if they are not known by another method (like rising of sun and setting of the sun).

This method is used by navigators of ships and aeroplanes. The directions are as shown in the figure. In all directions, E, W, N, and S are in the horizontal plane.

Magnetic Field NEET Class 12 Notes

The magnet rotates due to the earth’s magnetic field which we will discuss later in this chapter.

Pole Strength Magnetic Dipole And Magnetic Dipole Moment

A magnet always has two poles ‘N’ and ‘S’ and like poles of two magnets repel each other and the unlike poles of two magnets attract each other they form an action-reaction pair.

The poles of the same magnet do not come to meet each other due to attraction. They are maintained we cannot get two isolated poles by cutting the magnet from the middle. The other end becomes a pole of the opposite nature.

So, ‘N’ and ‘S’ always exist together therefore they are Known as +ve and –ve poles. The north pole is treated as a positive pole (or positive magnetic charge) and the south pole is treated as a –ve pole (or –ve magnetic charge).

They are quantitatively represented by their ”POLE STRENGTH” +m and –m respectively (just like we have charges +q and –q in electrostatics). Pole strength is a scalar quantity and represents the strength of the pole hence, of the magnet also).

A magnet can be treated as a dipole since it always has two opposite poles (just like in an electric dipole we have two opposite charges –q and +q). It is called a Magnetic Dipole and it has a Magnetic M Dipole Moment. It is represented by. It is a vector quantity. Its direction is from –m to +m which means from ‘S’ to ‘N’)

M = m.lm m here lm m = magnetic length of the magnet. Lm is slightly less than lg (it is the geometrical length of the magnet = end-to-end distance). The ‘N’ and ‘S’ are not located exactly at the ends of the magnet. For calculation purposes, we can assume lm = lg [Actually lm/lg ~ 0.84].

The units of m and M will be mentioned afterward so that you can remember and understand them.

Magnetic Field And Strength Of Magnetic Field.

The physical space around a magnetic pole has a special influence due to which other poles experience a force. That special influence is called magnetic field and that force is called ‘magnetic force’.

This field is qualitatively represented by the ‘strength of magnetic field’ or b “magnetic induction” or “magnetic flux density”. It is represented by \(\overrightarrow{\mathrm{b}}\). It is a vector quantity.

Definition of \(\overrightarrow{\mathrm{B}}\): The magnetic force experienced by a north pole of unit pole strength at a point due to some other poles (called source) is called the strength of the magnetic field at that point due to the source.

Mathematically \(\vec{B}=\frac{\vec{F}}{m}\)

Here \(\overrightarrow{\mathrm{F}}\) = magnetic force on the pole of pole strength m. m may be +ve or –ve and of any value. B S.\(\overrightarrow{\mathrm{B}}\). unit of is Tesla or Weber/m2 (abbreviated as T and Wb/m2).

We can also write \(\overrightarrow{\mathrm{F}}=\mathrm{m} \overrightarrow{\mathrm{B}}\) According to this direction of on +ve pole (North pole) will be in the direction B of field and on –ve pole (south pole) it will be opposite to the direction of \(\overrightarrow{\mathrm{B}}\)

The field generated by sources does not depend on the test pole (for its value and any sign).

⇒ \(\overrightarrow{\mathrm{B}}\) due to various source

Due to a single pole:

(Similar to the case of a point charge in electrostatics)

⇒ \(B=\left(\frac{\mu_0}{4 \pi}\right) \frac{m}{r^2} \text {. }\)

This is magnitude

The direction of B due to the north pole and south poles are as shown

in vector form \(\vec{B}=\left(\frac{\mu_0}{4 \pi}\right) \frac{m}{r^3} \vec{r}\) here m is with a sign and = position vector of the test point for the pole.

Due to a bar magnet:

(Same as the case of electric dipole in electrostatics) Independent case never found. Always ‘N’ and ‘S’ exist together as magnets.

at A (on the axis) \(=\left(\frac{\mu_0}{4 \pi}\right) \frac{\vec{M}}{r^3} \quad \text { for } \quad a \ll r\)

at B (on the equatorial) \(=-\left(\frac{\mu_0}{4 \pi}\right) \frac{\vec{M}}{r^3} \text { for } \mathrm{a} \ll \mathrm{r}\)

At General Point

⇒ \(B_r=2\left(\frac{\mu_0}{4 \pi}\right) \frac{M \cos \theta}{r^3} \quad \Rightarrow \quad B_n=2\left(\frac{\mu_0}{4 \pi}\right) \frac{M \sin \theta}{r^3}\)

⇒ \(\begin{aligned}
& B_{\text {res }}=\frac{\mu_0 M}{4 \pi r^3} \sqrt{1+3 \cos ^2 \theta} \\
& \tan \phi=\frac{B_n}{B_r}=\frac{\tan \theta}{2}
\end{aligned}\)

Magnetic lines of force of a bar magnet:

Solved Examples

Example 1. Find the magnetic field due to a dipole of magnetic moment 1.2 A-m2 at a point 1 m away from it in a direction making an angle of 60º with the dipole axis.
Solution: The magnitude of the field is

⇒ \(B=\frac{\mu_0}{4 \pi} \frac{M}{r^3} \sqrt{1+3 \cos ^2 \theta}\)

⇒ \(=\left(10^{-7} \frac{\mathrm{T}-\mathrm{m}}{\mathrm{A}}\right) \frac{1.2 \mathrm{~A}-\mathrm{m}^2}{1 \mathrm{~m}^3} \sqrt{1+3 \cos ^2 60^{\circ}}=1.6 \times 10^{-7} \mathrm{~T} \text {. }\)

The direction of the field makes an angle with the radial line where

⇒ \(\tan \alpha=\frac{\tan \theta}{2}=\frac{\sqrt{3}}{2}\)

Example 2. The figure shows two identical magnetic dipoles a and b of magnetic moments M each, placed at a separation d, with their axes perpendicular to each other. Find the magnetic field at the point P midway between the dipoles.

Solution: Point P is in the end-on position for dipole a and in the broadside-on position for dipole b.

The magnetic field at p due to a is \(\mathrm{B}_{\mathrm{a}}=\frac{\mu_0}{4 \pi} \frac{2 \mathrm{M}}{(\mathrm{d} / 2)^3}\) along the axis of a, and that due to b is \(B_b=\frac{\mu_0}{4 \pi} \frac{M}{(d / 2)^3}\) parallel to the axis of b as shown in figure. The resultant field at P is, therefore.

⇒ \(B=\sqrt{B_a^2+B_b^2}=\frac{\mu_0 M}{4 \pi(d / 2)^3} \sqrt{1^2+2^2}\)

⇒ \(=\frac{2 \sqrt{5} \mu_0 \mathrm{M}}{\pi d^2}\)

The direction of this field makes an angle α with Ba such that tanθ = Bb/Ba = 1/2.

Magnet in an external uniform magnetic field

(same as the case of the electric dipole)

Here θ is angle between and \(\vec{B} \text { and } \vec{M}\)

Note:

⇒ \(\vec{\tau}\) acts such that it tries to make \(\overrightarrow{\mathrm{M}} \times \vec{B}\)

⇒ \(\vec{\tau}\) is the same about every point of the dipole’s potential energy is

U = – MB cos θ = \(\overrightarrow{\mathrm{M}} \cdot \overrightarrow{\mathrm{B}}\)

θ = 0º is stable equilibrium

θ = π is an unstable equilibrium

For small ‘θ’ the dipole performs SHM about θ = 0º position

t= 0– MB sin θ ;

I α = – MB sin θ

for small θ, \(\sin \theta \simeq \theta\) \(\alpha=-\left(\frac{\mathrm{MB}}{\mathrm{I}}\right) \theta\)

Angular frequency of SHM

⇒ \(\omega=\sqrt{\frac{M B}{I}}=\frac{2 \pi}{T} \quad \Rightarrow \quad T=2 \pi \sqrt{\frac{I}{M B}}\)

Here = \(I_{c m}\) if the dipole is free to rotate

=\(I_{hinge}\) if the dipole is hinged.

Example 3. A bar magnet having a magnetic moment of 1.0 × 10^-4 J/T is free to rotate in a horizontal plane. A horizontal magnetic field B = 4 × 10^-5 T exists in the space. Find the work done in rotating the magnet slowly from a direction parallel to the field to a direction 60º from the field.
Solution: The work done by the external agent = change in potential energy
= (–MB cosθ₂) –(–MB cosθ₁) = –MB (cos 60º – cos 0º)

⇒ \(=\frac{1}{2} M B=\frac{1}{2} \times\left(1.0 \times 10^4 \mathrm{~J} / \mathrm{T}\right)\left(4 \times 10^{-5} \mathrm{~T}\right)=0.2 \mathrm{~J}\)

Example 4. A magnet of magnetic dipole moment M is released in a uniform magnetic field of induction B from the position shown in the figure. Find :

1. Its kinetic energy at θ = 90º
2. Its maximum kinetic energy during the motion.
3. Will it perform SHM? Oscillation? Periodic motion? What is its amplitude?

Solution: Apply energy conservation at θ= 120º and θ= 90º

= – MB cos 90º + (K.E.)

⇒ \(\mathrm{KE}=\frac{\mathrm{MB}}{2}\)

⇒ \(\mathrm{KE}=\frac{\mathrm{MB}}{2}\)

K.E. will be the maximum whereas P.E. is the minimum. P.E. is minimum at θ= 0º. Now apply energy conservation between θ= 120º and θ= 0º. – MB cos 120º + 0 = –mB cos 0º + (KE)_max

⇒ \((\mathrm{KE})_{\max }=\frac{3}{2} \mathrm{MB}\)

The K.E. is max at θ= 0º can also be proved by the torque method. From θ= 120º to θ= 0º the torque always acts on the dipole in the same direction (here it is clockwise) so its K.E. keeps on increasing till θ= 0º. Beyond that θ reverses its direction and then K.E. starts decreasing

θ = 0º is the orientation of M to here the maximum K.E.

Since ‘θ’ is not small.

θ = 0º is the orientation of M to here the maximum K.E.

Since ‘θ’ is not small.

Magnet In An External Nonuniform Magnetic Field

No special formulas are applied is such problems. Instead, see the force on individual poles and calculate the resistant force torque on the dipole.

Magnetic effects of current (and moving charge)

It was observed by OERSTED that a current-carrying wire produces a magnetic field near it.

It can be tested by placing a magnet in the nearby space, it will show some movement (deflection or rotation of displacement). This observation shows that a current or moving charge produces a magnetic field.

Oersted Experiment And Observations

Oersted experimented in 1819 whose arrangement is shown in the following figure. The following observations were noted from this experiment.

1. When no current is passed through the wire AB, the magnetic needle remains undeflected.
2. When current is passed through the wire AB, the magnetic needle gets deflected in a particular direction and the deflection increases as the current increases.
3. When the current flowing in the wire is reversed, the magnitude needle gets deflected in the opposite direction and its deflection increases as the current increases.
   1. Oersted concluded from this experiment that on passing a current through the conducting wire, a magnetic field is produced around this wire. As a result, the magnetic needle is deflected. This phenomenon is called the magnetic effect of current.
   2. In another experiment, it was found that the magnetic lines of force due to the current flowing in the wire are in the form of concentric circles around the conducting wire.

Frame Dependence Of \(\overrightarrow{\mathrm{B}}\)

The motion of anything is a relative term. A charge may appear at rest by an observer (say O₁) and \(\overrightarrow{\mathrm{v}}_1\)  1 moving at the same velocity concerning observer O₂ and at velocity concerning observer O₃ then due to that charge w.r.t. O₁ will be zero and w.r. to O₂ and O₃ it will be and (that means different).

In a current-carrying wire electrons move in the opposite direction to that of the current and +ve ions (of the metal) are static w.r.t. the wire.

Now if some observer (O₁) moves with velocity Vd in the direction of motion of the electrons then electrons will have zero velocity and +ve ions will have velocity Vd in the downward direction w.r.t. O₁. The density (n) of +ve ions is the same as the density of free electrons and their charges are of the same magnitudes.

So, w.r.t. O₁ electrons will produce zero magnetic field but +ve ions will produce +ve same due to the current carrying wire does not depend on the reference frame (this is true for any velocity of the observer).

\(\overrightarrow{\mathrm{B}}\) due to magnet:

B produced by the magnet does not contain the term of velocity
B So, we can say that the due magnet does not depend on the frame.

\(\overrightarrow{\mathrm{B}}\) Due To A Point Charge

r A charge particle ‘q’ has velocity v as shown in the figure. It is at position ‘A’ at some time. Is the position vector of point ‘P’ w.r.

To position of the charge. Then at P due to q is

⇒ \(B=\left(\frac{\mu_0}{4 \pi}\right) \frac{q v \sin \theta}{r^2}\); here θ angle between \(\vec{v} \text { and } \vec{r}\)

⇒ \(\vec{B}=\left(\frac{\mu_0}{4 \pi}\right) \frac{q \vec{V} \times \vec{r}}{r^3}\) ; q with sign \(\vec{B} \perp \vec{v} \text { and also } \vec{B} \perp \vec{r} \text {. }\).

The direction will be found by using the rules of vector product.

Self Practice Problems

Question 1. The magnetic field is produced by the flow of current in a straight wire. This phenomenon is based on-

1. Faraday’s Law
2. Maxwell’s Law
3. Coulbom’s Law
4. Oersted’s Law

Answer: 4. Oersted’s Law

Class 12 NEET Physics Magnetic Field Notes

Question 2. The field produced by a moving charged particle is-

1. Electric
2. Magnetic
3. Both electric and magnetic
4. Nothing can be predicted

Answer: 3. Both electric and magnetic

Question 3. The magnetic field due to a small bar magnet at a distance varies as

1. \(\frac{1}{d^2}\)
2. \(\frac{1}{d^{3 / 2}}\)
3. \(\frac{1}{d^{3 / 2}}\)
4. \(\frac{1}{d}\)

Answer: 3. \(\frac{1}{d}\)

Question 4. A magnetic dipole of magnetic moment M is situated with its axis along the direction of a magnetic field of strength B. How much work will have to be done to rotate it through 180°?

1. -MB
2. +MB
3. Zero
4. +2MB

Answer: 4. +2MB

Question 5. The magnetic field due to a small magnetic dipole of magnetic moment M, at distance r from the centre on the equatorial line, is given by- (in the MKS system)

1. \(\frac{\mu_0}{4 \pi} \times \frac{M}{r^2}\)
2. \(\frac{\mu_0}{4 \pi} \times \frac{M}{r^3}\)
3. \(\frac{\mu_0}{4 \pi} \times \frac{2 M}{r^2}\)
4. \(\frac{\mu_0}{4 \pi} \times \frac{2 M}{r^3}\)

Answer: 2. \(\frac{\mu_0}{4 \pi} \times \frac{M}{r^3}\)

Biot-Savant’s Law ( Due To A Wire)

It is an experimental law. A current ‘i’ flows in a wire (may be straight or curved). Due to θ the length of the wire the magnetic field at ‘P’ is

⇒ \(\mathrm{dB} \propto \text { id } \ell \quad \Rightarrow \quad \propto \frac{1}{\mathrm{r}^2} \quad \Rightarrow \quad \propto \sin \theta \quad \Rightarrow \quad \mathrm{dB} \propto \frac{\text { id } \ell \sin \theta}{\mathrm{r}^2}\)

⇒ \(\mathrm{dB}=\left(\frac{\mu_0}{4 \pi}\right) \frac{\mathrm{id} \ell \sin \theta}{\mathrm{r}^2} \quad \Rightarrow \quad \overrightarrow{\mathrm{dB}}=\left(\frac{\mu_0}{4 \pi}\right) \frac{\overrightarrow{i d} \times \overrightarrow{\mathrm{r}}}{\mathrm{r}^3}\)

Here = position vector of the test point w.r.t. \(\overrightarrow{\mathrm{d} \ell}\)

α = angle between \(\overrightarrow{\mathrm{d} \ell} \text { and } \overrightarrow{\mathrm{r}}\). The Resultant \(\overrightarrow{\mathrm{B}}=\int \overrightarrow{\mathrm{dB}}\)

Using this fundamental formula we can derive the expression of \(\vec{B}\) due to a long wire.

⇒ \(\vec{B}\) due to a straight wire:

Due to a straight wire ‘PQ’ carrying a current ‘i’ the \(\vec{B}\) at A is given by the formula \(B=\frac{\mu_0 I}{4 \pi \mathrm{r}}\left(\sin \theta_1+\sin \theta_2\right)\)

(Derivation can be seen in a standard textbook like your school book or concept of physics of HCV part 2) Direction:

B Due to every element of ‘PQ’ at A being directed inwards. So its resultant is also directed inwards. It is represented by (x)

The direction at various points is shown in the figure shown.

At points ‘C’ and ‘D’ = 0 (think how). For the case shown in figure B at \(A=\frac{\mu_0 i}{4 \pi r}\left(\sin \theta_2-\sin \theta_1\right)\)

Shortcut for Direction:

The direction of the magnetic field at point P due to a straight wire can be found by a slight variation in the right-hand thumb rule. If we stretch the thumb of the right hand along the current and curl our fingers to pass through point P, the direction of the fingers at P gives the direction of the magnetic field there.

We can draw magnetic field lines on the pattern of electric field lines. A tangent to a magnetic field line given the direction of the magnetic field existing at that point.

For a straight wire, the field lines are concentric circles with their centers on the wire and in the plane perpendicular to the wire. There will be an infinite number of such lines in the planes parallel to the above-mentioned plane.

Example 5. Find the resultant magnetic field at ‘C’ in the figure shown.

Solution: It is clear that ‘B’ is at ‘C’ due to all the wires being directed. Also, B at ‘C’ due to PQ and SR are the same. Also, due to QR and PS being the same

⇒ \(B_{r e s}=2\left(B_{P Q}+B_{S P}\right) \Rightarrow \quad B_{P Q}=\frac{\mu_0 \mathrm{i}}{4 \pi \frac{a}{2}}\left(\sin 60^{\circ}+\sin 60^{\circ}\right),\)

⇒ \(B_{s p}=\frac{\mu_0 i}{4 \pi \frac{\sqrt{3} a}{2}}\left(\sin 30^{\circ}+\sin 30^{\circ}\right) \Rightarrow B_{r e s}=2\left(\frac{\sqrt{3} \mu_0 i}{2 \pi a}+\frac{\mu_0 i}{2 \pi a \sqrt{3}}\right)=\frac{4 \mu_0 i}{\sqrt{3} \pi a}\)

Example 6. The figure shows a square loop made from a uniform wire. Find the magnetic field at the centre of the square if a battery is connected between points A and C.

Solution: The current will be equally divided at A. The fields at the center due to the currents in the wires AB and DC will be equal in magnitude and opposite in direction. The result of these two fields will be zero. Similarly, the resultant of the fields due to the wires AD and BC will be zero. Hence, the net field at the center will be zero.

Special case:

If the wire is infinitely long then the magnetic field at ‘P’ (as shown in the figure) is given by (using θ1 = θ2 = 90º and the formula of ‘B’ due to straight wire.

⇒ \(B=\frac{\mu_0 I}{2 \pi r} \quad \Rightarrow \quad B \propto \frac{I}{r}\)

The direction of at various is as shown in the figure. The magnetic lines of force will be concentric circles around the wire (as shown earlier)

If the wire is infinitely long but ‘P’ is as shown in the figure. The B direction at various points is as shown in the figure. At ‘P’.

⇒ \(B=\frac{\mu_0 I}{4 \pi r}\)

NEET Physics Chapter 1 Magnetic Field Notes and Key Concepts

Self Practice problems 

Question 6. A pair of stationary and infinitely long bent wires are placed in the xy plane as shown in The wires carry a current of i = 10 Amp. each as shown. The segments L and M are along the x-axis. The segments P and Q are parallel to the y-axis such that OS = OR = 0.02 m. The magnetic induction at the origin O is

1. \(10^{-4} \mathrm{~Wb} / \mathrm{m}^2\)
2. \(10^{-2} \mathrm{~Wb} / \mathrm{m}^2\)
3. \(10^{-6} \mathrm{~Wb} / \mathrm{m}^2\)
4. \(10^{-8} \mathrm{~Wb} / \mathrm{m}^2\)

Answer: 1. \(10^{-4} \mathrm{~Wb} / \mathrm{m}^2\)

Question 7. A current-carrying wire is bent into the shape of a square coil. The magnetic field produced at the center of the coil by one arm BC is B. Then the resultant magnetic field at the center due to all the arms will be

1. 4B
2. \(\frac{B}{2}\)
3. B
4. \(\frac{2}{B}\)

Answer: 1. 4B

Question 8. As shown in the diagram, two perpendicular wires are placed very close to each other, but they are not touching each other. The points where the intensity of the magnetic field is zero are-

1. A
2. B, D
3. A, B
4. B

Answer: 2. B, D

Question 9. At a distance of 10 cm. from a long straight wire carrying current, the magnetic field is 0.04. Tesla the magnetic field at the distance of 40 cm. will be

1. 0.001T
2. 0.02T
3. 0.08T
4. 0.16T

Answer: 1. 0.001T

⇒ \(\stackrel{\rightharpoonup}{B}\) due to circular loop

At centre: Due to each \(\overrightarrow{\mathrm{d} \ell}\) element of the loop \(\stackrel{\rightharpoonup}{B}\) At ‘c’ is inwards (in this case)

⇒ \(\overline{B_{r e s}} \text { at ‘ } c \text { ‘ is } \otimes . B=\frac{\mu_0 N I}{2 R} \text {, }\)

N = No. of turns in the loop =\(\frac{\ell}{2 \pi R}\) l= length of the loop.

N can be fraction \(\left(\frac{1}{4}, \frac{1}{3}, \frac{11}{3} \text { etc. }\right)\) or integer.

The direction of \(\stackrel{\rightharpoonup}{B}\): The direction of the magnetic field at the center of a circular wire can be obtained using the right-hand thumb rule. If the fingers are curled along the current, the stretched thumb will point toward the magnetic field.

Another way to find the direction is to look into the loop along its axis. If the current is in an anticlockwise direction, the magnetic field is towards the viewer. If the current is in a clockwise direction, the field is away from the viewer.

Semicircular And Quarter Of A Circle:

On the axis of the loop= \(B=\frac{\mu_0 N^2 R^2}{2\left(R^2+x^2\right)^{3 / 2}}\)

Direction can be obtained by the right-hand and thumb rule. Curl your fingers in the direction of the current then B the direction of the thumb points in the direction of at the points on the axis.

The magnetic field at a point not on the axis is mathematically difficult to calculate. We show qualitatively in the figure the magnetic field lines due to a circular current which will give some idea of the field.

A loop as a magnet:

The pattern of the magnetic field is comparable with the magnetic field produced by a bar magnet.

The side ‘I’ (the side from which the emerges out) of the loop acts as the ‘NORTH POLE’ and side II (the B side in which the enters) acts as the ‘SOUTH POLE’. It can be verified by studying the force on one loop due to a magnet or a loop.

Mathematically:

⇒ \(B_{\text {amis }}=\frac{\mu_0 N I R^2}{2\left(R^2+x^2\right)^{3 / 2}} \cong \frac{\mu_0 N I R^2}{2 x^3} \text { for } x>R=2\left(\frac{\mu_0}{4 \pi}\right)\left(\frac{I N \pi R^2}{x^3}\right)\)

It is similar to Baxis due to magnet \(=2\left(\frac{\mu_0}{4 \pi}\right) \frac{m}{x^3}\)

Magnetic dipole moment of the loop

M = INπR²

M = INA for any other shaped loop.

Unit of M is Amp. m²

Unit of m (pole strength) = Amp. m {since in magnet M = ml}

⇒ \({\mathrm{M}}=\mathrm{IN} \overrightarrow{\mathrm{A}} \text {, }\)

⇒ \(\vec{A}\) = unit normal vector for the loop.
To be determined by right hand rule which is also used to determine the direction of the axis. It is also from

‘S’ side to ‘N’ side of the loop.

Solenoid:

A solenoid contains a large number of circular loops wrapped around a non-conducting cylinder. (it may be a hollow cylinder or it may be a solid cylinder)

The winding of the wire is the uniform direction of the magnetic field is the same at all points of the axis.

⇒ \(\vec{B}\) on axis (turns should be very close to each other).

⇒ \(B=\frac{\mu_0 n i}{2}\left(\cos \theta_1-\cos \theta_2\right)\)

where n: number of turns per unit length.

⇒ \(\cos \theta_1=\frac{\ell_1}{\sqrt{\ell_1^2+\mathrm{R}^2}} ; \quad \cos \beta=\frac{\ell_2}{\sqrt{\ell_2^2+\mathrm{R}^2}}=-\cos \theta_2\)

⇒ \(B=\frac{\mu_0 n i}{2}\left[\frac{\ell_1}{\sqrt{\ell_1^2+R^2}}+\frac{\ell_2}{\sqrt{\ell_2^2+R^2}}\right]=\frac{\mu_0 n i}{2}\left(\cos \theta_1+\cos \beta\right)\)

Note: Use the right-hand rule for direction (same as the direction due to the loop).

Derivation:

Take an element of width dx at a distance x from point P. [point P is the point on the axis at which we are going to calculate the magnetic field. Total number of turns in the element dn = ndx where n: number of turns per unit length.

⇒ \(d B=\frac{\mu_0 i R^2}{2\left(R^2+x^2\right)^{3 / 2}}(n d x)\)

⇒ \(B=\int d B=\int_{-\ell_1}^2 \frac{\mu_0 i R^2 n d x}{2\left(R^2+x^2\right)^{3 / 2}}=\frac{\mu_0 n i}{2}\left[\frac{\ell_1}{\sqrt{\ell_1^2+R^2}}+\frac{\ell_2}{\sqrt{\ell_2^2+R^2}}\right]=\frac{\mu_0 n i}{2}\left[\cos \theta_1-\cos \theta_2\right]\)

For ‘Ideal Solenoid’:

Inside (at the midpoint)

⇒ \(\begin{aligned}
& \ell>R \quad \text { or length is infinite } \\
& \theta_1 \rightarrow 0 \\
& \theta_2 \rightarrow \pi \\
& B=\frac{\mu_0 n i}{2}[1-(-1)] \\
& \mathbf{B}=\mu_0 \mathbf{n i}
\end{aligned}\)

If the material of the solid cylinder has relative permeability \(\text { ‘ } \mu_t^{\prime} \text { then } B=\mu_0 \mu_t \text { ni }\)

At the ends B \(B=\frac{\mu_0 n i}{2}\)

Comparison between ideal and real solenoid:

1. Ideal Solenoid Real Solenoid

Self Practice Problems

Question 10. The radius of a circular coil is R and it carries a current of I ampere. The intensity of the magnetic field at a distance x from the centre (x >> R) will be:

1. \(\mathrm{B}=\frac{\mu_0}{2} \frac{\mathrm{IR}^2}{\mathrm{x}^2}\)
2. \(B=\frac{\mu_0 I^2}{2 x^3}\)
3. \(B=\frac{\mu_0 I R}{2 x^2}\)
4. \(B=\frac{\mu_0 \text { IR }}{2 x^3}\)

Answer: 2. \(B=\frac{\mu_0 I^2}{2 x^3}\)

Question 11. The magnetic field B at the centre of a circulate coil of radius r is times that due to a long straight wire at a distance r from it, for equal currents. Fig shows three cases; in all cases, the circular part has a radius of r and the straight ones are infinitely long. For the same current the field B at the centre P in cases 1,2, and 3 has the ratio.

Answer: 2. \(B=\frac{\mu_0 I^2}{2 x^3}\)

Question 12. If the intensity of the magnetic field at a point on the axis of the current-carrying coil is half of that at the centre of the coil, then the distance of that point from the centre of the coil will be

1. \(\left(-\frac{\pi}{2}\right): \frac{\pi}{2}:\left[\frac{3 \pi}{4}-\frac{1}{2}\right]\)
2. \(\left(-\frac{\pi}{2}+1\right):\left[\frac{\pi}{2}+1\right]:\left[\frac{3 \pi}{4}+\frac{1}{2}\right]\)
3. \(-\frac{\pi}{2}: \frac{\pi}{2}: \frac{3 \pi}{4}\)
4. \(\left(-\frac{\pi}{2}-1\right):\left[\frac{\pi}{4}-\frac{1}{4}\right]:\left[\frac{3 \pi}{4}+\frac{1}{2}\right]\)

Answer: 1. \(\left(-\frac{\pi}{2}\right): \frac{\pi}{2}:\left[\frac{3 \pi}{4}-\frac{1}{2}\right]\)

Question 13. If the intensity of the magnetic field at a point on the axis of current carrying coil is half of that at the centre of the coil, then the distance of that point from the centre of the coil will be

1. \(\frac{R}{2}\)
2. R
3. \(\frac{3 R}{2}\)
4. 0.766R

Answer: 4. \(\frac{3 R}{2}\)

Question 13. A current of 0.1 ampere flows through a coil of 100 turns and the radius is 5 cm. The magnetic field at the centre of the coil will be

1. \(4 \pi \times 10^{-5} \mathrm{~T}\)
2. \(8 \pi \times 10^{-5} \mathrm{~T}\)
3. \(4 \times 10^{-5} \mathrm{~T}\)
4. \(2 \times 10^{-5} \mathrm{~T}\)

Answer: 1. \(4 \pi \times 10^{-5} \mathrm{~T}\)

Question 14. A current I flows through a circular coil of radius r the intensity of the field at its centre is

1. Proportional to r
2. Inversely proportional I
3. Proportional to I
4. Proportional to I2

Answer: 3. Proportional to I

Question 15. In a current carrying long solenoid the field produced does not depend upon-

1. Number of turns per unit length
2. Current flowing
3. The radius of the solenoid
4. All of the above three

Answer: 3. Radius of the solenoid

Ampere’s Circuital Law :

The line integral \(\oint \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} \ell}\) on a closed curve of any shape is equal to (permeability of free space) times the net current through the area bounded by the curve.

⇒ \(\int \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} \ell}=\mu_0 \Sigma \mathrm{I}\)

Note:

A line integral is independent of the shape of the path and the position of the within in it.

The statement \(\int \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} \ell}=0\) does not necessarily mean that \(\vec{B}=0\) everywhere along the path but only that no net current is passing through the path.

Sign of current: The current due to which \(\vec{B}\) is produced in the same sense as \(\overrightarrow{\mathrm{d} \ell}\) (i.e \(\overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} \ell}\) positive will be taken positive and the current which produces \(\vec{B}\) in the sense opposite to \(\overrightarrow{\mathrm{d} \ell}\) will be negative

Solved Examples

Example 7. Find the values of \(\int \vec{B} \cdot \overrightarrow{d \ell}\) for the loops L1, L2, and L3 in the figure shown. The sense of \(\overrightarrow{\mathrm{d} \ell}\) is mentioned in the figure.

Solution: \(\text { for } L_1 \int \vec{B} \cdot \overrightarrow{d \ell}=\mu_0\left(I_1-\mathrm{I}_2\right)\)

here I1 is taken positively because magnetic lines of force produced by I1 are anti-clockwise as B d seen from the top. I2 produces lines of \(\overrightarrow{\mathrm{B}}\) in a clockwise sense as seen from the top. The sense of is anticlockwise as seen from the top.

For \(L_2: \int \vec{B} \cdot \vec{d}=\mu_0 \quad\left(I_1-I_2+I_4\right)\) for \(\mathrm{L}_3: \int \vec{B} \cdot \vec{d} \ell=0\)

To find out the magnetic field due to infinite current carrying wire

By B.S.L \(\overrightarrow{\mathrm{B}}\) will have circular lines. \(\overrightarrow{d \ell}\) is also taken tangent to the circle.

⇒ \(\int \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} \ell}=\) since \(\theta=0^{\circ} \text { so } \mathrm{B} \int \mathrm{d} \ell=\mathrm{B} 2 \pi \mathrm{R}\) (since B= const)

Now by amperes law: \(\text { B } 2 \pi R=\mu_0 I\) since \(B=\frac{\mu_0 i}{2 \pi R}\)

Hollow current carrying infinitely long cylinder : (I is uniformly distributed on the whole circumference)

For r > R By symmetry, the amperian loop is a circle.

⇒ \(\int \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} \ell}=\int \mathrm{B} \mathrm{d} \ell\) since 0=0

⇒ \(=\mathrm{B} \int_0^2 \mathrm{~d} \ell\) since b= const. \(B=\frac{\mu_0 I}{2 \pi r}\)

r<R = \(\int \overrightarrow{\mathrm{B}} \cdot \overrightarrow{\mathrm{d} \ell}=\int \mathrm{B} d \ell=\mathrm{B}(2 \pi \mathrm{r})=0\) = \(B_{\text {in }}=0\)

Graph:

Solid infinite current carrying cylinder:

Assume current is uniformly distributed on the whole cross-section area.

Current density \(\mathrm{J}=\frac{\mathrm{I}}{\pi \mathrm{R}^2}\)

Case \(r \leq R\)

Take an American loop inside the cylinder. By symmetry it should be a circle whose centre is on the axis of the cylinder and its axis also coincides with the cylinder axis on the loop.

⇒ \(\iint \vec{B} \cdot \vec{d} \ell=\int \mathrm{B} \cdot \mathrm{d} \ell=\mathrm{B} \int \mathrm{d} \ell=\mathrm{B} \cdot 2 \pi \mathrm{r}=\mu_0 \frac{1}{\pi \mathrm{R}^2} \pi \mathrm{r}^2\)

⇒ \(B=\frac{\mu_0 I r}{2 \pi R^2}=\frac{\mu_0 J r}{2} \quad \Rightarrow \quad \vec{B}=\frac{\mu_0(\vec{J} \times \vec{r})}{2}\)

Case 2: \(\int \overrightarrow{\mathrm{B}} \cdot \mathrm{d} \vec{\ell}=\int \mathrm{B} \mathrm{d} \ell=\mathrm{B} \int \mathrm{d} \ell=\mathrm{B} \cdot(2 \pi \mathrm{r})=\mu_0 \cdot \mathrm{I}\)

⇒ \(\Rightarrow \quad B=\frac{\mu_0 I}{2 \pi r} \text { also } \frac{\mu_0 I}{2 \pi r}(\hat{J} \times \hat{r})=\frac{\mu_0 J \pi R^2}{2 \pi r}\)

⇒ \(\vec{B}=\frac{\mu_0 R^2}{2 r^2}(\vec{J} \times \overrightarrow{\mathrm{r}})\)

Self Practice Problems

Question 16. The intensity of the magnetic field at a point situated at a distance r close to a long straight current carrying r wire is B the intensity of the field at a distance \(\frac{r}{2}\) from the wire will be-

1. \(\frac{B}{2}\)
2. \(\frac{B}{4}\)
3. 2B
4. 4B

Answer: 3. 2B

Question 17. Two straight infinitely long and thin wires are separated 0.1 m apart and carry a current of 10 Amp. each in opposite directions. The magnetic field on point at a distance of 0.1 m from both wires is

1. \(2 \times 10^{-5} \mathrm{~Wb} / \mathrm{m}^2\)
2. \(3 \times 10^{-5} \mathrm{~Wb} / \mathrm{m}^2\)
3. \(4 \times 10^{-5} \mathrm{~Wb} / \mathrm{m}^2\)
4. \(1 \times 10^{-5} \mathrm{~Wb} / \mathrm{m}^2\)

Answer: 1. \(3 \times 10^{-5} \mathrm{~Wb} / \mathrm{m}^2\)

Question 18. One ampere current is passed through a 2m long straight wire. The magnetic field in the air at a point distance of 3m from one end of the wire on its axis will be

1. \(\frac{\mu_0}{2 \pi}\)
2. \(\frac{\mu_0}{4 \pi}\)
3. \(\frac{\mu_0}{8 \pi}\)
4. zero

Answer: 4. Zero

Solved Examples 

Example 8. The figure shows a cross-section of a large metal sheet carrying an electric current along its surface. The current in a strip of width dl is Kdl where K is a constant. Find the magnetic field at a point P at a distance x from the metal sheet.

Solution: Consider two strips A and C of the sheet situated symmetrically on the two sides of P (figure). The magnetic field at P due to strip A is B 0 perpendicular to AP and that due to strip, C is BC perpendicular to CP. The resultant of these two is parallel to the width AC of the sheet. The field due to the whole sheet will also be in this direction. Suppose this field has magnitude B.

The field on the opposite side of the sheet at the same distance will also be B but in the opposite direction. Applying Ampere’s law to the rectangle shown in the figure.

⇒ \(2 \mathrm{~B} \ell=\mu_0 \mathrm{~K} \ell \quad \text { or, } \quad \mathrm{B}=\frac{1}{2} \mu_0 \mathrm{~K} \text {. }\)

Note that it is independent of x.

Example 9. Three identical long solenoids P, Q and R are connected as shown in the figure. If the magnetic field at the centre of P is 2.0 T, what would be the field at the centre of Q? Assume that the field due to any solenoid is confined within the volume of that solenoid only.

Solution: As the solenoids are identical, the currents in Q and R will be the same and will be half the current in P. The magnetic field within a solenoid is given by B = μ0ni. Hence the field in Q will be equal to the field in R and will be half the field in P i.e., will be 1.0 T.

Magnetic Field in a Toroid

1. A toroid is like an endless cylindrical solenoid, i.e. if a long solenoid is bent round in the form of a closed ring, then it becomes a toroid.
2. Electrically insulated wire is wound uniformly over the toroid as shown in the figure.
3. The thickness of the toroid is kept small in comparison to its radius and the number of turns is kept very large.
4. When a current i is passed through the toroid, each turn of the toroid produces a magnetic field along the axis at its centre. Due to the uniform distribution of turns this magnetic field has the same magnitude at their centres. Thus the magnetic lines of force inside the toroid are circular.
5. The magnetic field inside a toroid at all points is the same but outside the toroid, it is zero.
6. If the total number of turns in a toroid is N and R is its radius, then the number of turns per unit length of the toroid will be \(\mathrm{n}=\frac{\mathrm{N}}{2 \pi \mathrm{R}}\)
7. The magnetic field due to the toroid is determined by Ampere’s law.
8. The magnetic field due to toroid is \(B_0=\mu_0 \text { ni } \quad \text { or } \quad B_0=\mu_0\left(\frac{N}{2 \pi R}\right) \mathrm{i}\)
9. If a substance of permeability μ is placed inside the toroid, then B = uni
10. If ur is the relative magnetic permeability of the substance, then B = uru0 ni

Self Practice Problems

Question 19. A toroid has n turn density, current i then the magnetic field is

1. u0 ni
2. \(\mu_0 \frac{i}{n}\)
3. Zero
4. \(\mu_0 n^2 i\)

Answer: 1. u0 ni

Question 20. The current on the windings on a Toroid is 2.0 A. There are 400 turns and the mean circumferential length is 40 cm. If the inside magnetic field is 1.0 T, the relative permeability is near to

1. 100
2. 200
3. 300
4. 400

Answer: 4. 400

Current And Magnetic Field Due To Circular Motion Of A Charge

According to the theory of atomic structure every atom is made of electrons, protons and neutrons. Protons and neutrons are in the nucleus of each atom and electrons are assumed to be moving in different orbits around the nucleus.

An electron and a proton present in the atom constitute an electric dipole at every moment but the direction of this dipole changes continuously and hence at any time the average dipole moment is zero.

As a result static electric field is not observed.

Moving charge produces a magnetic field and the average value of this field in the atom is not zero.

In an atom, an electron moves in a circular path around the nucleus. Due to this motion current appears to be flowing in the electronic orbit and the orbit behaves like a current-carrying coil. If e is the electron charge, R is the radius of the orbit and f is the frequency of motion of an electron in the orbit, then

1. Current in the orbit = charge × frequency = ef
2. If T is the period, then \(f=\frac{1}{T}\) therefore \(\mathrm{i}=\frac{\mathrm{e}}{\mathrm{T}}\)
3. The magnetic field at the nucleus (centre) \(B_0=\frac{\mu_0 \mathrm{i}}{2 R}=\frac{\mu_0 \mathrm{ef}}{2 R}=\frac{\mu_0 \mathrm{e}}{2 R T}\)
4. If the angular velocity of the electron is, then \(\omega=2 \pi f \text { and } f=\frac{\omega}{2 \pi}\)
   • ∴ \(\mathrm{i}=\mathrm{ef}=\frac{\mathrm{e} \omega}{2 \pi}\)
   • ∴ \(B_0=\frac{\mu_0 i}{2 R}=\frac{\mu_0 \mathrm{e} \omega}{4 \pi R}\)
5. If the linear velocity of the electron is v, then v Rw R(2f) or \(f=\left(\frac{v}{2 \pi R}\right)\) or \(f=\left(\frac{v}{2 \pi R}\right)\)
   • ∴ \(i=e f=\frac{e v}{2 \pi R}\)
   • ∴ \(B_0=\frac{\mu_0 \mathrm{i}}{2 R}=\frac{\mu_0 e v}{4 \pi R^2}\)
6. Magnetic moment due to the motion of an electron in an orbit
   • \(M=i A=e f \pi R^2=\frac{e \pi R^2}{T}\) or, \(M=\frac{e \omega \pi R^2}{2 \pi}=\frac{e \omega R^2}{2}\) or, \(M=\frac{e v \pi R^2}{2 \pi R}=\frac{e v R}{2}\)

If the angular momentum of the electron is L, then
L mvR mR= mwR2

Writing M in terms of L

⇒ \(M=\frac{e m \omega R^2}{2 m}=\frac{e m v R}{2 m}=\frac{e L}{2 m}\)

According to Bohr’s second postulate \(m v R=n \frac{h}{2 \pi}\)

In ground state n = 1

⇒ \(L=\frac{h}{2 \pi}\)

∴ \(M=\frac{e h}{4 \pi m}\)

1. If a charge q (or a charged ring of charge q) is moving in a circular path of radius R with a frequency for angular velocity w, then
2. Current due to moving charge \(\mathrm{i}=\mathrm{qf}=\mathrm{q} \omega / 2 \pi\)
3. The magnetic field at the centre of the ring \(M=i\left(\pi R^2\right)=q f \pi R^2=\frac{1}{2} q \omega R^2\)
4. If a charge q is distributed uniformly over the surface of the plastic disc of radius R and it is rotated about its axis with an angular velocity w, then (a) the magnetic field produced at its centre will be \(B_0=\frac{\mu_0 q \omega}{2 \pi R}\)
5. The magnetic moment of the disc will be
   1. dM = (di) pix2
      • \(=\frac{\omega}{2 \pi} d q \pi x^2=\frac{\omega q}{R^2} x^3 d x\)
      • \(\Rightarrow \quad M=\int d M=\frac{\omega q}{R^2} \int_0^R x^3 d x\)
      • \(\Rightarrow \quad M=\frac{q \omega R^2}{4}\)
      • \(\Rightarrow \quad M=\frac{\mathrm{q} \omega \mathrm{R}^2}{4}\)

Question 21. A circular loop has a radius of 5 cm and it carries a current of 0.1 amp. Its magnetic moment is-

1. 1.32 × 10–4 amp. m2
2. 2.62 × 10–4 amp. m2
3. 5.25 × 10–4 amp. m2
4. 7.85 × 10–4 amp. m2

Answer: 4. 7.85 × 10–4 amp. m2

Question 22. The magnetic moment of a circular coil carrying current is-

1. Directly proportional to the length of the wire in the coil.
2. Inversely proportional to the length of the wire in the coil
3. Directly proportional to the square of the length of the wire in the coil
4. Inversely proportional to the square of the length of the wire in the coil.

Answer: 3. Directly proportional to the square of the length of the wire in the coil

Magnetic force on moving charge

When a charge q moves with velocity, in a magnetic field, then the magnetic force experienced by the moving charge is given by the following formula:

⇒ \(\vec{F}=q(\vec{v} \times \vec{B})\) Put q with sign.

⇒ \(\overrightarrow{\mathrm{v}}\): Instantaneous velocity

⇒ \(\overrightarrow{\mathrm{B}}\): Magnetic field at that point.

Note:

1. ⇒ \(\overrightarrow{\mathrm{F}} \perp \overrightarrow{\mathrm{V}} \text { and also } \overrightarrow{\mathrm{F}} \perp \overrightarrow{\mathrm{B}}\)
2. since \(\vec{F} \perp \vec{v}\) therefore power due to magnetic force on a charged particle is zero. (use the formula of power.
3. P= \(\overrightarrow{\mathrm{F}} \cdot \overrightarrow{\mathrm{V}}\) = for its proof).
4. Since the \(\overrightarrow{\mathrm{F}} \perp \overrightarrow{\mathrm{B}}\) work done by the magnetic force is zero in every part of the motion. The magnetic force cannot increase or decrease the speed (or kinetic energy) of a charged particle.
5. It can only change the direction of velocity.
6. On a stationary charged particle, the magnetic force is zero.
7. If \(\overrightarrow{\mathrm{V}} \| \overrightarrow{\mathrm{B}},\) then also magnetic force on charged particle is zero. It moves along a straight line if only a magnetic field is acting.

Solved Examples 

Example 10. A charged particle of mass 5 mg and charge q = +2uC has velocity \(\vec{v}=2 \hat{i}-3 \hat{j}+4 \hat{k}\). find out the magnetic force on the charged particle and its acceleration at this instant due to magnetic field \(\overrightarrow{\mathrm{B}}=3 \hat{\mathrm{j}}-2 \hat{\mathrm{k}} \quad \overrightarrow{\mathrm{v}} \text { and } \overrightarrow{\mathrm{B}}\) are in m/s and web/m2 respectively.

Solution:

⇒ \(\vec{F}=q \vec{v} \times \vec{B}=2 \times 10^{-6}(2 \hat{i}-3 \hat{j} \times 4 \hat{k}) \times(3 \hat{j}-2 \hat{k})=2 \times 10^{-6}[-6 \hat{i}+4 \hat{j}+6 \hat{k}] N\)

By newton’s law \(\vec{a}=\frac{\vec{F}}{m}=\frac{2 \times 10^{-6}}{5 \times 10^{-6}}(-6 \hat{i}+4 \hat{j}+6 \hat{k})\)

⇒ \(=0.8(-3 \hat{i}+2 \hat{j}+3 \hat{k}) \mathrm{m} / \mathrm{s}^2\)

Example 11. A charged particle has acceleration \(\vec{a}=2 \hat{i}+x \hat{j}\) in a magnetic field \(\vec{B}=-3 \hat{i}+2 \hat{j}-4 \hat{k}\). Find the value of x.
Solution: Since \(\vec{F} \perp \vec{B}\) since \(\overrightarrow{\mathrm{a}} \perp \overrightarrow{\mathrm{B}}\) since \(\overrightarrow{\mathrm{a}} \cdot \overrightarrow{\mathrm{B}}=0\) ∴ \((2 \hat{i}+x \hat{j}) \cdot(-3 \hat{i}+2 \hat{j}-4 \hat{k})=0\)

-6+2x=0

x=3

Motion of charged particles under the effect of magnetic force

Particle released if v = 0 then fm = 0

∴ The particle will remain at rest

⇒ \(\vec{V} \| \vec{B} \text { here } \theta=0 \text { or } \theta=180^{\circ}\)

∴ Fm= 0

∴ \(\overrightarrow{\mathrm{a}}=0\)

∴ \(\vec{V}\) = const.

∴ The particle will move in a straight line with constant velocity

Initial velocity \(\overrightarrow{\mathrm{u}} \perp \overrightarrow{\mathrm{B}} \text { and } \overrightarrow{\mathrm{B}}\) = uniform

In this case, since B is in the z direction the magnetic force in the z-direction will be zero. (since \(\overrightarrow{F_m} \perp \vec{B}\)

∴ the particle will always move in the xy plane.

∴ velocity vector is always \(\perp \vec{B}\)

∴ \(F_m=\mathrm{quB}=\text { constant. now } \mathrm{quB}=\frac{\mathrm{mu}^2}{\mathrm{R}} \Rightarrow \mathrm{R}=\frac{\mathrm{mu}}{\mathrm{qB}}=\text { constant. }\)

The particle moves in a curved path whose radius of curvature is the same everywhere,
such a curve in a plane is only a circle

∴ The path of the particle is circular.

⇒ \(R=\frac{m u}{q B}=\frac{p}{q B}=\frac{\sqrt{2 m k}}{q B}\) Here p= linear momentum; k= kinetic energy

Now \(v=\omega R \Rightarrow \omega=\frac{q B}{m}=\frac{2 \pi}{T}=2 \pi f\)

Time period T = 2πm/qB frequency f = Bq/2πm

Note: ω, f, T is independent of velocity.

Example 12. A proton (p), α-particle and deuteron (D) are moving in circular paths with the same kinetic energies in the same magnetic field. Find the ratio of their radii and periods. (Neglect interaction between particles).
Solution: \(R=\frac{\sqrt{2 m K}}{q B}\)

∴ \(R_p: R_a: R_D=\frac{\sqrt{2 m K}}{q B}: \frac{\sqrt{2.4 m K}}{2 q B}: \frac{\sqrt{2.2 m K}}{q B}=1: 1: \sqrt{2}\) t=2πm/qB

∴ \(T_p: T_\alpha: T_D=\frac{2 \pi m}{q B}: \frac{2 \pi 4 m}{2 q B}: \frac{2 \pi 2 m}{q B}=1: 2: 2\)

Example 13. In the figure shown the magnetic field on the left of ‘PQ’ is zero and on the right of ‘PQ’ it is uniform. Find the time spent in the magnetic field.

Example 14. A uniform magnetic field of strength ‘B’ exists in a region of width ‘d’. A particle of charge ‘q’ and mass ‘m’ is shot perpendicularly (as shown in the figure) into the magnetic field. Find the time spent by the particle in the magnetic field if

⇒ \(d>\frac{\mathrm{mu}}{\mathrm{qB}}\)

⇒ \(d<\frac{m u}{q B}\)

Solution: \(d>\frac{\mathrm{mu}}{\mathrm{qB}}\)

∴ \(\mathrm{t}=\frac{\mathrm{T}}{2}=\frac{\pi \mathrm{m}}{q B}\)

⇒ \(\sin \theta=\frac{d}{R} \Rightarrow \theta=\sin ^{-1}\left(\frac{d}{R}\right)\) \(\omega t=\theta \Rightarrow t=\frac{m}{q B} \sin ^{-1}\left(\frac{d}{R}\right)\)

Question 15. What should be the speed of a charged particle so that it can’t collide with the upper wall? Also, find the coordinates of the point where the particle strikes the lower plate in the limiting case of velocity.

Solution: The path of the particle will be circular larger the velocity, the larger will be the radius. For particle not to s strike R < d.

Since \(\frac{m v}{q B}<d \quad \Rightarrow \quad v<\frac{q B d}{m} .\)

For limiting case \(v=\frac{q B d}{m}\)

R=d

Therefore coordinate = (–2d, 0, 0) l

Self Practice Problems 

Question 23. In a hydrogen atom, an e– moves in Bohr’s orbit of radius r = 5 x 10–11 m. and makes 1017 revolutions per second. The magnetic moment produced due to the orbital motion of the e– is-

1. 0.40π x 10–22 A-m2
2. 2.2π x 10–22 A-m2
3. 2π x 10–22 A-m2
4. None of these

Answer: 1. 0.40π x 10–22 A-m2

Question 24. A charged particle is moving with velocity v under the magnetic field B. The force acting on the particle will be maximum if-

1. v and B are in the same direction
2. v and B are in the opposite direction
3. v and B are perpendicular
4. v does not depend on the direction B.

Answer: 3. v and B are perpendicular

Helical path:

If the velocity of the charge is not perpendicular to the magnetic field, we can break the velocity into two components – V11 parallel to the field and \(V_{\perp}\) perpendicular to the field.

The components v11 remains unchanged as the force \(\mathrm{q} \overrightarrow{\mathrm{v}} \times \overrightarrow{\mathrm{B}}\) is perpendicular to it. In the plane perpendicular to the field, the particle traces a circle of radius \(r=\frac{m v_{\perp}}{q B}\) as given by the equation. The resultant path is a helix.

Complete analysis:

Let a particle have an initial velocity in the plane of the paper and a constant and uniform magnetic field also in the plane of the paper.

The particle starts from point A1.

It completes its one revolution at A₂ 2nd revolution at A₃ and so on. X-axis is the tangent to the helix points.

A₁, A₂, A₃,……….all are on the x-axis. distance A₁ A₂ = A₃ A₄ = …………… = v cosθ. T = pitch where T = Period \(=\frac{\pi 2 m}{q B}\)

Let the particle’s initial position be (0,0,0) and v sinq in +y direction. Then
in x : Fx= 0, ax= 0, vx= constant = v cosθ, x = (v cosθ)t

In the y-z plane:

From the figure, it is clear that

⇒ \(\begin{aligned}
& y=R \sin \beta, v_y=v \sin \theta \cos \beta \\
& z=-(R-R \cos \beta) \\
& v_z=v \sin \theta \sin \beta
\end{aligned}\)

acceleration towards centre = (vsinθ)2/R = θ2R

∴ \(a_y=-\omega^2 R \sin \beta, a_z=-\omega^2 R \cos \beta\)

At any time: the position vector of the particle (or its displacement w.r.t. initial position)

⇒ \(\overrightarrow{\mathrm{r}}=x \hat{i}+y \hat{j}+z \hat{k}, x, y, z \text { already found }\)

Velocity \(\vec{v}=v_x \hat{i}+v_y \hat{j}+v_z \hat{k}, v_x, v_y, v_z \text { already found }\)

⇒ \(\vec{a}=a_x \hat{i}+a_y \hat{j}+a_z \hat{k}, a_x, a_y, a_z \text { already found }\)

Radius \(q(v \sin \theta) B=\frac{m(v \sin \theta)^2}{R} \quad \Rightarrow \quad R=\frac{m v \sin \theta}{q B}\)

⇒ \(\omega=\frac{v \sin \theta}{R}=\frac{q B}{m}=\frac{2 \pi}{T}=2 \pi f .\)

Charged Particle in \(\overrightarrow{\mathrm{E}} and \overrightarrow{\mathrm{B}}\)

When a charged particle moves with velocity in an electric field and magnetic field then. The net force experienced by it is given by the following equation.

⇒ \(\vec{F}=q \vec{E}+q(\vec{V} \times \vec{B})\)

Combine force is known as Lorentz force

image-

In the above situation, the particle passes undeviated but its velocity will change due to the electric field. Magnetic force on it = 0.

Case 1

⇒ \(\overrightarrow{\mathrm{E}} \| \overrightarrow{\mathrm{B}} \text { and uniform } \theta \neq 0 \text {, }\) (\(\text { } \vec{E} \text { and } \vec{B}\) are constant and uniform)

⇒ \(\text { in } x: F_x=q E, a_x=\frac{q E}{m}, v_x=v_0 \cos \theta+a_x t, x=v_0 t+\frac{1}{2} a_x t^2\)

in yz plane:

⇒ \(\begin{aligned}
& q v_0 \sin \theta B=m\left(v_0 \sin \theta\right)^2 / R \\
& \Rightarrow \quad R=\frac{m v_0 \sin \theta}{q B}, \quad \omega=\frac{v_0 \sin \theta}{R}=\frac{q B}{m}=\frac{2 \pi}{T}=2 \pi f
\end{aligned}\)

⇒ \(\vec{r}=\left\{\left(V_0 \cos \theta\right) t+\frac{1}{2} \frac{q E}{m} t^2\right\} \hat{i}+R \sin \omega t \hat{j}+(R-R \cos \omega t)(-\hat{k})\)

⇒ \(\vec{V}=\left(V_0 \cos \theta+\frac{q E}{m} t\right) \hat{i}+\left(V_0 \sin \theta\right) \cos \omega t \hat{j}+V_0 \sin \theta \sin \omega t(-\hat{k})\)

⇒ \(\vec{a}=\frac{q E}{m} \hat{i}+\omega^2 R[-\sin \beta \hat{j}-\cos \beta \hat{k}]\)

Magnetic force on a current-carrying wire:

B Suppose a conducting wire, carrying a current is placed in a magnetic field. Consider a small element dl of the wire (figure). The free electrons drift with a speed vd opposite to the direction of the current. The relation between the current i and the drift speed vd is

Here A is the area of the cross-section of the wire and n is the number of free electrons per unit volume. Each electron experiences an average (why average?) magnetic force.

⇒ \(\vec{f}=-e \vec{v}_d \times \vec{B}\)

The number of Free electrons in the small element is considered in nAdl. Thus, the magnetic force on the wire of length dl is

⇒ \(\mathrm{d} \overrightarrow{\mathrm{F}}=(\mathrm{nAd} \ell)\left(-\mathrm{e} \overrightarrow{\mathrm{v}}_{\mathrm{d}} \times \overrightarrow{\mathrm{B}}\right)\)

If we denote the length dl along the direction of the current, the above equation becomes

⇒ \(\begin{aligned}
& d \vec{F}=n A e v_d \vec{d} \ell \vec{B} \\
& d \vec{F}=i d \vec{\ell} \times \vec{B} .
\end{aligned}\)

using 1

The Quanity \(\text { id } \vec{\ell}\) is called a current element.

⇒ \(\overrightarrow{F_{\text {res }}}=\int \overrightarrow{\mathrm{dF}}=\int \mathrm{id} \vec{\ell} \times \overrightarrow{\mathrm{B}}=\mathrm{i} \int \overrightarrow{\mathrm{d} \ell} \times \overrightarrow{\mathrm{B}}\)

Since is the same at all points of the wire.

B If is uniform then \(\vec{F}_{\text {res }}=\mathrm{i}\left(\int \overrightarrow{\mathrm{d} \ell}\right) \times \overrightarrow{\mathrm{B}}\)

⇒ \(\overrightarrow{F_{\text {res }}}=\mathrm{i} \overrightarrow{\mathrm{L}} \times \overrightarrow{\mathrm{B}}\)

Here \(\overrightarrow{\mathrm{L}}=\int \mathrm{d} \vec{\ell}\) = vector length of the wire = vector connecting the endpoints of the wire.

The direction of magnetic force is perpendicular to the plane of \(\overrightarrow{\mathrm{I}} \text { and } \overrightarrow{\mathrm{B}}\) according to right-hand screw rule. The following two rules are used in determining the direction of the magnetic force.

Right-hand palm rule: If the right hand and the palm are stretched such that the thumb points in the direction of current and the stretched fingers in the direction of the magnetic field, then the force on the conductor will be perpendicular to the palm in the outward direction.

Fleming left-hand rule: If the thumb, forefinger, and central finger of the left hand are stretched such that the first finger points in the direction of the magnetic field and the central finger in the direction of current, then the thumb will point in the direction of force acting on the conductor.

Note: f a current loop of any shape is placed in a uniform

⇒ \(\left.\overrightarrow{\mathrm{B}} \text { then } \overrightarrow{\mathrm{F}_{\text {res }}}\right)_{\text {magnetic }}\) on it=0 (since \(\overrightarrow{\mathrm{L}}=0\)

Point of application of magnetic force:

On a straight current-carrying wire the magnetic force in a uniform magnetic field can be assumed to be acting at its midpoint.

This can be used for the calculation of torque.

Example 16. A wire is bent in the form of an equilateral triangle PQR of side 10 cm and carries a current of 5.0 A. It is placed in a magnetic field B of magnitude 2.0 T directed perpendicularly to the plane of the loop. Find the forces on the three sides of the triangle.
Solution: Suppose the field and the current have directions as shown in the figure. The force on PQ is

⇒ \(\vec{F}_1=\overrightarrow{i \ell} \times \vec{B} \quad \text { or, } \quad F_1=5.0 \mathrm{~A} \times 10 \mathrm{~cm} \times 2.0 \mathrm{~T}=1.0 \mathrm{~N}\)

The rule of vector product shows that the force F 1 is perpendicular to PQ and is directed towards the inside of the triangle. The forces \(\vec{F}_2 \text { and } \vec{F}_3\) on QR and RP can also be obtained similarly. Both the forces are 1.0 N
directed perpendicularly to the respective sides and towards the inside of the triangle.

The three forces \(\vec{F}_1, \vec{F}_2 \text { and } \vec{F}_3\) will have zero resultant so that there is no net magnetic force on the triangle. This result can be generalized. Any closed current loop, placed in a homogeneous magnetic field, does not experience a net magnetic force.

Example 17. Two long wires, carrying currents i1 and i2, are placed perpendicular to each other in such a way that they just avoid contact. Find the magnetic force on a small length dl of the second wire situated at a distance from the first wire.

Solution: The situation is shown in the figure. The magnetic field at the site of d, due to the first wire is, \(\mathrm{B}=\frac{\mu_0 i_1}{2 \pi \ell}\)

This field is perpendicular to the plane of the figure going into it. The magnetic force on the length dl is,

⇒ \(\mathrm{dF}=\mathrm{i}_2 \mathrm{~d} \ell \mathrm{B} \sin 90^{\circ}=\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 \mathrm{~d} \ell}{2 \pi \ell}\)

This force is parallel to the current i1.

Example 18. The figure shows two long metal rails placed horizontally and parallel to each other at a separation l. A uniform magnetic field B exists in the vertically downward direction. A wire of mass m can slide on the rails. The rails are connected to a constant current source which drives a current i in the circuit. The friction coefficient between the rails and the wire is u.

1. What soluble minimum value can prevent the wire from sliding on the rails?
2. Describe the motion of the wire if the value of u is half the value found in the previous part.

The force on the wire due to the magnetic field is

⇒ \(\overrightarrow{\mathrm{F}}=\mathrm{i} \vec{\ell} \times \overrightarrow{\mathrm{B}} \quad \text { or, } \quad \mathrm{F}=\mathrm{i} \ell \mathrm{B}\)

It acts towards the right in the given figure. If the wire does not slide on the rails, the force of friction by the rails should be equal to F. If u0 is the minimum coefficient of friction which can prevent sliding, this force is also equal to u0 mg. Thus,

⇒ \(\mu_0 \mathrm{mg}=\mathrm{i} \ell \mathrm{B} \quad \text { or, } \quad \mu_0=\frac{\mathrm{i} \ell \mathrm{B}}{\mathrm{mg}}\)

If the friction coefficient is \(\mu=\frac{\mu_0}{2}=\frac{i \ell B}{2 \mathrm{mg}}\) the wire will slide towards right. The frictional force by the rails is

⇒ \(f=\mu \mathrm{mg}=\frac{\mathrm{i} \ell \mathrm{B}}{2}\) towards left.

The resultant force is \(\mathrm{i} \ell \mathrm{B}-\frac{\mathrm{i} / \mathrm{B}}{2}=\frac{\mathrm{i} / \mathrm{B}}{2}\) towards right. The acceleration will be \(\mathrm{a}=\frac{\mathrm{i} \ell \mathrm{B}}{2 \mathrm{~m}}\) The
the wire will slide towards the right with this acceleration.

Example 19. In the figure shown a semicircular wire is placed in a uniform directed toward the right. Find the resultant magnetic force and torque on it.

Solution: The wire is equivalent to forces on individual parts marked in the figure by and . By symmetry there will be a pair of forces forming couples.

⇒ \(\tau=\int_0^{\pi / 2} i(R d \theta) B \sin (90-\theta) \cdot 2 R \cos \theta\)

⇒ \(\tau=\frac{i \pi R^2}{2} B \quad \Rightarrow \quad \vec{\tau}=\frac{i \pi R^2}{2} B(-\hat{j})\)

Example 20. Find the resultant magnetic force and torque on the loop

Solution: \(\overrightarrow{F_{\text {res }}}=0 \text {, }\) (since loop) and \(\vec{\tau}=i \pi R^2 B(-\hat{j})\) using the above method.

Example 21. In the figure shown find the resultant magnetic force and torque about ‘C’, and ‘P’.

Solution:

⇒ \(\begin{aligned}
& \mathrm{F}=\mathrm{I} \ell_{\mathrm{eq}} \mathrm{B} \\
& \overrightarrow{\mathrm{F}}_{\text {nett }}=\mathrm{I} .2 \mathrm{R} . \mathrm{B}
\end{aligned}\)

since the wire is equivalent to

Force on each element is radially outward: tc = 0 point about

Example 22. Prove that magnetic force per unit length on each of the infinitely long w ire due to each other is \(\mu_0 I_1 I_2 / 2 \pi d\). Here it is attractive also.

Solution:

on (2), B due to 1= \(=\frac{\mu_0 \mathrm{I}_1}{2 \pi \mathrm{d}} \otimes\)

therefore F on (2) on 1 m length

⇒ \(=I_2 \cdot \frac{\mu_0 I_1}{2 \pi d} \cdot 1\) towards left it is attractive

⇒ \(=\frac{\mu_0 \mathrm{I}_1 \mathrm{I}_2}{2 \pi \mathrm{d}}\) (hence proved)

Similarly on the other wire also.

Note:

Definition of ampere (the fundamental unit of current) using the above formula.

If I1 = I2 = 1A, d = 1m then F = 2 × 10–7 N

“When two very long wires carrying equal currents and separated by 1m distance exert on
each other a magnetic force of 2 × 10–7 N on 1m length then the current is 1 ampere.”

The above formula can also be applied if one wire is infinitely long and the other is of finite length. In this case, the force per unit length on each wire will not be the same.

Force per unit length on \(P Q=\frac{\mu_0 I_1 I_2}{2 \pi d}\) (attractive)

If the currents are in the opposite direction then the magnetic force on the wires will be repulsive.

Solved Examples

Example 23. Find the magnetic force on the loop ‘PQRS’ due to the loop wire.
Solution: \(\mathrm{F}_{\text {ras }}=\frac{\mu_0 \mathrm{I}_1 \mathrm{I}_2}{2 \pi \mathrm{a}} a(-\hat{\mathrm{i}})+\frac{\mu_0 \mathrm{I}_4 \mathrm{I}_2}{2 \pi(2 \mathrm{a})} \mathrm{a}(\hat{\mathrm{i}})=\frac{\mu_0 \mathrm{I}_4 \mathrm{I}_2}{4 \pi}(-\hat{\mathrm{i}})\)

Example 24. A current loop ABCD is held fixed on the plane of the paper as shown in the figure. The arcs BC (radius = b) and DA (radius = a) of the loop are joined by two straight wires AB and. CD. A steady current I is flowing in the loop. The angle made by AB and CD at the origin O is 30º. Another straight thin wire with a steady current I1 flowing out of the plane of the paper is kept at the origin.

The magnitude of the magnetic field due to the loop ABCD at the origin (O) is:

1. latex]\frac{\mu_0 I(b-a)}{24 a b}[/latex]
2. \(\frac{\mu_0 \mathrm{I}}{4 \pi}\left[\frac{\mathrm{b}-\mathrm{a}}{\mathrm{ab}}\right]\)
3. \(\frac{\mu_0 I}{4 \pi}\left[2(b-a)+\frac{\pi}{3}(a+b)\right]\)
4. Zero

Solution: Magnetic field due to loop ABCD

⇒ \(=\frac{\mu_0 1}{4 \pi}\left(\frac{\pi}{6}\right) \times\left[\frac{1}{a}-\frac{1}{b}\right]=\frac{\mu_0 1}{24}\left[\frac{b-a}{a b}\right]\)

Due to the presence of the current I1 at the origin:

1. The forces on AD and BC are zero.
2. The magnitude of the net force on the loop is given by \(\frac{\mu_0 I_1 I}{4 \pi}\left[2(b-a)+\frac{\pi}{3}(a+b)\right]\)
3. The magnitude of the net force on the loop is given by \(\frac{\mu_0 \mathrm{II}_1}{24 \mathrm{ab}}(\mathrm{b}-\mathrm{a}) \text {. }\)
4. The forces on AB and DC are zero.

Solution: \(\vec{F}=\mathrm{i}(\vec{\ell} \times \vec{B})\)

The magnetic field due to I1 is parallel to AD and BC. So that force On AD and BC is zero.

Self-practice problems

Question 25. The force on a conductor of length l placed in a magnetic field of magnitude B and carrying in current I is given by (θ is the angle which the conductor makes with the direction of B)

1. I l B sin θ
2. I2lB2 sin θ
3. IlB Cosθ
4. \(\frac{\mathrm{I}^2 \ell}{\mathrm{B}} \sin \theta\)

Answer: 1. I l B sin θ

Question 26. A charge ‘q’ moves in a region where an electric field and magnetic field both exist, then the net force on it-

1. \(q(\vec{v} \times \vec{B})\)
2. \(q \vec{E}+q(\vec{v} \times \vec{B})\)
3. \(q \vec{E}+q(\vec{B} \times \vec{v})\)
4. \(q \vec{B}+q(\vec{E} \times \vec{v})\)

Answer: 2. \(q \vec{E}+q(\vec{v} \times \vec{B})\)

Question 27. An electron moves with speed 2 × 105 m/s along the positive x-direction in the presence of a magnetic \(\vec{B}=\hat{i}+4 \hat{j}-3 \hat{k}\) induction (in tesla). The magnitude of the force experience by the electron in newtons is- (charge on the electron = 1.6 × 10–19 C)

1. 1.18 × 10–13
2. 1.28 × 10–13
3. 1.6 × 10–13
4. 1.72 × 10–13

Answer: 3. 1.6 × 10–13

Question 28. An electron (charge q coulomb) enters a magnetic field of H weber/m 2 with a velocity of v m/s in the same

1. Direction as that of the field. The force on its electron is-
2. Hqv newtons in the direction of the magnetic field
3. Hqv dynes in the direction of the magnetic field
4. Hqv newtons at a right angle to the direction of the magnetic field
5. Zero

Answer: 4. Zero

Question 29. A long wire A carries a current of 10 amp. Another long wire B, which is parallel to A and separated by 0.1 m from A, carries a current of 5 amp. in the opposite direction to that in A. What is the magnitude and nature of the force experience per unit length of B- \(\left[\mu_0=4 \pi \times 10^{-1}\right? \text { W/amp-m] }\)

1. Repulsive force of 10–4 N/m
2. Attractive force of 10–4 N/m
3. Repulsive force of 2π x 10–5 N/m
4. Attractive force of 2π × 10–5 N/m

Answer: 1. Repulsive force of 10–4 N/m.

Torque on a current loop:

When a current-carrying coil is placed in a uniform magnetic field the net force on it is always zero.

However, as its different parts experience forces in different directions so the loop may experience a torque (or couple) depending on the orientation of the loop and the axis of rotation. For this, consider a rectangular coil in a uniform field B which is free to rotate about a vertical axis PQ and normal to the plane of the coil making an angle  with the field direction

The arms AB and CD will experience forces B(NI)b vertically up and down respectively. These two forces together will give zero net force and zero torque (as are collinear with the axis of rotation), so will not affect the motion of the coil.

Now the forces on the arms AC and BD will be BINL in the direction out of the page and into the page respectively, resulting in zero net force, but an anticlockwise couple of value \(\tau=F \times A r m=B I N L \times(b \sin \theta)\)

ie. τ = BIA sinθ with A = NLb ………….(1)

M A=  Now treating the current–carrying coil as a dipole of the moment \(\overrightarrow{\mathrm{M}}=\mathrm{I} \overrightarrow{\mathrm{A}}\) Eqn.

Can be written in vector form as \(\vec{\tau}=\overrightarrow{\mathrm{M}} \times \overrightarrow{\mathrm{B}}\) \(\text { [with } \vec{M}=I \vec{A}=\text { NIA } \vec{n}\)

This is the required result and from this, it is clear that

Torque will be minimum (= 0) when sinθ = min = θ, i.e., θ = 0º, i.e. 180º i.e., the plane of the coil is perpendicular to the magnetic field i.e. normal to the coil is collinear with the field.

Torque will be maximum (= BINA) when sin = max = 1, i.e., θ = 90º i.e. the plane of the coil is parallel to the field i.e. normal to the coil is perpendicular to the field.

By analogy with dielectric or magnetic dipole in a field, in case of current–carrying in a field.

and W = MB(1 – cosθ)
The values of U and W for different orientations of the coil in the field.

Instruments such as electric motors, moving coil galvanometers tangent galvanometers etc. are based on the fact that a current–carrying coil in a uniform magnetic field experiences a torque (or couple).

Example 25: A bar magnet having a magnetic moment of 2 × 10 4 JT–1 is free to rotate in a horizontal plane. A horizontal magnetic field B= 6 × 10–4 T exists in the space. The work done in taking the magnet slowly from a direction parallel to the field to a direction 60° from the field is
Solution: The work done in rotating a magnetic dipole against the torque acting on it, when placed in a magnetic field is stored inside it in the form of potential energy. When magnetic dipole is rotated from initial position θ = θ1 to final position θ = θ2, then work done = MB(cos θ1– cos θ2)

⇒ \(=\operatorname{MB}\left(1-\frac{1}{2}\right)=\frac{2 \times 10^4 \times 6 \times 10^{-4}}{2}=6 \mathrm{~J}\)

Self-practice Problems

Due to the flow of current in a circular loop of radius R, the magnetic induction produced at the center of the loop is B. The magnetic moment of the loop is [u0 = Permeability of vacuum]

1. \(\frac{\mathrm{BR}^3}{2 \pi \mu_0}\)
2. \(\frac{2 \pi \mathrm{BR}^3}{\mu_0}\)
3. \(\frac{\mathrm{BR}^2}{2 \pi \mu_0}\)
4. \(\frac{2 \pi \mathrm{BR}^2}{\mu_0}\)

Answer: 2. \(\frac{2 \pi \mathrm{BR}^3}{\mu_0}\)

Question 31. A current i flows in a circular coil of radius r. If the coil is placed in a uniform magnetic field B with its plane parallel to the field magnitude of torque act on the coil is-

1. Zero
2. 2πriB
3. πr2iB
4. 2π2iB

Answer: 3. πr2iB

Question 32. To double the torque acting on a rectangular coil of n turns, when placed in a magnetic field-

1. The area of the coil and the magnetic induction should be doubled.
2. The area and current through the coil should be doubled.
3. Only the area of the coil should be doubled.
4. Some turns are to be halved.

Answer: 3. Only the area of the coil should be doubled.

Question 33. An arbitrarily shaped closed coil is made of a wire of length L and a current ampere is flowing in it. If B the plane of the coil is perpendicular to the magnetic field \(\vec{B}\) The force on the coil is

1. Zero
2. IBl
3. IBL
4. \(\frac{1}{2} \text { IBL }\)

Answer: 1. Zero

Question 34. A current-carrying loop is placed in a uniform magnetic field in four different orientations, 1,2, 3, and 4 arranged in the decreasing order of potential energy

1. 1>3>2>4
2. 1>2>3>4
3. 1>4>2>3
4. 3>4>1>2

Answer: 3. 1>4>2>3

Example: 26 (Read the following passage and answer the questions. They have only one correct option) In the given figure of a cyclotron, show the particle source S and the dees. A uniform magnetic field is directed up from the plane of the page. Circulating protons spiral outward within the hollow dees, gaining energy every time they cross the gap between the dees.

Suppose that a proton, injected by source S at the center of the cyclotron in Fig., initially moves toward a negatively charged dee. It will accelerate toward this dee and enter it. Once inside, it is shielded from the electric field by the copper walls of the dee; that is the electric field does not enter the dee.

The magnetic field, however, is not screened by the (nonmagnetic) copper dee, so the proton moves in a circular path whose radius, which depends on its speed, is given by

⇒ \(\text { Eq. } r=\frac{m v}{q B}\)

Let us assume that at the instant the proton emerges into the center gap from the first dee, the potential difference between the dees is reversed. Thus, the proton again faces a negatively charged dee and is again accelerated.

Thus, the proton again faces a negatively charged dee and is again accelerated. This process continues, the circulating proton always being in step, with the oscillations of the dee potential, until the proton has spiraled out to the edge of the dee system. There a deflector plate sends it out through a portal.

The key to the operation of the cyclotron is that the frequency f at which the proton circulates in the field (and that does not depend on its speed) must be equal to the fixed frequency fosc of the electrical oscillator, or \(\mathrm{f}=\mathrm{f}_{\text {oss }} \text { (resonance condition). }\)

This resonance condition says that, if the energy of the circulating proton is to increase, energy must be fed to it at a frequency fosc that is equal to the natural frequency f at which the proton circulates in the magnetic field.

Combining Eq. 1 and 2 allows us to write the resonance condition as \(\mathrm{qB}=2 \pi \mathrm{mf}_{\mathrm{osc}}\)

For the proton, q and m are fixed. The oscillator (we assume) is designed to work at a single fixed frequency fosc. We then “tune” the cyclotron by varying B until eq. 3 is satisfied and then many protons circulate through the magnetic field, to emerge as a beam.

Ratio of the radius of successive semi circular path

1. \(\sqrt{1}: \sqrt{2}: \sqrt{3}: \sqrt{4}\ldots \ldots \ldots \ldots\)
2. \(\sqrt{1}: \sqrt{3}: \sqrt{5}\ldots \ldots \ldots \ldots\)
3. \(\sqrt{2}: \sqrt{4}: \sqrt{6} \ldots \ldots \ldots \ldots\)
4. \(1: 2: 3\ldots \ldots \ldots \ldots\)

Solution: When the charge is accelerated by an electric field it gains energy for the first time \(K E_1=\frac{q V}{2}\)

For second time \(\mathrm{KE}_2=\frac{3}{2} \mathrm{qV}\)

For third time ,\(K E_3=\frac{5}{2} q V\)

Hence The ratio of radii are

⇒ \(r_1: r_2: r_3: \ldots \ldots \ldots \ldots: \frac{\sqrt{2 m \frac{q v}{2}}}{q B}: \frac{\sqrt{2 m \frac{3}{2} q v}}{q B}: \ldots \ldots . .\)

⇒ \(r_1: r_2: r_3 \ldots \ldots \ldots:: \sqrt{1}: \sqrt{3}: \sqrt{5}\)

Change in kinetic energy of charged particle after every period is:

1. 2qV
2. qV
3. 3qV
4. None of these

Solution: In one full cycle it gets accelerated two times so change in KE = 2 qV.

If q/m for a charged particle is 106, the frequency of applied AC is 106 Hz. Then the applied magnetic field is:

(1) 2π tesla (2) π tesla (3) 2 tesla (4) can not be defined

Solution: \(f=\frac{q B}{2 \pi m} \quad \Rightarrow 10^5=\frac{10^{\circ} B}{2 \pi} \quad \Rightarrow 2 \pi T .\)

Distance traveled in each period is in the ratio of:

1. \(\sqrt{1}+\sqrt{3}: \sqrt{5}+\sqrt{7}: \sqrt{9}+\sqrt{11}\)
2. \(\sqrt{2}+\sqrt{3}: \sqrt{4}+\sqrt{5}: \sqrt{6}+\sqrt{7}\)
3. \(\sqrt{1}: \sqrt{2}: \sqrt{3}\)
4. \(\sqrt{2}: \sqrt{3}: \sqrt{4}\)

Solution: Distance traveled by particle in one time period:

⇒ \(\pi\left(r_1+r_2\right): \pi\left(r_3+r_4\right): \pi\left(r_5+r_6\right)\)

⇒ \(\frac{\sqrt{2 m \frac{q V}{2}}}{q B}+\frac{\sqrt{2 m \frac{3 q V}{2}}}{q B}: \frac{\sqrt{2 m \frac{5 q V}{2}}}{q B}+\frac{\sqrt{2 m \frac{7 q V}{2}}}{q B}: \frac{\sqrt{2 m \frac{9 q V}{2}}}{q B}+\frac{\sqrt{2 m \frac{11 q V}{2}}}{q B} \ldots \ldots\)

⇒ \(S_1: S_2: S_3 \ldots \ldots \ldots \ldots \ldots:(\sqrt{1}+\sqrt{3}):(\sqrt{5}+\sqrt{7}):(\sqrt{9}+\sqrt{11})\)

For a given charge particle a cyclotron can be “tuned” by :

1. Changing applied a.c. Voltage only
2. Changing applied a.c. Voltage and magnetic field both
3. Changing the applied magnetic field only
4. By changing the frequency of applied a.c.

Solution: The frequency of A.C. depends on charge and mass only so it can be tuned by magnetic field only.

Terrestrial Magnetism (Earth’s Magnetism):

Introduction :

The idea that the earth is magnetized was first suggested towards the end of the sixteenth century by Dr. William Gilbert. The origin of Earth’s magnetism is still a matter of conjecture among scientists but it is agreed upon that the Earth behaves as a magnetic dipole inclined at a small angle (11.5º) to the Earth’s axis of rotation with its south pole pointing north.

The lines of force of the earth’s magnetic field are shown in the figure which is parallel to the earth’s surface near the equator and perpendicular to it near the poles.

While discussing the magnetism of the earth one should keep in mind that:

The magnetic meridian at a place is not a line but a vertical plane passing through the axis of a freely suspended magnet, i.e., it is a plane that contains the place and the magnetic axis.

The geographical meridian at a place is a vertical plane that passes through the line joining the geographical north and south, i.e., it is a plane that contains the place and earth’s axis of rotation, i.e., the geographical axis.

The magnetic Equator is a great circle (a circle with the center at the earth’s center) on the earth’s surface which is perpendicular to the magnetic axis. The magnetic equator passing through Trivandrum in South India divides the earth into two hemispheres.

The hemisphere containing the south polarity of the earth’s magnetism is called the northern hemisphere (NHS) while the other is the southern hemisphere (SHS).

The magnetic field of the earth is not constant and changes irregularly from place to place on the surface of the earth and even at a given place it varies with time too.

Elements of the Earth’s Magnetism:

The magnetism of Earth is completely specified by the following three parameters called elements of Earth’s magnetism:

Variation or Declination θ: At a given place the angle between the geographical meridian and the magnetic meridian is called declination, i.e., at a given place it is the angle between the geographical north-south direction and the direction indicated by a magnetic compass needle,

Declination at a place is expressed at θº E or θº W depending upon whether the north pole of the compass needle lies to the east (right) or to the west (left) of the geographical north-south direction. The declination at London is 10ºW means that at London the north pole of a compass needle points 10ºW, i.e., left of the geographical north.

Inclination or Angle of Dip Φ: It is the angle at which the direction of the resultant intensity of the earth’s magnetic field subtends with a horizontal line in the magnetic meridian at the given place.

It is the angle at which the axis of a freely suspended magnet (up or down) subtends with the horizontal in the magnetic meridian at a given place.

Here, it is worth noting that as the northern hemisphere contains the south polarity of earth’s magnetism, in it the north pole of a freely suspended magnet (or pivoted compass needle) will dip downwards, i.e., towards the earth while the opposite will take place in the southern hemisphere.

The angle of dip at a place is measured by the instrument called Dip-Circle in which a magnetic needle is free to rotate in a vertical plane which can be set in any vertical direction. The angle of dip at Delhi is 42º.

Horizontal Component of Earth’s Magnetic Field BH: At a given place it is defined as the component of Earth’s magnetic field along the horizontal in the magnetic meridian. It is represented by BH and is measured with the help of a vibration or deflection magnetometer.

At Delhi, the horizontal component of the earth’s magnetic field is 35 μT, i.e., 0.35 G. If at a place the magnetic field of the earth is BI and the angle of dip Φ, then under figure (a).

and \(\begin{aligned}
& \mathrm{B}_{\mathrm{H}}=\mathrm{B}_1 \cos \phi \\
& \mathrm{B}_{\mathrm{v}}=\mathrm{B}_1 \sin \phi
\end{aligned}\)

So that, \(\tan \phi=\frac{\mathrm{B}_{\mathrm{v}}}{\mathrm{B}_{\mathrm{H}}}\)

And \(I=\sqrt{B_H^2+B_v^2}\) …..(2)

Self Practice Problems

Question 35. At a place, the magnitudes of the horizontal component and total intensity of the magnetic field of the earth are 0.3 and 0.6 oersted respectively. The value of the angle of dip at this place will be

1. 60°
2. 45°
3. 30°
4. 0°

Answer: 1. 60°

Question 36. The angle of dip at a place on the earth gives-

1. The horizontal component of the earth’s magnetic field.
2. The location of the geographic meridian.
3. The vertical component of the earth’s field.
4. The direction of the earth’s magnetic field.

Answer: 4. The direction of the earth’s magnetic field.

Question 37. A bar magnet is placed north-south with its north pole due north. The points of zero magnetic field will be in which direction from the center of the magnet-

1. North and south
2. East and west
3. Northeast and southwest
4. Northwest and southeast

Answer: 2. East and west

Question 38. When the N-pole of a bar magnet points towards the south and the S-pole towards the north, the null points are at the-

1. Magnetic axis
2. Magnetic centre
3. Perpendicular divider of magnetic axis
4. N and s-pole

Answer: 3. Perpendicular divider of the magnetic axis

Magnetic Substances And Their Properties:

Classification of substances according to their magnetic behavior:

All substances show magnetic properties. An iron nail brought near a pole of a bar magnet is strongly attracted by it and sticks to it, Similar is the behavior of steel, cobalt, and nickel. Such substances are called ‘ferromagnetic ‘substances.

Some substances are only weakly attracted by a magnet, while some are repelled by it. They are called ‘paramagnetic’ and ‘diamagnetic ‘substances respectively. All substances, solids, liquids, and gases, fall into one or other of these classes.

Diamagnetic substance: Some substance, when placed in a magnetic field, are feebly magnetized opposite to the direction of the magnetizing field. These substances when brought close to a pole of a powerful magnet, are somewhat repelled away from the magnet. They are called ‘diamagnetic’ substances and their magnetism is called ‘diamagnetism’.

Examples of diamagnetic substances are bismuth, zinc, copper, silver, gold, lead, water, mercury, sodium chloride, nitrogen, hydrogen, etc.

Paramagnetic substances: Some substance when placed in a magnetic field, are feebly magnetized in the direction of the magnetizing field. This substance, when brought close to a pole of a powerful magnet, is attracted towards the magnet. These are called ‘paramagnetic’ substances and their magnetism is called ‘paramagnetism’.

Ferromagnetic substances: Some substance, when placed in a magnetic field, are strongly magnetized in the direction of the magnetizing field. They are attracted fast towards a magnet when brought close to either of the poles of the magnet. These are called ‘ferromagnetic’ substances and their magnetism is called ‘ferromagnetism’

Some important terms used in magnetism:

Magnetic induction:

When a piece of any substance is placed in an external magnetic field, the substance becomes magnetized. The magnetism so produced in the substance is called ‘induced magnetism’ and this phenomenon is called ‘magnetic induction’.

The number of magnetic lines of induction inside a magnetized substance crossing the unit area normal to their direction is called the magnitude of magnetic induction, or magnetic flux density, inside the substance. It is denoted by B.

Magnetic induction is a vector whose direction at any point is the direction of the magnetic line of induction at that point. The SI unit of magnetic induction is the tesla (T) or Weber/meter2 (Wb-m–2) or Newton/(amper-meter) (NA–1m–1). The CGS unit is ‘gauss’.

Intensity of magnetization (I):

The intensity of magnetization, or simply magnetization of a magnetized substance represents the extent to which the substance is magnetized.

It is defined as the magnetic moment per unit volume of the magnetized substance. It is denoted by I. Its SI unit is ampere/meter (Am–1). Numerically. I= M/V

In the case of a bar magnet, if m is the pole strength of the magnet, 2l is its magnetic length, and its area of cross-section, then

⇒ \(\mathrm{I}=\frac{\mathrm{M}}{\mathrm{V}}=\frac{\mathrm{m} \times 2 \ell}{\mathrm{a} \times 2 \ell}=\frac{\mathrm{m}}{\mathrm{a}}\)

Thus, magnetization may also be defined as pole strength per unit area of cross-section.

Magnetic Intensity or Magnetic Field strength:

When a substance is placed in an external magnetic field, it becomes magnetized. The actual magnetic field inside the substance is the sum of the external field due to its magnetization. The (H) capability of the magnetizing field to magnetize the substance is expressed through a vector, called the ‘magnetic intensity’ of the field. It is defined through the vector relation.

⇒ \((\vec{H})=\frac{B}{\mu_0}-(\overrightarrow{\mathrm{I}}) \text {. }\)

Where is magnetic field induction inside the substance and is the intensity of magnetization? µ 0 is the permeability of space.

The SI unit of is the same as of, that is, ampere/meter (Am–1). The C.G .S. unit is ‘oersted’.

Magnetic permeability (µ):

The magnetic permeability of a substance is a measure of its conduction of magnetic lines of force (B) through it. It is defined as the ratio of the magnetic induction inside the magnetized substance to the magnetic intensity of the magnetizing field, that is,

⇒ \(\mu=\frac{\vec{B}}{\vec{H}} .\)

Numerically, µ = B/H.

ts SI unit is Weber/amper-metre) (Wb A–1 m –1) or \(\frac{\text { Newton }}{\text { Ampere }^2}\left(\mathrm{NA}^{-2}\right) \text {. }^2\)

Relative magnetic permeability (µr): The relative magnetic permeability of a substance is the ratio of the magnetic permeability µ of the substance to the permeability of free space µ 0, that is, \(\mu_r=\frac{\mu}{\mu_0} .\)

It is a dimensionless quantity and is equal to 1 for vacuum (by definition). Alternatively, the relative permeability of a substance is defined as the ratio of the magnetic flux density B in the substance when placed in a magnetic field and the flux density B 0 in a vacuum in the same field, that is,

⇒ \(\mu_r=\frac{B}{B_0} .\)

We can classify substances in terms of µr:

µr < 1 (diamagnetic)
µr > 1 (paramagnetic)
µr > > 1 (ferromagnetic)

Magnetic susceptibility (xm):

It is a measure of how easily a substance is magnetized in a magnetizing field. For paramagnetic and (H) diamagnetic substances, the magnetization is directly proportional to the magnetic intensity of the magnetizing field. That is.

⇒ \(\overrightarrow{\mathrm{I}}=\chi_{\mathrm{m}}(\overrightarrow{\mathrm{H}})\)

The constant xm is called the ‘magnetic susceptibility of the substance. It may be defined as the ratio of the intensity of magnetization to the magnetic intensity of the magnetizing field, that is, \(\chi_m=\frac{I}{H} \text {. }\)

It is a pure number because I and H have the same unit). Its value for vacuum is zero as there can be no magnetization in a vacuum. We can classify substances in terms of xm. Substances with positive values of xm are paramagnetic and those with negative values of xm are diamagnetic. For ferromagnetic substances, xm is positive and very (H) x large. However, for them, is not accurately proportional to, and so xm is not strictly constant.

Relation between Relative permeability (µ r) and magnetic susceptibility (xm): When a substance is placed in a magnetizing field, it becomes magnetized. The total magnetic flux density B within the substance is the flux density that would have been produced by the magnetizing field in vacuum plus the flux density due to the magnetization of the substance. If I am the intensity of magnetization of the substance, then, by definition, the magnetic intensity of the magnetizing field is given by –

⇒ \(H=\frac{B}{\mu_0}-I\)

Or \(\text { But } I=\chi_m H \text {, where } \chi_m\) is the susceptibility of the substance. B = µ 0 (H + I).
But I = xm H, where µ is the permeability of the substance.

⇒ \(\mu=\mu_0\left(1+\chi_m\right) \text {. }\)

or \(\frac{\mu}{\mu_0}=1+\chi_m\)

Properties of dia, para, and ferromagnetic substance: Diamagnetic substance: These substances are feebly repelled by a magnet. When placed in a magnetizing field, they are feebly magnetized in a direction opposite to that of the field.

Thus, the susceptibility Im of a diamagnetic substance is negative: Further, the flux density in a diamagnetic substance placed in a magnetizing field is slightly less than in the free space. Thus, the relative permeability µ r is less than 1.

Diamagnetic substances show the following properties.

When a rod of diamagnetic material is suspended freely between two magnetic poles, then its axis becomes perpendicular to the magnetic field.

In a non-uniform magnetic field, a diamagnetic substance tends to move from the stronger to the weaker part of the field.

If a diamagnetic solution is poured into a U-tube and one arm of this U-tube is placed between the poles of a strong magnet, the level of the solution in that arm is depressed.

A diamagnetic gas when allowed to ascend in between the poles of a magnet spreads across the field.

The susceptibility of a diamagnetic substance is independent of temperature. Paramagnetic substance: These substances are feebly attracted by a magnet. When placed in a magnetizing field, they are feebly magnetized in the direction of the field. T

Thus, they have a positive susceptibility xm The relative permeability µ r for paramagnetics is slightly greater than 1:

When a rod of paramagnetic material is suspended freely between two magnetic poles, then its axis becomes parallel to the magnetic field The poles produced at the ends of the rod are opposite to the nearer magnetic poles.

In a non-uniform magnetic field, the paramagnetic substances tend to move from the weaker to the stronger part of the magnetic field.

If a paramagnetic solution is poured into a U-tube and one arm of the U-tube is placed between two strong poles, the level of the solution in that arm rises.

A paramagnetic gas when allowed to ascend between the pole-pieces of a magnet, spreads along the field.

The susceptibility of a paramagnetic substance varies inversely to the kelvin temperature of the substance, that is, \(\chi_m \propto \frac{1}{T}\)

This is known as Curie’s law.

Ferromagnetic substances: These substances which are strongly attracted by a magnet, show all the properties of a paramagnetic substance to a much higher degree.

For example, they are strongly magnetized in the relatively weak magnetizing field in the same direction as the field. They have relative permeabilities of the order of hundreds and thousands. Similarly, the susceptibilities of ferromagnetic have large positive values.

Curie temperature: Ferromagnetism decreases with rise in temperature. If we heat a ferromagnetic substance, then at a definite temperature the ferromagnetic property of the substance “suddenly” disappears and the substance becomes paramagnetic.

The temperature above which a ferromagnetic substance becomes paramagnetic is called the’ Curie temperature’ of the substance. The curie temperature of iron is 770ºC and that of nickel is 358ºC.

Explanation of Dia-, para- and ferromagnetism based on the atomic model of magnetism:

The diamagnetic, paramagnetic, and ferromagnetic behavior of substances can be explained based on the atomic model, we know that matter is made up of atoms.

Each atom of any substance has a positively charged nucleus at its center around which electrons revolve in various discrete orbits.

Each revolving electron is equivalent to a tiny current loop (or magnetic dipole) and gives a dipole moment to the atom.

Besides this, each electron “spins” about its axis and this spin also produces a magnetic dipole moment. However, most of the magnetic moment of the atom is produced by electron spin, the contribution of the orbital revolution is very small.

Explanation of Diamagnetism: The property of diamagnetism is generally found is those substances whose atoms, or molecules, have an “even’ number of electrons that form pairs. The direction of the spin of one electron is opposite to that of the other. So, the magnetic moment of one electron is neutralized by that of the other.

As such, the net magnetic moment of an atom of a diamagnetic substance is zero. Diamagnetism is temperature-independent.

Explanation of paramagnetism:

The property of paramagnetism is found in a substance whose atoms, or molecules, have an excess of electrons spinning in the same direction. Hence atoms of paramagnetic substance have a permanent magnetic moment and behave like tiny bar-magnets.

Even then the paramagnetic substances do not exhibit any magnetic effect in the absence of an external magnetic field. The reason is that the atomic magnets are randomly oriented so the magnetic moment of the bulk of the substance remains zero.

Paramagnetism is temperature-dependent:

Curie’s Law: In 1895, Curie discovered experimentally that the magnetization I (magnetic moment per unit volume) of a paramagnetic substance is directly proportional to the magnetic intensity H of the magnetizing field and inversely proportional to the kelvin temperature T. That is \(I=C\left(\frac{H}{T}\right) \text {, }\)

where C is constant. This equation is known as Curie’s law and the constant C is called the Curie constant. The law, however, holds so long the ratio H/T does not become too large.

I cannot increase without limit. It approaches a maximum value corresponding to the complete alignment of all the atomic magnets constant in the substance.

Curie’s law can be expressed in an alternative form. We know that the magnetic susceptibility xm is defined as \(\chi_{\mathrm{m}}=\mathrm{I} / \mathrm{H}\)

Making this substitution in the above expression, we get \(\chi_{\mathrm{m}}=\mathrm{C} / \mathrm{T} \quad \Rightarrow \quad \chi_{\mathrm{m}} \propto \frac{1}{\mathrm{~T}} .\)

Hysteresis: Retentivity and coercivity: Hysteresis curve: When a ferromagnetic substance is placed in a magnetic field, it is magnetized by induction. If we vary the magnetic intensity H of the magnetizing field, the intensity of magnetization and the flux density B in the (ferromagnetic) substance do not vary linearly with H.

In other words, the susceptibility Im (= I/H) and the permeability µ = (=B/H) of the substance are not constants, but vary with H and also depend upon the history of the substance.

The variation in I with variation in H is shown in the above figure. The point O represents the initial unmagnetized state of the substance (I = 0) and a zero magnetic intensity (H = 0). As H is increased, I increase (non-uniformly) along OA. At A the substance acquires a state of magnetic saturation. Any further increase in H does not produce any increase in I.

If now the magnetizing field H is decreased, the magnetization I of the substance also decreases following a new path AB (not the original path AO). Thus I lag behind H. When H becomes zero, I still have a value equal to OB. The magnetization remaining in the substance when the magnetizing field is reduced to zero is called “residual magnetism”.

The power of retaining this magnetism is called the “retentivity” or the remanence of the substance. Thus, the retentivity of a substance is a measure of the magnetization remaining in the substance when the magnetizing field is removed. In figure OB represents the retentivity of the substance If now the magnetizing field H is increased in the reverse direction, the magnetization I decrease along BC, still lagging behind H, until it becomes zero at C where H equals OC.

The value OC of the magnetizing field is called the “coercive “ or coercivity” of the substance. Thus, the coercivity of a substance is a measure of the reverse magnetizing field required to destroy the residual magnetism of the substance.

As H is increased beyond OC, the substance is increasingly magnetized in the opposite direction along CD, at D the substance is again magnetically saturated.

By taking H back from its maximum negative value (through zero) to its original maximum positive value, a symmetrical curve DEFA is obtained. At points B and E where the substance is magnetized in the absence of any external magnetizing field, it is said to be a “permanent magnet”.

It is thus found that the magnetization I (or of B) behind H is called “hysteresis”. The closed curve ABCDEFA which represents a cycle of magnetization of the substance is known as the “hysteresis curve (or loop)” of the substance. On repeating the process, the same closed curve is traced again but the portion OA is never obtained.

Hysteresis loss: A ferromagnetic substance consists of local regions called “domains”, each of which is spontaneously magnetized. In an unmagnetised substance the directions of magnetization in different domains are different so that, on average, the resultant magnetization is zero. It can be proved that the energy lost per unit volume of a substance in a complete cycle of magnetization is equal to the area of the hysteresis loop (I-Hcurve).

Difference in magnetic properties of soft iron and steel: A comparison of the magnetic properties of ferromagnetic substances can be made by the comparison of the shapes and sizes of their hysteresis loops.

In the figure are shown hystersis loops of soft iron and steel for the same values of I and H. We can draw the following conclusions regarding the magnetic properties of this substance from these loops.

The retentivity of soft iron (OB’) is greater than the retentivity of steel (OB).

The coercivity of soft iron (OC’) is less than the coercivity of steel (OC).

The hysteresis loss in soft iron is smaller than that in steel because the area of the soft iron is smaller than that of steel.

Curves between magnetic flux density B and magnetizing field H would reveal that the permeability of soft iron is greater than that of steel.

Section of magnetic materials:

The choice of a magnetic material for making a permanent magnet, electromagnet, core of transformer, or diaphragm of telephone earpiece can be decided from the hysteresis curve of the material.

Permanent magnets :

The material for a permanent magnet should have high retentivity so that the magnet is strong, and high coercivity so that the magnetization is not wiped out by stray external fields, mechanical ill-treatment, and temperature changes.

The hysteresis loss is immaterial because the material in this case is never put to cyclic changes of magnetization.

From these considerations, permanent magnets are made of steel. The fact that the retentivity of soft iron is a little greater than that of steel is outweighed by its much smaller coercivity, which makes it very easy to demagnetize.

Electromagnets: The material for the cores of electromagnets should have high permeability (or high susceptibility), especially at low magnetizing fields, and a high retentivity. Soft iron is a suitable material for electromagnets).

Transformer cores and telephone diaphragms: In these cases, the material goes through complete cycles of magnetization continuously. The material must therefore have a low hysteresis loss to have less dissipation of energy and hence a small heating of the material (otherwise the insulation of windings may break), a high permeability (to obtain a large flux density at low field), and a high specific resistance (to reduce eddy current loses).

Soft -iron is used for making transformer cores and telephone diaphragms: More effective alloys have now been developed for transformer cores. They are permalloys, mumetals, etc.

Electromagnet:

If we place a soft-iron rod in the solenoid, the magnetism of the solenoid increases hundreds of times. Then the solenoid is called an ‘electromagnet’. It is a temporary magnet.

An electromagnet is made by winding closely many turns of insulated copper wire over a soft-iron straight rod or a horse-shoe rod. On passing current through this solenoid, a magnetic field is produced in the space within the solenoid.

Example 27: A magnetizing field of 1600 Am–1 produces a magnetic flux of 2.4 × 10–5 wb in an iron bar of cross-sectional area 0.2cm2. Calculate the permeability and susceptibility of the bar.

Solution: \(\mathrm{B}=\frac{\Phi}{\mathrm{A}}=\frac{2.4 \times 10^{-5} \mathrm{~Wb}}{0.2 \times 10^{-4} \mathrm{~m}^2}=1.2 \mathrm{~Wb} / \mathrm{m}^2=1.2 \mathrm{~N} \mathrm{~A}^{-1} \mathrm{~m}^{-1} \text {. }\)

The magnetizing field (or magnetic intensity) H is 1600 Am – 1. Therefore, the magnetic permeability is given by

⇒ \(\mu=\frac{B}{H}=\frac{1.2 \mathrm{NA}^{-1} \mathrm{~m}^{-1}}{1600 \mathrm{Am}^{-1}}=7.5 \times 10^{-4} \mathrm{~N} / \mathrm{A}^2 \text {. }\)

Now, from the relation \(\mu=\mu_0\left(1+\chi_m\right)\) the susceptibility is given by \(\chi_m=\frac{\mu}{\mu_0}-1 .\) We known that µ 0 = 4π × 10 – 7 N/A2

therefore \(\chi_{\mathrm{m}}=\frac{7.5 \times 10^{-4}}{4 \times 3.14 \times 10^{-7}}-1=596 .\)

Example 28. The core of the toroid of 3000 turns has inner and outer radii of 11 cm and 12 cm respectively. A current of 0.6 A produces a magnetic field of 2.5 T in the core. Compute the relative permeability of the core. (µ 0 = 4π × 10–7 T m A – 1).

Solution: The magnetic field in the space enclosed by the windings of a toroid carrying a current I 0 is µ0 n i0 where n is the number of turns per unit length of the toroid and µ0 is the permeability of free space. If the space is filled by a core of some material of permeability µ, then the field is given by B = µ n i0 But µ = µ 0ur, where µ r is the relative permeability of the core material. Thus,

⇒ \(B=\mu_0 u_r n i_0 \quad \text { or } \quad \mu_r=\frac{B}{\mu_0 n i_0}\)

Here B= 2.5T, i0= 0.7 A and n \(\frac{3000}{2 \pi r} m^{-1} \text {, }\) where r is the mean radius of the toroid \(\left(\mathrm{r}=\frac{11+12}{2}=11.5 \mathrm{~cm} 11.5 \times 10^{-2} \mathrm{~m}\right)\)

Thus, \(\mu_r=\frac{2.5}{\left(4 \pi \times 10^{-7}\right) \times\left(3000 / 2 \pi \times 11.5 \times 10^{-2}\right) \times 0.7}=\frac{2.5 \times 11.5 \times 10^{-2}}{2 \times 10^{-7} \times 3000 \times 0.7}\)

µr = 684.5

Self Practice Problems

Question 39. A ferromagnetic material is heated above its curie temperature. Which one is a correct statement-

1. Ferromagnetic domains are perfectly arranged.
2. Ferromagnetic domains become random.
3. Ferromagnetic domains are not influenced.
4. Ferromagnetic material changes itself into diamagnetic material.

Answer: 2. Ferromagnetic domains become random.

Question 40. To protect a sensitive instrument from external magnetic jerks, it should be placed in a container made of-

1. Nonmagnetic substance
2. Diamagnetic substance
3. Paramagnetic substance
4. Ferromagnetic substance

Answer: 4. Ferromagnetic substance

Question 41. The ratio of the intensity of magnetization and magnetic field intensity is known as

1. Permeability
2. Magnetic flux
3. Magnetic susceptibility
4. Relative Permeability

Answer: 3. Magnetic susceptibility

Question 42. If a magnetic material, moves from stronger to weaker parts of a magnetic field, then it is known as

1. Diamagnetic
2. Paramagnetic
3. Ferromagnetic
4. Anti-ferromagnetic

Answer: 1. Diamagnetic

Question 43. The susceptibility of a magnetic substance is found to depend on temperature and the strength of the magnetizing field. The material is a-

1. Diamagnet
2. Ferromagnet
3. Paramagnet
4. Superconductor

Answer: 2. Ferromagnet

Question 44. Property possessed by ferromagnetic substance only is-

1. Attracting magnetic substance
2. Hysteresis
3. Susceptibility independent of temperature
4. Directional property

Answer: 2. Hysteresis

Solved Miscellaneous Problems

Problem 1. A bar magnet has a pole strength of 3.6 A-m and a magnetic length of 8 cm. Find the magnetic field at (a) a point on the axis at a distance of 6 cm from the center towards the north pole and (b) a point on the perpendicular bisector at the same distance.
Answer: 8.6 × 10–4 T; 7.7 × 10–5 T.

M = 3.6 × 8 × 102 A.m2

⇒ \(B=\frac{\mu_0}{4 \pi} \cdot \frac{2 \mathrm{Mr}}{\left(\mathrm{r}^2-\mathrm{a}^2\right)^2}=8.6 \times 10^{-4} \mathrm{~T} \text {. }\)

⇒ \(B=\frac{\mu_0}{4 \pi} \cdot \frac{M}{\left(r^2+a^2\right)^{3 / 2}}=7.7 \times 10^{-5} \mathrm{~T}\)

Problem 2. A loop in the shape of an equilateral triangle of side ‘a’ carries a current as shown in the figure. Find out the magnetic field at the center ‘C’ of the triangle.

Solution: B = B1 +B2 + B3 = 3B1

⇒ \(=3 \frac{\mu_0}{4 \pi} \times \frac{i}{\left(\frac{a}{2 \sqrt{3}}\right)} \times\left(\sin 60^{\circ}+\sin 60^{\circ}\right)=\frac{9 \mu_0 i}{2 \pi a}\)

Problem 3. Two long wires are kept along the x and y axes they carry currents  &  respectively in +ve x and B +ve y directions. Find at a point (0, 0, d).
Solution: \(\vec{B}=\vec{B}_1+\vec{B}_2=\frac{\mu_0}{2 \pi} \frac{\hat{i}}{d} \quad\left((-\hat{j})+\frac{\mu_0}{2 \pi} \frac{i}{d}(\hat{i})=\frac{\mu_0 I}{2 \pi d}(\hat{i}-\hat{j})\right.\)

Problem 4. Find ‘B’ at center ‘C’ in the following cases:

Answer:

1. \(\frac{\mu_0 I}{4 R} \otimes\)
2. \(\frac{\mu_0 \mathrm{I}}{4 \mathrm{R}}\left(1+\frac{1}{\pi}\right) \otimes\)
3. \(\frac{\mu_0 \mathrm{I}}{2 \mathrm{R}}\left(\frac{1}{2}+\frac{1}{\pi}\right) \otimes\)
4. \(\frac{\mu_0 I}{4}\left(\frac{1}{a}+\frac{1}{b}\right) \otimes\)
5. \(\frac{\mu_0 I}{4}\left(\frac{1}{a}-\frac{1}{b}\right) \otimes\)
6. \(\frac{\mu_0 I}{4}\left(\frac{1}{a}-\frac{1}{b}\right) \otimes\)
7. \(\frac{\mu_0 \mathrm{I}}{2 \mathrm{R}}\left(1-\frac{1}{\pi}\right) \otimes\)
8. \(\frac{\mu_0 \mathrm{I}}{2 \mathrm{R}}\left(1+\frac{1}{\pi}\right) \odot\)
9. \(\frac{\mu_0 I \theta}{4 \pi}\left(\frac{1}{a}-\frac{1}{b}\right) \odot\)
10. Solution: \(B=\frac{\mu_0 I}{2 R} \times \frac{1}{2}=\frac{\mu_0 I}{4 R}\)
11. \(B=B_1+B_2=\left(\frac{\mu_0 I}{2 R} \times \frac{1}{2}\right)+\left(\frac{\mu_0}{4 \pi} \cdot \frac{I}{R}\right)=\frac{\mu_0 I}{4 R}\left(1+\frac{1}{\pi}\right)\)
12. \(B=B_1+B_2=\frac{\mu_0}{2 a} \times \frac{1}{2}+\frac{\mu_0}{2 b} \times \frac{1}{2}=\frac{\mu_0 I}{4}\left(\frac{1}{a}+\frac{1}{b}\right)\)
13. \(B=B_1+B_2=\frac{\mu_0}{2 a} \times \frac{1}{2}+\frac{\mu_0}{2 b} \times \frac{1}{2}=\frac{\mu_0 I}{4}\left(\frac{1}{a}+\frac{1}{b}\right)\)
14. \(B=B_1+B_2=\frac{\mu_0}{2 a} \times \frac{1}{2}+\frac{\mu_0}{2 b} \times \frac{1}{2}=\frac{\mu_0 I}{4}\left(\frac{1}{a}+\frac{1}{b}\right)\)
15. \(B=B_1-B_2=\frac{\mu_0 I}{2 R}-\frac{\mu_0 I}{2 \pi R}=\frac{\mu_0 I}{2 R}\left(1-\frac{1}{\pi}\right)\)
16. \(B=B_1+B_2=\frac{\mu_0 I}{2 R}+\frac{\mu_0 I}{2 \pi R}=\frac{\mu_0 I}{2 R}\left(1+\frac{1}{\pi}\right)\)
17. \(B=B_1-B_2=\frac{\mu_0 I}{2 a}-\frac{\mu_0 \mathrm{I}}{2 b} \times \frac{\theta}{2 \pi}=\frac{\mu_0 \mathrm{I} \theta}{4 \pi}\left(\frac{1}{a}-\frac{1}{b}\right)\)

Problem 5. A thin solenoid of length 0.4 m and having 500 turns of wire carries a current 1A; then find the magnetic field on the axis inside the solenoid.
Answer: 5π × 10–4 T.

⇒\(B=\mu_0 n i=\frac{\mu_0 \mathrm{Ni}}{\ell}=5 \pi \times 10^{-4} \mathrm{~T} \text {. }\)

Problem 6. A charged particle of charge 2C is thrown vertically upwards with a velocity of 10 m/s. Find the magnetic force on this charge due to Earth’s magnetic field. Given vertical component of the earth = 3T and angle of dip = 37º.
Answer: 2 × 10 × 4 × 10–6 = 8 × 10–5 N towards west.

⇒ \(\tan 37^{\circ}=\frac{B_V}{B_H} \Rightarrow \quad B_H=\frac{4}{3} \times 3 \times 10^{-5} \mathrm{~T} \quad \Rightarrow \quad F=q v B_H=8 \times 10^{-5} \mathrm{~N}\)

Problem 7. A particle of charge q and mass m is projected in a uniform and constant magnetic field of B v strength B. The initial velocity vector makes an angle ‘θ’ with the. Find the distance traveled by the particle in time ‘t’.
Answer: vt

The speed of the particle does not change therefore distance covered by the particle is s = vt

Problem 8. Two long wires, carrying currents i 1 and i2, are placed perpendicular to each other in such a way that they just avoid contact. Find the magnetic force on a small length dl of the second wire situated at a distance l from the first wire.

Solution: The situation is shown in the figure. The magnetic field at the site of d, due to the first wire is, \(B=\frac{\mu_0 l_1}{2 \pi \ell}\)

This field is perpendicular to the plane of the figure going into it. The magnetic force on the
length dl is

⇒ \(\mathrm{dF}=\mathrm{i}_2 \mathrm{~d} \ell \mathrm{B} \sin 90^{\circ}=\frac{\mu_0 \mathrm{i}_1 \mathrm{i}_2 \mathrm{~d} \ell}{2 \pi \ell}\)

This force is parallel to the current i1.

Example 29: Curves in the graph shown to give, as functions of radial distance r (from the axis), the magnitude B of the magnetic field (due to individual wire) inside and outside four long wires a, b, c, and d, carrying currents that are uniformly distributed across the cross sections of the wires. Overlapping portions of the plots are indicated by double labels. All curves start from the origin.

Which wire has the greatest radius?

1. a
2. b
3. c
4. d

Answer: Inside the cylinder

⇒ \(\begin{aligned}
& B .2 \pi r=\mu_0 \cdot \frac{I}{\pi R^2} \pi r^2 \\
& \Rightarrow \quad B=\frac{\mu_0 I}{2 \pi R^2} \cdot
\end{aligned}\)

⇒ \(B=\frac{\mu_0 I}{2 \pi r}\)

Inside cylinder Bα r and outside \(\mathrm{B} \propto \frac{1}{\mathrm{r}}\)

So at the surface nature of the magnetic field changes. Hence clear from the graph, wire ‘c’ has the greatest radius

2. Which wire has the greatest magnitude of the magnetic field on the surface?

1. a
2. b
3. c
4. d

Answer: The magnitude of the magnetic field is maximum at the surface of wire ‘a’.

3. The current density in wire a is

1. Greater than in wire c.
2. Less than in wire c.
3. Equal to that in wire c.
4. Not comparable to that of wire c due to lack of information.

Solution: Inside the wire.

⇒ \(B(r)=\frac{\mu_0}{2 \pi} \cdot \frac{I}{R^2} \cdot r=\frac{\mu_0 J r}{2}\)

⇒ \(\frac{d B}{d r}=\frac{\mu_0 \mathrm{~J}}{2}\)

i.e slope \(\propto \mathrm{J}\)

⇒ \(\propto\) current density

It can be seen that the slope of the curve for wire A is greater than for wire C.