Joankessler

Class 8 Science Chapter 12 Some Natural Phenomena Very Short Answer Type Questions

Question 1. If an object is touched with the metal top of an electroscope its aluminium leaves diverge, then what conclusion do we get from this observation?
Answer: We conclude from this observation that the object has an electric charge on it.

NCERT Solutions for Some Natural Phenomena VSAQs Class 8

Question 2. How does earthing help to protect buildings?
Answer: Earthing helps to transfer unwanted electric charges in electrical circuits to flow to earth, and in such a way, it prevents electrical equipment from damage.

Some Natural Phenomena Class 8 VSAQs and Answers

Question 3. Briefly explain what the people thought the cause of lightning was in ancient times.
Answer: In ancient times, people were scared of lightning and thought that the wrath of God was visiting them. 

Question 4. During a thunderstorm, when we are in an open place nearby from home, where should we take shelter?
Answer: We should take shelter under a small tree

NCERT Solutions for Class 8 Science Some Natural Phenomena VSAQs

Question 5. To protect the building from lightning, briefly mention the place where the lightning rod should be attached.
Answer: The lightning rod should be attached to the top of the building.

NCERT Solutions For Class 8 Science Chapter 12 Some Natural Phenomena Short Answer Questions

Question 1. If scientists know so much about earthquakes, can they also predict when and where the next one will strike?
Answer: No, it is not yet possible to predict when and where the next earthquake might occur because they cause disturbance in the Earth’s crust.

NCERT Solutions for Some Natural Phenomena SAQs Class 8

Question 2. Which of the following cannot be charged easily by friction?

1. A plastic scale
2. A copper rod
3. An inflated balloon
4. A woollen cloth

Answer: 2. As copper is a conductor, when rubbing it, the charges start flowing across the length of the copper rod, which constitutes an electric current. So, copper cannot be charged easily by friction.

Question 3. When a glass rod is rubbed with a piece of silk cloth, the rod

1. And the cloth both acquire a positive charge
2. Becomes positively charged, while the cloth has a negative charge
3. And the cloth both acquires a negative charge
4. Becomes negatively charged, while the cloth has a positive charge

Answer: 2. Becomes positively charged, while the cloth has a negative charge.

NCERT Solutions for Class 8 Science Some Natural Phenomena SAQs

Question 4. Write True and F against False against the Statements

1. Like charges attract each other.
2. A charged glass rod attracts a charged plastic straw.
3. The lightning conductor cannot protect a building from lightning.
4. Earthquakes can be predicted in advance.

Answer:

1. F, as like charges repel each other and unlike charges attract each other.
2. T, but it may also repel if charges are similar.
3. F, as a lightning conductor, can protect a building from lightning.
4. F, as it is not possible to predict the occurrence of earthquakes.

Question 5. Sometimes, a crackling sound is heard while taking off a sweater during winter. Explain.
Answer: The crackling sound heard while taking off a sweater during winters is due to the rubbing of two objects, i.e. body and the wool. The rubbing of the static charges produces lightning or a spark in our clothes that produces a crackling sound. The electric charges produced by rubbing are called static charges.

NCERT Solutions for Some Natural Phenomena Chapter 12 SAQs

Question 6. Explain why a charged body loses its charge if we touch it with our hand.
Answer: When we touch a charged body, it loses its charge due to the process of earthing. As our body is a good conductor of electricity, and transfers the charge to the earth.

Question 7. Name the scale on which the destructive energy of an earthquake is measured. An earthquake measures 3 on this scale. Would it be recorded by a seismograph? Is it likely to cause much damage?
Answer: Destructive energy of an earthquake is measured on the Richter scale. Yes, the earthquake will be recorded by a seismograph in the form of seismic waves. The earthquake measuring 3 on the Richter scale cannot cause much damage.

Some Natural Phenomena Class 8 NCERT SAQs

Question 8. Suggest three measures to protect ourselves from lightning.
Answer: Lightning is an electric spark on a huge scale, which is caused by the accumulation of charges in clouds.

1. Some Measures to protect ourselves from lightning are as follows
2. We should stay under a covered area or inside the room.
3. We should not take a bath during lightning.
4. We should not use the TV, phone, or computers during lightning.

Question 9. Explain why a charged balloon is repelled by another charged balloon, whereas an uncharged balloon is attracted by another charged balloon.
Answer: Since both balloons acquire the same charges when being charged upon rubbing. Thus, they repel each other. On the other hand, one charged and the other uncharged balloon attract each other.

This is due to the property of charges that unlike charges attract each other.

The uncharged balloon, having the opposite charge, is attracted by the other charged balloon.

Question 10. List three states in India where earthquakes are more likely to strike.
Answer: Some earthquake-prone states of India are as follows

1. Kashmir
2. Gujarat
3. Rajasthan

Some Natural Phenomena SAQs NCERT Solutions Class 8

Question 11. Suppose you are outside your home and an earthquake strikes. What precautions would you take to protect yourself?
Answer: The precautions are as follows

1. We should move to an open space where trees and buildings are not available.
2. If we are driving, we should not come out. We should slow down the vehicle and move slowly away from that area to a safe spot.

Question 12. The weather department has predicted that a thunderstorm is likely to occur on a certain day. Suppose you have to go out on that day. Would you carry an umbrella? Explain.
Answer: Carrying an umbrella is not advisable during a thunderstorm. The rod of the umbrella and its supporting wires are made up of metal. Thus, during a thunderstorm, the conducting objects should be avoide.

NCERT Solutions For Class 8 Science Chapter 12 Some Natural Phenomena Long Answer Questions

Some Natural Phenomena Class 8 NCERT LAQs

Question 1. If the metal clip used in the electroscope is replaced by an ebonite rod, and a charged body is brought in contact with it, will there be any effect on the aluminium strips? Explain.
Answer: The ebonite rod acquires charge when rubbed. So, the charge transfer will be either too less or there will be no transfer of charges, so the strips of aluminium will not diverge and we will not be able to predict the object whether it is charged or not.

NCERT Solutions for Some Natural Phenomena LAQs Class 8

Question 2. Explain how lightning takes place.
Answer: Clouds having water droplets, coming from different directions, strike each other and due to striking, a friction force is created when they rub each other, and during rubbing, the charges appear on clouds (static charges).

They grow in number due to continuous charging and finally discharge when any region of moisture is found on the earth because they get a path of discharge to this place.

Question 3. Explain why It Is safer to use a wireless telephone instead of a landline telephone during lightning.
Answer: It nis ot safer to use a wired telephone during lightning because at that time lightning can enter the wire of the telephone, if it is open somewhere, that is, if there is any cut in the wire. On the other hand, there cannot be any possibility of this type in a wireless telephone.

NCERT Solutions for Class 8 Science Some Natural Phenomena LAQs

Question 4. During lightning, if you are outside the house, what precautions would you take?
Answer: Precautions during lightning while we are outside are as follows

1. Do not stand underneath a natural lightning rod, such as a tall and isolated tree.
2. Stand from any fountain or any water body.
3. Get away from tractors and other metal types of equipment like wire fences, metal pipes, rails, and another metallic paths.

Question 5. Priya went to school with an umbrella during the rainy season. One day, while returning from school, the rain started on the way. Priya opened her umbrella and saved herself from the rain.

After some time, she observed some lightning sparks in the sky. Suddenly, she folded her umbrella and went to a shelter under a closed building.

1. State the cause of lightning.
2. Priya folded her umbrella. Explain why?
   
3. Mention the method opted for by Priya here.

Answer:

1. In the clouds, the accumulation of charges causes lightning.
2. As we know that the top end of stretched umbrella is a metal part. Since, the metal is a good conductor of electricity, so if lightning strikes to the ground, then it can take the path towards umbrella. Therefore, to avoid herself from danger, Priya folded the umbrella and went to a closed building.
3. The immediate response and the scientific method are opted for by Priya here.

NCERT Solutions for Some Natural Phenomena Chapter 12 LAQs

Question 6. Mention the names of those regions of the Earth that are more prone to earthquakes.
Answer: Earthquakes are usually caused by the movement of plates on the outer layer ofearth. So, the regions which fall on the boundaries of these plates are called danger zones. In India, the most dangerous zones which are prone to earthquakes are Kashmir, western and central himalyas, the whole of North-East, Rann of Kutch, Rajasthan and the lndo-Gangetic plains.

NCERT Solutions For Class 8 Science Chapter 11 Chemical Effects Of Electric Current LAQs

Question 1. In the circuit given in the figure, Boojho observed that copper is deposited on the electrode connected to the negative terminal of the battery. Paheli tried to repeat the same experiment, but she could find only one copper plate. Therefore, she took a carbon rod as the negative electrode. Will copper still be deposited on the carbon rod? Explain your answer.

Answer: Copper will not be deposited on the carbon rod because, carbon rod is a poor conductor of electricity. For electroplating, the circuit must be completed, and that can be completed only by using the conducting material. Instead of a carbon rod, it should be any metal, then only it can be electroplated.

NCERT Class 8 Science Chapter 11 Chemical Effects of Electric Current LAQs

Question 2. Observe the circuit given in the figure

Boojho set up this circuit for the purification of copper. What will be the nature of (a) plate A, (b) plate B (c) the solution? Explain the process of purification.

Answer:

We take CuS04 solution and dip a pure copper plate as the cathode (-ve) and an impure copper plate as the anode (+ve). Due to the voltage of the battery, the impurities from the impure sample slowly deposit at the bottom, and the copper plate becomes purified.

NCERT Solutions for Chemical Effects of Electric Current Chapter 11

Question 3. The process that you saw in Activity 7 is used for the purification of copper. A thin plate of pure copper and a thick rod of impure copper are used as electrodes. Copper from the impure rod is sought to be transferred to the thin copper plate. Which electrode should be attached to the positive terminal of the
battery and why?
Answer:

The impure rod of copper should be attached to ihe positive terminal of the battery and pure copper plate should be attached to the negative terminal of the battery.

When electric current is passed through the copper sulphate solution, copper sulphate dissociates into copper and sulphate ions The free copper gets drawn to the electrode connected with negative terminal of the battery and starts depositing on it.

From the other electrode, a thick rod of impure copper, an equal amount of copper gets dissolved into the solution. Hence, the loss of copper from the solution is restored and the process continues. Thus, copper gets transferred from one electrode to the other.

NCERT Solutions For Class 8 Science Chapter 11 Chemical Effects Of Electric Current SAQs

Question 1. Explain in brief the procedure of glowing of bulb in a liquid.
Answer:

If the liquid between the two ends ofa tester allows the electric current to pass, then the circuit of the tester becomes complete.

The current flows in the circuit, and the bulb glows. When the liquid does not allow the electric current to pass, the circuit of the tester is not complete, and the bulb does not glow.

NCERT Class 8 Science Chapter 11 Chemical Effects of Electric Current SAQs

Question 2. State the reason why we need a magnetic compass to test the conduction of electric current.
Answer:

Sometimes the bulb does not glow on passing electric current. This is because the electric current flowing through a conductor is so small So in case ofsmall current, we need magnetic compass to test the conduction.

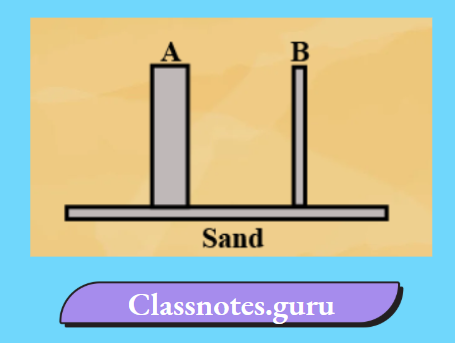
Question 3. Observe the figure.

image-

Which of these two circuits A or B shows the correct observation? It is not clear from the diagram that what u A and B. So. cannot predict the actual solution. But if wr compare with activity. this seems to be a potato and correct diagram is A because positive terminal makes the green spot on the potato.

Question 4. Explain how we can purify the impure metals.
Answer:

By an electrolysis process, we use a thick rod of impure metal as an anode and a thin strip of pure metal as a cathode. A water-soluble salt ofthe metal is taken as electrolyte.

On passing electric current, the metal dissolves from the impure anode and goes into electrolyte solution which is then deposited on the cathode in pure form.

Question 5. We should throw the conducting materials used in electroplating far away from residential areas. Explain why?
Answer:

As the conducting solutions or electrolytes contain various types of sites which may be poisonous and also usually addie in nature.

So, in electroplating factories. the disposal ofused conducting materials is a major problem and it should be disposed offin a proper way far away from the human population.

NCERT Solutions for Chemical Effects of Electric Current Chapter 11

Question 6. State some advantages of electroplating.
Answer: The advantages of electroplating are given below

1. It protects the metal from corrosion and rusting.
2. It is used to coat desired metals on other objects.
3. It can make more reactive metals like iron.
4. Coating of chromium on the metal gives luster to the objects.

Question 7. Paheli wants to deposit silver on an iron spoon. She took silver nitrate (AgNO.) solution in a beaker and set up a simple circuit for electroplating. Which terminal of the battery should the spoon be connected to? What material should the other electrode be made of
Answer:

The spoon should be connected to the negative terminal of the battery. The other electrode should be of silver, so that silver ions get deposited on an iron spoon.

Question 8. In case of a fire, before the firemen use the water hoses, they shut off the main electrical supply for the area. Explain why they do this.
Answer:

Since tap water is a very good conductor of electricity. So, if the main electrical supply remains ON, it can be fatal to human life because it can lead to electrocution due to water.

NCERT Class 8 Science Chapter 11 SAQ

Question 9. A child staying in a coastal region tests the drinking water and also the seawater with his tester. He finds that the compass needle deflects more in the case of seawater. Can you explain the reason?
Answer:

As we know that the current produces the magnetic effect and causes the deflection in a magnetic needle. In the case of seawater, the salt content is much higher than that of drinking water. Thus, it produces more current than drinking water.

Therefore, as a result, the deflection in the magnetic needle It is more in the case of seawater rather than drinking water.

Chemical Effects of Electric Current SAQs Class 8 NCERT Solutions

Question 10. Is it safe for the electrician to carry out electrical repairs outdoors during a heavy downpour? Explain.
Answer:

No, it is not safe for the electrician to carry out electrical repairs outdoors during heavy downpour. Because rainwater is a good conductor of electricity. So, during heavy downpour, there is a huge risk ofelectrocution.

Question 11. Paheli had heard that rainwater is as good as distilled water. So, she collected some rainwater in a clean glass tumbler and tested it using a tester. To her surprise, she found that the compass needle showed deflection. What could be the reasons?
Answer:

While it rains, the raindrops get mixed with the suspended particles of the air. So, they do not remain pure. It becomes a mixture of salts and other impurities. Thus, it shows the conduction of electricity.

But in case of distilled water, no conduction of electricity takes place as distilled water do not contain salts or impurities. Thus, it becomes a bad conductor of electricity.

Question 12. Prepare a list of objects around you that are electroplated.
Answer:

List of objects that are electroplated arc as follows;

1. Bath taps, kitchen gas burners,
2. Jewellery makers electroplate silver and gold on less expensive metals.
3. Electroplating iron cans with tin to store food.
4. Handlebars, bar cycles, and motorcycles.
5. Rims of cycles, buckles of clothes, and belts,

Question 13. Explain how we can purify the impure metals.
Answer:

By an electrolysis process, we use a thick rod of impure metal as an anode and a thin strip of pure metal as a cathode. A voter soluble salt ofthe metal is taken as electrolyte.

On passing electric current, the metal dissolves from the impure anode and goes into electrolyte solution which is then deposited on the cathode in pure form.

SAQs for Chemical Effects of Electric Current Chapter 11 Class 8

Question 14. We should throw away the conducting materials used in electroplating far away from residential areas. Explain why?
Answer:

As the conducting solutions or electrolytes contain various types of salts, which may be poisonous, and also usually addictive.

So, in electroplating factories. the disposal ofused conducting materials is a major problem and it should be disposed offin a proper way far away from the human population.

Question 15. State some advantages of electroplating.
Answer:

The advantages of electroplating are given below

1. It protects the metal from corrosion and rusting.
2. It is used to coat desired metals on other objects.
3. It can make more reactive metals like iron.
4. Coating of chromium on the metal gives luster to the objects.

Question 16. Paheli wants to deposit silver on an iron spoon. She took silver nitrate (AgNO.) solution in a beaker and set up a simple circuit for electroplating. Which terminal of the battery should the spoon be connected to? What material should the other electrode be made of
Answer:

The spoon should be connected to the negative terminal of the battery. The other electrode should be of silver, so that silver ions get deposited on an iron spoon.

Question 17. Last Monday, Ankush woke up late in the morning. So, he saw the time and suddenly realised that he had got late for an interview, which he was supposed to give after reaching the venue by the right time.

Immediately, he turned ON the geyser, but it did not work. He got more tense, then he used an electric iron rod through which he could get some boiled water for his bath.

There was an earthing problem in the switchboard, which he was unaware of.

He was barefoot and was just about to switch ON the electric iron rod, but at the same he was stopped from doing so by one of his room partner living with him. It could be dangerous for Ankush.

1. Explain in brief that what could be happened with Ankush. if he switched ON the electric iron rod (without wearing any slippers in his foot).
2. Mention the values shown by Ankush’s friend.

Answer:

If Ankush switched ON the electric iron rod and (without wearing any footwear), then he could have met with some accident, either in the form of electrical sparking or short circuit of the switchboard.

Ankush’s friend seems to be very intelligent and very much concerned for Ankush as well.

NCERT Solutions for SAQs on Chemical Effects of Electric Current

Question 18. Explain in brief the procedure for glowing of the bulb in a liquid.
Answer:

If the liquid between the two ends of a tester allows the electric current to pass, then the circuit of the tester becomes complete.

The current flows in the circuit and the bulb glows. When the liquid does not allow the electric current to pass, the circuit of the tester is not complete, and the bulb does not glow.

Question 19. State the reason why we need a magnetic compass to test the conduction of electric current.
Answer:

Sometimes the bulb does not glow on passing electric current. This is because the electric current flowing through a conductor is so small So in case of small current, we need magnetic compass to test the conduction.

NCERT Solutions For Class 8 Science Chapter 11 Chemical Effects Of Electric Current VSAQs

Question 1. It is dangerous to touch an electrical appliance with wet hands. Explain why?
Answer: A Wet hand acts as a good conductor. So, we feel an electric shock when we touch an electrical appliance with wet hands.

Question 2. Paheli and Boojho want to remind you that one should not experiment with the electric supply from the mains or a generator or an inverter. Why ?
Answer: The electrical supply which comes in our domestic main electrical line is about 120 V. We should not use this High voltage electricity for an experiment. This can cause serious injuries or instant death.

NCERT Class 8 Science Chapter 11 Chemical Effects of Electric Current VSAQs

Question 3. Sometimes we see that the liquid is conducting, but the bulb may not glow. Why?
Answer: The bulb does not glow because the current through it is too weak

Question 4. The bulb glows when the electric current passes through it. Explain why?
Answer: Due to the heating effect of the current, the filament of the bulb gets heated to a high temperature, and it starts glowing. However, if the current through a circuit is too weak, the filament does not get heated sufficiently, and it does not glow.

Question 5. When a compass needle is brought near a current-carrying wire, what happens?
Answer: When a compass needle is brought near a current-carrying wire, the needle deflects.

Question 6. Can we make another tester v/hich can detect a weak current?
Answer: Yes. we can use another effect of an electric current to make another kind of tester, i.e. magnetic effect of electric current.

Question 7. Do poor conductors also allow electricity to pass under certain conditions?
Answer: Yes, poor conductors can conduct electricity under certain conditions, like wet wood.

NCERT Solutions for Chemical Effects of Electric Current Chapter 11

Question 8. Give the names of these substances, which, when added to distilled water, make them good conductors of electricity
Answer: Acids, bases, and salts are those substances that, when added to distilled water, make it a good conductor of electricity.

Question 9. Give the names of the three effects of electric current.
Answer: The three effects of electric current are

1. The heating effect of the current
2. Magnetic effect of current
3. Chemical effect of the current

Question 10. An electric current is passed through a conducting solution. List any three possible observations.
Answer: Three possible observations are

1. The colour of the solution may change depending on the electrodes.
2. The temperature of the solution may increase.
3. Bubbles near the electrodes can be seen.

Class 8 Chapter 11 Chemical Effects of Electric Current VSAQs

Question 11. After doing the electroplating activity, Paheli interchanged the electrodes and repeated the activity. What do you think she would observe this time?
Answer: Paheli will observe the gas bubbles.

Question 12. In the electroplating process, what about the loss of copper from the solution?
Answer: An equal amount of copper gets dissolved in the solution from anode, thus the loss ofcopper from the solution is restored.

Question 13. The process of depositing a layer of any desired metal on another material employing electricity is called
Answer: Electroplating

Question 14. When the free ends of n tester arcs are dipped into solutions, the magnetic needle shows deflection. Can you explain the reason?
Answer: When the free ends of a tester arc are dipped into a solution, the liquid between the two ends allows the electric current to pass, and the circuit of the tester becomes complete.

NCERT Solutions for Chemical Effects of Electric Current VSAQ

Also, when the current passes through the tester, it establishes a magnetic effect, and hence, the magnetic needle shows deflection. In other words, we can say that the solution is a good conductor ofelectricity, so the needle gets deflected.

NCERT Solutions For Class 8 Science Chapter 10 Sound LAQs

Question 1. The town hall building is situated close to Boojho’s house. There is a clock on the top of the town hall building that rings the bell every hour. Boojho has noticed that the sound of the clock appears to be much clearer at night. Explain
Answer:

We know that speed, pitch, and loudness are all initiated with a vibration. During the day, there are several vibrations around us. So, the sound coming from the clock gets disturbed, and the amplitude of vibrations becomes small.

But during the night, there are no such multiple vibrations in the environment. So, the sound is clearer. Further, the dew factor at night increases the speed of sound as the moisture level increases.

NCERT Class 8 Science Chapter 10 Sound LAQs

Question 2. An alarm bell is kept inside a vessel as shown in the figure. A person standing close to it can distinctly hear the sound of the alarm. Now, if the alt inside the vessel is removed completely, how will the loudness of the alarm be affected for the same person?

Answer:

Initially, the person can hear the sound coming from the air and water distinctly. But after some time, when the air is completely removed from the bottle, the sound will not pass through the vacuum in the glass. So, the man will not hear the sound that was coming through the air initially.

Question 3. How is sound produced, and how is it transmitted and heard by us? 
Answer:

Sound is produced when any object starts vibrating by any means.

These vibrations travel from the sources all around the environment through the particles, and thus they reach their destination, i.e., our ear.

Now, it enters our ear and travels down a canal at the end of which a thin membrane is stretched tightly, known as the eardrum. The eardrum sends vibrations to the inner part of the ear, and finally reaches the brain, and we hear the sounds.

NCERT Solutions for LAQs on Sound Chapter 10

Question 4. Mention the property of vibrations that determines the pitch of the sound. Briefly explain along with some examples.
Answer:

The property that determines the shrillness or pitch of a sound is the frequency. If the frequency of vibration is higher, then we can say that the sound has a higher pitch. If the frequency of vibration is lower, we can say that the sound has a lower pitch.

Example: The drum vibrates with a low frequency.

Thus, it produces a low-pitched sound. Besides this, a whistle has a high frequency that produces a sound of a higher pitch. A bird makes a high-pitched sound while a lion makes a low-pitched roar. However, the roar of a lion is very loud while the sound of a bird is quite feeble.

NCERT Solutions for Sound Chapter 10

Question 5. Kanika switched ON the television to listen to her favourite music. After some time, she heard a loudspeaker sound coming from her neighbour’s house. Then, she switched OFF the television and closed her ears, so that the loudspeaker sound would not enter her ears.

• Slate the type of sound coming from the television.
• Explain how Kanika can distinguish between the categories of sound
• Mention whether the sound coming from the TV and the loudspeaker was audible or inaudible.
• Give the value displayed by Kanika here.

Answer: The sound of the music was coming from the television.

She realised after hearing both the sounds that the sound coming from the TV is pleasant and that ling from the loudspeaker outside is noisy and painful.

The sound coming from the TV and loudspeakers was in audible range, i.e., 20 Hz to 20 kHz.

The value displayed by Kanika is an attraction towards music and a hatred towards the loudspeakers.

NCERT Solutions For Class 8 Science Chapter 10 Sound SAQs

Question 1. Boojho saw a cracker burst at night at a distance from his house. He heard the sound of the cracker a
little later after seeing the cracker burst. Give a reason for the delay in hearing the sound.
Answer:

The light travels faster than sound, so the light from the cracker reaches faster than the sound of the cracker. Speed oflight in air = 3 x 10 8 m/s Speed ofsound in air = 330 m/s

Question 2. Explain the reason for not hearing the screeches of a bat by us.
Answer:

As we know, the audible frequency range for human beings is 20 Hz to 20 kHz. So, it is an obvious thing that the frequency of bats is beyond this range, due to which we are usually unable to hear the screams of a bat.

NCERT Class 8 Science Chapter 10 Sound SAQs

Question 3. Suggest three measures to limit noise pollution in your locality.
Answer:

Some measures to limit noise pollution in our locality are given as

1. The industries that produce noise should be set up away from the residential areas.
2. The television and the music systems should be run at low volumes.
3. The aircraft engines, transport vehicles, industrial machines, and home appliances must be installed with silencing devices.

Question 4. List three sources of noise pollution in your locality.
Answer:

Sources of noise pollution are

1. Horns of vehicles
2. Loudspeakers of temples
3. Generators running without silencers

Question 5. Briefly explain total hearing impairment.
Answer:

Hearing impairment means a person has damaged hearing ability and cannot hear properly. Some people are born with poor hearing ability. A person with very poor hearing ability is said to be deaf, so deafness is a total hearing impairment.

NCERT Solutions for Sound Chapter 10

Question 6. The sound from a mosquito is produced when it vibrates its wings at an average rate of 500 vibrations per second. What is the period of the vibration?
Answer:

Given, number of vibrations = 500

Time taken =ls

Period time taken/ number of vibrations

= 1/500= 0.002s

Question 7. Identify the part that vibrates to produce sound in the following instruments.

1. Dholak
2. Sitar
3. Flute

Answer:

Class 8 Chapter 10 Sound Short Answer Questions

Question 8. What is the difference between noise and music? Can music become noise sometimes?
Answer:

The Differences between noise and music are:

Question 9. List the sources of noise pollution in your surroundings.
Answer:

As we know that. Noise pollution is caused by excessive sound in our surroundings. The sources of such excessive sound are as follows

1. Television and transistor radio at high volume
2. Sounds of vehicles
3. Explosions, including the bursting of crackers, machines, loudspeakers, etc
4. Honking of horns

Question 10. Explain in what way noise pollution is harmful to humans.
Answer:

Lack of sleep, hypertension (high blood pressure), and temporary or permanent impairment of hearing are harmful effects of noise pollution.

NCERT Solutions for SAQs on Sound Chapter 10

Question 11. Your parents are going to buy a house. They have been offered one on the roadside and another three lanes from the roadside. Which house would you suggest your parents should buy? Explain your answer.
Answer:

We will suggest to our parents that they should buy a horn, which is three lanes away from the roadside. Taking a house on the roadside means bearing noise pollution, which leads to harmful effects on health.

Therefore, to attain a piece of mind and to avoid noise pollution, it is better to buy a house three lanes away from the roadside.

NCERT Solutions For Class 8 Science Chapter 8 Force And Pressure VSAQs

Question 1. Can you lift or push a book lying on a table without touching it?
Answer:

No, we cannot lift or push a book lying on a table without touching it because it is a type of contact force.

Question 2. What happens when you apply a force to an inflated balloon by pressing it between your palms?
Answer:

The shape of a balloon will change if we apply a force to an inflated balloon by pressing it between our palms.

Question 3. What does the force come from when we push an object like a school bag or lift a bucket of water?
Answer: This force is caused by the action of muscles in our body.

Question 4. List a few examples of the force exerted by the muscles in our body.
Answer: Chewing of food, lifting of luggage, and squeezing a sponge ball.

NCERT Class 8 Science Chapter 8 Force and Pressure VSAQs

Question 5. Leaves and fruits fall to the ground when they get detached from the plant. Have you ever wondered why it is so?
Answer:

Leaves and fruits fall towards the ground because Earth pulls them towards it, and this attractive force is known as the force of gravity or gravitational force.

Question 6. Is there any relation between pressure and force?
Answer:

Yes, pressure is force per unit area. Thus, we can say that pressure is directly proportional to force.

Question 7. Paheli wants to understand why porters place a round piece of cloth on their heads when they carry heavy loads.
Answer:

When a porter places a round piece of cloth on his head, it reduces the pressure on the head as the area ofcontact increases, and they find it easier to carry the load.

Question 8. Can you explain why shoulder bags are provided with broad straps and not thin straps?
Answer:

School bags are provided with broad straps because they increase the surface area of contact with the shoulder, which results in reducing the pressure on the shoulder.

NCERT Solutions for Force and Pressure Chapter 8

Question 9. Boojho has seen fountains of water coming out of the leaking joints or holes in pipes supplying water. Is it due to the pressure exerted by water on the walls of the pipes?
Answer:

Yes, water coming out of the leaking joints or holes in pipes supplying water is due to the pressure exerted by water on the surface of the pipes.

Question 10. Why is it easier to cut the fruit with a sharp knife as compared to a blunt knife?
Answer:

The surface area of a sharp knife is less than that of a blunt knife, so the pressure applied by a sharp knife is higher than blunt knife.

Question 11. In the following situation, identify the agent exerting the force and the object on which it acts. State the effect of the force in each case.

1. Squeezing a piece of lemon between the fingers to extract its juice.
2. Taking out paste from a toothpaste tube.
3. A load is suspended from a spring while its other end is on a hook fixed to a wall.
4. An athlete is making a high jump to clear the bar at a certain height.

Answer:

Force and Pressure VSAQs Class 8 NCERT Solutions

Question 12. A blacksmith hammers a hot piece of iron while making a tool. How does the force due to hammering affect the piece of iron?
Answer:

When a blacksmith hammers a hot piece of iron, the force due to hammering can change the shape of the piece of iron. In other words, we can say that the force applied through the hammer by the blacksmith can mould the hot piece of iron into any kind of tool.

Question 13. An inflated balloon was pressed against a wall after it had been rubbed with a piece of synthetic cloth. It was found that the balloon sticks to the wall. What force might be responsible for the attraction between the balloon and the wall?
Answer:

As the balloon has been rubbed with a piece of synthetic cloth, it has acquired some electrostatic charge and become a charged body. Now, when this charged body (which is a balloon) is pressed against the wall, it will get attracted. Thus, the electrostatic force is responsible for the attraction between the balloon and the wall.

Question 14. Name the forces acting on a plastic bucket containing water held above ground level in your hand. Discuss why the forces acting on the bucket do not bring a change in its state of motion.
Answer:

The forces acting on a plastic bucket are the gravitational force and the muscular force. These forces do not bring a change in its state of motion because, being equal and opposite in magnitude, the effect of the net force on the bucket becomes zero.

NCERT Solutions for VSAQs on Force and Pressure

Question 15. A rocket has been fired upwards to launch a satellite into orbit. Name the two forces acting on the rocket immediately after leaving the launching pad.
Answer: Two forces are as follows:

1. Gravitational force
2. Friction due to air or the force of friction

Question 16. When we press the bulb of a dropper with its nozzle kept in water, air in the dropper is seen to escape in the form of bubbles. Once we release the pressure on the bulb, water fills the dropper. The rise of water in the dropper is due to

1. Pressure of water
2. Gravity of the Earth
3. Shape of rubber bulb
4. Atmospheric pressure

Answer: 4. Atmospheric pressure.

NCERT Solutions For Class 8 Science Chapter 8 Force And Pressure SAQs

Question 1. The figure shows a magnet at the top of a ramp and paper clips at the base of the ramp. He observed that the paper clip moved up the ramp and attached to the magnet. What forces were acting on the paper clip as it moved up the ramp?

Answer:

The paper clip moved up the ramp because it was attracted to the magnet, therefore, there was a magnetic force acting on it.

Gravitational and frictional forces also continue to act on the paper clip as it moves up the ramp.

NCERT Solutions for Force and Pressure SAQs Class 8

Question 2. A chapati maker is a machine that converts balls of dough into chapatis. What effect of force comes into play in this process?
Answer:

The force per unit area is called pressure, which works on the chapatis. This is the pressure that works on the dough balls and makes them chapatis with the help of a machine.

Question 3. Wooden or concrete sleepers are kept below the railway line. Explain why?
Answer:

Since the area on which the weight of the train acts increases which resulting in a decrease in the pressure on the ground which the train moves easily on the railway line without any risk of an accident. So, this is the reason for keeping the wooden or concrete below the railway line.

NCERT Solutions for Class 8 Science Force and Pressure SAQs

Question 4. Determine the pressure when a force of 200 N acts on the area

1. 20 m² and
2. 8m²

Answer:

⇒ \(\text { Pressure }=\frac{\text { Force }}{\text { Area }}\)

Given, F = 200N

For area, A=20m2

⇒ \(p=\frac{200}{20}=10 \mathrm{~N} / \mathrm{m}^2 \text { or } 10 \mathrm{~Pa}\)

⇒ \(p=\frac{200}{8}=25 \mathrm{~N} / \mathrm{m}^2 \text { or } 25 \mathrm{~Pa}\)

Question 5. Raman was very curious to know how the porters carry a heavy load on their heads easily. Suddenly, he asked his teacher, and the teacher told him that by reducing the pressure on the head, the porters can carry a heavy load.

1. Explain how the porters carry heavy loads easily.
2. Mention your views about Raman.

Answer:

The porters usually cover their heads with thick, round cloths before carrying the load. This increases the area ofcontact, therefore reducing pressure on the head. So, the porters carry a heavy load easily.

According to me, Raman is very curious to know about science.

NCERT Solutions for Force and Pressure Chapter 8 SAQs

Question 6. Two rods of the same weight and equal length have different thicknesses. They are held vertically on the surface of the sand as shown in the figure. Which one of them will sink more? Why?

Answer:

As we know, pressure exerted by the body is inversely proportional to the area where force is applied. So, the thinner rod, i.e., rod B, will sink more because it has less area of cross-section in contact with the surface, hence it will exert more pressure on the sand than rod A.

Question 7. What type of force is involved in each of the given conditions? Put a tick mark for the response in terms of push or pull.
Answer:

Force and Pressure Class 8 NCERT SAQs

Question 8. If the area of my head were 15 cm x 15 cm, how much force would air exert on my head?
Answer:

We know that. 1 atmospheric pressure =10 s N/m: = 10N/cm2

⇒ \(\text { Pressure }=\frac{\text { Force }}{\text { Area }}\)

Force = Pressure x Area =10x(15xl5) =2250 N.

Question 9. Give two examples each of situations in which you push or pull to change the state of motion of objects.
Answer:

The two examples are as follows:

1. We push the door open.
2. We pull a drawer to open it.

Force and Pressure SAQs NCERT Solutions Class 8

Question 10. Give two examples of situations in which applied force causes a change in the shape of an object.
Answer: The two examples are as follows:

• Spring: When we compress or stretch the spring, it changes its shape.
• Foam: When we compress the foam or sponge, it changes its shape.